北师大版八年级下册数学期末试卷完整版
八年级数学下册期末考试卷及答案(北师大版)

八年级数学下册期末考试卷及答案(北师大版)(满分:120分;考试时间:120分钟)一.单选题。
(每小题4分,共40分) 1.若a <b ,则下列式子一定成立的是( )A.﹣a <﹣bB.﹣a2>﹣b2 C.ac >bc D.a -2>b -2 2.下列图案中,既是轴对称图形,又是中心对称图形的是( )A.等边三角形B.平行四边形C.矩形D.直角三角形 3.下列分式中,属于最简分式的是( ) A.42a B.yy 2 C.1-a a -1D.mm+34.要使分式a+2a+1有意义,x 的取值应满足( )A.a ≠﹣1B.a ≠﹣1且a ≠﹣2C.a ≠﹣2D.a=﹣15.为了推理出七边形的内角和,将七边形的某一个顶点分别与其它各顶点相连,这样把原来的七边形分割成 个三角形,最终求出七边形内角和是900°. A.4 B.5 C.6 D.76.下列各式中,能用公式法因式分解的是( )A.x 2-xB.4x 2+4x -1C.x 2+y 2D.4x 2-18.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,BE ∥AC ,AE ∥BD ,OE 与AB 交于点F ,若OE=5,AC=8,则菱形ABCD 的面积为( ) A.20 B.22 C.24 D.40A.﹣3≤x≤3B.﹣4≤x≤4C.﹣2≤x≤2D.﹣5≤x≤5二.填空题。
(每小题4分,共24分)11.因式分解:2a2-ab= .12.如果一个多边形的内角和等于外角和的两倍,则这个多边形是边形.13.如图,CD是△ABC的中线,电E,F分别是AC,DC的中点,EF=2,则BD= .(第13题图)(第14题图)(第16题图)14.如图,直线y=x+1与直线y=ax+b相交于点A(m,3),则关于x的不等式x+1<ax+b的解集是.15.若关于x的一元二次方程kx2-6x+9=0有实数根,则k的取值范围是.16.如图,在平行四边形ABCD中,AB=5,AD=3,∠A=60°,E是边AD上的一个点,且AE=2DE,F是射线AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG,连接BG,DG,则BG-DG的最大值为.三.解答题。
北师大版八年级下册数学期末试题附答案

北师大版八年级下册数学期末试卷一、单选题1.下列图形中,是中心对称图形但不是轴对称图形的是A .B .C .D . 2.若a >b ,则下列各式中一定成立的是A .a +2<b +2B .a -2<b -2C .2a >2b D .-2a >-2b 3.如图,Rt ABC 中,90,ACB CD AB ∠=︒⊥于点D ,若60,1A AD ∠=︒=,则BC 的长为A. B . C . D4.下列各式:①22k π;①1m n +;①224m n -;①23b a ;①()211x x +-;①1x .其中分式有 A .3个 B .4个 C .5个 D .6个5.在平行四边形ABCD 中,①A=2①B ,则①C 的度数是A .60°B .90°C .120°D .135°6.把分式22x y x y+-中的x ,y 都扩大2倍,则分式的值 A .不变 B .扩大2倍 C .扩大4倍 D .缩小2倍 7.下列四个命题中,假命题是A .“等边对等角”与“等角对等边”是互逆定理B .等边三角形是锐角三角形C .角平分线上的点到角两边的距离相等D .真命题的逆命题是真命题 8.某次列车平均提速20km/h ,用相同的时间,列车提速前行驶400km ,提速后比提速前多行驶100km ,设提速前列车的平均速度为km/h x ,下列方程正确是 A .40040010020x x +=+ B .40040010020x x -=-C .40040010020x x +=-D .40040010020x x -=+ 9.分式22x x -+有意义的条件是 A .2x ≠ B .2x ≠- C .2x ≠± D .2x >-10.若一个正多边形的一个外角是45︒,则这个正多边形的边数是A .10B .9C .8D .611.顺次连接平行四边形各边的中点得到的四边形是A .平行四边形B .菱形C .矩形D .正方形12.点(-4,1)关于原点的对称点是A .(-4,1)B .(-4,-1)C .(4,1)D .(4,-1)二、填空题13.如图,在①ABC 中,EF 是①ABC 的中位线,且EF=5,则AC 等于____.14.把多项式 x 2 + ax + b 分解因式得(x+1)(x ﹣3),则 a -b 的值是_____. 15.关于x 的分式方程21122m x x x +-=--有增根,则m =______. 16.如图,平行四边形ABCD 中,DE 平分①ADC 交边BC 于点E ,AD =8,AB =5,则BE =___.17.当x =______时,分式2136x x +-无意义. 三、解答题18.计算:(1)22-+11()2-02021 (2)解分式方程:11322x x x-+=--19.先化简,再求代数式的值:()2111x x ⎛⎫-÷-⎪+⎝⎭,其中x =2. 20.解不等式组:102332x x x ->⎧⎨-<-⎩21.因式分解:(1)2222416a x a y -;(2)()2(21)6219x x ---+. 22.如图,ABC 和BDE 是等边三角形,连接AD 、CE .求证:ABD △①CBE △.23.如图,已知平行四边形ABCD 的对角线AC 和BD 交于点O ,且28AC BD +=,12BC =,求AOD ∆的周长.24.如图,在ABC 中,4AB =,7BC =,60B ∠=︒,将ABC 绕点A 顺时针旋转一定角度得到ADE ,当点B 的对应点D 恰好落在BC 边上时,求CD 的长.25.如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD AB ⊥交BC 于点D ,2AD =,求BC 的长.26.①ABC 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.(1)画出①ABC 关于原点O 的中心对称图形①A 1B 1C 1;(2)写出中心对称图形①A 1B 1C 1的顶点坐标.27.已知:如图A 、C 是①DEBF 的对角线EF 所在直线上的两点,且AE =CF .求证:四边形ABCD 是平行四边形.28.某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球? 29.如图,ABCD 的对角线,AC BD 相交于点,,6,10O AB AC AB cm BC cm ⊥==,点P 从点A 出发,沿AD 方向以每秒1cm 的速度向终点D 运动,连接PO ,并延长交BC 于点Q .设点P 的运动时间为t 秒.(1)求BQ的长(用含t的代数式表示);(2)当四边形ABQP是平行四边形时,求t的值;(3)当325t 时,点O是否在线段AP的垂直平分线上?请说明理由.参考答案1.A2.C3.B4.B5.C6.A7.D8.A9.B10.C11.A12.D13.10【详解】解:在①ABC中,①EF是①ABC的中位线,①EF=12AC,①AC=2EF ,①EF=5,①AC=2×5=10,故答案为:10.14.1【详解】①()()21323x x x x +-=--又()()213x x x ax b +-=++①23a b ,=-=-①1a b -=故答案为1.15.5【详解】解:分式方程有增根20x ∴-=得:x=221122m x x x +-=-- 通分得:()2112m x x -+=-去分母得:212m x x --=-化简得:31m x =-将x=2代入得m=5故答案为5.【点睛】这道题考察的是分式方程增根的概念和分式方程未知参数的解法.解决这类题的关键在于:确定增根,化分为整,增根代入.16.3【解析】【分析】由平行四边形对边平行及根据两直线平行,内错角相等可得EDA DEC ∠=∠,而DE 平分ADC ∠,进一步推出EDC DEC ∠=∠,在同一三角形中,根据等角对等边得CE CD =,则BE 可求解.【详解】解:根据平行四边形的性质得//AD BC ,EDA DEC ∴∠=∠,又DE 平分ADC ∠,EDC ADE ∴∠=∠,EDC DEC ∴∠=∠,5CD CE AB ∴===,即853BE BC EC =-=-=.故答案为:3.【点睛】本题考查了平行四边形性质的应用,及等腰三角形的判定,解题的关键是值掌握平行四边形的性质.17.2【解析】【分析】分式无意义的条件是分母等于零.据此解答即可.【详解】 解:分式2136x x +-无意义, 360x ∴-=,解得2x =.故答案为:2.【点睛】本题考查了分式无意义的条件,熟知分式无意义的条件是分母等于零是解答本题的关键.18.(1)-2;(2)x=2是增根,原分式方程无解.【解析】【分析】(1)先乘方,再乘除,最后加减,注意负号的作用;(2)方程两边同时乘以2x -,将分式方程化为整式方程,再解方程、验根即可.【详解】解:(1)22-+11()2-02021 = -4+2-1+1= -2;(2)11322x x x-+=-- 方程两边同乘以2x -,得1+3(x -2)= x -11361x x +-=-解得x=2经检验:x=2是增根,原分式方程无解.【点睛】本题考查实数的混合运算、解分式方程,涉及零指数幂与负正整指数幂、分式有意义的条件等知识,是重要考点,掌握相关知识是解题关键.19.-x -1,-3【解析】【分析】根据题意将原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,进而将x 的值代入计算即可求出值.【详解】解:原式= ()21111x x x x +⎛⎫-÷- ⎪++⎝⎭ =()2111x x x --⎛⎫-÷ ⎪+⎝⎭()111x x x -⎛⎫=-÷ ⎪+⎝⎭=(1)x -+=1x --①当x=2时,①原式=213--=-【点睛】本题考查分式的化简求值,熟练掌握分式的运算法则是解答本题的关键. 20.1x >【解析】【分析】分别把两个不等式的解集求出来,再借助数轴求出两个解集的公共部分,即得不等式组的解集.【详解】解不等式(1)得:1x >解不等式(2)得:1x >-两个解集在数轴上表示如下:①不等式组的解集为:1x >【点睛】 本题考查了解不等式组及利用数轴求不等式组的解集.21.(1)()()2422a x y x y -+;(2)()242x - 【解析】【分析】(1)先提取公因式,再用 平方差公式分解即可;(2)先用完全平方公式分解,再提取公因式即可.【详解】解:(1)2222416a x a y -=()22246a x y -=()()2422a x y x y -+;(2)()2(21)6219x x ---+=2(213)x --=()242x -.【点睛】本题考查了因式分解,解题关键是熟练运用提取公因式和公式法进行因式分解,注意:因式分解要彻底.22.见解析.【解析】【分析】由等边三角形性质得到AB=BC ,BD=BE ,①ABC=①DBE=60°,从而有①ABD=①CBE ,即可得到结论【详解】证明:①ABC 和BDE 是等边三角形①60ABC DBE ∠=∠=︒①ABC DBC DBE DBC ∠-∠=∠-∠①ABD CBE ∠=∠又①AB BC =,BD BE =,∴在ABD △和CBE △中AB BC ABD CBE BD BE =⎧⎪∠=∠⎨⎪=⎩ ①ABD △①CBE △()SAS【点睛】本题考查了全等三角形的判定,以及等边三角形的性质,熟练掌握全等三角形的判定定理是解题关键.23.26【解析】【分析】根据平行四边形对角线互相平分的性质,由28AC BD +=,得到14AO OD +=,再根据平行四边形对边相等得到12AD BC ==,最后算出AOD ∆的周长.【详解】解:①四边形ABCD 是平行四边形, ①AO CO =,BO DO =,①28AC BD +=,①14AO OD +=,①12AD BC ==,①AOD ∆的周长141226AO OD AD =++=+=.【点睛】本题考查平行四边形的性质,解题的关键是熟练掌握平行四边形的性质. 24.3【解析】【分析】由旋转的性质可证得ABD △是等边三角形,则可求得BD 的长,再利用线段的和差即可求得答案.【详解】解:①将ABC 绕点A 顺时针旋转一定角度得到ADE ,①4AD AB ==.①60B ∠=︒,①ABD △是等边三角形,①4BD AD AB ===,①743CD BC AD =-=-=.【点睛】本题考查了旋转的性质、等边三角形的判定和性质、线段的和差等,证得ABD △是等边三角形是解题的关键.25.6BC =【解析】【分析】由题意易得①B=①C=30°,进而可得①CAD=①C=30°,则有2CD AD ==,由含30°的直角三角形的性质可得BD=4,进而问题可求解.【详解】解:①AB AC =,120BAC ∠=︒, ①()1180302B C BAC ∠=∠=︒-∠=︒,①AD AB ⊥,①90BAD ∠=︒,①1209030CAD BAC BAD C ∠=∠-∠=︒-︒=︒=∠,①2CD AD ==,在Rt BAD 中,30B ∠=︒,①24BD AD ==,①426BC BD CD =+=+=.【点睛】本题主要考查等腰三角形的性质与判定及含30°的直角三角形的性质,熟练掌握等腰三角形的性质与判定及含30°的直角三角形的性质是解题的关键. 26.(1)画图见解析;(2)A 1(1,-2),B 1(3,-3),C 1(4,0)【解析】【分析】(1)依据中心对称的性质,即可得到①ABC 关于原点O 的中心对称图形①A 1B 1C 1;(2)根据图象可得各点坐标.【详解】解:(1)如图所示:(2)由图可知:A 1(1,-2),B 1(3,-3),C 1(4,0).【点睛】本题主要考查了作图—中心对称,掌握中心对称的性质是解决问题的关键. 27.证明见解析【解析】【分析】根据平行四边形和平行线的性质,推导得DEA BFC ∠=∠,DFC BEA ∠=∠;根据全等三角形的判定和性质,证明DEA BFC △≌△、DFC BEA △≌△,得AD BC =、CD AB =,即可完成证明.【详解】证明:①平行四边形DEBF ,①//DE BF ,//DF BE ,①DEF BFE ∠=∠,DFE BEF ∠=∠,①180DEF DEA ∠+∠=︒,180BFE BFC ∠+∠=︒,180DFE DFC ∠+∠=︒,180BEF BEA ∠+∠=︒,①DEA BFC ∠=∠,DFC BEA ∠=∠,①平行四边形DEBF ,①DE BF =,DF BE =,在DEA △和BFC △中,DE BF DEA BFC AE CF =⎧⎪∠=∠⎨⎪=⎩①DEA BFC △≌△,①AD BC =,在DFC △和BEA △中,DF BE DFC BEA AE CF =⎧⎪∠=∠⎨⎪=⎩①DFC BEA △≌△,①CD AB =,①四边形ABCD 是平行四边形.【点睛】本题考查了平行四边形、平行线、全等三角形的知识;解题的关键是熟练掌握平行四边形、全等三角形的判定和性质,从而完成求解.28.(1)篮球、足球各买了20个,40个;(2)最多可购买篮球32个.【解析】【分析】(1)设篮球、足球各买了x ,y 个,根据等量关系:篮球、足球共60个,篮球、足球共用4600元,列出方程组,解方程组即可得;(2)设购买了a 个篮球,根据购买篮球的总金额不超过购买足球的总金额,列出不等式进行求解即可.【详解】(1)设篮球、足球各买了x ,y 个,根据题意,得6070804600x y x y +=⎧⎨+=⎩,解得2040xy=⎧⎨=⎩,答:篮球、足球各买了20个,40个;(2)设购买了a个篮球,根据题意,得()708060a a≤-,解得32a≤,①最多可购买篮球32个.【点睛】本题考查了二元一次方程组的应用,一元一次不等式的应用,弄清题意,找准等量关系或不等关系列出方程或不等式是解题的关键.29.(1)10-t;(2)5秒;(3)见解析【解析】【分析】(1)先证明①APO①①CQO,可得出AP=CQ=t,则BQ即可用t表示;(2)由题意知AP①BQ,根据AP=BQ,列出方程即可得解;(3)过点O作直线EF①AP,垂足为E,与BC交于F,利用三角形面积公式求出EF,得到OE,利用勾股定理求出AE,再说明AP=2AE即可.【详解】解:(1)①四边形ABCD是平行四边形,①OA=OC,AD①BC,①①PAO=①QCO,①①AOP=①COQ,①①APO①①CQO(ASA),①AP=CQ=t,①BC=10,①BQ=10-t;(2)①AP①BQ,当AP=BQ时,四边形ABQP是平行四边形,即t=10-t,解得:t=5,①当t为5秒时,四边形ABQP是平行四边形;(3)过点O作直线EF①AP,垂足为E,与BC交于F,在Rt①ABC中,①AB=6,BC=10,,①AO=CO=12AC=4,①S①ABC=12AB AC⋅=12BC EF⋅,①AB•AC=BC•EF,①6×8=10×EF,①EF=245,①OE=125,165,当325t=时,AP=325,①2AE=AP,即点E是AP中点,①点O在线段AP的垂直平分线上.【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、勾股定理,垂直平分线的判定等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.。
北师大版八年级下册数学期末试卷(完整)

北师大版八年级下册数学期末试卷(完整) 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.-2019的相反数是( )A .2019B .-2019C .12019D .12019- 2.矩形具有而平行四边形不一定具有的性质是( )A .对边相等B .对角相等C .对角线相等D .对角线互相平分3.对于函数y =2x ﹣1,下列说法正确的是( )A .它的图象过点(1,0)B .y 值随着x 值增大而减小C .它的图象经过第二象限D .当x >1时,y >04.已知a b 3132==,,则a b 3+的值为( ) A .1 B .2 C .3 D .275.如图,a ,b ,c 在数轴上的位置如图所示,化简22()a a c c b -++-的结果是( )A .2c ﹣bB .﹣bC .bD .﹣2a ﹣b 6.计算()22b a a -⨯的结果为( ) A .b B .b - C . ab D .b a7.四边形ABCD 中,对角线AC 、BD 相交于点O ,下列条件不能判定这个四边形是平行四边形的是( )A .AB ∥DC ,AD ∥BCB .AB=DC ,AD=BC C .AO=CO ,BO=DOD .AB ∥DC ,AD=BC8.如图,直线AB ∥CD ,∠C =44°,∠E 为直角,则∠1等于( )A .132°B .134°C .136°D .138°9.如图,将△ABC 放在正方形网格图中(图中每个小正方形的边长均为1),点A ,B ,C 恰好在网格图中的格点上,那么△ABC 中BC 边上的高是( )A .102B .104C .105D .510.下列选项中,不能判定四边形ABCD 是平行四边形的是( )A .AD //BC ,AB //CDB .AB //CD ,AB CD =C .AD //BC ,AB DC = D .AB DC =,AD BC =二、填空题(本大题共6小题,每小题3分,共18分)1.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.2.比较大小:23________13.3.若23(1)0m n -++=,则m -n 的值为________.4.如图,△ABC 中,CD ⊥AB 于D ,E 是AC 的中点.若AD=6,DE=5,则CD 的长等于________.5.如图:在△ABC 中,∠ABC ,∠ACB 的平分线交于点O ,若∠BOC =132°,则∠A 等于_____度,若∠A =60°时,∠BOC 又等于_____。
北师大版八年级下册数学期末试题及答案

北师大版八年级下册数学期末试卷一、单选题1.下列图形中,既是轴对称图形,又是中心对称图形的是A .B .C .D .2.a 、b 都是实数,且a<b ,则下列不等式正确的是A .a+x >b+xB .1-a<1-bC .5a <5bD .2a >2b 3.在平面直角坐标系内,将点M (3,1)先向上平移2个单位长度,再向右平移3个单位长度,则移动后的点的坐标是A .(6,3)B .(6,﹣1)C .(0,3)D .(0,﹣1)4.若()234a m a +-+能用完全平方公式进行因式分解,则常数m 的值是A .1或5B .1C .-1D .7或1-5.如图,l ∥m ,等边三角形ABC 的顶点B 在直线m 上,∠1=20°,则∠2的度数为A .60°B .45°C .40°D .30°6.化简22a b a b a b---的结果为A .-a b B .a b +C .a b a b+-D .a b a b-+7.函数y kx b =+的图象如图所示,则关于x 的不等式0kx b +≥的解集是A .2x ≤B .2x ≥C .0x ≤D .0x ≥8.如图,点P 在∠AOB 的平分线上,PC ⊥OA 于点C,∠AOB=30°,点D 在边OB 上,且OD=DP=2.则线段PC 的长度为()A .3B .2C .1D .129.若正多边形的一个外角是72 ,则该正多边形的内角和为()A .360B .540C .720D .900 10.下面式子从左边到右边的变形是因式分解的是()A .x 2﹣x ﹣2=x (x ﹣1)﹣2B .x 2﹣4x+4=(x ﹣2)2C .(x+1)(x ﹣1)=x 2﹣1D .x ﹣1=x (1﹣1x)11.四边形ABCD 中,对角线AC 、BD 相交于点O ,下列条件不能判定这个四边形是平行四边形的是()A .AB//DC ,AD//BCB .AB=DC ,AD=BC C .AO=CO ,BO=DOD .AB//DC ,AD=BC12.甲队修路120m 与乙队修路100m 所用天数相同,已知甲队比乙队每天多修10m ,设甲队每天修路xm.依题意,下面所列方程正确的是A .120100x x 10=-B .120100x x 10=+C .120100x 10x=-D .120100x 10x=+二、填空题13.一个纳米粒子的直径是0.000000035米,用科学记数法表示为______米.14.分式方程231xx =-的解是_____.15.当x =_________时,分式242x x -+的值为0.16.将直线5y x =--向上平移2个单位,得到直线_____,将直线3y x =-向左平移2个单位,得到直线_____;17.矩形ABCD 被两条对角线分成四个小三角形,如果四个小三角形周长的和是86cm ,矩形的对角线长是13cm ,那么该矩形的周长为_____.18.如图,菱形ABCD 的周长为16,面积为12,P 是对角线BD 上一点,分别作P 点到直线AB 、AD 的垂线段PE 、PF ,则PE +PF 等于____.19.将3x 2﹣27分解因式的结果是_______________________.20.关于x 的不等式3x m -<的解集中只有三个正整数,则m 的取值范围是_______.三、解答题21.解不等式组并把解集在数轴上表示出来.()32123232x x x ⎧--≥⎪⎨++>⎪⎩22.求下列分式的值:2224xx x x x x ⎛⎫+÷ ⎪-+-⎝⎭,并从x =0,﹣1,﹣2中选一个适当的值,计算分式的值.23.已知关于x 的方程233x k x x-=--(1)当3k =时,求x 的值?(2)若原方程的解是正数.求k 的取值范围?24.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A 、B ,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P 的位置.(作图不写作法,但要求保留作图痕迹.)25.如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:(1)ABC ∆的顶点都在方格纸的格点上,先将ABC ∆向右平移2个单位,再向上平移3个单位,得到111A B C ∆,其中点1A 、1B 、1C 分别是A 、B 、C 的对应点,试画出111A B C ∆;(2)连接11AA BB 、,则线段11AA BB 、的位置关系为____,线段11AA BB 、的数量关系为___;(3)平移过程中,线段AB 扫过部分的面积_____.(平方单位)26.如图,已知CAE ∠是ABC 外角,若①12∠=∠,②//AD BC ,③AB AC =,在这三个条件中任选两个作为已知条件,第三个作为结论进行证明.(1)已知12∠=∠,//AD BC ,求证:AB AC =.(请完成证明)(2)除上述方案,请再选一种方案加以证明.27.如图,在ABCD 中,点E ,F 分别在AD 、BC 上,且AE CF =,连接EF ,AC 交于点O .求证:OE OF =.28.已知:如图,AB CD =,DE AC ⊥,BF AC ⊥,E ,F 是垂足,DE BF =.(1)直接写出图中所有的全等三角形(不需要说明理由);(2)选取一组对第三问有帮助的全等进行证明;(3)证明四边形ABCD是平行四边形.参考答案1.C【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.【详解】解:A、不是轴对称图形,是中心对称图形,故本选项不符合题意;B、是轴对称图形,不是中心对称图形,故本选项不符合题意;C、既是轴对称图形,又是中心对称图形,故本选项符合题意;D、不是轴对称图形,是中心对称图形(不考虑颜色),故本选项不符合题意;故选:C.【点睛】本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2.C根据不等式的基本性质:(1)若a>b ,则a±c>b±c ,(2)若a>b ,c>0,则ac>bc ,a b c c>;(3)若a>b ,c<0,则ac<bc ,a b c c <;逐一判断得到答案即可【详解】解:A .∵a <b ,∴a+x <b+x ,计算错误;B .∵a <b ,∴-a >-b ,∴1-a >1-b ,计算错误;C .∵a <b ,∴5a <5b ,计算正确;D .∵a <b ,∴22ab <,计算错误.故答案为:C .【点睛】本题主要考查不等式的基本性质,熟练掌握不等式得基本性质是解题的关键.3.A 【解析】【分析】横坐标右移加,左移减;纵坐标上移加,下移减;依此即可求解.【详解】解:3+3=6,1+2=3.故点M 平移后的坐标为(6,3).故选:A .【点睛】本题主要考查坐标与图形变化-平移.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.4.D 【解析】【分析】直接利用完全平方公式进而分解因式得出答案.【详解】解:∵a 2+(m-3)a+4能用完全平方公式进行因式分解,∴m-3=±4,解得:m=-1或7.【点睛】本题考查了公式法分解因式,熟练掌握完全平方公式的结构特点是解题的关键.5.C【解析】【分析】过C作CM∥直线l,根据等边三角形性质求出∠ACB=60°,根据平行线的性质求出∠1=∠MCB,∠2=∠ACM,即可求出答案.【详解】解:过C作CM∥直线l,∵△ABC是等边三角形,∴∠ACB=60°,过C作CM∥直线l,∵直线l∥直线m,∴直线l∥直线m∥CM,∵∠ACB=60°,∠1=20°,∴∠1=∠MCB=20°,∴∠2=∠ACM=∠ACB-∠MCB=60°-20°=40°.故选:C.【点睛】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.6.B【解析】【分析】根据同分母的分式减法法则进行化简即可得到结果.【详解】解:22a b a b a b---22a b a b-=-()()a b a b a b+-=-a b =+,故选:B .【点睛】此题主要考查同分母分式的减法,熟练掌握运算法则是解答此题的关键.7.A 【解析】【分析】根据函数图象,找出图象在x 轴上方的部分的x 的取值范围即可得解.【详解】解:由图可知,当x≤2时,kx+b≥0.故选:A .【点睛】本题考查了一次函数与一元一次不等式,关键在于准确识图,找出符合不等式的图象的部分.8.C 【解析】【分析】过点P 作PE ⊥OB 于E ,根据角平分线上的点到角的两边距离相等可得PE=PC ,再根据直角三角形30°所对的边等于斜边的一半可得.【详解】解:如图,过点P 作PE ⊥OB 于E ,∵∠AOB=30°,点P 在∠AOB 的平分线上,∴∠AOP=∠POB=15°,∵OD=DP=2,∴∠OPD=∠POB=15°,∴∠PDE=30°,∴PE=12PD=1,∵OP 平分∠AOB ,PC ⊥OA ,PE ⊥OB ,∴PC=PE=1,故选:C .【点睛】此题考查的是角平分线的性质和直角三角形30°所对的边等于斜边的一半的应用、等腰三角形的性质,掌握角平分线上的点到角的两边距离相等和直角三角形30°所对的边是斜边的一半是解题关键.9.B 【解析】【分析】先根据正多边形的外角和为360°求出边数,然后再运用多边形的内角和公式解答即可.【详解】解:多边形的边数为360°÷72°=5则多边形的内角和为:(5-2)×180°=540°.故答案为B .【点睛】本题考查了正多边形的每一个外角都相等、多边形的外角和为360°以及多边形的内角和公式,求得正多边形的边数和掌握多边形内角和公式是解答本题的关键.10.B 【解析】【分析】根据因式分解的定义即可判断.【详解】A.()2212x x x x --=--右边含有加减,不是因式分解;B.()22442x x x -+=-是因式分解;C.()()2111x x x -+=-是整式的运算,不是因式分解;D.111x x x ⎛⎫-=- ⎪⎝⎭右边含有分式,不是因式分解.故选B 【点睛】此题主要考查因式分解的定义:把一个多项式化为几个整式的乘积形式.11.D 【解析】【详解】A 、由“AB//DC ,AD//BC”可知,四边形ABCD 的两组对边互相平行,则该四边形是平行四边形.故本选项不符合题意;B 、由“AB=DC ,AD=BC”可知,四边形ABCD 的两组对边相等,则该四边形是平行四边形.故本选项不符合题意;C 、由“AO=CO ,BO=DO”可知,四边形ABCD 的两条对角线互相平分,则该四边形是平行四边形.故本选项不符合题意;D 、由“AB//DC ,AD=BC”可知,四边形ABCD 的一组对边平行,另一组对边相等,据此不能判定该四边形是平行四边形.故本选项符合题意.故选D .12.A 【解析】【详解】甲队每天修路xm ,则乙队每天修(x -10)m ,因为甲、乙两队所用的天数相同,所以,120100x x 10=-.故选A.13.3.5×10-8.【解析】【分析】绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n ,与绝对值大于1数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.000000035=3.5×10-8.故答案为3.5×10-8.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n由原数左边起第一个不为零的数字前面的0的个数所决定.14.x=3【解析】【分析】首先去掉分母,观察可得最简公分母是x﹣1,方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解.【详解】解:23 1xx= -2=33x x-3x=.经检验x=3是分式方程的解,故答案为:x=3.【点睛】题目主要考查解分式方程,熟练掌握解分式方程的步骤是解题关键.15.2【解析】【分析】直接利用分式的值为零则分子为零,分母不为零,进而得出答案.【详解】∵242xx-+分式的值为0,∴x2-4=0,x+2≠0,解得:x=2.故答案为2.【点睛】此题主要考查了分式的值为零的条件,正确把握相关性质是解题关键.16.y=-x-3y=-3x-6【解析】【分析】由题意直接根据平移后解析式的变化规律横坐标右移减,左移加;纵坐标上移加,下移减进行分析即可.【详解】解:将直线y=−x−5向上平移2个单位,得到直线y=-x-3;将直线y=−3x 向左平移2个单位,得到直线y=-3(x+2)=-3x-6.故答案为:y=-x-3;y=-3x-6.【点睛】本题考查图形的平移变换和函数解析式之间的关系.在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.17.34cm【解析】【分析】根据四个小三角形的周长和为86cm ,列式得AD AO DO DC DO CO ++++++BC BO ++86CO AB AO BO +++=cm ,再由矩形的对角线相等解题即可.【详解】解:如图,矩形ABCD 中,13AC BD ==cm ,由题意得,86AOD DOC BOC AOB C C C C +++= cm ,86AD AO DO DC DO CO BC BO CO AB AO BO ∴+++++++++++=cm∴2286AD AC DB DC BC AB +++++=cm21321386AD DC BC AB ∴+⨯+⨯+++=cm8626234AD DC BC AB ∴+++=-⨯=cm故答案为:34cm .【点睛】本题考查矩形的性质,是重要考点,掌握相关知识是解题关键.18.3【解析】【分析】直接利用菱形的性质得出AB=AD=4,S △ABD=6,进而利用三角形面积求法得出答案.【详解】解:连接AP ,如图,∵菱形ABCD 的周长为16,∴AB=AD=4,∴S 菱形ABCD=2S △ABD ,∴S △ABD=12×12=6,而S △ABD=S △APB+S △APD ,PE ⊥AB ,PF ⊥AD ,∴12•PE•AB+12•PF•AD=6,∴2PE+2PF=6,∴PE+PF=3,故答案为:3.【点睛】本题考查了菱形的性质:菱形的对边分别平行,四条边都相等,两条对角线互相垂直平分,并且分别平分两组内角.也考查了三角形的面积公式.19.3(x-3)(x+3)【解析】先提取公因式3,再利用平方差公式进行因式分解.【详解】3x 2﹣27=3(x 2-9)=3(x-3)(x+3).故答案为:3(x-3)(x+3).【点睛】考查了综合因式分解,解题关键是先提取公式后再利用平方差公式进行因式分解.20.01m <≤【解析】【分析】根据不等式只有三个正整数解列出关于m 的不等式求解即可;【详解】解不等式3x m -<得3x m <+,∵只有三个正整数,∴334m <+≤,∴01m <≤.故答案是:01m <≤.【点睛】本题主要考查了根据一元一次不等式的整数解求参数,准确计算是解题的关键.21.-1<x≤3,把解集在数轴上表示见解析.【解析】【分析】分别解出不等式组中不等式的解集,然后在坐标轴上表示它们的公共部分,公共部分就是不等式的解集.【详解】解不等式3-(2x -1)≥-2,得x≤3;解不等式3232x x ++>,得x >-1.所以原不等式组的解集为-1<x≤3.把解集在数轴上表示如图.本题考查了解一元一次不等式组,掌握“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解题的关键.22.-2【解析】【分析】根据分式的加法和除法可以化简题目中的式子,然后从0,-1,-2中选一个使得原分式有意义的值代入即可解答本题【详解】解:2224x x x x x x ⎛⎫+÷⎪-+-⎝⎭=(2)(2)(2)(2)(2)(2)x x x x x x x x x++-+-+- =(x+2)+(x ﹣2)=x+2+x ﹣2=2x ,当x =﹣1时,原式=2×(﹣1)=﹣2.【点睛】此题考查分式的化简求值,掌握运算法则是解题关键23.(1)9x =是原方程的根;(2)6k >-且3k ≠-.【解析】【分析】(1)将3k =代入分式方程,再根据分式方程的求解方法,求解即可;(2)用k 表示出分式方程的解,再根据解为正数,列不等式求解即可,注意到3x ≠.【详解】解:(1)将3k =代入得3233x x x-=--两边同乘以()3x -,去分母得:()233x x --=-解得:9x =经检验9x =是原方程的根(2)两边同乘以()3x -,去分母得()23x x k--=-解得:6x k=+由原方程解是正数,易知60k +>得6k >-考虑分式方程产生增根3x =的情况,3x ≠即63k +≠,综上所述:6k >-且3k ≠-【点睛】此题考查了分式方程的求解方法,以及分式方程增根的情况,熟练掌握分式方程的求解方法是解题的关键.24.作图见解析.【解析】【分析】先画角的平分线,再画出线段AB 的垂直平分线,两线的交点就是P .【详解】解:作图如下:∴点P 为所求作.【点睛】本题主要考查了以下知识点:1.线段垂直平分线的性质;2.角平分线的性质.25.(1)见解析;(2)平行,相等;(3)15.【解析】【分析】(1)直接利用平移的性质分别得出对应点位置进而得出答案;(2)利用平移的性质得出线段AA 1、BB 1的位置与数量关系;(3)利用三角形面积求法进而得出答案.【详解】解:(1)如图所示:△A 1B 1C 1,即为所求;(2)线段AA1、BB1的位置关系为平行,线段AA1、BB1的数量关系为:相等.故答案为:平行,相等;×3×5=15.(3)平移过程中,线段AB扫过部分的面积为:2×12故答案为:15.【点睛】此题考查平移变换以及三角形面积求法,正确得出对应点位置是解题关键.26.(1)证明过程见解析;(2)见解析.【解析】【分析】(1)根据两直线平行,同位角相等、内错角相等,得到∠B=∠C相等,再利用等角对等边即可求解;(2)可以选择①和③作为条件,②作为结论证明;根据等腰三角形的性质得到∠B=∠C,根据三角形外角的性质得到∠1=∠B,根据平行线的判定定理即可得到AD∥BC.【详解】证明:(1)//AD BC,∠=∠,∴,2C∠=∠1B∠=∠,12∴∠=∠,B C∴=.AB AC(2)选择①和③作为条件,②作为结论加以证明.∵AB AC=,∴∠=∠,B C∵EAC ∠是ABC 的一个外角,∴2EAC B C B ∠=∠+∠=∠,又12EAC ∠=∠+∠,且12∠=∠,∴21EAC ∠=∠,∴1B ∠=∠,∴//AD BC .【总结】本题考查了平行线的性质和判定,等腰三角形的性质,三角形外角定理等知识点,熟练掌握各图形的性质及判定是解题的关键.27.见解析【解析】【分析】利用AAS 证得AOE COF ≅ 后即可证得结论.【详解】证明: 四边形ABCD 是平行四边形,//AD BC ∴,AEO CFO\Ð=Ð在AOE △和COF 中AOE COF AEO CFO AE CF ∠=∠⎧⎪∴∠=∠⎨⎪=⎩AOE COF∴≅ OE OF ∴=.【点睛】本题考查了平行四边形的性质及全等三角形的判定与性质,解题的关键是证得△AOE 和△COF 全等,难度不大.28.(1)△ABF ≌△CDE ,△ADE ≌△CBF ,△ADC ≌△CBA ;(2)见解析;(3)见解析.【解析】【分析】(1)根据全等三角形的判定方法,结合图形得出即可;(2)根据HL 证明三角形全等解答即可;(3)根据全等三角形的性质和平行四边形的判定解答即可.【详解】解:(1)图中所有全等的三角形为:△ABF ≌△CDE ,△ADE ≌△CBF ,△ADC ≌△CBA ;(2)DE AC ⊥ ,BF AC⊥90DEC AFB ∴∠=∠=o .在Rt ABF 和Rt CDE △中,AB CD DE BF=⎧⎨=⎩,()Rt ABF Rt CDE HL ∴≌△△;(3)由(2)知Rt Rt ABF CDE ≌△△,BAF DCE ∴∠=∠,//AB CD ∴,又AB CD = ,∴四边形ABCD 是平行四边形.【点睛】本题考查了全等三角形的判定和性质,平行四边形的判定方法等,熟练掌握各图形的性质和判定是解决此类题的关键.。
八年级数学下册期末考试卷附答案(北师大版)

八年级数学下册期末考试卷附答案(北师大版)(满分:120分;考试时间:120分钟)一.单选题。
(每小题4分,共40分)1.下列图形中,既是轴对称图形,又是中心对称图形的是( )2.若x >y ,则下列不等式一定成立的是( )A.x+4>y+6B.x -8<y -8C.x9>y9 D.﹣a >﹣b 3.下列各式:①3x ;②a+b 4;③y 3y ;④xyπ+2,其中是分式的是( )A.①③B.③④C.①②D.①②③④ 4.关于x 的方程5x x -2=ax -2+1有增根,则a 的值是( )A.0B.2或3C.2D.3 5.如果把5a a+b中的a ,b 同时扩大10倍,那么这个代数式的值( )A.不变B.扩大50倍C.扩大10倍D.缩小大原来的1106.如图,在四边形ABCD 中,AB ∥CD ,要使四边形ABCD 是平行四边形,下列添加的条件不正确的是( )A.AB=CDB.BC=ADC.∠A=∠CD.BC ∥AD(第6题图) (第7题图) (第8题图) 7.如图,正五边形ABCDE 中,连接BE ,则∠ABE 的度数为( ) A.30° B.36° C.54° D.72°8.如图,一个长为2,宽为1的长方形以所示姿态从直线l的左侧水平平移至右侧(图中的虚线是水平线),其中,平移的距离是()A.1B.2C.3D.2√29.若不等式组{x<1x<a的解集是x<a,则a的取值范围是()A.a≤1B.a=1C.a≥1D.a<1二.填空题。
(每小题4分,共24分)11.因式分解:a2-6a= .12.若分式x+1x-1的值为0,则x的值是 .13.如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE等于 .(第13题图)(第15题图)(第16题图)14.若不等式(a-4)x>1的解集是x<1a-4,则m的取值范围是 .15.如图,在平行四边形ABCD中,CE平分∠BCD,若CD=5,BC=3,则AE的长是 .16.如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移到△ECD,若四边形ABDC的面积为15,则点C的坐标为 .三.解答题。
北师大版八年级下册数学期末考试试题含答案
北师大版八年级下册数学期末考试试卷一、单选题1.若m n >,则下列不等式中不成立...的是()A .22m n +>+B .22m n->-C .2>2m n --D .22m n>2.下列图形:平行四边形、等腰三角形、线段、正六边形、圆,其中既是中心对称图形又是轴对称图形的有()A .1个B .2个C .3个D .4个3.下列各式从左到右的变形中,是因式分解的是()A .()()2339a a a +-=-B .()()2211a b a b a b -+=+-+C .()()2422m m m -=+-D .2211m m m m ⎛⎫+=+ ⎪⎝⎭4.下列各式中x 、y 的值均扩大为原来的2倍,则分式的值一定保持不变的是()A .2x y B .1x x y-+C .2x y-D .y x y+5.若关于x 的分式方程311-=-m x 的解为2x =,则m 的值为()A .5B .4C .3D .26.如图,在ABC 中,AB AC =,AD AB ⊥交BC 于点D ,120BAC ∠=︒,4=AD ,则BC 的长()A .8B .10C .11D .127.如图,将ABC 绕点A 按逆时针方向旋转80°,得到ADE ,连接BE ,若//AD BE ,CAE ∠的度数为()A .20°B .30°C .25°D .35°8.如图,一次函数1y kx b =+图象经过点()2,0A ,与正比例函数22y x =的图象交于点B ,则不等式02kx b x <+<的解集为()A .0x >B .1x >C .01x <<D .12x <<9.如图,在ABC 中,AB AC =,46BAC ∠=︒,BAC ∠的平分线与AB 的垂直平分线OD 交于点O ,点E 在BC 上,点F 在AC 上,连接EF ,将C ∠沿EF 折叠,点C 与点O 恰好重合时,则OEC ∠的度数()A .90°B .92°C .95°D .98°二、填空题10x 的取值范围是______.11.已知一个正多边形的一个内角是120º,则这个多边形的边数是_______.12.若1n m -=,则22242m mn n -+的值为______.13.如图:在ABC 中,90ACB ∠=︒,AD 平分CAB ∠交BC 于点D ,且2BD CD =,9BC cm =,则点D 到AB 的距离为______.14.不等式5132x x -+>-的正整数解为______.15.如图,ABC ∆,D 、E 分别是BC 、AC 的中点,BF 平分ABC ∠,交DE 于点F ,若10AB =,8BC =,则EF 的长是______.16.关于x 的分式方程2433x m mx x++=--的解为非负数,则实数m 的取值范围______.17.如图,四边形ABCD 中,//AB DC ,6DC =cm ,9AB =cm ,点P 以1cm/s 的速度由A 点向B 点运动,同时点Q 以2cm/s 的速度由C 点向D 点运动,其中一点到达终点时,另一点也停止运动,当线段PQ 将四边形ABCD 截出一个平行四边形时,此时的运动时间为______s .18.如图,BD 是ABC 的内角平分线,CE 是ABC 的外角平分线,过A 分别作AF BD ⊥、AG CE ⊥,垂足分别为F 、G ,连接FG ,若6AB =,5AC =,4BC =,则FG 的长度为____三、解答题19.(1)因式分解:32231212x x y xy -+(2)解不等式组:()3241213x x x x ⎧--<⎪⎨+>-⎪⎩,并把解集表示在数轴上.20.(1)先化简,再求值:236214422m m m m m m+-÷++++-,其中5m =.(2)解方:2231111x x x +=+--21.如图,在平面直角坐标系中,网格的每个小方格都是边长为1个单位长度的正方形,ABC 的顶点均落在格点上.(1)将ABC 先向右平移6个单位长度再向下平移1个单位长度,得到111A B C △,在网格中画出111A B C △;(2)作ABC 关于x 轴的轴对称图形,得到222A B C △,在网格中画出222A B C △.22.如图,在ABC 中,90BAC ∠=︒,AB AC =,点D 为BC 的中点,E 、F 分别是AB ,AC 上的点,且BE AF =,连接AD 、DE 、DF 、EF .求证:①BED ≌AFD V ②DE DF⊥23.某服装厂准备加工260套运动服,在加工了60套后,采用新技术,使每天的工作效率是原来的2倍,结果共用了8天完成,求该厂原来每天加工多少套运动服.24.如图,在ABCD 中,过点B 作BM AC ⊥,交AC 于点E ,交CD 于点M ,过点D 作DN AC ⊥,交AC 于点F ,交AB 于点N .(1)求证:四边形BMDN 是平行四边形;(2)已知125AF EM ==,,求AN 的长.25.甲、乙两家商场以相同的价格出售同样的商品,为了吸引顾客各自推出不同的优惠方案:在甲商场购买商品超过300元之后,超过部分按8折优惠;在乙商场购买商品超过200元之后,超过部分按8.5折优惠,设甲商场实际付费为1y 元,乙商场实际付费为2y 元,顾客购买商品金额为x 元()300x >.(1)分别求出1y ,2y 与x 的函数关系式;(2)比较顾客到哪个商场更优惠,并说明理由.26.在ABC 中,5AB BC ==,6AC =,将ABC 沿BC 方向平移得到DCE ,A ,C 的对应点分别是D 、E ,连接BD 交AC 于点O .(1)如图1,将直线BD 绕点B 顺时针旋转,与AC 、DC 、DE 分别相交于点I 、F 、G ,过点C 作//CH BG 交DE 于点H .①求证:IBC ≌HCE ②若DF CF =,求DG 的长;(2)如图2,将直线BD 绕点O 逆时针旋转()90αα<︒,与线段AD 、BC 分别交于点P 、Q ,在旋转过程中,四边形ABQP 的面积是否发生变化?若不变,求出四边形ABQP 的面积,若变化,请说明理由;(3)在(2)的旋转过程中,AOP 能否为等腰三角形,若能,请直接写出PQ 的长,若不能,请说明理由.参考答案1.B 【详解】解:A .∵m n >,不等式两边同时加2,不等号方向不变,∴22m n +>+,故A 不符合题意;B .∵m n >,不等式两边同时乘以-2,-2<0,不等号方向改变,∴22m n -<-,故B 符合题意;C .∵m n >,不等式两边同时加-2,不等号方向不变,∴22m n ->-,故C 不符合题意;D .∵m n >,不等式两边同时乘以12,12>0,不等号方向不变,∴22m n>,故D 不符合题意;故选B .2.C 【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【详解】解:平行四边形不是轴对称图形,但是中心对称图形;等腰三角形是轴对称图形,不是中心对称图形;线段、正六边形、圆既是中心对称图形又是轴对称图形,所以既是中心对称图形又是轴对称图形的有3个.故选:C .3.C 【分析】将多项式写成几个整式的积的形式,叫做将多项式分解因式,也叫因式分解,根据定义解答.【详解】解:A 、()()2339a a a +-=-不是因式分解;B 、()()2211a b a b a b -+=+-+不是因式分解;C 、()()2422m m m -=+-是因式分解;D 、2211m m m m ⎛⎫+=+ ⎪⎝⎭不是因式分解;故选:C .【点睛】此题考查因式分解,掌握因式分解的定义及因式分解的方法是解题的关键.4.D 【解析】【分析】根据分式的基本性质,分子分母同时乘除同一个不为零的数或式,分式的值不发生改变进行变形即可求解.【详解】解:根据题意,将x 变成2x,y 变成2y 化简求解:A.2x y 变成22222(2)4x x xy y y =≠,该选项不符合题意,B.1x x y -+变成21122x x x y x y --≠++,该选项不符合题意,C.2x y -变成2222x y x y ≠--,该选项不符合题意,D.yx y+变成22()y y x y x y =++,该选项符合题意,【点睛】本题考查了分式的基本性质,属于基础题,掌握分式的性质是解题关键. 5.B【解析】【详解】分析:直接解分式方程进而得出答案.详解:解分式方程311mx-=-得,x=m-2,∵关于x的分式方程311mx-=-的解为x=2,∴m-2=2,解得:m=4.故选B.点睛:此题主要考查了分式方程的解,正确解方程是解题关键.6.D【解析】【分析】依据等腰三角形的内角和,即可得到∠C=∠B=30°,依据AD⊥AB交BC于点D,即可得到BD=2AD=8,∠CAD=30°=∠B,CD=AD=4,进而得出BC的长.【详解】解:∵△ABC中,AB=AC,∠BAC=120°,∴∠C=∠B=30°,∵AD⊥AB交BC于点D,∴BD=2AD=8,∠CAD=30°=∠B,∴CD=AD=4,∴BC=BD+CD=8+4=12.故选:D.【点睛】本题主要考查了含30°角的直角三角形的性质以及等腰三角形的性质,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.【解析】【分析】由旋转的性质可知AB AE =,CAD BAE ∠=∠,即可求出50AEB ABE ∠=∠=︒.再由平行线的性质可知EAD AEB ∠=∠,最后由CAE CAD EAD ∠=∠-∠,即可求出CAE ∠的大小.【详解】∵ADE 是由ABC 绕点A 按逆时针方向旋转80︒得到,∴AB AE =,80CAD BAE ∠=∠=︒,∴1(180)502AEB ABE BAE ∠=∠=︒-∠=︒.∵//AD BE ,∴50EAD AEB ∠=∠=︒,∴805030CAE CAD EAD ∠=∠-∠=︒-︒=︒.故选:B .【点睛】本题考查旋转的性质,等腰三角形的判定和性质,平行线的性质.利用数形结合的思想是解答本题的关键.8.D 【解析】【分析】当x >1时,直线y=2x 都在直线y=kx+b 的上方,当x <2时,直线y=kx+b 在x 轴上方,于是可得到不等式0<kx+b <2x 的解集.【详解】解:当x >1时,2x >kx+b ,∵函数y=kx+b (k≠0)的图象经过点B (2,0),∴x <2时,kx+b >0,∴不等式0<kx+b <2x 的解集为1<x <2.故选D .【点睛】本题主要考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.9.B 【解析】【分析】连接OB 、OC .由角平分线和垂直平分线的性质可求出1232ABO BAC ∠=∠=︒,再由等腰三角形的性质可求出67ABC ACB ∠=∠=︒,由OBC ABC ABO ∠=∠-∠,即可求出OBC ∠的大小.在AOB 和AOC △中,利用“SAS”易证AOB AOC ≅ ,即得出OB=OC ,从而可求出44OBC OCB ∠=∠=︒.再由题意折叠可知OE=CE ,即得出44EOC ECO ∠=∠=︒,最后由180OEC EOC ECO ∠=︒-∠-∠,即可求出OEC ∠的大小.【详解】如图,连接OB 、OC.∵46BAC ∠=︒,BAC ∠的平分线与AB 的垂直平分线OD 交于点O ,∴1232OAB OAC ABO BAC ∠=∠=∠=∠=︒.∵AB=AC ,∴1(180)672ABC ACB BAC ∠=∠=︒-∠=︒,∴44OBC ABC ABO ∠=∠-∠=︒.在AOB 和AOC △中,AB AC OAB OAC AO AO =⎧⎪∠=∠⎨⎪=⎩,∴()AOB AOC SAS ≅ ,∴OB=OC ,∴44OBC OCB ∠=∠=︒.由题意将C ∠沿EF 折叠,点C 与点O 恰好重合,∴OE=CE ,∴44EOC ECO ∠=∠=︒,∴18092OEC EOC ECO ∠=︒-∠-∠=︒.故选:B .【点睛】本题考查角平分线、线段垂直平分线的性质,等腰三角形的性质,全等三角形的判定和性质,折叠的性质.作出辅助线构造等腰三角形是解答本题的关键.综合性强,较难.10.1≥x 且3x ≠【解析】【分析】直接利用二次根式有意义被开方数是非负数、分式有意义则分母不为零,进而得出答案.【详解】由题意知:x−1≥0且x−3≠0,解得:x≥1且x≠3.故答案为:x≥1且x≠3.【点睛】此题主要考查了二次根式有意义、分式有意义,正确掌握相关有意义的条件是解题关键.11.6【解析】【详解】一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.解:外角是180-120=60度,360÷60=6,则这个多边形是六边形.故答案为六.12.2【解析】先把所求式子的前三项分解因式得到()2222422m mn n m n -+=-,然后整体代入计算即得答案.【详解】解:∵1m n -=,∴()22222422212m mn n m n -+=-=⨯=.故答案为:2.【点睛】本题考查了多项式的因式分解和代数式求值,属于常考题型,熟练掌握分解因式的方法和整体的数学思想是解题的关键.13.3cm【解析】【分析】先求出CD 的长,再根据角平分线的性质证得DE=CD 即可.【详解】解:∵2BD CD =,9BC cm =,∴133CD BC ==cm ,过点D 作DE ⊥AB 于E ,∵AD 平分CAB ∠交BC 于点D ,90ACB ∠=︒,∴DE=CD=3cm ,故答案为:3cm .【点睛】此题考查角平分线的性质:角平分线上的点到角两边的距离相等,熟记性质定理是解题的关键.14.1,2【解析】【分析】根据解一元一次不等式基本步骤:去分母、移项、合并同类项、系数化为1可得.解:去分母得:x−5+2>2x−6,移项得:x−2x >−6+5−2,合并同类项得:−x >−3,系数化为1得:x <3.故不等式的正整数解是1,2,故答案为1,2.【点睛】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.15.1.【解析】【分析】根据三角形中位线定理得到DE ∥AB ,DE=0.5AB=5,根据平行线的性质、角平分线的定义求出DF ,计算即可.【详解】解:D Q 、E 分别是BC 、AC 的中点,152DE AB ∴==,//DE AB ,142BD BC ==,ABF DFB ∴∠=∠,BF 平分ABC ∠,ABF DBF ∴∠=∠,DBF DFB ∠=∠,4DF DB ∴==,1EF DE DF ∴=-=,故答案为1.【点睛】本题考查的是角平分线的定义、三角形中位线定理,掌握平行线的性质、角平分线的定义是解题的关键.16.12m ≤且3m ≠【分析】先解得分式方程的解为43m x =-,再由题意可得43m -≥0,又由x≠3,即可求m 的取值范围.【详解】解:2433x m m x x ++=--,方程两边同时乘以x−3,得x +m−2m =4(x−3),去括号得,x−m =4x−12,移项、合并同类项得,3x =12−m ,解得:43m x =-,∵解为非负数,∴43m -≥0,∴m≤12,∵x≠3,∴m≠3,∴m 的取值范围为m≤12且m≠3,故答案为为:m≤12且m≠3.【点睛】本题考查分式方程的解,熟练掌握分式方程的解法,注意增根的情况是解题的关键.17.2或3【解析】【分析】设运动时间为t ,有题意可得AP=tcm ,PB=(9-t )cm ,CQ=2tcm ,DQ=(6-2t )cm ,然后分当四边形APQD 是平行四边形时,DQ=AP 和当四边形BPQC 是平行四边形时,CQ=BP ,进行求解即可.【详解】解:设运动时间为t ,有题意可得AP=tcm ,PB=(9-t )cm ,CQ=2tcm ,DQ=(6-2t )cm ,∵AB ∥CD∴当四边形APQD 是平行四边形时,DQ=AP ,解得t=2;当四边形BPQC 是平行四边形时,CQ=BP ,∴9-t=2t ,解得t=3,∴当t=2或3时,线段PQ 将四边形ABCD 截出一个平行四边形,故答案为:2或3.【点睛】本题主要考查了平行四边形的性质,解题的关键在于能够熟练掌握相关知识进行求解.18.32【解析】【分析】延长AF 交BC 延长线于H ,延长AG 交BC 延长线于I ,由BD 平分∠ABC ,AF ⊥BF ,可得∠CBF=∠ABF ,∠HFB=∠AFB=90°,可证△HBF ≌△ABF (ASA ),可得BH=BA=6,HF=AF ,由CE 平分∠ACI ,AG ⊥CE ,可得∠ICG=∠ACG ,∠IGC=∠AGC=90°,可证△ICG ≌△ACG (ASA ),可得CI=CA=5,IG=AG,可证FG 为△AHI 的中位线即可.【详解】解:延长AF 交BC 延长线于H ,延长AG 交BC 延长线于I ,∵BD 平分∠ABC ,AF ⊥BF ,∴∠CBF=∠ABF ,∠HFB=∠AFB=90°,在△HBF 和△ABF 中,HBF ABF BF BF HFB AFB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△HBF ≌△ABF (ASA ),∴BH=BA=6,HF=AF ,∵CE 平分∠ACI ,AG ⊥CE ,∴∠ICG=∠ACG ,∠IGC=∠AGC=90°,在△ICG 和△ACG 中,ICG ACG CG CG IGC AGC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ICG ≌△ACG (ASA ),∴CI=CA=5,IG=AG ,∴IH=BC+CI-BH=4+5-6=3,∵HF=AF ,IG=AG ,∴FG 为△AHI 的中位线,∴FG=1133222HI =⨯=.故答案为32.【点睛】本题考查角平分线定义,垂线定义,三角形全等判定与性质,三角形中位线性质,线段和差,本题难度不大,训练画图构思能力,通过辅助线画出准确图形是解题关键.19.(1)()232x x y -;(2)14x <<,图见解析【解析】【分析】(1)先提公因式3x ,再利用完全平方公式进行因式分解即可;(2)先分别求出每一个不等式的解集,进而求出其公共解即可.【详解】解:(1)原式2223(44)3(2)x x xy y x x y =-+=-;(2)()3241213x x x x ⎧--<⎪⎨+>-⎪⎩①②解不等式①,得1x >,解不等式②,得4x <,在同一数轴上表示不等式①②的解集如下:∴不等式组的解集为:14x <<.【点睛】本题考查提公因式法、公式法分解因式,解一元一次不等式组,熟练掌握因式分解的方法以及解一元一次不等式组的基本步骤是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.20.(1)22m -,23;(2)0x =【解析】【分析】(1)先利用完全平方公式和分式混合运算法则进行化简,然后代值计算即可;(2)先把方程两边同时乘以()()11x x +-化为整式方程,然后求解即可.【详解】解:(1)236214422m m m m m m+-÷++++-()()23221222m m m m m ++=⨯---+3122m m =---22m =-,当5x =时,原式22523==-.(2)2231111x x x +=+--方程两边同时乘以()()11x x +-得()()21311x x -++=,整理得22331x x -++=,解得0x =.检验:将0x =代入原方程,左边1=-=右边,∴原方程的根是0x .【点睛】本题主要考查了分式的化简求值,解分式方程,解题的关键在于能够熟练掌握相关知识进行求解.21.(1)见解析;(2)见解析【解析】【分析】(1)利用点平移的坐标特征写出A 1、B 1、C 1的坐标,然后描点即可;(2)利用关于x 轴对称的点的坐标特征写出A 2、B 2、C 2的坐标,然后描点即可.【详解】解:(1)由图可得:A (-4,5)、B (-5,2)、C (-3,1)∴平移后的坐标:A 1(2,4)、B 1(1,1)、C 1(3,0)如图,111A B C △即为所求.(2)对称后的坐标:A 2(-4,-5)、B 2(-5,-2)、C 2(-3,-1)如图,222A B C △即为所求.【点睛】本题考查了作图−旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.22.①见解析;②见解析【解析】【分析】①证明:根据等腰直角三角形的性质推出1452DAF DAB BAC ∠=∠=∠=︒,45B C ∠=∠=︒,BD AD =,即可证得结论;②根据全等的性质证得BDE ADF ∠=∠,利用AD BC ⊥证得结论.【详解】解:①证明:在ABC 中,AB AC =,90BAC ∠=︒,点D 是BC 的中点,∴1452DAF DAB BAC ∠=∠=∠=︒,45B C ∠=∠=︒,∵B DAB ∠=∠,∴BD AD =,∵B DAF ∠=∠,BE AF =,∴BED ≌AFD V ;②证明:由①可知,BED ≌AFD V ,∴BDE ADF ∠=∠,∵AB AC =,点D 是BC 的中点,∴AD BC ⊥,∴90ADB ∠=︒,∴90ADE BDE ∠+∠=︒,∴90ADE ADF ∠+∠=︒,∴90EDF ∠=︒,∴DE DF ⊥.【点睛】此题考查了等腰直角三角形的性质,全等三角形的判定及性质,熟记等腰直角三角形的性质及全等三角形的判定定理是解题的关键.23.该厂原来每天加工20套运动服.【解析】【分析】设该厂原来每天加工x 套运动服,则采用新技术后每天加工2x 套运动服,由题意:某服装厂准备加工260套运动服,在加工了60套后,采用新技术,使每天的工作效率是原来的2倍,结果共用了8天完成,列出分式方程,解方程即可.【详解】解:设该厂原来每天加工x 套运动服,则采用新技术后每天加工2x 套运动服.根据题意得:602606082x x-+=解这个方程得20x =,经检验:20x =是原方程的根.答:该厂原来每天加工20套运动服.【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.24.(1)见解析;(2)13【解析】【分析】(1)只要证明DN ∥BM ,DM ∥BN 即可;(2)只要证明△CEM ≌△AFN ,可得FN =EM =5,在Rt △AFN 中,根据勾股定理AN =.【详解】(1)∵四边形ABCD 是平行四边形,∴CD AB .∵BM AC DN AC ⊥⊥,,∴DN BM ,∴四边形BMDN 是平行四边形.(2)∵四边形ABCD ,BMDN 都是平行四边形,∴AB CD DM BN CD AB ==,,∥,∴CM AN MCE NAF =∠=∠,.又∵90CEM AFN ∠=∠=︒,∴()CEM AFN AAS ≌,∴5FN EM ==.在Rt AFN 中,13AN =.【点睛】本题考查平行四边形的性质和判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.25.(1)10.860y x =+,20.8530y x =+;(2)当600x =时,选择甲、乙两个商场均可,当300600x <<时,选择乙商场更优惠,当x 600>时,选择甲商场更优惠.【解析】【分析】(1)在甲超市购物所付的费用:300元+0.8×超过300元的部分,在乙超市购物所付的费用:200+0.85×超过200元的部分;(2)根据(1)中解析式的费用分类讨论即可.【详解】(1)由题意得,()13000.8300y x =+-,即10.860y x =+,22000.85(200)y x =+-,即20.8530y x =+(2)当300x >时,由12y y <得:0.8600.8530x x +<+,解得:x 600>,由12y y =得:0.8600.8530x x +=+,解得:600x =,由12y y >得:0.8600.8530x x +>+,解得:600x <.∴当600x =时,选择甲、乙两个商场均可,当300600x <<时,选择乙商场更优惠,当x 600>时,选择甲商场更优惠.【点睛】本题考查了一次函数以及一元一次不等式的应用,根据题意列出正确的甲、乙两家商场的实际费用与购买商品金额x 之间的函数关系式是本题的关键.26.(1)①见解析;②2;(2)不变,12;(3)能,5PQ =或6【解析】【分析】(1)①由平移的特征可以推出三角形全等的条件,证明△IBC ≌△HCE ;②由①得IC =HE ,再证明四边形ICHG 是平行四边形,得IC =GH ,再证明△DFG ≌△CFI ,得DG =IC ,于是得DG =GH =HE =13DE =13AC ,可求出DG 的长;(2)由平行四边形的性质可证明线段相等和角相等,证明△AOP ≌△COQ ,将四边形ABQP 的面积转化为△ABC 的面积,说明四边形ABQP 的面积不变,求出△ABC 的面积即可;(3)按OP =OA 、PA =OA 、OP =AP 分类讨论,分别求出相应的PQ 的长,其中,当PA =OA 时,作OL ⊥AP 于点L ,构造直角三角形,用面积等式列方程求OL 的长,再用勾股定理求出OP 的长即可.【详解】(1)证明:①如图1,∵DCE 是由ABC 平移得到的,∴//AC DE BC CE =,∴ACB DEC ∠=∠,∵//CH BG ,∴GBC HCE∠=∠∴IBC ≌HCE②如图1,由①可知:IBC ≌HCE ,∴IC HE =,∵//AC DE ,//CH BG ,∴CI //GH ,CH //GH ,∴四边形ICHG 是平行四边形,∴IC GH =,∵//AC DE ,∴CDG DCI∠=∠∵CFI DFG ∠=∠,DF CF =,∴DFG ≌CFI △,∴DG IC =,∴DG GH HE ==,∴11233DG DE AC ===.(2)面积不变;如图2:由平移可知//AB CD ,AB CD =,∴四边形ABCD 是平行四边形,∴OA OC =,∵//AD BC ,∴APO CQO ∠=∠,∵AOP COQ ∠=∠,∴APO △≌CQO ,∴APO CQO S S =△△,APO CQO ABC ABQP AOQB AOQB S S S S S S =+=+=四边形四边形四边形△△△,∴四边形ABQP 的面积不变.∵5AB BC ==132OA OC AC ===,∴OB AC ⊥,∴90AOB ∠=︒,在Rt BOC 中222OB OC BC +=∴4OB ==,∴11641222ABC S AC OB ==⨯⨯= ,∴12ABQP S =四边形(3)如图3,OP =OA =3,由(2)得,△AOP ≌△COQ ,∴OQ =OP =3,∴PQ =3+3=6;如图4,PA =OA =3,作OL ⊥AP 于点L ,则∠OLA =∠OLP =90°,由(2)得,四边形ABCD是平行四边形,OA=3,∠AOB=90°,∴OD=OB=4,∠AOD=180°−∠AOB=90°,∵AO⊥BD,OD=OB,∴AO垂直平分BD,∴AD=AB=5,由12AD•OL=12OA•OD=AODS得,1 2×5OL=12×3×4,解得,OL=12 5,∴2222129355 AL OA OL⎛⎫=-=-=⎪⎝⎭,∴96355 PL=-=,∴222212665555OP OL PL⎛⎫⎛⎫=+=+=⎪ ⎪⎝⎭⎝⎭,∴PQ=2OP 125 5如图5,OP=AP,∵AD=AB,AC⊥BD,∴∠DAC=∠BAC,∴∠POA =∠DAC =∠BAC ,∴PQ //AB ,∵AP //BQ ,∴四边形ABQP 是平行四边形,∴PQ =AB =5,综上所述,5PQ 或6或5.【点睛】此题重点考查平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的判定、平移的特征、勾股定理以及根据面积等式列方程求线段的长度等知识与方法,解第(3)题时要进行分类讨论,求出所有符合条件的值,此题难度较大,属于考试压轴题.。
北师大版八年级下册数学期末考试试题及答案

北师大版八年级下册数学期末考试试卷一、单选题1.在下列四个标志中,既是中心对称又是轴对称图形的是()A .B .C .D .2.下列多边形中,不能够单独铺满地面的是()A .正三角形B .正方形C .正五边形D .正六边形3.多项式225a -与25a a -的公因式是()A .5a +B .5a -C .25a +D .25a -4.不等式组1{1x x >-≤的解集在数轴上可表示为()A .B .C .D .5.下列命题正确的是().A .在同一平面内,可以把半径相等的两个圆中的一个看成是由另一个平移得到的B .两个全等的图形之间必有平移关系C .三角形经过旋转,对应线段平行且相等D .将一个封闭图形旋转,旋转中心只能在图形内部6.如图所示,在ABC 中,AB AC =,点D 是边AC 上一点,BC BD AD ==,则A ∠的大小是()A .72°B .54°C .38°D .36°7.将分式24xx y-中的x ,y 的值同时扩大为原来的2019倍,则变化后分式的值()A .扩大为原来的2019倍B .缩小为原来的12019C .保持不变D .以上都不正确8.甲、乙二人做某种零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,若设乙每小时做x 个,则可列方程()A .90606x x=+B .90606x x=-C .90606x x =-D .90606x x =+9.平行四边形ABCD 的一边长为10,则它的两条对角线长可以是()A .10和12B .12和32C .6和8D .8和1010.如图,在平行四边形ABCD 中,120C ∠=︒,4=AD ,2AB =,点E 是折线BC CD DA --上的一个动点(不与A 、B 重合).则ABE △的面积的最大值是()A .2B .1C .D .二、填空题11.若分式33x x -+的值为0,则x 的值为_________;12.分解因式2242xy xy x ++=___________13.若一个多边形的每一个外角都等于30°,则这个多边形的边数为_________.14.若a 2﹣5ab ﹣b 2=0,则a bb a-的值为_____.15.如图,A 、B 、C 三点在同一条直线上,∠A =50°,BD 垂直平分AE ,垂足为D ,则∠EBC 的度数为_____.16.在平面直角坐标系中点A 、B 分别是x 轴、y 轴上的点且B 点的坐标是()0,3-,30OAB ∠=︒.点C 在线段AB 上,是靠近点A 的三等分点.点P 是y 轴上的点,当OCP △是等腰三角形时,点P 的坐标是__________.三、解答题17.因式分解:()2221x y xy ++-18.解不等式组:()2532121035x x x ⎧+≤+⎪⎨-+>⎪⎩19.解方程:214111x x x ++=--.20.ABC 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:(1)画出ABC 关于原点O 的中心对称图形111A B C △;(2)画出将ABC 绕点O 顺时针方向旋转90°得到的222A B C △.(3)设(),P a b 为ABC 边上一点,在222A B C △上与点P 对应的点是1P .则点1P 坐标为_______21.先化简,再求值:226939393m m m m m m -+-⎛⎫÷-- ⎪-+⎝⎭,其中3m =22.如图,已知E 是平行四边形ABCD 中BC 边的中点,AC 是对角线,连结AE 并延长AE 交DC 的延长线于点F ,连结BF .求证:四边形ABFC 是平行四边形.23.利用我们学过的知识,可以导出下面这个等式:()()()12222222a b c ab bc ac a b b c c a ⎡⎤++---=-+-+-⎣⎦.该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.(1)请你展开右边检验这个等式的正确性;(2)利用上面的式子计算:222201820192020201820192019202020182020++-⨯-⨯-⨯.24.某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.(1)甲、乙工程队每天各能铺设多少米?(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.25.(1)如图①所示,将ABC 绕顶点A 按逆时针方向旋转()090a a <<︒角,得到ADE ,90BAC DAE ∠=∠=︒,ED 分别与AC 、BC 交于点F 、G ,BC 与AD 相交于点H .求证:AH AF =;(2)如图②所示,ABC 和ADE 是全等的等腰直角三角形,90BAC D ∠=∠=︒,BC 与AD 、AE 分别交于点F 、G ,请说明BF ,FG ,GC 之间的数量关系.参考答案1.C【详解】解:A、不是中心对称图形,是轴对称图形,故本选项不合题意;B、既不是中心对称图形,也不是轴对称图形,故本选项不合题意;C、既是中心对称图形又是轴对称图形,故本选项符合题意;D、不是中心对称图形,是轴对称图形,故本选项不合题意.故选:C.2.C【详解】∵正三角形的内角=180°÷3=60°,360°÷60°=6,即6个正三角形可以铺满地面一个点,∴正三角形可以铺满地面;∵正方形的内角=360°÷4=90°,360°÷90°=4,即4个正方形可以铺满地面一个点,∴正方形可以铺满地面;∵正五边形的内角=180°-360°÷5=108°,360°÷108°≈3.3,∴正五边形不能铺满地面;∵正六边形的内角=180°-360°÷6=120°,360°÷120°=3,即3个正六边形可以铺满地面一个点,∴正六边形可以铺满地面.故选C .3.B 【分析】直接将原式分别分解因式,进而得出公因式即可.【详解】解:∵a2-25=(a+5)(a-5),a2-5a=a (a-5),∴多项式a2-25与a2-5a 的公因式是a-5.故选:B .4.D 【分析】先解不等式组11x x >-⎧⎨≤⎩可求得不等式组的解集是11x -<≤,再根据在数轴上表示不等式解集的方法进行表示.【详解】解不等式组11x x >-⎧⎨≤⎩可求得:不等式组的解集是11x -<≤,故选D.【点睛】本题主要考查不等组的解集数轴表示,解决本题的关键是要熟练掌握正确表示不等式组解集的方法.5.A 【解析】【分析】根据平移的性质:平移后图形的大小、方向、形状均不发生改变结合选项即可得出答案.【详解】解:A 、经过旋转后的图形两个图形的大小和形状也不变,半径相等的两个圆是等圆,圆还具有旋转不变性,故本选项正确;B 、两个全等的图形位置关系不明确,不能准确判定是否具有平移关系,错误;C 、三角形经过旋转,对应线段相等但不一定平行,所以本选项错误;D 、旋转中心可能在图形内部,也可能在图形边上或者图形外面,所以本选项错误.故选A.【点睛】本题考查平移、旋转的基本性质,注意掌握①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.6.D 【解析】【分析】由BD=BC=AD ,设∠A=∠ABD=x ,则∠C=∠CDB=2x ,又由AB=AC ,则∠ABC=∠C=2x ,在△ABC 中,根据三角形的内角和定理列方程求解.【详解】解:∵BD=BC=AD ,∴设∠A=∠ABD=x ,则∠C=∠CDB=2x ,又∵AB=AC ,∴∠ABC=∠C=2x ,在△ABC 中,∠A+∠ABC+∠C=180°,即x+2x+2x=180°,解得x=36°,即∠A=36°.故选:D .【点睛】本题考查了等腰三角形的性质.关键是利用等腰三角形的等边对等角的性质,三角形外角的性质,三角形内角和定理列方程求解.7.C 【解析】【分析】将分式24xx y中的x ,y 的值同时扩大为原来的2019倍,则x 、2x-4y 的值都扩大为原来的2019倍,所以根据分式的基本性质可得,变化后分式的值保持不变.【详解】解:∵将分式24xx y-中的x ,y 的值同时扩大为原来的2019倍,则201920192422019420192019(24)24x x x xx y x y x y x y===-⨯-⨯--,∴变化后分式的值保持不变.故选:C .【点睛】此题主要考查了分式的基本性质,解答此题的关键是要明确:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.8.A 【解析】【分析】设乙每小时做x 个零件,则甲每小时做(6)x +个零件,根据题意可得,甲做90个所用的时间与乙做60个所用的时间相等,据此列方程.【详解】解:设乙每小时做x 个零件,则甲每小时做(6)x +个零件,由题意得:90606x x=+,故选:A .【点睛】本题考查了由实际问题抽象出分式方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程.9.A 【解析】【分析】根据平行四边形的性质推出OA=OC=12AC ,OB=OD=12BD ,求出每个选项中OA 和OB 的值,再判断OA 、OB 、AD 的值是否能组成三角形即可.【详解】解:∵四边形ABCD 是平行四边形,∴OA=OC=12AC ,OB=OD=12BD ,A、∵AC=10,BD=12,∴OA=5,OD=6,∵6-5<10<6+5,∴此时能组成三角形,故本选项符合题意;B、∵AC=12,BD=32,∴OA=6,OD=16,∵16-6=10,∴此时不能组成三角形,故本选项不符合题意;C、∵AC=6,BD=8,∴OA=3,OD=4,∵3+4<10,∴此时不能组成三角形,故本选项不符合题意;D、∵AC=8,BD=10,∴OA=4,OD=5,∵4+5<10,∴此时不能组成三角形,故本选项不符合题意;故选:A.【点睛】本题考查了三角形的三边关系定理和平行四边形的性质,关键是判断OA、OB、AD的值是否符合三角形的三边关系定理.10.D【解析】【分析】分三种情况讨论:①当点E在BC上时,高一定,底边BE最大时面积最大;②当E在CD 上时,△ABE的面积不变;③当E在AD上时,E与D重合时,△ABE的面积最大,根据三角形的面积公式可得结论.【详解】解:分三种情况:①当点E在BC上时,E与C重合时,△ABE的面积最大,如图1,过A作AF⊥BC于F,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠C+∠B=180°,∵∠C=120°,∴∠B=60°,Rt △ABF 中,∠BAF=30°,∴BF=12AB=1,∴此时△ABE 的最大面积为:12②当E 在CD 上时,如图2,此时,△ABE 的面积=12S ▱ABCD =12③当E 在AD 上时,E 与D 重合时,△ABE 的面积最大,此时,△ABE 的面积综上,△ABE 的面积的最大值是故选:D .【点睛】本题考查平行四边形的性质,三角形的面积,含30°的直角三角形的性质以及勾股定理等知识,解题的关键是学会添加常用辅助线,并运用分类讨论的思想解决问题.11.3【解析】【详解】根据分式的值为0,分子为0,分母不为0,可得x-3=0且x+3≠0,即可得x=3.故答案为:x=3.12.22(1)x y 【解析】【分析】原式提取公因式,再利用完全平方公式分解即可.原式=2x (y 2+2y +1)=2x (y +1)2,故答案为2x (y +1)2【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.13.12【解析】【分析】多边形的外角和为360°,而多边形的每一个外角都等于30°,由此做除法得出多边形的边数.【详解】解:∵360°÷30°=12,∴这个多边形为十二边形,故答案为:12.【点睛】本题考查了多边形的外角,关键是明确多边形的外角和为360°.14.5【解析】【分析】由已知条件易得225a b ab -=,22a b a b b a ab --=,两者结合即可求得所求式子的值了.【详解】∵2250a ab b --=,∴225a b ab -=,∵22a b a b b a ab--=,∴2255a b a b ab b a ab ab--===.故答案为:5.【点睛】本题考查了分式的化简求值,“能由已知条件得到225a b ab -=和22a b a b b a ab --=是解答本题的关键.【解析】【分析】根据线段垂直平分线的性质,得BE BA =,根据等腰三角形的性质,得50E A ∠=∠=︒,再根据三角形外角的性质即可求解.【详解】∵BD 垂直平分AE ,∴BE BA =,∴50E A ∠=∠=︒,∴100EBC E A ∠=∠+∠=︒,故答案为100°.【点睛】考查线段垂直平分线的性质以及三角形外角的性质,掌握线段垂直平分线的性质是解题的关键.16.(0)或(0,0,-132)或(0,-2)【解析】【分析】根据条件可得AC=2,过点C 作CD ⊥OA ,由勾股定理得到再分以下三种情况求解:①当OP=OC 时,可直接得出点P 的坐标为(00,;②当PO=PC 时,点P 在OC 的垂直平分线PE 上,先求出直线OC 的解析式,从而可求出直线PE 的解析式,最后可求得P (0,-132);③当CO=CP 时,根据OP=2|y C |=2×1=2,求得P (0,-2).【详解】解:∵点B 坐标是(0,-3),∠OAB=30°,∴AB=2×3=6,∵点C 在线段AB 上,是靠近点A 的三等分点,∴AC=2,过点C 作CD ⊥OA 于D ,∴CD=12AC =1,∴33∴333∴2222(23)113OD CD +=+=∵△OCP 为等腰三角形,分以下三种情况:①当13P 的坐标为(0130,13;②当PO=PC 时,点P 在OC 的垂直平分线PE 上,其中E 为OC 的中点,∴点E 的坐标为3-12),设直线OC 的解析式为y=k 1x ,将点C (3-1)代入得k 13则可设直线PE 的解析式为y=k 2x+b ,则k 1·k 2=-1,∴k 23∴将点3-12)代入3,得b=-132,∴P(0,−132),③当CO=CP 时,OP=2|y C |=2×1=2,∴P (0,-2),综上所述,当△OCP 为等腰三角形时,点P 的坐标为(0,13)或(0,13或(0,-132)或(0,-2),故答案为:(0130,130,-132)或(0,-2).【点睛】本题考查了等腰三角形的判定和性质,含30°的直角三角形的性质,勾股定理以及一次函数解析式的求法等知识,正确作出辅助线是解题的关键.17.(x+y-1)(x+y+1)【解析】【分析】将前三项先利用完全平方公式分解因式,进而结合平方差公式分解因式得出即可.【详解】解:(x2+y2+2xy)-1=(x+y)2-1=(x+y-1)(x+y+1).【点睛】此题主要考查了分组分解法以及公式法分解因式,熟练利用公式法分解因式是解题关键.18.-1≤x<4 5【解析】【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】解:() 2532 121035x xx⎧+≤+⎪⎨-+>⎪⎩①②,解不等式①得x≥-1,解不等式②得x<4 5,∴不等式组的解集为-1≤x<4 5.【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.19.x=﹣3【解析】【分析】通过去分母,把分式方程化成整式方程,求解整式方程,再把解代入最简公分母检验即可.【详解】解:方程两边乘以(x+1)(x ﹣1)得:2(1)4(1)(1)x x x ++=+-解这个方程得:x=﹣3检验:当x=﹣3时,(x+1)(x ﹣1)≠0∴x=﹣3是原方程的解∴原方程的解是:x=﹣3.【点睛】本题考查了解分式方程,熟练掌握解分式方程的一般步骤是解题的关键.20.(1)见解析;(2)见解析;(3)(b ,-a ).【解析】【分析】(1)利用关于原点对称的点的坐标特征写出A1、B1、C1的坐标,然后描点,顺次连接即可;(2)利用网格特点和旋转的性质画出A 、B 、C 的对应点A2、B2、C2,从而得到△A2B2C2;(3)利用A 与A2、B 与B2、C 与C2的坐标特征确定对应点的坐标变换规律,从而写出点P1坐标.【详解】解:(1)如图,△A1B1C1即为所作;(2)如图,△A2B2C2即为所作;(3)点P1坐标为(b ,-a ).故答案为:(b ,-a ).【点睛】本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.21.13m ,【解析】【分析】先将括号里面的进行通分运算,再计算分式的除法运算,最后将m 的值代入即可得出答案.【详解】解:原式=2(3)(3)(3)3(3)(3)(3)3m m m m m m m -+---÷-++333(3)m m m m m -+=⨯+-=1m ,当=3.【点睛】此题主要考查了分式的化简求值,正确进行分式的混合运算是解题关键.22.见解析【解析】【分析】先证明△ABE 与△FCE 全等,根据全等三角形的对应边相等得到AB=CF ;再由AB 与CF 平行,根据一组对边平行且相等的四边形为平行四边形得到ABFC 为平行四边形.【详解】证明:∵四边形ABCD 为平行四边形,∴AB ∥DC ,∴∠ABE=∠ECF ,又∵E 为BC 的中点,∴BE=CE ,在△ABE 和△FCE 中,ABE ECF BE CE AEB FEC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABE ≌△FCE (ASA ),∴AB=CF ,又∵四边形ABCD 为平行四边形,∴AB∥CF,∴四边形ABFC为平行四边形.【点睛】此题考查了平行四边形的判定与性质,全等三角形的判定与性质,熟练掌握基本判定与性质是解本题的关键.23.(1)见解析;(2)3.【解析】【分析】(1)根据完全平方公式和合并同类项的方法可以将等式右边的式子进行化简,从而可以得出结论;(2)根据题目中的等式可以求得所求式子的值.【详解】解:(1)12[(a-b)2+(b-c)2+(c-a)2]=12(a2-2ab+b2+b2-2bc+c2+a2-2ac+c2)=12×(2a2+2b2+2c2-2ab-2bc-2ac)=a2+b2+c2-ab-bc-ac,故a2+b2+c2-ab-bc-ac=12[(a-b)2+(b-c)2+(c-a)2]正确;(2)20182+20192+20202-2018×2019-2019×2020-2018×2020=12×[(2018-2019)2+(2019-2020)2+(2020-2018)2]=12×(1+1+4)=12×6=3.【点睛】本题考查因式分解的应用,解答本题的关键是明确题意,熟练掌握完全平方公式并能灵活运用.24.(1)甲、乙工程队每天分别能铺设70米和50米.(2)所以分配方案有3种.方案一:分配给甲工程队500米,分配给乙工程队500米;方案二:分配给甲工程队600米,分配给乙工程队400米;方案三:分配给甲工程队700米,分配给乙工程队300米.【解析】【分析】(1)设甲工程队每天能铺设x 米.根据甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同,列方程求解;(2)设分配给甲工程队y 米,则分配给乙工程队(1000-y )米.根据完成该项工程的工期不超过10天,列不等式组进行分析.【详解】(1)解:设甲工程队每天能铺设x 米,则乙工程队每天能铺设(20x -)米.根据题意得:35025020x x =-.解得70x =.检验:70x =是原分式方程的解.答:甲、乙工程队每天分别能铺设70米和50米.(2)解:设分配给甲工程队y 米,则分配给乙工程队(1000y -)米.由题意,得107010001050y y ⎧≤⎪⎪⎨-⎪≤⎪⎩解得500700y ≤≤.所以分配方案有3种.方案一:分配给甲工程队500米,分配给乙工程队500米;方案二:分配给甲工程队600米,分配给乙工程队400米;方案三:分配给甲工程队700米,分配给乙工程队300米.25.(1)见解析;(2)FG2=BF2+GC2.理由见解析【解析】【分析】(1)利用ASA 证明△EAF ≌△BAH ,再利用全等三角形的性质证明即可;(2)结论:FG2=BF2+GC2.把△ABF 旋转至△ACP ,得△ABF ≌△ACP ,再利用三角形全等的知识证明∠ACP+∠ACB=90°,根据勾股定理进而可以证明BF 、FG 、GC 之间的关系.【详解】(1)证明:如图①中,∵AB=AC=AD=AE,∠CAB=∠EAD=90°,∴∠EAF=∠BAH,∠E=∠B=45°,∴△EAF≌△BAH(ASA),∴AH=AF;(2)解:结论:GF2=BF2+GC2.理由如下:如图②中,把△ABF旋转至△ACP,得△ABF≌△ACP,∵∠1=∠4,AF=AP,CP=BF,∠ACP=∠B,∵∠DAE=45°∴∠1+∠3=45°,∴∠4+∠3=45°,∴∠2=∠4+∠3=45°,∵AG=AG,AF=AP,∴△AFG≌△AGP(SAS),∴FG=GP,∵∠ACP+∠ACB=90°,∴∠PCG=90°,在Rt△PGC中,∵GP2=CG2+CP2,又∵BF=PC,GP=FG,∴FG2=BF2+GC2.【点睛】本题考查旋转变换,等腰直角三角形的性质,全等三角形的判定和性质以及勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.。
北师大版八年级下册数学期末考试试题及答案

北师大版八年级下册数学期末考试试卷一、单选题1.下列图案中既是中心对称图形,又是轴对称图形的是()A .B .C .D .2.分式1xx +在实数范围内有意义,则x 的取值范围是()A .x =﹣1B .x ≠﹣1C .x ≠0D .x >﹣13.已知两个不等式的解集在数轴上如右图表示,那么这个解集为()A .x≥-1B .x>1C .-3<x≤-1D .x>-34.下列从左到右的变形属于因式分解的是()A .(x +2)(x ﹣2)=x 2﹣4B .x ﹣1=x (1﹣1x)C .x 2+3x +1=x (x +3)+1D .x 2﹣9=(x +3)(x ﹣3)5.如图,在△ABC 中,AB=AC ,∠A=40°,CD ⊥AB 于D ,则∠DCB 等于()A .70°B .50°C .40°D .20°6.已知x y xy +=则22x y xy +的值为()A .B .9C .D .67.对于命题“若a >b ,则a 2>b 2”,小明想举一个反例说明它是一个假命题,则符合要求的反例可以是()A.a=﹣1,b=0B.a=2,b=﹣1C.a=2,b=1D.a=﹣1,b=﹣2 8.如图,OD平分∠AOB,DE⊥AO于点E,DE=4.2,F是射线OB上的任一点,则DF 的长度不可能是()A.3.9B.4.2C.4.7D.5.849.下列说法中,错误的是()A.对角线互相垂直的四边形是菱形B.有一个角是直角的平行四边形是矩形C.矩形的对角线相等D.菱形的面积等于两条对角线乘积的一半10.不等式组3xx m≤-⎧⎨>⎩有两个整数解,则实数m的取值范围为()A.﹣5≤m<﹣4B.﹣5<m<﹣4 C.﹣5<m≤﹣4D.﹣5≤m≤﹣4二、填空题11.用不等式表示“x+1是负数”:________.12.分解因式:2x2﹣6x=_______.13.若分式33xx+-的值为零,则x的值为_____.14.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AC=3km,AB=5km,则M,C两点间的距离为______km.15.如图,在Rt△ABC中,∠BAC=90°,AC的垂直平分线分别交BC、AC于点D,E,若AB=6cm,AC=8cm,则△ABD的周长为_____cm.16.如图,∠1=70°,直线a 平移后得到直线b ,则∠2-∠3=__________.17.在平面直角坐标系xOy 中,一次函数y 1=kx +b 与y 2=x +m 的图象如图所示,若它们的交点的横坐标为2,则下列三个结论中正确的是_______(填写序号).①直线y 2=x +m 与x 轴所夹锐角等于45°;②k +b >0;③关于x 的不等式kx +b <x +m 的解集是x <2.三、解答题18.解不等式组2131213x xx ->-⎧⎪+⎨≥-⎪⎩19.先化简,再求值:22441(1)11x x x x -+÷---,其中x =3.20.在平面直角坐标系中,已知△ABC 三个顶点的坐标分别为A(0,0),B(3,3),C(4,1).(1)画出△ABC 及△ABC 绕点A 逆时针旋转90°后得到的△AB 1C 1;(2)分别写出B1和C1的坐标.21.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.(1)求证:△ABC≌△DFE;(2)连接AF、BD,求证:四边形ABDF是平行四边形.22.如图,点P,M,N分别在等边△ABC的各边上,MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.(1)求证:△PMN是等边三角形;(2)若BP=2cm,求等边△ABC的边长.23.在2021年春季环境整治活动中,红旗社区计划对面积为1600m2的区域进行绿化.经投标由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.(1)求甲、乙两工程队每天能完成绿化的面积;(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务.已知甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,请问应该如何安排甲、乙两队施工的天数,使施工总费用最低?最低费用是多少?24.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②的方式拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积(直接用含m,n的代数式表示).方法一:;方法二:.(2)根据(1)中面积相等的关系,你能得出怎样的等量关系?(用含m的等式表示)(3)根据(2)题中的等量关系,解决如下问题:已知实数a,b满足:a+b=10,ab=8,求a﹣b的值.(4)根据图③,写出一个等式:.25.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.(1)∠EAF=°(直接写出结果不写解答过程);(2)①求证:四边形ABCD是正方形.②若BE=EC=3,求DF的长.(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是(直接写出结果不写解答过程).参考答案1.B【解析】根据中心对称图形和轴对称图形的概念逐项分析即可,轴对称图形:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.中心对称图形:在平面内,把一个图形绕着某个点旋转180 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.【详解】A.是轴对称图形,不是中心对称图形,故该选项不符合题意;B.既是轴对称图形,又是中心对称图形,故该选项符合题意;C.是轴对称图形,不是中心对称图形,故该选项不符合题意;D是轴对称图形,不是中心对称图形,故该选项不符合题意.故选B.2.B【解析】直接利用分式有意义的条件是分母不等于零,进而得出答案.【详解】解:∵分式1xx 在实数范围内有意义,∴x +1≠0,解得:x ≠﹣1.故选:B .【点睛】本题考查分式有意义的条件,熟练掌握分式有意义的条件是解题关键.3.A 【解析】>-3,≥-1,大大取大,所以选A4.D 【解析】根据因式分解是把一个多项式化为几个整式的积的形式,可得答案.【详解】解:A .(x +2)(x ﹣2)=x 2﹣4,是整式的乘法,不是因式分解,故此选项不符合题意;B .x ﹣1=x (1﹣1x),没把一个多项式化为几个整式的积的形式,不是因式分解,故此选项不符合题意;C .x 2+3x +1=x (x +3)+1,不是把一个多项式化为几个整式的积的形式,故此选项不符合题意;D .x 2﹣9=(x +3)(x ﹣3),把一个多项式化为几个整式的积的形式,故此选项符合题意;故选:D .【点睛】本题考查了因式分解的意义.掌握因式分解的定义:把一个多项式化为几个整式的积的形式是解题关键.5.D 【解析】解:∵AB=AC ,∠A=40°,∴∠B=∠C=(180°-40°)÷2=70°,又∵CD ⊥AB ,∴∠BDC=90°,∴∠DCB=90°-70°=20°.故选D .6.C【解析】根据x y xy+=x2y+xy2的值.【详解】解:∵x y xy+=∴x2y+xy2=xy(x+y)=故选C.【点睛】本题考查因式分解的应用,解答本题的关键是明确因式分解的方法,利用题目中的已知条件解答.7.D【解析】【分析】根据有理数的大小比较法则、有理数的乘方法则计算,判断即可.【详解】解:当a=﹣1,b=﹣2时,a>b,而a2<b2,∴“若a>b,则a2>b2”是假命题,故选:D.【点睛】本题考查的命题和定理,任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.8.A【解析】【分析】过D点作DH⊥OB于H,如图,根据角平分线的性质得到DH=DE=4.2,然后根据垂线段最短对各选项进行判断.解:过D点作DH⊥OB于H,如图,∵OD平分∠AOB,DE⊥AO,DH⊥OB,∴DH=DE=4.2,∵F是射线OB上的任一点,∴DF≥4.2.故选:A.【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了垂线段最短.9.A【解析】【分析】由矩形的判定与性质、菱形的判定与性质分别对各个选项进行判断即可.【详解】解:A、∵对角线互相垂直平分的四边形是菱形,∴选项A符合题意;B、∵有一个角是直角的平行四边形是矩形,∴选项B不符合题意;C、∵矩形的对角线相等,∴选项C不符合题意;D、∵菱形的面积等于两条对角线乘积的一半,∴选项D不符合题意;故选A.本题主要考查了矩形的性质与判定,菱形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.10.A 【解析】【分析】根据不等式组3x x m ≤-⎧⎨>⎩有两个整数解知不等式组的整数解为﹣3,﹣4,据此求解可得答案.【详解】解:∵不等式组3x x m≤-⎧⎨>⎩有两个整数解,∴不等式组的解集为3m x <≤-∴不等式组的整数解为﹣3,﹣4,则﹣5≤m <﹣4,故选A .【点睛】本题主要考查了不等式组的整数解,解题的关键在于能够熟练掌握相关知识进行求解.11.x +1<0【解析】【分析】根据负数都小于0,由此列出不等式即可.【详解】解:x +1<0.故答案为:x +1<0.【点睛】此题考查了列不等式;读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.12.2x (x ﹣3)【解析】【分析】因式分解的题,一般先考虑提公因数法,再考虑公式法,最后再用十字相乘即可分解到位.【详解】2x2﹣6x=2x(x﹣3).故答案为2x(x﹣3).13.﹣3【解析】【分析】直接利用分式为零的条件得出答案.【详解】解:∵分式33xx+-的值为零,∴x+3=0,解得:x=﹣3,此时满足分母不为零,故答案为:﹣3.【点睛】本题考查分式为零的条件,掌握分式为零的条件是解题关键. 14.2.5【解析】【分析】根据直角三角形斜边上的中线性质得出CM=12AB,再求出答案即可.【详解】解:∵公路AC,BC互相垂直,∴∠ACB=90°,∵M为AB的中点,∴CM=12 AB,∵AB=5km,∴CM=2.5km,即M,C两点间的距离为2.5km,故答案为:2.5.【点睛】本题主要考查了直角三角形斜边上的中线,解题的关键在于能够熟练掌握直角三角形斜边上的中线等于斜边的一半.15.16【解析】【分析】根据勾股定理求出BC,根据线段垂直平分线的性质得到DA=DC,根据三角形的周长公式计算,得到答案.【详解】解:在Rt△ABC中,∠BAC=90°,AB=6cm,AC=8cm,由勾股定理得:BC=10(cm),∵DE是AC的垂直平分线,∴DA=DC,∴△ABD的周长=AB+BD+DA=AB+BD=DC=AB+BC=16(cm),故答案为:16【点睛】本题考查的是线段垂直平分线的性质、勾股定理,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.16.110°【解析】【分析】先延长直线,然后根据平行线的性质和三角形的外角性质解答即可.【详解】解:如图:延长直线:∵a平移后得到直线b,∴a∥b,∴∠5=180°-∠1=180°-70°=110°,又∵∠2=∠4+∠5,∠3=∠4,∴∠2-∠3=∠5=110°故答案为:110°.【点睛】本题考查平移问题,解答本题的关键是根据平行线的性质和三角形的外角性质求角.17.①②【解析】【分析】①利用直线与两轴的截距相等即可判断;②利用x=1时的函数图象上点的位置来判断;③利用两函数图象的交点与两函数图象的位置来判断即可.【详解】解:由y 2=x +m 得,当x=0时,y 2=m,当y=0时,x=-m ,则直线与坐标轴的截距相等,所以直线y 2=x +m 与x 轴所夹锐角等于45°,故①的结论正确;由图知:当x =1时,函数y 1图象对应的点在x 轴的上方,因此k +b >0,故②的结论正确;由图知:两函数的交点横坐标为x=2,当x >2时,函数y 1图象对应的点都在y 2的图象下方,因此关于x 的不等式kx +b <x +m 的解集是x >2,故③的结论不正确;故答案为:①②.【点睛】本题考查一次函数与一元一次不等式,掌握一次函数与一元一次不等式的关系,会求截距,会求函数值,会比较两函数值的大小关系是解题关键.18.14x -<≤【解析】【分析】分别解出各不等式,再求出公共解集即可.【详解】2131213x x x ->-⎧⎪⎨+≥-⎪⎩①②解①得1x >-,解②得4x ≤,在数轴上表示为∴原不等式组的解集为14x -<≤.【点睛】此题主要考查不等式的解集,解题的关键是熟知不等式的性质.19.21x x -+;14【解析】【分析】首先将括号里面通分运算,再利用分式的混合运算法则计算得出答案.【详解】解:原式=()()()222111x x x x x --÷-+-,=()()()221112x x x x x --⨯-+-,=21x x -+,当x =3时,原式=321314-=+.【点睛】本题主要考查了分式的化简求值.化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.为了降低计算的难度,杜绝繁琐的计算,本题代数式结构复杂,化简后的结果简单,计算简单,把考查重点放在化简的规则和方法上.20.(1)画图见解析;(2)B 1(-3,3),C 1(-1,4).【解析】【分析】(1)根据网格结构找出点A 、B 、C 绕点A 逆时针旋转90°的对应点的位置,然后顺次连接即可;(2)根据关于y 轴对称的点的特征即可得到11,B C 的坐标.【详解】(1)如图所示,△ABC 和△AB 1C 1即为所求.(2)B 1(-3,3),C 1(-1,4).【点睛】本题考查了旋转变换的性质以及旋转作图,解题时要充分利用图形的特点和网格.21.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)由SSS 证明△ABC ≌△DFE 即可;(2)连接AF 、BD ,由全等三角形的性质得出∠ABC=∠DFE ,证出AB ∥DF ,即可得出结论.【详解】详解:证明:()1BE FC = ,BC EF ∴=,在ABC 和DFE 中,AB DF AC DE BC EF =⎧⎪=⎨⎪=⎩,ABC ∴≌()DFE SSS ;()2解:如图所示:由()1知ABC ≌DFE ,ABC DFE ∴∠=∠,//AB DF ∴,AB DF = ,∴四边形ABDF 是平行四边形.点睛:本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形的判定方法,证明三角形全等是解决问题的关键.22.(1)见解析;(2)等边△ABC 的边长为6cm 【解析】【分析】(1)根据等边三角形的性质得出∠A =∠B =∠C ,进而得出∠MPB =∠NMC =∠PNA =90°,再根据平角的意义即可得出∠NPM =∠PMN =∠MNP ,即可证得△PMN 是等边三角形;(2)先根据直角三角形30度的性质可得BM =4,证明△MPB ≌△NMC (AAS ),可得CM =PB =2,从而得结论.【详解】(1)证明:∵△ABC 是等边三角形,∴∠A =∠B =∠C ,∵MP ⊥AB ,MN ⊥BC ,PN ⊥AC ,∴∠MPB =∠NMC =∠PNA =90°,∴∠PMB =∠MNC =∠APN ,∴∠NPM =∠PMN =∠MNP ,∴△PMN 是等边三角形;(2)解:∵△PMN 是等边三角形∴PM=MN在Rt △BPM 中,∵∠B =60°,∴∠PMB =30°,∴BM =2PB =4,在△MPB 和△NMC 中,C B PMB CNM PM NM ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△MPB ≌△NMC (AAS ),∴CM =PB =2,∴BC =BM +CM =4+2=6(cm ),∴等边△ABC 的边长为6cm .本题考查了全等三角形的判定与性质、等边三角形的判定和性质等知识;证出∠NPM=∠PMN=∠MNP是本题的关键.23.(1)甲、乙两工程队每天能完成绿化的面积分别为80m2、40m2;(2)甲队施工15天,乙队施工10天,最低费用为11.5万元【解析】【分析】(1)设出两队的每天绿化的面积,以两队工作时间为等量构造分式方程;(2)以(1)为基础表示甲乙两队分别工作x天、y天的工作总量,工作总量和为1600;用甲乙两队施工的总天数不超过25天确定自变量x取值范围,用x表示总施工费用,根据一次函数增减性求得最低费用.【详解】解:(1)设乙队每天能完成绿化面积为am2,则甲队每天能完成绿化面积为2am2,根据题意得:4004005-=,a a2解得a=40,经检验,a=40为原方程的解,且符合题意,则甲队每天能完成绿化面积为80m2,答:甲、乙两工程队每天能完成绿化的面积分别为80m2、40m2;(2)由(1)得80x+40y=1600,整理:y=﹣2x+40,由已知y+x≤25,∴﹣2x+40+x≤25,解得x≥15,总费用W=0.6x+0.25y=0.6x+0.25(﹣2x+40)=0.1x+10,∵k=0.1>0,∴W随x的增大而增大,∴当x=15时,W最低=1.5+10=11.5,∴甲队施工15天,乙队施工10天,最低费用为11.5万元.本题考查了分式方程和一元一次不等式的应用、一次函数的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程和不等式求解.24.(1)方法一:(m﹣n)2,方法二:(m+n)2﹣4mn;(2)(m﹣n)2=(m+n)2﹣4mn;(3)a b-=±(4)(a+b)3=a3+b3+3a2b+3ab2【解析】【分析】(1)图2中阴影部分是边长为(m﹣n)的正方形,可根据正方形面积公式表示出来,也可以从边长为(m+n)的大正方形减去图1的面积即可;(2)由(1)的两种计算方法可得等式;(3)整体代入计算即可;(4)根据正方体的体积的计算方法,用两种不同的方法表示即可.【详解】解:(1)方法一:图2中阴影部分是边长为(m﹣n)的正方形,因此面积为(m﹣n)2,方法二:图2中阴影部分可以看作边长为(m+n)的大正方形减去图1的面积,即(m+n)2﹣4mn,故答案为:(m﹣n)2,(m+n)2﹣4mn;(2)由(1)可得,(m﹣n)2=(m+n)2﹣4mn;(3)由(2)可得(a﹣b)2=(a+b)2﹣4ab,当a+b=10,ab=8时,(a﹣b)2=102﹣4×8=68,∴a﹣b=(4)正方体的棱长为(a+b),因此体积为(a+b)3,大正方体的体积也可以表示为8块体积的和,即为a3+b3+3a2b+3ab2,所以有(a+b)3=a3+b3+3a2b+3ab2,故答案为:(a+b)3=a3+b3+3a2b+3ab2.【点睛】本题考查了完全平方公式的实际应用,完全平方公式与正方形的面积公式和长方形的面积公式经常联系在一起,要学会观察.25.(1)45;(2)①见解析;②DF的长为2;(3)15 7【解析】【分析】(1)根据平角的定义得到∠DFE+∠BEF=360°﹣90°=270°,根据角平分线的定义得到∠AFE=12∠DFE,∠AEF=12∠BEF,求得∠AEF+∠AFE=12(∠DFE+∠BEF),根据三角形的内角和定理即可得到结论;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,先证明四边形ABCD是矩形,再由角平分线的性质得出AB=AD,即可得出四边形ABCD是正方形;②设DF=x,根据已知条件得到BC=6,由①得四边形ABCD是正方形,求得BC=CD=6,根据全等三角形的性质得到BE=EG=3,同理,GF=DF=x,根据勾股定理列方程即可得到结论;(3)把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,得出MG=DG=MP=PH=6,GQ=4,设MR=HR=a,则GR=6﹣a,QR=a+2,在Rt△GQR 中,由勾股定理得出方程,解方程即可.【详解】解:(1)∵∠C=90°,∴∠CFE+∠CEF=90°,∴∠DFE+∠BEF=360°﹣90°=270°,∵AF平分∠DFE,AE平分∠BEF,∴∠AFE=12∠DFE,∠AEF=12∠BEF,∴∠AEF+∠AFE=12(∠DFE+∠BEF)=12⨯270°=135°,∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,故答案为:45;(2)①作AG⊥EF于G,如图1所示:则∠AGE =∠AGF =90°,∵AB ⊥CE ,AD ⊥CF ,∴∠B =∠D =90°=∠C ,∴四边形ABCD 是矩形,∵∠CEF ,∠CFE 外角平分线交于点A ,∴AB =AG ,AD =AG ,∴AB =AD ,∴四边形ABCD 是正方形;②设DF =x ,∵BE =EC =3,∴BC =6,由①得四边形ABCD 是正方形,∴BC =CD =6,在Rt △ABE 与Rt △AGE 中,AB AGAE AE =⎧⎨=⎩,∴Rt △ABE ≌Rt △AGE (HL ),∴BE =EG =3,同理,GF =DF =x ,在Rt △CEF 中,EC 2+FC 2=EF 2,即32+(6﹣x )2=(x +3)2,解得:x =2,∴DF 的长为2;(3)解:如图2所示:把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,∴MG=DG=MP=PH=5,∴GQ=3,设MR=HR=a,则GR=5﹣a,QR=a+2,在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,解得:a=157,即HR=157;故答案为:15 7.【点睛】本题考查了正方形的判定与性质、全等三角形的判定与性质、角平分线的性质、勾股定理、矩形的判定、翻折变换的性质等知识;本题综合性强,有一定难度.21。
北师大版初中数学八年级下册期末试卷及答案

北师大版八年级数学下册期末试卷及答案考试时间80分钟,满分120分一、选择题(每题3分共24分)1.不等式组⎩⎨⎧≥-->+021372x x x 的解集是A x <8B x ≥2C 2≤x<8D 2<x <82.多项式4x 2+1加上一个单项式后,使它能成为一个整式的完全平方,则加上的单项式不可以是 A 4x B -4x C 4x 4 D -4x 43..下列各式是分式的是 A.a 21. B.221a b +. C.4y -. D.xy 5421+. 4.已知311=-y x ,则yxy x y xy x ---+55的值为 A 、27- B 、27 C 、72 D 、72-5.△ABC ∽△A ‘B ’C ‘,且相似比为2:3,则对应边上的高的比等于 A 、2:3 ; B 、3:2; C 、4:9; D 、9:4。
6.下列说法正确的是A.两个等腰三角形相似B.两个直角三角形相似C.两个等腰直角三角形相似D.有一个角相等的两个等腰三角形相似7.甲、乙两组数据,它们都是由n 个数据组成,甲组数据的方差是 0.4,乙组数据的方差是0.2,那么下列说法正确的是A .甲的波动比乙大B .乙的波动比甲大C .甲、乙的波动一样大D .甲、乙的波动的大小无法比较8.三角形的三边长分别为3,a 21-,8,则a 的取值范围是A .-6<a <-3B .-5<a <-2C .a <-5或a >2D .2<a <5二、填空题9.因式分解:a3-a= ________.10.化简=-÷-ab b a b ab )(2 __________ 。
11.关于x 的方程3k-5x=9的解是非负数,则k 的取值范围是 _______12.如图,A 、B 两点被池塘隔开,在 AB 外选一点 C ,连结 AC 和 BC ,并分别找出它们的中点 M 、N .若测得MN =15m ,则A 、B 两点的距离为 ___________13. 为了让学生适应体育测试中新的要求某学校抽查了部分初二男生的身高身高取整数).经过整理和分析,估计出该校初二男生中身高在160cm 以上(包括160cm )的约占80%.右边为整理和分析时制成的频率分布表,其中a =__________14如图,在梯形ABCD 中,AD ∥BC,AC 交BD 于点O,9:1:=∆∆BOC AOD S S ,则=∆∆BOC DOC S S : 。
八年级下学期期末考试数学试卷带答案(北师大版)

八年级下学期期末考试数学试卷带答案(北师大版)(满分:120分;考试时间:120分钟)一.单选题。
(每小题4分,共40分) 1.下列图形中,其中是中心对称的是( )A. B. C. D.2.下列因式分解正确的是( )A.x 2+y 2=(x+y )2B.5a 2-20ab=m (5m -20n )C.﹣a 2+b 2=(b -a )(a+b )D.a 3-a=a (a 2-1) 3.若x >y ,下列不等式一定成立的是( )A.2x >y+2B.x -2023>y -2023C.﹣x >﹣yD.|x |>|y |4.如图,将平行四边形ABCD 沿对角线AC 折叠,使点B 落在B’处,若∠1=∠2=44°,则∠B 为( )A.124°B.114°C.104°D.66°(第4题图) (第5题图) (第7题图)5.如图,在五边形ABCDE 中,∠A+∠B+∠E=300°,DP ,CP 分别平分∠EDC ,∠BCD ,则∠P=( )A.45°B.60°C.90°D.120° 6.下列多项式中,不能用公式法因式分解的是( )A.﹣x 2+16y 2B.81(a 2-2ab+b 2)-(a+b )2C.m 2-13mn+19n 2 D.﹣a 2-b 2(第9题图)(第10题图)10.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,E、F、G分别是OC,OD,AB的中点,下列结论:①BE⊥AC;②四边形BEFG是平行四边形;③△EFG≌△GBE,其中正确的个数是()A.0B.1C.2D.3二.填空题。
(每小题4分,共24分)11.若xy=2,x-y=1,则代数式2x2y-2xy2= .12.如图,在△ABC中,AD为△ABC的平分线,DE⊥AB于点E,DF⊥AC于点F,若△ABC的面积是10cm2,AB=6cm,AC=4cm,则DF= cm.(第12题图)(第14题图)(第16题图)13.正多边形的一个内角等于150°,则这个正多边形的边数是.14.如图,在平行四边形ABCD 中,∠B=60°,AE ⊥BC ,AF ⊥CD ,垂足分别为E 、F ,若AB=6,CF=2,则CE= .15.按图中程序计算:规定输入一个值x 到结果是否≥17为一次程序操作,如果程序操作进行了两次才停止,则x 的取值范围是 .16.如图,等边△ABC 内有一点O ,OA=3,OB=4,OC=5,以点B 为旋转中心将OB 逆时针旋转60°得到线段O’B ,连接O’A ,下列结论:①△BO’A 可以看成是△BOC 绕点B 逆时针旋转60°得到的;②点O 到点O’的距离为5;③∠AOB=150°;④S 四边形AOBO’=6+4√2;⑤S △AOC +S △AOB =6+94√3.其中正确的结论有 .(只填序号) 三.解答题。
北师大版八年级下册数学期末试题带答案

北师大版八年级下册数学期末试卷一、单选题1.下列图形中,是轴对称图形,但不是中心对称图形的是 A .B .C .D .2.若x >y ,则下列式子中正确的是A .x ﹣2>y ﹣2B .x+2<y+2C .﹣2x >﹣2yD .22x y < 3.能判定四边形ABCD 是平行四边形的是 A .AB∥CD,AB =CD B .AB =BC,AD =CD C .AC =BD,AB =CD D .AB∥CD,AD =CB 4.等腰三角形的两边分别为7和4,则它的周长是A .15B .18C .15或18D .11 5.将2(2)(2)m a m a -+-分解因式,正确的是A .2(2)()a m n --B .(2)(1)m a m -+C .(2)(1)m a m --D .(2)(1)m a m --6.若分式211x x -+的值为0,则x 的值为A .0B .1C .﹣1D .±1 7.用反证法证明“若a∥c ,b∥c ,则a∥b”,第一步应假设A .a∥bB .a 与b 垂直C .a 与b 不一定平行D .a 与b 相交8.如图,在ABC 中,D ,E 分别是AB ,AC 边的中点,连接BE ,DE .若2BDE S =△,则BCE S的值为A .2B .4C .6D .89.如图,直线y 1=kx+2与直线y 2=mx 相交于点P(1,m),则不等式mx <kx+2的解集是A .x <0B .x <1C .0<x <1D .x >110.如图,将□ABCD 沿对角线AC 折叠,使点B 落在'B 处,若1240︒∠=∠=,则B =( )A .60︒B .100︒C .110︒D .120︒11.如图,四边形ABCD 是平行四边形,点E 是边CD 上一点,且BC =EC ,CF∥BE 交AB 于点F ,P 是EB 延长线上一点,下列结论:∥BE 平分∥CBF ;∥CF 平分∥DCB ;∥BC =FB ;∥PF =PC .其中正确结论的个数为( )A .1B .2C .3D .412.小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等.设小明打字速度为x 个/分钟,则列方程正确的是 A .1201806x x =+ B .1201806x x =- C .1201806x x =+ D .1201806x x=- 二、填空题13.不等式9﹣3x >0的非负整数解是_____. 14.若分式33x x --的值为零,则x =_______.15.若方程2111x m x x ++=--有一个增根,则m =_____. 16.若不等式组341x x x n +<-⎧⎨>⎩的解集是x >3,则n 的值是 ___.17.在平面直角坐标系中,线段AB 的端点A 的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A 对应点A′的坐标为____.18.如图所示,在∥ABC 中,∥C =90°,D 是CA 延长线上一点,∥BDC =15°,AD =AB =8,则BC =___.19.如图,一次函数1y kx b =+和2y mx n =+交于点A ,则kx b mx n +>+的解集为___.20.如图,在∥ABC 中,AB =AC ,AB 的垂直平分线 MN 交 AC 于 D 点.若 BD 平分∥ABC, 则∥A =________________ °.三、解答题21.分解因式:2x 2﹣12x+18.22.解不等式组()32226131x x x x -<+⎧⎨-≥--⎩. 23.解方程:2316111x x x +=+--. 24.先化简代数式22321(1)24a a a a -+-÷+-,再从-2,2,0三个数中选一个恰当的数作为a 的值代入求值.25.我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形. 如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,依次连接各边中点得到中点四边形EFGH . (1)这个中点四边形EFGH 的形状是____________; (2)证明你的结论.26.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,ABC 的顶点均在格点上,点C 的坐标为()41-,. (1)把ABC 向上平移5个单位后得到对应的111A B C △,画出111A B C △; (2)以原点O 为对称中心,画出与111A B C △关于原点O 对称的222A B C △.27.某服装店购进一批甲、乙两种款型时尚T 恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元,求甲、乙两种款型的T 恤衫各购进多少件?28.如图,在∥ABC 中,DM ,EN 分别垂直平分AC 和BC ,交AB 于M ,N 两点,DM 与EN 相交于点F .(1)若∥CMN 的周长为15cm ,求AB 的长; (2)若70MFN ∠=︒,求MCN ∠的度数.29.已知:如图,在平行四边形ABCD 中,点F 在AB 的延长线上,且BF=AB ,连接FD ,交BC 于点E . (1)说明∥DCE∥∥FBE 的理由; (2)若EC=3,求AD 的长.30.如图,在四边形ABCD 中,//AD BC ,6BC =厘米,9AD =厘米,点P ,Q 分别从点A ,C 同时出发,点P 以1厘米/秒的速度由点A 向点D 运动,点Q 以2厘米/秒的速度由点C 向点B 运动.当一点到达终点时,两点均停止运动. (1)经过几秒四边形ABQP 为平行四边形?(2)经过几秒直线PQ 将四边形ABCD 截出一个平行四边形?参考答案1.A2.A3.A4.C5.C6.B7.D8.B9.B10.D11.D12.C13.0、1、2【详解】解:9﹣3x>0,∥﹣3x>﹣9,∥x<3,∥x的非负整数解是0、1、2.故答案为0、1、2.14.-3【详解】根据题意得|x|-3=0且x-3≠0,解|x|-3=0得x=3或-3,而x-3≠0,所以x=-3.故答案为-3.15.2.【详解】解:去分母得:x+2=m+1,由分式方程有增根,得到x ﹣1=0,即x =1, 把x =1代入整式方程得:m+1=3, 解得:m =2, 故答案为:2 16.3 【详解】解:解不等式341x x +<-得:43x >, 不等式组的解集为3x >,3n ∴=.故答案为:3. 17.(1,-1) 【详解】解:将点A (-3,2)先向右平移4个单位,再向下平移3个单位, 即把A 点的横坐标加4,纵坐标减3即可,即A′的坐标为(1,-1). 故答案为:(1,-1). 18.4 【详解】 解:8AD AB ==,15ABD BDC ∴∠=∠=︒, 30BAC ABD BDC ∴∠=∠+∠=︒,在ABC ∆中,90C ∠=︒,142BC AB ∴==. 故答案为:4. 19.1x > 【详解】解:由函数图象可得:kx b mx n +>+的解集为:1x >, 故答案为:1x >. 20.36.【详解】试题分析:∥AB =AC , ∥∥C =∥ABC ,∥AB 的垂直平分线MN 交AC 于D 点. ∥∥A =∥ABD , ∥BD 平分∥ABC , ∥∥ABD =∥DBC , ∥∥C =2∥A =∥ABC , 设∥A 为x ,可得:x+x+x+2x =180°, 解得:x =36°, 故答案为36.点睛:此题考查了线段垂直平分线的性质以及等腰三角形的性质.根据垂直平分线的性质和等腰三角形的性质得出角相等,然后在一个三角形中利用内角和定理列方程即可得出答案. 21.2(x ﹣3)2. 【详解】原式=2(x 2﹣6x+9) =2(x ﹣3)2. 22.﹣1≤x <4. 【详解】解不等式3x ﹣2<2x+2,得:x <4, 解不等式6﹣x≥1﹣3(x ﹣1),得:x≥﹣1, 则不等式组的解集为﹣1≤x <4. 23.2x = 【详解】 解:2316111x x x +=+-- 两边同时乘以(x+1)(x -1)得: 3(x -1)+(x+1)=6,3x -3+x+1=6, 4x=8, x=2,检验:当x=2时,(x+1)(x -1)≠0, ∥x=2是原方程的根. 24.21a a --,2 【详解】试题分析:首先将括号里面的进行通分,然后将除法改成乘法进行分式的化简,选择a 的值时,不能使原分式没有意义,即a 不能取2和-2. 试题解析:原式=232a a +-+·2(2)(2)(1)a a a +--=21a a --当a=0时,原式=21a a --=2. 考点:分式的化简求值. 25.(1) 平行四边形;(2)见解析. 【详解】试题分析:(1)根据四边形的形状,及三角形中位线的性质可判断出四边形EFGH 是平行四边形;(2)连接AC 、利用三角形的中位线定理可得出HG=EF 、EF∥GH ,继而可判断出四边形EFGH 的形状; 试题解析:(1)平行四边形. (2)证明:连接AC ,∥E 是AB 的中点,F 是BC 的中点, ∥EF∥AC ,EF=12AC . 同理HG∥AC ,HG=12AC . ∥EF∥HG ,EF=HG .∥四边形EFGH 是平行四边形. 26.(1)见解析;(2)见解析 【详解】即111A B C △、222A B C △是所求作的三角形.27.甲种购进60件,乙种购进40件. 【详解】解:设乙种购进x 件,则甲种购进1.5x 件, 根据题意,得:78001.5x +30=6400x, 解得:x =40,经检验x =40是原分式方程的解, 1.5x =60,答:甲种购进60件,乙种购进40件.28.(1)AB 的长为15cm ;(2)MCN ∠的度数为40︒. 【详解】解:(1)∥DM ,EN 分别垂直平分AC 和BC ∥AM CM =,CN NB = ∥∥CMN 的周长为15cm ∥15CM CN MN cm ++= ∥15AM BN MN cm ++= ∥15AB cm = AB 的长为15cm(2)由(1)得AM CM==,CN NB∥A ACM∠=∠∠=∠,B BCN在MNF中,70∠=︒MFN∥110∠+∠=︒FMN FNM根据对顶角的性质可得:FMN AMD∠=∠,FNM BNE∠=∠在Rt ADM∠=︒-∠=︒-∠A AMD FMN△中,9090在Rt BNE中,9090∠=︒-∠=︒-∠B BNE FNM∥909070A B FMN FNM∠+∠=︒-∠+︒-∠=︒∥70∠+∠=︒MCA NCB在ABC中,70∠+∠=︒A B∥110∠=︒ACB∥()40∠=∠-∠+∠=︒MCN ACB MCA NCB29.(1)证明见解析(2)6【解析】(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∥CDE=∥F,又由BF=AB,即可利用AAS,判定∥DCE∥∥FBE.(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长.(1)证明:∥四边形ABCD是平行四边形,∥AB=DC,AB∥DC.∥∥CDE=∥F.又∥BF=AB,∥DC=FB.在∥DCE和∥FBE中,∥∥CDE=∥F,∥CED=∥BEF,DC=FB,∥∥DCE∥∥FBE(AAS).(2)解:∥∥DCE∥∥FBE,∥EB=EC.∥EC=3,∥BC=2EB=6.∥四边形ABCD是平行四边形,∥AD=BC.∥AD=6.30.(1)2秒;(2)2秒或3秒【解析】(1)设t秒后四边形ABQP是平行四边形;根据题意得:AP=t厘米,CQ=2t厘米,由AP=BQ得出方程,解方程即可;(2)由(1)知,2秒时四边形ABQP是平行四边形,第二种情况:四边形DCQP 是平行四边形,根据题意得:AP=x厘米,CQ=2x厘米,则PD=(9-x)厘米,进而可得方程2x=9-x,再解即可.【详解】解:(1)设经过t秒四边形ABQP是平行四边形,根据题意,得AP=t厘米,CQ=2t厘米,则BQ=(6-2t)厘米,∥AD∥BC,∥当AP=BQ时,四边形ABQP是平行四边形,∥t=6-2t,解得t=2,即经过2秒四边形ABQP为平行四边形;(2)由(1)知,经过2秒四边形ABQP是平行四边形,设经过x秒直线PQ将四边形ABCD截出另一个平行四边形DCQP,根据题意,得AP=x厘米,CQ=2x厘米,则PD=(9-x)厘米,∥AD∥BC,∥当CQ=PD时,四边形DCQP是平行四边形,∥2x=9-x,解得x=3.综上,经过2秒或3秒直线PQ将四边形ABCD截出一个平行四边形.。
(完美版)北师大版八年级下册数学期末测试卷及含答案(易错题)

北师大版八年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB 于点E,交BC于点D.CD=3,则BC的长为()A.6B.9C.6D.32、函数y= 中,自变量x的取值范围是()A.x>0B.x>1C.x>0且x≠1D.x≥0且x≠13、分式的值为0,则()A.x=﹣1B.x=1C.x=±1D.x=04、一个多边形的内角和比他的外角和的3倍少180°,这个多边形的边数是( )A.5B.6C.7D.85、下列各式:中,是分式的共有()A.1个B.2个C.3个D.4个6、下列说法正确的是()A.代数式是分式B.分式中,都扩大3倍,分式的值不变C.分式有意义D.分式是最简分式7、一个多边形的内角和是外角和的 3 倍,则多边形是( )A.五边形B.六边形C.八边形D.十二边形8、已知等腰三角形的两边长满足+(b﹣5)2=0,那么这个等腰三角形的周长为()A.13B.14C.13或14D.99、不等式组的解集在数轴上表示正确的是()A. B. C.D.10、已知直线y=x+ 与直线y=kx﹣1相交于点P,若点P的纵坐标为,则关于x的不等式x+ >kx﹣1的解集为()A.x>﹣1B.x≥﹣1C.x<﹣1D.x≤﹣111、已知一个多边形的内角和是900°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形12、下列交通标志中,既是轴对称图形,又是中心对称图形的是()A. B. C. D.13、如图,AC=AD,BC=BD,则()A.CD垂直平分ABB.AB垂直平分CDC.CD平分∠ACBD.以上结论都不正确14、若不等式组无解,则a的取值范围是()A.a≥﹣1B.a≤﹣1C.a>﹣1D.a<﹣115、若分式无意义,则x的值为()A.0B.1C.-1D.2二、填空题(共10题,共计30分)16、如果多边形的每个外角都是45°,那么这个多边形的边数是________.17、如图,AC、AD是正五边形的对角线,则∠CAD的度数是________.18、如图,在△ABC中,BC=6,将△ABC沿BC方向平移得到△A′B′C′,连接AA′,若A′B′恰好经过AC的中点O,则AA′的长度为________.19、如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作MN∥BC,分别交AB、AC于点M,N.若AB=8,AC=10,则△AMN的周长是________.20、小华将直角坐标系中的猫眼的图案向右平移了3个单位长度,平移前猫眼的坐标为(– 4,3)、(– 2,3),则移动后猫眼的坐标为________。
北师大版八年级下册数学期末考试试题附答案

北师大版八年级下册数学期末考试试卷一、单选题1.下列图形既是轴对称图形,又是中心对称图形的是()A .B .C .D .2.已知a b <,则下列不等式中不正确的是()A .44a b<B .44a b ++<C .4a 4b--<D .44a b --<3.当3x =-,下列分式中有意义的是()A .33x x --B .33x x -+C .()()()()3232x x x x ++--D .()()()()3232x x x x -++-4.不等式12x -≥的解集在数轴上表示正确的是()A .B .C .D .5.下列等式从左到右的变形正确的是()A .11b b a a +=+B .2b ab a a=C .22b b a a=D .32b b a a=6.下列多项式中,不能用平方差公式分解的是()A .22x y -B .22x y --C .224x y -D .24x -+7.如图,在菱形ABCD 中,不一定成立的是()A .四边形ABCD 是平行四边形B .AC BD ⊥C .ABD 是等边三角形D .CAB CAD∠=∠8.炎炎夏日,甲安装队为A 小区安装60台空调,乙安装队为B 小区安装50台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.设乙队每天安装x 台,根据题意,下面所列方程中正确的是A .6050x x 2=-B .6050x 2x=-C .6050x x 2=+D .6050x 2x=+9.若方程()()211120m m x m x +----=是关于x 的一元二次方程,则m 的值为()A .0B .±1C .1D .-110.若分式211x x -+的值为0,则x 的值为()A .0B .1C .﹣1D .±1二、填空题11.分解因式:2x y y -=_________.12.如图,函数y=2x 和y=ax+4的图象相交于点A(32,3),则不等式2x >ax+4的解集为___.13.已知关于x 的方程21+-x ax -1=0的解是正数,则a 的取值范围是________.14.如图,在△ABC 中,AB=AC=10cm ,DE 是AB 的中垂线,△BDC 的周长为16cm ,则BC 的长为______cm .15.已知关于x 的分式方程2233x kx x -=+--无解,则k 的值是__________.16.一个n 边形的各内角都等于120︒,则边数n 是_______.17.如图,在正方形ABCD 中,E 、F 分别是边BC 、CD 上的点,∠EAF =45°,△ECF 的周长为4,则正方形ABCD 的边长为_____.三、解答题18.在边长为1个单位长度的小正方形组成的网格中,点A 、B 、C 、O 都是格点.将ABC绕点O 按逆时针方向旋转180︒得到111A B C △,请画出111A B C △.19.(1)解方程:21233x x x-=+--(2)解不等式组64325213x x x x +≥-⎧⎪+⎨--⎪⎩>20.(1)用配方法解方程:2230x x --=(2)用因式分解法解方程:()()224219210x x +--=21.化简226921432a a a a a a a -++-----22.如图,过正方形ABCD 的顶点D 作DE ∥AC 交BC 的延长线于点E.(1)判断四边形ACED 的形状,并说明理由;(2)若BD=8cm ,求线段BE 的长.23.某物流公司要将300吨物资运往港口码头,现有A 、B 两种型号的车可供调用,已知A 型车每辆可装20吨,B 型车每辆可装15吨,在每辆车不超载的条件下,把300吨物资装完.如果已确定调用5辆A 型车,那么至少还需调用B 型车多少辆?24.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路钱一少用10分钟到达.求小明走路线一时的平均速度.25.如图,已知菱形ABCD ,AB=AC ,E 、F 分别是BC 、AD 的中点,连接AE 、CF .(1)求证:四边形AECF 是矩形;(2)若AB=6,求菱形的面积.26.如图,在ABC 中,点O 是AC 边上的一个动点,过点O 作直线//BC MN ,设MN 交BCA ∠的角平分线于点E ,交BCA ∠的外角ACG ∠的平分线于点F ,连接AF .(1)求证:EO FO =;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.(3)在(2)的条件下,ABC 满足什么条件时,四边形AECF 是正方形?并说明理由.参考答案1.D 【详解】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合.因此,A 、不是轴对称图形,是中心对称图形,故本选项错误;B 、是轴对称图形,但不是中心对称图形,故本选项错误;C 、是轴对称图形,但不是中心对称图形,故本选项错误;D 、既是轴对称图形,又是中心对称图形,故本选项正确.故选D .2.C【分析】根据不等式的性质逐个判断即可.【详解】解:A、∵a<b,∴4a<4b,故本选项不符合题意;B、∵a<b,∴a+4<b+4,故本选项不符合题意;C、∵a<b,∴-4a>-4b,故本选项符合题意;D、∵a<b,∴a-4<b-4,故本选项不符合题意;故选:C.【点睛】本题考查了不等式的性质,能熟记不等式的性质的内容是解此题的关键.3.C【解析】【分析】根据分式有意义的条件是分母不为0对各个选项进行判断即可.【详解】解:A、当x=-3时,x-3=0,故A不符合;B、当x=-3时,x+3=0,故B不符合;C、当x=-3时,(x-3)(x-2)≠0,故C符合;D、当x=-3时,(x+3)(x-2)=0,故D不符合;故选:C.【点睛】本题主要考查了分式有意义的条件,掌握分式有意义的条件是分母不等于0是解题的关键.4.A【解析】先求出已知不等式的解集,然后表示在数轴上即可.【详解】不等式1-x≥2,解得:x≤-1,表示在数轴上,如图所示:故选:A .【点睛】此题考查解一元一次不等式,在数轴上表示不等式的解集,解题关键在于把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画).在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆圈表示.5.B 【解析】【分析】根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项.【详解】解:A 、根据分式基本性质知道11b b a a ++≠,故选项错误;B 、2b ab a a =,其中a≠0,故选项正确;C 、等式的右边是左边的平方,显然不成立,故选项错误;D 、根据分式的基本性质可得:32b b a ab=(b≠0),故选项错误;故选B .【点睛】此题主要考查了分式的基本性质,关键是熟练掌握分式的基本性质.6.B 【解析】根据平方差公式的结构特点,两平方项的符号相反,对各选项分析判断后利用排除法求解.【详解】解:A 、x 2-y 2符合平方差公式,故本选项错误;B 、-x 2与-y 2符号相同,不能运用平方差公式,故本选项正确;C 、4x 2-y 2符合平方差公式,故本选项错误;D 、-4+x 2,符合平方差公式,故本选项错误.故选:B .【点睛】本题主要考查了运用公式法分解因式,熟记平方差公式的结构特点是解本题的关键.7.C 【解析】【分析】菱形是特殊的平行四边形,故A 正确,根据菱形的性质:对角线互相平分且平分对角得B 、D 正确.【详解】因为菱形是特殊的平行四边形,对角线互相垂直平分,且每一条对角线平分一组对角.故选:C.【点睛】考查菱形的性质,熟练掌握菱形的性质定理是解题的关键.8.D 【解析】【详解】试题分析:由乙队每天安装x 台,则甲队每天安装x+2台,则根据关键描述语:“两队同时开工且恰好同时完工”,找出等量关系为:甲队所用时间=乙队所用时间,据此列出分式方程:6050x 2x=+.故选D .9.D 【解析】【分析】根据一元二次方程的定义解答,(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.所以m 2+1=2,且m-1≠0,解得m 的值只能是-1.【详解】解:∵()()211120m m x m x +----=是关于x 的一元二次方程,∴21012m m -≠⎧⎨+=⎩,解得:m=-1,故选D .【点睛】本题考查了一元二次方程的定义,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.10.B 【解析】【分析】根据分式值为0的条件,分子为0分母不为0列式进行计算即可得.【详解】∵分式211x x -+的值为零,∴21010x x ⎧-=⎨+≠⎩,解得:x=1,故选B .【点睛】本题考查了分式值为0的条件,熟知分式值为0的条件是分子为0分母不为0是解题的关键.11.y (x+1)(x ﹣1).【解析】【详解】试题分析:x 2y ﹣y=y (x 2﹣1)=y (x+1)(x ﹣1),故答案为y (x+1)(x ﹣1).考点:提公因式法与公式法的综合运用;因式分解.12.x>3 2【解析】【分析】由于函数y=2x和y=ax+4的图象相交于点A(332,),观察函数图象得到当x>32时,函数y=2x的图象都在y=ax+4的图象上方,所以不等式2x>ax+4的解集为x>3 2.【详解】解:∵函数y=2x和y=ax+4的图象相交于点A(332,),∴当x>32时,2x>ax+4,即不等式2x>ax+4的解集为x>3 2.故答案为:x>3 2.【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x轴上(或下)方部分所有的点的横坐标所构成的集合.13.a<-1且a≠-2【解析】【分析】先求得方程的解,再解x>0,求出a的取值范围.【详解】解21+-x ax-1=0得:x=-a-1,∵于x的方程21+-x ax-1=0的解是正数,∴x〉0,即-a-1>0,∴a<-1,当x-1=0时,x=1,代入得:a=-2.此为增根,∴a≠-2,综合上述可得:a<-1且a≠-2.故答案是:a<-1且a≠-2.【点睛】考查了分式方程的解,先求出分式方程的解,再求出a的取值范围.14.6【解析】【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,然后推出△BDC的周长=AC+BC,代入数据进行计算即可得解.【详解】∵DE是AB的中垂线,∴AD=BD,∴△BDC的周长=BD+CD+BC=AD+CD+BC=AC+BC,∵△BDC的周长为16cm,AC=10cm,∴10+BC=16,解得BC=6.故答案为6.【点睛】此题考查等腰三角形的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,是基础题,熟记性质是解题的关键.15.1【解析】【分析】分式方程去分母转化为整式方程,由分式方程无解得到x-3=0求出x的值,代入整式方程求出k的值即可.【详解】解:分式方程去分母得:x-2=k+2(x-3),即x=4-k,由分式方程无解得到x-3=0,即x=3,代入整式方程得:3=4-k,解得:k=1,故答案为:1.【点睛】此题考查了分式方程的解,需注意在解分式方程时要考虑分母不为0.16.6【解析】【分析】首先求出外角度数,再用360°除以外角度数可得答案.【详解】解:∵n边形的各内角都等于120°,∴每一个外角都等于180°-120°=60°,∴边数n=360°÷60°=6.故答案为:6.【点睛】此题主要考查了多边形的外角和定理,外角与相邻的内角的关系,关键是掌握各知识点的计算公式.17.2【解析】【分析】根据旋转的性质得出∠EAF′=45°,进而得出△FAE≌△EAF′,即可得出EF+EC+FC=FC+CE+EF′=FC+BC+BF′=4,得出正方形边长即可.【详解】解:将△DAF绕点A顺时针旋转90度到△BAF′位置,由题意可得出:△DAF≌△BAF′,∴DF=BF′,∠DAF=∠BAF′,∴∠EAF′=45°,在△FAE 和△EAF′中''AF AF FAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△FAE ≌△EAF′(SAS ),∴EF=EF′,∵△ECF 的周长为4,∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4,∴2BC=4,∴BC=2.故答案为:2.【点睛】此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,得出△FAE ≌△EAF′是解题关键.18.见解析【解析】【分析】连接AO 并延长,然后截取OA 1=OA ,则A 1就是A 的对应点,同样可以作出B 、C 的对应点,然后顺次连接即可.【详解】解:所作图形111A B C △如图所示.【点睛】本题考查了利用旋转变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.19.(1)x=5;(2)45<x≤3【解析】【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.【详解】解:(1)21233x x x-=+--去分母得:()2231x x -=--,去括号得:2261x x -=--,移项合并得:x=5,经检验:x=5是原方程的解,∴原方程得解是x=5;(2)64325213x x x x +≥-⎧⎪⎨+--⎪⎩①>②,解不等式①得:x≤3,解不等式②得:x >45,∴不等式组的解集为:45<x≤3.【点睛】本题考查了解分式方程和解一元一次不等式组,解题的关键是掌握相应的解法.20.(1)x 1=-1,x 2=3;(2)x 1=110,x 2=52【解析】【分析】(1)方程两边加上4,再把方程左边分解得到()214x -=,然后利用直接开平方法求解;(2)利用平方差公式进行因式分解,然后求解即可.【详解】解:(1)2230x x --=,∴2214x x -+=,∴()214x -=,∴x-1=±2,解得:x 1=-1,x 2=3;(2)()()224219210x x +--=,()()2242630x x +--=,()()426342630x x x x ++-+-+=,()()101250x x --+=,10x-1=0或-2x+5=0,解得:x 1=110,x 2=52.【点睛】本题考查了解一元二次方程—因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.也考查了配方法解一元二次方程.21.22a --【解析】【分析】先将各分子和分母因式分解,再约分,最后计算减法.【详解】解:226921432a a a a a a a -++-⋅----=()()()23212232a a a a a a a -+-⋅-+---=3122a a a a -----=22a --【点睛】本题考查了分式的混合运算,解题的关键掌握运算法则以及因式分解的运用.22.(1)四边形ACED 是平行四边形.理由如下见解析(2).【解析】【分析】(1)根据正方形的对边互相平行可得AD ∥BC ,即为AD ∥CE ,然后根据两组对边互相平行的四边形是平行四边形解答.(2)根据正方形的四条边都相等,平行四边形的对边相等可得BC=AD=CE ,再根据正方形的边长等于对角线的2倍求出BC ,然后求出BE 即可.【详解】解:(1)四边形ACED 是平行四边形.理由如下:∵四边形ABCD 是正方形,∴AD ∥BC ,即AD ∥CE.∵DE ∥AC ,∴四边形ACED 是平行四边形.(2)由(1)知,BC=AD=CE=CD ,∵BD=8cm ,∴BC=2BD=2cm ,∴.23.14.【解析】【详解】试题分析:设还需要调用B 型车x 辆,根据关系式为:5辆A 型车的装载量+x 辆B 型车的装载量≥300列不等式进行求解即可得.试题解析:设还需要调用B 型车x 辆,根据题意得:20×5+15x≥300,解得x≥1313,由于x 是车的数量,应为整数,所以x 的最小值为14,答:至少需要调用14辆B 型车.【点睛】本题考查了一元一次不等式的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式.24.50千米/小时【解析】【分析】设小明走路线一的平均速度是x 千米/小时,则小明走路线二的平均速度是x (1+80%)千米/小时,根据走路线二比走路线一少用10分钟建立方程求出其解即可.【详解】解:设小明走路线一的平均速度是x 千米/小时,则走路线二的平均速度是x (1+80%)千米/小时,由题意,得()253010180%60x x =++,解得:x=50,经检验,x=50是原方程的解.故小明走路线一的平均速度是50千米/小时.答:小明走路线一的平均速度是50千米/小时.【点睛】本题考查了列分式方程解关于行程问题的运用题运用及分式方程的解法的运用,解答时根据条件找到等量关系建立方程是关键,解分式方程要验根是不可少的步骤.25.(1)证明见解析;(2)【解析】【详解】试题分析:(1)首先证明△ABC 是等边三角形,进而得出∠AEC=90°,四边形AECF 是平行四边形,即可得出答案;(2)利用勾股定理得出AE 的长,进而求出菱形的面积.试题解析:(1)∵四边形ABCD 是菱形,∴AB=BC ,又∵AB=AC ,∴△ABC 是等边三角形,∵E 是BC 的中点,∴AE ⊥BC ,∴∠AEC=90°,∵E 、F 分别是BC 、AD 的中点,∴AF=12AD ,EC=12BC ,∵四边形ABCD 是菱形,∴AD ∥BC 且AD=BC ,∴AF ∥EC 且AF=EC ,∴四边形AECF 是平行四边形,又∵∠AEC=90°,∴四边形AECF 是矩形;(2)在Rt △ABE 中,AE==,所以,S 菱形ABCD 考点:1.菱形的性质;2..矩形的判定.26.(1)见解析;(2)当点O 运动到AC 的中点时,四边形AECF 是矩形,理由见解析;(3)ABC 满足ACB ∠为直角时,四边形AECF 是正方形,理由见解析.【解析】【分析】(1)由平行线的性质和角平分线的定义得出32∠=∠,13∠=∠,得出EO=CO ,FO=CO ,即可得出结论;(2)先证明四边形AECF 是平行四边形,再由对角线相等,即可得出结论;(3)由//BC MN ,得出AOE ACB ∠=∠,当90ACB ∠=︒时,AC EF ⊥即可.【详解】(1)证明:如图,∵//BC MN ,∴32∠=∠.又∵CF 平分ACG ∠,∴12∠=∠,∴13∠=∠,∴FO CO =,同理,EO CO =,∴EO FO =.(2)解:当点O 运动到AC 的中点时,四边形AECF 是矩形,证明如下:当点O 运动到AC 的中点时,AO CO =.又∵EO FO =,∴四边形AECF 是平行四边形,由(1)可知,FO CO =,∴AO CO EO FO ===,∴AO CO EO FO +=+,即AC EF =,∴四边形AECF 是矩形.(3)当点O 运动到AC 的中点时,且△ABC 满足∠ACB 为直角的直角三角形时,四边形AECF 是正方形.在(2)的条件下,ABC 满足ACB ∠为直角时,四边形AECF 是正方形.理由:由(2)知,当点O 运动到AC 的中点时,四边形AECF 是矩形.∵//BC MN ,∴AOE ACB ∠=∠,当90ACB ∠=︒时,90AOE ∠=︒,即AC EF ⊥,∴四边形AECF 是正方形.【点睛】本题考查了平行线的性质、等腰三角形的判定、矩形的判定、正方形的性质;熟练掌握平行线的性质和矩形、正方形的判定方法,并能进行推理论证是解决问题的关键.。
(完整版)北师大版八年级下册数学期末测试卷及含答案(查漏补缺)

北师大版八年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,一次函数y=kx+b(k、b为常数,且k≠0)与正比例函数y=ax(a 为常数,且a≠0)相交于点P,则不等式kx+b<ax的解集是()A.x>1B.x<1C.x>2D.x<22、如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC 与∠A互补,其作法分别如下:(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;(乙)作过B点且与AB垂直的直线,作过C点且与AC垂直的直线,交于P点,则P即为所求.对于甲、乙两人的作法,下列叙述何者正确?()A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确3、下列命题:(1)如果a<0,b>0,那么;(2)同角的补角相等;(3)同位角相等;(4)如果,那么;(5)有公共顶点且相等的两个角是对顶角。
其中正确的个数是()A.1B.2C.3D.44、如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于()A.72°B.108°C.36°D.62°5、若不等式组的解集是x>4,则m的取值范围是()A.m>4B.m≥4C.m≤4D.m<46、已知整数x满足是不等式组,则x的算术平方根为()A.2B.±2C.D.47、下列基本图形中经过平移、旋转或轴对称变换后不能得到右图的是()A. B. C. D.8、若将分式中的x和y都扩大到原来的2倍,那么分式的值()A.扩大到原来的4倍B.扩大到原来的2倍C.不变D.缩小到原来的.9、如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4.将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )A. B. C. D.10、如图所示,在矩形ABCD中,AB= ,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A. B. C.1 D.1.511、如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,则MN=()A. B. C. D.12、如图,中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是()A. B. C.D.13、如图,△ABC的顶点都在⊙O上,∠BAO=50°,则∠C的度数为()A.30°B.40°C.45°D.50°14、如图,将边长相等的正方形、正五边形、正六边形纸板,按如图方式放在桌面上,则∠a的度数是( )A.42°B.40°C.36°D.32°15、若整数使得关于的不等式组的解集为,且关于的分式方程的解为负数,则所有符合条件的整数的和为()A.0B.-3C.-5D.-8二、填空题(共10题,共计30分)16、因式分解:________ .17、若m+n=2,计算6﹣2m﹣2n=________.18、如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有________个.19、如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为________.20、如图,在矩形中,,,那么的度数为________.21、若关于的分式方程有增根,则=________ .22、在函数y=中,自变量x的取值范围是________.23、在□ABCD中,若∠A=50°,则∠D的度数为________。
北师大版八年级数学下册期末试卷(完整版)

北师大版八年级数学下册期末试卷(完整版)班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.2020的相反数是( )A .2020B .2020-C .12020D .12020- 2.将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A .22(2)3y x =++;B .22(2)3y x =-+;C .22(2)3y x =--;D .22(2)3y x =+-.3.如果线段AB =3cm ,BC =1cm ,那么A 、C 两点的距离d 的长度为( )A .4cmB .2cmC .4cm 或2cmD .小于或等于4cm ,且大于或等于2cm4.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺.将绳子对折再量长木,长木还剩余1尺,问木长多少尺,现设绳长x 尺,木长y 尺,则可列二元一次方程组为( )A . 4.5112y x y x -=⎧⎪⎨-=⎪⎩B . 4.5112x y y x -=⎧⎪⎨-=⎪⎩C . 4.5112x y x y -=⎧⎪⎨-=⎪⎩D . 4.5112y x x y -=⎧⎪⎨-=⎪⎩ 5.下列说法中,错误的是( )A .不等式x <5的整数解有无数多个B .不等式x >-5的负整数解集有有限个C .不等式-2x <8的解集是x <-4D .-40是不等式2x <-8的一个解6.如图,正方形ABCD 中,AB=12,点E 在边CD 上,且BG=CG ,将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连接AG 、CF ,下列结论:①△ABG ≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC =725.其中正确结论的个数是()A.2个B.3个C.4个D.5个7.如图,在数轴上表示实数15的点可能是()A.点P B.点Q C.点M D.点N8.如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是()A.BF=DF B.∠1=∠EFD C.BF>EF D.FD∥BC9.如图,能判定EB∥AC的条件是()A.∠C=∠1 B.∠A=∠2C.∠C=∠3 D.∠A=∠110.下列选项中,不能判定四边形ABCD是平行四边形的是()A.AD//BC,AB//CD B.AB//CD,AB CDC .AD//BC ,AB DC =D .AB DC =,AD BC =二、填空题(本大题共6小题,每小题3分,共18分)1.8-的立方根是__________.2.已知AB//y 轴,A 点的坐标为(3,2),并且AB=5,则B 的坐标为________.3.若28n 是整数,则满足条件的最小正整数n 为________.4.如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm ,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物,则蚂蚁沿着台阶面爬到B 点的最短路程是__________dm.5.如图,在Rt △ABC 中,∠ACB=90°,点D ,E 分别是AB ,AC 的中点,点F 是AD 的中点.若AB=8,则EF=________.6.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,CE ∥BD ,DE ∥AC .若AC=4,则四边形CODE 的周长是__________.三、解答题(本大题共6小题,共72分) 1.解下列方程组:(1)75331x y x y +=⎧⎨+=⎩; (2)()346126x y y x y y ⎧+-=⎪⎨+-=⎪⎩.2.化简求值:[4(xy-1)2-(xy+2)(2-xy)]÷14xy,其中x=-2, y=15.3.已知:12x =-,12y =+,求2222x y xy x y +--+的值.4.如图,∠BAD=∠CAE=90°,AB=AD ,AE=AC ,AF ⊥CB ,垂足为F .(1)求证:△ABC ≌△ADE ;(2)求∠FAE 的度数;(3)求证:CD=2BF+DE .5.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x (h )之间的函数关系,其中线段AB 、BC 表示恒温系统开启阶段,双曲线的一部分CD 表示恒温系统关闭阶段.请根据图中信息解答下列问题:(1)求这天的温度y 与时间x (0≤x ≤24)的函数关系式;(2)求恒温系统设定的恒定温度;(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?6.某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.(1)甲、乙两种书柜每个的价格分别是多少元?(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.参考答案一、选择题(本大题共10小题,每题3分,共30分)1、B2、B3、D4、B5、C6、D7、C8、B9、D10、C二、填空题(本大题共6小题,每小题3分,共18分)1、-22、(3,7)或(3,-3)3、74、255、26、8三、解答题(本大题共6小题,共72分)1、(1)52xy=⎧⎨=⎩;(2)2xy=⎧⎨=⎩2、20xy-32,-40.3、4、(1)证明见解析;(2)∠FAE=135°;(3)证明见解析.5、(1)y关于x的函数解析式为210(05)20(510)200(1024)x xy xxx⎧⎪+≤<⎪=≤<⎨⎪⎪≤≤⎩;(2)恒温系统设定恒温为20°C;(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害.6、(1)设甲种书柜单价为180元,乙种书柜的单价为240元.(2)学校的购买方案有以下三种:方案一:甲种书柜8个,乙种书柜12个方案二:甲种书柜9个,乙种书柜11个,方案三:甲种书柜10个,乙种书柜10个.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版八年级下册数
学期末试卷
HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】
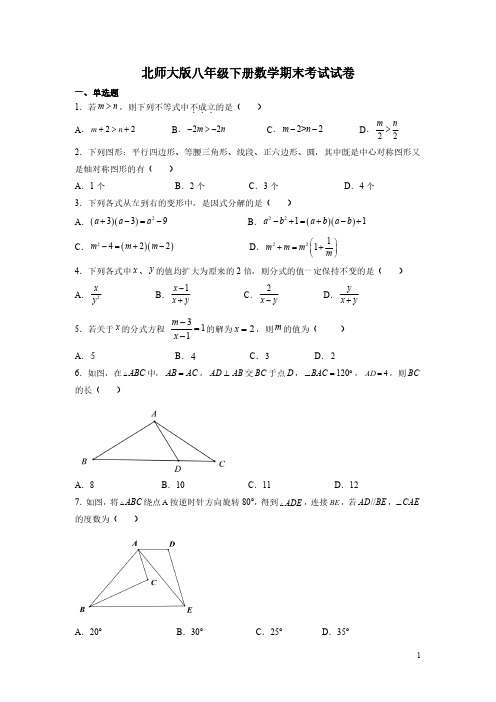
A B C E D 2016学年度第二学期八年级数学期末试题
一.选择题(共10小题,每题3分,计24分)
1. 下列从左边到右边的变形,是因式分解的是( )
322842(42)m n mn mn m n +=+ B.))((2233n mn m n m n m ++-=-
)1)(3()3)(1(+--=-+y y y y D.z yz z y z z y yz +-=+-)2(2242
2. 若a >b ,则下列式子正确的是( )
-4>b -3 12<12
b +2a >3+2b D.—3a >—3b 3. 若分式4242--x x 的值为零,则x 等于( ) B.-2 C.±2 4. 如图,在□ABCD 中,已知AD =5cm ,AB =3cm ,AE 平分 ∠BAD 交BC 边于点E ,则EC 等于( )
A.1.5cm
B. 2cm
C. 2.5cm
D. 3cm
5. 如下是一种电子计分牌呈现的数字图形,其中既是轴对称图形又是中心对称图形
的是( )
6. 如图所示,将矩形ABCD 纸对折,设折痕为MN ,再把B 点
叠在折痕线MN 上,(如图点B’),若AB =3,则折痕
AE 的长为( )
A. 323
B. 34
3 C. 2 D. 23 7. 在平面直角坐标系内,点P(3-m ,5-m )在第三象限,则m 的取值范围是( )
A.5<m
B.53<<m
C.3<m
D.3-<m 8. 如图,在周长为20cm 的□ABCD 中,AB ≠AD ,AC 、BD 相交于点
O , OE ⊥BD 交AD 于E ,则△ABE 的周长为D
A.4cm
B.6cm
C.8cm
D.10cm
9. 已知234221
x A B x x x x +=----+,其中A ﹑B 为常数,则4A-B 的值为( ) .9 C
10.如图,△ABC 的周长为26,点D ,E 都在边BC 上,∠ABC 的平
分线垂直于AE ,垂足为Q ,∠ACB 的平分线垂直于AD ,垂足
为
P ,若BC =10,则PQ 的长为
A.3
2 B.5
2
二.填空题(共6小题,每题3分,计18分)
A B C D O E
11.分解因式:2331212a a a -+- = .
12.如图,∠A =15°,AB =BC=CD=DE =EF ,则∠GEF=_______
13.直线b x k y l +=11:与直线x k y l 22:=在同一平面直角坐标系中的图象如图所示,则
关于x 的不等式x k b x k 21>+的解为___________
14.已知一个多边形中,除去一个内角外,其余内角的和为1160︒,则除去的那个内
角的度数是
15.关于x 的分式方程201
m x m x ++=-无解,则m = 16.如图,在△ABC 中,∠ACB=90°,D 是BC 的中点,DE⊥BC,CE 不等式组与方程(8分)
18. 先化简,再求值:3
116871419422-÷⎪⎭⎫ ⎝⎛+--+⋅--m m m m m m .其中m=5.(6分) 19. 如图,平行四边形ABCD 中,E 、F 分别是对角线BD 上的两点,且BE=DF ,连接AE 、AF 、CE 、CF 。
求证:AE ∥CF (6分) 20.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千
米,平均车速比走路线一时的平均车速能提高80%,因此
能比走路线一少用10分钟到达.求小明走路线一时的平均速度。
(7分)
21.如图,在等腰RT ABC ∆中,90ACB ∠=︒,D 为BC 中点,DE ⊥AB ,垂足为E ,
过点B 作BF ∥AC 交DE 延长线于F ,连接CF 。
(1) 求证:AD ⊥CF
(2) 连接AF ,试判断ACF ∆的形状,并说明理由。
(8
分) 22.某工厂现有甲种原料360千克,乙种原料290千克,计
划利用这两种原料生 产A ﹑B 两种产品共50件,已知生产一件A 种产品需用
甲种原料9千克,乙 种原料3千克,可获利润700元;生产一件B 种产品需
用甲种原料4千克,
乙种原料10千克,可获利润1200元。
(1) 按要求安排A ﹑B 两种产品的件数有几种方案?请你设计出来。
(2) 以上方案那种利润最大?是多少元?(8分)
23.如图,在ABC ∆中,点D 是边BC 中点。
点E 在ABC ∆内,AE 平分BAC ∠,
CE ⊥AE ,点P 在边AB 上,EF ∥BC 。
(1)求证:四边形BDEF 是平行四边形。
(2)线段BF ,AB ,AC 存在什么数量关系?证明你得到的结论。
(9分)
A
附加题:
如图,在平面直角坐标系中,有一Rt△ABC,且A (﹣1,3),B (﹣3,﹣1),C (﹣3,3),已知△A 1AC 1是由△ABC 旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)设线段AB 所在直线AB 表达式为y kx b =+,试求出当x 满
足什么要求时,2y >
(3)点Q 在x 轴上,点P 在直线AB 上,要使以Q 、P 、1A 、1C 为
顶点的四边形是平行四边形,求所有满足条件点P 的坐标。
