山西阳泉市统考14-15学年高二上学期期末考试理数试题(扫描版)
山西省阳泉市高二上学期期末数学试卷

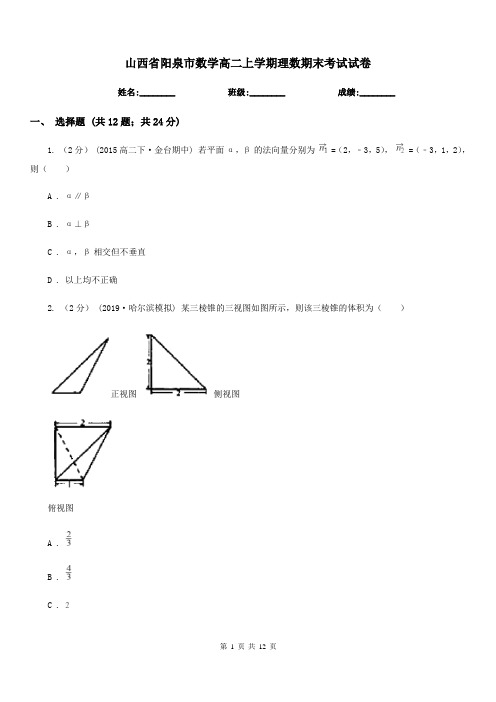
山西省阳泉市高二上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分)命题p:直线l与抛物线C有且仅有一个公共点;命题q:直线l与抛物线C相切.则p是q的()A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要2. (2分)下列命题正确的是()A . 函数在区间内单调递增B . 函数的最小正周期为2C . 函数的图像是关于点成中心对称的图形D . 函数的图像是关于直线成轴对称的图形3. (2分)(2017·泸州模拟) 已知函数,则满足不等式f(1﹣m2)>f(2m﹣2)的m 的取值范围是()A . (﹣3,1)B .C . (﹣3,1)∪D .4. (2分) (2015高二下·集宁期中) 抛物线y2=8x上一点P到顶点的距离等于它到准线的距离,则P的坐标是()A . (±4,2)B . (2,±4)C .D .5. (2分) (2018高三下·鄂伦春模拟) 甲、乙两个几何体的三视图如图所示(单位相同),记甲、乙两个几何体的体积分别为,,则()A .B .C .D .6. (2分)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的()A . 外接球的半径为B . 体积为C . 表面积为D . 外接球的表面积为7. (2分)(2017·安庆模拟) 已知双曲线C:的焦点到渐近线的距离为,则C的渐近线方程为()A .B .C .D . y=±x8. (2分) (2016高一上·金台期中) 下列选项正确的是()A . loga(x+y)=logax+logayB . loga =C . (logax)2=2logaxD . =loga二、填空题 (共7题;共7分)9. (1分)关于α的方程cos2α+(1﹣m)sinα﹣2=0在[﹣, ]上有解,则实数m的取值范围是________.10. (1分) (2019高二上·浙江期中) 实数x,y满足,则的最小值为________.11. (1分)点P(1,﹣2)到直线3x﹣4y﹣1=0的距离是________.12. (1分) (2018高二上·南通期中) 曲线与直线有两个交点,则实数的取值范围是________.13. (1分)已知弧长为πcm的弧所对的圆心角为,则这条弧所在的扇形面积为1cm2 .14. (1分) (2019高一上·丹东月考) 若,,为的三边且关于的一元二次方程有两个相等的实数根,则的形状为________.15. (1分)(2019·湖南模拟) 如图,在棱长为2的正方体中,、分别为棱、的中点,是线段上的点,且,若、分别为线段、上的动点,则的最小值为________.三、解答题 (共5题;共45分)16. (10分)如图,在四棱锥P﹣ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.(1)求证:直线AF∥平面PEC;(2)求PC与平面PAB所成角的正弦值.17. (5分)在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8.(Ⅰ)若a=2,b=,求cosC的值;(Ⅱ)若sinAcos2+sinBcos2=2sinC,且△ABC的面积S=sinC,求a和b的值.18. (10分)已知双曲线C:x2﹣y2=1及直线l:y=kx+1.(1)若l与C有两个不同的交点,求实数k的取值范围;(2)若l与C交于A,B两点,且AB中点横坐标为,求AB的长.19. (10分) (2015高二上·济宁期末) 已知函数f(x)=ax2﹣ax﹣1(a∈R).(1)若对任意实数x,f(x)<0恒成立,求实数a的取值范围;(2)当a>0时,解关于x的不等式f(x)<2x﹣3.20. (10分) (2017高二下·成都开学考) 已知F1、F2是椭圆 + =1的左、右焦点,O为坐标原点,点P(﹣1,)在椭圆上,线段PF2与y轴的交点M满足 + = ;(1)求椭圆的标准方程;(2)⊙O是以F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当=λ且满足≤λ≤ 时,求△AOB面积S的取值范围.参考答案一、选择题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共7题;共7分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题;共45分)16、答案:略17-1、18、答案:略19-1、19-2、20-1、20-2、。
易错汇总2014-2015年山西省太原市高二上学期期末数学试卷(理科)与解析

( 1)用向量 , , 表示向量 ;
( 2)求
.
19.( 10 分)已知抛物线 C; y2=2px( p> 0)的焦点为 F,准线为 l ,抛物线上的 点 M (3,y)( y>0)到焦点的距离 | MF| =4
≥0
2.(3 分)双曲线 x2﹣y2=2 的离心率是(
)
D.? x0∈R,x02
A.1
B.
C.2
D.2
3.(3 分)已知 =(2,y,2), =(x,﹣ 1,1),若 ⊥ ,则实数 x, y 满足的
关系式为( A.2x﹣ y=0
) B.2x+y=0
C.2x+y﹣2=0
D.2x﹣y+2=0
4.(3 分)椭圆 + =1 焦点坐标是(
A.( 1, 1)
B.( 2, 1)
C.(1,2)
D.以上都不正确
【解答】 解:联立两抛物线方程,即有
,消去 y,可得
( ) 2=2px, 解得 x=0 或 2p, 当 x=0 时, y=0, 当 x=2p 时, y=2p. 即有公共点为( 0,0),( 2p,2p). 对照选项, A 可能, B,C,D 均不可能.
故选: A.
6.(3 分)已知 A( 1, 0,0),B(0,1,0),C( 0, 0, 1),且 A,B,C,M 四
点共面,那么点 M 的坐标可以是(
)
A.( 1, 1, 1) B.( 2,﹣ 1,﹣ 1) C.(
) D.(
)
【解答】 解: =(﹣ 1,1,0), =(﹣ 1,0,1).
山西省阳泉市高二数学上学期期末考试试题理

山西省阳泉市—2020学年度第一学期期末考试试题高二理科数学注意事项:1.本试题分第Ⅰ卷(客观题)和第Ⅱ卷(主观题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至4页.2.答卷前考生务必将自己姓名、准考证号填写在答题卡相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将答题卡交回.5.考试时间90分钟,满分100分.第Ⅰ卷(30分)一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设命题R :∈∀x p ,使得20x ≥,则p ⌝为( )A .R 0∈∃x ,使得020<xB .R 0∈∃x ,使得020≥xC .R 0∉∃x ,使得020<xD .R ∈∀x ,使得02<x2.已知抛物线C :x 2=4y 的焦点为F ,点P 是抛物线C 上一点,若|PF|=5,则点P 的横坐标是( )A.-4B. 1C.4D.-4或43.已知向量a =(0,3,3)和b =(-1,1,0)分别是直线l 和m 的方向向量,则直线l 与m 所成的角为( )A .6πB .4πC .3πD .2π4.“m >0”是“方程1322=-+m y m x 表示双曲线”的( ) A .充分但不必要条件 B .必要但不充分条件C .充要条件D .既不充分也不必要条件5.如图,在四面体OABC 中,D 是BC 的中点,G 是AD 的中点 ,则OG 等于( )A .OC OB OA 313131++ B .413121++C .OC OB OA 414121++D .614141++ 6.与命题“若实数x ≠y ,则cos x ≠cos y ”等价的命题是( ) (第5 题图)A.若实数x =y ,则cos x =cos yB.若cos x =cos y ,则实数x =yC.若cos x ≠cos y ,则实数x ≠yD.若实数x ≥y ,则cos x ≥cos y7. 若直线l :x -y -1=0与椭圆C :1222=+y x 交于A 、B 两点,则|AB |=( )A. 322B. 223C. 423 D.324 8.若命题[],3,0∈∀x “都有”022≠--m x x 是假命题,则实数m 的取值范围是( )A . (-∞,3] B. [-1,+∞) C.[-1, 3] D.[3,+∞)9.正确使用远光灯对于夜间行车很重要.已知某家用汽车远光灯(如图)的。
山西省阳泉市高二上学期期末数学试卷(理科)

山西省阳泉市高二上学期期末数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)命题“,使得”的否定为()A . ,都有B . ,都有C . ,都有D . ,都有2. (2分)若直线ax+by+c=0经过一、三、四象限,则有()A . ab>0,bc>0B . ab>0,bc<0C . ab<0,bc>0D . ab<0,bc<03. (2分) (2016高二上·右玉期中) 设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是()①若m⊥α,α⊥β,则m∥β②若m⊥α,α∥β,n⊂β,则m⊥n③若m⊂α,n⊂β,m∥n,则α∥β④若n⊥α,n⊥β,m⊥β,则m⊥αA . ①②B . ③④C . ①③4. (2分)(2018·安徽模拟) 下列命题中,真命题是()A . ,有B .C . 函数有两个零点D . ,是的充分不必要条件5. (2分) (2018高一上·湘东月考) 圆,圆,M , N 分别是圆,上的动点,P为x轴上的动点,则的最小值()A .B .C .D .6. (2分)已知向量=(2cosα,2sinα),=(3cosβ,3sinβ),若与的夹角为60°,则直线xcosα-ysinα与圆(x-cosβ)2+(y+sinβ)2=的位置关系是()A . 相交但不过圆心B . 相交过圆心C . 相切D . 相离7. (2分) (2018高二下·中山月考) 是一个关于自然数的命题,若真,则真,现已知不真,那么:① 不真;② 不真;③ 真;④ 不真;⑤ 真;其中正确的结论为()B . ①、②C . ③、⑤D . ①、⑤8. (2分)如图,在多面体中,已知平面是边长为3的正方形,,,且EF与平面ABCD的距离为2,则该多面体的体积为()A .B .C . 5D . 69. (2分) (2019高二下·太原月考) 曲线 : ( 为参数)上的点到曲线 :(t为参数)上的点的最短距离为()A . 1B . 2C . 3D . 410. (2分) (2019高三上·西湖期中) 如图为一正方体的平面展开图,在这个正方体中,有以下结论:①,②CF与EN所成的角为,③ //MN ,④二面角的大小为 ,其中正确的个数是()A . 1B . 2C . 3D . 411. (2分) (2016高二上·诸暨期中) 圆心在曲线y= x2(x<0)上,并且与直线y=﹣1及y轴都相切的圆的方程是()A . (x+2)2+(y﹣1)2=2B . (x﹣1)2+(y﹣2)2=4C . (x﹣2)2+(y﹣1)2=4D . (x+2)2+(y﹣1)2=412. (2分)一个几何体的三视图如图所示,则此几何体的体积为()A . 1B . 2C . 3D . 4二、填空题 (共4题;共4分)13. (1分) (2017高一下·黄石期末) 一个正三棱柱顶点都在球面上,正三棱柱的底面是正三角形,正三角形的边长是3,正三棱柱的体积是,则球的体积是________.14. (1分) (2017高一下·包头期末) 圆x2+y2-1=0与圆x2+y2+3x+9y+2=0的公共弦长为________。
山西省阳泉市第十五中学高二数学理月考试卷含解析

山西省阳泉市第十五中学高二数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知复数,那么=( )A. B. C. D.参考答案:D略2. 若与都是非零向量,则“”是“”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件参考答案:C3. 观察数组:,,,------则的值不可能是()A.112 B.278 C. 704 D.1664参考答案:B由题意可得,,当时,;当时,;当时,所以A,C,D正确故选B. 4. 下列命题错误的是 ( )A.命题“若”的逆否命题为“若”B. “”是“”的充分不必要条件C. 若为假命题,则均为假命题D. 对于命题则参考答案:C略5. 设,若函数,,有大于零的极值点,则()A. B. C. D.参考答案:A6. 已知Z=﹣2+3i,求|Z|=()A.1 B.C.D.3参考答案:C【考点】A8:复数求模.【分析】直接由已知利用复数模的计算公式求解.【解答】解:∵Z=﹣2+3i,∴|Z|=.故选:C.【点评】本题考查复数模的求法,是基础的计算题.7. 设(其中),则的大小关系为()A. B. C. D.参考答案:D8. 某学习小组男女生共8人,现从男生中选2人,女生中选1人,分别去做3种不同的工作,共有90种不同的选法,则男女生人数为()A: 2,6 B:3,5 C:5,3 D:6,2参考答案:B略9. 设和为双曲线()的两个焦点, 若点和点是正三角形的三个顶点,则双曲线的离心率为( )。
A. B. C. D.3参考答案:C略10. 若圆的方程为则直线(为非零常数)与圆的位置关系是( )A 相交B 相切C 相离D 不能确定参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. 36的所有正约数之和可按如下方法得到:因为36=22×32,所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可求得200的所有正约数之和为.参考答案:465【考点】F4:进行简单的合情推理.【分析】这是一个类比推理的问题,在类比推理中,参照上述方法,200的所有正约数之和可按如下方法得到:因为200=23×52,所以200的所有正约数之和为(1+2+22+23)(1+5+52),即可得出答案.【解答】解:类比36的所有正约数之和的方法,有:200的所有正约数之和可按如下方法得到:因为200=23×52,所以200的所有正约数之和为(1+2+22+23)(1+5+52)=465.可求得200的所有正约数之和为465.故答案为:465.12. 如图,在梯形ABCD中,AB∥CD,AB=3,AD=2,CD=1,M为AD的中点,若?=4,则?=.参考答案:首先由已知求出角A的余弦值,然后利用平面向量的三角形法则将?用梯形的各边表示,展开分别求数量积即可.解:由已知得到cos ∠A=,AB∥CD,AB=3,AD=2,CD=1,M为AD的中点,若?=4,则?=()()==2×3×+﹣1×3=;故答案为:.13. 已知双曲线C:=1(a>0,b>0),P为x轴上一动点,经过P的直线y=2x+m(m≠0)与双曲线C有且只有一个交点,则双曲线C的离心率为________.参考答案:即双曲线的渐近线与直线y =2x +m 平行,即=2,所求的离心率e ===.14. 与平行线和等距离的直线的方程为参考答案:2x-7y+1=015. 函数的定义域是.参考答案:16. 若x ∈(1,+∞),则y=2x+的最小值是 .参考答案:2+2【考点】基本不等式.【分析】变形利用基本不等式的性质即可得出.【解答】解:∵x ∈(1,+∞),则y=2(x ﹣1)++2≥2+2=2+2,当且仅当x=1+时取等号.∴y=2x+的最小值是2+2.故答案为:2+2.17.______________. 参考答案:1 略三、 解答题:本大题共5小题,共72分。
山西省阳泉市数学高二上学期理数期末考试试卷
山西省阳泉市数学高二上学期理数期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2015高二下·金台期中) 若平面α,β的法向量分别为 =(2,﹣3,5), =(﹣3,1,2),则()A . α∥βB . α⊥βC . α,β相交但不垂直D . 以上均不正确2. (2分)(2019·哈尔滨模拟) 某三棱锥的三视图如图所示,则该三棱锥的体积为()正视图侧视图俯视图A .B .C .D .3. (2分)在平面直角坐标系中,若直线与直线是参数, )垂直,则()A .B .C .D .4. (2分)(2019·南平模拟) 已知双曲线的离心率为,则的渐近线方程为().A .B .C .D .5. (2分)已知命题p:∃x0∈R,lnx0≥x0﹣1.命题q:∀θ∈R,sinθ+cosθ<1,.则下列命题中为真命题的是()A . p∧qB . (¬p)∧qC . (¬p)∧(¬q)D . p∧(¬q)6. (2分)在正方体中,下列各式中运算的结果为向量的共有()①;②;③;④.A . 1个B . 2个C . 3个D . 4个7. (2分)α,β为平面,m为直线,如果α∥β,那么“m∥α”是“mβ”的()A . 充分非必要条件B . 必要非充分条件C . 充要条件D . 既非充分又非必要条件.8. (2分)如图2,在透明塑料制成的长方体容器内灌进一些水,将容器底面一边固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;②水面四边形的面积不改变;③棱始终与水面平行;④当时,是定值.其中所有正确的命题的序号是()A . ①②③B . ①③C . ②④D . ①③④9. (2分)某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是()A .B .C .D .10. (2分)若直线y=kx与圆的两个交点关于直线对称,则()A . k=-1,b=2B . k=1,b=2C . k=1,b=-2D . k=-1,b=-211. (2分)(2017·南阳模拟) 如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为()A .B . 8πC . 9πD .12. (2分)双曲线的渐近线与圆(x﹣3)2+y2=r2(r>0)相切,则r=()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)如图是一个几何体的表面展成的平面图形,则这个几何体是________.14. (1分)已知△ABC三顶点分别为A(1,3),B(3,1),C(﹣1,0),则AB边上的中线所在直线的一般式方程为________15. (1分)已知点,直线y=k与椭圆相交于A,B两点,则△ABM的周长为________16. (1分) (2018高一下·鹤岗期末) 已知球面上有四点满足两两垂直,,则该球的表面积是________.三、解答题 (共6题;共40分)17. (10分) (2015高二上·黄石期末) 已知圆A:(x+2)2+y2=1,圆B:(x﹣2)2+y2=49,动圆P与圆A,圆B均相切.(1)求动圆圆心P的轨迹方程;(2)已知点N(2,),作射线AN,与“P点轨迹”交于另一点M,求△MNB的周长.18. (5分) (2017高二上·太原月考) 双曲线与椭圆有相同的焦点,直线为的一条渐近线,求双曲线的方程.19. (5分)如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2,∠CAD=90°,以CD为轴,将△ACD 按逆时针方向旋转90°到△BCD位置,E为AD中点;证明:AB⊥CD.20. (5分)在极坐标系中,曲线C:ρsin2θ=2cosθ,过点A(5,α)(α为锐角且tanα= )作平行于θ= (ρ∈R)的直线l,且l与曲线C分别交于A,B两点.(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线C和直线l的普通方程;(Ⅱ)求|AB|的长.21. (10分) (2017高一下·鹤岗期末) 在如图所示的几何体中,四边形ABCD为正方形,为直角三角形,,且 .(1)证明:平面平面;(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.22. (5分)(2017·商丘模拟) 已知椭圆E:(a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为,过点M (m,0)(m>)作斜率不为0的直线l,交椭圆E于A,B两点,点P (,0),且为定值.(Ⅰ)求椭圆E的方程;(Ⅱ)求△OAB面积的最大值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共40分)17-1、17-2、18-1、19-1、20-1、21-1、21-2、22-1、。
山西省阳泉市高二上学期期末数学试卷(实验班)

山西省阳泉市高二上学期期末数学试卷(实验班)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ上一点,A∈β , AC=2,∠ACP=30°,则点A到平面α的距离为()A . 1B .C .D .2. (2分) (2018高二下·绵阳期中) 已知命题则为()A .B .C .D .3. (2分)下列命题中,否命题为假命题的是()A . 若同位角相等,则两直线平行B . 若x,y全为0,则x=0且y=0C . 若方程x2+2x+m=0有实根,则m≥0D . 若x2﹣3x+2>0,则x2﹣3x>04. (2分) (2016高三上·重庆期中) 设椭圆 =1的左右交点分别为F1 , F2 ,点P在椭圆上,且满足 =9,则| |•| |的值为()A . 8B . 10C . 12D . 155. (2分)已知菱形的边长为, ,则=()A .B .C .D .6. (2分)已知正四棱柱ABCD﹣A1B1C1D1中,AA1=4,AB=2,E是AA1的中点,则异面直线D1C与BE所成角的余弦值为()A .B .C .D .7. (2分)已知抛物线的焦点与椭圆的一个焦点重合,它们在第一象限内的交点为,且与轴垂直,则椭圆的离心率为()A .B .C .D .8. (2分)(2017·临汾模拟) 已知等边三角形的一个顶点坐标是(,0),另外两个顶点在抛物线y2=x上,则这个等边三角形的边长为()A . 3B . 6C . 2 ±3D . 2 +39. (2分)方程+=1的图象表示曲线C,则以下命题中甲:曲线C为椭圆,则1<t<4;乙:若曲线C为双曲线,则t>4或t<1;丙:曲线C不可能是圆;丁:曲线C表示椭圆,且长轴在x轴上,则1<t<.正确的有()A . 1个B . 2个C . 3个D . 4个10. (2分)已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若=4,则|QF|=()A .B . 3C .D . 211. (2分)若P是以F1 , F2为焦点的椭圆=1(a>b>0)上的一点,且=0,tan∠PF1F2=,则此椭圆的离心率为()A .B .C .D .12. (2分) (2018高二上·宜昌期末) 已知双曲线(m>0,n>0)的离心率为,则椭圆的离心率为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2015高二下·上饶期中) “∃x0∈R,ax02+ax0+1<0”为假命题,则a∈________.14. (1分) (2016高二上·常州期中) 已知双曲线的离心率,则该双曲线的虚半轴长b=________.15. (1分) (2019高二下·上海月考) 已知球的半径是1,三点都在球面上,两点和两点的球面距离都是,两点的球面距离是,则二面角的大小为________.16. (1分) (2018高二下·河池月考) 已知正方形,则以为焦点,且过两点的椭圆的离心率为________.三、解答题 (共6题;共70分)17. (10分)求适合下列条件的曲线的标准方程:(1)焦点在y轴上,长轴长等于10,离心率等于的椭圆标准方程;(2)经过点A(3,﹣1),并且对称轴都在坐标轴上的等轴双曲线的方程.18. (15分) (2016高二上·福田期中) 已知动点P与双曲线﹣ =1的两个焦点F1 , F2所连线段的和为6 ,(1)求动点P的轨迹方程;(2)若• =0,求点P的坐标;(3)求角∠F1PF2余弦值的最小值.19. (10分)如图,在四棱锥P-ABCD中,PC⊥底面ABCD ,底面ABCD是直角梯形,AB⊥AD ,AB∥CD ,AB=2AD=2CD=2,E是PB的中点.(1)求证:平面EAC⊥平面PBC;(2)若二面角P-AC-E的余弦值为,求直线PA与平面EAC所成角的正弦值.20. (15分) (2016高二上·桐乡期中) 如图,三棱锥P﹣ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2 ,PA= .(1)求证:平面ABC⊥平面PED;(2)求AC与平面PBC所成的角;(3)求平面PED与平面PAB所成锐二面角的余弦值.21. (10分)已知椭圆E:(a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为c.(1)求椭圆E的离心率(2)如图,AB是圆M:(x+2)2+(y-1)=的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.22. (10分) (2017高二上·四川期中) 已知抛物线顶点在原点,焦点在轴上,又知此抛物线上一点到焦点的距离为6.(1)求此抛物线的方程;(2)若此抛物线方程与直线相交于不同的两点、,且中点横坐标为2,求的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共70分) 17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、。
2021年山西省阳泉市第十四中学高二数学理上学期期末试题含解析

2021年山西省阳泉市第十四中学高二数学理上学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 在面积为S的△ABC的边AC上任取一点P,则△PBC的面积大于的概率是( )A. B.C. D.参考答案:C解析:如图,在△ABC中,点F是AC边的四等分点,设△ABC的高为AD,△FBC的高为FE,则FE=AD,∴S△FBC=S△ABC=,要使△PBC的面积大于,则点P需在线段FA上选取,故P==.答案:C2. 与圆相切,且在两坐标轴上截距相等的直线共有A. 3条B. 4条C. 5条D. 6条参考答案:B3. 已知双曲线的一个焦点与抛物线的焦点重合,则此双曲线的离心率为()(A)(B)(C)(D)ks5u参考答案:C略4. 命题:“若x2<1,则-1<x<1”的否命题是 ( )A.若x2≥1,则x≥1或x≤-1 B.若-1<x<1,则x2<1C.若x>1或x<-1,则x2>1 D.若x≥1或x≤-1,则x2≥1参考答案:A略5. 已知F1、F2为椭圆(a>b>0)的两个焦点,过F2作椭圆的弦AB, 若△AF1B的周长为16,椭圆的离心率, 则椭圆的方程为()A B C D参考答案:D6. 5.直线相切于点(2,3),则k的值为( ).A. 5 B. 6 C. 4D. 9参考答案:D直线相切于点(2,3),且7. 函数有( )A .极大值,极小值B .极大值,极小值C .极大值,无极小值D .极小值,无极大值参考答案:C 略 8. 为坐标原点,为抛物线的焦点,为上一点,若,则的面积为( )A .B .C .D .参考答案:C9. 曲线y =x 3-2x +1在点(1,0)处的切线方程为( )A. y =x -1B. y =-x +1C. y =2x -2D. y =-2x +2参考答案:A 略10. 某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有( )A.个B.个C.个D.个 参考答案: A某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有个,选A二、 填空题:本大题共7小题,每小题4分,共28分11. 已知双曲线的一条渐近线方程为,则实数等于 ▲.参考答案: 412.椭圆的一个顶点与两个焦点构成等边三角形,则离心率e=________。
山西省阳泉市高二上学期数学期末考试试卷

山西省阳泉市高二上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)已知直线l与过点M(- , ),N(,- )的直线垂直,则直线l的倾斜角是()A . 60°B . 120°C . 45°D . 135°2. (2分)(2018·南宁月考) 已知,则双曲线的离心率等于()A .B .C . 2D . 33. (2分) (2017高一下·定州期末) 关于空间直角坐标系O﹣xyz中的一点P(1,2,3),有下列说法:①点P到坐标原点的距离为;②OP的中点坐标为();③点P关于x轴对称的点的坐标为(﹣1,﹣2,﹣3);④点P关于坐标原点对称的点的坐标为(1,2,﹣3);⑤点P关于坐标平面xOy对称的点的坐标为(1,2,﹣3).其中正确的个数是()A . 2B . 3C . 4D . 54. (2分)一空间几何体的三视图如图,则该几何体的体积为()A .B .C .D .5. (2分)由直线y=x+1上的一点向圆引切线,则切线长的最小值为()A . 1B .C .D . 36. (2分)(2017·松江模拟) 已知a,b∈R,则“ab>0“是“ >2”的()A . 充分非必要条件B . 必要非充分条件C . 充要条件D . 既非充分也非必要条件7. (2分)已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点到焦点的距离等于5,则m等于()A .B .C .D .8. (2分)(2018·朝阳模拟) 已知是两个不同的平面,是一条直线,给出下列说法:①若,,则;②若,,则;③若,,则;④若,,则 .其中说法正确的个数为()A . 3B . 2C . 1D . 09. (2分) (2016高二下·惠阳期中) 已知双曲线E的中心在坐标原点,离心率为2,E的右焦点与抛物线C:y2=8x的焦点重合,A、B是C的准线与E的两个交点,则|AB|=()A . 3B . 6C . 9D . 1210. (2分) (2017高三上·张家口期末) 某几何体三视图如图所示,则该几何体的体积为()A . 2B . 4C . 6D . 12二、填空题 (共7题;共7分)11. (1分) (2019高三上·天津期末) 已知长方体的长、宽、高分别为2,1,2,则该长方体外接球的表面积为________.12. (1分) (2019高二下·吉林月考) 直线与的位置关系是________.13. (1分) (2016高二下·连云港期中) 若向量=(4,2,4),=(6,3,﹣2),则(2 ﹣3)•(+2 )=________.14. (1分)在平面直角坐标系xOy中,过动点P分别作圆C1:x2+y2+2x+2y+1=0和圆C2:x2+y2﹣4x﹣6y+9=0的切线PA,PB(A,B为切点),若|PA|=|PB|,则|OP|的最小值为________.15. (1分) (2016高二上·余姚期末) 直线l1:x+y+2=0在x轴上的截距为________;若将l1绕它与y轴的交点顺时针旋转,则所得到的直线l2的方程为________.16. (1分) (2016高二上·定兴期中) 已知椭圆C:9x2+y2=1,直线l不过原点O且不平行于坐标轴,l与C 有两个交点A,B,线段AB的中点为M.则直线OM的斜率与l的斜率的乘积为________.17. (1分)已知A点在x轴上,B点在y轴上,且满足|AB|=3,若,则点C的轨迹方程是________.三、解答题 (共5题;共25分)18. (5分) (2018高二下·牡丹江期末) 在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,已知圆的极坐标方程为,直线与圆相交于,两点.(1)求直线的普通方程和圆的直角坐标方程;(2)求弦长.19. (5分)(2013·江苏理) 如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.(1)求异面直线A1B与C1D所成角的余弦值;(2)求平面ADC1与ABA1所成二面角的正弦值.20. (5分)(2017·莆田模拟) 已知点P是圆F1:(x﹣1)2+y2=8上任意一点,点F2与点F1关于原点对称,线段PF2的垂直平分线分别与PF1 , PF2交于M,N两点.(1)求点M的轨迹C的方程;(2)过点的动直线l与点M的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.21. (5分)(2017·宜宾模拟) 如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=EA= ED,EF∥BD( I)证明:AE⊥CD( II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为?若存在,确定点M的位置;若不存在,请说明理由.22. (5分) (2018高二上·凌源期末) 已知椭圆的离心率为,且过点.(1)求椭圆的方程;(2)设不过原点的直线与椭圆交于两点,直线的斜率分别为,满足,试问:当变化时,是否为定值?若是,求出此定值,并证明你的结论;若不是,请说明理由.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共7分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共25分) 18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、第11 页共11 页。
山西省阳泉市玉泉中学高二数学理上学期期末试卷含解析

山西省阳泉市玉泉中学高二数学理上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 在下列命题中:①若、共线,则、所在的直线平行;②若、所在的直线是异面直线,则、一定不共面;③若、、三向量两两共面,则、、三向量一定也共面;④已知三向量、、,则空间任意一个向量总可以唯一表示为.其中正确命题的个数为()A.3 B.2 C.1 D.0参考答案:D略2. 下列各组向量中不平行的是()A.B.C.D.参考答案:D【考点】用向量证明平行.【分析】判断两向量共线,利用共线向量定理,只需找到一个实数λ,使得=λ,另外零向量与任意向量平行,于是可得本题答案.【解答】解:选项A中,;选项B中有:,选项C中零向量与任意向量平行,选项D,事实上不存在任何一个实数λ,使得,即:(16,24,40)=λ(16,24,40).故应选:D3. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于()A.2 B.3 C.4 D.5参考答案:C由程序框图可得,时,,继续循环;时,,继续循环;时,,继续循环;结束输出.4. 一元二次不等式的解集为,则不等式的解集为().A.B.C.D.参考答案:C由已知,得,∵,∴,,∴,,∵,,∴,是方程的两根,且,∴不等式的解集是.故选.5. 将名教师,名学生分成个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由名教师和名学生组成,不同的安排方案共有()A.种B.种C.种D.种参考答案:A略6. 已知集合()A. B. C. D.参考答案:D7. 已知双曲线的方程为,双曲线的一个焦点到一条渐近线的距离为(c 为双曲线的半焦距长),则双曲线的离心率为A. B. C. D.参考答案:B略8. 一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图为记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为().A.5 B.6 C.7 D.8参考答案:D由茎叶图可知=7,解得x=8.9. 不等式的解集是()A.(-∞,-1]∪[3,+∞) B.[-1,1)∪[3,+∞)C.[-1,3] D.(-∞,-3)∪(1,+∞)参考答案:B10. 个连续自然数按规律排列如下:根据规律,从2011到2013箭头方向依次是()A.↓→ B.→↑ C.↑→ D.→↓参考答案:D略二、填空题:本大题共7小题,每小题4分,共28分11. 已知A、B、C三点在球心为O,半径为3的球面上,且几何体O—ABC为正三棱锥,若A、B两点的球面距离为,则正三棱锥的侧面与底面所成角的余弦值为_____________参考答案:略12. 两个等差数列的前n项和分别是参考答案:13.的展开式中第3项的系数为 。
山西省阳泉市高二上学期期末数学试题(解析版)

高二上学期期末数学试题一、单选题1.已知数列满足,,则( ){}n a 12a =21n n a a n +=+3a =A .5 B .7 C .10 D .15【答案】B【分析】由递推关系求解即可.【详解】解:因为,所以,. 12a =2113a a =+=3247a a =+=故选:B2.如图,在三棱柱中,E ,F 分别是BC ,的中点,,则( )111ABC A B C -1CC 2AG GE = GF =A .1121332AB AC AA -+B .1121332AB AC AA ++C . 1211332AB AC AA -+- D .1121332AB AC AA -++【答案】D【分析】根据空间向量线性运算的几何意义进行求解即可. 【详解】23GF AF AG AC CF AE =-=+-,()11121121232332AC AA AB AC AB AC AA =+-⨯+=-++故选:D .3.函数的单调递增区间为( )21=ln 22y x x -+A .B .C .D .()1,1-()0,1[)1,+∞()0,∞+【答案】C【分析】先对函数求导,然后令导函数大于0解出不等式,并结合函数的定义域,即可得到本题答案.【详解】因为,所以,21=ln 22y x x -+211x y x x x -'=-=令,得或,0'>y 1x <-1x >又函数的定义域为,所以函数的单调递增区间为, {}0x x >[1,)+∞故选:C4.若两条直线与平行,则与间的距离是( ) 126:0l x y +-=2:50l x ay +-=1l 2lA B C D .【答案】B【分析】根据平行关系求解,进而根据平行线间距离公式即可求解. 2a =【详解】由与平行,可得, 126:0l x y +-=2:50l x ay +-=1122a a -=-⇒=当时,两直线不重合,故,进而与 2a =2a =1l 2l 故选:B5.圆内有一点,AB 为过点且倾斜角为的弦,则AB 的长为( ) 228x y +=()012P -,0P 135︒A B C .D .【答案】A【分析】先求得直线的方程,然后利用弦长公式求得.AB AB 【详解】直线AB 的斜率为,又直线AB 过点, 135tan 1k =︒=-()012P -,所以直线AB 的方程为:,即, ()21y x -=-+10x y +-=圆的圆心为,半径 228x y +=()0,0r =圆心到直线AB :的距离为 ()0,0O 10x y +-=d则 AB ===故选:A.6.已知函数的导函数图象如下图所示,则原函数的图象是( )()y f x =()y f x '=()y f x =A .B .C .D .【答案】B【分析】根据函数的单调性与导数的关系以及导数的变化可得结果.【详解】由图可知,当时,,则函数在上为增函数, 11x -<<()0f x ¢>()f x ()1,1-当时,单调递增,故函数在上的增长速度越来越快, 10x -<<()f x '()f x ()1,0-当时,单调递减,故函数在上的增长速度越来越慢. 01x <<()f x '()f x ()0,1B 选项中的图象满足题意. 故选:B.7.1202年意大利数学家斐波那契出版了他的《算盘全书》,在书中收录了一个有关兔子繁殖的问题.他从兔子繁殖规律中发现了“斐波那契数列”,具体数列为:1,1,2,3,5,8,13,…,即从该数列的第三项开始,每个数字都等于前两个相邻数字之和.已知数列为斐波那契数列,其前{}n a n 项和为,且满足,则当时,的值为( ) n S 12121,1,(2)n n n a a a a a n --===+>2n >2n n a S --A .1 B .2C .D .+1n 2n +【答案】A【分析】利用递推公式,得到 12n n n a a a --=+234512()n n n n a a a a a a ----=++++++ 21n S -=+【详解】,12n n n a a a --=+122322334n n n n n n n n n n a a a a a a a a a a ---------∴=+=++=+++23445n n n n n a a a a a -----=++++234512()n n n n a a a a a a ----=++++++ 21n S -=+ 21n n a S -∴-=故选:A8.过抛物线:的焦点作两条互相垂直的弦,,设为抛物线上的一动E ()220x py p =>F AB CD P 点,,若,则的最小值是( ) ()1,2Q 1114AB CD +=PF PQ +A .2 B .3C .4D .5【答案】B【分析】显然直线的斜率存在且不为0,设直线的斜率为,则直线的方程为AB AB k AB 2p y kx =+,与抛物线方程联立结合韦达定理可得:,因为,所以直线212||22AB y y p pk p =++=+AB CD ⊥CD的斜率为:,所以,由,解得,设点到准线的距1k-2222||p pk CD k +=111||||4AB CD +=2p =P 1y =-离为,由抛物线的性质可知:,而当垂直于轴时,的值最小,d ||||||PF PQ d PQ +=+QP x ||+d PQ 最小值为.213+=【详解】解:显然直线的斜率存在且不为0,设直线的斜率为,则直线的方程为AB AB k AB , 2py kx =+联立方程,消去得:, 222p y kx x py ⎧=+⎪⎨⎪=⎩y 2220x pkx p --=设,,,,1(A x 1)y 2(B x 2)y ,122x x pk ∴+=,∴21212()2y y k x x p pk p +=++=+由抛物线的性质可知:,212||22AB y y p pk p =++=+,直线的斜率为:, AB CD ⊥ ∴CD 1k-,22221222||2(22p p pk CD p p p k k k +∴=-+=+=, ∴2222211111||||2222224k k AB CD pk p p pk p pk ++=+==+++,222244p pk k ∴+=+,2p ∴=抛物线方程为:,准线方程为:,∴24x y =1y =-设点到准线的距离为,由抛物线的性质可知:, P 1y =-d ||||||PF PQ d PQ +=+而当垂直于轴时,的值最小,最小值为,如图所示:QP x ||+d PQ 213+=的最小值为3,||||PF PQ ∴+故选:B .二、多选题9.如图,在长方体中,,,,以直线,,分别1111ABCD A B C D -5AB =4=AD 13AA =DA DC 1DD 为轴、轴、轴,建立空间直角坐标系,则( )x y zA .点的坐标为,5,1B (43)B .点关于点对称的点为,8, 1C B (53)-C .点关于直线对称的点为,5, A 1BD (03)D .点关于平面对称的点为,5, C 11ABB A (80)【答案】ACD【分析】对A ,根据图示分析即可;对B ,设点关于点对称的点为,再根据为的中点列式求解即可; 1C B (),,P x y z B 1C P 对C ,根据四边形为正方形判断即可; 11ABC D 对D ,根据平面求解即可CB ⊥11ABB A 【详解】对A ,由图可得,的坐标为,5,,故A 正确;1B (43)对B ,由图,,,设点关于点对称的点为则()10,5,3C ()4,5,0B 1C B (),,P x y z ,解得,故,故B 错误; 0534,5,0222x y z+++===8,5,3x y z ===-()8,5,3P -对C ,在长方体中, 115AD BC AB ====所以四边形为正方形,与垂直且平分, 11ABC D 1AC 1BD 即点关于直线对称的点为,选项C 正确;A 1BD ()10,5,3C 对D ,因为平面,故点关于平面对称的点为,即,选项CB ⊥11ABB AC 11ABB A ()024,5,0+⨯()8,5,0D 正确; 故选:ACD.10.若存在实常数和,使得函数和对其定义域上的任意实数都满足k b ()F x ()G x x ()F x kx b≥+和恒成立,则称直线为和的“隔离直线”,已知函数()G x kx b ≤+y kx b =+()F x ()G x ()()2R f x x x =∈,,,下列命题正确的是( ) ()()10g x x x=<()2eln h x x =A .与有“隔离直线”()y g x =-()h x B .和之间存在“隔离直线”,且的取值范围为 ()f x ()g x b []4,0-C .和之间存在“隔离直线”,且的取值范围是 ()f x ()g x k (]4,0-D .和之间存在唯一的“隔离直线” ()f x ()h x e y =-【答案】ABD【分析】对于A ,取直线,讨论与的符号判断()2e R y x x =∈()2e (0)g x x x --<2e 2eln (0)x x x ->A ;对于B ,C ,令隔离直线为,利用二次不等式恒成立计算判断B ,C ;对于D ,函数与有 y kx b =+()f x ()h x公共点,求出在点处的切线,再证明此切线与图象关系作答.()f x ()h x【详解】对于A ,取直线,当时,,即2e (R)y x x =∈0x <()12e 2e 0g x x x x--=-->成立,()2e (0)g x x x -≥<当时,令,,则在递减,在上递增,0x >()2e 2eln F x x x =-1()2e(1F x x'=-()F x (0,1)(1,)+∞,,即成立,直线是与的“隔离直0x ∀>()(1)2e>0F x f ≥=()2e (0)h x x x ≤>2e y x =()y g x =-()h x 线”,A 正确;对于B ,C ,令和的“隔离直线”为,则,,()f x ()g x y kx b =+R x ∀∈220x kx b x kx b ≥+⇔--≥则,有,,有,当时,不2140k b ∆=+≤2104b k ≤-≤0x ∀<2110kx b kx bx x ≤+⇔+-≤0,0k b ==等式成立,当时,的对称轴,而时,,则,即0k <21y kx bx =+-02bx k=-≤0x =10y =-<2240b k ∆=+≤,24b k ≤-显然满足此不等式,有,而,解得,同理,,0,0k b ==421664b k b ≤≤-0b ≤40b -≤≤40k -≤≤B 正确,C 不正确;对于D ,因,即和的图象有公共点,若和有隔离直e f h ==()f x ()h x ()f x ()h x线,则该直线必过点,设过点的直线方程为,即,由,)e (y k x -=e y kx =-R x ∀∈()ef x kx ≥-+,即恒成立,则,解得2e 0x kx -+≥24(e)0k ∆=--≤k =e y =-,令,求导得: ()e 2eln (0)x x x ϕ=-->2e ()x x ϕ'==当时,,当,即在上递减,在上递0x <<()0x ϕ'<x >()0x ϕ'>()ϕx )+∞增,,即,,min ()0x ϕϕ==0x ∀>()2eln e h x x =≤-和之间存在唯一的“隔离直线”,D 正确. ()f x ()h x e y =-故选:ABD【点睛】思路点睛:涉及函数不等式恒成立问题,可以探讨函数的最值,借助函数最值转化解决问题.三、填空题11.已知函数的图象在点处的切线方程是,则______. ()y f x =()()1,1M f 21y x =+()()11f f '+=【答案】5【分析】由导数的几何意义可得的值,将点的坐标代入切线方程可得,即可得解. ()1f 'M ()1f 【详解】由导数的几何意义可得,将点的坐标代入切线方程可得, ()12f '=M ()12113f =⨯+=因此,. ()()115f f '+=故答案为:.5四、解答题12.已知数列的前n 项和公式为,则的通项公式为______.{}n a 221n S n =-+{}n a 【答案】 1,142,2n n a n n -=⎧=⎨-+≥⎩【分析】由题意,根据数列的通项与前n 项和之间的关系,即可求得数列的通项公式. n a n S 【详解】由题意,可知当时,;1n =111a S ==-当时,.2n ≥()2212121142;n n n a S S n n n -=-=-++--=-+又因为不满足,所以. 11a =-42n a n =-+1,142,2n n a n n -=⎧=⎨-+≥⎩故答案为: 1,142,2n n a n n -=⎧=⎨-+≥⎩五、填空题13.设椭圆C :的左、右焦点分别为F 1,F 2,P 是C 上的点,PF 2⊥F 1F 2,22221(0)x y a b a b +=>>,则C 的离心率为________. 1230PF F ︒∠=【解析】设,根据直角三角形中角所对的边等于斜边的一半以及勾股定理,得出、2PF m =30︒1PF、,根据椭圆的定义以及离心率公式求解即可.2PF 12F F 【详解】在中,设,因为,所以,21Rt PF F ∆2PF m =1230PF F ︒∠=12PF m = .12F F ==故. 121222F F c e a PF PF ===+【点睛】本题主要考查了椭圆的定义以及离心率的求法,属于基础题.14.当时,函数有两个极值点,则实数m 的取值范围___________.0x >()22x f x e mx =-+【答案】 2e m >【分析】函数有两个极值点转化为方程有两个不同的实数根,等价于与有两个2xe m x =y m =2x e y x=不同的交点,构造函数,即可求出结果.()(0)2xe h x x x =>【详解】有两个极值点, 2()2xf x e mx =-+所以有两个不同的实数根,'()20x f x e mx =-+=即有两个不同的实数根,2xe m x=等价于与有两个不同的交点,y m =2xe y x =设, ()(0)2x e h x x x =>2(1)'()(0)2x e x h x x x -=>当单调递减, (0,1),'()0,()x h x h x ∈<当单调递增, (1+),'()0,()x h x h x ∈∞>,所以 min ()(1)2eh x h ==当;0()x h x →→+∞,+()x h x →∞→+∞,所以与要有两个不同的交点,只需y m =2xey x=2e m >故答案为:2em >【点睛】方法点睛:含参方程有根的问题转化为函数图像的交点问题,数形结合,是常用的方法.本题考查了运算求解能力和数形结合思想,属于一般题目.六、解答题15.已知圆C 经过,两点,且圆心C 在直线上. ()4,1A ()3,0B 230x y +-=(1)求经过点A ,并且在两坐标轴上截距相等的直线方程; (2)求过点B 的圆C 的切线方程. 【答案】(1)或 40x y -=50x y --=(2) 260x y --=【分析】(1)分别讨论直线过原点和不过原点两种情况,设出直线方程,代入点坐标,求解()4,1A 即可.(2)设圆心坐标,借助于,解出C 点坐标,利用直线和切线垂()32,C b b -r AC BC ==BC 直求切线的斜率,进而写出切线方程.【详解】(1)经过点A ,在两坐标轴上的截距相等的直线,当直线过原点时, 设直线的方程为,代入点得,,即, y kx =()4,1A 41k =14k =14y x =即直线的方程为,40x y -=当直线不过原点时,设直线的方程为, x y a +=将点代入解得,即直线的方程为 ()4,1A 5a =50x y --=∴所求直线的方程为或;40x y -=50x y --=(2)因圆心C 在直线上,则设圆心, 230x y +-=()32,C b b -又圆C 经过,两点,于是得圆C 的半径, ()4,1A ()3,0B r AC BC ==,圆心,∴, =1b =-()5,1C -101532BC k --==--∴,∴切线l 的方程为:,即.2l k =()023y x -=-260x y --=16.已知等比数列的前n 项和为,且是与2的等差中项,等差数列中,,点{}n a n S n a n S {}n b 12b =在一次函数的图象上. 1(),n n P b b +2y x =+(1)求数列,的通项和; {}n a {}n b n a n b (2)设,求数列的前n 项和. n n n c a b ={}n c n T 【答案】(1),2n n a =2n b n =(2)2(1)24n n T n +=-+【分析】(1)结合已知条件,利用与之间的关系求的通项公式;将代入n a n S {}n a 1(),n n P b b +2y x =+中可得到公差,然后利用等差数列的通项公式即可求解;(2)利用错位相减法即可求解.【详解】(1)因为是与2的等差中项,n a n S 所以,即,22n n a S =+22n n S a =-则,1111222S a a a =-=⇒=当时,,2n ≥1122n n S a --=-从而, 111222n n n n n n n a a S S a a a ---=-=-⇒=则等比数列的公比,{}n a 2q =故; 112n n n a a q -==因为,点在一次函数的图象上,12b =1(),n n P b b +2y x =+所以,即等差数列的公差为2,1122n n n n b b b b ++=+⇒-={}n b 从而.12(1)2n b b n n =+-=(2)由,12n n n n c a b n +==⨯得:...①2341122232(1)22n n n T n n +=⨯+⨯+⨯++-⋅+⋅ ...②341221222(1)22n n n T n n ++=⨯+⨯++-⋅+⋅ ①-②得,2341222222n n n T n ++-=++++-⋅ , 222422(1)2412+++-=-⋅=-⋅--n n n n n 从而.2(1)24n n T n +=-+17.如图,在四棱锥中,PC ⊥底面ABCD ,ABCD 是直角梯形,AD ⊥DC ,AB DC ,P ABCD -A AB =2AD =2CD =2,点E 是PB 的中点.(1)证明:平面EAC ⊥平面PBC ;(2)若直线PB 与平面PAC P -AC -E 的余弦值. 【答案】(1)证明见解析【分析】(1)根据线面垂直的性质及勾股定理的逆定理可证出线面垂直,再由面面垂直的判定定理求证即可;(2)建立空间直角坐标系,利用向量法求解即可.【详解】(1)∵平面,平面,PC ⊥ABCD AC ⊂ABCD ∴.PC AC ⊥∵,由,且是直角梯形,2AB =1AD CD ==AD DC ⊥ABCD∴AC BC ===即,222AC BC AB +=∴.AC BC ⊥∵,平面,平面,PC BC C ⋂=PC ⊂PBC BC ⊂PBC ∴平面.AC ⊥PBC ∵平面,AC ⊂EAC ∴平面平面EAC ⊥PBC (2)∵平面,平面,PC ⊥ABCD BC ⊂ABCD ∴.PC BC ⊥由(1)知.AC BC ⊥∵,平面,平面,PC AC C ⋂=PC ⊂PAC AC ⊂PAC 所以平面,BC ⊥PAC ∴即为直线与平面所成角. BPC ∠PB PAC∴,sin BC BPC PB ∠===∴PB =2PC =取的中点G ,连接,以点C 为坐标原点,分别以、、为x 轴、y 轴、z 轴正方向,建AB CG CG CDCP 立如图所示的空间直角坐标系,则,,,,, ()0,0,0C ()002P ,,()1,1,0A ()1,1,0B -11,,122E ⎛⎫- ⎪⎝⎭∴,, ()1,1,0CA = ()0,0,2CP =u u r 11,,122CE ⎛⎫=- ⎪⎝⎭设为平面的法向量,则, ()111,,m x y z = PAC 111020m CA x y m CP z ⎧⋅=+=⎪⎨⋅==⎪⎩令,得,,得11x =10z =11y =-()1,1,0m =- 设为平面的法向量,()222,,x n y z = ACE 则,令,则,,得. 22222011022n CA x y n CE x y z ⎧⋅=+=⎪⎨⋅=-+=⎪⎩21x =21y =-21z =-()1,1,1n =-- ∴cos ,m n<>== 由图知所求二面角为锐角,所以二面角. P AC E --18.已知是椭圆的左焦点,上顶点B 的坐标是1F ()222210x y a b a b +=>>((1)求椭圆的标准方程;(2)O 为坐标原点,直线l 过点且与椭圆相交于P ,Q 两点,过点作,与直线相1F 1F 1EF PQ ⊥3x =-交于点E ,连接OE ,与线段PQ 相交于点M ,求证:点M 为线段PQ 的中点.【答案】(1) 22162x y +=(2)证明见解析【分析】(1)根据已知条件求得,从而求得椭圆的标准方程.,b a (2)设出直线的方程,求得直线的方程、直线的方程,求得点坐标,联立直线的方l 1EF OE M l 程与椭圆方程,化简写出根与系数关系,求得中点坐标,进而判断出是的中点.PQ M PQ 【详解】(1)因椭圆的上顶点,则c , ()222210x y a b a b +=>>(B b =,解得, c a 2222213b c a a -==26a =∴椭圆的标准方程为. 22162x y +=(2)由(1)知,,,显然直线l 不垂直于y 轴,设直线,2c =()12,0F -:2l x ty =-显然,直线l 不垂直于y 轴,因直线过点,且,则直线的方程可设为,1EF 1F 1EF PQ ⊥1EF20tx y t ++=由得点,直线OE 的方程为:, 320x tx y t =-⎧⎨++=⎩()3,E t -3t y x =-由解得:,因此点, 23x ty t y x =-⎧⎪⎨=-⎪⎩226323x t t y t ⎧=⎪⎪+⎨⎪=⎪+⎩2262,33t M t t ⎛⎫- ⎪++⎝⎭由消去x 并整理得:,设,, 22236x ty x y =-⎧⎨+=⎩()223420t y ty +--=()11,P x y ()22,Q x y 则,所以,, 12243t y y t +=+122223y y t t +=+1222262233x x t t t t +=⋅-=-++即线段PQ 中点坐标为,∴点M 为线段PQ 的中点. 2262,33t t t ⎛⎫- ⎪++⎝⎭19.已知函数. 1()ln ()f x a x a x ⎛⎫=-∈ ⎪⎝⎭R (1)若曲线在点处的切线方程为,求的值;()y f x =(1,(1))f 10x y +-=a (2)若的导函数存在两个不相等的零点,求实数的取值范围;()f x ()f x 'a (3)当时,是否存在整数,使得关于的不等式恒成立?若存在,求出的最大2a =λx ()f x λ≥λ值;若不存在,说明理由.【答案】(1);(2);(3)存在,最大值为.0a =()2,0e --1-【解析】(1)求出函数的导数,由题意得出从而可求出实数的值; ()y f x =()f x '()11f '=-a (2)令,可得知函数在上有两个零点,分和()21ln 0ax x f x x -+'==()1ln g x ax x =-+()0,∞+0a ≥两种情况讨论,利用导数分析函数在区间上的单调性和极值,由题意转化为函a<0()y g x =()0,∞+数极值相关的不等式,解出即可得出实数的取值范围;()y g x =a (3)将代入函数的解析式得出,对该函数求导得出2a =()y f x =()12ln f x x x ⎛⎫=- ⎪⎝⎭,构造函数,利用单调性结合零点存在定理找出函数()221ln x x f x x -+'=()21ln h x x x =-+()y f x =的极小值点,并满足,结合此关系式计算得出,从01,12x ⎛⎫∈ ⎪⎝⎭00ln 12x x =-()()()0min 1,0f x f x =∈-而可得出整数的最大值.λ【详解】(1), ()2111()ln f x x a x x x '=+-因为曲线在点处的切线方程为,()y f x =(1,(1))f 10x y +-=所以,得;(1)11f a '=-=-0a =(2)因为存在两个不相等的零点. 21ln ()ax x f x x -+'=所以存在两个不相等的零点,则.()1ln g x ax x =-+1()g x a x '=+①当时,,所以单调递增,至多有一个零点0a ≥()0g x '>()y g x =②当时,因为当时,,单调递增, a<01(0)x a∈-,()0g x '>()y g x =当时,,单调递减, 1(+)x a ∈-∞,()0g x '<()y g x =所以时,. 1x a=-max 11()(ln(2g x g a a =-=--因为存在两个零点,所以,解得.()g x 1ln(20a -->2e 0a --<<因为,所以. 2e 0a --<<21e 1a ->>因为,所以在上存在一个零点. (1)10g a =-<()y g x =1(0)a -,因为,所以.2e 0a --<<211(a a ->-因为,设,则, 22111[()]ln(1g a a a -=-+-1t a=-22ln 1(e )y t t t =-->因为,所以单调递减,20t y t -'=<22ln 1(e )y t t t =-->所以,所以,()2222ln e e 13e 0y <--=-<22111[(]ln()10g a a a -=-+-<所以在上存在一个零点. ()y g x =1()a -+∞,综上可知,实数的取值范围为;a 2(e ,0)--(3)当时,,, 2a =1()(2f x x x =-()2211121ln ()ln 2x x f x x x x x x -+'=+-=设,则.所以单调递增,()21ln h x x x =-+1()20h x x '=+>()y h x =且,,所以存在使得, 11(ln 022h =<(1)10h =>01(1)2x ∈,0()0h x =因为当时,,即,所以单调递减; 0(0)x x ∈,()0h x <()0f x '<()y f x =当时,,即,所以单调递增, 0(+)x x ∈∞,()0h x >()0f x '>()y f x =所以时,取得极小值,也是最小值,0x x =()y f x =此时, ()0000000111()(2)ln (2)12(4)4f x x x x x x x =-=--=-++因为,所以, 01(1)2x ∈,0()(10)f x ∈-,因为,且为整数,所以,即的最大值为.()f x λ≥λ1λ≤-λ1-【点睛】本题考查利用切线方程求参数、利用导数研究函数的零点,同时也考考查了利用导数研究不等式恒成立问题,涉及隐零点法的应用,考查分析问题和解决问题的能力,属于难题.。
山西省阳泉市高二上学期数学期末考试试卷

山西省阳泉市高二上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共10分)1. (1分) (2018高一下·双鸭山期末) 直线x-y=0的倾斜角为()A . 45°B . 60°C . 90°D . 35°2. (1分)已知抛物线y2=2px(p>0)的准线经过点(-1,1),则抛物线焦点坐标为()A . (-1,0)B . (1,0)C . (0,-1)D . (0,1)3. (1分) (2016高二下·黄冈期末) 给出下列四个命题:①f(x)=x3﹣3x2是增函数,无极值.②f(x)=x3﹣3x2在(﹣∞,2)上没有最大值③由曲线y=x,y=x2所围成图形的面积是④函数f(x)=lnx+ax存在与直线2x﹣y=0平行的切线,则实数a的取值范围是(﹣∞,2)其中正确命题的个数为()A . 1B . 2C . 3D . 44. (1分)“|x|<2”是“x2-x-6<0”的()A . 充分而不必要条件B . 必要而不充分条件C . 充要条件D . 既不充分也不必要条件5. (1分) (2017高一上·武邑月考) 若圆上总存在两点到原点的距离为1,则实数的取值范围是()A .B .C .D .6. (1分)下列命题中,真命题是()A . ∃x0∈R,≤0B . ∀x∈R,2x>x2C . 双曲线的离心率为D . 双曲线的渐近线方程为7. (1分)四棱锥P-ABCD中,底面ABCD为正方形,且平面ABCD,PA=AB,则直线PB与直线AC所成角的大小为()A .B .C .D .8. (1分)(2019·厦门模拟) 若抛物线的焦点到准线的距离为1,则()A . 2B . 4C .D .9. (1分)若椭圆x2+my2=1的焦距为2,则m的值是()A .B . 1C . 2D . 410. (1分)(2017高一下·沈阳期末) 在中,角所对的边分别为,若,则()A .B .C .D .二、填空题 (共7题;共7分)11. (1分) (2019高二上·哈尔滨月考) 双曲线的离心率是________.12. (1分)(2018·天津) 已知圆的圆心为C ,直线 ( 为参数)与该圆相交于A , B两点,则的面积为________.13. (1分)(2016·四川文) 已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.14. (1分)如图,矩形ABCD中,AB=1,BC= ,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[ , ]内变化,则点A所形成的运动轨迹的长度为________.15. (1分) (2017高二下·陕西期中) 已知椭圆x2+ky2=3k(k>0)的一个焦点与抛物线y2=12x的焦点重合,则该椭圆的离心率是________.16. (1分) (2016高二上·西湖期中) 已知两条不同直线m、l,两个不同平面α、β,给出下列命题:①若l垂直于α内的两条相交直线,则l⊥α;②若l∥α,则l平行于α内的所有直线;③若m⊂α,l⊂β且l⊥m,则α⊥β;④若l⊂β,l⊥α,则α⊥β;⑤若m⊂α,l⊂β且α∥β,则m∥l.其中正确命题的序号是________.(把你认为正确命题的序号都填上)17. (1分) (2015高二上·石家庄期末) 已知点A(1,0),曲线C:y=x2﹣2,点Q是曲线C上的一动点,若点P与点Q关于A点对称,则点P的轨迹方程为________.三、解答题 (共5题;共7分)18. (1分)已知a>0且a≠1,设p:函数y=loga(x+3)在(0,+∞)内单调递减,q:方程x2+(2a﹣3)x+1=0有两个不等负根,如果p∨q为真且p∧q为假,求实数a的取值范围.19. (2分)(2016·普兰店模拟) 如图,直三棱柱ABC﹣A1B1C1中,AC⊥AB,AB=2AA1 , M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.(1)若DE∥平面A1MC1,求;(2)求直线BC和平面A1MC1所成角的余弦值.20. (2分) (2016高二上·宁波期中) 已知抛物线x2=2py(p>0)与直线2x﹣y+1=0交于A,B两点,,点M在抛物线上,MA⊥MB.(1)求p的值;(2)求点M的横坐标.21. (1分)(2017·民乐模拟) 如图,在四棱锥P﹣ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.(1)设点E为PD的中点,求证:CE∥平面PAB;(2)线段PD上是否存在一点N,使得直线CN与平面PAC所成的角θ的正弦值为?若存在,试确定点N的位置,若不存在,请说明理由.22. (1分)(2017·南充模拟) 已知直线l:x+y+8=0,圆O:x2+y2=36(O为坐标原点),椭圆C: =1(a>b>0)的离心率为e= ,直线l被圆O截得的弦长与椭圆的长轴长相等.(I)求椭圆C的方程;(II)过点(3,0)作直线l,与椭圆C交于A,B两点设(O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在,求出直线l的方程,若不存在,说明理由.参考答案一、单选题 (共10题;共10分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共7分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共7分) 18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、。
山西省阳泉市中学高二数学理联考试卷含解析

山西省阳泉市中学高二数学理联考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知点和在直线的两侧,则的取值范围是()A. B. C. D.不确定参考答案:B2. 椭圆与圆(为椭圆半焦距)有四个不同交点,则椭圆离心率的取值范围是( )A. B. C. D.参考答案:A略3. 已知集合A={x|x2+2x﹣3<0},B={x|<0},则A∩B=( )A.{x|x<0} B.{x|x>1} C.{x|0<x≤1}D.{x|0<x<1}参考答案:D【考点】交集及其运算.【专题】计算题;集合.【分析】求出A与B中不等式的解集确定出A与B,找出两集合的交集即可.【解答】解:由A中不等式变形得:(x﹣1)(x+3)<0,解得:﹣3<x<1,即A={x|﹣3<x<1},由B中不等式变形得:x(x﹣2)<0,解得:0<x<2,即B={x|0<x<2},则A∩B={x|0<x<1},故选:D.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.4. 若点和点分别为椭圆的中心和右焦点,点为椭圆上的任意一点,则的最大值是()A. B. C. D.不存在参考答案:C5. 已知x与y之间的一组数据:则y与x的线性回归方程为y=bx+a必过()A.(2,2)点B.(1.5,0)点C.(1,2)点D.(1.5,4)点参考答案:D略6. 数列中,若,则的值为()A.-1 B.C.1 D.2参考答案:A略7. 若椭圆上离顶点A(0,a)最远点为(0,-a),则( ).(A) 0<a<1 (B) ≤a<1(C)<a<1 (D) 0<a<参考答案:B8. 如图21-7所示程序框图,若输出的结果y的值为1,则输入的x的值的集合为()图21-7A.{3} B.{2,3}C. D.参考答案:9.参考答案:A略10. 抛物线y2=6x的准线方程是()A.x=3 B.x=﹣3 C.x= D.x=﹣参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. =____________.参考答案:12. 在长方体ABCD-A1B1C1D1中,,E是AB的中点,则异面直线DE与D1C所成角的余弦值为_____.参考答案:【分析】过E作EF,则即为异面直线与所成角或其补角,在三角形DEF中,计算可得cos.【详解】取的中点F,连接EF,则EF,∴即为异面直线与所成角或其补角,不妨设,则在△DEF中,DE=,,∴在等腰三角形DEF中,可得cos,故答案为:.【点睛】本题考查异面直线所成角的余弦值的求法,考查异面直角所成角的定义,考查运算求解能力,是基础题.13. 已知直线l 1:3x ﹣y+2=0,l 2:x+my ﹣3=0,若l 1∥l 2,则m 的值等于 .参考答案:﹣【考点】直线的一般式方程与直线的平行关系. 【分析】利用平行线的充要条件即可得出.【解答】解:∵l 1∥l 2,∴,解得m=﹣. 故答案为:﹣.【点评】本题考查了平行线的充要条件,考查了推理能力与计算能力,属于基础题. 14. 已知是△的外心,且,,是线段上任一点(不含端点),实数,满足,则的最小值是 *** .参考答案:2略15. 已知正方体ABCD -A 1B 1C 1D 1的一个面A 1B 1C 1D 1在半径为的半球底面上,四个顶点A ,B ,C ,D 都在半球面上,则正方体ABCD -A 1B 1C 1D 1的体积为 .参考答案:16. 抛掷一枚均匀的硬币4次,则出现正面的次数多于反面此时的概率为参考答案:17. 函数的定义域是 .参考答案:{}略三、 解答题:本大题共5小题,共72分。
