扭转刚度矩阵
工程力学抗扭刚度计算公式

工程力学抗扭刚度计算公式引言。
在工程力学中,抗扭刚度是指材料或结构在受到扭转力作用时所表现出的抵抗扭转变形的能力。
抗扭刚度的计算对于设计和分析各种工程结构和机械元件都具有重要意义。
本文将从理论和公式两个方面介绍抗扭刚度的计算方法。
理论基础。
在进行抗扭刚度计算之前,首先需要了解一些基本的理论知识。
在工程力学中,材料或结构受到扭转力矩时会发生扭转变形,而扭转变形的大小与受到的扭转力矩成正比。
根据弹性力学理论,扭转变形与扭转力矩之间的关系可以用以下公式表示:θ = T/Gl。
其中,θ为扭转角度,T为扭转力矩,G为剪切模量,l为材料或结构的长度。
从上述公式可以看出,扭转角度与扭转力矩成正比,而与材料或结构的长度和剪切模量成反比。
因此,要提高材料或结构的抗扭刚度,可以通过增加剪切模量或减小长度来实现。
抗扭刚度计算公式。
在实际工程中,为了方便计算和分析,通常会使用一些简化的公式来计算抗扭刚度。
对于圆形截面的材料或结构,抗扭刚度可以用以下公式表示:J = (πr^4)/2。
其中,J为抗扭刚度,r为圆形截面的半径。
从上述公式可以看出,抗扭刚度与圆形截面的半径的四次方成正比。
因此,要提高材料或结构的抗扭刚度,可以通过增加圆形截面的半径来实现。
对于非圆形截面的材料或结构,抗扭刚度的计算则会更加复杂。
一般情况下,可以使用以下公式来计算非圆形截面的抗扭刚度:J = ∫(r^2)dA。
其中,J为抗扭刚度,r为截面上任意一点到截面中心的距离,dA为截面上的微元面积。
从上述公式可以看出,抗扭刚度可以通过对截面上的微元面积进行积分来计算。
这种方法虽然比较复杂,但可以适用于各种形状的截面。
应用举例。
为了更好地理解抗扭刚度的计算方法,下面将通过一个简单的应用举例来说明。
假设有一根圆形截面的钢杆,其半径为10mm,长度为1m。
现在需要计算该钢杆的抗扭刚度。
根据上述公式,可以得到该钢杆的抗扭刚度为:J = (π(10mm)^4)/2 = 785.4mm^4。
动力传动系统扭转振动的分析及控制

动力传动系统扭转振动的分析及控制任丽丽;施善;刘友波【摘要】随着国内汽车企业对车辆质量要求的升级,噪声振动的控制技术备受重视,来自系统设计相关的噪声振动需要靠实车测试及计算机模拟的配合来解决。
动力传动系统的扭转共振就是一个这样的噪声振动问题,利用系统化步骤解决这个问题的优点是它适用于各种类型的车辆,仿真模拟是解决这个问题的核心技术。
首先根据发动机到车桥整个动力系各单元部件的转动惯量、扭转刚度及阻尼来建振动力学模型,然后分析系统的自然频率、模态及频响,进行数模的开发过程与测试对比,这种方法对车辆性能优化问题非常有效。
%Vehicle NVH control has gained increasing attention of domestic auto makers in an effort to promote vehicle’s quality. To solve the problem, the integrated product testingand simulation modeling are necessary. One example of system NVH problem that can be benefited by this approach is the powertrain torsional vibration. The key technology in this approach is the development of an effective simulation model. First of all, dynamic parameters such as the torsional stiffness, moment of inertia and torsional damping of individual parts are measured or calculated. Then, these parameters are used to simulate the powertrain torsional vibration for its natural frequencies, mode shapes and frequency responses. With this method, the vehicle’s performance can be optimized easily.【期刊名称】《噪声与振动控制》【年(卷),期】2014(000)003【总页数】6页(P20-25)【关键词】振动与波;扭转振动;动力传动系统;频率;频响;阻尼【作者】任丽丽;施善;刘友波【作者单位】北汽福田汽车股份有限公司乘用车设计院,北京 102206;北汽福田汽车股份有限公司乘用车设计院,北京 102206;北汽福田汽车股份有限公司乘用车设计院,北京 102206【正文语种】中文【中图分类】U467.4+92近年来,随着生活水平的提高,选择车辆时,人们更注重车辆的各种性能,如NVH、操控性、舒适性等。
(仅供参考)第十九章-扭转的强度与刚度计算
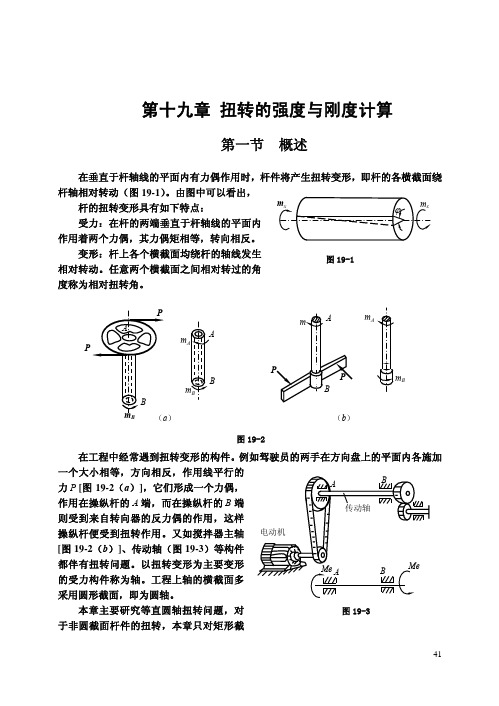
一、外力偶矩的计算
前面已经指出 ,使轴产生扭转变形的是外力偶矩。但是作用于轴上的外力偶矩往
往不是直接给出的,而是给定轴所传递的功率和轴的转速。以图 19-3 所示的传动轴为例,
由电动机的转速和功率可以求出传动轴 AB 的转速及通过皮带轮输入的功率。功率由皮
带轮传到轴 AB 上,再经右端的齿轮输出。设通过皮带轮给 AB 轴输入的功率为 N(kW),
因为 1kW=1000N·m/s 因此每秒钟输入功应为 : W = N ×1000(N ⋅ m)
(a)
电动机是通过皮带轮以力偶矩 Me 作用于 AB 轴上的,若 AB 轴的转速为每分钟 n 转,
则力偶矩 Me 在每秒内完成的功应为 :
W = 2π × n × Me(N ⋅ m)
(b)
60
因为 Me 所完成的功也就是皮带轮给 AB 轴输入的功,故(a)、(b)两式应相等,这
据微元的平衡要求,不仅左右一对面上有大小相等,方向相反的剪应力 τ ,在上下一对
面也必须有剪应力τ ′ ,而且由力矩平衡条件 ∑ mz = 0 有:
(τtdy)dx = (τ ′tdx)dy
由此得到:
τ =τ′
(19-2)
这表明,在相互垂直的两个微面上,剪应力总是成对出现的,它们数值相等,而方
向均垂直于两微面的交线,或指向或背离这一交线。这就是剪应力互等定理。
利用第三节中的(b)式和(c)式,上式可以写成:
φ
φ
图 19-9
u = 1 τγ 2
再由剪切胡克定律(式 19-3)得:
u = 1 τγ = τ 2 2 2G
46
第四节 圆轴扭转时的应力与变形
一、横截面上剪应力计算公式
圆轴扭转时,在已知横截面上的扭矩后,还应进一步研究横截面上的应力分布规律,
高层结构内力与位移计算的一般方法

a
2 1 2
;
b
1 1 2
6EJ GAL2 0
;
c
3 L0 1 2
;
e
6 1 2 L2 0
;
式中:
—截面剪应力分布不均匀系数; —中段截面的弹性模量、剪切模量、惯性矩和面积;
A E、 G 、J 、
L0 —分别为杆端刚域和中段的长度。 d j 、d k 、
j K jj Ks K kj
k K jk j K kk k
其中每个子矩阵为3×3,可叠加到总刚度矩阵 K f 中去,
叠加完毕、形成总刚度矩阵后,对于位移约束点(如底层固定点)的某一个 的位移为零时,可令相应于该位移分量的主对角元素为非常大的数(例 如 1016、 1017等),则求解时,这些位移分量自动等于零。 令荷载向量只在某一层(第i层)施加单位水平力 Pxi 1 ,其余荷载 值均为零,由下式可以求出相应的位移
GJ p , NS hNS
(1-24)
M K
(1-25)
1.1.4 在水平荷载作用下高层建筑结构空间协调工作分析的基本公式
y
us
P
( Ns ) xs
Lxs
p ys
pxs
s
vs
O′
O
lb2 hz 2 0.25hl
对于柱
lz1 hL1 0.25hz lz 2 hL 2 0.25hz
如果梁太高或太细,可按 hL hz的大小适当调整刚域长度。刚域长度当算得
为负值时,应取为零。
在进行高层建筑结构分析时,假定各片抗侧力结构在自身平面内的刚度
弹性力学 本构方程 刚度矩阵 柔度矩阵

弹性力学本构方程刚度矩阵柔度矩阵弹性力学本构方程刚度矩阵柔度矩阵中文名称:弹性力学英文名称:theory of elasticity其他名称:弹性理论定义:研究弹性体在荷载等外来因素作用下所产生的应力、应变、位移和稳定性的学科。
所属学科:水利科技(一级学科) ;工程力学、工程结构、建筑材料(二级学科) ;工程力学(水利)(三级学科)弹性力学也称弹性理论,主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移,从而解决结构或机械设计中所提出的强度和刚度问题。
在研究对象上,弹性力学同材料力学和结构力学之间有一定的分工。
材料力学基本上只研究杆状构件;结构力学主要是在材料力学的基础上研究杆状构件所组成的结构,即所谓杆件系统;而弹性力学研究包括杆状构件在内的各种形状的弹性体。
弹性力学是固体力学的重要分支,它研究弹性物体在外力和其它外界因素作用下产生的变形和内力,也称为弹性理论。
它是材料力学、结构力学、塑性力学和某些交叉学科的基础,广泛应用于建筑、机械、化工、航天等工程领域。
弹性体是变形体的一种,它的特征为:在外力作用下物体变形,当外力不超过某一限度时,除去外力后物体即恢复原状。
绝对弹性体是不存在的。
物体在外力除去后的残余变形很小时,一般就把它当作弹性体处理。
弹性力学的发展大体分为四个时期。
人类从很早时就已经知道利用物体的弹性性质了,比如古代弓箭就是利用物体弹性的例子。
当时人们还是不自觉的运用弹性原理,而人们有系统、定量地研究弹性力学,是从17世纪开始的。
发展初期的工作是通过实践,探索弹性力学的基本规律。
这个时期的主要成就是R.胡克于1678年发表的弹性体的变形与外力成正比的定律,后来被称为胡克定律。
第二个时期是理论基础的建立时期。
这个时期的主要成就是,从1822,1828年间,在A.-L?柯西发表的一系列论文中明确地提出了应变、应变分量、应力和应力分量概念,建立了弹性力学的几何方程、平衡(运动)微分方程,各向同性和各向异性材料的广义胡克定律,从而为弹性力学奠定了理论基础。
基于扭转-纵向振动耦合模型的汽车起步颤振分析

基于扭转-纵向振动耦合模型的汽车起步颤振分析栾文博【摘要】文章针对某装备干式AMT小型轿车的起步颤振现象,建立了传动系扭转振动、车辆纵向振动的耦合模型,以车身纵向加速度最大波动值为评价指标,对自激振动机理下起步颤振现象的影响因素进行分析,通过仿真发现:降低离合器摩擦系数随相对滑摩线速度的“负斜率”绝对值可以有效地抑制起步颤振;减小半轴的扭转刚度和整车质量、增大悬架纵向刚度,可以使起步颤振感减弱;并探讨了主动抑制自激颤振的干式离合器控制策略,采用与转速差呈“正斜率”关系的正压力来抵消与转速差呈“负斜率”关系的摩擦系数给传动系引入的负阻尼,以此来达到抑制起步颤振的目的.【期刊名称】《汽车实用技术》【年(卷),期】2019(000)006【总页数】5页(P158-162)【关键词】起步颤振;自激振动;扭转-纵向耦合振动;影响因素分析;主动颤振抑制【作者】栾文博【作者单位】泛亚汽车技术中心有限公司,上海201201【正文语种】中文【中图分类】U463引言汽车保有量的增大、拥堵的交通和复杂的路况使得在市区内行驶的汽车会频繁地处于停车起步状态。
离合器颤振现象就出现在起步过程中,是由于离合器的滑摩作用使汽车传动系发生剧烈的扭转振动[1],给乘员直观感受主要为整车出现的纵向抖动。
胡宏伟等研究了离合器在接合过程中的抖动及其影响因素,建立了四自由度传动系扭振模型,发现摩擦系数随相对滑摩线速度变化的曲线负斜率和正压力波动会引起和加剧离合器的抖动,通过降低该负斜率绝对值、提高最大静摩擦系数及适当提高传动轴刚度等可以有效降低接合抖动的程度[2]。
周林等针对某MPV车型起步颤振控制措施进行了研究,明确了离合器接合过程转速波动为问题根源,提出加大离合器直径、综合控制分离指端跳和压盘倾斜量工艺制造精度,可有效地解决起步颤振[3]。
吴光强等基于六自由度的传动系扭振模型对起步颤振现象进行了数值仿真,分析了传动系各部分阻尼对抑制起步颤振的影响程度,认为增大半轴和轮胎阻尼可以有效地抑制起步颤振[4]。
抗扭强度和抗扭刚度计算公式

抗扭强度和抗扭刚度计算公式抗扭强度和抗扭刚度是材料强度和刚度的两个重要参数之一。
抗扭强度指材料在扭转过程中所能承受的最大扭转应力,抗扭刚度则是指材料在扭转过程中所表现出的抵抗扭转的能力。
这两个参数的测量和计算都是非常重要的,因为它们对人们所关心的材料结构和性能均有着很大的影响。
在实际工程应用中,抗扭强度和抗扭刚度常常是决定材料使用和结构设计的关键因素之一。
例如,在机械制造和汽车工业中,材料的抗扭强度和抗扭刚度对于机器、发动机组件和汽车轮毂等大型结构件来说显得尤其重要。
计算抗扭强度和抗扭刚度可以使用以下的公式。
假设材料的截面形状是圆形,并且应力分布沿圆心方向均匀,那么:1. 抗扭强度公式:T = (π/2) × τ_max × R^3,其中,T是抗扭强度,τ_max是最大扭转应力,R是圆柱的半径。
2. 抗扭刚度公式:K = G × I,其中,K是抗扭刚度,G是剪切模量,I是截面惯性矩。
下面就计算材料的抗扭强度和抗扭刚度为例,进行简单的说明。
假设我们有一个直径为10 cm,长度为20 cm的纯铝杆,想计算它的抗扭强度和抗扭刚度。
首先,我们需要测量铝杆的圆柱半径R,它等于直径的一半,所以R=5 cm。
然后,我们需要确定材料的剪切模量G和截面惯性矩I。
对于铝杆这种确定奇形参数比较麻烦,我们可以选择一种计算常规圆形杆的抗扭刚度公式:K = (π/32) × d^4,其中,d是圆柱的直径。
将直径d=10 cm代入该公式中,我们得到K = 12.27 × 10^9 N·m^2。
然后,我们可以计算铝杆的抗扭强度T。
假设最大扭转应力τ_max = 80 MPa,将这个值和铝杆的半径R = 5 cm代入上述公式中,我们得到T = 15708 N·m。
这个数值告诉我们,在最大扭转应力为80 MPa的情况下,铝杆能够承受15708 N·m的扭矩。
船舶动力装置轴系扭转振动计算课程设计

船舶动力装置轴系扭转振动计算课程设计班级:轮机0801班学号:U200812201姓名:李弘扬一.设计任务及意义:在推进装置中,从主机到推进器之间,用传动轴及保证推进装置正常工作所需的全部设备连接在一起的中间机构成为轴系。
船舶轴系是船舶动力装置的重要组成部分之一。
轴系的工作好坏,将直接影响船舶的推进特性和正常航行,并对船舶主机的正常工作也有直接的影响。
如果轴系设计质量欠佳,将会引起机体振动、传动系统零部件损坏、轴承过度磨损、甚至轴件折断等事故,不仅会中止机械系统的正常运行,也会危急工作人员的生命安全。
因此对轴系必须进行深入的研究,以利于其正确的设计、制造、安装和检验。
船舶轴系振动控制就是设计及安装中采取措施,以保证动力装置的振动限制在容许的范围内。
这次设计主要是针对简化实际系统后的理想的轴系当量系统图进行分析,采用其参数,通过各种方法(矩阵特征值特征向量、HOLZER 法、专门解微分方程的软件等)求出系统的各阶频率及其主阵型,通过对着2个参数进行分析,得出所需的数据,并总结归纳出轴运转过程中要注意的问题,以保证轴能够安全有效的运转。
二.柴油机推进轴系布置图:图1所选主机的型号为6350ZC-1,其额定功率为661Kw,额定转速为350r/m。
三.轴系当量系统图:为了方便对船舶的推进轴系进行分析和振动计算,将实际的船舶推进轴系简化成当量系统,如下图:图2其中:1.空气压缩机2.水泵3.变速齿轮 4-8.柴油机气缸 9.飞轮 10.减速器 11.联轴节 12.螺旋浆各当量参数如下表:序号 1 2 3 4~7 8 9 10 11 12转动惯量5.98 1.08 1.04 2.913 2.913 51.463 0.6 1.115 3.944(kg·m2)扭转刚度×10-58.2 392.2 150 112.78 169.66 0.5 0.5 50.29 (N·m/rad)表1转动惯量与扭转刚度的等效计算原理:a,转动惯量:轴系作扭转振动时,其运动部件可分为旋转运动件和往复式运动件,其中,旋转运动件的转动惯量一般都是对圆盘这类有规则几何形状的物体进行积分:J=.比如真空心圆轴的转动惯量为J=ρ()L (kg ·m )。
结构中的各种刚度

结构中的各种刚度刚度:结构或构件抵抗变形的能力,包括构件刚度和截面刚度,按受力状态不同可分为轴向刚度、弯曲刚度、剪变刚度和扭转刚度等。
对于构件刚度,其值为施加于构件上的力(力矩)与它引起的线位移(角位移)之比。
对于截面刚度,在弹性阶段,其值为材料弹性模量或剪变模量与截面面积或惯性矩的乘积。
首先得从刚度说起。
刚度是指:单位变形条件下,结构或构件在变形方向所施加的力的大小。
在结构静力或动力分析时需要用到。
如用位移法分析结构内力时要用到刚度矩阵,计算地震作用或风振影响时需要用到结构的刚度参数。
还有在设计动力机器基础时也需要用到结构刚度参数。
可以看有关结构力学或结构动力学的书。
举个两个简单的例子以方便理解:用力弯折直径和长度相等的实心钢管和木头,哪个费劲哪个刚度(弯曲刚度)就大。
很显然是钢管的大,你有可能把木头弯折,但要弯折钢管就很难吧!用力弯折长度相等而直径不等的实心钢管,当然是直径小的容易弯折吧,那就是直径小的刚度小了。
所以刚度是和材料特性及截面特性直接相关,当然线刚度还和长度有关了!一般能满足F=k△,F为作用力,△为位移,k即为刚度,所以刚度物理意义为单位位移时所产生的力。
k可以是某些量的函数,即可为表达式。
由F的不同,叫法不同。
另外就是我们要说的刚度叫线刚度,即单位长度上的刚度。
比如,我们在用反弯点法计算多层框架水平荷载作用下内力近似计算时。
计算柱的水平剪力时,剪力与柱层间水平位移△的关系为V=(12ic/h2)△那么d=(12ic/h2)就叫柱的侧移刚度,表示柱上下两端相对有单位侧移时柱中产生的剪力。
其中ic表示柱的线刚度(即ic=EI/h),h为楼层高,EI是柱的抗弯刚度(M=EI(1/p),M为弯矩,(1/p)为曲率,也满足F=k△形式)。
另外还可用D值法,即考虑了梁柱的刚度比变化,因为柱两端梁的刚度不同,即对柱的约束不同,那么它的反弯点,即M=0的点会随之移动,那端强,反弯点离它越远。
optistruct 单元刚度矩阵

optistruct 单元刚度矩阵(实用版)目录1.什么是单元刚度矩阵2.单元刚度矩阵的作用3.如何计算单元刚度矩阵4.实例解释单元刚度矩阵在有限元法中的应用5.总结正文一、什么是单元刚度矩阵单元刚度矩阵是在结构力学中,描述单元(如梁、板、壳等)刚度特性的矩阵。
它可以用来表示单元在各个方向上的刚度,包括拉伸、压缩、弯曲、扭转等。
在有限元分析中,单元刚度矩阵是一个关键的组成部分,用于计算结构的整体刚度和解决节点平衡方程。
二、单元刚度矩阵的作用单元刚度矩阵的主要作用有以下几点:1.计算结构的整体刚度:通过组装各个单元的刚度矩阵,可以得到结构的整体刚度矩阵。
整体刚度矩阵反映了结构在各个方向上的刚度特性,从而可以分析结构的稳定性和变形情况。
2.解决节点平衡方程:在有限元法中,节点平衡方程是基于单元刚度矩阵建立的。
通过节点平衡方程,可以求解出节点处的荷载和位移。
3.计算结构的应力和应变:利用单元刚度矩阵,可以计算出结构在各个位置的应力和应变,从而分析结构的强度和刚度。
三、如何计算单元刚度矩阵单元刚度矩阵的计算方法取决于单元的类型和几何形状。
以下是计算单元刚度矩阵的一般步骤:1.确定单元的类型:根据结构的几何形状和受力特点,选择合适的单元类型,如梁单元、板单元、壳单元等。
2.计算单元的刚度:根据单元的类型和几何形状,计算单元在各个方向上的刚度。
对于梁单元,需要计算弯曲刚度和扭转刚度;对于板单元,需要计算弯曲刚度和扭转刚度;对于壳单元,需要计算弯曲刚度、扭转刚度和曲率刚度等。
3.组装单元刚度矩阵:根据单元的刚度,构建单元刚度矩阵。
对于梁单元,可以使用位移法或刚度法计算单元刚度矩阵;对于板单元和壳单元,需要考虑更多的因素,如材料性能、几何参数等。
四、实例解释单元刚度矩阵在有限元法中的应用假设有一个简支梁结构,我们需要分析其在承受均布荷载时的应力和应变。
首先,我们需要建立有限元模型,包括梁单元和节点。
然后,我们需要计算每个梁单元的刚度矩阵,包括弯曲刚度和扭转刚度。
单元刚度矩阵转换为整体刚度矩阵

单元刚度矩阵是在有限元分析中经常用到的一个概念,它描述了单个有限元单元的刚度性质。
而整体刚度矩阵则是描述了整个结构的刚度性质。
在有限元分析中,通常需要将单元刚度矩阵转换为整体刚度矩阵,以便对整个结构进行分析和计算。
本文将介绍单元刚度矩阵转换为整体刚度矩阵的方法和步骤。
1. 确定整体刚度矩阵的尺寸在将单元刚度矩阵转换为整体刚度矩阵之前,首先需要确定整体刚度矩阵的尺寸。
整体刚度矩阵的尺寸取决于整个结构的自由度数量。
通常情况下,整体刚度矩阵的尺寸为总自由度的数量乘以总自由度的数量。
在确定整体刚度矩阵的尺寸之后,可以开始进行单元刚度矩阵的转换了。
2. 单元刚度矩阵的转换单元刚度矩阵的转换是整体刚度矩阵计算的关键步骤。
假设有n个有限元单元,每个单元的刚度矩阵为K1、K2、...、Kn,对应的自由度编号为dof1、dof2、...、dofn。
单元刚度矩阵可以通过以下公式转换为整体刚度矩阵:[整体刚度矩阵] = [整体刚度矩阵] + [单元刚度矩阵]其中,整体刚度矩阵和单元刚度矩阵都是按照对应的自由度编号排列的。
转换的过程中需要将每个单元刚度矩阵根据对应的自由度编号放置到整体刚度矩阵的相应位置上,并进行累加。
这样就可以得到整体刚度矩阵。
3. 处理自由度约束在进行单元刚度矩阵转换为整体刚度矩阵的过程中,还需要处理自由度的约束。
通常情况下,整个结构中会存在一些自由度被约束的情况,这就需要在转换过程中进行处理。
一般来说,可以通过对整体刚度矩阵进行修改,将被约束的自由度对应的行和列删除,同时将约束后的位移值代入整体刚度矩阵中相关方程中进行处理。
4. 检验整体刚度矩阵转换完成后,需要对整体刚度矩阵进行检验,以确保计算的准确性。
通常可以通过一些验证计算、模拟和实验结果对比等方法,来验证整体刚度矩阵的正确性和可靠性。
通过以上步骤,就可以将单元刚度矩阵转换为整体刚度矩阵。
整体刚度矩阵描述了整个结构的刚度性质,对于有限元分析和结构设计具有重要的意义。
三维梁单元的刚度矩阵

三维梁单元的刚度矩阵
三维梁单元的刚度矩阵是指用于描述三维梁单元在受力情况下
的刚度性质的矩阵。
在建筑和结构工程中,梁是一种常见的结构元素,在承受荷载和力的作用下,需要具有足够的刚度和强度。
因此,对于梁单元的刚度矩阵研究具有重要意义。
三维梁单元的刚度矩阵通常包含12个自由度,分别为6个位移自由度和6个旋转自由度。
其中,位移自由度包括三个轴向位移和三个转角位移,旋转自由度包括三个轴向旋转和三个弯曲旋转。
这些自由度的变化会引起梁单元的变形和应力分布的改变,因此需要进行刚度矩阵的计算和分析。
三维梁单元的刚度矩阵的计算包括确定单元的几何参数、材料参数和荷载参数,并根据这些参数构造出单元的刚度矩阵。
通常采用有限元方法进行计算,利用矩阵乘法和逆矩阵运算来求解刚度矩阵。
刚度矩阵的求解可以通过手动计算或使用计算机软件进行。
三维梁单元的刚度矩阵在建筑和结构工程中具有重要的应用价值,可以用于分析和设计各种类型的梁结构。
通过对梁单元的刚度矩阵进行计算和分析,可以预测梁的刚度和强度,优化梁的结构设计,提高梁的使用寿命和安全性。
- 1 -。
第二章 刚度矩阵法

x lx mx nx x
y
l
y
my
n
y
y
z lz mz nz z
lx mx nx
T l y
my
n
y
lz mz nz
T
§2.5 基本步骤
•单元刚度矩阵的建立:
K e e f e f TF
K eTe TFe
T T K eTe F e Κe T T K eT Κee F e
x y z T
平面刚架
f x f y M z T
x y z T
空间刚架
f x f y f z M x M y M z x y z x y z
平面板架
f z M x M y T
z x y T
§2.2 位移模式
位移模式是建立起单元内任一点位移与节点之 间的关系 •轴向变形 •扭转变形 •弯曲变形
BT DBdV f
V
*T
*T
BT DBdV f
V
*T
*T
BT DBdV f V
BT DBdV f
V
BT DBdV f
V
K f
K BT DBdV V
§2.4 坐标变换
Z Y’
Z’ X
Y X’
x y z T
x y z T
x x cos(x, x' ) y cos(x, y' ) z cos(x, z' )
•轴向变形
ux a bx
I
J
ix a bx a jx a bL
i
b jx ix
L
L
ΔL
j L
ux
ix
jx
ix
L
cae 导出 刚度矩阵

cae 导出刚度矩阵刚度矩阵是计算机辅助工程(CAE)中一个重要的概念,它用于描述物体在受力作用下的刚度特性。
刚度矩阵是一个二维矩阵,表示物体在不同方向上的刚度。
在CAE中,刚度矩阵可以用来分析和预测物体在不同载荷下的变形和应力分布情况,从而指导设计和优化工作。
刚度矩阵的计算是基于有限元分析方法的。
有限元分析是一种数值计算方法,它将物体分割为许多小的有限元,然后通过求解方程组来获得物体的刚度矩阵。
在求解过程中,需要考虑物体的几何形状、材料特性和边界条件等因素。
通过对这些因素的建模和计算,可以得到刚度矩阵的数值结果。
刚度矩阵的形式与物体的几何形状和边界条件有关。
对于三维物体,刚度矩阵通常是一个6x6的矩阵,其中包含了物体在三个方向上的平移刚度和旋转刚度。
对于二维物体,刚度矩阵通常是一个4x4的矩阵,其中包含了物体在两个方向上的平移刚度和旋转刚度。
刚度矩阵的计算可以使用各种数值方法和软件工具来实现。
在CAE 领域,有许多流行的有限元分析软件,如ANSYS、ABAQUS和Nastran等,它们提供了强大的功能和用户友好的界面,可以方便地进行刚度矩阵的计算和分析。
刚度矩阵的应用非常广泛。
在工程设计中,刚度矩阵可以用来评估物体的结构强度和刚度,以及预测物体在不同载荷下的变形和应力分布情况。
例如,在汽车工程中,刚度矩阵可以用来评估车身的刚度和稳定性,以及预测车身在碰撞事故中的变形情况。
在航空航天工程中,刚度矩阵可以用来评估飞机的结构强度和疲劳寿命,以及预测飞机在高速飞行和大气扰动下的变形和应力分布情况。
除了工程设计,刚度矩阵还可以应用于材料力学、地震工程、生物力学等领域。
在材料力学中,刚度矩阵可以用来评估材料的刚度和弹性特性,以及预测材料在不同载荷下的应力应变行为。
在地震工程中,刚度矩阵可以用来评估建筑物的地震响应和抗震性能。
在生物力学中,刚度矩阵可以用来评估生物组织的刚度和弹性特性,以及预测生物组织在受力作用下的变形和应力分布情况。
