高考人教数学(理)大一轮复习检测:第七章 第二节 直线、平面的平行关系 Word版含解析
2023年新高考数学一轮复习8-4 直线、平面平行的判定及性质(知识点讲解)含详解

专题8.4 直线、平面平行的判定及性质(知识点讲解)【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理,运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题,凸显逻辑推理、直观想象、数学运算的核心素养.【知识点展示】(一)空间平行关系1.直线与平面平行的判定与性质a∥α,a⊂β,2.利用线面平行的定义,一般用反证法;利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β); 利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β). (二)平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a ⊥α,a ⊥β,则α∥β. (2)垂直于同一个平面的两条直线平行,即若a ⊥α,b ⊥α,则a ∥b. (3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.【常考题型剖析】题型一:与线、面平行相关命题的判定例1. (2023·全国·高三专题练习)已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列结论中正确的是( ) A .若m //α,m //n ,则n //α B .若m //α,n //α,则m //n C .若m //α,n ⊂α,则m //nD .若m //α,m ⊂β,αβ=n ,则m //n例2.(2022·上海静安·二模)在下列判断两个平面α与β平行的4个命题中,真命题的个数是( ). (1)α、β都垂直于平面r ,那么α∥β. (2)α、β都平行于平面r ,那么α∥β. (3)α、β都垂直于直线l ,那么α∥β.(4)如果l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β,那么α∥β A .0B .1C .2D .3例3.(四川·高考真题(文))下列命题正确的是( ) A .若两条直线和同一个平面所成的角相等,则这两条直线平行 B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行例4. (2022·云南师大附中模拟预测(理))若α,β是两个不同平面,m ,n 是两条不同直线,则下列4个推断中正确的是( )A .m α∥,m β∥,n ⊂α,n m n β⊂⇒∥B .m α⊂,n β⊂,m n αβ⇒∥∥C .m α∥,n α∥,m β⊂,n βαβ⊂⇒∥D .m α⊂,n β⊂,m n αβ⇒∥∥ 【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理,并注意定理中易忽视的条件. (2)结合题意构造或绘制图形,结合图形作出判断. (3)利用实物进行空间想象,比较判断.(4)熟记一些常见结论,如垂直于同一条直线的两个平面平行等. 题型二:直线与平面平行的判定例5.(2023·全国·高三专题练习)在直三棱柱111ABC A B C -中,D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点,给出下列四个判断:①//EF 平面1ADB ;②//EM 平面1ADB ; ③//EN 平面1ADB ; ④1//A M 平面1ADB , 错误的序号为___________.例6.【多选题】(2017·全国·高考真题(文))如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 平行的是( )A.B.C.D.例7.(2023·全国·高三专题练习)如图,AB是圆O的直径,点C是圆O上异于,A B的点,直线PC 平面ABC,,E F分别是PA,PC的中点.记平面BEF与平面ABC的交线为l,求证:直线l//平面PAC【总结提升】证明直线与平面平行的方法(1)线面平行的定义:一条直线与一个平面无公共点(不相交).(2)线面平行的判定定理:关键是找到平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线.注意内外平行三条件,缺一不可.题型三:线面平行性质定理的应用例8.(福建·高考真题(文))如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD 上.若EF∥平面AB1C,则线段EF的长度等于________.例9.(2019·全国卷Ⅰ改编)如图,直四棱柱ABCD A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.证明:MN ∥平面C 1DE .例10.如图,在直四棱柱ABCD A 1B 1C 1D 1中,E 为线段AD 上的任意一点(不包括A ,D 两点),平面CEC 1∩平面BB 1D =FG .证明:FG ∥平面AA 1B 1B .【总结提升】 1.思路方法:(1)通过线面平行可得到线线平行,其中一条线应是两平面的交线,要树立这种应用意识. (2)利用线面平行性质必须先找出交线. 2.易错提醒(1)在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.(2)线面平行关系证明的难点在于辅助面和辅助线的添加,在添加辅助线、辅助面时一定要以某一性质定理为依据,绝不能主观臆断.(3)解题中注意符号语言的规范应用. 题型四:平面与平面平行的判定与性质例11.(2023·全国·高三专题练习)已知长方体1111ABCD A B C D -中,4AB AD ==,12AA =,E ,F 分别为棱11A B 和11A D 的中点,M 为长方体表面上任意一点.若BM ∥平面AEF ,则BM 的最大值为( )A.B .C .D .6例12.(2020·全国·高三专题练习(文))如图,平面//α平面β,PAB △所在的平面与α,β分别交于CD 和AB ,若2PC =,3CA =,1CD =,则AB =______.例13.(2023·全国·高三专题练习)如图,在正方体1111ABCD A B C D -中,E ,F分别为棱11,DD CC 的中点.求证:平面1//AEC 平面BDF例14.(陕西·高考真题(文))如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 12AB AA ==.(1)证明: 平面A 1BD // 平面CD 1B 1;(2)求三棱柱ABD -A 1B 1D 1的体积.【规律方法】 1.证明面面平行的常用方法 (1)利用面面平行的定义.(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. (3)利用“垂直于同一条直线的两个平面平行”.(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”. (5)利用“线线平行”“线面平行”“面面平行”的相互转化.2.面面平行的应用(1)两平面平行,构造与之相交的第三个平面,可得交线平行.(2)两平面平行,其中一个平面内的任意一条直线与另一个平面平行,可用于证明线面平行.3.三种平行关系之间的转化其中线面平行是核心,线线平行是基础,要注意它们之间的灵活转化.专题8.4 直线、平面平行的判定及性质(知识点讲解)【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理,运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题,凸显逻辑推理、直观想象、数学运算的核心素养.【知识点展示】(一)空间平行关系1.直线与平面平行的判定与性质a∥α,a⊂β,2.利用线面平行的定义,一般用反证法;利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β); 利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β). (二)平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a ⊥α,a ⊥β,则α∥β. (2)垂直于同一个平面的两条直线平行,即若a ⊥α,b ⊥α,则a ∥b. (3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.【常考题型剖析】题型一:与线、面平行相关命题的判定例1. (2023·全国·高三专题练习)已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列结论中正确的是( ) A .若m //α,m //n ,则n //α B .若m //α,n //α,则m //n C .若m //α,n ⊂α,则m //n D .若m //α,m ⊂β,αβ=n ,则m //n【答案】D 【解析】 【分析】举例说明判断A ,B ,C ;利用线面平行的性质判断D 作答. 【详解】如图,长方体1111ABCD A B C D -中,平面1111D C B A 视为平面α,对于A ,直线AB 视为m ,直线11A B 视为n ,满足m //α,m //n ,而n ⊂α,A 不正确;对于B,直线AB视为m,直线BC视为n,满足m//α,n//α,而m与n相交,B不正确;A D视为n,满足m//α,n⊂α,显然m与n是异面直线,C不正确;对于C,直线AB视为m,直线11对于D,由直线与平面平行的性质定理知,D正确.故选:D例2.(2022·上海静安·二模)在下列判断两个平面α与β平行的4个命题中,真命题的个数是().(1)α、β都垂直于平面r,那么α∥β.(2)α、β都平行于平面r,那么α∥β.(3)α、β都垂直于直线l,那么α∥β.(4)如果l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,那么α∥βA.0B.1C.2D.3【答案】D【解析】【分析】由面面平行的判定定理及其相关结论分析可得结果.【详解】由面面平行的判定定理分析可知(1)错,(2),(3),(4)正确.故选:D例3.(四川·高考真题(文))下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行【答案】C【解析】【详解】若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D错;故选项C正确.例4. (2022·云南师大附中模拟预测(理))若α,β是两个不同平面,m ,n 是两条不同直线,则下列4个推断中正确的是( )A .m α∥,m β∥,n ⊂α,n m n β⊂⇒∥B .m α⊂,n β⊂,m n αβ⇒∥∥C .m α∥,n α∥,m β⊂,n βαβ⊂⇒∥D .m α⊂,n β⊂,m n αβ⇒∥∥【答案】A【解析】【分析】利用线面,面面位置关系逐项分析即得.【详解】对于A ,如图,n ⊂α,n n βαβ⊂⇒⋂=,结合m α,m β,可知m n ∥,故A 正确;对于B ,如图,m ,n 可能异面,故B 错误;对于C ,如图,α,β可能相交,故C 错误;对于D ,如图,αβ,可能相交,故D 错误.故选:A .【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理,并注意定理中易忽视的条件.(2)结合题意构造或绘制图形,结合图形作出判断.(3)利用实物进行空间想象,比较判断.(4)熟记一些常见结论,如垂直于同一条直线的两个平面平行等.题型二:直线与平面平行的判定例5.(2023·全国·高三专题练习)在直三棱柱111ABC A B C -中,D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点,给出下列四个判断:①//EF 平面1ADB ;②//EM 平面1ADB ;③//EN 平面1ADB ;④1//A M 平面1ADB ,错误的序号为___________.【答案】①②④【解析】【分析】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ,证明出平面1//A CE 平面1AD B ,利用面面平行的性质结合假设法可判断①②③④的正误.【详解】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ,在三棱柱111ABC A B C -中,因为11//BB CC 且11BB CC =,所以,四边形11BB C C 为平行四边形,则11//BC B C 且11BC B C =,D 、E 分别为BC 、11B C 的中点,则1//CD B E 且1CD B E =,故四边形1CDB E 为平行四边形,则1//CE B D ,CE ⊄平面1ADB ,1B D ⊂平面1ADB ,故//CE 平面1ADB ,同理可证四边形1BB ED 为平行四边形,则11////DE BB AA ,11DE BB AA ==,则四边形1AA ED 为平行四边形,所以,1//A E AD ,1A E ⊄平面1ADB ,AD ⊂平面1ADB ,则1//A E 平面1ADB ,1CE A E E =,故平面1//A CE 平面1AD B ,EN ⊂平面1A CE ,则//EN 平面1ADB ,③对;对于①,若//EF 平面1ADB ,EF EN E =,则平面//EFN 平面1ADB ,因为过点E 且与平面1ADB 平行的平面只有一个,矛盾,故①错,同理可知,②④均错.故答案为:①②④.例6.【多选题】(2017·全国·高考真题(文))如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 平行的是( )A .B .C .D .【答案】BCD【解析】【分析】利用线面平行判定定理逐项判断可得答案.【详解】对于选项A,OQ∥AB,OQ与平面MNQ是相交的位置关系,故AB和平面MNQ不平行,故A错误;对于选项B,由于AB∥CD∥MQ,结合线面平行判定定理可知AB∥平面MNQ,故B正确;对于选项C,由于AB∥CD∥MQ,结合线面平行判定定理可知AB∥平面MNQ:故C正确;对于选项D,由于AB∥CD∥NQ,结合线面平行判定定理可知AB∥平面MNQ:故D正确;故选:BCD例7.(2023·全国·高三专题练习)如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,,E F 分别是PA ,PC 的中点.记平面BEF 与平面ABC 的交线为l ,求证:直线l //平面PAC【答案】证明见解析【解析】【分析】先通过//EF AC 可得出//EF 平面ABC ,再利用线面平行的性质即可证明.【详解】因为,E F 分别是,PA PC 的中点,所以//EF AC ,又因为AC ⊂平面ABC ,EF ⊄平面ABC ,所以//EF 平面ABC ,又EF ⊂平面BEF ,平面BEF 与平面ABC 的交线为l ,所以//EF l ,而l ⊄平面PAC ,EF ⊂平面PAC ,所以//l 平面P AC .【总结提升】证明直线与平面平行的方法(1)线面平行的定义:一条直线与一个平面无公共点(不相交).(2)线面平行的判定定理:关键是找到平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线.注意内外平行三条件,缺一不可. 题型三:线面平行性质定理的应用例8.(福建·高考真题(文))如图,在正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.【解析】【分析】根据直线与平面平行的性质定理可得//EF AC ,再根据E 为AD 的中点可得F 为CD 的中点,从而根据三角形的中位线可得.【详解】如图:因为//EF 平面1AB C ,EF ⊂平面DABC ,且平面1A C B 平面ABCD AC =,所以//EF AC ,又因为E 为AD 的中点,所以F 为CD 的中点, 所以12EF AC =,因为正方体的棱长为2.所以AC =所以EF =故答案为.例9.(2019·全国卷Ⅰ改编)如图,直四棱柱ABCD A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M,N分别是BC,BB1,A1D的中点.证明:MN∥平面C1DE.【答案】见解析【解析】证明:连接B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=12B1C.又因为N为A1D的中点,所以ND=12A1D.由题设知A1B1//=DC,可得B1C//=A1D,故ME//=ND,因此四边形MNDE为平行四边形,所以MN∥ED.又MN⊄平面C1DE,ED⊂平面C1DE,所以MN∥平面C1DE.例10.如图,在直四棱柱ABCDA1B1C1D1中,E为线段AD上的任意一点(不包括A,D两点),平面CEC1∩平面BB1D=FG.证明:FG∥平面AA1B1B.【答案】见解析【解析】证明:在直四棱柱ABCDA1B1C1D1中,BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,所以CC1∥平面BB1D.又CC1⊂平面CEC1,平面CEC1∩平面BB1D=FG,所以CC1∥FG.因为BB1∥CC1,所以BB1∥FG.而BB1⊂平面AA1B1B,FG⊄平面AA1B1B,所以FG∥平面AA1B1B.【总结提升】1.思路方法:(1)通过线面平行可得到线线平行,其中一条线应是两平面的交线,要树立这种应用意识.(2)利用线面平行性质必须先找出交线.(1)在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.(2)线面平行关系证明的难点在于辅助面和辅助线的添加,在添加辅助线、辅助面时一定要以某一性质定理为依据,绝不能主观臆断.(3)解题中注意符号语言的规范应用.题型四:平面与平面平行的判定与性质例11.(2023·全国·高三专题练习)已知长方体1111ABCD A B C D -中,4AB AD ==,12AA =,E ,F 分别为棱11A B 和11A D 的中点,M 为长方体表面上任意一点.若BM ∥平面AEF ,则BM 的最大值为( )A.B .C .D .6【答案】C【解析】【分析】由面面平行的性质结合题意可确定点M 所在的平面,再由平面几何的性质即可确定BM 的值为最大值时的位置,即可求解【详解】如图所示,取G ,H 分别为棱11B C 和11D C 的中点,连接11,,,BG DH BD B D ,由题意易知1111,BF B D GH B D ∥∥,所以BF GH ∥;又易知AF BG ∥,故可以证明平面BGHD ∥平面AEF ;又BM ∥平面AEF ,由面面平行的性质可知M ∈平面BGHD ,所以由题意可知M 在等腰梯形BGHD 四条边上运动,过点H 作HQ BD ⊥,交BD 于点Q ,由题意可知BD GH DH BG DQ ====所以HQ BQ BD DQ =-=所以BH又BD BH ==,所以故当M 与D 点重合时,BM 的值为最大值,此时BM BD ==例12.(2020·全国·高三专题练习(文))如图,平面//α平面β,PAB △所在的平面与α,β分别交于CD 和AB ,若2PC =,3CA =,1CD =,则AB =______. 【答案】52【解析】【分析】根据面面平行的性质,证得//CD AB ,结合CD PC AB PA =,即可求解. 【详解】由题意,平面//α平面β,PAB △所在的平面与α,β分别交于CD 和AB , 根据面面平行的性质,可得//CD AB ,所以CD PC AB PA =, 因为2PC =,3CA =,1CD =,所以15522CD PA AB PC ⋅⨯===.故答案为:52. 例13.(2023·全国·高三专题练习)如图,在正方体1111ABCD A B C D -中,E ,F 分别为棱11,DD CC 的中点.求证:平面1//AEC 平面BDF【答案】证明见解析【解析】【分析】根据1//DF EC ,可证明1//EC 平面BDF ;又//BF AE ,可得//AE 平面BDF .进而根据线面平行证明面面平行.【详解】证明:在正方体1111ABCD A B C D -中,E ,F 分别为棱11,DD CC 的中点, 所以11111,22DE DD C F CC ==. 因为11CC DD =,且11//CC DD ,所以1DE C F =,且1//DE C F ,所以四边形1DEC F 是平行四边形,所以1//DF EC 又DF ⊂平面BDF ,1EC ⊄平面BDF ,所以1//EC 平面BDF .同理,//BF AE ,又BF ⊂平面BDF ,AE ⊄平面BDF , 所以//AE 平面BDF .又1AE EC E ⋂=,1,AE EC ⊂平面1AEC ,所以平面1//AEC 平面BDF 例14.(陕西·高考真题(文))如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 1AB AA =(1)证明: 平面A 1BD // 平面CD 1B 1;(2)求三棱柱ABD -A 1B 1D 1的体积.【答案】(1)证明见解析;(2)1.【解析】【详解】试题分析:(1)要证明1A C ⊥平面11BB D D ,只要证明1A C 垂直于平面11BB D D 内的两条相交直线即可,由已知可证出1A C ⊥BD ,取11B D 的中点为1E ,通过证明四边形11A OCE 为正方形可证1A C ⊥1E O .由线面垂直的判定定理问题得证;(2)由已知1A O 是三棱柱ABD ﹣A 1B 1D 1的高,由此能求出三棱柱ABD ﹣A 1B 1D 1的体积 试题解析:(Ⅰ)∵四棱柱ABCD ﹣A 1B 1C 1D 1的底面ABCD 是正方形,O 为底面中心,A 1O ⊥平面ABCD ,AB=AA 1=,由棱柱的性质可得BB 1和DD 1平行且相等,故四边形BB 1D 1D 为平行四边形,故有BD 和B 1D 1平行且相等.而BD 不在平面CB 1D 1内,而B 1D 1在平面CB 1D 1内,∴BD ∥平面CB 1D 1.同理可证,A 1BCD 1为平行四边形,A 1B ∥平面CB 1D 1.而BD 和A 1B 是平面A 1BD 内的两条相交直线,故有平面A 1BD ∥平面CD 1B 1 .(Ⅱ)由题意可得A 1O 为三棱柱ABD ﹣A 1B 1D 1的高.三角形A 1AO 中,由勾股定理可得A 1O===1,∴三棱柱ABD ﹣A 1B 1D 1的体积V=S △ABD •A 1O=•A 1O=×1=1.【规律方法】1.证明面面平行的常用方法 (1)利用面面平行的定义.(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3)利用“垂直于同一条直线的两个平面平行”.(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”.(5)利用“线线平行”“线面平行”“面面平行”的相互转化.2.面面平行的应用(1)两平面平行,构造与之相交的第三个平面,可得交线平行.(2)两平面平行,其中一个平面内的任意一条直线与另一个平面平行,可用于证明线面平行.3.三种平行关系之间的转化其中线面平行是核心,线线平行是基础,要注意它们之间的灵活转化.。
2024年高考数学一轮复习(新高考版) 第7章 空间直线、平面的垂直

§7.5空间直线、平面的垂直考试要求1.理解空间中直线与直线、直线与平面、平面与平面的垂直关系.2.掌握直线与平面、平面与平面垂直的判定与性质,并会简单应用.知识梳理1.直线与平面垂直(1)直线和平面垂直的定义一般地,如果直线l 与平面α内的任意一条直线都垂直,就说直线l 与平面α互相垂直.(2)判定定理与性质定理文字语言图形表示符号表示判定定理如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直m ⊂αn ⊂αm ∩n =P l ⊥m l ⊥n ⇒l ⊥α性质定理垂直于同一个平面的两条直线平行a ⊥αb ⊥α⇒a ∥b2.直线和平面所成的角(1)定义:平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.一条直线垂直于平面,我们说它们所成的角是90°;一条直线和平面平行,或在平面内,我们说它们所成的角是0°.(2)范围:0,π2.3.二面角(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角.(2)二面角的平面角:如图,在二面角α-l -β的棱l 上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱l 的射线OA 和OB ,则射线OA 和OB 构成的∠AOB 叫做二面角的平面角.(3)二面角的范围:[0,π].4.平面与平面垂直(1)平面与平面垂直的定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理与性质定理常用结论1.三垂线定理平面内的一条直线如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直.2.三垂线定理的逆定理平面内的一条直线如果和穿过该平面的一条斜线垂直,那么它也和这条斜线在该平面内的射影垂直.3.两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若直线l 与平面α内的两条直线都垂直,则l ⊥α.(×)(2)若直线a ⊥α,b ⊥α,则a ∥b .(√)(3)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.(×)(4)若α⊥β,a⊥β,则a∥α.(×)教材改编题1.(多选)下列命题中不正确的是()A.如果直线a不垂直于平面α,那么平面α内一定不存在直线垂直于直线aB.如果平面α垂直于平面β,那么平面α内一定不存在直线平行于平面βC.如果直线a垂直于平面α,那么平面α内一定不存在直线平行于直线aD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β答案ABD解析若直线a垂直于平面α,则直线a垂直于平面α内的所有直线,故C正确,其他选项均不正确.2.如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中必有()A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面答案A解析四面体S-EFG如图所示,由SG⊥GE,SG⊥GF,GE∩GF=G且GE,GF⊂平面EFG得SG⊥△EFG所在平面.3.已知PD垂直于正方形ABCD所在的平面,连接PB,PC,PA,AC,BD,则一定互相垂直的平面有________对.答案7解析如图,由于PD垂直于正方形ABCD,故平面PDA⊥平面ABCD,平面PDB⊥平面ABCD,平面PDC⊥平面ABCD,平面PDA⊥平面PDC,平面PAC⊥平面PDB,平面PAB⊥平面PAD,平面PBC⊥平面PDC,共7对.题型一直线与平面垂直的判定与性质例1(1)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题________.答案②③⇒①(或①③⇒②)解析已知l,m是平面α外的两条不同直线,由①l⊥m与②m∥α,不能推出③l⊥α,因为l 可以与α平行,也可以相交不垂直;由①l⊥m与③l⊥α能推出②m∥α;由②m∥α与③l⊥α可以推出①l⊥m.(2)(2023·娄底模拟)如图,在三棱柱ABC-A1B1C1中,点B1在底面ABC内的射影恰好是点C.①若点D是AC的中点,且DA=DB,证明:AB⊥CC1.②已知B1C1=2,B1C=23,求△BCC1的周长.①证明∵点B1在底面ABC内的射影是点C,∴B1C⊥平面ABC,∵AB⊂平面ABC,∴B1C⊥AB.在△ABC中,DA=DB=DC,∴BC⊥AB,∵BC∩B1C=C,BC,B1C⊂平面BCC1B1,∴AB⊥平面BCC1B1,∵CC1⊂平面BCC1B1,∴AB⊥CC1.②解如图,延长BC至点E,使BC=CE,连接C1E,则B1C1綉CE,四边形B1CEC1为平行四边形,则C1E綉B1C.由①知B1C⊥平面ABC,∴C1E⊥平面ABC,∵CE,BE⊂平面ABC,∴C1E⊥CE,C1E⊥BE,∵C1E=B1C=23,CE=BC=B1C1=2,BE=4,∴CC1=CE2+C1E2=4,BC1=BE2+C1E2=27,∴△BCC1的周长为2+4+27=6+27.思维升华证明线面垂直的常用方法及关键(1)证明直线和平面垂直的常用方法:①判定定理;②垂直于平面的传递性(a∥b,a⊥α⇒b⊥α);③面面平行的性质(a⊥α,α∥β⇒a⊥β);④面面垂直的性质.(2)证明线面垂直的关键是证线线垂直,而证明线线垂直则需借助线面垂直的性质.跟踪训练1如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱CD,A1D1的中点.(1)求证:AB1⊥BF;(2)求证:AE⊥BF;(3)棱CC1上是否存在点P,使BF⊥平面AEP?若存在,确定点P的位置,若不存在,说明理由.(1)证明如图,连接A1B,则AB1⊥A1B,因为A1F⊥平面ABB1A1,AB1⊂平面ABB1A1,所以A1F⊥AB1,又A1B∩A1F=A1,所以AB1⊥平面A1BF.又BF⊂平面A1BF,所以AB1⊥BF.(2)证明如图,取棱AD的中点G,连接FG,BG,则FG⊥AE,因为AB=DA,AG=DE,∠BAG=∠ADE,所以△BAG≌△ADE,所以∠ABG=∠DAE.所以AE ⊥BG .又因为BG ∩FG =G ,所以AE ⊥平面BFG .又BF ⊂平面BFG ,所以AE ⊥BF .(3)解存在.如图,取棱CC 1的中点P ,即为所求.连接EP ,AP ,C 1D ,因为EP ∥C 1D ,C 1D ∥AB 1,所以EP ∥AB 1.由(1)知AB 1⊥BF ,所以BF ⊥EP .又由(2)知AE ⊥BF ,且AE ∩EP =E ,所以BF ⊥平面AEP .题型二平面与平面垂直的判定与性质例2(2023·桂林模拟)如图所示,已知在四棱锥P -ABCD 中,底面ABCD 是矩形,平面PAD ⊥底面ABCD 且AB =1,PA =AD =PD =2,E 为PD 的中点.(1)求证:平面PCD ⊥平面ACE ;(2)求点B 到平面ACE 的距离.(1)证明由PA =AD =PD ,E 为PD 的中点,可得AE ⊥PD ,因为CD ⊥AD ,平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,CD ⊂平面ABCD ,所以CD ⊥平面PAD ,而AE ⊂平面PAD ,所以CD ⊥AE ,由CD ∩PD =D ,则AE ⊥平面PCD ,又AE ⊂平面ACE ,所以平面PCD ⊥平面ACE .(2)解如图,连接BD ,与AC 交于O ,则O 为BD 的中点,所以点D 到平面ACE 的距离即为点B 到平面ACE 的距离.由平面PCD ⊥平面ACE ,过D 作DM ⊥CE ,垂足为M ,则DM ⊥平面ACE ,则DM 为点D 到平面ACE 的距离.由CD ⊥平面PAD ,可得CD ⊥PD ,又CD =DE =1,所以DM =12CE =22,即点B到平面ACE的距离为2 2 .思维升华(1)判定面面垂直的方法①面面垂直的定义.②面面垂直的判定定理.(2)面面垂直性质的应用①面面垂直的性质定理是把面面垂直转化为线面垂直的依据,运用时要注意“平面内的直线”.②若两个相交平面同时垂直于第三个平面,则它们的交线也垂直于第三个平面.跟踪训练2(2022·邯郸模拟)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥平面ABCD,PA⊥AD,E和F分别是CD和PC的中点,求证:(1)PA⊥平面ABCD;(2)平面BEF∥平面PAD;(3)平面BEF⊥平面PCD.证明(1)∵平面PAD⊥平面ABCD,且PA垂直于这两个平面的交线AD,∴PA⊥平面ABCD.(2)∵AB∥CD,CD=2AB,E是CD的中点,∴AB∥DE,且AB=DE,∴四边形ABED是平行四边形,∴AD∥BE,∵BE⊄平面PAD,AD⊂平面PAD,∴BE∥平面PAD,∵E和F分别是CD和PC的中点,∴EF∥PD,∵EF⊄平面PAD,PD⊂平面PAD,∴EF∥平面PAD,∵BE∩EF=E,BE,EF⊂平面BEF,∴平面BEF∥平面PAD.(3)∵AB⊥AD,∴平行四边形ABED是矩形,∴BE⊥CD,AD⊥CD,由①知PA⊥平面ABCD,∴PA⊥CD,∵PA∩AD=A,∴CD⊥平面PAD,∴CD⊥PD,∵E和F分别是CD和PC的中点,∴PD∥EF,∴CD ⊥EF ,又∵BE ∩EF =E ,∴CD ⊥平面BEF ,∵CD ⊂平面PCD ,∴平面BEF ⊥平面PCD .题型三垂直关系的综合应用例3如图,已知ABCD -A 1B 1C 1D 1是底面为正方形的长方体,∠AD 1A 1=60°,AD 1=4,点P 是AD 1上的动点.(1)试判断不论点P 在AD 1上的任何位置,是否都有平面BPA ⊥平面AA 1D 1D ,并证明你的结论;(2)当P 为AD 1的中点时,求异面直线AA 1与B 1P 所成的角的余弦值;(3)求PB 1与平面AA 1D 1D 所成的角的正切值的最大值.解(1)是.∵BA ⊥平面AA 1D 1D ,BA ⊂平面BPA ,∴平面BPA ⊥平面AA 1D 1D ,∴无论点P 在AD 1上的任何位置,都有平面BPA ⊥平面AA 1D 1D .(2)过点P 作PE ⊥A 1D 1,垂足为E ,连接B 1E ,如图,则PE ∥AA 1,∴∠B 1PE (或其补角)是异面直线AA 1与B 1P 所成的角.在Rt △AA 1D 1中,∵∠AD 1A 1=60°,∴∠A 1AD 1=30°,∴A 1B 1=A 1D 1=12AD 1=2,∴A 1E =12A 1D 1=1,AA 1=3A 1D 1=23,∴PE =12AA 1=3,B 1E =A 1B 21+A 1E 2=5,∴在Rt △B 1PE 中,B 1P =B 1E 2+PE 2=22,cos ∠B 1PE =PE B 1P =322=64.∴异面直线AA 1与B 1P 所成的角的余弦值为64.(3)由(1)知,B 1A 1⊥平面AA 1D 1D ,∴∠B 1PA 1是PB 1与平面AA 1D 1D 所成的角,∴tan ∠B 1PA 1=A 1B 1A 1P =2A 1P ,∴当A 1P 最小时,tan ∠B 1PA 1最大,这时A 1P ⊥AD 1,A 1P =A 1D 1·AA 1AD 1=3,得tan ∠B 1PA 1=233,即PB 1与平面AA 1D 1D 所成的角的正切值的最大值为233.思维升华(1)三种垂直的综合问题,一般通过作辅助线进行线线、线面、面面垂直间的转化.(2)对于线面关系中的存在性问题,首先假设存在,然后在该假设条件下,利用线面关系的相关定理、性质进行推理论证.跟踪训练3(2023·柳州模拟)如图,在三棱锥P -ABC 中,AB =BC =2,PA =PB =PC =AC=22,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且PM 与平面ABC 所成角的正切值为6,求二面角M -PA -C 的平面角的余弦值.(1)证明方法一如图,连接OB .∵AB =BC =2,AC =22,∴AB2+BC2=AC2,即△ABC是直角三角形,又O为AC的中点,∴OA=OB=OC,又∵PA=PB=PC,∴△POA≌△POB≌△POC,∴∠POA=∠POB=∠POC=90°.∴PO⊥AC,PO⊥OB,∵OB∩AC=O,OB,AC⊂平面ABC,∴PO⊥平面ABC.方法二如图,连接OB,∵PA=PC,O为AC的中点,PA=PB=PC=AC=22,∴PO⊥AC,PO=6,又∵AB=BC=2,∴AB⊥BC,BO=2,∴PO2+OB2=PB2,∴PO⊥OB,∵OB∩AC=O,OB,AC⊂平面ABC,∴PO⊥平面ABC.(2)解由(1)知,PO⊥平面ABC,∴OM为PM在平面ABC上的射影,∴∠PMO为PM与平面ABC所成角,∵tan∠PMO=POOM=6OM=6,∴OM=1,在△ABC和△OMC中,由正弦定理可得MC=1,∴M为BC的中点.如图,作ME⊥AC交AC于E,则E为OC的中点,作EF⊥PA交PA于F,连接MF,∴MF ⊥PA ,∴∠MFE 即为所求二面角M -PA -C 的平面角,ME =22,EF =32AE =32×34×22=364,MF =ME 2+EF 2=624,∴cos ∠MFE =EF MF =39331,故二面角M -PA -C 的平面角的余弦值为39331.课时精练1.(多选)若平面α,β满足α⊥β,α∩β=l ,P ∈α,P ∉l ,则下列命题中是真命题的为()A .过点P 垂直于平面α的直线平行于平面βB .过点P 垂直于直线l 的直线在平面α内C .过点P 垂直于平面β的直线在平面α内D .过点P 且在平面α内垂直于l 的直线必垂直于平面β答案ACD 解析由于过点P 垂直于平面α的直线必平行于平面β内垂直于交线的直线,则直线平行于平面β,因此A 正确;过点P 垂直于直线l 的直线有可能垂直于平面α,不一定在平面α内,因此B 不正确;根据面面垂直的性质定理知,选项C ,D 正确.2.如图,在四棱锥P -ABCD 中,△PAB 与△PBC 是正三角形,平面PAB ⊥平面PBC ,AC ⊥BD ,则下列结论不一定成立的是()A .BP ⊥ACB .PD ⊥平面ABCDC .AC ⊥PDD .平面PBD ⊥平面ABCD 答案B 解析如图,取线段BP 的中点O ,连接OA ,OC ,易得BP ⊥OA ,BP ⊥OC ,又OA ∩OC =O ,所以BP ⊥平面OAC ,所以BP ⊥AC ,故选项A 正确;又AC ⊥BD ,BP ∩BD =B ,所以AC ⊥平面PBD ,所以AC ⊥PD ,故选项C 正确;又AC ⊂平面ABCD ,所以平面PBD ⊥平面ABCD,故选项D正确.3.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部答案A解析连接AC1(图略),由AC⊥AB,AC⊥BC1,AB∩BC1=B,得AC⊥平面ABC1.∵AC⊂平面ABC,∴平面ABC1⊥平面ABC.∴C1在平面ABC上的射影H必在平面ABC1与平面ABC 的交线AB上.4.(多选)如图,在以下四个正方体中,直线AB与平面CDE垂直的是()答案BD解析对于A,显然AB与CE不垂直,则直线AB与平面CDE不垂直;对于B,因为AB⊥CE,AB⊥ED,且CE∩ED=E,所以AB⊥平面CDE;对于C,显然AB与CE不垂直,所以直线AB与平面CDE不垂直;对于D,因为ED⊥平面ABC,则ED⊥AB,同理CE⊥AB,因为ED∩CE=E,所以AB⊥平面CDE.5.(多选)(2022·齐齐哈尔模拟)若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题错误的是()A.若m⊂β,α⊥β,则m⊥αB.若m∥α,n∥α,则m∥nC.若m⊥β,m∥α,则α⊥βD.若α⊥γ,α⊥β,则β⊥γ答案ABD解析由m ,n 是两条不同的直线,α,β,γ是三个不同的平面,在A 中,若m ⊂β,α⊥β,则m 与α相交、平行或m ⊂α,故A 错误;在B 中,若m ∥α,n ∥α,则m 与n 相交、平行或异面,故B 错误;在C 中,若m ⊥β,m ∥α,则由面面垂直的判定定理得α⊥β,故C 正确;在D 中,若α⊥γ,α⊥β,则β与γ相交或平行,故D 错误.6.(多选)在长方体ABCD -A 1B 1C 1D 1中,已知B 1D 与平面ABCD 和平面AA 1B 1B 所成的角均为30°,则下列说法正确的是()A .AB =2ADB .AB 与平面AB 1C 1D 所成的角为30°C .AC =CB 1D .B 1D 与平面BB 1C 1C 所成的角为45°答案AD 解析如图,连接BD ,易知∠BDB 1是直线B 1D 与平面ABCD 所成的角,所以在Rt △BDB 1中,∠BDB 1=30°,设BB 1=1,则B 1D =2BB 1=2,BD =B 1D 2-BB 21=3.易知∠AB 1D 是直线B 1D 与平面AA 1B 1B 所成的角,所以在Rt △ADB 1中,∠AB 1D =30°.因为B 1D =2,所以AD =12B 1D =1,AB 1=B 1D 2-AD 2=3,所以在Rt △ABB 1中,AB =AB 21-BB 21=2=2AD ,所以A 项正确;易知∠BAB 1是直线AB 与平面AB 1C 1D 所成的角,因为在Rt △ABB 1中,sin ∠BAB 1=BB 1AB 1=33≠12,所以∠BAB 1≠30°,所以B 项错误;在Rt △CBB 1中,CB 1=BC 2+BB 21=2,而AC =AB 2+BC 2=3,所以C 项错误;易知∠DB 1C 是直线B 1D 与平面BB 1C 1C 所成的角,因为在Rt △DB 1C 中,CB 1=CD =2,所以∠DB 1C =45°,所以D 项正确.7.如图所示,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,当点M 满足条件:①BM ⊥DM ,②DM ⊥PC ,③BM ⊥PC 中的________时,平面MBD ⊥平面PCD (只要填写一个你认为是正确的条件序号即可).答案②(或③)解析连接AC (图略)∵PA ⊥底面ABCD ,∴PA ⊥BD .∵底面各边都相等,∴AC ⊥BD .∵PA ∩AC =A ,∴BD ⊥平面PAC ,∴BD ⊥PC .当DM ⊥PC (或BM ⊥PC )时,即有PC ⊥平面MBD ,而PC ⊂平面PCD ,∴平面MBD ⊥平面PCD .8.在矩形ABCD 中,AB <BC ,现将△ABD 沿矩形的对角线BD 所在的直线进行翻折,在翻折的过程中,给出下列结论:①存在某个位置,使得直线AC 与直线BD 垂直;②存在某个位置,使得直线AB 与直线CD 垂直;③存在某个位置,使得直线AD 与直线BC 垂直.其中正确结论的序号是________.答案②解析①假设AC 与BD 垂直,过点A 作AE ⊥BD 于点E ,连接CE ,如图所示.则AE ⊥BD ⊥⇒BD ⊥平面AEC ,则BD ⊥CE ,而在平面BCD 中,CE 与BD 不垂直,故假设不成立,①不正确;②假设AB ⊥CD ,∵AB ⊥AD ,CD ∩AD =D ,∴AB ⊥平面ACD ,∴AB ⊥AC ,由AB <BC 可知,存在这样的直角三角形,使AB ⊥AC ,故假设成立,②正确;③假设AD ⊥BC ,∵CD ⊥BC ,AD ∩CD =D ,∴BC ⊥平面ACD ,∴BC ⊥AC ,即△ABC 为直角三角形,且AB 为斜边,而AB <BC ,故矛盾,假设不成立,③不正确.9.如图所示,在四棱锥P -ABCD 中,底面ABCD 是∠DAB =60°且边长为a 的菱形,侧面PAD 为正三角形,其所在平面垂直于底面ABCD ,若G 为AD 的中点.(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB;(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD?并证明你的结论.(1)证明在菱形ABCD中,∠DAB=60°,G为AD的中点,所以BG⊥AD.又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BG⊂平面ABCD,所以BG⊥平面PAD.(2)证明如图,连接PG,因为△PAD为正三角形,G为线段AD的中点,所以PG⊥AD.由(1)知BG⊥AD,又PG∩BG=G,所以AD⊥平面PGB.因为PB⊂平面PGB,所以AD⊥PB.(3)解能,当F为线段PC的中点时,平面DEF⊥平面ABCD.证明如下:如图,取线段PC的中点F,连接DE,EF,DF.在△PBC中,FE∥PB,在菱形ABCD中,GB∥DE.而FE⊂平面DEF,DE⊂平面DEF,EF∩DE=E,PB⊂平面PGB,GB⊂平面PGB,PB∩GB =B,所以平面DEF∥平面PGB.因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PG⊂平面PAD,PG⊥AD,所以PG⊥平面ABCD.又PG⊂平面PGB,所以平面PGB⊥平面ABCD,所以平面DEF⊥平面ABCD.10.(2023·广州模拟)如图,在三棱锥P-ABC中,平面PAC⊥平面PBC,PA⊥平面ABC.(1)求证:BC ⊥平面PAC ;(2)若AC =BC =PA ,求二面角A -PB -C 的平面角的大小.(1)证明如图,作AD ⊥PC 交PC 于点D ,因为平面PAC ⊥平面PBC ,平面PAC ∩平面PBC =PC ,AD ⊂平面PAC ,所以AD ⊥平面PBC ,又BC ⊂平面PBC ,所以AD ⊥BC ,又因为PA ⊥平面ABC ,BC ⊂平面ABC ,所以PA ⊥BC ,又PA ,AD ⊂平面PAC ,PA ∩AD =A ,所以BC ⊥平面PAC .(2)解如图,作AD ⊥PC 交PC 于点D ,DE ⊥PB 交PB 于点E ,连接AE ,由(1)知AD ⊥平面PBC ,因为PB ⊂平面PBC ,则AD ⊥PB ,又AD ,DE ⊂平面ADE ,AD ∩DE =D ,所以PB ⊥平面ADE ,因为AE ⊂平面ADE ,所以PB ⊥AE ,则∠AED 即为二面角A -PB -C 的平面角.又DE ⊂平面PBC ,则AD ⊥DE ,不妨设AC =BC =PA =1,则PC =2,AD =1×12=22,又由(1)知BC ⊥平面PAC ,因为AC ⊂平面PAC ,所以BC ⊥AC ,所以AB =2,PA ⊥平面ABC ,又AB ⊂平面ABC ,则PA ⊥AB ,则PB =3,AE =1×23=63,则sin ∠AED =AD AE =2263=32,由图知二面角A -PB -C 的平面角为锐角,所以∠AED =π3,即二面角A -PB -C 的平面角的大小为π3.11.如图,正三角形PAD 所在平面与正方形ABCD 所在平面互相垂直,O 为正方形ABCD的中心,M 为正方形ABCD 内一点,且满足MP =MC ,则点M 的轨迹为()答案A 解析如图,取AD 的中点E ,连接PE ,PC ,CE .因为△PAD 为正三角形,所以PE ⊥AD ,又平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,所以PE ⊥平面ABCD ,从而平面PEC ⊥平面ABCD ,分别取PC ,AB 的中点F ,G ,连接DF ,DG ,FG ,由PD =DC 知DF ⊥PC ,易得DG ⊥EC ,则DG ⊥平面PEC ,又PC ⊂平面PEC ,所以DG ⊥PC ,又DF ∩DG =D ,所以PC ⊥平面DFG ,又点F 是PC 的中点,因此,线段DG 上的点满足MP =MC .12.(多选)如图所示,一张A4纸的长、宽分别为22a ,2a ,A ,B ,C ,D 分别是其四条边的中点.现将其沿图中虚线折起,使得P 1,P 2,P 3,P 4四点重合为一点P ,从而得到一个多面体.下列关于该多面体的命题正确的是()A .该多面体是四棱锥B .平面BAD ⊥平面BCDC .平面BAC ⊥平面ACDD .该多面体外接球的表面积为54πa 2答案BC 解析由题意得该多面体是一个三棱锥,故A 错误;∵AP ⊥BP ,AP ⊥CP ,BP ∩CP =P ,∴AP ⊥平面BCD .又∵AP ⊂平面BAD ,∴平面BAD ⊥平面BCD ,故B 正确;同理可证平面BAC ⊥平面ACD ,故C 正确;通过构造长方体可得该多面体的外接球半径R =52a ,所以该多面体外接球的表面积为5πa 2,故D 错误.13.(多选)如图,在正方体ABCD -A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则下列说法正确的是()A .直线BD 1⊥平面A 1C 1DB .三棱锥P -A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范围是π4,π2D .直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为63答案ABD 解析A 项,如图,连接B 1D 1,由正方体可得A 1C 1⊥B 1D 1,且BB 1⊥平面A 1B 1C 1D 1,又A 1C 1⊂平面A 1B 1C 1D 1,则BB 1⊥A 1C 1,因为B 1D 1∩BB 1=B 1,所以A 1C 1⊥平面BD 1B 1,又BD 1⊂平面BD 1B 1,所以A 1C 1⊥BD 1.同理,连接AD 1,易证得A 1D ⊥BD 1,因为A 1D ∩A 1C 1=A 1,A 1D ,A 1C 1⊂平面A 1C 1D ,所以BD 1⊥平面A 1C 1D ,故A 正确;B 项,1111P A C D C A PD V V -=-三棱锥三棱锥,因为点P 在线段B 1C 上运动,所以1A DP S △=12A 1D ·AB ,为定值,且C 1到平面A 1PD 的距离即为C 1到平面A 1B 1CD 的距离,也为定值,故三棱锥P -A 1C 1D 的体积为定值,故B 正确;C 项,当点P 与线段B 1C 的端点重合时,AP 与A 1D 所成角取得最小值,最小值为π3,故C 错误;D 项,因为直线BD 1⊥平面A 1C 1D ,所以若直线C 1P 与平面A 1C 1D 所成角的正弦值最大,则直线C 1P 与直线BD 1所成角的余弦值最大,即点P 运动到B 1C 中点处,直线C 1P 与直线BD 1所成角为∠C 1BD 1,设正方体棱长为1,在Rt △D 1C 1B 中,cos ∠C 1BD 1=C 1B BD 1=23=63,故D 正确.14.如图,在矩形ABCD 中,点E ,F 分别在线段AB ,AD 上,AE =EB =AF =23FD =4,沿直线EF 将△AEF 翻折成△A ′EF ,使平面A ′EF ⊥平面BEF ,则二面角A ′-FD -C 的平面角的余弦值为________.答案33解析如图,取线段EF 的中点H ,AF 的中点G ,连接A ′G ,A ′H ,GH .由题意,知A ′E =A ′F 及H 是EF 的中点,所以A ′H ⊥EF .又因为平面A ′EF ⊥平面BEF ,平面A ′EF ∩平面BEF =EF ,A ′H ⊂平面A ′EF ,所以A ′H ⊥平面BEF .又AF ⊂平面BEF ,故A ′H ⊥AF .又因为G ,H 分别是AF ,EF 的中点,所以GH ∥AB ,所以GH ⊥AF ,又A ′H ∩GH =H ,于是AF ⊥平面A ′GH ,所以AF⊥A′G.所以∠A′GH为二面角A′-FD-C的平面角.在Rt△A′GH中,A′H=22,GH=2,A′G=23,所以cos∠A′GH=GHA′G=3 3,故二面角A′-FD-C的平面角的余弦值为3 3 .15.刘徽注《九章算术·商功》“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”如图1解释了由一个长方体得到“堑堵”“阳马”“鳖臑”的过程.堑堵是底面为直角三角形的直棱柱;阳马是一条侧棱垂直于底面且底面为矩形的四棱锥;鳖臑是四个面都为直角三角形的四面体.在如图2所示由正方体ABCD-A1B1C1D1得到的堑堵ABC-A1B1C1中,当点P在下列三个位置:A1A中点,A1B中点,A1C中点时,分别形成的四面体P-ABC中,鳖臑的个数为() A.0B.1C.2D.3答案C解析设正方体的棱长为a,则由题意知,A1C1=AC=2a,A1B=2a,A1C=3a,当点P 为A1A的中点时,因为PA⊥平面ABC,则∠PAC=∠PAB=90°,∠ABC=90°.由BC⊥平面PAB,得BC⊥PB,即∠PBC=90°,则△PAB,△PAC,△ABC,△PBC是直角三角形,即此时四面体P-ABC是鳖臑;当点P为A1B的中点时,因为BC⊥平面ABB1A1,所以BC⊥PB,BC⊥AB,所以△PBC,△ABC为直角三角形.因为ABB1A1是正方形,所以AP⊥BP,则△PAB是直角三角形,又AP⊥BC,BP∩BC=B,所以AP⊥平面PBC,所以AP⊥PC,所以△PAC是直角三角形,则此时四面体P-ABC是鳖臑;当点P 为A 1C 的中点时,此时PA =PC =12A 1C =3a 2,又AC =2a ,由勾股定理可知,△PAC 不是直角三角形,则此时四面体P -ABC 不是鳖臑.16.在长方体ABCD -A 1B 1C 1D 1中,已知AB =2,BC =t ,若在线段AB 上存在点E ,使得EC 1⊥ED ,则实数t 的取值范围是________.答案(0,1]解析因为C 1C ⊥平面ABCD ,ED ⊂平面ABCD ,可得C 1C ⊥ED ,由EC 1⊥ED ,EC 1∩C 1C =C 1,EC 1,C 1C ⊂平面ECC 1,可得ED ⊥平面ECC 1,所以ED ⊥EC ,在矩形ABCD 中,设AE =a ,0≤a ≤2,则BE =2-a ,由∠DEA +∠CEB =90°,可得tan ∠DEA ·tan ∠CEB =AD AE ·CB BE =t 2a (2-a )=1,即t 2=a (2-a )=-(a -1)2+1,当a =1时,t 2取得最大值1,即t 的最大值为1;当a =0或2时,t 2取得最小值0,但由于t >0,所以t 的取值范围是(0,1].。
【新教材】高三人教A版数学一轮复习课件:第7章 7.3 空间直线、平面的平行

(1)在AC上求作点P,使 PE∥平面ABF,请写出作法并说明理由;
(2)求三棱锥A-CDE的高.
解 (1)取BC的中点G,连接DG,交AC于点P,连接PE,此时P为所求作的点,如
图所示.
理由如下:∵BC=2AD,∴BG=AD.
又BC∥AD,∴四边形BGDA为平行四边形,
∴DG∥AB,即DP∥AB.
9.如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交
直线,那么这两个平面平行.
10.垂直于同一条直线的两个平面平行.
【知识巩固】
1.下列说法正确的画“√”,错误的画“×”.
(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.
( × )
(2)若一条直线平行于一个平面,则这条直线平行于这个平面内的任一条直
面内.
3.过两条异面直线中的一条可以作唯一一个平面与另一条直线平行.
4.两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.
5.夹在两个平行平面间的与两个平面都相交的平行线段相等.
6.经过平面外一点,有且只有一个平面和已知平面平行.
7.两条直线被三个平行平面所截,截得的对应线段成比例.
8.如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
同理连接B1Q,并延长,与CD也相交于点M.
1
由重心的性质可得 = 3 ,
1
1
所以 = ,所以 PQ∥A1B1.
1
1
=
又因为AB∥A1B1,所以PQ∥AB.
因为PQ⊄平面ABC,AB⊂平面ABC,
所以PQ∥平面ABC.
1
.
3
解题心得1.证明直线与平面平行的关键是设法在平面内找到一条与已知
新高考一轮复习人教版 直线、平面平行的判定和性质 作业

8.3直线、平面平行的判定和性质基础篇固本夯基考点一直线与平面平行的判定和性质1.(2021江苏扬州大学附中2月检测,5)已知直三棱柱ABC-A1B1C1中,M,N分别是A1B1,AB的中点,P点在线段B1C上,则NP与平面AMC1的位置关系是()A.垂直B.平行C.相交但不垂直D.要依P点的位置而定答案B2.(2021济南二模,7)已知正四面体ABCD的棱长为2,平面α与棱AB、CD均平行,则α截此正四面体所得截面面积的最大值为()A.1B.√2C.√3D.2答案A3.(多选)(2021山东青岛胶州调研,10)在三棱柱ABC-A1B1C1中,E,F,G分别为线段AB,A1B1,AA1的中点,下列说法正确的是()A.平面AC1F∥平面B1CEB.直线FG∥平面B1CEC.直线CG与BF异面D.直线C1F与平面CGE相交答案AC4.(2020福建漳州适应性测试,16)已知正方体ABCD-A1B1C1D1的棱长为3,点N是棱A1B1的中点,点T是棱CC1上靠近点C的三等分点,动点Q在正方形D1DAA1(包含边界)内运动,且QB∥平面D1NT,则动点Q的轨迹的长为.答案√105.(2022届山东潍坊10月过程性测试,18)如图,平面ABCD⊥平面AEBF,四边形ABCD为矩形,△ABE和△ABF 均为等腰直角三角形,且∠BAF=∠AEB=90°.(1)求证:平面BCE⊥平面ADE;(2)若点G为线段FC上任意一点,求证:BG∥平面ADE.证明(1)因为四边形ABCD为矩形,所以BC⊥AB,又因为平面ABCD⊥平面AEBF,BC⊂平面ABCD,平面ABCD∩平面AEBF=AB,所以BC⊥平面AEBF,又因为AE⊂平面AEBF,所以BC⊥AE.因为∠AEB=90°,即AE⊥BE,且BC、BE⊂平面BCE,BC∩BE=B,所以AE⊥平面BCE,又因为AE⊂平面ADE,所以平面ADE⊥平面BCE.(2)因为BC∥AD,AD⊂平面ADE,BC⊄平面ADE,所以BC∥平面ADE.因为△ABF和△ABE均为等腰直角三角形,且∠BAF=∠AEB=90°,所以∠EAB=∠ABF=45°,所以AE∥BF,又AE⊂平面ADE,BF⊄平面ADE,所以BF∥平面ADE,又BC∩BF=B,所以平面BCF∥平面ADE.又BG⊂平面FBC,所以BG∥平面ADE.6.(2022届广东佛山一中10月月考,20)如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=√2,四边形ABCD为等腰梯形,BC∥AD,BC=CD=1AD=1,E为PA的中点.2(1)证明:EB∥平面PCD;(2)求平面PAD与平面PCD所成的二面角θ的正弦值.解析(1)证明:取AD的中点O,连接EO,OB,∵E为PA的中点,O为AD的中点,∴OE∥PD,又OE⊄平面PCD,PD⊂平面PCD,∴OE∥平面PCD,又∵BC ∥AD,BC=12AD,∴四边形BCDO 为平行四边形,∴BO ∥CD, 又OB ⊄平面PCD,CD ⊂平面PCD,∴BO ∥平面PCD,又OE ∩BO=O,∴平面EBO ∥平面PCD, 又∵BE ⊂平面EBO,∴BE ∥平面PCD.(2)连接PO,∵PA=PD,O 为AD 的中点,∴PO ⊥AD, 又平面PAD ⊥平面ABCD,平面PAD ∩平面ABCD=AD, 所以PO ⊥平面ABCD,取BC 的中点M,连接OM, ∵四边形ABCD 是等腰梯形,∴OM ⊥AD, 建立如图所示的空间直角坐标系,则P(0,0,1),A(0,-1,0),D(0,1,0),C (√32,12,0),∴PD⃗⃗⃗⃗ =(0,1,-1),CD ⃗⃗⃗⃗ =(−√32,12,0),设平面PCD 的法向量为n=(x,y,z),则{n ·PD ⃗⃗⃗⃗ =y −z =0,n ·CD⃗⃗⃗⃗ =−√32x +12y =0,令x=1,则y=z=√3,则n=(1,√3,√3), 易知平面PAD 的一个法向量为m=(1,0,0), ∴|cos θ|=|cos<m,n>|=|m·n||m||n|=√7,则sin θ=√427. 7.(2019江苏,16,14分)如图,在直三棱柱ABC-A 1B 1C 1中,D,E 分别为BC,AC 的中点,AB=BC.求证: (1)A 1B 1∥平面DEC 1; (2)BE ⊥C 1E.证明(1)因为D,E分别为BC,AC的中点,所以ED∥AB.在直三棱柱ABC-A1B1C1中,AB∥A1B1,所以A1B1∥ED.又因为ED⊂平面DEC1,A1B1⊄平面DEC1,所以A1B1∥平面DEC1.(2)因为AB=BC,E为AC的中点,所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱,所以C1C⊥平面ABC.又因为BE ⊂平面ABC,所以C1C⊥BE.因为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C,所以BE⊥平面A1ACC1.因为C1E ⊂平面A1ACC1,所以BE⊥C1E.8.(2020江苏,15,14分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.证明(1)因为E,F分别是AC,B1C的中点,所以EF∥AB1,又EF⊄平面AB1C1,AB1⊂平面AB1C1,所以EF∥平面AB1C1.(2)因为B1C⊥平面ABC,AB⊂平面ABC,所以B1C⊥AB.又AB⊥AC,B1C⊂平面AB1C,AC⊂平面AB1C,B1C∩AC=C,所以AB⊥平面AB1C,又因为AB⊂平面ABB1,所以平面AB1C⊥平面ABB1.9.(2020北京,16,13分)如图,在正方体ABCD-A1B1C1D1中,E为BB1的中点.(1)求证:BC1∥平面AD1E;(2)求直线AA1与平面AD1E所成角的正弦值.解析 (1)证明:∵ABCD-A 1B 1C 1D 1为正方体,∴D 1C 1∥A 1B 1,D 1C 1=A 1B 1.又AB ∥A 1B 1,AB=A 1B 1,∴D 1C 1∥AB,D 1C 1=AB,∴四边形ABC 1D 1为平行四边形,∴AD 1∥BC 1,又AD 1⊂平面AD 1E,BC 1⊄平面AD 1E,∴BC 1∥平面AD 1E.(2)不妨设正方体的棱长为2,如图,以{AD ⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗ ,AA 1⃗⃗⃗⃗⃗⃗ }为正交基底建立空间直角坐标系A-xyz,则A(0,0,0),A 1(0,0,2),D 1(2,0,2),E(0,2,1),∴AA 1⃗⃗⃗⃗⃗⃗ =(0,0,2),AD 1⃗⃗⃗⃗⃗⃗ =(2,0,2),AE ⃗⃗⃗⃗ =(0,2,1),设平面AD 1E 的法向量为n=(x,y,z),直线AA 1与平面AD 1E 所成的角为θ, 则{n ·AD 1⃗⃗⃗⃗⃗⃗ =0,n ·AE ⃗⃗⃗⃗ =0,即{2x +2z =0,2y +z =0,令z=-2,则{x =2,y =1,此时n=(2,1,-2),∴sin θ=|cos<n,AA 1⃗⃗⃗⃗⃗⃗ >|=|n·AA 1⃗⃗⃗⃗⃗⃗⃗⃗ ||n||AA 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√4+1+4×2=23, ∴直线AA 1与平面AD 1E 所成角的正弦值为23.考点二 平面与平面平行的判定和性质1.(2022届重庆巴蜀中学11月月考,8)在棱长为2的正方体ABCD-A 1B 1C 1D 1中,点E,F,G,H 分别为棱AB,BC,C 1D 1,A 1D 1的中点,若平面α∥平面EFGH,且平面α与棱A 1B 1,B 1C 1,B 1B 分别交于点P,Q,S,其中点Q 是棱B 1C 1的中点,则三棱锥B 1-PQS 的体积为( ) A.1 B.12C.13D.16答案 D2.(2019课标Ⅱ文,7,5分)设α,β为两个平面,则α∥β的充要条件是( ) A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行 C.α,β平行于同一条直线D.α,β垂直于同一平面 答案 B3.(2021河北邢台月考,19)在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为正方形,AA 1=2AB=4,M,N,P 分别是AD,DD 1,CC 1的中点.(1)证明:平面MNC ∥平面AD 1P;(2)求直线DP 与平面MNC 所成角的正弦值.解析 (1)证明:因为M,N,P 分别是AD,DD 1,CC 1的中点,所以MN ∥AD 1,CN ∥PD 1.又AD 1⊄平面MNC,MN ⊂平面MNC,所以AD 1∥平面MNC,同理PD 1∥平面MNC, 又AD 1∩PD 1=D 1,所以平面MNC ∥平面AD 1P.(2)以D 为坐标原点,建立如图所示的空间直角坐标系D-xyz,则D(0,0,0),P(0,2,2),M(1,0,0),N(0,0,2),C(0,2,0),则DP ⃗⃗⃗⃗ =(0,2,2),MN ⃗⃗⃗⃗⃗ =(-1,0,2),MC⃗⃗⃗⃗⃗ =(-1,2,0). 设平面MNC 的法向量为n=(x,y,z),则{MN⃗⃗⃗⃗⃗ ·n =−x +2z =0,MC ⃗⃗⃗⃗ ·n =−x +2y =0,令z=1,得n=(2,1,1). 设直线DP 与平面MNC 所成角为θ,则sin θ=|cos<DP⃗⃗⃗⃗ ,n>|=|DP⃗⃗⃗⃗⃗ ·n||DP ⃗⃗⃗⃗⃗ ||n|=√33, 所以直线DP 与平面MNC 所成角的正弦值为√33.综合篇 知能转换A 组考法一 判断或证明线面平行的方法1.(2022届T8联考,7)如图,已知四棱柱ABCD-A 1B 1C 1D 1的底面为平行四边形,E,F,G 分别为棱AA 1,CC 1,C 1D 1的中点,则( )A.直线BC 1与平面EFG 平行,直线BD 1与平面EFG 相交B.直线BC 1与平面EFG 相交,直线BD 1与平面EFG 平行C.直线BC 1、BD 1都与平面EFG 平行D.直线BC 1、BD 1都与平面EFG 相交 答案 A2.(2022届湖南岳阳一中入学考试,18)如图,在三棱柱ABC-A 1B 1C 1中,侧面ABB 1A 1是菱形,∠BAA 1=60°,E 是棱BB 1的中点,CA=CB,F 在线段AC 上,且AF=2FC. (1)证明:CB 1∥平面A 1EF;(2)若CA ⊥CB,平面CAB ⊥平面ABB 1A 1,求二面角F-A 1E-A 的余弦值.解析 (1)证明:连接AB 1交A 1E 于点G,连接FG, 易得△AGA 1∽△B 1GE,所以AG GB 1=AA 1EB 1=2,又因为AF FC =2,所以AF FC =AGGB 1,所以FG ∥CB 1,又CB 1⊄平面A 1EF,FG ⊂平面A 1EF,所以CB 1∥平面A 1EF.(2)过C 作CO ⊥AB 于点O,因为CA=CB,所以O 是线段AB 的中点.因为平面CAB ⊥平面ABB 1A 1,平面CAB ∩平面ABB 1A 1=AB,所以CO ⊥平面ABB 1A 1.连接A 1B,OA 1,由题意易知△ABA 1是等边三角形,又O 是线段AB 的中点,所以OA 1⊥AB.以O 为坐标原点,OA ⃗⃗⃗⃗ ,OA 1⃗⃗⃗⃗⃗⃗ ,OC⃗⃗⃗⃗ 的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,不妨设AB=2,则A(1,0,0),A 1(0,√3,0),C(0,0,1),B(-1,0,0),F (13,0,23),B 1(-2,√3,0),E (−32,√32,0),则A 1E ⃗⃗⃗⃗⃗⃗ =(−32,−√32,0),A 1F ⃗⃗⃗⃗⃗ =13,-√3,23.设平面A 1FE 的法向量为n 1=(x 1,y 1,z 1), 则{A 1F ⃗⃗⃗⃗⃗ ·n 1=0,A 1E ⃗⃗⃗⃗⃗⃗ ·n 1=0,即{x 13−√3y 1+23z 1=0,−32x 1−√32y 1=0,令x 1=1,则n 1=(1,-√3,-5).易知平面ABB 1A 1的一个法向量为n 2=(0,0,1), 则cos<n 1,n 2>=n 1·n 2|n 1||n 2|=-5√2929,由题图可知,二面角F-A 1E-A 的平面角为锐角,所以二面角F-A 1E-A 的余弦值为5√2929. 3.(2022届南京二十九中10月月考,20)如图,在四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AD ∥BC,AB ⊥AD,AB=2BC=4,E 是棱PD 上的动点(除端点外),F,M 分别为AB,CE 的中点. (1)证明:FM ∥平面PAD;(2)若直线EF 与平面PAD 所成的最大角为30°,求平面CEF 与平面PAD 所成锐二面角的余弦值.解析 (1)证明:取CD 的中点N,连接FN,MN,因为F,N 分别为AB,CD 的中点,所以FN ∥AD,又FN ⊄平面PAD,AD ⊂平面PAD,所以FN ∥平面PAD,因为M,N 分别是CE,CD 的中点,所以MN ∥PD,又MN ⊄平面PAD,PD ⊂平面PAD,所以MN ∥平面PAD,又FN ∩MN=N,所以平面MFN ∥平面PAD,又因为FM ⊂平面MFN,所以FM ∥平面PAD.(2)连接AE,因为平面PAD ⊥平面ABCD,且平面PAD ∩平面ABCD=AD,AB ⊥AD,AB ⊂平面ABCD,所以AB ⊥平面PAD,所以∠AEF 即为直线EF 与平面PAD 所成的角,且tan ∠AEF=AF AE =2AE, 当AE 最小,即AE ⊥PD,亦即E 为PD 中点时,∠AEF 最大,为30°,又因为AF=2,所以AE=2√3,所以AD=4. 取AD 的中点O,连接PO,OC,易知PO ⊥平面ABCD,因为AO ∥BC 且AO=12AD=BC,所以四边形ABCO 为平行四边形,所以AB ∥CO,又AB ⊥AD,所以AO ⊥OC,以O 为坐标原点,建立如图所示的空间直角坐标系O-xyz.则O(0,0,0),C(4,0,0),D(0,2,0),P(0,0,2√3),E(0,1,√3),F(2,-2,0),则CE ⃗⃗⃗⃗ =(-4,1,√3),FC ⃗⃗⃗⃗ =(2,2,0),设平面CEF 的法向量为n 1=(x,y,z),则{n 1·FC⃗⃗⃗ =0,n 1·CE ⃗⃗⃗ =0,即{2x +2y =0,−4x +y +√3z =0,可取n 1=(√3,-√3,5).易知平面PAD 的一个法向量为n 2=(1,0,0), 所以cos<n 1,n 2>=n 1·n 2|n 1|·|n 2|=√3√31=√9331,所以平面CEF 与平面PAD 所成锐二面角的余弦值为√9331.4.(2019课标Ⅰ理,18,12分)如图,直四棱柱ABCD-A 1B 1C 1D 1的底面是菱形,AA 1=4,AB=2,∠BAD=60°,E,M,N 分别是BC,BB 1,A 1D 的中点. (1)证明:MN ∥平面C 1DE; (2)求二面角A-MA 1-N 的正弦值.解析 (1)证明:连接B 1C,ME.因为M,E 分别为BB 1,BC 的中点,所以ME ∥B 1C,且ME=12B 1C.又因为N 为A 1D 的中点,所以ND=12A 1D.由题设知A 1B 1 DC,可得B 1C A 1D,故ME ND,因此四边形MNDE 为平行四边形,则MN ∥ED.又MN ⊄平面EDC 1,所以MN ∥平面C 1DE.(2)由已知可得DE ⊥DA.以D 为坐标原点,DA⃗⃗⃗⃗ 的方向为x 轴正方向,建立如图所示的空间直角坐标系D-xyz, A(2,0,0),A 1(2,0,4),M(1,√3,2),N(1,0,2),A 1A ⃗⃗⃗⃗⃗⃗ =(0,0,-4),A 1M ⃗⃗⃗⃗⃗⃗⃗ =(-1,√3,-2),A 1N ⃗⃗⃗⃗⃗⃗ =(-1,0,-2),MN ⃗⃗⃗⃗⃗ =(0,-√3,0).设m=(x,y,z)为平面A 1MA 的法向量,则{m ·A 1M ⃗⃗⃗⃗⃗⃗⃗ =0,m ·A 1A ⃗⃗⃗⃗⃗⃗ =0.所以{−x +√3y −2z =0,−4z =0.可取m=(√3,1,0).设n=(p,q,r)为平面A 1MN 的法向量,则{n ·MN⃗⃗⃗⃗⃗ =0,n ·A 1N ⃗⃗⃗⃗⃗⃗ =0.所以{−√3q =0,−p −2r =0.可取n=(2,0,-1).于是cos<m,n>=m·n |m||n|=√32×√5=√155, 所以二面角A-MA 1-N 的正弦值为√105.5.(2021广东珠海一模,19)如图,三棱锥P-ABC 中,PA ⊥AB,AB ⊥AC,AB=AC=√2,PB=PC=√6,点M 是PA 的中点,点D 是AC 的中点,点N 在PB 上,且PN=2NB. (1)证明:BD ∥平面CMN;(2)求直线CN 与平面ABC 所成角的正切值.解析 (1)证明:如图,连接PD 交CM 于O,则O 为△PAC 的重心,PO=2OD,连接ON,因为PN=2NB,所以ON ∥BD,因为ON ⊂平面CMN,BD ⊄平面CMN,所以BD ∥平面CMN.(2)因为PB=PC,AB=AC,PA=PA,所以△PAB ≌△PAC,所以∠PAC=∠PAB=90°,所以PA=√PC 2−AC 2=√6−2=2,又因为PA ⊥AB,AB ∩AC=A,所以PA ⊥平面ABC,过N 作NH ⊥AB 于H,连接HC,因为NH ∥PA,所以NH ⊥平面ABC,所以NH ⊥HC,且AH=23AB,直线CN 与平面ABC 所成角为∠NCH,所以直线CN 与平面ABC 所成角的正切值tan ∠NCH=NH HC=13PA √AC 2+(23AB )2=13×2√(√2)2+(23×√2)2=√2613.6.(2017课标Ⅱ理,19,12分)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC=12AD,∠BAD=∠ABC=90°,E 是PD 的中点. (1)证明:直线CE ∥平面PAB;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为45°,求二面角M-AB-D 的余弦值.解析 (1)证明:取PA 的中点F,连接EF,BF.因为E 是PD 的中点,所以EF ∥AD,EF=12AD.由∠BAD=∠ABC=90°得BC ∥AD,又BC=12AD,所以EF BC,所以四边形BCEF 是平行四边形,所以CE ∥BF,又BF ⊂平面PAB,CE ⊄平面PAB,故CE ∥平面PAB.(2)由已知得BA ⊥AD,以A 为坐标原点,AB ⃗⃗⃗⃗ 的方向为x 轴正方向,|AB ⃗⃗⃗⃗ |为单位长,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,√3),则PC⃗⃗⃗⃗ =(1,0,-√3),AB ⃗⃗⃗⃗ =(1,0,0). 设M(x,y,z)(0<x<1),则BM ⃗⃗⃗⃗⃗ =(x-1,y,z),PM⃗⃗⃗⃗⃗ =(x,y-1,z-√3).因为BM 与底面ABCD 所成的角为45°,而n=(0,0,1)是底面ABCD 的一个法向量,所以|cos<BM⃗⃗⃗⃗⃗ ,n>|=sin45°,即√(x−1)+y 2+z 2=√22,即(x-1)2+y 2-z 2=0.①又M 在棱PC 上,设PM⃗⃗⃗⃗⃗ =λPC ⃗⃗⃗⃗ ,则 x=λ,y=1,z=√3-√3λ.②由①,②解得{ x =1+√22,y =1,z =−√62(舍去),或{ x =1−√22,y =1,z =√62,所以M (1−√22,1,√62),从而AM⃗⃗⃗⃗⃗ =(1−√22,1,√62).设m=(x 0,y 0,z 0)是平面ABM 的法向量,则{m ·AM⃗⃗⃗⃗⃗ =0,m ·AB⃗⃗⃗⃗ =0,即{(2−√2)x 0+2y 0+√6z 0=0,x 0=0,所以可取m=(0,-√6,2). 于是cos<m,n>=m·n |m||n|=√105. 易知所求二面角为锐二面角. 因此二面角M-AB-D 的余弦值为√105.考法二 判断或证明面面平行的方法(2021太原一模,19)如图,在三棱锥P-ABC 中,△PAB 是正三角形,G 是△PAB 的重心,D,E,H 分别是PA,BC,PC 的中点,点F 在BC 上,且BF=3FC. (1)求证:平面DFH ∥平面PGE;(2)若PB ⊥AC,AB=AC=2,BC=2√2,求二面角A-PC-B 的余弦值.解析 (1)证明:连接BG,GD,由题意得BG 与GD 共线,且BG=2GD, ∵E 是BC 的中点,BF=3FC,∴F 是CE 的中点, ∴BGGD =BEEF=2,∴GE ∥DF,∵GE ⊂平面PGE,DF ⊄平面PGE,∴DF ∥平面PGE, ∵H 是PC 的中点,∴FH ∥PE,∵HF ⊄平面PGE,PE ⊂平面PGE,∴FH ∥平面PGE, ∵DF ∩FH=F,∴平面DFH ∥平面PGE.(2)∵AB=AC=2,BC=2√2,∴AB 2+AC 2=8=BC 2,∴AB ⊥AC,又∵PB ⊥AC,AB ∩PB=B,∴AC ⊥平面PAB,以A 为坐标原点,向量AB ⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗ 的方向为x 轴,y 轴的正方向建立如图所示的空间直角坐标系A-xyz,由题意得A(0,0,0),B(2,0,0),C(0,2,0),P(1,0,√3),则AC⃗⃗⃗⃗ =(0,2,0),AP ⃗⃗⃗⃗ =(1,0,√3),PC ⃗⃗⃗⃗ =(-1,2,-√3),BC ⃗⃗⃗⃗ =(-2,2,0),设平面PAC 的法向量是m=(x 1,y 1,z 1),则{m ·AC⃗⃗⃗⃗ =0,m ·AP⃗⃗⃗⃗ =0,∴{2y 1=0,x 1+√3z 1=0,则y 1=0,令z 1=-1,则x 1=√3,∴m=(√3,0,-1), 设平面PBC 的法向量是n=(x 2,y 2,z 2),则{n ·PC⃗⃗⃗ =0,n ·BC⃗⃗⃗⃗ =0,∴{−x 2+2y 2−√3z 2=0,−2x 2+2y 2=0,令z 2=1,则{x 2=√3,y 2=√3,∴n=(√3,√3,1), ∴cos<m,n>=m·n |m||n|=√77,又知二面角A-PC-B 是锐二面角,∴二面角A-PC-B 的余弦值为√77. B 组1.(多选)(2021南京航空航天大学附中期中,10)已知棱长为1的正方体ABCD-A 1B 1C 1D 1,过对角线BD 1作平面α交棱AA 1于点E,交棱CC 1于点F,以下结论正确的是( ) A.四边形BFD 1E 不一定是平行四边形 B.平面α分正方体所得两部分的体积相等 C.平面α与平面DBB 1不可能垂直 D.四边形BFD 1E 面积的最大值为√2答案 BD2.(多选)(2021广东肇庆二模,12)在长方体ABCD-A 1B 1C 1D 1中,AB=AD=1,AA 1=2,P 是线段BC 1上的一动点,则下列说法中正确的是( ) A.A 1P ∥平面AD 1CB.A 1P 与平面BCC 1B 1所成角的正切值的最大值是2√55C.A 1P+PC 的最小值为√1705D.以A 为球心,√2为半径的球面与侧面DCC 1D 1的交线长是π2答案 ACD。
高三数学人教版A版数学(理)高考一轮复习试题:7.4直线、平面平行的判定及其性质Word版含答案
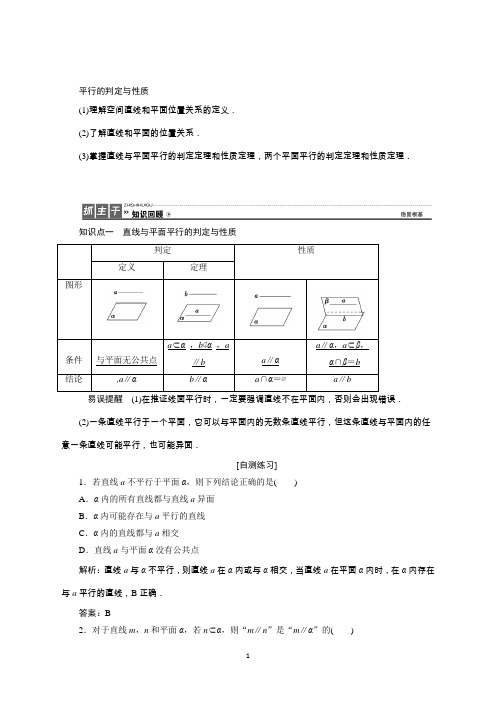
平行的判定与性质(1)理解空间直线和平面位置关系的定义.(2)了解直线和平面的位置关系.(3)掌握直线与平面平行的判定定理和性质定理,两个平面平行的判定定理和性质定理.知识点一直线与平面平行的判定与性质a∥α,a⊂β,_α∩β=b易误提醒(1)在推证线面平行时,一定要强调直线不在平面内,否则会出现错误.(2)一条直线平行于一个平面,它可以与平面内的无数条直线平行,但这条直线与平面内的任意一条直线可能平行,也可能异面.[自测练习]1.若直线a不平行于平面α,则下列结论正确的是()A.α内的所有直线都与直线a异面B.α内可能存在与a平行的直线C.α内的直线都与a相交D.直线a与平面α没有公共点解析:直线a与α不平行,则直线a在α内或与α相交,当直线a在平面α内时,在α内存在与a平行的直线,B正确.答案:B2.对于直线m,n和平面α,若n⊂α,则“m∥n”是“m∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:当m∥n时,m⊂α或m∥α,当m∥α时,m与n可能平行也可能为异面直线.答案:D知识点二平面与平面平行的判定与性质易误提醒(1)如果一个平面内的两条平行直线与另一个平面平行,则这两个平面相交或平行.(2)要证面面平行需证线面平行,要证线面平行需证线线平行,因此“面面平行”问题最终可转化为“线线平行”问题.必记结论平面与平面平行的几个有用性质(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两个平行平面之间的平行线段长度相等.(3)经过平面外一点有且只有一个平面与已知平面平行.(4)两条直线被三个平行平面所截,截得的对应线段成比例.(5)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.(6)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.[自测练习]3.已知m,n是两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是() A.若m∥n,m⊂α,则n∥αB.若m∥n,m⊂α,n⊂β,则α∥βC.若α⊥γ,α⊥β,则β∥γD.若m∥n,m⊥α,n⊥β,则α∥β解析:直线n可能在平面α内,A错误;两平面可相交,此时直线m,n均与交线平行即可,B错误;两平面可相交,C错误;因为m∥n,m⊥α,所以n⊥α,又n⊥β,所以α∥β,D正确.故选D.答案:D4.如图,L,M,N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是()A.垂直B.相交不垂直C.平行D.重合解析:如图,分别取另三条棱的中点A,B,C将平面LMN延展为平面正六边形AMBNCL,因为PQ∥AL,PR∥AM,且PQ与PR相交,AL与AM相交,所以平面PQR∥平面AMBNCL,即平面LMN∥平面PQR.答案:C考点一直线与平面平行的判定与性质|1.(2016·阜阳一中模拟)过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有()A.4条B.6条C.8条D.12条解析:如图所示,在平行六面体ABCD-A1B1C1D1中,E,F,G,H,M,N,P,Q分别为相应棱的中点,容易证明平面EFGH,平面MNPQ均与平面BDD1B1平行.平面EFGH和平面MNPQ 中分别有6条直线(相应四边形的四条边和两条对角线)满足要求,故共有12条直线符合要求.答案:D2.如图,正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱C1C,C1D1,D1D,DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件________时,就有MN∥平面B1BDD1(填上正确的一个条件即可,不必考虑全部可能情况).解析:当点M在线段FH上时,MN∥平面B1BDD1.答案:点M与点H重合(或点M在线段FH上)3.(2015·高考北京卷)如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=2,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB;(3)求三棱锥V-ABC的体积.解:(1)证明:因为O,M分别为AB,VA的中点,所以OM∥VB.又因为VB⊄平面MOC,所以VB∥平面MOC.(2)证明:因为AC=BC,O为AB的中点,所以OC⊥AB.又因为平面VAB⊥平面ABC,且OC⊂平面ABC,所以OC⊥平面VAB.所以平面MOC⊥平面VAB.(3)在等腰直角三角形ACB中,AC=BC=2,所以AB=2,OC=1,所以S△VAB=3,又因为OC⊥平面VAB,所以V C-VAB=13OC·S△VAB=33.又因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,所以三棱锥V-ABC的体积为3 3.判断或证明线面平行的常用三种方法(1)利用线面平行的定义(常用反证法).(2)利用线面平行的判定定理:关键是找平面内与已知直线平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面与已知平面相交找它们的交线.(3)利用面面平行的性质定理:当两平面平行时,其中一个平面内的任一直线平行于另一个平面.考点二面面平行的判定与性质|如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE 和CF的中点.(1)求证:平面BDGH∥平面AEF;(2)求多面体ABCDEF的体积.[解](1)证明:在△CEF中,因为G,H分别是CE,CF的中点,所以GH∥EF,又因为GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面AEF.设AC与BD的交点为O,连接OH,如图,在△ACF中,因为O,H分别是AC,CF的中点,所以OH∥AF,又因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF.又因为OH∩GH=H,OH,GH⊂平面BDGH,所以平面BDGH∥平面AEF.(2)因为AC ⊥平面BDEF ,又易知AO =2,S 矩形BDEF =3×22=62, 所以四棱锥A -BDEF 的体积V 1=13·AO ·S 矩形BDEF =4.同理可得四棱锥C -BDEF 的体积V 2=4. 所以多面体ABCDEF 的体积V =V 1+V 2=8.证明面面平行的五种常用方法(1)利用面面平行的定义.(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3)利用垂直于同一条直线的两个平面平行.(4)两个平面同时平行于第三个平面,那么这两个平面平行. (5)利用“线线平行”“线面平行”“面面平行”的相互转化.1.如图,在三棱锥S -ABC 中,平面SAB ⊥平面SBC ,AB ⊥BC ,AS =AB .过A 作AF ⊥SB ,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.求证:(1)平面EFG ∥平面ABC ; (2)BC ⊥SA .证明:(1)因为AS =AB ,AF ⊥SB ,垂足为F ,所以F 是SB 的中点.又因为E 是SA 的中点,所以EF ∥AB .因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC . 同理EG ∥平面ABC .又EF ∩EG =E , 所以平面EFG ∥平面ABC .(2)因为平面SAB ⊥平面SBC ,且交线为SB ,又AF ⊂平面SAB ,AF ⊥SB ,所以AF ⊥平面SBC ,因为BC ⊂平面SBC ,所以AF ⊥BC .又因为AB ⊥BC ,AF ∩AB =A ,AF ,AB ⊂平面SAB ,所以BC ⊥平面SAB . 因为SA ⊂平面SAB ,所以BC ⊥SA .考点三线面平行中的探索性问题|(2015·枣庄模拟)如图所示,在三棱柱ABC-A1B1C1中,D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,请确定点E的位置;若不存在,请说明理由.[解]法一:存在点E,且E为AB的中点时,DE∥平面AB1C1,下面给出证明:如图,取BB1的中点F,连接DF,则DF∥B1C1,∵AB的中点为E,连接EF,则EF∥AB1,B1C1∩AB1=B1,∴平面DEF∥平面AB1C1.而DE⊂平面DEF,∴DE∥平面AB1C1.法二:假设在棱AB上存在点E,使得DE∥平面AB1C1如图,取BB1的中点F,连接DF、EF,则DF∥B1C1,又DF⊄平面AB1C1,∴DF∥平面AB1C1,又DE∥平面AB1C1,DE∩DF=D,∴平面DEF∥平面AB1C1,∵EF⊂平面DEF,∴EF∥平面AB1C1,又∵EF⊂平面ABB1,平面ABB1∩平面AB1C1=AB1,∴EF∥AB1,∵点F是BB1的中点,∴点E是AB的中点.即当点E是AB的中点时,DE∥平面AB1C1.线面平行的探索性问题(1)对命题条件的探索常采用以下三种方法: ①先猜后证,即先观察与尝试给出条件再证明;②先通过命题成立的必要条件探索出命题成立的条件,再证明其充分性; ③把几何问题转化为代数问题,探索命题成立的条件. (2)对命题结论的探索常采用以下方法:首先假设结论存在,然后在这个假设下进行推理论证,如果通过推理得到了合乎情理的结论,就肯定假设,如果得到了矛盾的结论,就否定假设.2.四棱锥P -ABCD 的底面是边长为a 的正方形,侧棱P A ⊥底面ABCD ,在侧面PBC 内,有BE ⊥PC 于E ,且BE =63a ,试在AB 上找一点F ,使EF ∥平面P AD .解:在平面PCD 内,过E 作EG ∥CD 交PD 于G ,连接AG ,在AB 上取点F ,使AF =EG , ∵EG ∥CD ∥AF ,EG =AF ,∴四边形FEGA 为平行四边形,∴FE ∥AG . 又AG ⊂平面P AD ,FE ⊄平面P AD ,∴EF ∥平面P AD . ∴F 即为所求的点. 又P A ⊥面ABCD ,∴P A ⊥BC , 又BC ⊥AB ,∴BC ⊥面P AB .∴PB ⊥BC . ∴PC 2=BC 2+PB 2=BC 2+AB 2+P A 2. 设P A =x 则PC =2a 2+x 2,由PB ·BC =BE ·PC 得:a 2+x 2·a =2a 2+x 2·63a ,∴x =a ,即P A =a ,∴PC =3a ,PB =2a . ∴PE 2=PB 2-BE 2=2a 2-23a 2∴PE =233a ,∴PE PC =233a 3a =23, 即EG =23a ,∴AF =23a ,故在AB 上取AF =23AB ,连接EF 即可使EF ∥平面P AD .23.转化思想在平行关系判断与证明中的应用【典例】 如图,ABCD 与ADEF 均为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.(1)求证:BE ∥平面DMF ; (2)求证:平面BDE ∥平面MNG .[思维点拨] (1)利用判定定理及中位线性质证明.(2)抓住线线、线面、面面平行的转化关系证明.[证明] (1)连接AE ,则AE 必过DF 与GN 的交点O , 连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO , 又BE ⊄平面DMF ,MO ⊂平面DMF , 所以BE ∥平面DMF .(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点,所以DE ∥GN , 又DE ⊄平面MNG ,GN ⊂平面MNG , 所以DE ∥平面MNG . 又M 为AB 的中点,所以MN 为△ABD 的中位线,所以BD ∥MN ,又MN ⊂平面MNG ,BD ⊄平面MNG , 所以BD ∥平面MNG ,又DE ,BD ⊂平面BDE ,DE ∩BD =D , 所以平面BDE ∥平面MNG .[方法点评] (1)三种平行间的转化关系(2)对较复杂的综合问题往往需要反复运用线面平行的判定定理和性质定理来进行证明,有如下方法:线线平行→找过直线的平面→线面平行→找出或作出经过直线且与平面相交的平面,从而找出交线→线线平行[跟踪练习] (2016·咸阳模拟)如图所示,在四棱锥O -ABCD 中,底面ABCD 是边长为1的菱形,∠ABC =π4,OA ⊥底面ABCD ,OA =2,M 为OA 的中点,N 为BC 的中点.(1)求四棱锥O -ABCD 的体积; (2)证明:直线MN ∥平面OCD .解:(1)∵OA ⊥底面ABCD ,∴OA 是四棱锥O -ABCD 的高.∵四棱锥O -ABCD 的底面是边长为1的菱形,∠ABC =π4,∴底面面积S 菱形ABCD =22.∵OA =2,∴体积V O -ABCD =23. (2)证明:取OB 的中点E ,连接ME ,NE . ∵ME ∥AB ,AB ∥CD ,∴ME ∥CD .又∵NE ∥OC ,∵ME ∩EN =E ,CD ∩OC =C , ∴平面MNE ∥平面OCD .∵MN ⊂平面MNE ,∴MN ∥平面OCD .A 组 考点能力演练1.(2016·台州模拟)设m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是()A.若α⊥γ,β⊥γ,则α∥βB.若m⊥n,m⊥α,n∥β,则α∥βC.若m⊥α,m⊥β,则α∥βD.若m∥n,m∥α,n∥β,则α∥β解析:垂直于同一直线的两平面平行,故选C.答案:C2.若a,b,c为三条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的为() A.若a∥α,b∥α,则a∥bB.若α∥a,β∥a,则α∥βC.若a⊥α,b⊥α,则a∥bD.若α⊥β,α⊥γ,则β∥γ解析:对于A,空间中平行于同一个平面的两直线可能异面、相交或平行,故A错误;对于B,空间中平行于同一条直线的两平面平行或相交,故B错误;对于C,空间中垂直于同一个平面的两条直线平行,故C正确;对于D,空间中垂直于同一个平面的两平面相交或平行,故D错误.答案:C3.已知l,m,n是三条不重合的直线,α,β,γ是三个不重合的平面,给出下列四个命题:①若m∥n,n⊂α,则m∥α;②若直线m,n与平面α所成的角相等,则m∥n;③存在异面直线m,n,使得m∥α,m∥β,n∥α,则α∥β;④若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中真命题的个数为()A.1B.2C.3 D.4解析:对于①,m也可能在α内,①错误;对于②,直线m,n也可能相交或异面,②错误;对于③,命题成立;对于④,∵l∥γ,l⊂α,α∩γ=n,∴l∥n,同理l∥m,∴m∥n,④正确.综上可知③④正确,故选B.答案:B4.设a,b是两条直线,α,β是两个不同的平面,则α∥β的一个充分条件是()A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a、b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a、b,a⊂α,b⊂β,a∥β,b∥α解析:对于A,两个平面还可以相交,若α∥β,则存在一条直线a,a∥α,a∥β,所以A是α∥β的一个必要条件;同理,B也是α∥β的一个必要条件;易知C是一个必要条件;对于D,可以通过平移把两条异面直线平移到一个平面中,成为相交直线,则有α∥β,所以D是α∥β的一个充分条件.答案:D5.如图,正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与EF平行的直线()平面DA.不存在B.有1条C.有2条D.有无数条解析:由题设知平面ADD1A1与平面D1EF有公共点D1,由平面的基本性质中的公理知必有过该点的公共直线l,在平面ADD1A1内与l平行的线有无数条,且它们都不在平面D1EF内,由线面平行的判定定理知它们都与平面D1EF平行.答案:D6.已知正方体ABCD-A1B1C1D1,下列结论中正确的是________(只填序号).①AD1∥BC1;②平面AB1D1∥平面BDC1;③AD1∥DC1;④AD1∥平面BDC1.解析:由四边形ABC1D1是平行四边形可知AD1∥BC1,故①正确;根据线面平行与面面平行的判定定理可知,②④正确;AD1与DC1是异面直线,故③错.答案:①②④7.在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于D,E,F,H.D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为________.解析:取AC的中点G,连接SG,BG.易知SG⊥AC,BG⊥AC,故AC⊥平面SGB,所以AC⊥SB.因为SB∥平面DEFH,SB⊂平面SAB,平面SAB∩平面DEFH=HD,则SB∥HD.同理SB∥FE.又D,E分别为AB,BC的中点,则H ,F 也为AS ,SC 的中点,从而得HF 綊12AC 綊DE ,所以四边形DEFH 为平行四边形.又AC ⊥SB ,SB ∥HD ,DE ∥AC ,所以DE ⊥HD ,所以四边形DEFH 为矩形,其面积S =HF ·HD =⎝⎛⎭⎫12AC ·⎝⎛⎭⎫12SB =452.答案:4528.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是棱BC ,CC 1的中点,P 是侧面BCC 1B 1内一点,若A 1P ∥平面AEF ,则线段A 1P 长度的取值范围是________.解析:取B 1C 1中点M ,则A 1M ∥AE ;取BB 1中点N ,则MN ∥EF ,∴平面A 1MN ∥平面AEF .若A 1P ∥平面AEF ,只需P ∈MN ,则P 位于MN 中点时,A 1P 最短;当P 位于M 或N 时,A 1P 最长.不难求得A 1P 的取值范围为⎣⎡⎦⎤324,52. 答案:⎣⎡⎦⎤324,529.在如图所示的多面体中,四边形ABB 1A 1和ACC 1A 1都为矩形. 设D ,E 分别是线段BC ,CC 1的中点,在线段AB 上是否存在一点M ,使直线DE ∥平面A 1MC ?请证明你的结论.解:取线段AB 的中点M ,连接A 1M ,MC ,A 1C ,AC 1,设O 为A 1C ,AC 1的交点.由已知可知O 为AC 1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC 1的中位线, 所以MD 綊12AC ,OE 綊12AC ,因此MD 綊OE .连接OM ,从而四边形MDEO 为平行四边形, 则DE ∥MO .因为直线DE ⊄平面A 1MC ,MO ⊂平面A 1MC . 所以直线DE ∥平面A 1MC ,即线段AB 上存在一点M (线段AB 的中点), 使直线DE ∥平面A 1MC .10.(2016·成都模拟)如图所示,在三棱柱ABC -A1B 1C 1中,侧棱AA 1⊥底面ABC ,AB ⊥BC ,D 为AC 的中点,AA 1=AB =2.(1)求证:AB 1∥平面BC 1D ;(2)设BC =3,求四棱锥B -DAA 1C 1的体积.解:(1)证明:连接B 1C ,设B 1C 与BC 1相交于点O ,连接OD ,如图所示.∵四边形BCC 1B 1是平行四边形,∴点O 为B 1C 的中点. ∵D 为AC 的中点,∴OD 为△AB 1C 的中位线, ∴OD ∥AB 1.∵OD ⊂平面BC 1D ,AB 1⊄平面BC 1D , ∴AB 1∥平面BC 1D .(2)∵AA 1⊥平面ABC ,AA 1⊂平面AA 1C 1C , ∴平面ABC ⊥平面AA 1C 1C . ∵平面ABC ∩平面AA 1C 1C =AC ,作BE ⊥AC ,垂足为E ,则BE ⊥平面AA 1C 1C . ∵AB =AA 1=2,BC =3,AB ⊥BC , ∴在Rt △ABC 中,AC =AB 2+BC 2=4+9=13,∴BE =AB ·BC AC =613,∴四棱锥B -AA 1C 1D 的体积V =13×12(A 1C 1+AD )·AA 1·BE =16×3213×2×613=3.B 组 高考题型专练1.(2014·高考安徽卷)如图,四棱锥P -ABCD 的底面是边长为8的正方形,四条侧棱长均为217.点G ,E ,F ,H 分别是棱PB ,AB ,CD ,PC 上共面的四点,平面GEFH ⊥平面ABCD ,BC ∥平面GEFH .(1)证明:GH ∥EF ;(2)若EB =2,求四边形GEFH 的面积.解:(1)证明:因为BC ∥平面GEFH ,BC ⊂平面PBC ,且平面PBC ∩平面GEFH =GH ,所以GH ∥BC .同理可证EF ∥BC ,因此GH ∥EF .(2)如图,连接AC ,BD 交于点O ,BD 交EF 于点K ,连接OP ,GK . 因为P A =PC ,O 是AC 的中点,所以PO ⊥AC , 同理可得PO ⊥BD .又BD ∩AC =O ,且AC ,BD 都在底面ABCD 内, 所以PO ⊥底面ABCD .又因为平面GEFH ⊥平面ABCD , 且PO ⊄平面GEFH , 所以PO ∥平面GEFH .因为平面PBD ∩平面GEFH =GK , 所以PO ∥GK ,且GK ⊥底面ABCD , 从而GK ⊥EF .所以GK 是梯形GEFH 的高. 由AB =8,EB =2得EB ∶AB =KB ∶DB =1∶4, 从而KB =14DB =12OB ,即K 为OB 的中点.再由PO ∥GK 得GK =12PO ,即G 是PB 的中点,且GH =12BC =4.由已知可得OB =42, PO =PB 2-OB 2=68-32=6,所以GK =3.故四边形GEFH 的面积S =GH +EF2·GK =4+82×3=18.2.(2015·高考江苏卷)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E .求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.证明:(1)由题意知,E 为B 1C 的中点, 又D 为AB 1的中点,因此DE ∥AC . 又因为DE ⊄平面AA 1C 1C , AC ⊂平面AA 1C 1C , 所以DE ∥平面AA 1C 1C .(2)因为棱柱ABC -A 1B 1C 1是直三棱柱, 所以CC 1⊥平面ABC .因为AC ⊂平面ABC ,所以AC ⊥CC 1. 又因为AC ⊥BC ,CC 1⊂平面BCC 1B 1, BC ⊂平面BCC 1B 1, BC ∩CC 1=C , 所以AC ⊥平面BCC 1B 1.又因为BC 1⊂平面BCC 1B 1,所以BC 1⊥AC .因为BC =CC 1,所以矩形BCC 1B 1是正方形,因此BC 1⊥B 1C . 因为AC ,B 1C ⊂平面B 1AC , AC ∩B 1C =C ,所以BC 1⊥平面B 1AC .又因为AB1⊂平面B1AC,所以BC1⊥AB1.。
高考第一轮复习数学直线与平面平行

9.2直线与平面平行●知识梳理1.直线与平面的地点关系有且只有三种,即直线与平面平行、直线与平面订交、直线在平面内 .2.直线与平面平行的判断:假如平面外的一条直线与平面内的一条直线平行,那么这条直线与这个平面平行.3.直线与平面平行的性质:假如一条直线与一个平面平行,经过这条直线的平面与已知.平面订交,那么这条直线与交线平行●点击双基1.设有平面α、β和直线 m、 n,则 m∥α的一个充足条件是A. α⊥β且 m⊥βB.α∩β=n 且 m∥ nC.m∥ n 且 n∥αD. α∥β且mβ答案: D.给出2.( 2004 年北京,3)设m、n 是两条不一样的直线,α、β 、γ是三个不一样的平面以下四个命题,此中正确命题的序号是①若m⊥α,n∥α,则m⊥ n②若α∥β,β∥γ,m⊥α,则m⊥γ③若m∥α,n∥α,则m∥ n④若α⊥γ,β ⊥γ,则α∥βA. ①②B.②③C.③④D.①④分析:①②明显正确 .③中 m 与 n 可能订交或异面 .④考虑长方体的极点,α与β能够订交.答案: A3.一条直线若同时平行于两个订交平面,那么这条直线与这两个平面的交线的地点关系是A. 异面B.订交C.平行D.不可以确立分析:设α∩β=l,a∥α ,a∥β ,过直线 a 作与α、β都订交的平面γ,记α∩γ=b,β∩γ=c,则a∥b 且 a∥ c,∴ b∥ c.又 bα,α∩β=l,∴b∥l.∴a∥l.cal b答案: C4.(文)设平面α∥平面β,A、C∈α,B、D∈β,直线 AB 与 CD 交于点 S,且 AS=8,BS=9,CD =34,①当 S 在α、β之间时, SC=_____________ ,②当 S 不在α、β之间时,SC=_____________.分析:∵ AC∥ BD,∴△ SAC∽△ SBD,① SC=16,② SC=272.答案:① 16②272(理)设 D 是线段 BC 上的点, BC∥平面α,从平面α外必定点A(A 与 BC 分居平面双侧)作 AB 、 AD 、 AC 分别交平面 α 于 E 、 F 、 G 三点, BC=a , AD =b , DF=c ,则EG=_____________.分析:解法类同于上题.答案:ab acb5.在四周体 ABCD 中, M 、N 分别是面△ ACD 、△ BCD 的重心,则四周体的四个面中与MN 平行的是 ________.A.MB.N DC分析:连接 AM 并延伸, 交 CD 于 E ,连接 BN 并延伸交 CD 于 F ,由重心性质可知, E 、F 重合为一点,且该点为CD 的中点 E ,由EM =EN=1得 MN ∥AB ,MANB2所以, MN ∥平面 ABC 且 MN ∥平面 ABD .答案:平面 ABC 、平面 ABD●典例分析【例 1】 以以下图,两个全等的正方形ABCD 和 ABEF 所在平面订交于AB ,M ∈ AC , N∈FB 且 AM=FN ,求证: MN ∥平面 BCE .AFDN MBQEPC为垂足(如上图) ,连接 PQ. 证法一:过 M 作 MP ⊥ BC , NQ ⊥ BE ,P 、 Q ∵ MP ∥ AB ,NQ ∥ AB ,∴ MP ∥NQ.又 NQ=2 2 BN =CM =MP ,∴ MPQN 是平行四边形 .22∴ MN ∥ PQ , PQ 平面 BCE.而 MN 平面 BCE , ∴MN ∥平面 BCE.证法二:过 M 作 MG ∥ BC ,交 AB 于点 G (以以下图),连接 NG.A FGDNMBE∵ MG ∥ BC , BC 平面 BCE , CMG 平面 BCE ,∴ MG ∥平面 BCE.又BG =CM =BN , GA MA NF∴ GN ∥AF ∥BE ,相同可证明 GN ∥平面 BCE. 又面 MG ∩ NG=G ,∴平面 MNG ∥平面 BCE.又 MN平面 MNG .∴ MN ∥平面 BCE .特别提示证明直线和平面的平行往常采纳以下两种方法:①利用直线和平面平行的判断定理,过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,经过“面面”平行,证得“线面”平行 .【例 2】 以以下图, 正方体 ABCD — A 1B 1C 1D 1 中,侧面对角线 AB 1、BC 1 上分别有两点F ,且 B 1E=C 1F .求证: EF ∥平面 ABCD .通E 、D 1C 1A 1B 1 FEGDCN证法一:分别过MBE 、F 作 EM ⊥AB 于点 M ,FN ⊥BC 于点 N ,连接 MN. ∵ BB 1⊥平面 ABCD , ∴ BB 1⊥ AB , BB 1⊥BC .∴ EM ∥ BB 1, FN ∥ BB 1.∴ EM ∥ FN . 又 B 1E=C 1F ,∴ EM=FN. 故四边形 MNFE 是平行四边形 .∴ EF ∥ MN .又 MN 在平面 ABCD 中,∴ EF ∥平面 ABCD .证法二:过B 1 E B 1G E 作 EG ∥ AB 交 BB 1 于点 G ,连接 GF ,则=.B 1 A B 1 B∵ B 1E=C 1F ,B 1A=C 1 B ,∴C 1F =B 1G.C 1BB 1 B∴ FG ∥ B 1 C 1∥ BC.又∵ EG ∩ FG=G ,AB ∩BC=B ,∴平面 EFG ∥平面 ABCD .而 EF 在平面 EFG 中, ∴ EF ∥平面 ABCD .评论:证明线面平行的常用方法是:证明直线平行于平面内的一条直线;证明直线所在的平面与已知平面平行.【例 3】 已知正四棱锥P — ABCD的底面边长及侧棱长均为13,M 、N分别是PA 、 BD上的点,且 PM ∶ MA =BN ∶ND =5∶ 8.PMCD OE( 1)求证:直线 MN ∥平面 PBC ;NB(2)求直线 MN 与平面 ABCD 所成的角 .(1)证明:∵ P— ABCD 是正四棱锥,∴ABCD 是正方形 .连接 AN 并延伸交 BC 于点 E,连接 PE.∵AD∥ BC,∴ EN∶ AN=BN∶ ND.又∵ BN∶ ND=PM∶ MA,∴EN∶ AN=PM ∶MA .∴MN∥ PE.又∵ PE 在平面 PBC 内,∴ MN ∥平面 PBC.(2)解:由( 1)知 MN ∥ PE,∴ MN 与平面 ABCD 所成的角就是 PE 与平面 ABCD 所成的角 .设点 P 在底面 ABCD 上的射影为O,连接 OE,则∠ PEO 为 PE 与平面 ABCD 所成的角 .由正棱锥的性质知 PO= PB2OB2=13 2.2由( 1)知, BE∶ AD =BN∶ ND=5∶ 8,∴BE= 65.865在△ PEB 中,∠ PBE=60 °, PB=13 ,BE=,依据余弦定理,得PE= 91. 8在 Rt△POE 中, PO = 13 2, PE=91,28∴sin∠ PEO= PO=4 2. PE7故 MN 与平面 ABCD 所成的角为 arcsin 4 2.7思虑议论证线面平行,一般是转变为证线线平行.求直线与平面所成的角一般用结构法,作出线与面所成的角 .此题若直接求MN 与平面 ABCD 所成的角,计算困难,而平移转变为PE平面 ABCD 所成的角则计算简单.可见平移是求线线角、线面角的重要方法.与●闯关训练夯实基础1.两条直线a、b 知足a∥b, bα,则 a 与平面α的关系是A. a∥αB. a与α订交C.a 与α不订交D.aα答案: C2.a、 b 是两条异面直线, A 是不在 a、 b 上的点,则以下结论建立的是A. 过 A 有且只有一个平面平行于a、 bB. 过 A 起码有一个平面平行于a、 bC.过 A 有无数个平面平行于a、 bD.过 A 且平行 a、 b 的平面可能不存在分析:过点 A 可作直线 a′∥ a, b′∥ b,则 a′∩ b′ =A.∴ a′、 b′可确立一个平面,记为α.假如 aα,bα,则a∥α,b∥α.因为平面α可能过直线a、 b 之一,所以,过 A 且平行于a、b 的平面可能不存在.答案: D3.( 2004 年全国Ⅰ, 16)已知 a、b 为不垂直的异面直线,α 是一个平面,则a、b 在α上的射影有可能是①两条平行直线;②两条相互垂直的直线;③同一条直线;④一条直线及其外一点 .在上边结论中,正确结论的编号是__________.(写出全部正确结论的编号)分析: A1D 与 BC1在平面 ABCD 上的射影相互平行;AB1与 BC1在平面 ABCD 上的射影相互垂直;DD 1与 BC 1在平面 ABCD 上的射影是一条直线及其外一点 .D1C1A1B1DC答案:①②④B4.已知 Rt△ ABC 的直角极点 C 在平面α内,斜边 AB∥α, AB=2 6 ,AC、BC分别和平面α成45°和30°角,则AB到平面α的距离为__________.分析:分别过A、 B 向平面α引垂线 AA′、 BB′,垂足分别为 A′、 B′ .A BA' B 'C设 AA′ =BB′ =x,则 AC2=(x)2=2x2,sin 45x)2 =4x2.BC2=(sin 30又 AC2+BC2=AB2,∴ 6x2=( 2 6 )2,x=2.答案: 25.以以下图,四棱锥 P— ABCD 的底面是边长为a 的正方形,侧棱PA⊥底面 ABCD ,侧面PBC 内有 BE⊥ PC 于 E,且 BE=6a,试在 AB 上找一点 F,使 EF ∥平面 PAD . 3PGA E DFB C解:在面 PCD 内作 EG⊥ PD 于 G,连接 AG.∵PA⊥平面 ABCD ,CD⊥ AD,∴CD⊥PD .∴CD ∥ EG.又 AB∥ CD,∴ EG∥ AB.如有 EF ∥平面 PAD,则 EF∥ AG,∴四边形 AFEG 为平行四边形,得EG=AF .∵ CE=a2( 6a) 2 = 3 a ,△ PBC 为直角三角形,∴ BC 2=CE · CPCP= 3 a ,3 3AF EG PE 3a3 a23=== 3a= .ABCDPC3故得 AF ∶ FB=2∶1 时, EF ∥平面 PAD .6.以以下图,设 P 为长方形 ABCD 所在平面外一点,M 、 N 分别为 AB 、 PD 上的点,且AM =DN,求证:直线 MN ∥平面 PBC.MB NPPRNQDCA MBMN 所在的分析:要证直线 MN ∥平面 PBC ,只要证明 MN ∥平面 PBC 内的一条直线或某个平面∥平面 PBC.证法一:过 N 作 NR ∥ DC 交 PC 于点 R ,连接 RB ,依题意得DCNR =DN =AM =NRNP MBAB MB DC MB=NR=MB .∵ NR ∥ DC ∥AB ,∴四边形 MNRB 是平行四边形 .∴ MN ∥MBMBRB.又∵ RB 平面 PBC ,∴直线 MN ∥平面 PBC.证法二:过 N 作 NQ ∥AD 交 PA 于点 Q ,连接 QM ,∵AM =DN =AQ,∴ QM ∥PB.MB NPQP又 NQ ∥ AD ∥ BC ,∴平面 MQN ∥平面 PBC.∴直线 MN ∥平面 PBC.证法三:过N 作NR ∥DC交PC于点R ,连接RB ,依题意有BMAB=PN PD=NR DC,∴NR =MB ,BR = BM+ MN+ NR =MN.∴ MN ∥RB.又∵ RB平面PBC ,∴直线 MN ∥平面PBC.培育能力7.已知 l 是过正方体 ABCD — A 1B 1C 1D 1 的极点的平面 AB 1D 1 与下底面 ABCD 所在平面的交线,( 1)求证: D 1B 1∥ l ;( 2)若 AB=a ,求 l 与 D 1 间的距离 .D 1C 1A1B 1CDAB( 1)证明:lD1C1A1B1D CGB∵ D1B1∥ BD ,l∴D1B1∥平面 ABCD .又平面 ABCD ∩平面 AD 1B1=l,∴D1B1∥ l .( 2)解:∵ D1D ⊥平面 ABCD ,在平面 ABCD 内,由 D 作 DG ⊥ l 于 G,连接 D1G,则 D1G⊥ l , D1G 的长即等于点D1与 l 间的距离 .∵l ∥ D1B1∥ BD ,∴∠ DAG =45° .∴DG=2221a2a26 a,1DG D1 D== a.D G=222研究创新8.以以下图,在正四棱柱1AB,点 E、M 分别为 A1B、C1C 的ABCD — A1B1C1D 1中, AA 1=2中点,过点 A1、 B、 M 三点的平面 A1BMN 交 C1D1于点 N.D1NC 1A 1B1MDECA B(1)求证: EM∥平面 A1B1C1D1;(2)求二面角 B— A1N— B1的正切值;( 3)设截面A1BMN 把该正四棱柱截成的两个几何体的体积分别为V1、V2( V1< V2),求 V1∶V2的值 .( 1)证明:设A1B1的中点为F,连接 EF、 FC1.∵ E 为 A1B 的中点,∴ EF 1B1B.2P D1NC 1HA 1MF B1D CE又 C1M1A B B1B,∴ EF MC 1.2∴四边形 EMC 1F 为平行四边形.∴EM∥ FC 1.∵EM 平面 A1B1C1D 1,FC1平面A1B1C1D1,∴ EM∥平面 A1B1C1D 1.( 2)解:作 B 1H ⊥ A 1N 于 H ,连接 BH .∵ BB 1⊥平面 A 1B 1C 1D 1,∴ BH ⊥ A 1N.∴∠ BHB 1 为二面角 B —A 1N —B 1 的平面角 .∵ EM ∥平面 A 1B 1C 1D 1, EM 平面 A 1BMN ,平面 A 1BMN ∩平面 A 1B 1C 1D 1=A 1N , ∴ EM ∥ A 1N.又∵ EM ∥ FC 1,∴ A 1N ∥ FC 1 .又∵ A 1F ∥ NC 1,∴四边形 A 1FC 1N 是平行四边形 .∴ NC 1=A 1F.设 AA 1=a ,则 A 1B 1=2a , D 1N=a. 在 Rt △A 1D 1N 中,A 1N= A D2 D N 2 = 5 a ,1 11A 1 D 1 2∴ sin ∠ A 1ND 1==.A 1 N52 4 在 Rt △A 1B 1H 中, B 1H=A 1B 1sin ∠ HA 1B 1=2a ·=a.55在 Rt △BB 1H 中,tan ∠ BHB 1=BB 1= a= 5 .B 1 H4 a 45( 3)解:延伸 A 1N 与 B 1C 1 交于 P ,则 P ∈平面 A 1BMN ,且 P ∈平面 BB 1C 1C.又∵平面 A 1BMN ∩平面 BB 1C 1 C=BM ,∴ P ∈ BM ,即直线 A 1N 、 B 1C 1、 BM 交于一点 P. 又∵平面 MNC 1∥平面 BA 1B 1,∴几何体 MNC 1— BA 1B 1 为棱台 .(没有以上这段证明,不扣分)∵ S A 1 BB 1 = 1·2a · a=a 2,2 S MNC 1 = 1 · a ·1a=1 a 2,2 24棱台 MNC 1— BA 1B 1 的高为 B 1C 1=2a ,1 · 2a 21 a2 +1 2 ) = 73=2a · 2a · a -7 317 3V 1=2a ·( a +4 4a 6 a ,∴ V 26 a =6 a .3∴V 1=7.V 2 17●思悟小结1.直线与平面的地点关系有三种:直线在平面内、直线与平面订交、直线与平面平行,后者又统称为直线在平面外.2.协助线 (面)是解证线面平行的要点.为了能利用线面平行的判断定理及性质定理,往往需要作协助线(面)●教师下载中心.教课点睛1.一定使学生理解并掌握直线与平面的地点关系,以及直线与平面平行的判断定理及性质定理;联合本课时题目,使学生掌握解证线面平行的基本方法.2.证明线面平行是高考取常有的问题,常用的方法就是证明这条线与平面内的某条直线平行.拓展题例【例 1】以以下图,设 a、 b 是异面直线, AB 是 a、 b 的公垂线,过 AB 的中点 O 作平面α与a、b分别平行,M、N分别是a、b上的随意两点,MN与α 交于点P,求证:P是MN的中点 .A MaOPQB证明:连接AN,交平面α于点 Q,连接 PQ. Nb∵b∥α, b 平面 ABN,平面 ABN∩α =OQ ,∴ b∥OQ .又 O 为 AB 的中点,∴ Q 为 AN 的中点 .∵a∥ α,a平面AMN且平面AMN∩ α=PQ,∴a∥PQ .∴ P 为 MN 的中点 .评论:此题要点考察直线与平面平行的性质.【例 2】在直三棱柱ABC—A1B1C1中, AB1⊥ BC1, AB=CC1=a,BC=b.A1C1B1GE FA C(1)设 E、F 分别为 AB 1、 BC1的中点,求证B: EF ∥平面 ABC;(2)求证: A1C1⊥ AB;(3)求点 B1到平面 ABC1的距离 .(1)证明:∵ E、 F 分别为 AB1、 BC1的中点,∴EF∥ A1C1 .∵ A1C1∥ AC,∴ EF∥ AC.∴EF∥平面 ABC.( 2)证明:∵ AB=CC1,∴ AB =BB 1.又三棱柱为直三棱柱,∴四边形ABB1A1为正方形 .连接 A1B,则 A1B⊥ AB 1.又∵ AB1⊥ BC1,∴ AB1⊥平面 A1BC1.∴AB1⊥ A1C1.又 A1C1⊥ AA 1,∴ A1C1⊥平面 A1ABB1.∴A1C1⊥ AB .(3)解:∵ A1B1∥ AB,∴ A1B1∥平面 ABC1.∴ A1到平面 ABC1的距离等于B1到平面 ABC1的距离 .过 A1作 A1G⊥ AC1于点 G,∵AB⊥平面 ACC1A1,∴ AB⊥ A1G.进而 A1G⊥平面 ABC1,故 A1G 即为所求的距离,即 A1G= ab 2 a 2.b评论:此题(3)也可用等体积变换法求解 .。
2023年高考数学一轮复习第七章立体几何与空间向量3空间点直线平面之间的位置关系练习含解析

空间点、直线、平面之间的位置关系考试要求 1.借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系的定义.2.了解四个基本事实和一个定理,并能应用定理解决问题.知识梳理 1.平面基本事实1:过不在一条直线上的三个点,有且只有一个平面.基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内. 基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.基本事实4:平行于同一条直线的两条直线平行. 2.“三个”推论推论1:经过一条直线和这条直线外一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面. 3.空间中直线与直线的位置关系⎩⎪⎨⎪⎧共面直线⎩⎪⎨⎪⎧相交直线,平行直线,异面直线:不同在任何一个平面内,没有 公共点.4.空间中直线与平面的位置关系直线与平面的位置关系有:直线在平面内、直线与平面相交、直线与平面平行三种情况. 5.空间中平面与平面的位置关系平面与平面的位置关系有平行、相交两种情况. 6.等角定理如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补. 7.异面直线所成的角(1)定义:已知两条异面直线a ,b ,经过空间任一点O 分别作直线a ′∥a ,b ′∥b ,把直线a ′与b ′所成的角叫做异面直线a 与b 所成的角(或夹角).(2)范围:⎝⎛⎦⎥⎤0,π2.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)两个平面α,β有一个公共点A ,就说α,β相交于过A 点的任意一条直线.( × ) (2)两两相交的三条直线最多可以确定三个平面.( √ ) (3)如果两个平面有三个公共点,那么这两个平面重合.( × ) (4)没有公共点的两条直线是异面直线.( × ) 教材改编题1.(多选)如图是一个正方体的展开图,如果将它还原为正方体,则下列说法正确的是( )A .AB 与CD 是异面直线 B .GH 与CD 相交C .EF ∥CD D .EF 与AB 异面 答案 ABC解析 把展开图还原成正方体,如图所示.还原后点G 与C 重合,点B 与F 重合,由图可知ABC 正确,EF 与AB 相交,故D 错. 2.如果直线a ⊂平面α,直线b ⊂平面β.且α∥β,则a 与b ( ) A .共面 B .平行 C .是异面直线D .可能平行,也可能是异面直线 答案 D解析 α∥β,说明a 与b 无公共点, ∴a 与b 可能平行也可能是异面直线.3.如图,在三棱锥A -BCD 中,E ,F ,G ,H 分别是棱AB ,BC ,CD ,DA 的中点,则(1)当AC ,BD 满足条件________时,四边形EFGH 为菱形; (2)当AC ,BD 满足条件________时,四边形EFGH 为正方形. 答案 (1)AC =BD (2)AC =BD 且AC ⊥BD 解析 (1)∵四边形EFGH 为菱形, ∴EF =EH ,∵EF 綉12AC ,EH 綉12BD ,∴AC =BD .(2)∵四边形EFGH 为正方形, ∴EF =EH 且EF ⊥EH , ∵EF 綉12AC ,EH 綉12BD ,∴AC =BD 且AC ⊥BD .题型一 基本事实应用例1 如图所示,在正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是AB ,AA 1的中点,连接D 1F ,CE .求证:(1)E ,C ,D 1,F 四点共面; (2)CE ,D 1F ,DA 三线共点.证明 (1)如图所示,连接CD 1,EF ,A 1B , ∵E ,F 分别是AB ,AA 1的中点, ∴EF ∥A 1B ,且EF =12A 1B .又∵A 1D 1∥BC ,A 1D 1=BC , ∴四边形A 1BCD 1是平行四边形, ∴A 1B ∥CD 1,∴EF ∥CD 1,∴EF 与CD 1能够确定一个平面ECD 1F , 即E ,C ,D 1,F 四点共面.(2)由(1)知EF ∥CD 1,且EF =12CD 1,∴四边形CD 1FE 是梯形, ∴CE 与D 1F 必相交,设交点为P , 则P ∈CE ,且P ∈D 1F ,∵CE ⊂平面ABCD ,D 1F ⊂平面A 1ADD 1, ∴P ∈平面ABCD ,且P ∈平面A 1ADD 1. 又∵平面ABCD ∩平面A 1ADD 1=AD , ∴P ∈AD ,∴CE ,D 1F ,DA 三线共点. 教师备选如图所示,已知在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为D 1C 1,C 1B 1的中点,AC ∩BD =P ,A 1C 1∩EF =Q .求证:(1)D ,B ,F ,E 四点共面;(2)若A 1C 交平面DBFE 于R 点,则P ,Q ,R 三点共线. 证明 (1)∵EF 是△D 1B 1C 1的中位线, ∴EF ∥B 1D 1.在正方体ABCD -A 1B 1C 1D 1中,B 1D 1∥BD , ∴EF ∥BD .∴EF ,BD 确定一个平面,即D ,B ,F ,E 四点共面. (2)在正方体ABCD -A 1B 1C 1D 1中, 设平面A 1ACC 1为α, 平面BDEF 为β. ∵Q ∈A 1C 1,∴Q ∈α.又Q∈EF,∴Q∈β,则Q是α与β的公共点,同理,P是α与β的公共点,∴α∩β=PQ.又A1C∩β=R,∴R∈A1C.∴R∈α,且R∈β,则R∈PQ,故P,Q,R三点共线.思维升华共面、共线、共点问题的证明(1)证明共面的方法:先确定一个平面,然后再证其余的线(或点)在这个平面内.(2)证明共线的方法:先由两点确定一条直线,再证其他各点都在这条直线上.(3)证明共点的方法:先证其中两条直线交于一点,再证其他直线经过该点.跟踪训练1 (1)(多选)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点共面的图是( )答案ABC解析对于A,PS∥QR,故P,Q,R,S四点共面;同理,B,C图中四点也共面;D中四点不共面.(2)在三棱锥A-BCD的棱AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )A.一定在直线BD上B.一定在直线AC上C.在直线AC或BD上D.不在直线AC上,也不在直线BD上答案 B解析如图所示,因为EF⊂平面ABC,HG⊂平面ACD,EF∩HG=P,所以P∈平面ABC,P∈平面ACD.又因为平面ABC∩平面ACD=AC,所以P∈AC.题型二空间线面位置关系命题点1 空间位置关系的判断例2 (1)下列推断中,错误的是( )A.若M∈α,M∈β,α∩β=l,则M∈lB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A,B,C∈α,A,B,C∈β,且A,B,C不共线⇒α,β重合答案 C解析对于A,因为M∈α,M∈β,α∩β=l,由基本事实3可知M∈l,A对;对于B,A∈α,A∈β,B∈α,B∈β,故直线AB⊂α,AB⊂β,即α∩β=AB,B对;对于C,若l∩α=A,则有l⊄α,A∈l,但A∈α,C错;对于D,有三个不共线的点在平面α,β中,故α,β重合,D对.(2)已知在长方体ABCD-A1B1C1D1中,M,N分别是长方形A1B1C1D1与长方形BCC1B1的中心,则下列说法正确的是( )A.直线MN与直线A1B是异面直线B.直线MN与直线DD1相交C.直线MN与直线AC1是异面直线D.直线MN与直线A1C平行答案 C解析如图,因为M,N分别是长方形A1B1C1D1与长方形BCC1B1的中心,所以M,N分别是A1C1,BC1的中点,所以直线MN与直线A1B平行,所以A错误;因为直线MN经过平面BB1D1D内一点M,且点M不在直线DD1上,所以直线MN与直线DD1是异面直线,所以B错误;因为直线MN经过平面ABC1内一点N,且点N不在直线AC1上,所以直线MN与直线AC1是异面直线,所以C正确;因为直线MN经过平面A1CC1内一点M,且点M不在直线A1C上,所以直线MN与直线A1C是异面直线,所以D错误.命题点2 异面直线所成角例3 (1)(2021·全国乙卷)在正方体ABCD -A 1B 1C 1D 1中,P 为B 1D 1的中点,则直线PB 与AD 1所成的角为( ) A .π2B .π3C .π4D .π6答案 D解析 方法一 如图,连接C 1P ,因为ABCD -A 1B 1C 1D 1是正方体,且P 为B 1D 1的中点,所以C 1P ⊥B 1D 1,又C 1P ⊥BB 1,所以C 1P ⊥平面B 1BP .又BP ⊂平面B 1BP ,所以C 1P ⊥BP .连接BC 1,则AD 1∥BC 1,所以∠PBC 1为直线PB 与AD 1所成的角.设正方体ABCD -A 1B 1C 1D 1的棱长为2,则在Rt△C 1PB 中,C 1P =12B 1D 1=2,BC 1=22,sin∠PBC 1=PC 1BC 1=12,所以∠PBC 1=π6.方法二 如图所示,连接BC 1,A 1B ,A 1P ,PC 1,则易知AD 1∥BC 1,所以直线PB 与AD 1所成的角等于直线PB 与BC 1所成的角.根据P 为正方形A 1B 1C 1D 1的对角线B 1D 1的中点,易知A 1,P ,C 1三点共线,且P 为A 1C 1的中点.易知A 1B =BC 1=A 1C 1,所以△A 1BC 1为等边三角形,所以∠A 1BC 1=π3,又P 为A 1C 1的中点,所以可得∠PBC 1=12∠A 1BC 1=π6.(2)(2022·衡水检测)如图,在圆锥SO 中,AB ,CD 为底面圆的两条直径,AB ∩CD =O ,且AB ⊥CD ,SO =OB =3,SE =14SB ,则异面直线SC 与OE 所成角的正切值为( )A .222B .53C .1316D .113答案 D解析 如图,过点S 作SF ∥OE ,交AB 于点F ,连接CF ,则∠CSF (或其补角)为异面直线SC 与OE 所成的角.∵SE =14SB ,∴SE =13BE .又OB =3,∴OF =13OB =1.∵SO ⊥OC ,SO =OC =3, ∴SC =32.∵SO ⊥OF ,∴SF =SO 2+OF 2=10. ∵OC ⊥OF ,∴CF =10. ∴在等腰△SCF 中,tan∠CSF =102-⎝ ⎛⎭⎪⎫3222322=113. 教师备选1.(多选)设a ,b ,c 是三条不同的直线,α,β是两个不同的平面,则下列结论不正确的是( )A .若a ⊂α,b ⊂β,则a 与b 是异面直线B .若a 与b 异面,b 与c 异面,则a 与c 异面C .若a ,b 不同在平面α内,则a 与b 异面D .若a ,b 不同在任何一个平面内,则a 与b 异面 答案 ABC2.在长方体ABCDA 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A .15B .56C .55D .22 答案 C解析 如图,连接BD 1,交DB 1于O ,取AB 的中点M ,连接DM ,OM .易知O 为BD 1的中点,所以AD 1∥OM ,则∠MOD 为异面直线AD 1与DB 1所成角或其补角.因为在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,AD 1=AD 2+DD 21=2, DM =AD 2+⎝ ⎛⎭⎪⎫12AB 2=52, DB 1=AB 2+AD 2+BB 21=5. 所以OM =12AD 1=1,OD =12DB 1=52,于是在△DMO 中,由余弦定理,得cos∠MOD =12+⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫5222×1×52=55,即异面直线AD 1与DB 1所成角的余弦值为55. 思维升华 (1)点、直线、平面位置关系的判定,注意构造几何体(长方体、正方体)模型来判断,常借助正方体为模型. (2)求异面直线所成的角的三个步骤一作:根据定义作平行线,作出异面直线所成的角. 二证:证明作出的角是异面直线所成的角. 三求:解三角形,求出所作的角.跟踪训练2 (1)如图所示,G ,N ,M ,H 分别是正三棱柱的顶点或所在棱的中点,则表示直线GH 与MN 是异面直线的图形有________.(填序号)答案 ②④(2)若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则下列结论正确的是( ) A .l 与l 1,l 2都不相交 B .l 与l 1,l 2都相交C .l 至多与l 1,l 2中的一条相交D .l 至少与l 1,l 2中的一条相交 答案 D解析 如图1,l 1与l 2是异面直线,l 1与l 平行,l 2与l 相交,故A ,B 不正确;如图2,l 1与l 2是异面直线,l 1,l 2都与l 相交,故C 不正确.图1 图2题型三 空间几何体的切割(截面)问题例4 (1)在正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是棱DD 1和BB 1上的点,MD =13DD 1,NB =13BB 1,那么正方体中过M ,N ,C 1的截面图形是( ) A .三角形 B .四边形 C .五边形 D .六边形答案 C解析 先确定截面上的已知边与几何体上和其共面的边的交点,再确定截面与几何体的棱的交点.如图,设直线C 1M ,CD 相交于点P ,直线C 1N ,CB 相交于点Q ,连接PQ 交直线AD 于点E ,交直线AB 于点F ,则五边形C 1MEFN 为所求截面图形.(2)已知正方体ABCD -A 1B 1C 1D 1的棱长为2.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为______. 答案π2解析 以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线是以C 1为圆心,1为半径的圆与正方形BCC 1B 1相交的一段弧(圆周的四分之一),其长度为14×2π×1=π2.延伸探究 将本例(2)中正方体改为直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.答案2π2解析 如图,设B 1C 1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q ,连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形, ∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形, 则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心, 设截面圆的半径为r ,则r =R 2球-D 1E 2=5-3=2. 又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P =5,∴B 1P =D 1P 2-D 1B 21=1, 同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点, ∴∠PEQ =π2,知PQ ︵的长为π2×2=2π2,即交线长为2π2.教师备选如图,在正方体ABCD -A 1B 1C 1D 1中,E 是BC 的中点,平面α经过直线BD 且与直线C 1E 平行,若正方体的棱长为2,则平面α截正方体所得的多边形的面积为________.答案 92解析 如图,过点B 作BM ∥C 1E 交B 1C 1于点M ,过点M 作BD 的平行线,交C 1D 1于点N ,连接DN ,则平面BDNM 即为符合条件的平面α,由图可知M ,N 分别为B 1C 1,C 1D 1的中点, 故BD =22,MN =2, 且BM =DN =5, ∴等腰梯形MNDB 的高为h =52-⎝⎛⎭⎪⎫222=322, ∴梯形MNDB 的面积为 12×(2+22)×322=92. 思维升华 (1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线. (2)作交线的方法有如下两种:①利用基本事实3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线. 跟踪训练3 (1)(多选)正方体ABCD -A 1B 1C 1D 1的棱长为2,已知平面α⊥AC 1,则关于α截此正方体所得截面的判断正确的是( ) A .截面形状可能为正三角形 B .截面形状可能为正方形 C .截面形状可能为正六边形 D .截面面积最大值为3 3 答案 ACD解析 易知A ,C 正确,B 不正确,下面说明D 正确,如图,截面为正六边形,当六边形的顶点均为棱的中点时,其面积最大,MN =22,GH =2,OE =OO ′2+O ′E 2=1+⎝⎛⎭⎪⎫222=62, 所以S =2×12×(2+22)×62=33,故D 正确.(2)(2022·兰州模拟)如图,正方体A 1C 的棱长为1,点M 在棱A 1D 1上,A 1M =2MD 1,过M 的平面α与平面A 1BC 1平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为________.答案 3 2解析 在平面A 1D 1DA 中寻找与平面A 1BC 1平行的直线时,只需要ME ∥BC 1,如图所示,因为A 1M =2MD 1,故该截面与正方体的交点位于靠近D 1,A ,C 的三等分点处,故可得截面为MIHGFE ,设正方体的棱长为3a , 则ME =22a ,MI =2a ,IH =22a ,HG =2a ,FG =22a ,EF =2a ,所以截面MIHGFE 的周长为ME +EF +FG +GH +HI +IM =92a , 又因为正方体A 1C 的棱长为1,即3a =1, 故截面多边形的周长为32.课时精练1.下列叙述错误的是( )A .若P ∈α∩β,且α∩β=l ,则P ∈lB.若直线a∩b=A,则直线a与b能确定一个平面C.三点A,B,C确定一个平面D.若A∈l,B∈l且A∈α,B∈α,则l⊂α答案 C解析选项A,点P是两平面的公共点,当然在交线上,故正确;选项B,由基本事实的推论可知,两相交直线确定一个平面,故正确;选项C,只有不共线的三点才能确定一个平面,故错误;选项D,由基本事实2,直线上有两点在一个平面内,则这条直线在平面内.2.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列判断正确的是( ) A.若m⊥α,n⊥β,α⊥β,则直线m与n可能相交或异面B.若α⊥β,m⊂α,n⊂β,则直线m与n一定平行C.若m⊥α,n∥β,α⊥β,则直线m与n一定垂直D.若m∥α,n∥β,α∥β,则直线m与n一定平行答案 A解析m,n是两条不同的直线,α,β是两个不同的平面,对于A,若m⊥α,n⊥β,α⊥β,则直线m与n相交垂直或异面垂直,故A正确;对于B,若α⊥β,m⊂α,n⊂β,则直线m与n相交、平行或异面,故B错误;对于C,若m⊥α,n∥β,α⊥β,则直线m与n相交、平行或异面,故C错误;对于D,若m∥α,n∥β,α∥β,则直线m与n平行或异面,故D错误.3.(2022·营口模拟)已知空间中不过同一点的三条直线a,b,l,则“a,b,l两两相交”是“a,b,l共面”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 A解析空间中不过同一点的三条直线a,b,l,若a,b,l在同一平面,则a,b,l相交或a,b,l有两个平行,另一直线与之相交,或三条直线两两平行.所以a,b,l在同一平面,则a,b,l两两相交不一定成立;而若a,b,l两两相交,则a,b,l在同一平面成立.故“a,b,l两两相交”是“a,b,l共面”的充分不必要条件.4.如图所示,在正方体ABCD-A1B1C1D1中,E是平面ADD1A1的中心,M,N,F分别是B1C1,CC1,AB的中点,则下列说法正确的是( )A .MN =12EF ,且MN 与EF 平行B .MN ≠12EF ,且MN 与EF 平行C .MN =12EF ,且MN 与EF 异面D .MN ≠12EF ,且MN 与EF 异面答案 D解析 设正方体ABCD -A 1B 1C 1D 1的棱长为2a , 则MN =MC 21+C 1N 2=⎝ ⎛⎭⎪⎫2a 22+⎝ ⎛⎭⎪⎫2a 22 =2a ,作点E 在平面ABCD 内的射影点G ,连接EG ,GF ,所以EF =EG 2+GF 2=⎝ ⎛⎭⎪⎫2a 22+2a2=3a ,所以MN ≠12EF ,故选项A ,C 错误;连接DE ,因为E 为平面ADD 1A 1的中心, 所以DE =12A 1D ,又因为M ,N 分别为B 1C 1,CC 1的中点,所以MN ∥B 1C , 又因为B 1C ∥A 1D ,所以MN ∥ED , 且DE ∩EF =E ,所以MN 与EF 异面,故选项B 错误.5.(多选)(2022·临沂模拟)如图,在正方体ABCD -A 1B 1C 1D 1中,O 是DB 的中点,直线A 1C 交平面C 1BD 于点M ,则下列结论正确的是( )A.C1,M,O三点共线B.C1,M,O,C四点共面C.C1,O,B1,B四点共面D.D1,D,O,M四点共面答案AB解析∵O∈AC,AC⊂平面ACC1A1,∴O∈平面ACC1A1.∵O∈BD,BD⊂平面C1BD,∴O∈平面C1BD,∴O是平面ACC1A1和平面C1BD的公共点,同理可得,点M和C1都是平面ACC1A1和平面C1BD的公共点,∴三点C1,M,O在平面C1BD与平面ACC1A1的交线上,即C1,M,O三点共线,故A,B正确;根据异面直线的判定定理可得BB1与C1O为异面直线,故C1,O,B1,B四点不共面,故C不正确;根据异面直线的判定定理可得DD1与MO为异面直线,故D1,D,O,M四点不共面,故D不正确.6.(多选)(2022·厦门模拟)下列说法不正确的是( )A.两组对边分别相等的四边形确定一个平面B.和同一条直线异面的两直线一定共面C.与两异面直线分别相交的两直线一定不平行D.一条直线和两平行线中的一条相交,也必定和另一条相交答案ABD解析两组对边分别相等的四边形可能是空间四边形,故A错误;如图1,直线DD1与B1C1都是直线AB的异面直线,同样DD1与B1C1也是异面直线,故B错误;如图2,设直线AB与CD是异面直线,则直线AC与BD一定不平行,否则AC∥BD,有AC与BD确定一个平面α,则AC⊂α,BD⊂α,所以A∈α,B∈α,C∈α,D∈α,所以AB⊂α,CD⊂α,这与假设矛盾,故C正确;如图1,AB∥CD,而直线AA1与AB相交,但与直线CD不相交,故D错误.图1 图27.(2022·哈尔滨模拟)已知在直三棱柱ABC -A 1B 1C 1中,∠ABC =120°,AB =2,BC =CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为________. 答案105解析 如图所示,补成直四棱柱ABCD -A 1B 1C 1D 1,则所求角为∠BC 1D 或其补角,∵BC 1=2,BD =22+1-2×2×1×cos60°=3,C 1D =AB 1=5, 易得C 1D 2=BD 2+BC 21,即BC 1⊥BD , 因此cos∠BC 1D =BC 1C 1D =25=105. 8.(2022·本溪模拟)在空间中,给出下面四个命题,其中假命题为________.(填序号) ①过平面α外的两点,有且只有一个平面与平面α垂直; ②若平面β内有不共线三点到平面α的距离都相等,则α∥β; ③若直线l 与平面α内的任意一条直线垂直,则l ⊥α; ④两条异面直线在同一平面内的射影一定是两条相交直线. 答案 ①②④解析 对于①,当平面α外两点的连线与平面α垂直时,此时过两点有无数个平面与平面α垂直,所以①不正确;对于②,若平面β内有不共线三点到平面α的距离都相等,平面α与β可能平行,也可能相交,所以②不正确;对于③,直线l 与平面内的任意直线垂直时,得到l ⊥α,所以③正确;对于④,两条异面直线在同一平面内的射影可能是两条相交直线或两条平行直线或直线和直线外的一点,所以④不正确.9.(2022·上海市静安区模拟)如图所示,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是AB ,CC 1的中点.(1)求异面直线A 1E 与D 1F 所成的角的余弦值; (2)求三棱锥A 1-D 1EF 的体积.解 (1)如图,设BB 1的中点为H ,连接HF ,EH ,A 1H ,因为F 是CC 1的中点,所以A 1D 1∥CB ∥HF ,A 1D 1=CB =HF , 因此四边形A 1D 1FH 是平行四边形, 所以D 1F ∥A 1H ,D 1F =A 1H ,因此∠EA 1H 是异面直线A 1E 与D 1F 所成的角或其补角, 正方体ABCD -A 1B 1C 1D 1的棱长为2,E 是AB 的中点, 所以A 1E =A 1H =22+12=5,EH =12+12=2,由余弦定理可知,cos∠EA 1H =A 1E 2+A 1H 2-EH 22A 1E ·A 1H =5+5-22×5×5=45,所以异面直线A 1E 与D 1F 所成的角的余弦值为45.(2)因为A 1D 1∥HF ,HF ⊄平面A 1D 1E ,A 1D 1⊂平面A 1D 1E , 所以HF ∥平面A 1D 1E ,因此点H ,F 到平面A 1D 1E 的距离相等, 即111111F A D E H A D E D A EH V V V ---==,11D A EH V -=13D 1A 1·1A EH S △=13×2×⎝ ⎛⎭⎪⎫22-12×2×1×2-12×1×1=1,所以三棱锥A 1-D 1EF 的体积为1.10.如图,四棱柱ABCD -A 1B 1C 1D 1的侧棱AA 1⊥底面ABCD ,四边形ABCD 为菱形,E ,F 分别为AA 1,CC 1的中点,M 为AB 上一点.(1)若D 1E 与CM 相交于点K ,求证D 1E ,CM ,DA 三条直线相交于同一点; (2)若AB =2,AA 1=4,∠BAD =π3,求点D 1到平面FBD 的距离.(1)证明 ∵D 1E 与CM 相交于点K , ∴K ∈D 1E ,K ∈CM ,而D 1E ⊂平面ADD 1A 1,CM ⊂平面ABCD , 且平面ADD 1A 1∩平面ABCD =AD , ∴K ∈AD ,∴D 1E ,CM ,DA 三条直线相交于同一点K . (2)解 ∵四边形ABCD 为菱形,AB =2, ∴BC =CD =2,而四棱柱的侧棱AA 1⊥底面ABCD , ∴CC 1⊥底面ABCD ,又∵F 是CC 1的中点,CC 1=4,∴CF =2, ∴BF =DF =22,又∵四边形ABCD 为菱形,∠BAD =π3,∴BD =AB =2, ∴S △FBD =12×2×222-1=7.设点D 1到平面FBD 的距离为h ,点B 到平面DD 1F 的距离为d , 则d =2sin π3=3,又∵11D FBD B DD F V V --=, ∴13×S △FBD ×h =13×1DD F S △×d , ∴13×7×h =13×12×4×2×3, 解得h =4217.即点D1到平面FBD的距离为421 7.11.(多选)(2022·太原模拟)如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,下列结论正确的是( )A.GH与EF平行B.BD与MN为异面直线C.GH与MN成60°角D.DE与MN垂直答案BCD解析如图,还原成正四面体A-DEF,其中H与N重合,A,B,C三点重合,连接GM,易知GH与EF异面,BD与MN异面.又△GMH为等边三角形,∴GH与MN成60°角,易证DE⊥AF,MN∥AF,∴MN⊥DE.∴B,C,D正确.12.(多选)(2022·广州六校联考)如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,下列结论正确的是( )A.AP与CM是异面直线B.AP,CM,DD1相交于一点C.MN∥BD1D.MN∥平面BB1D1D答案 BD解析 如图,连接MP ,AC ,因为MP ∥AC ,MP ≠AC ,所以AP 与CM 是相交直线,又平面A 1ADD 1∩平面C 1CDD 1=DD 1,所以AP ,CM ,DD 1相交于一点,则A 不正确,B 正确;令AC ∩BD =O ,连接OD 1,ON .因为M ,N 分别是C 1D 1,BC 的中点,所以ON ∥D 1M ∥CD ,ON =D 1M =12CD , 则四边形MNOD 1为平行四边形,所以MN ∥OD 1,因为MN ⊄平面BB 1D 1D ,OD 1⊂平面BB 1D 1D ,所以MN ∥平面BB 1D 1D ,C 不正确,D 正确.13.(2022·玉林模拟)在正方体ABCD -A 1B 1C 1D 1中,E ,F ,P ,Q 分别为A 1B ,B 1D 1,A 1D ,CD 1的中点,则直线EF 与PQ 所成角的大小是________.答案 π3解析 如图,连接A 1C 1,BC 1,则F 是A 1C 1的中点,又E 为A 1B 的中点,所以EF ∥BC 1,连接DC 1,则Q 是DC 1的中点,又P 为A 1D 的中点,所以PQ ∥A 1C 1,于是∠A 1C 1B 是直线EF 与PQ 所成的角或其补角.易知△A 1C 1B 是正三角形,所以∠A 1C 1B =π3. 14.(2022·盐城模拟)在棱长为4的正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别为棱A 1D 1,CC 1的中点,过P ,Q ,A 作正方体的截面,则截面多边形的周长是________.答案 25+95+2133 解析 如图所示,过Q 作QM ∥AP 交BC 于M ,由A 1P =CQ =2,tan∠APA 1=2,则tan∠CMQ =2,CM =CQtan∠CMQ=1, 延长MQ 交B 1C 1的延长线于E 点,连接PE ,交D 1C 1于N 点,则多边形AMQNP 即为截面,根据平行线性质有C 1E =CM =1, C 1N ND 1=C 1E PD 1=12, 则C 1N =43,D 1N =83, 因此NQ =22+⎝ ⎛⎭⎪⎫432=2133, NP =22+⎝ ⎛⎭⎪⎫832=103, 又AP =42+22=25,AM =42+32=5,MQ =12+22=5,所以多边形AMQNP 的周长为AM +MQ +QN +NP +PA=5+5+2133+103+2 5 =25+95+2133.15.(2022·大连模拟)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的正方形,AA 1=3,E ,F 分别是AB ,BC 的中点,过点D 1,E ,F 的平面记为α,则下列说法中错误的是( )A .点B 到平面α的距离与点A 1到平面α的距离之比为1∶2B .平面α截直四棱柱ABCD -A 1B 1C 1D 1所得截面的面积为732C .平面α将直四棱柱分割成的上、下两部分的体积之比为47∶25D .平面α截直四棱柱ABCD -A 1B 1C 1D 1所得截面的形状为四边形 答案 D解析 对于A ,因为平面α过线段AB 的中点E ,所以点A 到平面α的距离与点B 到平面α的距离相等.由平面α过A 1A 的三等分点M 可知,点A 1到平面α的距离是点A 到平面α的距离的2倍,因此,点A 1到平面α的距离是点B 到平面α的距离的2倍.故选项A 正确;延长DA ,DC 交直线EF 的延长线于点P ,Q ,连接D 1P ,D 1Q ,交棱A 1A ,C 1C 于点M ,N .连接ME ,NF ,可得五边形D 1MEFN ,故选项D 错误;由平行线分线段成比例可得AP =BF =1,故DP =DD 1=3,则△DD 1P 为等腰三角形.由相似三角形可知,AM =AP =1,A 1M =2,则D 1M =D 1N =22,ME =EF =FN =2.连接MN ,则MN =22,因此五边形D 1MEFN 可分为等边三角形D 1MN 和等腰梯形MEFN .等腰梯形MEFN 的高h =22-⎝ ⎛⎭⎪⎫22-222=62, 则等腰梯形MEFN 的面积为22+22×62=332.又1D MN S △=12×22×6=23,所以五边形D 1MEFN 的面积为332+23=732,故选项B 正确;记平面将直四棱柱分割成上、下两部分的体积分别为V 1,V 2,则V 2=1D DPQ V --V M -PAE -V N -CFQ=13×12×3×3×3-13×12×1×1×1-13×12×1×1×1=256, 所以V 1=1111ABCD A B C D V --V 2=12-256=476, V 1∶V 2=47∶25,故选项C 正确.16.如图1,在边长为4的正三角形ABC 中,D ,F 分别为AB ,AC 的中点,E 为AD 的中点.将△BCD 与△AEF 分别沿CD ,EF 同侧折起,使得二面角A -EF -D 与二面角B -CD -E 的大小都等于90°,得到如图2所示的多面体.图1 图2(1)在多面体中,求证:A ,B ,D ,E 四点共面;(2)求多面体的体积.(1)证明 因为二面角A -EF -D 的大小等于90°,所以平面AEF ⊥平面DEFC ,又AE ⊥EF ,AE ⊂平面AEF ,平面AEF ∩平面DEFC =EF ,所以AE ⊥平面DEFC ,同理,可得BD ⊥平面DEFC ,所以AE ∥BD ,故A ,B ,D ,E 四点共面.(2)解 因为AE ⊥平面DEFC ,BD ⊥平面DEFC ,EF ∥CD ,AE ∥BD ,DE ⊥CD ,所以AE 是四棱锥A -CDEF 的高,点A 到平面BCD 的距离等于点E 到平面BCD 的距离, 又AE =DE =1,CD =23,EF =3,BD =2,所以V =V A -CDEF +V A -BCD =13S 梯形CDEF ·AE +13S △BCD ·DE =736.。
2019-2020年高考数学一轮复习 7-4 直线、平面平行的判定及其性质课时作业 文

2019-2020年高考数学一轮复习 7-4 直线、平面平行的判定及其性质课时作业文一、选择题1.(xx年正定摸底)已知直线a与平面α,β,α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线解析:设直线a和点B所确定的平面为γ,则α∩γ=a,记β∩γ=b,∵α∥β,∴a∥b,故存在唯一一条直线b与a平行.答案:D2.已知m,n是两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是() A.若m∥n,m⊂α,则n∥αB.若m∥n,m⊂α,n⊂β,则α∥βC.若α⊥γ,α⊥β,则β∥γD.若m∥n,m⊥α,n⊥β,则α∥β解析:直线n可能在平面α内,A错误;两平面可相交,此时直线m,n均于交线平行即可,B错误;两平面可相交,C错误;因为m∥n,m⊥α,所以n⊥α,又n⊥β,所以α∥β,D 正确.故选D.答案:D3.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,且m⊥α,则l⊥α;②若m∥l,且m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m.其中正确命题的个数是()A.1B.2C.3 D.4解析:易知①正确;②错误,l与α的具体关系不能确定;③错误,以墙角为例即可说明,④正确,可以以三棱柱为例证明,故选B.答案:B4.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是() A.若m∥α,n∥α,则m∥nB.若m∥n,n⊂α,则m∥αC.若m∥α,m∥β,则α∥βD.若α∥β,α∥γ,则β∥γ解析:m、n平行于α,m、n可能相交也可能异面,如图中正方体的棱A1B1,B1C1都与底面ABCD平行,但这两条棱相交,故选项A不正确;在正方体中,AB∥A1B1,A1B1⊂平面A1B1BA,而AB不平行于平面A1B1BA,故选项B不正确;正方体的棱B1C1既平行于平面ADD1A1,又平行于平面ABCD,但这两个平面相交,故选项C不正确;由平面与平面平行的传递性,得选项D正确.故选D.答案:D5.如图,L,M,N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是()A.垂直B.相交不垂直C.平行D.重合解析:如图,分别取另三条棱的中点A,B,C将平面LMN延展为平面正六边形AMBNCL,因为PQ∥AL,PR∥AM,且PQ与PR相交,AL与AM相交,所以平面PQR∥平面AMBNCL,即平面LMN∥平面PQR.答案:C二、填空题6.一个面截空间四边形的四边得到四个交点,如果该空间四边形的两条对角线与这个截面平行,那么此四个交点围成的四边形是________.解析:如图,由题意得AC∥平面EFGH,BD∥平面EFGH.∵AC⊂平面ABC,平面ABC∩平面EFGH=EF,∴AC∥EF,同理AC∥GH,所以EF∥GH.同理,EH∥FG,所以四边形EFGH为平行四边形.答案:平行四边形7.在正四棱柱ABCD -A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,则点Q满足条件________时,有平面D1BQ∥平面PAO.解析:假设Q为CC1的中点,因为P为DD1的中点,所以QB∥PA.连接DB,因为P,O 分别为DD1,DB的中点,所以D1B∥PO,又D1B⊄平面PAO,QB⊄平面PAO,所以D1B ∥平面PAO,QB∥平面PAO,又D1B∩QB=B,∴平面D1BQ∥平面PAO,故Q满足Q为CC1的中点时,有平面D1BQ∥平面PAO.答案:Q 为CC1的中点8.如图,在棱长为1的正方体ABCD -A1B1C1D1中,点E ,F 分别是棱BC ,CC1的中点,P 是侧面BCC1B1内一点,若A1P ∥平面AEF ,则线段A1P 长度的取值范围是________.解析:取B1C1中点M ,则A1M ∥AE ;取BB1中点N ,则MN ∥EF ,∴平面A1MN ∥平面AEF.若A1P ∥平面AEF ,只需P ∈MN ,则P 位于MN 中点时,A1P 最短;当P 位于M 或N 时,A1P 最长.不难求得A1P 的取值范围为⎣⎡⎦⎤324,52. 答案:⎣⎡⎦⎤324,52 三、解答题9.如图,已知平行四边形ABCD 中,BC =6,正方形ADEF 所在平面与平面ABCD 垂直,G ,H 分别是DF ,BE 的中点.(1)求证:GH ∥平面CDE ;(2)若CD =2,DB =42,求四棱锥F -ABCD 的体积.解析:(1)证明 解法一 ∵EF ∥AD ,AD ∥BC ,∴EF ∥BC.又EF =AD =BC ,∴四边形EFBC 是平行四边形,∴H 为FC 的中点.又∵G 是FD 的中点,∴HG ∥CD.∵HG ⊄平面CDE ,CD ⊂平面CDE ,∴GH ∥平面CDE.解法二 连接EA ,∵四边形ADEF 是正方形,∴G 是AE 的中点.∴在△EAB 中,GH ∥AB.又∵AB ∥CD ,∴GH ∥CD.∵HG ⊄平面CDE ,CD ⊂平面CDE ,∴GH ∥平面CDE.(2)∵平面ADEF ⊥平面ABCD ,交线为AD ,且FA ⊥AD ,∴FA ⊥平面ABCD.∵AD =BC =6,∴FA =AD =6. 又∵CD =2,DB =42,CD2+DB2=BC2,∴BD ⊥CD.∵S ▱ABCD =CD·BD =82,∴VF -ABCD =13S ▱ABCD·FA =13×82×6=16 2. 10.(xx 年开封摸底)已知四棱锥S -ABCD 中,四边形ABCD 是直角梯形,∠ABC =∠BAD=90°,SA ⊥平面ABCD ,SA =AB =BC =1,AD =12,E 是棱SC 的中点.(1)求证:DE ∥平面SAB ;(2)求三棱锥S -BED 的体积.解析:(1)取线段SB 的中点F ,连接EF ,AF ,则EF ∥BC 且EF =12BC , 由已知AD ∥BC 且AD =12BC , 所以EF ∥AD ,且EF =AD ,所以AF ∥DE ,又AF ⊂平面SAB ,DE ⊄平面SAB ,所以DE ∥平面SAB.(2)因为E 是棱SC 的中点,所以VS -BDE =VC -BDE =VE -BDC =13S △BDC·12SA =112. B 组 高考题型专练1.(xx 年高考四川卷)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC ⊥BC ,证明:直线BC ⊥平面ACC1A1;(2)设D ,E 分别是线段BC ,CC1的中点,在线段AB 上是否存在一点M ,使直线DE ∥平面A1MC ?请证明你的结论.解析:(1)证明:因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB ,AA1⊥AC.因为AB ,AC 为平面ABC 内两条相交直线,所以AA1⊥平面ABC.因为直线BC ⊂平面ABC ,所以AA1⊥BC.又AC ⊥BC ,AA1,AC 为平面ACC1A1内两条相交直线,所以BC ⊥平面ACC1A1.(2)取线段AB 的中点M ,连接A1M ,MC ,A1C ,AC1,设O 为A1C ,AC1的交点.由已知可知O 为AC1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC1的中位线,所以MD 綊12AC ,OE 綊12AC ,因此MD 綊OE.连接OM ,从而四边形MDEO 为平行四边形,则DE ∥MO.因为直线DE ⊄平面A1MC ,MO ⊂平面A1MC.所以直线DE ∥平面A1MC ,即线段AB 上存在一点M(线段AB 的中点),使直线DE ∥平面A1MC.2.(xx 年高考安徽卷)如图,四棱锥P -ABCD 的底面是边长为8的正方形,四条侧棱长均为217,点G ,E ,F ,H 分别是棱PB ,AB ,CD ,PC 上共面的四点,平面GEFH ⊥平面ABCD ,BC ∥平面GEFH.(1)证明:GH ∥EF ;(2)若EB =2,求四边形GEFH 的面积.解析:(1)证明:因为BC ∥平面GEFH ,BC ⊂平面PBC ,且平面PBC∩平面GEFH =GH ,所以GH ∥BC.同理可证EF ∥BC ,因此GH ∥EF.(2)连接AC ,BD 交于点O ,BD 交EF 于点K ,连接OP ,GK.因为PA =PC ,O 是AC 的中点,所以PO ⊥AC ,同理可得PO ⊥BD.又BD∩AC =O ,且AC ,BD 都在底面内,所以PO ⊥底面ABCD.又因为平面GEFH ⊥平面ABCD ,且PO ⊄平面GEFH ,所以PO ∥平面GEFH.因为平面PBD∩平面GEFH =GK ,所以PO ∥GK ,且GK ⊥底面ABCD ,从而GK ⊥EF.所以GK 是梯形GEFH 的高.由AB =8,EB =2得EB ∶AB =KB ∶DB =1∶4,从而KB =14DB =12OB ,即K 为OB 的中点.再由PO ∥GK 得GK =12PO ,即G 是PB 的中点,且GH =12BC =4. 由已知可得OB =42,PO =PB2-OB2=68-32=6,所以GK =3.故四边形GEFH 的面积S =GH +EF 2·GK =4+82×3=18. 3.如图,直三棱柱ABC -A1B1C1中,D ,E 分别是AB ,BB1的中点.(1)证明:BC1∥平面A1CD ;(2)设AA1=AC =CB =2,AB =22,求三棱锥C -A1DE 的体积. 解析:(1)证明:连接AC1交A1C 于点F ,则F 为AC1中点.又D 是AB 中点,连接DF ,则BC1∥DF.因为DF ⊂平面A1CD ,BC1⊄平面A1CD ,所以BC1∥平面A1CD.(2)因为ABC -A1B1C1是直三棱柱,所以AA1⊥CD.由已知AC =CB ,D 为AB 的中点,所以CD ⊥AB.又AA1∩AB =A ,于是CD ⊥平面ABB1A1.由AA1=AC =CB =2,AB =22得∠ACB =90°,CD =2,A1D =6,DE =3,A1E =3,故A1D2+DE2=A1E2,即DE ⊥A1D.所以V 三棱锥C -A1DE =13×12×6×3×2=1. .。
2025年新人教版高考数学一轮复习讲义 第七章 §7.4 空间直线、平面的平行

2025年新人教版高考数学一轮复习讲义第七章§7.4 空间直线、平面的平行1.理解空间中直线与直线、直线与平面、平面与平面的平行关系,并加以证明.2.掌握直线与平面、平面与平面平行的判定与性质,并会简单应用.第一部分 落实主干知识第二部分 探究核心题型课时精练第一部分落实主干知识1.线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果平面外一条直线与的一条直线平行,那么该直线与此平面平行⇒a∥α______________a⊄αb⊂αa∥b 此平面内文字语言图形语言符号语言性质定理一条直线与一个平面平行,如果过该直线的平面与此平面,那么该直线与交线平行⇒a∥b____________________a∥αa⊂βα∩β=b 相交2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果一个平面内的两条与另一个平面平行,那么这两个平面平行___________________________a⊂βb⊂βa∩b=Pa∥αb∥α⇒β∥α相交直线文字语言图形语言符号语言性质定理两个平面平行,如果另一个平面与这两个平面,那么两条平行⇒a∥b_______________________α∥βα∩γ=aβ∩γ=b相交交线常用结论1.垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.2.平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.3.垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.4.若α∥β,a⊂α,则a∥β.自主诊断1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的两条直线,则这条直线平行于这个平面.( )(2)若直线a 与平面α内无数条直线平行,则a ∥α.( )(3)若直线a ⊂平面α,直线b ⊂平面β,a ∥b ,则α∥β.( )(4)如果两个平面平行,那么分别在这两个平面内的两条直线也相互平行.( )××××2.(多选)下列命题中,正确的是A.平行于同一条直线的两个平面平行B.平行于同一平面的两个平面平行C.平行于同一平面的两直线关系不确定D.两平面平行,一平面内的直线必平行于另一平面√√√对于A,平行于同一条直线的两个平面也可能相交,故A错误;对于B,平行于同一平面的两个平面平行,故B正确;对于C,平行于同一平面的两直线关系不确定,可以平行、相交,也可以异面,故C正确;对于D,根据两个平面平行的性质定理,两平面平行,一平面内的直线必平行于另一平面,故D正确.3.(必修第二册P139T3改编)α,β是两个平面,m,n是两条直线,下列四个命题中正确的是A.若m∥n,n∥α,则m∥αB.若m∥α,n⊂α,则m∥n√C.若α∥β,m⊂α,则m∥βD.若m∥n,m⊂α,n⊂β,则α∥β若m∥n,n∥α,则m∥α或m⊂α,故A不正确;若m∥α,n⊂α,则m∥n或m与n异面,故B不正确;若α∥β,则α与β没有公共点,又因为m⊂α,所以m与β没有公共点,所以m∥β,故C正确;若m∥n,m⊂α,n⊂β,则α∥β或α与β相交,故D不正确.4.如图是长方体被一平面截后得到的几何体,四边形平行四边形EFGH为截面,则四边形EFGH的形状为___________.∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.返回第二部分探究核心题型命题点1 直线与平面平行的判定例1 如图,在四棱锥P -ABCD 中,底面ABCD 为梯形,AB ∥CD , PD =AD =AB =2,CD =4,E 为PC 的中点.题型一 直线与平面平行的判定与性质求证:BE ∥平面P AD .方法一 如图,取PD的中点F,连接EF,F A.又∵AB∥CD,AB=2,CD=4,∴AB綉EF,∴四边形ABEF为平行四边形,∴BE∥AF.又AF⊂平面P AD,BE⊄平面P AD,∴BE∥平面P AD.方法二 如图,延长DA,CB相交于H,连接PH,∵AB∥CD,AB=2,CD=4,即B为HC的中点,又E为PC的中点,∴BE∥PH,又BE⊄平面P AD,PH⊂平面P AD,∴BE∥平面P AD.方法三 如图,取CD 的中点H ,连接BH ,HE ,∵E 为PC 的中点,∴EH ∥PD ,又EH ⊄平面P AD ,PD ⊂平面P AD ,∴EH ∥平面P AD ,又由题意知AB 綉DH ,∴四边形ABHD 为平行四边形,∴BH ∥AD ,又AD ⊂平面P AD ,BH ⊄平面P AD ,∴BH ∥平面P AD ,又BH ∩EH =H ,BH ,EH ⊂平面BHE ,∴平面BHE ∥平面P AD ,又BE ⊂平面BHE ,∴BE ∥平面P AD .例2 如图所示,在四棱锥P-ABCD中,四边形ABCD是平行四边形,M是PC的中点,在DM上取一点G,过G和P A作平面交BD于点H.求证:P A∥GH.如图所示,连接AC交BD于点O,连接OM,∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴P A∥OM,又OM⊂平面BMD,P A⊄平面BMD,∴P A∥平面BMD,又P A⊂平面P AHG,平面P AHG∩平面BMD=GH,∴P A∥GH.思维升华(1)判断或证明线面平行的常用方法①利用线面平行的定义(无公共点).②利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).③利用面面平行的性质(α∥β,a⊂α⇒a∥β).④利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).(2)应用线面平行的性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面确定交线.=2,AD=4,点E,F分别为AD,PC的中点.设平面PDC∩平面PBE=l.证明:(1)DF∥平面PBE;取PB的中点G,连接FG,EG,因为点F为PC的中点,因为四边形ABCD为长方形,所以BC∥AD,且BC=AD,所以DE∥FG,DE=FG,所以四边形DEGF为平行四边形,所以DF∥GE,因为DF⊄平面PBE,GE⊂平面PBE,所以DF∥平面PBE.(2)DF∥l.由(1)知DF∥平面PBE,又DF⊂平面PDC,平面PDC∩平面PBE=l,所以DF∥l.例3 如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形.题型二 平面与平面平行的判定与性质(1)证明:平面A 1BD ∥平面CD 1B 1.由题设知BB 1∥DD 1且BB 1=DD 1,所以四边形BB 1D 1D 是平行四边形,所以BD ∥B 1D 1.又BD ⊄平面CD 1B 1,B 1D 1⊂平面CD 1B 1,所以BD ∥平面CD 1B 1.因为A 1D 1∥B 1C 1∥BC 且A 1D 1=B 1C 1=BC ,所以四边形A 1BCD 1是平行四边形,所以A 1B ∥D 1C .又A 1B ⊄平面CD 1B 1,D 1C ⊂平面CD 1B 1,所以A 1B ∥平面CD 1B 1.又因为BD ∩A 1B =B ,BD ,A 1B ⊂平面A 1BD ,所以平面A 1BD ∥平面CD 1B 1.(2)若平面ABCD∩平面CDB1=l,证明:B1D1∥l.由(1)知平面A1BD∥平面CD1B1,又平面ABCD∩平面CD1B1=l,平面ABCD∩平面A1BD=BD,所以l∥BD,又B1D1∥BD,所以B1D1∥l.思维升华(1)证明面面平行的常用方法①利用面面平行的判定定理.②利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β⇒α∥β).③利用面面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(α∥β,β∥γ⇒α∥γ).(2)当已知两平面平行时,可以得出线面平行,如果要得出线线平行,必须是与第三个平面的交线.跟踪训练2 如图所示,在三棱柱ABC-A1B1C1中,过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合).(1)求证:BC∥GH;∵在三棱柱ABC-A1B1C1中,∴平面ABC∥平面A1B1C1,又∵平面BCHG∩平面ABC=BC,且平面BCHG∩平面A1B1C1=HG,∴由面面平行的性质定理得BC∥GH.平面EF A1∥平面BCHG.∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1綉AB,∴A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又∵A1E∩EF=E,A1E,EF⊂平面EF A1,∴平面EF A1∥平面BCHG.例4 如图所示,四棱锥P -ABCD 的底面是边长为a 的正方形,侧棱PA ⊥底面ABCD ,在侧面PBC 内,有BE ⊥PC 于E ,且BE = ,试在AB 上找一点F ,使EF ∥平面P AD .题型三 平行关系的综合应用如图,在平面PCD内,过点E作EG∥CD交PD于点G,连接AG,在AB上取点F,使AF=EG,因为EG∥CD∥AF,EG=AF,所以四边形FEGA为平行四边形,所以EF∥AG.又AG⊂平面P AD,EF⊄平面P AD,所以EF∥平面P AD.所以点F即为所求的点.又BC⊥AB,P A∩AB=A,所以BC⊥平面P AB.所以PB⊥BC.所以PC2=BC2+PB2=BC2+AB2+P A2.由PB·BC=PC·BE,故点F是AB上靠近B点的一个三等分点.思维升华解决面面平行问题的关键点(1)在解决线面、面面平行的判定时,一般遵循从“线线平行”到“线面平行”,再到“面面平行”;而在应用性质定理时,其顺序恰好相反,但也要注意,转化的方向总是由题目的具体条件而定,绝不可过于“模式化”.(2)解答探索性问题的基本策略是先假设,再严格证明,先猜想再证明是学习和研究的重要思想方法.AB的中点.因为平面ABB1A1∥平面CDD1C1,且平面ABB1A1∩平面PQC=RQ,平面CDD1C1∩平面PQC=PC,所以RQ∥PC,根据空间等角定理可知,PQC,求λ的值.又RQ⊂平面PCQ, BE⊄平面PCQ,则BE∥平面PCQ.又BM∥平面PCQ,BM,BE⊂平面BME,且BM∩BE=B,所以平面BME∥平面PCQ,设DD1∩平面BME=F,连接EF,FM,CDD1C1=FM,平面PCQ∩平面CDD1C1=PC,所以FM∥PC,又CM∥PF,则四边形CPFM为平行四边形,同理四边形PREF也是平行四边形,返回。
2024届高考数学一轮复习+第七章《立体几何与空间向量》第三节+直线、平面平行的判定与性质+课件

文字语言
图形语言
符号语言
判定定理
性质定理
知识拓展1.与两个平面平行有关的结论(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)垂直于同一条直线的两个平面平行,即若 , ,则 .(3)平行于同一个平面的两个平面平行,即若 , ,则 .(4)经过平面外一点有且只有一个平面与已知平面平行.(5)两条直线被三个平行平面所截,截得的对应线段成比例.(6)同一条直线与两个平行平面所成角相等.
证明:①当 , 在同一平面内时,由平面 平面 ,平面 平面 ,平面 平面 ,知 . , .又 , , 平面 .
②当 与 异面时,如图所示,设平面 平面 ,且 .
∵平面 平面 ,平面 平面 , ,∴四边形 是平行四边形.在 上取一点 ,使 ,连接 , , ,则 , , .又 , ,且 , 平面 , , 平面 ,∴平面 平面 .又 平面 , 平面 .
因为 ,即 ,所以 ,所以 .又 平面 , 平面 ,所以 平面 ,又 平面 , , , 平面 ,所以平面 平面 .
角度1 直线与平面平行的判定
例1 (2022全国甲文,19,12分)小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示:底面 是边长为8(单位: )的正方形, , , , 均为正三角形,且它们所在的平面都与平面 垂直.
(1) 证明: 平面 ;
证明:如图所示,将几何体补形为长方体 ,过点 作 ,交 于点 ,过点 作 ,交 于点 ,连接 ,由于底面四边形 为正方形, , 均为正三角形,故 ,由面面垂直的性质可知 , 均与平面 垂直,则
迁移应用
3. 如图,四棱柱 的底面 是正方形.
(1) 证明:平面 平面 ;
2020年高考数学一轮复习人教班理科数学课件第七章 第二节 直线、平面的平行关系

求空间角.
知识点2
空间两直线的位置关系
(1)空间中两直线的位置关系
平行 ____________ 共面直线 相交 ____________ 任何 一个平面内 异面直线:不同在____________
(2)异面直线所成的角 ①定义:设a,b是两条异面直线,经过空间任一点O作直线 a′∥a,b′∥b,把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的 角(或夹角).
不重合的 平面有 公理3:如果两个____________
一个公共点,那么它们有且只有一条 过该点的公共直线
①证明:三点共线,三 线共点. ②确定两相交平面的交 线 证明:线线平行.
同一条直线 的两条直 公理4:平行于____________
线互相平行 定理:空间中如果一个角的两边与另
分别平行 ,那么这 一个角的两边____________
第二节
直线、平面的平行关系
教材细梳理 知识点1 平面的基本性质 语言表述 公理1:如果一条直线上的两点在 作用 证明“点在平面内”或 线在平面内
一个平面内 ,那么这条直线上所有 ____________
的点都在此平面内
公理2:过不在__________________ 的 同一条直线上 三点,有且只有一个平面 推论1:经过一条直线和直线外一点, ①判断两个平面是否重 有且只有一个平面 推论2:经过两条相交直线,有且只有 一个平面 推论3:经过两条平行直线,有且只有 一个平面 合 ②确定一个平面 ③证明点线共面
A.30° C.60°
B.45° D.90°
3.(知识点3)(2018· 浙江卷)已知平面α,直线m,n满足m⊄α ,n⊂ α ,则“m∥n”是“m∥α”的( A ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
2020高考人教数学(理)大一轮复习检测:第七章第二节直线、平面的平行关系

限时规范训练(限时练夯基练提能练)A 级基础夯实练1.给出三个命题:①若两条直线和一个平面所成的角相等,则这两条直线互相平行;②若两条直线与一个平面垂直,则这两条直线互相平行;③若两条直线与一个平面平行,则这两条直线互相平行.其中正确的命题的个数是( )A.0 B.1C.2 D.3解析:选B.若两条直线与同一个平面所成的角相等,则这两条直线与平面的法向量夹角相等,这些直线构成以法向量为轴的某个对顶圆锥.故①错误;两条直线与平面垂直,则这两条直线与平面的法向量平行,则根据公理4,两直线平行,故②正确;两条直线与一个平面平行,这两条直线可能异面、平行或相交.故③错误.2.下列命题中成立的个数是( )①直线I平行于平面a内的无数条直线,则I// a;②若直线I在平面a外,则I / a;③若直线I // b,直线b? a ,则I / a;④若直线I// b,直线b? a ,那么直线I就平行于平面a内的无数条直线.A.1 B.2C.3 D.4解析:选A・直线I平行于平面a内的无数条直线,包括I? a和I// a,故①不成立;直线I在平面a外,包括I与a相交和l//a,故②不成立;直线I // b,直线b? a,包括I? a和I// a,故③不成立;直线I// b,直线b? a ,那么I平行于a内与直线b平行的所有直线,所以直线I就平行于平面a内的无数条直线,故只有④成立.3.有如下三个命题:①分别在两个平面内的两条直线一定是异面直线;②垂直于同一个平面的两条直线是平行直线;③过平面a的一条斜线有一个平面与平面a垂直.其中正确命题的个数为( )A.0 B.1C.2 D.3解析:选C.①分别在两个平面中的两条直线不一定是异面直线,故①错误.②此命题是直线与平面垂直的性质定理,故②正确.③可过斜线与平面a的交点作一条垂直于平面a的直线,则斜线与垂线所确定的平面即与平面a垂直,这样的平面有且只有一个.故③正确.所以②③ 正确.4•设m, n是两条不同的直线,a , B是两个不同的平面,则下列命题正确的是( )A .若m / a n / a,贝U m / nB.若all p, m? a , n? B,贝y m II nC .若aA p= m, n? a ,贝卩n丄pD .若m丄a, m I n, n? p ,则a丄p解析:选D.若m l a, n I a ,则直线m , n可以是平行、相交、异面所以A 不正确.若aI p m? a n? p 贝直线m n 可能是平行或异面所以 B 不正确. C 选项显然不正确.5. (2018枣庄模拟)设a , b为两条不同的直线,a , p为两个不同的平面.贝下列四个命题中正确的是( )A. 若a , b与a所成的角相等,则a l bB. 若a la, b//p alp,贝y a l bC. 若a? a , b? p , a l b,贝U alpD .若a丄a, b丄p, a±p ,贝卩a丄b解析:选D.对于选项A , a , b不一定平行,也可能相交;对于选项B,只需找个平面Y使Y〃alp,且a? 丫, b? 丫即可满足题设, 但a b 不一定平行;对于选项 C 由直三棱柱模型可排除 C.6. 给出下列四个命题:①平面外的一条直线与这个平面最多有一个公共点;②若平面a内的一条直线a与平面p内的一条直线b相交,则a与p 相交;③若一条直线和两条平行线都相交贝这三条直线共面;④若三条直线交于同一点贝这三条直线共面.其中真命题的序号是________ .解析:①正确,因为直线在平面外,即直线与平面相交或直线平行于平面,所以最多有一个公共点.②正确,a,b 有交点,则两平面有公共点,则两平面相交. ③正确,两平行直线可确定一个平面,又直线与两平行直线的两交点在这两平行直线上,所以过这两交点的直线也在平面内,即三线共面.④错误,这三条直线可以交于同一点,但不在同一平面内.答案:①②③7. ______________________________________________ ( 201 8青岛模拟)将一个真命题中的“平面”换成“直线”“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”.给出下列四个命题:①垂直于同一平面的两直线平行;②垂直于同一平面的两平面平行;③平行于同一直线的两直线平行;④平行于同一平面的两直线平行.其中是“可换命题”的是 _______________________________________ .(填命题的序号)解析:由线面垂直的性质定理可知①是真命题,且垂直于同一直线的两平面平行也是真命题,故①是“可换命题”;因为垂直于同一平面的两平面可能平行或相交,所以②是假命题,不是“可换命题”;由公理4可知③是真命题,且平行于同一平面的两平面平行也是真命题,故③是“可换命题”;因为平行于同一平面的两条直线可能平行、相交或异面,故④是假命题,故④不是“可换命题”.答案:①③8•如图,平面a//平面B//平面Y两条直线a, b分别与平面 a B , 丫相交于点A, B , C 禾口点D, E, F.已知AB= 2 cm, DE = 4 cm, EF = 3 cm,贝S AC 的长为______________ cm.解析:因为平面a//平面B//平面Y 两条直线a , b 分别与平面 a, B, 丫相交于点A , B , C 和点D , E , F ,连接AD , BE , CF (图 略). 所以 AD // BE // CF , 因为 AB = 2 cm, DE = 4 cm, EF = 3 cm,2 4 3所以BC = 3解得BC = 2 cm ,所以 AC =AB + BC = 2+2 = 2(cm ).答案:79•如图,在三棱锥 S-ABC 中,平面SAB 丄平面SBC , AB 丄BC , AS = AB ,过点A 作AF 丄SB,垂足为F ,点E , G 分别是棱SA , SC 的中点.求证:(1)平面EFG //平面ABC.(2)BC 丄 SA.所以 AB BC =DE EF ,证明:(1)因为AS= AB, AF丄SB,垂足为F,所以F是SB的中点.又因为E是SA的中点,所以EF // AB.因为EF?平面ABC, AB?平面ABC,所以EF //平面ABC.同理EG //平面ABC.又因为EF A EG = E,所以平面EFG //平面ABC.(2)因为平面SAB丄平面SBC,且交线为SB,又因为AF?平面SAB, AF丄SB,所以AF丄平面SBC,因为BC?平面SBC,所以AF丄BC.又因为AB丄BC, AF AAB= A, AF?平面SAB, AB?平面SAB, 所以BC丄平面SAB.又因为SA?平面SAB,所以BC丄SA.10•如图,在四棱锥P-ABCD中,底面ABCD是菱形,/ DAB = 60°, PD丄平面ABCD, PD = AD = 1,点E, F分别为AB和PC的中点,连接EF , BF.(1) 求证:直线EF //平面PAD.(2) 求三棱锥F-PEB的体积.解:⑴如图,作FM // CD交PD于点M,连接AM.1因为点F为PC中点,所以FM = 2CD.1因为点E为AB的中点,所以AE = 2AB= FM.又AE // FM,所以四边形AEFM为平行四边形,又EF ?平面PAD, AM?平面PAD•所以EF // AM.所以直线EF //平面PAD.1(2)连接EC.已知/ DAB= 60°,AE = Q, AD = 1,由余弦定理,得DE丄AB,A E R又AB// DC,贝 S DE 丄DC,设F到平面BEC的距离为h.1因为点F为PC的中点,所以h= QPD.从而有V F - PBE = V P- BEF = V p- BEC —V F- BEC1 1 1=3SZ BEC •PD —h)= 3S佗EC 'Q PD48.B 级能力提升练11.如图,在四棱锥P-ABCD 中,四边形 ABCD 为 平行四边形,E 为AD 的中点,F 为PC 上一点,当PA // 平面EBF 时, 九2 解析:选D.如图,连接AC 交BE 于G ,连接 FG ,因为 PA //平面 EBF , PA ?平面 PAC ,平面又AD / BC , E 为AD 的中点,所以BC = £所以FCC = * 12.如图,在棱长为1的正方体ABCD-A i B i C i D i 中, 点E , F 分别是棱BC , CC 1的中点,P 是侧面BCC 1B 1 内一点,若A 1P //平面AEF ,则线段A 1P 长度的取值范 围是( )B. TPD . [ 2, 3]解析:选B.取B 1C 1的中点M , BB 1的中点N ,连接A 1M , A 1N , MN ,可以证明平面 AMN //平面AEF ,所以点P 位于线段MN 上, B . PAC A 平面 BEF FG,所以PA// FG ,所以 PF FC _ AG =GC . A. 1,d 2 y[5 (1 2 1 2 气[2因为A i M = A1N 1 + 2' =2,MN 2丿+ 2 =2,所以当点P位于M, N处时,A i P的长度最长,当P位于MN的中点0时,A i P的长度最短,此时A i O =寸惨j —乎/=所以A i O < A i P< A i M,即3J2< A i P W^,所以线段A i P长度的取值范围是选B.D Q cAt M &i3•如图,ABCD- A i B i C i D i是棱长为a的正方体,M, N分别是a棱A i B i, B i C i的中点,P是棱AD上一点,AP=3,过P, M , N的平面交上底面于PQ, Q在CD上,贝S PQ=(A.C.解析:选A・因为ABCD-A i B i C i D i是棱长为a的正方体,所以平面ABCD //平面A i B i C i D i,又P是棱AD上一点,过P, M , N的平面交上底面于PQ, Q在CD上,所以MN // PQ,又M , N分别是棱A iB i, B iC i的中点,AP = 3所以CQ=3所以DP = DQ =号,所以PQ = DP 2 + DQ 2 = 232a.解析:如图,取CD 的中点E.连接AE , BE ,由于M , N 分别是△ ACD ,伯CD 的重心,所以 AE , BE 分别过 M ,N ,贝卩 EM : MA = 1 : 2, EN : BN = 1 : 2,所以MN // AB •因为AB ?平面 ABD , MN ?平面ABD , AB ?平面 ABC , MN ?平面 ABC ,所以 MN // 平面 ABD , MN //平面 ABC.答案:平面ABD 与平面ABC15•如图,在正四棱柱ABCD-A 1B 1C 1D 1中,E , F , G , H 分别是棱CC 1, C 1D 1, DQ , DC 的中点,N 是BC 的 中点,点M 在四边形EFGH 上及其内部运动,贝S M 只 需满足条件 时,就有MN //平面B 1BDD 1(注:填 上你认为正确的一个条件即可).解析:连接 HN , FH , FN ,贝S FH // DD 1 , HN //BD ,二平面 FHN // 平面B 1BDD 1 ,当M € FH 时,MN ?平面FHN ,此时MN //平面 B 1BDD 仆答案:点M 在线段FH 上(包含端点)14•在四面体ABCD 中, 则四面体的四个面中与MNM , N 分别是△ ACD , △ BCD 的重心,平行的是 ________ . 3 F G16•如图,平面五边形ABCDE中,AB// CE,且AE = 2,/ AEC5=60°, CD = ED = 7, cosZ EDC = 7.将厶CDE 沿CE 折起,使点D到P的位置,且AP= 3,得到四棱锥P-ABCE・(1) 求证:AP I平面ABCE;(2) 记平面PAB与平面PCE相交于直线I,求证:AB//I.5 解:(1)在厶CDE 中,T CD = ED = . 7, cos/EDC = 7,由余弦定理得CE = 2•连接AC,vAE = 2,ZAEC = 60°, A C = 2.又AP= 3, •••在、PAE 中,PA2+ AE2= PE2, 即卩AP I AE.同理AP I AC.而AC? 平面ABCE, AE?平面ABCE, AC A AE = A,故AP 丄平面ABCE.(2) v AB// CE,且CE ?平面PCE, AB?平面PCE,• AB //平面PCE.又平面PAB A平面PCE = I,A AB//I.C级素养加强练17.(2018山西太原质检)如图,四边形ABCD中,AB丄AD, AD // BC, AD = 6, BC= 2AB= 4, E, F 分别在BC, AD 上, EF // AB, 现将四边形ABEF沿EF折起,使BE丄EC.(1)若BE= 1,在折叠后的线段AD上是否存在一点P,使得CP//平面ABEF ?若存在,求出pD的值;若不存在,说明理由;(2)求三棱锥A-CDF的体积的最大值,并求出此时点F至U平面ACD 的距离.解:⑴线段AD上存在一点P,使得CP//平面ABEF , “AP 3此时PD = 2.理由如下:当AP=3时AP=3当PD 2时,AD 5,过点P作PM // FD交AF于点M,连接EM ,由题意可得FD = 5,小亠MP AP 3 则有FD =AD =5,故MP = 3,由题意可得EC = 3,又MP // FD // EC, •••MP 綊EC,故四边形MPCE为平行四边形,•••CP//ME ,又T CP?平面ABEF , ME ?平面ABEF ,•••CP//平面ABEF成立.(2)设BE = x(0v x< 4),「•AF = x, FD = 6 —x,由题意可得EC丄EF,又BE丄EC, BE AEF = E,「EB丄平面ECDF ,VAF //BE,「AF 丄平面ECDF ・11 1 2故V A-CDF = 3X2X2X (6—x)x x= 3( —x2+ 6x),「当x= 3 时,V A CDF有最大值,且最大值为3,此时EC = 1, AF = 3, FD = 3, DC = 2 2, AD = 3 2, AC= 14,在厶ACD中,由余弦定理得AD2+ DC2—AC218+ 8—14 j cosZADC2AD DC =2X 3 2X 2 2=2、x/3「sinZADC =云,1「•S^DC = 2 DC DA s inZADC = 3 . 3,设点F到平面ACD的距离为h,由于V A-CDF = V F -ACD ,亦 1即3= 3 h S AACD ,•••h= .3,即点F到平面ACD的距离为.3.。
高考数学大一轮复习(备考基础查清+热点命题悟通)第七章 第二节 直线、平面平行的判定与性质配套课件
[类题通法] 判断面面平行的常用方法
(1)利用面面平行的判定定理; (2)面面平行的传递性(α∥β,β∥γ⇒α∥γ); (3)利用线面垂直的性质(l⊥α,l⊥β⇒α∥β).
第二十五页,共35页。
[针对训练] 如图,在直四棱柱 ABCD -A1B1C1D1 中,底面是正方形,E,F, G 分别是棱 B1B,D1D,DA 的中点.求证:
第四页,共35页。
[试一试] 1.下列说法中正确的是________(填序号).
①一条直线如果和一个平面平行,它就和这个平面内的无 数条直线平行;②一条直线和一个平面平行,它就和这个 平面内的任何直线无公共点;③过直线外一点,有且仅有 一个平面和已知直线平行;④如果直线 l 和平面 α 平行, 那么过平面 α 内一点和直线 l 平行的直线在 α 内. 解析:由线面平行的性质定理知①④正确;由直线与平面 平行的定义知②正确;③错误,因为经过一点可作一直线 与已知直线平行,而经过这条直线可作无数个平面. 答案:①②④
⇒l∥α
l⊄α
文字语言
图形(túxíng)语言
符号语言
一条直线与一个(yī ɡè)
性质 平面平行,则过这条
(xìngz
直线的任一平面与此
交线
hì)定 平面的 与该直线
理 平行(简记为“线面平
行⇒线线平行”)
l∥α l⊂β
⇒l∥b
α∩β=b
第二页,共35页。
2.平面与平面平行的判定定理和性质定理
第十二页,共35页。
[类题通法] 解决有关线面平行、面面平行的基本问题要注意
(1)判定定理与性质定理中易忽视的条件,如线面平行的 判定定理中条件线在面外易忽视.
(2)结合题意构造或绘制图形,结合图形作出判断. (3)举反例否定结论或用反证法推断命题是否正确.
高考人教数学(理)大一轮复习检测:第七章第三节 直线、平面的垂直关系Word版含解析

限时规范训练(限时练·夯基练·提能练)A级基础夯实练1.(·定州模拟)已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则()A.m∥l B.m∥nC.n⊥l D.m⊥n解析:选C.因为α∩β=l,所以l⊂β,又n⊥β,所以n⊥l.故选C.2.(·郑州测试)已知两条不重合的直线m,n和两个不重合的平面α,β,m⊥α,n⊂β.给出下列四个命题:①若α∥β,则m⊥n;②若m⊥n,则α∥β;③若m∥n,则α⊥β;④若α⊥β,则m∥n.其中正确命题的个数是()A.0 B.1C.2 D.3解析:选C.依题意,对于①,由“若一条直线与两个平行平面中的一个垂直,则该直线也垂直于另一个平面”得知,m⊥β,又n⊂β,因此m⊥n,①正确;对于②,当α⊥β时,设α∩β=n,在平面β内作直线m⊥n,则有m⊥α,因此②不正确;对于③,由m∥n,m⊥α得n⊥α,又n⊂β,因此有α⊥β,③正确;对于④,当m⊥α,α∩β=n,α⊥β时,直线m,n不平行,因此④不正确.综上所述,正确命题的个数为2,故选C.3.(·兰州重点中学联考)如图,四棱锥PABCD的底面是边长为1的正方形,侧棱PA=1,PB=PD=2,则它的五个面中,互相垂直的面共有()A.3对B.4对C.5对D.6对解析:选C.因为AB=AD=AP=1,PB=PD=2,所以AB2+AP2=PB2,PA2+AD2=PD2,则PA⊥AB,PA⊥AD,可得PA⊥底面ABCD,又PA⊂平面PAB,PA⊂平面PAD,所以平面PAB⊥平面ABCD,平面PAD⊥平面ABCD.又AB⊥AD,AD∩PA=A,所以AB⊥平面PAD,所以平面PAB⊥平面PAD.又BC⊥AB,BC⊥PA,AB∩PA=A,所以BC⊥平面PAB,所以平面PAB⊥平面PBC.又CD⊥AD,CD⊥AP,AD∩AP=A,所以CD⊥平面PAD,所以平面PAD⊥平面PCD.故选C.4.(·南阳模拟)已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是()A.AB∥m B.AC⊥mC.AB∥βD.AC⊥β解析:选D.因为直线m∥α,m∥β,α∩β=l,所以m∥l,所以AB∥m正确,AC⊥m正确;根据线面平行的判定定理可得AB∥β正确;当直线AC不在平面α内时,尽管AC⊥l,AC与平面β可以平行,也可以相交(不垂直),所以AC⊥β不一定成立.故选D.5.已知平面α与平面β相交,直线m⊥α,则()A.β内必存在直线与m平行,且存在直线与m垂直B.β内不一定存在直线与m平行,不一定存在直线与m垂直C.β内不一定存在直线与m平行,但必存在直线与m垂直D.β内必存在直线与m平行,不一定存在直线与m垂直解析:选C.如图,设平面α与平面β的交线为a,若在平面β内的直线与α,β的交线a平行,则该直线与m垂直.但β内不一定存在直线与m平行,只有当α⊥β时才存在.故选C.6.(·丽水模拟)如图,在四棱锥PABCD中,PA⊥底面ABCD且底面各边都相等,M是PC上一点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可)解析:如图,连接AC,因为PA⊥底面ABCD,所以PA⊥BD,因为四边形ABCD的各边相等,所以AC⊥BD,又PA∩AC=A,所以BD⊥平面PAC,所以BD⊥PC,要使平面MBD⊥平面PCD,只需PC垂直于平面MBD内与BD相交的直线即可,所以可填DM⊥PC(或BM⊥PC).答案:DM⊥PC(或BM⊥PC)7.若圆锥的侧面积是底面积的3倍,则其母线与底面夹角的余弦值为________.解析:设圆锥的底面半径为r,母线长为l,由题意πrl=3πr2,即l=3r,母线与底面夹角为θ,则cos θ=rl=13.答案:1 38.(·南宁模拟)如图,在正方形ABCD中,AC为对角线,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H.则下列说法错误的是________.(将符合题意的序号填到横线上)①AG⊥△EFH所在平面;②AH⊥△EFH所在平面;③HF⊥△AEF所在平面;④HG⊥△AEF所在平面.解析:根据折叠前AB⊥BE,AD⊥DF可得折叠后AH⊥HE,AH⊥HF,∴AH⊥平面EFH,即②正确;∵过点A只有一条直线与平面EFH垂直,∴①不正确;∵AG⊥EF,AH⊥EF,∴EF⊥平面HAG,∴平面HAG⊥平面AEF.过H作直线垂直于平面AEF,该直线一定在平面HAG内,∴③不正确;∵HG不垂直于AG,∴HG⊥平面AEF不正确,∴④不正确.综上,说法错误的是①③④.答案:①③④9.(·福建三明一中月考)如图,在四棱锥ABCD中,平面ABC⊥平面BCD,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(1)求证:EF⊥平面BCG;(2)求三棱锥DBCG的体积.解:(1)证明:由已知得,△ABC≌△DBC,因此AC=DC,因为G为AD的中点,所以CG⊥AD.同理BG ⊥AD ,又CG ∩BG =G ,CG ,BG ⊂平面BCG ,所以AD ⊥平面BCG ,由题意,EF 为△DAC 的中位线,所以EF ∥AD ,所以EF ⊥平面BCG .(2)在平面ABC 内作AO ⊥CB ,交CB 的延长线于O (图略), 因为平面ABC ⊥平面BCD ,平面ABC ∩平面BCD =BC ,所以AO ⊥平面BCD ,又G 为AD 的中点,所以G 到平面BCD 的距离h =12AO =12AB sin 60°=32, 又S △BCD =12BD ·BC ·sin 120°=3, 所以V D BCG =V G BCD =13S △BCD ×h =13×3×32=12.10.如图,在几何体ABC A 1B 1C 1中,点A 1,B 1,C 1在平面ABC 内的正投影分别为A ,B ,C ,且AB ⊥BC ,E 为AB 1的中点,AB =AA 1=BB 1=2CC 1.(1)求证:CE ∥平面A 1B 1C 1;(2)求证:平面AB 1C 1⊥平面A 1BC .证明:(1)由题意知AA 1⊥平面ABC ,BB 1⊥平面ABC ,CC 1⊥平面ABC ,∴AA 1∥BB 1∥CC 1.如图,取A 1B 1的中点F ,连接EF ,FC 1.∵E 为AB 1的中点,∴EF 綊12A 1A ,又AA 1=2CC 1,∴CC 1綊12AA 1,∴EF 綊CC 1,∴四边形EFC 1C 为平行四边形,∴CE ∥C 1F .又CE ⊄平面A 1B 1C 1,C 1F ⊂平面A 1B 1C 1,∴CE ∥平面A 1B 1C 1.(2)∵BB 1⊥平面ABC ,∴BB 1⊥BC .又AB ⊥BC ,AB ∩BB 1=B ,∴BC ⊥平面AA 1B 1B .∵AB 1⊂平面AA 1B 1B ,∴BC ⊥AB 1.∵AA 1=BB 1=AB ,AA 1∥BB 1,∴四边形AA 1B 1B 为正方形,∴AB 1⊥A 1B .∵A 1B ∩BC =B ,∴AB 1⊥平面A 1BC .∵AB 1⊂平面AB 1C 1,∴平面AB 1C 1⊥平面A 1BC .B 级 能力提升练11.直三棱柱ABC A 1B 1C 1中,侧棱长为2,AC =BC=1,∠ACB =90°,D 是A 1B 1的中点,F 是BB 1上的动点,AB 1,DF 相交于点E .要使AB 1⊥平面C 1DF ,则线段B 1F 的长为( )A.12 B .1C.32 D .2解析:选A.设B 1F =x ,因为AB 1⊥平面C 1DF ,DF ⊂平面C 1DF ,所以AB 1⊥DF .由已知可得A 1B 1=2, 设Rt △AA 1B 1斜边AB 1上的高为h ,则DE =12h . 又2×2=h 22+(2)2,所以h =233,DE =33. 在Rt △DB 1E 中,B 1E =⎝ ⎛⎭⎪⎫222-⎝ ⎛⎭⎪⎫332=66. 由面积相等得66× x 2+⎝ ⎛⎭⎪⎫222=22x ,得x =12.12.已知正方体ABCD A 1B 1C 1D 1中,点E ,F ,G 分别是线段DC ,D 1D 和D 1B 上的动点,给出下列结论①对于任意给定的点E ,存在点F ,使得AF ⊥A 1E ;②对于任意给定的点F ,存在点E ,使得AF ⊥A 1E ;③对于任意给定的点G ,存在点F ,使得AF ⊥B 1G ;④对于任意给定的点F ,存在点G ,使得AF ⊥B 1G .其中正确结论的个数是( )A .0B .1C .2D .3解析:选C.由DE ⊥平面A 1D ,根据三垂线定理,①对于任意给定的点E ,A 1E 在平面A 1D 的射影为A 1D ,所以存在点F ,使得AF⊥A1E,所以①正确;②如果对于任意给定的点F,存在点E,使得AF⊥A1E,那么,由A1D⊥AD1,可知过A有两条直线与A1D垂直,故②错误;③只有AF垂直B1G在平面AD1的射影时,AF⊥B1G,故③正确;④只有AF⊥平面BB1D1D时,④才正确,AF与平面BB1D1D不垂直,故④错误.13.(·郴州模拟)如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M,O分别为线段A1C,DE的中点,则在△ADE翻转过程中,下列说法错误的是() A.与平面A1DE垂直的直线必与直线BM垂直B.异面直线BM与A1E所成角是定值C.一定存在某个位置,使DE⊥MOD.三棱锥A1ADE外接球半径与棱AD的长之比为定值解析:选C.取CD的中点F,连接BF,MF,如图1,可知平面MBF∥平面A1DE,所以BM∥平面A1DE,A正确.取A1D中点G,可得EG∥BM,如图2,所以B正确.由题意可得点A关于直线DE 的对称点为F,则DE⊥平面A1AF,即过O与DE垂直的直线在平面A1AF内,而M不在平面A1AF内,故C错误.三棱锥A1ADE外接球的球心即为O点,所以外接球半径为22AD,故D正确.14.(·石家庄一模)已知一个直角三角形的三个顶点分别在底面边长为2的正三棱柱的侧棱上,则该直角三角形斜边的最小值为________.解析:记该直角三角形为△ABC,且AC为斜边.不妨令点A与正三棱柱的一个顶点重合,如图,取AC的中点O,连接BO,∴BO=12AC,∴当AC取得最小值时,BO取得最小值,即点B到平面ADEF的距离.∵△AHD是边长为2的正三角形,∴点B到平面ADEF的距离为3,∴AC的最小值为2 3.答案:2315.已知三棱锥SABC的底面是以AB为斜边的等腰直角三角形,AB=2,SA=SB=SC=2,则三棱锥的外接球的球心到平面ABC的距离是________.解析:因为三棱锥SABC的底面是以AB为斜边的等腰直角三角形,SA=SB=SC=2,∴S在平面ABC内的射影为AB中点,记为H,连接CH,SH,∴SH⊥平面ABC,∴SH上任意一点到A,B,C的距离相等,∴三棱锥的外接球的球心在线段SH上,记为O,连接OC,设外接球的半径为R,则SO=OC=R=3-OH,在△OCH中,由OH2+HC2=OC2,得OH2=(3-OH)2-12,得OH=3 3,故外接球的球心到平面ABC的距离是3 3.答案:3 316.如图,三棱柱ABCA1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=CC1=2,M是AB的中点.(1)求证:平面A1CM⊥平面ABB1A1;(2)求点M到平面A1CB1的距离.解:(1)证明:由A1A⊥平面ABC,CM⊂平面ABC,得A1A⊥CM.由AC=CB,M是AB的中点,得AB⊥CM.又A1A∩AB=A,则CM⊥平面ABB1A1,又CM⊂平面A1CM,所以平面A1CM⊥平面ABB1A1.(2)设点M到平面A1CB1的距离为h.连接MB1.由题意可知A1C=CB1=A1B1=2MC=22,A1M=B1M=6,则S△A1CB1=23,S△A1MB1=2 2.由(1)可知CM⊥平面ABB1A1,则CM是三棱锥CA1MB1的高,由VCA1MB1=13M M C·S△A1MB1=VMA1CB1=13M h·S△A1CB1,得h=2×2223=233,即点M到平面A1CB1的距离为23 3.C级素养加强练17.(·安徽淮北一中模拟)如图,四棱锥PABCD 的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.(1)求证:AF∥平面PEC;(2)求证:平面PEC⊥平面PCD.证明:(1)取PC的中点G,连接FG、EG,∵F为PD的中点,G为PC的中点,∴FG为△CDP的中位线,∴FG∥CD,FG=12CD.∵四边形ABCD为矩形,E为AB的中点,∴AE∥CD,AE=1 2CD.∴FG=AE,FG∥AE,∴四边形AEGF是平行四边形,∴AF∥EG,又EG⊂平面PEC,AF⊄平面PEC,∴AF∥平面PEC.(2)∵PA=AD,F为PD中点,∴AF⊥PD,∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD,又∵CD⊥AD,AD∩PA=A,∴CD⊥平面PAD,∵AF⊂平面PAD,∴CD⊥AF,又PD∩CD=D,∴AF⊥平面PCD,由(1)知EG∥AF,∴EG⊥平面PCD,又EG⊂平面PEC,∴平面PEC⊥平面PCD.18.(·四川泸州模拟)如图,在四棱锥SABCD中,底面ABCD是梯形,AB∥DC,∠ABC=90°,AD=SD,BC=CD=12AB,侧面SAD⊥底面ABCD.(1)求证:平面SBD⊥平面SAD;(2)若∠SDA=120°,且三棱锥SBCD的体积为612,求侧面△SAB的面积.解:(1)证明:设BC=a,则CD=a,AB=2a,由题意知△BCD 是等腰直角三角形,且∠BCD=90°,则BD=2a,∠CBD=45°,所以∠ABD=∠ABC-∠CBD=45°,在△ABD中,AD=AB2+DB2-2AB·DB·cos 45°=2a,因为AD2+BD2=4a2=AB2,所以BD⊥AD,由于平面SAD⊥底面ABCD,M平面SAD∩平面ABCD=AD,BD⊂平面ABCD,所以BD⊥平面SAD,又BD⊂平面SBD,所以平面SBD⊥平面SAD.(2)由(1)可知AD=SD=2a,在△SAD中,∠SDA=120°,SA =2SD sin 60°=6a,作SH⊥AD,交AD的延长线于点H,则SH=SD sin 60°=62a,由(1)知BD⊥平面SAD,因为SH⊂平面SAD,所以BD⊥SH,又AD∩BD=D,所以SH⊥平面ABCD,所以SH为三棱锥SBCD的高,所以V SBCD=13×62a×12×a2=612,解得a=1,由BD⊥平面SAD,SD⊂平面SAD,可得BD⊥SD,则SB=SD2+BD2=2+2=2,又AB=2,SA=6,在等腰三角形SBA中,边SA上的高为4-64=102,则△SAB的面积为12×6×102=152.。
2019-2020年高考数学大一轮复习第七章立体几何课时跟踪检测四十一直线平面平行的判定及其性质练习

2019-2020年高考数学大一轮复习第七章立体几何课时跟踪检测四^一直 线平面平行的判定及其性质练习文一抓基础,多练小题做到眼疾手快1 •已知直线a 与直线b 平行,直线a 与平面a 平行,则直线b 与a 的关系为()A. 平行B.相交C.直线b 在平面a 内D.平行或直线 b 在平面a 内解析:选D 依题意,直线a 必与平面a 内的某直线平行,又 a // b ,因此直线b 与平面a 的位置关系是平行或直线 b 在平面a 内.2. (xx •合肥模拟)在空间四边形 ABCDK E , F 分别是AB 和BC 上的点,若 AE : EB= CF : FB= 1 : 2,则对角线 AC 和平面DEF 勺位置关系是()A.平行B.相交C.在平面内D.不能确定过B 点的所有直线中( )A. 不一定存在与a 平行的直线B. 只有两条与a 平行的直线C. 存在无数条与a 平行的直线D. 存在唯一与a 平行的直线CD= 1,则 AB= ________解析:••• a// CD// AB…PC CD _ PAX CD 5X1 则 PA = AB : AB=W答案:5解析:选A AE CF如图,由甘韵得AC/ EF.又因为EF ? EB FB平面DEF AC ?平面 DEF 所以AC//平面 DEF3.若平面 a //平面3,直线a//平面a ,点B€ 3 ,则在平面 3内且 解析:选A 当直线a 在平面 3内且过B 点时,不存在与 a 平行的直线,故选 A . 4.如图,a / 3 ,△ PAB 所在的平面与 a , 3 分别交于 CD AB 若 PC= 2, CA= 3, A C5•如图所示,在四面体ABC即,点M N分别是△ ACD △ BCD勺重心,则四面体的四个面中与MN平行的是_____________ •解析:连接AM并延长,交CD于点E,连接BN并延长交CD于点F,由重心性质可知,E, F重合为一点,且该点为CD的中点E,连接MN由器EN// AB.因此,MIN/平面ABC且MIN/平面ABD答案:平面ABC平面ABD—保咼考,全练题型做到咼考达标1.在空间中,已知直线a, b,平面a,则以下三个命题:①若a / b, b? a ,贝U a / a ;②若a / b, a/ a ,贝U b/ a ;③若a/ a , b/ a,贝U a // b.其中真命题的个数是()A. 0C. 2D. 3解析:选A对于①,若a / b, b? a ,则应有a/ a或a? a ,所以①是假命题;对于②,若a / b a / a ,则应有b / a或b? a ,因此②是假命题;对于③,若a / a , b / a ,则应有a/ b或a与b相交或a与b异面,因此③是假命题.综上,在空间中,以上三个命题都是假命题.2.设m, n是平面a内的两条不同直线,I 1, I 2是平面3内的两条相交直线.则a //3的一个充分而不必要条件是()A. m// 3 且I 1 / a B.m//I 1 且n / 12C. m// 3 且n / 3D.m//3 且n / 12解析:选B因为m/ I i,且n / 12,又11与12是平面3内的两条相交直线,所以 a / 3,而当a / 3时不一定推出m//1 i且n / 12,可能异面.所以a / 3的一个充分而不必要条件是B.3.下列四个正方体图形中,A, B为正方体的两个顶点,M N, P分别为其所在棱的中点,能得出AB//平面MNP勺图形的序号是()B. 1.4 M①,\ 1③④A.①③B.②③C.①④D.②④解析:选C 对于图形①,平面MNPf AB所在的对角面平行,即可得到AB//平面MNR对于图形④,AB// PN即可得到AB//平面MNP图形②③无论用定义还是判定定理都无法证明线面平行.4•如图,透明塑料制成的长方体容器ABCDABCD内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:①没有水的部分始终呈棱柱形;②水面EFGH所在四边形的面积为定值;③棱AiD始终与水面所在平面平行;④当容器倾斜如图所示时,BE- BF是定值.其中正确命题的个数是()A. 1B. 2C. 3D. 4解析:选C由题图,显然①是正确的,②是错误的;对于③,••• A i D// BC BC// FG••• AD// FG且AD?平面EFGH••• AD//平面EFGH水面)••③是正确的;对于④,•••水是定量的(定体积V),1• &BEF- BC= V,即一BE- BF- BC= V2解析:选A 取AC 的中点G,连接SG BG易知 SGL AC BGL AC故ACL 平面SGB 所以ACL SB因为SB//平面 DEFH SB?平面SAB 平面SABH 平面DEFH + HD 贝U SB// HD 同理SB// FE1又D, E 分别为AB BC 的中点,贝U H F 也为AS SC 的中点,从而得 HF 綊^AC 綊DE所以四边形DEFH^平行四边形.又 AC L SB SB// HD DE// AC所以DEL HD 所以四边形 DEFF 为矩形,1 145其面积 S = HF- HD= 2AC- 2SB=—.6. 设a , 3 , Y 是三个平面,a , b 是两条不同直线,有下列三个条件: ① a //丫,b ? 3;② a //丫,b //3;③ b , a ? 丫.如果命题“ aQ3= a , b ? Y ,且 _________________ ,则a // b ”为真命题,则可以在横线处填入的条件是 ________ (把所有正确的序号填上).解析:由面面平行的性质定理可知,①正确;当 b //3, a ? 丫时,a 和b 在同一平面 内,且没有公共点,所以平行,③正确.故应填入的条件为①或③.答案:①或③7. 正方体 ABCD-A B C D 的棱长为1 cm ,过AC 作平行于对角线 BD 的截面,则截面面积为 ________ cm .解析:如图所示,截面ACE/ BD ,平面BDE T 平面ACE= EF ,其中F 为AC 与 BD 的交点, ••• E 为DD 的中点,• BE- BF = 2V品定值) ,即④是正确的,故选 C.5.在三棱锥 S -ABC 中, △ ABC 是边长为6的正三角形,SA= SB=SC= 15,平面 DEFH >别与 AB BC SC SA 交于 D, E, F , H,且 D, E分别是 AB BC 的中点,如果直线 SB//平面DEFH 那么四边形 DEFH 勺 面积为() A. 452B . 45, 3 2 C. 45 D. 45 ,3 cDE&如图,在直三棱柱ABCABG中,若BC丄AC, / BAG=nL, AC=34, M为AA的中点,点P为BM的中点,Q在线段CA上,且A i Q= 3QC 则PQ的长度为___________ .解析:由题意知,AB= 8,过点P作PD// AB交AA于点D,连接DQ1则D为AM中点,PD= 2AB= 4.AQ AD又 QC AD= 3,n3•••DQ/ AC / PDQ —, DQ=-AC= 3,3 4在厶PDC中,PQ= 42+ 32—2X 4X 3X cos ;=13.答案:139. (xx •长春质检)如图,在四棱锥P-ABCD^,底面ABCD1菱形,PDL平面ABCD点D为棱PD的中点,过D作与平面ABCD平行的平面与棱PA PB /p\c, PC相交于点A,B , C1,/ BAD= 60°.j | 胃入(1) 求证:B为PB的中点;賁盘*(2) 已知棱锥的高为3,且AB= 2, AC BD的交点为O,连接B0.求三棱4」锥B-ABO外接球的体积.解:(1)证明:连接BD.由题意知,平面ABCD平面ABCD,平面PBDn平面ABC= BD 平面PBDH平面ABCDi= BD,贝U BD/ BD,即BD PBD的中位线,即B为PB的中点.⑵由(1)可得,OB= |, AO=W, BO= 1,且OAL OB OAL OB, OB丄OB,即三棱锥B-ABO的外接球为以OA OB 0B为长,宽,高的长方体的外接球,则该长方体的体对角线长d= 即外接球半径•/ AB// CD4 4 '5^ 125 n则三棱锥B-ABC外接球的体积V=㊁冗R= 3X n X 14 3= 4810.如图所示,在正方体ABCDABGD中,CC, CD , AA的中点.求证:(1) BF// HD;(2) EG/平面BBDD(3) 平面BDF// 平面B i DH.证明:(1)如图所示,取BB的中点M连接MH MC,易证四边形HMGD是平行四边形,••• HD// MC.又••• MC// BF,「. BF// HD.1 1⑵取BD的中点O 连接EO DO,贝U OE綊-DC又DG綊2°C •- OE綊DG,•四边形OEG{是平行四边形,• GE/ DO又GE>平面BBDD, DC?平面BBD D,• EG/平面BBD D.(3)由(1 )知BF// HD,又BD/ B D , B D , HD?平面B D H, BF, BD?平面BDF 且B1 D A HD= D , DBH BF= B,•平面BDF//平面B DH.三上台阶,自主选做志在冲刺名校1•如图所示,设正方体ABCDA B CD的棱长为a,点P是棱aAD上一点,且AF= 3,过B , D , P的平面交平面ABCDF PQ Q在直线CD±,则FQ= _________ .解析:•••平面ABCD //平面ABCD而平面B D F A平面ABCD=FQ 平面B D P A平面A B C D = B1 D ,• BD// PQ又••• B D // BD • BD/ PQ设PC T AB= M•••晰AP= 2,即PQ= 2PM又知△ APMb^ ADB•PM AP 1•BD T A D=3,• PM= ^BD 又BD=后, 32•如图,四棱锥P-ABCDK AB// CD AB= 2CD E为PB的中点.⑴求证:CE//平面PAD(2)在线段AB上是否存在一点F,使得平面PAD/平面CEF若存在, 证明你的结论,若不存在,请说明理由.解:⑴证明:取PA的中点H,连接EH DH因为E为PB的中点,1所以EH/ AB, EH= ?AB1又AB// CD CD= 2AB所以EH/ CD EH= CD因此四边形DCE是平行四边形,所以CE/ DH又DF?平面PAD CE?平面PAD因此CE/平面PAD⑵存在点F为AB的中点,使平面PAD/平面CEF 证明如下:取AB的中点F,连接CF EF,1所以AF= 2AB又CD= 1AB所以AF= CD又AF// CD所以四边形AFCD^平行四边形,因此CF// AD又CF?平面PAD所以CF//平面PAD由⑴可知CE//平面PAD又CEH CF= C,故平面CEF//平面PAD故存在AB的中点F满足要求.2019-2020年高考数学大一轮复习第七章立体几何课时跟踪检测四十二直一抓基础,多练小题做到眼疾手快1 .设a , 3为两个不同的平面,直线I ? a ,则“ I丄是“ a丄B ”成立的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件解析:选A依题意,由I丄3 , I ? a可以推出a丄3 ;反过来,由a丄3 , I ? a 不能推出I丄3 .因此“ I丄3 ”是“ a丄3 ”成立的充分不必要条件,故选 A.2. 已知直线m I,平面a , 3,且m丄a, I? 3,给出下列命题:①若a // 3,则mL I ;②若a丄3,贝U m// I ;③若ml I,贝U a丄3 ;④若m// I,贝U a丄3,其中正确的命题的个数是()A. 1B. 2C. 3D. 4解析:选B①中,a / 3,且mL a ,则ml 3 ,因为I ? 3 ,所以mL I,所以①正确;②中,a丄3,且mLa,贝U m//3或m? 3,又I? 3,贝U m与I可能平行,可能异面,可能相交,所以②不正确;③中,mL I,且mL a , I? 3 ,则a与3可能平行,可能相交,所以③不正确;④中,m// I,且ml a ,则I丄a ,因为I ? 3 ,所以a丄3 ,所以④正确,故选B.3.已知在空间四边形ABCDh ADL BC AD L BD且厶BCD是锐角三角形,则必有()A.平面ABDL平面ADCB.平面ABDL平面ABCC.平面ADC L平面BDCD.平面ABC L平面BDC解析:选 C •/ ADL BC ADL BD B8 BD= B,「. ADL平面BDC 又AD?平面ADC・••平面ADCL平面BDC4•一平面垂直于另一平面的一条平行线,则这两个平面的位置关系是________ •解析:由线面平行的性质定理知,该面必有一直线与已知直线平行. 再根据“两平行线中一条垂直于一平面,另一条也垂直于该平面”得出两个平面垂直相交.答案:垂直相交5.设a, b为不重合的两条直线, a , 3为不重合的两个平面,给出下列命题:①若a// a且b// a ,贝U a // b;②若a丄a且a丄3 ,贝U a // 3 ;③若a丄3,则一定存在平面Y ,使得丫丄a , 丫丄3 ;④若a丄3,则一定存在直线I,使得I丄a , I // 3 •上面命题中,所有真命题的序号是___________ .解析:①中a与b可能相交或异面,故不正确.②垂直于同一直线的两平面平行,正确.③中存在丫,使得丫与a , 3都垂直.④中只需直线I丄a且1?3就可以.答案:②③④二保咼考,全练题型做到咼考达标1. (xx •青岛质检)设a, b是两条不同的直线,a , 3是两个不同的平面,则能得出a 丄b的是()A. a 丄a, b〃3,a 丄3B. a 丄a , b 丄3 , a / 3C. a? a , b 丄3 , a // 3D. a? a , b // 3 , a 丄3解析:选C 对于C项,由a / 3 , a? a可得a// 3 ,又b丄3,得a丄b,故选C.2. 如图,在Rt△ ABC中,/ ABC= 90°, PABC所在平面外一点,PA丄平面ABC则四面体P - ABC中直角三角形的个数为()A. 4B. 3C. 2D. 1解析:选A 由PAL平面ABC可得厶PAC △ PAB是直角三角形,且PA丄BC.又/ ABC= 90°,所以△ ABC是直角三角形,且BCL平面PAB所以BCL PB,即厶PBC为直角三角形,故四面体P - ABC中共有4个直角三角形.3. (xx •南昌模拟)设a, b是夹角为30°的异面直线,则满足条件“ a? a , b? 3 , 且a丄3 ”的平面 a , 3 ()A.不存在B.有且只有一对C.有且只有两对D.有无数对解析:选D过直线a的平面a有无数个,当平面a与直线b平行时,两直线的公垂线与b确定的平面3丄a,当平面a与b相交时,过交点作平面a的垂线与b确定的平面3丄a .故选D.4. (xx •吉林实验中学测试)设a, b, c是空间的三条直线,a , 3是空间的两个平面,则下列命题中,逆命题不成立的是()A. 当C丄a时,若C丄3,贝U a // 3B. 当b? a时,若b丄3,^U a丄3C. 当b? a,且c是a在a内的射影时,若b丄c,则a丄bD. 当b? a ,且C?a 时,若C/ a,贝U b/ C解析:选B A的逆命题为:当C丄a时,若a // 3,贝C丄3 .由线面垂直的性质知C丄3,故A正确;B的逆命题为:当b? a时,若a丄3,则b丄3,显然错误,故B错误;C的逆命题为:当b? a ,且C是a在a内的射影时,若a丄b,贝U b丄C.由三垂线逆定理知b丄C,故C正确;D的逆命题为:当b? a ,且C?a时,若b/ C,则C // a .由线面平行判定定理可得C/ a ,故D正确.5. (xx •贵阳市监测考试)如图,在三棱锥P-ABC中,不能证明APL BC的条件是()A. API PB API PCB. API PB BCL PBC. 平面BPCL平面APC BCL PCD. APL平面PBC解析:选B A中,因为AP I PB API PC PBn PC= P,所以API平面PBC又BQ 平面PBC所以AP I BC故A能证明AP I BC C中,因为平面BPCL平面APC BCL PC所以BCL平面APC AP?平面APC所以AP I BC故C能证明API BC由A知D能证明APL BQB中条件不能判断出API BC故选B.6.如图,已知/ BAC= 90° , PC L平面ABC则在△ ABC △ PAC勺边所在的直线中,与PC垂直的直线有______________ ;与AP垂直的直线有解析:••• PC L平面ABC••• PC垂直于直线AB BC AC•/ AB L AC AB丄PC ACn PC= C,•ABL平面PAC又AF?平面PAC•ABLAP,与AP垂直的直线是AB答案:AB BC AC AB7.如图所示,在四棱锥P-ABCD^ , PAL底面ABCD且底面各边都相等,M是PC上的一动点,当点M满足_______ 时,平面MB L平面PCD (只要填B写一个你认为是正确的条件即可)解析:连接AC BD 则ACL BD ••• PAL 底面 ABCD 二PAI BD. 又 PA? AC= A,「. BD 丄平面 PAC ••• BDLPC•••当DML PC 或BM L PC 时,即有 PC 丄平面MBD而PC ?平面PCD•平面MB L 平面PCD答案:DM L PQ 或 BM L PC&如图,直三棱柱 ABC -ABC 中,侧棱长为2, AC= BC= 1,/ ACB=90° , D 是AB 的中点,F 是BB 上的动点,AB , DF 交于点E 要使AB 丄平面GDF,贝懺段BF 的长为 _______________________ .解析:设BF = x ,因为AB 丄平面 CDF DF ?平面CDF,所以AB 丄DF.由已知可以得AB = 2,1设Rt △ AAB 斜边AB 上的高为h ,贝U DE= J.又 2X • 2= h X 22+ ;2 2,所以 h =233, DE =¥・ 1 即线段BF 的长为2.1答案:2 9. (xx •贵州省适应性考试)已知长方形 ABCDK AB= 3, AD = 4•现将长方形沿对角线BD 折起,使AC = a ,得到一个四面体 A-BCD 如图所示.(1) 试问:在折叠的过程中,直线 AB 与CD 能否垂直?若能,求出相应 a 的值;若不能, 请说明理由.(2) 求四面体A-BCD 体积的最大值.解:(1)直线AB 与CD 能垂直. 由面积相等得卡X2x +*,得 X =2. A因为ABL AD,若 ABL CD 因为 AD A CD= D,所以ABL 平面ACD又因为AC ?平面ACD 从而ABL AC此时,B C — A B =J l6 — 9 =,即当a = 7时,有AB 丄CD(2)由于△ BCD 面积为定值,所以当点 A 到平面BCD 的距离最大,即当平面 ABDL 平面 BCD 寸,该四面体的体积最大,此时,过点 A 在平面ABD 内作AH L BD 垂足为H,则有AH 丄平面BCD AH 就是该四面体的高.1&Bc =孑 3X 4= 6 1 24此时S BCD = ;S ^BCD - AH=—,即为该四面体体积的最大值. 3 510. (xx •河南省八市重点高中质量检测 )如图,过底面是矩形的四棱锥F -ABCD 勺顶点F 作EF// AB 使AB= 2EF,且平面 ABFEL 平面ABCD 若点G 在CD±且满足 DG= GC 求证:(1) FG/平面 AED(2) 平面DAFL 平面BAF证明:(1)因为 DG= GC AB= CD= 2EF, AB// EF// CD所以 EF// DG EF = DG所以四边形DEFG^平行四边形,所以FG/ ED.又因为FG ?平面AED ED ?平面AED所以FG/平面AED(2)因为平面 ABF 丄平面 ABCD 平面 ABFE?平面 ABC = AB AD L AB AD ?平面ABCD所以AD L 平面BAF又AD ?平面DAF所以平面DAFL 平面BAF三上台阶,自主选做志在冲刺名校1.(XX •兰州市实战考试)a , 3是两平面,AB CD 是两条线段,已知 a A 3 = EF ,ABL a 于B, CD L a 于D,若增加一个条件,就能得出 BD L EF.现有下列条件:① AC L 3 ;在厶 ABD 中, AH= AB- AD 12BD = 5②AC与a , 3所成的角相等;③AC与CD在3内的射影在同一条直线上;④ AC// EF.其中能成为增加条件的序号是解析:由题意得,AB// CD二代B, C, D四点共面,①:••• ACL 3 , EF? 3,- AC丄EF,又T AB! a , EF? a , ••• ABL EF, •/ ABA AC= A,二EF丄平面ABCD 又:BD?平面ABC D ••• BD L EF,故①正确;②不能得到BDL EF,故②错误;③:由AC与CD在3内的射影在同一条直线上可知平面ABC! 3 ,又AB L a , AB?平面ABCD ••平面ABC! a . :•平面ABCD 丄a ,平面ABC! 3 , aA3= EF, • EF丄平面ABCD 又BD?平面ABCD •- BD L EF,故③ 正确;④:由①知,若BD L EF,则EFL 平面ABCD则EFL AC故④错误,故填①③.答案:①③2.如图,在四棱锥S-ABCD中,平面SAD_平面ABCD四边形ABCD为正方形,且点P 为AD的中点,点Q为SB的中点.⑴求证:CD L平面SAD⑵求证:PQ/平面SCD(3)若SA= SD点M为BC的中点,在棱SC上是否存在点N,使得平面DM L平面ABCD 若存在,请说明其位置,并加以证明;若不存在,请说明理由.解:⑴ 证明:因为四边形ABC助正方形,所以CDLAD又因为平面SAD L平面ABCD且平面SADn平面ABC B AD所以CD L平面SAD(2)证明:如图,取SC的中点R连接QR DR1由题意知:PD// BC且PD=;BC .2 憑在厶SBC中 ,点Q为SB的中点,点R为SC的中点,所以QR/ BC且QR= 2BC所以PD// QR 且PD= QR所以四边形PDRQ^平行四边形,所以PQ// DR又因为PC P平面SCD DF?平面SCD所以PQ/平面SCD(3)存在点N为SC的中点,使得平面DMLL平面ABCD连接DN PM SP NM ND NQ证明如下:如图,连接PC DM交于点Q因为PD/ CM 且PD= CMa所以四边形PMC为平行四边形,所以PO= CO又因为点N为SC的中点,所以NO/ SP.易知SP1AD因为平面SADL平面ABCD平面SAD T平面ABC』AD并且SPL AD 所以SP!平面ABCD所以NOL平面ABCD 又因为NO? 平面DMN,所以平面DMILL平面ABCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
限时规范训练(限时练·夯基练·提能练)A级基础夯实练1.给出三个命题:①若两条直线和一个平面所成的角相等,则这两条直线互相平行;②若两条直线与一个平面垂直,则这两条直线互相平行;③若两条直线与一个平面平行,则这两条直线互相平行.其中正确的命题的个数是()A.0B.1C.2 D.3解析:选 B.若两条直线与同一个平面所成的角相等,则这两条直线与平面的法向量夹角相等,这些直线构成以法向量为轴的某个对顶圆锥.故①错误;两条直线与平面垂直,则这两条直线与平面的法向量平行,则根据公理4,两直线平行,故②正确;两条直线与一个平面平行,这两条直线可能异面、平行或相交.故③错误.2.下列命题中成立的个数是()①直线l平行于平面α内的无数条直线,则l∥α;②若直线l在平面α外,则l∥α;③若直线l∥b,直线b⊂α,则l∥α;④若直线l∥b,直线b⊂α,那么直线l就平行于平面α内的无数条直线.A.1 B.2C.3 D.4解析:选A.直线l平行于平面α内的无数条直线,包括l⊂α和l∥α,故①不成立;直线l在平面α外,包括l与α相交和l∥α,故②不成立;直线l∥b,直线b⊂α,包括l⊂α和l∥α,故③不成立;直线l∥b,直线b⊂α,那么l平行于α内与直线b平行的所有直线,所以直线l就平行于平面α内的无数条直线,故只有④成立.3.有如下三个命题:①分别在两个平面内的两条直线一定是异面直线;②垂直于同一个平面的两条直线是平行直线;③过平面α的一条斜线有一个平面与平面α垂直.其中正确命题的个数为()A.0 B.1C.2 D.3解析:选C.①分别在两个平面中的两条直线不一定是异面直线,故①错误.②此命题是直线与平面垂直的性质定理,故②正确.③可过斜线与平面α的交点作一条垂直于平面α的直线,则斜线与垂线所确定的平面即与平面α垂直,这样的平面有且只有一个.故③正确.所以②③正确.4.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是()A.若m∥α,n∥α,则m∥nB.若α∥β,m⊂α,n⊂β,则m∥nC.若α∩β=m,n⊂α,则n⊥βD.若m⊥α,m∥n,n⊂β,则α⊥β解析:选D.若m∥α,n∥α,则直线m,n可以是平行、相交、异面,所以A不正确.若α∥β,m⊂α,n⊂β,则直线m,n可能是平行或异面,所以B不正确.C选项显然不正确.5.(2018·枣庄模拟)设a,b为两条不同的直线,α,β为两个不同的平面.则下列四个命题中,正确的是()A.若a,b与α所成的角相等,则a∥bB.若a∥α,b∥β,α∥β,则a∥bC.若a⊂α,b⊂β,a∥b,则α∥βD.若a⊥α,b⊥β,α⊥β,则a⊥b解析:选D.对于选项A,a,b不一定平行,也可能相交;对于选项B,只需找个平面γ,使γ∥α∥β,且a⊂γ,b⊂γ即可满足题设,但a,b不一定平行;对于选项C,由直三棱柱模型可排除C.6.给出下列四个命题:①平面外的一条直线与这个平面最多有一个公共点;②若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交;③若一条直线和两条平行线都相交,则这三条直线共面;④若三条直线交于同一点,则这三条直线共面.其中真命题的序号是________.解析:①正确,因为直线在平面外,即直线与平面相交或直线平行于平面,所以最多有一个公共点.②正确,a,b有交点,则两平面有公共点,则两平面相交.③正确,两平行直线可确定一个平面,又直线与两平行直线的两交点在这两平行直线上,所以过这两交点的直线也在平面内,即三线共面.④错误,这三条直线可以交于同一点,但不在同一平面内.答案:①②③7.(2018·青岛模拟)将一个真命题中的“平面”换成“直线”“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”.给出下列四个命题:①垂直于同一平面的两直线平行;②垂直于同一平面的两平面平行;③平行于同一直线的两直线平行;④平行于同一平面的两直线平行.其中是“可换命题”的是________.(填命题的序号)解析:由线面垂直的性质定理可知①是真命题,且垂直于同一直线的两平面平行也是真命题,故①是“可换命题”;因为垂直于同一平面的两平面可能平行或相交,所以②是假命题,不是“可换命题”;由公理4可知③是真命题,且平行于同一平面的两平面平行也是真命题,故③是“可换命题”;因为平行于同一平面的两条直线可能平行、相交或异面,故④是假命题,故④不是“可换命题”.答案:①③8.如图,平面α∥平面β∥平面γ,两条直线a,b分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AB=2 cm,DE=4 cm,EF=3 cm,则AC的长为________cm.解析:因为平面α∥平面β∥平面γ,两条直线a,b分别与平面α,β,γ相交于点A,B,C和点D,E,F,连接AD,BE,CF(图略).所以AD∥BE∥CF,所以ABBC=DEEF,因为AB =2 cm ,DE =4 cm ,EF =3 cm ,所以2BC =43,解得BC =32cm , 所以AC =AB +BC =2+32=72(cm). 答案:729.如图,在三棱锥S -ABC 中,平面SAB ⊥平面SBC ,AB ⊥BC ,AS =AB ,过点A 作AF ⊥SB ,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.求证:(1)平面EFG ∥平面ABC .(2)BC ⊥SA .证明:(1)因为AS =AB ,AF ⊥SB ,垂足为F ,所以F 是SB 的中点.又因为E 是SA 的中点,所以EF ∥AB .因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC .同理EG ∥平面ABC .又因为EF ∩EG =E ,所以平面EFG ∥平面ABC .(2)因为平面SAB ⊥平面SBC ,且交线为SB ,又因为AF ⊂平面SAB ,AF ⊥SB ,所以AF ⊥平面SBC ,因为BC ⊂平面SBC ,所以AF ⊥BC .又因为AB ⊥BC ,AF ∩AB =A ,AF ⊂平面SAB ,AB ⊂平面SAB ,所以BC ⊥平面SAB .又因为SA ⊂平面SAB ,所以BC ⊥SA .10.如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,∠DAB =60°,PD ⊥平面ABCD ,PD =AD =1,点E ,F 分别为AB 和PC 的中点,连接EF ,BF .(1)求证:直线EF ∥平面PAD .(2)求三棱锥F -PEB 的体积.解:(1)如图,作FM ∥CD 交PD 于点M ,连接AM .因为点F 为PC 中点,所以FM =12CD . 因为点E 为AB 的中点,所以AE =12AB =FM . 又AE ∥FM ,所以四边形AEFM 为平行四边形,又EF ⊄平面PAD ,AM ⊂平面PAD .所以EF ∥AM .所以直线EF ∥平面PAD .(2)连接EC .已知∠DAB =60°,AE =12,AD =1,由余弦定理,得DE ⊥AB ,又AB ∥DC ,则DE ⊥DC ,设F 到平面BEC 的距离为h .因为点F 为PC 的中点,所以h =12PD . 从而有V F PBE =V P BEF =V P BEC -V F BEC=13S △BEC ·(PD -h )=13S △BEC ·12PD =13×12×12×32×12×1=348. B 级 能力提升练11.如图,在四棱锥P -ABCD 中,四边形ABCD 为平行四边形,E 为AD 的中点,F 为PC 上一点,当PA ∥平面EBF 时,PF FC=( ) A.23B .14 C.13 D .12解析:选D.如图,连接AC 交BE 于G ,连接FG ,因为PA ∥平面EBF ,PA ⊂平面PAC ,平面PAC ∩平面BEF =FG ,所以PA ∥FG ,所以PF FC =AG GC. 又AD ∥BC ,E 为AD 的中点,所以AG GC =AE BC =12,所以PF FC =12.12.如图,在棱长为1的正方体ABCD-A1B1C1D1中,ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ऐ8घ8म8888ॐ8ॲ8쳢ꚸࠀ肒銦銦ꚸ肒ꚸꚸ뢒噬l8888888888888888ᔪᘀ퉨譃㔀脈䩃??䩏8䩐䩑8䩞8䩡??⡯ᔧᘀ퉨譃㔀脈䩃??䩏8䩐䩑8䩞8䩡??ᔢᘀ퉨譃㔀脈䩃??䩑䩞8䩡??⡯ᔦᘀ퉨譃㔀脈䩃??䩏8䩑8䩞8䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩏8䩑8䩞8䩡??ᔧᘀ퉨譃㔀脈䩃??䩏8䩐䩑8䩞8䩡??ᔪᘀ퉨譃㔀脈䩃??䩏8䩐䩑8䩞8䩡??⡯ᔓը녟ᘀ퉨譃愀ꚸ漀Ĩᔔը녟ᘀ譃 愀ꚸ8ᔐը녟ᘀ퉨譃愀ꚸꚸ8ࠀ8൬8ï88888ࠀ888888Æ88888였888888Æࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ࠀ8ऒ8ल88੦8ઊ8ࠀ8ࠀ8ࠀ88ଡ଼8୮8ಢ8ಸ8೦8ഐ88888였888888Æ88888였888888Æ88888였888888Æ88888였888888Æ88888였888888Æ88888였888888Æ88888였888888Æ88888였888888Æ88888였888888Æ888888ᔓࠀ׆ᄀ㊄ሂ桤ā䜀Dec䑗È葠Ȳ摧䏒‹Ĥ옍ࠀ15萑Ȳ搒Ũ⑇圀졄怀㊄愂Ĥ摧䏒Ĥ옍ࠀ15搒Ũ⑇愀Ĥ摧弅±ࠀॲ9ࠀ9খ9ঘ999ড়9ࠀ9ࠀ9ࠀ9ਊ9ࠀ9ਖ9ਘ9ਚ9ਜ9ਸ9ࠀ99ਗ਼9ੜ9ਫ਼9ࠀ9੪9ઈ9ઊ9ઌ9ઐ9ࠀ9જ9ઞ9બ9મ9ર9લ9훪훪후훪훪훪훪후훪횮후袚皚抈抈骈抈99999999999ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ9ᔢᘀ퉨譃㔀脈䩃??䩑䩞9䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩏9䩑9䩞9䩡??ᔦᘀ퉨譃㔀脈䩃??䩏9䩑9䩞9䩡??⡯ᔪᘀ퉨譃㔀脈䩃??䩏9䩐䩑9䩞9䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩐䩑䩞9䩡??ᔧᘀ퉨譃㔀脈䩃??䩏9䩐䩑9䩞9䩡??ᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯∁લ9ࠀ9શ9સ9ࠀ999999ࠀ9ૐ9999ࠀ9ࠀ9ࠀ9ࠀ9ࠀ9૦9૨9૪9૬9ࠀ9ࠀ9ࠀ9ࠀ9ࠀ9ࠀ9ࠀ9ࠀ9ࠀ99ࠀ9ଆ9ଌ9ࠀ9ଐ9ࠀ9ଔ9ଘ9ଚ9ଜ9ଞ9ଠ9ନ9ପ9ࠀ뗉즣짛짛즵짛ꎵࠀࠀ즵跛땸ࠀࠀ뗉즣뗛ࠀ碍즵Ûᔩᘀ퉨譃㔀脈ꚸ䎁ࠀ伀J儀J帀J愀ꚸ漀Ĩᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔢᘀ퉨譃㔀脈䩃??䩑䩞10䩡??⡯ᔦᘀ퉨譃㔀脈䩃??䩏10䩑10䩞10䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩏10䩑10䩞10䩡??ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J 帀J愀ꚸ10ᔟᘀ퉨譃㔀脈䩃??䩑䩞10䩡??⼀ପ10ଶ10ସ1010୮10ࠀ10ࠀ10ࠀ10ࠀ10ࠀ10ஊ10ࠀ10ச10ஜ10ࠀ10ࠀ10த10ࠀ10ࠀ역鶱鶇鵱鵱鵛䕱10ᔭᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ漀Ĩᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯ᔪᘀ퉨譃㔀脈ꚸ䎁ࠀ伀JՊ儀J帀J愀ꚸ10ᔪᘀ퉨譃㔀脈䩃??䩏10䩐䩑10䩞10䩡??⡯ᔧᘀ퉨譃㔀脈䩃??䩏10䩐䩑10䩞10䩡??ᔧᘀ퉨譃㔀脈䩃??䩏10䩐䩑10䩞10䩡??ᔦᘀ퉨譃㔀脈䩃??䩏10䩑10䩞10䩡??⡯ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ10ᔣᘀ퉨譃㔀脈䩃??䩏10䩑10䩞10䩡??ᄀࠀ10ந10ப10ࠀ10ம10ர10ல10ழ101010101010ࠀ10101010ࠀ10ࠀ10ࠀ1010ࠀ10௦10௨10௪10௶10௸10௺10ࠀ10ࠀ1010ࠀ10ఆ10ఈ10ఊ10ఎ10ఐ10ఒ10ఔ10ఖ10ఘ10చ10헫헃韕쏕귕쏫헫헃臕굪헫檁헫Ã10ᔭᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ漀Ĩᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔪᘀ퉨譃㔀脈䩃??䩏11䩐䩑11䩞11䩡??⡯ᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩐䩑䩞11䩡??ᔪᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ11ᔧᘀ퉨譃㔀脈䩃??䩏11䩐䩑11䩞11䩡??⤀చ11జ11ఞ11ఠ11ఢ11మ11ర11ల11ࠀ11శ11ࠀ11111111111111ࠀ11ࠀ11ౘ11ࠀ11౨11౪11ࠀ11ࠀ11ࠀ1111ಐ11ಒ11ಘ11ಚ11ಠ11ದ11ಶ11ಸ11퓪껀샔飪풁퓀퓀껀淀浛11111111ᔣᘀ퉨譃㔀脈䩃??䩏11䩑11䩞11䩡??ᔦᘀ퉨譃㔀脈䩃??䩏11䩑11䩞11䩡??⡯ᔭᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ漀Ĩᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩐䩑䩞11䩡??ᔧᘀ퉨譃㔀脈䩃??䩏11䩐䩑11䩞11䩡??ᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯ᔪᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ∀ಸ12ࠀ12ࠀ12೦12೨12എ12ഐ12ഒ12ഘ12ച12ഴ12ശ12ࠀ12ൾ12ࠀ12ආ12ඊ12ඌ12බ12ම12ය12ࠀ12ෂ12ࠀ죜ࠀࠀࠀꃈ皌豢豌谺12ᔣᘀ퉨譃㔀脈䩃??䩐䩑䩞12䩡??ᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯ᔦᘀ퉨譃㔀脈䩃??䩐䩑䩞12䩡??⡯ᔪᘀ퉨譃㔀脈䩃??䩏12䩐䩑12䩞12䩡??⡯ᔧᘀ퉨譃㔀脈䩃??䩏12䩐䩑12䩞12䩡??ᔧᘀ퉨譃㔀脈䩃??䩏12䩐䩑12䩞12䩡??ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ12ᔦᘀ퉨譃㔀脈䩃??䩏12䩑12䩞12䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩏12䩑12䩞12䩡??ᔢᘀ퉨譃㔀脈䩃??䩑䩞12䩡??⡯ᘁ൬12ൾ12හ12෴12ࠀ12ຂ12໔12ࠀ12༜12ཀ12ཨ12ࠀ12ࠀ12Ⴊ12გ12ჺ12ᄢ12ᇚ12ᇲ12ሢ12ቦ12ኚ12ࠀ12ዬ12ᐪ12ᐸ12ì1212121212121212121212Ù1212121212ࠀ121212121212Ù121212121212121212 1212ì1212121212121212121212ì1212121212121212121212ì1212121212121212121212ì1212121212121212121212ì1212121212121212121212ì1212121212121212121212ì1212 121212121212121212ì1212121212121212121212ì1212121212121212121212ì12121212 12121212ᔓࠀ׆ᄀㆄሂ桤ā䜀Dec䑗È葠ȱ摧弅±ᔓࠀ׆ᄀ㊄ሂ桤ā䜀Dec䑗È葠Ȳ摧䏒‹ࠀෂ12හ12ෆ12ࠀ12ࠀ12ࠀ12ࠀ1212෴12ࠀ12ค12ฆ12ผ12พ12ฤ12ฦ12ๆ12121212ࠀ12ࠀ12ࠀ12ࠀ12ࠀ12ࠀ12ࠀ12ࠀ12ຈ12ຊ12ࠀ12훪냂슰슚슚싪슚싪슰싪슰璆虠12121212121212121212121212121212121212ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ12ᔣᘀ퉨譃㔀脈䩃??䩏12䩑12䩞12䩡??ᔦᘀ퉨譃㔀脈䩃??䩏12䩑12䩞12䩡??⡯ᔪᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ13ᔣᘀ퉨譃㔀脈䩃??䩐䩑䩞13䩡??ᔧᘀ퉨譃㔀脈䩃??䩏13䩐䩑13䩞13䩡??ᔦᘀ퉨譃㔀脈䩃??䩐䩑䩞13䩡??⡯ᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯ḁࠀ13ࠀ13ພ13ࠀ13ຢ13ࠀ13ࠀ131313໒13໘13ࠀ13ໜ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ࠀ13ༀ13༂13༄13༆13༈13༊1313༎13༐13༒13༔13༖1313༚13༠13༢13༤13༦13༨13༪13ࠀ쓘쓘냘날ࠀꂰ쒰냘날ࠀꂰ쒰냘날Øᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔢᘀ퉨譃㔀脈䩃??䩑䩞13䩡??⡯ᔟᘀ퉨譃㔀脈䩃??䩑䩞13䩡??ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ13ᔦᘀ퉨譃㔀脈䩃??䩏13䩑13䩞13䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩏13䩑13䩞13䩡??ᔩᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J 帀J愀ꚸ漀Ĩ⼀༪13༬13༮13༰13༲13༴13༶13༸13༺13༼1313ང13ཆ13ࠀ13ཊ13ཌ13ཎ13ཐ13དྷ13པ13བ13མ13ཚ13ཛྷ13ཞ13འ13ར13ཤ13ས13ཨ13ࠀ13ࠀ13ࠀ귃ࠀ鯘诬ࠀ秃ࠀ귃ࠀ旘Q13ᔧᘀ퉨譃㔀脈䩃??䩏13䩐䩑13䩞13䩡??ᔧᘀ퉨譃㔀脈䩃??䩏13䩐䩑13䩞13䩡??ᔢᘀ퉨譃㔀脈䩃??䩑䩞14䩡??⡯ᔟᘀ퉨譃㔀脈䩃??䩑䩞14䩡??ᔣᘀ퉨譃㔀脈䩃??䩏14䩑14䩞14䩡??ᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔩᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ漀Ĩᔦᘀ퉨譃㔀脈䩃??䩏14䩑14䩞14䩡??⡯ᔦᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸἀࠀ141414141414141414141414141414141414141414྾14 1414࿄1414࿈14࿊14࿌14ࠀ14ࠀ14ࠀ14ࠀ14ࠀ14ࠀ14훪껀飀涁颁샖膘飖샖삮膘腗膘腗횘飀ᔪᘀ퉨譃㔀脈䩃??䩏0䩐0䩑0䩞0䩡??⡯ᔦᘀ퉨譃㔀脈䩃??䩐䩑䩞14䩡??⡯ᔭᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ漀Ĩᔪᘀ퉨譃㔀脈䩃??䩏䩐䩑䩞䩡??⡯ᔣᘀ퉨譃㔀脈䩃??䩐䩑䩞15䩡??ᔪᘀ퉨譃㔀脈ࠀ䎁ꚸ伀JՊ儀J帀J愀ꚸ15ᔧᘀ퉨譃㔀脈䩃??䩏15䩐䩑15䩞15䩡??ᔪᘀ퉨譃㔀脈䩃??䩏15䩐䩑15䩞15䩡??⡯∁ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ151515151515ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15ࠀ15퓨풾풨풨肔婮䖔鑮鑅湅溔溔鑚1515ᔩᘀ퉨譃㔀脈ࠀ䎁ꚸ伀J儀J帀J愀ꚸ漀Ĩᔦᘀ。
