江苏省南京市2010届高考全真模拟数学试题
2010年江苏高考数学试题(含答案详解

2010年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题参考公式:锥体的体积公式: V 锥体=13Sh ,其中S 是锥体的底面积,h 是高。
一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答题卡相应的位.......置上...1、设集合A={-1,1,3},B={a+2,a 2+4},A ∩B={3},则实数a =______▲_____. [解析] 考查集合的运算推理。
3∈B, a+2=3, a=1.2、设复数z 满足z(2-3i)=6+4i (其中i 为虚数单位),则z 的模为______▲_____. [解析] 考查复数运算、模的性质。
z(2-3i)=2(3+2 i), 2-3i 与3+2 i 的模相等,z 的模为2。
3、盒子中有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是_ ▲__.[解析]考查古典概型知识。
3162p ==4、某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有_▲___根在棉花纤维的长度小于20mm 。
[解析]考查频率分布直方图的知识。
注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题)。
本卷满分160分,考试时间为120分钟。
考试结束后,请将本卷和答题卡一并交回。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答,在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整,笔迹清楚。
5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗。
再谈2010江苏高考数学的“难”

再谈2010江苏高考数学的“难”XXXXX2010年江苏省高考数学试卷从整体上看,更加突出数学学科特点,涉及考试说明中的五种能力和两种意识,特别注意从多种不同角度进行分析研究,引发多种不同的解法,展示考生的各种能力,试卷题型虽然常规,但梯度明显,区分度高,难度大,很多题目都有陷阱。
因此,考生们对2010年江苏高考数学考题普遍的评价和03年一样,又是一个字:难!1.今年江苏卷从知识与能力角度看真正地“难”在哪里?1.1.部分试题注重知识交汇点命题,综合性较强例1.(01江苏8)函数y=x 2(x>0)的图像在点(a k ,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数,a 1=16,则a 1+a 3+a 5=_________解析:在点(a k ,a k 2)处的切线方程为:时,解得,所以 数列是以为公比、16为首项的等比数列,因此,。
点评:本题考查抛物线的切线方程、数列的通项,是函数、导数、数列等三个知识点的结合。
它的难度至少达到B 级。
例2.(01江苏10)定义在区间上的函数y=6cosx 的图像与y=5tanx 的图像的交点为P ,过点P 作PP 1⊥x 轴于点P 1,直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为___________。
解析:线段P 1P 2的长即为sinx 的值,且6cosx=5tanx ,结合,解得sinx=。
线段P 1P 2的长为。
点评:本题考查三角函数的图象、同角三角函数关系、图形的交点计算等三个知识点,全面地考察了正弦、余弦、正切函数的图像的把握情况。
平时这类题目仅仅考到直线被两个函数图像截得的线段的长度大小等,现在更深入,增加了第三个函数。
1.2部分试题立意新颖,设问灵活,创新层次高例3.(01江苏12)设实数x,y 满足3≤≤8,4≤≤9,则的最大值是________解析一(后面还有两一种解法):设,,解得,, 则,其中,当,时,的最大值是27.点评:本题从表面上给人的第一感觉,它应该是线性规划问题,再仔细地想,这个题目类似如:已知,求的最大值。
2010届数学高考考前指导

2010届数学高考考前指导数学之战重中之重胆大心细一击而中------------------------------最后一课(一)、友情提醒:同学们在考前应做好以下三项准备工作----读、清、练:1、命题者与考生的共同财富—数学课本. 命题是在课本的基础上,源于课本又高于课本,因此,在考前应回归课本,将课本上的定义、定理、公式等重点内容“熟读”备用!!(公式熟了吗?)2、数学题在这之前已做得不少,试卷上有我们辛勤的血汗,更有我们的经验和教训. 此时此刻建议同学们将这些宝贵财富充分利用—将近期暴露出来的“地雷”逐一清除!逐一清除!!(错题本上题目过了吗?)3、数学题要天天练. 解数学题尤如“练歌”—天天练,“歌词”不记而熟;不练而突击死背,没有丝毫效果;建议同学们这几天每天完成部分选择题、填空题、中档解答题,练笔熟手!!(你练了吗?)(二)、数学一直有着高考“命门”之称,数学的成功与否可以说在很大程度上决定了你高考总分的高低。
一、高考数学网上阅卷基本情况:(已经了解)二、解题思考步骤、程序:1、观察⏹要求解(证)的问题是什么?它是哪种类型的问题?⏹已知条件(已知数据、图形、事项、及其与结论部分的联系方式)是什么?要求的结论(未知事项)是什么?⏹所给图形和式子有什么特点?能否用一个图形(几何的、函数的或示意的)或数学式子(对文字题)将问题表示出来?能否在图上加上适当的记号?⏹有什么隐含条件?解题思考步骤、程序:2、联想⏹这个题以前做过吗?⏹这个题以前在哪里见过吗?⏹以前做过或见过类似的问题吗?当时是怎样想的?⏹题中的一部分(条件,或结论,或式子,或图形)以前见过吗?在什么问题中见过的?⏹题中所给出的式子、图形,与记忆中的什么式子、图形相象?它们之间可能有什么联系?⏹解这类问题通常有哪几种方法?可能哪种方法较方便?试一试如何?⏹由已知条件能推得哪些可知事项和条件?要求未知结论,需要知道哪些条件(需知)?⏹与这个问题有关的结论(基本概念、定理、公式等)有哪些?解题思考步骤、程序:3、转化⏹能否将题中复杂的式子化简?⏹能否对条件进行划分,将大问题化为几个小问题?⏹能否将问题化归为基本命题?⏹能否进行变量替换、恒等变换或几何变换,将问题的形式变得较为明显一些?⏹能否形──数互化?利用几何方法来解代数问题?利用代数(解析)方法来解几何问题?⏹利用等价命题律(逆否命题律、同一法则、分断式命题律)或其他方法,可否将问题转化为一个较为熟悉的等价命题?⏹最终目的:将未知转化为已知。
高考出题神人葛军

数学帝”何许人士?因何受到如此关注?一切源于高考,2010年高考尘埃落定,众多江苏考生反映数学试题难度很大,有考生是哭着离开考场的。
附2010年江苏高考数学神题提供参加参考。
你可以先做做,看看能考多少分。
葛军,男,1964年10月生,江苏南通如东人。
南京师范大学副教授,硕士生导师,网称“数学帝”。
现任南京师范大学附属中学校长。
葛军老师“数学帝”葛军老师神话:2003年,葛军参与江苏高考数学命题工作,江苏数学全省均分68分(满分150分),2010年,葛军参与江苏高考数学命题工作,学生反映颇具难度。
当年高考平均分83.5分(总分160分)。
2012年,葛军参与全国新课标数学命题工作,学生反映颇具难度。
2012年11月16日,葛军就任南京师范大学附属中学校长。
2010年网友吐槽贴“2010年,江苏数学帝葛军!一个人——秒杀江苏52万考生!” “数学帝”何许人士?因何受到如此关注?一切源于高考,2010年高考尘埃落定,众多江苏考生反映数学试题难度很大,有考生是哭着离开考场的。
“考完数学,我的心都碎了”,一名江苏考生在网上发出如此感叹。
据报道称,江苏省2003年的数学高考卷被认为是难卷的标杆,当时150分的卷子平均分为68分。
而南京市有监考老师看过试卷后认为今年的数学考题难度已超越了2003年,堪称最难。
被网友“人肉”出题的老师葛军,拥有中国数学奥林匹克高级教练,南京师范大学附属实验学校校长等炫目头衔,曾在2003年出了江苏数学高考试卷,因为超难,直接将江苏上线分数直降50-60分,网称“数学帝”。
此次再次出手,网友称:“他,如神一般……秒杀了52万江苏考生”。
有学生家长跟帖说:“葛老师啊,女儿昨天下午从考场出来几乎瘫痪在地,整个晚上都是以泪洗面。
要知道她平时的成绩可是我们这儿重点高中的前几名啊。
”拿着该套数学试卷,我也感觉“蛋扯得疼”。
我的高中数学曾经还不错,现在要理解这种貌似奥林匹克数学竞赛题的题意,也找不着头绪,有些题目还用上了大学的知识。
江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03

2x
2π 3
.
试卷第 4页,共 5页
(1)求 f x 在0, π 上的单调递增区间;
(2)若当
x
0,
π 4
时,关于
x
的不等式
f
x
m
恒成立,求实数
m
的取值范围.
试卷第 5页,共 5页
信噪比.当信噪比比较大时,公式中真数中的 1 可以忽略不计.按照香农公式,若不改变
带宽W ,而将信噪比 S 从 1000 提升到 8000,则 C 大约增加了( ) lg 2 0.301
N
A.10%
B.20%
C.30%
D.50%
27.已知在
ABC
中,AB
2
,AC
3 ,BAC
3
,点
D
为边
BC
上靠近
江苏省 2024 年普通高中学业水平合格性考试数学全真模拟 数学试题 03
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知集合 A x x2 x 6 0 , B 0,1,2,3 ,则 A B ( )
A.1, 2
A.﹣1
B.1
C.2
D.4
14.已知 x R,则“ x 3 1”是“ x2 x 6 0 ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
15.青年大学习是共青团中央发起的青年学习行动,每期视频学习过程中一般有两个问
题需要点击回答.某期学习中假设同学小华答对第一、二个问题的概率分别为 1 , 3 ,且 35
D. x 0,1 , x2 x 0
数学_2010年江苏省南京市高考数学模拟试卷(含答案)

2010年江苏省南京市高考数学模拟试卷一、填空题(共14小题,每小题5分,满分70分) 1. 复数11+i+i2等于________.2. y =sin(2x +π6)的最小正周期是________.3. 已知集合A ={x|y =√4x −x 2},B =(−∞, a],若A ⊆B ,则实数a 的取值范围是_________.4. 为了保证信息安全传输必须使用加密方式,有一种方式其加密、解密原理如下:已知加密为y =a x −2(x 为明文、y 为密文),如果明文“3”通过加密后得到密文为“6”,再发送,接受方通过解密得到明文“3”,若接受方接到密文为“14”,则原发的明文是________. 5. 为了在运行下面的程序之后得到输出y =25,键盘输入x 应该是________. Input xIf x <0 tℎeny =(x +1)∗(x +1) Elsey =(x −1)∗(x −1) End if Print y End6. 已知向量a →=(1,sinθ),b →=(1,cosθ),则|a →−b →|的最大值为________.7. 在区间[−π, π]内随机取两个数分别记为a ,b ,则使得函数f(x)=x 2+2ax −b 2+π2有零点的概率为________.8. 若函数f(x)=x 3+x 2+mx +1是R 上的单调递增函数,则m 的取值范围是________. 9. 设f(x)=x 3+lg(x +√x 2+1),则对任意实数a ,b ,“a +b ≥0”是“f(a)+f(b)≥0”的________条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”之一) 10. 已知在平面直角坐标系中,A(−2, 0),B(1, 3),O 为原点,且OM →=αOA →+βOB →,(其中α+β=1,α,β均为实数),若N(1, 0),则|MN →|的最小值是________.11.若Rt △ABC 中两直角边为a 、b ,斜边c 上的高为ℎ,则1ℎ2=1a 2+1b 2,如图,在正方体的一角上截取三棱锥P −ABC ,PO 为棱锥的高,记M =1PO 2,N =1PA 2+1PB 2+1PC 2,那么M 、N 的大小关系是________.12. 直线l 是双曲线x 2a 2−y 2b 2=1(a >0,b >0)的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l 分成弧长为2:1的两段圆弧,则该双曲线的离心率是________.13. 设x ,y ,z 是正实数,满足xy +z =(x +z)(y +z),则xyz 的最大值是________. 14. 在数列{x n }中,已知x 1=x 2=1,x n+2=x n+1−x n (n ∈N),求得x 100=________.二、解答题(共6小题,满分0分) 15. 已知A ,B 是△ABC 的两个内角,a →=√2cos A+B 2i →+sinA−B 2j →(其中i →,j →是互相垂直的单位向量),若|a →|=√62. (1)试问tanA ⋅tanB 是否为定值,若是定值,请求出,否则说明理由;(2)求tanC 的最大值,并判断此时三角形的形状.16. 如图,PA 、PB 、PC 两两垂直,PA =PB =PC ,G 是△PAB 的重心,E 是BC 上的一点,且BE =13BC ,F 是PB 上的一点,且PF =13PB . 求证:(1)GF ⊥平面PBC ; (2)FE ⊥BC ;17. 如图,直角三角形ABC 的顶点坐标A(−2, 0),直角顶点B(0,−2√2),顶点C 在x 轴上,点P 为线段OA 的中点.(1)求BC 边所在直线方程;(2)M 为直角三角形ABC 外接圆的圆心,求圆M 的方程;(3)若动圆N 过点P 且与圆M 内切,求动圆N 的圆心N 的轨迹方程.18. 已知向量a →=(x 2−3,1),b →=(x,−y),(其中实数y 和x 不同时为零),当|x|<2时,有a →⊥b →,当|x|≥2时,a → // b →.(1)求函数式y =f(x);(2)求函数f(x)的单调递减区间;(3)若对∀x ∈(−∞, −2]∪[2, +∞),都有mx 2+x −3m ≥0,求实数m 的取值范围.19. 如图,一科学考察船从港口O出发,沿北偏东a角的射线OZ方向航行,其中tana=1,在距离港口O为3√13a(a为正常数)海里北偏东β角的A处有一个供科3,现指挥部紧急征调沿海岸线港口O正东方向m海里学考察船物资的小岛,其中cosβ=√13的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.(1)求S关于m的函数关系式S(m);(2)当m为何值时,补给最合适?20. 已知函数f(x)=(x−1)2,g(x)=k(x−1),函数f(x)−g(x)其中一个零点为5,数列{a n}满足a1=k,且(a n+1−a n)g(a n)+f(a n)=0.2(1)求数列{a n}通项公式;(2)求S{a n}的最小值(用含有n的代数式表示);(3)设b n=3f(a n)−g(a n+1),试探究数列{b n}是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.2010年江苏省南京市高考数学模拟试卷答案1. 122. π3. a≥44. 45. −6或66. √27. 1−π48. m≥139. 充要10. 3√2211. M=N12. 213. 12714. −115. 解:(1):|a→|2=2cos2A+B2+sin2A−B2=32,1+cos(A+B)+1−cos(A−B)2=32cosAcosB−sinAsinB−cosAcosB+sinAsinB2=01 2−3tanAtanB2=0则tanAtanB=13(2)由(1)可知A、B为锐角tanC=−tan(B+A)=−tanA+tanB1−tanAtanB=−3(tanA+tanB)2≤−3√tanAtanB=−√3所以tanC的最大值为−√3此时三角形ABC为钝角三角形.16. 证明:(1)连接BG和PG,并延长分别交PA、AB于M和D,在△PBM中,∵ PF=13PB,G是△PAB的重心,∴ MG=13BM,∴ GF // PM.又PA⊥PB,PA⊥PC,∴ PA⊥平面PBC,则GF⊥平面PBC.(2)在EC上取一点Q使CQ=13BC,连接FQ,又PF=13PB,∴ FQ // PC.∵ PB=PC,∴ FB=FQ.∵ BE=13BC,∴ E是BQ的中点,∴ FE⊥BQ,即FE⊥BC.17. 解:(1)∵ k AB=−√2,AB⊥BC,∴ k CB=√22,∴ BC:y=√22x−2√2(2)在上式中,令y=0,得C(4, 0),∴ 圆心M(1, 0)又∵ AM=3,∴ 外接圆的方程为(x−1)2+y2=9(3)∵ P(−1, 0),M(1, 0)∵ 圆N 过点P(−1, 0), ∴ PN 是该圆的半径又∵ 动圆N 与圆M 内切,∴ MN =3−PN ,即MN +PN =3∴ 点N 的轨迹是以M 、P 为焦点,长轴长为3的椭圆, ∴ a =32,c =1,b =√a 2−c 2=√54, ∴ 轨迹方程为x 294+y 254=118. 解:(1)当|x|<2时,由a →⊥b →得a →⋅b →=(x 2−3)x −y =0,y =x 3−3x ;(|x|<2且x ≠0)当|x|≥2时,由a → // b →.得y =−xx 2−3∴ y =f(x)={x 3−3x ,(−2<x <2且x ≠0)x3−x 2.(x ≥2或x ≤−2) (2)当|x|<2且x ≠0时,由y ′=3x 2−3<0,解得x ∈(−1, 0)∪(0, 1), 当|x|≥2时,y′=(3−x 2)−x(−2x)(3−x 2)2=3+x 2(3−x 2)2>0∴ 函数f(x)的单调减区间为(−1, 1);(3)对∀x ∈(−∞, −2]∪[2, +∞),都有mx 2+x −3m ≥0即m(x 2−3)≥−x , 也就是m ≥x 3−x 2对∀x ∈(−∞, −2]∪[2, +∞)恒成立,由(2)知当|x|≥2时,f′(x)=(3−x 2)−x(−2x)(3−x 2)2=3+x 2(3−x 2)2>0∴ 函数f(x)在(−∞, −2]和[2, +∞)都单调递增 又f(−2)=−23−4=2,f(2)=23−4=−2 当x ≤−2时f(x)=x 3−x 2>0,∴ 当x ∈(−∞, −2]时,0<f(x)≤2同理可得,当x ≥2时,有−2≤f(x)<0, 综上所述得,对x ∈(−∞, −2]∪[2, +∞),f(x)取得最大值2; ∴ 实数m 的取值范围为m ≥2.19. 解:以O 为原点,正北方向为轴建立直角坐标系,直线OZ 的方程为y =3x①,(1)设A(x 0, y 0),∵ cosβ=√13,sinβ=√13,则x 0=3√13asinβ=9a ,y 0=3√13acosβ=6a ,∴ A(9a, 6a). 又B(m, 0),则直线AB 的方程为y =6a9a−m (x −m) ② 由①、②解得,C(2amm−7a , 6amm−7a ),∴ S(m)=S △OBC =12|OB||yc|=12×m ×6amm−7a =3am 2m−7a (m >7a). (2)S(m)=3am 2m−7a=3a[(m −7a)+49a 2m−7a+14a]≥84a 2当且仅当m −7a =49a 2m−7a,即m =14a >7a 时,等号成立,故当m =14a 海里时,补给最合适. 20. 解:(1)函数f(x)−g(x)有一个零点为5,即方程(x −1)2−k(x −1)=0,有一个根为5,将x =5代入方程得16−4k =0, ∴ k =4, ∴ a 1=2由(a n+1−a n )g(a n )+f(a n )=0得4(a n+1−a n )(a n −1)+(a n −1)2=0(a n −1)(4a n+1−4a n +a n −1)=0∴ a n −1=0或4a n+1−4a n +a n −1=0 由(1)知a 1=2, ∴ a n −1=0不合舍去由4a n+1−4a n +a n −1=0得4a n+1=3a n +1 方法1:由4a n+1=3a n +1得a n+1−1=34(a n −1) ∴ 数列{a n −1}是首项为a 1−1=1,公比为34的等比数列∴ a n −1=(34)n−1,∴ a n =(34)n−1+1〔方法2:由4a n+1=3a n +1①得当n ≥2时4a n =3a n−1+1② ①-②得4(a n+1−a n )=3(a n −a n−1) ∴ an+1−a na n−an−1=34(n ≥2)即数列{a n −a n−1}是首项为a 2−a 1,公比为34的等比数列∵ a 2−a 1=14−14a 1=−14,∴ a n+1−a n =−14⋅(34)n−1③ 由①得a n+1=34a n +14代入③整理得a n =(34)n−1+1(2)由(1)知a n =(34)n−1+1∴ ∑a i n i=1=1+34+(34)2++(34)n−1+n =[1−(34)n ]1−34+n =4[1−(34)n ]+n∵ 对∀n ∈N ∗,有(34)n ≤34, ∴ 1−(34)n ≥1−34=14∴ 4[1−(34)n ]+n ≥1+n ,即∑a i n i=1≥1+n即所求S{a n }的最小值为1+n .(3)由b n =3f(a n )−g(a n+1)得b n =3(a n −1)2−4(a n+1−1) ∴ b n =3[(34)n−1]2−4(34)n =3{[(34)n−1]2−(34)n−1}令u =(34)n−1,则0<u ≤1,b n =3(u 2−u)=3[(u −12)2−14]∵ 函数b n =3[(u −12)2−14]在[12,1]上为增函数,在(0,12)上为减函数 当n =1时u =1, 当n =2时u =34,当n =3时,u =(34)2=916,当n =4时u =2764,∵ 2764<12<916<34<1,且|12−2764|>|12−916|∴ 当n =3时,b n 有最小值,即数列{b n }有最小项,最小项为b 3=3[(916)2−916]=−189256故当n =1即u =1时,b n 有最大值,即数列{b n }有最大项, 最大项为b 1=3(1−1)=0.。
2010年江苏高考数学模拟试卷(6)共10页

2010年江苏高考数学模拟试卷(6)参考公式: 样本数据x1,x2,…xn的方差s2=1nΣni=1(x1-x)2,其中x=1nΣni=1x1一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案直接填写在相应位置上.1.函数f(x)=1-2x的定义域为.2.直线4x-3y-12=0在两坐标轴上的截距之和.3.己知复数z满足z•i=3+4i,(i为虚数单位),则复数z的模为.4.在两个袋内分别装有标记数字1、2、3、4、5的5张卡片,现从每个袋中各任取一张卡片,则所得两数之和等于7的概率为.5.若函数f(x)=x2+ax,x∈[1,3]是单调函数,则实数a的取值范围是.6.使得函数y=cos(x+φ)为奇函数的φ的最小正值为.7.如图所示,是2009年底CCTV举办的全国钢琴、第8题图小提琴大赛比赛现场上七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的方差为.8.右图是一个算法的流程图,最后输出的S=.9.椭圆x29+y22=1的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则∠F1PF2的大小为.10.“a∈[2,+∞)”是“实系数一元二次方程x2-ax+1=0有实根”的.条件(从“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”中选出符合题意的一个填空)11.己知圆C:x2+y2-8y+12=0,直线l:ax+y+2a=0,若直线l与圆C相切,则实数a的值为.12.如图,在平面上,若直角三角形ABC的直角边BC和斜边AB的长分别为a、c,过直角顶点C作CD⊥AB于D,记BD的长为b,则a、b、c的关系为a2=bc.类似地.在空间,若四面体ABCD的棱AB、AC、AD两两垂直,过顶点A作AO⊥面BCD(如图所示),记△ABC、△BOC、△BCD的面积分别为S1,S2,S3,则S1,S2,S3的关系为.13.已知x>0,y>0,x,a,b,y成等差数列,x,c,d,y成等比数列,则(a+b)2cd的最小值是.14.己知等差数列{an}的各项都不为零,公差d>0,且a4+a7=0,记数列1an的前n项和为Sn,则使Sn>0成立的正整数n的最小值是.二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.)15.(本小题满分14分)A、B是直线y=1与函数f(x)=2cos2ωx2+cos(ωx+π3)(ω>0)图象的两个相邻交点,且|AB|=π2.(1)求ω的值;(2)在锐角△ABC中,a,b,c分别是角A,B,C的对边,若f(A)=-12,c=3,△ABC的面积为33,求a的值.16.(本小题满分14分)如图,正三棱柱ABC-A1B1C1的所有棱长都相等,D为CC1的中点,AB1与A1B相交于点O,连结OD.(1)求证:OD∥平面ABC;(2)求证:AB1⊥平面A1BD17.(本小题满分14分)如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地”△ABD,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值S1S2称为“草花比y”.(Ⅰ)设∠DAB=θ,将y表示成θ的函数关系式;(Ⅱ)当BE为多长时,y有最小值?最小值是多少?18.(本小题满分16分)已知数列{an}的各项均是正数,其前n项和为sn,满足(p-1)sn=p2-an,其中p为正常数,且p≠1(Ⅰ)求数列{an}的通项公式;(Ⅱ)设bn=12-logpan(n∈N*),数列{bnbn+2}的前n项和为Tn,求证Tnb>0;如图,半椭圆x2b2+y2a2=1(y≥0)内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点M(63,-33)时,△AGP的面积最大.(1)求曲线C的方程;(2)连PC、PD交AB分别于点E、F,求证:AE2+BF2为定值.20.(本小题满分16分)已知函数f(x)=12[3ln(x+2)-ln(x-2)].(I)求x为何值时,f(x)在[3,7]上取得最大值;(Ⅱ)设F(x)=aln(x-1)-f(x),若F(x)是单调递增函数,求a的取值范围.附加题部分1.选修4-1:几何证明选讲如图,在四边形ABCD中,△ABC≌△BAD.求证:AB∥CD2.选修4-2:矩阵与变换已知在一个二阶矩阵M的变换作用下,点A(1,2)变成了点A′(4,5),B(3,-1)变成了点B′(5,1),求矩阵M.3.选修4-4:坐标系与参数方程在极坐标系中,已知圆C的圆心坐标为C(2,π3),半径R=5,求圆C的极坐标方程.4.选修4-5:不等式选讲?ヒ阎?a+b+c=1,求证:a2+b2+c2≥135.某小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数ξ是一个随机变量,求随机变量ξ的分布列及数学期望E(ξ).6.已知a>0,b>0,n>1,n∈N*.用数学归纳法证明:an+bn2≥(a+b2)n.2010年江苏高考数学模拟试卷(6)参考答案一、填空题:1.(-∞,12]2.-1.3.54.4255.(-∞,-6]∪[-2,+∞)6.π27.858.309.120°10.充分不必要 11.-3412.s21=s2s3 13.4 14.11二、解答题:15.解析:(Ⅰ)f(x)=1+cosωx+12cosωx-32sinωx=1-3sin(ωx-π3).由函数的图象及|AB|=π2,得函数的周期T=2πω=2×π2,解得ω=2.又∵f(A)=1-3sin(2A-π3)=-12∴sin(2A-π3)=32.又∵△ABC是锐角三角形,-π3 则OE∥AB,又OE?て矫?ABC,AB?计矫?ABC,∴OE∥平面ABC,同理DE∥平面ABC又OE∩DE=E∴平面OED∥平面ABC而OD?计矫?OED,∴OD∥平面ABC(2)连B1D,AD,∵ABB1A1是正方形,∴AB1⊥A1B∵Rt△ACD≌Rt△B1C1D,∴AD=B1D又O是AB1的中点,∴AB1⊥DO,∵A1B∩DO=O∴AB1⊥平面A1BD.17.解:(Ⅰ)因为BD=atanθ,所以△ABD的面积为12a2tanθ(θ∈(0,π2))设正方形BEFG的边长为t,则由FGAB=DGDB,得ta=atanθ-tatanθ, 解得t=atanθ1+tanθ,则s2=a2tan2θ(1+tanθ)2所以s1=12a2tanθ-s2=12a2tanθ-a2tan2θ(1+tanθ)2,则y=s1s2=(1+tanθ)22tanθ-1(Ⅱ)因为tanθ∈(0,+∞),所以y=12(tanθ+1tanθ+2)-1=12(tanθ+1tanθ)≥1当且仅当tanθ=1时取等号,此时BE=a2.所以当BE长为a2时,y有最小值1.18.解析:(1)由题设知(p-1)a1=p2-a1,解得a1=p.由(p-1)sn=p2-an(p-1)sn+1=p2-an+1两式作差得(p-1)(sn+1-sn)=an-an+1所以(p-1)an+1=an-an+1,即an+1=1pan,可见,数列{an}是首项为p,公比为1p的等比数列.an=p(1p)n-1=(1p)n-2(Ⅱ)bn=12-logpp2-n=12-(2-n)=1nbnbn+2=1n(n+2)=12(1n-1n+2)Tn=b1b3+b2b4+b3b5+…bnbn+2=12[(11-13)+(12-14)+(13-15)+(14-16)+…(1n-1n+2)]=12(1+12-1n+1-1n+2)0,所以b=1,当半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行时,点P到直线AG的距离最大,此时△AGP的面积取得最大值,故半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行, 所以OM⊥AG,又KOM=yM-0xM-0=-22,所以KAG=2=ab,又b=1,所以a=2, 所以曲线C的方程为x2+y22=1(y≥0)或x2+y2=1(y≤0).(2)点C(1,2),点D(-1,2),设P(x0,y0),则有直线PC的方程为y-2=y0-2x0-1(x-1),令y=0,得xE=1-2(x0-1)y0-2,所以AE=2-2(x0-1)y0-2;直线PD的方程为y-2=y0-2x0+1(x+1),令y=0,得xF=-1-2(x0+1)y0-2 所以BF=2+2(x0+1)y0-2;则AE2+BF2=[2-2(x0-1)y0-2]2+[2+2(x0+1)y0-2]2=4x20+4(y0-2)2+82y0-2+ 8又由x20+y20=1,得x20=1-y20,代入上式得=8-4y20(y0-2)2+82y0-2+8=8-4y20+82(y0-2)(y0-2)2+8=-4(y0-2)2(y0-2)2+8=4,所以AE2+BF2为定值.20、解:(Ⅰ)f′(x)=12[3x+2-1x-2]=x-4x2-4.∴当24时,f′(x)>0.∴f(x)在(2,4)上是减函数,在(4,+∞)上是增函数.∴f(x)在[3,7]上取得最大值应在端点处取得.∵f(3)-f(7)=12[3ln5-ln1]-12[3ln9-ln5]=12[ln625-ln729]0恒成立∴(a-1)x2+5x-4(a+1)≥0在(2,+∞)恒成立下面分情况讨论(a-1)x2+5x-4(a+1)≥0在(2,+∞)恒成立时,a的解的情况,当a-10在(2,+∞)上恒成立当a-1>0,又有两种情况:①52+16(a-1)(a+1)≤0;?ア?-52(a-1)≤2且(a-1)•22+5×2-4(a+1)≥0由①得16a2+9≤0,无解,由②得a≥14 ∵a-1>0.∴a>1综上所述各种情况,当a≥1时,(a-1)x2+5x-4(a+1)≥0在(2,+∞)上恒成立∴所求的a的取值范围为[1,+∞)附加题部分1.A.选修4-1:几何证明选讲证明:由△ABC≌△BAD得∠ACB=∠BDA.∴A,B,CD四点共圆从而∠CAB=∠CDB再由△ABC≌△BAD得∠CAB=∠DBA∴∠DBA=∠CDB∴AB∥CD.2.解:设M=a bc d,则由a bc d12=45,a bc d3-1=51,得a+2b=4,c+2d=53a-b=53c-d=1所以a=2b=1c=1d=2因此2 11 2.3.解法一:设P(ρ,θ)是圆上的任意一点,则PC=R=5.由余弦定理,得ρ2+22-2×2×ρcos(θ-π3)=5.化简,得ρ2-4ρcos(θ-π3)+1=0,此即为所求的圆C的方程.解法二:将圆心C(2,π3)化成直角坐标为(1,3),半径R=5,故圆C的方程为(x-1)2+(y-3)2=5.再将C化成极坐标方程,得(ρcosθ-1)2+(ρcosθ-3)2=5.化简,得ρ2-4ρcos(θ-π3)+1=0,此即为所求的圆C的方程.4.证明:因为a2+b2+c2=(a+b+c)2-(2ab+2bc+2ac)≥(a+b+c)2-2(a2+b2+c2)所以.3(a2+b2+c2)≥(a+b+c)2=1,故a2+b2+c2≥13.5.解:(1)记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的A,则其概率为P(A)=C14C12C26=815.答:恰好选到1个曾经参加过数学研究性学习活动的同学的概率为815.(2)随机变量ξ=2,3,4P(ξ=2)=C24C26=25P(ξ=3)=C14C12C26=815P(ξ=4)=C22C26=115∴随机变量ξ的分布列为ξ234P2*******∴Eξ=2×25+3×815+4×115=836.证明(1)当n=2时,左边-右边=a2+b22=(a+b2)2=(a-b2)2≥0,不等式成立.(2)假设当n=k(k∈N*,k>1)时,不等式成立,即ak+bk2≥(a+b2)k.因为a>0,b>0,k>1,k∈N*,所以(ak+1+bk+1)-(akb+abk)=(ak-bk)(a-b)≥0,于是ak+1+bk+1≥akb+abk.当n=k+1时,(a+b2)k+1=(a+b2)k•a+b2≤ak+1+bk+12•a+b2= ak+1+bk+1+akb+abk4≤ak+1+bk+1+ak+1+bk+14=ak+1+bk+12.即当n=k+1时,不等式也成立.综合(1),(2)知,对于a>0,b>0,n>1,n∈N*,不等式an+bn2≥(a+b2)n总成立.希望以上资料对你有所帮助,附励志名言3条:1、宁可辛苦一阵子,不要苦一辈子。
2010年江苏省高三模拟试题(数学)Word版含答案
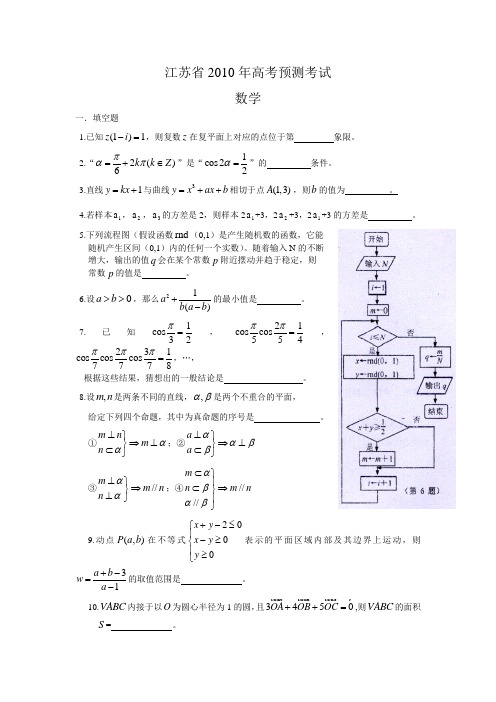
江苏省2010年高考预测考试数学一.填空题1.已知(1)1z i -=,则复数z 在复平面上对应的点位于第 象限。
2.“2()6k k Z παπ=+∈”是“1cos 22α=”的 条件。
3.直线1y kx =+与曲线3y x ax b =++相切于点(1,3)A ,则b 的值为 。
4.若样本1a ,2a ,3a 的方差是2,则样本21a +3,22a +3,21a +3的方差是 。
5.下列流程图(假设函数rnd (0,1)是产生随机数的函数,它能随机产生区间(0,1)内的任何一个实数)。
随着输入N 的不断增大,输出的值q 会在某个常数p 附近摆动并趋于稳定,则常数p 的值是 。
6.设0a b >>,那么21()a b a b +-的最小值是 。
7.已知1c o s 32π=,21cos cos 554ππ=,231cos cos cos 7778πππ=,…, 根据这些结果,猜想出的一般结论是 。
8.设,m n 是两条不同的直线,,αβ是两个不重合的平面,给定下列四个命题,其中为真命题的序号是 。
①m n m n αα⊥⎫⇒⊥⎬⊂⎭;②a a ααββ⊥⎫⇒⊥⎬⊂⎭③//m m n n αα⊥⎫⇒⎬⊥⎭;④////m n m n αβαβ⊂⎫⎪⊂⇒⎬⎪⎭9.动点(,)P a b 在不等式2000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩表示的平面区域内部及其边界上运动,则31a b w a +-=-的取值范围是 。
10.ABC 内接于以O 为圆心半径为1的圆,且3450OA OB OC ++=,则ABC 的面积 S = 。
11.过双曲线22221(0,0)x y a b a b+=>>的右顶点A 作斜率-1的直线,该直线与双曲线的两条渐近线的交点分别为,B C .若12AB BC =,则双曲线的离心率是 。
12.当θ取遍所有值时,直线cos sin )4x y πθθθ⋅+⋅=+所围成的图形面积为。
江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题04(3)

一、单选题二、多选题1. 设函数,则满足的整数的个数为( )A .2B .3C .4D .52. 复平面内表示复数的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3. 若向量,,满足,则A .1B .2C .3D .44. 如图,已知是双曲线的左、右焦点,若直线与双曲线交于两点,且四边形是矩形,则双曲线的离心率为()A.B.C.D.5. 已知三棱台中,三棱锥的体积为4,三棱锥的体积为8,则四面体的体积为( )A.B.C.D.6. “不等式在上恒成立”的一个充分不必要条件是A.B.C.D.7. 已知复数,则复数的共轭复数的虚部是( )A.B.C .2D .38.已知数列的前项和为.若,则( )A .512B .510C .256D .2549. 已知正方体的棱长为分别为的中点,为正方体的内切球上任意一点,则( )A.球被截得的弦长为B.球被四面体表面截得的截面面积为C .的范围为D .设为球上任意一点,则与所成角的范围是10.如图所示,在长方体中,是的中点,直线交平面于点,则( )江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题04(3)江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题04(3)三、填空题四、解答题A .三点共线B .的长度为1C .直线与平面所成角的正切值为D .的面积为11. 下列命题中正确的是( )A .设随机变量服从正态分布,若,则B.经验回归方程为时,变量x 和y 负相关C .某学生在上学的路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,那么该生在上学路上到第3个路口首次遇到红灯的概率为D .若,则取最大值时12. 已知函数的定义域都为为奇函数,且,,则( )A.B.C.D.13. 若,则______.14. 平面四边形ABCD 中,,E 为BC 的中点,用和表示______;若,则的最小值为______15.若过两点的直线l 与圆相切,则_____________.16. 已知a ,b ,c 分别为内角A ,B ,C的对边,.(1)求的值;(2)若,求的面积.17.设数列满足(1)求的通项公式;(2)设,记,证明:.18.在ABC 中,记角A ,B ,C 的对边为a ,b ,c ,角A为锐角,设向量,,且.(1)求角A 的大小及向量与的夹角;(2)若,求ABC 面积的最大值.19.四棱锥中,底面为矩形, ,,平面与平面的交线为.(1)求证:直线平行于平面;(2)求二面角的余弦值.20. 已知函数.(1)求的单调区间;(2)判断在上的零点的个数,并说明理由.(提示:)21. 如图,为圆的直径,点、在圆上,且,矩形所在的平面和圆所在的平面互相垂直,且,.(1)求证:平面;(2)设的中点为M,求证:平面DAF;(3)设平面将几何体分成的两个锥体的体积分别为,,求.。
江苏省南京市2010届期末迎一模高三数学期末模拟试卷(一)

南京市2010届期末迎一模高三数学期末模拟试卷(一)一、填空题:本大题共14小题,每小题5分,共70分.1.复数1ii+在复平面内对应的点位于第 象限. 2.集合2{0,2,},{1,}A a B a ==,若{0,1,2,4,16}A B = ,则a 的值为_____. 3.抛物线214x y =的准线方程为_______. 4.经过点(-2,3),且与直线250x y +-=垂直的直线方程为 . 5.若数列1,,,,4a b c 成等比数列,则b 的值为_______.6.已知函数3,100()(5),100x x f x f x x -≥⎧=⎨+<⎩,则(89)f = .7.已知两个点(2,1)A -和(1,3)B -分布在直线320x y a -++=的两侧,则a 的取值范围为_________.8.已知函数()f x 是二次函数,不等式()0f x >的解集是(0,4),且()f x 在区间[1,5]-上的最大值是12,则()f x 的解析式为 .9.已知命题p :函数y =lg x 2的定义域是R ,命题q :函数y =⎝⎛⎭⎫13x的值域是正实数集,给出命题:①p 或q ;②p 且q ;③非p ;④非q .其中真命题个数为_______.10.连续2次抛掷一枚骰子(六个面上分别标有数字1,2,3,4,5,6),记“两次向上的数字之和等于m ”为事件A ,则)(A P 最大时,m = .11.已知椭圆的方程为2221(0)16x y m m +=>,如果直线2y x =与椭圆的一个交点M 在x 轴的射影恰为椭圆的右焦点F ,则椭圆的离心率为__________.12.给出下列关于互不相同的直线l n m ,,和平面βα,的四个命题: (1),,,m A A l m ∉=⊂点αα 则l 与m 不共面;(2)l 、m 是异面直线,ααα⊥⊥⊥n m n l n m l 则且,,,//,//; (3)若ββαα//,//,,,m l A m l m l 点=⊂⊂ ,则βα//;(4)若m l m l //,//,//,//则βαβα 其中真命题是 (填序号)13.对于数列{n a },定义数列{n n a a -+1}为数列{n a }的“差数列”,若21=a ,{n a }的“差数列”的通项公式为n2,则数列{n a }的前n 项和n S = .14.如图已知在三棱柱ABC ——A 1B 1C 1中,AA 1⊥面ABC ,AC =BC ,M 、N 、P 、Q 分别是AA 1、BB 1、AB 、B 1C 1的中点.(1)求证:面PCC 1⊥面MNQ ; (2)求证:PC 1∥面MNQ .15.某工厂三个车间共有工人1000名,各车间男、女工人数如下表:已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.(1)求x 的值;(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名? (3)已知185,185y z ≥≥,求第三车间中女工比男工少的概率.A 1AB CPMNQ B 1C 116.已知不等式1)(1)ax x -+(<0 (a ∈R ).(1) 若x =a 时不等式成立,求a 的取值范围; (2) 当0a ≠时,解这个关于x 的不等式.17. 已知椭圆2214x y +=的左、右两个顶点分别为A ,B ,直线(22)x t t =-<<与椭圆相交于M ,N 两点,经过三点A ,M ,N 的圆与经过三点B ,M ,N 的圆分别记为圆C 1与圆C 2. (1)求证:无论t 如何变化,为圆C 1与圆C 2的圆心距是定值; (2)当t 变化时,求为圆C 1与圆C 2的面积的和S 的最小值.2009-2010学年度第一学期高三数学期末模拟一解答一、填空题:本大题共14小题,每小题5分,共70分.1.复数1ii+在复平面内对应的点位于第 一 象限. 2.集合2{0,2,},{1,}A a B a ==,若{0,1,2,4,16}A B = ,则a 的值为__4___. 3.抛物线214x y =的准线方程为___1x =-____. 4.经过点(-2,3),且与直线250x y +-=垂直的直线方程为280x y -+=. 5.若数列1,,,,4a b c 成等比数列,则b 的值为___2____. 6.已知函数3,100()(5),100x x f x f x x -≥⎧=⎨+<⎩,则(89)f = 101 .7.已知两个点(2,1)A -和(1,3)B -分布在直线320x y a -++=的两侧,则a 的取值范围为____.((9,8)-)8.已知函数()f x 是二次函数,不等式()0f x >的解集是(0,4),且()f x 在区间[1,5]-上的最大值是12,则()f x 的解析式为2()3(2)12f x x =--+.9.已知命题p :函数y =lg x 2的定义域是R ,命题q :函数y =⎝⎛⎭⎫13x的值域是正实数集,给出命题:①p 或q ;②p 且q ;③非p ;④非q .其中真命题个数为_______.(2)10.连续2次抛掷一枚骰子(六个面上分别标有数字1,2,3,4,5,6),记“两次向上的数字之和等于m ”为事件A ,则)(A P 最大时,m = 7 .11.已知椭圆的方程为2221(0)16x y m m+=>,如果直线y 与椭圆的一个交点M 在x 轴的射影恰为椭圆的右焦点F ,则椭圆的离心率为__________. 12.给出下列关于互不相同的直线l n m ,,和平面βα,的四个命题: (1),,,m A A l m ∉=⊂点αα 则l 与m 不共面;(2)l 、m 是异面直线,ααα⊥⊥⊥n m n l n m l 则且,,,//,//; (3)若ββαα//,//,,,m l A m l m l 点=⊂⊂ ,则βα//; (4)若m l m l //,//,//,//则βαβα 其中真命题是(1)、(2)、(3)(填序号)13.对于数列{n a },定义数列{n n a a -+1}为数列{n a }的“差数列”,若21=a ,{n a }的“差数列”的通项公式为n2,则数列{n a }的前n 项和n S =221-+n .二、解答题:本大题共6小题,共90分,解答应写出文字说明,证明过程或演算步骤.14.(本题满分14分)如图已知在三棱柱ABC ——A 1B 1C 1中,AA 1⊥面ABC ,AC =BC ,M 、N 、P 、Q 分别是AA 1、BB 1、AB 、B 1C 1的中点.(1)求证:面PCC 1⊥面MNQ ; (2)求证:PC 1∥面MNQ . 证明:(1)∵AC=BC , P 是AB 的中点 ∴AB ⊥PC∵AA 1⊥面ABC ,CC 1∥AA 1,∴CC 1⊥面ABC 而AB 在平面ABC 内 ∴CC 1⊥AB , ∵CC 1∩PC =C ∴AB ⊥面PCC 1;又∵M 、N 分别是AA 1、BB 1的中点,四边形AA 1B 1B 是平行四边形,MN ∥AB , ∴MN ⊥面PCC 1 ∵MN 在平面MNQ 内,∴面PCC 1⊥面MNQ ; 7分 (2)连PB 1与MN 相交于K ,连KQ ,∵MN ∥PB ,N 为BB 1的中点,∴K 为PB 1的中点. 又∵Q 是C 1B 1的中点∴PC 1∥KQ而KQ ⊂平面MNQ ,PC 1⊄平面MNQ ∴PC 1∥面MNQ . 14分 15.(本题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.(1)求x 的值;(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名? (3)已知185,185y z ≥≥,求第三车间中女工比男工少的概率. 解:(1)由题意可知0.15,1501000xx ==; 4分 (2)由题意可知第三车间共有工人数为1000(173177)(100150)400-+-+=名,则设应在第三车间级抽取m 名工人,则50,201000400mm ==. 8分 (3)由题意可知400y z +=,且185,185y z ≥≥,满足条件的(,)y z有(185,215),(186,214),……(215,185),共有31组.设事件A :第三车间中女工比男工少,即y z <,满足条件的(,)y z 有(185,215),(186,214),……(199,201),共有15组.故15()31P A =. 13分 A 1ABCP MNQ B 1C 1答:(1)150x =,(2)应在第三车间抽取20名工人,(3)第三车间中女工比男工少的概率为1531. 16.(本题满分15分)已知不等式1)(1)ax x -+(<0 (a ∈R ).(1) 若x =a 时不等式成立,求a 的取值范围; (2) 当0a ≠时,解这个关于x 的不等式. 解:(1)由x =a 时不等式成立,即2(1)(1)0a a -+<,所以2(1)(1)0a a +-<, 所以1a <且1a ≠-.所以a 的取值范围为(,1)(1,1)-∞-- . 6分 (2)当0a >时,11a>-,所以不等式的解:11x a -<<;当10a -<<时,11a <-,所以不等式的解:1x a<或1x >-; 当1a <-时,11a >-,所以不等式的解:1x <-或1x a>. 综上:当0a >时,所以不等式的解:11x a-<<; 当10a -<<时,所以不等式的解:1x a<或1x >-; 当1a <-时,所以不等式的解:1x <-或1x a>. 15分 17. (本题满分15分)已知椭圆2214x y +=的左、右两个顶点分别为A ,B ,直线(22)x t t =-<<与椭圆相交于M ,N 两点,经过三点A ,M ,N 的圆与经过三点B ,M ,N 的圆分别记为圆C 1与圆C 2.(1)求证:无论t 如何变化,为圆C 1与圆C 2的圆心距是定值;(2)当t 变化时,求为圆C 1与圆C 2的面积的和S 的最小值. 解:(1)易得A 的坐标)0,2(-,B 的坐标)0,2(M 的坐标)24,(2t t -,N 的坐标)24,(2t t --,线段AM 的中点P )44,22(2t t --,直线AM 的斜率t t k =+-=22421又AM PC ⊥1, ∴直线1PC 的斜率ttk -+-=2222 ∴直线1PC 的方程44)22(2222t t x t t y -+---+-=∴1C 的坐标为)0,863(-t 5分同理2C 的坐标为)0,863(+t∴4321=C C ,即无论t 如何变化,为圆C 1与圆C 2的圆心距是定值 8分 (2)圆1C 的半径为1AC 8103+=t 圆2C 的半径为83102tBC -=)1009(3222221+=+=t BC AC S πππ (2-<t <2)显然t 0=时,S 最小,825min π=S 15分。
2010年江苏高考数学模拟试卷(1)共5页word资料

2010年江苏高考数学模拟试卷(1)一、填空题:共14小题,每题5分,共70分. 1.已知集合A={x|1<2x<8,x∈R},B={x||x|<2,x∈R},则A∩B= .2.已知z=4i-zi,i为虚数单位,则复数z= .3.一位篮球运动员在最近的8场比赛中得分的茎叶图如图,则他在这8场比赛中得分的平均值是 .4.已知向量a=(1,n),b=(-1,n),若向量2a-b与向量b垂直,则|a|= .5.函数y=3x2-2alnx+a在(0,1)内有极小值,则实数a的取值范围是 .6.将一根木棒随意分成两段,较长一段的长度不超过较短一段的长度的2倍的概率是 .7.执行如图算法框图,若输入a=18,b=5,则输出的值为 .8.已知F1,F2是椭圆x2k+1+y2k=1的左、右焦点,经过F1的直线与椭圆交于A,B两点,若△ABF2的周长为12,则椭圆的离心率为 .9.曲线y=excosx在x=0处的切线方程为 .10.已知正四面体的表面积为43,则该四面体的体积为 .11.若函数f(x)=a-x+x+a2-2是偶函数,则实数a的值为 .12.用f(n)表示自然数n的各位数字的和,例如f(20)=2+0=2,f(2009)=2+0+0+9=11,若对任意n∈N,都有n+f(n)≠x,满足这个条件的最大的两位数x的值是 .13.函数y=23sinxcosx-cos2x+sin2x的图象在[0,m]上恰好有两个点的纵坐标为1,则实数m的取值范围是 .14.已知定义在R上的函数F(x)满足F(x+y)=F(x)+F(y),当x>0时,F(x)0且a≠1)图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.(1)试求p=f(t)的函数关系式;(2)老师在什么时段内安排核心内容能使得学生听课效果最佳?请说明理由.第17题18.已知圆C:(x+2)2+y2=4,相互垂直的两条直线l1、l2都过点A(a,0).(Ⅰ)若l1、l2都和圆C相切,求直线l1、l2的方程;(Ⅱ)当a=2时,若圆心为M(1,m)的圆和圆C外切且与直线l1、l2都相切,求圆M的方程;(Ⅲ)当a=-1时,求l1、l2被圆C所截得弦长之和的最大值.19.已知数列{an}的通项公式为an=nn+a(n,a∈N*).(1)若a1,a3,a15成等比数列,求a的值;(2)是否存在k(k≥3且k∈N),使得a1,a2,ak成等差数列,若存在,求出常数a的值;若不存在,请说明理由;(3)求证:数列中的任意一项an总可以表示成数列中的其他两项之积.20.已知正方形ABCD的中心在原点,四个顶点都在曲线y=ax3+bx上.(1)若正方形的一个顶点为(2,1),求a、b的值;(2)若a=1,求证:b=-22是正方形ABCD唯一确定的充要条件.数学附加题21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.A.选修4-1:几何证明选讲如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=210,AB=BC=3,求BD以及AC的长.B.选修4-2:矩阵与变换已知变换T把平面上的点(2,-1),(0,1)分别变换成点(0,-1),(2,-1),试求变换T对应的矩阵M.C.选修4-4:坐标系与参数方程圆C:ρ=2cos(θ-π4),与极轴交于点A(异于极点O),求直线CA的极坐标方程.D.选修4-5:不等式选讲证明:1+122+132+…+1n2 (2)连接A1B,连接A1C交AC1于点G,连接DG∵矩形A1ACC1,∴G为A1C的中点,又由(1)得D为BC的中点,∴△A1BC中,DG∥A1B又∵点E,F分别是BB1,A1B1的中点,∴△A1B1B中,EF∥A1B,∴EF∥DG,又EF?て矫?ADC1,DG?计矫?ADC1,∴EF∥平面ADC1.17.(本题满分14分)解:(1)t∈(0,14]时,设p=f(t)=c(t-12)2+82(c0,则n=mt,代入①得t(m2t2-22)+1=0即t[(t+22)t2-22]+1=0化简得(t-1t+2)2=0,又t-1t+2=0有且仅有一个正根,∴(m,n)唯一确定,即正方形ABCD唯一确定.2°必要性:若(m,n)唯一确定,则n=m3+bm-m=n3+bn,即nm=m2+b-mn=n2+b即(m2+b)(n2+b)+1=0――②令m2+b=t>0,则n=mt,代入①得t(m2t2+b)+1=0即t[(t-b)t2+b]+1=0化简得t2+1t2-b(t-1t)=0,即(t-1t)2-b(t-1t)+2=0――③又③有唯一解,∴b2=8,又∵b=-mn-n2=-25•5=-25.由于异面直线BE与AC所成的角是锐角,故其余弦值是25.(Ⅱ)AB=(2,0,-1),AE=(0,1,-1),设平面ABE的法向量为n1=(x,y,z),则由n1⊥AB,n1⊥AE,得2x-z=0,y-z=0.取n=(1,2,2),平面BEC的一个法向量为n2=(0,0,1),cos=n1•n2|n1|•|n2|=21+4+4=23.由于二面角A-BE-C的平面角是n1与n2的夹角的补角,其余弦值是-23.希望以上资料对你有所帮助,附励志名言3条:1、要接受自己行动所带来的责任而非自己成就所带来的荣耀。
南京市2010届全真高考模拟试卷

南京市2010届高考模拟试卷高 三 数 学 2010.03注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题)。
本卷满分160分,考试时间为120分钟。
考试结束后,请将本卷和答题卡一并交回。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答,在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整,笔迹清楚。
5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗。
6.请保持答题卡卡面清洁,不要折叠、破损。
一、填空题:本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.1、设集合1|2A x x ⎧⎫=<⎨⎬⎩⎭,{}|21x B x =>,则A B = ▲ .2、若i b i i a -=-)2(,其中i R b a ,,∈是虚数单位,则=+b a ▲ .3、函数R x x x y ∈+=,2cos 2sin 3的单调递增区间是 ▲ .4、已知向量a =(x,3), b =(2,1), 若a 与b 的夹角为锐角,则实数x 的取值范围是 ▲ .5、已知6π-=x 是方程3)tan(3=+αx 的一个解,)0(,πα-∈,则=α ▲ .6、已知函数y =ax 3+bx 2,当x =1时,有极大值3,则2a +b = ▲ .7、阅读下面的流程图,若输入a =6,b =1,则输出的结果是 ▲ .第1页 (共4页) 南京数学模拟8、在长为1的线段上任取两点,则这两点之间的距离小于12的概率为 ▲ .9、某商场在国庆黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为2.5万元,则11时至12时的销售额为 ▲ 万元.10、长方体1111ABC D A B C D -中,已知14AB =,13AD =,则对角线1AC 的取值范围是 ▲ . 11、若|(2)|0x x ->,则234x x y x-+=的取值范围是 ▲ .12、如图,在杨辉三角形中,斜线l 的上方从1按箭头方向可以构成一个“锯齿形”的数列{}n a :1,3,3,4,6,5,10,, 记其前n 项和为n S ,则19S 的值为 ▲ . 13、过双曲线1:222=-by x M 的左顶点A 作斜率为1的直线l , 若l 与双曲线M 的两条渐近线分别相交于点C B ,, 且||||BC AB =, 则双曲线M 的离心率是 ▲ . 14、在ABC Rt ∆中,c ,r ,S 分别表示它的斜边长,内切圆半径和面积,则Scr 的取值范围是 ▲ .二、解答题:本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤,并请将答案写在答题纸相应的位置上.15、【本小题满分14分】在△ABC 中,A 、B 、C 所对边的长分别为a 、b 、c ,已知向量→m =(1,2sinA), →n =(sinA ,1+cosA),满足→m ∥→n ,b +c =3a. (Ⅰ)求A 的大小; (Ⅱ)求sin(B +π6)的值.第2页 (共4页) 南京数学模拟BAC DOEF 16、【本小题满分14分】在多面体ABCDEF 中,点O 是矩形ABCD 的对角线的交点, 三角形CDE 是等边三角形,棱EF//BC 且EF =BC 21.(I )证明:FO ∥平面CDE ;(II )设BC =,3CD 证明EO ⊥平面CDF .17、【本小题满分14分】某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策,制定了如下实施方案:2009年底通过农民个人投保和政府财政投入,共集资1000万元作为全县农村医保基金,从2010年起,每年报销农民的医保费都为上一年底医保基金余额的10%,并且每年底县财政再向医保基金注资m 万元(m 为正常数).(Ⅰ)以2009年为第一年,求第n 年底该县农村医保基金有多少万元?(Ⅱ)根据该县农村人口数量和财政状况,县政府决定每年年底的医保基金要逐年增加,同时不超过1500万元,求每年新增医保基金m (单位:万元)应控制在什么范围内。
江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03 (2)

一、单选题二、多选题1. 已知不等式有实数解,则实数的取值范围为( )A.B.C.D.2. 已知,都是定义在上的函数,对任意,满足,且,则下列说法正确的是( )A.B .若,则C.函数的图像关于直线对称D.3.若为奇函数,则( )A .-8B .-4C .-2D .04. 如图,已知,,,,,则等于A.B.C.D.5. 已知实数集,集合,则( )A.B.C.D.6.已知等比数列的前项和为,,则数列的公比( )A .-1B .1C .1D .27. 设某圆锥的母线长和高分别为,,侧面积和底面积分别为,,若,则( )A.B.C.D.8.已知函数,下列对于函数性质的四个描述:①是的极小值点;②的图像关于点中心对称;③有且仅有三个零点;④若区间上递增,则的最大值为.其中正确的描述的个数是( )A .1B .2C .3D .49. 某高中学校积极响应国家“阳光体育运动”的号召,为确保学生每天一小时的体育锻炼,调查该校2000名高中学生每周平均参加体育锻炼时间的情况,现从高一、高二、高三三个年级学生中按照的比例分层抽样,收集了200名学生每周平均体育运动时间的样本数据(单位:小时),整理后得到如图所示的频率分布直方图,则下列说法中,正确的是()A .估计该校高中学生每周平均体育运动时间不足4小时的人数为500人B .估计该校高中学生每周平均体育运动时间不少于8小时的人数百分比为20%C .估计该校高中学生每周平均体育运动时间的中位数为5小时江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03 (2)江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03 (2)三、填空题四、解答题D .估计该校高中学生每周平均体育运动时间为5.8小时10. 双曲线C的两个焦点为,以C 的实轴为直径的圆记为D ,过作D 的切线与C 交于M ,N 两点,且,则C 的离心率为( )A.B.C.D.11.如图,在直三棱柱中,,,,分别为,和的中点,为棱上的一动点,且,则下列说法正确的是()A.B.三棱锥的体积为定值C.D .异面直线与所成角的余弦值为12. 中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关为了建立茶水温度随时间变化的函数模型,小明每隔1分钟测量一次茶水温度,得到若干组数据,,,,绘制了如图所示的散点图.小明选择了如下2个函数模型来拟合茶水温度随时间的变化情况,函数模型一:;函数模型二:,下列说法正确的是()A .变量与具有负的相关关系B .由于水温开始降得快,后面降得慢,最后趋于平缓,因此模型二能更好的拟合茶水温度随时间的变化情况C .若选择函数模型二,利用最小二乘法求得到的图象一定经过点D.当时,通过函数模型二计算得,用温度计测得实际茶水温度为65.2,则残差为0.113.(文)指数方程的解是__________.14. 已知函数的周期为,当时,函数恰有两个不同的零点,则实数的取值范围是__________.15. 若双曲线的渐近线方程为,则双曲线的离心率为________.16. 甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中3人答对的概率分别为且各人正确与否相互之间没有影响.用ε表示甲队的总得分.(Ⅰ)求随机变量分布列;(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).17. 如图,在长方体中,已知,E为BC中点,连接,F为线段上的一点,且.(1)证明:平面;(2)求平面与平面所成的锐二面角的余弦值.18. 已知椭圆C:()的左,右焦点分别为,,上,下顶点分别为A,B,四边形的面积和周长分别为2和.(1)求椭圆C的方程;(2)若直线l:()与椭圆C交于E,F两点,线段EF的中垂线交y轴于M点,且为直角三角形,求直线l的方程.19. 已知函数.(1)若对时,,求正实数a的最大值;(2)证明:;(3)若函数的最小值为m,证明:方程有唯一的实数根,(其中是自然对数的底数)20. 已知正整数数列满足:,,.(1)已知,,求和的值;(2)若,求证;(3)求的取值范围.21.已知抛物线C:的焦点为F,若点在C上,且.(1)求C的方程:(2)P为y轴上一点,过点F的直线l交C于A,B两点,若是以点P为直角顶点的等腰直角三角形,求线段AB的长.。
2010届高考数学复习必备试题7

空间几何体的表面积和体积一.【课标要求】了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
二.【命题走向】近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。
即使考查空间线面的位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解。
由于本讲公式多反映在考题上,预测2010年高考有以下特色:(1)用选择、填空题考查本章的基本性质和求积公式;(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;三.【要点精讲】1.多面体的面积和体积公式表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
2.旋转体的面积和体积公式表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台上、下底面半径,R表示半径四.【典例解析】题型1:柱体的体积和表面积例1.一个长方体全面积是20cm 2,所有棱长的和是24cm ,求长方体的对角线长. 解:设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得:⎩⎨⎧=++=++24)(420)(2z y x zx yz xy )2()1(由(2)2得:x 2+y 2+z 2+2xy+2yz+2xz=36(3)由(3)-(1)得x 2+y 2+z 2=16 即l 2=16所以l =4(cm)。
点评:涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察。
我们平常的学习中要多建立一些重要的几何要素(对角线、内切)与面积、体积之间的关系。
例2.如图1所示,在平行六面体ABCD —A 1B 1C 1D 1中,已知AB=5,AD=4,AA 1=3,AB ⊥AD ,∠A 1AB=∠A 1AD=3π。
江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03

一、单选题二、多选题1. 若两个等差数列,的前项和分别为和,且,则( )A.B.C.D.2.已知函数是奇函数,且,则A .9B.C.D .73.已知集合,,则( )A.B.C.D.4.已知都是锐角,,则( )A.B.C.D.5. 已知双曲线的左、右顶点分别为、,双曲线在第一象限的图象上有一点,,,,则( )A.B.C.D.6.的二项展开式中,奇数项的系数和为( )A.B.C.D.7. 已知命题:对任意,总有;:“”是“,”的充分不必要条件,则下列命题为真命题的是A.B.C.D.8. 在下面给出的函数中,哪一个函数既是区间上的增函数又是以为周期的偶函数( )A.B.C.D.9.有一组样本数据,其中是最小值,是最大值,则( )A.的平均数等于的平均数B .的中位数等于的中位数C.的标准差不小于的标准差D.的极差不大于的极差10. 我们把()叫做“费马数”(费马是十七世纪法国数学家).设,,表示数列的前项和,则使不等式成立的正整数的值可以是( )A .7B .8C .9D .1011. 已知O 为坐标原点,F为抛物线的焦点,C 的准线与x 轴的交点为,过F 的直线l 与C 交于A ,B 两点,与C 的准线交于点E ,直线l 的倾斜角,且点A 在第一象限,下列选项正确的有( )A .为定值B .为定值C .若F 为AE的中点,则D .若B 为AE的中点,则12.已知函数的图象如图所示,令,则下列说法正确的是( )江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03三、填空题四、解答题A.B.函数图象的对称轴方程为C.若函数的两个不同零点分别为,则的最小值为D .函数的图象上存在点P ,使得在P点处的切线斜率为13. 已知函数,若的最小值为,且,则实数的取值范围是________.14. 已知函数(,,是常数,,).若在区间上具有单调性,且.则的最小正周期为__.15. 请写出一个幂函数满足以下条件:①定义域为;②为增函数;③对任意的,,都有,则__________.16. 已知P 为椭圆()上一点,,分别是椭圆的左、右焦点,,且椭圆离心率为.(1)求椭圆的标准方程;(2)过的直线l 交椭圆于A ,B 两点,点C 与点B 关于x轴对称,求面积的最大值17. 如图,在四棱锥中,平面平面ABCD ,,,,,.(1)证明:;(2)若直线与平面PAD所成角的正切值等于,求平面PAD 与平面PBC 所成锐二面角的余弦值.18. 已知两点分别在轴和轴上运动,且,若动点满足,设动点的轨迹为曲线.(1)求曲线的方程;(2)过点作直线的垂线,交曲线于点(异于点),求面积的最大值.19.已知等差数列的前n 项和为,,,,成等差数列,,,成等比数列.(1)求及;(2)若,求数列的前n 项和.20. 在中,边所对的角分别为,,.(1)求角的大小;(2)若,求的面积.21. 如图,在三棱柱中,,.(1)证明:;(2)若,求二面角的余弦值.。
江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03(1)

一、单选题1. 已知为虚数单位,复数的共扼复数在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2. 在梯形中,,,且,若与交于点,则( )A.B.C.D.3. 已知集合,,则等于A.B.C.D.4. 设向量,且,则( )A .0B .1C .2D .35. 设i 是虚数单位,若复数,则z 的共轭复数为( )A.B.C.D.6. 如图l ,在高为h 的直三棱柱容器中,,,现往该容器内灌进一些水,水深为,然后固定容器底面的一边AB 于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为(如图2),则=()A.B.C.D.7. 已知函数的部分图象如图所示,且,,则( ).A.B.C.D.8.函数函数的零点个数为A .3B .2C .1D .0江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03(1)江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题03(1)二、多选题三、填空题四、解答题9. 高斯是德国著名数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德,牛顿并列为世界三大数学家,用表示不超过x 的最大整数,则称为高斯函数,例如,.则下列说法正确的是( )A .函数在区间上单调递增B .若函数,则的值域为C.若函数,则的值域为D .,10.已知函数的图象如图所示,令,则下列说法正确的是()A.B.函数图象的对称轴方程为C.若函数的两个不同零点分别为,则的最小值为D .函数的图象上存在点P ,使得在P点处的切线斜率为11. 已知双曲线满足条件:(1)焦点为,;(2)离心率为,求得双曲线C的方程为.若去掉条件(2),另加一个条件求得双曲线C 的方程仍为,则下列四个条件中,符合添加的条件可以为( )A .双曲线C 上的任意点P都满足B .双曲线C 的虚轴长为4C .双曲线C 的一个顶点与抛物线的焦点重合D .双曲线C的渐近线方程为12.如图,已知四棱锥的底面是直角梯形,,,,平面,,下列说法正确的是()A .与所成的角是B.与平面所成的角的正弦值是C .平面与平面所成的锐二面角余弦值是D.是线段上动点,为中点,则点到平面距离最大值为13.已知平面内两单位向量,若满足,则的最小值是___________.14. 在锐角三角形中,,,,则________15. 小张计划从个沿海城市和个内陆城市中随机选择个去旅游,则他至少选择个沿海城市的概率是__________.16. 为了调查某校高二学生是否需要学校提供学法指导,用简单随机抽样的方法从该校高二年级调查了55名学生,结果如下:男女需要2010不需要1015(1)估计该校高二年级学生中,需要学校提供学法指导的学生的比例;(用百分数表示,保留两位有效数字)(2)能否有95%的把握认为该校高二年级学生是否需要学校提供学法指导与性别有关?17. 中的内角的对边分别为,已知.(1)求角的大小;(2)求的最大值,并求出取得最大值时角的值.18. 已知等差数列的前n项和为,又对任意的正整数,都有,且.(1)求数列的通项公式;(2)设,求数列的前n项和.19. 已知函数,其中且的最小值为0.(1)求的值;(2)证明:当时,.20. 已知椭圆的长轴长为,离心率为,其中左顶点为,右顶点为,为坐标原点.(1)求椭圆的标准方程;(2)直线与椭圆交于不同的两点,,直线,分别与直线交于点,. 求证:为定值.21. 如图,在长方体中,相交于点,是线段的中点,已知.(1)求证:;(2)若是线段上异于端点的点,求过三点的平面被长方体所截面积的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省南京市2010届高考全真模拟数学试题2010.4注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题)。
本卷满分160分,考试时间为120分钟。
考试结束后,请将本卷和答题卡一并交回。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答,在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整,笔迹清楚。
5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗。
6.请保持答题卡卡面清洁,不要折叠、破损。
一、填空题:本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.1、复数1i1i 2++等于___ ★ ___ 2、函数sin(2)6π=-y x 的最小正周期为___ ★ ___ 3、已知集合⎭⎬⎫⎩⎨⎧-==24x x y x A ,(]a B ,∞-=,若A B ⊆,则实数a 的取值范围是___ ★ ___4、为了保证信息安全传输必须使用加密方式,有一种方式其加密、解密原理如下: 明文 密文 密文 明文已知加密为2-=xa y (x 为明文、y 为密文),如果明文“3”通过加密后得到密文为“6”, 再发送,接受方通过解密得到明文“3”,若接受方接到密文为“14”,则原发的明文 是___ ★ ___5、为了在运行下面的程序之后得到输出y =25,键盘输入x 应该是___ ★ ___ Input xIf x<0 theny=(x+1)*(x+1) Elsey=(x-1)*(x-1)End ifPrint y End6、已知向量 1),θ=a ,(1cos ),θ=b ,则⋅a b 的最大值为___ ★ ___ 7、在区间[-π,π]内随机取两个数分别记为a ,b ,则使得函数22()2π=+-+f x x ax b 有零点的概率为___ ★ ___解密 加密 发送8、若函数123+++=mx x x y 是R 上的单调函数,则实数m 的取值范围是___ ★ ___ 9、设0)()(0,,),1(log )(223≥+≥++++=b f a f b a b a x x x x f 是则对任意实数的___ ★ ___条件。
10、已知在平面直角坐标系中,O B A ),3,1(),0,2(-为原点,且,βα+=(其中1,,αβαβ+=均为实数),若N (1,0),则||的最小值是___ ★ ___ 11、若Rt ΔABC 中两直角边为a 、b,斜边c 上的高为h ,则222111ba h +=, 如图,在正方体的一角上截取三棱锥P-ABC ,PO 为棱锥的高, 记M =21PO , N =222111PC PB PA ++,那么M 、N 的大小关系是 M___ ★ ___N.(填<、>、=、≤、≥中的一种)12、直线l 是双曲线)0,0(12222>>=-b a by a x 的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l 分成弧长为2 : 1的两段圆弧,则该双曲线的离心率是___ ★ ___ 13、设x ,y ,z 是正实数,满足()()xy z x z y z +=++,则xyz 的最大值是___ ★ ___ 14、数列{}n a 定义如下:11a =,且当2n ≥时,211,1,n n n a n a n a -+⎧⎪⎪=⎨⎪⎪⎩当为偶数时,当为奇数时.已知3019n a =,则正整数n 为___ ★ ___ 二、解答题(本大题6小题,共90分。
解答时应写出文字说明,证明过程或演算步骤)15、(本小题满分14分,第一问7分,第二问7分。
)已知,A B 是△ABC的两个内角,sin 22A B A B a i j +-=+(其中,i j 是互相垂直的单位向量),若||2a =(1)试问tanB tanA ⋅是否为定值,若是定值,请求出,否则说明理由; (2)求tan C 的最大值,并判断此时三角形的形状。
16、(本小题满分14分,第一问7分,第二问7分。
)如图,PA 、PB 、PC 两两垂直,PA=PB=PC ,G 是△PAB 的重心, E 是BC 上的一点,且BE=31BC ,F 是PB 上的一点,且PF=31PB . 求证:(1)GF ⊥平面PBC ; (2)FE ⊥BC ; 17、(本小题满分15分,第一问3分,第二问4分,第三问8分。
) 如图,直角三角形ABC 的顶点坐标(2,0)A -,直角顶点(0,)B -,顶点C 在x 轴上,点P 为线段OA 的中点. (1)求BC 边所在直线方程;(2)M 为直角三角形ABC 外接圆的圆心,求圆M 的方程; (3)若动圆N 过点P 且与圆M 内切,求动圆N 的圆心N 的轨迹方程. 18、(本小题满分15分,第一问4分,第二问3分,第三问8分。
)已知向量2(3,1),(,)a x b x y =-=- ,(其中实数y 和x 不同时为零),当||2x <时,有a b ⊥ ,当||2x ≥时,//a b .(1) 求函数式()y f x =;(2)求函数()f x 的单调递减区间;(3)若对(,2]x ∀∈-∞-[2,)+∞ ,都有230mx x m +-≥,求实数m 的取值范围.NM G FEDC BPAQ19、(本小题满分14分,第一问9分,第二问5分。
) 如图,一科学考察船从港口O 出发,沿北偏东α角的射线OZ 方向航行,而在离港口O 13a (a 为正常数)海里的北偏东β角的A 处共有一个供给科考船物资的小岛,其中已知==βαcos ,31tan 132.现指挥部需要紧急征调沿海岸线港口O 正东m 海里的B 处的补给船,速往小岛A 装运物资供给科考船.该船沿BA 方向全速追赶科考船,并在C 处相遇.经测算当两船运行的航线与海岸线OB 围成的三角形OBC 的面积S 最小时,这种补给最适宜. (1)求S 关于m 的函数关系式S (m );(2)应征调m 为何值处的船只,补给最适宜?20、(本小题满分18分,第一问6分,第二问4分,第三问8分) 已知函数2()(1),()(1)f x x g x k x =-=-,函数()()f x g x -其中一个零点为5,数列{}n a 满足12ka =,且1()()()0n n n n a a g a f a +-+=. (1)求数列{}n a 通项公式;(2)求S {}n a 的最小值(用含有n 的代数式表示);(3)设13()()n n n b f a g a +=-,试探究数列{}n b 是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.南京市2010届高考全真模拟 数学试题参考答案及评分标准1、212、π3、4≥a4、45、6-或66、27、34 8、),31[+∞ 9、充要条件10、223 11、= 12、、2 13、12714、238 15、解:2223||2cos sin 222A B A B a +-=+= , 1cos()31cos()22A B A B --+++=【4分】02sin sin cos cos sin sin cos cos =+--BA B A B A B A13tan tan 022A B -= 【7分】 1tan tan 3A B =(定值)(2)由(1)可知A 、B为锐角tan tan 3(tan tan )tan tan()1tan tan 2A B A B C B A A B ++=-+=-=-≤-=-12分】所以tan C的最大值为ABC 为钝角三角形。
【14分】 16、证明:(1)连结BG 和PG ,并延长分别交PA 、AB 于M 和D ,在△PBM 中,∵PF=31PB ,G 是△PAB 的重心,【4分】 ∴MG=31BM ,∴GF ∥PM .又PA ⊥PB,PA ⊥PC ,∴PA ⊥平面PBC , 则GF ⊥平面PBC .【7分】 (2)在EC 上取一点Q 使CQ=31BC ,【9分】 连结FQ ,又PF=31PB ,∴FQ ∥PC .∵PB=PC ,∴FB=FQ .【12分】 ∵BE=31BC ,∴E 是BQ 的中点, ∴FE ⊥BQ ,即FE ⊥BC .【14分】N M G FE DCB P AQ17、(1)∵AB k =AB BC ⊥,∴2CB k =,∴:2BC y x =-【3分】(2)在上式中,令0y =,得(4,0)C ,∴圆心(1,0)M又∵3AM =,∴外接圆的方程为22(1)9x y -+=【7分】(3)∵(1,0)P -,(1,0)M∵圆N 过点(1,0)P -,∴PN 是该圆的半径又∵动圆N 与圆M 内切,∴3MN PN =-,即3MN PN +=【11分】∴点N 的轨迹是以M 、P 为焦点,长轴长为3的椭圆, ∴32a =,1c =,【13分】b ==∴轨迹方程为2219544x y += 【15分】 18、(1)当||2x <时,由a b ⊥ 得2(3)0a b x x y ⋅=--=,33y x x =-;(||2x <且0x ≠) 当||2x ≥时,由//a b.得23xy x =-- ∴323,(220)().(22)3x x x x y f x x x x x⎧--<<≠⎪==⎨≥≤-⎪-⎩且或【4分】(2)当||2x <且0x ≠时,由2'33y x =-<0,解得(1,0)(0,1)x ∈- ,【6分】当||2x ≥时,222222(3)(2)3'0(3)(3)x x x x y x x ---+==>--∴函数()f x 的单调减区间为(-1,0)和(0,1)【8分】(3)对(,2]x ∀∈-∞-[2,)+∞ ,都有230mx x m +-≥即2(3)m x x -≥-,也就是23xm x ≥-对(,2]x ∀∈-∞-[2,)+∞ 恒成立,由(2)知当||2x ≥时,222222(3)(2)3'()0(3)(3)x x x x f x x x ---+==>--∴函数()f x 在(-,-2]∞和[2,+)∞都单调递增【12分】又2(2)234f --==-,2(2)234f ==-- 当2x ≤-时2()03xf x x =>-,∴当(,2]x ∈-∞-时,0()2f x <≤ 同理可得,当2x ≥时,有2()0f x -≤<,综上所述得,对(,2]x ∈-∞-[2,)+∞ , ()f x 取得最大值2;∴实数m 的取值范围为2m ≥.【15分】 19、(I )以O 点为原点,指北的方向为y 轴建立直角坐标系,则直线OZ 的方程为y=3x , 设点A (x 0,y 0),则x 0=13asin β=3a ,y 0=13acos β=2a ,即A (3a ,2a ),又B (m ,0),则直线AB 的方程是y=)(32m x ma a--,由此得到C 点坐标为)736,732(am ama m am --, )37(733||||21)(2a m a m am y OB m S C >-=⨯=∴;【9分】(II )328]3149492[]314)37(949)37[()(222a a a a a a m a a m a m S =+≥+-+-=, ∴当且仅当)37(314,)37(949372a m a m a m a a m >=-=-即时等号成立,【13分】 答:征调a m 314=海里处的船只时,补给最适宜. 【14分】20、(1)函数()()f x g x -有一个零点为5,即方程2(1)(1)0x k x ---=,有一个根为5,将5x =代入方程得1640k -=,∴4k =,∴12a =【2分】由1()()()0n n n n a a g a f a +-+=得214()(1)(1)0n n n n a a a a +--+-=1(1)(441)0n n n n a a a a +--+-=∴10n a -=或14410n n n a a a +-+-=由(1)知12a =,∴10n a -=不合舍去由14410n n n a a a +-+-=得1431n n a a +=+【4分】方法1:由1431n n a a +=+得131(1)4n n a a +-=- ∴数列{1}n a -是首项为111a -=,公比为34的等比数列∴131()4n n a --=,∴13()14n n a -=+〔方法2:由1431n n a a +=+---①得当2n ≥时1431n n a a -=+----② ①-②得114()3()n n n n a a a a +--=- ∴1134n n n n a a a a +--=-(2n ≥)即数列1{}n n a a --是首项为21a a -,公比为34的等比数列∵211111444a a a -=-=-,∴1113()44n n n a a -+-=-⋅---------------③ 由①得13144n n a a +=+代入③整理得13()14n n a -=+【6分】(2)由(1)知13()14n n a -=+∴2113331()()444nn i i a n -==+++++∑ =3[1()]344[1()]3414n n n n -+=-+-------8分 ∵对,n N *∀∈有33()44n ≤,∴3311()1444n -≥-=【8分】∴34[1()]14nn n -+≥+,即11ni i a n =≥+∑即所求S {}n a 的最小值为1+n.【10分】(3)由13()()n n n b f a g a +=-得213(1)4(1)n n n b a a +=---∴12333[()]4()44n n n b -=-=121333{[()]()}44n n ---【12分】令13()4n u -=,则01u <≤,23()n b u u =-=2113[()]24u --∵函数2113[()]24n b u =--在1[,1]2上为增函数,在1(0,)2上为减函数【14分】当1n =时1u =,当2n =时34u =, 当3n =时,239()416u ==,当4n =时2764u =,∵2764<19312164<<<,且12719||||264216->-【16分】 ∴当3n =时,n b 有最小值,即数列{}n b 有最小项,最小项为23991893[()]1616256b =-=-故当1n =即1u =时,n b 有最大值,即数列{}n b 有最大项,最大项为13(11)0b =-=. 【18分】。
