人教版数学九年级上册24.3《正多边形和圆》word学案
人教版九年级数学上册教案:24.3正多边形和圆课堂优秀教学案例

3.结合学生的课堂表现、作业完成情况和小组合作情况,进行全面评价,关注学生的知识掌握、能力发展和情Байду номын сангаас态度。
四、教学内容与过程
(一)导入新课
1.利用图片展示正多边形的实际应用场景,如足球、蜂窝等,引发学生对正多边形的兴趣,激发学生的学习动机。
2.创设问题情境,如“为什么足球是正二十面体?”、“蜂窝为什么是正六边形?”等,引导学生思考正多边形的特征和性质。
3.小组合作:本节课鼓励学生进行小组合作学习和讨论,培养了学生的团队合作意识和沟通能力。通过小组合作,学生能够共同解决问题,分享自己的学习和研究成果,提高了学生的表达能力和批判性思维。
4.反思与评价:本节课在课堂结束前,引导学生进行自我反思,总结自己在课堂上的学习情况和收获。同时,设置了不同难度的题目,让学生在课后进行巩固练习。通过这种方式,学生能够及时巩固所学知识,提高自我认知和自我评价能力。
3.在解决问题的过程中,引导学生总结正多边形的性质和规律,提高学生的数学思维能力和逻辑推理能力。
(三)小组合作
1.将学生分成小组,鼓励学生进行合作学习和讨论,培养学生的团队合作意识和沟通能力。
2.设计小组合作任务,如:“观察并描述正多边形的性质”、“制作正多边形的模型”等,让学生在实践中掌握正多边形的知识。
3.利用多媒体课件展示正多边形的动态变化,让学生直观感受正多边形的魅力,引发学生的探究欲望。
(二)问题导向
1.设计一系列问题,引导学生逐步深入探究正多边形的定义、性质和与圆的关系。如:“正多边形有什么特点?”,“正多边形的边数与圆有什么关系?”,“如何判断一个多边形是正多边形?”等。
2024年人教版九年级数学上册教案及教学反思全册第24章 圆(教案)正多边形和圆(第1课时)

24.3 正多边形和圆第1课时一、教学目标【知识与技能】了解正多边形和圆的关系,了解正多边形半径和边长,边心距,中心,中心角等概念.会应用正多边形的有关知识解决圆中的计算问题.【过程与方法】结合生活中的正多边形形状的图案,发现正多边形和圆的关系.【情感态度与价值观】学生经历观察、发现、探究等数学活动,感受到数学来源于生活、又服务于生活.二、课型新授课三、课时第1课时,共2课时。
四、教学重难点【教学重点】正多边形与圆的相关概念及其之间的运算.【教学难点】探索正多边形和圆的关系,正多边形半径,中心角、边心距,边长之间的关系.五、课前准备课件、图片、直尺等.六、教学过程(一)导入新课出示课件2,3:观察上边的美丽图案,思考下面的问题:(1)这些都是生活中经常见到的利用正多边形得到的物体,你能找出正多边形吗?(2)你知道正多边形和圆有什么关系吗?怎样做一个正多边形呢?学生通过观察美丽的图案,欣赏生活中正多边形形状的物体.让学生感受到数学来源于生活,并从中感受到数学美.(板书课题)(二)探索新知探究一正多边形的对称性教师问:什么叫做正多边形?(出示课件5)学生答:各边相等,各角也相等的多边形叫做正多边形.教师问:矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?学生答:矩形不是正多边形,因为矩形不符合各边相等;菱形不是正多边形,因为菱形不符合各角相等;教师强调:正多边形:①各边相等;②各角相等,两个条件,缺一不可.教师问:正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?(出示课件6,7)学生动手操作,交流,感受正多边形的对称性.教师归纳:正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形既是轴对称图形又是中心对称图形.探究二正多边形的有关概念教师问:以正四边形为例,根据对称轴的性质,你能得出什么结论?(出示课件8,9)师生结合图形共同探究:EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.GH是边AD、BC的垂直平分线,∴OA=OD,OB=OC.∴OA=OB=OC=OD.∴正方形ABCD有一个以点O为圆心的外接圆.AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,∴OE=OH=OF=OG.∴正方形ABCD还有一个以点O为圆心的内切圆.出示课件10:教师问:所有的正多边形是不是也都有一个外接圆和一个内切圆?学生答:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.教师问:一个正多边形的各个顶点在同一个圆上?学生答:一个正多边形的各个顶点在同一个圆上,则这个正多边形就是这个圆的一个内接正多边形,圆叫做这个正多边形的外接圆.教师问:所有的多边形是不是都有一个外接圆和内切圆?学生答:多边形不一定有外接圆和内切圆,只有是正多边形时才有,任意三角形都有外接圆和内切圆.教师出示概念:(出示课件11)1.正多边形的外接圆和内切圆的公共圆心,叫做正多边形的中心.2.外接圆的半径叫做正多边形的半径.3.内切圆的半径叫做正多边形的边心距.4.正多边形每一条边所对的圆心角,叫做正多边形的中心角.正多边形的每个中心角都等于360.n练一练:(出示课件12)完成下面的表格:学生计算交流并填表.探究三 正多边形的有关计算出示课件13:如图,已知半径为4的圆内接正六边形ABCDEF :①它的中心角等于 度; ②OC BC(填>、<或=); ③△OBC 是 三角形;④圆内接正六边形的面积是△OBC 面积的 倍. ⑤圆内接正n 边形面积公式:_______________________. 学生计算交流后,教师抽学生口答.①60;②=;③等边;④6;⑤1=2S ⨯⨯正多边形周长边心距出示课件14:例 有一个亭子,它的地基是半径为4m 的正六边形,求地基的周长和面积(精确到0.1m 2).教师分析:根据题意作图,将实际问题转化为数学问题.师生共同解答:(出示课件15)解:过点O 作OM ⊥BC 于M.在Rt △OMB 中,OB =4,MB =4222BC ==,利用勾股定理,可得边心距r ==亭子地基的面积:2112441.6(m ).22S l r =⋅=⨯⨯≈ 巩固练习:(出示课件16)如图所示,正五边形ABCDE 内接于⊙O ,则∠ADE 的度数是( )A .60°B .45°C .36°D .30° 学生独立思考后自主解答:C.教师归纳:圆内接正多边形的辅助线(出示课件17)1.连半径,得中心角;2.作边心距,构造直角三角形. 巩固练习:(出示课件18)已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?学生独立思考后解答,一生板演.解:∵直角三角形两直角边之和为8,设一边长为x. ∴ 另一边长为8-x.则该直角三角形面积:S=(8-x )x ÷2,即214.2s x x =-+ 当x=2b a -=4,另一边为4时,S 有最大值244ac b a -=8.∴当两直角边都是4时,直角面积最大,最大值为8. (三)课堂练习(出示课件19-24)1.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=______度.2.填表:3.若正多边形的边心距与半径的比为1:2,则这个多边形的边数是_____.4.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为_____度.(不取近似值)5.要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.7.如图,正六边形ABCDEF的边长为点P为六边形内任一点.则点P 到各边距离之和是多少?8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.(1)求图①中∠MON=_______;图②中∠MON=_______;图③中∠MON=_______;(2)试探究∠MON的度数与正n边形的边数n的关系.参考答案:1.360°解析:由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°.2.3.34.412875.6.解:∵正方形的面积等于4, ∴正方形的边长AB=2. 则圆的直径AC=2, ∴⊙O 的半径=.∴⊙O 的面积为22.ππ=7.解:过P 作AB 的垂线,分别交AB 、DE 于H 、K ,连接BD ,作CG ⊥BD 于G.22∵六边形ABCDEF 是正六边形, ∴AB ∥DE ,AF ∥CD ,BC ∥EF ,∴P 到AF 与CD 的距离之和,及P 到EF 、BC 的距离之和均为HK 的长. ∵BC=CD ,∠BCD=∠ABC=∠CDE=120°, ∴∠CBD=∠BDC=30°,BD ∥HK ,且BD=HK.∴CG=12BC=.∵CG ⊥BD ,∴BD=2BG=2×=2×3=6.∴点P 到各边距离之和=3BD=3×6=18. 8.解:⑴①120°;②90°;③72°;⑵360MON n ︒∠=.(四)课堂小结通过这节课的学习,你知道正多边形和圆有怎样的关系吗?你知道正多边形的半径、边心距、内角、中心角等概念吗?(五)课前预习22BG BC-预习下节课(24.3第2课时)的相关内容.七、课后作业配套练习册内容八、板书设计:九、教学反思:本节课通过创设问题情境,将正多边形与圆紧密联系,让学生发现它们之间的密切关系,并将结论由特殊推广到一般,符合学生的认识规律,通过学习正多边形中的一些基本概念,引导学生将实际问题转化为数学问题,体现了化归的思想.。
人教版数学九年级上册第24章圆24.3正多边形和圆教学设计

2.在解决实际问题时,可能无法灵活运用所学的正多边形知识,需要加强练习和指导。
3.部分学生对几何图形的观察能力和空间想象力有待提高,需要在教学过程中给予关注和培养。
4.学生在小组合作中,可能存在沟通不畅、分工不明确等问题,需要教师在教学过程中引导学生形成良好的合作氛围。
3.培养学生的空间观念,提高学生对几何图形的观察力和想象力,为后续几何学习打下基础。
4.通过解决实际问题,培养学生的责任感、使命感和创新精神,使学生在面对问题时敢于挑战、勇于探索。
二、学情分析
九年级学生在经过前两年的数学学习后,已具备了一定的几何基础和逻辑思维能力。在本章节的学习中,他们能够运用已掌握的圆的相关知识,进一步探索正多边形与圆之间的关系。然而,学生在面对正多边形的性质和计算方法时,可能会出现以下情况:
-选择2-3道题目进行详细解答,要求步骤清晰,逻辑严谨。
-针对学生在课堂练习中出现的典型错误,设计类似题目进行针对性练习。
2.提高作业:结合生活实际,设计一道综合性的问题,让学生运用本节课所学的正多边形和圆的知识解决。
-鼓励学生运用数形结合、转化等数学思想方法,提高解决问题的能力。
-要求学生在解答过程中,注意逻辑推理和几何直观的运用。
3.通过小组合作,讨论解决正多边形和圆相关问题的方法,培养学生的团队协作能力和沟通能力。
4.运用数形结合、转化等数学思想方法,解决实际问题,提高学生解决问题的能力。
(三)情感态度与价值观
1.培养学生对正多边形和圆的美的认识,激发学生对数学美的追求,提高学生的审美情趣。
2.增强学生对数学学习的兴趣,使学生感受到数学与现实生活的密切联系,体会数学的实用价值。
人教版九年级数学上册《第二十四章圆24.3正多边形和圆》教学设计

人教版九年级数学上册《第二十四章圆24.3正多边形和圆》教学设计一. 教材分析人教版九年级数学上册《第二十四章圆24.3正多边形和圆》的内容包括正多边形的定义、性质和圆的定义、性质。
本章节的目的是让学生理解正多边形和圆的关系,掌握正多边形的计算方法,以及了解圆的性质和应用。
本节课的教学内容是24.3正多边形和圆,主要包括正多边形的定义、性质和圆的定义、性质。
二. 学情分析九年级的学生已经掌握了基本的代数和几何知识,对于图形的理解和计算能力有一定的基础。
但是,对于正多边形和圆的关系,以及圆的性质和应用可能还存在一定的困难。
因此,在教学过程中,需要引导学生通过观察、操作、思考、交流等活动,自主探索正多边形和圆的性质,提高他们的空间想象能力和思维能力。
三. 教学目标1.知识与技能:使学生掌握正多边形的定义、性质,理解圆的定义、性质,能够运用正多边形和圆的知识解决实际问题。
2.过程与方法:通过观察、操作、思考、交流等活动,培养学生的空间想象能力和思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识和自主学习能力。
四. 教学重难点1.重点:正多边形的定义、性质,圆的定义、性质。
2.难点:正多边形和圆的关系,圆的性质和应用。
五. 教学方法1.情境教学法:通过实物、图片、几何画板等直观教具,引导学生观察、操作、思考,激发学生的学习兴趣。
2.问题驱动法:提出问题,引导学生思考,激发学生的求知欲。
3.合作学习法:学生进行小组讨论,培养学生的团队合作意识和交流能力。
4.归纳总结法:引导学生通过总结归纳,形成系统的知识结构。
六. 教学准备1.教学课件:制作精美的课件,包括图片、几何画板等直观教具。
2.教学素材:准备相关的实物、图片等教学素材。
3.教学用具:准备黑板、粉笔、直尺、圆规等教学用具。
七. 教学过程1.导入(5分钟)利用实物、图片等教学素材,引导学生观察正多边形和圆的实例,激发学生的学习兴趣。
人教版数学九年级上册24.3.2《正多边形和圆》教案

人教版数学九年级上册24.3.2《正多边形和圆》教案一. 教材分析《正多边形和圆》是人民教育出版社出版的数学九年级上册第24章第三节的内容。
本节内容主要介绍了正多边形的定义、性质以及与圆的关系。
通过学习正多边形和圆,学生能够理解圆的定义,掌握圆的性质,并能够运用圆的知识解决实际问题。
二. 学情分析九年级的学生已经掌握了多边形的基本概念和性质,具备一定的逻辑思维能力。
但是对于正多边形和圆的关系的理解可能存在一定的困难。
因此,在教学过程中,需要通过实例和图形的演示,帮助学生建立直观的认识,引导学生主动探究正多边形和圆的性质。
三. 教学目标1.知识与技能:–能够理解正多边形的定义和性质。
–能够理解圆的定义和性质。
–能够运用正多边形和圆的知识解决实际问题。
2.过程与方法:–通过观察和操作,培养学生的观察能力和动手能力。
–通过小组合作,培养学生的合作能力和沟通能力。
3.情感态度与价值观:–培养学生对数学的兴趣和好奇心。
–培养学生的自主学习能力和解决问题的能力。
四. 教学重难点•正多边形的定义和性质。
•圆的定义和性质。
•正多边形和圆的关系的理解。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究正多边形和圆的性质。
2.通过实例和图形的演示,帮助学生建立直观的认识。
3.采用小组合作的学习方式,培养学生的合作能力和沟通能力。
六. 教学准备1.准备相关的图形和图片,用于演示和解释正多边形和圆的性质。
2.准备练习题和实际问题,用于巩固和拓展学生的知识。
七. 教学过程1.导入(5分钟)–利用图片和实例,引导学生回顾多边形的基本概念和性质。
–提出问题,引导学生思考正多边形和圆的关系。
2.呈现(15分钟)–通过图形和实例,展示正多边形的定义和性质。
–解释正多边形和圆的关系,引导学生理解圆的定义和性质。
3.操练(15分钟)–学生分组合作,进行实际操作,探究正多边形和圆的性质。
–教师引导学生进行讨论和交流,解答学生的疑问。
人教版数学九年级上册第24章圆24.3正多边形和圆优秀教学案例

3.总结本节课的学习方法,如观察、操作、探究、合作等。
4.布置课后作业,巩固所学知识。
(五)作业小结
1.教师发放课后作业,要求学生运用所学知识解决实际问题。
2.提醒学生在完成作业过程中注意审题、仔细计算、规范书写。
3.鼓励学生遇到问题时互相讨论、请教教师,提高解题能力。 Nhomakorabea五、案例亮点
1.生活情境的创设:本节课通过展示生活中的正多边形实例,让学生感受到了数学与生活的紧密联系,激发了学生的学习兴趣。这种情境的创设,不仅让学生在课堂上保持高度的热情,而且有助于提高学生的应用能力,使他们在解决实际问题时能够自然而然地想到运用所学知识。
1.教师展示一系列生活中常见的正多边形图片,如正方形、正三角形、正六边形等,引导学生关注正多边形的美感及其在生活中的应用。
2.提问:“同学们,你们能找出这些图片中的共同特征吗?这些图形有什么特别之处?”让学生思考并回答。
3.总结:正多边形具有对称性、边长相等、内角相等等特征。这些特征使得正多边形在生活中的应用非常广泛。
4.最后提问:“如何用圆规和直尺绘制正多边形?请同学们尝试绘制一个正六边形。”激发学生的动手操作欲望。
(三)小组合作
1.将学生分成若干小组,每组选定一个正多边形进行研究。
2.给出研究任务:“请同学们探究你们所选的正多边形的性质,并尝试用数学语言表达。”
3.组织小组讨论,鼓励学生发表自己的观点,培养学生的合作精神和团队意识。
本节课的教学策略旨在激发学生的学习兴趣,培养学生的探究能力和合作精神。通过情景创设、问题导向、小组合作和反思与评价等环节,引导学生主动参与课堂,提高学生的数学素养。同时,关注学生的情感态度与价值观的培养,使学生在知识与技能、过程与方法、情感态度与价值观等方面得到全面发展。
人教版九年级上册数学学案:24.3正多边形和圆
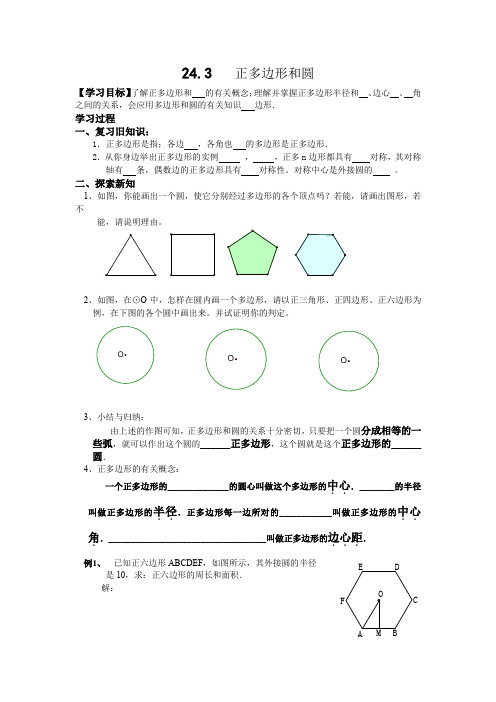
24.3 正多边形和圆【学习目标】了解正多边形和 的有关概念;理解并掌握正多边形半径和 、边心 、 角之间的关系,会应用多边形和圆的有关知识 边形. 学习过程一、复习旧知识:1.正多边形是指;各边 ,各角也 的多边形是正多边形.2.从你身边举出正多边形的实例 , ,正多n 边形都具有 对称,其对称轴有 条,偶数边的正多边形具有 对称性。
对称中心是外接圆的 。
二、探索新知1、如图,你能画出一个圆,使它分别经过多边形的各个顶点吗?若能,请画出图形,若不能,请说明理由。
2、如图,在⊙O 中,怎样在圆内画一个多边形,请以正三角形、正四边形、正六边形为例,在下图的各个圆中画出来。
并试证明你的判定。
3、小结与归纳:由上述的作图可知,正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的______正多边形,这个圆就是这个正多边形的______圆.4、正多边形的有关概念:一个正多边形的______________的圆心叫做这个多边形的中心...________的半径叫做正多边形的半径...正多边形每一边所对的____________叫做正多边形的中心..角..____________________________________叫做正多边形的边心距.... 例1、 已知正六边形ABCDEF ,如图所示,其外接圆的半径 是10,求:正六边形的周长和面积. 解:三、练习巩固1.如图1所示,正六边形ABCDEF 内接于⊙O ,则∠ADB 的度数是( ).A .60°B .45°C .30°D .22.5°(1) (2) (3)2.圆内接正五边形ABCDE 中,对角线AC 和BD 相交于点P ,则∠APB 的度数是( ). A .36° B .60° C .72° D .108° 3.若半径为5cm 的一段弧长等于半径为2cm 的圆的周长, 则这段弧所对的圆心角为( ) A .18° B .36° C .72° D .144° 4.已知正六边形边长为2,则它的内切圆面积为_______.5.在△ABC 中,∠ACB=90°,∠B=30°,以C 为圆心,CA 长为半径的圆交AB 于D ,如图2所示,若AC=6,则AD 的长为________.6.四边形ABCD 为⊙O 的内接梯形,如图3所示,AB ∥CD ,且CD 为直径,如果⊙O 的半径等于r ,∠C=60°,那图中△OAB 的边长AB 是______;△ODA 的周长是_______;∠BOC 的度数是________.四、综合提高题1.等边△ABC 的边长为4,求其内切圆的内接正方形DEFG 的面积.2.如图所示,已知⊙O 的周长等于6πcm ,求以它的半径为边长的正六边形ABCDEF 的面积.五、课后作业1.如图所示,•已知⊙O•的周长等于6πcm ,•求以它的半径为边长的正六边形ABCDEF 的面积.D BAC2.六、教学反思:。
九年级数学人教版上册24.3正多边形和圆优秀教学案例

在实际教学过程中,我将以知识与技能、过程与方法、情感态度与价值观为目标,设计丰富多样的教学活动和实例,引导学生积极参与,主动探究,使学生在掌握知识的同时,也能提高自身的综合素质和能力。同时,注重因材施教,关注每个学生的个体差异,充分调动学生的积极性和主动性,使每个学生都能在数学学科的学习中得到充分的发展和提高。
2.培养学生的动手操作能力,提高学生运用数学知识解决实际问题的能力。
3.引导学生运用归纳、推理等方法,总结正多边形的性质和规律,培养学生的创新思维能力。
(三)情感态度与价值观
1.培养学生对数学学科的兴趣和自信心,激发学生学习数学的内在动力。
2.培养学生独立思考、合作交流的习惯,提高学生的人际沟通能力和团队合作精神。
2.组织学生进行自我评价和同伴评价,让学生了解自己的学习成果和不足之处,提高学生的自我认知和评价能力。
3.教师对学生的学习情况进行总结和评价,关注学生的个体差异,给予有针对性的指导和鼓励,激发学生的学习动力和信心。
四、教学内容与过程
(一)导入新课
1.利用多媒体展示各种正多边形的实物图片,如正方形、正三角形等,引导学生关注正多边形在现实生活中的应用。
2.问题导向与小组合作相辅相成:在教学过程中,教师引导学生提出问题并自主探究,通过小组合作的形式进行研究讨论。这样的教学方式既培养了学生的提问意识和自主学习能力,又提高了学生的团队合作和交流沟通能力。
3.反思与评价注重个体差异:教师在教学过程中注重引导学生进行反思和评价,关注学生的个体差异,给予有针对性的指导和鼓励。这种教学方式既激发了学生的学习动力,又培养了学生的自我认知和评价能力。
2.设计一个正多边形的拼图游戏,让学生在游戏中体会正多边形的性质和特点,激发学生的学习兴趣。
人教版九年级数学上册24.3.1《正多边形和圆(1)》教学设计

人教版九年级数学上册24.3.1《正多边形和圆(1)》教学设计一. 教材分析《正多边形和圆》是人教版九年级数学上册第24章第三节的第一课时内容,主要介绍了正多边形的定义、性质以及与圆的关系。
本节课的内容是学生对几何图形学习的进一步深化,对于培养学生的空间想象能力和抽象思维能力具有重要意义。
教材通过生活中的实例引入正多边形和圆的概念,让学生感受数学与生活的紧密联系,激发学生的学习兴趣。
二. 学情分析九年级的学生已经具备了一定的几何基础知识,对图形的认识有一定的深度。
但是,对于正多边形和圆的性质和关系,可能还比较陌生。
因此,在教学过程中,需要教师通过生动形象的实例和直观的图形,帮助学生理解和掌握正多边形和圆的概念和性质。
三. 教学目标1.了解正多边形的定义和性质,能够识别和判断正多边形。
2.理解圆的概念,掌握圆的性质。
3.掌握正多边形与圆的关系,能够运用正多边形和圆的知识解决实际问题。
四. 教学重难点1.重难点:正多边形的定义和性质,圆的概念和性质。
2.难点:正多边形与圆的关系的理解和运用。
五. 教学方法1.采用问题驱动的教学方法,通过提问引导学生思考和探索,激发学生的学习兴趣和积极性。
2.采用直观演示法,通过实物和图形的展示,帮助学生直观地理解和掌握正多边形和圆的概念和性质。
3.采用归纳总结法,通过总结和归纳,使学生对正多边形和圆的知识有一个系统的认识。
六. 教学准备1.准备相关的图形和图片,如正多边形和圆的实物图片,正多边形和圆的模型等。
2.准备相关的教学PPT,内容包括正多边形和圆的定义、性质和关系等。
七. 教学过程1.导入(5分钟)通过提问方式引导学生回顾已学过的几何图形,如三角形、四边形等,激发学生的学习兴趣。
然后,展示一些生活中的实例,如五角星、车轮等,引导学生思考这些图形的共同特征。
2.呈现(10分钟)教师展示正多边形和圆的实物图片和模型,引导学生观察和描述正多边形和圆的特征。
然后,教师通过PPT呈现正多边形和圆的定义和性质,让学生初步了解和掌握。
人教版数学九年级上册24.3 正多边形和圆教案

教学过程
1.导入新课
“同学们,我们今天要学习的内容是关于正多边形和圆的相关知识。在正式开始学习之前,我想请大家观察一下我们周围的物体,看看是否有圆和正多边形的影子。”
(4)让学生利用教具模型进行观察和操作,加深对正多边形和圆的理解。
(5)鼓励学生参加数学竞赛和相关活动,提高学生的数学素养。
(6)建议学生在课后进行小组讨论,共同探讨正多边形和圆在现实生活中的应用,提高合作能力。
教学反思
今天讲授的是人教版数学九年级上册第24章《正多边形和圆》,这节课是九年级数学的重要内容,也是学生对几何图形认识的一次质的飞跃。在课后,我对本节课的教学进行了深刻的反思,有以下几点体会:
然而,我也发现了一些不足之处。在教学过程中,我发现部分学生在理解圆的定义和性质时存在一定的困难。对于这部分学生,我需要采取更加直观的教学方法,如利用实物模型、几何画板等教学媒体,帮助他们更好地理解圆的相关概念。此外,在课堂互动环节,我也要注意调动每一个学生的积极性,让每一个学生都能参与到课堂讨论中来,提高他们的合作能力。
5.课堂小结
“通过本节课的学习,我们了解了正多边形和圆的定义、性质和关系。希望大家能够将这些知识运用到实际生活中,不断提高自己的数学素养。”
(教师引导学生总结本节课6.课后作业
“请大家完成课后练习第2、3题,并预习下一节课的内容。”
(教师布置课后作业,为下一节课的学习做好铺垫。)
教学方法与策略
1.选择适合教学目标和学习者特点的教学方法:本节课的教学方法主要包括讲授法、直观演示法、小组合作探究法和实践活动法。通过讲授法向学生传授圆和正多边形的基本性质,直观演示法帮助学生形成清晰的表象,小组合作探究法鼓励学生共同探讨问题,实践活动法让学生动手操作,加深对知识的理解。
人教版数学九年级上册24.3《正多边形和圆》教学设计

人教版数学九年级上册24.3《正多边形和圆》教学设计一. 教材分析《正多边形和圆》是人教版数学九年级上册第24.3节的内容。
本节内容是在学生已经掌握了圆的概念和性质的基础上进行学习的,主要让学生了解正多边形的定义、性质及其与圆的关系。
通过本节内容的学习,学生能够理解正多边形的对称性,掌握正多边形的计算方法,并为后续学习圆的周长、面积等知识打下基础。
二. 学情分析九年级的学生已经具备了一定的几何基础知识,对圆的概念和性质有一定的了解。
但是,对于正多边形的定义和性质,以及与圆的关系,学生可能还比较陌生。
因此,在教学过程中,需要引导学生通过观察、思考、探究,逐步理解正多边形的性质,并能够运用到实际问题中。
三. 教学目标1.知识与技能:让学生掌握正多边形的定义、性质及其与圆的关系,能够运用正多边形的性质解决实际问题。
2.过程与方法:通过观察、思考、探究,培养学生的几何思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作精神。
四. 教学重难点1.重点:正多边形的定义、性质及其与圆的关系。
2.难点:正多边形的计算方法及其在实际问题中的应用。
五. 教学方法1.引导发现法:通过引导学生观察、思考、探究,发现正多边形的性质及其与圆的关系。
2.案例分析法:通过分析实际问题,让学生学会运用正多边形的性质解决实际问题。
3.小组合作学习:让学生在小组内进行讨论、交流,培养团队合作精神。
六. 教学准备1.教学课件:制作精美的教学课件,辅助讲解和展示。
2.教学素材:准备一些关于正多边形的实际问题,用于巩固和拓展。
3.教学工具:准备黑板、粉笔等教学工具。
七. 教学过程1.导入(5分钟)利用课件展示一些生活中常见的正多边形,如正方形、正三角形等,引导学生关注正多边形,激发学生的学习兴趣。
2.呈现(10分钟)介绍正多边形的定义和性质,引导学生通过观察、思考,发现正多边形的特点。
3.操练(10分钟)让学生分组讨论,分析一些实际问题,运用正多边形的性质解决问题。
人教版数学九年级上册教学设计24.3《正多边形和圆》

人教版数学九年级上册教学设计24.3《正多边形和圆》一. 教材分析《正多边形和圆》是人教版数学九年级上册第24章第三节的内容。
本节课主要介绍了正多边形的定义、性质以及与圆的关系。
通过本节课的学习,学生能够理解正多边形的概念,掌握正多边形的性质,并能运用这些性质解决一些实际问题。
教材中提供了丰富的实例和图示,有助于学生直观地理解和掌握知识。
二. 学情分析九年级的学生已经具备了一定的几何知识,对图形的认识和理解有一定的基础。
但是,对于正多边形的定义和性质,以及与圆的关系,可能还比较陌生。
因此,在教学过程中,需要引导学生通过观察、思考、探究,逐步理解和掌握知识。
三. 教学目标1.了解正多边形的定义和性质。
2.掌握正多边形与圆的关系。
3.能够运用正多边形的性质解决一些实际问题。
4.培养学生的观察能力、思考能力和动手能力。
四. 教学重难点1.正多边形的定义和性质。
2.正多边形与圆的关系。
五. 教学方法1.采用问题驱动的教学方法,引导学生通过观察、思考、探究,自主地学习和掌握知识。
2.利用多媒体辅助教学,展示正多边形的实例和图示,增强学生的直观感受。
3.采用小组合作学习的方式,鼓励学生互相交流、讨论,共同解决问题。
六. 教学准备1.多媒体教学设备。
2.正多边形的实例和图示。
3.练习题。
七. 教学过程1.导入(5分钟)利用多媒体展示一些正多边形的实例,如正方形、正三角形等,引导学生观察并思考:这些图形有什么特点?它们之间有什么联系?2.呈现(10分钟)介绍正多边形的定义和性质,以及正多边形与圆的关系。
通过图示和实例,让学生直观地理解和掌握知识。
3.操练(10分钟)让学生分组讨论,每组选择一个正多边形,分析其性质,并尝试用语言和图形表达出来。
然后,各组汇报自己的成果,其他组进行评价和补充。
4.巩固(10分钟)出示一些练习题,让学生独立完成。
题目包括判断题、填空题和解答题,内容涉及正多边形的性质和与圆的关系。
5.拓展(10分钟)让学生思考:如何判断一个多边形是否为正多边形?引导学生运用已学的知识,探索和解决问题。
数学人教版九年级上册24.3正多边形和圆教案、学案、教学反思
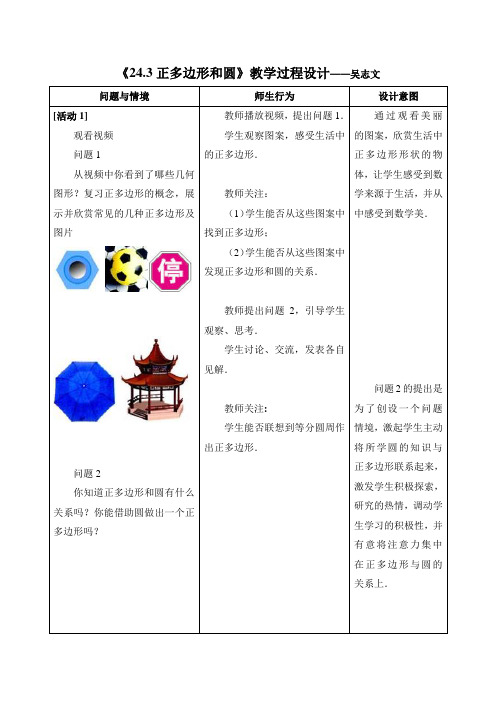
《24.3正多边形和圆》教学过程设计——吴志文问题与情境师生行为设计意图[活动1]观看视频问题1从视频中你看到了哪些几何图形?复习正多边形的概念,展示并欣赏常见的几种正多边形及图片问题2你知道正多边形和圆有什么关系吗?你能借助圆做出一个正多边形吗?教师播放视频,提出问题1.学生观察图案,感受生活中的正多边形.教师关注:(1)学生能否从这些图案中找到正多边形;(2)学生能否从这些图案中发现正多边形和圆的关系.教师提出问题2,引导学生观察、思考.学生讨论、交流,发表各自见解.教师关注:学生能否联想到等分圆周作出正多边形.通过观看美丽的图案,欣赏生活中正多边形形状的物体,让学生感受到数学来源于生活,并从中感受到数学美.问题2的提出是为了创设一个问题情境,激起学生主动将所学圆的知识与正多边形联系起来,激发学生积极探索,研究的热情,调动学生学习的积极性,并有意将注意力集中在正多边形与圆的关系上.[活动2]问题1将一个圆五等分,依次连接各分点得到一个五边形,这五边形一定是正五边形吗?如果是请你证明这个结论.教师演示作图:把圆分成相等的5段弧,依次连接各个分点得到五边形.教师引导学生从正多边形的定义入手,证明多边形各边都相等,各角都相等,引导学生观察、分析.教师关注:(1)学生能否看出:将圆分成五等份,可以得到5段相等的弧,这些弧所对的弦也是相等的,这些弦就是五边形的各边,进而证明五边形的各边相等;(2)学生能否观察发现圆内接五边形的各内角都是圆周角;(3)学生能否发现每一个圆周角所对弧都是三等份的弧;(4)学生能否利用这些圆周角所对的弧都相等,证明五边形的各内角相等,从而证明圆内接五边形是正五边形.教师带领学生完成证明过程.教师提出问题2,学生思考,同学间交流,回答问题.教师关注:学生是否会仿造证明圆内接正五边形的方法证明圆内接正n边形.在活动1中学生们发现了正多边形与圆有着密切的关系,只要把一个圆分成相等的一些弧,就可以做出这个圆的内接正多边形.活动2的设计就是要学生在教师的指导下进行逻辑推理,论证所发现的结论的正确性,从而培养学生科学严谨的治学态度,和运用所学知识解决问题的能力.问题2如果将圆n等分,依次连接各分点得到一个n边形,这n边形一定是正n边形吗?问题3各边相等的圆内接多边形是正多边形吗?各角相等的圆内接多边形呢?如果是,说明为什么?如果不是,举出反例.教师根据学生的回答给以总结:将圆n等分,依次连接各分点得到一个n边形,这n边形一定是正n边形.教师提出问题3,学生讨论,思考回答.教师关注:(1)学生能否利用正多边形定义进行判断;(2)学生能否由圆内接多边形各边相等,得到弦相等及弦所对的弧相等,进而证明圆内接多边形的各内角相等;(3)学生能否举出反例说明各角相等的圆内接多边形不一定是正多边形.教师讲评.问题2的设计是将结论由特殊推广到一般.这符合学生的认知规律.并教给学生一种研究问题的方法:由特殊到一般.问题3的提出是为了巩固所学知识,使学生明确判定圆内接多边形是正多边形,必须满足各边都相等,且各内角都相等,这两个条件缺一不可.同时教给学生学会举反例,培养学生思维的批判性.[活动3]学生观看课件,理解概念.例题1矗立在瑞金“一苏大”的革命烈士纪念亭,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2)变式练习 1.瑞金“一苏大”罕见的三角形纪念亭——公略亭,三个角寓意为黄公略将军在第三次反围剿中牺牲的,它的地基是边心距为m的正三角形,求地基的边长。
人教版数学九上24.3《正多边形和圆》WORD教案(一)

三、 典型例题:
例1 .已知正六边形ABCDEF,如图所示,其外接圆的半径是a,?求正六边形的周长和面积. ( 分析:要求正六边形的周长,只要求AB的长,已知条件是外接圆半径,因此自然而然,边长应与半径挂上钩,很自然应连接OA,过O点作OM⊥AB垂于M,在Rt△AOM?中便可求得AM,又应用垂径定理可求得AB的长.正六边形的面积是由六块正三角形面积组成的 )
24.3正多边形和圆
【学习目标】
了解正多边形和圆的有关概念;理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用多边形和圆的有关知识画多边形.
【学习过程】
一、温故知新:
1.什么叫正多边形?
2.从你身边举出两三个正多边形的实例,正多边形具有轴对称、?中心对称吗?其对称轴有几条,对称中心是哪一点?
3、 计算一下正五边形的中心角时多少?正五边形的一个内ห้องสมุดไป่ตู้是多少?正五边形的一个外角是多少?正六边形呢?
4、 通过上述计算,说明正n边形的一个内角的度数是多少?中心角呢?正多边形的中心角与外角的大小有什么关系?
5、 如何利用等分圆弧的方法来作正n边形? 方法一、用量角器作一个等于 的圆心角。 方法二、正六边形、正三角形、正十二边形等特殊正多边形的作法?
二、自主学习:
自学教材P 113--- P 116, 思考下列问题:
1、 正多边形和圆有什么关系?
只要把一个圆分成 的一些弧,就可以作出这个圆的 ,这个圆就是这个正多边形的 。
2、 通过教材图形,识别什么叫正多边形的中心、正多边形的中心角、正多边形的边心距?
人教版九年级数学上册24.3.2《正多边形和圆(2)》教案

人教版九年级数学上册24.3.2《正多边形和圆(2)》教案一. 教材分析人教版九年级数学上册第24章《圆》中的第3节《正多边形和圆(2)》是本章的重要内容。
本节主要让学生了解并掌握圆的性质,以及正多边形与圆的关系。
通过本节的学习,学生能够更深入地理解圆的性质,提高解决问题的能力。
二. 学情分析九年级的学生已经具备了一定的几何基础,对圆的概念有一定的了解。
但是,对于圆的性质和正多边形与圆的关系的理解还有待提高。
因此,在教学过程中,教师需要引导学生通过观察、思考、操作、讨论等方式,自主探索并掌握圆的性质,以及正多边形与圆的关系。
三. 教学目标1.了解圆的性质,掌握圆的基本概念。
2.理解正多边形与圆的关系,提高解决问题的能力。
3.培养学生的观察能力、思考能力和合作能力。
四. 教学重难点1.圆的性质的理解和运用。
2.正多边形与圆的关系的理解。
五. 教学方法采用问题驱动法、合作学习法和操作实践法。
通过提出问题,引导学生思考和探索;通过合作学习,培养学生之间的交流和合作能力;通过操作实践,让学生亲身体验和理解圆的性质和正多边形与圆的关系。
六. 教学准备1.准备相关的教学材料,如课件、黑板、粉笔等。
2.准备一些实际的例子,以便引导学生进行观察和操作。
七. 教学过程1.导入(5分钟)通过提出问题,如“什么是圆?圆有哪些性质?”引导学生回顾圆的基本概念,激发学生的学习兴趣。
2.呈现(10分钟)通过课件或黑板,呈现圆的性质,如圆的直径、半径、圆心等。
同时,给出一些实际的例子,让学生观察和理解圆的性质。
3.操练(10分钟)让学生进行一些实际的操作,如画圆、测量圆的直径、半径等。
通过操作,让学生更深入地理解圆的性质。
4.巩固(10分钟)通过一些练习题,让学生巩固所学的圆的性质。
同时,引导学生将这些性质与正多边形联系起来,理解正多边形与圆的关系。
5.拓展(10分钟)引导学生思考和探索正多边形与圆的更深层次的关系。
例如,讨论在给定边长的情况下,如何找到一个正多边形,使其与给定的圆相切。
人教版数学九年级上册24.3.2《正多边形和圆》教学设计

人教版数学九年级上册24.3.2《正多边形和圆》教学设计一. 教材分析《正多边形和圆》是人教版数学九年级上册第24章第三节的内容。
本节内容是在学生掌握了圆的概念、圆的性质、弧、弦、圆心角的基础上进行的。
本节主要介绍正多边形的定义、性质及正多边形与圆的关系。
教材通过生活中的实例引入正多边形和圆的概念,引导学生探究正多边形的性质,从而发现正多边形与圆的内在联系。
二. 学情分析初三学生已经具备了一定的几何基础知识,对圆的概念、性质有所了解。
但是,对于正多边形的定义、性质以及与圆的关系可能还比较模糊。
因此,在教学过程中,需要引导学生通过观察、操作、思考、探究等活动,自主发现正多边形的性质,理解正多边形与圆的关系。
三. 教学目标1.了解正多边形的定义、性质及正多边形与圆的关系。
2.能运用正多边形的性质解决实际问题。
3.培养学生的观察能力、操作能力、思考能力和探究能力。
四. 教学重难点1.正多边形的定义、性质。
2.正多边形与圆的关系。
五. 教学方法采用问题驱动法、探究法、合作学习法等,引导学生通过观察、操作、思考、探究等活动,自主发现正多边形的性质,理解正多边形与圆的关系。
六. 教学准备1.准备一些正多边形的图片,如正三角形、正方形、正五边形等。
2.准备一些圆的图片,如圆桌、轮子等。
3.准备黑板、粉笔。
七. 教学过程1.导入(5分钟)利用多媒体展示一些正多边形的图片,如正三角形、正方形、正五边形等,引导学生观察这些图形的特点。
同时,展示一些圆的图片,如圆桌、轮子等,引导学生思考圆的特点。
2.呈现(10分钟)教师在黑板上画出一个正三角形,提问:“这个图形是什么?”学生回答:“正三角形。
”教师继续提问:“正三角形有哪些性质?”学生回答:“正三角形的三个角都相等,三条边都相等。
”教师引导学生观察正三角形的特点,然后引入正多边形的定义:“像正三角形这样的图形,所有的边都相等,所有的角都相等,我们称之为正多边形。
”3.操练(10分钟)教师发放一些正多边形的卡片,让学生分组讨论,找出正多边形的性质。
人教版九年级上数学24.3正多边形和圆教案

2.教学难点
-正多边形内角与外角的关系:理解正多边形内角与外角互为补角,并能应用于解题。
-难点举例:证明正多边形内角和为(n-2)×180°,外角和为360°。
-正多边形圆心角、半径、边心距的计算:将圆心角、半径、边心距的关系应用于具体问题,进行计算。
5.增强学生的数学应用意识:通过实际应用案例,使学生体会数学知识在实际生活中的广泛应用,激发学生的数学应用意识。
三、教学难点与重点
1.教学重点
-正多边形的定义及其性质:理解正多边形的定义,掌握其内角、外角、对角线等基本性质。
-例如:正多边形内角和公式、外角和为360°、对角线相等且平分等。
-正多边形的圆心角、半径、边心距关系:掌握正多边形圆心角公式,理解半径与边心距的关系。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解正多边形和圆的基本概念。正多边形是指所有边相等、所有角相等的多边形;圆是由一条固定距离的点组成的图形。它们在几何学中有着广泛的应用,如建筑设计、艺术创作等领域。
2.案例分析:接下来,我们来看一个具体的案例。以正六边形为例,分析它在蜂巢中的应用,以及如何帮助我们解决实际问题。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了正多边形和圆的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对正多边形和圆的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
2.发展学生的逻辑思维与推理能力:引导学生运用定义、定理进行推理证明,培养学生严谨的逻辑思维和推理能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.3正多边形和圆
【学习目标】了解正多边形的有关概念;能根据条件进行正多边形的简单计算。
【学习重点】正多边形的有关概念和计算。
【学习难点】正多边形的有关计算。
【活动一】:基本训练(独立完成------5分钟)
阅读教材104~105
定义:一个正多边形的外接圆的叫做这个正多边形的中心,外接圆的叫做正多边形的半径,正多边形每一边所对的叫做正多边形的中心
角,中心到正多边形的一边的正多边形的边心距。
如下图所示都是圆内接正多边形,观察图形填空。
1、图(1)中圆心O是正多边形的,OB是正多边形的,
OD是,∠COB是。
2、请画出图(2)、(3)的边BC的边心距和一个中心角,并写出其中的一条半径,
图(2)中边心距是,中心角是,半径是;
图(3)中边心距是,中心角是,半径是。
【活动二】:问题探索(小组合作——15分钟)
3、观察图形,完成下表中有关正多边形的计算
(4)(5)(6)
(3)
(2)
(1)
正多边形边数
4、由以上计算填空:正n边形的一个内角是°,中心角= °,一个外角= °
【活动三】应用举例(自主探究--------8分钟)
【课后反思】_________________ ____________________________________________________.
24.3正多边形和圆课堂检测
1、半径是1的圆内接正三角形、正方形、正六边形的中心角分别是;
边心距分别是;边长分别是。
2、如图,求中心为原点O,顶点A、D在x轴上,半径为2cm的正六边形AB CDEF的各顶点
的坐标。
3、如图所示,已知⊙O的周长等于6 cm,求以它的半径为边长的正六边形ABCDEF的面积.。
