青岛版(五四制)八年级下册数学课件特殊的平行四边形(2)
青岛版八年级下册数学《三角形的中位线定理》PPT教学课件
高效上好每节课·快乐上好每天学
3.若△ABC的周长为12, 则△DEF的周长为 ____6
4.若△ABC的面积为20, 则△DEF的面积为_____5.
5.若△ABC的周长为a, 面积为
1a
1 s
2
4ADFra bibliotekFB
C
E
高效上好每节课·快乐上好每天学
课堂小结
1、三角形中位线是三角形中重要的线段,要与三角形 的中线区分开来. 2、三角形中位线定理有两个结论:
A
D
F
C
B
E
例: 求证三角形的一条中位线与第三边 上的中线互相平分.
已知:如图所示,在△ABC中,AD=DB,BE=EC,AF= FC. 求证:AE、DF互相平分.
图 24.4.3
证明 连结DE、EF. ∵ AD=DB,BE=EC, ∴ DE∥AC(三角形的中位线平行于 第三边并且等于第三边的一半). 同理EF∥AB. ∴四边形ADEF是平行四边形.
C
作业
习题6.4,第1、2题.
高效上好每节课·快乐上好每天学
A
结束
6.4 三角形的中位线定理
如图,有一块三角形的蛋糕,准备平 均分给四个小朋友,要求四人所分的形状 大小相同,请设计合理的解决方案。
获取新知
连结三角形两边中点的线段叫三角形的中位线 A
D
E
你还能画出几条三角形的中位线?
B
F
C
温馨提示 三角形有三条中位线
B
(2)顺次连结对角线垂 直的四边形各边中点所得 的四边形是什么?
(3)顺次连结对角线相等 B 且垂直的四边形各边中点 所得的四边形是什么?
青岛版八年级数学下册6.1《平行四边形及其性质》课件

∠BCD=180°-∠B=180°-56°=124° (2)∵四边形ABCD是平行四边形
∴AD=BC,AB=CD(平行四边形对边相等)
∵AD=30,CD=25 ∴BC=30,AB=25.
挑战自我
小结
1、什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
(1)根据题意,画出图形。 (2)结合图形,写出已知、求证。
(3)找出由已知推出求证的途径,写出证明。
证明:连接BD
∵四边形ABCD是平行四边形
∴AD∥BC ,AB∥CD(平行四边形的定义)
A
1 D ∴∠1=∠2, ∠3=∠4
4 3
在ABD和CDB中
2
B
C 1 2
已知:四边形ABCD
BD DB
6.1.1 平行四边形及其性质
视察思考
请同学们认真阅读课本第4页,完成以下内容: 1、什么叫平行四边形?怎么表示?如何读法?
两组对边分别平行的四边形叫做平行四边形.
A
D
平行四边形不相邻的两个顶
B
图2 C
点连成的线段叫它的对角线.
如图2所示的四边形ABCD是平行四边形.
记作: ABCD 读作:平行四边形ABCD
线段AC、BD就是 ABCD的对角线.
对平行四边形的理解:
对边分别平行的四边形
平行四边形
A
几何语言:
D
∵ AB∥CD,AD∥BC
B
C
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
∴ AB∥CD, AD∥BC
猜想:平行四边形的对边有什么样的关系?
平行四边形对边相等.
特殊平行四边形经典例题汇编(青岛版)
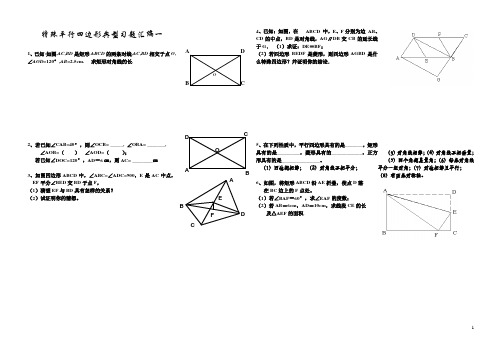
特殊平行四边形典型习题汇编一1、已知:如图,AC ,BD 是矩形ABCD 的两条对线,AC ,BD 相交于点O ,∠AOD =120°,AB =2.5cm.求矩形对角线的长.2、若已知∠CAB=40°,则∠OCB= _____, ∠OBA= _______,∠AOB=( ) ∠AOD=( ); 若已知∠DOC=120°,AD =6㎝,则AC= ________㎝3、如图四边形ABCD 中,∠ABC=∠ADC=900,E 是AC 中点,EF 平分∠BED 交BD 于点F ,(1)猜想EF 与BD 具有怎样的关系? (2)试证明你的猜想。
4、已知:如图,在 ABCD 中,E 、F 分别为边 AB 、CD 的中点,BD 是对角线,AG ∥DB 交CB 的延长线于G . (1)求证:DE =BF ;(2)若四边形 BEDF 是菱形,则四边形AGBD 是什么特殊四边形?并证明你的结论.5、在下列性质中,平行四边形具有的是_______,矩形具有的是_________,菱形具有的____________,正方形具有的是_______________。
(1)四边都相等; (2)对角线互相平分; 6、如图,将矩形ABCD 沿AE 折叠,使点D 落 在BC 边上的F 点处。
(1)若∠BAF =60°,求∠EAF 的度数;(2)若AB =6cm ,AD =10cm ,求线段CE 的长及△AEF 的面积.(3)对角线相等;(4)对角线互相垂直; (5)四个角都是直角;(6)每条对角线 平分一组对角;(7)对边相等且平行; (8)有两条对称轴。
D B C A O B B FAC DE7、如图,矩形纸片ABCD 中,现将A 、C 重合,使纸片折叠压平,设折痕为EF 。
(1)连结CF ,四边形AECF 是什么特殊的四边形?为什么? 8、在四边形ABCD 中O 是对角线的交点,能判定这个四边形是正方形的是( )A 、AC = BD ,AB ∥CD ,AB = CDB 、AD ∥BC ,∠A =∠ C C 、AO=BO=CO=DO ,AC ⊥BD D 、AO=CO ,BO=DO ,AB=BC9、如图,边长为a 的菱形ABCD 中,∠DAB=60度,E 是异于A 、D 两点的动点,F 是CD 上的动点,满足AE+CF=a 。
(青岛版五年制)五年级数学下册课件_平行四边形的认识_1

Copyright 2004-2009 版权所有 盗版必究
想一想
长方形、正方形和平 行四边形有什么相同点和 不同点?
Copyright 2004-2009 版权所有 盗版必究
•
请同学们用你的直 尺和三角板推一推、量 一量长方形、正方形的 边有什么样的特征。
Copyright 2004-20009 版权所有 盗版必究
×
• 6.平行四边形的两组对边平行却不相等 (× ) • 7.平行四边形的高都相等 (× )
• 8.平行四边形有无数条高
(
√
)
Copyright 2004-2009 版权所有 盗版必究
平行四边形、长方形和正方形 的关系可以用下图表示:
平行四边形 长方形 正方形
平行四边形
Copyright 2004-2009 版权所有 盗版必究
本节课我们主要来认识平行 四边形,同学们结合日常生 活中的实际例子要理解并掌 握平行四边形的概念以及组 成,能够解决相关的实际问 题。
Copyright 2004-2009 版权所有 盗版必究
Copyright 2004-2009 版权所有 盗版必究
Copyright 2004-2009 版权所有 盗版必究
平行四边形的特性
1) 两组对边分别相等
7厘米
5厘米
5厘米
Copyright 2004-2009 版权所有 盗版必究
7厘米
观察下面的平行四边形。角有什么特点?
Copyright 2004-2009 版权所有 盗版必究
下面图形中是平行四边形的打上“√”
9个
Copyright 2004-2009 版权所有 盗版必究
高
底
Copyright 2004-2009 版权所有 盗版必究
《6.3特殊的平行四边形》作业设计方案-初中数学青岛版12八年级下册

《特殊的平行四边形》作业设计方案(第一课时)一、作业目标本作业设计旨在巩固学生对特殊平行四边形概念的理解,掌握特殊平行四边形的性质及其在实际生活中的应用,提高学生分析问题和解决问题的能力。
二、作业内容本次作业包括以下内容:1. 概念复习:学生需复习特殊平行四边形的定义及其类型(如矩形、菱形等),理解各类特殊平行四边形的性质特点。
2. 题目练习:通过典型例题和练习题,巩固对特殊平行四边形性质的运用。
例如,让学生通过图形的拼接、翻折或旋转等方式,找出特殊的平行四边形并证明其性质。
3. 思考探究:要求学生分析并尝试解答日常生活中遇到的特殊平行四边形问题,如建筑物的窗户设计、桥梁的构造等。
三、作业要求1. 作业量适中:本课时作业量不宜过大,以避免学生因疲劳而影响学习效果。
同时,也要保证学生有足够的思考时间。
2. 内容清晰:作业中涉及的知识点要明确,每一题的目标和解题步骤要清晰,以便学生能够明确解题思路。
3. 难度递进:题目设置应遵循由易到难的原则,先让学生掌握基础知识点,再逐步提高难度,引导学生深入思考。
4. 格式规范:要求学生按照规范的格式完成作业,如题目编号、解题步骤、答案等,以方便教师批改。
四、作业评价教师将根据以下标准对作业进行评价:1. 正确性:答案是否准确无误,是否完全符合题目要求。
2. 解题思路:学生的解题思路是否清晰,是否有创新性。
3. 书写规范:学生书写是否工整,格式是否规范。
4. 独立思考能力:学生在解决问题过程中是否能够独立思考,并运用所学知识解决实际问题。
五、作业反馈1. 及时批改:教师将及时批改作业,并对学生的答题情况进行统计和分析。
2. 反馈形式:教师将通过课堂讲解、小组讨论等形式,对学生在作业中出现的错误进行纠正,对优秀答案进行表扬和分享。
3. 个性化指导:针对学生在作业中表现出的不同特点和问题,教师将给予个性化的指导和建议,帮助学生更好地掌握知识和技能。
4. 家长沟通:教师将与家长保持沟通,及时反馈学生的学习情况,以便家长更好地配合学校的教育工作。
6.3特殊的平行四边形(2)课件(2014年新青岛版八年级下)

10
㎝,
120°
矩形的定义: 有一个角是直角的平行四边形是矩形。 ABCD ∠A=900 四边形ABCD是矩形
你还有其它的判定方法吗?
情境一:李芳同学用“边—
—直角、边——直角、边—— 直角、边”这样四步,画出了 一个四边形,她说这就是一个 矩形,她的判断对吗?为什么 ?
猜想:有三个角是直角的四边形是矩形 。
D
Hale Waihona Puke 例3:已知,如图.矩形ABCD的对角线 AC、BD相交于点O,且E、F、G、H分 别是AO、BO、CO、DO的中点, 求证:四边形EFGH是矩形.
方法1:
有一个角是直角的平行四边形是矩形。
方法2:
对角线相等的平行四边形是矩形 。
(对角线相等且互相平分的四边形是矩形。)
方法3:
有三个角是直角的四边形是矩形 。
C) 2.下列说法错误的是( A.有一个内角是直角的平行四边形是矩形 B.矩形的四个角都是直角,并且对角线相等 C.对角线相等的平行四边形是矩形 D.有两个角是直角的四边形是矩形
例1:如图,M为平行四边形ABCD 边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。
A
M
D
B
C
例2:如图, ABCD四个内角的平分线围成四边 形EFGH,猜想四边形EFGH的形状,并说明理 由 证明: A ∵四边形ABCD是平行四边形 H ∴∠DAB+∠ABC=180 ° E G ∵AE、BE分别平分 F B C ∠DAB、∠ABC ∴∠EAB+∠EBA=90 ° ∴∠AEB=90° 即∠HEF=90° 同理:∠EFG=90°、∠FGH=90° ∴四边形EFGH是矩形
你能证明上述结论吗?
八年级数学下册6.1平行四边形及其性质平行四边形的性质的应用素材(新版)青岛版.doc

平行四边形的性质的应用一、求平行四边形的周长【例1】如图所示,在□ABCD中,AB=18cm,PC=6cm,AP是∠DAB的平分线,求□ABCD的周长.【思考与分析1】欲求□ABCD的周长,已知AB=18cm,PC=6cm,只需求出AD、BC的长.我们可以过点P作P Q∥BC交AB于Q,构造△AQP与△ADP全等.方法1:过点P 作PQ∥BC交AB于Q,由平行四边形的定义可知四边形ADPQ,BCPQ也是平行四边形.∴AQ=D P,QB=PC.∴AQ=AB-PC=18cm-6cm=12cm.∵AP是∠DAB的平分线,∴∠1=∠2.又∵∠D =∠AQP,AP=AP,∴△ADP≌△AQP.∴AD=AQ=12c.m∴□ABCD的周长为:2(AB+AD)=60cm.【思考与分析2】欲求□ABCD的周长,我们可以延长A P交BC的延长线于Q,构造等腰三角形ABQ.方法2:延长A P交BC的延长线于Q.在□ABCD中,AD∥BC,AB∥CD,∴∠1=∠Q,∠2=∠3.又∵∠1=∠2,∴∠Q=∠2=∠3.∴AB=BQ,P=C C Q.∴BC=BQ-C Q=AB-PC=18cm-6cm=12cm.∴□ABCD的周长为:2(AB+BC)=60cm.【小结】求平行四边形的周长时往往只需要求出平行四边形的相邻两边长,在求解过程中可以构造特殊的三角形,如等腰三角形、全等三角形等等.二、等分面积【例2】如图,ABCD是王老六家的一块平行四边形田地,P 为水井,现要把这块田平均分给两个儿子, 为了方便用水,要求两个儿子分到的地都与水井相邻,请你来设计一下,并说明你的理由.【思考与分析】我们说只要满足所分的两块地面积相等,且都与水井相邻就可以. 那么可以考虑利用平行四边形的性质(平行四边形的对角线互相平分)来解题. 找到两条对角线的交点,则交点和水井所在的直线将田地分成面积相等的两块.解:设对角线AC,BD交于O,如下图,过O、P 作直线交BC,AD于E、F,则线段EF分割的这两块田地符合要求. 理由如下:易证OE=OF,BE=DF,AF=CE(把证线段相等转化为证三角形全等),四边形ABEF绕点O旋转180°,就与四边形CDFE重合,这两部分面积相等, 又点P(井)在EF上,符合水井和两块地相邻的要求,故此种分法符合要求.【反思】实际生活中有很多需要直接或间接用平行四边形的性质来解决的问题,我们要牢牢把握住性质以便可以灵活地运用它来解题.三、探究相等的线段【例3】如图,在平行四边形ABCD中,点E、F 在对角线AC上,且AE=CF,请你以 F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并说明它和图象中已有的某2一条线段相等(只需说明一组线段相等即可).(1)连接.(2)猜想:=___________.(3)理由:.【思考与分析】本题立足于一个常见的基本图形,把传统的几何题,改造成一个发现猜想、说明理由的几何题,对平面几何的学习有着重要的意义.解:答案1:(1)连接BF.(2)猜想:BF=DE.(3)理由1:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∴∠DAE=∠BCF.在△BCF与△DAE中,∴△BCF≌△DAE. ∴BF=DE.理由2:如图,连接DB、D F,设D B、CA交于点O.∵四边形ABCD是平行四边形,∴AO=OC,DO=OB.∵AE=FC,∴AO-AE=OC-FC.即EO=OF.∴四边形EBFD为平行四边形.∴BF=DE.答案2:(1)连接DF.(2)猜想:DF=BE.(3)理由:略.【小结】理由 1 中把线段相等问题转化为求三角形全等问题;理由 2 中把线段相等问题转化为平行四边形判定的问题. 通过解转化后的问题,线段相等成为明显的事实.四、证明角相等【例4】如图,已知点M、N分别是□ABCD的边A B、DC的中点,试说明:∠DAN=∠BCM.【思考与分析】先找这两个角的位置,但没有什么联系.题中给出点M、N分别是平行四边形ABCD的边A B、DC的中点,很容易想到连接MN,得到三个四边形AMC、N AMND、BCNM是平行四边形,推出∠DAN=∠ANM,∠BCM=∠CMN,而只要能推出∠ANM∠=CMN,题中结论即可证明.解:连接MN.∵M、N分别是平行四边形ABCD的边A B、DC的中点,∴AM、CN平行且相等.∴四边形AMCN是平行四边形.同理,四边形AMND、四边形BCNM是平行四边形.∴∠DAN=∠ANM∠=CMN∠= BCM.五、证明线段平行【例5】已知:如图,E、F 是平行四边形ABCD的对角线A C上的两点,AE=CF.试说明:(1)△ADF≌△CBE;(2)EB∥DF.【思考与分析】要说明△ADF≌△CBE,就要找全等的条件. 猛一看,题中只有AE=CF一个条件,其实还有一个条件四边形ABCD是平行四边形,则A D=BC,∠DAF=∠BCE,所以△ADF≌△CBE.所以∠DFA=∠BEC,所以(2)的结论成立.4解:(1)∵AE=CF,∴AE+EF=CF+FE即AF=CE .又四边形ABCD是平行四边形,∴AD=CB,AD∥BC .∴∠DAF=∠BCE .在△ADF与△CBE中∴△ADF≌△CBE(SAS). (2)∵△ADF≌△CBE,∴∠DFA=∠BEC .∴DF∥EB .。
初中数学青岛版八年级下册第6章 平行四边形6.3特殊的平行四边形-章节测试习题(8)

章节测试题1.【题文】如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?【答案】见解答.【分析】首先根据定理:到角两边距离相等的点在角的平分线上,可得到∠DAC=∠CAE,然后证明∠DAC=∠DCA,可得到DA=DC,再根据菱形的判定定理:邻边相等的平行四边形是菱形,进而可得到结论.【解答】是菱形.理由如下:∵PE⊥AB,PF⊥AD,且PE=PF,∴AC是∠DAB的角平分线,∴∠DAC=∠CAE,∵四边形ABCD是平行四边形,∴DC∥AB,∴∠DCA=∠CAB,∴∠DAC=∠DCA,∴DA=DC,∴平行四边形ABCD是菱形.【点评】此题主要考查了菱形的判定,证明∠DAC=∠DCA是解此题的关键.2.【题文】如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点.(1)求证:四边形EFGH是平行四边形;(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论.【答案】见解答.【分析】(1)根据中位线的判定GH=EF= AB,EH=FG= CD,所以四边形EFGH是平行四边形.(2)根据菱形的判定,四边都相等的四边形是菱形,只要证明EF=FG=GH=HE就可以了,这就需要AB=CD这个条件.【解答】(1)证明:∵E、F分别是AD,BD的中点,G、H分别中BC,AC的中点,∴EF∥AB,EF= AB;GH∥AB,GH= AB.(2分)∴EF∥GH,EF=GH.∴四边形EFGH是平行四边形.(2分)(2)当AB=CD时,四边形EFGH是菱形.(1分)理由:∵E、F分别是AD,BD的中点,H,G分别是AC,BC的中点,G、F分别是BC,BD的中点,E,H分别是AD,AC的中点,∴EF= AB,HG= AB,FG= CD,EH= CD,又∵AB=CD,∴EF=FG=GH=EH.∴四边形EFGH是菱形.(3分)【点评】此题考查了三个判定:平行四边形的判定、菱形的判定、中位线的判定,牢记这几个判定,解此类问题就轻而易举了.3.【题文】如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作A G∥BD,交CB的延长线于点G.(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.【答案】见解答.【分析】(1)利用平行四边形的性质证得△AED是等边三角形,从而证得DE=BE,问题得证;(2)利用平行四边形的性质证得∠ADB=90°,利用有一个角是直角的平行四边形是矩形判定矩形.【解答】(1)证明:∵四边形ABCD是平行四边形∴AB∥CD且AB=CD,AD∥BC且AD=BCE,F分别为AB,CD的中点,∴BE= AB,DF= CD,∴BE=BF,∴四边形DEBF是平行四边形在△ABD中,E是AB的中点,∴AE=BE= AB=AD,而∠DAB=60°∴△AED是等边三角形,即DE=AE=AD,故DE=BE∴平行四边形DEBF是菱形.(2)解:四边形AGBD是矩形,理由如下:∵AD∥BC且AG∥DB∴四边形AGBD是平行四边形由(1)的证明知AD=DE=AE=BE,∴∠ADE=∠DEA=60°,∠EDB=∠DBE=30°故∠ADB=90°∴平行四边形AGBD是矩形.【点评】本题考查了矩形的性质、等边三角形的判定及性质、三角形中位线定理等知识,解题的关键是弄清菱形及矩形的判定方法.4.【题文】如图,△ABC中,AB=AC,AD、CD分別是△ABC两个外角的平分线.(1)求证:AC=AD;(2)若∠B=60°,求证:四边形ABCD是菱形.【答案】见解答.【分析】(1)根据角平分线的性质得出∠FAD=∠B,以及AD∥BC,再利用∠D=∠ACD,证明AC=AD;(2)根据平行四边形的判定方法得出四边形ABCD是平行四边形,再利用菱形的判定得出.【解答】证明:(1)∵AB=AC,∴∠B=∠BCA,∵AD平分∠FAC,∴∠FAD=∠DAC= ∠FAC,∵∠B+∠BCA=∠FAC,∴∠B= ∠FAC,∴∠B=∠FAD,∴AD∥BC,∴∠D=∠DCE,∵CD平分∠ACE,∴∠ACD=∠DCE,∴∠D=∠ACD,∴AC=AD;(2)∵∠B=60°,AB=AC,∴△ABC为等边三角形,∴AB=BC,∴∠ACB=60°,∠FAC=∠ACE=120°,∴∠BAD=∠BCD=120°,∴∠B=∠D=60°,∴四边形ABCD是平行四边形,∵AB=BC,∴平行四边形ABCD是菱形.【点评】此题主要考查了平行四边形的判定以及菱形的判定和角平分线的性质等内容,注意菱形与平行四边形的区别,得出AB=BC是解决问题的关键.5.【题文】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(1)求证:BE=DF;(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM,FM,判断四边形AEMF是什么特殊四边形?并证明你的结论.【答案】见解答.【分析】(1)求简单的线段相等,可证线段所在的三角形全等,即证△ABE≌△ADF;(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相垂直平分,根据对角线互相垂直且平分的四边形是菱形,即可判定四边形AEMF 是菱形.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,在Rt△ABE和Rt△ADF中,∵,∴Rt△ADF≌Rt△ABE(HL)∴BE=DF;(2)解:四边形AEMF是菱形,理由为:证明:∵四边形ABCD是正方形,∴∠BCA=∠DCA=45°(正方形的对角线平分一组对角),BC=DC(正方形四条边相等),∵BE=DF(已证),∴BC-BE=DC-DF(等式的性质),即CE=CF,在△COE和△COF中,,∴△COE≌△COF(SAS),∴OE=OF,又OM=OA,∴四边形AEMF是平行四边形(对角线互相平分的四边形是平行四边形),∵AE=AF,∴平行四边形AEMF是菱形.【点评】本题主要考查对正方形的性质,平行四边形的判定,菱形的判定,平行线分线段成比例定理,全等三角形的性质和判定等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.6.【题文】如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.求证:四边形AECD是菱形.【答案】见解答.【分析】首先证明四边形AECD是平行四边形,再由AB∥CD,得∠EAC=∠DCA,AC平分∠BAD,得∠DAC=∠CAE,从而得到∠ACD=∠DAC,即AD=DC,有一组邻边相等的平行四边形是菱形.【解答】证明:∵AB∥CD,CE∥AD,∴四边形AECD是平行四边形.(3分)∵AC平分∠BAD,∴∠BAC=∠DAC,(4分)又∵AB∥CD,∴∠ACD=∠BAC=∠DAC,(5分)∴AD=DC,(6分)∴四边形AECD是菱形.(8分)【点评】考查了平行四边形和菱形的判定,比较简单.7.【题文】两块完全相同的三角板Ⅰ(△ABC)和Ⅱ(△A 1 B 1 C 1)如图①放置在同一平面上(∠C=∠C 1 =90°,∠ABC=∠A 1 B 1 C 1 =60°),斜边重合.若三角板Ⅱ不动,三角板Ⅰ在三角板Ⅱ所在的平面上向右滑动,图②是滑动过程中的一个位置.(1)在图②中,连接BC 1、B 1 C,求证:△A 1 BC 1≌△AB 1 C;(2)三角板Ⅰ滑到什么位置(点B 1落在AB边的什么位置)时,四边形BCB 1 C 1是菱形?说明理由.【答案】见解答.【分析】利用全等三角形的性质得出一些条件,然后再进行证明.【解答】(1)证明:∵三角板Ⅰ(△ABC)和Ⅱ(△A 1 B 1 C 1)是两块完全相同的三角板,∴AC=A 1 C 1 AB=A 1 B 1∠A=∠A 1∴在图②中A 1 B=AB 1∴△A 1 BC 1≌△AB 1 C.(2)解:点B 1落在AB边的中点.理由如下:如图②所示,由已知条件知BC=B 1 C 1,BC∥B 1 C 1∴四边形BCB 1 C 1是平行四边形.要使四边形BCB 1 C 1是菱形,则BC=CB 1∵∠ABC=∠A 1 B 1 C 1 =60°,∴△BCB 1为等边三角形.∴BB 1 =B 1 C=BC,又∵∠A=30°,在直角三角形ABC中,BC= AB,∴BB 1 = AB,∴点B 1落在AB边的中点.【点评】(1)灵活把握题中隐含的条件是解题的关键.(2)菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.8.【题文】将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.【答案】见解答.【分析】第一次折叠,AC落在AB边上,则折痕AD平分∠BAC,∠EAD=∠FAD;第二次折叠,A、D重合,则∠EAF=∠EDF、∠EDA=∠FDA;AE=ED、AF=FD;易证得△AED≌△AFD,得AE=AF、DE=DF,再根据第二次折叠所得到的AE=DE、AF=FD,可证得四边形AEDF的四边相等,由此可判定四边形AEDF是菱形.【解答】证明:由第一次折叠可知:AD为∠CAB的平分线,∴∠1=∠2(2分)由第二次折叠可知:∠CAB=∠EDF,∵AE=ED,AF=FD,∴∠1=∠3,∠2=∠4,∵∠1=∠2,∴∠3=∠4(4分),在△AED与△AFD中1=∠2,AD=AD,∠3=∠4∴△AED≌△AFD(ASA)(6分)∴AE=AF,DE=DF,∴EO=FO,AO=DO,AD⊥EF,故四边形AEDF是菱形.(9分)【点评】此题考查了折叠的性质、全等三角形的判定和性质及菱形的判定方法.9.【题文】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并说明理由;(2)若AB=6,BC=8,求四边形OCED的面积.【答案】见解答.【分析】(1)首先可根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形,然后根据矩形的性质:矩形的对角线相等且互相平分,可得OC=OD,由此可判定四边形OCED是菱形.(2)连接OE,通过证四边形BOEC是平行四边形,得OE=BC;根据菱形的面积是对角线乘积的一半,可求得四边形ODEC的面积.【解答】解:(1)四边形OCED是菱形.(2分)∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,(3分)又在矩形ABCD中,OC=OD,∴四边形OCED是菱形.(4分)(2)连接OE.由菱形OCED得:CD⊥OE,(5分)又∵BC⊥CD,∴OE∥BC(在同一平面内,垂直于同一条直线的两直线平行),又∵CE∥BD,∴四边形BCEO是平行四边形;∴OE=BC=8(7分)∴S 四边形OCED = OE•CD=×8×6=24.(8分)【点评】本题主要考查矩形的性质,平行四边形、菱形的判定,菱形面积的求法;菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.10.【题文】如图,在▱ABCD中,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于点E、F.已知BE=BP.求证:(1)∠E=∠F;(2)▱ABCD是菱形.【答案】见解答.【分析】(1)四边形ABCD是平行四边形,则BC∥AF,可得同位角∠BPE=∠F;在等腰△BEP中,∠E=∠BPE,等量代换后即可证得所求的结论;(2)由EF∥BD,可得同位角∠ABD=∠E,∠ADB=∠F;由(1)知∠E=∠F,等量代换后可证得∠ABD=∠ADB,即AB=AD,根据一组邻边相等的平行四边形是菱形即可判定四边形ABCD是菱形.【解答】证明:(1)在▱ABCD中,BC∥AF,∴∠1=∠F,∵BE=BP,∴∠E=∠1,∴∠E=∠F;(2)∵BD∥EF,∴∠2=∠E,∠3=∠F,∵∠E=∠F,∴∠2=∠3,∴AB=AD,∴▱ABCD是菱形.【点评】此题主要考查了平行四边形的性质及菱形的判定:一组邻边相等的平行四边形是菱形.11.【题文】如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF,求证:四边形AEOF是菱形.【答案】见解答.【分析】要证明四边形AEOF是菱形,可根据“四条边相等的四边形是菱形”或“一组邻边相等的平行四边形是菱形”进行证明.【解答】证明:∵点E,F分别为AB,AD的中点∴AE= AB,AF= AD (2分),又∵四边形ABCD是菱形,∴AB=AD,∴AE=AF (4分),又∵菱形ABCD的对角线AC与BD相交于点O∴O为BD的中点,∴OE,OF是△ABD的中位线.(6分)∴OE∥AD,OF∥AB,∴四边形AEOF是平行四边形(8分),∵AE=AF,∴四边形AEOF是菱形.【点评】菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.12.【题文】某同学用两个完全相同有一个角为60°的直角三角尺重叠在一起(如图)固定△ABC不动,将△DEF沿线段AB向右平移,当D移至AB中点时(如图②).(1)求证:△ACD≌△DFB;(2)猜想四边形CDBF的形状,并说明理由.【答案】见解答.【分析】(1)根据已知可以得出∠CAB=∠FDE,AC=DF,BD=AD,即可得出△ACD≌△DFB;(2)根据直角三角形斜边上的中线等于斜边的一半和平移的性质,即可得到该四边形的四条边都相等,则它是一个菱形;【解答】(1)证明:∵两个完全相同有一个角为60°的直角三角尺重叠在一起(如图②)固定△ABC不动,将△DEF沿线段AB向右平移,∴∠CAB=∠FDE=60°,AC=DF,∵D移至AB中点时,∴BD=AD,∴在△ACD与△DFB中,,∴△ACD≌△DFB;(2)菱形.理由:∵在直角三角形ABC中,AD=BD,∴CD=AD=BD,根据平移的性质,图形平移前后对应线段相等,对应点平移距离相等,得到CF=BD,BF=CD,∴CF=BD=BF=CD,∴四边形CDBF是菱形;【点评】此题主要考查了菱形的判定,综合运用直角三角形的性质和平移的性质进行分析计算,考查学生综合运用数学知识的能力.13.【题文】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.(1)求证:△BDF≌△CDE;(2)若AB=AC,求证:四边形BFCE是菱形.【答案】见解答.【分析】(1)由CE、BF的内错角相等,可得出△CED和△BFD的两组对应角相等;已知D是BC的中点,即BD=DC,由AAS即可证得两三角形全等;(2)若AB=AC,则△ABC是等腰三角形,而D是底边BC的中点,根据等腰三角形三线合一的性质可证得AD⊥BC;由(1)的全等三角形,易证得四边形BFCE的对角线互相平分;根据对角线互相垂直平分的四边形是菱形即可判定四边形BFCE是菱形.【解答】证明:(1)∵CE∥BF,∴∠ECD=∠FBD,∠DEC=∠DFB;又∵D是BC的中点,即BD=DC,∴△BDF≌△CDE;(AAS)(2)∵AB=AC,∴△ABC是等腰三角形;又∵BD=DC,∴AD⊥BC(三线合一),由(1)知:△BDF≌△CDE,则DE=DF,DB=DC;∴四边形BFCE是菱形(对角线互相平分且互相垂直的四边形为菱形).【点评】此题主要考查的是全等三角形的判定和性质、等腰三角形的性质及菱形的判定方法.14.【题文】如图,在梯形ABCD中,AC平分∠BAD,在底边AB上截AE=CD.(1)求证:四边形AECD是菱形;(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.【答案】见解答.【分析】(1)根据四边形ABCD是梯形得到AB∥DC,从而得到∠DCA=∠EAC,利用EC平分∠BAD,得到∠BAC=∠DAC,从而∠DAC=∠DCA,所以AD=CD,利用邻边相等的平行四边形是菱形判定四边形AECD是菱形;(2)利用若点E是AB的中点,得到AE=BE,根据CE=AE,得到CE=BE,从而得到△ABC为直角三角形.【解答】(1)证明:∵四边形ABCD是梯形,∴AB∥DC,又∵AE=CD,∴四边形AECD是平行四边形.∴∠DCA=∠EAC,∵AC平分∠BAD,∴∠BAC=∠DAC,∴∠DAC=∠DCA,∴AD=CD,∴四边形AECD是菱形;(2)解:∵若点E是AB的中点,∴AE=BE,∵CE=AE,∴CE=BE,∴∠EBC=∠ECB,∠EAC=∠ECA∴∠ECB+∠ECA=90°∴△ABC为直角三角形.【点评】本题考查了梯形的性质及菱形的判定,解题的关键是熟知梯形的性质,并理解其基本辅助线的作法.15.【题文】如图,在Rt△ABC中,∠ABC=90°,∠BAC=60°,D为AC的中点,以BD为折痕,将△BCD折叠,使得C点到达C 1点的位置,连接AC 1.求证:四边形ABDC 1是菱形.【答案】见解答.【分析】要证四边形ABDC 1为菱形,则要通过题中的条件证出四边相等即可得出答案.【解答】证明:∵∠ABC=90°,∠BAC=60°,∴∠C=30°∴BA= AC.又∵BD是斜边AC的中线,∴BD=AD= AC=CD.∴BD=AB=CD,∴∠C=∠DBC=30°,∵将△BCD沿BD折叠得△BC 1 D,∴△CBD≌△C 1 BD,∴CD=DC 1,∴AB=BD=DC 1,∴∠C 1 BA=∠BC 1 D=30°,∴BA∥DC 1,DC 1 =AB,∴四边形ABDC 1为平行四边形,又∵AB=BD,∴平行四边形ABDC 1为菱形.【点评】此题考查的是图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.16.【题文】如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E.DF平分∠ADC交BC于F.(1)求证:△ABE≌△CDF;(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.【答案】见解答.【分析】(1)由平行四边形ABCD可得出的条件有:①AB=CD,②∠A=∠C,③∠ABC=∠CDA;已知BE、CD分别是等角∠ABD、∠CDA的平分线,易证得∠ABE=∠CDF④;联立①②④,即可由ASA判定所求的三角形全等;(2)由(1)的全等三角形,易证得DE=BF,那么DE和BF平行且相等,由此可判定四边形BEDF 是平行四边形,根据对角线垂直的平行四边形是菱形即可得出EBFD的形状.【解答】(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AB=CD,∠ABC=∠ADC,∵BE平分∠ABC,DF平分∠ADC,∴∠ABE=∠CDF,∴△ABE≌△CDF(ASA);(2)解:若BD⊥EF,则四边形EBFD是菱形.证明:由△ABE≌△CDF,得AE=CF,在平行四边形ABCD中,AD平行BC,AD=BC,∴DE∥BF,DE=BF,∴四边形EBFD是平行四边形,∴若BD⊥EF,则四边形EBFD是菱形.【点评】此题主要考查了平行四边形的性质、全等三角形的判定和性质及菱形的判定方法.17.【题文】如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点.(1)求证:四边形DECF是平行四边形;(2)若AC=BC,则四边形DECF是什么特殊四边形?请说明理由.【答案】见解答.【分析】(1)根据一组对边平行且相等的四边形是平行四边进行证明;(2)根据一组邻边相等的平行四边形是菱形进行证明.【解答】(1)证明:方法一:∵D、E、F分别是边AB、BC、CA的中点,∴DE∥AC,DE= AC,CF= AC.(3)分∴DE∥CF,DE=CF.∴四边形DECF是平行四边形,5分)方法二:∵D、E、F分别是边AB、BC、CA的中点,∴DE∥AC,DF∥BC,(3分)∴四边形DECF是平行四边形.(5分)(2)解:四边形DECF是菱形(6分)理由:∵E、F分别是边BC、CA的中点,∴CE= BC,CF= AC,又∵AC=BC,∴CE=CF.(8分)由(1)知,四边形DECF是平行四边形,∴四边形DECF是菱形.(10分)【点评】考查了平行四边形和菱形的判定.形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.18.【题文】如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且∠BAE=∠DCF.(1)求证:△ABE≌△CDF;(2)若AC⊥EF,试判断四边形AECF是什么特殊四边形,并证明你的结论.【答案】见解答.【分析】(1)平行四边形的对边相等,对角相等,即∠B=∠D,AB=CD,根据已知给出的∠BAE=∠DCF,可证明两个三角形全等.(2)可先证明四边形AECF中对角线的关系,根据AC⊥EF,从而判断出到底是什么特殊的四边形.【解答】解:(1)∵在平行四边形ABCD中,∴∠B=∠D,AB=CD,又∵∠BAE=∠DCF.∴△ABE≌△CDF;(2)∵△ABE≌△CDF,∴BE=DF,∴BC-BE=AD-FD,∴EC=AF,∵AD∥BC,∴∠FAC=∠ECA,∠CEF=∠AFE,∴△AOF≌△COE,∴AO=CO,EO=FO,又∵AC⊥EF,∴四边形AECF是菱形.【点评】本题考查了平行四边形的判定和性质,平行四边形的对边平行且相等,对角相等,全等三角形的判定和性质,菱形的判定.19.【题文】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE 是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.(1)如图(a)所示,当点D在线段BC上时.①求证:△AEB≌△ADC;②探究四边形BCGE是怎样特殊的四边形?并说明理由;(2)如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立;(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.【答案】见解答.【分析】(1)根据等边三角形的性质可得AB=AC,AE=AD,∠BAC=∠EAD=60°,然后求出∠BAE=∠CAD,再利用“边角边”证明△AEB和△ADC全等;②四边形BCGE是平行四边形,因为△AEB≌△ADC,所以可得∠ABE=∠C=60°,进而证明∠ABE=∠BAC,则可得到EB∥GC又EG∥BC,所以四边形BCGE是平行四边形;(2)根据(1)的思路解答即可.(3)当CD=CB时,四边形BCGE是菱形,由(1)可知△AEB≌△ADC,可得BE=CD,再证明BE=CB,即邻边相等的平行四边形是菱形.【解答】证明:(1)①∵△ABC和△ADE都是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°.又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,∴∠EAB=∠DAC,∴△AEB≌△ADC(SAS).②方法一:由①得△AEB≌△ADC,∴∠ABE=∠C=60°.又∵∠BAC=∠C=60°,∴∠ABE=∠BAC,∴EB∥GC.又∵EG∥BC,∴四边形BCGE是平行四边形.方法二:证出△AEG≌△ADB,得EG=AB=BC.∵EG∥BC,∴四边形BCGE是平行四边形.(2)①②都成立.(3)当CD=CB (∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.理由:方法一:由①得△AEB≌△ADC,∴BE=CD又∵CD=CB,∴BE=CB.由②得四边形BCGE是平行四边形,∴四边形BCGE是菱形.方法二:由①得△AEB≌△ADC,∴BE=CD.又∵四边形BCGE是菱形,∴BE=CB∴CD=CB.方法三:∵四边形BCGE是平行四边形,∴BE∥CG,EG∥BC,∴∠FBE=∠BAC=60°,∠F=∠ABC=60°∴∠F=∠FBE=60°,∴△BEF是等边三角形.又∵AB=BC,四边形BCGE是菱形,∴AB=BE=BF,∴AE⊥FG∴∠EAG=30°,∵∠EAD=60°,∴∠CAD=30°.【点评】本题主要考了平行线四边形的判定和性质、等边三角形的性质、全等三角形的判定和性质以及菱形的判定,解题关键在于根据题意画出图形,通过求证三角形全等,推出等量关系,即可推出结论.20.【题文】如图,在△ABC中,AB=2BC,点D、点E分别为AB、AC的中点,连接DE,将△ADE 绕点E旋转180°,得到△CFE.试判断四边形BCFD的形状,并说明理由.【答案】见解答.【分析】四边形BCFD应该是菱形,要证四边形AFCE是菱形,只需通过定义证明它是一组邻边相等的平行四边形即可,此题实际是对判定菱形的方法“一组邻边相等的平行四边形是菱形”的证明.【解答】解:四边形BCFD是菱形,理由如下:∵点D、点E分别是AB、AC的中点,∴DE∥BC,DE= BC,又∵△CFE是由△ADE旋转而得,∴DE=EF,∴DF∥BC,DF=BC,∴四边形BCFD是平行四边形,又∵AB=2BC,且点D为AB的中点,∴BD=BC,∴BCFD是菱形.【点评】菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.还有就是本题中一组邻边相等的平行四边形是菱形.。
6.1平行四边形的性质(1)课件(2014年新青岛版八年级下)

练一练
3、已知O是 4、已知O是 ABCD两条对角线的交点,若AC=24mm, ABCD两条对角线的交点,若已知AB= BD=38mm,BC=28mm,则△OBC的周长为_____ 59mm 5,△OAB的周长比△OBC的周长短3,
则BC=_____ 8
中,周长为20cm,对角线AC交BD于点 O,△OBC比△OAB的周长多4,则边AB=________ ,BC=____. A
O (0,0)
Y
D(2,3)
C B(5,0) x
D. (8,2)
ABCD中, 对角线AC﹑BD相交于 点O,且AC+BD=20, △AOB的周长等于15,
5 则CD=______.
2.如图,在
A
B
D O
C
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到 晚年的时候,终于拥有了一块平行四边形的土地,由于年 迈体弱,他决定把这块土地分给他的四个孩子,他是这样 分的:
D
●
A
●
D
●
E
O
●
O
F
●
F
B
(1)
C
B
(2)
C
在上述问题中,若将直线EF绕点O旋转至下 图(3)的位置时,上述结论是否仍然成立?
若此时再与两边延长线相交呢?
●
E
A E
E
●
D
A
E
●
D
●
O
F
●
O
B
(3) F (1)
C
B
(4) (3) F (4)
C F●
小结:过平行四边形的对角线交点作直线与平行四边形 的一组对边或对边的延长线相交,得到线段总相等。
青岛版数学八年级下册6.2《平行四边形的判定》教学设计1

青岛版数学八年级下册6.2《平行四边形的判定》教学设计1一. 教材分析《平行四边形的判定》是青岛版数学八年级下册第六章第二节的内容。
本节课的主要内容是让学生掌握平行四边形的判定方法,能够运用这些方法判断一个四边形是否为平行四边形。
教材通过引入平行四边形的定义和性质,引导学生探究并发现平行四边形的判定方法,从而提高学生的空间想象能力和逻辑思维能力。
二. 学情分析学生在学习本节课之前,已经学习了四边形的性质,对四边形有了一定的了解。
同时,学生已经掌握了平行线的性质,能够熟练地画出平行线。
但是,学生对平行四边形的判定方法可能还不够熟悉,需要通过本节课的学习来进一步掌握。
三. 教学目标1.让学生掌握平行四边形的判定方法,能够运用这些方法判断一个四边形是否为平行四边形。
2.培养学生的空间想象能力和逻辑思维能力。
3.提高学生的合作交流能力,培养学生的团队精神。
四. 教学重难点1.重点:平行四边形的判定方法。
2.难点:如何运用判定方法判断一个四边形是否为平行四边形。
五. 教学方法1.采用问题驱动的教学方法,引导学生探究并发现平行四边形的判定方法。
2.利用多媒体辅助教学,展示平行四边形的判定过程,提高学生的空间想象能力。
3.采用小组合作交流的方式,让学生在探究过程中互相学习,共同进步。
4.通过练习题巩固所学知识,提高学生的应用能力。
六. 教学准备1.多媒体教学设备。
2.练习题。
3.平行四边形的模型或图片。
七. 教学过程1.导入(5分钟)利用多媒体展示一些生活中的平行四边形图片,引导学生观察并思考:这些图形有什么共同特征?你能否用已学的知识解释这些特征?2.呈现(10分钟)介绍平行四边形的定义和性质,引导学生发现并总结平行四边形的判定方法。
3.操练(15分钟)让学生分组合作,运用判定方法判断一些给定的四边形是否为平行四边形。
每组选出一个代表进行讲解,其他组进行评价。
4.巩固(10分钟)让学生独立完成一些判断题,检验是否掌握了平行四边形的判定方法。
青岛版八年级数学下册平行四边形的判定教学课件

已知:平行四边形ABCD
A
则可得:AB∥CD AD∥BC
(平行四边形的定义)
B
边: AB=CD AD=BC (平行四边形的两组对边分别相等)
角: ∠A= ∠C ∠B= ∠D (平行四边形的对角相等)
D
O
C
对角线: AO=CO BO=DO 平行四边形的对角线互相平分
已知:如图 ,在平行四边形ABCD中, E,F分别是边AD,BC的中点.
又∵ AB=CD(已知) AC=AC(公共边)
∴△ABC≌△CDA(SAS) ∴∠3=∠4(两直线平行,内错角相等) ∴ AD ∥ BC(内错角相等,两直线平行) ∴四边形ABCD是平行四边形(平行四边形的定义)
判定定理1 一组对边平行且相等的四边形是平行四边形
已知:在四边形ABCD中,AB=CD, AD=BC , 求证:四边形ABCD是平行四边形.
证明:连结AC.
︶ ︵
得: ∠1=∠2
A
D
AB=CD
1 3
AC=AC
4
可能是假命题!
B
2C
E
等腰梯形ABED
例1 如图, 证明:
填空:
A
D
1、∵AB=CD _A_B∥_CD_
B
C
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
2、 ∵AB ∥ CD
_A_D ∥ _BC_
∴四边形ABCD是平行四边形
作为命题的题设,结论是四边形ABCD是平行四边形.
A
D
你有几种选法?得到了几个命题?
√ 1、AB=CD AB ∥ CD
B
C
√ 2、AB = CD AD=BC
青岛版八年级数学下册平行四边形的判定课件

【例3】已知:如图3,□ABCD中,E、F分别是AC上
两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形 BEDF是平行四边形。
【答案】证明:连接BD,交AC于点O.因为四边形 ABCD是平行四边形,所以 AO=CO,BO=DO.ΔABE≌ ΔCDE,所以即AE=CF, 所以EO=FO,所以四边
返回 首页
问题:如图(1),将两长两短的四根细木条用小钉绞合 在一起,做成一个四边形,使等长的木条作为对边.在转 动过程中它一直是平行四边形吗?
如图(2)将两根细木条AC、BD的中点重叠,用小钉绞 合在一起,用橡皮筋连接木条的顶点,做成一个四边 形ABCD,在转动过程中,四边形ABCD一直是平行四边形 吗?
平行四边形的判定 (1)两组对边分别相等的四边形是平行四边形; (2)对角线互相平分的四边形是平行四边形。
问题:你能证明这两个结论吗?
如图,连接AC,因为AD=BC,AB=CD, 又AC是公共边, 所以△ABC≌△CDA, 所以∠ACB=∠CAD, 所以AD∥BC, 同理AB∥CD。
问题:如图,取两根相等的木条AB,CD,将他们平行 放置,再用两根木条BC、AD加固,得到的四边形 ABCD是平行四边形吗?
图3
4.判断题: (1)相邻的两个角都互补的四边形是平行四边形; (√ )
(2)两组对角分别相等的四边形是平行四边形; (√ ) (3)一组对边平行,另一组对边相等的四边形是平行 四边形;( × ) (4)一组对边平行且相等的四边形是平行四边形; (√ ) (5)对角线相等的四边形是平行四边形;( × ) (6)对角线互相平分的四边形是平行四边形.( √ )
问题:如上图,四边形 ABCD, AB∥CD,且AB=CD, 求证:四边形ABCD是平行 四边形。
青岛版初中八年级下册数学课件 《图形的平移》PPT教学课件(第1课时)

在平面内,将一个图形沿一个方向移动一定的距离, 这样的变换叫做图形的平移。
A
B
C
平移两要素:平移后图形的位置由平移方向和距离确定。
A
B
C
平移性质:
①一个图形和它经过平移得到的图形中,两组对应点的连线 平行(或在同一直线上)且相等。
②平移不改变图形的形状和大小。
③由平移得到的图形与原来的图形是全等的。
的面积是cm2
28
3.如下图∠ABC是∠O经过平移而得的角,若 ∠O=65°,则∠ABC等于多少度?
A
B
C 解:∠ABC是∠O平移过程
中的对应角,所以∠ABC=
O
D
∠O=65°
4.由△ABC平移而得的三角形共有多少个?
A
C
B
解:共有5个。
课堂小结
通过本课时的学习,我们学习了:
1.平移的定义 2.平移的性质 (1)图形平移前后,两个图形的对应点的连线平行(或 在同一条直线上)且相等。 (2)图形平移后,图形的形状、大小都不变,即平移前 后的图形全等。于是平移前后的图形中,对应线段相等、 对应角相等。
图形的平移
第1课时
1.通过具体的实例认识图形的平移变换,去体会平移变换的过 程。 2.经历对图形进行观察、分析、欣赏和动手操作、画图等过程, 掌握有关画图的操作技能,能找出一个图形的对应点,按要求 作出一个图形的平移图形,发展初步的审美能力。(重、难点) 3.体会以局部带动整体的思想。
阅读课本,回答以下问题: 一、什么是平移? 二、平移的两要素是什么? 三、平移的性质是什么?
B′
C′
例1如图,在四边形ABCD中,AD∥BC,AD<BC,AB=CD你能 利用平移的方法判断∠B和∠C是否相等吗?说明你的理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•
•
阅读课文第17页到第20页,思考以下问题: 1、什么叫矩形?
ZXXK
2、矩形有哪些性质定理和推论?
•
•
2. 矩形的性质:
பைடு நூலகம்
学科网
矩形的性质定理1:矩形的四个角都是直角. 矩形的性质定理2:矩形的两条对角线相等. 性质定理的推论:直角三角形斜边上的中线 等于斜边长的一半.
2.判断题
(1).矩形是平行四边形( )
(2).矩形的两条对角线将矩形分成四个面积相等的
等腰三角形(
•
)
A O D
B
•
C
•
主要内容: 有一个角是直角的平行四边形叫矩形 1、矩形的定义: 2、矩形的性质:
Z.X.X.K
矩形的对边平行且相等.
矩形的四个角都是直角. 矩形的两条对角线相等 且互相平分.
矩形是轴对称图形. 直角三角形斜边上的中线等于斜边长的一半 .
•
练一练
1. 矩形的短边长为3cm,两对角线所成的钝角是120 °, 6cm 则它的对角线长是_______.
