《4.玻尔的原子模型》课件2
合集下载
人教版物理选修—玻尔的原子模型-ppt精品课件

多学一点: 2、使原子能级跃迁的两种粒子——光子与实物粒子 (1)原子若是吸收光子的能量而被激发,其光子的能量必须等于两能 级的能量差,否则不被吸收。
(2)原子还可吸收实物粒子(如自由电子)的能量而被激发,由于实物粒 子的动能可部分地被原子吸收,所以只要入射粒子的能量大于两能级 的能量差值,就可使原子发生能级跃迁。
1.玻尔理论的成功之处:玻尔的原子理论第一次将量子观念引入原子领域, 提出了定态和跃迁的概念,成功地解释了氢原子光谱的实验规律。轨道 量子化假设把量子观念引入原子理论,这是玻尔的原子理论之所以成功 的根本原因 2.玻尔理论的局限性:对更复杂的原子发光,玻尔理论却无法解释,它过多 地保留了经典粒子的概念。把电子运动看成是经典力学描述下的轨道运 动。 3.电子云:根据量子观念,核外电子的运动服从统计规律,而没有固定的轨 道,我们只能知道它们在核外某处出现的概率大小,画出来的图像就像云 雾一样,稠密的地方就是电子出现概率大的地方,把它形象地称作电子云。
1、玻尔理论提出的历史背景是怎样的? 2、玻尔理论要解决什么问题? 3、玻尔理论是怎样解决所面对的问题的? 4、玻尔理论的成功和局限分别有哪些?
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
五、玻尔理论的成功与局限性: 人教版物理选修3—518.4玻尔的原子模型(共24张PPT)
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
更组电 基成子 本部是 的分原 单,子 元是的
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
本章知识结构:
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
•
1.某林场中繁殖力极强老鼠种群数量 的增长 会受密 度制约
(2)原子还可吸收实物粒子(如自由电子)的能量而被激发,由于实物粒 子的动能可部分地被原子吸收,所以只要入射粒子的能量大于两能级 的能量差值,就可使原子发生能级跃迁。
1.玻尔理论的成功之处:玻尔的原子理论第一次将量子观念引入原子领域, 提出了定态和跃迁的概念,成功地解释了氢原子光谱的实验规律。轨道 量子化假设把量子观念引入原子理论,这是玻尔的原子理论之所以成功 的根本原因 2.玻尔理论的局限性:对更复杂的原子发光,玻尔理论却无法解释,它过多 地保留了经典粒子的概念。把电子运动看成是经典力学描述下的轨道运 动。 3.电子云:根据量子观念,核外电子的运动服从统计规律,而没有固定的轨 道,我们只能知道它们在核外某处出现的概率大小,画出来的图像就像云 雾一样,稠密的地方就是电子出现概率大的地方,把它形象地称作电子云。
1、玻尔理论提出的历史背景是怎样的? 2、玻尔理论要解决什么问题? 3、玻尔理论是怎样解决所面对的问题的? 4、玻尔理论的成功和局限分别有哪些?
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
五、玻尔理论的成功与局限性: 人教版物理选修3—518.4玻尔的原子模型(共24张PPT)
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
更组电 基成子 本部是 的分原 单,子 元是的
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
本章知识结构:
人教版 物理 选修3—5 18.4 玻尔的原子模型(共24张PPT)
•
1.某林场中繁殖力极强老鼠种群数量 的增长 会受密 度制约
玻尔的原子模型(共16张)PPT课件
You Know, The More Powerful You Will Be
14
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX
时 间:XX年XX月XX日
15
即hν=Em-En
称为频率条件,又称辐射条件
针对原子光谱是线状谱提出
Em n
En
光子的发射和吸收
低
(电子克服库仑引力做功增大电势能,原子的能量增加)
高
能 量 态
吸收光子
跃迁 跃迁
跃迁
辐射光子
(电子所受库仑力做正功减小电势能,原子的能量减少)
能 量 态
10
二.玻尔理论对氢光谱的解释
玻尔从上述假设出发,利用经典电磁学和经典力学,计算 出了氢的电子可能的轨道半径及相应的能量.
e
v
F
r+ e
认 终落在原子核上,而使
为 原子变得不稳定.
e
事
实
e+
3
卢瑟福的核式结构学说与经典电磁理论的矛盾(
经 由于电子轨道的变 典 化是连续的,辐射 理 电磁波的频率等于 论 绕核运动的频率, 认 连续变化,原子光 为 谱应该是连续光谱
事 原子光谱是不 实 连续的线状谱
4
玻尔的原子模型
5
1:轨道量子化
18-4 玻尔的原子模型
回顾科学家对原子结构的认识史
汤姆孙发现电子
否定
原子不可割
建立
汤姆孙的西 瓜模型
出现矛盾
α粒子散射实验
否定
原子稳定性事实 氢光谱实验
否定
汤姆孙的西 瓜模型
14
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX
时 间:XX年XX月XX日
15
即hν=Em-En
称为频率条件,又称辐射条件
针对原子光谱是线状谱提出
Em n
En
光子的发射和吸收
低
(电子克服库仑引力做功增大电势能,原子的能量增加)
高
能 量 态
吸收光子
跃迁 跃迁
跃迁
辐射光子
(电子所受库仑力做正功减小电势能,原子的能量减少)
能 量 态
10
二.玻尔理论对氢光谱的解释
玻尔从上述假设出发,利用经典电磁学和经典力学,计算 出了氢的电子可能的轨道半径及相应的能量.
e
v
F
r+ e
认 终落在原子核上,而使
为 原子变得不稳定.
e
事
实
e+
3
卢瑟福的核式结构学说与经典电磁理论的矛盾(
经 由于电子轨道的变 典 化是连续的,辐射 理 电磁波的频率等于 论 绕核运动的频率, 认 连续变化,原子光 为 谱应该是连续光谱
事 原子光谱是不 实 连续的线状谱
4
玻尔的原子模型
5
1:轨道量子化
18-4 玻尔的原子模型
回顾科学家对原子结构的认识史
汤姆孙发现电子
否定
原子不可割
建立
汤姆孙的西 瓜模型
出现矛盾
α粒子散射实验
否定
原子稳定性事实 氢光谱实验
否定
汤姆孙的西 瓜模型
波尔的原子模型(课堂PPT)

E1
轨道半径: rn n2r1 (n=1,2,3……)
式中r1 =0.53×10-10m 、E1=-13.6ev
频率条件 hEmEn
4 3 21
轨道假设
1
43 2
定态假设
E4 E3 E2
E1
43 2
跃迁假设
E4 E3 E2
1
E1
9
Hδ
n=1 n=2 n=3 n=4 n=5 n=6
(巴尔末系)
Hγ
Hβ
Hα
1R(212n12) n3,4,5,...
巴 耳 末 公 式R=1.10107m1 里 德 伯 常 量
根据:E=hv,λ=c/v
又Eδ =1.89eV= 3.03 ×10-19J 所以, λ δ=hc/ Eδ = 6.63×10-34 ×3.0 ×10-8 / 3.03 ×10-19J
A、原子要发出一系列频率的光子
B、原子要吸收一系列频率的光子
C、原子要发出某一频率的光子
D、原子要吸收某一频率的光子
4、根据玻尔理论,氢原子中,量子数n越大,则下列说 法中正确的是( ACD) A、电子轨道半径越大 B、核外电子的速率越大 C、氢原子能级的能量越大 D、核外电子的电势能越大
5、如图所示是某原子的能级图,a、b、c 为原子跃迁所
2、根据玻尔的原子理论,原子中电子绕核运动的半径 ( D) A、可以取任意值 B、可以在某一范围内取任意值 C、可以取一系列不连续的任意值 D、是一系列不连续的特定值
3、按照玻尔理论,一个氢原子中的电子从一半径为ra 的圆轨道自发地直接跃迁到一半径为rb的圆轨道上,已 知ra>rb,则在此过程中( C )
在普朗克关于黑体辐射的量子论和爱因斯坦关于 光子概念的启发下,波尔于1913年把微观世界中物理 量取分立值的观念应用到原子系统,提出了自己的原 子结构假说。
玻尔的原子模型PPT教学课件

汉初,接秦之敝,诸 侯并起,民失作业而大饥 谨。凡米石五千,人相食, 死者过半。高祖乃令民得 卖子,就食蜀、汉。天下 既定,民亡盖藏,自天子 不能具醇驷 (同一颜色的四匹 马),而将相或乘牛车。
——《汉书.食货志》
经济残败、百废待兴
修养生息、轻徭薄赋
西汉初年的社会状况
西汉建立之初, 经过秦末农民战争, 经济受到严重破坏。 为了恢复元气,汉 初实行休养生息的 政策。对外与匈奴 “和亲”,对内轻 徭薄赋。
罢 1、“无为而治” 不能适应中央集权的需要。 匈奴南下侵汉;
黜 诸侯“自为法令,拟于天子”—七国之乱 2、儒学的自我调节符合中央集权的要求——
百 吸收大一统的思想。 家 3、汉的强大使其统治者不满足于“无为”,推
崇
“有为”而治。
独 尊 儒 术
罢黜百家 独尊儒术
董仲舒: 中国古代著名的思想家。 (前179——前104年)广
川人(今河北景县人)向 汉武帝提出“罢黜百家 独尊儒术”的主张,创立 新儒学。
2、董仲舒的新儒学的思想内涵
#思想来源: 以《公羊春秋》为骨干, 融合阴阳家,黄老之学 以及法家思想而形成的 新的思想体系。
#理论基础: “天人感应”学说。
#思想核心: 大一统(“新”所在)
天人感应
“天子受命于天,天下受命于天子”;“古之造文者,三画 连其中,谓之王,三画者,天地人,而连其中,通其道也, 谓之王。”
光子的发射和吸收
原子在始、 末两个能级Em和 En( Em>En )间 跃迁时发射光子 的频率可以由下 式决定:
h Em En
人们早在了解原子内部结构之前就已经观 察到了气体光谱,不过那时候无法解释为什么气 体光谱只有几条互不相连的特定谱线,玻尔理论 很好的解释了氢原子的光谱.
——《汉书.食货志》
经济残败、百废待兴
修养生息、轻徭薄赋
西汉初年的社会状况
西汉建立之初, 经过秦末农民战争, 经济受到严重破坏。 为了恢复元气,汉 初实行休养生息的 政策。对外与匈奴 “和亲”,对内轻 徭薄赋。
罢 1、“无为而治” 不能适应中央集权的需要。 匈奴南下侵汉;
黜 诸侯“自为法令,拟于天子”—七国之乱 2、儒学的自我调节符合中央集权的要求——
百 吸收大一统的思想。 家 3、汉的强大使其统治者不满足于“无为”,推
崇
“有为”而治。
独 尊 儒 术
罢黜百家 独尊儒术
董仲舒: 中国古代著名的思想家。 (前179——前104年)广
川人(今河北景县人)向 汉武帝提出“罢黜百家 独尊儒术”的主张,创立 新儒学。
2、董仲舒的新儒学的思想内涵
#思想来源: 以《公羊春秋》为骨干, 融合阴阳家,黄老之学 以及法家思想而形成的 新的思想体系。
#理论基础: “天人感应”学说。
#思想核心: 大一统(“新”所在)
天人感应
“天子受命于天,天下受命于天子”;“古之造文者,三画 连其中,谓之王,三画者,天地人,而连其中,通其道也, 谓之王。”
光子的发射和吸收
原子在始、 末两个能级Em和 En( Em>En )间 跃迁时发射光子 的频率可以由下 式决定:
h Em En
人们早在了解原子内部结构之前就已经观 察到了气体光谱,不过那时候无法解释为什么气 体光谱只有几条互不相连的特定谱线,玻尔理论 很好的解释了氢原子的光谱.
课件2:18.4 波尔的原子模型

第十八章 第四节 玻尔的原子模型
1 学习目标定位
2
课堂情景切入
3 知识自主梳理
4 重点难点突破 5 考点题型设计
6
课时作业
学习目标定位
※
了解玻尔原子模型及能级的概念
※ 理解原子发射和吸收光子的频率与能级差的关系
※ 知道玻尔对氢光谱的解释以及玻尔理论的局限性
课堂情景切入
霓虹灯发出的光,线条结构丰 富,色彩鲜艳、绚丽多姿,形状、 色彩变幻莫测,令人赏心悦目。一 幅幅流动的画面,似天上彩虹,像 人间银河,更酷似一个梦幻世界, 使人难以忘怀。霓虹灯是一种增添节日欢快气氛和进行广告宣 传的最佳光源,霓虹灯的亮、美、动特点,在各类新型光源中 独领风骚。同学们,你们知道霓虹灯的发光原理吗?
(黄冈中学2014~2015学年高二下学期期中)如图所示 为氢原子的能级图,在具有下列能量的光子或者电子 中,不能让基态氢原子吸收能量而发生跃迁的是 ()
A.13eV的光子
B.13eV的电子
C.10.2eV的光子
D.10.2eV的电子
答案:A
解析:基态氢原子吸收 13eV 的光子,能量为-13.6eV+ 13eV=-0.6eV,该光子不能被吸收而发生跃迁;基态氢原子 与 13eV 的电子碰撞,可能只有部分能量被吸收,跃迁到第 2、 3 或者 4 能级;基态氢原子吸收 10.2eV 的光子,能量为-13.6eV +10.2eV=-3.4eV,该光子能被吸收而跃迁到第二能级,基态 氢原子与 10.2eV 的电子碰撞,能量可以全部被吸收,跃迁到第 二能级。综上所述,本题选 A。
个轨道上,玻尔将这种现象称跃迁。
电子在核外的运动真的有固定轨道吗?玻尔理论中的轨道 量子化又如何解释?
答案: 在原子内部,电子绕核运动并没有固定的轨道只 不过当原子处于不同的定态时,电子出现在rn=n2r1处的 几率大。
1 学习目标定位
2
课堂情景切入
3 知识自主梳理
4 重点难点突破 5 考点题型设计
6
课时作业
学习目标定位
※
了解玻尔原子模型及能级的概念
※ 理解原子发射和吸收光子的频率与能级差的关系
※ 知道玻尔对氢光谱的解释以及玻尔理论的局限性
课堂情景切入
霓虹灯发出的光,线条结构丰 富,色彩鲜艳、绚丽多姿,形状、 色彩变幻莫测,令人赏心悦目。一 幅幅流动的画面,似天上彩虹,像 人间银河,更酷似一个梦幻世界, 使人难以忘怀。霓虹灯是一种增添节日欢快气氛和进行广告宣 传的最佳光源,霓虹灯的亮、美、动特点,在各类新型光源中 独领风骚。同学们,你们知道霓虹灯的发光原理吗?
(黄冈中学2014~2015学年高二下学期期中)如图所示 为氢原子的能级图,在具有下列能量的光子或者电子 中,不能让基态氢原子吸收能量而发生跃迁的是 ()
A.13eV的光子
B.13eV的电子
C.10.2eV的光子
D.10.2eV的电子
答案:A
解析:基态氢原子吸收 13eV 的光子,能量为-13.6eV+ 13eV=-0.6eV,该光子不能被吸收而发生跃迁;基态氢原子 与 13eV 的电子碰撞,可能只有部分能量被吸收,跃迁到第 2、 3 或者 4 能级;基态氢原子吸收 10.2eV 的光子,能量为-13.6eV +10.2eV=-3.4eV,该光子能被吸收而跃迁到第二能级,基态 氢原子与 10.2eV 的电子碰撞,能量可以全部被吸收,跃迁到第 二能级。综上所述,本题选 A。
个轨道上,玻尔将这种现象称跃迁。
电子在核外的运动真的有固定轨道吗?玻尔理论中的轨道 量子化又如何解释?
答案: 在原子内部,电子绕核运动并没有固定的轨道只 不过当原子处于不同的定态时,电子出现在rn=n2r1处的 几率大。
玻尔的原子模型【公开课教学PPT课件】高中物理

对于能量大于或等于 对于能量小于13.6eV的光子 13.6eV的光子(电离) (要么全被吸收,要么不吸收)
(2)吸收实物粒子能量
只要实物粒子动能足以使氢原子向高能级跃迁, 就能被氢原子吸收全部或部分动能而使氢原子向高能 级跃迁,多余能量仍为实物粒子动能。
思考与讨论 巴耳末公式有正
整数n出现,这里我们 也用正整数n来标志氢 原子的能级。它们之 间是否有某种关系?
同时又应用了“粒子、 轨道”等经典概念和 有关牛顿力学规律
除了氢原子光谱外,在解决其 他问题上遇到了很大的困难.
)
hc
E1 52
E1 22
E1
(
1 22
1 52
)
hc
E1 62
E1 22
1 E1( 22
1 62
)
巴耳末系:
1 E1 ( 1 1 )
hc 22 32
1
E1 hc
(
1 22
1 42
)
1
E1 hc
(
1 22
1 52
)
1
E1 hc
52
1 n2
n 6,7,8,
二、玻尔理论对氢光谱的解释
氢 原 子激 的发 能态 级 图
n
E/eV
∞----------------- 0 eV
5
-0.54
4 3
2
巴
帕 邢 系
布 喇 开 系
普 丰 德 系
-0.85 -1.51
(2)吸收实物粒子能量
只要实物粒子动能足以使氢原子向高能级跃迁, 就能被氢原子吸收全部或部分动能而使氢原子向高能 级跃迁,多余能量仍为实物粒子动能。
思考与讨论 巴耳末公式有正
整数n出现,这里我们 也用正整数n来标志氢 原子的能级。它们之 间是否有某种关系?
同时又应用了“粒子、 轨道”等经典概念和 有关牛顿力学规律
除了氢原子光谱外,在解决其 他问题上遇到了很大的困难.
)
hc
E1 52
E1 22
E1
(
1 22
1 52
)
hc
E1 62
E1 22
1 E1( 22
1 62
)
巴耳末系:
1 E1 ( 1 1 )
hc 22 32
1
E1 hc
(
1 22
1 42
)
1
E1 hc
(
1 22
1 52
)
1
E1 hc
52
1 n2
n 6,7,8,
二、玻尔理论对氢光谱的解释
氢 原 子激 的发 能态 级 图
n
E/eV
∞----------------- 0 eV
5
-0.54
4 3
2
巴
帕 邢 系
布 喇 开 系
普 丰 德 系
-0.85 -1.51
人教版物理选修-玻尔的原子模型-ppt精品课件
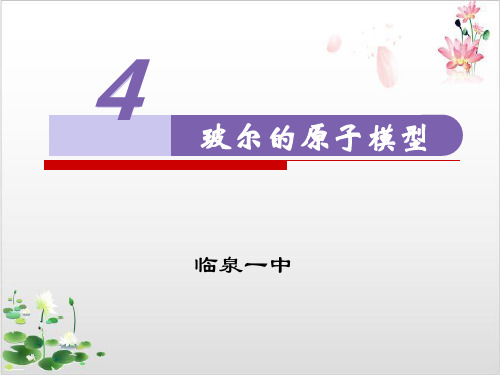
E/eV
0 -0.54 -0.85 -1.51
-3.4
1
人教版物理选修3-5 18.4 玻尔的原子模型(共28张PPT)【PPT优秀 课件】 -精美 版
赖曼系
-13.6
20
人教版物理选修3-5 18.4 玻尔的原子模型(共28张PPT)【PPT优秀 课件】 -精美 版
思考与讨论:
1. 根据氢原子能级取值量子化,如何解释 原子的光谱是分立的线状谱?
7.先用低 倍镜找 到叶肉 细胞, 然后换 用高倍 镜观察 。注意 观察叶 绿体随 着细胞 质流动 的情况 ,仔细 看看每 个细胞 中细胞 质流动 的方向 是否一 致致。
8.内质网 以类似 于“出 芽”的 形式形 成具有 膜的小 泡,小 泡离开 内质网 ,移动 到高尔 基体与 高尔基 体融合 ,成为 高尔基 体的一 部分。 高尔基 体又以 “出芽 ”方式 形成小 泡,移 动到细 胞膜与 细胞膜 融合, 成为细 胞膜的 一部分 。
hc
1 n2
2π2e4k 2me h2
1 ( 22
2π2e4k h2
2me
)
1 2π2e4k 2me ( 1 1 )
h3c
22 n2
17
人教版物理选修3-5 18.4 玻尔的原子模型(共28张PPT)【PPT优秀 课件】 -精美 版
1
1 R( 22
1 n2 )
1 2π2e4k 2me ( 1 1 )
4
原子光谱对玻尔创立原子结构具有重 要作用,然而最初玻尔没有意识到这一点.
玻尔曾这样说道: “人们总以为[光谱是]神奇的,但在 那儿不可能取得进步.这就彷佛你有蝴蝶的 翅膀,那么其色彩等等当然是非常有规律的, 但是没有人想到能从蝴蝶翅膀的颜色推出生 物学的基础”
《4 玻尔的原子模型》PPT课件(安徽省县级优课)

事 原子光谱是不连续 实 的,是线状谱
新课导入
以上矛盾表明,从宏观现象总结出来的经典 电磁理论不适用于原子世界的现象。引入新观念 是必须的!
1913年丹麦的物理学家玻尔在卢瑟福的基础 上,把普朗克的量子理论和爱因斯坦的光子理 论运用到原子系统上,提出了玻尔原子结构假 说。
学习目标
1.知道玻尔原子理论的基本假设的主要内容。 2.了解能级、跃迁、能量量子化以及基态、激发态等概念。 3.能用玻尔原子理论简单解释氢原子模型。 4.了解玻尔模型的不足之处及其原因。
除了氢原子光谱外,在解决其 他问题上遇到了很大的困难
? 汤 原α 粒氢姆子子光孙稳散发定谱思 关射现性实实想 键电事验怎验子实: :样必 用修须 电观察与实验所获得的事实否否否彻子改定定定底云玻放概尔弃念模原 汤 卢 式经取瓜子 姆 瑟结型典代模不 孙 福构?概经型可 的 的模念典割 西 核型的轨出出道现建建 建建立科学模型提出科学假说现矛概矛立立立盾念盾
巴
耳
n=2
末
系
-1.51 eV -3.40 eV
n=1
-13.6 eV
1
巴尔末公式:
1 R( 22
1 n2
) n
3,4,
5,
R=1.10 107m1
想一想
Hα
Hβ
Hγ
Hδ
H
n=1 n=2 n=3 n=4
n=5 n=6
1
1 R( 22
1 n2
)
n 3,4, 5,
R=1.10 107m1
小结提升
( ACD )
A. 用 10.2 eV 的光子照射 B. 用 11 eV 的光子照射 C. 用 14 eV 的光子照射 D. 用 11 eV 的电子碰撞
新课导入
以上矛盾表明,从宏观现象总结出来的经典 电磁理论不适用于原子世界的现象。引入新观念 是必须的!
1913年丹麦的物理学家玻尔在卢瑟福的基础 上,把普朗克的量子理论和爱因斯坦的光子理 论运用到原子系统上,提出了玻尔原子结构假 说。
学习目标
1.知道玻尔原子理论的基本假设的主要内容。 2.了解能级、跃迁、能量量子化以及基态、激发态等概念。 3.能用玻尔原子理论简单解释氢原子模型。 4.了解玻尔模型的不足之处及其原因。
除了氢原子光谱外,在解决其 他问题上遇到了很大的困难
? 汤 原α 粒氢姆子子光孙稳散发定谱思 关射现性实实想 键电事验怎验子实: :样必 用修须 电观察与实验所获得的事实否否否彻子改定定定底云玻放概尔弃念模原 汤 卢 式经取瓜子 姆 瑟结型典代模不 孙 福构?概经型可 的 的模念典割 西 核型的轨出出道现建建 建建立科学模型提出科学假说现矛概矛立立立盾念盾
巴
耳
n=2
末
系
-1.51 eV -3.40 eV
n=1
-13.6 eV
1
巴尔末公式:
1 R( 22
1 n2
) n
3,4,
5,
R=1.10 107m1
想一想
Hα
Hβ
Hγ
Hδ
H
n=1 n=2 n=3 n=4
n=5 n=6
1
1 R( 22
1 n2
)
n 3,4, 5,
R=1.10 107m1
小结提升
( ACD )
A. 用 10.2 eV 的光子照射 B. 用 11 eV 的光子照射 C. 用 14 eV 的光子照射 D. 用 11 eV 的电子碰撞
《4 玻尔的原子模型》PPT课件(广东省市级优课)

第四节
玻尔的原子模型
温故知新
卢瑟福核式结构模型无法解释的2种情况? 1、无法解释原子的稳定性 2、无法解释原子光谱分离特性
一、玻尔理论的基本假设
假设1:轨道假设:电子的轨道量子化
rn=n2r1 (n=1、2、3、….)
假设2:能级假设:原子能量量子化 定态 量子化的能量
值叫做能级
En E1 (n=1、2、3、….)
电离:因为,原子一旦电离,原子结构即被破 坏,因而不再遵守有关原子结构的理论。如基态氢原 子的电离能为13.6eV,只要大于或等于13.6eV的光子 都被基态的氢原子吸收而发生电离,只不过入射光子 的能量越大,原子电离后产生的自由电子的动能越大。
实物粒子碰撞:至于实物粒子和原子碰撞的情况, 由于实物粒子的动能可全部或部分地为原子吸收,所 以只要入射粒子的动能大于或等于原子某两定态能量 之差,也可使原子受激发而向较高能级跃迁。
n2
原子能量包含哪些能?
动能和势能
n=1是基态,能量最低,原子最稳定,其余为激发态,能量高, 原子不稳定。
假设3:跃迁假设 跃迁公式:h = Em- En
跃迁 过程中辐射或吸收是特定的特定频率的光子 。
高能级
∞
45 3
2
二、氢原子能级图
n
1
低能级
以无穷远处为参考位置
0 eV -0.54eV -0.85eV -1.51eV -3.4eV
En
-13.6eV
氢原子能级跃迁规律1
激发态跃迁到基态可辐射几种频率的光子
∞
0 eV
45
-0.54eV -0.85eV
3
-1.51eV
2
-3.4eV
n
hv1= E3- E1 hv2= E3- E2
玻尔的原子模型
温故知新
卢瑟福核式结构模型无法解释的2种情况? 1、无法解释原子的稳定性 2、无法解释原子光谱分离特性
一、玻尔理论的基本假设
假设1:轨道假设:电子的轨道量子化
rn=n2r1 (n=1、2、3、….)
假设2:能级假设:原子能量量子化 定态 量子化的能量
值叫做能级
En E1 (n=1、2、3、….)
电离:因为,原子一旦电离,原子结构即被破 坏,因而不再遵守有关原子结构的理论。如基态氢原 子的电离能为13.6eV,只要大于或等于13.6eV的光子 都被基态的氢原子吸收而发生电离,只不过入射光子 的能量越大,原子电离后产生的自由电子的动能越大。
实物粒子碰撞:至于实物粒子和原子碰撞的情况, 由于实物粒子的动能可全部或部分地为原子吸收,所 以只要入射粒子的动能大于或等于原子某两定态能量 之差,也可使原子受激发而向较高能级跃迁。
n2
原子能量包含哪些能?
动能和势能
n=1是基态,能量最低,原子最稳定,其余为激发态,能量高, 原子不稳定。
假设3:跃迁假设 跃迁公式:h = Em- En
跃迁 过程中辐射或吸收是特定的特定频率的光子 。
高能级
∞
45 3
2
二、氢原子能级图
n
1
低能级
以无穷远处为参考位置
0 eV -0.54eV -0.85eV -1.51eV -3.4eV
En
-13.6eV
氢原子能级跃迁规律1
激发态跃迁到基态可辐射几种频率的光子
∞
0 eV
45
-0.54eV -0.85eV
3
-1.51eV
2
-3.4eV
n
hv1= E3- E1 hv2= E3- E2
《4 玻尔的原子模型》PPT课件(湖南省县级优课)

(2)几个概念:
①能级:在玻尔理论中,原子各个状态的能量值。
②基态:原子能量 最低 的状态。
③激发态:在原子能量状态中除基态之外的其他较高的状态。 ④量子数:原子的状态是不连续的,用于表示原子状态的 __正__整__数_。
(3)氢原子的轨道半径和能级:
①氢原子的半径公式:rn=_n_2r1(n=1,2,3…),其中 r1 为基态半
(2)实物粒子和原子作用而使原子激发或电离,是通过实 物粒子和原子碰撞来实现的。在碰撞过程中,实物粒子的动 能可以全部或部分地被原子吸收,所以只要入射粒子的动能 大于或等于原子某两个能级差值,就可以使原子受激发而跃 迁到较高的能级;当入射粒子的动能大于原子在某能级的能 量值时,也可以使原子电离。
结论:
②实验结果:α粒子穿过金箔后,绝大多数沿 原方向前进,少 数发生较大角度偏转,极少数偏转角度大于90°,甚至被弹回。
(3)核式结构模型:原子中心有一个很小的核,叫做原子 核,原子的全部正电荷和几乎全部质量都集中在原子核里,带 负电的电子在核外空间绕核旋转。
二、玻尔的原子模型 (1)玻尔理论: ①轨道假设:原子中的电子在库仑引力的作用下,绕原子 核做圆周运动,电子绕核运动的可能轨道是 不连续的 。
探究点二、原子跃迁时光谱线条数的确定方法 (1) 一个氢原子跃迁发出可能的光谱线条数最多为(n-1);
(2)
一群氢原子跃迁发出可能的光谱线条数为N
C
2 n
n(n 1) 2
。
探究点三、原子跃迁的两种类型
(1)原子吸收光子的能量时,原子将由低能级态跃迁到高 能级态。但只吸收能量为能级差的光子,原子发光时是由高 能级态向低能级态跃迁,发出的光子能量仍为能级差。
②定态假设:电子在不同的轨道上运动时,原子处于不同 的状态,因而具有不同的能量,即原子的能量是不连续的。这 些具有确定能量的稳定状态称为定态,在各个定态中,原子是 稳定的,不向外辐射能量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的激发态,电子克服库仑力做
1
E1 功,增大电势能,原子能量增
大,要吸收光子
c.无论是 吸收光子还是辐射光子,其频率都不是随意的,而都 是一定的,其频率由两个能级差决定 hν=Em-En
光子的发射和吸收
(电子克服库仑引力做功,增大
基 电势能,原子的能量增加) 吸收光子 激
跃迁
发
态
态
辐射光子 (电子所受库仑力做正功,
如何解释原子的发光呢?
针对原子光谱是线状谱提出
5 4E∞Leabharlann 原子从较高的E5 E4
能级Em跃迁到较
3
E3
低的能级En
2
E2
( Em>En )会发
出一个光子。即
1
E1
h Em En
针对原子光谱是线状谱提出
原子在始、末
5 4
E∞
E5 E4
两个能级Em和En ( Em>En )间跃
3
E3
迁时发射(或吸
说明2:
1 从高能级向低能级跃迁– 发射光子 以光子形式辐射出去(原子发光现象)
2 从低能级向高能级跃迁 (1) 吸收光子 对于能量大于或等于13.6eV的光子(电离) 对于能量小于13.6eV的光子(要么全被吸收,要么 不吸收)吸收满足 hν=Em-En
第4节:玻尔的原子模型
汤姆孙发现电子 枣糕模型
否定
α粒子散射实验
为什么光谱是特征明线? 原子为什么会稳定存在?
核式结构模型
原子稳定性 氢光谱实验
由上节课的学习可知:从氢气放电管可以获得氢原子光谱
氢原子光谱的谱线系可用一个简单的公式表达如下:
莱曼系 巴耳末系 帕邢系 布喇开系 普丰德系
1
R
1 12
玻 尔 是 谁 ?
围绕原子核运动的电子 的轨道半径只能是满足一
定条件的不连续、分立的
数值。且电子在这些轨道 上绕核的转动是稳定的, 不产生电磁辐射,也就是 说,电子的轨道是量子化 的 即电子的可能轨道是
分立的、不连续的
针对原子核式结构模型提出
不同的轨道对应不同的状 态,在这些状态中,尽管 电子在做变速运动却不辐 射电磁波,因此,这些状 态是稳定的
动时的能量(包括动能和势能)公式:
轨道半径: rn = n2r1 (n=1,2,3……)
能
量:
En
1 n2
E1
(n=1,2,3……)
式中r1、E1、分别代表第一条(即离核最近的)
可能轨道的半径和电子在这条轨道上运动时的能量,
rn、En 分别代表第n条可能轨道的半径和电子在第n
条轨道上运动时的能量,n是正整数,叫量子数。
2
E2
收)光子的频率
可以由前后能级
的能量差决定:
1
E1
h Em En
针对原子光谱是线状谱提出
说明:a.原子从激发态回到基
5 4 3
E∞ 态,或从较高的激发态跃迁到
E5 E4 E3
较低的激发态,库仑力对电子 做正功,减小电势能,原子能 量减小,原子要辐射光子
2
E2
b.原子从基态跃迁到激发态,
或从较低的激发态跃迁到较高
1 n2
n=2,3,4……
紫外光区域
1
R
1 22
1 n2
n=3,4,5……
可见光区域
} 1
R
1 32
1 n2
n=4,5,6……
红
外
1
R
1 42
1 n2
n=5,6,7……
光 区 域
1
R
1 52
1 n2
n=6,7,8……
经 电子绕核运动将不断 典 向外辐射电磁波,电 理 子损失了能量,其轨 论 道半径不断缩小,最 认 终落在原子核上,而使 为 原子变得不稳定.
针对原子核式结构模型提出
对氢原子:轨道半径rn = n2r1 n=1,2,3……
氢原子的轨道半径满足的条件
轨道最小半径r1 = 0.053nm 则r2 = 0.212nm r3 = 0.477nm
电子在不同的轨道上 运动,原子处于不同的状 态.玻尔指出,原子在不 同的状态中具有不同的能 量,所以原子的能量也是 量子化的。在这些状态中 原子是稳定的。
对氢原子:轨道最小半径r1 = 0.053nm
r2 = 0.212nm
r3 = 0.477nm
对氢原子:基态能量E1 = -13.6eV
其它激发态的能量E2 = -3.4eV E3 = -1.51eV
氢原子各定态的能量值,为电子绕核 运动的动能Ek和电势能Ep的代数和,因为 在选无穷远处电势能为零的情况下,各定 态的电势能均为负值,且其大小总大于同 一定态的动能值,所以各定态能量值均为 负值。
(2)这里的电势能Ep<0,原因是规定了无限远处的电 势能为零。这样越是里面轨道电势能越少,负得越多。
(3)量子数n=1定态,能量值最小,电子动能最大, 电势能最小;量子数越大,能量值越大,电子动能越 小,电势能越大.
(4)跃迁时电子动能、原子电势能与原子能量的变化
当轨道半径减小时,库仑引力做正功,原子的电势能 Ep减小,电子动能增大,原子能量减小.反之,轨道 半径增大时,原子电势能增大,电子动能减小,原子 能量增大.
针对原子的稳定性提出
➢能级:量子化的能量值。
➢定态:原子中具有确定能量的稳定状态
定态 基态:能量最低的状态(离核最近) 激发态:其他的状态
5
4
3
量
2
子
数
1
能级图
E∞
E5
EE34 激发态
E2
1 2
3
E1 ——基态
轨道与能级相对应
玻尔根据经典电磁理论和牛顿力学计算出氢原子
的电子的各条可能轨道半径和电子在各条轨道上运
事 实
e
e +
e
F
r + e
经 由于电子轨道的变 典 化是连续的,辐射 理 电磁波的频率等于 论 绕核运动的频率, 认 连续变化,原子光 为 谱应该是连续光谱
事
原子光谱是不
实
连续的,是线
状谱
以上矛盾表明,从宏观现象总结出来 的经典电磁理论不适用于原子这样小的物 体产生的微观现象。为了解决这个矛盾, 1913年丹麦的物理学家玻尔在卢瑟福学说 的基础上,把普朗克的量子理论运用到原 子系统上,提出了玻尔理论。
减小电势能,原子的能量
减少)
h Em En
( Em>En )
【小组讨论】
➢ 巴尔末公式有正整数n出现,这里我们也用正整数n 来标志氢原子的能级。它们之间是否有某种关系?
➢ 气体导电发光机理是什么? ➢ 原子光谱为什么是线状光谱? ➢ 不同元素的原子为什么具有不同的特征谱线?
二、玻尔理论对氢光谱的解释
玻尔从上述假设出发,利用库仑定律和牛顿运动定律, 计算出了氢的电子可能的轨道半径和对应的能量.
rn n 2 r1
氢
(r1=0.053nm)
原 子 能
En
1 n2
E1
级
(E1 13.6eV )
n 1,2,3
说明1:
(1)这里的能量指总能量(即E=Ek+Ep) 例如:E1=-13.6eV 实际上,其中Ek1=13.6eV, Ep1=-27.2eV。
