找规律填数
找规律填数字

(1)17、4、14、4、11、4、( )、( )
(2)2、40、7、34、12、28、( )、( )
(3)2、4、7、11、16、( )、( )
例4:观察下列各图的规律,然后填上合适的数。
解析:前面三个圆圈中四个数字之间的关系是:把左上方的一个数看作第一个数,然后,按照顺时针方向后面依次是第二个数、第三个数和第四个数。第一个数+4=第二个数,第二个数÷2=第三个数,第三个数×3=第四个数。即6+4=10,10÷2=5,5×3=15;8+4=12,12÷2=6,6×3=18,......的规律。因此,我们可以确定第四个圆圈内分别应填16、8、24。
(3)100、95、90、85、( )、( )......
(4)3、4、6、9、13、( )、( )......
学 习 内 容 与 过 程
例2:根据前面三个圆圈中三个数字之间的关系,在第四个圆圈中填上合适的数。
解析:前面三个圆圈中三个数字之间的关系是:把左上方的一个数看作第一个数是自己的1倍,然后,按照顺时针方向后面两个数分别是第一个数的2倍、3倍。即2×2=4,2×3=6;3×2=6,3×3=9;4×2=8,4×3=12的规律。因此,第四个圆圈分别应填10、15。
(2)在2、4、8、16、( )、( )......中,前一个数×2=后一个数,即2×2=4,4×2=8,8×2=16,......因此,根据这一规律,可以确定括号内应填上32,64。
(3)在1、4、9、16、( )、( )......中,第一个数是1×1=1,第二个数是2×2=4,第三个数是3×3=9,第四个数是4×4=16,......因此,根据这一规律,可以确定括号内应填上25,36。
找规律填数

找规律填数[问题一]你知道()里应该填几吗?1,3,5,7,(),()。
[思路分析]要知道()里填几,必须首先仔细观察这一串数中的每一个数,找到相邻两个数之间有什么排列规律。
仔细观察前面的四个数,发现这四个数在逐渐变大,第一个数是1,1加上2得到第二个数3, 3加上2得到第三个数5,5再加上2则得到了第四个数7,这样我们就找到了这一串数的规律:前面一个数加上2就能得到后面一个数:1 3 5 7 ()()(+2)(+2)(+2)(+2)(+2)小朋友,在填数的时候,要善于观察,找到已知数之间的排列规律,还要会动脑分析,有的时候,我们不妨动手填一填,试一试。
[试一试]按照给出的数的规律,在()填上合适的数。
(1)1,4,7,10,(),()(2)20,18,16,(),()10,()(3)3,6,9,12,(),()[问题二]你能在下面的括号中填上合适的数吗?1,5,2,5,3,5,4,5,(),()[思路分析]仔细观察这一串数,我们发现,光看相邻两个数似乎很难找到其中的规律,因此,有时候就要看间隔的数之间有什么规律,通过观察前面几个数,我们发现:第2、第4、第6、第8个数都是5;而第一个数加上1得第三个数2,第三个数加上1得第五个数3,第五个数加上1又得到了第七个数4;,由此可见这一串数的规律如下:+1 +1 +1 +11, 5, 2, 5, 3, 5, 4, 5,(),()试一试:找规律在()里填上适当的数。
(1) 1,2,2,2,3,2,4,2,(),(),(),()(2)5,15,5,10,5,5,(),()(3)1,1,2,1,1,3,1,1,4,,1,1(),1,1,()练一练:1、找规律在横线上填上合适的数。
(1)1,3,6,10,,。
(2)1,7,13,19,,。
(3)20,1,20,2,20,3,20,4,,,,。
(4)1,2,3,5,,。
(5)19,10,17,10,15,10,,。
小学数学二年级按规律填数

找规律填数知识导航找规律在奥数题目中属于常见题型,主要分为找规律填图和找规律填数。
在之前的课程里面我们已经接触过这一类型的题,这一讲我们继续加深对这一类型题目的认识和理解。
小朋友们,要认真观察、勇敢地去探索规律,相信你们都能找出空缺的数。
精典例题例1:找规律填数。
(1)1,3,5,7,(),()。
(2)65,60,55,50,(),()。
(3)1,10,100,1000,(),()。
(4)1,2,4,7,11,(),()。
(5)1,2,4,8,(),()。
(6)1,3,4,7,11,(),(),()。
思路点拨第(1)题,从左往右依次增加;第(2)题从左往右依次减少;第(3)题,从左往右依次在末尾添加一个,或者说依次乘;第(4)题从左往右,相邻两个数相差1,2,3,4……第(5)题中,1×2=2,2×2=4,4×2=8,所以,8×2=……第(6)题中,从第三个数开始,每个数都等于前面两个数的和。
模仿练习找规律填数。
(1)2,4,6,8,(),()。
(2)1,5,9,13,(),()。
(3)2,20,200,2000,(),()。
(4)1,2,2,4,3,6,4,8,(),()。
(5)49,42,35,(),(),()。
(6)4,6,9,13,(),24,()。
(7)100,81,64,(),36,25,(),9,4,1例2:仔细观察下列组图,在每一组的“?”处填上合适的数。
(1)(2)(3)(4)(5)思路点拨第(1)题中,3+4+8=15;第(2)题中,2×3+1=7;第(3)题中,3×4+5=17;第(4)题中4×5-5=20;第(5)题中,5+3+7=15,15+15=30。
模仿练习仔细观察每组图的规律,在空白处填合适的数。
(1)(2)例3:根据下表中的排列规律,在空格里填上适当的数。
思路点拨分析表格中的数可以发现,按行看,12+6=18,8+7=15,也就是说每一行中间的数等于两边的两个数的和。
二年级第六讲 找规律填数

找出每组数字的规律,然后在( ) 内填上适当的数。
1,2,3,6,7 ,( ) ,( )。 2, 3,6,7,14, 15,30, ( ) 。 32,16,8, 4,( ) ,( ) 。
1、找规律画出第五个图形; 2、第10个图形有多少个点?
(1)
(2)
(3)
(4)
1、找规律画出第5个图形; 2、第10个图形有多少个点?
找出每组数字的规律,然后在( ) 内填上适当的数。
1,2,4,8,16 , ( ),( )。 1, 3,9,27,( ) , ( ) 。 16,8,4, 2,( ) 。
找出每组数字的规律,然后在( ) 内填上适当的数。
2,3,5,8,12 , ( ),( )。 4, 6,9,13,18,( ) , ( ) 。 2,5,9, 14,20 ,( ) ,( ) 。
二年级第六讲 找规律 填数
找出每组数字的规律,然后在( ) 内填上适当的数。
1,3,5,7,9 ,( ),( )。 12,10,8,( ),( ),2。 5,10,15 ,( ) ,( )。
找出每组数字的规律,然后在( ) 内填上适当的数。
1,7,13,19,( ),( ),37。 1,2,4,5 , 7 , 8 , ( ),( )。 3,5,9, 11, 15,17,( ) ,( )。
(1)
(2)
(3)
(4)
1、找规律画出第5个图形; 2、第10个图形有多少个点?
(1)
(2)
(3)
(4)
找规律填数
12345 22345 33345
找规律填数,使得每一横 行,每一竖行都有1,2,3,4,5。
12345 51234 45123
找规律填数
老师解析
(1) 65、45、30、20、( )、( )。
(2) 90、78、68、60、( )、( )。
(3) 11、16、26、41、( )、( )。
(4) 27、26、24、21、17、( )、( )。
(5) 10、15、21、28、( )、( )。
例3:
(1) 1、2、3、2、5、2、( )、( )。
(2) 17、2、14、4、11、6、( )、( )。
(3) 3、6、9、12、( )、( )。
(4) 30、28、26、24、22、( )、( )。
按照找出的规律,把所缺的数填写出来。
知识难点:
会举一反三,不仅仅能找出数字排列的规律,还可以运用到图形当中,
在图形中找到规律并画出来。
1、前后两个数依次逐一增加(减少)相同项
2、前后两个数依次逐一增加(减少)自然数
3、间隔数之间依次增加(减少)
4、第三项数字为前两项数字之和
(1) 0、10、0、12、0、14、( )、( )。
(2) 8、13、11、11、14、9、( )、( )。
(2) 1、13、2、14、3、15、( )、( )。
(3) 10、20、11、19、12、18、( )、( )。
(4) 3、2、3、4、3、6、3、( )、( )。
(5) 77、10、66、20、55、30、( )、( )。
这一讲,我们就来学习找规律的方法!
例1: 15、13、11、( )、( )、5、3。
自我尝试
老师解析
(1)( )、( )、5、7、9、11。
(2)90、80、70、60、( )、( )。
(3)1、4、7、10、( )、( )。
(4)5、10、15、20、( )、( )。
找规律填数
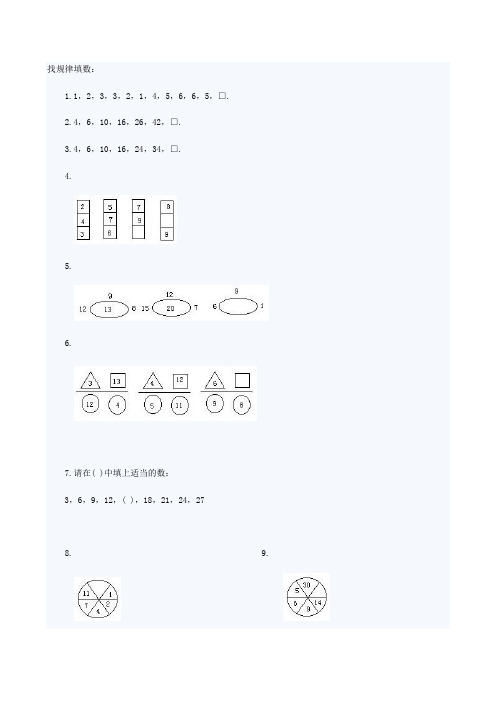
找规律填数:1.1,2,3,3,2,1,4,5,6,6,5,□.2.4,6,10,16,26,42,□.3.4,6,10,16,24,34,□.4.5.6.7.请在( )中填上适当的数:3,6,9,12,( ),18,21,24,278. 9.习题解答1.解:.每三个数一组,前后两组数是对称排列的.2.解:.从第3个数开始,后面的数是它前面两个数的和.4+6=10,6+10=16,10+16=26,16+26= 42,∴26+42=68.3.解:.从第2个数开始,后面的数是它前面的数依次加2,4,6,8,10,12得到的,即4+2=6 6+4=1010+6=16,16+8=24,24+10=34∴34+12=46.4.解:,每一竖排中的三个数按上、下、中的顺序依次排列,所以第3列中最下面一个数是8,第4列中间的数为10·5.解:14.每个图中,圈左边的数减去圈右边的数再加上圈上边的数得到圈里的数.6.解:.把横线下面图中的两个数相加减去三角形中的数就得到正方形里的数.7.解答:15,因为后面的数和前面的数都是相差3,所以12+3=158.解:16.从右上方开始,顺时针方向旋转,依次加上1,2,3,4,5得到后面的数.9.解:21.从左上方开始.逆时针方向旋转,依次加上1,3,5,7,9得到后面的数.一、在下面算式添上适当的运算符号,使等式成立。
(1)4 4 4 4 = 0 (2)4 4 4 4 = 1(3)4 4 4 4 = 2 (4)4 4 4 4 = 7二、填空1、( )÷( )×( )=242、( )×( )+( )=213、由2、9、0、5组成的最大四位数是(),最小四位数是()。
4、用0、1、2、3能组成()个不同的三位数。
5、一根绳子长16米,对折以后,再对折,每折长()米。
6、一个星期你在学校上学()天,在家()天。
7、小明、小亮和小刚3个小朋友进行乒乓球比赛,小明比赛了5场,小亮比赛了4场,小刚比赛了3场,这三名小朋友一共比赛了()场比赛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、1,3,6,10,(),(),()。
2、4.9.16.25.(),(),()。
3、60,63,66,69,(),(),()。
4、180,160,140,120,(),(),()。
5、2,5,8,11,(),(),()。
6、64,32,16,8,(),(),()。
7、1,1,2,3,5,8,(),(),()。
8、5,8,8,6,11,4,(),()。
9、1.2.2.4.3.8.4.16.5,(),()。
10、1,2,2,4,8,(),()。
11、100,95,90,85,80,()7012、5,9,13,17,21,(),()13、2,6,18,54,162,(),()14、2,3,5,8,12,(),()15、2,3,5,9,17,(),()16、8,16,17,34,35,(),(),142,14317、1,1/2,1/4,1/8,1/16,(),()18、1,1,1,3,5,9,(),()19、2,98,96,2,94,92,(),()20、1,8,27,64,125,(),343,()21、1,9,2,8,3,(),4,6,5,522、0,1,3,4,5,9,7,(),()下面数列的每一项由3个数组成,它们依次是:(1,5,9),(2,10,18),(3,15,27),……,请问第50个数组内三个数的和是多少?(用两种方法解)○、△、☆分别代表什么数?(1)、○+○+○=18(2)、△+○=14(3)、☆+☆+☆+☆=20○=()△=()☆=()△+○=9 △+△+○+○+○=25△=()○=()珠珠和立立一共有40支铅笔,珠珠的铅笔是立立的3倍,珠珠和立立各有多少支铅笔?珠珠比立立多40支铅笔,珠珠的铅笔是立立的3倍,珠珠和立立各有多少支铅笔?知识要点:数图形时我们要按照一定的顺序、有条理、有计划、有方法的去解答题目,可由单个图形数起,再数两个图形合成的图形,依此规律一个一个往下数。
{例1}数一数图中共有几条线段?DA BC这样想:数之前,先将每条线段写上字母,写好后,先数AB这条线段上有4条小线段,再数两条合并成的有3条,再数三条合并成的有2条,最后数四条合并成的有1条,4+3+2+1=10条。
同样CD这条线段上也有10条,和起来一共有20条。
{例2}数一数图中共有几个小长方体?这样想:从上面先数,第一排有2个小长方体,再数第二排有4个小长方体,最后数第三排有6个小长方体,所以2+4+6=12,有12个小长方体。
{例3}数一数图中共有几个三角形?这样想:数之前,先将每个图形编号,编好后,先数单个三角形共10个。
再数两个图形合成的三角形,按顺序两个两个合并,共8个三角形。
所以10+8=18,共18个三角形。
{例4}数一数图中共有几个三角形?这样想:先数单个三角形共4个。
再数两个三角形合成的三角形,按顺序两个两个合并,共2个三角形。
最后数由3个小三角形组成的大三角形,有1个。
所以4+2+1=7,共7个三角形。
{例5}数一数图中共有几个三角形?这样想:先数每个角上三角形共5个,再数由两个不靠着的角和中间五边形合成的三角形,按顺序数共3个三角形,所以5+3=8,共8个三角形。
下面各图中各有多少个长方形?【解析】:我们把上面的图形分拆成两个部分:一、蓝色方框里的部分;二黑色方框里的部分。
这两部分正中心有一个公共的长方形。
第一部分,这个长方形底边上有(1+2+3=)6条线段,对应其中每一条线段都有一个长方形,因此蓝色方框里有6个长方形;同理,第二部分同样是6个长方形,共有12个长方形。
去掉中间公共的长方形重复计算了一次,所以,这个图形中共有11个长方形。
【题目】:下面各图中各有多少个正方形?【解析】:正方形的数法与长方形的数法有所不同。
先根据正方形的边长把上图中出现的正方形分为四类:一、边长为1个单位长度的正方形;二、边长为2个单位长度的正方形;三、边长为3个单位长度的正方形;四、边长为4个单位长度的正方形。
再分类数出所有正方形的个数。
第一类:边长为1个单位长度的正方形,也就是图中的基本图形。
每行4个,4行,共有正方形:4×4=16(个)。
第二类:边长为2个单位长度的正方形。
如下图,用这样大的正方形框一框,图中每行有3个这样的正方形【图(一)】;每列也有这样的3个正方形【图(二)】。
即图中这样的正方形有3行,每行3个,共有正方形:3×3=9(个)。
第三类:边长为3个单位长度的正方形。
与第二类正方形的数法相同,可以数出图中边长为3个单位长度的正方形有2行,每行2个,共有正方形:2×2=4(个)。
第四类:边长为4个单位长度的正方形只有1个。
所以图中共有正方形:16+9+4+1=30(个)。
规律:任意一个有n2个基本小正方形拼成的大正形中,所有正方形的个数为:n2+(n-1)2+ (12)一、找规律填数1、1 , 3 , 9 , 27 , ( ) , ( )2、5, 6, 11, 17, 28, ( ), ( )3、1,4 ,13,40,(),()4、1,5,2,10,3,15,4,20,(),()5、1,2,6,24,120,(),50406、0,3,8,15,24,(),48,637、1,1,3,7,13,(),318、3,2,5,2,7,2,9,2,(),()9、2,5,14,41,122,(),()10、1,1/2,1/3,1/4,(),()11、1,8,27,64,(),()二、下面数列的每一项由3个数组成的数组表示,它们依次是:(1、5、9)、(2、10、18)、(3、15、27)、。
第10项的三个数的和是多少?第20项呢?第50项呢?(用两种方法解)三、先观察下面各算式,找出规律,然后填数。
1、1*9+2=1112*9+3=111123*9+4=11111234*9+5=()()*9+6=1111112、21*9=189321*9=28894321*9=38889--------------------------------------------654321*9=5888889---------------------------------------------87654321*9=7888888893、81-9=72882-9=8738883-9=887488884-9=()8888885-9=()四、(1)4,5,6,7,8,9,。
第20个数是()(2)4,7,10,13,16,19,。
第20个数是()(3)12,18,24,30,36,42,。
第10个数是(),第30个数是(),T引50个数是()。
五、在下面5个数中选出与其他4个数不同的数,并把它划去,再从括号里选一个合适的数替换。
1、42,20,18,48,24(21,54,45,10)2、15,75,60,45,27(51,72,30,9)3、42,126,168,63,882(27,210,33,25).已知等差数列5,9,13,17,…,它的第15项为_______.已知等差数列2,7,12,…,122,这个等差数列共有_____项。
6.下面的算式是按一定规律排列的,4+3,5+6,6+9,7+12,…那么第100个算式的得数是()例1 观察下列各图,并按照变化规律在“?”处填上合适的图形.分析:首先,每幅图中都只有三角形、长方形、圆、正方形这四种图形,所以,我们可以知道(d)中的图形也是三角形、长方形、圆、正方形四种;其次,从第二幅图形开始,每个图形都是由前一幅图形逆时针方向旋转90°而得到的,所以,我们又可以得到(d)中各个图形的位置关系.解题:1.在空白处填上合适的图形.(1)(2)2.在空白处填上合适的字母.3.在空白处填上适当的图形.(1)(2)4.观察下图,按照(a)(b)的变化规律,根据(c),在(d)中填上适当的图形.参考答案(答案为红色部分)1.(1)(2)2. 3.(1)(2)4.前面两幅图形,后一幅是将前一幅的每一个图形,沿顺时针方向向前进一格,并且把圆也顺时针转过90°,阴影变为原来的一半,所以(d)处图形如下:教学目的:1)使学生进一步理解周长的含义,熟练掌握计算周长的方法.能灵活运用长方形、正方形周长公式解决实际问题.2)培养学生的观察能力,思维能力,灵活的解题能力和语言表达能力.3)培养学生初步的空间观念.教学重点:掌握求解由小正方形拼合成的长方形周长的方法.教学难点:理解拼合处与周长的关系.教学过程:一、复习引入.1.什么是周长2.长方形周长公式3.正方形周长公式二、运用平移、翻转的方法改变图形的形状,巧算周长.1.移动哪几根火柴,就能使它变成正方形?怎样移?火柴的总根数变没变?周长是多少根?你是怎样算的?2.下面各图形行、列之间点与点的距离都是一厘米,几号图形的周长与其它3个不同?你是怎样想的?小结:有些图形通过将线段平移或翻转,可转化成标准的长方形、正方形,从而便于计算他们的周长.对于这些图形,这是一个巧方法.三、重新认识长、宽或去掉拼合处的边,巧算周长.1.求边长是1厘米的正方形的周长.1×4=4(cm)2.用2个正方形拼成一个长方形,这个长方形的周长是正方形的2倍吗?(拼一拼,算一算)(2+1)×2=6(cm)4×2-1×2=6(cm)(板书:去掉拼合处的边)3.你能用4个小正方形拼成一个长方形或正方形,并算出它们的周长吗?①(4+1)×2=10(cm)②2×4=8(cm)①4×4-2×3=10(cm)②4×4-2×4=8(cm)问:(1)为什么图②的周长比图①的周长小?(讨论)(板书:拼合处越多,周长越小)验证结论(2)4个小正方形还可以怎样拼?你能想出与众不同的拼法,并算出它的周长吗?(反馈)(3)你发现了周长的大小与什么有关系?四、综合练习1.两个长7厘米,宽3厘米的长方形,拼成一个大长方形,怎样拼周长最大?2.有两个相同的长方形,长7cm,宽3cm,如图叠放,求图形的周长.(1)指一指周长是哪一部分.(2)拼一拼,算一算.(3)选择答案:①平移,翻转7×4=28(cm)②(7+3)×2=20(cm)20×2-3×2=34(cm)③7-3=4(cm)(7+3+4)×2=28(cm)电脑演示,验证学生结论.比较:哪种方法最巧?小结:你有什么收获?四、作业:1.用7张边长都是3cm的正方形纸,这样叠放,求周长,怎样求最简便?(21页7题)2.23页6题五、板书设计:加法的巧算(凑整数、找补数、或加减括号改变运算顺序进行巧算)2458+503 574+798 784+25+1752803+(2178+5497)+ 4722 999+99+9+358+238+44 47+48+49+50+51+52+53 1057+(332-57)256+503 327+798 2497+18336+87+64 1361+972+639+28376+(174+24)864+(673+136)+227 65+75+3632+81+23+19+68 (24+37+15)+(16+45+13)99999+9999+999+99+9 7523+(653-1523)576+(224-16)3993+2996+7994+13576+79+79+80+81+83+84 54+47+50+57+48+45536+(541+464)+459 588+264+148 8996+3458+7546 83+82+78+79+80+81+78+79+77+84+83103+99+103+96+105+102+98+98+101+102+97+102减法的巧算1、可将减数结合起来一起减。
