子午线收敛角计算
陀螺定向中子午线收敛角的计算方法

工程技术研究2021年第7期242陀螺定向中子午线收敛角的计算方法李泽军中铁一局集团天津建设工程有限公司,天津 300000摘 要:陀螺仪定向是提高隧道定向精度的必要手段,其定向精度不随距离的长短产生误差传递,子午线收敛角γ计算结果的精度直接影响坐标方位角的精度。
文章结合实例计算,表明采用公式γ=sin B ·L 和公式γ=Ky 分别计算得到的子午线收敛角和陀螺推算方位角均可满足工程施工精度要求,因此陀螺定向可为隧道内平面控制网联测和开挖方向的正确性提供检测复核依据,适用于地下工程定向测量。
关键词:子午线收敛角;坐标方位角;陀螺仪中图分类号:P213文献标志码:A文章编号:2096-2789(2021)07-0242-021 子午线收敛角的概念以真子午线为参考,坐标系纵轴X 北端在其东侧时,子午线收敛角为正,反之则为负。
地面上的点纬度B 和中央子午线的距离经差ΔL 决定了子午线收敛角的大小,计算其角值可以用如下近似计算公式:γ=ΔL ·sin B (1)在一个投影带内,高斯平面子午线收敛角的变化遵循一定规律。
距离中央子午线越远,收敛角越大,在中央子午线上收敛角等于零;距离赤道线越远,收敛角越大,在赤道线上收敛角等于零。
2 坐标方位角的换算陀螺仪北方向与真北方向间存在角度偏差,角度的偏差值就是陀螺仪的仪器常数,偏东为正、偏西为负。
坐标北方向与真北方向间的角度偏差就是子午线收敛角,相对真北方向,坐标方位角偏东为正、偏西为负。
陀螺北、真北、坐标北方向关系如图1所示。
陀螺北、真北、坐标北方向之间的角度关系可用如下公式表示:午线与坐标纵线之间的夹角。
坐标纵线东偏为正,西偏为负。
图1陀螺北、真北、坐标北方向关系示意图图2 子午线收敛角概述图赫里斯托夫给出的展至第7次项的计算公式:γ=cos B ×t ×L +cos 3B ×t (1+3η2+2η4)L 3÷3+cos 5B ×t (2t 2+15η2-15η2t 2)L 5÷15+cos 7B ×t (17-26t 2+2t 4)L 7÷315+O(L 7)(3)式中:t =tan B ;η=e′×cos 2B ,e′为第二偏心率;B 为纬度;L 为经差。
子午收敛角计算

子午收敛角计算
【实用版】
目录
1.子午收敛角的定义与重要性
2.子午收敛角的计算方法
3.子午收敛角在实际应用中的案例分析
正文
【子午收敛角的定义与重要性】
子午收敛角,又称子午聚散度,是指地球表面上某一点的子午线方向与地球赤道面之间的夹角。
子午收敛角是地球形状和地球表面重力场研究的一个重要参数,它直接影响到地球表面上的测量、定位和地图制图等。
【子午收敛角的计算方法】
子午收敛角的计算公式为:
α = 2 * arcsin[(R * Δlat) / (2 * R * Δlon)]
其中,α表示子午收敛角,R 为地球半径,Δlat 为两点的纬度差,Δlon 为两点的经度差。
根据该公式,可以计算出任意两点之间的子午收敛角。
【子午收敛角在实际应用中的案例分析】
在我国,子午收敛角被广泛应用于大地测量、导航定位、地图制图等领域。
例如,在测量某个地区的经纬度时,需要考虑子午收敛角的影响,以提高测量的精度。
此外,子午收敛角在航空、航天、航海等领域也具有重要意义,因为它直接影响到导航定位的准确性。
总之,子午收敛角是地球形状和地球表面重力场研究的一个重要参数,它在实际应用中具有很高的价值。
第1页共1页。
子午收敛角计算

子午收敛角计算
(实用版)
目录
1.子午收敛角的定义
2.子午收敛角的计算方法
3.子午收敛角的应用
正文
一、子午收敛角的定义
子午收敛角,又称为子午聚光角,是指在光学系统中,光线通过透镜或反射镜等光学元件后,汇聚于一点时的入射光线与出射光线之间的夹角。
子午收敛角通常用符号α表示,单位为度(°)。
二、子午收敛角的计算方法
子午收敛角的计算方法有多种,下面介绍两种常用的计算方法:
1.公式法
对于一个理想的凸透镜,其子午收敛角可以通过以下公式计算:
α = (n - 1) * β
其中,n 为透镜的折射率,β为入射光线与光轴的夹角。
2.作图法
对于一个理想的凹透镜,其子午收敛角可以通过作图法计算。
具体步骤如下:
(1)画出凹透镜的轴截面图,并标出光轴和两个曲率半径 R1 和 R2;
(2)画出入射光线,并标出入射光线与光轴的夹角β;
(3)从透镜的顶点向入射光线作一条射线,与入射光线的延长线相
交;
(4)在射线与入射光线的延长线相交处作一个圆,圆的半径为 R1;
(5)连接圆上的两个交点,得到出射光线;
(6)测量出射光线与光轴的夹角,即为子午收敛角α。
三、子午收敛角的应用
子午收敛角在光学系统中有着广泛的应用,例如:
1.在照相机中,通过调整透镜的子午收敛角,可以控制照片的景深;
2.在望远镜中,通过调整透镜的子午收敛角,可以提高望远镜的成像质量;
3.在激光器中,通过调整透镜的子午收敛角,可以调整激光束的聚焦性能。
子午线收敛角的计算知识分享

子午线收敛角的计算子午线收敛角的计算探讨摘要:利用给定的高斯坐标值(x,y)可以通过公式2,3得到其大地经纬度(B,L),得到(B,L)经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。
关键字:子午线坐标正算(反算)大地坐标投影长度比引言:为了求取子午线收敛角,我们可以有多种方法。
我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{(x,y)—>(B,L)},然后利用L,B就可以求取子午线收敛角。
在测量工作中,经常需要进行正算、反算、换带和子午线收敛角的计算工作。
如图1所示,以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。
显然它与以子午线方向为起始方向的大地方位角A是不相同的,其间的差异即为点P上的大地平行线与子午线之问的夹角y,可称为大地坐标系中点P上的子午线收敛角,显然就有:γ=A-a+δ,a=A-γ+δ式中γ为子午线收敛角,δ为坐标方位角,A为大地方位角,为曲率改正。
正文:一、通过“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不同大地坐标L、B。
1. 对于54和80参心坐标系统而言,其坐标系特点比较如下表格。
对于求解大地纬度B,大地经度L需要迭代计算,可以用以下公式直接编写程序求解L、B,理论计算结果2,数值结果2: (2) (3)式中,X为由赤道至纬度B的子午线弧长,为计算点P点与中央子午线的经差。
N为卯酉圈曲率半径,t=tanB,η=e′cosB。
L-L0若以度为单位,则ρ=57.295779513;L-L0若以分为单位,则ρ=3437.7467708;L-L0若以秒为单位,则ρ=206264.80625。
上式中,我们利用(x,y)就可以得到(B,L)54年北京坐标系克拉索夫斯基椭球;参心坐标系长半轴a=6378245m;短半轴扁率α=1:298.3。
大地原点在原苏联的普尔科沃采用多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳;参心坐标系长半轴a=637814m;短半轴b=6356755.29m;扁率α=1:298.257;大地原点在陕西省泾阳县永乐镇;椭球短轴平行于地球地轴起始子午面平行于格林威治天文台平均子午面二、利用B、L进行高斯投影平面的坐标的计算的变形分析。
子午线收敛角计算公式及计算精度分析

子午线收敛角计算公式及计算精度分析以《子午线收敛角计算公式及计算精度分析》为标题,本文将对子午线收敛角的定义、物理意义和计算公式进行详细分析,并对子午线收敛角计算的精度做出评估。
子午线收敛角是一种定义在空间曲率理论上的角度,它描述在一个曲率空间中两个不同子午线之间角度的变化情况。
它被用来描述万有引力场的形状,如地球表面的地貌等。
子午线收敛角是非常重要的度量,具有重要的物理意义。
子午线收敛角的计算公式可以从拉格朗日系数表示法中推出:$$ phi= frac{1}{2} sum_{i=1}^{3} (gamma_{ii} - gamma_{jj}) cdot Delta theta_{ij} $$其中,$gamma_{ij}$表示拉格朗日系数; $Delta theta_{ij}$表示两个子午线之间的夹角。
这里要计算子午线收敛角可以使用上述公式。
此公式计算结果对于子午线收敛角的精度有一定要求,如果计算结果误差大,会对实际应用造成影响。
为了评估子午线收敛角的计算精度,一种常用的方法是使用仿真数据。
在仿真实验中,通过改变空间曲率参数,产生不同子午线收敛角的情况,从而获得理想的测量结果。
用这些理想结果与计算结果比较,就可以评估子午线收敛角计算的精度了。
此外,为了提高子午线收敛角计算精度,还可以使用多种数值计算方法,比如拉格朗日元法、二阶中心差分法等。
这些方法都可以得到更精确的子午线收敛角计算结果,可以提供更准确的计算结果以满足应用需求。
综上所述,子午线收敛角是一种定义在空间曲率理论上的角度,可以用来描述万有引力场的形状,具有重要的物理意义。
计算子午线收敛角可以使用拉格朗日系数表示法中推导出的公式。
为了评估子午线收敛角计算的精度,可以使用仿真数据,也可以使用多种数值计算方法来提高计算精度。
本文根据子午线收敛角的定义、物理意义和计算公式,以及计算精度,对子午线收敛角做出了全面分析。
子午线收敛角计算公式及计算精度分析

子午线收敛角计算公式及计算精度分析子午线收敛角,也叫做子午线弯曲角,是衡量地球的一种重要的球面度量。
当地球的子午线既不是完全水平也不是完全垂直的时候,它就会产生弯曲,这种弯曲就叫做子午线收敛角。
子午线收敛角的弯曲大小决定了地球的子午线的收缩和延伸,从而决定地球的经纬度系统及坐标坐标形式。
子午线收敛角的计算方法有多种,其中最常用的就是基于子午线收敛角的计算公式。
1.子午线收敛角的计算公式基于子午线收敛角的计算公式有两种,第一种是WaIters公式(WaIters formula),它的公式为:$$Δ= arccos(frac {s_1-s_2}{s_1+s_2} )$$其中,Δ是子午线收敛角,s1、s2分别是子午线两点的大圆距离。
WaIters公式利用大圆距离来计算子午线收敛角,它可以用来计算椭圆面子午线收敛角,但是它计算精度受到大圆距离精度的限制,其精度为1分。
第二种是瓦特斯-贝塞尔公式(Waters-Bessel formula),它的公式为:$$Δ=arccos(frac {s_1^2-s_2^2}{s_1^2+s_2^2})$$ 其中,Δ是子午线收敛角,s1、s2分别是子午线两点的球面坐标的经纬差。
瓦特斯-贝塞尔公式利用球面坐标经纬差计算子午线收敛角,是WaIters公式的一种改进,它可以用来计算椭圆及偏心率修正后的球体子午线收敛角,其精度可以达到1厘米。
2.子午线收敛角计算精度分析子午线收敛角的计算精度受多种因素的影响,其中最主要的是地球的椭球体模型精度和地理坐标测量精度。
(1)影响地球椭球体模型精度的因素地球椭球体模型的精度受到各种因素的影响,例如,地球的大小、形状、弹性模量、重力系数、质量、质心定位等。
由于这些因素都是比较复杂的物理模型,因此,地球椭球体模型精度受到较大的影响,其精度通常在3到5厘米之间。
(2)影响地理坐标测量精度的因素地理坐标测量精度受多种因素的影响,如地理坐标测量仪器、标定结果、大圆距离测量精度等。
真子午线与中央子午线的收敛角

真子午线与中央子午线的收敛角真子午线与中央子午线的收敛角其实是测量地球表面上两条纵向线之间的角度,它们的区别在于位置不同。
真子午线是指贯穿地球北极和南极的线,也就是地球表面上的0度经线;而中央子午线则是指某个特定区域内经度为中心的经线。
在测量中,真子午线与中央子午线的收敛角是非常重要的参考参数。
此处,我们将从以下四个方面来探讨真子午线与中央子午线的收敛角:一、概念定义真子午线收敛角与中央子午线收敛角都是指地球表面上两条经线(纵向线)之间的角度。
其中,真子午线收敛角是指两条经线穿过地球两极的情况下的角度,而中央子午线收敛角则是指任意两条经线之间的角度。
二、计算方法真子午线收敛角和中央子午线收敛角的计算方法是不同的。
计算真子午线收敛角时,需要考虑地球的椭球形状,以及两条经线间的距离。
而计算中央子午线收敛角时,则只需要考虑两条经线之间的距离。
三、影响因素真子午线与中央子午线的收敛角都受到多种因素的影响。
其中,地理位置、对地面的曲率半径、大气密度、温度等因素都会对收敛角产生一定的影响。
由于真子午线跨越了整个地球,因此受到的影响也更加复杂和多样。
四、实际应用真子午线与中央子午线的收敛角在实际应用中也有较为广泛的应用。
例如,对于地图绘制和GPS导航等场景,在计算距离和方位角时都需要考虑真子午线与中央子午线的收敛角,以获得更为准确的结果。
综述以上四点,真子午线与中央子午线的收敛角是测量地球表面上两条纵向线之间的角度,它们的计算方法、影响因素以及在实际应用中的重要性都各有不同。
对于地理信息、航海、测量等领域的专业人士来说,熟练掌握真子午线与中央子午线的收敛角是十分必要的。
子午线收敛角名词解释

子午线收敛角名词解释子午线收敛角是指表示光波在子午线方向上辐射能量减弱的程度。
1子午线收敛角的概念及其定义子午线收敛角是指表示光波在子午线方向上辐射能量减弱的程度。
子午线又称经线,是经过地球表面两点并与纬线垂直相交的直线,它把地球平分为南北两半球。
子午线与经线垂直,并与纬线垂直相交形成两个大圆,把地球平分为东西两半球。
每条子午线长度都相等。
子午线收敛角是指表示光波在子午线方向上辐射能量减弱的程度。
2。
计算子午线收敛角的基本原理及主要公式:当子午线收敛角的数值较小时,在给定方向上测量所得的真实面积、表面积或总体积与给定的面积之比很接近于理想表面面积。
此时测量结果更接近于真实表面面积。
3。
用子午线收敛角估算被测物体面积时应注意的问题: 3。
用子午线收敛角估算被测物体面积时应注意的问题:(1)准确求出物体表面与待估表面的面积。
(2)根据被测物体与理想表面面积关系式确定待估表面面积。
(3)选取适当参数。
(4)计算精度的误差分析和提高的方法。
在实际应用中,一般不使用理想表面,而是直接采用近似表面面积计算。
在特殊情况下,必须保证计算的精度时,则需引入理想表面进行换算。
1.高斯-波尔兹曼原理:由高斯公式和波尔兹曼公式可知,被测物体表面面积( s)的二次积分与测量长度L的平方根成正比,且成正弦级数的形式关系,即:(2)(3)(4)应用时,将式(4)按实际尺寸在其边界上任意点取样,利用理想和近似表面面积公式求出几何表面的面积S(D),代入公式(1)计算物体表面的面积S(D)。
(5)作为评价估算方法的精度指标,估算的表面面积越接近于实际的表面面积,测量的精度越高。
4。
测量工具误差对子午线收敛角的影响:测量工具对子午线收敛角的影响有多种形式。
一般说来,测量工具越粗糙、越简单,子午线收敛角测量的精度就越高。
对于已知子午线收敛角的区域,测量工具在给定方向上的相对移动会引起子午线收敛角发生变化,因此测量工具的质量对子午线收敛角也有影响。
子午线收敛角的计算公式与计算精度分析

在 B 取 35°时取得最大值,6.11857″;
(2)可以看出在同一子午线上,差值 △在中纬(20°-55°)之间误差较大;
(3)在中低纬度(B=5°-80°)时, 公式(3)的计算精度能达到秒级。
绘制纬度 B 和差值△的函数图象,如 图 3:
图 3.B 与△的函数图像 为便于实际应用,同时考虑我国所处的 经纬度,我们选择四次三项式来拟合经差为 3.5°时的纬度 B 和子午线收敛角差值△ 间的关系[1],得到拟合多项式公式如下(y 代表 B;x 代表子午线收敛角差值△):
地球的形状接近于旋转椭球面,椭球面 是一个不可直接展开的曲面,大地坐标经过 高斯投影得到平面直角坐标后,必然有投影
变形,子午线投影后向中央子午线弯曲,并 向两极收敛。
如图 1 所示,地球椭球体面上一点处子 午线收敛角是该点真子午线与位于此点所 在的投影带的中央子午线之间的夹角,即在 高斯平面上的真子午线与坐标纵线的夹角, 通常用γ表示。
1573 1900 0. 95
1666 2000 0. 95
1759 2100 0. 97
1854 2200 0. 97
1949 2300 0. 99
2046 2400 0. 100
2143 2500 0. 102
2242 2600 0. 103
2342 2700 0. 104
2444 2800 0. 107
2 子午线收敛角的计算公式
2.1 用大地坐标计算
2.1.1 文献[2]中给出的展开五次项公
式
γ = l *sinB[1+ l2 cos2 B(1+ 3η2
3
+ 2η4) + l4 cos4 B(2 − t 2)]
最新子午线收敛角的计算
子午线收敛角的计算探讨摘要:利用给定的高斯坐标值(x,y)可以通过公式2,3得到其大地经纬度(B,L),得到(B,L)经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。
关键字:子午线坐标正算(反算)大地坐标投影长度比引言:为了求取子午线收敛角,我们可以有多种方法。
我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{(x,y)—>(B,L)},然后利用L,B就可以求取子午线收敛角。
在测量工作中,经常需要进行正算、反算、换带和子午线收敛角的计算工作。
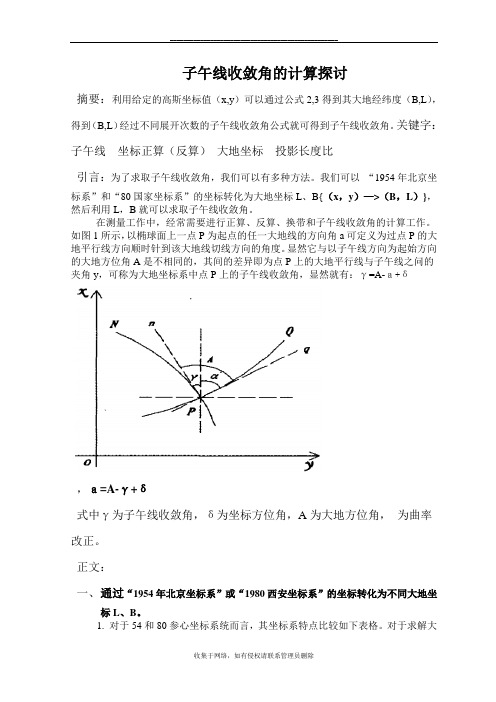
如图1所示,以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。
显然它与以子午线方向为起始方向的大地方位角A是不相同的,其间的差异即为点P上的大地平行线与子午线之问的夹角y,可称为大地坐标系中点P上的子午线收敛角,显然就有:γ=A-a+δ,a=A-γ+δ式中γ为子午线收敛角,δ为坐标方位角,A为大地方位角,为曲率改正。
正文:一、通过“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不同大地坐标L、B。
1. 对于54和80参心坐标系统而言,其坐标系特点比较如下表格。
对于求解大地纬度B,大地经度L需要迭代计算,可以用以下公式直接编写程序求解L、B,理论计算结果2,数值结果2: (2) (3)式中,X为由赤道至纬度B的子午线弧长,为计算点P点与中央子午线的经差。
N为卯酉圈曲率半径,t=tanB,η=e′cosB。
L-L0若以度为单位,则ρ=57.295779513;L-L0若以分为单位,则ρ=3437.7467708;L-L0若以秒为单位,则ρ=206264.80625。
上式中,我们利用(x,y)就可以得到(B,L)54年北京坐标系克拉索夫斯基椭球;参心坐标系长半轴a=6378245m;短半轴扁率α=1:298.3。
大地原点在原苏联的普尔科沃采用多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳;参心坐标系长半轴a=637814m;短半轴b=6356755.29m;扁率α=1:298.257;大地原点在陕西省泾阳县永乐镇;椭球短轴平行于地球地轴起始子午面平行于格林威治天文台平均子午面二、利用B、L进行高斯投影平面的坐标的计算的变形分析。
不同国家坐标系下子午线收敛角计算公式及其精度分析

( 1 . S c h o o l o f E n v i r o n me n t a n d S p a i f M I n f o r ma t i e s , C h i n a U n i v e r s i t y o f Mi in n g a n d T e c h n o l o g y , Xu z h o u 2 2 1 0 0 8 , C h i n a ; 2 . E me r g e n c y R e p a i  ̄ n g C o mp a n y o f C h i n a p e t r d u m P i p e H n e P o u r e a u , L ng a f a n g 0 6 5 0 0 0, C h i n a )
Ab s t r a c t :T h e p a p e r i n t r o d u c e s t h e c o n c e p t a n d f o r mu l a s o f me r i d i a n c o n v e r g e n c e a n g l e a n d c o d e s Ga u s s p o s i t i v e a n d i n v e r s e c lc a u l a — t i o n nd a me r i d i n a c o n v e r g e n c e a n g l e b y u s i n g C+ + l a n g u a g e .w h i c h i mp ov r e s t h e c a l c u l a t i o n e ic f i e n c y . 1 4 p o i n t s o f Xu z h o u a r e s e — l e c t e d a n d i t i s f o u n d t h a t me r i d i a n c o n v e r g e n c e a n g l e f o m u r l a s c a n b e u s e d i n e i t h e r g e o d e t i c c o o r d i n a t e s y s t e m 1 9 5 4 o r g e o d e t i c c o o r -
子午线收敛角和垂线偏差对陀螺方位角的影响

未知点子午线收敛角之差的影响,计算可按式(7) 进行.当两点间经差小于1。时,计算精度可 达0.001tt.
(2)垂线偏差可用式(10)和式(12)计算.根据 试验表明,垂线偏差最大值一般小于20”[_7。10].试验 地区的垂线偏差平均值为2.9”,同一点不同方向或 不同点的垂线偏差较差最大在30”左右.若有可能, 最好实测垂线偏差值,然后进行改正.
万方数据
第3期
邬熙娟等:子午线收敛角和垂线偏差对陀螺方位角的影响
95
精度和垂线偏差对坐标方位角的影响大小进行深入 探讨.
1子午线收敛角
Fig l
图1 方位角和坐标方位角关系
Relations between azimuth and c00rdinate azimuth
井下定向边的坐标方位角计算公式为
d=“7T+△+“7一y
(2)
式中:d’,为井下定向边的实测陀螺方位角;“’为井
下设站点的垂线偏差;y为井下设站点的子午线收
敛角.
将式(1)中的仪器常数△代人式(2),则有
d=do一(aT—d 7T)+6l+62
(3)
式中:6l=yo一7;62=M 7一u.
由此可知,影响坐标方位角测量结果准确性的
因素主要有2个,即2个不同测站的子午线收敛角
由表3可知,同一点上不同方向的垂线偏差差 值最大可达28”,平均值一般达8.7”.
3 工程实例
由南京工业大学负责完成的某超长盾构隧道的 精密导向控制工作,单向推进2 271 m,由两段圆弧 和一段直线组成s形隧道.按常规布设了井下控制 导线和施工导线(吊篮),要求贯通点的横向误差在 ±50 mm范围内,为了限制支导线的端点横向误差, 在导线中间位置加测了3条陀螺方位角(图3).
子午线收敛角计算公式及计算精度分析

子午线收敛角计算公式及计算精度分析子午线收敛角是测量我们在地球上的位置的方法之一。
然而,它的计算精度至关重要,因为它是一种3D投影的基础。
因此,本文的主要目的是探讨子午线收敛角的计算公式和精度,以及如何减少计算的错误。
一、子午线收敛角的定义子午线收敛角是地图学上的一项基本概念,它指的是把地球上的一点线性投射到地图上时,投射端点与子午线之间的夹角。
子午线是地球上经度方向上的一条线,与地球赤道平行,地球上每一点的子午线都不同。
子午线收敛角用θ(θ <90°)表示,其计算公式为:θ=arccos(cosφ1cosφ2sin(λ2-λ1)+sinφ1sinφ2)其中,λ和φ是投影点的经度和纬度。
二、子午线收敛角的计算精度计算子午线收敛角的精度主要取决于地球模型的精度,它是空间位置信息计算的基础。
如果地球模型精度低,会影响子午线收敛角计算的精度,甚至产生误差。
例如,在地球表面变形较重的地区,如山区,可能会产生较大的误差。
实际计算过程中,计算机还会对数字的计算和精度有一定的影响。
例如,在电脑上使用浮点精度(float),这种计算精度远远不及双精度(double),因此会出现精度丢失的情况。
三、如何减少计算误差以上是子午线收敛角的计算公式和精度分析,下面我们来讨论如何减少计算误差。
首先,对地球模型进行精确测量,以减少误差。
其次,有必要采用更高精度的计算方式,例如双精度计算法,减少计算误差。
再者,可以使用更精确的坐标系统,例如WGS84,准确计算子午线收敛角。
此外,在计算过程中使用合适的中间计算空间,例如椭球面,有助于计算子午线收敛角的精度。
本文简要介绍了子午线收敛角的计算公式及其计算精度分析,以及如何减少计算误差的方法。
通过有效的采用更精准的计算方法,选择更好的投影体系,以及使用适合的计算空间,可以有效提高子午线收敛角的计算精度,从而更好地实现地理空间信息计算。
射向标定中的子午线收敛角改正计算

射向标定中的子午线收敛角改正计算
子午线收敛角改正是一项在测地学中常用的数学计算,它不仅可以在大地测量中及早发现测量错误,而且可以提高测量的精度与准确性。
因此,对子午线收敛角的改正计算加以了解非常有必要。
子午线收敛角改正计算是基于球面坐标系下,把子午线收敛角加入到大地坐标平面坐标系当中来进行计算的。
其实子午线收敛角是代表一个基准线到任意一点的球面距离,是整体投影畸变最大变形量所在位置。
它可以将大地测量中潜在的误差转换成子午线收敛角,使得解决方案能够更准确。
子午线收敛角计算可以在很多地方得到应用,比如可以在坐标的测绘中用来确定精度,以及定位测量距离等,更可以在地理信息管理当中得到应用,根据子午线收敛角的参数可以处理许多关于地球的变形和导数问题来改正数据,从而提高数据的准确性。
总之,子午线收敛角改正计算是大地测量学中最重要的一个因素,它在提高测量准确性和发现潜在错误上发挥了至关重要的作用。
因此,学习和掌握大地测量学中的子午线收敛角改正计算及其应用对于提高学生的学业成绩和理解力来说是必须的。
谈大地坐标及子午线收敛角的计算方法

谈大地坐标及子午线收敛角的计算方法常惠宗【摘要】就工程测量中的坐标系做了简要的介绍,从而引出高斯—克吕格坐标系中的点位如果不在中央子午线上点位的子午线收敛角的概念,并通过实例讲解子午线收敛角的计算,以供实际工程参考借鉴.【期刊名称】《山西建筑》【年(卷),期】2013(039)001【总页数】2页(P183-184)【关键词】基准面;坐标系;高斯—克吕格坐标;子午线收敛角【作者】常惠宗【作者单位】山西路桥第一工程有限责任公司,山西太原030006【正文语种】中文【中图分类】TU1980 引言工程测量是一门测定地面点位的科学,广泛应用于公路、建筑、铁路等各种建筑工程的勘测、设计、施工的各个环节。
本文就子午线收敛角做简单的介绍,在介绍子午线收敛角之前我们应该先剖析一下公路及建筑测量中所用的测量坐标系。
1 测量坐标系测量的基本值说到底其实就是点、线、面,将大地实际的三维体系转换和绘制在电脑或者图纸,在图纸上标定和计算,再将图纸上的点线面放样到大地的实际点位,组成新的三维实体。
测量上确定地面点的位置,是通过在基准面上建立坐标系,测定点位之间的距离角度和高差三个值来实现的。
1.1 基准面地球的形状可以使用两级近似,第一级我们可以将地球近似为一个圆球,半径为6 371 km;第二级近似概况为一个椭球体,其长半轴为 6 378.137 km,短半轴为6 356.752 km,扁率为1/298.257。
自由静止的水面即是水准面,水准面包围的地球形体称为大地体。
测量工作就是以椭球面作为基准面,把大地体作为地球的数学模型,在上面建立一一对应的数学坐标关系。
1.2 坐标轴系坐标轴系分为两部分,即平面坐标轴系及竖直坐标轴系。
本文主要对平面坐标轴系进行阐述。
平面坐标轴系分为地理坐标,平面直角坐标及高斯—克吕格坐标。
1.2.1 地理坐标地理坐标是以经度λ、纬度φ来确定地面点位的球面坐标,其中通过一点和地球南北极的平面称为该点的子午面,子午面与地球表面的交线称为子午线也叫真子午线。
子午线收敛角的计算

子午线收敛角的盘算商量摘要:运用给定的高斯坐标值(x,y)可以经由过程公式2,3得到其大地经纬度(B,L),得到(B,L)经由不合睁开次数的子午线收敛角公式就可得到子午线收敛角.症结字:子午线坐标正算(反算)大地坐标投影长度比引言:为了求取子午线收敛角,我们可以有多种办法.我们可以“1954年北京坐标系”和“80国度坐标系”的坐标转化为大地坐标L.B{(x,y)—>(B,L)},然后运用L,B就可以求取子午线收敛角.在测量工作中,经常须要进行正算.反算.换带和子午线收敛角的盘算工作.如图1所示,以椭球面上一点P为起点的任一大地线的偏向角a可界说为过点P的大地平行线偏向顺时针到该大地线切线偏向的角度.显然它与以子午线偏向为肇端偏向的大地方位角A是不雷同的,其间的差别即为点P上的大地平行线与子午线之问的夹角y,可称为大地坐标系中点P上的子午线收敛角,显然就有:γ=A-a+δ,a=A-γ+δ式中γ为子午线收敛角,δ为坐标方位角,A为大地方位角, 为曲率纠正.正文:一、经由过程“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不合大地坐标L.B.1. 对于54和80参心坐标体系而言,其坐标系特色比较如下表格.对于求解大地纬度B,大地经度L须要迭代盘算,可以用以下公式直接编写程序求解L.B,理论盘算成果2,数值成果2: (2) (3)式中,X为由赤道至纬度B的子午线弧长,为盘算点P 点与中心子午线的经差.N为卯酉圈曲率半径,t=tanB,η=e′cosB.L-L0若以度为单位,则ρ=57.295779513;L-L0若以分为单位,则ρ=3437.7467708;L-L0若以秒为单位,则ρ=206264.80625.上式中,我们运用(x,y)就可以得到(B,L)54年北京坐标系克拉索夫斯基椭球;参心坐标系长半轴a=6378245m;短半轴扁率α=1:298.3.大地原点在原苏联的普尔科沃采取多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳;参心坐标系长半轴a=637814m;短半轴b=6356755.29m;扁率α=1:298.257;大地原点在陕西省泾阳县永乐镇;椭球短轴平行于地球地轴肇端子午面平行于格林威治天文台平均子午面二、运用B.L进行高斯投影平面的坐标的盘算的变形剖析.起首因为运用高斯投影得到的成果会有投影变形,变形成果如下1.用大地坐标暗示的高斯投影长度比m:上式中,用平面坐标暗示的高斯投影长度比m其变形情形如下:从上式可以发明不合的地位投影长度比m不合,而在统一点处与偏向无关.这相符正形投影特色.当y=0;m=1,中心子午线投影长度变形为零.并随其y的变更而变更.因而高斯投影得到极大的运用.三、子午线收敛角的求取2.. 当带入克拉索夫斯基椭球参数进行七次睁开,得如下盘算公式: (4)上式中,t=tanB ,η=e/`cos2B, B为纬度,l经差.假如将其参数数值带入,可得成果请拜见[2]第191页3.在工程掌握测量上我们一般运用如下公式:…………5经由过程参考文献[1]我们发明公式5得到的成果足以达到精度请求.当得到B.L,就可以并进行公式5就可以得到其子午线收敛角了.四、成果剖析我们拔取器械跨度为41公里.南北跨度21公里规模内平均散布的38个1980西安坐标系的掌握点.将(x.y)成果带入,运用编写程序进行带入成果可得子午线收敛角有正负之分.以网格北相对于真北的偏向进行断定.,在中心子午线以东,网格北都在真北以东,可称为东收敛角,收敛角为正值;在中心子午线以西,网格北都在真北以西,可称为西收敛角,收敛角为负值.得到成果;五、总结经由过程结算我们发明可以经由过程多种办法进行求解子午线收敛角,运用不合的测量精度请求可以进行不合的处理办法(转变睁开参数次数),可以大大削减处理速度,进步精度,并可以知足其精度请求.参考文献:[1] 邬熙娟,江国焰,高俊强子午线收敛角盘算公式及盘算精度剖析(南京工业大学土木匠程学院.江苏南京210009)[2] 张华海王宝山赵长胜韩晓东等《运用大地测量学》中国矿业大学出版社[3] B.H.巴兰金高斯一克吕格投影的子午线收敛角和长度比的盘算[4] 刘福山高斯投影坐标换带和子午线收敛角盘算编程长軎邮电学院面授部长軎 130012[5] 韩志勇关于子午线收敛角校订问题(中国石油大学(华东)石油丁程学院,山东东营 257061)。
子午线收敛角在煤矿测量中的应用

子午线收敛角在煤矿测量中的应用赵世杰【期刊名称】《《中州煤炭》》【年(卷),期】2019(041)009【总页数】4页(P99-102)【关键词】子午线收敛角; 坐标方位角; 陀螺方位角; 仪器常数; 精度评定【作者】赵世杰【作者单位】河南国控建设集团有限公司河南郑州450009【正文语种】中文【中图分类】TD1780 引言我国煤炭资源储量丰富,煤炭资源的开采利用是我国国民经济发展的重要组成部分。
相对而言,储量丰富的煤矿大多分布在地形复杂多变、水文地质条件千差万别的煤田。
环境恶劣意味着安全威胁。
煤矿测量作为煤矿生产的“眼睛”,指导煤矿建设和资源开采。
目前,煤矿生产安全形势日益严峻,为提高煤矿建设和资源开采的安全系数,保障国家和人民的生命财产安全不受损害,必须不断提高煤矿测量精度[1-5]。
1 子午线收敛角的概念子午线收敛角是地球椭球体面上一点的真子午线与位于此点所在的投影带的中央子午线之间的夹角。
即在高斯平面上的真子午线与坐标纵线的夹角,通常用γ表示。
此角有正负之分:以真子午线北方向为准,当坐标纵轴线北端位于以东时称东偏,其角值为正;位于以西时称西偏,其角值为负。
某地面点此角的大小与此点相对于中央子午线的经差ΔL和此点的纬度B有关,其角值可以用近似计算公式γ=ΔL·sin B计算。
在一个投影带内,高斯平面子午线收敛角的变化遵循一定规律。
距离中央子午线越远,收敛角越大,在中央子午线上收敛角等于零。
距离赤道线越远,收敛角越大。
在赤道线上收敛角等于零。
子午线收敛角[6-10]如图1所示。
图1 子午线收敛角Fig.1 Meridian convergence angle2 子午线收敛角的计算公式及实例子午线收敛角的计算精度直接影响坐标方位角的精度,目前关于子午线收敛角计算公式在许多测量书籍中都已经导出,因精度要求不同其公式推导不同。
赫里斯托夫给出的展至7次项的计算公式[11-12]:γ=cos B·t·l+cos3B·t(1+3η2+2η4)l3/3+cos5B·t(2t2+15η2-15η2t2)l5/15+cos7B·t(17-26t2+2t4)l7/315+O(l7)式中,t=tan B;η=e′ ·cos2B(e′第二偏心率);B为纬度;l为经差。
平面子午线收敛角

平面子午线收敛角
平面子午线收敛角,又称偏向角,是指平面子午线在连续大地测
量中,会收敛到一条折线上。
其中包括两个重要的参数,即收敛角θ
和收敛率R,它们是衡量子午线收敛情况的重要指标。
收敛角θ,是指在地理坐标系中,当子午线收敛时,该折线与位
置轴夹角的弧度值,通常用弧度表示,表示的是子午线的收敛变化趋势。
收敛率R,是指在地理坐标系中,当子午线收敛时,该折线每百米
收敛量的值,通常用弧度表示,表示子午线沿着某一方向的收敛速率。
平面子午线收敛角的计算通常是靠曲率半径的积分计算,也就是说,当子午线收敛时,它的收敛率和收敛角的值会随每百米的曲率变
化而变化,而每百米的曲率变化又是由曲率半径的积分计算得到的。
平面子午线收敛角有助于对空间坐标系中的经纬度坐标信息进行
精确的转换,例如,在地图投影过程中,可以将经纬度坐标转换为相
对应的实际空间坐标,而收敛角θ和收敛率R,就是在此过程中所使
用的重要工具。
