数独：链的入门学习与运用

合集下载

数独快速入门及数独技巧

数独快速入门及数独技巧数独是一种经典的数字游戏，它的规则简单，但要想成为一个高手并不容易。

本文将介绍数独的快速入门方法和一些常用的数独技巧，希望能帮助读者迅速提高数独水平。

一、快速入门方法1.观察法：观察法是数独问题的基本解题方法。

通过观察已有的数字，找出能够唯一确定的数字。

首先，找到已经填入数字最多的九宫格，然后观察一行、一列、一宫格中已经填入的数字，根据规则推断缺失的数字。

2.排除法：排除法也是数独问题的常用解题方法。

通过排除已经确定的数字，缩小其他数字的范围，进而确定其位置。

首先，找到一个数字的可能位置，然后观察该数字在同行、同列、同宫格中是否有其他的可能位置，如果没有则确定该数字的位置。

3.假设法：假设法适用于数独问题的困难级别较高的情况。

当观察法和排除法都无法解决问题时，可以假设一个数字的可能位置，并在此基础上进行推理。

如果出现矛盾，则回溯到上一步，重新假设其他数字的位置，直到解决问题。

二、常用数独技巧1.唯一候选数法：当一些格子中只有一个可能的数字时，该数字就是该格的解。

这种情况通常出现在一行、一列或一个九宫格内已经填入了大量数字，只剩下一个数字可填时。

2.剪枝法：当一些数字在行、列或宫格中已经出现一次时，可以排除其他位置的该数字候选数。

例如，如果数字1已经在行的一个格子出现了，那么该行的其他格子就不能填入数字13.区块切割法：当一些九宫格内已经确定了一些数字，可以利用这些数字来确定其他九宫格的数字。

例如，如果一个九宫格中的行已经填入了数字1，那么该行在其他九宫格中就不能再填入数字14. X-Wing技巧：X-Wing技巧适用于多个九宫格中两个数字分别在两行或两列中成“X”字形排列的情况。

通过观察X字形排列的行或列，可以排除其他行或列中的该数字。

5.链接法：链接法适用于困难级别的数独问题。

它通过连接多个数字的可能位置来推导出一些数字的位置。

例如，如果数字1只能出现在A格和B格中，数字2只能出现在B格和C格中，那么可以确定数字2出现在C格，进而推导出数字1出现在A格。

数独高级技巧入门链地逻辑及AIC

数独高级技巧入门链地逻辑及AIC
数独高级技巧入门包括链地逻辑和AIC（Advanced Implications Chains）。

链地逻辑是利用数独细节的一种有效的解题技巧，它允许有经验的数独玩家解决一些更棘手的题目，因此它又被称为逻辑链技巧。

AIC 是一种强大的数独技巧，可以有效地排除一些数字，并在解数独时使用更多的细节。

其次是AIC技巧，它是数独解题中更高级的技巧之一、AIC技巧是将假设和推断结合起来，以便从一系列地逻辑和技巧中得出结论。

它可以让数独玩家分析每个单元格中的可能数字，从而有助于解决更棘手的题目。

AIC技巧通常都是基于高级覆盖、数字组合和限制推理来进行解答的。

最后，值得一提的是，在使用高级技巧解数独时，玩家需要仔细观察数独板上的每一个单元格，以及每一个位置上可用的值。

数独九宫格中链的应用

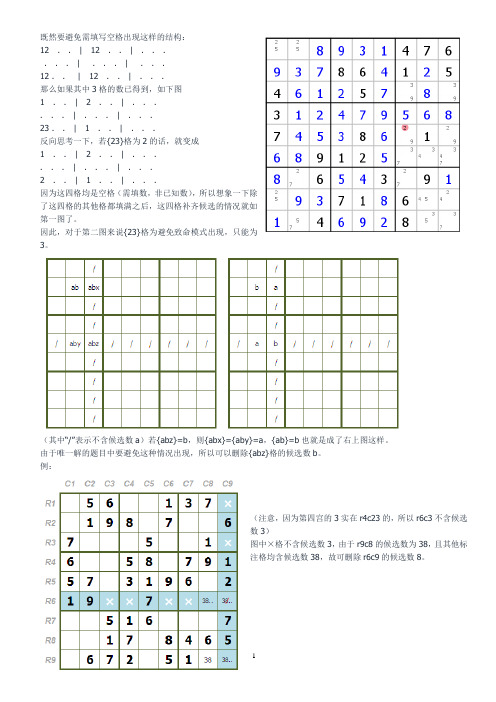
既然要避免需填写空格出现这样的结构：12 . . | 12 . . | . . .. . . | . . . | . . .12 . . | 12 . . | . . .那么如果其中3格的数已得到，如下图1 . . |2 . . | . . .. . . | . . . | . . .23 . . | 1 . . | . . .反向思考一下，若{23}格为2的话，就变成1 . . |2 . . | . . .. . . | . . . | . . .2 . . | 1 . . | . . .因为这四格均是空格（需填数，非已知数），所以想象一下除了这四格的其他格都填满之后，这四格补齐候选的情况就如第一图了。

因此，对于第二图来说{23}格为避免致命模式出现，只能为3。

（其中“/”表示不含候选数a）若{abz}=b，则{abx}={aby}=a，{ab}=b也就是成了右上图这样。

由于唯一解的题目中要避免这种情况出现，所以可以删除{abz}格的候选数b。

例：（注意，因为第四宫的3实在r4c23的，所以r6c3不含候选数3）图中×格不含候选数3，由于r9c8的候选数为38，且其他标注格均含候选数38，故可删除r6c9的候选数8。

若{abz}=b，则{aby}=a，{ab}=b，{abx}=a。

由于唯一解的题目中要避免这种情况出现，所以可以删除{abz}格的候选数b。

（注意下，因为第六宫的4在r46c7，即在第七列，所以r2c7不为4）图中×格不含候选数4，由于r8c9的候选数为34，且其他标注格均含候选数34，故可删除r2c8的候选数3。

第1题：{238,378,38,38}构成UR3，第1宫形成27对，删除R2C1的2，R2C5=1。

第2题：{18,18,1289,128}构成UR3，第9宫形成29对，删除R7C6的9，R9C5=9。

Unique Rectangle type 112 . . | 21 . . | . . .21 . . | 12 . . | . . .. . . | . . . | . . .可以反推在一道唯一解的标准数独题目中未填空格的候选数是不会出现下述情况的。

数独强链弱链的用法

数独强链弱链的用法
1. 嘿，你知道吗？数独里的强链用法可神奇啦！就好像是给你指出了一条明确的道路。

比如说在一个数独中，有两个格子只能是 5 或者 6，当其他地方都排除了 5，那这两个格子不就强烈指向 6 嘛，这就是强链的厉害之处呀！
2. 哎呀呀，数独的弱链可是很巧妙的哦！就像是一条若隐若现的线索。

好比有三个格子分别是 3、4、5，其中两个格子有弱链关联，那我们就能通过这个关系来进一步推理呀！
3. 哇塞，强链的用法真的是太重要啦！这就好比是游戏中的必杀技一样。

比如在某个角落，通过强链我们可以迅速确定一个数字的位置，那感觉超爽的啊！
4. 嘿，你想想看，弱链在数独中不就像是隐藏的辅助线嘛！就像有一次我玩数独，就是靠找出弱链才解开难题的呢！
5. 数独里的强链呀，那可是能给你带来惊喜的哟！像有时候苦苦思索不得其解，突然发现强链，哇，一下子就豁然开朗啦！比如确定了一条强链后，数字的分布突然就清晰了呢！
6. 哎呀，弱链的作用可别小瞧呀！这就跟找宝藏的小线索一样。

比如说在一片区域中，通过分析弱链，我们能逐渐缩小范围，找到正确的数字呢！
7. 强链在数独里简直就是秘密武器呀！就好比走在迷雾中突然亮起了一盏明灯。

有次解一个很难的数独，就是靠强链才打破僵局的，厉害吧！
8. 哟呵，弱链可是有着意想不到的魔力哦！就像在迷宫中找到的那一丝曙光。

我有回玩数独，靠着微弱的弱链关联，居然就解开了关键的一步呢！
9. 总之啊，数独强链弱链的用法太有趣也太有用啦！只要我们善于运用，就能在数独的世界里畅游无阻啊！。

数独九宫格各种链关系

第一种情况：A==B--C==D由A的真假情况可以做出以下BCD关系的枚举。

再次请大家注意本文开头所提到的强弱关系本质1.强关系是说A与B两个事件，假如A不成立，则B一定成立。

2.弱关系是说A与B两个事件，假如A成立，则B一定不成立。

XY-Wing了，下面是一个XY-Wing的例子：•通常解释XY-Wing原理的时候会用如果r4c2=1则r5c1=4；如果r4c2=9则r4c8=4，所以不论r4c2是1还是9，r5c1与r4c8中至少有一个是4，从而得到r5c1与r4c8的等位群格位交集部分（图中蓝色格）不含4。

•这样是不是有点猜测的味道呢？很多人都说高级技巧是把猜的东西合理化，其实不然。

•用强弱强链的观点可以这样看r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4)，也是得到r5c1与r4c8中至少有一个是4。

•与XY-Wing较相近的要数XY-Chain。

•XY-Wing由三格组成，分别为xy格，xz格，yz格。

XY-Chain不止三格，需要把一些格合并当作XY-Wing组成格之一来看。

•单数链以强、弱方式构成环，称为X-Cycle，无法构成环，则称为X-Chain。

•X-Cycle 的弱环节除节点外，单元内其它格位的相同候选数均可删除。

•X-Chain 在开口处之两节点共同作用格的相同候选数均可删除。

本质上X-Cycle 只是X-Chain 的特例，因此统称为单链。

•单链若由两条强链与一条弱链构成，就是习称的双强链，有摩天楼、双线风筝、鱼三种连结方式。

•单链若由两条强链与两条弱链构成环，就是习称的X-Wing。

XY-Wing的结构可以分为两种：1. xy格与xz格或者xy格与yz格同宫。

2. xy格、xz格、yz格在三个不同宫。

XY-Chian首尾若能连接起来就成为了XY-Cycle（Multi X-Wing）r4c1(7)==r5c4(7)--r5c2(7)=={r1c2, r2c2}(7) 断开任意一条弱链（绿色表示）即成为XY-Chain的结构。

数独链的正确使用方法

数独链的正确使用方法
1. 嘿呀，数独链可是个宝啊！就比如在解一个超级难的数独时，你可以把它想象成一根救命稻草！当你看到一些数字有奇妙联系的时候，就赶紧抓住这条数独链呀！就像在大海里抓住了浮木一样。

2. 哇塞，要学会找数独链的起始点哦！好比你要开启一场冒险，得先找到入口呀！比如看到某个格子里只有两种可能数字，那这不就是个绝佳的起始点嘛。

3. 嘿，数独链中强弱链的运用很关键呀！这就像是武林高手的不同功夫，各有奇妙之处。

比如说在一个区域里，强链就像大力金刚掌，直截了当，弱链呢则像绵里藏针，暗藏玄机。

4. 哈哈，可别小看了对数独链的观察呀！这可是寻找宝藏的关键步骤呢！就好像侦探在找线索一样，比如看到几个数字总是同时出现或不出现，那这里面肯定有数独链的踪迹。

5. 哎呀呀，使用数独链的时候要灵活多变呀！不能死脑筋哦。

就跟跳舞一样，要随着节奏灵活转动。

比如遇到复杂的局面，就得像个机灵鬼一样去发现那些隐藏的数独链。

6. 哇哦，数独链还可以组合起来用呢！这多厉害呀，就像把不同的武器组合成超级武器一样。

比如说用几条数独链一起推理出某个关键数字。

7. 嘿嘿，一定要多练习使用数独链啊！就跟练功一样，越练越厉害。

你想想，如果天天练习，那解数独不就手到擒来啦，就像孙悟空耍金箍棒一样轻松！
我的观点结论：数独链真的是解数独的绝妙方法，只要用心去发现和运用，就能在数独的世界里畅游无阻！。

数独强弱链详解

数独强弱链详解引言数独是一种经典的逻辑推理游戏，通过填写9x9的方格中的数字，使得每一行、每一列和每一个3x3的方块内都包含了1到9的数字，且不重复。

数独游戏的难度取决于初始给出的数字数量和位置，而解决数独的关键在于找到合适的数字填入空白格中。

在解决数独的过程中，数独强弱链是一种常用的策略。

本文将详细探讨数独强弱链的原理、应用和解题技巧。

数独强弱链的原理数独强弱链是一种基于候选数的推理方法，通过确定某个数字的位置，进而推断其他数字的位置。

强弱链的原理基于以下两个观察：1.强链：如果一个数字在某行、某列或某个3x3方块中只能出现在两个候选格中，那么这两个格子就形成了一个强链。

强链中的数字必须出现在其中一个格子中，从而排除了其他格子的该数字候选。

2.弱链：如果一个数字在某行、某列或某个3x3方块中只能出现在两个候选格中，那么这两个格子就形成了一个弱链。

弱链中的数字必须出现在其中一个格子中，从而确定了该格子的数字。

数独强弱链的关键在于不断地寻找强链和弱链，并利用它们推断其他格子的数字，从而逐步解决数独。

数独强弱链的应用数独强弱链在解决数独问题时具有广泛的应用。

通过寻找强链和弱链，可以有效地减少候选数的数量，从而缩小解空间，简化解题过程。

数独强弱链的应用包括以下几个方面：1. 排除候选数通过找到强链，我们可以确定某个数字必须出现在其中一个格子中，从而排除了其他格子的该数字候选。

这样可以减少候选数的数量，缩小解空间。

2. 确定格子的数字通过找到弱链，我们可以确定某个数字必须出现在其中一个格子中，从而确定了该格子的数字。

这样可以直接填入数字，简化解题过程。

3. 推断其他格子的数字通过不断地应用强链和弱链，我们可以逐步推断其他格子的数字。

当所有格子都被推断出数字后，数独就被解决了。

数独强弱链的解题技巧在应用数独强弱链解题时，我们可以采用以下一些技巧：1. 优先寻找强链在解题过程中，我们应该首先寻找强链。

强链可以排除候选数，从而减少解空间。

[数独高级技巧]单数链及其延伸的运用

[数独高级技巧]单数链及其延伸的运用
•本帖将讨论单一数字利用强弱链关系所形成的一些技巧，有X-Wing、Skyscraper、Turbot Fish等等不同的结构，但是他们的本质都是相同的。

•构成矩形摒除（X-Wing）需要四个节点（节点指需要观察的数字个数），要直接观察到并不容易。

•箭鱼摒除（Swordfish）有6～9 个节点，观察极度困难，即使懂得这种方法，也很难运用在解题过程中。

•有一种解法叫做简易分色法（Simple Coloring）是利用单数的强链导出矛盾的删减法。

•简易分色法是解析出一条色链之后，可同时得到多个格位的解，在使用候选数时，是很不错的观察方向，但要观察的格位太多，因此不适用于直观。

•有一种解法称做多宝鱼（Turbotfish）解法，它是由五个节点所构成，观察比较容易。

•多宝鱼解法与简易分色法不同之处是简易分色法全部由强链构成，而多宝鱼解法则由强链与弱链构成，因此结构形成的机会很大。

•多宝鱼解法虽然只有 5 个格位，但要观察也是不容易的，因此我们将之解构为双强链 (Two Strong Link)，观察两条强链容易多了。

数独高级技巧入门链的逻辑及

[数独高级技巧入门]链的逻辑及AIC这个帖子主要想阐述链是什么，怎么使用链，以及链的逻辑过程，帮助大家首先了解原理，那么以后关于chain、wing之类的按照这个思路都非常容易理解。

首先我想说明下什么是“强”关系，什么是“弱”关系强关系是说A与B两个事件，假如A不成立，则B一定成立。

弱关系是说A与B两个事件，假如A成立，则B一定不成立。

举一个简单的例子帮助大家体会：（图中被划短横线的格表示不含候选数1）这是一个数独的宫，根据数独规则一个宫内出现数字1-9各一次，可以做出以下两点推断：1.左上格不是1，则右中格一定是1；2.左上格是1，则右中格一定不是1。

第一种推断得到这两格的1是强关系，所以可以说两格之间形成一条强链，强链我们通常以双横线表示（==）；第二种推断得到这两格的1是弱关系，所以可以说两格之间形成一条弱链，弱链我们通常以单横线表示（——）。

再举一个例子：（图中被划短横线的格表示不含候选数1）上图可以做出三大点推断：1.左上格是1，则中上格及右中格一定不是1；2.中上格是1，则左上格及右中格一定不是1；3.右中格是1，则左上格及中上格一定不是1。

这个例子里，存在着3条弱链，分别是（左上--中上）、（左上--右中）、（中上--右中）。

上面说的是同一数字的强弱关系，当然强弱关系可以不局限于一个数字，下面用例子来说明：（图中被短横线划掉的格说明未知其候选数情况）根据右上格的候选数仅有1与2可以做出以下推断：1.如果该格不能是1，则一定为2；2.如果该格是1，则一定不是2。

推断一说明数字1与2之间是强关系，形成强链；推断二说明其为弱关系，形成弱链。

（图中被短横线划掉的格说明未知其候选数情况）右上格有3个候选数，我们可以做出以下推断：1.如果这格为1，则不能为2或3；2.如果这格为2，则不能为1或3；3.如果这格为3，则不能为1或2。

数字1与2、2与3、1与3之间分别为一条弱链。

像第二张图这样的关系推断，大家可能会不以为意，但是这是理解强弱关系的一个很好的例子，对于后面将要叙述的内容也会有所帮助。

数独_链

链1.链是什么？链是数独高级技巧的核心，它表示两个命题间的关系。

命题有真假之分，我们可以通过分析链来判断某个命题是真还是假。

在数独中，我们要判断真假的命题都是：“某某格子应该填入某某数。

”“A1=3”，“E7=8”，……诸如此类。

分析出了它们的真假，我们就相当于是填出了一个数字。

本文中约定把这些命题表示为“格子（数）”，例如A1(3)，E7(8)，等等。

链分强链关系、弱链关系两种：强链：两个命题不可以同时为假，本文中用==（双横线）表示；弱链：两个命题不可以同时为真，本文中用--（单横线）表示。

讲了这么多，我们来先找几条链试试吧。

例1：1. H2(4)—H4(4)如果H2和H4都填4，会有什么结果？结果是一行里出现了重复数字，违反了数独规则。

于是我们可以判断H2(4)和H4(4)不能同时为真，即它们呈弱链关系。

2. D1(4)==I1(4)我们仔细观察，会发现第1列除了D1和I1，其他格子都不可能填入4了。

那么无论如何，它们两格中至少有一个4，即不能同假，呈强链关系。

3. G2(1)==G2(6)刚才的两条链都是不同格子间的同一个候选数，这条却是同一个格子中不同的两个候选数。

我们可以把上面两条叫做单链，这条和第4条叫做多链。

G2要么填入1要么填入6，不可能是其他的数字了。

所以它们俩不能同假（要不然G2就没数填了），呈强链。

其实，第2、3两条链也可以看成是弱链，因为他们即符合强链的定义，又符合弱链的定义（不能同真）。

4.G6(1)—G6(8)一个格子内只能填一个数，而如果1和8都成立那么G6就有2个数了。

所以它们不能同时成立，呈弱链。

上面这些都是链的4种基本情况，理解它们后我们就可以往下看第2节了。

2.链的基本应用链之所以被称作链，是因为它们能够像链条一样串起来用：例2：这是一条长度为3的2的单链。

乍看一下它只是3条单链连在一起罢了，难道它还有什么别的性质吗？当然。

由E3(2)==H3(2)—H4(2)==D4(2)我们可以推理出E3(2)==D4(2)，即它们不同假。

数独策略解密最有效的方法

数独策略解密最有效的方法数独是一种非常受欢迎的逻辑推理游戏，它的规则简单而又富有挑战性。

在解答数独谜题的过程中，我们常常需要运用一系列策略来帮助我们揭开谜底。

本文将介绍一些最有效的数独策略，让你能够更好地解密数独。

【基础策略】在解密数独之前，我们首先需要掌握一些基础策略。

这些策略更加侧重于观察并填写已知的数字，以便为后续推理提供基础。

1. 唯一候选数法：当一个空格的可能数字只有一个的时候，那么该数字就是该空格的解答。

通过观察其他行、列和九宫格中已经填入的数字，我们可以确定一个数字在某个空格的唯一性。

2. 排除法：在每一行、每一列以及每一个九宫格中，如果某个数字已经在该行、该列或该九宫格中出现过，那么该数字就不能出现在该行、该列或该九宫格的其他空格。

通过排除一些已知的数字，我们可以缩小其他空格的候选数字范围。

【进阶策略】除了基础策略之外，还有一些进阶策略可以帮助我们解密更加复杂的数独谜题。

这些策略需要更多的逻辑思考和观察能力。

1. 唯余法：当某个数字在某行、某列或某九宫格中只剩下一个空格可填时，该空格必然是该数字的解答。

在解密数独过程中，我们需要仔细观察每行、每列和每个九宫格中数字的分布情况，判断出哪些数字的唯余空格可以确定。

2. 隐性唯余法：当一个数字在某行、某列或某九宫格中只有一个位置可填时，即使该位置有多个候选数，也可以确定该数字就是要填入的数。

这是因为其他空格上的候选数会被其他规则所排除。

3. X-Wing法：当某个数字在两行或两列中只出现两次，且这两个位置满足特定条件时，可以排除其他行或列上相同位置的该数字。

X-Wing法需要观察不同行和列中数字的分布情况，找到特定形态的重复数字并进行排除。

4. 锁定候选数法：当一个数字在某行或某列中只出现在一个九宫格的两个空格中，可以排除该九宫格中其他行或其他列上相同位置的该数字。

锁定候选数法需要观察不同行和列中数字的分布情况，找到特定形态的数字分布以及包含候选数字的九宫格。

数独解法知多少？—高级技巧入门：链的逻辑

数独解法知多少？—高级技巧入门：链的逻辑2011-09-29本文行家：林敏舫由成立到不成立即是弱，由不成立到成立即是强首先我想说明下什么是“强”关系，什么是“弱”关系？强关系是说A与B两个事件，假如A不成立，则B一定成立。

弱关系是说A与B两个事件，假如A成立，则B一定不成立。

这个例子里，存在着3条弱链，分别是（左上--中上）、（左上--右中）、（中上--右中）。

推断一说明数字1与2之间是强关系，形成强链；推断二说明其为弱关系，形成弱链。

数字1与2、2与3、1与3之间分别为一条弱链。

像第二张图这样的关系推断，大家可能会不以为意，但是这是理解强弱关系的一个很好的例子，对于后面将要叙述的内容也会有所帮助。

数独九宫格各种链的关系

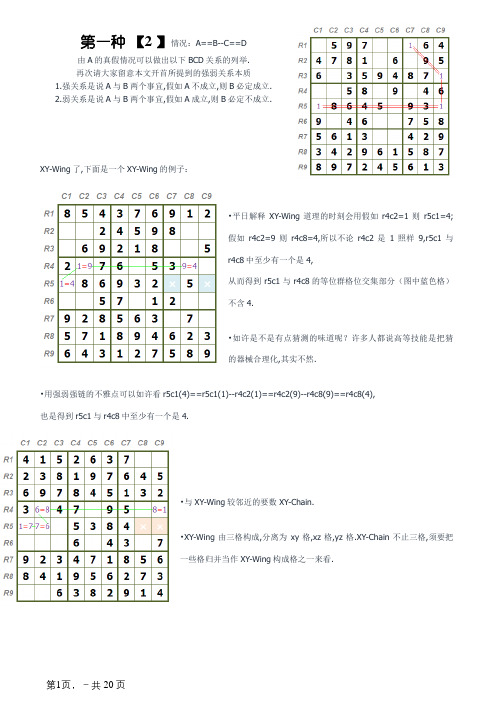
第一种【2 】情况：A==B--C==D由A的真假情况可以做出以下BCD关系的列举.再次请大家留意本文开首所提到的强弱关系本质1.强关系是说A与B两个事宜,假如A不成立,则B必定成立.2.弱关系是说A与B两个事宜,假如A成立,则B必定不成立.XY-Wing了,下面是一个XY-Wing的例子：•平日解释XY-Wing道理的时刻会用假如r4c2=1则r5c1=4;假如r4c2=9则r4c8=4,所以不论r4c2是1照样9,r5c1与r4c8中至少有一个是4,从而得到r5c1与r4c8的等位群格位交集部分（图中蓝色格）不含4.•如许是不是有点猜测的味道呢？许多人都说高等技能是把猜的器械合理化,其实不然.•用强弱强链的不雅点可以如许看r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4),也是得到r5c1与r4c8中至少有一个是4.•与XY-Wing较邻近的要数XY-Chain.•XY-Wing由三格构成,分离为xy格,xz格,yz格.XY-Chain不止三格,须要把一些格归并当作XY-Wing构成格之一来看.•单数链以强.弱方法构成环,称为 X-Cycle,无法构成环,则称为 X-Chain.•X-Cycle 的弱环节除节点外,单元内其它格位的雷同候选数均可删除.•X-Chain 在启齿处之两节点配合感化格的雷同候选数均可删除.本质上 X-Cycle 只是 X-Chain 的特例,是以统称为单链.•单链若由两条强链与一条弱链构成,就是习称的双强链,有摩天楼.双线风筝.鱼三种贯穿连接方法. •单链若由两条强链与两条弱链构成环,就是习称的 X-Wing.XY-Wing的构造可以分为两种：1. xy格与xz格或者xy格与yz格同宫.2. xy格.xz格.yz格在三个不同宫.XY-Chian首尾若能衔接起来就成为了XY-Cycle（Multi X-Wing）r4c1(7)==r5c4(7)--r5c2(7)=={r1c2, r2c2}(7)断开随意率性一条弱链（绿色表示）即成为XY-Chain的构造.得到{r1c2, r2c2}与r4c1至少有一个为7.例如断开上端r8c57的弱链后,可以得到r8c5(7)与r8c7(7)所以可以删除{r1c2, r2c2}与r4c1等位群格位的交至少有一个成立,即可删除这两格等位群格位交集的7,集r1c3的候选数7.其他三种断开弱链可以或许做何删减,大家可以本身尝试推导.Guardians（守护者）的技能,也有地方称之为Broken Wings或者Turbot-Fish.其描写的是某一个候选数X的情况,当有偶数条强链,且两个端点处于统一unit时,这时可以删除两个端点上的候选数X,假如该unit出这两头点非分特别只有一格含有候选数X,则该格必定就是X.下图：从蓝色格动身到达红色格,依据它们之间的逻辑关系,可以得到红色格有雷同的真假值.•红色格若为假,没问题两个都可删除,红色格若为真,则违背数独原则也应该删除. •结论：红色格应予删除•用链的不雅点来看：r3c8(9)==r3c8(2)--r6c8(2)==r6c6(2)--r9c6(2)==r9c6(9),是以可以删除r9c8的候选数9.•亦可如许懂得,假如r3c8不为9,r3c8为2,则r6c8不为2,r6c6为2,r9c6不为2,即r9c6为9;反过来,假如r9c6不为9,则r9c6为2,r6c6不为2,r6c8为2,r3c8不为2,即r3c8为9;可见r3c8与r9c6至少有一个为9,是以可以删除r9c8的候选数9.•双强链的按其强链地点区域及构成可分为三种.1. 摩天楼（Skyscraper）2. 鱼（Fish）3. 双线风筝（Two Strings Kite）摩天楼以下是双线风筝（Two Strings Kite）.鱼（Fish）的构造及其删减情况.1. 上左图,两条强链一条在「行」另一条在「列」,红色顶端之配合感化格（红色「X」）就是不能有构成强链数字之处,这个构造称为双线风筝.2. 上右图,两条强链一条在「宫」另一条在「列」,红色顶端之配合感化格（红色「X」）就是不能有构成强链数字之处,这个构造称为鱼.（C2.C5各有一个{XY}数对,是以R5的两格也为{XY}数对）当r2c2是X时,可以得到r5c2为Y,继而r5c5为X,r3c5为Y;反之,当r2c2是Y时,可以得到r5c2为X,继而r5c5为Y,r3c5为X.也就是说r2c2与r3c5也为{XY}数对,是以可以删除其等位群格位的交分散候选数XY.•双强链的基座（Base）必须在统一单元,且链顶（Top）必须有雷同感化格才有删减后果. •有时两条强链虽有雷同的基座,但链顶没有配合感化格,如斯将达不到删减的后果.•是以就有所谓的进阶型的双强链.•因为 A==B==C==D 三条强链会造成 A 与 D 有相反的真假值,是以可以当一条强链应用.•不雅察一.三条形成的双强链不会太庞杂,是以以下我们就以如许的构形提出实例加以解释.•在数独的解题技法称这种解法为 X-Chain.如右图附一道题的七种解法.解法1解法 #2解法 #3解法 #4解法 #5解法 #6解法 #7单数链解法的三要素就是：1. 有强关系的两头点.2. 两头点有配合感化格.3. 配合感化格有删减后果.•右图是这是摩天楼的扩充型的思虑办法,黄色为底（起点）,红色为顶（终点）.•当黄色为真,则往绿色偏向推动,当黄色为假则往红色偏向推动.•无论黄色为真或假,经推导的成果,红色的两个端点必定有一点为真,是以它们是强关系.•强关系的配合感化格可以将候选数 2 删除,如图上彀点标示之格位.左图的别的一种推法：•这是摩天楼的扩充型,黄色为底（起点）,红色为顶（终点）.•当黄色为真,则往绿色偏向推动,当黄色为假则往红色偏向推动.•无论黄色为真或假,经推导的成果,红色的两个端点必定有一点为真,是以它们是强关系.•强关系的配合感化格可以将候选数 2 删除,如图上彀点标示之格位.点算图示格的候选数,可以发明形成XY-Cycle,可以删的数比jcvb 提到XY-Chain略多一些.右图：重要应用了r2c5的8的删减,可以得到第五列的摒除解r7c5=8.欠一数对Almost Locked Pair数对.三链数.四链数被统称为Locked Candidates,假如还差一点的也就是Almost Locked Candidates.我们取个中的数对部分,也就是Almost Locked Pair来讲授.起首讲一下构造与结论：（“/”失落格表示不含候选数XY）看R1,数字“XY”中的一个在r1c4,另一个在r1c123,也就是说r1c123含有“XY”中的一个数,第一宫的数字“XY”中的另一个在r2c1,所以可以得到第一宫的其他格不含有候选数XY,因为{r1c123, r2c1} 为 {XY}数对.反之亦然.R8的“78”在r8c679三格,因为r9c8的候选数为78,所以r8c79只能有“78”中的一个,所以R8的“78”另一个在r8c6,所以r8c6的候选数为78.数字1对第八宫摒除,得到r8c5=1.微变一下构造：（“/”部分表示不含候选数XYZ）r1c45的部分个中一个会是Z,一个是{XY}之一,是以r1c123含有{XY}中的另一个,{r1c123, r1c45}为{XY}数对（{r1c123, r1c4, r1c5}为{XYZ}三链数）,所以{r1c123, r2c1}为{XY}数对,所以可以删除第一宫其他格的候选数XY.r4c1的候选数为68,第四宫{68}中的另一个在r5c12之中;r5c12含有{68}中的一个,与r5c7的68形成{68}数对,可以删除r5c9的候选数6.数字78对C7摒除可以得到r89c7的{78}数对;中图：数字8对第六宫摒除,得到第六宫的8在C8;右图：数字78对R8摒除,得到r8c67为{78}数对.左图：r4c1的候选数为68,第四宫{68}中的另一个在r5c12之中;r5c12含有{68}中的一个,与r5c7的68形成{68}数对,可以删除r5c9的候选数6.右图：看r6c3的候选数为17,第四宫{17}中的另一个在r5c23中,R5的其他格只有r5c9含候选17,所以可以肯定r5c9的候选数为17,即删除6.（图中标示候选数表示该格仅含这些候选数）•看到这个构造,大家头脑里会有冒出什么结论呢？想不到也没紧要,可以跟着我们的思绪来.•先看r1c5的候选数为wx,所以r1c23中要不不含wx,要不只能有wx之一;再看r2c1候选数为yz,同样的r1c23中要不不含yz,要不只含个中一个;但r1c23没有其他候选数,按照上述剖析,其构成即为有『wx』中的一个和『yz』中的一个.也就是说我们可以将{r1c23,r1c5}看作wx数对,{r1c23,r2c1}看作yz数对,继而这两个“数对”所影响规模的对应数字即可删减.•这题有比较显著的单链,但用“欠一数对”尝尝要怎么不雅察呢？•因为橙色的23,蓝色至多含有23中的一个,又因为绿色的16,蓝色至多含有16中的一个,蓝色仅含候选数1236,故蓝色构成为16中的一个和23中的一个,{r1c23,r1c5}构成23数对,{r1c23,r2c2}构成16数对.故可以删除第一行其他格的候选数23,第一宫其他格的候选数16.Y-Wing（可能与XY-Wing混杂）,有的地方称为W-Wing（可能与WXYZ-Wing混杂）,本帖采用Y-Wing的名称."数对"为蓝色格所示{23},加之第四行数字3,构成Y-Wing,可以删除r5c7与r6c6的候选数2.M-Wing的构造：•大家可以比较一下上两图,差别在于r5c2的候选数情况,但是他们的推导进程是雷同的.•橙格仅含候选数ab,即只有2种情况：1. 为b;2. 为a,则绿格不为a->蓝格为a（即蓝格不为b）->紫格为b.•以链的不雅点：r2c7(b)==r2c7(a)--r2c2(a)==r5c2(a)--r5c2(b)==r5c5(b),即r2c7==r5c5为b的强链.•那么为什么他们会有雷同的结论呢？•因为无论是用什么不雅点来剖析这个成果,用到的都是r5c2是a则不是b,是b则不是a的弱关系不雅点,而是否消失其他候选数并不影响弱关系的成立.所以,M-wing的链关系可以总结为右上图.个中X为任何数.•涂色四格构成M-Wing的构造,可以删除r6c2的候选数9;•可以按照以下思绪推导：r6c5有两种情况：1. 为9;2. 为3->r6c7不为3->r3c7为3->r3c7不为4->r3c2为9.•则r6c5与r3c2至少有一格为9,可以删除它们配合感化格r6c2的9.R6C4<>8(=49)->R3C4=8(<>5)->R2C4=5->R2C3=2->R5C3=6->R5C7=49->R56C4,R56C7=独一矩形.即R6C4=8.看一个Swordfish的例子：X-Cycle演习题。

数独链的技巧

数独链的技巧
1. 尝试解决一个完整的数独，先从单元格开始。

从中可以找到唯一可能的可能性；
2. 检查每个横行、竖行和九宫格，寻找其中重复的数字；
3. 检查每行、每列和每个九宫格，并尝试从单元格中发现有助于解决数独的模式；
4. 扫描每行和每列，如果可以，从一行或一列中确定数字的位置；
5. 尝试突出一个数字，并找到它在每一行和每一列中的其他可能位置；
6. 尝试找出模式，使用像字谜游戏一样的技巧，看看能否将某个位置的数字确定出来；
7. 使用“数独链”，这是一种可以连接预设和排除分组中的数字的特殊技巧；
8. 如果一切都失败，请反复检查答案，以确保一切正确；
9. 如果还是失败，请尝试重新开始。

数独高阶技巧入门之二：简单的单数链结构——双强链

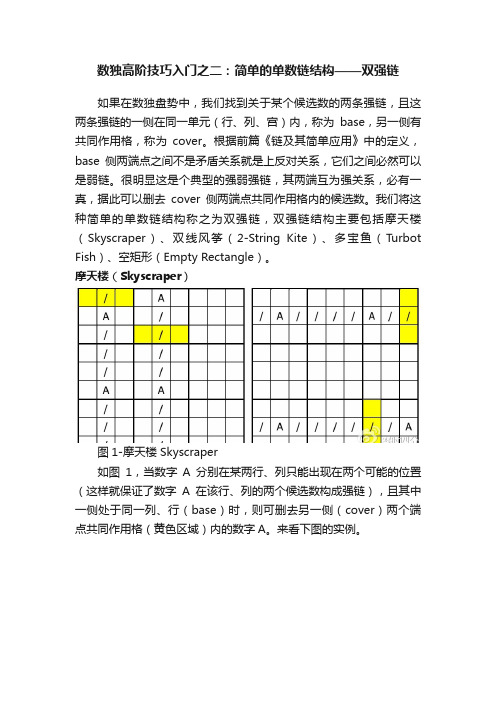
数独高阶技巧入门之二：简单的单数链结构——双强链如果在数独盘势中，我们找到关于某个候选数的两条强链，且这两条强链的一侧在同一单元（行、列、宫）内，称为base，另一侧有共同作用格，称为cover。

根据前篇《链及其简单应用》中的定义，base侧两端点之间不是矛盾关系就是上反对关系，它们之间必然可以是弱链。

很明显这是个典型的强弱强链，其两端互为强关系，必有一真，据此可以删去cover侧两端点共同作用格内的候选数。

我们将这种简单的单数链结构称之为双强链，双强链结构主要包括摩天楼（Skyscraper）、双线风筝（2-String Kite）、多宝鱼（Turbot Fish）、空矩形（Empty Rectangle）。

摩天楼（Skyscraper）图1-摩天楼 Skyscraper如图1，当数字A分别在某两行、列只能出现在两个可能的位置（这样就保证了数字A在该行、列的两个候选数构成强链），且其中一侧处于同一列、行（base）时，则可删去另一侧（cover）两个端点共同作用格（黄色区域）内的数字A。

来看下图的实例。

图2-SK01在图2中，数字1在C6、C9列只能出现在两个位置，且R5C6和R5C9同处于R5行（base），显然这是个典型的强弱强链（R1C6==R5C6 —R5C9==R3C9），cover侧R1C6和R3C9之间为强关系，必有一真，可以删去它们共同作用格内的数字1（红色）。

上例是数字A在两列中只出现于两个位置的摩天楼结构，我们再看一个位于两行的摩天楼。

图3中数字4在R2、R8中只出现在两个位置，R2C1和R8C1同处于C1列（base），可删去cover侧R2C5与R8C4共同作用格内的候选数4（红色）。

图3-SK02双线风筝（2-String Kite）图4-双线风筝 Two Strings Kite当数字A在一行、一列均只能出现在2个可能位置（保证是强链），且该行和列的一个端点同处于同一宫（base），则可以删除另两个端点（cover）的共同作用格（黄色区域）内的候选数A。

九宫数独高阶技巧（2）单数链之摩天楼

九宫数独高阶技巧（2）单数链之摩天楼
今天来学习简单的单数链，在开始今天的学习之前，先回顾一下上一节讲强链和弱链的定义。

强链：若A&B不能同时为假，即为强链，记为A==B；
弱链：若A&B不能同时为真，即为弱链，记为A——B。

今天我们学习的单数链结构是强弱强链结构，我们称之为双强链，其结构为：两个强链之间用一个弱链链接，这样就可以将两强链的顶端所共同作用的区域进行删减。

首先看一个简单的摩天楼（skyscaper）结构
如图，当数字A只能出现在某两列的两个位置（这样就保证了这两链的关系是强链），且其中一侧处于同一行（这两个A一定不能同时为真，这样就是弱链关系，所以这一行当中还有没有其他的单元格能不能出现A都没有关系），则另外一侧必为一真一假或者两个都真。

（推理如下：若C2不是A，则H2必是A，则H5必不是A，则B5必是A；若B5不是A，则H5必是A，则H2必不是A，则C2必是A），这样C2和B5共同作用的单元格B1、B2、B3和C3、C5、C6中必不能是A，这样就可以对这几个单元格的数字A做删减。

当然，也可以将上面的列的强链换成行的强链，且其一侧处于同一列，如图所示：
下面用一个实际的例子来看看这种结构的单数链。

如图所示：数字1在第6列和第9列只能出现在两个位置E6、A6和E9、C9，正好符合我们刚刚分析的摩天楼结构，这样A6和C9共同覆盖的区域A7、A8和C7、C8一定不能是1，将这两个单元格的候选数1删去，即可得C9=1。

再来看一个在两行中出现摩天楼结构的例子，如图所示：
注意观察数字4在B行和H行只能出现在两个位置B1、B5和H1、H4，正好符合摩天楼结构，因此可以将B5和H4共同作用的单元格A4中的4删去，这样A4就只能是6。

(完整版)数独：链的入门学习与运用

数独：链的入门学习和运用链是什么？分析候选数之间的关系以获得线索就是链。

在学习链前我想先说明下什么是“强”关系，什么是“弱”关系？强关系是说A与B两个事件，假如A不成立，则B一定成立，即A、B不能同假。

弱关系是说A与B两个事件，假如A成立，则B一定不成立，即A、B不能同真。

如上图，在5宫仅存两个候选5，这两个5无论哪个为假，另一个必定为真，因而5宫的这两个候选5成强关系。

现在我们来看看2列仅存的候选7，不难发现这两个候选7在2列呈强关系。

同样候选6在7行呈强关系。

我们再来看看F7仅存两个的候选1、5在格内形成强关系。

我们注意到3宫的候选8画得特别漂亮，根据之前学过的知识你能否描述一下它们是怎样呈现什么样的关系的呢？在这里我就不说太多，留待下文慢慢解释，不过先做一点提示，如果你把同色染色格看成一个整体怎样看？细心的同学应该注意到，上面描述的都是A、B非假即真的强关系，貌似我们给强关系的定义是A、B不能同假，似乎忽略了A、B同真的介绍。

这并不是疏忽，而是要说明A、B同真需要更深入的学习，对入门者来说有点难度。

在弄懂强关系后，弱关系就不难理解了，只要A、B不能同真均是弱关系。

我们注意到5宫的候选5应该是强关系，为什么跑来弱关系图了。

弱关系的定义是A、B不能同真，5宫的候选5是一种A、B非假即真的强关系，换句话说就是A、B不可能同真，符合弱关系的定义，因此5宫的候选5同是弱关系，更确切的描述是同时兼有强、弱关系。

在完全弄清强与弱的关系后，我们再来学习一下画链，懂得如何看图作图对阅读本文有莫大的帮助。

如上图，强关系候选数以实线链接，以实线表示为强链，文字表达为“==”（双横线）；弱关系候选数以虚线链接，以虚线表示为弱链，文字表达为“--”（单横线）；格内链无论强弱均不另行标示；双箭头是把同色候选数视为一个整体。

在理解上述基础概念后，我们现在就开始链的学习。

链之所以被称作链，是因为它们能够像链条一样串起来。