数独高级技巧入门链的逻辑及
数独的规则与技巧

数独的规则与技巧
以下是 6 条关于数独的规则与技巧:
1. 数独的规则其实很简单呀,每行每列和每个小九宫里都得填上 1 到9 数字,而且不能重复哟!就像搭积木一样,每个位置都有它特定的要求。
比如说,这一行已经有了 1、2、3,那你再填个 4 试试,是不是马上就能发现不对劲啦?
2. 技巧之一就是从出现次数多的数字入手呀!你想想,如果一个数字在很多地方都没出现,那它肯定在某个地方很重要嘛。
就好像找宝藏,先从线索多的地方开始找呀!像这个九宫格只有一个地方能填 5,那你还不赶紧抓住这个机会呀!
3. 要善于观察空白处的限制呀!每个空白都不是孤立的呢,它们都和周围的数字相互关联。
好比是走迷宫,看清楚前面的路才能找到出口嘛。
你看这个位置,根据周围的数字,不就能判断出这里只能填 8 嘛!
4. 遇到难题别着急,慢慢试也是个办法呀!有时候感觉走进死胡同了,那就一个一个试呗。
这就像解开一团乱麻,一点点地捋清楚呀。
比如说实在不知道填啥,那就把可能的数字都填上试试,说不定就柳暗花明了呢!
5. 注意利用唯一性呀!如果一个数字在某一行或某一列只有一个位置能填,那就是它啦!这就好比是一个独一无二的宝贝,一眼就能认出来。
像这个情况,除了这里能填 7,其他地方都不行,那还犹豫啥呢!
6. 特别要关注那些交叉点呀!这些地方往往是关键所在。
就好像打仗时候的战略要地,守住了就胜利在望啦。
你看看这个交叉位置,对整个数独的解决起着关键作用呢!
我觉得吧,数独真的很有趣,掌握了这些规则和技巧,就像有了一把打开智慧大门的钥匙,让你在数独的世界里尽情探索和挑战!。
数独高级技巧入门链地逻辑及AIC

数独高级技巧入门链地逻辑及AIC
数独高级技巧入门包括链地逻辑和AIC(Advanced Implications Chains)。
链地逻辑是利用数独细节的一种有效的解题技巧,它允许有经验的数独玩家解决一些更棘手的题目,因此它又被称为逻辑链技巧。
AIC 是一种强大的数独技巧,可以有效地排除一些数字,并在解数独时使用更多的细节。
其次是AIC技巧,它是数独解题中更高级的技巧之一、AIC技巧是将假设和推断结合起来,以便从一系列地逻辑和技巧中得出结论。
它可以让数独玩家分析每个单元格中的可能数字,从而有助于解决更棘手的题目。
AIC技巧通常都是基于高级覆盖、数字组合和限制推理来进行解答的。
最后,值得一提的是,在使用高级技巧解数独时,玩家需要仔细观察数独板上的每一个单元格,以及每一个位置上可用的值。
数独诀窍和技巧

数独是一种基于逻辑推理的数字填充游戏,其解题诀窍和技巧众多,以下是几个关键的解题策略:1. **唯一解法(唯一候选数法/唯一余数法)**:- 在一个单元格(行、列或宫格)中,如果只剩下唯一一个位置可以放置某个数字,那么这个数字就应该填在那里。
2. **排除法(隐性唯一候选数法)**:- 在一个单元格所在的行、列或宫格中,如果一个数字在其他位置都已经出现,那么这个数字就不能出现在当前单元格中。
3. **区块排除法(区块唯一候选数法)**:- 在一个较大的连续空间里,如果一个数字仅在一个小的区块(比如两个行或列的交叉部分)内有候选位置,那么这个数字就在那个区块内唯一的空格里。
4. **单元内排除法**:- 观察某一行、列或宫格中已知的数字,可以排除掉同一行、列或宫格内剩余单元格的对应数字。
5. **对角线分析**:- 在某些变形数独(如对角线数独)中,需要考虑对角线上数字的唯一性和排除法。
6. **连锁反应(显性或隐性数对、三元组、四元组等)**:- 数对:在同一个宫格、行或列内,如果两个单元格共享相同的两个候选数字,那么这两个数字只能分别填在这两个单元格中。
- 类似的逻辑还可扩展到三元组(三个单元格共享三个候选数字)和四元组等更复杂的情形。
7. **区块分析**:- 在某些特定区域(如宫格内部、宫格外围等)内,通过观察数字的分布情况,可以进一步缩小其他单元格的候选数字范围。
8. **十字交叉法**:- 当某行或某列只剩下一个宫格未填数字,而这个宫格在对应的行或列中也只有唯一一个候选数字时,可以确定这个数字的位置。
通过反复应用这些技巧和不断的逻辑推理,即使是复杂的数独也能逐一破解。
记住,数独解题的关键是观察和逻辑推理,而不是盲目的猜测。
数独九宫格各种链的关系

第一种情况:A==B--C==D由A的真假情况可以做出以下BCD关系的枚举。
再次请大家注意本文开头所提到的强弱关系本质1.强关系是说A与B两个事件,假设A不成立,则B一定成立。
2.弱关系是说A与B两个事件,假设A成立,则B一定不成立。
*Y-Wing了,下面是一个*Y-Wing的例子:•通常解释*Y-Wing原理的时候会用如果r4c2=1则r5c1=4;如果r4c2=9则r4c8=4,所以不管r4c2是1还是9,r5c1与r4c8中至少有一个是4,从而得到r5c1与r4c8的等位群格位交集局部〔图中蓝色格〕不含4。
•这样是不是有点猜想的味道呢?很多人都说高级技巧是把猜的东西合理化,其实不然。
•用强弱强链的观点可以这样看r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4),也是得到r5c1与r4c8中至少有一个是4。
•与*Y-Wing较相近的要数*Y-Chain。
•*Y-Wing由三格组成,分别为*y格,*z格,yz格。
*Y-Chain不止三格,需要把一些格合并当作*Y-Wing组成格之一来看。
•单数链以强、弱方式构成环,称为 *-Cycle,无法构成环,则称为 *-Chain。
•*-Cycle 的弱环节除节点外,单元内其它格位的一样候选数均可删除。
•*-Chain 在开口处之两节点共同作用格的一样候选数均可删除。
本质上 *-Cycle 只是 *-Chain 的特例,因此统称为单链。
•单链假设由两条强链与一条弱链构成,就是习称的双强链,有摩天楼、双线风筝、鱼三种连结方式。
•单链假设由两条强链与两条弱链构成环,就是习称的 *-Wing。
*Y-Wing的构造可以分为两种:1. *y格与*z格或者 *y格与yz格同宫。
2. *y格、*z格、yz格在三个不同宫。
*Y-Chian首尾假设能连接起来就成为了*Y-Cycle〔Multi *-Wing〕r4c1(7)==r5c4(7)--r5c2(7)=={r1c2, r2c2}(7) 断开任意一条弱链〔绿色表示〕即成为*Y-Chain的构造。
数独的方法技巧与规律

数独的方法技巧与规律数独是一种经典的逻辑推理游戏,其解题方法可以分为基本技巧和高级技巧两个方面。
下面将详细介绍数独的解题技巧与规律。
数独游戏的目标是在一个9x9的方格中填入数字1-9,使得每一行、每一列和每一个3x3的宫都包含1-9中的每个数字,且每个数字在每一行、每一列和每一个3x3的宫中只能出现一次。
数独的解题过程也就是根据已知的数字,通过逻辑推理逐步填充其他空格的过程。
首先介绍数独的基本技巧和规律:1. “唯一候选数法”:在某个空格中,根据所在行、所在列和所在宫中已经填入的数字来确定该空格的候选数字。
如果某数字只在某个空格的候选数字中出现一次,那么该数字就是该空格的唯一填入数字。
2. “唯余候选数法”:在某个宫中,如果某个数字在该宫中的空格的候选数字中只出现在一个行或一列中,那么该行或该列就是该数字的唯一位置,可以确定该数字的位置。
3. “唯余候选宫法”:在某个行或某个列中,如果某个数字在该行或列中的空格的候选数字中只出现在一个宫中,那么该宫就是该数字的唯一位置,可以确定该数字的位置。
4. “摒弃法”:在某个空格的候选数字中,如果某数字出现在该空格所在的行、列或宫的其他空格的候选数字中,那么该数字就不可能是该空格的填入数字,可以将该数字从该空格的候选数字中摒弃。
5. “排除法”:当某个数字已经出现在某行、某列或某宫的九个空格中的八个空格的候选数字中时,那么该数字一定是出现在剩下的那个空格中,可以确定该空格的填入数字。
以上是数独的基本技巧和规律,可以帮助解题者逐步填充空格。
接下来介绍数独的高级技巧和规律:1. “观察交叉”:在某行、某列或某宫中,如果某数字只出现在两个空格的候选数字中,那么该数字一定是出现在这两个空格中的一个,可以根据这个推理来确定该数字的位置。
2. “数对法”:在某行、某列或某宫中,如果两个空格的候选数字都是两个数字的组合,那么这两个空格一定分别是这两个数字的位置,可以根据这个推理来确定这两个数字的位置。
数独高级解题思路

数独高级解题思路数独是一种用数字填充方格的逻辑游戏,以数字1至9填入每个空格,使得每行、每列和每个九宫格内的数字均不重复。
对于初学者来说,数独可能会有些困难,但是通过掌握一些高级解题思路,你将能够更加迅速、准确地解决数独难题。
一、唯余法唯余法是数独中最基础、最常用的解题方法之一。
其基本思想是通过排除可能性,确定特定位置的数字。
具体步骤如下:1. 扫描整个数独盘面,找到空格(没有数字的方块);2. 对于每个空格,检查同行、同列、同九宫格内已有的数字。
将1至9依次填入空格,检查是否满足数独规则;3. 若填入的数字在同行、同列、同九宫格中均没有重复出现,则该数字为唯一解,可以确定该位置的数字。
二、格局排除法格局排除法是一种高级解题思路,可以通过观察不同空格的数字关系,进一步确定某个位置的数字。
具体步骤如下:1. 扫描整个数独盘面,找到特定数字已经填入的位置;2. 对于这个数字已经填入的位置,观察该数字所在的行、列和九宫格内其他空格;3. 如果其他空格已经确定了相同数字,或者确定了不可能填入该数字的其他数字,那么可以排除该位置的该数字。
三、候选数法候选数法可以理解为一种逆向思维,通过确定每个空格可能填入的数字,从而推出该空格的确定数字。
具体步骤如下:1. 扫描整个数独盘面,找到空格;2. 对于每个空格,推断该位置可能填入的数字,并将其罗列出来;3. 根据该位置所在行、列和九宫格内已有的数字,排除不可能填入的数字;4. 如果某个空格的候选数字只有一个,那么可以确定该位置的数字。
四、数对法数对法是一种通过解决数对(对偶)进行推理的方法。
具体步骤如下:1. 找到数独盘面中有两个空格,这两个空格在同行、同列或同九宫格中,都只能填入相同的两个数字;2. 如果这两个空格中的某一个数字已经确定,那么另一个空格的数字也可以确定;3. 针对第二步中确定的数字,进行必要的唯余法、格局排除法和候选数法等进一步推理。
五、多数对法多数对法是一种进一步发展的解题思路,其基本思想是通过找出两个或多个空格,在同行、同列或同九宫格中只能填入相同的两个或多个数字,从而推断其他位置的数字。
数独九宫格各种链的关系

第一种情况:A==B--C==D由A的真假情况可以做出以下BCD关系的枚举。
再次请大家注意本文开头所提到的强弱关系本质1.强关系是说A与B两个事件,假如A不成立,则B一定成立。
2.弱关系是说A与B两个事件,假如A成立,则B一定不成立。
XY-Wing了,下面是一个XY-Wing的例子:•通常解释XY-Wing原理的时候会用如果r4c2=1则r5c1=4;如果r4c2=9则r4c8=4,所以不论r4c2是1还是9,r5c1与r4c8中至少有一个是4,从而得到r5c1与r4c8的等位群格位交集部分(图中蓝色格)不含4。
•这样是不是有点猜测的味道呢?很多人都说高级技巧是把猜的东西合理化,其实不然。
•用强弱强链的观点可以这样看r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4),也是得到r5c1与r4c8中至少有一个是4。
•与XY-Wing较相近的要数XY-Chain。
•XY-Wing由三格组成,分别为xy格,xz格,yz格。
XY-Chain不止三格,需要把一些格合并当作XY-Wing组成格之一来看。
•单数链以强、弱方式构成环,称为X-Cycle,无法构成环,则称为X-Chain。
•X-Cycle 的弱环节除节点外,单元内其它格位的相同候选数均可删除。
•X-Chain 在开口处之两节点共同作用格的相同候选数均可删除。
本质上X-Cycle 只是X-Chain 的特例,因此统称为单链。
•单链若由两条强链与一条弱链构成,就是习称的双强链,有摩天楼、双线风筝、鱼三种连结方式。
•单链若由两条强链与两条弱链构成环,就是习称的X-Wing。
XY-Wing的结构可以分为两种:1. xy格与xz格或者xy格与yz格同宫。
2. xy格、xz格、yz格在三个不同宫。
XY-Chian首尾若能连接起来就成为了XY-Cycle(Multi X-Wing)r4c1(7)==r5c4(7)--r5c2(7)=={r1c2, r2c2}(7) 断开任意一条弱链(绿色表示)即成为XY-Chain的结构。
数独链的正确使用方法

数独链的正确使用方法
1. 嘿呀,数独链可是个宝啊!就比如在解一个超级难的数独时,你可以把它想象成一根救命稻草!当你看到一些数字有奇妙联系的时候,就赶紧抓住这条数独链呀!就像在大海里抓住了浮木一样。
2. 哇塞,要学会找数独链的起始点哦!好比你要开启一场冒险,得先找到入口呀!比如看到某个格子里只有两种可能数字,那这不就是个绝佳的起始点嘛。
3. 嘿,数独链中强弱链的运用很关键呀!这就像是武林高手的不同功夫,各有奇妙之处。
比如说在一个区域里,强链就像大力金刚掌,直截了当,弱链呢则像绵里藏针,暗藏玄机。
4. 哈哈,可别小看了对数独链的观察呀!这可是寻找宝藏的关键步骤呢!就好像侦探在找线索一样,比如看到几个数字总是同时出现或不出现,那这里面肯定有数独链的踪迹。
5. 哎呀呀,使用数独链的时候要灵活多变呀!不能死脑筋哦。
就跟跳舞一样,要随着节奏灵活转动。
比如遇到复杂的局面,就得像个机灵鬼一样去发现那些隐藏的数独链。
6. 哇哦,数独链还可以组合起来用呢!这多厉害呀,就像把不同的武器组合成超级武器一样。
比如说用几条数独链一起推理出某个关键数字。
7. 嘿嘿,一定要多练习使用数独链啊!就跟练功一样,越练越厉害。
你想想,如果天天练习,那解数独不就手到擒来啦,就像孙悟空耍金箍棒一样轻松!
我的观点结论:数独链真的是解数独的绝妙方法,只要用心去发现和运用,就能在数独的世界里畅游无阻!。
数独九宫格各种链的关系

第一种情况:A==B--C==D由A的真假情况可以做出以下BCD关系的枚举。
再次请大家注意本文开头所提到的强弱关系本质1.强关系是说A与B两个事件,假如A不成立,则B一定成立。
2.弱关系是说A与B两个事件,假如A成立,则B一定不成立。
XY-Wing了,下面是一个XY-Wing的例子:•通常解释XY-Wing原理的时候会用如果r4c2=1则r5c1=4;如果r4c2=9则r4c8=4,所以不论r4c2是1还是9,r5c1与r4c8中至少有一个是4,从而得到r5c1与r4c8的等位群格位交集部分(图中蓝色格)不含4。
•这样是不是有点猜测的味道呢?很多人都说高级技巧是把猜的东西合理化,其实不然。
•用强弱强链的观点可以这样看r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4),也是得到r5c1与r4c8中至少有一个是4。
•与XY-Wing较相近的要数XY-Chain。
•XY-Wing由三格组成,分别为xy格,xz格,yz格。
XY-Chain不止三格,需要把一些格合并当作XY-Wing组成格之一来看。
•单数链以强、弱方式构成环,称为 X-Cycle,无法构成环,则称为 X-Chain。
•X-Cycle 的弱环节除节点外,单元其它格位的相同候选数均可删除。
•X-Chain 在开口处之两节点共同作用格的相同候选数均可删除。
本质上 X-Cycle 只是 X-Chain 的特例,因此统称为单链。
•单链若由两条强链与一条弱链构成,就是习称的双强链,有摩天楼、双线风筝、鱼三种连结方式。
•单链若由两条强链与两条弱链构成环,就是习称的 X-Wing。
XY-Wing的结构可以分为两种:1. xy格与xz格或者 xy格与yz格同宫。
2. xy格、xz格、yz格在三个不同宫。
XY-Chian首尾若能连接起来就成为了XY-Cycle(Multi X-Wing)r4c1(7)==r5c4(7)--r5c2(7)=={r1c2, r2c2}(7) 断开任意一条弱链(绿色表示)即成为XY-Chain的结构。
数独规律与技巧

数独规律与技巧1. 哎呀呀,数独规律里有一条超重要的,就是每行每列每个小九宫格都得有1 到9 数字,还不能重复!就像拼图一样,得把每个数字都摆对地方。
比如说,看到一行里已经有了 1、2、3、5、7、8、9,那剩下的不就是 4和 6 嘛,这不是很明显嘛!2. 嘿,还有个技巧呢,先找出现次数多的数字呀!假如一个数字在很多地方都露了点苗头,那咱就顺着这个线索去找它的位置呀。
就像是警察抓小偷,先锁定那个最可疑的家伙。
比如 5 老是在几个地方晃悠,那咱肯定得重点盯着它呀!3. 哇塞,再告诉你们一个厉害的,要关注那些只剩下几个空格的地方呀!这就好比快到终点的比赛,就剩那么几步了,肯定得全力以赴呀。
像有个小九宫格就剩 3 个空格了,那范围一下子就缩小了呀,肯定容易多了嘛!4. 呀,观察数字之间的关系也很关键嘞!某个数字的旁边可能就暗示了它的“小伙伴”在哪。
就跟好朋友似的,一个出现了,另一个也不远啦。
比如 7 的旁边有个 8,那 8 可能就在附近的几个格子里呀!5. 嘿嘿,别忘了特殊位置哦!比如四角呀,边缘呀。
这些地方可特别啦,它们的限制可能更多。
就像站在舞台边缘的演员,一举一动都很显眼呢。
要是在边上的一个格子只能填某个数字,那不就一下子找到了嘛!6. 哟呵,有时候还可以用排除法呀!把不可能的都排除掉,剩下的就是答案啦。
这就好像排除掉坏苹果,好的那个不就出来了嘛。
比如一个格子不可能是 1 和 2,那不是 3 就是 4 咯!7. 哇哦,还要注意那些重复出现的模式呀!就像一首歌的旋律,一旦你发现了,就能顺着往下唱啦。
要是两个小九宫格有类似的地方,那很可能答案也是相似的呀。
8. 哈哈,数独可是很有趣的嘞!只要掌握了这些规律与技巧,就像有了魔法钥匙,难题都能迎刃而解啦!不信你们试试看呀!我的观点结论就是:数独虽然有难度,但只要熟练运用这些规律与技巧,就能体会到其中的乐趣和成就感!。
(完整版)数独:链的入门学习与运用

数独:链的入门学习和运用链是什么?分析候选数之间的关系以获得线索就是链。
在学习链前我想先说明下什么是“强”关系,什么是“弱”关系?强关系是说A与B两个事件,假如A不成立,则B一定成立,即A、B不能同假。
弱关系是说A与B两个事件,假如A成立,则B一定不成立,即A、B不能同真。
如上图,在5宫仅存两个候选5,这两个5无论哪个为假,另一个必定为真,因而5宫的这两个候选5成强关系。
现在我们来看看2列仅存的候选7,不难发现这两个候选7在2列呈强关系。
同样候选6在7行呈强关系。
我们再来看看F7仅存两个的候选1、5在格内形成强关系。
我们注意到3宫的候选8画得特别漂亮,根据之前学过的知识你能否描述一下它们是怎样呈现什么样的关系的呢?在这里我就不说太多,留待下文慢慢解释,不过先做一点提示,如果你把同色染色格看成一个整体怎样看?细心的同学应该注意到,上面描述的都是A、B非假即真的强关系,貌似我们给强关系的定义是A、B不能同假,似乎忽略了A、B同真的介绍。
这并不是疏忽,而是要说明A、B同真需要更深入的学习,对入门者来说有点难度。
在弄懂强关系后,弱关系就不难理解了,只要A、B不能同真均是弱关系。
我们注意到5宫的候选5应该是强关系,为什么跑来弱关系图了。
弱关系的定义是A、B不能同真,5宫的候选5是一种A、B非假即真的强关系,换句话说就是A、B不可能同真,符合弱关系的定义,因此5宫的候选5同是弱关系,更确切的描述是同时兼有强、弱关系。
在完全弄清强与弱的关系后,我们再来学习一下画链,懂得如何看图作图对阅读本文有莫大的帮助。
如上图,强关系候选数以实线链接,以实线表示为强链,文字表达为“==”(双横线);弱关系候选数以虚线链接,以虚线表示为弱链,文字表达为“--”(单横线);格内链无论强弱均不另行标示;双箭头是把同色候选数视为一个整体。
在理解上述基础概念后,我们现在就开始链的学习。
链之所以被称作链,是因为它们能够像链条一样串起来。
数独高级技巧入门链的逻辑及

[数独高级技巧入门]链的逻辑及AIC这个帖子主要想阐述链是什么,怎么使用链,以及链的逻辑过程,帮助大家首先了解原理,那么以后关于chain、wing之类的按照这个思路都非常容易理解。
首先我想说明下什么是“强”关系,什么是“弱”关系强关系是说A与B两个事件,假如A不成立,则B一定成立。
弱关系是说A与B两个事件,假如A成立,则B一定不成立。
举一个简单的例子帮助大家体会:(图中被划短横线的格表示不含候选数1)这是一个数独的宫,根据数独规则一个宫内出现数字1-9各一次,可以做出以下两点推断:1.左上格不是1,则右中格一定是1;2.左上格是1,则右中格一定不是1。
第一种推断得到这两格的1是强关系,所以可以说两格之间形成一条强链,强链我们通常以双横线表示(==);第二种推断得到这两格的1是弱关系,所以可以说两格之间形成一条弱链,弱链我们通常以单横线表示(——)。
再举一个例子:(图中被划短横线的格表示不含候选数1)上图可以做出三大点推断:1.左上格是1,则中上格及右中格一定不是1;2.中上格是1,则左上格及右中格一定不是1;3.右中格是1,则左上格及中上格一定不是1。
这个例子里,存在着3条弱链,分别是(左上--中上)、(左上--右中)、(中上--右中)。
上面说的是同一数字的强弱关系,当然强弱关系可以不局限于一个数字,下面用例子来说明:(图中被短横线划掉的格说明未知其候选数情况)根据右上格的候选数仅有1与2可以做出以下推断:1.如果该格不能是1,则一定为2;2.如果该格是1,则一定不是2。
推断一说明数字1与2之间是强关系,形成强链;推断二说明其为弱关系,形成弱链。
(图中被短横线划掉的格说明未知其候选数情况)右上格有3个候选数,我们可以做出以下推断:1.如果这格为1,则不能为2或3;2.如果这格为2,则不能为1或3;3.如果这格为3,则不能为1或2。
数字1与2、2与3、1与3之间分别为一条弱链。
像第二张图这样的关系推断,大家可能会不以为意,但是这是理解强弱关系的一个很好的例子,对于后面将要叙述的内容也会有所帮助。
数独_链

链1.链是什么?链是数独高级技巧的核心,它表示两个命题间的关系。
命题有真假之分,我们可以通过分析链来判断某个命题是真还是假。
在数独中,我们要判断真假的命题都是:“某某格子应该填入某某数。
”“A1=3”,“E7=8”,……诸如此类。
分析出了它们的真假,我们就相当于是填出了一个数字。
本文中约定把这些命题表示为“格子(数)”,例如A1(3),E7(8),等等。
链分强链关系、弱链关系两种:强链:两个命题不可以同时为假,本文中用==(双横线)表示;弱链:两个命题不可以同时为真,本文中用--(单横线)表示。
讲了这么多,我们来先找几条链试试吧。
例1:1. H2(4)—H4(4)如果H2和H4都填4,会有什么结果?结果是一行里出现了重复数字,违反了数独规则。
于是我们可以判断H2(4)和H4(4)不能同时为真,即它们呈弱链关系。
2. D1(4)==I1(4)我们仔细观察,会发现第1列除了D1和I1,其他格子都不可能填入4了。
那么无论如何,它们两格中至少有一个4,即不能同假,呈强链关系。
3. G2(1)==G2(6)刚才的两条链都是不同格子间的同一个候选数,这条却是同一个格子中不同的两个候选数。
我们可以把上面两条叫做单链,这条和第4条叫做多链。
G2要么填入1要么填入6,不可能是其他的数字了。
所以它们俩不能同假(要不然G2就没数填了),呈强链。
其实,第2、3两条链也可以看成是弱链,因为他们即符合强链的定义,又符合弱链的定义(不能同真)。
4.G6(1)—G6(8)一个格子内只能填一个数,而如果1和8都成立那么G6就有2个数了。
所以它们不能同时成立,呈弱链。
上面这些都是链的4种基本情况,理解它们后我们就可以往下看第2节了。
2.链的基本应用链之所以被称作链,是因为它们能够像链条一样串起来用:例2:这是一条长度为3的2的单链。
乍看一下它只是3条单链连在一起罢了,难道它还有什么别的性质吗?当然。
由E3(2)==H3(2)—H4(2)==D4(2)我们可以推理出E3(2)==D4(2),即它们不同假。
数独解法知多少?—高级技巧入门:链的逻辑

数独解法知多少?—高级技巧入门:链的逻辑2011-09-29本文行家:林敏舫由成立到不成立即是弱,由不成立到成立即是强首先我想说明下什么是“强”关系,什么是“弱”关系?强关系是说A与B两个事件,假如A不成立,则B一定成立。
弱关系是说A与B两个事件,假如A成立,则B一定不成立。
举一个简单的例子帮助大家体会:(图中被划短横线的格表示不含候选数1)这是一个数独的宫,根据数独规则一个宫内出现数字1-9各一次,可以做出以下两点推断:1.左上格不是1,则右中格一定是1;2.左上格是1,则右中格一定不是1。
第一种推断得到这两格的1是强关系,所以可以说两格之间形成一条强链,强链我们通常以双横线表示(==);第二种推断得到这两格的1是弱关系,所以可以说两格之间形成一条弱链,弱链我们通常以单横线表示(——)。
再举一个例子:(图中被划短横线的格表示不含候选数1)上图可以做出三大点推断:1.左上格是1,则中上格及右中格一定不是1;2.中上格是1,则左上格及右中格一定不是1;3.右中格是1,则左上格及中上格一定不是1。
这个例子里,存在着3条弱链,分别是(左上--中上)、(左上--右中)、(中上--右中)。
上面说的是同一数字的强弱关系,当然强弱关系可以不局限于一个数字,下面用例子来说明:(图中被短横线划掉的格说明未知其候选数情况)根据右上格的候选数仅有1与2可以做出以下推断:1.如果该格不能是1,则一定为2;2.如果该格是1,则一定不是2。
推断一说明数字1与2之间是强关系,形成强链;推断二说明其为弱关系,形成弱链。
(图中被短横线划掉的格说明未知其候选数情况)右上格有3个候选数,我们可以做出以下推断:1.如果这格为1,则不能为2或3;2.如果这格为2,则不能为1或3;3.如果这格为3,则不能为1或2。
数字1与2、2与3、1与3之间分别为一条弱链。
像第二张图这样的关系推断,大家可能会不以为意,但是这是理解强弱关系的一个很好的例子,对于后面将要叙述的内容也会有所帮助。
数独的方法技巧与规律

数独的方法技巧与规律数独是一种受欢迎的逻辑解谜游戏,玩家需要根据已有的数字确定未知格子的数值。
下面是一些常见的数独解题方法、技巧和规律:1.单个候选数法:如果一些格子只有一个候选数字,那么可以确定该数字为格子的数值。
2.唯一候选数法:如果一些数字在行/列/九宫格中只有一个候选位置,那么可以确定该位置的数字为该数字。
3.唯一数字法:如果一些数字在行/列/九宫格中只出现了一次,那么可以确定该位置的数字为该数字。
4.排除法:当候选数法和唯一候选数法无法继续推进时,可以通过排除法进行解题。
通过观察行/列/九宫格中已经确定的数字,可以排除其它候选数,进而确定格子的数值。
5.摒除法:当行/列/九宫格中已经确定的8个数字,只缺一个数字时,可以通过摒除法确定该数字的位置。
6.回溯法:当以上方法都无法继续推进时,可以使用回溯法进行求解。
回溯法是一种穷举的方法,尝试填充一个格子,然后继续向后寻找解,如果无法找到满足要求的解,则回溯到上一个格子,重新尝试新的数值。
7.四宫格法:对于一些数字,在九宫格区域内只能存在于四个格子中,那么即使无法确定具体位置,也可以缩小候选范围。
8.对角线法:对于一些数字,在对角线上只能存在于一些九宫格区域中,那么即使无法确定具体位置,也可以缩小候选范围。
9.链接法:通过连接一些数字在不同行/列/九宫格中的候选位置,来缩小具体位置的候选数。
10. X-Wing法:当一些数字在两行/两列的两个九宫格中都有两个候选位置,且这四个位置恰好形成一个矩形,那么即使无法确定具体位置,也可以推导出该数字在这四行/四列中的另外两个位置。
11. XY-Wing法:对于三个格子A、B、C,如果A和B都是C的候选数,那么如果A和C构成了一对唯一候选单元,且B在这两个唯一候选单元中的第三个格子的候选数,那么可以确定B不是这个数字。
12.双数对法:当一些九宫格中只剩下两个候选数,且这两个候选数只在这两个格子中出现时,可以确定这两个候选数分别在这两个格子中。
数独九宫格各种链的关系
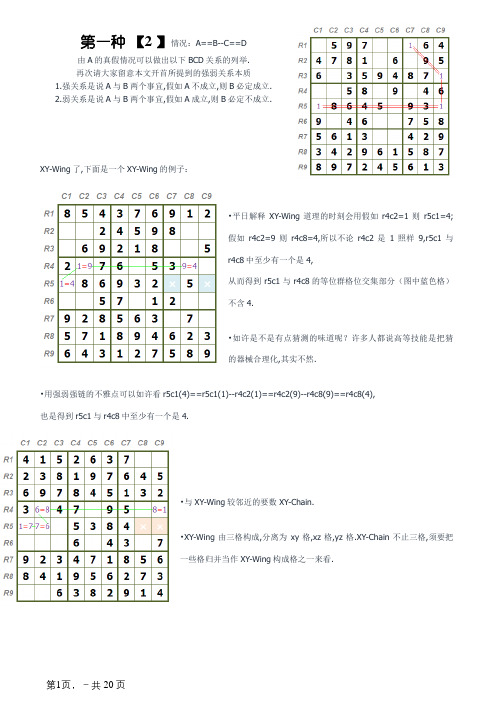
第一种【2 】情况:A==B--C==D由A的真假情况可以做出以下BCD关系的列举.再次请大家留意本文开首所提到的强弱关系本质1.强关系是说A与B两个事宜,假如A不成立,则B必定成立.2.弱关系是说A与B两个事宜,假如A成立,则B必定不成立.XY-Wing了,下面是一个XY-Wing的例子:•平日解释XY-Wing道理的时刻会用假如r4c2=1则r5c1=4;假如r4c2=9则r4c8=4,所以不论r4c2是1照样9,r5c1与r4c8中至少有一个是4,从而得到r5c1与r4c8的等位群格位交集部分(图中蓝色格)不含4.•如许是不是有点猜测的味道呢?许多人都说高等技能是把猜的器械合理化,其实不然.•用强弱强链的不雅点可以如许看r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4),也是得到r5c1与r4c8中至少有一个是4.•与XY-Wing较邻近的要数XY-Chain.•XY-Wing由三格构成,分离为xy格,xz格,yz格.XY-Chain不止三格,须要把一些格归并当作XY-Wing构成格之一来看.•单数链以强.弱方法构成环,称为 X-Cycle,无法构成环,则称为 X-Chain.•X-Cycle 的弱环节除节点外,单元内其它格位的雷同候选数均可删除.•X-Chain 在启齿处之两节点配合感化格的雷同候选数均可删除.本质上 X-Cycle 只是 X-Chain 的特例,是以统称为单链.•单链若由两条强链与一条弱链构成,就是习称的双强链,有摩天楼.双线风筝.鱼三种贯穿连接方法. •单链若由两条强链与两条弱链构成环,就是习称的 X-Wing.XY-Wing的构造可以分为两种:1. xy格与xz格或者xy格与yz格同宫.2. xy格.xz格.yz格在三个不同宫.XY-Chian首尾若能衔接起来就成为了XY-Cycle(Multi X-Wing)r4c1(7)==r5c4(7)--r5c2(7)=={r1c2, r2c2}(7)断开随意率性一条弱链(绿色表示)即成为XY-Chain的构造.得到{r1c2, r2c2}与r4c1至少有一个为7.例如断开上端r8c57的弱链后,可以得到r8c5(7)与r8c7(7)所以可以删除{r1c2, r2c2}与r4c1等位群格位的交至少有一个成立,即可删除这两格等位群格位交集的7,集r1c3的候选数7.其他三种断开弱链可以或许做何删减,大家可以本身尝试推导.Guardians(守护者)的技能,也有地方称之为Broken Wings或者Turbot-Fish.其描写的是某一个候选数X的情况,当有偶数条强链,且两个端点处于统一unit时,这时可以删除两个端点上的候选数X,假如该unit出这两头点非分特别只有一格含有候选数X,则该格必定就是X.下图:从蓝色格动身到达红色格,依据它们之间的逻辑关系,可以得到红色格有雷同的真假值.•红色格若为假,没问题两个都可删除,红色格若为真,则违背数独原则也应该删除. •结论:红色格应予删除•用链的不雅点来看:r3c8(9)==r3c8(2)--r6c8(2)==r6c6(2)--r9c6(2)==r9c6(9),是以可以删除r9c8的候选数9.•亦可如许懂得,假如r3c8不为9,r3c8为2,则r6c8不为2,r6c6为2,r9c6不为2,即r9c6为9;反过来,假如r9c6不为9,则r9c6为2,r6c6不为2,r6c8为2,r3c8不为2,即r3c8为9;可见r3c8与r9c6至少有一个为9,是以可以删除r9c8的候选数9.•双强链的按其强链地点区域及构成可分为三种.1. 摩天楼(Skyscraper)2. 鱼(Fish)3. 双线风筝(Two Strings Kite)摩天楼以下是双线风筝(Two Strings Kite).鱼(Fish)的构造及其删减情况.1. 上左图,两条强链一条在「行」另一条在「列」,红色顶端之配合感化格(红色「X」)就是不能有构成强链数字之处,这个构造称为双线风筝.2. 上右图,两条强链一条在「宫」另一条在「列」,红色顶端之配合感化格(红色「X」)就是不能有构成强链数字之处,这个构造称为鱼.(C2.C5各有一个{XY}数对,是以R5的两格也为{XY}数对)当r2c2是X时,可以得到r5c2为Y,继而r5c5为X,r3c5为Y;反之,当r2c2是Y时,可以得到r5c2为X,继而r5c5为Y,r3c5为X.也就是说r2c2与r3c5也为{XY}数对,是以可以删除其等位群格位的交分散候选数XY.•双强链的基座(Base)必须在统一单元,且链顶(Top)必须有雷同感化格才有删减后果. •有时两条强链虽有雷同的基座,但链顶没有配合感化格,如斯将达不到删减的后果.•是以就有所谓的进阶型的双强链.•因为 A==B==C==D 三条强链会造成 A 与 D 有相反的真假值,是以可以当一条强链应用.•不雅察一.三条形成的双强链不会太庞杂,是以以下我们就以如许的构形提出实例加以解释.•在数独的解题技法称这种解法为 X-Chain.如右图附一道题的七种解法.解法1解法 #2解法 #3解法 #4解法 #5解法 #6解法 #7单数链解法的三要素就是:1. 有强关系的两头点.2. 两头点有配合感化格.3. 配合感化格有删减后果.•右图是这是摩天楼的扩充型的思虑办法,黄色为底(起点),红色为顶(终点).•当黄色为真,则往绿色偏向推动,当黄色为假则往红色偏向推动.•无论黄色为真或假,经推导的成果,红色的两个端点必定有一点为真,是以它们是强关系.•强关系的配合感化格可以将候选数 2 删除,如图上彀点标示之格位.左图的别的一种推法:•这是摩天楼的扩充型,黄色为底(起点),红色为顶(终点).•当黄色为真,则往绿色偏向推动,当黄色为假则往红色偏向推动.•无论黄色为真或假,经推导的成果,红色的两个端点必定有一点为真,是以它们是强关系.•强关系的配合感化格可以将候选数 2 删除,如图上彀点标示之格位.点算图示格的候选数,可以发明形成XY-Cycle,可以删的数比jcvb 提到XY-Chain略多一些.右图:重要应用了r2c5的8的删减,可以得到第五列的摒除解r7c5=8.欠一数对Almost Locked Pair数对.三链数.四链数被统称为Locked Candidates,假如还差一点的也就是Almost Locked Candidates.我们取个中的数对部分,也就是Almost Locked Pair来讲授.起首讲一下构造与结论:(“/”失落格表示不含候选数XY)看R1,数字“XY”中的一个在r1c4,另一个在r1c123,也就是说r1c123含有“XY”中的一个数,第一宫的数字“XY”中的另一个在r2c1,所以可以得到第一宫的其他格不含有候选数XY,因为{r1c123, r2c1} 为 {XY}数对.反之亦然.R8的“78”在r8c679三格,因为r9c8的候选数为78,所以r8c79只能有“78”中的一个,所以R8的“78”另一个在r8c6,所以r8c6的候选数为78.数字1对第八宫摒除,得到r8c5=1.微变一下构造:(“/”部分表示不含候选数XYZ)r1c45的部分个中一个会是Z,一个是{XY}之一,是以r1c123含有{XY}中的另一个,{r1c123, r1c45}为{XY}数对({r1c123, r1c4, r1c5}为{XYZ}三链数),所以{r1c123, r2c1}为{XY}数对,所以可以删除第一宫其他格的候选数XY.r4c1的候选数为68,第四宫{68}中的另一个在r5c12之中;r5c12含有{68}中的一个,与r5c7的68形成{68}数对,可以删除r5c9的候选数6.数字78对C7摒除可以得到r89c7的{78}数对;中图:数字8对第六宫摒除,得到第六宫的8在C8;右图:数字78对R8摒除,得到r8c67为{78}数对.左图:r4c1的候选数为68,第四宫{68}中的另一个在r5c12之中;r5c12含有{68}中的一个,与r5c7的68形成{68}数对,可以删除r5c9的候选数6.右图:看r6c3的候选数为17,第四宫{17}中的另一个在r5c23中,R5的其他格只有r5c9含候选17,所以可以肯定r5c9的候选数为17,即删除6.(图中标示候选数表示该格仅含这些候选数)•看到这个构造,大家头脑里会有冒出什么结论呢?想不到也没紧要,可以跟着我们的思绪来.•先看r1c5的候选数为wx,所以r1c23中要不不含wx,要不只能有wx之一;再看r2c1候选数为yz,同样的r1c23中要不不含yz,要不只含个中一个;但r1c23没有其他候选数,按照上述剖析,其构成即为有『wx』中的一个和『yz』中的一个.也就是说我们可以将{r1c23,r1c5}看作wx数对,{r1c23,r2c1}看作yz数对,继而这两个“数对”所影响规模的对应数字即可删减.•这题有比较显著的单链,但用“欠一数对”尝尝要怎么不雅察呢?•因为橙色的23,蓝色至多含有23中的一个,又因为绿色的16,蓝色至多含有16中的一个,蓝色仅含候选数1236,故蓝色构成为16中的一个和23中的一个,{r1c23,r1c5}构成23数对,{r1c23,r2c2}构成16数对.故可以删除第一行其他格的候选数23,第一宫其他格的候选数16.Y-Wing(可能与XY-Wing混杂),有的地方称为W-Wing(可能与WXYZ-Wing混杂),本帖采用Y-Wing的名称."数对"为蓝色格所示{23},加之第四行数字3,构成Y-Wing,可以删除r5c7与r6c6的候选数2.M-Wing的构造:•大家可以比较一下上两图,差别在于r5c2的候选数情况,但是他们的推导进程是雷同的.•橙格仅含候选数ab,即只有2种情况:1. 为b;2. 为a,则绿格不为a->蓝格为a(即蓝格不为b)->紫格为b.•以链的不雅点:r2c7(b)==r2c7(a)--r2c2(a)==r5c2(a)--r5c2(b)==r5c5(b),即r2c7==r5c5为b的强链.•那么为什么他们会有雷同的结论呢?•因为无论是用什么不雅点来剖析这个成果,用到的都是r5c2是a则不是b,是b则不是a的弱关系不雅点,而是否消失其他候选数并不影响弱关系的成立.所以,M-wing的链关系可以总结为右上图.个中X为任何数.•涂色四格构成M-Wing的构造,可以删除r6c2的候选数9;•可以按照以下思绪推导:r6c5有两种情况:1. 为9;2. 为3->r6c7不为3->r3c7为3->r3c7不为4->r3c2为9.•则r6c5与r3c2至少有一格为9,可以删除它们配合感化格r6c2的9.R6C4<>8(=49)->R3C4=8(<>5)->R2C4=5->R2C3=2->R5C3=6->R5C7=49->R56C4,R56C7=独一矩形.即R6C4=8.看一个Swordfish的例子:X-Cycle演习题。
数独的技巧口诀及解释

数独的技巧口诀及解释数独是一种逻辑推理游戏,通过填写9×9网格中的数字,使得每一行、每一列、每一个3×3宫格中的数字都是1到9且不重复。
下面是数独游戏中常用的技巧和口诀及其解释:1.唯一候选数法:如果一些格子只剩下一个候选数,那么这个格子就只能填入这个数。
这个技巧是数独解题的基本法则。
2.找宫限制法:通过排除法,找到一些宫格中唯一的候选数,然后填入相应的格子中。
这个技巧在寻找宫格的唯一候选数时非常有用。
3.唯一数法:如果一些格子是其所在行、列、宫内唯一的候选数,那么这个格子就只能被填入这个数。
4.隐性唯一候选者法:如果一些数在其中一行、列或宫中只有一个格子可以填入,那么该格子只能填入这个数。
这个技巧常用于解决九宫格中的难题。
5.锁定候选数法:当一些数只能在一个宫格的其中一行或其中一列中填入,那么这个数所在行(列)其它的宫格就不能填入这个数。
这个技巧常用于解决九宫格中的难题。
6.链接数法:当两个宫格有相同的两个候选数,并且这两个宫格在同一行(列)上,那么这两个宫格中其它的格子就不能填入这两个候选数。
这个技巧常用于解决难度较高的数独题目。
7.排除法:通过排除一些候选数,缩小格子可能填入的数字范围,从而减少后续填写的可能性。
这个技巧是数独解题时常用的策略之一8.先试填法:当在一些格子中填入一个候选数后,可以通过推理和验证来判断这个数是否正确。
如果不正确,则需要回退到之前的状态重新尝试。
这个方法适用于解决难度较高的数独题目。
9.分支法:当无法通过上述技巧解出数独时,可以选择一种可能的填数方案,填写一个候选数,并在此基础上继续推理和验证。
如果结果正确,则可以继续推理;如果结果错误,则需要回退到之前的状态重新尝试。
这个方法适用于解决难度非常高的数独题目。
10.逻辑推理法:数独游戏的核心在于通过逻辑推理来确定每个格子的填数结果。
这包括根据已知的数字关系,通过上述技巧进行推理,逐步揭示每个格子的候选数,并最终确定每个格子的填数结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[数独高级技巧入门]链的逻辑及AIC
这个帖子主要想阐述链是什么,怎么使用链,以及链的逻辑过程,帮助大家首先了解原理,那么以后关于chain、wing之类的按照这个思路都非常容易理解。
首先我想说明下什么是“强”关系,什么是“弱”关系强关系是说A与B两个事件,假如A不成立,则B一定成立。
弱关系是说A与B两个事件,假如A成立,则B 一定不成立。
举一个简单的例子帮助大家体会:
(图中被划短横线的格表示不含候选数1)这是一个数独的宫,根据数独规则一个宫内出现数字1-9各一次,可以做出以下两点推断:1.左上格不是1,则右中格一定是1;2.左上格是1,则右中格一定不是1。
第一种推断得到这两格的1是强关系,所以可以说两格之间形成一条强链,强链我们通常以双横线表示(==);第二种推断得到这两格的1是弱关系,所以可以说两格之间形成一条弱链,弱链我们通常以单横线表示(——)。
再举一个例子:(图中被划短横线的格表示不含候选数1)上图可以做出三大点推断:1.左上格是1,则中上格及右中格一定不是1;2.中上格是1,则左上格及右中格一定不是1;3.右中格是1,则左上格及中上格一定不是1。
这个例子里,存在着3条弱链,分别是(左上--中上)、(左上--右中)、(中上--右中)。
上面说的是同一数字的强弱关系,当然强弱关系可以不局限于一个数字,下面用例子来说明:(图中被短横线划掉的格说明未知其候选数情况)根据右上格的候选数仅有1与2可以做出以下推断:1.如果该格不能是1,则一定为2;2.如果该格是1,则一定不是2。
推断一说明数字1与2之间是强关系,形成强链;推断二说明其为弱关系,形成弱链。
(图中被短横线划掉的格说明未知其候选数情况)右上格有3个候选数,我们可以做出以下推断:1.如果这格为1,则不能为2或3;2.如果这格为2,则不能为1或3;3.如果这格为3,则不能为1或2。
数字1与2、2与3、1与3之间分别为一条弱链。
像第二张图这样的关系推断,大家可能会不以为意,但是这是理解强弱关系的一个很好的例子,对于后面将要叙述的内容也会有所帮助。
相信通过上面的说明大家已经了解了强弱链是什么,接下来我们将强弱链连接起来。
第一种情况:A==B--C==D由A的真假情况可以做出以下BCD关系的枚举。
再次请大家注意本文开头所提到的强弱关系本质1.强关系是说A与B 两个事件,假如A不成立,则B一定成立。
2.弱关系是说A与B两个事件,假如A成立,则B一定不成立。
(图中红色部分表示根据上一个的真假情况必然是这样的推导)可见A与D不全为假,即A与D一定有一个为真。
当A 与D有等位群格位的交集时,即可做出相应删减。
(图示技巧名为Skyscraper)根据强弱关系,我们找到了一条符合
A==B--C==D的强弱链组:r3c1(2)==r3c7(2)--r9c7(2)==r9c2(2)。
根据上文提到的逻辑关系,可以得到r3c1=2与r9c2=2至少有一个成立,所以可以删去它们等位群格位的交集(即橙色区域)的候选数2。
补充说明:发现很多人对于第七列的画法存在疑问,为什么不标双线(强链),因为这里运用的是“是A非B”的弱关系,所以只能是标单线(弱链)的,关于“强强强”
的链接我们在后文提到是无法得到任何结论的。
我们可以从强弱关系的逻辑把上述这条链走一遍,共有以下两种情形:1)r3c1=2;2)r3c1<>2->r3c7=2
(强关系,非A是B)->r9c7<>2(弱关系,是A非B)->r9c2(强关系,非A是B)。
也就是r3c1和r9c2至少有一个是2(强关系,非A即B),如果r3c7和r9c7之间用强关系的逻辑(非A即B)看的话,从r3c7=2是无法得到r9c7<>2的,这条推理也就到此为止,无法进行下去。
若换一种观点,仍然看2,有r1c2==r9c2--r9c7==r3c7,此时就需要使用r9c7和r3c7的强关系了。
所以强弱关系是按照需要来使用的,将逻辑连贯起来;另一方面,很多人会认为强关系包括了弱关系,因为“非A即B”的逻辑是不包括“是A 非B”的逻辑的,所以这当然是错误的观点,强弱关系是两种不同的逻辑,且是相互独立的。
根据叶卡林娜前面对于强链的叙述,以下是一个双强链的实例,也是大家耳熟能详的X-Wing。
1.上左图,数字4在C4,C8形成X-Wing。
2.上右图,R2,R4除了形成X-Wing的四格之外,其它格位不能存在数字4,因此画X处就是可以删减候选数4的格位。
●X-Wing用之前提到的强弱强链观察可以找到2组,以上图为例:
r2c4==r4c4--r4c8==r2c8,得到r2c4与r2c8的4至少有一个成立,所以可以删除R2其他格的候选数4;r4c4==r2c4--r2c8==r4c8,得到r4c4与r4c8的4至少有一个成立,所以可以删除R4其他格的候选数4。
有时运用不同的强弱强链,能达到相同的删减效果,下面就是一个例子:
左侧使用的是r5c1==r5c9--r3c9==r1c7的强弱强链;
右侧使用的是r3c2==r3c9--r5c9==r5c1的强弱强链。
两种观察方法均可以删除r1c1的候选数1。
上面的几个例子都是关于单一数的强弱强链的,在数独的解题技巧里我们将这类成为X-Chain。
关于单一数链应用我们放在双强链解法的运用这个主题中继续讨论。
当把链的条数增加的时候,也就是A==B--C==D--E==F时,也能够推导出A 与F至少有一个为真,这边就不做枚举了,大家可以自行推导下。
下面来看一些牵扯到异数的强弱强链的例子。
要说异数强弱强的关系肯定要提到XY-Wing了,下面是一个XY-Wing的例子:(图中三格的候选数由点算即得)
通常解释XY-Wing原理的时候会用如果r4c2=1则r5c1=4;如果r4c2=9则
r4c8=4,所以不论r4c2是1还是9,r5c1与r4c8中至少有一个是4,从而得到r5c1与r4c8的等位群格位交集部分(图中蓝色格)不含4。
这样是不是有点猜测的味道呢很多人都说高级技巧是把猜的东西合理化,其实不然。
用强弱强链的观点可以这样看
r5c1(4)==r5c1(1)--r4c2(1)==r4c2(9)--r4c8(9)==r4c8(4),也是得到r5c1与r4c8中至少有一个是4,这样的观察是不是更逻辑化呢欢迎大家提出你的看法。
与XY-Wing较相近的要数XY-Chain。
XY-Wing由三格组成,分别为xy格,xz格,yz格。
XY-Chain不止三格,需要把一些格合并当作XY-Wing组成格之一来看。
(这些我们会在相应主题再讨论)
下面来看一个例子:
这里就不用如果怎么则怎么来解释了,毕竟通过上面一些介绍,大家可以用强弱强这样的逻辑关系解释,不需要用如果怎么样的解释。
以XY-Wing的观点来看的话可以将r4c2作xy格,r4c9作xz格,{r5c1,r5c2}作为yz格。
以强弱链的观点来看略复杂,因为由4条强链组成,请大家以r4c9为起点依次观察交替的强链(红色)、弱链(绿色)。
可以得到两端点r5c1(1)、r4c9(1)至少有一个成立,所以可删除两者交集
r5c89的候选数1。
有的时候我们可以把两格看作一组,例如在双强链解法运用中的第六题:
r1c4(7)==r5c4(7)--r5c2(7)=={r1c2,r2c2}(7)得到{r1c2,r2c2}与r1c4至少有一个为7。
所以可以删除{r1c2,r2c2}与r1c4等位群格位的交集r1c3
的候选数7。
XY-Chian的首尾若能连接起来就成为了XY-Cycle(Multi X-Wing)
上图中断开任意一条弱链(绿色表示)即成为XY-Chain的结构。
例如断开上端r8c57的弱链后,可以得到r8c5(7)与r8c7(7)至少有一个成立,即可删除这两格等位群格位交集的7(这里交集是R8除这两格外的格)。
其他三种断开弱链能够做何删减,大家可以自己尝试推导。
再来看另一种涉及双数关系的技巧Y-Wing的逻辑关系:
用链的观点来看:
r3c8(9)==r3c8(2)--r6c8(2)==r6c6(2)--r9c6(2)==r9c6(9),因此可以删除r9c8的候选数9。
亦可这样理解,如果r3c8不为9,r3c8为2,则r6c8不为2,r6c6为2,r9c6不为2,即r9c6为9;反过来,如果r9c6不为9,则r9c6为2,r6c6不为2,r6c8为2,r3c8不为2,即r3c8为9;可见r3c8与r9c6至少有一个为9,因此可以删除r9c8的候选数9。
