图论专题 二分图
图论——二分图1:二分图以及判定
图论——⼆分图1:⼆分图以及判定图,有有向图,⽆向图,稠密图,简单图······算法,有贪⼼法,⼆分法,模拟法,倍增法······那,⼆分图是啥?⼆分法+有向图?于是,我查了许多资料,才对它有⼀定了解。
⼆分图:⼆分图,是图论中的⼀种特殊模型,设G=(V,E)是⼀个⽆向图,如果顶点V可分割为两个互不相交的⼦集(A,B),并且同⼀集合中不同的两点没有边相连。
这就是⼆分图。
举个栗⼦吧:这是不是⼆分图?反正我第⼀次看觉得不是其实,是的,他是⼆分图,尽管看上去是连着的。
若我们将图中的⼀些边转⼀下,变成:这就是⼀个明显的⼆分图。
集合A与B中的点互不相连。
因此,在⼿动判定⼆分图时学会转边!辣魔,⼆分图要⽤计算机判定怎么实现?数竞⼤佬:简单!!!!染⾊⼤法!!!有没有熟悉的感觉0表⽰还未访问,1表⽰在集合A中,2表⽰在集合B中。
col(color)储存颜⾊。
初始化为0.上代码:其实是模板可以记忆。
1 vector <int> v[N];2void dfs(int x,int y){3 col[x]=y;4for (int i=0; i<v[x].size(); i++) {5if (!col[v[x][i]]) dfs(v[x][i],3-y);6if (col[v[x][i]]==col[x]) FLAG=true; //产⽣了冲突7 }8 }9for (i=1; i<=n; i++) col[i]=0; //初始化10for (i=1; i<=n; i++) if (!col[i]) dfs(i,1); //dfs染⾊11if (FLAG) cout<<"NO"; else cout<<"YES";下⼀章我们将讲到⼆分图的匹配,我们明天见。
二分体 图论

二分体图论
1.定义
二分图,又称二部图,是图论中的一种特殊模型。
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G是一个二分图。
2.判定
无向图G={V, E},如果可以把结点分成不相交的两部分,即X和Y,使得每条边的其中一个端点在X中,另一个端点在Y中,则称图G 是二分图。
二分图-无奇数图
无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
3.性质
1.最小点覆盖=最大匹配数
2.最小边覆盖=点数-最小点覆盖(最大匹配数)
3.最小路径覆盖=原图的结点数-新图的最大匹配数。
4.最大独立集=点数-最小点覆盖(最大匹配数)
4.匹配
二分图匹配:给定一个二分图G={V, E},将E的子集M称作一个匹配,如果M中的任意两条边都没有公共端点。
多重匹配:二分图中某些点可以被匹配多次。
最大匹配:包含的边数最多的匹配。
X(Y) -完全匹配:X(Y)中的所有顶点都出现在匹配M中。
完全匹配:所有的点都在匹配边上的匹配(M既是X-完全匹配,又是Y-完全匹配)。
最佳匹配:如果G为加权二分图,则权值和最大的完美匹配称为最佳匹配。
5.相关算法:
二分图最大匹配:匈牙利算法、HK算法、网络流最大流
二分图多重匹配:网络流最大流
二分图最佳匹配:KM算法、网络流最大流。
完全二分图

图2
若 (这里表示顶点集中元素的个数),且中无相邻的顶点对,中亦然,则称图为二分图;特别地,若对任意, 与中每个顶点相邻,则称图G为完全二分图(complete bipartite graph),或称完全偶图,记为。
相关概念
图G=(V,E)各条边都加上方向的图称为有向图,否则称为无向图。如果有的边有方向,有的边无方向,则称 为混合图。
完全二分图
数学术语
01 基本概念
03 相关结论
目录
02 相关概念
设G=(V,E)为二分图,V=XUY,且X中的任一顶点与Y中每一个顶点均有且仅有唯一的一条边相连,则称G为完 全二分图或完全偶图。
基本概念
直观地讲,对于平面上的n个点,把其中的一些点对用曲线或直线连接起来,不考虑点的位置与连线曲直长短, 这样形成的一个关系结构就是一个图。记成G=(V,E),V是以上述点为元素的顶点集,E是以上述连线为元素的边 集。
赋权图是指每条边都有一个(或多个)实数对应的图,这个(些)实数称为这条边的权(每条边可以具有多个权)。 赋权图在实际问题中非常有用。根据不同的实际情况,权数的含义可以各不相同。例如,可用权数代表两地之间 的实际距离或行车时间,也可用权数代表某工序所需的加工时间等。
相关结论
定理1 推论1
定理2 推论2
如果图的两顶点间有边相连.则称此两顶点相邻,每一对顶点都相邻的图称为完全图,否则称为非完全图.设 为n阶无向简单图,若中每个顶点均与其余的个顶点相邻,则称为n阶无向完全图,简称n阶完全图,记做。设为n 阶有向简单图,若中每个顶点都邻接到其余的个顶点,又邻接于其余的个顶点,则称是n阶有向完全图。
图1分别列出了。图2分别列出了1阶有向完全图、2阶有向完全图、3阶有向完全图。
图论:二分图多重匹配

图论:⼆分图多重匹配使⽤最⼤流和费⽤流解决⼆分图的多重匹配之前编辑的忘存了好⽓啊。
本来打算学完⼆分图的乱七⼋糟的匹配之后再去接触⽹络流的,提前撞到了之前我们说的⼆分图最⼤匹配和⼆分图最⼤权匹配有⼀个特点,那就是没个点只能与⼀条边相匹配如果规定⼀个点要与L条边相匹配,这样的问题就是⼆分图的多重匹配问题然后根据边是否带权重,⼜可以分为⼆分图最⼤多重匹配和⼆分图最⼤权多重匹配(⼆分图多重最佳完美匹配)⾸先给出⼆分图多重最⼤匹配的做法:在原图上建⽴源点S和汇点T,S向每个X⽅点连⼀条容量为该X⽅点L值的边,每个Y⽅点向T连⼀条容量为该Y⽅点L值的边原来⼆分图中各边在新的⽹络中仍存在,容量为1(若该边可以使⽤多次则容量⼤于1),求该⽹络的最⼤流,就是该⼆分图多重最⼤匹配的值然后给出⼆分图多重最优匹配(⼆分图多重最⼤权匹配)的做法:在原图上建⽴源点S和汇点T,S向每个X⽅点连⼀条容量为该X⽅点L值、费⽤为0的边,每个Y⽅点向T连⼀条容量为该Y⽅点L值、费⽤为0的边原来⼆分图中各边在新的⽹络中仍存在,容量为1(若该边可以使⽤多次则容量⼤于1),费⽤为该边的权值。
求该⽹络的最⼤费⽤最⼤流,就是该⼆分图多重最优匹配的值这道题⾥⾯,⼀共有X⽅点这么多的电影,每个电影需要拍摄多少天就是对应的X⽅点L值,然后每⼀天是⼀个Y⽅点,由于每⼀天只能拍摄⼀部电影,所有Y⽅点的L值均为1下⾯介绍⼀下实现:int n,sum,cnt,ans;int g[maxn],cur[maxn];int str[25][10];struct Edge{int u,v,next,cap,flow;}e[maxm];这⾥⾯的cur数组是g数组的临时数组str⽤来保存每⼀个电影可以在哪⼀天拍摄Edge是⽹络流图⾥⾯的边void addedge(int u,int v,int c){e[++cnt].u=u;e[cnt].v=v;e[cnt].cap=c;e[cnt].flow=0;e[cnt].next=g[u];g[u]=cnt;e[++cnt].u=v;e[cnt].v=u;e[cnt].cap=0;e[cnt].flow=0;e[cnt].next=g[v];g[v]=cnt;}建图的时候,注意怎么赋值的接下来根据题意建图:for(int i=1;i<=n;i++){for(int j=1;j<=7;j++)scanf("%d",&str[i][j]);scanf("%d%d",&d,&w);sum+=d;addedge(0,i,d); //容量为需要多少天for(int j=1;j<=7;j++)for(int k=0;k<w;k++)if(str[i][j]) addedge(i,20+k*7+j,1);}for(int i=21;i<=370;i++) addedge(i,371,1);ans=maxflow(0,371);0为源点,371为汇点sum最后进⾏⼀个统计,和源点出发的最⼤流量进⾏⽐较,如果相等,说明电影排的开然后是求最⼤流的⼀个板⼦int maxflow(int st,int ed){int flowsum=0;while(bfs(st,ed)){memcpy(cur,g,sizeof(g));flowsum+=dfs(st,ed,INF);//cout<<"#"<<flowsum<<" ";}return flowsum;}具体的DFS和BFS这⾥不作为重点,以后再说下⾯给出完整的实现:1 #include<cstdio>2 #include<cstring>3 #include<algorithm>4using namespace std;5const int INF=1000000000;6const int maxn=1005;7const int maxm=20005;8int n,sum,cnt,ans;9int g[maxn],cur[maxn];10int str[25][10];11struct Edge{int u,v,next,cap,flow;}e[maxm];12void addedge(int u,int v,int c)13 {14 e[++cnt].u=u;e[cnt].v=v;e[cnt].cap=c;15 e[cnt].flow=0;e[cnt].next=g[u];g[u]=cnt;1617 e[++cnt].u=v;e[cnt].v=u;e[cnt].cap=0;18 e[cnt].flow=0;e[cnt].next=g[v];g[v]=cnt;19 }20int q[maxn],vis[maxn],d[maxn];21bool bfs(int st,int ed)22 {23 memset(q,0,sizeof(q));24 memset(vis,0,sizeof(vis));25 memset(d,-1,sizeof(d));26 vis[st]=1;d[st]=0;27int h=0,t=1;28 q[t]=st;29while(h!=t)30 {31 h=h%maxn+1;32int u=q[h];33for(int tmp=g[u];tmp;tmp=e[tmp].next)34 {35if(!vis[e[tmp].v]&&e[tmp].cap>e[tmp].flow)36 {37 vis[e[tmp].v]=1;38 d[e[tmp].v]=d[u]+1;39if(e[tmp].v==ed) return true;40 t=t%maxn+1;41 q[t]=e[tmp].v;42 }43 }44 }45return false;46 }47int getpair(int x)48 {49if(x%2==0)50return x-1;51else return x+1;52 }53int dfs(int x,int ed,int a)54 {55if(x==ed||a==0) return a;56int flow=0,f;57for(int tmp=cur[x];tmp;tmp=e[tmp].next)58 {59if(d[e[tmp].v]==d[x]+1&&(f=dfs(e[tmp].v,ed,min(a,e[tmp].cap-e[tmp].flow)))>0)60 {61 e[tmp].flow+=f;62 e[getpair(tmp)].flow-=f;63 a-=f;64 flow+=f;65if(a==0) break;66 }67 }68return flow;69 }70int maxflow(int st,int ed)71 {72int flowsum=0;73while(bfs(st,ed))74 {75 memcpy(cur,g,sizeof(g));76 flowsum+=dfs(st,ed,INF);77//cout<<"#"<<flowsum<<" ";78 }79return flowsum;8081 }82void init()83 {84 sum=cnt=0;85 memset(g,0,sizeof(g));86 }87int main()88 {89int T,d,w;90 scanf("%d",&T);91while(T--)92 {93 init();94 scanf("%d",&n);95for(int i=1;i<=n;i++)96 {97for(int j=1;j<=7;j++)98 scanf("%d",&str[i][j]);99 scanf("%d%d",&d,&w);100 sum+=d;101 addedge(0,i,d); //容量为需要多少天102for(int j=1;j<=7;j++)103for(int k=0;k<w;k++)104if(str[i][j]) addedge(i,20+k*7+j,1);105 }106for(int i=21;i<=370;i++) addedge(i,371,1);107 ans=maxflow(0,371);108if(ans==sum) printf("Yes\n");109else printf("No\n");110 }111return0;112 }据说这是典型的最⼤流题⽬,然⽽为了强⾏安利⼀波⼆分图的多重匹配,就不说成那个了。
二分图理论

*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图,本节先介绍二部图的基本概念和主要结论,然后介绍它的一个重要应用—匹配。
定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ,满足(1)12V V V =,12V V φ=;(2)(,)e u v E ∀=∈,均有1u V ∈,2v V ∈。
则称G 为二部图或偶图(Bipartite Graph 或Bigraph),1V 和2V 称为互补顶点子集,常记为12,,G V V E =。
如果1V 中每个顶点都与2V 中所有顶点邻接,则称G 为完全二部图或完全偶图(Complete Bipartite Graph),并记为,r s K ,其中12,r V s V ==。
由定义可知,二部图是无自回路的图。
图7-55中,(),(),(),(),()a b c d e 都是二部图,其中(),(),(),()b c d e 是完全二部图1,32,32,43,3,,,K K K K 。
图7-55二部图示例显然,在完全二部图中,r s K 中,顶点数n r s =+,边数m rs =。
一个无向图如果能画成上面的样式,很容易判定它是二部图。
有些图虽然表面上不是上面的样式,但经过改画就能成为上面的样式,仍可判定它是一个二部图,如图7-56中()a 可改画成图()b ,图()c 可改画成图()d 。
可以看出,它们仍是二部图。
图7-56二部图示例定理7.5.1 无向图,G E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。
证明 先证必要性。
设G 是具有互补节点子集1V 和2V 的二部图。
121(,,,,)k v v v v 是G 中任一长度为k 的回路,不妨设11v V ∈,则211m v V +∈,22m v V ∈,所以k 必为偶数,不然,不存在边1(,)k v v 。
再证充分性。
设G 是连通图,否则对G 的每个连通分支进行证明。
算法学习:图论之二分图的最优匹配(KM算法)

二分图的最优匹配(KM算法)KM算法用来解决最大权匹配问题:在一个二分图内,左顶点为X,右顶点为Y,现对于每组左右连接XiYj有权wij,求一种匹配使得所有wij的和最大。
基本原理该算法是通过给每个顶点一个标号(叫做顶标)来把求最大权匹配的问题转化为求完备匹配的问题的。
设顶点Xi的顶标为A[ i ],顶点Yj的顶标为B[ j ],顶点Xi与Yj之间的边权为w[i,j]。
在算法执行过程中的任一时刻,对于任一条边(i,j),A[ i ]+B[j]>=w[i,j]始终成立。
KM算法的正确性基于以下定理:若由二分图中所有满足A[ i ]+B[j]=w[i,j]的边(i,j)构成的子图(称做相等子图)有完备匹配,那么这个完备匹配就是二分图的最大权匹配。
首先解释下什么是完备匹配,所谓的完备匹配就是在二部图中,X点集中的所有点都有对应的匹配或者是Y点集中所有的点都有对应的匹配,则称该匹配为完备匹配。
这个定理是显然的。
因为对于二分图的任意一个匹配,如果它包含于相等子图,那么它的边权和等于所有顶点的顶标和;如果它有的边不包含于相等子图,那么它的边权和小于所有顶点的顶标和。
所以相等子图的完备匹配一定是二分图的最大权匹配。
初始时为了使A[ i ]+B[j]>=w[i,j]恒成立,令A[ i ]为所有与顶点Xi关联的边的最大权,B[j]=0。
如果当前的相等子图没有完备匹配,就按下面的方法修改顶标以使扩大相等子图,直到相等子图具有完备匹配为止。
我们求当前相等子图的完备匹配失败了,是因为对于某个X顶点,我们找不到一条从它出发的交错路。
这时我们获得了一棵交错树,它的叶子结点全部是X顶点。
现在我们把交错树中X顶点的顶标全都减小某个值d,Y顶点的顶标全都增加同一个值d,那么我们会发现:1)两端都在交错树中的边(i,j),A[ i ]+B[j]的值没有变化。
也就是说,它原来属于相等子图,现在仍属于相等子图。
2)两端都不在交错树中的边(i,j),A[ i ]和B[j]都没有变化。
二分图概念及性质

⼆分图概念及性质 段段续续的看⼆分图已经有些时⽇了。
现在借着周末整理⼀下这么多天对⼆分图的掌握程度。
也好对⼆分图有个整体的认知。
另外,此⽂只针对与⼆分图的⼀些概念和性质,不涉及求最⼤匹配的算法。
好吧,切⼊正题: ⾸先我们抛开⼆分图严谨准确的定义,从⼀个感性的⾓度来认识⼀下什么是⼆分图。
所谓⼆分图,就是能够把图中的定点分成两个X,Y两部分;并且整个图的边只存在于X与Y之间。
就是说,X与Y的内部是不存在边的,否则的话就不是⼆分图了。
举个例⼦:如果把整个⼈类中的男⼈和⼥⼈看成顶点,⼈与⼈之间的恋爱关系(这⾥只讨论异性之间的正常恋爱,同性恋是不被承认的)为边来建⽴图模型的话。
那么这其实就是⼀个⼆分图,其中的男⼈为X部分,⼥⼈为Y部分。
好了,现在我们给出⼆分图严谨的科学定义: 假设图G=(V,E)是⼀个⽆向图,若顶点集 V 可以分解成两个互不相交的⼦集(A,B),并且图中的所有边(i,j)的端点 i,j 分别属于⼦集 A,B 中的元素,则称图 G 是⼀个⼆分图。
为了更好的叙述下⽂,先让我们清楚⼀个概念: 匹配:⽆公共点的边集合。
(形象点就是 X与Y之间的边的个数) 匹配数:边集中边的个数。
最⼤匹配:匹配数最⼤的匹配。
边独⽴集:指图中边集的⼀个⼦集,且该⼦集中的任意两条边之间没有公共点。
(对⽐匹配的概念我们发现,其实边独⽴集和匹配是⼀个概念) 最⼤边独⽴集:包含边数最多的边独⽴集。
(其实就是最⼤匹配,为了⽅便,以后统称最⼤匹配)图1如图1,如果<1,4>是⼀个合法匹配,那么<1,5>就不是⼀个合法的匹配,因为它们有公共点1 。
同样的如果<2,5>是⼀个合法的匹配,那么<2,6>和<3,5>就不是⼀个合法的匹配。
不难看出,其中最⼤匹配是边集:{1, 4, 5},最⼤匹配数为3 。
独⽴集: 是指图的顶点集的⼀个⼦集,且该⼦集中的任意两个顶点之间不存在边。
第五章_图论2

通路定理
[定理]通路定理 在n阶图G中,如果有顶点u到v (u v) 的通路,那么u到v必有一条长度小于等
于n1的基本通路。
7
通路定理证明
定理:在有n个顶点的图G中,如果有顶点u到v的通路,必有长 度不大于n-1的基本通路。
证明:(1)先证明u和v之间存在基本通路 若uv之间的通路P中有相同的顶点,则从P中删除相同顶点之间
路径,直到P中没有相同顶点,这样得到的路径为u和v之间的基 本通路。
(2) 再证基本通路长度不大于n-1 (反证法)设u和v之间的基本通路的长度≥n。 ∵ 一条边关联两个顶点, ∴长度≥n的基本通路上至少有n+1个顶点。 ∴至少有两个相同顶点在u和v之间的基本通路上,这与基本通路 的性质“任意两个顶点不同”相矛盾。
图G从vi点到vj点有通路当且仅当?
bij = 1
21
图的连通性与可达矩阵
有向图的连通性(n1): 设有向图G的可达矩阵为B
(1) G强连通 B中元素全为1 (2) G是单向连通的 B中所有关于主对角线对称
的两个元素中至少一个值为1
无向图的连通性(n1): 设无向图G的可达矩阵为B
G连通 B中元素全为1
[定义]基本通(回)路
结点各不相同的通路称为基本通路。 中间结点各不相同的回路称为基本回路。
A
基本通路:ACEBD
B
E
基本回路:ABCDEA
C
D
5
有向通(回)路
[定义]有向通(回)路 若通路v0v1 … vn各边是有向边,且vi-1和vi 分别是有向边的始点与终点,则称该通路为 有向通(回)路。
通路uxv相连。
由u和v的任意性,可知~G是连通的。
27
二分图的讲解

例 3个图的匹配数 依次为3, 3, 4.
4
匹配 (续)
设M为G中一个匹配 vi与vj被M匹配: (vi,vj)M v为M饱和点: M中有边与v关联 v为M非饱和点: M中没有边与v关联 M为完美匹配: G的每个顶点都是M饱和点
例 关于M1, a,b,e,d是饱和点 f,c是非饱和点
M1不是完美匹配
(1)
(2)
(3)
6
Hall定理
定理(Hall定理) 设二分图G=<V1,V2,E>中,|V1||V2|. G中存 在从V1到V2的完备匹配当且仅当V1中任意k 个顶点至少与V2 中的k个顶点相邻(k=1,2,…,|V1|). 由Hall定理不难证明, 上一页图(2)没有完备匹配.
定理 设二部图G=<V1,V2,E>中, 如果存在t1, 使得V1中每个 顶点至少关联 t 条边, 而V2中每个顶点至多关联t条边,则G 中存在V1到V2的完备匹配.
注意: n 阶零图为二分图.
2
二分图的判别法
定理 非平凡无向图G=<V,E>是二分图当且仅当G中 无奇数长度的回路
例 下述各图都是二分图
3
匹配
设G=<V,E>, 匹配(边独立集): 任2条边均不相邻的边子集 极大匹配: 添加任一条边后都不再是匹配的匹配 最大匹配: 边数最多的匹配
匹配数: 最大匹配中的边数, 记为1
M2是完美匹配
M1
M2
5
二分图中的匹配
定义 设G=<V1,V2,E>为二部图, |V1||V2|, M是G中最 大匹配, 若V1中顶点全是M饱和点, 则称M为G中V1 到V2的完全匹配. 当|V1|=|V2|时, 完备匹配变成完美 匹配.
什么是二分图

我们定义匹配点、匹配边、未匹配点、未匹配边,它们的含 义非常显然。例如图3中1,4,5,7为匹配点,其他顶点为未匹 点;1-5、4-7为匹配边,其他边为非匹配边。
最大匹配&完美匹配
最大匹配:一个图所有的匹配中,所匹配的边数最多 的匹配,称为这个图的最大匹配。图4是一个最大匹 配。 完美匹配:如果一个图的某个匹配中,所有的顶点都 是匹配点,那么它就是一个完美匹配。图 4 是一个完 美匹配。显然,完美匹配一定是最大匹配(完美匹配 的任何一个点都已经匹配,添加一条新的匹配边一定 会与已有的匹配边冲突)。但并非每个图都存在完美 匹配。
交替路:图的一条简单路径,满足任意相邻的两条边, 一条在匹配内,一条不在匹配内 。
增广路:从一个未匹配点出发,走交替路, 如果途径另一个未匹配点(出发的点不算), 则这条交替路称为增广路(agumenting path)。 例如,图 5 中的一条增广路如图 6 所示 (图中的匹配点均用红色标出)
/*==================================================*\ | 二分图匹配(匈牙利算法BFS 实现) | INIT: g[][]邻接矩阵; | CALL: res = MaxMatch (); Nx, Ny 初始化!!! | 优点:适用于稀疏二分图,边较少,增广路较短。 | 匈牙利算法的理论复杂度是O(VE) \*==================================================*/ const int MAXN = 1000; int g[MAXN][MAXN], Mx[MAXN], My[MAXN], Nx, Ny; int chk[MAXN], Q[MAXN], prev[MAXN]; int MaxMatch(void) { int res = 0; int qs, qe; memset(Mx, -1, sizeof(Mx)); memset(My, -1, sizeof(My)); memset(chk, -1, sizeof(chk)); for (int i = 0; i < Nx; i++) { if (Mx[i] == -1) {//对于x集合中的每个没有匹配的点i进行一次bfs找 交错轨 qs = qe = 0; Q[qe++] = i; prev[i] = -1; bool flag = 0;//判断是否找到
二分图最大匹配及其应用
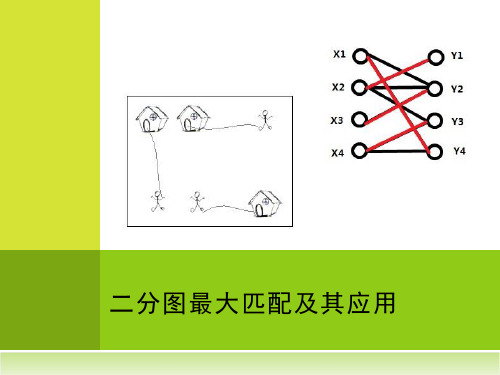
例 1. T HE P ERFECT S TALL
本题就是要求从图中选出尽可能多的边, 满足每个顶点至多是其中一条边的端点。 设G=(V, E)是一个图,M是E的一个子集。 如果M中的任何两条边都没有共同的端点, 则称M为G的一个匹配。G中边数最多的 匹配称为G的最大匹配。 要求一般图的最大匹配是比较困难的,但 是求二分图的匹配就容易得多。本题就是 求二分图最大匹配的问题。
y2
X2
y2
X2
y2
X3
y3
X3
y3
X3
y3
X4
y4
X4
y4
X4
y4
X5
y5
X5
y5
X5
y5
匈牙利算法
function find(i): boolean for j ← 1 to m if g[i][j] and (not c[j]) c[j] ← true if (l[j] = 0) or find(l[j]) l[j] ← i return true end if end if end for return false end function
例 3. 最小路径覆盖
题目来源:经典问题 给出一个含N个顶点的有向无环图G。用 尽量少的不相交路径覆盖G的所有顶点, 即每个顶点严格属于一条路径。允许路径 的长度为0,即只含一个顶点。
例 3. 最小路径覆盖
因为含n条边的路径共覆盖了n+1个顶点, 所以对于任何一个路径覆盖,有一个显然 的关系:路径数+路径覆盖中的边数=N。
匈牙利算法
形象化地说,就是从二分图中找出一条路 径,使得路径的起点和终点都是没有被匹 配的点,而且路径经过的边是一条没被匹 配,一条已经匹配过,再下一条又没匹配 这样交替地出现。找到这样的路径后,显 然路径里没被匹配的边比已经匹配了的边 多一条,于是修改匹配图,把路径里所有 匹配过的边去掉,把没有匹配的边变成匹 配的,这样一来匹配数就比原来多了1。 不断执行上述操作,直到找不到这样的路 径为止。
二分图匹配与最短路径问题

的顶点之间的最短路的长度)。 (2)通过形成特殊顶点的集合完成算法。 Sk 表示标记过程中第 k 次迭代之后的特殊顶点的集合。集合 Sk
是把不属于 Sk1 的带最小标记的顶点 u 添加到 Sk1 里来形成的,即 Sk = Sk1 +u
地的公路网纵横交错,因此有多种行车路线,这名司机应选择哪条线路呢?假设货 柜车的运行速度是恒定的,那么这一问题相当于需要找到一条从甲地到乙地的最短 路。
定义 (1) 设 P(u,v)是赋权图 G 中从 u 到 v 的路径,
则称 w(P) w(e) 为路径 P 的权. eE ( P )
(2) 在赋权图 G 中,从顶点 u 到顶点 v 的具有最小权的路
}
//读取数据
void dfs1(int v) {
//第一次遍历确定点的顺序
int i;
vis[v]=1;
for(i = 1; i <= n; i++)
if(map[v][i]<INF && vis[i]!=1)
dfs1(i);
order[number] = v; //出栈的时候记录顺序于ORDER数组
(3)更新 v 的标记( v Sk )。 从 a 到 v 的只包含 Sk 中顶点的最短通路,或者是从 a 到
v 的只包含 Sk1 中顶点(即不包括 u 在内的特殊顶点)的最短 通路,或者是在第 k-1 阶段从 a 到 u 的最短通路加上边(u, v)。即:
Lk(v ) min{Lk 1(v ),Lk 1(u) w(u,v )}
(2)非连通图
二分图

二分图二分图又称作二部图,是图论中的一种特殊模型。
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
1定义简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集。
2辨析示例区别二分图,关键是看点集是否能分成两个独立的点集。
上图中U和V构造的点集所形成的循环圈不为奇数,所以是二分图。
上图中U和V和W构造的点集所形成的的循环圈为奇数,所以不是二分图。
3必要条件无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
证先证必要性。
设G为二分图<X,E,Y>。
由于X,Y非空,故G至少有两个顶点。
若C为G 中任一回路,令C=(v0,v1,v2,…,v l-1,v l=v0)其中诸vi(i=0,1,…,l)必定相间出现于X及Y中,不妨设{v0,v2,v4,…,v l=v0}ÍX{v1,v3,v5,…,v l-1}ÍY因此l必为偶数,从而C中有偶数条边。
再证充分性。
设G的所有回路具有偶数长度,并设G为连通图(不失一般性,若G不连通,则可对G的各连通分支作下述讨论)。
令G的顶点集为V,边集为E,现构作X,Y,使<X,E,Y>=G。
取v0ÎV,置X={v|v=v0或v到v0有偶数长度的通路}Y=V-XX显然非空。
现需证Y非空,且没有任何边的两个端点都在X中或都在Y中。
由于|V|≥2并且G为一连通图,因此v0必定有相邻顶点,设为v1,那么v1ÎY;故Y不空。
设有边(u,v),使uÎX,vÎX。
那么,v0到u有偶数长度的通路,或u=v0;v0到v有偶数长度的通路,或v=v0。
二分图的判定与C++实现

二分图的判定与C++实现一、二分图定义二分图,是图论中的一种特殊模型,设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且同一集合中不同的两点没有边相连。
看一个例子:图中点集合分为U和V,并且U,V集合中的点没有形成连接关系,显然这是一个二分图。
二、二分图判定定理1:无向图G为二分图的一个充要条件是:1、G中至少包含两个顶点2、G中所有的回路长度都必须是偶数也就是说,一个图是二分图的充分必要条件是这个图不包含长度为奇数的圈。
那么,怎么实现呢?很简单,采用染色的方法,对于一个无向图,起初图中所有顶点都是无色,我们从任意未染色顶点出发,对这个顶点进行染色,对于与这个顶点相邻的的顶点,有三种情况:1、未染色那么将这个顶点染色,染与当前顶点不相同的颜色。
2、已经染色但是当前顶点颜色不同那么跳过该顶点3、已经染色但是与当前顶点相同。
则该图不是一个二分图,返回失败。
图中所有顶点已经进行染色,并且没有出现相邻顶点颜色相同的情况,则该图是一个二分图。
三、代码实现1、DFS实现思想也就是上面二分图判定所描述的。
描述:给定一个无向图,判断是否是二分图思想:通过dfs染色的方法,从任意未遍历过的顶点出发进行染色,如果有与当前顶点染色相同的,则不是二分图否则继续搜索与当前顶点相连的未染色的节点,并且染上相反的颜色,最后遍历完所有的顶点,相邻顶点没有同色,则为二分图。
时间复杂度O(n^2),空间复杂度O(n^2),若采用邻接表作为存储结构,则时间复杂度为O(n+m)1.#include<bits/stdc++.h>ing namespace std;3.const int maxn=1005;4.int edge[maxn][maxn];//邻接矩阵存储5.int color[maxn];//标记顶点颜色6.int n,m;7.bool dfs(int u,int c)8.{9. color[u]=c;//对u点进行染色10.for(int i=1;i<=n;i++)//遍历与u点相连的点11. {12.if(edge[u][i]==1)//如果i点与u点相连13. {14.if(color[i]==c) return false;//i点的染色重复,则不是二分图15.if(!color[i]&&!dfs(i,-c)) return false;//该点未染色,染上相反的颜色.dfs继续搜索16. }17. }18.return true;//所有点染色完成之后,并且相邻顶点没有同色,则为二分图19.}20.int main()21.{22.while(scanf("%d%d",&n,&m)!=EOF)23. {24.memset(edge,0,sizeof(edge));25.memset(color,0,sizeof(color));26.for(int i=0;i<m;i++)27. {28.int u,v;29.scanf("%d%d",&u,&v);30. edge[u][v]=1;//无向图,因此uv和vu都需要31. edge[v][u]=1;32. }33.bool flag=false; //默认为二分图34.for(int i=1;i<=n;i++)35. {36.if(!color[i])37. {38.if(!dfs(i,1))39. {40.printf("No\n");41. flag=true;42. }43. }44. }45.if(!flag) printf("Yes\n");46. }47.return0;48.}2、BFS思想主要是遍历这个图中每一层的时候,检查每一层是否有圈,有圈则不是二分图。
K M 算 法 详 解 ( 2 0 2 0 )

【原创】我的KM算法详解0.二分图二分图的概念二分图又称作二部图,是图论中的一种特殊模型。
设G=(V, E)是一个无向图。
如果顶点集V可分割为两个互不相交的子集X和Y,并且图中每条边连接的两个顶点一个在X中,另一个在Y中,则称图G为二分图。
可以得到线上的driver与order之间的匹配关系既是一个二分图。
二分图的判定无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
判断无向连通图是不是二分图,可以使用深度优先遍历算法(又名交叉染色法)。
下面着重介绍下交叉染色法的定义与原理首先任意取出一个顶点进行染色,和该节点相邻的点有三种情况:1.如果节点没有染过色,就染上与它相反的颜色,推入队列,2.如果节点染过色且相反,忽视掉,3.如果节点染过色且与父节点相同,证明不是二分图,return二分图博客推荐交叉染色法博客推荐:交叉染色法判断二分图另外附上二分图的性质博客:二分图的一些性质1.KM算法初步KM算法全称是Kuhn-Munkras,是这两个人在1957年提出的,有趣的是,匈牙利算法是在1965年提出的。
?增广路径增广路径定义:若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M 的一条增广路径(举例来说,有A、B集合,增广路由A中一个点通向B中一个点,再由B中这个点通向A中一个点……交替进行)增广路径有如下特性:?1. 有奇数条边?2. 起点在二分图的X边,终点在二分图的Y边?3. 路径上的点一定是一个在X边,一个在Y边,交错出现。
?4. 整条路径上没有重复的点?5. 起点和终点都是目前还没有配对的点,其他的点都已经出现在匹配子图中?6. 路径上的所有第奇数条边都是目前还没有进入目前的匹配子图的边,而所有第偶数条边都已经进入目前的匹配子图。
奇数边比偶数边多一条边?7. 于是当我们把所有第奇数条边都加到匹配子图并把条偶数条边都删除,匹配数增加了1.例如下图,蓝色的是当前的匹配子图,红色表示未匹配的路径,目前只有边x0y0,然后通过x1找到了增广路径:x1y0-y0x0-x0y2?增广路径有两种寻径方法,一个是深搜,一个是宽搜。
算法学习:图论之二分图最小覆盖(顶点以及边的最小覆盖)

二分图最小覆盖的Konig定理及其证明点的最小覆盖二分图:顶点可以分类两个集合X和Y,所有的边关联在两个顶点中,恰好一个属于集合X,另一个属于集合Y。
最小覆盖:最小覆盖要求用最少的点(X集合或Y集合的都行)让每条边都至少和其中一个点关联。
可以证明:最少的点(即覆盖数)=最大匹配数Konig定理:二分图的最小顶点覆盖数等于最大匹配数。
证明:为主便叙述,假设G分为左边X和右边Y两个互不相交的点集。
假设G经过匈牙利算法后找到一个最大匹配M,则可知G中再也找不到一条增广路径。
标记右边未匹配边的顶点,并从右边未匹配边的顶点出发,按照边:未匹配->匹配->未匹配...,的原则标记途中经过的顶点,则最后一条经过的边必定为匹配边。
重复上述过程,直到右边不再含有未匹配边的点。
记得到的左边已标记的点和右边未标记的点为S,以下证明S即为所求的最小顶点集。
1。
| S | == M因为每个点都是某个匹配边的其中一个端点。
如果右边的哪个点是没有匹配过的,那么它早就当成起点被标记了;如果左边的哪个点是没有匹配过的,那就走不到它那里去(否则就找到了一条完整的增广路)。
而一个匹配边又不可能左端点是标记了的,同时右端点是没标记的(不然的话右边的点就可以经过这条边到达了)。
因此,最后我们圈起来的点与匹配边一一对应。
2。
S能覆盖G中所有的边。
反证:如果最大匹配边的两个端点不能覆盖所有边,证明存在至少一条边的两个端点都不是最大匹配边的两个端点(根据覆盖的定义,每条边都至少和其中一个点关联),而这就得到了更大的覆盖,所以S能覆盖所有边!3。
S是最小的覆盖。
覆盖M条匹配边至少需要|S|来覆盖转自:/post.2801156.html#边的最小覆盖在一个PXP的有向图中,路径覆盖就是在图中找一些路经,使之覆盖了图中的所有顶点,且任何一个顶点有且只有一条路径与之关联;(如果把这些路径中的每条路径从它的起始点走到它的终点,那么恰好可以经过图中的每个顶点一次且仅一次);如果不考虑图中存在回路,那么每每条路径就是一个弱连通子集.由上面可以得出:1.一个单独的顶点是一条路径;2.如果存在一路径p1,p2,......pk,其中p1 为起点,pk为终点,那么在覆盖图中,顶点p1,p2,......pk不再与其它的顶点之间存在有向边.最小路径覆盖就是找出最小的路径条数,使之成为P的一个路径覆盖.路径覆盖与二分图匹配的关系:最小路径覆盖=|P|-最大匹配数;其中最大匹配数的求法是把P中的每个顶点pi分成两个顶点pi'与pi'',如果在p中存在一条pi到pj的边,那么在二分图P'中就有一条连接pi'与pj''的无向边;这里pi' 就是p中pi 的出边,pj''就是p中pj 的一条入边;对于公式:最小路径覆盖=|P|-最大匹配数;可以这么来理解;如果匹配数为零,那么P中不存在有向边,于是显然有:最小路径覆盖=|P|-最大匹配数=|P|-0=|P|;即P的最小路径覆盖数为|P|;P'中不在于匹配边时,路径覆盖数为|P|;如果在P'中增加一条匹配边pi'-->pj'',那么在图P的路径覆盖中就存在一条由pi连接pj的边,也就是说pi与pj 在一条路径上,于是路径覆盖数就可以减少一个;如此继续增加匹配边,每增加一条,路径覆盖数就减少一条;直到匹配边不能继续增加时,路径覆盖数也不能再减少了,此时就有了前面的公式;但是这里只是说话了每条匹配边对应于路径覆盖中的一条路径上的一条连接两个点之间的有向边;下面来说明一个路径覆盖中的每条连接两个顶点之间的有向边对应于一条匹配边;与前面类似,对于路径覆盖中的每条连接两个顶点之间的每条有向边pi--->pj,我们可以在匹配图中对应做一条连接pi'与pj''的边,显然这样做出来图的是一个匹配图(这一点用反证法很容易证明,如果得到的图不是一个匹配图,那么这个图中必定存在这样两条边 pi'---pj'' 及pi' ----pk'',(j!=k),那么在路径覆盖图中就存在了两条边pi-->pj, pi--->pk ,那边从pi出发的路径就不止一条了,这与路径覆盖图是矛盾的;还有另外一种情况就是存在pi'---pj'',pk'---pj'',这种情况也类似可证);至此,就说明了匹配边与路径覆盖图中连接两顶点之间边的一一对应关系,那么也就说明了前面的公式成立!。
二分图匹配匈牙利算法和KM算法简介

❖
end else
匈牙利算法
❖ begin
❖ j := queue[st];
❖
while true do
❖
begin
❖
t := match1[j];
❖
match1[j] := i;
❖
match2[i] := j;
❖
if t = 0 then break;
❖
i := t; j := father[t];
1 2
3 4
例题1 Place the Robots(ZOJ)
小结
比较前面的两个模型:模型一过于简单,没有给问 题的求解带来任何便利;模型二则充分抓住了问题的内 在联系,巧妙地建立了二部图模型。为什么会产生这种 截然不同的结果呢?其一是由于对问题分析的角度不同: 模型一以空地为点,模型二以空地为边;其二是由于对 原型中要素的选取有差异:模型一对要素的选取不充分, 模型二则保留了原型中“棋盘”这个重要的性质。由此 可见,对要素的选取,是图论建模中至关重要的一步。
例题3 打猎
❖ 猎人要在n*n的格子里打鸟,他可以在某一行 中打一枪,这样此行中的所有鸟都被打掉, 也可以在某一列中打,这样此列中的所有鸟 都打掉。问至少打几枪,才能打光所有的鸟?
❖ 建图:二分图的X部为每一行,Y部为每一列, 如果(i,j)有一只鸟,那么连接X部的i与Y部的j。
❖ 该二分图的最大匹配数则是最少要打的枪数。
匈牙利算法
❖ for i:=1 to n do
❖ if (father[i]=0)and(a[queue[st],i]=1) then
❖ begin
❖ if match2[i]<>0 then
❖
图论——染色法判定二分图

图论——染⾊法判定⼆分图 ⾸先明确概念: ⼆分图:设G=(V,E)是⼀个⽆向图,如果顶点V可分割为两个互不相交的⼦集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为⼀个⼆分图。
奇数环:⼀个图中边数为奇数的环。
染⾊法原理: ⾸先任意取出⼀个顶点进⾏染⾊,和该节点相邻的点有三种情况: 1.如果未染⾊,那么继续染⾊此节点(染为另⼀种颜⾊) 2.如果已染⾊但和当前节点颜⾊不同,则跳过该点 3.如果已染⾊并且和当前节点颜⾊相同,返回失败(该图不是⼆分图) 明确⼆分图、奇数环、染⾊法之间的关系: 如果⼀个图中存在奇数环,那么这个图⼀定不是⼆分图;这⼀点显然成⽴。
如果⼀个图中不存在奇数环,那么这个图⼀定是⼆分图: 证明:⽤染⾊法。
从某个点开始逐层交叉染⾊,在染⾊过程中: 若发现有某条边的两个端点着⾊相同,则必定存在奇数环①,与题意相⽭盾。
若没有发现,则根据染⾊法原理,每⼀条边的两端着⾊必然不同,那么根据⼆分图的定义,就可知这个图是⼀个⼆分图。
①的证明: 不妨设这条边的两个端点着⾊都为1,且这两点必然是由同⼀个源点扩展⽽来。
那么根据染⾊法原理,因为这两个点的着⾊相同,那么从源点到这两个点所经过的边数(假设分别为x和y)的奇偶性必然相同,那么这个环的总边数为x+y+1,由数学知识得这个数必然是奇数。
证毕! 模板题链接: 代码如下:#include <iostream>#include <algorithm>#include <cstring>#include <cstdio>using namespace std;const int N = 100010, M = 200010;struct Edge{int to,next;}edge[M];int cnt;int n,m;int h[N],color[N];void add_edge(int u,int v){edge[++cnt].to=v;edge[cnt].next=h[u];h[u]=cnt;}bool dfs(int u,int c){color[u]=c;for(int i=h[u]; ~ i;i=edge[i].next){int to=edge[i].to;if(color[to]==c){return false;}else if(!color[to]&&!dfs(to,3-c))return false; }return true;}int main(){scanf("%d%d",&n,&m);memset(h,-1,sizeof h);for(int i=1;i<=m;i++){int a,b;scanf("%d%d",&a,&b);add_edge(a,b);add_edge(b,a);}bool flag=true;for(int i=1;i<=n;i++){if(!color[i]){if(!dfs(i,1)){flag=false;break;}}}if(flag)printf("Yes\n");else printf("No\n");}。
二分图及匹配算法

Chapter 3
二分图最佳匹配
-二分图最佳匹配-
定义:图G中权值和最大的完全匹配。
Kuhn-Munkras算法:该算法是通过给每个顶点一个标号(叫做顶标) 来把求最大权匹配的问题转化为求完备匹配的问题的。设顶点Xi的顶标 为A[ i ],顶点Yj的顶标为B[ j ],顶点Xi与Yj之间的边权为w[i,j]。在算法 执行过程中的任一时刻,对于任一条边(i,j),A[ i ]+B[j]>=w[i,j]始终成立。 KM算法的正确性基于以下定理: 若由二分图中所有满足A[ i ]+B[j]=w[i,j]的边(i,j)构成的子图(称做相等 子图)有完备匹配,那么这个完备匹配就是二分图的最大权匹配。 KM算法流程: (1)初始化可行顶标的值; (2)用匈牙利算法寻找完备匹配; 这样做是O(n^4)的
-稳定婚姻问题-
Байду номын сангаас
求婚拒绝算法(Gale-Shapley算法/延迟认可算法): 先对所有男生进行单身标记,称其为单身狗男。当存在单身狗男时,进行 以下操作:
①选择一位单身狗男在所有尚未拒绝她的女生中选择一位被他排名最优先 的女神;
②女神将正在追求她的单身狗男与其现任进行比较,选择其中排名优先的 男生作为其男友,即若单身狗男优于现任,则现任被抛弃为前任;否则保 留其男友,拒绝单身狗男。 ③若某男生被其女友抛弃,则重新变成单身狗男,至①重复。
Chapter 5
稳定婚姻问题
-稳定婚姻问题-
你们班上有n位男生和n位女生,每个人对异性都有一个排序,表示对他们 的爱恋程度。现在你的任务是使他们凑成CP,使他们的爱情坚不可摧! 满足一下条件的爱情不是坚不可摧的: 男生u和女生v不是CP,但他们爱恋对方的程度都大于爱恋现任 的程度。 因为这样男生u和女生v会抛下已经是CP的那个她/他,另外组成一对。于 是乎多出了两位前任,这样就会让人再也无法相信爱情了! 怎么能避免悲剧的发生呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论专题二分图朝花夕拾2010-12-28 17:56:46 阅读66 评论0 字号:大中小订阅二分图:二分图是这样一个图,它的顶点可以分类两个集合X和Y,所有的边关联的两个顶点恰好一个属于集合X,另一个属于集合Y。
二分图匹配:给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
最大匹配:图中包含边数最多的匹配称为图的最大匹配。
完美匹配:如果所有点都在匹配边上,则称这个最大匹配是完美匹配。
二分图匹配基本概念:未盖点设VI是G的一个顶点,如果VI不与任意一条属于匹配M的边相关联,就称VI是一个未盖点。
交错轨设P是图G的一条轨,如果P的任意两条相邻的边一定是一条属于M而另一条不属于M,就称P是交错轨。
可增广轨(增广路)两个端点都是未盖点的交错轨称为可增广轨。
可增广轨的性质:1:P的路径长度必定为奇数,第一条边和最后一条边都不属于M。
2:P经过取反操作可以得到一个更大的匹配M’。
3:M为G的最大匹配当且仅当不存在相对于M的增广路径。
二分图最大匹配匈牙利算法:算法的思路是不停的找增广轨,并增加匹配的个数,增广轨顾名思义是指一条可以使匹配数变多的路径,在匹配问题中,增广轨的表现形式是一条"交错轨",也就是说这条由图的边组成的路径,它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且始点和终点还没有被选择过.这样交错进行,显然他有奇数条边.那么对于这样一条路径,我们可以将第一条边改为已匹配,第二条边改为未匹配...以此类推.也就是将所有的边进行"取反",容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对.另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路。
代码://匈牙利算法复杂度o(nm)#include<iostream>using namespace std;const int MAXN = 1001,MAXM = 1001;int n1,n2,m,ans;//n1,n2分别为二分图两边节点的个数,两边的节点分别用1..n1,1..n2编号,m为边数bool g[MAXN][MAXM];//图G邻接矩阵g[x][y]bool y[MAXM];//Y集合中点i访问标记int link[MAXM];//link[y]表示当前与y节点相邻的x节点void init(){int x,y;memset(g,0,sizeof(g));memset(link,-1,sizeof(link));ans = 0;scanf("%d%d%d",&n1,&n2,&m);for (int i = 1;i <= m;i++){scanf("%d%d",&x,&y);g[x][y] = true;}}bool find(int x)//是否存在X集合中节点x开始的增广路{for (int i = 1;i <= n2;i++)if (g[x][i] && !y[i])//如果节点i与x相邻并且未访问过{y[i] = true;if (link[i] == -1 || find(link[i]))//如果找到一个未盖点i中或从与i相邻的节点出发有增广路{link[i] = x;return true;}}return false;}int main(){init();/*for (int j = 1;j <= n2;j++)for (int i = 1;i <= n1;i++)if (g[i][j] && !link[j])link[j] = i;//贪心初始解优化*/for (int i = 1;i <= n1;i++){memset(y,0,sizeof(y));if (find(i))ans++;}printf("%d\n",ans);return0;}真正求二分图的最大匹配的题目很少,往往做一些简单的变化:变种1:二分图的最小顶点覆盖最小顶点覆盖要求用最少的点(X或Y中都行),让每条边都至少和其中一个点关联。
knoig定理:二分图的最小顶点覆盖数= 二分图的最大匹配数(m)。
变种2:DAG图的最小路径覆盖用尽量少的不相交简单路径覆盖有向无环图(DAG)G的所有顶点,这就是DAG图的最小路径覆盖问题。
结论:DAG图的最小路径覆盖数= 节点数(n)- 最大匹配数(m)变种3:二分图的最大独立集结论:二分图的最大独立集数 = 节点数(n)—最大匹配数(m)附上一些题目1:pku 1466 Girls and Boys /problem?id=1466这是一道典型的二分匹配的题目,并且非常简单,使用模板即可AC。
题目大意:在N个点的图G中选出m个点,使这m个点两两之间没有边.求m最大值.如果图G满足二分图条件,则可以用二分图匹配来做.最大独立集点数= N - 最大匹配数。
最大独立数=未匹配的节点+匹配数/2 (1)(设n=匹配数/2,可以理解为去掉二分图某侧匹配好的n个节点,在另一侧对应的n个节点就没有相匹配的了)未匹配的节点=顶点数-匹配数(2)由(1)(2)得: 最大独立数=顶点数-匹配数的一半参考:/zjut_nizhenyang/blog/static/1695700292010920914230/2:pku 1719 Shooting Contest 二分图匹配/zjut_nizhenyang/blog/static/169570029201010199320592/建图,输出匹配就行了//题目分析:题目其实要求你以x,y坐标作为二分图的两个节点部分,然后让你找到一个匹配,然后根据一个部分的节点顺序把对应的另一个节点输出//思路分析:直接用dfs实现的匈牙利算法来解决二分图参考:/zjut_nizhenyang/blog/static/169570029201010199320592/3:pku 1422 二分图,最小路径覆盖/problem?id=1422参考:/zjut_nizhenyang/blog/static/16957002920101025922340/4:pku 2594 Treasure Exploration floyd 重新建图+最小路径覆盖+二分图/problem?id=2594参考:/zjut_nizhenyang/blog/static/1695700292010102583552414/5:pku 3216 Repairing Company floyd 最短路+二分图最大匹配/problem?id=3216参考:/zjut_nizhenyang/blog/static/169570029201010257563738/6:pku 1904 King's Quest 强连通分支,二分图/problem?id=1904参考:/zjut_nizhenyang/blog/static/1695700292010102572022595/7:pku 3041 二分图最小点覆盖数=最大匹配数/problem?id=3041参考:/zjut_nizhenyang/blog/static/1695700292010102462244415/8:zjut 1321 Dividing 二分图匹配/ShowProblem.aspx?ShowID=1321参考:/zjut_nizhenyang/blog/static/1695700292010102454153206/9:pku 2771 Guardian of Decency 二分图,最大独立集/problem?id=2771参考:/zjut_nizhenyang/blog/static/1695700292010111065019932/10:pku 1325 Machine Schedule 二分图最小点覆盖/problem?id=1325参考:/zjut_nizhenyang/blog/static/1695700292010111035942586/11:pku 1486 Sorting Slides 二分图必须边/problem?id=1486参考:/zjut_nizhenyang/blog/static/1695700292010111032443864/12:pku 2536 Gopher II 二分图匹配/problem?id=2536参考:/zjut_nizhenyang/blog/static/1695700292010117113611862/13:pku 2239 Selecting Courses 二分图匹配/problem?id=2239参考:/zjut_nizhenyang/blog/static/16957002920101171151319/ 14:pku 1274 The Perfect Stall 二分图匹配/problem?id=1274参考:/zjut_nizhenyang/blog/static/1695700292010117102245344/ 15:pku 2724 Purifying Machine 二分图最小路径覆盖/problem?id=2724参考:/zjut_nizhenyang/blog/static/1695700292010111495830231/ 16:pku 3020 Antenna Placement 二分图最小路径覆盖/problem?id=3020参考:/zjut_nizhenyang/blog/static/1695700292010111485846859/ 17:pku 2446 二分图最大匹配的应用/problem?id=2446参考:/zjut_nizhenyang/blog/static/169570029201011148555347/ 18:pku 2226 Muddy Fields 二分图最小点覆盖/problem?id=2226参考:/zjut_nizhenyang/blog/static/1695700292010111365944100/ 19:zjut 1478 挽救损失二分图最小点覆盖/ShowProblem.aspx?ShowID=1478参考:/zjut_nizhenyang/blog/static/1695700292010111365248521/20:pku 2060 Taxi Cab Scheme 二分图最小路径覆盖/problem?id=2060参考:/zjut_nizhenyang/blog/static/16957002920101111433360/ 21:pku 1548 Robots 二分图最小路径覆盖/problem?id=1548参考:/zjut_nizhenyang/blog/static/169570029201011113748927/ 22:pku 3692 Kindergarten 二分图最大独立集,求补图的最大独立集/problem?id=3692参考:/zjut_nizhenyang/blog/static/1695700292010111075931537/。
