新沪科版八年级上册《11.2 图形在坐标系中的平移》专题训练(含答案)
沪科版-数学-八年级上册-11.2.1 图形在坐标系中的平移 同步训练

11.2.1 图形在坐标系中的平移同步训练一、选择题:1、将点P(2,-3)向左平移3个单位得到点P′,则点P′的坐标为 ( )A、(5,一3)B、(一1,一3)C、(2,0)D、(一5,一3)2、点M(一2,5)是由点N向上平移3个单位得到的.则点N的坐标为 ( )A、(一2,2)B、(一5,5)C、(一2,8)D、(1,5)3、将点P(3,4)先关于x轴对称得P1,再将P1关于y轴对称得P2,则P2的坐标为( )A、(一3,4)B、(3,一4)C、(一3,一4)D、(4,3)4、在平面直角坐标系中,将点(x,y)向左平移a个单位长度,再向下平移b个单位长度,则平移后点的坐标是 ( )A、(x+a,y)B、(x+a,y-b)C、(x-a,y-b)D、(x+a,y+b)5、将点P(1,-m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点K(m,n)的坐标为 ( )A、(3,一2)B、(2,一3)C、(3,2)D、(一2,3)6、将△ABC的各顶点的横坐标分别加3,纵坐标不变,连接三个新的点所成的三角形是由△ABC( )A、向左移3个单位所得B、向右平移3个单位所得C、向上平移3个单位所得D、向下平移3个单位所得二、填空题:7、将△ABC在平面内先向左平移3个单位,再向下平移2个单位与先向平移2个单位.再向平移3个单位得到的是同一个图形.8、已知△ABC中顶点的坐标分别为A(2,3),B(0,0),C(4,0),若只将点A移动到A′(4,3),则△ABC与△A′BC的面积关系为.9、中国象棋的走棋规则中有“象飞田字”,如右图,象在点P处,走一步可到达的点的坐标可以记作.10、在平面直角坐标系内△ABC的三个顶点的坐标分别是A(-1,3),B(2,5),C(2,0).△ABC经过平移后点C的坐标为C′(5,6),则A、B的坐标变为.11、已知点M(a-1,5),现在将平面直角坐标系先向左平移3个单位,之后又向下平移4个单位.得到点N(2,b-1).则a=,b=.12、根据指令(s≥0, 0°≤A<360°)机器人在平面上能完成如下动作:先在原地顺时针旋转角度A,再朝其面对的方向沿直线行走距离s. 现在机器人在平面直角坐标系的原点,且面对y轴的负方向,为使其移动到点(-3,0),应下的指令是 .三、计算与解答:13、如图,点A坐标为(-1,1),将此小船向左平移2个单位后,画出图形,并指出A,B,C,D各点坐标.14、如图是小明家周边地区的平面示意图。
2015年秋季新版沪科版八年级数学上学期11.2、图形在坐标系中的平移同步练习1

11.2图形在坐标中的平移练习二第1题. 在直角坐标系中,写出如图所示的图形各顶点坐标,将图形向右平移3个单位,作出相应的图形,并写出平移后相应5个顶点的坐标.第2题. 如图,将梯形ABCD 什么结论?画出得到的图形.第3题. 将图中的小猫向右平移2个单位.第4题. 在平面直角坐标系中,如果将一个图形先向左平移3个单位,再向下平移4个单位,即是将图形各顶点横坐标 ,纵坐标 可得到.第5题. 如果将三角形ABC 的三个顶点的横坐标都加上5 ,纵坐标都减去4,得到三角形A B C ''',则三角形A B C '''在三角形ABC 的基础上( ) A.先向左平移5个单位长度,再向下平移4个单位长度 B.先向右平移5个单位长度,再向上平移4个单位长度 C.先向左平移5个单位长度,再向上平移4个单位长度 D.先向右平移5个单位长度,再向下平移4个单位长度第6题. 如图,三角形111A B C 是由三角形ABC 平移后得到的,三角形ABC 中任意一点0(P x ,0)y 经平移后对应点为10(5P x +,03)y +.求1A,1B ,1C 的坐标.第7题. 将点(224)P m m ++,向右平移1轴上,那么( )A.(20)-,B.(02)-, C.(1,第8题. 点(35)M --,向上平移7个单位得到点M ',则点M '的坐标为( )A.(32)-,B.(312)--, C.(45)-, D.(105)--,第9题. 点(00)R ,先向右平移1个单位,再向下平移2个单位到点S ,则点S 的坐标为( ) A.(12),B.(12)-, C.(12)-, D.(12)--,第10题. 在平面直角坐标系中,点(58)--,是由下面的( )点沿x 轴负方向平移3个单位得到的A.(28)--,B.(55)--, C.(85)--, D.(511)--,第11题. 将点(53)-,沿x 轴的正方向平移3个单位后的坐标是( ) A.(83),B.(83)-, C.(23)-, D.(50)-,第12题. 把原点向下移动4个单位后,再向左移动3个单位,所得到的点在原坐标系中的坐标为( )A.(43),B.(34)-, C.(34)--,D.(43)-,第13题. 在直角坐标系中,点(2P -,3)向右平移3个单位长度后的坐标为( )A.(36),B.(13),C.(16),D.(33),第14题. 下列说法不正确的是( )A.把一个图形平移到一个确定位置大小形状都不变B.在平移图形的过程中,图形上的各点坐标发生同样的变化 C.在平移过程中图形上的个别点的坐标不变D.平移后的两个图形的对应角相等,对应边相等,对应边平行或共线第15题. 将OBA △进行怎样的平移得到O B A '''△?并写出各顶点的坐标.第16题. 如图,三角形PQR点P,点B与点Q,点C与点R意一点M的坐标为(x,)y第17题. 纪检委的小王科长为了了解公款吃喝情况,准备去调查几大宾馆,并且事先知道下面的信息:⑴“会宾楼”在他现在所在地的北偏东45°的方向,距离此处2km的地方;⑵“临湖宾馆”在他现在所在地的北偏西60°的方向,距离他现在所在地3.6km的地方;⑶“红玫瑰酒楼”在他现在所在地的南偏西38°的方向,距离他现在所在地1.5km的地方.根据这此信息,请你画一张表示各处位置的简图.第18题. 在直角坐标系中,作出如图所示的图形关于x 轴、y 轴及坐标原点O 的对称图形.第19题. 在如图所示的直角坐标系中,多边形ABCDEF 的各个顶点的坐标分别是(1A ,0),(2B ,3),(5C ,6),(7D ,4),(6E ,2),(9F ,0),确定这个多边形的面积,你是怎样做的?与你的同伴进行交流.第20题. 已知点E ,F 为矩形ABCD 长为6,宽为4,求AEF △的面积.第21题. 已知点(M a ,)b ,过M 作MH x ⊥轴于H N 点坐标为(2-,3)-,则()a b +=A.0B.1C.-1D.-5第22题. 已知线段AB ,点A 的坐标为(3,5),点B 的坐标为(1-,1),则线段AB 的中点坐标为 .第23题. 如图,求图中阴影部分的面积之和(用两种方法)第24题. 如图,设点(2A -,3)米,又向东跑300米,再向北跑100米,再向东跑500米.⑴在图中画出小猫的跑步路线.⑵小猫跑步路线圈起的土地面积是多少平方米?第25题. 达了终点……,用1S ,2S 相吻合的是 ( )第A ,-⒈观察图形,你觉得它像什么字?⒉若将A 组所在线段上移1个单位,B 组线段不变,C 组线段向右,E 组向左各移动1个单位,D 组对应变为(0,1),(2-,1)-,F 组变为(0,1),(2,1)-,图形会发生怎样的变化?第27题. 如图是一种放大图形的方法:ABCD⑴在原来的图片上画一些小方格子. ⑵在另一张纸上画同样数量的大方格子.⑶将小方格子的内容画在相应的大方格子中.第28题. (1)画出1A MN (2)画出A(3) 11A B ⑴⑵1. 答案:略.2. 答案:略.3. 答案:略.4. 答案:减去3,减去4.5.答案:D.6. 答案:1(3A ,6),1(1B ,2),1(7C ,3).7. 答案:B. 8. 答案:A. 9. 答案:B. 10. 答案:A. 11. 答案:C. 12. 答案:C. 13. 答案:B. 14. 答案:C.15. 答案:将OBA △向上平移6个单位长度,再向右平移3个单位长度,即能得到O B A '''△.(0O ,0),(6B -,3)-,(4A -,6)-,(3O ',6),(3B '-,3),(1A '-,0).16. 答案:(4A ,3),(4P -,3)-;(3B ,1),(3Q -,1)-;(1C ,2),(1R -,2)-.分析发现A 与P ,B 与Q ,C 与R ,都是关于原点的对称点,由此可知,ABC △与PQR △是关于原点对称的,点(M x ,)y 的对应点N 的坐标是(x -,)y -.17. 答案:略.18. 答案:略.19. 答案:多边形的面积是25,由计算相关的矩形面积转化而来. 20. 答案:(2A -,4),(2B -,0),(4C ,0),(4D ,4)24AEF ABE CEF ADF S S S S =---△△△△11124423361222=-⨯⨯-⨯⨯-⨯⨯10.5=21. 答案:B.22. 答案:(1,3).23. 答案:方法一:求三阴影部分面积;方法二:把三阴影部分合理拼成一个图形,面积25. 24. 答案:2(5100)(2100)100230000⨯-⨯⨯=(平方米) 25. 答案:D. 26. 答案:略. 27. 答案:略.28. 答案:解:(1)如图,1111A B C D ,就是所求的平行四边形. (2)如图,2222A B C D ,就是所求的平行四边形. (3)是轴对称图形,对称轴是直线EF . `212B。
沪科版数学八年级上册专题训练11.2 图形在坐标系中的平移

11.2 图形在坐标系中的平移1.将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是()A. 将原图向左平移两个单位B. 关于原点对称C. 将原图向右平移两个单位D. 关于y轴对称2.已知直角坐标系中的点A,点B的坐标分别为A(-2,6),B(0,-4),且P为AB的中点,若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标为________ .3.如图,已知正方形ABCD,顶点A(1,3)、B(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2 014次变换后,正方形ABCD的对角线交点M的坐标变为________.4.如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为________.5.如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为________.6.在如图所示的平面直角坐标系中表示下面各点:A(0,3);B(1,﹣3);C(3,﹣5);D (﹣3,﹣5);E(3,5);F(5,7)G(5,0).(1)A点到原点的距离是.(2)将点C向x轴的负方向平移6个单位,它与点重合.参考答案1.A 【解析】∵将三角形三个顶点的横坐标都减2,纵坐标不变,∴所得三角形与原三角形的关系是:将原图向左平移两个单位.故选A.2.(2,1)【解析】根据中点坐标的求法可知点P点坐标为(-1,1),因为左右平移点的纵坐标不变,由题意向右平移3个单位,则各点的横坐标加3,所以点Q的坐标是(2,1).3.(﹣2012,2)【解析】∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).∴对角线交点M的坐标为(2,2).根据题意,得第1次变换后的点M的对应点的坐标为(2﹣1,﹣2),即(1,﹣2),第2次变换后的点M的对应点的坐标为(2﹣2,2),即(0,2),第3次变换后的点M的对应点的坐标为(2﹣3,﹣2),即(﹣1,﹣2),第n次变换后的点M的对应点的坐标:当n为奇数时为(2﹣n,﹣2),当n为偶数时为(2﹣n,2),∴连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(﹣2012,2).4.(14,44)【解析】设粒子运动到A1,A2,…,A n时所用的间分别为a1,a2,…,a n,a n ﹣a1=2×n+…+2×3+2×2=2 (2+3+4+…+n),a n=n(n+1),44×45=1 980,故运动了1 980秒时它到点A44(44,44),则运动了2 010秒时,粒子所处的位置为(14,44).5.(2,5)【解析】∵点A的坐标为(﹣2,6),∴对应点A1的坐标为(﹣2+4,6﹣1),即(2,5).6.【解】(1)如图,A点到原点的距离是3.(2)将点C向x轴的负方向平移6个单位,它与点D重合.。
精选2019-2020年数学八年级上册[第11章 平面直角坐标系11.2 图形在 坐标中的 平移]沪科版习题精选[含答案
![精选2019-2020年数学八年级上册[第11章 平面直角坐标系11.2 图形在 坐标中的 平移]沪科版习题精选[含答案](https://img.taocdn.com/s3/m/3ebcf22625c52cc58ad6be14.png)
精选2019-2020年数学八年级上册[第11章平面直角坐标系11.2 图形在坐标中的平移]沪科版习题精选[含答案解析]三十八第1题【单选题】已知点P (3, ?2),点Q(?3, 2),点R(?3, ?2),点H(3, 2),下面选项中关于y轴对称的是( ).A、P和QB、P和HC、Q和RD、P和R【答案】:【解析】:第2题【单选题】已知点A的坐标为(﹣2,3),则点A关于y轴的对称点的坐标是( )A、(﹣2,3)B、(2,3)C、(2,﹣3)D、(﹣2,﹣3)【答案】:【解析】:第3题【单选题】在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1 ,已知在AC上一点P(2.4,2)平移后的对应点为P1 ,点P1绕点O逆时针旋转180°,得到对应点P2 ,则P2点的坐标为( )A、(1.4,﹣1)B、(1.5,2)C、(1.6,1)D、(2.4,1)【答案】:【解析】:第4题【单选题】已知点A(2,﹣2),如果点A关于x轴的对称点是B,点B关于原点的对称点是C,那么C点的坐标是( )A、(2,2)B、(﹣2,2)C、(﹣1,﹣1)D、(﹣2,﹣2)【答案】:【解析】:第5题【单选题】点A(﹣3,4)与点B(m,n)关于x轴对称,则点B的坐标为( )A、(﹣3,﹣4)B、(﹣3,4)C、(3,﹣4)D、(3,4)【答案】:【解析】:第6题【单选题】已知点A与点B关于x轴对称,点A的坐标为(﹣1,2),则点B的坐标是( )A、(﹣1,2)B、(﹣1.﹣2)C、(1,2)D、(﹣2,1)【答案】:【解析】:第7题【填空题】已知P1点关于x轴的对称点P2(3-2a,2a-5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是______【答案】:【解析】:第8题【填空题】在平面直角坐标系中,将点A(﹣1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C 的坐标是______.A、(2,﹣2)【答案】:【解析】:第9题【填空题】如图,在菱形OABC中,点B在x轴上,点A的标为(2,3),则点C的坐标为______.【答案】:【解析】:第10题【填空题】已知点M(b,5)与点N(9,2a+b)关于y轴对称,则a=______,b=______.A、7B、-9【答案】:【解析】:第11题【填空题】一般地,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向______(或向左)平移a个单位长度;如果把一个图形各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向______(或向下)平移______个单位长度.【答案】:【解析】:第12题【填空题】点(2,5)关于直线x=1的对称点的坐标为______.A、(0,5)【答案】:【解析】:第13题【作图题】如图,在平面直角坐标系中,A(-2,-1),B(2,-2),C(3,1).在图中作出△ABC关于x轴的对称图形△A1B1C1(A和A1 ,B和B1 ,C和C1分别是对应顶点).写出点A1 ,B1 ,C1的坐标:A1______, B1______, C1______.△A1B1C1的面积为______.【答案】:【解析】:。
沪科版八年级数学上册 11.2 图形在坐标系中的平移 随堂练习

安徽省濉溪县2021—2021学八年级数学随堂练习考试范围:11.2图形在坐标系中的平移;考试时间:60分钟一、选择题(本大题共8小题,共32.0分)1.在平面直角坐标系中,把点先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是A. B. C. D.2.点平移后变为点,下列关于平移的说法中,正确的是A. 先向左平移1个单位,再向上平移4个单位B. 先向右平移1个单位,再向上平移4个单位C. 先向左平移1个单位,再向下平移4个单位D. 先向右平移1个单位,再向下平移4个单位3.在平面直角坐标系中,将点向右平移5个单位长度,再向下平移3个单位长度后与点重合,则点A的坐标是A. B. C. D.4.已知线段AB是线段CD平移得到的,点,,,则点C的对应点A的坐标为A. B. C. D.5.如图所示,在图形B到图形A的变化过程中,下列描述正确的是A. 向上平移2个单位,向左平移4个单位B. 向上平移1个单位,向左平移4个单位C. 向上平移2个单位,向左平移5个单位D. 向上平移1个单位,向左平移5个单位6.如果点和点关于x轴对称,则的值是A. B. 1 C. D. 57.在平面直角坐标系中,点先向左平移3个单位,再向下平移4个单位,得到点的坐标为A. B. C. D.8.在平面直角坐标系内,将进行平移后得到,其中点的对应点为,那么是A. 向右平移了4个单位长度B. 向左平移了4个单位长度C. 向上平移了4个单位长度D. 向下平移了4个单位长度二、填空题(本大题共6小题,共18.0分)9.在平面直角坐标系中有一点,将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为______.10.将点P向下平移3个单位,向左平移2个单位后得到点,则点P坐标为______ .11.已知的三个顶点分别为、、,现将平移至处,且坐标为,则点的坐标为______.12.点沿x轴正方向平移2个单位,再沿y轴负方向平移4个单位,所得到的点的坐标为______.13.通过平移把点移到点,按同样的平移方式,点移动到点,则点的坐标是______ .14.将点向左平移1个单位长度,再向下平移2个单位长度得到点,则点的坐标为______ .三、计算题(本大题共1小题,共10.0分)15.在直角坐标平面内,已点、,将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.写出C点、D点的坐标:C______,D______;把这些点按顺次连接起来,这个图形的面积是______.四、解答题(本大题共2小题,共22.0分)16.如图,在网格中有点.将点A向左平移4个单位,得到点,请在图上标出这个点,并写出它的坐标.将点A向上平移4个单位,得到点,请在图上标出这个点,并写出它的坐标.你能判断直线与x轴,直线与y轴的位置关系吗?17.本小题满分6分如图,直角坐标系中,的顶点都在网格点上,已知C点坐标为。
沪科版八年级上册《图形在坐标系中的平移》同步练习(含详细答案)

图形在坐标系中的平移课堂练习1. 如图是在方格纸上画出的小旗图案,若用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为()图12-2-3A.(0,3)B.(2,3)C.(3,2)D.(3,0)2.如图所示,小颖从家到达莲花中学要穿过一个居民小区,若小区的道路均是正南或正东方向,小颖走下面哪条线路不能到达学校()A.(0,4)⇒(0,0)⇒(4,0)B.(0,4)⇒(4,4)⇒(4,0)C.(0,4)⇒(1,4)⇒(1,1)⇒(4,1)⇒(4,0)D.(0,4)⇒(3,4)⇒(4,2)⇒(4,0)3. (2012·监利县期末)课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成()图12-2-5A .(5,4)B .(4,5)C .(3,4)D .(4,3)4.在方格纸中,把一个图形先沿水平方向平移a 格(当a 为正数时,表示向右平移;当a 为负数时,表示向左平移),再沿竖直方向平移b 格(当b 为正数时,表示向上平移;当b 为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为【a ,b 】.例如,把△ABC 先向右平移3格,再向下平移5格得到△A1B1C1,可以把这个过程记为【3,-5】.若再将△A1B1C1经过【5,2】得到△A2B2C2,则△ABC 经过平移得到△A2B2C2的过程是( )A .【2,7】B .【8,-3】C .【8,-7】D .【-8,-2】5.如果甲图形上的点P (-2,4)经平移变换后是Q (3,-2),则甲图上的点M (1,-2)经这样平移后的对应点的坐标是( )A .(6,-8)B .(-4,4)C .(5,3 )D .(3,-5)6. 在平面直角坐标系中,线段11A B 是由线段AB 平移得到的,已知A B,两点的坐标分别为(23)A -,,(31)B -,,若点A 的对应点1A 的坐标为(34),,则1B 的坐标为 .7. 将点Q (-2,3)向左平移1个单位长度,再向下平移2个单位长度得到点Q ′,则点Q ′的坐标为 .8.如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(___,___)2-)、B(___,___)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(___,___)、B′(___,___)、C′(___,___).(3)△ABC的面积为___。
沪科版八年级上册数学第11章 平面直角坐标系 图形在坐标系中的平移

D
8.【芜湖月考】如图,三角形ABC中任意一点P(x0,y0)经平移后其对应点为
P1(x0+3,y0-1),将三角形ABC作同样的平移,得到三角形A1B1C1,则
A1的坐标是( )
A.(-4,3)
B.(-4,5)
3.点P(a,b)先向左平移3个单位,再向上平移2个单位得到 点P′(-5,-1),则( A )
A.a=-2,b=-3 B.a=-2,b=3 C.a=2,b=-3 D.a=2,b=3
4.【合肥蜀山区期末】在第四象限内有一点A到x轴的距离是2,到y轴的距
离是3,则点A向左平移1个单位后的坐标是( )
(3)求三角形A′B′C′的面积.
1 1 解:S三角形A′B′C′=4×3- ×3×1- ×3×2-
2 ×1×4=12- -3-2= .
2
1
3
11
2
2
2
13.【六安霍邱期中】已知点P的等于它到y轴的距离,求点P的坐标;
解:由题意得|2-a|=|3a+6|, 所以2-a=3a+6或2-a=-(3a+6), 解得a=-1或a=-4, 所以点P的坐标为(3,3)或(6,-6).
上平移3个单位得到点A1,则点A1的坐标为( )
A.(1,2)
B.(2,9)
C.(5,3)
D.(-9,-4) A
2.【2021·亳州涡阳期末】点P(x,y)平移后得到点P′(x+1,y-2),其平 移的方式是( ) A.先向左平移1个单位,再向上平移2个单位 D B.先向左平移1个单位,再向下平移2个单位 C.先向右平移1个单位,再向上平移2个单位 D.先向右平移1个单位,再向下平移2个单位
新沪科版八年级上册《11.2 图形在坐标系中的平移》专题训练(含答案)

11.2 图形在坐标系中的平移专题一 图形平移中的规律探究题1. )在平面直角坐标系中 ,一蚂蚁从原点O 出发 ,按向上、向右、向下、向右的方向依次不断移动 ,每次移动1个单位.其行走路线如以下图所示.(1 )填写以下各点的坐标:A 4( , ) ,A 8 ( , ) ,A 12 ( , );(2 )写出点A 4n 的坐标 (n 是正整数 );(3 )指出蚂蚁从点A 100到点A 101的移动方向.2.如下图 ,矩形ABCD 的顶点坐标分别为A (1,1),B (2,1),C (2,3),D (1,3).(1)将矩形ABCD 向上平移2个单位 ,画出相应的图形 ,并写出各点的坐标;(2)将矩形ABCD 各个顶点的横坐标都减去3 ,纵坐标不变 ,画出相应的图形;(3)观察 (1 )、 (2 )中的到的矩形 ,你发现了什么 ?3.在直角坐标系中 ,△ABC 的三个顶点的位置如下图 ,现将△ABC 平移使得点A 移至|图中的点A ′的位置.(1)在直角坐标系中 ,画出平移后所得△A′B′C′ (其中B ′、C ′分别是B 、C 的对应点 ).(2)计算:对应点的横坐标的差:=-A A x x ' ,=-B B x x ' ,=-C C x x ';对应点的纵坐标的差:=-A A y y ' ,=-B B y y ' ,=-C C y y ' .(3)从 (2 )的计算中 ,你发现了什么规律 ?请你把发现的规律用文字表述出来.(4)根据上述规律 ,假设将△ABC 平移使得点A 移至|A ″ (2 , -2 ) ,那么相应的点O 1 A 1 A 2 A 3 A 4 A 5 A 6 A 7A 8 A 9 A 10A 11 A 12 xyB ″、C ″ (其中B ″、C ″分别是B 、C 的对应点 )的坐标分别是 、 .专题二 图形平移中的规律探究题4.初三年级|某班有54名学生 ,所在教室有6行9列座位 ,用 (m ,n )表示第m 行第n 列的座位 ,新学期准备调整座位 ,设某个学生原来的座位为 (m ,n ) ,如果调整后的座位为 (i ,j ),那么称该生作了平移[a ,b ] =[m - i ,n - j ] ,并称a +b 为该生的位置数.假设某生的位置数为10 ,那么当m +n 取最|小值时 ,m •n 的最|大值为 .5.国际象棋、中|国象棋和围棋号称世|界三大棋种. 国际象棋中的 "皇后〞的威力可比中|国象棋中的 "车〞大得多: "皇后〞不仅能控制她所在的行与列中的每一个小方格 ,而且还能控制 "斜〞×4的小方格棋盘 ,图中的 "皇后Q 〞能控制图中虚线所经过的每一个小方格.(1)在如图乙的小方格棋盘中有一 "皇后Q 〞 ,她所在的位置可用 " (2 ,3 )〞来表示 ,请说明 "皇后Q 〞所在的位置 " (2 ,3 )〞的意义 ,并用这种表示法分别写出棋盘中不能被该 "皇后Q 〞所控制的四个位置.(2)如图丙也是一个4×4的小方格棋盘 ,请在这个棋盘中放入四个 "皇后Q 〞 ,使这四个 "皇后Q 〞之间互不受对方控制 (在图丙中的某四个小方格中标出字母Q 即可 ).【知识要点】1.点的平移变换与坐标的变化规律是:点(x ,y )右 (左 )移m 个单位 ,得对应点(x ±m ,y ) ,点(x ,y )上 (下 )移n 个单位 ,得对应点(x ,y ±n ).2.图形的平移变换与坐标的变化规律一般是通过从图形中特殊点,转化为点的平移变换解决.【温馨提示】1.平移只改变物体的位置,不改变的物体的形状和大小,因此,平移前后图形的面积不变.2.一个图形进行平移,这个图形上所有的点的坐标都要发生相应的变化;反之,如果图形上的点的坐标发生变化,那么这个图形进行了平移.【方法技巧】1.点的平移与其坐标的变化规律是解决平移问题的关键,平移的方向决定了坐标是加还是减,平移的距离决定了加(或减)的数值.1 23 4 甲1 2 3 4 行 乙1 2 3 4 丙 第5题图2.作平移后的图形时,可先作出平移后图形中某些特殊点,然后再连结即可得到所需要的图形.参考答案1.⑴ A 4 (2 ,0 ); A 8 (4 ,0 ); A 12 (6 ,0 ); ⑵ A 4n (2n ,0 );⑶ 向上.2.(1)将矩形向上平移2个单位 ,画出图形 (略 ) ,矩形相应点的坐标为11(1,3),(2,3)A B ,11(2,5),(1,5)C D .(2) 22(2,1),(1,1)A B -- ,22(1,3),(2,3)C D --.图形略. (3 )发现 (1 )、 (2 )中的两图形形状、大小完全相同.3.(1)平移后的图形如图; (2)5 5 5 1 1 1(3)对应点的横坐标的差都相等;对应点的纵坐标的差都相等 (保持不变 );(4) (4 , -3 ) , (6 ,0 ).4.36 提示:由 ,得a +b =m -i +n -j ,即m -i +n -j =10 ,所以m +n =10 +i +j ,当m +n 取最|小值时 ,i +j 最|小为2 ,所以m +n 的最|小值为12 ,因为m +n =12 =3 +9 =4 +8=5 +7 =6 +6 =… ,m •n 的最|大值为6×6 =36.5.(1)说明皇后在第2列,第3行的位置,不能被控制的位置有(4,4),(1,1),(3,1),(4,2);(2)放在如(1,2),(2,4),(3,1),(4,3)四个位置.。
沪科版-数学-八年级上册-11.2.2 图形在坐标系中的平移 同步训练

11.2.2 图形在坐标系中的平移同步训练一、选择题:1、将点A(-4,2)向上平移3个单位长度得到的点B的坐标是()A (-1,2)B (-1,5)C (-4,-1)D (-4,5)2、已知正方形ABCD的三个顶点坐标为A(2,1),B(5,1),D(2,4),现将该正方形向下平移3个单位长度,再向左平移4个单位长度,得到正方形A'B'C'D',则C’点的坐标为()A (5,4)B (5,1)C (1,1)D (-1,-1)3、三角形ABC中,A(-1,0),B(5,0),C(2,5),则三角形ABC的面积为()A 30B 15C 20D 104、在平面直角坐标系中,若一图形各点的横坐标不变,纵坐标分别减3,那么图形与原图形相比()A向右平移了3个单位长度 B向左平移了3个单位长度C向上平移了3个单位长度 D向下平移了3个单位长度5、到x轴的距离等于2的点组成的图形是()A过点(0,2)且与x轴平行的直线 B过点(2,0)且与y轴平行的直线C过点(0,-2)且与x轴平行的直线D分别过(0,2)和(0,-2)且与x轴平行的两条直线6、下列现象中不属于平移的是()A滑雪运动员在平坦的雪地上滑雪B彩票打转盘在旋转C高楼的电梯在上上下下D火车在一段笔直的铁轨上行驶二、填空题:7、点P(-3,2)沿x轴的负方向平移3个单位长度,得到点Q的坐标是,在将Q 沿y轴正方向平移5个单位长度,得到点R的坐标是。
三、解答题:8、段AB的端点坐标为A(2,-1),B(3,1)。
试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状。
(画出图形,不必说明理由)9、当建立直角坐标系,描出点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),并用线段顺次连接各点。
⑴. 看图案像什么?⑵. 作如下变化:纵坐标不变,横坐标减2,并顺次连接各点,所得的图案与原来相比有什么变化?10、直角坐标系中,画出三角形AOB,使A、B两点的坐标分别为A(-2,-4),B(-6,-2)。
沪科版-数学-八年级上册-11.2.3 图形在坐标系中的平移同步练习
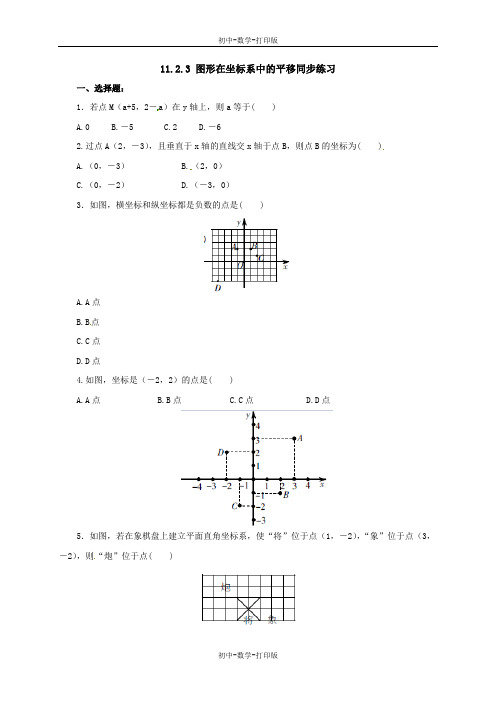
11.2.3 图形在坐标系中的平移同步练习一、选择题:1.若点M(a+5,2-a)在y轴上,则a等于( )A.0B.-5C.2D.-62.过点A(2,-3),且垂直于x轴的直线交x轴于点B,则点B的坐标为( )A.(0,-3)B.(2,0)C.(0,-2)D.(-3,0)3.如图,横坐标和纵坐标都是负数的点是( )A.A点B.B点C.C点D.D点4.如图,坐标是(-2,2)的点是( )A.A点B.B点C.C点D.D点5.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )A.(1,-1)B.(-1,1)C.(-1,2)D.(1,-2)6.已知点P1(a-1, 5)和P2(2,b-1)关于x轴对称,则(a+b)2013的值为( )A.1B.-1C.0D.2二、填空题:7.若点A在x轴上,且到点(3,0)的距离为5,则点A的坐标为_____________.8.线段AB=4,且AB平行于y轴,若A点坐标为(-3,2),则B点坐标为_____.9.若点P(x,y)在x轴的下方,y轴的右方,则xy 0.(填“>”、“<”、“≥”或“≤”)10.在平面直角坐标系中,A点的坐标为(5,-3),B点的坐标为(-2,-4),将线段AB平移到A′B′位置,且A′的坐标为(1,4),则B′的坐标为 .三、计算与解答11.已知(a-2)2+(b+3)2=0,试判断点M(-a,1b)所在的象限.12.大雁是一种候鸟,每年秋季,它们将结队而行,集体迁往南方,飞行时,它们保持一定的队形飞行,如图是它们的飞行示意图,当领头雁A飞到A′时,队尾的两只雁B、C飞到了什么位置?这期间,队形未发生变化,分别写出这三只大雁的新位置A′、B′、C′的坐标.13.如图,(1)请写出在直角坐标系中房子上的A、B、C、D、E、F、G的坐标;(2)强强想把房子向左平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标.14.如图,平面直角坐标系中,三角形ABC的顶点分别为A(0,0)、B(5,5)、C(6,0).(1)求三角形ABC的面积;(2)如果将三角形ABC向上平移1个单位长度,得到三角形A1B1C1,再将所得三角形向右平移2个单位长度,得到三角形A2B2C2,试求三角形A2B2C2的顶点坐标.参考答案一、选择题1.B 提示:a+5=0,解得a=-5.2. B 提示:x 轴上的点纵坐标为0.3.D 提示:据图可知.4.D 提示:据图可知. 5.B 提示:以图中“米”字型左上角的点为原点建立平面直角坐标系.6.B二、填空题7.(-2,0)或(8,0) 提示:分A 在点(3,0)左侧、右侧两种情况.8.(-3,-2)或(-3,6) 提示:分B 点在A 点上面或下面两种情况.9.< 提示:据题意有x>0,y<0,即xy <0.10.(-6,3)三、解答题11.解:因为(a -2)2+(b+3)2=0,所以a=2,b=-3,所以点M (-a ,1b)的坐标为(-2,-13 ),所以点M (-a ,1b)在第三象限. 12.解:由图可知,点B 的坐标为(-5,0),点C 的坐标为(1,-1),点A 的坐标为(-1,3),点A ′的坐标为(4,5).坐标的变化情况是:横坐标加上5,纵坐标加上2,由于雁群飞行时图形是在平移,所以点B ′的坐标为(0,2),点C ′的坐标为(6,1).13.解:(1)A (2,3),B (6,5),C (10,3),D (3,3),E (9,3),F (3,0),G (9,0).(2)能,(图略)平移后的坐标分别为A (-1,3),B (3,5),C (7,3),D (0,3),E (6,3),F (0,0),G (6,0).14.解:(1)三角形ABC 的面积为12 AC ·BD =12×6×5=15;(2)三角形A 1B 1C 1的顶点坐标分别为A 1(0,1),B 1(5,6),C 1(6,1),三角形A 2B 2C 2的顶点坐标分别为A 2(2,1),B 2(7,6),C 2(8,1).。
沪科版-数学-八年级上册-11.2 图形在坐标中的平移 练习

11.2图形在坐标中的平移一、单选题1.将△ABC的三个顶点的横坐标都加上6,纵坐标都减去5,则所得图形与原图形的关系是()A.将原图形向x轴的正方向平移了6个单位,向y轴的正方向平移了5个单位B.将原图形向x轴的负方向平移了6个单位,向y轴的正方向平移了5个单位C.将原图形向x轴的负方向平移了6个单位,向y轴的负方向平移了5个单位D.将原图形向x轴的正方向平移了6个单位,向y轴的负方向平移了5个单位2.将点P(2m+3,m﹣2)向上平移1个单位得到P′,且P′在x轴上,那么点P的坐标是()A.(9,1)B.(5,﹣1)C.(7,0)D.(1,﹣3)3.如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(﹣1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为()A.(a,b)B.(﹣a,﹣b)C.(a+2,b+4)D.(a+4,b+2)4.如图,在平面直角坐标系中,将点A(﹣2,3)向右平移3个长度单位,那么平移后对应的点A′的坐标是()A.(﹣2,﹣3)B.(﹣2,6)C.(1,3)D.(﹣2,1)5.把点A (2,5)向下平移3个单位长度后,再向右平移2个单位长度,它的坐标是( )A.(﹣1,5)B.(2,2)C.(4,2)D.(﹣1,7)6.在平面直角坐标系xOy 中,点P (﹣3,5)关于x 轴的对称点的坐标是( )A.(3,﹣5)B.(﹣3,﹣5)C.(3,5)D.(5,﹣3)7.如图,A ,B 的坐标为(2,0),(0,1),若将线段AB 平移至11B A , 则a+b 的值为( )A.2B.3C.4D.58、如图,在一张无穷大的格纸上,格点的位置可用数对(m ,n )表示,如点A 的位置为(3,3),点B 的位置为(6,2).点M 从(0,0)开始移动,规律为:第1次向右移动1个单位到(1,0),第2次向上移动2个单位到(1,2),第3次向右移动3个单位到(4,2),…,第n 次移动n 个单位(n 为奇数时向右,n 为偶数时向上),那么点M 第27次移动到的位置为( )A.(182,169)B.(169,182)C.(196,182)D.(196,210)二、填空题9.把点(3,﹣1)向________平移________个单位长度,再向________平移________个单位长度,可以得到对应点(﹣1,4).10.如图,在平面直角坐标系中,△ABC 的顶点都在方格纸的格点上,如果将△ABC 先向右平移4个单位长度,再向下平移1个单位长度,得到111C B A , 那么点A 的对应点A1的坐标为________.11.若将P (1,﹣m )向右平移2个单位长度后,再向上平移1个单位长度得到点Q (n ,3),则点(m ,n )的实际坐标是________.12.点P (2,﹣3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是________.13.如果点P (m ,1﹣2m )关于x 轴对称的点Q 在第四象限,则m 的取值范围是________.14.点P 在平面直角坐标系的位置如图所示,将点P 向下平移a 个单位得点P′,若点P′到x 轴和y 轴的距离均相等,且点P′在第三象限,则a 的值是________.三、解答题15.在平面直角坐标系中指出下列各点A (5,1),B (5,0),C (2,1),D (2,3),并顺次连接,且将所得图形向下平移3个单位,写出对应点A′、B′、C′、D′的坐标.16、若点M (1,a )与点N (b ﹣5,2)关于x 轴对称,求a+b 的值.17、在平面直角坐标系中,已知点A (﹣2,﹣3)关于x 轴对称的点为B ,关于y 轴对称的点为C ,求△ABC 的面积.18、如图,在直角坐标系中,A (﹣1,5),B (﹣3,0),C (﹣4,3).19、(1)在图中作出△ABC 关于y 轴对称的图形111C B A .20、(2)写出点1C 的坐标.参考答案与解析一、单选题1. D解:∵将△ABC的三个顶点的横坐标都加上6,纵坐标都减去5,∴所得图形与原图形的位置关系是△ABC先向右平移6个单位,再向下平移5个单位即可.故选D.2. B解:∵将点P(2m+3,m﹣2)向上平移1个单位得到P′,∴P′的坐标为(2m+3,m﹣1),3. D解:∵△A′B′O′是由△ABO平移得到的,点A的坐标为(﹣1,2),它的对应点A′的坐标为(3,4),∴△ABO平移的规律是:先向右平移4个单位,再向上平移2个单位,∴△ABO内仼意点P(a,b)平移后的对应点P′的坐标为(a+4,b+2).故选D.4. C解:点A(﹣2,3)向右平移3个长度单位后对应的点A′的坐标是(1,3),故选C.5.C解:点A(2,5)向下平移3个单位长度后,再向右平移2个单位长度,横坐标变为2+2=4,纵坐标变为5﹣3=2,所以,平移后的坐标为(4,2).故选C.6.B解:点P(﹣3,5)关于x轴的对称点的坐标是(﹣3,﹣5).故选B.7. A解:由B点平移前后的纵坐标分别为1.2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2.3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A.B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.8. C解:根据题意可知:当向右移动时,列的数字发生变化,行的数字不变,当向上移动时,行的数字发生变化,列的数字不变,所以点M第27次移动到的位置时,列的数字是1﹣﹣27中所有奇数的和,行的数字是1﹣﹣27中所有偶数的和,即1+3+5+7+9+…+27=196,2+4+6+8+…+26=182,所以,点M第27次移动到的位置为(196,182),故选C.二、填空题9. 左;4;上;5解:横坐标的变化为:﹣1﹣3=﹣4,说明向左平移了4个单位长度;纵坐标的变化为:4﹣(﹣1)=5,说明向上平移了5个单位长度.故四空分别填:左、4.上、5.10. (2,5)A的坐标为(﹣2+4,6﹣1),解:∵点A的坐标为(﹣2,6),∴对应点1即(2,5),故答案为:(2,5).11. (﹣2,3)解:将P(1,﹣m)向右平移2个单位长度后,可得到:(3,﹣m),再向上平移1个单位长度得到(3,﹣m+1),与点Q(n,3)重合,故3=n,﹣m+1=3,解得:n=3,m=﹣2,故(m,n)的实际坐标是:(﹣2,3).故答案为:(﹣2,3).12. (﹣2,﹣2)解:点(2,﹣3),向左平移4个单位,横坐标:2﹣4=﹣2,向上平移1个单位,纵坐标:﹣3+1=﹣2,∴点P'(﹣2,﹣2),故答案为:(﹣2,﹣2)13.0<m <21 解:∵点P (m ,1﹣2m )关于x 轴对称的点Q 在第四象限, ∴点P 在第一象限, ∴ ⎩⎨⎧>->0210m m ,解得0<m <21. 故答案为:0<m <21. 14. 6解:由图得知:P (﹣2,4), ∵将点P 向下平移a 个单位得点P′,∴P′(﹣2,4﹣a ),∵点P′到x 轴和y 轴的距离均相等,且点P′在第三象限,∴4﹣a=﹣2,∴a=6,故答案为:6.三、解答题15.解:如图:∵将所得图形向下平移3个单位,∴点A′(5,﹣2),B (5,﹣3),C (2,﹣2),D (2,0)16.解:∵M(1,a )与点(b ﹣5,2)关于x 轴对称 ∴b﹣5=1,a=﹣2, 解得:b=6,a=﹣2,∴a+b=6+(﹣2)=4,即:a+b 的值为417.解:∵点A (﹣2,﹣3)关于x 轴对称的点为B ,关于y 轴对称的点为C , ∴B(﹣2,3),C (2,﹣3),故△ABC 的面积为:21×AB×AC=21×6×4=12.18.解:(1)如图所示:(2)点1C 的坐标为:(4,3).。
新泸教版数学八年级上册同步练习:11.2 图形在坐标系中的平移

11.2图形在坐标系中的平移知识要点基础练知识点1点在坐标系中的平移1.将点( -5,3 )沿x轴的正方向平移3个单位后的坐标是( C)A.( 8,3 )B.( -8,3 )C.( -2,3 )D.( -5,0 )2.通过平移把点A( 2,-3 )移到点A'( 4,-2 ),按同样的平移方式可将点B( -3,1 )移到点B',则点B'的坐标是( -1,2 ).知识点2图形在坐标系中的平移3.( 2019·合肥庐阳中学期中)在如图所示的5×5方格纸中,图1中的图形N平移后如图2所示,则下列关于图形N的平移方法中,正确的是( C)A.先向下平移1格,再向左平移1格B.先向下平移1格,再向左平移2格C.先向下平移2格,再向左平移1格D.先向下平移2格,再向左平移2格4.在平面直角坐标系中,已知线段AB的两个端点分别是A( 4,-1 ),B( 1,1 ).将线段AB平移后得到线段A'B',若点A'的坐标为( -2,2 ),则点B'的坐标为( -5,4 ).知识点3图形的平移与坐标变化的互逆关系5.在平面直角坐标系中,将三角形各点的横坐标都减去3,纵坐标保持不变,所得图形与原图形相( B)A.向右平移了3个单位B.向左平移了3个单位C.向上平移了3个单位D.向下平移了3个单位6.( 教材P14练习第3题变式)在平面直角坐标系中,若点P( x-3,y+1 )平移后得到点P1( x,y),则点Q( 5,3 )作同样的平移后的坐标为( 8,2 ).综合能力提升练7.在平面直角坐标系中,将点P( 1,-2 )向右平移3个单位,再向上平移4个单位,得到的点P1的坐标为( B)A.( -2,2 )B.( 4,2 )C.( 5,1 )D.( 5,-5 )【变式拓展】在平面直角坐标系中,将点A( x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B( -3,2 )重合,则点A的坐标是( D )A.( 2,5 )B.( -8,5 )C.( -8,-1 )D.( 2,-1 )8.( 青岛中考)如图,线段AB经过平移得到线段A'B',其中点A,B的对应点分别为点A',B',这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A'B'上的对应点P'的坐标为( A)A.( a-2,b+3 )B.( a-2,b-3 )C.( a+2,b+3 )D.( a+2,b-3 )9.将点P( -3,y)先向下平移3个单位长度,再向左平移2个单位长度后得到点Q( x,-1 ),则xy=-10.10.已知坐标平面内点A( -2,5 ),如果将坐标轴先向左平移3个单位,再向上平移4个单位,那么点A在新坐标系中的坐标为( 1,1 ).11.( 改编)如图,将边长为6的等边△ABC沿BC方向平移3个单位得到△DEF,则四边形ABFD的周长为24.12.写出下列各点平移后的点的坐标.( 1 )将点A( -3,2 )向右平移3个单位;( 2 )将点B( 1,-2 )向左平移3个单位;( 3 )将点C( 4,7 )向上平移2个单位;( 4 )将点D( -1,2 )向下平移1个单位;( 5 )将点E( 2,-3 )先向右平移1个单位,再向下平移1个单位.解:( 1 )( 0,2 ).( 2 )( -2,-2 ).( 3 )( 4,9 ).( 4 )( -1,1 ).( 5 )( 3,-4 ).13.一个△ABC的三个顶点坐标分别为A( 0,0 ),B( 3,0 ),C( 2,3 ).( 1 )把△ABC向右平移3个单位,再向下平移2个单位,得到△A'B'C',写出点A',B',C'的坐标. ( 2 )若△A″B″C″三个顶点的坐标分别是A″( -2,-3 ),B″( 1,-3 ),C″( 0,0 ),则△A″B″C″是由△ABC经过怎样的平移得到的?解:( 1 )A'( 3,-2 ),B'( 6,-2 ),C'( 5,1 ).( 2 )将△ABC先向左平移2个单位,再向下平移3个单位,得到△A″B″C″.14.如图,有8×8的正方形网格,按要求操作并计算.( 1 )在8×8的正方形网格中建立平面直角坐标系,使点A的坐标为( 2,4 ),点B的坐标为( 4,2 );( 2 )将点A向下平移5个单位,再关于y轴对称得到点C,求点C的坐标;( 3 )画出△ABC,并求其面积.解:( 1 )如图所示.( 2 )点A向下平移5个单位得到点( 2,-1 ),关于y轴对称的点C的坐标为( -2,-1 ). ( 3 )△ABC如图所示.S△ABC=5×6-×6×3-×4×5-×2×2=9.拓展探究突破练15.阅读理解:在平面直角坐标系xOy中,对于任意两点P1( x1,y1)与P2( x2,y2)的“非常距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.例如:点P1( 1,2 ),点P2( 3,5 ),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值( 点Q为垂直于y轴的直线P1Q与垂直于x 轴的直线P2Q的交点).已知点A-,B为y轴上的一个动点.( 1 )若已知点B( 0,2 ),则点A与点B的“非常距离”为2;( 2 )若点A与点B的“非常距离”为3,求点B的坐标;( 3 )点A与点B的“非常距离”的最小值为. 解:( 2 )( 0,3 )或( 0,-3 ).。
11.2 图形在坐标中的平移(基础达标提升训练解析答案)

沪科版数学八年级上册第11章平面直角坐标系11.2图形在坐标系中的平移基础达标提升训练1. 将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是()A. (2,3)B. (2,-1)C. (4,1)D. (0,1)2.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是()A. (-1,1)B. (-1,-2)C. (-1,2)D. (1,2)3. 在平面直角坐标系中,将点M向右平移2个单位长度,则()A. 横坐标减2,纵坐标不变B. 横坐标加2,纵坐标不变C. 纵坐标减2,横坐标不变D. 纵坐标加2,横坐标不变4. 若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为()A. (-2,-1)B. (-1,0)C. (-1,-1)D. (-2,0)5. 如图所示,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A1的坐标是()A. (6,1)B. (0,1)C. (0,-3)D. (6,-3)6. 已知△ABC顶点坐标分别是A(0,6),B(-3,-3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为()A. (7,1)B. (1,7)C. (1,1)D. (2,1)7. 如图所示,把图(1)中的☉A经过平移得到☉O[如图(2)],如果图(1)中☉A上一点P的坐标为(m,n).那么平移后在图(2)中的对应点P′的坐标是()图(1) 图(2)A. (m+2,n+1)B. (m-2,n-1)C. (m-2,n+1)D. (m+2,n-1)8. 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为()A. (a-2,b+3)B. (a-2,b-3)C. (a+2,b+3)D. (a+2,b-3)9. 在平面直角坐标系中,已知线段AB的两个端点坐标分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′(点A的对应点为点A′),若点A′的坐标为(-2,2),则点B′的坐标为.10. 将点A(1,-3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为.11. 将点P(-3,y)向右平移3个单位,向上平移2个单位后得到点Q(x,-1),则xy=.12. 如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为.第12题第13题13. 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为.14. 如图,在网格中有点A(3,-1).(1)将点A向左平移4个单位,得到点A1,请在图上标出这个点,并写出它的坐标;(2)将点A向上平移4个单位,得到点A2,请在图上标出这个点,并写出它的坐标;(3)你能判断直线AA1与x轴,直线AA2与y轴的位置关系吗?15. 在边长为1的小正方形网格中,△AOB的顶点均在格点上,(1)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;(2)在(1)的条件下,A1的坐标为.16. 三角形A1B1C1是由三角形ABC平移后得到的,三角形ABC中任意一点P(x,y)经平移后对应点为P1(x-3,y-5),求A1,B1,C1的坐标.拓展探究 综合训练17. 如图所示,三角形A 1B 1C 1是三角形ABC 平移后得到的,三角形ABC 内任意一点M (x 0,y 0)经平移后对应点M 1(x 0-5,y 0-3).(1)试说明三角形ABC 是经过怎样的平移后变为三角形A 1B 1C 1的;(2)求A 1,B 1,C 1的坐标;(3)求 111A B C S 三角形 的值.。
沪科版数学 八年级上册 11.2 图形在坐标系中的平移 课后练习题

一、单选题1. 将点向下平移个单位长度后,再向左平移个单位长度的点为()A.B.C.D.2. 如果点向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是,那么a,b的值分别是( )A.B.C.D.3. 在平面直角坐标系中,将点向右平移3单位长度,再向上平移2个单位长度正好与原点重合,那么点的坐标是()A.B.C.D.4. 在平面直角坐标系中,将点(-2,6)沿轴向右平移5个单位后的对应点的坐标为()A.(3,6)B.(-2,11)C.(-7,6)D.(-2,1)5. 点先向右平移3个单位长度,再向下平移4个单位长度,得到的对应点的坐标是()A.B.C.D.二、填空题6. 点向右平移2个单位长度得到,则的坐标为_________.7. 在平面直角坐标系内,把点P(﹣5,﹣2)向右平移2个单位长度得到的点的坐标是_____.8. 点P的坐标是,把点P向左平移2m个单位,向上平移m个单位后,得到的点Q在第三象限,则m的取值范围为___________.三、解答题9. 如图,市政府的坐标是,某酒店的坐标是.(1)请你根据上述信息,画出这个平面直角坐标系;(2)某人所在位置的坐标为.①请你在图中用字母A标出某人的位置;②某人向北走了3个单位长度,又向东走了2个单位长度,此时某人所在位置的坐标是.10. 如图,已知,.(1)在表格中建立直角坐标系,并写出点的坐标;(2)若将点B向上平移3个单位得到点C,标出点C并连接,求的面积.11. 在下面所给的平面直角坐标系中,解答下列问题(1)描出点A(﹣2,0),B(2,﹣1),C(3,3),并用线段依次连接起来.(2)将三角形ABC向左平移2个单位长度,再向下平移3个单位长度,得到三角形A′B′C′.(3)写出三角形A′B′C′各个顶点的坐标.。
新沪科版数学八年级上册同步练习:11.2图形在坐标系中的平移

11.2图形在坐标系中的平移2. 点N( — 1, 3)可以看作由点 M( — 1, — 1)(个单位,则所得点的坐标是知识点2图形在坐标系中的平移4.在平面直角坐标系中,将三角形各点的横坐标都减去 与原图形相比( )5 .教材习题11.2第3题变式题如图11 — 2— 1,已知三角形ABC 经过平移后得到三角形A 1B 1C 1,点A 与点A 1,点B 与点B 1,点C 与点C 1分别是对应点,观察各对应点坐标之间的知识要点分类练 知识点1 点在坐标系中的平移 1.已知点 A 的坐标为(2, 1). (1)将点 向左平移 则点 B 的坐标为 ⑵将点 向右平移 C , 则点 C 的坐标为 ⑶将点 向上平移 2则点D 的坐标为 ⑷将点 向下平移 个单位后得E , 则点 E 的坐标为A .向上平移4个单位得到的B . 向左平移C .向下平移4个单位得到的D . 向右平移 4个单位得到的3. 2018宿迁在平面直角坐标系中,将点(3, —2)先向右平移 2个单位,再向上平移3 3,纵坐标保持不变,所得图形A .向右平移了 3个单位B .向左平移了 3个单位C .向上平移了 3个单位D .向下平移了 3个单位关系,解答下列问题:⑴分别写出点A与点A i,点B与点B i,点C与点C i的坐标;(2)若点P(x, y)通过上述的平移规律平移得到的对应点为Q(3, 5),求点P的坐标.图11 — 2 — 1 知识点3平面直角坐标系中的平移作图6.如图11 —2 —2所示,在平面直角坐标系中画出将“小船”先向下平移3个单位,再向右平移2个单位后得到的图形.7.已知三角形ABC三个顶点的坐标分别是(一2, 1), (2, 3), (—3, —1),把三角形ABC 平移到一个确定位置,则平移后各顶点的坐标可能是()A . (0, 3), (0, 1), (—1 , —1)B . (—3, 2), (3, 2), (—4, 0)C. (1 , —2), (3, 2), (—1, —3)D . (—1, 3), (3, 5), (—2, 1)&若将点P(1, —m)向右平移2个单位,再向上平移1个单位后得到点Q(n, 3),则点K(m, n)的坐标为 __________________ .A拓厂探究创新练9.如图11 —2—3,在平面直角坐标系中,P(a, b)是三角形ABC的边AC上的一点,三角形ABC 经平移后点P的对应点为P i(a+ 6, b+ 2).(1) 请画出经过上述平移后得到的三角形A i B i C i,并写出点A, C, A i, C i的坐标;(2) 求线段AC扫过的面积.... 牛…—■ I ■ I I [| ■图11 —2— 3教师详解详析1. (1)(0 , 1) (2)(4 , 1) (3)(2, 3) (4)(2, —1)2. A3. (5, 1)4. B [解析]只有横坐标变化,则图形左右平移,根据“左减右加”,可知选B.5. 解:(1)由图知A(1 , 2), A i( —2, —1), B(2 , 1), B i(—1 , —2) , C(3 , 3) , C i(0 , 0).⑵由(1)知,平移的方向和距离为向左平移3个单位,向下平移3个单位.x —3= 3 , x = 6 ,所以,解得I•y—3 = 5 , l y= 8.则点P的坐标为(6, 8).6. 略7. D [解析]平移后各顶点的坐标与原顶点坐标相比,必须有统一的变化规律,即每个顶点的横坐标要有相同的变化,纵坐标也有相同的变化.通过计算可知,只有D项各点坐标符合这一要求,这一组坐标的变化规律是“横坐标都加1,纵坐标都加2”.& (—2, 3)9.解:(1)如图,三角形A i B i C i即为所求.各点的坐标分别为A( —3, 2), C( —2, 0), A i(3, 4), C i (4 , 2).⑵如图,连接AA i, CC i.i iS三角形ACiAi= 7 X 2 = 7, S三角形ACiC= 7 X 2= 7,所以四边形ACC i A i的面积为7 +7= i4,即线段AC扫过的面积为i4.。
2018-2019学年数学沪科版八年级上册11.2 图形在坐标系中的平移 同步练习

2018-2019学年数学沪科版八年级上册11.2 图形在坐标系中的平移同步练习一、选择题1.在平面直角坐标系中,将点向右平移个单位长度后得到的对应点的坐标的().A、B、C、D、+2.在直角坐标系内,将点P(1,﹣2)向左平移2个单位长度,再向上平移3个单位长度,可以得到对应点P1的坐标为()A、(﹣1,1)B、(﹣1,﹣5)C、(3,1)D、(3,﹣5)+3.将点A(﹣1,2)向右平移4个单位长度,再向下平移3个单位长度,则平移后点的坐标是()A、(3,1)B、(﹣3,﹣1)C、(3,﹣1)D、(﹣3,1)+4.将点A(2,1)向上平移2个单位长度得到点A′,则点A′的坐标是()A、(2,3)B、(0,1)C、(4,1)D、(2,-1)+5.线段平移得到的,点(-2,3)的对应点为(2,-1),则点是由线段(1,1)的对应点的坐标为()A、(-1,-3)B、(5,3)C、(5,-3)D、(0,3)+将点A(﹣3,﹣2)向左平移5个单位,再向下平移4个单位得到点B,则点B的坐标为()A、(﹣8,2)B、(﹣8,﹣6)C、(2,﹣2)D、(2,2)+7.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比()A、向右平移了3个单位长度B、向左平移了3个单位长度C、向上平移了3个单位长度D、向下平移了3个单位长度+8.如图,线段AB经过平移得到线段,其中点A、B的对应点分别为点、,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在上的对应点的坐标为()A、(a+2,b?3)B、(a+2,b+3)C、(a?2,b?3)D、(a?2,b+3)+二、填空题9.在坐标平面内,圆心坐标为(4,3),将圆向左平移4个单位长度时圆心坐标为,再向下平移3个单位长度时圆心坐标为.+10.将点P(-3,4)先向下平移3个单位长度,再向右平移2个单位长度后得到点Q,则点Q的坐标是11.将点P(-3,y)向下平移2个单位,向左平移3个单位后得到点Q(x,-1),则xy=.+12.把向上平移3个单位长度再向下平移1个单位长度所到达位置的坐标是+13.已知A(2,﹣3),先将点A向左平移3个单位,再向上平移2个单位得到点B,则点B的坐标是.+14.△ABC中,A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,则对应点A′、B′、C′的坐标分别为、、.+15.线段是由线段平移得到的,点的对应点为,则点的对应点的坐标为.+三、解答题16.将△ABC向右平移4个单位长度,再向下平移5个单位长度,(1)(1)、作出平移后的△A′B′C′.(2)、分别写出A′,B′,C′的坐标;+17.一个正方形在平面直角坐标系内的位置如图所示,已知点 A 的坐标为(3,0),线段AC与BD的交点是M.(1)、写出点M、B、C、D的坐标;(2)、当正方形中的点M由现在的位置经过平移后,得到点M(﹣4,6)时,写出点A、B、C、D的对应点A′、B′、C′、D′的坐标,并求出四边形A′B′C′D′的面积+18.在如图所示的网格中,三角形ABC的顶点A(0,5),B(-2,2).(1)、根据A,B坐标在网格中建立平面直角坐标系,并写出点C坐标:();(2)、平移三角形ABC,使点C移动到点F(7,-4),画出平移后的三角形DEF,其中点D与点A对应,点E与点B对应.+19.如图,A、B两点的坐标分别为(2,3)、(4,1).(1)、求△ABO的面积;(2)、把△ABO向下平移3个单位后得到一个新三角形△O′A′B′,求△O′A′B′的3 个顶点的坐标.+20.三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图:(1)、分别写出下列各点的坐标:A' (2)、三角形A'B'C'由三角形ABC 经过怎样的平移得到?(3)、若点P (a ,b )是三角形ABC 内部一点,则平移后三角形A'B'C'内的对应点P '的坐标为 ; B' ;C'; ; ;(4)、求三角形ABC 的面积. +21.在如图所示的平面直角坐标系中表示下面各点:A (2,0);B (1,-3);C (3,-5);D (-3,-5);E (3,5);F(5,7).(1)、A 点到原点O 的距离是. (2)、将点C 向x 轴的负方向平移6个单位,它与点(3)、连接CE ,则直线CE 与x 轴,y 轴分别是什么关系?(4)、点F 到x 、y 轴的距离分别是多少?重合. +22.在平面直角坐标系中,有点(1)、当点在第一象限的角平分线上时,的值为(2)、若线段 轴. , . .①求点、的坐标.②若将线段 A B 平移至线段 E F ,点 A 、 B 分别平移至 A ′ ( x 1 , 3 x 1 + 1 ) , B ′ ( x 2 , 2 x 2 ? 3 ),求 A ′、 B ′的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.2 图形在坐标系中的平移
专题一 图形平移中的规律探究题
1.)在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.
(1)填写下列各点的坐标:A 4( , ),A 8( , ),A 12( , ); (2)写出点A 4n 的坐标(n 是正整数);
(3)指出蚂蚁从点A 100到点A 101的移动方向.
2.如图所示,矩形ABCD 的顶点坐标分别为A (1,1),B (2,1),C (2,3),D (1,3).
(1)将矩形ABCD 向上平移2个单位,画出相应的图形,并写出各点的坐标;
(2)将矩形ABCD 各个顶点的横坐标都减去3,纵坐标不变,画出相应的图形;
(3)观察(1)、(2)中的到的矩形,你发现了什么?
3.在直角坐标系中,△ABC 的三个顶点的位置如图所示,现将△ABC 平移使得点A 移至图中的点A ′的位置.
(1)在直角坐标系中,画出平移后所得△A′B′C′(其中
B ′、
C ′分别是B 、C 的对应点).
(2)计算:
对应点的横坐标的差:=-A A x x ' ,
=-B B x x ' ,=-C C x x ' ;
对应点的纵坐标的差:=-A A y y ' ,
=-B B y y ' ,=-C C y y ' .
(3)从(2)的计算中,你发现了什么规律?请你把发现的规律用文字表述出来.
(4)根据上述规律,若将△ABC 平移使得点A 移至A ″(2,-2),那么相应的点B ″、C ″(其中B ″、C ″分别是B 、C 的对应点)的坐标分别是 、 .
O 1 A 1 A 2 A 3 A 4 A 5 A 6 A 7
A 8 A 9 A 10
A 11 A 12 x
y
专题二 图形平移中的规律探究题
4.初三年级某班有54名学生,所在教室有6行9列座位,用(m ,n )表示第m 行第n 列的座位,新学期准备调整座位,设某个学生原来的座位为(m ,n ),如果调整后的座位为(i ,j ),则称该生作了平移[a ,b ]=[m - i ,n - j ],并称a +b 为该生的位置数.若某生的位置数为10,则当m +n 取最小值时,m •n 的最大值为 .
5.国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q ”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q ”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q ”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q ”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q ”,使这四个“皇后Q ”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q 即可).
【知识要点】
1.点的平移变换与坐标的变化规律是:点(x ,y )右(左)移m 个单位,得对应点(x ±m ,y ),点(x ,y )上(下)移n 个单位,得对应点(x ,y ±n ).
2.图形的平移变换与坐标的变化规律一般是通过从图形中特殊点,转化为点的平移变换解决.
【温馨提示】
1.平移只改变物体的位置,不改变的物体的形状和大小,因此,平移前后图形的面积不变.
2.一个图形进行平移,这个图形上所有的点的坐标都要发生相应的变化;反之,如果图形上的点的坐标发生变化,那么这个图形进行了平移.
【方法技巧】
1.点的平移与其坐标的变化规律是解决平移问题的关键,平移的方向决定了坐标是加还是减,平移的距离决定了加(或减)的数值.
2.作平移后的图形时,可先作出平移后图形中某些特殊点,然后再连结即可得到所需要
1 2
3 4 甲
1 2 3 4 行 乙
1 2 3 4 丙 第5题图
的图形.
参考答案
1.⑴ A 4(2,0); A 8(4,0); A 12(6,0); ⑵ A 4n (2n ,0);⑶ 向上.
2.(1)将矩形向上平移2个单位,画出图形(略),矩形相应点的坐标为11(1,3),(2,3)A B ,11(2,5),(1,5)C D .(2) 22(2,1),(1,1)A B --,22(1,3),(2,3)C D --.图形略.
(3)发现(1)、(2)中的两图形形状、大小完全相同.
3.(1)平移后的图形如图; (2)5 5 5 1 1 1
(3)对应点的横坐标的差都相等;对应点的纵坐标的差都相
等(保持不变);(4)(4,-3),(6,0).
4.36 提示:由已知,得a +b =m -i +n -j ,即m -i +n -j =10,
所以m +n =10+i +j ,当m +n 取最小值时,i +j 最小为2,所以
m +n 的最小值为12,因为m +n =12=3+9=4+8=5+7=6+6=…,
m •n 的最大值为6×6=36.
5.(1)说明皇后在第2列,第3行的位置,不能被控制的位置有(4,4),(1,1),(3,1),(4,2);(2)放在如(1,2),(2,4),(3,1),(4,3)四个位置.。
