海珠区2017-2018学年第一学期期末联考试题含答案

合集下载

广州市海珠区2017-2018学年第一学期期末考试五年级语文试卷及参考答案

1读拼音，写词语。

2写出下列拼音的汉字，组成词语。

3把下面的四字词语补充完整。

4选择正确答案，把序号写在括号里。

5根据提示填空。

6按要求完成句子练习。

阅读短文，完成练习。

7阅读文章，回答下列小题。

8按要求作文。

9按要求作文。

102017~2018学年广州海珠区五年级上学期期末语文试卷一、基础知识1忽略（1）（2）糟糕稀罕（3）谨慎（4）（5）殿堂盗窃（6）爱慕（7）（8）皎洁颤抖（9）坠落（10）（1）21．崎2．骑（2）1．旅2．侣（3）1．付2．附（4）1．剧2．惧3倾盆（1）翼翼（2）（3）1．失2．落厉（4）（5）1．欺2．压（6）1．滚2．烂1．披2．斩（7）崖（8）4（1）B 1A 2C3C（2）B （3）51．只怕有心人2．万事能成3．十事九空（1）1．香自苦寒来2．江南几度梅花发3．明月何时照我还（2）1．更喜岷山千里雪，三军过后尽开颜2．金沙水拍云崖暖，大渡桥横铁索寒（3）6王懿荣是第一个发现和研究甲骨文的人。

（1）示例：父母的爱，是温暖的拥抱，是细心的叮咛。

（2）7如果，就；虽然，但是；语气，倒不如（1）廉价失败坚硬坚持不懈（2）1．积累2．基础3．自私4．公平（3）王羲之20年临池习书，才换来现在书法上的成功；李时珍跋山涉水，遍尝百草，才有《本草纲目》的问世；司马迁博览群书，忍辱负重，却从不停止书写，才有（4）二、古诗词默写三、语言运用四、现代文阅读了《史记》的诞生。

懒汉因为不努力不奋斗，就很难获得成功，所以说成功是“自私”的，但是奋斗者（5）会坚持不懈地努力，总有一天会成功，所以说成功是“公平”的。

8（1）恍然大悟1以身作则2油然而生3蔚然成风4（2）要他和群众同吃同住同劳动外貌外貌的变化说明毛岸英生活艰苦，说明毛主席并没有因为他是自己儿子就（3）特殊对待，而是与农民同吃同住，体现了领导以身作则的艰苦奋斗精神。

（4）A（5）略五、作文略9略10。

2017~2018学年广东广州海珠区初一上学期期末英语试卷(解析)

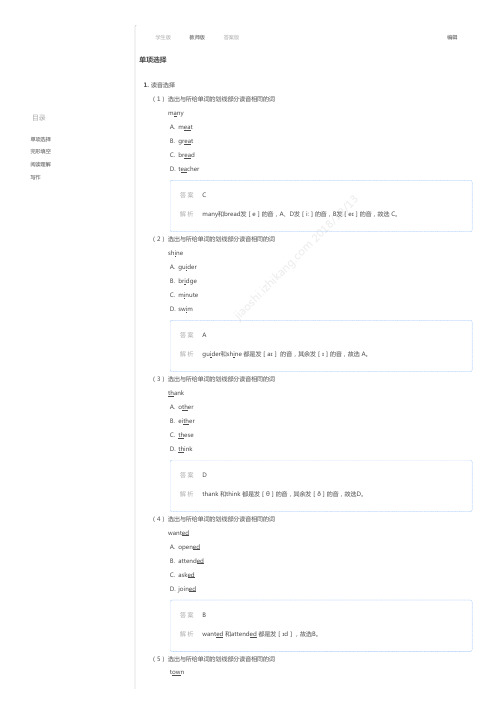
目录单项选择完形填空阅读理解写作单项选择j i ao s h i.i zh ik an g.co m2018/12/131.（1）选出与所给单词的划线部分读音相同的词many A.B.C.D.答案解析（2）选出与所给单词的划线部分读音相同的词shine A.B.C.D.答案解析（3）选出与所给单词的划线部分读音相同的词thank A.B.C.D.答案解析（4）选出与所给单词的划线部分读音相同的词wanted A.B.C.D.答案解析（5）选出与所给单词的划线部分读音相同的词town读音选择meat great bread teacherCmany和bread发［e］的音，A、D发［i:］的音，B发［e ɪ］的音，故选 C。

guider bridge minute swimAguider和shine 都是发［a ɪ］的音，其余发［ɪ］的音，故选 A。

other either these thinkDthank 和think 都是发［θ］的音，其余发［ð］的音，故选D。

opened attended asked joinedBwanted 和attended 都是发［ɪd］，故选B。

学生版教师版答案版编辑目录单项选择完形填空阅读理解写作jiaoshi.izhikang.com218/12/13jiaoshi.izhikang.com218/12/13A.B.C.D.答案解析yellowfollowbrownthrowCtown和brown 都是发［aʊ］的音，其余发［əʊ］的音，故选 C。

2.A.aB.anC.theD.不填答案解析Tom likes maths and science. He hopes to be engineer.B考察不定冠词a/an的辨析。

engineer的读音以元音开头，因此，前面要用an，故选 B。

3.A.readB.readsC.readingD.to read答案解析Many teenagers in China enjoy now. They often read books in the library.C考察动词的固定搭配。

广东省广州市2017-2018学年第一学期海珠区七年级期末英语试卷及参考答案

海珠区2017-2018学年第一学期期末调研测试七年级英语试题（满分100分，考试时间90分钟）注意事项：1. 答题前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的考生号、姓名，再用2B铅笔将对应号码的标号涂黑。

2. 答案必须填涂在答题卡上。

每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试卷上。

一、语法选择（共15小题；每小题1分，满分15分）阅读下面短文，按照句子结构的语法性和上下文连贯的要求，从1-15各题所给的A、B、C和D项中选出最佳选项，并在答题卡上将该项涂黑。

(A)I'm so happy! Tomorrow I'll be one of the first (1)________ to travel into space. The Moon is around380,000 kilometers from the Earth, so it (2)________ us about four days to get there. There's no gravity inspace, so we'll (3)________ able to float around in the spaceship. We'll have to tie ourselves to our beds so thatwe won't float(4)________ in our sleep. Without gravity, our bodies may get weak, (5)________ we'll have to doexercises every day.(1). A. student B. students C. a student D. the student(2). A. will take B. took C. take D. takes(3). A. are B. is C. am D. be(4). A. away B. down C. up D. along(5). A. because B. and C. so D. but(B)John is thirteen years now. He began (6)________ in a middle school two years ago. His family is in asmall village and it's far away (7)________ the school. Every day, he gets up early in the morning. After a quickbreakfast, he has to run to school to get there on time. His father hopes to borrow (8)________ money to buy abike forhim, but he knows his mother is always ill and his father spends much money (9)________ hermedicine. If his father buys him a bike, their life (10)________ harder than before. So he(11)________agree with him and keeps running there every day. Now he'svery strong and never late for class.Last week there was (12)________ sports meeting in their school. John ran faster than the other boys, and it was (13)________for him to win three matches. He (14)________ three gold medals and thewhole school knew him.How happy the boy was! He told (15)________ grandma about the good news as soon as he got home.“I broke two school records today, Granny.” called out the boy.She was surprised and said, "I am sorry to hear that. We have no money to pay for them!”(6). A. to study B. study C. studies D. studied(7). A. to B. at C. from D. with(8). A. many B. few C. a few D. some(9). A. buys B. buying C. to buy D.buy(10). A.will be B. is C. was D. are(11). A.don’t B. won’t C. isn’t D. doesn’t(12). A.a B. an C. the D. /(13). A.exciting B. excited C. excitement D. excitedly(14). A.get B. got C. gets D. will get(15). A.he B. him C. his D. himself二、完形填空（共10小题；每小题1.5分，满分15分）阅读下面短文，掌握其大意，然后从16~25各题所给的A、B、C和D项中选出最佳选项并在答题卡上将该项涂黑。

2017-2018学年广东省广州市海珠区高一(上)期末数学试卷

2017-2018学年广东省广州市海珠区高一（上）期末数学试卷副标题一、选择题（本大题共12小题，共60.0分）1.若M={x|x2-px+6=0}，N={x|x2+6x-q=0}，若M∩N={2}，则p+q=（）A. 21B. 8C. 6D. 72.下列四组函数中，表示相同函数的一组是（）A. f(x)=x2−1x−1，g(x)=x+1 B. f(x)= x2，g(x)=(x)2C. f(x)=|x|，g(x)=2D. f(x)=x+1⋅x−1,g(x)=x2−13.下列函数中，值域为[0，+∞）的偶函数是（）A. y=x2+1B. y=lg xC. y=x3D. y=|x|4.下列函数在其定义域内既是奇函数，又是增函数的是（）A. y=xB. y=3xC. y=lg|x|D. y=x135.设a=0.60.6，b=0.61.5，c=1.50.6，则a，b，c的大小关系（）A. a<b<cB. a<c<bC. b<a<cD. b<c<a6.函数f（x）=2x+3x的零点所在的一个区间（）A. (−2,−1)B. (−1,0)C. (0,1)D. (1,2)7.设函数f（x）=1+log2(2−x)，x＜12x−1，x≥1，则f（-2）+f（log212）=（）A. 3B. 6C. 9D. 128.函数y=xa x|x|（0＜a＜1）的图象的大致形状是（）A. B.C. D.9.直线kx-y-k=0（k∈R）和圆x2+y2=2交点的个数为（）A. 2个B. 1个C. 0个D. 不确定10.圆C1：（x-1）2+（y-1）2=1和圆C2：（x+2）2+（y-5）2=36的位置关系是（）A. 相离B. 外切C. 相交D. 内切11.设α，β是两个不同的平面，l是一条直线，以下命题正确的是（）A. 若l⊥α，α⊥β，则l⊂βB. 若l⊥α，α//β，则l⊥βC. 若l//α，α//β，则l⊂βD. 若l//α，α⊥β，则l⊥β12.某几何体的三视图如图所示，它的体积为（）A. 72πB. 48πC. 30πD. 24π二、填空题（本大题共4小题，共20.0分）13.计算log216=______．log2414.经过P（1，3），Q（3，5）两点的直线的倾斜角是______．15.若函数f（x）=a x-1（a＞1）在区间[2，3]上的最大值比最小值大a，则a=______．216.体积为8的正方体的顶点都在同一个球面上，则该球面的表面积为______．三、解答题（本大题共6小题，共70.0分）17.三角形的三个顶点为A（-2，4），B（-3，-1），C（1，3）．（1）求BC边上高所在直线的方程；（2）求△ABC的面积S．18.如图，在直三棱柱ABC-A1B1C1中，已知AC⊥BC，BC=CC1，设AB1的中点为D，BC1∩B1C=E．求证：（Ⅰ）DE∥平面AA1C1C；（Ⅱ）BC1⊥AB1．19.已知函数f（x）=a x−1（a＞1）．a x+1（1）根据定义证明：函数f（x）在（-∞，+∞）上是增函数；（2）根据定义证明：函数f（x）是奇函数．20.如图，在三棱锥S-ABC中，SA=SB=AC=BC=2，AB=23，SC=1．（1）画出二面角S-AB-C的平面角，并求它的度数；（2）求三棱锥S-ABC的体积．21.在平面直角坐标系xOy中，圆C经过P（3+22，0），Q（3-22，0），R（0，1）三点．（1）求圆C的方程；（2）若圆C与直线x-y+a=0交于A，B两点，且OA⊥OB，求a的值．22.已知函数f（x）=ax2+mx+m-1（a≠0）．（1）若f（-1）=0，判断函数f（x）的零点个数；（2）若对任意实数m，函数f（x）恒有两个相异的零点，求实数a的取值范围；[f（x1）+f（x2）]（3）已知x1，x2∈R且x1＜x2，f（x1）≠f（x2），求证：方程f（x）=12在区间（x1，x2）上有实数根．答案和解析1.【答案】A【解析】解：∵M∩N={2}，∴2∈M，2∈N，即4-2p+6=0且4+12-q=0，得p=5，q=16，则p+q=5+16=21，故选：A根据交集的定义，得到方程根的关系，进行求解即可．本题主要考查集合交集的应用，根据元素转化为一元二次方程的根是解决本题的关键．2.【答案】C【解析】解：A．函数f（x）==x+1，x≠1，则定义域为{x|x≠1}，所以两个函数的定义域不同，所以A不是相同函数B．f（x）=（）2=x，x≥0，g（x）==|x|，所以两个函数的定义域和对应法则不同，所以B不是相同函数C．g（x）==|x|，两个函数的定义域和对应法则，所以C表示的是相同函数．D．由即x≥1，由x2-1≥0得x≥1或x≤-1，则两个函数的定义域不同，不是相同函数．故选：C．分别判断两个函数的定义域和对应法则是否相同即可．本题考查了判断两个函数是否是同一个函数．判断的标准是看两个函数的定义域和对应法则是否相同．3.【答案】D【解析】解：y=x2+1为偶函数，值域为[1，+∞）；y=lgx为对数函数，不为偶函数，且值域为R；y=x3为奇函数，值域为R；y=|x|为偶函数，值域为[0，+∞）．故选D．运用常见函数的奇偶性和值域，即可得到符合题意的函数．本题考查函数的奇偶性和值域的求法，掌握常见函数的奇偶性和值域是解题的关键，属于基础题．4.【答案】D【解析】解：函数为非奇非偶函数，不满足条件；函数y=3x为非奇非偶函数，不满足条件；函数y=lg|x|为偶函数，不满足条件；只有函数既是奇函数，又是增函数，满足条件；故选D根据指数函数，幂函数，对数函数及函数对折变换法则，我们逐一分析四个答案中的四个函数的性质，然后和题目中的条件进行比照，即可得到答案．本题考查的知识点是函数奇偶性与单调性的综合应用，其中熟练掌握基本初等函数的性质是解答本题的关键．5.【答案】C【解析】解：函数y=0.6x为减函数；故a=0.60.6＞b=0.61.5，函数y=x0.6在（0，+∞）上为增函数；故a=0.60.6＜c=1.50.6，故b＜a＜c，故选：C．利用指数函数和幂函数的单调性，可判断三个式子的大小．本题考查的知识点是指数函数和幂函数的单调性，难度中档．6.【答案】B【解析】解：函数f（x）=2x+3x是增函数，f（-1）=＜0，f（0）=1+0=1＞0，可得f（-1）f（0）＜0．由零点判定定理可知：函数f（x）=2x+3x的零点所在的一个区间（-1，0）．故选：B．判断函数的单调性，利用f（-1）与f（0）函数值的大小，通过零点判定定理判断即可．本题考查零点判定定理的应用，考查计算能力，注意函数的单调性的判断．7.【答案】C【解析】解：函数f（x）=，即有f（-2）=1+log2（2+2）=1+2=3，12）==2×=12×=6，f（log则有f（-2）+f（log212）=3+6=9．故选：C．先求f（-2）=1+log2（2+2）=1+2=3，再由对数恒等式，求得f（log212）=6，进而得到所求和．本题考查分段函数的求值，主要考查对数的运算性质，属于基础题．8.【答案】D【解析】解：当x＞0时，|x|=x，此时y=a x（0＜a＜1）；当x＜0时，|x|=-x，此时y=-a x（0＜a＜1），则函数（0＜a＜1）的图象的大致形状是：，故选：D．分x＞0与x＜0两种情况将函数解析式化简，利用指数函数图象即可确定出大致形状．此题考查了函数的图象，熟练掌握指数函数的图象与性质是解本题的关键．9.【答案】A【解析】解：直线kx-y-k=0（k∈R）转化为：y=k（x-1），则：直线经过定点（1，0），由于定点（1，0）在圆x2+y2=2的内部．故经过定点的直线与圆有两个交点．故选：A．首先求出直线所经过的定点，进一步判断定点和圆的位置关系，进一步求出直线和圆的位置关系．本题考查的知识要点：经过定点的直线系的应用，点和圆的位置关系的应用．10.【答案】D【解析】解：圆心坐标分别为C1：（1，1），C2：（-2，5），两圆半径分别为R=6，r=1，圆心距离|C1C2|===5，则|C1C2|=R-r，即两圆相内切，故选：D求出两圆圆心距离以及半径，根据圆心距和半径之间的关系进行判断即可．本题主要考查圆与圆的位置关系的判断，求出圆心距，判断圆心距和半径之间的关系是解决本题的关键．11.【答案】B【解析】解：由设α，β是两个不同的平面，l是一条直线，知：在A中，若l⊥α，α⊥β，则l∥β或l⊂β，故A错误；在B中，若l⊥α，α∥β，则由线面垂直的判定定理得l⊥β，故B正确；在C中，若l∥α，α∥β，则l∥β或l⊂β，故C错误；在D中，若l∥α，α⊥β，则l与β相交\平行或l⊂β，故D错误．故选：B．在A中，l∥β或l⊂β；在B中，由线面垂直的判定定理得l⊥β；在C中，l∥β或l⊂β；在D中，l与β相交\平行或l⊂β．本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．12.【答案】C【解析】解：由图知，该几何体是圆锥和半球体的组合体，球的半径是3，圆锥底面圆的半径是3，圆锥母线长为5，由圆锥的几何特征可求得圆锥的高为4，==30π则它的体积V=V圆锥+V半球体故选：C．由题意，结合图象可得该几何体是圆锥和半球体的组合体，根据图中的数据即可计算出组合体的体积选出正确选项本题考查由三视图求体积，解题的关键是由三视图得出几何体的几何特征及相关的数据，熟练掌握相关几何体的体积公式也是解题的关键13.【答案】2【解析】解：=．故答案为：2．直接由对数的运算性质计算得答案．本题考查了对数的运算性质，是基础题．14.【答案】45°【解析】解：∵P（1，3），Q（3，5），∴，设经过P（1，3），Q（3，5）两点的直线的倾斜角为α，（0°≤α＜180°），则tanα=1，∴α=45°．故答案为：45°．由两点坐标求出直线的斜率，再由倾斜角的正切值等于斜率求得直线的倾斜角．本题考查直线倾斜角的求法，考查倾斜角与斜率的关系，是基础题．15.【答案】32【解析】解：∵函数f（x）=a x-1（a＞1）在区间[2，3]上为增函数，∴，f（x）min=a．由题意可得：，解得a=（a＞1）．故答案为：．由题意可得关于a的一元二次方程，求解得答案．本题考查指数函数的单调性，考查一元二次方程的解法，是基础题．16.【答案】12π【解析】解：∵体积为8的正方体的顶点都在同一个球面上，∴该正方体的棱长a==2，∴球半径R==，∴该球面的表面积S=4=12π．故答案为：12π．先求出该正方体的棱长a==2，再求出球半径R==，由此能求出该球面的表面积．本题考查正方体的外接球的表面积的求法，考查正方体、球等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．17.【答案】解：（1）k BC=−1−3−3−1=1，∴BC边上高所在直线的斜率k=-1，可得BC边上高所在直线的方程：y-4=-（x+2），即为：x+y-2=0．（2）|BC|=(−3−1)2+(−1−3)2=42，直线BC的方程为：y-3=x-1，化为：x-y+2=0．点A到直线BC的距离d=2=22．∴△ABC的面积S=12|BC|•d=12×42×22=8．【解析】（1）利用斜率直线计算公式可得k BC，可得BC边上高所在直线的斜率k=-，利用点斜式可得可得BC边上高所在直线的方程．（2）利用两点之间的距离公式可得|BC|，利用点斜式可得直线BC的方程．利用点到直线的距离公式可得点A到直线BC的距离d，可得△ABC的面积S=|BC|•d．本题考查了斜率计算公式、相互垂直的直线斜率之间的关系、两点之间的距离公式、点到直线的距离公式、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．18.【答案】证明：（1）∵在直三棱柱ABC-A1B1C1中，BC1∩B1C=E，∴E是B1C的中点，∵AB1的中点为D，∴DE∥AC，∵AC⊂平面AA1C1C，DE⊄平面AA1C1C，∴DE∥平面AA1C1C．（2）∵在直三棱柱ABC-A1B1C1中，BC=CC1，∴BC1⊥B1C，AC⊥CC1，又AC⊥BC，BC∩CC1=C，∴AC⊥平面BCC1B1，∴AC⊥BC1，∵AC∩B1C=C，∴BC1⊥平面ACB1，∴BC1⊥AB1．【解析】（1）由三角形中位线定理得DE∥AC，由此能证明DE∥平面AA1C1C．（2）推导出BC1⊥B1C，AC⊥CC1，AC⊥BC，从而AC⊥平面BCC1B1，进而AC⊥BC1，由此能证明BC1⊥AB1．本题考查线面平行的证明，考查线线垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．19.【答案】证明：（1）f（x）=1-2a x+1，令m＜n，则f（m）-f（n）=1-2a+1-1+2a+1=2(a m−a n)(a n+1)(a m+1)，∵a＞1，m＜n，则a m＜a n，（a n+1）（a m+1）＞0，故2(a m−a n)(a n+1)(a m+1)＜0，故f（m）-f（n）＜0，故f（x）在R递增；（2）由题意函数的定义域是R，关于原点对称，又f（-x）=a −x−1a−x+1=-a x−1a x+1=-f（x），故f（x）是奇函数．【解析】（1）根据函数的单调性的定义证明函数的单调性即可；（2）根据函数的奇偶性的定义证明函数的奇偶性即可．本题考查了函数的单调性和函数的奇偶性问题，考查定义的应用，是一道基础题．20.【答案】解：（1）取AB中点O，连结SO，CO，∵SA=SB=AC=BC=2，SC=1．∴SO⊥AB，CO⊥AB，∴∠SOC是二面角S-AB-C的平面角，∵SO=CO=22−12=3，∴cos∠SOC=SO2+CO2−SC22×SO×CO =2×3×3=56，∴二面角S-AB-C的大小为：∠SOC=arccos56．（2）过S作SE⊥平面ABC，交CO于E，OE=13CO=1322−12=33，SE= SO2−OE2=3−13=263，S△ABC=12×2×3=3，∴三棱锥S-ABC的体积：V S-ABC=13S△ABC×SE=1 3×3×263=223．【解析】（1）取AB中点O，连结SO，CO，推导出SO⊥AB，CO⊥AB，从而∠SOC是二面角S-AB-C的平面角，由此能求出二面角S-AB-C的大小．（2）过S作SE⊥平面ABC，交CO于E，求出OE=，SE==，=，由此能求出三棱锥S-ABC的体积．本题考查二面角的大小的求法，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．21.【答案】解（1）设圆的方程为：x2+y2+Dx+Ey+F=0，圆C经过P（3+22，0），Q（3-22，0），R（0，1）三点．则：1+E+F=0，令y=0，则：圆的方程转化为：x2+Dx+F=0，则：3+22+3−22=−D，解得：D=-6．利用：(3+22)(3−22)=F，解得：F=1．故：E=-2．所以圆的方程为：x2+y2-6x-2y+1=0．（2）圆x2+y2-6x-2y+1=0，转化为标准式为：（x-3）2+（y-1）2=9．由于圆C与直线x-y+a=0交于A，B两点，且OA⊥OB，则：|AB|=32+32=32，所以：圆心（3，1）到直线x-y+a=0的距离d=2=322，解得：a=1或-5．【解析】（1）利用已知条件求出圆的一般式方程．（2）首先求出弦AB的值，进一步利用点到直线的距离公式求出结果．本题考查的知识要点：圆的方程的求法，直线和圆的位置关系的应用．点到直线的距离公式的应用．22.【答案】（1）解：∵函数f（x）=ax2+mx+m-1（a≠0），且f（-1）=0，∴a-m+m-1=0，则a=1，f（x）=x2+mx+m-1=（x+1）（x-1+m），∴当m=2时，此函数f（x）有一个零点-1；当m≠2时，函数f（x）有两个零点-1，1-m；（2）解：对任意实数m，函数f（x）恒有两个相异的零点，可得△1＞0恒成立，即m2-4a（m-1）＞0，即为m2-4am+4a＞0对任意实数m恒成立，可得△2＜0，即16a2-16a＜0，解得0＜a＜1；[f（x1）+f（x2）]，（3）证明：令F（x）=f（x）-12[f（x1）+f（x2）]则F（x1）=f（x1）-12[f（x1）-f（x2）]，=12F（x2）=f（x2）-1[f（x1）+f（x2）]2=1[f（x2）-f（x1）]，2∵f（x1）≠f（x2）∴F（x1）F（x2）=-1[f（x2）-f（x1）]2＜0，4所以F（x）=0在（x1，x2）内必有一个实根，[f（x1）+f（x2）]在区间（x1，x2）上有实数根．则方程f（x）=12【解析】（1）由f（-1）=0可求得a=1，利用因式分解，讨论m=2与m不为2，分析判断即可；（2）由题意可得可得△1＞0恒成立，即m2-4am+4a＞0对任意实数m恒成立，可得△2＜0，即16a2-16a＜0，解不等式即可得到所求范围；（3）令F（x）=f（x）-[f（x1）+f（x2）]，可证得F（x1）F（x2）＜0，由零点存在定理可知方程f（x）=[f（x1）+f（x2）]在区间（x1，x2）上有实数根．本题考查二次函数的性质，考查函数零点的判定定理，考查化归思想与构造函数的思想的综合应用，属于难题．。

2017_2018学年广东广州海珠区初一上学期期末英语试卷及参考答案

C. brown D. throw
2. Tom likes maths and science. He hopes to be
A. a
B. an
engineer. C. the
D. 不填
3. Many teenagers in China enjoy
now. They often read books in the library.
happy about that. "You are a growing boy," his mother said "You need meat. Don't you want to become healthy
and 2 ?" His mother put some 3
, rice and carrots in front of him. "I want you to eat all your food
C. to
D. at
14. Linda and Leo felt A. surprise
when they saw the rocket disappear into the sky.
B. surprising
C. surprised
D. surprisingly
15. This is not A. my; your
me some Chinese exercises every day.
B. gives
C. giving
D. is giving
6. Today is a A. sun; bright
day. The Sun shines
.
B. sun; brightly

2017~2018学年广东广州海珠区初一上学期期末语文试卷(解析)

（选自浙江文艺出版社《粽子里的乡愁》，有删改）（1）通读全文，在横线上填写恰当的内容。
老人送“我”小山薯——______________——“我”给老人铜钱老人再送“我”小山薯——______________
答案二婶买山薯少给老人一个铜板；“我”把事情告诉老师老师教育我要体谅做小贩的
目录
积累与运用古诗文积累与默写古诗文阅读现代文阅读写作
答案 A
解析 2分。
B“着”应读“ zhuó ”；“怯”应读“qiè”；
C“蜷”应读“quán”
D“哄”应读“hōng ”。 2. 下列词语中，没有错别字的一项是
2018/12/10
A. 缥缈博学翻来复去
C. 安祥分歧见异思迁
答案 D 解析 2分。
答案 C 解析 3分。“乃悟前狼假寐”可以看出不是“早就明白”。
10. 阅读下面的诗歌，然后回答问题。
观沧海曹操
东临碣石，以观沧海。水何澹澹，山岛竦峙。树木丛生，百草丰茂。秋风萧瑟，洪波涌起。日月之行，若出其中；星汉灿烂，若出其里。幸甚至哉，歌以咏志。
/10
目录
积累与运用古诗文积累与默写古诗文阅读现代文阅读写作
，
”（《闻王昌龄左迁龙标遥有此
寄》），将同情和思念之心托付给多情的明月。
答案 1．逝者如斯夫 2．不舍昼夜 3．我寄愁心与明月 4．随君直到夜郎西
解析 4分。 ①中“河边”、“时间像河水一样流去，日夜不停”可以看出； ②“将同情和思念之心托付给多情的明月”可以看出。
8. 根据课本，解释下面句子中加粗词的意义。
（1）下列句子中，加粗词的意义相同的一组是
A. 恐前后受其敌盖以诱敌

2017-2018学年广东广州海珠区初二上学期期末语文试卷(带答案)

2017-2018学年广东广州海珠区初二上学期期末语文试卷积累与运用1、下列词语中，加粗字的读音全都正确的一项是（）A.抖擞sǒu 镜léng正襟危坐jīnB.镌刻juān教诲huì不折不挠ráoC.滞留zhì蹒跚pán惟妙惟肖qiàoD.洗涤dí翘首qiào刨根问底páo2、下列词语中，没有错别字的一项是（）A.秀颀落第眼花瞭乱B.愚钝磷峋筋疲力尽C.宣嚣濒临截然不同D.睫毛安详因地制宜3、下列句子中，加粗词语使用有误的一项是（）A.人民解放军百万大军横渡长江，以锐不可当之势占领南岸广大地区。

B.他口才非常好，不论是演讲还是平时聊天，一说起话来就络绎不绝。

C.鲁迅先生的作品往往能入木三分地揭露出国民的劣根性，引人深思。

D.他是一位尽职尽责的班干部，总能一丝不苟地完成老师布置的任务。

4、下列句子中，没有语病的一项是（）A.十九大提出了把我国建成富强民主文明和谐美丽的社会主义现代化强国。

B.同学们能否学好语文这门基础学科，关键在于平时勤于阅读和认真积累。

C.在当今的移动互联网时代，电子阅读已经成为人们阅读的一种常见方式。

D.通过参观广州五羊石像，让我了解了五羊降福的传说，使我增长了见识。

5、下列句子中，语言表达得体的一项是（）A.学生会主席在给校长的建议书里写道：“我的看法不是很成熟，请校长批评指正。

”B.小明对老师说：“我昨天在班群里都说了请假，你怎么忘了呢？真是贵人多忘事！”C.会议开始前，主持人提醒：“为保持会场安静，请各位关闭手机，否则后果自负！”D.听完讲座后，学员对专家说：“感谢你的指导！你确实有较高的水平，我很欣赏。

”6、阅读下面材料，回答问题。

大洋网讯8月10日，2017年南国书香节暨羊城书展在广州琶洲会展中心正式开幕。

本届书香节以“把读书作为一种生活态度”为年度口号，整个展区的面积有4万平方米，将举办名人名家、中华优秀传统文化、2016年度中国好书、新锐和网络、儿童及青少年、岭南文化名家等系列活动240多场次，出席名人嘉宾300多名。

2017-2018学年广东省广州市海珠区高二第一学期期末联考文科数学参考答案与评分标准

2017 学年第一学期期末考试
高二文科数学试题答案及评分标准
评分说明: 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据
试题的主要考查内容比照评分参考制订相应的评分细则． 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该
题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
得 2 a3 2 28 a3 ,解得, a3 8 .

a2

a4

20

a1q a1q a1q2 8
3

20
……………………2分
q 2 q 1
解之得
或 2
a1 2 a1 32
又数列an 是递增数列,q 2 an a1qn1 2n .
i1
2 2 3 3.5 4 6 5 6.5 6 7
=113.0
……………………3分
23456
x
4，
5
……………………4 分
2 3.5 6 6.5 7
y
5
5
……………………5 分
文科数学试题答案第 2 页（共 6 页）
5
xi2 x12 x22 x32 x42 x52 =90，
（2）当 n 1时, b1 S1 1 ,
当 n 2 时, bn Sn Sn1 n2 n 12 2n 1,
……………………4分
……………………5分 ……………………6分 ……………………7分
2 1 1 1,an 2n 1 an bn 2n 2n 1

2017-2018学年广东省广州市海珠区等五区高一数学上期末联考试题

海珠区2017-2018 学年第一学期期末联考试题高一数学本试卷共4页，22小题，满分150分，考试用时120分钟。

第I卷（选择题共60分）每小题5分，共60分，在每小题所给的四个选项中，只有一项是符合题目要求的.1 To g2 (2 —x), x ::: 15= 2心_1 ，贝《2)"9212)=A. 3B. 6C. 9D.函数yxxa=———（0 ::: a ：：:1）的图象的大致形状是、选择题：本大题共12小题,1. 若M = x —px !：「6 = 0 J ,•6x_q=0?,且M「lN ={2}，贝p ■ q =A. 21B. 8C.D. 72. F列四组函数中，表示相同函数的一组是2x —1A. f (x) , g( x) = x 1x -1B. f (x) =x? , g (x) = ( •.. x )2C. f (x) =| x |, g( x)D. f(x)二x x - 1, g (x)3. F列函数中，值域为 1.0，•::的偶函数是B. y = lg xC.D.4. F列函数在其定义域内既是奇函数，又是增函数的是1B. y = x 3C. y =ig I x |D.5. 0.6设 a 二0.6 , b0.6=0.6 1.5 , c =1.5 0.6，则a,b,c 的大小关系是A. b ::: a ::: cB. a ::: c ::: bC. a ::: b ::: cD. b ::: c ::: a6. 函数f x =2 3x的零点所在的一个区间是A. -2, -1B. -1,0C. 0,1D. 1,27. 设函数x。

2017_2018学年广东广州海珠区初一上学期期末语文试卷答案

积累与运用古诗文积累与默写1.【答案】A2.【答案】D3.【答案】B4.【答案】C5.【答案】D6.【答案】美丽的花朵像少女一样娇媚。

7.【答案】1归雁洛阳边2岐王宅里寻常见3非宁静无以致远4人不知而不愠5便引诗情到碧霄6终古高云簇此城（1）（2）1．2．3．4．逝者如斯夫不舍昼夜我寄愁心与明月随君直到夜郎西8.【答案】1．大体现代文阅读写作1眼睛好像闭起来，神情悠闲得很。

2禽兽狡辩诡诈的方法能有多少呢？（2）（3）C10.【答案】（1）登上；耸立。

（2）太阳和月亮的运行，好像是从这浩瀚的海洋中发出的。

银河星光灿烂，好像是从这浩瀚的海洋中产生出来的。

表达了诗人博大的情怀和开阔的胸襟，以及一统天下的豪情壮志。

11.【答案】（1）二婶买山薯少给老人一个铜板；“我”把事情告诉老师老师教育我要体谅做小贩的（2）老人“愣愣地”表现了二婶少给了他一个铜板时他的生气与无奈；“我愣愣地”表现了我对老人的同情以及我对自己免费吃了老人山薯的惭愧。

（3）我认为二婶不会补给老人。

因为如果烤山薯的老人经常来这里卖山薯的话。

应该与周围的邻居很熟，因此二婶少给了他一个铜板，他不会这么在意；其次，二婶来买山薯的时候应该知道自己的钱够买多少的山薯，但是她依旧是捡了很大的几个山薯，可以看出她是个爱贪便宜的人。

因此她不会补回一枚铜板给老人。

12.【答案】（1）1．2．爬树摘下人参果贪吃（2）用动作描写的方法，一连串的动作，写孙悟空偷人参果的一气呵成，表现了他的动作敏捷、本领高超。

（3）名号：齐天大圣得名缘由：孙悟空因不满在天庭只做弼马温，打出南天门，回到花果山，接受独角鬼王的建议，自封为“齐天大圣”。

13.【答案】略。

2017-2018学年广东省广州市海珠区八年级第一学期期末数学试卷带答案

2017-2018学年广东省广州市海珠区初二（上）期末数学试卷一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）下面四个手机应用图标中是轴对称图形的是（）A．B．C．D．2．（3分）用科学记数法表示0.000002017=（）A．20.17×10﹣5 B．2.017×10﹣6 C．2.017×10﹣7 D．0.2017×10﹣73．（3分）以下列长度的线段为边，可以作一个三角形的是（）A．6cm，16cm，21cm B．8cm，16cm，30cmC．6cm，16cm，24cm D．8cm，16cm，24cm4．（3分）若△ABC有一个外角是锐角，则△ABC一定是（）A．钝角三角形B．锐角三角形C．等边三角形D．等腰三角形5．（3分）（x2y）2的结果是（）A．x6y B．x4y2C．x5y D．x5y26．（3分）如果把分式中的x和y都扩大3倍，那么分式的值（）A．扩大3倍B．扩大9倍C．扩大4倍D．不变7．（3分）计算4x3yz÷2xy正确的结果是（）A．2xyz B．xyz C．2x2z D．x2z8．（3分）如图所示，小李用直尺和圆规作∠CAB的平分线AD，则得出∠CAD=∠DAB的依据是（）A．ASA B．AAS C．SSS D．SAS9．（3分）如图，AD是△ABC的中线，点E是AD的中点，连接BE、CE，若△ABC的面积是8，则阴影部分的面积为（）A．2 B．4 C．6 D．810．（3分）如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为（）A．2 B．2 C．4 D．4二、填空题（本大题共6小题，每小题3分，共18分）11．（3分）如果10m=12，10n=3，那么10m+n=．12．（3分）若一个多边形每个外角都是30°，则这个多边形的边数有条．13．（3分）已知分式的值为零，那么x的值是．14．（3分）如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是．15．（3分）已知a2+b2=12，a﹣b=4，则ab=．16．（3分）对实数a、b，定义运算☆如下：a☆b=，例如：2☆3=2﹣3=，则计算：[2☆（﹣4）]☆1=．。

2017_2018学年广东广州海珠区初二上学期期末语文试卷及参考答案

2017~2018学年广东广州海珠区初二上学期期末语
文试卷
A.B.C.D.下列词语中，加粗字的读音全都正确的一项是
抖擞s ǒu 棱镜l éng 正襟危坐j īｎ
镌刻ju ān 教诲hu ì 不折不挠r áｏ
滞留zh ì
蹒跚p án 惟妙惟肖qi àｏ洗涤d í 翘首qi ào 刨根问底p áｏ
1 A.秀颀
落第眼花瞭乱 B.愚钝磷峋筋疲力尽C.宣嚣濒临截然不同 D.睫毛安详因地制宜下列词语中，没有错别字的一项是
2 A.B.C.D.下列句子中，加粗词语使用有误的一项是
人民解放军百万大军横渡长江，以锐不可当之势占领南岸广大地区。

他口才非常好，不论是演讲还是平时聊天，一说起话来就
络绎不绝。

鲁迅先生的作品往往能入木三分地揭露出国民的劣根性，引人深思。

他是一位尽职尽责的班干部，总能
一丝不苟地完成老师布置的任务。

3 A.B.C.D.下列句子中，没有语病的一项是
十九大提出了把我国建成富强民主文明和谐美丽的社会主义现代化强国。

同学们能否学好语文这门基础学科，关键在于平时勤于阅读和认真积累。

在当今的移动互联网时代，电子阅读已经成为人们阅读的一种常见方式。

通过参观广州五羊石像，让我了解了五羊降福的传说，使我增长了见识。

4下列句子中，语言表达得体的一项是5一、积累与运用。

2017-2018学年广东省广州市海珠区等五区高一上学期期末联考数学试题

海珠区 2017-2018 学年第一学期期末联考试题高一数学本试卷共 4 页， 22 小题，满分 150 分，考试用时120 分钟。

第Ⅰ卷 ( 选择题共 60 分)一、选择题：本大题共12 小题，每题 5 分，共 60 分，在每题所给的四个选项中，只有一项为哪一项切合题目要求的．．若 M = x x2px 6 0， N = x x26x q 0 ，且M N{2}，则 p q1A.21B.8C. 6D.7 2．以下四组函数中，表示同样函数的一组是A. f (x)x21, g( x) x 1 B. f ( x)x2 , g( x) ( x) 2 x1C. f (x)| x |, g( x)x2D. f ( x)x 1x1, g( x)x2 1 3．以下函数中，值域为0，的偶函数是A. y x21B. y lg xC. y x3D. y x4．以下函数在其定义域内既是奇函数，又是增函数的是1A. y xB.y x 3C. y lg | x |D. y 3x5．设a0.60.6 , b0.61.5 , c 1.50.6，则 a,b, c 的大小关系是A. b a cB. a c bC. a b cD. b c a6．函数f x2x3x 的零点所在的一个区间是A.2,1B.1,0C.0,1D.1,27．设函数f (x)1log 2 (2x), x1则f( 2) f (log 2 12) 2x 1, x 1,A.3B.6C.9D.12 8．函数yxa x(0 a 1) 的图象的大概形状是xA B C D 9．直线kx y k0 k R 与圆x2y2 2 交点的个数为A.2 个B.1 个C.0个D. 不确立C1 :x2y21与圆C2:x252．圆112y36的地点关系是10A. 相离B. 外切C. 订交D.内切11.设 ,是两个不一样的平面，l 是一条直线，以下命题正确的选项是A. 若l,，则 lB. 若l,/ / ，则 lC. 若l / /,/ / ，则 lD. 若l / /,，则 l12．某几何体的三视图如下图，它的体积为A. 72B.48C.D.第12题图第Ⅱ卷 ( 非选择题共90分)二、填空题：本大题共 4 小题，每题 5 分，共 20 分．log 13．计算log 169. 43．经过 P(1,3)，Q 3,5两点的直线的倾斜角是.1415．若函数f x a x 1 a 1 在区间[ 2,3]上的最大值比最小值大a ,则2a.16．体积为8 的正方体的极点都在同一球面上，则该球面的表面积为.三、解答题：本大题共 6 小题，满分70 分．解答应写出文字说明，证明过程或演算步骤．17．（本小题满分10 分）已知ABC 的三个极点 A 2,4 , B 3, 1 ,C 1,3 ．（1）求BC边上高所在直线的方程；（2）求ABC的面积S．18.（本小题满分12 分）如图，在直三棱柱 ABC A1 B1C1中，已知AC BC ，BC CC1，设 AB1的中点为 D ，B1C BC1 E .求证：A CB （ 1）DE //平面AA1C1C；（ 2）BC1AB1.D EA1C1 19. （本小题满分12 分）B1a x1第18题图已知函数 f x a 1 .a x1（1）依据定义证明：函数（2）依据定义证明：函数f x 在,上是增函数；f x 是奇函数.20.（本小题满分12 分）如图，在三棱锥S ABC 中，SA=SB AC BC 2, AB 2 3, SC 1 .（1）画出二面角S AB C的平面角，并求它的度数；（2）求三棱锥S ABC的体积 .第20题图21.（本小题满分 12 分）在平面直角坐标系 xOy 中，圆C经过 P 3 2 2,0 ,Q 3 2 2,0 , R 0,1 三点．（ 1）求圆C的方程；（ 2）若圆C与直线x y a 0 交于 A, B 两点，且 OA OB ，求a的值．22.（本小题满分 12 分）已知函数 f x ax2mx m 1 a 0 .（ 1）若f10 ，判断函数 f x 的零点个数；（ 2）若对随意实数m，函数f x恒有两个相异的零点，务实数 a 的取值范围；（ 3）已知x1, x2R 且x1x2， f x1 f x2，求证：方程 f x 1f x2f x12在区间x1, x2上有实数根 .2017 学年第一学期期末联考高一数学试题参照答案与评分标准说明：1．参照答案与评分标准指出了每道题要考察的主要知识和能力，并给出了一种或几种解法供参照，假如考生的解法与参照答案不一样，可依据试题主要考察的知识点和能力比较评分准以相的分数．2．解答中的算，当考生的解答在某一步出，假如后部分的解答未改的内容和度，可影响的程度决定后部分的得分，但所分数不得超部分正确解答得分数的一半；假如后部分的解答有重的，就不再分．3．解答右端所注分数，表示考生正确做到一步得的累加分数． 4．只整数分数，和填空不中分．一、题号123 456781 1 191 2答案A CＤ BＡBCDADBC二、填空13. 1；14.450；15. 3 ；16. 12．2三、解答（本大共6 个小，共 70 分．解答写出文字明、演算步聚或推理程．）17．（本小分10 分）已知ABC 的三个点 A 2,4 , B 3,1,C1,3．⑴求 BC 上高所在直的方程；⑵求 ABC 的面 S ．解 (1)BC 上高所在直 l ，因为直BC 的斜率 k BC 3+1 =1, ⋯⋯⋯⋯⋯⋯⋯⋯. ⋯2分1+3因此直l 的斜率 k11. ⋯⋯⋯⋯⋯⋯⋯⋯. ⋯3分kBC又直 l 点 A2,4 ，因此直 l 的方程 y 41x 2 ， ⋯⋯⋯⋯⋯ . ⋯4分即 xy 2 0.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ .. ⋯4 分⑵ BC 所在直方程：y+1＝ 1 x3 , 即 xy20, ⋯⋯⋯⋯⋯⋯⋯⋯. ⋯5分点 A 2,4 到直 BC 的距离| 2 42 |d2 2 , ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分1221又BC=123 1 22 ⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分3 =4 SABC1BC d 1 4 2 2 2 8. ⋯⋯⋯⋯⋯ . ⋯ 10分2 218．（本小分12 分）如，在直三棱柱 ABCA 1B 1C 1中，已知 ACBC ，BCCC 1 ， AB 1 的中点 D ， B 1C BC 1 E .ACBEDA1C1B 12017-2018学年广东省广州市海珠区等五区高一上学期期末联考数学试题求：⑴ DE // 平面 AA 1C 1C ； ⑵ BC 1 AB 1 .明：⑴在直三棱柱ABCA 1B 1C 1 中，CC 1 平面 A 1 B 1C 1 ，且 BC CC 1矩形BB 1C 1C 是正方形， ⋯⋯⋯....................⋯⋯⋯分 . ⋯ .................⋯1EBC 1 的中点， ⋯⋯⋯⋯⋯⋯.⋯分.................................................又 D AB 1的中点，.3DE / / AC ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分又 DE平面 AACC 1 1， AC 平面 AACC 11 ， ⋯⋯⋯⋯⋯ .. 分⋯⋯4DE // 平面 AACC1. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分. ⋯51⑵在直三棱柱 ABCA 1B 1C 1 中，CC 1平面 ABC , AC平面 ABC ,ACCC 1 . ⋯⋯⋯⋯⋯⋯6分又AC BC ， CC 1 平面 BCC 1B 1 ， BC 平面 BCC 1 B 1 ， BCCC 1 C ， ⋯ ..... 7分AC平面 BCC 1 B 1 ， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯....................................分BC 1 平面 BCC 1 B 1 ，AC B 1C . ⋯⋯⋯⋯⋯⋯⋯.... ⋯ .................................. 分矩形 BCC BBCBC，⋯⋯⋯⋯⋯⋯⋯⋯ ...............................分1 1 是正方形，11AC, B 1C平面 B 1AC ， C1CC ， BC 1 平面 B 1 AC . ⋯⋯ .............分⋯ 11又AB 1平面 B 1 AC ， BC 1AB 1 . ⋯⋯⋯⋯⋯⋯⋯⋯. ⋯ ................................. 分19.（本小分12 分）x已知函数 fxa x 1 a 1 .a1⑴依据定明：函数 f x 在 ,上是增函数；⑵依据定明：函数 fx 是奇函数 .明：⑴ 随意的x 1 , x 2,，且 x 1 x 2 ， ⋯⋯⋯⋯1 分fx 1f x 2 a x 11 a x 21a x 11a x 2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分1⋯2⋯8⋯⋯ 10⋯ 12a x11a x21a x21a x11⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分a x11a x212 a x1a x2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分a x11a x21x x , a1，a x1a x2 ，即a x1a x20，⋯⋯⋯.⋯5分12又a x11a x210 ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯. ⋯6分f x1f x20 ，即 f x1f x2，⋯⋯⋯⋯⋯⋯7分f x在,上是增函数 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分⑵f x f x a x1 a x1，⋯⋯⋯⋯⋯⋯⋯⋯9分a x1 a x111 a x1=a x10,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分a x1a x a x10⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分111a x a x1f x f x =0 ，即 f x = f x因此函数 f x是奇函数 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分 1220.（本小分12 分）如，在三棱 S ABC 中， SA=SB AC BC 2,AB 23, SC 1.⑴画出二面角 S AB C 的平面角，并求它的度数；⑵求三棱 S ABC 的体.解：⑴取 BC 中点 D ，接 SD 、 CD ，⋯⋯....................................⋯⋯....1 分SA=SB2， AC BC 2 ，SD AB,CD AB ，⋯...⋯......... 2 分且 SD平面 SAB ， CD平面 CAB ，⋯.............................................⋯...3 分SDC 是二面角 S AB C 的平面角.⋯.....................................⋯⋯....4 分在直角三角形 SDA 中，SDSA2AD 222321⋯...5分在直角三角形 CDA 中，SCA2AD 2222CD31⋯...6分ACODBSD CD SC1SDC 是等三角形，⋯⋯⋯⋯⋯⋯⋯.7分SDC 600. ⋯...⋯⋯⋯⋯⋯⋯⋯⋯⋯...8分⑵解法 1：SD AB,CD AB, SD CD D ， AB SDC ......................9 分又AB 平面ABC，平面 ABC平面 SDC ，且平面 ABC平面 SDC CD .............10 分在平面 SDC 内作 SO DC 于 O ， SO平面 ABC ，..................11 分即 SO是三棱 S ABC 的高.3在等SDC 中， SO，三棱S ABC 的体2VS ABC 1S ABC SO11 2 3 131. ....................................12 分33222解法 2：SD AB,CD AB, SD CD D AB 平面 SDC .........9 分在等SDC 中，SDC 的面 S SDC 3 SD2344三棱 S ABC 的体， .......................10 分VS ABC VA SDCVB SDC1S SDC AB13 2 31. ..................12 分334221.（本小分12 分）在平面直角坐系 xOy 中，C P 322,0,Q3 22,0, R 0,1 三点．⑴求 C 的方程；⑵若 C 与直x y a0交于 A, B 两点，且OA OB, 求a的．解：⑴因 C 的心在段PQ 的直均分上，因此可 C 的心3,t ，⋯⋯⋯⋯⋯⋯⋯⋯.⋯⋯⋯.1分有 32(t 1)2(2 2 )2t 2 , 解得 t 1. ⋯⋯⋯⋯⋯⋯⋯2分C 的半径32(t1) 2 3. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分因此 C的方程(x 3) 2(y1) 29. ⋯⋯⋯⋯⋯⋯⋯⋯分4⑵ A x , y , B x , y，其坐足方程：x y a0,5 分(x 3)( y 1)29. ............11222消去 y ，获得方程2x 2(2a8)x a2210. ⋯⋯分a (6)由根与系数的关系可得，x1x24a, x1x2a22a1①. ⋯⋯⋯⋯8分2由OA OB于可得 ,x1 x2y1 y20.⋯⋯⋯⋯⋯⋯⋯⋯⋯.....10 分.....................................又 y x a, y2x a,因此2x1x2a( x1x2 )20② .⋯⋯⋯分112a (11)由①，②得a1，足0, 故a 1. ⋯⋯......................................⋯⋯⋯⋯⋯12 分22.（本小分 12 分）已知函数 f x ax2mx m 1 a 0 .⑴若 f10，判断函数f x 零点个数；⑵若对随意实数 m ，函数f x 恒有两个相异的零点，务实数 a 的取值范围；⑶已知 x1 , x2R 且 x1 x2， f x1f x2，求：方程 f x1f x1 f x22在区x , x2上有数根 .1解: ⑴ f 1 0, a m m 1 0, a1f x x2mx m 1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分m2 4 m 1m 2 2,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分当 m 2 ，0，函数f x 当 m 2 ，0，函数f x 有一个零点；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分有两个零点 .⋯⋯⋯⋯⋯⋯⋯⋯.⋯4⋯分⑵已知 a0 ，则m24a m10 关于m R恒建立,⋯⋯⋯⋯⋯⋯⋯⋯ (6)即 m24am4a0 恒建立；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯...⋯⋯⋯6分因此16a216a0 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分进而解得 0 a 1.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯...8分⑶ g xf x1 f x 1 f x 2，2gx 1fx 11 f x 1 f x 21 f x 1 f x2 ⋯⋯⋯.⋯9 分22g x 2f1f x 1f x 21 f x 2f x 1⋯⋯⋯.⋯10 分x 222f x 1f x 2g x 1 gx 21 f x 1f x 220 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11分4g x0在区 x 1, x 2 上有数根， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.⋯12⋯分即方程 fx1 f x 1 f x 2在区x 1, x 2 上有数根 . ⋯⋯..⋯12 分2。

2017-2018学年广东省广州市海珠区九年级(上)期末数学试卷

2017-2018学年广东省广州市海珠区九年级（上）期末数学试卷一．选择题（本题有10个小题，每小题3分，共30分.下面每小题给出的四个选项中，只有一个是正确的）1．（3分）下面图形中，是中心对称图形的是（）A．B．C．D．2．（6分）在平面直角坐标系中，点P（﹣3，4）关于原点对称的点的坐标是（）A．（3，4） B．（3，﹣4）C．（4，﹣3）D．（﹣3，4）3．（3分）下列事件中是不可能事件的是（）A．三角形内角和小于180°B．两实数之和为正C．买体育彩票中奖 D．抛一枚硬币2次都正面朝上4．（3分）如果两个相似正五边形的边长比为1：10，则它们的面积比为（）A．1：2 B．1：5 C．1：100 D．1：105．（3分）把抛物线y=x2向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为（）A．y=（x+1）2+2 B．y=（x﹣1）2+2 C．y=（x+1）2﹣2 D．y=（x﹣1）2﹣2 6．（3分）如图，△ABC为直角三角形，∠C=90°，AC=6，BC=8，以点C为圆心，以CA为半径作⊙C，则△ABC斜边的中点D与⊙C的位置关系是（）A．点D在⊙C上B．点D在⊙C内C．点D在⊙C外D．不能确定7．（3分）点M（﹣3，y1），N（﹣2，y2）是抛物线y=﹣（x+1）2+3上的两点，则下列大小关系正确的是（）A．y1＜y2＜3 B．3＜y1＜y2C．y2＜y1＜3 D．3＜y2＜y18．（3分）今年“十一”长假某湿地公园迎来旅游高峰，第一天的游客人数是1.2万人，第三天的游客人数为2.3万人，假设每天游客增加的百分率相同且设为x，则根据题意可列方程为（）A．2.3 （1+x）2=1.2B．1.2（1+x）2=2.3C．1.2（1﹣x）2=2.3 D．1.2+1.2（1+x）+1.2（1+x）2=2.39．（3分）如图，抛物线y=ax2+bx+c（a＞0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（）A．﹣1＜P＜0 B．﹣2＜P＜0 C．﹣4＜P＜﹣2 D．﹣4＜P＜0二．填空题（本题有6个小题，每小题3分，共18分）10．（3分）在一个有15万人的小镇，随机调查了1000人，其中200人会在日常生活中进行垃圾分类，那么在该镇随机挑一个人，会在日常生活中进行垃圾分类的概率是．11．（3分）如图，在平面直角坐标系中，点A的坐标为（﹣1，2），AB⊥x轴于点B，以原点O为位似中心，将△OAB放大为原来的2倍得到△OA1B1，且点A1在第二象限，则点A1的坐标为．12．（3分）已知方程x2+mx+2=0的一个根是1，则它的另一个根是．13．（3分）如图，在Rt△ABC中，∠BAC=90°．将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为．14．（3分）如图，△ABC的周长为8，⊙O与BC相切于点D，与AC的延长线相切于点E，与AB的延长线相切于点F，则AF的长为．15．（3分）如图，正方形ABCD的边长为2，点O是边AB上一动点（点O不与点A，B重合），以O为圆心，2为半径作⊙O，分别与AD，BC相交于M，N，则劣弧MN长度a的取值范围是．三．解答题（本题共9个小题，共102分，解答要求写出文字说明，证明过程或计算步骤）16．（10分）解方程（1）x2+4x﹣5=0（2）（x﹣3 ）（x+3 ）=2x+6．17．（10分）如图，在正方形网格中，每个小正方形的边长均为1 个单位．（1）把△ABC绕着点C逆时针旋转90°，画出旋转后对应的△A1B1C；（2）求△ABC旋转到△A1B1C时线段AC扫过的面积．18．（10分）如图，甲分为三等分数字转盘，乙为四等分数字转盘，自由转动转盘．（1）转动甲转盘，指针指向的数字小于3的概率是；（2）同时自由转动两个转盘，用列举的方法求两个转盘指针指向的数字均为奇数的概率．19．（10分）已知关于x的一元二次方程有两个实数x2+2x+a﹣2=0，有两个实数根x1，x2．（1）求实数a的取值范围；（2）若x12x22+4x1+4x2=1，求a的值．20．（10分）如图，一天晚上，小颖由路灯A下的B处走到C处时，测得影子CD的长为1米，当她继续往前走到D处时，测得影子DE的长刚好是自己的身高，已知小颖的身高为1.5米，求路灯A的高度AB．21．（12分）已知某种产品的进价为每件40元，现在的售价为每件59元，每星期可卖出300件，市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．（1）求w与x之间的函数关系式，并写出自变量x的取值范围；（2）求该厂产品销售定价为每件多少元时，每星期的销售利润最大？最大利润是多少元？22．（12分）如图，圆C过原点并与坐标轴分别交于A、D两点，已知点B为圆C圆周上一动点，且∠ABO=30°，点D的坐标为（0，2 ）．（1）直接写出圆心 C 的坐标；（2）当△BOD为等边三角形时，求点B的坐标；（3）若以点B为圆心、r为半径作圆B，当圆B与两个坐标轴同时相切时，求点B的坐标．23．（14分）如图，已知CE是圆O的直径，点B在圆O上由点E顺时针向点C 运动（点B不与点E、C重合），弦BD交CE于点F，且BD=BC，过点B作弦CD 的平行线与CE的延长线交于点A．（1）若圆O的半径为2，且点D为弧EC的中点时，求圆心O到弦CD的距离；（2）在（1）的条件下，当DF•DB=CD2时，求∠CBD的大小；（3）若AB=2AE，且CD=12，求△BCD的面积．24．（14分）如图，已知二次函数y=ax2+bx+c（a＜0，c＞0）与x轴交于点A、B，与y轴交于点C，且以AB为直径的圆经过点C．（1）若点A（﹣2，0），点B（8，0），求ac的值；（2）若点A（x1，0），B（x2，0），试探索ac是否为定值？若是，求出这个定值；若不是，请说明理由．（3）若点D是圆与抛物线的交点（D与A、B、C 不重合），在（1）的条件下，坐标轴上是否存在一点P，使得以P、B、C为顶点的三角形与△CBD相似？若存在，请直接写出点P坐标；若不存在，请说明理由．2017-2018学年广东省广州市海珠区九年级（上）期末数学试卷参考答案与试题解析一．选择题（本题有10个小题，每小题3分，共30分.下面每小题给出的四个选项中，只有一个是正确的）1．（3分）下面图形中，是中心对称图形的是（）A．B．C．D．【分析】根据中心对称图形的概念判断即可．【解答】解：A、不是中心对称图形；B、不是中心对称图形；C、不是中心对称图形；D、是中心对称图形．故选：D．【点评】本题考查的是中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后两部分重合．2．（6分）在平面直角坐标系中，点P（﹣3，4）关于原点对称的点的坐标是（）A．（3，4） B．（3，﹣4）C．（4，﹣3）D．（﹣3，4）【分析】直接利用关于原点对称点的性质得出答案．【解答】解：点P（﹣3，4）关于原点对称的点的坐标是：（3，﹣4）．故选：B．【点评】此题主要考查了关于原点对称点的性质，正确把握横纵坐标的关系是解题关键．3．（3分）下列事件中是不可能事件的是（）A．三角形内角和小于180°B．两实数之和为正C．买体育彩票中奖 D．抛一枚硬币2次都正面朝上【分析】根据事件发生的可能性大小判断相应事件的类型即可．【解答】解：A、三角形的内角和小于180°是不可能事件，故A符合题意；B、两实数之和为正是随机事件，故B不符合题意；C、买体育彩票中奖是随机事件，故C不符合题意；D、抛一枚硬币2次都正面朝上是随机事件，故D不符合题意；故选：A．【点评】本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．4．（3分）如果两个相似正五边形的边长比为1：10，则它们的面积比为（）A．1：2 B．1：5 C．1：100 D．1：10【分析】根据相似多边形面积的比等于相似比的平方即可得出结论．【解答】解：∵两个相似多边形的相似比为1：10，∴它们的面积比=12：102=1：100．故选：C．【点评】本题考查的是相似多边形的性质，熟知相似多边形面积的比等于相似比的平方是解答此题的关键．5．（3分）把抛物线y=x2向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为（）A．y=（x+1）2+2 B．y=（x﹣1）2+2 C．y=（x+1）2﹣2 D．y=（x﹣1）2﹣2【分析】按照“左加右减，上加下减”的规律平移则可．【解答】解：原抛物线的顶点为（0，0），向左平移1个单位，再向下平移2个单位，那么新抛物线的顶点为（﹣1，﹣2）．可设新抛物线的解析式为：y=（x﹣h）2+k，代入得：y=（x+1）2﹣2．故选：C．【点评】此题考查了二次函数图象与几何变换以及一般式转化顶点式，正确将一般式转化为顶点式是解题关键．6．（3分）如图，△ABC为直角三角形，∠C=90°，AC=6，BC=8，以点C为圆心，以CA为半径作⊙C，则△ABC斜边的中点D与⊙C的位置关系是（）A．点D在⊙C上B．点D在⊙C内C．点D在⊙C外D．不能确定【分析】要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系，本题先由勾股定理求出斜边AB的长，再根据直角三角形斜边上的中线等于斜边的一半得出CD的长，然后根据点到圆心距离与半径的关系即可确定该点与圆的位置关系．【解答】解：∵Rt△ABC中，∠C=Rt∠，AC=6，BC=8，∴AB==10，∵D为斜边AB的中点，CD=AB=5，d=5，r=6，∴d＜r，∴点D与⊙C内，故选：B．【点评】本题根据点到圆心的距离和圆的半径之间的数量关系，来判断点和圆的位置关系．点与圆的位置关系有3种．设⊙O的半径为r，点P到圆心的距离OP=d，则有：①点P在圆外⇔d＞r；②点P在圆上⇔d=r；③点P在圆内⇔d＜r．7．（3分）点M（﹣3，y1），N（﹣2，y2）是抛物线y=﹣（x+1）2+3上的两点，则下列大小关系正确的是（）A．y1＜y2＜3 B．3＜y1＜y2C．y2＜y1＜3 D．3＜y2＜y1【分析】根据抛物线的性质，抛物线上的点离对称轴越远，对应的函数值就越小，点（﹣1，3）在对称轴上，即可得到答案．【解答】解：∵抛物线y=﹣（x+1）2+3开口向下，对称轴是直线x=﹣1，∴抛物线上的点离对称轴越远，对应的函数值就越大，∵点（﹣1，3）在对称轴上，﹣3＜﹣2，∴y1＜y2＜3．故选：A．【点评】本题考查了二次函数图象上点的坐标特征．解题时，需熟悉抛物线的有关性质：抛物线的开口向下，则抛物线上的点离对称轴越远，对应的函数值就越小．8．（3分）今年“十一”长假某湿地公园迎来旅游高峰，第一天的游客人数是1.2万人，第三天的游客人数为2.3万人，假设每天游客增加的百分率相同且设为x，则根据题意可列方程为（）A．2.3 （1+x）2=1.2B．1.2（1+x）2=2.3C．1.2（1﹣x）2=2.3 D．1.2+1.2（1+x）+1.2（1+x）2=2.3【分析】利用平均增长率问题，一般用增长后的量=增长前的量×（1+增长率），参照本题，如果设平均每年增产的百分率为x，分别用x表示出第二天和第三天游客数量，即可得出方程．【解答】解：设每天游客增加的百分率相同且设为x，第二天的游客人数是：1.2（1+x）；第三天的游客人数是：1.2（1+x）（1+x）=1.2（1+x）2；依题意，可列方程：1.2（1+x）2=2.3．故选：B．【点评】本题考查了由实际问题抽象出一元二次方程中求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．9．（3分）如图，抛物线y=ax2+bx+c（a＞0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（）A．﹣1＜P＜0 B．﹣2＜P＜0 C．﹣4＜P＜﹣2 D．﹣4＜P＜0【分析】先利用待定系数法求出经过点（1，0）和（0，﹣2）的直线解析式为y=2x﹣2，则当x=﹣1时，y=2x﹣2=﹣4，再利用抛物线的顶点在第三象限，所以x=﹣1时，对应的二次函数值为负数，从而得到所以﹣4＜a﹣b+c＜0．【解答】解：经过点（1，0）和（0，﹣2）的直线解析式为y=2x﹣2，当x=﹣1时，y=2x﹣2=﹣4，而x=﹣1时，y=ax2+bx+c=a﹣b+c，所以﹣4＜a﹣b+c＜0，即﹣4＜P＜0．故选：D．【点评】本题考查了二次函数图象与系数的关系：二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时，对称轴在y轴左；当a与b异号时，对称轴在y轴右．常数项c决定抛物线与y轴交点：抛物线与y轴交于（0，c）．抛物线与x轴交点个数由判别式确定：△=b2﹣4ac ＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．二．填空题（本题有6个小题，每小题3分，共18分）10．（3分）在一个有15万人的小镇，随机调查了1000人，其中200人会在日常生活中进行垃圾分类，那么在该镇随机挑一个人，会在日常生活中进行垃圾分类的概率是．【分析】用所抽样本中会进行垃圾分类的人数除以抽取的总人数即可得．【解答】解：在该镇随机挑一个人，会在日常生活中进行垃圾分类的概率是=，故答案为：．【点评】本题考查概率公式和用样本估计总体，概率计算一般方法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．11．（3分）如图，在平面直角坐标系中，点A的坐标为（﹣1，2），AB⊥x轴于点B，以原点O为位似中心，将△OAB放大为原来的2倍得到△OA1B1，且点A1在第二象限，则点A1的坐标为（﹣2，4）．【分析】直接利用位似图形的性质以及结合A点坐标直接得出点A1的坐标．【解答】解：∵点A的坐标为（﹣1，2），以原点O为位似中心，将△OAB放大为原来的2倍，得到△OA1B1，且点A1在第二象限，∴点A1的坐标为（﹣2，4）．故答案为：（﹣2，4）．【点评】此题主要考查了位似变换以及坐标与图形的性质，正确把握位似图形的性质是解题关键．12．（3分）已知方程x2+mx+2=0的一个根是1，则它的另一个根是2．【分析】设方程的另一个根为x1，根据两根之积等于，即可得出关于x1的一元一次方程，解之即可得出结论．【解答】解：设方程的另一个根为x1，根据题意得：1×x1=2，∴x1=2．故答案为：2．【点评】本题考查了根与系数的关系、一元二次方程的解以及解一元一次方程，牢记两根之积等于是解题的关键．13．（3分）如图，在Rt△ABC中，∠BAC=90°．将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为42°．【分析】根据题意：Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，即旋转角为48°，则：∠ACA′=48°，根据直角三角形的两锐角互余求出∠B′的大小．【解答】解：由旋转得：∠ACA′=48°，∵∠BAC=90°，∴∠B′A′C=∠BAC=90°，∴∠B′=90°﹣48°=42°，故答案为：42°．【点评】本题考查了旋转的性质和直角三角形的性质，比较简单；明确旋转前后的两个角相等，及两直角三角形的两锐角互余．14．（3分）如图，△ABC的周长为8，⊙O与BC相切于点D，与AC的延长线相切于点E，与AB的延长线相切于点F，则AF的长为4．【分析】根据切线长定理得出AF=AE，CE=CD，BF=BD，再根据△ABC的周长等于16得出AF+AE=16，即可求出AE．【解答】解：∵AB、AC的延长线与圆分别相切于点E、F，∴AF=AE，∵圆O与BC相切于点D，∴CE=CD，BF=BD，∴BC=DC+BD=CE+BF，∵△ABC的周长等于8，∴AB+AC+BC=8，∴AB+AC+CE+BF=8，∴AF+AE=8，∴AF=4．故答案为4【点评】此题考查了切线长定理，掌握切线长定理即从圆外一点引圆的两条切线，切线长相等是本题的关键．15．（3分）如图，正方形ABCD的边长为2，点O是边AB上一动点（点O不与点A，B重合），以O为圆心，2为半径作⊙O，分别与AD，BC相交于M，N，则劣弧MN长度a的取值范围是π≤l＜π．【分析】观察图象可知，扇形OMN的圆心角∠MON的最大值90°，最小值为60°，由此即可解决问题．【解答】解：∵O是边AB上一动点，∴观察图象可知，扇形OMN的圆心角∠MON的最大值90°，最小值为60°，①当∠OMN=90°时，l==π，②当∠OMN=60°时，l==π，∴π≤l＜π．故答案为π≤l＜π．【点评】本题考查正方形的性质、扇形的面积公式等知识，解题的关键是确定圆心角∠MON的最大值和最小值，属于中考常考题型．三．解答题（本题共9个小题，共102分，解答要求写出文字说明，证明过程或计算步骤）16．（10分）解方程（1）x2+4x﹣5=0（2）（x﹣3 ）（x+3 ）=2x+6．【分析】（1）十字相乘法分解因式求解可得；（2）移项后，提取公因式（x+3）分解因式，求解可得．【解答】解：（1）∵x2+4x﹣5=0，∴（x﹣1）（x+5）=0，则x﹣1=0或x+5=0，解得：x=1或x=﹣5；（2）∵（x﹣3）（x+3）﹣2（x+3）=0，∴（x+3）（x﹣5）=0，则x+3=0或x﹣5=0，解得：x=﹣3或x=5．【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．17．（10分）如图，在正方形网格中，每个小正方形的边长均为1 个单位．（1）把△ABC绕着点C逆时针旋转90°，画出旋转后对应的△A1B1C；（2）求△ABC旋转到△A1B1C时线段AC扫过的面积．【分析】（1）找出点A、B、C绕着点C逆时针旋转90°所得的对应点A1、B1、C1的位置，然后顺次连接即可；（2）根据扇形的面积公式计算可得．【解答】解：（1）如图所示，△A1B1C即为所求；（2）∵CA==2，∴S==2π．【点评】本题主要考查作图﹣旋转变换，解题的关键是熟练掌握旋转变换的定义和性质及扇形的面积公式．18．（10分）如图，甲分为三等分数字转盘，乙为四等分数字转盘，自由转动转盘．（1）转动甲转盘，指针指向的数字小于3的概率是；（2）同时自由转动两个转盘，用列举的方法求两个转盘指针指向的数字均为奇数的概率．【分析】（1）直接利用概率公式即可得出结论；（2）画出树状图，再利用概率公式即可得出结论．【解答】解：（1）甲转盘共有1，2，3三个数字，其中小于3的有1，2，=，∴P（转动甲转盘，指针指向的数字小于3）故答案为．（2）树状图如下：由树状图知，共有12种等可能情况，其中两个转盘指针指向的数字为奇数的有4种情况，所以两个转盘指针指向的数字均为奇数的概率P==．【点评】此题主要考查了树状图的画法，概率公式，解本题的关键是熟练掌握概率公式．19．（10分）已知关于x的一元二次方程有两个实数x2+2x+a﹣2=0，有两个实数根x1，x2．（1）求实数a的取值范围；（2）若x12x22+4x1+4x2=1，求a的值．【分析】（1）由方程根的个数，根据根的判别式可得到关于a的不等式，可求得a的取值范围；（2）由根与系数的关系可用a表示出x1x2和x1+x2的值，代入已知条件可得到关于a的方程，则可求得a的值．【解答】解：（1）∵方程有两个实数根，∴△≥0，即22﹣4×1×（a﹣2）≥0，解得a≤3；（2）由题意可得x1+x2=﹣2，x1x2=a﹣2，∵x12x22+4x1+4x2=1，∴（a﹣2）2﹣8=1，解得a=5或a=﹣1，∵a≤3，∴a=﹣1．【点评】本题主要考查根的判别式及根与系数的关系，掌握根的个数与根的判别式的关系及一元二次方程的两根之和、两根之积与方程系数的关系是解题的关键．20．（10分）如图，一天晚上，小颖由路灯A下的B处走到C处时，测得影子CD的长为1米，当她继续往前走到D处时，测得影子DE的长刚好是自己的身高，已知小颖的身高为1.5米，求路灯A的高度AB．【分析】直接利用相似三角形的判定与性质得出BC的长，进而求出AB的长．【解答】解：由题MC=FD=DE=1.5m，CD=1m，∵MC∥AB，∴△DMC∽△DAB，∴=，∵△EFD∽△EAB，∴=，∵MC=FD，∴=，即=，解得：BC=2m，将BC=2m代入=，即=，解得：AB=4.5，答：路灯A的高度AB为4.5m．【点评】此题主要考查了相似三角形的应用，正确得出BC的长是解题关键．21．（12分）已知某种产品的进价为每件40元，现在的售价为每件59元，每星期可卖出300件，市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．（1）求w与x之间的函数关系式，并写出自变量x的取值范围；（2）求该厂产品销售定价为每件多少元时，每星期的销售利润最大？最大利润是多少元？【分析】（1）根据“总利润=每件产品的利润×销售量”可得函数解析式；（2）将（1）中所得函数解析式配方成顶点式，利用二次函数的性质求解可得．【解答】解：（1）根据题意，w=（59﹣40﹣x）（300+20x）=﹣20x2+80x+5700，由300+20x≤380可得x≤4；所以0≤x≤4，且x为整数；（2）∵w=﹣20x2+80x+5700=﹣20（x﹣2）2+5780，∴当x=2时，w取得最大值，最大值为5780，答：该厂产品销售定价为每件57元时，每星期的销售利润最大，最大利润是5780元．【点评】本题主要考查二次函数的应用，解题的关键是理解题意找到题目蕴含的相等关系，据此列出函数解析式．22．（12分）如图，圆C过原点并与坐标轴分别交于A、D两点，已知点B为圆C圆周上一动点，且∠ABO=30°，点D的坐标为（0，2 ）．（1）直接写出圆心 C 的坐标；（2）当△BOD为等边三角形时，求点B的坐标；（3）若以点B为圆心、r为半径作圆B，当圆B与两个坐标轴同时相切时，求点B的坐标．【分析】（1）直接利用圆周角定理结合锐角三角函数关系得出ED的长进而得出答案；（2）利用等边三角形的性质求出B点坐标即可；（3）分别利用若B在第二象限，设B（﹣a，a），（a＞0），以及B在第一象限，设B（a，a），（a＞0），表示出线段长进而得出答案．【解答】解：（1）如图1，连接OC并延长，交⊙C于点E，连接EA、ED．因为∠ABO=30°，∴∠AEO=30°，又因为OE是直径，∠AOE=60°，∠EOD=30°，∠EDO=90°∵OD=2，∴ED=DO•tan30°=2．过点C作CF⊥OD，垂足为F，则CF是△DEO的中位线，所以OF=，CF=1．∴点C的坐标为（﹣1，）故圆心C的坐标为（﹣1，）；（2）如图2，作BH⊥x轴交x轴于点H，当△BOD是等边三角形，则OB=OD=2，∠BOD=60°，故∠BOA=30°，则BH=OB=×2=，OH===3，∴B（﹣3，）；（3）若B在第二象限，设B（﹣a，a），（a＞0），则BC=，∴AD===4，∴AC=2，∵BC=AC，∴=2，∴（﹣a+1）2+（a﹣）2=4，解得：a1=0（舍去），a2=1+，故B（﹣﹣1，+1），若B在第一象限，设B（a，a），（a＞0），∴BC=，同理：=2，解得：a3=0（舍去），a4=﹣1，∴B（﹣1，﹣1），综上所述：B（﹣﹣1，+1）或B（﹣1，﹣1）．【点评】此题主要考查了圆的综合以及勾股定理和等边三角形的性质，正确应用分类讨论是解题关键．23．（14分）如图，已知CE是圆O的直径，点B在圆O上由点E顺时针向点C 运动（点B不与点E、C重合），弦BD交CE于点F，且BD=BC，过点B作弦CD 的平行线与CE的延长线交于点A．（1）若圆O的半径为2，且点D为弧EC的中点时，求圆心O到弦CD的距离；（2）在（1）的条件下，当DF•DB=CD2时，求∠CBD的大小；（3）若AB=2AE，且CD=12，求△BCD的面积．【分析】（1）过O作OH⊥CD于H，根据点D为弧EC的中点，可得∠OCH=45°，进而得出OH=CH，再根据圆O的半径为2，即可得到OH=；（2）先判定△CDF∽△BDC，可得∠DCF=∠DBC，再根据∠DCF=45°，即可得出∠DBC=45°；（3）连接BE，BO，DO，并延长BO至H点，依据∠ABE=∠OBC=∠OCB，∠A=∠A，判定△ABE∽△ACB，即可得到AC=，设AE=x，再根据△AOB∽△COH，可得，即，解得x=5，OH=4.5，OB=7.5，即可得到△BCD的面积=×12×12=72．【解答】解：（1）如图，过O作OH⊥CD于H，∵点D为弧EC的中点，∴弧ED=弧CD，∴∠OCH=45°，∴OH=CH，∵圆O的半径为2，即OC=2，∴OH=；（2）∵当DF•DB=CD2时，，又∵∠CDF=∠BDC，∴△CDF∽△BDC，∴∠DCF=∠DBC，由（1）可得∠DCF=45°，∴∠DBC=45°；（3）如图，连接BE，BO，DO，并延长BO至H点，∵BD=BC，OD=OC，∴BH垂直平分CD，又∵AB∥CD，∴∠ABO=90°=∠EBC，∴∠ABE=∠OBC=∠OCB，又∵∠A=∠A，∴△ABE∽△ACB，∴，即AB2=AE×AC，∴AC=，设AE=x，则AB=2x，∴AC=4x，EC=3x，∴OE=OB=OC=，∵CD=12，∴CH=6，∵AB∥CH，∴△AOB∽△COH，∴，即，解得x=5，OH=4.5，OB=7.5，∴BH=BO+OH=12，∴△BCD的面积=×12×12=72．【点评】本题属于圆的综合题，主要考查了相似三角形的判定与性质，垂径定理以及等腰三角形的性质的综合运用，解决问题的关键是作辅助线构造相似三角形，依据相似三角形的对应边成比例得到方程得出结论．在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．24．（14分）如图，已知二次函数y=ax2+bx+c（a＜0，c＞0）与x轴交于点A、B，与y轴交于点C，且以AB为直径的圆经过点C．（1）若点A（﹣2，0），点B（8，0），求ac的值；（2）若点A（x1，0），B（x2，0），试探索ac是否为定值？若是，求出这个定值；若不是，请说明理由．（3）若点D是圆与抛物线的交点（D与A、B、C 不重合），在（1）的条件下，坐标轴上是否存在一点P，使得以P、B、C为顶点的三角形与△CBD相似？若存在，请直接写出点P坐标；若不存在，请说明理由．【分析】（1）先求出OC的长，即可得出点C的坐标，最后用待定系数法即可得出结论；（2）先判断出△OAC∽△OCB，得出，即：c2=﹣x1•x2，利用根与系数的关系打得出x1•x2=，即可得出结论；（3）分点P在x轴和y轴上，利用相似三角形的性质得出比例式建立方程即可求出点P的坐标．【解答】解：（1）设圆心为点M，∵A（﹣2，0），B（8，0），∴M（3，0），⊙M的半径为5，∴OC==4，∴C（0，4），设抛物线解析式为y=a（x+2）（x﹣8），∵点C在抛物线上，∴a×2×（﹣8）=4，∴a=﹣，∴y=﹣（x+2）（x﹣8）=﹣x2+x+4，∴a=﹣，c=4，∴ac=﹣1；（2）ac的值是定值，为﹣1，理由：∵点A（x1，0），B（x2，0），∴OA=﹣x1，OB=x2，OC=c，∵∠OAC+∠OCA=90°，∠OCB+∠OCA=90°，∴∠OAC=∠OCB，∵∠AOC=∠BOC=90°，∴△OAC∽△OCB，∴，∴OC2=OA•OB，∴c2=﹣x1•x2，令y=0时，0=ax2+bx+c，∴x1•x2=，∴c2=﹣，∴ac=﹣1；（3）∵点D是圆与抛物线的交点（D与A、B、C 不重合），C（0，4），∴D（6，4），即：CD∥AB，当点P在x轴上时，如图1，设点P的坐标为（m，0），∵C（0，4），D（6，4），B（8，0），∴BC=4，CD=6，BP=8﹣m，∵CD∥AB，∴∠BCD=∠ABC，∵以P、B、C为顶点的三角形与△CBD相似，∴①，∴，∴m=2，∴P2（2，0），或②，∴，∴m=﹣，∴P1（﹣，0），当点P在y轴上时，如图2，∵CD∥AB，∴，∵，∴，∴∠ABD=∠BCO，∵CD∥AB，∴∠BDC+∠ABC=180°，∵∠BCO+∠BCy=180°，∴∠BDC=∠BCy，设P（0，n），∵C（0，4），D（6，4），B（8，0），∴BC=4，CD=6，BD=2，CP=n﹣4，∵以P、B、C为顶点的三角形与△CBD相似，∴①，∴，∴n=，∴P3（0，）或②，∴，∴n=16，∴P4（0，16），即：满足条件的点P的坐标为（2，0）或（﹣，0）或（0，）或（0，16）．【点评】此题是二次函数综合题，主要考查了圆的性质，待定系数法，相似三角形的判定和性质，平行线的性质，分类讨论的思想，解本题的关键是用方程的思想思考问题．。

2017_2018学年广东广州海珠区初一上学期期末英语试卷答案

13. 【答案】B
14. 【答案】C
15. 【答案】C
16. 【答案】B
完形填空
17. 【答案】CBADA BADBA
阅读理解
18. 【答案】（1）A （2）B （3）B （4）C （5）D
19. 【答案】（1）C （2）B （3）B （4）DБайду номын сангаас（5）A
20. 【答案】（1）A （2）A （3）C （4）D （5）B
写作
21. 【答案】（1）goes （2）had （3）hardly
（4）swimming （5）pollution
22. 【答案】（1）dream （2）dry （3）protect （4）able （5）light
23. 【答案】（1）1．in 2．the 3．centre 4．of
（2）1．is 2．harmful 3．for 4．put
（3）1．have 2．a 3．good 4．time
（4）1．make 2．friends 3．with 4．her
（5）1．as 2．many 3．as 4．possible
24. 【答案】（1）Some animals fly in the sky. （2）We love our country. （3）I am a middle school student. （4）They show me how to make cakes. （5）We must keep the classroom clean.
2017~2018学年广东广州海珠区初一上学期期末英语试卷
单项选择
1. 【答案】（1）C （2）A （3）D （4）B （5）C
2. 【答案】B 3. 【答案】C 4. 【答案】A 5. 【答案】B 6. 【答案】D 7. 【答案】A 8. 【答案】B 9. 【答案】D 10. 【答案】B 11. 【答案】A 12. 【答案】A

广东省广州市海珠区2017-2018学年上学期期末考试九年级物理试卷(解析版)

广东省广州市海珠区2017-2018学年上学期期末考试九年级物理试卷一、单项选择题（选一个最优选项，每题3分，共39分）1．以下四个温度中，最接近20℃的是（）A．健康成年人的体温B．老年病人洗澡时，热水的温度C．广州全年的最低气温D．秋高气爽时，广州的气温【专题】估算法；温度计、熔化和凝固．【分析】此题考查我们对常见物体或环境温度的认识，结合对生活的了解和对温度单位摄氏度的认识，选出符合题意的选项。

【解答】解：A、正常情况下，人的体温在37℃左右，变化幅度很小，故A不符合实际；B、正常情况下，人的体温在37℃左右，老年病人高于37℃，低于40℃，故洗澡时，热水的温度约为40℃，故B不符合实际；C、广州全年的最低气温约为10℃，故C不符合实际；D、秋高气爽时，广州的气温约为20℃，故D符合实际。

故选：D。

【点评】对物体长度、质量、温度等进行估测，是初中物理的一项基本要求，平时结合所学知识对身边的如：人高、教室高、一步长、步行速度、体温、气温等等，多观察多思考，必要时做出正确判断。

2．在气体扩散现象的演示实验中，一瓶装有空气，另一瓶装有密度大于空气的红棕色二氧化氮气体，按正确的方式放置（如图所示），抽出玻璃板并合上两瓶，过一段时间后两瓶气体会混合在一起，且颜色都变得同样均匀，本实验中（）A．甲瓶装的是二氧化氮气体B．人眼能直接观察到：气体分子不停地作无规则运动C．两瓶气体颜色都一样时，分子不再运动D．若温度越高，瓶内气体颜色变化会越快【专题】应用题；分子热运动、内能．【分析】密度小的气体总是浮在密度大的气体上面；分子在永不停息地做无规则运动的现象属于扩散现象，分子的运动速度和温度有关，温度越高分子的运动速度越快，即扩散越快；分子的扩散现象在任何温度都能进行。

【解答】解：A、二氧化氮气体的颜色是红棕色的，而且比空气的密度大。

如果将两个瓶口对在一起，则二氧化氮气体分子会向空气中运动，所以应该在下面的瓶中装有二氧化氮气体，故A错误；B、扩散现象说明气体分子不停地做无规则运动，分子运动人眼不能直接观察到，要通过颜色和味道来体现，故B错误；C、分子在永不停息地做无规则运动，所以两瓶气体颜色都一样时，分子仍然再做无规则运动，故C错误；D、由于分子的运动跟温度有关，所以分子的无规则运动叫做分子的热运动，温度越高，热运动越剧烈，瓶内气体颜色变化会越快，故D正确。