北京大学ACM暑期课讲义-Bellman-ford算法培训讲学
北京大学ACM暑期课讲义-计算几何教程

计算几何教程
计算几何的恶心之处
代码长,难写。
需要讨论各种边界情况。后面所介绍的算
法,有些对于边界情况的处理很完美,不 需要再做讨论;有些则不然,需要自行处 理边界情况。
精度误差
二维矢量
2-Dimension Vector
矢量
既有大小又有方向的量。
算法演示
2 被弹出栈,3 进栈。
算法演示
没有点被弹出栈,4 进栈。
算法演示
4 被弹出栈,5 进栈。
算法演示
5 被弹出栈,6 进栈。
算法演示
6 被弹出栈,7 进栈。
算法演示
如此直到下凸壳被找到。
算法演示
倒序进行扫描找到上凸壳。
Graham 扫描的时间复杂度
这太傻缺了。算法的瓶颈在排序,所以时
总时间复杂度 O(N2 log N)。
算法扩展
SPOJ CIRUT
求恰好被覆盖 1 次、2 次、„、N 次的面积。
算法的本质在于对“裸露”部分进行处理。
这种方法也可以用于求很多圆与很多凸多 边形的面积并——但是情况复杂得多,要 讨论的情况也多得多。
三维矢量
3-Dimension Vector
总体来说讨论比较辛苦,写起来不算很难。
精度存在比较大的问题,而且半平面交的
题目一般都容许 O(N2) 算法,所以并不是 很常用。
半平面交练习题
POJ 1279 POJ 3525 POJ 2451 POJ 3384
求多边形的核。核中的点满足其到多边形边 界上任一点之间的线段只与多边形在那一点相交。 求凸多边形最大内切圆半径。 裸的半平面交。朱泽园专门为他的算法出的 题,要求 O(N log N) 算法。 求在凸多边形内部放两个半径为 r 的圆所能 覆盖的最大面积。两圆可以重叠,但不能与多边形相交。 需要用到旋转卡壳。
北京大学ACM国际大学生程序设计竞赛课件4

1048
输入:
Follow My Logic
输入数据包含多个输入数据块.每个输入数据块包含以 下部分:
一个电路图,以上述形式表示,用只含'*'的单独一行结束. 多行01字符串,每行对应一组数据,包含26个0或1,分别对应AZ的值.用只含'*'的单独一行结束
输出:
对每组输入数据,输出对应的电路输出值. 每个结果占一行. 不同输入数据块的输出结果之间用空行隔开.
问题求解与程序设计 第三讲 模拟问题李Βιβλιοθήκη 新 2004.2 – 2004.6
内容提要
作业总结 - 1016 作业总结 - 1048 讨论 – 1207 作业 – 1207
1016 Numbers That Count
题意 count the numbers of each digit to form the new number 123321 -〉212223 1)Self-inventory 2) enter self inventory after k steps 3) enter inventory loop of length k 4) can not determined after 15 steps
Can not be classified
源程序
1016 c0400348274.txt 1016 c0400348198.txt
1048
Follow My Logic
对于一个逻辑电路和给定的输入值,计算该电路 对于一个逻辑电路和给定的输入值, 的输出值.该逻辑电路有一个或多个输入端, 的输出值.该逻辑电路有一个或多个输入端, 零 个或多个逻辑门电路,和一个输出端. 个或多个逻辑门电路,和一个输出端.本题中用 标准ASCll字符来表示逻辑电路:横竖导线分别 字符来表示逻辑电路: 标准 字符来表示逻辑电路 表示, 表示, 用'-'和'|'表示,转折点用'+'表示,输入端用 和 表示 转折点用' 表示 大写字母' 表示, 表示, 大写字母'A'-'Z'表示,输出端用问号'?'表示, 表示 输出端用问号' 表示 小写字母' 表示取反 与门, 表示取反. 小写字母'o'表示取反.与门,或门及电路各部 分示例如下: 分示例如下:
ACM培训资料

ACM培训资料目录第一篇入门篇 (3)第1章新手入门 (5)1ACM国际大学生程序设计竞赛简介 (5)2ACM竞赛需要的知识 (8)3团队配合 (14)4练习、练习、再练习 (15)5对新手的一些建议 (16)第2章C++语言介绍 (22)1C++简介 (22)2变量 (23)3C++数据类型 (25)4C++操作符 (30)5数组 (35)6字符数组 (38)7字串操作函数 (41)8过程控制 (45)9C++中的函数 (54)10函数规则 (59)第3章STL简介 (61)1泛型程序设计 (61)2STL 的组成 (67)第二篇算法篇 (102)第1章基本算法 (103)1算法初步 (103)2分治算法 (115)3搜索算法 (124)4贪婪算法 (135)第2章进阶算法 (165)1数论基础 (165)2图论算法 (180)3计算几何基础 (222)第三篇实践篇 (246)第1章《多边形》 (247)第2章《灌溉问题》 (255)第3章《L GAME》 (263)第4章《NUMBER》解题报告 (271)第5章《J OBS》解题报告 (275)第6章《包裹运送》 (283)第7章《桶的摆放》 (290)第一篇入门篇练就坚实的基础,总有一天……我们可以草木皆兵!第1章新手入门1ACM国际大学生程序设计竞赛简介1.1背景与历史1970年在美国TexasA&M大学举办了首次区域竞赛,从而拉开了国际大学生程序设计竞赛的序幕。
1977年,该项竞赛被分为两个级别,即区域赛和总决赛,这便是现代ACM竞赛的开始。
在亚洲、美国、欧洲、太平洋地区均设有区域赛点。
1995至1996年,来自世界各地的一千多支高校的代表队参加了ACM区域竞赛。
ACM 大学生程序设计竞赛由美国计算机协会(ACM)举办,旨在向全世界的大学生提供一个展示和锻炼其解决问题和运用计算机能力的机会,现已成为全世界范围内历史最悠久、规模最大的大学生程序设计竞赛。
最短路问题的Bellman-Ford算法 (2)

0 2 0123 3 312365 61236 9123687 1012368
基本表 空格为无穷大
v1
5
-3
v3
6
v6 2
4
4
v4
P1(jk ) Min{ P1(i k 1 ) wij }
1 i n
7
v7
利用 下标 追踪 路径
wij
v1 v1 v2 v3 v4 v5 v6 v7 v8 0 v2 2 0 v3 5 -2 0 4 v4 -3 4 6 0 0 -3 7 3 2 v5 v6 v7 v8
第10页
Floyd算法(路矩阵法)思想
dij 表示D中vi到vj的最 网络D=(V,A,W),令U=(dij)nn, 短路的长度。 考虑D中任意两点vi,vj,如将D中vi,vj以外的点都删掉, 得只剩vi,vj的一个子网络D0,记
当 vi ,v j A wij d 否 vi wij为弧( vi,vj)的权。
(0) ij
(0) i1
d
(0) 1j
再在D1中加入v2及D中与vi,vj,v1, v2相关联的弧,得D2, (2) D2中vi到vj的最短路长记为 ,则有 d ij
(2) (1) (1) dij min dij , di(1) d 2 2j
第12页
Floyd算法(路矩阵法)步骤
(k) ( k 1) P 3.当出现 P 时, 1j 1j
v3
其元素即是v1到vj的最短路长。
第 4页
例
计算从点v1到所有其它顶点的最短路
2 v1 -3 v4 v2 4 v5
-2
5 4
-3 v3
6 v6 2 v7 4
最短路算法(bellman-Ford算法)

最短路算法(bellman-Ford算法)贝尔曼-福特算法与迪科斯彻算法类似,都以松弛操作为基础,即估计的最短路径值渐渐地被更加准确的值替代,直⾄得到最优解。
在两个算法中,计算时每个边之间的估计距离值都⽐真实值⼤,并且被新找到路径的最⼩长度替代。
然⽽,迪科斯彻算法以贪⼼法选取未被处理的具有最⼩权值的节点,然后对其的出边进⾏松弛操作;⽽贝尔曼-福特算法简单地对所有边进⾏松弛操作,共|V | − 1次,其中 |V |是图的点的数量。
在重复地计算中,已计算得到正确的距离的边的数量不断增加,直到所有边都计算得到了正确的路径。
这样的策略使得贝尔曼-福特算法⽐迪科斯彻算法适⽤于更多种类的输⼊。
贝尔曼-福特算法的最多运⾏O(|V|·|E|)次,|V|和|E|分别是节点和边的数量)。
贝尔曼-福特算法与迪科斯彻算法最⼤的不同:bellman-Ford算法可以存在负权边,⽽dijkstra算法不允许出现负权边;bellman-Ford算法的步骤: 步骤1:初始化图 步骤2 :对每⼀条边进⾏松弛操作 步骤3:检查负权环procedure BellmanFord(list vertices, list edges, vertex source)// 该实现读⼊边和节点的列表,并向两个数组(distance和predecessor)中写⼊最短路径信息// 步骤1:初始化图for each vertex v in vertices:if v is source then distance[v] := 0else distance[v] := infinitypredecessor[v] := null// 步骤2:重复对每⼀条边进⾏松弛操作for i from1 to size(vertices)-1:for each edge (u, v) with weight w in edges:if distance[u] + w < distance[v]:distance[v] := distance[u] + wpredecessor[v] := u// 步骤3:检查负权环for each edge (u, v) with weight w in edges:if distance[u] + w < distance[v]:error "图包含了负权环"View Code题意:John在N个农场之间有path与wormhole ,path+时间,wormhole-时间;求是否存在某点满⾜,John 旅⾏⼀些 paths和wormholes,回到原点时间为负。
北京大学ACM国际大学生程序设计竞赛课件3

Problem
Conqueror's batalion
Table of Contents
The problem Solution
The problem
CENTRAL EUROPEAN OLYMPIAD IN INFORMATICS
30 June – 6 July 2002 Day 1: conquer Conqueror's battalion Time limit: 1 s Memory limit: 16 MB
The problem
If at least one of your soldiers reaches the uppermost stair, you will be the winner, in the other case, you will be the loser.
The problem
The problem
In case the game ends (either because you won or there are no more soldiers in the game), the library will terminate your program correctly. Your program may not terminate in any other way.
The problem
For each stair, you are given the number of soldiers standing on it, with number 1 being the uppermost stair and N the bottom one. None of your soldiers stands on stair 1 at the beginning.
ACM竞赛要掌握的知识

ACM竞赛要掌握的知识图论路径问题最短路径0/1边权最短路径BFS非负边权最短路径Dijkstra可以用Dijkstra解决的问题的特征负边权最短路径Bellman-FordBellman-Ford的Yen-氏优化差分约束系统Floyd广义路径问题传递闭包极小极大距离/ 极大极小距离Euler Path / Tour圈套圈算法混合图的Euler Path / TourHamilton Path / Tour特殊图的Hamilton Path / Tour 构造生成树问题最小生成树第k小生成树最优比率生成树0/1分数规划度限制生成树连通性问题强大的DFS算法无向图连通性割点割边二连通分支有向图连通性强连通分支2-SAT最小点基有向无环图拓扑排序有向无环图与动态规划的关系二分图匹配问题一般图问题与二分图问题的转换思路最大匹配有向图的最小路径覆盖0 / 1矩阵的最小覆盖完备匹配最优匹配网络流问题网络流模型的简单特征和与线性规划的关系最大流最小割定理最大流问题有上下界的最大流问题循环流最小费用最大流/ 最大费用最大流弦图的性质和判定组合数学解决组合数学问题时常用的思想逼近递推/ 动态规划概率问题Polya定理计算几何/ 解析几何计算几何的核心:*积/ 面积解析几何的主力:复数基本形点直线,线段多边形凸多边形/ 凸包凸包算法的引进,卷包裹法Graham扫描法水平序的引进,共线凸包的补丁完美凸包算法相关判定两直线相交两线段相交点在任意多边形内的判定点在凸多边形内的判定经典问题最小外接圆近似O(n)的最小外接圆算法点集直径旋转卡壳,对踵点多边形的三角剖分数学/ 数论最大公约数Euclid算法扩展的Euclid算法同余方程/ 二元一次不定方程同余方程组线性方程组高斯消元法解mod 2域上的线性方程组整系数方程组的精确解法矩阵行列式的计算利用矩阵乘法快速计算递推关系分数分数树连分数逼近数论计算求N的约数个数求phi(N)求约数和……素数问题概率判素算法概率因子分解数据结构:组织结构二*堆左偏树胜者树Treap统计结构树状数组虚二*树线段树矩形面积并圆形面积并关系结构Hash表并查集路径压缩思想的应用STL中的数据结构vectordequeset / map动态规划/ 记忆化搜索动态规划和记忆化搜索在思考方式上的区别最长子序列系列问题最长不下降子序列最长公共子序列一类NP问题的动态规划解法树型动态规划背包问题动态规划的优化四边形不等式状态设计规划方向(?)常用思想二分最小表示法。
ACM培训大纲

实用标准文案ACM培训大纲基础内容:数据结构——》搜索——》图论DP数论博弈中级内容数据结构网络流第一章搜索1.二分搜索三分搜索2.栈 3.队列 4.深搜 5.广搜 6.第二章数据结构1.优先队列并查集 2.二叉搜索树3.线段树(单点更新) 4.Trie5.精彩文档.实用标准文案第三章图论1.图的表示1.1二维数组1.2邻接表1.3前向星2.图的遍历2.1双连通分量2.2拓扑排序3.最短路3.1迪杰斯特拉3.2弗洛伊德3.3SPFA4.匹配匈牙利算法5.生成树6.网络流简介第四章动态规划1.状态转移方程2.引入2.10-1背包2.2硬币问题2.3矩阵链乘3.区间DP4.按位DP5.树形DP6.状压DP第五章数论1.欧几里得扩展欧几里得 2.因数分解3.费马小定理 4.欧拉定理 5.素数6.6.1筛法6.2素数判定6.2.1O(√n)方法精彩文档.实用标准文案6.2.2Miller-rabin测试第六章博弈1.Nim和2.SG函数第七章中级数据结构1.树状数组RMQ 2.KMP3.AC自动机4.线段树(区间更新)5.第八章图论进阶1.网络流问题精彩文档.实用标准文案综述在很多人眼里,东北大学秦皇岛分校不算是985高校。
所以我们要用自己的能力证明我们有985的实力。
ACM是计算机界认可度最高的一个比赛,可以说只要区域赛有过奖牌,国内任何IT公司没有理由不要。
同时,在高校之中,对一个大学计算机专业的评价,大部分人也会首先看ACM 的水平。
将ACM打出学校,在国内打出一定成绩,对扩大我校影响力很有帮助。
考虑到本校暂时没有进行专题训练的出题能力,专题训练的题目主要从UESTC 2014年集训队专题训练中获取,再加上从别的OJ上找一些题目。
训练的平台设置在华中科技大学的vertual judge上面。
本人将在毕业之前承担培训任务。
在2015学年开始之前,培训计划为每两周一次,中间空闲的时间由大二或者大一熟悉C++的同学给不熟悉C++的同学进行基础的讲解。
ACM暑期培训资料(ppt28张)

大整数除法
1、链接地址
/problem?id=2737
2、问题描述
– 求两个大的正整数相除的商
输入数据
第1 行是测试数据的组数n,每组测试数据占2 行,第1 行是被除数,第2 行是除数。每组测试数据之间有一个空 行,每行数据不超过100 个字符
输出要求
n 行,每组测试数据有一行输出是相应的整数商
规律:一个数的第i 位和另一个数的第j 位相乘所得的数,一 定是要累加到结果的第i+j 位上。这里i, j 都是从右往左,从 0 开始数。
POJ2389 参考程序
#include<iostream> #include<string> using namespace std; const int MAXLEN=200+10; int a[MAXLEN],b[MAXLEN]; int c[2*MAXLEN]; string st1,st2; int i,j,k; //字符串s转换为整型数组t void tran(string s,int *t) { int m,l; l=s.length(); for(m=0;m<l;m++) t[m]=s[l-1-m]-'0'; }
//下面判断p1 是否比p2 大,如果不是,返回-1 if( nLen1 == nLen2 ) { for( i = nLen1-1; i >= 0; i -- ) { if( p1[i] > p2[i] ) break; //p1>p2 else if( p1[i] < p2[i] ) return -1; //p1<p2 } } for( i = 0; i < nLen1; i ++ ) { //要求调用本函数确保当i>=nLen2 时,p2[i] = 0 p1[i] -= p2[i]; if( p1[i] < 0 ) { p1[i]+=10; p1[i+1] --; } } for( i = nLen1 -1 ; i >= 0 ; i-- ) if( p1[i] )//找到最高位第一个不为0 return i + 1; return 0;//全部为0,说明两者相等 }
Bellman_ford算法

Bellman-Ford算法思想Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。
对于给定的带权(有向或无向)图G=(V,E),其源点为s,加权函数w是边集 E 的映射。
对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。
若不存在这样的回路,算法将给出从源点s到图G的任意顶点v的最短路径d[v]。
Bellman-Ford算法流程分为三个阶段:(1)初始化:将除源点外的所有顶点的最短距离估计值d[v]←+∞, d[s] ←0;(2)迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)(3)检验负权回路:判断边集E中的每一条边的两个端点是否收敛。
如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在d[v]中。
算法描述如下:Bellman-Ford(G,w,s) :boolean //图G ,边集函数w ,s为源点1 for each vertex v∈V(G)do //初始化1阶段2 d[v]←+∞3 d[s] ←0; //1阶段结束4 for i=1 to |v|-1 do //2阶段开始,双重循环。
5 for each edge(u,v)∈E(G) do //边集数组要用到,穷举每条边。
6 If d[v]> d[u]+ w(u,v) then //松弛判断7 d[v]=d[u]+w(u,v) //松弛操作2阶段结束8 for each edge(u,v)∈E(G) do9 If d[v]> d[u]+ w(u,v) then10 Exit false11 Exit true下面给出描述性证明:首先指出,图的任意一条最短路径既不能包含负权回路,也不会包含正权回路,因此它最多包含|v|-1条边。
acm-icpc暑期课_最短路

acm-icpc暑期课_最短路北京⼤学暑期课《ACM/ICPC 竞赛训练》最短路算法本讲义为四处抄袭后改编⽽成,来源已不可考。
仅⽤于内部授课北京⼤学信息学院郭炜 guo_wei@/doc/d83c4f84bb68a98270fefa4a.html/doc/d83c4f84bb68a98270fefa4a.html /guoweiofpkuDijkstra 算法●解决⽆负权边的带权有向图或⽆向图的单源最短路问题●贪⼼思想,若离源点s 前k-1近的点已经被确定,构成点集P ,那么从s 到离s 第k 近的点t 的最短路径,{s,p 1,p 2…p i ,t}满⾜s,p 1,p 2…p i ∈P 。
●否则假设pi ?P ,则因为边权⾮负,pi 到t 的路径≥0,则d[pi]≤d[t],pi 才是第k 近。
将pi 看作t ,重复上⾯过程,最终⼀定会有找不到pi 的情况●d[i]=min(d[p i ]+cost(p i ,i)),i ?P,p i ∈P d[t]=min(d[i]) ,i ?P基本思想●初始令d[s]=0,d[i]=+∞,P=?●找到点i?P,且d[i]最⼩●把i添⼊P,对于任意j?P,若d[i]+cost(i,j)d[j]=d[i]+cost(i,j)。
●⽤邻接表,不优化,时间复杂度O(V2+E)●Dijkstra+堆的时间复杂度 o(ElgV)●⽤斐波那契堆可以做到O(VlogV+E)●若要输出路径,则设置prev数组记录每个节点的前趋点,在d[i]更新时更新prev[i]4 23 150200200 100080005000v Dist[v]0 01234 50100001000300025025082505250源点0加⼊P后:Dijkstra's AlgorithmDijkstra 算法也适⽤于⽆向图。
但不适⽤于有负权边的图。
231-234d[1,2] = 2但⽤Dijkstra 算法求得 d[1,2] = 3有N个孩⼦(N<=3000)分糖果。
Bellman-Ford

最短路径算法—Bellman-Ford(贝尔曼-福特)算法分析与实现(C/C++)ByTanky Woo– 2011年01月17日Posted in:我的原创|My Original Creation, 算法|Algorithms相关文章:1.Dijkstra算法:/?p=18902.Floyd算法:/?p=1903Dijkstra算法是处理单源最短路径的有效算法,但它局限于边的权值非负的情况,若图中出现权值为负的边,Dijkstra算法就会失效,求出的最短路径就可能是错的。
这时候,就需要使用其他的算法来求解最短路径,Bellman-Ford算法就是其中最常用的一个。
该算法由美国数学家理查德•贝尔曼(Richard Bellman, 动态规划的提出者)和小莱斯特•福特(Lester Ford)发明。
Bellman-Ford算法的流程如下:给定图G(V, E)(其中V、E分别为图G的顶点集与边集),源点s,∙数组Distant[i]记录从源点s到顶点i的路径长度,初始化数组Distant[n]为, Distant[s]为0;∙以下操作循环执行至多n-1次,n为顶点数:对于每一条边e(u, v),如果Distant[u] + w(u, v) < Distant[v],则另Distant[v] = Distant[u]+w(u, v)。
w(u, v)为边e(u,v)的权值;若上述操作没有对Distant进行更新,说明最短路径已经查找完毕,或者部分点不可达,跳出循环。
否则执行下次循环;∙为了检测图中是否存在负环路,即权值之和小于0的环路。
对于每一条边e(u, v),如果存在Distant[u] + w(u, v) < Distant[v]的边,则图中存在负环路,即是说改图无法求出单源最短路径。
否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
可知,Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).首先介绍一下松弛计算。
北京大学 acm程序设计 图论讲义

for (w=G->first(v); w<G->n(); w = G>next(v,w))
if (G->getMark(w) == UNVISITED) { G->setMark(w, VISITED); Q->enqueue(w); }
PostVisit(G, v); // Take action }}
Q Q
31
() ((1,1)) ((1,1) (2,3)) ((1,1) (2,4)) ((1,1) (2,4) (3.2))
Q Q
Q
32
() ((1,1)) ((1,1) (2,3)) ((1,1) (2,4)) ((1,1) (2,4) (3.2))
Q Q
33
Q () ((1,1)) ((1,1) (2,3)) ((1,1) (2,4)) ((1,1) (2,4) (3.2))
求解算法
穷举法 贪心法 深度/广度优先搜索
图和树的搜索 回溯法(深度优先)
递归
分治
动态规划法
55
谢谢!
56
49
动态规划法的思想
自底向上构造 在原问题的小子集中计算 每一步列出局部最优解,并用一张
表保留这些局部最优解,以避免重 复计算 子集越来越大,最终在问题的全集 上计算,所得出的就是整体最优 解。
50
Fib(1)=Fib(2)=1
Fibonacci数列 Fib(n)=Fib(n-1) + Fib (n-2)
23
八数码 深度优先搜索
1
23 184 765
2
c
3
283 164 75
283 14 765
Bellman-ford算法ppt课件
实现(具体应用见ZOJ2770的代码)
假设图中有关边的数据结构如下:
#define MAX 999999
#define EDGE_MAX 100 //边数最大值
#define VER_MAX 50
//顶点个数最大值
struct Edge
{
int u, v, w;
//边:起点、终点、权值
};
Edge edges[EDGE_MAX];
#define MAX 1000000 int Edge[MAX_VER_NUM][MAX_VER_NUM]; //图的邻接矩阵 int vexnum; //顶点个数
void BellmanFord(int v) //假定图的邻接矩阵和顶点个数已经读进来了
{
int i, k, u;
for(i=0; i<vexnum; i++)
8
算法复杂度分析
§ 假设图的顶点个数为n,边的个数为e。算法中有一个三重 嵌套的for循环,假如:
§ 使用邻接矩阵存储图,最内层if语句的总执行次数为O(n3), 因此算法的复杂度为O(n3);
§ 使用邻接表存储图,内层的两个for循环改成while循环,可 以使算法的复杂度降为O(n*e)。
9
Bellman-Ford算法思想的另一种理解
for(k = 0; k < m; k ++)
{
if(dist[edges[k].u] != MAX &&
dist[edges[k].u] + edges[k].w < dist[edges[k].v])
{
return false;
}
最短路径问题—Bellman-Ford算法
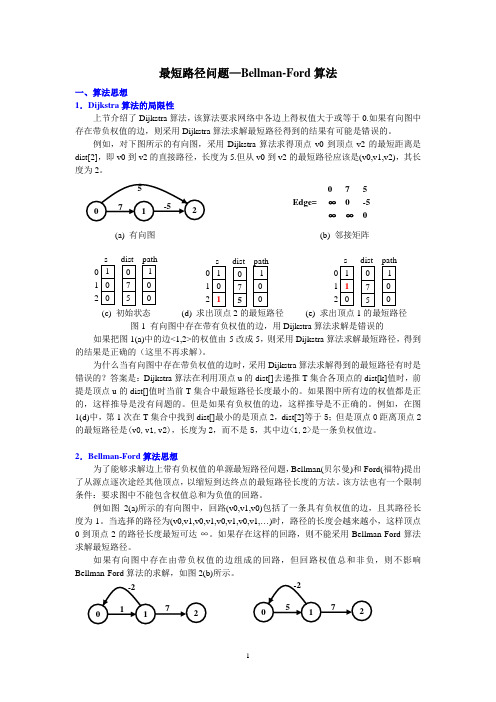
最短路径问题—Bellman-Ford 算法一、算法思想1.Dijkstra 算法的局限性上节介绍了Dijkstra 算法,该算法要求网络中各边上得权值大于或等于0.如果有向图中存在带负权值的边,则采用Dijkstra 算法求解最短路径得到的结果有可能是错误的。
例如,对下图所示的有向图,采用Dijkstra 算法求得顶点v0到顶点v2的最短距离是dist[2],即v0到v2的直接路径,长度为5.但从v0到v2的最短路径应该是(v0,v1,v2),其长度为2。
(a) 有向图 (b) 邻接矩阵(c) 初始状态(d) 求出顶点2的最短路径 (e) 求出顶点1的最短路径 图1 有向图中存在带有负权值的边,用Dijkstra算法求解是错误的如果把图1(a)中的边<1,2>的权值由-5改成5,则采用Dijkstra 算法求解最短路径,得到的结果是正确的(这里不再求解)。
为什么当有向图中存在带负权值的边时,采用Dijkstra 算法求解得到的最短路径有时是错误的?答案是:Dijkstra 算法在利用顶点u 的dist[]去递推T 集合各顶点的dist[k]值时,前提是顶点u的dist[]值时当前T 集合中最短路径长度最小的。
如果图中所有边的权值都是正的,这样推导是没有问题的。
但是如果有负权值的边,这样推导是不正确的。
例如,在图1(d)中,第1次在T 集合中找到dist[]最小的是顶点2,dist[2]等于5;但是顶点0距离顶点2的最短路径是(v0,v1,v2),长度为2,而不是5,其中边<1,2>是一条负权值边。
2.Bellman-Ford 算法思想为了能够求解边上带有负权值的单源最短路径问题,Bellman(贝尔曼)和Ford(福特)提出了从源点逐次途经其他顶点,以缩短到达终点的最短路径长度的方法。
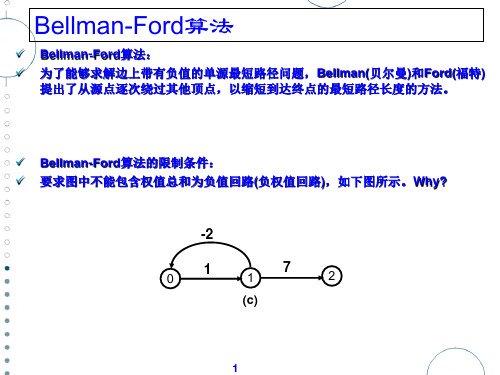
该方法也有一个限制条件:要求图中不能包含权值总和为负值的回路。
例如图2(a)所示的有向图中,回路(v0,v1,v0)包括了一条具有负权值的边,且其路径长度为-1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int vexnum; //顶点个数
int path[MAX_VER_NUM]; //path[i]是i在最短路径中的上一个节点
void BellmanFord(int v) //假定图的邻接矩阵和顶点个数已经读进来了
{
int i, k, u;
for(i=0; i<vexnum; i++)
{
dist[i]=Edge[v][i];
是否成立,如果成立,则说明存在从源点可达的负权值回路。代码如 下:
//对dist[ ]初始化
if( i!=v && dis[i]<MAX ) path[i] = v; //对path[ ]初始化
else path[i] = -1;
}
5
for(k=2; k<vexnum; k++) //从dist1[u]递推出dist2[u], …,distn-1[u]
{ for(u=0; u< vexnum; u++)//修改每个顶点的dist[u]和path[u]
01 23456
4
3
0 6
0
5 5 0
1
1
2 0 1 2
6
2 0
1
3
0 3 4
3
5
0 3 5 0 6
dist 2 [1] = min{ dist 1 [1], min{ dist 1 [j] + Edge[j][1] } } = min{6, min{dist1[0]+Edge[0][1], dist1[2]+Edge[2][1], … } }
-2
1
0
7
1
2
(c)
1
Bellman-Ford算法思想
✓ Bellman-Ford算法构造一个最短路径长度数组序列dist 1 [u], dist 2 [u], …, dist n-1 [u]。其中: ❖ dist 1 [u]为从源点v到终点u的只经过一条边的最短路径长度,并 有dist 1 [u] =Edge[v][u]; ❖ dist 2 [u]为从源点v最多经过两条边到达终点u的最短路径长度; ❖ dist 3 [u]为从源点v出发最多经过不构成负权值回路的三条边到 达终点u的最短路径长度; …… ❖ dist n-1 [u]为从源点v出发最多经过不构成负权值回路的n-1条边 到达终点u的最短路径长度;
{
if( u != v )
{ for(i=0; i<vexnum; i++)//考虑其他每个顶点
{
if( Edge[i][u]<MAX &&
dist[u]>dist[i]+Edge[i][u] )
{
dist[u]=dist[i]+Edge[i][u];
path[u]=i;
}
}
} } }
如果dist[ ]各元素的初值为 MAX,则循环应该n-1次,
Bellman-Ford算法
✓ Bellman-Ford算法: ✓ 为了能够求解含负权边的带权有向图的单源最短路径问题, Bellman(贝尔曼)和Ford(福特)提出了从源点逐次绕过其他顶点, 以缩短到达终点的最短路径长度的方法。不能处理带负权边的无 向图。
✓ Bellman-Ford算法的限制条件: ✓ 要求图中不能包含权值总和为负值回路(负权值回路),如下图所 示。Why?
✓ 算法的最终目的是计算出dist n-1 [u],为源点v到顶点u的最短路径长 度。
2
dist k [u]的计算
✓ 采用递推方式计算 dist k [u]。 ❖ 设已经求出 dist k-1 [u] , u = 0, 1, …, n-1,此即从源点v最多经 过不构成负权值回路的k-1条边到达终点u的最短路径的长度。 ❖ 从图的邻接矩阵可以找到各个顶点j到达顶点u的距离 Edge[j][u],计算min{ dist k-1 [j] + Edge[j][u] } ,可得从源点 v绕过各个顶点,最多经过不构成负权值回路的k条边到达终点 u的最短路径的长度。 ❖ 比较dist k-1 [u]和min{ dist k-1 [j] + Edge[j][u] } ,取较小者作 为dist k [u]的值。
即k的初值应该改成1。
}
6
Dijkstra算法与Bellman算法的区别
§Dijkstra算法和Bellman算法思想有很大的区别: Dijkstra算法在求解过程中,源点到集合S内各顶点 的最短路径一旦求出,则之后不变了,修改的仅仅 是源点到T集合中各顶点的最短路径长度。 Bellman算法在求解过程中,每次循环都要修改所 有顶点的dist[ ],也就是说源点到各顶点最短路径长 度一直要到Bellman算法结束才确定下来。
7
如果存在从源点可达的负权值回路,则最短路径不存在,因 为可以重复走这个回路,使得路径无穷小。
在Bellman算法中判断是否存在从源点可达的负权值回路的 方法:
思路:在求出distn-1[ ]之后,再对每条边<u,v>判断一下:加入这条 边是否会使得顶点v的最短路径值再缩短,即判断:
dist[u]+w(u,v)<dist[v]
1, …, n-1。算法结束时中存放的是dist n-1 [u] 。 2. path数组含义同Dijkstra算法中的path数组。
#define MAX_VER_NUM 10 //顶点个数最大值
#define MAX 1000000
int Edge[MAX_VER_NUM][MAX_VER_NUM]; //图的邻接矩阵
递推公式(求顶点u到源点v的最短路径): dist 1 [u] = Edge[v][u] dist k [u] = min{ dist k-1 [u], min{ dist k-1 [j] + Edge[j][u] } }, j=0,1,…,n-
1,j≠u
3
例子
-1
1
6
-2
05
2
1
5 -2
-1
3 (c)
k dist k [0] dist k [1] dist k [2] dist k [3] dist k [4] dist k [5] dist k [6]
1
0
6
5
5
∞
∞
∞
2
0
3
3
5
5
4
∞
3
0
1
3
5
2
4
7
4
0
1
35Leabharlann 0455
0
1
3
5
0
4
3
6
0
1
3 45
0
4
3
算法实现
注意: 1. 本算法使用同一个数组dist [u]来存放一系列的dist k [u] 。其中k = 0,
