2021届安徽省六安中学高三上学期开学考试数学(文)试题(解析版)
安徽省六安中学2021届高三上学期开学考试语文试题 Word版含答案

Evaluation Only. Created with Aspose.Words. Copyright 2003-2016 Aspose Pty Ltd.六安中学2020—2021学年度高三上学期入学考试语文试卷时间:150分钟分值:150分第I卷阅读题(70分)一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
○1书法与国学有诸多联系,但不能直接画等号。
书法是艺术,国学是学问。
把书法当成国学,与把传统文化当成国学如出一辙。
书法是传统文化的一部分,而且是重要组成部分,但只有用国学方法研究传统文化的学问才是国学。
○2那么研究书法的学问是不是就是国学了?不全是。
举个例子,用传统文献学方法研究的传统书学,可称得上国学。
○3古代书论文献大多是文学性描述,多运用比喻、夸张和想象等文学手法,且行文简略,如孙过庭《书谱》中有一句经典概括“古不乖时,今不同弊”。
意思是取法古人,不能背离时代条件,同时又不能随大流,过于迎合今人。
写不出自己,看不到古人,是书法大忌。
孙过庭以简短八个字,把古今书学的道理说通了。
而这用短短几个字就能说透的问题,今人千言万语也未必能达其真谛。
所以,凡遇古书论,都需用文献学方法,对所涉字词进行训诂学研究,这些自然属于国学范畴。
○4按照国学大师梁启超的划分,国学研究总体分为两类:一类是关于智识的学问,一类是关于人生的学问。
前者侧重于认识,后者侧重于实践体悟。
书学也是如此。
○5书学是关于智识的学问。
书法的基础是汉字,研究书法必须研究汉字本体,故此,书学的基础是字学,也即小学,小学又融于国学之中。
所以,国学中的字学或小学,对书学研究有直接作用和影响。
辑校和注疏是国学研究的重要方法,也是传统书学研究的重要方法。
在阅读和运用古代书论文献时,必须对其中的字词进行训诂或校注,否则易发生误读。
譬如现在我们时常用“天真烂漫”一词形容书法作品至高的美学境界,但从包世臣《艺舟双楫》中对“烂漫”一词的注解可知,“烂漫”的本意是花开十分,已渐有凋疏之意,用在书法上,则是指笔法粗疏导致的墨法凋疏,字法散乱。
2021届安徽省六安市示范高中高三上学期教学质量检测数学(文)试题解析

绝密★启用前2021年六安市省示范高中高三教学质量检测文科数学试题注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数1z i =+(i 为虚数单位),则一在复平面内对应的点在() A .第一象限B .第二象限C .第三象限D .第四象限2.已知集合(){}ln 1A x y x ==-,{}2B x y x ==,则A B ⋂=() A .()0,1B .(]0,1C .[)0,1D .[]0,13.设120212020a =,2000log 2021b =,20211log 2020c =则() A .a c b >>B .b c a >>C .b a c >>D .a b c >>4.已知命题2:20p x x --<,:24xq <,则p 是q 的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.已知函数()y f x =的部分图象如图所示,则()f x 的解析式可能为()A .()1sin 2f x x x =- B .()1sin 2f x x x =+ C .()1cos 2f x x x =-D .1()cos 2f x x x =+6.已知()0,1A ,()0,3B ,C 在抛物线24y x =上,且到焦点的距离为5,则ABC 的面积为() A .4B .5C .8D .107.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A .86π+B .483π+C .166π+D .4163π+8.六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r 米,在最小口径上方h 米处的口径为4r 米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为()A .3hy x =±B .3h y x =±C .3r y x =±D .3r y x =±9.设等差数列{}n a 的前n 项和为n S ,公差0d >且2217a a =,则n S 取得最小值时,n 的值为()A .3B .4C .3或4D .4或510.《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,这是一个伟大创举。
安徽省六安市城南中学2021届高三语文上学期开学考试试题

安徽省六安市城南中学2021届高三语文上学期开学考试试题一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
《古诗十九首》(以下简称《古诗》)是古代文人五言诗的代表,其意义不仅在于标志着五言诗由产生发展到最终的成熟,更在于诗歌精神的拓进:将中国诗歌精神推向了最本质的深度,即对人的生存、生活之关注与关怀,体现了中国文学对人及其命运的探索与追问、对大地苍生的悲悯情怀。
《古诗》对人的现实存在、生活状态没有任何回避与粉饰。
在《古诗》中,读者能够感受到一般感伤哀怨诗所没有的诗歌精神。
诗歌的意义并不在于功利的教化,或是成就经国之大业,而在于悲悯。
这对中外诗歌来说都是普适的,是共同的诗歌精神。
东汉直至魏晋,战乱频仍,社会动荡,民不聊生,“铠甲生虮虱,万姓以死亡。
白骨露于野,千里无鸡鸣”。
《古诗》以怨而不怒的态度揭示人们的栖居状态,正是要让人们勇于直面无法回避的死亡、离乱、孤独、悲观、绝望等人世之悲;而诗歌的写作者也对人世间的这些悲苦怀有一种感同身受的情感,而不是以高高在上的旁观者自居。
这种悲悯情怀是凄凉人世间的一抹温柔,是灰暗生活中的一道光亮。
在混乱的时代,人的生命无法得到保障,所以“死亡”成为《古诗》中悲苦的深源。
“生年不满百,常怀千岁忧”“去者日以疏,生者日以亲。
出郭门直视,但见丘与坟”。
死亡是人之存在的最根本困境,可是人又渴望永恒。
愿之不得而生忧,所以人在现实人世中常感到悲苦。
《古诗》的时代,因羁旅天涯、交通阻隔等客观因素,人世间的常态是离散,不是团聚。
“行行重行行,与君生别离。
相去万余里,各在天一涯”“同心而离居,忧伤以终老”,挥之不去的孤独与离愁,是诗歌要让人直面的又一个悲观现实。
孤独并不以空间为限,它不仅是客观存在的处境,更是心灵的寂寞无人知:“不惜歌者苦,但伤知音稀。
”其实,心灵悲苦,在现代社会仍然是一个生存困境。
即使交通、通信的问题解决了,为什么心灵的孤独仍难解脱?因为人在本质上就是孤独的。
2021-2022学年安徽省六安市中学高三数学文测试题含解析

2021-2022学年安徽省六安市中学高三数学文测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 命题“”的否定为()A. B.C. D.参考答案:C2. 数列{a n}的前n项和为S n,若,则S5等于( )A.1 B.C.D.参考答案:B考点:数列的求和.专题:等差数列与等比数列.分析:利用“裂项求和”即可得出.解答:解:∵,∴…+==.∴.故选B.点评:熟练掌握“裂项求和”的方法是解题的关键.3. 如图,某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆,则该几何体的体积为()A.4 B.8 C.2πD.4π参考答案:C【考点】由三视图求面积、体积.【专题】空间位置关系与距离.【分析】根据几何体的三视图,得该几何体是底面为半圆的圆锥,求出几何体的体积即可.【解答】解:根据几何体的三视图,得该几何体是底面为半圆的圆锥,∴该几何体的体积为V几何体=S底面h=××π××3=2π.故选:C.【点评】本题考查了空间几何体的三视图的应用问题,解题时应根据三视图,得出该几何体是什么几何图形.4. △ABC的三个内角A,B,C所对的边分别为a,b,c,,则等于( )A.B. C. D.参考答案:D略5. 将函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象关于对称,则ω的最小值是( )A.6B.C.D.参考答案:【知识点】函数的性质 C4【答案解析】D 解析:将函数的图像向右平移个单位后,可得到函数的图像,又因为所得图像关于对称,所以,即,ω>0,所以当时,取最小值,故选:D【思路点拨】由条件根据函数的图象变换规律,正弦函数的图象的对称性可得,即,由此可计算出取最小值。
6. 若集合,集合,则等于()A. B. C.D.参考答案:C试题分析:,,又,.故选C.考点:集合运算.7. 直线,圆,直线与圆交于两点,则等于()A. 2 B.3 C.4D.参考答案:A8. 已知函数,则实数的值等于A.1B.2C.3D.4参考答案:B略9. 已知全集,集合则集合中的元素的个数为 ( )A.1B.1C.3D.4参考答案:【知识点】集合的运算 A1B因为集合,所以,求得,所以,故选择B.【思路点拨】先求得集合,可得,根据补集定义求的其补集.10. 设等比数列的前项和为,若,则下列式子中数值不能确定的是( )A. B. C. D.参考答案:D略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数则的零点是_____;的值域是_____.参考答案:和, 当时,由得,。
安徽省六安中学2021届高三数学上学期开学考试试题文 【含答案】

组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前 n 项和为
Sn ,则 S21 =__________.
三、解答题 17.某校高一年级 1000 名学生期中考试生物学科成绩的频率分布直方 图如图所示,其中成绩分组情况如下表:
A.36π
B.45π
C.54π
D.63π
4.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上 有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈 皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中各随机选取 1 个数,则选 取的两数之和能被 5 整除的概率( )
出结果.
【详解】
设点
P
x0
,
y0
,则
x02 4
y02 5
1
①.
OP OF 4 5 3
安徽省六安中学 2021 届高三数学上学期开学考试试题 文
时间:120 分钟 分值:150 分
一、单选题
1.已知 R 是实数集,集合
A
x Z
|
x
2 B ,
x | 2x 1
0 ,则
A CRB ( )
A.
1 2
,1
1
B.
1, 0
C.
D.
,
1 2
z 4i 2. i 是虚数单位, 1 i
由等比数列性质可知
a10
a7 2 a4
8, a1
a42 a7
1 a10
或
a7 2 a4
1, a1
a42 a7
8
a1 a10 7
安徽省六安市城南中学2021届高三数学上学期第一次月考试题文

安徽省六安市城南中学2021届高三数学上学期第一次月考试题 文一、单选题(共12题;共60分)1.已知集合{}|M x x N =∈,则( )A A 、0M ∈ B 、M π∈ C 、2M ∈ D 、1M ∉2. “-1x =”是“2230x x --=”的( )AA 、充分不必要条件B 、充要条件C 、必要不充分条件D 、既不充分也不必要条件3.已知集合{}212,4,2A a a a =+-,且3A -∈,则a =( )DA 、1-B 、31--或C 、3D 、3-4.如果函数f (x )=x 2-ax -3在区间(-∞,2]上单调递减,那么实数a 满足的条件是( )CA .a ≥2B .a ≤2C .a ≥4D .a ≥-45.命题“若 ,则 ”的否命题为( ) DA.若 ,则 且B.若 ,则 或C.若 ,则 且D.若 ,则 或6.若函数满足, 则=( )BA. B.C. D. 或7.函数2(33)x y a a a =--是指数函数,则有( ) BA .14a a =-=或B .4a =C .1a =-D .01a a >≠或8.与函数f (x )=表示同一函数提( ) D A. g (x )=B. g (x )=()2 C. g(x)=x D. g (x )=|x| 9.已知2()355f x ax bx a b =+-+是偶函数,且其定义域为[]31,a a -,则a b +=( ) CA. 17B. 12C. 14D.7 10.幂函数y =f (x )的图象经过点(2,4),则f (x )是( ) AA.偶函数,且在(0,+∞)上是增函数B.偶函数,且在(0,+∞)上是减函数C.奇函数,且在(0,+∞)上是减函数D.非奇非偶函数,且在(0,+∞)上是增函数11.如果函数f (x )=x 2+bx +c 对任意的实数x ,都有f (-1+x )=f (-x ),那么( ) BA .f (0)<f (2)<f (-2)B .f (0)<f (-2)<f (2)C .f (2)<f (0)<f (-2)D .f (-2)<f (0)<f (2)12.已知函数是R 上的单调递增函数,则实数 的取值范围是( )CA. B. C. D.二、填空题(共4题;共20分)13.已知命题2:,10p x R x x ∀∈-+≤,则P ⌝为________2000,10x R x x ∃∈-+>14.函数1()214x f x x =---的定义域为________ [0,4)(4,)+∞ 15. 化简2112333324()3a b a b -⋅÷-的结果为________ 136ab --16.函数f (x )是定义在[-4,4]上的偶函数,其在[0,4]上的图象如下图所示,那么不等式f (x )<0的解集为________.三、解答题(共6题;共70分)17.函数2()(31)m f x m m x =--是幂函数,且在(0,)x ∈+∞上为增函数,则实数m 的值是多少?解:由2311m m --=得,23m m =-或=1 又(0,)x ∈+∞上为增函数,则1m =18.已知集合 ,. (1)当5a =时,求 ;(2)若 ,求实数a 的取值范围.解:(1)当时,{}37A x x =-≤≤, , ∴ {}3147A B x x x =-≤≤-≤≤或(2)若 ,此时 ,∴ ,满足 ,当 时, ,∵ ,∴,∴ . 综上可知,实数a 的取值范围是 .19.已知函数f (x )为(0,+∞)上的增函数,若2()(8)f a a f a ->+,则实数a 的取值范围是多少?解析:由已知可得220880a a a a a a ⎧->⎪->+⎨⎪+>⎩,解得(8,2)(4,)a ∈--⋃+∞20.已知函数()2x f x x =- . (1)求函数的定义域和值域; (2)判断函数 在区间 上单调性,并用定义来证明所得结论. 解:(1)222()122x f x x x -+==+-- , 的定义域为{}2x x ≠ .值域 (2)由函数解析式得该函数在为减函数,下面证明: 任取 ,且 ,, 211212122()22()()1(1)22(2)(2)x x f x f x x x x x --=+-+=---- ,,1220,20x x ->-> ,. 函数在 ()2x f x x =- 为减函数21. 函数f (x )=k ·a -x (k ,a 为常数,a >0且a ≠1)的图象过点A (0,1),B (3,27).(1)求函数f (x )的解析式;(2)若函数g (x )=f (x )-1f (x )+1,试判断函数g (x )的奇偶性,并给出证明. [解析] (1)由已知得3127k k a -=⎧⎨⋅=⎩,∴k =1,a =13,∴f (x )=3x . (2)函数g (x )为奇函数.证明:31()31x x g x -=+,其定义域为R , 又311331()()311331x x x x x x g x g x ------===-=-+++,∴函数g (x )为奇函数.22.已知函数f (x )=|3x +1|-2|x -1|.(1)画出y=f(x)的图象;(2)求不等式f(x)>1的解集.解析:(1)由题设知f(x)=⎩⎪⎨⎪⎧-x-3,x≤-13,5x-1,-13<x≤1,x+3,x>1.y=f(x)的图象如图所示.(2)24,5x x x⎧⎫<->⎨⎬⎩⎭。
2021届安徽省六安市第一中学高三上学期第二次月考数学(文)试题(解析版)

2021届安徽省六安市第一中学高三上学期第二次月考数学(文)试题一、单选题1.已知全集U =R ,集合(){}20A x x x =-≤,{}1,0,1,2,3B =-,则()UA B =( ) A .{}1- B .{}1,3-C .{}1,2,3D .{}1,0,2,3-【答案】B【分析】解出集合A 中的不等式即可.【详解】因为(){}{}2002A x x x x x =-≤=≤≤,所以()(),02,UA =-∞⋃+∞所以()UA B ={}1,3-故选:B2.已知角α的终边经过点(-,则sin α的值为( )A .B .12-C .D 【答案】C【分析】利用三角函数的定义可计算出sin α的值.【详解】由三角函数的定义得sin α== C.【点睛】本题考查任意角三角函数的定义,要熟记正弦、余弦以及正切三个三角函数值的定义,考查计算能力,属于基础题.3.已知0.12a =,0.50.5b =,8log 4c =,则( ) A .a b c >> B .c a b >>C .a c b >>D .c b a >>【答案】A【分析】判断出1a >,2b =,23c =即可.【详解】因为0.10221a =>=,120.510.522b ⎛⎫=== ⎪⎝⎭,32822log 4log 23c ===所以a b c >>4.下列函数中,周期为π,且在0,2π⎛⎫⎪⎝⎭上为减函数的是( ) A .sin 22y x π⎛⎫=+⎪⎝⎭B .cos 22y x π⎛⎫=+⎪⎝⎭C .sin 2y x π⎛⎫=+ ⎪⎝⎭D .cos 2y x π⎛⎫=+⎪⎝⎭【答案】A【分析】逐个分析各个函数周期以及在0,2π⎛⎫⎪⎝⎭上为单调性,即可作出判断选择. 【详解】sin 2cos 22y x x π⎛⎫=+= ⎪⎝⎭,因为0,2x π⎛⎫∈ ⎪⎝⎭,所以()20,x π∈,所以sin 22y x π⎛⎫=+ ⎪⎝⎭的周期为π,且在0,2π⎛⎫ ⎪⎝⎭上为减函数,同理cos 2sin 22y x x π⎛⎫=+=- ⎪⎝⎭得周期为π,但在0,2π⎛⎫⎪⎝⎭上有增有减;sin cos 2y x x π⎛⎫=+= ⎪⎝⎭的周期为2π,在0,2π⎛⎫ ⎪⎝⎭上为减函数;cos sin 2y x x π⎛⎫=+=- ⎪⎝⎭的周期为2π,在0,2π⎛⎫ ⎪⎝⎭上为减函数;故选:A【点睛】本题考查三角函数周期以及单调性,考查基本分析求解能力,属基础题. 5.已知a ,b 均为单位向量,3a b +=,则()()2a b a b +⋅-=( ) A .12-B .12C .32-D .32【答案】B【分析】利用向量的积的运算求解即可【详解】a ,b 均为单位向量,故1a =,1b =,由3a b +=,得23a b +=, 则有2223a b ab ++=,化简得12ab =,所以, ()()2211222122a b a b a b ab +⋅-=--=--=6.《九章算术》有这样一个问题:今有女子善织,日增等尺,七日共织二十八尺,第二日、第五日、第八日所织之和为十五尺,则第十日所织尺数为( ) A .9 B .10C .11D .12【答案】B【解析】设第一天织布1a 尺,从第二天起每天比第一天多织d 尺由已知得:1111721284715a d a d a d a d +=⎧⎨+++++=⎩解得11a =,1d =∴第十日所织尺数为101910a a d =+=故选B7.将函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象向左平移6π个单位长度后,所得图象对应的函数为( ) A .2sin 2y x =B .2sin 26y x π⎛⎫=+⎪⎝⎭ C .2sin 23y x π⎛⎫=- ⎪⎝⎭D .2sin 22y x π⎛⎫=-⎪⎝⎭【答案】B【分析】根据三角函数的平移原则,直接得出结果. 【详解】将函数2sin 26y x π⎛⎫=-⎪⎝⎭的图象向左平移6π个单位长度后, 所得函数解析式为2sin 22sin 2366y x x πππ⎛⎫⎛⎫=+-=+ ⎪ ⎪⎝⎭⎝⎭. 故选:B.8.已知函数()f x 是定义在R 上的奇函数,()()22f x f x +=-,且()2,0x ∈-时,()()2log 31f x x =-+,则()2021f =( )A .4B .2log 7C .2D .-2【答案】D【分析】先求出函数的周期,再利用函数的周期性和奇偶性计算求解.【详解】因为()()22f x f x +=-, 所以函数()f x 是周期为4的周期函数,则(2021)(50541)f f f =⨯+=(1)22(1)log (31)log 42f =--=-+=-=-, 故选:D .9.函数2()ln(1)f x x x x =+-的图象大致为( )A .B .C .D .【答案】D【分析】利用排除法,先判断奇偶性,再取特殊值即可得结果. 【详解】解:由题意知函数的定义域为R())2ln1f x x x x =+,则())2ln1f x x x x -=-+,有()()()22ln 10x x f x x f x ⎡⎤-=+-=⎣⎦-,得()()f x f x =-,所以函数()f x 为偶函数,排除选项A ,B ;又())1ln 10f =<,排除选项C.故选:D.【点睛】此题考查了函数图像的识别,注意奇偶性、特殊值的使用,属于基础题. 10.已知ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,满足222cos cos cos 1sin sin A B C A C -+=+,且sin sin 1A C +=,则ABC 的形状为( ) A .等边三角形B .等腰直角三角形C .顶角为120的非等腰三角形D .顶角为120的等腰三角形【答案】D【分析】利用平方关系式和正弦定理得222122a c b ac +-=-,根据余弦定理求出120B =,再根据sin sin 1A C +=求出30A C ==,从而可得解.【详解】因为222cos cos cos 1sin sin A B C A C -+=+, 所以2221sin (1sin )1sin 1sin sin A B C A C ---+-=+, 所以222sin sin sin sin sin A C B A C +-=-,根据正弦定理可得222a cb ac +-=-,即222122a cb ac +-=-,所以1cos 2B =-,因为0B π<<,所以120B =,所以60A C +=, 由sin sin 1A C +=得sin sin(60)1A A +-=, 得sin sin 60cos cos60sin 1A A A +-=,得1sin cos sin 122A A A +-=,得1sin 12A A +=, 得sin(60)1A +=,因为A 为三角形的内角,所以30A =,30C =, 所以ABC 为顶角为120的等腰三角形. 故选:D【点睛】思路点睛:判断三角形形状从两个方面入手:①利用正余弦定理角化边,利用边的关系式判断形状,②利用正余弦定理边化角,利用角的关系式判断形状. 11.已知函数()()ln f x a x x a a R =--∈有两个零点,则a 的取值范围( ) A .(),e -∞ B .()2,e-∞C .(),e +∞D .()2,e +∞【答案】D【分析】求导,分类讨论a ,当0a ≤时,函数()f x 在(0,)+∞上为增函数,()f x 最多只有一个零点,不符合题意;当0a >时,()f x 在(0,)a 上递增,在(,)a +∞上递减,()f x 取得最大值()ln 2f a a a a =-,由()ln 20f a a a a =->解得结果即可得解. 【详解】()f x 的定义域为(0,)+∞,()1a a xf x x x'-=-=, 当0a ≤时,()0f x '≤,函数()f x 在(0,)+∞上为增函数,()f x 最多只有一个零点,不符合题意;当0a >时,由()0f x '<得x a >,由()0f x '>得0x a <<, 所以()f x 在(0,)a 上递增,在(,)a +∞上递减, 所以当x a =时,()f x 取得最大值()ln 2f a a a a =-,因为x 趋近于0时,()f x 趋近于负无穷大,x 趋近于正无穷大时,()f x 趋近于负无穷大,所以要使()f x 有两个零点,只需()ln 20f a a a a =->,因为0a >,所以ln 2a >, 所以2a e >. 故选:D【点睛】方法点睛:已知函数零点的个数求参数值(取值范围)常用的方法:利用导数判断函数的单调性,研究函数的极值与最值,根据函数变化趋势作出大致图象,通过图象直观分析解决问题.12.在直角梯形ABCD 中,AB AD ⊥,//AD BC ,22AB BC AD ===,E ,F 分别为BC ,CD 的中点,以A 为圆心,AD 为半径的圆交AB 于G ,点P 在弧DG 上运动(如图).若AP AE BF λμ=+,其中,R λμ∈,则32μλ+的取值范围是( )A .12,2⎡⎤⎢⎥⎣⎦B .1,22⎡⎤⎢⎥⎣⎦C .2,22⎡⎤⎢⎥⎣ D .1,2⎡⎤⎣⎦【答案】D【分析】建立空间直角坐标系,求得()cos ,sin AP αα=,()2,1AE =,()2,0AB =,31,2BF ⎛⎫=- ⎪⎝⎭,由AP AE BF λμ=+,得到()()32,1co 1n 2,i ,s s λμαα⎛⎫=+- ⎪⎝⎭,,λμ用α表示,利用辅助角公式化简,再利用三角函数性质求解. 【详解】建立如图所示直角坐标系:则()()()()()()30,0,2,0,2,2,0,1,2,1,1,,cos ,sin 0,22A B C D E F P πααα⎛⎫⎛⎫⎡⎤∈ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭,所以()cos ,sin AP αα=,()2,1AE =,()2,0AB =,31,2BF ⎛⎫=- ⎪⎝⎭, 因为AP AE BF λμ=+, 所以()()32,1co 1n 2,i ,s s λμαα⎛⎫=+- ⎪⎝⎭, 所以3cos 2,sin 2αλμαλμ=-=+,解得1311sin cos ,sin cos 4824λααμαα=+=-,所以3sin cos 24μπλααα⎛⎫+=+=+ ⎪⎝⎭, 因为0,2απ⎡∈⎤⎢⎥⎣⎦, 所以3,444πππα⎡⎤⎢⎥⎣∈⎦+,所以sin 4πα⎤⎛⎫+∈⎥ ⎪⎝⎭⎣⎦,所以32μλ+的取值范围是⎡⎣. 故选:D【点睛】方法点睛:(1)用平面向量解决平面几何问题时,在便于建立直角坐标系的情况下建立平面直角坐标系,可以使向量的运算更简便一些.在解决这类问题时,共线向量定理和平面向量基本定理起主导作用.(2)解决平面向量与三角函数问题,关键是准确利用向量的坐标运算化简已知条件,将其转化为三角函数中的有关问题解决.二、填空题13.已知平面向量()2,3m =-,()6,n λ=.若m n ⊥,则n =______.【答案】【分析】由m n ⊥得出0m n ⋅=,利用平面向量数量积的坐标运算可求出实数λ的值,然后利用平面向量模的坐标运算可求出n 的值.【详解】依题意,0m n ⋅=,则1230λ-=,解得4λ=,则()6,4n =,故3616n =+=故答案为:【点睛】本题考查利用坐标处理向量垂直的问题,同时也考查了平面向量模的坐标运算,考查运算求解能力,属于基础题. 14.曲线1ln e xy x x ⎛⎫=+⋅ ⎪⎝⎭在点(1,e )处的切线方程为______.【答案】e y x = 【分析】先对1ln e xy x x ⎛⎫=+⋅ ⎪⎝⎭求导,再代入1x =算得在点(1,)e 处的切线斜率,再利用点斜式算出切线方程即可. 【详解】依题意,2111e ln e x x y x x x x ⎛⎫⎛⎫'=-⋅++⋅ ⎪ ⎪⎝⎭⎝⎭,故1e x k y ='==,故所求切线方程为e y x = 故答案为e y x =【点睛】导数的几何意义为在某点处导函数的值等于在该点处切线的斜率.算得斜率之后再代入点斜式即可求得切线方程.15.已知112n a n =-,数列{}n a 的前n 项和为n S ,若650k S =,则k =_______. 【答案】30【分析】根据数列通项公式,分5,6n n ≤≥分别求出数列的前n 项和公式,根据650k S =即可求解.【详解】当5n ≤时,112n a n =-,2(9112)102n n n S n n +-∴==-,令265010k S k k ==-,无解,当6n ≥时,211n a n =-,6257510(1211)(5)()1050.22n n n n S S a a a n n ⨯+--=++++=+=-+ 令21065005k S k k =-+=,解得30k =或20k =-(舍去), 综上30k =, 故答案为:30【点睛】关键点点睛:112n a n =-,去掉绝对值号可得分段函数,分别计算前n 项和,代入650k S =,分别求k 即可.考查了等差数列的求和公式,属于中档题. 16.函数()cos 2|sin |f x x x =+的值域为______.【答案】90,8⎡⎤⎢⎥⎣⎦【分析】观察到()cos 2|sin |f x x x =+中有二倍角关系,故考虑用二倍角公式,化简成关于|sin |x 的函数表达式,再进行二次复合函数的分析求值域即可.【详解】2219()cos 2|sin |12|sin ||sin |2|sin |48f x x x x x x ⎛⎫=+=-+=--+ ⎪⎝⎭,所以当1sin 4x =时, ()f x 取到最大值98,当sin 1x =时,()f x 取到最小值0,所以()f x 的值域为90,8⎡⎤⎢⎥⎣⎦故答案为90,8⎡⎤⎢⎥⎣⎦【点睛】本题主要考查二倍角公式,代换后再利用二次复合函数的方法求对称轴分析最值.三、解答题17.在ABC 中,6B π=,25AC =,D 是AB 边上的一点,2CD =.若ACD ∠为锐角,ACD △的面积为4.(1)求边AD 的长; (2)求边BC 的长. 【答案】(1)4;(2)4.【分析】(1)利用三角形的面积公式计算出sin ACD ∠,利用同角三角函数的基本关系求得cos ACD ∠的值,再利用余弦定理可求得边AD 的长; (2)推导出CD AB ⊥,可得出sin CDB BC=,进而可求得边BC 的长. 【详解】(1)因为1252sin 42ACD S ACD =⋅⋅∠=△,所以25sin ACD ∠=. 因为ACD ∠为锐角,所以25cos 1sin 5ACD ACD ∠=-∠=.所以(222222165AD =+-⨯⨯=,所以4=AD . (2)2AC =2CD =,4=AD ,222AD CD AC ∴+=,所以AD CD ⊥,所以sin CD B BC=,所以2412BC ==. 18.设函数233()cos cos 24f x x x x =-+. (1)求函数()f x 图象的对称中心; (2)求()f x 在[]0,π内的单调增区间.【答案】(1)(),062k k Z ππ⎛⎫+∈⎪⎝⎭;(2)50,12π⎡⎤⎢⎥⎣⎦和11,12ππ⎡⎤⎢⎥⎣⎦. 【分析】(1)先化简()23f x x π⎛⎫=- ⎪⎝⎭,再令23x k ππ-=,()k Z ∈即可求解;(2)令222232k x k πππππ-+≤-≤+,k Z ∈,解得x 的范围即为单调增区间.【详解】解:31cos 23()2224x f x x +=-⋅+32cos 2243x x x π⎛⎫=-=- ⎪⎝⎭ (1)令23x k ππ-=,得()62k x k Z ππ=+∈. 所以()f x 图象的对称中心为(),062k k Z ππ⎛⎫+∈ ⎪⎝⎭. (2)令222232k x k πππππ-+≤-≤+,得51212k x k ππππ-+≤≤+,k Z ∈, 当0k =时,51212x ππ-≤≤,当1k =时,11171212x ππ≤≤, 又因为0x π≤≤,所以()f x 在[]0,π内的单调增区间为50,12π⎡⎤⎢⎥⎣⎦和11,12ππ⎡⎤⎢⎥⎣⎦.19.已知等差数列{}n a 的公差为2,且2a ,4a ,8a 成等比数列. (1)求数列{}n a 的通项公式;(2)若()*12nn n a b n N +=∈,求数列{}n b 的前n 项和n T ; (3)在(2)的条件下,32n n n T λ-≤-对一切*n N ∈恒成立,求λ最大值.【答案】(1)2n a n =;(2)222n n +-;(3)54.【分析】(1)由等比数列的性质可得2428a a a =,结合等差数列的通项公式可解得12a =,即可得解;(2)利用错位相减法运算即可得解; (3)由321222n n n n n T ---=-,令2122n nn C -=-,通过作差确定n C 的最小值,即可得解.【详解】(1)由题意,2428a a a =,即()()()21116214a a a +=++,解得12a =, 所以22(1)2na n n =+-=;(2)由题意,122n n n na nb +==, 231123122222n n n n n T --=++++, 231112122222n n n n nT +-=++++, 两式相减得2111111221*********222212nn nn n n n n n T +++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭+⎢⎥⎣⎦=++-=-=--,所以222n n n T +=-; (3)由题意,32321222222n n n n nn n n n T -+---=--=-,令2122n nn C -=-,11121212322222n n n n n n n n C C ++++--⎛⎫⎛⎫-=---= ⎪ ⎪⎝⎭⎝⎭, 所以当1n =时,210C C -<,故21C C <; 当2n ≥时,10n n C C +->,即1n n C C +>; 所以()2min 54n C C ==, 由已知,只需()min n C λ≤,所以54λ≤, 所以max 54λ=.【点睛】关键点点睛:解决本题的关键是错位相减法的应用及利用作差法确定数列的最小项.20.如图,某校园有一块半径为20m 的半圆形绿化区域(以O 为圆心,AB 为直径),现对其进行改建,在AB 的延长线上取点D ,40m OD =,在半圆上选定一点C ,改建后绿化区域由扇形区域AOC 和三角形区域COD 组成,设AOC θ∠=.(1)当3πθ=时,求改建后的绿化区域边界AC 与线段CD 长度之和;(2)若改建后绿化区域的面积为S ,写出S 关于θ的函数关系式()S θ,试问θ为多大时,改建后的绿化区域面积S 取得最大值. 【答案】(1)202073π+;(2)()S θ=200400sin θθ+,()0,θπ∈;23πθ=. 【分析】(1)利用弧长公式和余弦定理可算出答案;(2)利用扇形和三角形的面积公式可得()S θ,然后利用导数求出其单调性即可. 【详解】(1)弧2222020204022040cos7333AC CD πππ+=⨯+-⨯⨯⨯=+(2)()211202040sin()22COD AOC S S S θθπθ==⨯⨯+⨯+⨯⨯-△扇形 200400sin θθ=+,()0,θπ∈.由()'200400cos S θθ=+,得20,3πθ⎛⎫∈ ⎪⎝⎭,()'0S θ>,()S θ单调递增, 得2,3πθπ⎛⎫∈⎪⎝⎭,()'0S θ<,()S θ单调递减. 所以当23πθ=时,S 取得最大值. 21.已知数列{}n a 的前n 项和为n S ,2326n n S a n =+-. (1)求1a ,2a ,3a ;(2)数列{}n a k +为等比数列,求k 的值; (3)求证:()*1211112n n N a a a +++<∈. 【答案】(1)14a =,210a =,328a =;(2)1-;(3)证明见解析. 【分析】(1)分别令1n =,2n =,3n =,即可求解;(2)由2326n n S a n =+-,得11232(1)6n n S a n --=+--,利用当2n ≥时,1n n n a S S -=-,化简整理得1311n n a a ,证{}1n a -是等比数列,即求得1k =-.(3)由(2)得111313n nn a =<+,利用等比数列求和,即可证得结论. 【详解】(1)令1n =,得112326a a =+-,解得14a =, 令2n =,()122232a a a +=-,解得210a =; 令3n =,()123323a a a a ++=,解得328a =.(2)由2326n n S a n =+-,得11232(1)6n n S a n --=+--,2n ≥. 两式相减得:12332n n n a a a -=-+,即132n n a a -=-,所以1311n n a a ,故{}1n a -是首项为3,公比为3的等比数列,所以1k =-.(3)由(2)13nn a -=,所以111313n n n a =<+, 所以2121113311111111113332313nnn n a a a ⎡⎤⎛⎫-⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎣⎦++<+++==-⎢⎥⎪⎝⎭⎢⎥⎣⎦-, 103n>,1113n ∴-<,1111232n⎡⎤⎛⎫∴-<⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 即()*1211112n n N a a a +++<∈ 【点睛】方法点睛:求数列通项公式常用的方法:(1)由n a 与n S 的关系求通项公式;(2)累加法;(3)累乘法;(4)两边取到数,构造新数列法.22.已知函数321()1()32x a f x x ax a R +=-++∈.(1)若2x =是函数()f x 的一个极值点,求a 的值; (2)当2a <时,[]12,0,2x x ∀∈,()()1223f x f x -≤恒成立,求a 的取值范围. 【答案】(1)2;(2)15,33⎡⎤⎢⎥⎣⎦.【分析】(1)由解析式得到导函数fx ,结合2x =是函数()f x 的一个极值点,()20f '=即可求a 的值;(2)由题设分析知,在[]0,2x ∈内有()()max min 23f x f x -≤,结合已知2a <,讨论0a ≤、01a <<、1a =、12a <<分别求a 的范围,然后求并集即可.【详解】解:(1)由函数解析式知:()()21f x x a x a '=-++,由题意,得()()24210f a a '=-++=,故2a =. 经检验,2a =满足题意.(2)由已知,当2a <时,只需[]0,2x ∈,()()max min 23f x f x -≤. ()()()()211f x x a x a x x a '=-++=--.①当0a ≤时,()f x 在0,1单减,在[]1,2单增.所以()()min 5162a f x f ==+,而()01f =,()523f =,故()max 53f x =. 所以()()max min 5523623f a x f x =--≤-,解得13a ≥(舍去).②当01a <<时,()f x 在[]0,a 单增,在[],1a 单减,在[]1,2单增.由于()()2203f f -=,所以只需()()()()210fa f ff ⎧≤⎪⎨≥⎪⎩,即()()2144013a a a a ⎧+-+≥⎪⎨≥⎪⎩, 所以113a ≤<. ③当1a =时,()()2'10f x x =-≥,()f x 在[]0,2单增, 所以()()()()max min 2203f x f x f f -=-=,满足题意. ④当12a <<时,()f x 在0,1单增,在[]1,a 单减,在[],2a 单增.由于()()2203f f -=,所以只需()()()()120f f f a f ⎧≤⎪⎨≥⎪⎩,即533a a ⎧≤⎪⎨⎪≤⎩,所以513a <≤. 综上,知:15,33a ⎡⎤∈⎢⎥⎣⎦. 【点睛】思路点睛:已知函数极值点求参数时,一般应用极值点处的导数为0列方程;函数在闭区间内任意两个函数值的差小于定值转化为最值间的距离小于该定值, (1)当0x x =有极值则0()0f x '=,即可得有关参数的方程; (2)[]12,,x x a b ∀∈,()()1223f x f x -≤恒成立转化为[],x a b ∈,()()max min 23f x f x -≤;。
安徽省六安市城南中学2021届高三上学期开学考试数学(文)试题 PDF版含答案

(2)由
f′(-1)=0,得
a=1,此时有
f(x)=(x2-4)
x-1 2
,
2
f′(x)=3x2-x-4.由 f′(x)=0,得 x=4或 x=-1. 3
4
又
f
3
=-50,f(-1)=9,f(-2)=0,f(2)=0,
27
2
所以 f(x)在[-2,2]上的最大值为9, 最小值为-50.
2
27
…………12 分
……………7 分
根据表中数据得 K2 的观测值 k=
第2页共3页
≈33.333>6.635,
故在犯错误的概率不超过 0.010 的前提下,认为高一、高二两个年级学生这次读书读 报知识竞赛的成绩有差异.
………………12 分
第3页共3页
(参考公式:
,其中
)
参考答案
1~5 ACBCC
6~10 CDAAC
13. x0 R,x0 x02 0
14. 1
16. n (n 1) (3n 2) (2n 1)2
11~12 DC 15. 5
17.∵
x 2 5
y
1
x3 y 1
(1 i)x y (1 i)2 2i
…………10 分
安徽六安城南中学 2020 年秋考试高三数学
时长:120 分钟
总分:150 分 命题人:经 纬
一、选择题(本题共 12 道小题,每小题 5 分,共 60 分)
1.下列各式的运算结果为纯虚数的是(
A. 1 i2
B. i2 1 i
)
C. i 1 i2
D. i1 i
2.已知命题 p:“若 x≥a2+b2,则 x≥2ab”,则下列说法正确的是( )
安徽省六安中学2021届高三数学上学期开学考试试题文
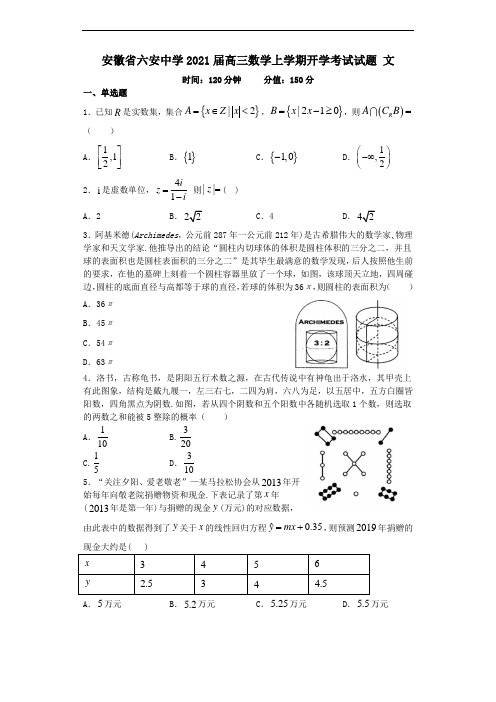
安徽省六安中学2021届高三数学上学期开学考试试题 文 时间:120分钟 分值:150分一、单选题1.已知R 是实数集,集合{}|2A x Z x =∈<,{}|210B x x =-≥,则()R AC B =( )A .1,12⎡⎤⎢⎥⎣⎦B .{}1C .{}1,0-D .1,2⎛⎫-∞ ⎪⎝⎭ 2.i 是虚数单位,41i z i =- 则||z =( ) A .2 B .22 C .4 D .423.阿基米德(Archimedes ,公元前287年一公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为( )A .36πB .45πC .54πD .63π4.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中各随机选取1个数,则选取的两数之和能被5整除的概率( ) A .110B.320C.15 D .310 5.“关注夕阳、爱老敬老”—某马拉松协会从2013年开始每年向敬老院捐赠物资和现金.下表记录了第x 年(2013年是第一年)与捐赠的现金y (万元)的对应数据,由此表中的数据得到了y 关于x 的线性回归方程ˆ0.35y mx =+,则预测2019年捐赠的x 34 5 6 y 2.5 34 4.5 A .5万元B .5.2万元C .5.25万元D .5.5万元6.若实数a ,b 满足3412a b ==,则11a b +=( ) A .12 B .15 C .16 D .17.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( ).A .4B .5C .6D .78.函数()sin(2)(0)f x x ϕϕπ=+<<的图象如图所示,为了得到()sin 2g x x =的图象,可将()f x 的图象( )A.向右平移6π个单位 B .向右平移12π个单位 C .向左平移12π个单位 D .向左平移6π个单位 9.执行如图所示的程序框图,输出的结果是31,则判断框中应填入( )A .4A <?B .4A >?C .5A <?D .5A >?10.已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( )A .7B .5C .5-D .7-11.已知F 是双曲线22:145x y C 的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为( )A .32B .52C .72D .9212.已知三棱锥D -ABC 中,AB =BC =1,AD =2,BD =5,AC =2,BC ⊥AD ,则该三棱锥的外接球的表面积为( )A .6πB .6πC .5πD .8π二、填空题13.设,x y满足约束条件22022x yxy+-≥⎧⎪≤⎨⎪≤⎩,则2z x y=-的最小值是____________. 14.已知向量||1a=,1,2b m⎛⎫= ⎪⎝⎭,若()()a b a b+⊥-,则实数m的值为________. 15.已知函数f(x)=axlnx﹣bx(a,b∈R)在点(e,f(e))处的切线方程为y=3x﹣e,则a+b=_____.16.如图,在杨辉三角形中,斜线1的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n项和为n S,则21S=__________.三、解答题17.某校高一年级1000名学生期中考试生物学科成绩的频率分布直方图如图所示,其中成绩分组情况如下表:组号第一组第二组第三组第四组第五组分组[)50,60[)60,70[)70,80[)80,90[]90,100(1)求生物成绩在[50,60)内的人数;(2)若同组中的每个数据用该组区同中点值代替,根据频率分布直方图,估计这1000名学生生物成绩的平均分:(3)现有5名同学,其中3人的成绩在第三组内,2人的成绩在第四组内,从这5名同学中随机抽取2名,求这2名同学来自不同组的概率.18.ABC的内角A,B,C的对边分别为a,b,c,已知2222sin sinsinb c a B Aab A+--=.(1)求C的大小;(2)若ABC 的周长为18,面积为63,求ABC 外接圆的面积.19.如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面,(I )证明:平面AEC ⊥平面BED ;(II )若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -的体积为6,求该三棱锥的侧面积.20.设函数()3xf x e ax =-+(a R ∈). (1)讨论函数()f x 的极值;(2)若函数()f x 在区间[]1,2上的最小值是4,求a 的值.21.已知椭圆()222210x y a b a b+=>>的左右焦点分别为1F 、2F ,上顶点为M ,若直线1MF 的斜率为1,且与椭圆的另一个交点为N ,2F MN ∆的周长为42(1)求椭圆的标准方程;(2)过点1F 的直线l (直线l 的斜率不为1)与椭圆交于P 、Q 两点,点P 在点Q 的上方,若1123F NQ F MP S S ∆∆=,求直线l 的斜率.22.[选修4-5:不等式选讲]已知函数()225f x x =+-.(1)解不等式:()|1|f x x ≥-;(2)当1m ≥-时,函数()()||g x f x x m =+-的图象与x 轴围成一个三角形,求实数m 的取值范围.参考答案1.C【解析】【分析】先求得的集合{}1,0,1A =-,1|2B x x ⎧⎫=≥⎨⎬⎩⎭,进而得到R C B ,再根据集合的交集的运算,即可求解.【详解】 由题意,集合{}{}|21,0,1A x Z x =∈<=-,{}1|210|2B x x x x ⎧⎫=-≥=≥⎨⎬⎩⎭, 所以1|2R C B x x ⎧⎫=<⎨⎬⎩⎭,所以(){}1,0R A C B =-.故选:C .【点睛】 本题主要考查了集合的表示方法,以及集合的混合运算,其中解答中熟记集合运算的概念,准确运算是解答的关键,着重考查了推理与运算能力.2.B【解析】【分析】根据复数的除法运算求出z 的代数形式,然后再求出z .【详解】 由题意得44(1)2(1)221(1)(1)i i i z i i i i i i +===+=-+--+,∴ ||z ==故选B .【点睛】本题考查复数的除法运算和复数的模,解题的关键是正确进行复数的运算,属于简单题.3.C【解析】【分析】先设球的半径为r ,根据体积求出3r =,再由题意,得出圆柱的底面圆半径,以及圆柱的高,根据圆柱的表面积公式,即可求出结果.【详解】因为球的体积为36π,设球的半径为r ,则34363r ππ=,所以3r =, 又圆柱的底面直径与高都等于球的直径,所以圆柱的底面圆半径为3r =,高为26h r ==,因此圆柱的表面积为22222654S r r r r ππππ=+⋅==.故选:C.【点睛】本题主要考查圆柱与球内切的相关计算,熟记圆柱的表面积公式,以及球的体积公式即可,属于基础题型.4.C【解析】【分析】由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9. 各选一个数,求出所有的选法,求出其和能被5整除的选法种数,根据古典概型的概率计算公式,即得答案.【详解】由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9.各选一个数,共有4520⨯=种选法.其和能被5整除的分别为:2,3;4,1;6,9;8,7,共4种选法, ∴选取的两数之和能被5整除的概率41205P ==. 故选:C.【点睛】 本题考查古典概型和计数原理,属于基础题.5.C【解析】【分析】 由已知求出,x y ,代入回归直线的方程,求得m ,然后取7x =,求得y 的值,即可得到答案.【详解】 由已知得,29t =, 所以样本点的中心点的坐标为(4.5,3.5),代入ˆ0.35ymx =+, 得3.5 4.50.35m =+,即0.7m =,所以ˆ0.70.35yx =+, 取7x =,得ˆ0.770.35 5.25y=⨯+=, 预测2019年捐赠的现金大约是5.25万元.【点睛】本题主要考查了线性回归方程以及应用,其中解答中熟记回归直线的方程经过样本中心点是解答的关键,着重考查了推理与计算能力,属于基础题.6.D【解析】【分析】先将指数式化成对数式,求出,a b ,再利用换底公式的推论log log 1a b b a ⋅=以及对数的运算法则即可求出.【详解】因为3412a b ==,所以34log 12,log 12a b ==,121212341111log 3log 4log 1211212a b log log +=+=+==. 故选:D .【点睛】本题主要考查指数式与对数式的互化、换底公式推论log log 1a b b a ⋅=的应用以及对数的运算法则的应用.7.A【解析】【分析】求出圆心C 的轨迹方程后,根据圆心M 到原点O 的距离减去半径1可得答案.【详解】设圆心(),C x y ,则()()22341x y -+-=, 化简得()()22341x y -+-=,所以圆心C 的轨迹是以(3,4)M 为圆心,1为半径的圆,所以||1||OC OM +≥22345+=,所以||514OC ≥-=, 当且仅当C 在线段OM 上时取得等号,故选:A. 【点睛】本题考查了圆的标准方程,属于基础题.8.A【解析】【分析】函数过7(,1)12π- 代入解得ϕ,再通过平移得到()sin 2g x x =的图像. 【详解】()sin(2)(0)f x x ϕϕπ=+<<,函数过7(,1)12π- 71sin()63ππϕϕ-=+⇒= ()sin(2)3f x x π=+向右平移6π个单位得到()sin 2g x x =的图象 故答案选A本题考查了三角函数图形,求函数表达式,函数平移,意在考查学生对于三角函数图形的理解.9.C【解析】【分析】首先判断循环结构类型,得到判断框内的语句性质,然后对循环体进行分析,找出循环规律.判断输出结果与循环次数以及A 的关系,最终得出选项.【详解】解:经判断此循环为“当型”结构,判断框内为跳出循环的语句第1次循环:3S =,2A =;第2次循环:7=S ,3A =;第3次循环:15S =,4A =;第4次循环:31S =,5A =;此时退出循环,根据判断框内为跳出循环的语句“5A <?”5?A ∴<故选:C .【点睛】本题考查程序框图,考查循环结构.对循环体每次循环需要进行分析并找出内在规律是解题的关键,属于基础题.10.D【解析】【分析】由条件可得47a a ,的值,进而由27104a a a =和2417a a a =可得解. 【详解】56474747822,4a a a a a a a a ==-+=∴=-=或474,2a a ==-.由等比数列性质可知2274101478,1a a a a a a ==-==或2274101471,8a a a a a a ====- 1107a a ∴+=-【点睛】本题主要考查了等比数列的下标的性质,属于中档题.11.B【解析】【分析】设()00,P x y ,因为=OP OF 再结合双曲线方程可解出0y ,再利用三角形面积公式可求出结果.【详解】设点()00,P x y ,则2200145x y -=①.又3OP OF ===,22009x y ∴+=②. 由①②得20259y =, 即053y =, 0115532232OPF S OF y ∆∴==⨯⨯=, 故选B .【点睛】本题易错在忽视圆锥曲线方程和两点间的距离公式的联系导致求解不畅.12.B【解析】【分析】由题意结合平面几何、线面垂直的判定与性质可得BC ⊥BD ,AD ⊥AC ,再由平面几何的知识即可得该几何体外接球的球心及半径,即可得解.【详解】AB =BC =1,AD =2,BD AC ,∴222AB BC AC +=,222AD AB DB +=,∴DA ⊥AB ,AB ⊥BC ,由BC ⊥AD 可得BC ⊥平面DAB ,DA ⊥平面ABC ,∴BC ⊥BD ,AD ⊥AC ,∴CD ,由直角三角形的性质可知,线段CD 的中点到点A ,B ,C ,D 的距离均为2CD =故三棱锥的外接球的表面积为4π2⋅⎝⎭=6π.故选:B.【点睛】本题考查了三棱锥几何特征的应用及其外接球表面积的求解,考查了运算求解能力与空间思维能力,属于中档题.13.-6【解析】【分析】由约束条件画出可行域,再变形2z x y =-为2y x z =-,即在可行域内找到使该直线截距最大的点,进而求解.【详解】由题,可行域如图所示,设2y x z =-,平移直线,当直线与点()2,2A -相交时,直线的截距最大,所以z 的最小值为()2226⨯--=-,故答案为:6-【点睛】本题考查利用目标函数的几何意义求最值,考查简单的线性规划问题,考查数形结合思想. 14.32± 【解析】【分析】由()()a b a b +⊥-可得|||==|1a b ,由||=1b 即可求得m 值.【详解】∵()()a b a b +⊥-,∴()()0a b a b +⋅-=,即22||||0a b -=,|||==|1a b 可得2221||2=1b m ⎛⎫=+ ⎪⎝⎭,得出234m =,32m =±. 故答案为:3 【点睛】 本题考查两个向量垂直的应用,考查向量的模的求解,属于基础题.15.0【解析】【分析】由题意()()'2,3f e e fe ==,列方程组可求,a b ,即求+a b . 【详解】∵在点()(),e f e 处的切线方程为3y x e =-, ()2f e e ∴=,代入()ln f x ax x bx =-得2a b -=①.又()()()''1ln ,23f x a x b f e a b =+-∴=-=②.联立①②解得:1,1a b ==-.0a b ∴+=.故答案为:0.【点睛】本题考查导数的几何意义,属于基础题.16.361【解析】【分析】将n 按照奇偶分别计算n a :当n 为偶数时,42n n a +=;当n 为奇数时,2438n n n a ++=, 11102113212420(...)(...)S a a a a a a =+++++个个计算得到答案.【详解】解法一:根据杨辉三角形的生成过程,当n 为偶数时,42n n a +=, 当n 为奇数时,1=1a ,3=3a ,2-132n n n n n a a a a ++=+=+, 312a a -=,533a a -=,212n n n a a -+-=,2438n n n a ++=, 11102113212420(...)(...)S a a a a a a =+++++个个136...66(345...12)28675361=+++++++++=+=()解法二:当*21()n m m N =-∈时,221(1)22n m m m m m a a -++===, 当*2()n m m N =∈时,22n m a a m ==+,11102113212420(...)(...)S a a a a a a =+++++个个222110(312)[(12...11)(12...11)]22⋅+=+++++++ 1111223111127525333753612622⨯⨯⨯=⨯+⨯+=++= 【点睛】本题考查了数列的前N 项和,意在考查学生的应用能力和解决问题的能力.17.(1)50人;(2)平均分为74.5;(3)35. 【解析】【分析】(1)根据频率分布直方图求出在[)50,60内的频率,进而可求出成绩在[50,60)内的人数.(2)由平均数等于小矩形的面积乘以小矩形底边中点横坐标之和即可求解.(3)这2名同学来自不同组”为事件A ,设第三组的3名同学为a ,b ,c ,第四组的2位同学为x ,y ,列举法求出基本事件个数,再利用古典概型的概率计算公式即可求解.【详解】解:(1)由题意,生物成绩在[)50,60内的频率为1-(0.01×10+0.02×10+0.03×10+0.035×10)=0.05,所以生物成绩在[)50,60内的人数为0.05×1000=50.答:生物成绩在[)50,60内的人数为50人.(2)由频率分布直方图,分数在[50,60)内的频率为0.05,[60,70)内的频率为0.35,[70,80)内的频率为0.3,[80,90)的频率为0.2,[90,100]的频率为0.1,所以这1000名学生期中考试生物成绩的平均分的估计值为:55×0.05+65×0.35+75×0.3+85×0.2+95×0.1=74.5.答:这1000名学生生物成绩的平均分为74.5.(3)设“这2名同学来自不同组”为事件A ,设第三组的3名同学为a ,b ,c ,第四组的2位同学为x ,y ,则样本空间为Ω={(a ,b ),(a ,c ),(a ,x ),(a ,y ),(b ,c ),(b ,x ),(b ,y ),(c ,x ),(c ,y ),(x ,y )},事件A ={(a ,x ),(a ,y ),(b ,x ),(b ,y ),(c ,x ),(c ,y )}. 所以63()105P A ==. 答:这2名同学来自不同组的概率为35 . 【点睛】本题考查了频率分布直方图求平均数、样本容量、古典概型的概率计算公式,属于基础题.18.(1)3π;(2)493π. 【解析】【分析】(1)根据正弦定理,得到222ab b a c =+-,再由余弦定理即可求出角C ;(2)根据题意,由三角形面积公式,以及余弦定理,求出7c =,再由正弦定理,得到外接圆半径,进而可求出外接圆的面积.【详解】(1)根据题意,由正弦定理可得:2222sin sin 2sin b c a B A b a ab A a+---==, ∴222ab b a c =+-,∴2221cos 22b a c C ab +-==, ∵(0,)x π∈,∴3C π=;(2)由题意,18a b c ++=,1sin 2ABC S ab C ==△ ∴24ab =,18a b c +=-, 又2222()3c b a ab a b ab =+-=+-,∴22(18)72c c =--,∴7c =; 由正弦定理得外接圆直径2sin c R C ==R =,ABC 外接圆的面积2493S ππ==. 【点睛】本题主要考查解三角形,熟记正弦定理以及余弦定理即可,属于常考题型.19.(1)见解析(2)【解析】试题分析:(Ⅰ)由四边形ABCD 为菱形知AC ⊥BD ,由BE ⊥平面ABCD 知AC ⊥BE ,由线面垂直判定定理知AC ⊥平面BED ,由面面垂直的判定定理知平面AEC ⊥平面BED ;(Ⅱ)设AB=x ,通过解直角三角形将AG 、GC 、GB 、GD 用x 表示出来,在Rt ∆AEC 中,用x 表示EG ,在Rt ∆EBG 中,用x 表示EB ,根据条件三棱锥E ACD -求出x ,即可求出三棱锥E ACD -的侧面积.试题解析:(Ⅰ)因为四边形ABCD 为菱形,所以AC ⊥BD ,因为BE ⊥平面ABCD ,所以AC ⊥BE ,故AC ⊥平面BED.又AC ⊂平面AEC ,所以平面AEC ⊥平面BED(Ⅱ)设AB=x ,在菱形ABCD 中,由∠ABC=120°,可得AG=GC=2x ,GB=GD=2x .因为AE ⊥EC ,所以在Rt ∆AEC 中,可得EG=2x .由BE ⊥平面ABCD ,知∆EBG 为直角三角形,可得BE=2x .由已知得,三棱锥E-ACD 的体积31132E ACD V AC GD BE x -=⨯⋅⋅==.故x =2从而可得.所以∆EAC 的面积为3,∆EAD 的面积与∆ECD故三棱锥E-ACD 的侧面积为考点:线面垂直的判定与性质;面面垂直的判定;三棱锥的体积与表面积的计算;逻辑推理能力;运算求解能力20.(1)当0a ≤时,函数()f x 在R 上无极值;当0a >时,()f x 的极小值为ln 3a a a -+,无极大值.(2)1e -【解析】【分析】(1)求得函数的导数()xf x e a '=-,分类讨论即可求解函数的单调区间,得到答案. (2)由(1)知,当0a ≤时,函数()f x 在R 上单调递增,此时最小值不满足题意;当0a >时,由(1)得ln x a =是函数()f x 在R 上的极小值点,分类讨论,即可求解.【详解】解:(1)()xf x e a '=-. 当0a ≤时,()0f x '>,()f x 在R 上单调递增;无极值当0a >时,()0f x '>,解得ln x a >,由()0f x '<,解得ln x a <.函数()f x 在(),ln a -∞上单调递减,函数()f x 在()ln ,a +∞上单调递增,()f x 的极小值为()ln ln 3f a a a a =-+,无极大值综上所述:当0a ≤时,函数()f x 在R 上无极值;当0a >时,()f x 的极小值为ln 3a a a -+,无极大值.(2)由(1)知,当0a ≤时,函数()f x 在R 上单调递增,∴函数()f x 在[]1,2上的最小值为()134f e a =-+=,即10a e =->,矛盾.当0a >时,由(1)得ln x a =是函数()f x 在R 上的极小值点.①当ln 1a ≤即0a e <≤时,函数()f x 在[]1,2上单调递增,则函数()f x 的最小值为()134f e a =-+=,即1a e =-,符合条件.②当ln 2a ≥即2a e ≥时,函数()f x 在[]1,2上单调递减,则函数()f x 的最小值为()22234f e a =-+=即2212e a e -=<,矛盾. ③当1ln 2a <<即2e a e <<时,函数()f x 在[]1,ln a 上单调递减,函数()f x 在[]ln ,2a 上单调递增,则函数()f x 的最小值为()ln ln ln 34a f a e a a =-+=,即ln 10a a a --=.令()ln 1h a a a a =--(2e a e <<),则()ln 0h a a '=-<,∴()h a 在()2,e e 上单调递减,而()1h e =-,∴()h a 在()2,e e 上没有零点,即当2e a e <<时,方程ln 10a a a --=无解.综上,实数a 的值为1e -.【点睛】本题主要考查导数在函数中的综合应用,着重考查了转化与化归思想、逻辑推理能力与计算能力,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,求解曲线在某点处的切线方程;(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数;(3)利用导数求函数的最值(极值),解决函数的恒成立与有解问题,同时注意数形结合思想的应用;本题属于难题.21.(1)2212x y +=;(2). 【解析】【分析】(1)由椭圆的定义得出2F MN ∆的周长为4a =可求出a 的值,又由直线1MF 的斜率得出1b c=,可求出b 、c 的值,从而得出椭圆的标准方程; (2)将直线1MF 的方程与椭圆方程联立,求出点N 的坐标,设直线l 的方程为1x my =-,设点()11,P x y 、()22,Q x y ,将直线l 的方程与椭圆的方程联立,列出韦达定理,由题意分析得出212y y =-,代入韦达定理可求出实数m 的值,即可得出直线l 的斜率.【详解】(1)根据题意,因为1F MN ∆的周长为4a =,即a =由直线1MF 的斜率1,得1b c =, 因为222a b c =+,所以1b c ==,所以椭圆的标准方程为2212x y +=; (2)由题意可得直线1MF 方程为1y x =+,联立得22112y x x y =+⎧⎪⎨+=⎪⎩,得2340x x +=, 解得41,33N ⎛⎫-- ⎪⎝⎭,所以1113NF MF =,因为1123F NQ F MP S S ∆∆=, 即111111121sin sin 232NF QF MF P Q F F F N P M ⎛⎫⋅∠=⋅∠ ⎪⎝⎭,所以112QF PF =, 当直线l 的斜率为0时,不符合题意;故设直线l 的方程为1x my =-,设点()11,P x y 、()22,Q x y ,由点P 在点Q 的上方,且212y y =,则有212y y =-, 联立22112x my x y =-⎧⎪⎨+=⎪⎩,所以()222210m y my +--=, 由韦达定理得12222m y y m +=+,12212y y m =-+, 消去2y 得1221222122m y m y m -⎧=⎪⎪+⎨⎪=⎪+⎩,所以()22228122m m m =++,得227m =,m ∴=又由画图可知7m =7m =-,故直线l的斜率为12m =-. 【点睛】本题考查椭圆方程的求解,同时也考查了椭圆中的三角形面积比的计算,解题时要结合已知条件将三角形的面积比转化为共线向量来处理,并结合韦达定理进行求解,考查运算求解能力,属于中等题. 22.(1)(][),82,-∞-⋃+∞(2){}3,412⎡⎫⋃-⎪⎢⎣⎭【解析】试题分析:(Ⅰ)由已知,可按不等中两个绝对值式的零点将实数集分为三部分进行分段求解,然后再综合其所得解,从而求出所求不等式的解集;(Ⅱ)由题意,可将m 的值分为1m =-和1m >-进行分类讨论,当1m =-时,函数()315g x x =+-不过原点,且最小值为5-,此时满足题意;当1m >-时,函数()37,13,133,x m x g x x m x m x m x m -+-≤-⎧⎪=+--<≤⎨⎪-->⎩,再由函数()g x 的单调性及值域,求出实数m 的范围,最后综合两种情况,从而得出实数m 的范围.试题解析:(Ⅰ)由题意知,原不等式等价于12251x x x ≤-⎧⎨---≥-⎩或112251x x x -<≤⎧⎨+-≥-⎩或12251x x x >⎧⎨+-≥-⎩, 解得8x ≤-或∅或2x ≥,综上所述,不等式()1f x x ≥-的解集为(][),82,-∞-⋃+∞.(Ⅱ)当1m =-时,则()2251g x x x =+-++ 315x =+-,此时()g x 的图象与x 轴围成一个三角形,满足题意: 当1m >-时,()225g x x x m =+-+- 37,13,133,x m x x m x m x m x m -+-≤-⎧⎪=+--<≤⎨⎪-->⎩,则函数()g x 在(),1-∞-上单调递减,在()1,-+∞上单调递增.要使函数()g x 的图象与x 轴围成一个三角形,则()()140230g m g m m ⎧-=-<⎪⎨=-≥⎪⎩,解得342m ≤<; 综上所述,实数m 的取值范围为{}3,412⎡⎫⋃-⎪⎢⎣⎭.。
安徽省六安市高三上学期数学开学考试试卷

安徽省六安市高三上学期数学开学考试试卷姓名:________ 班级:________ 成绩:________一、填空题:本大题共14个小题,每小题5分,共70分,把答案填在 (共14题;共15分)1. (1分) (2016高一上·洛阳期中) 已知集合A={1,2},集合B满足A∪B=A,则集合B有________个.2. (1分) (2015高三上·石景山期末) 在复平面内,复数对应的点到原点的距离为________.3. (1分) (2016高一下·赣州期中) 若向量 =(1,﹣x)与向量 =(x,﹣6)方向相反,则x=________.4. (2分) (2017高二下·山西期末) 已知离散型随机变量X的分布列如下:X012P x4x5x由此可以得到期望E(X)=________,方差D(X)=________.5. (1分)(2017·南通模拟) 根据如图所示的伪代码,当输入x的值为e(e为自然对数的底数)时,则输出的y的值为________.6. (1分)(2018·鞍山模拟) 点分别为双曲线的焦点、实轴端点、虚轴端点,且为直角三角形,则双曲线的离心率为________.7. (1分) (2019高一下·海珠期末) 如图,⊙O的半径为,六边形是⊙O的内接正六边形,从六点中任意取两点,并连接成线段,则线段的长为的概率是________.8. (1分) (2017高二上·常熟期中) 已知正三棱锥的体积为9 cm3 ,高为3cm.则它的侧面积为________ cm2 .9. (1分) (2019高二上·丽水期中) 当直线l:kx-y+1-3k=0被圆x2+y2=16所截得的弦长最短时,k=________.10. (1分)要得到函数的图象,只需将函数y=2sin3x的图象向________.11. (1分)(2020·上饶模拟) 已知等比数列的前项和为,且,则________.12. (1分) (2019高二上·洛阳期中) 设,则四个数,,,中最小的是________.13. (1分) (2018高一下·伊通期末) 已知向量,,则________.14. (1分) (2017高三上·襄阳期中) 若函数在区间(﹣2,2)上有两个零点,则实数a的取值范围为________.二、解答题 (共6题;共60分)15. (10分) (2016高一下·漳州期末) 已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c,且2acosA=ccosB+bcosC.(1)求cosA及a的值;(2)若b2+c2=4,求△ABC的面积.16. (10分) (2019高三上·新疆月考) 如图,在四棱锥中,平面,,四边形满足且,点为的中点,点为边上的动点,且 .(1)求证:平面平面;(2)是否存在实数,使得二面角的余弦值为?若存在,试求出实数的值;若不存在,说明理由.17. (10分) (2017高三上·汕头开学考) 在数列{an}中,首项,前n项和为Sn ,且(1)求数列{an}的通项(2)如果bn=3(n+1)×2n•an,求数列{bn}的前n项和Tn.18. (10分)(2017·白山模拟) 如图,椭圆 =1(a>b>0)的左、右顶点分别为A,B,焦距为2 ,直线x=﹣a与y=b交于点D,且|BD|=3 ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.(1)求椭圆的方程;(2)证明:为定值.19. (10分) (2016高一上·辽宁期中) “城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因.暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数.当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,0.2≤x≤2时,排水量V 是垃圾杂物密度x的一次函数.(1)当0≤x≤2时,求函数V(x)的表达式;(2)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时)f(x)=x•V(x)可以达到最大,求出这个最大值.20. (10分) (2016高一上·埇桥期中) 已知函数f(x)=x+ ,且此函数图象过点(1,5).(1)求函数m的值;(2)判断函数f(x)在[2,+∞)上的单调性?并证明你的结论.参考答案一、填空题:本大题共14个小题,每小题5分,共70分,把答案填在 (共14题;共15分) 1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共60分)15-1、15-2、16-1、16-2、17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、。
安徽省六安市第一中学2021届高三数学上学期第五次月考试题文(含解析)

安徽省六安市第一中学2021届高三数学上学期第五次月考试题文(含解析)文科数学试卷一、选择题:本大题共12个小题,每小题5分,共60分.每一小题给出的四个选项中只有一项是符合题目要求的.1. 已知集合,则()A. B. C. D.【答案】D【解析】由题意得,故可排除选项A,B,C.关于D,由于,因此,故正确.选D.2. 设,则“”是“直线与直线垂直”的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】由直线垂直可得,解得.因此“”是“直线与直线垂直”的充分不必要条件.选A.3. 己知是两相异平面,,是两相异直线,则下列错误的是()A. 若,则B. 若,,则C. 若,则D. 若,则【答案】D【解析】选项A,由线面垂直的性质及判定可得,故A正确.选项B,由可得,又,因此,故B正确.选项C,由线面垂直的性质可得正确.选项D,由条件可得可能平行、相交或异面,故D不正确.综上选D.4. 水平放置的,用斜二测画法作出的直观图是如图所示的,其中,则绕所在直线旋转一周后形成的几何体的表面积为()A. B. C. D.【答案】B【解析】由斜二测画法的规则可得在中.把绕所在直线旋转一周后形成的几何体为有相同底面的两个相同圆锥的组合体,其中圆锥的底面圆半径为,母线长为4,故该几何体的表面积为.选B.5. 己知成等差数列,成等比数列,则的值是()A. 或B.C.D.【答案】C【解析】由题意得,又与第一项的符号相同,故.因此.选C.点睛:(1)在等差(比)数列的差不多运算中要注意数列性质的运用,专门是下标和的性质,利用性质解题可简化运算,提高运算的速度.(2)依照等比中项的定义可得,在等比数列中,下标为奇数的项的符号相同,下标为偶数的项的符号相同,在求等比数列的项时要注意这一性质的运用,幸免显现符号上的错误.6. 己知函数!处有极值,则()A. -1B. 1C. 1或-1D. -1或3【答案】A【解析】,若在处有极值,故,解得且,符合题意;或且,现在,单调递减,在处不存在极值,故且,不合题意,因此=,故选A.7. 若是圆上任一点,则点到直线距离的最大值()A. 4B. 6C.D.【答案】B【解析】由题意得直线过定点.圆的圆心为,半径.因此圆心到直线的最大距离为.故点到直线距离的最大值为.选B.8. —个四棱锥的三视图如图所示,关于那个四棱锥,下列说法正确的是()A. 最长的棱长为B. 该四棱锥的体积为C. 侧面四个三角形差不多上直角三角形D. 侧面三角形中有且仅有一个等腰三角形【答案】B【解析】还原四棱锥,如图所示,由主视图可知,底面运算可知B正确,故选B.点睛: 摸索三视图还原空间几何体第一应深刻明白得三视图之间的关系,遵循“长对正,高平齐,宽相等”的差不多原则,其内涵为正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽.由三视图画出直观图的步骤和摸索方法:1、第一看俯视图,依照俯视图画出几何体地面的直观图;2、观看正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再依照三视图进行调整.9. 已知为双曲线上不同三点,且满足(为坐标原点),直线的斜率记为,则的最小值为()A. 8B. 4C. 2D. 1【答案】B【解析】由有点为线段的中点,设 ,则 ,因此 ,故 ,由于点A,B,P在双曲线上,因此,代入上式中,有 ,因此 ,故最小值为4.选B.点睛:本题要紧考查了双曲线的有关运算,涉及到的知识点有平面向量中线定理,直线斜率的运算公式,差不多不等式等,属于中档题. 第一得出原点为线段AB的中点,再求出直线PA,PB 斜率的表达式, 算出为定值,再由差不多不等式求出最小值.10. 已知二次函数有两个零点,且,则直线的斜率的取值范畴是()A. B. C. D.【答案】A【解析】由题意0,在坐标系作出点表示的平面区域,如图内部(不含边界),已知直线的斜率为,表示点与点连线的斜率,,,,,因此斜率的范畴是.故选A.11. 设函数是定义在上的偶函数,且,当时,,若在区间内关于的方程有且只有4个不同的根,则实数的取值范畴是()A. B. C. D.【答案】D【解析】∵,∴函数图象的对称轴为,即,又函数为偶函数,即,∴,∵函数为周期函数,且是一个周期.结合函数为偶函数,且当时,,画出函数在区间上的图象(如图所示),同时.∵在区间内方程有且只有4个不同的根,∴函数和的图象在区间内仅有4个不同的公共点.结合图象可得只需满足,解得.∴实数的取值范畴是.点睛:已知函数零点个数(方程根的个数)求参数值(取值范畴)的方法(1)直截了当法:通过解方程得到方程的根,再通过解不等式确定参数的值(或范畴);(2)分离参数法:先将参数分离,转化成求函数的值域的问题,并结合题意加以解决;(3)数形结合法:先对函数解析式变形,化为两个函数的形式,然后在同一平面直角坐标系中画出两个函数的图象,然后依照两个图象的位置关系得到关于参数的不等式(组),求得解集后可得范畴,解题时要注意一些专门点的相对位置.12. 已知是椭圆的左、右焦点,点在椭圆上,且,线段与轴的交点为,为坐标原点,若与四边形的面积之比为1:2,则该椭圆的离心率等于()A. B. C. D.【答案】C【解析】画出图形如图所示.设,∵与四边形的面积之比为1:2,∴与的面积之比为1:3,∴,解得.又,∴.∵,∴,∴.将和代入椭圆方程得,整理得,即,解得或(舍去),∴.选C.点睛:椭圆的离心率及其范畴是每年高考的热点,应用平面几何知识是解决这类问题的关键.求离心率的常用方法为:(1)由条件求得的值,再由直截了当求离心率.(2)列出含有的方程(或不等式),借助于消去b,然后转化成关于e的方程(或不等式)求解.二、填空题:本大题共4小题,每小题5分,共20分.请将答案填写在答题卷相应位置上.13. 若方程表示椭圆,则实数的取值范畴是__________.【答案】【解析】试题分析:由椭圆方程可知,解不等式得实数的取值范畴为考点:椭圆方程14. 已知集合,集合,若有两个元素,则实数的取值范畴是__________.【答案】【解析】集合表示直线,集合表示圆心为(0,1),半径为2的圆的下半部分.如图所示.∵有两个元素,∴直线与半圆有两个交点.当直线与圆相切时,即图中直线,则有,解得或(舍去).当直线过点(2,1)时,即图中直线,则有,解得.结合图形可得.∴实数的取值范畴是.答案:.15. 已知三棱锥的底面是以为斜边的等腰直角三角形,,则三棱锥的外接球的球心到平面的距离为__________.【答案】【解析】∵三棱锥中,∴顶点在底面ABC上的射影为的外心,又是以为斜边的等腰直角三角形,∴点为的中点.∴.如上图,设点O为三棱锥外接球的球心,则的长即为外接球的球心到平面的距离.设球半径为,则.由题意得,,在中,有,即,解得,∴,即三棱锥的外接球的球心到平面的距离为.答案:..............................16. 已知直线交抛物线于和两点,以为直径的圆被轴截得的弦长为,则__________.【答案】【解析】由消去y整理得,设,则,∴.由抛物线的定义可得,∴以为直径的圆的半径为,圆心到x轴的距离为.由题意得,解得.答案:三、解答题:本大题共6小题,共70分,解承诺写出文字说明、证明过程或演算步骤.17. 设的内角所对的边长分别为且.(1)若,求的值;(2)若的面积为3,求的值.【答案】(1)(2).【解析】试题分析:(Ⅰ)因为,可得,由正弦定理求出a的值.(Ⅱ)因为△ABC的面积,可得,再由余弦定理可得a2+c2=20=(a+c)2-2ac,由此求出a+c的值.试题解析:(Ⅰ)∵∴由正弦定理可知:,∴(Ⅱ)∵∴∴由余弦定理得:∴,即则:故:18. 如图所示,已知是直角梯形,,,平面.(1)证明:;(2)若是的中点,证明:平面;(3)若,求三棱锥的体积.【答案】(1)见解析(2)见解析(3).【解析】试题分析:(1)先证得,由平面可得,从而可得平面,故可得.(2)取的中点,连,,可证得四边形是平行四边形,故,从而可得平面;又可得平面,因此平面平面,故可得平面.(3)利用等积法可得,可求得三棱锥的体积.试题解析:(1)由已知易得,.∵,∴ ,即.又平面,平面,∴ .∵ ,∴ 平面.∵ 平面,∴ .(2)取的中点,连,.∵ ,,∴ ,且,∴ 四边形是平行四边形,∴ .∵ 平面,平面,∴ 平面.∵分别是的中点,∴ .∵ 平面,平面,∴ 平面.∵ ,∴平面平面.∵平面,∴ 平面.(3)由已知得,因此.即三棱锥的体积为.19. 已知圆过,两点,且圆心在直线上.(1)求圆的方程;(2)若直线过点且被圆截得的线段长为,求的方程.【答案】(1).(2)或【解析】试题分析:(1)把点P、Q的坐标和圆心坐标代入圆的一样方程,利用待定系数法求得系数的值;(2)分类讨论,斜率存在和斜率不存在两种情形.①当直线l的斜率不存在时,满足题意,易得直线方程;②当直线l的斜率存在时,设所求直线l的斜率为k,则直线l的方程为:y-5=kx,由点到直线的距离公式求得k的值.试题解析:(1)设圆的方程为,圆心,依照题意有,运算得出,故所求圆的方程为.(2)如图所示,,设是线段的中点,则,∴,.在中,可得.当直线的斜率不存在时,满足题意,现在方程为.当直线的斜率存在时,设所求直线的斜率为,则直线的方程为:,即,由点到直线的距离公式:,得,现在直线的方程为.∴所求直线的方程为或20. 已知动点到点的距离比到直线的距离小1,动点的轨迹为.(1)求曲线的方程;(2)若直线与曲线相交于两个不同点,且,证明: 直线通过一个定点.【答案】(1)(2).【解析】试题分析:(1)利用题意结合抛物线的定义可得动点的轨迹的方程为;(2)设出点的坐标,将直线方程与圆锥曲线方程联立,设而不求可得直线必通过定点. 试题解析:(1)由题意可得动点到点的距离等于到直线的距离,曲线是以点为焦点,直线为准线的抛物线,设其方程为,,,动点的轨迹的方程为;(2)设,由得,,.,,,或.,舍去,,满足,直线的方程为,直线必通过定点.21. 已知函数.(1)当时,求的最小值;(2)若在上为单调函数,求实数的取值范畴.【答案】(1)(2).【解析】试题分析:(1)依照导函数的符号判定函数的单调性,并依照单调性求极值,进而可得最值。
安徽省六安市舒城中学2021届高三上学期第一次统考数学(文)试卷 Word版含解析

2022-2021学年安徽省六安市舒城中学高三(上)第一次统考数学试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合要求的,请你将符合要求的项的序号填在括号内)1.集合A={x|﹣1≤2x+1≤3},B={x|x(x﹣2)≤0},则A∩B=()A. {x|﹣1≤x<0} B. {x|0<x≤1} C. {x|0≤x≤2} D. {x|0≤x≤1}2.设x,y∈R,则“x≥2且y≥2”是“x2+y2≥4”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件3.已知0<a<b<1,则()A. 3b<3a B.log a3>log b3 C.(lga)2<(lgb)2 D.()a <()b4.若x,y 满足约束条件,则z=x﹣y的最小值是()A.﹣3 B. 0 C. D. 35.若方程x3﹣x+1=0在区间(a,b)(a,b,∈Z,且b﹣a=1)上有一根,则a+b的值为() A.﹣1 B.﹣2 C.﹣3 D.﹣46.一个几何体的三视图如图所示,则此几何体的体积是()A. 112 B. 80 C. 72 D. 647.函数y=x2﹣lnx的单调递减区间为()A.(﹣1,1] B.(0,1] C. [1,+∞) D.(0,+∞)8.已知函数y=f(x)的大致图象如图所示,则函数y=f(x)的解析式应为()A. f(x)=x ﹣ B. f(x)=x+ C. f(x)= D. f(x)=x+9.定义在(﹣∞,+∞)上的奇函数f(x)和偶函数g(x)在区间(﹣∞,0]上的图象关于x轴对称,且f (x)为增函数,则下列各选项中能使不等式f(b)﹣f(﹣a)>g(a)﹣g(﹣b)成立的是() A. a>b>0 B. a<b<0 C. ab>0 D. ab<010.已知椭圆C :(a>b>0)的离心率为,过右焦点F且斜率为k(k>0)的直线于C相交于A、B 两点,若.则k=()A. 1 B. C. D. 2二.填空题(本大题共5小题,每小题5分,共25分,请你将正确的答案填在空格处)11.若cosα=﹣,且α∈(π,),则tan α= .12.已知A(2,3),B(4,5),则与共线的单位向量是.13.垂直于直线2x﹣6y+1=0并且与曲线y=x3+3x2﹣5相切的直线方程是14.已知等差数列{a n}的前n项和为S n,且S2=10,S5=55,则过点P(n,a n)和Q(n+2,a n+2)(n∈N*)的直线的斜率是.15.以下四个命题,其中正确的是.①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②抛掷两个骰子,则两个骰子点数之和大于4的概率为;③在回归直线方程y=0.2x+12中,当解释变量x每增加一个单位时,预报变量y平均增加0.2单位;④对分类变量X与Y,它们的随机变量K2(χ2)的观测值k来说,k越大,“X与Y有关系”的把握程度越大.三、解答题(本大题共6小题,共75分.请你留意解答本题时,肯定要具体地写出文字说明、证明过程及演算步骤等)16.已知A、B、C是△ABC 的三个内角,向量,且(1)求角A;(2)若的值.17.为了解某班同学宠爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:宠爱打篮球不宠爱打篮球合计男生20525女生101525合计302050(1)用分层抽样的方法在宠爱打蓝球的同学中抽6人,其中男生抽多少人?(2)在上述抽取的6人中选2人,求恰有一名女生的概率.(3)为了争辩宠爱打蓝球是否与性别有关,计算出K2≈8.333,你有多大的把握认为是否宠爱打蓝球与性别有关?下面的临界值表供参考:P(K2≥k)0.150.100.050.0250.0100.0050.001k 2.072 2.706 3.841 5.024 6.6357.87910.82818.如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,E、F分别为DD1、DB的中点.(1)求证:EF∥平面ABC1D1;(2)求证:EF⊥B1C;(3)求三棱锥的体积.19.已知函数.(Ⅰ)若f′(2)=0,求函数y=f(x)的解析式;(Ⅱ)若函数f(x)在其定义域内为增函数,求实数k的取值范围.20.已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).(1)求椭圆E的标准方程;(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.21.已知数列{a n}满足a1=0且S n+1=2S n+n(n+1),(n∈N*)(Ⅰ)求a2,a3,并证明:a n+1=2a n+n,(n∈N*);(Ⅱ)设b n=a n+1﹣a n(n∈N*),求证:b n+1=2b n+1;(Ⅲ)求数列{a n}(n∈N*)的通项公式.2022-2021学年安徽省六安市舒城中学高三(上)第一次统考数学试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合要求的,请你将符合要求的项的序号填在括号内)1.集合A={x|﹣1≤2x+1≤3},B={x|x(x﹣2)≤0},则A∩B=()A. {x|﹣1≤x<0} B. {x|0<x≤1} C. {x|0≤x≤2} D. {x|0≤x≤1}考点:交集及其运算.专题:集合.分析:求出A与B中不等式的解集确定出A与B,找出两集合的交集即可.解答:解:由A中不等式解得:﹣1≤x≤1,即A={x|﹣1≤x≤1},由B中不等式解得:0≤x≤2,即B={x|0≤x≤2},则A∩B={x|0≤x≤1}.故选:D.点评:此题考查了交集及其运算,娴熟把握交集的定义是解本题的关键.2.设x,y∈R,则“x≥2且y≥2”是“x2+y2≥4”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的推断.专题:简易规律.分析:由“x≥2且y≥2”推出“x2+y2≥4”可证明充分性;由满足“x2+y2≥4”可举出反例推翻“x≥2且y ≥2”,则证明不必要性,综合可得答案.解答:解:若x≥2且y≥2,则x2≥4,y2≥4,所以x2+y2≥8,即x2+y2≥4;若x2+y2≥4,则如(﹣2,﹣2)满足条件,但不满足x≥2且y≥2.所以“x≥2且y≥2”是“x2+y2≥4”的充分而不必要条件.故选A.点评:本题主要考查充分条件与必要条件的含义.3.已知0<a<b<1,则()A. 3b<3a B. log a3>log b3 C.(lga)2<(lgb)2 D.()a <()b考点:对数值大小的比较.专题:常规题型;综合题.分析:由于是选择题,所以可利用排解法去做.依据指数函数y=3x为增函数,y=()x为减函数,排解A,D,依据对数函数y=lgx为(0,+∞)上的增函数,就可得到正确选项.解答:解:∵y=3x为增函数,排解A,∵y=()x为减函数,排解D∵y=lgx为(0,+∞)上的增函数,∴lga<lgb<0,排解C故选B点评:本题主要考查指数函数与对数函数单调性的推断,另外对于选择题,解答时可利用排解法去做.4.若x,y 满足约束条件,则z=x﹣y的最小值是()A.﹣3 B. 0 C. D. 3考点:简洁线性规划.专题:计算题.分析:画出约束条件表示的可行域,推出三角形的三个点的坐标,直接求出z=x﹣y的最小值.解答:解:约束条件,表示的可行域如图,解得A(0,3),解得B(0,)、解得C(1,1);由A(0,3)、B(0,)、C(1,1);所以t=x﹣y的最大值是1﹣1=0,最小值是0﹣3=﹣3;故选A.点评:本题考查简洁的线性规划的应用,正确画出约束条件的可行域是解题的关键,常考题型.5.(5分)(2022秋•安徽校级月考)若方程x3﹣x+1=0在区间(a,b)(a,b,∈Z,且b﹣a=1)上有一根,则a+b的值为()A.﹣1 B.﹣2 C.﹣3 D.﹣4考点:二分法求方程的近似解.专题:函数的性质及应用.分析:令f(x)=x3﹣x+1,由题意可得 f(x)在区间(a,b)上有一零点.再利用函数零点的判定定理求得f(x)在区间(﹣2,﹣1)有一零点,可得a和b的值,从而求得a+b的值.解答:解:令f(x)=x3﹣x+1,由题意可得 f(x)在区间(a,b)(a,b,∈Z,且b﹣a=1)上有一零点.再依据f(﹣2)=﹣5<0,f(﹣1)=1>0,f(﹣2)f(﹣1)<0,故 f(x)在区间(﹣2,﹣1)有一零点,可得a=﹣2、b=﹣1,∴a+b=﹣3,故选:C.点评:本题主要考查函数的零点的判定定理的应用,依据函数的解析式求函数的值,推断函数的零点所在的区间的方法,属于基础题.6.一个几何体的三视图如图所示,则此几何体的体积是()A. 112 B. 80 C. 72 D. 64考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:由三视图可知此几何体是由一个棱柱和一个棱锥构成的组合体,代入数据分别求棱柱与棱锥的体积即可.解答:解:由三视图可知,此几何体是由一个棱柱和一个棱锥构成的组合体,棱柱的体积为4×4×4=64;棱锥的体积为×4×4×3=16;则此几何体的体积为80;故选B.点评:本题考查了三视图的识图与计算力量,属于基础题.7.函数y=x2﹣lnx的单调递减区间为()A.(﹣1,1] B.(0,1] C. [1,+∞) D.(0,+∞)考点:利用导数争辩函数的单调性.专题:计算题.分析:由y=x2﹣lnx得y′=,由y′≤0即可求得函数y=x2﹣lnx的单调递减区间.解答:解:∵y=x2﹣lnx的定义域为(0,+∞),y′=,∴由y′≤0得:0<x≤1,∴函数y=x2﹣lnx的单调递减区间为(0,1].故选:B.点评:本题考查利用导数争辩函数的单调性,留意标根法的考查与应用,属于基础题.8.已知函数y=f(x)的大致图象如图所示,则函数y=f(x)的解析式应为()A. f(x)=x ﹣ B. f(x)=x+ C. f(x)= D. f(x)=x+考点:函数的图象;函数解析式的求解及常用方法.专题:数形结合.分析:函数y=f(x)的解析求不出来,依据选项结合图象接受排解法进行排解,以及利用特殊值法进行排解.解答:解:依据图象不关于原点对称,则该函数不是奇函数,可排解选项D,取x=时,依据图象可知函数值大于0,而选项B,f ()=+=﹣e2<0,故B不正确,由题上图象可以看出当x→﹣∞时,有f(x)<0,但C选项,f(x)=,当x→﹣∞时,f(x)=>0,∴C错误故选A.点评:本题主要考查了识图力量,以及函数的对称性和单调性,数形结合的思想和特殊值法的应用,属于中档题.本题正面确定不易,排解法做此类题是较好的选择9.定义在(﹣∞,+∞)上的奇函数f(x)和偶函数g(x)在区间(﹣∞,0]上的图象关于x轴对称,且f (x)为增函数,则下列各选项中能使不等式f(b)﹣f(﹣a)>g(a)﹣g(﹣b)成立的是() A. a>b>0 B. a<b<0 C. ab>0 D. ab<0考点:奇偶性与单调性的综合.专题:综合题;函数的性质及应用.分析:利用函数的奇偶性,条件可转化为(b)+f(a)>g(a)﹣g(b),利用偶函数g(x)在区间(﹣∞,0]上的图象关于x轴对称,可得f(x)和g(x)在区间[0,+﹣∞)上图象重合,由此可得结论.解答:解:∵函数f(x)是奇函数,∴f(﹣x)=﹣f(x),∴f(b)﹣f(﹣a)=f(b)+f(a)∵函数g(x)是偶函数,∴g(﹣x)=g(x),∴g(a)﹣g(﹣b)=g(a)﹣g(b)∵f(b)﹣f(﹣a)>g(a)﹣g(﹣b),∴f(b)+f(a)>g(a)﹣g(b)∵偶函数g(x)在区间(﹣∞,0]上的图象关于x轴对称,∴f(x)和g(x)在区间[0,+∞)上图象重合∴a>b>0成立.故选A点评:本题考查函数奇偶性与单调性的结合,考查同学分析解决问题的力量,属于中档题.10.已知椭圆C :(a>b>0)的离心率为,过右焦点F且斜率为k(k>0)的直线于C相交于A、B 两点,若.则k=()A. 1 B. C. D. 2考点:直线与圆锥曲线的综合问题.专题:计算题;压轴题.分析:设A(x1,y1),B(x2,y2),依据求得y1和y2关系依据离心率设,b=t,代入椭圆方程与直线方程联立,消去x,依据韦达定理表示出y1+y2和y1y2,进而依据y1和y2关系求得k.解答:解:A(x1,y1),B(x2,y2),∵,∴y1=﹣3y2,∵,设,b=t,∴x2+4y2﹣4t2=0①,设直线AB 方程为,代入①中消去x ,可得,∴,,解得,故选B点评:本题主要考查了直线与圆锥曲线的综合问题.此类题问题综合性强,要求考生有较高地转化数学思想的运用力量,能将已知条件转化到基本学问的运用.二.填空题(本大题共5小题,每小题5分,共25分,请你将正确的答案填在空格处)11.若cosα=﹣,且α∈(π,),则tan α= .考点:任意角的三角函数的定义.专题:三角函数的求值.分析:依据α∈(π,),cos α=﹣,求出sinα,然后求出tanα,即可.解答:解:由于α∈(π,),cosα=﹣,所以sinα=﹣,所以tanα==故答案为:点评:本题是基础题,考查任意角的三角函数的定义,留意角所在的象限,三角函数值的符号,是本题解答的关键.12.已知A(2,3),B(4,5),则与共线的单位向量是±.考点:平行向量与共线向量.专题:平面对量及应用.分析:利用与共线的单位向量=即可得出.解答:解:=(2,2),∴与共线的单位向量==±=±.故答案为:±.点评:本题考查了单位向量的计算公式,属于基础题.13.垂直于直线2x﹣6y+1=0并且与曲线y=x3+3x2﹣5相切的直线方程是3x+y+6=0考点:利用导数争辩曲线上某点切线方程.专题:计算题;压轴题.分析:欲求切线方程,只须求出切点坐标即可,设切点为P(a,b),先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率列出等式求出a,b值.从而问题解决.解答:解:设切点为P(a,b),函数y=x3+3x2﹣5的导数为y′=3x2+6x切线的斜率k=y′|x=a=3a2+6a=﹣3,得a=﹣1,代入到y=x3+3x2﹣5,得b=﹣3,即P(﹣1,﹣3),y+3=﹣3(x+1),3x+y+6=0.故答案为:3x+y+6=0.点评:本小题主要考查相互垂直的直线的斜率间的关系、导数的几何意义、利用导数争辩曲线上某点切线方程等基础学问,考查运算求解力量.属于基础题.14.已知等差数列{a n}的前n项和为S n,且S2=10,S5=55,则过点P(n,a n)和Q(n+2,a n+2)(n∈N*)的直线的斜率是 4 .考点:数列与解析几何的综合.专题:计算题.分析:由题意等差数列{a n}的前n项和为S n,且S2=10,S5=55,利用前n项和概念建立首项与公差的方程,再利用已知直线上两点的坐标求其斜率公式求得答案.解答:解:由题意得:,消去a1得d=4.直线的斜率为,故答案为4.点评:此题重点考查了等差数列的前n项和公式,及利用方程的思想解出数列的首项及公差,还考查了直线的斜率公式.15.以下四个命题,其中正确的是②③④.①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②抛掷两个骰子,则两个骰子点数之和大于4的概率为;③在回归直线方程y=0.2x+12中,当解释变量x每增加一个单位时,预报变量y平均增加0.2单位;④对分类变量X与Y,它们的随机变量K2(χ2)的观测值k来说,k越大,“X与Y有关系”的把握程度越大.考点:命题的真假推断与应用.专题:阅读型;概率与统计.分析:由系统抽样的特点,可知①错误;由古典概率的求法,可得抛掷两个骰子的基本大事的总数为36,两个骰子点数之和大于4的大事有30种,即可推断②;由回归直线方程的一次项系数的符号,即可推断③;对分类变量X与Y,它们的随机变量K2(χ2)的观测值k来说,k越小,“X与Y有关系”的把握程度越小;k越大,“X与Y有关系”的把握程度越大.即可推断④.解答:解:对于①,从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样.故①错误;对于②,抛掷两个骰子的基本大事的总数为36,两个骰子点数之和大于4的大事有30种,则两个骰子点数之和大于4的概率为,故②正确;对于③,在回归直线方程y=0.2x+12中,当解释变量x每增加一个单位时,预报变量y平均增加0.2单位,故③正确;对于④,对分类变量X与Y,它们的随机变量K2(χ2)的观测值k来说,k越大,“X与Y有关系”的把握程度越大,故④正确.故答案为:②③④点评:本题考查命题的真假推断和应用,考查抽样方法和回归直线方程、随机变量的观测值,同时考查古典概率的计算,属于基础题.三、解答题(本大题共6小题,共75分.请你留意解答本题时,肯定要具体地写出文字说明、证明过程及演算步骤等)16.已知A、B、C是△ABC的三个内角,向量,且(1)求角A;(2)若的值.考点:三角函数中的恒等变换应用.专题:计算题.分析:(1)利用,直接得到A的关系式,利用两角差的余弦函数,求出A的值,留意A是三角形内角.(2)依据,利用C=π﹣(A+B),利用诱导公式,通过两角和的正切,求出tanC 的值.解答:解:(1)由于,所以,(2分)所以(4分)由于(6分)(2)由于,所以(8分)所以tanB=2(9分)所以tanC=tan(π﹣(A+B))=﹣tan(A+B)=,(11分)即(12分)点评:本题是基础题,考查三角恒等变换,利用向量数量积,留意三角形的内角的范围,求出角的大小,三角形中:A+B+C=π是常用结论.17.为了解某班同学宠爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:宠爱打篮球不宠爱打篮球合计男生20525女生101525合计302050(1)用分层抽样的方法在宠爱打蓝球的同学中抽6人,其中男生抽多少人?(2)在上述抽取的6人中选2人,求恰有一名女生的概率.(3)为了争辩宠爱打蓝球是否与性别有关,计算出K2≈8.333,你有多大的把握认为是否宠爱打蓝球与性别有关?下面的临界值表供参考:P(K2≥k)0.150.100.050.0250.0100.0050.001k 2.072 2.706 3.841 5.024 6.6357.87910.828考点:独立性检验的应用;独立性检验的基本思想;列举法计算基本大事数及大事发生的概率.分析:(1)依据分层抽样的方法,在宠爱打蓝球的同学中抽6人,先计算了抽取比例,再依据比例即可求出男生应当抽取人数.(2)在上述抽取的6名同学中,女生的有2人,男生4人.女生2人记A,B;男生4人为c,d,e,f,列出其一切可能的结果组成的基本大事个数,通过列举得到满足条件大事数,求出概率.(3)依据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明打篮球和性别有关系.解答:解:(1)在宠爱打蓝球的同学中抽6人,则抽取比例为∴男生应当抽取人….(4分)(2)在上述抽取的6名同学中,女生的有2人,男生4人.女生2人记A,B;男生4人为c,d,e,f,则从6名同学任取2名的全部状况为:(A,B)、(A,c)、(A,d)、(A,e)、(A,f)、(B,c)、(B ,d)、(B,e)、(B,f)、(c,d)、(c,e)、(c,f)、(d,e)、(d,f)、(e,f)共15种状况,其中恰有1名女生状况有:(A,c)、(A,d)、(A,e)、(A,f)、(B,c)、(B,d)、(B,e)、(B,f),共8种状况,故上述抽取的6人中选2人,恰有一名女生的概率概率为.….(8分)(3)∵K2≈8.333,且P(k2≥7.879)=0.005=0.5%,那么,我们有99.5%的把握认为是否宠爱打蓝球是与性别有关系的….(12分)点评:本题是一个统计综合题,包含独立性检验和概率,本题通过创设情境激发同学学习数学的情感,挂念培育其严谨治学的态度.18.如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,E、F分别为DD1、DB的中点.(1)求证:EF∥平面ABC1D1;(2)求证:EF⊥B1C;(3)求三棱锥的体积.考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的性质.专题:计算题.分析:(1)欲证EF∥平面ABC1D 1,依据直线与平面平行的判定定理可知只需证EF 与平面ABC1D1内始终线平行,连接BD1,在△DD1B 中,E、F分别为D1D,DB的中点,依据中位线定理可知EF∥D1B,满足定理所需条件;(2)先依据线面垂直的判定定理证出B1C⊥平面ABC1D1,而BD1⊂平面ABC1D1,依据线面垂直的性质可知B1C ⊥BD1,而EF∥BD1,依据平行的性质可得结论;(3)可先证CF⊥平面EFB1,依据勾股定理可知∠EFB1=90°,依据等体积法可知=V C﹣B1EF,即可求出所求.解答:解:(1)证明:连接BD1,如图,在△DD1B中,E、F分别为D1D,DB的中点,则平面ABC1D1.(2)(3)∵CF⊥平面BDD1B1,∴CF⊥平面EFB1且,∵,,∴EF2+B1F2=B1E2即∠EFB1=90°,∴==点评:本题主要考查了线面平行的判定,以及线面垂直的性质和三棱锥体积的计算,同时考查了空间想象力量、运算求解力量、转化与划归的思想,属于中档题.19.已知函数.(Ⅰ)若f′(2)=0,求函数y=f(x)的解析式;(Ⅱ)若函数f(x)在其定义域内为增函数,求实数k的取值范围.考点:利用导数争辩函数的单调性;函数解析式的求解及常用方法.专题:计算题;转化思想.分析:(Ⅰ)依据题意,对f(x)求导,依据f'(2)=0,即可求得k的值,从而求的函数y=f(x)的解析式;(Ⅱ)要使函数f(x)在其定义域内为增函数,只需函数f′(x)≥0在区间(0,+∞)上恒成立,即,kx2﹣2x+k≥0在区间(0,+∞)上恒成立,然后利用分别参数法,转化为求函数的最值,即可求得实数k的取值范围.解答:解:f′(x)=k+﹣=由f'(2)=0,得k=,函数f(x)=,(Ⅱ)函数y=f(x)的定义域为(0,+∞),要使函数f(x)在其定义域内为增函数,只需函数f′(x)≥0在区间(0,+∞)上恒成立,即,kx2﹣2x+k≥0在区间(0,+∞)上恒成立,即k ≥在区间(0,+∞)上恒成立,令g(x)=,x∈(0,+∞),g(x)==,当且仅当x=1时取等号,∴k≥1.点评:此题是个中档题.本题主要考查用导数法争辩函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题,体现了转化的数学思想,很好的考查了同学的计算力量.20.已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).(1)求椭圆E的标准方程;(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线的定义、性质与方程.分析:(1)由两个焦点分别为A(﹣1,0),B(1,0),上顶点为D(2,0),得到椭圆的半长轴a,半焦距c,再求得半短轴b,最终由椭圆的焦点在X轴上求得方程.(2)利用向量垂直即可求得M点的横坐标x0,从而解决问题.解答:解:(1)由题意得,c=1,a=2,则b=故所求的椭圆标准方程为;(2)设M(x0,y0)(x0≠±2),则①又由P(t,0),H(2,0).则,由MP⊥MH 可得,即(t﹣x0,﹣y0)•(2﹣x0,﹣y0)=由①②消去y0,整理得②∵x0≠2,∴∵﹣2<x0<2,∴﹣2<t<﹣1故实数t的取值范围为(﹣2,﹣1).点评:本题考查直线和椭圆的位置关系、考查存在性问题,解题时要认真审题,认真解答.21.已知数列{a n}满足a1=0且S n+1=2S n +n(n+1),(n∈N*)(Ⅰ)求a2,a3,并证明:a n+1=2a n+n,(n∈N*);(Ⅱ)设b n=a n+1﹣a n(n∈N*),求证:b n+1=2b n+1;(Ⅲ)求数列{a n}(n∈N*)的通项公式.考点:数列递推式;数列的求和.专题:综合题;等差数列与等比数列.分析:(Ⅰ)利用a1=0且S n+1=2S n +n(n+1),代入计算,可得a2,a3,n≥2时,a n+1=S n +n(n+1),a n=S n ﹣1+n(n﹣1),两式相减,即可得出结论;(Ⅱ)利用a n+1=2a n+n,结合b n=a n+1﹣a n(n∈N*),即可证明:b n+1=2b n+1;(Ⅲ)利用叠加法,即可求数列{a n}(n∈N*)的通项公式.解答:解:(Ⅰ)∵a1=0且S n+1=2S n +n(n+1),∴S2=2S1+1,∴a2=1,同理可得,a3=4;∵S n+1=2S n +n(n+1),∴a n+1=S n +n(n+1),①∴n≥2时,a n=S n﹣1+n(n﹣1),②①﹣②:a n+1﹣a n=a n+n,∴a n+1=2a n+n,n=1时也成立;(Ⅱ)∵a n+1=2a n+n,∴a n+1﹣a n=2(a n﹣a n﹣1)+1,∵b n=a n+1﹣a n,∴b n+1=2b n+1;(Ⅲ)∵b n+1=2b n+1,∴b n+1+1=2(b n+1),∴数列{b n}是以2为首项,2为公比的等比数列,∴b n=2n,∴a n+1﹣a n=2n,∴a n=a1+(a2﹣a1)+…+(a n﹣a n﹣1)=0+2+…+2n﹣1==2n﹣2.点评:本题考查数列递推式,考查数列的求和,考查等比数列的证明,考查同学分析解决问题的力量,属于中档题.。
六安中学2021高三语文上学期开学考试试题

安徽省六安中学2021届高三语文上学期开学考试试题时间:150分钟分值:150分第I卷阅读题(70分)一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
错误!书法与国学有诸多联系,但不能直接画等号.书法是艺术,国学是学问。
把书法当成国学,与把传统文化当成国学如出一辙。
书法是传统文化的一部分,而且是重要组成部分,但只有用国学方法研究传统文化的学问才是国学.○2那么研究书法的学问是不是就是国学了?不全是。
举个例子,用传统文献学方法研究的传统书学,可称得上国学。
○,3古代书论文献大多是文学性描述,多运用比喻、夸张和想象等文学手法,且行文简略,如孙过庭《书谱》中有一句经典概括“古不乖时,今不同弊”。
意思是取法古人,不能背离时代条件,同时又不能随大流,过于迎合今人。
写不出自己,看不到古人,是书法大忌。
孙过庭以简短八个字,把古今书学的道理说通了。
而这用短短几个字就能说透的问题,今人千言万语也未必能达其真谛。
所以,凡遇古书论,都需用文献学方法,对所涉字词进行训诂学研究,这些自然属于国学范畴。
错误!按照国学大师梁启超的划分,国学研究总体分为两类:一类是关于智识的学问,一类是关于人生的学问。
前者侧重于认识,后者侧重于实践体悟。
书学也是如此。
错误!书学是关于智识的学问.书法的基础是汉字,研究书法必须研究汉字本体,故此,书学的基础是字学,也即小学,小学又融于国学之中。
所以,国学中的字学或小学,对书学研究有直接作用和影响。
辑校和注疏是国学研究的重要方法,也是传统书学研究的重要方法。
在阅读和运用古代书论文献时,必须对其中的字词进行训诂或校注,否则易发生误读。
譬如现在我们时常用“天真烂漫”一词形容书法作品至高的美学境界,但从包世臣《艺舟双楫》中对“烂漫"一词的注解可知,“烂漫"的本意是花开十分,已渐有凋疏之意,用在书法上,则是指笔法粗疏导致的墨法凋疏,字法散乱。
2021-2022学年安徽省六安市裕安中学高三数学文联考试卷含解析

2021-2022学年安徽省六安市裕安中学高三数学文联考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知函数在处取得极值,令函数,程序框图如图所示,若输出的结果,则判断框内可填入的条件为()A.B. C. D.参考答案:B由题意,,而,解得,故.由程序框图可知,当时,,选B.2. 若实数a,b,c满足,则下列关系中不可能成立的是()(A) (B)(C) (D)参考答案:A3. 直线与曲线的公共点的个数是() A.1 B.2 C.3 D.4参考答案:C4. 将函数的图象向右平移个单位长度后得到的图象,则()A.B.C.D.参考答案:D5. 已知a=2,b=ln2,c=,则的大小为().(A) (B) (C). (D)参考答案:C略6. 已知集合,,则=A. B. C. D.参考答案:BA=,所以.7. 设i是虚数单位,,则实数a=()A.B.C.﹣1 D.1参考答案:A【考点】复数代数形式的乘除运算.【分析】直接由复数代数形式的乘除运算化简,再由复数相等的充要条件计算得答案.【解答】解:由===,得,解得a=﹣.故选:A.8. 设数列是由正数组成的等比数列,为其前n项和,已知,则(A) (B) (C) (D)参考答案:B.设此数列的公比为,由已知,得所以,由,知即解得,进而,所以.9. 在△ABC中,AB =AC =3,∠BAC= 30o,CD是边AB上的高,则·=A.B. C.D.参考答案:B10. 若.则()A. B. C. D.参考答案:A【分析】利用诱导公式及同角三角函数的商数关系可得,再利用诱导公式及同角三角函数的平方关系化简,求值即可。
【详解】,,即,又,故答案选A。
【点睛】本题考查同角三角函数的基本关系的应用以及诱导公式的应用,考查学生的转化思想与运算能力,属于中档题。
二、填空题:本大题共7小题,每小题4分,共28分11. 设实数满足不等式,若的最大值为1,则常数的取值范围是。
2021年8月安徽省六安市新安中学2022届高三上学期8月开学考试数学(文)试卷及答案

2021年8月安徽省六安市新安中学2022届高三上学期8月开学考试数学(文)试卷★祝考试顺利★(含答案)第I 卷(选择题)一、单选题1.已知全集{}1,2,3,4,5U =,集合{}1,2A =,集合{}2,4B =,则()U A B =( )A .{}4B .{}2,3,4,5C .{}3,5D .{}2,3,52.复数z 满足条件23z z i +=+,则复数1z 在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.若()f x 是R 上周期为5的奇函数,且满足()11f =,()22f =,则()()124f f --等于()A .-2B .2C .-1D .14.“2(2)log 0x x ->”是“39x >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.函数()()lg 1f x x =- )A .(]1,4B .()1,4C .[]1,4D .[)1,46.命题“*N n ∀∈,x R ∃∈,使得2n x <”的否定是A .*N n ∀∈, x R ∃∈,使得2n x ≥B .*N n ∀∈,x R ∀∈,使得2n x ≥C .*N n ∃∈,x R ∀∈,使得2n x ≥D .*N n ∃∈,x R ∃∈,使得2n x ≥7.已知函数1()3()3x xf x =-,则()f xA .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数8.已知函数是定义在上的偶函数, 且在区间上单调递增. 若实数满足, 则的最小值是A .B .1C .D .2 9.已知函数321()393f x x x x =--+,给出四个函数①|f (x )|,②f (-x ),③f (|x |),④-f (-x ),又给出四个函数的大致图象,则正确的匹配方案是( )A .甲-②,乙-③,丙-④,丁-①B .甲-②,乙-④,丙-①,丁-③C .甲-④,乙-②,丙-①,丁-③D .甲-①,乙-④,丙-③,丁-②10.已知函数()2,11,12x a x f x x a x ⎧+≤⎪=⎨+>⎪⎩,其中a R ∈.如果函数()f x 恰有两个零点,则a 的取值范围为( )A .1,2⎛⎤-∞- ⎥⎝⎦B .[)2,-+∞C .12,2⎡⎤--⎢⎥⎣⎦D .12,2⎡⎫--⎪⎢⎣⎭ 11.已知()()21cos f x x x =+-,则不等式()ln 11f x -<的解集为A .()0,eB .()1,+∞C .()e,+∞D .()1,e12.若1x 是方程x xe 1=的解,2x 是方程ln 1x x =的解,则12x x 等于A .eB .1C .1eD .-1第II 卷(非选择题)二、填空题13.若2()(1)m f x m x =-是幂函数且在(0,)+∞单调递增,则实数m =_______.14.已知定义在R 上的函数()f x 满足(2)()f x f x +=,当01x <≤时,()21x f x =-,则(5)f =___________.15.若x 0是函数f (x )=2x +3x 的零点,且x 0∈(a ,a +1),a ∈Z ,则a =_____.16.若函数32()36f x x x ax =-+存在两个极值点1x ,2x ,(12x x <),则()1f x 的取值范围是_____.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021届安徽省六安中学高三上学期开学考试数学(文)试题一、单选题1.已知R 是实数集,集合{}|2A x Z x =∈<,{}|210B x x =-≥,则()R A C B =( ) A .1,12⎡⎤⎢⎥⎣⎦B .{}1C .{}1,0-D .1,2⎛⎫-∞ ⎪⎝⎭【答案】C【解析】先求出集合A 、B ,再进行补集和交集运算. 【详解】{}{}{}|2=|221,0,1A x Z x x Z x =∈<∈-<<=-, {}1|210|2B x x x x ⎧⎫=-≥=≥⎨⎬⎩⎭,1|2R C B x x ⎧⎫=<⎨⎬⎩⎭,所以()R A C B ={}1,0-,故选:C 【点睛】本题主要考查了集合的交集、补集运算,属于基础题. 2.i 是虚数单位,41iz i=- 则||z =( )A .2B .C .4D .【答案】B【解析】根据复数的除法运算求出z 的代数形式,然后再求出z . 【详解】 由题意得44(1)2(1)221(1)(1)i i i z i i i i i i +===+=-+--+,∴ ||z == 故选B . 【点睛】本题考查复数的除法运算和复数的模,解题的关键是正确进行复数的运算,属于简单题. 3.阿基米德(Archimedes ,公元前287年一公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的表面积为( )A .36πB .45πC .54πD .63π【答案】C【解析】先设球的半径为r ,根据体积求出3r =,再由题意,得出圆柱的底面圆半径,以及圆柱的高,根据圆柱的表面积公式,即可求出结果. 【详解】因为球的体积为36π,设球的半径为r ,则34363r ππ=,所以3r =, 又圆柱的底面直径与高都等于球的直径,所以圆柱的底面圆半径为3r =,高为26h r ==, 因此圆柱的表面积为22222654S r r r r ππππ=+⋅==. 故选:C. 【点睛】本题主要考查圆柱与球内切的相关计算,熟记圆柱的表面积公式,以及球的体积公式即可,属于基础题型.4.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中各随机选取1个数,则选取的两数之和能被5整除的概率( )A .110B .320C .15D .310【答案】C【解析】由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9. 各选一个数,求出所有的选法,求出其和能被5整除的选法种数,根据古典概型的概率计算公式,即得答案. 【详解】由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9. 各选一个数,共有4520⨯=种选法.其和能被5整除的分别为:2,3;4,1;6,9;8,7,共4种选法,∴选取的两数之和能被5整除的概率41205P ==. 故选:C. 【点睛】本题考查古典概型和计数原理,属于基础题.5.“关注夕阳、爱老敬老”—某马拉松协会从2013年开始每年向敬老院捐赠物资和现金.下表记录了第x 年(2013年是第一年)与捐赠的现金y (万元)的对应数据,由此表中的数据得到了y 关于x 的线性回归方程ˆ0.35y mx =+,则预测2019年捐赠的现金大约是( )x3 4 5 6y2.5344.5A .5万元B .5.2万元C .5.25万元D .5.5万元【答案】C【解析】由已知求出,x y ,代入回归直线的方程,求得m ,然后取7x =,求得y 的值,即可得到答案. 【详解】 由已知得,3456 2.534 4.54.5, 3.544x y ++++++====,所以样本点的中心点的坐标为(4.5,3.5),代入ˆ0.35ymx =+, 得3.5 4.50.35m =+,即0.7m =,所以ˆ0.70.35yx =+, 取7x =,得ˆ0.770.35 5.25y=⨯+=, 预测2019年捐赠的现金大约是5.25万元. 【点睛】本题主要考查了线性回归方程以及应用,其中解答中熟记回归直线的方程经过样本中心点是解答的关键,着重考查了推理与计算能力,属于基础题. 6.若实数a ,b 满足3412a b ==,则11a b+=( ) A .12B .15C .16D .1【答案】D【解析】先将指数式化成对数式,求出,a b ,再利用换底公式的推论log log 1a b b a ⋅=以及对数的运算法则即可求出. 【详解】因为3412a b ==,所以34log 12,log 12a b ==,121212341111log 3log 4log 1211212a b log log +=+=+==. 故选D . 【点睛】本题主要考查指数式与对数式的互化、换底公式推论log log 1a b b a ⋅=的应用以及对数的运算法则的应用.7.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( ). A .4 B .5C .6D .7【答案】A【解析】求出圆心C 的轨迹方程后,根据圆心M 到原点O 的距离减去半径1可得答案. 【详解】设圆心(),C x y ,则()()22341x y -+-=,化简得()()22341x y -+-=,所以圆心C 的轨迹是以(3,4)M 为圆心,1为半径的圆,所以||1||OC OM +≥22345=+=,所以||514OC ≥-=, 当且仅当C 在线段OM 上时取得等号, 故选:A. 【点睛】本题考查了圆的标准方程,属于基础题.8.函数()sin(2)(0)f x x ϕϕπ=+<<的图象如图所示,为了得到()sin 2g x x =的图象,可将()f x 的图象( )A .向右平移6π个单位 B .向右平移12π个单位C .向左平移12π个单位D .向左平移6π个单位 【答案】A【解析】函数过7(,1)12π- 代入解得ϕ,再通过平移得到()sin 2g x x =的图像. 【详解】()sin(2)(0)f x x ϕϕπ=+<<,函数过7(,1)12π-71sin()63ππϕϕ-=+⇒= ()sin(2)3f x x π=+向右平移6π个单位得到()sin 2g x x =的图象故答案选A 【点睛】本题考查了三角函数图形,求函数表达式,函数平移,意在考查学生对于三角函数图形的理解.9.执行如图所示的程序框图,输出的结果是31,则判断框中应填入( )A .4A <?B .4A >?C .5A <?D .5A >?【答案】C【解析】首先判断循环结构类型,得到判断框内的语句性质,然后对循环体进行分析,找出循环规律.判断输出结果与循环次数以及A 的关系,最终得出选项. 【详解】解:经判断此循环为“当型”结构,判断框内为跳出循环的语句第1次循环:3S =,2A =;第2次循环:7=S ,3A =;第3次循环:15S =,4A =;第4次循环:31S =,5A =;此时退出循环, 根据判断框内为跳出循环的语句“5A <?”5?A ∴<故选:C . 【点睛】本题考查程序框图,考查循环结构.对循环体每次循环需要进行分析并找出内在规律是解题的关键,属于基础题.10.已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( ) A .7 B .5C .5-D .7-【答案】D【解析】由条件可得47a a ,的值,进而由27104a a a =和2417a a a =可得解.【详解】56474747822,4a a a a a a a a ==-+=∴=-=或474,2a a ==-.由等比数列性质可知2274101478,1a a a a a a ==-==或2274101471,8a a a a a a ====-1107a a ∴+=-故选D. 【点睛】本题主要考查了等比数列的下标的性质,属于中档题.11.已知F 是双曲线22:145x y C 的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为( )A .32B .52C .72D .92【答案】B【解析】设()00,P x y ,因为=OP OF 再结合双曲线方程可解出0y ,再利用三角形面积公式可求出结果. 【详解】设点()00,P x y ,则2200145x y -=①.又3OP OF ===,22009x y ∴+=②.由①②得20259y =, 即053y =, 0115532232OPF S OF y ∆∴==⨯⨯=, 故选B . 【点睛】本题易错在忽视圆锥曲线方程和两点间的距离公式的联系导致求解不畅.12.已知三棱锥D -ABC 中,AB =BC =1,AD =2,BD =5,AC =2,BC ⊥AD ,则该三棱锥的外接球的表面积为( )A 6πB .6πC .5πD .8π【答案】B【解析】由题意结合平面几何、线面垂直的判定与性质可得BC ⊥BD ,AD ⊥AC ,再由平面几何的知识即可得该几何体外接球的球心及半径,即可得解. 【详解】AB =BC =1,AD =2,BD 5AC 2,∴222AB BC AC +=,222AD AB DB +=,∴DA ⊥AB ,AB ⊥BC ,由BC ⊥AD 可得BC ⊥平面DAB ,DA ⊥平面ABC , ∴BC ⊥BD ,AD ⊥AC , ∴CD 226BD BC +=,由直角三角形的性质可知,线段CD的中点O到点A,B,C,D的距离均为622CD=,∴该三棱锥外接球的半径为6,故三棱锥的外接球的表面积为4π262⎛⎫⋅ ⎪⎪⎝⎭=6π.故选:B.【点睛】本题考查了三棱锥几何特征的应用及其外接球表面积的求解,考查了运算求解能力与空间思维能力,属于中档题.二、填空题13.设,x y满足约束条件22022x yxy+-≥⎧⎪≤⎨⎪≤⎩,则2z x y=-的最小值是____________.【答案】-6【解析】由约束条件画出可行域,再变形2z x y=-为2y x z=-,即在可行域内找到使该直线截距最大的点,进而求解.【详解】由题,可行域如图所示,设2y x z =-,平移直线,当直线与点()2,2A -相交时,直线的截距最大, 所以z 的最小值为()2226⨯--=-, 故答案为:6- 【点睛】本题考查利用目标函数的几何意义求最值,考查简单的线性规划问题,考查数形结合思想.14.已知向量||1a =,1,2b m ⎛⎫= ⎪⎝⎭,若()()a b a b +⊥-,则实数m 的值为________.【答案】3 【解析】由向量垂直得数量积为0,即由()()0a b a b +⋅-=求解. 【详解】∵()()a b a b +⊥-,∴()()0a b a b +⋅-=,即22||||0a b -=,|||==|1a b可得2221||2=1b m ⎛⎫=+ ⎪⎝⎭,得出234m =,32m =±. 故答案为:3【点睛】本题考查两个向量垂直的数量积表示,考查向量的模的求解,属于基础题.15.已知函数f (x )=axlnx ﹣bx (a ,b ∈R )在点(e ,f (e ))处的切线方程为y =3x ﹣e ,则a +b =_____. 【答案】0【解析】由题意()()'2,3f e e f e ==,列方程组可求,a b ,即求+a b .【详解】∵在点()(),e f e 处的切线方程为3y x e =-,()2f e e ∴=,代入()ln f x ax x bx =-得2a b -=①.又()()()''1ln ,23f x a x b f e a b =+-∴=-=②.联立①②解得:1,1a b ==-.0a b ∴+=.故答案为:0. 【点睛】本题考查导数的几何意义,属于基础题.16.如图,在杨辉三角形中,斜线1的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n 项和为n S ,则21S __________.【答案】361【解析】将n 按照奇偶分别计算n a :当n 为偶数时,42n n a +=;当n 为奇数时,2438n n n a ++=, 11102113212420(...)(...)S a a a a a a =+++++个个计算得到答案.【详解】解法一:根据杨辉三角形的生成过程, 当n 为偶数时,42n n a +=, 当n 为奇数时,1=1a ,3=3a ,2-132n n n n n a a a a ++=+=+, 312a a -=,533a a -=,212n n n a a -+-=,2438n n n a ++=,11102113212420(...)(...)S a a a a a a =+++++个个136...66(345...12)28675361=+++++++++=+=()解法二:当*21()n m m N =-∈时,221(1)22n m m m m m a a -++===, 当*2()n m m N =∈时,22n m a a m ==+,11102113212420(...)(...)S a a a a a a =+++++个个222110(312)[(12...11)(12...11)]22⋅+=+++++++1111223111127525333753612622⨯⨯⨯=⨯+⨯+=++= 【点睛】本题考查了数列的前N 项和,意在考查学生的应用能力和解决问题的能力.三、解答题17.某校高一年级1000名学生期中考试生物学科成绩的额率分布直方图如图所示,其中成绩分组情况如下表:组号 第一组 第二组 第三组 第四组 第五组分组 [)50,60 [)60,70 [)70,80 [)80,90 []90,100(1)求生物成绩在[50,60)内的人数;(2)若同组中的每个数据用该组区同中点值代替,根据频率分布直方图,估计这1000名学生生物成绩的平均分:(3)现有5名同学,其中3人的成绩在第三组内,2人的成绩在第四组内,从这5名同学中随机抽取2名,求这2名同学来自不同组的概率.【答案】(1)50人;(2)平均分为74.5;(3)3 5 .【解析】(1)根据频率分布直方图求出在[)50,60内的频率,进而可求出成绩在[50,60)内的人数.(2)由平均数等于小矩形的面积乘以小矩形底边中点横坐标之和即可求解.(3)这2名同学来自不同组”为事件A,设第三组的3名同学为a,b,c,第四组的2位同学为x,y,列举法求出基本事件个数,再利用古典概型的概率计算公式即可求解. 【详解】解:(1)由题意,生物成绩在[)50,60内的频率为1-(0.01×10+0.02×10+0.03×10+0.035×10)=0.05,所以生物成绩在[)50,60内的人数为0.05×1000=50.答:生物成绩在[)50,60内的人数为50人.(2)由频率分布直方图,分数在[50,60)内的频率为0.05,[60,70)内的频率为0.35,[70,80)内的频率为0.3,[80,90)的频率为0.2,[90,100]的频率为0.1,所以这1000名学生期中考试生物成绩的平均分的估计值为:55×0.05+65×0.35+75×0.3+85×0.2+95×0.1=74.5.答:这1000名学生生物成绩的平均分为74.5.(3)设“这2名同学来自不同组”为事件A,设第三组的3名同学为a,b,c,第四组的2位同学为x,y,则样本空间为Ω={(a,b),(a,c),(a,x),(a,y),(b,c),(b,x),(b,y),(c,x),(c,y),(x,y)},事件A={(a,x),(a,y),(b,x),(b,y),(c,x),(c,y)}.所以63 ()105P A==.答:这2名同学来自不同组的概率为35.【点睛】本题考查了频率分布直方图求平均数、样本容量、古典概型的概率计算公式,属于基础题.18.ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2222sin sin sin b c a B Aab A+--=. (1)求C 的大小;(2)若ABC 的周长为18,面积为ABC 外接圆的面积. 【答案】(1)3π;(2)493π. 【解析】(1)根据正弦定理,得到222ab b a c =+-,再由余弦定理即可求出角C ; (2)根据题意,由三角形面积公式,以及余弦定理,求出7c =,再由正弦定理,得到外接圆半径,进而可求出外接圆的面积. 【详解】(1)根据题意,由正弦定理可得:2222sin sin 2sin b c a B A b aab A a +---==, ∴222ab b a c =+-,∴2221cos 22b ac C ab +-==,∵(0,)x π∈,∴3C π=;(2)由题意,18a b c ++=,1sin 2ABC S ab C ==△ ∴24ab =,18a b c +=-,又2222()3c b a ab a b ab =+-=+-,∴22(18)72c c =--,∴7c =; 由正弦定理得外接圆直径2sin c R C ==R = ABC 外接圆的面积2493S ππ==.【点睛】本题主要考查解三角形,熟记正弦定理以及余弦定理即可,属于常考题型. 19.如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面, (I )证明:平面AEC ⊥平面BED ;(II )若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -,求该三棱锥的侧面积.【答案】(1)见解析(2)5【解析】(1)由四边形ABCD为菱形知AC⊥BD,由BE⊥平面ABCD知AC⊥BE,由线面垂直判定定理知AC⊥平面BED,由面面垂直的判定定理知平面AEC⊥平面BED;(2)设AB=x,通过解直角三角形将AG、GC、GB、GD用x表示出来,在Rt∆AEC 中,用x表示EG,在Rt∆EBG中,用x表示EB,根据条件三棱锥E ACD-的体积为6 3求出x,即可求出三棱锥E ACD-的侧面积.【详解】(1)因为四边形ABCD为菱形,所以AC⊥BD,因为BE⊥平面ABCD,所以AC ⊥BE,故AC⊥平面BED. 又AC⊂平面AEC,所以平面AEC ⊥平面BED(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC 3x,GB=GD=2x.因为AE⊥EC,所以在Rt∆AEC中,可得EG 3x.连接EG,由BE⊥平面ABCD,知∆EBG为直角三角形,可得BE=22x.由已知得,三棱锥E -ACD 的体积3116632243E ACD V AC GD BE x -=⨯⋅⋅==.故 x =2 从而可得AE =EC =ED 6. 所以∆EAC 的面积为3,∆EAD 的面积与∆ECD 的面积均为 5故三棱锥E -ACD 的侧面积为3+25【点睛】本题考查线面垂直的判定与性质;面面垂直的判定;三棱锥的体积与表面积的计算;逻辑推理能力;运算求解能力.20.设函数()3xf x e ax =-+(a R ∈).(1)讨论函数()f x 的极值;(2)若函数()f x 在区间[]1,2上的最小值是4,求a 的值.【答案】(1)当0a ≤时,函数()f x 在R 上无极值;当0a >时,()f x 的极小值为ln 3a a a -+,无极大值.(2)1e -【解析】(1)求得函数的导数()xf x e a '=-,分类讨论即可求解函数的单调区间,得到答案.(2)由(1)知,当0a ≤时,函数()f x 在R 上单调递增,此时最小值不满足题意;当0a >时,由(1)得ln x a =是函数()f x 在R 上的极小值点,分类讨论,即可求解.【详解】解:(1)()xf x e a '=-.当0a ≤时,()0f x '>,()f x 在R 上单调递增;无极值当0a >时,()0f x '>,解得ln x a >, 由()0f x '<,解得ln x a <.函数()f x 在(),ln a -∞上单调递减,函数()f x 在()ln ,a +∞上单调递增,()f x 的极小值为()ln ln 3f a a a a =-+,无极大值综上所述:当0a ≤时,函数()f x 在R 上无极值; 当0a >时,()f x 的极小值为ln 3a a a -+,无极大值. (2)由(1)知,当0a ≤时,函数()f x 在R 上单调递增,∴函数()f x 在[]1,2上的最小值为()134f e a =-+=,即10a e =->,矛盾. 当0a >时,由(1)得ln x a =是函数()f x 在R 上的极小值点. ①当ln 1a ≤即0a e <≤时,函数()f x 在[]1,2上单调递增,则函数()f x 的最小值为()134f e a =-+=,即1a e =-,符合条件. ②当ln 2a ≥即2a e ≥时,函数()f x 在[]1,2上单调递减,则函数()f x 的最小值为()22234f e a =-+=即2212e a e -=<,矛盾.③当1ln 2a <<即2e a e <<时,函数()f x 在[]1,ln a 上单调递减,函数()f x 在[]ln ,2a 上单调递增,则函数()f x 的最小值为()ln ln ln 34af a ea a =-+=,即ln 10a a a --=.令()ln 1h a a a a =--(2e a e <<),则()ln 0h a a '=-<, ∴()h a 在()2,e e上单调递减,而()1h e =-,∴()h a 在()2,e e上没有零点,即当2e a e <<时,方程ln 10a a a --=无解. 综上,实数a 的值为1e -. 【点睛】本题主要考查导数在函数中的综合应用,着重考查了转化与化归思想、逻辑推理能力与计算能力,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,求解曲线在某点处的切线方程;(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数;(3)利用导数求函数的最值(极值),解决函数的恒成立与有解问题,同时注意数形结合思想的应用;本题属于难题.21.已知椭圆()222210x y a b a b+=>>的左右焦点分别为1F 、2F ,上顶点为M ,若直线1MF 的斜率为1,且与椭圆的另一个交点为N ,2F MN ∆的周长为 (1)求椭圆的标准方程;(2)过点1F 的直线l (直线l 的斜率不为1)与椭圆交于P 、Q 两点,点P 在点Q 的上方,若1123F NQ F MP S S ∆∆=,求直线l 的斜率. 【答案】(1)2212x y +=;(2)2-. 【解析】(1)由椭圆的定义得出2F MN ∆的周长为4a =可求出a 的值,又由直线1MF 的斜率得出1bc=,可求出b 、c 的值,从而得出椭圆的标准方程; (2)将直线1MF 的方程与椭圆方程联立,求出点N 的坐标,设直线l 的方程为1x my =-,设点()11,P x y 、()22,Q x y ,将直线l 的方程与椭圆的方程联立,列出韦达定理,由题意分析得出212y y =-,代入韦达定理可求出实数m 的值,即可得出直线l 的斜率.【详解】(1)根据题意,因为1F MN ∆的周长为4a =,即a =由直线1MF 的斜率1,得1bc=, 因为222a b c =+,所以1b c ==,所以椭圆的标准方程为2212x y +=;(2)由题意可得直线1MF 方程为1y x =+,联立得22112y x x y =+⎧⎪⎨+=⎪⎩,得2340x x +=, 解得41,33N ⎛⎫-- ⎪⎝⎭,所以1113NF MF =,因为1123F NQ F MP S S ∆∆=, 即111111121sin sin 232NF QF MF P Q F F F N P M ⎛⎫⋅∠=⋅∠ ⎪⎝⎭,所以112QF PF =, 当直线l 的斜率为0时,不符合题意;故设直线l 的方程为1x my =-,设点()11,P x y 、()22,Q x y , 由点P 在点Q 的上方,且212y y =,则有212y y =-,联立22112x my x y =-⎧⎪⎨+=⎪⎩,所以()222210m y my +--=, 由韦达定理得12222m y y m +=+,12212y y m =-+, 消去2y 得1221222122m y m y m -⎧=⎪⎪+⎨⎪=⎪+⎩,所以()22228122m m m =++,得227m =,m ∴=,又由画图可知7m =不符合题意,所以7m =-,故直线l的斜率为12m =-. 【点睛】本题考查椭圆方程的求解,同时也考查了椭圆中的三角形面积比的计算,解题时要结合已知条件将三角形的面积比转化为共线向量来处理,并结合韦达定理进行求解,考查运算求解能力,属于中等题. 22.[选修4-5:不等式选讲] 已知函数()225f x x =+-. (1)解不等式:()|1|f x x ≥-;(2)当1m ≥-时,函数()()||g x f x x m =+-的图象与x 轴围成一个三角形,求实数m 的取值范围.【答案】(1)(][),82,-∞-⋃+∞(2){}3,412⎡⎫⋃-⎪⎢⎣⎭【解析】试题分析:(Ⅰ)由已知,可按不等中两个绝对值式的零点将实数集分为三部分进行分段求解,然后再综合其所得解,从而求出所求不等式的解集;(Ⅱ)由题意,可将m 的值分为1m =-和1m >-进行分类讨论,当1m =-时,函数()315g x x =+-不过原点,且最小值为5-,此时满足题意;当1m >-时,函数()37,13,133,x m x g x x m x m x m x m -+-≤-⎧⎪=+--<≤⎨⎪-->⎩,再由函数()g x 的单调性及值域,求出实数m 的范围,最后综合两种情况,从而得出实数m 的范围.试题解析:(Ⅰ)由题意知,原不等式等价于12251x x x ≤-⎧⎨---≥-⎩或112251x x x -<≤⎧⎨+-≥-⎩或12251x x x >⎧⎨+-≥-⎩, 解得8x ≤-或∅或2x ≥,综上所述,不等式()1f x x ≥-的解集为(][),82,-∞-⋃+∞. (Ⅱ)当1m =-时,则()2251g x x x =+-++ 315x =+-, 此时()g x 的图象与x 轴围成一个三角形,满足题意:当1m >-时,()225g x x x m =+-+- 37,13,133,x m x x m x m x m x m -+-≤-⎧⎪=+--<≤⎨⎪-->⎩,则函数()g x 在(),1-∞-上单调递减,在()1,-+∞上单调递增. 要使函数()g x 的图象与x 轴围成一个三角形,则()()140230g m g m m ⎧-=-<⎪⎨=-≥⎪⎩,解得342m ≤<;综上所述,实数m 的取值范围为{}3,412⎡⎫⋃-⎪⎢⎣⎭.。
