八下数学《同步练习》9.4矩形、菱形、正方形(1)

合集下载

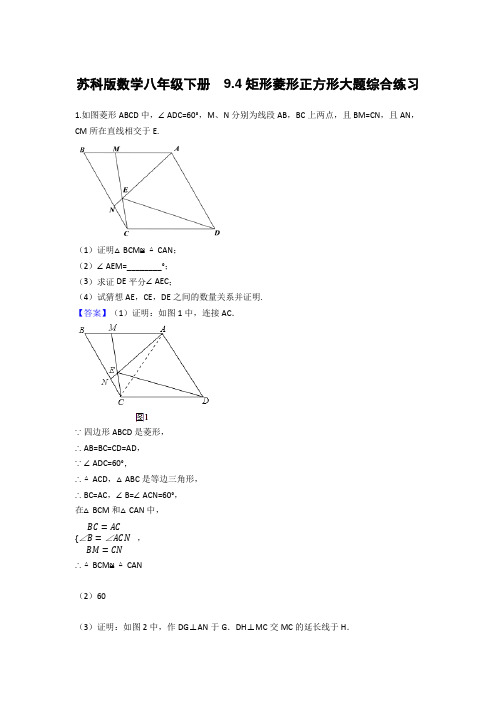
苏科版八下 9.4矩形、菱形、正方形同步课时训练(word版含答案)

9.4矩形、菱形、正方形同步课时训练一、单选题1．如图，已知矩形纸片ABCD 中，9cm,3cm AD AB ==，将其折叠，使点D 与点B 重合，那么折叠后DE 的长和折痕EF 的长分别是（）A ．4cmB ．5cmC ．4cm 、D ．5cm 、 2．如图，已知△ABC 中，AB ＝AC ，AD 是∠BAC 的平分线，AE 是∠BAC 的外角平分线，ED ∥AB 交AC 于点G ．下列结论：①AD ⊥BC ；②AE ∥BC ；③AE ＝AG ；④AD 2＋AE 2＝4AG 2，其中正确结论的个数是（）A ．1B ．2C ．3D ．4 3．如图，在四边形ABCD 中，BD 平分ABC ∠，//AD BC ，90C ∠=︒，5AB =，4CD =，则四边形ABCD 的周长是（）．A ．18B ．20C ．22D ．24 4．如图，将矩形ABCD 的四个角向内折叠铺平，恰好拼成一个无缝隙无重叠的矩形EFGH ，若EH ＝5，EF ＝12，则CD 长为（）A．13 B．12013C．12 D．175．如图，将矩形纸片ABCD沿BE折叠，使点A落在对角线BD上的A'处．若∠DBC ＝24°，则∠A'EB等于（）A．66°B．60°C．57°D．48°6．一次数学课上，老师请同学们在一张长为18厘米，宽为16厘米的矩形纸板上，剪下一个腰长为10厘米的等腰三角形，且要求等腰三角形的一个顶点与矩形的一个顶点重合，其它两个顶点在矩形的边上，则剪下的等腰三角形的面积为（）A．50或40或30 B．50或40 C．50 D．50或30或20 7．如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）A．AB=BE B．DE⊥DC C．∠ADB=90°D．CE⊥DE 8．顺次连结对角线互相垂直的四边形各边的中点，所得的四边形是( )A．矩形B．菱形C．正方形D．梯形9．如图，在正方形ABCD中，点E，F将对角线AC三等分，且18AC=，点P在正方形的边上，则满足PE PF+，则的点P的个数是（）A ．0B ．4C ．6D ．810．如图，在△ABC 中，∠ACB ＝90°，以△ABC 的各边为边作三个正方形，点G 落在HI 上，若AC ＋BC ＝6，空白部分面积为10.5，则AB 的长为（）A ．B C ．D二、填空题 11．如图，在边长为1的菱形ABCD 中，∠ABC ＝60°，将△ABD 沿射线BD 的方向平移得到△A 'B 'D '，分别连接A 'C ，A 'D ，B 'C ，则A 'C +B 'C 的最小值为_____．12．如图，在矩形ABCD 中，4,3AB AD ==，点E 在AB 上，且1AE =，点P Q 、分别是直线CD AD 、上的两个动点，将AEQ ∆沿EQ 翻折，使点A 落在矩形中的点F 处，连接PF PB 、，则PB PF +的最小值是__________．13．在Rt ABC △中，90ABC ∠=︒，D 为斜边AC 中点，8AC =，则BD =______． 14．在矩形ABCD 中，AB ＝5，BC ＝7，点P 是直线BC 一动点，若将△ABP 沿AP 折叠，使点B落在平面上的点E处，连结AE、PE．若P、E、D三点在一直线上，则BP ＝_________．15．如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E．若点P、Q分别是AD和AE上的动点，则DQ＋PQ的最小值是________．16．如图，在菱形ABCD中，AB＝∠ABC＝60°，点M、N分别是BC、CD上任意一点，点P是BD上一点，连接PM、PN，则PM＋PN的最小值为________．三、解答题17．如图所示，AD∥BC，∠BAD＝90°，以B为圆心，BC长为半径画弧，与射线AD 相交于点E，连接BE，过C作CF⊥BE于点F．（1）线段BF与图中哪条线段相等？写出来并加以证明：（2）若AB＝12，BC＝13，P从E沿ED方向运动，Q从C出发向B运动，两点同时出发且速度均为每秒1个单位．①当t＝秒时，四边形EPCQ是矩形；②当t＝秒时，四边形EPCQ是菱形．18．如图，在等腰Rt△ABC中，∠BAC＝90°，延长BA至点D，连结DC，过点B作BE⊥DC于点E，F为BC上一点，FC＝FE．连结AF，AE．（1）求证：F A ＝FE ．（2）若∠D ＝60°，BC ＝10，求△AEF 的周长．19．如图，四边形ABCD 中，∠B=60°，AC=BC ，点E 在AB 上，将CE 绕点C 顺时针旋转60°得CF ，且点F 在AD 上．（1）求证：AF=BE ；（2）若AE=DF ，求证：四边形ABCD 是菱形；（3）若BC=AFCE 的面积．20．如图，在Rt ABC △中，AB AC =，90BAC ∠=︒，O 为BC 的中点．（1）写出点O 到ABC 的三个顶点A ，B ，C 的距离的关系（不要求证明）；（2）如果点M ，N 分别在线段AB ，AC 上移动，在移动过程中保持AN BM =，请判断OMN 的形状，并证明你的结论．参考答案1．B2．C3．C4．B5．C6．A7．B8．A9．D10．B1112．-1．13．414．或7﹣15．16．617．（1）BF ＝AE ，证明见解析；（2）①8，②13【详解】解：（1）BF ＝AE ．理由如下：∵AD ∥BC ，∴∠CBF ＝∠AEB ，在△BCF 和△EBA ，BFC A CBF AEB BC EB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCF ≌△EBA ，∴BF ＝EA ；（2）EP＝t，CQ＝t，在Rt△ABE中，AE5，∵EP＝CQ，EP∥CQ，∴四边形EPCQ为平行四边形，①当CP⊥AD时，∠CPE＝90°，则平行四边形EPCQ为矩形，此时AP＝BC＝13，即5+t＝13，解得t＝8，即当t＝8时，四边形EPCQ是矩形；②作CH⊥AD于H，如图，当CP＝CQ＝EP＝t，平行四边形EPCQ为菱形，而PH＝t+5﹣13＝t﹣8，在Rt△PCH中，122+（t﹣8）2＝t2，解得t＝13，即当t＝13，四边形EPCQ是菱形．故答案为：8，13．18．（1）见解析；（2）15【详解】（1）证明：∵BE⊥DC，∴∠EBC+∠ECB＝∠CEF+∠BEF＝90°，∵FC＝FE，∴∠ECB＝∠CEF，∴∠EBC＝∠BEF，∴BF＝FE＝FC，在Rt△BAC中，AF是斜边BC上的中线，∴F A＝FE；（2）解：∵∠D＝60°，∠BAC＝90°，∴∠ACD＝30°，∵△ABC为等腰直角三角形，∴∠ABC＝∠ACB＝45°，∴∠ECF＝∠ACD+∠ACB＝30°+45°＝75°，由（1）得：F A＝FE，AF是斜边BC上的中线，∴AF⊥BC，AF＝12BC＝5，∵FC＝FE，∴∠EFC＝180°﹣2∠ECF＝180°﹣2×75°＝30°，∴∠AFE＝90°﹣30°＝60°，∴△AEF是等边三角形，∴△AEF的周长＝3AF＝3×5＝15．19．（1）见解析；（2）见解析；（3）四边形AFCE的面积=．【详解】(1)证明:∵AC=BC,∠B=60°,∴△ABC是等边三角形,∴AB=BC=AC,∠ACB=60°.∵∠ECF=60°,∴∠ACB=∠ECF, ∴∠ECB=∠ACF.在△BCE和△ACF中,,,,BC ACECB ACF EC FC∠∠=⎧⎪=⎨⎪=⎩∴△BCE≌△ACF(SAS),∴AF=BE.(2)证明:由(1)得∠FAC=∠EBC=∠ACB=60°, ∴AF∥BC.∵AF=BE,AE=DF,∴AD=BC,∴四边形ABCD 是平行四边形.∵AB=BC,∴▱ABCD 是菱形.(3)∵△BCE ≌△ACF,∴四边形AFCE 的面积=△AFC 的面积+△ACE 的面积 =△BEC 的面积+△ACE 的面积=△ABC 的面积,∵△ABC 是一个等边三角形且,∴四边形AFCE 的面积=12×20．（1） OA OB OC ==；（2）等腰直角三角形，见解析【详解】解：（1）点O 到ABC 的三个顶点A ，B ，C 的距离的关系是B OA O OC ==．（2）OMN 的形状是等腰直角三角形．证明如下：在ABC 中，AB AC =，90BAC ∠=︒，O 为BC 的中点， OA OB OC ∴==，AO 平分BAC ∠，AO BC ⊥， 90AOB ∠=︒∴，45B C ∠=∠=︒，45BAO CAO ∠=∠=︒， CAO B ∠=∠．在BOM 和AON 中，AN BM =，CAO B ∠=∠，OA OB =，()BOM AON SAS ∴△≌△，OM ON ∴=，AON BOM ∠=∠．90AOB BOM AOM ∠=∠+∠=︒，90AON AOM ∴∠+∠=︒，即90MON ∠=︒，OMN ∴是等腰直角三形．。

2024年苏科版八年级下册同步练习9.4矩形、菱形、正方形练习 (新版)苏含答案

2024年苏科版八年级下册同步练习9.4矩形、菱形、正方形练习（新版）苏矩形、菱形、正方形1．正方形具有而菱形不一定具有的性质是 ( )A．对角线互相垂直B．对角线互相平分C．对角线相等D．对角线平分一组对角2．下列判断中正确的是 ( )A．四边相等的四边形是正方形B．四角相等的四边形是正方形C．对角线互相垂直的平行四边形是正方形D．对角线互相垂直平分且相等的四边形是正方形3．如图，已知正方形ABCD的边长为3，E为CD边上一点，DE＝1．以点A为中心，把△ADE顺时针旋转90°，得△ABE'，连接EE'，则EE'的长等于_______．4．如图，过正方形ABCD的顶点B作直线l，过A、C作l的垂线，垂足分别为E、F．若AE＝1，CF＝3，则AB的长度为_______．5．如图，三个边长均为2的正方形重叠在一起，O1、O2是其中两个正方形的中心，则阴影部分的面积是_______．6．（2013．铁岭）如图，△ABC中，AB＝AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE＝OD，连接AE、BE．(1)求证：四边形AEBD是矩形；(2)当△ABC满足什么条件时，矩形AEBD是正方形？并说明理由．7．已知四边形ABCD中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是 ( )A．∠D＝90° B．AB＝CD C．AD＝BC D．BC＝CD8．如图所示，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB＝S四边形DEOF中，错误的有( ) A．1个 B．2个 C．3个 D．4个9．(2013．枣庄)如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD至点E，使ME＝MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为 ( )A．3－1 B．3－5C．5＋1 D．5－110．(2013．钦州)如图，在正方形ABCD中，E是AB上一点，BE＝2，AE＝3BE，P是AC上一动点，则PB＋PE的最小值是_______．11．已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是_______．12．(2013．锦州)如图①，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC、DC于点E、F，连接EF．(1)猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；(2)在图①中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；(3)如图②．将Rt△ABC沿斜边AC翻折得到Rt△ADC，E、F分别是BC、CD边上的点，∠EAF＝12∠BAD，连接EF，过点A作AM⊥EF于点M．试猜想AM与AB之间的数量关系，并证明你的猜想．参考答案1．C 2．D 3．204．105．2 6．略7．D 8．A 9．D 10．10 11．15°或 75° 12．(1) EF＝BE＋DF．(2)AM＝AB； (3)AM＝AB．三角形的中位线1．如图，DE是△ABC的中位线，若BC的长为3 cm，则DE的长是 ( )A．2 cm B．1.5 cm C．1.2 cm D．1cm2．如图，小区的一角有一块形状为等腰梯形的空地，为了美化小区，社区居委会计划在空地上建一个四边形的水池，使水池的四个顶点恰好在梯形各边的中点上，则水池的形状一定是( )A．梯形 B．矩形 C．菱形 D．正方形3．如图，在△ABC中，点D、E、F分别是AB、BC、CA的中点，若△ABC的周长为10 cm，则△DEF的周长是_______cm．4．（2013．宿迁）如图，为测量位于一水塘旁的两点A、B间的距离，在地面上确定点O，分别取OA、OB的中点C、D，量得CD＝20 m，则A、B之间的距离是_______m．5．将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如图所示）．若∠C＝90°，BC＝8 cm，则折痕DE的长度是_______cm．6．如图，在四边形ABCD中，AD＝BC，E、F、G分别是AB、CD、AC的中点，试说明△EFG 的形状．7．（2013．河池）一个三角形的周长是36 cm，则以这个三角形各边中点为顶点的三角形的周长是 ( )A．6 cm B．12 cm C．18 cm D．36 cm8．如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是 ( )A．AB∥DC B．AB＝DCC．AC⊥BD D．AC＝BD9．（2013．北京）如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB＝5，AD＝12，则四边形ABOM的周长为_______．10．如图，在Rt△ABC中，∠ACB＝90°，D、E、F分别是AB、BC、CA的中点，若CD＝5 cm，则EF＝_______cm．11．如图，点D、E、F分别是△ABC的边AB、BC、CA的中点，连接DE、EF、FD，则图中平行四边形的个数为_______．12．如图，M是△ABC的边BC的中点，AN平分∠BAC，且BN⊥AN，垂足为N，且AB＝6，BC＝10，MN＝1.5，求△ABC的周长．13．如图，在四边形ABCD中，AD∥BC，AB与CD不平行，H、G分别是两条对角线BD、AC的中点，求证：GH∥AD，且GH＝12(BC－AD)．14．如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三角形，AB、BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN为怎样的四边形，并说明你的理由．参考答案1．B 2．C 3．5 4．40 5．4 6．略7．C 8．C 9．20 10．5 11．3 12．25 13．14．四边形PQMN 为菱形．分式一选择1 下列运算正确的是（）A -40=1B （-3）-1=31C （-2m-n ）2=4m-nD （a+b ）-1=a -1+b -1 2 分式28,9,12z y x xy z x x z y -+-的最简公分母是（） A 72xyz 2 B 108xyz C 72xyz D 96xyz 23 用科学计数法表示的树-3.6×10-4写成小数是（）A 0.00036B -0.0036C -0.00036D -360004 若分式6522+--x x x 的值为0，则x 的值为（）A 2B -2C 2或-2D 2或35计算⎪⎭⎫ ⎝⎛-+÷⎪⎭⎫ ⎝⎛-+1111112x x 的结果是（） A 1 B x+1 C x x 1+ D 11-x 6 工地调来72人参加挖土和运土，已知3人挖出的土1人恰好能全部运走，怎样调动劳动力才能使挖出的土能及时运走，解决此问题，可设派x 人挖土，其它的人运土，列方程 ①3172=-x x ②72-x=3x ③x+3x=72 ④372=-xx 上述所列方程，正确的有（）个A 1B 2C 3D 47 在ma y x xy x x 1,3,3,21,21,12+++π中，分式的个数是（） A 2 B 3 C 4 D 58 若分式方程xa x a x +-=+-321有增根，则a 的值是（） A -1 B 0 C 1 D 29 若3,111--+=-b a a b b a b a 则的值是（） A -2 B 2 C 3 D -3 10 已知k b a c c a b c b a =+=+=+，则直线y=kx+2k 一定经过（） A 第1、2象限 B 第2、3象限 C 第3、4象限 D 第 1、4象限二填空1 一组按规律排列的式子：()0,,,,41138252≠--ab ab a b a b a b ，其中第7个式子是第n 个式子是 2 7m =3,7n =5,则72m-n =3 ()2312008410-+⎪⎭⎫ ⎝⎛--+-= 4 若2222,2ba b ab a b a ++-=则= 三化简1 ()d cd b a cab 234322222-•-÷ 2 111122----÷-a a a a a a3 ⎪⎭⎫ ⎝⎛---÷--225262x x x x四解下列各题1 已知b ab a b ab a b a ---+=-2232,311求的值2 若0<x<1,且xx x x 1,61-=+求的值五（5）先化简代数式()()n m n m mn n m n m n m n m -+÷⎪⎪⎭⎫ ⎝⎛+---+222222，然后在取一组m,n 的值代入求值六解方程1 12332-=-x x2 1412112-=-++x x x七 2008年5月12日，四川省发生8.0级地震，我校师生积极捐款，已知第一天捐款4800元，第二天捐款6000元，第二天捐款人数比第一天捐款人数多50人，且两天人均捐款数相等，那么两天共参加捐款的人数是多少？分式(二)一、选择题：1．已知230.5x y z ==，则32x y z x y z +--+的值是（）A ．17 B.7 C.1 D.132．一轮船从A 地到B 地需7天，而从B 地到A 地只需5天，则一竹排从B 地漂到A 地需要的天数是（）A ．12 B.35 C.24 D.473．已知226a b ab +=，且0a b >>，则a b a b +-的值为（） A ．2 B ．2± C ．2 D ．2±二、填空题：4. 若关于x 的分式方程3232-=--x m x x 无解，则m 的值为__________.5.若分式231-+x x 的值为负数，则x 的取值范围是__________． 6. 已知2242141x y y x y y +-=-+-，则的24y y x ++值为______. 三、解答题：7. 计算： ()3322232n m n m --⋅8. 计算（1）168422+--x x x x （2）mn n n m m m n n m -+-+--29. 先化简，后求值：222222()()12a a a a a b a ab b a b a b -÷-+--++-，其中2,33a b ==- 10. 解下列分式方程．1412112-=-++x x x11. 计算：（1）1111-÷⎪⎭⎫ ⎝⎛--x x x （2）4214121111xx x x ++++++-12．已知x 为整数，且918232322-++-++x x x x 为整数，求所有符合条件的x 的值．13．先阅读下面一段文字，然后解答问题：一个批发兼零售的文具店规定：凡一次购买铅笔301支以上（包括301支）可以按批发价付款；购买300支以下（包括300支）只能按零售价付款．现有学生小王购买铅笔，如果给初三年级学生每人买1支，则只能按零售价付款，需用()12-m 元，（m 为正整数，且12-m ＞100）如果多买60支，则可按批发价付款，同样需用()12-m 元．设初三年级共有x 名学生，则①x 的取值范围是；②铅笔的零售价每支应为元；③批发价每支应为元．（用含x 、m 的代数式表示）．14． A 、B 两地相距20 km ，甲骑车自A 地出发向B 地方向行进30分钟后，乙骑车自B 地出发，以每小时比甲快2倍的速度向A 地驶去，两车在距B 地12 km 的C 地相遇，求甲、乙两人的车速.分式(三)一、填空题1、在有理式22xy ，πx ，11+a ，y x +1，122-m 中属于分式的有 .2、分式33+-x x 的值为0，则x= .3、分式x x 2-和它的倒数都有意义，则x 的取值范围是 .4、当_____=x 时，x --11的值为负数；当x 、y 满足时，)(3)(2y x y x ++的值为32；5、若分式y x y -3的值为4，则x,y 都扩大两倍后，这个分式的值为6、当x= 时，分式11+x 与11-x 互为相反数.7、若分式方程=-1x m 1-x -11有增根，则m= .8、要使方程=-11x a x -2有正数解，则a 的取值范围是9、+++)2)(1(1 x x )3)(2(1++x x +)2007)(2006(1.....+++x x =_____________10、若=a 3b 4=c 5，则分式222c b a acbc ab +++-=____________二、选择题11、已知m 、n 互为相反数，a 、b 互为倒数,|x|=2,则ab x x nm -++2的值为（） A 、2 B 、3 C 、4 D 、512. 下列式子:（1）y x y x y x -=--122；（2）c a ba a c ab --=--；（3）1-=--b a ab ；（4）y x yx y x yx +-=--+-中正确的是（）A 、1个B 、2 个C 、3 个D 、4 个13. 下列分式方程有解的是（）A 、++12x 13-x =162-x B 、012=+x x C 、0122=-x D 、111=-x14. 若分式m x x ++212不论m 取何实数总有意义，则m 的取值范围是（）A 、m ≥1B 、m ＞1C 、m ≤1D 、m ＜115、晓晓根据下表，作了三个推测：x 1 lO 100 1000 10000…3-x-1x 3 2.1 2．Ol 2.001 2.0001…①3-x-1x (x>0)的值随着x 的增大越来越小；②3-x-1x (x>0)的值有可能等于2；③3-x-1x (x>O)的值随着x 的增大越来越接近于2．则推测正确的有( ) A 、0个 B 、1个 C 、2个 D 、3个16. 已知分式xyy x -+1的值是a ，如果用x 、y 的相反数代入这个分式所得的值为b ，则a 、b 关系（）A 、相等B 、互为相反数C 、互为倒数D 、乘积为－1三、解答题17、化简：[22222a b a ab b -+++2ab ÷(1a +1b )2]·2222a b ab-+.18、当21,23-==b a 时，求⎪⎭⎫ ⎝⎛-+⋅⎪⎭⎫ ⎝⎛-+-b a ab b a b a ab b a ＋44的值.19、A 玉米试验田是边长为a 米的正方形减去一个边长为1米的正方形蓄水池后余下部分，B 玉米试验田是边长为（a －1）米的正方形，两块试验田的玉米都收获了500千克.（1）那种玉米的单位面积产量高？（2）高的单位面积产量是低的单位面积产量的多少倍？四、探索题20、观察以下式子：1112122132+→=+＞，5527544264+→=+＜，3354355555+→=+＞， 773722232+→=+＜.请你猜想，将一个正分数的分子分母同时加上一个正数，这个分数的变化情况，并证明你的结论.21、甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000千克，乙每次用去800元，而不管购买多少饲料.谁的购货方式更合算？22、一个批发兼零售的文具店规定：凡一次购买铅笔300枝以上，（不包括300枝），可以按批发价付款，购买300枝以下，（包括300枝）只能按零售价付款.小明来该店购买铅笔，如果给八年级学生每人购买1枝，那么只能按零售价付款，需用120元，如果多购买60枝，那么可以按批发价付款，同样需要120元，①这个八年级的学生总数在什么范围内？②若按批发价购买6枝与按零售价购买5枝的款相同，那么这个学校八年级学生有多少人？分式（一）参考答案一 CACBC CBBA B二 1 -()n n n ab a b 137201,--， 2 9/5， 3 2， 4 53 三 1 ac 1 ， 2 1-a a ， 3 32+-x 四 1 提示：将所求式子的分子、分母同时除以ab 。

苏科版数学八年级下《9.4矩形、菱形、正方形》同步练习含答案初二数学试卷分析.docx

9-4矩形、菱形.正方形（选择.填空题）一.选择题矩形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标为（3, 4） , D是0A 的中点，点E 在AB 上，当厶CDE 的周长最小时，点E 的坐标为（）4RA. （3, 1）B. （3,令）C. （3,寻）D. （3, 2） O 04. 如图，在矩形ABCD 中，AB=4, BC=6，点E 为BC 的中点，将AABE 沿AE 折叠，使点B 落在矩形内点F 处，连接CF,则CF 的长为（）A. 4B.半C.芈D.半55555. 如图，矩形ABCD 的顶点A 、C 分别在直线a 、b±,且a 〃b, Zl=60°,则Z 2的度数为（）1.菱形具有而一般平行四边形不具有的性质是（）A. 对边相等B.对角相等C. 对角线互相平分D.对角线互相垂直2. 如图, 四边形ABCD 是菱形，AC=8, DB=6, DH 丄AB 于H ，则DH 等于A.D. 43.A. 30°B. 45°C. 60°D. 75°246. 如图，点P 是矩形ABCD 的边AD 上的一动点，矩形的两条边AB 、BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离Z 和是（）7.如图，矩形ABCD 与菱形EFGH 的对角线均交于点0,且EG 〃BC,将矩形折叠，使点C 与点0重合，折痕MN 恰好过点G 若AB=V6, EF=2, ZH=120°,则 DN 的长为（）8. 如图，矩形ABCD 中，0为AC 中点，过点0的直线分别与AB 、CD 交于点 E 、F,连结BF 交AC 于点M,连结DE 、B0.若ZCOB=60°, F0=FC,则下列结论：①FB 垂直平分 0C ；②△EOB9ZXCMB ；③DE=EF ；④S A A OE ： S A B CM =2： 3.其屮正确结论的个数是（）9. 如图，在矩形ABCD 中，AD=6, AE 丄BD, 别在BD, AD 上，则AP+PQ 的最小值为（）10. 有3个正方形如图所示放置，阴影部分的面积依次记为S’ S2,则Sx S2等A. 4.8B. 5C. 6D. 7.2A. 4个B. 3个C. 2个D. 1个垂足为E, ED=3BE,点P 、Q 分 A. 2^2B. V2C. 2^3D. 3^311・如图，正方形ABCD 的边长为9,将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH.若BE ： EC=2： 1,则线段CH 的长是（）12. 如图是出三个边长分别为6、9、x 的正方形所组成的图形，若直线AB 将它分成面积相等的两部分，则x 的值是（）13.如图，在正方形ABCD 中，连接BD,点0是BD 的中点，若M 、N是边AD 上的两点，连接MO 、NO,并分別延长交边BC 于两点M ，、N\则图中的全等三角形共有（）15. 如图，面积为24的正方形ABCD 中，有一个小正方形EFGH,其中E 、F 、GA. 1 或9B. 3 或 5C. 4 或 6D. 3 或 6A. 2对B. 3对C. 4对D. 5对14. 如图，有一平行四边形ABCD 与一正方形CEFG, 其中E 点在AD 上・若ZECD=35。

八年级数学下册第9章 9.4 矩形、菱形、正方形同步练习(含解析)苏科版(2021-2022学年)

第9章9.4矩形、菱形、正方形一、单选题(共12题；共２4分）1、下面说法中,正确的是( )A、有一个角是直角的四边形是矩形B、两条对角线相等的四边形是矩形ﻫC、两条对角线互相垂直的四边形是矩形ﻫD、四个角都是直角的四边形是矩形２、在▱ABCD中增加下列条件中的一个,这个四边形就是矩形,则增加的条件是（ )A、对角线互相平分ﻫB、AB＝ＢCＣ、∠A+∠Ｃ＝18０°ﻫD、AＢ= AC3、检查一个门框是矩形的方法是( ）A、测量两条对角线是否相等ﻫB、测量有三个角是直角ﻫＣ、测量两条对角线是否互相平分ﻫＤ、测量两条对角线是否互相垂直４、在下列所给出的4个图形中，对角线一定互相垂直的是( ）A、长方形ﻫＢ、平行四边形C、菱形ﻫＤ、直角梯形5、如图，矩形ABCＤ对角线相交于点O，∠AOB＝6０°,AB=４，则AC的为（）ﻫＡ、４ﻫB、8ﻫＣ、4 ﻫD、106、如图,菱形ABCD中，∠BAD＝12０°．若△ABC的周长是15,则菱形ABＣＤ的周长是( ）A、2５ﻫB、20C、１5D、1０7、如图,以正方形AＢＣD的一边向形外作等边△ABE，BＤ与EC交于点F,则∠ＡFD等于（)A、60°ﻫB、50°Ｃ、45°Ｄ、4０°8、如图,将矩形ABCD分成１5个大小相等的正方形，Ｅ、Ｆ、G、Ｈ分别在ＡD、AB、BC、ＣD边上，且都是某个小正方形的顶点,若四边形EＦＧH的面积为1,则矩形ＡBCＤ的面积为（)A、２B、３ﻫＣ、ﻫＤ、9、如图，在矩形ABＣD中，若AC＝2ＡB,则∠ＡOB的大小是（）A、３０°ﻫB、4５°ﻬC、6０°D、90°１0、如图,四边形ＡBCD的四边相等,且面积为120cm2，对角线ＡＣ＝２４cm,则四边形AＢCD的周长为( )A、52cmﻫＢ、40cmＣ、３9cｍﻫD、２6cｍ11、在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、２、3，正放置的四个正方形的面积依次是Ｓ1、S2、Ｓ３、S4，则S１+2S２＋2Ｓ3+S4＝( ）A、５B、4C、6D、1012、八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( ）A、ﻫB、y= x+C、ﻫD、二、填空题(共６题;共7分）ﻬ１３、如图,平行四边形ABCＤ的对角线AC，ＢD交于点Ｏ,△AＯＤ是正三角形,AD=4,则平行四边形ABCＤ的面积为＿_＿_＿___．1４、如图,两条宽度为1的带子，相交成∠α,那么重叠部分（阴影部分)的面积是_＿__＿_＿_. 15、如图，ＢF平行于正方形ABCD的对角线AC,点E在BF上,且AE＝AC,CF∥AE，则∠BCF的度数为________．16、在四边形AＢCD中,∠Ａ＝∠B＝∠C=∠D,则四边形ＡBＣD是___＿____.17、一组邻边相等的＿_____＿＿是正方形，有一个角是___＿_＿__角的菱形是正方形.1８、如图,在菱形ＡBCD中，对角线AＣ与ＢD相交于点O，OE⊥AB,垂足为Ｅ点,若∠ＡDC=130°,ﻫ则∠AOE=＿____＿__．三、解答题(共5题；共25分)19、如图,△ＡＢC中,∠C=９０°,∠BAＣ、∠AＢＣ的平分线相交于点D,DE⊥BC，ＤＦ⊥AC,垂足分别为E、F．问四边形ＣFDE是正方形吗?请说明理由．2０、如图所示,在Rt△AＢＣ中,CＦ为直角的平分线,ＦＤ⊥CA于Ｄ,FE⊥BＣ于E，则四边形ＣDFE是怎样的四边形,为什么？21、如图所示,四边形EFＧＨ是由矩形ABCD的外角平分线围成的. 求证：四边形EFＧH是正方形．2２、如图,在△ABC中,AＢ=ＡＣ，Ｄ为边BＣ上一点，以AB、BＤ为邻边作平行四边形ＡＢDE ,连接AD、EC. 若BＤ＝ＣＤ , 求证:四边形ADCE是矩形.ﻫ２3、正方形的边长为2,建立合适的直角坐标系，写出各个顶点的坐标．答案解析部分一、单选题１、【答案】D【考点】矩形的判定【解析】【解答】解：A、有一个直角的平行四边形是矩形,故错误； B、两条对角线相等的平行四边形是矩形，故错误;C、两条对角线互相垂直的四边形可能是梯形等，故错误；D、四个角都是直角的四边形是矩形，正确，故选D.【分析】利用矩形的判定定理及矩形的定义进行判断后即可确定本题的答案．２、【答案】C【考点】矩形的判定【解析】【解答】解:根据矩形的判定(有一个角是直角的平行四边形是矩形) 可得∠A+∠B=180°，∠A+∠C=180°故∠B＝∠C＝９0°ﻫ增加的条件是∠A+∠Ｃ＝1８0°．故选C.ﻫ【分析】根据矩形的判定(有一个角是直角的平行四边形是矩形）.3、【答案】B ﻫ【考点】矩形的判定ﻫ【解析】【解答】解:∵有三个角是直角的四边形是矩形, ∴检查一个门框是矩形的方法是:测量有三个角是直角．∵对角线相等的平行四边形是矩形,∴检查一个门框是矩形的另一个方法是:先测得门框的两组对边是否分别相等，再测其对角线的是否相等.故选B.【分析】由对角线相等的平行四边形是矩形与有三个角是直角的四边形是矩形,可求得答案．4、【答案】Ｃﻫ【考点】平行四边形的性质，菱形的性质,矩形的性质,直角梯形ﻫ【解析】【解答】解:菱形的对角线互相垂直，而长方形、平行四边形、直角梯形的对角线不一定互相垂直. 故选:C.ﻫ【分析】根据菱形的对角线互相垂直即可判断．5、【答案】B ﻫ【考点】等边三角形的判定与性质，矩形的性质【解析】【解答】∵矩形ABCＤ,ﻫ∴AC=BD,AC=2OA＝2ＯＢﻫ∵∠AOB=60度，ﻫ∴△AOB是等边三角形，∴OA=ＡB＝4,则AC＝2OA=８.故选B。

2020-2021学年苏科版八年级下册数学9.4矩形、菱形、正方形同步练习 (含解析)

9.4矩形、菱形、正方形同步练习一．选择题1．下列说法中不正确的是（）A．对角线垂直的平行四边形是菱形B．对角线相等的平行四边形是矩形C．菱形的面积等于对角线乘积的一半D．对角线互相垂直平分的四边形是正方形2．下列说法正确的是（）A．一组对边平行，另一组对边相等的四边形是平行四边形B．对角线相等的平行四边形是菱形C．三个角都是直角的四边形是矩形D．一组邻边相等的平行四边形是正方形3．如图，矩形ABCD中，AB＝2，点E在边AD上，EB平分∠AEC，∠DCE＝45°，则AE长（）A．B．2﹣2C．2﹣D．24．如图，在菱形ABCD中，对角线AC、BD交于点O，且AC＝6，BD＝8，过A点作AE垂直BC，交BC于点E，则的值为（）A．B．C．D．5．如图，点E是矩形ABCD的边CD上一点，作AF⊥BE于F，连接DF，若AB＝6，DF＝BC，则CE的长度为（）A．2B．C．3D．6．如图，在菱形ABCD中，∠ABC＝80°，E是线段BD上一动点（点E不与点B，D重合），当△ABE是等腰三角形时，∠DAE＝（）A．30°B．70°C．30°或60°D．40°或70°7．如图，菱形ABCD的边AB的垂直平分线交AB于点E，交AC于点F，连接DF．当∠BAD ＝100°时，则∠CDF＝（）A．15°B．30°C．40°D．50°8．如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE＝22.5°，EF⊥AB，垂足为F，则EF的长为（）A．4﹣2B．3﹣4C．1D．9．如图所示，在菱形ABCD中，AC、BD相交于O，∠ABC＝70°，E是线段AO上一点，则∠BEC的度数可能是（）A．100°B．70°C．50°D．20°10．如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与AD，AC，BC相交于点E，O，F．下列结论正确的个数有（）①四边形AFCE为菱形；②△ABF≌△CDE；③当F为BC中点时，∠ACD＝90°．A．0个B．1个C．2个D．3个二．填空题11．如图，在矩形ABCD中，对角线AC与BD相交于点O，∠ACB＝30°，BD＝4，则矩形ABCD 的面积是．12．如图，正方形ABCD边长为2，点P在BC边上，DP交AC于点E，∠ADE＝∠AED，则BP的长度是．13．如图，点E为正方形ABCD外一点，ED＝CD，AE与BD相交于点F．若∠CDE＝52°，则∠DCF＝°．14．在长方形ABCD中，AB＝，BC＝4，CE＝CF，延长AB至点E，连接CE，CF平分∠ECD，则BE＝．15．如图，在菱形ABCD中，∠B＝60°，E，H分别为AB，BC的中点，G，F分别为线段HD，CE的中点．若线段FG的长为2，则AB的长为．三．解答题16．如图，点E在矩形ABCD的边BC上，延长EB到点F，使BF＝CE，连接AF．求证：AD ＝EF．17．如图，正方形ABCD中，点P是对角线AC上一点，连接PB，边作PE⊥PB交AD边于于点E，且点E不与点A，D重合，作PM⊥AD，PN⊥AB，垂足分别为点M和N．（1）求证：PM＝PN；（2）求证：EM＝BN．18．已知：在矩形ABCD中，点E在BC边上，连接DE，且DE＝BC，过点A作AF⊥DE于点F．（1）如图1，求证：AB＝AF；（2）如图2，连接AE，当BE＝DF时，在不添加任何辅助线的情况下，请直接写出图2中所有长度等于AB的线段．参考答案一．选择题1．解：A、对角线垂直的平行四边形是菱形，正确，故不符合题意；B、对角线相等的平行四边形是矩形，正确，故不符合题意；C、菱形的面积等于对角线乘积的一半，正确；故不符合题意；D、对角线互相垂直平分且相等的四边形是正方形，故选项错误，故符合题意．故选：D．2．解：A、一组对边平行，另一组对边也平行的四边形是平行四边形，所以A选项错误，不符合题意；B、对角线相等的平行四边形是矩形，所以B选项错误，不符合题意；C、三个角都是直角的四边形是矩形，所以C选正确；符合题意；D、一组邻边相等的平行四边形是正方形，所以D选项错误，不符合题意．故选：C．3．解：∵四边形ABCD是矩形，∴AB＝CD＝2，∠A＝∠D＝∠DCB＝90°，∵∠DCE＝45°，∴DE＝DC＝2，∴EC＝2，∵∠DCE＝45°，∴∠DEC＝45°，∵EB平分∠AEC，∴∠BEC＝∠AEB＝∠AEC＝，∴∠EBC＝180°﹣67.5°﹣45°＝67.5°，∴∠BEC＝∠EBC，∴BC＝CE＝2，∴AD＝BC＝2，∴AE＝AD﹣DE＝2﹣2，故选：B．4．解：∵四边形ABCD是菱形，∴CO＝AC＝3，BO＝BD＝4，AO⊥BO，∴BC＝＝＝5，∵S菱形ABCD＝AC•BD＝BC×AE，∴AE＝＝．在Rt△ABE中，BE＝＝＝，∴CE＝BC﹣BE＝5﹣＝，∴的值为，故选：C．5．解：过D作DH⊥AF于点H，延长DH与AB相交于点G，∵四边形ABCD为矩形，∴AD＝BC，∵DF＝BC，∴DA＝DF，∴AH＝FH，∵AF⊥BE，∴DG∥BE，∴AG＝BG＝，∵矩形ABCD中，AB＝DC＝6，AB∥DC，∴四边形BEDG为平行四边形，∴DE＝BG＝3，∴CE＝CD﹣DE＝6﹣3＝3．故选：C．6．解：∵在菱形ABCD中，∠ABC＝80°，∴∠ABD＝ABC＝40°，AD∥BC，∴∠BAD＝180°﹣∠ABC＝100°，∵△ABE是等腰三角形，∴AE＝BE，或AB＝BE，当AE＝BE时，∴∠ABE＝∠BAE＝40°，∴∠DAE＝100°﹣40°＝60°；当AB＝BE时，∴∠BAE＝∠AEB＝（180°﹣40°）＝70°，∴∠DAE＝100°﹣70°＝30°，综上所述，当△ABE是等腰三角形时，∠DAE＝30°或60°，故选：C．7．解：如图，连接BF，∵四边形ABCD是菱形，∴CD＝BC，∠DCF＝∠BCF，在△BCF和△DCF中，∵，∴△BCF≌△DCF（SAS）∴∠CBF＝∠CDF∵FE垂直平分AB，∠BAF＝×100°＝50°∴∠ABF＝∠BAF＝50°∵∠ABC＝180°﹣100°＝80°，∠CBF＝80°﹣50°＝30°∴∠CDF＝30°．故选：B．8．解：在正方形ABCD中，∠ABD＝∠ADB＝45°，∵∠BAE＝22.5°，∴∠DAE＝90°﹣∠BAE＝90°﹣22.5°＝67.5°，在△ADE中，∠AED＝180°﹣45°﹣67.5°＝67.5°，∴∠DAE＝∠AED，∴AD＝DE＝4，∵正方形的边长为4，∴BD＝4，∴BE＝BD﹣DE＝4﹣4，∵EF⊥AB，∠ABD＝45°，∴△BEF是等腰直角三角形，∴EF＝BE＝×（4﹣4）＝4﹣2．故选：A．9．解：∵四边形ABCD是菱形，∠ABC＝70°，∴∠ABO＝35°，AC⊥BD，∴∠BAC＝55°，∵∠BEC＝∠BAC+∠ABE，∴55°≤∠BEC≤90°，故选：B．10．解：∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC，AB＝CD，∠B＝∠D，AB∥CD，∴∠EAC＝∠FCA，∵EF垂直平分AC，∴OA＝OC，EA＝EC，∴∠EAC＝∠ECA，∴∠FCA＝∠ECA，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE＝OF，∴四边形AFCE为平行四边形，∵EF垂直平分AC，∴平行四边形AFCE是菱形，①正确；∴AE＝CF，∴BF＝DE，在△ABF和△CDE中，，∴△ABF≌△CDE（SAS），②正确；∵四边形AFCE是菱形，∴AF＝CF，∵F为BC的中点，∴BF＝CF，∴AF＝CF＝BC，∴∠BAC＝90°，∵AB∥CD，∴∠ACD＝∠BAC＝90°，③正确；正确的个数有3个，故选：D．二．填空题11．解：∵四边形ABCD是矩形，BD＝4，∴AC＝BD＝4，∠ABC＝90°，∵∠ACB＝30°，∴AB＝2，BC＝＝＝2，∴矩形ABCD的面积是：2×2＝4，故答案为：4．12．解：∵正方形ABCD，边长为2，∴AD∥BC，AC＝2，∴∠ADE＝∠DPC，∵∠ADE＝∠AED，∴AE＝AD＝2，∠DPC＝∠AED＝∠CEP，∴CP＝CE＝AC﹣AE＝2﹣2，∴BP＝BC﹣CP＝2﹣（2﹣2）＝4﹣2．故答案为：4﹣2．13．解：∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝90°，∴∠ADB＝∠BDC＝45°，∵DC＝DE，∴AD＝DE，∴∠DAE＝∠DEA，∵∠ADE＝90°+52°＝142°，∴∠DAE＝19°，在△ADF和△CDF中，，∴△ADF≌△CDF（SAS），∴∠DAE＝∠DCF＝19°，故答案为：19．14．解：如图，延长CF，BA交于点G，连接EF，过点F作FH⊥CE于H，过点E作EM⊥CF 于M，∵四边形ABCD是矩形，且AB＝，BC＝4，∴AB∥CD，AB＝CD＝，∠D＝∠ABC＝∠CBE＝90°，∴∠DCF＝∠G，∵CF平分∠ECD，∴∠DCF＝∠FCE，FH＝DF，∴∠G＝∠ECF，∴EC＝EG，∴∠ECG是等腰三角形，∴CM＝MG，∵CE＝CF，∴△ECF是等腰三角形，∵EM⊥CF，FH⊥CE，∴EM和FH是等腰三角形腰上的高，∴EM＝FH＝DF，∴Rt△CDF≌Rt△CME（HL），∴CM＝CD＝，∴CG＝5，Rt△CBG中，BG＝＝＝3，设BE＝x，则EC＝EG＝3+x，Rt△CBE中，（3+x）2＝x2+42，解得：x＝，∴BE＝．故答案为：．15．解：如图，连接CG并延长，交AD于点M，连接EM，∵四边形ABCD为菱形，∠B＝60°，∴AD∥BC，∴∠A＝120°，∠MGD＝∠CGH，∵点G为HD的中点，∴HG＝DG，∵∠MGD＝∠CGH，∴△MGD≌△CGH（ASA），∴MG＝CG，MD＝CH＝BC＝AD，∴点G为MC的中点，点M为AD的中点，∵F，G分别为CE和CM的中点，∴FG是△CEM的中位线，∴FG＝EM，∴EM＝2FG＝4，∵E，M分别为AB和AD的中点，∴AE＝AM，∵∠A＝120°，∴EM＝AE＝4，∴AE＝4，∴AB＝2AE＝8．故答案为：8．三．解答题16．证明：∵四边形ABCD是矩形，∴AD＝BC，∵EF＝BF+BE，∵BC＝CE+BE，BF＝CE，∴EF＝BC，∴AD＝EF．17．证明：（1）∵四边形ABCD为正方形，∴AC平分∠BAD，又∵PM⊥AD，PN⊥AB，∴PM＝PN．（2）∵PM⊥AD，PN⊥AB，∠MAN＝90°，PM＝PN，∴四边形PMAN为正方形，∴∠MPN＝90°，即∠MPE+∠EPN＝90°．∵PE⊥PB，∴∠EPN+∠NPB＝90°，∴∠MPE＝∠NPB．∵PM⊥AD，PN⊥AB，∴∠PME＝∠PNB＝90°．在△PME和△PNB中，，∴△PME≌△PNB（ASA），∴EM＝BN．18．证明：（1）∵四边形ABCD是矩形，AF⊥DE，∴AD∥BC，AD＝BC，AB＝CD，∠C＝∠AFD＝90°，∴∠ADE＝∠DEC，∵DE＝BC，∴AD＝DE，在△ADF和△DEC中，，∴△ADF≌△DEC（AAS），∴AF＝CD，∴AF＝AB；（2）AD，BC，DE的长度等于AB，理由如下：∵△ADF≌△DEC，∴CE＝DF，∴BE＝EF，∵BE＝DF，∴BE＝EC＝DF＝EF，∴DE＝2EC，∵DE2＝EC2+CD2，∴DE＝AB，∴AD＝BC＝DE＝AB．。

《9.4矩形、菱形、正方形》同步优生提高训练苏科版八年级数学下册

2021学年苏科版八年级数学下册《9.4矩形、菱形、正方形》同步优生提高训练（附答案）1．如图所示的木质活动衣帽架是由三个全等的菱形组成，根据实际需要可调节A，E间的距离，已知菱形ABCD的边长为20cm，若A，E间的距离调节到60cm时，则这个活动衣帽架所围成的面积为（）A．600cm2B．600cm2C．450cm2D．900cm22．如图，正方形ABCD中，E、F是对角线BD上的两点，BD＝12，BE＝DF＝8，则四边形AECF的面积为（）A．24B．12C．4D．23．如图，在矩形ABCD中，AB＝4，BC＝8，对角线AC、BD相交于点O，过点O作OE 垂直AC交AD于点E，则DE的长是（）A．3B．5C．2.4D．2.54．如图，菱形中，对角线、BD交于点O，E为AD边中点，菱形ABCD的面积为24，OA ＝3，则OE的长等于（）A．B．C．5D．5．如图，在菱形ABCD中，AB＝BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE＝DF，连接BF与DE相交于点G，连接CG与BD相交于点H．给出如下几个结论：①∠DBC＝60°：②△AED≌△DFB；③GC与BD一定不垂直；④∠BGE的大小为定值．其中结论正确的是（）A．①②③B．①②④C．①③④D．②③④6．如图，在▱ABCD中，M，N是BD上两点，BM＝DN，连接AM，MC，CN，NA，添加一个条件，使四边形AMCN是菱形，这个条件是（）A．OM＝AC B．MB＝MO C．BD⊥AC D．∠AMB＝∠CND 7．如图，在菱形ABCD中，∠BAD＝60°，AC与BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE分别交AC、AD于点F、G，连接OG，则下列结论中一定成立的是（）①OG＝AB；②与△DEG全等的三角形共有5个；③四边形ODEG与四边形OBAG面积相等；④由点A、B、D、E构成的四边形是菱形．A．①③④B．①④C．①②③D．②③④8．如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形ABCD中，AB＝3，AC＝2，则四边形ABCD的面积为（）A．B．C．D．59．如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与AD，AC，BC相交于点E，O，F．下列结论正确的个数有（）①四边形AFCE为菱形；②△ABF≌△CDE；③当F为BC中点时，∠ACD＝90°．A．0个B．1个C．2个D．3个10．下列说法中，正确的是（）A．当x≠﹣1时，有意义B．对角线相等的四边形是矩形C．三角形三边垂直平分线的交点到三个顶点的距离相等D．若a＜b，则m2a＜m2b一定成立11．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，CD为中线，延长CB至点E，使BE＝BC，连接DE，F为DE的中点，连接BF，若BF＝3，则BC的长为（）A．6B．3C．8D．612．如图，矩形ABCD的对角线相交于点O，OF⊥AB，BE⊥AC，E是OC的中点，OF＝4，则BD的长为（）A．16B．8C．4D．813．如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，则EF的最小值为（）A．1.2B．1.25C．2.4D．2.514．如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE，设AC＝12，BD＝16，则OE的长为（）A．8B．9C．10D．1215．如图，四边形ABCD是正方形，它的四个顶点都在坐标轴上，且正方形边长为8，则点A的坐标为（）A．（8，0）B．（4，0）C．（4，0）D．（8，0）16．如图，平面内三点A、B、C，AB＝5，AC＝4，以BC为对角线作正方形BDCE，连接AD，则AD的最大值是（）A．5B．9C．9D．17．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC 交EF于G，下列结论：①BE＝DF；②∠DAF＝15°，③AC垂直平分EF，④，其中正确结论有（）个．A．1B．2C．3D．418．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，H是AF的中点，CH ＝3，那么CE的长是（）A．3B．4C．D．19．如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC，PF⊥CD，垂足分别为点E，F，连接AP，EF，给出下列四个结论：①AP＝EF；②∠PFE＝∠BAP；③PD＝EC；④△APD一定是等腰三角形．其中正确的结论有（）A．①②④B．①②③C．②③④D．①②③④20．如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列结论：①OA＝OD；②AD⊥EF；③AE+DF＝AF+DE；④当∠BAC＝90°时，四边形AEDF是正方形．其中一定正确的是（）A．①②③B．②③④C．①③④D．①②③④21．如图，A（0，4），B（8，0），点C是x轴正半轴上一点，D是平面内任意一点，若以A、B、C、D为顶点的四边形是菱形，则点D的坐标为．22．如图，在△ABC中，点D、E、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA，下列四种说法：①四边形AEDF是平行四边形；②如果∠BAC＝90°，那么四边形AEDF是菱形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果AB＝AC，那么四边形AEDF是菱形．其中，正确的有．（只填写序号）23．有两个全等矩形纸条，长与宽分别为11和7，按如图所示的方式交叉叠放在一起，则重合部分构成的四边形BGDH的周长为．24．如图，在菱形ABCD中，∠BAD＝60°，AC与BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE分别交AC、AD于点F、G，连接OG，则下列结论中一定成立的是．（把所有正确结论的序号都填在横线上）①OG＝AB；②与△EGD全等的三角形共有5个；③S四边形ODGF＞S△ABF；④由点A、B、D、E构成的四边形是菱形．25．如图，已知四边形ABCD是菱形，点E，F分别在线段AB，AD上，EG∥BC，FH∥DC，点G，H分别在线段CD，BC上，EG和FH相交于点P，BE＝DF．（1）求证：四边形HCGP是菱形．（2）若四边形BHPE是菱形，求证：点E是线段AB的中点．26．如图，已知四边形ABCD为正方形，AB＝4，点E为对角线AC上一动点，连接DE、过点E作EF⊥DE．交BC点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．27．如图，在平行四边形ABCD中，点E、F在对角线BD上，且BE＝DF．（1）求证：AF＝CE；（2）若AF＝CF，说明四边形AFCE为菱形．28．如图1，四边形ABCD为菱形，对角线AC，BD相交于点O，点E为OC上的动点．（1）当AD＝AE时，OE＝1，OD＝5，求菱形ABCD的面积；（2）如图2，当OE＝OD时，过点A作CD的垂线，垂足为F，交ED延长线于点G，求证：GE＝AO．29．如图，在菱形ABCD中，AC，BD相交于点O，过B，C两点分别作AC，BD的平行线，相交于点E．（1）求证：四边形BOCE是矩形；（2）连接EO交BC于点F，连接AF，若∠ABC＝60°，AB＝2，求AF的长．30．正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF＝45°．（1）求证：EF＝AE+CF；（2）当AE＝1时，求EF的长．参考答案1．解：连接AE，如图所示：∵AE间的距离调节到60cm，木质活动衣帽架是由三个全等的菱形组成，∴AC＝AE＝20（cm），∵菱形ABCD的边长为20cm，∴AC＝AB＝BC，∴△ABC是等边三角形，∴这个活动衣帽架所围成的面积为：3S菱形ABCD＝3×2S△ABC＝3×2×AC2＝×202＝600（cm2），故选：B．2．解：连接AC，∵四边形ABCD是正方形，∴AO＝CO，BO＝DO，AC⊥BD，AC＝BD＝12，∴AO＝CO＝BO＝DO，∵BE＝DF＝8，∴BF＝DE＝BD﹣BE＝4，∴OE＝OF，EF＝DF﹣DE＝4，∴四边形AECF是菱形，∴菱形AECF的面积＝AC•EF＝×12×4＝24，故选：A．3．解：连接CE，如图：在矩形ABCD中，AB＝4，BC＝8，∴∠CDE＝90°，AD＝BC＝8，AB＝DC＝4，AO＝OC，∵OE⊥AC，∴AE＝CE，设DE＝x，则AE＝CE＝8﹣x，在Rt△CDE中，由勾股定理得：DE2+DC2＝CE2，∴x2+42＝（8﹣x）2，解得x＝3．∴DE的长为3．故选：A．4．解：∵菱形的对角线、BD交于点O，OA＝3，∴AC＝2AO＝6，∵菱形ABCD的面积为24，∴＝24，∴BD＝8，DO＝4，又∵AC⊥BD，∴AD＝＝＝5，又∵E为AD边中点，∴OE＝AD＝，故选：A．5．解：∵ABCD为菱形，∴AB＝AD，∵AB＝BD，∴△ABD为等边三角形，∴∠A＝∠BDF＝60°＝∠DBC，又∵AE＝DF，AD＝BD，∴△AED≌△DFB，故①、②正确；当点E，F分别是AB，AD中点时，由（1）知，△ABD，△BDC为等边三角形，∵点E，F分别是AB，AD中点，∴∠BDE＝∠DBG＝30°，∴DG＝BG，∴△GDC≌△BGC，∴∠DCG＝∠BCG，∴CH⊥BD，即CG⊥BD，故③错误；∵∠BGE＝∠BDG+∠DBF＝∠BDG+∠GDF＝60°，为定值，故④正确；综上所述，正确的结论有①②④，故选：B．6．证明：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD∵对角线BD上的两点M、N满足BM＝DN，∴OB﹣BM＝OD﹣DN，即OM＝ON，∴四边形AMCN是平行四边形，∵BD⊥AC，∴MN⊥AC，∴四边形AMCN是菱形．故选：C．7．解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA，AB∥CD，OA＝OC，OB＝OD，AC⊥BD，∴∠BAG＝∠EDG，△ABO≌△BCO≌△CDO≌△AOD，∵CD＝DE，∴AB＝DE，在△ABG和△DEG中，，∴△ABG≌△DEG（AAS），∴AG＝DG，∴OG是△ACD的中位线，∴OG＝CD＝AB，①正确；∵AB∥CE，AB＝DE，∴四边形ABDE是平行四边形，∵∠BCD＝∠BAD＝60°，∴△ABD、△BCD是等边三角形，∴AB＝BD＝AD，∠ODC＝60°，∴OD＝AG，四边形ABDE是菱形，④正确；∴AD⊥BE，由菱形的性质得：△ABG≌△BDG≌△DEG，在△ABG和△DCO中，，∴△ABG≌△DCO（SAS），∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG，②不正确；∵OB＝OD，∴S△BOG＝S△DOG，∵四边形ABDE是菱形，∴S△ABG＝S△DGE，∴四边形ODEG与四边形OBAG面积相等，故③正确；故选：A．8．解：过点A作AE⊥CD于E，AF⊥BC于F，连接AC，BD交于点O，∵两条纸条宽度相同，∴AE＝AF．∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形．∵S▱ABCD＝BC•AF＝CD•AE．又∵AE＝AF．∴BC＝CD，∴四边形ABCD是菱形，∴AO＝CO＝1，BO＝DO，AC⊥BD，∴BO＝＝＝2，∴BD＝4，∴四边形ABCD的面积＝＝4，故选：A．9．解：∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC，AB＝CD，∠B＝∠D，AB∥CD，∴∠EAC＝∠FCA，∵EF垂直平分AC，∴OA＝OC，EA＝EC，∴∠EAC＝∠ECA，∴∠FCA＝∠ECA，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE＝OF，∴四边形AFCE为平行四边形，∵EF垂直平分AC，∴平行四边形AFCE是菱形，①正确；∴AE＝CF，∴BF＝DE，在△ABF和△CDE中，，∴△ABF≌△CDE（SAS），②正确；∵四边形AFCE是菱形，∴AF＝CF，∵F为BC的中点，∴BF＝CF，∴AF＝CF＝BC，∴∠BAC＝90°，∵AB∥CD，∴∠ACD＝∠BAC＝90°，③正确；正确的个数有3个，故选：D．10．解：A、∵当x＞﹣1时，有意义，∴选项A不符合题意；B、∵对角线相等的平行四边形是矩形，∴选项B不符合题意；C、∵三角形三边垂直平分线的交点到三个顶点的距离相等，∴选项C符合题意；D、∵0＜a＜b，若m＝0时，则m2a＝m2b，∴选项D不符合题意；故选：C．11．解：∵BE＝BC，∴点B为CE的中点，∵点F为DE的中点，∴BF为△CDE的中位线，∴CD＝2BF＝2×3＝6，在Rt△ABC中，∵∠ACB＝90°，CD为中线，∴CD＝AD＝BD＝6，∴AB＝BD+AD＝6+6＝12，在Rt△ABC中，∵AB2＝BC2+AC2，AC＝6，AB＝12，∴BC＝＝＝6．故选：A．12．解：∵E是OC的中点，BE⊥AC，∴直线BE是线段OC的垂直平分线，∴BO＝BC，∵四边形ABCD为矩形，∴BO＝CO，∴BO＝BC＝CO，∴△OBC为等边三角形，∴∠CBO＝60°，∵四边形ABCD为矩形，∴AO＝BO，∠ABC＝∠DAB＝90°，∵OF⊥AB，∴AF＝BF，∴OF为△BAD的中位线，∴AD＝2OF＝8，在Rt△BAD中，∠DBA＝90°﹣60°＝30°，∴BD＝2AD＝16．故选：A．13．解：连接AP，如图：∵PE⊥AB，PF⊥AC，∴∠AEP＝∠AFP＝90°，∵∠BAC＝90°，∴四边形AFPE是矩形，∴EF＝AP，要使EF最小，只要AP最小即可，当AP⊥BC时，AP最短，∵∠BAC＝90°，AB＝3，AC＝4，∴BC＝＝＝5，∵△ABC的面积＝×4×3＝×5×AP，∴AP＝2.4，即EF＝2.4，故选：C．14．解：∵DE∥AC，CE∥BD，∴四边形OCED为平行四边形，∵四边形ABCD是菱形，AC＝12，BD＝16，∴AC⊥BD，OA＝OC＝AC＝6，OB＝OD＝BD＝8，∴∠DOC＝90°，CD＝＝＝10，∴平行四边形OCED为矩形，∴OE＝CD＝10，故选：C．15．解：∵四边形ABCD是正方形，边长为8，∴∠AOB＝90°，OA＝OB，AB＝8，设OA＝OB＝x，Rt△AOB中，OA2+OB2＝AB2，∴x2+x2＝82，解得x＝4，∴OA＝4，即A（4，0），故选：C．16．解：如图，将△BDA绕点D顺时针旋转90°得到△CDM，由旋转不变性可知：AB＝CM＝5，DA＝DM，∠ADM＝90°，∴△ADM是等腰直角三角形，∴AD＝AM，∴当AM的值最大时，AD的值最大，∵AM≤AC+CM，∴AM≤9，∴AM的最大值为9，∴AD的最大值为．故选：D．17．解：∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，∠B＝∠BCD＝∠D＝∠BAD＝90°，∵△AEF等边三角形，∴AE＝EF＝AF，∠EAF＝60°，∴∠BAE+∠DAF＝30°，在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF，∠BAE＝∠DAF，故①正确；∵∠BAE+∠DAF＝30°，∴∠DAF+∠DAF＝30°，即∠DAF＝15°，故②正确；∵BC＝CD，∴BC﹣BE＝CD﹣DF，即CE＝CF，∵Rt△ABE≌Rt△ADF，∴AE＝AF，∴AC垂直平分EF，∴EG＝FG，故③正确；∵∠ECF＝90°，EG＝FG，∴CG＝EF，设EC＝FC＝x，由勾股定理，得EF＝＝x，∴CG＝EF＝x＝CE，故④正确；综上所述，正确的有①②③④，共4个．故选：D．18．解：连接AC，CF，如图，∵四边形ABCD和四边形CEFG为正方形，∴AB＝BC＝1，CE＝EF，∠ACD＝∠GCF＝45°．∴∠ACF＝45°×2＝90°．∵H是AF的中点，CH＝3，∴AF＝2CH＝6．在Rt△ABC中，AC＝BC＝．在Rt△ACF中，CF＝＝．在Rt△ECF中，∵CE2+EF2＝CF2，CE＝EF，∴CE＝CF＝＝．故选：D．19．解：延长PF交AB于点G，∵PF⊥CD，AB∥CD，∴PG⊥AB，即∠PGB＝90°．∵PE⊥BC，PF⊥CD，∴四边形GBEP为矩形，又∵∠PBE＝∠BPE＝45°，∴BE＝PE，∴四边形GBEP为正方形，四边形PFCE为矩形．∴GB＝BE＝EP＝GP，∴GP＝PE，AG＝CE＝PF，又∠AGP＝∠C＝90°，∴△AGP≌△FPE（SAS）．∴AP＝EF，∠PFE＝∠BAP，故①、②正确；在Rt△PDF中，由勾股定理得PD＝，故③正确；∵P在BD上，∴当AP＝DP、AP＝AD、PD＝DA时，△APD才是等腰三角形，∴△APD是等腰三角形共有3种情况，故④错误．∴正确答案有①②③，故选：B．20．解：如果OA＝OD，则四边形AEDF是矩形，∠A＝90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠F AD，在△AED和△AFD中，，∴△AED≌△AFD（AAS），∴AE＝AF，DE＝DF，∴AE+DF＝AF+DE，∴③正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO＝FO，又∵AE＝AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A＝90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE＝DF，∴四边形AEDF是正方形，∴④正确．综上，可得正确的是：②③④．故选：B．21．解：当AB为菱形的对角线时，如图1，设菱形的边长为m，∵A（0，4），B（8，0），∴OA＝4，OB＝8，∵四边形ABCD为菱形，∴CA＝AD＝BC，AD∥BC，∴CA＝CB＝8﹣m，在Rt△AOC中，42+（8﹣m）2＝m2，解得m＝5，∴D（5，4）；当AB为菱形的边时，如图2，AB＝＝4，∵四边形ABCD为菱形，∴BC＝AB＝AD＝4，AD∥BC，∴D（4，4），综上所述，D点坐标为（5，4）或（4，4）．故答案为（5，4）或（4，4）．22．解：∵DE∥CA，DF∥BA，∴四边形AEDF是平行四边形，故①正确；∵∠BAC＝90°，四边形AEDF是平行四边形，∴四边形AEDF是矩形，故②错误；∵AD平分∠BAC，四边形AEDF是平行四边形，∴四边形AEDF是菱形，故③正确；∵AB＝AC，四边形AEDF是平行四边形，不能得出AE＝AF，故四边形AEDF不一定是菱形，故④错误；故答案为：①③．23．解：由题意得：矩形ABCD≌矩形BEDF，∴∠A＝90°，AB＝BE＝7，AD∥BC，BF∥DE，AD＝11，∴四边形BGDH是平行四边形，∴平行四边形BGDH的面积＝BG×AB＝BH×BE，∴BG＝BH，∴四边形BGDH是菱形，∴BH＝DH＝DG＝BG，设BH＝DH＝x，则AH＝11﹣x，在Rt△ABH中，由勾股定理得：72+（11﹣x）2＝x2，解得：x＝，∴BH＝，∴四边形BGDH的周长＝4BH＝，故答案为：．24．解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA，AB∥CD，OA＝OC，OB＝OD，AC⊥BD，∴∠BAG＝∠EDG，△ABO≌△BCO≌△CDO≌△AOD，∵CD＝DE，∴AB＝DE，在△ABG和△DEG中，，∴△ABG≌△DEG（AAS），∴AG＝DG，∴OG是△ACD的中位线，∴OG＝CD＝AB，①正确；∵AB∥CE，AB＝DE，∴四边形ABDE是平行四边形，∵∠BCD＝∠BAD＝60°，∴△ABD、△BCD是等边三角形，∴AB＝BD＝AD，∠ODC＝60°，∴OD＝AG，四边形ABDE是菱形，④正确；∴AD⊥BE，由菱形的性质得：△ABG≌△BDG≌△DEG，在△ABG和△DCO中，，∴△ABG≌△DCO（SAS），∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG，②不正确；∵OB＝OD，AG＝DG，∴OG是△ABD的中位线，∴OG∥AB，OG＝AB，∴△GOD∽△ABD，△ABF∽△OGF，∴△GOD的面积＝△ABD的面积，△ABF的面积＝△OGF的面积的4倍，AF：OF＝2：1，∴△AFG的面积＝△OGF的面积的2倍，又∵△GOD的面积＝△AOG的面积＝△BOG的面积，∴S四边形ODGF＝S△ABF；不正确；正确的是①④．故答案为：①④．25．证明：（1）∵四边形ABCD是菱形，∴AB∥CD，AD∥BC，∵EG∥BC，FH∥DC，∴四边形HCGP、四边形BCGE、四边形CDFH都是平行四边形，∴BE＝CG，CH＝DF，∵BE＝DF，∴CG＝CH，∴平行四边形HCGP是菱形；（2）由（1）可知，BE＝CG＝CH，∵四边形BHPE是菱形，∴BE＝BH，∴BE＝BH＝CH＝BC，∵四边形ABCD是菱形，∴AB＝BC，∴BE＝AB，∴点E是线段AB的中点．26．解：（1）如图所示，过E作EM⊥BC于M点，过E作EN⊥CD于N点，∵正方形ABCD，∴∠BCD＝90°，∠ECN＝45°，∴∠EMC＝∠ENC＝∠BCD＝90°，且NE＝NC，∴四边形EMCN为正方形，∵四边形DEFG是矩形，∴EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，∴∠DEN＝∠MEF，又∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴ED＝EF，∴矩形DEFG为正方形，（2）CE+CG的值为定值，理由如下：∵矩形DEFG为正方形，∴DE＝DG，∠EDC+∠CDG＝90°，∵四边形ABCD是正方形，∵AD＝DC，∠ADE+∠EDC＝90°，∴∠ADE＝∠CDG，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴AE＝CG，∴AC＝AE+CE＝AB＝×4＝8，∴CE+CG＝8是定值．27．（1）证明：连接AC交BD于O，如图所示：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∵BE＝DF，∴OE＝OF，∴四边形AFCE是平行四边形，∴AF＝CE；（2）说明如下：由（1）得：四边形AFCE是平行四边形，又∵AF＝CF，∴平行四边形AFCE为菱形．28．解：（1）∵四边形ABCD是菱形，∴AC⊥BD，AC＝2AO，BD＝2DO＝10，∵AD＝AE，∴AD＝AE＝AO+OE＝1+OEA，∵AD2＝OD2+AO2，∴（1+OA）2＝25+AO2，∴AO＝12，∴AC＝24，∴菱形ABCD的面积＝＝120；（2）如图，过点G作GH⊥AC于H，∵四边形ABCD是菱形，∴AC⊥BD，AO＝CO，AD＝CD，∠DAC＝∠DCA，∵OE＝OD，∴∠DEO＝∠EDO＝45°，∵GH⊥AC，∴∠HED＝∠HGE＝45°，∴GH＝HE，GE＝GH，设∠DAC＝∠DCA＝x，∴∠EDC＝45°﹣x＝∠GDF，∵AF⊥CF，∴∠FGD＝90°﹣∠GDF＝45°+x，∵∠DAF＝90°﹣2x，∴∠ADC＝180°﹣∠GAD﹣∠AGD＝45°+x，∴∠ADC＝∠AGD，∴AG＝AD，在△AHG和△DOA中，，∴△AHG≌△DOA（AAS），∴GH＝AO，∴GE＝GH＝AO．29．（1）证明：∵BE∥AC，EC∥BD，∴四边形BOCE是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD，∴∠BOC＝90°，∴平行四边形BOCE是矩形；（2）解：如图，∵四边形ABCD是菱形，∴AB＝BC，∵∠ABC＝60°，∴△ABC是等边三角形，∴BC＝AB＝2，∠BAC＝60°，∵四边形BOCE是矩形，∴BF＝CF＝BC＝1，∴AF⊥BC，∠BAF＝∠BAC＝30°，∴∠AFB＝90°，∴AF＝BF＝．30．解：（1）证明：延长BC至H，使CH＝AE，连接DH，如图，∵四边形ABCD是正方形，∴AD＝CD，∠A＝∠DCE＝90°．∴△DAE≌△DCH（SAS）．∴DE＝DH，∠ADE＝∠CDH．∵∠ADC＝90°，∠EDF＝45°，∴∠ADE+∠FDC＝45°．∴∠FDC+∠CDH＝45°．即∠FDH＝45°．∴∠EDF＝∠FDH＝45°．在△EDF和△HDF中，．∴△EDF≌△HDF（SAS）．∴EF＝FH．∵FH＝FC+CH＝FC+AE，∴EF＝AE+FC．（2）设EF＝x，则FH＝x．∵正方形ABCD的边长为3，∴AB＝BC＝3．∵AE＝1，∴BE＝2，CH＝1．∴FC＝x﹣1．∴BF＝BC﹣CF＝3﹣（x﹣1）＝4﹣x．在Rt△BEF中，∵BE2+BF2＝EF2，∴22+（4﹣x）2＝x2．解得：x＝．∴EF＝。

苏教版八年级数学下册第9章矩形、菱形、正方形同步练习题 (1)

第7课时矩形、菱形、正方形(2)1．下列说法中，正确的是( )A．有1个角是直角的四边形是矩形B．2条对角线相等的四边形是矩形．C．2条对角线互相垂直的四边形是矩形D．有3个角是直角的四边形是矩形2．下列关于矩形的说法中正确的是( )A．对角线相等的四边形是矩形B．对角线互相平分的四边形是矩形C．矩形的对角线互相垂直且平分D．矩形的对角线相等且互相平分3．如图，工人师傅砌门时，要想检验门框ABCD是否符合设计要求（即门框是否为矩形），在确保两组对边分别平行的前提下，只要测量出对角线AC、BD 的长度，然后看它们是否相等就可判断了．(1)当AC_______（填“等于”或“不等于”）BD时，门框符合要求；(2)这种做法的根据是___________________________________．4．如图，在四边形ABCD中，已知AB∥DC，AB＝D C．在不添加任何辅助线的前提下，要想该四边形成为矩形，只需再加上一个条件是_______（填上你认为正确的一个答案即可）．5．如图，在△ABC中，AB＝AC，D为BC中点，四边形ABDE是平行四边形，则四边形ADCE的形状是_______．6．如图，O是矩形ABCD的对角线的交点，E、F、G、H分别是OA、OB、OC、OD上的点，且AE＝BF＝CG＝DH．(1)四边形EFGH是矩形吗？请证明你的结论；(2)若E、F、G、H分别是OA、OB、OC、OD的中点，且DG⊥AC，OF＝2 cm，求矩形ABCD的面积．7．平行四边形ABCD中，AC、BD是两条对角线，如果添加一个条件，即可推出平行四边形ABCD是矩形，那么这个条件是( )A．AB＝BC B．AC＝BD C．AC⊥BD D．AB⊥BD8．下列说法正确的是( )A．两个角为直角的四边形是矩形B．有一组对边相等，一组对角是直角的四边形是矩形C．一组对边平行，一个角是直角的四边形是矩形D．两条对角线垂直且相等的四边形是矩形9．□ABCD中，AC交BD于点O，再添加一个条件，仍不能判定四边形ABCD 是矩形的是( )A．AB＝AD B．OA＝OB C．AC＝BD D．DC⊥BC 10．如图所示，已知□ABCD，下列条件：①AC＝BD．②AB＝AD，③∠1＝∠2，④AB⊥BC中，能说明□ABCD是矩形的有_______（填写序号）．11．如图，在△ABC中，AB＝AC，将△ABC绕点C旋转180°得到△FEC，连接AE、BF．当∠ACB为_______度时，四边形ABFE为矩形．12．如图，在△ABC中，AB＝AC，AD⊥BC于点D，AN是△ABC的外角∠CAM 的平分线，CE⊥AN于点E．求证：四边形ADCE为矩形．13．如图，将□ABCD的边DC延长到点E，使CE＝DC，连接AE，交BC于点F．(1)求证：△ABF≌△ECF．(2)若∠AFC＝2∠D，连接AC、BE．求证：四边形ABEC是矩形．参考答案1．D 2．D 3．(1)等于(2)对角线相等的平行四边形是矩形4．∠A＝90°5．矩形6．(1)四边形EFGH是矩形．(2)16(cm2)7．B 8．B 9．A 10．①④11．60 12．略13．略考点综合专题：一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1．(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2－4x＋3＝0的根，则该三角形的周长可以是（）A．5 B．7 C．5或7 D．102．(广安中考)一个等腰三角形的两条边长分别是方程x2－7x＋10＝0的根，则该等腰三角形的周长是（）A．12 B．9C．13 D．12或93．(罗田县期中)菱形ABCD的一条对角线长为6，边AB的长是方程x2－7x＋12＝0的一个根，则菱形ABCD的周长为（）A．16 B．12 C．16或12 D．244．(烟台中考)等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2－6x＋n－1＝0的两根，则n的值为（）A．9 B．10C．9或10 D．8或105．(齐齐哈尔中考)△ABC的两边长分别为2和3，第三边的长是方程x2－8x＋15＝0的根，则△ABC的周长是．6．(西宁中考)若矩形的长和宽是方程2x2－16x＋m＝0(0＜m≤32)的两根，则矩形的周长为．【方法8】7．已知一直角三角形的两条直角边是关于x的一元二次方程x2＋(2k－1)x ＋k2＋3＝0的两个不相等的实数根，如果此直角三角形的斜边是5，求它的两条直角边分别是多少．【易错4】◆类型二一元二次方程与函数的综合8．(泸州中考)若关于x的一元二次方程x2－2x＋kb＋1＝0有两个不相等的实数根，则一次函数y＝kx＋b的大致图象可能是（）9．(安顺中考)若一元二次方程x2－2x－m＝0无实数根，则一次函数y＝(m ＋1)x＋m－1的图象不经过（）A．第四象限B．第三象限C．第二象限D．第一象限10．(葫芦岛中考)已知k、b是一元二次方程(2x＋1)(3x－1)＝0的两个根，且k＞b，则函数y＝kx＋b的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限11．(广元中考)从3，0，－1，－2，－3这五个数中抽取一个数，作为函数y＝(5－m2)x和关于x的一元二次方程(m＋1)x2＋mx＋1＝0中m的值．若恰好使函数的图象经过第一、三象限，且使方程有实数根，则满足条件的m的值是．12．(甘孜州中考)若函数y＝－kx＋2k＋2与y＝kx(k≠0)的图象有两个不同的交点，则k的取值范围是．.◆类型三一元二次方程与二次根式的综合13．(达州中考)方程(m －2)x 2－3－mx ＋14＝0有两个实数根，则m 的取值范围为（）A ．m ＞52B ．m ≤52且m ≠2 C ．m ≥3 D ．m ≤3且m ≠214．(包头中考)已知关于x 的一元二次方程x 2＋k －1x －1＝0有两个不相等的实数根，则k 的取值范围是．考点综合专题：一元二次方程与其他知识的综合1．B 2.A 3.A 4.B 5.86．16 解析：设矩形的长和宽分别为x 、y ，根据题意得x ＋y ＝8，所以矩形的周长为2(x ＋y)＝16.7．解：∵一元二次方程x 2＋(2k －1)x ＋k 2＋3＝0有两个不相等的实数根，∴Δ>0，∴(2k －1)2－4(k 2＋3)>0，即－4k －11>0，∴k<－114，令其两根分别为x 1，x 2，则有x 1＋x 2＝1－2k ，x 1·x 2＝k 2＋3，∵此方程的两个根分别是一直角三角形的两条直角边，且此直角三角形的斜边长为5，∴x 21＋x 22＝52，∴(x 1＋x 2)2－2x 1·x 2＝25，∴(1－2k)2－2(k 2＋3)＝25，∴k 2－2k －15＝0，∴k 1＝5，k 2＝－3，∵k<－114，∴k ＝－3, ∴把k ＝－3代入原方程得到x 2－7x ＋12＝0，解得x 1＝3，x 2＝4，∴直角三角形的两直角边分别为3和4.8．B9．D 解析：∵一元二次方程x2－2x－m＝0无实数根，∴Δ＜0，∴Δ＝4－4×1×(－m)＝4＋4m＜0，∴m＜－1，∴m＋1＜1－1，即m＋1＜0，m－1＜－1－1，即m－1＜－2，∴一次函数y＝(m＋1)x＋m－1的图象不经过第一象限．故选D.10．B 11.－2 12.k>－12且k≠013．B 14.k≥1。

9.4苏科版八年级数学下册9.2矩形、菱形、正方形——正方形练习及答案

八年级数学（正方形习题训练）一．（填空题，共7小题，每小题5分）1、如图，己知P是正方形ABCD对角线BD上--点，且BP=BC,则∠ACP= 度.2、己知正方形ABCD中，CM=CD, MN丄AC,连接CN,则∠DCN= .第1题图第2题图第3题图第4题图3.如图，以正方形ABCD的边CD为一边，在正方形ABCD内作等边△CDE，BE交AC于点M，则∠AMD= .4.如图，正方形ABCD的边长为2, E为CD的中点，以点A为中心把△ADE顺时针旋转90°,得到△ABF，连接EF，则EF的长等_______________.5.如图，正方形ABCD的边长为a, AE平分∠DAC, EF⊥AC交于F,则EF=_________.第5题图第6题图第7题图6.6.如图，已知正方形的边长为2, △BPC是等边三角形，则△CDP的面积是__________，△BPD的面积是_________________.7.如图,正方形ABCD中，点E、F分别在边BC、CD上，且AE=EF=FA.下列结论:①△ABE≌△ADF；②CE=CF；③∠AEB=75°；④BE+DF=EF；⑤S△ABE+S△ADF=S△CEF，其中正确的是___________.二.（解答题，共4小题，共65分）1.（15分）如图，点B、C分别在两条直线y=2x和y=kx上.,点A、D是x轴上两点，已知四边形ABCD是正方形，则求k的值2.（15分）如图，正方形ABCD中，E是BD上一-点，AE的延长线交CD于F,交BC的延长线于G, M 是FG的中点.（1）求证：①∠1 = ∠2；②EC丄MC.（2）试问当∠1等于多少度时，△ECG为等腰三角形？请说明理由.3.（15分）如图所示，正方形ABCD中，在AD的延长线上取点E、F,使DE=AD, DF=BD,连接BF 分别交CD、CE于H、G。

求证：△GHD是等腰三角形.4.（20分）点E 是正方形ABCD 外一点，点F 在DE 上，且AF=AE=2, ∠EAF=90°, FB=3. （1）求证：△AFD≌△AEB；（2）求∠DEB的度数.（3）求正方形ABCD的面积答案及解析一．（填空题，共7小题）1.22.5°2.22.5°3.120°4.102-5.()a13-6.17.二.（解答题，共4小题）1.2.3.4.。

苏科版数学八年级下册 9.4矩形菱形正方形大题综合练习(含答案解析)

苏科版数学八年级下册9.4矩形菱形正方形大题综合练习1.如图菱形ABCD中，∠ADC=60°，M、N分别为线段AB，BC上两点，且BM=CN，且AN，CM所在直线相交于E.（1）证明△BCM≌△CAN；（2）∠AEM=________°；（3）求证DE平分∠AEC；（4）试猜想AE，CE，DE之间的数量关系并证明.【答案】（1）证明：如图1中，连接AC．∵四边形ABCD是菱形，∴AB=BC=CD=AD，∵∠ADC=60°，∴△ACD，△ABC是等边三角形，∴BC=AC，∠B=∠ACN=60°，在△BCM和△CAN中，{BC=AC∠B=∠ACNBM=CN，∴△BCM≌△CAN（2）60（3）证明：如图2中，作DG⊥AN于G．DH⊥MC交MC的延长线于H．∵∠AEM=60°，∴∠AEC=120°，∵∠DGE=∠H=90°，∴∠GEH+∠GDH=180°，∴∠GDH=∠ADC=60°，∴∠ADG=∠CDH ，在△DGA 和△DHC 中，{∠DGA =∠H =90∘∠ADG =∠CDH DA =DC，∴△DGA ≌△DHC ，∴DG=DH ，∵DG ⊥AN ，DH ⊥MC ，∴∠DEG=∠DEH ．∴DE 平分∠AEC ．（4）证明：结论：EA+EC=ED ．理由如下：如图2中，由（3）可知，∠GED=60°，在Rt △DEG 中，∵∠EDG=30°，∴DE=2EG ，易知△DEG ≌△DEH ，∴EG=EH ，∴EA+EC=EG+AG+EH-CH ，∵△DGA ≌△DHC ，∴GA=CH ，∴EA+EC=2EG=DE ，∴EA+EC=ED.【解析】【解答】解：（2）如图1中，∵△BCM ≌△CAN ，∴∠BCM=∠CAN ，∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°．故答案为60．【分析】(1)连接AC，因为∠ADC=60°，利用菱形四边相等的性质，可知△ADC为等边三角形，所以AC=BC ,又因为菱形的对角线平分一组对角，所以∠ACN=60°=∠B，因为BM=CN，所以△BCM≌△CAN；（2）因为∠AEM=∠CEN，对顶角相等，由全等可知∠AEM=∠CEN=∠B=60°；（3）过点D做AE、CM两边的垂线，利用角角边可得到△DHC≌△DGA，可得DH=DG，再用角平分线的性质，到一个角两边距离相等的点在这个角的角平分线上；（4）由全等可知EA+EC=2EG，又因为在Rt△中30°的角所对的边等于斜边的一半，所以EA +EC=DE.2.综合：（1）如图1，纸片▱ABCD中，AD=5，S▱ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE'的位置，拼成四边形AEE'D，则四边形AEE'D的形状为A. 平行四边形B. 菱形C. 矩形D. 正方形（2）如图2，在（1）中的四边形纸片AEE'D中，在EE'上取一点F，使EF=4，剪下△AEF，剪下△AEF，将它平移至△DE'F'的位置，拼成四边形AFF'D．①求证：四边形AFF'D是菱形；②求四边形AFF'D的两条对角线的长．【答案】（1）C（2）解：如图2中，①证明：∵AD=5，S□ABCD=15，∴AE=3．又∵在图2中，EF=4，∴在Rt△AEF中，AF═5．∴AF=AD=5，又∵AF∥DF'，AF=DF，∴四边形AFF'D是平行四边形．∴四边形AFF'D是菱形．②解：连接AF'，DF，在Rt△DE'F中，∵E'F=E'E﹣EF=5﹣4=1，DE'=3，∴DF═√E′D2+E′F2= √10．在Rt△AEF'中，∵EF'=E'E+E'F'=5+4=9，AE=3，∴AF'═√AE2+EF′2= √32+92=3 √10【解析】【解答】（1）解：如图1中，∵四边形ABCD是平行四边形，∴AD=BC，∵BE=CE′，∴AD∥EE′，AD=EE′，∴四边形AEE′D是平行四边形，∵∠AEE′=90°，∴四边形AEE′D是矩形，故选C．【分析】（1）根据矩形的判定方法即可判定；（2）①通过计算证明AF=AD=5，证明四边形AFF′D是平行四边形即可；②连接AF'，DF，分别利用勾股定理计算即可；3.如图，正方形ABCD中，AB=4，P是CD边上的动点（P点不与C、D重合），过点P作直线与BC的延长线交于点E，与AD交于点F，且CP=CE，连接DE、BP、BF，设CP═x，△PBF 的面积为S1，△PDE的面积为S2．（1）求证：BP⊥DE．（2）求S1﹣S2关于x的函数解析式，并写出x的取值范围．（3）分别求当∠PBF=30°和∠PBF=45°时，S1﹣S2的值．【答案】（1）解：如图1中，延长BP交DE于M．∵四边形ABCD是正方形，∴CB=CD，∠BCP=∠DCE=90°，∵CP=CE，∴△BCP≌△DCE，∴∠BCP=∠CDE，∵∠CBP+∠CPB=90°，∠CPB=∠DPM，∴∠CDE+∠DPM=90°，∴∠DMP=90°，∴BP⊥DE．（2）解：由题意S1﹣S2= 12（4+x）•x﹣12•（4﹣x）•x=x2（0＜x＜4）．（3）解：①如图2中，当∠PBF=30°时，∵∠CPE=∠CEP=∠DPF=45°，∠FDP=90°，∴∠PFD=∠DPF=45°，∴DF=DP，∵AD=CD，∴AF=PC，∵AB=BC，∠A=∠BCP=90°，∴△BAF≌△BCP，∴∠ABF=∠CBP=30°，∴x=PC=BC•tan30°= 4√3，3∴S1﹣S2=x2= 16．3②如图3中，当∠PBF=45°时，在CB上截取CN=CP，理解PN．由①可知△ABF≌△BCP，∴∠ABF=∠CBP，∵∠PBF=45°，∴∠CBP=22.5°，∵∠CNP=∠NBP+∠NPB=45°，∴∠NBP=∠NPB=22.5°，∴BN=PN= √2x，∴√2x+x=4，∴x=4 √2﹣4，∴S1﹣S2=（4 √2﹣4）2=48﹣32 √2．【解析】【分析】（1）首先延长BP交DE于M．然后依据SAS可证明△BCP≌△DCE，依据全等三角形的性质可得到∠BCP=∠CDE，由∠CBP+∠CPB=90°，∠CPB=∠DPM，即可推出∠CDE+∠DPM=90°；（2）根据题意可得到S1-S2=S△PBE-S△PDE，然后依据三角形的面积公式列出函数关系式即可；（3）分当∠PBF=30°和∠PBF=45°两种情形分别求出PC 的长，最后再利用（2）中结论进行计算即可.4.如图，在矩形ABCD 中，BC ＞AB ，∠BAD 的平分线AF 与BD ，BC 分别交于点E ，F ，点O 是BD 的中点，直线OK ∥AF ，交AD 于点K ，交BC 于点G ．（1）求证：△DOK ≌△BOG ；（2）探究线段AB 、AK 、BG 三者之间的关系，并证明你的结论；（3）若KD=KG ，BC=2 √2 ﹣1，求KD 的长度．【答案】（1）证明：∵在矩形ABCD 中，AD ∥BC ，∴∠KDO=∠GBO ，∠DKO=BGO ．∵点O 是BD 的中点；∴DO=BO ．在△DOK 和△BOG 中， {∠KDO =∠GBO∠DKO =∠BGO DO =BO∴△DOK ≌△BOG （AAS ）．（2）解：AB+AK=BG ；证明如下：∵四边形ABCD 是矩形；∴∠BAD=∠ABC=90°，AD ∥BC ．又∵AF 平分∠BAD ，∴∠BAF=∠BFA=45°．∴AB=BF ．∵OK ∥AF ，AK ∥FG ，∴四边形AFGK 是平行四边形．∴AK=FG ．∵BG=BF+FG ；∴BG=AB+AK ．（3）解：∵四边形AFGK 是平行四边形．∴AK=FG ，AF=KG又∵△DOK ≌△BOG ，且KD=KG ，∴AF=KG=KD=BG ．设AB=a ，则AF=KG=KD=BG= √2 a ．∴AK=2 √2 ﹣1﹣ √2 a ，FG=BG ﹣BF= √2 a ﹣a ．∴2 √2﹣1﹣√2a= √2a﹣a．解得a=1．∴KD= √2a= √2．【解析】【分析】（1）在矩形ABCD中，AD∥BC，得到∠KDO=∠GBO，∠DKO=BGO，DO=BO，得到△DOK≌△BOG（AAS）；（2）四边形ABCD是矩形，得到∠BAD=∠ABC=90°，AD∥BC，又AF平分∠BAD，得到∠BAF=∠BFA=45°，AB=BF，由OK∥AF，AK∥FG，得到四边形AFGK 是平行四边形，得到AK=FG，BG=BF+FG，即BG=AB+AK；（3）四边形AFGK是平行四边形，得到AK=FG，AF=KG，又△DOK≌△BOG，且KD=KG，得到AF=KG=KD=BG，设AB=a，则AF=KG=KD=BG=√2a，得到AK=2√2﹣1-√2a，FG=BG﹣BF=√2a﹣a，解得a=1，得到KD=√2a=√2．5.综合题（1）感知：如图①，四边形ABCD、CEFG均为正方形．易知BE=DG．（2）探究：如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．（3）如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上．若AE=3ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为________ ．【答案】（1）证明：∵四边形ABCD、四边形CEFG均为正方形，∴BC=CD，CE=CG，∠BCD=∠ECG=90°，∴∠BCD﹣∠ECD=∠ECG﹣∠ECD，即∠BCE=∠DCG，在△BCE和△DCG中，{CB=CD∠BCE=∠DCGCE=CG，∴△BCE≌△DCG，∴BE=DG．（2）∵四边形ABCD、四边形CEFG均为菱形，∴BC=CD，CE=CG，∠BCD=∠A，∠ECG=∠F，∵∠A=∠F，∴∠BCD=∠ECG，∴∠BCD﹣∠ECD=∠ECG﹣∠ECD，即∠BCE=∠DCG，∴△BCE≌△DCG．，∴BE=DG．（3）20【解析】【解答】解：应用：∵四边形ABCD是菱形，S△EBC=8，∴S△AEB+S△EDC=8，∵AE=3DE，∴S△AEB=3S△EDC，∴S△EDC=6，S△EDC=2，∵△BCE≌△DCG，∴S△DGC=S△EBC=8，∴S△ECG=8+2=10，∴菱形CEFG的面积=2•S△EGC=20，故答案为20．【分析】感知：根据正方形的性质，得到BC=CD，CE=CG，∠BCD=∠ECG=90°，得到∠BCE=∠DCG，得到△BCE≌△DCG，BE=DG；探究：由四边形ABCD、四边形CEFG均为菱形，得到BC=CD，CE=CG，∠BCD=∠A，∠ECG=∠F，由∠A=∠F，得到∠BCE=∠DCG，△BCE≌△DCG，BE=DG；应用：由四边形ABCD是菱形，△EBC的面积为8，AE=3DE，得到S△AEB=3S△EDC，得到S△EDC=6，S△EDC=2，由△BCE≌△DCG，得到S△DGC=S△EBC=8，S△ECG=8+2=10，所以菱形CEFG的面积=2•S△EGC=20.6.如图，矩形OABC的顶点A、C分别在x、y的正半轴上，点B的坐标为（3，4），一次函x+b的图象与边OC、AB分别交于点D、E，并且满足OD=BE．点M是线段DE 数y=23上的一个动点．（1）求b的值；（2）连结OM，若三角形ODM的面积与四边形OAEM的面积之比为1：3，求点M的坐标；（3）设点N是x轴上方平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点N 的坐标．【答案】（1）解：y=23x+b中，令x=0，解得y=b，则D的坐标是（0，b），OD=b，∵OD=BE，∴BE=b，则E的坐标是（3，4﹣b），把E的坐标代入y=23x+b得4﹣b=﹣2+b，解得：b=3（2）解：S四边形OAED= 12（OD+AE）•OA= 12×（3+1）×3=6，∵三角形ODM的面积与四边形OAEM的面积之比为1：3，∴S△ODM=1.5．设M的横坐标是a，则12×3a=1.5，解得：a=1，把x=a=1代入y=﹣23x+3得y=﹣23× 43+3= 73．则M的坐标是（1，73）（3）解：当四边形OMDN是菱形时，如图（1），M的纵坐标是32，把y= 32代入y=﹣23x+3，得﹣23x+3= 32，解得：x= 94，则M的坐标是（94，32），则N的坐标是（﹣94，32）；当四边形OMND是菱形时，如图（2）OM=OD=3，设M的横坐标是m，则纵坐标是﹣23m+3，则m2+（﹣23m+3）2=9，解得：m= 3613或0（舍去）．则M的坐标是（3613，1513）．则DM的中点是（1813，2713）．则N的坐标是（3613，5413）．故N的坐标是（﹣94，32）或（3613，5413）．【解析】【分析】（1）首先在一次函数的解析式中令x=0，即可求得D的坐标，则OD的长度即可求得，OD=b，则E的坐标即可利用b表示出来，然后代入一次函数解析式即可得到关于b的方程，求得b的值；（2）首先求得四边形OAED的面积，则△ODM的面积即可求得，设出M的横坐标，根据三角形的面积公式即可求得M的横坐标，进而求得M的坐标；（3）分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论，四边形OMDN 是菱形时，M是OD的中垂线与DE的交点，M关于OD的对称点就是N；四边形OMND是菱形，OM=OD，M在直角DE上，设出M的坐标，根据OM=OD即可求得M的坐标，则根据ON和DM的中点重合，即可求得N的坐标．7.如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上，AH=2．（1）若DG=6，求AE的长；（2）若DG=2，求证：四边形EFGH是正方形．【答案】（1）解：∵AD=6，AH=2∴DH=AD﹣AH=4∵四边形ABCD是矩形∴∠A=∠D=90°∴在Rt△DHG中，HG2=DH2+DG2在Rt△AEH中，HE2=AH2+AE2∵四边形EFGH是菱形∴HG=HE∴DH2+DG2=AH2+AE2即42+62=22+AE2∴AE= =4（2）证明：∵AH=2，DG=2，∴AH=DG，∵四边形EFGH是菱形，∴HG=HE，在Rt△DHG和Rt△AEH中，，∴Rt△DHG≌Rt△AEH（HL），∴∠DHG=∠AEH，∵∠AEH+∠AHE=90°，∴∠DHG+∠AHE=90°，∴∠GHE=90°，∵四边形EFGH是菱形，∴四边形EFGH是正方形【解析】【分析】（1）先根据矩形的性质，利用勾股定理列出表达式：HG2=DH2+DG2，HE2=AH2+AE2，再根据菱形的性质，得到等式DH2+DG2=AH2+AE2，最后计算AE的长；（2）先根据已知条件，用HL判定Rt△DHG≌Rt△AEH，得到∠DHG=∠AEH，因为∠AEH+∠AHE=90°，∠DHG+∠AHE=90°，可得菱形的一个角为90°，进而判定该菱形为正方形．8.如图1，直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=8，BC=6，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AD 于点P，连接AC交NP于点Q，连接MQ．设运动时间为t秒．（1）AM=________，AP=________．（用含t的代数式表示）（2）当四边形ANCP为平行四边形时，求t的值（3）如图2，将△AQM沿AD翻折，得△AKM，是否存在某时刻t，①使四边形AQMK为为菱形，若存在，求出t的值；若不存在，请说明理由②使四边形AQMK为正方形，则AC等于．【答案】（1）8﹣2t；2+t（2）解：∵四边形ANCP为平行四边形时，CN=AP，∴6﹣t=8﹣（6﹣t），解得t=2（3）解：①存在时刻t=1，使四边形AQMK为菱形．理由如下：∵NP⊥AD，QP=PK，∴当PM=PA时有四边形AQMK为菱形，∴6﹣t﹣2t=8﹣（6﹣t），解得t=1，②要使四边形AQMK为正方形．∵∠ADC=90°，∴∠CAD=45°．∴四边形AQMK为正方形，则CD=AD，∵AD=8，∴CD=8，∴AC=8 √2．【解析】【解答】解：（1）如图1．∵DM=2t，∴AM=AD﹣DM=8﹣2t．∵在直角梯形ABCD中，AD∥BC，∠ADC=90°，NP⊥AD于点P，∴四边形CNPD为矩形，∴DP=CN=BC﹣BN=6﹣t，∴AP=AD﹣DP=8﹣（6﹣t）=2+t；故答案为：8﹣2t，2+t．【分析】（1）由DM=2t，根据AM=AD﹣DM即可求出AM=8﹣2t；先证明四边形CNPD为矩形，得出DP=CN=6﹣t，则AP=AD﹣DP=2+t；（2）根据四边形ANCP为平行四边形时，可得6﹣t=8﹣（6﹣t），解方程即可；（3）①由NP⊥AD，QP=PK，可得当PM=PA时有四边形AQMK为菱形，列出方程6﹣t﹣2t=8﹣（6﹣t），求解即可，②要使四边形AQMK为正方形，由∠ADC=90°，可得∠CAD=45°，所以四边形AQMK为正方形，则CD=AD，由AD=8，可得CD=8，利用勾股定理求得AC即可．9.已知▱OABC的顶点A、C分别在直线x=2和x=4上，O为坐标原点，直线x=2分别与x轴和OC边交于D、E，直线x=4分别与x轴和AB边的交于点F、G．（1）如图，在点A、C移动的过程中，若点B在x轴上，①直线AC是否会经过一个定点，若是，请直接写出定点的坐标；若否，请说明理由．②▱OABC是否可以形成矩形？如果可以，请求出矩形OABC的面积；若否，请说明理由．③四边形AECG是否可以形成菱形？如果可以，请求出菱形AECG的面积；若否，请说明理由．（2）在点A 、C 移动的过程中，若点B 不在x 轴上，且当▱OABC 为正方形时，直接写出点C 的坐标．【答案】（1）解：①是，经过定点（3，0）．理由如下：如图1中，连接AC 交OB 于K ．∵四边形OABC 是平行四边形，∴OK=KB ，BC ∥OA ，BC=OA ，∴∠CBF=∠AOD ，在△DOA 和△FBC 中，{∠ODA =∠CFB =90°∠AOD =∠CBF OA =BC，∴△DOA ≌△FBC ，∴OD=FB=2，∴OB=6，∵OK=KB ，∴OK=3，∴K （3，0），∴直线AC 经过定点K （3，0）．②可以．利用如下：当∠OCB=90°时，四边形OABC 是矩形，由（1）可知△DOA ≌△FBC ，∴OD=BF=2，∵∠OCF+∠FCB=90°，∠FCB+∠CBF=90°，∴∠OCF=∠CBF，∵∠CFO=∠CFB，∴△CFO∽△BFC，∴CFBF = OFCF，∴CF2= 4CF，∴CF=2 √2，∴S矩形OABC=2•S△OBC=2× 12× 6×2√2=12 √2．③可以．理由如下：如图3中，易知当OE=EC=AE时，四边形AECG是菱形．由（1）可知，△DOA≌△FBC，∴AD=CF，∵DE= 12CF，设DE=x，则AD=CF=2x，OE=AE=3x，在Rt△ADE中，∵OE2=OD2+DE2，∴9x2=x2+4，∴x= √22，∴AE= 3√22，∴S菱形AECG=AE•DF= 3√22×2=3 √2（2）解：如图4中，当四边形OABC是正方形时，易证△DOA≌△FCO，∴OD=CF=2，∴点C坐标（4，2），根据对称性C′（4，﹣2）时，也满足条件．综上所述，点C坐标为（4，2）或（4，﹣2）【解析】【分析】（1）①是，经过定点（3，0）．如图1中，连接AC交OB于K，只要证明OD=FB=2，推出OB=6，即可解决问题．②当∠OCB=90°时，四边形OABC是矩形，由（1）可知△DOA≌△FBC，推出OD=BF=2，由△CFO∽△BFC，可得CFBF = OFCF，由此即可解决问题．③可以．如图3中，易知当OE=EC=AE时，四边形AECG是菱形．由（1）可知，△DOA≌△FBC，推出AD=CF，易知DE= 12CF，设DE=x，则AD=CF=2x，OE=AE=3x，在Rt△ADE中，根据OE2=OD2+DE2，列出方程即可解决问题．（2）如图4中，当四边形OABC是正方形时，易证△DOA≌△FCO，推出OD=CF=2，推出点C坐标（4，2），根据对称性C′（4，﹣2）时，也满足条件．10.如图1，在平面直角坐标系中，正方形ABCO的顶点C、A分别在x、y轴上，A（0，6）、E（0，2），点H、F分别在边AB、OC上，以H、E、F为顶点作菱形EFGH（1）当H（﹣2，6）时，求证：四边形EFGH为正方形（2）若F（﹣5，0），求点G的坐标（3）如图2，点Q为对角线BO上一动点，D为边OA上一点，DQ⊥CQ，点Q从点B出发，沿BO方向移动．若移动的路径长为3，直接写出CD的中点M移动的路径长为________．【答案】（1）证明：如图1中，∵E（0，2），H（﹣2，6），∴OE=AH=2，∵四边形ABCO是正方形，∴∠HAE=∠EOF=90°，∵四边形EFGH是菱形，∴EH=EF，在Rt△AHE和Rt△OEF中，{AH=EOHE=EF，∴Rt△AHE≌△Rt△OEF，∴∠AEH=∠EFO，∵∠EFO+∠FEO=90°，∴∠AEH+∠FEO=90°，∴∠HEF=90°，∴四边形EFGH是正方形（2）解：如图1中，连接GE、FH交于点K．∵F（﹣5，0），E（0，2），∴OF=5，OE=2，EA=4，∵HE=EF，∴52+22=42+AH2，∴AH= √13，∴H（﹣√13，6），∵四边形EFGH是菱形，∴HK=KF，KE=KG，设G（m，n），则有m+02= −5−√132，n+22= 6+02，∴m=﹣5﹣√13，n=4，∴G（﹣5﹣√13，4）（3）3√22【解析】【解答】（3）解：如图2中，如图2中，作MN⊥CO于M．∵MN∥OD，CM=MD，∴CN=ON，∴MN垂直平分线段CO，∴点M在线段OC的垂直平分线上运动，如图3中，易知当点Q与B重合时，点M与BD的中点N重合，当BQ=3时，作EQ⊥BC于E，延长EQ交OA于F，延长OM交BC于H，连接NM（线段MN的长即为点M的运动轨迹的长），∵QC=QD，∠CEQ=∠QFD，易证∠ECQ=∠FQD，∴△EQC≌△FDQ，∴EQ=DF=BE= 3√22，CE=OF=6﹣3√22，∴DO=6﹣3 √2，∵CM=DM，∠CMH=∠OMD，∠CHM=∠DOM，∴△HMC≌△OMD，∴OM=HM，CH=OD=6﹣3 √2，BH=3 √2，∵ON=NB，∴MN= 12BH= 3√22，∴点M的运动的路径的长为3√22．故答案为3√2．2【分析】（1）只要证明Rt△AHE≌△Rt△OEF，推出∠AEH=∠EFO，由∠EFO+∠FEO=90°，推出∠AEH+∠FEO=90°，推出∠HEF=90°，即可解决问题．（2）如图1中，连接GE、FH交于点K．首先求出点H的坐标，设G（m，n），根据中点坐标公式，列出方程组即可解决问题．（3）如图2中，作MN⊥CO于M．由MN∥OD，CM=MD，推出CN=ON，推出MN 垂直平分线段CO，推出点M在线段OC的垂直平分线上运动，如图3中，易知当点Q与B 重合时，点M与BD的中点N重合，当BQ=3时，作EQ⊥BC于E，延长EQ交OA于F，延长OM交BC于H，连接NM（线段MN的长即为点M的运动轨迹的长），想办法求出BH 的长，即可利用三角形的中位线定理解决问题．11.如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB, AC上的一动点,且满足BP=AQ,D 是BC的中点.（1）求证:△PDQ是等腰直角三角形.（2）当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.【答案】（1）证明：连接AD.∵△ABC是等腰直角三角形,D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,又∵BP=AQ,∴△BPD≌△AQD,∴PD=QD,∠BDP=∠ADQ,∵∠BDP+∠ADP=90°,∴∠ADP+∠ADQ=∠PDQ=90°,∴△PDQ为等腰直角三角形（2）解：当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:由(1)知△ABD为等腰直角三角形,当P为AB的中点时,DP⊥AB,即∠APD=90°,又∵∠BAC=90°,∠PDQ=90°,∴四边形APDQ为矩形,AB,∴四边形APDQ为正方形又∵DP=AP= 12【解析】【分析】连接AD，根据直角三角形的性质可得AD=BD=DC，从而证明△BPD≌△AQD，得到PD=QD，∠ADQ=∠BDP，则△PDQ是等腰三角形；由∠BDP+∠ADP=90°，得出∠ADP+∠ADQ=90°，得到△PDQ是直角三角形，从而证出△PDQ是等腰直角三角形；若四边形APDQ是正方形，则DP⊥AB，得到P点是AB的中点．12.如图，在等边三角形ABC中，点D是BC边的中点，以AD为边作等边三角形ADE.（1）求∠CAE的度数；（2）取AB边的中点F，连结CF、CE，试证明四边形AFCE是矩形．【答案】（1）解：在等边三角形ABC中，∵点D是BC边的中点，∴∠DAC＝30°.又∵△ADE为等边三角形，∴∠DAE＝60°.∴∠CAE＝∠DAE－∠DAC＝30°（2）解：由(1)知，∠EAF＝90°，由F为AB的中点知，∠CFA＝90°，∴CF∥EA.在等边三角形ABC中，CF＝AD.在等边三角形ADE中，AD＝EA.∴CF＝EA.∴四边形AFCE为平行四边形．又∵∠CFA＝90°，∴四边形AFCE为矩形．【解析】【分析】根据等边三角形三线合一的特点，易求得∠DAC=30°，则∠CAE=∠DAE-∠DAC．先证明四边形AECF是平行四边形，然后根据∠CFA=∠FAE=90°，由矩形的定义判定四边形AFCE是矩形.13.如图，以△ABC的三边为边在BC的同一侧分别作三个等边三角形，即△ABD、△BCE、△ACF，请回答下列问题：（1）四边形ADEF是什么四边形？（2）当△ABC满足什么条件时，四边形ADEF是矩形？（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在？【答案】（1）解：四边形ADEF是平行四边形．理由：∵△ABD，△EBC都是等边三角形．∴AD=BD=AB，BC=BE=EC∠DBA=∠EBC=60°∴∠DBE+∠EBA=∠ABC+∠EBA．∴∠DBE=∠ABC．在△DBE和△ABC中∵BD=BA∠DBE=∠ABCBE=BC，∴△DBE≌△ABC．∴DE=AC．又∵△ACF是等边三角形，∴AC=AF．∴DE=AF．同理可证：AD=EF，∴四边形ADEF平行四边形（2）解：∵四边形ADEF是矩形，∴∠FAD=90°．∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°．∴∠BAC=150°时，四边形ADEF是矩形（3）解：当∠BAC=60°时，以A，D，E，F为顶点的四边形不存在．理由如下：若∠BAC=60°，则∠DAF=360°﹣∠BAC﹣∠DAB﹣∠FAC=360°﹣60°﹣60°﹣60°=180°．此时，点A、D、E、F四点共线，∴以A、D、E、F为顶点的四边形不存在【解析】【分析】可先证明△DBE≌△ABC ，又∵△ACF是等边三角形，∴AC=AF．∴DE=AF，同理可得AD=EF，根据两组对边分别相等的四边形是平行四边形，可证四边形ADEF是平行四边形；若四边形ADEF是矩形，则∠DAF=90°，又有∠BAD=∠FAC=60°，可得∠BAC=150°，故∠BAC=150°时，四边形ADEF是矩形；根据∠BAC=60°时，∠DAF=180°，此时D、A、F三点在同一条直线上，A，D，E，F为顶点的四边形就不存在.14.如图1，在Rt△ABC中，∠ACB=90°，点D是边AB的中点，点E在边BC上，AE=BE，点M是AE的中点，联结CM，点G在线段CM上，作∠GDN=∠AEB交边BC于N．（1）如图2，当点G和点M重合时，求证：四边形DMEN是菱形；（2）证明：如图1，当点G和点M、C不重合时，求证：DG=DN．【答案】（1）证明：如图2中，∵AM=ME．AD=DB，∴DM∥BE，∴∠GDN+∠DNE=180°，∵∠GDN=∠AEB，∴∠AEB+∠DNE=180°，∴AE∥DN，∴四边形DMEN是平行四边形，∵DM== BE，EM== AE，AE=BE，∴DM=EM，∴四边形DMEN是菱形（2）证明：如图1中，取BE的中点F，连接DM、DF．由（1）可知四边形EMDF是菱形，∴∠AEB=∠MDF，DM=DF，∴∠GDN=∠AEB，∴∠MDF=∠GDN，∴∠MDG=∠FDN，∵∠DFN=∠AEB=∠MCE+∠CME，∠GMD=∠EMD+∠CME，、在Rt△ACE中，∵AM=ME，∴CM=ME，∴∠MCE=∠CEM=∠EMD，∴∠DMG=∠DFN，∴△DMG≌△DFN，∴DG=DN【解析】【分析】（1）如图2中，首先证明四边形DMEN是平行四边形，再证明ME=MD 即可证明．（2）如图1中，取BE的中点F，连接DM、DF．只要证明△DMG≌△DFN即可．15.如图，四边形ABCD是菱形，对角线AC、BD相交于点O，分别延长OB，OD到点E，F，使BE=DF，顺次连接A、E、C、F各点．（1）求证：∠FAD=∠EAB．（2）若∠ADC=130°，要使四边形AECF是正方形，求∠FAD的度数．【答案】（1）证明：∵菱形ABCD的对角线AC，BD相交于点O，∴AD=AB，∠ADB=∠ABD，∴∠ADF=∠ABE，在△FAD与△EAB中，∴△FAD≌△EAB（SAS），∴∠FAD=∠EAB；（2）解：∵四边形AECF对角线互相垂直平分，∴只要∠EAF=90°即得四边形BFDE是正方形，∵∠ADC=130°，∴∠DAB=180°﹣130°=50°∴∠FAD+∠EAB=40°，∵∠FAD=∠EAB，∴∠FAD= ×40°=20°【解析】【分析】（1）由题意易证∠ADF=∠ABE，又因为DF=EB，AD=AB，于是可△FAD≌△EAB，；（2）由已知可得四边形AECF对角线互相垂直平分，只要∠EAF=90°即得四边形AECF是正方形，由∠FAD=∠EAB，再证得∠DAB=50°，可得∠FAD+∠EAB=40°，于是∠FAD= 1×40°=20°．216.某数学兴趣小组在数学课外活动中，研究三角形和正方形的性质时，做了如下探究：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD 为边在AD右侧作正方形ADEF，连接CF．（1）观察猜想如图1，当点D在线段BC上时，①BC与CF的位置关系为：________，②BC，DC，CF之间的数量关系为：________；（将结论直接写在横线上）（2）数学思考如图2，当点D在线段CB的延长线上时，（1）中的①，②结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．（3）拓展延伸如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2，CD=BC，请直接写出GE的长．【答案】（1）垂直；BC=CF+CD（2）解：CF⊥BC成立；BC=CD+CF不成立，CD=CF+BC．理由如下：∵正方形ADEF中，AD=AF，∵∠BAC=∠DAF=90°，∴∠BAD=∠CAF，在△DAB与△FAC中，{AD=AF∠BAD=∠CAFAB=AC，∴△DAB≌△FAC（SAS），∴∠ABD=∠ACF，∵∠BAC=90°，AB=AC，∴∠ACB=∠ABC=45°．∴∠ABD=180°﹣45°=135°，∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°，∴CF⊥BC．∵CD=DB+BC，DB=CF，∴CD=CF+BC ．（3）解：过A 作AH ⊥BC 于H ，过E 作EM ⊥BD 于M ，EN ⊥CF 于N ，如图3所示：∵∠BAC=90°，AB=AC ，∴BC= √2 AB=2 √2 ，AH= 12 BC= √2 ，∴CD= 14 BC= √22 ，CH= 12 BC= √2 ，∴DH= 3√22 ，由（2）证得BC ⊥CF ，CF=BD= 5√22 ，∵四边形ADEF 是正方形，∴AD=DE ，∠ADE=90°，∵BC ⊥CF ，EM ⊥BD ，EN ⊥CF ，∴四边形CMEN 是矩形，∴NE=CM ，EM=CN ，∵∠AHD=∠ADC=∠EMD=90°，∴∠ADH+∠EDM=∠EDM+∠DEM=90°，∴∠ADH=∠DEM ，在△ADH 与△DEM 中， {∠ADH =∠DEM∠AHD =∠DMEAD =DE， ∴△ADH ≌△DEM （AAS ），∴EM=DH= 3√22 ，DM=AH= √2 ，∴CN=EM= 3√22 ，EN=CM= 3√22 ，∵∠ABC=45°，∴∠BGC=45°，∴△BCG 是等腰直角三角形，∴CG=BC=2 √2 ，∴GN=CG ﹣CN= √22 ， ∴EG= √GN 2+EN 2 = (√22)(3√22)= √5 ．【解析】【解答】解：（1）①正方形ADEF 中，AD=AF ，∵∠BAC=∠DAF=90°，∴∠BAD=∠CAF ，在△DAB 与△FAC 中， {AD =AF∠BAD =∠CAFAB =AC，∴△DAB ≌△FAC （SAS ），∴∠B=∠ACF ，∴∠ACB+∠ACF=90°，即BC ⊥CF ；故答案为：垂直；②△DAB ≌△FAC ，∴CF=BD ，∵BC=BD+CD ，∴BC=CF+CD ；故答案为：BC=CF+CD ；【分析】（1）①根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB ≌△FAC ，根据全等三角形的性质即可得到结论；②由正方形ADEF 的性质可推出△DAB ≌△FAC ，根据全等三角形的性质得到CF=BD ，∠ACF=∠ABD ，根据余角的性质即可得到结论；（2）根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB ≌△FAC ，根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论．（3）根据等腰直角三角形的性质得到BC= √2 AB=2 √2 ，AH= 12 BC= √2 ，求得DH= 3√22 ，根据正方形的性质得到AD=DE ，∠ADE=90°，根据矩形的性质得到NE=CM ，EM=CN ，由角的性质得到∠ADH=∠DEM ，根据全等三角形的性质得到EM=DH= 3√22 ，DM=AH= √2 ，等量代换得到CN=EM= 3√22 ，EN=CM= 3√22，根据等腰直角三角形的性质得到CG=BC=2 √2 ，根据勾股定理即可得到结论．17.如图，四边形ABCD 中，对角线AC 、BD 相交于点O ，AO=CO ，BO=DO ，且∠ABC+∠ADC=180°．（1）求证：四边形ABCD 是矩形．（2）DF ⊥AC ，若∠ADF ：∠FDC=3：2，则∠BDF 的度数是多少？【答案】（1）证明：∵AO=CO ，BO=DO ，∴四边形ABCD 是平行四边形，∴∠ABC=∠ADC，∵∠ABC+∠ADC=180°，∴∠ABC=∠ADC=90°，∴四边形ABCD是矩形（2）解：∵∠ADC=90°，∠ADF：∠FDC=3：2，∴∠FDC=36°，∵DF⊥AC，∴∠DCO=90°﹣36°=54°，∵四边形ABCD是矩形，∴CO=OD，∴∠ODC=∠DCO=54°，∴∠BDF=∠ODC﹣∠FDC=18°．【分析】（1）根据平行四边形的判定得出四边形ABCD是平行四边形，求出∠ABC=90°，【解析】根据矩形的判定得出即可；（2）求出∠FDC的度数，根据三角形内角和定理求出∠DCO，根据矩形的性质得出OD=OC，求出∠CDO，即可求出答案．18.如图①，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PE=PA，PE交CD于F．（1）求证：PC=PE；（2）求∠CPE的度数；（3）如图②，把正方形ABCD改为菱形ABCD，其它条件不变，若∠ABC=65°，则∠CPE=________度．【答案】（1）证明：在正方形ABCD中，AB=BC，∠ABP=∠CBP=45°，在△ABP和△CBP中，{AB＝BC∠ABP＝∠CBPPB＝PB，∴△ABP≌△CBP（SAS），∴PA=PC，∵PA=PE，∴PC=PE（2）解：由（1）知，△ABP≌△CBP，∴∠BAP=∠BCP，∵PA=PE，∴∠PAE=∠PEA，∴∠CPB=∠AEP，∵∠AEP+∠PEB=180°，∴∠PEB+∠PCB=180°，∴∠ABC+∠EPC=180°，∵∠ABC=90°，∴∠EPC=90°（3）115°【解析】【解答】（3）∠EPC=115°，理由：在菱形ABCD中，AB=BC，∠ABP=∠CBP，在△ABP和△CBP中，{AB＝BC∠ABP＝∠CBPPB＝PB，∴△ABP≌△CBP（SAS），∴∠BAP=∠BCP，∵PA=PE，∴∠DAP=∠DCP，∴∠PAE=∠PEA，∴∠CPB=∠AEP，∵∠AEP+∠PEB=180°，∴∠PEB+∠PCB=180°，∴∠ABC+∠EPC=180°．∴∠CPE=180°-∠ABC=180°-65°=115°【分析】（1）根据正方形的性质得到△ABP≌△CBP，得到对应边相等，得到PC=PE；（2）由（1）知△ABP≌△CBP，得到对应边对应角相等，根据等边对等角和两直线平行同旁内角互补，求出∠CPE的度数；（3）根据菱形的性质，得到△ABP≌△CBP，得到得到对应边对应角相等，根据等边对等角和两直线平行同旁内角互补，求出∠CPE的度数.19.实践探究，解决问题如图1，△ABC中，AD为BC边上的中线，则S△ABD=S△ACD．（1）在图2中，E、F分别为矩形ABCD的边AD、BC的中点，且AB=4，AD=8，则S阴影=________；（2）在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S阴影和S平行四边形ABCD 之间满足的关系式为________；（3）在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S阴影和S四边形ABCD之间还满足（2）中的关系式吗？若满足，请予以证明，若不满足，说明理由．解决问题：（4）在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和（即S1+S2+S3+S4的值）．【答案】（1）16（2）S阴影=12S平行四边形ABCD（3）解：满足（2）中的关系式，理由如下：连接BD，由图1得S△EBD= 12 S△ABD同理S△BDF= 12S△BDC∴S四边形EBFD=S△EBD+S△BDF= 12S四边形ABCD（4）解：设四边形的空白区域分别为a，b，c，d 由上述性质可以得出：a+S2+S3= 12S△ACD①，c+S1+S4= 12S△ACB②，b+S2+S1= 12S△ABD③，d+S4+S3= 12S△ACD④，①+②+③+④得，a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四边形ABCD⑤而S四边形ABCD=a+b+c+d+S1+S2+S3+S4+S阴影⑥所以联立⑤⑥得S1+S2+S3+S4=S阴影=20平方米．【解析】【解答】解：（1）∵E、F分别为矩形ABCD的边AD、BC的中点，且AB=4，AD=8，∴S阴影= 12×8×4=16，故答案为：16；（2）∵E、F分别为平行四边形ABCD的边AD、BC的中点，∴S阴影= 12S平行四边形ABCD；故答案为：S阴影= 12S平行四边形ABCD；【分析】（1）由矩形的性质容易得出结果；（2）由平行四边形的性质容易得出结果；（3）连接BD，由题意得出S△EBD= 12 S△ABD同理S△BDF= 12S△BDC，即可得出结论；（4）设四边形的空白区域分别为a，b，c，d，由（3）可以得出：a+S2+S3= 12S△ACD①，c+S1+S4= 12S△ACB②，b+S2+S1= 12S△ABD③，d+S4+S3= 12S△ACD④，进一步得出结论即可．20.如图，E、F分别是□ABCD的边BC、AD上的点，且BE＝DF．（1）求证：四边形AECF是平行四边形；（2）若BC＝10，∠BAC＝90°，且四边形AECF是菱形，求BE的长．【答案】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，且AD=BC，∴AF∥EC，∵BE=DF，∴AF=EC，∴四边形AECF是平行四边形．（2）解：∵四边形AECF是菱形，如图所示：∴AE=EC，∴∠1=∠2，∵∠3=90°﹣∠2，∠4=90°﹣∠1，∴∠3=∠4，∴AE=BE，∴BE=AE=CE= 12BC=5．【解析】【分析】（1）利用平行四边形的性质得出对边平行且相等，结合已知，可证出AECF是平行四边形；（2）利用菱形的邻边相等的性质，可证出BE=AE=CE= 12BC=5.。

八年级数学下册第9章中心对称图形—平行四边形 9.4 矩形、菱形、正方形同步练习苏科版

9.4矩形、菱形、正方形一、选择题AB，以点O为圆心，OC长为半径画圆，延长CO交⊙O于点D，1.在△ABC中，CO为AB边上的中线，且OC=12连结AD，BD，则四边形ADBC是( )A。

正方形 B. 矩形C. 菱形D. 邻边相等的四边形2.符合下列条件的四边形不一定是菱形的是( )A。

四边都相等的四边形B。

两组邻边分别相等的四边形C. 对角线互相垂直平分的四边形D. 两条对角线分别平分一组对角的四边形3.如图，菱形ABCD的对角线AC、BD的长分别是6cm和8cm，AE⊥BC于点E,则AE的长是( )cmA. 245B。

2√5cmcmC。

485D. 5√3cm4.如图，矩形ABCD的两条对角线相交于点O，∠AOB=60∘，AO=4，则AB的长是( )A。

4 B。

5 C。

6 D。

85.菱形的两条对角线长分别为12与16，则此菱形的周长是( )A。

10 B。

30 C。

40 D。

1006.如图,在矩形ABCD中，对角线AC、BD交于点O，∠AOB=60∘，BD=8cm，则CD的长度为( )A。

8cmB. 6cmC。

4cmD。

2cm7.已知,在四边形ABCD中,∠A=∠B=90∘,要使四边形ABCD为矩形，那么需要添加的一个条件是( )A。

AB=BC B. AD=BC C. AD=AB D。

BC=CD8.如图，EF过矩形ABCD对角线的交点O,且分别交AD、BC于点E、F已知AB=3，BC=4，则图中阴影部分的面积是( )A。

3 B。

4 C. 6 D。

129.如图,ABCD、AEFC都是矩形，而且点B在EF上，这两个矩形的面积分别是S1，S2，则S1，S2的关系是( )A. S1>S2B。

S1<S2C. S1=S2D. 3S1=2S210.如图,在菱形ABCD中,对角线AC、BD相交于点O，且AC=2,若AB=2，则BD的长为( )A. √3B. √32C. 2√3D. 4√311.用边长为1的正方形覆盖3×3的正方形网格，最多覆盖边长为1的正方形网格(覆盖一部分就算覆盖)的个数是( )A。

八年级数学苏科版下册课时练第9单元《9.4矩形、菱形、正方形》(含答案解析)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练9.4矩形菱形正方形一、选择题1.菱形、矩形、正方形都具有的性质是()A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角线平分一组对角2.如图，E是正方形ABCD的边BC延长线上一点，且CE＝AC，则∠E＝()A.90°B.45°C.30°D.22.5°3.如图，将一正方形纸片沿图(1)、(2)的虚线对折，得到图(3)，然后沿图(3)中虚线的剪去一个角，展开得平面图形(4)，则图(3)的虚线是()A. B. C. D.4.如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD 上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有()A.2对B.3对C.4对D.5对5.如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE.若AB的长为2，则FM 的长为()A.2B.3C.2D.16.下列叙述，错误的是()A.对角线互相垂直且相等的平行四边形是正方形B.对角线互相垂直平分的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线相等的四边形是矩形7.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD.中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①②B.②③C.①③D.②④8.如图，把一张正方形纸对折两次后，沿虚线剪下一角，展开后所得图形一定是()A.三角形B.菱形C.矩形D.正方形9.如图，把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是()A.62B.6C.32D.3＋3210.如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD 内，在对角线AC上有一点P，使PD＋PE最小，则这个最小值为()A.3B.23C.26D.6二、填空题11.如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF＝20°，则∠AED等于．12.把正方形ABCD沿对边中点所在直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE，若AB的长为2，则FM＝．13.如图所示，直线a经过正方形ABCD的顶点A，分别过此正方形的顶点B、D 作BF⊥a于点F、DE⊥a于点E，若DE＝4，BF＝3，则EF的长为____________.14.如图，已知正方形ABCD边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE＝.15.如图，已知正方形ABCD的边长为1，点E在边DC上，AE平分∠DAC，EF⊥AC，点F为垂足，那么FC＝．16.如图，四边形ABCD是边长为3的正方形，∠BDC的平分线DE交BC于点E，点M、点N分别是CD和DE上的动点，连接AM，则当MN＋CN的值最小时，AM ＝.三、解答题17.如图，在正方形ABCD中，BC＝2，E是对角线BD上的一点，且BE＝AB.求△EBC的面积．18.如图，正方形ABCD的对角线AC、BD相交于点O，E是OC上一点，连接EB．过点A作AM⊥BE，垂足为M，AM与BD相交于点F．求证：OE＝OF．19.如图，在正方形ABCD中，F为DC的中点，E为BC上一点，BC＝4CE.求证：AF⊥FE.20.如图，在四边形ABCD中，AB＝BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N.(1)求证：∠ADB＝∠CDB；(2)若∠ADC＝90°，求证：四边形MPND是正方形.21.如图，正方形ABCD中，AB＝3，点E、F分别在BC、CD上，且∠BAE＝30°，∠DAF＝150.(1)求证：DF＋BE＝EF；(2)求∠EFC的度数；(3)求△AEF的面积.答案1.C2.D3.D.4.C5.B6.D.7.D8.B.9.A10.B11.65°.12.3．13.7.14.2﹣1.15.2﹣1.16.326.17.解：作EF⊥BC于F，如图所示：则∠EFB＝90°，∵四边形ABCD是正方形，∴AB＝BC＝2，∠DAB＝∠ABC＝90°，∴∠ABD＝∠DBC＝12∠ABC＝45°，∴△BEF是等腰直角三角形，∴EF＝BF，∵BE＝AB，∴BE＝BC＝2，∴EF＝BF＝22BE＝2，∴△EBC的面积＝12BC•EF＝12×2×2＝2．18.证明：∵四边形ABCD是正方形．∴∠BOE＝∠AOF＝90°，OB＝OA．又∵AM⊥BE，∴∠MEA＋∠MAE＝90°＝∠AFO＋∠MAE，∴∠MEA＝∠AFO．∴△BOE≌△AOF(AAS)．∴OE＝OF．19.证明：连接AE，设正方形的边长为4a.在Rt△ADF中，AD＝4a，DF＝2a，据勾股定理得，AF2＝AD2＋DF2，解得AF2＝20a2.在Rt△ABE中，AB＝4a，BE＝3a，据勾股定理得，AE2＝AB2＋BE2，解得AE2＝25a2.在Rt△ECF中，FC＝2a，CE＝a，据勾股定理得，EF2＝CF2＋CE2，解得EF2＝5a2.∴AE2＝AF2＋EF2，∴AF⊥FE.20.证明：(1)∵对角线BD平分∠ABC，∴∠ABD＝∠CBD，在△ABD和△CBD中，，∴△ABD≌△CBD(SAS)，∴∠ADB＝∠CDB；(2)∵PM⊥AD，PN⊥CD，∴∠PMD＝∠PND＝90°，∵∠ADC＝90°，∴四边形MPND是矩形，∵∠ADB＝∠CDB，∴∠ADB＝45°∴PM＝MD，∴四边形MPND是正方形.21.解：(1)延长EB至G，使BG＝DF，连接AG，∵正方形ABCD，∴AB＝AD，∠ABG＝∠ADF＝∠BAD＝90°，∵BG＝DF，∴△ABG≌△ADF，∴AG＝AF，∵∠BAE＝30°，∠DAF＝15°，∴∠FAE＝∠GAE＝45°，∵AE＝AE，∴△FAE≌△GAE，∴EF＝EG＝GB＋BE＝DF＋BE；(2)∵△AGE≌△AFE，∴∠AFE＝∠AGE＝75°，∵∠DFA＝90°﹣∠DAF＝75°，∴∠EFC＝180°﹣∠DFA﹣∠AFE＝180°﹣75°﹣75°＝30°，∴∠EFC＝30°(3)∵AB＝BC＝3，∠BAE＝30°，∴BE＝1，CE＝3﹣1，∵∠EFC＝30°，∴CF＝3﹣3，∴S△CEF＝12CE•CF＝23﹣3，由(1)知，△ABG≌△ADF，△FAE≌△GAE，∴S△AEF ＝S正方形ABCD﹣S△ADF﹣S△AEB﹣S△CEF＝S正方形ABCD﹣S△AEF﹣S△CEF，S△AEF ＝12(S正方形ABCD﹣S△AEF﹣S△CEF)＝3﹣ 3.。

八年级数学下册同步训练：必刷知识点9.4.1 矩形(含答案及解析)(苏科版)

2019-2020学年八年级数学下册同步必刷题闯关练（苏科版）第9章《中心对称图形》9.4.1 矩形1. 理解矩形的概念.2. 掌握矩形的性质定理与判定定理.知识点1：矩形的定义有一个角是直角的平行四边形叫做矩形.细节剖析矩形定义的两个要素：①是平行四边形；②有一个角是直角.即矩形首先是一个平行四边形，然后增加一个角是直角这个特殊条件.知识点2：矩形的性质矩形的性质包括四个方面：1.矩形具有平行四边形的所有性质；2.矩形的对角线相等；3.矩形的四个角都是直角；4.矩形是轴对称图形，它有两条对称轴.细节剖析（1）矩形是特殊的平行四边形，因而也是中心对称图形.过中心的任意直线可将矩形分成完全全等的两部分.（2）矩形也是轴对称图形，有两条对称轴（分别通过对边中点的直线）.对称轴的交点就是对角线的交点（即对称中心）.（3）矩形是特殊的平行四边形，矩形具有平行四边形的所有性质，从而矩形的性质可以归结为从三个方面看：从边看，矩形对边平行且相等；从角看，矩形四个角都是直角；从对角线看，矩形的对角线互相平分且相等.知识点3：矩形的判定矩形的判定有三种方法：1.定义：有一个角是直角的平行四边形叫做矩形.2.对角线相等的平行四边形是矩形.3.有三个角是直角的四边形是矩形.细节剖析在平行四边形的前提下，加上“一个角是直角”或“对角线相等”都能判定平行四边形是矩形.知识点4：直角三角形斜边上的中线的性质直角三角形斜边上的中线等于斜边的一半.细节剖析（1）直角三角形斜边上的中线的性质是矩形性质的推论.性质的前提是直角三角形，对一般三角形不可使用.（2）学过的直角三角形主要性质有：①直角三角形两锐角互余；②直角三角形两直角边的平方和等于斜边的平方；③直角三角形中30°所对的直角边等于斜边的一半.（3）性质可以用来解决有关线段倍分的问题.。

八下数学《同步练习》9.4矩形、菱形、正方形(1)

苏科版 八下 9.4矩形、菱形、正方形同步课时训练(word版含答案)

2024年苏科版八年级下册同步练习9.4矩形、菱形、正方形练习 (新版)苏含答案

苏科版数学八年级下《9.4矩形、菱形、正方形》同步练习含答案初二数学试卷分析.docx

八年级数学下册 第9章 9.4 矩形、菱形、正方形同步练习(含解析)苏科版(2021-2022学年)

最新苏科版八年级下册数学第9章矩形、菱形、正方形1同步练习题及答案.docx

2020-2021学年苏科版八年级下册数学9.4矩形、菱形、正方形 同步练习 (含解析)

《9.4矩形、菱形、正方形》同步优生提高训练 苏科版八年级数学下册