【9A文】霍尔效应测磁场实验报告

合集下载

霍尔效应测量磁场实验报告

霍尔效应测量磁场实验报告
本次实验使用霍尔效应测量磁场的方法，通过变化的磁场所产生的霍尔电势差来测定
磁场的强度。

本实验包括两部分，一是以电流为变量，测量霍尔电势与磁场的关系。

二是
以磁场大小为变量，测量霍尔电势随磁场的大小变化。

1.实验器材
霍尔效应测量仪、磁场发生器、数字万用表、导线等。

2.实验步骤
首先，将霍尔效应测量仪接入数字万用表的设置好电流和电压。

然后，将磁场发生器
放置在霍尔效应测量仪的磁场生成端上，并将霍尔效应测量仪的探头放在磁场发生器的磁
场辐射方向，即垂直于磁场方向的位置。

接着，将数字万用表调至电压测量模式，再通过
磁场发生器的旋钮变化磁场强度，记录下每一组数据。

在每组记录前，要等待电流稳定。

3.实验结果
根据实验数据的统计和分析，我们发现灯光颜色对人类的生理和心理都有一定的影响。

灯光颜色不同，可以引发人体机能的不同变化。

光强度越强，越易引发及加剧疲劳感、头
痛等症状。

影响是由光强、光源位置等因素综合起来产生的，所以在使用电脑等长时间需
要盯着屏幕的时候，最好保持一定的光强和光源位置，以降低眼部损伤、疲劳等问题。

通过本次实验，我们得到了霍尔电势与磁场强度之间的函数关系，验证了霍尔效应的
基本原理。

同时，我们还发现在特定的磁场强度下，霍尔电势与电流大小成正比关系。

在
实验过程中，我们也注意到灯光对人的生理和心理健康存在一定的影响，需要注意保持合
适的灯光强度和光源位置。

霍尔效应法测磁场实验报告

霍尔效应法测磁场实验报告霍尔效应法测磁场实验报告引言：磁场是我们日常生活中常常接触到的物理现象之一。

为了准确测量磁场的强度和方向，科学家们提出了多种方法和仪器。

本实验采用了霍尔效应法来测量磁场的强度，并通过实验数据分析和讨论，探究霍尔效应的原理和应用。

实验目的：1. 了解霍尔效应的基本原理和测量磁场的方法。

2. 掌握霍尔效应实验的操作步骤和数据处理方法。

3. 分析实验结果，验证霍尔效应的理论模型。

实验器材：1. 霍尔效应实验仪器：包括霍尔元件、电源、磁铁、直流电流源等。

2. 万用表：用于测量电流和电压。

实验步骤：1. 将霍尔元件连接到电源和万用表上，保证电路的正常工作。

2. 调节电源，使得通过霍尔元件的电流保持恒定。

3. 将磁铁靠近霍尔元件，并测量霍尔元件两侧的电压差。

4. 改变磁铁的位置和方向，多次测量电压差，并记录数据。

5. 根据实验数据，绘制电压差与磁场强度的关系曲线。

实验结果与分析：通过实验测量得到的电压差与磁场强度的关系曲线如下图所示。

曲线呈线性关系，即电压差与磁场强度成正比。

图1：电压差与磁场强度的关系曲线根据霍尔效应的原理，当电流通过霍尔元件时，磁场会引起霍尔元件两侧的电压差。

而电压差的大小与磁场的强度成正比。

因此，我们可以利用霍尔效应来测量磁场的强度。

实验中，我们改变了磁铁的位置和方向，多次测量了电压差。

通过对实验数据的分析，我们可以得出以下结论：1. 磁场的强度与电压差成正比：根据实验数据绘制的曲线可以看出，电压差随着磁场强度的增加而增加，两者呈线性关系。

2. 磁场的方向与电压差的正负有关：实验中我们发现，当磁铁的方向改变时，电压差的正负也会相应改变。

这说明电压差的正负与磁场的方向有关，电压差的正负可以用来判断磁场的方向。

3. 霍尔元件的材料和几何形状对实验结果有影响：在实验中，我们采用了一种特定的霍尔元件。

实际上，不同材料和几何形状的霍尔元件对实验结果可能会有一定的影响。

因此，在实际应用中，选择合适的霍尔元件也是非常重要的。

霍尔效应测磁场-实验报告

V B
'C
(mV
)
=
◆ (不计分)样品导电类型=
◆ (不计分)霍尔系数 RH(单位：103cm3 / c )=
◆ (10 分)样品电导率 σ(s/m)=
◆ (10 分)载流子的浓度（单位：1020 /m3 ）=
◆ (10 分)载流子迁移率 µ(单位： m2 /(V s) )=
思考题
总分值：10
思考题 1
这种效应建立需要一定时间，如果采用直流电测量时会因此而给霍尔电压测量带来误差，如
果采用交流电，则由于交流变化快使得爱延豪森效应来不及建立，可以减小测量误差。
（2）不等位电动势引起的误差
这是因为霍尔电极 B、 B' 不可能绝对对称焊在霍尔片两侧产生的。由于目前生产工艺水平
较高，不等位电动势很小，故一般可以忽略，也可以用一个电位器加以平衡。
b
为薄片宽度， FE
随着电荷累积而增大，当达到稳定状态时 FE FB ，即 qUB qVBB' / b 这时在 B、 B' 两侧
建立的电场称为霍尔电场，相应的电压称为霍尔电压，电极 B、 B' 称为霍尔电极。
另一方面，射载流子浓度为 n,薄片厚度为 d,则电流强度 I 与 u 的关系为：
RH 称为霍尔系数，它体现了材料的霍尔效应大小。根据霍尔效应制作的元件称为霍尔元件。
通过霍尔效应测量磁场
创建人：系统管理员总分：100
实验目的
通过用霍尔元件测量磁场，判断霍尔元件载流子类型，计算载流子的浓度和迁移速度，以及了解霍尔效应测试中的各种副效应及消除方法。
实验仪器
QS-H 霍尔效应组合仪，小磁针，测试仪。霍尔效应组合仪包括电磁铁，霍尔样品和样品架，换向开关和接线柱，如下图所示：

霍尔效应实验

《霍尔效应测量磁场》实验报告姓名学号学院专业班级一、实验目的通过用霍尔元件测量磁场，判断霍尔元件载流子类型，计算载流子的浓度和迁移速度，以及了解霍尔效应测试中的各种副效应及消除方法。

二、实验仪器QS-H霍尔效应组合仪，小磁针，测试仪。

霍尔效应组合仪包括电磁铁，霍尔样品和样品架，换向开关和接线柱。

测试仪由励磁恒流源I M，样品工作恒流源I S，数字电流表，数字毫伏表等组成。

三、实验原理1、通过霍尔效应测量磁场详见实验指导书2、霍尔效应实验中的副效应详见实验指导书3、材料的电导率和载流电子浓度及迁移率详见实验指导书四、实验内容将测试仪上I M输出，I S输出和V h输入三对接线柱分别与实验台上对应接线柱连接。

打开测试仪电源开关，预热数分钟后开始实验。

1. 保持I M不变，取I M＝0.45A，I S取1.00,1.50……,4.50mA，测绘V h-I S曲线，计算R h。

2. 保持I S不变，取I S＝4.50mA，I M取0.100,0.150……,0.450mA，测绘V h-I M曲线，计算R h。

3. 在零磁场下，取I S=0.1mA，测感应电动势V B’C（即V）。

4. 确定样品导电类型，并求载流子浓度n , 迁移率m, 电导率s。

电子的迁移率，表示每秒钟每伏特电压下电子的运动范围大小。

用来描述载流子在电场下运动的难易程度，其定义是：在弱电场作用下，载流子平均漂移速率与电场强度的比值。

它的量纲是速度除以电场强度，常用的单位是cm2/V·s。

计算涉及相关公式：电磁线圈的磁场大小：B=励磁参数×励磁电流，（1T=10000GS）霍尔系数：R h =V h·d/(Is·B)载流子浓度：n=1/(R h·e)材料的电导率：σ=Is·L/(V·b·d)载流子的迁移率：μ=σ·R h五、数据记录及处理5. 计算霍尔效应系数R h，确定霍尔元件导电类型，求载流子浓度n，迁移率µ，电导率σ。

霍尔效应实验报告(共8篇)

篇一：霍尔效应实验报告大学本(专)科实验报告课程名称：姓名：学院：系：专业：年级：学号：指导教师：成绩：年月日（实验报告目录）实验名称一、实验目的和要求二、实验原理三、主要实验仪器四、实验内容及实验数据记录五、实验数据处理与分析六、质疑、建议霍尔效应实验一．实验目的和要求：1、了解霍尔效应原理及测量霍尔元件有关参数.2、测绘霍尔元件的vh?is，vh?im曲线了解霍尔电势差vh与霍尔元件控制（工作）电流is、励磁电流im之间的关系。

3、学习利用霍尔效应测量磁感应强度b及磁场分布。

4、判断霍尔元件载流子的类型，并计算其浓度和迁移率。

5、学习用“对称交换测量法”消除负效应产生的系统误差。

二．实验原理：1、霍尔效应霍尔效应是导电材料中的电流与磁场相互作用而产生电动势的效应，从本质上讲，霍尔效应是运动的带电粒子在磁场中受洛仑兹力的作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷在不同侧的聚积，从而形成附加的横向电场。

如右图（1）所示，磁场b位于z的正向，与之垂直的半导体薄片上沿x正向通以电流is（称为控制电流或工作电流），假设载流子为电子（n型半导体材料），它沿着与电流is相反的x负向运动。

由于洛伦兹力fl的作用，电子即向图中虚线箭头所指的位于y轴负方向的b侧偏转，并使b侧形成电子积累，而相对的a侧形成正电荷积累。

与此同时运动的电子还受到由于两种积累的异种电荷形成的反向电场力fe的作用。

随着电荷积累量的增加，fe增大，当两力大小相等（方向相反）时，fl=-fe，则电子积累便达到动态平衡。

这时在a、b两端面之间建立的电场称为霍尔电场eh，相应的电势差称为霍尔电压vh。

设电子按均一速度向图示的x负方向运动，在磁场b作用下，所受洛伦兹力为fl=-eb式中e为电子电量，为电子漂移平均速度，b为磁感应强度。

同时，电场作用于电子的力为 fe??eeh??evh/l 式中eh为霍尔电场强度，vh为霍尔电压，l为霍尔元件宽度当达到动态平衡时，fl??fe ?vh/l （1）设霍尔元件宽度为l，厚度为d，载流子浓度为n，则霍尔元件的控制（工作）电流为 is?ne （2）由（1），（2）两式可得 vh?ehl?ib1isbrhs （3）nedd即霍尔电压vh（a、b间电压）与is、b的乘积成正比，与霍尔元件的厚度成反比，比例系数rh?1称为霍尔系数，它是反映材料霍尔效应强弱的重要参数，根据材料的电导ne率σ=neμ的关系，还可以得到：rh??/ （4）式中?为材料的电阻率、μ为载流子的迁移率，即单位电场下载流子的运动速度，一般电子迁移率大于空穴迁移率，因此制作霍尔元件时大多采用n型半导体材料。

霍尔效应测磁场实验报告

实验报告（一）学生姓名：学号：指导教师：实验地点：实验时间：一、实验室名称：霍尔效应实验室二、实验项目名称：霍尔效应法测磁场三、实验学时：四、实验原理：（一）霍耳效应现象将一块半导体（或金属）薄片放在磁感应强度为B 的磁场中，并让薄片平面与磁场方向（如Y 方向）垂直。

如在薄片的横向（X 方向）加一电流强度为H I 的电流，那么在与磁场方向和电流方向垂直的Z 方向将产生一电动势H U 。

如图1所示，这种现象称为霍耳效应，H U 称为霍耳电压。

霍耳发现，霍耳电压H U 与电流强度H I 和磁感应强度B 成正比，与磁场方向薄片的厚度d 反比，即d BI RU H H =（1）式中，比例系数R 称为霍耳系数，对同一材料R 为一常数。

因成品霍耳元件（根据霍耳效应制成的器件）的d 也是一常数，故d R /常用另一常数K 来表示，有B KI U H H =（2）式中，K 称为霍耳元件的灵敏度，它是一个重要参数，表示该元件在单位磁感应强度和单位电流作用下霍耳电压的大小。

如果霍耳元件的灵敏度K 知道（一般由实验室给出），再测出电流H I 和霍耳电压H U ，就可根据式HH KI U B =（3）算出磁感应强度B 。

图1霍耳效应示意图图2霍耳效应解释（二）霍耳效应的解释现研究一个长度为l 、宽度为b 、厚度为d 的N 型半导体制成的霍耳元件。

当沿X 方向通以电流H I 后，载流子（对N 型半导体是电子）e 将以平均速度v 沿与电流方向相反的方向运动，在磁感应强度为B 的磁场中，电子将受到洛仑兹力的作用，其大小为evB f B =方向沿Z 方向。

在B f 的作用下，电荷将在元件沿Z 方向的两端面堆积形成电场H E （见图2），它会对载流子产生一静电力E f ，其大小为H E eE f =方向与洛仑兹力B f 相反，即它是阻止电荷继续堆积的。

当B f 和E f 达到静态平衡后，有E B f f =，即b eU eE evB H H /==，于是电荷堆积的两端面（Z 方向）的电势差为vbB U H =（4）通过的电流H I 可表示为nevbd I H -=式中n 是电子浓度，得nebd I v H-=（5）将式（5）代人式（4）可得ned B I U H H -=可改写为B KI d BI RU H H H ==该式与式（1）和式（2）一致，ne R 1-=就是霍耳系数。

霍尔效应法测磁场的实验报告

霍尔效应法测磁场的实验报告一、实验目的本实验旨在通过霍尔效应法测量磁场强度，并掌握霍尔效应的基本原理和测量方法。

二、实验原理1. 霍尔效应霍尔效应是指在一个导体中，当有电流通过时，在该导体中产生横向磁场时，将会出现一种电势差，这种现象就称为霍尔效应。

该电势差与磁场强度、电流大小以及材料特性有关。

2. 霍尔元件霍尔元件是利用霍尔效应制造的元器件，它可以将磁场转化为电信号输出。

通常采用n型半导体材料制成，具有高灵敏度和线性度好等特点。

3. 测量方法利用霍尔元件可以测量磁场强度。

首先将待测磁场垂直于霍尔元件所在平面，然后通过调整外加直流电压的大小和方向，使得霍尔元件输出的电势差为零。

此时所加直流电压即为待测磁场强度。

三、实验器材1. 霍尔元件2. 直流稳压电源3. 万用表4. 磁铁5. 铜线四、实验步骤1. 将霍尔元件固定在试验台上，并将其与直流稳压电源和万用表连接好。

2. 将磁铁放置在霍尔元件旁边，调整其位置和方向，使得磁场垂直于霍尔元件所在平面。

3. 通过调整直流稳压电源的输出电压大小和方向，使得万用表读数为零。

此时所加直流电压即为待测磁场强度。

4. 更换不同大小的磁铁，重复以上步骤，记录不同磁场下的电势差和电流值。

五、实验结果分析1. 数据处理根据实验数据计算出不同磁场下的电势差和电流值，并绘制出它们之间的关系图。

通过拟合曲线可以得到待测磁场强度与输出电势差之间的函数关系式。

2. 实验误差分析在实际操作中，由于仪器精度、环境温度等因素的影响，可能会产生一定误差。

此时需要对数据进行处理，并考虑误差来源及其影响程度。

六、实验结论通过本次实验可以得出以下结论：1. 霍尔效应是一种将磁场转化为电信号输出的现象，其电势差与磁场强度、电流大小以及材料特性有关。

2. 利用霍尔元件可以测量磁场强度，通过调整外加直流电压的大小和方向，使得霍尔元件输出的电势差为零，此时所加直流电压即为待测磁场强度。

3. 在实际操作中，需要考虑仪器精度、环境温度等因素对实验结果的影响，并进行误差分析和数据处理。

霍尔效应测磁场实验报告

实验报告学生姓名：学号：指导教师：实验地点：实验时间：一、实验室名称：霍尔效应实验室实验项目名称：霍尔效应法测磁场三、实验学时:四、实验原理:（一）霍耳效应现象将一块半导体（或金属）薄片放在磁感应强度为B的磁场中，并让薄片平面与磁场方向（如P方向）垂直。

如在薄片的横向（ P方向）加一电流强度为|H的电流，那么在与磁场方向和电流方向垂直的Z方向将产生一电动势U H。

如图1所示，这种现象称为霍耳效应，U H称为霍耳电压。

霍耳发现，霍耳电压U H与电流强度I H和磁感应强度 B成正比，与磁场方向薄片的厚度d反比，即U H二只楽（1）H d式中，比例系数 R称为霍耳系数，对同一材料 R为一常数。

因成品霍耳元件（根据霍耳效应制成的器件）的d也是一常数，故R/d常用另一常数K来表示，有U H = KI H B （2）式中，K称为霍耳元件的灵敏度，它是一个重要参数，表示该元件在单位磁感应强度和单位电流作用下霍耳电压的大小。

如果霍耳元件的灵敏度K知道（一般由实验室给出），再测出电流I H和霍耳电压U H，就可根据式(3)图1霍耳效应示意图图2霍耳效应解释（二）霍耳效应的解释现研究一个长度为I 、宽度为b 、厚度为d 的N 型半导体制成的霍耳元件。

当沿 P 方向通以电流I H 后，载流子（对 N 型半导体是电子）e 将以平均速度v 沿与电流方向相反的方向运动，在磁感应强度为 B 的磁场中，电子将受到洛仑兹力的作用，其大小为f B 二 evB方向沿Z 方向。

在f B 的作用下，电荷将在元件沿 Z 方向的两端面堆积形成电场 E H （见图2），它会对载流子产生一静电力f E ，其大小为方向与洛仑兹力 f B 相反，即它是阻止电荷继续堆积的。

当f B 和f E 达到静态平衡后，有f B 二f E ，即evB 二eE H 二e5 / b ，于是电荷堆积的两端面（U H 二 vbB (4)该式与式（1）和式（2）一致，五、实验目的：研究通电螺线管内部磁场强度六、实验内容：（一）测量通电螺线管轴线上的磁场强度的分布情况，并与理论值相比较；（二）研究通电螺线管内部磁场强度与励磁电流的关系。

用霍尔效应测量磁场的实验报告

用霍尔效应测量磁场的实验报告
实验目的：掌握用霍尔效应测量磁场的方法，并测量出磁场的大小。

实验原理：当一个电流通过一块导体板时，如果与该板垂直方向的磁场发生变化，板上就会产生电势差，即霍尔电压，这就是霍尔效应。

霍尔效应的公式为：VH=B·IB·d，其中VH为霍尔电压，B为磁场大小，IB为电流大小，d为针对霍尔元件的厚度。

实验材料：磁铁、霍尔元件、导线、电流表、电压表、万用表。

实验步骤：
1. 在实验板上固定霍尔元件，并将元件上的三个接头与接线柱连接。

2. 连接电路：电流表与霍尔元件串联，接线柱连接电流源，电源的正电极通过导线连接与霍尔元件的横向端子相接，负极通过导线连接与霍尔元件的竖向端子相接。

3. 调节电流源的纹波电流为零，保证恒流源的输出电流稳定在一个合适的电流值。

4. 将磁铁从霍尔元件上方经过，记录其所在位置和霍尔电压。

5. 依次改变磁铁的位置，记录每个位置的霍尔电压。

6. 将上述实验结果整理，根据霍尔效应公式求出磁场大小B。

实验结果：
磁铁位置（cm）霍尔电压（V）
0 0
1 0.14
2 0.28
3 0.42
4 0.56
公式计算：B=VH÷IB÷d，VH=0.56V，IB=0.5A，d=0.1mm。

B=0.56÷0.5÷0.1=11.2T。

实验结论：通过霍尔效应测量出磁场大小为11.2T。

霍尔效应测量磁场实验报告

实
验
报
告
实验名称霍尔效应测量磁场
专业班级：组别：
姓名：学号：
合作者：日期：
B
图3.4-1N型半导体
图1N型半导体
图2励磁电流与磁感应强度的B-I曲线图
轴方向磁感应强度的分布
0.0 2.0 4.0 6.08.010.015.020.0-43-65-119-189-198-198-193-188图3电磁铁间隙内B-x 曲线图
电磁铁间隙内磁感应强度的y 方向分布（500=B
I mA ，S I =10.00mA
．电磁铁中心处磁感应强度为T 15.1=B 。

图4电磁铁间隙内B-y 曲线图
H eE evB
=霍尔电压H U 的大小为
1S S
H H H I B I B
U E b R ne d d
==
=H R 称为霍尔系数，令1H H R K d ned
=
=，则H H S U K I B
=（3）结合电路图可以判断工作电流流入霍尔元件的方向，通过判断螺线管的绕行方向和励磁电流的流向可以判断电磁铁中的磁感应强度方向，最后结合霍尔电压表头上读数的正负可判断半导体的类型。

（4）若霍尔元件与磁场方向不垂直，则测量出的磁感应强度值减小。

若稍微转动霍尔元件在磁场中的方向，若霍尔电压值变小，则说明霍尔元件表面与磁场方向垂直。

霍尔效应测磁场实验报告(共7篇)

篇一：霍尔元件测磁场实验报告用霍尔元件测磁场前言：霍耳效应是德国物理学家霍耳（a.h.hall 1855—1938）于1879年在他的导师罗兰指导下发现的。

由于这种效应对一般的材料来讲很不明显，因而长期未得到实际应用。

六十年代以来，随着半导体工艺和材料的发展，这一效应才在科学实验和工程技术中得到了广泛应用。

利用半导体材料制成的霍耳元件，特别是测量元件，广泛应用于工业自动化和电子技术等方面。

由于霍耳元件的面积可以做得很小，所以可用它测量某点或缝隙中的磁场。

此外，还可以利用这一效应来测量半导体中的载流子浓度及判别半导体的类型等。

近年来霍耳效应得到了重要发展，冯﹒克利青在极强磁场和极低温度下观察到了量子霍耳效应，它的应用大大提高了有关基本常数测量的准确性。

在工业生产要求自动检测和控制的今天，作为敏感元件之一的霍耳器件，会有更广阔的应用前景。

了解这一富有实用性的实验，对今后的工作将大有益处。

教学目的：1. 了解霍尔效应产生的机理，掌握测试霍尔器件的工作特性。

2. 掌握用霍尔元件测量磁场的原理和方法。

3. 学习用霍尔器件测绘长直螺线管的轴向磁场分布。

教学重难点： 1. 霍尔效应2. 霍尔片载流子类型判定。

实验原理如右图所示，把一长方形半导体薄片放入磁场中，其平面与磁场垂直，薄片的四个侧面分别引出两对电极（m、n和p、s），径电极m、n 通以直流电流ih，则在p、s极所在侧面产生电势差，这一现象称为霍尔效应。

这电势差叫做霍尔电势差，这样的小薄片就是霍尔片。

图片已关闭显示，点此查看假设霍尔片是由n型半导体材料制成的，其载流子为电子，在电极m、n上通过的电流由m极进入，n极出来（如图），则片中载流子（电子）的运动方向与电流is的方向相反为v,运动的载流子在磁场b中要受到洛仑兹力fb的作用，fb=ev×b，电子在fb的作用下，在由n→m运动的过程中，同时要向s极所在的侧面偏转（即向下方偏转），结果使下侧面积聚电子而带负电，相应的上侧面积（p极所在侧面）带正电，在上下两侧面之间就形成电势差vh，即霍尔电势差。

霍尔效应及磁场的测定实验报告

霍尔效应及磁场的测定实验报告霍尔效应及磁场的测定实验报告实验目的：1.了解霍尔效应的概念及其表现形式；2.掌握霍尔元件的使用和原理；3.探究磁场对于霍尔效应的影响及其测定方法。

实验原理：霍尔效应是指在垂直于导体芯片的方向上，当导体内部流动电荷受外磁场力作用弯曲轨迹时，在芯片两端被电极接收时所产生的电势差的现象。

霍尔效应是一种利用磁场和电流来测量电学参数的重要方法。

常用的霍尔元件由具有导电性的半导体材料经特殊处理后制成，通过对霍尔电压和磁场的测量，可以确定材料中载流子的类型、浓度、迁移率等参数。

实验装置：霍尔元件、恒流源、电子万用表、多用万用表、直流稳压电源、磁铁。

实验过程：1.连接实验电路：将霍尔元件放在磁场中心，使用恒流源连接霍尔元件的两端，同时使用电子万用表测量霍尔电势差；2.调整磁场：将磁铁放置在霍尔元件下方，并调整磁铁的位置，使得磁场与芯片法向垂直；3.测量数据：固定电流值，分别测量不同磁场下的霍尔电势差，并记录测量数据。

实验结果：1.横向霍尔电势差随着磁场的增加呈线性增长关系；2.随着电流的增大，横向霍尔电势差的值也增大；3.改变磁场方向，横向电势差的正负号随之改变。

实验分析：在固定电流的情况下，横向霍尔电势差的大小与磁场的大小呈线性关系，符合霍尔效应的理论预测。

横向电势差的正负号与磁场的方向有关，这是因为电子在磁场力的作用下，被弯曲侧向流动，而侧向电场的方向随之方向改变。

此外，仪器误差也会对测量结果造成影响。

实验结论：通过对横向霍尔电势差与磁场的关系的测量，初步探究了霍尔效应的表现形式，并明确了磁场方向对霍尔电势差的影响。

通过对测量数据的处理和分析，了解了霍尔元件的使用及其参数的测量方法，为今后在电学和材料科学领域的实际应用提供了基础。

霍尔效应法测磁场实验报告

竭诚为您提供优质文档/双击可除霍尔效应法测磁场实验报告篇一：物理实验报告3_利用霍尔效应测磁场实验名称：利用霍耳效应测磁场实验目的：a．了解产生霍耳效应的物理过程；b．学习用霍尔器件测量长直螺线管的轴向磁场分布；c．学习用“对称测量法”消除负效应的影响，测量试样的Vh?Is和Vh?Im曲线；d．确定试样的导电类型、载流子浓度以及迁移率。

实验仪器：Th－h型霍尔效应实验组合仪等。

实验原理和方法：1.用霍尔器件测量磁场的工作原理如下图所示，一块切成矩形的半导体薄片长为l、宽为b、厚为d，置于磁场中。

磁场b垂直于薄片平面。

若沿着薄片长的方向有电流I通过，则在侧面A和b间产生电位差Vh?VA?Vb。

此电位差称为霍尔电压。

半导体片中的电子都处于一定的能带之中，但能参与导电的只是导带中的电子和价带中的空穴，它们被称为载流子。

对于n型半导体片来说，多数载流子为电子；在p型半导体中，多数载流子被称为空穴。

再研究半导体的特性时，有事可以忽略少数载流子的影响。

霍尔效应是由运动电荷在磁场中收到洛仑兹力的作用而产生的。

以n型半导体构成的霍尔元件为例，多数载流子为电子，设电子的运动速度为v，则它在磁场中收到的磁场力即洛仑兹力为Fm??ev?bF的方向垂直于v和b构成的平面，并遵守右手螺旋法则，上式表明洛仑兹力F的方向与电荷的正负有关。

自由电子在磁场作用下发生定向便宜，薄片两侧面分别出现了正负电荷的积聚，以两个侧面有了电位差。

同时，由于两侧面之间的电位差的存在，由此而产生静电场，若其电场强度为ex，则电子又受到一个静电力作用，其大小为Fe?eex电子所受的静电力与洛仑兹力相反。

当两个力的大小相等时，达到一种平衡即霍尔电势不再变化，电子也不再偏转，此时，ex?bV两个侧面的电位差Vh?exb由I?nevbd及以上两式得Vh?[1/(ned)]Ib其中：n为单位体积内的电子数；e为电子电量；d为薄片厚度。

令霍尔器件灵敏度系数则Vh?IsVh?KhIb若常数Kh已知，并测定了霍尔电动势Vh和电流I就可由上式求出磁感应强度b的大小。

霍尔效应法测磁场实验报告

霍尔效应法测磁场实验报告一、实验目的1、了解霍尔效应的基本原理。

2、学习用霍尔效应法测量磁场的原理和方法。

3、掌握霍尔元件的特性和使用方法。

二、实验原理1、霍尔效应将一块半导体薄片置于磁场中（磁场方向垂直于薄片平面），当有电流通过时，在垂直于电流和磁场的方向上会产生一个横向电位差，这种现象称为霍尔效应。

这个横向电位差称为霍尔电压，用＄U_H$ 表示。

霍尔电压的大小与电流＄I$、磁感应强度＄B$ 以及薄片的厚度＄d$ 等因素有关，其关系式为：＄U_H ＝ K_H IB$其中，＄K_H$ 称为霍尔系数，它与半导体材料的性质有关。

2、用霍尔效应法测磁场若已知霍尔元件的灵敏度＄K_H$ ，通过测量霍尔电压＄U_H$ 和电流＄I$ ，就可以计算出磁感应强度＄B$ ：＄B ＝＼frac{U_H}｛K_H I}＄三、实验仪器霍尔效应实验仪、直流电源、毫安表、伏特表、特斯拉计等。

四、实验步骤1、仪器连接（1）将霍尔效应实验仪的各个部件按照说明书正确连接。

（2）将直流电源、毫安表、伏特表等仪器与实验仪连接好。

2、调节仪器（1）调节直流电源的输出电压，使通过霍尔元件的电流达到预定值。

（2）调节特斯拉计，使其归零。

3、测量霍尔电压（1）在不同的磁场强度下，测量霍尔元件两端的电压。

（2）改变电流的方向，再次测量霍尔电压。

4、数据记录将测量得到的数据记录在表格中，包括电流、磁场强度、霍尔电压等。

五、实验数据及处理1、实验数据记录｜电流（mA）｜磁场强度（T）｜霍尔电压（mV）（正电流）｜霍尔电压（mV）（负电流）｜｜｜｜｜｜｜50|01|256|－258|｜50|02|512|－515|｜50|03|768|－771|｜100|01|512|－515|｜100|02|1024|－1028|｜100|03|1536|－1542|2、数据处理（1）计算每个测量点的平均霍尔电压：＄U_{H平均} ＝＼frac{U_{H正} ＋ U_{H负}｝｛2}＄（2）根据霍尔系数＄K_H$ 和平均霍尔电压、电流计算磁场强度：＄B ＝＼frac{U_{H平均}｝｛K_H I}＄3、绘制曲线以磁场强度为横坐标，霍尔电压为纵坐标，绘制霍尔电压与磁场强度的关系曲线。

利用霍尔效应测磁场实验报告

同理，计算其他组数据的霍尔系数，并取平均值。
六、实验误差分析
1、系统误差
实验仪器本身的精度限制，如电源输出的稳定性、电表的测量精度等。
磁场的不均匀性，可能导致测量的磁场值与实际值存在偏差。
2、随机误差
读数误差，在读取电表数据时，由于人的视觉和反应时间等因素，可能会产生一定的误差。
实验环境的干扰，如电磁场的干扰等。
｜01｜50｜25｜－24｜245｜
｜பைடு நூலகம்2｜50｜48｜－47｜475｜
｜03｜50｜72｜－71｜715｜
｜04｜50｜96｜－95｜955｜
根据实验数据，计算霍尔系数RH。由于VH＝RHIB，所以RH＝VH／（IB）
以第一组数据为例，RH＝245×10^－3／（01×50×10^－3）＝49×10^－3（m³/C）
三、实验仪器
霍尔效应实验仪、直流电源、毫安表、伏特表、特斯拉计。
四、实验步骤
1、连接实验仪器
将霍尔效应实验仪的电源、毫安表、伏特表等按照正确的方式连接好。
确保连接线路牢固，接触良好。
2、校准仪器
使用特斯拉计对实验仪器进行校准，确保测量磁场的准确性。
3、测量霍尔电压
接通电源，调节电流I为某一固定值。
改变磁场B的大小，测量不同磁场下对应的霍尔电压VH。
eEH＝e（v×B）
设导体的宽度为b，厚度为d，则霍尔电压VH＝EHb＝（v×B）bd
又因为电流I＝nevbd，其中n为单位体积内的电子数，所以v＝I／（nebd）
将v代入霍尔电压的表达式，可得：
VH＝IB／（ned）
令RH＝1／（ned），称为霍尔系数，则VH＝RHIB
通过测量霍尔电压VH、电流I和导体的几何尺寸b、d，就可以计算出磁场B的大小。

霍尔效应测磁场-实验报告

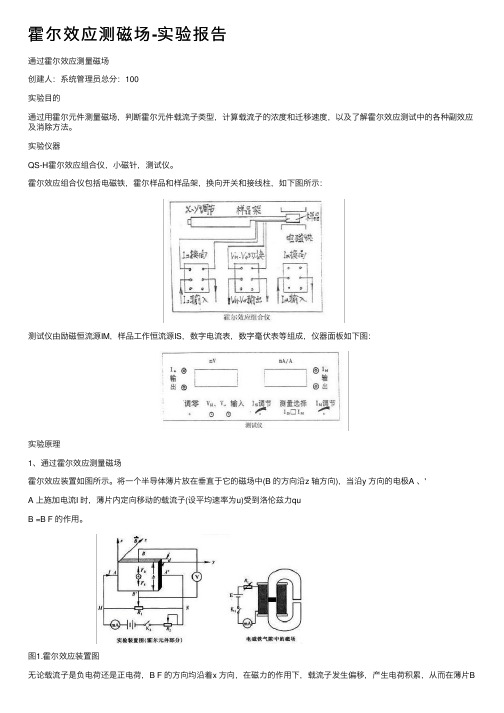
霍尔效应测磁场-实验报告通过霍尔效应测量磁场创建⼈：系统管理员总分：100实验⽬的通过⽤霍尔元件测量磁场，判断霍尔元件载流⼦类型，计算载流⼦的浓度和迁移速度，以及了解霍尔效应测试中的各种副效应及消除⽅法。

实验仪器QS-H霍尔效应组合仪，⼩磁针，测试仪。

霍尔效应组合仪包括电磁铁，霍尔样品和样品架，换向开关和接线柱，如下图所⽰：测试仪由励磁恒流源IM，样品⼯作恒流源IS，数字电流表，数字毫伏表等组成，仪器⾯板如下图：实验原理1、通过霍尔效应测量磁场霍尔效应装置如图所⽰。

将⼀个半导体薄⽚放在垂直于它的磁场中(B 的⽅向沿z 轴⽅向)，当沿y ⽅向的电极A 、'A 上施加电流I 时，薄⽚内定向移动的载流⼦(设平均速率为u)受到洛伦兹⼒quB =B F 的作⽤。

图1.霍尔效应装置图⽆论载流⼦是负电荷还是正电荷，B F 的⽅向均沿着x ⽅向，在磁⼒的作⽤下，载流⼦发⽣偏移，产⽣电荷积累，从⽽在薄⽚B、'B 两侧产⽣⼀个电位差'BB V ,形成⼀个电场E 。

电场使载流⼦⼜受到⼀个与⽅向相反的电场⼒b qV qE F BB E /'==。

其中b 为薄⽚宽度，EF 随着电荷累积⽽增⼤，当达到稳定状态时B E F F =，即b qV qUB BB /'=这时在B 、'B 两侧建⽴的电场称为霍尔电场，相应的电压称为霍尔电压，电极B 、'B 称为霍尔电极。

另⼀⽅⾯，射载流⼦浓度为n,薄⽚厚度为d,则电流强度I 与u 的关系为：H R 称为霍尔系数，它体现了材料的霍尔效应⼤⼩。

根据霍尔效应制作的元件称为霍尔元件。

在应⽤中IB K V H BB ='，式中若I 、H K 已知，只要测出霍尔电压'BB V ，即可算出磁场B 的⼤⼩；并且若知载流⼦类型(n 型半导体多数载流⼦为电⼦，P 型半导体多数载流⼦为空⽳),则由'BB V 的正负可测出磁场⽅向，反之，若已知磁场⽅向，则可判断载流⼦类型。

用霍尔效应测量磁场实验报告

实验名称:用霍尔效应测量磁场
实验目的:
实验仪器:霍尔效应仪、稳流电源、稳压电源、安培表、数字万用表两块、电阻箱实验原理:
霍尔效应原理如图,将通有电流的导体置于磁场B 中,磁场B 垂直与电流H I 的
方向,在导体中垂直于磁场B 方向和H I 方向上会产生一个横向电势差H
U 。

霍
尔电势与通过霍尔元件的电流H I 和磁场强度B 有线性关系B I K U H H H =
霍尔效应装置如图,运用此装置可测量霍尔电流H I 与霍尔电势H U 的关系,测
量励磁电流μI 和磁场强度B 的关系,测量电磁铁磁场沿水平方向的分布
实验操作步骤:
(1) 连接电路如图
(2) 改变霍尔电流H I ,测量霍尔电流H I 与霍尔电势H U 的关系
(3) 改变励磁电流μI ,测量励磁电流μI 和磁场强度B 的关系
(4) 改变霍尔片在磁场中的空间位置,测量电磁铁磁场沿水平方向的分布实验数据记录:
(1)测量霍尔电流H I 与霍尔电势H U 的关系
(2)测量励磁电流μI 和磁场强度B 的关系
(3)测量电磁铁磁场沿水平方向的分布)/(A I H μ=? )/(mA I μ=600
数据处理:(1)测量霍尔电流H I 与霍尔电势H U 的关系
(2)测量励磁电流μI 和磁场强度B 的关系
(3)测量电磁铁磁场沿水平方向的分布。