新课标2020年高考数学一轮总复习第八章平面解析几何8_5椭圆课时规范练理含解析新人教A
2020年高考数学一轮总复习 第八章平面解析几何 课时规范练理含解析

8-1 直线的倾斜角与斜率、直线的方程课时规范练(授课提示:对应学生用书第299页)A 组 基础对点练1.如图中的直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则( D )A .k 1<k 2<k 3B .k 3<k 1<k 2C .k 3<k 2<k 1D .k 1<k 3<k 22.如果AB <0,且BC <0,那么直线Ax +By +C =0不通过( D ) A .第一象限 B .第二象限 C .第三象限D .第四象限3.已知直线l 过圆x 2+(y -3)2=4的圆心,且与直线x +y +1=0垂直,则l 的方程是( D ) A .x +y -2=0 B .x -y +2=0 C .x +y -3=0D .x -y +3=04.设a ∈R ,则“a =1”是“直线l 1:ax +2y -1=0与直线l 2:x +2y +4=0平行”的( C ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件5.直线(2m +1)x +(m +1)y -7m -4=0过定点( C ) A .(1,-3) B .(4,3) C .(3,1)D .(2,3)6.直线x +(a 2+1)y +1=0的倾斜角的取值范围是( B )A.⎣⎢⎡⎦⎥⎤0,π4B .⎣⎢⎡⎭⎪⎫3π4,πC.⎣⎢⎡⎭⎪⎫0,π4∪⎝ ⎛⎭⎪⎫π2,π D .⎣⎢⎡⎭⎪⎫π4,π2∪⎣⎢⎡⎭⎪⎫3π4,π 7.直线3x -4y +5=0关于x 轴对称的直线的方程是( A )A .3x +4y +5=0B .3x +4y -5=0C .-3x +4y -5=0D .-3x +4y +5=08.已知两点M (2,-3),N (-3,-2),直线l 过点P (1,1),且与线段MN 相交,则直线l的斜率k 的取值范围是( A ) A .k ≥34或k ≤-4B .-4≤k ≤34C.34≤k ≤4 D .-34≤k ≤4解析:如图所示,∵k PN =1--1--=34,k PM =1--1-2=-4,∴要使直线l 与线段MN 相交, 当l 的倾斜角小于90°时,k ≥k PN ; 当l 的倾斜角大于90°时,k ≤k PM , ∴k ≥34或k ≤-4.9.已知过点P (2,2)的直线与圆(x -1)2+y 2=5相切,且与直线ax -y +1=0垂直,则a =( C ) A .-12B .1C .2D .1210.垂直于直线y =x +1且与圆x 2+y 2=1相切于第一象限的直线方程是( A ) A .x +y -2=0 B .x +y +1=0 C .x +y -1=0D .x +y +2=011.平行于直线2x +y +1=0且与圆x 2+y 2=5相切的直线的方程是( A ) A .2x +y +5=0或2x +y -5=0 B .2x +y +5=0或2x +y -5=0 C .2x -y +5=0或2x -y -5=0 D .2x -y +5=0或2x -y -5=012.“a =14”是“直线(a +1)x +3ay +1=0与直线(a -1)x +(a +1)y -3=0互相垂直”的( A )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件13.已知点M (0,-1),点N 在直线x -y +1=0上,若直线MN 垂直于直线x +2y -3=0, 则点N 的坐标是( B ) A .(-2,-1) B .(2,3) C .(2,1)D .(-2,1)14.已知m ,n 为正整数,且直线2x +(n -1)y -2=0与直线mx +ny +3=0互相平行,则2m +n 的最小值为 9 .解析:由题意知,2n =m (n -1),即m +2n =mn , 得2m +1n=1,又m ,n 为正整数,∴2m +n =(2m +n )⎝ ⎛⎭⎪⎫2m +1n =5+2n m +2m n ≥9.当且仅当2n m =2m n时取等号.B 组 能力提升练1.已知f (x )=a sin x -b cos x ,若f ⎝ ⎛⎭⎪⎫π4-x =f ⎝ ⎛⎭⎪⎫π4+x ,则直线ax -by +c =0的倾斜角为( D ) A.π3 B .π6C.π4D .3π4解析:令x =π4,得f (0)=f ⎝ ⎛⎭⎪⎫π2,得a =-b ,易得直线斜率k =a b =-1. 2.过点P (1,1)的直线,将圆形区域{(x ,y )|x 2+y 2≤4}分为两部分,使得这两部分的面积之差最大,则该直线的方程为( A ) A .x +y -2=0 B .y -1=0 C .x -y =0D .x +3y -4=03.过点(3,1)作圆(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为( A ) A .2x +y -3=0 B .2x -y -3=0 C .4x -y -3=0D .4x +y -3=04.一条光线从点(-2,-3)射出,经y 轴反射后与圆(x +3)2+(y -2)2=1相切,则反射光线所在直线的斜率为( D ) A .-53或-35B .-32或-23C .-54或-45D .-43或-345.已知点O (0,0),A (0,b ),B (a ,a 3).若△OAB 为直角三角形,则必有( C ) A .b =a 3B .b =a 3+1aC .(b -a 3)⎝ ⎛⎭⎪⎫b -a 3-1a =0D .|b -a 3|+⎪⎪⎪⎪⎪⎪b -a 3-1a =06.若θ是直线l 的倾斜角,且sin θ+cos θ=55,则l 的斜率为( D ) A .-12B .-12或-2C.12或2 D .-2解析:∵sin θ+cos θ=55,① ∴(sin θ+cos θ)2=1+sin 2θ=15,∴2sin θcos θ=-45,∴(sin θ-cos θ)2=95,易知sin θ>0,cos θ<0,∴sin θ-cos θ=355,②由①②解得⎩⎪⎨⎪⎧sin θ=255,cos θ=-55,∴tan θ=-2,即l 的斜率为-2,故选D.7.已知倾斜角为θ的直线与直线x -3y +1=0垂直,则23sin 2θ-cos 2θ=( C ) A.103 B .-103C.1013D .-10138.已知点A (-1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( B ) A .(0,1) B .⎝ ⎛⎭⎪⎫1-22,12 C.⎝ ⎛⎦⎥⎤1-22,13 D .⎣⎢⎡⎭⎪⎫13,129.过点A (1,2)且与直线x -2y +3=0垂直的直线方程为 2x +y -4=0 .解析:直线x -2y +3=0的斜率为12,所以由垂直关系可得要求直线的斜率为-2,所以所求方程为y -2=-2(x -1),即2x +y -4=0.10.已知直线l 经过点(-5,0)且方向向量为(2,-1),则直线l 的方程为 x +2y +5=0 .解析:∵直线l 的方向向量为(2,-1),∴直线l 的斜率为-12,∵直线l 过点(-5,0),∴直线l 的方程为x +2y +5=0.11.直线y =k (x -1)与以A (3,2),B (2,3)为端点的线段有公共点,则k 的取值范围是 [1,3] .解析:直线y =k (x -1)恒过点P (1,0),且与以A (3,2),B (2,3)为端点的线段有公共点,画出图形(如图所示),则直线落在阴影区域内.∵k PA =2-03-1=1,k PB =3-02-1=3,∴k 的取值范围是[1,3].12.若ab >0,且A (a,0),B (0,b ),C (-2,-2)三点共线,则ab 的最小值为 16 .解析:根据A (a,0),B (0,b )确定直线的方程为x a +y b=1,又C (-2,-2)在该直线上,故-2a+-2b=1,所以-2(a +b )=ab .又ab >0,故a <0,b <0.根据基本不等式ab =-2(a +b )≥4ab ,从而ab ≤0(舍去)或ab ≥4,故ab ≥16,当且仅当a =b =-4时取等号,即ab 的最小值为16.8-2 直线的交点与距离公式课时规范练(授课提示:对应学生用书第301页)A 组 基础对点练1.(2016·高考北京卷)圆(x +1)2+y 2=2的圆心到直线y =x +3的距离为( C ) A .1 B .2 C. 2D .2 22.(2018·邢台模拟)“a =-1”是“直线ax +3y +3=0和直线x +(a -2)y +1=0平行”的 ( C )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:由题意得,直线ax +3y +3=0和直线x +(a -2)y +1=0平行的充要条件是⎩⎪⎨⎪⎧a a -=3×1,a ×1≠3×1,解得a =-1,故选C.3.过点P (-3,-1)的直线l 与圆x 2+y 2=1有公共点,则直线l 的倾斜角的取值范围是( D )A.⎝ ⎛⎦⎥⎤0,π6B .⎝ ⎛⎦⎥⎤0,π3C.⎣⎢⎡⎦⎥⎤0,π6 D .⎣⎢⎡⎦⎥⎤0,π3 4.若直线y =-2x +3k +14与直线x -4y =-3k -2的交点位于第四象限,则实数k 的取值范围是( A ) A .-6<k <-2 B .-5<k <-3 C .k <-6D .k >-25.若直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,则直线l 2过定点( B ) A .(0,4) B .(0,2) C .(-2,4)D .(4,-2)6.已知点A (x,5)关于点(1,y )的对称点是(-2,-3),则点P (x ,y )到原点的距离是( D ) A .4 B .13 C.15D .177.已知直线3x +2y -3=0与直线6x +my +7=0互相平行,则它们之间的距离是( B )A .4B .132C.21313D .713268.圆C :x 2+y 2-4x -4y -10=0上的点到直线l :x +y -14=0的最大距离与最小距离的差是( C ) A .36 B .18 C .6 2D .5 2解析:圆x 2+y 2-4x -4y -10=0的圆心为(2,2),半径为32, 圆心到直线x +y -14=0的距离为|2+2-14|2=52>32,圆上的点到直线的最大距离与最小距离的差是2R =6 2.9.若直线3x -4y +5=0与圆x 2+y 2=r 2(r >0)相交于A ,B 两点,且∠AOB =120°(O 为坐标原点),则r = 2 .解析:圆x 2+y 2=r 2的圆心为原点,则圆心到直线3x -4y +5=0的距离为|0-0+5|32+-2=1,在△OAB 中,点O 到边AB 的距离d =r sin 30°=r2=1,所以r =2.10.若在平面直角坐标系内过点P (1,3)且与原点的距离为d 的直线有两条,则d 的取值范围为 0<d <2 .解析:|OP |=2,当直线l 过点P (1,3)且与直线OP 垂直时,有d =2,且直线l 有且只有一条;当直线l 与直线OP 重合时,有d =0,且直线l 有且只有一条;当0<d <2时,有两条. 11.已知直线l 1与直线l 2:4x -3y +1=0垂直且与圆C :x 2+y 2=-2y +3相切,则直线l 1的方程是 3x +4y +14=0或3x +4y -6=0 .解析:圆C 的方程为x 2+(y +1)2=4,圆心为(0,-1),半径r =2.由已知可设直线l 1的方程为3x +4y +c =0,则|3×0+-+c |32+42=2,解得c =14或c =-6.即直线l 1的方程为3x +4y +14=0或3x +4y -6=0. 12.已知直线l 经过直线2x +y -5=0与x -2y =0的交点. (1)若点A (5,0)到l 的距离为3,求l 的方程; (2)求点A (5,0)到l 的距离的最大值.解析:(1)易知点A 到直线x -2y =0的距离不等于3,可设经过两已知直线交点的直线系方程为(2x +y -5)+λ(x -2y )=0, 即(2+λ)x +(1-2λ)y -5=0.由题意得|10+5λ-5|+λ2+-2λ2=3,即2λ2-5λ+2=0,∴λ=2或12.∴l 的方程为4x -3y -5=0或x =2.(2)由⎩⎪⎨⎪⎧2x +y -5=0,x -2y =0,解得交点为P (2,1),如图,过P 作任一直线l ,设d 为点A 到l 的距离,则d ≤|PA |(当l ⊥PA 时等号成立).∴d max =|PA |=10.B 组 能力提升练1.在直角三角形ABC 中,点D 是斜边AB 的中点,点P 为线段CD 的中点,则|PA |2+|PB |2|PC |2=( D ) A .2 B .4 C .5D .102.已知直线y =2x 是△ABC 中∠C 的平分线所在的直线,若点A ,B 的坐标分别是(-4,2),(3,1),则点C 的坐标为( C ) A .(-2,4) B .(-2,-4) C .(2,4)D .(2,-4)解析:设A (-4,2)关于直线y =2x 的对称点为(x ,y ),则⎩⎪⎨⎪⎧y -2x +4×2=-1,y +22=2×-4+x2,解得⎩⎪⎨⎪⎧x =4,y =-2,∴BC 所在直线方程为y -1=-2-14-3(x -3),即3x +y -10=0. 联立y =2x ,解得⎩⎪⎨⎪⎧x =2,y =4,则C (2,4).故选C.3.已知圆C :(x -1)2+(y -2)2=2与y 轴在第二象限所围区域的面积为S ,直线y =2x +b 分圆C 的内部为两部分,其中一部分的面积也为S ,则b =( D ) A .- 6B .± 6C .- 5D .± 54.设m ∈R ,过定点A 的动直线x +my =0和过定点B 的动直线mx -y -m +3=0交于点P (x ,y ),则|PA |·|PB |的最大值是 5 .解析:易求定点A (0,0),B (1,3).当P 与A 和B 均不重合时,不难验证PA ⊥PB ,所以|PA |2+|PB |2=|AB |2=10,所以|PA |·|PB |≤|PA |2+|PB |22=5(当且仅当|PA |=|PB |=5时,等号成立),当P 与A 或B 重合时,|PA |·|PB |=0,故|PA |·|PB |的最大值是5.5.已知动直线l :ax +by +c -2=0(a >0,c >0)恒过点P (1,m ),且Q (4,0)到动直线l 的最大距离为3,则12a +2c 的最小值为 94.解析:因为动直线l :ax +by +c -2=0(a >0,c >0)恒过点P (1,m ),所以a +bm +c -2=0,又Q (4,0)到动直线l 的最大距离为3, 所以-2+-m2=3,解得m =0.所以a +c =2,则12a +2c =12(a +c )·⎝ ⎛⎭⎪⎫12a +2c =12⎝ ⎛⎭⎪⎫52+c 2a +2a c ≥12⎝ ⎛⎭⎪⎫52+2c 2a ·2a c =94, 当且仅当c =2a =43时取等号.6.在平面直角坐标系内,到点A (1,2),B (1,5),C (3,6),D (7,-1)的距离之和最小的点的坐标是 (2,4) .解析:由已知得k AC =6-23-1=2,k BD =5--1-7=-1,所以AC 的方程为y -2=2(x -1), 即2x -y =0,①BD 的方程为y -5=-(x -1),即x +y -6=0,②联立①②解得⎩⎪⎨⎪⎧x =2,y =4.所以直线AC 与直线BD 的交点为P (2,4), 此点即为所求点.因为|PA |+|PB |+|PC |+|PD |=|AC |+|BD |, 取异于P 点的任一点P ′,则|P ′A |+|P ′B |+|P ′C |+|P ′D | =(|P ′A |+|P ′C |)+(|P ′B |+|P ′D |)>|AC |+|BD |=|PA |+|PB |+|PC |+|PD |. 故P 点就是到A ,B ,C ,D 的距离之和最小的点.7.在平面直角坐标系xOy 中,将直线l 沿x 轴正方向平移3个单位,沿y 轴正方向平移5个单位,得到直线l 1.再将直线l 1沿x 轴正方向平移1个单位,沿y 轴负方向平移2个单位,又与直线l 重合.若直线l 与直线l 1关于点(2,3)对称,则直线l 的方程是 6x -8y +1=0 . 解析:由题意知直线l 的斜率存在,设直线l 的方程为y =kx +b ,将直线l 沿x 轴正方向平移3个单位,沿y 轴正方向平移5个单位,得到直线l 1:y =k (x -3)+5+b ,再将直线l 1沿x 轴正方向平移1个单位,沿y 轴负方向平移2个单位,则平移后的直线方程为y =k (x-3-1)+b +5-2,即y =kx +3-4k +b .∴b =3-4k +b ,解得k =34.∴直线l 的方程为y=34x +b ,直线l 1为y =34x +114+b ,设直线l 上的一点P ⎝ ⎛⎭⎪⎫m ,b +3m 4,则点P 关于点(2,3)的对称点为⎝ ⎛⎭⎪⎫4-m ,6-b -34m ,∴6-b -34m =34(4-m )+b +114,解得b =18.∴直线l 的方程是y =34x +18,即6x -8y +1=0.8.著名数学家华罗庚曾说过:“数形结合百般好,割裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:x -a2+y -b2可以转化为平面上点M (x ,y )与点N (a ,b )的距离.结合上述观点,可得f (x )=x 2+4x +20+ x 2+2x +10的最小值为 5 2 .解析:∵f (x )=x 2+4x +20+x 2+2x +10=x +2+-2+x +2+-2,∴f (x )的几何意义为点M (x,0)到两定点 A (-2,4)与B (-1,3)的距离之和.设点 A (-2,4)关于x 轴的对称点为A ′,则A ′为(-2,-4).要求f (x )的最小值,可转化为|MA |+|MB |的最小值,利用对称思想可知|MA |+|MB |≥|A ′B |=-1+2++2=52,即f (x )=x 2+4x +20+x 2+2x +10的最小值为5 2.9.已知直线l :(2+m )x +(1-2m )y +4-3m =0. (1)求证:不论m 为何实数,直线l 过一定点M ;(2)过定点M 作一条直线l 1,使夹在两坐标轴之间的线段被M 点平分,求直线l 1的方程. 解析:(1)证明:直线l 的方程整理得(2x +y +4)+m (x -2y -3)=0,由⎩⎪⎨⎪⎧2x +y =-4,x -2y =3,解得⎩⎪⎨⎪⎧x =-1,y =-2,所以无论m 为何实数,直线l 过定点M (-1,-2).(2)过定点M (-1,-2)作一条直线l 1,使夹在两坐标轴之间的线段被M 点平分,则直线l 1过点(-2,0),(0,-4), 设直线l 1的方程为y =kx +b ,把两点坐标代入得⎩⎪⎨⎪⎧-2k +b =0,b =-4,解得⎩⎪⎨⎪⎧k =-2,b =-4,∴直线方程为y =-2x -4.8-3 圆的方程课时规范练(授课提示:对应学生用书第303页)A 组 基础对点练1.圆心为(1,1)且过原点的圆的方程是( D ) A .(x -1)2+(y -1)2=1 B .(x +1)2+(y +1)2=1 C .(x +1)2+(y +1)2=2 D .(x -1)2+(y -1)2=22.直线x -2y -2k =0与直线2x -3y -k =0的交点在圆x 2+y 2=9的外部,则k 的取值范围为( A )A .k <-35或k >35B .-35<k <35C .-34<k <34D .k <-34或k >343.已知圆C 1:(x -2)2+(y -3)2=1,圆C 2:(x -3)2+(y -4)2=9,M ,N 分别是圆C 1,C 2上的动点,P 为x 轴上的动点,则|PM |+|PN |的最小值为( B ) A .6-2 2 B .52-4 C.17-1D .174.点P (4,-2)与圆x 2+y 2=4上任一点连线的中点的轨迹方程是( A ) A .(x -2)2+(y +1)2=1 B .(x -2)2+(y +1)2=4C .(x +4)2+(y -2)2=4 D .(x +2)2+(y -1)2=15.(2018·长沙二模)圆x 2+y 2-2x -2y +1=0上的点到直线x -y =2的距离的最大值是( A ) A .1+ 2 B .2 C .1+22D .2+2 2解析:将圆的方程化为(x -1)2+(y -1)2=1,圆心坐标为(1,1),半径为1,则圆心到直线x -y =2的距离d =|1-1-2|2=2,故圆上的点到直线x -y =2的距离的最大值为d +1=2+1,故选A.6.(2016·高考天津卷)已知圆C 的圆心在x 轴的正半轴上,点M (0,5)在圆C 上,且圆心到直线2x -y =0的距离为455,则圆C 的方程为 (x -2)2+y 2=9 .解析:设圆心为(a,0)(a >0),则圆心到直线2x -y =0的距离d =|2a -0|4+1=455,得a =2,半径r =a -2+-52=3,所以圆C 的方程为(x -2)2+y 2=9.7.(2016·高考浙江卷)已知a ∈R ,方程a 2x 2+(a +2)y 2+4x +8y +5a =0表示圆,则圆心坐标是 (-2,-4) ,半径是 5 .解析:由题可得a 2=a +2,解得a =-1或a =2.当a =-1时,方程为x 2+y 2+4x +8y -5=0,表示圆,故圆心为(-2,-4),半径为5.当a =2时,方程不表示圆.8.(2018·高考天津卷)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为x 2+y 2-2x =0 .解析:设圆的方程为x 2+y 2+Dx +Ey +F =0,圆经过三点(0,0),(1,1),(2,0),则⎩⎪⎨⎪⎧F =0,1+1+D +E +F =0,4+0+2D +F =0,解得⎩⎪⎨⎪⎧D =-2,E =0,F =0,则圆的方程为x 2+y 2-2x =0.9.过点M (1,2)的直线l 与圆C :(x -3)2+(y -4)2=25交于A ,B 两点,C 为圆心,当∠ACB 最小时,直线l 的方程是 x +y -3=0 .解析:验证得M (1,2)在圆内,当∠ACB 最小时,直线l 与CM 垂直,又圆心为(3,4),则k CM =4-23-1=1,则k l =-1,故直线l 的方程为y -2=-(x -1),整理得x +y -3=0. 10.已知圆C 经过点(0,1),且圆心为C (1,2). (1)写出圆C 的标准方程;(2)过点P (2,-1)作圆C 的切线,求该切线的方程及切线长. 解析:(1)由题意知,圆C 的半径r =-2+-2=2,所以圆C 的标准方程为(x -1)2+(y -2)2=2.(2)由题意知切线斜率存在,故设过点P (2,-1)的切线方程为y +1=k (x -2),即kx -y -2k -1=0,则|-k -3|1+k 2=2,所以k 2-6k -7=0,解得k =7或k =-1,故所求切线的方程为7x -y -15=0或x +y -1=0.由圆的性质易得所求切线长为PC 2-r 2=-2+-1-2-2=2 2.11.在平面直角坐标系xOy 中,经过函数f (x )=x 2-x -6的图象与两坐标轴交点的圆记为圆C .(1)求圆C 的方程;(2)求经过圆心C 且在坐标轴上截距相等的直线l 的方程.解析:(1)设圆的方程为x 2+y 2+Dx +Ey +F =0,函数f (x )=x 2-x -6的图象与两坐标轴交点为(0,-6),(-2,0),(3,0), 由⎩⎪⎨⎪⎧ 36-6E +F =0,4-2D +F =0,9+3D +F =0,解得⎩⎪⎨⎪⎧D =-1,E =5,F =-6,所以圆的方程为x 2+y 2-x +5y -6=0.(2)由(1)知圆心坐标为⎝ ⎛⎭⎪⎫12,-52,若直线经过原点,则直线l 的方程为5x +y =0;若直线不过原点,设直线l 的方程为x +y =a ,则a =12-52=-2,即直线l 的方程为x +y +2=0.综上可得,直线l 的方程为5x +y =0或x +y +2=0.B 组 能力提升练1.方程|y |-1=1-x -2表示的曲线是( D )A .一个椭圆B .一个圆C .两个圆D .两个半圆2.圆C 的圆心在y 轴正半轴上,且与x 轴相切,被双曲线x 2-y 23=1的渐近线截得的弦长为3,则圆C 的方程为( A )A .x 2+(y -1)2=1 B .x 2+(y -3)2=3 C .x 2+(y +1)2=1D .x 2+(y +3)2=33.已知圆C :(x -3)2+(y -4)2=1和两点A (-m,0),B (m,0)(m >0),若圆C 上存在点P ,使得∠APB =90°,则m 的最大值为( B ) A .7 B .6 C .5D .44.已知圆M 的圆心在抛物线x 2=4y 上,且圆M 与y 轴及抛物线的准线都相切,则圆M 的方程是( A )A .x 2+y 2±4x -2y +1=0 B .x 2+y 2±4x -2y -1=0 C .x 2+y 2±4x -2y +4=0 D .x 2+y 2±4x -2y -4=05.已知△ABC 的三个顶点坐标分别为A (-2,3),B (-2,-1),C (6,-1),以原点为圆心的圆与此三角形有唯一的公共点,则该圆的方程为( D ) A .x 2+y 2=1 B .x 2+y 2=4 C .x 2+y 2=4D .x 2+y 2=1或x 2+y 2=37解析:直线AC 为x +2y -4=0,点O 到直线AC 的距离为d =|-4|5=455>1,又|OA |=13,|OB |=5,|OC |=37.由题意知公共点为(0,-1)或(6,-1).故半径为1或37. 6.圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为 (x -2)2+(y -1)2=4 .解析:依题意,设圆心的坐标为(2b ,b )(其中b >0),则圆C 的半径为2b ,圆心到x 轴的距离为b ,所以24b 2-b 2=23,b >0,解得b =1,故所求圆C 的标准方程为(x -2)2+(y -1)2=4.7.(2018·运城二模)已知圆C 截y 轴所得的弦长为2,圆心C 到直线l :x -2y =0的距离为55,且圆C 被x 轴分成的两段弧长之比为3∶1,则圆C 的方程为 (x +1)2+(y +1)2=2或(x -1)2+(y -1)2=2 .解析:设圆C 的方程为(x -a )2+(y -b )2=r 2,则点C 到x 轴,y 轴的距离分别为|b |,|a |.由题意可知⎩⎪⎨⎪⎧r 2=2b 2,r 2=a 2+1,|a -2b |5=55,∴⎩⎪⎨⎪⎧ a =-1,b =-1,r 2=2或⎩⎪⎨⎪⎧a =1,b =1,r 2=2.故所求圆C 的方程为(x +1)2+(y +1)2=2或(x -1)2+(y -1)2=2.8.在平面直角坐标系xOy 中,以点(2,1)为圆心且与直线mx +y -2m =0(m ∈R )相切的所有圆中,半径最大的圆的标准方程为 (x -2)2+(y -1)2=1 .解析:直线mx +y -2m =0过定点(2,0),则以点(2,1)为圆心且与直线mx +y -2m =0(m ∈R )相切的所有圆中,半径最大的圆的半径为1,∴半径最大的圆的标准方程为(x -2)2+(y -1)2=1.9.已知平面区域⎩⎪⎨⎪⎧x ≥0,y ≥0,x +2y -4≤0恰好被面积最小的圆C :(x -a )2+(y -b )2=r 2及其内部所覆盖,则圆C 的方程为 (x -2)2+(y -1)2=5 .解析:由题意知,此平面区域表示的是以O (0,0),P (4,0),Q (0,2)所构成的三角形及其内部,∴覆盖它的且面积最小的圆是其外接圆.∵△OPQ 为直角三角形,∴圆心为斜边PQ 的中点(2,1),半径r =|PQ |2=5,∴圆C 的方程为(x -2)2+(y -1)2=5.10.如图,已知圆C 与x 轴相切于点T (1,0),与y 轴正半轴交于两点A ,B (B 在A 的上方),且|AB |=2.(1)圆C 的标准方程为 (x -1)2+(y -2)2=2 ; (2)圆C 在点B 处的切线在x 轴上的截距为 -2-1 .解析:(1)过点C 作CM ⊥AB 于M ,连接AC (图略),则|CM |=|OT |=1,|AM |=12|AB |=1,所以圆的半径r =|AC |=|CM |2+|AM |2=2,从而圆心C (1,2),即圆的标准方程为(x -1)2+(y -2)2=2.(2)令x =0得,y =2±1,则B (0,2+1), 所以直线BC 的斜率为k =2+-20-1=-1,由直线与圆相切的性质知,圆C 在点B 处的切线的斜率为1,则圆C 在点B 处的切线方程为y -(2+1)=1×(x -0),即y =x +2+1, 令y =0得,x =-2-1,故所求切线在x 轴上的截距为-2-1.11.在平面直角坐标系xOy 中,已知圆P 在x 轴上截得线段长为22,在y 轴上截得线段长为2 3.(1)求圆心P 的轨迹方程; (2)若P 点到直线y =x 的距离为22,求圆P 的方程. 解析:(1)设P (x ,y ),圆P 的半径为r . 由题意可得y 2+2=r 2,x 2+3=r 2, 从而y 2+2=x 2+3.故P 点的轨迹方程为y 2-x 2=1. (2)设P (x 0,y 0).由已知得|x 0-y 0|2=22. 又P 点在双曲线y 2-x 2=1上,从而得⎩⎪⎨⎪⎧|x 0-y 0|=1,y 20-x 20=1.由⎩⎪⎨⎪⎧x 0-y 0=1,y 20-x 20=1得⎩⎪⎨⎪⎧x 0=0,y 0=-1.此时,圆P 的半径r = 3. 由⎩⎪⎨⎪⎧x 0-y 0=-1,y 20-x 20=1得⎩⎪⎨⎪⎧x 0=0,y 0=1.此时,圆P 的半径= 3.∴圆的方程为x 2+(y +1)2=3或x 2+(y -1)2=3.12.如图,在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4.设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使|MA |=2|MO |,求圆心C 的横坐标a 的取值范围.解析:(1)由题意知,圆心C 是直线y =2x -4和y =x -1的交点,解得点C (3,2),于是切线的斜率必存在.设过A (0,3)的圆C 的切线方程为y =kx +3, 由题意得,|3k +1|k 2+1=1, 解得k =0或-34,故所求切线方程为y =3或3x +4y -12=0. (2)因为圆心在直线y =2x -4上,所以圆C 的方程为(x -a )2+[y -2(a -2)]2=1. 设点M (x ,y ),因为|MA |=2|MO |, 所以x 2+y -2=2x 2+y 2,化简得x 2+y 2+2y -3=0, 即x 2+(y +1)2=4,所以点M 在以D (0,-1)为圆心,2为半径的圆上. 由题意,点M (x ,y )在圆C 上, 所以圆C 与圆D 有公共点, 则|2-1|≤|CD |≤2+1, 即1≤a 2+a -2≤3.整理,得-8≤5a 2-12a ≤0. 由5a 2-12a +8≥0,得a ∈R ; 由5a 2-12a ≤0,得0≤a ≤125. 所以圆心C 的横坐标a 的取值范围为⎣⎢⎡⎦⎥⎤0,125.8-4 直线与圆、圆与圆的位置关系课时规范练(授课提示:对应学生用书第305页)A组基础对点练1.已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( B ) A.相切B.相交C.相离D.不确定2.设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( B )A.6 B.4C.3 D.23.直线3x+4y=b与圆x2+y2-2x-2y+1=0相切,则b的值是( D )A.-2或12 B.2或-12C.-2或-12 D.2或124.圆x2+2x+y2+4y-3=0上到直线x+y+1=0的距离为2的点共有( C )A.1个B.2个C.3个D.4个解析:圆的方程可化为(x+1)2+(y+2)2=8,圆心(-1,-2)到直线的距离d=|-1-2+1|2=2,半径是22,结合图形可知有3个符合条件的点.5.若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( C ) A.[-3,-1]B.[-1,3]C.[-3,1]D.(-∞,-3]∪[1,+∞)6.(2016·高考山东卷)已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是22,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是( B )A.内切B.相交C.外切D.相离7.过点(3,1)作圆(x-1)2+y2=r2的切线有且只有一条,则该切线的方程为( B )A .2x +y -5=0B .2x +y -7=0C .x -2y -5=0D .x -2y -7=08.过点(1,-2)作圆(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( B ) A .y =-34 B .y =-12C .y =-32D .y =-149.已知圆C :(x -1)2+(y -2)2=2,y 轴被圆C 截得的弦长与直线y =2x +b 被圆C 截得的弦长相等,则b =( D ) A .- 6 B .± 6 C .- 5D .± 5解析:易求得圆C 被y 轴截得的弦长为2,得|2×1-2+b |5=1,解得b =± 5.10.若圆x 2+y 2-4mx +(2m -3)y +4=0被直线2x -2y -3=0所截得的弦最长,则实数m 的值为 1 .解析:圆x 2+y 2-4mx +(2m -3)y +4=0的圆心坐标为⎝⎛⎭⎪⎫2m ,-m +32.∵圆x 2+y 2-4mx +(2m -3)y +4=0被直线2x -2y -3=0所截得的弦最长,∴圆心在直线上, ∴4m +2m -3-3=0,解得m =1,满足圆的方程, ∴m =1.11.已知矩形ABCD 的对角线交于点P (2,0),边AB 所在的直线方程为x +y -2=0,点(-1,1)在边AD 所在的直线上. (1)求矩形ABCD 的外接圆方程;(2)已知直线l :(1-2k )x +(1+k )y -5+4k =0(k ∈R ),求证:直线l 与矩形ABCD 的外接圆相交,并求最短弦长.解析:(1)依题意得AB ⊥AD ,∵k AB =-1, ∴k AD =1,∴直线AD 的方程为y -1=x +1, 即y =x +2.联立方程⎩⎪⎨⎪⎧x +y -2=0,x -y +2=0,解得⎩⎪⎨⎪⎧x =0,y =2,即A (0,2).∵矩形ABCD 的外接圆是以P (2,0)为圆心,|AP |=22为半径的圆,∴方程为(x -2)2+y 2=8.(2)直线l 的方程可整理为(x +y -5)+k (y -2x +4)=0,k ∈R ,∴联立方程⎩⎪⎨⎪⎧x +y -5=0,y -2x +4=0,解得⎩⎪⎨⎪⎧x =3,y =2,∴直线l 过定点M (3,2).又∵点M (3,2)在圆内,∴直线l 与圆相交. ∵圆心P 与定点M 的距离d =5, ∴最短弦长为28-5=2 3. 12.已知方程x 2+y 2-2x -4y +m =0. (1)若此方程表示圆,求实数m 的取值范围;(2)若(1)中的圆与直线x +2y -4=0相交于M ,N 两点,且OM ⊥ON (O 为坐标原点),求m 的值;(3)在(2)的条件下,求以MN 为直径的圆的方程.解析:(1)由D 2+E 2-4F >0得(-2)2+(-4)2-4m >0,解得m <5.(2)设M (x 1,y 1),N (x 2,y 2),由x +2y -4=0得x =4-2y .将x =4-2y 代入x 2+y 2-2x -4y +m =0得5y 2-16y +8+m =0,∴y 1+y 2=165,y 1y 2=8+m 5.∵OM ⊥ON ,∴x 1x 2+y 1y 2=0.∵x 1x 2=(4-2y 1)(4-2y 2)=16-8(y 1+y 2)+4y 1y 2, ∴x 1x 2+y 1y 2=16-8(y 1+y 2)+5y 1y 2=0, 即(8+m )-8×165+16=0,解得m =85.(3)设圆心C 的坐标为(a ,b ),则a =12(x 1+x 2)=45,b =12(y 1+y 2)=85,半径r =|OC |=455,∴所求圆的方程为⎝ ⎛⎭⎪⎫x -452+⎝ ⎛⎭⎪⎫y -852=165.B 组 能力提升练1.在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2x +y -4=0相切,则圆C 面积的最小值为( A ) A.45π B .34π C .(6-25)πD .54π 2.已知直线l :y =kx +b ,曲线C :x 2+y 2=1,则“b =1”是“直线l 与曲线C 有公共点”的( A )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.若圆x 2+y 2+Dx +Ey +F =0关于直线l 1:x -y +4=0和直线l 2:x +3y =0都对称,则D +E 的值为( D ) A .-4 B .-2 C .2D .44.过点P (1,3)作圆O :x 2+y 2=1的两条切线,切点分别为A 和B ,则弦长|AB |=( A ) A. 3 B .2 C. 2D .45.过点P (1,3)作圆x 2+y 2=1的两条切线,切点分别为A ,B ,则PA →·PB →= 32.解析:由题意,得圆心为O (0,0),半径为1.如图所示. ∵P (1,3),∴PB ⊥x 轴,|PA |=|PB |= 3. ∴△POA 为直角三角形,其中|OA |=1,|AP |=3, 则|OP |=2,∴∠OPA =30°,∴∠APB =60°.∴PA →·PB →=|PA →||PB →|·cos∠APB =3×3×cos 60°=32.6.(2016·高考全国卷Ⅲ)已知直线l :x -3y +6=0与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别作l 的垂线与x 轴交于C ,D 两点.则|CD |= 4 .解析:设A (x 1,y 1),B (x 2,y 2),C (x 3,0),D (x 4,0),由x -3y +6=0,得x =3y -6,代入圆的方程,并整理,得y 2-33y +6=0,解得y 1=23,y 2=3,所以x 1=0,x 2=-3,所以直线AC 的方程为y -23=-3x ,令y =0得x 3=2,直线BD 的方程为y -3=-3(x +3),令y =0得x 4=-2,则|CD |=|x 3-x 4|=4.7.已知圆C 的圆心与抛物线y 2=4x 的焦点关于直线y =x 对称,直线4x -3y -2=0与圆C 相交于A ,B 两点,且|AB |=6,则圆C 的方程为 x 2+(y -1)2=10 .解析:设所求圆的半径是r ,依题意得,抛物线y 2=4x 的焦点坐标是(1,0),则圆C 的圆心坐标是(0,1),圆心到直线4x -3y -2=0的距离d =|4×0-3×1-2|42+-2=1,则r 2=d 2+⎝ ⎛⎭⎪⎫|AB |22=10,故圆C 的方程是x 2+(y -1)2=10.8.在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2-8x +15=0,若直线y =kx -2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是 43 .解析:圆C 的标准方程为(x -4)2+y 2=1,圆心为(4,0). 由题意知(4,0)到kx -y -2=0的距离应不大于2, 即|4k -2|k 2+1≤2,整理得3k 2-4k ≤0,解得0≤k ≤43.故k 的最大值是43.9.若圆O :x 2+y 2=5与圆O 1:(x -m )2+y 2=20(m ∈R )相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长是 4 .解析:圆O 1与圆O 在A 处的切线互相垂直,如图,可知两切线分别过另一圆的圆心,∴O 1A ⊥OA .又∵|OA |=5,|O 1A |=25,∴|OO 1|=5. 又A ,B 关于OO 1所在直线对称, ∴AB 长为Rt △OAO 1斜边上的高的2倍, ∴|AB |=2×5×255=4. 10.已知过点A (0,1)且斜率为k 的直线l 与圆C :(x -2)2+(y -3)2=1交于M ,N 两点. (1)求k 的取值范围;(2)若OM →·ON →=12,其中O 为坐标原点,求|MN |. 解析:(1)设直线l 的方程为y =kx +1. 因为直线l 与圆交于两点,所以|2k -3+1|1+k 2<1,解得4-73<k <4+73. 所以k 的取值范围为⎝⎛⎭⎪⎫4-73,4+73.(2)设M (x 1,y 1),N (x 2,y 2).将y =kx +1代入圆C 的方程(x -2)2+(y -3)2=1,整理得(1+k 2)x 2-4(1+k )x +7=0,所以x 1+x 2=+k 1+k 2,x 1x 2=71+k2.OM →·ON →=x 1x 2+y 1y 2=(1+k 2)x 1x 2+k (x 1+x 2)+1=4k +k1+k2+8. 由题设可得4k+k1+k2+8=12,解得k =1, 所以l 的方程为y =x +1.又因为圆C 的圆心(2,3)在l 上,所以|MN |=2.11.已知直线l :4x +3y +10=0,半径为2的圆C 与l 相切,圆心C 在x 轴上且在直线l 的右上方. (1)求圆C 的方程;(2)过点M (1,0)的直线与圆C 交于A ,B 两点(A 在x 轴上方),问在x 轴正半轴上是否存在定点N ,使得x 轴平分∠ANB ?若存在,请求出点N 的坐标;若不存在,请说明理由. 解析:(1)设圆心C (a,0)⎝ ⎛⎭⎪⎫a >-52,则|4a +10|5=2,解得a =0或a =-5(舍).所以圆C 的方程为x 2+y 2=4.(2)当直线AB ⊥x 轴时,x 轴平分∠ANB .当直线AB 的斜率存在时,设直线AB 的方程为y =k (x -1),N (t,0),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧x 2+y 2=4,y =k x -,得(k 2+1)x 2-2k 2x +k 2-4=0,所以x 1+x 2=2k 2k 2+1,x 1x 2=k 2-4k 2+1.若x 轴平分∠ANB ,则k AN =-k BN , 即y 1x 1-t +y 2x 2-t=0,则k x 1-x 1-t+k x 2-x 2-t=0,即2x 1x 2-(t +1)(x 1+x 2)+2t =0, 即k 2-k 2+1-2k 2t +k 2+1+2t =0,解得t =4,所以当点N 坐标为(4,0)时,能使x 轴平分∠ANB .8-5 椭圆课时规范练(授课提示:对应学生用书第307页)A 组 基础对点练1.已知椭圆x 225+y 2m2=1(m >0)的左焦点为F 1(-4,0),则m =( B )A .2B .3C .4D .92.方程kx 2+4y 2=4k 表示焦点在x 轴上的椭圆,则实数k 的取值范围是( D ) A .k >4 B .k =4 C .k <4D .0<k <43.若对任意k ∈R ,直线y -kx -1=0与椭圆x 22+y 2m=1恒有公共点,则实数m 的取值范围是( C ) A .(1,2] B .[1,2)C .[1,2)∪(2,+∞)D .[1,+∞)4.(2017·河北衡水中学二调)设椭圆x 216+y 212=1的左、右焦点分别为F 1,F 2,点P 在椭圆上,且满足PF 1→·PF 2→=9,则|PF 1|·|PF 2|的值为( D ) A .8 B .10 C .12D .15解析:由椭圆方程x 216+y 212=1,可得c 2=4,所以|F 1F 2|=2c =4,而F 1F 2→=PF 2→-PF 1→,所以|F 1F 2→|=|PF 2→-PF 1→|,两边同时平方,得|F 1F 2→|2=|PF 1→|2-2PF 1→·PF 2→+|PF 2→|2,所以|PF 1→|2+|PF 2→|2=|F 1F 2→|2+2PF 1→·PF 2→=16+18=34.根据椭圆定义,得|PF 1|+|PF 2|=2a =8,(|PF 1|+|PF 2|)2=|PF 1|2+|PF 2|2+2|PF 1|·|PF 2|=64,所以34+2|PF 1|·|PF 2|=64,所以|PF 1|·|PF 2|=15,故选D.5.已知椭圆的中心在原点,离心率e =12,且它的一个焦点与抛物线y 2=-4x 的焦点重合,则此椭圆方程为( A ) A.x 24+y 23=1 B.x 28+y 26=1C.x 22+y 2=1 D.x 24+y 2=1 6.若椭圆x 2a 2+y 2b2=1(a >b >0)的右焦点F 是抛物线y 2=4x 的焦点,两曲线的一个交点为P ,且|PF |=4,则该椭圆的离心率为( A ) A.7-23B .2+13C.23 D .127.椭圆C :x 2a 2+y 2b2=1(a >b >0)的左焦点为F ,若F 关于直线3x +y =0的对称点A 是椭圆C上的点,则椭圆C 的离心率为( D ) A.12 B .3-12C.32D .3-18.若x 2+ky 2=2表示焦点在y 轴上的椭圆,则实数k 的取值范围是 (0,1) .解析:将椭圆的方程化为标准形式得y 22k+x 22=1,因为x 2+ky 2=2表示焦点在y 轴上的椭圆,所以2k>2,解得0<k <1.9.如图,在平面直角坐标系xOy 中,F 是椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点,直线y =b2与椭圆交于B ,C 两点,且∠BFC =90°,则该椭圆的离心率是63.解析:由题意可得B ⎝ ⎛⎭⎪⎫-32a ,b 2,C ⎝ ⎛⎭⎪⎫32a ,b 2,F (c,0),则由∠BFC =90°得BF →·CF →=⎝ ⎛⎭⎪⎫c +32a ,-b 2·⎝ ⎛⎭⎪⎫c -32a ,-b 2=c 2-34a 2+14b 2=0,化简得3c =2a ,则离心率e =c a =23=63.10.(2018·湖南江西十四校联考)已知椭圆E :x 2a 2+y 2b2=1()a >b >0上的点到椭圆一个焦点的距离的最大值是最小值的3倍,且点P ⎝ ⎛⎭⎪⎫1,32在椭圆E 上. (1)求椭圆E 的方程;(2)过点M ()1,1任作一条直线l ,l 与椭圆E 交于不同于P 点的A ,B 两点,l 与直线m :3x +4y -12=0交于C 点,记直线PA ,PB ,PC 的斜率分别为k 1,k 2,k 3.试探究k 1+k 2与k 3的关系,并证明你的结论.解析:(1)∵椭圆E :x 2a 2+y 2b2=1()a >b >0上的点到椭圆一个焦点的距离的最大值和最小值分别为a +c ,a -c ,依题意有a +c =3()a -c ⇒a =2c , ∵a 2=b 2+c 2,∴b =3c .故可设椭圆E 的方程为x 24c 2+y 23c2=1,∵点P ⎝ ⎛⎭⎪⎫1,32在椭圆E 上,所以将其代入椭圆E 的方程得14c 2+943c 2=1⇒c 2=1.∴椭圆E 的方程为x 24+y 23=1.(2)依题意,直线l 不可能与x 轴垂直,故可设直线l 的方程为y -1=k ()x -1,即y =kx -k +1,设A ()x 1,y 1,B ()x 2,y 2为l 与椭圆E 的两个交点.将y =kx -k +1代入方程3x 2+4y 2-12=0,化简得()4k 2+3x 2-8()k 2-k x +4k 2-8k -8=0.∴x 1+x 2=8k 2-8k 4k 2+3,x 1x 2=4k 2-8k -84k 2+3. ∴k 1+k 2=y 1-32x 1-1+y 2-32x 2-1=k ()x 1-1-12x 1-1+k ()x 2-1-12x 2-1=2k -12⎝ ⎛⎭⎪⎫1x 1-1+1x 2-1=2k -12x 1+x 2-2x 1x 2-()x 1+x 2+1=2k -128k 2-8k -2()4k 2+34k 2-8k -8-()8k 2-8k +()4k 2+3=6k -35. 又由⎩⎪⎨⎪⎧y =kx -k +1,3x +4y -12=0⇒3x +4()kx -k +1-12=0,解得x =4k +84k +3,y =9k +34k +3,即C 点的坐标为C ⎝⎛⎭⎪⎫4k +84k +3,9k +34k +3,∴k 3=9k +34k +3-324k +84k +3-1=6k -310.∴k 1+k 2与k 3的关系为k 1+k 2=2k 3.B 组 能力提升练1.已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F (3,0),过点F 的直线交E 于A ,B 两点.若AB 的中点坐标为(1,-1),则E 的方程为( D )A.x 245+y 236=1 B .x 236+y 227=1 C.x 227+y 218=1 D .x 218+y 29=1 2.设F 1,F 2是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左,右焦点,P 为直线x =3a2上一点,△F 2PF 1是底角为30°的等腰三角形,则椭圆E 的离心率为( C ) A.12 B .23 C.34D .453.从椭圆x 2a 2+y 2b2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是( C ) A.24 B .12 C.22D .32解析:易得P ⎝⎛⎭⎪⎫-c ,b 2a ,k AB =k OP ,即-b a =-b 2ac , 又a 2=b 2+c 2,可得c a =22. 4.已知直线l :y =kx +2过椭圆x 2a 2+y 2b2=1(a >b >0)的上顶点B 和左焦点F ,且被圆x 2+y 2=4截得的弦长为L ,若L ≥455,则椭圆离心率e 的取值范围是( B )A.⎝ ⎛⎭⎪⎫0,55 B .⎝⎛⎦⎥⎤0,255C.⎝ ⎛⎦⎥⎤0,355D .⎝⎛⎦⎥⎤0,4555.已知椭圆E :x 2a 2+y 2b2=1(a >b >0)的右焦点为F ,短轴的一个端点为M ,直线l :3x -4y =0交椭圆E 于A ,B 两点.若|AF |+|BF |=4,点M 到直线l 的距离不小于45,则椭圆E 的离心率的取值范围是( A ) A.⎝ ⎛⎦⎥⎤0,32 B .⎝ ⎛⎦⎥⎤0,34 C.⎣⎢⎡⎭⎪⎫32,1 D .⎣⎢⎡⎭⎪⎫34,1 6.(2016·高考浙江卷)已知椭圆C 1:x 2m 2+y 2=1(m >1)与双曲线C 2:x 2n2-y 2=1(n >0)的焦点重合,e 1,e 2分别为C 1,C 2的离心率,则( A ) A .m >n 且e 1e 2>1 B .m >n 且e 1e 2<1 C .m <n 且e 1e 2>1 D .m <n 且e 1e 2<17.(2018·湖北重点中学联考)已知椭圆C 1:x 2a 2+y 2b 2=1(a >b >0)与椭圆C 2:y 2a 2+x 2b2=1(a >b >0)相交于A ,B ,C ,D 四点,若椭圆C 1的一个焦点F (-2,0),且四边形ABCD 的面积为163,则椭圆C 1的离心率e 为22. 解析:联立⎩⎪⎨⎪⎧x 2a 2+y 2b 2=1,y 2a 2+x2b 2=1,两式相减得x 2-y 2a 2=x 2-y 2b 2,又a ≠b ,所以x 2=y 2=a 2b 2a 2+b 2,故四边形ABCD 为正方形,面积为4x 2=4a 2b 2a 2+b 2=163,(*)又由题意知a 2=b 2+2,将其代入(*)式整理得3b 4-2b 2-8=0,所以b 2=2,则a 2=4, 所以椭圆C 的离心率e =22.8.(2017·湖南东部六校联考)设P ,Q 分别是圆x 2+(y -1)2=3和椭圆x 24+y 2=1上的点,则P ,Q 两点间的最大距离是733. 解析:由圆的性质可知,P ,Q 两点间的最大距离可以转化为圆心到椭圆上点的距离的最大值加上圆的半径3,设Q (x ,y ),则圆心(0,1)到椭圆上点的距离为d =x 2+y -2=-3y 2-2y +5=-3⎝ ⎛⎭⎪⎫y +132+163, ∵-1≤y ≤1,∴当y =-13时,d 取最大值433,∴P ,Q 两点间的最大距离为d max +3=733. 9.(2018·高考天津卷)设椭圆x 2a 2+y 2b2=1(a >b >0)的右顶点为A ,上顶点为B .已知椭圆的离心率为53,|AB |=13. (1)求椭圆的方程;(2)设直线l :y =kx (k <0)与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若△BPM 的面积是△BPQ 面积的2倍,求k 的值.解析:(1)设椭圆的焦距为2c ,由已知得c 2a 2=59,又由a 2=b 2+c 2,可得2a =3b .由|AB |=a 2+b 2=13,从而a =3,b =2. 椭圆的方程为x 29+y 24=1.(2)设点P 的坐标为(x 1,y 1),点M 的坐标为(x 2,y 2),由题意知x 2>x 1>0,点Q 的坐标为(-x 1,-y 1).由△BPM 的面积是△BPQ 面积的2倍, 可得|PM |=2|PQ |,从而x 2-x 1=2[x 1-(-x 1)],即x 2=5x 1.易知直线AB 的方程为2x +3y =6,由方程组⎩⎪⎨⎪⎧2x +3y =6,y =kx消去y ,可得x 2=63k +2.由方程组⎩⎪⎨⎪⎧x 29+y 24=1,y =kx消去y ,可得x 1=69k 2+4.由x 2=5x 1,可得9k 2+4=5(3k +2),两边平方,整理得18k 2+25k +8=0,解得k =-89或k =-12.。
(新课标)2020年高考数学一轮总复习第八章平面解析几何8_5椭圆课件文新人教A版

点,P为C上一点,满足|OP|=|OF|,且|PF|=6,则椭圆C的方程为( )
A.3x62 +1y62 =1 C.4x92 +2y42 =1
B.4x02 +1y52 =1 D.4x52 +2y02 =1
[解析]
(1)因为O,M分别为F1F2和PF1的中点,所以OM∥PF2,且|OM|=
1 2
|PF2|,
中心到l的距离为其短轴长的14,则该椭圆的离心率为( )
1
1
A.3
B.2
2
3
C.3
D.4
(2)如图,焦点在x轴上的椭圆
x2 4
+
y2 b2
=1的离心率e=
1 2
,F,A分别是椭圆的左焦点
和右顶点,P是椭圆上任意一点.则P→F·P→A的最大值为________.
[解析] (1)如图,|OB|为椭圆中心到l的距离,则|OA|·|OF|=|AF|·|OB|,即bc=a·b2, 所以e=ac=12.故选B.
②设直线 AM 的方程为 y=k(x+2)(k>0),
代入x2+y2=1 得(3+4k2)x2+16k2x+16k2-12=0. 43
由
x1·(-2)=163k+2-4k122得
x1=
2(3 4k 2 ) 3 4k 2
,
故|AM|=|x1+2| 1+k2=123+14+k2k2.
由题设直线 AN 的方程为 y=-1(x+2), k
点,则△AF1B的周长为________.
答案:20
考点一|椭圆的定义及方程 (易错突破)
【例 1】 (1)椭圆 C:ax22+y2=1(a>0)的左、右焦点分别为 F1,F2,P 为椭圆上异
于端点的任意一点,PF1,PF2 的中点分别为 M,N.O 为坐标原点,四边形 OMPN
2020届高考数学一轮复习第八章平面解析几何8
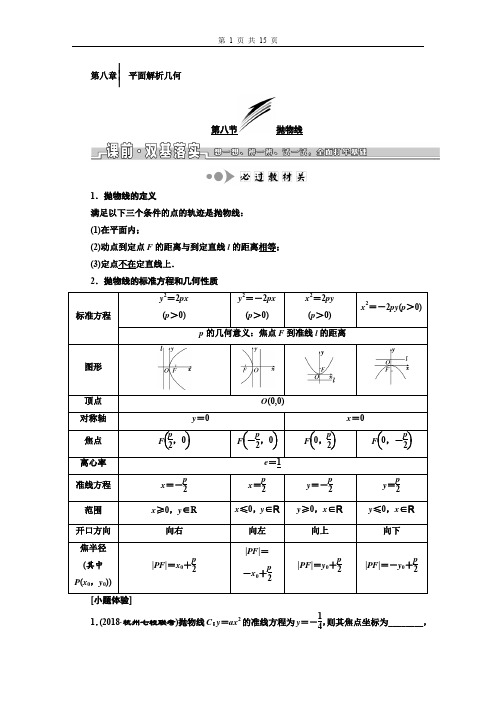
第八章⎪⎪⎪平面解析几何第八节抛物线1.抛物线的定义满足以下三个条件的点的轨迹是抛物线:(1)在平面内;(2)动点到定点F 的距离与到定直线l 的距离相等; (3)定点不在定直线上.2.抛物线的标准方程和几何性质1.(2018·杭州七校联考)抛物线C :y =ax 2的准线方程为y =-14,则其焦点坐标为________,实数a 的值为________.解析:由题意得焦点坐标为⎝⎛⎭⎫0,14,抛物线C 的方程可化为x 2=1a y ,由题意得-14a =-14,解得a =1. 答案:⎝⎛⎭⎫0,14 1 2.焦点在直线2x +y +2=0上的抛物线的标准方程为________. 答案:y 2=-4x 或x 2=-8y3.(教材习题改编)抛物线y =4x 2的焦点坐标为__________;准线方程为____________. 解析:抛物线的标准方程为x 2=14y ,所以焦点坐标为⎝⎛⎭⎫0,116,准线方程为y =-116. 答案:⎝⎛⎭⎫0,116 y =-1161.抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与直线垂直的直线.2.抛物线标准方程中参数p 易忽视,只有p >0才能证明其几何意义是焦点F 到准线l 的距离,否则无几何意义.3.抛物线的标准方程的形式要注意,根据方程求焦点坐标或准线方程时,要注意标准形式的确定.[小题纠偏]1.平面内到点(1,1)与到直线x +2y -3=0的距离相等的点的轨迹是( ) A .椭圆 B .双曲线 C .抛物线 D .一条直线答案:D2.抛物线8x 2+y =0的焦点坐标为________. 解析:由8x 2+y =0,得x 2=-18y .∴2p =18,p =116,∴焦点为⎝⎛⎭⎫0,-132. 答案:⎝⎛⎭⎫0,-132考点一 抛物线定义及应用(重点保分型考点——师生共研)[典例引领]1.(2019·温州十校联考)设抛物线C :y =14x 2的焦点为F ,直线l 交抛物线C 于A ,B 两点,|AF |=3,线段AB 的中点到抛物线C 的准线的距离为4,则|BF |=( )A.72 B .5 C .4D .3解析:选B 抛物线C 的方程可化为x 2=4y ,由线段AB 的中点到抛物线C 的准线的距离为4,可得|AF |+|BF |=8,又|AF |=3,所以|BF |=5.2.已知M 是抛物线x 2=4y 上一点,F 为其焦点,点A 在圆C :(x +1)2+(y -5)2=1上,则|MA |+|MF |的最小值是( )A .4B .5C .6D .7解析:选B 依题意,由点M 向抛物线x 2=4y 的准线l :y =-1引垂线,垂足为M 1(图略),则有|MA |+|MF |=|MA |+|MM 1|,结合图形可知|MA |+|MM 1|的最小值等于圆心C (-1,5)到y =-1的距离再减去圆C 的半径,即等于6-1=5,因此|MA |+|MF |的最小值是5,故选B.[由题悟法]应用抛物线定义的2个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P (x ,y )到焦点F 的距离|PF |=|x |+p 2或|PF |=|y |+p 2.[即时应用]1.如图,设抛物线y 2=4x 的焦点为F ,不经过焦点的直线上有三个不同的点A ,B ,C ,其中点A ,B 在抛物线上,点C 在y 轴上,则△BCF 与△ACF 的面积之比是( )A.|BF |-1|AF |-1 B.|BF |2-1|AF |2-1C.|BF |+1|AF |+1D.|BF |2+1|AF |2+1解析:选A 由图形可知,△BCF 与△ACF 有公共的顶点F ,且A ,B ,C 三点共线,易知△BCF 与△ACF 的面积之比就等于|BC ||AC |.由抛物线方程知其焦点F (1,0),作准线l ,则l 的方程为x =-1.∵点A ,B 在抛物线上,过A ,B 分别作AK ,BH 与准线垂直,垂足分别为点K ,H ,且与y 轴分别交于点N ,M .由抛物线定义,得|BM |=|BF |-1,|AN |=|AF |-1.在△CAN 中,BM ∥AN ,∴|BC ||AC |=|BM ||AN |=|BF |-1|AF |-1. 2.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是( )A.355B .2 C.115D .3解析:选B 由题可知l 2:x =-1是抛物线y 2=4x 的准线,设抛物线的焦点为F (1,0),则动点P 到l 2的距离等于|PF |,则动点P 到直线l 1和直线l 2的距离之和的最小值,即焦点F 到直线l 1:4x -3y +6=0的距离,所以最小值是|4-0+6|5=2.考点二 抛物线的标准方程与几何性质(题点多变型考点——多角探明) [锁定考向]抛物线的标准方程及性质是高考的热点,多以选择题、填空题形式出现. 常见的命题角度有: (1)求抛物线方程;(2)抛物线的对称性.[题点全练]角度一:求抛物线方程1.(2019·台州重点校联考)已知直线l 过抛物线y 2=-2px (p >0)的焦点,且与抛物线交于A ,B 两点,若线段AB 的长是8,AB 的中点到y 轴的距离是2,则此抛物线的方程是( )A .y 2=-12xB .y 2=-8xC .y 2=-6xD .y 2=-4x解析:选B 过A ,B 分别作抛物线的准线的垂线,垂足分别为A 1,B 1,由抛物线定义知|AF |=|AA 1|,|BF |=|BB 1|,则|AA 1|+|BB 1|=2⎝⎛⎭⎫2+p2=8,解得p =4,所以此抛物线的方程是y 2=-8x .角度二:抛物线的对称性2.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与抛物线y 2=2px (p >0)分别交于O ,A ,B 三点,O 为坐标原点.若双曲线的离心率为2,△AOB 的面积为3,则p =( )A .1 B.32C .2D .3解析:选B 双曲线的渐近线方程为y =±ba x , 因为双曲线的离心率为2, 所以1+b 2a 2=2,ba = 3.由⎩⎨⎧y =3x ,y 2=2px , 解得⎩⎪⎨⎪⎧x =0,y =0或⎩⎨⎧x =2p 3,y =23p 3.由曲线的对称性及△AOB 的面积得, 2×12×23p 3×2p 3=3, 解得p 2=94,即p =32⎝⎛⎭⎫p =-32舍去. [通法在握]求抛物线方程的3个注意点(1)当坐标系已建立时,应根据条件确定抛物线方程属于四种类型中的哪一种; (2)要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系; (3)要注意参数p 的几何意义是焦点到准线的距离,利用它的几何意义来解决问题.[演练冲关]1.(2019·宁波质检)已知点M 是抛物线C :y 2=2px (p >0)上一点,F 为C 的焦点,MF 的中点坐标是(2,2),则p 的值为( )A .1B .2C .3D .4解析:选D 抛物线C :y 2=2px (p >0)的焦点为F ⎝⎛⎭⎫p 2,0,设M ⎝⎛⎭⎫y 212p ,y 1,由中点坐标公式可知p 2+y 212p=2×2,y 1+0=2×2,解得p =4.2.(2019·丽水高三质检)过抛物线C :y 2=4x 的焦点F 的直线l 与抛物线C 交于P ,Q 两点,与抛物线准线交于M ,且FM =3FP ,则|FP |=( )A.32B.23C.43D.34解析:选C 设直线l 的倾斜角为θ,如图所示,过点P 作PN 垂直准线于点N ,由抛物线定义知|PN |=|PF |.∵FM =3FP ,∴|FM |=3|FP |,即|PM |=2|PN |.在Rt △MNP 中,cos ∠MPN =12,∵PN ∥x 轴,∴cos θ=12,由抛物线焦半径的性质可得|PF |=p 1+cos θ=21+12=43,即|FP |=43. 考点三 直线与抛物线的位置关系(重点保分型考点——师生共研)[典例引领](2018·长兴中学模拟)已知抛物线C 1:y 2=2px (p >0)的焦点为F ,P 为C 1上一点,|PF |=4,点P 到y 轴的距离等于3.(1)求抛物线C 1的标准方程;(2)设A ,B 为抛物线C 1上的两个动点,且使得线段AB 的中点D 在直线y =x 上,P (0,2)为定点,求△PAB 面积的最大值.解:(1)由题意,p2+3=4,∴p =2,所以抛物线C 1的标准方程为y 2=4x .(2)设直线AB :x =ty +b ,A (x 1,y 1),B (x 2,y 2).联立方程⎩⎪⎨⎪⎧x =ty +b ,y 2=4x消元化简得y 2-4ty -4b =0, Δ=16t 2+16b >0.且y 1+y 2=4t ,x 1+x 2=t (y 1+y 2)+2b =4t 2+2b , 所以D (2t 2+b,2t ),2t 2+b =2t . 由Δ>0得0<t <2.所以点P 到直线AB 的距离d =|-2t -b |1+t 2=|2t 2-4t |1+t 2, 所以|AB |=1+t 216t 2+16b =41+t 22t -t 2,所以S △ABP =12|AB |d =12×41+t 22t -t 2|2t 2-4t |1+t2=22t -t 2·|2t 2-4t |. 令m =2t -t 2,则m ∈(0,1],且S △ABP =4m 3. 由函数单调性可知,(S △ABP )max =4.[由题悟法]解决直线与抛物线位置关系问题的2种常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用弦长公式.[即时应用]如图所示,已知抛物线C :y 2=4x 的焦点为F ,直线l 经过点F 且与抛物线C 相交于A ,B 两点.(1)若线段AB 的中点在直线y =2上,求直线l 的方程; (2)若线段|AB |=20,求直线l 的方程. 解:(1)由已知,得抛物线的焦点为F (1,0). 因为线段AB 的中点在直线y =2上, 所以直线l 的斜率存在,设直线l 的斜率为k ,A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),由⎩⎪⎨⎪⎧y 21=4x 1,y 22=4x 2,得(y 1+y 2)(y 1-y 2)=4(x 1-x 2),所以2y 0k =4.又y 0=2,所以k =1,故直线l 的方程是y =x -1.(2)设直线l 的方程为x =my +1,与抛物线方程联立得⎩⎪⎨⎪⎧x =my +1,y 2=4x ,消去x ,得y 2-4my-4=0,所以y 1+y 2=4m ,y 1y 2=-4,Δ=16(m 2+1)>0. |AB |=m 2+1|y 1-y 2| =m 2+1·(y 1+y 2)2-4y 1y 2 =m 2+1·(4m )2-4×(-4) =4(m 2+1).所以4(m 2+1)=20,解得m =±2,所以直线l 的方程是x =±2y +1,即x ±2y -1=0.一抓基础,多练小题做到眼疾手快1.(2019·湖州质检)已知抛物线y 2=2px (p >0),点C (-4,0),过抛物线的焦点作垂直于x 轴的直线,与抛物线交于A ,B 两点,若△CAB 的面积为24,则以直线AB 为准线的抛物线的标准方程是( )A .y 2=4xB .y 2=-4xC .y 2=8xD .y 2=-8x解析:选D ∵AB ⊥x 轴,且AB 过点F ,∴AB 是焦点弦,∴|AB |=2p ,∴S △CAB =12×2p ×⎝⎛⎭⎫p 2+4=24,解得p =4或p =-12(舍去),∴直线AB 的方程为x =2,∴以直线AB 为准线的抛物线的标准方程是y 2=-8x ,故选D.2.(2018·江山质检)在抛物线y 2=2px (p >0)上,横坐标为4的点到焦点的距离为5,则p 的值为( )A.12 B .1 C .2D .3解析:选C 由抛物线的定义可知,4+p2=5,解得p =2.3.(2018·珠海模拟)已知抛物线y 2=4x 的焦点为F ,准线为l ,点P 为抛物线上一点,且在第一象限,PA ⊥l ,垂足为A ,|PF |=4,则直线AF 的倾斜角等于( )A.7π12B.2π3C.3π4D.5π6解析:选B 由抛物线y 2=4x 知焦点F (1,0),准线l 的方程为x =-1,由抛物线定义知|PA |=|PF |=4,所以点P 的坐标为(3,23),因此点A 的坐标为(-1,23),所以k AF =23-0-1-1=-3,所以直线AF 的倾斜角为2π3.4.(2019·宁波六校联考)已知抛物线C :y 2=23x ,过焦点F 且斜率为3的直线与C 相交于P ,Q 两点,且P ,Q 两点在准线上的投影分别为M ,N 两点,则S △MFN =( )A .8B .2 3C .4 3D .8 3解析:选B 法一:由题意可得p =3,F⎝⎛⎭⎫32,0.不妨设点P 在x 轴上方,由抛物线定义可知|PF |=|PM |,|Q F |=|Q N |,设直线P Q 的倾斜角为θ,则tan θ=3,∴θ=π3,由抛物线焦半径的性质可知,|PF |=p 1-cos θ=31-cos π3=23,|Q F |=p 1+cos θ=31+cosπ3=233,∴|MN |=|P Q |sin θ=(|PF |+|Q F |)·sin π3=833×32=4,∴S △MFN =12|MN |·p =12×4×3=2 3.法二:由题意可得F⎝⎛⎭⎫32,0,直线P Q 的方程为y =3⎝⎛⎭⎫x -32=3x -32,与抛物线方程y 2=23x 联立,得⎝⎛⎭⎫3x -322=23x ,即3x 2-53x +94=0,设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=533,∴|P Q |=x 1+x 2+p =533+3=833,∵直线P Q 的斜率为3,∴直线P Q 的倾斜角为π3.∴|MN |=|P Q |sinπ3=833×32=4,∴S △MFN =12×4×3=2 3. 5.已知点P 在抛物线y 2=4x 上,且点P 到y 轴的距离与其到焦点的距离之比为12,则点P 到x 轴的距离为________.解析:设点P 的坐标为(x P ,y P ),抛物线y 2=4x 的准线方程为x =-1,根据抛物线的定义,点P 到焦点的距离等于点P 到准线的距离,故x P x P -(-1)=12,解得x P =1,所以y 2P =4,所以|y P |=2. 答案:2二保高考,全练题型做到高考达标1.(2018·临海期初)动圆过点(0,1),且与直线y =-1相切,则动圆圆心的轨迹方程为( ) A .y =0 B .x 2+y 2=1 C .x 2=4yD .y 2=4x解析:选C 设动圆圆心M (x ,y ),则x 2+(y -1)2=|y +1|,解得x 2=4y .2.(2018·绍兴二模)已知抛物线C :y 2=4x 的焦点为F ,直线y =3(x -1)与抛物线C 交于A ,B 两点(A 在x 轴上方).若AF =mFB ,则m 的值为( )A. 3B.32C .2D .3解析:选D 直线方程为x =33y +1,代入y 2=4x 可得y 2-433y -4=0,则y A =23,y B =-233,所以|y A |=3|y B |,因为AF =mFB ,所以m =3.3.(2018·宁波十校联考)已知抛物线x 2=4y ,过焦点F 的直线l 交抛物线于A ,B 两点(点A 在第一象限),若直线l 的倾斜角为30°,则|AF ||BF |的值等于( )A .3B.52C .2D.32解析:选A 由题可得,F (0,1),设l :y =33x +1,A (x 1,y 1),B (x 2,y 2).将直线方程与抛物线方程联立,消去x ,化简得3y 2-10y +3=0,解得y 1=3,y 2=13.由抛物线的定义可知|AF ||BF |=y 1+1y 2+1=3+113+1=3. 4.已知P 为抛物线y =12x 2上的动点,点P 在x 轴上的射影为点M ,点A 的坐标是⎝⎛⎭⎫6,172,则|PA |+|PM |的最小值是( )A .8 B.192C .10D.212解析:选B 依题意可知焦点F ⎝⎛⎭⎫0,12,准线方程为y =-12,延长PM 交准线于点H (图略).则|PF |=|PH |,|PM |=|PF |-12,|PM |+|PA |=|PF |+|PA |-12,即求|PF |+|PA |的最小值. 因为|PF |+|PA |≥|FA |, 又|FA |=62+⎝⎛⎭⎫172-122=10.所以|PM |+|PA |≥10-12=192,故选B.5.(2019·嘉兴六校联考)已知抛物线C :y 2=2px (p >0)的焦点为F ,点M 在抛物线C 上,且|MO |=|MF |=32(O 为坐标原点),则OM ·MF =( )A .-74B.74C.94D .-94解析:选A 设M (m ,2pm ),抛物线C 的焦点F 的坐标为⎝⎛⎭⎫p 2,0,因为|MO |=|MF |=32,所以m 2+2pm =94 ①,m +p 2=32 ②,由①②解得m =12,p =2,所以M ⎝⎛⎭⎫12,2,F (1,0),所以OM =⎝⎛⎭⎫12,2,MF =⎝⎛⎭⎫12,-2,故OM ·MF =14-2=-74.6.(2018·宁波期初)已知抛物线x 2=4y 的焦点为F ,若点M 在抛物线上,|MF |=4,O 为坐标原点,则∠MFO =________.解析:由题可得,p =2,焦点在y 轴正半轴,所以F (0,1). 因为|MF |=4,所以M (±23,3).所以tan ∠MFO =-tan(π-∠MFO )=-233-1=-3,所以∠MFO =2π3. 答案:2π37.设O 为坐标原点,P 是以F 为焦点的抛物线y 2=2px (p >0)上任意一点,M 是线段PF 上的点,且|PM |=2|MF |,则直线OM 的斜率的最大值为________.解析:如图,由题可知F ⎝⎛⎭⎫p 2,0,设P 点坐标为⎝⎛⎭⎫y 202p ,y 0(y 0>0),则OM ―→=OF ―→+FM ―→=OF ―→+13FP ―→=OF ―→+13(OP ―→-OF ―→)=13OP ―→+23OF ―→=⎝⎛⎭⎫y 206p +p 3,y 03,k OM =y 03y 206p +p 3=2y 0p +2p y 0≤222=22,当且仅当y 2=2p 2时等号成立,所以直线OM 的斜率的最大值为22. 答案:228.(2018·嵊州一模)设抛物线y 2=4x 的焦点为F ,过点M (5,0)的直线与抛物线相交于A ,B 两点,与抛物线的准线相交于C 点,|BF |=3,则△BCF 与△ACF 的面积之比S △BCFS △ACF=________.解析:设点A 在第一象限,B 在第四象限,A (x 1,y 1),B (x 2,y 2),直线AB 的方程为x =my + 5.由y 2=4x ,得p =2,因为|BF |=3=x 2+p2=x 2+1,所以x 2=2,则y 22=4x 2=4×2=8,所以y 2=-22,由⎩⎨⎧y 2=4x ,x =my +5,得y 2-4my -45=0,则y 1y 2=-45,所以y 1=10,由y 21=4x 1,得x 1=52.过点A 作AA ′垂直于准线x =-1,垂足为A ′,过点B 作BB ′垂直于准线x =-1,垂足为B ′,易知△CBB ′∽△CAA ′,所以S △BCF S △ACF =|BC ||AC |=|BB ′||AA ′|.又|BB ′|=|BF |=3,|AA ′|=x 1+p 2=52+1=72,所以S △BCF S △ACF =372=67.答案:679.(2018·杭州高三检测)如图,过抛物线M :y =x 2上一点A (点A 不与原点O 重合)作抛物线M 的切线AB 交y 轴于点B ,点C 是抛物线M 上异于点A 的点,设G 为△ABC 的重心(三条中线的交点),直线CG 交y 轴于点D .(1)设A (x 0,x 20)(x 0≠0),求直线AB 的方程; (2)求|OB ||OD |的值. 解:(1)因为y ′=2x ,所以直线AB 的斜率k =y ′|x =x 0=2x 0, 所以直线AB 的方程为y -x 20=2x 0(x -x 0), 即y =2x 0x -x 20.(2)由(1)得,点B 的纵坐标y B =-x 20, 所以AB 的中点坐标为⎝⎛⎭⎫x 02,0.设C (x 1,y 1),G (x 2,y 2),直线CG 的方程为x =my +x 02.由⎩⎪⎨⎪⎧x =my +x 02,y =x 2,得m 2y 2+(mx 0-1)y +x 204=0.因为G 为△ABC 的重心,所以y 1=3y 2. 由根与系数的关系,得y 1+y 2=4y 2=1-mx 0m 2,y 1y 2=3y 22=x 204m 2. 所以y 22=(1-mx 0)216m4=x 2012m 2, 解得mx 0=-3±2 3.所以点D 的纵坐标y D =-x 02m =x 206±43,故|OB ||OD |=⎪⎪⎪⎪y B y D =43±6. 10.(2018·台州模拟)已知抛物线C 1:y 2=4x 和C 2:x 2=2py (p >0)的焦点分别为F 1,F 2,点P (-1,-1),且F 1F 2⊥OP (O 为坐标原点).(1)求抛物线C 2的方程;(2)过点O 的直线交C 1的下半部分于点M ,交C 2的左半部分于点N ,求△PMN 面积的最小值.解:(1)由题意知F 1(1,0),F 2⎝⎛⎭⎫0,p 2,则F 1F 2―→=⎝⎛⎭⎫-1,p 2, ∵F 1F 2⊥OP ,∴F 1F 2―→·OP ―→=⎝⎛⎭⎫-1,p 2·(-1,-1)=1-p 2=0, ∴p =2,∴抛物线C 2的方程为x 2=4y . (2)设过点O 的直线为y =kx (k <0),联立⎩⎪⎨⎪⎧ y =kx ,y 2=4x 得M ⎝⎛⎭⎫4k 2,4k , 联立⎩⎪⎨⎪⎧y =kx ,x 2=4y得N (4k,4k 2),从而|MN |=1+k 2·⎪⎪⎪⎪4k 2-4k =1+k 2·⎝⎛⎭⎫4k 2-4k , 又点P 到直线MN 的距离d =|k -1|1+k 2,故S △PMN =12·|k -1|1+k 2·1+k 2·⎝⎛⎭⎫4k 2-4k =2(1-k )(1-k 3)k 2=2(1-k )2(1+k +k 2)k 2=2⎝⎛⎭⎫k +1k -2⎝⎛⎭⎫k +1k +1, 令t =k +1k (t ≤-2), 则S △PMN =2(t -2)(t +1)≥8,当t =-2,即k =-1时,S △PMN 取得最小值.即当过点O 的直线为y =-x 时,△PMN 面积的最小值为8. 三上台阶,自主选做志在冲刺名校1.(2018·台州高三模拟)已知抛物线x 2=2py (p >0),点M 是抛物线的准线与y 轴的交点,过点A (0,λp )(λ∈R)的动直线l 交抛物线于B ,C 两点.(1)求证:MB ·MC ≥0,并求等号成立时实数λ的值;(2)当λ=2时,设分别以OB ,OC (O 为坐标原点)为直径的两圆相交于另一点D ,求|DO |+|DA |的最大值.解:(1)由题意知动直线l 的斜率存在,且过点A (0,λp ), 则可设动直线l 的方程为y =kx +λp ,代入x 2=2py (p >0),消去y 并整理得x 2-2pkx -2λp 2=0, Δ=4p 2(k 2+2λ)>0, 设B (x 1,y 1),C (x 2,y 2), 则x 1+x 2=2pk ,x 1x 2=-2λp 2,y 1y 2=(kx 1+λp )(kx 2+λp )=k 2x 1x 2+λpk (x 1+x 2)+λ2p 2=λ2p 2,y 1+y 2=k (x 1+x 2)+2λp =2pk 2+2λp =2p (k 2+λ). 因为抛物线x 2=2py 的准线方程为y =-p2,所以点M 的坐标为⎝⎛⎭⎫0,-p 2, 所以MB =⎝⎛⎭⎫x 1,y 1+p 2,MC =⎝⎛⎭⎫x 2,y 2+p2, 所以MB ·MC =x 1x 2+⎝⎛⎭⎫y 1+p 2⎝⎛⎭⎫y 2+p2 =x 1x 2+y 1y 2+p 2(y 1+y 2)+p 24=-2λp 2+λ2p 2+p 2[2p (k 2+λ)]+p 24=p 2⎣⎡⎦⎤k 2+⎝⎛⎭⎫λ-122≥0, 当且仅当k =0,λ=12时等号成立.(2)由(1)知,当λ=2时,x 1x 2=-4p 2,y 1y 2=4p 2, 所以OB ·OC =x 1x 2+y 1y 2=0, 所以OB ⊥OC .设直线OB 的方程为y =mx (m ≠0),与抛物线的方程x 2=2py 联立可得B (2pm,2pm 2), 所以以OB 为直径的圆的方程为x 2+y 2-2pmx -2pm 2y =0. 因为OB ⊥OC ,所以直线OC 的方程为y =-1m x .同理可得以OC 为直径的圆的方程为 x 2+y 2+2p m x -2pm2y =0, 即m 2x 2+m 2y 2+2pmx -2py =0,将两圆的方程相加消去m ,得x 2+y 2-2py =0, 即x 2+(y -p )2=p 2,所以点D 的轨迹是以OA 为直径的圆, 所以|DA |2+|DO |2=4p 2, 由|DA |2+|DO |22≥⎝⎛⎭⎫|DA |+|DO |22, 得|DA |+|DO |≤22p ,当且仅当|DA |=|DO |=2p 时,等号成立. 故(|DA |+|DO |)max =22p .2.如图所示,抛物线关于x 轴对称,它的顶点在坐标原点,点P (1,2),A (x 1,y 1),B (x 2,y 2)均在抛物线上.(1)写出该抛物线的方程及其准线方程.(2)当PA 与PB 的斜率存在且倾斜角互补时,求y 1+y 2的值及直线AB 的斜率.解:(1)由已知条件,可设抛物线的方程为y 2=2px (p >0). 因为点P (1,2)在抛物线上, 所以22=2p ×1, 解得p =2.故所求抛物线的方程是y 2=4x ,准线方程是x =-1. (2)设直线PA 的斜率为k PA ,直线PB 的斜率为k PB . 则k PA =y 1-2x 1-1(x 1≠1),k PB =y 2-2x 2-1(x 2≠1), 因为PA 与PB 的斜率存在且倾斜角互补, 所以k PA =-k PB .由A (x 1,y 1),B (x 2,y 2)均在抛物线上,得⎩⎪⎨⎪⎧y 21=4x 1, ①y 22=4x 2, ②所以y 1-214y 21-1=-y 2-214y 22-1,所以y 1+2=-(y 2+2). 所以y 1+y 2=-4.由①-②得,y 21-y 22=4(x 1-x 2),所以k AB =y 1-y 2x 1-x 2=4y 1+y 2=-1(x 1≠x 2).。
2020版高考数学一轮复习第8章平面解析几何第5讲课后作业理含解析

第8章 平面解析几何 第5讲A 组 基础关1.已知椭圆的标准方程为x 2+y 210=1,则椭圆的焦点坐标为( )A .(10,0),(-10,0)B .(0,10),(0,-10)C .(0,3),(0,-3)D .(3,0),(-3,0)答案 C解析 椭圆x 2+y 210=1的焦点在y 轴上,a 2=10,b 2=1,故c 2=a 2-b 2=9,c =3.所以椭圆的焦点坐标为(0,3),(0,-3).2.(2018·合肥三模)已知椭圆E :y 2a 2+x 2b2=1(a >b >0)经过点A (5,0),B (0,3),则椭圆E 的离心率为( )A.23 B .53C .49D .59答案 A解析 由题意得a =3,b =5,所以c =a 2-b 2=9-5=2,离心率e =c a =23.3.设椭圆x 216+y 212=1的左、右焦点分别为F 1,F 2,点P 在椭圆上,且满足PF 1→·PF 2→=9,则|PF 1|·|PF 2|的值为( )A .8B .10C .12D .15答案 D解析 由椭圆方程x 216+y 212=1,可得c 2=4,所以|F 1F 2|=2c =4,而F 1F 2→=PF 2→-PF 1→,所以|F 1F 2→|=|PF 2→-PF 1→|,两边同时平方,得|F 1F 2→|2=|PF 1→|2-2PF 1→·PF 2→+|PF 2→|2,所以|PF 1→|2+|PF 2→|2=|F 1F 2→|2+2PF 1→·PF 2→=16+18=34,根据椭圆定义得|PF 1|+|PF 2|=2a =8,所以34+2|PF 1||PF 2|=64,所以|PF 1|·|PF 2|=15.故选D.4.(2018·武汉调研)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)及点B (0,a ),过点B 与椭圆相切的直线交x 轴的负半轴于点A ,F 为椭圆的右焦点,则∠ABF =( )A .60°B .90°C .120°D .150°答案 B解析 由题意知,切线的斜率存在,设切线方程y =kx +a (k >0),与椭圆方程联立,⎩⎪⎨⎪⎧y =kx +a ,x 2a 2+y2b2=1,消去y 整理得(b 2+a 2k 2)x 2+2ka 3x +a 4-a 2b 2=0,由Δ=(2ka 3)2-4(b 2+a 2k 2)(a 4-a 2b 2)=0,得k =c a ,从而y =c a x +a 交x 轴于点A ⎝ ⎛⎭⎪⎫-a 2c ,0,又F (c,0),易知BA →·BF →=0,故∠ABF =90°.5.过椭圆x 25+y 24=1的右焦点作一条斜率为2的直线与椭圆交于A ,B 两点,O 为坐标原点,则△OAB 的面积为( )A.43 B .53 C .54 D .103答案 B解析 由题意知椭圆的右焦点F 的坐标为(1,0),则直线AB 的方程为y =2x -2.联立⎩⎪⎨⎪⎧x 25+y 24=1,y =2x -2,解得交点(0,-2),⎝ ⎛⎭⎪⎫53,43,∴S △OAB =12·|OF |·|y A -y B |=12×1×⎪⎪⎪⎪⎪⎪-2-43=53.故选B.6.(2018·南宁模拟)已知椭圆x 2a 2+y 2b2=1(a >b >0)的一条弦所在的直线方程是x -y +5=0,弦的中点坐标是M (-4,1),则椭圆的离心率是( )A.12 B .22 C .32D .55答案 C解析 设直线x -y +5=0与椭圆x 2a 2+y 2b2=1相交于A (x 1,y 1),B (x 2,y 2)两点,因为AB 的中点M (-4,1),所以x 1+x 2=-8,y 1+y 2=2.易知直线AB 的斜率k =y 2-y 1x 2-x 1=1.⎩⎪⎨⎪⎧x 21a 2+y 21b2=1,x 22a 2+y 22b 2=1,两式相减得,x 1+x 2x 1-x 2a 2+y 1+y 2y 1-y 2b 2=0,所以y 1-y 2x 1-x 2=-b 2a 2·x 1+x 2y 1+y 2,所以b 2a 2=14,于是椭圆的离心率e =ca=1-b 2a 2=32.故选C.7.过椭圆x 225+y 216=1的中心任意作一条直线交椭圆于P ,Q 两点,F 是椭圆的一个焦点,则△PQF 周长的最小值是( )A .14B .16C .18D .20答案 C解析 如图,设F 1为椭圆的左焦点,右焦点为F 2,根据椭圆的对称性可知|F 1Q |=|PF 2|,|OP |=|OQ |,所以△PQF 1的周长为|PF 1|+|F 1Q |+|PQ |=|PF 1|+|PF 2|+2|PO |=2a +2|PO |=10+2|PO |,易知2|OP |的最小值为椭圆的短轴长,即点P ,Q 为椭圆的上、下顶点时,△PQF 1即△PQF 的周长取得最小值为10+2×4=18.8.已知椭圆的中心在原点,焦点在x 轴上,离心率为55,且过点P (-5,4),则椭圆的标准方程为________.答案x 245+y 236=1 解析 由题意设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0).由离心率e =55可得a 2=5c 2,所以b 2=4c 2,故椭圆的方程为x 25c 2+y 24c 2=1,将P (-5,4)代入可得c 2=9,故椭圆的方程为x 245+y 236=1.9.设P ,Q 分别是圆x 2+(y -1)2=3和椭圆x 24+y 2=1上的点,则P ,Q 两点间的最大距离是________.答案733解析 根据已知条件作出如图所示的图形.记圆x 2+(y -1)2=3的圆心为M ,由三角形的性质可得|PQ |≤|PM |+|MQ |=3+|MQ |,设点Q 坐标为(x ,y ),那么x 24+y 2=1,所以|QM |2=x 2+(y -1)2=4(1-y 2)+(y -1)2=-3y 2-2y +5,y ∈[-1,1],因此|QM |2≤163,即|QM |≤433,所以|PQ |≤433+3=733,所以P ,Q 两点间的最大距离为733. 10.(2018·厦门模拟)已知椭圆x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2,点P 在椭圆上,且PF 2垂直于x 轴,若直线PF 1的斜率为33,则该椭圆的离心率为________. 答案33解析 因为点P 在椭圆上,且PF 2垂直于x 轴,所以点P 的坐标为⎝ ⎛⎭⎪⎫c ,b 2a . 又因为直线PF 1的斜率为33,所以在Rt △PF 1F 2中, PF 2F 1F 2=33,即b 2a 2c =33.所以3b 2=2ac . 3(a 2-c 2)=2ac ,3(1-e 2)=2e , 整理得3e 2+2e -3=0, 又0<e <1,解得e =33. B 组 能力关1.如果椭圆x 236+y 29=1的弦AB 被点M (x 0,y 0)平分,设直线AB 的斜率为k 1,直线OM (O 为坐标原点)的斜率为k 2,则k 1k 2的值为( )A .4B .14C .-1D .-14答案 D解析 解法一:设A (x 1,y 1),B (x 2,y 2),因为弦AB 被点M (x 0,y 0)平分,所以x 1+x 2=2x 0,y 1+y 2=2y 0.易知k 1=y 1-y 2x 1-x 2,k 2=y 0x 0. ⎩⎪⎨⎪⎧x 2136+y 219=1,x 2236+y 229=1,两式相减得,x 1+x 2x 1-x 236+y 1+y 2y 1-y 29=0,所以y 1-y 2x 1-x 2=-14·x 1+x 2y 1+y 2=-14·x 0y 0, ∴k 1k 2=-14.解法二:设直线AB 的方程为y =k 1x +m ,A (x 1,y 1),B (x 2,y 2).代入椭圆方程并整理得,(1+4k 21)x 2+8k 1mx +4m 2-36=0,x 1+x 2=-8k 1m 1+4k 21,又中点M (x 0,y 0)在直线AB 上,所以y 1+y 22=k 1⎝ ⎛⎭⎪⎫x 1+x 22+m =m1+4k 21,从而得弦中点M 的坐标为⎝ ⎛⎭⎪⎫-4k 1m 1+4k 21,m 1+4k 21,∴k 2=m1+4k 21-4k 1m 1+4k 21=-14k 1,∴k 1k 2=-14. 2.(2018·昆明诊断)椭圆x 29+y 225=1上的一点P 到两焦点的距离的乘积为m ,当m 取最大值时,点P 的坐标是________.答案 (-3,0)或(3,0)解析 记椭圆的两个焦点分别为F 1,F 2,有|PF 1|+|PF 2|=2a =10. 则m =|PF 1|·|PF 2|≤⎝⎛⎭⎪⎫|PF 1|+|PF 2|22=25,当且仅当|PF 1|=|PF 2|=5,即点P 位于椭圆的短轴的顶点处时,m 取得最大值25.∴点P 的坐标为(-3,0)或(3,0).3.(2018·内江三模)设P 是椭圆x 29+y 24=1第一象限弧上任意一点,过P 作x 轴的平行线与y轴和直线y =-23x 分别交于点M ,N .过P 作y 轴的平行线与x 轴和直线y =-23x 分别交于点R ,Q ,设O 为坐标原点,则△OMN 和△ORQ 的面积之和为________.答案 3解析 设P (x 0,y 0)(0<x 0<3,0<y 0<2),则M (0,y 0),联立⎩⎪⎨⎪⎧y =y 0,y =-23x ,解得y =y 0,x =-32y 0,所以N ⎝ ⎛⎭⎪⎫-32y 0,y 0, 所以S △OMN =12y 0×32y 0=34y 20.同理可得R (x 0,0),联立⎩⎪⎨⎪⎧x =x 0,y =-23x ,解得x =x 0,y =-23x 0,可得Q ⎝ ⎛⎭⎪⎫x 0,-23x 0.所以S △ORQ =12x 0×23x 0=13x 20.又x 209+y 204=1,所以△OMN 和△ORQ 的面积之和为34y 20+13x 20=3⎝ ⎛⎭⎪⎫x 209+y 204=3. 4.在平面直角坐标系xOy 中,点P 到两点(0,-3),(0,3)的距离之和等于4,设点P 的轨迹为C .(1)写出C 的方程;(2)设直线y =kx +1与C 交于A ,B 两点,k 为何值时O A →⊥O B →?此时|AB |的值是多少? 解 (1)设P (x ,y ),由椭圆定义可知,点P 的轨迹C 是以(0,-3),(0,3)为焦点,长半轴长为2的椭圆.它的短半轴长b = 22-32=1,故曲线C 的方程为x 2+y 24=1.(2)设A (x 1,y 1),B (x 2,y 2),其坐标满足⎩⎪⎨⎪⎧x 2+y 24=1,y =kx +1,消去y ,并整理得(k 2+4)x 2+2kx -3=0, 故x 1+x 2=-2k k 2+4,x 1x 2=-3k 2+4. ∵OA →⊥OB →,∴x 1x 2+y 1y 2=0. ∵y 1y 2=k 2x 1x 2+k (x 1+x 2)+1,于是x 1x 2+y 1y 2=-3k 2+4-3k 2k 2+4-2k 2k 2+4+1=-4k 2+1k 2+4.又x 1x 2+y 1y 2=0,∴k =±12.当k =±12时,x 1+x 2=∓417,x 1x 2=-1217.|AB |=x 2-x 12+y 2-y 12=1+k 2x 2-x 12,而(x 2-x 1)2=(x 2+x 1)2-4x 1x 2 =42172+4×1217=43×13172, ∴|AB |=54×43×13172=46517. C 组 素养关1.(2018·东北三省四市教研联合体模拟)在平面直角坐标系中,椭圆C :x 2a 2+y 2b2=1(a >b >0)的离心率为12,点M ⎝ ⎛⎭⎪⎫1,32在椭圆C 上. (1)求椭圆C 的方程;(2)已知P (-2,0)与Q (2,0)为平面内的两个定点,过(1,0)点的直线l 与椭圆C 交于A ,B 两点,求四边形APBQ 面积的最大值.解 (1)∵c a =12,∴a =2c ,椭圆的方程为x 24c 2+y 23c2=1,将⎝ ⎛⎭⎪⎫1,32代入得14c 2+912c 2=1,∴c 2=1.∵椭圆的方程为x 24+y 23=1. (2)设l 的方程为x =my +1,联立⎩⎪⎨⎪⎧x 24+y 23=1,x =my +1,消去x ,得(3m 2+4)y 2+6my -9=0, 设点A (x 1,y 1),B (x 2,y 2), 有y 1+y 2=-6m 3m 2+4,y 1y 2=-93m 2+4,有|AB |=1+m 2·121+m 23m 2+4=121+m23m 2+4,点P (-2,0)到直线l 的距离为31+m2,点Q (2,0)到直线l 的距离为11+m2,从而四边形APBQ 的面积S =12×121+m23m 2+4×41+m2=241+m 23m 2+4(或S =12|PQ ||y 1-y 2|). 令t =1+m 2,t ≥1,有S =24t 3t 2+1=243t +1t,设函数f (t )=3t +1t ,f ′(t )=3-1t2>0,所以f (t )在[1,+∞)上单调递增,有3t +1t ≥4,故S =24t 3t 2+1=243t +1t≤6,所以当t =1,即m =0时,四边形APBQ 面积的最大值为6.2.(2018·全国卷Ⅲ)已知斜率为k 的直线l 与椭圆C :x 24+y 23=1交于A ,B 两点.线段AB 的中点为M (1,m )(m >0).(1)证明:k <-12;(2)设F 为C 的右焦点,P 为C 上一点,且FP →+FA →+FB →=0.证明:|FA →|,|FP →|,|FB →|成等差数列,并求该数列的公差.解 (1)证明:设A (x 1,y 1),B (x 2,y 2),则x 214+y 213=1,x 224+y 223=1.两式相减,并由y 1-y 2x 1-x 2=k 得x 1+x 24+y 1+y 23·k =0. 由题设知x 1+x 22=1,y 1+y 22=m ,于是k =-34m.①由题设得m < ⎝ ⎛⎭⎪⎫1-14×3=32,且m >0,即0<m <32, 故k <-12.(2)由题意得F (1,0).设P (x 3,y 3),则由(1)及题设得(x 3-1,y 3)+(x 1-1,y 1)+(x 2-1,y 2)=(0,0),x 3=3-(x 1+x 2)=1,y 3=-(y 1+y 2)=-2m <0.又点P 在C 上,所以m =34,从而P ⎝⎛⎭⎪⎫1,-32,|FP →|=32. 于是|FA →|=x 1-12+y 21= x 1-12+3⎝ ⎛⎭⎪⎫1-x 214=2-x 12.同理| FB →|=2-x 22. 所以| FA →|+|FB →|=4-12(x 1+x 2)=3.故2|FP →|=|FA →|+|FB →|,即|FA →|,|FP →|,|FB →|成等差数列.设该数列的公差为d ,则 2|d |=||FB →|-|FA →||=12|x 1-x 2|=12x 1+x 22-4x 1x 2. ②将m =34代入①得k =-1.所以l 的方程为y =-x +74,代入C 的方程,并整理得7x 2-14x +14=0.故x 1+x 2=2,x 1x 2=128,代入②解得|d |=32128.所以该数列的公差为32128或-32128.。
新课标2020年高考数学一轮总复习第八章平面解析几何8_5椭圆课件理新人教A

第五节 椭圆
教 材 回 顾 考 点 突 破
栏目导航
最新考纲考情考向分析
1.了解椭圆的实际背景,了解椭圆在刻画现实世界和解决实际问题中的作用.
2.掌握椭圆的定义、几何图形、标准方程及简单几何性质.3.利用椭圆的几何性质研究直线与椭圆的关系.椭圆的定义、标准方程、几何性质通常以小题形式考查,直线与椭圆的位置关系主要出现在解答题中.题型主要以选择、填空题为主,一般为中档题,椭圆方程的求解经常出现在解答题的第一问.
之和
焦点焦距。
2020版高考数学一轮复习第八章平面解析几何8_5_1椭圆课件文新人教A版

解析 (1)设圆 M 的半径为 r,则|MC1|+|MC2|=(13-r)+(3+r)=16, 所以 M 的轨迹是以 C1,C2 为焦点的椭圆,且 2a=16,2c=8,故所求的轨迹 方程为6x42 +4y82 =1。
答案 (1)D
(2)设 F1,F2 分别是椭圆 E:x42+by22=1(0<b<2)的左、右焦点,过点 F1 的直线交椭圆 E 于 A,B 两点。若 3|AF1|=5|AF2|,AF2⊥x 轴,则椭圆 E 的 方程为________。
常数}。 (1)若 a>c ,则 M 点的轨迹为椭圆。 (2)若 a=c ,则 M 点的轨迹为线段 F1F2。 (3)若 a<c ,则 M 点不存在。
2.椭圆的标准方程和几何性质
1.椭圆方程中的 a,b,c (1)a,b,c 关系:a2=b2+c2。 (2)e 与ba:因为 e=ac= a2a-b2= 1-ba2,所以离心率 e 越大,则ba越小, 椭圆就越扁;离心率 e 越小,则ba越大,椭圆就越圆。 2.在求焦点在 x 轴上椭圆的相关量的范围时,要注意应用以下不等关系: -a≤x≤a,-b≤y≤b,0<e<1。 3.焦点三角形 椭圆上的点 P 与焦点 F1,F2 若构成三角形,则称△PF1F2 为焦点三角形, 焦点三角形问题注意与椭圆定义、正弦定理、余弦定理的联系。
【变式训练】 (1)(2019·惠州调研)设 F1,F2 为椭圆x92+y52=1 的两个焦
点,点 P 在椭圆上,若线段 PF1 的中点在 y 轴上,则||PPFF21||的值为(
)
A.154
B.59
C.49
D.153
解析 (1)如图,设线段 PF1 的中点为 M,因为 O 是 F1F2 的中点,所以 OM∥PF2,可得 PF2⊥x 轴,可求得|PF2|=53,|PF1|=2a-|PF2|=133,||PPFF12||= 153。故选 D。
2020版高考数学一轮复习第八章平面解析几何8_5_2椭圆的综合问题课件理新人教版

设 A(x1,y1),B(x2,y2), 则 x1+x2=41+0k52k2,x1x2=54k+2-5k220。 设 N(5,y0),因为 A,M,N 三点共线, 所以3--yx11=y20,所以 y0=x12-y13。 而 y0-y2=x12-y13-y2=2kx1x-1-31-k(x2-1) =3kx1+xx21--k3x1x2-5k =3k·41+0k52k2-x1k-·543k+2-5k220-5k=0。
【变式训练】 已知椭圆 C 的方程为x42+y22=1,点 A 为椭圆的右顶点, 直线 y=k(x-1)与椭圆 C 交于不同的两点 M,N。当△AMN 的面积为49 7时, 求 k 的值。
y=kx-1, 解 由x42+y22=1,
得(1+2k2)x2-4k2x+2k2-4=0。 设点 M,N 的坐标分别为(x1,y1),(x2,y2), 则 y1=k(x1-1),y2=k(x2-1),
解 由题意知,F(1,0),E(5,0),M(3,0)。 (1)因为直线 l1 的倾斜角为π4,所以斜率 k=1。 所以直线 l1 的方程为 y=x-1。 代入椭圆方程,可得 9x2-10x-15=0。 设 A(x1,y1),B(x2,y2), 则 x1+x2=190,x1x2=-53。 所以|AB|= 2· x1+x22-4x1x2
Δ>0⇒m2<4, 所以 x1+x2=-32m,x1x2=3m24-3。
|AB|= 1+k2|x1-x2| = 2x2-x12 = 2[x1+x22-4x1x2] = 12-23m2。 当 m=0,即直线 l 过原点时,|AB|最大,最大值为 6。
2020版高考数学一轮复习 第8章 平面解析几何 第5讲 椭圆讲义 理(含解析)

A.3
B.6
C.9
D.12
答案 A
解析 画出图形如图所示.
∵椭圆方程为错误!+错误!=1, ∴a=3,b= 5,c=2。 又△ABF2 的内切圆的面积为 π, ∴△ABF2 内切圆的半径 r=1, ∴S△ABF2=12×(|AB|+|BF2|+|AF2|)×r =错误!×4a×r=2ar=6, 又 S△ABF2=错误!×|y1-y2|×2c=2|y1-y2|, ∴2|y1-y2|=6,∴|y1-y2|=3。
(3)椭圆上一短轴顶点到一焦点的距离等于实半轴长 a. 2.待定系数法求椭圆的标准方程的四步骤
提 醒 : 当 椭 圆 的 焦 点 位 置 不 明 确 时 , 可 设 为 错误! + 错误! = 1(m 〉 0 , n>0,m≠n),也可设为 Ax2+By2=1(A>0,B〉0,且 A≠B).可简记为“先定 型,再定量”.
1.“2〈m〈6"是“方程错误!+错误!=1 表示椭圆"的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 B 解析 方程错误!+错误!=1 表示椭圆⇔错误! 解得 2<m〈6 且 m≠4, 所以“2〈m〈6"是“方程错误!+错误!=1 表示椭圆"的必要不充分条 件. 2.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为 10,一个焦点的 坐标是(- 5,0),则椭圆的标准方程为________. 答案 错误!+错误!=1 解析 由题意得,该椭圆的焦点在 x 轴上, c=错误!,2a+2b=10,即 a+b=5, 又因为 a2-b2=c2=5, 所以 a-b=1,解得 a=3,b=2。 所以椭圆的标准方程是错误!+错误!=1. 3.已知 A错误!,B 是圆错误!2+y2=4(F 为圆心)上一动点,线段 AB 的垂 直平分线交 BF 于点 P,则动点 P 的轨迹方程为________. 答案 x2+错误!y2=1
高考数学总复习第八章解析几何8.5椭圆理新人教A版

4.理解数形结合的思想. 以解答题的形式呈现,具有
一定的综合性.
课堂探究 考点突破
真题模拟演练
课堂探究 考点突破
考点一 椭圆的定义及标准方程
(1)已知椭圆 C:x42+y32=1,M,N 是坐标平面内的两点,
且 M 与 C 的焦点不重合.若 M 关于 C 的焦点的对称点分别为 A,B,
线段 MN 的中点在 C 上,则|AN|+|BN|=( B )
解:设弦的端点为 P(x1,y1),Q(x2,y2),其中点是 M(x,y).
x221+y21=1,① x222+y22=1,②
①-②得yx22--yx11=-2xy22++xy11=-2xy,
所以-2xy=yx--12, 化简得 x2-2x+2y2-2y=0(包含在椭圆x22+y2=1 内部的部
圆 E 的方程为 x2+32y2=1 .
解析:设点 B 的坐标为(x0,y0). ∵x2+by22=1, ∴F1(- 1-b2,0),F2( 1-b2,0). ∵AF2⊥x 轴,设点 A 在 x 轴上方, 则 A( 1-b2,b2).
∵|AF1|=3 1-b2,y0). ∴x0=-53 1-b2,y0=-b32. ∴点 B 的坐标为-53 1-b2,-b32. 将 B-53 1-b2,-b32代入 x2+by22=1, 得 b2=23.
B.
32-1,12
D.0,12
解析:由题意可得,|PF2|2=|F1F2|2+|PF1|2-2|F1F2|·|PF1|cos
∠ PF1F2 = 4c2 + 4c2 - 2·2c·2c·cos ∠ PF1F2 , 即 |PF2| = 2 2
c· 1-cos∠PF1F2 , 所 以
1.椭圆定义的应用技巧 (1)椭圆定义的应用主要有:求椭圆的标准方程,求焦点三角 形的周长、面积及弦长、最值和离心率等. (2)通常定义和余弦定理结合使用,求解关于焦点三角形的周 长和面积问题. 2.椭圆方程的求解方法 (1)求椭圆的标准方程多采用定义法和待定系数法. (2)利用定义法求椭圆方程,要注意条件 2a>|F1F2|;利用待 定系数法要先定形(焦点位置),再定量,也可把椭圆方程设为 mx2 +ny2=1(m>0,n>0,m≠n)的形式.
2020版高考数学一轮复习第八章平面解析几何8_5_1椭圆课件理新人教A版

(2)已知椭圆4x92 +2y42 =1 上一点 P 与椭圆的两焦点 F1,F2 的连线夹角为 直角,则|PF1|·|PF2|=________。
解析 (2)依题意 a=7,b=2 6,c= 49-24=5,|F1F2|=2c=10,由 于 PF1⊥PF2,所以由勾股定理得|PF1|2+|PF2|2=|F1F2|2,即|PF1|2+|PF2|2= 100。又由椭圆定义知|PF1|+|PF2|=2a=14,所以(|PF1|+|PF2|)2-2|PF1|·|PF2| =100,即 196-2|PF1|·|PF2|=100。解得|PF1|·|PF2|=48。
-b≤x≤b -a≤y≤a ;对称中心: 原点
顶点
A1 (-a,0),A2 (a,0) A1(0,-a),A2 (0,a) B1(0,-b),B2 (0,b) B1 (-b,0) ,B2 (b,0)
性 轴 长轴 A1A2 的长为 2a ;短轴 B1B2 的长为 2b
质 焦距
|F1F2|= 2c
离心率
二、走近高考 3.(2018·全国卷Ⅱ)已知 F1,F2 是椭圆 C:ax22+by22=1(a>b>0)的左、右焦
点,A 是 C 的左顶点,点 P 在过 A 且斜率为 63的直线上,△PF1F2 为等腰三
角形,∠F1F2P=120°,则 C 的离心率为( )
A.23
B.12
C.13
D.14
解析 由题意可得椭圆的焦点在 x 轴上,如图所示,设|F1F2|=2c,因 为△PF1F2 为等腰三角形,且∠F1F2P=120°,所以|PF2|=|F1F2|=2c。因为 |OF2|=c,所以点 P 坐标为(c+2ccos60°,2csin60°),即点 P(2c, 3c)。因 为点 P 在过 A 且斜率为 63的直线上,所以2c+3ca= 63,解得ac=14,所以 e =14,故选 D。
2020年高考数学一轮总复习第八章平面解析几何8-5椭圆课时规范练文(含解析)

8—5 椭圆课时规范练A组基础对点练1.(2018·长春质检)已知椭圆错误!+错误!=1的左、右焦点分别为F1,F2,过点F2的直线交椭圆于A,B两点,则△ABF1的周长为( C ) A.4 B。
6C.8 D.162.(2018·武汉调研)曲线C1:错误!+错误!与曲线C2:错误!+错误!=1(0〈k<9)的( D )A.长轴长相等B。
短轴长相等C.离心率相等 D.焦距相等解析:因为0<k〈9,所以25-k>9-k>0,所以曲线C2是焦点在x轴上的椭圆,记其长半轴长为a2,短半轴长为b2,半焦距为c2,则c2,2=a22-b错误!=25-k-(9-k)=16。
曲线C1也是焦点在x轴上的椭圆,记其长半轴长为a1,短半轴长为b1,半焦距为c1,则c错误!=a错误!-b错误!=25-9=16,所以曲线C1和曲线C2的焦距相等,故选D。
3.若对任意k∈R,直线y-kx-1=0与椭圆错误!+错误!=1恒有公共点,则实数m的取值范围是( C )A.(1,2] B.[1,2)C.[1,2)∪(2,+∞) D.[1,+∞)4.(2017·高考浙江卷)椭圆错误!+错误!=1的离心率是( B )A。
错误! B.错误!C.错误!D。
错误!5.已知椭圆的中心在原点,离心率e=错误!,且它的一个焦点与抛物线y2=-4x的焦点重合,则此椭圆方程为( A )A。
x24+错误!=1 B.错误!+错误!=1C.错误!+y2=1 D。
错误!+y2=16.若椭圆错误!+错误!=1(a〉b>0)的右焦点F是抛物线y2=4x的焦点,两曲线的一个交点为P,且|PF|=4,则该椭圆的离心率为( A ) A。
错误! B.错误!C。
23D。
127.已知椭圆错误!+错误!=1,其中α∈错误!,则椭圆形状最圆时的方程为( A )A.x2+错误!=1 B。
x2+错误!=1C.x2+错误!=1 D.x2+错误!=18.若x2+ky2=2表示焦点在y轴上的椭圆,则实数k的取值范围是__(0,1)__.9.(2018·福州质量)在三角形MAB中,点A(-1,0),B(1,0),且它的周长为6,记点M的轨迹为曲线E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-5 椭圆课时规范练(授课提示:对应学生用书第307页)A 组 基础对点练1.已知椭圆+=1(m >0)的左焦点为F 1(-4,0),则m =( B )x 225y 2m2A .2 B .3C .4D .92.方程kx 2+4y 2=4k 表示焦点在x 轴上的椭圆,则实数k 的取值范围是( D )A .k >4 B .k =4C .k <4D .0<k <43.若对任意k ∈R ,直线y -kx -1=0与椭圆+=1恒有公共点,则实数m 的取值范围x 22y 2m是( C )A .(1,2]B .[1,2)C .[1,2)∪(2,+∞)D .[1,+∞)4.(2017·河北衡水中学二调)设椭圆+=1的左、右焦点分别为F 1,F 2,点P 在椭圆上,x 216y 212且满足·=9,则|PF 1|·|PF 2|的值为( D )PF 1→ PF 2→A .8B .10C .12D .15解析:由椭圆方程+=1,可得c 2=4,所以|F 1F 2|=2c =4,而=-,所以||=x 216y 212F 1F 2→ PF 2→ PF 1→ F 1F 2→|-|,两边同时平方,得||2=||2-2·+||2,所以||2+||2=|PF 2→ PF 1→ F 1F 2→ PF 1→ PF 1→ PF 2→ PF 2→ PF 1→ PF 2→|2+2·=16+18=34.根据椭圆定义,得|PF 1|+|PF 2|=2a =8,(|PF 1|+|PF 2|)2=F 1F 2→PF 1→PF 2→|PF 1|2+|PF 2|2+2|PF 1|·|PF 2|=64,所以34+2|PF 1|·|PF 2|=64,所以|PF 1|·|PF 2|=15,故选D.5.已知椭圆的中心在原点,离心率e =,且它的一个焦点与抛物线y 2=-4x 的焦点重合,12则此椭圆方程为( A )A.+=1x 24y 23B.+=1x 28y 26C.+y 2=1x 22D.+y 2=1x 246.若椭圆+=1(a >b >0)的右焦点F 是抛物线y 2=4x 的焦点,两曲线的一个交点为P ,x 2a 2y 2b2且|PF |=4,则该椭圆的离心率为( A )A.B .7-232+13C. D .23127.椭圆C :+=1(a >b >0)的左焦点为F ,若F 关于直线x +y =0的对称点A 是椭圆Cx 2a 2y 2b23上的点,则椭圆C 的离心率为( D )A. B .123-12C.D .-13238.若x 2+ky 2=2表示焦点在y 轴上的椭圆,则实数k 的取值范围是 (0,1) .解析:将椭圆的方程化为标准形式得+=1,因为x 2+ky 2=2表示焦点在y 轴上的椭圆,y 22kx 22所以>2,解得0<k <1.2k9.如图,在平面直角坐标系xOy 中,F 是椭圆+=1(a >b >0)的右焦点,直线y =与椭x 2a 2y 2b2b2圆交于B ,C 两点,且∠BFC =90°,则该椭圆的离心率是 .63解析:由题意可得B ,C ,F (c,0),则由∠BFC =90°得·=(-32a ,b 2)(32a ,b 2)BF → CF →·=c 2-a 2+b 2=0,化简得c =a ,则离心率e ===(c +32a ,-b 2)(c -32a ,-b2)341432c a 23.6310.(2018·湖南江西十四校联考)已知椭圆E :+=1上的点到椭圆一个焦x 2a 2y 2b2(a >b >0)点的距离的最大值是最小值的3倍,且点P 在椭圆E 上.(1,32)(1)求椭圆E 的方程;(2)过点M 任作一条直线l ,l 与椭圆E 交于不同于P 点的A ,B 两点,l 与直线m :3x +4y -(1,1)12=0交于C 点,记直线PA ,PB ,PC 的斜率分别为k 1,k 2,k 3.试探究k 1+k 2与k 3的关系,并证明你的结论.解析:(1)∵椭圆E :+=1上的点到椭圆一个焦点的距离的最大值和最小值x 2a 2y 2b2(a >b >0)分别为a +c ,a -c ,依题意有a +c =3⇒a =2c ,(a -c )∵a 2=b 2+c 2,∴b =c .3故可设椭圆E 的方程为+=1,x 24c 2y 23c2∵点P 在椭圆E 上,所以将其代入椭圆E 的方程得+=1⇒c 2=1.(1,32)14c 2943c2∴椭圆E 的方程为+=1.x 24y 23(2)依题意,直线l 不可能与x 轴垂直,故可设直线l 的方程为y -1=k ,即y =kx -k +(x -1)1,设A ,B 为l 与椭圆E 的两个交点.(x 1,y 1)(x 2,y 2)将y =kx -k +1代入方程3x 2+4y 2-12=0,化简得x 2-8x +4k 2-8k -8=0.(4k 2+3)(k 2-k )∴x 1+x 2=,x 1x 2=.8k 2-8k 4k 2+34k 2-8k -84k 2+3∴k 1+k 2=+=+=2k -y 1-32x 1-1y 2-32x 2-1k (x 1-1)-12x 1-1k (x 2-1)-12x 2-112(1x 1-1+1x 2-1)=2k -12x 1+x 2-2x 1x 2-(x 1+x 2)+1=2k -=.128k 2-8k -2(4k 2+3)4k 2-8k -8-(8k 2-8k )+(4k 2+3)6k -35又由Error!⇒3x +4-12=0,解得x =,y =,(kx -k +1)4k +84k +39k +34k +3即C 点的坐标为C,(4k +84k +3,9k +34k +3)∴k 3==.9k +34k +3-324k +84k +3-16k -310∴k 1+k 2与k 3的关系为k 1+k 2=2k 3.B 组 能力提升练1.已知椭圆E :+=1(a >b >0)的右焦点为F (3,0),过点F 的直线交E 于A ,B 两点.若ABx 2a 2y 2b2的中点坐标为(1,-1),则E 的方程为( D )A.+=1 B .+=1x 245y 236x 236y 227C.+=1D .+=1x 227y 218x 218y 292.设F 1,F 2是椭圆E :+=1(a >b >0)的左,右焦点,P 为直线x =上一点,△F 2PF 1是x 2a 2y 2b 23a2底角为30°的等腰三角形,则椭圆E 的离心率为( C )A. B .1223C. D .34453.从椭圆+=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正x 2a 2y 2b2半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是( C )A. B .2412C.D .2232解析:易得P ,k AB =k OP ,即-=-,(-c ,b 2a )b a b 2ac又a 2=b 2+c 2,可得=.c a 224.已知直线l :y =kx +2过椭圆+=1(a >b >0)的上顶点B 和左焦点F ,且被圆x 2+y 2=4x 2a 2y 2b2截得的弦长为L ,若L ≥,则椭圆离心率e 的取值范围是( B )455A. B .(0,55)(0,255]C.D .(0,355](0,455]5.已知椭圆E :+=1(a >b >0)的右焦点为F ,短轴的一个端点为M ,直线l :3x -4y =0x 2a 2y 2b2交椭圆E 于A ,B 两点.若|AF |+|BF |=4,点M 到直线l 的距离不小于,则椭圆E 的离心45率的取值范围是( A )A.B .(0,32](0,34]C.D .[32,1)[34,1)6.(2016·高考浙江卷)已知椭圆C 1:+y 2=1(m >1)与双曲线C 2:-y 2=1(n >0)的焦点重x 2m 2x 2n2合,e 1,e 2分别为C 1,C 2的离心率,则( A )A .m >n 且e 1e 2>1B .m >n 且e 1e 2<1C .m <n 且e 1e 2>1D .m <n 且e 1e 2<17.(2018·湖北重点中学联考)已知椭圆C 1:+=1(a >b >0)与椭圆C 2:+=1(a >b >0)x 2a 2y 2b 2y 2a 2x 2b2相交于A ,B ,C ,D 四点,若椭圆C 1的一个焦点F (-,0),且四边形ABCD 的面积为,2163则椭圆C 1的离心率e 为 .22解析:联立Error!两式相减得=,又a ≠b ,x 2-y 2a 2x 2-y 2b2所以x 2=y 2=,a 2b 2a 2+b 2故四边形ABCD 为正方形,面积为4x 2==,(*)4a 2b 2a 2+b 2163又由题意知a 2=b 2+2,将其代入(*)式整理得3b 4-2b 2-8=0,所以b 2=2,则a 2=4,所以椭圆C 的离心率e =.228.(2017·湖南东部六校联考)设P ,Q 分别是圆x 2+(y -1)2=3和椭圆+y 2=1上的点,x 24则P ,Q 两点间的最大距离是 .733解析:由圆的性质可知,P ,Q 两点间的最大距离可以转化为圆心到椭圆上点的距离的最大值加上圆的半径,设Q (x ,y ),则圆心(0,1)到椭圆上点的距离为d =3==,x 2+ y -1 2-3y 2-2y +5-3(y +13)2+163∵-1≤y ≤1,∴当y =-时,d 取最大值,13433∴P ,Q 两点间的最大距离为d max +=.37339.(2018·高考天津卷)设椭圆+=1(a >b >0)的右顶点为A ,上顶点为B .已知椭圆的离x 2a 2y 2b2心率为,|AB |=.5313(1)求椭圆的方程;(2)设直线l :y =kx (k <0)与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若△BPM 的面积是△BPQ 面积的2倍,求k 的值.解析:(1)设椭圆的焦距为2c ,由已知得=,又由a 2=b 2+c 2,可得2a =3b .c 2a 259由|AB |==,从而a =3,b =2.a 2+b 213椭圆的方程为+=1.x 29y 24(2)设点P 的坐标为(x 1,y 1),点M 的坐标为(x 2,y 2),由题意知x 2>x 1>0,点Q 的坐标为(-x 1,-y 1).由△BPM 的面积是△BPQ 面积的2倍,可得|PM |=2|PQ |,从而x 2-x 1=2[x 1-(-x 1)],即x 2=5x 1.易知直线AB 的方程为2x +3y =6,由方程组Error!消去y ,可得x 2=.63k +2由方程组Error!消去y ,可得x 1=.由x 2=5x 1,可得=5(3k +2),两边平方,69k 2+49k 2+4整理得18k 2+25k +8=0,解得k =-或k =-.8912当k =-时,x 2=-9<0,不合题意,舍去;89当k =-时,x 2=12,x 1=,符合题意.12125所以k 的值为-.12。
