2013-2014学年高一数学上学期期中试题及答案(新人教A版第105套)

合集下载

2013-2014学年度上学期期中考试(高一数学)附答案

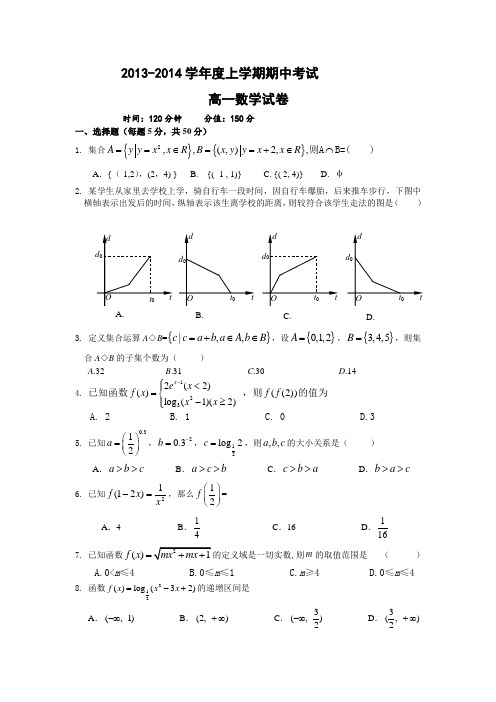
2013-2014学年度上学期期中考试高一数学试卷时间：120分钟分值：150分一、选择题（每题5分，共50分）1. 集合{}{}2,,(,)2,,A y y x x R B x y y x x R ==∈==+∈⋂则A B=( )A ．{（-1,2），(2，4) } B. {( -1 , 1)} C. {( 2, 4)} D. φ2. 某学生从家里去学校上学，骑自行车一段时间，因自行车爆胎，后来推车步行，下图中横轴表示出发后的时间，纵轴表示该生离学校的距离，则较符合该学生走法的图是（）3. 定义集合运算A ◇B =|,,c c a b a A b B =+∈∈，设0,1,2A =，3,4,5B =，则集合A ◇B 的子集个数为（）A .32B .31C .30D .144. 已知函数1232(2)()log (1)(2)x e x f x x x -⎧<⎪=⎨-≥⎪⎩ ，则))2((f f 的值为 A. 2 B. 1 C. 0 D.35. 已知0.312a ⎛⎫= ⎪⎝⎭，20.3b -=，12log 2c =，则,,a b c 的大小关系是（）A ．a b c >>B ．a c b >>C ．c b a >>D ．b a c >> 6. 已知21)21(x x f =-，那么12f ⎛⎫⎪⎝⎭= A ．4 B ．41 C ．16 D ．1617. 已知函数()=f x 的定义域是一切实数,则m 的取值范围是（）A.0<m ≤4B.0≤m ≤1C.m ≥4D.0≤m ≤48. 函数212()log (32)f x x x =-+的递增区间是A ． (,1)-∞B ． (2,)+∞C ． 3(,)2-∞ D ．3(,)2+∞　9. 已知函数()f x 是定义在R 上的偶函数，在(),0-∞上单调递减，且有()3=0f ，则使得()0<f x 的x 的范围为（）A.(),3-∞B. ()3,+∞C.()(),33,-∞+∞D.()3,3-10.对实数a 和b 定义运算“⊗”：,1,,1a ab a b b a b -≤⎧⊗=⎨->⎩．设函数22()(2)()f x x x x =-⊗-，x ∈R ，若函数()y f x c =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是（）A ．3(,2](1,)2-∞--B ．3(,2](1,)4-∞---C ．11(1,)(,)44-+∞D ．31(1,)[,)44--+∞二、填空题（每题5分，共25分） 11．函数)12(log 741)(2++-=x x x f 的定义域为 .12．幂函数()22211m m y m m x--=--在()0,x ∈+∞时为减函数，则m= ．13. 已知2510m n==，则11m n+= ． 14. 如果函数()f x 满足：对任意实数,a b 都有()()()f a b f a f b +=,且()11f =，则()()()()()()()()()()2342011201212320102011f f f f f f f f f f +++++= _________．15. 给出下列命题：①()f x 既是奇函数，又是偶函数；②()f x x =和2()x f x x=为同一函数；③已知()f x 为定义在R 上的奇函数，且()f x 在(0,)+∞上单调递增，则()f x 在(,)-∞+∞上为增函数；④函数y =[0,4) 其中正确命题的序号是 .三、解答题（共75分）16.（本小题满分12分）⑴计算：0.25-2-25.0log 10log 2)161(85575.032----⑵已知函数)(x f 是定义域为R 的奇函数，当x ≤0时，)(x f =x(1+x).求函数)(x f 的解析式并画出函数)(x f 的图象.17.（本小题满分12分）已知集合{}|5239A x x =-≤+≤，{}|131B x m x m =+≤≤- （1）求集合A ；（2）若B A ⊆，求实数m 的取值范围.18．（本小题满分12分）某商品在近30天内每件的销售价格p （元）与时间t （天）的函数关20,025,,100,2530,.t t t N p t t t N +<<∈⎧=⎨-+≤≤∈⎩该商品的日销售量Q （件）与时间t （天）的函数关系是40+-=t Q ),300(N t t ∈≤<，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？19．（本小题满分12分）定义运算：a bad bc c d=- （1）若已知1k =,求解关于x 的不等式101x x k< -（2）若已知1()1x f x k x=- -，求函数()f x 在[1,1]-上的最大值。

吉林省吉林市普通高中2013-2014学年高一上学期期中教学质量检测数学试题含答案

吉林市普通中学2013—2014学年度上学期期中教学质量检测高一数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题)两部分，共21小题，共120分，共8页,考试时间90分钟，考生作答时将答案答在答题卡上，在本试卷上答题无效。

注意事项:1、答题前，考生务必将自己的学校、班级、姓名、准考证号填写在答题卡上,2、请按照题号在各题的答题区域(黑色线框）内作答，超出答题区域书写的答案无效.3、保持卡面清洁,不折叠、不破损。

第Ⅰ卷（选择题，共48分）一、选择题（本大题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求。

）1．下列几个关系中正确的是 A. 0{0}∈B 。

0{0}= C. 0{0}⊆ D 。

{0}∅=2。

函数()lg(31)f x x =+的定义域是A.(0,)+∞B 。

(1,0)-C 。

1(,)3-+∞ D 。

1(,0)3- 3。

下列函数中与函数y x =是同一个函数的是A 。

2)(x y =B 。

33)(x y =C.2xy = D.xx y 2=4. 函数2()1log f x x =-的零点是A 。

(1,1)B 。

1C 。

(2,0)D 。

25. 如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上单调递减，那么实数a 的取值范围是 A.5a ≥B. 5a ≤C. 3a ≥- D 。

3a ≤-6. 三个数6log 6,7.07.07.06的大小关系为A 。

7.067.067.06log << B. 6log 67.07.07.06<<C 。

67.07.07.066log <<D.6.07.0676log 7.0<<7。

已知函数2log ,0()3,xx x f x x >⎧=⎨≤⎩则1[()]4f f 的值是A. 14B. 4C. 19D 。

8。

设,P Q是两个非空集合，定义运算“⊙”：{|,}PQ x x P Q x P Q =∈∉且如果,0{|{|2}x x P y y Q y y >====,则PQ ＝A ．[0,1](2,)+∞B ． [0,1](4,)+∞C ．[1,4]D ．(4,)+∞ 9。

2013-2014学年高一数学上学期期中试题文及答案(新人教A版第211套)

高一上期中数学试题一、选择题（每小题5分，共60分）1. 已知集合{}10，=S ，集合{}0=T ，Φ表示空集，那么=T S ( ) A.ΦB.{}0C.{}10，D.{}010，，2．设{1,2,3,4,5},{1,,5},{2,,4}U A B ===,则()U BC A =（）A.}4,3,2{B.}2{C.}4,2{D.}5,4,3,1{6. 设全集U ＝{1,2,3,4,5,6}，A ＝{1,3,5}，则∁U A 的所有非空子集的个数为( )A ．8B ．3C ．4D ．77.已知312.01.0)2(,)22(,2.1-===c b a ，则c b a ,,的大小关系是（）A.c b a >> B ．c a b >> C.a c b >> D ．b a c >> 8. 设函数||)(x x x f =定义在(－∞，＋∞)上，则f (x )( )A ．既是偶函数，又是减函数B ．既是奇函数，又是减函数C ．既是偶函数，又是增函数D ．即是奇函数，又是增函数9.已知g （x ）=1-2x,f [g （x ）]=)0(122≠-x xx ,则f （21）等于（）A ．1B ．3C ．15D ．3010.若函数y=x 2﹣3x ﹣4的定义域为[0，m]，值域为，则m 的取值范围是（）A. （0，4]B.C.D.11.已知函数f （x ）满足：当x ≥4时，f （x ）=（12），当x<4时，f （x ）=f （x+1），则f（2+log 23）=（）A ．241 B.121 C.81 D.8312.()()()(){}()=>-≥-=02|,042x f x x x f x f x 则满足设偶函数A.{}42|>-<x x x 或 B.{}40|><x x x 或C.{}60|><x x x 或 D.{}22|>-<x x x 或三、解答题（共六个小题，满分70分，要求写出必要的文字说明、推理过程和演算步骤） 17.计算（满分10分，每小题5分）（1）21134320212)12(])2[(])73(2[)25.0(--+-⨯⨯---（2）21324lg (lg 2)lg 50lg 52493-∙+18.（满分12分）已知集合A＝ X∣1≤X＜7 ，Ｂ＝ X∣2＜X＜10 ，C＝ X∣X＜a ,全集为实数集R，（Ⅰ）求A∪B，（C R A）∩B；（Ⅱ）如果A∩C≠ ，求a 取值范围。

2013-2014学年高一数学上学期期中联考试题及答案(新人教A版第73套)

广东省东莞市五校2013-2014学年第一学期期中联考高一数学试卷本试卷共4页，20小题，满分150分．考试用时120分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上．将条形码横贴在答题卡右上角“条形码粘贴处”．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案．答案不能答在试卷上．3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须填写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用2B 铅笔填涂选做题的题号（或题组号）对应的信息点，再作答．漏涂、错涂、多涂的，答案无效．5．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}1,2,3A =，{}2,3,4,5B =，则A B ⋂=A ．{}6,7,8B ．{}1,4,5,6,7,8C ．{}2,3D ．{}1,2,3,4,52.下列函数中哪个与函数x y =相等A.2)(x y = B. xx y 2= C.2x y = D.33x y =3.已知函数()()()210,10.x x x f x x x ->⎧⎪=⎨-≤⎪⎩，，则函数(1)f 的值为 A ．1- B ．0 C ．1 D ．44.设函数y =M ，那么 A ．{|10}x x x >-≠且 B ． {|1}x x >-C ．{|10}或M x x x =<->D ．{|1100}或或M x x x x =<--<<>5. 函数()2x f x e x =+-的零点所在的一个区间为A ．()2,1--B ．()1,0-C ．()0,1D ．()1,2 6.偶函数)(x f y =在区间[]4,0-上单调递增，则有A.)()3()1(ππ->>-f f fB. )()1()3(ππ->->f f fC.)3()1()(ππf f f >->-D. )3()()1(ππf f f >->-7.函数xy 2=的值域为A ．)1,0(B ．]1,0(C ．),0(+∞D ．),1[+∞ 8. 设217.0=a ，218.0=b ，c 7.0log 3=，则 A ．c b a << B ．ab c << C ．c a b <<D ． b a c<<9.函数log (23)2a y x =-+的图象恒过定点P ，P 在指数函数)(x f 的图象上，则(1)f -的值为2 C.2- 10.定义在]1,1[-的函数)(x f 满足下列两个条件：①任意的]1,1[-∈x ，都有()()f x f x -=-；②任意的]1,0[,∈n m ，当n m ≠，都有0)()(<--nm n f m f ，则不等式)1()31(-<-x f x f 的解集是A.)21,0[B. ]32,21( C.)21,1[- D.]1,32[ 二、填空题：本大题共4小题，每小题5分，满分20分． 11.已知幂函数()y f x =的图象经过点11,42⎛⎫⎪⎝⎭，则该幂函数的解析式为 . 12.若21{,x x ∈}，则x = .13.函数log a y x =在(1,)x ∈+∞上恒有0y <，则a 的取值范围是 . 14.在实数运算中, 定义新运算“⊕”如下: 当a b ≥时, a b a ⊕=; 当a b <时,2a b b ⊕=. 则函数()(1)(2)f x x x =⊕-⊕(其中[2,2x ∈-)的最大值是 .三、解答题：本大题共6小题，满分80分．解答须写出文字说明，证明过程或演算步骤． 15. （本题满分12分）已知{2-≤=x x A 或}5>x ，{}71≤<=x x B ．求：（1）B A ；（2）B A ；（3）()R A C B ．16. （本题满分12分）计算（1）01242--+（2）23511log 25log log 169⋅⋅17. （本题满分14分）设函数xx f 11)(+=. （1）用定义证明函数)(x f 在），（∞+0上为减函数；（2）判断函数)(x f 的奇偶性.18. （本题满分14分）,A B 两地相距150千米，某人开汽车以60千米/小时的速度从A 地到达B 地，在B 地停留1小时后再以50千米/小时的速度返回A 地.（1）试把汽车离开A 地的距离y (千米)表示为时间x （小时）的函数；（2）根据（1）中的函数表达式，求出汽车距离A 地100千米时x 的．19. （本小题满分14分）已知函数2()2f x x ax a =-+，（1）当1a =时，求函数()f x 在[]0,3上的值域；（2）是否存在实数a ，使函数2()2f x x ax a =-+的定义域为[]1,1-，值域为[]22-，？若存在，求出a 的值；若不存在，说明理由．20.（本小题满分14分）已知函数212(),03()11,02x x f x x x x ⎧-≤⎪⎪=⎨⎪-+>⎪⎩（1）当0x ≤时，解不等式()1f x ≥-；（2）写出该函数的单调区间；(3) 若函数()()g x f x m =-恰有3个不同零点，求实数m 的取值范围．2013-2014学年第一学期五校联考高一数学一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1 2 3 4 5 6 7 8 9 10 CDBBCADDBA二、填空题：本大题共6小题，每小题5分，满分30分．11. 12y x =(或y =)12.若1-13. ()0,1或{}|01x x <<或01x <<均给分。

2013-2014第一学期高一数学期中考试(附答案)

普宁一中2013～2014学年度第一学期期中考试高一级数学科试题注意事项：1．本试卷分试题卷和答题卷两部分，考试结束后交答题卷，总分150分，考试时间120分钟。

2．答题前，考生须将自己的姓名、班级、座位号填写在答题卡指定的位置上。

3．选择题的每小题选出答案后，用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其答案，不能答在试题卷上。

4．非选择题必须按照题号顺序在答题卡上各题目的答题区域内用黑色字迹的钢笔或签字笔作答，超出答题区域或在其它题的答题区域内书写的答案无效。

第Ⅰ卷选择题部分（满分50分）一、单项选择题（本大题共10小题，每小题5分，共50分。

）1. 已知全集{12345}U =，，，，，集合{1,3}A =，{1,3,4}B =，则集合()U C A B =（ * ）A ．{3}B ．{4,5}C ．{245}，，D ．{3,4,5} 2. 若全集{}{}1,2,3,41U U C A ==且，则集合A 的真子集共有（ * ）A. 3个B. 5个C. 7个D. 8个 3. 函数()lg(23)f x x =-的定义域是（ * ）A. 3[,)2+∞B. 3(,)2+∞C. 3(,]2-∞D. 3(,)2-∞4. 下列函数中,既是奇函数又是增函数的为（ * ）A ．1y x =+B ．2y x =-C ．1y x=D ．||y x x = 5. 三个数20.40.40.42log 2，，的大小关系为（ * ）A. 20.40.40.42log 2<<B. 20.40.4log 20.42<< C ．20.40.40.4log 22<< D ．0.420.4log 220.4<< 6. 函数1()34x f x -=-的零点所在区间为（ * ）A ．（0， 1）B ．（1，2）C ．（2，3）D ．（3，4）D CB A7. 定义在R 上的偶函数在[0，6]上是增函数，在[6，+∞]上是减函数，又(6)5f =，则()f x （ * ）A ．在[－6，0]上是增函数，且最大值是5B ．在[－6，0]上是增函数，且最小值是5C ．在[－6，0]上是减函数，且最小值是5D ．在[－6，0]上是减函数，且最大值是5 8. 已知幂函数()f x3），则(2)f 的值是（ * ）A ． 4B ．2C ．41D ．219.某同学家门前有一笔直公路直通长城，星期天，他骑自行车匀速前往旅游，他先前进了a km ，觉得有点累，就休息了一段时间，想想路途遥远，有些泄气，就沿原路返回骑了b km(b <a ), 当他记起诗句“不到长城非好汉”，便调转车头继续前进. 则该同学离起点的距离s 与时间t 的函数关系的图象大致为（ * ）10. 已知y ＝f (x )是定义在R 上的奇函数，当0x >时，()3f x x =-，那么不等式0)(<x f 的解集是（ * ） A. {}03x x <<B. {}3x x <-C. {}30,03x x x -<<<<或D. {}3,03x x x <-<<或第Ⅱ卷非选择题部分（满分100分）二、填空题（本大题共4小题，每小题5分，共20分。

2013-2014学年高一上学期期中考试数学试题 Word版含答案

2013-2014学年度第一学期期中考试高一年级数学（满分160分，考试时间120分钟）一、填空题1、设集合}3,1{=A ，集合}5,4,2,1{=B ，则集合=B A2、若1)(+=x x f ，则(3)f =3、函数3)1()(+-=x k x f 在R 上是增函数，则k 的取值范围是4、指数函数x a y =的图像经过点（2，16）则a 的值是5、幂函数2-=x y 在区间]2,21[上的最大值是6、已知31=+aa ，则 =+aa 17、函数321)(-=x x f 的定义域是________．8、化简式子82log 9log 3的值为9、已知函数()y f x =是定义在R 上的单调减函数，且(1)(2)f a f a +>，则a 的取值范围是10、下列各个对应中, 从A 到B 构成映射的是（填序号）A B A B A B A B（1）（2）（3）（4）11、满足82>x 的实数x 的取值范围12、设()x f 为定义在()+∞∞-,上的偶函数，且()x f 在[)+∞,0上为增函数，则()2-f ，()π-f ，()3f 的大小顺序是____________13、当0>a 且1≠a 时，函数3)(-=x a x f 的图像必过定点14、已知⎩⎨⎧≥+<-=)0(1)0(2)(2x x x x x x f 若,3)(=x f 则=x二、解答题15、全集R U =,若集合},103|{<≤=x x A }72|{≤<=x x B ，则（结果用区间表示）（1）求)()(,,B C A C B A B A U U ；（2）若集合C A a x x C ⊆>=},|{，求a 的取值范围16、对于二次函数2483y x x =-+-，（1）求函数在区间]2,2[-上的最大值和最小值；（2）指出函数的单调区间17、化简或求值：（1）)3()4)(3(656131212132b a b a b a -÷-；（2）()281lg500lg lg 6450lg 2lg552+-++18、已知某皮鞋厂一天的生产成本c(元)与生产数量n(双)之间的函数关系是n=c504000+（1）求一天生产1000双皮鞋的成本；（2）如果某天的生产成本是48000元，那么这一天生产了多少双皮鞋？（3）若每双皮鞋的售价为90元，且生产的皮鞋全部售出，试写出这一天的利润P关于这一天生产数量n的函数关系式，并求出每天至少生产多少双皮鞋，才能不亏本？19、已知21()log 1xf x x+=- （1）求()f x 的定义域；（2）求证：()f x 为奇函数（3）判断()f x 的单调性，并求使()0f x >的x 的取值范围。

河南省商丘市六校2013-2014学年高一上期期中联考数学试题 Word版含答案

2013---2014学年度上期期中联考高一数学试题一．选择题：（本大题共12小题，每小题5分，共60分）. 1．已知错误！未找到引用源。

，则错误！未找到引用源。

=（）（A ） 2 （B ） 1 （C ）2或 1 （D ）1或3 2．下列各组函数中表示同一函数的是（） A ．()f x x = 与()2g x =B ．()f x x = 与()g x =C ．()f x x x = 与()()()2200x x g x x x ⎧ >⎪=⎨- <⎪⎩D ．()211x f x x -=- 与()()11g x x x =+ ≠ 3．函数1()lg(1)1f x x x=++-的定义域是（） A ．(,1)-∞- B.(1,)+∞ C.(1,1)(1,)-+∞ D. (,)-∞+∞4．下列函数中,既是奇函数又是增函数的为（） A 、1y x =+ B 、||y x x = C 、1y x= D 、2y x =- 5．已知函数2,0()1,0x x f x x x >⎧=⎨+≤⎩，若f(a)＋f(1)＝0，则实数a 的值等于( )A ．3B ．1C ．－1D ．－3 6．已知则f(x)=( ) A ．f(x)=x+2B ．f(x)=x+2(x ≥0) C ．f(x)=x 2-1 D ．f(x)=x 2-1(x ≥1)7．已知1(4)()2(1)(4)x x f x f x x ⎧≥⎪=⎨⎪+<⎩，则=)3(log 2f （）A.124 B. 238- C. 111 D. 1198．函数1()322xf x x =+-的零点所在的一个区间是( )A ．(－2，－1)B ．(－1，0)C ．(0，1)D ．(1，2)9．设)(x f 为定义在R 上的奇函数，当0≥x 时，b x x f x++=22)((b 为常数)，则)1(-f =（）A .3 B.1 C.－1 D.－3 10．如图，设a,b,c,d>0，且不等于1，y=a x, y=b x,y=a xy=c x ,y=d x在同一坐标系中的图象如图，则a,b,c,d 的大小顺序（） A. a<b<c<d B ．a<b<d<c C ．b<a<d<c D ．b<a<c<d 11．下列说法中：①．所有幂函数的图象都经过点（1，1）和（0，0）②．所有幂函数的图象都不经过第四象限 ③.函数0x y =的图象是一条直线 ④.幂函数可能是奇函数，也可能是偶函数，也可能既不是奇函数也不是偶函数正确说法的个数是（） A ．0B ．1C ．2D ．312．已知a 是函数13()3log x f x x =-的零点，若00x a <<，则)(0x f 的值满足( ) A ．0()0f x < B ．0()0f x > C ．0()0f x = D ．)(0x f 的符号不确定二、填空题（本大题共4小题，每小题5分，共20分）. 13．函数4()f x x x=+的单调递减区间为________ 14．设44log ,32log ,21log 33131===c b a ，则c b a ,,大小关系是__ _错误！未找到引用源。

2013-2014学年高一数学上学期期中考试及答案(新人教A版第56套)

梁山一中2013—2014学年高一上学期期中检测数学一、选择题:(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.)22. 函数)5(log 5.0-=x y 的定义域是( )A.（5，)∞+B. [5，)∞+C. （5，)6D.[5，6）3.函数xy ⎪⎭⎫⎝⎛=31在[]2,1上的值域为( )()+∞,0.A ⎥⎦⎤ ⎝⎛91,0.B ⎥⎦⎤ ⎝⎛31,0.C ⎥⎦⎤⎢⎣⎡31,91.D4. 已知全集{}3,1,1-=U ，集合{}2,22++=a a A ，且{}1-=A C U ，则a 的值是（） A ．1- B ．1 C ． 3 D ．1±5. 设1232,2()log (1),2x e x f x x x -⎧ <⎪=⎨-≥⎪⎩，则[(2)]f f 的值为（） A.0 B.1 C.2 D.3 6. 已知0.9 1.7 1.51.7,0.9,0.9,a b c ===则有( )A.a b c <<B.a c b <<C. b a c <<D. b c a <<7. 方程220xx +-=的解所在的区间为( )A.（-1，0）B.（0，1） C.（1，2） D.（2，3）8. 图中阴影部分所表示的集合是( )A. [()]U BAC ð B. (A ∪B) ∪(B ∪C) C. (A ∪C)∩(ðU B) D.[()]U AC B ð9. 已知函数2,5()(2),5x x x f x f x x ⎧-<=⎨-≥⎩则(8)f 的值为 ( )A.－12B.20C.－56D.5610.函数y ＝a x在区间[0,1]上的最大值与最小值的和为3，则函数y ＝3ax －1在区间[0,1]上的最大值是( ) A ．6B ．1C ．5D.3211.函数|1|ln )(-=x x f 的图象大致是( )12．若11|log |log 44aa =，且|log |logb b a a =-，则,a b 满足的关系式是（） A ．1,1a b >>且 B ．1,01a b ><<且 C ．1,01b a ><<且 D ．01,01a b <<<<且二、填空题（本大题共4个小题，每小题5分，共20分.） 13. 函数2()23x f x -=-的图象恒过定点________.14. 函数f (x )＝ax 3＋bx ＋4(a ，b 不为零)，且f (5)＝10，则f (－5)等于_____.15. 若函数2()(21)1f x x a x a =--++是[1,2]上的单调函数，则实数a 的取值范围为________．16. 若函数y ＝f (x )在(－∞，0)∪(0，＋∞)上为奇函数，且在(0，＋∞)上为增函数，f (－2)＝0，则不等式x ·f (x )<0的解集为________．三、解答题：（写出必要的计算步骤、解答过程，只写最后结果的不得分，共70分.）17．（本小题满分10分）已知全集U=R ，A={x|x ＜﹣2或x ＞5}，B={x|4≤x≤6}，求∁U A ，∁U B ，A∩B，及∁U （A∪B）．18．（本小题满分12分）已知函数21()1x f x x +=+. (1) 证明函数()f x 在区间[1,)+∞上是增函数； (2) 求该函数在区间[1,4]上的最大值与最小值．19．（本小题满分12分）已知函数f (x )是定义在R 上的奇函数，且当x ＞0时，f (x )＝(12)x.(1) 求函数f (x )的解析式；(2) 在所给坐标系中画出函数()f x 的图像，并根据图象写出函数f (x )的单调区间．20．（本小题满分12分）已知函数f (x )的定义域为(－2,2)，函数g (x )＝f (x －1)＋f (3－2x )． (1) 求函数g (x )的定义域；(2) 若f (x )是奇函数，且在定义域上单调递减，求不等式g (x )≤0的解集． 21．（本题满分12分）某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.（1）当每辆车的月租金定为3600元时，能租出多少辆车？（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？22．（本题满分12分）已知定义域为R 的函数12()22x x b f x +-+=+是奇函数.（1）求b 的值；（2）判断函数()f x 的单调性; （3）若对任意的t R ∈，不等式22(2)(2)0f t t f t k -+-<恒成立，求k 的取值范围．参考答案:1-5 BADAC 6-10 DBAAC 11-12 BC13. (2,-2) 14. －2 15. 35(,][,)22-∞+∞ 16. (－2,0)∪(0,2) 17.根据题意，A={x|x ＜﹣2或x ＞5}，则∁U A={x|﹣2≤x≤5}， B={x|4≤x≤6}，则∁U B={x|x ＜4或x ＞6}，又由A={x|x ＜﹣2或x ＞5}，B={x|4≤x≤6}，则A∩B={x|5＜x≤6}， A∪B={x|x＜﹣2或x≥4}，则∁U （A∪B）={x|﹣2≤x＜4}．18．解: (1) 任取x 1，x 2∈[1，＋∞)，且x 1＜x 2，则210x x x ∆=->21()()y f x f x ∆=-=2121212111x x x x ++-++2112(1)(1)x x x x -=++ ∵210x x x ∆=->，(x 1＋1)(x 2＋1)＞0，所以0y ∆>，所以函数f (x )在[1,)+∞上是增函数． (2)由(1)知函数f (x )在[1,4]上是增函数．所以最大值为f (4)＝2×4＋14＋1＝95，最小值为f (1)＝2×1＋11＋1＝32.19．(1)因为f (x )是定义在R 上的奇函数，所以f (0)＝0，当x ＜0时，－x ＞0，f (x )＝－f (－x )＝1()2x --＝－2x .所以函数的解析式为f (x )＝⎩⎪⎨⎪⎧－2x，x ＜0，0，x ＝0，⎝ ⎛⎭⎪⎫12x， x ＞0.(2)列表如下：函数图象如图所示：通过函数的图象可以知道，f (x )的单调递减区间是(－∞，0)，(0，＋∞)．20．解：(1)由题意可知⎩⎪⎨⎪⎧－2＜x －1＜2，－2＜3－2x ＜2，∴⎩⎪⎨⎪⎧－1＜x ＜3，12＜x ＜52.解得12<x <52.故函数f (x )的定义域为⎝ ⎛⎭⎪⎫12，52. (2)由g (x )≤0，得f (x －1)＋f (3－2x )≤0， ∴f (x －1)≤－f (3－2x )．∵f (x )为奇函数，∴f (x －1)≤f (2x －3)．而f (x )在(－2,2)上单调递减，∴⎩⎪⎨⎪⎧x －1≥2x －3，12＜x ＜52.解得12＜x ≤2.∴g (x )≤0的解集为⎝ ⎛⎦⎥⎤12，2.… 21．（1）当每辆车的月租金定为3600元时，未租出的车辆数为：5030003600- =12，所以这时租出了88辆车（2）设每辆车的月租金定为x 元，则租赁公司的月收益为：f （x ）=（100－503000-x ）（x －150）－503000-x ×50，整理得f （x ）=－502x +162x －21000=－501（x －4050）2+307050所以，当x =4050时，f （x ）最大，其最大值为f （4050）=307050.即当每辆车月租金定为4050元时，租赁公司月收益最大，最大收益为307050元.……12分 22.(1)因为()f x 在定义域为R 上是奇函数，所以(0)f =0，即10122b b -=∴=+ （2）由(1)知11211()22221x x x f x +-==-+++，设12x x <则211212121122()()2121(21)(21)x x x x x x f x f x --=-=++++ 因为函数y=2x在R 上是增函数且12x x < ∴2122x x->0 又12(21)(21)x x++>0 ∴12()()f x f x ->0即12()()f x f x > ∴()f x 在(,)-∞+∞上为减函数.（3）因()f x 是奇函数，从而不等式： 22(2)(2)0f t t f t k -+-< 等价于222(2)(2)(2)f t t f t k f k t -<--=-，因()f x 为减函数，由上式推得：2222t t k t ->-．即对一切t R ∈有：2320t t k -->，从而判别式14120.3k k ∆=+<⇒<-。

2013-2014学年高一上学期期中考试数学试题Word版含答案.docx

2013-2014 学年度第一学期期中考试高一年级数学（满分 160 分，考试时间 120 分钟）一、填空题1 、设集合 A {1,3} ，集合 B {1,2,4,5} ，则集合 AB2 、若 f ( x) x 1 ，则 f (3)3 、函数 f (x) (k 1)x 3 在 R 上是增函数，则 k 的取值范围是4 、指数函数 y a x 的图像经过点（ 2 ，16 ）则 a 的值是5 、幂函数 yx 2在区间 [ 1,2] 上的最大值是26 、已知1 3 ，则1aaaa1 7 、函数 f (x)2 x 3的定义域是 ________．8 、化简式子 log 8 9的值为log 2 39 、已知函数 y f ( x) 是定义在 R 上的单调减函数，且 f (a 1)f (2 a) ，则 a 的取值范围是10、下列各个对应中, 从 A 到 B 构成映射的是（填序号）A B ABAB A B1 4 1 1 3 1 a 22 54 2 b 3536253c（ 1 ）（ 2 ）（3 ）（ 4 ）11 、满足 2 x 8 的实数 x 的取值范围12 、设 f x 为定义在 ,上的偶函数，且 f x 在 0, 上为增函数，则 f2 ， f， f 3 的大小顺序是 ____________13 、当 a 0 且 a 1 时，函数 f ( x) a x3 的图像必过定点x 2 2x ( x 0) 3, 则 x14 、已知 f (x)1(x若 f ( x) x0)二、解答题15 、全集 UR ,若集合 A { x | 3 x 10}, B { x | 2 x 7} ，则（结果用区间表示）（1）求 AB, A B,(C U A)(C U B)；（2 ）若集合C{ x | x a},A C ，求a的取值范围16 、对于二次函数y4x28x 3 ，（1 ）求函数在区间[ 2,2]上的最大值和最小值；（2 ）指出函数的单调区间17、化简或求值：211115（1 ）(3a3b2)( 4a2b3)( 3a 6 b 6 ) ；（2 ）lg500lg 81 lg 64 50 lg2 lg5 2 5 218 、已知某皮鞋厂一天的生产成本c(元)与生产数量 n (双)之间的函数关系是 c 400050 n（1 ）求一天生产 1000 双皮鞋的成本；（2）如果某天的生产成本是 48000 元，那么这一天生产了多少双皮鞋？（3）若每双皮鞋的售价为 90 元，且生产的皮鞋全部售出，试写出这一天的利润 P 关于这一天生产数量 n 的函数关系式，并求出每天至少生产多少双皮鞋，才能不亏本？1x19 、已知f (x) log21x（1 ）求f (x)的定义域；（2 ）求证：f ( x)为奇函数（3 ）判断f ( x)的单调性，并求使 f (x)0 的x的取值范围。

2013-2014学年高一第一学期期中数学试题2

2013-2014学年度第一学期期中考试高一数学科试题（考试时间：120分钟满分：150）注意事项：1、选择题每题有且仅有一个正确答案，用2B 铅笔将前10小题正确代码涂在答题卷对应位置；2、用0.5毫米的黑色签字笔填答填空题和解答题，谨防答题错位和将答题内容超出扫描区域外，否则评卷时对应部分不给分；一、选择题（每题5分，共50分）1、已知集合U ＝{1,3,5,7,9}，A ＝{1,5,7}，则A C U ＝( )A 、{1,3}B 、{3,7,9}C 、{3,5,9}D 、{3,9}2、下列各组函数中，定义域相同的一组是( )A 、x a y =与x y a log = (a ＞0，且a ≠1)B 、x y =与x y =C 、x y lg =与x y lg =D 、2x y =与2lg x y =3、函数x x y +-=1的定义域是( )A 、{x|x ≤1}B 、{x|x ≥0}C 、{x|x ≥1或x ≤0}D 、{x|0≤x ≤1}4、对数函数的图象过点M(16,4)，则此对数函数的解析式为( )A 、 x y 2log =B 、x y 41log =C 、x y 21log = D 、 x y 4log =5、设5.1348.029.01)21(,8,4-===y y y ，则( )A 、123y y y >>2B 、 231y y y >>C 、321y y y >>D 、 312y y y >>6、设A ＝{x|1＜x ＜2}，B ＝{x|x ＜a}，若A B ，则a 的取值范围是( )A 、a ≥2B 、a ≤1C 、a ≥1D 、a ≤27．若log m 3<log n 3<0，则m ，n 应满足的条件是（）A 、m > n > 1B 、n > m > 1C 、1> n > m > 0D 、1> m > n > 08、已知函数y=⎩⎨⎧>≤+)0(2)0(12x x x x ，若10)(=a f ，则a 的值是（）A 、3或-3B 、-3或5C 、-3D 、3或-3或59、定义A －B ＝{x|x ∈A 且x ∉B}，若A ＝{1,3,5,7,9}，B ＝{2,3,5}，则A －B 等于( )A 、AB 、BC 、{2}D 、{1,7,9}10、已知⎩⎨⎧≥〈-=,0,1,0,1)(x x x f 则不等式)2()2(+⋅++x f x x ≤5的解集是（） A 、]1,2[- B 、]2,(--∞ C 、]23,2[- D 、]23,(-∞二、填空题（每题5分，共20分）11、函数x x x f 23)1()(0--=的定义域是________．12、设指数函数()(1)x f x a =-是R 上的减函数，则a 的取值范围是________13、幂函数的图象过点(2，14)，则它的单调递增区间是________________ 14、已知全集U ＝{2,3，12--a a }，A ＝{2,3}，若A C U ＝{1}，则实数a 的值是________．三、解答题（共六题，总分80分）15、（满分：13分）设函数)4lg()(x x f -=的定义域为集合A ，函数 32)(2--=x x x g 的定义域为集合B 。

2013-2014学年高一数学上学期期中试题及答案(新人教A版第160套)

湖北省孝感高级中学2013—2014学年度高中一年级上学期期中考试数学满分150分，考试用时150分钟。

考试时间：2013年11月16日一、选择题（每题的四个选项中，只有一个符合题意，每题5分，共50分） 1．集合{(,)}A x y y x ==和21(,)45x y B x y x y ⎧⎫-=⎧⎪⎪=⎨⎨⎬+=⎩⎪⎪⎩⎭，则以下结论中正确的是（） A ．1A ∈B ．B A ⊆C ．(1,1)B ⊆D ． A ∅∈2．33xy +和2234x xy y --的公因式为（）A ．4x y +B ． 4x y -C ． x y -D ．x y +3．已知函数31()(0)()2(0),xx f x x x ⎧≤⎪=⎨⎪>⎩那么()1f f ⎡-⎤⎣⎦的值为（）A ．8B ．18C ．9D ．194．若14x x-+=，则1122x x-+的值等于（） A ．2或－2B ．2CD ． 65．已知集合{}0,1,2A =，集合B 满足AB A =，则可能的集合B 共有（）A ．4个B ．7个C ．8个D ．9个6．已知 ()Q x 是幂函数，则以下结论中正确的一个是（） A ．()Q x 在区间(0,)+∞上总是增函数. B ．()Q x 的图像总过点(1,1). C ．()Q x 的值域一定是实数集RD ．()Q x 一定是奇函数或者偶函数7．函数()log (0a f x x a =>且1)a ≠对任意正实数,m n 都有( ) A ．()()()f mn f m f n =+ B ．()()()f mn f m f n = C ．()()()f m n f m f n +=D ．()()()f m n f m f n +=+8．若不等式20mx px q ++<的解集为(1,3)，则不等式2px qx m ++>0的解集为（）A．1(,1)4-B．(4,1)-C．(,4)(1,)-∞-+∞D．1(,)(1,)4-∞-+∞9．已知2ln2,loga b c e===，（e是自然对数的底数）则它们的大小顺序是（）A．a c b>>B．c b a>>C．c a b>>D．b c a>> 10．已知线段AB的长为4,以AB形ABCD，其中AB CD长的最大值为是( )A．8 B．10 C．1) D二、填空题：（本大题共5小题，每小题5分，满分2511．已知幂函数)(xfy=的图象过点1(,8)2，则-)2(f12．定义在实数集R上的偶函数()f x在[0,)+∞解集是_____________．13．函数()f x的定义域是[4,1]-，则函数22()1f xyx=-的定义域为．14．若函数()(1)x af x a x=-+（0a>，1a≠）的图像恒过点P，则点P的坐标为．15．由声强I(单位:2/w cm)计算声压级D(单位: dB)的公式为：1610lg()10ID-=．（1）人低声说话的声压级为30dB，则它的声强是____________2/w cm；（2）音乐会上的声压级约为100dB，那么它的声强约是人低声说话时声强的_________倍（用数字作答）．三、解答题：（本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤）16．（本小题满分12分）已知全集U= R，{|36,}A x x x R=-<≤∈，2{|560,}B x x x x R=--<∈．求：（1）A B；（2）()B AUð∩17．（本题满分12分）设()f x 是定义在R 上的函数，且对任意实数x ,有2(1)33f x x x -=-+．（1）求函数()f x 的解析式;（2）若函数()()51g x f x x =-+在[,1]m m +上的最小值为2-，求实数m 的取值范围．18．（本题满分12分）提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度()v x （单位：千米/小时）是车流密度x （单位：辆/千米）的函数．高考资源网当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当20200x ≤≤时，车流速度()v x 是车流密度x 的一次函数．（Ⅰ）当0200x ≤≤时，求函数()v x 的表达式；（Ⅱ）当车流密度x 为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）()()f x x v x =⋅可以达到最大值，并求出这个最大值．（精确到1辆/小时）.19．（本题满分12分）已知函数32()32x x x xf x ---=+．（1）判断()f x 的奇偶性；（2）若1()2f m =，试用m 表示3log 8．20．（本题满分13分）已知定义在实数集R 上的函数()f x ，同时满足以下三个条件：①(1)2f -=；②0x <时，()1f x >；③对任意实数,x y 都有()()()f x y f x f y +=；（1）求(0)f ，(4)f -的值；高考资源网（2）判断函数()f x 的单调性，并求出不等式21(4)(10)16f x f x -≥的解集．21．（本题满分14分）对于在区间[,]p q 上有意义的两个函数(),()f x g x ，若对于所有的[,]x p q ∈，都有()()1f x g x -≤，则称()f x 和()g x 在区间[,]p q 上是接近的两个函数，否则称它们在区间[,]p q 上是非接近的两个函数. 现在给定区间[2,3]D a a =++，有两个函数1()log (3),()log 01a af x x ag x a a x a=-=>≠-，其中且．（1）若()f x 和()g x 在区间D 上都有意义，求a 的取值范围；（2）讨论()f x 和()g x 在区间D 上是否为接近的两个函数．湖北省孝感高级中学2013—2014学年度高中一年级上学期期中考试11. 8-12. (,1)(1,)-∞-+∞13. (1,1)-14. (0,0)15. (1)1310-(2) 71016．解：(1) B={x | -1<x<6}； …………………………..3分{|36}A B x x ⋃=-<< ……………………………6分（2） ∁U B ={x | x ≤-1或x ≥6} …………………………………………9分( ∁U B )∩A= {x | －3<x ≤－1或x=6}. …………………………….12分 17．解：(1)令1x t -=得2()(1)3(1)3f t t t =---+ …………………..3分化简得2()1f t t t =++即2()1,f x x x x R =++∈，------------------------------------6分（2）()22()4222g x x x x =-+=-- (1m x m ≤≤+)-------------8分因为1m x m ≤≤+，min ()2g x =-21m m ∴≤≤+ ………………………….10分 12m ∴≤≤ ………………………….12分18．解析：（Ⅰ）由题意：当200≤≤x 时，()60=x v ； …………..2分当20020≤≤x 时，设()b ax x v +=， 20002060a b a b +=⎧⎨+=⎩，解得132003a b ⎧=-⎪⎪⎨⎪=⎪⎩ …….5分故函数()v x 的表达式为60020()1(200)202003x v x x x ≤≤⎧⎪=⎨-≤≤⎪⎩ ………….6分（Ⅱ）依题意并由（Ⅰ）可得60020()1(200)202003x x f x x x x ≤≤⎧⎪=⎨-≤≤⎪⎩当020x ≤≤时，()f x 为增函数，故当20=x 时，其最大值为12002060=⨯；……….9分当20200x ≤≤时，2min 120010000()()(100)333f x x x f x f =-+⇒==所以，综上当100x =时，()f x 在区间[0,200]上取得最大值1000033333≈．……….12分即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时．19．解：（1）3223161()3223161x x x x x x x x x x f x ---⋅--===+⋅++所以6116()(),6116x xxxf x f x x R -----===-∈++，则()f x 是奇函数. .…………6分（2）6611()log 3612m mf m m -==⇒=+ .…………8分663366log (63)1log 3log 83log 233log 3log 3÷-=== 31log 83(1)m∴=- .…………12分 20．解：（1）()(10)1(0),(0)1f f f f -+=-∴= .…………2分2(2)(11)(1)4f f f -=--=-= 2(4)(22)(2)16f f f -=--=-=.…….…….……4分（2）1(0)(())()()1()()f f x x f x f x f x f x =+-=-=⇒-=任取12x x <，则112122()()()()1()f x f x f x f x x f x =-=->，故12()()f x f x >，()f x 在R 上是单调递减函数 .…… .…………8分所以1(4)(4)1(4)16f f f -=⇒=，即2(410)(4)f x x f -+≥ .…………9分又∵()f x 是R 的减函数，∴244x -+10x ≤∴原不等式的解集为1{|2}2x x x ≥≤或 ….………13分21．解：（1）01,a a >≠∴且3030x a x a x a ->⎧⇒>⎨->⎩，23,01a a a ∴+>∴<<…4分（2）2222()()log (43)log [(2)]a a f x g x x ax a x a a -=-+=--，当x D ∈时，22(2)[44,96]x a a a a --∈--，令22()log (43)a h x x ax a =-+，则min ()(3)log (96)a h x h a a =+=-，max ()(2)log (44)a h x h a a =+=-，…8分要使得()()1f x g x -≤，则019log (96)1(0,12log (44)1a a a a a a <<⎧⎪-≥-⇒∈⎨⎪-≤⎩， ………………12分所以当9(0,]12a ∈时，()f x 和()g x 在区间D 上是接近的两个函数当a ∈时，()f x 和()g x 在区间D 上是非接近的两个函数 ……14分。

山东省临沂市重点中学2013-2014学年高一上学期期中考试数学 Word版含答案.pdf

高一数学质量调研试题 2013.11 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分．测试时间120分钟．第Ⅰ卷1至2页，第Ⅱ卷3至4页. 注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选择其它答案标号．不能答在试题卷上．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题；每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的，把正确选项的代号涂在答题卡上． 1.已知集合则=A．B． C． D． 2. 下列函数中,是偶函数又在区间上递增的函数为 A．B．C．D． 3．函数的零点一定位于的区间是 A．（2，3）B．（3，4）C．（1，2）D．（0，1） 4. 已知，，，，那么 A. B. C. D. 5.已知函数的定义域为，且为偶函数，则实数的值可以是 A. B. C. D. 6. 如果幂函数的图象不过原点，则的取值范围是 A． B.或 C.或 D. 7. 函数的图象 A．关于原点对称 B．关于直线对称 C．关于轴对称 D．关于轴对称 8.已知函数，若实数是方程的解，且，则的值A.等于0B.恒为负值C.恒为正值D.不能确定 9.函数的图象为 10．设是R上的偶函数, 且在上递增, 若，那么x的取值范围是 A． B． C． D． 11.已知函数满足:对任意实数,当时,总有,那么实数的取值范围是 A. B. C. D. 12.定义域与值域相同的奇函数称为“八卦函数”，下列函数中是“八卦函数”的是 A． B． C． D．第Ⅱ卷（非选择题共90分）注意事项： 1．用蓝黑钢笔或圆珠笔答在答题纸上，直接答在试题卷上无效． 2．答题前将答题纸密封线内的项目填写清楚．二、填空题：（本大题共4个小题.每小题4分；共16分．） 13．设，集合，则 ________． 14. 已知，，用 “二分法”求方程在区间内的实根，取区间中点为，那么下一个有根的区间是 . 15.已知，函数的图象恒过定点，若在幂函数的图象上，则_________. 16. 若对任意,, (.)有唯一确定的,与之对应,称,为关于,的二元函数. 现定义满足下列性质的二元函数为关于实数.的广义“距离”. (1)非负性:时取等号； (2)对称性:； (3)三角形不等式:对任意的实数z均成立.今给出三个二元函数,请选出所有能够成为关于.的广义“距离”的序号: ①； ②； ③ 能够成为关于的.的广义“距离”的函数的序号是___________. 三、解答题：本大题共6个小题. 共74分．解答应写出文字说明，证明过程或演算步骤． 17.（本小题满分12分）已知集合,，. （1）求,；（2）若，求实数的取值范围. 18.（本小题满分12分） (1) 计算：； (2) 解关于的方程：. 19.（本小题满分12分）已知函数的图象经过点A (2，1)、 B（5，2）. （1）求函数的解析式及定义域；（2）求的值． 20.（本小题满分12分）已知函数满足（1）求常数的值；（2）解关于的方程，并写出的解集. 21.（本小题满分13分）为了预防甲型流感，某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，y与t的函数关系式为（a为常数），如图所示，根据图中提供的信息，回答下列问题：（1）求从药物释放开始，每立方米空气中的含药量y（毫克）与时间t（小时）之间的函数关系式；（2）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过多少小时后，学生才能回到教室． 22. （本小题满分13分）已知函数. （1）求函数的定义域并判断函数的奇偶性；（2）用单调性定义证明:函数在其定义域上都是增函数；（3）解不等式:. 高一数学参考答案 2013.11 一、选择题：本大题共12小题；每小题5分，共60分．BCADB BDCDA AC 二、填空题：本大题共4个小题.每小题4分；共16分． 13. 2 14. 15. 16.① 三、解答题：本大题共6个小题. 共74分． 17.解：（1）,， ∴或，又，……………………4分 ∴；………………………6分（2）若，则需，解得， …………………10分故实数的取值范围为.…………………………………………………12分 18. 解：(1)原式==－3；………………………………………6分（2）原方程化为，从而,解得或，经检验，不合题意，故方程的解为.………………………………………………………………12分 19. 解：∵函数的图象经过点A (2，1)、 B（5，2）， ∴ ，……………2分即，∴ ，解得，……………6分 ∴ ，定义域为.……………………………………8分（2）=.……………………12分20．解：（1）∵，∴，即得 ∴. ………………４分（2）由（1），方程就是，即或解得，…………11分 ∴方程的解集是. ……………12分 21．解：（1）依题意：当时，设为常数），由图可知，图象过点（0.1, 1），∴， ∴， ∴ ……3分当时，（a为常数）. 由图可知，图象过点（0.1,1），∴， ∴，综上： ………………8分（2）依题意 ∴ ∵在上是减函数，∴，即 ∴至少需要经过0.6小时后，学生才能回到教室. …………13分 22.解：（1），，∴函数的定义域为，…………2分的定义域为，又，∴是定义在上的奇函数.…4分（2）证明：任取，且，则=，…………………6分，∴,∴, 又,∴,即 ∴函数在其定义域上是增函数. ………………8分（3）由, 得,………………………………………………………9分函数为奇函数， ∴，由（2）已证得函数在Ｒ上是增函数， ∴ . ………………………………………………………12分即，，∴ 不等式的解集为 ………………13分。

2013-2014学年高一数学上学期期中试题及答案(新人教A版第128套)

河南省沈丘县县直高级中学2013-2014学年高一数学上学期期中试题新人教A 版一、选择题（本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1、设集合{}{}1,2,3,4,3,4,5A B ==,则集合=⋂B A （）A 、{}5,4,3,2,1B 、{}4,3C 、{}5,4,3D 、{}4,3,2,1 2、下列各组函数中表示同一函数的是（）A 、 ()()2f x xg x ==与 B 、()()f x x g x ==与C 、()()f x g x ==D 、 ()()()21111x f x g t t t x -==+≠-与 3、使根式21--x x 与分别有意义的x 的允许值集合依次为M 、F,则使根式21-+-x x 有意义的x 的允许值集合可表示为（）A 、F M ⋃B 、F M ⋂C 、F C MD 、M C F4、在映射中B A f →:，},|),{(R y x y x B A ∈==，且),(),(:y x y x y x f +-→，则与A 中的元素)2,1(-对应的B 中的元素为（） A 、)1,3(-B 、)3,1(C 、)3,1(--D 、)1,3(5、已知集合{}{}1|,1|2+==+==x y y B x y x A ，则=⋂B A （）A 、∅B 、[]1,1-C 、[)+∞-,1D 、[)+∞,1 6、满足条件{}{}c b a M b a ,,,⊆⊆的集合M 的个数为（）A 、8B 、6C 、2D 、412、若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为 “孪生函数”，那么函数解析式为()12+=x x f ，值域为{}5,10的“孪生函数”共有（）A.、4个 B 、8个 C 、9个 D 、12个二、填空题（本题共4小题，每小题5分，共20分。

）13、县直高中某班有48学生，其中喜爱学习数学的有38人，喜爱学习英语的有36人，4人两科都不喜爱，则既喜爱学习数学又喜爱学习英语的有________人 14、若()561++=+x x x f，则()=x f ________________________15、已知函数()[]4,1,322-∈+-=x x x x f ，则函数()x f 的值域为__________________ 16、下列描述正确的序号为_______________________________（1）2A B A B A =⋂⊆则,（4（5）集合{x x A |=}，对应关系f 三、解答题（617、(10分)计算：()430311681064.01+⎪⎭⎫ ⎝⎛---(2218、(12分)已知()()为常数b a b a x f x ,+=为指数函数，且图像经过点()9,2，求函数()x f 的解析式。

山东省潍坊市某区县2013-2014学年高一上学期期中考试_数学_Word版含答案

2013-2014学年第一学期普通高中模块监测高一数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

试卷共4页，满分150分，考试时间120分钟. 注意事项：1．答题前，考生在答题卡上务必将自己的姓名、准考证号涂写清楚.2．第Ⅰ卷，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效.一、选择题:本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知{}{}|10,2,1,0,1A x x B =+>=--,则()R A B =I ðA ．{}2,1--B ．{}2-C ．{}1,0,1-D ．{}0,12.化简34的结果为A ．5B ．5C ．－5D ．－53. 下列集合A 到集合B 的对应中，构成映射的是4. 函数210)2()5(--+-=x x y 的定义域是A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或 5.下列函数为偶函数的是A ．f (x )＝x 2(－1<x <3)B ．f (x )＝x 4xC ．f (x )＝x 4－1D ．f (x )＝x ＋1x6. 已知0.9 1.7 1.51.7,0.9,0.9,a b c ===则有A.a b c <<B.a c b <<C. b a c <<D. b c a << 7. 方程220x x +-=的解所在的区间为A.（-1，0）B.（0，1）C.（1，2）D.（2，3）8. 图中阴影部分所表示的集合是A. [()]U B A C I U ðB. (A ∪B) ∪(B ∪C)C. (A ∪C)∩(ðU B)D.[()]U A C B I U ð9. 已知函数2,5()(2),5x x x f x f x x ⎧-<=⎨-≥⎩则(8)f 的值为A.－12B.20C.－56D.5610.函数y ＝a x 在区间[0,1]上的最大值与最小值的和为3，则函数y ＝3ax －1在区间[0,1]上的最大值是 A ．6B ．1C ．5D.3211. 已知函数g (x )=1－2x ，[()]f g x =)0(122≠-x xx ,则f (21)等于 A ．1B ．3C ．15D ．3012.已知函数()f x ＝(a －x )|3a －x |，a 是常数，且a >0，下列结论正确的是A ．当x ＝2a 时, ()f x 有最小值0B ．当x ＝3a 时，()f x 有最大值0C ．()f x 无最大值且无最小值D ．()f x 有最小值，但无最大值第Ⅱ卷 (非选择题共90分)注意事项:请务必用黑色碳素笔在答题纸上各题的答题区域内作答，在试题卷上作答无效. 二、填空题（本大题共4个小题，每小题4分，共16分.） 13. 函数2()23x f x -=-的图象恒过定点________.14. 函数f (x )＝ax 3＋bx ＋4(a ，b 不为零)，且f (5)＝10，则f (－5)等于_____.15. 若函数2()(21)1f x x a x a =--++是[1,2]上的单调函数，则实数a 的取值范围为________． 16. 若函数y ＝f (x )在(－∞，0)∪(0，＋∞)上为奇函数，且在(0，＋∞)上为增函数，f (－2)＝0，则不等式x ·f (x )<0的解集为________．三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤．20017．（本小题满分12分）已知集合{|36},{|2,23}xA x xB y y x =≤<==≤<. （Ⅰ）分别求,R A B B A I U ð；（Ⅱ）已知{|1},C x a x a =<<+若C B ⊆，求实数a 的取值范围．18．（本小题满分12分）已知函数21()1x f x x +=+. (Ⅰ) 证明函数()f x 在区间[1,)+∞上是增函数； (Ⅱ) 求该函数在区间[1,4]上的最大值与最小值． 19．（本小题满分12分）已知函数f (x )是定义在R 上的奇函数，且当x ＞0时，f (x )＝(12)x .(Ⅰ) 求函数f (x )的解析式；(Ⅱ) 在所给坐标系中画出函数()f x 的图像，并根据图象写出函数f (x )的单调区间．20．（本小题满分12分）已知函数f (x )的定义域为(－2,2)，函数g (x )＝f (x －1)＋f (3－2x )． (Ⅰ) 求函数g (x )的定义域；(Ⅱ) 若f (x )是奇函数，且在定义域上单调递减，求不等式g (x )≤0的解集． 21．（本小题满分12分）某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价又不高于800元/件，经试销调查，发现销售量y （件）与销售单价x （元/件），可近似看做一次函数y kx b =+的关系（如下图所示）.（Ⅰ）根据图象，求一次函数y kx b =+的表达式；（Ⅱ）设公司获得的利润（利润＝销售总价－成本总价）为S 元, 写出S 关于x 的函数表达式,并求该公司可获得的最大利润.22．（本小题满分14分）已知二次函数()f x 的图像过点（0,4），对任意x 满足(3)()f x f x -=,且有最小值是74.()2g x x m =+. （Ⅰ）求()f x 的解析式;(Ⅱ) 求函数()()(23)h x f x t x =--在区间 [0,1]上的最小值,其中R t ∈;(Ⅲ)设()f x 与()g x 是定义在同一区间[,]p q 上的两个函数,若函数()()()F x f x g x =-在[,]x p q ∈上有两个不同的零点,则称()f x 和()g x 在[,]p q 上是“关联函数”,区间[,]p q 称为“关联区间”.若()f x 与()g x 在[0,3]上是“关联函数”,求m 的取值范围.2013-2014学年第一学段模块监测高一数学参考答案 2013.11一、选择题:本大题共12小题，每小题5分，共60分.ABDDC DBAAC CC二、填空题（本大题共4个小题，每小题4分，共16分.）13. (2,-2) 14. －2 15. 35(,][,)22-∞+∞U 16. (－2,0)∪(0,2) 三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）解：（Ⅰ）∵{|36}[3,6),A x x =≤<={|2,23}{|48}[4,8)x B y y x y y ==≤<=≤<=…………………2分[4,6)A B ∴=I , …………………4分 Q (,4)[8,)R B =-∞+∞U ð,…………………6分(,6)[8,)R B A ∴=-∞+∞U U ð.…………………8分（Ⅱ）A B ⊆Q ，∴418a a ≥⎧⎨+≤⎩ …………………11分解得47a ≤≤,∴实数a的取值范围[4,7]．…………………12分18．（本小题满分12分）解: (Ⅰ) 任取x1，x2∈[1，＋∞)，且x1＜x2，…………………2分则21x x x∆=->21()()y f x f x∆=-=2121212111x xx x++-++2112(1)(1)x xx x-=++…………6分∵21x x x∆=->，(x1＋1)(x2＋1)＞0，所以0y∆>，所以函数f(x)在[1,)+∞上是增函数．…………8分(Ⅱ)由(Ⅰ)知函数f(x)在[1,4]上是增函数．所以最大值为f(4)＝2×4＋14＋1＝95，…………………10分最小值为f(1)＝2×1＋11＋1＝32.…………………………12分19．（本小题满分12分）解(Ⅰ)因为f(x)是定义在R上的奇函数，所以f(0)＝0，……………………2分当x＜0时，－x＞0，f(x)＝－f(－x)＝1()2x--＝－2x.……………………5分所以函数的解析式为f(x)＝⎩⎪⎨⎪⎧－2x，x＜0，0，x＝0，⎝⎛⎭⎫12x，x＞0.……………………6分(Ⅱ)列表如下：x 0 121 2 3 ……y 0 22121418…………………………8分函数图象如图所示：………………10分通过函数的图象可以知道，f (x )的单调递减区间是(－∞，0)，(0，＋∞)．………12分 20．（本小题满分12分）解：(Ⅰ)由题意可知⎩⎪⎨⎪⎧－2＜x －1＜2，－2＜3－2x ＜2，……………………3分∴⎩⎪⎨⎪⎧－1＜x ＜3，12＜x ＜52. ……………………5分解得12<x <52.故函数f (x )的定义域为⎝⎛⎭⎫12，52.……………………6分 (Ⅱ)由g (x )≤0，得f (x －1)＋f (3－2x )≤0， ∴f (x －1)≤－f (3－2x )．∵f (x )为奇函数，∴f (x －1)≤f (2x －3)．……………………9分而f (x )在(－2,2)上单调递减，∴⎩⎪⎨⎪⎧x －1≥2x －3，12＜x ＜52. ……………………10分解得12＜x ≤2.∴g (x )≤0的解集为⎝⎛⎦⎤12，2.……………………12分 21．（本小题满分12分）解：（Ⅰ）由图象知，当x =600时，y =400，当x =700时，y =300，代入y kx b =+中，得400600300700k bk b+⎧⎨=+⎩=，………………………………2分解得11000k b =-⎧⎨=⎩.∴1000(500800)y x x =-+≤≤ ……………4分(Ⅱ)依题意得，500(1000)500(1000)S xy y x x x =-=-+--+ =21500500000x x -+-…………7分2(750)62500(500800)x x =--+≤≤.……………10分∴当750x =时，max 62500y =.答：该公司可获得的最大利润是62500元. ……12分22．（本小题满分14分）解: （Ⅰ）由题知二次函数图象的对称轴为32x =,又最小值是74，则可设()f x =a (x -237)24+, ……………………………………2分又图像过点(0,4)，则237(0)424a -+=,解得1a =,2237()()3424f x x x x ∴=-+=-+.………………………………4分(Ⅱ) 2()()(23)24h x f x t x x tx =--=-+=22()4x t t -+- 其对称轴为x t =,………………………………………………5分①当0t ≤时，函数在[0,1]上单调递增，最小值为(0)4h =.………………6分 ②当01t <<时，函数的最小值为2()4h n t =-；……………………7分③当1t ≥时，函数在[0,1]上单调递减，最小值为(1)52h t =-.………………8分(Ⅲ)若函数2()34f x x x =-+与()2g x x m =+在[0,3]上是“关联函数”,则函数2()()()54F x f x g x x x m =-=-+-在[0,3]上有两个不同的零点,………………10分则222(5)4(4)0(0)05040(3)35340m F m F m ⎧∆=--->⎪=-⨯+-≥⎨⎪=-⨯+-≥⎩………………………………………………13分解得924m -<≤-.…………………………14分。

山西省康杰中学2013-2014学年高一上学期期中数学试题Word版含答案

康杰中学2013—2014学年度第一学期期中考试高一数学试题2013.11一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．集合A ＝{1,3}，B ＝{2,3,4}则A∩B ＝( )A ．{1}B ．{2}C ．{3}D ．{1,2,3,4}2．下列集合中结果是空集的是( )A ．{x ∈R|x 2－4＝0}B ．{x|x>9或x<3}C ．{(x ，y)|x 2＋y 2＝0}D ．{x|x>9且x<3}3．下列函数中，定义域为(0，＋∞)的是( )A ．y ＝1xB ．y ＝xC ．y ＝1x 2D ．y ＝12x4．函数f(x)＝125x x -+-的零点所在区间为( )A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)5．函数f(x)＝|lgx|，则f(14)、f(13)、f(2)的大小关系是( )A ．f(2)>f(13)>f(14)B ．f(14)>f(13)>f(2)C ．f(2)>f(14)>f(13)D ．f(13)>f(14)>f(2)6．若函数y ＝f(x)的定义域是[2,4]，则y ＝f(12log x )的定义域是( )A ．[12，1]B ．[116，14]C ．[4,16]D ．[2,4]7．函数y ＝－1x －1＋1的图象是下列图象中的( )8．已知f(x)＝ax 7－bx 5＋cx 3＋2，且f(－5)＝m ，则f(5)＋f(－5)的值为( )A ．0B ．4C ．2mD ．－m ＋49．函数y ＝log 0.6(6＋x －x 2)的单调增区间是( )A ．(－∞，12]B ．[12，＋∞)C ．(－2，12]D ．[12，3)10．函数32++=bx ax y 在(]1,-∞-上是增函数，在[)+∞-,1上是减函数，则（） A ．00<>a b 且B ．02<=a bC ．02>=a bD ．的符号不确定b a ,11．下面四个结论：①偶函数的图象一定与y 轴相交；②奇函数的图象一定通过原点； ③偶函数的图象关于y 轴对称；④既是奇函数又是偶函数的函数一定是()f x ＝0（x ∈R ），其中正确命题的个数是（） A ．4 B. 3C ． 2 D. 112．函数()log |1|a f x x =+，当(1,0)x ∈-时，恒有()0f x >，有（）A ．()f x 在(,1)-∞-上是增函数B ．()f x 在(,0)-∞上是减函数C ．()f x 在(0,)+∞上是增函数D ．()f x 在(,)-∞+∞上是减函数二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．设集合A ＝{－1,0,3}，B ＝{a ＋3,2a ＋1}，A∩B ＝{3}，则实数a 的值为________． 14. 函数11x y a-=+(a>0,且a≠1)的图象恒过定点 .15．已知函数{2log 0()20xx x f x x >=≤,则满足1()2f a <的a 的取值范围是________. 16. 若幂函数y=(m 2-2m-2)x -4m-2在x ∈(0,+∞)上为减函数,则实数m 的值是 . 三、解答题(本大题共6个小题，共70分，解答应写出文字说明) 17．(本小题满分10分)已知集合A ＝{x|x≤a ＋3}，B ＝{x|x<－1或x>5}．(1)若a ＝－2，求A∩∁R B ； (2)若A ⊆B ，求a 的取值范围．18．(本小题满分12分) (1)计算：3333212log 2log 3log 92--； (2)已知27,64x y ==.化简并计算：19．(本小题满分12分)已知函数f(x)＝x 2＋2ax ＋2，x ∈[－5,5]． (1)当a ＝－1时，求函数的最大值和最小值；(2)求实数a 的取值范围，使y ＝f(x)在区间[－5,5]上是单调函数．20．(本小题满分12分)已知函数f(x)＝log a (1＋x)，g(x)＝log a (1－x)，(a ＞0，a≠1)．(1)设a ＝2，函数f(x)的定义域为[3,63]，求f(x)的最值； (2)求使f(x)－g(x)＞0的x 的取值范围．21．(本小题满分12分)函数f (x )＝ax ＋b x 2＋1是定义在(－∞，＋∞)上的函数，且f (12)＝25，f (1)=1.(1)求实数a 、b ，并确定函数f (x )的解析式；(2)判断f (x )在(－1,1)上的单调性，并用定义证明你的结论．22．(本小题满分12分)已知定义域为R 的单调函数()f x 是奇函数，当0x >时，()23x f x x=-. （I ）求()1f -的值；（II ）求()f x 的解析式；（III ）若对任意的t R ∈，不等式22(2)(2)0f t t f t k -+-<恒成立，求实数k 的取值范围.高一数学参考答案一、选择题1-5 CDACB 6-10 BABDB 11-12 DA 二、填空题13． a ＝0或1 14. (1,2) 15． (－∞，－1)∪(0，2) 16. m=3 三、解答题17．[解析] (1)当a ＝－2时，集合A ＝{x|x ≤1}，∁R B ＝{x|－1≤x ≤5}；∴A ∩∁R B ＝{x|－1≤x ≤1}．(2)∵A ＝{x|x ≤a ＋3}，B ＝{x|x<－1或x>5}， A ⊆B ，∴a ＋3<－1， ∴a<－4.18．[解析] (1) 原式＝log 34－log 3329－1233log= log 34－log 3329＋log 38＝log 3(4×932×8)＝log 39＝2∴原式＝24×(26)16＝48.19．[解析] (1)a ＝－1，f(x)＝x 2－2x ＋2.对称轴x ＝1，f(x)min ＝f(1)＝1，f(x)max ＝f(－5)＝37， ∴f(x)max ＝37，f(x)min ＝1.(2)对称轴x ＝－a ，当－a ≥5时，f(x)在[－5,5]上单调减函数， ∴a ≤－5. 当－a ≦－5时f(x)在[－5,5]上单调减函数， ∴a ≥5.综上a ≤－5或a ≥5。

河北衡水中学2013-2014学年高一上学期期中考试_数学试题

2013—2014学年度上学期期中考试高一数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.做答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·第Ⅰ卷第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合{}*∈<<=N x x x U ,100，若{}3,2=B A ，{}7,5,1=B C A U ，{}9=B C A C U U ，则集合B=（）A ．}4,3,2{B ．}6,4,3,2{C ．}8,6,4,2{D ． }8,6,4,3,2{ 2．函数0)2()1lg(4)(-+-+-=x x x x f 的定义域为（）A. }41|{≤<x x B. }2,41|{≠≤<x x x 且 C. }241|{≠≤≤x ，x x 且 D. }4|{≥x x3．下列各式正确的是（）A ．327.17.1> B. 32.09.07.1>C. 7.2log 8.1log 3.03.0<D. 9.2lg 4.3lg <4．已知2)(35+++=bx ax x x f ，且3)2(-=-f ，则)2(f =（）A ．3B ．5C ．7D ．-15．函数122++-=x x y 在区间[-3,a]上是增函数，则a 的取值范围是（）A ． 13≤<-aB ．23≤<-aC ． 3-≥aD ．13-≤<-a6.已知[0,1]x ∈，则函数y = ）A ．]13,12[--B ．]3,1[C ．]3,12[-D ．]12,0[-7．设f(x)=⎪⎩⎪⎨⎧>+≤--1||,111||,2|1|2x xx x ，则1(())2f f 等于（） A ．21 B ．134 C ．59- D ． 4125 8．若2()21x f x a =-+是奇函数，则a 的值为（） A ． 0 B ．－1 C ．1 D ． 29．若14log 3=x ，则xx -+44的值为（） A ．38 B ．310 C ．2 D ．1 10．已知}1,0{}1,0,1{=- A ，且}2,1,0,2{}2,0,2{-=- A ，则满足上述条件的集合A 共有（）A ．2个B ． 4个C ． 6个D ．8个11．若函数f(x)=)2(log ax a -在[0，1]上是减函数，则实数a 的取值范围是（）A.20<<aB.1>aC.21<<aD.10<<a12．下列所给4个图象中，与所给3件事吻合最好的顺序为（）（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

南昌三中2013—2014学年度上学期期中考试
高一数学试卷
一、选择题（3'1030'⨯=）
1
、已知{|||}M x x x N =∈，则（）
（A
M （B ）2M ∈（C
2M M ∈且（D ）以上结论都不正确 2、函数lg(1)2x y x -=-+的定义域为（）（A ）(,1)-∞（B ）(,0)-∞（C ）(1,)+∞（D ）(0,)+∞
3、函数3()4(0,1)x f x a a a -=+>≠的图像恒过定点坐标为（）（A ）(3,5)（B ）(3,4)（C ）(0,4)（D ）(0,5)
4、已知函数22,1
(),12
x x f x x x +≤-⎧=⎨-<<⎩，若()3f a =，则a 的取值个数为（）
（A ）1 （B ）2 （C ）3 （D ）4 5、已知幂函数()f x
的图像经过点(2,2
，则(4)f 的值为（）（A ）16 （B ）
116 （C ）1
2
（D ）2 6、设5.1348
.020.91)2
1(,8,4y -===y y ，则（）
（A ）213y y y >>（B ）312y y y >>（C ）321y y y >>（D ）231y y y >> 7、设x 、y 为非零实数，0,1a a >≠，则下列正确的是（）（A ）2log 2log a a x x = （B ）log ||log ||log ||a a a x y x y ⋅=⋅ （C ）2
log 2log ||a a x x = （D ）log log ()log a a a x
x y y
-=
8、不等式2
log (23)1a x x -+≤-在x R ∈时恒成立，则a 的取值范围是（）（A ）[2,)+∞ （B ）(1,2] （C ）1[,1)2 （D ）1(0,]2
9、函数(10)x
f x =，则(3)f 的值为（）
（A ）3log 10（B ）lg 3（C ）310（D ）10
3
10、若函数()x b
f x x a
-=
-在区间(,4]-∞上是增函数，则有（）（A ）4a b >>（B ）4a b >>（C ）4a b <<（D ）4a b << 二、填空题（4'520'⨯=）
11、方程|lg |20x x +-=有个实数根
12、函数101
()101
x x f x -=+是（填偶函数、奇函数、非奇非偶函
数）
13、计算：2lg 5lg2lg5lg20++=
14、已知x
x 1
,5x
x 22
12
1+=+-则的值是 15、函数1()42(2)x x f x x -=+≤的值域是
南昌三中2013—2014学年度上学期期中考试
高一数学答卷
一、选择题（3'1030'⨯=）
二、填空题（）
11、 12、 13、
14、 15、三、解答题
16、（8分）若全集为R ，若集合{|1},{|0}5
x
A x x
B x x =≥=≤- （1）求A B ；（2）求U A
B ð
17、（10分）若函数2
())f x x =-，（1）求定义域（2）求值域（3）求单调增区间
18、（10分）解关于x 的不等式22
231
251()x x x x a a
-+--+>（0,1a a >≠）
19、（10分）设2
221()2(log )2log f x x a b x =++，已知当1
2
x =时，()f x 有最小值8-，（1）求,a b ；（2）满足()0f x >的x 集合
20、（12分）已知定义域为R 的函数12()2x x b
f x a
+-+=+为奇函数
（1）求,a b 的值；
（2）若对任意的正数t ，不等式2
2
(2)(2)0f t t f t k -+-<恒成立，求k 的取值范围
南昌三中2013—2014学年度上学期期中考试
高一数学答案
二、填空题（）
11、1个 12、奇函数 13、2 14、23 15、(0,18] 三、解答题
16、{|05}
2B x x =≤<分；{|15}4A B x x =≤<分；
{|1}6U A x x =<分ð；{|01}8U A
B x x =≤<分ð 17、（1）{|11}3x x -<<分；
（2）{|0}6y y ≤分；（3）(1,0]
10-分（(1,0)-也对）
18、当1,{|23}
5a x x x ><>时或分；当01,{|23}10a x x <<<<时分
19、（1）246
a b =-⎧⎨
=-⎩分；
（2）1
{|02}108
x x x <<>或分 20、（1）[解析] (1)∵f (x )是奇函数，
∴f (0)＝0，即－1＋b 2＋a ＝0，解得b ＝1，从而有f (x )＝－2x
＋12x ＋1＋a
.
又由f (1)＝－f (－1)知－2＋1
4＋a ＝－－12＋11＋a ，
解得a ＝2.经检验a ＝2适合题意， ∴所求a ，b 的值为2,1
4分
(2)由(1)知f (x )＝－2x
＋12x ＋1＋2＝－12＋1
2x ＋1.
由上式易知f (x )在(－∞，＋∞)上为减函数6分
又因f (x )是奇函数，
从而不等式f (t 2
－2t )＋f (2t 2
－k )<0，等价于
f (t 2－2t )<－f (2t 2－k )＝f (－2t 2＋k
8分．
因f (x )是减函数，由上式推得t 2
－2t >－2t 2
＋k .
即对一切0t <有3t 2
－2t >k 0
12k ⇒<分。

2013-2014学年高一数学上学期期中试题及答案(新人教A版 第105套)