二次函数表达式专项练习
专题训练(二)确定二次函数的表达式五种方法

专题训练(二)确定二次函数的表达式五种方法 ► 方法一 利用一般式求二次函数表达式1.已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2.则这条抛物线的表达式为( )A.y=x2-x-2B.y=-x2+x+2C.y=x2-x-2或y=-x2+x+2D.y=-x2-x-2或y=x2+x+22.若二次函数y=x2+bx+c的图象经过点(-4,0),(2,6),则这个二次函数的表达式为______________.3.一个二次函数,当自变量x=-1时,函数值y=2;当x=0时,y=-1;当x=1时,y=-2.那么这个二次函数的表达式为____________.4.如图2-ZT-1,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2,0)三点.(1)求抛物线的表达式;(2)若M是该抛物线的对称轴上的一点,求AM+OM的最小值.图2-ZT-1► 方法二 利用顶点式求二次函数表达式5.已知二次函数y =ax 2+bx +c ,当x =1时,有最大值8,其图象的形状、开口方向与抛物线y =-2x 2相同,则这个二次函数的表达式是( )A .y =-2x 2-x +3B .y =-2x 2+4C .y =-2x 2+4x +8D .y =-2x 2+4x +66.已知y 是x 的二次函数,根据表中的自变量x 与函数y 的部分对应值,可判断此函数的表达式为( )x …-1012…y…-154254…A .y =x 2B .y =-x 2C .y =(x -1)2+234D .y =-(x -1)2+2347.[2018·巴中改编]一位篮球运动员在距离篮框中心水平距离4m 处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m 时,达到最大高度3.5m ,然后准确落入篮框内.已知篮框中心距离地面高度为3.05m .在如图2-ZT -2所示的平面直角坐标系中,此抛物线的表达式是________.8.已知抛物线y 1=ax 2+bx +c 的顶点坐标是(1,4),它与直线y 2=x +1的一个交点的横坐标为2.(1)求抛物线的函数表达式;(2)在如图2-ZT -3所示的平面直角坐标系中画出抛物线y 1=ax 2+bx +c 及直线y 2=x +1,并根据图象,直接写出使得y 1≥y 2成立的x 的取值范围.图2-ZT -3► 方法三 利用交点式求二次函数表达式9.若抛物线的最高点的纵坐标是,且过点(-1,0),(4,0),则该抛物线的表达式为( )254A .y =-x 2+3x +4 B .y =-x 2-3x +4C .y =x 2-3x -4D .y =x 2-3x +410.抛物线y =ax 2+bx +c 与x 轴的两个交点坐标为(-1,0),(3,0),其形状及开口方向与抛物线y =-2x 2相同,则抛物线的函数表达式为( )A .y =-2x 2-x +3B .y =-2x 2+4x +5C .y =-2x 2+4x +8D .y =-2x 2+4x +6► 方法四 利用平移求二次函数表达式11.[2018·广西]将抛物线y =x 2-6x +21向左平移2个单位后,得到新抛物线的表达式12为( )A .y =(x -8)2+5B .y =(x -4)2+51212C .y =(x -8)2+3D .y =(x -4)2+3121212.如果将抛物线y =2x 2+bx +c 先向左平移3个单位,再向下平移2个单位,得到了抛物线y=2x2-4x+3.(1)试确定b,c的值;(2)求出抛物线y=2x2+bx+c的顶点坐标和对称轴.► 方法五 利用对称轴求二次函数表达式13.如图2-ZT-4,已知抛物线y=-x2+bx+c的对称轴为直线x=1,且与x轴的一个交点坐标为(3,0),那么它对应的函数表达式是______________.图2-ZT-414.如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图2-ZT-5,二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.(1)直接写出两条“关于y轴对称二次函数”图象所具有的特点.(2)二次函数y=2(x+2)2+1的“关于y轴对称二次函数”的表达式为__________;二次函数y=a(x-h)2+k的“关于y轴对称二次函数”的表达式为____________;(3)平面直角坐标系中,记“关于y轴对称二次函数”的图象与y轴的交点为A,它们的两个顶点分别为B,C,且BC=6,顺次连接点A,B,O,C,得到一个面积为24的菱形,求“关于y轴对称二次函数”的表达式.图2-ZT-5教师详解详析1.[解析]C 由题意可知点C 的坐标是(0,2)或(0,-2).设抛物线的表达式为y =ax 2+bx +c .由抛物线经过点(2,0),(-1,0),(0,2),得解得{4a +2b +c =0,a -b +c =0,c =2,)则抛物线的表达式是y =-x 2+x +2.同理,由抛物线经过点(2,0),(-1,0),(0,-2)求{a =-1,b =1,c =2,)得该抛物线的表达式为y =x 2-x -2.故这条抛物线的表达式为y =-x 2+x +2或y =x 2-x -2.2.[答案]y =x 2+3x -4[解析]将点(-4,0),(2,6)代入y =x 2+bx +c ,得解得{16-4b +c =0,4+2b +c =6,){b =3,c =-4,)∴这个二次函数的表达式为y =x 2+3x -4.3.y =x 2-2x -14.解:(1)把A (-2,-4),O (0,0),B (2,0)代入y =ax 2+bx +c ,得{4a -2b +c =-4,4a +2b +c =0,c =0,)解这个方程组,得{a =-12,b =1,c =0,)所以抛物线的表达式为y =-x 2+x .12(2)由y =-x 2+x =-(x -1)2+,可得抛物线的对称轴为直线x =1,并且对称轴垂直121212平分线段OB ,∴OM =BM ,∴AM +OM =AM +BM .连接AB 交直线x =1于点M ,则此时AM +OM 的值最小.过点A 作AN ⊥x 轴于点N ,在Rt △ABN 中,AB ===4,因此AM +OM 的最小值为4.AN 2+BN 242+42225.D6.[解析]D ∵函数图象过点(0,)和(2,),∴函数图象的对称轴为直线x =1,故该函数5454图象的顶点坐标为(1,2).设函数表达式为y =a (x -1)2+2.把(-1,-1)代入,得4a +2=-1,解得a =-,∴此函数表达式为y =-(x -1)2+2.34347.[答案]y =-x 2+3.515[解析]∵抛物线的顶点坐标为(0,3.5),∴可设抛物线的表达式为y =ax 2+3.5.∵篮框中心(1.5,3.05)在抛物线上,将它的坐标代入表达式,得3.05=a ×1.52+3.5,∴a =-,∴y =-x 2+3.5.15158.解:(1)∵抛物线与直线y 2=x +1的一个交点的横坐标为2,∴交点的纵坐标为2+1=3,即此交点的坐标为(2,3).设抛物线的表达式为y 1=a (x -1)2+4.把(2,3)代入,得3=a (2-1)2+4,解得a =-1,∴抛物线的表达式为y 1=-(x -1)2+4=-x 2+2x +3.(2)令y 1=0,即-x 2+2x +3=0,解得x 1=3,x 2=-1,∴抛物线与x 轴的交点坐标为(3,0)和(-1,0).在平面直角坐标系中画出抛物线与直线,如图所示:根据图象可知,使得y 1≥y 2成立的x 的取值范围为-1≤x ≤2.9.[解析]A 由抛物线的轴对称性可知该抛物线的对称轴为直线x =×(-1+4)=,故1232该抛物线的顶点坐标为(,).设该抛物线的表达式为y =a (x +1)(x -4).将(,)代入,得3225432254=a (+1)(-4),解得a =-1,故该抛物线的表达式为y =-(x +1)(x -4)=-x 2+3x +4.注2543232意:本题也可运用顶点式求抛物线的表达式.10.[解析]D 设抛物线的函数表达式为y =a (x -x 1)(x -x 2).因为抛物线y =ax 2+bx +c 与x 轴的两个交点坐标为(-1,0),(3,0),所以y =a (x -3)(x +1).又因为其形状及开口方向与抛物线y =-2x 2相同,所以y =-2(x -3)(x +1),即y =-2x 2+4x +6.11.[解析]D y =x 2-6x +2112=(x 2-12x )+2112=[(x -6)2-36]+2112=(x -6)2+3,12故y =(x -6)2+3向左平移2个单位后,12得到新抛物线的表达式为y =(x -4)2+3.1212.解:(1)∵y =2x 2-4x +3=2(x 2-2x +1-1)+3=2(x -1)2+1,∴将其向上平移2个单位,再向右平移3个单位可得原抛物线,即y =2(x -4)2+3,∴y =2x 2-16x +35,∴b =-16,c =35.(2)由y =2(x -4)2+3得顶点坐标为(4,3),对称轴为直线x =4.13.[答案]y =-x 2+2x +3[解析]∵抛物线y =-x 2+bx +c 的对称轴为直线x =1,∴=1,解得b =2,b2又∵抛物线与x 轴的一个交点坐标为(3,0),∴0=-9+6+c ,解得c =3,故函数表达式为y =-x 2+2x +3.14.解:(1)(答案不唯一)顶点关于y 轴对称,对称轴关于y 轴对称.(2)y =2(x -2)2+1 y =a (x +h )2+k (3)若点A 在y 轴的正半轴上,如图所示:顺次连接点A ,B ,O ,C ,得到一个面积为24的菱形,由BC =6,得OA =8,则点A 的坐标为(0,8),点B 的坐标为(-3,4).设一个抛物线的表达式为y =a (x +3)2+4.将点A 的坐标代入,得9a +4=8,解得a =.49二次函数y =(x +3)2+4的“关于y 轴对称二次函数”的表达式为y =(x -3)2+4.4949根据对称性,开口向下的抛物线也符合题意,则“关于y 轴对称二次函数”的表达式还可以为y =-(x +3)2-4,y =-(x -3)2-4.4949综上所述,“关于y 轴对称二次函数”的表达式为y =(x +3)2+4,y =(x -3)2+4或4949y =-(x +3)2-4,y =-(x -3)2-4.4949。
初三数学二次函数的专项培优练习题(含答案)含详细答案

初三数学二次函数的专项培优练习题(含答案)含详细答案一、二次函数1.某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量(y 万件)与销售单价(x 元)之间符合一次函数关系,其图象如图所示.()1求y 与x 的函数关系式;()2物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x 定为每件多少元时,厂家每月获得的利润()w 最大?最大利润是多少?【答案】(1)2280y x =-+;(2)当销售单价x 定为每件80元时,厂家每月获得的利润()w 最大,最大利润是4800元.【解析】【分析】()1根据函数图象经过点()40,200和点()60,160,利用待定系数法即可求出y 与x 的函数关系式;()2先根据利润=销售数量(⨯销售单价-成本),由试销期间销售单价不低于成本单价,也不高于每千克80元,结合电子产品的成本价即可得出x 的取值范围,根据二次函数的增减性可得最值.【详解】解:()1设y 与x 的函数关系式为()0y kx b k =+≠,Q 函数图象经过点()40,200和点()60,160,{4020060160k b k b +=∴+=,解得:{2280k b =-=, y ∴与x 的函数关系式为2280y x =-+.()2由题意得:()()224022802360112002(90)5000w x x x x x =--+=-+-=--+. Q 试销期间销售单价不低于成本单价,也不高于每千克80元,且电子产品的成本为每千克40元,∴自变量x 的取值范围是4080x ≤≤.20-<Q ,∴当90x <时,w 随x 的增大而增大,80x ∴=时,w 有最大值,当80x =时,4800w =,答:当销售单价x 定为每件80元时,厂家每月获得的利润()w 最大,最大利润是4800元.【点睛】本题考查了一次函数和二次函数的应用,根据点的坐标利用待定系数法求出函数关系式是解题的关键,并注意最值的求法.2.抛物线y =ax 2+bx ﹣3(a≠0)与直线y =kx+c (k≠0)相交于A (﹣1,0)、B (2,﹣3)两点,且抛物线与y 轴交于点C .(1)求抛物线的解析式;(2)求出C 、D 两点的坐标(3)在第四象限抛物线上有一点P ,若△PCD 是以CD 为底边的等腰三角形,求出点P 的坐标.【答案】(1)y =x 2﹣2x ﹣3;(2)C (0,﹣3),D (0,﹣1);(3)P (2,﹣2).【解析】【分析】(1)把A (﹣1,0)、B (2,﹣3)两点坐标代入y =ax 2+bx ﹣3可得抛物线解析式. (2)当x =0时可求C 点坐标,求出直线AB 解析式,当x =0可求D 点坐标. (3)由题意可知P 点纵坐标为﹣2,代入抛物线解析式可求P 点横坐标.【详解】解:(1)把A (﹣1,0)、B (2,﹣3)两点坐标代入y =ax 2+bx ﹣3可得 304233a b a b --=⎧⎨+-=-⎩ 解得12a b =⎧⎨=-⎩∴y =x 2﹣2x ﹣3(2)把x =0代入y =x 2﹣2x ﹣3中可得y =﹣3∴C (0,﹣3)设y =kx+b ,把A (﹣1,0)、B (2,﹣3)两点坐标代入023k b k b -+=⎧⎨+=-⎩解得11 kb=-⎧⎨=-⎩∴y=﹣x﹣1∴D(0,﹣1)(3)由C(0,﹣3),D(0,﹣1)可知CD的垂直平分线经过(0,﹣2)∴P点纵坐标为﹣2,∴x2﹣2x﹣3=﹣2解得:x=1±2,∵x>0∴x=1+2.∴P(1+2,﹣2)【点睛】本题是二次函数综合题,用待定系数法求二次函数的解析式,把x=0代入二次函数解析式和一次函数解析式可求图象与y轴交点坐标,知道点P纵坐标带入抛物线解析式可求点P 的横坐标.3.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).(1)求抛物线y=x2+bx+c的表达式;(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.【答案】(1)y=x2﹣4x+3;(2)(2,﹣1);(3)42【解析】试题分析:(1)利用待定系数法求抛物线解析式;(2)如图1,设D(2,y),利用两点间的距离公式得到BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,然后讨论:当BD为斜边时得到18+4+(y﹣3)2=1+y2;当CD 为斜边时得到4+(y﹣3)2=1+y2+18,再分别解方程即可得到对应D的坐标;(3)先证明∠CEF=90°得到△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,则PE 2,PF2,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,这样PE+EF=2PE+PF=﹣2t2+42t,然后利用二次函数的性质解决问题.试题解析:解:(1)把B(3,0),C(0,3)代入y=x2+bx+c得:9303b cc++=⎧⎨=⎩,解得:43bc=-⎧⎨=⎩,∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3;(2)如图1,抛物线的对称轴为直线x=﹣42-=2,设D(2,y),B(3,0),C(0,3),∴BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得:y=5,此时D点坐标为(2,5);当△BCD是以BC为直角边,CD为斜边的直角三角形时,BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,解得:y=﹣1,此时D点坐标为(2,﹣1);(3)易得BC的解析式为y=﹣x+3.∵直线y=x+m与直线y=x平行,∴直线y=﹣x+3与直线y=x+m垂直,∴∠CEF=90°,∴△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,PE=22PG,PF=2PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=2PH=2t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=22PG=﹣22t2+322t,∴PE+EF=PE+PE+PF=2PE+PF=﹣2t2+32t+2t=﹣2t2+42t=﹣2(t﹣2)2+42,当t=2时,PE+EF的最大值为42.点睛:本题考查了二次函数的综合题.熟练掌握等腰直角三角形的性质、二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,记住两点间的距离公式.4.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(4)如图2,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.【答案】(1)y=﹣x2﹣2x+3;(2)存在符合条件的点P,其坐标为P(﹣1,10)或P(﹣1,﹣10)或P(﹣1,6)或P(﹣1,53);(3)存在,Q(﹣1,2);(4)63 8,315,24E⎛⎫-⎪⎝⎭.【解析】【分析】(1)已知抛物线过A、B两点,可将两点的坐标代入抛物线的解析式中,用待定系数法即可求出二次函数的解析式;(2)可根据(1)的函数解析式得出抛物线的对称轴,也就得出了M点的坐标,由于C是抛物线与y轴的交点,因此C的坐标为(0,3),根据M、C的坐标可求出CM的距离.然后分三种情况进行讨论:①当CP=PM时,P位于CM的垂直平分线上.求P点坐标关键是求P的纵坐标,过P作PQ⊥y轴于Q,如果设PM=CP=x,那么直角三角形CPQ中CP=x,OM的长,可根据M 的坐标得出,CQ=3﹣x,因此可根据勾股定理求出x的值,P点的横坐标与M的横坐标相同,纵坐标为x,由此可得出P的坐标.②当CM=MP时,根据CM的长即可求出P的纵坐标,也就得出了P的坐标(要注意分上下两点).③当CM=C P时,因为C的坐标为(0,3),那么直线y=3必垂直平分PM,因此P的纵坐标是6,由此可得出P的坐标;(3)根据轴对称﹣最短路径问题解答;(4)由于四边形BOCE不是规则的四边形,因此可将四边形BOCE分割成规则的图形进行计算,过E作EF⊥x轴于F,S四边形BOCE=S△BFE+S梯形FOCE.直角梯形FOCE中,FO为E的横坐标的绝对值,EF为E的纵坐标,已知C的纵坐标,就知道了OC的长.在△BFE中,BF=BO﹣OF,因此可用E的横坐标表示出BF的长.如果根据抛物线设出E的坐标,然后代入上面的线段中,即可得出关于四边形BOCE的面积与E的横坐标的函数关系式,根据函数的性质即可求得四边形BOCE的最大值及对应的E的横坐标的值.即可求出此时E的坐标.【详解】(1)∵抛物线y =ax 2+bx+3(a≠0)与x 轴交于点A (1,0)和点B (﹣3,0), ∴309330a b a b ++=⎧⎨-+=⎩, 解得:12a b =-⎧⎨=-⎩. ∴所求抛物线解析式为:y =﹣x 2﹣2x+3;(2)如答图1,∵抛物线解析式为:y =﹣x 2﹣2x+3,∴其对称轴为x =22-=﹣1, ∴设P 点坐标为(﹣1,a ),当x =0时,y =3,∴C (0,3),M (﹣1,0)∴当CP =PM 时,(﹣1)2+(3﹣a )2=a 2,解得a =53, ∴P 点坐标为:P 1(﹣1,53); ∴当CM =PM 时,(﹣1)2+32=a 2,解得a =±10,∴P 点坐标为:P 2(﹣1,10)或P 3(﹣1,﹣10);∴当CM =CP 时,由勾股定理得:(﹣1)2+32=(﹣1)2+(3﹣a )2,解得a =6, ∴P 点坐标为:P 4(﹣1,6).综上所述存在符合条件的点P ,其坐标为P (﹣1,10)或P (﹣1,﹣10)或P (﹣1,6)或P (﹣1,53); (3)存在,Q (﹣1,2),理由如下:如答图2,点C (0,3)关于对称轴x =﹣1的对称点C′的坐标是(﹣2,3),连接AC′,直线AC′与对称轴的交点即为点Q .设直线AC′函数关系式为:y=kx+t(k≠0).将点A(1,0),C′(﹣2,3)代入,得23 k tk t+=⎧⎨-+=⎩,解得11kt=-⎧⎨=⎩,所以,直线AC′函数关系式为:y=﹣x+1.将x=﹣1代入,得y=2,即:Q(﹣1,2);(4)过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0)∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a∴S四边形BOCE=12BF•EF+12(OC+EF)•OF=12(a+3)•(﹣a2﹣2a+3)+12(﹣a2﹣2a+6)•(﹣a)=﹣32a2﹣92a+92=﹣32(a+32)2+638,∴当a=﹣32时,S四边形BOCE最大,且最大值为638.此时,点E坐标为(﹣32,154).【点睛】本题主要考查了二次函数的综合知识,要注意的是(2)中,不确定等腰三角形哪条边是底边的情况下,要分类进行求解,不要漏解.5.如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B.抛物线过A、B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)如图1,设抛物线顶点为M,且M的坐标是(12,92),对称轴交AB于点N.①求抛物线的解析式;②是否存在点P,使四边形MNPD为菱形?并说明理由;(2)是否存在这样的点D,使得四边形BOAD的面积最大?若存在,求出此时点D的坐标;若不存在,请说明理由.【答案】(1)①y=﹣2x2+2x+4;;②不存在点P,使四边形MNPD为菱形;;(2)存在,点D的坐标是(1,4).【解析】【分析】(1)①由一次函数图象上点的坐标特征求得点B的坐标,设抛物线解析式为y=a21922x⎛⎫-+⎪⎝⎭,把点B的坐标代入求得a的值即可;②不存在点P,使四边形MNPD为菱形.设点P的坐标是(m,﹣2m+4),则D(m,﹣2m2+2m+4),根据题意知PD∥MN,所以当PD=MN时,四边形MNPD为平行四边形,根据该等量关系列出方程﹣2m2+4m=32,通过解方程求得m的值,易得点N、P的坐标,然后推知PN=MN是否成立即可;(2)设点D的坐标是(n,﹣2n2+2n+4),P(n,﹣2n+4).根据S四边形BOAD=S△BOA+S△ABD =4+S△ABD,则当S△ABD取最大值时,S四边形BOAD最大.根据三角形的面积公式得到函数S△ABD=﹣2(n﹣1)2+2.由二次函数的性质求得最值.【详解】解:①如图1,∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭,∴设抛物线解析式为y=21922a x⎛⎫-+⎪⎝⎭(a≠0).∵直线y=﹣2x+4交y轴于点B,∴点B的坐标是(0,4).又∵点B在该抛物线上,∴21922a⎛⎫-+⎪⎝⎭=4,解得a=﹣2.故该抛物线的解析式为:y=219222x⎛⎫--+⎪⎝⎭=﹣2x2+2x+4;②不存在.理由如下:∵抛物线y=219222x⎛⎫--+⎪⎝⎭的对称轴是直线x=12,且该直线与直线AB交于点N,∴点N的坐标是1,32⎛⎫ ⎪⎝⎭.∴93322MN=-=.设点P的坐标是(m,﹣2m+4),则D(m,﹣2m2+2m+4),∴PD=(﹣2m2+2m+4)﹣(﹣2m+4)=﹣2m2+4m.∵PD∥MN.当PD=MN时,四边形MNPD是平行四边形,即﹣2m2+4m=32.解得 m1=12(舍去),m2=32.此时P(32,1).∵PN∴PN≠MN,∴平行四边形MNPD不是菱形.∴不存在点P,使四边形MNPD为菱形;(2)存在,理由如下:设点D的坐标是(n,﹣2n2+2n+4),∵点P在线段AB上且直线PD⊥x轴,∴P(n,﹣2n+4).由图可知S四边形BOAD=S△BOA+S△ABD.其中S△BOA=12OB•OA=12×4×2=4.则当S△ABD取最大值时,S四边形BOAD最大.S△ABD=12(y D﹣y P)(x A﹣x B)=y D﹣y P=﹣2n2+2n+4﹣(﹣2n+4)=﹣2n2+4n=﹣2(n﹣1)2+2.当n=1时,S△ABD取得最大值2,S四边形BOAD有最大值.此时点D的坐标是(1,4).【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.6.(10分)(2015•佛山)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.【答案】(1)(2,4);(2)(,);(3);(4)(,).【解析】试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;(2)联立两解析式,可求出交点A的坐标;(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,将P(2,4)代入,求出直线PM的解析式为y=x+3.再与抛物线的解析式联立,得到方程组,解方程组即可求出点M的坐标.试题解析:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,故二次函数图象的最高点P的坐标为(2,4);(2)联立两解析式可得:,解得:,或.故可得点A的坐标为(,);(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×(+4)×(﹣2)﹣××=4+﹣=;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,∵P的坐标为(2,4),∴4=×2+b,解得b=3,∴直线PM的解析式为y=x+3.由,解得,,∴点M的坐标为(,).考点:二次函数的综合题7.已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)(1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.【答案】(1)y=﹣x2﹣2x+3;(2)抛物线与x轴的交点为:(﹣3,0),(1,0)(3)15.【解析】【分析】(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B 点坐标代入,即可求出二次函数的解析式;(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.【详解】(1)设抛物线顶点式y=a(x+1)2+4,将B(2,﹣5)代入得:a=﹣1,∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与x轴的交点为:(﹣3,0),(1,0);(3)设抛物线与x轴的交点为M、N(M在N的左侧),由(2)知:M(﹣3,0),N(1,0),当函数图象向右平移经过原点时,M与O重合,因此抛物线向右平移了3个单位,故A'(2,4),B'(5,﹣5),∴S△OA′B′=12×(2+5)×9﹣12×2×4﹣12×5×5=15.【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识.熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.8.在平面直角坐标系xOy中(如图).已知抛物线y=﹣12x2+bx+c经过点A(﹣1,0)和点B(0,52),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.(1)求这条抛物线的表达式;(2)求线段CD的长;(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.【答案】(1)抛物线解析式为y=﹣12x 2+2x+52;(2)线段CD 的长为2;(3)M 点的坐标为(0,72)或(0,﹣72). 【解析】【分析】(1)利用待定系数法求抛物线解析式; (2)利用配方法得到y=﹣12(x ﹣2)2+92,则根据二次函数的性质得到C 点坐标和抛物线的对称轴为直线x=2,如图,设CD=t ,则D (2,92﹣t ),根据旋转性质得∠PDC=90°,DP=DC=t ,则P (2+t ,92﹣t ),然后把P (2+t ,92﹣t )代入y=﹣12x 2+2x+52得到关于t的方程,从而解方程可得到CD 的长;(3)P 点坐标为(4,92),D 点坐标为(2,52),利用抛物线的平移规律确定E 点坐标为(2,﹣2),设M (0,m ),当m >0时,利用梯形面积公式得到12•(m+52+2)•2=8当m <0时,利用梯形面积公式得到12•(﹣m+52+2)•2=8,然后分别解方程求出m 即可得到对应的M 点坐标.【详解】(1)把A (﹣1,0)和点B (0,52)代入y=﹣12x 2+bx+c 得 10252b c c ⎧--+=⎪⎪⎨⎪=⎪⎩,解得252b c =⎧⎪⎨=⎪⎩,∴抛物线解析式为y=﹣12x 2+2x+52; (2)∵y=﹣12(x ﹣2)2+92, ∴C (2,92),抛物线的对称轴为直线x=2, 如图,设CD=t ,则D (2,92﹣t ),∵线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P 处, ∴∠PDC=90°,DP=DC=t , ∴P (2+t ,92﹣t ), 把P (2+t ,92﹣t )代入y=﹣12x 2+2x+52得﹣12(2+t )2+2(2+t )+52=92﹣t , 整理得t 2﹣2t=0,解得t 1=0(舍去),t 2=2, ∴线段CD 的长为2;(3)P 点坐标为(4,92),D 点坐标为(2,52), ∵抛物线平移,使其顶点C (2,92)移到原点O 的位置, ∴抛物线向左平移2个单位,向下平移92个单位,而P 点(4,92)向左平移2个单位,向下平移92个单位得到点E , ∴E 点坐标为(2,﹣2), 设M (0,m ),当m >0时,12•(m+52+2)•2=8,解得m=72,此时M 点坐标为(0,72);当m <0时,12•(﹣m+52+2)•2=8,解得m=﹣72,此时M 点坐标为(0,﹣72);综上所述,M 点的坐标为(0,72)或(0,﹣72).【点睛】本题考查了二次函数的综合题,涉及到待定系数法、抛物线上点的坐标、旋转的性质、抛物线的平移等知识,综合性较强,正确添加辅助线、运用数形结合思想熟练相关知识是解题的关键.9.如图,抛物线25(0)y ax bx a =+-≠经过x 轴上的点A (1,0)和点B 及y 轴上的点C ,经过B 、C 两点的直线为y x n =+. ①求抛物线的解析式.②点P 从A 出发,在线段AB 上以每秒1个单位的速度向B 运动,同时点E 从B 出发,在线段BC 上以每秒2个单位的速度向C 运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t 秒,求t 为何值时,△PBE 的面积最大并求出最大值.③过点A 作AM BC ⊥于点M ,过抛物线上一动点N (不与点B 、C 重合)作直线AM 的平行线交直线BC 于点Q .若点A 、M 、N 、Q 为顶点的四边形是平行四边形,求点N 的横坐标.【答案】①265y x x =-+-;②当2t =时,△PBE 的面积最大,最大值为22③点N 的横坐标为:4或5412+或5412. 【解析】 【分析】①点B 、C 在直线为y x n =+上,则B (﹣n ,0)、C (0,n ),点A (1,0)在抛物线上,所以250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩,解得1a =-,6b =,因此抛物线解析式:265y x x =-+-;②先求出点P 到BC 的高h 为2sin 45(4)2BP t ︒=-,于是21122)22)2222PBE S BE h t t t ∆=⋅=-⨯=-+2t =时,△PBE 的面积最大,最大值为22③由①知,BC 所在直线为:5y x =-,所以点A 到直线BC 的距离22d =N 作x 轴的垂线交直线BC 于点P ,交x 轴于点H .设()2,65N m m m -+-,则(,0)H m 、(,5)P m m -,易证△PQN 为等腰直角三角形,即22NQ PQ ==4PN =,Ⅰ.4NH HP +=,所以265(5)4m m m -+---=解得11m =(舍去),24m =,Ⅱ.4NH HP +=,()25654m m m ---+-=解得1541m +=,2541m -=去),Ⅲ.4NH HP -=,()265[(5)]4m m m --+----=,解得15412m =(舍去),252m =. 【详解】解:①∵点B 、C 在直线为y x n =+上, ∴B (﹣n ,0)、C (0,n ), ∵点A (1,0)在抛物线上,∴250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩, ∴1a =-,6b =,∴抛物线解析式:265y x x =-+-; ②由题意,得,4PB t =-,2BE t =,由①知,45OBC ︒∠=, ∴点P 到BC 的高h为sin 45)BP t ︒=-,∴211)22)22PBE S BE h t t t ∆=⋅=-⨯=-+ 当2t =时,△PBE的面积最大,最大值为 ③由①知,BC 所在直线为:5y x =-, ∴点A 到直线BC的距离d =过点N 作x 轴的垂线交直线BC 于点P ,交x 轴于点H . 设()2,65N m m m -+-,则(,0)H m 、(,5)P m m -, 易证△PQN为等腰直角三角形,即NQ PQ == ∴4PN =, Ⅰ.4NH HP +=, ∴265(5)4m m m -+---= 解得11m =,24m =,∵点A 、M 、N 、Q 为顶点的四边形是平行四边形, ∴4m =;Ⅱ.4NH HP +=, ∴()25654m m m ---+-=解得1m =,2m =∵点A 、M 、N 、Q 为顶点的四边形是平行四边形,5m >,∴541m +=, Ⅲ.4NH HP -=,∴()265[(5)]4m m m --+----=, 解得15412m +=,25412m -=,∵点A 、M 、N 、Q 为顶点的四边形是平行四边形,0m <,∴5412m -=, 综上所述,若点A 、M 、N 、Q 为顶点的四边形是平行四边形,点N 的横坐标为:4或541+或541-. 【点睛】本题考查了二次函数,熟练掌握二次函数的性质、平行四边形的判定与性质是解题的关键.10.已知抛物线C 1:y=ax 2﹣4ax ﹣5(a >0). (1)当a=1时,求抛物线与x 轴的交点坐标及对称轴;(2)①试说明无论a 为何值,抛物线C 1一定经过两个定点,并求出这两个定点的坐标; ②将抛物线C 1沿这两个定点所在直线翻折,得到抛物线C 2,直接写出C 2的表达式; (3)若(2)中抛物线C 2的顶点到x 轴的距离为2,求a 的值.【答案】(1)(﹣1,0)或(5,0)(2)①(0,﹣5),(4,﹣5)②y=﹣ax 2+4ax ﹣5(3)a=或【解析】试题分析:(1)将a=1代入解析式,即可求得抛物线与x轴交点;(2)①化简抛物线解析式,即可求得两个点定点的横坐标,即可解题;②根据抛物线翻折理论即可解题;(3)根据(2)中抛物线C2解析式,分类讨论y=2或﹣2,即可解题试题解析:(1)当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,∴对称轴为y=2;∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0);(2)①抛物线C1解析式为:y=ax2﹣4ax﹣5,整理得:y=ax(x﹣4)﹣5;∵当ax(x﹣4)=0时,y恒定为﹣5;∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);②这两个点连线为y=﹣5;将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;∴抛物线C2解析式为:y=﹣ax2+4ax﹣5,(3)抛物线C2的顶点到x轴的距离为2,则x=2时,y=2或者﹣2;当y=2时,2=﹣4a+8a﹣5,解得,a=;当y=﹣2时,﹣2=﹣4a+8a﹣5,解得,a=;∴a=或;考点:1、抛物线与x轴的交点;2、二次函数图象与几何变换11.(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线()与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.【答案】(1)A(-1,0),;(2);(3)P的坐标为(1,)或(1,-4).【解析】试题分析:(1)在中,令y=0,得到,,得到A(-1,0),B(3,0),由直线l经过点A,得到,故,令,即,由于CD=4AC,故点D的横坐标为4,即有,得到,从而得出直线l的函数表达式;(2)过点E作EF∥y轴,交直线l于点F,设E(,),则F(,),EF==,S△ACE=S△AFE-S△CFE==,故△ACE的面积的最大值为,而△ACE的面积的最大值为,所以,解得;(3)令,即,解得,,得到D (4,5a),因为抛物线的对称轴为,设P(1,m),然后分两种情况讨论:①若AD是矩形的一条边,②若AD是矩形的一条对角线.试题解析:(1)∵=,令y=0,得到,,∴A(-1,0),B(3,0),∵直线l经过点A,∴,,∴,令,即,∵CD=4AC,∴点D的横坐标为4,∴,∴,∴直线l的函数表达式为;(2)过点E作EF∥y轴,交直线l于点F,设E(,),则F(,),EF==,S△ACE=S△AFE-S△CFE===,∴△ACE的面积的最大值为,∵△ACE的面积的最大值为,∴,解得;(3)令,即,解得,,∴D(4,5a),∵,∴抛物线的对称轴为,设P(1,m),①若AD是矩形的一条边,则Q(-4,21a),m=21a+5a=26a,则P(1,26a),∵四边形ADPQ为矩形,∴∠ADP=90°,∴,∴,即,∵,∴,∴P1(1,);②若AD 是矩形的一条对角线,则线段AD 的中点坐标为( ,),Q (2,),m =,则P (1,8a ),∵四边形APDQ 为矩形,∴∠APD =90°,∴,∴,即,∵,∴,∴P 2(1,-4).综上所述,以点A 、D 、P 、Q 为顶点的四边形能成为矩形,点P 的坐标为(1,)或(1,-4).考点:二次函数综合题.12.如图,已知抛物线2(0)y ax bx a =+≠过点3,-3) 和3,0),过点A 作直线AC//x 轴,交y 轴与点C . (1)求抛物线的解析式;(2)在抛物线上取一点P ,过点P 作直线AC 的垂线,垂足为D ,连接OA ,使得以A ,D ,P 为顶点的三角形与△AOC 相似,求出对应点P 的坐标;(3)抛物线上是否存在点Q ,使得13AOC AOQ S S ∆∆=?若存在,求出点Q 的坐标;若不存在,请说明理由.【答案】(1)21332y x x =-;(2)P 点坐标为(383,- 43);(3)Q 点坐标(30)或(315) 【解析】 【分析】(1)把A 与B 坐标代入抛物线解析式求出a 与b 的值,即可确定出解析式;(2)设P 坐标为2133,22x x x ⎛⎫- ⎪ ⎪⎝⎭,表示出AD 与PD ,由相似分两种情况得比例求出x 的值,即可确定出P 坐标;(3)存在,求出已知三角形AOC 边OA 上的高h ,过O 作OM ⊥OA ,截取OM=h,与y 轴交于点N ,分别确定出M 与N 坐标,利用待定系数法求出直线MN 解析式,与抛物线解析式联立求出Q 坐标即可. 【详解】(1)把3A 3)-和点(33B 0)代入抛物线得:33327330a b a b ⎧+=-⎪⎨+=⎪⎩,解得:12a =,332b =-, 则抛物线解析式为213322y x x =-; (2)当P 在直线AD 上方时,设P 坐标为2133,2x x x ⎛⎫ ⎪ ⎪⎝⎭,则有3AD x =213332PD x x =+, 当OCA ADP ∆∆∽时,OC CA AD DP =2331333x x x =--+, 整理得:239318236x x x -+=-,即23113240x x -+=,解得:6x =,即3x =或x =此时P 4)3-;当OCA PDA ∆∆∽时,OC CA PD AD =22=,296x x -+=-2120x -+=,解得:x =x =此时P 6);当点()0,0P 时,也满足OCA PDA ∆∆∽; 当P 在直线AD 下方时,同理可得:P的坐标为10)3-,综上,P的坐标为,4)3-或6)或10)3-或()0,0;(3)在Rt AOC ∆中,3OC =,AC =根据勾股定理得:OA =Q 11··22OC AC OA h =, 32h ∴=,132AOC AOQ S S ∆∆==Q , AOQ ∴∆边OA 上的高为92, 过O 作OM OA ⊥,截取92OM =,过M 作//MN OA ,交y 轴于点N ,如图所示:在Rt OMN ∆中,29ON OM ==,即()0,9N , 过M 作MH x ⊥轴,在Rt OMH ∆中,1924MH OM ==,393OH ==,即93(M ,9)4, 设直线MN 解析式为9y kx =+,把M 坐标代入得:99394=+,即3k =39y x =+, 联立得:23913322y x y x x ⎧=-+⎪⎨=-⎪⎩,解得:330x y ⎧=⎪⎨=⎪⎩315x y ⎧=-⎪⎨=⎪⎩(33Q 0)或(23-,15),则抛物线上存在点Q ,使得13AOC AOQ S S ∆∆=,此时点Q 的坐标为(330)或(23-15).【点睛】二次函数综合题,涉及的知识有:待定系数法求函数解析式,相似三角形的判定与性质,点到直线的距离公式,熟练掌握待定系数法是解本题的关键.13.如图1,抛物线y=ax 2+2x+c 与x 轴交于A (﹣4,0),B (1,0)两点,过点B 的直线y=kx+23分别与y 轴及抛物线交于点C ,D . (1)求直线和抛物线的表达式;(2)动点P 从点O 出发,在x 轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t 秒,当t 为何值时,△PDC 为直角三角形?请直接写出所有满足条件的t 的值;(3)如图2,将直线BD 沿y 轴向下平移4个单位后,与x 轴,y 轴分别交于E ,F 两点,在抛物线的对称轴上是否存在点M ,在直线EF 上是否存在点N ,使DM+MN 的值最小?若存在,求出其最小值及点M ,N 的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为:y=228233x x +-,BD 解析式为y=﹣2233x +;(2)t 的值为4915129±、233.(3)N 点坐标为(﹣2,﹣2),M 点坐标为(﹣32,﹣54),213 【解析】分析:(1)利用待定系数法求解可得;(2)先求得点D 的坐标,过点D 分别作DE ⊥x 轴、DF ⊥y 轴,分P 1D ⊥P 1C 、P 2D ⊥DC 、P 3C ⊥DC 三种情况,利用相似三角形的性质逐一求解可得;(3)通过作对称点,将折线转化成两点间距离,应用两点之间线段最短. 详解:(1)把A (﹣4,0),B (1,0)代入y=ax 2+2x+c ,得168020a c a c -+=⎧⎨++=⎩,解得:2383a c ⎧=⎪⎪⎨⎪=-⎪⎩,∴抛物线解析式为:y=228233x x +-, ∵过点B 的直线y=kx+23, ∴代入(1,0),得:k=﹣23, ∴BD 解析式为y=﹣2233x +;(2)由2282332233y x xy x﹣⎧=+-⎪⎪⎨⎪=+⎪⎩得交点坐标为D(﹣5,4),如图1,过D作DE⊥x轴于点E,作DF⊥y轴于点F,当P1D⊥P1C时,△P1DC为直角三角形,则△DEP1∽△P1OC,∴DEPO=PEOC,即4t=523t-,解得t=151296±,当P2D⊥DC于点D时,△P2DC为直角三角形由△P2DB∽△DEB得DBEB=2P BDB,5252,解得:t=233;当P3C⊥DC时,△DFC∽△COP3,∴DFOC=3CFP O,即523=103t,解得:t=49,∴t的值为49、151296、233.(3)由已知直线EF解析式为:y=﹣23x﹣103,在抛物线上取点D的对称点D′,过点D′作D′N⊥EF于点N,交抛物线对称轴于点M过点N 作NH ⊥DD′于点H ,此时,DM+MN=D′N 最小. 则△EOF ∽△NHD′ 设点N 坐标为(a ,﹣21033a -), ∴OE NH =OF HD ',即52104()33a ---=1032a -, 解得:a=﹣2,则N 点坐标为(﹣2,﹣2),求得直线ND′的解析式为y=32x+1, 当x=﹣32时,y=﹣54, ∴M 点坐标为(﹣32,﹣54), 此时,DM+MN 的值最小为22D H NH '+=2246+=213.点睛:本题是二次函数和几何问题综合题,应用了二次函数性质以及转化的数学思想、分类讨论思想.解题时注意数形结合.14.如图,已知抛物线2y ax bx c =++(a≠0)经过A (﹣1,0)、B (3,0)、C (0,﹣3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当点P 到点A 、点B 的距离之和最短时,求点P 的坐标;(3)点M 也是直线l 上的动点,且△MAC 为等腰三角形,请直接写出所有符合条件的点M 的坐标.【答案】(1)223y x x =--;(2)P (1,0);(3).【解析】试题分析:(1)直接将A 、B 、C 三点坐标代入抛物线的解析式中求出待定系数即可; (2)由图知:A .B 点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l 与x 轴的交点,即为符合条件的P 点;(3)由于△MAC 的腰和底没有明确,因此要分三种情况来讨论:①MA=AC 、②MA=MC 、③AC=MC ;可先设出M 点的坐标,然后用M 点纵坐标表示△MAC 的三边长,再按上面的三种情况列式求解.试题解析:(1)将A (﹣1,0)、B (3,0)、C (0,﹣3)代入抛物线2y ax bx c=++中,得:0{9303a b c a b c c -+=++==-,解得:1{23a b c ==-=-,故抛物线的解析式:223y x x =--.(2)当P 点在x 轴上,P ,A ,B 三点在一条直线上时,点P 到点A 、点B 的距离之和最短,此时x=2ba-=1,故P (1,0); (3)如图所示:抛物线的对称轴为:x=2ba-=1,设M (1,m ),已知A (﹣1,0)、C (0,﹣3),则:2MA =24m +,2MC =2(3)1m ++=2610m m ++,2AC =10;①若MA=MC ,则22MA MC =,得:24m +=2610m m ++,解得:m=﹣1; ②若MA=AC ,则22MA AC =,得:24m +=10,得:m=6±;③若MC=AC ,则22MC AC =,得:2610m m ++=10,得:10m =,26m =-; 当m=﹣6时,M 、A 、C 三点共线,构不成三角形,不合题意,故舍去;综上可知,符合条件的M 点,且坐标为 M (1,6)(1,6-)(1,﹣1)(1,0).考点:二次函数综合题;分类讨论;综合题;动点型.15.如图1,四边形OABC 是矩形,点A 的坐标为(3,0),点c 的坐标为(0,6).点P 从点O 出发,沿OA 以每秒1个单位长度的速度向点A 运动,同时点Q 从点A 出发,沿AB 以每秒2个单位长度的速度向点B 运动,当点P 与点A 重合时运动停止.设运动时间为t 秒.(1)当2t =时,线段PQ 的中点坐标为________; (2)当CBQ ∆与PAQ ∆相似时,求t 的值;(3)当1t =时,抛物线2y x bx c =++经过P 、Q 两点,与y 轴交于点M ,抛物线的顶点为K ,如图2所示.问该抛物线上是否存在点D ,使12MQD MKQ ∠=∠,若存在,求出所有满足条件的D 点坐标;若不存在,说明理由. 【答案】(1)PQ 的中点坐标是(2.5,2);(2)9352t -=或3t 4=;(3)124(,)39D ,2240(,)39D -. 【解析】分析:(1)先根据时间t=2,和速度可得动点P 和Q 的路程OP 和AQ 的长,再根据中点坐标公式可得结论;(2)根据矩形的性质得:∠B=∠PAQ=90°,所以当△CBQ 与△PAQ 相似时,存在两种情况:①当△PAQ ∽△QBC 时,PA QB AQ BC =,②当△PAQ ∽△CBQ 时,PA BC AQ QB=,分别列方程可得t 的值;(3)根据t=1求抛物线的解析式,根据Q (3,2),M (0,2),可得MQ ∥x 轴,∴KM=KQ ,KE ⊥MQ ,画出符合条件的点D ,证明△KEQ ∽△QMH ,列比例式可得点D 的坐标,同理根据对称可得另一个点D .详解:(1)如图1,∵点A 的坐标为(3,0), ∴OA=3,当t=2时,OP=t=2,AQ=2t=4, ∴P (2,0),Q (3,4),。
【经典必考】待定系数法求二次函数表达式30题含详细答案

…………○……………○…………线……学校:_______________…………○……………○…………线……待定系数法求二次函数表达式30题含详细答案1.如图,已知抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =-,且抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(1,0)A ,(0,3)C .(1)若直线y mx n =+经过B 、C 两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴1x =-上找一点M ,使点M 到点A 的距离与到点C 的距离之和最小,求出点M 的坐标;(3)设点P 为抛物线的对称轴1x =-上的一个动点,求使BPC ∆为直角三角形的点P 的坐标.2.如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A (﹣1,0)B (3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点. (1)求抛物线的解析式和直线AC 的解析式;(2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;(3)试探究:在拋物线上是否存在点P ,使以点A ,P ,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.3.如图,已知二次函数y=ax 2+bx+3的图象交x 轴于点A (1,0),B (3,0),交y 轴于点C .(1)求这个二次函数的表达式;(2)点P 是直线BC 下方抛物线上的一动点,求△BCP 面积的最大值;(3)直线x=m 分别交直线BC 和抛物线于点M ,N ,当△BMN 是等腰三角形时,直接写出m 的值.试卷第2页,总11页○…………装……○…………订………线…………○……※※请※※不※※要※※※※订※※线※※内※※答○…………装……○…………订………线…………○……4.如图,抛物线y =x 2 +bx +c 与x 轴交于A (﹣1,0),B (3,0)两点. (1)求该抛物线的解析式;(2)求该抛物线的对称轴以及顶点坐标;(3)设(1)中的抛物线上有一个动点P ,当点P 在该抛物线上滑动到什么位置时,满足S △P AB =8,并求出此时P 点的坐标.5.如图,已知抛物线2y ax bx c =++的顶点为()4,3A ,与y 轴相交于点()0,5B -,对称轴为直线l ,点M 是线段AB 的中点.(1)求抛物线的表达式;(2)写出点M 的坐标并求直线AB 的表达式;(3)设动点P ,Q 分别在抛物线和对称轴l 上,当以A ,P ,Q ,M 为顶点的四边形是平行四边形时,求P ,Q 两点的坐标.6.如图所示抛物线2y ax bx c =++过点()1,0A -,点()0,3C ,且OB OC = (1)求抛物线的解析式及其对称轴;(2)点,D E 在直线1x =上的两个动点,且1DE =,点D 在点E 的上方,求四边形…外…………○…………装…………○…………线………学校:___________姓名:____________…内…………○…………装…………○…………线………ACDE 的周长的最小值;(3)点P 为抛物线上一点,连接CP ,直线CP 把四边形CBPA 的面积分为3∶5两部分,求点P 的坐标.7.如图,抛物线y=ax 2+6x+c 交x 轴于A ,B 两点,交y 轴于点C .直线y=x ﹣5经过点B ,C .(1)求抛物线的解析式;(2)过点A 的直线交直线BC 于点M .①当AM ⊥BC 时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标; ②连接AC ,当直线AM 与直线BC 的夹角等于∠ACB 的2倍时,请直接写出点M 的坐标.8.如图,已知抛物线y=2x +mx+3与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0),(1)求m 的值及抛物线的顶点坐标.(2)点P 是抛物线对称轴l 上的一个动点,当PA+PC 的值最小时,求点P 的坐标.试卷第4页,总11页○…………外………装…………○…………订……………○……※※要※※在※※装※※订※※线※※内※※答○…………内………装…………○…………订……………○……9.如图,抛物线y=a (x ﹣1)(x ﹣3)(a >0)与x 轴交于A 、B 两点,抛物线上另有一点C 在x 轴下方,且使△OCA ∽△OBC (1)求线段OC 的长度;(2)设直线BC 与y 轴交于点M ,点C 是BM 的中点时,求直线BM 和抛物线的解析式;(3)在(2)的条件下,直线BC 下方抛物线上是否存在一点P ,使得四边形ABPC 面积最大?若存在,请求出点P 的坐标;若不存在,请说明理由.10.抛物线y=﹣x 2+bx +c 与x 轴交于A (﹣3,0),B (1,0)两点,与y 轴交于点C . (1)求该抛物线的解析式;(2)在抛物线上求一点P ,使S △PAB =S △ABC ,写出P 点的坐标;(3)在抛物线的对称轴上是否存在点Q ,使得△QBC 的周长最小?若存在,求出点Q 的坐标,若不存在,请说明理由.11.如图,在平面直角坐标系中,二次函数2y x bx c =++的图象与x 轴交于A 、B 两…………○…………………线…………学校:_________…………○…………………线…………点,B 点的坐标为(3,0),与y 轴交于点C (0,-3),点P 是直线BC 下方抛物线上的一个动点.(1)求二次函数解析式;(2)连接PO ,PC ,并将△POC 沿y 轴对折,得到四边形POP'C .是否存在点P ,使四边形POP'C 为菱形?若存在,求出此时点P 的坐标;若不存在,请说明理由; (3)当点P 运动到什么位置时,四边形ABPC 的面积最大?求出此时P 点的坐标和四边形ABPC 的最大面积.12.如图,已知A (﹣2,0),B (4,0),抛物线y=ax 2+bx ﹣1过A 、B 两点,并与过A 点的直线y=﹣12x ﹣1交于点C . (1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P ,使四边形ACPO 的周长最小?若存在,求出点P 的坐标,若不存在,请说明理由;(3)点M 为y 轴右侧抛物线上一点,过点M 作直线AC 的垂线,垂足为N .问:是否存在这样的点N ,使以点M 、N 、C 为顶点的三角形与△AOC 相似,若存在,求出点N 的坐标,若不存在,请说明理由.13.如图,已知抛物线y=13x 2+bx+c 经过△ABC 的三个顶点,其中点A (0,1),点B (-9,10),AC ∥x 轴,点P 是直线AC 下方抛物线上的动点. (1)求抛物线的解析式;(2)过点P 且与y 轴平行的直线l 与直线AB 、AC 分别交于点E 、F ,当四边形AECP 的面积最大时,求点P 的坐标;(3)当点P 为抛物线的顶点时,在直线AC 上是否存在点Q ,使得以C 、P 、Q 为顶点试卷第6页,总11页…………装…………○…………线…………○…※※请※※不※※要※※在※※装※※订…………装…………○…………线…………○…的三角形与△ABC 相似,若存在,求出点Q 的坐标,若不存在,请说明理由.14.如图,已知抛物线经过点A (﹣1,0),B (4,0),C (0,2)三点,点D 与点C 关于x 轴对称,点P 是x 轴上的一个动点,设点P 的坐标为(m ,0),过点P 做x 轴的垂线l 交抛物线于点Q ,交直线BD 于点M . (1)求该抛物线所表示的二次函数的表达式; (2)已知点F (0,12),当点P 在x 轴上运动时,试求m 为何值时,四边形DMQF 是平行四边形?(3)点P 在线段AB 运动过程中,是否存在点Q ,使得以点B 、Q 、M 为顶点的三角形与△BOD 相似?若存在,求出点Q 的坐标;若不存在,请说明理由.15.抛物线y=﹣x 2+bx+c 经过点A 、B 、C ,已知A (﹣1,0),C (0,3). (1)求抛物线的解析式;(2)如图1,P 为线段BC 上一点,过点P 作y 轴平行线,交抛物线于点D ,当△BDC 的面积最大时,求点P 的坐标;(3)如图2,抛物线顶点为E ,EF ⊥x 轴于F 点,M (m ,0)是x 轴上一动点,N 是线段EF 上一点,若∠MNC=90°,请指出实数m 的变化范围,并说明理由.……○…………外……装…………○…线…………○……____姓名:___________班……○…………内……装…………○…线…………○……16.已知抛物线2y x bx c =-++经过点A (3,0),B (﹣1,0). (1)求抛物线的解析式; (2)求抛物线的顶点坐标.17.在平面直角坐标系中,二次函数y=ax 2+53x+c 的图象经过点C (0,2)和点D (4,﹣2).点E 是直线y=﹣13x+2与二次函数图象在第一象限内的交点. (1)求二次函数的解析式及点E 的坐标.(2)如图①,若点M 是二次函数图象上的点,且在直线CE 的上方,连接MC ,OE ,ME .求四边形COEM 面积的最大值及此时点M 的坐标.(3)如图②,经过A 、B 、C 三点的圆交y 轴于点F ,求点F 的坐标.18.如图,抛物线y=ax 2+bx+2交x 轴于点A(-3,0)和点B(1,0),交y 轴于点C (1)求这个抛物线的函数表达式.(2)点D 的坐标为(-1,0),点P 为第二象限内抛物线上的一个动点,求四边形ADCP 面积的最大值.(3)点M 为抛物线对称轴上的点,问:在抛物线上是否存在点N ,使△MNO 为等腰直角三角形,且∠MNO 为直角?若存在,请直接写出点N 的坐标;若不存在,请说明理由.试卷第8页,总11页………○………………订…………○※※请※※不※※※内※※答※※题※※………○………………订…………○19.若二次函数y=ax 2+bx+c 的图象的顶点是(2,1)且经过点(1,﹣2),求此二次函数解析式.20.已知二次函数的图象以A (﹣1,4)为顶点,且过点B (2,﹣5) (1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A 、B 两点随图象移至A′、B′,求△O A′B′的面积.21.如图,已知二次函数212y x bx c =-++的图象经过()2,0A ,()0,6B -两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x 轴交于点C ,连接BA ,BC ,求ABC ∆的面积. 22.如图,二次函数y=(x+2)2+m 的图象与y 轴交于点C ,点B 在抛物线上,且与点C 关于抛物线的对称轴对称,已知一次函数y=kx+b 的图象经过该二次函数图象上的点A (﹣1,0)及点B .(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足(x+2)2+m≥kx+b 的x 的取值范围.23.在平面直角坐标系中,点()0,0O ,点1,0A .已知抛物线22y x mx m =+-(m 是常数),顶点为P .(Ⅰ)当抛物线经过点A 时,求顶点P 的坐标;(Ⅱ)若点P 在x 轴下方,当45AOP ∠=︒时,求抛物线的解析式;(Ⅲ) 无论m 取何值,该抛物线都经过定点H .当45AHP ∠=︒时,求抛物线的解析式.○…………装…………○…………○…………学校:___________姓名:___________班:___________○…………装…………○…………○…………24.如图,抛物线y=ax 2+bx(a <0)过点E(10,0),矩形ABCD 的边AB 在线段OE 上(点A 在点B 的左边),点C ,D 在抛物线上.设A(t,0),当t=2时,AD=4. (1)求抛物线的函数表达式.(2)当t 为何值时,矩形ABCD 的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD 不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G ,H ,且直线GH 平分矩形的面积时,求抛物线平移的距离.25.在平面直角坐标系中,将二次函数()20y axa =>的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x 轴交于点A 、B (点A 在点B 的左侧),1OA =,经过点A 的一次函数()0y kx b k =+≠的图象与y 轴正半轴交于点C ,且与抛物线的另一个交点为D ,ABD ∆的面积为5.(1)求抛物线和一次函数的解析式;(2)抛物线上的动点E 在一次函数的图象下方,求ACE ∆面积的最大值,并求出此时点E 的坐标;(3)若点P 为x 轴上任意一点,在(2)的结论下,求35PE PA +的最小值. 26.如图,抛物线顶点P (1,4),与y 轴交于点C (0,3),与x 轴交于点A ,B . (1)求抛物线的解析式.(2)Q 是抛物线上除点P 外一点,△BCQ 与△BCP 的面积相等,求点Q 的坐标. (3)若M ,N 为抛物线上两个动点,分别过点M ,N 作直线BC 的垂线段,垂足分别为D ,试卷第10页,总11页…装…………○…………………线…………不※※要※※在※※装※※订※※线※※…装…………○…………………线…………E .是否存在点M ,N 使四边形MNED 为正方形?如果存在,求正方形MNED 的边长;如果不存在,请说明理由.27.已知抛物线y =ax 2+bx +c 经过A(-1,0)、B(3,0)、C(0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标;(3)在直线l 上是否存在点M ,使△MAC 为等腰三角形?若存在,直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.28.已知k 是常数,抛物线y =x 2+(k 2+k -6)x +3k 的对称轴是y 轴,并且与x 轴有两个交点.(1)求k 的值:(2)若点P 在抛物线y =x 2+(k 2+k -6)x +3k 上,且P 到y 轴的距离是2,求点P 的坐标. 29.如图,已知抛物线2y x bx c =-++与x 轴交于A 、B 两点,4AB =,交y 轴于点C ,对称轴是直线1x =.…外…………○…………线…………○……学校:_____…内…………○…………线…………○…… (1)求抛物线的解析式及点C 的坐标;(2)连接BC ,E 是线段OC 上一点,E 关于直线1x =的对称点F 正好落在BC 上,求点F 的坐标; (3)动点M 从点O 出发,以每秒2个单位长度的速度向点B 运动,过M 作x 轴的垂线交抛物线于点N ,交线段BC 于点Q .设运动时间为()0t t >秒. ①若AOC ∆与BMN ∆相似,请直接写出t 的值; ②BOQ ∆能否为等腰三角形?若能,求出t 的值;若不能,请说明理由. 30.在平面直角坐标系xOy 中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=14x 与抛物线交于A 、B 两点,直线l 为y=﹣1. (1)求抛物线的解析式; (2)在l 上是否存在一点P ,使PA+PB 取得最小值?若存在,求出点P 的坐标;若不存在,请说明理由. (3)知F (x 0,y 0)为平面内一定点,M (m ,n )为抛物线上一动点,且点M 到直线l 的距离与点M 到点F 的距离总是相等,求定点F 的坐标.参考答案1.(1)抛物线的解析式为223y x x =--+,直线的解析式为3y x .(2)2()1,M -;(3)P 的坐标为(1,2)--或(1,4)-或3(1,2+-或3(1,)2-. 【解析】分析:(1)先把点A ,C 的坐标分别代入抛物线解析式得到a 和b ,c 的关系式,再根据抛物线的对称轴方程可得a 和b 的关系,再联立得到方程组,解方程组,求出a ,b ,c 的值即可得到抛物线解析式;把B 、C 两点的坐标代入直线y=mx+n ,解方程组求出m 和n 的值即可得到直线解析式;(2)设直线BC 与对称轴x=-1的交点为M ,此时MA+MC 的值最小.把x=-1代入直线y=x+3得y 的值,即可求出点M 坐标;(3)设P (-1,t ),又因为B (-3,0),C (0,3),所以可得BC 2=18,PB 2=(-1+3)2+t 2=4+t 2,PC 2=(-1)2+(t-3)2=t 2-6t+10,再分三种情况分别讨论求出符合题意t 值即可求出点P 的坐标.详解:(1)依题意得:1203b a a b c c ⎧-=-⎪⎪++=⎨⎪=⎪⎩,解得:123a b c =-⎧⎪=-⎨⎪=⎩,∴抛物线的解析式为223y x x =--+.∵对称轴为1x =-,且抛物线经过()1,0A ,∴把()3,0B -、()0,3C 分别代入直线y mx n =+, 得303m n n -+=⎧⎨=⎩,解之得:13m n =⎧⎨=⎩, ∴直线y mx n =+的解析式为3y x =+.(2)直线BC 与对称轴1x =-的交点为M ,则此时MA MC +的值最小,把1x =-代入直线3y x =+得2y =,∴()1,2M -.即当点M 到点A 的距离与到点C 的距离之和最小时M 的坐标为()1,2-. (注:本题只求M 坐标没说要求证明为何此时MA MC +的值最小,所以答案未证明MA MC +的值最小的原因).(3)设()1,P t -,又()3,0B -,()0,3C ,∴218BC =,()2222134PB t t =-++=+,()()222213610PC t t t =-+-=-+, ①若点B 为直角顶点,则222BC PB PC +=,即:22184610t t t ++=-+解得:2t =-, ②若点C 为直角顶点,则222BC PC PB +=,即:22186104t t t +-+=+解得:4t =, ③若点P 为直角顶点,则222PB PC BC +=,即:22461018t t t ++-+=解得:1t =2t =.综上所述P 的坐标为()1,2--或()1,4-或⎛- ⎝⎭或⎛- ⎝⎭. 点睛:本题综合考查了二次函数的图象与性质、待定系数法求函数(二次函数和一次函数)的解析式、利用轴对称性质确定线段的最小长度、难度不是很大,是一道不错的中考压轴题. 2.(1)抛物线解析式为y=﹣x 2+2x+3;直线AC 的解析式为y=3x+3;(2)点M 的坐标为(0,3);(3)符合条件的点P 的坐标为(73,209)或(103,﹣139), 【解析】分析:(1)设交点式y=a (x+1)(x-3),展开得到-2a=2,然后求出a 即可得到抛物线解析式;再确定C (0,3),然后利用待定系数法求直线AC 的解析式;(2)利用二次函数的性质确定D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,∴﹣2a=2,解得a=﹣1,∴抛物线解析式为y=﹣x2+2x+3;当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM 的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M 的坐标为(0,3);(3)存在.过点C 作AC 的垂线交抛物线于另一点P ,如图2,∵直线AC 的解析式为y=3x+3,∴直线PC 的解析式可设为y=﹣13x+b , 把C (0,3)代入得b=3,∴直线PC 的解析式为y=﹣13x+3, 解方程组223133y x x y x ⎧-++⎪⎨-+⎪⎩==,解得03x y =⎧⎨=⎩或73209x y ⎧=⎪⎪⎨⎪=⎪⎩,则此时P 点坐标为(73,209); 过点A 作AC 的垂线交抛物线于另一点P ,直线PC 的解析式可设为y=﹣x+b ,把A (﹣1,0)代入得13+b=0,解得b=﹣13, ∴直线PC 的解析式为y=﹣13x ﹣13, 解方程组2231133y x x y x ⎧-++⎪⎨--⎪⎩==,解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩,则此时P 点坐标为(103,﹣139). 综上所述,符合条件的点P 的坐标为(73,209)或(103,﹣139). 点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.3.(1)这个二次函数的表达式是y=x 2﹣4x+3;(2)S △BCP 最大=278;(3)当△BMN 是等腰三角形时,m,1,2.【解析】分析:(1)根据待定系数法,可得函数解析式;(2)根据平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PE 的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;(3)根据等腰三角形的定义,可得关于m 的方程,根据解方程,可得答案.详解:(1)将A (1,0),B (3,0)代入函数解析式,得309330a b a b ++⎧⎨++⎩==, 解得14a b ⎧⎨-⎩==, 这个二次函数的表达式是y=x 2-4x+3;(2)当x=0时,y=3,即点C (0,3),设BC 的表达式为y=kx+b ,将点B (3,0)点C (0,3)代入函数解析式,得300k b b +⎧⎨⎩==, 解这个方程组,得13k b -⎧⎨⎩== 直线BC 的解析是为y=-x+3,过点P 作PE ∥y 轴,交直线BC于点E(t,-t+3),PE=-t+3-(t2-4t+3)=-t2+3t,∴S△BCP=S△BPE+S CPE=12(-t2+3t)×3=-32(t-32)2+278,∵-32<0,∴当t=32时,S△BCP最大=278.(3)M(m,-m+3),N(m,m2-4m+3)MN=m2-3m,|m-3|,当MN=BM时,①m2(m-3),解得②m2(m-3),解得当BN=MN时,∠NBM=∠BMN=45°,m2-4m+3=0,解得m=1或m=3(舍)当BM=BN时,∠BMN=∠BNM=45°,-(m2-4m+3)=-m+3,解得m=2或m=3(舍),当△BMN是等腰三角形时,m,1,2.点睛:本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用面积的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用等腰三角形的定义得出关于m的方程,要分类讨论,以防遗漏.4.(1)y=x2﹣2x﹣3;(2)抛物线的对称轴x=1,顶点坐标(1,﹣4);(3)(1+4)或(1-4)或(1,﹣4).【分析】(1)由于抛物线y=x 2+bx+c 与x 轴交于A (﹣1,0),B (3,0)两点,那么可以得到方程x 2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b 、c 的值.(2)根据S △PAB =8,求得P 的纵坐标,把纵坐标代入抛物线的解析式即可求得P 点的坐标.【详解】解:(1)∵抛物线y=x 2+bx+c 与x 轴交于A (﹣1,0),B (3,0)两点,∴方程x 2+bx+c=0的两根为x=﹣1或x=3,∴﹣1+3=﹣b ,﹣1×3=c , ∴b=﹣2,c=﹣3,∴二次函数解析式是y=x 2﹣2x ﹣3.(2)∵y=﹣x 2﹣2x ﹣3=(x ﹣1)2﹣4,∴抛物线的对称轴x=1,顶点坐标(1,﹣4).(3)设P 的纵坐标为|y P |,∵S △PAB =8, ∴12AB•|y P |=8, ∵AB=3+1=4,∴|y P |=4,∴y P =±4,把y P =4代入解析式得,4=x 2﹣2x ﹣3,解得,x=1±, 把y P =﹣4代入解析式得,﹣4=x 2﹣2x ﹣3,解得,x=1,∴点P 在该抛物线上滑动到(4)或(1﹣,4)或(1,﹣4)时,满足S △PAB =8.【点睛】考点:1.待定系数法求二次函数解析式;2.二次函数的性质;3.二次函数图象上点的坐标特征.5.(1)21452=-+-y x x ;(2)()2,1M -,25y x =-;(3)点P 、Q 的坐标分别为(6,1)、(4,-3)或(2,1)、(4,5)或(2,1)、(4,1).【分析】(1)函数表达式为:y=a (x-4)2+3,将点B 坐标代入上式,即可求解;(2)A (4,3)、B (0,-5),则点M (2,-1),设直线AB 的表达式为:y=kx-5,将点A 坐标代入上式,即可求解;(3)分当AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况,分别求解即可.【详解】解:(1)设函数表达式为:()243y a x =-+,将点B 坐标代入上式并解得:12a =-, 故抛物线的表达式为:21452=-+-y x x ; (2)()4,3A 、()0,5B -,则点()2,1M -,设直线AB 的表达式为:5y kx =-,将点A 坐标代入上式得:345k =-,解得:2k =,故直线AB 的表达式为:25y x =-;(3)设点()4,Q s 、点21,452P m m m ⎛⎫-+- ⎪⎝⎭, ①当AM 是平行四边形的一条边时,当点Q 在A 的下方时,点A 向左平移2个单位、向下平移4个单位得到M ,同样点P (m ,-12m 2+4m-5)向左平移2个单位、向下平移4个单位得到Q (4,s ), 即:m-2=4,-12m 2+4m-5-4=s , 解得:m=6,s=-3,故点当点Q 在点A 上方时,AQ=MP=2,同理可得点Q 的坐标为(4,5),②当AM 是平行四边形的对角线时,由中点定理得:4+2=m+4,3-1=-12m 2+4m-5+s ,解得:m=2,s=1,故点P 、Q 的坐标分别为(2,1)、(4,1);综上,P 、Q 的坐标分别为(6,1)、(4,-3)或(2,1)、(4,5)或(2,1)、(4,1).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,避免遗漏.6.(1)2y x 2x 3=-++,对称轴为直线1x =;(2)四边形ACDE 的周长最小值为1;(3)12(4,5),(8,45)P P --【分析】(1)OB=OC ,则点B (3,0),则抛物线的表达式为:y=a (x+1)(x-3)=a (x 2-2x-3)=ax 2-2ax-3a ,即可求解;(2)CD+AE=A′D+DC′,则当A′、D 、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,即可求解;(3)S △PCB :S △PCA =12EB×(y C -y P ):12AE×(y C -y P )=BE :AE ,即可求解. 【详解】(1)∵OB=OC ,∴点B (3,0),则抛物线的表达式为:y=a (x+1)(x-3)=a (x 2-2x-3)=ax 2-2ax-3a ,故-3a=3,解得:a=-1,故抛物线的表达式为:y=-x 2+2x+3…①;对称轴为:直线1x =(2)ACDE 的周长=AC+DE+CD+AE ,其中、DE=1是常数,故CD+AE 最小时,周长最小,取点C 关于函数对称点C (2,3),则CD=C′D ,取点A′(-1,1),则A′D=AE ,故:CD+AE=A′D+DC′,则当A′、D 、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,四边形ACDE 的周长的最小值(3)如图,设直线CP 交x 轴于点E ,直线CP 把四边形CBPA 的面积分为3:5两部分,又∵S △PCB :S △PCA =12EB×(y C -y P ):12AE×(y C -y P )=BE :AE , 则BE :AE ,=3:5或5:3,则AE=52或32, 即:点E 的坐标为(32,0)或(12,0), 将点E 、C 的坐标代入一次函数表达式:y=kx+3,解得:k=-6或-2,故直线CP 的表达式为:y=-2x+3或y=-6x+3…②联立①②并解得:x=4或8(不合题意值已舍去),故点P 的坐标为(4,-5)或(8,-45).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、图象面积计算、点的对称性等,其中(1),通过确定点A′点来求最小值,是本题的难点.7.(1)抛物线解析式为y=﹣x 2+6x ﹣5;(2)①P 点的横坐标为4或2或2;②点M 的坐标为(136,﹣176)或(236,﹣76). 【解析】 分析:(1)利用一次函数解析式确定C (0,-5),B (5,0),然后利用待定系数法求抛物线解析式;(2)①先解方程-x 2+6x-5=0得A (1,0),再判断△OCB 为等腰直角三角形得到∠OBC=∠OCB=45°,则△AMB 为等腰直角三角形,所以,接着根据平行四边形的性质得到,PQ ⊥BC ,作PD ⊥x 轴交直线BC 于D ,如图1,利用∠PDQ=45°得到PQ=4,设P (m ,-m 2+6m-5),则D (m ,m-5),讨论:当P 点在直线BC 上方时,PD=-m 2+6m-5-(m-5)=4;当P 点在直线BC 下方时,PD=m-5-(-m 2+6m-5),然后分别解方程即可得到P 点的横坐标;②作AN ⊥BC 于N ,NH ⊥x 轴于H ,作AC 的垂直平分线交BC 于M 1,交AC 于E ,如图2,利用等腰三角形的性质和三角形外角性质得到∠AM 1B=2∠ACB ,再确定N (3,-2),AC 的解析式为y=5x-5,E 点坐标为(12,-52),利用两直线垂直的问题可设直线EM 1的解析式为y=-15x+b ,把E (12,-52)代入求出b 得到直线EM 1的解析式为y=-15x-125,则解方程组511255y x y x -⎧⎪⎨--⎪⎩==得M 1点的坐标;作直线BC 上作点M 1关于N 点的对称点M 2,如图2,利用对称性得到∠AM 2C=∠AM 1B=2∠ACB ,设M 2(x ,x-5),根据中点坐标公式得到3=13+62x ,然后求出x 即可得到M 2的坐标,从而得到满足条件的点M 的坐标.详解:(1)当x=0时,y=x ﹣5=﹣5,则C (0,﹣5),当y=0时,x ﹣5=0,解得x=5,则B (5,0),把B (5,0),C (0,﹣5)代入y=ax 2+6x+c 得253005a c c ++=⎧⎨=-⎩,解得15a b =-⎧⎨=-⎩, ∴抛物线解析式为y=﹣x 2+6x ﹣5;(2)①解方程﹣x 2+6x ﹣5=0得x 1=1,x 2=5,则A (1,0),∵B (5,0),C (0,﹣5),∴△OCB 为等腰直角三角形,∴∠OBC=∠OCB=45°,∵AM ⊥BC ,∴△AMB 为等腰直角三角形,∴AM=2AB=2×, ∵以点A ,M ,P ,Q 为顶点的四边形是平行四边形,AM ∥PQ ,∴PQ ⊥BC ,作PD ⊥x 轴交直线BC 于D ,如图1,则∠PDQ=45°,∴×=4, 设P (m ,﹣m 2+6m ﹣5),则D (m ,m ﹣5),当P 点在直线BC 上方时,PD=﹣m 2+6m ﹣5﹣(m ﹣5)=﹣m 2+5m=4,解得m 1=1,m 2=4,当P 点在直线BC 下方时,PD=m ﹣5﹣(﹣m 2+6m ﹣5)=m 2﹣5m=4,解得m 1,m 2综上所述,P 点的横坐标为4; ②作AN ⊥BC 于N ,NH ⊥x 轴于H ,作AC 的垂直平分线交BC 于M 1,交AC 于E ,如图2,∵M1A=M1C,∴∠ACM1=∠CAM1,∴∠AM1B=2∠ACB,∵△ANB为等腰直角三角形,∴AH=BH=NH=2,∴N(3,﹣2),易得AC的解析式为y=5x﹣5,E点坐标为(12,﹣52,设直线EM1的解析式为y=﹣15x+b,把E(12,﹣52)代入得﹣110+b=﹣52,解得b=﹣125,∴直线EM1的解析式为y=﹣15x﹣125解方程组511255y xy x=-⎧⎪⎨=--⎪⎩得136176xy⎧=⎪⎪⎨⎪=-⎪⎩,则M1(136,﹣176);作直线BC上作点M1关于N点的对称点M2,如图2,则∠AM2C=∠AM1B=2∠ACB,设M2(x,x﹣5),∵3=13+ 62x∴x=236,∴M2(236,﹣76).综上所述,点M 的坐标为(136,﹣176)或(236,﹣76). 点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角的判定与性质和平行四边形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会运用分类讨论的思想解决数学问题.8.(1)m=2,顶点为(1,4);(2)(1,2).【分析】(1)首先把点B 的坐标为(3,0)代入抛物线y=2x -+mx+3,利用待定系数法即可求得m 的值,继而求得抛物线的顶点坐标;(2)首先连接BC 交抛物线对称轴l 于点P ,则此时PA+PC 的值最小,然后利用待定系数法求得直线BC 的解析式,继而求得答案.【详解】解:(1)把点B 的坐标为(3,0)代入抛物线y=2x -+mx+3得:0=23-+3m+3,解得:m=2,∴y=2x -+2x+3=()214x --+,∴顶点坐标为:(1,4).(2)连接BC 交抛物线对称轴l 于点P ,则此时PA+PC 的值最小,设直线BC 的解析式为:y=kx+b ,∵点C (0,3),点B (3,0),∴033k b b =+⎧⎨=⎩,解得:13k b =-⎧⎨=⎩, ∴直线BC 的解析式为:y=﹣x+3,当x=1时,y=﹣1+3=2,∴当PA+PC 的值最小时,点P 的坐标为:(1,2).考点:二次函数的性质.9.(1);(2)y=3x ,抛物线解析式为y=3x 2﹣3;(3)点P 存在,坐标为(94,﹣8). 【分析】 (1)令y=0,求出x 的值,确定出A 与B 坐标,根据已知相似三角形得比例,求出OC 的长即可;(2)根据C 为BM 的中点,利用直角三角形斜边上的中线等于斜边的一半得到OC=BC ,确定出C 的坐标,利用待定系数法确定出直线BC 解析式,把C 坐标代入抛物线求出a 的值,确定出二次函数解析式即可;(3)过P 作x 轴的垂线,交BM 于点Q ,设出P 与Q 的横坐标为x ,分别代入抛物线与直线解析式,表示出坐标轴,相减表示出PQ ,四边形ACPB 面积最大即为三角形BCP 面积最大,三角形BCP 面积等于PQ 与B 和C 横坐标之差乘积的一半,构造为二次函数,利用二次函数性质求出此时P 的坐标即可.【详解】解:(1)由题可知当y=0时,a (x ﹣1)(x ﹣3)=0,解得:x 1=1,x 2=3,即A (1,0),B (3,0),∴OA=1,OB=3∵△OCA ∽△OBC ,∴OC :OB=OA :OC ,∴OC 2=OA•OB=3,则(2)∵C 是BM 的中点,即OC 为斜边BM 的中线,∴OC=BC ,∴点C 的横坐标为32,又C 在x 轴下方,∴C (32设直线BM的解析式为y=kx+b,把点B(3,0),C(323032k bk b+=⎧⎪⎨+=⎪⎩,解得:b=∴x又∵点C(3 2解得:a=3,∴抛物线解析式为x2(3)点P存在,设点P坐标为(xx2,过点P作PQ⊥x轴交直线BM于点Q,则Q(x∴2)=x2x﹣当△BCP面积最大时,四边形ABPC的面积最大,S △BCP =12PQ (3﹣x )+12PQ (x ﹣32)=34PQ=2 当x=﹣9=24b a 时,S △BCP 有最大值,四边形ABPC 的面积最大,此时点P 的坐标为(94,﹣). 【点睛】此题属于二次函数综合题,涉及的知识有:二次函数图象与性质,待定系数法确定函数解析式,相似三角形的判定与性质,以及坐标与图形性质,熟练掌握各自的性质是解本题的关键.10.(1)y=﹣x 2﹣2x +3;(2)所求P 点的坐标为(﹣2,3)或(﹣1,﹣3)或(﹣1,﹣3);(3)点Q 的坐标是(﹣1,2).【分析】(1)将A (-3,0),B (1,0)两点代入y=-x 2+bx+c ,利用待定系数法求解即可求得答案; (2)首先求得点C 的坐标为(0,3),然后根据同底等高的两个三角形面积相等,可得P点的纵坐标为±3,将y=±3分别代入抛物线的解析式,求出x 的值,即可求得P 点的坐标; (3)根据两点之间线段最短可得Q 点是AC 与对称轴的交点.利用待定系数法求出直线AC 的解析式,将抛物线的对称轴方程x=-1代入求出y 的值,即可得到点Q 的坐标.【详解】(1)∵抛物线y=﹣x 2+bx+c 与x 轴交于A (﹣3,0),B (1,0)两点,∴930{10b c b c -++=-++=,解得23b c =-⎧⎨=⎩, ∴抛物线的解析式为:y=﹣x 2﹣2x+3;(2)∵y=﹣x 2﹣2x+3,∴x=0时,y=3,∴点C 的坐标为(0,3).设在抛物线上存在一点P (x ,y ),使S △PAB =S △ABC ,则|y|=3,即y=±3. 如果y=3,那么﹣x 2﹣2x+3=3,解得x=0或﹣2,x=0时与C 点重合,舍去,所以点P (﹣2,3);如果y=﹣3,那么﹣x 2﹣2x+3=﹣3,解得x=﹣,所以点P (﹣,﹣3);综上所述,所求P 点的坐标为(﹣2,3)或(﹣,﹣3)或(﹣1,﹣3); (3)连结AC 与抛物线的对称轴交于点Q ,此时△QBC 的周长最小.设直线AC 的解析式为:y=mx+n ,∵A (﹣3,0),C (0,3),∴30{3m n n -+==,解得:13m n ==⎧⎨⎩, ∴直线AC 的解析式为:y=x+3.∵y=﹣x 2﹣2x+3的对称轴是直线x=﹣1,∴当x=﹣1时,y=﹣1+3=2,∴点Q 的坐标是(﹣1,2).【点睛】此题考查了抛物线与x 轴的交点,待定系数法求函数的解析式,二次函数的性质,三角形的面积以及轴对称-最短路线问题.正确求出函数的解析式是解此题的关键.11.(1)223y x x =--;(2)存在这样的点,此时P ,32-);(3)P 点的坐标为(32,−154),四边形ABPC 的面积的最大值为758. 【分析】 (1)将B 、C 的坐标代入抛物线的解析式中即可求得待定系数的值;.(2)由于菱形的对角线互相垂直平分,若四边形POP′C 为菱形,那么P 点必在OC 的垂直平分线上,据此可求出P 点的纵坐标,代入抛物线的解析式中即可求出P 点的坐标;. (3)由于△ABC 的面积为定值,当四边形ABPC 的面积最大时,△BPC 的面积最大;过P 作y 轴的平行线,交直线BC 于Q ,交x 轴于F ,易求得直线BC 的解析式,可设出P 点的横坐标,然后根据抛物线和直线BC 的解析式求出Q 、P 的纵坐标,即可得到PQ 的长,以PQ 为底,B 点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ACPB 的面积与P 点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC 的最大面积及对应的P 点坐标.【详解】。
第二章 二次函数专题训练(三)求二次函数表达式的常见类型(含答案)
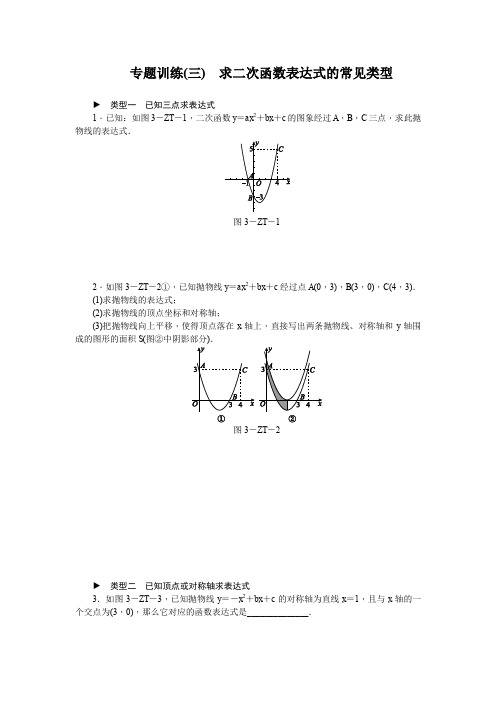
专题训练(三)求二次函数表达式的常见类型►类型一已知三点求表达式1.已知:如图3-ZT-1,二次函数y=ax2+bx+c的图象经过A,B,C三点,求此抛物线的表达式.图3-ZT-12.如图3-ZT-2①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).(1)求抛物线的表达式;(2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).图3-ZT-2►类型二已知顶点或对称轴求表达式3.如图3-ZT-3,已知抛物线y=-x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数表达式是______________.图3-ZT-34.在平面直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0),求该二次函数的表达式.5.已知抛物线经过点A(1,0),B(0,3),且对称轴是直线x=2,求该抛物线的表达式.6.如图3-ZT-4,已知抛物线的顶点为A(1,4),与y轴交于点B(0,3),与x轴交于C,D两点,点P是x轴上的一个动点.(1)求此抛物线的表达式;(2)当P A+PB的值最小时,求点P的坐标.图3-ZT-4►类型三已知抛物线与x轴的交点求表达式7.抛物线与x轴交于点(-1,0)和(3,0),与y轴交于点(0,-3),则此抛物线的表达式为()A.y=x2+2x+3 B.y=x2-2x-3C.y=x2-2x+3 D.y=x2+2x-38.如图3-ZT-5,已知抛物线过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(3,0),且3AB=4OC,则抛物线的表达式为______________.图3-ZT-59.已知抛物线的顶点坐标为(1,9),它与x轴有两个交点,两交点间的距离为6,求抛物线的表达式.► 类型四 根据图形平移求表达式10.一个二次函数图象的形状与抛物线y =-2x 2相同,顶点坐标为(2,1),则这个二次函数的表达式为______________________________.11.将抛物线y =12x 2平移,使顶点的坐标为(t ,t 2),并且经过点(1,1),求平移后抛物线对应的函数表达式.12.把抛物线y =x 2先向左平移1个单位长度,再向下平移4个单位长度,得到如图3-ZT -6所示的抛物线.(1)求此抛物线的表达式;(2)在抛物线上存在一点M ,使△ABM 的面积为20,请直接写出点M 的坐标.图3-ZT -613.如图3-ZT -7,经过点A (0,-6)的抛物线y =12x 2+bx +c 与x 轴相交于B (-2,0),C 两点.(1)求此抛物线的表达式和顶点D 的坐标;(2)将(1)中求得的抛物线先向左平移1个单位长度,再向上平移m (m >0)个单位长度得到新抛物线y 1,若新抛物线y 1的顶点P 在△ABC 内,求m 的取值范围.图3-ZT -7详解详析1.解:把(-1,0),(0,-3),(4,5)代入y =ax 2+bx +c ,得⎩⎨⎧a -b +c =0,c =-3,16a +4b +c =5,解得⎩⎪⎨⎪⎧a =1,b =-2,c =-3.所以此抛物线的表达式为y =x 2-2x -3.2.解:(1)把(0,3),(3,0),(4,3)代入y =ax 2+bx +c ,得⎩⎨⎧c =3,9a +3b +c =0,16a +4b +c =3,解得⎩⎪⎨⎪⎧a =1,b =-4,c =3.所以抛物线的表达式为y =x 2-4x +3. (2)因为y =x 2-4x +3=(x -2)2-1,所以抛物线的顶点坐标为(2,-1),对称轴是直线x =2. (3)阴影部分的面积为2. 3.[答案] y =-x 2+2x +3[解析] ∵抛物线y =-x 2+bx +c 的对称轴为直线x =1,∴b2=1,解得b =2.∵抛物线与x 轴的一个交点为(3,0),∴0=-9+6+c ,解得c =3, 故抛物线对应的函数表达式为y =-x 2+2x +3. 4.解:∵二次函数图象的顶点为A (1,-4),∴设该二次函数的表达式为y =a (x -1)2-4.将(3,0)代入表达式,得a =1, 故该二次函数的表达式为y =(x -1)2-4,即y =x 2-2x -3.5.解:∵抛物线的对称轴是直线x =2且经过点A (1,0), ∴由抛物线的对称性可知,抛物线还经过点(3,0). 设抛物线的表达式为y =a (x -1)(x -3). 把(0,3)代入表达式,得3=3a , ∴a =1,∴该抛物线的表达式为y =(x -1)(x -3), 即y =x 2-4x +3.6.解:(1)∵抛物线的顶点坐标为(1,4), ∴设此抛物线的表达式为y =a (x -1)2+4. ∵抛物线过点B (0,3),∴3=a (0-1)2+4,解得a =-1,∴此抛物线的表达式为y =-(x -1)2+4,即y =-x 2+2x +3.(2)作点B 关于x 轴的对称点E (0,-3),连接AE 交x 轴于点P . 设直线AE 的表达式为y =kx +b ,则⎩⎨⎧k +b =4,b =-3,解得⎩⎨⎧k =7,b =-3,∴直线AE 的表达式为y =7x -3. 当y =0时,x =37,∴当P A +PB 的值最小时,点P 的坐标为(37,0).7.[解析] B 由抛物线与x 轴交于点(-1,0)和(3,0),设此抛物线的表达式为y =a (x +1)(x -3).又因为抛物线与y 轴交于点(0,-3),把x =0,y =-3代入y =a (x +1)(x -3),得-3=a (0+1)(0-3),即-3a =-3,解得a =1,故此抛物线的表达式为y =(x +1)(x -3)=x 2-2x -3.故选B.8.[答案] y =-x 2+2x +39.解:由抛物线的对称性可知抛物线与x 轴的两个交点分别为(-2,0)和(4,0),所以设其表达式为y =a (x +2)(x -4).将(1,9)代入表达式,得9=a (1+2)(1-4), 解得a =-1.所以抛物线的表达式为y =-(x +2)(x -4), 即y =-x 2+2x +8.10.[答案] y =-2x 2+8x -7或y =2x 2-8x +911.解:根据题意,得平移后的抛物线的表达式为y =12(x -t )2+t 2.∵平移后的抛物线经过点(1,1), ∴1=12(1-t )2+t 2,解得t =1或t =-13,∴平移后抛物线对应的函数表达式为y =12(x -1)2+1或y =12(x +13)2+19,即y =12x 2-x +32或y =12x 2+13x +16.12.解:(1)此抛物线的表达式为y =(x +1)2-4,即y =x 2+2x -3.(2)∵当y =0时,x 2+2x -3=0,解得x 1=-3,x 2=1,∴A (1,0),B (-3,0),∴AB =4.设点M 的坐标为(m ,n ). ∵△ABM 的面积为20, ∴12AB ·|n |=20,解得n =±10. 当n =10时,m 2+2m -3=10,解得m =-1+14或m =-1-14,∴M (-1+14,10)或M (-1-14,10);当n =-10时,m 2+2m -3=-10,此方程无解. 故点M 的坐标为(-1+14,10)或(-1-14,10). 13.解:(1)∵点A 的坐标为(0,-6),∴y =12x 2+bx -6.∵该抛物线过点B (-2,0),∴12×(-2)2-2b -6=0,解得b =-2, ∴此抛物线的表达式为y =12x 2-2x -6.∵y =12x 2-2x -6=12(x -2)2-8,∴抛物线的顶点D 的坐标为(2,-8).(2)平移后所得新抛物线的表达式为y 1=12(x -2+1)2-8+m ,即y 1=12(x -1)2-8+m ,∴顶点P 的坐标为(1,m -8).对于y =12x 2-2x -6,令y =0,得12x 2-2x -6=0,解得x 1=6,x 2=-2,∴C (6,0),∴直线AC 的表达式为y =x -6,当x =1时,y =-5. ∵点P 在△ABC 内,∴⎩⎨⎧m -8<0,m -8>-5,解得3<m <8.。
九年级数学二次函数表达式常见类型专项练习附答案

求二次函数表达式的常见类型名师点金:求二次函数的表达式是解决二次函数问题的重要保证,在求解二次函数的表达式时一般选用待定系数法,但在具体题目中要根据不同条件,设出恰当的表达式,往往可以使解题过程简便.)由函数的基本形式求表达式方法1 利用一般式求二次函数表达式1.【2016·黔南州】如图,已知二次函数y =x 2+bx +c 的图象与y 轴交于点C(0,-6),与x 轴的一个交点是A(-2,0). (1)求二次函数的表达式,并写出图象的顶点D 的坐标; (2)将二次函数的图象沿x 轴向左平移52个单位长度,当y<0时,求x 的取值范围.方法2 利用顶点法求二次函数表达式2.已知二次函数y =ax 2+bx +c ,当x =1时,有最大值8,其图象的形状、开口方向与抛物线y =-2x 2相同,则这个二次函数的表达式是( )A .y =-2x 2-x +3B .y =-2x 2+4C .y =-2x 2+4x +8D .y =-2x 2+4x +63.已知某个二次函数的最大值是2,图象顶点在直线y =x +1上,并且图象经过点(3,-6).求这个二次函数的表达式.方法3 利用交点式求二次函数表达式4.已知抛物线与x 轴交于A(1,0),B(-4,0)两点,与y 轴交于点C ,且AB =BC ,求此抛物线对应的函数表达式.方法4 利用平移法求二次函数表达式5.【中考·绥化】把二次函数y =2x 2的图象向左平移1个单位长度,再向下平移2个单位长度,平移后抛物线对应的函数表达式是______________.6.已知y =x 2+bx +c 的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数表达式为y =x 2-2x -3.(1)b =________,c =________; (2)求原函数图象的顶点坐标;(3)求两个图象顶点之间的距离.方法5 利用对称轴法求二次函数表达式 7.如图,已知抛物线y =-x 2+bx +c 的对称轴为直线x =1,且与x 轴的一个交点为(3,0),那么它对应的函数表达式是________________.8.如图,抛物线与x 轴交于A ,B 两点,与y 轴交于C 点,点A 的坐标为(2,0),点C 的坐标为(0,3),抛物线的对称轴是直线x =-12. (1)求抛物线对应的函数表达式;(2)M 是线段AB 上的任意一点,当△MBC 为等腰三角形时,求点M 的坐标.方法6 灵活运用方法求二次函数的表达式9.已知抛物线的顶点坐标为(-2,4),且与x 轴的一个交点坐标为(1,0),求抛物线对应的函数表达式.由函数图象中的信息求表达式10.如图是某个二次函数的图象,根据图象可知,该二次函数的表达式是()A.y=x2-x-2B.y=-12x2-12x+2C.y=-12x2-12x+1D.y=-x2+x+211.【中考·南京】某企业生产并销售某种产品,假设销售量与产量相等.如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义.(2)求线段AB所表示的y1与x之间的函数表达式.(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?由表格信息求表达式12.若y=ax2+bx+c,则由表格中信息可知y与x之间的函数关系式是()x -1 0 1ax2 1ax2+bx+c 8 3A.y=x2-4x+3B.y=x2-3x+4C.y=x2-3x+3 D.y=x2-4x+813.已知二次函数y=ax2+bx+c(a≠0)的自变量x和函数值y的部分对应值如下表:x …-32-1-1212132…y …-54-2-94-2-5474…则该二次函数的表达式为______________.几何应用中求二次函数的表达式14.【2016·安顺】某校校园内有一个大正方形花坛,如图①所示,它由四个边长为3 m的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图②所示,DG=1 m,AE=AF=x m,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是()(第14题)实际问题中求二次函数表达式15.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m,花园的面积为S m2.(1)求S与x之间的函数表达式;(2)若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.(第15题)答案1.解:(1)∵把C 点坐标(0,-6)代入二次函数的表达式得c =-6,把A 点坐标(-2,0)代入y =x 2+bx -6得b =-1, ∴二次函数的表达式为y =x 2-x -6. 即y =()x -122-254. ∴图象的顶点D 的坐标为()12,-254.(2)将二次函数的图象沿x 轴向左平移52个单位长度所得图象对应的函数表达式为y =(x +2)2-254. 令y =0,得(x +2)2-254=0, 解得x 1=12,x 2=-92.∵a>0,∴当y<0时,x 的取值范围是-92<x<12.2.D3.解:设二次函数图象的顶点坐标为(x ,2),则2=x +1,所以x =1,所以图象的顶点坐标为(1,2).所以设二次函数的表达式为y =a(x -1)2+2.将点(3,-6)的坐标代入上式,可得a =-2.所以该函数的表达式为y =-2(x -1)2+2,即y =-2x 2+4x.4.解:由A(1,0),B(-4,0)可知AB =5,OB =4. 又∵BC =AB ,∴BC =5.在Rt △BCO 中,OC =BC 2-OB 2=52-42=3, ∴C 点的坐标为(0,3)或(0,-3).设抛物线对应的函数表达式为y =a(x -1)(x +4),将点(0,3)的坐标代入得3=a(0-1)×(0+4),解得a =-34.将点(0,-3)的坐标代入得-3=a(0-1)×(0+4),解得a =34.∴该抛物线对应的函数表达式为y =-34(x -1)(x +4)或y =34(x -1)(x +4),即y =-34x 2-94x +3或y =34x 2+94x -3.点拨:若给出抛物线与x 轴的交点坐标或对称轴及抛物线与x 轴的两交点间的距离,通常可设交点式求解. 5.y =2x 2+4x 6.解:(1)2;0(2)原函数的表达式为y =x 2+2x =(x +1)2-1.∴其图象的顶点坐标为(-1,-1).(3)原函数图象的顶点为(-1,-1),新函数图象的顶点为(1,-4).由勾股定理易得两个顶点之间的距离为13. 7.y =-x 2+2x +38.解:(1)设抛物线对应的函数表达式为y =a ()x +122+k.把点(2,0),(0,3)的坐标代入,得⎩⎪⎨⎪⎧254a +k =0,14a +k =3.解得⎩⎪⎨⎪⎧a =-12,k =258.∴y =-12()x +122+258, 即y =-12x 2-12x +3.(2)由y =0,得-12()x +122+258=0, 解得x 1=2,x 2=-3,∴B(-3,0).①当CM =BM 时,∵BO =CO =3,即△BOC 是等腰三角形,∴当M 点在原点O 处时,△MBC 是等腰三角形. ∴M 点坐标为(0,0).②当BC =BM 时,在Rt △BOC 中,BO =CO =3,由勾股定理得BC =OC 2+OB 2=32,∴BM =3 2. ∴M 点坐标为(32-3,0).综上所述,点M 的坐标为(0,0)或(32-3,0).9.解:方法一:设抛物线对应的函数表达式为y =ax 2+bx +c ,由题意得⎩⎪⎨⎪⎧-b2a=-2,4ac -b 24a=4,a +b +c =0.解得⎩⎨⎧a =-49,b =-169,c =209.∴抛物线对应的函数表达式为y =-49x 2-169x +209.方法二:设抛物线对应的函数表达式为y =a(x +2)2+4,将点(1,0)的坐标代入得0=a(1+2)2+4,解得a =-49.∴抛物线对应的函数表达式为y =-49(x +2)2+4.即y =-49x 2-169x +209.方法三:∵抛物线的顶点坐标为(-2,4),与x 轴的一个交点坐标为(1,0),∴抛物线的对称轴为直线x =-2,与x 轴的另一个交点坐标为(-5,0).设抛物线对应的函数表达式为y =a(x -1)(x +5),将点(-2,4)的坐标代入得4=a(-2-1)×(-2+5), 解得a =-49.∴抛物线对应的函数表达式为y =-49(x -1)(x +5),即y =-49x 2-169x +209.点拨:本题分别运用了一般式、顶点式、交点式求二次函数表达式,求二次函数的表达式时要根据题目条件灵活选择方法,如本题中,第一种方法列式较复杂,且计算量大,第二、三种方法较简便,计算量小. 10.D11.解:(1)点D 的横坐标、纵坐标的实际意义:当产量为130 kg 时,该产品每千克生产成本与销售价相等,都为42元. (2)设线段AB 所表示的y 1与x 之间的函数表达式为y 1=k 1x +b 1. 因为y 1=k 1x +b 1的图象过点(0,60)与(90,42), 所以⎩⎨⎧b 1=60,90k 1+b 1=42.解方程组得⎩⎨⎧k 1=-0.2,b 1=60.所以所求函数表达式为y 1=-0.2x +60(0≤x ≤90).(3)设y 2与x 之间的函数表达式为y 2=k 2x +b 2.因为y 2=k 2x +b 2的图象过点(0,120)与(130,42), 所以⎩⎨⎧b 2=120,130k 2+b 2=42.解方程组得⎩⎨⎧k 2=-0.6,b 2=120.所以y 2与x 之间的函数表达式为y 2=-0.6x +120(0≤x ≤130). 设产量为x kg 时,获得的利润为W 元.当0≤x ≤90时,W =x[(-0.6x +120)-(-0.2x +60)]=-0.4(x -75)2+2 250.所以当x =75时,W 的值最大,最大值为2 250.当90<x ≤130时,W =x[(-0.6x +120)-42]=-0.6(x -65)2+2 535.当x =90时,W =-0.6×(90-65)2+2 535=2 160.由-0.6<0知,当x >65时,W 随x 的增大而减小,所以90<x ≤130时,W<2 160.因此,当该产品产量为75 kg 时,获得的利润最大,最大利润是2 250元.12.A 13. y =x 2+x -214.A 点拨:先求出△AEF 和△DEG 的面积,然后可得到五边形EFBCG 的面积,继而可得y 与x 的函数表达式.S △AEF =12AE ×AF =12x 2,S △DEG =12DG ×DE =12×1×(3-x)=3-x 2, S五边形EFBCG=S正方形ABCD-S △AEF -S △DEG =9-12x 2-3-x 2=-12x 2+12x +152, 则y =4×()-12x 2+12x +152=-2x 2+2x +30. ∵0<AE<AD ,∴0<x<3. ∴y =-2x 2+2x +30(0<x<3). 故选A .15.解:(1)∵AB =x m ,∴BC =(28-x)m . 于是易得S =AB·BC =x(28-x)=-x 2+28x. 即S =-x 2+28x(0<x <28). (2)由题意可知,⎩⎨⎧x ≥6,28-x ≥15.解得6≤x ≤13.由(1)知,S =-x 2+28x =-(x -14)2+196.易知当6≤x ≤13时,S 随x 的增大而增大,∴当x =13时,S 最大值=195,即花园面积的最大值为195 m 2.。
(完整版)二次函数表达式三种形式练习题

1.把二次函数y=x2﹣4x+5化成y=a(x﹣h)2+k(a≠0)的形式,结果正确的是()A.y=(x﹣2)2+5 B.y=(x﹣2)2+1 C.y=(x﹣2)2+9 D.y=(x﹣1)2+12.将y=(2x﹣1)•(x+2)+1化成y=a(x+m)2+n的形式为()A. B.C. D.3.与y=2(x﹣1)2+3形状相同的抛物线为()A.y=1+x2 B.y=(2x+1)2 C.y=(x﹣1)2 D.y=2x24.二次函数的图象的顶点坐标是(2,4),且过另一点(0,﹣4),则这个二次函数的解析式为()A.y=﹣2(x+2)2+4 B.y=﹣2(x﹣2)2+4 C.y=2(x+2)2﹣4 D.y=2(x﹣2)2﹣45.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )A.y=﹣3(x﹣1)2+3 B.y=3(x﹣1)2+3 C.y=﹣3(x+1)2+3 D.y=3(x+1)2+36.顶点为(6,0),开口向下,开口的大小与函数y=x2的图象相同的抛物线所对应的函数是()A.y=(x+6)2 B.y=(x﹣6)2 C.y=﹣(x+6)2 D.y=﹣(x﹣6)27.已知二次函数的图象经过点(﹣1,﹣5),(0,﹣4)和(1,1),则这二次函数的表达式为()A.y=﹣6x2+3x+4 B.y=﹣2x2+3x﹣4 C.y=x2+2x﹣4 D.y=2x2+3x﹣48.若二次函数y=x2﹣2x+c图象的顶点在x轴上,则c等于()A.﹣1 B.1C.D.29.如果抛物线经过点A(2,0)和B(﹣1,0),且与y轴交于点C,若OC=2.则这条抛物线的解析式是()A.y=x2﹣x﹣2 B.y=﹣x2﹣x﹣2或y=x2+x+2 C.y=﹣x2+x+2 D.y=x2﹣x﹣2或y=﹣x2+x+210.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于()A.8 B.14 C.8或14 D.﹣8或﹣1411.二次函数的图象如图所示,当﹣1≤x≤0时,该函数的最大值是( )A.3.125 B.4 C.2 D.012.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值3,则实数m的值为( )A.或﹣ B.或﹣ C.2或﹣ D.或﹣13.如果一条抛物线经过平移后与抛物线y=﹣x2+2重合,且顶点坐标为(4,﹣2),则它的解析式为.14.二次函数的图象如图所示,则其解析式为.15.若函数y=(m2﹣4)x4+(m﹣2)x2的图象是顶点在原点,对称轴是y轴的抛物线,则m= .16.二次函数图象的开口向上,经过(﹣3,0)和(1,0),且顶点到x轴的距离为2,则该二次函数的解析式为.17.如图,已知抛物线y=﹣x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是.18.二次函数y=ax2+bx+c的图象经过A(﹣1,0)、B(0,﹣3)、C(4,5)三点,求出抛物线解析式.19.二次函数图象过点(﹣3,0)、(1,0),且顶点的纵坐标为4,此函数关系式为.20.如图,一个二次函数的图象经过点A,C,B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C 在y轴的正半轴上,且AB=OC.则这个二次函数的解析式是.21.坐标平面内向上的抛物线y=a(x+2)(x﹣8)与x轴交于A、B两点,与y轴交于C点,若∠ACB=90°,则a的值是.22.平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.(1)求此抛物线的解析式.(2)求此抛物线顶点D的坐标和四边形ABCD的面积.23.已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.(1)求m、n的值;(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.24.已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.25.二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(1,0),与y轴的交点坐标为(0,﹣3).(1)求出b、c的值,并写出此二次函数的解析式;(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围.26.二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5).(1)求函数的关系式;(2)求函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△OA′B′的面积.27.二次函数y=﹣x2+bx+c的图象经过坐标原点,且与x轴交于A(﹣2,0).(1)求此二次函数解析式及顶点B的坐标;(2)在抛物线上有一点P,满足S△AOP=3,直接写出点P的坐标.28.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),A(﹣1,0),B(3,0),与y轴交于点C(0,3)连接BC.(1)求抛物线的解析式;(2)点D与点C关于抛物线对称轴对称,连接DB、DC,直线PD交直线BC于点P,且直线PD把△BCD分成面积相等的两部分,请直接写出直线PD的解析式.29.如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.(1)求点C的坐标;(2)求二次函数的解析式,并化成一般形式.30.已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图,点P是第一象限内抛物线上的一个动点,若点P使四边形ABPC的面积最大,求点P的坐标.1.B;2.C;3.D;4.B;5.A;6.D;7.D; 8.B;9.D;10.C; 11.C; 12.A;13.y=—(x—4)2-2; 14.y=-x2+2x+3; 15.—2; 16.y=x2+x-;17.y=-x2+2x+3;18.y=x2-2x-3;19.y=-x2-2x+3; 20.y=—x2+x+5;21.;。
求二次函数的表达式练习题(含答案)

二次函数的表达式一、选择题1.函数y =21x 2+2x +1写成y =a (x -h)2+k 的形式是=21(x -1)2+2 =21(x -1)2+21 =21(x -1)2-3 =21(x +2)2-1 2.抛物线y =-2x 2-x +1的顶点在第_____象限A.一B.二C.三D.四 3.不论m 取任何实数,抛物线y =a (x +m )2+m (a ≠0)的顶点都A.在y =x 直线上B.在直线y =-x 上C.在x 轴上D.在y 轴上4.任给一些不同的实数n ,得到不同的抛物线y =2x 2+n ,如当n =0,±2时,关于这些抛物线有以下结论:①开口方向都相同;②对称轴都相同;③形状都相同;④都有最低点,其中判断正确的个数是个 个 个 个 5.二次函数y =x 2+p x +q 中,若p+q=0,则它的图象必经过下列四点中A.(-1,1)B.(1,-1)C.(-1,-1)D.(1,1)图36.下列说法错误的是A.二次函数y =-2x 2中,当x =0时,y 有最大值是0B.二次函数y =4x 2中,当x >0时,y 随x 的增大而增大C.在三条抛物线y =2x 2,y =-,y =-x 2中,y =2x 2的图象开口最大,y =-x 2的图象开口最小D.不论a 是正数还是负数,抛物线y =ax 2(a ≠0)的顶点一定是坐标原点 7.已知二次函数y =x 2+(2k +1)x +k 2-1的最小值是0,则k 的值是A.43B.-43C.45D.-458.小颖在二次函数y =2x 2+4x +5的图象上,依横坐标找到三点(-1,y 1),(21,y 2), (-321,y 3),则你认为y 1,y 2,y 3的大小关系应为>y 2>y 3 >y 3>y 1 >y 1>y 2 >y 2>y 1 二、填空题9.抛物线y =21(x +3)2的顶点坐标是______.10.将抛物线y =3x 2向上平移3个单位后,所得抛物线的顶点坐标是______.11.函数y =34x -2-3x 2有最_____值为_____.12.已知抛物线y =ax 2+bx +c 的图象顶点为(-2,3),且过(-1,5),则抛物线的表达式为______.13.二次函数y =mx 2+2x +m -4m 2的图象过原点,则此抛物线的顶点坐标是______. 三、解答题14.根据已知条件确定二次函数的表达式(1)图象的顶点为(2,3),且经过点(3,6);(2)图象经过点(1,0),(3,0)和(0,9);(3)图象经过点(1,0),(0,-3),且对称轴是直线x=2。
九年级数学二次函数专项训练含答案-精选5篇

九年级数学二次函数专题精练含答案一、单选题1.关于二次函数22(4)6y x =-+的最大值或最小值,下列说法正确的是( ) A .有最大值4 B .有最小值4 C .有最大值6 D .有最小值6 2.已知抛物线24y x x c =-++经过点(4,3),那么下列各点中,该抛物线必经过的点是( )A .(0,2)B .(0,3)C .(0,4)D .(0,5) 3.在平面直角坐标系中,已知抛物线245y x x =-+,将该抛物线沿y 轴翻折所得的抛物线的表达式为( )A .245y x x =--+B .245y x x =++C .245y x x =-+-D .245y x x =--- 4.正方形的边长为4,若边长增加x ,那么面积增加y ,则y 关于x 的函数表达式为( ) A .216y x =+ B .2(4)y x =+ C .28y x x =+ D .2164y x =- 5.把抛物线22y x =向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( )A .22(2)1y x =-+-B .22(2)1y x =--+C .22(2)1y x =++D .22(2)1y x =--6.如图,二次函数2y ax bx c =++的图象关于直线1x =对称,与x 轴交于1(,0)A x ,2(,0)B x 两点,若121x -<<-,则下列四个结论:①234x <<,①320a b +>,①24b a c ac >++,①a c b >>.正确结论的个数为( )A .1个B .2个C .3个D .4个7.对于抛物线23(1)2y x =-+-,下列说法正确的是( )A .抛物线开口向上B .当1x >-时,y 随x 增大而减小C .函数最小值为﹣2D .顶点坐标为(1,﹣2)8.关于二次函数()215y x =-+,下列说法正确的是( )A .函数图象的开口向下B .函数图象的顶点坐标是()1,5-C .该函数有最大值,是大值是5D .当1x >时,y 随x 的增大而增大 9.已知A (−3,−2) ,B (1,−2),抛物线y =ax 2+bx +c (a >0)顶点在线段AB 上运动,形状保持不变,与x 轴交于C ,D 两点(C 在D 的右侧),下列结论:①c ≥−2 ;①当x >0时,一定有y 随x 的增大而增大;①若点D 横坐标的最小值为−5,点C 横坐标的最大值为3;①当四边形ABCD 为平行四边形时,a =12. 其中正确的是( )A .①①B .①①C .①①D .①①① 10.已知二次函数2243y mx m x =--(m 为常数,0m ≠),点(),p p P x y 是该函数图象上一点,当04p x ≤≤时,3p y ≤-,则m 的取值范围是( )A .m 1≥或0m <B .m 1≥C .1m ≤-或0m >D .1m ≤-11.已知函数()211y ax a x =-++,则下列说法不正确的个数是( )①若该函数图像与x 轴只有一个交点,则1a =①方程()2110ax a x -++=至少有一个整数根①若11x a<<,则()211y ax a x =-++的函数值都是负数 ①不存在实数a ,使得()2110ax a x -++≤对任意实数x 都成立A .0B .1C .2D .312.如图,在正方形ABCD 中,4AB =,点P 从点A 出发沿路径A B C →→向终点C 运动,连接DP ,作DP 的垂直平分线MN 与正方形ABCD 的边交于M ,N 两点,设点P 的运动路程为x ,PMN 的面积为y ,则下列图象能大致反映y 与x 函数关系的是( )A .B .C .D .二、填空题13.已知点(3,a )在抛物线y =-2x 2+2x 上,则=a ______.14.如图是二次函数21y ax bx c =++ 和一次函数y 2=kx +t 的图象,当y 1≥y 2时,x 的取值范围是_____.15.小亮同学在探究一元二次方程2ax bx c 0++=的近似解时,填好了下面的表格:根据以上信息请你确定方程2ax bx c 0++=的一个解的范围是________.16.已知二次函数223y x x =--+,当12a x时,函数值y 的最小值为1,则a 的值为_______.17.已知抛物线2122y x bx =+-与x 轴交于A ,B 两点,与y 轴交于C 点.(1)若(1,0)A -,则b =______.(2)若(1,0)M -,(1,0)N ,抛物线2122y x bx =+-与线段MN 没有交点,则b 的取值范围为______.三、解答题18.已知抛物线经过点()1,0A -,()5,0B ,()0,5C ,求该抛物线的函数关系式 19.如图,抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点,其中点A 在y 轴上,且此抛物线与x 轴的一个交点为()3,0C -.(1)求抛物线的解析式(2)在抛物线对称轴l 上找一点M ,使MBC ∆的周长最小,请求出这个周长的最小值.20.如图,一次函数y A 、B ,二次函数2y bx c ++图象过A 、B 两点.(1)求二次函数解析式;(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.21.如图,二次函数y =ax 2+bx +c 的图象与x 轴交于点A (﹣2,0)和点B (8,0),与y 轴交于点C (0,﹣8),连接AC ,D 是抛物线对称轴上一动点,连接AD ,CD ,得到①ACD .(1)求该抛物线的函数解析式.(2)①ACD 周长能否取得最小值,如果能,请求出D 点的坐标;如果不能,请说明理由.(3)在(2)的条件下,在抛物线上是否存在点E ,使得①ACE 与①ACD 面积相等,如果存在,请求出点的坐标;如果不存在,请说明理由.参考答案1--10DBCCD BBDDA 11--12CA13.-1214.﹣1≤x ≤215.3.24x 3.25<<16.1-17. 32- 3322b -<< 18.解:①抛物线经过点()1,0A -,()5,0B ,()0,5C ,①设抛物线的表达式为()()15y a x x =+-,将点()0,5C 代入得:55a =-,解得:1a =-,①()()21545y x x x x =-+-=-++.①该抛物线的函数关系式为245y x x =-++.19..解:(1)抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A , 令0,x = 则3,y = ∴ 点()0,3A把()0,3A ,()3,0C -代入212y x bx c =++得: 39302c b c =⎧⎪⎨-+=⎪⎩, 解得:523b c ⎧=⎪⎨⎪=⎩, ∴抛物线的解析式是215322y x x =++; (2)将直线132y x =+与二次函数215322y x x =++联立得方程组: 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得:0x =或4x =-,04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ,()4,1B ∴-BC ∴==如图,要使MBC △的周长最小,则MB MC +最小,设二次函数215322y x x =++与x 轴的另一交点为D ,抛物线的对称轴为:552,1222x=-=-⨯()3,0C-∴点()2,0D-,连接,BD交对称轴于,MMD MC∴=,此时,MB MC MB MD BD+=+=最小,此时:BD=MBC∴20.解:(1)对于y x=x=0时,y=当y=0时,03x-=,妥得,x=3①A(3,0),B(0,把A(3,0),B(0,2y bx c++得:+=0b cc⎧⎪⎨=⎪⎩解得,bc⎧=⎪⎨⎪=⎩①抛物线的解析式为:2y x x=-(2)抛物线的对称轴为直线12bxa=-==故设P(1,p),Q(m,n)①当BC为菱形对角线时,如图,①B ,C 关于对称没对称,且对称轴与x 轴垂直,①①BC 与对称轴垂直,且BC //x 轴①在菱形BQCP 中,BC ①PQ①PQ ①x 轴①点P 在x =1上,①点Q 也在x =1上,当x =1时,211y①Q (1,); ①当BC 为菱形一边时,若点Q 在点P 右侧时,如图,①BC //PQ ,且BC =PQ①BC //x 轴,①令y =2y 解得,120,2x x ==①(2,C①PQ=BC=22①PB=BC=2①迠P在x轴上,①P(1,0)①Q(3,0);若点Q在点P的左侧,如图,同理可得,Q(-1,0)综上所述,Q点坐标为(1,)或(3,0)或(-1,0)21.解:(1)由题意可得:0=4206488a b ca b cc-+⎧⎪=++⎨⎪=-⎩,解得:1238abc⎧=⎪⎪=-⎨⎪=-⎪⎩,①抛物线的解析式为:y=12x2﹣3x﹣8;(2)△ACD周长能取得最小值,①点A(﹣2,0),点B(8,0),①对称轴为直线x=3,①①ACD周长=AD+AC+CD,AC是定值,①当AD+CD取最小值时,△ACD周长能取得最小值,①点A,点B关于对称轴直线x=3对称,①连接BC交对称轴直线x=3于点D,此时AD+CD有最小值,设直线BC 解析式为:y =kx ﹣8,①0=8k ﹣8,①k =1,①直线BC 解析式为:y =x ﹣8,当x =3,y =﹣5,①点D (3,﹣5);(3)存在,①点A (﹣2,0),点C (0,﹣8),①直线AC 解析式为y =﹣4x ﹣8,如图,①①ACE 与①ACD 面积相等,①DE ①AC ,①设DE 解析式为:y =﹣4x +n ,①﹣5=﹣4×3+n ,①n =7,①DE 解析式为:y =﹣4x +7, 联立方程组可得:2471382y x y x x =-+⎧⎪⎨=--⎪⎩,解得:12111x y ⎧=⎪⎨=-⎪⎩,22111x y ⎧=⎪⎨=⎪⎩, ①点E1,﹣1,).九年级上册数学二次函数同步练习一、单选题1.下列函数中,是二次函数的是( ) A .y =(2x ﹣1)2 B .y =(x +1)2﹣x 2 C .y =ax 2D .y =2x +32.若抛物线258(3)23m m y m x x -+=-+-是关于x 的二次函数,那么m 的值是( )A .3B .2-C .2D .2或33.若抛物线y =x 2-x -2经过点A (3,a ),则a 的值是( ) A .2B .4C .6D .84.已知二次函数2135y x x =-+,则其二次项系数a ,一次项系数b ,常数项c 分别是( ) A .1,3,5a b c ==-= B .1,3,5a b c ===C .5,3,1a b c ===D .5,3,1a b c ==-=5.如果函数2(2)25y a x x =-+-是二次函数,则a 的取值范围是( ) A .2a ≠ B .a≥0C .a=2D .a>06.下列函数中①31y x ;①243y x x =-;①1y x=;①225=-+y x ,是二次函数的有() A .①①B .①①C .①①D .①①7.若抛物线2y x bx c =-++经过点()2,3-,则247c b --的值是( ) A .6B .7C .8D .208.函数y=ax2+bx+c(a ,b ,c 是常数)是二次函数的条件是( ) A .a≠0,b≠0,c≠0 B .a<0,b≠0,c≠0 C .a>0,b≠0,c≠0 D .a≠0二、填空题 9.若()2321m m y m x --=+是二次函数,则m 的值为______.10.若22ay x -=是二次函数,则=a ________.11.在二次函数21y x =-+中,二次项系数、一次项系数、常数项的和为_____. 12.下列函数一定是二次函数的是__________.①2y ax bx c =++;①3y x =-;①2431y x x =-+;①2(1)y m x bx c =-++;①y =(x -3)2-x 213.当常数m ≠______时,函数y =(m 2﹣2m ﹣8)x 2+(m +2)x +2是二次函数;当常数m =___时,这个函数是一次函数. 14.已知函数2135m y x -=-① 当m = _________时,y 是关于x 的一次函数; ① 当m =_________时,y 是关于x 的二次函数 .15.二次函数()22339y m x x m =+++-的图象经过原点,则m =__________.16.已知二次函数2y x bx 3=-++,当x 2=时,y 3=.则这个二次函数的表达式是________. 三、解答题17.下列函数中(x ,t 是自变量),哪些是二次函数? 22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++.18.已知函数y =(m 2-2)x 2+(m x +8. (1)若这个函数是一次函数,求m 的值; (2)若这个函数是二次函数,求m 的取值范围.19.若函数y=(a -1)x b+1+x 2+1是二次函数,试讨论a 、b 的取值范围.20.篱笆墙长30m ,靠墙围成一个矩形花坛,写出花坛面积y(m 2)与长x 之间的函数关系式,并指出自变量的取值范围.参考答案:1.A 2.C 3.B 4.D 5.A 6.B 7.B 8.D 9.4 10.2± 11.0 12.①13. 4,-2 4 14. 1 3215.316.2y x 2x 3=-++17.2132y x =-+和215s t t =++是二次函数18.(1)m (2)m ≠m ≠19.①a≠0;①b=0或-1,a 取全体实数①当a=1,b 为全体实数时,y=x 2+1是二次函数 20.y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数的图象与性质练习题(附答案)一.选择题1.如果在二次函数的表达式y =ax 2+bx +c 中,a >0,b <0,c <0,那么这个二次函数的图象可能是( )A.B.C.D.2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为()A.﹣2B.2C.±2D.03.已知A(,y1),B(2,y2),C(﹣,y3)是二次函数y=3(x﹣1)2+k图象上三点,则y1、y2、y3的大小关系为()A.y1>y2>y3B.y2>y1>y3C.y3>y2>y1D.y2>y3>y14.二次函数的部分图象如图所示,对称轴是直线x=﹣1,则这个二次函数的表达式为()A.y=﹣x2+2x+3B.y=x2+2x+3C.y=﹣x2+2x﹣3D.y=﹣x2﹣2x+3 5.在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为()A.B.C.D.6.关于抛物线y=﹣x2+2x﹣3的判断,下列说法正确的是()A.抛物线的开口方向向上B.抛物线的对称轴是直线x=﹣1C.抛物线对称轴左侧部分是下降的D.抛物线顶点到x轴的距离是27.已知二次函数y=x2﹣4x+5(0≤x≤3),则它的最大值是()A.1B.2C.3D.58.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有()A.①②④B.①②⑤C.①③⑤D.②④⑤9.已知函数y=2(x+1)2+1,则()A.当x<1 时,y随x的增大而增大B.当x<1 时,y随x的增大而减小C.当x<﹣1 时,y随x的增大而增大D.当x<﹣1 时,y随x的增大而减小10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的有()个.①abc>0;②2a+b=0;③9a+3b+c<0;④4ac﹣b2<0;⑤a+b≥m(am+b)(m为任意实数).A.3B.2C.1D.0二.填空题11.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是.(请用“>”连接排序)12.抛物线y=3x2+6x+11的顶点坐标为.13.二次函数y=3(x﹣1)2+5的最小值为.14.已知二次函数y=2x2+bx+4顶点在x轴上,则b=.15.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为.16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号).三.解答题17.已知二次函数的顶点坐标为A(1,﹣4),且经过点B(3,0).(1)求该二次函数的解析式;(2)判断点C(2,﹣3)是否在该函数图象上,并说明理由.18.如图,已知直线l过点A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP=4,试求二次函数的表达式.19.如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).(1)求m的值;(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.20.已知二次函数y=a(x+a)(x+a﹣1).(1)当a=2时,求该二次函数图象的对称轴.(2)当a<0时,判断该二次函数图象的顶点所在的象限,并说明理由.(3)当0<x<3时,y随着x增大而增大,求a的取值范围.21.已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),求△OAB的面积.22.抛物线y=﹣x2+bx+c经过点A(3,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.(1)求抛物线的解析式;(2)连接AB、AC、BC,求△ABC的面积.23.如图,在平面直角坐标系中,直线AB与抛物线y=﹣x2+bx+c交于A(﹣1,0)和B(2,3)两点,抛物线与y轴交于点C.(1)求一次函数和二次函数的解析式;(2)求△ABC的面积.参考答案一.选择题1.解:∵a>0,b<0,c<0,∴﹣>0,∴抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴,故选:C.2.解:∵y=(m+2)x|m|+2是y关于x的二次函数,∴|m|=2且m+2≠0.解得m=2.故选:B.3.解:∵二次函数y=3(x﹣1)2+k图象的对称轴为直线x=1,而A(,y1)到直线x=1的距离最近,C(﹣,y3)到直线x=1的距离最远,∴y3>y2>y1.故选:C.4.解:由图象知抛物线的对称轴为直线x=﹣1,设抛物线解析式为y=a(x+1)2+k,将(﹣3,0)、(0,3)代入,得:,解得:,则抛物线解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,故选:D.5.解:A、由抛物线可知,a<0,x=﹣<0,得b<0,由直线可知,a<0,b<0,故本选项正确;B、由抛物线可知,a>0,由直线可知,a<0,故本选项错误;C、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b>0,故本选项错误;D、由抛物线可知,a>0,由直线可知,a<0,故本选项错误.故选:A.6.解:∵y=﹣x2+2x﹣3=﹣(x﹣1)2﹣2,∴抛物线开口向下,对称轴为x=1,顶点坐标为(1,﹣2),在对称轴左侧,y随x的增大而增大,∴A、B、C不正确;∵抛物线顶点到x轴的距离是|﹣2|=2,∴D正确,故选:D.7.解:y=x2﹣4x+5=(x﹣2)2+1,由于0≤x≤3,所以当x=2时,y有最小值1,当x=0时,y有最大值5.故选:D.8.解:根据图象可知:①对称轴﹣>0,故ab<0,正确;②方程ax2+bx+c=0的根为x1=﹣1,x2=3,正确;③x=1时,y=a+b+c<0,错误;④当x<1时,y随x值的增大而减小,错误;⑤当y>0时,x<﹣1或x>3,正确.正确的有①②⑤.故选:B.9.解:∵y=2(x+1)2+1,∴当x>﹣1时,y随x的增大而增大,故选项A错误,当x<﹣1时,y随x的增大而减小,故选项B错误、选项C错误、选项D正确;故选:D.10.解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a>0,∵抛物线与y轴的交点坐标在x轴上方,∴c>0,∴abc<0,所以①错误;∵b=﹣2a,∴2a+b=0,所以②正确;∵x=3时,y<0,∴9a+3b+c<0,所以③正确.∵抛物线与x轴有2个交点,∴Δ=b2﹣4ac>0,即4ac﹣b2<0,所以④正确;∵抛物线的对称轴为直线x=1,∴函数的最大值为a+b+c,∴a+b+c≥am2+bm+c(m为任意实数),即a+b≥m(am+b),所以⑤正确.故选:C.二.填空题11.解:如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,③y=a3x2的开口大于④y=a4x2的开口,开口向下,则a4<a3<0,故a1>a2>a3>a4.故答案为:a1>a2>a3>a412.解:∵y=3x2+6x+11=3(x+1)2+8,∴抛物线y=3x2+6x+11的顶点坐标为(﹣1,8),故答案为(﹣1,8).13.解:由于二次函数y=3(x﹣1)2+5中,a=3>0,所以当x=1时,函数取得最小值为5,故答案为5.14.解:∵二次函数y=2x2+bx+4顶点在x轴上,∴=0,解得b=,故答案为:±4.15.解:∵二次函数y=x2﹣2x+1=(x﹣1)2,∴当x>1时,y随x的增大而增大,∴在2≤x≤5范围内,当x=2时,y取得最小值,此时y=(2﹣1)2=1,故答案为:1.16.解:∵抛物线的对称轴为直线x=﹣=1,∴2a+b=0,所以①正确;∵x=﹣1时,y<0,∴a﹣b+c<0,即a+c<b,所以②错误;∵抛物线与x轴的一个交点为(﹣2,0)而抛物线的对称轴为直线x=1,∴抛物线与x轴的另一个交点为(4,0),所以③错误;∵抛物线开口向上,∴a>0,∴b=﹣2a<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以④正确.故答案为①④.三.解答题17.解:(1)设二次函数的解析式是y=a(x﹣h)2+k,∵二次函数的顶点坐标为A(1,﹣4),∴y=a(x﹣1)2﹣4,∵经过点B(3,0),∴代入得:0=a(3﹣1)2﹣4,解得:a=1,∴y=(x﹣1)2﹣4,即二次函数的解析式为y=x2﹣2x﹣3;(2)点C(2,﹣3)在该函数图象上,理由是:把C(2,﹣3)代入y=x2﹣2x﹣3得:左边=﹣3,右边=4﹣4﹣3=﹣3,即左边=右边,所以点C在该函数的图象上.18.解:设直线l的解析式为y=kx+b,把A(4,0),B(0,4)分别代入得,解得,∴直线l的关系式为y=﹣x+4,设P(t,﹣t+4),∵S△AOP=4,∴×4×(﹣t+4)=4,解得t=2,∴P(2,2),把P(2,2)代入y=ax2得4a=2,解得a=,∴二次函数的表达式为y=x2.19.解:(1)把B(1,1)代入y=ax2得:a=1,∴抛物线解析式为y=x2.把A(m,4)代入y=x2得:4=m2,∴m=±2.∵点A在二象限,∴m=﹣2.(2)观察函数图象可知:当﹣2<x<1时,直线在抛物线的上方,∴n的取值范围为:﹣2<n<1.20.解:(1)当a=2时,y=2(x+2)(x+1),∴二次函数的对称轴为x=.(2)由题知二次函数与x轴的交点坐标为(﹣a,0),(1﹣a,0);∵a<0,∴二次函数的开口方向向下;又﹣a>0,1﹣a>0,所以对称轴所在直线为x==>0,当x=时,y=﹣>0,所以顶点坐标(,﹣)在第一象限.(3)由(2)知,二次函数的对称轴为直线x=,∵当0<x<3时,y随着x增大而增大,∴当a>0时,≤0,解得a≥;当a<0,≥3,解得a≤﹣.∴a的取值范围为a≥或a≤﹣.21.解:∵一次函数y=kx﹣2的图象相过点A(﹣1,﹣1),∴﹣1=﹣k﹣2,解得k=﹣1,∴一次函数表达式为y=﹣x﹣2,∴令x=0,得y=﹣2,∴G(0,﹣2),∵y=ax2过点A(﹣1,﹣1),∴﹣1=a×1,解得a=﹣1,∴二次函数表达式为y=﹣x2,由一次函数与二次函数联立可得,解得,,∴S△OAB=OG•|A的横坐标|+OG•点B的横坐标=×2×1+×2×2=1+2=3.22.解:(1)∵抛物线经过A、B(0,3)∴由上两式解得∴抛物线的解析式为:;(2)由(1)抛物线对称轴为直线x=把x=代入,得y=4则点C坐标为(,4)设线段AB所在直线为:y=kx+b,则有,解得∴AB解析式为:∵线段AB所在直线经过点A、B(0,3)抛物线的对称轴l于直线AB交于点D∴设点D的坐标为D将点D代入,解得m=2∴点D坐标为,∴CD=CE﹣DE=2过点B作BF⊥l于点F∴BF=OE=∵BF+AE=OE+AE=OA=∴S△ABC=S△BCD+S△ACD=CD•BF+CD•AE∴S△ABC=CD(BF+AE)=×2×=23.解:(1)∵抛物线y=﹣x2+bx+c交于A(﹣1,0)和B(2,3)两点∴,解得:,∴抛物线解析式为y=﹣x2+2x+3,设直线AB的解析式为y=mx+n(m≠0),则,解得,∴直线AB的解析式为y=x+1;(2)令x=0,则y=﹣x2+2x+3=3,∴C(0,3),则OC=3,BC=2,BC∥x轴,∴S△ABC=×BC×OC==3.九年级数学上册二次函数单元综合测试卷一.选择题(共10小题)1.下列各式中,是y关于x的二次函数的是()A.y=4x B.y=3x﹣5C.y=D.y=2x2+12.已知:a>b>c,且a+b+c=0,则二次函数y=ax2+bx+c的图象可能是下列图象中的()A.B.C.D.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2 5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣66.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+17.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1 8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.49.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°二.填空题(共6小题)11.函数是二次函数,则m的值为.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,则点B的横坐标.x B的值为.13.已知二次函数y=ax2开口向上,且|2﹣a|=3,则a=.14.已知抛物线y=x2﹣3x+1的图象上有一点A(m,n),则m﹣n的最大值是.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,交抛物线于另一点D,若AB+CD=3,则c的值为.16.如图,在矩形ABCD中,AB=12,BC=16,点E、F分别是边AB、BC上的动点,且EF=10,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为.三.解答题(共7小题)17.看图回答.(1)当y=0时,求x的值;(2)当y>5时,求x的范围;(3)y随x的增大而增大时,求x的范围.18.已知二次函数y=x2﹣6x+8.(1)将解析式化成顶点式;(2)写出它的开口方向、对称轴和顶点坐标;(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.19.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.20.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在云南省广泛种植.长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售,平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)若降价2元,则每天的销售利润是多少元(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)(3)将商品的销售单价定为多少元时,商场每天销售该商品获得的利润w最大?最大利润是多少元?21.如图,抛物线与x轴交于A(﹣1,0)、B(4,0),与y轴交于C.(1)求抛物线的解析式;(2)如图1,已知线段DE与线段BC关于平面内某点成中心对称,其中DE的两端点刚好一个落在抛物线上,一个落在对称轴上,求落在对称轴上的点的坐标;(3)如图2,点M为第二象限抛物线上,作MN∥BC交抛物线于点N,直线NB、MC 交于点P,求P点的横坐标.22.在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y'),给出如下定义:若y'=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)点(﹣5,﹣2)的“可控变点”坐标为;(2)若点P在函数y=﹣x2+16的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;(3)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,求实数a的取值范围.23.在平面直角坐标系中,抛物线y=x2+bx+c经过A(﹣4,0),点M为抛物线的顶点,点B在y轴上,直线AB与抛物线在第一象限交于点C(2,6),如图①.(1)求抛物线解析式;(2)直线AB的函数解析式为,点M的坐标为.(3)在y轴上找一点Q,使得△AMQ的周长最小,具体作法如图②,作点A关于y轴的对称点A',连接MA′交y轴于点Q,连接AM,AQ,此时△AMQ的周长最小,请求出点Q的坐标;(4)在坐标平面内是否存在点N,使以点A,O,C,N为顶点的四边形是平行四边形?若存在请直接写出点N的坐标;若不存在,请说明理由.参考答案一.选择题(共10小题)1.下列各式中,是y关于x的二次函数的是()A.y=4x B.y=3x﹣5C.y=D.y=2x2+1解:A.根据二次函数的定义,y=4x是一次函数,不是二次函数,故A不符合题意.B.根据二次函数的定义,y=3x﹣5不是二次函数,是一次函数,故B不符合题意.C.根据二次函数的定义,y=是反比例函数,不是二次函数,故C不符合题意.D.根据二次函数的定义,y=2x2+1是二次函数,故D符合题意.故选:D.2.已知:a>b>c,且a+b+c=0,则二次函数y=ax2+bx+c的图象可能是下列图象中的()A.B.C.D.解:A、由图知a>0,﹣=1,c>0,即b<0,∵已知a>b>c,故本选项错误;B、由图知a<0,而已知a>b>c,且a+b+c=0,必须a>0,故本选项错误;C、图C中条件满足a>b>c,且a+b+c=0,故本选项正确;D、∵a+b+c=0,即当x=1时a+b+c=0,与图中与x轴的交点不符,故本选项错误.故选:C.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)解:∵二次函数可化为y=(x﹣3)2+5,∴二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是(3,5),故选:D.4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2解:y=x2+2x﹣1=(x2+2x+1)﹣2=(x+1)2﹣2,即y=(x+1)2﹣2.故选:D.5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣6解:y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2,∴当x<2时,y随着x增大而增大,∴当x=时有最大值y=﹣2(﹣2)2+2=﹣2.5,故选:C.6.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+1解:设所求的抛物线解析式为y=a(x﹣3)2+1,∵所求抛物线与函数y=的图象相同且开口方向相反,∴a=﹣,∴所求的抛物线解析式为y=﹣(x﹣3)2+1.故选:D.7.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1解:当x=﹣1时,y1=(x﹣1)2=(﹣1﹣1)2=4;当x=1时,y2=(x﹣1)2=(1﹣1)2=0;当x=2时,y3=(x﹣1)2=(2﹣1)2=1,所以y2<y3<y1.故选:C.8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.4解:根据表格数据可知:抛物线的对称轴是直线x==,∴③错误;∵抛物线与x轴的一个交点为(﹣2,0),∴抛物线与x轴的另一个交点为(3,0),∴方程ax2+bx+c=0有两根为x1=﹣2,x2=3;故①正确;从表格可知当x=0时,y=6,∴抛物线与y轴的交点为(0,6);∴②正确;从表格可知:当x<时,y随x的增大而增大,当x>时,y随x的增大而减小,∴抛物线开口向下,故④错误.故选:B.9.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对解:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∴∠OBE=∠OCF=45°,∵BE=CF,∴△BOE≌△COF,∴OE=OF,∠BOE=∠COF,∴∠BOE+∠COE=∠COF+∠COE,即∠EOF=∠BOC=90°,且S△COE+S△COF=S△COE+S△BOE,即S四边形OECF=S△BOC=S正方形ABCD=×4×4=4,由垂线段最短可得,当OE⊥BC时,OE=BC=×4=2,△OEF面积取最小值为×2×2=2,∴结论Ⅰ和Ⅱ都对,结论Ⅲ错,故选:A.10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°解:把(25,0.725),(50,0.06),(60,0.09)代入y=ax2+bx+c得:,解得,∴y=0.0001x2﹣0.008x+0.21=0.0001(x﹣40)2+0.05,∵0.0001>0,∴x=40时,y最小为0.05,∴燃气灶烧开一壶水最节省燃气的旋钮角度约为40°,故选:B.二.填空题(共6小题)11.函数是二次函数,则m的值为3.解:∵函数是二次函数,∴m2﹣7=2且m+3≠0,解得:m=3.则m的值为3.故答案为:3.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,则点B的横坐标.x B的值为5.解:∵y=x2﹣4x+c,∴抛物线开口向上,对称轴为直线x=﹣=2,∴点A,B关于直线x=2对称,∵点A横坐标为﹣1,∴点B横坐标为5,故答案为:5.13.已知二次函数y=ax2开口向上,且|2﹣a|=3,则a=5.解:∵|2﹣a|=3,∴2﹣a=±3,解得:a=﹣1或5,又二次函数y=ax2开口向上,则a>0,故a=5.故答案为:5.14.已知抛物线y=x2﹣3x+1的图象上有一点A(m,n),则m﹣n的最大值是3.解:∵点A(m,n)在抛物线y=x2﹣3x+1上,∴n=m2﹣3m+1,∴m﹣n=﹣m2+4m﹣1=﹣(m﹣2)2+3,∴当m=2时,m﹣n有最大值为3,故答案为:3.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,交抛物线于另一点D,若AB+CD=3,则c的值为﹣.解:设A(x1,0),B(x2,0),令y=0,则y=﹣x2+2x+c=0,由根与系数的关系得:x1+x2=2,x1•x2=﹣c,则AB=|x1﹣x2|===2,令x=0,则y=c,∴C(0,c),∵CD∥x轴,∴点D纵坐标为c,当y=c时,则﹣x2+2x+c=c,解得:x=2,或x=0,∴D(2,c),∴CD=2,∵AB+CD=3,∴2+2=3,解得:c=﹣,故答案为:﹣.16.如图,在矩形ABCD中,AB=12,BC=16,点E、F分别是边AB、BC上的动点,且EF=10,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为142.解:连接AC,过B作BH⊥AC于H,以B为圆心,BG为半径作圆,交BH于G',如图:∵四边形ABCD是矩形,∴∠EBF=90°,∵EF=10,点G是EF的中点,∴BG=EF=10=5,∴G在以B为圆心,5为半径的弧上,当G运动到G'时,S△ACG最小,此时四边形AGCD 面积的最小值,最小值即为四边形AG'CD的面积,∵AB=12=CD,BC=16=AD,∴AC=20,S△ACD=×12×16=96,∴BH==,∴G'H=BH﹣5=﹣5=,∴S△ACG'=AC•G'H=×20×=46,∴S四边形AG'CD=S△ACD+S△ACG'=46+96=142,即四边形AGCD面积的最小值是142.故答案为:142.三.解答题(共7小题)17.看图回答.(1)当y=0时,求x的值;(2)当y>5时,求x的范围;(3)y随x的增大而增大时,求x的范围.解:(1)由图象可知,抛物线经过点(﹣1,0),对称轴为直线x=1,∴抛物线与x轴的另一个交点为(3,0),∴当y=0时,x的值为﹣1和3;(2)∵抛物线经过点(﹣1,0),(3,0),(0,﹣3),∴设抛物线的解析式为y=a(x+1)(x﹣3),代入(0,﹣3)得,﹣3=﹣3a,解得a=1,∴抛物线的解析式为y=(x+1)(x﹣3),令y=5得5=(x+1)(x﹣3),解得x1=4,x2=﹣2,∴当y>5时,求x的范围是x>4或x<﹣2;(3)∵y=(x+1)(x﹣3)=(x﹣1)2+4,∴抛物线开口向上,顶点为(1,4),对称轴为直线x=1,∴y随x的增大而增大时,x的范围是x>1.18.已知二次函数y=x2﹣6x+8.(1)将解析式化成顶点式;(2)写出它的开口方向、对称轴和顶点坐标;(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.解:(1)y=x2﹣6x+8=x2﹣6x+9﹣1=(x﹣3)2﹣1;(2)开口向上,对称轴是直线x=3,顶点坐标是(3,﹣1);(3)x>3时,y随x的增大而增大;x<3时,y随x增大而减小.19.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.解:∵h=﹣5t2+20t=﹣5(t﹣2)2+20,且﹣5<0,∴当t=2时,h取最大值20,答:小球飞行高度达到最高时的飞行时间为2s.20.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在云南省广泛种植.长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售,平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)若降价2元,则每天的销售利润是多少元(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)(3)将商品的销售单价定为多少元时,商场每天销售该商品获得的利润w最大?最大利润是多少元?解:(1)根据题意,降价2元则销售量为60+2×10=80(斤),销售利润为:(30﹣15﹣2)×80=1040(元),。
求二次函数解析式专项练习60题(含解析)

文档从网络中收集,已重新整理排版.word版本可编辑.欢迎下载支持.求二次函数解析式专项练习60题(含解析)1.已知二次函数图象的顶点坐标是(1,﹣4),且与y轴交于点(0,﹣3),求此二次函数的解析式.2.已知二次函数y=x2+bx+c的图象经过点A(﹣1,12),B(2,﹣3).(1)求这个二次函数的解析式.(2)求这个图象的顶点坐标及与x轴的交点坐标.3.在平面直角坐标系xOy中,直线y=﹣x绕点O顺时针旋转90°得到直线l,直线l与二次函数y=x2+bx+2图象的一个交点为(m,3),试求二次函数的解析式.4.已知抛物线y=ax2+bx+c与抛物线形状相同,顶点坐标为(﹣2,4),求a,b,c的值.5.已知二次函数y=ax2+bx+c,其自变量x的部分取值及对应的函数值y如下表所示:(1)求这个二次函数的解析式;x …﹣2 0 2 …y …﹣1 1 11 …6.已知抛物线y=x+(m+1)x+m,根据下列条件分别求m的值.(1)若抛物线过原点;(2)若抛物线的顶点在x轴上;(3)若抛物线的对称轴为x=2.7.已知抛物线经过两点A(1,0)、B(0,3),且对称轴是直线x=2,求其解析式.8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:(1)写出y>0时,x的取值范围_________;(2)写出y随x的增大而减小的自变量x的取值范围_________;(3)求函数y=ax2+bx+c的表达式.9.已知二次函数y=x2+bx+c的图象经过点A(﹣2,5),B(1,﹣4).(1)求这个二次函数解析式;(2)求这个图象的顶点坐标、对称轴、与坐标轴的交点坐标;(3)画出这个函数的图象.10.已知:抛物线经过点A(﹣1,7)、B(2,1)和点C(0,1).(1)求这条抛物线的解析式;(2)求该抛物线的顶点坐标.11.若二次函数y=ax2+bx+c的图象与y轴交于点A(0,3),且经过B(1,0)、C(2,﹣1)两点,求此二次函数的解析式.12.二次函数y=x2+bx+c的图象过A(2,3)和B(﹣1,0)两点,求此二次函数的解析式.13.已知:一抛物线y=ax2+bx﹣2(a≠0)经过点(3,4)和点(﹣1,0)求该抛物线的解析式,并用配方法求它的对称轴.14.二次函数y=2x2+bx+c的图象经过点(0,﹣6)、(3,0),求这个二次函数的解析式,并用配方法求它的图象的顶点坐标.15.如图,抛物线y=﹣x2+5x+m经过点A(1,0),与y轴交于点B,(1)求m的值;(2)若抛物线与x轴的另一交点为C,求△CAB的面积;(3)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.16.如图,抛物线y=﹣x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).(1)求这条抛物线对应函数的表达式;(2)若P点在该抛物线上,求当△PAB的面积为8时,点P的坐标.17.已知二次函数的图象经过点(0,﹣1)、(1,﹣3)、(﹣1,3),求这个二次函数的解析式.并用配方法求出图象的顶点坐标.18.已知:二次函数的顶点为A(﹣1,4),且过点B(2,﹣5),求该二次函数的解析式.19.已知一个二次函数y=x2+bx+c的图象经过(1,2)、(﹣1,6),求这个函数的解析式.20.已知二次函数y=x2+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)求该二次函数图象与x轴的另一个交点.21.已知抛物线最大值为3,其对称轴为直线x=﹣1,且过点(1,﹣5),求其解析式.22.已知二次函数图象顶点坐标为(﹣2,3),且过点(1,0),求此二次函数解析式.23.已知抛物线y=﹣x2+bx+c,它与x轴的两个交点分别为(﹣1,0),(3,0),求此抛物线的解析式.24.一个二次函数的图象经过点(0,0),(﹣1,﹣1),(1,9)三点,求这个函数的关系式.25.已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(1,﹣4).(1)求这个函数的解析式;(2)求这个函数图象与x轴、y轴的交点坐标.26.已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).求二次函数的解析式.27.已知二次函数y=ax2+bx+c,当x=0时,函数值为5,当x=﹣1或﹣5时,函数值都为0,求这个二次函数的解析式.28.已知抛物线的图象经过点A(1,0),顶点P的坐标是.(l)求抛物线的解析式;(2)求此抛物线与两坐标轴的三个交点所围成的三角形的面积.29.如图为抛物线y=﹣x2+bx+c的一部分,它经过A(﹣1,0),B(0,3)两点.(1)求抛物线的解析式;(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.30.已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).(1)试求二次函数的解析式;(2)求y的最大值;(3)写出当y>0时,x的取值范围.31.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.32.抛物线y=﹣x2+bx+c的对称轴是x=l,它与x轴有两个交点,其中的一个为(3,0),求此抛物线的解析式.33.已知二次函数的图象经过点(0,﹣3),且顶点坐标为(﹣1,﹣4).(1)求该二次函数的解析式;(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.34.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(2,0),B(5,3).(1)求m的值和抛物线的解析式;(2)求不等式ax2+bx+c≤x+m的解集(直接写出答案);(3)若抛物线与y轴交于C,求△ABC的面积.35.二次函数的图象经过点(1,2)和(0,﹣1)且对称轴为x=2,求二次函数解析式.36.如图所示,二次函数y=﹣x2+bx+c的图象经过坐标原点O和A(4,0).(1)求出此二次函数的解析式;(2)若该图象的最高点为B,试求出△ABO的面积;(3)当1<x<4时,y的取值范围是_________.37.已知:一个二次函数的图象经过(﹣1,10),(1,4),(2,7)三点.(1)求出这个二次函数解析式;(2)利用配方法,把它化成y=a(x+h)2+k的形式,并写出顶点坐标和y随x变化情况.38.已知抛物线y=x2﹣2(k﹣2)x+1经过点A(﹣1,2)(1)求此抛物线的解析式;(2)求此抛物线的顶点坐标与对称轴.39.根据条件求下列抛物线的解析式:(1)二次函数的图象经过(0,1),(2,1)和(3,4);(2)抛物线的顶点坐标是(﹣2,1),且经过点(1,﹣2).40.已知二次函数的图象的顶点坐标为(3,﹣2)且与y轴交于(0,)(1)求函数的解析式;(2)当x为何值时,y随x增大而增大.41.已知二次函数的图象经过点(0,﹣2),且当x=1时函数有最小值﹣3.(1)求这个二次函数的解析式;(2)如果点(﹣2,y1),(1,y2)和(3,y3)都在该函数图象上,试比较y1,y2,y3的大小.42.已知二次函数y=x2+bx+c的图象经过点(0,3)、(4,3)(1)求二次函数的解析式,并在给定的坐标系中画出该函数的图象(不用列表);(2)直接写出x2+bx+c>3的解集.43.不论m取任何实数,y关于x的二次函数y=x2+2mx+m2+2m﹣1的图象的顶点都在一条直线上,求这条直线的函数解析式.44.抛物线y=ax2+bx+c过点A(﹣2,1),B(2,3),且与y轴负半轴交于点C,S△ABC=12,求其解析式.45.直线y=kx+b过x轴上的A(2,0)点,且与抛物线y=ax2相交于B、C两点,已知B点坐标为(1,1),求直线和抛物线所表示的函数解析式,并在同一坐标系中画出它们的图象.46.已知二次函数y=x2+bx+c的图象经过点P(2,7)、Q(0,﹣5).(1)试确定b、c的值;(2)若该二次函数的图象与x轴交于A、B两点(其中点A在点B的左侧),试求△PAB的面积.47.抛物线y=ax2﹣3ax+b经过A(﹣1,0),C(3,﹣2)两点.(1)求此抛物线的解析式;(2)求出这个二次函数的对称轴和顶点坐标.48.已知二次函数y=x2+bx+c的图象经过点A(0,4),且对称轴是直线x=﹣2,求这个二次函数的表达式.49.已知关于x的二次函数的图象的顶点坐标为(﹣4,3),且图象过点(l,﹣2).(1)求这个二次函数的关系式;(2)写出它的开口方向、对称轴.50.如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.(1)求m的值和二次函数的解析式.(2)二次函数交y轴于C,求△ABC的面积.51.若二次函数的图象的对称轴是直线x=1.5,并且图象过A(0,﹣4)和B(4,0)(1)求此二次函数的解析式;(2)求此二次函数图象上点A关于对称轴对称的点A′的坐标.52.若二次函数y=ax2+bx+c中,c=3,图象的顶点坐标为(2,﹣1),求该二次函数的解析式.53.过点A(﹣1,4),B(﹣3,﹣8)的二次函数y1=ax2+bx+c与二次函数的图象的形状一样,开口方向相同,只是位置不同,求这个函数的解析式及顶点坐标.54.二次函数的图象与x轴的两交点的横坐标为1和﹣7,且经过点(﹣3,8).求:(1)这个二次函数的解析式;(2)试判断点A(﹣1,2)是否在此函数的图象上.55.已知二次函数y=ax2+bx+c的图象经过点(0,﹣9)、(1,﹣8),对称轴是y轴.(1)求这个二次函数的解析式;(2)将上述二次函数图象沿x轴向右平移2个单位,设平移后的图象与y轴的交点为C,顶点为P,求△POC的面积.56.如图,抛物线y=ax2+bx经过点A(4,0)、B(2,2),连接OB、AB.(1)求抛物线的解析式;(2)求证:△OAB是等腰直角三角形.57.如图,抛物线y=x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;(2)若将上述抛物线先向下平移3个单位,再向右平移2个单位,请直接写出平移后的抛物线的解析式.58.已知二次函数y=﹣x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.59.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标.60.已知函数y=x2+bx+c过点A(2,2),B(5,2).(1)求b、c的值;(2)求这个函数的图象与x轴的交点C的坐标;(3)求S△ABC的值.二次函数解析式60题参考答案:1.∵顶点坐标是(1,﹣4)因此,设抛物线的解析式为:y=a(x﹣1)2﹣4,∵抛物线与y轴交于点(0,﹣3)把(0,﹣3)代入解析式:﹣3=a(0﹣1)2﹣4解之得:a=1(14分)∴抛物线的解析式为:y=x2﹣2x﹣3.2.(1)把点A(﹣1,12),B(2,﹣3)的坐标代入y=x2+bx+c 得得∴y=x2﹣6x+5.(2)y=x2﹣6x+5,y=(x﹣3)2﹣4,故顶点为(3,﹣4).令x2﹣6x+5=0解得x1=1,x2=5.与x轴的交点坐标为(1,0),(5,0).3.由题意,直线l的解析式为y=x,将(m,3)代入直线l的解析式中,解得m=3.将(3,3)代入二次函数的解析式,解得,∴二次函数的解析式为4.抛物线y=ax2+bx+c 与抛物线形状相同,则a=±.当a=时,解析式是:y=(x+2)2+4=x2+x+5.即a=,b=1,c=5;当a=﹣时,解析式是:y=﹣(x+2)2+4=﹣x2﹣x+3.即a=﹣,b=﹣1,c=3.5.(1)依题意,得,解得;∴二次函数的解析式为:y=x2+3x+1.(2)由(1)知:y=x2+3x+1=(x+)2﹣,故其顶点坐标为(﹣,﹣)6.(1)∵抛物线过原点,∴0=02+(m+1)×0+m.解得m=0;(2)∵抛物线的顶点在x轴上.∴△=(m+1)2﹣4m=0.解得:m=1;(3)∵抛物线的对称轴是x=2,∴﹣=2.解得m=﹣57.∵抛物线对称轴是直线x=2且经过点A(1,0)由抛物线的对称性可知:抛物线还经过点(3,0)设抛物线的解析式为y=a(x﹣x1)(x﹣x2)(a≠0)即:y=a(x﹣1)(x﹣3)把B(0,3)代入得:3=3a∴a=1∴抛物线的解析式为:y=x2﹣4x+3.8.(1)抛物线开口向下,与x轴交于(1,0),(3,0),当y>0时,x的取值范围是:1<x<3;(2)抛物线对称轴为直线x=2,开口向下,y随x的增大而减小的自变量x的取值范围是x>2;(3)抛物线与x轴交于(1,0),(3,0),设解析式y=a(x﹣1)(x﹣3),把顶点(2,2)代入,得2=a(2﹣1)(2﹣3),解得a=﹣2,∴y=﹣2(x﹣1)(x﹣3),即y=﹣2x2+8x﹣6.9.(1)把A(﹣2,5),B(1,﹣4)代入y=x2+bx+c,得,解得b=﹣2,c=﹣3,∴二次函数解析式为y=x2﹣2x﹣3.(2)∵y=x2﹣2x﹣3,∴﹣=1,=﹣4,∴顶点坐标(1,﹣4),对称轴为直线x=1;又当x=0时,y=﹣3,∴与y轴交点坐标为(0,﹣3);y=0时,x=3或﹣1,∴与x轴交点坐标为(3,0),(﹣1,0).(3)图象如图.10.(1)设所求抛物线解析式为y=ax2+bx+c.根据题意,得,解得.故所求抛物线的解析式为y=2x2﹣4x+1.(2)∵,∴该抛物线的顶点坐标是(1,﹣1)11.∵二次函数y=ax2+bx+c的图象与y轴交于点A(0,3),∴c=3.又∵二次函数y=ax2+bx+c的图象经过B(1,0)、C(2,﹣1)两点,∴代入y=ax2+bx+c得:a+b+c=0,①4a+2b+c=﹣1,②由①②及c=3解得∴二次函数的解析式为y=x2﹣4x+312.由题意得解得,.此二次函数的解析式为y=x2﹣1.13.把点(3,4)、(﹣1,0)代入y=ax2+bx﹣2得:解得:则抛物线的解析式是y=x2﹣x﹣2=(x ﹣)2﹣则抛物线的对称轴是:x=14.由题意得,解得.∴这个二次函数的解析式是y=2x2﹣4x﹣6.y=2(x2﹣2x)﹣6=2(x2﹣2x+1)﹣2﹣6(1分)=2(x﹣1)2﹣8.(1分)∴它的图象的顶点坐标是(1,﹣8).15.(1)根据题意,把点A的坐标代入抛物线方程得:0=﹣1+5+m,即得m=﹣4;(2)根据题意得:令y=0,即﹣x2+5x﹣4=0,解得x1=1,x2=4,∴点C坐标为(4,0);令x=0,解得y=﹣4,∴点B的坐标为(0,﹣4);∴由图象可得,△CAB的面积S=×OB×AC=×4×3=6;(3)根据题意得:①当点O为PB的中点,设点P的坐标为(0,y),(y>0)则y﹣4=0,即得y=4,∴点P的坐标为(0,4).②当AB=BP时,AB=,∴OP 的长为:﹣4,∴P(0,﹣4),∴P(0,﹣4),或(0,4)16.(1)点(1,0),(3,0)在抛物线y=﹣x2+bx+c上.则有解得:则所求表达式为y=﹣x2+4x﹣3.(2)依题意,得AB=3﹣1=2.设P点坐标为(a,b)当b>0时,×2×b=8.则b=8.故﹣x2+4x﹣3=8即x2+4x+11=0△=(﹣4)2﹣4×1×11=16﹣44=﹣28<0,方程﹣x2+4x+11=0无实数根.当b<0时,×2×(﹣b)=8,则b=﹣8故﹣x2+4x﹣3=﹣8 即﹣x2+4x﹣5=0.解得x1=﹣1,x2=5所求点P坐标为(﹣1,﹣8),(5,﹣8)17.设二次函数的解析式为y=ax2+bx+c,由题意得,解得.故二次函数的解析式为y=x2﹣3x﹣1;y=x2﹣3x﹣1=x2﹣3x+()2﹣()2﹣1=(x ﹣)2﹣,所以抛物线的顶点坐标为(,﹣).18.设此二次函数的解析式为y=a(x+1)2+4.∵其图象经过点(2,﹣5),∴a(2+1)2+4=﹣5,∴a=﹣1,∴y=﹣(x+1)2+4=﹣x2﹣2x+3.故答案为:y=﹣x2﹣2x+319.∵二次函数y=x2+bx+c的图象经过(1,2)、(﹣1,6),∴,解得,∴所求的二次函数的解析式为y=x2﹣2x+3.20.(1)把A(2,0)、B(0,﹣6)代入y=x2+bx+c得,4+2b+c=0,c=﹣6,∴b=1,c=﹣6,∴这个二次函数的解析式y=x2+x﹣6;(2)令y=0,则x2+x﹣6=0,解方程得x1=2,x2=﹣3,∴二次函数图象与x轴的另一个交点为(﹣3,0).21.∵已知抛物线最大值为3,其对称轴为直线x=﹣1,∴抛物线的顶点坐标为(﹣1,3)设抛物线的解析式为:y=a(x+1)2+3,∵(1,﹣5)在抛物线y=a(x+1)2+3上,∴解得a=﹣2,∴此抛物线的解析式y=﹣2(x+1)2+322.设二次函数式为y=k(x+2)2+3.将(1,0)代入得9k+3=0,解得k=.∴所求的函数式为 y=(x+2)2+323.根据题意得,,解得,∴抛物线的解析式为y=﹣x2+2x+3;或:由已知得,﹣1、3为方程﹣x2+bx+c=0的两个解,∴﹣1+3=b,(﹣1)×3=c,解得b=2,c=3,∴抛物线的解析式为y=﹣x2+2x+3.24.设二次函数的关系式为y=ax2+bx+c(a≠0),∵二次函数的图象经过点(0,0),(﹣1,﹣1),(1,9)三点,∴点(0,0),(﹣1,﹣1),(1,9)满足二次函数的关系式,∴,解得,所以这个函数关系式是:y=4x2+5x25.(1)由题意,将A与B 代入代入二次函数解析式得:,解得:,则二次函数解析式为y=x2﹣2x﹣3;(2)令y=0,则x2﹣2x﹣3=0,即(x+1)(x﹣3)=0,解得:x1=﹣1,x2=3,∴与x轴交点坐标为(﹣1,0),(3,0);令x=0,则y=﹣3,∴与y轴交点坐标为(0,﹣3)26.根据题意,得,解得,;∴该二次函数的解析式为:y=x2﹣2x﹣3.27.由题意得,二次函数y=ax2+bx+c,过(0,5)(﹣1,0)(﹣5,0)三点,∴,解得a=1,b=6,c=5,∴这个二次函数的解析式y=x2+6x+528.(1)由题意,可设抛物线解析式为y=a(x ﹣)2+,把点A(1,0)代入,得a(1﹣)2+=0,解之得a=﹣1,∴抛物线的解析式为y=﹣(x ﹣)2+,即y=﹣x2+5x﹣4;(2)令x=0,得y=﹣4,令y=0,解得x1=4,x2=1,S=×(4﹣1)×4=6.所以抛物线与两坐标轴的三个交点所围成的三角形的面积为6.29.(1)∵抛物线经过A(﹣1,0),B(0,3)两点∴解得∴抛物线的解析式为y=﹣x2+2x+3.(2)∵y=﹣x2+2x+3可化为y=﹣(x﹣1)2+4,∴抛物线y=﹣x2+2x+3的顶点坐标为(1,4),又∵此抛物线向左平移3个单位,再向下平移1个单位,∴平移后的抛物线的顶点坐标为(﹣2,3).∴平移后的抛物线的解析式为y=﹣(x+2)2+3=﹣x2﹣4x﹣1.30.(1)∵二次函数图象与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3),∴x=﹣1,y=0代入y=﹣x2+bx+c得:﹣1﹣b+c=0①,把x=0,y=3代入y=﹣x2+bx+c得:c=3,把c=3代入①,解得b=2,则二次函数解析式为y=﹣x2+2x+3;(2)∵二次函数y=﹣x2+2x+3的二次项系数a=﹣1<0,∴抛物线的开口向下,则当x=﹣=﹣=1时,y有最大值,最大值为=4;(3)令二次函数解析式中的y=0得:﹣x2+2x+3=0,可化为:(x﹣3)(x+1)=0,解得:x1=3,x2=﹣1,由函数图象可知:当﹣1<x<3时,y>031.∵函数的最大值是2,则此函数顶点的纵坐标是2,又顶点在y=x+1上,那么顶点的横坐标是1,设此函数的解析式是y=a(x﹣1)2+2,再把(2,1)代入函数中可得a(2﹣1)2+2=1,解得a=﹣1,故函数解析式是y=﹣x2+2x+1.32.∵﹣=﹣=1,∴b=2,又∵点(3,0)在函数上,∴﹣9+6+c=0,∴c=3,∴函数的解析式是y=﹣x2+2x+3.33.(1)设y=a(x+1)2﹣4,把点(0,﹣3)代入得:a=1,∴函数解析式y=(x+1)2﹣4或y=x2+2x﹣3;(2)∵x2+2x﹣3=0,解得x1=1,x2=﹣3,∴A(﹣3,0),B(1,0),C(0,﹣3),∴△ABC的面积=.34.(1)解:∵直线y=x+m经过A点,∴当x=2时,y=0,∴m+2=0,∴m=﹣2,∵抛物线y=x2+bx+c过A(2,0),B(5,3),∴,解得,∴抛物线的解析式为y=x2﹣6x+8;(2)由图可知,不等式ax2+bx+c≤x+m的解集为2≤x≤5;(3)解:设直线AB与y轴交于D,∵A(2,0)B(5,3),∴直线AB的解析式为y=x﹣2,∴点D(0,﹣2),由(1)知C(0,8),∴S△BCD =×10×5=25,∵S△ACD =×10×2=10,∴S△ABC=S△BCD﹣S△ACD=25﹣10=15.35.设二次函数的解析式为y=ax2+bx+c,由题意得,二次函数的图象对称轴为x=2且图象过点(1,2),(0,﹣1),故可得:,解得:.即可得二次函数的解析式为:y=﹣x2+4x﹣136.(1)由条件得解得所以解析式为y=﹣x2+4x,(2)∵该图象的最高点为B,∴点B的坐标为(2,4),∴△ABO的面积=×4×4=8,(3)∵当x=1时,y=3,∴当1<x<4时,y的取值范围是0<y<4.故答案为:0<y<4.37.(1)这个二次函数解析式y=ax2+bx+c(a≠0),把三点(﹣1,10),(1,4),(2,7)分别代入得:,解得:,故这个二次函数解析式为:y=2x2﹣3x+5;(2)y=2x2﹣3x+5=2(x2﹣x+﹣)+5=2(x ﹣)2﹣+5=2(x ﹣)2+,则抛物线的顶点坐标是(,),因为抛物线的开口向上,所以当x >时,y随x的增大而增大,当x时,y随x的增大而减小.38.(1)将A(﹣1,2)代入y=x2﹣2(k﹣2)x+1得:2=1﹣2(k ﹣2)+1,解得:k=2,则抛物线解析式为y=x2+1;(2)对于二次函数y=x2+1,a=1,b=0,c=1,∴﹣=0,=1,则顶点坐标(0,1);对称轴为直线x=0(y轴)39.(1)设抛物线的解析式是y=ax2+bx+c,把(0,1),(2,1),(3,4)代入得:,解得:,∴y=x2﹣2x+1.(2)设抛物线的解析式是:y=a(x+2)2+1,把(1,﹣2)代入得:﹣2=a(1+2)2+1,∴a=﹣,∴y=﹣(x+2)2+1,即y=﹣x2﹣x ﹣.40.(1)设函数的解析式是:y=a(x﹣3)2﹣2根据题意得:9a﹣2=,解得:a=;∴函数解析式是:y=﹣2;(2)∵a=>0 ∴二次函数开口向上又∵二次函数的对称轴是x=3.∴当x>3时,y随x增大而增大.41.(1)由题意知:抛物线的顶点坐标为(1,﹣3)设二次函数的解析式为y=a(x﹣1)2﹣3,由于抛物线过点(0,﹣2),则有:a(0﹣1)2﹣3=﹣2,解得a=1;因此抛物线的解析式为:y=(x﹣1)2﹣3.(2)∵a=1>0,∴故抛物线的开口向上;∵抛物线的对称轴为x=1,∴(1,y2)为抛物线的顶点坐标,∴y2最小.由于(﹣2,y1)和(4,y1)关于对称轴对称,可以通过比较(4,y1)和(3,y3)来比较y1,y3的大小,由于在y轴的右侧是增函数,所以y1>y3.于是y2<y3<y1.42.(1)由于二次函数y=x2+bx+c的图象经过点(0,3)、(4,3),则,解得:,∴此抛物线的解析式为:y=x2﹣4x+3.函数图象如下:(2)由函数图象可直接写出x2+bx+c>3的解集为:x<0或x>4.43.二次函数可以变形为y=(x+m)2+2m﹣1,抛物线的顶点坐标为(﹣m,2m﹣1).由,消去m,得y=﹣2x﹣1.所以这条直线的函数解析式为y=﹣2x﹣144.设直线AB的解析式为y=kx+b,∴,解得,直线AB的解析式为y=x+2,令x=0,则y=2,∴直线AB与y轴的交点坐标(0,2),∵S△ABC=12,∴C(0,﹣4),∵抛物线y=ax2+bx+c过点A(﹣2,1),B(2,3),且与y轴负半轴交于点C,∴,解得,∴抛物线的解析式为y=x2+x﹣445.∵直线y=kx+b过点A(2,0)和点B(1,1),∴,解得,∴直线AB所表示的函数解析式为y=﹣x+2,∵抛物线y=ax2过点B(1,1),∴a×12=1,解得a=1,∴抛物线所表示的函数解析式为y=x2.它们在同一坐标系中的图象如下所示:46.(1)∵二次函数y=x2+bx+c的图象经过点P(2,7)、Q(0,﹣5),,解得b=4,c=﹣5.∴b、c的值是4,5;(2)∵二次函数的图象与x轴交于A、B两点,(其中点A在点B 的左侧),∴A(1,0),B(﹣5,0),∴AB=6,∵P点的坐标是:(2,7),∴△PAB的面积=×6×7=2147.(1)根据题意得,解得,所以抛物线的解析式为y=﹣x﹣2;(2)y=﹣x﹣2=(x ﹣)2﹣,所以抛物线的对称轴为直线x=,顶点坐标为(,﹣)48.∵二次函数的图象过A(0,4),∴c=4,∵对称轴为x=﹣1,∴x=﹣=﹣2,解得b=4;∴二次函数的表达式为y=x2+4x+4.49.(1)∵关于x的二次函数的图象的顶点坐标为(﹣4,3),∴设该二次函数的关系式为:y=a(x+4)2+3(a≠0);又∵图象过点( l,﹣2),∴﹣2=a(1+4)2+3,解得,a=﹣;∴设该二次函数的关系式为:y=﹣(x+4)2+3;(2)由(1)知,该二次函数的关系式为:y=﹣(x+4)2+3,∴a=﹣<0,∴该抛物线的方向向下;∵关于x的二次函数的图象的顶点坐标为(﹣4,3),∴对称轴方程为:x=﹣4.50.(1)把A(﹣1,0)代入y1=﹣x+m得﹣(﹣1)+m=0,解得m=1,把A(﹣1,0)、B(2,﹣3)代入y2=ax2+bx﹣3得,解得.故二次函数的解析式为y2=x2﹣﹣2x﹣3;(2)因为C点坐标为(0,﹣3),B(2,﹣3),所以BC⊥y轴,所以S△ABC =×2×3=3.51.(1)设此二次函数的解析式为y=ax2+bx+c,把A(0,﹣4)和B(4,0),即对称轴x=1.5代入解析式得:,解得:故y=x2﹣3x﹣4;(2)∵A(0,﹣4),对称轴是x=1.5,∴A′(3,﹣4)52.∵二次函数y=ax2+bx+c的顶点坐标为(﹣,),二次函数y=ax2+bx+c中,c=3,图象的顶点坐标为(2,﹣1),∴﹣=2,=﹣1,解得a=1,b=﹣4,∴二次函数的解析式y=x2﹣4x+353.∵二次函数y1=ax2+bx+c 与二次函数的图象的形状一样,开口方向相同,∴a=﹣2,将点A(﹣1,4),B(﹣3,﹣8)代入y1=﹣2x2+bx+c,得,解得,∴y1=﹣2x2﹣2x+4;∵y1=﹣2x2﹣2x+4=﹣2(x2+x)+4=﹣2(x+)2+,∴顶点坐标为(﹣,).故这个函数的解析式为y1=﹣2x2﹣2x+4,顶点坐标为(﹣,).54.(1)∵二次函数的图象与x轴的两交点的横坐标为1和﹣7,且经过点(﹣3,8),∴两交点的横坐标为:(1,0),(﹣7,0),且经过点(﹣3,8),∴代入解析式:y=a(x﹣1)(x+7),8=a(﹣3﹣1)×(﹣3+7),解得:a=﹣,∴y=﹣(x﹣1)(x+7);(2)∵将点A(﹣1,2)此函数的解析式,∴左边=2,右边=﹣(﹣1﹣1)(﹣1+7)=6;∴左边≠右边,∴点A(﹣1,2)不在此函数的图象上.55.(1)∵二次函数的对称轴为y轴,即x=0,∴b=0,即二次函数解析式为y=ax2+c,又二次函数的图象经过点(0,﹣9)、(1,﹣8),∴,解得:,则二次函数的解析式为y=x2﹣9;(2)由平移规律得:二次函数向右平移2个单位的解析式为:y=(x﹣2)2﹣9,即y=x2﹣4x﹣5,令x=0,解得:y=﹣5,∴C(0,﹣5),即OC=5,又平移后抛物线的顶点P的坐标为(2,9),即P的横坐标为2,则S△POC =OC•x P的横坐标=×5×2=5.56.1)解:由题意得,解得;∴该抛物线的解析式为:y=﹣x2+2x;(2)证明:过点B作BC⊥x轴于点C,则OC=BC=AC=2;∴∠BOC=∠OBC=∠BAC=∠ABC=45°;∴∠OBA=90°,OB=AB;∴△OAB是等腰直角三角形;57.(1)将A(﹣1,0)代入抛物线y=x2+bx﹣2得,×(﹣1)2﹣b﹣2=0,解得,b=﹣,则函数解析式为y=x2﹣x﹣2.配方得,y=(x ﹣)2﹣,可见,顶点坐标为(,﹣).(2)将上述抛物线先向下平移3个单位,再向右平移2个单位,可得,y=(x ﹣﹣2)2﹣﹣3=(x ﹣)2﹣=x2﹣x.58.(1)把(2,0)、(0,﹣6)代入二次函数解析式,可得,解得,故解析式是y=﹣x2+4x﹣6;(2)∵对称轴x=﹣=4,∴C点的坐标是(4,0),∴AC=2,OB=6,AB=2,BC=2,∴S△ABC =AC•OB=×2×6=6,△ABC的周长=AC+AB+BC=2+2+2.59.(1)A坐标是(﹣1,﹣1),B点的坐标是(3,﹣9),代入y=ax2﹣4x+c 得:解得:a=1,c=﹣6.则二次函数表达式是:y=x2﹣4x﹣6(2)y=x2﹣4x﹣6=(x﹣2)2﹣10,因此对称轴为直线x=2,顶点坐标为(2,﹣10)60.(1)把A(2,2),B(5,2)分别代入y=x2+bx+c,文档从网络中收集,已重新整理排版.word版本可编辑.欢迎下载支持. 可得,解得;(2)由b=﹣7,c=12,知y=x2﹣7x+12令y=0,得x2﹣7x+12=0,∴x=3或x=4,∴C(3,0)或C(4,0);(3)∵A(2,2)B(5,2)∴AB=|2﹣5|=3,且△ABC的AB边上的高h=2,∴S△ABC =AB•h=×3×2=311word版本可编辑.欢迎下载支持.。
中考数学《二次函数》专项练习(附答案解析)

中考数学《二次函数》专项练习(附答案解析)一、综合题1.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是()(填方案一,方案二,或方案三),则B点坐标是(),求出你所选方案中的抛物线的表达式;(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.2.如图,抛物线 y =-x2+3x +4 与x轴负半轴相交于A点,正半轴相交于B点,与 y 轴相交于C 点.(1)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线 BC 对称的点的坐标;(2)在(1)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.3.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.4.已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.(1)求点A的坐标;(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.5.如图,抛物线G:y=−x2+2mx−m2+m+3的顶点为P(x P,y P),抛物线G与直线l:x=3交于点Q.(1)x P=,y P=(分别用含m的式子表示);y P与x P的函数关系式为;(2)求点Q的纵坐标y Q(用含m的式子表示),并求y Q的最大值;(3)随m的变化,抛物线G会在直角坐标系中移动,求顶点P在y轴与l之间移动(含y轴与l)的路径的长.6.如图,抛物线的顶点D的坐标为(﹣1,4),抛物线与x轴相交于A.B两点(A在B的左侧),与y轴交于点C(0,3).(1)求抛物线的表达式;(2)如图1,已知点E(0,﹣3),在抛物线的对称轴上是否存在一点F,使得△CEF的周长最小,如果存在,求出点F的坐标;如果不存在,请说明理由;(3)如图2,连接AD,若点P是线段OC上的一动点,过点P作线段AD的垂线,在第二象限分别与抛物线、线段AD相交于点M、N,当MN最大时,求△POM的面积.7.已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).(1)求该抛物线的解析式;(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.8.如图,在平面直角坐标系xOy中,O为坐标原点,点A(4,0),点B(0,4),ΔABO的中线AC与y轴交于点C,且⊙M经过O,A,C三点.(1)求圆心M的坐标;(2)若直线AD与⊙M相切于点A,交y轴于点D,求直线AD的函数表达式;(3)在过点B且以圆心M为顶点的抛物线上有一动点P,过点P作PE∥y轴,交直线AD于点E.若以PE为半径的⊙P与直线AD相交于另一点F.当EF=4√5时,求点P的坐标.9.如图1所示,已知抛物线y=−x2+4x+5的顶点为D,与x轴交于A、B两点(A左B右),与y轴交于C点,E为抛物线上一点,且C、E关于抛物线的对称轴对称,作直线AE.(1)求直线AE的解析式;(2)在图2中,若将直线AE沿x轴翻折后交抛物线于点F,则点F的坐标为(直接填空);(3)点P为抛物线上一动点,过点P作直线PG与y轴平行,交直线AE于点G,设点P的横坐标为m,当S△PGE∶S△BGE=2∶3时,直接写出所有符合条件的m值,不必说明理由.10.综合与探究如图,直线y=−23x+4与x轴,y轴分别交于B,C两点,抛物线y=ax2+43x+c经过B,C两点,与x轴的另一个交点为A(点A在点B的左侧),抛物线的顶点为点D.抛物线的对称轴与x轴交于点E.(1)求抛物线的表达式及顶点D的坐标;(2)点M是线段BC上一动点,连接DM并延长交x轴交于点F,当FM:FD=1:4时,求点M的坐标;(3)点P是该抛物线上的一动点,设点P的横坐标为m,试判断是否存在这样的点P,使∠PAB+∠BCO=90°,若存在,请直接写出m的值;若不存在,请说明理由.11.如图,点A,B在函数y=14x2的图像上.已知A,B的横坐标分别为-2、4,直线AB与y轴交于点C,连接OA,OB.(1)求直线AB的函数表达式;(2)求ΔAOB的面积;(3)若函数y=14x2的图像上存在点P,使得ΔPAB的面积等于ΔAOB的面积的一半,则这样的点P共有个.12.如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y 轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.(1)求一次函数解析式;(2)求顶点P的坐标;,求点M (3)平移直线AB使其过点P,如果点M在平移后的直线上,且tan∠OAM=32坐标;(4)设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值.13.如图,抛物线y=ax2+bx+4经过点A(−1,0),B(2,0)两点,与y轴交于点C,点D是拋物线在x轴上方,对称轴右侧上的一个动点,设点D的横坐标为m.连接AC,BC,DB,DC.(1)求抛物线的解析式;(2)当△BCD的面积与△AOC的面积和为7时,求m的值;2(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.(x+m)(x−3m)图象的顶点为M,图象交x轴于A、14.如图,y关于x的二次函数y=−√33mB两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(−3,0),连接ED.(m>0)(1)写出A、B、D三点的坐标;(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.15.在图1中,抛物线y=ax2+2ax﹣8(a≠0)与x轴交于点A、B(点A在B左侧),与y轴负半轴交于点C,OC=4OB,连接AC,抛物线的对称轴交x轴于点E,交AC于点F.(1)AB的长为,a的值为;(2)图2中,直线ON分别交EF、抛物线于点M、N,OM=√17,连接NC.①求直线ON的解析式;②证明:NC∥AB;③第四象限存在点P使△BFP与△AOC相似,且BF为△BFP的直角边,请直接写出点P坐标.16.如图,直线AB的解析式为y=−43x+4,抛物线y=−13x2+bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.(1)求抛物线的解析式;(2)如图(1),当点P在第一象限内的抛物线上时,求△ABP面积的最大值,并求此时点P的坐标;(3)过点A作直线l//x轴,过点P作PH⊥l于点H,将△APH绕点A顺时针旋转,使点H的对应点恰好落在直线AB上,同时恰好落在坐标轴上,请直接写出点P的坐标.参考答案与解析1.【答案】(1)解:方案一:点B的坐标为(5,0),设抛物线的解析式为:y=a(x+5)(x−5).由题意可以得到抛物线的顶点为(0,5),代入解析式可得:a=−15,∴抛物线的解析式为:y=−15(x+5)(x−5)方案2:点B的坐标为(10,0).设抛物线的解析式为:y=ax(x−10).由题意可以得到抛物线的顶点为(5,5),代入解析式可得:a=−15,∴抛物线的解析式为:y=−15x(x−10);方案3:点B的坐标为(5,−5),由题意可以得到抛物线的顶点为(0,0).设抛物线的解析式为:y=ax2,把点B的坐标(5,−5),代入解析式可得:a=−15,∴抛物线的解析式为:y=−15x2;(2)解:方案一:由题意:把x=3代入y=−15(x+5)(x−5),解得:y=165=3.2,∴水面上涨的高度为3.2m方案二:由题意:把x=2代入y=−15x(x−10)解得:y=165=3.2,∴水面上涨的高度为3.2m.方案三:由题意:把x=3代入y=−15x2解得:y=−95= −1.8,∴水面上涨的高度为5−1.8= 3.2m.2.【答案】(1)解: 将点D( m,m+1 )代入y=−x2+3x+4中,得:m+1=−m2+3m+4,解得:m=−1或3,∵点D在第一象限,∴m=3,∴点D的坐标为(3,4);令y=0,则−x2+3x+4=0,解得:x1=−1,x2=4,令x=0,则y=4,由题意得A(-1,0),B(4,0),C(0,4),∴OC=OB=4,BC= 4√2,CD=3,∵点C、点D的纵坐标相等,∴CD∥AB,∠OCB=∠OBC=∠DCB=45°,∴点D关于直线BC的对称点E在y轴上.根据对称的性质知:CD=CE=3 ,∴OE=OC−CE=4−3=1,∴点D关于直线BC对称的点E的坐标为(0,1);(2)解: 作PF⊥AB于F,DG⊥BC于G,由(1)知OB=OC=4,∠OBC=45°.∵∠DBP=45°,∴∠CBD=∠PBF.∵CD=3,∠DCB=45°,∴CG=DG= 3√22,∵BC= 4√2,∴BG= 4√2−3√22=5√22∴tan∠PBF=tan∠CBD=DGBG =35.设PF=3t,则BF=5t,OF=5t−4.∴P(−5t+4,3t),∵P点在抛物线上,∴3t=−(−5t+4)2+3(−5t+4)+4解得:t=2225或t=0(舍去).∴点P的坐标为( −25,6625).3.【答案】(1)解:在Rt△AOB中,OA=1,tan∠BAO= OBOA=3,∴OB=3OA=3.∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).代入解析式为{a+b+c=09a−3b+c=0c=3,解得: {a =−1b =−2c =3.∴抛物线的解析式为y=﹣x 2﹣2x+3(2)解:①∵抛物线的解析式为y=﹣x 2﹣2x+3,∴对称轴l=﹣ b2a =﹣1,∴E 点的坐标为(﹣1,0).如图, 当∠CEF=90°时,△CEF ∽△COD .此时点P 在对称轴上,即点P 为抛物线的顶点,P (﹣1,4);当∠CFE=90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于点M ,则△EFC ∽△EMP . ∴EMMP =EFFC =DO OC=13 ,∴MP=3EM .∵P 的横坐标为t ,∴P (t ,﹣t 2﹣2t+3).∵P 在第二象限,∴PM=﹣t 2﹣2t+3,EM=﹣1﹣t ,∴﹣t 2﹣2t+3=﹣(t ﹣1)(t+3),解得:t 1=﹣2,t 2=﹣3(因为P 与C 重合,所以舍去),∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.∴P (﹣2,3).∴当△CEF 与△COD 相似时,P 点的坐标为:(﹣1,4)或(﹣2,3); ②设直线CD 的解析式为y=kx+b ,由题意,得{−3k +b =0b =1 ,解得: {k =13b =1,∴直线CD 的解析式为:y= 13 x+1.设PM 与CD 的交点为N ,则点N 的坐标为(t , 13 t+1),∴NM= 13 t+1.∴PN=PM ﹣NM=﹣t 2﹣2t+3﹣( 13 t+1)=﹣t 2﹣ 73t +2. ∵S △PCD =S △PCN +S △PDN ,∴S △PCD = 12 PN •CM+ 12 PN •OM= 12 PN (CM+OM )= 12 PN •OC= 12 ×3(﹣t 2﹣ 73t +2)=﹣ 32 (t+76)2+ 12124 ,∴当t=﹣ 76 时,S △PCD 的最大值为 12124 . 4.【答案】(1)解:∵抛物线C 1:y=ax 2+4ax+4a+b (a ≠0,b >0)经过原点O , ∴0=4a+b ,∴当ax 2+4ax+4a+b=0时,则ax 2+4ax=0, 解得:x=0或﹣4,∴抛物线与x 轴另一交点A 坐标是(﹣4,0)(2)解:∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b(a≠0,b>0),(如图1)∴顶点M坐标为(﹣2,b),∵△AMO为等腰直角三角形,∴b=2,∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,∴a(0+2)2+2=0,解得:a=﹣12,∴抛物线C1:y=﹣12x2﹣2x(3)解:∵b=1,抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,(如图2)∴a=﹣14,∴y=﹣14(x+2)2+1=﹣14x2﹣x,设N(n,﹣1),又因为点P(m,0),∴n﹣m=m+2,∴n=2m+2即点N的坐标是(2m+2,﹣1),∵顶点N在抛物线C1上,∴﹣1=﹣14(2m+2+2)2+1,解得:m=﹣2+ √2或﹣2﹣√2 5.【答案】(1)m;m+3;y P=x P+3(2)解:∵抛物线 G :y =−x 2+2mx −m 2+m +3 与直线 l :x =3 交于点 Q , ∴把 x =3 代入 y =−x 2+2mx −m 2+m +3 , 得 y Q =−m 2+7m −6 .∵y Q =−m 2+7m −6=−(m −72)2+254,∴当 m =72 时, y Q 的最大值为 254 .(3)解:∵点 P 在 y 轴与 l 之间沿直线 l 1:y =x +3 运动, 如图,设直线 l 1:y =x +3 与 y 轴和直线 l 分别交于点 B 和点 P 1 ,线段 BP 1 的长即为点 P 路径长.把 x B =0 , x P 1=3 代入 y =x +3 得点 B(0,3) ,点 P 1(3,6) , 过点 P 1 作 P 1M ⊥y 轴,垂足为M , 则 P 1M =3,BM =3 , 在 Rt △BMP 1 中, BP 1=√BM 2+MP 12=√32+32=3√2 ,∴点 P 路径长为 3√2 .6.【答案】(1)解:设抛物线的表达式为:y =a (x+1)2+4, 把x =0,y =3代入得:3=a (0+1)2+4,解得:a =﹣1 ∴抛物线的表达式为y =﹣(x+1)2+4=﹣x 2﹣2x+3(2)解:存在.如图1,作C 关于对称轴的对称点C ′,连接EC ′交对称轴于F ,此时CF+EF的值最小,则△CEF的周长最小.∵C(0,3),∴C′(﹣2,3),易得C′E的解析式为:y=﹣3x﹣3,当x=﹣1时,y=﹣3×(﹣1)﹣3=0,∴F(﹣1,0)(3)解:如图2,∵A(﹣3,0),D(﹣1,4),易得AD的解析式为:y=2x+6,过点D作DH⊥x轴于H,过点M作MG⊥x轴交AD于G,AH=﹣1﹣(﹣3)=2,DH=4,∴AD=√AH2+DH2=√22+42=2√5,设M(m,﹣m2﹣2m+3),则G(m,2m+6),(﹣3≤m≤﹣1),∴MG=(﹣m2﹣2m+3)﹣(2m+6)=﹣m2﹣4m﹣3,由题易知△MNG∽△AHD,∴MGMN =ADAH即MN=AH×MGAD =22√5=−√55(m+2)2+√55∵√55<0∴当m =﹣2时,MN 有最大值;此时M (﹣2,3),又∵C (0,3),连接MC ∴MC ⊥y 轴∵∠CPM =∠HAD ,∠MCP =∠DHA =90°, ∴△MCP ∽△DHA , ∴PCAH =MCDH 即 PC2=24 ∴PC =1∴OP =OC ﹣PG =3﹣1=2, ∴S △POM = 12×2×2 =2,7.【答案】(1)解:由题意,得 {0=16a −8a +c 4=c解得 {a =−12c =4∴所求抛物线的解析式为:y=﹣ 12 x 2+x+4(2)解:设点Q 的坐标为(m ,0),过点E 作EG ⊥x 轴于点G .由﹣ 12 x 2+x+4=0, 得x 1=﹣2,x 2=4∴点B 的坐标为(﹣2,0) ∴AB=6,BQ=m+2 ∵QE ∥AC ∴△BQE ∽△BAC∴EG CO =BQBA 即 EG4=m+26 ∴EG =2m+43∴S △CQE =S △CBQ ﹣S △EBQ = 12 BQ •CO ﹣ 12 BQ •EG = 12 (m+2)(4﹣2m+43)= −13m 2+23m +83 =﹣ 13 (m ﹣1)2+3 又∵﹣2≤m ≤4∴当m=1时,S △CQE 有最大值3,此时Q (1,0) (3)解:存在.在△ODF 中. (ⅰ)若DO=DF ∵A (4,0),D (2,0) ∴AD=OD=DF=2又在Rt △AOC 中,OA=OC=4 ∴∠OAC=45度 ∴∠DFA=∠OAC=45度∴∠ADF=90度.此时,点F 的坐标为(2,2) 由﹣ 12 x 2+x+4=2, 得x 1=1+ √5 ,x 2=1﹣ √5此时,点P 的坐标为:P (1+ √5 ,2)或P (1﹣ √5 ,2). (ⅱ)若FO=FD ,过点F 作FM ⊥x 轴于点M由等腰三角形的性质得:OM= 12OD=1∴AM=3∴在等腰直角△AMF中,MF=AM=3∴F(1,3)由﹣12x2+x+4=3,得x1=1+ √3,x2=1﹣√3此时,点P的坐标为:P(1+ √3,3)或P(1﹣√3,3).(ⅲ)若OD=OF∵OA=OC=4,且∠AOC=90°∴AC= 4√2∴点O到AC的距离为2√2,而OF=OD=2 <2√2,与OF≥2 √2矛盾,所以AC上不存在点使得OF=OD=2,此时,不存在这样的直线l,使得△ODF是等腰三角形综上所述,存在这样的直线l,使得△ODF是等腰三角形所求点P的坐标为:P(1+ √5,2)或P(1﹣√5,2)或P(1+ √3,3)或P(1﹣√3,3)8.【答案】(1)解:∵C为OB的中点,点B(0,4),∴点C(0,2),又∵M为AC中点,点A(4,0),0+4 2=2,2+02=1,∴点M(2,1)(2)解:∵⊙P与直线AD,则∠CAD=90°,设:∠CAO=α,则∠CAO=∠ODA=∠PEH=α,tan∠CAO=OCOA =12=tanα,则sinα=√5,cosα=√5,AC=√10,则CD=ACsin∠CDA =√10sinα=10,则点D(0,−8),设直线AD的解析式为:y=mx+n,将点A、D的坐标分别代入得:{0=4m+n−8=n,解得:{m=2n=−8,所以直线AD的表达式为:y=2x−8(3)解:设抛物线的表达式为:y=a(x−2)2+1,将点B坐标代入得:4=a(0-2)2+1,解得:a=34,故抛物线的表达式为:y=34x2−3x+4,过点P作PH⊥EF,则EH=12EF=2√5,cos∠PEH=EHPE =2√5PE=cosα=√5,解得:PE=5,设点P(x,34x2−3x+4),则点E(x,2x−8),则PE=34x2−3x+4−2x+8=5,解得x=143或2(舍去2),则点P(143,193) .9.【答案】(1)解:∵抛物线的解析式为y=−x2+4x+5,∴该抛物线的对称轴为:x=−42×(−1)=2,令y=−x2+4x+5中x=0,则y=5,∴点C的坐标为(0,5),∵C、E关于抛物线的对称轴对称,∴点E的坐标为(2×2−0,5),即(4,5),令y =−x 2+4x +5中y =0,则−x 2+4x +5=0, 解得:x 1=−1,x 2=5,∴点A 的坐标为(−1,0)、点B 的坐标为(5,0), 设直线AE 的解析式为y =kx +b ,将点A(−1,0)、E(4,5)代入y =kx +b 中, 得:{0=−k +b 5=4k +b ,解得:{k =1b =1,∴直线AE 的解析式为y =x +1; (2)(6,-7)(3)解:符合条件的m 值为0、3、3−√412和3+√412.10.【答案】(1)解:当x =0时,得y =4, ∴点C 的坐标为(0,4),当y =0时,得−23x +4=0,解得:x =6, ∴点B 的坐标为(6,0), 将B ,C 两点坐标代入,得{36a +43×6+c =0,c =4. 解,得{a =−13,c =4.∴抛物线线的表达式为y =−13x 2+43x +4.∵y =−13x 2+43x +4=−13(x 2−4x +4−4)+4=−13(x −2)2+163.∴顶点D 坐标为(2,163). (2)解:作MG ⊥x 轴于点G ,∵∠MFG =∠DFE ,∠MGF =∠DEF =90°, ∴ΔMGF ∽ΔDEF .∴FM FD =MG DE.∴14=MG163.∴MG =43当y =43时,43=−23x +4 ∴x =4.∴点M 的坐标为(4,43).(3)解:∵∠PAB +∠BCO =90°,∠CBO +∠BCO =90°, ∴∠PAB =∠CBO ,∵点B 的坐标为(6,0),点C 的坐标为(0,4), ∴tan ∠CBO =46=23, ∴tan ∠PAB =23, 过点P 作PQ ⊥AB , 当点P 在x 轴上方时,−13m 2+4m +12m +2=23解得m=4符合题意, 当点P 在x 轴下方时,13m 2−4m −12m +2=23解得m=8符合题意, ∴存在,m 的值为4或8.11.【答案】(1)解:∵A ,B 是抛物线 y =14x 2 上的两点,∴当 x =−2 时, y =14×(−2)2=1 ;当 x =4 时, y =14×42=4 ∴点A 的坐标为(-2,1),点B 的坐标为(4,4) 设直线AB 的解析式为 y =kx +b , 把A ,B 点坐标代入得 {−2k +b =14k +b =4解得, {k =12b =2所以,直线AB 的解析式为: y =12x +2 ; (2)解:对于直线AB : y =12x +2 当 x =0 时, y =2 ∴OC =2∴S ΔAOB =S ΔAOC +S ΔBOC = 12×2×2+12×2×4 =6 (3)412.【答案】(1)解:∵A (﹣1,0), ∴OA=1 ∵OB=3OA , ∴B (0,3)∴图象过A 、B 两点的一次函数的解析式为:y=3x+3(2)解:∵二次函数y=ax 2﹣2ax+c (a <0)的图象与x 轴负半轴交于点A (﹣1,0),与y 轴正半轴交于点B (0,3), ∴c=3,a=﹣1,∴二次函数的解析式为:y=﹣x 2+2x+3 ∴抛物线y=﹣x 2+2x+3的顶点P (1,4) (3)解:设平移后的直线的解析式为:y=3x+m ∵直线y=3x+m 过P (1,4), ∴m=1,∴平移后的直线为y=3x+1 ∵M 在直线y=3x+1,且 设M (x ,3x+1)①当点M 在x 轴上方时,有 3x+1x+1=32 ,∴x =13 , ∴M 1(13,2)②当点M 在x 轴下方时,有 −3x+1x+1=32 ,∴x =−59 , ∴M 2(−59 , −23)(4)解:作点D 关于直线x=1的对称点D ′,过点D ′作D ′N ⊥PD 于点N , 当﹣x 2+2x+3=0时,解得,x=﹣1或x=3, ∴A (﹣1,0), P 点坐标为(1,4),则可得PD 解析式为:y=2x+2, 根据ND ′⊥PD ,设ND ′解析式为y=kx+b , 则k=﹣ 12 ,将D ′(2,2)代入即可求出b 的值, 可得函数解析式为y=﹣ 12 x+3,将两函数解析式组成方程组得: {y =−12x +3y =2x +2 ,解得 {x =25y =145 ,故N ( 25 , 145 ),由两点间的距离公式:d= √(2−25)2+(2−145)2 = 4√55, ∴所求最小值为4√5513.【答案】(1)解:把A (-1,0),B (2,0)代入抛物线解析式得: {a −b +4=04a +2b +4=0,解得: {a =−2b =2∴抛物线的解析式为: y =−2x 2+2x +4 (2)解:如图,连接OD ,由 y =−2x 2+2x +4 可得: 对称轴为 x =−22×(−2)=12 ,C (0,4)∵D(m,−2m 2+2m +4)(12<m <2) ,A (-1,0),B (2,0) ∴∴S △BCD =S △OCD +S △BCD −S △OBC=12×4m +12×2·(−2m 2+4m +2)−12×2×4=−2m 2+4m S △AOC =12×1×4=2又∵S △BCD +S △AOC =72 ∴−2m 2+4m +2=72 ,∴4m 2−8m +3=0解得: m 1=12 , m 2=32 ,当 m 1=12 时,点在对称轴上,不合题意,舍去,所以取 m 2=32 , 综上, m =32(3)解: M 1(0,0) , M 2(4,0) , M 3(√142,0) , M 4(−√142,0)14.【答案】(1)解:令y =0,则−√33m (x +m)(x −3m)=0,解得x 1=−m ,x 2=3m ;令x =0,则y =−√33m (0+m)(0−3m)=√3m .故A(−m ,0),B(3m ,0),D(0,√3m).(2)解:设直线ED 的解析式为y =kx +b ,将E(−3,0),D(0,√3m)代入得:{−3k +b =0b =√3m解得,k =√33m ,b =√3m .∴直线ED 的解析式为y =√33mx +√3m .将y =−√33m (x +m)(x −3m)化为顶点式:y =−√33m (x −m)2+4√33m . ∴顶点M 的坐标为(m ,4√33m).代入y =√33mx +√3m 得:m 2=m∵m >0,∴m =1.所以,当m =1时,M 点在直线DE 上. 连接CD ,C 为AB 中点,C 点坐标为C(m ,0). ∵OD =√3,OC =1, ∴CD =2,D 点在圆上又∵OE =3,DE 2=OD 2+OE 2=12, EC 2=16,CD 2=4, ∴CD 2+DE 2=EC 2.∴∠EDC =90°∴直线ED 与⊙C 相切.(3)解:当0<m <3时,S △AED =12AE ⋅OD =√32m(3−m)S =−√32m 2+3√32m . 当m >3时,S ΔAED =12AE ⋅OD =√32m(m −3).即S =√32m 2_3√32m . S 关于m 的函数图象的示意图如右:15.【答案】(1)6;1(2)解:①由抛物线的表达式知,抛物线的对称轴为x=﹣1,故设点M的坐标为(﹣1,m),则OM=12+m2=(√17)2,解得m=4(舍去)或﹣4,故点M的坐标为(﹣1,﹣4),由点O、M的坐标得,直线OM(即ON)的表达式为y=4x②,故答案为y=4x;②联立①②并解得{x=−2y=−8,故点N(﹣2,﹣8),∵点C、N的纵坐标相同,故NC∥x轴,即NC∥AB;③当∠BFP为直角时,由A(﹣4,0),C(0,-8)可求AC解析式为y=-2x﹣8,把x=-1,代入y=-2x﹣8得,y=-6,点F的坐标为:(-1,-6),由点F、B的坐标得,直线BF的表达式为y=2x﹣4,当x=﹣2时,y=2x﹣4=﹣8,故点N在直线BF上,连接FN,过点F作FP⊥BF交NC的延长线于点K,由直线BF 的表达式知,tan ∠BNK =2,则tan ∠FKN = 12 , 故设直线PF 的表达式为y =﹣ 12 x+t , 将点F 的坐标代入上式并解得t =﹣ 132 ,则直线PF 的表达式为y =﹣ 12 x ﹣ 132 ,故设点P 的坐标为(m ,﹣ 12 m ﹣ 132 ), 在Rt △AOC 中,tan ∠ACO = AOCO = 12 ,则tan ∠OCA =2, ∵△BFP 与△AOC 相似, 故∠FBP =∠ACO 或∠OAC ,则tan ∠FBP =tan ∠ACO 或tan ∠OAC ,即tan ∠FBP = 12 或2, 由点B 、F 的坐标得:BF = √32+62=3√5 , 则PF =BFtan ∠FBP =3√52或6 √5 ,由点P 、F 的坐标得:PF 2=(m+1)2+(﹣ 12 m ﹣ 132 +6)2=( 3√52)2或(6 √5 )2, 解得m =2或﹣4(舍去)或11或﹣13(舍去), 故点P 的坐标为(11,﹣12)或(2,﹣ 152 ); 当∠PBF 为直角时,过点B 作BP ⊥BF ,同理可求直线PF 的表达式为y =﹣ 12 x+1,故设点P 的坐标为(m ,﹣ 12 m ﹣1),同理可得,PB =BFtan ∠FBP =3√52或6 √5 ,由点P 、B 的坐标得:PB 2=(m-2)2+(﹣ 12 m+1)2=(3√52)2或(6 √5 )2,解得m=-1(舍去)或5或14或﹣10(舍去),点P的坐标为(5,﹣32)或(14,-6);综上,点P的坐标为(11,﹣12)或(2,﹣152)或(5,﹣32)或(14,-6);16.【答案】(1)解:当x=0时,y=−43x+4=4,则A(0,4),把A(0,4),C(6,0)代入y=−13x2+bx+c得{−12+6b+c=0c=4,解得{b=43c=4,∴抛物线解析式为y=−13x2+43x+4;(2)连接OP,设P(m,−13m2+43m+4),当y=0时,−43x+4=0,解得x=3,则B(3,0),S△ABP=S△AOP+S△POB−S△AOB=12⋅4⋅m+12⋅3⋅(−13m2+43m+4)−12⋅3⋅4=−12m2+4m,=−12(m−4)2+8,当m=4时,△ABP面积有最大值,最大值为8,此时P点坐标为(4,4);(3)在Rt△OAB中,AB=√32+42=5,当点P′落在x轴上,如图2,∵△APH绕点A顺时针旋转,使点H的对应点恰好落在直线AB上,同时恰好落在x 轴上∴P′H′=PH=4−(−13m2+43m+4)=13m2−43m,AH′=AH=m,∠P′H′A=∠PHA=90∘,∵∠P′BH′=∠ABO,∴△BP ′H ′ ∽ △BAO ,∴P ′H ′ : OA =BH ′ :OB ,即 (13m 2−43m) : 4=BH ′ :3, ∴BH ′=14m 2−m , ∵AH ′+BH ′=AB ,∴m +14m 2−m =5 ,解得 m 1=2√5 , m 2=−2√5( 舍去 ) ,此时P 点坐标为 (2√5,−8+8√53) ; 当点 P ′ 落在y 轴上,如图3,同理可得 P ′H ′=PH =13m 2−43m , AH ′=AH =m , ∠P ′H ′A =∠PHA =90∘ , ∵∠P ′AH ′=∠BAO , ∴△AH ′P ′′ ∽ △AOB ,∴P ′H ′ : OB =AH ′ :AO ,即 (13m 2−43m) : 3=m :4, 整理得 4m 2−25m =0 ,解得 m 1=254, m 2=0( 舍去 ) ,此时P 点坐标为 (254,−4348) ; 综上所述,P 点坐标为 (2√5,−8+8√53) 或 (254,−4348) ;。
求二次函数的表达式

(5)抛物线L:y=-x2+bx+c经过点A(0,1),与它的对称轴直 线x=1交于点B,则抛物线L的表达式为 y=-x2+2x+1 .
类型2 已知三点坐标(用“一般式”)求二次函数表达式
2.已知抛物线y=ax2+bx+c经过点(-1,-5),(0,-4)和 (1,1),则该抛物线的表达式为y=2x2+3x-4.
类型5 由平移或翻折求二次函数表达式
5.如图,将二次函数y=
1 2
(x-2)2+1的图象沿y轴向上平移得到一条
新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点
A′,B′.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数
表达式是 y=21(x-2)2+4.
6.已知二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到 的抛物线的表达式为 y=3x2-1.
(5)已知二次函数图象的顶点坐标为(-1,3),且与y轴的交点到 x轴的距离为1,则该函数的表达式为 y=-2(x+1)2+3或y=-4(x+ 1)2+3 .
类型4 设“交点式”求二次函数表达式
4.求下列二次函数表达式: (1)已知二次函数的图象如图所示,则这个二次函数的表达式 为 y=(x+1)(x-3)(或写成y=x2-2x-3) ;
(3)已知抛物线y=ax2+bx+c(a≠0)经过原点和点B(4,8),对
称轴为直线x=-2,则抛物线的表达式为 y=41x2+x);
y=41(x+2)2-1(或写成
(4)已知二次函数的图象经过点(-1,
7 2
)和(-3,
7 2
),且该二
次函数的最小值为3, 则该二次函数的表达式为 y=12(x+2)2+3(或写成y=12x2+2x+5);
求二次函数表达式 知识点+例题+练习 (非常好 分类全面)

二.二次函数解析式的确定1、设顶点式,即:设2、设一般式,即:设3、设交点式,即:设注意:(1)如抛物线顶点在原点,可设(2)以y轴为对称轴,可设(3)顶点在x轴上,可设(4)抛物线过原点,可设题型一例1.如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.(1)写出该二次函数的表达式及点C的坐标;2.(3分)(2014秋•无锡期末)若二次函数y=(a+1)x2+3x+a2﹣1的图象经过原点,则a 的值必为()A.1或﹣1B.1C.﹣1D.03.(9分)已知二次函数的图象经过A(3,0),B(0,﹣3),C(﹣2,5)三点.(1)求这个函数的解析式及函数图象顶点P的坐标;(2)画出二次函数的图象(要列表画图)并求四边形OBPA的面积.4.已知二次函数y=x2+bx+c的图象经过点(1,0)、(4,3).(1)求这个二次函数的表达式;(2)指出这个二次函数的顶点坐标、对称轴;(3)在所给的坐标系中画出y=x2+bx+c的图象;(4)x在什么范围内,y随x的增大而减小.例2 、如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围.2.如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).(1)求此抛物线的解析式;(2)写出顶点坐标及对称轴;(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.A BCO x y3.(8分)(2016秋•徐州期末)如图,平面直角坐标系中,矩形ABCO的边OA,OC分别在坐标轴上,OA=2,OC=1,以点A为顶点的抛物线经过点C(1)求抛物线的函数表达式;(2)将矩形ABCO绕点A旋转,得到矩形AB′C′O′,使点C′落在x轴上,抛物线是否经过点C′?请说明理由.4.(3分)如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为()A.B.C.﹣2D.例3 、若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>14;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0 B.1 C.2 D.32.如图,已知抛物线与x 轴的一个交点A (1,0),对称轴是x=-1,则该抛物线与x 轴的另一交点坐标是( )A .(-3,0)B .(-2,0)C .x=-3D .x=-23.已知二次函数212y x x =+-(1)求这个二次函数图像与x 轴交点的坐标;(2)求以这个二次函数图像与x 轴的两个交点及与y 轴的交点为顶点的三角形的面积。
专题训练(一) 二次函数表达式的三种常见求解方法
专题训练(一)二次函数表达式的三种常见求解方法▶方法一已知图象上任意三点,通常设一般式1.已知二次函数的图象经过A(0,0),B(-1,-11),C(1,9)三点,则这个二次函数的表达式是()A.y=-10x2+xB.y=-10x2+19xC.y=10x2+xD.y=-x2+10x2.已知抛物线y=ax2+bx+c(a≠0)经过点(1,6),(-1,0),(2,12),则该抛物线的函数表达式为.3.如图1所示,二次函数y=ax2+bx+c(a≠0)的图象经过A,B,C三点.观察图象,写出A,B,C三点的坐标,并求出二次函数的表达式.图14.已知一个二次函数的图象经过原点及点(-2,-2),且图象与x轴的另一个交点到原点的距离为4,求该二次函数的表达式.▶方法二已知顶点、对称轴、最值,通常设顶点式5.已知抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-1,3),且过点(0,5),那么该抛物线的函数表达式为() A.y=-2(x-1)2+3 B.y=-2(x+1)2+3C.y=2(x-1)2+3D.y=2(x+1)2+36.某广场中心标志性建筑处有高低不同的各种喷泉,其中一个高度为1 m的喷水管喷水的最大高度为3 m,此时喷出的水距喷水管的水平距离为12m.在如图1-ZT-2所示的平面直角坐标系中,这个喷泉喷出的水所在的抛物线的函数表达式为()图2A.y=-x-122+3 B.y=3x-122+1C.y=-8x-122+3 D.y=-8x+122+37.如图3,抛物线经过点A,B,C,则此抛物线的函数表达式为.图-38.已知抛物线经过点(3,0),(2,-3),并以直线x=0为对称轴,则该抛物线的函数表达式为. 9.如图4,二次函数y=ax2+bx+c(a≠0)的图象的顶点坐标为(-2,4),且经过原点.(1)求二次函数的表达式;(2)在抛物线上存在点P,使S△AOP=8,请直接写出点P的坐标.图4▶方法三已知图象与x轴的两个交点坐标和另一个点的坐标,通常设交点式10.若抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别为(-1,0),(3,0),其形状及开口方向与抛物线y=-2x2相同,则该抛物线的函数表达式为() A.y=-2(x-1)(x-3) B.y=-2(x+1)(x+3)C.y=-2(x+1)(x-3)D.y=-2(x-1)(x+3)11.已知二次函数的图象经过点(2,-3),对称轴为直线x=1,与x轴的两交点间的距离为4,求这个二次函数的表达式.12.如图5,在平面直角坐标系xOy中,一条抛物线经过A,O,B三点,点B在x轴的正半轴上,且OA=OB=4,∠AOB=120°.求这条抛物线的函数表达式.图513.已知抛物线C1经过点A(-1,0),B(3,0),C(0,-3).(1)求抛物线C1的函数表达式;(2)将抛物线C1向左平移几个单位,可使所得的抛物线C2经过坐标原点?写出抛物线C2的函数表达式.专题一 教师详解详析1.D2.y=x 2+3x+23.解:A (-1,0),B (0,-3),C (4,5),二次函数的表达式为y=x 2-2x-3.4.解:设二次函数的表达式为y=ax 2+bx+c (a ≠0). ∵二次函数的图象经过原点,∴c=0.∵二次函数的图象与x 轴的另一个交点到原点的距离为4,∴二次函数的图象与x 轴的另一个交点坐标为(4,0)或(-4,0).当二次函数的图象与x 轴的另一个交点坐标为(-4,0)时,可得{4a -2b =-2,16a -4b =0, 解得{a =12,b =2.当二次函数的图象与x 轴的另一个交点坐标为(4,0)时,可得{4a -2b =-2,16a +4b =0, 解得{a =-16,b =23.综上所述,该二次函数的表达式为 y=12x 2+2x 或y=-16x 2+23x.5.D6.C7.y=(x-1)2-4 [解析] ∵抛物线的顶点坐标为(1,-4), ∴可设抛物线的表达式为y=a (x-1)2-4. 把A (-1,0)代入上式,得4a-4=0, 解得a=1, ∴此抛物线的表达式为y=(x-1)2-4. 8.y=35x 2-275[解析] 设抛物线的函数表达式为y=ax 2+c (a ≠0),则{9a +c =0,4a +c =-3,解得{a =35,c =-275, ∴抛物线的函数表达式为y=35x 2-275.9.解:(1)∵二次函数y=ax 2+bx+c (a ≠0)的图象的顶点坐标为(-2,4),∴二次函数的表达式可写成y=a (x+2)2+4. 又∵二次函数的图象经过原点, ∴0=a (0+2)2+4,解得a=-1, ∴y=-(x+2)2+4=-x 2-4x.故二次函数的表达式为y=-x 2-4x. (2)易求得点A 的坐标为(-4,0), ∴AO=4.设点P 到x 轴的距离为h , 则S △AOP =12×4h=8,解得h=4.①当点P 在x 轴上方时,-x 2-4x=4,解得x 1=x 2=-2,∴点P 的坐标为(-2,4).②当点P 在x 轴下方时,-x 2-4x=-4,解得x 1=-2+2√2,x 2=-2-2√2,∴点P 的坐标为(-2+2√2,-4)或(-2-2√2,-4).综上所述,点P 的坐标是(-2,4)或(-2+2√2,-4)或(-2-2√2,-4). 10.C11.解:∵二次函数的图象与x 轴的两交点间的距离为4,且以直线x=1为对称轴,∴图象与x 轴两交点的坐标分别为(-1,0),(3,0). 设二次函数的表达式为y=a (x+1)(x-3)(a ≠0). 又∵抛物线过点(2,-3),∴-3=(2+1)(2-3)a ,解得a=1,∴二次函数的表达式为y=(x+1)(x-3)=x 2-2x-3. 12.解:过点A 作AC ⊥x 轴于点C ,如图.∵∠AOB=120°, ∴∠AOC=60°, ∴∠OAC=30°. ∵OA=OB=4,∴OC=2,AC=2√3, ∴A (-2,2√3).由题意可知B (4,0).设抛物线的函数表达式为y=ax (x-4)(a ≠0). 把A (-2,2√3)代入得a×(-2)×(-2-4)=2√3,解得a=√36,∴抛物线的函数表达式为y=√36x (x-4), 即y=√36x 2-2√33x. 13.解:(1)∵抛物线C 1经过点A (-1,0),B (3,0),∴可设其函数表达式为y=a (x+1)(x-3)(a ≠0). 将C (0,-3)代入,得a=1, ∴y=(x+1)(x-3)=x 2-2x-3.(2)将抛物线C 1向左平移3个单位,可使所得的抛物线C 2经过坐标原点. ∵y=x 2-2x-3=(x-1)2-4,∴抛物线C 2的函数表达式为y=(x-1+3)2-4, 即抛物线C 2的函数表达式为y=x 2+4x.。
初中数学精品试题:二次函数求表达式

求二次函数表达式 一、一般式 1、一个二次函数的图象经过点A (0,0),B (−1,−11),C (1,9)三点,则这个二次函数的关系式是________2、一个二次函数的图象经过点A (1,0),B (−1,−6),C (2,6)三点,则这个二次函数与y 轴的交点是____________3、如图,二次函数2y x bx c =++的图象过点B (0,-2)。
它与反比例函数8y x=-,的图象交于点A (m ,4),则这个二次函数的解析式为____________4、如图,二次函数2y ax bx c =++的图象经过A . B . C 三点。
(1)求出抛物线解析式;(2)求此抛物线的顶点坐标和对称轴;(3)观察图象,当x 取何值时,y <0?5、已知:在平面直角坐标系xOy 中,抛物线2y ax bx c =++经A (3,0),B (2,−3),C (0,−3)(1)求抛物线的表达式;(2)设点D 是抛物线上一点,且点D 的横坐标为−2,求△AOD 的面积。
二、顶点式1、已知二次函数的图象经过点(4,-3),且当x =3时,y 有最大值4,则二次函数的表达式是 _________2、已知抛物线2y ax bx c =++与x 轴相交于点A (−3,0),对称轴为x =−1,顶点M 到x 轴的距离为2,求此抛物线的解析式。
3、(杭州中考)设抛物线2y ax bx c =++过A (0,2),B (4,3),C 三点,其中点C 在直线x =2上,且点C 到抛物线的对称轴的距离等于1,求抛物线的函数表达式.4、如图所示,二次函数2-4y ax x c =+(a ≠0)的图像经过坐标原点,与x 轴交于点A (-4,0).(1)求二次函数的表达式;(2)在抛物线上存在点P ,满足S △AOP =8,请直接写出点P 的坐标.三、交点式1、经过A (4,0),B (−2,0),C (0,3)三点的抛物线解析式是_____________2、抛物线2y ax bx c =++与x 轴的两个交点坐标为(-1,0),(3,0),其形状、开口方向与抛物线y =-2x 2相同,则该抛物线所对应的函数关系式为_____________3、已知二次函数2y ax bx c =++的图椽过A (0,−5),B (5,0)两点,它的对称轴为直线x =2,求这个二次函数的解析式四、利用平移求表达式1、将抛物线y =2(x −4)2−1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为______________2、将抛物线244y x x =--向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为___________3、如图,把抛物线y =x 2沿直线y =x 平移2个单位后,其顶点在直线上的A 处,则平移后的抛物线解析式是___________4、如图,抛物线29++2y x bx =与y 轴相交于点A ,与过点A 平行于x 轴的直线相交于点B (点B 在第一象限).抛物线的顶点C 在直线OB 上,对称轴与x 轴相交于点D . 平移抛物线,使其经过点A . D ,则平移后的抛物线的解析式为_______________5、如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y =x 2+1,则原抛物线的解析式不可能的是( )A .y =x 2+4x +4B .y =x 2+6x +5C .y =x 2-1D .y =x 2+8x +176、已知抛物线21-++c 2y x bx =经过点(1,0),(0,32). (1)求物线的函数表达式; (2)将抛物线21-++c 2y x bx =平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.四、综合1、根据条件求二次函数(1)与x 轴的两个交点的横坐标为1-2、32,与y 轴交点的纵坐标为-5,求这个二次函数的表达式(2)二次函数顶点在x 轴上,且图象经过(2,-2),(-1,-8),求此函数表达式(3)已知二次函数2y ax bx c =++图象经过原点及点(-2,-2),且与x 轴的另一个交点到原点的距离4,求表达式2、如图,Rt △AOB 的直角边OA 在x 轴上,OA =2,AB =1,将Rt △AOB 绕点O 逆时针旋转90°得到Rt △COD ,抛物线25-6y x bx c =++经过B ,D 两点. (1)求二次函数的表达式;(2)连接BD ,P 是抛物线上一点,直线OP 把△BOD 的周长分成相等的两部分,求点P 的坐标.3、如图,二次函数2y ax bx c =++ (a ≠0)的图象交x 轴于A . B 两点,交y 轴于点D ,点B 的坐标为(3,0),顶点C 的坐标为(1,4).(1)求二次函数的解析式和直线BD 的解析式;(2)点P 是直线BD 上的一个动点,过点P 作x 轴的垂线,交抛物线于点M ,当点P 在第一象限时,求线段PM 长度的最大值;(3)在抛物线上是否存在异于B . D 的点Q ,使△BDQ 中BD 边上的高为22?若存在求出点Q 的坐标;若不存在请说明理由。
九年级数学:二次函数表达式的确定 练习(含解析)

九年级数学:二次函数表达式的确定练习1.求下列函数的最大值或最小值。
(1)y=-x2-4x+2 (2)y=x2-5x+1
4
(3)y=5x2+10
(4)y=-2x2+8x
2.已知一个矩形的周长是24cm。
(1)写出矩形面积S与一边长a的函数关系式。
(2)当a 长多少时,S最大?
3.填空:
(1)二次函数y=x2+2x-5取最小值时,自变量x的值是______;
(2)已知二次函数y=x2-6x+m的最小值为1,那么m的值是______。
4.如图(1)所示,要建一个长方形的养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆的养鸡场,没靠墙的篱笆长度为xm。
(1)要使鸡场的面积最大,鸡场的长应为多少
米?
(2)如果中间有n(n是大于1的整数)道篱笆隔
墙,要使鸡场面积最大,鸡场的长应为多少米?
(3)比较(1)、(2)的结果,你能得到什么结论?
5.如图(2),已知平行四边形ABCD的周长为8cm,∠B=30°,若边长AB=x(cm)。
(1)写出□ABCD的面积y(cm2)与x的函数
关系式,并求自变量x的取值范围。
(2)当x取什么值时,y的值最大?并求最大
值。
(3).求二次函数的函数关系式。
《求二次函数的表达式》练习题

(1)抛物线的表达式为 y=2x2-8x+6.(2)设动点 P 的坐标为(n,n+2),则点 C 的 坐标为(n,2n2-8n+6),∴PC=(n+2)-(2n2-8n+6)=-2n2+9n-4=-2(n
-94)2+489,∵12<n<4,∴当 n=94时,线段 PC 最大且为489.
(3)∵△PAC 为直角三角形,(ⅰ)若点 P 为直角顶点,则∠APC=90°,由题意易知, PC∥y 轴,∠APC=45°,因此这种情形不存在.(ⅱ)若点 A 为直角顶点,则∠PAC =90°,如图①,过点 A(12,52)作 AN⊥x 轴于点 N,则 ON=12,AN=52.过点 A 作 AM⊥ 直线 AB,交 x 轴于点 M,则由题意易知,△AMN 为等腰直角三角形,∴MN=AN =52,∴OM=ON+MN=12+52=3,∴M(3,0).
4.已知二次函数的图象开口向上,且对称轴在y轴的右侧,请你写出一个满足 条件的二次函数的表达式___答__案__不__唯__一__,__如__y_=__x_2_-__x_,__y_=__x_2_-__2_x_+__8______.
5.有一个抛物线形桥拱,其最大高度为16 m,跨度为40 m,现把它的示意图 放在如图所示的平面直角坐标系中,则此抛物线的表达式为 _______y_=__-__21_5_x_2_+__85_x__________.
8.牡丹江如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).请解答下列 问题: (1)求抛物线的表达式; (2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE的中点, 连结FH,求线段FH的长.
(1)抛物线的表达式为:y=x2-2x-3. (2)∵点 E(2,m)在抛物线上,∴m=4-4-3=-3,∴E(2,-3),∴由勾 股定理,得 BE= (3-2)2+32= 10,∵点 F 是 AE 的中点,抛物线的对称 轴与 x 轴交于点 H,即 H 为 AB 的中点,连结 BE(图略),则 FH 是三角形 ABE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数表达式专项练习
顶点式
当已知条件有抛物线的顶点坐标时,可以设这个二次函数的表达式为___________________ 例:已知二次函数图象顶点坐标(-3,
21)且图象过点(2,2
11),求二次函数解析式
练习:1、抛物线顶点坐标为(-1,-2)且通过点(1,10)。
2、已知二次函数的图象顶点是(-1,2),且经过(1,-3),求这个二次函数。
3、当x=3时,y 最小值=-1,且图象过(0,7);
交点式
当已知条件有抛物线与x 轴的交点时,可以设这个二次函数的表达式为______________ 例:已知二次函数图象与x 轴交点(2,0)(-1,0)与y 轴交点是(0,-1)求解析式及顶点坐标。
练习:1、图象经过(0,1)(1,0)(3,0);
2、当二次函数图象与x 轴交点的横坐标分别是x 1= -3,x 2=1时,且与y 轴交点为(0,-2),求这个二次函数的解析式
一般式
练习:1、图象过点(0,-2)(1,2)且对称轴为直线x=23;
2、当x=1时,y=0;x=0时,y= -2,x=2 时,y=3;。
