化学动力学基础二
大学物理化学第12章 化学动力学基础(二)(1)

第12章化学动力学基础(二)1.在简单碰撞理论中,有效碰撞的定义是: ( )A、互撞分子的总动能超过EcB、互撞分子的相对总动能超过EcC、互撞分子联心线上的相对平动能超过EcD、互撞分子的内部动能超过Ec2.简单碰撞理论属基元反应速率理论,以下说法不正确的是: ( )A、反应物分子是无相互作用的刚性硬球B、反应速率与分子的有效碰撞频率成正比C、从理论上完全解决了速率常数的计算问题D、反应的判据之一是联线上的相对平动能大于某临界值3. 根据碰撞理论,温度增加反应速率提高的主要原因是: ( )A、活化能降低B、碰撞频率提高C、活化分子所占比例增加D、碰撞数增加4.化学反应的过渡态理论的要点是: ( )A、反应物通过简单碰撞就变成产物B、在气体分子运动论的基础上提出来的C、反应物首先形成活化络合物,反应速率决定于活化络合物分解为产物的分解速率D、引入了方位因子的概念,并认为它与熵变化有关5. 过渡态理论对活化络合物的假设中,以下说法不正确的为: ( )A、是处在鞍点时的分子构型B、正逆反应的过渡态不一定相同C、存在着与反应物间化学平衡D、生成的过渡态不能返回反应始态6. Lindemann 单分子反应机理是假定反应分子经碰撞激发后 ( )A、立即分解B、有一时滞C、发出辐射D、引发链反应7. 电解质溶液中的反应速率受离子强度影响的规律,下述说法中正确的应是: ( )A、离子强度I越大,反应速率越大;B、I越大,反应速率越小C、同号离子间反应,原盐效应为正;D、电解质与中性反应物作用,原盐效应为负[Co(NH3)5Br]2++OH-→[Co(NH3)5OH]2++Br-CH2ICOOH+SCN-→CH2(SCN)COOH+I-8. 除多光子吸收外,一般引起化学反应的光谱,其波长范围应是: ( )A、可见光(400 - 800 nm)及紫外光(150 - 400 nm)B、X射线 (5 -10-4nm)C、远红外射线D、微波及无线电波9.对光化学第二定律的认识下述说法正确的是:( )A、对初级,次级过程均适用B、对任何光源均适用C、对激光光源及长寿命激发态不适用D、对大、小分子都适用10. 与光化学基本定律有关的说法中正确的是:( )A、凡是被物质吸收了的光都能引起光化学反应;B、光化学反应所得到的产物数量与被吸收的光能的量成正比;C、在光化学反应中,吸收的光子数等于被活化的反应物微粒数;D、在其它条件不变时,吸收系数越大,透过溶液的光强度也越大11. 已知 HI 的光分解反应机理是:HI + h→ H·+ I·H·+ HI→ H2 + I·I·+ I·+ M→I2 + M 则该反应,反应物消耗的量子效率为: ( )A、 1B、 2C、 4D、 10612. 光化反应与热反应(黑暗反应)的相同之处在于 ( )A、反应都需要活化能;B、温度系数小;C、反应都向G(恒温恒压,W'=0时)减小的方向进行;D、平衡常数可用通常的热力学函数计算13. 温度对光化学反应速率的影响为:()A、与热反应大致相同;B、与热反应大不相同,温度增高,光化学反应速率下降;C、与热反应大不相同,温度增高,光化学反应速率不变;D、与热反应大不相同,温度的变化对光化学反应速率的影响较小14. 催化剂能极大地改变反应速率,以下说法不正确的是: ( )A、催化剂改变了反应历程B、催化剂降低了反应的活化能C、催化剂改变了反应的平衡,以致使转化率大大地提高了D、催化剂能同时加快正向和逆向反应速率15. 称为催化剂毒物的主要行为是: ( )A、和反应物之一发生化学反应;B、增加逆反应的速度;C、使产物变得不活泼;D、占据催化剂的活性中心;16.乙醛的光解机理拟定如下:(1)CH3CHO + hνCH3· + CHO·(2)CH3· + CH3CHO CH4 + CH3CO·(3) CH3CO·CO + CH3·(4) CH3· + CH3· C2H6试推导出CO的生成速率表达式和CO的量子产率表达式。
物理化学全程导学及习题全解259-186 第十二章化学动力学基础(二)

第十二章 化学动力学基础 (二)本章知识要点与公式1. 碰撞理论双分子碰撞频率 :2AB AB A B Z pd L c = 22AA AA A 2Z d L π= 临界能c E 与活化能a E 的关系:12a c E E RT =+ 用简单碰撞理论计算双 分子反应的速率常数:2AB aEk d RT π⎛⎫=- ⎪⎝⎭ 2AA 2a E k d RT π⎛⎫=- ⎪⎝⎭ 概率子Pexp a E k PA RT ⎛⎫=- ⎪⎝⎭2ABA d π= A P A =n n n n 2. 过渡态理论用统计热力学方法计算速率常数:,0B B B exp E k T f k h f RT π≠⎛⎫=- ⎪⎝⎭用热力学方法计算速率常数:()0010B r m r m exp exp nk T S H k c h R RT ≠≠-⎛⎫⎛⎫∆∆=- ⎪ ⎪⎝⎭⎝⎭对于双分子理想气体反应:1n000B r m r m exp exp k T S H P k h RT R RT -≠≠⎛⎫⎛⎫⎛⎫∆∆=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3.原盐效应稀溶液中,离子强度对反应速率的影响: A B 0lg2kz z k = A z 与B z 同号,产生正的原盐效应,I ↑ k ↑;A z 与B z 昇号,产生负的原盐效应,I k ↑↓。
4. 光化学反应光化学第一定律:只有被分子吸收的光才能引起分子的光化学反应。
光化学第二定律:在初级反应中, 一个反应分子吸收一个光子而被活化。
1 mol 光子能量(1 Einstein ) 101197J m mol Lhcu Lh νλλ-.===⋅⋅量子产率 ar I ϕ=5. 催化反应催化剂通过改变反应历程,改变反应的表观活化能来改变反应速率,只能缩短达到平蘅的时间,而不能改变平蘅的组成。
酶催化反应历程( Michaelis – Menten 机理)米氏常数12m 1k kK k -+=当[]S →∞ 时 []m m m111S K r r r =⋅+将1r对[]1S 作图,可求m K 和m r .典型俐题讲解例 1 500K 时,实验测得 NO 2 分解反应的提前因子为 61312.0010mol m s --⨯⋅⋅,碰撞截面为1921.0010m -⨯,试计算该反应的概率因子 P解 :2AA2A d π=c 2σ= ()()19223-12 1.0010m 602310mol-=⨯⨯⨯.⨯7-13133710mol m s -=.⨯⋅⋅61371320010mol m s 33710mol m s A P A --1∞--1∞.⨯⋅⋅==.⨯⋅⋅ 例 2 实验测得 N 2O 5 分解反应在不同温度时的反应速率常数,数据列于表中。
第十二章化学动力学基础(二)练习题及答案

第十二章 化学动力学基础(二)练习题一、 选择题1.以下有关催化剂不正确的说法,是催化剂(A )改变反应物的平衡转化率 (B )改变反应途径(C )改变频率因子 (D )降低活化能 2.催化剂加快反应速率,是由于它能使(A )指前因子增大 (B )几率因子增大 (C )碰撞频率增加 (D )活化分子数增加 3.反应本性、温度、反应途径、浓度与活化能关系正确的是(A )反应途径与活化能无关 (B )反应物浓度与活化能有关(C )反应温度与活化能无关 (D )反应本性与活化能有关 4.气固相催化反应Pt<700K 2CO(g) + O 2(g)2CO 2(g)的速率方程是: r = k p (o 2)/p (co), 其反应级数应为:(A) 一级反应 (B) 二级反应 (C) 对 O 2是一级,对 CO 是负一级 (D) 级数不能确定 5.某反应速率常数与各基元反应速率常数的关系为 12124()2k k k k , 则该反应的表观活化能E a 与各基元反应活化能的关系为:(A) E a =E 2 +12E 1 - E 4 (B) E a = E 2+12(E 1- E 4)(B) E a = E 2+ (E 1- 2E 4)1/2 (D) E a = E 2+ E 1- E 46.在平行反应中要提高活化能较低的反应的产率,应采取的措施为: (A) 升高反应温度 (B) 降低反应温度 (C) 反应温度不变(D) 不能用改变温度的方法。
7.化学反应速率常数的 Arrhenius 关系式能成立的范围是:(A) 对任何反应在任何温度范围内 (B) 对某些反应在任何温度范围内 (C) 对任何反应在一定温度范围内 (D) 对某些反应在一定温度范围内8.一个基元反应,正反应的活化能是逆反应活化能的2倍,反应时吸热120 kJ·mol-1,则正反应的活化能是(kJ·mol-1):(A) 120 (B) 240 (C) 360 (D) 609.物质A 发生两个一级平行反应A B,A C,设两反应的指前因子相近且与温度无关,若E1> E2,则有:(A) k1> k2 (B) k2 > k1 (C) k2= k1 (D) 无法比较k1, k2 的大小10.催化剂能极大地改变反应速率,以下说法不正确的是:(A) 催化剂改变了反应历程(B) 催化剂降低了反应的活化能(C) 催化剂改变了反应的平衡,以致使转化率大大地提高了(D) 催化剂能同时加快正向和逆向反应速率11.下面四种说法中不正确的是:(A)在具有速控步的反应历程中,达到稳态后,速控步后的各个步骤的反应速率都等于速控步的反应速率,速控步前的各步骤均处于平衡状态(B) 根据微观可逆性原理,在反应历程中不可能出现2A → C + 3D 这样的基元反应(C) 在光化学反应中,体系的Gibbs自由能总是在不断地降低(D) 在采用温度跃变的驰豫法来研究溶液中的快速反应时,该反应必须是放热或吸热反应12.除多光子吸收外,一般引起化学反应的光谱,其波长范围应是:(A) 可见光(400 - 800 nm) 及紫外光(150 - 400 nm)(B) X射线(5 - 10-4 nm)(C) 远红外射线(D) 微波及无线电波13.在光的作用下,O2可转变为O3,当1 mol O3生成时,吸收了3.01×1023个光子,则该反应之总量子效率Φ为:(A) Φ=1 (B) Φ=1.5(C) Φ=2 (D) Φ=314.根据微观可逆性原理,反应物分子能量消耗的选择性和产物能量分配的特殊性 有对应关系,因此对正向反应产物主要是平动激发,则对逆向反应更有利于促进反 应进行的能量形式应为:(A)振动能 (B)转动能(C)平动能 (D)能量形式不限,只要足够高 15.对Einstain 光化当量定律的认识下述说法正确的是:(A) 对初级,次级过程均适用 (B) 对任何光源均适用 (C) 对激光光源及长寿命激发态不适用 (D) 对大、小分子都适用 16.在简单碰撞理论中,有效碰撞的定义是:(A) 互撞分子的总动能超过E c (B) 互撞分子的相对总动能超过E c (C)互撞分子联心线上的相对平动能超过E c (D)互撞分子的内部动能超过E c 17.在碰撞理论中校正因子P 小于1的主要因素是:(A) 反应体系是非理想的 (B) 空间的位阻效应 (C) 分子碰撞的激烈程度不够 (D) 分子间的作用力 18.Lindemann 单分子反应机理是假定多原子分子被振动激发后 (A) 立即分解 (B) 有一时滞 (C) 发出辐射 (D) 引发链反应19.同一个反应在相同反应条件下未加催化剂时平衡常数及活化能为k 及E a ,加入正催化剂后则为k '、E a ',则存在下述关系: (A) k '=k , E a =E a ' (B) k '≠k , E a ≠E a ' (C) k '=k , E a >E a ' (D) k '<k , E a '<E a20.过渡态理论的速率常数的公式为()()()k k T h q q q E RT =≠-B AB//exp /∆0,下述说法正确的是(A) q ≠不是过渡态的全配分函数 (B) q A , q B 是任意体积中分子的配分函数 (C) q A , q B , q ≠均是分子在基态时的配分函数(D) ()k T h B /是过渡态M≠中任一个振动自由度配分函数二、 判断题1.关于催化剂特征的不正确描述是在反应前后催化剂的物理性质和化学性质全不改变。
物理化学(第五版傅献彩)第12_化学动力学基础2

k
=ν
K
≠ c
=
kBT h
f fA
≠'
fBC
exp
−
E0 RT
一般基元反应 k 的计算式为
k
=
kBT h
f ≠' ΠfB
exp
−
E0 RT
常温
kBT ≈ 1013 s−1 h
36
A (单原子) + B(单原子) ‡ˆˆˆ†ˆ[ALB]≠ (双原子)
( ) k = kBT ( ) ( ) h
25
势能面
Ep
OT ≠
rAB
A+RBC
D
P
rBC
AB+C
A+B+C
26
R点:是反应物A+BC分子的基态。随A原子靠近, 势能沿RT 升高,到T点形成活化络合物 随C原子离去,势能沿TP线下降
P点:是生成物AB+C分子 的基态
D点:是离解为A,B,C原 子时的势能
OEP一侧是原子间 的相斥能,很高
f
3 t
fr2
≠
f
3 t
A
f
3 t
B
exp
−
E0 RT
1个振动自由度用于活化络合物的分解
37
A
(
N
,非线型多原子分子
A
)
+
B
(
N
,非线型多原子分子
B
)
‡ˆˆˆ†ˆ[ALB]≠ ( NA + NB,非线型多原子分子)
( ) k = kBT
( ) ( ) h
南京大学《物理化学》练习第十一章化学动力学基础_二_

南京⼤学《物理化学》练习第⼗⼀章化学动⼒学基础_⼆_第⼗⼀章化学动⼒学基础(⼆)返回上⼀页1. 将1.0 g氧⽓和0.1 g氢⽓于300 K时在1 dm3的容器内混合,试计算每秒钟内单位体积内分⼦的碰撞数为若⼲?设O2和H2为硬球分⼦,其直径分别为0.339和0.247 nm.2. 某双原⼦分⼦分解反应的阈能为83.68 kJ/mol,试分别计算300 K及500 K时,具有⾜够能量可能分解的分⼦占分⼦总数的分数为多少?3. 某⽓相双分⼦反应, 2A(g) ---> B(g)+C(g),能发⽣反应的临界能为100 kJ/mol.已知A的相对分⼦量为60,分⼦直径为0.35 nm,试计算在300 K 时,该分解作⽤的速率常数k 值.4. 松节油萜(液体)的消旋作⽤上⼀级反应,在457.6 K和510.1 K时的速率常数分别为2.2×和3.07×min-1,试求反应的实验活化能E a,在平均温度时的活化焓和活化熵.5. 在298 K时某化学反应,如加了催化剂后使其活化熵和活化焓⽐不加催化剂是时分别下降了10 J/(mol·K)和10 kJ/mol,试求不加催化剂与加了催化剂的两个速率常数的⽐值.6. 在298 K时有两个级数相同的基元反应A和B,其活化焓相同,但速率常数k A=10k B,求两个反应的活化熵相差多少?7. 某顺式偶氮烷烃在⼄醇溶液中不稳定,通过计量其分解放出的N2⽓来计算其分解的速率常数k值,⼀系列不同温度下测定的k值如下所⽰:T/ k 248 252 256 260 264k×/s-1 1.22 2.31 4.39 8.50 14.3试计算该反应在298K时的实验活化能,活化焓,活化熵和活化吉布斯⾃由能.8. 对下述⼏个反应,若增加溶液中的离⼦强度,则其反应速率常数是增⼤,减⼩还是不变?(1) NH4+ +CNO- --->CO(NH2)2(2) 酯的皂化作⽤.(3) S2O82- + I- --->P9. 在298 K时,反应N2O4(g)2NO2(g)的速率常数k1=4.80×s-1,已知NO2和N2O4的⽣成吉布斯⾃由能分别为51.3和97.8 kJ/mol,试求(1)298 K时, N2O4的起始压⼒为101.325 kPa时, NO2(g)的平衡分压?(2)该反应的弛豫时间?10. ⽤温度跳跃技术测量⽔的离解反应: H2O H+ + OH-,在298 K时的弛豫时间τ=37×s,试求该反应正向和逆向反应的速率常数k1和k-2.11. 在光的影响下,蒽聚合为⼆蒽.由于⼆蒽的热分解作⽤⽽达到光化平衡.光化反应的温度系数(即温度每增加10K反应速率所增加的倍数)是1.1,热分解的温度系数是2.8,当达到光化平衡时,温度每升⾼10K.⼆蒽产量是原来的多少倍?12. ⽤波长为313nm的单⾊光照射⽓态丙酮,发⽣下列分解反应:(CH3)2CO +hv---> C2H6 + CO ,若反应池的容量是0.059 dm3,丙酮吸收⼊射光的分数为0.915,在反应过程中,得到下列数据:反应温度:840 K 照射时间t=7 h起始压⼒:102.16 kPa ⼊射能48.1×J/s,终了压⼒:104.42 kPa计算此反应的量⼦效率.13. 有⼀酸催化反应A+B C+D,已知该反应的速率公式为d[C]/dt=k[H+][A][B] ,当[A]0=[B]0=0.01 mol·dm-3时,在pH=2的条件下,在298 K时的反应的半衰期为1 h,若其他条件不变,在288 K时t1/2为2 h,试计算(1)在298 K时反应的速率常数k值。
物理化学12章_化学动力学基础(二)
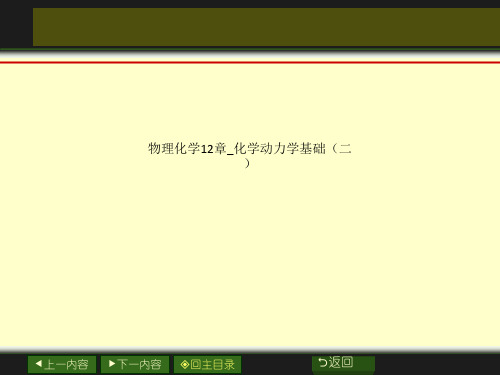
Eb。Eb。是活化络合物与反应物最 低势能之差,E0是两者零点能
之间的差值。
这个势能垒的存在说明了实验活化能的实质。
上一内容 下一内容 回主目录
返回
2021/1/16
势能面剖面图
上一内容 下一内容 回主目录
返回
2021/1/16
三原子系统振动方式
式中r0是分子中双原子分子间的平衡核间 距,De是势能曲线的井深,a为与分子结构有 关的常数.
上一内容 下一内容 回主目录
返回
2021/1/16
双原子分子的莫尔斯势能曲线
AB双原子分子根据该公式 画出的势能曲线如图所示。
当r>r0时,有引力,即化学键力。 当r<r0时,有斥力。 0时的能级为振动基态能级,E0为零点能。
物理化学12章_化学动力学基础(二 )
上一内容 下一内容 回主目录
返回
物理化学电子教案—第十二章
上一内容 下一内容 回主目录
返回
2021/1/16
第十二章 化学动力学基础(二)
§12.1 碰撞理论 *§12.2 过渡态理论
§12.3 单分子反应理论 * §12.4 分子反应动态学简介
§12.5 在溶液中进行的反应 * §12.6 快速反应的几种测试手段
Ea≈ E
上一内容 下一内容 回主目录
返回
2021/1/16
概率因子(probability factor)
由于简单碰撞理论所采用的模型过于简单, 没有考虑分子的结构与性质,所以用概率因子 来校正理论计算值与实验值的偏差。
P=k(实验)/k(理论)
概率因子又称为空间因子或方位因子。
上一内容 下一内容 回主目录
傅献彩《物理化学》(第5版)笔记和课后习题(含考研真题)详解(化学动力学基础(二))【圣才出品】

二、过渡态理论 1.过渡态理论基本要点
3 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
(1)反应物到产物必须经过一种过渡状态,即反应物分子活化形成活化络合物的中间 状态,反应物与活化络合物之间能很快速成化学平衡。
(2)活化络合物又可分解为产物,活化络合物分解步骤为慢步骤,化学反应速率由活 化络合物分解步骤决定。
Ep (r) De[exp{2a(r r0)} 2exp{a(r r0)}]
计算双原子分子势能 Ep 最常用的经验公式。式中 r0 是分子中双原子分子间的平衡核间
4 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
距,De 是势能曲线的井深,a 为与分子结构有关的常数。
③活化络合物,就向产物转化,这步是反应的速决步。
(2)对于一般基元反应,速率常数的计算式为
k kBT f ' exp( E0 )
h fB
RT
B
4.过渡状态理论的优缺点
(1)优点
①形象地描绘了基元反应进展的过程。
②原则上可以从原子结构的光谱数据和势能面计算宏观反应的速率常数。
(3)反应物分子间相互作用势能是分子间相对位置的函数,反应物转化为产物的过程 是体系势能不断变化的过程。
(4)过渡状态理论提供了由物质基本结构系数[υ(振动频率),m(质量),r(核间距) 等]计算反应速率常数的方法。
过渡态理论:由反应物分子变成生成物分子,中间一定要经过一个过渡态,而形成这个过 渡态必须吸取一定的活化能,即反应物分子活化形成活化络合物的中间状态,所以又称为活 化络合物理论。用该理论,只要知道分子的振动频率、质量、核间距等基本物性,就能计算 反应的速率常数,所以又称为绝对反应速率理论。
第十一章_化学动力学基础(二)

第十一章化学动力学基础(二)通过本章学习理解碰撞、过渡态和单分子反应理论,了解一些特殊反应的动力学规律。
(一)基本要求和基本内容:基本要求1.了解化学反应动力学的碰撞、过渡态和单分子反应理论的基本内容,弄清几个能量的不同物理意义及相互关系。
2.了解溶液中反应的特点和溶剂对反应的影响。
3.了解快速反应所常用的测定方法及弛豫时间4.了解光化学反应和催化反应的特点。
重点和难点:过渡态理论中E c、E b、E0、ϑmrH#∆、ϑmrS#∆与Ea之间的关系:基本内容一、碰撞理论1.双分子的互碰频率2.硬球碰撞模型3.微观反应和宏观反应之间的关系4.反应阈能与实际活化能的关系5.概率因子二、过渡态理论1.势能面2.由过渡态理论计算反应速率3.E c、E b、E0、θmrH∆、θmrS∆与Ea和指前因子A之间的关系三、单分子反应理论四、在溶液中进行的反应1.溶剂对反应速率的影响2.原盐效应3.扩散控制反应五、快速反应的测试1.弛豫法2.闪光光解六、光化学反应1.光化学基本定律2.量子产率3.分子的能态4.光化反应动力学5.光化平衡和温度对光化学反应的影响6.感光反应、化学发光七、催化反应动力学1.催化剂与催化作用2.均相酸碱催化3.络合催化(配位催化)4.酶催化反应(二) 基本理论及公式1. 碰撞理论 ⑴ 要点① 反应物分子必须经过碰撞过程才有可能变成产物 ② 只有能量较大的活化分子的碰撞才能发生化学反映⑵ 计算公式① 不同种物质分子间的碰撞次数 [][]B A RTLdB dA Z ABπμπ222⎪⎭⎫ ⎝⎛+=② 同种物质分子间的碰撞次数 []2222A RTLd Z AA AA πμπ=③ 有效碰撞分数)e x p (RTE q C -= E C 为临界能,是基元反应所必需的能量。
④ 不同种分子间碰撞反应的速率常数⎪⎭⎫⎝⎛-=RT E M RTLd k C AB exp 82ππ ⑤ 同种分子间碰撞反应的速率常数⎪⎭⎫⎝⎛-=RT E M RTLd k C AA exp 22ππ ⑶ 解决的问题① 揭示了反应究竟是如何进行的一个简明﹑清晰的物理现象 ② 解释了简单反应速率公式及阿累尼乌斯公式成立的依据③ 解决了反应速率常数的求算问题 ④ 说明了Ea 与T 间的关系RT E E C a 21+=2. 过渡状态理论 ⑴ 要点反应物先形成不稳定的活化络合物,活化络合物与反应物之间迅速达成化学平衡,另一方面活化络合物转化为产物[]C B A C B A C B A +-→⋅⋅⋅⋅⋅⋅⇔-+≠⑵ 计算公式① 用统计热力学方法计算速率常数⎪⎭⎫ ⎝⎛-⋅⋅=∏≠RT E f f hT k k BBB 0'exp② 用热力学方法计算速率常数 (ⅰ) ()()⎪⎪⎭⎫ ⎝⎛∆-⋅⋅=≠-ΘRT G Ch T k k l nB exp 1 或,≠⋅=C B K h Tk k 或,()⎪⎪⎭⎫⎝⎛∆-⋅⎪⎪⎭⎫⎝⎛∆-⋅⋅=Θ≠-ΘRT H R S ChT k k m r mr nB exp exp 1 (ⅱ) ⎪⎪⎭⎫⎝⎛∆-⋅⎪⎭⎫⎝⎛⋅=≠-RTG RT P h T k k PnB exp 1 或 ⎪⎪⎭⎫⎝⎛∆-⋅⎪⎪⎭⎫⎝⎛∆-⋅⎪⎭⎫⎝⎛⋅=Θ≠-RT H RS RT P h T k k P r Pr nB exp exp 1 ③ 几个能量及其关系 (ⅰ) RT E EC a 21+=Ea 活化能,Ec 分子发生有效反应所必须超过的临界能 (ⅱ)mRT E E a +=0E 0 活化络合物的零点能与反应物零点能之差式中m 包括了普适常数项中及配分函数项中所有与T 有关的因子,对一定的反应体系,m 有定值。
第十二章-化学动力学基础(二)

第十二章 化学动力学基础〔二〕1.在K 300时,将)(0.12g gO 和)(1.02g gH 在30.1gdm 的容器内混合,试计算每秒钟、每单位体积内分子碰撞的总数?设)(2g O 和)(2g H 为硬球分子,其直径分别为nm 339.0和nm 247.0。
解:)(1093.2102247.0339.0210922m d d d H O AB --⨯=⨯+=+=)(10896.110016.200.32016.200.321332222---⋅⨯=⨯+⨯=+⋅=mol kg M M M M H O H O μ)(10881.110111002.600.320.13253232--⨯=⨯⨯⨯⨯==m n n O A )(10968.210111002.6016.21.03253232--⨯=⨯⨯⨯⨯==m n n H B 25253210210986.210881.110896.114.3300314.88)1093.2(14.38⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯==--B A ABAB n n RTd Z πμπ )(1077.21335--⋅⨯=s m Z AB2.请计算恒容下,温度每增加K 10时, 〔1〕碰撞频率增加的百分数;〔2〕碰撞时在分子连心线上的对平动能超过180-⋅=mol kJ E c 的活化分子对的增加百分数;〔3〕由上述计算结果可得出什么结论?解:〔1〕B A ABAB n n RTd Z πμπ82=T n n Rd Z B A ABAB ln 21)8ln(ln 2+=∴πμπ TdT Z d AB 21ln =或T dT Z dZ AB AB 2= 当温度变化范围不太大时,有TTZ Z AB AB 2∆=∆ 如K T 298=,K T 10=∆时,有%68.1298210=⨯=∆ABAB Z Z〔2〕)exp(RTE q c-= RTE q q d c=∴ln dT RTE q dqc 2= 当K T 298=,180-⋅=mol kJ E c ,K T 10=∆时%10810)298(314.81080232=⨯⨯⨯=∆=∆T RT E q q c 〔3〕通过计算结果可以看出,温度升高时,碰撞频率的增加并不明显,而活化分子数成倍增加。
第十一章 化学动力学基础(二)

k(T) ( 1 )1/ 2 ( 2 )3/ 2 kBT
0
r
exp(
r kBT
)r
(r
)dr
将硬球碰撞模型:
r ( r ) = dAB2 (1 c / r 数 k SCT ( T ):
8RT M A
单位体积内所有 A 分子间的碰撞频率即为:
ZAA
1 2
NA V
ZAA
乘以系数
1 2
是因为每一对碰撞
Ai Aj
被重复计算了两次:Ai
A
;
j
Ai
Aj
ZAA
2d2AA
NA V
ZAA
1 2
NA V
ZAA
8RT M A
2 2
d
2 AA
(
NA V
g
r
1 2
(mA
mB ) ug2
1 2
ur2
显然,质心整体运动能 g 对两个分子的 碰撞反应没有贡献;
而相对平动能 r 则能衡量两个分子接近 时的相互作用能的大小。
2. 碰撞参数与反应截面:
考虑相对动能 r 时,可设 A 分子以相对于 B 的速度 ur向相对静止的 B 分子的运动。如图:
f
(ur
,
T)
4(
2k BT
)3/
2
exp(
u
2 r
2k BT
)
ur2
(3)
k (ur) = urr (ur)
化学动力学

RT
1
k2dA 2BLRT Me
2
eEa
RT
1
A2dA2BLRTMe 2
1
A2dA2BLRM T 2
kkB hTcθ1nexp R Sm θ exp R H Tm θ
适用范围:凝聚相反应
kkB h T R pT 1nexp R Sm θ exp R H Tm θ
Carbon Dioxide Fixation into Chemicals Methyl Formate at High Yields by Surface Coupling over a Pd/Cu/ZnO Nanocatalyst
Gm θRTlnKcθ
G m θRTlnKc
cθ
n1
Gm θ RT
lnKc
cθ
n1
cθ
K n1 c
expRG Tm θ
Kc cθ 1nexpRG Tm θ
k
kBT h
K
c
kkBT h
cθ
1nexpR G Tm θ
G
m
标准摩尔反应活化Gibbs自由能变
G m θ H m θT Sm θ
kkB h Tcθ1nexp R Sm θ exp E aR T R T
kkB hTcθ1nexp R Sm θ exp R T R TE a
kkBTcθ h
1nexp R Sm θexp1R E T a
kkBTecθ h
1nexp R Sm θexp R E Ta
rk2KccAcBC
根据过渡状态理论的假设活化络合物只 进行一次非对称伸缩振动就能断裂发生 反应因此反应速率为
k2
rr K cccAcBC
苏州大学物理化学考研、期末考试复习-第十二章化学动力学基础二练习题及答案

第十二章化学动力学基础二练习题一、选择题1. 化学反应发生的条件是:()(A) (Δr G m)T, p<0 (B) (Δr G m)T, p>0(C) (Δr G m)T, p=0 (D) (Δr G m)T, p≠03. 单原子分子A,B间发生反应,若忽略振动基态能量之差,则实验活化能E a,临界能E c,势垒E b间存在关系为:( )(A) E a=E c+12RT=E b+12RT(B) E a=E b+12RT=E c+RT(C) E a=E c-12RT=E b-12RT(D) E a=E b+RT=E c+RT4. 在T = 300 K,如果分子A和B要经过每一千万次碰撞才能发生一次反应,这个反应的临界能将是:( )(A) 170 kJ·mol-1(B) 10.5 kJ·mol-1(C) 40.2 kJ·mol-1(D) -15.7 kJ·mol-15. 选用适当的催化剂后,使反应活化能比未加催化剂时降低了8500J·mol-1,则二者速率常数比(k cat/k0) ( )(A) 31倍 (B) 61倍(C) 92倍 (D) 4.5倍6. 下列双分子反应中:(1) Br + Br → Br2(2) CH3CH2OH + CH3COOH → CH3CH2COOCH3+ H2O(3) CH4+ Br2→ CH3Br + HBr碰撞理论中方位因子P的相对大小是∶( )(A) P(1) > P(2) > P(3)(B) P(1) > P(3) > P(2)(C) P(1) < P(2) < P(3)(D) P(1) < P(3) < P(2)7. 破坏臭氧的反应机理为:NO + O3 NO→2+ O2NO2+ O NO + O→2在此机理中,NO 是:( )(A) 总反应的产物(B) 总反应的反应物(C) 催化剂(D) 上述都不是8. 对于水溶液中的反应[ Co(NH 3)5Br]2+ + OH - [Co(NH →3)5OH]2+ + Br -如果增加离子强度,此反应的速率将: ( ) (A) 不变 (B) 降低(C) 达到爆炸极限 (D) 增大9. 根据活化络合物理论,液相分子重排反应之活化能E a 和活化焓Δ≠H m 之间的关系是:( )(A) E a = Δ≠H m(B) E a = Δ≠H m - RT(C) E a = Δ≠H m + RT(D) E a = Δ≠H m / RT二、填空题11. 化学反应的简单碰撞理论中能发生化学反应的判据有两个,即__________________________________ _______________________________,____________________________________________。
第十一章化学动力学基础(二) 本章内容:介绍碰撞理论,过渡状态理论

第十一章化学动力学基础(二)本章内容:介绍碰撞理论,过渡状态理论和单分子反应理论。
了解分子反应动力学的常用实验方法,快速反应所常用的测试方法,说明溶液中反应的特点和溶剂对反应的影响;了解光化学反应的特点及量子产率的计算;介绍催化反应的特点和常见的催化反应的类型。
第一节碰撞理论(simple collision theory)一、碰撞理论基本论点分子碰撞理论是在接受了阿仑尼乌斯活化态、活化能概念的基础上,利用分子运动论于1918 年由路易斯建立起来的。
其基本论点是:1.反应物分子要发生反应必须碰撞,反应物分子间的接触碰撞是发生反应的前提;2.不是任何反应物分子间的碰撞均能发生反应,只有那些能量较高的活化分子、并满足一定的空间配布几何条件的碰撞反应才能发生;3.活化分子的能量较普通能量高,它们碰撞时,松动并部分破坏了反应物分子中的旧键,并可能形成新键,从而发生反应,这样的碰撞称为有效碰撞或非弹性碰撞,活化分子愈多,发生化学反应的可能性就愈大;4.若从Z A,B表示单位时间、单位体积内A,B分子碰撞总数,以q代表有效碰撞在总碰撞数Z A,B中所占的百分数,则反应速率可表示为二、双分子的互碰频率设A、B两种分子都是完全弹性的、无压缩性的刚球,二者半径各为1/2d A, 1/2d B, 单位体积中A的分子数为nN A/V, A分子运动的平均速率为〈U A〉。
假定B分子是静止的,那么一个A 分子与静止B 分子的碰撞次数为,A、B 分子的碰撞直径为d AB = 1/2(d A +d B),碰撞截面为πd2AB,,在时间t内,A分子走过的路程为〈U A〉t,碰撞截面所掠过的体积为〈U A〉tπd2AB, 凡是质心落在这个体积内的静态B分子都可能与A碰撞。
所以移动着的A分子在单位时间内与静止B分子相碰的次数(即碰撞频率)为,由于B分子也在运动,因此要用相对速率u r来代替平均速率(u),A与B的相对速率有几种情况考虑平均情况,则那么,一个运动着的A 分子与运动着的B 分子互相碰撞频率为那么,单位时间、单位体积内所有运动着的A、B 分子碰撞的总次数为对于浓度为[A]的同种分子,则三、硬球碰撞摸型设A.和B为两个没有结构的硬球分子,质量分别为m A和m B,折合质量为μ,运动速度分别为u A、u B,总能量E为'四、微观反应与宏观反应之间的关系反应截面是微观反应动力学基本参数,而速率常数k和实验活化能E a 等是宏观反应动力学参数。
第2章 化学反应动力学基础
1.3.2 活化能因素: 对于基元反应来说,如果体系中一个组分有两 个以上的基元反应发生,则以活化能最低的发生反 应几率最大,这也是探索历程的一个重要线索依 据,由此因素,我们可以确定基元反应那些反应可 以发生,那些反应的发生可能性最小。
1.3.3 中间物和分子结构因素: 如果能从反应中检验某种中间物,则对反应历 程的确定将起重要作用,某些物质容易捕捉自由 基,反应体系加入这些物质,观察反应速率是否 下降,以判断体系中是否有自由基存在,而自由 基的存在常能导致链反应,此外,所设想的中间 物应与结构化学规律相符合,这就是需要考虑的 结构因素。
cCH3CHO(0)为乙醛的初始浓度。 式中,
上一内容 下一内容 返回
反应级数 当固定乙醛的初始浓度,可见在不同反应时间 测量反应速率时,r与
cCH3CHO 的平方成正比,
即称其时间级数为二级。如果以不同的初始浓
度进行试验,测定反应的初始反应速率,则与 乙醛的初始浓度的一次方成正比,即称为反应 级数为一级。许多反应的时间级数与浓度级数 是相同的,但也有一些不同。
在我们通过考虑三因素后,则基本上对反应的历 程有了某些线索和启发,然后可以进行初步探索 拟定历程,当初步拟定历程后,如何检验所草拟 的历程有一定的正确性和认为可以接受呢? 这就要求我们必须记住服从下面两个一致性:由 拟定的反应历程所得到的反应动力学方程应该和 由实验得到的动力学方程相一致。由拟定的反应 历程所得到的表观活化能应该和由实验测得的活 化能相一致。
t1/2 =
1 n-1-1 ] [ (2) (n-1)αkcA(0)n-1
上一内容 下一内容
[n(≠1)级反应]
返回
八、收率、转化率和选择收率 收率是指一个反应过程的产物量占反应物量的 百分数
第十二章 化学动力学(二)自测题

第十二章 化学动力学基础(二)自测题Ⅰ.选择题1.在简单硬球碰撞理论中,有效碰撞的定义是(c ) (a)互撞分子的总动能超过E c (b)互撞分子的相对动能超过E c(c)互撞分子的相对平动能在连心线上的分量超过E c (d)互撞分子的内部动能超过E c2.某双原子分子分解反应的阀能E c =83.68 kJ·mol -1,则在300 k 时活化分子所占的分数是(d ) (a)3.719×10-14 (b)6.17×10-15 (c)2.69×10-11 (d)2.69×10-153.有一稀溶液反应33CH COOCH OH P -+→,根据原盐效应,当溶液总的离子强度增加时,反应速率常数k 值将(c )(a)变大 (b)变小 (c)不变 (d)无确定关系 4.已知HI 的光分解反应机理如下:HI H +I hv +→⋅⋅ 2H HI H I ⋅+→+⋅ 2I I M I M ⋅+⋅+→+则该反应的反应物消耗的量子效应(b ) (a)1 (b)2 (c)4 (d)1065.某一反应在一定条件下的平衡转化率为25%,当加入合适的催化剂后,反应速率提高10倍,其平衡转化率将(c )(a)大于25% (b)小于25% (c)不变 (d)不确定 6.设某基元反应在500 K 时的实验活化能为83.14 kJ·mol -1,则此反应的阀能E c 为(d ) (a)2.145 kJ·mol -1 (b)162.1 kJ·mol -1 (c)83.14 kJ·mol -1 (d)81.06 kJ·mol -1 7.根据过渡态理论,液相双分子反应的实验活化能E a 与活化焓r m H ≠∆之间的关系为(b ) (a)a r m E H ≠=∆ (b)a r m E H RT ≠=∆+ (c)a r m E H RT ≠=∆- (d)a r m 2E H RT ≠=∆+ 8.设两个单原子气体A 和B 发生化合反应。
化学动力学基础二
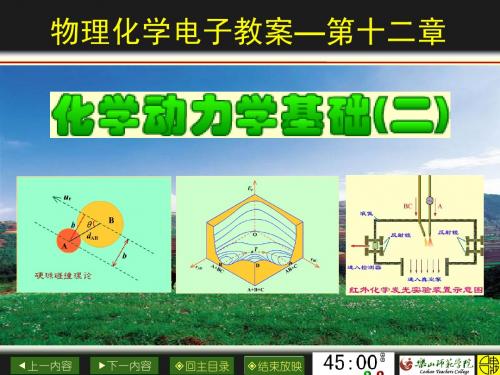
反应截面的定义
r def b d
2 r
2 AB
r c r c
上一内容 下一内容
r 0 r 的值随着 r 的增加而增加
回主目录 结束放映
c 1 r
*宏观速率常数
1 2 r ur 2 r 也是 u r 的函数 2 c 2 r ur d AB 1 2 ur
*宏观速率常数
若用物质的量浓度表示,则速率常数的计算式为
ksct (T ) d L
2 AB
8kBT
exp(
c
kBT
)
或
ksct (T ) d L
2 AB
8RT
Ec exp( ) RT
对于相同分子的双分子反应,则有
c 2 8kBT 2 kSCT T d AA L exp 2 MA kBT
称为能发生化学反应的临界能或阈能
上一内容 下一内容
回主目录 结束放映
c
bmax
0
2 bdb b
2 max
d
2 AB
*反应截面 发生反应的必要条件是
设碰撞参数为某一数值时
b2 r 1 2 c d AB
2 br c 2 2 r 1 2 c br d AB 1 d AB r 凡是 b br 的所有碰撞都是有效的
dcA Z AB r e dt L
上一内容 下一内容
qe
d L
2 AB
E RT
E RT
E RT
8 RT
e
cA cB kcA cB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章化学动力学基础(二)11.1 碰撞理论11.1.1 速率理论的共同点与热力学的经典理论相比,动力学理论发展较迟。
先后形成的碰撞理论、过渡态理论都是20世纪后建立起来的,尚有明显不足之处。
理论的共同点是:首先选定一个微观模型,用气体分子运动论(碰撞理论)或量子力学(过渡态理论)的方法,并经过统计平均,导出宏观动力学中速率系数的计算公式。
由于所采用模型的局限性,使计算值与实验值不能完全吻合,还必须引入一些校正因子,使理论的应用受到一定的限制。
11.1.2 两个分子的一次碰撞过程两个分子在相互的作用力下,先是互相接近,接近到一定距离,分子间的斥力随着距离的减小而很快增大,分子就改变原来的方向而相互远离,完成了一次碰撞过程。
粒子在质心体系中的碰撞轨线可用示意图表示为:有效碰撞直径和碰撞截面运动着的A分子和B分子,两者质心的投影落在直径为d AB的圆截面之内,都有可能发生碰撞。
d AB称为有效碰撞直径,数值上等于A分子和B分子的半径之和。
虚线圆的面积称为碰撞截面(collision cross section)。
数值上等于。
A与B分子互碰频率将A和B分子看作硬球,根据气体分子运动论,它们以一定角度相碰。
相对速度为:互碰频率为:2ABdπ221/2AB AB8()[A B]][RTZ d Lππμ=或A BM Mμ=式中A B[A][B]N NL L==两个A 分子的互碰频率当体系中只有一种A 分子,两个A 分子互碰的相对速度为:每次碰撞需要两个A 分子,为防止重复计算,在碰撞频率中除以2,所以两个A 分子互碰频率为:221/2A AA A 2()()N RT d V M ππ= 硬球碰撞模型设A 和B 为没有结构的硬球分子,质量分别为 和 ,折合质量为 ,运动速度分别为 和 ,总的动能为 将总的动能表示为质心整体运动的动能 和分子相对运动的动能 ,两个分子在空间整体运动的动能对化学反应没有贡献,而相对动能可以衡量两个分子相互趋近时能量的大小,有可能发生化学反应。
碰撞参数(impact parameter )碰撞参数用来描述粒子碰撞激烈的程度,通常用字母b 表示。
在硬球碰撞示意图上,A 和B 两个球的连心线 等于两个球的半径之和,它与相对速度 之间的夹角为 。
通过A 球质心,画平行于 的平行线,两平行线间的距离就是碰撞参数b 。
数值上: max AB b d =有效碰撞分数 分子互碰并不是每次都发生反应,只有相对平动能在连心线上的分量2/1Ar )82(M RT u π⨯=221/2A AA AA A8()() 2N RT Z d V M π=221/22AA A2()[A]RT d L M ππ=A u B u 2B B 2A A 2121u m u m E +=A m B m g εr ε22g r A B g r 11()22E m m u u εεμ=+=++g u AB d r u θr u AB sin b d θ=⋅0 b b =值越小,碰撞越激烈。
迎头碰撞,最激烈.大于阈能的碰撞才是有效的,所以绝大部分的碰撞是无效的。
要在碰撞频率项上乘以有效碰撞分数q 。
反应截面(cross section of reaction)反应截面 的定义式为: 式中b r 是碰撞参数临界值,只有碰撞参数小于b r 的碰撞才是有效的。
为反应阈能,从图上可以看出,反应截面是相对平动能的函数,相对平动能至少大于阈能,才有反应的可能性,相对平动能越大,反应截面也越大。
反应阈能(threshold energy of reaction)反应阈能又称为反应临界能。
两个分子相撞,相对动能在连心线上的分量必须大于一个临界值 E c ,这种碰撞才有可能引发化学反应,这临界值E c 称为反应阈能。
E c 值与温度无关,实验尚无法测定,而是从实验活化能E a 计算。
碰撞理论计算速率系数的公式11.1.3碰撞理论计算速率系数的公式(1)(2)式完全等效,(1)式以分子计,(2)式以1mol 计算。
11.1.4 反应阈能与实验活化能的关系碰撞理论计算速率系数的公式:r σ)1(rc 2AB 2r r εεππσ-==d b c ε]A][B [d ]A [d P B A k t r =-=−→−+有(2) )exp()8( :(1) )exp()8( c 2/12AB B c 2/1B 2AB RT E RT L d k T k T k L d k -=-=πμπεπμπ则21/2c AA A 8 2A p )exp( ) (3)2E RT k d L M RTπ−−→=-(将与T 无关的物理量总称为B :实验活化能的定义:比较得 总结:阈能E c 与温度无关,但无法测定,要从实验活化能E a 计算。
在温度不太高时,E a ≈ E c11.1.5 概率因子(probability factor )由于简单碰撞理论所采用的模型过于简单,没有考虑分子的结构与性质,所以用概率因子来校正理论计算值与实验值的偏差。
P=k (实验)/k (理论)概率因子又称为空间因子或方位因子。
理论计算值与实验值发生偏差的原因主要有:(1)从理论计算认为分子已被活化,但由于有的分子只有在某一方向相撞才有效;(2)有的分子从相撞到反应中间有一个能量传递过程,若这时又与另外的分子相撞而失去能量,则反应仍不会发生;(3)有的分子在能引发反应的化学键附近有较大的原子团,由于位阻效应,减少了这个键与其它分子相撞的机会等等。
碰撞理论的优缺点优点: 碰撞理论为我们描述了一幅虽然粗糙但十分明确的反应图像,在反应速率理论的发展中起了很大作用。
对阿仑尼乌斯公式中的指数项、指前因子和阈能都提出了较明确的物理意)exp()8(c 2/12AB RTE RT d k -=πμπTRT E T k 21d ln d 2c +=c 1 ln ln ln 2E k T B RT =-++有kRT E ln d 2a =义,认为指数项相当于有效碰撞分数,指前因子A 相当于碰撞频率。
它解释了一部分实验事实,理论所计算的速率系数k 值与较简单的反应的实验值相符。
缺点:但模型过于简单,所以要引入概率因子,且概率因子的值很难具体计算。
阈能还必须从实验活化能求得,所以碰撞理论还是半经验的。
11.2 过渡态理论11.2.1 过渡态理论(transition state theory)过渡态理论是1935年由艾林(Eyring)和波兰尼(Polany)等人在统计热力学和量子力学的基础上提出来的。
他们认为由反应物分子变成生成物分子,中间一定要经过一个过渡态,而形成这个过渡态必须吸取一定的活化能,这个过渡态就称为活化络合物,所以又称为活化络合物理论。
用该理论,只要知道分子的振动频率、质量、核间距等基本物性,就能计算反应的速率系数,所以又称为绝对反应速率理论(absolute rate theory)。
11.2.2 双原子分子的莫尔斯势能曲线该理论认为反应物分子间相互作用的势能是分子间相对位置的函数。
莫尔斯(Morse)公式是对双原子分子最常用的计算势能E p 的经验公式:式中r 0是分子中双原子分子间的平衡核间距,D e 是势能曲线的井深,a 为与分子结构有关的常数.AB 双原子分子根据该公式画出的势能曲线如图所示。
当r>r 0时,有引力,即化学键力。
当r<r 0时,有斥力。
时的能级为振动基态能级,E 0为零点能。
D 0为把基态分子离解为孤立原子所需的能量,它的值可从光谱数据得到。
11.2.3 三原子分子的核间距以三原子反应为例:p e 00()[exp{2()}2exp{()}]E r D a r r a r r =-----0ν=A BC [A B C]AB C≠+⋅⋅⋅⋅⋅⋅→+当A 原子与双原子分子BC 反应时首先形成三原子分子的活化络合物,该络合物的势能是3个内坐标的函数:这要用四维图表示,现在令∠ABC=180°,即A 与BC 发生共线碰撞,活化络合物为线型分子,则E P=E P(r AB,r BC),就可用三维图表示。
11.2.4 势能面对于反应: 令∠ABC=180o, E P=E P(r AB,r BC)。
随着核间距r AB 和r BC 的变化,势能也随之改变。
这些不同点在空间构成高低不平的曲面,称为势能面,如图所示。
图中R 点是反应物BC 分子的基态,随着A 原子的靠近,势能沿着RT 线升高,到达T 点形成活化络合物。
随着C 原子的离去,势能沿着TP 线下降,到P 点是生成物AB 分子的稳态。
D 点是完全离解为A,B,C 原子时的势能;OE P 一侧,是原子间的相斥能,也很高。
势能面的类型目前常见的势能面有两种:一种是Eyring 和Polanyi 利用London 对三原子体系的量子力学势能近似式画出的势能面称为London-Eyring-Polanyi 势能面,简称LEP 势能面。
另一种是Sato 又在这个基础上进行了修正,使势垒顶端不合理的势阱消失,这样得到的势能面称为 London-Eyring-Polanyi-Sato 势能面,简称LEPS 势能面。
反应坐标(reaction coordinate)反应坐标是一个连续变化的参数,其每一个值都对应于沿反应体系中各原子的相对位置。
如在势能面上,反应沿着RT →TP 的虚线进行,反应进程不同,各原子间相对位置也不同,体系的能量也不同。
如以势能为纵坐标,反应坐标为横坐标,画出的图可以表示反应过),,( ),,(A BC BC A B P P CA BC A B P P ∠==r r E E r r r E E 或[A B C]A BC AB C≠⋅⋅⋅⋅⋅→⋅++程中体系势能的变化,这是一条能量最低的途径。
马鞍点(saddle point)在势能面上,活化络合物所处的位置T点称为马鞍点。
该点的势能与反应物和生成物所处的稳定态能量R点和P点相比是最高点,但与坐标原点一侧和D点的势能相比又是最低点。
如把势能面比作马鞍的话,则马鞍点处在马鞍的中心。
从反应物到生成物必须越过一个能垒。
势能面投影图将三维势能面投影到平面上,就得到势能面的投影图。
图中曲线是相同势能的投影,称为等势能线,线上数字表示等势能线的相对值。
等势能线的密集度表示势能变化的陡度。
靠坐标原点(O点)一方,随着原子核间距变小,势能急剧升高,是一个陡峭的势能峰。
在D点方向,随着r AB和r BC的增大,势能逐渐升高,这平缓上升的能量高原的顶端是三个孤立原子的势能,即D点。
反应物R经过马鞍点T到生成物P,走的是一条能量最低通道。
势能面剖面图沿势能面上R-T-P虚线切剖面图,把R-T-P曲线作横坐标,这就是反应坐标。
