2018年人教版八年级下《第18章平行四边形》同步测试题含答案
八年级数学下第18章平行四边形单元测试题2018人教版附答案
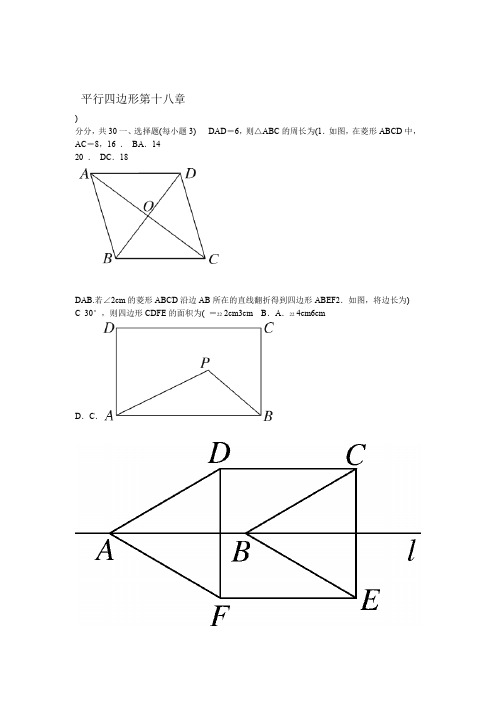
平行四边形第十八章)分分,共30一、选择题(每小题3) DAD=6,则△ABC的周长为(1.如图,在菱形ABCD中,AC=8,16 .BA.1420 .DC.18DAB.若∠2cm的菱形ABCD沿边AB所在的直线翻折得到四边形ABEF2.如图,将边长为)C30°,则四边形CDFE的面积为(=22 2cm3cm B.A.22 4cm6cmD.C.题图第3 2第题图S内,且满足3,动点P在矩形ABCD3.如图,在矩形ABCD中,AB=5,AD=ABP△1) 的最小值为(D P到A,B两点距离之和PA+PBS,则点ABCD矩形3D.412 C.529 B.34 A.4、矩形具有而菱形不具有的性质是( B )A.两组对边分别平行B.对角线相等C.对角线互相平分D.两组对角分别相等5.已知在?ABCD中,BC-AB=2cm,BC=4cm,则?ABCD的周长是(B)A.6cm B.12cm C.8cm D.10cm6.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为(D)A.25cm B.50cmC.75cm D.100cm8题图第第7题图第6题图的延长BAEAD于,交,BC=8,∠BCD的平分线交.如图,在7?ABCD中,AB=6)(A线于F,则AF的长等于6 . D 4 C 3 2 A.B..) C CPQ的度数为(CDQABCD.如图,在正方形中,P、分别为BC、的中点,则∠8 .45°C .50°A.B60°.D70°9.小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是(D).①④B .①② A D.②③.③④C10、如图,下列四组条件中,能判定□ABCD是正方形的有( D )①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.A.1个 B.2个 C.3个 D.4个二、填空题(每小题3分,共24分)11.已知平行四边形ABCD中,∠B+∠D=270°,则∠C=________.12.在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.13.如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是________.题图第15 第13题图.AOB,AB=1,∠=60°,则AD=________交于点.14在矩形ABCD中,对角线AC、BDOAD90°,点D,E分别是AB,AC的中点,点F是ACB15.如图,在Rt△ABC中,∠=的中点.若.EF=________AB=8,则2处.若∠1=∠落在点BD折叠,使点AA′16.如图,将平行四边形ABCD沿对角线________.50°=,则∠A′的度数为第18题图第17题图第16题图22,则菱形AECF的面积为ABCD17.如图,已知菱形的面积为120cm50cm,正方形________cm. 的边长为,BCG的边长分别为3和1,点F,分别在边EFCG18.如图,正方形ABCD和正方形PG,则PG的长为________.AECD上,P为的中点,连接)分(共66三、解答题,的延长线于BAF并延长交的中点,连接的边?E)(819.分如图,是ABCDADCE CD若=BF6,求的长.20.(8分)如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.(1)求证:四边形ABCD是平行四边形;(2)若AC⊥BD,求?ABCD的面积.21.(8分)如图,在?ABCD中,已知AD>AB.(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF(要求:尺规作图,保留作图痕迹,不写作法);(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.22.(8分)如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:(1)△ODE≌△FCE;(2)四边形ODFC是菱形.23.(10分)如图,E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE.(1)判断四边形EFGH的形状,并证明你的结论;(2)当BD,AC满足什么条件时,四边形EFGH是正方形?请说明理24.(10分)如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.(1)求证:DF=AE;2的值.2时,求BEAB(2)当=25.(14分)如图①,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD 上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动.①当点Q与点C重合时(如图②),求菱形BFEP的边长;②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.答案17.1316.105°15.212.3013.914.311.45°18.519.解:∵E是?ABCD的边AD的中点,∴AE=DE.(2分)∵四边形ABCD是平行四边形,∴AB=CD=6,AB∥CD,∴∠F=∠DCE.(4分)在△AEF和△DEC中,∠F=∠DCE,???∠AEF=∠DEC,∴△AEF≌△DEC(AAS),(6分)∴AF=CD=6,∴BF=AB +AF=??AE=DE,12.(8分)20.(1)证明:∵O是AC的中点,∴OA=OC.∵AD∥BC,∴∠ADO=∠CBO.(2分)在∠ADO =∠CBO,???中,COB和△△AOD∠AOD=∠COB,??OA=OC,∴△AOD≌△COB,∴OD=OB,∴四边形ABCD是平行四边形.(4分)(2)解:∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,(6分)∴S?ABCD1AC·BD =24.(8分) 221.解:(1)如图所示.(3分)(2)四边形ABEF是菱形.(4分)证明如下:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE =∠AEB.∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴BE=AB.(6分)由(1)得AF=AB,∴BE=AF.又∵BE∥AF,∴四边形ABEF是平行四边形.(7分)∵AF=AB,∴四边形ABEF是菱形.(8分)22.证明:(1)∵CF∥BD,∴∠DOE=∠CFE.∵E是CD的中点,∴CE=DE.(2分)在△ODE和△FCE中,∠DOE=∠CFE,???∠DEO=∠CEF,∴△ODE≌△FCE(AAS).(4分)??DE=CE,(2)∵△ODE≌△FCE,∴OD=FC.(5分)∵CF∥BD,∴四边形ODFC是平行四边形.(6分)在矩形ABCD中,∵OC=OD,∴四边形ODFC是菱形.(8分)23.解:(1)四边形EFGH为平行四边形.(1分)理由如下:在△ABC中,∵E,F分别11是边AB,BC的中点,∴EF∥AC,且EF=AC,同理有GH∥AC,且GH=AC,(3分)∴EF∥GH 22且EF=GH,故四边形EFGH是平行四边形.(5分)1,BDEFGH当AC=BD且AC⊥BD时,四边形是正方形.(6分)理由如下:∵EH=(2)21EFGH ∴四边形=AC,∴若AC=BD,则有EH=EF.又∵四边形EFGH是平行四边形,EF2))∵AC⊥BD,∴∠EHG=90°.∴四边形EFGH为正方形.(10分是菱形.(8分AEF,在正方形ABCD中,∠D=90°.CEF=∠EF⊥AC,∴∠∵24.(1)证明:连接CF,=CFCF??.(2EF,∴DF =RtRt△CDF≌△CEF(HL).=90°在Rt△CDF和Rt△CEF中,∴?,CECD=??=AE,∴△AEF 是等腰直角三角形,∴是正方形ABCD的对角线,∴∠EAF=45°)分∵AC)AE.(4分DFEF,∴=中,由勾股定△ABC=AB=2.在RtBC(2)解:在正方形ABCD中,∠ABC =90°,CD=22)22-2.(6AC-CD+BC=分=2AB=∴22.∵CE=CD,AE=AC-CE理得AC==AB是等腰直角三角形,AEH是正方形ABCD的角平分线,∴△于H.∵AC过点E作EH⊥AB22在=2.(8AH=2-分(2-)AE-=(222)=2)2-2,∴BH=AB∴EH=AH-=2222222)2.(108分+-(2BERt△BEH中,由勾股定理得-=BH2)+EH4==(2)关于与点EPQ,∴点B点落在边(1)证明:∵折叠纸片使BAD上的E处,折痕为25.,EFPBPFAB,∴∠=∠.(2分)又∵EF∥,PQ对称,∴PB=PEBF=EF,∠BPF=∠EPF)分BFEP为菱形.(4BF=EF=EP,∴四边形∴∠EPF=∠EFP,∴EP=EF,∴BP=∵.=90°,∠A=∠D=AD=5cm,CD=AB=3cmBC(2)解:①∵四边形ABCD是矩形,∴22=4cmCE,-在Rt△CDE中,CDDE=5cm.(5关于点B与点EPQ对称,∴CE=BC=分)2EP,∴-EPPB=3-=3AE(7.分)在Rt△APE中,=1,AP4DEAE∴=AD-=5-=1(cm)5522,∴EP=cm,∴菱形BFEP的边长为1EP+(3-)cm.(9分)=33②当点Q与点C重合时,如图②所示.点E离点A最近,由①知,此时AE=1cm.(11分)当点P与点A重合时,如图③所示.点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,(13分)∴点E在边AD上移动的最大距离为2cm.(14分)。
人教版八年级下册数学第18章平行四边形同步资料及答案

《平行四边形边、角的性质》基础训练知识点1 平行四边形边、角的性质1.在下列性质中,平行四边形不一定具有的是( ) A.对边相等 B.对边平行C.对角互补D.内角和为3602.如图,在ABCD 中,M 是BC 延长线上的一点.若135A ︒∠=,则MCD ∠的度数是( )A.45︒B.55︒C.65︒D.75︒3.如图,若平行四边形ABCD 的周长是28cm ,△ABC 的周长是22cm ,则AC 的长为( )A.14cmB.12cmC.10cmD.8cm4.(1)在ABCD 中,若200B D ︒∠+∠=,则A ∠=______;若:5:4A B ∠∠=,则C ∠=______________; (2)已知ABCD 的周长为28cm ,若:3:4AB BC =,则AB =________,BC =_____.5.(2019·吉林)如图,在ABCD 中,点E 在边AD 上,以C 为圆心,AE 长为半径画弧,交边BC 于点F ,连接,,BE DF .求证:△ABE ≌△CDF .6.(2019·广安)如图,点E 是ABCD 的边CD 的中点,,AE BC 的延长线交于点,3,2F CF CE ==,求ABCD 的周长.知识点2 平行线间的距离7.如图,//,//,,a b AB CD CE b FG b ⊥⊥,点,E G 为垂足,则下列说法不正确的是( )A.AB CD =B.EC GF =C.,A B 两点的距离就是线段AB 的长度D.a 与b 的距离就是线段CD 的长度 8.如图,//,AB CD AB BC ⊥.若24cm,12cm ABCAB S ==,则△ABD 中AB 边上的高等于____________cm .易错点1 位置不确定,造成漏解9.已知直线////,a b c a 与b 的距离是5cm,b 与c 的距离是3cm ,则a 与c 的距离是__________.易错点2 不注意分情况讨论,造成漏解10.在ABCD中,A的平分线把BC边分成长度是3和4的两部分,则ABCD的周长是___________.参考答案1.C2.A3.D4.(1)80100︒︒(2)6cm 8cm5.证明:由题意可得:AE FC =,在ABCD 中,,AB DC A C =∠=∠.在△ABE和△CDF 中,,,,AE CF A C AB CD =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF (SAS ).6.解:∵四边形ABCD 是平行四边形,//.AD BC DAE ∴∴∠=,F D ECF ∠∠=∠. 又E 是CD 的中点,.ED EC ∴=∴△ADE ≌△FCE (AAS ).3AD CF ∴==,2, 4. DE CE DC ABCD ==∴=∴的周长为2()14AD DC +=.7.D 8.6 9.8cm 或2cm 10.22或20《平行四边形边、角的性质》提升训练1.如图,在ABCD 中,4,6,AB BC AC ==的垂直平分线交AD 于点E ,则△CDE的周长是( )A.7B.10C.11D.122.如图所示,直线//,a b A 是直线a 上的一个定点,线段BC 在直线b 上移动,那么在移动过程中△ABC 的面积( )A.变大B.变小C.保持不变D.无法确定3.如图,将ABCD 沿对角线BD 折叠,使点A 落在点E 处,DE 交BC 于点F ,连接CE ,则下列结论:①BE CD =;②BF DF =;③BEFDCFS S=;④//BD CE ,其中正确的有( )A.1个B.2个C.3个D.4个4.(2019·梧州)如图,在ABCD 中,119,ADC BE DC ︒∠=⊥于点,E DF BC ⊥于点,F BE 与DF 交于点H ,则BHF ∠=______________.5.(2019·福建)在平面直角坐标系xOy 中,OABC 的三个顶点坐标分别为(0,0),(3,0),(4,2)O A B ,则其第四个顶点的坐标是____________.6.如图,在ABCD 中,CM AD ⊥于点,M CN AB ⊥于点N .(1)若45B ︒∠=,求MCN ∠的大小; (2)若ABCD 的周长等于15,2,3CM CN ==,求,AB AD 的长.7.(原创题)已知四边形ABCD 是平行四边形,,DAB ABC ∠∠的平分线相交于点P .(1)如图1,若点P 刚好落在CD 边上,5cm,8cm AD AP ==,求△APB 的周长; (2)如图2,若点P 落在ABCD 的内部,5cm,8cm AD AB ==,求EF 的长;(3)若点P 落在ABCD 的外部,画出图形并直接写出ABCD 应满足的条件.参考答案 1.B 2.C 3.D 4.61 5.(1,2)6.解:(1)45MCN ︒∠=.(2)3, 4.5AB AD ==7.解:(1)∵四边形ABCD 是平行四边形,//,//,,AD BC AB DC AD BC AB DC ∴==.180DAB CBA ︒∴∠+∠=.又AP 和BP 分别平分DAB ∠和CBA ∠,1()902PAB PBA DAB CBA ︒∴∠+∠=∠+∠=.180()90APB PAB PBA ︒︒∴∠=-∠+∠=.AP 平分,//DAB AB CD ∠,DAP PAB DPA ∴∠=∠=∠.5cm AD DP ∴==.同理:5cm PC BC AD ===. 10cm AB DC DP PC ∴==+=.在Rt △APB 中,10cm,8cm AB AP ==,221086(cm)BP ∴=-=.∴△APB 的周长为681024(cm)++=. (2)由(1)可知,,.5cm AD DE BC CF AD ===,5cm DE CF ∴==.又8cm AB =,8cm.2cm CD EF DE CF CD ∴=∴=+-=.(3)当ABCD 满足2AB AD >时,点P 落在ABCD 的外部,如图所示.《平行四边形对角线的性质》基础训练知识点1 平行四边形的对角线互相平分1.如图,在ABCD 中,O 是对角线,AC BD 的交点,下列结论错误的是( )A.//AB CDB.AB CD =C.AC BD =D.OA OC =2.(教材P44练习T1变式)如图,ABCD 的对角线,AC BD 相交于点O ,已知8,12,6AD BD AC ===,则△OBC 的周长为( )A.13B.17C.20D.263.如图,在ABCD 中,已知90,10cm,6cm ODA AC BD ︒∠===,则AD 的长为( )A.4cmB.5cmD.8cm4.如图,若ABCD的周长为22cm,,AC BD相交于点O,△AOD的周长比△AOB 的周长小3cm,则AD=_________,AB=________.5.在ABCD中,3,5AB BCAC BD相交于点O,则OA的取值范围==,对角线,是________________.6.如图所示,在ABCD中,对角线AC与BD相交于点O,点,M N在对角线AC上,且AM CNBM DN.=,求证//知识点2 平行四边形的面积7.如图,在ABCD中,O是对角线,AC BD的交点.若△AOD的面积是5,则ABCD的面积是()A.10B.15C.208.如图,若ABCD的面积为20,5BC=,则边AD与BC间的距离为_____________.9.如图,在ABCD中,对角线,==,AC BD相交于点O.若 1.5cm,5cmDO ABBC=,则ABCD的面积为___________.4cm易错点考虑不全面而致错10.如图,在ABCD中,对角线AC与BD相交于点,O AE BD⊥于⊥于点,E CF BD点F,则图中全等三角形共有()A.7对B.6对C.5对D.4对参考答案1.C2.B3.A4. 4cm 7cm5.14OA <<6.证明:四边形ABCD 是平行四边形,,.OA OC OB OD AM CN ∴===,OM ON ∴=.在△BOM 和△DON 中,,,,OB OD BOM DON OM ON =⎧⎪∠=∠⎨⎪=⎩∴△BOM ≌△DON (SAS)..//OBM ODN BM DN ∴∠=∠∴7.C 8.4 9.12 10.A《平行四边形对角线的性质》提升训练1.【整体思想】如图,ABCD 的对角线相交于点O ,且5AB =,△OCD 的周长为23,则ABCD 的两条对角线的和是( )A.18B.28C.36D.462.如图,ABCD 的对角线AC 的长为10cm,30,CAB AB ︒∠=的长为6cm ,则ABCD 的面积为( )A.260cmB.230cmC.220cmD.216cm3.(2019·遂宁)如图,在ABCD 中,对角线,AC BD 相交于点,O OE BD ⊥交AD 于点E ,连接BE .若ABCD 的周长为28,则△ABE 的周长为( )A.28B.24C.21D.144.如图,在ABCD 中,,AC BD 为对角线,6,BC BC =边上的高为4,则阴影部分的面积为___________.5.(2018·福建改编)(1)如图1,ABCD 的对角线,AC BD 相交于点O ,过点O 作直线EF 分别交,AD BC 于点,E F .求证OE OF =;(2)如图2,在ABCD 中,若过点O 的直线与,BA DC 的延长线分别交于点,E F ,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?6.(2019·荆门)如图,已知在ABCD 中,5,3,213AB BC AC === (1)求ABCD 的面积; (2)求证:BD BC ⊥.7.如图,在ABCD 中,对角线AC 与BD 相交于点,45,2E AEB BD ︒∠==,将△ABC 沿AC 所在直线翻折.若点B 的落点记为B ',则DB '的长为___________.参考答案1.C2.B3.D4.125.解:(1)证明:四边形ABCD 为平行四边形,∴//,AD BC OA OC =.,EAO FCO AEO CFO ∴∠=∠∠=∠.∴△AEO ≌△CFO (AAS ). OE OF ∴=.(2)能得到(1)中的结论.证明如下:四边形ABCD 为平行四边形,//,.,AB CD OA OC EAO FCO AEO CFO ∴=∴∠=∠∠=∠.∴△AEO ≌△CFO(AAS ). OE OF ∴=.一般性结论是:过平行四边形对角线的交点O 作一条直线与平行四边形相对的两边或其延长线相交于,E F 两点,则OE OF =.6.解:(1)作CE AB ⊥交AB 的延长线于点E .设,BE x CE h ==,在Rt △CEB 中,229x h +=①,在Rt △CEA 中,22(5)52x h ++=②,联立①②,解得95x =,12.5h ABCD =∴的面积为12AB h ⋅=.(2)证明:作DF AB ⊥,垂足为,90F DFA CEB ︒∴∠=∠=.四边形ABCD 是平行四边形,,//AD BC AD BC ∴=.DAF CBE ∴∠=∠.又90DFA CEB ︒∠=∠=,,AD BC =∴△ADF ≌△BCE (AAS ). 9916,5555AF BE BF ∴===-=,125DF CE ==.在Rt △DFB 中,2222212161655BD DF BF ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭,4BD ∴=.2223,5,BC DC CD DB BC ==∴=+.BD BC ∴⊥.《平行四边形的判定1》基础训练平行四边形的判定定理1:已知:四边形ABCD, AB=CD ,AD=BC 求证:四边形ABCD 是平行四边形平行四边形的判定定理2: 已知:四边形ABCD, ∠A=∠C ,∠B=∠D 求证:四边形ABCD 是平行四边形平行四边形的判定定理3已知:四边形ABCD, AC 、BD 交于点O 且OA=OC ,OB=OD 求证:四边形ABCD 是平行四边形例题解析例:已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且OE=OF 。
人教版数学八年级下册 第18章 平行四边形 测试题(含答案)

第18章测试卷(满分120分,时间120分钟)题号一二三总分得分一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是符合要求的)1.在▱ABCD中,若∠A=50°,则下列各式中,不能成立的是( )A.∠B=130°B.∠B+∠C=180°C.∠C=50°D.∠B+∠D=180°2.如图,在平行四边形ABCD中,下列结论一定正确的是( )A. AB=ADB. OA=OCC. AC=BDD.∠BAD=∠ABC3.正方形具有而菱形不具有的性质是( )A.四边相等B.对角线相等C.两组对边分别平行D.一条对角线平分一组对角4.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别为AB,AC,AD 的中点,若AB=4,则 EF 的长度为( )A.12B.1C.32D.35.如图,□ABCD的对角线AC与BD 相交于点O,AB⊥AC.若AB=4,AC=6,则 BD 的长为( )A.11B.10C.9D.86.已知四边形ABCD 中,对角线AC,BD相交于点O,下列对于四边形 ABCD 的说法中正确的是( )A.若AC=BD,则它是矩形B.若AB∥CD且AB=CD,则它是平行四边形C.若AC⊥BD,则它是菱形D.若AO=BO=CO=DO,则它是正方形7.如图,P为线段AB上的一个点,分别以AP,PB 为边在AB 的同侧作菱形APCD 和菱形PBFE,点 P,C, E在一条直线上.若∠DAP=60°,AP²+3PB²=1,M,N分别是对角线AC,BE的中点. MN长为( )A.12B.14C.1D.48.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED为( )A.15°B.35°C.45°D.55°9.如图,□ABCD中,对角线AC,BD 相交于O,BD=2AD,E,F,G 分别是OC,OD,AB 的中点,下列结论:①BE ⊥AC;②四边形 BEFG是平行四边形;③EG=GF;④EA平分∠GEF.其中正确的是( )A.①②③B.①②④C.①③④D.②③④10.如图,在矩形ABCD中,AD=2,点 P为直线AD 上一动点,若满足△PBC是等腰三角形的点P 有且只有3个,则AB的长为( )A.2B.3C.2或3D.4或23二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)11.在菱形ABCD 中,∠BAD=80°,EF⊥AB交对角线AC 于点 F,垂足为 E,则.∠AFE等于 .12.已知矩形ABCD,给出三个关系式:①AB=BC;②AC=BD;③AC⊥BD,如果选择关系式作为条件(写出一个即可),那么可以判定矩形 ABCD为正方形,理由是.13.菱形的两对角线长分别为 8和6,则它的周长为 .14.如图,□ABCD的对角线AC 与BD 相交于点O,AB⊥AC,若.AB=4,BD=10,,点E是AB 边的中点,则OE的长是 .15.如图,在平面直角坐标系xOy中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A 的坐标为(12,13),则点C的坐标是 .16.已知:正方形ABCD 的边长为8,点E、F分别在AD、CD上,AE=DF=2,,BE 与AF 相交于点G,点H为BF 的中点,连接GH,则GH 的长为 .17.如图所示,在四边形ABCD 中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是 .18.如图1,有一张菱形纸片ABCD,BC=6,∠ABC=120°.先将其沿较短的对角线BD剪开,固定△DBC,并把△ABD沿着BC 方向平移,得到△A'B'D'(点 B 在边 BC 上)如图2.当两个三角形重叠部分的面积为43时,它移动的距离BB'等于 .三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)19.(8分)如图,在▱ABCD中,BE平分∠ABC交CD 的延长线于点E,作(CF⊥BE于F.(1)求证:BF=EF;(2)若AB=8,DE=4,求□ABCD的周长.20.(9分)如图,矩形ABCD 中,AB=6,BC=4,,过对角线 BD的中点O的直线分别交AB,CD 边于点E,F.(1)求证:四边形BEDF 是平行四边形;(2)当四边形 BEDF 是菱形时,求 DF 的长.21.(9分)如图,正方形ABCD 中,对角线.AC=8cm..射线.AF⊥AC,,垂足为A.动点 P 从点C 出发在CA 上运动,动点 Q 从点 A 出发在射线AF 上运动,两点的运动速度都是22cm/s..若两点同时出发,多长时间后,四边形 AQBP 是特殊四边形?请说明特殊四边形的名称及理由.22.(10分)矩形,菱形由于其特殊的性质,为拼图提供了方便,因而墙面瓷砖一般设计为矩形,图案也以菱形居多.如图,是一种长30cm,宽20cm的矩形瓷砖,E、F、G、H分别是矩形各边的中点,阴影部分为淡黄色,中间部分为白色,现有一面长4.2m,宽2.8m的墙壁准备贴瓷砖.问:这面墙壁最少要贴这种瓷砖多少块?全部贴满瓷砖后,这面墙壁最多会出现多少个面积相等的菱形?其中淡黄色的菱形有多少个?23.(10分)在△ABC中,BC=2AC,点 D、E分别是边AB、BC的中点,过点 A作.AF‖BC交ED的延长线于点F,连接BF.(1)求证:四边形 ACEF 是菱形;(2)若四边形AEBF也是菱形,写出线段AB 与线段AC 的关系并说明理由.24.(12分)如图,在△ABC中,∠ACB=90°,,D为AB 的中点,四边形 BCED为平行四边形,DE,AC 相交于点 F.连接DC,AE.(1)试确定四边形ADCE 的形状,并说明理由;(2)若AB=16,AC=12,,求四边形 ADCE的面积;(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.第18章测试题1. D2. B3. B4. B5. B6. B7. A8. C9. B 10. C11.50°12.③对角线互相垂直的矩形是正方形13.20 14. 13 15.(0,—5) 16.5 17.2 3 18.2或 419.(1)证明:∵在平行四边形ABCD中,AB∥CD,∴∠ABE=∠E.∵BE平分∠ABC,∴∠ABE=∠CBE.∴∠E=∠CBE.∴BC=CE.∵CF⊥BE,∴BF=EF;(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.∴CE=12.∴由(1)得BC=CE=12.∴平行四边形ABCD的周长=2(AB+BC)=40.20.(1)证明:∵四边形ABCD是矩形,O是BD的中点,∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,∴∠OBE=∠ODF,∴△BOE≌△DOF(ASA),∴EO=FO,∴四边形BEDF是平行四边形;(2)解:当四边形BEDF是菱形时,BE=DE=DF=BF,设BE=x,则DE=x,AE=6-x,在Rt△ADE中,DE²=AD²+AE²,∴x²=4²+(6−x)²,解得x=133,∴DF=133.21.解:当P,Q运动2s后,四边形AQBP是正方形,理由如下:∵四边形ABCD是正方形,∴AB=BC.当 P,Q运动2 s后,CP=AQ=4 cm,∵AC=8 cm,∴AP=CP=4 cm,∴BP⊥AC,且BP=AP=AQ=4 cm,∵AF⊥AC,∴AF∥BP,∴四边形APBQ是平行四边形,∵BP⊥AC,AP=BP,∴四边形AQBP 是正方形.22.解:4.2m=420 cm,2.8m=280 cm,∵420÷30=14,280÷20=14,∴贴满墙壁需要14行14列瓷砖,共14×14=196块;∵每一块瓷砖都有一个白色菱形,∴白色菱形有196个,∵E、F、G、H分别是矩形各边的中点,∴淡黄色菱形有(14-1)×(14-1)=169个,所以,共有菱形:196+169=365个.23.(1)证明:∵点D、E分别是边AB、BC的中点,∴DE是△ABC的中位线,BC=2CE,∴DE∥AC.∵AF∥BC,∴四边形ACEF是平行四边形,∵BC=2AC,∴CE=AC,∴四边形 ACEF是菱形;(2)解:AB=3AC,理由如下:∵四边形AEBF也是菱形,∴AB⊥EF,∵DE∥AC,∴AC⊥AB,∴∠BAC=90°,∵BC=2AC,∴∠ABC=30°,∴AB=3AC.24.解:(1)四边形ADCE为菱形,理由如下:∵四边形DBEC为平行四边形,∴CE∥BD,CE=BD,∵D为AB中点,∴AD=BD,∴CE∥AD,CE=AD,∴四边形ADCE为平行四边形,又BC∥DE,∴∠AFD=∠ACB=90°,∴AC⊥DE,∴四边形 ADCE为菱形;(2)在Rt△ABC中,∵AB=16,AC=12,∴BC=47.∵D为AB中点,F也为AC的中点,∴DF=27,∴四边形ADCE的面积=AC×DF=247;(3)证明如下:当△ABC中AC=BC时,四边形ADCE为正方形.∵AC=BC,D为AB 中点,∴CD⊥AB(三线合一的性质),即∠ADC=90°.∵四边形 BCED为平行四边形,四边形ADCE 为平行四边形,∴DE=BC=AC,∠AFD=∠ACB=90°.∴四边形ADCE为正方形.(对角线互相垂直且相等的四边形是正方形)。
人教版八年级下册《第18章 平行四边形》单元测试试卷及答案(共五套)

人教版八年级下册《第18章平行四边形》单元测试试卷(一)一、选择题(每题4分,共40分)1.不能判定四边形ABCD为平行四边形的题设是()(A)AB平行且等于CD。
(B)∠A=∠C,∠B=∠D。
(C)AB=AD,BC=CD。
(D)AB=CD,AD=BC。
2.正方形具有而菱形不一定具有的性质是()(A)四条边相等(B)对角线互相垂直平分(C)对角线平分一组对角(D)对角线相等3、顺次连结任意四边形四边中点所得的四边形一定是()A、平行四边形B、矩形C、菱形D、正方形4.正多边形的一个内角是120°,则这个正多边形的边数为( )A.4B.8C.6D.125.如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )A.18°B.36°C.72°D.108°6.下列命题中,真命题是()A、有两边相等的平行四边形是菱形B、对角线垂直的四边形是菱形C、四个角相等的菱形是正方形D、两条对角线相等的四边形是矩形7.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )A.6B.7C.8D.98.菱形的周长是它的高的4倍,则菱形中较大的一个角是( )A.100°B.120°C.135°D.150°9.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是( )A.20B.15C.10D.510.如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是( )A.8B.9C.10D.12二、填空题(每题4分,共24分)11、菱形ABCD的周长为36,其相邻两内角的度数比为1:5,则此菱形的面积为_________。
12、对角线长为2的正方形的周长为___________,面积为__________。
2018年人教版八年级下第18章平行四边形同步测试题含答案

选择题1. 下列四边形中,对角线相等且互相垂直平分的是()A. 平行四边形B.正方形C.等腰梯形D.矩形2. 如图,由六个全等的正三角形拼成的图,图中平行四边形的个数是()3. 在四边形ABCD中,对角线AC BD 相交于点0, ____二_工_,添加下列一个条则Z P=( )5. 如图,将n个边长都为2的正方形按如图所示摆放,点方形的中心,则这n个正方形重叠部分的面积之和是()6. 在平面中,下列命题为真命题的是()A. 四个角相等的四边形是矩形第18章平行四边形B. 6个C. 8个D. 10 个件后,仍不能判定四边形ABCD是平行四边形的是A BC ____ DZBCDZDJC=ZBC44.如图,在四边形ABCD中,/ A+Z D=a,/ ABC的平分线与/ BCD勺平分线交于点P,11aA. 90°aB. 90°+ aC. —7D. 360 ° aA 1 , A 2 ,…A n分别是正A. nB. n1C.( )n11D. n44B. 只有对角线互相平分且垂直的四边形是菱形,C. 对角线互相平分且垂直的四边形是矩形D. 四边相等的四边形是菱形 7.如图,把一个长方形的纸片对折两次, 然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()8. 下列性质中,正方形具有而矩形不一定具有的性质是 A .对角线互相垂直 B .对角线互相平分 C.对角线相等D.四个角都是直角9.如图,大正方形中有 2个小正方形,如果它们的面积分别是S i 、S 2,那么S i 、S2的大小关系是( )B . S i =S 2D. S i 、S 2的大小关系不确定10. 如图,等腰梯形 ABCD 中, AD// BC AE// DC / B=60°, BC=3 △ ABE 的周长为 6 ,则等腰梯形的周长是( ) A . 8 B . iO C. i2 D. i6ii.下列命题正确的是( )A. 同一边上两个角相等的梯形是等腰梯形B. —组对边平行,一组对边相等的四边形是平行四边形C. 如果顺次连接一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方 形A. 15° 或 30°B. 30° 或 45C. 45° 或 60 °D. 30 °或 60°C. S i v S 2D. 对角线互相垂直的四边形面积等于对角线乘积的一半12. 平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等二、填空题13. 已知平行四边形的三个顶点坐标分别为(-1 , 0)(0, 2)(2, 0),则在第四象限的第四个顶点的坐标为_____________ 。
人教版八年级数学下册 第十八章 平行四边形 单元测试卷(包含答案)

第十八章 平行四边形 综合测试一、选择题(每小题3分,共30分)1.顺次连接对角线相等的四边形各边中点所形成的四边形是( )A .平行四边形B .菱形C .矩形D .正方形2.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB BC =;②90ABC =︒∠;③AC BD =;④AC BD ⊥中选两个作为补充件,使ABCD 成为正方形(如图).现有下列四种选法,你认为其中错误是( )A .①②B .②③C .①③D .②④3.如图,已知D 为ABC △边AB 的中点,E 在AC 上,将ABC △沿着DE 折叠,使A 点落在BC 上的F 处,若65B ∠=︒,则BDF ∠等于( )A .65︒B .50︒C .60︒D .57.5︒4.如图,在菱形ABCD 中,AC 、BD 是对角线,若50BAC ∠=︒,则ABC ∠等于( )A .40︒B .50︒C .80︒D .100︒5.已知:如图,在ABCD Y 中,CE AB ⊥,E 为垂足,如果125A ∠=︒,则BCE ∠的度数是( )A .25︒B .30︒C .35︒D .55︒6.已知ABCD Y 中,4B A ∠=∠,则A ∠=( )A .18︒B .36︒C .72︒D .144︒7.已知:菱形ABCD 中,对角线AC 与BD 相交于点O ,OE DC ∥交BC 于点E , 6 cm AD =,则OE 的长为( )A .6 cmB .4 cmC .3 cmD .2 cm8.如图,在矩形ABCD 中,E 点在BC 上,且AE 平分BAC ∠.若4BE =,15AC =,则AEC △面积为( ) A .15 B .30 C .45 D .609.如图,点E 在正方形ABCD 内,满足90AEB ∠=︒,6AE =,8BE =,则阴影部分的面积是( )A .48B .60C .76D .8010.如图,在ABCD Y 中,对角线AC 与BD 交于点O ,90OBC ∠=︒,8AC =,4BD =,则BCO △的面积是( )A .B .CD .3二、填空题(每小题3分,共24分)11.如图,在ABCD Y 中,AC 、BD 相交于点O ,10 cm AB =,8 cm AD =,AC BC ⊥,则OB =___________cm .12.如图,在正方形ABCD 的外侧,作等边三角形ADE ,则BED ∠为___________度.13.如图,在矩形ABCD 中,M 、N 分别是边AD 、BC 的中点,E 、F 分别是线段BM 、CM 的中点,若8AB =,12AD =,则四边形ENFM 的周长为___________.14.如图,ABCD 是对角线互相垂直的四边形,且OB OD =,请你添加一个适当的条件___________,使ABCD 成为形(只需添加一个即可).15.如图,在ABCD Y 中,10 cm AD =, 6 cm CD =.E 为AD 上一点,有BE BC =,CE CD =,则DE =___________cm .16.如图,在平行四边形ABCD 中,AE 平分BAD ∠,若110D ∠=︒,则DAE ∠的度数为___________.17.如图,在MBN △中,6BM =,点A ,C ,D 分别在MB ,BN ,NM 上,四边形ABCD 为平行四边形,NDC MDA ∠=∠,那么平行四边形ABCD 的周长是___________.18.如图,在正方形ABCD 中,1AB =,延长AB 到E ,使AE AC =,则ACE △的面积是___________.三、解答题(共46分)19.(5分)已知:如图,在ABCD Y 中,5AB =,8AD =,ABC ∠的平分线BE 交AD 于点E ,求线段ED 的长.20.(5分)将矩形纸片ABCD 折叠,使点C 与点A 重合,然后展开,折痕为EF ,连接AE ,CF .求证:四边形AECF 是菱形。
【3套】人教版八年级下册 第十八章平行四边形单元测试及答案

图2OEDCBA人教版八年级下册 第十八章平行四边形单元测试及答案一、选择题(共10题,每题3分,共30分)1、下列哪组条件能够判别四边形ABCD 是平行四边形?( )A :AB ∥CD ,AD =BC B :AB =CD ,AD =BC C :∠A =∠B ,∠C =∠D D :AB =AD ,CB =CD 2、对角线互相垂直平分的四边形是 ( ) A 、平行四边形 B 、矩形 C 、菱形 D 、梯形 3、正方形具有而菱形不具有的性质是( )A. 对角线互相平分B. 对角线互相垂直C. 对角线相等D. 对角线平分一组对角4、 已知,在平行四边形ABCD 中,下列结论不一定正确的是( )A. AB ﹦CDB. 当AC ⊥BD 时,它是菱形C. AC ﹦BDD.当∠ABC ﹦90°时,它是矩形5、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( ).A .测量对角线是否相互平分B .测量两组对边是否分别相等C .测量一组对角是否都为直角D .测量其中三角形是否都为直角6、A 、B 、C 、D 在同一平面内,从①AB ∥CD ;②AB =CD ;③BC ∥AD ;④BC =AD ;这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法共有( ) A.3种 B 4种 C 5种 D 6种7.如图1,在ABCD 中,∠BAD 的平分线交BC 于E ,且AE ﹦BE,则∠BCD 的度数为( )A. 30° B . 60°或120° C.60° D. 120°8、如图2所示,矩形ABCD 中AE 平分∠BAD 交BC 于E, ∠CAE=15°,则下面的结论:①△ODC 是等边三角形; ②BC=2AB; ③∠AOE=135°; ④COE AOE S S ∆∆=,其中正确结论有( )A. 1个B. 2个C. 3个D. 4个9、平行四边形ABCD 的周长32,5AB=3BC,则对角线AC 的取值范围为( )D C BA 图1ED CBA图5D CBAA 、 6<AC<10B 、 6<AC<16C 、 10<AC<16D 、 4<AC<16 10、如图,□ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE=3 cm ,则AB 的长为 ( )A .3 cmB .6 cmC .9 cmD .12 cm 二、填空题(共8小题、每小题3分,共24分) 11、在ABCD 中,∠A ﹦100°,则∠B 。
人教版八年级下册数学第十八章 平行四边形 含答案

人教版八年级下册数学第十八章平行四边形含答案一、单选题(共15题,共计45分)1、正方形具有而菱形不具有的性质是( )A.对角线相等B.对角线互相平分C.对角线平分一组对角D.对角线互相垂直2、将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC 的长为()A. B.2 C.1.5 D.3、如图3,∠AOP=∠BOP=15°,PC∥OA,若PC=4,则PD等于()A.1B.3C.4D.24、下列说法中正确的是()A.对角线相等的四边形是正方形B.对角线互相平分的矩形是正方形 C.对角线互相垂直且平分的四边形是正方形 D.邻边相等的矩形是正方形5、如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD =10cm2, S△ACD为()A.10B.9C.8D.76、如图所示,为的内接三角形,则的内接正方形的面积为()A.2B.4C.8D.167、如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,顶点A,C分别在x轴、y轴上,反比例函数y= (k≠0,x>0)的图象与正方形OABC的两边AB,BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是()A.△ONC≌△OAMB.四边形DAMN与△OMN面积相等C.ON=MND.若∠MON=45°,MN=2,则点C的坐标为(0,+1)8、下列命题错误的是()A.矩形的对角线相等B.平行四边形的对角线互相平分C.对角线相等的四边形是矩形D.对角线互相垂直平分的四边形是菱形9、已知菱形的周长是20cm,一条对角线长是6cm,则这个菱形面积为()A.48cm 2B.30cm 2C.24cm 2D.25cm 210、如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有 )A.0个B.1个C.2个D.3个11、如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB.DM⊥AN于点M,CN⊥AN于点N,则DM+CN的值为(用含有a的代数式表示)( )A.aB. aC. aD. a12、边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1, S2,则S1+S2的值为( )A.16B.17C.18D.1913、如图所示,在菱形ABCD中,对角线AC,BD相交于点O,若∠ABC=60°,则AC:BD等于()A. :1B.1:2C. :3D.1:14、如图,在▱ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是()A.BG平分∠ABCB.BE=BFC.AD=CHD.CH=DH15、如果三角形的两条边分别为8和6,那么连接该三角形三边中点所得的周长可能是下列数据中的()A.8B.10C.14D.16二、填空题(共10题,共计30分)16、数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)请根据上图完成这个推论的证明过程.证明:S矩形NFGD =S△ADC-(S△ANF+S△FGC),S矩形EBMF =S△ABC-(________+________).易知,S△ADC =S△ABC, ________=________,________=________.可得S矩形NFGD =S矩形EBMF.17、如图,在菱形ABCD中,AC与BD相较于点O,点P是AB的中点,PO=3,则菱形ABCD的周长是________.18、如图,菱形的边长为1,;作于点,以为一边,作第二个菱形,使;作于点,以为一边,作第三个菱形,使;…依此类推,这样作出第个菱形.则________.________.19、如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣2,﹣1),则点A坐标为________,点B坐标为________.20、如图所示,在矩形中,,.矩形绕着点逆时针旋转一定角度得到矩形.若点的对应点落在边上,则的长为________.21、如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为________.22、如图,四边形ABCD中,AD∥BC,AD=3,BC=8,E是BC的中点,点P 以每秒1个单位长度的速度从A点出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动.当运动时间t=________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.23、如图,在▱ABCD中,AD=8,点E、F分别是BD、CD的中点,则EF=________.24、如图,,是正方形的边上的两个动点,满足,连接交于点,连接交于点,若正方形的边长为2,则线段的长度的最小值是________.25、如图,四边形OABC是菱形,点B,C在以点O为圆心的弧EF上,且∠1=∠2,若扇形OEF的面积为3π,则菱形OABC的边长为________.三、解答题(共5题,共计25分)26、如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.</div>27、如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F.求证:AE=DF.28、如图,▱ABCD中,O是AB的中点,CO=DO.求证:▱ABCD是矩形.29、如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,求四边形CODE的周长.30、如图,E、F分别为正方形ABCD的边DC、BC中点.求证:.参考答案一、单选题(共15题,共计45分)1、A2、D3、D4、D5、A6、A7、C8、C9、C10、D11、C12、B13、C14、D15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、29、。
人教版八年级数学下《第十八章平行四边形》同步练习含答案.doc

F E D C B A O ED C B A D C B A O D C B A 第十八章 平行四边形 练习题一、选择题(每小题5分,共30分)1.如图,下列四组条件中,不能判定四边形ABCD 是平行四边形的是( )A.AB=DC ,AD=BCB.AB ∥DC ,AD ∥BCC.AB ∥DC ,AD=BCD.AB ∥DC ,AB=DC(第1题) (第2题)2.如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,下列结论中不一定成立的是( )A.AB ∥DCB.AC=BDC.AC ⊥BDD.OA=OC3.顺次连接矩形四边中点得到的四边形一定是( )A.正方形B.矩形C.菱形D.等腰梯形4.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,CE ∥BD ,DE ∥AC.若AC=4,则四边形OCED 的周长为( )A.4B.6C.8D.105.如图,将一个边长分别为4,8的矩形纸片ABCD 折叠,使点C 与点A 重合,则折痕EF 的长为( )6.如图,正方形ABCD 的边长为8,点M 在DC 上,且DM=2,N 是AC 上一动点,则DN+MN 的最小值为( )(第4题) (第5题) (第6题)二、填空题(每小题6分,共24分)7.如图,在四边形ABCD 中,AB ∥CD ,AD ∥BC ,AC ,BD 相交于点O ,若AC=6,则AO 的长度等于________________.8.如图,若将四根木条钉成的矩形木框变形为□ABCD 的形状,并使其面积变为O F E D C BA D CB A 矩形面积的一半,则□ABCD 的最小内角的大小为______________.(第7题) (第8题)9.如图,将两条宽度都为3的纸片重叠在一起,使∠ABC=600,则四边形ABCD 的面积为__________10.如图,设四边形ABCD 是边长为1的正方形,以对角线AC 为边作第二个正方形ACEF ,再以对角线AE 为边作第三个正方形AEGH ,如此下去.则第n 个正方形的边长为________.(第9题) (第10题)三、解答题(第11题14分,第12,13题各16分,共46分)11.如图,在四边形ABCD 中,AB=CD ,BE=DF ;AE ⊥BD ,CF ⊥BD ,垂足分别为E ,F.(1)求证:△ABE ≌△CDF ;(第11题)(2)若AC 与BD 交于点O ,求证:AO=CO.O D C B AF E D C B A12.如图,在△ABC 中,∠CAB=900,DE ,DF 是△ABC 的中位线,连结EF ,AD.求证:EF=AD.(第12题)∵AE⊥BD,CF ⊥BD,∴∠AEB=∠CFD=90°∵AB =CD,BE=DF ∴ABE≌CDF参考答案:1.C.2.B.3.C.4.C.5.D.6.D7.3. 8.300. 11.(1)证明:(2)提示:证明四边形ABCD 是平行四边形由(1)△ABE ≌△CDF ,可得∠ABE=∠CDF ,AB ∥CD ,可得四边形ABCD 是平行四边形,于是AO=CO.12.提示:由DE ,DF 是△ABC 的中位线,可得四边形EAFD 是平行四边形,又∠CAB=900.可知□EAFD 是矩形,根据矩形对角线相等即可得证.13.提示:(1)证明△AOF ≌△BOE ;(2)结论仍然成立,证明△AOF ≌△BOE.。
(完整版)新人教版八年级下第十八章(平行四边形)同步练习及答案

AB // CD
AB CD
又 BE DF
B
.∠ A=∠ B,∠ C=∠ D
C. AB=CD,AD=BC
D
. AB=AD,CB=CD
2 、两直角边不等的两个全等的直角三角形能拼成平行四边形的个数
()
A.4
B.3
C.2
D.1
3. 如图,已知 □ABCD的对角线交点是 O,直线 EF过 O点,且平行于 BC,直线 GH过且平行
于 AB,则图中共有 ( ) 个平行四边形 .
C 、对角线互相平分
D、对角相等
2、下列叙述错误的是(
)
A. 平行四边形的对角线互相平分。 B. 平行四边形的四个内角相等。
C.矩形的对角线相等。
D. 有一个角时 90o 的平行四边形是矩形
3、下列图形中既是轴对称图形,又是中心对称图形的是(
)
A、平行四边形
B 、等边三角形
C、矩形
D
、直角三角形
4、如果矩形的一边长为 8,一条对角线长为 10,那么这个矩形面积是
18.1.2 平行四边形的判定(一)
1.A 、2. ×、×、√、√、√、×、
3. 证明: 1 2
AD // BC
又34
AB // CD
四边形 ABCD为平行四边形。(两条对边平行 )
4. 证明:∵ AB=CD,BC=AD,
∴四边形 ABCD是平行四边形.
∴AB∥ CD. ∴∠ BAE=∠DCF.
又∵ AE=CE,
AC
AD BC
又 DE AB 、 BF CD 、
AED CFB 90
ADE BCF ( AAS)
DE BF
9. 解:∵四边形 ABCD是平行四边形, ∵△ AOB的周长为 15,AB=6,
人教版八年级数学下册 第18章 平行四边形 单元练习卷含答案

人教版八年级数学下册第18章平行四边形单元练习卷含答案一.选择题(共6小题)1.在下列条件中,能判定四边形为平行四边形的是()A.两组对边分别平行B.一组对边平行且另一组对边相等C.两组邻边相等D.对角线互相垂直2.如图在▱ABCD中,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD 于点F,点G为CD的中点,连接EG,BG.则△BEG的面积为()A.16B.14C.8D.73.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB;②与△EGD 全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形,其中正确的是()A.①④B.①③④C.①②③D.②③④4.在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD,垂足为P,则∠EPF=()A.35°B.45°C.50°D.55°5.如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE ⊥AC于E,PF⊥BC于点F,连结EF,则线段EF的最小值为()A.B.C.D.56.如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD 于G,取DG的中点H,连结AH,EH,FH.下列结论:①FH∥AE;②AH=EH且AH⊥EH;③∠BAH=∠HEC;④△EHF≌△AHD;⑤若,则.其中哪些结论是正确()A.①②④⑤B.②③④C.①②③D.②③④⑤二.填空题(共6小题)7.如图,E、F是平行四边形ABCD的对角线BD上的点,要使四边形AFCE是平行四边形,还需添加的一个条件是(只需添加一个正确的即可).8.如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE=,DF=2,则∠EDF=°,线段AB的长度=.9.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为.10.如图,在矩形ABCD中,过点D作DE⊥AC,垂足为E,延长线ED至F,使DF=AC,连接BF交AD于G.若AB=1,AD=2,则∠ABG=,GF=.11.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是.12.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是.三.解答题13.如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.(1)求证:四边形CMAN是平行四边形.(2)已知DE=2,FN=1,求BN的长.14.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,交AC于G,F是AD的中点.(1)求证:四边形ADCE是为平行四边形;(2)若EB是∠AEC的角平分线,请写出图中所有与AE相等的边.15.如图,已知E是▱ABCD中BC边的中点,AC是对角线,连结AE并延长AE交DC的延长线于点F,连结BF.(1)求证:四边形ABFC是平行四边形;(2)若∠AEC=2∠ABC,求证:四边形ABFC为矩形.16.如图,以△ABC的各边为边长,在边BC的同侧分别作正方形ABDI,正方形BCFE,正方形ACHG,连接AD,DE,EG.(1)求证:△BDE≌△BAC;(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;②求证:四边形ADEG是平行四边形;(3)当△ABC满足什么条件时,四边形ADEG是正方形?请说明理由.17.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.(1)求证:四边形MANP是正方形;(2)求证:EM=BN.18.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=CG.19.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.(1)求证:四边形BPEQ是菱形;(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.参考答案与试题解析一.选择题(共6小题)1.在下列条件中,能判定四边形为平行四边形的是()A.两组对边分别平行B.一组对边平行且另一组对边相等C.两组邻边相等D.对角线互相垂直【分析】根据平行四边形的判定定理逐个判断即可.【解答】解:A、两组对边分别平行的四边形是平行四边形,故本选项符合题意;B、一组对边平行且另一组对边相等的四边形是等腰梯形,不是平行四边形,故本选项不符合题意;C、两组邻边相等的四边形不一定是平行四边形,故本选项不符合题意;D、对角线互相平分的四边形才是平行四边形,故本选项不符合题意;故选:A.2.如图在▱ABCD中,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD 于点F,点G为CD的中点,连接EG,BG.则△BEG的面积为()A.16B.14C.8D.7【分析】如图,取BC中点H,连接AH,连接EC交AD于N,作EM⊥CD交CD的延长线于M.构建S△BEG=S△BCE+S ECG﹣S△BCG计算即可;【解答】解:如图,取BC中点H,连接AH,连接EC交AD于N,作EM⊥CD交CD的延长线于M.∵BC=2AB,BH=CH,∠ABC=60°,∴BA=BH=CH,∴△ABH是等边三角形,∴HA=HB=HC,∴∠BAC=90°,∴∠ACB=30°,∵EC⊥BC,∠BCD=180°﹣∠ABC=120°,∴∠ACE=60°,∠ECM=30°,∵BC=2AB=8,∴CD=4,CN=EN=2,∴EC=4,EM=2,∴S△BEG=S△BCE+S ECG﹣S△BCG=×8×4+×2×2﹣S平行四边形ABCD=16+2﹣4=14故选:B.3.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB;②与△EGD 全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形,其中正确的是()A.①④B.①③④C.①②③D.②③④【分析】由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG =CD=AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,④正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG∥AB,OG=AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;③不正确;即可得出结果.【解答】解:∵四边形ABCD是菱形,∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,∵CD=DE,∴AB=DE,在△ABG和△DEG中,,∴△ABG≌△DEG(AAS),∴AG=DG,∴OG是△ACD的中位线,∴OG=CD=AB,∴2OG=AB,①正确;∵AB∥CE,AB=DE,∴四边形ABDE是平行四边形,∵∠BCD=∠BAD=60°,∴△ABD、△BCD是等边三角形,∴AB=BD=AD,∠ODC=60°,∴OD=AG,四边形ABDE是菱形,④正确;∴AD⊥BE,由菱形的性质得:△ABG≌△DEG(SAS),△BDG≌△DEG(SAS),在△ABG和△DCO中,,∴△ABG≌△DCO(SAS),∴△ABO≌△DEG(SAS),△BCO≌△DEG(SAS),△CDO≌△DEG(SAS),△AOD≌△DEG(AAS),△ABG≌△DEG(SAS),△BDG≌△DEG(SAS),∴②不正确;∵OB=OD,AG=DG,∴OG是△ABD的中位线,∴OG∥AB,OG=AB,∴△GOD∽△ABD(ASA),△ABF∽△OGF(ASA),∴△GOD的面积=△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,∴△AFG的面积=△OGF的面积的2倍,又∵△GOD的面积=△AOG的面积=△BOG的面积,∴S四边形ODGF=S△ABF;③不正确;正确的是①④.故选:A.4.在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD,垂足为P,则∠EPF=()A.35°B.45°C.50°D.55°【分析】延长PF交AB的延长线于点G.根据已知可得∠B,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而求得∠FPC的度数,根据余角的定义即可得到结果.【解答】解:如图,延长PF交AB的延长线于点G.在△BGF与△CPF中,,∴△BGF≌△CPF(ASA),∴GF=PF,∴F为PG中点.又∵∠BEP=90°,∴EF=PG=PF,∴∠FEP=∠EPF,∵∠BEP=∠EPC=90°,∴∠BEP﹣∠FEP=∠EPC﹣∠EPF,即∠BEF=∠FPC,∵四边形ABCD为菱形,∴AB=BC,∠ABC=180°﹣∠A=70°,∵E,F分别为AB,BC的中点,∴BE=BF,∠BEF=∠BFE=(180°﹣70°)=55°,∴∠FPC=55°,∴∠EPF=90°﹣55°=35°,故选:A.5.如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE ⊥AC于E,PF⊥BC于点F,连结EF,则线段EF的最小值为()A.B.C.D.5【分析】连接PC,当CP⊥AB时,PC最小,利用三角形面积解答即可.【解答】解:连接PC,∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=∠C=90°,∴四边形ECFP是矩形,∴EF=PC,∴当PC最小时,EF也最小,即当CP⊥AB时,PC最小,∵AC=8,BC=6,∴AB=10,∴PC的最小值为:=4.8.∴线段EF长的最小值为4.8.故选:B.6.如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD 于G,取DG的中点H,连结AH,EH,FH.下列结论:①FH∥AE;②AH=EH且AH⊥EH;③∠BAH=∠HEC;④△EHF≌△AHD;⑤若,则.其中哪些结论是正确()A.①②④⑤B.②③④C.①②③D.②③④⑤【分析】①根据正方形对角线互相垂直、过一点有且只有一条直线与已知直线垂直即可得结论;②根据矩形的判定和性质、直角三角形的性质,证明三角形全等即可得结论;③根据全等三角形性质、矩形的性质进行角的计算即可得结论;④根据边边边证明三角形全等即可得结论;⑤根据割补法求四边形的面积,再求等腰直角三角形的面积,即可得结论.【解答】证明:①在正方形ABCD中,∠ADC=∠C=90°∵EF∥CD∴∠EFD=90°,得矩形EFDC.在Rt△FDG中,H是DG中点,∴FH⊥BD∵正方形对角线互相垂直,过A点只能有一条垂直于BD的直线,∴AE不垂直于BD,∴FH与AE不平行.所以①不正确.②∵四边形ABEF是矩形,∴AF=EB,∠BEF=90°,∵BD平分∠ABC,∴∠EBG=∠EGB=45°,∴BE=GE,∴AF=EG.在Rt△FGD中,H是DG的中点,∴FH=GH,FH⊥BD∴∠AFH=∠AFE+∠GFH=90°+45°=135°∠EGH=180°﹣∠EGB=180°﹣45°=135°∴∠AFH=∠EGH∴△AFH≌△EGH,∴AH=EH,∠AHF=∠EHG∴∠AHF+AHG=∠EHG+∠AHG即∠FHG=∠AHE=90°∴AH⊥EH.所以②正确.③∵△AFH≌△EGH,∴∠FAH=∠GEH,∵∠BAF=CEG=90°∴∠BAH=∠HEC.所以③正确.④∵EF=AD,FH=DH,EH=AH∴△EHF≌△AHD所以④正确.⑤设EC=FD=x,则BE=AF=EG=2x,∴BC=DC=AB=AD=3x,AH2=(x)2+(x)2=x2,S四边形DHEC=S梯形EGDC﹣S△EGH=(2x+3x)•x﹣×=2x2S△AHE=AH•EH=AH2=x2∴==.所以⑤不正确.故选:B.二.填空题(共6小题)7.如图,E、F是平行四边形ABCD的对角线BD上的点,要使四边形AFCE是平行四边形,还需添加的一个条件是BF=DE(答案不唯一)(只需添加一个正确的即可).【分析】由平行四边形的判定定理,通过对角线互相平分得出结论.【解答】解:添加的一个条件为BF=DE;理由如下:∵四边形ABCD是平行四边形,∴AO=CO、BO=DO,∵BF=DE,∴OE=OF,∴四边形AFCE是平行四边形;故答案为:BF=DE(答案不唯一).8.如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE=,DF=2,则∠EDF=45 °,线段AB的长度=2.【分析】延长FD到M使得DM=DF,连接AM、EM、EF,作EN⊥DF于N,先证明∠EDF=45°,在Rt△EMN中求出EM,再证明△AEM是等腰直角三角形即可解决问题.【解答】解:如图,延长FD到M使得DM=DF,连接AM、EM、EF,作EN⊥DF于N.∵∠C=90°,∴∠BAC+∠B=90°,∵AE=AD,BF=BD,∴∠AED=∠ADE,∠BDF=∠BFD,∴2∠ADE+∠BAC=180°,2∠BDF+∠B=180°,∴2∠ADE+2∠BDF=270°,∴∠ADE+∠BDF=135°,∴∠EDF=180°﹣(∠ADE+∠BDF)=45°,∵∠END=90°,DE=,∴∠EDF=∠DEN=45°,∴EN=DN=1,在△DAM和△DBF中,,∴△ADM≌△BDF(SAS),∴BF=AM=BD=AD=AE,∠MAD=∠B,∴∠MAE=∠MAD+∠BAC=90°,∴EM=AM,在Rt△EMN中,∵EN=1,MN=DM+DN=3,∴EM==,∴AM=,AB=2AM=2.故答案为:45,2.9.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为(4,4)或(﹣5,).【分析】作AM⊥BC于M,由题意得出AD∥BC,OB=4,OC=1,OM=1得出AD=BC=5,BM=3,CM=2,①当点D在y轴的右侧时,由菱形的性质得出AB=BC=5,由勾股定理得出AM==4,得出点D的坐标为(4,4);②当点D在y轴的左侧时,由菱形的性质得出AB=BC=5,由勾股定理得出AM==,得出点D的坐标为(﹣6,).【解答】解:作AM⊥BC于M,∵A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,∴AD∥BC,OB=4,OC=1,OM=1,∴AD=BC=5,BM=3,CM=2,分两种情况:①当点D在y轴的右侧时,如图1所示:∵以点A、B、C、D为顶点的四边形是菱形,∴AB=BC=5,∴AM===4,∴点D的坐标为(4,4);②当点D在y轴的左侧时,如图2所示:∵以点A、B、C、D为顶点的四边形是菱形,∴AB=BC=5,∴AM===,∴点D的坐标为(﹣6,);综上所述,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为(4,4)或(﹣6,);故答案为:(4,4)或(﹣6,).10.如图,在矩形ABCD中,过点D作DE⊥AC,垂足为E,延长线ED至F,使DF=AC,连接BF交AD于G.若AB=1,AD=2,则∠ABG=45°,GF=2.【分析】如图,作FH⊥AD交AD的延长线于H.由△ADC≌△FHD(AAS),推出FH=AD=2,DH=CD=1,由AB∥FH,推出AG:GH=AB:FH=1:2,由AH=AD+DH=2+1=3,推出AG =1,GH=2,由此即可解决问题;【解答】解:如图,作FH⊥AD交AD的延长线于H.∵四边形ABCD是矩形,∴AD=BC=2,AB=CD=1,∠ADC=∠CDH=∠H=∠BAD=90°,∵∠ACD+∠CDE=90°,∠CDE+∠FDH=90°,∴∠ACD=∠FDH,∵AC=DF,∴△ADC≌△FHD(AAS)∴FH=AD=2,DH=CD=1,∵AB∥FH,∴AG:GH=AB:FH=1:2,∵AH=AD+DH=2+1=3,∴AG=1,GH=2,∴AB=AG=1,GH=FH=2,∴∠ABG=45°,FG==2,故答案为45°,2.11.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是①②③.【分析】根据矩形的判定和性质,菱形的判定,正方形的判定,平行四边形的判定定理即可得到结论.【解答】解:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,过点O直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,则四边形MNPQ是平行四边形,故当MQ∥PN,PQ∥MN,四边形MNPQ是平行四边形,故存在无数个四边形MNPQ是平行四边形;故正确;②如图,当PM=QN时,四边形MNPQ是矩形,故存在无数个四边形MNPQ是矩形;故正确;③如图,当PM⊥QN时,存在无数个四边形MNPQ是菱形;故正确;④当四边形MNPQ是正方形时,MQ=PQ,则△AMQ≌△DQP,∴AM=QD,AQ=PD,∵PD=BM,∴AB=AD,∴四边形ABCD是正方形与任意矩形ABCD矛盾,故错误;故答案为:①②③.12.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是 6.5 .【分析】根据三角形中位线定理得到AC=2DE=5,AC∥DE,根据勾股定理的逆定理得到∠ACB=90°,根据线段垂直平分线的性质得到DC=BD=AB.【解答】解:∵D,E分别是AB,BC的中点,∴AC=2DE=5,AC∥DE,AC2+BC2=52+122=169,AB2=132=169,∴AC2+BC2=AB2,∴∠ACB=90°,∵AC∥DE,∴∠DEB=90°,又∵E是BC的中点,∴直线DE是线段BC的垂直平分线,∴DC=BD=AB=6.5,故答案是:6.5.三.解答题13.如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.(1)求证:四边形CMAN是平行四边形.(2)已知DE=2,FN=1,求BN的长.【分析】(1)欲证明四边形AMCN是平行四边形,只要证明CM∥AN,AM∥CN即可;(2)首先证明△MDE≌△NBF,推出ME=NF=1,在Rt△DME中,根据勾股定理即可解决问题;【解答】证明:∵四边形ABCD是平行四边形,∴CD∥AB,∵AM⊥BD,CN⊥BD,∴AM∥CN,∴CM∥AN,AM∥CN,∴四边形AMCN是平行四边形.(2)∵四边形AMCN是平行四边形,∴CM=AN,∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∴DM=BN,∠MDE=∠NBF,在△MDE和△NBF中,,∴△MDE≌△NBF,∴ME=NF=1,在Rt△DME中,∵∠DEM=90°,DE=4,ME=3,∴BN=DM===.14.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,交AC于G,F是AD的中点.(1)求证:四边形ADCE是为平行四边形;(2)若EB是∠AEC的角平分线,请写出图中所有与AE相等的边.【分析】(1)首先证明△AFE≌△DFB可得AE=BD,进而可证明AE=CD,再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;(2)图中所有与AE相等的边有:AF、DF、BD、DC.理由平行四边形的性质、等腰三角形的判定即可解决问题;【解答】(1)证明:∵AD是△ABC的中线,∴BD=CD,∵AE∥BC,∴∠AEF=∠DBF,在△AFE和△DFB中,,∴△AFE≌△DFB(AAS),∴AE=BD,∴AE=CD,∵AE∥BC,∴四边形ADCE是平行四边形;(2)图中所有与AE相等的边有:AF、DF、BD、DC.理由:∵四边形ADCE是平行四边形,∴AE=DC,AD∥EC,∵BD=DC,∴AE=BD,∵BE平分∠AEC,∴∠AEF=∠CEF=∠AFE,∴AE=AF,∵△AFE≌△DFB,∴AF=DF,∴AE=AF=DF=CD=BD.15.如图,已知E是▱ABCD中BC边的中点,AC是对角线,连结AE并延长AE交DC的延长线于点F,连结BF.(1)求证:四边形ABFC是平行四边形;(2)若∠AEC=2∠ABC,求证:四边形ABFC为矩形.【分析】(1)由△ABE与△FCE全等,根据全等三角形的对应边相等得到AB=CF;再由AB与CF平行,根据一组对边平行且相等的四边形为平行四边形得到ABFC为平行四边形,(2)根据平行四边形的对角线互相平分得到AE=EF,BE=EC;再由∠AEC为三角形ABE 的外角,利用外角的性质得到∠AEC等于∠ABE+∠EAB,再由∠AEC=2∠ABC,得到∠ABE =∠EAB,利用等角对等边可得出AE=BE,可得出AF=BC,利用对角线相等的平行四边形为矩形可得出ABFC为矩形.【解答】证明:(1)∵四边形ABCD为平行四边形,∴AB∥DC,∴∠ABE=∠ECF,又∵E为BC的中点,∴BE=CE,在△ABE和△FCE中,∵,∴△ABE≌△FCE(ASA);∴AB=CF,又∵四边形ABCD为平行四边形,∴AB∥CF,∴四边形ABFC为平行四边形,(2)∵四边形ABFC为平行四边形,∴BE=EC,AE=EF,又∵∠AEC=2∠ABC,且∠AEC为△ABE的外角,∴∠AEC=∠ABC+∠EAB,∴∠ABC=∠EAB,∴AE=BE,∴AE+EF=BE+EC,即AF=BC,则四边形ABFC为矩形.16.如图,以△ABC的各边为边长,在边BC的同侧分别作正方形ABDI,正方形BCFE,正方形ACHG,连接AD,DE,EG.(1)求证:△BDE≌△BAC;(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;②求证:四边形ADEG是平行四边形;(3)当△ABC满足什么条件时,四边形ADEG是正方形?请说明理由.【分析】(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC,(2)由△BDE≌△BAC,可得全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°,易证ED∥GA;最后由“一组对边平行且相等”的判定定理证得结论;(3)由“正方形的内角都是直角,四条边都相等”易证∠DAG=90°,且AG=AD.由▱ABDI 和▱ACHG的性质证得,AC=AB.【解答】(1)证明:∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,,∴△BDE≌△BAC(SAS),(2)①解:∵△BDE≌△BAC,∠ADB=45°,∴∠EDA=α﹣45°,∵∠DAG=360°﹣45°﹣90°﹣α=225°﹣α,②证明:∵△BDE≌△BAC,∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等).(3)解:结论:当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.理由:由①知,当∠DAG=90°时,∠BAC=135°.∵四边形ABDI是正方形,∴AD=AB.又∵四边形ACHG是正方形,∴AC=AG,∴AC=AB.∴当∠BAC=135°且AC=AB时,四边形ADEG是正方形.17.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.(1)求证:四边形MANP是正方形;(2)求证:EM=BN.【分析】(1)根据有三个角是直角的四边形是矩形证明四边形MANP是矩形,再根据角平分线的性质得:PM=PN,可得结论;(2)证明△EPM≌△BPN,可得结论.【解答】证明:(1)∵四边形ABCD是正方形,∴∠DAB=90°,AC平分∠DAB,(1分)∵PM⊥AD,PN⊥AB,∴∠PMA=∠PNA=90°,∴四边形MANP是矩形,(2分)∵AC平分∠DAB,PM⊥AD,PN⊥AB,∴PM=PN,(3分)∴四边形MANP是正方形;(4分)(2)∵四边形ABCD是正方形,∴PM=PN,∠MPN=90°,∵∠EPB=90°,∴∠MPE+∠EPN=∠NPB+∠EPN=90°,∴∠MPE=∠NPB,(5分)在△EPM和△BPN中,∵,∴△EPM≌△BPN(ASA),(6分)∴EM=BN.(7分)18.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=CG.【分析】(1)利用勾股定理即可得出BH的长,进而运用公式得出△ABE的面积;(2)过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,判定△AME≌△BNG(AAS),可得ME=NG,进而得出BE=GC,再判定△AFO≌△CEO(AAS),可得AF=CE,即可得到DF=BE=CG.【解答】解:(1)∵AH=3,HE=1,∴AB=AE=4,又∵Rt△ABH中,BH==,∴S△ABE=AE×BH=×4×=;(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,∵∠ACB=45°,∴∠MAC=∠NGC=45°,∵AB=AE,∴BM=EM=BE,∠BAM=∠EAM,又∵AE⊥BG,∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,∴∠MAE=∠NBG,设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,∴AB=BG,∴AE=BG,在△AME和△BNG中,,∴△AME≌△BNG(AAS),∴ME=NG,在等腰Rt△CNG中,NG=NC,∴GC=NG=ME=BE,∴BE=GC,∵O是AC的中点,∴OA=OC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠OAF=∠OCE,∠AFO=∠CEO,∴△AFO≌△CEO(AAS),∴AF=CE,∴AD﹣AF=BC﹣EC,即DF=BE,∴DF=BE=CG.19.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.(1)求证:四边形BPEQ是菱形;(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.【分析】(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论;(2)根据三角形中位线的性质可得AE+BE=2OF+2OB=18,设AE=x,则BE=18﹣x,在Rt△ABE中,根据勾股定理可得62+x2=(18﹣x)2,BE=10,得到OB=BE=5,设PE =y,则AP=8﹣y,BP=PE=y,在Rt△ABP中,根据勾股定理可得62+(8﹣y)2=y2,解得y=,在Rt△BOP中,根据勾股定理可得PO==,由PQ=2PO 即可求解.【解答】(1)证明:∵PQ垂直平分BE,∴PB=PE,OB=OE,∵四边形ABCD是矩形,∴AD∥BC,∴∠PEO=∠QBO,在△BOQ与△EOP中,,∴△BOQ≌△EOP(ASA),∴PE=QB,又∵AD∥BC,∴四边形BPEQ是平行四边形,又∵QB=QE,∴四边形BPEQ是菱形;(2)解:∵O,F分别为PQ,AB的中点,∴AE+BE=2OF+2OB=18,设AE=x,则BE=18﹣x,在Rt△ABE中,62+x2=(18﹣x)2,解得x=8,BE=18﹣x=10,∴OB=BE=5,设PE=y,则AP=8﹣y,BP=PE=y,在Rt△ABP中,62+(8﹣y)2=y2,解得y=,在Rt△BOP中,PO==,∴PQ=2PO=.。
人教版初中数学八年级下册第十八章《18.1平行四边形》同步练习题(含答案)

《18.1平行四边形》同步练习题一、选择题(每小题只有一个正确答案)1.如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是()A. 1<m<11B. 2<m<22C. 10<m<12D. 2<m<62.如图所示,在▱ABCD中,CE⊥AB,E为垂足.若∠A=125°,则∠BCE等于()A. 55°B. 35°C. 30°D. 25°3.如图,E、F分别为平行四边形ABCD两对边AD、BC的中点,AF与BE交于点G,CE 与DF交于点H,则图中平行四边形的个数为()A. 4B. 5C. 7D. 84.四边形ABCD中,从∠A,∠B,∠C,∠D的度数之比中,能判定四边形ABCD是平行四边形的是()A. 1:2:3:4B. 2:3:2:3C. 2:2:3:3D. 1:2:2:35.如图,在□ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①C F=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是()A. 4B. 3C. 2D. 16.如图,在四边形ABCD中,E是AB边的中点,连结DE并延长,交CB的延长=.添加一个条件,使四边形ABCD是平行四边形,你认为下面线于F点,BC BF四个条件中可选择的是().7.如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是()A. S△BEC=2S△CEFB. EF=CFC. ∠DCF=12∠BCD D. ∠DFE=3∠AEF二、填空题8.如图,在▱ABCD中,AM=AD,BD与MC相交于点O,则S△MOD:S△BOC=_____.9.9.已知平行四边形的三个顶点坐标分别为(-1,0),(0,2),(2,0),则在第四象限的第四个顶点的坐标为___________.10.如图,在□ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC+BD=___________.11.如图,在四边形ABCD中,AD∥BC,点E是BC边的中点,连接DE并延长,交AB的延长线于F点.已知AB=4,∠F=∠CDE,则BF的长为________.12.如图,▱ABCD中,BE平分∠ABC交AD于点E,且CE平分∠DCB,若BC=10,则平行四边形ABCD的周长是________.三、解答题13.已知:如图,在□ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.14.如图,在□ABCD 中,点E、F 是对角线BD 上的两点,且BF=DE,连接AE、CF.求证:AE∥CF.15.如图,□ABCD的对角线AC,BD相较于点O,且E,F,G,H分别是AO,BO,CO,DO的中点.求证:四边形EFGH是平行四边形.16.已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.(1)如图1,求证:四边形ADCF是平行四边形;(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。
人教版八年级下册数学第十八章 平行四边形 含答案

人教版八年级下册数学第十八章平行四边形含答案一、单选题(共15题,共计45分)1、直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为()A. B. C.12 D.252、如图,在平行四边形ABCD中,AC,BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是()A.∠BAC=∠ACBB.∠BAC=∠ACDC.∠BAC=∠DACD.∠BAC=∠ABD3、设A,B表示两个集合,我们规定“A∩B”表示A与B的公共部分,并称之为A与B的交集.例如:若A={正数},B={整数},则A∩B={正整数}.如果A={矩形},B={菱形},则所对应的集合A∩B是A.{平行四边形}B.{矩形}C.{菱形}D.{正方形}4、如图,反比例函数y= 的图象经过▱ABCD对角线的交点P,已知点A,C,D 在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k的值为()A. B. C. D.5、如图,长方形ABCD是由6个正方形组成,其中有两个一样大的正方形,且最小正方形边长为1,则长方形ABCD的边长DC为()A.10B.13C.16D.196、如图,M是菱形ABCD的边AB中点,MO=5cm,则菱形ABCD的周长为()A.5 cmB.10 cmC.20 cmD.40 cm7、如图,若平行四边形的顶点的坐标分别是,则顶点的坐标是()A. B. C. D.8、用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是()A.一组邻边相等的四边形是菱形B.四边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.每条对角线平分一组对角的平行四边形是菱形9、如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是()A.15B.16C.19D.2010、如图,顺次连结四边形ABCD各中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是()A. AB∥DCB. AB=DCC. AC⊥BDD. AC=BD11、如图,将边长为 6 的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD 方向平移,得到△A′B′C′,当两个三角形重叠部分为菱形时,则DA′为()A.3B.4C.2 ﹣1D.6 ﹣612、若正方形的对角线长为2 cm,则这个正方形的面积为()A.4B.2C.D.13、圆柱形纸筒沿母线AB剪开铺平,得到一个矩形(如图).如果将这个纸筒沿线路B⇒M⇒A剪开铺平,得到的图形是()A.矩形B.半圆C.三角形D.平行四边形14、如图,平行四边形中,对角线与相交于点,、分别是对角线BD上的两点,给出下列四个条件:①;②;③;④.其中能判断四边形是平行四边形的个数是()A.1个B.2个C.3个D.4个15、如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A. B. C. D.二、填空题(共10题,共计30分)16、如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为________.17、如图,四边形为菱形,以为斜边的的面积为3,,点E,C在BD的同侧,点P是BD上的一动点,则的最小值是________.18、如图,在□ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.19、在平行四边形ABCD中,∠A=110°,则∠D=________.20、在▱ABCD中,AB:BC=4:3,周长为28cm,则AD=________cm.21、如图是长为20cm,宽为8cm的矩形纸片,M点为长BC边上的中点,沿过M 的直线翻折.若顶点B落在对边AD上,那么折痕长度为________cm.22、如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为________.23、如图,正方形ABCD的边长为4,对角线AC,BD交于点O,以边BC为直径作半圆,则图中阴影部分的面积为________.24、已知菱形的两条对角线长分别为2cm,3cm,则它的面积是________ cm2.25、等腰梯形ABCD中,AB∥DC,AD=BC=CD,点E为AB上一点,连结CE,请添加一个你认为合适的条件________ ,使四边形AECD为菱形.三、解答题(共5题,共计25分)26、如图,在每个小正方形的边长为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上。
人教版八年级下册数学第十八章 平行四边形 含答案

人教版八年级下册数学第十八章平行四边形含答案一、单选题(共15题,共计45分)1、若面积为6cm2的平行四边形的一条边长为x(cm),这条边上的高为y(cm),则y关于x的函数表达式为()A.xy=12B.xy=6C.D.2、如图在Rt△ABC中,∠BAC= ,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )A.①②③④B.②③④C.①③④D.①②④3、如图所示,、分别是正方形的边、上的点,且,,,现有如下结论:①;②;③;④.其中,正确的结论有()A.4个B.3个C.2个D.1个4、如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为()A. B. C. D.5、已知▱ABCD中,对角线AC、BD相交于点O,添加一个适当的条件,使▱ABCD 成为一个矩形.下列所加条件中,不符合要求的是()A.∠ABC=90°B.AC=BDC.AC 2=AB 2+BC 2D.AC⊥BD6、如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC 的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为()A. B. C. D.7、菱形在平面直角坐标系中的位置如图所示,点的坐标是,点的纵坐标是,则点的坐标是()A. B. C. D. </div>8、已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4 ,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为()A.(2,2)B.(2,)C.(,)D.(,)9、在下列图形中,各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大()A. B. C. D.10、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()A.AB=24mB.MN∥ABC.△CMN∽△CABD.CM:MA=1:211、如图:将的对角线的交点与直角坐标系的原点重合,点和分别对应的D点,A点的坐标是()A. 和B. 和C. 和D. 和12、如图,在矩形中,、相交于点,平分交于点,若,则的度数为()A.60°B.75°C.72°D.90°13、如图,在ABCD中,对角线AC、BD相交于O,α=60°.若AB=OD=2,则ABCD的面积是()A.8B.C.2D.414、如图,四边形ABCD是平行四边形,下列说法不正确的是( )A.当AC=BD时,四边形ABCD是矩形B.当AC⊥BD时,四边形ABCD是菱形C.当AC平分∠BAD时,四边形ABCD是菱形D.当∠DAB=90°时,四边形ABCD是正方形15、如图,直线a∥b,则直线a,b之间距离是()A.线段AB的长度B.线段CD的长度C.线段EF的长度D.线段GH的长度二、填空题(共10题,共计30分)16、已知四边形,点是对角线与的交点,且,请再添加一个条件,使得四边形成为平行四边形,那么添加的条件可以是________.(用数学符号语言表达)17、如图,在正方形ABCD内作一个等边△BEC,连接AE、DE,则∠BEA=________.18、如图,在直角坐标系中,四边形OABC为菱形,OA在x轴的正半轴上,∠AOC=60°,过点C的反比例函数的图象与AB交于点D,则△COD的面积为________.19、如图所示,在ABCD中,∠A=50°,则∠B=________,∠C=________.20、如图,正方形ABCD的边长为4,点M在DC上,且,N是AC上的一点,则的最小值为________.21、如图所示,在中,与相交于点O,若,,,则的面积为________.22、面积为的正方形的边长是________.23、如图,菱形ABCD的对角线AC和BD交于点O,点G在射线OD上,且,过点G作交射线OC于点E,过点E作OE的垂线,与过点G作OG的垂线交于点P,得到矩形OEFG.射线AD交线段GF于点H,将沿直线AH折叠,得到,当点M在矩形OEFG的边上时,________.24、设,,是同一平面内三条互相平行的直线,已知与的距离是,与的距离是,则与的距离等于________ .25、我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN 经过点O,若MH=3ME,BD=2MN=4 .则△APD的面积为________.三、解答题(共5题,共计25分)26、如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).27、如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,AE=CF.(1)求证:△ABF≌△CDE;(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?28、如图,在所给方格纸中,每个小正方形边长都是1,标号为①,②,③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图甲、图乙中的指定图形分割成三个三角形,使它们与标号为①,②,③的三个三角形分别对应全等.(1)图甲中的格点正方形ABCD;(2)图乙中的格点平行四边形ABCD.注:分割线画成实线.29、如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?30、如图,在▱ABCD中,AB=10,AD=6,AC⊥BC.求BD的长度.参考答案一、单选题(共15题,共计45分)1、D2、D3、C4、A5、D6、A7、B8、D9、B10、D11、A12、B13、D15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第18章平行四边形
一、选择题
1. 下列四边形中,对角线相等且互相垂直平分的是()
A.平行四边形B.正方形C.等腰梯形D.矩形
2. 如图,由六个全等的正三角形拼成的图,图中平行四边形的个数是()
A.4个B.6个C.8个D.10个
3. 在四边形ABCD中,对角线AC、BD相交于点O,,添加下列一个条
件后,仍不能判定四边形ABCD是平行四边形的是
A B
C D
4. 如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()
A.90°αB.90°+ αC.D.360°α
5. 如图,将n个边长都为2的正方形按如图所示摆放,点A 1 ,A 2 ,…A n 分别是正方形的中心,则这n个正方形重叠部分的面积之和是()
A.n B.n1 C.()n1 D.n
6. 在平面中,下列命题为真命题的是()
B.只有对角线互相平分且垂直的四边形是菱形,
C.对角线互相平分且垂直的四边形是矩形
D.四边相等的四边形是菱形
7. 如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()
A.15°或30°B.30°或45°C.45°或60°D.30°或60°
8. 下列性质中,正方形具有而矩形不一定具有的性质是
A.对角线互相垂直B.对角线互相平分
C.对角线相等D.四个角都是直角
9. 如图,大正方形中有2个小正方形,如果它们的面积分别是S 1 、S 2 ,那么S 1 、S
的大小关系是()
2
A.S 1 >S 2 B.S 1 =S 2
C.S 1 <S 2 D.S 1 、S 2 的大小关系不确定
10. 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠B=60°,BC=3,△ABE的周长为6,则等腰梯形的周长是()
A.8 B.10 C.12 D.16
11. 下列命题正确的是()
A.同一边上两个角相等的梯形是等腰梯形
B.一组对边平行,一组对边相等的四边形是平行四边形
C.如果顺次连接一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形
12. 平行四边形的对角线一定具有的性质是()
A.相等B.互相平分C.互相垂直D.互相垂直且相等
二、填空题
13. 已知平行四边形的三个顶点坐标分别为(-1,0)(0,2)(2,0),则在第四象限的第四个顶点的坐标为___________。
14. 已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图),把线段AE绕点A 旋转,使点E落在直线BC上的点F处,则F、C两点的距离为____________ .
15. 已知平行四边形ABCD中,AC,BD交于点O,若AB=6,AC=8,则BD的取值范围是.
16. 如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是
_________ .
17. 如图,矩形ABCD中,AB=2,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD= _________ .
18. 将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= 度.
三、解答题
19. 如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q在边AD上,将△CBP和△QAP分别沿PC、PQ折叠,使B点与E点重合,A点与F点重合,且P、E、F三点共线.
(1)若点E平分线段PF,则此时AQ的长为多少?
(2)若线段CE与线段QF所在的平行直线之间的距离为2,则此时AP的长为多少?(3)在“线段CE”、“线段QF”、“点A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时AP的长;若不存在,请说明理由.
20. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
21. 如图,矩形ABCD中,点E在CD边的延长线上,且∠EAD=∠CAD.求证:AE=BD.
22. 如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.
(1)写出图中所有的全等三角形;
(2)求证:BE=DF.
答案
一、选择题
1、 B.
2、 B.
3、 D.
4、 C.
5、 B.
6、 D.
7、 D.
8、 A.
9、 A.
10、 A. 11、 D. 12、 B.
二、填空题
13、 (-3,2).
14、 1或5.
15、 4<BD<20.
16、.
17、 2 .
18、 70°.
三、解答题
19、(1)由△CBP和△QAP分别沿PC、PQ折叠,得到△QFP和△PCE,则△AQP≌△FQP,△CPB≌△CPE
∴PA=PF,PB=PE,∠QPA=∠QPF,∠CPB=∠CPE.
∵EF=EP,
∴AB=AP+PB=FP+PB=EF+EP+PB=3PB.
∵AB=4,
∴PB= AB = ,
∴AP AB = .
∵180°=∠QPA+∠QPF+∠CPB+∠CPE=2(∠QPA+∠CPB),
∴∠QPA+∠CPB=90°.
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠CPB+∠PCB=90°,
∴∠QPA=∠PCB,
∴△QAP∽△PBC,
∴,
∴,
∴;
(2)由题意,得PF=EP+2或EP=FP+2.
当EPPF=2时,
∵EP=PB,PF=AP,
∴PBAP=2.
∵AP+PB=4,
∴2BP=6,
∴BP=3,
∴AP=1.
当PFEP=2时,
∵EP=PB,PF=AP,
∴APPB=2.
∵AP+PB=4,
∴2AP=6.
∴AP=3.
故AP的长为1或3;
(3)①若CE与点A在同一直线上,如图2,连接AC,点E在AC上,
在△AEP和△ABC中,
∠APE=∠B=90°,∠EAP=∠BAC,
∴△AEP∽△ABC,
∴.
设AP=x,则EP=BP=4x,
在Rt△ABC中,
∵AB=4,BC=2,
∴AC=2 ,
∴.
解得.
②若CE与QF在同一直线上,如图3,
∵△AQP≌△EQP,△CPB≌△CPE,
∴AP=EP=BP,
∴2AP=4,
∴AP=2.
20、(1)在正方形ABCD中,
∵,
∴△CBE≌△CDF(SAS).
∴CE=CF;
(2)GE=BE+GD成立.理由是:
∵△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵,
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
21、∵四边形ABCD是矩形,
∴∠CDA=∠EDA=90°,AC=BD.
在△ADC和△ADE中.
∵∠EAD=∠CAD
AD="AD"
∠ADE=∠ADC,
∴△ADC≌△ADE(ASA).
∴AC=AE.
∴BD=AE.
22、(1)图中全等的图形有:△ADF≌△CBE,△ABE≌△CDF,△ABC≌△DCA;(2)∵ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
又∵AE=CF,
∴△ABE≌△DCF(SAS),
∴BE=DF.。
