(通用版)2018年中考数学总复习专题检测21 与圆有关的计算试题
全国各地2018年中考数学真题汇编圆(填空+选择46题)

C.70° D.80°
【答案】 D
6. 如图, 蒙古包可近似看作由圆锥和圆柱组成,
圆锥高为 2m的蒙古包,则需要毛毡的面积是(
若用毛毡搭建一个底面圆面积为 )
25π m2 , 圆柱高为 3m,
A. B.40 πm2 C. D.55 πm2 【答案】 A
B. C. D.
的长为(
)
A.
B.
C.
【答案】 C 4. 如图,在
中,
D.
,
的半径为 3,则图中阴影部分的面积是(
)
A.
B.
C.
D.
【答案】 C
5. 如图,AB是圆 O的弦,OC⊥ AB,交圆 O于点 C,连接 OA,OB,BC,若∠ ABC=20°,则∠ AOB的度数是(
)
A.40 °
B.50 °
2018 年中考数学真题汇编 : 圆( 填空 +选择 46 题)
一、选择题
1. 已知
的半径为
,
是( )
A. 外离
切ห้องสมุดไป่ตู้
交
【答案】 C
2. 如图,
为
的直径,
的半径为
,圆心距
是
的弦,
,则
与
的位置关系
B. 外 C. 相 D. 内切
,则
的度数为(
)
A.
【答案】 C 3. 已知半径为 5 的⊙ O是△ ABC的外接圆,若∠ ABC=25°,则劣弧
河南2018中考数学总复习专题检测:圆(含答案)

圆(建议时间:90分钟总分:100分)一、选择题(本大题共7个小题,每小题4分,共28分)1.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于(D) A.180°-2αB.2αC.90°+αD.90°-α第1题图第2题图2.如图,AB是⊙O的直径,P A切⊙O于点A,PO交⊙O于点C.连接BC,若∠P=40°,则∠B等于(B)A.20°B.25°C.30°D.40°3.如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于(B)A.100°B.112.5°C.120°D.135°第3题图第5题图4.已知圆锥的底面面积为9π cm2,母线长为6 cm,则圆锥的侧面积是(A) A.18π cm2B.27π cm2C.18 cm2D.27 cm2 5.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为(A)A.2 B.-1 C.2D.46.已知一个扇形的圆心角为60°,它所对的弧长为2π cm,则这个扇形的半径为(A)A .6 cmB .12cmC .2 3 cm D. 6 cm7.如图,AB 是⊙O 的直径,C ,D 是⊙O 上的点,且OC ∥BD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论:①AD ⊥BD ;②∠AOC =∠AEC ;③BC 平分∠ABD ;④AF =DF ;⑤DB =2OF ; ⑥△CEF ≌△BED ,其中一定成立的是( D )A .②④⑤⑥B .①③⑤⑥C .②③④⑥D .①③④⑤二、填空题(本大题共6个小题,每小题4分,共24分)8.如图,AB 是⊙O 的直径,AC 与⊙O 相切,CO 交⊙O 于点D .若∠CAD =30°,则∠BOD = 120 °.第8题图 第9题图 9.如图,AB 为⊙O 的直径,C ,D 为⊙O 上的点,︵AD =︵CD .若∠CAB =40°,则∠CAD = 25° .10.在半径为20的⊙O 中,弦AB =32,点P 在弦AB 上,且OP =15,则AP =7或25 .11.如图,小明自制一块乒乓球拍,正面是半径为8 cm 的⊙O ,︵AB =90°,弓形ACB (阴影部分)粘贴胶皮,则胶皮面积为 (48π+32)cm 2 .第11题图 第12题图12.如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在︵AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为2π-4. 13.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长线于点F,若图中两个阴影部分的面积相等,则AF的长为π(结果保留根号).三、解答题(本大题共4个小题,共48分)14.(12分)如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF,BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.证明:(1)∵E是△ABC的内心,∴∠BAE=∠CAE,∠EBA=∠EBC.∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,∴∠DBE=∠DEB,∴DB=DE;(2)连接CD ,如解图所示.∵E 是△ABC 的内心,∴∠DAB =∠DAC ,∴BD =CD .∵BD =DF ,∴CD =DB =DF ,∴∠BCF =90°,∴BC ⊥CF ,∴CF 是⊙O 的切线.15.(12分)如图,AB 为⊙O 的直径,C ,D 为⊙O 上两点,∠BAC =∠DAC ,过点C 作直线EF ⊥AD ,交AD 的延长线于点E ,连接BC .(1)求证:EF 是⊙O 的切线;(2)若DE =1,BC =2,求劣弧BC ︵)的长l .(1)证明:连接OC ,如解图所示.∵OA =OC ,∴∠OAC =∠OCA .又∵∠OAC =∠DAC ,∴∠DAC =∠OCA ,∴AD ∥OC .∵EF ⊥AD ,∴EF ⊥OC ,∴EF 是⊙O 的切线;。
中考数学专题复习《圆的证明与计算》检测题(含答案)

专题二 圆的证明与计算类型一 圆基本性质的证明与计算1.如图,⊙O 的半径为5,点P 在⊙O 外,PB 交⊙O 于A 、B 两点,PC 交⊙O 于D 、C 两点. (1)求证:P A ·PB =PD ·PC ;(2)若P A =454,AB =194,PD =DC +2,求点O 到PC 的距离.第1题图2. 如图,△ABC 是⊙O 的内接三角形,AB =AC ,点P 是AB ︵的中点,连接P A ,PB ,PC .(1)如图①,若∠BPC =60°,求证:AC =3AP ; (2)如图②,若sin ∠BPC =2425,求tan ∠P AB 的值.第2题图3. 已知⊙O 中弦AB ⊥弦CD 于E ,tan ∠ACD =32. (1)如图①,若AB 为⊙O 的直径,BE =8,求AC 的长;(2)如图②,若AB 不为⊙O 的直径,BE =4,F 为BC ︵上一点,BF ︵=BD ︵,且CF =7,求AC 的长.第3题图4.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O ,交BC 于点D ,交CA 的延长线于点E ,连接AD 、DE .(1)求证:D 是BC 的中点;(2)若 DE =3,BD -AD =2,求⊙O 的半径; (3)在(2)的条件下,求弦AE 的长.第4题图5.如图,⊙O 的半径为1,A ,P ,B ,C 是⊙O 上的四个点, ∠APC =∠CPB =60°.(1)判断△ABC 的形状:________;(2)试探究线段P A ,PB ,PC 之间的数量关系,并证明你的结论; (3)当点P 位于AB ︵的什么位置时,四边形APBC 的面积最大?求出最大面积.第5题图 备用图类型二与切线有关的证明与计算(一、与三角函数结合1.已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD 交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)求证:AC与⊙O相切;(2)当BD=6,sin C=35时,求⊙O的半径.第1题图2.如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:∠PCA=∠ABC;(2)过点A作AE∥PC,交⊙O于点E,交CD于点F,连接BE.若sin ∠P =35,CF =5,求BE 的长.第2题图3. 如图①,在⊙O 中,直径AB ⊥CD 于点E ,点P 在BA 的延长线上,且满足∠PDA =∠ADC .(1)判断直线PD 与⊙O 的位置关系,并说明理由;(2)延长DO 交⊙O 于M (如图②),当M 恰为BC ︵的中点时,试求DE BE 的值;(3)若P A =2,tan ∠PDA =12,求⊙O 的半径.第3题图二、与相似三角形结合1.如图,在Rt △ABC 中,∠ACB =90°,E 是BC 的中点,以AC 为直径的⊙O 与AB 边交于点D ,连接DE . (1)求证:△ABC ∽△CBD ; (2)求证:直线DE 是⊙O 的切线.第1题图2. 如图,⊙O 的圆心在Rt △ABC 的直角边AC 上,⊙O 经过C 、D 两点,与斜边AB 交于点E ,连接BO 、ED ,有BO ∥ED ,作弦EF ⊥AC 于G ,连接DF .(1)求证:CO ·CD =DE ·BO ;(2)若⊙O 的半径为5,sin ∠DFE =35,求EF 的长.第2题图3. 如图,在△ABC 中,AB =AC ,以AB 为直径作半圆⊙O ,交BC 于点D ,连接AD ,过点D 作DE ⊥AC ,垂足为点E ,交AB 的延长线于点F .(1)求证:EF 是⊙O 的切线;(2)若⊙O 的半径为5,sin ∠ADE =45,求BF 的长.第3题图4.如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形;(2)若AC=6,AB=10,连接AD,求⊙O的半径和AD的长.第4题图5.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD =DC,延长CB交⊙O于点E.(1)图①的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图②,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)第5题图6.已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,OF延长线交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH·EA;(3)若⊙O 的半径为5,sin A =35,求BH 的长.第6题图7.如图①,△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交BC 于点E (BE >EC ),且BD =2 3.过点D 作DF ∥BC ,交AB 的延长线于点F .(1)求证:DF 为⊙O 的切线;(2)若∠BAC =60°,DE =7,求图中阴影部分的面积;(3)若AB AC =43,DF +BF =8,如图②,求BF 的长.第7题图三、与全等三角形结合1.如图,已知PC 平分∠MPN ,点O 是PC 上任意一点,PM 与⊙O 相切于点E ,交PC 于A 、B 两点. (1)求证:PN 与⊙O 相切;(2)如果∠MPC =30°,PE =23,求劣弧BE ︵的长.第1题图2.如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M是⊙O上一点,并且∠BMC =60°.(1)求证:AB是⊙O的切线;(2)若E、F分别是边AB、AC上的两个动点,且∠EDF=120°,⊙O 的半径为2.试问BE+CF的值是否为定值,若是,求出这个定值;若不是,请说明理由.第2题图3. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.(1)求证:AE与⊙O相切;(2)连接BD,若ED∶DO=3∶1,OA=9,求AE的长和tan B的值.第3题图4. 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O 交于点C,连接BC,AF.(1)求证:直线P A为⊙O的切线;(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;(3)若BC=6,tan∠F=12,求cos∠ACB的值和线段PE的长.第4题图5. 如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,∠ACB 的平分线CD 交⊙O 于点D ,过点D 作⊙O 的切线PD ,交CA 的延长线于点P ,过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥CD 于点F . (1)求证:PD ∥AB ; (2)求证:DE =BF ;(3)若AC =6,tan ∠CAB =43,求线段PC 的长.第5题图6.如图,点P 是⊙O 外一点,P A 切⊙O 于点A ,AB 是⊙O 的直径,连接OP ,过点B 作BC ∥OP 交⊙O 于点C ,连接AC 交OP 于点D . (1)求证:PC 是⊙O 的切线;(2)若PD =163,AC =8,求图中阴影部分的面积;(3)在(2)的条件下,若点E 是AB ︵的中点,连接CE ,求CE 的长.第6题图7. 如图①,AB是⊙O的直径,OC⊥AB,弦CD与半径OB相交于点F,连接BD,过圆心O作OG∥BD,过点A作⊙O的切线,与OG 相交于点G,连接GD,并延长与AB的延长线交于点E.(1)求证:GD=GA;(2)求证:△DEF是等腰三角形;(3)如图②,连接BC,过点B作BH⊥GE,垂足为点H,若BH=9,⊙O的直径是25,求△CBF的周长.第7题图专题二圆的证明与计算类型一圆基本性质的证明与计算1. (1)证明:如解图,连接AD,BC,∵四边形ABCD内接于⊙O,∴∠P AD=∠PCB,∠PDA=∠PBC,∴△P AD ∽△PCB , ∴P A PD =PC PB , ∴P A ·PB =PD ·PC ;(2)解:如解图,连接OD ,过O 点作OE ⊥DC 于点E , ∵P A =454,AB =194,PD =DC +2,∴PB =P A +AB =16,PC =PD +DC =2DC +2, ∵P A ·PB =PD ·PC ,∴454×16=(DC +2)(2DC +2), 解得DC =8或DC =-11(舍去), ∴DE =12DC =4, ∵OD =5,∴在Rt △ODE 中,OE =OD 2-DE 2=3, 即点O 到PC 的距离为3.2. (1)证明:∵∠BAC 与∠BPC 是同弧所对的圆周角, ∴∠BAC =∠BPC =60°, 又∵AB =AC ,∴△ABC 为等边三角形, ∴∠ACB =60°, ∵点P 是AB ︵的中点, ∴P A ︵=PB ︵,∴∠ACP =∠BCP =12∠ACB =30°,而∠APC =∠ABC =60°, ∴△APC 为直角三角形, ∴tan ∠APC =AC AP , ∴AC =AP tan60°=3AP ;(2)解:连接AO 并延长交PC 于点E ,交BC 于点F ,过点E 作EG ⊥AC 于点G ,连接OC ,BO ,如解图,∵AB =AC , ∴AF ⊥BC , ∴BF =CF , ∵点P 是AB ︵中点, ∴∠ACP =∠PCB , ∴EG =EF .∵∠BPC =∠BAC =12∠BOC =∠FOC , ∴sin ∠FOC =sin ∠BPC =2425, 设FC =24a ,则OC =OA =25a ,∴OF =OC 2-FC 2=7a ,AF =25a +7a =32a , 在Rt △AFC 中,∵AC 2=AF 2+FC 2, ∴AC =(32a )2+(24a )2=40a , ∵∠EAG =∠CAF , ∴△AEG ∽△ACF , ∴EG CF =AE AC ,又∵EG =EF ,AE =AF -EF ,第2题解图∴EG 24a =32a -EG 40a , 解得EG =12a ,在Rt △CEF 中,tan ∠ECF =EF FC =12a 24a =12, ∵∠P AB =∠PCB ,∴tan ∠P AB =tan ∠PCB =tan ∠ECF =12. 3. 解:(1)如解图①,连接BD , ∵直径AB ⊥弦CD 于点E , ∴CE =DE ,∵∠ACD 与∠ABD 是同弧所对的圆周角, ∴∠ACD =∠ABD , ∴tan ∠ABD =tan ∠ACD =32, ∴ED EB =AE CE =32,即ED 8=32, ∴ED =12, ∴CE =ED =12, 又∵AE =32CE =18, ∴AC =AE 2+CE 2=613;(2)连接CB ,过B 作BG ⊥CF 于G ,如解图②, ∵BF ︵=BD ︵, ∴∠BCE =∠BCG , 在△CEB 和△CGB 中第3题解图①⎩⎪⎨⎪⎧∠BCE =∠BCG ∠BEC =∠BGC BC =BC, ∴△CEB ≌△CGB (AAS), ∴BE =BG =4,∵四边形ACFB 内接于⊙O , ∴∠A +∠CFB =180°, 又∵∠CFB +∠BFG =180°, ∴∠BFG =∠A , ∵∠FGB =∠AEC =90°, ∴△BFG ∽△CAE , ∴FG BG =AE CE =32, ∴FG =32BG =6, ∴CE =CG =13, ∴AE =32CE =392,∴AC =AE 2+CE 2=13213. 4. (1)证明:∵AB 是⊙O 的直径, ∴∠ADB =90°, 即AD ⊥BC , ∵AB =AC ,∴等腰△ABC ,AD 为BC 边上的垂线, ∴BD =DC , ∴D 是BC 的中点; (2)解:∵AB =AC ,∴∠ABC =∠C ,∵∠ABC 和∠AED 是同弧所对的圆周角, ∴∠ABC =∠AED , ∴∠AED =∠C , ∴CD =DE =3, ∴BD =CD =3, ∵BD -AD =2, ∴AD =1,在Rt △ABD 中,由勾股定理得AB 2=BD 2+AD 2=32+12=10, ∴AB =10,∴⊙O 的半径=12AB =102; (3)解:如解图,连接BE , ∵AB =10, ∴AC =10,∵∠ADC =∠BEA =90°,∠C =∠C , ∴△CDA ∽△CEB , ∴AC BC =CD CE ,由(2)知BC =2BD =6,CD =3, ∴106=3CE , ∴CE =9510,∴AE =CE -AC =9510-10=4510. 5. 解:(1)等边三角形.第4题解图【解法提示】∵∠APC =∠CPB =60°,又∵∠BAC 和∠CPB 是同弧所对的圆周角,∠ABC 和∠APC 是同弧所对的圆周角,∴∠BAC =∠CPB =60°,∠ABC =∠APC =60°, ∴∠BAC =∠ABC =60°, ∴AC =BC ,又∵有一个角是60°的等腰三角形是等边三角形, ∴△ABC 是等边三角形. (2)P A +PB =PC .证明如下:如解图①,在PC 上截取PD =P A ,连接AD , ∵∠APC =60°, ∴△P AD 是等边三角形, ∴P A =AD =PD ,∠P AD =60°, 又∵∠BAC =60°, ∴∠P AB =∠DAC , 在△P AB 和△DAC 中, ∵⎩⎪⎨⎪⎧AP =AD ∠P AB =∠DAC ,AB =AC ∴△P AB ≌△DAC (SAS), ∴PB =DC , ∵PD +DC =PC , ∴P A +PB =PC ,(3)当点P 为AB ︵的中点时,四边形APBC 的面积最大. 理由如下:如解图②,过点P 作PE ⊥AB ,垂足为E ,第5题解图①第5题解图②过点C 作CF ⊥AB ,垂足为F , ∵S △P AB =12AB ·PE ,S △ABC =12AB ·CF , ∴S 四边形APBC =12AB ·(PE +CF ).当点P 为AB ︵的中点时,PE +CF =PC ,PC 为⊙O 的直径, 此时四边形APBC 的面积最大, 又∵⊙O 的半径为1,∴其内接正三角形的边长AB = 3 , ∴四边形APBC 的最大面积为12×2×3= 3 . 类型二 与切线有关的证明与计算 一、与三角函数结合 针对演练1. (1)证明:连接OE ,如解图, ∵AB =BC 且D 是AC 中点, ∴BD ⊥AC , ∵BE 平分∠ABD , ∴∠ABE =∠DBE , ∵OB =OE , ∴∠OBE =∠OEB , ∴∠OEB =∠DBE , ∴OE ∥BD ,第1题解图∵BD ⊥AC , ∴OE ⊥AC , ∵OE 为⊙O 半径, ∴AC 与⊙O 相切;(2)解:∵BD =6,sin C =35,BD ⊥AC , ∴BC =BDsin C =10, ∴AB =BC =10.设⊙O 的半径为r ,则AO =10-r , ∵AB =BC , ∴∠C =∠A , ∴sin A =sin C =35, ∵AC 与⊙O 相切于点E , ∴OE ⊥AC ,∴sin A =OE OA =r 10-r =35,∴r =154, 即⊙O 的半径是154.2. (1)证明:连接OC ,如解图, ∵PC 切⊙O 于点C , ∴OC ⊥PC , ∴∠PCO =90°, ∴∠PCA +∠OCA =90°, ∵AB 为⊙O 的直径,第2题解图∴∠ACB =90°, ∴∠ABC +∠OAC =90°, ∵OC =OA , ∴∠OCA =∠OAC , ∴∠PCA =∠ABC ; (2)解:∵AE ∥PC , ∴∠PCA =∠CAF , ∵AB ⊥CG , ∴AC ︵=AG ︵, ∴∠ACF =∠ABC , ∵∠PCA =∠ABC , ∴∠ACF =∠CAF , ∴CF =AF , ∵CF =5, ∴AF =5, ∵AE ∥PC , ∴∠F AD =∠P , ∵sin ∠P =35, ∴sin ∠F AD =35,在Rt △AFD 中,AF =5,sin ∠F AD =35, ∴FD =3,AD =4, ∴CD =CF +FD =8, 在Rt △OCD 中,设OC =r , ∴r 2=(r -4)2+82,∴r =10, ∴AB =2r =20, ∵AB 为⊙O 的直径, ∴∠AEB =90°,在Rt △ABE 中,sin ∠EAD =35, ∴BE AB =35, ∵AB =20, ∴BE =12.3. 解:(1)直线PD 与⊙O 相切, 理由如下:如解图①,连接DO ,CO , ∵∠PDA =∠ADC , ∴∠PDC =2∠ADC , ∵∠AOC =2∠ADC , ∴∠PDC =∠AOC , ∵直径AB ⊥CD 于点E , ∴∠AOD =∠AOC , ∴∠PDC =∠AOD , ∵∠AOD +∠ODE =90°, ∴∠PDC +∠ODE =90°, ∴OD ⊥PD , ∵OD 是⊙O 的半径, ∴直线PD 与⊙O 相切; (2)如解图②,连接BD , ∵M 恰为BC ︵的中点,第3题解图①∴∠CDM =∠BDM , ∵OD =OB , ∴∠BDM =∠DBA , ∴∠CDM =∠DBA , ∵直线PD 与⊙O 相切, ∴∠PDA +∠ADO =90°, 又∵AB 是⊙O 的直径,∴∠ADB =90°,即∠ADO +∠BDM =90°, ∴∠PDA =∠BDM , ∴∠PDA =∠DBA =∠CDM , 又∵∠PDA =∠ADC , ∴∠PDM =3∠CDM =90°, ∴∠CDM =30°, ∴∠DBA =30°, ∴DE BE =tan30°=33; (3)如解图③,∵tan ∠PDA =12,∠PDA =∠ADC , ∴AE DE =12,即DE =2AE ,在Rt △DEO 中,设⊙O 的半径为r , DE 2+EO 2=DO 2, ∴(2AE )2+(r -AE )2=r 2, 解得r =52AE ,在Rt △PDE 中,DE 2+PE 2=PD 2,第3题解图②第3题解图③∴(2AE )2+(2+AE )2=PD 2, ∵直线PD 与⊙O 相切,连接BD , 由(2)知∠PDA =∠DBA ,∠P =∠P , ∴△P AD ∽△PDB , ∴PD PB =P A PD ,∴PD 2=P A ·PB ,即PD 2=2×(2+2r ), ∴(2AE )2+(2+AE )2=2×(2+2r ), 化简得5AE 2+4AE =4r , ∵r =52AE , 解得r =3. 即⊙O 的半径为3. 二、与相似三角形结合 针对演练1. 证明:(1)∵AC 为⊙O 的直径, ∴∠ADC =90°, ∴∠CDB =90°, 又∵∠ACB =90°, ∴∠ACB =∠CDB , 又∵∠B =∠B , ∴△ABC ∽△CBD ; (2)连接DO ,如解图,∵∠BDC =90°,E 为BC 的中点, ∴DE =CE =BE , ∴∠EDC =∠ECD ,第1题解图又∵OD =OC , ∴∠ODC =∠OCD ,而∠OCD +∠DCE =∠ACB =90°, ∴∠EDC +∠ODC =90°,即∠EDO =90°, ∴DE ⊥OD , ∵OD 为⊙O 的半径, ∴DE 与⊙O 相切.2. (1)证明:连接CE ,如解图, ∵CD 为⊙O 的直径, ∴∠CED =90°, ∵∠BCA =90°, ∴∠CED =∠BCO , ∵BO ∥DE , ∴∠BOC =∠CDE , ∴△CBO ∽△ECD , ∴CO DE =BO CD , ∴CO ·CD =DE ·BO ;(2)解:∵∠DFE =∠ECO ,CD =2·OC =10,∴在Rt △CDE 中,ED =CD ·sin ∠ECO =CD ·sin ∠DFE = 10×35=6,∴CE =CD 2-ED 2=102-62=8, 在Rt △CEG 中,EG CE =sin ∠ECG =35, ∴EG =35×8=245,第2题解图根据垂径定理得:EF =2EG =485. 3. (1)证明:如解图,连接OD , ∵AB 是⊙O 的直径, ∴∠ADB =90°, ∵AB =AC ,∴AD 垂直平分BC ,即DC =DB , ∴OD 为△BAC 的中位线, ∴OD ∥AC . 而DE ⊥AC , ∴OD ⊥DE , ∵OD 是⊙O 的半径, ∴EF 是⊙O 的切线;(2)解:∵∠DAC =∠DAB ,且∠AED =∠ADB =90°, ∴∠ADE =∠ABD ,在Rt △ADB 中,sin ∠ADE =sin ∠ABD =AD AB =45,而AB =10, ∴AD =8,在Rt △ADE 中,sin ∠ADE =AE AD =45, ∴AE =325, ∵OD ∥AE , ∴△FDO ∽△FEA ,∴OD AE =FO F A ,即5325=BF +5BF +10,第3题解图∴BF =907.4. (1)证明:如解图①,连接OD 、OE 、ED . ∵BC 与⊙O 相切于点D , ∴OD ⊥BC ,∴∠ODB =90°=∠C , ∴OD ∥AC , ∵∠B =30°, ∴∠A =60°, ∵OA =OE ,∴△AOE 是等边三角形, ∴AE =AO =OD ,∴四边形AODE 是平行四边行, ∵OA =OD ,∴平行四边形AODE 是菱形; (2)解:设⊙O 的半径为r . ∵OD ∥AC , ∴△OBD ∽△ABC ,∴OD AC =OBAB ,即10r =6(10-r ). 解得r =154, ∴⊙O 的半径为154.如解图②,连接OD 、DF 、AD . ∵OD ∥AC , ∴∠DAC =∠ADO ,第4题解图①∵OA =OD , ∴∠ADO =∠DAO , ∴∠DAC =∠DAO , ∵AF 是⊙O 的直径, ∴∠ADF =90°=∠C , ∴△ADC ∽△AFD , ∴AD AC =AF AD , ∴AD 2=AC ·AF ,∵AC =6,AF =154×2=152, ∴AD 2=152×6=45,∴AD =45=3 5.(9分) 5. 解:(1)存在,AE =CE . 理由如下:如解图①,连接AE ,ED , ∵AC 是△ABC 的斜边, ∴∠ABC =90°, ∴AE 为⊙O 的直径, ∴∠ADE =90°, 又∵D 是AC 的中点, ∴ED 为AC 的中垂线, ∴AE =CE ;(2)①如解图②,∵EF 是⊙O 的切线, ∴∠AEF =90°.第5题解图①由(1)可知∠ADE=90°,∴∠AED+∠EAD=90°,∵∠AED+∠DEF=90°,∴∠EAD=∠DEF.又∵∠ADE=∠EDF=90°∴△AED∽△EFD,∴ADED=EDFD,∴ED2=AD·FD.又∵AD=DC=CF,∴ED2=2AD·AD=2AD2,在Rt△AED中,∵AE2=AD2+ED2=3AD2,由(1)知∠AED=∠CED,又∵∠CED=∠CAB,∴∠AED=∠CAB,∴sin∠CAB=sin∠AED=ADAE=13=33.②sin∠CAB=a+2 a+2.【解法提示】由(2)中的①知ED2=AD·FD,∵CF=aCD(a>0),∴CF=aCD=aAD,∴ED2=AD·DF=AD(CD+CF)=AD(AD+aAD)=(a+1)AD2,在Rt△AED中,AE2=AD2+ED2=(a+2)AD2,∴sin ∠CAB =sin ∠AED =ADAE =1a +2=a +2a +2. 6. (1)证明:∵∠ODB =∠AEC ,∠AEC =∠ABC , ∴∠ODB =∠ABC , ∵OF ⊥BC , ∴∠BFD =90°,∴∠ODB +∠DBF =90°, ∴∠ABC +∠DBF =90°, 即∠OBD =90°, ∴BD ⊥OB , ∵OB 为⊙O 的半径, ∴BD 是⊙O 的切线;(2)证明:连接AC ,如解图①所示: ∵OF ⊥BC , ∴BE ︵=CE ︵, ∴∠ECH =∠CAE , ∵∠HEC =∠CEA , ∴△CEH ∽△AEC , ∴CE EH =EA CE , ∴CE 2=EH ·EA ;(3)解:连接BE ,如解图②所示: ∵AB 是⊙O 的直径, ∴∠AEB =90°,∵⊙O 的半径为5,sin ∠BAE =35,第6题解图①第6题解图②∴AB =10,BE =AB ·sin ∠BAE =10×35=6, 在Rt △AEB 中,EA =AB 2-BE 2=102-62=8, ∵BE ︵=CE ︵, ∴BE =CE =6, ∵CE 2=EH ·EA , ∴EH =CE 2EA =628=92,在Rt △BEH 中,BH =BE 2+EH 2=62+(92)2=152.7. (1)证明:连接OD ,如解图①, ∵AD 平分∠BAC 交⊙O 于D , ∴∠BAD =∠CAD , ∴BD ︵=CD ︵, ∴OD ⊥BC , ∵BC ∥DF , ∴OD ⊥DF , ∴DF 为⊙O 的切线;(2)解:连接OB ,连接OD 交BC 于P ,作BH ⊥DF 于H ,如解图①,∵∠BAC =60°,AD 平分∠BAC , ∴∠BAD =30°,∴∠BOD =2∠BAD =60°, 又∵OB =OD ,∴△OBD 为等边三角形, ∴∠ODB =60°,OB =BD =23,第7题解图①∴∠BDF =30°, ∵BC ∥DF , ∴∠DBP =30°,在Rt △DBP 中,PD =12BD =3,PB =3PD =3, 在Rt △DEP 中, ∵PD =3,DE =7,∴PE =(7)2-(3)2=2, ∵OP ⊥BC , ∴BP =CP =3,∴CE =CP -PE =3-2=1, 易证得△BDE ∽△ACE , ∴BE AE =DE CE ,即5AE =71, ∴AE =577. ∵BE ∥DF , ∴△ABE ∽△AFD ,∴BE DF =AE AD ,即5DF =5771277,解得DF =12,在Rt △BDH 中,BH =12BD =3, ∴S 阴影=S △BDF -S 弓形BD =S △BDF -(S 扇形BOD -S △BOD )=12·12·3-60·π·(23)2360+34·(23)2=93-2π;(7分)(3)解:连接CD ,如解图②,由AB AC =43可设AB =4x ,AC =3x ,BF =y , ∵BD ︵=CD ︵, ∴CD =BD =23, ∵DF ∥BC ,∴∠F =∠ABC =∠ADC , ∴∠FDB =∠DBC =∠DAC , ∴△BFD ∽△CDA , ∴BD AC =BF CD ,即233x =y 23,∴xy =4,∵∠FDB =∠DBC =∠DAC =∠F AD , 而∠DFB =∠AFD , ∴△FDB ∽△F AD , ∴DF AF =BF DF , ∵DF +BF =8, ∴DF =8-BF =8-y , ∴8-y y +4x =y 8-y , 整理得:16-4y =xy , ∴16-4y =4,解得y =3, 即BF 的长为3.(10分) 三、与全等三角形结合第7题解图②针对演练1. (1)证明:连接OE ,过点O 作OF ⊥PN ,如解图所示, ∵PM 与⊙O 相切, ∴OE ⊥PM ,∴∠OEP =∠OFP =90°, ∵PC 平分∠MPN , ∴∠EPO =∠FPO , 在△PEO 和△PFO 中, ⎩⎪⎨⎪⎧∠EPO =∠FPO ∠OEP =∠OFP OP =OP, ∴△PEO ≌△PFO (AAS), ∴OF =OE ,∴OF 为圆O 的半径且OF ⊥PN, 则PN 与⊙O 相切;(2)解:在Rt △EPO 中,∠MPC =30°,PE =23, ∴∠EOP =60°,OE =PE ·tan30°=2, ∴∠EOB =120°,则劣弧BE ︵的长为120π×2180=4π3.2. (1)证明:如解图①,连接BO 并延长交⊙O 于点N ,连接CN , ∵∠BMC =60°, ∴∠BNC =60°, ∵∠BNC +∠NBC =90°, ∴∠NBC =30°,又∵△ABC 为等边三角形,第1题解图∴∠BAC =∠ABC =∠ACB =60°, ∴∠ABN =30°+60°=90°, ∴AB ⊥BO ,即AB 为⊙O 的切线.(2)解:BE +CF =3,是定值. 理由如下:如解图②,连接D 与AC 的中点P , ∵D 为BC 中点, ∴AD ⊥BC , ∴PD =PC =12AC , 又∵∠ACB =60°,∴PD =PC =CD =BD =12AC , ∴∠DPF =∠PDC =60°, ∴∠PDF +∠FDC =60°, 又∵∠EDF =120°, ∴∠BDE +∠FDC =60°, ∴∠PDF =∠BDE , 在△BDE 和△PDF 中, ⎩⎪⎨⎪⎧∠EBD =∠DPF BD =PD∠BDE =∠PDF, ∴△BDE ≌△PDF (ASA), ∴BE =PF ,∴BE +CF =PF +CF =CP =BD , ∵OB ⊥AB ,∠ABC =60°,第2题解图②∴∠OBC =30°, 又∵OB =2,∴BD =OB ·cos30°=2×32=3, 即BE +CF = 3.3. (1)证明:连接OC ,如解图①, ∵OD ⊥AC ,OC =OA , ∴∠AOD =∠COD . 在△AOE 和△COE 中, ⎩⎪⎨⎪⎧OA =OC ∠AOE =∠COE OE =OE, ∴△AOE ≌△COE (SAS), ∴∠EAO =∠ECO . 又∵EC 是⊙O 的切线, ∴∠ECO =90°, ∴∠EAO =90°. ∴AE 与⊙O 相切;(2)解:设DO =t ,则DE =3t ,EO =4t , 在△EAO 和△ADO 中,⎩⎪⎨⎪⎧∠EOA =∠AOD ∠EAO =∠ADO, ∴△EAO ∽△ADO , ∴AO DO =EO AO ,即9t =4t 9, ∴t =92,即EO =18.第3题解图①∴AE =EO 2-AO 2=182-92=93;延长BD 交AE 于点F ,过O 作OG ∥AE 交BD 于点G , 如解图②, ∵OG ∥AE , ∴∠FED =∠GOD 又∵∠EDF =∠ODG , ∴△EFD ∽△OGD , ∴EF OG =ED OD =31,即EF =3GO . 又∵O 是AB 的中点, ∴AF =2GO ,∴AE =AF +FE =5GO , ∴5GO =93, ∴GO =935, ∴AF =1835, ∴tan B =AF AB =35.4. (1)证明:如解图,连接OB , ∵PB 是⊙O 的切线, ∴∠PBO =90°,∵OA =OB ,BA ⊥PO 于点D , ∴AD =BD ,∠POA =∠POB , 又∵PO =PO ,∴△P AO ≌△PBO (SAS), ∴∠P AO =∠PBO =90°,第3题解图②第4题解图∴OA ⊥P A ,∴直线P A 为⊙O 的切线;(2)解:线段EF 、OD 、OP 之间的等量关系为EF 2=4OD ·OP . 证明:∵∠P AO =∠PDA =90°,∴∠OAD +∠AOD =90°,∠OP A +∠AOP =90°,∴∠OAD =∠OP A ,∴△OAD ∽△OP A ,∴ OD OA =OA OP ,即OA 2=OD ·OP ,又∵EF =2OA ,∴EF 2=4OD ·OP ;(3)解:∵OA =OC ,AD =BD ,BC =6,∴OD =12BC =3,设AD =x ,∵tan ∠F =12,∴FD =2x ,OA =OF =FD -OD =2x -3,在Rt △AOD 中,由勾股定理,得(2x -3)2=x 2+32,解之得,x 1=4,x 2=0(不合题意,舍去),∴AD =4,OA =2x -3=5,∵AC 是⊙O 直径,∴∠ABC =90°,又∵AC =2OA =10,BC =6,∴ cos ∠ACB =610=35.∵OA 2=OD ·OP ,∴3(PE +5)=25,∴PE =103.5. (1)证明:连接OD ,如解图,∵AB 为⊙O 的直径,∴∠ACB =90°,∵∠ACB 的平分线交⊙O 于点D ,∴∠ACD =∠BCD =45°,∴∠DAB =∠ABD =45°,∴△DAB 为等腰直角三角形,∴DO ⊥AB ,∵PD 为⊙O 的切线,∴OD ⊥PD ,∴PD ∥AB ;(2)证明:∵AE ⊥CD 于点E ,BF ⊥CD 于点F ,∴AE ∥BF ,∴∠FBO =∠EAO ,∵△DAB 为等腰直角三角形,∴∠EDA +∠FDB =90°,∵∠FBD +∠FDB =90°,∴∠FBD =∠EDA ,在△FBD 和△EDA 中,⎩⎪⎨⎪⎧∠BFD =∠DEA ∠FBD =∠EDA BD =DA, ∴△FBD ≌△EDA (AAS),∴DE =BF ;第5题解图(3)解:在Rt △ACB 中,∵AC =6,tan ∠CAB =43,∴BC =6×43=8,∴AB =AC 2+BC 2=62+82=10,∵△DAB 为等腰直角三角形,∴AD =AB 2=52, ∵AE ⊥CD ,∴△ACE 为等腰直角三角形,∴AE =CE =AC 2=62=32, 在Rt △AED 中,DE =AD 2-AE 2=(52)2-(32)2=42,∴CD =CE +DE =32+42=72,∵AB ∥PD ,∴∠PDA =∠DAB =45°,∴∠PDA =∠PCD ,又∵∠DP A =∠CPD ,∴△PDA ∽△PCD ,∴PD PC =P A PD =AD DC =5272=57, ∴P A =57PD ,PC =75PD ,又∵PC =P A +AC ,∴57PD +6=75PD ,解得PD =354,∴PC =57PD +6=57×354+6=254+6=494.6. (1)证明:如解图①,连接OC ,∵P A 切⊙O 于点A ,∴∠P AO =90°,∵BC ∥OP ,∴∠AOP =∠OBC ,∠COP =∠OCB ,∵OC =OB ,∴∠OBC =∠OCB ,∴∠AOP =∠COP ,在△P AO 和△PCO 中,⎩⎪⎨⎪⎧OA =OC ∠AOP =∠COP OP =OP, ∴△P AO ≌△PCO (SAS),∴∠PCO =∠P AO =90°,∴OC ⊥PC ,∵OC 为⊙O 的半径,∴PC 是⊙O 的切线;(2)解:由(1)得P A ,PC 都为圆的切线,∴P A =PC ,OP 平分∠APC ,∠ADO =∠P AO =90°, ∴∠P AD +∠DAO =∠DAO +∠AOD ,又∵∠ADP =∠ADO ,∴∠P AD =∠AOD ,∴△ADP ∽△ODA ,∴AD PD =DO AD ,第6题解图①∴AD 2=PD ·DO ,∵AC =8,PD =163, ∴AD =12AC =4,OD =3,在Rt △ADO 中,AO =AD 2+OD 2=5,由题意知OD 为△ABC 的中位线,∴BC =6,AB =BC 2+AC 2=10.∴S 阴影=12S ⊙O -S △ABC =12·π·52-12×6×8=25π2-24;(3)解:如解图②,连接AE 、BE ,作BM ⊥CE 于点M , ∴∠CMB =∠EMB =∠AEB =90°,∵点E 是AB ︵的中点,∴AE =BE ,∠EAB =∠EBA =45°,∴∠ECB =∠CBM =∠ABE =45°,CM =MB =BC ·sin45°=32,BE =AB ·cos45°=52,∴EM =BE 2-BM 2=42,则CE =CM +EM =7 2.7. (1)证明:连接OD ,如解图①所示,∵OB =OD ,∴∠ODB =∠OBD .∵OG ∥BD ,∴∠AOG =∠OBD ,∠GOD =∠ODB ,∴∠DOG =∠AOG ,在△DOG 和△AOG 中,第6题解图②第7题解图①⎩⎪⎨⎪⎧OD =OA ∠DOG =∠AOG OG =OG, ∴△DOG ≌△AOG (SAS),∴GD =GA ;(2)证明:∵AG 切⊙O 于点A ,∴AG ⊥OA ,∴∠OAG =90°,∵△DOG ≌△AOG ,∴∠OAG =∠ODG =90°,∴∠ODE =180°-∠ODG =90°,∴∠ODC +∠FDE =90°,∵OC ⊥AB ,∴∠COB =90°,∴∠OCD +∠OFC =90°,∵OC =OD ,∴∠ODC =∠OCD ,∴∠FDE =∠OFC ,∵∠OFC =∠EFD ,∴∠EFD =∠EDF ,∴EF =ED ,∴△DEF 是等腰三角形;(3)解:过点B 作BK ⊥OD 于点K ,如解图②所示: 则∠OKB =∠BKD =∠ODE =90°,∴BK ∥DE ,∴∠OBK =∠E ,∵BH ⊥GE ,∴∠BHD =∠BHE =90°, ∴四边形KDHB 为矩形, ∴KD =BH =9,∴OK =OD -KD =72,在Rt △OKB 中,∵OK 2+KB 2=OB 2,OB =252, ∴KB =12,∴tan ∠E =tan ∠OBK =OK KB =724,sin ∠E =sin ∠OBK =OK OB =725,∵tan ∠E =OD DE =724,∴DE =3007,∴EF =3007,∵sin ∠E =BH BE =725,∴BE =2257,∴BF =EF -BE =757,∴OF =OB -BF =2514,在Rt △COF 中,∠COB =90°, ∴OC 2+OF 2=FC 2,∴FC =125214,在Rt △COB 中,∵OC 2+OB 2=BC 2,OC =OB =252, ∴BC =2522,∴BC +CF +BF =1502+757, ∴△CBF 的周长=1502+757.。
2018 初三数学中考复习 与圆有关的计算 专项复习练习题 含答案

2018 初三数学中考复习 与圆有关的计算 专项复习练习题1.将半径为12 cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( D )A .2 cmB .3 cmC .4 cmD .6 cm2.半径相等圆的内接正三角形、正方形、正六边形的边长之比为( B )A .1∶2∶ 3 B.3∶2∶1 C .3∶2∶1 D .1∶2∶33.如图,▱ABCD 中,∠B =70°,BC =6,以AD 为直径的⊙O 交CD 于点E ,则DE︵的长为( B )A.13πB.23πC.76πD.43π 4.如图,正方形ABCD 内接于半径为2的⊙O,则图中阴影部分的面积为( D )A .π+1B .π+2C .π-1D .π-25.如图,圆锥的底面半径为2,母线长为6,则侧面积为( C )A .4πB .6πC .12πD .16π6.如图,在扇形AOB 中,∠AOB =90°,正方形CDEF 的顶点C 是AB ︵的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为22时,则阴影部分的面积为( A )A .2π-4B .4π-8C .2π-8D .4π-47.如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 的夹角为120°,AB 长为30厘米,则BC ︵的长为__20π__厘米.(结果保留π)8.如图,⊙O 的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ,AE =2,则EG 的长是.9.圆锥的底面半径为 2 cm ,圆锥高为 3 cm ,则此圆锥侧面展开图的周长为10.如图,分别以正五边形ABCDE 的顶点A ,D 为圆心,以AB 长为半径画BE ︵,CE ︵.若AB =1,则阴影部分图形的周长为__65π+1__(结果保留π).11.如图,P ,Q 分别是⊙O 的内接正五边形的边AB ,BC 上的点,BP =CQ ,则∠POQ =__72°__.12.如图,在扇形OAB 中,C 是OA 的中点,CD ⊥OA ,CD 与AB ︵交于点D ,以O 为圆心,OC 的长为半径作CE ︵交OB 于点E ,若OA =4,∠AOB =120°,则图中阴影部分的面积为3.(结果保留π)13.如图,在Rt △ABC 中,∠C =90°,AC =BC ,点O 在AB 上,经过点A 的⊙O 与BC 相切于点D ,交AB 于点E.(1)求证:AD 平分∠BAC;(2)若CD =1,求图中阴影部分的面积(结果保留π).解:(1)证明:连结DE ,OD.∵BC 相切⊙O 于点D ,∴∠CDA =∠AED,∵∠ADE =∠ACD=90°,∴∠DAO =∠CAD.∴AD 平分∠BAC.(2)∵在Rt △ABC 中,∠C =90°,AC =BC ,∴∠B =∠BAC=45°.∵∠ODB =90°,∴OD =BD.∴∠BOD=45°.设BD =x ,则OD =OA =x ,OB =2x ,∴BC =AC =x +1,∵AC 2+BC 2=AB 2,∴2(x +1)2=(2x +x)2,∴x =2.∴BD=OD =2.∴图中阴影部分的面积=S △BOD -S 扇形DOE =12×2×2-45·π×(2)2360=1-π4.14.如图,AB 为⊙O 的直径,C ,D 为⊙O 上的两点,∠BAC =∠DAC,过点C 作直线EF⊥AD,交AD 的延长线于点E ,连结BC.(1)求证:EF 是⊙O 的切线;(2)若DE =1,BC =2,求劣弧BC ︵的长l.解:(1)证明:连结OC ,∵OA =OC ,∴∠OAC =∠OCA,∴∠DAC =∠OCA.∴AD//OC,∴∠OCF =∠AEC=90°.∴EF 是⊙O 的切线.(2)连结OD ,DC ,∵∠DAC =∠OAC,∴DC =BC =2.∵ED=1,DC =2,∴sin ∠ECD =DE DC =12.∴∠ECD=30°.∴∠OCD =60°.∵OC =OD ,∴△DOC 是等边三角形,∴∠BOC =∠COD=60°,OC =2.∴l=60π×2180=23π.15.如图,在△ABC 中,∠ACB =90°,O 是边AC 上一点,以O 为圆心,OA 为半径的圆分别交AB ,AC 于点E ,D ,在BC 的延长线上取点F ,使得BF =EF ,EF 与AC 交于点G.(1)试判断直线EF 与⊙O 的位置关系,并说明理由;(2)若OA =2,∠A =30°,求图中阴影部分的面积.解:(1)连结OE ,∵OA =OE ,∴∠A =∠AEO,∵BF =EF ,∴∠B =∠BEF.∵∠A +∠B=90°,∴∠AEO +∠BEF=90°,即∠OEG=90°.∴EF 是⊙O 的切线.(2)∵AD 是⊙O 的直径,∴∠AED =90°.∵∠A =30°,∴∠EOD =60°.∵OE =OA =2,∴EG =23.∴阴影部分的面积=12×2×23-60·π×22360=23-23π.16.如图为一个圆锥形粮堆,从正面看是边长为6米的正三角形ABC ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时,小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路线是多少米?(结果保留根号)解:∵BC=6,∴圆锥的底面周长为6π,则6π=n π×6180,∴n =180°.∵AP =3,AB =6,将圆锥展开后∠BAP=90°,∴BP =32+62=3 5.故小猫所经过的最短路线是35米.。
2018中考真题圆综合题
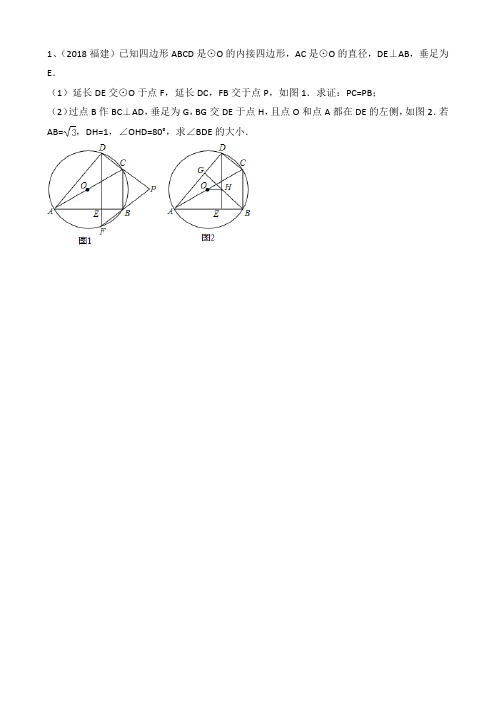
1、(2018福建)已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;(2)过点B作BC⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=,DH=1,∠OHD=80°,求∠BDE的大小.2、(2018广东)如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.(1)证明:OD∥BC;(2)若tan∠ABC=2,证明:DA与⊙O相切;(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.3、(2018深圳)如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB=.(1)求AB的长度;(2)求AD•AE的值;(3)过A点作AH⊥BD,求证:BH=CD+DH.4、(2018桂林)如图1,已知⊙O是△ADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.(1)求证:AC=BC;(2)如图2,在图1的基础上做⊙O的直径CF交AB于点E,连接AF,过点A做⊙O的切线AH,若AH∥BC,求∠ACF的度数;(3)在(2)的条件下,若△ABD的面积为,△ABD与△ABC的面积比为2:9,求CD 的长.5、(2018贵阳)如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.6、(2018哈尔滨)已知:⊙O是正方形ABCD的外接圆,点E在上,连接BE、DE,点F在上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.(1)如图1,求证:∠CBE=∠DHG;(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER 的面积与△DHK的面积的差为,求线段BR的长.7、(2018大庆)如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC ⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.(1)求证:AC平分∠FAB;(2)求证:BC2=CE•CP;(3)当AB=4且=时,求劣弧的长度.8、(2018恩施州)如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P 点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE 交CD于F点.(1)求证:DE为⊙O切线;(2)若⊙O的半径为3,sin∠ADP=,求AD;(3)请猜想PF与FD的数量关系,并加以证明.9、(2018荆门)如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.(1)求证:AC平分∠DAE;(2)若cosM=,BE=1,①求⊙O的半径;②求FN的长.10、(2018十堰)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.(1)求证:FG是⊙O的切线;(2)若tanC=2,求的值.11、(2018常德)如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.(1)求证:EA是⊙O的切线;(2)求证:BD=CF.12、(2018湘潭)如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.(1)若半圆的半径为10.①当∠AOM=60°时,求DM的长;②当AM=12时,求DM的长.(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.13、(2018株州)如图,已知AB为的直径,,点C和点D是上关于直线AB对称的两个点,连接OC、AC,且,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且.求证:直线CG为的切线;若点H为线段OB上一点,连接CH,满足,∽;求的最大值.14、(2018淮安)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.(1)试判断直线DE与⊙O的位置关系,并说明理由;(2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.15、(2018南通)如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;(2)若的长为π,求“回旋角”∠CPD的度数;(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13,直接写出AP的长.16、(2018年江苏省南京市)如图,在正方形ABCD中,E是AB上一点,连接DE.过点A 作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.(1)求证:△AFG∽△DFC;(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.17、(2018年江苏省南京市)结果如此巧合!下面是小颖对一道题目的解答.题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?请你帮她完成下面的探索.已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.可以一般化吗?(1)若∠C=90°,求证:△ABC的面积等于mn.倒过来思考呢?(2)若AC•BC=2mn,求证∠C=90°.改变一下条件……(3)若∠C=60°,用m、n表示△ABC的面积.,18、(2018大连)如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.(1)求证:DE是⊙O的切线;(2)若AC∥DE,当AB=8,CE=2时,求AC的长.19、(2018通辽)如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△ABD∽△DCP;(3)当AB=5cm,AC=12cm时,求线段PC的长.20、(2018陕西)问题提出问题提出 (1)如图①,在△ABC 中,∠A =120°,AB =AC =5,则△ABC 的外接圆半径R 的值为 . 问题探究(2)如图②,⊙O 的半径为13,弦AB =24,M 是AB 的中点,P 是⊙O 上一动点,求PM 的最大值.问题解决(3)如图③所示,AB 、AC 、BC 是某新区的三条规划路其中,AB =6km ,AC =3km ,∠BAC =60°,BC 所对的圆心角为60°.新区管委会想在BC 路边建物资总站点P ,在AB 、AC 路边分别建物资分站点E 、F .也就是,分别在BC 线段AB 和AC 上选取点P 、E 、F .由于总站工作人员每天要将物资在各物资站点间按P →E →F →P 的路径进行运输,因此,要在各物资站点之间规划道路PE 、EF 和FP .为了快捷环保和节约成本要使得线段PE 、EF 、FP 之和最短,试求PE +EF +FP 的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).C B ABA M O PA图① 图② 图③21、(2018陕西)如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 上的中线CD 为直径作⊙O ,分别与AC 、BC 相交于点M 、N .(1)过点N 作⊙O 的切线NE 与AB 相交于点E ,求证:NE ⊥AB ;(2)连接MD ,求证:MD =NB . E N M OD A BC22(2018上海)已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.(1)如图1,如果AC=BD,求弦AC的长;(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.23、(2018杭州)如图,在ABC ∆中,︒=∠90ACB ,以点B 为圆心,BC 的长为半径画弧,交线段AB 于点D,以点A 为圆心,AD 长为半径画弧,交线段AC 于点E ,连结CD(1)若︒=∠28A ,求ACD ∠的度数;(2)设b AC a BC ==,①线段AD 的长度是方程0222=-+b ax x 的一个根吗?说明理由。
2018年中考数学圆综合题

2017年初三圆综合题1.如图,△ABC 中,以BC 为直径的圆交AB 于点D ,∠ACD =∠ABC .(1)求证:CA 是圆的切线;(2)若点E 是BC 上一点,已知BE =6,tan ∠ABC =32,tan ∠AEC =35,求圆的直径.2如图,已知AB 是⊙O 的弦,OB =2,∠B=30°,C 是弦AB 上的任意一点(不与点A 、B 重合),连接CO 并延长CO 交于⊙O 于点D ,连接AD .(1)弦长AB 等于 ▲ (结果保留根号); (2)当∠D=20°时,求∠BOD 的度数;(3)当AC 的长度为多少时,以A 、C 、D 为顶点的三角形与以B 、C 、O 为顶点的三角形相似?请写出解答过程.3. 如图右,已知直线PA 交⊙0于A 、B 两点,AE 是⊙0的直径.点C 为⊙0上一点,且AC 平分∠PAE,过C 作CD⊥PA,垂足为D 。
(1)求证:CD 为⊙0的切线;(2)若DC+DA=6,⊙0的直径为l0,求AB 的长度.4.(已知四边形ABCD 是边长为4的正方形,以AB 为直径在正方形内作半圆,P 是半圆上的动点(不与点A 、B 重合),连接PA 、PB 、PC 、PD . (1)如图①,当PA 的长度等于 ▲ 时,∠PAB=60°;当PA 的长度等于 ▲ 时,△PAD 是等腰三角形;(2)如图②,以AB 边所在直线为x 轴、AD 边所在直线为y 轴,建立如图所示的直角坐标系(点A 即为原点O ),把△PAD、△PAB、△PBC 的面积分别记为S 1、S 2、S 3.坐标为(a ,b ),试求2 S 1 S 3-S 22的最大值,并求出此时a ,b 的值.6.(11金华)如图,射线PG 平分∠EPF ,O 为射线PG 上一点,以O 为圆心,10为半径作⊙O ,分别与∠EPF 的两边相交于A 、B 和C 、D ,连结OA ,此时有OA//PE . (1)求证:AP =AO ;(2)若tan∠OPB =12,求弦AB 的长;四边形,则能构成菱形的四个点为,能构成等腰梯形的四个点为或或 . 7.(芜湖市)如图,BD是⊙O的直径,OA⊥OB,M是劣弧AB⌒上一点,过点M点作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.(1)求证:PM=PN;(2)若BD=4,PA=32AO,过点B作BC∥MP交⊙O于C点,求BC的长.8.(黄冈市)(6分)如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB·AE,求证:DE是⊙O的切线.9.(义乌市)如图,以线段AB 为直径的⊙O 交线段AC 于点E ,点M是AE 的中点,OM 交AC 于点D ,60BOE ∠=°,1cos 2C =,BC = (1)求A ∠的度数;(2)求证:BC 是⊙O 的切线; (3)求MD 的长度.10. (兰州市2017)(本题满分10分)如图,已知AB 是⊙O 的直径,点C 在⊙O 上,过点C 的直线与AB 的延长线交于点P ,AC=PC ,∠COB=2∠PCB. (1)求证:PC 是⊙O的切线; (2)求证:BC=21AB ;(3)点M 是弧AB 的中点,CM 交AB 于点N ,若AB=4,求MN·MC 的值.11.(本题满分14分)如图(1),两半径为r 的等圆1O 和2O 相交于M N ,两点,且2O 过点1O .过M 点作直线AB 垂直于MN ,分别交1O 和2O 于A B ,两点,连结NA NB ,. (1)猜想点2O 与1O 有什么位置关系,并给出证明; (2)猜想NAB △的形状,并给出证明;(3)如图(2),若过M 的点所在的直线AB 不垂直于MN ,且点A B ,在点M 的两侧,那么(2)中的结论是否成立,若成立请给出证明.12.如图12,已知:边长为1的圆内接正方形ABCD 中,P 为边CD 的中点,直线AP 交圆于E 点. (1)求弦DE 的长.(2)若Q 是线段BC 上一动点,当BQ 长为何值时,三角形ADP 与以Q C P ,,为顶点的三角形相似.13..(本小题满分10分)如图,⊙O 是Rt△ABC 的外接圆,AB 为直径,∠ABC =30°,CD 是⊙O 的切线,ED ⊥AB 于F , (1)判断△DCE 的形状;(2)设⊙O 的半径为1,且OF =213-,求证△DCE ≌△OCB .15、 ⊙O 的半径OD 经过弦AB (不是直径)的中点C ,过AB 的延长线上一点P 作⊙O 的切线PE ,E 为切点,PE ∥OD ;延长直径AG 交PE 于点H ;直线DG 交OE 于点F ,交PE 于点K .(1)求证:四边形OCPE 是矩形;(2)求证:HK =HG ; (3)若EF =2,FO =1,求KE 的长.14(2017湖北襄樊24题)如图,直线AB 经过O 上的点C ,并且OA OB =,CA CB =,O 交直线OB 于E D ,,连接EC CD ,.(1)求证:直线AB 是O 的切线;(2)试猜想BC BD BE ,,三者之间的等量关系,并加以证明; (3)若1tan 2CED ∠=,O 的半径为3,求OA 的长16、如图,直角坐标系中,已知两点O(0,0) A(2,0),点B 在第一象限且△OAB 为正三角形,△OAB 的外接圆交y 轴的正半轴于点C ,过点C 的圆的切线交X 轴于点D . (1)求B C ,两点的坐标;(2)求直线CD 的函数解析式;(3)设E F ,分别是线段AB AD ,上的两个动点,且EF 平分四边形ABCD 的周长. 试探究:AEF △的最大面积?17、如图,在平面直角坐标系中,ABC △的边AB 在x 轴上,且OA OB >,以AB 为直径的圆过点C .若点C 的坐标为(02),,5AB =,A 、B 两点的横坐标A x ,B x 是关于x 的方程2(2)10x m x n -++-=的两根.(1)求m 、n 的值;(2)若ACB ∠平分线所在的直线l 交x 轴于点D ,试求直线l 对应的一次函数解析式; (3)过点D 任作一直线l '分别交射线CA 、CB (点C 除外)于点M 、N .则11CM CN+的是否为定值?若是,求出该定值;若不是,请说明理由.18、如图,在ABC △中90ACB ∠=,D 是AB 的中点,以DC 为直径的O 交ABC △的三边,交点分别是G F E ,,点.GE CD ,的交点为M ,且ME =:2:5MD CO =. (1)求证:GEF A ∠=∠. (2)求O 的直径CD 的长.。
2018年中考数学圆的综合题试题

圆的综合题1.如图,AB是⊙O的弦,AB=4,过圆心O的直线垂直AB于点D,交⊙O于点C和点E,连接AC、BC、OB,cos∠ACB=13,延长OE到点F,使EF=2OE.(1)求证:∠BOE=∠ACB;(2)求⊙O的半径;(3)求证:BF是⊙O的切线.2. 如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且AD DE,过点D作DF⊥BC于点F,连接BD、DE、AE.(1)求证:DF是⊙O的切线;(2)试判断△DEC的形状,并说明理由;(3)若⊙O的半径为5,AC=12,求sin∠EAB的值.3. (2016长沙9分)如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=25DE,求tan∠ABD的值.4. (2016德州10分)如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC 于点D,过点E作直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.5. (2015永州)如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.(1)求证:BE=CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.6 (2017原创)如图,AB切⊙O于点B,AD交⊙O于点C 和点D,点E为DC的中点,连接OE交CD于点F,连接BE交CD于点G.(1) 求证:AB =AG ;(2) (2)若DG =DE ,求证:GB 2=GC ·GA ;(3)在(2)的条件下,若tan D =34,EG =10,求⊙O 的半径.7.(2015达州)在△ABC 的外接圆⊙O 中,△ABC 的外角平分线CD 交⊙O 于点D ,F 为AD 上一点,且AF BC ,连接DF ,并延长DF 交BA 的延长线于点E . (1)判断DB 与DA 的数量关系,并说明理由;(2)求证:△BCD ≌△AFD ;(3)若∠ACM =120°,⊙O 的半径为5,DC =6,求DE 的长.8. 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为点D.(1)求证:△ACD∽△ABC;(2)求证:∠PCA=∠ABC;(3)过点A作AE∥PC交⊙O于点E,交CG于点F,连接BE,若sin P=35,CF=5,求BE的长.9、(2016大庆9分)如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB 于点M,若H是AC的中点,连接MH。
2018年人教版中考数学6.3与圆有关的计算-复习课件+检测试卷含真题分类汇编解析
回归教材
考点聚焦
考向探究
第29课时┃与圆有关的计算
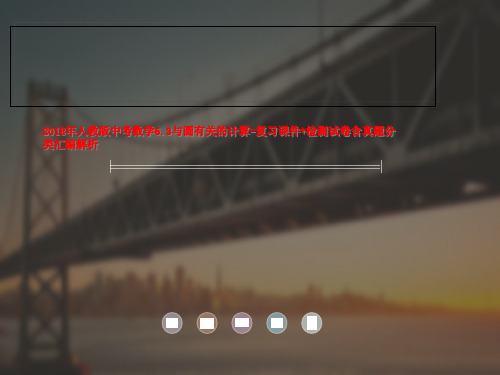
|针对训练| 1.【2017·台州】如图 29-4,扇形纸扇完全打开后,外侧 两竹条 AB,AC 的夹角为 120°,AB 长为 30 厘米,则B︵C的长 为___2_0_π___厘米.(结果保留π)
解析
图 29-4
B︵C的长=120·1π80·30=20π(厘米).
如图③,∵OA=2,∴OF=2×cos30°= 3,
则该三角形的三边分别为:1, 2, 3.
∵12+( 2)2=( 3)2,∴该三角形是直角三角形,
∴该三角形的面积是12×1× 2= 22,故选 A.
回归教材
考点聚焦
考向探究
第29课时┃与圆有关的计算
方法模型
(1)正 n 边形的半径 R、边心距 r 和边长的一半构成直角三 角形.在正 n 边形中,共有 2n 个这样的直角三角形;(2)在正 n 边形中,构造直角三角形或特殊的三角形是常用方法.
回归教材
考点聚焦
考向探究
第29课时┃与圆有关的计算
考点4 圆锥的侧面积与全面积
图形
(1)h 是圆锥的高;
(2)a 是圆锥的母线,其长为侧面展开后所得扇形的
圆锥简介
__半__径____; (3)r 是底面圆半径;
(4)圆锥的侧面展开图是半径等于__母__线____长,弧
长等于圆锥底面__周__长____的扇形
A.60π cm2 B.65π cm2 C.120π cm2 D.130π cm2
回归教材
图 29-7
考点聚焦
考向探究
第29课时┃与圆有关的计算
解析
AB= BC2+AC2= 122+52=13(cm).这个几何 体是圆锥,圆锥的底面半径 AC=5 cm,母线 AB=13 cm,圆锥的侧面积=πAC·AB=π×5×13=65π (cm2).故选 B.
2018年中考数学总复习圆试题

2018年中考数学总复习圆试题D∠ABC=60°,∠ACB=40°,则∠BOC=(A)A.130°B.135°C.120°D.150°二、填空题(每小题5分,共20分)11.如图,☉O的两条弦AB,CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则☉O的半径是.(第11题图)(第12题图)12.如图,AB是☉O的直径,OA=1,AC是☉O的弦,过点C的切线交AB的延长线于点 D.若BD=-1,则∠ACD=112.5°.13.如下图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是.14.如图,从☉O外的两点C和D分别引圆的两线DA,DC,CB,切点分别为点A、点E和点B,AB是☉O的直径,连接OC,连接OD交CB延长线于F,给出如下结论:①AD+BC=CD;②OD2=DE·CD;③OD=OC;④CD=CF.其中正确的是①②④.(把所有正确结论序号都填在横线上)三、解答题(共70分)15.(6分)如图,PA,PB是☉O的两条切线,A,B分别是切点,点C是上任意一点,连接OA,OB,CA,CB,∠P=70°,求∠ACB的度数.解∵PA,PB是☉O的切线,OA,OB是半径,∴∠PAO=∠PBO=90°.又∵∠PAO+∠PBO+∠AOB+∠P=360°,∠P=70°,∴∠AOB=110°.∵∠AOB是圆心角,∠ACB是圆周角,∴∠ACB=55°.16.(6分)已知在以点O为圆心的两个同心圆中,大圆的弦AB 交小圆于点C,D(如图所示).(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.(1)证明过点O作OE⊥AB于点E,则CE=DE,AE=BE.∴AE-CE=BE-DE,即AC=BD.(2)解由(1)可知,OE⊥AB且OE⊥CD,∴CE===2.AE===8.∴AC=AE-CE=8-2.〚导学号92034207〛17.(6分)已知A,B,C,D是☉O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求☉O的半径.图1图2(1)证明∵∠ADC=∠BCD=90°,∴AC,BD是☉O的直径,且交点为圆心O.∵AD=CD,AO=CO,∴AC⊥BD.(2)解如图,画直径CK,连接DK,BC,则∠KDC=90°,∴∠K+∠KCD=90°.∵AC⊥BD,∴∠ACB+∠EBC=90°.∵∠EBC=∠K,∴∠ACB=∠KCD,∴=,∴DK=AB=2.∵DC=4,∴KC==2,∴☉O的半径为.〚导学号92034208〛18.(6分)如图,O是△ABC的内心,BO的延长线和△ABC 的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC 为平行四边形.(1)求证:△BOC≌△CDA:(2)若AB=2,求阴影部分的面积.(1)证明∵O为△ABC的内心,∴∠2=∠3,∠5=∠6.∵∠1=∠2,∴∠1=∠3,由AD∥CO,AD=CO,∴∠4=∠5,∴∠4=∠6,∴△BOC≌△CDA.(2)解由(1)得BC=AC,∠3=∠4=∠6,∴∠ABC=∠ACB,∴AB=AC,△AB C为等边三角形,∴O为△ABC的内外心,∴OA=OB=OC.设E为BD与AC的交点,BE垂直平分AC.在Rt△O CE 中,CE=AB=1,∠OCE=30°,∴OA=OB=OC=,∵∠AOB=120°,∴S阴=S扇形AOB-S△AOB=-×2×=.19.(8分)如图,在边长为1的正方形网格中,△ABC 的顶点均在格点上,点A,B的坐标分别是A(4,3),B(4,1),把△ABC绕点C逆时针旋转90°后得到△A 1B1C.(1)画出△A1B1C,直接写出点A1,B1的坐标;(2)求在旋转过程中,△ABC所扫过的面积.解(1)所求作△A1B1C如图所示:由A(4,3),B(4,1)可建立如图所示坐标系,则点A1的坐标为(-1,4),点B1的坐标为(1,4);(2)∵AC===,∠ACA1=90°,∴在旋转过程中,△ABC所扫过的面积为+S△ABC=+×3×2=+3.20.(10分)已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB 于点E.(1)求证:AC·AD=AB·AE;(2)如果BD是☉O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.(1)证明连接DE.∵AE是直径,∴∠ADE=90°,∴∠ADE=∠ABC.在Rt△ADE和Rt△ABC中,∠A是公共角,故△ADE∽△ABC,则=,即AC·AD=AB·AE.(2)解连接OD.∵BD是圆O的切线,∴OD⊥BD.在Rt△OBD中,OE=BE=OD,∴OB=2OD,∴∠OBD=30°.同理∠BAC=30°.在Rt△ABC中,AC=2BC=2×2=4.〚导学号92034209〛21.(8分)如图,AB为☉O的直径,F为弦AC的中点,连接OF并延长交于点D,过点D作☉O的切线,交BA的延长线于点E.(1)求证:AC∥DE;(2)连接CD,若OA=AE=a,求四边形ACDE的面积.(1)证明∵ED与☉O相切于D,∴OD⊥DE.∵F为弦AC 中点,∴OD⊥AC,∴AC∥DE.(2)解作DM⊥OA于M,连接CD,CO,AD.∵AC∥DE,AE=AO,∴OF=DF.∵AF⊥DO,∴AD=AO,∴AD=AO=OD,∴△ADO是等边三角形,同理△CDO也是等边三角形,∴∠CDO=∠DOA=60°,AE=CD=AD=AO=CO=a,∴AO ∥CD,又AE=CD,∴四边形ACDE是平行四边形,易知DM=a,∴平行四边形ACDE面积为a2.22.(10分)已知:如图,☉O是△ABC的外接圆,=,点D 在边BC上,AE∥BC,AE=BD.(1)求证:AD=CE;(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.(1)证明在☉O 中,∵=,∴AB=AC,∴∠B=∠ACB.∵AE∥BC,∴∠EA C=∠ACB,∴∠B=∠EAC.在△ABD和△CAE 中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE.(2)解连接AO并延长,交边BC于点H,∵=,OA为半径,∴AH⊥BC,∴BH=CH.∵AD=AG,∴DH=HG,∴BH-DH= CH-GH,即BD=CG.∵BD=AE,∴CG=AE.∵CG∥AE,∴四边形AGCE是平行四边形.23.(10分)如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.(1)求证:∠ACD=∠B.(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;①求tan∠CFE的值;②若AC=3,BC=4,求CE的长.图1图2(1)证明如图中,连接OC.∵OA=OC,∴∠1=∠2.∵CD是☉O切线,∴OC⊥CD,∴∠DCO=90°,∴∠3+∠2=90°.∵AB是直径,∴∠1+∠B=90°,∴∠3=∠B.∴∠ACD=∠B.(2)解①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,∴∠CEF=∠CFE,∵∠ECF=90°,∴∠CEF=∠CFE=45°,∴tan∠CFE=tan 45°=1.②在Rt△ABC中,∵AC=3,BC=4,∴AB==5.∵∠CDA=∠BDC,∠DCA=∠B,∴△DCA∽△DBC,∴===.∵∠CDE=∠BDF,∠DCE=∠B,∴△DCE∽△DBF,∴=.设EC=CF=x,∴=,∴x=.∴CE=.。
武汉市2018年中考数学21题圆的有关证明和计算4
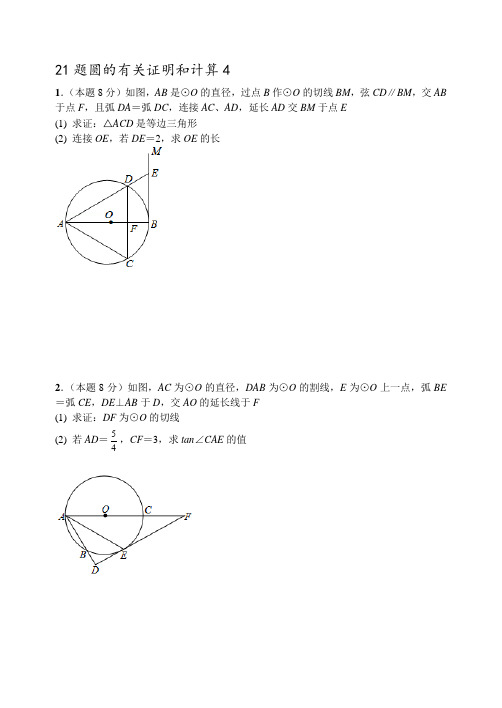
4. (本题 8 分)如图,在正方形 ABCD 中,以 BC 为直径的正方形内,作半圆 O,AE 切 半圆于点 F 交 CD 于 E (1) 求证:AO⊥EO (2) 连接 DF,求 tan∠FDE 的值
21 题圆的有关证明和计算 4
1. (本题 8 分)如图,AB 是⊙O 的直径,过点 B 作⊙O 的切线 BM,弦 CD∥BM,交 AB 于点 F,且弧 DA=弧 DC,连接 AC、AD,延长 AD 交 BM 于点 E (1) 求证:△ACD 是等边三角形 (2) 连接 OE,若 DE=2,求 OE 的长
ቤተ መጻሕፍቲ ባይዱ
2. (本题 8 分)如图,AC 为⊙O 的直径,DAB 为⊙O 的割线,E 为⊙O 上一点,弧 BE =弧 CE,DE⊥AB 于 D,交 AO 的延长线于 F (1) 求证:DF 为⊙O 的切线 (2) 若 AD=
5 ,CF=3,求 tan∠CAE 的值 4
3. (本题 8 分)如图,BC 为⊙O 的直径,AB 为⊙O 的弦,D 为弧 BC 的中点,CE⊥AD 于 E,AD 交 BC 于点 F,tanB= (1) 求证:DE=2AE (2) 求 sin∠BFD 的值
武汉市2018年中考数学21题圆的有关证明和计算2
21题圆的有关证明和计算2
1、如图,四边形ABCD 内接于⊙O ,对角线AC 为⊙O 的直径,过点C 作AC 的垂线交AD 的延长线于点E ,点F 为CE 的中点,连接DB ,DC ,DF.
(1)求∠CDE 的度数;
(2)求证:DF 是⊙O 的切线;
(3)若AC =25DE ,求tan ∠ABD 的值.
2、如图,AB 是⊙O 的直径,弦CD ⊥AB 于点G ,点F 是CD 上一点,且满足CF FD =1
3
,
连接AF 并延长⊙O 于点E ,连接AD ,DE ,若CF =2,AF =3.
(1)求证:△ADF ∽△AED ; (2)求FG 的长; (3)求tan E 的值.
A
C
E F
3、如图,AB 为⊙O 的直径,点C 为弧AB 上一点,弦CD 交AB ①若点C 为弧AB 的中点,4
5
DE CE =,求tanB 的值.
②在①中,若E 是OB 的中点,连AC ,求tan ∠ACD 的值.
③如图,DC =DB ,若5
8
DE CE =,求tan ∠CDB 的值.
4、等腰直角△AOB ,F 是以OA 为半径的⊙O 上一点.
(1) FC ⊥AB 于C , 若∠BCF =1
2
∠BOF ,求证:CF
为⊙O 的切线;
(2)连BF ,D 在直线BF 上,DC ⊥AB 于C ,交AF 的延长线于E ,若,CE =4,DE =3,求AE 的长.。
2018中考数学圆试题解析

2018中考数学圆试题解析以下是查字典数学网为您推荐的2018中考数学圆试题解析,希望本篇文章对您学习有所帮助。
2018中考数学圆试题解析一、选择题1. (2018江苏常州2分)已知两圆半径分别为7,3,圆心距为4,则这两圆的位置关系为【】A.外离B.内切C.相交D.内含【答案】B。
【考点】两圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
因此,∵两半径之差7-3等于两圆圆心距4,两圆内切。
故选B。
2. (2018江苏淮安3分)如图,AB是⊙O的直径,点C在⊙O 上,若A=400,则B的度数为【】A、800B、600C、500D、400【答案】C。
【考点】圆周角定理,三角形内角和定理。
【分析】根据直径所对圆周角不直角的性质,由AB是⊙O的直径,点C在⊙O上得根据三角形内角和定理,由A=400,得B=1800-900-400=500。
故选C。
3. (2018江苏苏州3分)如图,已知BD是⊙O直径,点A、C 在⊙O上,,AOB=60,则BDC的度数是【】A.20B.25C.30D. 40【答案】C。
【考点】圆周角定理,圆心角、弧、弦的关系。
【分析】利用在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得BDC的度数:∵ ,AOB=60,BDC= AOB=30。
故选C。
4. (2018江苏宿迁3分)若⊙O1,⊙O2的半径是r1=2, r2=4,圆心距d=5,则这两个圆的位置关系是【】A.内切B.相交C.外切D.外离【答案】B。
【考点】两圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
2018全国各地中考数学试题《圆》试题汇编(解答题)

2018全国各地中考数学试题《圆》试题汇编(解答题)2018全国各地中考数学试题《圆》解答题汇编1. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.求证:∠CBP=∠ADB.若OA=2,AB=1,求线段BP的长.2.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O 于点D.已知⊙O的半径为6,∠C=40°.求∠B的度数.求AD的长.3.如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E,点C是BF的中点.求证:AD⊥CD;若∠CAD=30°,⊙O的半径为3,一只蚂蚁从点B出发,沿着BE-EC-CB爬回至点B,求蚂蚁爬过的路程.第 1 页共 27 页4. 如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.求证:OP ⊥CD;连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.5. 如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O 于点F,AC平分∠BAD,连接BF.求证:AD⊥ED;若CD=4,AF=2,求⊙O的半径.6. 如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE 丄AB,交AB的延第 2 页共 27 页长线于点E.求证:CB平分∠ACE;若BE=3,CE=4,求⊙O的半径.7.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB 于点F.求证:BC是⊙O的切线;若⊙O的半径是2cm,E 是AD的中点,求阴影部分的面积8.已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,如图①,若D为AB的中点,求∠ABC和∠ABD的大小;如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,第 3 页共 27 页求∠OCD的大小.9. 如图,D是△ABC外接圆上的动点,且B,D位于AC 的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG ⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.求证:BG∥CD;设△ABC外接圆的圆心为O,若AB=3DH,∠OHD=80°,求∠BDE的大小.10. 如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.求证:AE与⊙O相切于点A;若AE∥BC,BC=27,AC=22,求AD的长.第 4 页共 27 页11.如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC.BC平分∠ABD.求证:CD为⊙O的切线.12.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.求证:DA=DE;若AB=6,CD=43,求图中阴影部分的面积.13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC 于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.求证:DF是⊙O的切线;已知BD=25 第 5 页共27 页25. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.求证:PC是⊙O的切线;若∠ABC=60°,AB=10,求线段CF的长.26. 如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.试判断直线DE与⊙O的位置关系,并说明理;若⊙O的半径为2,∠B=50°,AC=,求图中阴影部分的面积.第 11 页共 27 页27.如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.求证:MD=MC;若⊙O的半径为5,AC=45,求MC的长.27. 如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.判断CM与⊙O的位置关系,并说明理;若∠ECF=2∠A,CM=6,CF=4,求MF的长.第 12 页共 27 页28.如图,在△ABC中,AB=AC,以AB为直径的圆交AC 于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.求证:四边形ABFC是菱形;若AD=7,BE=2,求半圆和菱形ABFC的面积.29.如图,已知A、B、C、D、E是⊙O上五点,⊙O的直径BE=23,∠BCD=120°,A为BE的中点,延长BA到点P,使BA=AP,连接PE.求线段BD的长;求证:直线PE是⊙O的切线.第 13 页共 27 页30.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.求证:EF是⊙O的切线;若AC=4,CE=2,求 BD的长度.31.已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.求扇形OBC的面积;求证:CD是⊙O的切线.32.已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.求证:DF是⊙O的切线;若等边△ABC的边长为8,求第 14 页共 27 页DE、DF、EF围成的阴影部分面积.33.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.求证:AE=ED;若AB=10,∠CBD=36°,求AC的长.34.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.求证:AC是⊙O 的切线;若BD=3,BE=1.求阴影部分的面积.第 15 页共 27 页35.如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.求证:EA是⊙O的切线;求证:BD=CF.36. 如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.若∠ADE=25°,求∠C的度数;若AB=AC,CE=2,求⊙O半径的长.37. 如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,连接OD,过点B作BE∥OD交⊙O于点E,连接DE并延长交BN于点C.求证:DE是⊙O的切线;第 16 页共 27 页若AD=l,BC=4,求直径AB的长.38. 如图所示,PB是⊙O的切线,B为切点,圆心O在PC上,∠P=30°,D为弧BC的中点.求证:PB=BC;试判断四边形BOCD的形状,并说明理.39. 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.40. 如图,AB是⊙O的直径,弦CD⊥AB于点E,过点C 的切线交AB的延长线于点F,连接DF.求证:DF是⊙O的切线;连接BC,若∠BCF=30°,BF=2,求CD的长.第 17 页共 27 页41. 已知,如图AB是⊙O的直径,点P在BA的延长线上,弦BC平分∠PBD,且BD⊥PD于点D.求证:PD是⊙O 的切线.若AB=8cm,BD=6cm,求CD的长.42. 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC 是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.求证:CF是⊙O的切线;若∠F=30°,EB=8,求图中阴影部分的面积.43.如图,已知△ABC内接于⊙O,AB是直径,OD∥AC, AD=OC.求证:四边形OCAD是平行四边形;第 18 页共 27 页探究:①当∠B= °时,四边形OCAD是菱形;②当∠B满足什么条件时,AD与⊙O相切?请说明理.43. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.若∠AOD=52°,求∠DEB的度数;若OC=3,OA=5,求AB的长.44.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.求证:AB=CD;如果⊙O的半径为5,DE=1,求AE的长.第 19 页共 27 页45.如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD. AB,BD,AD围成的阴影部分的面积是;求线段DE的长.46.如图,在△ABC中,AB=AC,O为边AC上一点,以OC 为半径的圆分别交边BC,AC于点D,E,过点D作DF⊥AB于点F.求证:直线DF是⊙O的切线;若∠A=45°,OC=2,求劣弧DE的长.第 20 页共 27 页2018全国各地中考数学试题《圆》解答题汇编1. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.求证:∠CBP=∠ADB.若OA=2,AB=1,求线段BP的长.2.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O 于点D.已知⊙O的半径为6,∠C=40°.求∠B的度数.求AD的长.3.如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E,点C是BF的中点.求证:AD⊥CD;若∠CAD=30°,⊙O的半径为3,一只蚂蚁从点B出发,沿着BE-EC-CB爬回至点B,求蚂蚁爬过的路程.第 1 页共 27 页4. 如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.求证:OP ⊥CD;连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.5. 如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O 于点F,AC平分∠BAD,连接BF.求证:AD⊥ED;若CD=4,AF=2,求⊙O的半径.6. 如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE 丄AB,交AB的延第 2 页共 27 页长线于点E.求证:CB平分∠ACE;若BE=3,CE=4,求⊙O的半径.7.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB 于点F.求证:BC是⊙O的切线;若⊙O的半径是2cm,E是AD的中点,求阴影部分的面积8.已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,如图①,若D为AB的中点,求∠ABC和∠ABD的大小;如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,第 3 页共 27 页求∠OCD的大小.9. 如图,D是△ABC外接圆上的动点,且B,D位于AC 的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG ⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.求证:BG∥CD;设△ABC外接圆的圆心为O,若AB=3DH,∠OHD=80°,求∠BDE的大小.10. 如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.求证:AE与⊙O相切于点A;若AE∥BC,BC=27,AC=22,求AD的长.第 4 页共 27 页11.如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC.BC平分∠ABD.求证:CD为⊙O的切线.12.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.求证:DA=DE;若AB=6,CD=43,求图中阴影部分的面积.13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC 于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.求证:DF是⊙O的切线;已知BD=25 第 5 页共27 页。
2018中考圆解答题集合(完整答案)

2018中考圆解答题集合(完整答案)一.解答题(共35小题)1.如图,▱ABCD中,⊙O过点A、C、D,交BC于E,连接AE,∠BAE=∠ACE.(1)求证:AE=CD;(2)求证:直线AB是⊙O的切线.2.如图,PA、PB分别切⊙O于点A、B,M为劣弧AB上一点(不与A、B重合)过点M的切线分别与PA、PB相交于点C、D,Q为优弧AB上一点(不与A、B重合).(1)若PA=10,求△PCD的周长;(2)若∠P=40°,求∠AQB的度数.3.如图,⊙O的弦AB、CD相交于点E,点C为弧AB的中点,过点D作⊙O的切线交AB的延长线于点F.(1)求证:DF=EF;(2)连接AC,若AC∥DF,BE=AE,CE=,求⊙O的半径.4.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB 于点E,且交AC于点P,连结AD.(1)求证:∠DAC=∠DBA;(2)求证:PD=PF;(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.5.如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE,连接OC.(1)求证:DE是⊙O的切线;(2)若⊙O半径为4,∠D=30°,求图中阴影部分的面积(结果用含π和根号的式子表示).6.如图,点O是△ABC的边AB上一点,以OB为半径的⊙O交BC于点D,过点D的切线交AC于点E,且DE⊥AC.(1)证明:AB=AC;(2)设AB=cm,BC=2cm,当点O在AB上移动到使⊙O与边AC所在直线相切时,求⊙O的半径.7.如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.(1)求证:CD是⊙O的切线.(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.8.如图,已知直线PT与⊙O相交于点T,直线PO与⊙O相交于A,B两点.已知∠PTA=∠B.(1)求证:PT是⊙O的切线;(2)若PT=6,PA=4,求⊙O的半径;(3)若PT=TB=,求图中阴影部分的面积.9.如图,AB是⊙O直径,C是半圆上一点,连接BC、AC,过点O作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)求证:DE是⊙O的切线;(2)若AE=3,CE=,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).10.如图,圆O是△ABC的外接圆,AE平分∠BAC交圆O于点E,交BC于点D,过点E作直线l∥BC.(1)判断直线l与圆O的关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=5,DF=3,求AF的长.11.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED.(1)求证:ED=EC;(2)若CD=3,EC=2,求AB的长.12.如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.(1)求证:DC是⊙O的切线;(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.13.如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.(1)求证:DC是⊙O切线;(2)若AO=6,DC=3,求DE的长;(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3,求图中阴影部分面积.14.如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.(1)求证:AB是⊙O的切线;(2)若AB=4cm,AD=2cm,求CD的长.15.如图AB为⊙O的直径,C为⊙O上半圆的一个动点,CE⊥AB于点E,∠OCE的角平分线交⊙O于D 点.(1)当C点在⊙O上半圆移动时,D点位置会变吗?请说明理由;(2)若⊙O的半径为5,弦AC的长为6,连接AD,求线段AD、CD的长.16.在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF(1)求证:BF是⊙A的切线.(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.17.如图,PC是⊙O的弦,作OB⊥PC于点E,交⊙O于点B,延长OB到点A,连接AC,OP,使∠A=∠P.(1)求证:AC是⊙O的切线;(2)若BE=2,PC=4,求AC的长.18.如图,AB为⊙O的直径,P在BA的延长线上,C为圆上一点,且∠PCA=∠B.(1)求证:PC与⊙O相切;(2)若PA=4,⊙O的半径为6,求BC的长.19.如图,AB是⊙O的直径,AC平分∠DAB交⊙O于点C,过点C的直线垂直于AD交AB的延长线于点P,弦CE交AB于点F,连接BE.(1)求证:PD是⊙O的切线;(2)若PC=PF,试证明CE平分∠ACB.20.如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明:(1)BD=DC;(2)DE是⊙O切线.21.如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),D为⊙C在第一象限内的一点且∠ODB=60°.求:(1)求线段AB的长及⊙C的半径;(2)求B点坐标及圆心C的坐标.22.如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;(3)求证:CD=HF.23.如图,已知AB是⊙O的直径,点C,D在⊙O上,BC=6cm,AC=8cm,∠BAD=45°.点E在⊙O外,做直线AE,且∠EAC=∠D.(1)求证:直线AE是⊙O的切线.(2)求图中阴影部分的面积.24.已知AB是⊙O的直径,点P是AB延长线上的一点.(I)如图1,过P作⊙O的切线PC,切点为C.作AD⊥PC于点D,求证:∠PAC=∠DAC;(II)如图2,过P作⊙O的割线,交点为M、N,作AD⊥PN于点D,求证:∠PAM=∠DAN.25.如图,△ABC内接于⊙O,且∠B=60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.(1)求证:△ACF≌△ACG;(2)若AF=4,求图中阴影部分的面积.26.如图1,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60度.(1)求∠AOC的度数;(2)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;=S△CAO时,求动点M所经过(3)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO的弧长.27.已知扇形的圆心角为120°,面积为300πcm2.(1)求扇形的弧长;(2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少?28.圆锥的底面半径是1,母线长是4,求它的侧面展开图的圆心角的度数.29.扇形的圆心角为90°,面积为16π.(1)求扇形的弧长.(2)若将此扇形卷成一个无底圆锥形筒,则这个圆锥形筒的高是多少?30.如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于F,∠A=30°.(1)求⊙O的半径;(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.31.如图,AB是⊙O的直径,CD是⊙O的弦,且CD⊥AB于点E.(1)求证:∠BCO=∠D;(2)若CD=2,AE=1,求劣弧BD的长.32.如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求弧BC的长;(2)求弦BD的长.33.如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.(1)由AB,BD,围成的阴影部分的面积是;(2)求线段DE的长.34.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).35.如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.(1)求点O到AB的距离;(2)求阴影部分的面积.2018中考圆解答题集合(完整答案)参考答案与试题解析一.解答题(共35小题)1.如图,▱ABCD中,⊙O过点A、C、D,交BC于E,连接AE,∠BAE=∠ACE.(1)求证:AE=CD;(2)求证:直线AB是⊙O的切线.【解答】解:(1)∵四边形ABCD是平行四边形∴AB=CD,∠B=∠ADC∵四边形ADCE是⊙O内接四边形∴∠ADC+∠AEC=180°∵∠AEC+∠AEB=180°∴∠ADC=∠AEB∴∠B=∠AEB∴AE=CD(2)如图:连接AO,并延长AO交⊙O交于点F,连接EF.∵AF是直径∴∠AEF=90°∴∠AFE+∠EAF=90°∵∠BAE=∠ECA,∠AFE=∠ACE∴∠AFE=∠BAE∴∠BAE+∠EAF=90°∴∠BAF=90°且AO是半径∴直线AB是⊙O的切线2.如图,PA、PB分别切⊙O于点A、B,M为劣弧AB上一点(不与A、B重合)过点M的切线分别与PA、PB相交于点C、D,Q为优弧AB上一点(不与A、B重合).(1)若PA=10,求△PCD的周长;(2)若∠P=40°,求∠AQB的度数.【解答】解:(1)∵PA、PB分别切⊙O于点A、B,∴PA=PB=10,∵CD切⊙O于M,∴CA=CM,DB=DM,∵△PCD的周长=PC+CD+PD=PC+CM+PD+DM=PA+PB,∴△PCD的周长=20;(2)连接OA,OB,∵PA、PB分别切⊙O于点A、B,∴∠PAO=∠PBO=90°,∵∠P=40°,∴∠AOB=140°,∴∠AQB=∠AOB=70°.3.如图,⊙O的弦AB、CD相交于点E,点C为弧AB的中点,过点D作⊙O的切线交AB的延长线于点F.(1)求证:DF=EF;(2)连接AC,若AC∥DF,BE=AE,CE=,求⊙O的半径.【解答】解:(1)连接OC,OD,∵C为的中点,∴OC⊥AB,∴∠OCE+∠CEA=∠OCE+∠FED=90°,∵DF是⊙O的切线,∴OD⊥DF,∴∠ODC+∠EDF=90°,∵OC=OD,∴∠OCD=∠ODC,∴∠DEF=∠EDF,∴EF=DF;(2)如图,连接OA、OC;由(1)知OC⊥AB,∴AH=BH;∵AC∥DF,∴∠ACD=∠CDF;而EF=DF,∴∠DEF=∠CDF=∠ACD,∴AC=AE;设AE=5λ,则BE=3λ,∴AH=4λ,HE=λ,AC=AE=5λ;∴由勾股定理得:CH=3λ;CE2=CH2+HE2=9λ2+λ2,∴CE=λ=;∴λ=1,∴AH=4,CH=3,∴OH=AO﹣3,在直角△AOH中,由勾股定理得:AO2=AH2+OH2,∴AO2=42+(AO﹣3)2,∴AO=,∴⊙O的半径为:.4.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB 于点E,且交AC于点P,连结AD.(1)求证:∠DAC=∠DBA;(2)求证:PD=PF;(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.【解答】(1)证明:∵BD平分∠CBA,∴∠CBD=∠DBA,∵∠DAC与∠CBD都是弧CD所对的圆周角,∴∠DAC=∠CBD,∴∠DAC=∠DBA,∵AB是⊙O的直径,DE⊥AB,∴∠ADB=∠AED=90°,∴∠ADE+∠DAE=90°,∠DBA+∠DAE=90°,∴∠ADE=∠DBA,∴∠DAC=∠ADE,∴∠DAC=∠DBA;(2)证明:∵AB为直径,∴∠ADB=90°,∵DE⊥AB于E,∴∠DEB=90°,∴∠ADE+∠EDB=∠DFA+∠DAC=90°,又∵∠ADE=∠DAP,∴∠PDF=∠PFD,∴PD=PF;(3)解:连接CD,∵∠CBD=∠DBA,∴CD=AD,∵CD﹦3,∴AD=3,∵∠ADB=90°,∴AB=5,故⊙O的半径为2.5,∵DE×AB=AD×BD,∴5DE=3×4,∴DE=2.4.即DE的长为2.4.5.如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE,连接OC.(1)求证:DE是⊙O的切线;(2)若⊙O半径为4,∠D=30°,求图中阴影部分的面积(结果用含π和根号的式子表示).【解答】(1)证明:∵OA=OC∴∠OAC=∠OCA∵AC平分∠BAE∴∠OAC=∠CAE∴∠OCA=∠CAE∴OC∥AE∴∠OCD=∠E∵AE⊥DE∴∠E=90°=∠OCD即OC⊥CD∴CD是圆O的切线(2)在Rt△ODC中,∵∠D=30°,OC=4∴∠COD=60°,OD=2OC=8∴CD===4∴S阴影=S△OCD﹣S扇形OBC=××4﹣=8﹣π.6.如图,点O是△ABC的边AB上一点,以OB为半径的⊙O交BC于点D,过点D的切线交AC于点E,且DE⊥AC.(1)证明:AB=AC;(2)设AB=cm,BC=2cm,当点O在AB上移动到使⊙O与边AC所在直线相切时,求⊙O的半径.【解答】(1)证明:连接OD.∵DE是⊙O的切线,∵DE⊥OD,∵AC⊥DE,∴OD∥AC,∴∠ODB=∠C,∵OB=OD,∴∠B=∠ODB,∴∠B=∠C,∴AB=AC.(2)设AC与⊙O相切于点F,连接OF,作AH⊥BC于H.设半径为r.∵AB=AC,AH⊥BC,∴BH=CH=1,∴AH==2,∴tan∠C==2,∵∠OFE=∠ODE=∠DEF=90°,∴四边形ODEF是矩形,∵OD=OF,∴四边形ODEF是正方形,∴EF=DE=r,∵tanC==2,∴EC=,∴AF=﹣r﹣r=﹣r,在Rt△AOF中,∵OA2=AF2+OF2,∴(﹣r)2=r2+(﹣r)2,解得r=.7.如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.(1)求证:CD是⊙O的切线.(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.【解答】(1)证明:如图1,连结OC,∵点O为直角三角形斜边AB的中点,∴OC=OA=OB.∴点C在⊙O上,∵BD=OB,∴AB=DO,∵CD=CA,∴∠A=∠D,∴△ACB≌△DCO,∴∠DCO=∠ACB=90°,∴CD是⊙O的切线;(2)解:如图2,在Rt△ABC中,BC=ABsin∠A=2×8×sin30°=8,∵∠ABC=90°﹣∠A=90°﹣30°=60°,∴BE=BCcos60°=8×=4.8.如图,已知直线PT与⊙O相交于点T,直线PO与⊙O相交于A,B两点.已知∠PTA=∠B.(1)求证:PT是⊙O的切线;(2)若PT=6,PA=4,求⊙O的半径;(3)若PT=TB=,求图中阴影部分的面积.【解答】(1)证明:连接OT,∵AB是⊙O的直径,∴∠ATB=90°,∴∠B+∠OAT=90°,∵OA=OT,∴∠OAT=∠2,∵∠PTA=∠B,∴∠PTA+∠2=90°,即∠OTP=90°,∴直线PT与⊙O相切;(2)解:∵∠PTA=∠B,∠P=∠P,∴△PTA∽△PBT,∴,设⊙O的半径为r,∵PT=6,PA=4,∴,解得r=,∴⊙O的半径是;(3)∵TP=TB=,∴∠P=∠B=∠PTA,∵∠TAB=∠P+∠PTA,∴∠TAB=2∠B,∵∠TAB+∠B=90°,∴∠TAB=60°,∠B=30°,在Rt△ABT中,设AT=a,则AB=2AT=2a,∴,解得:a=1,∴AT=1,∵OA=OT,∠TAO=60°,∴△AOT为等边三角形,∴OT=AT=OA=1,∠AOT=60°∴图中阴影部分的面积=S扇形OAT ﹣S△AOT=﹣=﹣.9.如图,AB是⊙O直径,C是半圆上一点,连接BC、AC,过点O作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)求证:DE是⊙O的切线;(2)若AE=3,CE=,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).【解答】解:(1)如图,连接OC,∵AD是过点A的切线,AB是⊙O的直径,∴AD⊥AB,∴∠DAB=90°.∵OD∥BC,∴∠1=∠2,∠3=∠4.∵OC=OB,∴∠2=∠4.∴∠1=∠3.在△COD和△AOD中,∵,∴△COD≌△AOD(SAS)∴∠OCD=∠DAB=90°,即OC⊥DE于点C.∵OC是⊙O的半径,∴DE是⊙O的切线;(2)设AD=x,由△COD≌△AOD知CD=AD=x,在Rt△ADE中,由AD2+AE2=DE2可得x2+32=(+x)2,解得:x=,则AD=、DE=2,∴sin∠E===,∴∠E=30°,∵∠ACE=90°,∴∠COB=60°,设圆的半径为r,在Rt△OCE中,由OC2+CE2=OE2可得r2+()2=(3﹣r)2,解得:r=1,则S=S△COE ﹣S扇形BOC=×1×﹣=﹣.10.如图,圆O是△ABC的外接圆,AE平分∠BAC交圆O于点E,交BC于点D,过点E作直线l∥BC.(1)判断直线l与圆O的关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=5,DF=3,求AF的长.【解答】解:(1)直线l与⊙O相切.理由:如图1所示:连接OE.∵AE平分∠BAC,∴∠BAE=∠CAE.∴=,∴OE⊥BC.∵l∥BC,∴OE⊥l.∴直线l与⊙O相切.(2)∵BF平分∠ABC,∴∠ABF=∠CBF.又∵∠CBE=∠CAE=∠BAE,∴∠CBE+∠CBF=∠BAE+∠ABF.又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB.∴BE=EF.(3)由(2)得BE=EF=DE+DF=8.∵∠DBE=∠BAE,∠DEB=∠BEA,∴△BED∽△AEB.∴=,即=,解得;AE=.∴AF=AE﹣EF=﹣8=.11.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED.(1)求证:ED=EC;(2)若CD=3,EC=2,求AB的长.【解答】解:(1)∵∠EDC+∠EDA=180°、∠B+∠EDA=180°,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠EDC=∠C,∴ED=EC;(2)连接AE,∵AB是直径,∴AE⊥BC,又∵AB=AC,∴BC=2EC=4,∵∠B=∠EDC、∠C=∠C,∴△ABC∽△EDC,∴AB:EC=BC:CD,又∵EC=2、BC=4、CD=3,∴AB=8.12.如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.(1)求证:DC是⊙O的切线;(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.【解答】(1)证明:连接DO,如图,∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD,又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB.在△COD和△COB中∴△COD≌△COB(SAS),∴∠CDO=∠CBO.∵BC是⊙O的切线,∴∠CBO=90°,∴∠CDO=90°,∴OD⊥CE,又∵点D在⊙O上,∴CD是⊙O的切线;(2)解:由(1)可知∠OCB=∠OCD=30°,∴∠DCB=60°,又BC⊥BE,∴∠E=30°,在Rt△ODE中,∵tan∠E=,∴DE==4,同理DC=OD=4,=•OD•CE=×4×8=16.∴S△OCE13.如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.(1)求证:DC是⊙O切线;(2)若AO=6,DC=3,求DE的长;(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3,求图中阴影部分面积.【解答】(1)证明:连接OC,如图1,∵AC平分∠EAB,∴∠1=∠2,∵OA=OC,∴∠2=∠3,∴∠1=∠3,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,∴DC是⊙O切线;(2)解:连接BE交OC于H,如图1,∵AB为⊙O的直径,∴∠AEB=90°,∵OC∥AD,∴∠OHB=90°,∴EH=BH,四边形CDEH为矩形,∴CD=EH=3,CH=ED,∴BH=3,在Rt△OBH中,OH==3,∴CH=6﹣3=3,∴DE=3;(3)解:连接OC,如图2,设⊙O的半径为r,∵AC平分∠BAD,CD⊥AD,CF⊥AB,∴AD=AF=AO+OF,∵AD﹣OA=1.5,∴AO+OF﹣OA=1.5,即OF=1.5,∵AB为⊙O的直径,∴∠ACB=90°,∵∠CAF=∠BAC,∴△ACF∽△ABC,∴=,即=,解得r=﹣(舍去)或r=3,在Rt△OCF中,cos∠COF==,∴∠COF=60°,∴CF=OF=,∴图中阴影部分面积=S扇形BOC ﹣S△OCB=﹣×3×=π﹣.14.如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.(1)求证:AB是⊙O的切线;(2)若AB=4cm,AD=2cm,求CD的长.【解答】(1)证明:连接OB,如图,∵DC是⊙O的直径,∴∠CBD=90°,即∠1+∠2=90°,∴∠1=∠C,∵∠C=∠ABD,∴∠ABD+∠2=90°,即∠ABO=90°,∴OB⊥AB,∴AB是⊙O的切线;(2)解:∵∠BAD=∠CAB,∠ABD=∠C,∴△ABD∽△ACB,∴=,即=,∴AC=8,∴CD=AC﹣AD=8﹣2=6.15.如图AB为⊙O的直径,C为⊙O上半圆的一个动点,CE⊥AB于点E,∠OCE的角平分线交⊙O于D 点.(1)当C点在⊙O上半圆移动时,D点位置会变吗?请说明理由;(2)若⊙O的半径为5,弦AC的长为6,连接AD,求线段AD、CD的长.【解答】解:(1)当C点在⊙O上半圆移动时,D点位置不会变;理由如下:连接OD.∵CD平分∠OCE,∴∠1=∠3,而OC=OD,∴∠1=∠2,∴∠2=∠3,∴CE∥OD,∵CE⊥AB,∴OD⊥AB,∴=,即点D为半圆AB的中点.(2)∵在直角△AOD中,OA=OD=5,∴AD=5.过点A作CD的垂线,垂足为G,∵∠ACD=∠AOD=45°,∴△AGC是等腰直角三角形,∵AC=6,∴AG=CG=3.在直角△AGD中,DG==4,∴CD=CG+DG=3+4=7,∴线段AD的长度为5,线段CD的长度为7.16.在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF(1)求证:BF是⊙A的切线.(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.【解答】(1)证明:∵EF∥AB,∴∠E=∠CAB,∠EFA=∠FAB,∵∠E=∠EFA,∴∠FAB=∠CAB,在△ABC和△ABF中,,∴△ABC≌△ABF(SAS),∴∠AFB=∠ACB=90°,∴BF⊥AF,∵AF是⊙A的半径,∴BF是⊙A的切线;(2)解:当∠CAB=60°时,四边形ADFE为菱形.理由如下:∵∠CAB=60°,∴∠FAB=∠EAF=60°,∵AE=AF=AD,∴△AEF和△ADF都为等边三角形,∴AE=EF=AD=DF,∴四边形ADFE是菱形.17.如图,PC是⊙O的弦,作OB⊥PC于点E,交⊙O于点B,延长OB到点A,连接AC,OP,使∠A=∠P.(1)求证:AC是⊙O的切线;(2)若BE=2,PC=4,求AC的长.【解答】(1)证明:连接OC,如图,∵OP=OC,∴∠P=∠OCP,∵∠P=∠A,∴∠A=∠OCP,∵OB⊥PC,∴∠A+∠ACP=90°,∴∠ACP+∠OCP=90°,即∠OCA=90°,∴OC⊥AC,∴AC是⊙O的切线;(2)解:∵OB⊥PC,∴PE=CE=PC=2,设⊙O的半径为r,则OE=r﹣2,在Rt△OCE中,(2)2+(r﹣2)2=r2,解得r=4,∴OE=2,OC=4,∴∠OCE=30°,∠COE=60°,在Rt△AOC中,AC=OC=4.18.如图,AB为⊙O的直径,P在BA的延长线上,C为圆上一点,且∠PCA=∠B.(1)求证:PC与⊙O相切;(2)若PA=4,⊙O的半径为6,求BC的长.【解答】(1)证明:连接OC,如图,∵AB为⊙O的直径,∴∠ACB=90°,即∠2+∠3=90°,∵∠1=∠B,∠3=∠B,∴∠1=∠3,∴∠1+∠2=90°,即∠PCO=90°,∴OC⊥PC,∴PC与⊙O相切;(2)解:在Rt△POC中,PC===8,∵∠CPA=∠BPC,∠1=∠B,∴△PAC∽△PCB,∴===,在Rt△ABC中,∵AC2+BC2=AB2,∴BC2+BC2=122,∴BC=.19.如图,AB是⊙O的直径,AC平分∠DAB交⊙O于点C,过点C的直线垂直于AD交AB的延长线于点P,弦CE交AB于点F,连接BE.(1)求证:PD是⊙O的切线;(2)若PC=PF,试证明CE平分∠ACB.【解答】证明:(1)连接OC,如图,∵AC平分∠DAB,∴∠1=∠2,∵OA=OC,∴∠1=∠3,∴∠2=∠3,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,∴PD是⊙O的切线;(2)∵OC⊥PC,∴∠PCB+∠BCO=90°,∵AB为直径,∴∠ACB=90°,即∠3+∠BCO,∴∠3=∠PCB,而∠1=∠3,∴∠1=∠PCB,∵PC=PF,∴∠PCF=∠PFC,而∠PCF=∠PCB+∠BCF,∠PFC=∠1+∠ACF,∴∠BCF=∠ACF,即CE平分∠ACB.20.如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明:(1)BD=DC;(2)DE是⊙O切线.【解答】证明:如右图所示,(1)连接AD,∵AB是直径,∴∠ADB=90°,又∵AB=AC,∴BD=CD;(2)连接OD,∵∠BAC=2∠BAD,∠BOD=2∠BAD,∴∠BAC=∠BOD,∴OD∥AC,又∵DE⊥AC,∴∠AED=90°,∴∠ODB=∠AED=90°,∴DE是⊙O的切线.21.如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),D为⊙C在第一象限内的一点且∠ODB=60°.求:(1)求线段AB的长及⊙C的半径;(2)求B点坐标及圆心C的坐标.【解答】解:(1)∵点A的坐标为(0,3),∴OA=3,∵∠ODB=∠OAB,∠ODB=60°∴∠OAB=60°,∵∠AOB是直角,∴AB是⊙C的直径,∴∠OBA=30°,∴AB=2OA=6,∴⊙C的半径r=3;(2)过C点作CE⊥OB于E,在Rt△OAB中,∠OBA=30°,∴OB=AB=×6=3,∴B的坐标为:(3,0),由垂径定理得:OE=OB=,∵AC=BC,OE=BE,∴CE=OA=×3=∴C的坐标为(,).22.如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;(3)求证:CD=HF.【解答】(1)证明:(1)如图,连接OE.∵BE⊥EF,∴∠BEF=90°,∴BF是圆O的直径,∴OB=OE,∴∠OBE=∠OEB,∵BE平分∠ABC,∴∠CBE=∠OBE,∴∠OEB=∠CBE,∴OE∥BC,∴∠AEO=∠C=90°,∴AC是⊙O的切线;(2)证明:∵∠C=∠BHE=90°,∠EBC=∠EBA,∴BEC=∠BEH,∵BF是⊙O是直径,∴∠BEF=90°,∴∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,∴∠FEH=∠FEA,∴FE平分∠AEH.(3)证明:如图,连结DE.∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,∴EC=EH.∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,∴∠CDE=∠HFE,∵∠C=∠EHF=90°,∴△CDE≌△HFE(AAS),∴CD=HF,23.如图,已知AB是⊙O的直径,点C,D在⊙O上,BC=6cm,AC=8cm,∠BAD=45°.点E在⊙O外,做直线AE,且∠EAC=∠D.(1)求证:直线AE是⊙O的切线.(2)求图中阴影部分的面积.【解答】解:(1)∵AB是⊙O的直径,∴∠ACB=90°,∴∠CBA+∠CAB=90°,∵∠EAC=∠D,∠B=∠D,∴∠EAC=∠B,∴∠CAE+∠BAC=90°,即BA⊥AE.∴AE是⊙O的切线.(2)如图:连接OD.在Rt△ABC中,AB==10,∴BA=10,∴r=5.∵∠BAD=45°,∴∠BOD=2∠BAD=90°.∴∠DOA=90°.∴阴影部分的面积=S扇形DOA ﹣S△AOD=π×52﹣×5×5=﹣.24.已知AB是⊙O的直径,点P是AB延长线上的一点.(I)如图1,过P作⊙O的切线PC,切点为C.作AD⊥PC于点D,求证:∠PAC=∠DAC;(II)如图2,过P作⊙O的割线,交点为M、N,作AD⊥PN于点D,求证:∠PAM=∠DAN.【解答】证明:(Ⅰ)如图1,连接OC,∵OA=OC,∴∠1=∠2,∵PC是⊙O的切线,∴OC⊥PC,∵AD⊥PC,∴AD∥OC,∴∠2=∠3,∴∠1=∠3,即∠PAM=∠DAN;(Ⅱ)如图2,连接BM,∵AB是⊙O的直径,∴∠1+∠2=90°,∵AD⊥PN,∴∠AND+∠3=90°,∵ABMN时⊙O的内接四边形,∴∠AND=∠2,∴∠1=∠3,即∠PAM=∠DAN.25.如图,△ABC内接于⊙O,且∠B=60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.(1)求证:△ACF≌△ACG;(2)若AF=4,求图中阴影部分的面积.【解答】(1)证明:如图,连接CD,OC,则∠ADC=∠B=60°.∵AD是圆的直径,∴∠ACD=90°又∵∠ADC=∠B=60°∴∠CAD=30°∵EF与圆相切,∴∠FCA=∠ADC=60°∴直角△ACF中,∠FAC=30°,∴∠FAC=∠CAD,又∵CG⊥AD,AF⊥EF∴FC=CG则在△ACF和△ACG中:∴△ACF≌△ACG(AAS).(2)解:在Rt△ACF中,∠ACF=60°,AF=4,∴∠FAC=30°,∴FC=AC,设FC=x,则AC=2x,(2x)2﹣x2=(4)2,解得:x=4,∴CF=4.在Rt△OCG中,∠COG=60°,CG=CF=4,得OC==.在Rt△CEO中,OE=.于是S阴影=S△CEO﹣S扇形COD==﹣=.26.如图1,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60度.(1)求∠AOC的度数;(2)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;(3)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.【解答】解:(1)∵在△ACO中,∠OAC=60°,OC=OA∴△ACO是等边三角形∴∠AOC=60°.(2)∵CP与⊙O相切,OC是半径.∴CP⊥OC,又∵∠OAC=∠AOC=60°,∴∠P=90°﹣∠AOC=30°,∴在Rt△POC中,CO=PO=4,则PO=2CO=8;(3)如图,(每找出一点并求出弧长得1分)①作点C关于直径AB的对称点M1,连接AM1,OM1.易得S=S△CAO,∠AOM1=60°△M1AO∴=S△CAO,∴当点M运动到M1时,S△MAO此时点M经过的弧长为.②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO.∴∠AOM1=∠M1OM2=∠BOM2=60°∴或∴当点M运动到M2时,S=S△CAO,此时点M经过的弧长为.△MAO=S△CAO③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO∴∠BOM3=60°,∴或=S△CAO,此时点M经过的弧长为.∴当点M运动到M3时,S△MAO=S△CAO,④当点M运动到C时,M与C重合,S△MAO此时点M经过的弧长为或.27.已知扇形的圆心角为120°,面积为300πcm2.(1)求扇形的弧长;(2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少?【解答】解:(1)设扇形的半径为R,则300π=,解得,R=30,扇形的弧长==20π(cm);(2)设圆锥的底面半径为r,则20π=2πr,解得,r=10,又R=30,圆锥的高为:=20,∴S=×2×10×20=200(cm2),轴截面因此,扇形的弧长是20πcm,卷成圆锥的轴截面是200cm2.28.圆锥的底面半径是1,母线长是4,求它的侧面展开图的圆心角的度数.【解答】解:设圆锥侧面展开图的圆心角为n°,根据题意得2π×1=,解得:n=90,故圆锥侧面展开图的圆心角的度数90°.29.扇形的圆心角为90°,面积为16π.(1)求扇形的弧长.(2)若将此扇形卷成一个无底圆锥形筒,则这个圆锥形筒的高是多少?【解答】解:(1)设扇形的半径是R,则=16π,解得:R=8,设扇形的弧长是l,则lR=16π,即4l=16π,解得:l=4π.(2)圆锥的底面圆的半径为r,根据题意得2πr=,解得r=2,所以个圆锥形桶的高==2.故答案为2.30.如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于F,∠A=30°.(1)求⊙O的半径;(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.【解答】解:∵AC⊥BD于F,∠A=30°,∴∠BOC=60°,∠OBF=30°,∠BOD=120°,∵AB=4∴BF=2,∴OB====πcm2.∴S扇形(2)设圆锥的底面圆的半径为r,则周长为2πr,∴2πr=∴r=.∴这个圆锥底面圆的半径为.31.如图,AB是⊙O的直径,CD是⊙O的弦,且CD⊥AB于点E.(1)求证:∠BCO=∠D;(2)若CD=2,AE=1,求劣弧BD的长.【解答】(1)证明:∵OB=OC,∴∠BCO=∠B,∵∠B=∠D,∴∠BCO=∠D;(2)解:连接OD.∵AB是⊙O的直径,CD⊥AB,∴CE=DE=CD=,∵∠B=∠D,∠BEC=∠DEC,∴△BCE∽△DAE,∴AE:CE=DE:BE,∴1:=:BE,解得:BE=3,∴AB=AE+BE=4,∴⊙O的半径为2,∵tan∠EOD==,∴∠EOD=60°,∴∠BOD=120°,∴的长==π.32.如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求弧BC的长;(2)求弦BD的长.【解答】解:(1)如图,连接OC,OD,,∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,在Rt△ABC中,∵cos∠BAC===,∴∠BAC=60°,∴∠BOC=2∠BAC=2×60°=120°,∴的长==π.(2)∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠AOD=∠BOD,∴AD=BD,∴∠ABD=∠BAD=45°,在Rt△ABD中,BD=AB×sin45°=10×=5.33.如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.(1)由AB,BD,围成的阴影部分的面积是9π+18;(2)求线段DE的长.【解答】解:(1)连接OD,∵⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,∴∠ADB=90°,AD=BD,∴∠OBD=∠ODB=45°,∴OB=OD=6,∴由AB,BD,围成的阴影部分的面积是:=9π+18,故答案为:9π+18;(2)作AF⊥DE于点F,则AF=OD=6,∵AB∥DE,∠OAB=45°,∴∠ADF=∠OAB=45°,∴DF=AF=6,∵∠ACB=90°,AC=6,AB=12,∴∠CBA=30°,∴∠CAB=60°,∵AB∥DE,∴∠E=∠CAB=60°,∵AF=6,∠AFE=90°,∴EF=,∴DE=EF+DF=2+6.34.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).【解答】解:连接OD,∵OA=OD,∠A=45°,∴∠A=∠ADO=45°,∴∠DOB=90°,即OD⊥AB,∵BC∥AD,CD∥AB,∴四边形ABCD是平行四边形,∴CD=AB=2∴S梯形OBCD===,∴图中阴影部分的面积S=S梯形OBCD ﹣S扇形OBD=﹣=﹣.35.如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.(1)求点O到AB的距离;(2)求阴影部分的面积.【解答】解:(1)过点O作OE⊥AB于点E,∵对角线AC是圆O的直径,DB平分∠ADC,∴∠ADC=90°,则∠ADB=∠CDB=45°,∴∠AOB=90°,∵AO=BO,∴△AOB是等腰直角三角形,则EO=AO•sin45°=5×=(cm);(2)阴影部分的面积为:﹣×5×5=﹣.。
2018年中考数学真题专题汇编------圆综合题

① 若 AB 5 ,求 BC 的长; AC 3
② 当 AB 为何值时, AB AC 的值最大? AC
26.(2018 四川内江) 如图,以 Rt ABC 的直角边 AB 为直径作 O 交斜边 AC 于
长线上一点,且 BC CD , CE AD 于点 E .
( 1)求证:直线 EC 为 ⊙ O 的切线; ( 2)设 BE 与⊙ O 交于点 F , AF 的延长线与 CE 交于点 P .已知 PCF , PC 5 , PF 4 ,求 sin PEF 的值 .
CBF
21. (2018 浙江金华) 如图,在 Rt△ABC 中,点 O 在斜边 AB 上,以 O 为圆心,
OB 为 半 径 作 圆 , 分 别 与 BC,AB 相 交 于 点 D,E, 连 结 AED.已 知 ∠ 的切线 .
( 2)若 BC=8, tanB= 1 ,求 ⊙O 的半径 .
A
2
O
C
D
B
22.( 2018 浙江衢州) 如图,已知 AB 为⊙ O 直径, AC 是⊙ O 的切线,连接 BC 交 ⊙O 于点 F,取 的中点 D,连接 AD 交 BC 于点 E,过点 E 作 EH⊥AB 于 H. ( 1)求证: △HBE∽△ ABC ; ( 2)若 CF=4, BF=5,求 AC 和 EH 的长.
2018 年中考数学真题专题汇编 ------ 圆综合题
20.(2018 安徽) 如图 ,⊙O 为锐角 △ABC 的外接圆 ,半径为 5. ( 1)用尺规作图作出 ∠BAC 的平分线,并标出它与劣弧 BC 的交点 E(保留作 图痕迹 ,不写作法 ); ( 2)若( 1)中的点 E 到弦 BC 的距离为 3,求弦 CE 的长 .
中考数学总复习《圆的有关计算》专项测试卷含答案

中考数学总复习《圆的有关计算》专项测试卷含答案学校:___________班级:___________姓名:___________考号:___________【A层·基础过关】⏜的长为( )1.(2024·安徽中考)若扇形AOB的半径为6,∠AOB=120°,则ABA.2πB.3πC.4πD.6π2.如图,☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )A.144°B.130°C.129°D.108°3.如图,AB,AC分别为☉O的内接正方形、内接正三角形的一边,BC是圆内接n边形的一边,则n等于( )A.8B.10C.12D.164.如图,在☉O中,OA=2,∠C=45°,则图中阴影部分的面积为( )A.π-√2 B.π-√22C.π2-2 D.π-25.如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得到扇形DAE(阴影部分,点E在对角线AC上).若扇形DAE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )A.√2B.1C.√22D.126.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24 cm,若∠ACB=60°,则劣弧AB的长是( )A.8π cmB.16π cmC.32π cmD.192π cm7.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,DO⊥BE于点O,连接AD交BC于点F,若AC=FC.(1)求证:AC是☉O的切线;(2)若BF=8,DF=2√10,求☉O的半径;(3)若∠ADB =60°,BD =1,求阴影部分的面积.(结果保留根号)【B 层·能力提升】8.如图,已知点C 为圆锥母线SB 的中点,AB 为底面圆的直径,SB =6,AB =4,一只蚂蚁沿着圆锥的侧面从A 点爬到C 点,则蚂蚁爬行的最短路程为( )A .5B .3√3C .3√2D .6√39.如图,在△ABC 中,AB =5,AC =3,BC =4,将△ABC 绕点A 逆时针旋转40°得到△ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积为( )A.143π-6B.259πC.338π-3D.√33+π10.(2024·乐山中考)如图,☉O 是△ABC 的外接圆,AB 为直径,过点C 作☉O 的切线CD 交BA 延长线于点D ,点E 为CB⏜上一点,且AC ⏜=CE ⏜.(1)求证:DC ∥AE ;(2)若EF 垂直平分OB ,DA =3,求阴影部分的面积.【C 层·素养挑战】11.(2024·唐山二模)一个工件槽的两个底角∠A =∠B =90°,点A ,B 的初始高度相同,尺寸如图1所示(单位:cm),将一个形状规则的铁球放入槽内,测得球落在槽内的最大深度为2 cm(E 为球的最低点).(1)求该铁球的半径;(2)如图2,将这个工件槽的右边升高2 cm(BC =2 cm)后,求该平面图中铁球落在槽内的弧AB 的长度.(参考数据:sin 56°≈√175,cos 34°≈√175,tan 40°≈√175) 参考答案【A 层·基础过关】1.(2024·安徽中考)若扇形AOB 的半径为6,∠AOB =120°,则AB ⏜的长为(C) A .2π B .3π C .4π D .6π2.如图,☉O 与正五边形ABCDE 的两边AE ,CD 相切于A ,C 两点,则∠AOC 的度数是(A)A.144°B.130°C.129°D.108°3.如图,AB,AC分别为☉O的内接正方形、内接正三角形的一边,BC是圆内接n边形的一边,则n等于(C)A.8B.10C.12D.164.如图,在☉O中,OA=2,∠C=45°,则图中阴影部分的面积为(D)A.π-√2 B.π-√22C.π-2 D.π-225.如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得到扇形DAE(阴影部分,点E在对角线AC上).若扇形DAE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是(D)A.√2B.1C.√22D.126.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24 cm,若∠ACB=60°,则劣弧AB的长是(B)A.8π cmB.16π cmC.32π cmD.192π cm7.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,DO⊥BE于点O,连接AD交BC于点F,若AC=FC.(1)求证:AC是☉O的切线;【解析】(1)连接OA∵OA=OD,∴∠OAD=∠ODA∵AC=CF,∴∠CAF=∠CFA∵OD⊥BE,∴∠DOB=∠DOF=90°∴∠OFD+∠ODA=90°.∵∠OFD=∠CFA∴∠CAF+∠OAD=90°,∴OA⊥AC∵OA是☉O的半径,∴AC是☉O的切线.(2)若BF=8,DF=2√10,求☉O的半径;【解析】(2)设☉O的半径为r,∴BO=DO=r∵BF=8,∴OF=8-r.∵∠DOF=90°∴在Rt△ODF中,由勾股定理得OF2+OD2=DF2,∵DF=2√10∴(8-r)2+r2=(2√10)2解得r=6或r=2(不符合题意,舍去)故☉O的半径为6.(3)若∠ADB=60°,BD=1,求阴影部分的面积.(结果保留根号)【解析】(3)∵BO=DO,BD=1,∠DOB=90°∴在Rt△BOD中,由勾股定理得BO2+OD2=BD2∴BO=DO=√22即☉O的半径为√2.2∵∠ADB=60°∴∠AOB=2∠ADB=120°∴∠AOC=180°-∠AOB=60°.∵OA⊥AC∴∠OAC=90°.∴在Rt △OAC 中,tan ∠AOC =tan 60°=ACOA=√3.∵OA =√22,∴AC =√3OA =√62∴S △OAC =12OA ·AC =12×√22×√62=√34,S 扇形OAE =60π×(√22) 2360=π12∴S 阴影=S △OAC -S 扇形OAE =√34-π12.【B 层·能力提升】8.如图,已知点C 为圆锥母线SB 的中点,AB 为底面圆的直径,SB =6,AB =4,一只蚂蚁沿着圆锥的侧面从A 点爬到C 点,则蚂蚁爬行的最短路程为(B)A .5B .3√3C .3√2D .6√39.如图,在△ABC 中,AB =5,AC =3,BC =4,将△ABC 绕点A 逆时针旋转40°得到△ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积为(B)A.143π-6B.259πC.338π-3D.√33+π10.(2024·乐山中考)如图,☉O 是△ABC 的外接圆,AB 为直径,过点C 作☉O 的切线CD 交BA 延长线于点D ,点E 为CB⏜上一点,且AC ⏜=CE ⏜.(1)求证:DC∥AE;【解析】(1)连接OC(图略)∵CD为☉O的切线,点C在☉O上∴∠OCD=90°,∴∠DCA+∠OCA=90°∵AB为☉O的直径∴∠ACB=90°,∴∠B+∠OAC=90°.∵OC=OA,∴∠OAC=∠OCA⏜=CE⏜∴∠B=∠DCA,∵AC∴∠B=∠CAE,∴∠CAE=∠DCA∴CD∥AE.(2)若EF垂直平分OB,DA=3,求阴影部分的面积.【解析】(2)连接OE,BE(图略)∵EF垂直平分OB,∴OE=BE∵OE=OB,∴△OEB为等边三角形.∴∠BOE=60°,∴∠AOE=180°-60°=120°∵OA=OE,∴∠OAE=∠OEA=30°.∵DC∥AE,∴∠D=∠OAE=30°.∵∠OCD=90°,∴OD=2OC=OA+AD∵OA=OC,∴OC=AD=3∴AO=OE=OC=3,∴EF=√32OE=3√32∴S△OAE=12AO·FE=9√34∵S扇形OAE=120π×32360=3π∴S阴影=S扇形OAE-S△OAE=3π-9√34.【C层·素养挑战】11.(2024·唐山二模)一个工件槽的两个底角∠A=∠B=90°,点A,B的初始高度相同,尺寸如图1所示(单位:cm),将一个形状规则的铁球放入槽内,测得球落在槽内的最大深度为2 cm(E为球的最低点).(1)求该铁球的半径;【解析】(1)连接AB,OA,OE,且OE,AB交于点D由题意,得AB=8,DE=2,OE⊥AB∴AD=12AB=4设铁球的半径为r,则OA=OE=r,OD=OE-DE=r-2第 11 页 共 11 页 由勾股定理,得OA 2=OD 2+AD 2即r 2=(r -2)2+42解得r =5∴铁球的半径为5 cm .(2)如图2,将这个工件槽的右边升高2 cm(BC =2 cm)后,求该平面图中铁球落在槽内的弧AB 的长度.(参考数据:sin 56°≈√175,cos 34°≈√175,tan 40°≈√175) 【解析】(2)连接OA ,OB ,AB ,过点O 作OF ⊥AB 于点F则AF =BF =12AB ,OA =OB在Rt △ACB 中,由勾股定理,得AB =√AC 2+BC 2=√82+22=2√17∴AF =BF =12AB =√17 由(1)知OA =OB =5∴cos ∠OBF =BF OB =√175 ∴∠OBF =34°∴∠OAB =∠OBA =34°∴∠AOB =180°-2∠OBA =112°∴弧AB 的长度为112π180×5=28π9.。
【中考专题】2018年九年级中考数学 圆 解答题 中考专题汇编(含答案)

2018年九年级中考数学圆解答题中考专题汇编一、解答题:1、如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.(1)求证:BD是⊙O的切线;(2)若AB=12,DB=5,求△AOB的面积.2、如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.(1)求证:BD是⊙O的切线;(2)若AB=10,cos∠BAC=0.6,求BD的长及⊙O的半径.3、如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.(1)求证:MD=MC;(2)若⊙O的半径为5,AC=4,求MC的长.4、如图,△ABC 中,AB=AC ,以AB 为直径的⊙O 交BC 于点D ,交AC 于点E ,过点D 作FG ⊥AC 于点F ,交AB 的延长线于点G .(1)求证:FG 是⊙O 的切线; (2)若tanC=2,求BG :AG 的值.5、如图,在⊙O 中,AB 为直径,AC 为弦.过BC 延长线上一点G ,作GD ⊥AO 于点D ,交AC 于点E ,交⊙O 于点F ,M 是GE 的中点,连接CF ,CM . (1)判断CM 与⊙O 的位置关系,并说明理由; (2)若∠ECF=2∠A ,CM=6,CF=4,求MF 的长.6、如图,AB 是⊙O 的直径,点E 为线段OB 上一点(不与O ,B 重合),作EC ⊥OB ,交⊙O 于点C ,作直径CD ,过点C 的切线交DB 的延长线于点P ,作AF ⊥PC 于点F ,连接CB . (1)求证:AC 平分∠FAB ; (2)求证:BC 2=CE •CP ; (3)当AB=43且43CP CF 时,求劣弧BD 的长度.7、如图,在△ABC中,以AB为直径作⊙O交BC于点D,∠DAC=∠B.(1)求证:AC是⊙O的切线;(2)点E是AB上一点,若∠BCE=∠B,tan∠B=0.5,⊙O的半径是4,求EC的长.8、如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.(1)求证:AC平方DAE;(2)若cosM=0.8,BE=1,①求⊙O的半径;②求FN的长.9、如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且.(1)求AB的长度;(2)求AD·AE的值;(3)过A点作AH⊥BD,求证:BH=CD+DH.10、如图,AB 为⊙O 直径,P 点为半径OA 上异于O 点和A 点的一个点,过P 点作与直径AB 垂直的弦CD ,连接AD ,作BE ⊥AB ,OE ∥AD 交BE 于E 点,连接AE 、DE 、AE 交CD 于F 点. (1)求证:DE 为⊙O 切线;(2)若⊙O 的半径为3,sin ∠ADP=,求AD ; (3)请猜想PF 与FD 的数量关系,并加以证明.11、如图,AB 是以O 为圆心的半圆的直径,半径CO ⊥AO ,点M 是上的动点,且不与点A 、C 、B 重合,直线AM 交直线OC 于点D ,连结OM 与CM . (1)若半圆的半径为10.①当∠AOM=60°时,求DM 的长;②当AM=12时,求DM 的长.(2)探究:在点M 运动的过程中,∠DMC 的大小是否为定值?若是,求出该定值;若不是,请说明理由.12、如图,D 是△ABC 的BC 边上一点,连接AD ,作△ABD 的外接圆,将△ADC 沿直线AD 折叠,点C 的对应点E 落在上.(1)求证:AE=AB . (2)若∠CAB=90°,cos ∠ADB=31,BE=2,求BC 的长.13、如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=0.6时,求AF的长.14、如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.(1)试说明点D在⊙O上;(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.15、如图,已知D,E分别为△ABC的边AB,BC上两点,点A,C,E在⊙D上,点B,D在⊙E上.F为弧BD上一点,连接FE并延长交AC的延长线于点N,交AB于点M.(1)若∠EBD为α,请将∠CAD用含α的代数式表示;(2)若EM=MB,请说明当∠CAD为多少度时,直线EF为⊙D的切线;(3)在(2)的条件下,若AD=,求MN:MF的值.参考答案1、解:2、3、解:4、5、解:6、7、8、9、解:10、11、解:12、解:13、解:14、解:15、解:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题检测21 与圆有关的计算
(时间90分钟满分100分)
一、选择题(每小题4分,共40分)
1.已知一个扇形的圆心角是120°,面积是3π cm2,则这个扇形的半径是(B)
A.1 cm
B.3 cm
C.6 cm
D.9 cm
2.如图,4个正方形的边长均为1,则图中阴影部分三个小扇形的面积和为(A)
A.B.C.D.
(第2题图)
(第3题图)
3.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A'OB',则点A运动的路径的长为(B)
A.π
B.2π
C.4π
D.8π
4.如图,点A,B,C在☉O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为(C)
A.π-4
B.π-1
C.π-2
D.-2
(第4题图)
(第5题图)
5.如图,PA,PB是☉O的切线,切点分别为A,B.若OA=2,∠P=60°,则的长为(C)
A.π
B.π
C.π
D.π
6.如图,分别以五边形ABCDE的顶点为圆心,1为半径作五个圆,则图中阴影部分的面积之和为(C)
A.π
B.3π
C.π
D.2π
(第6题图)
(第7题图)
7.如图,圆锥的底面半径为r cm,母线长为10 cm,其侧面展开图是圆心角为216°的扇形,则r的值是(B)
A.3
B.6
C.3π
D.6π
8.
如图,△PQR是☉O的内接正三角形,四边形ABCD是☉O的内接正方形,BC∥QR,则∠AOR=(D)
A.60°
B.65°
C.72°
D.75°〚导学号92034204〛
9.
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作,过点O作AC的平行线交两弧于点D,E,则阴影部分的面积是(A)
A.-2
B.+2
C.2-
D.+〚导学号92034205〛
10.
如图,在矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次翻滚,则点B在两次翻滚过程中经过的路径的长是(A)。
