2.5厦门大学概率统计
厦大高等数学教材

厦大高等数学教材厦门大学高等数学教材厦门大学高等数学教材是厦门大学数学系编写的一本面向本科生的高等数学教材。
该教材旨在全面介绍高等数学的各个分支和重要概念,帮助学生建立扎实的数学基础,并培养学生的数学思维和解决实际问题的能力。
下面将对该教材的特点和内容进行详细介绍。
一、教材特点1.全面系统:该教材内容涵盖了高等数学的主要分支,如微积分、数列、级数、多元函数等,为学生提供了一个全面系统学习高等数学的机会。
2.逻辑清晰:教材在编写过程中经过精心策划,各个章节的内容逻辑清晰,层次分明。
每个知识点都有详细解释和推导,学生可以轻松地理解和掌握。
3.解题实例丰富:教材中精选了大量的解题实例,每个知识点都有相应的例题和习题,帮助学生巩固所学内容,并提供了相关的解题思路和方法。
4.注重应用:教材注重将数学理论与实际应用相结合,通过丰富的实例和案例,引导学生将数学知识应用到实际问题的解决中,培养学生的实际应用能力。
二、教材内容教材内容按照难易程度和知识关联度进行了合理的划分,下面列举了教材主要包含的内容:1.微积分部分:介绍了函数、极限、导数、微分、积分等基本概念和运算技巧,包括一元函数和多元函数的微积分。
2.数列和级数:讲解了数列和级数的概念及其性质,包括等差数列、等比数列、幂级数等。
3.多元函数与偏导数:介绍了多元函数的定义和性质,讲解了偏导数的概念和计算方法。
4.曲线积分与曲面积分:详细说明了曲线积分和曲面积分的定义和计算方法,引导学生理解曲线和曲面与积分之间的关系。
5.常微分方程:介绍了常微分方程的基本概念和解法,包括一阶和高阶常微分方程。
6.概率统计:讲解了概率统计的基本概念和方法,包括概率、随机变量、概率分布、样本调查等。
三、教材使用建议为了更好地学习和掌握该教材,建议学生按照以下步骤进行学习:1.预习教材:在课前预习教材内容,了解将要学习的知识点,尝试理解和记忆相关概念和公式。
2.听课和笔记:认真听课,做好笔记,将重点和难点整理出来,方便复习和回顾。
高等数学教材 厦大会计系

高等数学教材厦大会计系高等数学是会计系学生必修的一门重要课程,它主要涵盖了微积分、线性代数、概率论和数理统计等内容。
这门课程对于会计学专业的学生来说至关重要,因为它为他们打下了数学基础,为后续的专业课程奠定了坚实的基础。
本文将重点介绍厦门大学会计系采用的高等数学教材和教学方法。
1. 高等数学教材选择厦门大学会计系在高等数学课程中使用了《高等数学(上册)》和《高等数学(下册)》两本教材。
这两本教材由知名的高等教育出版社出版,内容丰富、结构清晰、知识点覆盖全面。
教材的选用考虑了会计专业的特点,注重应用与实践,将抽象的数学理论与实际问题相结合,帮助学生更好地理解和应用数学知识。
2. 教学方法在高等数学的教学中,厦大会计系采用了多种教学方法,旨在提高学生的学习效果和兴趣。
首先,讲授与实例相结合。
教师在讲解数学理论的同时,引入相关实例和应用,通过具体案例的演示,帮助学生理解抽象的数学概念和定理。
其次,启发式教学方法被广泛采用。
教师注重培养学生的逻辑思维能力和解决问题的能力,通过提出问题、引导学生思考和讨论,激发学生的学习兴趣和主动性。
此外,厦大会计系还组织了课外辅导班和习题讲解班,为学生提供更多的学习支持和帮助。
学生可以在辅导班中与教师和同学进行互动,解决自己在学习过程中遇到的难题。
3. 教学成果与展望由于采用了合适的教材和教学方法,厦大会计系的高等数学教学取得了良好的效果。
学生在这门课程中掌握了基本的数学理论和方法,提高了数学思维能力和问题解决能力。
未来,厦大会计系将继续不断改进教学方法和内容,确保高等数学课程的质量和教学效果。
同时,会计系还将加强与其他专业的合作,推动跨学科的交流与融合,为学生提供更广阔的学习空间和发展机会。
总结:高等数学是会计系学生不可或缺的一门课程,厦大会计系通过选择合适的教材和采用多种教学方法,帮助学生更好地掌握数学知识。
未来,会计系将继续致力于提高教学质量,为学生的学习提供更好的支持和帮助。
概率论与数理统计专业大学排名

排名
学校名称
等级
排名
学校名称
等级
排名
学校名称
等级
1
中国科学技术大学
A+
5
华东师范大学
A
9
山东大学
A
2
北京大学
A+
6
浙江大学
A
10
中南大学
A
3
南开大学
A+
7
武汉大学
A
11
东北师范大学
A
4
北京师范大学
8
华中科技大学
A
12
复旦大学
A
B+等(18个):北京工业大学、四川大学、大连理工大学、中山大学、云南大学、吉林大学、北京理工大学、中国人民大学、西安交通大学、湖南师范大学、华中师范大学、清华大学、同济大学、上海师范大学、兰州大学、安徽大学、南京大学、江苏大学
B等(18个):广西师范大学、湖北大学、暨南大学、湖南大学、首都师范大学、上海财经大学、厦门大学、燕山大学、云南师范大学、东南大学、武汉科技大学、河南师范大学、西北工业大学、苏州大学、重庆大学、新疆大学、长沙理工大学、山西大学
C等(13个):名单略
厦门大学《概率论与数理统计》2016-2017学年第二学期期末试卷A卷

(说明:共10题,每题10分)1.设6件产品中有2次品,采用不放回抽样方式,每次抽一件,记A 为“第一次抽到正品”的事件,B “第二次抽到正品”的事件,求P (A ),P (AB ),P (B|A ),P (B ).2.某类电灯泡使用时数在1000小时以上的概率为0.2,求三个灯泡在使用1000小时以后最多只有一个坏的概率.3.设两箱内装有同种零件,第一箱装50件,其中有10 件一等品,第二箱装30件,其中有18件一等品,先从两箱中任挑一箱,再从此箱中前后不放回任取两个零件,求(1)先取出的零件是一等品的概率p 。
(2)在先取出的 是一等品的条件下,后取 的仍是一等品的条件概率q.4. 设随机变量X 服从参数为0λ>的泊松分布,且已知E[(X+1)(X-2)]=2,求(1)λ(2)P{X>1}. 5 设随机变量X 服从参数为2λ=的指数分布,试证21X Y e −=−在(0,1)上服从均匀分布. 6 设连续型随机变量X 的密度函数为0()1/40202x ke x f x x x ⎧<⎪=≤<⎨⎪≥⎩,求(1)系数k;(2)X 的分布函数;(3)P{X=1},P{1<X<2}.7.设随机变量X 在 [-1,2]区间上服从均匀分布,随机变量Y 与X 的关系是100010X Y X X −<⎧⎪==⎨⎪>⎩若求EY ,DY.8.设(X ,Y )的联合分布律为XY0 1 20 2/15 3/15 1 1/15 6/15 3/15 求:(1) E (X ),EY;(2) X 和Y 是否独立?(3)在Y=0条件下X 的条件分布. 厦门大学《概率论与数理统计》试卷____学院____系____年级____专业主考教师:____试卷类型:(A 卷)9.设二维随机向量(X ,Y)的联合密度函数为⎧≤<<=⎨⎩801(,)0其它xy x y f x y (1) 分别求X 和Y 的边缘密度函数;(2) 判断X 与Y 是否独立;(3) 求条件密度函数|(|)X Y f x y 在y=1/2时的函数值。
厦门大学统计学简答题整理+答案

统计学简答题整理第一章1.时期指标与时点指标(定义.特点),也可能多选,课件⏹时期数据是反映现象在某一段时期内活动过程的总结果。
例如,人口出生数、粮食产量、商品销售额等。
⏹时点数据是反映现象在某一时刻(瞬间)上的数量状况。
例如,人口数、职工人数、商品库存量等。
⏹1)时期指标数值是连续登记、累计的结果。
例如,月产量是对每天的生产量进行登记后累计得到的,而年产量是将12个月产量累计得到的。
⏹2)不同时期的时期指标数值具有可加性,相加后表示较长时期现象总的发展水平。
例如,将一年内12个月的钢产量相加就得到全年的钢产量。
⏹3)时期指标数值大小与包含的时期长短成正比。
⏹⏹1)时点指标数值只能间断计数,它的每个数据都表示社会经济现象发展到一定时点上所处的水平。
⏹2)不同的时点的指标数值不具有可加性,即相加后不具有实际意义。
⏹3)时点指标的数值大小与其时间间隔长短无直接关系。
⏹2.总体与总体单位、指标与标志的区别联系,见课件1统计总体(Population):简称总体,是指根据统计任务要求所确定的,由客观存在的,在同一性质基础上结合起来的许多个别事物的集合或整体。
2总体单位(unit):又称单位。
是指构成总体的个别事物(或个体)。
3.总体和单位是可以变换的。
⏹总体和单位的概念是相对而言的,随着研究目的不同,总体范围不同而相互变换。
同一个研究对象,在一种情况下为总体,但在另一种情况下又可能变成单位。
⏹标志:总体各单位普遍具有的属性或特征。
⏹指标:反映总体现象数量特征的概念。
区别:⏹(1)标志是说明总体单位的特征和属性;而指标则是说明总体的数量特征。
⏹(2)标志有不能用数值表示的品质标志与能用数值表示的数量标志;而指标都是能用数值表示的。
联系:⏹(1)有许多统计指标的数值是从总体单位的数量标志值汇总而来的。
如一个学校的教师工资总额是由每个教师工资加总得到的。
⏹(2)指标与数量标志之间存在变换关系。
例如,研究福建省各县人口情况时,福建省是总体,各县是总体单位,福建省人口总数是指标;而当要研究全国各省的人口情况时,全国是总体,福建省是总体单位之一,则福建省人口是它的标志。
厦门大学2009级概率论期中考试试卷及答案

1. (6分)设B A ,都出现的概率与B A ,都不出现的概率相等, 且p A P =)(, 求)(B P .2. (6分)设某光学仪器厂制造的透镜, 第一次落下时打破的概率为1/2, 若第一次落下未打破, 第二次落下打破的概率为7/10, 若前两次落下未打破, 第三次落下打破的概率为9/10. 试求透镜落下三次而未打破的概率.3. (8分)人们为了解一支股票未来一定时期内价格的变化, 往往会去分析影响股票价格的基本因素, 比如利率的变化. 现假设人们经分析估计利率下调的概率为60%, 利率不变的概率为40%. 根据经验, 人们估计, 在利率下调的情况下, 该支股票价格上涨的概率为80%,而在利率不变的情况下, 其价格上涨的概率为40%, 求该支股票将上涨的概率.4. (12分)一条自动生产线上的产品, 次品率为4%, 求解以下两个问题:(1) 从中任取10件, 求至少有两件次品的概率;(2) 一次取1件, 无放回地抽取,求当取到第二件次品时, 之前已取到8件正品的概率. 5.(14分)设随机变量X 具有概率密度⎪⎪⎩⎪⎪⎨⎧≤≤-<≤=.,0,43,22,30,)(其它x x x kx x f}.2/71{)3();()2(;)1(≤<X P x F X k 求的分布函数求确定常数6.(12分)具有概率密度设二维随机变量),(Y X⎪⎩⎪⎨⎧>>=+-.,0,0,0,2),()2(其它y x ey x f y x(1) 求分布函数);,(y x F (2) 求概率}.{X Y P ≤厦门大学概率统计课程期中试卷____学院___系___年级___专业考试时间 2010.11.207. (12分)设店主在每日开门营业时,放在柜台上的货物量为Y ,当日销售量为X 假定一天中不再往柜台上补充货物,于是Y X ≤. 根据历史资料,),(Y X 的概率密度函数为⎩⎨⎧≤≤≤≤=.,0200,0,200/1),(其它时,当y y x y x f即),(Y X 服从直角三角形区域OAB 上的均匀分布, 见右图. 求(1) 给定y Y =条件下,X 的条件分布.(2)假定某日开门时,10=Y 件,求这天顾客买走5≤X 件的概率. 如果20=Y 件呢?8.(10分)某商店对某种家用电器的销售采用先使用后付款的方式. 记使用寿命为X (以年计), 规定:.3000,3;2500,32;2000,21;1500,1元一台付款元一台付款元一台付款元一台付款>≤<≤<≤X X X X设寿命X 服从指数分布, 概率密度为()⎪⎩⎪⎨⎧≤>=-.0,00,10110/x x e x f x试求该类家用电器一台收费Y 的数学期望. 9.(20分)设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<=-.,0;0,),(其它y x e y x f y(1) 求X 与Y 的边际概率密度, 并判断X 与Y 是否相互独立;(2) 求在y Y =的条件下, X 的条件概率密度; (3) 求概率{}{}.4|21|2/10},12{=≥≤≤≤≤+Y X P Y X P Y X P厦门大学2009年概率统计期中答案1. 解 由题设条件得)P()P()P(1)P(1)P()P(AB B A B A B A AB +--=-== --------4分故 p A B -=-=1)P(1)P(。
考研资料_厦门大学卫生综合_卫生统计厦大内部习题集_第五章 常用概率分布

第五章常用概率分布习题一、是非题1.在确定某个指标的医学参考值范围时,必须选取足够多的健康人来进行计算。
2.对于服从正态分布的资料,变量取值位于-1.96到1.96之间的可能性为0.95。
3.Poisson分布有两个参数:n和μ。
4.在μ足够大时,Poisson分布就是正态分布。
5.设X服从Poisson分布,则Y=2X也服从Poisson分布。
6.用X表示某个放射性物体的每分钟脉冲数,其平均每分钟脉冲数为5次(可以认为服从Poisson分布),用Y表示连续观察20分钟的脉冲数,则可以认为近似服从正态分布,但不能认为X近似服从正态分布。
二、选择题1.关于二项分布,错误的是( )。
A.服从二项分布随机变量为离散型随机变量B.当n很大,π接近0.5时,二项分布图形接近正态分布C.当π接近0.5时,二项分布图形接近对称分布D.服从二项分布随机变量,取值的概率之和为1E.当nπ>5时,二项分布接近正态分布2.关于泊松分布,错误的是( )。
A.当二项分布的n很大而π很小时,可用泊松分布近似二项分布B.泊松分布由均数λ唯一确定C.泊松分布的均数越大,越接近正态分布D.泊松分布的均数与标准差相等E.如果X1和X2分别服从均数为λl和λ2的泊松分布,且相互独立。
则X1+X2服从均数为λl+λ2泊松分布3.正态曲线下、横轴上,从μ到μ+2.58σ的面积占曲线下总面积的( ) A.99%B.95%C.47.5%D.49.5%E.90%4.标准正态曲线下,中间95%的面积所对应的横轴范围是( )。
A.-∞到+1.96 B.-1.96到+1.96 C.-∞到+2.58D.-2.58到+2.58 E.-1.64到+1.645.服从二项分布的随机变量的总体均数为( )。
A.n(1-π) B.(n-1)π(1-π) C.nπ(1-π) D.nπE.6.服从二项分布的随机变量的总体标准为( )。
A B.(n-1)π(1-π) C.nπ(1-π) D E7.以下方法中,确定医学参考值范围的最好方法是( )A.百分位数法B.正态分布法C.对数正态分布法D.标准化法E.结合原始数据分布类型选择相应的方法8.下列叙述中.错误的是( )。
厦门大学 级会计学课程表
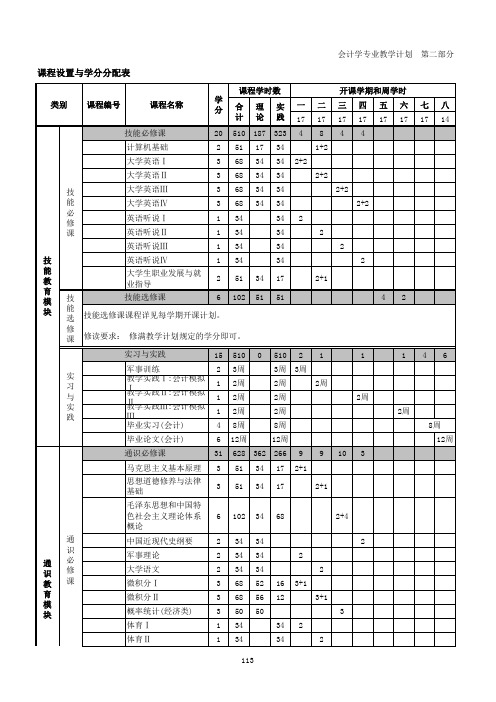
2+4
概论
中国近现代史纲要
2 34 34
2
军事理论
2 34 34
2
大学语文
2 34 34
2
微积分Ⅰ
3 68 52 16 3+1
微积分Ⅱ
3 68 56 12
3+1
概率统计(经济类)
3 50 50
3
体育Ⅰ
1 34
34 2
体育Ⅱ
1 34
34
2
七八 17 14
46 8周 12周
113
通 识 通必 识修 教课
块
114
会计学专业教学计划 第二部分
课程设置与学分分配表
专 业类别 教 育 模 块
课程编号
课程名称
基础会计模拟 高级财务管理
课程学时数
开课学期和周学时
学 分
合
理
实
一
二
三
四
五
六
七
八
计 论 践 17 17 17 17 17 17 17 14
2 34 34
2
2 34 34
2
跨国公司财务管理
2 34 34
2 34 34
2
专
宏观经济学原理
2 34 34
业
统计学原理
3 50 50
必
修
中级财务会计(A)Ⅰ 3 50 50
课
中级财务会计(A)Ⅱ 3 50 50
2 3
3 3
高级财务会计
2 34 34
2
成本会计
3 50 50
3
财务管理(A)Ⅰ
3 50 50
3
财务管理(A)Ⅱ
3 50 50
计算语言学厦大应用语言学

利用深度学习模型,如卷积神经网络(CNN)和循环神经网络 (RNN),对文本进行情感分析和意见挖掘。
方面级情感分析
针对特定方面或属性进行情感分析,如产品评价中的性能、外观等方 面。
机器翻译技术进展与挑战
神经机器翻译
基于深度学习的神经机器翻译模型,如Transformer和Seq2Seq, 实现了更高的翻译质量和效率。
• 深度学习技术融合:随着深度学习技术的不断发展,未来计算语言学将更加注 重与深度学习技术的融合,利用神经网络模型强大的特征提取和学习能力,提 高自然语言处理的效果和效率。
• 知识图谱与语义理解:知识图谱作为一种重要的知识表示和推理工具,将在未 来计算语言学中发挥越来越重要的作用。结合知识图谱和语义理解技术,可以 实现更加准确、全面的自然语言理解和分析。
认知科学对语言生成的影响
认知科学研究人类如何获取、存储、处理和运用知识的科学,对计算语言学在语言生成方面提供了重要的启示。 例如,认知语言学将语言视为一种认知活动,关注语言与认知、文化等因素的相互作用,为自然语言生成提供了 更广阔的研究视角。
人工智能技术在教育、出版等领域应用
人工智能技术在教育领域的应用
计算语言学厦大应用 语言学
目录
• 引言 • 计算语言学基础理论 • 应用语言学实践案例分析 • 跨领域合作与交叉研究趋势 • 挑战与未来发展方向 • 总结回顾与展望未来
01
引言
计算语言学与应用语言学关系
计算语言学是应用语言学的一个分支,它利用计算机技术 和方法来研究自然语言处理(NLP)问题。
多模态数据处理与跨媒体智能
多模态数据处理
多模态数据处理是指处理包含文本、图像、音频、视频等多种模态的数据。在计算语言学中,多模态 数据处理可以帮助我们更全面地理解语言信息,例如通过图像和文本的结合来识别情感、场景等。
2021年厦门大学868概率论与数理统计考研精编资料

2021 年厦门大学 868 概率论与数理统计考研精编资料一、厦门大学 868 概率论与数理统计考研真题汇编及考研大纲1 .厦门大学 868 概率论与数理统计(回忆版) 2014 年考研真题,暂无答案。
2. 厦门大学 868概率论与数理统计考研大纲①2018年厦门大学868概率论与数理统计考研大纲。
二、 2021 年厦门大学 868 概率论与数理统计考研资料3 .茆诗松《概率论与数理统计教程》考研相关资料( 1 )茆诗松《概率论与数理统计教程》 [ 笔记 + 课件 + 提纲 ]①厦门大学 868 概率论与数理统计之茆诗松《概率论与数理统计教程》考研复习笔记。
②厦门大学 868 概率论与数理统计之茆诗松《概率论与数理统计教程》本科生课件。
③厦门大学 868 概率论与数理统计之茆诗松《概率论与数理统计教程》复习提纲。
( 2 )茆诗松《概率论与数理统计教程》考研核心题库(含答案)①厦门大学 868 概率论与数理统计考研核心题库之综合题精编。
( 3 )茆诗松《概率论与数理统计教程》考研模拟题 [ 仿真 + 强化 + 冲刺 ]① 2021 年厦门大学 868 概率论与数理统计考研专业课六套仿真模拟题。
② 2021 年厦门大学 868 概率论与数理统计考研强化六套模拟题及详细答案解析。
③ 2021 年厦门大学 868 概率论与数理统计考研冲刺六套模拟题及详细答案解析。
三、V资料X获取:ky21985四、 2021 年研究生入学考试指定 / 推荐参考书目(资料不包括教材)5 .厦门大学 868 概率论与数理统计考研初试参考书茆诗松《概率论与数理统计教程》五、 2021 年研究生入学考试招生专业目录6 .厦门大学 868 概率论与数理统计考研招生专业目录院系所专业学制(年)学习方式研究方向考试科目备注022统计系 071400统计学3 (1)全日制01数理统计① 101思想政治理论②201英语一③301数学一④868概率论与数理统计本专业授予理学学位。
理学 概率论与数理统计_第三版龙永红完整答案

概率论与数理统计龙永红,第三版,高等教育出版社课后习题详细答案厦门大学 经济学院08经济 周玉龙08金融 王骁 李政宵09金融 孙士慧 许彩灵 唐艺烨联合编写2011年2月16日 第一版注意:若要打印,请不要打印34页之后的内容!只有34页之前的内容才是校对过的!2010年的时候半期考试考到3.1,即34页之前的内容。
目录前言 (3)编写任务记录 (4)练习1‐1 (5)练习1‐2 (6)练习1‐3 (7)练习1‐4 (9)练习1‐5 (12)习题一 (13)练习2‐1 (15)练习2‐2 (17)练习2‐3 (18)练习2‐4 (20)练习2‐5 (23)习题二 (26)练习3‐1 (29)练习3‐2 (35)练习3‐3 (40)练习3‐4 (43)练习3‐5 (48)练习4‐1 (49)练习4‐2 (50)练习4‐3 (51)练习4‐4 (53)练习5‐2 (54)练习5‐3 (55)练习5‐4 (56)练习5‐5 (56)练习5‐6 (58)前言各位学弟学妹们,大家好。
这份答案是我在2010年学习概率统计的时候,和几个好朋友一起编写的。
我在大二上学线性代数的时候,当时找不到习题答案,于是很多不会做的题目,我就直接放弃了,期末线性代数成绩很不理想。
大二下在学概率统计的时候,我决定要把书上的题目都做会,但当时找不到一本参考答案,于是便想到了自己来编写一本答案书。
这样我不仅可以强迫自己把书上的题目都做了,更重要的是,我还可以帮助今后很多的学弟学妹学习概率统计。
于是找到08经济系的周玉龙同学,由他撰写手写初稿答案;我又找了几个愿意加入的朋友,我们一起将手写初稿录入进电脑,他们是09金融的孙士慧、许彩灵、唐艺烨和08金融的李政宵;我再将电子版初稿打印下来,并在上面进行打印错误的校正,再由我将这些错误在电脑中改过来。
最后整理排版,这就是你眼前的这本电子书。
撰写初版答案是辛苦的,将初版手写答案录入电脑更是非常辛苦。
厦门大学应用多元统计分析第判别分析

AB 102 52 125 ; CD 12 102 101
如果我们将长度单位变为 mm,那么,有
AB 102 502 2600 ; CD 12 1002 10001
量纲的变化,将影响欧氏距离计算的结果。
为此,我们引入一种由印度著名统计学家马哈拉诺比斯 (Mahalanobis, 1936)提出旳“马氏距离”旳概念。
其
中
μ
1 2
(μ1
μ2)
是
两
个
总
体
均
值
的
平
均
值
,
α Σ1 (μ1 μ 2 ) ,记 W (X) α(X μ)
(4.5)
则判别规则(4.4)式可表示为
X X
G1 G2
, ,
如果 如果
W (X) 0 W (X) 0
(4.6)
这里称W (X) 为两总体距离判别的判别函数,由于它是 X 的线性
设 X 和 Y 是来自均值向量为 μ ,协方差为 Σ( 0) 的总体 G
中的 p 维样本,则总体 G 内两点 X 与 Y 之间的马氏距离定
义为
D2 (X, Y) (X Y)Σ1(X Y) (4.2)
定义点 X 到总体 G 的马氏距离为
D2 (X,G) (X μ)Σ1(X μ)
(4.3)
一 Bayes鉴别旳基本思想 二 Bayes鉴别旳基本措施
从上节看距离鉴别法虽然简朴,便于使用。但是该措施也有 它明显旳不足之处。
第一,鉴别措施与总体各自出现旳概率旳大小无关;
第二,鉴别措施与错判之后所造成旳损失无关。Bayes鉴别 法就是为了处理这些问题而提出旳一种鉴别措施。
一、Bayes鉴别旳基本思想
《概率论及数理统计》课程标准

精选文档《概率论与数理统计》课程标准课程编号课程性质必修参照学时36学分2查核方式理论考试合用范围金融管理专业开设单位教育学院先修课程经济数学 / 高等数学主笔人苏明(教育学院)一、课程概括第一部分序言《概率论与数理统计》 (Probability Theory and Mathematical Statistics),由概率论和数理统计两部分构成。
它是研究随机现象并找出其统计规律的一门学科,是宽泛应用于社会、经济、科学等各个领域的定量和定性剖析的科学系统。
一、课程性质《概率论与数理统计》是理、工科有关专业的基础干课。
对高校的统计专业本科生它也是一门学科基础课程。
从学科性质讲,它是一门基础性学科,它为统计专业学生后继专业课程的学习供给方法论的指导。
学生对这门课程的掌握程度直接关系到统计学科培育目标—“经济和管理领域中擅长在定性剖析基础上从事定量剖析的特意统计人材”的实现。
二、基本理念第一,侧重基础,侧重标准。
在我国,迄今为止,有关数理统计教材许多,这些教材和理论参照文件各自保持了自己的特点。
只有侧重基础、侧重标准,精选文档才能与国际先进的理论研究趋向保持一致。
第二,力争在简短的基础上使学生能从整体上认识和掌握该课程的内容系统,使学生可以在实质工作中、其余学科的学习中能灵巧、自如地应用这些理论。
三、课程标准的设计思路第一,浙江大学盛骤、谢式千、潘承毅主编的《概率论与数理统计》为蓝本, 全力用较为平常的语言阐释概率论的基本理论和数理统计思想方法; 第二,密切联合财经特点和计算机应用加以论述和学习 ;第三,理论和方法相联合,以重申数理统计理论的应用价值。
总之,重申治论与实质应用相联合的特点, 力争在实质应用方面做些有利的探究,也为其余学科的进一步学习打下一个优异的基础。
第二部分课程目标一、总目标《概率论与数理统计》是一门几乎遍布全部的科学技术领域以及工农业生产和公民经济各部门之中。
经过学习该课程使学生掌握概率、统计的基本概念,熟习数据办理、数据剖析、数据推测的各样基本方法,并能用所掌握的方法详细解决社会经济所碰到的各样问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这里 min{g (a), g (b)}, max{g (a), g (b)}.
2014年7月24日
20 / 31
证明:
设随机变量Y g X 的分布函数为FY y , 则有 FY y P Y y Pg X y
由题设,不妨假设g x 0,则 g x 是严格增 加的函数.
5 / 31
例 1
设离散型随机变量X 的分布律为
X P
-3
1 252
-1
5 252
0
15 252
2
35 252
6
70 252
9
126 252
随机变量Y 2 X 3 ,试求Y 的分布律.
解:
随机变量Y 2 X 3 的取值为
9, 5, 3, 1, 9, 15,
2014年7月24日
此时称Y 服从自由度为1的 2分布。
2014年7月24日
18 / 31
定理
设随机变量 X 具有概率密度 f X ( x) , x ,
又设函数 g ( x) 处处可导,且有 g ( x) 0 (或恒有 g ( x) 0).
则 Y =g(X ) 是一个连续型随机变量,其概率密度为
6 / 31
例 1(续)
这些取值两两互不相同 . 由此得随机变量
Y 2X 3
的分布律为
Hale Waihona Puke Y P-91 252
-5
5 252
-3
15 252
1
35 252
9
70 252
15
126 252
2014年7月24日
7 / 31
例 2
设随机变量 X 具有以下的分布律,试求
Y = (X-1)2
的分布律.
2014年7月24日
27 / 31
例 8(续)
1 f X ( x) e 2 ( x )2 2 2
, x .
由定理的结论得:
y b 1 x h( y ) , 且h( y ) . a a
2014年7月24日
19 / 31
定理(续)
若 f ( x) 在有限区间[a, b] 以外等于零,则只须假 设 在 [a, b] 上恒有g ( x) 0(或恒有g ( x) 0), 此时仍有:
f X [h( y )] | h( y ) |, y , fY ( y ) 0, 其它.
2014年7月24日
2 / 31
一、离散型随机变量的函数
设 X 是离散型随机变量,其 分布律为
P X xn pn
n 1,
2,
或
X P
x1 p1
x2 p2
, ,
xn pn
Y是X 的函数:Y g X ,则Y也是离散型随机变 量,它的取值为 y1 , y2 , , yn ,
(2) 利用 fY ( y ) FY ( y )可以求得:
y 8 y 8 fY ( y ) f X ( )( ) 2 2 y 8 1 y 8 1 8 ( 2 ) 2 , 0 2 4, 0, 其它.
2014年7月24日
x , 0 x 4, f X (X ) 8 其它. 0,
由此得随机变量Y e 的密度函数为
1 ln y 2 exp 2 fY y 2 y 2 0 y0 y0
X
2014年7月24日
26 / 31
例 8
设随机变量X ~ N ( , 2 ), 试证明X的线性函数Y aX b (a 0)也服从正态分布 .
证
X的概率密度为:
1 f X ( x) e 2 ( x )2 2 2
, x .
y g ( x) ax b, g ( x) a, 满足定理的条件,
y b 1 y g ( x)的反函数为: x h( y ) , 且h( y ) . a a
§5
随机变量的函数的分布
• 离散型 • 连续型 • 定理及其应用
2014年7月24日
1 / 31
随机变量的函数
设 X 是一随机变量, Y 是 X 的函数, Y g X , 则 Y
也是一个随机变量.当 X 取值 x时,Y 取值 y g x
本节的任务就是:
已知随机变量 X 的分布,并且已知Y g X , 要求随机变量Y 的分布.
因此, FY y P X g 1 y PX h y
FX h y
2014年7月24日
21 / 31
定 理 的 证 明
由题设,当随机变量X 在区间 , 上变化时, 随机变量Y 在区间 , 上变化.
其中,
ming , g , maxg , g
PY yn pn
或
Y P
y1 p1
y2 p2
, ,
yn pn
4 / 31
2014年7月24日
第 二 种 情 形
如果
y1 , y2 , , yn , 有相同的项,
则把这些相同的项合并(看作是一项),并把相 应的概率相加,即可得随机变量Y g X 的分布律.
2014年7月24日
解:(1) 先求 Y =2X+8 的分布函数 FY(y):
FY ( y ) P{Y y} y 8 y 8 P{2 X 8 y} P{ X } FX 2 2
2014年7月24日
13 / 31
例 4(续)
y 8 FY ( y ) FX 2
14 / 31
例 4(续)
整理得 Y=2X+8 的概率密度为:
y 8 32 , 8 y 16, fY ( y ) 0, 其它.
2014年7月24日
15 / 31
例5
设随机变量 X 具有概率密度 f X ( x ), x , 求 Y = X 2 的概率密度.
解:(1) 先求 Y = X 2 的分布函数 FY(y):
10 由于 Y X 2 0, 故当 y 0 时 FY ( y) 0.
2
0
当 y 0 时, FY ( y ) P{Y y} P{ X 2 y} P{ y X FX
X
y F y
f X h y h y f X h y h y
P X g 1 y PX h y 1 FX h y
d 所以,f y FY y 1 FX h y dy
2014年7月24日
2014年7月24日
17 / 31
例如,设 X~N(0,1),其概率密度为:
1 ( x) e 2
x2 2
, x .
则 Y = X 2 的概率密度为:
1 y 1 2 2 y e , fY ( y ) 2 0,
y 0, y 0.
P{Y=1}=P{X=0}+P{X=2}=0.3+ 0.4=0.7, P{Y=4}= P{X= -1}= 0.2,
所以,Y=(X-1)2 的分布律为:
4 Y 0 1 p k 0 . 1 0. 7 0 . 2
2014年7月24日
9 / 31
例 3
设离散型随机变量X 的分布律为
X P
1
1 2
2
1 22
16 / 31
y}
2014年7月24日
例
5(续)
FY ( y) FX
y F y
X
(2)利用fY ( y ) FY ( y )及变限定积分求导公式得:
1 [ f X ( y ) f X ( y )], y 0, fY ( y ) 2 y 0, y 0.
其中 yn g xn
n 1, 2,
3 / 31
2014年7月24日
第 一 种 情 形
如果
y1 , y2 , , yn ,
两两不相同,则由
P Y yn PX xn
可知随机变量Y 的分布律为
n 1, 2, n 1,
2,
f X [h( y )] | h( y ) |, y , fY ( y ) 0, 其它.
其中 h(y) 是 g(x) 的反函数, min{g (), g ()}, max{g (), g ()}. 即 x g 1 ( y ) h( y )
23 / 31
定 理 的 证 明
f X h y h y f X h y h y
综上所述,得 Y g X 的密度函数为
f X h y h y fY y 0
y
其它
2014年7月24日
24 / 31
… …
n
1 2n
… …
1 若X为奇数 Y gX 1 若X为偶数
试求随机变量Y 的分布律.
2014年7月24日
10 / 31
例 3(续)
P Y 1
n为 奇 数
PX n PX 2k 1
k 0
1
2 k 1 2 k 0
我们要求的是Y g X 的密度函数 f Y y . 随机变量.
再设Y g X 是 X 的函数,我们假定Y 也是连续型
解题思路
⑴.先求Y g X 的分布函数 FY y P Y y Pg X y
