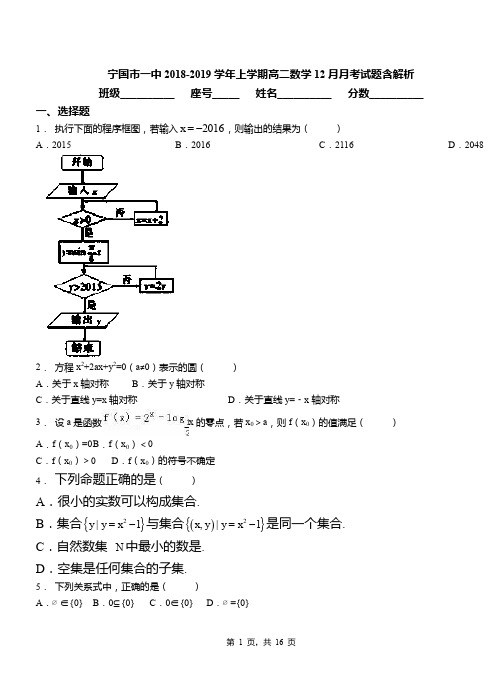
最新-安徽省宁国中学2018-2018学年高一数学第二学期第一次段考新人教A版精品

合集下载

高中数学模块1 高考真题(含解析)新人教A版必修1-新人教A版高一必修1数学试题

模块1高考真题对应学生用书P81剖析解读高考全国Ⅰ、Ⅱ、Ⅲ卷都是由教育部按照普通高考考试大纲统一命题，适用于不同省份的考生．但在难度上会有一些差异，但在试卷结构、命题方向上基本上都是相同的．“稳定”是高考的主旋律．在今年的高考试卷中，试题分布和考核内容没有太大的变动，三角、数列、立体几何、圆锥曲线、函数与导数等都是历年考查的重点．每套试卷都注重了对数学通性通法的考查，淡化特殊技巧，都是运用基本概念分析问题，基本公式运算求解、基本定理推理论证、基本数学思想方法分析和解决问题，这有利于引导中学数学教学回归基础．试卷难度结构合理，由易到难，循序渐进，具有一定的梯度．今年数学试题与去年相比整体难度有所降低．“创新”是高考的生命线．与历年试卷对比，Ⅰ、Ⅱ卷解答题顺序有变，这也体现了对于套路性解题的变革，单纯地通过模仿老师的解题步骤而不用心去理解归纳，是难以拿到高分的．在数据处理能力以及应用意识和创新意识上的考查有所提升，也符合当前社会的大数据处理热潮和青少年创新性的趋势．全国Ⅰ、Ⅱ、Ⅲ卷对必修1集合与函数知识的考查，相对来说比较常规，难度不大，变化小，综合性低，属于基础类必得分试题，主要考查集合的概念及运算，函数的图象及定义域、值域、单调性、奇偶性、对称性、周期、最值等基本性质．做题时若能熟练应用概念及性质，掌握转化的技巧和方法，基本不会丢分。

若综合其他省市自主命题卷研究，必修1的知识又能与命题、不等式、导数、分段函数等知识综合，强化了数形结合思想、分类讨论思想、转化与化归的数学思想的运用，提高了试题的难度，所以作为高一学生来说，从必修1就应该打好牢固的基础，培养最基本的能力．下面列出了2018年全国Ⅰ、Ⅱ、Ⅲ卷及其他自主命题省市试卷必修1所考查的全部试题，请同学们根据所学必修1的知识，测试自己的能力，寻找自己的差距，把握高考的方向，认清命题的趋势！(说明：有些试题带有综合性，是与以后要学习内容的小综合试题，同学们可根据目前所学内容，有选择性地试做！)穿越自测一、选择题1．(2018·全国卷Ⅰ，文1)已知集合A＝{0,2}，B＝{－2，－1,0,1,2}，则A∩B＝( ) A．{0,2} B．{1,2}C．{0} D．{－2，－1,0,1,2}答案A解析根据集合交集中元素的特征，可以求得A∩B＝{0,2}，故选A.2．(2018·全国卷Ⅱ，文2)已知集合A＝{1,3,5,7}，B＝{2,3,4,5}，则A∩B＝( ) A．{3} B．{5}C．{3,5} D．{1,2,3,4,5,7}答案C解析∵A＝{1,3,5,7}，B＝{2,3,4,5}，∴A∩B＝{3,5}，故选C.3．(2018·某某卷，1)已知全集U＝{1,2,3,4,5}，A＝{1,3}，则∁U A＝( )A．∅B．{1,3}C．{2,4,5} D．{1,2,3,4,5}答案C解析因为全集U＝{1,2,3,4,5}，A＝{1,3}，所以根据补集的定义得，∁U A＝{2,4,5}，故选C.4．(2018·全国卷Ⅲ，文1)已知集合A＝{x|x－1≥0}，B＝{0,1,2}，则A∩B＝( ) A．{0} B．{1} C．{1,2} D．{0,1,2}答案C解析由集合A＝{x∈R|x≥1}，所以A∩B＝{1,2}，故选C.5．(2018·某某卷，文1)设集合A＝{1,2,3,4}，B＝{－1，0,2,3}，C＝{x∈R|－1≤x<2}，则(A∪B)∩C＝( )A．{－1,1} B．{0,1}C．{－1,0,1} D．{2,3,4}答案 C解析由并集的定义可得，A∪B＝{－1,0,1,2,3,4}，结合交集的定义可知，(A∪B)∩C ＝{－1,0,1}．故选C.6．(2018·某某卷，理1)设全集为R，集合A＝{x|0<x<2}，B＝{x|x≥1}，则A∩(∁R B)＝( )A．{x|0<x≤1} B．{x|0<x<1}C．{x|1≤x<2} D．{x|0<x<2}答案 B解析由题意可得，∁R B＝{x|x<1}，结合交集的定义可得，A∩(∁R B)＝{x|0<x<1}．故选B.7．(2018·卷，文1)已知集合A ＝{x ||x |<2}，B ＝{－2,0,1,2}，则A ∩B ＝( ) A ．{0,1} B ．{－1,0,1} C ．{－2,0,1,2} D ．{－1,0,1,2} 答案 A解析 A ＝{x ||x |<2}＝{x |－2<x <2}，B ＝{－2,0,1,2}，∴A ∩B ＝{0,1}．故选A. 8．(2018·全国卷Ⅰ，理2)已知集合A ＝{x |x 2－x －2>0}，则∁R A ＝( ) A ．{x |－1<x <2} B ．{x |－1≤x ≤2} C ．{x |x <－1}∪{x |x >2} D ．{x |x ≤－1}∪{x |x ≥2} 答案 B解析解不等式x 2－x －2>0，得x <－1或x >2，所以A ＝{x |x <－1或x >2}，于是∁R A ＝{x |－1≤x ≤2}，故选B.9．(2018·全国卷Ⅲ，文7)下列函数中，其图象与函数y ＝ln x 的图象关于直线x ＝1对称的是( )A ．y ＝ln (1－x )B ．y ＝ln (2－x )C ．y ＝ln (1＋x )D ．y ＝ln (2＋x ) 答案 B解析函数y ＝ln x 过定点(1,0)，(1,0)关于x ＝1对称的点还是(1,0)，只有y ＝ln (2－x )过此点．故B 正确．10．(2018·某某卷，理5)已知a ＝log 2e ，b ＝ln 2，c ＝log 1213，则a ，b ，c 的大小关系为( )A ．a >b >cB ．b >a >cC ．c >b >aD ．c >a >b 答案 D解析由题意结合对数函数的性质可知，a ＝log 2e>1，b ＝ln 2＝1log 2e ∈(0,1)，c ＝log1213＝log 23>log 2e ，据此可得，c >a >b .故选D.11．(2018·全国卷Ⅱ，文3)函数f (x )＝e x －e－xx2的图象大致为( )答案 B解析 ∵x ≠0，f (－x )＝e －x－e xx2＝－f (x )， ∴f (x )为奇函数，排除A ，∵f (1)＝e －e －1>0，∴排除D ；∵f (2)＝e 2－e －24＝4e 2－4e 216；f (4)＝e 4－e－416＝e 2·e 2－1e 416，∴f (2)<f (4)，排除C.因此选B.12．(2018·全国卷Ⅰ，理9)已知函数f (x )＝⎩⎪⎨⎪⎧e x，x ≤0，ln x ，x >0，g (x )＝f (x )＋x ＋a .若g (x )存在2个零点，则a 的取值X 围是( )A ．[－1,0)B ．[0，＋∞)C ．[－1，＋∞) D．[1，＋∞) 答案 C解析画出函数f (x )的图象，再画出直线y ＝－x ，之后上下移动，可以发现当直线过点A 时，直线与函数图象有两个交点，并且向下可以无限移动，都可以保证直线与函数的图象有两个交点，即方程f (x )＝－x －a 有两个解，也就是函数g (x )有两个零点，此时满足－a ≤1，即a ≥－1，故选C.13．(2018·全国卷Ⅰ，文12)设函数f (x )＝⎩⎪⎨⎪⎧2－x，x ≤0，1，x >0，则满足f (x ＋1)<f (2x )的x 的取值X 围是( )A ．(－∞，－1]B ．(0，＋∞)C ．(－1,0)D ．(－∞，0) 答案 D解析将函数f (x )的图象画出来，观察图象可知⎩⎪⎨⎪⎧2x <0，2x <x ＋1，解得x <0，所以满足f (x ＋1)<f (2x )的x 的取值X 围是(－∞，0)，故选D.14．(2018·全国卷Ⅲ，理12)设a ＝log 0.20.3，b ＝log 20.3，则( ) A ．a ＋b <ab <0 B ．ab <a ＋b <0 C ．a ＋b <0<ab D ．ab <0<a ＋b 答案 B解析 ∵a ＝log 0.20.3，b ＝log 20.3，∴1a ＝log 0.30.2，1b ＝log 0.32，∴1a ＋1b＝log 0.30.4，∴0<1a ＋1b <1，即0<a ＋b ab<1.又∵a >0，b <0，∴ab <0，即ab <a ＋b <0，故选B.二、填空题15．(2018·某某卷，1)已知集合A ＝{0,1,2,8}，B ＝{－1，1,6,8}，那么A ∩B ＝________. 答案 {1,8}解析由题设和交集的定义可知，A ∩B ＝{1,8}．16．(2018·某某卷，5)函数f (x )＝log 2x －1的定义域为________．答案 [2，＋∞)解析要使函数f (x )有意义，则log 2x －1≥0，解得x ≥2，即函数f (x )的定义域为[2，＋∞)．17．(2018·全国卷Ⅰ，文13)已知函数f (x )＝log 2(x 2＋a )，若f (3)＝1，则a ＝________. 答案－7解析根据题意有f (3)＝log 2(9＋a )＝1，可得9＋a ＝2，所以a ＝－7.18．(2018·全国卷Ⅲ，文16)已知函数f (x )＝ln (1＋x 2－x )＋1，f (a )＝4，则f (－a )＝________.答案－2解析 f (x )＋f (－x )＝ln (1＋x 2－x )＋1＋ln (1＋x 2＋x )＋1＝ln (1＋x 2－x 2)＋2＝2，∴f (a )＋f (－a )＝2，则f (－a )＝－2.19．(2018·卷，理13)能说明“若f (x )>f (0)对任意的x ∈(0,2]都成立，则f (x )在[0,2]上是增函数”为假命题的一个函数是________．答案 y ＝sin x (答案不唯一)解析令f (x )＝⎩⎪⎨⎪⎧0，x ＝0，4－x ，x ∈0，2]，则f (x )>f (0)对任意的x ∈(0,2]都成立，但f (x )在[0,2]上不是增函数．又如，令f (x )＝sin x ，则f (0)＝0，f (x )>f (0)对任意的x ∈(0,2]都成立，但f (x )在[0,2]上不是增函数．20．(2018·某某卷，9)函数f (x )满足f (x ＋4)＝f (x )(x ∈R )，且在区间(－2,2]上，f (x )＝⎩⎪⎨⎪⎧cos πx2，0<x ≤2，x ＋12，－2<x ≤0，则f [f (15)]的值为________．答案22解析由f (x ＋4)＝f (x )得函数f (x )的周期为4，所以f (15)＝f (16－1)＝f (－1)＝－1＋12＝12，因此f [f (15)]＝f 12＝cos π4＝22. 21．(2018·某某卷，15)已知λ∈R ，函数f (x )＝⎩⎪⎨⎪⎧x －4，x ≥λ，x 2－4x ＋3，x <λ，当λ＝2时，不等式f (x )<0的解集是________．若函数f (x )恰有2个零点，则λ的取值X 围是________．答案 (1,4) (1,3]∪(4，＋∞)解析由题意，得⎩⎪⎨⎪⎧x ≥2，x －4<0或⎩⎪⎨⎪⎧x <2，x 2－4x ＋3<0，所以2≤x <4或1<x <2，即1<x <4，不等式f (x )<0的解集是(1,4)，当λ>4时，f (x )＝x －4>0，此时f (x )＝x 2－4x ＋3＝0，x ＝1,3，即在(－∞，λ)上有两个零点；当λ≤4时，f (x )＝x －4＝0，x ＝4，由f (x )＝x 2－4x ＋3在(－∞，λ)上只能有一个零点，得1<λ≤3.综上，λ的取值X 围为(1,3]∪(4，＋∞)．22．(2018·某某卷，理14)已知a >0，函数f (x )＝⎩⎪⎨⎪⎧x 2＋2ax ＋a ，x ≤0，－x 2＋2ax －2a ，x >0.若关于x的方程f (x )＝ax 恰有2个互异的实数解，则a 的取值X 围是________．答案 (4,8)解析当x ≤0时，方程f (x )＝ax ，即x 2＋2ax ＋a ＝ax ，整理可得，x 2＝－a (x ＋1)，很明显x ＝－1不是方程的实数解，则a ＝－x 2x ＋1，当x >0时，方程f (x )＝ax ，即－x 2＋2ax －2a ＝ax ，整理可得，x 2＝a (x －2)，很明显x ＝2不是方程的实数解，则a ＝x 2x －2，令g (x )＝⎩⎪⎨⎪⎧－x 2x ＋1，x ≤0，x 2x －2，x >0，其中－x 2x ＋1＝－x ＋1＋1x ＋1－2，x 2x －2＝x －2＋4x －2＋4，原问题等价于函数g (x )与函数y ＝a 有两个不同的交点，求a 的取值X 围．结合对勾函数和函数图象平移的规律绘制函数g (x )的图象，同时绘制函数y ＝a 的图象如图所示，考查临界条件，结合a >0观察可得，实数a 的取值X 围是(4,8)．。

安徽省宁国中学2020-2021学年高一上学期第一次段考数学试题及答案

宁国中学20～21学年第一学期高一年级第一次段考数学试卷本试卷满分150分，考试时间120分钟.一、单项选择题:本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 全集U R =,{}20N x x =-<<,{}1-<=x x M ,则图中阴影部分表示的集合是A ．{}21x x -<<-B ．{}20x x -<<C ．{}|10x x -≤<D ．{}10x x -≤≤2. 满足条件{1,2,3}⊆M ⊂≠{1,2,3,4,5,6}的集合M 的个数是A. 6B. 7C. 8D. 53. 已知不等式的解集是，则a b +=A. 10-B. 6-C. 0D. 2 4. 设函数()02,0x f x x x≥=⎨<⎪⎩,若()()12f a f +-=,则=a A.12B. 2±C. 4D. 16 5. 函数()1y x x =-的图象的大致形状是A ．B ．C ．D ．6. 已知实数0,0x y >>，且24x y +=，则11x y+的最小值为 A B ．32 C ．34+ D ． 24+ 7. 已知偶函数()f x 在区间[)0,+∞上单调递增，则满足(21)(3)f x f -<的x 的范围是 A ．(1,2)- B ．[)0,2 C ．(),2-∞ D ．(,1)(2,)-∞-+∞8. 设函数{}22()min 3,f x x x x=--，x R ∈,若函数()y f x c =-的图象与x 轴恰有两个公共点,则实数c的取值范围是 A ．3[3,)4-- B ．3(3,)4-- C ．3(,3][2,]4-∞--- D ．3(,3)(2,)4-∞---二、多项选择题:本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，选对但不全的得3分，有选错的得0分.9. 下面四个条件中，是成立的充分条件的有A. B. C.a b > D. >10. 若命题为假命题，则a 的取值可以是A. 3-B.C.D. 20a -≤<11. 关于x 的方程2210x x m --+=的实数根情况，下列说法正确的有A. 当0m =时，方程有两个不等的实数根B. 当2m >时，方程没有实数根C. m R ∃∈, 方程有三个不等的实数根D. 不论m 取何值，方程不可能有4个实数根12. 已知函数()2+=x f y 是偶函数，且()x f y =在()2,0上是增函数，则下列结论中一定正确的有A. 函数()2y f x =- 是偶函数B. ()x f y =的图像关于直线2x =对称C. ()75122f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭ D. ()2y f x =在()1,2上单调递减三、填空题：本大题共4小题，每小题5分，共20分.13. 设命题2:,2p n N n n ∃∈>，则命题p 的否定是：．14. 函数1()2f x x =-的定义域是．15. 已知幂函数2()(3)m f x m x =- 在()0,+∞上为减函数，则(4)f -= ．16. 已知不等式224xy ax y ≤+对于0,0x y >>恒成立，则a 的取值范围是．四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算过程．17.（本题满分10分）已知集合{}{}|26,|18A x x B x x =≤<=<<,{}|3C x a x a =-<<．（Ⅰ）求,()R A B C A B ；（Ⅱ）若()C AB ⊆，求a 的取值范围．18．（本题满分12分）已知函数()f x 是定义在上的奇函数，且当时，2()2f x x x =+．（Ⅰ）求出函数()f x 在上的解析式，并补出函数()f x 在轴右侧的图像；（Ⅱ）①根据图像写出函数()f x 的单调递减区间；②若[]1,x m ∈-时,函数()f x 的值域是[]1,1-，求m 的取值范围．19.（本题满分12分）设集合2|04x A x x +⎧⎫=<⎨⎬-⎩⎭，集合{}22|320B x x ax a =-+=．（Ⅰ）当1a =时，判断""x B ∈是""x A ∈的什么条件，说明理由；（充分不必要，必要不充分，充要，既不充分也不必要）；（Ⅱ）是否存在实数a ，使A B ≠∅成立？若存在，求出实数a 的取值范围；若不存在，请说明理由．R 0x ≤Ry20. (本题满分12分)已知函数()2()326()f x ax a x a R =-++∈（Ⅰ）当1a =时，求()f x 在[)1,6x ∈上的值域；（Ⅱ）当0a >时,解关于x 的不等式：()0f x >．21. (本题满分12分)某书商为提高某套丛书的销售量，准备举办一场展销会.据市场调查，当每套丛书售价定为x 元时，销售量可达到()100.1x -万套.现出版社为配合该书商的活动，决定进行价格改革,每套丛书的供货价格分成固定价格和浮动价格两部分，其中固定价格为20元，浮动价格（单位：元）与销售量（单位：万套）成反比，比例系数为10.假设不计其他成本，即销售每套丛书的利润=售价-供货价格．（Ⅰ）求每套丛书利润y 与售价x 的函数关系，并求出每套丛书售价定为80元时，书商能获得的总利润是多少万元？（Ⅱ）每套丛书售价定为多少元时，每套丛书的利润最大？并求出最大利润．22. (本题满分12分)已知函数2()h x x bx c =++是偶函数，()(2)0,()h x h f x x-==．（Ⅰ）求函数()f x 的解析式，并证明在[]1,2上单调递增；（Ⅱ）设函数[]22164()2(),1,2,F x x a x x a R x x=+--∈∈，求函数()F x 的最小值()g a ．宁国中学20～21学年第一学期高一年级第一次段考数学参考答案一、选择题1~4：CBAD ， 5~8： BCAD ， 9：AD ， 10：ABD ， 11：ABC ， 12：BCD三、填空题13. 2,2n N n n ∀∈≤， 14. [)2,2−或{}|22x x −≤<， 15.116， 16. 4a ≥ 四、解答题17.解：（1）{}{}|18,|26R A B x x C A x x x =<<=<≥或，{}()|1268R C A B x x x =<<≤<或————————————5分（2）当C =∅时，332a a a −≥⇒≤————————————————7分当C ≠∅时，此时32a > 且3132282a a a a −≥⎧⇒≤<≤⎨≤⎩即——————————————9分综上：2a ≤——————————————————————10分18.解：（1）当0x >时，0x −<，则22()()22f x x x x x −=−−=−————2分因为()f x 为奇函数，则()()f x f x −=−，即0x >时，2()2f x x x =−+————————————————3分所以222,0()2,0x x x f x x x x ⎧+≤⎪=⎨−+>⎪⎩————————————————4分图略（注意关键点）———————————————————————6分，（2）如图可知，减区间为：()(),11+−∞−∞和，——————————————8分 (1)1f −=− ，(1)1f =———————————————————————9分令2222121012x x x x x ±−+=−⇒−−=⇒==11x x >∴=故由图可知1m ⎡⎤∈+⎣⎦————————————————————12分19.解：（1）{}{}|24,|()(2)0A x x B x x a x a =−<<=−−=当1a =时，{}1,2B =,—————————————————————2分1,2,,A A x B x A ∈∈∴∀∈∈——————————————————4分又,x A x B ∃∈∉,如3x =，则x B x A ∈∈是的充分不必要条件————6分（2）当0a =时，{}0B =,则{}0AB =,满足题意————————8分当0a ≠时，{},2B a a =，要使A B ≠∅,只要24224a a −<<−<<或————————10分即240a a −<<≠且综上：24a −<<—————————————————————12分20.解：（1）2()56f x x x =−+对称轴为[)51,62x =∈，——————————1分则最小值为52551()562424f =−⋅+=− ——————————3分又(1)2,(6)12f f ==，结合图像知值域为1,124⎡⎫−⎪⎢⎣⎭——————6分（2）2(32)6(3)(2)0ax a x ax x −++=−−>因为0a >所以当① 32a =时，2x ≠，解集为：{}|2x x ≠———————8分 ②302a <<时，32x x a <>或，解集为：3|2x x x a ⎧⎫<>⎨⎬⎩⎭或——10分 ③32a >时，32x x a <>或，解集为：3|2x x x a ⎧⎫<>⎨⎬⎩⎭或———12分 21.解：（1） 00100100.10x x x >⎧∴<<⎨−>⎩ ——————————————1分 10100(20)20(0100)100.1100y x x x x x=−+=−−<<−− ————3分当80x =时，10080205510080y =−−=−（元）————————4分此时销量为100.1802−⨯=（万件）总利润为255110⨯=（万元）————————————————6分（2）10020100y x x=−−− 01001000x x <<∴−>100[(100)]808060100y x x ∴=−+−+≤−+=−————10分当且仅当10010090100x x x=−⇒=− 即定价为90元时，每套利润最大为60元.————————————————12分 22.解：（1）因为()h x 为偶函数，所以()()h x h x −=————————————————1分即2220x bx c x bx c bx ++=−+⇒=因为x 为一切实数，所以0b =————————————————————2分又(2)404h c c −=+=⇒=− 则2()44()h x x f x x x x x−===−———————————————————3分证明：1212x x ∀≤<≤，12121212214444()()()()()f x f x x x x x x x x x −=−−−=−+− 12124()(1)x x x x =−⋅+⋅————————————————4分因为1212x x ≤<≤，则12124()(1)0x x x x −⋅+<⋅ 所以1212()()0()()f x f x f x f x −<⇒<即()f x 在[]1,2上单调递增——————————————————————6分（2）令4x t x−=，则由（1）知[]3,0t ∈−———————————————————7分则2()28F t t at =−+当3a <−时，min ()(3)617F t F a =−=+————————————————9分当30a −≤≤时，2min ()()8F t F a a ==−+——————————————10分当0a >时，min ()(0)8F t F ==————————————————————————11分故2617,3()8,308,0a a g a a a a +<−⎧⎪=−+−≤≤⎨⎪>⎩————————————————————————12分。

2018-2019学年第二学期期末考试高一年级数学试卷(含答案)

2018-2019学年第二学期期末考试高一年级数学试卷一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．某电视台在因特网上就观众对其某一节目的喜爱程度进行调查，参加调查的人数为20000人，其中持各种态度的人数如表所示：电视台为了了解观众的具体想法和意见，打算从中抽选出100人进行更为详细的调查，为此要进行分层抽样，那么在分层抽样时，每类人中各应抽选出的人数为（）A．25，25，25，25 B．48，72，64，16 C．20，40，30，10 D．24，36，32，82．某校为了解学生学习的情况，采用分层抽样的方法从高一1000人、高二1200人、高三n人中，抽取81人进行问卷调查．已知高二被抽取的人数为30，那么n=（）A．860 B．720 C．1020 D．10403. 在中，，，则等于（）A. 3B.C. 1D. 24．（1+tan20°）（1+tan25°）=（）A．2 B．1 C．﹣1 D．﹣25．在△ABC中，若sin2A+sin2B＜sin2C，则△ABC的形状是（）A．锐角三角形B．直角三角形C．钝角三角形D．不能确定6．如图，给出的是的值的一个程序框图，判断框内应填入的条件是（）A．i＜99 B．i≤99 C．i＞99 D．i≥997. 已知直线平面，直线平面，则下列命题正确的是（）A. 若，则B. 若，则C. 若，则D. 若，则8．已知过点P（0，2）的直线l与圆（x﹣1）2+y2=5相切，且与直线ax﹣2y+1=0垂直，则a=（）A．2 B．4 C．﹣4 D．19．《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂减上，余四约之，为实．一为从隔，开平方得积．”若把以上这段文字写成公式，即S=．现有周长为2+的△ABC满足sinA：sinB：sinC=（﹣1）：：（ +1），试用以上给出的公式求得△ABC的面积为（）A． B． C． D．10．天气预报说，在今后的三天中，每一天下雨的概率均为40%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数：907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计，这三天中恰有两天下雨的概率近似为（）A．0.35 B．0.25 C．0.20 D．0.1511．在区间（0，3]上随机取一个数x，则事件“0≤log2x≤1”发生的概率为（）A．B．C．D．12．已知函数f（x）=sin2x向左平移个单位后，得到函数y=g（x），下列关于y=g（x）的说法正确的是（）A．图象关于点（﹣，0）中心对称B．图象关于x=﹣轴对称C．在区间[﹣，﹣]单调递增D．在[﹣，]单调递减二、填空题（共4小题，每小题5分，满分20分）13．函数f（x）=Asin（ωx+φ）+b的图象如图所示，则f（x）的解析式为．14．在△ABC中，内角A、B、C所对应的边分别为a、b、c，若bsinA﹣acosB=0，则A+C= ．15. 已知直线的倾斜角为，则直线的斜率为__________．16．已知正实数x，y满足x+2y﹣xy=0，则x+2y的最小值为8y的取值范围是．三、解答题（本大题共6小题，共70分．第17题10分，其它均12分）17．某同学用“五点法”画函数f （x ）=Asin （ωx+φ）（ω＞0，|φ|＜）在某一个周期内的图象时，列表并填入了部分数据，如表：（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f （x ）的解析式；（2）将y=f （x ）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g （x ）的图象．若y=g （x ）图象的一个对称中心为（，0），求θ的最小值．18. 在中，内角所对的边分别为，且.（1）求；（2）若，且的面积为，求的值.19．设函数f （x ）=mx 2﹣mx ﹣1．若对一切实数x ，f （x ）＜0恒成立，求实数m 的取值范围．20．已知函数f （x ）=cosx （sinx+cosx ）﹣．（1）若0＜α＜，且sin α=，求f （α）的值；（2）求函数f （x ）的最小正周期及单调递增区间．21．根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如表（1）从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中，随机抽取2天，求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率；（2）将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图．①求图中a的值；②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．22．（12分）（2016秋•德化县校级期末）已知f（x）=sin2（2x﹣）﹣2t•sin（2x﹣）+t2﹣6t+1（x∈[，]）其最小值为g（t）．（1）求g（t）的表达式；（2）当﹣≤t≤1时，要使关于t的方程g（t）=kt有一个实根，求实数k的取值范围．参考答案：一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1.D2．D3.D4．A5．C6．B7. B8．C9．A10．B11．C12.C二、填空题（共4小题，每小题5分，满分20分）13．．14．120°． 15. 16． 8；（1，+∞）．三、解答题（本大题共6小题，共70分．第17题10分，其它均12分）17．（1）根据表中已知数据，解得A=5，ω=2，φ=﹣．数据补全如下表：且函数表达式为f（x）=5sin（2x﹣）．（2）由（Ⅰ）知f（x）=5sin（2x﹣），得g（x）=5sin（2x+2θ﹣）．因为y=sinx的对称中心为（kπ，0），k∈Z．令2x+2θ﹣=kπ，解得x=，k∈Z．由于函数y=g（x）的图象关于点（，0）成中心对称，令=，解得θ=，k∈Z．由θ＞0可知，当K=1时，θ取得最小值．18. (1) ；（2）. 19．（﹣4，0]．20．（1）∵0＜α＜，且sinα=，∴cosα=，∴f（α）=cosα（sinα+cosα）﹣=×（+）﹣=；（2）∵函数f（x）=cosx（sinx+cosx）﹣=sinxcosx+cos2x﹣=sin2x+﹣=（sin2x+cos2x）=sin（2x+），∴f（x）的最小正周期为T==π；令2kπ﹣≤2x+≤2kπ+，k∈Z，解得kπ﹣≤x≤kπ+，k∈Z；∴f（x）的单调增区间为[kπ﹣，kπ+]，k∈Z．．21．1） P==．（2）a=0.00422．（1）∵x∈[，]，∴sin（2x﹣）∈[﹣，1]，∴f（x）=[sin（2x﹣﹣t]2﹣6t+1，当t＜﹣时，则当sinx=﹣时，f（x）min=；当﹣≤t≤1时，当sinx=t时，f（x）min=﹣6t+1；当t＞1时，当sinx=1时，f（x）min=t2﹣8t+2；∴g（t）=（2）k≤﹣8或k≥﹣5．。

安徽省宁国中学2018-2019学年高一数学上学期期中试题(扫描版)

安徽省宁国中学2018-2019学年高一数学上学期期中试题（扫描版）宁国中学2018—2019学年度第一学期高一年级期中考试数学参考答案一、选择题二、填空题13、214、(,2)(2,4]-∞-- 15、n 16、[0,2] 三、简答题 17．(1) 1 (2) 2…………………………………………………………………………10分18．（1）{}|25A x x =≤<，{}{}|(3)(8)0|38B x x x x x =--<=<<， {}|38R C B x x x =≤≥或,……………………………………………………………………2分 {}{}|28,()|28R A B x x C A B x x x =≤<=<≥或………………………………5分 {}())|23R C B A x x =≤≤…………………………………………………………………8分(2) {}|3C x a x a =≤<+，{}|38B x x =<<若C B ⊆,则338a a <⎧⎨+≤⎩，35a a >⎧⎨≤⎩故35a <≤……………………………………………12分 19． (1)…………………………………………3分根据图像写出函数()f x 的增区间为[]1,1-……………………………………………………6分(2)函数()f x 在R 上的解析式为2220()20x x x f x x x x ⎧+≤⎪=⎨-+>⎪⎩，………………………………9分当[]1,3x ∈-时最小值为：(3)3f =- 最大值为：(1)1f =，()f x 的值域为[]3,1-…12分20．（1）()log (1)log (3)a a f x x x =++-的定义域为(1,3)-……………………………1分令log (1)log (3)0a a x x ++-=, log (1)(3)0a x x ⇒+-=(1)(3)1x x ⇒+-= ，即2220x x --= ， 1x =±经检验：1x =±()f x 的零点为15分(2)设()(1)(3)(1,3)g x x x x =+-∈-，()(0,4]g x ∈……………………………………7分当1a >时，函数()f x 有最大值log 4a ，无最小值。

安徽省宁国中学高一英语第二学期第一次段考新人教版

宁国中学高一年级第二学期第一次段考试卷英语学科第Ⅰ卷（三部分，共115分）第一部分：听力（共两小节，满分30分）第一节（共5小题；每小题1.5分,满分7.5分）听下面5段对话.每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What is the man doing?A. Making a phone call.B. Making a visitC. Making an appointment2. When did the man leave the gate?A. At about 12:00B. At about 12:30C. At about 1:00What3. Where does the conversation most probably take place?A. At a railway stationB. At a booking office.C. On a bridge.4. What does the man do?A. A taxi driverB. A policemanC. A cinema manager5. How did the woman go to school today?A. By bikeB. By busC. On foot.第二节（共15小题；每小题1.5分,满分22.5分）听下面5段对话或独白.每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

6. What will the woman do tomorrow morning?A. Have a restB. Go shoppingC. Visit London7. Where are the speakers going to have lunch?A. At homeB. In a shopping centerC. In a restaurant.听第7段材料，回答第8至10题。

宁国市第一中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市第一中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1．如图是某几何体的三视图，则该几何体任意两个顶点间的距离的最大值为（）A ．4B ．5C ．D．2．数列{a n }满足a n+2=2a n+1﹣a n ，且a 2014，a 2016是函数f （x ）=+6x ﹣1的极值点，则log 2（a 2000+a 2012+a 2018+a 2030）的值是（）A ．2B ．3C ．4D ．53．边长为2的正方形ABCD 的定点都在同一球面上，球心到平面ABCD 的距离为1，则此球的表面积为（）A ．3πB ．5πC ．12πD ．20π4．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若﹣+1=0，则角B 的度数是（）A ．60°B ．120°C ．150°D ．60°或120°5．若实数x ，y 满足不等式组则2x+4y 的最小值是（）A ．6B ．﹣6C ．4D ．26．若，，则不等式成立的概率为（）[]0,1b ∈221a b +≤A ．B ．C ．D ．16π12π8π4π7．已知向量=（1，），=（，x ）共线，则实数x 的值为（）A ．1B ．C ．tan35°D ．tan35°8．经过点且在两轴上截距相等的直线是（）()1,1M A ． B ．20x y +-=10x y +-=C ．或D ．或1x =1y =20x y +-=0x y -=9．函数f （x ）=e ln|x|+的大致图象为（）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．B ．C ．D ．10．已知幂函数y=f （x ）的图象过点（，），则f （2）的值为（）A ．B ．﹣C ．2D ．﹣211．设公差不为零的等差数列的前项和为，若，则（）{}n a n n S 4232()a a a =+74S a = A ．B ．C ．7D ．1474145【命题意图】本题考查等差数列的通项公式及其前项和，意在考查运算求解能力.n 12．已知是虚数单位，若复数在复平面内对应的点在第四象限，则实数的值可以是（）22aiZ i+=+A ．-2B ．1C ．2D ．3二、填空题13．【盐城中学2018届高三上第一次阶段性考试】已知函数f （x ）=，对任意的m ∈[﹣2，2]，f （mx ﹣3x x +2）+f （x ）＜0恒成立，则x 的取值范围为_____．14．已知[2,2]a ∈-，不等式2(4)420x a x a +-+->恒成立，则的取值范围为__________.15．在中，角的对边分别为，若，的面积，ABC ∆A B C 、、a bc 、、1cos 2c B a b ⋅=+ABC∆S =则边的最小值为_______．c 【命题意图】本题考查正弦定理、余弦定理、三角形面积公式、基本不等式等基础知识，意在考查基本运算能力．16．已知双曲线﹣=1（a ＞0，b ＞0）的一条渐近线方程是y=x ，它的一个焦点在抛物线y 2=48x 的准线上，则双曲线的方程是．17．定义为与中值的较小者，则函数的取值范围是 )}(),(min{x g x f )(x f )(x g },2min{)(2x x x f -=18．【启东中学2018届高三上学期第一次月考（10月）】在平面直角坐标系xOy 中，P 是曲线上xC y e ：＝一点，直线经过点P ，且与曲线C 在P 点处的切线垂直，则实数c 的值为________．20l x y c ：＋＋＝三、解答题19．已知函数f （x ）=log 2（m+）（m ∈R ，且m ＞0）．（1）求函数f （x ）的定义域；（2）若函数f （x ）在（4，+∞）上单调递增，求m 的取值范围．20．已知函数，，．()xf x e x a =-+21()x g x x a e=++a R ∈（1）求函数的单调区间；()f x （2）若存在，使得成立，求的取值范围；[]0,2x ∈()()f x g x <（3）设，是函数的两个不同零点，求证：．1x 2x ()f x 121x x e +<21．设数列{a n }的前n 项和为S n ，a 1=1，S n =na n ﹣n （n ﹣1）．（1）求证：数列{a n }为等差数列，并分别求出a n 的表达式；（2）设数列的前n 项和为P n ，求证：P n ＜；（3）设C n =，T n =C 1+C 2+…+C n ，试比较T n 与的大小．22．在等比数列{a n }中，a 2=3，a 5=81．（Ⅰ）求a n ；（Ⅱ）设b n =log 3a n ，求数列{b n }的前n 项和S n ．　23．如图，已知AC，BD为圆O的任意两条直径，直线AE，CF是圆O所在平面的两条垂线，且线段AE=CF=，AC=2．（Ⅰ）证明AD⊥BE；（Ⅱ）求多面体EF﹣ABCD体积的最大值．24．已知函数f（x）=e x﹣ax﹣1（a＞0，e为自然对数的底数）．（1）求函数f（x）的最小值；（2）若f（x）≥0对任意的x∈R恒成立，求实数a的值．宁国市第一中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1．【答案】D 【解析】试题分析：因为根据几何体的三视图可得，几何体为下图相互垂直，面面,,AD AB AG AEFG ⊥,根据几何体的性质得：,//,3,1ABCDE BC AE AB AD AG DE ====AC GC ==,所以最长为．GE ===4,BG AD EF CE ====GC =考点：几何体的三视图及几何体的结构特征．2．【答案】C【解析】解：函数f （x ）=+6x ﹣1，可得f ′（x ）=x 2﹣8x+6，∵a 2014，a 2016是函数f （x ）=+6x ﹣1的极值点，∴a 2014，a 2016是方程x 2﹣8x+6=0的两实数根，则a 2014+a 2016=8．数列{a n }中，满足a n+2=2a n+1﹣a n ，可知{a n }为等差数列，∴a 2014+a 2016=a 2000+a 2030，即a 2000+a 2012+a 2018+a 2030=16，从而log 2（a 2000+a 2012+a 2018+a 2030）=log 216=4．故选：C ．【点评】熟练掌握利用导数研究函数的极值、等差数列的性质及其对数的运算法则是解题的关键．　3．【答案】C【解析】解：∵正方形的边长为2，∴正方形的对角线长为=2，∵球心到平面ABCD 的距离为1，∴球的半径R==，则此球的表面积为S=4πR 2=12π．故选：C ．【点评】此题考查了球的体积和表面积，求出球的半径是解本题的关键．　4．【答案】A【解析】解：根据正弦定理有： =，代入已知等式得：﹣+1=0，即﹣1=，整理得：2sinAcosB﹣cosBsinC=sinBcosC，即2sinAcosB=sinBcosC+cosBsinC=sin（B+C），又∵A+B+C=180°，∴sin（B+C）=sinA，可得2sinAcosB=sinA，∵sinA≠0，∴2cosB=1，即cosB=，则B=60°．故选：A．【点评】此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．　5．【答案】B【解析】解：作出不等式组对应的平面区域如图：设z=2x+4y得y=﹣x+，平移直线y=﹣x+，由图象可知当直线y=﹣x+经过点C时，直线y=﹣x+的截距最小，此时z最小，由，解得，即C（3，﹣3），此时z=2x+4y=2×3+4×（﹣3）=6﹣12=﹣6．故选：B【点评】本题主要考查线性规划的应用，利用目标函数的几何意义是解决本题的关键．6．【答案】D【解析】考点：几何概型．7．【答案】B【解析】解：∵向量=（1，），=（，x）共线，∴x====，故选：B．【点评】本题考查了向量的共线的条件和三角函数的化简，属于基础题．8．【答案】D【解析】考点：直线的方程.9．【答案】C【解析】解：∵f（x）=e ln|x|+∴f（﹣x）=e ln|x|﹣f（﹣x）与f（x）即不恒等，也不恒反，故函数f（x）为非奇非偶函数，其图象不关于原点对称，也不关于y轴对称，可排除A，D，当x→0+时，y→+∞，故排除B故选：C．10．【答案】A【解析】解：设幂函数y=f （x ）=x α，把点（，）代入可得=α，∴α=，即f （x ）=，故f （2）==，故选：A ．　11．【答案】C.【解析】根据等差数列的性质，，化简得，∴4231112()32(2)a a a a d a d a d =+⇒+=+++1a d =-，故选C.1741767142732a dS d a a d d⋅+===+12．【答案】A 【解析】试题分析：，对应点在第四象限，故，A 选项正确.()()()()2224(22)2225ai i ai a a ii i i +-+++-==++-40220a a +>⎧⎨-<⎩考点：复数运算．二、填空题13．【答案】22,3⎛⎫- ⎪⎝⎭【解析】14．【答案】(,0)(4,)-∞+∞U 【解析】试题分析：把原不等式看成是关于的一次不等式,在2]，[-2a ∈时恒成立,只要满足在2]，[-2a ∈时直线在轴上方即可，设关于的函数44)2(24)4(x f(x)y 22+-+-=-+-+==x x a x a x a 对任意的2]，[-2a ∈，当-2a =时，044)42(x )2(f(a)y 2>++--+=-==x f ，即086x )2(2>+-=-x f ，解得4x 2x ><或；当2a =时，044)42(x )2(y 2>-+-+==x f ，即02x )2(2>-=x f ，解得2x 0x ><或，∴的取值范围是{x|x 0x 4}<>或；故答案为：(,0)(4,)-∞+∞U ．考点：换主元法解决不等式恒成立问题.【方法点晴】本题考查了含有参数的一元二次不等式得解法，解题时应用更换主元的方法，使繁杂问题变得简洁，是易错题．把原不等式看成是关于的一次不等式,在2]，[-2a ∈时恒成立,只要满足在2]，[-2a ∈时直线在轴上方即可.关键是换主元需要满足两个条件，一是函数必须是关于这个量的一次函数，二是要有这个量的具体范围.15．【答案】116．【答案】【解析】解：因为抛物线y 2=48x 的准线方程为x=﹣12，则由题意知，点F （﹣12，0）是双曲线的左焦点，所以a 2+b 2=c 2=144，又双曲线的一条渐近线方程是y=x ，所以=，解得a 2=36，b 2=108，所以双曲线的方程为．故答案为：．【点评】本题考查双曲线的标准方程，以及双曲线的简单性质的应用，确定c 和a 2的值，是解题的关键．　17．【答案】(],1-∞【解析】试题分析：函数的图象如下图：(){}2min 2,f x x x =-观察上图可知：的取值范围是。

2017-2018学年度人教版高一第一学期期末质量检测语文试题含答案

2017-2018学年度人教版高一第一学期期末质量检测语文试题含答案2017-2018学年高一第一学期期末质量检测语文科试卷考试时间：150分钟；满分：150分；共23小题友情提示：请将答案填涂在答题卡的相应位置上，答在本试卷上一律无效一、现代文阅读（每小题3分，共9分）读下面文字，完成1-3题。

很多人说：什么是意境？意境就是“情”“景”交融。

其实这种解释应该是从近代开始的。

XXX在《人间词话》中所使用的“意境”或“境界”，他的解释就是情景交融。

但是在中国传统美学中，情景交融所规定的是“意象”，而不是“意境”。

中国传统美学认为艺术的本体就是意象，任何艺术作品都要创造意象，都应该情景交融，而意境则不是任何艺术作品都具有的。

意境除了有意象的一般规定性之外，还有自己的特殊规定性，意境的内涵大于意象，意境的外延小于意象。

那么意境的特殊规定性是什么呢？唐代XXX有句话：“境生于象外。

”“境”是对于在时间和空间上有限的“象”的突破，只有这种象外之“境”才能体现作为宇宙的本体和生命的“道”。

从审美活动的角度看，所谓“意境”，就是超越具体的有限的物象、事件、场景，进入无限的时间和空间，从而对整个人生、历史、宇宙获得一种哲理性的感受和领悟。

西方古代艺术家，他们给自己提出的任务是要再现一个具体的物象，所以他们，比如古希腊雕塑家追求“美”，就把人体刻画得非常逼真、非常完美。

而中国艺术家不是局限于刻画单个的人体或物体，把这个有限的对象刻画得很逼真、很完美。

相反，他们追求一种“象外之象”、“景外之景”。

中国园林艺术在审美上的最大特点也是有意境。

中国古典园林中的楼、台、亭、阁，它们的审美价值主要不在于这些建筑本身，而是如同XXX《兰亭集序》所说，在于可使人“仰观宇宙之大，俯察品类之盛。

我们生活的世界是一个成心味的世界。

XXX有两句诗说得好：“此中有真意，欲辩已忘言。

”艺术就是要去寻找、发现、体验生活中的这种意味。

成心境的作品和普通的艺术作品在这一点的区别，就在于它不但揭示了生活中某一个具体事物或具体事件的意味，并且超出了具体的事物和事件，从一个角度揭示了整个人生的意味。

安徽省宁国中学高一数学第二次段考

宁国中学度第一学期高一年级第二次段考数学试卷本试卷分第I 卷和第II 卷两部分。

全卷满分150分，考试时间120分钟。

第I 卷（选择题共50分）一．选择题：（本大题共10小题，每小题5分，共50分）1．已知集合A=｛x|x －m=0｝，B=｛x|mx －1=0｝，若A ∩B=B ，则m 等于（）A ．1B ．0或1C ．－1或1D ．0或1或－12．若23=a ，则=-8363log log 2（）A ．12+-a a B. a a 32- C. a -2 D. a 52-3. 已知0tan cos <⋅θθ，那么角θ是（）A ．第一或第二象限角 B. 第二或第三象限角C. 第三或第四象限角D. 第一或第四象限角4. 函数是R 上的偶函数，则ϕ的值是（）A B C D 5 设是定义域为R ，最小正周期为的函数，若则等于（） A 1B 2C 0 D2- 6．方程521=+-x x 的解所在的区间是（） A ．（0, 1） B （1, 2） C （2, 3） D （3, 4）7．若0lg lg =+b a ,（1,1≠≠b a ）,则函数x a x f =)( 与x b x g =)(的图像（）A ．关于直线y =x 对称B ．关于x 轴对称C ．关于y 轴对称D ．关于原点对称cos ,(0)(),2sin ,(0)x x f x x x ππ⎧-≤<⎪=⎨⎪≤<⎩sin(2)(0)y x ϕϕπ=+≤≤4π2π()f x 32π15()4f π-π08. 如果函数()sin()(02)f x x πθθπ=+<<的最小正周期是T ,且当2x =时取得最大值,那么（） A 2,2T πθ==B 1,T θπ==C 2,T θπ==D 1,2T πθ==9．函数sin()(0,,)2y A x x R πωϕωϕ=+><∈的部分图象如图所示，则函数表达（）A ．)48sin(4π+π-=x yB ．)48sin(4π-π=x y C ．)48sin(4π-π-=x y D ． )48sin(4π+π=x y10.将函数sin()3y x π=-的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是（） A. 1sin 2y x = B 1sin()22y x π=- C 1sin()26y x π=- D sin(2)6y x π=-第II 卷（非选择题共100分）二．填空题：（共5小题，每小题5分，共25分）11.函数tan()3y x π=+的定义域为。

宁国市第一中学校2018-2019学年高二上学期第二次月考试卷数学

宁国市第一中学校2018-2019学年高二上学期第二次月考试卷数学班级__________ 姓名__________ 分数__________一、选择题1．设=（1，2），=（1，1），=+k ，若，则实数k 的值等于（）A ．﹣B ．﹣C ．D ．2．在△ABC 中，b=，c=3，B=30°，则a=（）A ．B ．2C ．或2D ．23．已知双曲线和离心率为4sinπ的椭圆有相同的焦点21F F 、，P 是两曲线的一个公共点，若 21cos 21=∠PF F ，则双曲线的离心率等于（） A ． B ．25 C ．26 D ．274．已知函数f （x ）=Asin （ωx ﹣）（A ＞0，ω＞0）的部分图象如图所示，△EFG 是边长为2 的等边三角形，为了得到g （x ）=Asin ωx 的图象，只需将f （x ）的图象（）A ．向左平移个长度单位B ．向右平移个长度单位C ．向左平移个长度单位 D ．向右平移个长度单位5．命题“∀x ∈R ，2x 2+1＞0”的否定是（）A ．∀x ∈R ，2x 2+1≤0B ．C ．D ．6．设复数z 满足z （1+i ）=2（i 为虚数单位），则z=（）A ．1﹣iB ．1+iC ．﹣1﹣iD ．﹣1+i7．函数f （x ）=tan （2x+），则（）A ．函数最小正周期为π，且在（﹣，）是增函数B ．函数最小正周期为，且在（﹣，）是减函数C ．函数最小正周期为π，且在（，）是减函数D ．函数最小正周期为，且在（，）是增函数8．是z 的共轭复数，若z+=2，（z ﹣）i=2（i 为虚数单位），则z=（） A ．1+i B ．﹣1﹣iC ．﹣1+iD ．1﹣i9．如图所示，函数y=|2x ﹣2|的图象是（）A ．B ．C ．D ．10．四面体ABCD 中,截面 PQMN 是正方形，则在下列结论中，下列说法错误的是（）A ．AC BD ⊥B ．AC BD =C.AC PQMN D ．异面直线PM 与BD 所成的角为4511．已知抛物线C ：24y x =的焦点为F ，定点(0,2)A ，若射线FA 与抛物线C 交于点M ，与抛物线C 的准线交于点N ，则||:||MN FN 的值是（）A ．B ．C ．1:D (1 12．某人以15万元买了一辆汽车，此汽车将以每年20%的速度折旧，如图是描述汽车价值变化的算法流程图，则当n=4吋，最后输出的S 的值为（）A ．9.6B ．7.68C ．6.144D ．4.9152二、填空题13在这段时间内，该车每100千米平均耗油量为升．14．在ABC ∆中，有等式：①sin sin a A b B =；②sin sin a B b A =；③cos cos a B b A =；④sin sin sin a b cA B C+=+.其中恒成立的等式序号为_________. 15．等比数列{a n }的前n 项和为S n ，已知S 3=a 1+3a 2，则公比q= ． 16．定义在R 上的偶函数f （x ）在[0，+∞）上是增函数，且f （2）=0，则不等式f （log 8x ）＞0的解集是．17．在△ABC 中，点D 在边AB 上，CD ⊥BC ，AC=5，CD=5，BD=2AD ，则AD 的长为．18．命题：“∀x ∈R ，都有x 3≥1”的否定形式为．三、解答题19．已知数列a1，a2，…a30，其中a1，a2，…a10，是首项为1，公差为1的等差数列；列a10，a11，…a20，是公差为d的等差数列；a20，a21，…a30，是公差为d2的等差数列（d≠0）．（1）若a20=40，求d；（2）试写出a30关于d的关系式，并求a30的取值范围；（3）续写已知数列，使得a30，a31，…a40，是公差为d3的等差数列，…，依此类推，把已知数列推广为无穷数列．提出同（2）类似的问题（（2）应当作为特例），并进行研究，你能得到什么样的结论？20．等差数列{a n}的前n项和为S n．a3=2，S8=22．（1）求{a n}的通项公式；（2）设b n=，求数列{b n}的前n项和T n．21．本小题满分12分某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求，剩余商品全部退回，但每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利30元.Ⅰ若商店一天购进该商品10件,求当天的利润y单位:元关于当天需求量n单位:件,n∈N的函数解析式；,整理得下表:,求这50天的日利润单位:元的平均数；②若该店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间[400,550]内的概率.22．已知函数，且．（Ⅰ）求的解析式；（Ⅱ）若对于任意，都有，求的最小值；（Ⅲ）证明：函数的图象在直线的下方．23．为了培养中学生良好的课外阅读习惯，教育局拟向全市中学生建议一周课外阅读时间不少于t0小时．为此，教育局组织有关专家到某“基地校”随机抽取100名学生进行调研，获得他们一周课外阅读时间的数据，整理得到如图频率分布直方图：（Ⅰ）求任选2人中，恰有1人一周课外阅读时间在[2，4）（单位：小时）的概率（Ⅱ）专家调研决定：以该校80%的学生都达到的一周课外阅读时间为t0，试确定t0的取值范围24．（本题满分15分）如图AB 是圆O 的直径，C 是弧AB 上一点，VC 垂直圆O 所在平面，D ，E 分别为VA ，VC 的中点. （1）求证：DE ⊥平面VBC ；（2）若6VC CA ==，圆O 的半径为5，求BE 与平面BCD 所成角的正弦值.【命题意图】本题考查空间点、线、面位置关系，线面等基础知识，意在考查空间想象能力和运算求解能力．宁国市第一中学校2018-2019学年高二上学期第二次月考试卷数学（参考答案）一、选择题1．【答案】A【解析】解：∵ =（1，2），=（1，1），∴=+k =（1+k ，2+k ）∵，∴ =0，∴1+k+2+k=0，解得k=﹣故选：A【点评】本题考查数量积和向量的垂直关系，属基础题．2．【答案】C 【解析】解：∵b=，c=3，B=30°，∴由余弦定理b 2=a 2+c 2﹣2accosB ，可得：3=9+a 2﹣3，整理可得：a 2﹣3a+6=0，∴解得：a=或2．故选：C ．3．【答案】C 【解析】试题分析：设椭圆的长半轴长为1a ，双曲线的实半轴长为2a ，焦距为c 2，m PF =1，n PF =2，且不妨设n m >，由12a n m =+，22a n m =-得21a a m +=，21a a n -=，又21c os 21=∠PF F ，∴由余弦定理可知：mn n m c -+=2224，2221234a a c +=∴，432221=+∴c a c a ，设双曲线的离心率为，则4322122=+e）（，解得26=e .故答案选C ．考点：椭圆的简单性质．【思路点晴】本题主要考查圆锥曲线的定义和离心率.根据椭圆和双曲线的定义，由P 为公共点，可把焦半径1PF 、2PF 的长度用椭圆的半长轴以及双曲线的半实轴21,a a 来表示，接着用余弦定理表示21cos 21=∠PF F ，成为一个关于21,a a 以及的齐次式，等式两边同时除以2c ，即可求得离心率.圆锥曲线问题在选择填空中以考查定义和几何性质为主. 4．【答案】 A【解析】解：∵△EFG是边长为2的正三角形，∴三角形的高为，即A=，函数的周期T=2FG=4，即T==4，解得ω==，即f（x）=Asinωx=sin（x﹣），g（x）=sin x，由于f（x）=sin（x﹣）=sin[（x﹣）]，故为了得到g（x）=Asinωx的图象，只需将f（x）的图象向左平移个长度单位．故选：A．【点评】本题主要考查三角函数的图象和性质，利用函数的图象确定函数的解析式是解决本题的关键，属于中档题．5．【答案】C【解析】解：∵命题∀x∈R，2x2+1＞0是全称命题，∴根据全称命题的否定是特称命题得命题的否定是：“”，．故选：C．【点评】本题主要考查含有量词的命题的否定，要求掌握特称命题的否定是全称命题，全称命题的否定是特称命题，比较基础．6．【答案】A【解析】解：∵z（1+i）=2，∴z===1﹣i．故选：A．【点评】本题考查了复数的运算法则、共轭复数的定义，属于基础题．7．【答案】D【解析】解：对于函数f（x）=tan（2x+），它的最小正周期为，在（，）上，2x+∈（，），函数f（x）=tan（2x+）单调递增，故选：D．8．【答案】D【解析】解：由于，（z ﹣）i=2，可得z ﹣=﹣2i ①又z+=2 ②由①②解得z=1﹣i 故选D ．9．【答案】B【解析】解：∵y=|2x﹣2|=，∴x=1时，y=0， x ≠1时，y ＞0．故选B ．【点评】本题考查指数函数的图象和性质，解题时要结合图象进行求解．10．【答案】B 【解析】试题分析：因为截面PQMN 是正方形，所以//,//PQ MN QM PN ，则//PQ 平面,//ACD QM 平面BDA ，所以//,//PQ AC QM BD ,由PQ QM ⊥可得AC BD ⊥，所以A 正确；由于//PQ AC 可得//AC 截面PQMN ，所以C 正确；因为PN PQ ⊥，所以AC BD ⊥，由//BD PN ，所以MPN ∠是异面直线PM 与BD所成的角，且为045，所以D 正确；由上面可知//,//BD PN PQ AC ，所以,PN AN MN DN BD AD AC AD==，而,AN DN PN MN ≠=，所以BD AC ≠，所以B 是错误的，故选B. 1考点：空间直线与平面的位置关系的判定与证明.【方法点晴】本题主要考查了空间中直线与平面的位置关系的判定与证明，其中解答中涉及到直线与平面平行的判定定理和性质定理、正方形的性质、异面直线所成的角等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，属于中档试题，此类问题的解答中熟记点、线、面的位置关系的判定定理和性质定理是解答的关键. 11．【答案】D 【解析】考点：1、抛物线的定义；2、抛物线的简单性质.【方法点睛】本题主要考查抛物线的定义和抛物线的简单性质，属于难题.与焦点、准线有关的问题一般情况下都与拋物线的定义有关，解决这类问题一定要注意点到点的距离与点到直线的距离的转化：（1）将抛物线上的点到准线距转化为该点到焦点的距离；（2）将抛物线上的点到焦点的距离转化为到准线的距离，使问题得到解决.本题就是将M到焦点的距离转化为到准线的距离后进行解答的.12．【答案】C【解析】解：由题意可知，设汽车x年后的价值为S，则S=15（1﹣20%）x，结合程序框图易得当n=4时，S=15（1﹣20%）4=6.144．故选：C．二、填空题13．【答案】8升．【解析】解：由表格信息，得到该车加了48升的汽油，跑了600千米，所以该车每100千米平均耗油量48÷6=8．故答案是：8．14．【答案】②④【解析】试题分析：对于①中，由正弦定理可知sin sin a A b B =，推出A B =或2A B π+=，所以三角形为等腰三角形或直角三角形，所以不正确；对于②中，sin sin a B b A =，即sin sin sin sin A B B A =恒成立，所以是正确的；对于③中，cos cos a B b A =，可得sin()0B A -=，不满足一般三角形，所以不正确；对于④中，由正弦定理以及合分比定理可知sin sin sin a b cA B C+=+是正确，故选选②④．1 考点：正弦定理；三角恒等变换． 15．【答案】 2 ．【解析】解：设等比数列的公比为q ，由S 3=a 1+3a 2，当q=1时，上式显然不成立；当q ≠1时，得，即q 2﹣3q+2=0，解得：q=2．故答案为：2．【点评】本题考查了等比数列的前n 项和，考查了等比数列的通项公式，是基础的计算题．16．【答案】（0，）∪（64，+∞）．【解析】解：∵f （x ）是定义在R 上的偶函数， ∴f （log 8x ）＞0，等价为：f （|log 8x|）＞f （2），又f （x ）在[0，+∞）上为增函数， ∴|log 8x|＞2，∴log 8x ＞2或log 8x ＜﹣2，∴x ＞64或0＜x ＜．即不等式的解集为{x|x ＞64或0＜x ＜}故答案为：（0，）∪（64，+∞）【点评】本题考查函数奇偶性与单调性的综合，是函数性质综合考查题，熟练掌握奇偶性与单调性的对应关系是解答的关键，根据偶函数的对称性将不等式进行转化是解决本题的关键．17．【答案】 5 ．【解析】解：如图所示：延长BC，过A做AE⊥BC，垂足为E，∵CD⊥BC，∴CD∥AE，∵CD=5，BD=2AD，∴，解得AE=，在RT△ACE，CE===，由得BC=2CE=5，在RT△BCD中，BD===10，则AD=5，故答案为：5．【点评】本题考查平行线的性质，以及勾股定理，做出辅助线是解题的关键，属于中档题．18．【答案】∃x0∈R，都有x03＜1．【解析】解：因为全称命题的否定是特称命题．所以，命题：“∀x∈R，都有x3≥1”的否定形式为：命题：“∃x0∈R，都有x03＜1”．故答案为：∃x0∈R，都有x03＜1．【点评】本题考查全称命题与特称命题的否定关系，基本知识的考查．三、解答题19．【答案】【解析】解：（1）a10=1+9=10．a20=10+10d=40，∴d=3．（2）a30=a20+10d2=10（1+d+d2）（d≠0），a30=10，当d∈（﹣∞，0）∪（0，+∞）时，a30∈[7.5，+∞）（3）所给数列可推广为无穷数列{a n]，其中a1，a2，…，a10是首项为1，公差为1的等差数列，当n ≥1时，数列a 10n ，a 10n+1，…，a 10（n+1）是公差为d n的等差数列．研究的问题可以是：试写出a 10（n+1）关于d 的关系式，并求a 10（n+1）的取值范围．研究的结论可以是：由a 40=a 30+10d 3=10（1+d+d 2+d 3），依此类推可得a 10（n+1）=10（1+d+…+d n）=．当d ＞0时，a 10（n+1）的取值范围为（10，+∞）等．【点评】此题考查学生灵活运用等差数列的性质解决实际问题，会根据特例总结归纳出一般性的规律，是一道中档题．20．【答案】【解析】解：（1）设等差数列{a n }的公差为d ，∵a 3=2，S 8=22．∴，解得，∴{a n }的通项公式为a n =1+（n ﹣1）=．（2）∵b n ===﹣，∴T n =2+…+=2=．21．【答案】【解析】：Ⅰ当日需求量10n ≥时,利润为5010(10)3030200y n n =⨯+-⨯=+；当需求量10n <时，利润50(10)1060100y n n n =⨯--⨯=-. 所以利润y 与日需求量n 的函数关系式为：30200,10,60100,10,n n n Ny n n n N+≥∈⎧=⎨-<∈⎩Ⅱ50天内有9天获得的利润380元，有11天获得的利润为440元，有15天获得利润为500元，有10天获得的利润为530元，有5天获得的利润为560元.① 38094401150015530105605477.250⨯+⨯+⨯+⨯+⨯= ② 若利润在区间[400,550]内的概率为111510185025P ++==22．【答案】【解析】【知识点】导数的综合运用利用导数研究函数的单调性【试题解析】（Ⅰ）对求导，得，所以，解得，所以．（Ⅱ）由，得，因为，所以对于任意，都有．设，则．令，解得．当x 变化时，与的变化情况如下表：所以当时，．因为对于任意，都有成立，所以．所以的最小值为．（Ⅲ）证明：“函数的图象在直线的下方”等价于“”，即要证，所以只要证．由（Ⅱ），得，即（当且仅当时等号成立）．所以只要证明当时，即可．设，所以，令，解得．由，得，所以在上为增函数．所以，即．所以．故函数的图象在直线的下方． 23．【答案】【解析】解：（Ⅰ）一周课外阅读时间在[0，2）的学生人数为0.010×2×100=2人，一周课外阅读时间在[2，4）的学生人数为0.015×2×100=3人，记一周课外阅读时间在[0，2）的学生为A ，B ，一周课外阅读时间在[2，4）的学生为C ，D ，E ，从5人中选取2人，得到基本事件有AB ，AC ，AD ，AE ，BC ，BD ，BE ，CD ，CE ，DE 共有10个基本事件，记“任选2人中，恰有1人一周课外阅读时间在[2，4）”为事件M ，其中事件M 包含AC ，AD ，AE ，BD ，BC ，BE ，共有6个基本事件，所以P （M ）==，即恰有1人一周课外阅读时间在[2，4）的概率为．（Ⅱ）以该校80%的学生都达到的一周课外阅读时间为t 0，即一周课外阅读时间未达到t 0的学生占20%，由（Ⅰ）知课外阅读时间落在[0，2）的频率为P 1=0.02，课外阅读时间落在[2，4）的频率为P 2=0.03，课外阅读时间落在[4，6）的频率为P 3=0.05，课外阅读时间落在[6，8）的频率为P 1=0.2，因为P 1+P 2+P 3＜0.2，且P 1+P 2+P 3+P 4＞0.2，故t 0∈[6，8），所以P 1+P 2+P 3+0.1×（t 0﹣6）=0.2，解得t 0=7，所以教育局拟向全市中学生的一周课外阅读时间为7小时．【点评】本题主要考查了用列举法计算随机事件的基本事件，古典概型概以及频率分布直方图等基本知识，考查了数据处理能力和运用概率知识解决实际问题的能力，属于中档题．24．【答案】（1）详见解析；（2. 【解析】（1）∵D ，E 分别为VA ，VC 的中点，∴//DE AC ，…………2分 ∵AB 为圆O 的直径，∴AC BC ⊥，…………4分又∵VC ⊥圆O ，∴VC AC ⊥，…………6分 ∴DE BC ⊥，DE VC ⊥，又∵VCBC C =，∴DE VBC ⊥面；…………7分（2）设点E 平面BCD 的距离为d ，由D BCE E BCD V V --=得1133BCE BCD DE S d S ∆∆⨯⨯=⨯⨯，解得d =12分设BE 与平面BCD 所成角为θ，∵8BC =，BE =sin d BE θ==.…………15分。

宁国市一中2018-2019学年上学期高二数学12月月考试题含解析

宁国市一中2018-2019学年上学期高二数学12月月考试题含解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题1．执行下面的程序框图，若输入2016x =-，则输出的结果为（）A ．2015B ．2016C ．2116D ．20482．方程x 2+2ax+y 2=0（a ≠0）表示的圆（）A ．关于x 轴对称B ．关于y 轴对称C ．关于直线y=x 轴对称D ．关于直线y=﹣x 轴对称3．设a 是函数x 的零点，若x 0＞a ，则f （x 0）的值满足（）A ．f （x 0）=0B ．f （x 0）＜0C ．f （x 0）＞0D ．f （x 0）的符号不确定4．下列命题正确的是（）A ．很小的实数可以构成集合.B ．集合{}2|1y y x =-与集合(){}2,|1x y y x =-是同一个集合.C ．自然数集 N 中最小的数是.D ．空集是任何集合的子集.5．下列关系式中，正确的是（） A ．∅∈{0} B ．0⊆{0}C ．0∈{0}D ．∅={0}6．函数y=sin（2x+）图象的一条对称轴方程为（）A．x=﹣B．x=﹣C．x=D．x=7．“”是“一元二次方程x2+x+m=0有实数解”的（）A．充分非必要条件B．充分必要条件C．必要非充分条件D．非充分非必要条件8．若函数f（x）=ax2+bx+1是定义在[﹣1﹣a，2a]上的偶函数，则该函数的最大值为（）A．5 B．4 C．3 D．29．下列函数在（0，+∞）上是增函数的是（）A．B．y=﹣2x+5 C．y=lnx D．y=x ，则输出的所有x的值的和为（）10．执行如图所示的程序，若输入的3A．243B．363C．729D．1092【命题意图】本题考查程序框图的识别和运算，意在考查识图能力、简单的计算能力． 11．若复数2b ii++的实部与虚部相等，则实数b 等于（）（A ） 3 （ B ） 1 （C ）13 （D ） 12- 12．某单位综合治理领导小组成员之问的领导关系可以用框图表示，这种框图通常称为（）A ．程序流程图B ．工序流程图C ．知识结构图D ．组织结构图二、填空题13．圆心在原点且与直线2x y +=相切的圆的方程为_____ .【命题意图】本题考查点到直线的距离公式，圆的方程，直线与圆的位置关系等基础知识，属送分题.14．一个正四棱台，其上、下底面均为正方形，边长分别为2cm 和4cm ,侧棱长为2cm ,则其表面积为__________2cm .15．已知实数x ，y 满足约束条，则z=的最小值为．16．曲线y ＝x 2＋3x 在点（－1，－2）处的切线与曲线y ＝ax ＋ln x 相切，则a ＝________． 17．设全集______.18．在直角梯形,,DC//AB,AD DC 1,AB 2,E,F ABCD AB AD ⊥===分别为,AB AC 的中点，点P 在以A 为圆心，AD 为半径的圆弧DE 上变动（如图所示）．若AP ED AF λμ=+，其中,R λμ∈，则2λμ-的取值范围是___________．三、解答题19．在直角坐标系xOy 中，以原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线C 1的极坐标方程为ρ（sin θ+cos θ）=1，曲线C 2的参数方程为（θ为参数）．（Ⅰ）求曲线C 1的直角坐标方程与曲线C 2的普通方程；（Ⅱ）试判断曲线C 1与C 2是否存在两个交点？若存在，求出两交点间的距离；若不存在，说明理由．20．如图所示，在正方体ABCD﹣A1B1C1D1中，E、F分别是棱DD1、C1D1的中点．（Ⅰ）证明：平面ADC1B1⊥平面A1BE；（Ⅱ）证明：B1F∥平面A1BE；（Ⅲ）若正方体棱长为1，求四面体A1﹣B1BE的体积．21．设函数f（x）=lg（a x﹣b x），且f（1）=lg2，f（2）=lg12（1）求a，b的值．（2）当x∈[1，2]时，求f（x）的最大值．（3）m为何值时，函数g（x）=a x的图象与h（x）=b x﹣m的图象恒有两个交点．22．已知椭圆的左、右焦点分别为F1（﹣c，0），F2（c，0），P是椭圆C上任意一点，且椭圆的离心率为．（1）求椭圆C的方程；（2）直线l1，l2是椭圆的任意两条切线，且l1∥l2，试探究在x轴上是否存在定点B，点B到l1，l2的距离之积恒为1？若存在，求出点B的坐标；若不存在，请说明理由．23．已知集合P={x|2x2﹣3x+1≤0}，Q={x|（x﹣a）（x﹣a﹣1）≤0}．（1）若a=1，求P∩Q；（2）若x∈P是x∈Q的充分条件，求实数a的取值范围．24．已知函数f（x）=cosx（sinx+cosx）﹣．（1）若0＜α＜，且sinα=，求f（α）的值；（2）求函数f（x）的最小正周期及单调递增区间．宁国市一中2018-2019学年上学期高二数学12月月考试题含解析（参考答案）一、选择题1．【答案】D 【解析】试题分析：由于20160-<，由程序框图可得对循环进行加运算，可以得到2x =，从而可得1y =，由于20151>，则进行2y y =循环，最终可得输出结果为2048．1考点：程序框图． 2．【答案】A【解析】解：方程x 2+2ax+y 2=0（a ≠0）可化为（x+a ）2+y 2=a 2，圆心为（﹣a ，0），∴方程x 2+2ax+y 2=0（a ≠0）表示的圆关于x 轴对称，故选：A ．【点评】此题考查了圆的一般方程，方程化为标准方程是解本题的关键．3．【答案】C【解析】解：作出y=2x和y=logx 的函数图象，如图：由图象可知当x 0＞a 时，2＞log x 0，∴f （x 0）=2﹣logx 0＞0．故选：C ．4．【答案】D 【解析】试题分析：根据子集概念可知，空集是任何集合的子集，是任何非空集合的真子集，所以选项D是正确，故选D.考点：集合的概念；子集的概念.5．【答案】C【解析】解：对于A∅⊆{0}，用“∈”不对，对于B和C，元素0与集合{0}用“∈”连接，故C正确；对于D，空集没有任何元素，{0}有一个元素，故不正确．6．【答案】A【解析】解：对于函数y=sin（2x+），令2x+=kπ+，k∈z，求得x=π，可得它的图象的对称轴方程为x=π，k∈z，故选：A．【点评】本题主要考查正弦函数的图象的对称性，属于基础题．7．【答案】A【解析】解：由x2+x+m=0知，⇔．（或由△≥0得1﹣4m≥0，∴．），反之“一元二次方程x2+x+m=0有实数解”必有，未必有，因此“”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件．故选A．【点评】本题考查充分必要条件的判断性，考查二次方程有根的条件，注意这些不等式之间的蕴含关系．8．【答案】A【解析】解：函数f（x）=ax2+bx+1是定义在[﹣1﹣a，2a]上的偶函数，可得b=0，并且1+a=2a，解得a=1，所以函数为：f（x）=x2+1，x∈[﹣2，2]，函数的最大值为：5．故选：A．【点评】本题考查函数的最大值的求法，二次函数的性质，考查计算能力．9．【答案】C【解析】解：对于A ，函数y=在（﹣∞，+∞）上是减函数，∴不满足题意；对于B ，函数y=﹣2x+5在（﹣∞，+∞）上是减函数，∴不满足题意；对于C ，函数y=lnx 在（0，+∞）上是增函数，∴满足题意；对于D ，函数y=在（0，+∞）上是减函数，∴不满足题意．故选：C ．【点评】本题考查了基本初等函数的单调性的判断问题，是基础题目．10．【答案】D【解析】当3x =时，y 是整数；当23x =时，y 是整数；依次类推可知当3(*)nx n N =∈时，y 是整数，则由31000nx =≥，得7n ≥，所以输出的所有x 的值为3，9，27，81，243，729，其和为1092，故选D ． 11．【答案】C【解析】b ＋i 2＋i ＝(b ＋i)(2－i)(2＋i)(2－i)＝2b ＋15＋2－b 5i ，因为实部与虚部相等，所以2b ＋1＝2－b ，即b ＝13.故选C.12．【答案】D【解析】解：用来描述系统结构的图示是结构图，某单位综合治理领导小组成员之问的领导关系可以用组织结构图表示．故选D ．【点评】本题考查结构图和流程图的概念，是基础题．解题时要认真审题，仔细解答．二、填空题13．【答案】222x y +=【解析】由题意，圆的半径等于原点到直线2x y +=的距离，所以r d ===222x y +=.14．【答案】20 【解析】考点：棱台的表面积的求解.15．【答案】．【解析】解：作出不等式组对应的平面区域如图：（阴影部分）．由z==32x+y，设t=2x+y，则y=﹣2x+t，平移直线y=﹣2x+t，由图象可知当直线y=﹣2x+t经过点B时，直线y=﹣2x+t的截距最小，此时t最小．由，解得，即B（﹣3，3），代入t=2x+y得t=2×（﹣3）+3=﹣3．∴t最小为﹣3，z有最小值为z==3﹣3=．故答案为：．【点评】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．16．【答案】【解析】由y ＝x 2＋3x 得y ′＝2x ＋3， ∴当x ＝－1时，y ′＝1，则曲线y ＝x 2＋3x 在点（－1，－2）处的切线方程为y ＋2＝x ＋1，即y ＝x －1，设直线y ＝x －1与曲线y ＝ax ＋ln x 相切于点（x 0，y 0），由y ＝ax ＋ln x 得y ′＝a ＋1x（x ＞0），∴⎩⎪⎨⎪⎧a ＋1x 0＝1y 0＝x 0－1y 0＝ax 0＋ln x，解之得x 0＝1，y 0＝0，a ＝0. ∴a ＝0. 答案：017．【答案】{7，9}【解析】∵全集U={n ∈N|1≤n ≤10}，A={1，2，3，5，8}，B={1，3，5，7，9}， ∴（∁U A ）={4，6，7，9 }，∴（∁U A ）∩B={7，9}，故答案为：{7，9}。

宁国市高级中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1．已知实数满足不等式组，若目标函数取得最大值时有唯一的最优解，则y x ,⎪⎩⎪⎨⎧≤-≥+≤-5342y x y x x y mx y z -=)3,1(实数的取值范围是（）m A ．B ．C ．D ．1-<m 10<<m 1>m 1≥m 【命题意图】本题考查了线性规划知识，突出了对线性目标函数在给定可行域上最值的探讨，该题属于逆向问题，重点把握好作图的准确性及几何意义的转化，难度中等.2．在等比数列中，，前项和为，若数列也是等比数列，则等于（）A ．B ．C ．D ．3．甲、乙、丙、丁四人参加某运动会射击项目选拔赛，四人的平均成绩和方差如表所示：甲乙丙丁平均环数x 8.38.88.88.7方差s s 3.53.6 2.25.4从这四个人中选择一人参加该运动会射击项目比赛，最佳人选是（）A ．甲B ．乙C ．丙D ．丁4．在区间上恒正，则的取值范围为（）()()22f x ax a =-+[]0,1A ． B ． C ．D ．以上都不对0a >0a <<02a <<5．等比数列的前n 项，前2n 项，前3n 项的和分别为A ，B ，C ，则（）A ．B 2=ACB ．A+C=2BC ．B （B ﹣A ）=A （C ﹣A ）D ．B （B ﹣A ）=C （C ﹣A ）6．已知定义在R 上的函数f （x ）满足f （x ）=，且f （x ）=f （x+2），g （x ）=，则方程g（x ）=f （x ）﹣g （x ）在区间[﹣3，7]上的所有零点之和为（）A ．12B ．11C ．10D ．97．如图框内的输出结果是（）A ．2401B ．2500C ．2601D ．2704班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________8．某大学的名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽8车，每车限坐名同学（乘同一辆车的名同学不考虑位置），其中大一的孪生姐妹需乘同一辆车，则乘44坐甲车的名同学中恰有名同学是来自同一年级的乘坐方式共有（）种.42A ．B ．C ．D ．24184836【命题意图】本题考查排列与组合的基础知识，考查学生分类讨论，运算能力以及逻辑推理能力．9．不等式≤0的解集是（）A ．（﹣∞，﹣1）∪（﹣1，2）B ．[﹣1，2]C ．（﹣∞，﹣1）∪[2，+∞）D ．（﹣1，2]10．在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知a=3，，A=60°，则满足条件的三角形个数为（）A ．0B ．1C ．2D ．以上都不对11．若，则等于（）A ．B ．C ．D ．12．复数是虚数单位）的虚部为（）i iiz (21+=A ．B ．C ．D ．1-i -i 22【命题意图】本题考查复数的运算和概念等基础知识，意在考查基本运算能力．二、填空题13．若全集，集合，则14．已知函数为定义在区间[﹣2a ，3a ﹣1]上的奇函数，则a+b= ．15．已知，则不等式的解集为________．,0()1,0x e x f x x ì³ï=í<ïî2(2)()f x f x ->【命题意图】本题考查分段函数、一元二次不等式等基础知识，意在考查分类讨论思想和基本运算能力．16．已知（1+x+x 2）（x）n （n ∈N +）的展开式中没有常数项，且2≤n ≤8，则n= ．17．如图是某赛季甲乙两名篮球运动员每场比赛得分的茎叶图，则甲乙两人比赛得分的中位数之和是．18．已知数列{a n }中，a 1=1，a n+1=a n +2n ，则数列的通项a n = ．三、解答题19．已知复数z=．（1）求z 的共轭复数；（2）若az+b=1﹣i ，求实数a ，b 的值．20．（本小题满分12分）从2016年1月1日起，广东、湖北等18个保监局所辖地区将纳入商业车险改革试点范围，其中最大的变化是上一年的出险次数决定了下一年的保费倍率，具体关系如下表：上一年的出险次数01234次以上（含次）55下一年保费倍率85%100%125%150%175%200%连续两年没有出险打折，连续三年没有出险打折76 经验表明新车商业车险保费与购车价格有较强的线性相关关系，下面是随机采集的8组数据（其中(,)x y x （万元）表示购车价格，（元）表示商业车险保费）：、、、、y (8,2150)(11,2400)(18,3140)(25,3750)、、、，设由这8组数据得到的回归直线方程为：．(25,4000)(31,4560)(37,5500)(45,6500)$1055y bx =+$（1）求；b （2）广东李先生2016年1月购买一辆价值20万元的新车，（i ）估计李先生购车时的商业车险保费；（ii ）若该车今年2月已出过一次险，现在又被刮花了，李先生到店询价，预计修车费用为元，保险4S 800专员建议李先生自费（即不出险），你认为李先生是否应该接受建议？说明理由．（假设车辆下一年与上一年都购买相同的商业车险产品进行续保）21．已知椭圆C ： =1（a ＞2）上一点P 到它的两个焦点F 1（左），F 2 （右）的距离的和是6．（1）求椭圆C 的离心率的值；（2）若PF 2⊥x 轴，且p 在y 轴上的射影为点Q ，求点Q 的坐标．22．定义在R 上的增函数y=f （x ）对任意x ，y ∈R 都有f （x+y ）=f （x ）+f （y ），则（1）求f （0）；（2）证明：f （x ）为奇函数；（3）若f （k •3x ）+f （3x ﹣9x ﹣2）＜0对任意x ∈R 恒成立，求实数k 的取值范围．　23．已知函数f （x ）=|x ﹣10|+|x ﹣20|，且满足f （x ）＜10a+10（a ∈R ）的解集不是空集．（Ⅰ）求实数a 的取值集合A（Ⅱ）若b ∈A ，a ≠b ，求证a a b b ＞a b b a ．24．（本小题满分10分）已知圆过点，.P )0,1(A )0,4(B （1）若圆还过点，求圆的方程； P )2,6( C P （2）若圆心的纵坐标为，求圆的方程.P P宁国市高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案C D CCCBBADB题号1112答案BA二、填空题13．{|0＜＜1｝14．　2　．15．(-16．　5　．　17．　64　．18．　2n ﹣1　．三、解答题19． 20．21． 22． 23．24．（1）；（2）.047522=++-+y x y x 425)2(25(22=-+-y x。

宁国市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1．设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b ⊥m ，则“α⊥β”是“a ⊥b ”的（） A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件2．设双曲线焦点在y轴上，两条渐近线为，则该双曲线离心率e=（）A ．5B．C．D．3．若双曲线C ：x 2﹣=1（b ＞0）的顶点到渐近线的距离为，则双曲线的离心率e=（）A ．2B．C ．3 D．4．已知数列{}n a 的各项均为正数，12a =，114n n n na a a a ++-=+，若数列11n n a a +⎧⎫⎨⎬+⎩⎭的前n 项和为5，则n =（）A ．35B ． 36C ．120D ．1215．函数2(44)x y a a a =-+是指数函数，则的值是（）A ．4B ．1或3C ．3D ．16．已知一元二次不等式f （x ）＜0的解集为{x|x ＜﹣1或x＞}，则f （10x ）＞0的解集为（） A ．{x|x ＜﹣1或x ＞﹣lg2} B ．{x|﹣1＜x ＜﹣lg2} C ．{x|x ＞﹣lg2} D ．{x|x ＜﹣lg2}7．如图，棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中，M 为线段A 1B 上的动点，则下列结论正确的有（） ①三棱锥M ﹣DCC 1的体积为定值 ②DC 1⊥D 1M ③∠AMD 1的最大值为90° ④AM+MD 1的最小值为2．A ．①②B ．①②③C ．③④D ．②③④8．函数y=f ′（x ）是函数y=f （x ）的导函数，且函数y=f （x ）在点p （x 0，f （x 0））处的切线为l ：y=g （x ）=f ′（x 0）（x ﹣x 0）+f （x 0），F （x ）=f （x ）﹣g （x ），如果函数y=f （x ）在区间[a ，b]上的图象如图所示，且a ＜x 0＜b ，那么（）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．F ′（x 0）=0，x=x 0是F （x ）的极大值点B ．F ′（x 0）=0，x=x 0是F （x ）的极小值点C ．F ′（x 0）≠0，x=x 0不是F （x ）极值点D ．F ′（x 0）≠0，x=x 0是F （x ）极值点9． cos80cos130sin100sin130︒︒-︒︒等于（）A B ．12 C ．12- D ．10．A 是圆上固定的一定点，在圆上其他位置任取一点B ，连接A 、B 两点，它是一条弦，它的长度大于等于半径长度的概率为（）A ．B ．C ．D ．11．62)21(x x -的展开式中，常数项是（） A ．45- B ．45 C ．1615- D ．161512．“x ＞0”是“＞0”成立的（）A ．充分非必要条件B ．必要非充分条件C ．非充分非必要条件D ．充要条件二、填空题13．设集合A={x|x+m ≥0}，B={x|﹣2＜x ＜4}，全集U=R ，且（∁U A ）∩B=∅，求实数m 的取值范围为． 14．设全集U={0，1，2，3，4}，集合A={0，1，2}，集合B={2，3}，则（∁U A ）∪B= ． 15．函数()y f x =图象上不同两点()()1122,,,A x y B x y 处的切线的斜率分别是A B k k ，，规定(),A Bk k A B ABϕ-=（AB 为线段AB 的长度）叫做曲线()y f x =在点A 与点B 之间的“弯曲度”，给出以下命题：①函数321y x x =-+图象上两点A 与B 的横坐标分别为1和2，则(),A B ϕ> ②存在这样的函数，图象上任意两点之间的“弯曲度”为常数； ③设点A,B 是抛物线21y x =+上不同的两点，则(),2A B ϕ≤；④设曲线xy e =（e 是自然对数的底数）上不同两点()()112212,,,,1A x y B x y x x -=且，若(),1t A B ϕ⋅<恒成立，则实数t 的取值范围是(),1-∞.其中真命题的序号为________.（将所有真命题的序号都填上）16．已知函数f （x ）=，点O 为坐标原点，点An （n ，f （n ））（n ∈N +），向量=（0，1），θn 是向量与i 的夹角，则++…+= ．17．自圆C ：22(3)(4)4x y -++=外一点(,)P x y 引该圆的一条切线，切点为Q ，切线的长度等于点P 到原点O 的长，则PQ 的最小值为（） A ．1310 B ．3 C ．4 D ．2110【命题意图】本题考查直线与圆的位置关系、点到直线的距离，意在考查逻辑思维能力、转化能力、运算求解能力、数形结合的思想．18．已知数列{}n a 的首项1a m =，其前n 项和为n S ，且满足2132n n S S n n ++=+，若对n N *∀∈，1n n a a +< 恒成立，则m 的取值范围是_______．【命题意图】本题考查数列递推公式、数列性质等基础知识，意在考查转化与化归、逻辑思维能力和基本运算能力．三、解答题19．定义在R 上的增函数y=f （x ）对任意x ，y ∈R 都有f （x+y ）=f （x ）+f （y ），则（1）求f （0）；（2）证明：f （x ）为奇函数；（3）若f （k •3x ）+f （3x ﹣9x﹣2）＜0对任意x ∈R 恒成立，求实数k 的取值范围．20．已知不等式的解集为或（1）求，的值（2）解不等式.21．已知椭圆，过其右焦点F且垂直于x轴的弦MN的长度为b．（Ⅰ）求该椭圆的离心率；（Ⅱ）已知点A的坐标为（0，b），椭圆上存在点P，Q，使得圆x2+y2=4内切于△APQ，求该椭圆的方程．22．设数列{a n}的前n项和为S n，a1=1，S n=na n﹣n（n﹣1）．（1）求证：数列{a n}为等差数列，并分别求出a n的表达式；（2）设数列的前n项和为P n，求证：P n＜；（3）设C n=，T n=C1+C2+…+C n，试比较T n与的大小．23．已知在△ABC中，A（2，4），B（﹣1，﹣2），C（4，3），BC边上的高为AD．（1）求证：AB⊥AC；（2）求向量．24．已知双曲线过点P（﹣3，4），它的渐近线方程为y=±x．（1）求双曲线的标准方程；（2）设F1和F2为该双曲线的左、右焦点，点P在此双曲线上，且|PF1||PF2|=41，求∠F1PF2的余弦值．宁国市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1．【答案】B【解析】解：∵b ⊥m ，∴当α⊥β，则由面面垂直的性质可得a ⊥b 成立，若a ⊥b ，则α⊥β不一定成立，故“α⊥β”是“a ⊥b ”的充分不必要条件，故选：B ．【点评】本题主要考查充分条件和必要条件的判断，利用线面垂直的性质是解决本题的关键．2．【答案】C【解析】解：∵双曲线焦点在y 轴上，故两条渐近线为 y=±x ，又已知渐近线为，∴=，b=2a ，故双曲线离心率e====，故选C ．【点评】本题考查双曲线的标准方程，以及双曲线的简单性质的应用，判断渐近线的斜率=，是解题的关键．3．【答案】B【解析】解：双曲线C ：x 2﹣=1（b ＞0）的顶点为（±1，0），渐近线方程为y=±bx ，由题意可得=，解得b=1，c==，即有离心率e==．故选：B ．【点评】本题考查双曲线的离心率的求法，注意运用点到直线的距离公式，考查运算能力，属于基础题．4．【答案】C【解析】解析：本题考查等差数列的定义通项公式与“裂项法”求数列的前n 项和．由114n n n na a a a ++-=+得2214n n a a +-=，∴{}2n a 是等差数列，公差为4，首项为4，∴244(1)4n a n n =+-=，由0n a >得n a =．1112n n a a +==+，∴数列11n n a a +⎧⎫⎨⎬+⎩⎭的前n 项和为11111)(11)52222n ++++==，∴120n =，选C ． 5．【答案】C 【解析】考点：指数函数的概念． 6．【答案】D【解析】解：由题意可知f （x ）＞0的解集为{x|﹣1＜x ＜}，故可得f （10x ）＞0等价于﹣1＜10x＜，由指数函数的值域为（0，+∞）一定有10x＞﹣1，而10x＜可化为10x ＜，即10x＜10﹣lg2，由指数函数的单调性可知：x ＜﹣lg2故选：D7．【答案】A【解析】解：①∵A 1B ∥平面DCC 1D 1，∴线段A 1B 上的点M 到平面DCC 1D 1的距离都为1，又△DCC 1的面积为定值，因此三棱锥M ﹣DCC 1的体积V==为定值，故①正确．②∵A 1D 1⊥DC 1，A 1B ⊥DC 1，∴DC 1⊥面A 1BCD 1，D 1P ⊂面A 1BCD 1，∴DC 1⊥D 1P ，故②正确． ③当0＜A 1P ＜时，在△AD 1M 中，利用余弦定理可得∠APD 1为钝角，∴故③不正确；④将面AA 1B 与面A 1BCD 1沿A 1B 展成平面图形，线段AD 1即为AP+PD 1的最小值，在△D 1A 1A 中，∠D 1A 1A=135°，利用余弦定理解三角形得AD 1==＜2，故④不正确．因此只有①②正确．故选：A ．8．【答案】 B【解析】解：∵F （x ）=f （x ）﹣g （x ）=f （x ）﹣f ′（x 0）（x ﹣x 0）﹣f （x 0），∴F'（x ）=f'（x ）﹣f ′（x 0） ∴F'（x 0）=0，又由a ＜x 0＜b ，得出当a ＜x ＜x 0时，f'（x ）＜f ′（x 0），F'（x ）＜0，当x 0＜x ＜b 时，f'（x ）＜f ′（x 0），F'（x ）＞0， ∴x=x 0是F （x ）的极小值点故选B ．【点评】本题主要考查函数的极值与其导函数的关系，即当函数取到极值时导函数一定等于0，反之当导函数等于0时还要判断原函数的单调性才能确定是否有极值．9．【答案】D 【解析】试题分析：原式()()cos80cos130sin80sin130cos 80130cos210cos 30180cos30=︒︒-︒︒=︒+︒=︒=︒+︒=-︒= 考点：余弦的两角和公式.10．【答案】B【解析】解：在圆上其他位置任取一点B ，设圆半径为R ，则B 点位置所有情况对应的弧长为圆的周长2πR ，其中满足条件AB 的长度大于等于半径长度的对应的弧长为2πR ，则AB 弦的长度大于等于半径长度的概率P==．故选B ．【点评】本题考查的知识点是几何概型，其中根据已知条件计算出所有基本事件对应的几何量及满足条件的基本事件对应的几何量是解答的关键．11．【答案】D【解析】2612316611()()()22rr r r r rr T C x C xx --+=-=-，令1230r -=，解得4r =．∴常数项为446115()216C -=． 12．【答案】A【解析】解：当x ＞0时，x 2＞0，则＞0∴“x ＞0”是“＞0”成立的充分条件；但＞0，x 2＞0，时x ＞0不一定成立∴“x ＞0”不是“＞0”成立的必要条件；故“x ＞0”是“＞0”成立的充分不必要条件；故选A【点评】判断充要条件的方法是：①若p ⇒q 为真命题且q ⇒p 为假命题，则命题p 是命题q 的充分不必要条件；②若p ⇒q 为假命题且q ⇒p 为真命题，则命题p 是命题q 的必要不充分条件；③若p ⇒q 为真命题且q ⇒p 为真命题，则命题p 是命题q 的充要条件；④若p ⇒q 为假命题且q ⇒p 为假命题，则命题p 是命题q 的即不充分也不必要条件．⑤判断命题p 与命题q 所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p 与命题q 的关系．二、填空题13．【答案】 m ≥2 ．【解析】解：集合A={x|x+m ≥0}={x|x ≥﹣m}，全集U=R ，所以C U A={x|x ＜﹣m}，又B={x|﹣2＜x ＜4}，且（∁U A ）∩B=∅，所以有﹣m ≤﹣2，所以m ≥2．故答案为m ≥2．14．【答案】 {2，3，4} ．【解析】解：∵全集U={0，1，2，3，4}，集合A={0，1，2}， ∴C U A={3，4}，又B={2，3}，∴（C U A ）∪B={2，3，4}，故答案为：{2，3，4}15．【答案】②③ 【解析】试题分析：①错：(1,1),(2,5),|||7,A B A B AB k k -=(,)A B ϕ∴=<②对：如1y =；③对；(,)2A B ϕ==≤；④错；1212(,)x x x x A B ϕ==，1211,(,)A B ϕ==>因为1(,)t A B ϕ<恒成立，故1t ≤.故答案为②③.111] 考点：1、利用导数求曲线的切线斜率；2、两点间的距离公式、最值问题、不等式恒成立问题.【方法点晴】本题通过新定义“弯曲度”对多个命题真假的判断考查利用导数求曲线的切线斜率、两点间的距离公式、最值问题、不等式恒成立问题以及及数学化归思想，属于难题.该题型往往出现在在填空题最后两题，综合性较强，同学们往往因为某一点知识掌握不牢就导致本题“全盘皆输”，解答这类问题首先不能慌乱更不能因贪快而审题不清，其次先从最有把握的命题入手，最后集中力量攻坚最不好理解的命题.16．【答案】．【解析】解：点An（n，）（n∈N+），向量=（0，1），θn是向量与i的夹角，=，=，…，=，∴++…+=+…+=1﹣=，故答案为：．【点评】本题考查了向量的夹角、数列“裂项求和”方法，考查了推理能力与计算能力，属于中档题．17．【答案】D【解析】18．【答案】15 (,)43三、解答题19．【答案】【解析】解：（1）在f（x+y）=f（x）+f（y）中，令x=y=0可得，f（0）=f（0）+f（0），则f（0）=0，（2）令y=﹣x，得f（x﹣x）=f（x）+f（﹣x），又f（0）=0，则有0=f（x）+f（﹣x），即可证得f（x）为奇函数；（3）因为f（x）在R上是增函数，又由（2）知f（x）是奇函数，f（k•3x）＜﹣f（3x﹣9x﹣2）=f（﹣3x+9x+2），即有k•3x＜﹣3x+9x+2，得，又有，即有最小值2﹣1，所以要使f（k•3x）+f（3x﹣9x﹣2）＜0恒成立，只要使即可，故k的取值范围是（﹣∞，2﹣1）．20．【答案】【解析】解：（1）因为不等式的解集为或所以，是方程的两个解所以，解得（2）由（1）知原不等式为，即，当时，不等式解集为当时，不等式解集为;当时，不等式解集为;21．【答案】【解析】解：（Ⅰ）设F（c，0），M（c，y1），N（c，y2），则，得y1=﹣，y2=，MN=|y1﹣y2|==b，得a=2b，椭圆的离心率为：==．（Ⅱ）由条件，直线AP、AQ斜率必然存在，设过点A且与圆x2+y2=4相切的直线方程为y=kx+b，转化为一般方程kx﹣y+b=0，由于圆x2+y2=4内切于△APQ，所以r=2=，得k=±（b＞2），即切线AP、AQ关于y轴对称，则直线PQ平行于x轴，∴y Q=y P=﹣2，不妨设点Q在y轴左侧，可得x Q=﹣x P=﹣2，则=，解得b=3，则a=6，∴椭圆方程为：．【点评】本题考查了椭圆的离心率公式，点到直线方程的距离公式，内切圆的性质．22．【答案】【解析】解：（1）证明：∵S n=na n﹣n（n﹣1）∴S n+1=（n+1）a n+1﹣（n+1）n…∴a n+1=S n+1﹣S n=（n+1）a n+1﹣na n﹣2n…∴na n+1﹣na n﹣2n=0∴a n+1﹣a n=2，∴{a n}是以首项为a1=1，公差为2的等差数列…由等差数列的通项公式可知：a n=1+（n﹣1）×2=2n﹣1，数列{a n}通项公式a n=2n﹣1；…（2）证明：由（1）可得，…=…（3）∴，=，两式相减得…=，=，=，=，∴…∴…∵n∈N*，∴2n＞1，∴，∴…23．【答案】【解析】解（1）∵=（﹣1，﹣2）﹣（2，4）=（﹣3，﹣6），=（4，3）﹣（2，4）=（2，﹣1），=﹣3×2+（﹣6）×（﹣1）=0，∴AB⊥AC．（2）=（4，3）﹣（﹣1，﹣2）=（5，5）．设=λ=（5λ，5λ）则=+=（﹣3，﹣6）+（5λ，5λ）=（5λ﹣3，5λ﹣6），由AD⊥BC得5（5λ﹣3）+5（5λ﹣6）=0，解得λ=，∴=（，﹣）．【点评】本题考查向量的垂直与共线的应用，向量的数量积的应用，考查计算能力．24．【答案】【解析】解：（1）设双曲线的方程为y2﹣x2=λ（λ≠0），代入点P（﹣3，4），可得λ=﹣16，∴所求求双曲线的标准方程为（2）设|PF1|=d1，|PF2|=d2，则d1d2=41，又由双曲线的几何性质知|d1﹣d2|=2a=6，∴d12+d22﹣2d1d2=36即有d12+d22=36+2d1d2=118，又|F1F2|=2c=10，∴|F1F2|2=100=d12+d22﹣2d1d2cos∠F1PF2∴cos∠F1PF2=【点评】本题给出双曲线的渐近线，在双曲线经过定点P的情况下求它的标准方程，并依此求∠F1PF2的余弦值．着重考查了双曲线的标准方程与简单几何性质、利用余弦定理解三角形等知识，属于中档题．。

宁国市第一高级中学2018-2019学年高二上学期数学期末模拟试卷含解析

宁国市第一高级中学2018-2019学年高二上学期数学期末模拟试卷含解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题1．下列命题正确的是（）A ．已知实数,a b ，则“a b >”是“22a b >”的必要不充分条件B ．“存在0x R ∈，使得2010x -<”的否定是“对任意x R ∈，均有210x ->” C ．函数131()()2xf x x =-的零点在区间11(,)32内D ．设,m n 是两条直线，,αβ是空间中两个平面，若,m n αβ⊂⊂，m n ⊥则αβ⊥ 2．已知平面向量(12)=，a ，(32)=-，b ，若k +a b 与a 垂直，则实数k 值为（） A ．15- B ．119 C ．11 D ．19【命题意图】本题考查平面向量数量积的坐标表示等基础知识，意在考查基本运算能力．3．如图是七位评委为甲，乙两名参赛歌手打出的分数的茎叶图（其中m ，n 为数字0～9中的一个），则甲歌手得分的众数和乙歌手得分的中位数分别为a 和b ，则一定有（）A ．a ＞bB ．a ＜bC ．a=bD ．a ，b 的大小与m ，n 的值有关 4． i 是虚数单位，计算i+i 2+i 3=（）A ．﹣1B ．1C ．﹣iD ．i5．已知函数()2sin()f x x ωϕ=+(0)2πϕ<<与y 轴的交点为(0,1)，且图像上两对称轴之间的最小距离为2π，则使()()0f x t f x t +--+=成立的t 的最小值为（）1111] A ．6π B ．3π C ．2π D ．23π6．设函数y=x 3与y=（）x 的图象的交点为（x 0，y 0），则x 0所在的区间是（） A ．（0，1） B ．（1，2） C ．（2，3） D ．（3，4）7．已知函数211,[0,)22()13,[,1]2x x f x x x ⎧+∈⎪⎪=⎨⎪∈⎪⎩，若存在常数使得方程()f x t =有两个不等的实根12,x x（12x x <），那么12()x f x ∙的取值范围为（）A ．3[,1)4B．1[8 C ．31[,)162 D ．3[,3)88．已知两条直线12:,:0L y x L ax y =-=，其中为实数，当这两条直线的夹角在0,12π⎛⎫⎪⎝⎭内变动时，的取值范围是（） A ． ()0,1 B．⎝ C．()1,3⎫⎪⎪⎝⎭D ．(9．函数g （x）是偶函数，函数f （x ）=g （x ﹣m ），若存在φ∈（，），使f （sin φ）=f （cos φ），则实数m 的取值范围是（） A ．（）B ．（，]C ．（） D ．（]10．圆心在直线2x ＋y ＝0上，且经过点（－1，－1）与（2，2）的圆，与x 轴交于M ，N 两点，则|MN |＝（） A ．4 2 B ．4 5 C ．2 2D ．2 511．在△ABC 中，a ，b，c 分别是角A ，B ，C 的对边，a=5，b=4，cosC=，则△ABC 的面积是（） A ．16B ．6C ．4D ．812．数列{a n }的通项公式为a n =﹣n+p，数列{b n }的通项公式为b n =2n ﹣5，设c n =，若在数列{c n }中c 8＞c n （n ∈N *，n ≠8），则实数p 的取值范围是（）A ．（11，25）B ．（12，16]C ．（12，17）D ．[16，17）二、填空题13．如图，是一回形图，其回形通道的宽和OB 1的长均为1，回形线与射线OA 交于A 1，A 2，A 3，…，若从点O 到点A 3的回形线为第1圈（长为7），从点A 3到点A 2的回形线为第2圈，从点A 2到点A 3的回形线为第3圈…依此类推，第8圈的长为．14．如图，已知m ，n 是异面直线，点A ，B m ∈，且6AB =；点C ，D n ∈，且4CD =.若M ，N 分别是AC ，BD 的中点，MN =m 与n 所成角的余弦值是______________.【命题意图】本题考查用空间向量知识求异面直线所成的角，考查空间想象能力，推理论证能力，运算求解能力.15．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知sinAsinB+sinBsinC+cos2B=1．若C=，则= ．16．函数f （x ）=a x +4的图象恒过定点P ，则P 点坐标是． 17．抽样调查表明，某校高三学生成绩（总分750分）X 近似服从正态分布，平均成绩为500分．已知P （400＜X ＜450）=0.3，则P （550＜X ＜600）= ．18．有三个房间需要粉刷，粉刷方案要求：每个房间只用一种颜色的涂料，且三个房间的颜色各不相同．三个房间的粉刷面积和三种颜色的涂料费用如下表：那么在所有不同的粉刷方案中，最低的涂料总费用是 _______元．三、解答题19．坐标系与参数方程线l ：3x+4y ﹣12=0与圆C ：（θ为参数）试判断他们的公共点个数．20．已知函数（a≠0）是奇函数，并且函数f（x）的图象经过点（1，3），（1）求实数a，b的值；（2）求函数f（x）的值域．21．已知椭圆x2+4y2=4，直线l：y=x+m（1）若l与椭圆有一个公共点，求m的值；（2）若l与椭圆相交于P、Q两点，且|PQ|等于椭圆的短轴长，求m的值．22．已知函数f（x）=lg（2016+x），g（x）=lg（2016﹣x）（1）判断函数f（x）﹣g（x）的奇偶性，并予以证明．（2）求使f（x）﹣g（x）＜0成立x的集合．23．已知不等式ax2﹣3x+6＞4的解集为{x|x＜1或x＞b}，（1）求a，b；（2）解不等式ax2﹣（ac+b）x+bc＜0．24．（本小题满分12分）成都市某中学计划举办“国学”经典知识讲座.由于条件限制，按男、女生比例采取分层抽样的方法，从某班选出10人参加活动，在活动前，对所选的10名同学进行了国学素养测试，这10名同学的性别和测试成绩（百分制）的茎叶图如图所示.（1）根据这10名同学的测试成绩，分别估计该班男、女生国学素养测试的平均成绩；（2）若从这10名同学中随机选取一男一女两名同学，求这两名同学的国学素养测试成绩均为优良的概率.（注：成绩大于等于75分为优良）宁国市第一高级中学2018-2019学年高二上学期数学期末模拟试卷含解析（参考答案）一、选择题1．【答案】C 【解析】考点：1.不等式性质；2.命题的否定；3.异面垂直；4.零点；5.充要条件．【方法点睛】本题主要考查不等式性质，命题的否定，异面垂直，零点，充要条件.充要条件的判定一般有①定义法:先分清条件和结论（分清哪个是条件,哪个是结论），然后找推导关系（判断,p q q p ⇒⇒的真假），最后下结论（根据推导关系及定义下结论）. ②等价转化法:条件和结论带有否定性词语的命题,常转化为其逆否命题来判断. 2．【答案】A3．【答案】C【解析】解：根据茎叶图中的数据，得；甲得分的众数为a=85，乙得分的中位数是b=85；所以a=b ．故选：C ．4．【答案】A【解析】解：由复数性质知：i 2=﹣1 故i+i 2+i 3=i+（﹣1）+（﹣i ）=﹣1故选A【点评】本题考查复数幂的运算，是基础题．5．【答案】A 【解析】考点：三角函数的图象性质． 6．【答案】A【解析】解：令f （x ）=x 3﹣，∵f ′（x ）=3x 2﹣ln =3x 2+ln2＞0，∴f （x ）=x 3﹣在R 上单调递增；又f （1）=1﹣=＞0， f （0）=0﹣1=﹣1＜0，∴f （x ）=x 3﹣的零点在（0，1），∵函数y=x 3与y=（）x的图象的交点为（x 0，y 0），∴x 0所在的区间是（0，1）．故答案为：A ．7．【答案】C 【解析】试题分析：由图可知存在常数，使得方程()f x t =有两上不等的实根，则314t <<，由1324x +=，可得14x =，由213x =，可得x =12111,422x x ≤<≤≤，即221143x ≤≤，则()212123133,162x f x x x ⎡⎫=⋅∈⎪⎢⎣⎭.故本题答案选C.考点：数形结合．【规律点睛】本题主要考查函数的图象与性质,及数形结合的数学思想方法.方程解的个数问题一般转化为两个常见的函数图象的交点个数问题来解决.要能熟练掌握几种基本函数图象,如二次函数,反比例函数,指数函数,对数函数,幂函数等.掌握平移变换,伸缩变换,对称变换,翻折变换,周期变换等常用的方法技巧来快速处理图象.8．【答案】C 【解析】1111]试题分析：由直线方程1:L y x =，可得直线的倾斜角为045α=，又因为这两条直线的夹角在0,12π⎛⎫⎪⎝⎭，所以直线2:0L ax y -=的倾斜角的取值范围是03060α<<且045α≠，所以直线的斜率为00tan30tan 60a <<且0tan 45α≠1a <<或1a << C. 考点：直线的倾斜角与斜率. 9．【答案】A【解析】解：∵函数g （x ）是偶函数，函数f （x ）=g （x ﹣m ）， ∴函数f （x ）关于x=m 对称，若φ∈（，），则sin φ＞cos φ，则由f （sin φ）=f （cos φ），则=m ，即m==（sin φ×+cos αφ）=sin （φ+）当φ∈（，），则φ+∈（，），则＜sin （φ+）＜，则＜m＜，故选：A【点评】本题主要考查函数奇偶性和对称性之间的应用以及三角函数的图象和性质，利用辅助角公式是解决本题的关键．10．【答案】【解析】选D.设圆的方程为（x －a ）2＋（y －b ）2＝r 2（r ＞0）．由题意得⎩⎪⎨⎪⎧2a ＋b ＝0（－1－a ）2＋（－1－b ）2＝r 2（2－a ）2＋（2－b ）2＝r2，解之得a ＝－1，b ＝2，r ＝3，∴圆的方程为（x ＋1）2＋（y －2）2＝9，令y ＝0得，x ＝－1±5，∴|MN |＝|（－1＋5）－（－1－5）|＝25，选D. 11．【答案】D【解析】解：∵a=5，b=4，cosC=，可得：sinC==，∴S △ABC=absinC==8．故选：D ．12．【答案】C【解析】解：当a n ≤b n 时，c n =a n ，当a n ＞b n 时，c n =b n ，∴c n 是a n ，b n 中的较小者， ∵a n =﹣n+p ，∴{a n }是递减数列， ∵b n =2n ﹣5，∴{b n }是递增数列，∵c 8＞c n （n ≠8），∴c 8是c n 的最大者，则n=1，2，3，…7，8时，c n 递增，n=8，9，10，…时，c n 递减， ∴n=1，2，3，…7时，2n ﹣5＜﹣n+p总成立，当n=7时，27﹣5＜﹣7+p ，∴p ＞11，n=9，10，11，…时，2n ﹣5＞﹣n+p 总成立，当n=9时，29﹣5＞﹣9+p ，成立，∴p ＜25，而c 8=a 8或c 8=b 8，若a 8≤b 8，即23≥p ﹣8，∴p ≤16，则c 8=a 8=p ﹣8，∴p﹣8＞b7=27﹣5，∴p＞12，故12＜p≤16，若a8＞b8，即p﹣8＞28﹣5，∴p＞16，∴c8=b8=23，那么c8＞c9=a9，即8＞p﹣9，∴p＜17，故16＜p＜17，综上，12＜p＜17．故选：C．二、填空题13．【答案】63．【解析】解：∵第一圈长为：1+1+2+2+1=7第二圈长为：2+3+4+4+2=15第三圈长为：3+5+6+6+3=23…第n圈长为：n+（2n﹣1）+2n+2n+n=8n﹣1故n=8时，第8圈的长为63，故答案为：63．【点评】本题主要考查了归纳推理，解答的一般步骤是：先通过观察第1，2，3，…圈的长的情况发现某些相同性质，再从相同性质中推出一个明确表达的一般性结论，最后将一般性结论再用于特殊情形．14．【答案】5 12【解析】15．【答案】=．【解析】解：在△ABC中，角A，B，C的对边分别为a，b，c，∵已知sinAsinB+sinBsinC+cos2B=1，∴sinAsinB+sinBsinC=2sin2B．再由正弦定理可得ab+bc=2b2，即a+c=2b，故a，b，c成等差数列．C=，由a，b，c成等差数列可得c=2b﹣a，由余弦定理可得（2b﹣a）2=a2+b2﹣2abcosC=a2+b2+ab．化简可得5ab=3b2，∴=．故答案为：．【点评】本题主要考查等差数列的定义和性质，二倍角公式、余弦定理的应用，属于中档题．16．【答案】（0，5）．【解析】解：∵y=a x的图象恒过定点（0，1），而f（x）=a x+4的图象是把y=a x的图象向上平移4个单位得到的，∴函数f（x）=a x+4的图象恒过定点P（0，5），故答案为：（0，5）．【点评】本题考查指数函数的性质，考查了函数图象的平移变换，是基础题．17．【答案】0.3．【解析】离散型随机变量的期望与方差．【专题】计算题；概率与统计．【分析】确定正态分布曲线的对称轴为x=500，根据对称性，可得P（550＜ξ＜600）．【解答】解：∵某校高三学生成绩（总分750分）ξ近似服从正态分布，平均成绩为500分，∴正态分布曲线的对称轴为x=500，∵P（400＜ξ＜450）=0.3，∴根据对称性，可得P（550＜ξ＜600）=0.3．故答案为：0.3．【点评】本题考查正态分布曲线的特点及曲线所表示的意义，正确运用正态分布曲线的对称性是关键．18．【答案】1464【解析】【知识点】函数模型及其应用【试题解析】显然，面积大的房间用费用低的涂料，所以房间A用涂料1，房间B用涂料3，房间C用涂料2，即最低的涂料总费用是元。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

宁国中学高一年级第二学期第一次段考
数学试题
第Ⅰ卷（选择题，共50分）
一、选择题（本大题共10小题，每小题5分.在每小题给出的四个选项中，只有一项是符
合题目要求的，请把正确答案的代号填在题后的括号内．）
1、若sin x +
12
cos x =sin(x +φ)，则φ的一个可能值为
（）Ａ、6π-
Ｂ、3π- Ｃ、6π Ｄ、3
π 2、
27tan 33tan 327tan 33tan ++的结果为（）
Ｃ、Ｄ、33-
3、将一个棱长为a 的正方体切成8个全等的小正方体，表面积增加了（）
A 、 2
4a B 、2
6a C 、 2
8a
D 、2
12a
4、△ABC 三内角满足c B a =cos 2，则△ABC 的形状为（）
A 、等腰三角形
B 、等边三角形
C 、直角三角形
D 、等腰直角三角形 5、两等角的一组对应边平行，则
（）
A 、另一组对应边一定平行
B 、另一组对应边一定不平行
C 、另一组对应边不可能垂直
D 、以上都不对
6、三棱锥P —ABC 的侧棱PA 、PB 、PC 两两互相垂直，侧面面积分别是1，1，2，则三棱锥的体积是( ) A 、
3
1 B 、
3
2 C 、
3
4 D 、 2
7、已知41
)6
cos(=
-
π
x ，则=-+)3
cos(cos πx x （）Ａ、
43 Ｂ、 43- Ｃ、 41 Ｄ、4
3
±
8、已知高与底面的直径之比为1：2的圆柱内接于球，且圆柱体积为64π，则球的体积（）
A 、
3
80π
B 、
3
5160π
C 、π80
D 、π5160
9、在△ABC 中，已知5
4
sin ,135cos ==
B A ，则cos
C 的值为（）
Ａ、
6533 Ｂ、 6563 Ｃ、 6533或65
63 Ｄ、 6533-
10、用若干个体积为1的正方体搭成一个几何体，其正视图、侧视图都
是如图所示的图形，则这个几何体的最大体积与最小体积的差是（）. A 、5 B 、6 C 、7 D 、8
第Ⅱ卷（非选择题，共100分）
二、填空题(本大题共5小题，每小题5分，共25分，把答案填在题中的横线上) 11、在ABC ∆中，若， 45=C ， 60=B ，则=a 12、若tan α=
3
1
,则αα2cos 2sin +的值是 13、圆锥的高为1,底面半径为3,过圆锥两条母线所作的截面面积最大值__ _ __ 14、如果满足 60=∠ABC ，6=AC 的△ABC 恰有一个，那么BC 的取值集合 15．某几何体的三视图如图所示，则它的体积是
三、解答题(本大题共6小题，16-18题每题
12分，19-21每题13分，共75分，解答应写出文字说明、证明过程或演算步骤) 16、已知函数f (x )＝2cos
2
2
x
＋sin x -1. （Ⅰ) 求f (x )的单调递增区间；
（Ⅱ）当x∈[0,π]时，求f (x )的值域。

17、如图，已知长方体中1111D C B A ABCD
，1AB BC AA ===
，
（Ⅰ）求异面直线11AB BC 与所成的角；（Ⅱ）求长方体外接球表面积。

18、右图为一简单组合体，其底面ABCD 为平行四边形，四边形PDCE 是梯形，//EC PD .
（Ⅰ）作出平面PEB 与平面ABCD 的交线，不要求写作法；（Ⅱ）求证：//BE 平面PDA ．
19、甲船在A 处、乙船在甲船正南方向距甲船40海里的B 处，乙船以每小时20海里的速度
向正北方向行驶，而甲船同时以每小时10海里的速度由A 处向南偏西60o
方向行驶，问经过多少小时后，甲、乙两船相距最近？
1
A 1
第17题图
第19题图 B
第18题图
20、设,,A B C 为ABC ∆的三个内角，)0,(c b m +=，),0(a n =，且bc n m n m 3)()(=-⋅+（Ⅰ）求角A 的大小；
（Ⅱ）求sin sin B C +的取值范围。

21、如图在四棱锥P —ABCD 中，底面ABCD 是菱形，CD PA ⊥，AB=2，PA=2，PC=3，,E 是PC 的中点，F 是AB 的中点。

（Ⅰ）求证：BE ∥平面PDF ；（Ⅱ）求BE 的长；
（Ⅲ）求BE 与AD 所成角的余弦值。

第21题图
宁国中学高一年级第二学期第一次段考Array数学试题答题卡
主观题分数：
一、选择题（每小题5分，共50分，填在答题卡上）
三、解答题（共75分，填写在每一题对应格子内，不要超出答题框）
18、（本小题12分）17、（本小题12分）
1
A1
第17题图
B
第18题图。

最新-安徽省宁国中学2018-2018学年高一数学第二学期第一次段考新人教A版精品

高中数学模块1 高考真题(含解析)新人教A版必修1-新人教A版高一必修1数学试题

最新-安徽省宁国中学2018-2018学年高一物理第二学期第一次段考新人教版精品

安徽省宁国中学2020-2021学年高一上学期第一次段考数学试题及答案

2018-2019学年第二学期期末考试高一年级数学试卷(含答案)

安徽省宁国中学2018-2019学年高一数学上学期期中试题(扫描版)

安徽省宁国中学高一英语第二学期第一次段考新人教版

宁国市第一中学2018-2019学年高三上学期11月月考数学试卷含答案

2017-2018学年度人教版高一第一学期期末质量检测语文试题含答案

最新-安徽省宣城市2018学年高一数学下学期期中试题新

安徽省宁国中学高一数学第二次段考

最新-安徽省宁国市2018学年高一英语上学期18月月考试

宁国市第一中学校2018-2019学年高二上学期第二次月考试卷数学

宁国市一中2018-2019学年上学期高二数学12月月考试题含解析

宁国市高级中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市第一高级中学2018-2019学年高二上学期数学期末模拟试卷含解析

最新-安徽省宁国中学2018-2018学年高一数学第二学期第一次段考新人教A版 精品

高中数学 模块1 高考真题(含解析)新人教A版必修1-新人教A版高一必修1数学试题

最新-安徽省宁国中学2018-2018学年高一物理第二学期第一次段考新人教版 精品

安徽省宁国中学2020-2021学年高一上学期第一次段考数学试题及答案

2018-2019学年第二学期期末考试高一年级数学试卷(含答案)

安徽省宁国中学2018-2019学年高一数学上学期期中试题(扫描版)

安徽省宁国中学高一英语第二学期第一次段考新人教版

宁国市第一中学2018-2019学年高三上学期11月月考数学试卷含答案

2017-2018学年度人教版高一第一学期期末质量检测语文试题含答案

最新-安徽省宣城市2018学年高一数学下学期期中试题新

安徽省宁国中学 高一 数学 第二次段考

最新-安徽省宁国市2018学年高一英语上学期18月月考试

宁国市第一中学校2018-2019学年高二上学期第二次月考试卷数学

宁国市一中2018-2019学年上学期高二数学12月月考试题含解析

宁国市高级中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案

宁国市第一高级中学2018-2019学年高二上学期数学期末模拟试卷含解析

最新-安徽省宁国中学2018-2018学年高一数学第二学期第一次段考新人教A版精品

高中数学模块1 高考真题(含解析)新人教A版必修1-新人教A版高一必修1数学试题

最新-安徽省宁国中学2018-2018学年高一物理第二学期第一次段考新人教版精品

安徽省宁国中学高一数学第二次段考