人教版九年级旋转题型汇总
人教版九年级数学上册 旋转专题综合练习经典题目 (无答案)

旋转专题一类型一:旋60°造等边1.如图, P是等边△ABC内部一点.若PC = 3, PA = 4, PB = 5,求△ABC的边长.2.如图, P是等边△ABC外一点,若PA = 3, PB = 4, PC = 5,求∠APB的度数.3.如图,四边形ABCD中,AB = BD=AD,∠BCD= 30°.求证:DC2 +BC2=AC2.类型二:旋90°,造垂直4.如图,四边形ABCD被对角线BD分为等腰直角三角形ABD和直角三角形CBD,其中∠A和∠C都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.5.如图5,△PAB 中,∠APB= 45°,PA = 2,PB= 4,以AB为一边作正方形 ABCD.求PD的长.6.如图,△ABC中,AC=BC= 90°,D为AB的中点,若E是直线AC上任意一点,DF丄DE,交直线BC于F点。
G为EF的中点,延长CG交AB于点H.(1)证明:DE=DF;(2)证明:CG=GH.7.如图, E是正方形ABCD的边CD上任意一点,F是边AD上的点,且FB平分∠ABE. 证明:BE = AF+CE.8.如图,已知△ABC中,∠ACB= 135° ,将△ABC绕点A顺时针旋转90°,得到△AED,连接 CD, CE.(1)求证:△ACD为等腰直角三角形;(2)若BC=1, AC=2,求四边形ACED的面积.类型三:旋180°,造中心对称9.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8 时,则阴影部分的面积为多少?10.如图,在△ABC中,AB = 2AC, AD为BC边上的中线,AD⊥AC,求∠BAC的度数.类型四:大角夹半角11.如图, △ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC= 120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.(1)求证:MN = BM+ NC;(2)△AMN的周长为多少?12.已知:正方形ABCD中,∠MAN = 45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC (或它们的延长线)于点M,N.如图 (1),当∠MAN绕点A旋转到BM = DN 时,易证BM+ DN = MN.(1)如图 (2),当∠MAN绕点A旋转到BM≠DN时,线段BM, DN和MN之间有怎样的数量关系?写出猜想,并加以证明.(2)当∠MAN绕点A旋转到如图(3)的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.旋转专题二类型三:旋180°,造中心对称1.已知矩形ABCD的一条边AD = 8,将矩形ABCD折叠,使得顶点B落在CD边上的 P点处.(1)如图 (1),已知折痕与边BC交于点O,连接AP,OP, OA.若△OCP与△PDA的面积比为 1 : 4,求边CD的长;(2)如图 (2),在(1)的条件下,擦去折痕AO,线段OP,连接BP.动点M在线段AP上(点M与点P, A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB 于点F,作ME丄BP于点E.试问当动点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明变化规律;若不变,求出线段EF的长度.类型四:大角夹半角2.数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且 60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB, AD于点E, F (不包括线段的端点).(1 )初步尝试:如图2 (1),若 AD = AB,求证:①△BCE ≌△ACF,②AE + AF = AC;(2)类比发现:如图 (2),若AD = 2AB,过点C作CH丄AD于点H.求证:AE = 2FH;(3)深入探究:如图 (3),若AD = 3AB,探究得:AC AF3AE 的值为常数t,则t= .类型五:旋转任意角3.如图,△ABC 与△ADE 中,∠BAC=∠DAE=ɑ°,AD = AE, AB = AC,连接CE.请你在图中确定一个以已知点为顶点的多边形,使它的面积等于S△ABC-S△ADE的差,并说明理由.4.如图,点E是菱形ABCD对角线CA延长线上的任意一点,以线段AE为边作一个菱形AEFG,使菱形AEFG∽菱形ABCD,且面积之比为2 : 5,EC = 8,610AF,连接DG,求DG的长.55.如图 (1),△ABC是等腰直角三角形,四边形ADEF是正方形,D, F分别在AB, AC 边上,此时BD=CF, BD丄CF成立.(1)当正方形ADEF绕点A逆时针旋转θ(θ)090时,如图 (2) , BD= CF成立吗?若成立,请证明;若不成立,请说明理由.(2)当正方形ADEF绕点A逆时针旋转45°时,如图 (3),延长BD交CF于点G.①求证:BD丄CF;②当,42AB AD时,求线段BG的长.6.如图,已知△ABC是等腰直角三角形,∠BAC = 90°,点D是BC的中点,作正方形DEFG, 连接AE.若BC=DE = 2,将正方形DEFG绕点D逆时针方向旋转,在旋转过程中,当AE为最大值时,求AF的值.1 7.拓展.(1)如图 (1),在四边形 ABCD 中,AB = AD,∠B = ∠D = 90°,E, F 分别是边BC, CD 上的点,且12EAF BAD .求证:EF = BE + FD. (2)如图 (2),在四边形 ABCD 中,AB = AD,∠B +∠D=180°,E,F 分别是边 BC,CD 上的点且12EAF BAD . (1)中的结论是否仍然成立?不用证明. (3)如图(3),在四边形 中,AB = AD, ∠B + ∠ADC= 180°,E 、F 分别是边 BC,CD 上的点,且12EAF BAD .(1)中的结论是否仍然成立?若成立,请证明; 若不成立,请写出它们之间的数量关系,并证明.。
(完整版)人教版九年级数学上册《旋转》知识点及复习题

第三单元旋转一、旋转1、定义把一个图形绕某一点O转动一个角度的图形变换叫做旋转,其中O叫做旋转中心,转动的角叫做旋转角。
2、性质(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角等于旋转角。
二、中心对称1、定义把一个图形绕着某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
2、性质(1)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
(3)关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3、判定如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。
4、中心对称图形把一个图形绕某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个店就是它的对称中心。
考点五、坐标系中对称点的特征(3分)1、关于原点对称的点的特征两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y)2、关于x轴对称的点的特征两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y)3、关于y轴对称的点的特征两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)单元测试1.下列正确描述旋转特征的说法是()A.旋转后得到的图形与原图形形状与大小都发生变化.B.旋转后得到的图形与原图形形状不变,大小发生变化.C.旋转后得到的图形与原图形形状发生变化,大小不变.D.旋转后得到的图形与原图形形状与大小都没有变化.2.下列描述中心对称的特征的语句中,其中正确的是()A.成中心对称的两个图形中,连接对称点的线段不一定经过对称中心B.成中心对称的两个图形中,对称中心不一定平分连接对称点的线段C.成中心对称的两个图形中,对称点的连线一定经过对称中心,但不一定被对称中心平分D.成中心对称的两个图形中,对称点的连线一定经过对称中心,且被对称中心平分3.4.下列图形中即是轴对称图形,又是旋转对称图形的是()A.(l)(2)B.(l)(2)(3)C.(2)(3)(4)D.(1)(2)(3(4)5.下列图形中,是中心对称的图形有()①正方形;②长方形;③等边三角形;④线段;⑤角;⑥平行四边形。
人教版九年级数学上册第二十三章旋转必刷常考题附答案

人教版九年级数学上册第二十三章旋转必刷常考题附答案一.选择题(共5小题)1.如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,那么∠AOB'的度数是()A.15°B.30°C.45°D.60°2.在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P′的坐标是()A.(3,1)B.(﹣3,﹣1)C.(﹣3,1)D.(﹣1,3)3.如图,AC、BD为四边形ABCD的对角线,将△ACD绕点A顺时针旋转60°,得到△AEB(点C、D的对应点分别为点E、B),若点C、B、E在一条直线上,则下列说法错误的是()A.∠ABC+∠ADC=180°B.∠BCD=120°C.AC=BC+CD D.AE=BD4.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△A′B′C′,若点B′恰好落在BC边上,AB′=CB′,则∠C′的度数为()A.18°B.20°C.22°D.24°5.如图所示,已知点A(﹣1,2),将长方形ABOC沿x轴正方向连续翻转2021次,点A 依次落在点A1,A2,A3,…,A2021的位置,则A2021的坐标是()A.(3038,1)B.(3032,1)C.(2021,0)D.(2021,1)二.填空题(共5小题)6.如图,这个正六边形是由Rt△ABC绕点O经过多次旋转变换得到,则∠ABC=.7.如图,正方形ABCD中,点E,F分别在BC和AB上,BE=2,AF=2,BF=4,将△BEF绕点E顺时针旋转,得到△GEH,当点H落在CD边上时,F,H两点之间的距离为.8.如图,将△ABC绕点A逆时针旋转得到△AB′C′,延长CB交B′C′于点D,若∠BAB ′=40°,则∠C′DC的度数是°.9.如图,已知正方形ABCD的边长为4,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是.10.如图,正方形ABCD中,E为DC边上一点,且DE=2,将AE绕点E逆时针旋转90°得到EF,连接AF、FC,则线段FC的长度是.三.解答题(共5小题)11.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,连接BE、DF、BF.(1)证明:△CFD≌△ABC;(2)证明:四边形BEDF是平行四边形.12.如图,四边形ABCD是矩形,以点B为中心,顺时针旋转矩形ABCD得到矩形GBEF,点A,D,C的对应点分别为点G,F,E,点D恰好在FG的延长线上,BG与CD相交于点H,求证:DH=BH.13.如图,是由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A、B、C、D均在格点上,在网格中将点D按下列步骤移动:第一步:点D绕点A顺时针旋转180°得到点D1;第二步:点D1绕点B顺时针旋转90°得到点D2;第三步:点D2绕点C顺时针旋转90°回到点D;(1)请用圆规画出点D→D1→D→D经过的路径;(2)所画图形是对称图形;(3)写出所画图形围成的面积.(结果保留π)14.如图1,在△ABC中,BA=BC,D、E是AC边上的两点,且满足∠DBE=∠ABC.以点B为旋转中心,将△CBE按逆时针方向旋转得到△ABF,连接DF.(1)求证:DF=DE;(2)如图2,若AB⊥BC,其他条件不变.求证:DE2=AD2+EC2.15.在平面直角坐标系中,已知点A(2,0),点B在y轴正半轴上,且∠BAO=60°,点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.(1)如图1,A'B'恰好经过点A时,①求此时旋转角α的度数;②求出此时点B'的坐标;(2)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,猜测AA'与BB'的位置关系,并说明理由.2022-2023学年上学期初中数学人教版九年级期末必刷常考题之旋转参考答案与试题解析一.选择题(共5小题)1.如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,那么∠AOB'的度数是()A.15°B.30°C.45°D.60°【考点】旋转的性质.【专题】平移、旋转与对称;推理能力.【分析】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角,进而得出答案即可.【解答】解:∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,∴∠A′OA=45°,∠AOB=∠A′OB′=15°,∴∠AOB′=∠A′OA﹣∠A′OB′=45°﹣15°=30°,故选:B.【点评】此题主要考查了旋转的性质,根据旋转的性质得出∠A′OA=45°,∠AOB=∠A′OB′=15°是解题关键.2.在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P′的坐标是()A.(3,1)B.(﹣3,﹣1)C.(﹣3,1)D.(﹣1,3)【考点】关于原点对称的点的坐标.【专题】平面直角坐标系;平移、旋转与对称;模型思想;应用意识.【分析】根据关于原点对称的两个点的坐标之间的关系,即纵横坐标均互为相反数,可得答案.【解答】解:点P(3,﹣1)关于坐标原点中心对称的点P′的坐标为(﹣3,1),故选:C.【点评】本题考查关于原点对称的点的坐标,掌握关于原点对称的两个点坐标之间的关系是得出正确答案的前提.3.如图,AC、BD为四边形ABCD的对角线,将△ACD绕点A顺时针旋转60°,得到△AEB(点C、D的对应点分别为点E、B),若点C、B、E在一条直线上,则下列说法错误的是()A.∠ABC+∠ADC=180°B.∠BCD=120°C.AC=BC+CD D.AE=BD【考点】全等三角形的判定与性质;旋转的性质.【专题】平移、旋转与对称;运算能力;推理能力.【分析】由旋转的性质可得出∠ADC=∠ABE,AC=AE,AD=AB,∠ACD=∠AEB,∠CAE=∠DAB=60°,得出△CAE和△DAB都是等边三角形,可判断A,B,C选项正确,则可得出结论.【解答】解:∵将△ACD绕点A顺时针旋转60°,得到△AEB,∴∠ADC=∠ABE,∵∠ABE+∠ABC=180°,∴∠ADC+∠ABC=180°,故选项正确,不符合题意,∵将△ACD绕点A顺时针旋转60°,得到△AEB,∴AC=AE,AD=AB,∠ACD=∠AEB,∠CAE=∠DAB=60°,∴△CAE和△DAB都是等边三角形,∴∠ACD=∠AEB=60°,∠ACE=60°,∴∠BCD=120°,故B选项正确,不符合题意;∵△ACE为等边三角形,∴AC=CE=BE+BC,又∵BE=CD,∴AC=CD+BC,故C选项正确,不符合题意,∵BD=AB,AB≠AE,∴AE≠BD,故D选项错误,符合题意.故选:D.【点评】本题主要考查旋转的性质,等边三角形的判定与性质,熟练掌握旋转的性质是解题的关键.4.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△A′B′C′,若点B′恰好落在BC边上,AB′=CB′,则∠C′的度数为()A.18°B.20°C.22°D.24°【考点】等腰三角形的性质;旋转的性质.【专题】图形的相似;应用意识.【分析】根据图形的旋转性质,得AB=AB′,已知AB′=CB′,结合等腰三角形的性质及三角形的外角性质,得∠B、∠C的关系为解决问题的关键.【解答】解:∵AB′=CB′,∴∠C=CAB′,∴∠AB′B=∠C+∠CAB′=2∠C,∵将△ABC绕点A按逆时针方向旋转得到△AB′C′,∴∠C=∠C′,AB=AB′,∴∠B=∠AB′B=2∠C,∵∠B+∠C+∠CAB=180°,∴3∠C=180°﹣108°,∴C=24°,∴∠C′=∠C=24°,故选:D.【点评】本题主要考查了等腰三角形的性质及图形的旋转性质.5.如图所示,已知点A(﹣1,2),将长方形ABOC沿x轴正方向连续翻转2021次,点A 依次落在点A1,A2,A3,…,A2021的位置,则A2021的坐标是()A.(3038,1)B.(3032,1)C.(2021,0)D.(2021,1)【考点】规律型:点的坐标;坐标与图形变化﹣旋转.【专题】规律型;平移、旋转与对称;几何直观;运算能力;推理能力.【分析】分析A1,A2,A3,A4,A5点坐标,找到规律求解.【解答】解:根据图形分析,从A开始旋转,当旋转到A4,时,A回到矩形的起始位置,4次一循环.A1(2,1),A2(3,0),A3(3,0),A4(5,2),A5(8,1),A6(9,0),A7(9,0),A8(11,2),A9(14,1),A10(15,0),A11(15,0),A12(17,2),A4n+1(6n+2,1),A4n+2(6n+3,0),A4n+3(6n+3,0),A4n+4(6n+5,0),当A2021时,即4n+1=2021,解得n=505,∴横坐标为6n+2=6×505+2=3032,纵坐标为1,则A2021的坐标(3032,1),故选:B.【点评】本题主要考查图形的旋转变换,解题关键是找到图形在旋转的过程中,点坐标变化规律进而求解.二.填空题(共5小题)6.如图,这个正六边形是由Rt△ABC绕点O经过多次旋转变换得到,则∠ABC=30°.【考点】多边形内角与外角;旋转对称图形.【专题】平移、旋转与对称;几何直观.【分析】依据多边形内角和公式求得正六边形每个角的度数,再根据角的和差关系进行计算即可.【解答】解:由旋转可得,该多边形是正六边形,∴该正六边形每个角为=120°,∴∠ABC=120°﹣90°=30°,故答案为:30°.【点评】本题主要考查了旋转对称图形,如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.7.如图,正方形ABCD中,点E,F分别在BC和AB上,BE=2,AF=2,BF=4,将△BEF绕点E顺时针旋转,得到△GEH,当点H落在CD边上时,F,H两点之间的距离为2.【考点】勾股定理;正方形的性质;旋转的性质.【专题】矩形菱形正方形;平移、旋转与对称;运算能力;推理能力.【分析】连接FH,由正方形的性质得出∠B=∠C=90°,AB=BC,由旋转的性质得出EF=EH,证明Rt△EBF≌Rt△HCE(HL),得出∠EFB=∠HEC,证出∠FEH=90°,由勾股定理可得出答案.【解答】解:连接FH,∵四边形ABCD是正方形,∴∠B=∠C=90°,AB=BC,∵AF=2,BF=4,∴AB=6,∵BE=2,∴CE=4,∴BF=CE,∵将△BEF绕点E顺时针旋转,得到△GEH,∴EF=EH,在Rt△EBF和Rt△HCE中,,∴Rt△EBF≌Rt△HCE(HL),∴∠EFB=∠HEC,∵∠EFB+∠BEF=90°,∴∠BEF+∠CEH=90°,∴∠FEH=90°,∵BF=4,BE=2,∴EF===2,∴FH=EF=2.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质,勾股定理.8.如图,将△ABC绕点A逆时针旋转得到△AB′C′,延长CB交B′C′于点D,若∠BAB′=40°,则∠C′DC的度数是40°.【考点】旋转的性质.【专题】平移、旋转与对称;推理能力.【分析】由旋转的性质得到∠BAC=∠B′AC′,∠C=∠C′,进而推出∠CAC′=40°,根据三角形内角和定理证得∠C′DC=∠CAC′,即可求得∠C'DC的度数.【解答】解:∵将△ABC绕点A逆时针旋转得到△AB'C',∴△ABC≌△AB'C',∴∠BAC=∠B′AC′,∠C=∠C′,∵∠BAB'=40°,∴∠CAC′=40°,∵∠C'DC=180°﹣∠DEC′﹣∠C′,∠CAC′=180°﹣C﹣∠AEC,∠DEC′=∠AEC,∠C′DC=∠CAC′=40°,故答案为:40.【点评】本题主要考查了旋转的性质,三角形内角和定理,能灵活运用旋转的性质是解决问题的关键.9.如图,已知正方形ABCD的边长为4,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是4.【考点】正方形的性质;轴对称﹣最短路线问题;旋转的性质.【专题】图形的全等;平移、旋转与对称;推理能力.【分析】连接BF,过点F作FG⊥AB交AB延长线于点G,通过证明∴△AED≌△GFE (AAS),确定F点在BF的射线上运动,作点C关于BF的对称点C',由三角形全等得到∠CBF=45°,从而确定C'点在AB的延长线上,当D,F,C'三点共线时,DF+CF=DC'最小,在Rt△ADC'中,AD=4,AC'=8,求出DC'=4即可.【解答】解:连接BF,过点F作FG⊥AB交AB延长线于点G,∵将ED绕点E顺时针旋转90°到EF,∴EF⊥DE,且EF=DE,∴∠EDA=∠FEG,在△AED与△GFE中,,∴△AED≌△GFE(AAS),∴FG=AE,∴F点在BF的射线上运动,作点C关于BF的对称点C',∵EG=DA,FG=AE,∴AE=BG,∴BG=FG,∴∠FBG=45°,∴∠CBF=45°,∴BF是∠CBC'的角平分线,即F点在∠CBC'的角平分线上运动,∴C'点在AB的延长线上,当DF+CF=DC'最小,在Rt△ADC'中,AD=4,AC'=8,∴DC'===4,故答案为4.【点评】本题考查了旋转的性质,正方形的性质,轴对称求最短路径,能够将线段和通过轴对称转化为共线线段是解题的关键.10.如图,正方形ABCD中,E为DC边上一点,且DE=2,将AE绕点E逆时针旋转90°得到EF,连接AF、FC,则线段FC的长度是2.【考点】勾股定理;正方形的性质;旋转的性质.【专题】矩形菱形正方形;平移、旋转与对称;运算能力;推理能力.【分析】过点F作FH⊥CD于H,如图,利用正方形的性质得DA=CD,∠D=90°,再根据旋转的性质得EA=EF,∠AEF=90°,接着证明△ADE≌△EHF得到DE=FH=2,AD=EH,所以EH=DC,则DE=CH=2,然后利用勾股定理计算FC的长.【解答】解:过点F作FH⊥于H,如图,∵四边形ABCD为正方形,∴DA=CD,∠D=90°,∵AE绕点E顺时针旋转90°得到EF,∴EA=EF,∠AEF=90°,∵∠DAE+∠AED=90°,∠FEH+∠AED=90°,∴∠EAD=∠FEH,在△ADE和△EHF中,,∴△ADE≌△EHF(AAS),∴DE=FH=2,AD=EH,∴EH=DC,即DE+CE=CH+EC,∴DE=CH=2,在Rt△CFH中,FC===2,【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.三.解答题(共5小题)11.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,连接BE、DF、BF.(1)证明:△CFD≌△ABC;(2)证明:四边形BEDF是平行四边形.【考点】全等三角形的判定与性质;直角三角形斜边上的中线;平行四边形的判定;旋转的性质.【专题】图形的全等;多边形与平行四边形;推理能力.【分析】(1)由旋转的性质可得CB=CE,AB=DE=BF,由“SSS”可证△ABC≌△CFD;(2)延长BF交CE于点G,可证BF∥ED,由一组对边平行且相等可证四边形BEDF 是平行四边形.【解答】证明:(1)∵点F是边AC中点,∴CF=AC,∵∠BCA=30°,∴BA=AC,∠A=60°,∴AB=CF,∵将△ABC绕点C顺时针旋转60°得到△DEC,∴AC=CD,∠ACD=60°,∴∠ACB=∠DCE,在△ABC和△CFD中,,∴△ABC≌△CFD(SAS);(2)延长BF交CE于点G,由(1)得,FC=BF,∴∠BCF=∠FBC=30°,∵∠BCE=60°,∴∠BCE+∠CBG=∠BGE=90°,∵∠DEC=∠ABC=90°∴∠BGE=∠DEC,∴BF∥ED,∵,AB=DE,∴BF=DE,∴四边形BEDF是平行四边形.【点评】本题考查了旋转的性质,全等三角形的判定和性质,平行四边形的判定等知识,灵活运用这些知识进行推理是本题的关键.12.如图,四边形ABCD是矩形,以点B为中心,顺时针旋转矩形ABCD得到矩形GBEF,点A,D,C的对应点分别为点G,F,E,点D恰好在FG的延长线上,BG与CD相交于点H,求证:DH=BH.【考点】全等三角形的判定与性质;矩形的性质;旋转的性质.【专题】图形的全等;矩形菱形正方形;平移、旋转与对称;推理能力.【分析】证明Rt△BDA≌Rt△BDG,得到∠ABD=∠GBD,再利用矩形性质求解.【解答】证明:∵旋转矩形ABCD得到矩形GBEF,∴AB=BG,∠A=∠DGB=90°,在Rt△BDA和Rt△BDG中,,∴Rt△BDA≌Rt△BDG(HL),∴∠ABD=∠GBD,∵四边形ABCD是矩形,∴∠ABD=∠BDH,∴∠BDH=∠HBD,∴DH=BH.【点评】本题主要考查了旋转的性质、矩形的性质、解题关键是证明Rt△BDA≌Rt△BGA,得到∠ABD=∠GBD,再利用矩形性质求解.13.如图,是由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A、B、C、D均在格点上,在网格中将点D按下列步骤移动:第一步:点D绕点A顺时针旋转180°得到点D1;第二步:点D1绕点B顺时针旋转90°得到点D2;第三步:点D2绕点C顺时针旋转90°回到点D;(1)请用圆规画出点D→D1→D2→D经过的路径;(2)所画图形是轴对称图形;(3)写出所画图形围成的面积.(结果保留π)【考点】作图﹣旋转变换.【专题】平移、旋转与对称;几何直观;运算能力.【分析】(1)根据要求画出图形即可.(2)根据轴对称图形的定义判断即可.S+S﹣S矩形,利用扇形的面积公式(3)根据所画图形的面积=S计算可得.【解答】解:(1)点D→D1→D2→D经过的路径如图所示.(2)所画图形是轴对称图形;故答案为:轴.S+S﹣S矩形(3)所画图形的面积=S半圆+=•π•42+×2﹣4×8=8π+4π+4π﹣32=16π﹣32.【点评】本题考查作图﹣旋转变换,扇形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.14.如图1,在△ABC中,BA=BC,D、E是AC边上的两点,且满足∠DBE=∠ABC.以点B为旋转中心,将△CBE按逆时针方向旋转得到△ABF,连接DF.(1)求证:DF=DE;(2)如图2,若AB⊥BC,其他条件不变.求证:DE2=AD2+EC2.【考点】全等三角形的判定与性质;等腰三角形的性质;勾股定理;旋转的性质.【专题】图形的全等;等腰三角形与直角三角形;平移、旋转与对称;推理能力.【分析】(1)先根据∠DBE=∠ABC可知∠ABD+∠CBE=∠DBE=∠ABC,再由图形旋转的性质可知BE=BF,∠ABF=∠CBE,故可得出∠DBF=∠DBE,由全等三角形的性质即可得出△DBE≌△DBF,故可得出结论;(2)把△CBE逆时针旋转90°,由于△ABC是等腰直角三角形,故可知图形旋转后点C与点A重合,∠FAB=∠BCE=45°,所以∠DAF=90°,由(1)证DE=DF,再根据勾股定理即可得出结论.【解答】(1)证明:∵∠DBE=∠ABC,∴∠ABD+∠CBE=∠DBE=∠ABC,∵△ABF由△CBE旋转而成,∴BE=BF,∠ABF=∠CBE,∴∠DBF=∠DBE,在△DBE与△DBF中,,∴△DBE≌△DBF(SAS),∴DF=DE;(2)证明:∵将△CBE按逆时针方向旋转得到△ABF,∴BA=BC,∠ABC=90°,∴∠BAC=∠BCE=45°,∴图形旋转后点C与点A重合,CE与AF重合,∴AF=EC,∴∠FAB=∠BCE=45°,∴∠DAF=90°,在Rt△ADF中,DF2=AF2+AD2,∵AF=EC,∴DF2=EC2+AD2,同(1)可得DE=DF,∴DE2=AD2+EC2.【点评】本题考查的是图形的旋转及勾股定理,熟知旋转前、后的图形全等是解答此题的关键.15.在平面直角坐标系中,已知点A(2,0),点B在y轴正半轴上,且∠BAO=60°,点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.(1)如图1,A'B'恰好经过点时,①求此时旋转角α的度数;②求出此时点B'的坐标;(2)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,猜测AA'与BB'的位置关系,并说明理由.【考点】含30度角的直角三角形;坐标与图形变化﹣旋转.【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.【分析】(1)①根据旋转的性质得到OA=OA',∠A'=∠BAO=60°,推出△OAA'是等边三角形,于是得到α=∠AOA'=60°;②如图1,过B'作B'C⊥x轴于C,根据三角形的内角和定理得到∠OBA=30,根据勾股定理得到,求得,得到,于是得到答案;(2)如图2,等腰三角形的性质得到,推出∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,由垂直的定义得到结论.【解答】解:(1)①由旋转得:OA=OA',∠A'=∠BAO=60°,∴△OAA'是等边三角形,∴α=∠AOA'=60°;②如图1,过B'作B'C⊥x轴于C,∵∠BAO=60°,∴∠OBA=30°,在Rt△OAB中,∠OBA=30°,∴AB=2OA=4,∴,∴,又∵∠AOA'=60°,∴∠B'OC=90°﹣∠AOA'=30°,∵∠B'CO=90°,∴,∴,∴;(2)AA'⊥BB',理由:如图2,∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',∴,∵∠BOA'=90°﹣α,四边形OBPA'的内角和为360°,∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,即AA'⊥BB'.【点评】主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和定理,解决问题的关键是熟练掌握旋转的性质.考点卡片1.规律型:点的坐标规律型:点的坐标.2.全等三角形的判定与性质(1)全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.(2)在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.3.等腰三角形的性质(1)等腰三角形的概念有两条边相等的三角形叫做等腰三角形.(2)等腰三角形的性质①等腰三角形的两腰相等②等腰三角形的两个底角相等.【简称:等边对等角】③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】(3)在①等腰;②底边上的高;③底边上的中线;④顶角平分线.以上四个元素中,从4.含30度角的直角三角形(1)含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.(2)此结论是由等边三角形的性质推出,体现了直角三角形的性质,它在解直角三角形的相关问题中常用来求边的长度和角的度数.(3)注意:①该性质是直角三角形中含有特殊度数的角(30°)的特殊定理,非直角三角形或一般直角三角形不能应用;②应用时,要注意找准30°的角所对的直角边,点明斜边.5.直角三角形斜边上的中线(1)性质:在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点)(2)定理:一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.该定理可以用来判定直角三角形.6.勾股定理(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.(2)勾股定理应用的前提条件是在直角三角形中.(3)勾股定理公式a2+b2=c2的变形有:a=,b=及c=.(4)由于a2+b2=c2>a2,所以c>a,同理c>b,即直角三角形的斜边大于该直角三角形中的每一条直角边.7.多边形内角与外角(1)多边形内角和定理:(n﹣2)•180°(n≥3且n为整数)此公式推导的基本方法是从n边形的一个顶点出发引出(n﹣3)条对角线,将n边形分割为(n﹣2)个三角形,这(n﹣2)个三角形的所有内角之和正好是n边形的内角和.除此方法之和还有其他几种方法,但这些方法的基本思想是一样的.即将多边形转化为三角形,这也是研究多边形问题常用的方法.(2)多边形的外角和等于360①多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.②借助内角和和邻补角概念共同推出以下结论:外角和=180°n﹣(n﹣2)•180°=360°.8.平行四边形的判定(1)两组对边分别平行的四边形是平行四边形.符号语言:∵AB∥DC,AD∥BC∴四边行ABCD是平行四边形.(2)两组对边分别相等的四边形是平行四边形.符号语言:∵AB=DC,AD=BC∴四边行ABCD是平行四边形.(3)一组对边平行且相等的四边形是平行四边形.符号语言:∵AB∥DC,AB=DC∴四边行ABCD是平行四边形.(4)两组对角分别相等的四边形是平行四边形.符号语言:∵∠ABC=∠ADC,∠DAB=∠DCB∴四边行ABCD是平行四边形.(5)对角线互相平分的四边形是平行四边形.符号语言:∵OA=OC,OB=OD∴四边行ABCD是平行四边形.9.矩形的性质(1)矩形的定义:有一个角是直角的平行四边形是矩形.(2)矩形的性质①平行四边形的性质矩形都具有;②角:矩形的四个角都是直角;③边:邻边垂直;④对角线:矩形的对角线相等;⑤矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中点连线所在的直线;对称中心是两条对角线的交点.(3)由矩形的性质,可以得到直角三角形的一个重要性质,直角三角形斜边上的中线等于斜边的一半.10.正方形的性质(1)正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.(2)正方形的性质①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③正方形具有四边形、平行四边形、矩形、菱形的一切性质.④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.11.轴对称-最短路线问题1、最短路线问题在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点.2、凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.12.旋转的性质(1)旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.(2)旋转三要素:①旋转中心;②旋转方向;③旋转角度.注意:三要素中只要任意改变一个,图形就会不一样.13.旋转对称图形(1)旋转对称图形如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.(214.关于原点对称的点的坐标关于原点对称的点的坐标特点(1)两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y).(2)关于原点对称的点或图形属于中心对称,它是中心对称在平面直角坐标系中的应用,它具有中心对称的所有性质.但它主要是用坐标变化确定图形.注意:运用时要熟练掌握,可以不用图画和结合坐标系,只根据符号变化直接写出对应点的坐标.15.坐标与图形变化-旋转(1)关于原点对称的点的坐标P(x,y)⇒P(﹣x,﹣y)(2)旋转图形的坐标图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.16.作图-旋转变换(1)旋转图形的作法:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.(2)旋转作图有自己独特的特点,决定图形位置的因素较多,旋转角度、旋转方向、旋转中心,任意不同,位置就不同,但得到的图形全等。
图形的旋转(中考专题提升)2022—2023学年人教版数九年级学上册

图形的旋转(中考专题提升)一、单选题1.有一个正n边形旋转90后与自身重合,则n为()A.6 B.9 C.12 D.152.如图所示的运动员只经过旋转不能得到的是( )3.如图,OAB绕点O逆时针旋转80到OCD的位置,已知45∠等于()AOB∠=,则AODA.55B.45C.40D.35△,点B'恰好落在CA的延长线上,4.如图,将直角三角板ABC绕顶点A顺时针旋转到AB C''B C,则BAC'∠为(),∠=︒∠=︒3090A.90︒B.60︒C.45︒D.305.如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=70°且AD⊥BC于点F,则∠BAC的度数为( )A.65°B.70°C.75°D.80°6.如图,在ABC 中,90ACB ∠=︒,30A ∠=︒,将ABC 绕点C 逆时针旋转90°得到DEC ,则AED ∠的度数为( )A .105°B .120°C .135°D .150°7.将矩形ABCD 绕点A 顺时针旋转()0360αα︒<<︒,得到矩形AEFG .当GC GB =时,下列针对α值的说法正确的是( )A .60︒或300︒B .60︒或330︒C .30D .60︒8.如图,在Rt △ABC 中,∠BAC=90°,AB=AC=3,将一个无限大的直角尺MON 的直角顶点O 与BC 边上的中点D 重合并绕点D 旋转,分别交AB 、AC 所在的直线于点E 、F,连接EF,若BE=1,则EF 的长度为( )A.B. C.或 D.无法确定9.如图,在边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接CE,将线段CE绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是()A.6 B.3 C.2 D.1.510.如图,边长为3的正五边形ABCDE,顶点A、B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE 绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为()A.12°B.16°C.20°D.24°二、填空题11.如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(4,0),连接AB,若将△ABO绕点B顺时针旋转90°,得到△A'BO',则点A'的坐标为.12.如图,将正方形ABCD 绕点A 按逆时针方向旋转到正方形AB ' C ' D ' ,旋转角为α( 0︒<α< 180︒),连接B ' D 、C ' D ,若B ' D =C ' D ,则∠α =____.13.如图,AB=BC=CD,AB⊥BC,∠BCD=30°,则∠BAD=________°.14.如图,点E 在正方形ABCD 的边CB 上,将△DCE 绕点D 顺时针旋转90°到△DAF 的位置,连接EF,过点D 作EF 的垂线,垂足为点H,与AB 交于点G,若AG=4,BG=3,则BE 的长为 .15.如图,△ABC ,△ADE 均为等腰直角三角形,∠BAC=∠DAE=90°,将△ADE 绕点A 在平面内自由旋转,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点,若AD=3,AB=7,则线段MN 的取值范围是______.16.如图,在ABC 中,3AB =,2AC =,60BAC ∠=︒,P 为ABC 内一点,则PA PB PC ++的最小值为__________.三、解答题17.如图,以点O 为旋转中心,将△ABC 按顺时针方向旋转60°,作出旋转后的图形(不用写作法).18.阅读下面材料:小伟遇到这样一个问题:如图1,在正三角形ABC 内有一点P ,且3PA =,4PB =,5PC =,求∠APB 的度数. 小伟是这样思考的:如图2,利用旋转和全等的知识构造AP C '△,连接PP ',得到两个特殊的三角形,从而将问题解决.参考小伟同学思考问题的方法,解决下列问题.(1)请你计算图1中∠APB 的度数.(2)如图3,在正方形ABCD 内有一点P ,且2PA =,1PB =,3PD =,求∠APB 的度数.19.已知ABC 是等边三角形,点B ,D 关于直线AC 对称,连接AD ,CD .(1)求证:四边形ABCD 是菱形;(2)在线段AC 上任取一点Р(端点除外),连接PD .将线段PD 绕点Р逆时针旋转,使点D 落在BA 延长线上的点Q 处.请探究:当点Р在线段AC 上的位置发生变化时,DPQ ∠的大小是否发生变化?说明理由.(3)在满足(2)的条件下,探究线段AQ 与CP 之间的数量关系,并加以证明.20.如图,在平面直角坐标系中,已知△ABC 的三个顶点的坐标分别为A(1,4),B(4,1),C(4,3).(1)画出将△ABC 向左平移5个单位长度得到的△A 1B 1C 1;(2)画出将△ABC 绕原点O 顺时针旋转90°得到的△A 2B 2C 2.21.已知:如图,在ABC ∆中,120BAC ∠=︒,以BC 为边向形外作等边三角形BCD ∆,把ABD ∆绕着点D 按顺时针方向旋转60︒后得到ECD ∆,若3AB =,2AC =,求BAD ∠的度数与AD 的长.22.已知,四边形ABCD 是正方形,DEF 绕点D 旋转(DE AB <),90EDF ∠=︒,DE DF =,连接AE ,CF.(1)如图1,求证:ADE≌CDF;(2)直线AE与CF相交于点G.①如图2,BM AGBN CF于点N,求证:四边形BMGN是正方形;⊥于点M,⊥②如图3,连接BG,若4DE=,直接写出在DEF旋转的过程中,线段BG长度的最小值.AB=,2参考答案1--10CCBBD AACCA11.812.60°13.15 14.15.22≤MN ≤5216.1917.解析 如图所示,△A'B'C'即为所求.18.(1)150APB ∠=︒(2)135APB ∠=︒19.(1)连接BD ,ABC 是等边三角形,AB BC AC ∴==,点B ,D 关于直线AC 对称,∴AC 垂直平分BD ,,DC BC AD AB ∴==,AB BC CD AD ∴===,∴四边形ABCD 是菱形;(2)当点Р在线段AC 上的位置发生变化时,DPQ ∠的大小不发生变化,始终等于60°,理由如下: 将线段PD 绕点Р逆时针旋转,使点D 落在BA 延长线上的点Q 处,PQ PD ∴=, ABC 是等边三角形,,60AB BC AC BAC ABC ACB ∴==∠=∠=∠=︒,连接PB ,过点P 作PE CB ∥交AB 于点E ,PF ⊥AB 于点F ,则60,60APE ACB AEP ABC ∠=∠=︒∠=∠=︒,60APE BAC AEP ∴∠=∠=︒=∠,APE ∴是等边三角形,AP EP AE ∴==,PF AB ⊥,APF EPF ∴∠=∠,点B ,D 关于直线AC 对称,点P 在线段AC 上,∴PB = PD ,∠DPA =∠BPA ,∴PQ = PD ,PF AB ⊥,QPF BPF ∴∠=∠,∴∠QPF -∠APF =∠BPF -∠EPF ,即∠QPA = ∠BPE ,∴∠DPQ =∠DPA - ∠QPA =∠BPA -∠BPE = ∠APE = 60°;(3)AQ = CP ,证明如下:AC = AB ,AP = AE ,∴AC - AP = AB – AE ,即CP = BE ,AP = EP ,PF ⊥AB ,∴AF = FE ,PQ = PD ,PF ⊥AB ,∴QF = BF ,∴ QF - AF = BF – EF ,即AQ = BE ,∴AQ = CP .20. (1)如图所示,△A 1B 1C 1即为所求.(2)如图所示,△A 2B 2C 2即为所求.21.60BAD ∠=︒,AD=5【解析】只要证明A 、B 、D 、C 四点共圆,即可推出∠BAD=∠BCD =60°,然后证明A 、C 、E 三点共线,根据旋转的性质,推出AD=AE=AC+CE=AC+AB=2+3=5.解:∵ABC ∆的120BAC ∠=︒,以BC 为边向形外作等边BCD ∆,∴12060180BAC BDC ∠+∠=︒+︒=︒.∴A ,B ,D ,C 四点共圆,∴60BAD BCD ∠=∠=︒,180ACD ABD ∠+∠=︒,又∵ABD ECD ∠=∠,∴180ACD ECD ∠+∠=︒,∴180ACE ∠=︒,即A ,C ,E 共线.∵把ABD ∆绕D 点按顺时针方向旋转60︒到ECD ∆位置且3AB =,∴3AB CE ==,∴235AD AE AC AB ==+=+=.本题考查旋转变换、等边三角形的性质、四边形内角和定理等知识,解题的关键是充分利用旋转不变性解决问题,本题的突破点是证明A 、C 、E 共线,△AED 是等边三角形即可. 22(1)证明:四边形ABCD 是正方形,AD DC ∴=,90ADC ∠=︒.DE DF =,90EDF ∠=︒.ADC EDF ∴∠=∠,ADE CDF ,在ADE 和CDF 中,DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩ADE ∴≌()SAS CDF △;(2)①证明:如图2中,设AG 与CD 相交于点P .90ADP ∠=︒,90DAP DPA ∴∠+∠=︒. ADE ≌CDF ,DAE DCF ∴∠=∠.DPA GPC ∠∠=,90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒.90PGN ∠∴=︒,BM AG ⊥,BN GN ⊥,∴四边形BMGN 是矩形,90MBN ∴∠=︒.四边形ABCD 是正方形,AB BC ∴=,90ABC MBN ∠∠==︒.ABM CBN ∴∠=∠.又90AMB BNC ∠∠==︒,AMB ∴≌CNB △.MB NB ∴=.∴矩形BMGN 是正方形;②解:作DH AG ⊥交AG 于点H ,作BM AG ⊥于点M ,∵90,90,DHA AMB ADH DAH BAM AD AB ∠=∠=︒∠=︒-∠=∠= ∴AMB ≌DHA .BM AH ∴=.222AH AD DH =-,4=AD ,DH ∴最大时,AH 最小,2DH DE ==最大值.23BM AH ∴==最小值最小值由()2①可知,BGM 是等腰直角三角形,226BG BM ∴=最小值。
人教版初中九年级数学上册第二十三章《旋转》经典题(含答案解析)

一、选择题1.下列图形中,不是中心对称图形的是()A.B.C.D.A解析:A【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A、是轴对称图形,不是中心对称图形,故本选项符合题意;B、是中心对称图形,故本选项不符合题意;C、是中心对称图形,故本选项不符合题意;D、是中心对称图形,故本选项不符合题意;故选:A.【点睛】本题考查了中心对称图形的概念.中心对称是要寻找对称中心,旋转180°后与原图重合.2.以原点为中心,将点P(3,4)旋转90°,得到的点Q所在的象限为()A.第二象限B.第三象限C.第四象限D.第二或第四象限D 解析:D【分析】根据旋转的性质,以原点为中心,将点P(3,4)旋转90°,分两种情况讨论即可得到点Q 所在的象限.【详解】Q,如图,点P(3,4)按逆时针方向旋转90°,得到点1Q,按顺时针方向旋转90°,得到点2得点Q所在的象限为第二、四象限.【点睛】本题考查了坐标与图形变化-旋转,解决本题的关键是掌握旋转的性质.注意分类讨论.3.以下四幅图案,其中图案是中心对称图形的是()A.B.C.D.A解析:A【分析】根据中心对称图形的定义逐一分析即可.【详解】解:A、是中心对称图形,故此选项符合题意;B、不是中心对称图形,故此选项不合题意;C、不是中心对称图形,故此选项不合题意;D、不是中心对称图形,故此选项不合题意.故选:A.【点睛】本题考查中心对称图形的识别,掌握中心对称图形的定义是解题的关键.4.如图,△ABC中,AB=6,AC=4,以BC为对角线作正方形BDCF,连接AD,则AD长不可能是()A.2 B.4 C.6 D.8D解析:D【分析】将△ABD绕点D顺时针旋转90º得△ECD,AB=EC,DE=AD,等腰Rt△ADE中2AD,在△ACE中由三边关系得,CE-AC<AE<CE+AC,即2<2AD<10求出AD的范围即可.【详解】将△ABD绕点D顺时针旋转90º得△ECD,AB=EC=6,DE=AD,在Rt△ADE中由勾股定理得2AD,在△ACE中由三边关系得,CE-AC<AE<CE+AC,即2<2AD<10,<,2<AD<52=508【点睛】本题考查AD 的范围问题,掌握正方形的性质,和旋转性质,由条件分散,将已知与未知化归一个三角形中,利用旋转构造等腰直角三角形△ACE 实现转化,利用三边关系确定AE 的范围是解题关键.5.如图,在Rt ABC 中,90ACB ∠=︒,60B ∠=︒,1BC =,A B C ''由ABC 绕点C 顺时针旋转得到,其中点A '与点A 、点B '与点B 是对应点,连接AB ',且点A 、B '、A '在同一条直线上,则AA '的长为( )A .3B .3C .4D .45解析:A【分析】 先利用互余计算出∠BAC =30°,再根据含30度的直角三角形三边的关系得到AB =2BC =2,接着根据旋转的性质得A 'B '=AB =2,B 'C =BC =1,A 'C =AC ,∠A '=∠BAC =30°,∠A 'B ' C =∠B =60°,于是可判断CA A '为等腰三角形,所以∠CA A '=∠A '=30°,再利用三角形外角性质计算出∠B 'CA =30°,可得B 'A =B 'C =1,然后利用A A '=A B '+A 'B '进行计算.【详解】解:∵∠ACB =90°,∠B =60°,∴∠BAC =30°,∴AB =2BC =2×1=2,∵ABC绕点C顺时针旋转得到A'B'C,∴A'B'=AB=2,B'C=BC=1,A'C=AC,∠A'=∠BAC=30°,∠A'B'C=∠B=60°,∴CA A'为等腰三角形,∴∠CA A'=∠A'=30°,∵A、B'、A'在同一条直线上,∴∠A'B'C=∠B'AC+∠B'CA,∴∠B'CA=60°﹣30°=30°,∴B'A=B'C=1,∴A A'=A B'+A'B'=2+1=3.故选:A.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系.6.若点P(-m,m-3)关于原点对称的点是第二象限内的点,则m满足( )A.m>3 B.0<m≤3C.m<0 D.m<0或m>3C 解析:C【分析】两个点关于原点对称时,它们的坐标符号相反,即点P(-m,m-3)关于原点O的对称点是P′(m,3-m),再由第二象限内的点横坐标为负数,纵坐标为正数,可得m的取值范围.【详解】解:点P(-m,m-3)关于原点O的对称点是P′(m,3-m),∵P′(m,3-m),在第二象限,∴30 mm<⎧⎨->⎩,∴m<0.故选:C.【点睛】本题考查了关于原点对称的点的坐标,注意掌握:两个点关于原点对称时,它们的坐标符号相反.7.如图,点E,F,G,H分别为四边形ABCD四条边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的是()A.不是平行四边形B.不是中心对称图形C.一定是中心对称图形D.当AC=BD时,它为矩形C 解析:C【分析】先连接AC,BD,根据EF=HG=12AC,EH=FG=12BD,可得四边形EFGH是平行四边形,当AC⊥BD时,∠EFG=90°,此时四边形EFGH是矩形;当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,据此进行判断即可.【详解】连接AC,BD,如图:∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,∴EF=HG=12AC,EH=FG=12BD,∴四边形EFGH是平行四边形,故选项A错误;∴四边形EFGH一定是中心对称图形,故选项B错误;当AC⊥BD时,∠EFG=90°,此时四边形EFGH是矩形,当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,故选项D错误;∴四边形EFGH可能是轴对称图形,∴四边形EFGH是平行四边形,四边形EFGH一定是中心对称图形.故选:C.【点睛】本题主要考查了中点四边形的运用,解题时注意:平行四边形是中心对称图形.解决问题的关键是掌握三角形中位线定理.8.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为().A.60 °B.75°C.85°D.90°C解析:C【解析】试题分析:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.如图,设AD⊥BC于点F.则∠AFB=90°,∴在Rt△ABF中,∠B=90°-∠BAD=25°,∴在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,即∠BAC的度数为85°.故选C.考点: 旋转的性质.9.如图,在△ABC中,AB=2.2,BC=3.6,∠B=60°,将△ABC绕点A按逆时针方向旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为()A.1.5 B.1.4 C.1.3 D.1.2B解析:B【分析】运用旋转变换的性质得到AD=AB,进而得到△ABD为等边三角形,求出BD即可解决问题.【详解】解:如图,由题意得:AD=AB,且∠B=60°,∴△ABD为等边三角形,∴BD=AB=2,∴CD=3.6﹣2.2=1.4.故选:B.【点睛】该题主要考查了旋转变换的性质、等边三角形的判定等几何知识点及其应用问题;牢固掌握旋转变换的性质是解题的关键.10.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE 与△COF成中心对称.其中正确的个数为 ( )A.2 B.3 C.4 D.5D解析:D【分析】由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.【详解】△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,因此点O就是▱ABCD的对称中心,则有:(1)点E和点F;B和D是关于中心O的对称点,正确;(2)直线BD必经过点O,正确;(3)四边形ABCD是中心对称图形,正确;(4)四边形DEOC与四边形BFOA的面积必相等,正确;(5)△AOE与△COF成中心对称,正确;其中正确的个数为5个,故选D.【点睛】熟练掌握平行四边形的性质和中心对称图形的性质是解决此题的关键.二、填空题11.如图.面积为8的正方形ABCD的顶点A在数轴上,点A表示实数2-,正方形ABCD绕点A旋转时,顶点B的运动轨迹与数轴的交点表示的数为______________或﹣【分析】先由正方形的面积公式求出AB=再根据点A表示实数即可求出顶点B的运动轨迹与数轴的交点表示的数【详解】解:∵正方形ABCD的面积为8∴AB=∵点A表示实数∴顶点B 的运动轨迹与数轴的交点表示2或﹣32【分析】先由正方形的面积公式求出AB=22A表示实数2-,即可求出顶点B的运动轨迹与数轴的交点表示的数.【详解】解:∵正方形ABCD 的面积为8,∴AB=22, ∵点A 表示实数2-,∴顶点B 的运动轨迹与数轴的交点表示的数为2-+22=2或2-﹣22=﹣32, 故答案为:2或﹣32.【点睛】本题考查了正方形的面积、实数和数轴、旋转的性质、算术平方根、二次根式的加减运算,理解实数与数轴的关系是解答的关键.12.如图,正方形ABCD 的边长为6,点E 在边CD 上.以点A 为中心,把ADE 顺时针旋转90︒至ABF 的位置,若2DE =,则FC =________.8【分析】先根据旋转的性质和正方形的性质证明CBF三点在一条直线上又知BF =DE =2可得FC 的长【详解】∵四边形ABCD 是正方形∴∠ABC =∠D =90°AD =AB 由旋转得:∠ABF =∠D =90°BF 解析:8【分析】先根据旋转的性质和正方形的性质证明C 、B 、F 三点在一条直线上,又知BF =DE =2,可得FC 的长.【详解】∵四边形ABCD 是正方形,∴∠ABC =∠D =90°,AD =AB ,由旋转得:∠ABF =∠D =90°,BF =DE =2,∴∠ABF +∠ABC =180°,∴C 、B 、F 三点在一条直线上,∴CF =BC +BF =6+2=8,故答案为:8.【点睛】本题主要考查了正方形的性质、旋转变换的性质,难度适中.由旋转的性质得出BF =DE 是解答本题的关键.13.如图,在ABC 中,4AB =, 5.8BC =,60B ∠=︒,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为________.【分析】先根据旋转的性质可得再根据等边三角形的判定与性质可得然后根据线段的和差即可得【详解】由旋转的性质得:是等边三角形故答案为:【点睛】本题考查了旋转的性质等边三角形的判定与性质等知识点熟练掌握旋解析:1.8【分析】先根据旋转的性质可得AB AD =,再根据等边三角形的判定与性质可得4BD AB ==,然后根据线段的和差即可得.【详解】由旋转的性质得:4AB AD ==,60B ∠=︒,ABD ∴是等边三角形,4BD AB ∴==,5.8BC =,5.84 1.8CD BC BD ∴=-=-=,故答案为:1.8.【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点,熟练掌握旋转的性质是解题关键.14.在平面直角坐标系中,点()4,6P -与点()4,1Q m -+关于原点对称,那么m =______.5【分析】先根据关于原点对称的点坐标规律可得一个关于m 的一元一次方程再解方程即可得【详解】关于原点对称的点坐标规律:横纵坐标均互为相反数则解得故答案为:5【点睛】本题考查了关于原点对称的点坐标规律熟解析:5【分析】先根据关于原点对称的点坐标规律可得一个关于m 的一元一次方程,再解方程即可得.【详解】关于原点对称的点坐标规律:横、纵坐标均互为相反数,则610m -++=,解得5m =,故答案为:5.【点睛】本题考查了关于原点对称的点坐标规律,熟练掌握关于原点对称的点坐标规律是解题关键.15.如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360°),得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值和最大值的和为_____.﹣1【分析】由轴对称的性质可知AM=AD故此点M在以A圆心以AD为半径的圆上故此当点AMC在一条直线上时CM有最小值【详解】解:如图所示:连接AM∵四边形ABCD为正方形∴AC==∵点D与点M关于A解析:2﹣1【分析】由轴对称的性质可知AM=AD,故此点M在以A圆心,以AD为半径的圆上,故此当点A、M、C在一条直线上时,CM有最小值.【详解】解:如图所示:连接AM.∵四边形ABCD为正方形,∴AC2222AD CD+=+211∵点D与点M关于AE对称,∴AM=AD=1.∴点M在以A为圆心,以AD长为半径的圆上.如图所示,当点A、M、C在一条直线上时,CM有最小值.∴CM的最小值=AC﹣AM′2﹣1,21.【点睛】本题主要考查的是旋转的性质,正方形的性质,依据旋转的性质确定出点M 运动的轨迹是解题的关键.16.如图,在ABC 中,AB =2,AC =1,∠BAC =30°,将ABC 绕点A 逆时针旋转60°得到11AB C △,连接BC 1,则BC 1的长为__________ .【分析】先根据旋转的定义和性质可得从而可得再利用勾股定理即可得【详解】由旋转的定义和性质得:在中故答案为:【点睛】本题考查了旋转的定义和性质勾股定理熟练掌握旋转的性质是解题关键 解析:5 【分析】 先根据旋转的定义和性质可得111,60A AC C CAC ==∠=︒,从而可得190BAC ∠=︒,再利用勾股定理即可得.【详解】由旋转的定义和性质得:111,60A AC C CAC ==∠=︒,30BAC ∠=︒,1190AC BAC AC B C ∴∠=+=∠∠︒,在1Rt ABC 中,222211215BC AB AC =+=+=,故答案为:5.【点睛】本题考查了旋转的定义和性质、勾股定理,熟练掌握旋转的性质是解题关键.17.如图,在△ABC 中,AB =6,将△ABC 绕点B 按逆时针方向旋转30°后得到△A 1BC 1,则阴影部分的面积为________. 9【分析】根据旋转的性质得到△ABC ≌△A1BC1A1B=AB=6所以△A1BA 是等腰三角形依据∠A1BA=30°得到等腰三角形的面积由图形可以知道S 阴影=S △A1BA+S △A1BC1﹣S △ABC=解析:9【分析】根据旋转的性质得到△ABC ≌△A 1BC 1,A 1B=AB=6,所以△A 1BA 是等腰三角形,依据∠A 1BA=30°得到等腰三角形的面积,由图形可以知道 S 阴影=S △A1BA +S △A 1BC 1﹣S △ABC=S △A 1BA ,最终得到阴影部分的面积.【详解】解:∵在△ABC 中,AB=6,将△ABC 绕点 B 按逆时针方向旋转 30°后得到△A1BC1,∴△ABC≌△A1BC1,∴A1B=AB=6,∴△A1BA 是等腰三角形,∠A1BA=30°,∴S△A1BA= 12×6×3=9,又∵S 阴影=S△A1BA+S△A1BC1﹣S△ABC,S△A1BC1=S△ABC,∴S阴影=S△A1BA=9.故答案为9.【点睛】本题主要考查旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决此题的关键是运用面积的和差关系解决不规则图形的面积.18.如图,在Rt△ABC中,∠ABC=90°,∠BAC=32°,斜边AC=6,将斜边AC绕点A逆时针方向旋转26°到达AD的位置,连接CD,取线段CD的中点N,连接BN,则BN的长为_________.【分析】设M为AC中点连接ANBMMN根据直角三角形斜边中点定理得出MB=MN=同时算出∠BMN=90°最后利用勾股定理算出BN的长【详解】解:设M为AC中点连接ANBMMN由旋转可知:AC=AD=解析:32【分析】设M为AC中点,连接AN,BM,MN,根据直角三角形斜边中点定理得出MB=MN=132AC ,同时算出∠BMN=90°,最后利用勾股定理算出BN的长.【详解】解:设M为AC中点,连接AN,BM,MN,由旋转可知:AC=AD=6,∠CAD=26°,∵∠BAC=32°,∠ABC=90°,∴∠ACB=58°,∵AC=AD,N为CD中点,M为AC中点,∴MB=MC=MN=3,∴∠MBC=∠MCB=58°,∠MCN=∠MNC=(180-26)÷2=77°,∴∠BMC=64°,∠CMN=26°,∴∠BMN=90°,即△BMN为等腰直角三角形,∴BN=22+=.3332故答案为:32.【点睛】本题考查了直角三角形的性质,等腰三角形的判定和性质,旋转的性质,三角形内角和,解题的关键是找出AC中点M,构造等腰直角三角形.19.如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD 绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.【分析】由旋转的性质可知BD=DE∠C=90°则容易想到构造一个直角三角形与Rt△BCD全等即过E点作EH⊥AD于点H设CD=x则可用x表示AE的长从而判断什么时候AE取得最小值【详解】设CD=x则解析:2【分析】由旋转的性质可知BD=DE,∠C=90°,则容易想到构造一个直角三角形与Rt△BCD全等,即过E点作EH⊥AD于点H,设CD=x,则可用x表示AE的长,从而判断什么时候AE取得最小值.【详解】设CD=x,则AD=5﹣x,过点E作EH⊥AD于点H,如图:由旋转的性质可知BD=DE,∵∠ADE+∠BDC=90°,∠BDC+∠CBD=90°,∴∠ADE=∠CBD,∴△BCD ≌△DHE ,∴EH =CD =x ,DH =BC =3.∵AD =5﹣x ,∴AH =AD ﹣DH =5﹣x ﹣3=2﹣x ,∵在Rt △AEH 中,AE 2=AH 2+EH 2=(2﹣x )2+x 2=2x 2+4x +4=2(x ﹣1)2+2,所以当x =1时,AE 2取得最小值2,即AE 取得最小值2.故答案是:2.【点睛】考查了全等三角形的性质和判定,解此题的关键灵活其相关的知识点进行推理证明. 20.如图,在正方形ABCD 内部有一点P ,PB =1,PC =2,135BPC ∠=︒,则PA = ____.【分析】将△PBA 沿B 点顺时针旋转90°此时A 与C 点重合P 点旋转到E 点连接PE 易证△BPE 是等腰直角三角形利用勾股定理可求出PE 的长再证明△PCE 是直角三角形利用勾股定理求出CE 的长即可得到PA 的长 解析:6【分析】将△PBA 沿B 点顺时针旋转90°,此时A 与C 点重合,P 点旋转到E 点,连接PE ,易证△BPE 是等腰直角三角形,利用勾股定理可求出PE 的长,再证明△PCE 是直角三角形.利用勾股定理求出CE 的长,即可得到PA 的长.【详解】将△PBA 沿B 点顺时针旋转90°,此时A 与C 点重合,P 点旋转到E 点,连接PE ,∴PB=BE=1,PA=EC ,∠BPE=90°∴△PEB 是等腰直角三角形,∴∠PEB=∠EPB =45°,∴22,∴∠EPC=135°-45°=90°,∴在直角△PEC 中,EC=()2222226PC PE +=+=, ∴PA=EC 6=,故答案为:6.【点睛】本题考查了正方形的性质、旋转的性质、等腰直角三角形的判断和性质以及勾股定理的运用,解答此题的关键是利用旋转构建直角三角形,由勾股定理求解.三、解答题21.如图,△ABC 的顶点坐标分别为(﹣2,﹣4),B (0,﹣4),C (2,﹣1). (1)画出△ABC 关于点O 的中心对称图形△A 1B 1C 1,直接写出点C 1的坐标为 . (2)画出△ABC 绕原点O 逆时针旋转90°的△A 2B 2C 2,直接写出点C 2的坐标为 . (3)若△ABC 内一点P (m ,n )绕原点O 逆时针旋转180°的对应点为Q ,则Q 的坐标为 .解析:(1)图见解析,()2,1-;(2)图见解析,()1,2;(3)(),m n --【分析】(1)分别画出A ,B ,C 的对应点A 1,B 1,C 1即可.(2)分别画出A ,B ,C 的对应点A 2,B 2,C 2即可.(3)根据中心旋转图形的性质解决问题即可.【详解】解:(1)如图,△A 1B 1C 1即为所求,点C 1的坐标为(﹣2,1).故答案为:(﹣2,1).(2)如图,△A 2B 2C 2即为所求,点C 2的坐标为(1,2),故答案为:(1,2).(3)若△ABC 内一点P (m ,n )绕原点O 逆时针旋转180°的对应点为Q ,则Q 的坐标为(﹣m ,﹣n ).故答案为:(﹣m ,﹣n ).【点睛】本题考查作图-旋转变换,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.22.(1)问题发现:如图1,ACB △和DCE 均为等边三角形,当DCE 旋转至点A ,D ,E 在同一直线上,连接BE .①填空:AEB ∠的度数为______.②线段AD 、BE 之间的数量关系是_______.(2)拓展研究:如图2,ACB △和DCE 均为等腰三角形,且90ACB DCE ∠∠==,点A 、D 、E 在同一直线上,若15AE =,7DE =,求AB 的长度.(3)探究发现:图1中的ACB △和DCE ,在DCE 旋转过程中当点A ,D ,E 不在同一直线上时,设直线AD 与BE 相交于点O ,试在备用图中探索AOE ∠的度数,直接写出结果,并说明理由.解析:(1)①60°;②AD BE =;(2)AB 的长度为17;(3)60°或120°,证明见解析.【分析】(1)由条件易证△ACD ≌△BCE ,从而得到:AD=BE ,∠ADC=∠BEC .由点A ,D ,E 在同一直线上可求出∠ADC ,从而可以求出∠AEB 的度数.(2)仿照(1)中的解法可求出∠AEB 的度数,证出AD=BE ;由△DCE 为等腰直角三角形及CM 为△DCE 中DE 边上的高可得CM=DM=ME ,从而证到AE=2CH+BE .(3)由(1)知△ACD ≌△BCE ,得∠CAD=∠CBE ,由∠CAB=∠ABC=60°,可知∠EAB+∠ABE=120°,根据三角形的内角和定理可知∠AOE=60°.【详解】(1)①如图1,∵ACB △和DCE 均为等边三角形,∴CA CB =,CD CE =,60ACB BCE ∠=∠=,∴ACD BCE ∠=∠,在ACD △和BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴()?ACD BCE SAS ≌, ∴ADC BEC ∠∠=, ∵DCE 为等边三角形,∴60CDE CED ∠=∠=,∵点A ,D ,E 在同一直线上,∴120ADC ∠=,∴120BEC ∠=,∴60AEB BEC CED ∠=∠-∠=.故答案为:60°.②∵≌ACD BCE ,∴AD BE =,故答案为:AD BE =.(2)∵ACB △和DCE 均为等腰直角三角形, ∴CA CB =,CD CE =,90ACB DCE ∠∠==,∴ACD BCE ∠=∠,在ACD △和BCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴()ACD BCE SAS △≌△,∴8AD BE AE DE ==-=,ADC BEC ∠∠=,∵DCE 为等腰直角三角形,∴45CDE CED ∠=∠=,∵点A ,D ,E 在同一直线上,∴135ADC ∠=,∴135BEC ∠=,∴90AEB BEC CED ∠=∠-∠=, ∴2217AB AE BE =+=.(3)如图3,由(1)知≌ACD BCE ,∴CAD CBE ∠=∠,∵60CAB CBA ∠=∠=,∴120OAB OBA ∠+∠=,∴18012060AOE ∠=-=,如图4,同理求得60AOB ∠=,∴120AOE ∠=,∵AOE ∠的度数是60°或120°.【点睛】此题是几何变换综合题,主要考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识,得出△ACD ≌△BCE (SAS )是解本题的关键.23.如图,在Rt ABC 中,90ACB ∠=︒,点D ,E 分别在AB ,AC 上,CE BC =,连结CD ,将线段CD 绕点C 按顺时针方向旋转90︒后得CF ,连结EF .(1)补充完成图形;(2)求证:BD EF =.解析:(1)见解析;(2)见解析【分析】(1)根据题意补全图形,如图所示;(2)由旋转的性质得到∠DCF 为直角,由EF 与CD 平行,得到∠EFC 为直角,利用SAS 得到三角形BDC 与三角形EFC 全等,利用全等三角形的性质即可得证.【详解】解:(1)补全图形,如图所示(2)由旋转的性质得:CD CF =,90DCF ∠=︒,∴90DCE ECF ∠+∠=︒,∵90ACB ∠=︒,∴90DCE BCD ∠+∠=︒,∴BCD ECF ∠=∠,在BDC 和EFC 中=DC FC BCD ECF BC EC =⎧⎪⎨⎪=⎩∠∠,∴()SAS BDC EFC △≌△∴BD EF =.【点睛】此题考查了旋转的性质,以及全等三角形的判定与性质,熟练掌握旋转的性质是解本题的关键.24.如图,将矩形ABCD 绕点C 旋转得到矩形EFGC ,点E 在AD 上.延长AD 交FG 于点H .求证:EDC HFE ≅.解析:证明见解析.【分析】先根据矩形的性质可得,90AB CD A B ADC =∠=∠=∠=︒,再根据旋转的性质可得,90,90EF AB F A CEF B =∠=∠=︒∠=∠=︒,从而可得,90CD EF EDC F =∠=∠=︒,然后根据直角三角形的性质、角的和差可得DCE FEH ∠=∠,最后根据三角形全等的判定定理即可得证.【详解】四边形ABCD 是矩形,,90AB CD A B ADC ∴=∠=∠=∠=︒,由旋转的性质得:,90,90EF AB F A CEF B =∠=∠=︒∠=∠=︒,,90CD EF EDC F ∴=∠=∠=︒,又90,90EDC CEF ∠=︒∠=︒,90CED DCE CED FEH ∴∠+∠=∠+∠=︒,DCE FEH ∴∠=∠,在EDC △和HFE 中,EDC F CD EF DCE FEH ∠=∠⎧⎪=⎨⎪∠=∠⎩,()DC A∴≅.E ASHFE【点睛】本题考查了矩形的性质、旋转的性质、三角形全等的判定定理等知识点,熟练掌握矩形和旋转的性质是解题关键.25.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1)、B(-3,1)、C(-1,4).(1)画出△ABC绕点C顺时针旋转90°后得到的△A1B1C;(2)画出△ABC关于点P(1,0)对称的△A2B2C2.解析:(1)见解析;(2)见解析【分析】(1)分别作出点A、B绕点C顺时针旋转90°后得到的对应点,再顺次连接可得;(2)分别作出点A、B、C关于点P的对称点,再顺次连接可得.【详解】(1)如图,△A1B1C即为所求;(2)如图,△A2B2C2即为所求.【点睛】本题考查了作图-旋转变换,中心对称等知识,解题的关键是熟练掌握旋转变换的定义和性质.26.在Rt ABC ∆中,,90,,AC BC ACB M N ︒=∠=在直线AB 上,且222MN AM BN =+.(1)如图1,当点,M N 在线段AB 上时,求证:45MCN ︒∠=.(2)如图2,当点M 在BA 的延长线上且点N 在线段AB 上时,上述结论是否成立?若成立,请证明,若不成立,请说明理由.解析:(1)证明见解析;(2)成立,证明见解析.【分析】(1)将ACM ∆绕点C 逆时针旋转90︒,得到'BCM ∆,利用旋转的性质和等腰三角形的性质证明'NBM ∆为直角三角形,可证明'MN M N =,利用全等三角形的判定(SSS )可证明()'CMN CM N SSS ∆≅∆,即可证得1'452MCN MCM ︒∠=∠=; (1)仿照(1)中方法将CMA ∆绕点C 逆时针旋转90︒得到CDB ∆,证明DBN ∆为直角三角形,再证DN=MN ,进而证明()CMN CDN SSS ∆≅∆即可得出结论.【详解】()1如图1,,90AC BC ACB ︒=∠=,将ACM ∆绕点C 逆时针旋转90︒,得到'BCM ∆,则'ACM NCM ∆≅∆,',','ACM BCM CM CM AM BM ∴∠=∠==,连接'M N ,'CAM CNM ∠=∠=45°,''90M BN CBM CBA ︒∴∠=∠+∠=,'NBM ∴∆为直角三角形,22222''NM BN BM BN AM ∴=+=+,又222MN AM BN =+,'MN M N ∴=,在CMN ∆和'CM N ∆中''CM CM MC M N CN CN =⎧⎪=⎨⎪=⎩,()'CMN CM N SSS ∴∆≅∆,'MCN M CN ∴∠=∠, 1'452MCN MCM ︒∴∠=∠=, 即45MCN ︒∠=;()2如图2,,90AC BC ACB ︒=∠=,将CMA ∆绕点C 逆时针旋转90︒得到CDB ∆,CMA CDB ∴∆≅∆,,,135CM CD AM BD CAM CBD ︒∴==∠=∠=,90DBN CBD CBA ︒∴∠=∠-∠=,DBN ∴∆为直角三角形,22222DN BD BN AM BN ∴=+=+,又222MN AM BN =+,DN MN ∴=, 在CMN ∆和CDN ∆中CM CD CN CN MN DN =⎧⎪=⎨⎪=⎩,()CMN CDN SSS ∴∆≅∆,1452MCN DCN MCD ︒∴∠=∠=∠=, 45MCN ︒∴∠=.【点睛】本题考查了等腰三角形的性质、旋转的性质、全等三角形的判定与性质、勾股定理,熟练掌握全等三角形的判定与性质,利用旋转性质旋转△ACM 构造直角三角形是解答的关键. 27.江都大润发超市销售一种利润为每千克10元的水产品,一个月能销售出500千克.经市场分析,销售单价每涨价1元,月销售量就减少10千克.针对这种水产品的销售情况,若设单价每千克涨价x元,请解答以下问题:(1)填空:每千克水产品获利元,月销售量减少千克;(2)要使得月销售利润达到8000元,又要“薄利多销”,销售单价应涨价为多少元?解析:(1)(10+x);10x;(2)10【分析】(1)根据获利=原利润+涨价即可得出答案;根据销售单价每涨价1元,月销售量就减少10千克即可得出月销售量减少的数量;(2)利用“每千克水产品获利×月销售量=总利润”列出方程,解方程即可求出结果.【详解】解:(1)(10+x),10x;(2)由题意,得:(10+x)(500﹣10x)=8000;化简为:x2﹣40x+300=0;解得:x1=10,x2=30.∵“薄利多销”,∴x=30不符合题意,舍去.答:销售单价应涨价10元.【点睛】本题考查了一元二次方程的应用,正确表示出月销售量是解题的关键.28.在图中网格上按要求画出图形,并回答下列问题:(1)把△ABC平移,使点A平移到图中点D的位置,点B、C的对应点分别是点E、F,请画出△DEF;A B C;(2)画出△ABC关于点D成中心对称的△111A B C(填“是”或“否”)关于某个点成中心对称,如果是,请在图(3)△DEF与△111中画出对称中心,并记作点O.解析:(1)见解析;(2)见解析;(3)是,见解析【分析】(1)由题意得出,需将点B与点C先向左平移3个单位,再向下平移1个单位,据此可得;(2)分别作出三顶点分别关于点D的对称点,再首尾顺次连接可得;(3)连接两组对应点即可得.【详解】(1)如图所示,△DEF即为所求.(2)如图所示,△A1B1C1即为所求;(3)如图所示,△DEF与△A1B1C1是关于点O成中心对称,故答案为:是.【点睛】本题主要考查了作图-旋转变换和平移变换,解题的关键是熟练掌握旋转变换和平移变换的定义和性质,并据此得出变换后的对应点.。
九年级数学上册专题23.1 旋转【十大题型】(举一反三)(人教版)(原卷版)

专题23.1 旋转【十大题型】【人教版】【题型1 关于原点对称的点的坐标】 (1)【题型2 利用旋转的性质求角度】 (2)【题型3 利用旋转的性质求线段长度】 (3)【题型4 旋转中的坐标与图形变换】 (4)【题型5 作图-旋转变换】 (6)【题型6 中心对称图形及旋转对称图形】 (8)【题型7 旋转中的周期性问题】 (9)【题型8 旋转中的多结论问题】 (10)【题型9 旋转中的最值问题】 (12)【题型10 旋转的综合】 (13)【题型1 关于原点对称的点的坐标】【例1】(2022春•平阴县期末)点A(﹣2,3)与点B(a,b)关于坐标原点对称,则a+b的值为.【变式1-1】(2022秋•雨花区期末)若点A(m,5)与点B(2,n)关于原点对称,则3m+2n的值为.【变式1-2】(2022秋•常熟市期末)已知点P(2m﹣1,﹣m+3)关于原点的对称点在第三象限,则m的取值范围是.【变式1-3】(2022春•永新县期末)已知点P(3+2a,2a+1)与点P′关于原点成中心对称,若点P′在=3的解是.第二象限,且a为整数,则关于x的分式方程2x−ax+1【题型2 利用旋转的性质求角度】【例2】(2022春•梅州校级期末)如图,点O是等边△ABC内一点,∠AOB=110°,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,若OD=AD,则∠BOC的度数为.【变式2-1】(2022•南充)如图,将直角三角板ABC绕顶点A顺时针旋转到△AB′C′,点B′恰好落在CA的延长线上,∠B=30°,∠C=90°,则∠BAC′为()A.90°B.60°C.45°D.30°【变式2-2】(2022•天津一模)如图,在△ABC中,AB=AC,∠BAC=40°,点D在边AB上,将△ADC 绕点A逆时针旋转40°,得到△AD'B,且D',D,C三点在同一条直线上,则∠ACD的大小为()A.20°B.30°C.40°D.45°【变式2-3】(2022•城步县模拟)如图,P为等边三角形ABC内一点,∠APB:∠APC:∠CPB=5:6:7,则以P A,PB,PC为三边构成的三角形的三个内角从小到大的度数之比为()A.1:2:3B.2:3:4C.3:4:5D.5:6:7【题型3 利用旋转的性质求线段长度】【例3】(2022春•仪征市期末)如图,边长为1的正方形ABCD绕点A逆时针旋转60°得到正方形AEFG,连接CF,则CF的长是()A.1B.√2C.√3D.3√2−3【变式3-1】(2022春•如皋市期末)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.将△ABC绕点A 逆时针旋转得到△AB′C′,使点C′落在AB边上,连接BB′,则B′B的长为()A.2√3B.5C.2√5D.6【变式3-2】(2022•东莞市校级一模)如图,△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O 逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为()A.3√5B.12√55C.9√55D.16√55【变式3-3】(2022春•和平区期末)如图,△ABC与△CDE都是等边三角形,连接AD,BE,CD=4,BC =2,若将△CDE绕点C顺时针旋转,当点A、C、E在同一条直线上时,线段BE的长为()A.2√3B.2√7C.√3或√7D.2√3或2√7【题型4 旋转中的坐标与图形变换】【例4】(2022秋•黄石期末)如图,线段AB与线段CD关于点P对称,若点A(a,b)、B(5,1)、D (﹣3,﹣1),则点C的坐标为()A.(﹣a,﹣b)B.(﹣a+2,﹣b)C.(﹣a﹣1,﹣b+1)D.(﹣a+1,﹣b﹣1)【变式4-1】(2022秋•本溪期末)如图,在△AOB中,OA=4,OB=6,AB=2√7,将△AOB绕原点O逆时针旋转90°,则旋转后点A的对应点A′的坐标是()A.(﹣4,2)B.(﹣2√3,4)C.(﹣2√3,2)D.(﹣2,2√3)【变式4-2】(2022秋•西湖区期末)如图,在平面直角坐标系中,△MNP绕原点逆时针旋转90°得到△M1N1P1,若M(1,﹣2),则点M1的坐标为()A.(﹣2,﹣1)B.(1,2)C.(2,1)D.(﹣1,﹣2)【变式4-3】(2022•新抚区模拟)如图,Rt△AOB的斜边AO在y轴上,OB=√3,∠AOB=30°,直角顶点B在第二象限,将Rt△AOB绕原点O顺时针旋转120°后得到△A′OB',则A点的对应点A′的坐标是()A.(√3,﹣1)B.(1,−√3)C.(2,0)D.(√3,0)【题型5 作图-旋转变换】【例5】(2022春•化州市校级期中)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2.【变式5-1】(2022春•洪雅县期末)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)将△ABC向下平移5个单位得△A1B1C1,画出平移后的△A1B1C1.(2)画出△ABC关于点B成中心对称的图形.(3)在直线l上找一点P,使△ABP的周长最小.【变式5-2】(2022春•蒲城县期末)在如图所示的平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点坐标分别为A(1,1),B(3,0),C(2,3).(1)将△ABC向左平移4个单位长度得到△A1B1C1,点A、B、C的对应点分别为A1、B1、C1,请画出△A1B1C1,并写出点C1的坐标;(2)以原点O为旋转中心,将△ABC顺时针旋转90°得到△A2B2C2,点A、B、C的对应点分别为A2、B2、C2,请画出△A2B2C2.【变式5-3】(2022秋•利通区期末)方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.(1)画出△ABC绕B点顺时针旋转90°后的△A1B1C1;并写出A1、B1、C1的坐标;(2)画出△ABC关于原点O对称的△A2B2C2;并写出A2、B2、C2的坐标.【题型6 中心对称图形及旋转对称图形】【例6】(2022秋•单县校级月考)如图所示的图案中,是轴对称图形而不是中心对称图形的个数是.【变式6-1】(2022秋•普陀区期末)在下列图形中:等腰三角形、等边三角形、正方形、正五边形、平行四边形,等腰梯形,其中有个旋转对称图形.【变式6-2】(2022秋•孝义市期中)2022年2月4日﹣2月20日,北京冬奥会将隆重开幕,北京将成为世界上第一个既举办过夏季奥运会,又举办过冬季奥运会的城市.下面图片是在北京冬奥会会徽征集过程中,征集到的一幅图片,整个图片由“京字组成的雪花图案”、“beijing2022”、“奥运五环”三部分组成.对于图片中的“雪花图案”,至少旋转°能与原雪花图案重合.【变式6-3】(2022春•景德镇期中)如图,由4个全等的正方形组成的L形图案,请按下列要求画图:(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);(2)在图案②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);(3)在图案③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.【题型7 旋转中的周期性问题】【例7】(2022春•高新区校级月考)如图,在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转30°得到点P1,延长OP1到P2,使得OP2=2OP1;再将点P2绕着原点O 按逆时针方向旋转30°得到P3,延长OP3到P4,使得OP4=2OP3……如此继续下去,点P2023坐标为()A.(﹣21010,√3•21010)B.(0,21011)C.(21010,√3•21010)D.(√3•21010,21010)【变式7-1】(2022秋•中原区校级期末)将△OBA按如图方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(1,√3),将△OBA绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点A对应点的坐标为()A.(−1,√3)B.(−√3,1)C.(−√33,1)D.(−1,√33)【变式7-2】(2022•开封一模)如图,在平面直角坐标系中,将正方形OABC绕O点顺时针选择45°后,得到正方形OA1B1C1,以此方式,绕O点连续旋转2022次得到正方形OA2022B2022C2022,如果点C的坐标为(0,1),那么点B2022的坐标为()A.(0,−√2)B.(−√2,0)C.(﹣1,1)D.(﹣1,﹣1)【变式7-3】(2022春•高州市期中)如图,矩形ABCD的顶点A,B分别在x轴、y轴上,OA=OB=2,AD=4√2,将矩形ABCD绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点C的坐标为()A.(6,4)B.(﹣6,4)C.(4,﹣6)D.(﹣4,6)【题型8 旋转中的多结论问题】【例8】(2022•益阳)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有()A.①②③B.①②④C.①③④D.②③④【变式8-1】(2022春•邗江区期末)如图,在正方形ABCD中,AB=8,若点E在对角线AC上运动,将线段DE绕点D逆时针旋转90°得到线段DF,连接EF、CF.点P在CD上,且CP=3PD.给出以下几个结论①EF=√2DE,②EF2=AE2+CE2,③线段PF的最小值是4√2,④△CFE的面积最大是16.其中正确的是()A.①②④B.②③④C.①②③D.①③④【变式8-2】(2022春•双牌县期末)一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,AC =4.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:①MF=NF;②四边形CMFN有可能是正方形:③MN长度的最小值为2;④四边形CMFN的面积保持不变.其中正确结论的个数是()A.1B.2C.3D.4【变式8-3】(2022春•德州期中)如图,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.给出如下四个结论:①∠OEF=45°;②正方形A1B1C1O绕点O旋转时,四边形OEBF的面积随EF的长度变化而变化;③△BEF周长的最小值为(1+√2)OA;④AE2+CF2=2OB2.其中正确的结论有()A.①③B.②③C.①④D.③④【题型9 旋转中的最值问题】【例9】(2022•黄石)如图,等边△ABC中,AB=10,点E为高AD上的一动点,以BE为边作等边△BEF,连接DF,CF,则∠BCF=,FB+FD的最小值为.【变式9-1】(2022春•大埔县期中)如图,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AC=AD =3,AB=AE=5.连接BD,CE,将△ADE绕点A旋转一周,在旋转的过程中当∠DBA最大时,S△ACE =()A.6B.6√2C.9D.9√2【变式9-2】(2022春•龙岗区期末)如图,点E是等边三角形△ABC边AC的中点,点D是直线BC上一动点,连接ED,并绕点E逆时针旋转90°,得到线段EF,连接DF.若运动过程中AF的最小值为√3+1,则AB的值为()A.2B.4√3C.2√3D.4【变式9-3】(2022春•南京期末)如图,在正方形ABCD中,AB=4,E为AB边上一点,点F在BC边上,且BF=1,将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为()A.2B.2√2C.3D.√10【题型10 旋转的综合】【例10】(2022春•长沙期末)如图,有一副直角三角板如图1放置(其中∠D=45°,∠C=30°),P A,PB与直线MN重合,且三角板P AC,三角板PBD均可以绕点P逆时针旋转.(1)在图1中,∠DPC=;(2)①如图2,若三角板PBD保持不动,三角板P AC绕点P逆时针旋转,转速为10°/秒,转动一周三角板P AC就停止转动,在旋转的过程中,当旋转时间为多少时,有PC∥DB成立;②如图3,在图1基础上,若三角板P AC的边P A从PN处开始绕点P逆时针旋转,转速为3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/秒,当PC转到与P A重合时,两三角板都停止转动,在旋转过程中,当∠CPD=∠BPM时,求旋转的时间是多少?【变式10-1】(2022春•南川区期末)如图,四边形ABCD是正方形,点E在AB的延长线上,连接EC,EC绕点E逆时针旋转90°得到EF,连接CF、AF,CF与对角线BD交于点G.(1)若BE=2,求AF的长度;(2)求证:AF+2BG=√2AD.【变式10-2】(2022•平邑县一模)在正方形ABCD中,点E在射线BC上(不与点B、C重合),连接DB,DE,将DE绕点E逆时针旋转90°得到EF,连接BF.(1)如图1,点E在BC边上.①依题意补全图1;②若AB=6,EC=2,求BF的长;(2)如图2,点E在BC边的延长线上,用等式表示线段BD,BE,BF之间的数量关系.【变式10-3】(2022•泰安一模)如图,将矩形ABCD绕着点B逆时针旋转得到矩形GBEF,使点C恰好落到线段AD上的E点处,连接CE,连接CG交BE于点H.(1)求证:CE平分∠BED;(2)取BC的中点M,连接MH,求证:MH∥BG;(3)若BC=2AB=4,求CG的长.。
人教版九年级上册数学 期末专题复习---《旋转的性质》(含答案)

人教版九年级上册数学期末专题复习---《旋转的性质》一、选择题1.如图,在正方形网格中,将△ABC顺时针旋转后得到△A'B′C′,则下列4个点中能作为旋转中心的是( )A.点PB.点QC.点RD.点S2.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )A.55°B.60°C.65°D.70°3.在平面直角坐标系中,把点P(﹣5,4)向右平移9个单位得到点P1,再将点P1绕原点顺时针旋转90°得到点P2,则点P2的坐标是( )A.(4,﹣4)B.(4,4)C.(﹣4,﹣4)D.(﹣4,4)4.如图所示,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2).若将△ABC绕着点C顺时针旋转90º,得到△A'B'C',点A,B的对应点A',B'的坐标分别为(a,b),(c,d),则(ab-cd)2023的值为()A.0B.1C.-1D.无法计算5.在下列几何图形中:(1)两条互相平分的线段;(2)两条互相垂直的直线;(3)两个有公共顶点的角;(4)两个有一条公共边的正方形.其中是中心对称图形的有( )A.1个B.2个C.3个D.4个6.在如图所示的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )A.1个 B.2个 C.3个 D.4个7.将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6,则AC长是()A.6+2B.9C.10D.6+68.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB/C/,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是()A.πB.πC.2πD.4π9.如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60º,得到△BAE,连接ED,则下列结论中:①AE∥BC;②∠DEB=60º;③∠ADE=∠BDC.其中正确结论的序号是()A.①②B.①③C.②③D.只有①10.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE.给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③四边形ODBE的面积始终等于;④△BDE周长的最小值为6.上述结论中正确的个数是( )A.1B.2C.3D.4二、填空题11.如图,在△BDE中,∠BDE=90°,2D的坐标是(5,0),∠BDO=15°,将△BDE旋转到△ABC 的位置,点C在BD 上,则旋转中心的坐标为_______.12.如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是 .13.在Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD,把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_______.14.如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:①AD=CD;②∠ACD的大小随着α的变化而变化;③当α=30°时,四边形OADC为菱形;④△ACD面积的最大值为a2;其中正确的是 .(把你认为正确结论的序号都填上).15.P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC 重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC= .16.如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为.三、解答题17.在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得到△A′BO′,点A,O旋转后的对应点分别为A′,O′,记旋转角为α.(1)如图①,若α=90°,求AA′的长;(2)如图②,若α=120°,求点O′的坐标.18.如图所示,正方形ABCD的边BC上有一点E,∠DAE的平分线交CD于点F.求证:AE=DF+BE.19.如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,在Rt△ABC中,已知直角边BC=5,AC=7,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到如图②所示的“数学风车”.⑴这个风车是中心对称图形吗?若是,指出这个风车至少需要绕着它的中心旋转多少度才能和它本身重合;⑵求这个风车的外围周长(即求图②中的实线的长).20.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:(1)EA是∠QED的平分线;(2)EF2=BE2+DF2.答案1. A.2. C;3. A;4. C.5. C6. B.7. A;8. C.9.A10.C11. (3,23)12.①②③13. 80或120.14.:①③④.15. 3:4:2.16.(36,0).17.解:(1)∵点A(4,0),点B(0,3),∴OA=4,OB=3.∴AB=5.∵△ABO绕点B逆时针旋转90°,得△A′BO′,∴BA=BA′,∠ABA′=90°.∴△ABA′为等腰直角三角形,(2)作O′H⊥y轴于点H.∵△ABO绕点B逆时针旋转120°,得△A′BO′,∴BO=BO′=3,∠OBO′=120°.∴∠HBO′=60°.在Rt△BHO′中,∵∠BO′H=90°-∠HBO′=30°,18.解:如图,将△ADF绕点A顺时针旋转90°得△ABF′,则∠3=∠1,∠AFD=∠F′,∠ABF′=∠D,BF′=DF.∵四边形ABCD为正方形,∴AB∥CD,∠ABC=∠D=90°,∴∠AFD=∠FAB,∠ABF′=∠D=90°,∴∠ABF′+∠ABC=180°,∴F′,B,C三点共线.∵∠FAB=∠2+∠BAE,∴∠AFD=∠2+∠BAE.又∵∠DAE的平分线交CD于点F,∴∠1=∠2,∴∠3=∠2,∴∠AFD=∠3+∠BAE,∴F′=∠3+∠BAE.∵∠F′AE=∠3+∠BAE,∴∠F′AE=∠F′,∴AE=EF′=BF′+BE=DF+BE.19.解:⑴这个风车是中心对称图形,这个风车至少需要绕着它的中心旋转90度才能和它本身重合;⑵风车的其中一个直角三角形的较短直角边长为5,较长直角边长为7+5=12,则斜边长为13,所以这个风车的外围周长为4×(5+13)=4×18=72.20.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,∴QB=DF,AQ=AF,∠BAQ=∠DAF,∵∠EAF=45°,∴∠DAF+∠BAE=45°,∴∠QAE=45°,∴∠QAE=∠FAE,在△AQE和△AFE中,∴△AQE≌△AFE(SAS),∴∠AEQ=∠AEF,∴EA是∠QED的平分线;(2)由(1)得△AQE≌△AFE,∴QE=EF,在Rt△QBE中,QB2+BE2=QE2,又∵QB=DF,∴EF2=BE2+DF2.。
人教版初中九年级数学上册第二十三章《旋转》经典题(含答案解析)

一、选择题1.下面四个图案是常用的交通标志,其中为中心对称图形的是( )A .B .C .D . 2.如图,OAB 绕点O 逆时针旋转80°到OCD 的位置,已知45AOB ∠=︒,则AOD ∠等于( )A .45°B .35°C .25°D .15°3.如图,在等边△ABC 中,AC=8,点O 在AC 上,且AO=3,点P 是边AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,要使点D 恰好落在BC 上,则AP 的长是( ).A .4B .5C .6D .84.如图所示,把ABC 绕C 点旋转35︒,得到A B C ''',A B ''交AC 于点D ,若90A DC '∠=︒,则A ∠等于( )A .35︒B .65︒C .55︒D .45︒5.下列图形中,是中心对称图形的是( )A .B .C .D.6.在一个无盖的正方体玻璃容器内装了一些水,把容器按不同方式倾斜一点,容器内的水面的形状可能是()A.B.C.D.7.把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的()A.内部B.外部C.边上D.以上都有可能8.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为().A.60 °B.75°C.85°D.90°9.如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转90 得到月牙②,则点A的对应点A’的坐标为()A.(2,2)B.(2,4)C.(4,2)D.(1,2)10.如图所示的图形中,是中心对称图形的是( )A.B.C.D.11.下列图标中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.12.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.13.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A.B.C.D.14.如图,以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′(点B、C的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为()A.45°B.60°C.70°D.90°15.如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的12,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的()A .12B .14C .16D .18二、填空题16.如图,在边长为1的正方形ABCD 中,将射线AC 绕点A 按顺时针方向旋转α度(0<α≤360°),得到射线AE ,点M 是点D 关于射线AE 的对称点,则线段CM 长度的最小值和最大值的和为_____.17.如图,四边形ABCD 是菱形,O 是两条对角线的交点,过O 点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm 2,则阴影部分的面积为_____cm 2.18.将边长为1的正方形ABCD 绕点C 按顺时针方向旋转到FECG 的位置(如图),使得点D 落在对角线CF 上,EF 与AD 相交于点H ,则HD =_________.(结果保留根号)19.△ABC 是等边三角形,点O 是三条高的交点.若△ABC 以点O 为旋转中心旋转后能与原来的图形重合,则△ABC 旋转的最小角度是____________.20.在直角坐标系中,点(﹣1,2)关于原点对称点的坐标是_____.21.如图,平行四边形ABCD 的两条对角线AC 与BD 相交于直角坐标系的原点.若点A 的坐标为(-2,3),则点C 的坐标为___________.22.如图,在平面直角坐标系中,将ABC 绕点A 顺时针旋转到111A B C △的位置,点,B O 分别落在点11,B C 处,点1B 在x 轴上,再将111A B C △绕点1B 顺时针旋转到112A B C的位置,点2C 在x 轴上,再将112A B C 绕点2C 顺时针旋转到222A B C △的位置,点2A 在x轴上,依次进行下去,······,若点()3,0,0,2,2A B ⎛⎫ ⎪⎝⎭则点2020B 的坐标为__________________.23.如图,△ABC 中,∠BAC =20°,△ABC 绕点A 逆时针旋转至△AED ,连接对应点C 、D ,AE 垂直平分CD 于点F ,则旋转角度是_____°.24.如图,在Rt △ABC 中,∠ABC =90°,∠BAC =32°,斜边AC =6,将斜边AC 绕点A 逆时针方向旋转26°到达AD 的位置,连接CD ,取线段CD 的中点N ,连接BN ,则BN 的长为_________.25.直角坐标系中,已知A (3,2),作点A 关于y 轴对称点A 1,点A 1关于原点对称点A 2,点A 2关于x 轴对称点A 3,A 3关于y 轴对称点A 4,……,按此规律,则点A 2019的坐标为_____.26.如图,把Rt ABC ∆绕点A 逆时针旋转40︒,得到Rt AB C ''∆,点C '恰好落在边AB 上,连接BB ',则BB C ''∠=___________度.三、解答题27.如图,已知正方形ABCD 的边长为3,E 、F 分别是AB 、BC 边上的点,且∠EDF=45°,将△DAE 绕点D 逆时针旋转90°,得到△DCM .若AE=1,求FM 的长.28.如图,在10×10的正方形方格之中,ABC 的顶点都在格点上(1)在图1中画出ABC 关于格点O 成中心对称的A B C '''.(2)在图2中画出格点ABEF ,使得ABE A C F B S S =.29.如图,ABC ∆和ECD ∆都是等边三角形,直线AE ,BD 交于点F .(1)如图1,当A ,C ,D 三点在同一直线上时,AFB ∠的度数为_____,线段AE 与BD 的数量关系为_____.(2)如图2,当ECD ∆绕点C 顺时针旋转α()0360α︒≤<︒时,(1)中的结论是否还成立?若不成立,请说明理由:若成立,请就图2给予证明.(3)若4AC =,3CD =,当ECD ∆绕点C 顺时针旋转一周时,请直接写出BD 长的取值范围.30.如图,己知点()2,4A ,()1,1B ,()3,2C .(1)将MBC 绕点O 逆时针旋转90°得111A B C △,画出111A B C △,并写出点C 的对应点1C 的坐标为_____;(2)画出ABC 关于原点成中心对称的图形222A B C △,并写出点A 的对称点2A 的坐标为______.。
九年级旋转经典题型

九年级旋转经典题型一、旋转性质的基础应用1. 题目- 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE。
若∠CAE = 65°,∠E = 70°,且AD⊥BC,求∠BAC的度数。
- 解析- 因为△ABC绕点A逆时针旋转得到△ADE,所以△ABC≌△ADE。
- 根据全等三角形的性质,∠C = ∠E = 70°。
- 因为AD⊥BC,在Rt△ADC中,∠DAC = 90° - ∠C = 90° - 70°= 20°。
- 又因为∠CAE = 65°,所以∠BAC = ∠DAE=∠DAC + ∠CAE = 20°+ 65°= 85°。
2. 题目- 已知正方形ABCD的边长为3,点E在边CD上,且DE = 1。
将△ADE绕点A 顺时针旋转90°得到△ABF,求EF的长。
- 解析- 因为△ADE绕点A顺时针旋转90°得到△ABF,所以AE = AF,∠EAF = 90°。
- 在正方形ABCD中,AD = 3,DE = 1,根据勾股定理可得:AE=√(AD^2)+DE^{2}=√(3^2)+1^{2}=√(10)。
- 在等腰直角三角形AEF中,EF=√(2)AE=√(2)×√(10) = 2√(5)。
二、旋转与坐标的结合1. 题目- 在平面直角坐标系中,点A的坐标为(1,3),将点A绕原点O逆时针旋转90°得到点A',求点A'的坐标。
- 解析- 设点A(x = 1,y = 3)绕原点O逆时针旋转90°后的点A'(x',y')。
- 根据旋转坐标变化规律:对于点(x,y)绕原点逆时针旋转90°后变为(-y,x)。
- 所以点A'的坐标为(-3,1)。
2. 题目- 已知点P(2, - 1),把点P绕坐标原点O顺时针旋转135°后得到点Q,求点Q的坐标。
(常考题)人教版初中数学九年级数学上册第三单元《旋转》测试(包含答案解析)

一、选择题1.如图,在△ABC 中,AB =AC ,∠BAC =45°,点D 在AC 边上.将△ABD 绕点A 逆时针旋转45°得到△ACD ′,且D ′、D 、B 三点在同一条直线上,则∠ABD 的大小为( )A .15°B .22.5°C .25°D .30°2.下列图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D . 3.直线26y x =-+与x 轴交于A 点,与y 轴交于B 点,将AOB 绕点A 顺时针旋转90°得到AO B ''△,则点B '的坐标是( )A .()9,9B .()3,9-C .()9,3D .()3,9 4.如图所示,把ABC 绕C 点旋转35︒,得到A B C ''',A B ''交AC 于点D ,若90A DC '∠=︒,则A ∠等于( )A .35︒B .65︒C .55︒D .45︒5.下列图形中,是中心对称图形的是( )A .B .C .D .6.在一个无盖的正方体玻璃容器内装了一些水,把容器按不同方式倾斜一点,容器内的水面的形状可能是( )A .B .C .D . 7.如图,Rt OCB ∆的斜边在y 轴上,3OC =,含30︒角的顶点与原点重合,直角顶点C 在第二象限,将Rt OCB ∆绕原点顺时针旋转120︒后得到'OC B ∆',则B 点的对应点B ′的坐标是( )A .(3,1)-B .(1,3)-C .(2,0)D .(3,0) 8.既是中心对称图形又是轴对称图形,且只有两条对称轴的四边形是( ) A .正方形 B .矩形 C .菱形 D .矩形或菱形 9.如图,在正方形ABCD 中,AB=3,点M 在CD 的边上,且DM=1,ΔAEM 与ΔADM 关于AM 所在的直线对称,将ΔADM 按顺时针方向绕点A 旋转90°得到ΔABF ,连接EF ,则线段EF 的长为( )A .3B .23C .13D .1510.下列图形既是轴对称图形,又是中心对称图形的是( )A .B .C .D .11.如图,将Rt △ABC 绕点A 按顺时针方向旋转一定角度得到Rt △ADE ,点B 的对应点D恰好落在BC 边上,若DE =12,∠B =60°,则点E 与点C 之间的距离为( )A .12B .6C .62D .6312.如图,已知△ABC 与△CDA 关于点O 成中心对称,过点O 任作直线EF 分别交AD,BC 于点E,F,则下则结论:①点E 和点F,点B 和点D 是关于中心O 的对称点;②直线BD 必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC 与四边形BFOA 的面积必相等;⑤△AOE 与△COF 成中心对称.其中正确的个数为 ( )A .2B .3C .4D .5二、填空题13.如图,在ABC 中,4AB =, 5.8BC =,60B ∠=︒,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为________.14.如图,正方形AEFG 与正方形ABCD 的边长都为2,正方形AEFG 绕正方形ABCD 的顶点A 旋转一周,在此旋转过程中,线段DF 的长可取的整数值可以为______________.15.如图,BD 为正方形ABCD 的对角线,BE 平分∠DBC ,交DC 与点E ,将△BCE 绕点C 顺时针旋转90°得到△DCF ,若CE =1 cm ,则BF =__________cm .16.如图,在Rt ABC 中,5AB =,4BC =,如果ABC 绕点B 旋转,使点C 落在AB 边上的点D 处得到EBD △,则点A 到BE 的距离是__________.17.如图,在Rt ABC 中,∠C =90°,AC =6cm ,BC =8cm .将Rt ABC 绕点A 逆时针旋转得到Rt AB C ''△,使点C '落在AB 边上,连结BB ',则BB '的长度为_________.18.一副直角三角尺叠放,如图①所示,现将含45°角的三角尺ADE 固定不动,将含30°角的三角尺ABC 绕顶点A 顺时针转动(旋转角不超过180度),使两个三角尺有一组边互相平行.例如图②,当∠BAD =15°时,BC ∥DE ,当90°<∠BAD <180°时,∠BAD 的度数为___.19.点()1,5A a -与点()2,5B b +-关于原点对称,则(a +b )2 020=____ . 20.如图,在正方形ABCD 内部有一点P ,PB =1,PC =2,135BPC ∠=︒,则PA = ____.三、解答题21.如图,已知正方形ABCD 的边长为3,E 、F 分别是AB 、BC 边上的点,且∠EDF=45°,将△DAE 绕点D 逆时针旋转90°,得到△DCM .若AE=1,求FM 的长.22.如图,△ABC 三个顶点的坐标分别是A (1,1),B (4,2),C (3,4). (1)请画出△ABC 关于原点对称的△A 1B 1C 1;通过作图,你发现了△ABC 中任意一点(x ,y )关于原点中心对称后的点坐标为 .(2)已知点M 坐标为(m ,n ),点P 的坐标为(2,-3),则点M 关于点P 中心对称的点N 的坐标为 .23.已知ABC 是边长为4的等边三角形,边AB 在射线OM 上,且6OA =,点D 是射线OM 上的动点,当点D 不与点A 重合时,将ACD △绕点C 逆时针方向旋转60°得到BCE ,连接DE .(1)如图1,求证:CDE △是等边三角形.(2)设OD t =,①如图2,当610t <<时,CDE △的周长存在最小值,请求出此最小值; ②如图1,若06t <<,直接写出以D 、E 、B 为顶点的三角形是直角三角形时t 的值.24.如图,四边形ABCD 中,45ABC ADC ∠=∠=︒,将BCD △绕点C 顺时针旋转一定角度后,点B 的对应点恰好与点A 重合,得到ACE △.(1)请求出旋转角的度数;(2)请判断AE与BD的位置关系,并说明理由.25.如图,P是正方形ABCD内一点,△ABP绕着点B旋转后能到达△CBE的位置.(1)旋转的角度是多少度?(2)若BP=3cm,求线段PE的长.26.在正方形ABCD中,点E是BC上的一点,连结AE.(1)画出△ABE绕点A逆时针旋转90°后的图形(点E的对应点为F);(2)若AB=3,则四边形AECF的面积为.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】由旋转的性质可得∠BAC=∠CAD'=45°,AD=AD',由等腰三角形的性质可得∠AD'D=67.5°,∠D'AB=90°,即可求∠ABD的度数.【详解】解:∵将△ABD绕点A逆时针旋转45°得到△ACD′,∴∠BAC=∠CAD'=45°,AD=AD',∴∠AD'D=1(180°-45°)=67.5°,∠D'AB=90°,2∴∠ABD=90°-67.5°=22.5°;故选:B.【点睛】本题考查了旋转的性质,等腰三角形的性质,直角三角形两锐角互余等知识;熟练运用旋转的性质和等腰三角形的性质是解题的关键.2.D解析:D【分析】根据轴对称图形的定义和中心对称图形的定义逐一判断即可.【详解】解:A选项是轴对称图形,不是中心对称图形,故本选项不符合题意;B选项不是轴对称图形,是中心对称图形,故本选项不符合题意;C选项不是轴对称图形,是中心对称图形,故本选项不符合题意;D选项既是轴对称图形,也是中心对称图形,故本选项符合题意.故选D.【点睛】此题考查的是轴对称图形的识别和中心对称图形的识别,掌握轴对称图形的定义和中心对称图形的定义是解决此题的关键.3.C解析:C【分析】由题意可求点A(3,0),点B(0,6),根据旋转的性质可得OA=O'A=3,BO=B'O'=6,B'O'∥OA,即可求点B'坐标.【详解】解:如图:∵直线y=-2x+6与x轴交于A点,与y轴交于B点,∴当x=0时,y=6;当y=0时,x=3.∴点A (3,0),点B (0,6)∴OA=3,OB=6∵将△AOB 绕点A 顺时针旋转90°得到△AO′B′,∴OA=O'A=3,BO=B'O'=6,∠OAO'=∠B'O'A=90°∴B'O'∥OA∴点B'(9,3)故选:C .【点睛】本题考查了一次函数图象上点的坐标特征,旋转的性质,熟练运用旋转的性质是本题的关键.4.C解析:C【分析】先根据旋转的性质可得,35A A ACA ''∠=∠∠=︒,再根据三角形的内角和定理可得A '∠的度数,由此即可得.【详解】由旋转的性质得:,35A A ACA ''∠=∠∠=︒,90A DC '∠=︒,18055A A DC ACA '''∴∠=︒-∠-∠=︒,55A A '∴∠=∠=︒,故选:C .【点睛】本题考查了旋转的性质、三角形的内角和定理,熟练掌握旋转的性质是解题关键. 5.C解析:C【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心可得答案.【详解】解:A 、不是中心对称图形,故此选项不合题意;B 、不是中心对称图形,故此选项不符合题意;C 、是中心对称图形,故此选项符合题意;D 、不是中心对称图形,故此选项不合题意;故选:C .【点睛】此题主要考查了中心对称图形,关键是掌握中心对称图形的概念.6.A解析:A【分析】结合题意,相当于把正方体一个面,即正方形截去一个角,可以得到三角形、四边形、五边形.【详解】解:根据题意,结合实际,容器内水面的形状不可能是正方形、六边形、七边形. 故选A .【点睛】此类问题也可以亲自动手操作一下,培养空间想象力.7.A解析:A【分析】如图,利用含30度的直角三角形三边的关系得到1BC =,再利用旋转的性质得到3,1,90OC OC B C BC B C O BCO ====∠''''=='∠︒,然后利用第四象限点的坐标特征写出点B ′的坐标. 【详解】如图,在Rt OCB ∆中,30BOC ∠=︒,333133BC OC ∴===, Rt OCB ∆绕原点顺时针旋转120︒后得到'OC B ∆',3,1,90OC OC B C BC B C O BCO ∴====''''∠'=∠=︒,∴点B ′的坐标为(3,1)-.故选A .本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30456090180︒︒︒︒︒,,,,. 8.D解析:D【分析】根据轴对称图形与中心对称图形的概念求解.【详解】正方形是轴对称图形,也是中心对称图形,有4条对称轴;矩形是轴对称图形,也是中心对称图形,有2条对称轴;菱形是轴对称图形,也是中心对称图形,有2条对称轴.故选D.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.9.C解析:C【分析】连接BM.证明△AFE≌△AMB得FE=MB,再运用勾股定理求出BM的长即可.【详解】连接BM,如图,由旋转的性质得:AM=AF.∵四边形ABCD是正方形,∴AD=AB=BC=CD,∠BAD=∠C=90°,∵ΔAEM与ΔADM关于AM所在的直线对称,∴∠DAM=∠EAM.∵∠DAM+∠BAM=∠FAE+∠EAM=90°,∴∠BAM=∠EAF,∴△AFE≌△AMB∴FE=BM.在Rt△BCM中,BC=3,CM=CD-DM=3-1=2,∴2222+=+=BC CM3213∴13故选C.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.10.D解析:D【解析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合.因此,A、不是轴对称图形,是中心对称图形,故本选项错误;B、是轴对称图形,但不是中心对称图形,故本选项错误;C、是轴对称图形,但不是中心对称图形,故本选项错误;D、既是轴对称图形,又是中心对称图形,故本选项正确.故选D.11.D解析:D【分析】由旋转的性质可得DE=BC=12,AD=AB,AC=AE,∠DAB=∠EAC,由直角三角形的性质可得AB=12BC=6,AC=3,AB=63,通过证明△ACE是等边三角形,可得AC=AE=EC=63.【详解】解:如图,连接EC,∵将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE,∴DE=BC=12,AD=AB,AC=AE,∠DAB=∠EAC,∵∠B=60°,∴∠ACB=30°,∴AB=12BC=6,AC3AB=3∵AD=AB,∠B=60°,∴△ABD是等边三角形,∴∠DAB=60°=∠EAC,∴△ACE是等边三角形,∴AC=AE=EC=3故选:D.【点睛】本题考查了旋转的性质,直角三角形的性质,等边三角形的判定和性质,求出AC的长是本题的关键.12.D解析:D【分析】由于△ABC 与△CDA 关于点O 对称,那么可得到AB=CD 、AD=BC ,即四边形ABCD 是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.【详解】△ABC 与△CDA 关于点O 对称,则AB=CD 、AD=BC ,所以四边形ABCD 是平行四边形, 因此点O 就是▱ABCD 的对称中心,则有:(1)点E 和点F ;B 和D 是关于中心O 的对称点,正确;(2)直线BD 必经过点O ,正确;(3)四边形ABCD 是中心对称图形,正确;(4)四边形DEOC 与四边形BFOA 的面积必相等,正确;(5)△AOE 与△COF 成中心对称,正确;其中正确的个数为5个,故选D .【点睛】熟练掌握平行四边形的性质和中心对称图形的性质是解决此题的关键.二、填空题13.【分析】先根据旋转的性质可得再根据等边三角形的判定与性质可得然后根据线段的和差即可得【详解】由旋转的性质得:是等边三角形故答案为:【点睛】本题考查了旋转的性质等边三角形的判定与性质等知识点熟练掌握旋 解析:1.8【分析】先根据旋转的性质可得AB AD =,再根据等边三角形的判定与性质可得4BD AB ==,然后根据线段的和差即可得.【详解】由旋转的性质得:4AB AD ==,60B ∠=︒,ABD ∴是等边三角形,4BD AB ∴==,5.8BC =,5.84 1.8CD BC BD ∴=-=-=,故答案为:1.8.【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点,熟练掌握旋转的性质是解题关键.14.1或2或3或4【分析】如图连接AF 由题意可知AF-AD≤DF≤AD+AF 即2-2≤DF≤2+2由此即可解决问题【详解】解:如图连接AF 易知AF=2∵AF-AD≤DF≤AD+AF ∴2-2≤DF≤2+2解析:1或2或3或4【分析】如图连接AF,由题意可知AF-AD≤DF≤AD+AF,即22-2≤DF≤2+22,由此即可解决问题.【详解】解:如图连接AF.易知AF=22,∵AF-AD≤DF≤AD+AF,∴22-2≤DF≤2+22,∵DF是整数,∴DF=1或2或3或4.故答案为:1或2或3或4【点睛】本题考查了旋转变换、正方形的性质、三角形的三边关系等知识,解题的关键是学会用转化的思想思考问题,把最短问题转化为三边关系解决.15.2+【详解】过点E作EM⊥BD于点M如图所示:∵四边形ABCD为正方形∴∠BAC=45°∠BCD=90°∴△DEM为等腰直角三角形∵BE平分∠DBCEM⊥BD∴EM=EC=1cm∴DE=EM=cm由解析:2+2【详解】过点E作EM⊥BD于点M,如图所示:∵四边形ABCD为正方形,∴∠BAC=45°,∠BCD=90°,∴△DEM为等腰直角三角形.∵BE平分∠DBC,EM⊥BD,∴EM=EC=1cm,∴DE =2EM =2cm .由旋转的性质可知:CF =CE =1cm ,∴BF =BC +CF =CE +DE +CF =1+2+1=2+2cm . 故答案为2+2.16.3【分析】连接AE 作AH ⊥BE 于H 根据勾股定理求出AC 的值根据旋转的性质可知BE=AB=5DE=AC=3然后根据等面积法求解即可【详解】解:连接AE 作AH ⊥BE 于H ∵在中∴AC=由旋转的性质得BE=解析:3【分析】连接AE ,作AH ⊥BE 于H ,根据勾股定理求出AC 的值,根据旋转的性质可知BE=AB=5,DE=AC=3,然后根据等面积法求解即可.【详解】解:连接AE ,作AH ⊥BE 于H ,∵在Rt ABC 中,5AB =,4BC =,∴AC=2254=3-,由旋转的性质得BE=AB=5,DE=AC=3,∵1122BE AH AB DE ⋅=⋅, ∴5AH=5×3,∴AH=3,故答案为:3.【点睛】本题考查了勾股定理,旋转的性质,等面积法求线段的长,熟练掌握各知识点是解答本题的关键.17.4【分析】由勾股定理得到AB=10然后根据旋转的性质求出△BB′C′的边长最后根据勾股定理求出BB′即可【详解】∵在Rt △ABC 中∠C=90°AC =6cmBC =8cm ∴又由旋转的性质知AC′=AC=解析:5【分析】由勾股定理得到AB=10,然后根据旋转的性质求出△BB′C′的边长,最后根据勾股定理求出BB′即可.【详解】∵在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,∴2210=+=.AB AC BC又由旋转的性质知,AC′=AC=6,B′C′=BC=8∴BC′= AB-AC′=4∵B′C′⊥AB,∴在Rt△BB′C′中,2245BB B C BC''=''.=+故答案为45.【点睛】本题主要考查了旋转的性质和勾股定理,此题实际上是利用直角三角形的性质和旋转的性质将所求线段BB'与已知线段AC、BC的长度联系起来求解的.18.105°或135°【分析】根据题意画出图形再由平行线的判定定理即可得出结论【详解】解:如图(1)当AC∥DE时∠BAD=∠DAE=45°;如图(2)当BC∥AD时∠DAB=∠B=60°;如图(3)当解析:105°或135°【分析】根据题意画出图形,再由平行线的判定定理即可得出结论.【详解】解:如图(1),当AC∥DE时,∠BAD=∠DAE=45°;如图(2),当BC∥AD时,∠DAB=∠B=60°;如图(3),当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;如图(4),当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.∴当90°<∠BAD<180°时,∠BAD=105°或135°.故答案为:105°或135°.【点睛】本题考查的是旋转的性质,平行线的判定与性质,根据题意画出图形,利用平行线的性质及直角三角板的性质求解是解答此题的关键.19.【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数求出ab 的值然后相加计算即可得解【详解】∵点与点关于原点对称∴∴∴故答案为1【点睛】本题考查了关于原点对称的点的坐标关于原点的对称点横纵坐标都 解析:1【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数求出a 、b 的值,然后相加计算即可得解.【详解】∵点()1,5A a -与点()2,5B b +-关于原点对称 ∴1+2=0a b -+∴1,2a b ==- ∴()()2 020 2 020211a b =++=- 故答案为1. 【点睛】本题考查了关于原点对称的点的坐标,关于原点的对称点,横纵坐标都变成相反数. 20.【分析】将△PBA 沿B 点顺时针旋转90°此时A 与C 点重合P 点旋转到E 点连接PE 易证△BPE 是等腰直角三角形利用勾股定理可求出PE 的长再证明△PCE 是直角三角形利用勾股定理求出CE 的长即可得到PA 的长解析:6【分析】将△PBA 沿B 点顺时针旋转90°,此时A 与C 点重合,P 点旋转到E 点,连接PE ,易证△BPE 是等腰直角三角形,利用勾股定理可求出PE 的长,再证明△PCE 是直角三角形.利用勾股定理求出CE 的长,即可得到PA 的长.【详解】将△PBA 沿B 点顺时针旋转90°,此时A 与C 点重合,P 点旋转到E 点,连接PE ,∴PB=BE=1,PA=EC ,∠BPE=90°∴△PEB 是等腰直角三角形,∴∠PEB=∠EPB =45°,∴,又∵∠BPC=135°,∴∠EPC=135°-45°=90°,∴在直角△PEC 中,==∴PA=EC =.【点睛】本题考查了正方形的性质、旋转的性质、等腰直角三角形的判断和性质以及勾股定理的运用,解答此题的关键是利用旋转构建直角三角形,由勾股定理求解.三、解答题21.52【分析】由旋转可得DE=DM ,∠EDM 为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF 为45°,可得出∠EDF=∠MDF ,再由DF=DF ,利用SAS 可得出三角形DEF 与三角形MDF 全等,由全等三角形的对应边相等可得出EF=MF ;则可得到AE=CM=1,正方形的边长为3,用AB-AE 求出EB 的长,再由BC+CM 求出BM 的长,设EF=MF=x ,可得出BF=BM-FM=BM-EF=4-x ,在直角三角形BEF 中,利用勾股定理列出关于x 的方程,求出方程的解得到x 的值,即为FM 的长.【详解】解:∵∆DAE 逆时针旋转90°得到∆DCE ,∴∠FCM=∠FCD+∠DCM=180°,∴F 、C 、M 三点共线,∴DE=DM ,∠EDM=90°,∴∠EDF+∠FDM=90°,∵∠EDF=45°,∴∠FDM=∠EDF=45°,在∆DEF 和∆DMF 中,DE DM EDF FDM DF DF =⎧⎪∠=∠⎨⎪=⎩∴∆DEF ≌∆DMF(SAS),∴EF=MF ,设EF=MF=x ,∵AE=CM=1,且BC=3,∴BM=BC+CM=4,∴BF=BM-MF=BM-EF=4-x ,∵EB=AB-AE=3-1=2,在Rt∆EBF 中222EB BF EF +=即2222(4)x x +-=解得x=52, ∴FM=52【点睛】此题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,以及勾股定理.此题难度适中,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想与方程思想的应用.22.(1)画图见解析,(-x ,-y ),(2)(-m +4,-n -6)【分析】(1)依据中心对称画图,即可得到△A 1B 1C 1;根据关于原点对称的坐标变化规律,可得坐标;(2)将P 点平移到原点,利用(1)的结论,求出N 点坐标.【详解】解:(1)△ABC 关于原点对称的△A 1B 1C 1如图所示,(x ,y )关于原点中心对称后的点坐标为(-x ,-y )(2)将点P (2,-3)平移到原点,对应的点M 坐标变为M 1(m-2,n+3),M 1(m-2,n+3)关于原点(即现在的点P )对称点M 2的坐标为(-m+2,-n-3),再将点P 平移回原来的位置,点M 2的坐标变为(-m+4,-n-6),即点N 的坐标为(-m+4,-n-6)【点睛】本题考查了中心对称的画法以及关于原点对称点的坐标变化规律,通过平移点P ,把关于任意一点成中心对称的问题转化为关于原点对称的问题是解决问题的关键,体现了数学的转化思想.23.(1)见解析;(2)①②2【分析】(1)由旋转的性质得到∠DCE=60°,DC=EC ,即可得到结论;(2)①存在,由等边三角形的性质可得△CDE 的周长=3CD ,当CD ⊥AB 时,CD 有最小值,即可求解;②由题意可得∠BED=90°,由直角三角形的性质可求解.【详解】解:(1)∵证明:将ACD △绕点C 逆时针方向旋转60°得到BCE ,∴60DCE ∠=︒,DC EC =,∴CDE △是等边三角形:(2)①∵CDE △是等边三角形,∴CDE △的周长3CD =,当610t <<时,由垂线段最短可知,当CD AB ⊥时,CDE △的周长最小,此时,CD =∴CDE △的最小周长3CD ==②存在,当0<t <6时,由旋转可知,∠ABE=60°,∠BDE <60°,∴∠BED=90°,由(1)可知,△CDE 是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA ,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA-DA=6-4=2,∴t=2.【点睛】本题是几何变换综合题,考查了旋转的性质,等边三角形的性质,直角三角形的性质,垂线段最短等知识,灵活运用这些性质解决问题是本题的关键.24.(1)旋转角的度数为90°;(2)AE 与BD 互相垂直,理由见详解.【分析】(1)由题意易得BC=AC ,则有∠CBA=∠CAB=45°,进而问题可求解;(2)由(1)可得∠DBC=∠EAC ,如图∠1=∠2,∠2+∠DBC=90°,进而问题可求解.【详解】解:(1)由将BCD △绕点C 顺时针旋转一定角度后,点B 的对应点恰好与点A 重合,得到ACE △可得:BCD ACE ≌,∴BC=AC ,∵45ABC ADC ∠=∠=︒,∴∠CBA=∠CAB=45°,∴∠ACB=90°,即旋转角度为对应边的夹角,故旋转角为∠ACB=90°;(2)AE ⊥BD ,理由如下:如图所示,由(1)可得:BCD ACE ≌,∴∠DBC=∠EAC ,∵∠ACB=90°,∴∠2+∠DBC=90°,∵∠1=∠2,∴∠1+∠EAC=90°,∴BD ⊥AE .【点睛】本题主要考查旋转的性质,熟练掌握旋转的性质是解题的关键.25.(1)90,(2)2cm .【分析】(1)找出对应边AB 、BC 的夹角的度数就是旋转角的度数;(2)根据旋转变换的性质可知BP=BE ,∠PBE=∠ABC ,再根据勾股定理列式求解即可得到PE 的长度.【详解】解:(1)∵△ABP 绕着点B 旋转后能到达△CBE 的位置,∴∠ABC 为旋转角.∵四边形ABCD 是正方形,∴∠ABC =90°,即旋转的角度是90度;(2)∵△ABP 绕着点B 旋转后能到达△CBE 的位置,∴BP =BE =3cm ,∠PBE =∠ABC =90°,∴PE 222233BP BE =+=+=2cm .【点睛】本题主要考查了旋转变换的性质,根据对应边的夹角的度数就等于旋转角的度数求解是解题的关键.26.(1)见解析;(2)9【分析】(1)根据旋转的性质即可画出△ABE绕点A逆时针旋转90°后的图形(点E的对应点为F);(2)根据AB=3和旋转的性质可得四边形AECF的面积即为正方形ABCD的面积.【详解】(1)如图,△ADF即为△ABE绕点A逆时针旋转90°后的图形;(2)根据旋转可知:四边形AECF的面积=正方形ABCD的面积=AB2=9.故答案为:9.【点睛】本题考查了作图-旋转变换、正方形的性质、旋转的性质,解决本题的关键是掌握旋转的性质.。
人教版九年级上册数学第二十三章 旋转含答案(精品)

人教版九年级上册数学第二十三章旋转含答案一、单选题(共15题,共计45分)1、下面图形中,既是轴对称图形又是中心对称图形的是()A. B. C. D.2、在下列图案中,中心对称图形的个数是().A.1 个B.2个C.3 个D.4个3、下图中是中心对称图形而不是轴对称图形的共有()A.1个B.2个C.3个D.4个4、四边形ABCD的对角线相交于点O,且AO=BO=CO=DO,则这个四边形()A.仅是轴对称图形B.仅是中心对称图形C.既是轴对称图形又是中心对称图形D.既不是轴对称图形,又不是中心对称图形5、如图.在△ABC中,∠CAB=80°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=()A.20B.35C.40D.456、下列既是轴对称又是中心对称图形的是A. B. C. D.7、下列图形中,既是轴对称图形也是中心对称图形的是()A. B. C. D.8、如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.30°B.40°C.50°D.65°9、如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是()A.45°B.60°C.75°D.90°10、下列汽车标志中,既是轴对称图形又是中心对称图形的是()A. B. C. D.11、从图中的四张图案中任取一张,取出图案是中心对称图形的概率是()A. B. C. D.112、如图,△ABC是⊙O的内接三角形,∠A=30°,BC=,把△ABC绕点O 按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为()A.1B.C.D.213、如图,在△ABC中,AB=2.2,BC=3.6,∠B=60°,将△ABC绕点A按逆时针方向旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为()A.1.5B.1.4C.1.3D.1.214、民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是A. B. C. D.15、如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是()A. B.13π C.25π D.25二、填空题(共10题,共计30分)16、如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是________.17、如图,把△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC 于D点.若∠A′DC=90°,则∠A=________度.18、如图,四边形ABCD中,AB=AD,AC=6,∠DAB=∠DCB=90°,则四边形ABCD的面积为________.19、如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2 ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=________.20、如图所示,图案绕中心至少旋转________ 可以和原来图形互相重合.21、如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点F旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了________cm.22、如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有________ 种.23、如图,在平面直角坐标系xOy中,将线段OA绕点O顺时针旋转得到线段,其中,则的坐标是________.24、如图,△ABC顶点的坐标分别为A(1,﹣1),B(4,﹣1),C(3,﹣4).将△ABC绕点A逆时针旋转90°后,得到△AB1C1.在所给的直角坐标系中画出旋转后的△AB1C1,并直接写出点B1的坐标:B1(________,________);C1(________,________).25、如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O意旋转.当时.的值为________.三、解答题(共5题,共计25分)26、如图,将△ABC绕点C顺时针旋转90°后得△DEC,若BC∥DE,求∠B的度数.27、如图,在平面直角坐标系中,每个小正方形的边长为1cm,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣1,2)、(0,-1),结合所给的平面直角坐标系解答下列问题:(1)AC的长等于多少?的坐(2)画出△ABC向右平移2个单位得到的△,求A点的对应点A1标。
人教版 九年级数学 第23章 旋转 复习题(含答案)

人教版九年级数学第23章旋转复习题一、选择题(本大题共10道小题)1. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是()2. 若点A(-3,2)关于原点的对称点是点B,点B关于x轴的对称点是点C,则点C的坐标是()A.(3,2) B.(-3,2)C.(3,-2) D.(-2,3)3. 如图,四边形ABCD与四边形FGHE关于一个点中心对称,则这个点是()A.O1B.O2C.O3D.O44. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为()A.10 B.2 2C.3 D.2 55. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为()A.A2P的中点B.A1B2的中点C.A1O的中点D.PO的中点6. 在平面直角坐标系中,点A的坐标为(1,3),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为()A.(3,1) B.(3,-1) C.(2,1) D.(0,2)7. 如图,已知菱形ABCD与菱形EFGH关于直线BD上的某个点中心对称,则点B的对称点是()A.点E B.点FC.点G D.点H8. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2n A2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是()A.(4n-1,3) B.(2n-1,3)C.(4n+1,3) D.(2n+1,3)9. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为()A.90°-αB.αC.180°-αD.2α10. 2018·桂林如图,在正方形ABCD中,AB=3,点M在边CD上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM绕点A按顺时针方向旋转90°得到△ABF,连接EF,则线段EF的长为()A.3 B.2 3 C.13 D.15二、填空题(本大题共8道小题)11. 若将等腰直角三角形AOB按图所示的方式放置,OB=2,则点A关于原点对称的点的坐标为________.12. 如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=________°.13. 如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.14. 已知▱ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB 与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.15. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.16. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.17. 如图,等边三角形ABC内有一点P,分别连接AP,BP,CP,若AP=6,B P=8,CP=10,则S△ABP+S△BPC=________.18. 如图,在平面直角坐标系中,对点P(1,0)作如下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2020的坐标为____________.三、解答题(本大题共4道小题)19. 如图,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D 分别在OE和OF上,现将△OEF绕点O逆时针旋转角α(0°<α<90°),连接AF,DE(如图②).(1)在图②中,∠AOF=________;(用含α的式子表示)(2)猜想图②中AF与DE的数量关系,并证明你的结论.20. 如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC 的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD =30,DM=10.(1)在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长;②当A,D,M三点为同一直角三角形的顶点时,求AM的长.(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外部的点D1处转到其内部的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.21. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD. 求证:BD2=AB2+BC2.22. 2019·福建如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A,B的对应点分别是D,E.(1)当点E恰好在AC上时,如图①,求∠ADE的度数;(2)若α=60°,F是边AC的中点,如图②,求证:四边形BEDF是平行四边形.人教版九年级数学第23章旋转复习题-答案一、选择题(本大题共10道小题)1. 【答案】C2. 【答案】A3. 【答案】A[解析] 如图,连接HC和DE交于点O1.4. 【答案】A[解析] ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5. ∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,∴AE=4,DE=3,∴BE=1.在Rt△BED中,BD=BE2+DE2=10.故选A.5. 【答案】D[解析] 因为P,O是对称点,所以PO的中点是对称中心.6. 【答案】A[解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,∴∠AEO =∠A′FO =90°.∵点A 的坐标为(1,3),∴AE =1,OE =3,∴OA =2,∠AOE =30°,由旋转可知∠AOA′=30°,OA′=OA =2,∴∠A′OF =90°-30°-30°=30°,∴A′F =12OA′=1,OF =3,∴A′(3,1). 故选A.7. 【答案】D[解析] 由于点B ,D ,F ,H 在同一条直线上,根据中心对称的定义可知,只能是点B 和点H 是对称点,点F 和点D 是对称点.故选D.8. 【答案】C[解析] A 1(1,3),A 2(3,-3),A 3(5,3),A 4(7,-3),…,∴点A n 的坐标为⎩⎨⎧(2n -1,3)(n 为奇数),(2n -1,-3)(n 为偶数).∵2n +1是奇数,∴点A 2n +1的坐标是(4n +1,3).故选C.9. 【答案】C[解析] 由题意可得∠CBD =α,∠C =∠EDB.∵∠EDB +∠ADB =180°, ∴∠C +∠ADB =180°.由四边形的内角和定理,得∠CAD +∠CBD =180°. ∴∠CAD =180°-∠CBD =180°-α.故选C.10. 【答案】C[解析] 如图,连接BM .∵△AEM 与△ADM 关于AM 所在的直线对称, ∴AE =AD ,∠MAD =∠MAE .∵△ADM绕点A按顺时针方向旋转90°得到△ABF,∴AF=AM,∠F AB=∠MAD,∴∠F AB=∠MAE,∴∠F AB+∠BAE=∠BAE+∠MAE,即∠F AE=∠MAB,∴△F AE≌△MAB(SAS),∴EF=BM.∵四边形ABCD是正方形,∴BC=CD=AB=3.∵DM=1,∴CM=2.∵在Rt△BCM中,BM=22+32=13,∴EF=13.二、填空题(本大题共8道小题)11. 【答案】(-1,-1)[解析] 如图,过点A作AD⊥OB于点D.∵△AOB是等腰直角三角形,OB=2,∴OD=AD=1,∴A(1,1),∴点A关于原点对称的点的坐标为(-1,-1).12. 【答案】90[解析] 连接AA1,CC1,分别作AA1和CC1的垂直平分线,两直线相交于点D,则点D即为旋转中心,连接AD,A1D,则∠ADA1=α=90°.13. 【答案】(0,1)14. 【答案】(-2-a,-b)或(2-a,-b)[解析] 如图①,∵点A的坐标为(a,b),AB与x轴平行,∴B(2+a,b).∵点D与点B关于原点对称,∴D(-2-a,-b).如图②,∵B(a-2,b),且点D与点B关于原点对称,∴D(2-a,-b).15. 【答案】y =-x 2-2x -3[解析] 旋转前二次项的系数a =1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a =-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y =-(x +1)2-2,即y =-x 2-2x -3.16. 【答案】18[解析] 如图.∵∠BAD =∠BCD =90°,∴∠B +∠ADC =180°.又∵AB =AD ,∴将△ABC 绕点A 逆时针旋转90°后点B 与点D 重合,点C 的对应点E 落在CD 的延长线上,∴AE =AC =6,∠CAE =90°,∴S 四边形ABCD =S △ACE =12AC·AE =12×6×6=18.17. 【答案】24+163 [解析] 如图,将△BPC 绕点B 逆时针旋转60°后得到△BP ′A ,连接PP ′.根据旋转的性质可知,旋转角∠PBP ′=∠CBA =60°,BP =BP ′, ∴△BPP ′为等边三角形, ∴BP ′=BP =8=PP ′.由旋转的性质可知,AP ′=PC =10, 在△APP ′中,PP ′=8,AP =6,AP ′=10, 由勾股定理的逆定理,得△APP ′是直角三角形,∴S△ABP+S△BPC=S四边形AP′BP=S△BPP′+S△AP′P=34BP2+12PP′·AP=24+16 3.故答案为24+16 3.18. 【答案】(1,-505)[解析] 根据题意可列出下面的表格:观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2020÷4=505,所以点P2020在第四象限,坐标为(1,-505).三、解答题(本大题共4道小题)19. 【答案】解:(1)∵△OEF绕点O逆时针旋转角α,∴∠DOF=∠COE=α.∵四边形ABCD为正方形,∴∠AOD=90°,∴∠AOF=90°-α.故答案为90°-α.(2)猜想:AF=DE.证明:∵四边形ABCD为正方形,∴∠AOD=∠COD=90°,OA=OD.∵∠DOF=∠COE=α,∴∠AOF=∠DOE.∵△OEF 为等腰直角三角形,∴OF =OE.在△AOF 和△DOE 中,⎩⎨⎧OA =OD ,∠AOF =∠DOE ,OF =OE ,∴△AOF ≌△DOE(SAS),∴AF =DE.20. 【答案】解:(1)①当A ,D ,M 三点在同一直线上时,AM =AD +DM =40或AM =AD -DM =20.②当A ,D ,M 三点为同一直角三角形的顶点时,显然∠MAD 不能为直角. 当∠AMD 为直角时,AM 2=AD 2-DM 2=302-102=800,∵AM>0, ∴AM =20 2.当∠ADM =90°时,AM 2=AD 2+DM 2=302+102=1000,∵AM>0, ∴AM =10 10.综上所述,满足条件的AM 的长为20 2或10 10.(2)如图,连接CD 1,由题意得,∠D 1AD 2=90°,AD 1=AD 2=30,∴∠AD 2D 1=45°,D 1D 2=30 2.∵∠AD 2C =135°,∴∠CD 2D 1=∠AD 2C -∠AD 2D 1=90°,∴CD 1=(30 2)2+602=30 6.∵∠BAC =∠D 1AD 2=90°,∴∠BAC -∠CAD 2=∠D 1AD 2-∠CAD 2,∴∠BAD 2=∠CAD 1.又∵AB =AC ,AD 2=AD 1,∴△BAD2≌△CAD1(SAS),∴BD2=CD1=30 6.21. 【答案】证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.又∵∠ADC=60°,∴∠BDE=60°,∴△DBE是等边三角形,∴BD=BE.又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,∴△ECB是直角三角形,∴BE2=CE2+BC2,即BD2=AB2+BC2.22. 【答案】解:(1)∵△ABC绕点C顺时针旋转角α得到△DEC,点E恰好在AC上,∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°.∵CA=CD,∴∠CAD=∠CDA=12(180°-30°)=75°,∴∠ADE=90°-75°=15°.(2)证明:连接AD.∵F是边AC的中点,∠ABC=90°,∴BF=12AC.∵∠ACB=30°,∴AB=12AC,∴BF=AB.∵△ABC绕点C顺时针旋转60°得到△DEC,∴∠BCE=∠ACD=60°,BC=CE,CD=CA,DE=AB,∴DE=BF,△ACD和△BCE均为等边三角形,∴BE=CB.∵F为△ACD的边AC的中点,∴DF⊥AC,易证得△CFD≌△ABC,∴DF=BC,∴DF=BE.又∵BF=DE,∴四边形BEDF是平行四边形.。
初三旋转题型

初三旋转题型旋转题型的题目有很多,以下是一些常见的题型和解题思路:1. 题目:在等腰三角形ABC中,∠BAC=120°,AB=AC,点E、F是BC边上的两点,∠BAE=∠CAF=30°,连接AE、AF、EF,则△AEF的面积与△ABC的面积之比为 _______.首先,由于∠BAC=120°,AB=AC,所以∠ABC=∠ACB=30°。
然后,由于∠BAE=∠CAF=30°,所以∠EAF=∠BAC−∠BAE−∠CAF=60°。
接着,因为∠ABC=∠ACB=30°和AB=AC,我们可以得出△ABE≌△ACF。
因此,△ABE 和△ACF的面积相等。
2. 题目:在平面直角坐标系中,点A的坐标为$(2,3)$,将线段OA绕点O 按顺时针方向旋转90°得到线段OB,则点B的坐标是____.首先,点A的坐标为$(2,3)$,那么点A和原点O之间的向量是$(2,3)$。
按照题目要求,线段OA绕原点O按顺时针方向旋转90°。
根据向量旋转的性质,新的向量应该是原向量乘以单位旋转矩阵。
单位旋转矩阵是一个2x2矩阵,其形式为:$\begin{bmatrix} \cos 90^\circ & -\sin 90^\circ \\ \sin 90^\circ &\cos 90^\circ \end{bmatrix}$将原向量$(2,3)$乘以这个单位旋转矩阵,得到新的向量$(-3, 2)$。
因此,点B的坐标是$(-3, 2)$。
3. 题目:将正方形绕着它的旋转中心至少旋转多少度才能和原来的图形重合.正方形有4个对称轴,每个角都是90度。
因此,正方形绕着它的旋转中心至少需要旋转90度才能和原来的图形重合。
人教版九年级旋转题型汇总
人教版九年级旋转题型汇总一、旋转中心及旋转角的确定1.如图,△ABC 绕着点O 旋转到△DEF 的位置,则旋转中心是______.旋转角是______.AO =______,AB =______,∠ACB =∠______.2.如图,△ABC 绕着点O 逆时针旋转到△DEF 的位置,则旋转中心及旋转角分别是()A.点B ,?ABOB.点O ,?AOBC.点B ,?BOED.点O ,?AOD 3.如图,在44⨯的正方形网格中,MNP ∆绕某点旋转︒90,得到111P N M ∆,则其旋转中心可以是()A .点EB .点FC .点GD .点H4.如图,正方形ABCD 中,点F 在边BC 上,E 在边BA 的延长线上.(1)若DCF △按顺时针方向旋转后恰好与DAE △重合.则旋转中心是点;最少旋转了度;(2)在(1)的条件下,若3,2AE BF ==,求四边形BFDE 的面积.二、旋转图形的做法: 1.在平面直角坐标系中,等腰Rt △OAB 斜边OB 在y 轴上,且OB =4. (1)画出△OAB 绕原点O 顺时针旋转90°后得到的三角形△OA’B’;(2)求点A 在旋转过程中经过的路径长. 2.如图,在8×11的方格纸中,每个小正方形的边长均为1,△ABC 的顶点均在小正方形的顶点处. (1)画出△ABC 绕点A顺时针方向旋转90°得到的△AB C ''; (2)求点B 运动到点B′所经过的路径的长.3.已知,如图,在平面直角坐标系中, △ABC 三个顶点的坐标分别为A (0,0), B (1,0),C (2,2).以A 为旋转中心, 把△ABC 逆时针旋转90︒,得到△''AB C . (1)画出△''AB C ; (2)点'B 的坐标为________; (3)求点C 旋转到'C 所经过的路线长.、4.如图,ABC Rt ∆中,︒=∠90C ,︒=∠30A ,2=AB 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
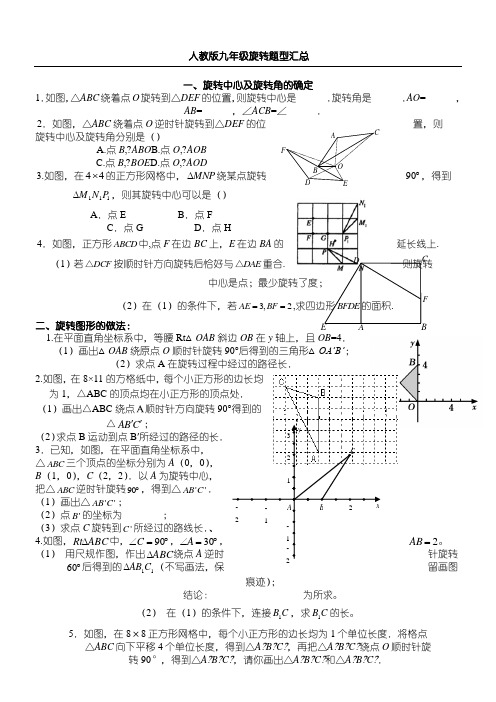
人教版九年级旋转题型汇总一、旋转中心及旋转角的确定1.如图,△ABC 绕着点O 旋转到△DEF 的位置,则旋转中心是______.旋转角是______.AO =______,AB =______,∠ACB =∠______.2.如图,△ABC 绕着点O 逆时针旋转到△DEF 的位置,则旋转中心及旋转角分别是() A.点B ,?ABO B.点O ,?AOB C.点B ,?BOE D.点O ,?AOD 3.如图,在44⨯的正方形网格中,MNP ∆绕某点旋转︒90,得到111P N M ∆,则其旋转中心可以是()A .点EB .点FC .点GD .点H 4.如图,正方形ABCD 中,点F 在边BC 上,E 在边BA 的延长线上.(1)若DCF △按顺时针方向旋转后恰好与DAE △重合.则旋转中心是点;最少旋转了度;(2)在(1)的条件下,若3,2AE BF ==,求四边形BFDE 的面积.二、旋转图形的做法:1.在平面直角坐标系中,等腰Rt △OAB 斜边OB 在y 轴上,且OB =4.(1)画出△OAB 绕原点O 顺时针旋转90°后得到的三角形△OA’B’;(2)求点A 在旋转过程中经过的路径长.2.如图,在8×11的方格纸中,每个小正方形的边长均为1,△ABC 的顶点均在小正方形的顶点处.(1)画出△ABC 绕点A顺时针方向旋转90°得到的△AB C ''; (2)求点B 运动到点B′所经过的路径的长. 3.已知,如图,在平面直角坐标系中, △ABC 三个顶点的坐标分别为A (0,0),B (1,0),C (2,2).以A 为旋转中心, 把△ABC 逆时针旋转90︒,得到△''AB C .(1)画出△''AB C ; (2)点'B 的坐标为________; (3)求点C 旋转到'C 所经过的路线长.、4.如图,ABC Rt ∆中,︒=∠90C ,︒=∠30A ,2=AB 。
E D O C B A F y x-1 -2 -2 -1 3 2 2 1 B A C D C F B E AF A B C E D (1) 用尺规作图,作出ABC ∆绕点A 逆时针旋转︒60后得到的11C AB ∆(不写画法,保留画图痕迹);结论:__________________为所求。
(2) 在(1)的条件下,连接C B 1,求C B 1的长。
5.如图,在8×8正方形网格中,每个小正方形的边长均为1个单位长度.将格点△ABC 向下平移4个单位长度,得到△A ?B ?C ?,再把△A ?B ?C ?绕点O 顺时针旋转90°,得到△A ?B ?C ?,请你画出△A ?B ?C ?和△A ?B ?C ?.解: 6.在平面直角坐标系xoy 中,已知ABC △三个顶点的坐标分别为()()()1,2,3,4,2,9.A B C ---⑴画出ABC △;⑵画出ABC △绕点A 顺时针旋转90o 后得到的11AB C △,并求出CC 的长. .三、对称中心的找法:1.已知:如图,四边形ABCD 与四边形EFGH 成中心对称,试画出它们的对称中心,并简要说明理由.四、中心对称图形的做法:1.如图,在正方形网络中,已知格点ABC △,请画出ABC △关于点B 成中心对称的''A BC △五、旋转的应用:1.如图,将含30︒角的直角三角尺ABC 绕点B 顺时针旋转150︒后得到EBD △,连结CD 。
若BCD△的面积为23cm ,则AC =cm .2.如图,在正方形ABCD 中,E 为DC 边上的点,连接BE ,将△BCE 绕点C 顺时针方向旋转90°得到△DCF ,连接 EF ,则∠CEF =度.3.△ABC 在平面直角坐标系中的位置如图所示,其中A (1,2),B (1,1),C (3,1),将△ABC 绕原点O顺时针旋转90o 后得到△'''C B A ,则点A 旋转到点'A所经过的路线长为A .π25B .π45C .π25D .5 O C B Ax y -3-4-2-1-2-3-412344-1321O B A C4.如图,△ABC 为等边三角形,D 是△ABC 内一点,且AD =3,将△ABD 绕点A 旋转到△ACE 的位置,连接DE ,则DE 的长为.5.ABCD 绕顶点A 逆时针旋转30°到正方形A ′B ′C ′D ______.6中,AD ∥BC ,∠B =90°,AD =3,BC =5,AB =1,把线段90°到DE 位置,连结AE ,则AE 的长为______. 7.如图,已知D ,E 分别是正三角形的边BC 和CA 上的点,且AE =CD ,AD 与BE 交于P ,则∠BPD ______°.8.如图,用等腰直角三角板画∠AOB =45°,并将三角板沿OB 方向平移到如图所示的虚线处后绕点M 按逆时针方向旋转22°,则三角板的斜边与射线OA 的夹角?为______°.9.如图,以等腰直角三角形ABC 的斜边AB 为边作等边△ABD ,连结DC ,以DC 为边作等边△DCE ,B ,E 在C ,D 的同侧.若,2=AB 则BE =______.六、旋转的综合应用:1.已知:如图,四边形ABCD 中,∠D =60°,∠B =30°,AD =CD .求证:BD 2=AB 2+BC 2.2.阅读下面材料:小阳遇到这样一个问题:如图(1),O 为等边△ABC 内部一点,且3:2:1::=OC OB OA ,求AOB ∠的度数.小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△CO A 绕点A 逆时针旋转60°,使点C 与点B 重合,得到△O AB ',连结O O '.则△O AO '是等边三角形,故OA O O =',至此,通过旋转将线段OA 、OB 、OC 转移到同一个三角形B O O '中.(1)请你回答:︒=∠AOB .(2)参考小阳思考问题的方法,解决下列问题:已知:如图(3),四边形ABCD 中,AB=AD ,∠DAB =60°,∠DCB =30°,AC =5,CD =4.求四边形ABCD 的面积.3.(1)如图①所示,P 是等边△ABC 内的一点,连结PA 、PB 、PC ,将△BAP 绕B 点顺时针旋转60°得△BCQ ,连结PQ .若PA 2+PB 2=PC 2,证明∠PQC =90°.(2)如图②所示,P 是等腰直角△ABC (∠ABC =90°)内的一点,连结PA 、PB 、PC ,将△BAP 绕B 点顺时针旋转90°得△BCQ ,连结PQ .当PA 、PB 、PC 满足什么条件时,∠PQC =90°?请说明理由.4.如图①,△ABC 是正三角形,△BDC 是顶角∠BDC =120°的等腰三角形,以D 为顶点图⑴图⑵图⑶ QC P A B第6题图① A B C P Q 第6题图②①F E D C B A F E DC B A H F ED C B A FE B D A C 作一个60°角,角的两边分别交AB 、AC 边于M 、N 两点,连接MN .(1)探究:线段BM 、MN 、NC 之间的关系,并加以证明.(2)若点M 、N 分别是射线AB 、CA 上的点,其它条件不变,再探线段BM 、MN 、NC 之间的关系,在图②中画出图形,并说明理由.图②例2、如图,已知△ABC 为等腰直角三角形,∠BAC =90°,E 、F 是BC 边上点,且∠EAF =45°.求证:222BE CF EF +=. 2.(1)如图1,△ABC 中,∠BAC=90°,AB=AC ,D 、E 在BC 上,∠DAE=45°,为了探究BD 、DE 、CE 之间的等量关系,现将△AEC 绕A 顺时针旋转90°后成△AFB ,连接DF ,经探究,你所得到的BD 、DE 、CE 之间的等量关系式是.(2)如图2,在△ABC 中,∠BAC=120°,AB=AC ,D 、E 在BC 上,∠DAE=60°、∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD 、DE 、CE 之间的等量关系,并证明你的结论.七、旋转的应用(4)正方形中的旋转例1已知:如图,E 是正方形ABCD 边BC 上任意一点,AF 平分∠EAD 交CD于F ,试说明BE +DF =AE .例2.已知:在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,(1)如图(1),若有∠EAF =45o.求证:BE +DF =EF . (2)如图(2),若有BE +DF =EF ,求:∠EAF 的度数.(3)如图(3),若∠EAF =45o ,AH ⊥EF .求证:AH =AB .(4)如图(4),若正方形ABCD 边长为1,△CEF 的周长为2.求∠EAF 的大小.(5)如图(5),若AB =3,且∠BAE =30o ,∠DAF =15o ,求△AEF 的面积.(6).如图17,正方形ABCD ,E 、F 分别为BC 、CD 边上一点.(1)若∠EAF=45o .求证:EF=BE+DF .(2)若⊿AEF 绕A 点旋转,保持∠EAF=45o ,问⊿CEF的周长是否随⊿AEF 位置的变化而变化?(3)已知正方形ABCD 的边长为1,如果⊿CEF 的周长为2.求∠EAF 的度数.八、应用: (2009东城期末)23.已知:正方形ABCD 中,45MAN ∠=o ,MAN ∠绕点A 顺时针旋转,它的两边分别交CB DC ,(或它们的延长线)于点M N ,. 当MAN ∠绕点A 旋转到BM DN =时(如图1),易证BM DN MN +=. A C B F E A B CE F F'F E D C BA图17(1)当MAN ∠绕点A 旋转到BM DN ≠时(如图2),线段BM DN ,和MN 之间有怎样的数量关系?写出猜想,并加以证明.(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间又有怎样的数量关系?请直接写出你的猜想.图1图2图36、①如图①,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,求证:EF =BE +FD .②如图②,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是BC 、CD 上的点,且∠EAF 是∠BAD 的一半,那么结论EF =BE +FD 是否仍然成立?若成立,请证明;若不成立,请说明理由.(怀柔2012)24.探究:(1)如图1,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,试判断BE 、DF 与EF 三条线段之间的数量关系,直接写出判断结果:;(2)如图2,若把(1)问中的条件变为“在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF=21∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AEF 绕点A 逆时针旋转,当点分别E 、F 运动到BC 、CD 延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明..2013东城24.问题1:如图1,在等腰梯形ABCD 中,AD ∥BC ,AB =BC =CD ,点M ,N 分别在AD ,CD 上,若∠MBN =12∠ABC ,试探究线段MN ,AM ,CN 有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD 中,AB =BC ,∠ABC +∠ADC =180°,点M ,N分别在DA ,CD 的延长线上,若∠MBN =12∠ABC 仍然成立,请你进一步探究线段MN ,AM ,CN 又有怎样的数量关系?写出你的猜想,并给予证明. 4(08天津市卷)25.(本小题10分)已知Rt △ABC 中,︒=∠90ACB ,CB CA =,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(Ⅰ)当扇形CEF 绕点C 在ACB ∠的内部旋转时,如图①,求证:222BN AM MN +=;C A B E F M N 图① CA B E F M N 图② 思路点拨:考虑222BN AM MN +=符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM 沿直线CE 对折,得△DCM ,连DN ,只需证BN DN =,︒=∠90MDN 就可以了.请你完成证明过程:(Ⅱ)当扇形CEF 绕点C 旋转至图②的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由. 5.已知:如图,在四边形ABCD 中,∠B +∠D =180°,AB =AD ,E ,F 分别是线段BC ,CD 上的点,且BE +FD =EF .求证:.21BAD EAF ∠=∠ 6.已知:如图,Rt △ABC 中,∠ACB =90°,D 为AB 中点,DE 、DF 分别交AC于E ,交BC 于F ,且DE ⊥DF .(1)如果CA =CB ,求证:AE 2+BF 2=EF 2;(2)如果CA <CB ,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.10.如图,在正方形ABCD 中,E 、F 分别是AB 、BC 的中点,求证:AM AD =.九、中心对称图形的认识1.下列图形是中心对称图形的是A.B.C.D.2.下列图形中,既是中心对称图形又是轴对称图形的是A .B.C.D.3.下列图形中,既是中心对称图形又是轴对称图形的是().A .等边三角形B .菱形C .等腰梯形D .平行四边形。
