物理化学第二、三章习题
第五版物理化学第二章习题答案

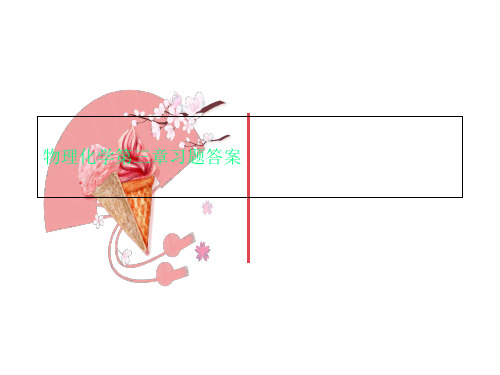
第二章热力学第一定律1mol理想气体在恒定压力下温度升高1℃,求过程中系统与环境交换的功。
解:理想气体n = 1mol对于理想气体恒压过程,应用式(2.2.3)W =-p ambΔV =-p(V2-V1) =-(nRT2-nRT1) =-1mol水蒸气(H2O,g)在100℃,下全部凝结成液态水。
求过程的功。
假设:相对于水蒸气的体积,液态水的体积可以忽略不计。
解: n = 1mol恒温恒压相变过程,水蒸气可看作理想气体, 应用式(2.2.3)W =-p ambΔV =-p(V l-V g ) ≈ pVg = nRT =在25℃及恒定压力下,电解1mol水(H2O,l),求过程的体积功。
H2O(l) = H2(g) + 1/2O2(g)解: n = 1mol恒温恒压化学变化过程, 应用式(2.2.3)W=-p ambΔV =-(p2V2-p1V1)≈-p2V2 =-n2RT=-系统由相同的始态经过不同途径达到相同的末态。
若途径a的Q a=,Wa=-;而途径b的Q b=-。
求W b.解: 热力学能变只与始末态有关,与具体途径无关,故ΔU a= ΔU b 由热力学第一定律可得Qa + Wa = Q b + W b∴ W b = Q a + W a-Q b = -始态为25℃,200 kPa的5 mol某理想气体,经途径a,b两不同途径到达相同的末态。
途经a先经绝热膨胀到 -28.47℃,100 kPa,步骤的功;再恒容加热到压力200 kPa的末态,步骤的热。
途径b为恒压加热过程。
求途径b的及。
解:先确定系统的始、末态3111061902000001529831485m ...P nRT V =××==32101601000005824431485m ...P nRT V V =××=== kJ .kJ )..(Q W U Δa a 85194225575=+=+=-对于途径b ,其功为kJ .J ..V Δp W b 932706190101602000001-)-(--===根据热力学第一定律4mol 某理想气体,温度升高20℃, 求ΔH-ΔU 的值。
第五版物理化学第二章习题答案

第二章热力学第一定律2、1 1mol理想气体在恒定压力下温度升高1℃,求过程中系统与环境交换的功。
解:理想气体n = 1mol对于理想气体恒压过程,应用式(2、2、3)W =-p ambΔV =-p(V2-V1) =-(nRT2-nRT1) =-8、314J2、2 1mol水蒸气(H2O,g)在100℃,101、325kPa下全部凝结成液态水。
求过程的功。
假设:相对于水蒸气的体积,液态水的体积可以忽略不计。
解: n = 1mol恒温恒压相变过程,水蒸气可瞧作理想气体, 应用式(2、2、3)W =-pambΔV =-p(Vl-Vg) ≈ pVg = nRT = 3、102kJ 2、3 在25℃及恒定压力下,电解1mol水(H2O,l),求过程的体积功。
H2O(l) =H2(g) + 1/2O2(g)解: n = 1mol恒温恒压化学变化过程, 应用式(2、2、3)W=-pambΔV =-(p2V2-p1V1)≈-p2V2=-n2RT=-3、718kJ2、4 系统由相同的始态经过不同途径达到相同的末态。
若途径a的Q a=2、078kJ,Wa=-4、157kJ;而途径b的Q b=-0、692kJ。
求W b、解: 热力学能变只与始末态有关,与具体途径无关,故ΔU a= ΔU b由热力学第一定律可得 Qa + Wa = Q b + W b∴ W b = Q a + W a-Q b = -1、387kJ2、5 始态为25℃,200 kPa的5 mol某理想气体,经途径a,b两不同途径到达相同的末态。
途经a先经绝热膨胀到 -28、47℃,100 kPa,步骤的功;再恒容加热到压力200 kPa 的末态,步骤的热。
途径b为恒压加热过程。
求途径b的及。
解:先确定系统的始、末态3111061902000001529831485m ...P nRT V =××==32101601000005824431485m ...P nRT V V =××===kJ .kJ )..(Q W U Δa a 85194225575=+=+=-对于途径b,其功为kJ .J ..V Δp W b 932706190101602000001-)-(--===根据热力学第一定律2、6 4mol 某理想气体,温度升高20℃, 求ΔH -ΔU 的值。
物理化学 答案 第二章_习题解答

=
(0.3 × 48.66 +
0.7 ×12) KJ·mol-1
=
23.0KJ·mol-1
B
∑ ∑ ∑ S
2-2 已知当 NaCl 溶液在 1kg 水中含物质的量为 n(单位为 mol)的 NaCl 时,体积 V 随 n 的变化关系为:
V/m3 = 1.00138×10-3 + 1.66253×10-5n/mol +1.7738×10-3(n/mol)3/2 + 1.194×10-7(n/mol)2
求当 n 为 2mol 时 H2O 和 NaCl 的偏摩尔体积为多少? 解:设水用“A”表示,NaCl 用“B”表示,由题意得:
1
⎜⎜⎝⎛
∂V ∂n B
⎟⎟⎠⎞ = 1.66253 ×10−5
+ 1.7738 ×10−3
×
3 2
1
× (n / mol) 2
+ 1.194 × 10−7
× 2(n / mol)
那么当 n=2 时,NaCl 的偏摩尔体积
VB
= 1.66253 × 10−5
+ 1.7738 × 10−3
×
3
×
2
1 2
mol·dm3 = 0.547mol·dm-3
bB
=
nB mA
=
wB M (1 − wB )
=
0.095 0.18 × (1 − 0.095)
mol·kg-1 = 0.583mol·kg-1
2-4 若将 25℃、101.325KPa 纯理想气体的状态定为气体的标准状态,则氧气的标准
熵 S1O =205.03J·K-1·mol-1,现改为 25℃、100Kpa 的纯理想气体作为气体的标准态,氧气
物理化学第三章 习题解答

第三章 习题解答1. 在298 K 和标准压力下,含甲醇(B)的摩尔分数x B 为0.458的水溶液的密度为0.89463kg dm -⋅,甲醇的偏摩尔体积313(CH OH)39.80 cm mol V -=⋅,试求该水溶液中水的偏摩尔体积2(H O)V 。
解:3322(CH OH)(CH OH)(H O)(H O)V n V n V =+3330.45832(10.458)18()dm 0.02729 dm 0.894610mV ρ⨯+-⨯===⨯ 3313120.027290.45839.8010(H O)() cm mol 16.72 cm mol 10.458V ----⨯⨯=⋅=⋅-2. 298 K 和标准压力下,有一甲醇物质的量分数为0.4的甲醇-水混合物。
如果往大量的此混合物中加入1 mol 水,混合物的体积增加17.35 cm 3;如果往大量的此混合物中加1 mol 甲醇,混合物的体积增加39.01 cm 3。
试计算将0.4 mol 的甲醇和0.6 mol 的水混合时,此混合物的体积为若干?此混合过程中体积的变化为若干?已知298 K 和标准压力下甲醇的密度为0.79113g cm -⋅,水的密度为0.99713g cm -⋅。
解:312(H O)17.35cm mol V -=⋅313(CH OH)39.01 cm mol V -=⋅33322(CH OH)(CH OH)(H O)(H O)26.01 cm V n V n V =+=混合前的体积为:33[(18/0.9971)0.6(32/0.7911)0.4] cm 27.01 cm ⨯+⨯=31.00 cm V ∆=3. 298 K 时,K 2SO 4在水溶液中的偏摩尔体积V B 与其质量摩尔浓度的关系式为:1/2B 32.28018.220.222V m m =++,巳知纯水的摩尔体积V A , m = 17.96 cm 3·mol -1,试求在该溶液中水的偏摩体积与K 2SO 4浓度m 的关系式。
物理化学习题与答案

第一章热力学第一定律练习题下一章返回一、判断题(说法对否):1.1.当系统的状态一定时,所有的状态函数都有一定的数值。
当系统的状态发生变化时,所有的状态函数的数值也随之发生变化。
2.2.体积是广度性质的状态函数;在有过剩NaCl(s) 存在的饱和水溶液中,当温度、压力一定时;系统的体积与系统中水和NaCl的总量成正比。
3.3.在101.325kPa、100℃下有lmol的水和水蒸气共存的系统,该系统的状态完全确定。
4.一定量的理想气体,当热力学能与温度确定之后,则所有的状态函数也完全确定。
5.系统温度升高则一定从环境吸热,系统温度不变就不与环境换热。
6.从同一始态经不同的过程到达同一终态,则Q和W的值一般不同,Q + W 的值一般也不相同。
7.因Q P= ΔH,Q V= ΔU,所以Q P与Q V都是状态函数。
8.封闭系统在压力恒定的过程中吸收的热等于该系统的焓。
9.对于一定量的理想气体,当温度一定时热力学能与焓的值一定,其差值也一定。
10.在101.325kPa下,1mol l00℃的水恒温蒸发为100℃的水蒸气。
若水蒸气可视为理想气体,那么由于过程等温,所以该过程ΔU = 0。
11.1mol,80.1℃、101.325kPa的液态苯向真空蒸发为80.1℃、101.325kPa 的气态苯。
已知该过程的焓变为30.87kJ,所以此过程的Q = 30.87kJ。
12.1mol水在l01.325kPa下由25℃升温至120℃,其ΔH= ∑C P,m d T。
13.因焓是温度、压力的函数,即H = f(T,p),所以在恒温、恒压下发生相变时,由于d T = 0,d p = 0,故可得ΔH = 0。
14.因Q p = ΔH,Q V = ΔU,所以Q p - Q V = ΔH - ΔU = Δ(p V) = -W。
15.卡诺循环是可逆循环,当系统经一个卡诺循环后,不仅系统复原了,环境也会复原。
16.一个系统经历了一个无限小的过程,则此过程是可逆过程。
物理化学 第03章习题(含答案)

第三章 化学平衡测试练习题选择题:1、化学反应若严格遵循体系的“摩尔吉布斯函数—反应进度”曲线进行,则该反应在( A )[A].曲线的最低点[B].最低点与起点或终点之间的某一侧[C].曲线上的每一点[D].曲线以外某点进行着热力学可逆过程.2、有一理想气体反应A+B=2C ,在某一定温度下进行,按下列条件之一可以用θm r G ∆直接判断反应方向和限度:( C )[A].任意压力和组成[B].总压101.325kPa ,物质的量分数31===C B A x x x [C].总压303.975kPa ,31===C B A x x x [D].总压405.300kPa ,41==B A x x ,21=C x 3、298K 的理想气体化学反应AB=A+B ,当温度不变,降低总压时,反应的转化率( A )[A].增大 [B].减小 [C].不变 [D].不能确定4、已知气相反应)()(3)(126266g H C g H g H C =+在373K 时的143.192-⋅-=∆mol kJ H mr θ,当反应达平衡时,可采用下列哪组条件,使平衡向右移动( C )[A].升温与加压 [B].升温与减压[C].降温与加压 [D].降温与减压5、化学反应的平衡状态随下列因素当中的哪一个面改变? ( A )[A].体系组成 [B].标准态 [C].浓度标度[D].化学反应式中的计量系数νB6、在相同条件下有反应式(1)C B A 2=+,(θ1,m r G ∆);(2) C B A =+2121,(θ2,m r G ∆)则对应于(1),(2)两式的标准摩尔吉不斯函数变化以及平衡常数之间的关系为:( B )[A].θθ2,1,2m r m r G G ∆=∆,θθ21K K =[B].θθ2,1,2m r m r G G ∆=∆,221)(θθK K =[C].θθ2,1,m r m r G G ∆=∆,221)(θθK K =[D].θθ2,1,m r m r G G ∆=∆,θθ21K K = 7、反应)()()()(222g H g CO g O H g CO +=+,在600℃、100 kPa 下达到平衡后,将压力增大到5000kPa ,这时各气体的逸度系数为09.12=CO γ,10.12=H γ,23.1=CO γ,77.02=O H γ。
物理化学第二章热力学第二定律练习题及答案

物理化学第二章热力学第二定律练习题及答案第二章 热力学第二定律练习题一、判断题(说法正确否):1.自然界发生的过程一定是不可逆过程。
2.不可逆过程一定是自发过程。
3.熵增加的过程一定是自发过程。
4.绝热可逆过程的∆S = 0,绝热不可逆膨胀过程的∆S > 0,绝热不可逆压缩过程的∆S < 0。
5.为了计算绝热不可逆过程的熵变,可以在始末态之间设计一条绝热可逆途径来计算。
6.由于系统经循环过程后回到始态,∆S = 0,所以一定是一个可逆循环过程。
7.平衡态熵最大。
8.在任意一可逆过程中∆S = 0,不可逆过程中∆S > 0。
9.理想气体经等温膨胀后,由于∆U = 0,所以吸的热全部转化为功,这与热力学第二定律矛盾吗?10.自发过程的熵变∆S > 0。
11.相变过程的熵变可由T H S ∆=∆计算。
12.当系统向环境传热时(Q < 0),系统的熵一定减少。
13.一切物质蒸发时,摩尔熵都增大。
14.冰在0℃,p 下转变为液态水,其熵变TH S ∆=∆>0,所以该过程为自发过程。
15.自发过程的方向就是系统混乱度增加的方向。
16.吉布斯函数减小的过程一定是自发过程。
17.在等温、等压下,吉布斯函数变化大于零的化学变化都不能进行。
18.系统由V 1膨胀到V 2,其中经过可逆途径时做的功最多。
19.过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的,由基本方程可得∆G = 0。
20.理想气体等温自由膨胀时,对环境没有做功,所以 -p d V = 0,此过程温度不变,∆U = 0,代入热力学基本方程d U = T d S - p d V ,因而可得d S = 0,为恒熵过程。
21.是非题:⑴“某体系处于不同的状态,可以具有相同的熵值”,此话对否?⑵“体系状态变化了,所有的状态函数都要变化”,此话对否?⑶ 绝热可逆线与绝热不可逆线能否有两个交点?⑷ 自然界可否存在温度降低,熵值增加的过程?举一例。
物理化学各章复习题 附答案

第一章化学热力学基础1.4 练习题1.4.1 判断题1.可逆的化学反应就是可逆过程。
2.Q和W不是体系的性质,与过程有关,所以Q + W也由过程决定。
3.焓的定义式H = U + pV是在定压条件下推导出来的,所以只有定压过程才有焓变。
4.焓的增加量DH等于该过程中体系从环境吸收的热量。
5.一个绝热过程Q = 0,但体系的DT不一定为零。
6.对于一定量的理想气体,温度一定,热力学能和焓也随之确定。
7.某理想气体从始态经定温和定容两过程达终态,这两过程的Q、W、DU及DH是相等的。
8.任何物质的熵值是不可能为负值和零的。
9.功可以全部转化为热,但热不能全部转化为功。
10.不可逆过程的熵变是不可求的。
11.某一过程的热效应与温度相除,可以得到该过程的熵变。
12.在孤立体系中,一自发过程由A→B,但体系永远回不到原来状态。
13.绝热过程Q = 0,即,所以d S = 0。
14.可以用一过程的熵变与热温熵的大小关系判断其自发性。
15.绝热过程Q = 0,而由于DH = Q,因而DH等于零。
16.按Clausius不等式,热是不可能从低温热源传给高温热源的。
17.在一绝热体系中,水向真空蒸发为水蒸气 (以水和水蒸气为体系),该过程W>0,DU>0。
18.体系经过一不可逆循环过程,其DS体>0。
19.对于气态物质,C p-C V = n R。
20.在一绝热体系中有一隔板,两边分别是空气和真空,抽去隔板,空气向真空膨胀,此时Q= 0,所以DS=0。
1.4.2 选择题1.273K, p q时,冰融化为水的过程中,下列关系式正确的有 .A.W<0 B. DH = Q P C. DH<0 D. DU<02.体系接受环境作功为160J,热力学能增加了200J,则体系 .A.吸收热量40J B.吸收热量360JC.放出热量40J D.放出热量360J3.在一绝热箱内,一电阻丝浸入水中,通以电流。
若以水和电阻丝为体系,其余为环境,则 .A.Q> 0,W = 0,DU > 0 B.Q =0,W = 0,DU > 0C.Q = 0,W> 0,DU > 0 D.Q< 0,W = 0,DU < 04.任一体系经一循环过程回到始态,则不一定为零的是 .A.DG B.DS C.DU D.Q5.对一理想气体,下列哪个关系式不正确 .A. B.C. D.6.当热力学第一定律写成d U = δQ–p d V时,它适用于 .A.理想气体的可逆过程 B.封闭体系的任一过程C.封闭体系只做体积功过程 D.封闭体系的定压过程7.在一绝热钢壁体系内,发生一化学反应,温度从T1→T2,压力由p1→p2,则 .A.Q>0,W>0,DU > 0 B.Q = 0,W<0,DU <0C.Q = 0,W>0,DU >0 D.Q = 0,W = 0,DU = 08.理想气体混合过程中,下列体系的性质,不正确的是 .A.DS>0 B.DH =0 C.DG = 0 D. DU = 09.任意的可逆循环过程,体系的熵变 .A.一定为零 B.一定大于零 C.一定为负 D.是温度的函数10.一封闭体系,从A→B变化时,经历可逆(R)和不可逆(IR)途径,则 .A.Q R = Q IR B. C.W R = W IR D.11.理想气体自由膨胀过程中 .A.W = 0,Q>0,DU>0,DH=0 B.W>0,Q=0,DU>0,DH>0C.W<0,Q>0,DU=0,DH=0 D.W = 0,Q=0,DU=0,DH=012.H2和O2在绝热定容的体系中生成水,则 .A.Q=0,DH>0,DS孤 = 0 B.Q>0,W = 0,DU>0C.Q>0,DU>0,DS孤>0 D. Q=0,W = 0,DS孤>013.理想气体可逆定温压缩过程中,错误的有 .A. DS体= 0 B. DU=0 C.Q<0 D. DH=014.当理想气体反抗一定的外压做绝热膨胀时,则 .A. 焓总是不变的 B.热力学能总是不变的C.焓总是增加的 D.热力学能总是减小的15.环境的熵变等于 .A. B. C. D.1.4.3 填空题1.理想气体的定温可逆膨胀体系做的功最,定温可逆压缩过程环境做的功最。
物理化学习题

物理化学习题第一章热力学第一定律一、问答题1.什么是系统?什么是环境?2.什么是状态函数?3.什么是等压过程?4.什么是热力学能?5.什么是热力学第一定律?6.什么是体积功7.可逆过程有哪些特点?8.什么是理想气体?9.什么是标准摩尔生成焓?10.夏天为了降温,采取将室内电冰箱门打开,接通电源并紧闭门窗(设墙壁门窗均不传热)。
该方法能否使室内温度下降?为什么?二、判断题(正确打√,错误打×)1.由于p和V都是状态函数,则pV也是状态函数。
()2.状态函数改变后,状态一定改变。
()3.孤立系统内发生的一切变化过程,其UΔ必定为零。
()4.温度越高,Q值越大。
()5.等压过程是指系统在变化过程中系统的压力等于环境的压力。
()6.不做非体积功是指系统的始态和终态的体积相同。
()7.在标准状态下,最稳定单质的焓值等于零。
()8.O2(g)的标准摩尔燃烧焓等于零。
()9.H2O(l)的标准摩尔燃烧焓等于零。
()10.H2和O2在绝热钢瓶中发生反应的U△等于零。
()三、选择题(选1个答案)1. 是状态函数。
( )A .GB .U △C .WD .Q2. 不是状态函数。
( )A .HB .UC .SD .G △3. 具有广度性质。
( )A .TB 、UC .PD .ρ(密度)4. 具有强度性质。
( ) A .S B .V C .G D .η(粘度)5. 的标准摩尔生成焓等于零。
( ) A .C (石墨) B .C (金刚石) C .CO 2 D .CO6. 的标准摩尔燃烧焓等于零。
( ) A .C (石墨) B .C (金刚石) C .CO 2 D .CO7. 理想气体在外压为101.325kPa 下的等温膨胀,该过程的 。
( ) A .Q>0 B .Q<0 C .U △>0 D .U △<08. 101.325kPa 和273.15K 的水等温等压变为冰,该过程的 。
《物理化学》第二章-热力学第一定律练习题(含标准答案)

《物理化学》第二章-热力学第一定律练习题(含答案)————————————————————————————————作者:————————————————————————————————日期:第二章练习题一、填空题1、根据体系和环境之间能量和物质的交换情况,可将体系分成、、。
2、强度性质表现体系的特征,与物质的数量无关。
容量性质表现体系的特征,与物质的数量有关,具有性。
3、热力学平衡状态同时达到四种平衡,分别是、、、。
4、体系状态发生变化的称为过程。
常见的过程有、、、、。
5、从统计热力学观点看,功的微观本质是,热的微观本质是。
6、气体各真空膨胀膨胀功W= 07、在绝热钢瓶中化学反应△U= 08、焓的定义式为。
二、判断题(说法对否):1、当体系的状态一定时,所有的状态函数都有一定的数值。
(√)2、当体系的状态发生变化时,所有的状态函数的数值也随之发生变化。
(χ)3.因= ΔH, = ΔU,所以与都是状态函数。
(χ)4、封闭系统在压力恒定的过程中吸收的热等于该系统的焓。
(χ)错。
只有封闭系统不做非膨胀功等压过程ΔH=Q P5、状态给定后,状态函数就有定值;状态函数确定后,状态也就确定了。
(√)6、热力学过程中W的值应由具体过程决定( √ )7、1mol理想气体从同一始态经过不同的循环途径后回到初始状态,其热力学能不变。
( √ )三、单选题1、体系的下列各组物理量中都是状态函数的是( C )A 、T、P、V、QB 、m、W、P、HC、T、P、V、n、D、T、P、U、W2、对于内能是体系的单值函数概念,错误理解是( C )A体系处于一定的状态,具有一定的内能B对应于某一状态,内能只能有一数值不能有两个以上的数值C状态发生变化,内能也一定跟着变化D对应于一个内能值,可以有多个状态3下列叙述中不具有状态函数特征的是(D )A体系状态确定后,状态函数的值也确定B体系变化时,状态函数的改变值只由体系的始终态决定C经循环过程,状态函数的值不变D状态函数均有加和性4、下列叙述中正确的是( A )A物体温度越高,说明其内能越大B物体温度越高,说明其所含热量越多C凡体系温度升高,就肯定是它吸收了热D凡体系温度不变,说明它既不吸热也不放热5、下列哪一种说法错误( D )A焓是定义的一种具有能量量纲的热力学量B只有在某些特定条件下,焓变△H才与体系吸热相等C焓是状态函数D焓是体系能与环境能进行热交换的能量6、热力学第一定律仅适用于什么途径(A)A同一过程的任何途径B同一过程的可逆途径C同一过程的不可逆途径D不同过程的任何途径7. 如图,将CuSO4水溶液置于绝热箱中,插入两个铜电极,以蓄电池为电源进行电解,可以看作封闭系统的是(A)(A) 绝热箱中所有物质; (B) 两个铜电极;(C) 蓄电池和铜电极;(D) CuSO4水溶液。
物理化学第三章习题答案
S3 nC p,m(s)lnT T21 ?
S2
nfusHm T2
?
S ?
G H T S ?
12. 在400K、标准压力下,理想气体间进行下列 恒温、恒压化学反应:A(g)+ 2B(g)→ 3C(g)+ D (g)
求进行1mol上述反应的AΔrGmθ已B知25℃数C据如下:D
G H T S 56 2 21 .6 1 0 ( 3 5-2 05) . 5 22 1 .4J 27
8. 1 mol液体水于298.15K,101.325 kPa下蒸发为水蒸气,
试计算此过程的W、Q、∆U、∆H、∆S及 ∆G,
并判断此过程能否自发进行.已知在298.15K、3.167 kPa
H 2
H 2 O (l) H 2 O (g)
H H 2
29 .18 K 5 ,p23.16 k7 Pa 29.185K,3.16k7Pa
U H p ( V g V l) H p g V H n R ? T
S S 1 S 2 S 3
S1 0
S3
nRln 3.167 10.1325
何者可以作为上述过程是否自发进行的判据。 请计算出具体数值来说明。
C 6H 6(l) 不 可 C 逆 6H 6(g) H
35.23K 5,10.312k5Pa 35.23K 5,10.312k5Pa
可逆
H n v a H p m3.7 0k 7J
U H p ( V g V l) H p g V H n R 2 . 0 k 8 T 8 J
已知H2O(l)在298.15K时饱和蒸气压为3.168kPa, H2O(l)的摩尔体积为 18.02 mL/mol 。
p1
北京大学《物理化学》课后章节练习题第2章习题及答案

ΔS = ΔSA + ΔSB
=
nACv,m
(
A)
ln
T2 T1
+
nBC
p,
m
(B)
ln
T2 T1
+ nBR ln
pB,1 pB,2
由此得 T2=254.84K
所以
W = −ΔU = −nACv,m ( A)(T2 − T1) − nBCv,m (B)(T2 − T1) = 2440.5J
5. 解:(1)
21.
已知纯物质的平衡稳定条件为 ( ∂p ∂V
)T
<
0 ,请证明任一物质绝热可逆膨胀后
压力必然降低。
-4-
第二章 习题答案
∫ 1.解: ΔS = nR ln
p1 p2
+
C T2 p T T1
dT
= nR ln
p1 p2
+
n(Cv,m
+
R) ln
T2 T1
= −86.67J.K −1
2.解:设终态温度为 T
等式右边可以转化为
W = WB = p外 (VB,2 −VB,1) = p B,2 (VB,2 − VB,1) = pB,2VB,2 − p B V,2 B,1
=
nB R(T2
− TB,1
pB,2 ) pB,1
=
2R(T
− (300K ) 1)...........(2) 2
联立(1)和(2)式,得T2=264.7K
4. 一导热良好的固定隔板将一带无摩擦绝热活塞的绝热气缸分为左右两室,左
室中充入 1mol A,右室中充入 2mol B,设A和B均为理想气体且A为单原子 气体,B为双原子气体,起始温度均为 300K,压力均为 101.325kPa,始态如 图所示,图中C为销钉,p外为 50.663kPa。 (a)若将绝热活塞上的销钉 C 拔掉,求平衡时,该过程的功及体系的熵变。 (b)若拔掉销钉后使其可逆膨胀至p外,则该过程的功和体系熵又为何值。
物理化学傅献彩习题课-第二、三、四章
8.卡诺循环过程包括——、——、———、———。 9.理想气体在等温下向真空膨胀,则ΔU=———,ΔH=—— ——,ΔS————。 10.在隔离系统中发生某剧烈化学反应,使系统的温度及压力 皆明显升高,则系统的:ΔS—;ΔU—;ΔH——;ΔA—; Δ G——。(填>0,=0,<0或无法确定。) 11.使一个过程的熵变等于零,应满足的条件是—————— ——————————。 12.给自行车打气时,把气筒内的空气作为系统,打气筒、橡 皮管和轮胎均不导热,则该过程中Q—0,W—0。 13.理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨 胀到达相同的终态压力,则终态的温度T可逆——T不可逆;V可 逆—V不可逆;ΔH可逆—ΔH不可逆。 14.在恒熵、恒容、不做非膨胀功的封闭系统中,当热力学函 数——到达最——值的状态为平衡状态。 15
13
填空题
1.Qv=ΔU应用条件是__________, _________, __________。
2.纯物质完美晶体___________________时熵值为零。 3.热力学第三定律的普朗克说法的数学表达式是——。
4.熵增原理表述为
_______________________________________________________ _________________________________。 5.物理量Q、T、P、V、W、U、H、S、A、G ,其中属于状态函数 的是————;与过程有关的是————;状态函数中属于容 量性质的是—————;属于强度性质的是————。 6.节流膨胀过程是————,膨胀后温度将———。 7.热力学第二定律的经典表述之一是——-————————; 其数学表达公式是——————————。
椐,因 W = 0 ∴ −W ≤ − ∆vapA ∴ ∆vapA < 0,过程不可逆 ∵ 过程不恒压,不能用 ∆vapG 来判别
第五版物理化学第二章习题答案解析

第二章 热力学第一定律2.1 1mol 理想气体在恒定压力下温度升高1℃,求过程中系统与环境交换的功。
解:理想气体n = 1mol对于理想气体恒压过程,应用式(2.2.3)W =-p amb ΔV =-p(V 2-V 1) =-(nRT 2-nRT 1) =-8.314J2.2 1mol 水蒸气(H 2O,g)在100℃,101.325kPa 下全部凝结成液态水。
求过程的功。
假设:相对于水蒸气的体积,液态水的体积可以忽略不计。
解: n = 1mol恒温恒压相变过程,水蒸气可看作理想气体, 应用式(2.2.3)W =-p amb ΔV =-p(V l -V g ) ≈ pVg = nRT = 3.102kJ2.3 在25℃及恒定压力下,电解1mol 水(H 2O,l),求过程的体积功。
H 2O(l) = H 2(g) + 1/2O 2(g) 解: n = 1mol恒温恒压化学变化过程, 应用式(2.2.3)W=-p amb ΔV =-(p 2V 2-p 1V 1)≈-p 2V 2 =-n 2RT=-3.718kJ2.4 系统由相同的始态经过不同途径达到相同的末态。
若途径a 的Q a =2.078kJ,Wa=-4.157kJ ;而途径b 的Q b =-0.692kJ 。
求W b .解: 热力学能变只与始末态有关,与具体途径无关,故 ΔU a = ΔU b由热力学第一定律可得 Qa + Wa = Q b + W b ∴ W b = Q a + W a -Q b = -1.387kJ2.5 始态为25℃,200 kPa 的5 mol 某理想气体,经途径a ,b 两不同途径到达相同的末态。
途经a 先经绝热膨胀到 -28.47℃,100 kPa ,步骤的功;再恒容加热到压力200 kPa 的末态,步骤的热。
途径b 为恒压加热过程。
求途径b 的及。
解:先确定系统的始、末态3111061902000001529831485m ...P nRT V =××==32101601000005824431485m ...P nRT V V =××=== kJ .kJ )..(Q W U Δa a 85194225575=+=+=-对于途径b ,其功为kJ .J ..V Δp W b 932706190101602000001-)-(--===根据热力学第一定律2.6 4mol 某理想气体,温度升高20℃, 求ΔH-ΔU 的值。
物理化学第二、三章习题及答案

主要计算公式
总结
1. 热力学第一定律的数学表达式 :
dU Q W 或 U Q W
适用于封闭体系中的单纯PVT变化、相变化、化学变化
2. 恒容热和恒压热
Qv U
Qp H
适用于dV=0,W’=0条件下的三类反应
适用于dP=0,W’=0条件下的三类反应
3. 摩尔定压热容和摩尔定容热容之间的关系:
n= 1 mol T1=300.15K P1=101.32 KPa V1
dT 0 n= 1 mol T2=300.15K P2 V2
习题
n= 1 mol T3=370.15K P3=250.00 KPa V3 = V2
dV 0
因为V2=V3,则p2/T2=p3/T3, p2=p3T2/T3=250.00×300.15/370.15 kPa=202.72 kPa nRT p 1 W2=0 W p (V V ) nRT p nRT ( 2 1)
vap H m 1 1 p2 ( ) 克-克方程 ln p1 R T2 T1
可用来计算不同温度下的蒸气压或摩尔蒸发热。
热力学第一定律
习题
1、 1 mol 某理想气体于27oC ,101.325 kPa 的始态下,先受 某恒定外压恒温压缩至平衡态,再恒容升温至97oC , 250.00 kPa。求过程的W,Q, △U, △H。已知气体的
热力学第一定律
n= 5 mol T1=300 P1=200 KPa
dTV 0 n= 5 mol T2=300K P2=50 KPa
习题
T3 P3=200 KPa
Qr 0 n= 5 mol
整个过程由于第二步为 绝热过程,计算热是方 便的,而第一步 为恒温可逆过程,则: U1 0 Q1 W1 , Q1 -W1 V2 p1 Q Q1 Q2 W1 0 nRT ln nRT ln V1 p2 (5 8.314 300 ln 200/ 50) J 17.29kJ W U Q (15.15 17.29)kJ 2.14kJ
物理化学-第二章-热力学第一定律-经典习题及答案

。由始态 100 kPa,50 dm3,先恒容加热使
压力体积增大到 150 dm3,再恒压冷却使体积缩小至 25 dm3。求整个过程的
。
解:过程图示如下
n = 2mol
n = 2mol
n = 2mol
理想气体
理想气体
T1 = ?
恒容 → T2 = ?
理想气体 恒压 → T3 = ?
p1 = 100kPa
解:环境对体系做最小的功,必然是一个可逆过程
(1)
n = 1mol
n = 1mol
理想气体 T1 = 300K p1 = p外
理想气体 恒温可逆压缩 → T2 = 300K
p2 = p外
V1 = 0.040m3
V2 = 0.010m3
∫ ∫ Wr = −
pdV = − V2 nRT dV = nRT ln V1
n = 5mol 理想气体
T3 = ? p3 = 200kPa V3 = V2
两种过程始终态相同,先确定系统的始、末态 由理想气体状态方程
V1
=
nRT1 p1
=
5×8.314× 298.15 200 ×103
=
0.06197m3
V3
= V2
=
nRT2 p2
=
5×8.314× 244.18 100 ×103
解:
CV ,m = 20.92J ⋅ mol−1 ⋅ K −1
n = 1mol
n = 1mol
n = 1mol
理想气体
理想气体
理想气体
恒温
恒容
T1 = 300.15K p1 = 101.325kPa
→ p外 = p2
T2 p2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
烧焓
cH m
B
=(-393.51-1.9)kJ mol-1 = -395.41 kJ mol-1
4. (c) (c) (c) (a) 同样T、P下,冰的有序度大于水的,恒温恒 压下过冷水结冰是自发过程, △G<0; △S环=-Q/T>0
5. (c); 6. (c); 7. (d); 8. (c)
封闭系统,T、P、W’=0 的过程
不等式判别过程自发进行的方向;等式作为系统平衡的判据
热力学部分
10. △G 及△A 的计算
恒T过程
总结
A U T S
G H T S
1)单纯 PVT 变化 非恒T
G H T 2 S 2 T1 S 1 理想气体 V2 P1 G nR T ln nR T ln V1 P2
热力学部分
主要计算公式 1. 热力学第一定律的数学表达式 :
dU Q W
总结
或 U Q W
适用于封闭体系中的单纯PVT变化、相变化、化学变化
2. 恒容热和恒压热
Qv U
Q p H
适用于dV=0,W’=0条件下的三类反应
适用于dP=0,W’=0条件下的三类反应
3. 摩尔定压热容和摩尔定容热容之间的关系:
n= 2 mol T2 P2=200 KPa V2 = 50 dm3
dp 0
p1V1=p3V3,则T3=T1,对于理想气体△H和△U只是温 度的函数,所以△H=△U=0
该途径只涉及恒容和恒压过程,因此先计算功更为方便。
W p 外 V p 3 V [ 200 10 ( 25 10
1) 自由膨胀过程-向真空膨胀 ∵
2) 等容过程
∵ dV=0 ,W = 0
Wr V2 nRT ln V 1
3) 等温可逆膨胀
4)理想气体绝热可逆体积功计算
热力学部分
8. 熵的定义
PBiblioteka 总结Q p ΔH
S 2 S1 S
S nC
P .m
2
(
Qr T
)
1
2. 在一保温良好、门窗紧闭的房间内,放有电冰箱,若将电
冰箱门打开,不断向冰箱供给电能,室内的温度将(
(a) 逐渐降低; (b)逐渐升高; (c)不变;
)
(d)无法确定
热力学第一定律
二、选择题
习题
3. 已知25 oC时,金刚石的标准摩尔生成焓 f H m =1.90 kJ
mol-1
,石墨的标准摩尔燃烧焓 c H m
热力学第一定律
二、选择题答案
1. (c)
习题
W= △U =nCv,m △T,W(绝热可逆)> W(绝热不
可逆),所以T2’>T2 2. (b) 因环境对系统做了电功,所以室内温度将升高
3.
(c) C(石墨) : →
C(金刚石),由公式
可计算金刚石的标准摩尔燃
r H m (T ) B c H m ( B , , T )
n= 1 mol T1=300.15K P1=101.32 KPa V1
dT 0
习题
n= 1 mol T3=370.15K P3=250.00 KPa V3 = V2
n= 1 mol T2=300.15K P2 V2
dV 0
因为V2=V3,则p2/T2=p3/T3, p2=p3T2/T3=250.00×300.15/370.15 kPa=202.72 kPa nRT 1 p W2=0 W p (V V ) nRT p nRT ( 2 1)
习题
2.10 2 mol 某理想气体 Cp,m=3.5R。由始态 100 kPa,50 dm3, 先恒容加热使压力升高到 200KPa,再恒压冷却使体积缩 小至25 dm3。求整个过程的W,Q, △U, △H。 解:过程图示如下:
n= 2 mol T1 P1=100 KPa V1= 50 dm3
dV 0
3. 一系列无限接近平衡条件下进行的
热力学部分
二、选择题
习题
1. 一定量的某种理想气体从 同一始态T1,p1,V1出发,经
绝热可逆过程膨胀至T2,p2,V2,和反抗恒定外压p2绝 热膨胀至T2’,V2’,则T2’( )T2,在数值上W(不可逆) ( )W(可逆)。 (a) >,>; (b)<,>; (c)>,<; (d) <, <
热力学第一定律
三、计算题
习题
2.5 始态为 25 oC,200KPa的5 mol 某理想气体,经 a,b两 个不同途径到达相同的末态。途径a先绝热膨胀到 -28.57
oC,
100 kPa,步骤的功Wa=-5.57 kJ;再恒容加热到压力
200kPa的末态,步骤的热Qa=25.24 kJ。途径b为恒压加热
过程,求途径b的Wb 及Qb。
热力学第一定律
2.5 解: 先确定系统的始、末态
n= 5 mol Q a T1= 298.15 K P1=200 KPa V1
0
习题
n= 5 mol n= 5 mol dV a 0 T2= 244.58 K T3 P2=100 KPa P3 V2 V3=V2
恒T
2)
热力学部分
3)化学反应的 r G ( T ) 计算
m
总结
rG
m
T
rH
B
m
T T r S m T
r H m (T )
B
f H m (B , T )
B CH m
(B , T )
r S m T
pV
TV
Tp
常数 , 或 p 1V 1 p 2V 2
常数 , 或 T1V 1
1
1
T 2V 2
1
C
p ,m
(1 ) /
p2 常数 , 或 p T1 1 T2
( 1) /
C v ,m
,
热力学部分
热力学部分
一、填空题
习题
1. 在300K的常压下, 2 mol 的某固体物质完全升 华过程的体积功W=( )
2. 一定量单原子理想气体经历某过程的△(pV)
=20 kJ,则此过程的△U=(
); △H=( )
)
3. 系统内部及系统与环境之间,在(
过程,称为可逆过程。
热力学部分
一、填空题答案 1. -4.99 kJ
1 2 2 1 2
p1
1
p1
所以 W=W2+W1=2.497 kJ,
U nC H nC
v ,m
202 . 72 1 8 . 314 300 . 15 1 J 2 . 497 kJ 101 . 325
3 3
50 10
3
)] J 5 . 00 kJ
根据热一律
Q U W ( 0 5 . 00 ) kJ 5 . 00 kJ
热力学第一定律
习题
2.11 1 mol 某理想气体于27oC ,101.325 kPa 的始态下,先受 某恒定外压恒温压缩至平衡态,再恒容升温至97oC , 250.00 kPa。求过程的W,Q, △U, △H。已知气体的
Cv,m=20.92 J mol-1K-1
解:过程图示如下:
n= 1 mol T1=300.15K P1=101.32 KPa V1
dT 0
n= 1 mol T2=300.15K P2 V2
dV 0
n= 1 mol T3=370.15K P3=250.00 KPa V3 = V2
热力学第一定律
ln
T2 T1
恒压变温 恒容变温
变温过程 pVT 变化
V S n C V . m ln T2 T1
QV Δ U
V2 V1 nR ln P1 P2
系 统 熵 变 的 计 算
等温气体膨胀、压缩 可逆相变 相变化 不可逆相变 化学变化
r S m T
T S nR ln
B
B S
B ,m
(T )
热力学部分
9. S、A、G 判据
def
总结
A U TS
判据 S A G 适用范围
def
G H TS
自发过程方向 S增大,△S≥0, dS≥0 A减小,△A≤0, dA≤0 G减小,△G≤0, dG≤0
孤立系统中任何过程 封闭系统,T、V、W’=0 的过程
n= 2 mol T2 P2=200 KPa V2 = 50 dm3
dp 0
n= 2 mol T3 P3=200 KPa V3 = 25 dm3
热力学第一定律
n= 2 mol T1 P1=100 KPa V1= 50 dm3
dV 0
习题
n= 2 mol T3 P3=200 KPa V3 = 25 dm3
dp b 0
对于途径b,其功为:
W a p 1 (V 3 V 1 ) p 1 ( nRT p2
2
nRT p1
1
) nRp 1 (
T2 p2
T1 p1
)
298 . 15 244 . 58 3 5 8 . 314 200 10 3 3 200 10 100 10
J 7 . 940 kJ
