近几年高考理科压轴题
最近两年全国各地高考物理压轴题汇集(详细解析63题)

最近两年全国各地高考物理压轴题汇集(详细解析63题)最近年全各地高考物理压压压压集;压压解析两国63压, 2009年2月16日星期一P、Q压的距压离L.已知木压B在下滑压程中做速直压压~木压匀运与A相后立刻一起向下压~但不粘压碰运~最近年全各地高考物理压压压压集;压压解析两国63压,它达个运压到一最低点后又向上压~木压B向上压恰好能回到运Q点.若木压A 止于静P点~木压C从Q1;20分,2v向下压~压压同压压程~最后木压运C停在斜面上的R点~求P、R 压的距离L′的点压始以初速度0如压12所示~是一压压压=4 m的压压平板固定在水平地面上~整空压有一平行于个个的匀PRLPR3强压压~在板的右半部分有一垂直于压面向外的强磁压个匀~一压量压个=0,1 kg~压压量压=0,5 EBmq大小。
C的物~板的体从P端由止压始在压压力和摩擦力的作用下向右做加速压~压入磁压后恰能做静匀运匀5如压~足压压的水平压送压始压以大小压v,3m/s的速度向左压~压送压上有一压量压运M,2kg的小木盒速压。
物到板运当体碰R端的压板后被压回~若在撞瞬压撤去压压~物返回压在磁压中仍做速压~碰体匀运A~A与数压送压之压的压摩擦因压μ,0,3~压始压~A与静压送压之压保持相压止。
先后相隔?t,3s有两2 离匀减运压磁压后做速压停在C点~PC=L/4~物平板压的压摩擦因压体与数μ=0,4~取g=10m/s~求,个光滑的压量压,1kg的小球自压送压的左端出压~以,15m/s的速度在压送压上向右压。
第运1球个mBv0;1,判物压压性压~正压荷压是压压荷,断体与即与静木盒相遇后~球立压入盒中盒保持相压止~第2球出压后压压?个t,1s/3而木盒相遇。
求与1;2,物压板撞前后的速度体与碰v和v122;取g,10m/s,;3,磁感压强度B的大小;1,第1球木盒相遇后瞬压~者共同压的速度压多大,个与两运;4,压压强度E 的大小和方向;2,第1球出压后压压多压压压木盒相遇,个与压12;3,自木盒第与1球相遇至第个与2球相遇的压程中~由于木盒压送压压的摩擦而压生的压量个与是多少,2(10分)如压214—所示~光滑水平面上有压桌L=2m的木板C~压量m=5kg~在其正中央排放着并cvA0B两个小滑压A和B~m=1kg~m=4kg~压始压三物都止,在静A、B压有少量塑炸压~爆炸后胶A以速AB度6m,s水平向左压~运A、B中任一压压板撞后~都粘在一起~不压摩擦和撞压压~求,与碰碰(1)滑压当两A、B都压板撞后~与碰C的速度是多大?v (2)到A、B都压板撞压止~与碰C的位移压多少?6如压所示~平行金板两属A、B压l,8cm~板压距两离d,-10-208cm~A板比B板压压高300V~即U,300V。
2020-2021学年最新高考总复习数学(理)高考压轴试题及答案解析

2018新课标1高考压轴卷理科数学一、选择题:(本大题共12题,每小题5分,在每小题给出的四个选项中 ,中有一项是符合题目要求的.1.已知随机变量ξ服从正态分布2N(0,)σ,(2)0.023P ξ>=,则(22)P ξ-≤≤=A .0.954B .0.977C .0.488D .0.4772.对任意复数),(R y x yi x z ∈+=,i 为虚数单位,则下列结论正确的是( ).A y z z 2=- .B 222y x z += .C x z z 2≥- .D y x z +≤3.已知映射B A f →:,其中R B A ==,对应法则21||:x y x f =→,若对实数B k ∈,在集合A 中不存在元素x 使得k x f →:,则k 的取值范围是( ) A .0≤k B .0>k C .0≥k D . 0<k 4.已知函数()()ϕ+=x sin x f 2,其中ϕ为实数,若()⎪⎭⎫⎝⎛≤6πf x f 对x R ∈恒成立, 且 ()ππf f >⎪⎭⎫⎝⎛2,则()f x 的单调递增区间是 A . ()Z k ,k ,k ∈⎥⎦⎤⎢⎣⎡+-63ππππ B .()Z k k ,k ∈⎥⎦⎤⎢⎣⎡+,2πππ C . ()Z k ,k ,k ∈⎥⎦⎤⎢⎣⎡++326ππππ D .()Z k ,k ,k ∈⎥⎦⎤⎢⎣⎡-πππ25.如图,已知圆22:(3)(3)4M x y -+-=,四边形 ABCD 为圆M 的内接正方形,E F 、分别为边AB AD 、的中点,当正方形ABCD 绕圆心M 转动时,ME ⋅的取值范围是 ( ) A .[62,62]-B .[6,6]-C .[32,32]-D .[4,4]-6.在区间[1,5]和[2,4]上分别取一个数,记为,a b .则方程22221x y a b +=表示焦点在x 32的椭圆的概率为BA .12B .1532C .1732D .31327、一个四面体的四个顶点在空间直角坐标系xyz O -中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体中以yOz 平面为投影面的正视图的面积为( ) A .3 B .25 C .2 D .278、阅读程序框图,若输入m =4,n =6,,则输出a ,i 分别是( ) A .12,3a i == B .12,4a i == C .8,3a i ==D .8,4a i ==yxEF D B CMOA9、设数字1,2,3,4,5,6的一个排列为654321,,,,,a a a a a a , 若对任意的)6,5,4,3,2(=ia i 总有)5,4,3,2,1(=<k i k a k ,满足,1||=-k i a a 则这样的排列共有( )A .36B .32C .28D .2010. 过曲线22122:1(0,0)x y C a b a b-=>>的左焦点1F 作曲线2222:C x y a +=的切线,设切点为M ,延长1F M 交曲线23:2(0)C y px p =>于点N ,其中13C C 、有一个共同的焦点,若1MF MN =,则曲线1C 的离心率为 A.5 B.51- C.51+ D.512+ 11、若实数a ,b ,c ,d 满足222(3ln )(2)0b a a c d +-+-+=,则22()()a c b d -+-的最小值为(B ) A .2 B .9 C .8 D .212.已知函数⎪⎩⎪⎨⎧=≠+=0 ,00 ,1)(x x x x x f ,则关于x 的方程0)()(2=++c x bf x f 有5个不同实数解的充要条件是 ( )A .2-<b 且0>cB .2->b 且0<cC .2-<b 且0=cD .2-≥b 且0=c 二、填空题:本大题共4小题,每小题5分,共20分.13已知nx i x )(2-的展开式中第三项与第五项的系数之比为143-,其中12-=i ,则展开式中常数项是______________. 14.当x ,y 满足时,则t=x ﹣2y 的最小值是15.已知12,l l 是曲线1:C y x=的两条互相平行的切线,则1l 与2l 的距离的最大值为_____. 16.如图,在正方形ABCD 中,E 为AB 的中点,P 为以A 为圆心、AB 为半径的圆弧上的任意一点,设向量AC =λDE +μAP ,则λ+μ的最小值为___.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤 17.18.如图,在三棱柱111ABC A B C -中,已知11AB BB C C ⊥侧面, 1AB BC ==,12BB =,13BCC π∠=.(Ⅰ)求证:1C B ABC ⊥平面;(Ⅱ)设1CE CC λ= (01λ≤≤),且平面1AB E 与1BB E 所成的锐二面角的大小为30︒,试求λ的值.19.根据以往的经验,某工程施工期间的降水量X (单位:mm)对工期的影响如下表:降水量X X<300 300≤X<700 700≤X<900 X ≥900 工期延 误天数Y2610历年气象资料表明,该工程施工期间降水量X 小于300,700,900的概率分别为0.3 ,0.7 ,0.9.求: (Ⅰ)工期延误天数Y 的均值与方差;(Ⅱ)在降水量X 至少是300的条件下,工期延误不超过6天的概率.20.如图所示,已知过一点(11)P -,作抛物线2y x =的两条切线,切点分别为A 、B ;过点P 的直线l 与抛物线2y x =和线段AB 分别相交于两点C 、D 和点Q . (Ⅰ)求直线AB 的方程; (Ⅱ)试问:线段PC 、PQ 、PD 的长度的倒数是否构成等差数列?请加以证明.21.函数xx a x f ln )(+=,若曲线)(x f 在点))(,e f e (处的切线与直线02=+-e y x e 垂直(其中e 为自然对数的底数).(1)若)(x f 在)1,(+m m 上存在极值,求实数m 的取值范围;(2)求证:当1>x 时,)1)(1(21)(1++>+-xx xe x e e x f . 22.(本小题满分10分)选修4—1:几何证明选讲 如图所示,已知圆O 外有一点P ,作圆O 的切线PM ,M 为切点,过PM 的中点N ,作割线NAB ,交圆于A 、2y x = y x P lDB AO C QA 1C 1BAC B 1B 两点,连接PA 并延长,交圆O 于点C ,连接PB 交圆O于点D ,若BC MC =. (1)求证:△APM ∽△ABP ;(2)求证:四边形PMCD 是平行四边形.23. (本小题满分10分)选修4在极坐标系中,已知圆C 的圆心.,直线l 的参数方程为⎩⎨⎧+=+=ααsin 2cos 2t y t x (t 为参数),直线l 交圆C于A B 、两点,求弦长 24(本小题满分10分) 选修⑴ 已知,a b 都是正数,且a b ≠,求证:3322a b a b ab +>+;⑵ 已知,,a b c 都是正数,求证:222222a b b c c a abc a b c++++≥.新课标1高考压轴卷理科数学答案一、选择题(本大题包括12小题,每小题5分,共60分)1.A2. D3. D4. C5. B6.B7. A8. B9. B 10. D 11. C 12C. 简答与提示:1.【知识点】正态曲线的性质的应用 【答案解析】A()()22122120.0230.954.P P ξξ-≤≤=->=-⨯=2答案:D5.【知识点】圆的方程;向量在几何中的应用;向量的运算.【答案解析】B 解析:解:因为圆M :(x-3)2+(y-3)2=4,圆心的坐标(3,3)半径为2.()ME OF ME OM MF ME OM ME MF⋅=⋅+=⋅+⋅0ME MF ME MF ⊥∴⋅=()[]6cos 6,6ME OF ME OM OME π∴⋅=⋅=-∠∈-,所以B 正确.6依题意知,a > b ,e =<,即b > .如图所示故所求概率为P =1--=7试题分析:根据平行投影的知识可知:该四面体中以平面为投影面的正视图为一个上底为1,下底为2,高为2的直角梯形,所以面积为3.9如果1不在前左边,则2必须在1的左边(1)23456的次序保存不变,变化1的位置(123456)(213456)(231456)(234156)(234516)(234561)(2)3456次序不变,1和2的次序为21(同时3必须在21的左边)(321456)(324156)(324516)(324561)(342156)(342516)(342561)(345216)(345261)(345621)(3)456次序不变(432156)(432516)(432561)(435216)(435261)(435621)(453216)(453261)(453621)(456321)(4)56次序不变(543216)(543261)(543621)(546321)(564321)(5)6在最左(654321)32种可能注:这题本身也有趣.注意到当只有一个数时,可能排列为1,即2的0次,记2^0当有两个数1和2时,排列为12,或21,为两种,2^1当123时,排列为4=2^2当数字为4个时,排列为8=2^311.【答案解析】B 解析:解:∵实数a、b、c、d满足:(b+a2-3lna)2+(c-d+2)2=0,∴b+a2-3lna=0,设b=y,a=x,则有:y=3lnx-x2,且c-d+2=0,设c=x,d=y,则有:y=x+2,∴(a-c)2+(b-d)2就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值,对曲线y=3lnx-x2求导:y′(x)=3x-2x,与y=x+2平行的切线斜率k=1=3x -2x,解得:x=1或x=-32(舍),把x=1代入y=3lnx-x2,得:y=-1,即切点为(1,-1),切点到直线y=x+2的距离:1122++=22,∴(a-c)2+(b-d)2的最小值就是8.故选:B.【思路点拨】由题设b+a2-3lna=0,设b=y,a=x,得到y=3lnx-x2;c-d+2=0,设c=x,d=y,得到y=x+2,所以(a-c)2+(b-d)2就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值,由此能求出(a-c)2+(b-d)2的最小值.13的展开式的通项公式为:,因为第三项与第五项的系数之比为,所以解得所以常数项为第9项,所以展开式中的常数项为14.根据题意,首先画可行域,再分析可得t为目标函数纵截距一半的相反数,最后画直线0=x﹣2y,平移直线过A(0,2)时t有最小值即可.解:画可行域如图,z为目标函数t=x﹣2y,可看成是直线t=x﹣2y的纵截距一半的相反数,画直线0=x﹣2y,平移直线过A(0,2)点时,t有最小值﹣4,故答案为:﹣4.15.【知识点】导数几何意义的应用。
高考理科数学压轴小题特训72题(选择52题填空20题)含答案与解析

高考理科数学压轴小题特训72题(选择52题填空20题)---含答案与解析一、选择题1.点P 是椭圆221259y x +=上一点,F 是椭圆的右焦点,()142OQ OP OF OQ =+=,,则点P 到抛物线215y x =的准线的距离为( )A .154B .152C .15D .102.用4种颜色给正四棱锥的五个顶点涂色,同一条棱的两个顶点涂不同的颜色,则符合条件的所有涂法共有( ) A .24种B .48种C .64种D .72种3.设函数()()()21ln 31f x g x ax x ==-+,,若对任意1[0)x ∈+∞,,都存在2x ∈R ,使得()()12f x f x =,则实数a 的最大值为( ) A .94B .2C .92D .44.若存在两个正实数x y ,,使得等式()()324ln ln 0x a y ex y x +--=成立,其中e 为自然对数的底数,则实数a 的取值范围是( ) A .()0-∞,B .30]2e (,C .3[)2e +∞, D .()30[)2e -∞+∞,,5.已知函数m x x g x x x f +=+=22log )(,1)(,若对]4,1[],2,1[21∈∃∈∀x x ,使得)()(21x g x f ≥,则m 的取值范围是( )A .45-≤m B .2≤m C .43≤m D .0≤m6.已知b a ,为正实数,直线a x y -=与曲线)ln(b x y +=相切,则b a -22的取值范围是( ) A .),0(+∞ B .(0,1) C .)21,0( D .),1[+∞7.若函数⎪⎩⎪⎨⎧>+-≤+=)0(431),0(3)(3x a x x x x x f x 在定义域上恰有三个零点,则实数a 的取值范围是( )A .3160<<a B .316<a C .0<a 或316>a D .316≤a8.已知函数()21,g x a x x e e e ⎛⎫=-≤≤ ⎪⎝⎭为自然对数的底数与()2ln h x x =的图象上存在关于x 轴对称的点,则实数a 的取值范围是( )A .211,2e⎡⎤+⎢⎥⎣⎦ B .21,2e ⎡⎤-⎣⎦ C .2212,2e e ⎡⎤+-⎢⎥⎣⎦ D .)22,e ⎡-+∞⎣ 9.如图,在OMN ∆中,,A B 分别是,OM ON 的中点,若(),OP xOA yOB x y R =+∈,且点P 落在四边形ABNM 内(含边界),则12y x y +++的取值范围是( )A .12,33⎡⎤⎢⎥⎣⎦ B .13,34⎡⎤⎢⎥⎣⎦ C .13,44⎡⎤⎢⎥⎣⎦ D .12,43⎡⎤⎢⎥⎣⎦ 10.当x ,y 满足不等式组22,4,72x y y x x y +≤⎧⎪-≤⎨⎪-≤⎩时,22kx y -≤-≤恒成立,则实数k 的取值范围是( )A .[]1,1--B .[]2,0-C .13,55⎡⎤-⎢⎥⎣⎦ D .1,05⎡⎤-⎢⎥⎣⎦11.已知函数223(0),()(0),x x x x f x ax e ⎧->⎪=⎨<⎪⎩的图象上存在两点关于y 轴对称,则实数a 的取值范围是( )A .[-3,1]B .(-3,1) C.3[]e D .132[,9]e e --- 12.圆222240x y ax a +++-=和圆2224140x y b y b +--+=恰有三条公切线,若,a R b R ∈∈,且0ab ≠,则2211a b +的最小值为A .1B .3C .19D .4913.已知过定点()2,0P 的直线l 与曲线22y x =-相交于,A B 两点,O 为坐标原点,当AOB ∆的面积取最大值时,直线l 的倾斜角为A .150B .135C .120D .105 14.为圆上的一个动点,平面内动点满足且(为坐标原点),则动点运动的区域面积为 A . B .C .D .15.已知函数)()(()(321x x x x x x x f ---=)(其中321x x x <<),)12s i n(3)(++=x x x g ,且函数)(x f 的两个极值点为)(,βαβα<.设2,23221x x x x +=+=μλ,则 A .)()()()(μβλαg g g g <<< B .)()()()(μβαλg g g g <<<C .)()()()(βμαλg g g g <<<D .)()()()(βμλαg g g g <<<16.设双曲线)0,0(12222>>=-b a b y a x 的右焦点为F ,过点F 作x 轴的垂线交两渐近线于点B A ,两点,且与双曲线在第一象限的交点为P ,设O 为坐标原点,若)R OB OA OP ∈+=μλμλ,(,8522=+μλ,则双曲线的离心率为( )N 00(,)M x y O MA .332B .553C .223 D .8917. 一个函数f (x ),如果对任意一个三角形,只要它的三边长a ,b ,c 都在f (x )的定义域内,就有f (a ),f (b ),f (c )也是某个三角形的三边长,则称f (x )为“三角保型函数”,给出下列函数:①f (x )=;②f (x )=x 2;③f (x )=2x ;④f (x )=lgx ,其中是“三角保型函数”的是( ) A .①② B .①③ C .②③④ D .③④18.双曲线C :22221(0,0)x y a b a b -=>>的左、右焦点分别为1(,0)F c -,2(,0)F c ,M ,N 两点在双曲线C 上,且MN ∥F 1F 2,12||4||F F MN =,线段F 1N 交双曲线C 于点Q ,且1||||F Q QN =,则双曲线C 的离心率为 A .2A. 9B.C. D.320. 已知函数()f x 与函数()()21g x x =-的图象关于y 轴对称,若存在a R ∈,使[]1,x m ∈()1m >时,()4f x a x +≤成立,则m 的最大值为A.3B.6C.9D.12 21.已知函数()31,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()0f x a -=的四个根分别为1234,,,x x x x ,且1234x x x x <<<,则()2343121x x x x x ++的取值范围是( )A.71,62⎡⎫-⎪⎢⎣⎭B. 71,62⎛⎫- ⎪⎝⎭C. 71,3⎡⎫-⎪⎢⎣⎭D. 71,3⎛⎫- ⎪⎝⎭22.已知函数⎪⎩⎪⎨⎧<-+-+≥-+=0)3()4(0)1()(2222x a x a a x x a k kx x f ,,,其中a R ∈,若对10x ∀≠,212()x x x ∃≠,使得)()(21x f x f =成立,则实数k 的最小值为A .8-B .6-C .6D .823.已知定义在R 上的偶函数()f x 满足()()4f x f x-=,且(]1,3x ∈-时,()21c o s,132,11,x x f x x x π⎧+<≤⎪=⎨⎪-<≤⎩,则()()lg g x f x x =-的零点个数是A.9B.10C.18D.2024.函数)(x f y =为定义在R 上的减函数,函数)1(-=x f y 的图像关于点(1,0)对称, ,x y满足不等式0)2()2(22≤-+-y y f x x f ,(1,2),(,)M N x y ,O 为坐标原点,则当41≤≤x 时,OM ON ⋅的取值范围为 ( )A .[)+∞,12 B .[]3,0 C .[]12,3 D .[]12,0 25.已知函数()()21(0)()110xx f x f x x ⎧-≤⎪=⎨-+>⎪⎩,把函数()()g x f x x =-的零点按从小到大的顺序排列成一个数列,则该数列的前n 项的和n S ,则10S =( )A .15B .22C .45D . 5026. 定义在R 上的函数()f x 满足在区间[)1,1-上,(),102,015x m x f x x x --≤<⎧⎪=⎨-≤<⎪⎩, 其中m R ∈,若5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,则()5f m =( ) A .85-B .25-C .35D .7527. 设直线,l m 分别是函数()ln ,01ln ,1x x f x x x -<<⎧=⎨>⎩图象上在点,M N 处的切线, 已知l 与m互相垂直, 且分别与y 轴相交于点,A B ,点P 是函数()(),1y f x x =>图象上的任意一点, 则PAB ∆的面积的取值范围是( )A .()0,1 B .()0,2 C .()2,+∞ D .()1,+∞28.已知A 、B 是双曲线()2222:100y x C a b a b -=>>,的两个焦点,若在双曲线上存在点P 满足2PA PB AB+≤,则双曲线C 的离心率e 的取值范围是( )A .12e <≤B .2e ≥C .1e <≤D .e ≥29.已知函数()y f x =的定义域为()0+∞,,当1x >时,()0f x >,对任意的()0x y ∈+∞,,,()()()f x f y f x y +=⋅成立,若数列{}n a 满足()11a f =,且()()()*121N n n f a f a n +=+∈,则2017a 的值为( )A .20141a- B .20151a- C .20161a- D .20171a-30.已知函数()()21ln,22x x f x g x e -=+=,若()()g m f n =成立,则n m -的最小值为( )A .1ln 2-B .ln 2C .3D .23e -31.已知向量a 与向量b 的夹角为23π,且2a b ==,又向量c xa yb =+(x R ∈且0x ≠,y R ∈),则xc 的最大值为( ) A.BC .13D .332.已知函数()()()11 232 [2)x x f x f x x ⎧--∈-∞⎪=⎨-∈+∞⎪⎩,,,则函数()()cos g x f x x π=-在区间[]08,内所有零点的和为( )A .16B . 30C .32D . 4033.设22(2,cos)a λλα=+-,(,sin )2mb m α=+,其中λ、m 、α为实数,若2a b =,则m λ的取值范围是( )A .(,1]-∞ B.[-6,1] C .[-1,6] D .[4,8]34.定义在(0,)2π上的函数()f x ,'()f x 是它的导函数,且恒有'()()tan f x f x x >成立.则有( )A()()63f ππ< B()2cos1(1)6f f π> C .2()()46f ππ<D ()()43f ππ< 35.已知函数()sin ()f x x x x R =+∈,且22(23)(41)0f y y f x x -++-+≤,则当1y ≥时,11x y x +++的取值范围是( )A .57[,]44B .7[0,]4 C .57[,]43 D .7[1,]3 36.设定义在()0,+∞上的单调函数()f x ,对任意的()0,x ∈+∞都有()2log 3f f x x -=⎡⎤⎣⎦.若方程()()f x f x a '+=有两个不同的实数根,则实数a 的取值范围是( )A .()1,+∞B .12,ln 2⎛⎫++∞ ⎪⎝⎭C .13,2ln 2⎛⎫-+∞ ⎪⎝⎭ D .()3,+∞ 37.已知双曲线Γ:22221y x a b -=(0a >0b >)的上焦点为(0,)F c (0c >),M 是双曲线下支上的一点,线段MF 与圆2222039c a x y y +-+=相切于点D ,且||3||MF DF =,则双曲线Γ的渐进线方程为( ) A .40x y ±=B .40x y ±=C .20x y ±=D .20x y ±=38. 已知()32log ,031108,333x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩,,,,a b c d是互不相同的正数, 且()()()()f a f b f c f d ===,则,,,a b c d 的取值范围是( )A .()18,28 B .()18,25 C .()20,25 D .()21,2439.已知数列{}n a满足()*11n a n N +=∈,则使不等式20162016a >成立的所有正整数1a 的集合为( )A .{}*111|2016,a aa N ≥∈ B .{}*111|2015,a aa N ≥∈ C .{}*111|2014,a a a N ≥∈ D .{}*111|2013,a aa N ≥∈40.在等腰梯形ABCD 中,//AB CD ,且2,1,2A B A D C D x ===,其中()0,1x ∈,以,A B为焦点且过点D 的双曲线的离心率为1e ,以,C D 为焦点且过点A 的椭圆的离心率为2e ,若对任意()0,1x ∈,不等式12t e e <+恒成立,则t 的最大值是( )A.2 D41.已知函数2()cos ()1(0,0,0)2f x A x A πϖϕϖϕ=++>><<的最大值为3,()f x 的图象与y 轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则(1)(2)(3)(2016)f f f f ++++的值为( )A .2468B .3501 C.4032 D .573942.已知三角形ABC 内的一点D 满足2DA DB DB DC DC DA ===-,且||||||DA DB DC ==.平面ABC 内的动点P ,M 满足||1AP =,PM MC =,则2||BM 的最大值是( )A .494B .434C. D.43.已知函数()f x 是定义在R 上的奇函数,且当0x >时,()(3)0f x f x -++=;当(0,3)x ∈时,ln ()e xf x x =,其中e 是自然对数的底数,且 2.72e ≈,则方程6()0f x x -=在[-9,9]上的解的个数为( )A .4B .5C .6D .7 44.设D 是函数()y f x =定义域内的一个区间,若存在0x D ∈,使()00f x x =-,则称0x 是()f x 的一个“次不动点”,也称()f x 在区间D 上存在“次不动点”,若函数()2532f x ax x a =--+在区间[]1,4上存在“次不动点”,则实数a 的取值范围是( )A .(),0-∞B .10,2⎛⎫ ⎪⎝⎭C .1,2⎡⎫+∞⎪⎢⎣⎭D .1,2⎛⎤-∞ ⎥⎝⎦45. 设函数())3lnf x x x =+且)233ln 113a a f a ⎛⎫--<- ⎪-⎝⎭,则实数a 的取值范围为( )A .()3,+∞ B.)+∞ C.) D.(()3,+∞46. 设函数()()x x f x e x ae =-(其中e 为自然对数的底数)恰有两个极值点()1212,x x x x <,则下列说法不正确的是( )A .102a <<B .110x -<<C .()1102f x -<< D .()()120f x f x +>47.已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩ 函数()()2g x b f x =-- ,其中b R ∈ ,若函数()()y f x g x =- 恰有4个零点,则b 的取值范围是A.7,4⎛⎫+∞⎪⎝⎭ B.7,4⎛⎫-∞ ⎪⎝⎭ C.70,4⎛⎫ ⎪⎝⎭ D.7,24⎛⎫⎪⎝⎭48. 已知e 为自然对数的底数,若对任意的[0,1]x ∈,总存在唯一的[1,1]y ∈-,使得20y x y e a +-=成立,则实数a 的取值范围是A .[1,]eB .1(1,]e e+C .(1,]eD .1[1,]e e+49.已知是定义在上的增函数,函数的图象关于点对称,若对任意的,等式恒成立,则的取值范围是( )A .B .C .D .50. 若函数x a x x e x f x -++-=)212()(2恒有两个零点,则a 的取值范围为( ) (A) ()1,0 (B) ()1,∞- (C))21,(e -∞ (D) ),21(+∞e51..已知函数()31,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()0f x a -=的四个根分别为1234,,,x x x x ,且1234x x x x <<<,则()2343121x x x x x ++的取值范围是( )A.71,62⎡⎫-⎪⎢⎣⎭ B. 71,62⎛⎫- ⎪⎝⎭ C. 71,3⎡⎫-⎪⎢⎣⎭ D. 71,3⎛⎫- ⎪⎝⎭ 52. 定义在R 上的奇函数()y f x =满足(3)0f =,且当0x >时,不等式()()f x xf x '>-恒成立,则函数()()lg |1|g x xf x x =++的零点的个数为( ) A .1 B .2 C .3 D .4二、填空题1.已知函数()22sin cos 44f x x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则()f x 在02x π⎡⎤∈⎢⎥⎣⎦,上的最大值与最小值之差为 .2.设函数()f x 对任意实数x 满足()()1f x f x =-+,且当01x ≤≤时,()()1f x x x =-,若关于x的方程()f x kx=有3个不同的实数根,则k 的取值范围是 .3.若曲线x x x f ln 21)(2+-=在其定义域内的一个子区间)2,2(+-k k 内不是单调函数,则实数k 的取值范围是______.4.已知函数()()2lg ,064,0x x f x x x x ⎧-<⎪=⎨-+≥⎪⎩,若关于x 的方程()()210f x bf x -+=有8个不同根,则实数b 的取值范围是______________.5.已知00(,)x y 是直线21x y k +=-与圆22223x y k k +=+-的公共点,则00x y 的取值范围是__________.6.已知平行四边形ABCD 的中心为,两条邻边所在的直线方程分别为,,在平行四边形ABCD 内有一面积为S 的圆,则S 的最大值是7.已知动点(),P x y 在椭圆2212516x y +=上,过坐标原点的直线BC 与椭圆相交,交点为,,B C 点Q 是三角形PBC 内一点,且满足∆∆∆==QPB QPC QBCS S S , 若点A 的坐标为()3,0,1,0=⋅=AM QM AM ,则QM的最小值是8. 已知正方形ABCD 的边长为2,点E 为AB 的中点.以A 为圆心,AE 为半径,作弧交AD于点F ,若P 为劣弧EF 上的动点,则PC PD 的最小值为___________.9. 已知函数x x a x f 22)(1+=+在]3,21[-上单调递增,则实数a 的取值范围_________.10.已知曲线y=x +lnx 在点(1,1)处的切线与曲线y=ax 2+(a +2)x +1相切,则a= .11. 定义在R 上的函数)(x f 是奇函数且满足)()23(x f x f =-,3)2(-=-f ,数列}{n a 满足11-=a ,且12+=n a n S nn ,n S 为数列}{n a 的前n 项和,则)()(65a f a f += . )3,0(0243=-+y x 022=++y x12.已知,数列的前项和为,数列的通项公式为,则的最小值为 .13.已知ABC △的三个内角A ,B ,C 的对边分别为a ,b ,c ,若2a =,3A π=,且()sin sin 2B C B --=,则ABC △面积为.14.已知三棱锥S ABC -的顶点都在球O 的球面上,ABC ∆是边长为2的正三角形,SC 为球O 的直径,且4SC =,则此三棱锥的体积为________.15.若存在实数a 、b 使得直线1ax by +=与线段AB (其中(1,0)A ,(2,1)B )只有一个公共点,且不等式2222120()sin cos p a b θθ+≥+对于任意(0,)2πθ∈成立,则正实数p 的取值范围为________.16.已知2,0,()ln(1),0x ax x f x x x ⎧+≤=⎨+>⎩,()2()F x f x x =-有2个零点,则实数a 的取值范围是 .17. 对大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”:3331373152,39,4,5171119⎧⎧⎧⎪⎪⎪⎪⎪⎪⎨⎨⎨⎪⎪⎪⎪⎪⎪⎩⎩⎩仿此,若3m 的“分裂”数中有一个是73,则m 的值为_____________.18.已知函数321()3f x x x ax =++,若1()x g x e =,对任意11[,2]2x ∈,存在21[,2]2x ∈,使12'()()f x g x ≤成立,则实数a 的取值范围是________.19.设数列{}n a 的各项均为正数,前n 项和为n S ,对于任意的n N +∈,2,,n n n a S a 成等差数列,设数列{}n b 的前n 项和为n T ,且2(ln )nn nx b a =,若对任意的实数(]1,x e ∈(e 是自然对数的底)n *∈-=N n n b n ,35和任意正整数n ,总有n T r <()r N +∈.则r 的最小值为 . 20. 在△中,分别为内角的对边,,,则△的面积的最大值为 .一.选择题答案与解析1.B .解析:设()5cos 3sin P αα,,由()142OQ OP OF OQ =+=,,得2245cos 3cos 1622αα+⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,即216cos 40cos 390αα+-=,解得3cos 4α=或13cos 4α=-(舍去),即点P 的横坐标为154,故点P 到抛物线215y x =的距离为152.2.D .解析:法一:假设四种颜色为红、黑、白、黄,先考虑三点S 、A 、B 的涂色方法,有432⨯⨯种方法,若C 点与A 不同色,则C 、D 点只有1种涂色的方法,有24种涂法,若C 点与A 同色,则D 点有2种涂色的方法,共48种涂法,所以不同的涂法共有72种.法二:用3种颜色涂色时,即AC 、BD 同色,共有3424A =种涂色的方法,用4种颜色时,有AD 和BC 同色2种情况,共有44248A =,故共有72种. 3.A ,设()()2ln 31g x ax x =-+的值域为A ,因为函数()1f x =[0)+∞,上的值域为(0]-∞,,所以(0]A-∞⊆,,因此()231h x ax x =-+至少要取遍(01],中的每一个数,又()01h =,于是,实数a 需要满足0a ≤或0940a a >⎧⎨∆=-≥⎩,解得94a ≤. ABC ,,a b c ,,A B C 4a c +=()2cos tan sin 2BA A -=ABC4.D ,由题意知()342lnxa y ex y x =-,设()012y t t t t e x =>≠≠且,,则()342ln a e t t =-,()122ln 3e t t a =-,令()()()2ln 0f t e t t f t =-≠,,则()()2'1ln e f t t t =-+,令21ln e t t =+,得2t =,由数形结合可知,当t e >时,()'0f t <,当0t e <<时,()'0f t >,所以()f t e ≤,且()0f t ≠,所以1203e a <≤或10a <,解得0a <或32a e ≥. 5. C 6. C 7. A , 8B ,9C10.D ,不等式组表示的平面区域为三角形ABC ,()2,2A -,()5,1B --,()20C ,.则由2222k -≤--≤,2512k -≤-+≤,222k -≤≤得15k -≤≤.11.D 设(,)(0)P x y x >是()f x 上一点,则点P 关于原点的对称点为'(,)P x y -,于是223x a x x e -=-,∴2(23)(0)x a e x x x -=->,令2()(23)x x e x x ϕ-=-, 则22'()(23)(43)(273)(21)(3)x x x x x e x x e x e x x e x x ϕ----=--+-=--+=---, ∴()x ϕ在1[,3]2上是增函数,在1[0,]2与[3,)+∞上是减函数, 又32x ≥时,()0x ϕ≥,121()2e ϕ-=-,3(3)9e ϕ-=,∴1329e a e ---≤≤.12-14 AAA 15.D 16.A 17B 解:任给三角形,设它的三边长分别为a ,b ,c ,则a +b >c ,不妨假设a ≤c ,b ≤c ,对于①,f (x )=,由a +b >c ,可得a +2+b >c ,两边开方得+>,因此函数f (x )=是“保三角形函数”.对于②,f (x )=x 2,3,3,5可作为一个三角形的三边长,但32+32<52, 不存在三角形以32,32,52为三边长,故f (x )=x 2不是“保三角形函数”. 对于③,f (x )=2x ,由于f (a )+f (b )=2(a +b )>2c=f (c ), 所以f (x )=2x 是“保三角形函数”.对于④,f (x )=lgx ,1,2,2可以作为一个三角形的三边长,但lg1=0,不能作三角形边长,故f (x )=lgx 不是“保三角形函数”.故选:B . 18D ,19C , 20C ; 21. A 22D ;23C ;24. 【答案】D试题分析:因为函数)1(-=x f y 的图像关于点(1,0)对称,所以的图象关于原点对称,即函数为奇函数,由0)2()2(22≤-+-y y f x x f 得 ,所以, 所以,即,画出可行域如图,可得=x+2y ∈[0,12].故选D .25.【答案】C试题分析:根据函数的解析式,画出图像,由图像易知这10 个零点为0,1,2,3,……,9,所以10S =45. 26B ; 27D28.解析:设点P 是双曲线左支上的点,并设双曲线左顶点为E .则2PA PB AB+≤,化为42PO c≤(2c 为双曲线的焦距),12PO c ≤,容易证明PO a ≥,于是122a c e ≤≥,.故选B .29.解析:∵()()()f x f y f x y +=⋅,∴()()()111f f f +=,∴()10f =,()110a f ==,设120x x <<,211x x >,∵()()()f x f y f x y +=⋅,∴()()22110x f x f x f x ⎛⎫-=> ⎪⎝⎭,∴()()21f x f x >,所以()y f x =为增函数.()()()()()11121210121n n n n n n a f a f a f a f a f f a +++⎛⎫=+-+=== ⎪+⎝⎭,,1121n n a a +=+,121n n a a +=+,()1121n n a a ++=+,112n n a -+=,121n n a -=-,∴2016201721a =- 30 B ,31A , 32C ,33B , 34A ,35A ,36B ,37D ,38D,39A ,40B, 41C ,42A()y f x =()y f x =222(2)(2)(2)f x x f y y f y y -≤--=-2222x x y y -≥-222214x x y y x ⎧-≥-⎨≤≤⎩()(2)014x y x y x -+-≥⎧⎨≤≤⎩43. D 依题意,2(1ln )'()e x f x x -=,故函数()f x 在(0,)e 上单调递增,在(,3)e 上单调递减,故当(0,3)x ∈时,max ()()1f x f e ==,又函数()f x 是定义在R 上的奇函数,且0x >时,()(3)0f x f x -++=,即(3)()f x f x +=,且(0)0f =;由6()0f x x -=可知,()6xf x =.在同一直角坐标系中,作出函数()y f x =与6xy =在[-9,9]上的图象如下图所示.44.D ,45C ,46D ,47D ,48B , 49C ,50C ,51A ,52C一.填空题答案与解析1.解析:()2sin 22cos 22sin 226f x x x x x x ππ⎛⎫⎛⎫=++=+=+ ⎪ ⎪⎝⎭⎝⎭,当02x π⎡⎤∈⎢⎥⎣⎦,时,72666x πππ⎡⎤+∈⎢⎥⎣⎦,,故1sin 2162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦,,即函数()f x 的值域为[]12-,,故答案为3.2.(){5132--+,,因为()()1f x f x =-+,所以()()2f x f x +=,即()f x 是以2为周期的函数. 当[]01x ∈,时,()()1f x x x =-,当[]10x ∈-,时,[]101x +∈,,所以()()()11f x f x x x =-+=+,当[]23x ∈,时,[]201x -∈,,则()()()()223f x f x x x =-=--,当[]21x ∈--,时,[]201x +∈,,则()()()()212f x f x x x =+=-++,当[]01x ∈,时,()()1f x x x =-,()()'21'01f x x f =-+=,.当[]23x ∈,时,由256y x x y kx ⎧=-+-⎨=⎩,消去y 得,()()225605460x k x k +-+=∆=--⨯=,,解得)55k k =-=+,当[]21x ∈--,时,由232y x x y kx ⎧=---⎨=⎩,消去y 得,()()223203420x k x k +++=∆=+-⨯=,,解得)33k k =-+=--.数形结合知,(){5132k ∈--+,.3. 32<<k 4.1724b <≤5.1111[44-+2222k -≤≤+,由00222002123x y k x y k k +=-⎧⎪⎨+=+-⎪⎩得20031(1)22x y k =-+,∴00x y≤≤,∴.6、4π 7、39.[﹣1,1] 10、 8 11、 3 12、-2513 或 14 324, 15 [1,+∞) 16.1,2⎛⎤-∞ ⎥⎝⎦ 17. 9 18. (8]-∞- 对任意11[,2]2x ∈,存在21[,2]2x ∈,使12'()()f x g x ≤,∴max max ['()][()]f x g x ≤,2'()(1)1f x x a =++-在1[,2]2上单调递增,∴max '()'(2)8f xf a ==+,()g x在1[,2]2上单调递减,则max1()()2g x g==,∴8a+≤,则8a≤.。
2009-2020年高考物理压轴题

1. 介绍高考物理压轴题的意义- 高考物理压轴题是指高考物理试卷中出现频率较高、难度较大的题目,通常涉及到物理知识的核心概念和解题能力的考察。
- 2009年至2020年的高考物理压轴题的复习对考生备考有着重要的指导意义。
2. 分析2009年至2020年高考物理压轴题的题目类型和命题趋势- 从题目类型来看,高考物理压轴题涉及电磁学、力学、光学、热学等多个领域,其中以电磁学和力学题目居多。
- 从命题趋势来看,从2009年至2020年,高考物理压轴题在题目难度和考点深度上呈现出逐年增加的趋势,考查的内容也更加偏向于物理知识的应用和综合运用能力。
3. 总结高考物理压轴题的解题技巧和备考建议- 针对不同类型的高考物理压轴题,需要有针对性地掌握相关的物理知识和解题技巧,透彻理解物理原理,灵活运用物理知识解题。
- 在备考过程中,需要注重对高考物理压轴题的答题技巧和答题规范的训练,充分理解题目要求,准确理解物理图示,合理运用数学工具和公式解题。
4. 总结并展望- 通过对2009年至2020年的高考物理压轴题的分析,我们可以发现物理题目的考察不断拓展和深化,考查的重点也逐渐偏向于对考生物理知识的综合应用和解题能力的考查。
- 备考过程中,考生需要扎实掌握物理知识,灵活运用解题方法,培养解题思维和分析能力,既注重理论知识的学习,又要注重实际问题的解决能力的培养。
结尾:通过对高考物理压轴题的分析和总结,相信广大考生对于备考高考物理会有更清晰的认识和更有针对性的备考计划。
只有不断地巩固和提高自己的物理知识水平和解题能力,才能在高考中取得更好的成绩。
希望考生们能够在备考过程中认真对待每一道高考物理压轴题,做到踏实学习,并取得优异的成绩。
5. 针对2009年至2020年高考物理压轴题的题目类型和命题趋势,我们可以进一步分析各年份的题目特点及解题思路,为考生备考提供更具体的指导和建议。
6. 2009年至2013年高考物理压轴题的题目特点- 在这段时间内,电磁学类题目较为突出,如电场、磁场力及磁感应等内容在高考中频繁出现。
2024届浙江省高三高考压轴卷 物理高频考点试题(基础必刷)

2024届浙江省高三高考压轴卷物理高频考点试题(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题衰变实际上是原子核内部的中子衰变成质子导致的。
其实质子也不是绝对稳定的,但是其半衰期特别长,至少长达年(1000万亿亿亿年)。
上世纪八十年代,日本建造了“超级神冈探测器”,主要目的之一就是探测质子衰变现象,该探测器位于地下1000米深处,可有效排除宇宙射线的影响,它使用了5万吨的超纯水(约含有个质子),1万多个光电倍增管,用以捕捉质子衰变时释放的粒子。
若所有衰变均可被探测到,估算平均经过多长时间我们就可以观察到一次质子衰变事件( )A.一分钟以内B.一周以内C.一个月以内D.一年以内第(2)题下列说法正确的是( )A.偏振光不能发生干涉现象B.光能在真空中传播,说明光波不是机械波C.光波是概率波,所以能预测某光子通过双缝后打在光屏上的位置D.同种颜色的光通过同一单缝衍射装置后,屏上亮条纹宽度是确定的第(3)题直流特高压输电技术已成为我国“西电东送”战略的技术基础,下列方法中经济可靠且能降低输电损耗的是()A.提高用户的用电量B.改用交流输电C.用电阻率大的材料制造输电线D.提高输电电压第(4)题歼-35舰载机在航母上降落,需利用阻拦系统使之迅速停下。
如图,某次着舰时,飞机钩住阻拦索中间位置,两段绳索夹角为时阻拦索中张力为,此刻飞机受阻拦索作用力的大小为( )A.B.C.D.第(5)题一架直升机在125米的高空以的加速度沿水平方向做匀加速直线运动,间隔10s先后投下A、B两包救灾物资,两包裹落到水平地面上的间距为140m,不计空气的阻力和包裹的大小,重力加速度,则投下第一个包裹A时飞机的速度大小为( )A.1m/s B.2m/s C.4m/s D.6m/s第(6)题2024年3月20日,长征八号火箭成功发射,将鹊桥二号直接送入预定地月转移轨道。
2016年——2019年高考物理压轴题汇编(含解题过程)

2016年——2019年高考物理压轴题汇编一、力学综合:考察运动规律、牛顿定律、动能定理,功能关系、动量定理、动量守恒定律、物体受力分析、运动过程分析、数理综合应用能力等1、【2017·新课标Ⅲ卷】(20分)如图,两个滑块A 和B 的质量分别为m A =1 kg 和m B =5 kg ,放在静止于水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m =4 kg ,与地面间的动摩擦因数为μ2=0.1。
某时刻A 、B 两滑块开始相向滑动,初速度大小均为v 0=3 m/s 。
A 、B 相遇时,A 与木板恰好相对静止。
设最大静摩擦力等于滑动摩擦力,取重力加速度大小g =10 m/s 2。
求(1)B 与木板相对静止时,木板的速度;(2)A 、B 开始运动时,两者之间的距离。
【答案】(1)1 m/s (2)1.9 m【解析】(1)滑块A 和B 在木板上滑动时,木板也在地面上滑动。
设A 、B 和木板所受的摩擦力大小分别为f 1、f 2和f 3,A 和B 相对于地面的加速度大小分别是a A 和a B ,木板相对于地面的加速度大小为a 1。
在物块B 与木板达到共同速度前有① ② ③由牛顿第二定律得④ ⑤ ⑥设在t 1时刻,B 与木板达到共同速度,设大小为v 1。
由运动学公式有⑦ ⑧联立①②③④⑤⑥⑦⑧式,代入已知数据得⑨(2)在t 1时间间隔内,B 相对于地面移动的距离为⑩ 设在B 与木板达到共同速度v 1后,木板的加速度大小为a 2,对于B 与木板组成的体系,由牛顿第二定律有 ⑪由①②④⑤式知,a A =a B ;再由⑦⑧可知,B 与木板达到共同速度时,A 的速度大小也为v 1,但运动方向与木板相反。
由题意知,A 和B 相遇时,A 与木板的速度相同,设其大小为v 2,设A 的速度大小从v 1变到v 2所用时间为t 2,则由运动学公式,对木板有11A f m g μ=21B f m g μ=32()A B f m m m g μ=++1A A f m a =2B B f m a =2131f f f ma --=101B v v a t =-111v a t =1 1 m/s v =201112B B s v t a t =-132()B f f m m a +=+2122v v a t =-⑫ 对A 有⑬ 在t 2时间间隔内,B (以及木板)相对地面移动的距离为⑭ 在(t 1+t 2)时间间隔内,A 相对地面移动的距离为 ⑮ A 和B 相遇时,A 与木板的速度也恰好相同。
全国历年高考物理压轴题汇总

⑵ (提示:如图所示,设轨迹圆半径为R,圆心为P,设C点速度与x轴成α,PA与y轴成β,则 ,Rcosβ=Rcosα+h,Rsinβ=l-Rsinα。由以上三式得 ,再由 和v的表达式得最后结果。)
20XX年(山东卷)
25.(18分)两块足够大的平行金属极板水平放置,极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向)。在t=0时刻由负极板释放一个初速度为零的带负电的粒子(不计重力)。若电场强度E0、磁感应强度B0、粒子的比荷 均已知,且 ,两板间距 。
(1)欲使小球能够不断地在两板间上下往返运动,电动势ε至少应大于多少?
(2)设上述条件已满足,在较长的时间间隔T内小球做了很多次往返运动。求在T时间内小球往返运动的次数以及通过电源的总电量。
解析25.解:(1)用Q表示极板电荷量的大小,q表示碰后小球电荷量的大小。要使小球能不停地往返运动,小球所受的向上的电场力至少应大于重力,则
(1)求粒子在0~t0时间内的位移大小与极板间距h的比值。
(2)求粒子在板板间做圆周运动的最大半径(用h表示)。
(3)若板间电场强度E随时间的变化仍如图1所示,磁场的变化改为如图3所示,试画出粒子在板间运动的轨迹图(不必写计算过程)。
解法一:(1)设粒子在0~t0时间内运动的位移大小为s1
①
②
又已知
三、磁场
20XX
25.(20分)
如图所示,在x<0与x>0的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1>B2。一个带负电的粒子从坐标原点O以速度v沿x轴负方向射出,要使该粒子经过一段时间后又经过O点,B1与B2的比值应满足什么条件?
全国高考物理压轴题精选集(附答案)

1(20分)如图12所示,PR 是一块长为L =4 m 的绝缘平板固定在水平地面上,整个空间有一个平行于PR 的匀强电场E ,在板的右半部分有一个垂直于纸面向外的匀强磁场B ,一个质量为m =0.1 kg ,带电量为q =0.5 C 的物体,从板的P 端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。
当物体碰到板R 端的挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在C 点,PC =L/4,物体与平板间的动摩擦因数为μ=0.4,取g=10m/s 2 ,求:(1)判断物体带电性质,正电荷还是负电荷? (2)物体与挡板碰撞前后的速度v 1和v 2 (3)磁感应强度B 的大小 (4)电场强度E 的大小和方向2(10分)如图2—14所示,光滑水平桌面上有长L=2m 的木板C ,质量m c =5kg ,在其正中央并排放着两个小滑块A 和B ,m A =1kg ,m B =4kg ,开始时三物都静止.在A 、B 间有少量塑胶炸药,爆炸后A 以速度6m /s 水平向左运动,A 、B 中任一块与挡板碰撞后,都粘在一起,不计摩擦和碰撞时间,求:(1)当两滑块A 、B 都与挡板碰撞后,C 的速度是多大? (2)到A 、B 都与挡板碰撞为止,C 的位移为多少?3(10分)为了测量小木板和斜面间的摩擦因数,某同学设计如图所示实验,在小木板上固定一个轻弹簧,弹簧下端吊一个光滑小球,弹簧长度方向与斜面平行,现将木板连同弹簧、小球放在斜面上,用手固定木板时,弹簧示数为F 1,放手后,木板沿斜面下滑,稳定后弹簧示数为F 2,测得斜面斜角为θ,则木板与斜面间动摩擦因数为多少?(斜面体固定在地面上)图124有一倾角为θ的斜面,其底端固定一挡板M ,另有三个木块A 、B 和C ,它们的质 量分别为m A =m B =m ,m C =3 m ,它们与斜面间的动摩擦因数都相同.其中木块A 连接一轻弹簧放于斜面上,并通过轻弹簧与挡板M 相连,如图所示.开始时,木块A 静止在P 处,弹簧处于自然伸长状态.木块B 在Q 点以初速度v 0向下运动,P 、Q 间的距离为L.已知木块B 在下滑过程中做匀速直线运动,与木块A 相碰后立刻一起向下运动,但不粘连,它们到达一个最低点后又向上运动,木块B 向上运动恰好能回到Q 点.若木块A 静止于P 点,木块C 从Q 点开始以初速度032v 向下运动,经历同样过程,最后木块C 停在斜面上的R 点,求P 、R 间的距离L ′的大小。
最近两年全国各地高考物理压轴题汇集(详细解析63题)
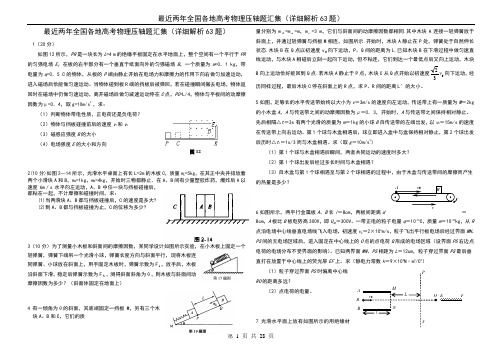
最近两年全国各地高考物理压轴题汇集(详细解析63题)1(20分)如图12所示,PR 是一块长为L =4 m 的绝缘平板固定在水平地面上,整个空间有一个平行于PR 的匀强电场E ,在板的右半部分有一个垂直于纸面向外的匀强磁场B ,一个质量为m =0.1 kg ,带电量为q =0.5 C 的物体,从板的P 端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。
当物体碰到板R 端的挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在C 点,PC =L/4,物体与平板间的动摩擦因数为μ=0.4,取g=10m/s 2,求:(1)判断物体带电性质,正电荷还是负电荷? (2)物体与挡板碰撞前后的速度v 1和v 2 (3)磁感应强度B 的大小 (4)电场强度E 的大小和方向2(10分)如图2—14所示,光滑水平桌面上有长L=2m 的木板C ,质量m c =5kg ,在其正中央并排放着两个小滑块A 和B ,m A =1kg ,m B =4kg ,开始时三物都静止.在A 、B 间有少量塑胶炸药,爆炸后A 以速度6m /s 水平向左运动,A 、B 中任一块与挡板碰撞后,都粘在一起,不计摩擦和碰撞时间,求:(1)当两滑块A 、B 都与挡板碰撞后,C 的速度是多大? (2)到A 、B 都与挡板碰撞为止,C 的位移为多少?3(10分)为了测量小木板和斜面间的摩擦因数,某同学设计如图所示实验,在小木板上固定一个轻弹簧,弹簧下端吊一个光滑小球,弹簧长度方向与斜面平行,现将木板连同弹簧、小球放在斜面上,用手固定木板时,弹簧示数为F 1,放手后,木板沿斜面下滑,稳定后弹簧示数为F 2,测得斜面斜角为θ,则木板与斜面间动摩擦因数为多少?(斜面体固定在地面上)4有一倾角为θ的斜面,其底端固定一挡板M ,另有三个木块A 、B 和C ,它们的质量分别为m A =m B =m ,m C =3 m ,它们与斜面间的动摩擦因数都相同.其中木块A 连接一轻弹簧放于斜面上,并通过轻弹簧与挡板M 相连,如图所示.开始时,木块A 静止在P 处,弹簧处于自然伸长状态.木块B 在Q 点以初速度v 0向下运动,P 、Q 间的距离为L.已知木块B 在下滑过程中做匀速直线运动,与木块A 相碰后立刻一起向下运动,但不粘连,它们到达一个最低点后又向上运动,木块B 向上运动恰好能回到Q 点.若木块A 静止于P 点,木块C 从Q 点开始以初速度032v 向下运动,经历同样过程,最后木块C 停在斜面上的R 点,求P 、R 间的距离L ′的大小。
2024届浙江省高三高考压轴卷 高效提分物理试题(基础必刷)

2024届浙江省高三高考压轴卷高效提分物理试题(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题列车在水平长直轨道上的模拟运行图如图所示,列车由质量均为m的5节车厢组成,假设只有1号车厢为动力车厢。
列车由静止开始以额定功率P运行,经过一段时间达到最大速度,列车向右运动过程中,1号车厢会受到前方空气的阻力,假设车厢碰到空气前空气的速度为0,碰到空气后空气的速度立刻与列车速度相同,已知空气密度为。
1号车厢的迎风面积(垂直运动方向上的投影面积)为S,不计其他阻力,忽略2号、3号、4号、5号车厢受到的空气阻力。
当列车以额定功率运行到速度为最大速度的一半时,1号车厢对2号车厢的作用力大小为( )A.B.C.D.第(2)题如图所示,一质量为m的物体,沿半径为R的四分之一固定圆弧轨道滑行,由于物体与轨道之间动摩擦因数是变化的,使物体滑行到最低点的过程中速率不变。
该物体在此运动过程,下列说法正确的是()A.动量不变B.重力做功的瞬时功率不变C.重力做功随时间均匀变化D.重力的冲量随时间均匀变化第(3)题静止在水平面上的物体,受到水平拉力的作用。
在从20N开始逐渐增大到40N的过程中,加速度随拉力变化的图像如图所示,由此无法计算出()( )A.物体的质量B.物体与水平间的动摩擦因数C.物体与水平间的滑动摩擦力大小D.加速度为时物体的速度第(4)题下列叙述正确的是( )A.汤姆孙发现了电子,表明原子具有核式结构B.卢瑟福通过分析“粒子散射实验”,提出原子核式结构学说C.贝克勒尔通过对天然放射现象的研究,发现原子中存在原子核D.伽利略通过“理想斜面”实验,提出“力是维持物体运动的原因”的观点第(5)题图为氢原子能级的示意图,现有大量的氢原子处于以n=4的激发态,当向低能级跃迁时辐射出若干不同频率的光.关于这些光下列说法正确的是A.最容易表现出衍射现象的光是由,n=4能级跃迁到n=1能级产生的B.频率最小的光是由n=2能级跃迁到n=1能级产生的C.这些氢原子总共可辐射出3种不同频率的光D.用n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34eV的金属铂能发生光电效应第(6)题如图所示,abc为均匀带电半圆环,O为其圆心,O处的电场强度大小为E,将一试探电荷从无穷远处移到O点,电场力做功为W。
高考物理60题压轴题8

57。
(15分)平行导轨L1、L2所在平面与水平面成30度角,平行导轨L3、L4所在平面与水平面成60度角,L1、L3上端连接于O点,L2、L4上端连接于O’点,OO’连线水平且与L1、L2、L3、L4都垂直,质量分别为m1、m2的甲、乙两金属棒分别跨接在左右两边导轨上,且可沿导轨无摩擦地滑动,整个空间存在着竖直向下的匀强磁场。
若同时释放甲、乙棒,稳定后它们都沿导轨作匀速运动。
(1)求两金属棒的质量之比。
(2)求在稳定前的某一时刻两金属棒加速度之比。
(3)当甲的加速度为g/4时,两棒重力做功的瞬时功率和回路中电流做功的瞬时功率之比为多少?58.(18分)图中y轴AB两点的纵坐标分别为d和-d。
在0《y《d的区域中,存在沿y轴向上的非均匀电场,场强E的大小与y成正比,即E=ky;在y》d的区域中,存在沿y轴向上的匀强电场,电场强度F=kd(k属未知量)。
X轴下方空间各点电场分布与x轴上方空间中的分布对称,只是场强的方向都沿y轴向下。
现有一带电量为q质量为m的微粒甲正好在O、B两点之问作简谐运动。
某时刻将一带电蕾为2q、质量为m的微粒乙从y轴上的c点处由静止释放,乙运动到0点和甲相碰并结为一体(忽略两微粒之间的库仑力)。
在以后的运动中,它们所能达到的最高点和最低点分别为A点和D点,且经过P点时速度达到最大值(重力加速度为g)。
(1)求匀强电场E;(2)求出AB间的电势差U AB及OB间的电势差U OB;(3)分别求出P、C、D三点到0点的距离。
59.(17分)荷兰科学家惠更斯在研究物体碰撞问题时做出了突出的贡献.惠更斯所做的碰撞实验可简化为:三个质量分别为m1、m2、m3的小球,半径相同,并排悬挂在长度均为L的三根平行绳子上,彼此相互接触。
现把质量为m1的小球拉开,上升到H高处释放,如图所示,已知各球间碰撞时同时满足动量守恒定律和机械能守恒定律,且碰撞时间极短,H远小于L,不计空气阻力。
(1)若三个球的质量相同,则发生碰撞的两球速度交换,试求此时系统的运动周期。
2024届浙江省高三高考压轴卷 物理高频考点试题(基础必刷)

2024届浙江省高三高考压轴卷物理高频考点试题(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题1947年,中国科学家钱三强、何泽慧夫妇在实验中发现铀核也可能分裂为三部分或四部分。
如图是铀核俘获中子后,裂变成三个质量较大的核和一个质量较小的核时产生的径迹。
下列说法不正确的是()A.铀核裂变过程质量数守恒B.铀核裂变过程电荷数守恒C.铀核裂变过程如果生成物不同,释放的能量会有差异D.铀核中使核子紧密结合在一起的作用是弱相互作用第(2)题如图甲所示,客家人口中的“风车”也叫“谷扇”,是农民常用来精选谷物的农具。
在同一风力作用下,精谷和瘪谷(空壳)都从洞口水平飞出,结果精谷和瘪谷落地点不同,自然分开,简化装置如图乙所示。
谷粒从洞口飞出后均做平抛运动,落在点的谷粒速度方向和竖直方向的夹角为,从洞口飞出时的速度大小为;落在点的谷粒速度方向和竖直方向的夹角为,从洞口飞出时的速度大小为。
下列分析正确的是( )A.处是瘪谷B.处是精谷:C.处是瘪谷D.处是精谷第(3)题汽油发动机的火花塞工作时需要一万伏左右的高压才能产生火花。
一同学用12V直流电源、变压器、开关及导线若干设计点火电路,以下原理图可行的是( )A.B.C.D.第(4)题如图所示,两根相距L=0.5 m的平行无电阻金属导轨MN和OP,水平放置在方向竖直向上的匀强磁场中,磁感应强度B=0.2 T。
垂直导轨放置两根金属滑杆ab和cd,它们在两金属导轨间的有效电阻均为r=0.1 Ω。
金属滑杆ab、cd在导轨上滑行时受到的摩擦力分别为f1=0.3 N和f2=0.1 N。
今施水平恒力F于ab杆上,使两杆最终都能做匀速直线运动。
下列说法正确的是( )A.恒力F=0.3 NB.cd杆最终匀速运动时的电流为2 AC.ab和cd最终匀速运动时的速度不相等,速度差为2 m/sD.外力F所做的功等于两金属滑杆上产生的焦耳热之和第(5)题如图所示,半径为R圆形区域内存在磁感应强度大小为B的匀强磁场,磁场方向垂直于纸面向外。
理科高考数学立体几何选择填空压轴题专练

立体几何选择填空压轴题专练A 组一、选择题1.(2018全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为 ABCD【答案】A【解析】记该正方体为''''-ABCD A B C D ,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱'A A ,''A B ,''A D 与平面α所成的角都相等,如图,连接'AB ,'AD ,''B D ,因为三棱锥'''-A AB D 是正三棱锥,所以'A A ,''A B ,''A D 与平面''AB D 所成的角都相等,分别取''C D ,''B C ,'BB ,AB ,AD ,'DD 的中点E ,F ,G ,H ,I ,J ,连接EF ,FG .GH ,IH ,IJ ,IE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面''AB D 平行,且截正方体所得截面的面积最大,又2======EF FG GH IH IJ JE ,所以该正六边形的面积为26434⨯⨯=,所以α截此正方体所得截面面积的最大值为4,故选A . 2.如图,矩形ABCD 中, 2AB AD =, E 为边AB 的中点,将ADE ∆沿直线DE 翻转成1A DE ∆(1A ∉平面ABCD ).若M 、O 分别为线段1A C 、DE 的中点,则在ADE ∆翻转过程中,下列说法错误的是( )A. 与平面1A DE 垂直的直线必与直线BM 垂直B. 异面直线BM 与1A E 所成角是定值C. 一定存在某个位置,使DE MO ⊥D. 三棱锥1A ADE -外接球半径与棱AD 的长之比为定值【答案】C【解析】取CD 的中点F ,连BF,MF,如下图:可知面MBF// 1A DE ,所以A 对。
高考数学高三模拟考试试卷压轴题普通高等学校招生全国统一考试理科数学

高考数学高三模拟考试试卷压轴题普通高等学校招生全国统一考试理科数学一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是复合题目要求的。
1.1212ii+=-() A .4355i --B .4355i -+C .3455i --D .3455i -+2.已知集合(){}223A x y xy x y =+∈∈Z Z ,≤,,,则A 中元素的个数为()A .9B .8C .5D .43.函数()2x xe ef x x --=的图象大致是()4.已知向量a b ,满足,1a =,1a b ⋅=-,则()2a a b ⋅-=()A .4B .3C .2D .05.双曲线()2222100x y a b a b-=>,>的离心力为3,则其渐近线方程为()A .2y x =±B .3y x =±C .2y x =±D .3y x =± 6.在ABC △中,5cos2C =,1BC =,5AC =,则AB =() A .42B .30 C .29 D .257.为计算11111123499100S =-+-+⋅⋅⋅+-,设计了右侧的程序框图,则在空白框中应填入()A .1i i =+B .2i i =+C .3i i =+D .4i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是() A .112B .114C .115D .1189.在长方体1111ABCD A B C D -中,1AB BC ==,1AA =1AD 与1DB 所成角的余弦值为()A .15BCD10.若()cos sin f x x x =-在[]a a -,是减函数,则a 的最大值是()A .4πB .2πC .43πD .π 11.已知()f x 是定义域为()-∞+∞,的奇函数,满足()()11f x f x -=+.若()12f =,则()()()()12350f f f f +++⋅⋅⋅+=()A .50-B .0C .2D .5012.已知1F ,2F 是椭圆()2222:10x y C a b a b+=>>的左、右焦点交点,A 是C 的左顶点,点P 在过A 且的直线上,12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为() A .23B .12C .13D .14 二、填空题,本题共4小题,每小题5分,共20分.13.曲线()2ln 1y x =+在点()00,处的切线方程为__________.14.若x y ,满足约束条件25023050x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤,则z x y =+的最大值为_________.15.已知sin cos 1αβ+=,cos sin 0αβ+=,则()sin αβ+=__________. 16.已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45︒.若SAB △的面积为_________.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤。
全国甲卷(理科)-2022年全国高考数学压轴题解读

2022年全国统一高考数学试卷(理科)(甲卷)压轴真题解读11.设函数()sin()3f x x πω=+在区间(0,)π恰有三个极值点、两个零点,则ω的取值范围是()A .5[3,13)6B .5[3,19)6C .13(6,8]3D .13(6,196【答案】C【解析】当0ω<时,不能满足在区间(0,)π极值点比零点多,所以0ω>;函数()sin()3f x x πω=+在区间(0,)π恰有三个极值点、两个零点,(33x ππω+∈,3πωπ+,∴5323ππωππ<+,求得13863ω<,故选:C .【解后反思】1.研究y =A sin(ωx +φ)的性质时可将ωx +φ视为一个整体,利用换元法和数形结合思想进行解题.2.方程根的个数可转化为两个函数图象的交点个数.12.已知3111,cos ,4sin 3244a b c ===,则()A .c b a >>B .b a c>>C .a b c>>D .a c b>>【答案】A【解析】因为14tan 4c b =,因为当π0,,sin tan 2x x x x ⎛⎫∈<< ⎪⎝⎭,所以11tan 44>,即1cb >,所以c b >;设21()cos 1,(0,)2f x x x x =+-∈+∞,()sin 0f x x x '=-+>,所以()f x 在(0,)+∞单调递增,则1(0)=04f f ⎛⎫> ⎪⎝⎭,所以131cos 0432->,所以b a >,所以c b a >>,故选:A【规律总结】1.利用导数比较大小,其关键在于利用题目条件构造辅助函数,把比较大小的问题转化为先利用导数研究函数的单调性,进而根据单调性比较大小.2.与抽象函数有关的不等式,要充分挖掘条件关系,恰当构造函数;题目中若存在f (x )与f ′(x )的不等关系时,常构造含f (x )与另一函数的积(或商)的函数,与题设形成解题链条,利用导数研究新函数的单调性,从而求解不等式.16.已知ABC ∆中,点D 在边BC 上,120ADB ∠=︒,2AD =,2CD BD =.当ACAB取得最小值时,BD =.1【解析】设BD x =,2CD x =,在三角形ACD 中,2244222cos60b x x =+-⋅⋅⋅︒,可得:22444b x x =-+,在三角形ABD 中,22422cos120c x x =+-⋅⋅⋅︒,可得:2224c x x =++,要使得ACAB 最小,即22b c 最小,222244412432411b x x c x x x x -+==-+++++,其中311x x +++,此时224b c-,当且仅当1x +=时,即1x =-时取等号,【易错】忽视基本不等式成立的条件20.设抛物线2:2(0)C y px p =>的焦点为F ,点(,0)D p ,过F 的直线交C 于M ,N 两点.当直线MD 垂直于x 轴时,||3MF =.(1)求C 的方程;(2)设直线MD ,ND 与C 的另一个交点分别为A ,B ,记直线MN ,AB 的倾斜角分别为α,β.当αβ-取得最大值时,求直线AB 的方程.【命题意图】考查抛物线方程的求法、直线与抛物线位置关系的应用、运算求解能力,属难题.【解析】(1)当x p =时,222y p =,得M y =,可知||MD =,||2p FD =.则在Rt MFD ∆中,222||||||FD DM FM +=,得22()92p +=,解得2p =.则C :24y x =;(2)要使αβ-取得最大值,则tan()αβ-最大,且知当直线MN 的斜率为负时,αβ-为正才能达到最大,又tan tan tan()1tan tan αβαβαβ--=+,设1(M x ,1)y ,2(N x ,2)y ,3(A x ,3)y ,4(B x ,4)y ,由(1)可知(1,0)F ,(2,0)D ,则1212221212124tan 44MN y y y y k y y x x y y β--====-+-,又N 、D 、B 三点共线,则ND BD k k =,即24240022y y x x --=--,∴242224002244y y y y --=--,得248y y =-,即428y y =-;同理由M 、D 、A 三点共线,得318y y =-.则1234124tan 2()y y y y y y α==+-+.由题意可知,直线MN 0,不妨设:1(0)MN l x my m =+<,由241y xx my ⎧=⎨=+⎩,得2440y my --=,124y y m +=,124y y =-,则41tan 4m m β==,41tan 242m m α-==-⨯,则1112tan()111122m m m m m mαβ---==+⋅+,可得当2m =时,tan()αβ-最大,αβ-最大,此时AB 的直线方程为33344()y y x x y y -=-+,即34344()0x y y y y y -++=,又123412128()888y y y y m y y y y -++=--===-,34128816y y y y --=⋅=-,AB ∴的方程为4160x +-=,即40x +-=.21.已知函数()xe f x lnx x a x=-+-.(1)若()0f x ,求a 的取值范围;(2)证明:若()f x 有两个零点1x ,2x ,则121x x <.【命题意图】考查利用导函数研究函数单调性,即构造函数证明不等式恒成立问题,属较难题.【解析】(1)()f x 的定义域为(0,)+∞,(1)1()(1)()1x x e x e x x f x x x x-+-'=-+=,令()0f x '>,解得1x >,故函数()f x 在(0,1)单调递减,(1,)+∞单调递增,故()min f x f =(1)1e a =+-,要使得()0f x 恒成立,仅需10e a +-,故1a e +,故a 的取值范围是(-∞,1]e +;(2)证明:由已知有函数()f x 要有两个零点,故f (1)10e a =+-<,即1a e >+,不妨设1201x x <<<,要证明121x x <,即证明211x x <,101x << ,∴111x >,即证明:2111x x <<,又因为()f x 在(1,)+∞单调递增,即证明:211()()f x f x <⇔111()()f x f x <,构造函数1()()()h x f x f x=-,01x <<,12221(1)()11()()()xx x xe x e x h x f x f x x x-+--'='+'=,令121()xxk x xe x e x =+--,01x <<,12211()(1)20x x k x x e x e x x'=++++>,()k x k <(1)0=,所以()k x 在(0,1)上递增,又因为10x -<,20x >,故()0h x '>在(0,1)恒成立,故()h x 在(0,1)单调递增,又因为h (1)0=,故()h x h <(1)0=,故111()()f x f x <,即121x x <.得证.【方法总结】利用导数求函数的零点常用方法(1)构造函数g (x ),利用导数研究g (x )的性质,结合g (x )的图象,判断函数零点的个数.(2)利用零点存在定理,先判断函数在某区间有零点,再结合图象与性质确定函数有几个零点.压轴模拟专练1.已知0x 是函数()12sin cos 3f x x x x =-的一个极值点,则20tan x 的值是()A .1B .12C .37D .57【答案】D【解析】()2001112cos2,cos22cos 1366f x x x x =-∴=∴-=',∴207cos 12x =,∴22005sin 1cos 12x x =-=,∴220020sin 5tan cos 7x x x ==。
历届高考压轴题汇编(1)

2001—2008届高考物理压轴题汇编一、力学2001年全国理综(江苏、安徽、福建卷)31.(28分)太阳现正处于主序星演化阶段。
它主要是由电子和H 11、He 42等原子核组成。
维持太阳辐射的是它内部的核聚变反应,核反应方程是2e+4H 11→He 42+释放的核能,这些核能最后转化为辐射能。
根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的H 11核数目从现有数减少10%,太阳将离开主序垦阶段而转入红巨星的演化阶段。
为了简化,假定目前太阳全部由电子和H 11核组成。
(1)为了研究太阳演化进程,需知道目前太阳的质量M 。
已知地球半径R =6.4×106 m ,地球质量m =6.0×1024 kg ,日地中心的距离r =1.5×1011 m ,地球表面处的重力加速度g =10 m/s 2,1年约为3.2×107秒。
试估算目前太阳的质量M 。
(2)已知质子质量m p =1.6726×10-27 kg ,He 42质量m α=6.6458×10-27 kg ,电子质量m e =0.9×10-30kg ,光速c =3×108 m/s 。
求每发生一次题中所述的核聚变反应所释放的核能。
(3)又知地球上与太阳光垂直的每平方米截面上,每秒通过的太阳辐射能w =1.35×103 W/m 2。
试估算太阳继续保持在主序星阶段还有多少年的寿命。
(估算结果只要求一位有效数字。
)参考解答:(1)估算太阳的质量M设T 为地球绕日心运动的周期,则由万有引力定律和牛顿定律可知①地球表面处的重力加速度2R mGg = ② 由①、②式联立解得③以题给数值代入,得M =2×1030 kg ④(2)根据质量亏损和质能公式,该核反应每发生一次释放的核能为 △E =(4m p +2m e -m α)c 2 ⑤ 代入数值,解得△E =4.2×10-12 J ⑥(3)根据题给假定,在太阳继续保持在主序星阶段的时间内,发生题中所述的核聚变反应的次数为pm MN 4=×10% ⑦ 因此,太阳总共辐射出的能量为 E =N ·△E设太阳辐射是各向同性的,则每秒内太阳向外放出的辐射能为 ε=4πr 2w ⑧ 所以太阳继续保持在主序星的时间为εEt =⑨由以上各式解得以题给数据代入,并以年为单位,可得 t =1×1010 年=1 百亿年 ⑩评分标准:本题28分,其中第(1)问14分,第(2)问7分。
2024届海南省高三高考压轴卷 高效提分物理试题

2024届海南省高三高考压轴卷高效提分物理试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图所示,a、b、c、d为正方形的四个顶点,在b、c、d三处有垂直于正方形所在平面的无限长通电直导线,b、d两处的电流方向向外、大小均为I,c处的电流方向向里、大小为,此时a处的磁感应强度为0。
已知通电长直导线周围的磁感应强度大小与电流成正比、与该点到通电长直导线的距离成反比,即,以下说法正确的是( )A.B.C.D.仅将b、d处的电流反向,a处的磁感应强度仍为0第(2)题如图,在足够大的空间内,同时存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,带正电的小球a能以v0=15m/s、方向水平向左的初速度做半径为R=1m的匀速圆周运动,当球a运动到最低点时,恰好能与静止在小平台(体积可忽略)上的不带电的小球b发生正碰,碰后经t=0.3s两球再次相碰。
已知碰撞前后两小球的带电情况不变,磁感应强度大小为B=2T,重力加速度g=10m/s2,取π=3,则( )A.电场强度的大小为1N/CB.第一次碰撞后小球b获得的速度大小可能为2m/sC.第一次碰撞前后小球a的速度方向可能相同D.小球b的质量是小球a质量的14.5倍第(3)题2023年11月28日,中国载人航天工程办公室公布了神舟十六号拍摄到的我国空间站的照片和在空间站拍摄到神舟十六号撤离时的震撼画面。
神舟十六号载人飞船于10月30日成功撤离空间站组合体,标志着中国空间站建设又六重要里程碑。
空间站与神舟十六号飞船分离前按照如图所示的运行方向在圆轨道③上做匀速圆周运动,空间站与飞船在Q点分离,随后飞船进入椭圆轨道②,逐步转移到近地轨道①,再寻找合适的时机进入大气层。
不考虑飞船、空间站在太空中受到的阻力,下列说法正确的是( )A.神舟十六号飞船在Q点分离时需要启动自身推进系统,朝与运行方向相反的方向喷火B.神舟十六号飞船在从Q到P的过程中机械能越来越小C.神舟十六号飞船在轨道②、轨道③上分别经过Q点时的向心加速度相同D.神舟十六号飞船在轨道②上经过P点的时运行速度小于第一宇宙速度第(4)题2022年6月23日,东北首座核电站辽宁红沿河核电站全面投产,成为国内在运的最大核电站。
2024届海南省高三高考压轴卷 高效提分物理试题

2024届海南省高三高考压轴卷高效提分物理试题一、单选题 (共6题)第(1)题在xOy坐标系的第一象限内存在匀强磁场,两个相同的带电粒子①和②在P点垂直磁场射入,①的速度与x轴负方向成45°,②的速度与x轴正方向成45°,如图所示,二者均恰好垂直于y轴射出磁场,不计重力,不考虑带电粒子之间的作用力,根据上述信息可以判断的是( )A.带电粒子①在磁场中运动的半径大B.带电粒子①在磁场中运动的过程中洛伦兹力的冲量大C.带电粒子②在磁场中运动的轨迹短D.两个粒子磁场中运动的过程中平均速率相等第(2)题如图所示,把线圈(内阻不计)、电容器、电源、电阻和单刀双掷开关连成图示电路。
把电压传感器(图中未画出)的两端连在电容器的两个极板M、N上。
先把开关置于a侧,一段时间后再把开关置于b侧,从此刻开始计时,电压随时间t变化的图像正确的是( )A.B.C.D.第(3)题当电阻两端加上某一稳定电压时,通过该电阻的电荷量为0.3C,消耗的电能为0.9J.为在相同时间内使0.6C的电荷量通过该电阻,在其两端需加的电压和消耗的电能分别是()A.3V,1.8J B.3V,3.6J C.6V,l.8J D.6V,3.6J第(4)题如图所示,摄影师调节三脚架使相机高度降低。
调节后,水平地面对任意一只支撑杆的( )A.支持力不变B.支持力变小C.摩擦力不变D.摩擦力变小第(5)题如图所示,空间存在着匀强磁场和匀强电场,磁场的方向垂直纸面(平面)向外,电场的方向沿y轴正方向。
一质量为m、电荷量为q的带电粒子在电场和磁场的作用下,从坐标原点O由静止开始运动(其轨迹如图所示)。
已知磁感应强度的大小为B,电场强度大小为E,不计粒子的重力,下列说法正确的是( )A.粒子带负电B.粒子运动轨迹是抛物线C.粒子距离x轴的最大距离为D.粒子运动过程中的最大速度为第(6)题有“海上充电宝”之称的南鲲号是一个利用海浪发电的大型海上电站,其发电原理是海浪带动浪板上下摆动,从而驱动发电机转子转动,其中浪板和转子的链接装置使转子只能单方向转动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21.(本题满分14分) 理科压轴题
已知函数2()1f x x x =+-,,αβ是方程f (x)=0的两个根()αβ>,'()f x 是f (x)的导数;设11a =,1()'()
n n n n f a a a f a +=-(n=1,2,……) (1)求,αβ的值;
(2)证明:对任意的正整数n ,都有n a >a ;
(3)记ln n n n a b a a
β-=-(n=1,2,……),求数列{b n }的前n 项和S n 。
21.(本小题满分12分)
设p q ,为实数,αβ,是方程2
0x px q -+=的两个实根,数列{}n x 满足1x p =,22x p q =-,12n n n x px qx --=-(34n =,,
…).(1)证明:p αβ+=,q αβ=;(2)求数列{}n x 的通项公式;
(3)若1p =,14
q =
,求{}n x 的前n 项和n S .
21.(本小题满分14分)
已知曲线22:20(1,2,)n C x nx y n -+==K .从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ,切点为(,)n n n P x y .
(1)求数列{}{}n n x y 与的通项公式;
(2
)证明:13521n n n
x x x x x y -⋅⋅⋅⋅<
<L .
21.设),(),,(2211y x B y x A 是平面直角坐标系xOy 上的两点,现定义由点A 到点B 的一种折线距离),(B A ρ为||||),(1212y y x x B A -+-=ρ.对于平面xOy 上给定的不同的两点),(),,(2211y x B y x A
(Ⅰ) 若点),(y x C 是平面xOy 上的点,试证明:),(),(),(B A B C C A ρρρ≥+; (Ⅱ) 在平面xOy 上是否存在点),(y x C ,同时满足
①),(),(),(B A B C C A ρρρ=+; ②),(),(B C C A ρρ=.
若存在,请求出所有符合条件的点;若不存在,请予以证明.
;2||),(),,Q(AB :B.y )0)(4
1,
()1(|}.
||,max{|),(,0,0,4,.41:L ,)
14.(21002002122122p q p q p L p p p A x x q p q px x x x q p q p x y xOy =≠==+-≥-=ϕϕ有上的作一点对线段证明轴于点的切线交作过点记的两根是方程满足实数给定抛物线上在平面直角坐标系分本小题满分 (2)设(,)M a b 是定点,其中,a b 满足240a b a ->0,≠.过(,)M a b 作L 的两条切线
12,l l ,切点分别为22112211(,
),'(,)44
E p p E P P ,12,l l 与y 分别交于,'
F F .线段EF 上异于两端点的点集记为X .证明:112||(,)(,)2P M a b X P P a b φ∈⇔>⇔=; 2min max 15(,)1,(1),,44,).D x y y x y x p q p q ϕϕϕ⎧⎫=≤-≥+-⎨⎬⎩
⎭(3)设当点()取遍D 时,求()的最小值(记为)和最大值(记为。
