振动力学1112(A卷) - 360文档中心

《振动力学》习题集(含答案)【精选】精心总结

，即
令引起的静变形为，则有：
，即
令 + 引起的静变形为，同理有：
得：
则系统的自由振动可表示为：
其中系统的固有频率为：
注意到与方向相反，得系统的自由振动为：
1.9质量为m、长为l的均质杆和弹簧k及阻尼器c构成振动系统，如图E1.9所示。以杆偏角为广义坐标，建立系统的动力学方程，给出存在自由振动的条件。若在弹簧原长处立即释手，问杆的最大振幅是多少？发生在何时？最大角速度是多少？发生在何时？是否在过静平衡位置时？
解：
（1）保持水平位置：
（2）微幅转动：
故：
2.10求图T 2-10所示系统的固有频率，刚性杆的质量忽略不计。
图T 2-10答案图T 2-10
解：
m的位置：
，，
，
，
2.11图T 2-11所示是一个倒置的摆。摆球质量为m，刚杆质量可忽略，每个弹簧的刚度为。
（1）求倒摆作微幅振动时的固有频率；
（2）摆球质量m为0.9 kg时，测得频率为1.5 Hz，m为1.8 kg时，测得频率为0.75 Hz，问摆球质量为多少千克时恰使系统处于不稳定平衡状态？
图E1.2
解：
如图，令为柱体的转角，则系统的动能和势能分别为：
利用和可得：
1.3转动惯量为J的圆盘由三段抗扭刚度分别为，和的轴约束，如图E1.3所示。求系统的固有频率。
图E1.3
解：
系统的动能为：
和相当于串联，则有：
以上两式联立可得：
系统的势能为：
利用和可得：
1.4在图E1.4所示的系统中，已知，横杆质量不计。求固有频率。
图E1.4答案图E1.4
解：
对m进行受力分析可得：

振动力学》习题集(含答案)

《振动力学》习题集（含答案）质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图所示。

求系统的固有频率。

图解：系统的动能为：()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得： ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图所示。

求系统的固有频率。

图解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得： ()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图所示。

求系统的固有频率。

图解：系统的动能为：221θ&J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得： ()()3232132k k J k k k k k n +++=ω在图所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学(高教版)部分课后习题答案

3c 1 2a mk 1 c 2m n l 3
l mgl k 0 a a ， 0 2 2ka2 1.12 面积为 S、质量为 m 的薄板连接于弹簧下端，在粘性流体中振动，如图 E1.12 所示。作用于 mg
薄板的阻尼力为 Fd 2Sv ，2S 为薄板总面积，v 为速度。若测得薄板无阻尼自由振动的周期为 T0 ，在粘性流体中自由振动的周期为 Td 。求系数。
k2 m x1 k1 c1 m c2 k2 x2 k1
c2
k2 x
m x
m
c2 x
c1 x1
x 1 k1 x x1 c1 x
图 E2.1 解：
答案图 E2.1(a)
答案图 E2.1(b)
等价于分别为 x1 和 x2 的响应之和。先考虑 x1 ，此时右端固结，系统等价为图（a），受力为图（b），故：
考虑到 x2 t 的影响，则叠加后的 xt 为：
xt
i 1
2
k
Ai ki2 ci2i2 k2 m
2 2 i
1

c c c sin it tg 1 1 2 2i tg 1 i i 2 k1 k2 i m ki c1 c2 i2
ax2 x1 a 2 k1 b 2 k2 mg ab a b2 k1k2
a 2 k1 b 2 k2 1 1 x x0 x3 mg mg 2 k0 a b k1k2 k3
则等效弹簧刚度为：
ke
则固有频率为：
a b2 k1k2k3 2 a 2 k1k3 b 2 k2 k3 a b k1k2

《振动力学》习题集(含问题详解)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》作业资料(含答案解析)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学习题集含答案

图T 2-2答案图T 2-2
解：
，
动量守恒：
，
平衡位置：
，
，
故：
故：
2.4在图E2.4所示系统中，已知m，，，和，初始时物块静止且两弹簧均为原长。求物块运动规律。
图E2.4答案图E2.4
解：
取坐标轴和，对连接点A列平衡方程：
即：
（1）
对m列运动微分方程：
即：
（2）
由（1），（2）消去得：
图E2.7
解：
，
s=1时共振，振幅为：
（1）
远离共振点时，振幅为：
（2）
由（2）
由（1）
，，
故：
2.7求图T 2-7中系统的固有频率，悬臂梁端点的刚度分别是及，悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解：
和为串联，等效刚度为：。（因为总变形为求和）
和为并联（因为的变形等于的变形），则：
图E1.9答案图E1.9
解：
利用动量矩定理得：
，
，
，
，
1.12面积为S、质量为m的薄板连接于弹簧下端，在粘性流体中振动，如图E1.12所示。作用于薄板的阻尼力为，2S为薄板总面积，v为速度。若测得薄板无阻尼自由振动的周期为，在粘性流体中自由振动的周期为。求系数。
图E1.12
解：
平面在液体中上下振动时：
和为串联（因为总变形为求和），故：
故：
2.9如图T 2-9所示，一质量m连接在一刚性杆上，杆的质量忽略不计，求下列情况系统作垂直振动的固有频率：
（1）振动过程中杆被约束保持水平位置；
（2）杆可以在铅锤平面内微幅转动；
（3）比较上述两种情况中哪种的固有频率较高，并说明理由。

振动力学习题集含答案

图答案图
解：
利用动量矩定理得：
，
，
，
，
面积为S、质量为m的薄板连接于弹簧下端，在粘性流体中振动，如图所示。作用于薄板的阻尼力为，2S为薄板总面积，v为速度。若测得薄板无阻尼自由振动的周期为，在粘性流体中自由振动的周期为。求系数。
图
解：
平面在液体中上下振动时：
，
，
图所示系统中，已知m，c，，，和。求系统动力学方程和稳态响应。
（2）
若取下面为平衡位置，求解如下：
，
图T 2-17所示的系统中，四个弹簧均未受力，k1=k2=k3=k4=k，试问：
（1）若将支承缓慢撤去，质量块将下落多少距离？
（2）若将支承突然撤去，质量块又将下落多少距离？
图T 2-17
解：
（1），
（2），
如图T 2-19所示，质量为m2的均质圆盘在水平面上可作无滑动的滚动，鼓轮绕轴的转动惯量为I，忽略绳子的弹性、质量及各轴承间的摩擦力，求此系统的固有频率。
因此有：
图所示阶梯杆系统中已知m，ρ，S，E和k。求纵向振动的频率方程。
图
解：
模态函数的一般形式为：
题设边界条件为：
，
边界条件可化作：
，
导出C2= 0及频率方程：
，其中
长为l、密度为ρ、抗扭刚度为GIp的的等直圆轴一端有转动惯量为J的圆盘，另一端连接抗扭刚度为k的弹簧，如图所示。求系统扭振的频率方程。
《振动力学》习题集（含答案）
质量为m的质点由长度为l、质量为m1的均质细杆约束在铅锤平面内作微幅摆动，如图所示。求系统的固有频率。
图
解：
系统的动能为：
其中I为杆关于铰点的转动惯量：

《振动力学》作业资料(含答案解析)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集[含答案]

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学习题集

《振动力学》习题集（含答案）质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图所示。

求系统的固有频率。

图解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图所示。

求系统的固有频率。

图解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn = 和U T =可得：()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图所示。

求系统的固有频率。

图解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn = 和U T =可得：()()3232132k k J k k k k k n +++=ω在图所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集(含答案)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

1112(2)工程力学试题A(11级机电.数48时附答案)

1112 （2）工程力学试题A 卷（试题页）to朱濯宅考前须知：1.请在本页左侧准确填写上班级、姓名和学号；2.所有试题答案填写在答题纸页上，试鹿页上答题无效。

一、选择题（按题意将正确选择填在答题纸页上，2"XI5=300I 、图示结构中（）是二力构件。

/仍杆；BC 杆；C7）杆； AB 杆和C 。

杆；2、活动较支座约束力的方向（沿中心线背离向物体：沿支承面公法线指向物体：3、平面任意力系，可列出一组（一个二个顾图）»沿接触面公法线指向物体: 不确定，用正交分力表示:）独立的平衡方程。

三个四个4、图示F 力作用使重G 的物块处「摩擦临界状态时，己知摩擦因数外.接触面最大摩擦力Ra>G 小的为 <）图。

5、工程实际中把构件抵抗变形的能力称为构件的（）» 强度；刚度：力度：承载能力；6、研究构件的变形和破坏规律，对丁•脆性材料来说，破坏是指材料发生了（）。

断裂；屈服；断裂或屈服：颈缩；7、低碳钢拉伸实验，有四个阶段,缶£曲线直线局部最高点所对应的应力值称为（）。

比例极限。

P ；屈服点G ：抗拉强度。

b ；8、冷作硬化工艺是将载荷加到低碳钢的（）阶段后卸载，重新加载使材料的比例极限提高。

弹性；屈服：强化；缩颈断裂；9、低碳钢拉伸实脸,屈服阶段曲线（）所对应的应力值作为材料的屈服点。

最高点：最低点；中间点：10、对于塑性材料，其许用应力［5=（）.II 、材料的塑性用（）来衡量。

Op ： Os ： Oh ： 3:12、图所示三种材料的应力-应变曲线，对其力学性质说法正确的选项是（）。

a 强度高,b 刚度大,c 型性好：b 强度高,c 刚度大,a 塑性好：a 强度高,a 刚度大,c 塑性好: 13、空心圆轴扭转时.横截而上正确的切应力分布图为图中的（）。

14、圆截面的直径为d.那么该截面的极惯性矩为（）。

nd'血4 mV7ul 4加‘4"~32'16~'"iT ；"64-；育15、圆轴的抗扭刚度用（）表示。

《振动力学》习题集(含答案解析)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学答案

2
k1
k1k 2 k1 k2
k 2 ，
k3
k1k 2 k1 k2
，
k
k1k2k4 k2k3k4 k1k2k4
k1k3 k2k3 k1k2 k1k4 k2k4
p2
k1k2k4 k2k3k4 k1k2k4
m(k1k3 k2k3 k1k2 k1k4 k2k4 )
word 文档可自由复制编辑
振幅。解：列出平衡方程可得：
word 文档可自由复制编辑
W
k(st
x)
Q g
w2e sin wt
W g
x
W x kx Q w2esin(wt )
g
g
x kg x Q w2esin(wt ) WW
所以：
Pn
kg W
h Q w2e W
W
又因为
kst即k
W st
将结果代入B
h
4.875cos4.875
当 x =0 时，振幅最大，此时 t=0.03s 。当
t=0.03s 时，x=0.005m）
代入初始条件，得
C1
x0
0, C2
nx0 x0 pd
x0 pd
0.006 ，得
x C2ent sin pd t 物体达到最大振幅时，有
x nC2ent sin pd t C2ent pd cos pd t 0 既得 t = 0.30 s 时，物体最大振幅为 x 0.006 e0.490.3 sin(4.875 0.3) 0.528 cm
撞后一起作自由振动。已知 k =48020 N/m，c
=1960 Ns/m，问重
物在碰撞后多少时
间达到最大振幅?

振动力学考题集[]资料讲解

振动力学考题集[]1、四个振动系统中，自由度为无限大的是（）。

A. 单摆；B. 质量-弹簧；C. 匀质弹性杆；D. 无质量弹性梁；2、两个分别为c1、c2的阻尼原件,并连后其等效阻尼是（）。

A. c1+c2；B. c1c2/(c1+c2)；C. c1-c2；D. c2-c1；3、（）的振动系统存在为0的固有频率。

A. 有未约束自由度；B. 自由度大于0；C. 自由度大于1；D. 自由度无限多；4、多自由度振动系统中，质量矩阵元素的量纲应该是（）。

A. 相同的，且都是质量；B. 相同的，且都是转动惯量；C. 相同的，且都是密度；D. 可以是不同的；5、等幅简谐激励的单自由度弹簧-小阻尼-质量振动系统，激励频率（）固有频率时，稳态位移响应幅值最大。

A. 等于；B. 稍大于；C. 稍小于；D. 为0；6、自由度为n的振动系统，且没有重合的固有频率，其固有频率的数目（A ）。

A. 为n；B. 为1；C. 大于n；D. 小于n；7、无阻尼振动系统两个不同的振型u(r)和u(s)，u(r)T Mu(s)的值一定（）。

A. 大于0；B. 等于0；C. 小于0；D. 不能确定；8、无阻尼振动系统的某振型u(r)，u(r)T Ku(r)的值一定（）。

A. 大于0；B. 等于0；C. 小于0；D. 不能确定；9、如果简谐激励力作用在无约束振动系统的某集中质量上，当激励频率为无限大时，该集中质量的稳态位移响应一定（）。

A. 大于0；B. 等于0；C. 为无穷大；D. 为一常数值；10、相邻固有频率之间的间隔呈近似无限等差数列的振动系统是（）。

A. 杆的纵向振动；B. 弦的横向振动；C. 一般无限多自由度系统；D. 梁的横向振动；11、两个刚度分别为k1、k2串连的弹簧,其等效刚度是（）。

A. k1+k2；B. k1k2/(k1+k2)；C. k1-k2；D. k2-k1；12、无阻尼振动系统两个不同的振型u(r)和u(s)，u(r)T Ku(s)的值一定（）。

《振动力学》习题集(含答案)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学12-13(A卷)

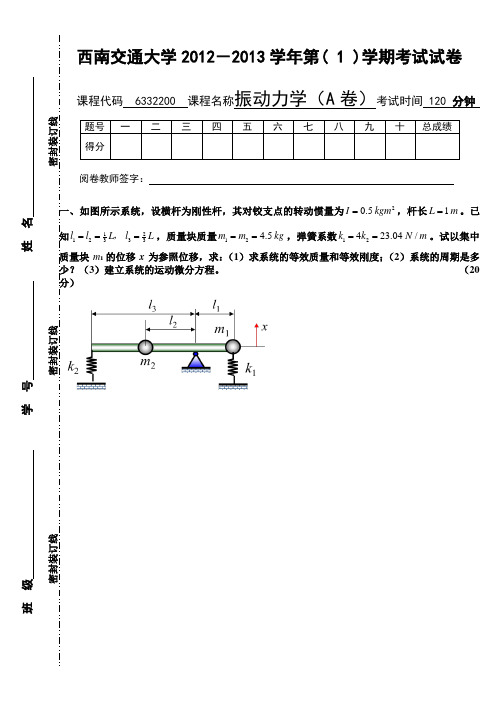
西南交通大学2012－2013学年第( 1 )学期考试试卷课程代码6332200课程名称振动力学（A卷）考试时间120分钟阅卷教师签字：一、如图所示系统，设横杆为刚性杆，其对铰支点的转动惯量为20.5I kgm=，杆长1L m=。

已知1212333l l L l L===，，质量块质量124.5m m kg==，弹簧系数12423.04/k k N m==。

试以集中质量块m1的位移x为参照位移，求：（1）求系统的等效质量和等效刚度；（2）系统的周期是多少？（3）建立系统的运动微分方程。

（20分）班级学号姓名密封装订线密封装订线密封装订线二、横截面面积为A、质量为m的圆柱形浮子，静止在密度为ρ的液体中。

设从静平衡位置压低距离x0，然后无初速地释放，假定阻尼可以忽略不计。

（1）试建立浮子的运动方程；（2）给出浮子的固有频率及初始条件；（3）求浮子自由运动的响应。

(20分)三、如图所示两层楼房，假设各层的等效质量分别为12,m m ，剪切刚度分别为12,k k 。

若已知()2112122,,10/k m m m k k k rad s m=====，试求：（1）系统的运动方程；（2）系统的频率及正则振型；（3）给出系统的解耦运动方程。

（20分）四、已知系统的运动方程为：112233210200012003000010040x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦（1）假设系统的一阶振型近似为{}110.50.1=x ，采用瑞利商估算系统的基频；（2）采用矩阵迭代法求系统的基频及振型（精确到小数点后4位），并与瑞利商的计算结果进行比较，两者的相对误差是多少？。

（10分）五、两端自由的等截面均匀直杆，设杨氏模量为E，截面积为A，长为L，材料密度为ρ。

（1）试建立杆纵向自由振动微分方程；（2）列出相应的边界条件；（3）求系统的固有频率。

2008级华南理工大学工程硕士振动力学课试题A

………………………………………密………………………………………………封………………………………………线…………………………………… ………………………………
华南理工大学专业学位研究生课程考试
《振动力学》试卷 A
2009 年 1 注意事项：1. 请考生考前将密封线内各项信息填写清楚； 2. 考试形式：闭卷（√）开卷（） 3. 考生类别：工程硕士（√）法律硕士（）风景园林硕士（）工商管理硕士（）公共管理硕士（）高校教师（ 4. 本试卷共七大题，满分 100 分，考试时间为 150 分钟。月 5 日
学号
学院
三、一个物体放在水平台面上，当台面沿铅垂方向作频率为 10Hz 的简谐振动时，要使物体不跳离平台，对台面的振幅应如何限制？(10 分) 四、推导单自由度系统( mx(t ) kx(t ) 0, x(0) x0 , x(0) x0 )的自由振动响应。(10 分)
《振动力学》试卷第 1 页共 2 页
姓名
五、建立如图所示系统的运动微分方程并求稳态响应。(10 分)
x c
m k
x1 A sin t
六、写出图示弹簧质量系统运动的作用力方程。（10 分）
பைடு நூலகம்
七、详细写出求解多自由系统对周期激励的振动稳态响应的思路和步骤。(5 分)
《振动力学》试卷第 2 页共 2 页
任课教师
）
_____________ ________ 工程硕士领域名称（工程硕士填写）：
题号得分评卷人
一
二
三
四
五
六
七
总分
一、基本概念 40 分
1．振动的定义及振动三要素。(5 分) 2．简谐激励下系统的响应由哪三部分组成。(5 分) 3．振动的激励主要有哪几种？(5 分) 4．刚度矩阵中元素 kij 的物理意义。(5 分) 5．多自由系统的模态是什么？模态参数有哪些？(5 分) 6．写出振动系统输入 x(t ) 、输出 y(t ) 和系统频率响应函数 H ( f ) 的时域和频域的