中考中的费马点详解加测试
初三数学费马点练习题

初三数学费马点练习题费马点(Fermat Point)是指在一个三角形中,距离三个顶点的距离之和最小的点。
它被称为费马点,是为了纪念法国数学家皮埃尔·费马(Pierre de Fermat)。
在本文中,将提供一些初三数学费马点练习题,通过这些题目的解答,读者将更好地理解费马点的概念和特性。
题目一:已知△ABC中,∠ABC = 60°,AD为边BC上的高,点E为三角形内部一点,满足∠BAE = ∠CAE = 30°。
证明:点E为△ABC的费马点。
解答一:我们需要证明点E到三个顶点A、B、C的距离之和最小。
首先,连接AE、BE、CE,构造△BAE和△CAE。
由已知条件可知,∠BAE = ∠CAE = 30°,而∠ABC = 60°。
观察三角形△BAE,角度和为180°,因此∠AEB = 180° - 30° - 30°= 120°。
同理,在三角形△CAE中,∠AEC = 180° - 30° - 30° = 120°。
现在我们可以继续分析三角形△ABC,∠ABC = 60°,∠BAC = 180°- 60° - 30° - 30° = 60°。
接下来,我们来考虑三角形△BAE和△CAE的外角。
对于△BAE,∠BEA = 180° - 120° = 60°;对于△CAE,∠CEA = 180° - 120° = 60°。
现在,我们可以观察到三角形△BAE、△CAE和△ABC中都有一个60°的角,并且对应的外角也是60°。
根据确定费马点的性质,可知点E为△ABC的费马点。
题目二:已知△ABC中,∠BAC = 90°,点D为边BC上的一点,满足BD = DC。
费马点与中考试题(可编辑修改word版)

识别“费马点” 思路快突破例1 探究问题:(1)阅读理解:①如图(A),在已知△ABC 所在平面上存在一点P,使它到三角形顶点的距离之和最小,则称点P 为△ABC 的费马点,此时PA+PB+PC 的值为△ABC 的费马距离.②如图(B),若四边形ABCD 的四个顶点在同一圆上,则有AB·CD+BC·DA=AC·BD.此为托勒密定理.(2)知识迁移:①请你利用托勒密定理,解决如下问题:如图(C),已知点P 为等边△ABC 外接圆的B C上任意一点.求证:PB+PC=PA.②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C 均小于120°)的费马点和费马距离的方法:第一步:如图(D),在△ABC 的外部以BC 为边长作等边△BCD 及其外接圆;第二步:在B C上任取一点P′,连结P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+;第三步:请你根据(1)①中定义,在图(D)中找出△ABC 的费马点P,并请指出线段的长度即为△ABC 的费马距离.(3)知识应用:2010 年4 月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难,为解决老百姓的饮水问题,解放军某部来到云南某地打井取水.已知三村庄A、B、C 构成了如图(E)所示的△ABC(其中∠A、∠B、∠C 均小于120°),现选取一点P 打水井,使从水井P 到三村庄A、B、C 所铺设的输水管总长度最小,求输水管总长度的最小值.AB 2 +BD 2 32 + 42 简解:(2)①证明:由托勒密定理可知 PB ·AC +PC ·AB =PA ·BC∵△ABC 是等边三角形∴ AB =AC =BC∴PB +PC =PA②P ′D AD(3)解:如图,以 BC 为边长在△ABC 的外部作等边△BCD ,连接 AD ,则知线段 AD 的长即为△ABC 的费马距离.∵△BCD 为等边三角形,BC =4,∴∠CBD =60°,BD =BC =4.∵∠ABC =30°, ∴∠ABD =90°.在 Rt △ABD 中,∵AB =3,BD =4∴AD = = =5(km )∴从水井 P 到三村庄 A 、B 、C 所铺设的输水管总长度的最小值为 5km.点评:此题集阅读理解、创新探究、实际应用于一体,题型新颖别致,综合考查自主探究、创新应用能力,是一道不可多得的好题.命题者设置成递进式问题,后续问题的思路获取、求解都靠对上一结论的解读、利用,这也是近年“课题学习”考查的一大风向,值得重视.如果说例 1 只是以“费马点”为课题学习的素材进行了考查,为了帮助同学们更好的理解三角形的费马点,我们补充几点:(1) 平面内一点 P 到△ABC 三顶点的之和为 PA+PB+PC ,当点 P 为费马点时,距离之和最小.特殊三角形中:(2) 三内角皆小于 120°的三角形,分别以 AB ,BC ,CA ,为边,向三角形外侧做正三角形 ABC 1,ACB 1,BCA 1,然后连接 AA 1,BB 1,CC 1,则三线交于一点 P ,则点 P 就是所求的费马点.(3) 若三角形有一内角大于或等于 120 度,则此钝角的顶点就是所求.(4)当△ABC 为等边三角形时,此时外心与费马点重合.可见,永州卷这道考题对于费马点只是以课题学习为问题载体,考得比较直截了当;巧合的是 2010 年福建宁德一道考题对这个知识考查显得隐蔽了,请看:例 2 如图,四边形 ABCD 是正方形,△ABE 是等边三角形,M 为对角线 BD (不含 B 点)上任意一点,将 BM 绕点 B 逆时针旋转 60°得到 BN ,连接 EN 、AM 、CM .⑴ 求证:△AMB ➴△ENB ;⑵ ①当 M 点在何处时,AM +CM 的值最小;②当 M 点在何处时,AM +BM +CM 的值最小,并说明理由;⑶ 当 AM +BM +CM 的最小值为 1时,求正方形的边长.A DEB C 3 NM3 2 2 思路探求:⑴略;⑵ ①要使 AM +CM 的值最小,根据“两点之间线段最短”,需设法将 AM +CM 转化为一条线段, 连接 AC 即可获取;②要使 AM +BM +CM 的值最小,由例 3 积累的知识经验:点 M 应该是△ABC 的费马点.由例 3 中(2)的求解示范,只要连接 CE 即可获得 CE 为 AM +BM +CM 的值最小.这样获到 M 点至少帮助我们在思路获取上提高了效率.理由说明供助于第(1)问的全等获得 BM=BN ,将三条线段转化到 CE 上去,问题化为两点之间线段最短.⑶根据题意,添加辅助线,构造直角三角形,过 E 点作 EF ⊥BC 交 CB 的延长线于 F . 设正方形 的边长为 x ,则 BF,EF = x .在 Rt △EFC 中,由勾股定理得( x )2+( 3 x +x )2= (+ 1)2, 2 2 2 2 解得即可.简答:⑴略;⑵①当 M 点落在 BD 的中点时,AM +CM 的值最小.②如图,连接 CE ,当 M 点位于 BD 与 CE 的交点处时,A D AM +BM +CM 的值最小.理由如下:连接 MN.由⑴知,△AMB ➴△ENB ,∴AM =EN .∵∠MBN =60°,MB =NB ,∴△BMN 是等边三角形.∴BM =MN .∴AM +BM +CM =EN +MN +CM .F B C 根据“两点之间线段最短”,得 EN +MN +CM =EC 最短∴当 M 点位于 BD 与 CE 的交点处时,AM +BM +CM 的值最小,即等于 EC 的长.⑶过 E 点作 EF ⊥BC 交 CB 的延长线于 F ,∴∠EBF =90°-60°=30°. 设正方形的边长为 x ,则 BF = 3x ,EF = x . 2 2在 Rt △EFC 中,∵EF 2+FC 2=EC 2,∴( x )2x +x )2= ( + 1)2. 2 2 解得,x = (舍去负值).∴正方形的边长为 .点评:本题中“AM +BM +CM 的值最小”如果没有费马点的知识积累,会在探究点 M 的位置上花费不少时间,这对紧张的考试来说,势必造成“隐性失分”. 3 E N M。
2024年中考数学几何模型之动点最值之费马点模型(讲+练)(原卷版[001]
![2024年中考数学几何模型之动点最值之费马点模型(讲+练)(原卷版[001]](https://img.taocdn.com/s3/m/f2f8ba4cbfd5b9f3f90f76c66137ee06eef94e7f.png)
专题12 动点最值之费马点模型费马点模型:如图,在△ABC内部找到一点P,使得PA+PB+PC的值最小.当点P满足∠APB=∠BPC=∠CPA=120º,则PA+PB+PC的值最小,P点称为三角形的费马点.特别地,△ABC中,最大的角要小于120º,若最大的角大于或等于120º,此时费马点就是最大角的顶点A(这种情况一般不考,通常三角形的最大顶角都小于120°)费马点的性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值解法:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值证明过程:将△APC边以A为顶点逆时针旋转60°,得到AQE,连接PQ,则△APQ为等边三角形,PA=PQ。
即PA+PB+PC=PQ+PB+PC,当B、P、Q、E四点共线时取得最小值BE例题1. 已知:△ABC是锐角三角形,G是三角形内一点。
△AGC=△AGB=△BGC=120°.求证:GA+GB+GC的值最小.例题2. 已知正方形ABCD 内一动点E 到A 、B 、C 26求正方形的边长.【变式训练1】已知点P 是△ABC 内一点,且它到三角形的三个顶点距离之和最小,则P 点叫△ABC 的费马点。
已经证明:在三个内角均小于120°的△ABC 中,当∠APB =∠APC =∠BPC =120°时,P 就是△ABC 的费马点。
若点P 的等腰直角三角形DEF 的费马点,则PD +PE +PF = .【变式训练2】如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.【变式训练3】如图,P 是锐角△ABC 所在平面上一点,如果∠APB =∠BPC =∠CPA =120°,则点P 就叫做△ABC 费马点。
中考中的费马点详解加练习

皮耶·德·费马(Pierre de Fermat)是一个17世纪的法国律师,也是一位业余数学家。
之所以称业余,是由于皮耶·德·费马具有律师的全职工作。
他的姓氏根据法文与英文实际发音也常译为“费尔玛”(注意“玛”字)。
费马最后定理在中国习惯称为费马大定理,西方数学界原名“最后”的意思是:其它猜想都证实了,这是最后一个。
著名的数学史学家贝尔(E. T. Bell)在20世纪初所撰写的著作中,称皮耶·德·费马为”业余数学家之王。
“贝尔深信,费马比皮耶·德·费马同时代的大多数专业数学家更有成就,然而皮耶·德·费马并未在其他方面另有成就,本人也渐渐退出人们的视野,考虑到17世纪是杰出数学家活跃的世纪,因而贝尔认为费马是17世纪数学家中最多产的明星。
费马点问题最早是由法国数学家皮埃尔·德·费马在一封写给意大利数学家埃万杰利斯塔·托里拆利(气压计的发明者)的信中提出的。
托里拆利最早解决了这个问题,而19世纪的数学家斯坦纳重新发现了这个问题,并系统地进行了推广,因此这个点也称为托里拆利点或斯坦纳点,相关的问题也被称作费马-托里拆利-斯坦纳问题。
这一问题的解决极大推动了联合数学的发展,在近代数学史上具有里程碑式的意义。
“费马点”是指位于三角形内且到三角形三个顶点距离之和最短的点。
若给定一个三角形△ABC的话,从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和比从其它点算起的都要小。
这个特殊点对于每个给定的三角形都只有一个。
1.若三角形3个内角均小于120°,那么3条距离连线正好三等分费马点所在的周角,即该点所对三角形三边的X角相等,均为120°。
所以三角形的费马点也称为三角形的等角中心。
2.若三角形有一内角大于等于120°,则此钝角的顶点就是距离和最小的点。
费马点与中考试题

识别“费马点”思路快突破例1 探究问题:(1)阅读理解:①如图(A),在已知△ABC所在平面上存在一点P,使它到三角形顶点的距离之和最小,则称点P为△ABC的费马点,此时P A+PB+PC的值为△ABC的费马距离.②如图(B),若四边形ABCD的四个顶点在同一圆上,则有AB·CD+BC·DA=AC·BD.此为托勒密定理.(2)知识迁移:①请你利用托勒密定理,解决如下问题:如图(C),已知点P为等边△ABC外接圆的»BC上任意一点.求证:PB+PC=P A.②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120°)的费马点和费马距离的方法:第一步:如图(D),在△ABC的外部以BC为边长作等边△BCD及其外接圆;第二步:在»BC上任取一点P′,连结P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+;第三步:请你根据(1)①中定义,在图(D)中找出△ABC的费马点P,并请指出线段的长度即为△ABC的费马距离.(3)知识应用:2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难,为解决老百姓的饮水问题,解放军某部来到云南某地打井取水.已知三村庄A、B、C构成了如图(E)所示的△ABC(其中∠A、∠B、∠C均小于120°),现选取一点P打水井,使从水井P到三村庄A、B、C所铺设的输水管总长度最小,求输水管总长度的最小值.(1)平面内一点P到△ABC三顶点的之和为PA+PB+PC,当点P为费马点时,距离之和最小.特殊三角形中:(2)三内角皆小于120°的三角形,分别以AB,BC,CA,为边,向三角形外侧做正三角形ABC1,ACB1,BCA1,然后连接AA1,BB1,CC1,则三线交于一点P,则点P就是所求的费马点.(3)若三角形有一内角大于或等于120度,则此钝角的顶点就是所求.(4)当△ABC为等边三角形时,此时外心与费马点重合.可见,永州卷这道考题对于费马点只是以课题学习为问题载体,考得比较直截了当;巧合的是例2 如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.⑴求证:△AMB≌△ENB;⑵①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;3 时,求正方形的边长.⑶当AM+BM+CM的最小值为1A DB C思路探求:⑴略;⑵ ①要使AM +CM 的值最小,根据“两点之间线段最短”,需设法将AM +CM 转化为一条线段,连接AC 即可获取;②要使AM +BM +CM 的值最小,由例3积累的知识经验:点M 应该是△ABC 的费马点.由例3中(2)的求解示范,只要连接CE 即可获得CE 为AM +BM +CM 的值最小.这样获到M 点至少帮助我们在思路获取上提高了效率.理由说明供助于第(1)问的全等获得BM=BN ,将三条线段转化到CE 上去,问题化为两点之间线段最短.⑶根据题意,添加辅助线,构造直角三角形,过E 点作EF ⊥BC 交CB 的延长线于F . 设正方形的边长为x ,则BF =23x ,EF =2x .在Rt △EFC 中,由勾股定理得(2x )2+(23x +x )2=()213+,解得即可.简答:⑴略;⑵①当M 点落在BD 的中点时,AM +CM 的值最小.②如图,连接CE ,当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小.理由如下:连接MN.由⑴知,△AMB ≌△ENB∴AM =EN .∵∠MBN =60°,MB =NB ,∴△BMN 是等边三角形.∴BM =MN .∴AM +BM +CM =EN +MN +CM .根据“两点之间线段最短”,得EN +MN +CM =EC 最短∴当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小,即等于EC 的长.⑶过E 点作EF ⊥BC 交CB 的延长线于F ,∴∠EBF =90°-60°=30°.设正方形的边长为x ,则BF =23x ,EF =2x . 在Rt △EFC 中,∵EF 2+FC 2=EC 2,∴(2x )2+(23x +x )2=()213+. 解得,x =2(舍去负值).∴正方形的边长为2.F A D B C点评:本题中“AM+BM+CM的值最小”如果没有费马点的知识积累,会在探究点M的位置上花费不少时间,这对紧张的考试来说,势必造成“隐性失分”.。
费马点与中考试题

“费马点”与中考试题费尔马,法国业余数学家,拥有业余数学之王的称号,他是解析几何的发明者之一.费马点——就是到三角形的三个顶点的距离之和最小的点.费尔马的结论:对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点,对于有一个角超过120°的三角形,费马点就是这个内角的顶点.△三个顶点的距离之和P A+PB+PC最小?这就下面简单说明如何找点P使它到ABC是所谓的费尔马问题.图1解析:如图1,把△APC绕A点逆时针旋转60°得到△AP′C′,连接PP′.则△APP′为等边三角形,AP= PP′,P′C′=PC,所以P A+PB+PC= PP′+ PB+ P′C′.点C′可看成是线段AC绕A点逆时针旋转60°而得的定点,BC′为定长,所以当B、P、P′、C′四点在同一直线上时,P A+PB+PC最小.这时∠BP A=180°-∠APP′=180°-60°=120°,∠APC=∠A P′C′=180°-∠AP′P=180°-60°=120°,∠BPC=360°-∠BP A-∠APC=360°-120°-120°=120°△的每一个内角都小于120°时,所求的点P对三角形每边的张角都是因此,当ABC120°,可在AB、BC边上分别作120°的弓形弧,两弧在三角形内的交点就是P点;当有一内角大于或等于120°时,所求的P点就是钝角的顶点.费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.本文列举近年“费马点”走进中考试卷的实例,供同学们学习参考.例1 (2008年广东中考题)已知正方形ABCD内一动点E到A、B、C三点的距离26图2 图3 分析:连接AC ,发现点E 到A 、B 、C 三点的距离之和就是到ABC △三个顶点的距离之和,这实际是费尔马问题的变形,只是背景不同.解 如图2,连接AC ,把△AEC 绕点C 顺时针旋转60°,得到△GFC ,连接EF 、BG 、A G ,可知△EFC 、△AGC 都是等边三角形,则EF =CE .又FG =AE ,∴AE +BE +CE = BE +EF +FG (图4).∵ 点B 、点G 为定点(G 为点A 绕C 点顺时针旋转60°所得).∴ 线段BG 即为点E 到A 、B 、C 三点的距离之和的最小值,此时E 、F 两点都在BG 上(图3).设正方形的边长为a ,那么BO =CO 2,GC 2a , GO 6. ∴ BG=BO +GO =22+62a . ∵ 点E 到A 、B 、C 26∴ 22a 6a 26a =2. 注 本题旋转△AEB 、△BEC 也都可以,但都必须绕着定点旋转,读者不妨一试. 例2 (2009年北京中考题) 如图4,在平面直角坐标系xOy 中,△ABC 三个顶点的坐标分别为()6,0A -,()6,0B ,(0,43C ,延长AC 到点D , 使CD =12AC ,过点D 作DE ∥AB 交BC 的延长线于点E .(1)求D 点的坐标;(2)作C 点关于直线DE 的对称点F ,分别连结DF 、EF ,若过B 点的直线y kx b =+将四边形CDFE 分成周长相等的两个四边形,确定此直线的解析式;(3)设G 为y 轴上一点,点P 从直线y kx b =+与y 轴的交点出发,先沿y 轴到达G 点,再沿GA 到达A 点,若P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定G 点的位置,使P 点按照上述要求到达A 点所用的时间最短.分析和解:(1)D 点的坐标(3,(过程略).(2) 直线BM的解析式为y =+.图4(3)如何确定点G 的位置是本题的难点也是关健所在.设Q 点为y 轴上一点,P 在y 轴上运动的速度为v ,则P 沿M →Q →A 运动的时间为2MQ AQ v v +,使P 点到达A 点所用的时间最短,就是12MQ +AQ 最小,或MQ +2AQ 最小. 解法1 ∵ BQ =AQ , ∴MQ +2AQ 最小就是MQ +AQ +BQ 最小,就是在直线MO 上找点G 使他到A 、B 、M 三点的距离和最小.至此,再次发现这又是一个费尔马问题的变形,注意到题目中等边三角形的信息,考虑作旋转变换.把△MQB 绕点B 顺时针旋转60°,得到△M ′Q ′B ,连接QQ ′、MM ′(图5),可知△QQ ′B 、△MM ′B 都是等边三角形,则QQ ′=BQ .又M ′Q ′=MQ ,∴MQ +AQ +BQ = M ′Q ′+ QQ ′+AQ .∵点A 、M ′为定点,所以当Q 、Q ′两点在线段A M ′上时,MQ +AQ +BQ 最小.由条件可证明Q ′点总在AM ′上,所以A M ′与OM 的交点就是所要的G 点(图6).可证OG =12MG .图5 图6 图7解法2 考虑12MQ+AQ最小,过Q作BM的垂线交BM于K,由OB=6,OM=63,可得∠BMO=30°,所以QK=12 MQ.要使12MQ+AQ最小,只需使AQ+QK最小,根据“垂线段最短”,可推出当点A、Q、K在一条直线上时,AQ+QK最小,并且此时的QK垂直于BM,此时的点Q即为所求的点G(图7).过A点作AH⊥BM于H,则AH与y轴的交点为所求的G点.由OB=6,OM=63,可得∠OBM=60°,∴∠BAH=30°在Rt△OAG中,OG=AO·tan∠BAH=23∴G点的坐标为(0,23)(G点为线段OC的中点).例3 (2009年湖州中考题)若点P 为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°, 则点P叫做△ABC的费马点.(1)若P为锐角△ABC的费马点,且∠ABC=60°,P A=3,PC=4, 则PB的值为;(2)如图8,在锐角△ABC的外侧作等边△ACB′,连结BB′.求证:BB′过△ABC的费马点P,且BB′=P A+PB+PC.图8解:(1)利用相似三角形可求PB的值为3(2)设点P为锐角△ABC的费马点,即∠APB=∠BPC=∠CP A=120°如图8,把△ACP绕点C顺时针旋转60°到△B′CE,连结PE,则△EPC为正三角形.∵∠B′EC = ∠APC =120°,∠PEC=60°∴∠B′EC+∠PEC=180°即P、E、B′三点在同一直线上∵∠BPC=120°,∠CPE=60°,∴∠BPC +∠CPE =180°,即B、P、E 三点在同一直线上∴B、P、E、B′四点在同一直线上,即BB′过△ABC的费马点P.又PE=PC,B′E= P A,∴BB′=E B′+PB+PE=P A+PB+PC.注通过旋转变换,可以改变线段的位置,优化图形的结构.在使用这一方法解题时需注意图形旋转变换的基础,即存在相等的线段,一般地,当题目出现等腰三角形(等边三角形)、正方形条件时,可将图形作旋转60°或90°的几何变换,将不规则图形变为规则图形,或将分散的条件集中在一起,以便挖掘隐含条件,使问题得以解决.费尔马问题是个有趣的数学问题,这些问题常常可通过旋转变换来解决.。
专题40中考最值难点突破费马点问题(原卷版)

专题40 中考最值难点突破费马点问题(原卷版)模块一典例剖析+针对训练费马点问题解题技巧:旋转变换.类型一费马点模型典例1(2020秋•仓山区校级期中)如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点,此时P A+PB+PC的和最小,称为△ABC的费马距离.(1)若点P是等边三角形三条高的交点,点P(填是或不是)该三角形的费马点.(2)如图(2),分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD相交于P点.求证:P点为△ABC的费马点.(3)若图(2)中,AB=5,AC=4,BC=a,BD=b,则△ABC的费马距离=.针对训练1.(2021春•滨海县期中)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B 点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)当M点在何处时,2AM的值最小,并说明理由;(3)当M点在何处时,2AM+BM的值最小,并说明理由.2.(2021春•历下区期末)【操作发现】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.①请按要求画图:将ABC绕点A按顺时针方向旋转90°,点B的对应点为B',点C的对应点为C′;②连接BB′,此时∠ABB′=°;【问题解决】在某次数学兴趣小组活动中,小明同学遇到了如下问题:(2)如图2,在等边△ABC中,点P在内部,且P A=3,PC=4,∠APC=150°,求PB的长.经过同学们的观察、分析、思考、交流,对上述问题形成了如下想法:将△APC绕点A按顺时针方向旋转60°,得到△ABP′,连接PP′,寻找P A、PB、PC三边之间的数量关系.…请参考他们的想法,完成该问题的解答过程;【学以致用】(3)如图3,在等腰直角△ABC中,∠ACB=90°,P为△ABC内一点,且P A=5,PC=2√2,∠BPC =135°,求PB;【思维拓展】(4)注意:从以下①②中,你任意选择一道题解答即可.①等腰直角△ABC中,∠ACB=90°,P为△ABC内部一点,若BC=4,则AP+BP+CP的最小值=;②如图4,若点P是正方形ABCD外一点,P A=3,PB=√3,PC=√15,求∠APB的度数.3.(2019春•金水区校级期中)在△ABC中,∠ACB=90°,点P为△ABC内一点.(1)如图1,连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.如果BP⊥CE,BP=3,AB=6,则CE=.(2)如图2,连接P A,PB,PC,当AC=BC=8时,求P A+PB+PC的最小值.类型二费马点模型变式典例2(2021春•碑林区校级期中)[问题发现]如图①,在△OAB中,OB=3,若将△OAB绕点O逆时针旋转120°得△OA′B′,连接BB'.则BB'=.[问题探究]如图②,已知△ABC是边长为4√3的等边三角形,以BC为边向外作等边△BCD,P为△ABC 内一点,将线段CP绕点C逆时针旋转60°,P的对应点为Q.求P A+PB+PC的最小值.[实际应用]如图③,在长方形ABCD中,其中AB=600,AD=800,点P是长方形内一动点,且S△P AD =2S△PBC,点Q为△ADP内的任意一点,是否存在一点P和一点Q,使得AQ+DQ+PQ有最小值?若存在,请求出这个最小值,并求出此时PQ的长度,若不存在,请说明理由.针对训练1.(2021•雁塔区校级模拟)【问题情境】如图1,在△ABC中,∠A=120°,AB=AC,BC=5√3,则△ABC的外接圆的半径值为.【问题解决】如图2,点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.【问题解决】如图3,正方形ABCD是一个边长为3√3cm的隔离区域设计图,CE为大门,点E在边BC上,CE=√3cm,点P是正方形ABCD内设立的一个活动岗哨,到B、E的张角为120°,即∠BPE=120°,点A、D为另两个固定岗哨.现需在隔离区域内部设置一个补水供给点Q,使得Q到A、D、P三个岗哨的距离和最小,试求QA+QD+QP的最小值.(保留根号或结果精确到1cm,参考数据√3≈1.7,10.52=110.25).模块二2023中考押题预测一.选择题1.(2017秋•义乌市月考)已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermatpoint).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为√2的等腰直角三角形DEF的费马点,则PD+PE+PF=()A.2√3B.1+√3C.6D.3√32.(2022春•山亭区期中)如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.40°B.30°C.50°D.65°二.填空题3.(2019秋•开福区校级月考)法国数学家费马提出:在△ABC内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时P A+PB+PC的值为费马距离.经研究发现:在锐角△ABC中,费马点P满足∠APB=∠BPC=∠CP A=120°,如图,点P为锐角△ABC的费马点,且P A=3,PC=4,∠ABC=60°,则费马距离为.4.(2019秋•梁溪区期末)如图,已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为1+√3,则这个正方形的边长为.5.(2021•丹东)已知:到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果△ABC是锐角(或直角)三角形,则其费马点P是三角形内一点,且满足∠APB=∠BPC=∠CP A=120°.(例如:等边三角形的费马点是其三条高的交点).若AB=AC=√7,BC=2√3,P为△ABC的费马点,则P A+PB+PC =;若AB=2√3,BC=2,AC=4,P为△ABC的费马点,则P A+PB+PC=.6.(2022秋•洪山区校级期中)如图,以等边△ABC的一边BC为底边作等腰△BCD,已知AB=3,CD=BD=√3,且∠BDC=120°,在△BCD内有一动点P,则PB+PC+PD的最小值为.7.(2022秋•大冶市期末)如图,D是等边三角形ABC外一点,连接AD,BD,CD,已知BD=8,CD=3,则当线段AD的长度最小时,①∠BDC=;②AD的最小值是.三.解答题8.(2009•湖州)自选题:若P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点.(1)若点P为锐角△ABC的费马点,且∠ABC=60°,P A=3,PC=4,则PB的值为;(2)如图,在锐角△ABC外侧作等边△ACB′连接BB′.求证:BB′过△ABC的费马点P,且BB′=P A+PB+PC.9.问题探究:(1)如图1,已知,在四边形ABCD中,AB=BC,AD=DC,则对角线AC、BD的位置关系是.(2)如图2,已知,在△ABC中,AC=BC,∠ACB=90°.△ABC内一动点E到A、B、C三点的距离之和的最小值为2,求AC的长.问题解决:(3)如图3,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣6,0),B(6,0),C(0,4√3),延长AC至点D,使CD=12AC,过点D作DE⊥y轴于点E.设G为y轴上一点,点P从点E出发,先沿y轴到达G点,再沿GA到达A点.若点P在直线GA上运动速度为定值v,在y轴上运动速度为2v,试确定点G的位置,使P点按照上述要求到达A点所用的时间最短,并求此时点G的坐标.10.(2017•利辛县一模)如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点.(1)若点P是等边三角形三条中线的交点,点P(填是或不是)该三角形的费马点.(2)如果点P为锐角△ABC的费马点,且∠ABC=60°.求证:△ABP∽△BCP;(3)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD交于P点.如图(2)①求∠CPD的度数;②求证:P点为△ABC的费马点.12.(2022春•兰溪市校级月考)定义:在一个等腰三角形底边的高线上所有点中,到三角形三个顶点距离之和最小的点叫做这个等腰三角形的“近点”,“近点”到三个顶点距离之和叫做这个等腰三角形的“最近值”.【基础巩固】(1)如图1,在等腰Rt△ABC中,∠BAC=90°,AD为BC边上的高,已知AD上一点E满足∠DEC =60°,AC=4√6,求AE+BE+CE=;【尝试应用】(2)如图2,等边三角形ABC边长为4√3,E为高线AD上的点,将三角形AEC绕点A逆时针旋转60°得到三角形AFG,连接EF,请你在此基础上继续探究求出等边三角形ABC的“最近值”;【拓展提高】(3)如图3,在菱形ABCD中,过AB的中点E作AB垂线交CD的延长线于点F,连接AC、DB,已知∠BDA=75°,AB=6,求三角形AFB“最近值”的平方.。
中考复习之线段和差最值之费马点问题-附练习题含参考答案
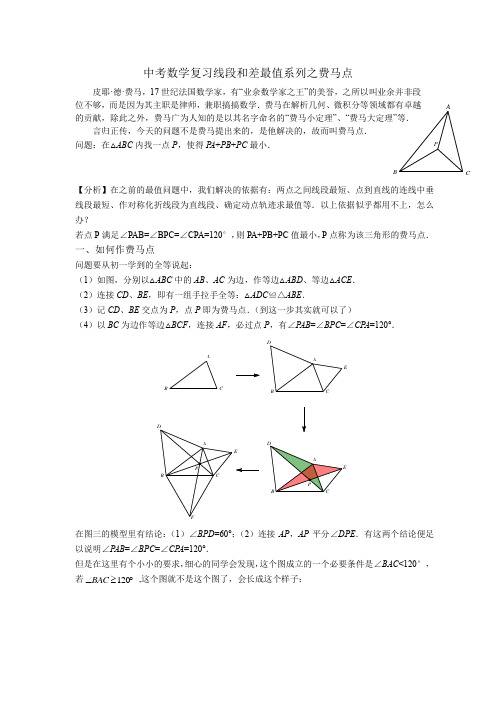
ABCP中考数学复习线段和差最值系列之费马点皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.言归正传,今天的问题不是费马提出来的,是他解决的,故而叫费马点. 问题:在△ABC 内找一点P ,使得P A +PB +PC 最小.【分析】在之前的最值问题中,我们解决的依据有:两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等.以上依据似乎都用不上,怎么办?若点P 满足∠PAB=∠BPC=∠CPA=120°,则PA+PB+PC 值最小,P 点称为该三角形的费马点.一、如何作费马点问题要从初一学到的全等说起:(1)如图,分别以△ABC 中的AB 、AC 为边,作等边△ABD 、等边△ACE . (2)连接CD 、BE ,即有一组手拉手全等:△ADC ≌△ABE .(3)记CD 、BE 交点为P ,点P 即为费马点.(到这一步其实就可以了)(4)以BC 为边作等边△BCF ,连接AF ,必过点P ,有∠P AB =∠BPC =∠CP A =120°.在图三的模型里有结论:(1)∠BPD =60°;(2)连接AP ,AP 平分∠DPE .有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°.但是在这里有个小小的要求,细心的同学会发现,这个图成立的一个必要条件是∠BAC <120°,若120BAC ∠≥︒ ,这个图就不是这个图了,会长成这个样子:EB ACAB CDE此时CD 与BE 交点P 点还是我们的费马点吗?显然这时候就不是了,显然P 点到A 、B 、C 距离之和大于A 点到A 、B 、C 距离之和.所以,是的,你想得没错,此时三角形的费马点就是A 点!当然这种情况不会考的,就不多说了.二、为什么是这个点为什么P 点满足∠P AB =∠BPC =∠CP A =120°,P A +PB +PC 值就会最小呢?归根结底,还是要重组这里3条线段:P A 、PB 、PC 的位置,而重组的方法是构造旋转!在上图3中,如下有△ADC ≌△ABE ,可得:CD =BE .类似的手拉手,在图4中有3组,可得:AF =BE =CD .巧的,它们仨的长度居然一样长!更巧的是,其长度便是我们要求的P A +PB +PC 的最小值,这一点是可以猜想得到的,毕竟最小值这个结果,应该也是个特别的值! 接下来才是真正的证明:考虑到∠APB =120°,∴∠APE =60°,则可以AP 为边,在PE 边取点Q 使得PQ =AP ,则△APQ 是等边三角形.△APQ 、△ACE 均为等边三角形,且共顶点A ,故△APC ≌△AQE ,PC =QE . 以上两步分别转化P A =PQ ,PC =QE ,故P A +PB +PC =PB +PQ +QE =BE .没有对比就没有差别,我们换个P 点位置,如下右图,同样可以构造等边△APQ ,同样有△APC ≌△AQE ,转化P A =PQ ,PC =QE ,显然,P A +PB +PC =PB +PQ +QE >BE .还剩下第3个问题!如果说费马点以前还算是课外的拓展内容,那现在,已经有人把它搬上了中考舞台!【中考再现】问题背景:如图1,将△ABC 绕点A 逆时针旋转60°得到△ADE ,DE 与BC 交于点P ,可推出结论:P A +PC =PE .问题解决:如图2,在△MNG 中,MN =6,∠M =75°,MG=O 是△MNG 内一点,则点O 到△MNG 三个顶点的距离和的最小值是______.【分析】本题的问题背景实际上是提示了解题思路,构造60°的旋转,当然如果已经了解了费马点问题,直接来解决就好了!如图,以MG 为边作等边△MGH ,连接NH ,则NH 的值即为所求的点O 到△MNG 三个顶点的距离和的最小值.(此处不再证明)过点H 作HQ ⊥NM 交NM 延长线于Q 点,根据∠NMG =75°,∠GMH =60°,可得∠HMQ =45°,∴△MHQ 是等腰直角三角形, ∴MQ =HQ =4,∴NH== 练习题1.如图,在△ABC 中,△ACB=90°,AB=AC=1,P 是△ABC 内一点,求P A +PB +PC 的最小值.2. 如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.NG图2图1ABCD EPHGN M464Q HGN MABCDME3.如图,矩形ABCD中,AB=10,BC=15,现在要找两点E、F,则EA+EB+EF+FC+FD的最小值为__________4.如图,等腰Rt∆ABC中,AB=4,P为∆ABC内部一点,则PA+PB+PC的最小值为_______5.如图,∆ABC中,AB=4,,∠ABC=75°,P为∆ABC内的一个动点,连接PA、PB、PC,则PA+PB+PC的最小值为________6.如图,P为正方形ABCD对角线BD上一动点,若AB=2,则PA+PB+PC的最小值为______7.在Rt∆ABC中,∠ACB=90°,AC=1,,点O为Rt∆ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=_______8.如图,在四边形ABCD中,∠B=60°,AB=BC=3,AD=4,∠BAD=90°,点P是四边形内部一点,则PA+PB+PD的最小值是______9.如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,,则PA+PB+PC 的最小值为_______10.如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则PA+PB+PD的最小值为__________11.已知,在∆ABC中,∠ACB=30°点P是ABC内一动点,则PA+PB+PC的最小值为__________12.如图,设点P到等边三角形ABC两顶点A、B的距离分别为2则PC的最大值为______13.如图,设点P到正方形ABCD两顶点A、D的距离为2PC的最大值为________14.如图,设点P到正方形ABCD两顶点A、D的距离为2则PO的最大值为_________.15.如图,在Rt∆ABC中,∠BAC=90⁰,AB=AC,点D是BC边上一动点,连接AD,把AD 绕点A逆时针旋转90⁰,得到AE,连接CE、DE,点F是DE的中点,连接CF问题:在点D运动的过程中,在线段AD上存在一点P,使PA+PB+PC的值最小,当PA+PB+PC 取最小值时,AP的长为m,用含有m的式子表示CE的长.参考答案1.7.8.7 9.3 10. 12.2+13.2+1 15.32m +。
2024成都中考数学二轮复习专题 三条线段最值专项训练(含答案)

2024成都中考数学二轮复习专题三条线段最值专项训练(学生版)目标层级图课中讲解一.费马点问题内容讲解费马,法国业余数学家,拥有业余数学之王的称号,他是解析几何的发明者之一,费马点——就是到三角形的三个顶点的距离之和最小的点。
费尔马的结论:对于一个各角不超过120︒的三角形,费马点是对各边的张角都是120︒的点,对于有一个角超过120︒的三角形,费马点就是这个内角的顶点。
下面简单说明如何找点P 使它到ABC ∆三个顶点的距离之和PA PB PC ++最小?这就是所谓的费尔马问题。
解析:如图,把APC ∆绕A 点逆时针旋转60︒得到''AP C ∆,连接'PP ,则'APP ∆为等边三角形,'AP PP =,''P C PC =,所以'''PA PB PC PP PB P C ++=++。
点'C 可看成是线段AC 绕A 点逆时针旋转60︒而得的定点,'BC 为定长。
所以当''B P P C 、、、四点在同一直线上时,PA PB PC ++最小。
这时'180********BPA APP ∠=︒-∠=︒-︒=︒'''180********APC AP C AP P ∠=∠=︒-∠=︒-︒=︒360360*********BPC BPA APC ∠=︒-∠-∠=︒-︒-︒=︒因此,当ABC ∆的每一个内角都小于120︒时,所求的点P 对三角形每边的张角都是120︒,可在AB BC 、边上分别作120︒的弓形弧,两弧在三角形内的交点就是点P ;当有一内角大于或等于120︒时,所求的P 点就是钝角的顶点。
费马问题-告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换。
例1.如图,在Rt ABC ∆中,90C ∠=︒,1AC =,3BC =,点O 为Rt ABC ∆内一点,连接0A 、BO 、CO ,且120AOC COB BOA ∠=∠==︒,按下列要求画图(保留画图痕迹):以点B 为旋转中心,将AOB ∆绕点B 顺时针方向旋转60︒,得到△A O B ''(得到A 、O 的对应点分别为点A '、)O ',则A BC ∠'=,OA OB OC ++=.例2.在ABC ∆中,60BAC ∠=︒,23AB =,43AC =-,点P 为ABC ∆内一点,连接PA ,PB ,PC ,则PA PB PC ++的最小值为()A .231-B .23C .5D .53例3.如图①,四边形ABCD是正方形,ABE∆是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60︒得到BN,连接EN、AM、C M.(1)连结M N,BM N∆是等边三角形吗?为什么?(2)求证:AMB ENB∆≅∆;(3)①当M点在何处时,AM CM+的值最小;②如图②,当M点在何处时,AM BM CM++的值最小,请你画出图形,并说明理由.例4.阅读理解题(1)阅读理解:如图①,等边ABC∆内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求APB∠的大小.思路点拨:考虑到PA,PB,PC不在一个三角形中,采用转化与化归的数学思想,可以将ABP∆绕顶点A逆时针旋转60︒到ACP∆≅∆,这样,就可以利用全∆’处,此时ACP ABP等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出APB∠的度数.请你写出完整的解题过程.(2)变式拓展:请你利用第(1)题的解答思想方法,解答下面问题:已知如图②,ABC=,E、F为BC上的点且45∠=︒,EAF∆中,90CAB∠=︒,AB ACCF=,求EF的大小.BE=,45(3)能力提升:如图③,在Rt ABCABC∠=︒,点O为AC=,30∆中,90ACB∠=︒,1∠=∠=∠=︒,请直接写出AOC COB BOA∆内一点,连接AO,BO,CO,且120Rt ABC++=.OA OB OC++的值,即OA OB OC过关检测1.如图,在ABC ∆中,90ACB ∠=︒,点P 为ABC ∆内一点,连接PA 、PB 、PC ,当3AC =,6AB =时,则PA PB PC ++的最小值是.2.如图,已知等腰三角形ABC ,6CA CB cm ==,8AB cm =,点O 为ABC ∆内一点(点O 不在ABC ∆边界上)。
中考专题费马点讲义与练习

图4—11PC BA从“费马点”说起前言解题 题海战术 通性通法 过程与结果 内化 一、走近费马点 1.(浙教版数学八下P82)设计题 你听说过费马点吗?如图4—11,P 为△ABC 所在平面上一点。
如果∠APB=∠BPC=∠CPA=120°,则点P 就叫做费马点。
费马点有许多有趣并且有意义的性质,例如,平面内一点P 到△ABC 三顶点的距离之和为PA+PB+PC ,当点P 为费马点时,距离之和最小。
假设A,B,C 表示三个村庄,要选一处建车站,使车站到三个村庄的公路路程的和最短。
若不考虑其他因素,那么车站应建在费马点上。
请按下列步骤对费马点进行探究:(1) 查找有关资料,了解费马点被发现的历史背景;(2) 在特殊三角形中寻找并验证费马点。
例如,当△ABC 是等边三角形、等腰三角形或直角三角形时,费马点有哪些性质?(3) 把你的研究结果写成一篇小论文,并通过与同学交流来修改完善你的小论文。
2.(2009年浙江省湖州市中考题)若P 为ABC △所在平面上一点,且120APB BPC CPA ∠=∠=∠=°,则点P 叫做ABC △的费马点. (1)若点P 为锐角ABC △的费马点,且60ABC PA PC ∠===°,3,4,则PB 的值为________; (2)如图,在锐角ABC △外侧作等边ACB △′连结BB ′. 求证:BB ′过ABC △的费马点P ,且BB ′=PA PB PC ++.3.(2010年湖南省永州市中考数学试题)探究问题:(1)阅读理解:①如图(1),在已知△ABC 所在平面上存在一点P ,使它到三角形三顶点的距离之和最小,则称点P 为△ABC 的费马点,此时PA+PB+PC 的值为△ABC 的费马距离.②如图(2),若四边形ABCD 的四个顶点在同一圆上,则有AB ·CD+BC ·DA=AC ·BD ,此为托勒密定理.(2)知识迁移:HPDCBA①请你利用托勒密定理,解决如下问题:如图(3),已知点P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC=PA ②根据(2)①的结论,我们有如下探寻△ABC(其中∠A 、∠B 、∠C 均小于120度)的费 马点和费马距离的方法:第一步:如图(4)在△ABC 的外部以BC 为边长作等边△BCD 及其外接圆; 第二步:在弧BC 上任取一点'P ,连结'P A 、'P B 、'P C 、'P D易知''''('')'P A P B P C P A P B P C P A ++=++=+ ; 第三步:请你根据(1)①中定义,在图(4)中找出△ABC 的费马点P ,并请指出 线段 的长度即为△ABC 的费马距离(3)知识应用:2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难,为解决老百姓的饮水问题,解放军某部来到云南某地打井取水.已知三村庄A 、B,C 构成了如图(5)所示的△ABC(其中∠A 、∠B 、∠C 均小于120o),现选取一点P 打水井,使从水井P 到三村庄A 、B 、C 所铺设的 输水管总长度最小,求输水管总长度的最小值. 4.(2008年广东省中考题)已知正方形ABCD 内一动点E 到A,B,C 三点的距离之和的最小值为62+,求此正方形的边长。
(完整版)“费马点”与中考试题

“费马点”与中考试题费马,法国业余数学家,拥有业余数学之王的称号,他是解析几何的发明者之一. 费马点一一就是到三角形的三个顶点的距离之和最小的点. 费尔马的结论:对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点,对于有一个角超过120°的三角形,费马点就是这个内角的顶点.下面简单说明如何找点P使它到△ ABC三个顶点的距离之和PA+PB+PC最小?这就是所谓的费马问题.解析:如图1,把△ APC绕A点逆时针旋转60°得到△ APC',连接PP'.则厶APP为等边三角形,AP= PP P C = PC,所以PA+PB+PC= PP + PB+ PC'.点C'可看成是线段AC绕A点逆时针旋转60°而得的定点,BC为定长,所以当B、P、P、C '四点在同一直线上时,FA+PB+PC最小.这时/ BPA=180°- / APP =180°-60 °=120°,/ APC= / A P C =180°-Z AP P=180° -60 °=120°,/ BPC=360°-Z BPA- Z APC=360° -120。
-120 °=120°因此,当厶ABC的每一个内角都小于120。
时,所求的点P对三角形每边的张角都是120 °可在AB、BC边上分别作120 的弓形弧,两弧在三角形内的交点就是P点;当有一内角大于或等于120°时,所求的P点就是钝角的顶点.费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.本文列举近年“费马点”走进中考试卷的实例,供同学们学习参考.例1 (2008年广东中考题)已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为2 -.6,求此正方形的边长.分析:连接AC ,发现点E 到A 、B 、C 三点的距离之和就是到 △ ABC 三个顶点的距离 之和,这实际是费尔马问题的变形,只是背景不同.解 如图2,连接人6把厶AEC 绕点C 顺时针旋转60°得到△ GFC ,连接EF 、BG 、 AG ,可知△ EFC 、△ AGC 都是等边三角形,则 EF=CE .又 FG =AE ,••• AE+BE+CE = BE+EF+FG (图 4).•••点B 、点G 为定点(G 为点A 绕C 点顺时针旋转60°所得). •线段BG 即为点E 到A 、B 、C 三点的距离之和的最小值,此时 E 、F 两点都在BG上(图3).设正方形的边长为 a ,那么BG=BO+GO =』a +2点E 到A 、B 、C 三点的距离之和的最小值为.2,6 .注 本题旋转厶AEB 、△ BEC 也都可以,但都必须绕着定点旋转,读者不妨一试. 例2(2009年北京中考题) 如图4,在平面直角坐标系 xOy 中,△ ABC 三个顶点的坐标分别为A 6,0 , B 6,0 , C 0,4-. 3,延长AC 到点D,使CD=1 AC ,过点D 作2DE // AB 交BC 的延长线于点 E.(1)求D 点的坐标;BO=CO=GC=」2a , GO=「6,解得 a =2.(2)作C点关于直线DE的对称点F,分别连结DF、EF,若过B点的直线y kx b将四边形CDFE分成周长相等的两个四边形,确定此直线的解析式;(3)设G为y轴上一点,点P从直线y kx b与y轴的交点出发,先沿y轴到达G 点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短.分析和解:(1)D点的坐标(3, 3 )(过程略).(2)直线BM的解析式为y ,3x 6.3 (过程略).解法1 •/ BQ=AQ, ••• MQ + 2AQ最小就是MQ + AQ+ BQ最小,就是在直线MO上找点G使他到A、B、M三点的距离和最小•至此,再次发现这又是一个费尔马问题的变形,注意到题目中等边三角形的信息,考虑作旋转变换.把厶MQB绕点B顺时针旋转60。
中考数学试卷费马点

的位置关系是()A. 共线B. 共圆C. 共点D. 无规律2. 已知三角形ABC的边长分别为a、b、c,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()A. DE=EF=FDB. ∠ABC=∠DEFC. AB+BC+CA=DE+EF+FDD. ABC≌DEF3. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定不成立?()A. AB=ACB. ∠ABC=∠DEFC. DE=EF=FDD. ABC≌DEF4. 在三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()A. ∠ABC=∠DEFB. ∠ABD=∠BCDC. ∠ACF=∠BCED. ∠BAC=∠BCF5. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()A. AB=ACB. ∠ABC=∠DEFC. AB+BC+CA=DE+EF+FDD. ABC≌DEF二、填空题6. 在三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么点D、E、F 的位置关系是()7. 已知三角形ABC的边长分别为a、b、c,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()8. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定不成立?()9. 在三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()10. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()三、解答题点D、E、F在同一直线上。
12. (15分)已知三角形ABC的边长分别为a、b、c,点D、E、F分别满足AD=BD,BE=CE,CF=AF,求证:DE=EF=FD。
费马点问题(含答案)

费马点的问题定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
3. 费马点与3个顶点连成的线段是沟通3点的最短路线,容易理解,这个路线是唯一的。
我们称这一结果为最短路线原理。
性质:费马点有如下主要性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
3.费马点为三角形中能量最低点。
4.三力平衡时三力夹角皆为120°,所以费马点是三力平衡的点。
例1:已知:△ABH是等边三角形。
求证:GA+GB+GH最小证明:∵△ABH是等边三角形。
G是其重心。
∴∠AGH=∠AGB=∠BGH=120°。
以HB为边向右上方作等边三角形△DBH.以HG为边向右上方作等边三角形△GHP.∵ AH=BH=AB=12.∴∠AGH=120°, ∠HGP=60°.∴ A、G、P三点一线。
再连PD两点。
∵△ABH、△GHP和△BDH都是等边三角形,∠GHB=30°.∴∠PHD=30°,.在△HGB和△HPD中∵ HG=HP∠GHB=∠PHD;HB=HD;∴△HGB≌△HPD;(SAS)∴∠HPD=∠HGB=120°;∵∠HPG=60°.∴ G、P、D三点一线。
∴ AG=GP=PD,且同在一条直线上。
∵ GA+GH+GB=GA+GP+PD=AD.∴ G点是等边三角形内到三个顶点的距离之和最小的哪一点,费马点。
也就是重心。
例2:已知:△ABC是等腰三角形,G是三角形内一点。
∠AGC=∠AGB=∠BGC=120°。
求证:GA+GB+GC最小证明:将△BGC逆时针旋转60°,连GP,DB.则△HGB≌△HPD;∴∠CPD=∠CGB=120°,CG=CP,GB=PD, BC=DC,∠GCB=∠PCD.∵∠GCP=60°,∴∠BCD=60°,∴△GCP和△BCD都是等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精心整理
皮耶·德·费马(PierredeFermat)是一个17世纪的法国律师,也是一位业余数学家。
之所以称业余,是由于皮耶·德·费马具有律师的全职工作。
他的姓氏根据法文与英文实际发音也常译为“费尔玛”(注意“玛”
2若在≥120°的钝角三角形中,其顶点即是。
另外,当刚好120°,且三角形BCD为等边三角形时,有个结论:AD=AB+AC
我们拓展一道几何题,第二问对很多学生或者老师还是很酥爽的。
2011房山一摸2009石景山A
25.(本小题满分7分)
已知:等边三角形ABC
如图1,P为等边△ABC外一点,且∠BPC=120°.
试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
(2)如图2,P为等边△ABC内一点,且∠APD=120°.
25.
∠
A、
(1
(2
(3以及m 2013
24
AD
(2外
CF
①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°;
(3)如图2,在(2)的条件下,求证:PB+PC+PD=BE.
29.阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值。
他的方法是以点B
为旋转中心将△ABP逆时针旋转60°得到△A’BC,连接A’A,当点A落在A’C上时,此题可解(如图2).
(1)请你回答:AP的最大值是.
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把⊿ABP绕B点逆时针旋转60,得到'
'BP
A
. Array
①
②
2016
28.
(1
60
(2
2017年一月昌平
29.如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点
分别为点D,A,E,连接CE.
① 依题意,请在图2中补全图形;
② 如果BP ⊥CE ,BP =3,AB =6,求
CE 的长.
3
PB ,PC
得到△AMN ,那么就将PA+PB+PC CP 上时,此题可解.
3CP +PM +MN . 2017海淀2
α
.连
(11所示.APC (2)如图2,当α=120°时,请参考(1)中的方法,探究P A ,PB ,PC 满足的等量关系,并给出证明;
(3)P A ,PB ,PC 满足的等量关系为. 2016年顺义一摸
28.已知:在△ABC 中,∠BAC =60°. 图1B
图2图3
(1)如图1,若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC 绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP
①依题意补全图1;
②直接写出PB的长;
(2)如图2,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;(3)如图3,若AB=2AC,点P在△ABC内,且PA=3,PB=5,∠APC=120°,请直接写出PC的长.
26、如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
在矩形ABCD中,点P在矩形内,点Q在BC上,AD=5,AB=3,
求AP+DP+PQ的最小值。
