几何05_四下09_格点割补
高思导引-四年级第十九讲-格点与割补教师版

第19讲ﻩﻩ格点与割补内容概述明确格点多边形的概念,学会通过分割和添补的方法计算其面积;学会利用割补法计算不规则图形的面积;掌握格点多边形的面积计算公式.典型问题兴趣篇1.图19-l中相邻两格点问的距离均为1厘米.三个多边形的面积分别是多少平方厘米?答案:4平方厘米2平方厘米8平方厘米【分析】方法:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=0,L=10,则用粗线围成图形的面积为:(0+10÷2-1)×1=4(平方厘米)有N=0,L=10,则用粗线围成图形的面积为:(1+4÷2-1)×1=2(平方厘米)有N=5,L=8,则用粗线围成图形的面积为:(5+8÷2-1)×1=8(平方厘米)2.图19-2中相邻两格点问的距离均为l厘米.三个阴影图形的面积分别是多少平方厘米? 答案:5平方厘米5平方厘米0.5平方厘米【分析】方法:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=4,则用粗线围成图形的面积为:(4+4÷2-1)×1=5(平方厘米) 有N=4,L=4,则用粗线围成图形的面积为:(4+4÷2-1)×1=5(平方厘米)有N=0,L=3,则用粗线围成图形的面积为:(0+3÷2-1)×1=0.5(平方厘米)3.图19-3中每个小正方形的面积均为2平方厘米.阴影多边形的面积是多少平方厘米?答案:19平方厘米【分析】方法:交点组成了正方形格点,正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=7,L=17,则用粗线围成图形的面积为:(7+7÷2-1)×2=19(平方厘米)4.图19-4是一个三角形点阵,其中能连出的最小的等边三角形的面积为l平方厘米.三个多边形的面积分别为多少平方厘米?答案:6平方厘米6平方厘米14平方厘米【分析】方法:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=0,L=8,所以用粗线围成的图形的面积为:(0×2+8-2)×1=6(平方厘米).有N=2,L=4,所以用粗线围成的图形的面积为:(2×2+4-2)×1=6(平方厘米).有N=4,L=7,所以用粗线围成的图形的面积为:(4×2+7-2)×1=14(平方厘米).5.如图19-5所示,如果每个小等边三角形的面积都是1平方厘米.四边形ABCD和三角形EFG的面积分别是多少平方厘米?答案:20平方厘米10平方厘米【分析】方法:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).有N=4,L=4,所以用粗线围成的图形的面积为:(4×2+4-2)×1=10(平方厘米).6.图19-6中的数字分别表示对应线段的长度,试求这个多边形的面积.(单位:厘米)答案:32平方厘米【分析】3×2+2×4+(5-2)×(3+1+2)=327.如图19-7所示,在正方形A BCD 内部有一个长方形.EFGH .已知正方形A BCD的边长是6厘米,图中线段AE 、AH 都等于2厘米.求长方形EFGH 的面积.答案:16平方厘米【分析】先算正方形面积6×6=36 再算左上角和右下角三角形面积2×2÷2×2=4 后算左下角和右上角三角形面积4×4÷2×2=16 36-4-16=168.如图19-8所示,四边形ABCD 是长方形,长AD 等于7厘米,宽AB 等于5厘米,四边形C DEF 是平行四边形.如果BH 的长是3厘米,那么图中阴影部分面积是多少平方厘米?答案:25平方厘米【分析】 CDEF S 平行四边形=DC×BC=5×7=35,HC=BC-B H=7-3=4,所以CDH S =12×CD×HC=12×5×4=10. S 阴影=CDEF S 平行四边形-CDHS =35-10=25(平方厘米).9.如图19-9所示,大正方形的边长为10厘米.连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连.请问:图中阴影部分的面积总和等于多少平方厘米?答案:50平方厘米【分析】如下图,我们将大正方形中的所有图形分成A、B两种三角形.其中含有A形三角形8个,B形三角形16个,其中阴影部分含有A形三角形4个,B形三角形8个.方形面积的12,即为12×1所以,阴影部分面积恰好为大正0×10=50(平方厘米).10.在图19-10中,五个小正方形的边长都是2厘米,求三角形ABC的面积.答案:14平方厘米【分析】方法:转化为正方形格点,正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=3,L=3,则用粗线围成图形的面积为:(3+3÷2-1)×4=14(平方厘米)拓展篇1. 图19-11中相邻格点围成的最小正方形或正三角形的面积均为l平方厘米.这三个多边形的面积分别是多少平方厘米?答案:7.5平方厘米 6.5平方厘米9平方厘米【分析】方法:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=9,则用粗线围成图形的面积为:(4+9÷2-1)×1=7.5(平方厘米)有N=3,L=9,则用粗线围成图形的面积为:(3+9÷2-1)×1=6.5(平方厘米)有N=4,L=12,则用粗线围成图形的面积为:(4+12÷2-1)×1=9(平方厘米)2.(1)图19-12中每个小正方形的面积是2平方厘米.阴影部分面积是多少平方厘米?(2)图19-13中每个小正三角形的面积是4平方厘米.阴影部分面积是多少平方厘米? 答案:17平方厘米56平方厘米【分析】方法:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=3,L=13,则用粗线围成图形的面积为:(3+13÷2-1)×2=17(平方厘米)【分析】方法:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=8,所以用粗线围成的图形的面积为:(4×2+8-2)×4=56(平方厘米).3.图19-14中每个小正方形的边长为1厘米.阴影部分的面积是多少平方厘米?答案:14平方厘米【分析】方法:可用公式先算出整个图形的面积,在减去中间空白部分的面积。
【讲义】四年级下第05讲_割补法巧算面积

第五讲割补法巧算面积在上一讲中,我们学习了如何计算格点图形的面积,介绍了正方形格点图形和三角形格点图形的面积计算公式.根据公式,我们可以求出正方形格点图形的面积是最小正方形面积的几倍,或者求出三角形格点图形面积是最小正三角形面积的几倍.随着几何学习的步步深入,大家会发现除了用公式法直接求面积之外,还有很多间接求面积的方法.尤其是对于不规则图形,我们并不知道这些图形的面积公式,但是可以把它们通过分割、添补等各种方式变换为规则的图形.例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)「分析」这是一个不规则图形,我们能不能把它切成很多规则的小块,一块一块地求面积呢?练习1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)我们可以看到,在没有格点的情况下,割补的方法仍然可以使用.我们将来做几何面积计算时,就要视情况灵活运用割补法.例题2如图所示,在正方形ABCD 内部有一个长方形EFGH .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 都等于2厘米.求长方形EFGH 的面积.「分析」所求长方形的长、宽都是未知且不可求的,但是正方形面积以及周围四个直角三角形面积都是可以计算出来的,那么长方形面积怎么计算呢?1 2234 5 3 2 4 3412 4 9 DG如图所示,在正方形ABCD 内部有三角形CEF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AF 都等于2厘米.求三角形CEF 的面积.例题3如图所示,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?「分析」阴影部分零零散散,能不能通过割补的方法把它变成规则的图形嗯?练习3如图所示,大正三角形的面积为10平方厘米.连接大正三角形的各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分的面积总和等于多少平方厘米?例题4如图,把两个相同的正三角形的各边分别三等分和四等分,并连接这些等分点.已知图1中阴影部分的面积是48平方分米.请问:图2中阴影部分的面积是多少平方分米?「分析」图1和图2中最小正三角形的面积是不一样的,但两个大正三角形面积却是一样的,你能求出大正三角形的面积吗?D图2如图,把两个同样大小的正方形分别分成55⨯和33⨯的方格表.图1阴影部分的面积是162,请问图2中阴影部分的面积是多少?例题4中的阴影部分都是同样形状的花图形,我们不能直接看出花图形和大正三角形的面积之间有什么倍数关系,但是借助一块块小正三角形,我们把花图形和大正三角形之间联系起来,看看它们各自占了多少个小正三角形.找到面积之间的联系,是解决类似问题的钥匙.有些图形看起来没有分割成一些相同的小图形,实际上不过是将分割线隐藏起来或者只出现了其中的一部分,需要我们自己进行分割.例题5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A 的面积是36平方厘米,那么正方形B 的面积是多少平方厘米?「分析」乍一看上去和例题2有些相似,我们能不能求出大等腰直角三角形的面积呢?它的面积和正方形A 、B 之间有什么关系呢?例题6如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)「分析」这个四边形并不规则,直接求面积似乎有些困难.我们已经知道了其中的三个角,其中有直角也有45°角.你能从这两种“特殊角”发现图形的特点吗?图1课堂内外毕式定理据说毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形瓷砖,但毕达哥拉斯不仅仅是欣赏瓷砖的美丽,而是想到它们和数之间的关系,于是拿了画笔并且蹲在地板上,选了一块瓷砖以它的对角线AB为边画一个正方形,他发现这个正方形面积恰好等于两块瓷砖的面积和.他很好奇……于是再以两块瓷砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块瓷砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.这就是著名的毕式定理:在任何一个直角三角形中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方.实际上,早在毕达哥拉斯之前,许多民族已经发现了这个事实,而且巴比伦、埃及、中国、印度等的发现都有真凭实据,有案可查.相反,毕达哥拉斯的著作却什么也没有留传下来,关于他的这个故事都是后人辗转传播的.可以说真伪难辨.这个现象的确不太公平,之所以这样,是因为现代的数学和科学来源于西方,而西方的数学及科学又来源于古希腊,古希腊流传下来的最古老的著作是欧几里得的《几何原本》,而其中许多定理再往前追溯,自然就落在毕达哥拉斯的头上.他常常被推崇为“数论的始祖”,而在他之前的泰勒斯被称为“几何的始祖”,西方的科学史一般就上溯到此为止了.至于希腊科学的起源只是近一二百年才有更深入的研究.因此,毕达哥拉斯定理这个名称一时半会儿改不了.不过,在中国,因为我们的老祖宗也研究过这个问题,因此称为商高定理,更普遍地则称为勾股定理.中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.作业1. 下图中的数字分别表示对应线段的长度,图中多边形的面积是多少?2. 如下图所示,在正方形ABCD 内部有梯形EHGF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 、BF 、DG 都等于2厘米.则梯形EHGF 的面积是多少平方厘米?3. 如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连.图中阴影部分的面积总和是多少?4. 下图中空白部分的面积是100,那么阴影正方形的面积是多少?5. 如图所示,正六边形ABCDEF 的面积是36.阴影正六边形的面积是多少? D G 32 434 12 423 3 3 3。
第1讲.格点与割补.提高班

例 5
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
图中相邻三点所形成的等边三角形的面积为 1 ,计算三角形 ABC 的面积.
【分析】 方法一(分割法) :
四年级 第 1 讲 格点与割补 (提高班)
【分析】方法一:同正方形格点相似,将目标三角形分成容易求出面积的两个小三角形,如图. 易知左边小三角形面积为 2,右边小三角形面积为 4,则所求三角形面积为 6.
方法二:三角形毕克定理:图形内部有 1 个点,边上有 6 个点,由 S ( N (1+6÷2-1)×2=6.
L 1) 2 得面积为 2
S1
S1
S2
(a)
S3
S2(Leabharlann )方法三(正方形毕克定理) :图形内部(N)有 8 个格点,图形边上(L)有 6 个格点,根据正方形
L 1 得面积为 8+6÷2-1=10. 2 注:请老师强调扩展法和割补法,避免孩子过分依赖毕克定理,为高年级的几何学习打好基础.
毕克定理: S N
图 2: 用毕克定理: 图形内部没有格点, 图形边上 (L) 有 6 个格点, 根据正方形毕克定理: SN
笔记整理
6
四年级 第 1 讲 格点与割补 (提高班)
毕克定理:如果用 S 表示面积,N 表示图形内包含的格点数,L 表示图形边界上的格点数, L 正方形格点: S N 1 2 三角形格点: S ( N
L 1) 2 2
1. 图中相邻两个格点的距离都是 1,请你求出葫芦和锤子的面积各是多少.
【分析】 (1)面积为 2 应当包含 2 个面积为 1 的“4 个相邻点组成的小正方形” ; (2)直角三角形的面积=两条直角边长的乘积÷2; (3)梯形面积=(上底+下底)×高÷2. 【答案】
第6讲格点与割补

【内容概述】正方形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题. 通过恰当地分割与拼补进行计算的面积问题. 【典型问题】1 •如图6-1,每一个小方格的面积都是I平方厘米,那么用粗线围成的图形的面积是多少平方厘米图6-1【分析与解】方法一:正方形格点阵中多边形面积公式:(N+L-1)X单位正方形面2积,其中N为图形内格点数,L为图形周界上格点数.有N=4, L=7,贝U用粗线围成图形的面积为:(4+7-1 ) X 1=(平方厘米)2方法二:如下图,先求出粗实线外格点内的图形的面积,有①=3- 2=,②=2- 2=1,③=2- 2=1,④=2 - 2=1,⑤=2- 2=1,⑥=2- 2=1,还有三个小正方形,所以粗实线外格点内的图形面积为+1+1+1+1+1+3=,而整个格点阵所围成的图形的面积为16, 所以粗线围成的图形的面积为:=平方厘米.2.如图6-2,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD勺面积是多少平方厘米【分析与解】方法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9, L=4,所以用粗线围成的图形的面积为:(9 X 2+4- 2)XI =20(平方厘米).方法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为4,所以①部分的面积为2, ②、③、④部分对应的平行四边形面积分别为2, 8, 6,所以②、③、④部分的面积分别为1, 4, 3•所以粗实线内图形的面积为10+2+1+4+3=20(平方厘米).北京市第十二矿'迎春杯”数学竟轟快骞弟一题第3题3.如果图6-3是常见的一副七巧板的图,图6-4是用这副七巧板的7块板拼成的小房 子图,那么,第2块板的面积等于整幅图的面积的几分之几第 4块板与第7块板面积的和等于整幅图的面积的几分之几【分析与解】 如下图,我们在图6-3中标出图6-4中各块图形的位置.1 积为-x2所以第2块板的面积等于整幅图面积的1 2,第4块板与第7块板面积和为整幅图面积8的 - +] = ?.16 8 164 .把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六 角形.再将这个六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向 外作更小的正三角形,这样就得到图 6-5所示的图形.如果这个图形面积是 1,那么原来1有S a =S 4 ,S 2=S 5 = S 7=2S 3,有2、3、4、5、7五块图形的面积之和为-,所以S 4=S 长方形品,21 S7= 8设整个七巧板组成的正方形的边长为 1,显然整幅图形的面积为1,且有第2块的面图—3的正三角形面积是多少【分析与解】 方法一:如右图,我们将图6-5分成若干个大小、形状完全相同的小 正三角形,由40块小正三角形组成图6-5,而由27块小正三角形组成了图中最大的正三 角形.120 块小正三角形的面积为1,所以每块为丄,那么原来的正三角形由120方法二:如下图,我们把图6-5中的三角形分成 A B C 三种,设A 形正三角形面积在图6-5中,A 种、B 种、C 种正三角形的个数依次为1, 3,12,所以图6-5中图形的第五届“华罗廉金杯"艺年数曾邀请赛♦决賽口试第4題5.如图6-6,正六边形ABCDE 的面积是6平方厘米,M 是AB 中点,N 是CD 中点,P81块小正三角形组成,其面积显然为27 401 1 40面积为1+3X 丄+12X -=40•所以有981 2727T 对应27,而原来的正三角形即为三角形 40A ,所以原来的正三角形的面积为27 40为“1”是EF 中点•问:三角形MNP 的面积是多少平方厘米【分析与解】 如下图,我们将图6-6分成大小、形状相同的三角形,有正六边形ABCDEF 包含有24个小正三角形,而阴影部分 MNP 包含有9个小正三角形.正六边形ABCDE 的面积为6,所以每个小正三角形的面积为1的面积为9X 丄=(平方厘米).4般觀级数:車* ■-厂I第四届“小学柚学报橄數学竟决赛填空题第3題6 .把同一个三角形的三条边分别五等分、七等分,适当连接这些分点,便得到了若 干个面积相等的小三角形•已知图 6-7中阴影部分的面积是294平方分米,那么图6-8中 的阴影部分的面积是多少平方分米【分析与解】 在图6-7中,原正三角形被分成25个小正三角形,而阴影部分含有 12个小正三角形,所以每个小正三角形的面积为294-12=,所以原正三角形的面积为X 25=(平方分米)•16-24=-,所以三角形MNP4A' S6-6而在图6-8中,原正三角形被分成49块,而阴影部分含有16块,所以阴影部分的面积为十49 X 16=200(平方分米).T992年仝国小学數学真林匹克・初* C雄第7題7. 图6-9是5X 5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求选出的点中任意3点都不在同一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么所围图形的面积是多少平方厘米【分析与解】我们知道满足题意的7个点可以组成一个七边形,适当的切去正方形的一个角可以得到一个五边形,切出2个角可以得到一个六边形,切去3个角可以得到七边形•为了使最后留下的七边形的面积尽可能大,那么切去的3个角面积应尽可能的小.如下切法得到的七边形的面积最大,为25-3 X =(平方厘米).鑛錮级数;車車8. 在图6-10中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米, CF长3厘米,那么阴影部分的面积是多少平方厘米圈20【分析与解】 方法一:如图(a ),将原题中图形分为12个完全一样的小等腰三角形. △ ABC 占有9个小等腰三角形,其中阴影部分占有6个小等腰三角形, S^ABC =9X 9十2=(平方厘米),所以阴影部分的面积为宁9X 6=27(平方厘米).方法二:如图(b ),连接IG ,有四边形ADGI 为正方形,易知FG=FC=3厘米),所以 DG=DF-FG=9-3=6厘米),于是=- X s 正方形逍=-X 62 =9.44而四边形IGFB 为长方形,有BF=AD=DG 二厘米),GF=3(厘米),所以S 长方形品=6X 3=18.阴影部分面积为A HIG 与长方形IGFB 的面积和,即为9+18=27(平方厘米).方法三:如图(C ),为了方便叙述,将图6-10中某些交点标上字母. 易知三角形BIE 、CGF AIH 、DGH 匀为等腰直角三角形.先求出等腰直角三角形 AHI 、CGF 的面积,再用已知的等腰三角形 ABC 的面积与其作差, 即为需求阴影部分的面积.因为 CF=FG=3 所以 DG=DF-FG=6如图(d ),可以将4个三角形DGH 拼成一个边长为DG 的正方形.所以,S^ACD S^DGH =4X DG>< DG=9,而 S^AIH S]ABC-S^CGF - ^AIH =81 - 9 -9=27(平方厘米).即阴影部分的面积为27平方厘米.有 S^ABC =S 』DEF=—2X EF X DF=81, i 19 Si^cGF = X CF X FG=—. 2 2=9,所以S 阴影 BFGHI图(町9. 如图6-11,在长方形ABCD 中,0是长方形的中心,BC 长20厘米,AB 长12厘米, DE=4AE CF=3DF 那么阴影部分的面积是多少平方厘米由题意知 AE=4 ED=16 DF=3 FC=9有 S^AOD = — S 矩形 ABCD 4=-X 20 X 12=60,41 1=丄 X DF X( 3 4 AD)=2 41 X 3X 1 X 20=15.2 211丄 X 4X 1 X12=12,221 1=丄 X EDX DFr 1 X 16X 3=24. 2 2有S 阴影 =(S^AOD +S^ODF )- S J A EO - S EFD =60+15-12-24=39(平方厘米).即阴影部分的面积为39平方厘米.越酸徴鞍译章・导呼全珂小垄敬学奥林匹克*主膵芒卷心题3 1=丄 X AE X(丄 AB)= 4 2【分析与解】 我们只用先求出四边形 ADFO 勺面积,再将其减去两个三角形 AEO EFD的面积和,即为所求阴影部分的面积.而四边形ADFO 勺面积等于两个三角形 AOD ODF 的面积和.10. 如图6-12,大正方形的边长为10厘米•连接大正方形的各边中点得小正方形, 将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影 部分的面积总和等于多少平方厘米【分析与解】 如下图,我们将大正方形中的所有图形分成 A 、B 两种三角形.其中含有A 形三角形8个,B 形三角形16个,其中阴影部分含有 A 形三角形4个,B 形三角形8个.11 .如图6-13,ABCD 是边长为8厘米的正方形,梯形 AEBD 勺对角线相交于0,三角 形AOE 的面积比三角形BOD 勺面积小16平方厘米,则梯形AEBD 勺面积是多少平方厘米【分析与解】如下图,将梯形AEBD 内 4个三角形的面积分别记为①、②、③、④.在梯形AEBD 中,有厶EBD △ ABD 同底等高,所以有S EBD =S ABD ,即③+②二①+②.显 然有①=③.由题意知S /D - S^AOE =16,即②-④=16,于是有(①+②)-(③+④)=16 .已知①所以,阴影部分面积恰好为大正方形面积的1 1-,即为-X 10X 10=50(平方厘米). 2 26 - 12BC\国 6- 13+②二 S^BD 冷 X 8X 8=32,所以③ +④=(① +®) -16=16 .所以有S 梯形AEBD =(①+②)+(③+④)=32+16=48(平方厘米).评注:在任意梯形ABCD 中,两条对角线将其分成四个部分,记它们的面积为“上”、 “下”、“左”、“右”,有:左二右;左X 右=±X 下;上:下=AD 2 : B C 2 .㈱矽级数;車* ‘二I1994年全国小学数学奥沐匹克•决宴民族毎第3建12.如图6-14 , ABCD 是长方形,长 AD 等于厘米,宽 AB 等于5厘米,CDEF 是平行四 边形.如果BH 的长是3厘米,那么图中阴影部分的面积是多少平方厘米 IL8 £ /DC【分析与解】 S 平行四边形CDEF =DC X BC=X =36, HC=BC-BH==所以S'ICDH =X CD^ HC^ X 5X =.2 21期年金段小学數学真林匹克z 决纂第6理13 .如图6-15,已知一个四边形的两条边的长度和三个角,那么这个四边形的面积是 多少S 阴影=$平行四边形CDEF -S^cDH ==(平方厘米).级数:車車車H【分析与解】 将AD BC 延长交于E ,有/ EDC=45,/ ECD=90,所以△ CDE 为等腰直角三角形,有EC=DC而/ ECD =45,/ EAB=90,所以△ ABE 也是等腰直角三角形,有 EA=AB1 9 =—X EC X DC=-2 21994年仝国小辛數学凑棘匹丸•利賽B 卷鈿10题14•图6-16是边长为1的正方形和一个梯形拼成的“火炬” •梯形的上底长 1.5米,A 为上底的中点,B 为下底的中点,线段AB 恰好是梯形的高,长为0.5米,CD 长为丢米.那 么图中阴影部分的面积是多少平方米【分析与解】 方法一:为了方便叙述. 母•延长AB 交正方形边EF 于H 点,我们先求出梯形JICK 与正方形IFEC 的面积和,再求 AFH 与梯形AHEM 面积和,将前者与后者做差所得到的值 影部分的面积.有S四边形ABCD==1 X ABX EA=4949ABE2级数:审車車出三角形 即为所求阴1s 梯形 J |CK =2 X +1) X=,S 正方形 IFEC =1 X 1=1.L 11 1 11S^FH =^x AH X FH=1 X( AB+BH X( 1 FE)= 1 X +1)-(1 X 1)=,111 X (AH+DE X HE= 1X (AB+BH+CECD)X( 丄 FE)= 1X2 22213有S阴影=S梯形JICK+S正方形IFEC-SlAFH- S梯形AHED=+刃=万(平方米),17即阴影部分的面积为 乂平方米.24方法二:如下图,连接AI 、AC 将阴影部分分成四个部分.△ AJI 可以看作以AJ 为底,AB 的长为高的三角形;△ AKC 可以看作以AK 为底,AB 的 长为高的三角形;△ AJF 可以看作以IF 为底,IB 的长为高的三角形;△ ACD 可以看作CD 为底.CB 的长为高的三角形.阴影部分面积为S^AJI+ SAKC+SL AIF +s£ACD1= X 十 2+X 十 2+l X 十 2+ — X 十 2 3 1=+++ 12=口(平方米)24觀題级皺♦♦♦♦鷲一心更盒赫”少年敕学還请赛•决赛一试第S梯形AHED11 13+ 1+1--) X(丄 X 1)=3 2 2415.从一块正方形木板锯下宽为1米的一个木条以后,剩下的面积是 色平方米•问锯2 18下的木条面积是多少平方米【分析与解】 我们画出示意图(a ),则剩下的木块为图(b ),将4块剩下的木块如下 拼成一个正方形得到图(c ).1 11,所以图(c )中心的小正方形边长为5 6,2-65 1 1 529 23 23 23 于是大正方形AEHK 勺面积为65 X 4+丄X 1 =529=23 X 23,所以AK 长为竺.1822 36666即,长+宽=空,已知:长-宽=丄,得长=空,于是锯去部分的木条的面积为13X6 2 6 65=13=11(平方米).6 12 2我们称AB 为长,AD 为宽,有长与宽的差为 图T。
高斯小学奥数四年级下册含答案第05讲_割补法巧算面积

第五讲割补法巧算面积在上一讲中,我们学习了如何计算格点图形的面积,介绍了正方形格点图形和三角形格点图形的面积计算公式.根据公式,我们可以求出正方形格点图形的面积是最小正方形面积的几倍,或者求出三角形格点图形面积是最小正三角形面积的几倍.随着几何学习的步步深入,大家会发现除了用公式法直接求面积之外,还有很多间接求面积的方法.尤其是对于不规则图形,我们并不知道这些图形的面积公式,但是可以把它们通过分割、添补等各种方式变换为规则的图形.例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)「分析」这是一个不规则图形,我们能不能把它切成很多规则的小块,一块一块地求面积呢? 练习1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)我们可以看到,在没有格点的情况下,割补的方法仍然可以使用.我们将来做几何面积计算时,就要视情况灵活运用割补法.例题2如图所示,在正方形ABCD 内部有一个长方形EFGH .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 都等于2厘米.求长方形EFGH 的面积.「分析」所求长方形的长、宽都是未知且不可求的,但是正方形面积以及周围四个直角三角形面积都是可以计算出来的,那么长方形面积怎么计算呢?1 223 453 2 4341249 DG如图所示,在正方形ABCD 内部有三角形CEF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AF 都等于2厘米.求三角形CEF 的面积.例题3如图所示,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?「分析」阴影部分零零散散,能不能通过割补的方法把它变成规则的图形嗯? 练习3如图所示,大正三角形的面积为10平方厘米.连接大正三角形的各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分的面积总和等于多少平方厘米?例题4如图,把两个相同的正三角形的各边分别三等分和四等分,并连接这些等分点.已知图1中阴影部分的面积是48平方分米.请问:图2中阴影部分的面积是多少平方分米?「分析」图1和图2中最小正三角形的面积是不一样的,但两个大正三角形面积却是一样的,你能求出大正三角形的面积吗?D图2如图,把两个同样大小的正方形分别分成55⨯和33⨯的方格表.图1阴影部分的面积是162,请问图2中阴影部分的面积是多少?例题4中的阴影部分都是同样形状的花图形,我们不能直接看出花图形和大正三角形的面积之间有什么倍数关系,但是借助一块块小正三角形,我们把花图形和大正三角形之间联系起来,看看它们各自占了多少个小正三角形.找到面积之间的联系,是解决类似问题的钥匙.有些图形看起来没有分割成一些相同的小图形,实际上不过是将分割线隐藏起来或者只出现了其中的一部分,需要我们自己进行分割. 例题5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A 的面积是36平方厘米,那么正方形B 的面积是多少平方厘米?「分析」乍一看上去和例题2有些相似,我们能不能求出大等腰直角三角形的面积呢?它的面积和正方形A 、B 之间有什么关系呢? 例题6如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)「分析」这个四边形并不规则,直接求面积似乎有些困难.我们已经知道了其中的三个角,其中有直角也有45°角.你能从这两种“特殊角”发现图形的特点吗?图1课堂内外毕式定理据说毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形瓷砖,但毕达哥拉斯不仅仅是欣赏瓷砖的美丽,而是想到它们和数之间的关系,于是拿了画笔并且蹲在地板上,选了一块瓷砖以它的对角线AB为边画一个正方形,他发现这个正方形面积恰好等于两块瓷砖的面积和.他很好奇……于是再以两块瓷砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块瓷砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.这就是著名的毕式定理:在任何一个直角三角形中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方.实际上,早在毕达哥拉斯之前,许多民族已经发现了这个事实,而且巴比伦、埃及、中国、印度等的发现都有真凭实据,有案可查.相反,毕达哥拉斯的著作却什么也没有留传下来,关于他的这个故事都是后人辗转传播的.可以说真伪难辨.这个现象的确不太公平,之所以这样,是因为现代的数学和科学来源于西方,而西方的数学及科学又来源于古希腊,古希腊流传下来的最古老的著作是欧几里得的《几何原本》,而其中许多定理再往前追溯,自然就落在毕达哥拉斯的头上.他常常被推崇为“数论的始祖”,而在他之前的泰勒斯被称为“几何的始祖”,西方的科学史一般就上溯到此为止了.至于希腊科学的起源只是近一二百年才有更深入的研究.因此,毕达哥拉斯定理这个名称一时半会儿改不了.不过,在中国,因为我们的老祖宗也研究过这个问题,因此称为商高定理,更普遍地则称为勾股定理.中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.作业1. 下图中的数字分别表示对应线段的长度,图中多边形的面积是多少?2. 如下图所示,在正方形ABCD 内部有梯形EHGF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 、BF 、DG 都等于2厘米.则梯形EHGF 的面积是多少平方厘米?3. 如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连.图中阴影部分的面积总和是多少?4. 下图中空白部分的面积是100,那么阴影正方形的面积是多少?5. 如图所示,正六边形ABCDEF 的面积是36.阴影正六边形的面积是多少?D G324 34 1242 3 33 3第五讲 割补法巧算面积1. 例题1答案:32平方厘米详解:对这个图形进行简单分割后,分别求面积再相加. 32243632⨯+⨯+⨯=平方厘米.也可对图形进行添补.(如右图)2.例题2答案:16平方厘米详解:正方形面积是36平方厘米,三角形AEH 、FCG 的面积是2平方厘米,三角形EBF 、GDH 的面积是8平方厘米.长方形EFGH 的面积是36228216-⨯-⨯=平方厘米.3. 例题3答案:50平方厘米详解:首先可把小正方形中间的阴影部分添补到相对应的空白处,中间小正方形的面积等于四个角上的阴影三角形的面积和.可连接正方形对边的中点,也可以把四个三角形向中间对折都可以说明阴影部分的面积是正方形面积的一半,即为1010250⨯÷=平方厘米. 4. 例题4答案:27平方厘米详解:图1中大三角形被分成9块,阴影部分面积占3块,面积是48平方分米,那么每个小三角面积是16平方分米,大三角形面积是169144⨯=平方分米. 图2中大三角形被分成了16块,那么每个小三角形的面积是144169÷=平方分米,阴影部分面积是9327⨯=平方分米. 5. 例题5答案:32平方厘米详解:对图形进行如左图的分割,通过第一个图,我们知道等腰直角三角形的面积8平方厘米,正方形B 的面1 2 2 3 4 5 1 22 3 45积是32平方厘米.6. 例题6答案:20平方厘米详解:如图所示,把原图添补成一个大的等腰直角三角形.需要将多余的小直角三角形去掉才是原图.大等腰直角三角形的底是7厘米,高是7厘米,所以面积是77224.5⨯÷=平方厘米;小等腰直角三角形的底是3厘米,高是3厘米,所以面积是332 4.5⨯÷=平方厘米.所以四边形的面积是24.5 4.520-=平方厘米.7. 练习1答案:78平方厘米详解:492331278⨯+⨯+⨯=平方厘米.8. 练习2答案:10平方厘米详解:正方形面积是36平方厘米,三角形AEF 的面积是2平方厘米,三角形BEC 、DFC 的面积都是12平方厘米.三角形EFC 的面积是362121210---=平方厘米.9. 练习3答案:5简答:大正三角形被分成12块,阴影部分占6块,占总个数的一半,面积为5平方厘米.10. 练习4答案:1503 243 4124 9简答:图1中大正方形被分成25块,阴影部分面积占18块,面积是162,那么每个小正方形面积是9,大正方形面积是259225⨯=.图2中大正方形被分成了9块,那么每个小正方形的面积是225925÷=,阴影部分面积是256150⨯=.11. 作业1答案:84简答:()312433332284⨯+⨯+++⨯⨯=平方厘米.12. 作业2答案:18简答:首先求出大正方形的面积,再求出各个角上的小三角形的边长和面积.然后把大正方形的面积减去四个小三角形的面积就得梯形的面积. 13. 作业3答案:6简答:将右上两个阴影三角形切下来添到左侧空白处,使其拼成一个大的三角形.阴影面积是平行四边形面积的一半.所以阴影部分的面积是6. 14. 作业4答案:80简答:对三角形进行分割,能知道每个小三角形的面积是100520÷=,阴影正方形的面积是80.15. 作业5答案:9简答:把大六边形划分为24个小正三角形,其中阴影部分可以分成6个小正三角形,所以大六边形是阴影部分面积的4倍,正六边形面积是36,阴影部分的面积是3649÷=.。
格点与割补

趣味数学
• 体育运动会授奖台的图形如下,你能否 只剪一刀,把它拼成一个正方形?
基础热身
• 1.有一块长方形麦地,长200米,宽50 米,这块麦地的面积有多少公顷?
• 2.某乡沿江种植一个长15千米,宽8米的 林带,如果每公顷植树2000棵,这个林 带共植树多少棵?
知识导学
• 这一讲我们来研究借助格点计算图形面积的方 法.
• (1)数格子 • (2)合理分割法:把图形分割成若干个可直
接计算面的规则图行 • (3)扩展法:把图形先扩展成易算面积的规
则图形,在减去扩展的部分 • (4)毕克公式:若N表示内部的格点数,L表
示边界上的格点数,S表示面积。
知识导学
• 正方形格点: • S=N+L÷2-1 • 三角形格点: • S=(N+L÷2-1)×2
• (1)多边形内包含的格点数有7个,多 边形周界上的格点数是7个,所以面积 是2×7+7-2=19(面积单位)
• (2)多边形包含的格点数有8个,多边 形周界上的格点数是5个,所以面积是 2×8+5-2=19(面积单位)
一题一练
• 下面是一个漂亮礼盒的平面图,请你求 出它的面积。
• (图见课本29页“课堂练习 ”)
一题一练
• 计算下例题各多边形的面积(点与点之 间的距离都是1厘米)
• (图见课本26页“课堂练习”)
• 例4. 在下图中有21个点,每相邻三点 构成一个单位面积的等边三角形,计算 三角形ABC的面积
A
C
B 图1
• 方法一:(图2)三角形ABC的面积是:
• 25-3-4-8=10(面积单位)
•.
例1:计算下图中各图形的 面积.
几何格点与割补

第十一、十二讲格点与割补本讲知识点1.分割法1)正所谓“大事化小”,把不规则的大图形化为规则的小图形,来进行计算.2)在对格点图形的分割计算时,不一定要分到最小的基本单位。
一般来说分为中等大小的,可以计算的规则形状比较方便。
2.割补法1)是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.2)此外,在图形中进行适当的分割拼补,把不规则的形状拼成规则形状,也是常见的方法.3.格点面积公式1)在最小的正方形面积为1的图形中:正方形格点多边形面积=边界格点数÷2+内部格点数-1.2)在最小正三角形面积为1的图形中:三角形格点多边形面积=边界格点数+内部格点数×2-1.3)在使用公式法计算格点多边形面积时,要注意公式的适用条件.4)在多个格点图形相关的问题中,要注重利用它们之间的共同点来帮助计算.5)对于很多非格点图形的面积计算,分割和添补的方法依然适用.6)特别的,在图形中恰当的添加格线进行分制,能更好的体现围形的结构,以及整体和部分的数量关系,而在添补中,看见某些特殊角度,如45°、60°、120°等时,可以联想到一些特殊的图形,如,等腰直角三角形,正三角形等等.精选例题例题1.如图,分别在如下三种情况中,求出图中格点图形的面积:(1)相邻格点距离为1;(2)相邻格点距离为2;(3)最小正方形面积为2.例题2.如图,下图的正方形格点,单位正方形面积为1,分别求出两个图形的面积.例题3.如图,下图的正方形格点中,单位正方形面积为3,求出图形面积.练习1.如图,分别在如下两种情况中,求出图中格点图形的面积:(1)最小正三角形面积为1;(2)最小正三角形形面积为2.例题4.如图,下图的三角形格点,单位正三角形面积为1,分别求出两个图形的面积.例题5.如图,下图的正三角形格点中,单位正三角形面积为5,求出图形面积.例题6.下图点阵间隔为1,请利用方形格点公式,填出下表:练习2.下图三角形点阵所能连出的最小三角形面积为1,请利用三角形格点公式,填出下表:例题7.如图,单位正方形面积为1,利用格点公式计算下面阴影图形的面积,并再用一种其他方法计算检查.例题8.(1)在图1的正方形格点中,左图面积是45,那么右图的面积是多少?(2)图2的左右两个大三角形相同,左图的单位正三角形面积为100,右图的单位正三角形面积是多少?例题9.把同一个三角形的三条边分别四等分、六等分,适当连接这些分点,便得到了若干个面积相等的小三角形,已知图1中副影部分的面积是63平方厘米,那么图2中的阴影部分的面积是多少平方厘米?例题10.如图,对下列图形进行适当的格线划分,使得能恰当的体现出阴影部分与总面积的关系,并进行相应计算:(1)大正方形面积为90,连结各边中点得到阴影正方形,求阴影面积.(2)大正三角形面积为90.每边取三等分点,连结得到阴影正六边形,求阴影面积.(3)大正六边形面积为90,连结其中3个顶点得到阴影正三角形,求阴影面积.(4)大等腰直角三角形面积为90,如图放入一个阴影正方形,求阴影面积.例题11.在面积为72平方厘米的正六边形中,按图中不同方式切割(切割点均为等分),形成的阴影部分面积分别是多少?例题12.如图,大正方形和小正方形的边长分别为6厘米和2厘米,G、N、M分别为AF、AB、ED边上的中点,求四边形GNME的面积.例题13.如图,在长方形ABCD中,O是长方形的中心,BC长20厘米,AB长12厘米,=,3DE AE4=,那么阴影部分的面积是多少平方厘米?CF DEBE=,三角形AEF的面积是37,那么长例题14.如图,在长方形ABCD中,3DF=,11方形ABCD的面积是多少?例题15.甲乙两个六边形的内角都是120°,其边长如图所示,那么甲,乙面积分别是边长为1的正三角形面积的多少倍?例题16.求阴影部分面积:例题17.两个等腰直角三角形直角边分别长10厘米和6厘米,那么三角形DGE面积是多少平方厘米?思考创新思考1.下图为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点面一个面积为13的三角形.思考2.如图,平面上有16个点,每个点都钉上钉子,形成间隔为1厘米的4行4列的正方形钉阵,现在有许多皮筋,可以套出几种面积的三角形?请各举一例.思考3.正方形格点如图,原有格点的单位正方形面积为68,利用原有格点在图中划分新的格线,分别划出两种新的情况,那么这两种新格线的单位小正方形的面积分别是多少?思考4.如图,把长方形纸片ABCD的一角折起,使点D恰好与AB的中点F重合,若三角形EDC的面积是10.那么长方形ABCD的面积是多少?思考5.如下图,在一平行四边形纸片上割去了①,②两个直角三角形,已知三角形①两条直角边分别为2厘米和5厘米,三角形②两条直角边分别为5厘米和8厘米,求图中阴影部分的面积.第十一讲格点割补(一)思维冲浪1.如图所示,每一个小方格的面积都是1,那么用祖线围成的图形的面积是________.2.已知图中相邻两格点的距离均为2厘米,那么图中连出多边形的面积是______平方厘米.3.如图所示,图中最小的“□”面积是2,那么阴影部分面积分别为________.4.如图,如果每个小三角形的面积都是1cm2,那么连接A,B,C三点的三角形的面积是________cm2.5.如图,如果每一个小三角形的面积是2平方厘米,那么四边形ABCD的面积是________平方厘米.6.如图所示,图中最小的“Δ”面积是2,那么阴影部分面积分别为_______.7.如图所示,每个小方格格的边长为1.那么阴影部分的面积是多少?8.图中相邻三点所形成的等边三角形的面积为1,求五边形的面积.9.如图,大正六边形的面积为108,求阴影部分的面积为多少?10.图中水平,竖直方向相邻两个格点的距离都是1,请你求出图中“8”、“0”,“9”的面积各是多少.第十二讲格点割补(二)思维冲浪1.把同一个三角形的三条边分别五等分、七等分,连接这账分点,便得到了若干个面积相等的小三角形,左图中阴影部分的面积是294平方分米,那么右图中阴影部分的面积是________平方分米.2.下图是一个面积为24的正六边形,阴影部分的面积是__________.3.如图所示,ABCD是长方形,长AD等于7.2厘米,宽AB等于5厘米,CDEF是平行四边形,如果BH的长是3厘米,那么图中阴影部分面积是________平方厘米.4.在下图中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,那么阴影部分的面积是________平方厘米.5.如图,大正方形和小正方形的边长分别为6厘米和2厘米,G、N分别为AF、AB边上的中点,那么四边形GNCE的面积是__________平方厘米.6.如图所示,三个长方形APHM、BNHP、CQHN的面积分别是7、4、6、则阴影部分的面积是__________.7.如图所示,为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点画一个面积为7的三角形.8.如图所示,为一个边长为2的正方形,其中阴影部分的面积为多少?9.图中大正方形边长为8,小正方形边长为4,求阴影部分面积.10.如图,一个正方形,与4个等腰直角三角形,恰好拼成了一个长方形,如果正方形的面积是16,那么,长方形的面积是________.。
2017年小学奥数几何专题——格点与割补

2017年小学奥数几何专题——格点与割补注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、填空题(题型注释)1、如图,的方格纸上放了16枚棋子,以棋子为顶点的正方形有( ) 个.2、的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是( )平方厘米.3、把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.4、如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC 的面积是_____平方厘米.二、判断题(题型注释)5、判断下列图形哪些是格点多边形?三、解答题(题型注释)6、用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少? 面积等于2平方厘米的三角形有多少个?7、如图,计算各个格点多边形的面积.8、如图(a),计算这个格点多边形的面积.9、右图是一个方格网,计算阴影部分的面积.10、分别计算图中两个格点多边形的面积.⑴ ⑵11、我们开始提到的“乡村小屋”的面积是多少?12、右图是一个面积单位的图形.求矩形内的箭形的面积.13、右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?14、第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?15、两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.16、图中正六边形ABCDEF 的面积是54,AP=2PF ,CQ=2BQ ,求阴影四边形CEPQ 的面积.17、如图(a),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC 的面积.18、求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).19、把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.20、如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD 的面积是多少平方厘米?21、如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?22、正六边形ABCDEF 的面积是6平方厘米.M 是AB 中点,N 是CD 中点,P 是EF 中点.问:三角形MNP 的面积是多少平方厘米?23、如图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算ABC 的面积.24、求下列各个格点多边形的面积.25、如图,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?参考答案1、202、23.53、2004、665、(1)6、87、16,15,10,15,12,188、109、410、9,1011、1812、4613、62.514、2715、1916、3117、1018、19,19,18,2119、5220、2021、4822、2.2523、1124、15,20,14,1725、6.5【解析】1、根据正方形的大小,分类数正方形.共能组成五种大小不同的正方形(如下图).的正方形:9个;的正方形:4个;的正方形:1个;以正方形对角线为边长的正方形:4个;以长方形对角线为边长的正方形:2个.故可以组成(个)正方形.2、为了使这7个点围成最大的面积,这7个点应尽量在正方形的边或顶点上,如图选取7个点,围成面积最大.最大面积为(平方厘米).3、图1中阴影部分占整个三角形面积的,图2中阴影部分占整个三角形面积的,故图2中阴影部分的面积为294÷=200(平方分米).4、5、根据格点多边形的定义可知,图形的边必须是直线段,顶点要在格点上!所以只有⑴是格点多边形.6、面积等于1平方厘米的三角形有32个.面积等于2平方厘米的三角形有8个.(1)面积等于1平方厘米的分类统计如下:①②③底为2,高为1 底为2,高为1 底为1,高为23×2=6(个) 3×2=6(个) 3×2=6(个)④⑤⑥底为1,高为2 底为2,高为1 底为1,高为23×2=6(个) 2×2=4(个) 2×2=4(个)所以,面积等于1平方厘米的三角形的个数有:6+6+6+6+4+4=32(个).(2)面积等于2平方厘米的分类统计如下:3×2=6(个) 1×2=2(个)所以,面积等于2平方厘米的三角形的个数有:6+2=8(个).7、本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断出相应的有关数据就行了.方法一:图⑴是正方形,边长是4,所以面积是(面积单位);图⑵是矩形,长是5,宽是3,所以面积是(面积单位);图⑶是三角形,底是5,高是4,所以面积是(面积单位);图⑷是平行四边形,底是5,高是3,所以面积是(面积单位);图⑸是直角梯形,上底是3,下底是5,高是3,所以面积是(面积单位);图⑹是梯形,上底是3,下底是6,高是4,所以面积是(面积单位).如果两格点之间的距离是2,能利用刚计算的结果说出相应面积么?(教师总结:面积数值均扩大4倍.)方法二:以上部分图形除了利用各自的面积公式直接求出外,我们还可以从推导它们的面积公式过程中得到启发,即用“割补法”或“扩展法”分别转化成长方形来求.这一种方法很重要,在下面的题目中我们还将使用这种方法!如图⑶,我们利用“扩展法”将其转化,如图所示,从图中易知三角形面积是长方形面积的一半.如图⑷,我们利用“割补法”将其阴影部分面积平移到右边,转化成一个长方形,从中易得平行四边形面积.同理,图⑸、⑹也可利用同样的思想.8、方法一(扩展法).这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能另想别的办法:这个三角形是处在长是6、宽是4的矩形内,除此之外还有其他三个直角三角形,如下右图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积.矩形面积是;直角三角形Ⅰ的面积是:;直角三角形Ⅱ的面积是:;直角三角形Ⅲ面积是;所求三角形的面积是(面积单位).方法二(割补法).将原三角形分割成两个我们方便计算面积的三角形,如(c)图.因此三角形的面积是:(面积单位).9、扩展法.把所求三角形扩展成正方形ABCD中.这个正方形中有四个三角形:一个是要求的;另外三个分别是:ABE、FEC、DAF,它们都有一条边是水平放置的,易求它们的面积分别为,,.所以,图中阴影部分的面积为:().10、利用“扩展法”和“割补法”我们都可以简单的得到⑴的面积均为9面积单位.⑵的面积均为10面积单位.“一个格点多边形面积的大小很可能是由哪些因素决定呢?”“格点多边形内部的格点数和周界上的格点数与格点多边形的面积有没有什么内在联系呢?”下面我们就来探讨一下!在巩固中,我们发现两个图形面积相等.进一步还可以发现第一个图形边界上的格点数是8个;第二个图形边界上的格点数是10个,包含在图形内的格点数也相等,都是6个.11、图形内部格点数;图形边界上的格点数;根据毕克定理,则(单位面积).12、箭形的面积(面积单位).13、图形内部格点数为54,图形周界上格点数为19.所以图形的面积为:(面积单位).14、要计算三个数字所占的面积之和,可以先分别求出每个数字所占的面积.显然,图中的三个数字都可以看作格点多边形,根据毕克定理,可以很方便地求出每个数字所占的面积.值得注意的是:数字“7”内部有两个格点,而数字“2”和“1”内部都没有格点.7所占的面积为:;2所占的面积为:;1所占的面积为:.所以,这三个数字所占的面积之和为:.15、块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.16、如图,将正六边形ABCDEF等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积,面积,面积,四边形ABQP面积.上述三块面积之和为.因此,阴影四边形CEPQ面积为.17、方法一:如图(b)所示,在ABC内连接相邻的三个点成DEF,再连接DC、EA、FB后是ABC可看成是由DEF分别延长FD、DE、EF边一倍、一倍、二倍而成的,由等积变换不难得到,,,所以(面积单位).方法二:如图(c)所示,作辅助线把图Ⅰ′、Ⅱ′、Ⅲ′分别移拼到Ⅰ、Ⅱ、Ⅲ的位置,这样可以通过数小正三角形的方法,求出ABC的面积为10.方法三:如图(d)所示:作辅助线可知:平行四边形ARBE中有6个小正三角形,而ABE 的面积是平行四边形ARBE面积的一半,即,平行四边形ADCH中有4个小正三角形,而ADC的面积是平行四边形ADCH面积的一半,即.平行四边形FBGC中有8个小正三角形,而FBC的面积是平行四边形FBGC的一半,即:.所以(面积单位).18、⑴∵;,∴(面积单位);⑵∵;,∴(面积单位);⑶∵;,∴(面积单位);⑷∵;,∴(面积单位).19、图中有(个)小三角形,那么一个小三角形的面积是,图形内部格点数为12,图形周界上格点数为4;图形的面积为:(面积单位),进而得图形的面积为:.20、法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为4,所以①部分的面积为2,②、③、④部分对应的平行四边形面积分别为2,8,6,所以②、③、④部分的面积分别为1,4,3.所以粗实线内图形的面积为10+2+1+4+3=20(平方厘米).21、如图,涂阴影部分的小正六角星形可分成12个与三角形PMN全等(能完全重叠地放在一起)的小三角形.而图中的大正六角星形除去小正六角星形后.有6×4=24个与三角形PMN全等的小三角形,所以大正六角星形的面是小正六角星形的3倍,即48平方厘米.22、将正六边形分成六个面积为1平方厘米的正三角形,再取它们各边的中点将每个正三角形分为4个小正三角形.于是正六边形ABCDEF被分成了24个小正三角形,每一个小正三角形的面积是(平方厘米),三角形MNP由9个小正三角形所组成,所以三角形MNP的面积(平方厘米).23、因为;:所以(面积单位).24、⑴∵;,∴(面积单位);⑵∵;,∴(面积单位);⑶∵;,∴(面积单位);⑷∵;,∴(面积单位).25、方法一:正方形格点阵中多边形面积公式:(N+-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=7,则用粗线围成图形的面积为:(4+-1)×1=6.5(平方厘米)方法二:如右上图,先求出粗实线外格点内的图形的面积,有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:16-9.5=6.5平方厘米.。
割补法在立体几何中的应用

WS自动填充功能快速填写重复内容自动填充功能是工作表软件(WS)中一个高效的工具,它可以帮助用户快速填写重复内容。
通过利用这一功能,用户可以大大提高数据录入的效率,节省时间和精力。
本文将介绍WS自动填充功能的使用方法和一些注意事项。
一、使用方法使用WS自动填充功能十分简便。
以下是具体操作步骤:1. 创建一个新的工作表或打开一个已有的工作表。
2. 在需要填写重复内容的单元格中输入第一个数值或文本。
3. 鼠标选中填写内容的单元格,使其被选中。
4. 在选中的单元格的右下角会出现一个小黑色方块,将鼠标放置在该方块上,鼠标指针会变成一个加号(+)。
5. 按住鼠标左键,拖动该小黑色方块至需要填充的单元格区域,可以是横向、纵向或是一个矩形区域。
6. 松开鼠标左键,重复内容会被自动填充至选中的单元格区域。
二、应用场景WS自动填充功能在很多场景下都非常实用。
以下是几个常见的应用场景:1. 数字序列的填充:有时候我们需要填写一列连续的数字,如1、2、3等。
使用WS自动填充功能,只需输入前几个数字,然后拖动填充方块即可快速生成整个序列。
2. 日期序列的填充:在某些情况下,我们需要填写一系列连续的日期,如每月的第一天或每周的某一天。
借助自动填充功能,我们只需输入一个日期,然后拖动填充方块即可轻松生成整个日期序列。
3. 文本的填充:有时候需要在表格中填写一些重复的文本,如产品名称或客户姓名。
使用自动填充功能,只需输入第一个文本,然后拖动填充方块即可快速将文本填充至其他单元格。
三、注意事项在使用WS自动填充功能时,需要注意以下几点:1. 填充方块大小的调整:在拖动填充方块之前,可以根据需要调整其大小。
只需将鼠标放置在填充方块的右下角,鼠标指针会变成双向箭头,然后按住鼠标左键拖动即可调整填充方块的大小。
2. 自动填充的规律:WS自动填充功能会根据已有的数据规律进行填充。
对于数字序列和日期序列,可以根据需要选择自增、自减或是使用特定的间隔。
第6讲 格点与割补

正方形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题.通过恰当地分割与拼补进行计算的面积问题.1.如图6-1,每一个小方格的面积都是l平方厘米,那么用粗线围成的图形的面积是多少平方厘米?-1)×单位正方形面【分析与解】方法一:正方形格点阵中多边形面积公式:(N+L2积,其中N为图形内格点数,L为图形周界上格点数.-1)×1=6.5(平方厘米)有N=4,L=7,则用粗线围成图形的面积为:(4+72方法二:如下图,先求出粗实线外格点内的图形的面积,有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:16-9.5=6.5平方厘米.2.如图6-2,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD的面积是多少平方厘米?【分析与解】方法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).方法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为4,所以①部分的面积为2,②、③、④部分对应的平行四边形面积分别为2,8,6,所以②、③、④部分的面积分别为1,4,3.所以粗实线内图形的面积为lO+2+1+4+3=20(平方厘米).3.如果图6-3是常见的一副七巧板的图,图6-4是用这副七巧板的7块板拼成的小房子图,那么,第2块板的面积等于整幅图的面积的几分之几?第4块板与第7块板面积的和等于整幅图的面积的几分之几?【分析与解】 如下图,我们在图6-3中标出图6-4中各块图形的位置.设整个七巧板组成的正方形的边长为1,显然整幅图形的面积为1,且有第2块的面积为12×12×12=18.有3S =4S ,2S =5S =7S =23S ,有2、3、4、5、7五块图形的面积之和为12,所以4S =IGFB S 长方形,7S =18.所以第2块板的面积等于整幅图面积的18,第4块板与第7块板面积和为整幅图面积的116+18=316.4.把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形.再将这个六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向外作更小的正三角形,这样就得到图6-5所示的图形.如果这个图形面积是1,那么原来的正三角形面积是多少?【分析与解】方法一:如右图,我们将图6-5分成若干个大小、形状完全相同的小正三角形,由40块小正三角形组成图6-5,而由27块小正三角形组成了图中最大的正三角形.120块小正三角形的面积为1,所以每块为1120,那么原来的正三角形由81块小正三角形组成,其面积显然为2740.方法二:如下图,我们把图6-5中的三角形分成A、B、C三种,设A形正三角形面积为“1”,则B、C两种正三角形的面积依次为“19”、“181”.在图6-5中,A种、B种、C种正三角形的个数依次为1,3,12,所以图6-5中图形的面积为1+3×19+12×181=4027.所以有“1”对应2740,而原来的正三角形即为三角形A,所以原来的正三角形的面积为2740.5.如图6-6,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米?【分析与解】如下图,我们将图6-6分成大小、形状相同的三角形,有正六边形ABCDEF包含有24个小正三角形,而阴影部分MNP包含有9个小正三角形.正六边形ABCDEF的面积为6,所以每个小正三角形的面积为6÷24=14,所以三角形MNP的面积为9×14=2.25(平方厘米).6.把同一个三角形的三条边分别五等分、七等分,适当连接这些分点,便得到了若干个面积相等的小三角形.已知图6-7中阴影部分的面积是294平方分米,那么图6-8中的阴影部分的面积是多少平方分米?【分析与解】在图6-7中,原正三角形被分成25个小正三角形,而阴影部分含有12个小正三角形,所以每个小正三角形的面积为294÷12=24.5,所以原正三角形的面积为24.5×25=612.5(平方分米).而在图6-8中,原正三角形被分成49块,而阴影部分含有16块,所以阴影部分的面积为612.5÷49×16=200(平方分米).7.图6-9是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求选出的点中任意3点都不在同一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么所围图形的面积是多少平方厘米?【分析与解】我们知道满足题意的7个点可以组成一个七边形,适当的切去正方形的一个角可以得到一个五边形,切出2个角可以得到一个六边形,切去3个角可以得到七边形.为了使最后留下的七边形的面积尽可能大,那么切去的3个角面积应尽可能的小.如下切法得到的七边形的面积最大,为25-3×0.5=23.5(平方厘米).8.在图6-10中,三角形ABC 和DEF 是两个完全相同的等腰直角三角形,其中DF 长9厘米,CF 长3厘米,那么阴影部分的面积是多少平方厘米?【分析与解】 方法一:如图(a),将原题中图形分为12个完全一样的小等腰三角形.△ABC 占有9个小等腰三角形,其中阴影部分占有6个小等腰三角形,SABC=9×9÷2=40.5(平方厘米),所以阴影部分的面积为40.5÷9×6=27(平方厘米).方法二:如图(b),连接IG ,有四边形ADGI 为正方形,易知FG=FC=3(厘米),所以DG=DF-FG=9-3=6(厘米),于是SHIG =14×AIGD S 正方形=14×26=9. 而四边形IGFB 为长方形,有BF=AD=DG=6(厘米),GF=3(厘米),所以IGFB S 长方形=6×3=18.阴影部分面积为A HIG 与长方形IGFB 的面积和,即为9+18=27(平方厘米).方法三:如图(C),为了方便叙述,将图6-10中某些交点标上字母. 易知三角形BIE 、CGF 、AIH 、DGH 均为等腰直角三角形.先求出等腰直角三角形AHI 、CGF 的面积,再用已知的等腰三角形ABC 的面积与其作差,即为需求阴影部分的面积.有S ABC =DEFS=12×EF ×DF=812,CGF S =12×CF×FG=92.因为CF=FG=3,所以DG=DF-FG=6.如图(d),可以将4个三角形DGH 拼成一个边长为DG 的正方形. 所以,ACD S DGHS=14×DG×DG=9,而AIHS =DGHS=9,所以BFGHI S 阴影=SABC -CGF S-AIH S=812 -92-9=27(平方厘米).即阴影部分的面积为27平方厘米.9.如图6-11,在长方形ABCD 中,O 是长方形的中心,BC 长20厘米,AB 长12厘米,DE=4AE ,CF=3DF ,那么阴影部分的面积是多少平方厘米?【分析与解】 我们只用先求出四边形ADFO 的面积,再将其减去两个三角形AEO 、EFD 的面积和,即为所求阴影部分的面积.而四边形ADFO 的面积等于两个三角形AOD 、ODF 的面积和.由题意知AE=4,ED=16,DF=3,FC=9. 有AOD S =14ABCD S 矩形=14×20×12=60,ODF S=12×DF×(14AD)= 12×3×12×20=15.AEO S=12×AE×(12AB)= 12×4×12×12=12,EFD S=12×ED×DF=12×16×3=24.有S 阴影=(AODS +ODFS)-AEOS-EFDS=60+15-12-24=39(平方厘米).即阴影部分的面积为39平方厘米.10.如图6-12,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【分析与解】 如下图,我们将大正方形中的所有图形分成A 、B 两种三角形.其中含有A 形三角形8个,B 形三角形16个,其中阴影部分含有A 形三角形4个,B 形三角形8个.所以,阴影部分面积恰好为大正方形面积的12,即为12×10×10=50(平方厘米).11.如图6-13,ABCD 是边长为8厘米的正方形,梯形AEBD 的对角线相交于0,三角形AOE 的面积比三角形BOD 的面积小16平方厘米,则梯形AEBD 的面积是多少平方厘米?【分析与解】如下图,将梯形AEBD 内4个三角形的面积分别记为①、②、③、④.在梯形AEBD 中,有△EBD、△ABD 同底等高,所以有EBDS =ABDS,即③+②=①+②.显然有①=③.由题意知BODS -AOES=16,即②-④=16,于是有(①+②)-(③+④)=16.已知①+②=ABD S=12×8×8=32,所以③+④=(①+②)-16=16.所以有AEBD S 梯形=(①+②)+(③+④)=32+16=48(平方厘米).评注:在任意梯形ABCD 中,两条对角线将其分成四个部分,记它们的面积为“上”、“下”、“左”、“右”,有:左=右;左×右=上×下;上:下=A 2D :B 2C .12.如图6-14,ABCD 是长方形,长AD 等于7.2厘米,宽AB 等于5厘米,CDEF 是平行四边形.如果BH 的长是3厘米,那么图中阴影部分的面积是多少平方厘米?【分析与解】 CDEF S 平行四边形=DC×BC=5×7.2=36,HC=BC-BH=7.2-3=4.2,所以CDH S=12×CD×HC=12×5×4.2=10.5.S 阴影=CDEF S 平行四边形-CDHS=36-10.5=25.5(平方厘米).13.如图6-15,已知一个四边形的两条边的长度和三个角,那么这个四边形的面积是多少?【分析与解】 将AD 、BC 延长交于E ,有∠EDC=45°,∠ECD=90°,所以△CDE为等腰直角三角形,有EC=DC.而∠ECD =45°,∠EAB=90°,所以△ABE 也是等腰直角三角形,有EA=AB . 有ABE S =12×AB×EA =492,EDC S =12×EC×DC=92.有ABCD S 四边形=ABE S-EDC S=492-92=20.14.图6-16是边长为1的正方形和一个梯形拼成的“火炬”.梯形的上底长1.5米,A 为上底的中点,B 为下底的中点,线段AB 恰好是梯形的高,长为0.5米,CD 长为丢米.那么图中阴影部分的面积是多少平方米?【分析与解】 方法一:为了方便叙述.将下图中一些点标上字母.延长AB 交正方形边EF 于H 点,我们先求出梯形JICK 与正方形IFEC 的面积和,再求出三角形AFH 与梯形AHED 的面积和,将前者与后者做差所得到的值即为所求阴影部分的面积.JICK S 梯形=12×(1.5+1)×0.5=0.625, IFEC S 正方形=1×1=1.AFH S=12×AH ×FH=12×(AB+BH )×(12FE)= 12×(0.5+1)-(12×1)=0.375,AHED S 梯形=12×(AH+DE)×HE=12×(AB+BH+CE -CD)×(12FE)=12×(0.5+1+1-13)×(12×1)=1324.有S 阴影=JICK S 梯形+IFEC S 正方形-AFH S -AHED S 梯形=0.625+l-0.375-1324=1724(平方米).即阴影部分的面积为1724平方米.方法二:如下图,连接AI 、AC ,将阴影部分分成四个部分.△AJI 可以看作以AJ 为底,AB 的长为高的三角形;△AKC 可以看作以AK 为底,AB 的长为高的三角形;△AJF 可以看作以IF 为底,IB 的长为高的三角形;△ACD 可以看作CD 为底.CB 的长为高的三角形.阴影部分面积为AJIS+AKCS+AIFS+ACDS=0.75×0.5÷2+O .75×O .5÷2+l×O .5÷2+13×0.5÷2=0.1875+O.1875+0.25+112=1724(平方米)15.从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米?【分析与解】我们画出示意图(a),则剩下的木块为图(b),将4块剩下的木块如下拼成一个正方形得到图(c).我们称AB为长,AD为宽,有长与宽的差为12,所以图(c)中心的小正方形边长为12,于是大正方形AEHK的面积为6518×4+12×12=52936=236×236,所以AK长为236.即,长+宽=236,已知:长-宽=12,得长=136,于是锯去部分的木条的面积为136×1 2=1312=112(平方米).如有侵权请联系告知删除,感谢你们的配合!。
【详解】四年级下第04讲_格点图形面积计算
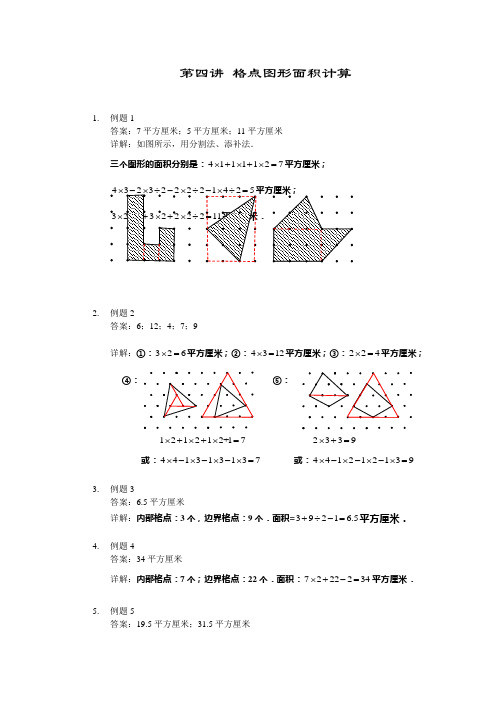
第四讲 格点图形面积计算1. 例题1答案:7平方厘米;5平方厘米;11平方厘米详解:如图所示,用分割法、添补法.三个图形的面积分别是:4111127⨯+⨯+⨯=平方厘米; 4⨯⨯÷32⨯⨯÷2. 例题2答案:6;12;4;7;9详解:①:326⨯=平方厘米;②:4312⨯=平方厘米;③:224⨯=平方厘米;3. 例题3答案:6.5平方厘米 详解:内部格点:3个,边界格点:9个.面积=3921 6.5+÷-=平方厘米.4. 例题4答案:34平方厘米详解:内部格点:7个;边界格点:22个.面积:7222234⨯+-=平方厘米.5.例题5答案:19.5平方厘米;31.5平方厘米④: ⑤: 121212+17⨯+⨯+⨯= 或:441313137⨯-⨯-⨯-⨯= 2339⨯+= 或:441212139⨯-⨯-⨯-⨯=详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:7个.面积:()7241319.5÷+-⨯=平方厘米;(2)内部格点:8个;边界格点:7个.面积:()7281331.5÷+-⨯=平方厘米.6. 例题6答案:28平方厘米;56平方厘米详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:8个.面积:()4282228⨯+-⨯=平方厘米;(2)内部格点:3个;边界格点:10个.面积:()32102456⨯+-⨯=平方厘米.7. 练习1答案:3平方厘米;10平方厘米详解:如图,分别用分割法、添补法.8. 练习2答案:12;20;5;18 详解:①:3412⨯=平方厘米; ②:直接数,每层4个,共5层,4520⨯=9. 练习3答案:13 简答:内部格点:1个,边界格点:13个.面积=()11321213+÷-⨯=.10. 练习4答案:17平方厘米简答:内部格点:1个;边界格点:17个.面积:1217217⨯+-=平方厘米. ③: ④:1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案:6;6.5简答:可用分割或添补法完成.12.作业2答案:7;12简答:使用割补法分别计算.13.作业3答案:56简答:大正三角形的面积是254100⨯=平方厘米,利用添补法可得.14.作业4答案:29简答:综合利用分割法与添补法.也可以用正方形格点图形面积公式计算.注意每个最小正方形面积是2.15.作业5答案:44简答:综合利用分割法与添补法.也可以用三角形格点图形面积公式计算.注意每个最小正三角形面积是2.。
第五讲 割补法巧算面积

例题5:如图,在两个相同的等腰直角三角形中各画一个正方形, 如果正 方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?
例题6:如图所示, 已知一个四边形的两条边的长度和三个角的度数,这 个四边形的面积是多少平方厘米?(单位:厘米)
练习3:如图所示,大正三角形的面积为10平方厘米.连接大正三角形的 各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正 三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分 的面积总和等于多少平方厘米?
例题4:如图,把两个相同的正三角形的各边分别三等分和四等分,并连 接这些等分点.已知图1中阴影部分的面积是48平方分米.请问:图2中 阴影部分的面积是多少平方分米?
4、右图中空白部分的面积是100,那么阴影正方形的面积是多少?
5、如图所示,正六边形ABCDEF的面积是36. 阴影正六边形的面积是多少?
第五讲 割补法巧算面积
在上一讲中, 我们学习了如何计算格点图形的面积,介绍了正方 形格点图形和三角形格点图形的面积计算公式 根据公式,我们可以求 出正方形格点图形的面积是最小正方形面积的几倍, 或者求出三角形 格点图形面积是最小正三角形面积的几倍. 随着几何学习的步步深入, 大家会发现除了用公式法直接 求面积之外,还有很多间接求面积的方 法. 尤其是对于不规则图形,我们并不知道这些图形的面积公式, 但 是可以把它们通过分割、添补等各种方式变换为规则的图形.
巩固练习 1、右图中的数字分别表示对应线段的长度,图中多边形的面积是多少?
2、如右图所示,在正方形ABCD内部有梯形EHGF.已知正方形ABCD的 边长是6厘米,图中线段AE、AH、BF、DG都等于2厘米.则梯形EHGF 的面积是多少平方厘米?
2011年学而思春季第三讲(格点与割补)

第三讲 格点与割补一、格点多边形满足两个条件1、顶点都在格点上2、图形的边是直线段二、格点多边形面积计算方法1:数格子方法2:分割法——把图形分割成若干个可直接计算面积的规则图形方法3:扩展法——把图形先扩展成易算面积的规则图形,再减去扩展的部分方法4:毕克公式若N表示内部的格点数,L表示边界上的格点数,S表示面积正方形格点 S = N + L÷2 -1三角形格点 S = (N + L÷2 -1)×2注意:公式所得结果为面积单位,即有多少个格子。
例1 略例2 计算格点多边形的面积解析:这是一个规则的三角形,可以直接用面积公式吗?好像不行,因为我们现在的知识还算不出相应边的长度,无法用面积公式。
如果分割成知道一条边长度的三角形不就可以了吗? 分割法:如左图,连结辅助线,将原图分割成两个三角形,这 两个三角形都知道一天边,且高也很容易观察出。
上面的三角形:5×2÷2=5下面的三角形:5×2÷2=5共计:5+5=10(面积单位)如左图,将原图扩展为一个规则的长方形,再用长方形面积减去三个三角形A,B,C的面积即可。
长方形:6×4=24A:6×2÷2=6 B:4×2÷2=4 C:2×4÷2=4结果为:24‐6‐4‐4=10(面积单位)毕克公式法:8+6÷2‐1=10例3 已知相邻两个格点距离是1,求图形面积。
解析:本题需要注意的是,这是三个独立的图形组合而成的图形,所以最好是分开算,特别是想用毕克公式的同学,一定要分成三个图形用,不能看成一个图形用公式。
同学们自己练习一下吧,不管你用什么方法,看看结果对不对。
A=5 B=4 C=12 合计:5+4+12=21(尖子)学案2 图中每个小正方形的面积都是4平方厘米,求图中阴影部分的面积。
解析:第一个图可以分割为4个一样的三角形和中间的一个田字格。
(完整版)格点与割补

学科:奥数教学内容:格点与面积生活中我们常借助一些工具来迅速简便的解决一些问题,如为了能捕到鱼,人们制作了鱼钩和网。
同样在数学的学习中,为了更好的解决问题聪明的人类也创造了一些“工具”。
这一讲我们主要介绍利用格点求几何图形的面积。
先来介绍什么是“格点”。
见下图:这是一张由水平线和垂直线组成的方格纸,我们把水平线和垂直线的交点称为“格点”,水平线和垂直线围成的每个小正方形称为“面积单位”。
图中带阴影的小方格就是一个面积单位。
借助格点图,我们可以很快的比较或计算图形的面积大小。
利用格点求图形的面积通常有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
例1 计算下图中各图形的面积:分析:先仔细观察图中的每个图形,选择方法。
显然第一、三、六图可以直接数出包含多少个面积单位即可。
而二、四、五图显然不适合用数单位面积的方法来求面积,可以采用虚线把这些图形扩展或割补成长方形,通过求长方形面积来求这些图形面积。
解答:(1)图中长方形包括3×2=6(个)面积单位,所以它的面积为6。
(2)将图中平行四边形割补成一个长方形,长方形的面积为3×2=6,而平行四边形的面积等于长方形面积,所以平行四边形的面积为3×2=6。
(3)将图中三角形用虚线分成3块,它包含有1个面积单位和2个面积单位的一半,合起来有2个面积单位,所以它的面积为2。
(4)图中将三角形扩展成一个长方形,长方形的面积为3×2=6,而三角形面积为长方形面积的一半,则三角形面积为3。
(5)将图中梯形的互相平行的一组对边延长,补出一个和原来梯形方向颠倒,但面积一样的梯形,形成一个大的长方形。
长方形的面积为(2+4)×3=18,而梯形的面积为长方形的面积的一半。
所以梯形的面积为:(2+4)×3÷2=9。
四年级下册数学讲义奥数导引第3讲格点与割补全国通用

一、 掌握格点多边形面积的计算方法,以及这些方法的推广和拓展.二、 分割法,正所谓“大事化小”,把不规则的大图形化为规则的小图形,来进行计算. 三、 添补法,则正好相反,是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.四、 遇在图形中进行适当的分割拼补,把不规则的形状拼成规则形状,也是常见的方法. 五、 公式法:在最小的正方形面积为1的图形中:21=÷+−正方形格点多边形面积边界格点数内部格点数. 在最小正三角形面积为1的图形中:22=+×−三角形格点多边形面积边界格点数内部格点数.六、 对于很多非格点图形的面积计算,分割和添补的方法依然适用.知识精讲第三讲格点与割补【例1】 图17-27中每个小正方形的边长为1厘米,阴影部分的面积是多少平方厘米?【例2】 如图17-28,平面上有16个点,相邻两点间隔为1厘米,在每个点都钉上钉子,形成4行4列的正方形钉阵.现在有许多皮筋,请问:可以套出多少种不同面积的三角形?(面积相同但形状不同的三角形算一种)图17‐28图17‐27例题解析【例3】 已知大的正六边形面积是72平方厘米,按图17-29中不同方式切割(切割点均为等分点),形成的阴影部分面积各是多少平方厘米?【例4】 图17-30为一个边长为2厘米的正方形,分别连接顶点与对应边中点.围成的阴影部分的面积为多少平方厘米?【例5】如图17-31所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)图17‐3111图17‐3011图17‐29【例6】如图17-32所示,这个多边形六条边的长度分别是1,2,3,4,5,7.问:这个图形的面积最大可能是多少?【例7】如图17-33,有一个80100×的长方形网格,它的四个顶点分别为A,B,C,D.已知图中每一个小方格的面积都是1,请选出一个合适的格点P,使得三角形P AC的面积尽可能小(不能等于0),那么这个最小的面积是多少?【例8】正12边形的边长为1厘米,阴影部分都是正三角形(边长也为1厘米),如图17-34.那么空白部分面积等于多少平方厘米?图17‐34A BCD图17‐33图17‐32。
立体几何割补法

立体几何割补法立体几何中的割补法解题技巧邹启文※ 高考提示立体几何中常用割补法解题.特别是高考中的立体几何题很多可用割补法解,有时解起来还比较容易.※ 解题钥匙例1 (2005湖南高考,理5)如图,正方体ABCD—ABCD的棱长为1,O是底面ABCD11111111的中心,则O到平面ACD的距离为( ) 112231A、 B、 C、 D、 4222分析:求点到面的距离通常是过点做面的垂线,而由于该图的局限性显然不太好做垂线,考虑O为AC的中点,故将要求的距离 11与A到面ACD的距离挂钩,从而与棱锥知识挂钩,所以可在该 111图中割出一个三棱锥A—ACD而进行解题。
111解:连AC,可得到三棱锥A—ACD,我们把这个正方体的其 1111它部分都割去就只剩下这个三棱锥,可以知道所求的距离正好为这个三棱锥的高的一半。
这个三棱锥底面为直角边为1与的直 2角三角形。
这个三棱维又可视为三棱锥C—AAC,后者高为1,底为腰是1的等腰直角三角111 2形,利用体积相等,立即可求得原三棱锥的高为,故应选B。
2例2 (2007湖南高考,理8)棱长为1的正方体ABCD—ABCD1111 的8个顶点都在球O的表面上,E,F分别是棱AA、DD的中点, 11则直线EF被球O截得的线段长为( )22A、 B、1 C、1+ D、 222分析:在该题中我们若再在正方体上加上一个球,则该图形变得复杂而烦琐,而又考虑到面AADD截得的球的截面为圆,且EF 11在截面内,故可连接球心抽出一个圆锥来。
解:如图,正方体ABCD—ABCD,依题O亦为此正方体的中心,补侧面 1111 可得圆锥0—AD(如下图), AD为平面AD,球0截平面A D1111其底面圆心正为线段AD之中点,亦为线段EF之中点,割去正方体和球 1 的其它部分,只看这个圆锥,容易看出球O截直线EF所得线段长就等于这个圆锥底面圆的直径AD之长,故选D。
1例3 (2005全国高考I,理5)如图,在多面体ABCDEF中,已知 ABCD是边长为1的正方形,且?ADE、?BCF均为正三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级下学期第九讲,几何问题第05讲格点与割补【内容概述】通过割补的办法来计算格点图形的面积,了解格点图形的面积公式.计算较复杂的图形面积时可以借助构造格点阵,或直接进行恰当的分割与拼补.【典型问题】1.【40901】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★)如图6-1,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?图6-12.【40902】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★)如图6-2,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD的面积是多少平方厘米?CDB图6-23.【40903】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★)如果图6-3是常见的一副七巧板的图,图6-4是用这副七巧板的7块板拼成的小房子图,那么,第2块板的面积等于整幅图的面积的几分之几?第4块板与第7块板面积的和等于整幅图的面积的几分之几?4. 【40904】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★)把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形.再将这个六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向外作更小的正三角形,这样就得到图6-5所示的图形.如果这个图形面积是1,那么原来的正三角形面积是多少?5. 【40905】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★★)如图6-6,正六边形ABCDEF 的面积是6平方厘米,M 是AB 中点,N 是CD 中点,P 是EF 中点.问:三角形MNP 的面积是多少平方厘米?6. 【40906】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★)把同一个三角1 23 4 56 7图6-3 图6-4图6-5 图6-6形的三条边分别五等分、七等分,适当连接这些分点,便得到了若干个面积相等的小三角形.已知图6-7中阴影部分的面积是294平方分米,那么图6-8中的阴影部分的面积是多少平方分米?7. 【40907】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★)图6-9是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求选出的点中任意3点都不在同一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么所围图形的面积是多少平方厘米?8. 【40908】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★)在图6-10中,三角形ABC 和DEF 是两个完全相同的等腰直角三角形,其中DF 长9厘米,CF 长3厘米,那么阴影部分的面积是多少平方厘米?9. 【40909】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★)如图6-11,在图6-10图6-7 图6-8长方形ABCD 中,O 是长方形的中心,BC 长20厘米,AB 长12厘米,DE =4AE ,CF =3DF ,那么阴影部分的面积是多少平方厘米?10. 【40910】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★)如图6-12,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?11. 【40911】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★★)如图6-13,ABCD 是边长为8厘米的正方形,梯形AEBD 的对角线相交于O ,三角形AOE 的面积比三角形BOD 的面积小16平方厘米,则梯形AEBD 的面积是多少平方厘米?12. 【40912】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★)如图6-14,ABCD C 图6-11 图6-12 AD C BE O图6-13是长方形,长AD 等于7.2厘米,宽AB 等于5厘米,CDEF 是平行四边形.如果BH 的长是3厘米,那么图中阴影部分面积是多少平方厘米?13. 【40913】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★★)如图6-15,已知一个四边形的两条边的长度和三个角,那么这个四边形的面积是多少?14. 【40914】(导引偶数题,四下第9讲格点与割补,几何问题第5讲★★★)图6-16是边长为1米的正方形和一个梯形拼成的“火炬”.梯形的上底长1.5米,A 为上底的中点,B 为下底的中点,线段AB 恰好是梯形的高,长为0.5米,CD 长为13米.那么图中阴影部分的面积是多少平方米?图6-14图6-15图6-1615.【40915】(导引奇数题,四下第9讲格点与割补,几何问题第5讲★★★★)从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米?16.【40916】(题解议,葛颢,四下第9讲格点与割补,几何问题第5讲★★)在同样大的正六边形中,按图1中不同方式切割(切割点均为等分),形成的阴影部分面积分别占原正六边形的几分之几?(1)93248=;(2)183244=;(3)61244=;(4)61183=。
17.【40917】(李川,四下第9讲格点与割补,几何问题第5讲★★)已知图中相邻两格点的距离均为1厘米,那么图中连出多边形的面积是多少厘米?图16.5平方厘米.可以采取分割的办法,把图形分成长方形和三角形进行计算;也可以采取添补的办法,把所围成的多边形外面的面积算出,再用总面积16减去即可;也可以采取格点面积公式进行计算.18. 【40918】(王坤,四下第9讲格点与割补,几何问题第5讲★★★)如图11,这个“凸”形的八条边长分别为1~8这8个整数,那么它的面积最大能是多少?70。
补齐长方形,周长为36,面积最大为8×10=80,最小减去如图15的两个小长方形。
19. 【40919】(题解议,葛颢,四下第9讲格点与割补,几何问题第5讲★★★)图3为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点画一个面积为137图15图11图7的三角形。
总面积是25,所以该三角形外面还有面积12。
而原图形是有3个方向等价的,因此可以考虑在每个角上去掉一个面积为4的图形。
20. 【40920】(题解议,葛颢,四下第9讲格点与割补,几何问题第5讲★★★)图4为一个边长为2的正方形,其中阴影部分的面积为多少?阴影部分的面积=2×2÷5=0.8。
21. 【40921】(李川,四下第9讲格点与割补,几何问题第5讲★★★★)在正六边形中,图3图4 1 1先通过连接各边中点画出一个六角星,并在其内部连接顶点又画出一个小六角星,如果阴影部分的面积为1,那么原来的正六边形面积是多少?12平方厘米.从外到里,依次有大、中、小三个六边形.把图形按格点分割成一个个小块的三角形,可以得到大六边形是中六边形的4倍,中六边形是小六边形的3倍,所以原来大六边形的面积为1⨯3⨯4=12平方厘米.22. 【40922】(题解议,葛颢,四下第9讲格点与割补,几何问题第5讲★★★★)图5中含有7个面积为1的小正六边形,那么阴影部分面积为多少?如图,S1的面积是412122429⨯=+++,所以阴影部分的总面积是211()615923+⨯+=。
23. 【40923】(题解议,葛颢,四下第9讲格点与割补,几何问题第5讲★★★★)如图2,平面上有16个点,每个点都钉上钉子,形成间隔为1厘米的4行4列的正方形钉阵,现在有许多皮筋,可以套出几种面积的三角形?请各举一例。
9种。
注意三角形面积在0.5和4.5之间,且为0.5的整数倍24.【40924】(题解议,葛颢,四下第9讲格点与割补,几何问题第5讲★★★★)如图6,正方形ABCD是面积为240平方厘米,HF=17厘米,EG=16厘米,则阴影EFGH的面积是多少平方厘米?图2图6AEFH如图做辅助线,由勾股定理知中间小长方形的长和宽分别是7和4,因此阴影EFGH 的面积是120+14=134平方厘米。
25. 【40925】(王坤,四下第9讲格点与割补,几何问题第5讲★★★★)如图6,两个六边形的角都是120°,其边长如图所示,那么甲的面积是乙的多少倍?6765倍。
将它们都分为边长为1的小三角形即可。
26. 【40926】(试题与详解,四下第09讲,格点与割补,几何第05讲 )图1中每个小方格的边长为1.那么阴影部分的面积是 .甲 1 62435乙416325图6 AE B图1答案:14.图3如图3,阴影区域的面积=大正方形的面积-4⨯区域1的面积-区域2的面积.区域1的面积=6⨯1÷2=3,区域2的面积=10.所以阴影区域的面积=6⨯6-4⨯3-10=14.本题还可以直接用公式计算:阴影区域的边界上一共有20个格点,内部一共有4个格点.总面积为20÷2+4=14.27.【40927】(杨笑山,四下第9讲格点与割补,几何问题第5讲★★)图点阵间隔为1,请利用方形格点公式,填出下表;答案:28. 【40928】(杨笑山,四下第9讲格点与割补,几何问题第5讲 ★★)下图三角形点阵所能连出的最小三角形面积为1,请利用三角形格点公式,填出下表答案:29. 【40929】(杨笑山,四下第9讲格点与割补,几何问题第5讲 ★★)图中最小的“□”和“△”面积都是2那么,图中左右两块阴影部分面积分别为______、______; 答案:(56、34)30. 【40930】(杨笑山,四下第9讲格点与割补,几何问题第5讲 ★★★)右图中每个小方格的边长为1.那么阴影部分的面积是_______; 答案:31. 【40931】(汪岩,四下第9讲格点与割补,几何问题第5讲★)如图21,大正方形和小正方形的边长分别为6厘米和2厘米,G 、N 、M 分别为AF 、AB 、ED 边上的中点,求四边形GNME 的面积。
答案:答案:13.5平方厘米。
32. 【40932】(汪岩,四下第9讲格点与割补,几何问题第5讲★★★)如图22,大正方形和小正方形的边长分别为7厘米和3厘米,求阴影部分的面积。
答案:7.35平方厘米。
图22图21BNA33. 【40933】(汪岩,四下第9讲格点与割补,几何问题第5讲★)在图11中,五个小正方形的边长都是2厘米,求三角形ABC 的面积。
答案:14平方厘米。
34. 【40934】(汪岩,四下第9讲格点与割补,几何问题第9讲★★)如图,两个大正三角20平方厘米,小星形的面积是多少?答案:5平方厘米。
35. 【40935】(李川,四下第09讲,格点与割补,几何第05讲★★)如图,每相邻两个格点的距离都是1,那么两个阴影图形的面积分别是多少? (6;7.5)图11ABC图1136. 【40936】(李川,四下第09讲,格点与割补,几何第05讲★★★)每个小正方形面积为1,则图中阴影部分的面积是多少?(14.5)37. 【40937】(李川,四下第09讲,格点与割补,几何第05讲★★★)每个小三角形的面积是1平方厘米,那么阴影部分的面积是多少平方厘米?(14)38. 【40938】(李川,四下第09讲,格点与割补,几何第05讲★★)如图,三角形ABC的面积为1,D 、E 、F 分别为AB 、BC 、CA 的三等分点,求三角形DEF 的面积为多少?(1/3)39. 【40939】(李川,四下第09讲,格点与割补,几何第05讲★★)如图,正方形ABCDC的边长是10厘米,BO =8厘米,那么AE 的长度是多少厘米?(12.5)40. 【40940】(李川,四下第09讲,格点与割补,几何第05讲★★)如图,△ABE 和△DCE都是等腰直角三角形,且BC =22厘米,那么直角梯形ABCD 的面积是多少平方厘米?(242)41. 【40941】(李川,四下第09讲,格点与割补,几何第05讲★★★)如图,大正六边形的面积为1,求阴影部分的面积为多少?(5/9)42. 【40942】(李川,四下第09讲,格点与割补,几何第05讲★★)已知图中大正方形和小正方形的边长分别是6和4,则图中阴影部分的面积是多少?如果大正方形的边长是8呢?如果大正方形的边长是10呢?(8)ACDD43. 【40943】(李川,四下第09讲,格点与割补,几何第05讲★★★)如图,若三个长方形APHM 、BNHP 、CQHN 的面积分别是7、4、6,则阴影部分的面积是多少?(8.5)44. 【40944】(李川,四下第09讲,格点与割补,几何第05讲★★★)如图,把长方形纸片ABCD 的一角折起,使点D 恰好与AB 的中点F 重合,若三角形EDC 的面积是10,那么长方形ABCD 的面积是多少?(30)1. (2004年ABC 卷)如下图所示,A 1,A 2,A 3,A 4⋅⋅⋅⋅⋅⋅与原点O 的距离依次是1,2,3,4⋅⋅⋅⋅⋅⋅.由A 7,A 8,A 9三点为顶点的三角形的面积为_________.(64)B CN2.(2004年ABC卷)如左下图所示,图中的小三角形和右下图中的六角形每条边的长度都是1.那么想拼成一个右下图中的六角形,需要_______个小三角形.(12)3.(2003ABC卷)如右图,如果每个小三角形的面积都是1cm2那么连接A,B,C三点的三角形的面积是_______cm2(5)4.(2003ABC卷)将边长为正整数n的正方形平均分成n 2个小正方形,每个小正方形的顶点称为格点.例如,左下图中的黑点是边长为2的正方形的格点.(33)A2A1A3A5A7A4A6O如右上图,在边长为12的正方形中有四个完全相同的直角三角形.如果三角形的一条直角边是3,那么这四个三角形各边共经过多少个格点?(每个格点只计一次)5.(2003ABC卷)下面是一座“迎春杯”奖杯的正面设计图,图中每一个小正方形的面积是1平方厘米.那么阴影部分的面积(精确到个位)是( )平方厘米.(π取值3.14) (61)6.(1999ABC卷)设上题的答数是S(8).下图是一张设计图,表示一块由10 11个方格构成的矩形土地.设计人员计划在五边形ABCDE内建一所少年宫.其余地方为绿化带.设计要求,平均每个等于方格面积的绿化地内要种S棵树.那么,在绿化地带需要种树______棵.(576)7.(1999ABC卷)下图中每个小方格的面积都是1,阴影部分是艺术字“1999”.“1999”四个字所占的面积是_______.(19.5)8.(1999ABC卷)左下图是一个面积为24的正六边形,阴影部分的面积是_______.(8)。
