数方块图形练习题
人教版小学一年级数学上学期第四单元《认识图形(一)》专项(数方块)检测题及答案

人教版小学一年级数学上学期第四单元
《认识图形(一)》专项(数方块)训练题及答案例下面图形中共有多少个小方块?你是怎样数的?
1.下面图形各有几个是看不见的?
2.数一数,填一填。
看得见的有()个;看不见的
有()个;一共有()个。
看得见的有()个;看不见的
有()个;一共有()个。
看得见的有()个;看不见的
有()个;一共有()个。
3.选一选。
(填序号)
(1)10个可以摆出()。
(2)看得见的超过8个的图形是
()。
(3)看不见的有2个的图形是()。
参考答案
例 7个
1. 1 2 2 2 提示:注意要数看不见的正方体。
2. 10 2 12 9 3 12 12 6 18 提示:数的时候可以一层一层地数。
3.(1)①③⑥(2)②④⑦
(3)①②③⑤提示:先数出看得见的正方体和看不见的正方体数量之后再填空。
数方块习题附答案-幼小衔接小学生数学思维
4/4
数方块习题-思维训练
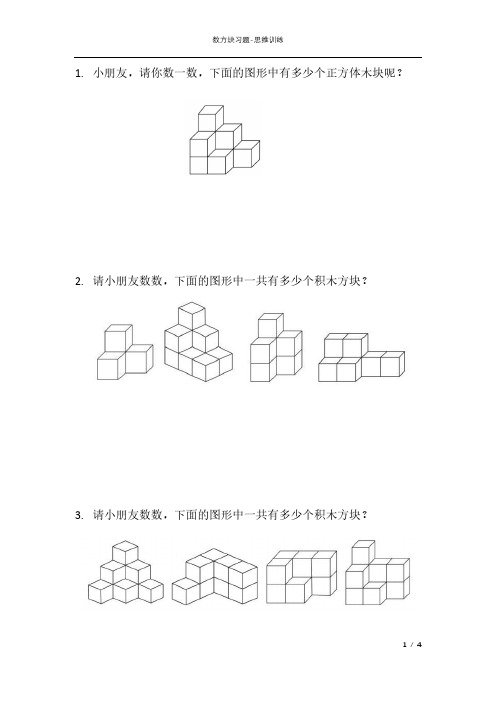
1. 小朋友,请你数一数,下面的图形中有多少个正方体木块呢?
2. 请小朋友数数,下面的图形中一共有多少个积木方块?
3. 请小朋友数数,下面的图形中一共有多少个积木方块?
1/4
数方块习题-思维训练
4. 请小朋友数数,下面的图形中一共有多少个积木方块?
5. 请小朋友数数,下面的图形中一共有多少个积木方块?
2Байду номын сангаас4
数方块习题-思维训练
6. 请小朋友数数,下面的图形中一共有多少个积木方块?
3/4
数方块习题-思维训练
答案: 1. 9 2. 4 块、10 块、7 块、8 块。 3. 10 块、9 块、9 块、10 块。 4. 11 块、15 块、14 块、9 块。 5. 7 块、20 块、9 块、8 块。 6. 13 块、20 块、19 块、17 块、11 块、13 块、8 块、11 块、8 块、
小学奥数~平面图形计数-数正方形--不规则图形
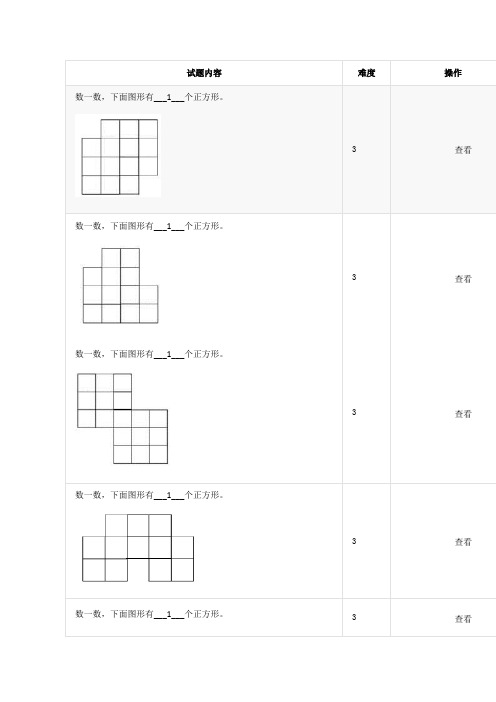
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看
数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
一年级数学学方块练习题

一年级数学学方块练习题在一年级的数学学习中,方块练习题是非常重要的一部分。
通过解决方块练习题,学生可以培养自己的逻辑思维能力,并提高数学运算的能力。
本文将为大家提供一系列适合一年级学生的方块练习题,帮助他们巩固数学知识,提高学习兴趣。
1. 填空题(1)已知有两个方块,一个方块上有3,另一个方块上有5,将它们放在一起,一共有的方块数是___。
(2)请你画一个有3个方块的长方形,并写出方块的数量是___。
(3)将以下数集中的数填入方块中:4 1 23 52. 计算题(1)有3块方块,每块方块上有3个小圆圈,请你计算一共有___个小圆圈。
(2)如果一个方块上有2个小圆圈,另一个方块上有3个小圆圈,将它们放在一起,一共有的小圆圈数是___。
(3)请你计算:2 + 3 - 1 = ___。
3. 分组题把下面的方块分成两组,每组方块的数量相等。
□□□ □□ □□ □□ □□□4. 排序题请按照方块上的数字从小到大的顺序排列方块:□ □ □ □1 42 35. 应用题小明有3块红色方块,小红有2块蓝色方块。
请你帮忙回答以下问题:(1)小明和小红一共有几块方块?(2)小明手中的方块比小红多几块?(3)小明和小红共有几种颜色的方块?通过以上一系列的方块练习题,一年级学生可以逐步巩固他们对方块、数字和计算的理解。
同时,这些练习题的设计也能引导学生进行逻辑思考,并培养他们对问题的分析能力。
希望这些练习题可以帮助学生们更好地掌握数学知识,提高他们的学习兴趣和成绩。
(字数:383)。
数学思维数方块

数学思维数方块
例1、下面的图形各有几个方块?为什么呢?
例2、左边的方块拼起来后,变成了右边的样子,左边每堆各有几个方块?右边的图中有几个看得见的,有几个看不见的?右图中一共有几个方块?
最右边组合完的图形里面,有( )块是看不见的,有( )块是我们可以看见的.
最右边组合完的图形里面,有( )块是看不见的,有( )块是我们可以看见的.
学生练习:
1、下列图形中,左边的图形均可以拆分成右边的样子.左图中有几个方块是看不见的,把它拆成右图后,就看得见了,在这些方块上面画上斜线.
拆分之后,我们多看到了( )块. 在图上标示出来.
拆分之后,我们多看到了( )块. 在图上标示出来.
3、数数下图中各有多少个方块?
4、左边的两堆方块拼起来,是右边的哪一堆?用直线连起来。
(1)
2)
3)
(4)
5、数一数,算一算,下面图中有多少块方块?
6、下面的图形表示由一些方砖堆起来的“宝塔”.仔细观察后,请你回答:
(1)从上往下数,第四层包含几块方砖?
(2)整个四层的“宝塔”共包含多少块方砖?
(3)若另有一座这样的九层宝塔,共包含多少块方砖?。
一年级数学练习题关于方块

一年级数学练习题关于方块方块的数学练习题方块是我们数学学习中常见的几何形状之一。
在一年级的数学学习中,学生将开始探索和认识方块,并通过练习题来巩固对方块的理解。
本文将为一年级学生提供一些关于方块的数学练习题,帮助他们更好地掌握这个几何图形。
练习题一:认识方块在下面的图片中,圈出所有的方块。
[图片:包含不同形状的几何图形,要求圈出方块]练习题二:方块的特征1. 方块有多少个面?2. 方块有多少个顶点?3. 方块有多少条边?4. 方块的所有面都是什么形状?练习题三:方块的比较比较下面两个方块,回答问题。
[图片:两个不同大小的方块]1. 哪个方块更大?2. 哪个方块的面积更大?3. 哪个方块的周长更长?练习题四:组合方块根据下面的提示,用不同的方块组合出下面的图形。
提示:可以使用2个或3个方块。
[图片:包含一个使用方块组成的图形]练习题五:方块的拼图根据给出的方块图案,用合适的方块填充空缺的位置。
[图片:包含一个未完成的方块拼图]练习题六:方块的数量数一数下面的图片中,每种颜色的方块各有多少个。
[图片:包含若干个不同颜色的方块]练习题七:方块的排序按照大小顺序排列下面的方块,从最小到最大。
[图片:包含不同大小的方块]练习题八:方块的分类将下面的方块分成两类,圈出每组方块。
[图片:包含不同形状的方块]练习题九:方块的填充用适当的方块填充下面的空格,使每行每列的方块数相等。
[图片:包含一个未填充完整的表格]练习题十:方块的图形组合根据给出的图形,选择合适的方块进行组合,填充每个方格。
[图片:包含一个未完成的图形组合]通过这些练习题,一年级的学生可以加深对方块的理解。
同时,这些练习题也可以帮助他们培养观察、比较和解决问题的能力。
希望同学们能够通过不断练习,逐渐掌握方块相关的数学知识,为未来的学习打下坚实的基础。
注意:以上练习题仅为示例,实际的练习题可以根据一年级学生的学习进度和能力水平进行适当调整。
不同学校和教材可能会有所不同,可以根据实际情况进行编写和修改。
一年级数学上册方块练习题

一年级数学上册方块练习题方块练习题一、填空题1. 将⃝的图形涂黑,使每一行、每一列和每一个宫都有且只有一个黑色方块。
2. 在图中,一共有___个正方形。
3. ⃝与⃝的面积之比是____。
4. 将图中的正方形按照红色部分的标记进行分组,请写出每一组的个数。
二、选择题1. 在以下图形中,哪一个图形的边数最多?(A)⃝(B)⃝(C)⃝(D)⃝2. 以下哪个图形是矩形?(A)⃝(B)⃝(C)⃝(D)⃝3. 以下哪一个是不规则图形?(A)⃝(B)⃝(C)⃝(D)⃝三、判断题1. 以下哪一个图形具有对称轴?(A)⃝(B)⃝(C)⃝(D)⃝2. 在一个宫内,不能出现相同的颜色方块。
(A)正确(B)错误3. 在一个宫内,不能出现相同的形状。
(A)正确(B)错误四、解答题1. 有一个3x3的方格,其中有一些方块被涂黑,使得每一行、每一列和每一个宫都没有相同的颜色方块。
请你根据下图填写正确的颜色。
(请在此处插入图1)2. 下图中有一些方块被涂黑,使得每一行、每一列和每一个宫都没有相同的形状。
请你根据图2填写正确的形状。
(请在此处插入图2)五、应用题小明有一块8x8的方格,他想将其分成若干个宫,使得每一个宫内的方块数量都相同。
请你帮小明计算,他最多可以将方格分成几个宫?每个宫内有几个方块?六、拓展思考请你设计一个5x5的方格,按照规则填充颜色和形状,使得每一行、每一列和每一个宫都没有相同的颜色和形状的方块。
你设计的方格应该满足什么条件?七、挑战题有一个9x9的方格,其中有一些方块被涂黑,使得每一行、每一列和每一个宫都没有相同的颜色方块。
请你尝试填满剩余的方块,使得整个方格中每一行、每一列和每一个宫的黑色方块数量都相同。
你能找到一种解法吗?以上是一年级数学上册方块练习题,希望你能认真思考并且正确解答。
加油!。
人教版小学一年级数学上学期第四单元《认识图形(一)》专项(数方块)检测题及答案

人教版小学一年级数学上学期第四单元
《认识图形(一)》专项(数方块)训练题及答案例下面图形中共有多少个小方块?你是怎样数的?
1.下面图形各有几个是看不见的?
2.数一数,填一填。
看得见的有()个;看不见的
有()个;一共有()个。
看得见的有()个;看不见的
有()个;一共有()个。
看得见的有()个;看不见的
有()个;一共有()个。
3.选一选。
(填序号)
(1)10个可以摆出()。
(2)看得见的超过8个的图形是
()。
(3)看不见的有2个的图形是()。
参考答案
例 7个
1. 1 2 2 2 提示:注意要数看不见的正方体。
2. 10 2 12 9 3 12 12 6 18 提示:数的时候可以一层一层地数。
3.(1)①③⑥(2)②④⑦
(3)①②③⑤提示:先数出看得见的正方体和看不见的正方体数量之后再填空。
图形计数(及答案)

图形计数姓名:日期:【专项训练】NO1.下图中一共有多少个长方形NO2.数一数下图共有多少个正方形NO3.下图中,AB、CD、EF、MN互相平行,则图中梯形个数与三角形个数的差是多少NO4. 图中共有多少条线段N MFEDCBAO1350NO5.如图所示,图中共有个三角形。
NO6.把一个长方体分割如下图。
这图中有多少个长方体(包括正方体)多少个正方体NO7.用小方块搭成的一个几何体,从不同的方向观察得到三视图如下图,试确定该几何体用了多少块小方块.NO8. 下图中共有____个正方形。
主视图左视图俯视图NO9. 由20个边长为1的小正方形拼成一个45长方形中有一格有“☆”图中含有“☆”的所有长方形(含正方形)共有个,它们的面积总和是。
NO10. 图中共有多少个三角形【实战训练】1、计算:55555×666667+44445×666666-155555=________。
2、计算:☆3、甲、乙两队学生参加郊外夏令营,只有一辆车接送,坐不下。
甲队学生坐车从学校出发的同时,乙队学生开始步行,车到途中某处让甲队学生下车步行去营地,车立即返回接乙队学生并直接开到营地,结果是两队学生同时到达。
已知学生步行速度为4千米/小时,汽车载学生时的速度为40千米/小时,空车速度为50千米/小时,那么甲队学生步行路程与全程的比是。
4、一个三位数,如果它的每一位数字都不超过另一个三位数对应数位上的数字,那么就称它被另一个三位数“吃掉”。
又规定“任何数都可以被它相同的数吃掉”。
比如,241被342“吃掉”,123被123“吃掉”,但是240和223互相都不能被“吃掉”。
现请你设计出6个三位数,它们中的任何一个都不能被另外5个“吃掉”,并且它们的百位数字只允许取1,2;十位数字只允许取1,2,3;个位数字只允许取1,2,3,4,那么这6个三位数之和是。
图形计数(答案)【专项训练】NO1. 下图中一共有多少个长方形解:(4+3+2+1)×(3+2+1)=60个NO2. 数一数下图共有多少个正方形解:4×7+3×6+2×5+1×4=60个NO3. 下图中,AB 、CD 、EF 、MN 互相平行,则图中梯形个数与三角形个数的差是多少解:梯形:(4+3+2+1)×(3+2+1)=60个 三角形:(4+3+2+1)×4 =40个 相差:20个NO4. 图中共有多少条线段解:49+48+47+……+1=1225条NO5.如图所示,图中共有 个三角形。
一年级数正方体练习题

一年级数正方体练习题
1. 观察下面的正方体,数一数一共有几个小正方体组成。

2. 请在下面的空白处画出一个由4个小正方体组成的大正方体。
_ _ _
_ _ _
3. 用小正方体搭建一个长方体,需要几个小正方体?(提示:长方体的长、宽、高各为2个小正方体)
长方体的长:____ 个
长方体的宽:____ 个
长方体的高:____ 个
总共需要:____ 个小正方体
4. 一个正方体的每个面都是正方形,每个面的边长都是2厘米。
请问这个正方体的体积是多少立方厘米?
5. 如果一个正方体的体积是27立方厘米,那么这个正方体的边长是多少厘米?
6. 用小正方体搭建一个长方体,长方体的长是3个小正方体,宽是2个小正方体,高是1个小正方体。
请问一共需要多少个小正方体?
7. 一个正方体的体积是64立方厘米,它的边长是多少厘米?
8. 用小正方体搭建一个长方体,长方体的长是4个小正方体,宽是2个小正方体,高是1个小正方体。
请问一共需要多少个小正方体?
9. 一个正方体的边长是5厘米,它的体积是多少立方厘米?
10. 用小正方体搭建一个长方体,长方体的长是5个小正方体,宽是3个小正方体,高是2个小正方体。
请问一共需要多少个小正方体?。
图形计数专项练习题

图形计数专项练习题在图形计数中,我们需要根据给定的图形,计算出其中的几何形状的数量。
这是一个很有趣的数学问题,也是培养孩子逻辑思维和观察力的好方法。
本文将为大家提供一些图形计数的专项练习题,帮助读者加深对图形计数的理解和运用能力。
练习一请计算下图中不同形状的数量,并将答案填写在括号中:```□□ □■■■■■■■正方形:( )个长方形:( )个三角形:( )个```练习二请计算下图中不同形状的数量,并将答案填写在括号中:```△▢ ■▢▢△■ ■ △正方形:( )个长方形:( )个三角形:( )个```练习三请计算下图中不同形状的数量,并将答案填写在括号中:```▢□ △△△△ □ ▢▢□ □ □正方形:( )个长方形:( )个三角形:( )个```练习四请计算下图中不同形状的数量,并将答案填写在括号中:```△▢ ■■ ■ □□ ▢▢正方形:( )个长方形:( )个三角形:( )个```练习五请计算下图中不同形状的数量,并将答案填写在括号中:```□ ■ △ □■ ■ △ ■■ ■ ■ ■正方形:( )个长方形:( )个```练习六请计算下图中不同形状的数量,并将答案填写在括号中:```■ ■ ■ ■ △■ △ □ □ □■ △ ■ ▢ □正方形:( )个长方形:( )个三角形:( )个```练习七请计算下图中不同形状的数量,并将答案填写在括号中:```■ ■ ■ ● □ □■ △ ● □ □ △□ □ □ ■ ■ ■长方形:( )个三角形:( )个```练习八请计算下图中不同形状的数量,并将答案填写在括号中:```△ □ ■ ■ ■■ ■ ■ ▪ ▢■ □ △ ■ ■正方形:( )个长方形:( )个三角形:( )个```以上是图形计数的专项练习题,通过对每个图形中不同形状的数量进行计数,可以提高我们的观察力和计数能力。
希望大家能够通过这些练习题,更好地掌握图形计数的方法和技巧。
祝大家学习进步!。
立体图形计数 小学数学 测试题

一、填空题
1. 如图所示的立方体图形是由______个小立方体组成的。
2. 将个相同的小正方体拼成一个体积为立方厘米的长方体,将表面涂上红漆,然后分开,其中有个面涂红的小正方体有个,则有个面涂红的小正方体有( )个。
3. 数数下面图形各有几个正方体?
( )个
( )个
( )个
4. 将一个棱长为整数的(单位:分米)的长方体6个面都涂上红色,然后把它全
部切成棱长为1分米的小正方体.在这些小正方体中,6个面都没有涂红色的有12块,仅有两个面涂红色的有28块,仅有一面涂红色的有____块.原来长方体的体积是____立方分米.
5. 用同样大小的正方体小木块堆成如下图的立体图形,那么一共用了__________块小正方体。
二、解答题
6. 一个3×3×3的正方体.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?
7. 如图,原来的大正方体是由个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?
8. 如图,125个黑色与白色小立方体相间排列拼成了一个大立方体,其中露在表面上的黑色小立方体有多少个?
9. 有一个3×4×5的长方体,先把其中相邻的两个面染红,再把它切成60个1×1×1的小正方体,请问:这些小正方体中最多有多少个是恰有一个面被染红的?。
二年级奥数计数黑白方块试题及答案

二年级奥数计数黑白方块试题及答案计数的黑白方块试题及答案例题:数一数,图2-1和图2-2中各有多少黑方块和白方块?【解析】仔细观察图2-1,可发现黑方块和白方块同样多.因为每一行中有4个黑方块和4个白方块,共有8行,所以:黑方块是:4×8=32(个)白方块是:4×8=32(个)再仔细观察图2-2,从上往下看:第一行白方块5个,黑方块4个;第二行白方块4个,黑方块5个;第三、五、七行同第一行,第四、六、八行同第二行;但最后的第九行是白方块5个,黑方块4个.可见白方块总数比黑方块总数多1个.白方块总数:5+4+5+4+5+4+5+4+5=41(个)黑方块总数:4+5+4+5+4+5+4+5+4=40(个)再一种方法是:每一行的白方块和黑方块共9个.共有9行,所以,白、黑方块的总数是:9×9=81(个).由于白方块比黑方块多1个,所以白方块是41个,黑方块是40个.总结:原理是解决问题的重要依据,只有熟练掌握并运用奥数计数问题的乘法原理才能解决更多此类题型。
递推方法的概述及解题技巧在不少计数问题中,要很快求出结果是比较困难的,有时可先从简单情况入手,然后从某一种特殊情况逐渐推出与以后比较复杂情况之间的关系,找出规律逐步解决问题,这样的方法叫递推方法。
线段AB上共有10个点(包括两个端点),那么这条线段上一共有多少条不同的线段?分析与解答:从简单情况研究起:AB上共有2个点,有线段:1条AB上共有3个点,有线段:1+2=3(条)AB上共有4个点,有线段:1+2+3=6(条)AB上共有5个点,有线段:1+2+3+4=10(条)AB上共有10个点,有线段:1+2+3+4+…+9=45(条)一般地,AB上共有n个点,有线段:1+2+3+4+…+(n-1)=n×(n-1)÷2即:线段数=点数×(点数-1)÷2。
