浅议自由网平差与程序设计
平差实验报告及完整matlab程序
fprintf(fn,'%6.3f\n',v);
fprintf(fn,'%s\n','未知参数估值x');
fprintf(fn,'%6.3f\n',x1);
fprintf(fn,'%s\n','各点高程平差值');
fprintf(fn,'%6.3f\n',x2);
86.806
3
31.225
344.8
14.846
4
-71.952
149.2
25.706
5
-61.084
142.9
31.216
6
-44.178
250.0
42.626
7
10.847
128.2
8
16.350
98.0
9
11.409
196.1
五、计算过程
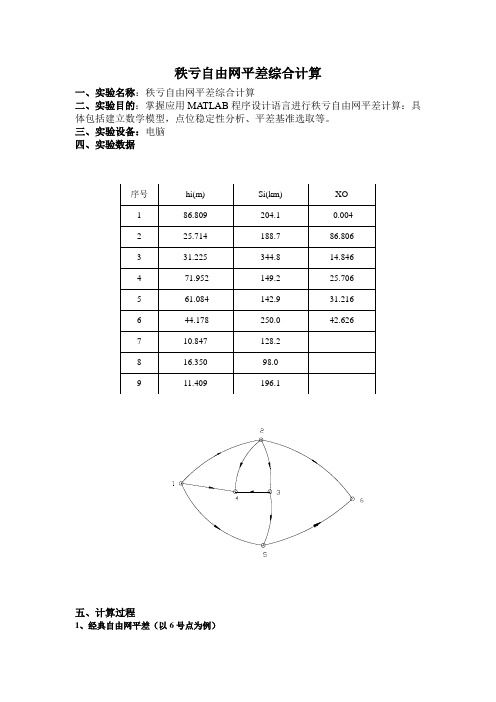
1、经典自由网平差(以6号点为例)
由已知可列出误差方程
(1)
fnal=strcat(p1,f);fpath=p1;
fm=fopen(fnal,'r');
while (~feof(fm))
s=fscanf(fm,'%f',inf)
end
%---------------从文件获取数据----------------------------------------------
switch dh_index
case 1
b=b(:,2:6);
x0=x0(2:6,:);
自由网平差

求导
ˆ T P 2 K T N 0 得到 K N 1P X ˆ 2X 1 X1 11 11 X 1 1 ˆ1 x
ˆ T P 2K T N 0 得到 X ˆ Q N K 2X 2 X2 12 2 X 2 21 X 2
于是
1 ˆ ˆ X 2 QX 2 N 21 N11 PX1 X 1
V BT ( BBT ) 1W
BR BT ( BBT ) 1
右逆
第三讲 秩亏平差(Free Net Adjustment)
关于广义逆 2、广义逆(generalized Inverse)
设A是m×n矩阵,秩R(A)=r<=min(m,n), 如果G满足如下方程,
AGA A
定义为A的广义逆,G为n×m矩阵,并记为 A 一般不唯一。
第三讲 秩亏平差(Free Net Adjustment)
一、自由网平差概述
4、秩亏网平差方法分类(根据约束条件)
加权最小二乘最小范数解
V T PV min ˆTP X ˆ min X
X
最小二乘最小范数解
逆稳平差
V T PV min ˆTX ˆ min X
ˆ X ˆ 1 X ˆ X 2 V T PV min ˆ TX ˆ min X 2 2
关于向量范数(Norm of Vector) ——范数是比长度更广泛的概念
设
X ( x1, x2 xn )
1-范数
X xi
i 1
n
X
p
( xi )1/ p
i 1
n
p
p-范数
X
( x x x )
2 1 2 2
测绘数据处理自由网平差

的秩R(B)等于未知参数 的个数t.即 (1-7-2)
2020/7/9
2
在最小二乘准则下,得其法方程为
(1-7-3)
其中N= PB,W=
。此时,系数阵N为满秩方阵,即
det(N) ,N为非奇异阵,有唯一解,其解为
(1-7-4)
当平差网没有起算数据时,网中所有的点均为待定点。设未知
方程,从而可以按附有限制条件的间接平差法求解。
等价于约束条件
的限制条件方程为
式中
BG=0
故加权秩亏网平差函数模型为
(1-7-9) (1-7-10)
(1-7-11)
2020/7/9 11
此处的系数矩阵B不是列满矩阵,而是列亏矩阵。 将式(1-7-11)组成法方程,得
(1-7-12)
式中
, 因N为降秩方阵,无正常逆,所以
2020/7/9
5
(2)、秩亏网平差。它是在最小二乘
和最小范数
的条件
下求定未知参数的最佳估值。
(3)、加权秩亏网平差。它是在最小二乘
和加权最
小范数的条件
下求定未知参数的最佳估值。式
中, 为表示未知参数稳定程度的先验权矩阵。
(4)、拟稳平差。若将平差网中的未知参数分为两类,即
(s>d)
(1-7-7)
平均距离)。 对于一维的高程网,这种约束是使平差前后网店的平均高程保持 不变。 这些约束条件我们称之为重心基准条件。
2020/7/9
9
(三)加权秩亏自由网平差基准 和秩亏自由网平差基准类似,但应考虑各网点的权重,采用了带 权重心基准条件。 (四)拟稳平差基准 也和秩亏自由网平差基准类似,但仅仅是采用所有拟稳点的重心 基准条件。
导线网平差及精度评定程序设计平差

导线网平差及精度评定程序设计平差引言导线网平差是测量领域中的一项重要工作,它对于保证测量结果的准确性和可靠性具有重要意义。
本文将介绍导线网平差的基本原理和流程,并且设计一个用于导线网平差及精度评定的程序。
程序设计平差流程数据预处理•导入原始测量数据:从测量仪器或文件中导入导线网的原始测量数据。
数据应包括导线长度、角度观测值以及观测仪器的精度等信息。
•数据格式检查:对导入的测量数据进行检查,确保数据的完整性和准确性。
•数据转换:将角度观测值转换为弧度制,便于后续计算。
•建立导线网模型:根据导线的连接关系,建立导线网的拓扑模型。
进行平差计算•确定已知点:根据实际情况,选取导线网中已知点,作为平差计算的基准点。
•建立平差方程:根据导线网模型和已知点的观测值,建立平差方程组。
•进行平差计算:使用最小二乘法或其他适当的方法,求解平差方程组,得到未知点的坐标和精度估计。
•检查计算结果:对平差结果进行检查,确保计算的准确性。
精度评定•计算精度指标:根据计算结果和观测数据的精度,计算导线网的精度指标,如相对误差、中误差等。
•统计分析:对计算结果进行统计分析,得出导线网的整体精度评定。
•生成报告:将计算结果和精度评定结果输出到报告中,方便用户阅读和使用。
程序设计考虑用户界面设计在程序设计过程中,为了方便用户使用,需要设计一个用户友好的界面。
该界面应允许用户导入原始测量数据、选择计算参数、查看计算结果和精度评定结果等。
可以使用图形界面或命令行界面来实现。
程序性能优化导线网平差是一项计算量较大的工作,特别是在处理大规模的导线网时。
为了提高程序的运行效率,可以采用一些优化技术,如矩阵运算优化、并行计算等。
同时,还可以合理选择数据结构和算法,减少计算和存储的开销。
错误处理和异常处理在程序设计中,要考虑到可能出现的数据错误和计算异常情况,为程序添加相应的错误处理和异常处理机制。
当程序发生错误或异常时,应给出合适的提示和错误信息,方便用户及时发现和解决问题。
水准网平差程序设计

程序设计中的关键问题
数据处理
如何高效地读取和处理大规模数据, 避免内存占用过多或计算效率低下。
算法优化
如何优化算法以提高程序的运行效率, 减少计算时间和资源消耗。
可扩展性
如何设计程序结构,使其具有良好的 可扩展性,便于未来功能扩展和维护。
健壮性
如何提高程序的健壮性,使其能够处 理异常情况,避免因数据错误或异常 输入导致程序崩溃。
05
程序测试与验证
测试环境与测试数据
测试环境
选择合适的硬件和软件环境,确保测试结果的准确性和可靠性。
测试数据
准备充足的水准网平差数据,包括已知的控制点数据和待处理的观测数据,以覆盖各种实际情况。
测试结果分析
精度分析
01
对测试结果进行精度分析,包括闭合差、中误差等指标,评估
程序的精度水平。
效率分析
06
总结与展望
工作总结
完成了水准网平差程序设 计的需求调研和分析,明 确了程序设计的目的和功 能要求。
实现了水准网平差程序的 基本功能,包括数据导入、 平差计算、结果输出等。
ABCD
完成了程序设计方案的制 定,包括算法选择、数据 结构设计和界面设计等。
对程序进行了全面的测试 和调试,确保程序的稳定 性和正确性。
水准网平差程序设计
• 引言 • 水准网平差基础 • 水准网平差程序设计 • 水准网平差程序实现 • 程序测试与验证 • 总结与展望
目录
01
引言
目的和背景
目的
水准网平差程序设计的主要目的是对水准网进行精度分析和优化,以提高测量 数据的准确性和可靠性。
背景
随着测量技术的发展,水准网在各种工程领域中得到了广泛应用,如建筑、水 利和交通等。然而,由于测量过程中存在误差,需要对水准网进行平差处理, 以消除或减小误差的影响。
测绘数据处理-自由网平差

4
d就是网中必要的起算数据个数。且有:
二、秩亏自由网平差思路 为了求得未知参数的唯一确定解,除了遵循最小二乘准则外 ,还必须增加新的约束条件,从而达到求得唯一解的目的 。由于约束条件不同,秩亏自由网平差可分为如下几种情 况: (1)、经典自由网平差。它是在假设网中有d个必要起算数据 的条件下,求定未知参数的最佳估计。这种方法早就已为 人们所熟知。不难理解,该法的平差结果(未知参数X的 解及其协因数阵 )将随着假设的d个必要起算数据的不同 而不同,即随着已知点位置的改变而改变。
第七行划去,剩下的6三行u列的阵即为三维测边网平差时的附
加阵。 很明显,上述的附加阵G均未标准化,即只是满足了BG=0, 但尚未满足的条件。
2019/2/15
17
阵标准化
1、用原始阵 2、设 和 阵,求出相应的阵 ; 相应 中第i行主对角元素为gii,把原始阵
的第i行数据均乘以
即可得到标准化阵的相应数据;
2019/2/15
2
在最小二乘准则下,得其法方程为 (1-7-3) 其中N= PB,W= 。此时,系数阵N为满秩方阵,即 (1-7-4) 当平差网没有起算数据时,网中所有的点均为待定点。设未知 参数的个数为u,误差方程为 (1-7-5) 组成的法方程为
2019/2/15
det(N)
,N为非奇异阵,有唯一解,其解为
2019/2/15
26
点号
P1 P2 P3 P4
/m
2019/2/15
27
(1)计算网的重心点坐标
(2)计算以加权重心点坐标为坐标原点的各待定点的坐标值
点号
P1 P2 P3
/km
P4
2019/2/15
自 由 网 平 差

自由网平差班级:测绘0911 学号:姓名:日期:一、实验分析(1)实验的目的1.熟悉广义逆的概念和计算当观测值之间不存在着函数相关,是满秩的,以间接平差为例,在求解NX=BTPl的时候,N=BTPB,其秩R(N)=R(BTPB)=R(B)=t,N为非奇异的,存在凯利逆,所以法方程存在唯一的解,称为经典自由网平差,而当网中不设起始数据或不存在必要的起始数据,而且又设网点坐标为待平差参数,误差方程系数阵列亏,这样的平差称为秩亏自由网平差,而这里就引入了广义逆的概念,广义逆是对任何矩阵定义的一种逆矩阵,设A为n*m阵,秩R(A)=γ<=min(m,n),满足方程AGA=A,的G定义为A的广义逆,G为m*n阵,记为A-不唯一,称为A-型广义逆。
(仅当A为m=n阶非奇异方阵时,A-1=A-,唯一)2.了解秩亏自由网平差的原理和方法秩亏自由网平差的原理:误差方程式为V=BX-l,权阵P为D=σ02Q=σ02P-1平差原则:V T PV=min,X T X=min法方程及其解为 NX=B T Pl X=N M-B T Pl=N(NN)-B T Pl因N+也满足最小范数逆的两个条件,故N+∈Nm-,其解也可以用N+表达,即有X=N+B T Pl=N(NN)-N(NN)-NB T Pl,单位权方差估值仍为σ02=V T PV/f=V T PV/(n-R(B))X的协因数阵为 Q XX=Nm-B T PQPB(Nm-)T=N(NN)-N(NN)-N=N+ 或者Q XX=N+ B T PQPBN+=N+NN+=N+ 法方程系数阵N的伪逆N+就是参数估值X的协因数阵。
由误差方程式,顾及Q XV=Q-BQ XX B T=Q-BN+B T秩亏自由网平差的方法:第一步:求得误差方程:V=BX-l第二步:组成法方程:NX=B T Pl第三步:计算N(NN)-和Nm-=N(NN)-第四步:计算X=Nm-B T l第五步:平差结果的计算第六步:X的协因数计算Q XX=N+3.掌握如何使用自由网拟稳平差解决变形监测数据处理在监测自由网中,假定有一部分对于另一部分点是相对稳定的。
控制网平差软件设计与实现共51页文档

6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
控制网平差软件设计与实现
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于ቤተ መጻሕፍቲ ባይዱ的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
自由网平差

L0
=
113
中央子午线
N0
=
0.0000
北向加常数
E0
=
500000.0000
东向加常数
回到顶部
2三维无约束平差
2.1平差参数
基准
WGS-84
迭代次数
2
参考因子
1.00
χ平方检验(α=95%)
通过
自由度
27
2.2基线向量及改正数
基线
起点->终点.时段
DX/改正数
(m)
DY/改正数
(m)
DZ/改正数
DY04->HG67.328K
0.4721
0.0277
0.2793
DY04->HG67.328L
0.1347
0.4665
0.3476
DY04->HG67.328M
0.3580
0.7991
0.3396
EY02->G021.331K
0.0693
0.0920
0.1366
EY02->HG67.328K
0.4309
-0.0003
0.0024
0.0007
-0.0003
1: 394858
DY04->HG67.328K
-1964.3727
-700.9887
-188.7706
2094.2253
0.0032
0.0038
0.0003
-0.0033
-0.0034
1: 647896
DY04->HG67.328L
-1964.3727
-700.9887
-188.7706
第8章自由网平差

2、秩亏自由网平差 如果不设起始已知高程, 设网中全部待定点为参数, 则误差方程为:
ˆ1 l1 v1 1 0 1 x v 1 1 0 x l ˆ 2 2 2 ˆ3 v3 0 1 1 x l3
自由网: 当控制网中仅没有必要的起算数据时,通常称为自由网。 附合网: 当控制网中除必要起算数据时外,还有多余的起算数据 的网,称为附合网。 自由网平差方法分为: 经典自由网平差和秩亏自由网平差两种。
一些特殊用途的控制网,如变形观测网、沉降监测网等, 一般为自由网。
1、经典自由网平差
例:
选定x3的高程为已知,则可列出误差方程为:
v1 1 0 l1 ˆ1 v 1 1 x l 2 2 x ˆ2 v3 0 1 l3
法方程:
ˆ1 l1 l2 2 1 x 0 1 2 x ˆ2 l2 l3
ˆ X 1 t11 B2 f ˆ n1 nt1 X 2 t2 1
2、拟稳平差附加基准条件
ˆ 0 GT Px X 0 0 t1t1 T T 其中:Px , G G1 0 I du dt1 t t 2 2 则基准约束条件变为: ˆ 0 GT X
系数阵的行列式不为零,即R(N)=2,非奇异, 方程有唯一解:
ˆ1 2 1 l1 l2 x x ˆ2 1 2 l2 l3
经典平差法的条件:
是在控制网中必需设定(或已有)足够的坐标起算数据;
如果“设定”的坐标起算数据等于必要起始数据,则称为经 典自由网平差。
第二章2自由网平差基准

1 0 0 ...
...
GCT
42t
0
ac1132
1 b12 d13
0 a12
0
... b12
0
0 c13
... d13
... ... 0 ...
3、二维测边网、边角网、导线网 ①基准条件:一个已知点坐标、一条边上的方位角
Xˆ1 0 Yˆ1 0
a12 Xˆ1 b12Yˆ1 a12 Xˆ 2 b12Yˆ2 0
M
GTG
M
H
m
m
, H
(Yi 2
X
2 i
)
S
2 i
H
i 1
i 1
标准化后G:
1
m
0
GT
Y1
m
X1
m
0
1
m
1
0
m
X 1 Y2
mm
Y1 X 2
mm
0 ....
1
...
m
X2
...
m
Y2
...
m
基准条件也可写为:
1 m
m i 1
Xˆ i
1 m
m
Yˆi
i 1
0 0
S02i
(S00i )2
2(
X
0 i
X 0 )Xˆ i
2(Yi0
Yi )Yˆi
(S00i )2
2(
X
0 i
Xˆ
i
Yi0Yˆ) 2X 0 Xˆ i
2YYˆi
将m个点至重心点的边长取和得:
m
m
m
m
m
S
2 0i
(
S
0 0i
测绘数据处讲义理自由网平差

的秩R(B)等于未知参数 的个数t.即 (1-7-2)
2021/4/13
2
在最小二乘准则下,得其法方程为
(1-7-3)
其中N= PB,W=
。此时,系数阵N为满秩方阵,即
det(N) ,N为非奇异阵,有唯一解,其解为
(1-7-4)
当平差网没有起算数据时,网中所有的点均为待定点。设未知
必须对法方程作适当变动。将式(1-7-12)中第二个方程左乘后再
加到第一个方程上去,即得变形后的法方程为
式中,
(1-7-13)
解法方程,得
(1-7-14)
2021/4/13
12
(1-7-15) 可以证明(证明略),当G满足条件BG=0时,连系数向量K必
等于零。故可简化为
(1-7-16)
将代入式(1-7-11),可求得V,再根据
2021/4/13
5
(2)、秩亏网平差。它是在最小二乘
和最小范数
的条件
下求定未知参数的最佳估值。
(3)、加权秩亏网平差。它是在最小二乘
和加权最
小范数的条件
下求定未知参数的最佳估值。式
中, 为表示未知参数稳定程度的先验权矩阵。
(4)、拟稳平差。若将平差网中的未知参数分为两类,即
(s>d)
(1-7-7)
2021/4/13 26
点号
/m
P1
P2
P3
P4
2021/4/13 27
(1)计算网的重心点坐标
(2)计算以加权重心点坐标为坐标原点的各待定点的坐标值
点号
/km
P1
P2
P3
自由网平差基准PPT演示文稿

算法优化
随着技术的发展,自由网平差 基准的算法不断得到优化和完 善,提高了数据处理效率和精
度。
02
自由网平差基准的基本原理
Chapter
自由网平差的数学模型
01
自由网平差是一种基于最小二乘法的数学模型,通过构建误差方程式和法方程 式,求解出最优解,得到待定点坐标。
02
自由网平差模型中,待定点坐标是未知数,而观测值是已知数,通过观测值之 间的相互关系,可以求解出待定点坐标的最优解。
给定初始值,为模型求解做准备。
迭代计算
通过迭代计算,逐步逼近最优解。
收敛判定
判断模型是否收敛,若收敛则停止迭代,否则继 续迭代计算。
平差结果的后处理
结果输出
将平差结果以图表、表格等形式进行展示。
精度评估
对平差结果进行精度评估,判断其可靠性和稳定性。
异常值检测
利用平差结果对观测数据进行异常值检测,提高数据质量。
自由网平差基准ppt演示文稿
目录
• 引言 • 自由网平差基准的基本原理 • 自由网平差基准的实现细节 • 自由网平差基准的优点与局限性 • 自由网平差基准的应用实例 • 总结与展望
01
引言
Chapter
什么是自由网平差基准
自由网平差基准是一种测量数据处理方法,通过数学模 型和算法对测量数据进行处理,以获得更准确的位置信 息。 它是一种相对定位方法,通过最小化观测值之间的误差 来获得更准确的位置信息。
机器视觉中的应用
总结词
关键技术、高精度要求
详细描述
自由网平差基准是机器视觉中的关键技术之一,能够提供高精度的图像几何校正和配准,广泛应用于 工业自动化、智能交通等领域。
测绘技术中的水准网设计和水准平差

测绘技术中的水准网设计和水准平差测绘技术在现代社会起着重要的作用,它不仅能够帮助我们了解地形地貌,还能为工程建设提供精确的数据支持。
其中,水准网设计和水准平差是测绘技术中的重要环节,对于保证测量结果的准确性和可靠性至关重要。
水准网设计是指在测量过程中选择合理的控制点和水准路线,确保观测数据的连贯性和全面性。
水准路线的选择应考虑地理条件、地形地貌、工程建设要求等多种因素,以达到最佳的观测效果。
在设计水准网时,需要根据具体测量任务制定相应的测量计划,并考虑到观测设备和人力资源的限制。
合理的水准网设计能够在较短的时间内获取较高的观测精度,提高工作效率。
水准平差是根据测量数据对水准路线进行调整,消除测量误差,得到最终的水准高程。
水准平差是一个复杂的数学运算过程,需要考虑到各种误差源,如仪器误差、观测误差、大地水准面的不规则性等。
在水准平差中,重力对大地水准面的影响也需要进行修正,并引入高程纲领面以确保高程系统的整体一致性。
通过水准平差,可以得到高程精度较高且整体连贯的地形高程数据,为后续工程建设和地图制图提供可靠的基础数据。
在实际的水准网设计和水准平差中,有几个关键问题需要注意。
首先是观测精度的控制,精确的观测数据是水准平差的基础,因此,在测量过程中要选择精度较高的仪器设备,并进行适当的校正和调试。
其次是高程控制的提供,选择合适的控制点来定位水准路线的起点和终点,以及中途的控制点,可以提高水准平差的精度和可靠性。
此外,还需要根据操作地形的具体情况选择合适的水准工具和观测方法,以确保测量的顺利进行。
随着科技的不断发展,现代测绘技术中的水准网设计和水准平差也在不断进步和完善。
例如,借助全球卫星导航系统(GNSS)和激光测距技术,可以实现更高精度的水准测量。
同时,计算机与信息技术的应用也为水准平差提供了更加高效准确的工具和方法。
这些技术的迅速发展不仅提高了测绘工作的效率,还提高了数据的精度和可靠性。
总之,水准网设计和水准平差是测绘技术中的重要环节,对于测量结果的准确性和可靠性至关重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V=AX.L .
√
12 假设检 验 的原理 与公 式 .
两期变形点坐标值之差异 , 并不一定反 映点 位的
变 动 , 也可 能 是测 量 误 差 引起 的。 为 了探 明 这 些 差 它 异主要 是误差 干 扰还 是 变 形 造成 的位 移 , 要 进 行 位 需
附加 的最 小范 数条 件 :
X x2=ri an 两期 观 测 数 据 结 果 表1 图 1 水 准 路 线 图
M =N控一NnN Nl 2
Mm ( = MM) 一
O= 一 2 l Ⅳ 4 Ⅳ
Ol=
= ( — Ⅳ N: )
其中( M)为 M M 一 M的广义逆矩阵, 得到方程解如下:
信。
13 拟 稳平差 的原 理与公 式 .
式中 R N a = ( )= < ,a 为奇异阵, ( a) R A tu N a 其凯利 逆不存在 , 得不到唯一解 。秩亏数 d “ t = 一 等于控制 网 的必要起算个数 , 对于水准 网, 必要一个点 的起算高 程, 所以 d 1 = 。本例采用 M tr ae 9 2 ie yr 7 年发表的附 tm 1
中 图分 类 号 :2 7 P0
文 献 标 识 码 : B
浅议 自由网平差与程 序设计
壬娟 , 王东
( 南通市现代测绘工程 院 , 江苏 南通
网平差计算过程 , 并用实例进行水 准测量数据平差处理。
关键词 : 自由 网 平 差 ; 亏 自由 网平 差 ; 稳 平 差 ; B 秩 拟 V
Q x N a S ~一 S x =( a + S ) S
网, 各期都进行 固定基准或拟稳基准的经典平差, 但要 对基准的稳定性进行假设检验。对于后一类型的监测 网, 一般先按重心基准进行秩亏 自由网平差 , 通过观测 数据统计检验分析 , 找出网中相对稳定点 , 用拟稳平差 对监测点的位移进行分析。 设某水准观测 数为 n 必要观测数为 t控制 网中 , ,
13 2
按 最小 二乘 法原 理 :
PV:mi n
高差 年变 化量 在 1m m以 内 , 因此 可 以作 为变形 监测 网 内的所谓 不 动 点 。水 准路 线 图如 图 1所 示 , 期 的 野 两 外观 测数 据如 表 1所示 。
法方 程 为 :
N1 l
其中:
一
得 到法方 程 : Na +K { aX S :
S X :0 K=0
是所布 网中部分点是不动点或相对不动点构成基
得 到解 为 :
:
准, 对网中其他点进行监测 ; 二是网中全部点是否移动
要通 过观 测 数 据 分 析才 能 判 定 。对 于前 一类 型监 测
( a+ S f N a S
N】aP 1 l TA =
Ⅳ 2 P 2 1 1 :A = =
Ⅳ2 P 2 2= A
N : PA 靖 吕_ 6 4
尺 N 1 =t, 1 秩 , N) ,『 异 , 式 不 ( 1 ) lN1 满 尺( =r. 奇 7 、 上 能得 到唯 一解 。本 文 中的拟 稳平 差解 算方 法采 用 我 国 周 江 文研 究员 针对 变形 监测 网提 出的广义 逆 的方 法 。
2 60 ) 2 0 8
摘 要 : 简单讨论 自由网平差 中的秩亏 自由网平差和 自由网拟稳平差的原理 , 分析公式 , 结合 V B语 言编程 , 简化 自由
1 秩亏 自由网平差 。 拟稳平差 以及假设检 验的
原 理 与公 式
1 1 秩 亏 自由网平差原 理与公 式 . 变 形观测 中 , 水准监 测 网一般 可归纳 为两 种类 型 :
如果检测 网中的确有一部分点相对于另一部分点 是相对稳定的, 则以网中点的高程或坐标作为未知数 , 就有稳定未知点和不稳定知点两类 。设不稳定未知数
加条件法 , 运用数学工具使法方程系数阵零特征值对 应的特征向量构成矩阵 L s 。附加条件 :
J X:0 s
的改正值为 x , l稳定未知数的改正值为 x , 2设有 t 个 1 稳定点 , 进行拟稳平差 。误差方程为 :
移量显著性检验 , 本文采用 t 检验法 , 步骤如下 :
() I 检验 的原 假 设 H 0是 = , I 即该 点 坐 标 理 论值 两期相 同 , 自然无位 移存在 ; 如果拒 绝 原假 设 H 0, 则接 受备假 设 H1认 为 位移存 在 。 , ( ) 统计量 £当原假 设 H 2做 , 0成 立 , : 则
=
按照最小二乘原则 , 作函数 :
v PV 2 S X) T + K ( T :mi n
c ,) 4 (一 。 己
收稿 日 :0O 9 2 期 2 1 —O —O 作者简介 : (9 2 ) 女 , 王娟 18 一 , 助理工程师 , 主要从事软件开发。
第 3期
王娟等 .浅议 自由网平差与程序 设计
2 1 年 6月 01 第 3期 文章 编号 :62 8 6 (0 0 0 — 2 — 4 17 — 22 2 1 )3 12 0
城
市
勘
测
J n 2 1 u .0 1
No 3 .
U b n Ge t c n c lI v s g t n & S r e i g r a oe h ia n e t ai i o u v yn
△
一
一 一
按最小二乘法原理 :
v PV=mi T n
法方 程为 :
Na f 0 aX- = f AP = L
Na a:A PA
△
√ lQ m5 Q+ 2 / x
( ) 定显著 水平 , t 布表 得 t , 3选 查 分 如果 fl > t
t , 则拒绝 H , 0 位移显著 可信 , 否则 , 认为变形 不 可
X1:8PL
X2= p JL
V=A — L
