三维自由网平差
自由网平差

求导
ˆ T P 2 K T N 0 得到 K N 1P X ˆ 2X 1 X1 11 11 X 1 1 ˆ1 x
ˆ T P 2K T N 0 得到 X ˆ Q N K 2X 2 X2 12 2 X 2 21 X 2
于是
1 ˆ ˆ X 2 QX 2 N 21 N11 PX1 X 1
V BT ( BBT ) 1W
BR BT ( BBT ) 1
右逆
第三讲 秩亏平差(Free Net Adjustment)
关于广义逆 2、广义逆(generalized Inverse)
设A是m×n矩阵,秩R(A)=r<=min(m,n), 如果G满足如下方程,
AGA A
定义为A的广义逆,G为n×m矩阵,并记为 A 一般不唯一。
第三讲 秩亏平差(Free Net Adjustment)
一、自由网平差概述
4、秩亏网平差方法分类(根据约束条件)
加权最小二乘最小范数解
V T PV min ˆTP X ˆ min X
X
最小二乘最小范数解
逆稳平差
V T PV min ˆTX ˆ min X
ˆ X ˆ 1 X ˆ X 2 V T PV min ˆ TX ˆ min X 2 2
关于向量范数(Norm of Vector) ——范数是比长度更广泛的概念
设
X ( x1, x2 xn )
1-范数
X xi
i 1
n
X
p
( xi )1/ p
i 1
n
p
p-范数
X
( x x x )
2 1 2 2
三维自由网平差。。
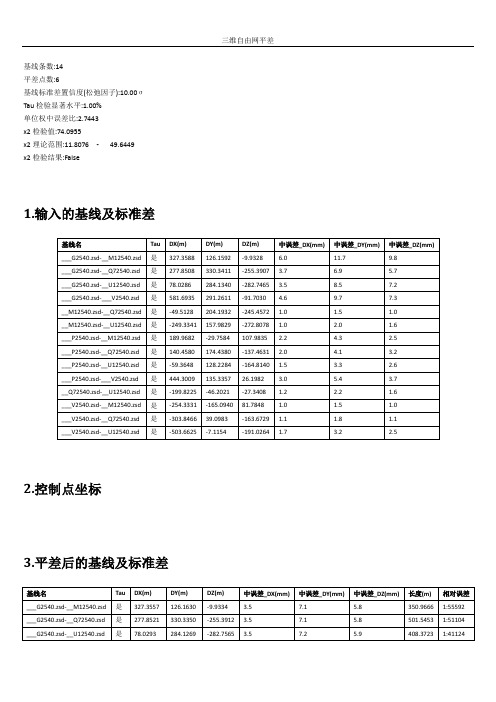
7.2
5.8
6.
站点名
Lat.
Lon.
H(m)
中误差_Lat(mm)
中误差_Lon(mm)
中误差_H(mm)
G
040:37:15.67245N
109:49:46.11362E
1026.7267
0.0
0.0
0.0
M1
040:37:15.26688N
109:49:31.19336E
1026.0589
0.0
___G2540.zsd-__U12540.zsd
是
0.0006
-0.0070
-0.0100
4.5
12.0
10.3
0.0
0.0
0.0
___G2540.zsd-___V2540.zsd
是
-0.0011
0.0115
0.0135
6.7
14.3
10.5
0.0
0.0
0.0
__M12540.zsd-__Q72540.zsd
dVDX(mm))
dVDY(mm)
dVDZ(mm)
___G2540.zsd-__M12540.zsd
是
-0.0031
0.0038
-0.0006
9.4
18.0
15.2
0.0
0.0
0.0
___G2540.zsd-__Q72540.zsd
是
0.0013
-0.0060
-0.0005
5.1
9.1
7.4
0.0
0.0
4131120.0894
3.8
7.7
6.2
Q7
第二章2自由网平差基准

(4‘)
平差前和平差后重心点至各点的边长平方和相等。
经典自由网平差
基准:一个点坐标,一条边方位,一边长,平差前后保持不变,
秩亏网平差中,以(1’)——(4‘)式代替,其中(1’)(2‘)式为网的平移, (3’) 式定向,(4)式边长缩放,
根据重心坐标,为了计算方便,当近似值取定后。可先进行重心化—— 就是把坐标原点移至重心点处。
2. 二维测角网
假设所有点的纵横坐标为未知数,给定网中两个点的坐标为 固定(已知)坐标或一个点的纵横坐标、一条边方位角、一条边的边 长为固定值(已知)。
——这些固定数据构成网的平差基准。
设
GCT Xˆ 0
为基准方程
①当1、2两点已知(固定)坐标,则:
Xˆ 1 Yˆ1 Xˆ 2
0
V3 1
1 1 0
110XXXˆˆˆ132
0 0 6
(2)
X3 X30 设 X3X30Xˆ3
Xˆ3 0
称为基准条件方程
GCT 0 0 1 ,GCTXˆ 0 ,其中 X ˆX ˆ1 X ˆ2 X ˆ3 13
(Yi2Xi2) Si2
H
i1
i1
标准化后G:
1
m
0
0 1
1 m 0
0
....
1
...
GT
Y1
m X1
Y2
m
X2
...
m m m m
X
1
m
Y1 X 2 mm
Y2
...
测绘数据处理自由网平差

的秩R(B)等于未知参数 的个数t.即 (1-7-2)
2020/7/9
2
在最小二乘准则下,得其法方程为
(1-7-3)
其中N= PB,W=
。此时,系数阵N为满秩方阵,即
det(N) ,N为非奇异阵,有唯一解,其解为
(1-7-4)
当平差网没有起算数据时,网中所有的点均为待定点。设未知
方程,从而可以按附有限制条件的间接平差法求解。
等价于约束条件
的限制条件方程为
式中
BG=0
故加权秩亏网平差函数模型为
(1-7-9) (1-7-10)
(1-7-11)
2020/7/9 11
此处的系数矩阵B不是列满矩阵,而是列亏矩阵。 将式(1-7-11)组成法方程,得
(1-7-12)
式中
, 因N为降秩方阵,无正常逆,所以
2020/7/9
5
(2)、秩亏网平差。它是在最小二乘
和最小范数
的条件
下求定未知参数的最佳估值。
(3)、加权秩亏网平差。它是在最小二乘
和加权最
小范数的条件
下求定未知参数的最佳估值。式
中, 为表示未知参数稳定程度的先验权矩阵。
(4)、拟稳平差。若将平差网中的未知参数分为两类,即
(s>d)
(1-7-7)
平均距离)。 对于一维的高程网,这种约束是使平差前后网店的平均高程保持 不变。 这些约束条件我们称之为重心基准条件。
2020/7/9
9
(三)加权秩亏自由网平差基准 和秩亏自由网平差基准类似,但应考虑各网点的权重,采用了带 权重心基准条件。 (四)拟稳平差基准 也和秩亏自由网平差基准类似,但仅仅是采用所有拟稳点的重心 基准条件。
第十四章、GPS网三维平差

第十四章、GPS网三维平差
多基线解模式
多基线解模式(Multi-Baseline Mode):采用逐时段 解算方式,也就是在进行基线解算时,一次提取一 个观测时段中所有同步观测的n台GPS接收机所采集 的同步观测数据,在一个单一解算过程中共同求出 所有n-1条函数独立的基线。在每一个完整的多基线 解中,包含了所有解算出的n-1条基线向量的结果。 也成为时段模式(Session Mode)。
第十四章、GPS网三维平差
❖ 0、基线残差 理论上,载波相位观测精度为1%周,即对
L1载波信号观测的误差只有2mm。
第十四章、GPS网三维平差
第十四章、GPS网三维平差
1 RMS
RMS 即均方根误差(Root Mean Square),即:
其中:
VT PV RMS
n f
V为观测值的残差;P为观测值的权;n-f为观测值的
在解算时,究竟采用哪n-1条基线,有不同的选择方 法。常用的有射线法和导线法。虽然这两种方法在 理论上是等价的,但由于基线解算模型的不完善, 其结果并不完全相同。基本原则是选择数据质量好 的点作为基准点,选择距离较短的基线进行解算。 当两个原则无法同时满足时,需要进行权衡。
第十四章、GPS网三维平差
(3)基线解算中所需的起算点坐标,应按以下优先顺序 采用
国家 GPS A、B级网控制点或其他高级GPS网控制点已 有的WGS-84坐标系坐标。 国家或城市较高等级控制点转到WGS-84坐标系后的坐 标值。
第十四章、GPS网三维平差
不少于观测30分钟的单点定位结果的平差值提供 的WGS-84系坐标。
高速铁路CPⅢ三角高程网构网与平差计算方法

为克 服高 速铁路 C 1控 制 网将平 面 和高 程数 P1 I
据分开测量的不足 , 高高速铁路 C 1控制 网的 提 P1 I 建 网效率 , 保证 达 到高精 度要 求 , 文 在 C I 并 本 PI平 I
平 差计 算原 理 , 建立 了平差计 算 和精度 评定 的数 并
学 模 型 , 后 , 绍 根 据 该 数 学 模 型 开 发 的 实 用 最 介
C 1三角 高程 网平 差计算 软 件. P1 I
间距 约为 l 2 精度 要 求很 高 , 面 网要 求 相 0~ 0m; 平
邻点 的相 对 点 位 中误 差 不 大 于 -1mm , 程 网 4 j高 -
o sna os sb i ,ad teprm t dut e t eh di ue oo ti teacrt e v t n be Tl ,i ul n aa ee ajs n m to s sd t ba h cua l a o tn t h r m n e e i
法, 又有 中国的矩形 法 .
站 到 C Ⅲ点 的水 平方 向值 、 P 斜距 和竖 直 角. 采用 自
由测 站观 测 , 没有 仪 器 对 中的 问题 , 镜 中心就 是 棱 C Ⅲ三维控 制 点 的 点 位 , 有 目标 对 中和 棱 镜 高 P 没 度 问题 . 样 , 据 自由测站 到 C H点 的斜距 和竖 这 根 PI 直角 , 就可 以计算 测 站到 C Ⅲ点 的三角 高差 . P 一个 C 1平 面 网测 站 一般观 测 1 P1 I 2个 C I点 , 个 自 PI 由单 I 由测站观 测值 形 成 的 三 角 高差 情 况 , 图 1 示. 如 所
【精】三维自由网平差(学习资料)
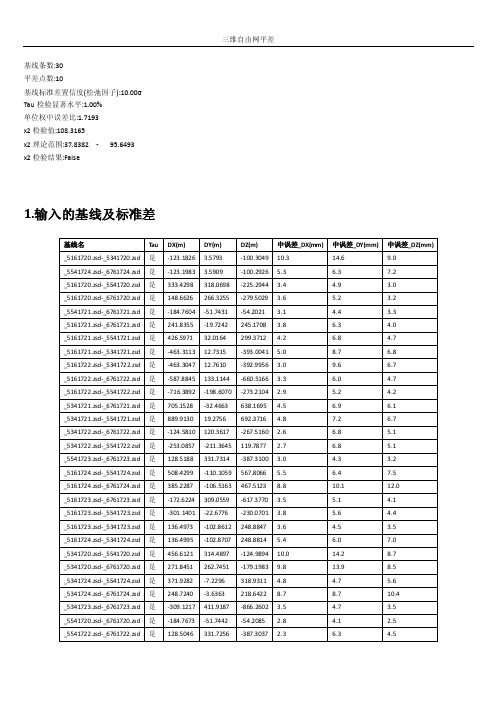
_5341722.zsd-_5541722.zsd 是
_5541723.zsd-_6761723.zsd 是
_5161724.zsd-_5541724.zsd 是
_5161724.zsd-_6761724.zsd 是
_5161723.zsd-_6761723.zsd 是
_5161723.zsd-_5541723.zsd 是
三维自由网平差
4.基线改正数及标准差
基线名
Tau
_5161720.zsd-_5341720.zsd 是 _5541724.zsd-_6761724.zsd 是 _5161720.zsd-_5541720.zsd 是 _5161720.zsd-_6761720.zsd 是 _5541721.zsd-_6761721.zsd 是 _5161721.zsd-_6761721.zsd 是 _5161721.zsd-_5541721.zsd 是 _5161721.zsd-_5341721.zsd 是 _5161722.zsd-_5341722.zsd 是 _5161722.zsd-_6761722.zsd 是 _5161722.zsd-_5541722.zsd 是 _5341721.zsd-_6761721.zsd 是 _5341721.zsd-_5541721.zsd 是 _5341722.zsd-_6761722.zsd 是 _5341722.zsd-_5541722.zsd 是 _5541723.zsd-_6761723.zsd 是 _5161724.zsd-_5541724.zsd 是 _5161724.zsd-_6761724.zsd 是 _5161723.zsd-_6761723.zsd 是 _5161723.zsd-_5541723.zsd 是 _5161723.zsd-_5341723.zsd 是 _5161724.zsd-_5341724.zsd 是 _5341720.zsd-_5541720.zsd 是 _5341720.zsd-_6761720.zsd 是 _5341724.zsd-_5541724.zsd 是 _5341724.zsd-_6761724.zsd 是 _5341723.zsd-_6761723.zsd 是 _5541720.zsd-_6761720.zsd 是 _5541722.zsd-_6761722.zsd 是 _5341723.zsd-_5541723.zsd 是
WGS-84三维无约束平差坐标在GPS测量中的运用

WGS-84平差坐标在GPS测量中的运用韶关市国土资源信息中心郭建华摘要:本文基于GPS相对定位和坐标转换原理,针对GPS测量中的WGS-84与本地坐标系转换参数的选择进行研究,结合实际测量工作,介绍WGS-84平差坐标在实际测量过程运用,提高工作效率的作业方法。
关键词:WGS-84坐标系,网平差,坐标转换,RTKAbstract: Based on GPS relative positioning and coordinate conversion mechanism for GPS measurements in WGS-84 coordinate system with the local transformation parameters of selection, in combination with the actual measurements, introduced Adjustment WGS-84 coordinates the use of the actual measurement process, improve efficient way of operating.Key words: WGS-84 coordinate system, network adjustment, coordinate transformation,RTK1.引言全球定位系统(GPS)技术的出现,以其高精度、全天候、低成本、高效率等特点被广泛应用到测绘及其他领域,大大的提高了测绘工作的效率,减轻了测绘工作者的外业劳动强度。
由于GPS系统是一个全球性的定位和导航系统,其坐标也是全球性的。
目前GPS测量所使用的协议地球坐标系成果WGS-84世界大地坐标系(World Geodetic System),所有的GPS测量成果都是基于WGS-84坐标系的,包括单点定位的坐标以及相对定位中解算的基线向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中误差_DZ(mm)
长度(m)
相对误差
_5161720.zsd-_5341720.zsd
是
-123.1719
3.5687
-100.3121
4.2
5.3
4.6
158.8917
1:19537
_5541724.zsd-_6761724.zsd
是
-123.2033
3.5921
-100.2875
2.7
3.4
3.0
301.9220
1:56996
_5341720.zsd-_5541720.zsd
是
456.6011
314.5024
-124.9806
4.6
6.1
4.8
568.3454
1:63048
_5341720.zsd-_6761720.zsd
是
271.8322
262.7564
-179.1913
是
248.7240
-3.6363
218.6422
8.7
8.7
10.4
_5341723.zsd-_6761723.zsd
是
-309.1217
411.9187
-866.2602
3.5
4.7
3.5
_5541720.zsd-_6761720.zsd
是
-184.7673
-51.7442
-54.2085
2.8
4.1
是
-716.3892
-198.6070
-273.2104
2.9
5.2
4.2
_5341721.zsd-_6761721.zsd
是
705.1528
-32.4663
638.1695
4.5
6.9
6.1
_5341721.zsd-_5541721.zsd
是
889.9130
19.2756
692.3716
4.8
7.2
1.8
3.3
2.5
525.9086
1:115882
_5161724.zsd-_5541724.zsd
是
508.4318
-110.1096
567.8021
3.5
4.4
4.3
770.0820
1:108644
_5161724.zsd-_6761724.zsd
是
385.2227
-106.5203
467.5111
基线条数:30
平差点数:10
基线标准差置信度(松弛因子):10.00σ
Tau检验显著水平:1.00%
单位权中误差比:1.7193
x2检验值:108.3165
x2理论范围:37.8382 - 95.6493
x2检验结果:False
1.
基线名
Tau
DX(m)
DY(m)
DZ(m)
中误差_DX(mm)
中误差_DY(mm)
4.4
3.4
894.2082
1:148873
_5161722.zsd-_5541722.zsd
是
-716.3841
-198.5966
-273.2089
2.4
4.3
3.3
792.0163
1:134184
_5341721.zsd-_6761721.zsd
是
705.1618
-32.4706
638.1674
2.7
4.0
3.2
379.6501
1:65356
_5161723.zsd-_5341723.zsd
是
136.4955
-102.8558
248.8871
2.7
3.4
3.0
301.9190
1:56996
_5161724.zsd-_5341724.zsd
是
136.4998
-102.8748
248.8805
14.2
8.7
_5341720.zsd-_6761720.zsd
是
271.8451
262.7451
-179.1983
9.8
13.9
8.5
_5341724.zsd-_5541724.zsd
是
371.9282
-7.2296
318.9311
4.8
4.7
5.6
_5341724.zsd-_6761724.zsd
4.6
6.1
4.8
418.3816
1:46391
_5341724.zsd-_5541724.zsd
是
371.9277
-7.2237
318.9333
3.4
4.1
4.0
490.0009
1:73145
_5341724.zsd-_6761724.zsd
是
248.7125
-3.6269
218.6533
4.7
5.7
4.2
5.3
4.6
158.9010
1:19539
_5161720.zsd-_5541720.zsd
是
333.4299
318.0728
-225.2929
2.9
4.2
2.7
512.9354
1:88430
_5161720.zsd-_6761720.zsd
是
148.6603
266.3274
-279.5029
12.8
18.4
10.9
0.0
0.0
0.0
_5541724.zsd-_6761724.zsd
是
-0.0050
0.0011
0.0051
5.6
6.4
8.2
0.0
0.0
0.0
_5161720.zsd-_5541720.zsd
是
0.0000
0.0030
0.0015
3.4
4.9
2.9
0.0
0.0
0.0
_5161720.zsd-_6761720.zsd
是
333.4298
318.0698
-225.2944
3.4
4.9
3.0
_5161720.zsd-_6761720.zsd
是
148.6626
266.3255
-279.5029
3.6
5.2
3.2
_5541721.zsd-_6761721.zsd
是
-184.7604
-51.7431
-54.2021
3.1
4.4
2.3
4.7
3.6
318.7052
1:50558
_5341722.zsd-_5541722.zsd
是
-253.0859
-211.3713
119.7820
2.2
4.6
3.6
350.8248
1:55947
_5541723.zsd-_6761723.zsd
是
128.5279
331.7361
-387.3133
3.0
4.8
3.9
951.6118
1:138777
_5341721.zsd-_5541721.zsd
是
889.9172
19.2700
692.3644
3.0
4.8
3.9
1127.6934
1:162660
_5341722.zsd-_6761722.zsd
是
-124.5861
120.3542
-267.5186
3.3
2.1
199.3893
1:44473
_5541722.zsd-_6761722.zsd
是
128.4996
331.7244
-387.3006
1.8
3.3
2.5
525.8850
1:115877
_5341723.zsd-_5541723.zsd
是
-437.6429
80.1811
-478.9512
2.7
2.5
_5541722.zsd-_6761722.zsd
是
128.5046
33Hale Waihona Puke .7256-387.3037
2.3
6.3
4.5
_5341723.zsd-_5541723.zsd
是
-437.6394
80.1868
-478.9518
3.5
4.8
3.7
2.
3.
基线名
Tau
DX(m)
DY(m)
DZ(m)
中误差_DX(mm)
12.0
_5161723.zsd-_6761723.zsd
是
-172.6224
309.0559
-617.3770
3.5
5.1
4.1
_5161723.zsd-_5541723.zsd
是
-301.1401
-22.6776
-230.0701
3.8
5.6
4.4
_5161723.zsd-_5341723.zsd
是
-0.0022
0.0019
0.0000
3.7
5.4
3.2
0.0
0.0
0.0
_5541721.zsd-_6761721.zsd
是
0.0046
