第九章磁路
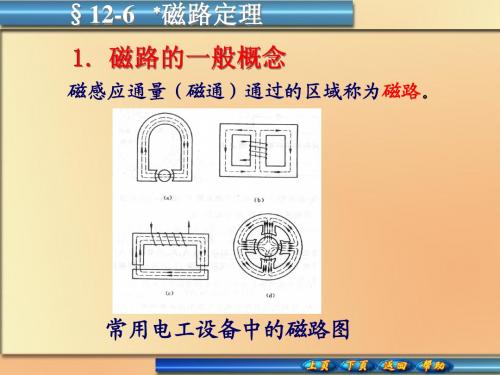
磁路

3、基本磁化曲线
对同一铁磁材料,选择不同的Hm反复磁化,得到不同 的磁滞回线。将各条回线的顶点连接起来,所得曲线称为 基本磁化曲线或平均磁化曲线。虽然不同于起始磁化曲线, 但差别不大。
23
三. 铁磁材料
按照磁滞回线形状的不同,铁磁材料可分为软材和硬磁材料两大类。
软磁材料
磁滞回线形状较窄,Br和Hc较小的铁磁材料。如铸铁、铸钢、硅钢片等,其 磁导率较高,常用来制造电机和变压器的铁芯。
1
§1.1磁路的基本定律
磁场的几个常用量
磁感应强度(又称磁通密度)B —— 表征磁场强弱 及方向的物理量。单位:Wb/m2 磁通量Φ —— 垂直穿过某截面积的磁力线总和。 单位:Wb 磁场强度H —— B=μH ,单位:A/m
一. 磁路的概念
磁路——磁通所通过的路径。如图1-1所示,图a是 变压器的磁路,图b是两极直流电机的磁路。 2 磁通所通过的路径称为磁路:
硬磁(永磁)材料
磁滞回线较宽 ,Br和Hc较大的铁磁材料。由于剩磁Br较大,可以作成永久 磁铁。因而硬磁材料也称为永磁材料。永磁材料的种类很多。 永磁材料三个性能指标:(一般而言,越大越好) 剩磁Br、矫顽力Hc、最大磁能积(BH)max 永磁材料的种类介绍以及性能对比参见书12页:
24
三、铁磁材料 1、软磁材料 2、硬磁材料 四、铁心损耗
对于一般硅钢片,在正常磁通密度工作范围内(1T—1.8T),上式可以近似 写成:
pFe cFe f
1.3
Bm G
28
2
CFe为铁芯损耗系数;G为铁芯重量。上式表明:铁芯损耗 于频率的1.3次方、磁通密度的平方和铁芯重量成正比。
交流铁心损耗
(工程/ 50 Bm 50
磁路和磁性材料

铁心线圈的电感不是常数,当磁 路饱和程度增加时,自感下降。
精品资料
互感(hùgǎn)
M
Ψ 21 i1
N2Φ21 i1
N2 (F1m ) i1
N2 (N1i1m ) i1
N1 N 2 m
N1 ----线圈1的匝数 N2 ----线圈2的匝数 Λm----互感(hùgǎn)磁通所经磁路的
和最大磁能积(BH)max三项指标表征
精品资料
精品资料
常见(chánɡ jiàn)永磁材
料
铸造型/粉末 型铝钴镍
铁氧体
Br(T)
1.35
0.405
Hc(kA/m)
59
294
(BH)max(kJ/m3) Br温度系数 允许温度
59.7 -0.02
30.5
-0.2 受温度影响
变化大
价格
便宜/较贵
便宜
F Ni, N为绕组匝数
磁通量(磁通)Φ(Wb):穿过曲面S的磁通是磁感应密度 B的法线分量的面积分
B均匀时
sB da
BcSc
精品资料
磁场强度H与磁感应密度B对比 H和B均可表征磁场性质(即磁场强弱和方向) 均匀磁介质,若包括介质因磁化(cíhuà)而产生的磁场在内时,
用B表示,其单位为特斯拉T,是一个基本物理量 单独由电流或者运动电荷所引起的磁场(不包括介质磁化
稀土钴 1.06 748 206.9 -0.025
200~250℃
贵
钕铁硼
1.12 843 238.7 -0.1 100 ℃ 较稀土钴低 廉
精品资料
铸造(zhùzào)型铝钴镍铁芯
铁氧体铁芯
back
磁学

A1=6.5×5×0.92=30cm2 A2=8×5=40cm2 A3=ab+(a+b)l0
=5×6.5+(5+6.5) ×0.1=33.65cm2
JIE
⑶ 求各段磁路磁感应强度
⑷ 求各段磁路磁场强度
B1
A1
3103 30104
1T
3103 B2 A2 40104 0.75T
B0
A0
的系数。
Φ
Φ
ie
ie
i
+
ue
–
§9.6交流铁心线圈的电路模型
一、励磁电流的计算
U E I a
I
IM
E
损耗角
arc
tan
I IM
2
1.求磁化电流
U m Bm Hm Im IM
IM
Im 2
>1
2.求磁损耗电流
磁损耗 pFe pFe0V
磁损耗电流 Ia PFe / E
3.求励磁电流
l0 l2 30
30
0.1 8
为cm,铁心由D21硅钢片叠成,叠装因 数KFe=0.92,衔铁材料为铸钢。要使电 磁铁空气隙中的磁通为3×10-3 Wb。 求:⑴所需磁通势;⑵若线圈匝数
N=1000匝,求线圈的励磁电流。
解:⑴ 将磁路分成铁心、衔铁、气隙三段。
⑵ 求各段长度和截面积 l1=(30-6.5)+2(30-3.25)=77cm l2=30-6.5+4×2=31.5cm 2l0=0.1×2=0.2cm
I Ia IM
I
2 a
I
2 M
求励磁电流
设铁心是由D21硅钢片叠制而成,片厚0.5mm,铁心截面A=6.6cm2, 磁路平均长度l =66cm,励磁线圈匝数N=1000匝,接至频率f=50HZ U=220V的正弦电压。求励磁电流有效值及相位角(忽略线圈电阻 及漏磁通)。
磁路

磁
路
学习目标
知识目标——认识磁路的基本概念, 掌握磁路的欧姆定律。
技能目标——会运用磁路欧姆定律进 行定性分析。
情感目标——培养勤于思考的工作作 风。
学习重难点
学习重点——磁路的欧姆定律。
学习难点——磁路的欧姆定律的应用。
课教学
一、磁路的基本概念
磁通(磁感线)通过的闭合路径称为磁路。 磁路按其结构不同来分,可分为无分支磁路和有
分支磁路两种。(例如,图1为无分支磁路,图2为有
分支磁路。)
由于铁磁物质的磁导率远大于空气,故磁通主要沿铁 心而闭合,只有很少部分磁通经过空气或其他物质闭合。
我们把通过铁心的磁通称为主磁通,铁心外的磁通称为
漏磁通。(如图1中所示。)
图1
无分支磁路
图2
有分支磁路
二、磁路的欧姆定律
1.磁动势( Em ) 通电线圈产生的磁通 与线圈的匝数 N 和线圈中 所通过的电流 I 的乘积成正比。 把通过线圈的电流 I 与线圈匝数 N 的乘积,称为
磁动势,即
Em = IN
磁动势 Em 的单位是A (安)。
2.磁阻( Rm ) 磁阻就是磁通通过磁路时所受到的阻碍作用 ,用 Rm 表示。磁路中磁阻的大小与磁路的长度 l 成正比, 与磁路的横截面积 S 成反比,并与组成磁路的材料性 质有关。因此有
Rm =
l
mS
式中,m 为磁导率,单位 H/m;长度 l 和截面积 S 的单位分别为 m 和 m2 。因此,磁阻 Rm 的单位为 1/亨(H1)。由于磁导率 m 不是常数,所以 Rm 也不是 常数。
3.磁路的欧姆定律 (1) 定律内容 通过磁路的磁通与磁动势成正比,与磁阻成反比,
磁路计算

磁路与电感计算一个空心螺管线圈,或是带气隙的磁芯线圈,通电流后磁力线分布在它周围的整个空间。
对于静止或低频电磁场问题,可以根据电磁理论应用有限元分析软件进行求解,获得精确的结果,但是不能提供简单的、指导性的和直观的物理概念。
在开关电源中,为了用较小的磁化电流产生足够大的磁通(或磁通密度),或在较小的体积中存储较多的能量,经常采用一定形状规格的软磁材料磁芯作为磁通的通路。
因磁芯的磁导率比周围空气或其他非磁性物质磁导率大得多,把磁场限制在结构磁系统之内,即磁结构内磁场很强,外面很弱,磁通的绝大部分经过磁芯而形成一个固定的通路。
在这种情况下,工程上常常忽略次要因素,只考虑导磁体内磁场或同时考虑较强的外部磁场,使得分析计算简化。
通常引入磁路的概念,就可以将复杂的场的分析简化为我们熟知的路的计算。
3.1 磁路的概念从磁场基本原理知道,磁力线或磁通总是闭合的。
磁通和电路中电流一样,总是在低磁阻的通路流通,高磁阻通路磁通较少。
所谓磁路指凡是磁通(或磁力线)经过的闭合路径称为磁路。
3.2 磁路的欧姆定律以图3.1(a)为例,在一环形磁芯磁导率为μ的磁芯上,环的截面积A ,平均磁路长度为l ,绕有N 匝线圈。
在线圈中通入电流I ,在磁芯建立磁通,同时假定环的内径与外径相差很小,环的截面上磁通是均匀的。
根据式(1.7),考虑到式(1.1)和(1.3)有 F NI Hl BlAl R m =====μφμφ (3.1) 或φ=F /R m (3.2) 式中F =NI 是磁动势;而R m =lA μ (3.3)R m —称为磁路的磁阻,与电阻的表达式相似,正比于路的长度l ,反比于截面积A 和材料的磁导率μ;其倒数称为磁导G m m R A l==1μ (3.3a) 式(3.1)即为磁路的欧姆定律。
在形式上与电路欧姆定律相似,两者对应关系如表3.1所示。
磁阻的单位在SI 制中为安/韦,或1/亨;在CGS 制中为安/麦。
磁路

磁路第一节 磁路的基本定律磁场作为电机实现机电能量转换的耦合介质,其强弱程度和分布状况不仅关系到电机的参数和性能,还决定电机的体积、重量。
然而电机的结构、形状比较复杂,并有铁磁材料和气隙并存,很难用麦克斯韦尔方程直接求解。
因此,在实际工程中,将电机各部分磁场等效为各段磁路,并认为各段磁路中磁通沿其截面积均匀分布,各段磁路中磁场强度保持为恒值,其意义是各段磁路的磁压降应等于磁场内对应点之间的磁位差。
从工程观点来说,将复杂的磁场问题简化为磁路计算,其准确度是足够的。
一、磁场的几个常用物理量1.磁感应强度B磁场是电流通入导体后产生的,表征磁场强弱及方向的物理量是磁感应强度B ,它是一个矢量。
磁场中各点的磁感应可以用闭合的磁感应矢量线来表示,它与产生它的电流方向可以用右手螺旋定则来确定,如图1-1所示。
磁感应矢量线图1-1 磁感应矢量线回转方向与电流方向的关系国际单位制中,B 的单位为T (特[斯拉]),211T Wb m =。
2.磁通Φ在均匀磁场中,磁感应强度B 的大小与垂直于磁场方向面积A 的乘积,为通过该面积的通量,简称磁通Φ(一般情况下,磁通量的定义为BdA Φ=⎰)。
由于B A =Φ,B 也称为磁通量密度,可简称磁通密度。
若用磁感应矢量线来描述磁场,通过单位面积磁感应矢量线的疏密反映了磁感应强度(磁通密度)的大小以及磁通量的多少。
国际单位制中,Φ的单位为Wb (韦[伯])。
μ。
二、磁路的概念如同把电流流过的路径称为电路一样,是磁通的路径可以是铁磁物质,也可以是非磁体。
图量转换或传递。
围绕载流线圈,在部分铁心和铁心周围的空间,还存在少量分散的磁通,这部分磁通称为漏磁通,漏磁通不参与能量转换或传递。
主磁通和漏磁通所通过的路径分别构成主磁路和漏磁路。
图1-2中示意地表示出了这两种磁路。
用以激励磁路中磁通的载流线圈称为励磁线圈,励磁线圈中的电流称为励磁电流。
若励磁电流为直流,磁路中的磁通是恒定的不随时间变化而变化,这种磁路称为直流磁路,直流电机的磁路就属于这一类。
第九章磁路

N m
2
2f N m
2
4.44 fNm
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(三)
B
S
O
H Ni
l
O
i
图 9.15 B-H曲线与Φ-i曲线
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(四)
0
t
0
i
0 i
t
图 9.16 电流i的波形的求法
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(五)
Fav t
第9章 磁路与铁芯线圈
9.5.2 交流电磁铁(三)
衔铁
′
短路环
″
铁芯
图9.27 有短路环时的磁通
第9章 磁路与铁芯线圈
9.5.3 交流电磁铁的特点
表 9.1 直流电磁铁与交流电磁铁比较
内容
直流电磁铁
交流电磁铁
铁芯结构
由整块软钢制成, 无短路环 由硅钢片制成, 有短路环
吸合过程
电流不变, 吸力逐渐加大
重点:磁化曲线 难点:磁化曲线
第9章 磁路与铁芯线圈
9.1.1 铁磁性物质的磁化
磁化:铁磁物质会在外加磁场的作用下, 产生一个与外磁场 同方向的附加磁场, 这种现象叫做磁化。
(a)
(b)
(c)
图 9.1 铁磁性物质的磁化
第9章 磁路与铁芯线圈
9.1.2
磁化曲线:铁磁性物质的磁感应强度B与外磁场的磁场强 度H之间的关系曲线, 所以又叫B-H曲线。
第9章 磁路与铁芯线圈
9.4.3 交流铁芯线圈的等效电路(二)
U E
I
Ia
I
R0
Im
磁 路

以说磁路是封闭在一定范围里的磁场,所以描述磁场的物理量也适用
于磁路。
1.1 磁场的基本物理量
1.磁感应强度
磁感应强度是表示磁场内某点的磁场强弱和方向的物理量,是个矢量,
用符号B表示。
对于电流产生的磁场,磁感应强度的方向和电流方向满足右手螺旋定
则,其大小可用式(1.1)表示
B=F/lI
(1.1)
材料的磁滞性。
1.3 磁路的基本定律
1.安培环路定律(全电流定律)
安培环路定律可用来确定磁场与电流之间的关系,是计算磁路的基本
公式。其数学表达式为
H dl I
(1.5)
2.磁路的欧姆定律
磁路欧姆定律是分析磁路的基本定律。以图1.1铁心线圈为例。媒质
是均匀的,磁导率为,根据式(1.5)得
式(1.1)中F表示磁通势,l表示磁路平均长度,I表示电流。感应强 度的单位是特斯拉(T)即韦伯/米2。
如果磁场内各点磁感应强度大小相等,方向相同的磁场,这样的称为
匀强磁场。
2. 磁通
磁感应强度B与垂直于磁场方向面积S的乘积,称为通过该面积的磁
通。用符号Φ表示,单位是Wb(韦伯)。在均匀磁场中
在没有外磁场作用时,小磁畴排列无序,对外部不显示磁性。在外磁
场作用下,一些小磁畴就会顺向外磁场方向而形成规则的排列,此时
磁性材料对外显示出磁性。随着外磁场的增强,大量磁畴都转到与外
磁场相同的方向,这样便产生了一个很强的与外磁场同方向的磁化磁
场,使磁性材料内的磁感应强度大大增强。磁性材料的磁化如图1.2
NI Hl B l l S
ቤተ መጻሕፍቲ ባይዱ
(N为线圈匝数)
(1.6)
因此,有
NI F l Rm S
磁 路

磁 路电机是一种机电能量转换装置,变压器是一种电能传递装置,它们的工作原理都以电磁感应原理为基础,且以电场或磁场作为其耦合场。
在通常情况下,由于磁场在空气中的储能密度比电场大很多,所以绝大多数电机均以磁场作为耦合扬。
磁场的强弱和分布,不仅关系到电机的性能,而且还将决定电机的体积和重量;所以磁场的分析扣计箅,对于认识电机是十分重要的。
由于电机的结构比校复杂,加上铁磁材料的非线性性质,很难用麦克斯韦方程直接解析求解;因此在实际工作中.常把磁场问题简化成磁路问题来处理。
从工程观点来说,准确度已经足够。
本章先说明磁路的基本定律,然后介绍常用铁磁材料及其性能,最后说明磁路的计算方法。
1-1 磁路的基本定律 一、磁路的概念磁通所通过的路径称为磁路。
图1—1表示两种常见的磁路,其中图a 为变压器的磁路,图b 为两极直流电机的磁路。
在电机和变压器里,常把线圈套装在铁心上。
当线圈内通有电流时、在线圈周围的空间(包括铁心内、外)就会形成磁场。
由于铁心的导磁性能比空气要好得多,所以绝大部分磁通将在铁心内通过,并在能量传递或转换过程中起耦合场的作用,这部分磁通称为主磁通。
围绕裁流线圈、部分铁心和铁心周围的空间,还存在少量分散的磁通,这部分磁通称为漏磁通。
主磁通和漏磁通所通过的路径分别构成主磁路和漏磁路,图1—l 中示意地表出了这两种磁路。
用以激励磁路中磁通的载流线圈称为励磁线圈(或称励磁绕组),励磁线圈中的电流称为励磁电流(或激磁电流)。
若励磁电流为直流,磁路中的磁通是恒定的,不随时间而变化,这种磁路称为直流磁路;直流电机的磁路就属于这一类。
若励磁电流为交流(为把交、直流激励区分开,本书中对文流情况以后称为激磁电流),磁路中的磁通随时间交变变化,这种磁路称为交流磁路;交流铁心线圈、变压器和感应电机的磁路都属于这一类。
二、磁路的基本定律进行磁路分析和计算时,往往要用到以下几条定律。
安培环路定律 沿着任何一条闭合回线L ,磁场强度H 的线积分值dl H L∙⎰ 恰好等于该闭合回线所包围的总电流值∑i ,(代数和).这就是安培环路定律(图l —2)。
磁路及其基本定律

磁路及其基本定律磁路的概念为了使较小的励磁电流产生足够大的磁通(或磁感应强度),在电机、变压器及各种铁磁元件中常用磁性材料做成一定形状的铁心。
铁心的磁导率比周围空气或其它物质的磁导率高得多,磁通的绝大部分经过铁心形成闭合通路,磁通的闭合路径称为磁路。
如四极直流电机、交流接触器等,的磁路如图。
磁路的欧姆定律磁路的欧姆定律是分析磁路的基本定律环形线圈如图,其中媒质是均 匀的,磁导率 为μ, 试计算线圈内部 的磁通Φ 。
【解】根据安培环路定律,有 l S l Hl NI μΦμ===B⎰∑=I l H d 设磁路的平均长度为 l ,则有 一、引例SxΦH x I N 匝m R F =Φ式中:F=NI 为磁通势,由其产生磁通;R m 称为磁阻,表示磁路对磁通的阻碍作用;l 为磁路的平均长度;S 为磁路的截面积。
二、磁路的欧姆定律若某磁路的磁通为Φ,磁通势为F ,磁阻为R m ,则即有: mRFSl NI ==Φμ此即磁路的欧姆定律。
三、 磁路与电路的比较1、形式比较 磁路磁通势F 磁通Φ磁阻 电路 电动势 E 电流密度 J 电阻 磁感应强度B电流 I S l R μ=m Sl NI R F μΦ==mS l R γ=S lE R E I γ==Φ N I+_E I R2、磁路分析的特点(1)在处理电路时不涉及电场问题,在处理磁路时离不开磁场的概念;(2)在处理电路时一般可以不考虑漏电流,在处理磁路时一般都要考虑漏磁通;(3)磁路欧姆定律和电路欧姆定律只是在形式上相似。
由于μ不是常数,其随励磁电流而变,磁路欧姆定律不能直接用来计算,它只能用于定性分析;(4)在电路中,当E=0时,I=0;但在磁路中,由于有剩磁,当F=0 时,Φ不为零;(5)磁路的基本物理量单位较复杂,学习时应注意。
磁路的分析计算主要任务: 预先选定磁性材料中的磁通Φ (或磁感应强度),按照所定的磁通、磁路各段的尺寸和材料,求产生预定的磁通所需要的磁通势F=NI , 确定线圈匝数和励磁电流。
磁路
l′ 10−3 ′ Rm = = A/Wb = 20×105 A/Wb - µ0S 4π ×10 7 × 4×10−4
环长度的微小变化可略而不计, 环长度的微小变化可略而不计 , 它的磁阻与 先前相同, 92× A/Wb. 先前相同 , 即 1.92×105A/Wb. 那么空气隙虽然只 mm,它的磁阻却比铁环大近10 10倍 长1mm,它的磁阻却比铁环大近10倍,这时全部磁 路的磁阻为 欲维持同样的磁通所需的磁通势为
解 磁阻 l 0.5 Rm = = A/W =1.92×105 A/W µS 65×10−4 × 4×10−4 磁通势
F = φRm = 4×10 ×1.92×10 A = 77A m
−4 5
385A 当有空气隙时, 因 Fm=NI, 所以 I=0.385A , 当有空气隙时 , 空 气隙的磁阻为
磁路定理
H = NI l QΦ = BS = µHS
NI ∴Φ = l µS
磁路定理
NI Φ= l µS
I=
ε
R
=
ε
l γS
I
F m Φ= Rm
磁路的欧 姆定理
其中 F = NI 为磁路的 m 磁通势, 磁通势,单位为 A 。
l Rm = b 为闭合磁路的磁阻,单位为 A/W 。 为闭合磁路的磁阻, 磁阻 µS
BAD =1.3T
φ2 = BADSAD =1.3×12.5×10−4Wb =1.625×10−3Wb 于是
根据磁通量的连续性可得
磁路定理
BDEA =
则DEA铁芯中的磁感应强度为 φ3 3.625×10−3
SDEA = 37.5×10
−4
T = 0.964T
从磁化曲线查得相应的 磁场强度为 HDEA = 575A/ m 根据安培环路定理得
磁路

H
H
5
磁性材料按磁滞回线形状分成三类: (1)软磁材料:剩磁和矫顽磁力均较小,如硅 钢片、坡莫合金等,常用来做成电机、变压器的 铁心等。 (2)硬磁材料:剩磁和矫顽磁力都较大,如碳 钢、钨钢、钴钢及铁镍合金等。适宜做永久磁铁。 (3)矩磁材料:磁滞回线接近矩形,如镁锰铁 氧体、1J51型铁镍合金等。在计算机和控制系统 中,可用作记忆元件、开关元件和逻辑元件。
1. 磁路
1.1 磁场的基本物理量
(磁通密度) 一、磁感应强度
与磁场方向相垂直的单位面积上通过的磁 通(磁力线)。
B S
B 的单位:特斯拉(Tesla)
1 Tesla = 104 高斯
单位:韦伯
1
二、磁通
磁感应强度B与垂直与磁场方向的面积S 的乘积,称为通过该面积的磁通。
BS
d e N dt
(线圈中没有反电动势)
磁动势 F=IN 一定 磁通和磁阻成反比(Φ U
I
F
Rm
)
直流磁路和电路中的恒压源类似 直流磁路中 直流电路中
F
F 固定
Rm 随 Rm 变化
I E
R I 随 R 变化
15
E 固定
二.交流磁路的分析 (交流铁心线圈电路)
1. 电磁关系
i u
Φ
Φ
Φ :主磁通
Φ
(亨/米)
和真空中的磁导率之比,
称为这种材料的相对磁导率
r 0
r 1,则称为磁性材料
r 1 ,则称为非磁性材料
4
r
1.2
磁性材料的磁性能
c
Bμ B 1.高导磁性 在外磁场作用下,磁性材 b 料磁化,使磁性材料内的B大大增加,图 μ 中ab段。 a 2.磁饱和性 磁性材料磁化所产生的磁 O 图 磁化曲线 场不会随外磁场的增强而无限增强。当 外磁场增大到一定值时,B达到饱和值。 B 图中bc段。 Br 3.磁滞性和剩磁性 磁性材料在H值作正 –H Hc O –Br 负变化的反复磁化过程中,B的变化总是 H的变化,称磁滞;当H=0时,Br≠0,称 图 磁滞回线 剩磁。当B=0时,H=-HC,称为矫顽磁力, 进行去磁,图中的磁滞回线。
磁路

L
Ni RmL
RmL为自感磁通所经过路径的磁阻,所以:
Ni
N
L L NL
ii
RmL i
N 2L
32
N Ni
L L NL
ii
RmL i
N 2L
L 是自感磁通所经路径的磁导,它与磁阻的关系为:
L
1 RmL
表明: 线圈自感与线圈匝数的平方成正比,与磁通所经 过磁路的磁导成正比。
损耗,发热。
铁损耗包括磁滞损耗和涡流损耗。
18
铁磁材料的铁损耗
• 磁滞损耗:铁磁材料置于交变磁场中时,磁畴相 互间不停地摩擦、消耗能量、造成损耗,这种损 耗称为磁滞损耗。
HH
i
1800 3600
i
0
t
随电流的反复变化,外加H方向也变化,小磁畴的方向随H 的方向来回变化,在磁畴之间摩擦生热,消耗功率; 电流越大,损耗越大; 磁滞回线面积越大,Bm幅值也越大,磁滞损耗越大。
M 21
21
i2
N121
i2
N1
N 2i2 RM 21
i2
N1 N 2 M 21
M 21 M12
M12 M 21 M
36
电磁力定律
载流导体在磁场中将要受到力的作用,由于这种 力是磁场和载流导体相互作用产生的,所以称为电磁 力。若磁场与导体垂直,则作用在导体上的电磁力为:
硅钢片等。
软磁材料特点:导磁率
H
高,可做电机,变压器
铁心。
软磁材料的磁滞曲1线6
铁磁材料的分类
硬磁材料:磁滞回线宽, 硬
B
剩磁Br与矫顽力Hc均较大 磁
磁路

比较
磁路磁路与电路有某些相似之处。例如,若磁路中有一磁通经过若干段磁路,则此各段磁路的总磁位降等于 各段磁路上磁位降之和。每一段磁路的磁位降等于该段磁路的磁阻与磁通的乘积,从而可得总磁阻等于各段磁路 磁阻之和。这相当于串联电阻电路的总电阻等于其中各电阻之和。同样,磁路中若有多个磁路支路并联,则各支 路的两端有相同的磁位降,各磁路支路的磁通之和即等于总磁通,从而可得这些并联支路的总磁导等于各支路磁 导之和。这相当于并联电路的总电导等于其中各电导之和。
磁通(主磁通和漏磁通)经过的闭合路径叫做磁路。分为有分支磁路和无分支磁路。 有分支磁路 无分支磁路
简介
磁路永久磁铁、铁磁性材料,以及电磁铁中都存在磁路。磁路又是一种模型,用以研究含有用来导磁的铁心 的电磁器件,在这些器件中利用磁路在其中获得所需的磁场。磁路一般由通电流以激励磁场的线圈(有些场合也 可用永磁体作为磁场的激励源)、由软磁材料制成的铁心,以及适当大小的空气隙组成。
分析目的
磁路磁路分析的主要目的是要确定励磁磁通势和它所产生的磁通的关系,这对了解器件的性能和进行相应的 设计、诸如确定磁路形状、尺寸、励磁电流的大小,选择适用的材料等,都是必要的。
感谢观看
在有些场合下,用永磁体作为磁场的激励源,其作用相当于通有电流的励磁线圈。如图《磁路》所示b是一直 流电机的磁路。它由磁极、气隙、电枢、磁轭构成,励磁线圈绕在磁极上。a是一个常见于一些电工仪器中的含永 久磁铁的磁路。
磁路中有关的物理量有磁通、磁通势、磁阻、磁位差。研究磁路在于确定励磁磁通势和它所产生的磁通的关 系。这对了解器件的性能,以进行相应的设计是必要的。
磁路
由于电工中常用铁磁材料作铁心,铁磁材料的磁导率与其中的磁通密度或磁场强度有关而非恒定值,这就使 磁路分析成为非线性问题。
磁路设计课件

II
l1 A1
A2 l0/2
l2
【例4题】 图示磁路由硅钢制成。磁通势 F1 = N1 I1 = F2 = N2 I2 ,线圈的绕向及各量的方向如图所示。 磁路左右对称,具体尺寸为: A1 = A2 = 8 2 ,l1 = l2 = 30 ,A3 = 20 2,l3 = 10 。若已知 3 = 0.002 ,问两个线圈的磁通势各是多少?
ph ChfBm nV
2).涡流损耗 涡流:当通过铁心的磁通随时间变化时,根据电磁感应定律,铁心中将产生感应电动势,并引起环流,环流在
铁心内部围绕磁通作旋涡状流动 称为涡流。 定义:涡流在铁心中引起的损耗。 公式: 应用:为减小涡流损耗,电机和变压器的铁心都用含硅量较高的薄硅钢片叠成。
pe Ce2f2Bm 2V
0.35
Φ
0.30
0.27
0.22
(a) 涡流损耗
Φ (b)
3).铁心损耗 定义: 铁心中磁滞损耗和涡流损耗之和。 表达式:
pFephpe
pFeCFef1.3Bm 2G
铁心损耗及频率的1.3次方,磁通密度的平方和铁心重量成正比。
磁路和电路的区别
1、电路中有电流就有功率损耗。磁路中恒定磁通下没有功率损耗; 2、电流全部在导体中流动,而在磁路中没有绝对的磁绝缘体; 3、对于线性电路可应用叠加原理,而当磁路饱和时为非线性,不能应用叠加原理。 可见,磁路及电路仅是形式上的类似,而本质是不同的。
铁心内的磁场强度:
气隙磁场强度: 铁心磁位降: 气隙磁位降: 励磁磁动势:
HHFeB 0B F F7ee7115049A A//m m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i(t ) I m sin t
0
i
0
0 i
图 9.18 i为正弦量时Φ的波形
t
第9章 磁路与铁芯线圈
9.4.2 磁滞和涡流的影响
铁芯的磁滞损耗PZ和涡流损耗PW可分别由下式计算:
PZ K Z fB V (W )
n m
P (W ) W KW f B V
2 2 m
PFe PZ P W
-1
a 铸铁
0.8 0.9 1.0× 10
3
图 9.6 几种常用铁磁材料的基本磁化曲线
第9章 磁路与铁芯线圈
教学方法
联系实际讲解本节
第9章 磁路与铁芯线圈
思考题
1、铁磁性物质为什么会有高的导磁性能?
2、制造电喇叭时要用到永久磁铁,制造变压器时要用到铁心, 试说明它们在铁磁性材料时有何不同?
3、什么是基本磁化曲线?什么是起始磁化曲线? 4、铁磁性材料的μ不是常数, μ的最大值处在起始磁化曲线的 哪个部位?
(b )
图9.7 直流电机和单相变压器磁路
第9章 磁路与铁芯线圈
9.2.1 磁路(二)
边缘 效应 主磁 通
I
漏磁 通
图 9.8 主磁通、 漏磁通和边缘效应
第9章 磁路与铁芯线圈
9.2.2 磁路定律(一)
1. 磁路的基尔霍夫第一定律
0
1 2 3 0
第9章 磁路与铁芯线圈
1. 电压为正弦量
i u E N
图9.14 交流铁芯线圈各电磁量参考方向
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(二)
d (t ) d (t ) u ( t ) e( t ) N dt dt
设Φ(t)=Φmsinωt, 则有
d (t ) 1 u ( t ) e( t ) N N ( m sin t ) dt dt N m sin(t
的磁动势? 若线圈的匝数为1000匝, 求激磁电流应为多大?
解 (1) 按照截面和材料不同, 将磁路分为三段l1, l2, l3。
第9章 磁路与铁芯线圈
例9.1(二)
(2) 按已知磁路尺寸求出:
l1 275 220 275 770m m 77cm S1 50 60 3000m m2 30cm2 l2 35 220 35 290m m 29cm S2 60 70 4200m m2 42cm2 l3 2 2 4m m 0.4cm S3 60 50 (60 50) 2 3220m m2 32.2cm2
9.2.2 磁路定律(二)
1
I1 D l1′ I2 N1 l1 A
2
l3′
3
N2 l2 l0
C
l1″
B
l3″
图 9.9 磁路示意图
第9章 磁路与铁芯线圈
9.2.2 磁路定律(三)
2. 磁路的基尔霍夫第二定律
( Hl) ( IN )
对于如图9.9所示的ABCDA回路, 可以得出
H1l1 H l H l H 2l2 I1 N1 I 2 N 2
l1 l2 l3 l4 l5
图 9.13 思考题 2 图
第9章 磁路与铁芯线圈
9.4 交流铁芯线圈 及等效电路
第9章 磁路与铁芯线圈
目的与要求
理解交流铁芯线圈及其等效电路
第9章 磁路与铁芯线圈
重点与难点
重点: 交流铁芯线圈及其等效电路 难点: 交流铁芯线圈的等效电路
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(一)
' ' 11
" " 1 1
U
m
Fm
第9章 磁路与铁芯线圈
9.2.3 磁路的欧姆定律
Hl U m U m HS l l Rm S 讲解本节
第9章 磁路与铁芯线圈
思考题
1、已知线圈电感L=Ψ/I=NΦ/I,试用磁路欧姆定律证明
9.3 简单直流磁路的计算(三)
(3) 由已知磁通Φ, 算出各段磁路的磁感应强度B=Φ/S。
(4) 根据每一段的磁感应强度求磁场强度, 对于铁磁材料 可查基本磁化曲线(如图9.6所示)。 对于空气隙可用以下公式:
B0 6 3 H0 0.8 10 B0 ( A / m) 8 10 B0 ( A / cm) 7 0 4 10
第9章 磁路与铁芯线圈
9.2 磁路和磁路定律
第9章 磁路与铁芯线圈
目的与要求
掌握磁路基尔霍夫定律,磁路欧姆定律
第9章 磁路与铁芯线圈
重点与难点
重点: 磁路基尔霍夫定律,磁路欧姆定律 难点: 磁路基尔霍夫定律,磁路欧姆定律
第9章 磁路与铁芯线圈
9.2.1 磁路(一)
N
I
S
S
U
N
(a )
第9章 磁路与铁芯线圈
第9章 磁路与铁芯线圈
9.1 铁磁性物质 9.2 磁路与磁路定律 9.3 简单直流磁路的计算 9.4 交流铁芯线圈及等效电路 9.5 电磁铁
第9章 磁路与铁芯线圈
9.1 铁 磁 性 物 质
第9章 磁路与铁芯线圈
目的与要求
掌握铁磁性物质及其分类
第9章 磁路与铁芯线圈
重点与难点
t
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(五)
m m 0 U E j 4.44 fN m I m I m 0
E
E U
I m
. m
图9.17 电压、 电流相量图
第9章 磁路与铁芯线圈
9.4.1 电压、电流和磁通(六)
2. 电流为正弦量 设线圈电流为
H1l1 1.4 77 107.8 A H 2l2 1.5 29 43.5 A H 3l3 4942 0.4 1976 .8 A
(6) 所需的磁通势为
NI H1l1 H2l2 H3l3 107.8 43.5 1976 .8 2128 .1A
I
. m
U
R0
jX0
E
图 9.20 图 9.19的相量图
图9.21 串联等效模型
I a G0 U , I m jB0 U , I I 0 I m
第9章 磁路与铁芯线圈
例9. 2(一)
将一个匝数 N=100 的铁芯线圈接到电 压Us=220V的工频正弦电源上, 测得线圈的电 流I=4A, 功率P=100W。 不计线圈电阻及漏 磁通, 试求铁芯线圈的主磁通Φm, 串联电路模 型的Z0, 并联电路模型的Y0。
第9章 磁路与铁芯线圈
例9. 2(二)
解 由Us=4.44fNΦm得
m
Us 220 9.91 103Wb 4.44 fN 4.44 50 100
第9章 磁路与铁芯线圈
例9.1(三)
50 170 l1 I 硅钢 50 60
70
铸钢
图9.12 例9.1图
70
1 l3 2
l2
2
310
第9章 磁路与铁芯线圈
例9.1(四)
(3) 各段磁感应强度为
2.0 10 B1 0.667Wb / cm2 0.667T S1 30 2.0 103 B2 0.476 104Wb / cm2 0.476T S2 42 2.0 103 B3 0.621 104Wb / cm2 0.621 T S3 32.2
第9章 磁路与铁芯线圈
9.1.3 铁磁性物质的分类(一)
B
软磁 硬磁
O
H
图9.5 软磁和硬磁材料的磁滞回线
第9章 磁路与铁芯线圈
9.1.3 铁磁性物质的分类(二)
1 1.8 1.6 1.4 1.2 c b c 硅钢 片 b 铸钢 2 3 H / A· m 4 5
-1
6
7
8
9
10× 10
3
B/T
1.0 0.8 0.6 0.4 0.2 0 a 0.1 0.2 0.3 0.4 0.5 0.6 0.7 H / A· m
3
第9章 磁路与铁芯线圈
例9.1(五)
(4) 由图9.6 所示硅钢片和铸钢的基本磁化曲线得
H1 1.4 A / cm H 2 1.5 A / cm
空气中的磁场强度为
0.621 H3 4942A / cm 7 0 4 10
B3
第9章 磁路与铁芯线圈
例9.1(六)
(5) 每段的磁位差为
重点:磁化曲线 难点:磁化曲线
第9章 磁路与铁芯线圈
9.1.1 铁磁性物质的磁化
磁化:铁磁物质会在外加磁场的作用下, 产生一个与外磁场 同方向的附加磁场, 这种现象叫做磁化。
(a)
(b)
(c)
图 9.1 铁磁性物质的磁化
第9章 磁路与铁芯线圈
9.1.2 磁化曲线(一)
磁化曲线:铁磁性物质的磁感应强度B与外磁场的磁场强
第9章 磁路与铁芯线圈
9.4.3 交流铁芯线圈的等效电路(一)
1. 不考虑线圈电阻及漏磁通的情况
I
I m
U
G0
I a
jB0
图9.19 考虑磁饱和、磁滞、涡流影响的等效电路
第9章 磁路与铁芯线圈
9.4.3 交流铁芯线圈的等效电路(二)
E U
I
I a I m
第9章 磁路与铁芯线圈
9.3 简单直流磁路的计算(二)
Sa (a )(b ) ab (a b) Sb ( r ) r r 2
