河南省豫南九校2020-2021学年高二上学期第三次联考数学(文)试题
豫南九校2011---2012学年高三第一次联考语文试题参考答案

甲 必考题
一、现代文阅读(9分,每小题3分) 阅读下面的文字,完成l~3题。 名士与名流
1.下列关于“名流”与“名士”的解说,不正确的一项是( B ) (3分) A.名流与名士都有一定的才气与悟性,但人生姿态不同,人 生境界不同。 B. 名流与名士对社会的意义不可相提并论,前者务实,后者 务虚。 C.名流与名士的流变与时代的发展和社会的变化有着密切的 关系。 D.名流与名士都有一定的知名度,前者常常是刻意求得,后 者往往是无意而得。 B(“前者务实,后者务虚”意思和原文不符。)
上问:“谁也?”对曰:“安昌侯张禹。”上大怒, 曰:“小臣居下讪上,廷辱师傅,罪死不赦。”御史 将云下,云攀殿槛,槛折。云呼曰:“臣得下从龙逢、 比干游于地下,足矣!未知圣朝何如耳?”御史遂将 云去。 成帝问:“你要斩的是谁呀 “朱云答道:“安昌侯张禹。” 成帝大怒,道:“你一个小官居于下位而毁谤上级,在 朝廷上侮辱我的老师,罪死不赦!”御史拉朱云下朝 堂,朱云攀住殿上的栏杆,栏杆被他拉断。朱云大呼 道:“微臣我得以和龙逢(夏桀时忠臣,因谏被杀),比 干(商纣时忠臣,因谏被杀)在九泉之下交往,也就满 足了,只是不知圣朝将要怎样。”御史便把朱云拉了 下去。
C(3分)E(2分)A(1分) (A“情节的发展过程也是朱丹精神的发展过程”不确切。 B朱丹 “小心谨慎地”从绒套中取出木笛,说明他对木笛 的珍爱,而木笛是一种中国民族乐器,其意图显而易见, 表现朱丹对民族音乐的挚爱。 D考查情节及主题:大师最后录取朱丹是因为认识到他既 有出色的音乐才华,更有崇高的民族精神,因而能够理解 他,接受他。)
9.梅尧臣在艺术上注重诗歌的形象性,请结合颔联和颈联, 分析作者是如何表现抽象的“春寒”的。(6分) 答:中间两联,通过具体物象,来表现春寒,(1分)三四 句写因寒气袭来,蝴蝶收敛双翅,花蕾无力舒展,这是选 取春天最有代表性的蝶和花写天气之寒。(2分) 五六句写压挂在树枝上的酒旗翻动,足见风很猛;依傍山 丘的阴云挟带着阵雨压来,表明雨势之急。(2分) 这四句从不同视角形容春寒,这一派峭寒,使天宇充塞着 凄冷寥落的气氛,这就把春寒真切地刻画出来。(1分)
河南省中原名校(即豫南九校)2017-2018学年高一上学期期末联考数学试题 Word版含解析

豫南九校2017-2018学年上期期末联考高一数学试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,则集合中元素的个数为()A. 1B. 2C. 3D. 4【答案】D【解析】集合B中元素有(1,1),(1,2),(2,1),(2,2),共4个.故选D.2. 已知:直线与直线平行,则的值为()A. 1B. -1C. 0D. -1或1【答案】A【解析】由于直线l1:ax+y-1=0与直线l2:x+ay+=0平行所以,即-1或1,经检验成立.故选A.3. 函数,则()A. B. 4 C. D. 8【答案】D【解析】∵,∴.故选D4. 设是两个不同的平面,是直线且,,若使成立,则需增加条件()A. 是直线且,B. 是异面直线,C. 是相交直线且,D. 是平行直线且,【答案】C【解析】要使成立,需要其中一个面的两条相交直线与另一个面平行,是相交直线且,,,,由直线和平面平行的判定定理可得.故选C.5. 已知函数在区间上是单调增函数,则实数的取值范围为()A. B. C. D.【答案】B【解析】函数f(x)=x2-2ax-3的图象开口向上,对称轴为直线x=a,画出草图如图所示.由图象可知,函数在[a,+∞)上是单调增函数,因此要使函数f(x)在区间[1,2]上是单调增函数,,只需a≤1,从而a∈(-∞,1].故选B.6. 已知矩形,,,沿矩形的对角线将平面折起,若四点都在同一球面上,则该球面的面积为()A. B. C. D.【答案】C【解析】矩形ABCD,AB=6,BC=8,矩形的对角线AC=10为该球的直径,所以该球面的面积为. 故选C.7. 设是定义在实数集上的函数,且,若当时,,则有()A. B.C. D.【答案】B【解析】由f(2-x)=f(x)可知函数f(x)的图象关于x=1对称,所以,,又当x≥1时,f(x)=ln x单调递增,所以,故选B.8. 已知是定义在上的偶函数,那么的最大值是()A. 0B.C.D. 1【答案】C【解析】∵f(x)=ax2+bx是定义在[a-1,2a]上的偶函数,∴a-1+2a=0,∴a=.又f(-x)=f(x),∴b=0,∴,所以.故选C.9. 某四面体的三视图如图,则该四面体的体积是()A. 1B.C.D. 2【答案】B【解析】在正方体ABCDA1B1C1D1中还原出三视图的直观图,其是一个三个顶点在正方体的右侧面、一个顶点在左侧面的三棱锥,即为D1BCB1,如图所示,该四面体的体积为. 故选B.点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.10. 已知实数满足方程,则的最小值和最大值分别为()A. -9,1B. -10,1C. -9,2D. -10,2【答案】A【解析】即为y-2x可看作是直线y=2x+b在y轴上的截距,.....................故选A.11. 已知函数,若对一切,都成立,则实数的取值范围为()A. B. C. D.【答案】C【解析】由题意得,对一切,f(x)>0都成立,即,而,则实数a的取值范围为.故选C.点睛:函数问题经常会遇见恒成立的问题:(1)根据参变分离,转化为不含参数的函数的最值问题;(2)若就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为,若恒成立;(3)若恒成立,可转化为(需在同一处取得最值) .12. 已知为圆的两条互相垂直的弦,且垂足为,则四边形面积的最大值为()A. 10B. 13C. 15D. 20【答案】B【解析】如图,作OP⊥AC于P,OQ⊥BD于Q,则|OP|2+|OQ|2=|OM|2=5,∴|AC|2+|BD|2=4(9-|OP|2)+4(9-|OQ|2)=52.则|AC|·|BD|=,当时,|AC|·|BD|有最大值26,此时S四边形ABCD=|AC|·|BD|=×26=13,∴四边形ABCD面积的最大值为13.故选B.点睛:直线与圆的位置关系常用处理方法:(1)直线与圆相切处理时要利用圆心与切点连线垂直,构建直角三角形,进而利用勾股定理可以建立等量关系;(2)直线与圆相交,利用垂径定理也可以构建直角三角形;(3)直线与圆相离时,当过圆心作直线垂线时长度最小.二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 函数的单调递增区间为__________.【答案】(-∞,-1)【解析】试题分析:因为,所以当时,而,所以函数的单调递增区间为.考点:复合函数单调性14. 已知集合,,则集合中子集个数是__________【答案】4【解析】由题意知中的元素为圆与直线交点,因为圆心(1,-2)到直线2x+y-5=0的距离,所以直线与圆相交.集合有两个元素.故集合中子集个数为4.故答案为:4.15. 如图,已知圆柱的轴截面是矩形,,是圆柱下底面弧的中点,是圆柱上底面弧的中点,那么异面直线与所成角的正切值为__________.【答案】【解析】取圆柱下底面弧AB的另一中点D,连接C1D,AD,因为C是圆柱下底面弧AB的中点,所以AD∥BC,所以直线AC1与AD所成角等于异面直线AC1与BC所成角,因为C1是圆柱上底面弧A1B1的中点,所以C1D⊥圆柱下底面,所以C1D⊥AD,因为圆柱的轴截面ABB1A1是矩形, AA1=2AB所以C1D=2AD,所以直线AC1与AD所成角的正切值为2,所以异面直线AC1与BC所成角的正切值为2.故答案为:2.点睛:求两条异面直线所成角的关键是作为这两条异面直线所成角,作两条异面直线所成角的方法是:将其中一条一条直线平移与另一条相交相交或是将两条异面直线同时平移到某个位置使他们相交,然后再同一平面内求相交直线所成角,值得注意的是:平移后相交所得的角必须容易算出,因此平移时要求选择恰当位置.16. 已知函数,则函数的零点个数为__________.【答案】3【解析】由,得,作出y=f(x),的图象,由图象可知共有3个交点,故函数的零点个数为3.故答案为:3三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知全集,集合,集合.(1)当时,求,;(2)若,求实数的取值范围.【答案】(1)A∪B={x|-2<x<3},;(2)(-∞,-2].【解析】试题分析:(1)求解集合A,B根据集合交并补的定义求解即可;(2)由A∩B=A,得A⊆B,从而得,解不等式求解即可.试题解析:(1)由题得集合A={x|0<<1}={x|1<<3}当m=-1时,B={x|-2<x<2},则A∪B={x|-2<x<3}.(2)由A∩B=A,得A⊆B..解得m≤-2,即实数m的取值范围为(-∞,-2].18. 已知直线及点.(1)证明直线过某定点,并求该定点的坐标;(2)当点到直线的距离最大时,求直线的方程.【答案】(1)证明见解析,定点坐标为;(2)15x+24y+2=0.【解析】试题分析:(1)直线l的方程可化为 a(2x+y+1)+b(-x+y-1)=0,由,即可解得定点;(2)由(1)知直线l恒过定点A,当直线l垂直于直线PA时,点P到直线l的距离最大,利用点斜式求直线方程即可.试题解析:(1)证明:直线l的方程可化为 a(2x+y+1)+b(-x+y-1)=0,由,得,所以直线l恒过定点.(2)由(1)知直线l恒过定点A,当直线l垂直于直线PA时,点P到直线l的距离最大.又直线PA的斜率,所以直线l的斜率k l=-.故直线l的方程为,即15x+24y+2=0.19. 设是定义在上的奇函数,当时,.(1)求的解析式;(2)解不等式.【答案】(1);(2)(-∞,-2)∪(0,2).【解析】试题分析:(1)奇函数有f(0)=0,再由x<0时,f(x)=-f(-x)即可求解;(2)由(1)分段求解不等式,最后取并集即可.试题解析:(1)因为f(x)是定义在上的奇函数,所以当x=0时,f(x)=0,当x<0时,f(x)=-f(-x),-x>0,又因为当x>0时,f(x)=,.所以当x<0时,f(x)=-f(-x)=-=..综上所述:此函数的解析式.(2)f(x)<-,当x=0时,f(x)<-不成立;当x>0时,即<-,所以<-,所以>,所以3x-1<8,解得x<2,当x<0时,即<-,所以>-,所以3-x>32,所以x<-2,综上所述解集是(-∞,-2)∪(0,2).20. 已知圆经过点,和直线相切.(1)求圆的方程;(2)若直线经过点,并且被圆截得的弦长为2,求直线的方程.【答案】(1)(x-1)2+(y+2)2=2;(2)x=2或3x-4y-6=0.【解析】试题分析:(1)先求线段AB的垂直平分线方程为,设圆心的坐标为C(a,-a-1),由圆心到点的距离和到切线的距离相等求解即可;(2)由题知圆心C到直线l的距离,进而讨论直线斜率存在不存在两种情况求解即可.试题解析:(1)由题知,线段AB的中点M(1,-2),,线段AB的垂直平分线方程为,即,设圆心的坐标为C(a,-a-1),则,化简,得a2-2a+1=0,解得a=1.∴C(1,-2),半径r=|AC|==.∴圆C的方程为(x-1)2+(y+2)2=2.(解二:可设原方程用待定系数法求解)(2)由题知圆心C到直线l的距离,①当直线l的斜率不存在时,直线l的方程为x=2,此时直线l被圆C截得的弦长为2,满足条件.②当直线l的斜率存在时,设直线l的方程为,由题意得,解得k=,∴直线l的方程为y=(x-2).综上所述,直线l的方程为x=2或3x-4y-6=0.点睛:直线与圆的位置关系常用处理方法:(1)直线与圆相切处理时要利用圆心与切点连线垂直,构建直角三角形,进而利用勾股定理可以建立等量关系;(2)直线与圆相交,利用垂径定理也可以构建直角三角形;(3)直线与圆相离时,当过圆心作直线垂线时长度最小.21. 如图,四面体中,平面,,,,.(1)求四面体的四个面的面积中,最大的面积是多少?(2)证明:在线段上存在点,使得,并求的值.【答案】(1);(2)证明见解析.【解析】试题分析:(1)易得,,,均为直角三角形,且的面积最大,进而求解即可;(2)在平面ABC内,过点B作BN⊥AC,垂足为N.在平面PAC内,过点N作MN∥PA交PC于点M,连接BM,可证得AC⊥平面MBN,从而使得AC⊥BM,利用相似和平行求解即可.试题解析:(1)由题设AB=1,AC=2,BC=,可得,所以,由PA⊥平面ABC,BC、AB⊂平面ABC,所以,,所以,又由于PA∩AB=A,故BC⊥平面PAB,PB⊂平面PAB,所以,所以,,,均为直角三角形,且的面积最大,.(2)证明:在平面ABC内,过点B作BN⊥AC,垂足为N.在平面PAC内,过点N作MN∥PA 交PC于点M,连接BM.由PA⊥平面ABC知PA⊥AC,所以MN⊥AC.由于BN∩MN=N,故AC⊥平面MBN.又BM⊂平面MBN,所以AC⊥BM.因为与相似,,从而NC=AC-AN=.由MN∥PA,得==.22. 已知函数,.(1)当时,求函数的值域;(2)如果对任意的,不等式恒成立,求实数的取值范围;(3)是否存在实数,使得函数的最大值为0,若存在,求出的值,若不存在,说明理由.【答案】(1)[0,2];(2)(-∞,);(3)答案见解析.【解析】试题分析:(1)由h(x)=-2(log3x-1)2+2,根据log3x∈[0,2],即可得值域;(3)由,假设最大值为0,因为,则有,求解即可.试题解析:(1)h(x)=(4-2log3x)·log3x=-2(log3x-1)2+2,因为x∈[1,9],所以log3x∈[0,2],故函数h(x)的值域为[0,2].(2)由,得(3-4log3x)(3-log3x)>k,令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],所以(3-4t)(3-t)>k对一切t∈[0,2]恒成立,令,其对称轴为,所以当时,的最小值为,综上,实数k的取值范围为(-∞,)..(3)假设存在实数,使得函数的最大值为0,由.因为,则有,解得,所以不存在实数,使得函数的最大值为0.点睛:函数问题经常会遇见恒成立的问题:(1)根据参变分离,转化为不含参数的函数的最值问题;(2)若就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为,若恒成立;(3)若恒成立,可转化为(需在同一处取得最值) .。
河南省豫南九校2015届上期高三第三次联考数学(理)试题
河南豫南九校2015届上期高三第三次联考数学(理)试题(考试时间:120分钟 试卷满分:150分)第Ⅰ卷 选择题(共60分)一、选择题:本大题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项符合题目要求的。
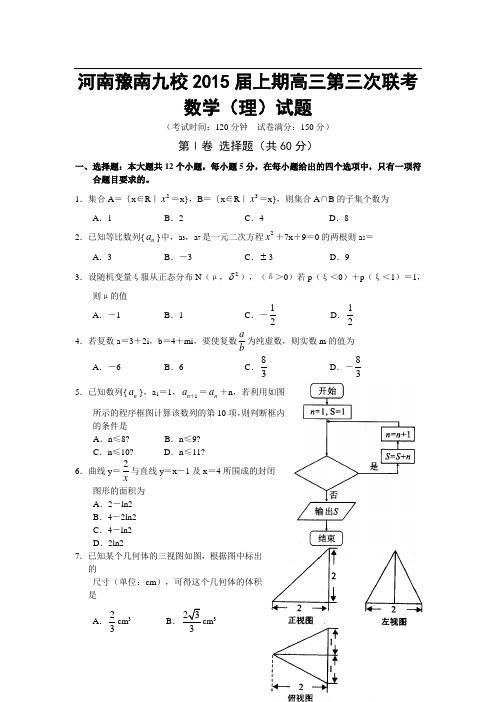
1.集合A ={x ∈R |2x =x},B ={x ∈R |3x =x},则集合A ∩B 的子集个数为A .1B .2C .4D .8 2.已知等比数列{n a }中,a 3,a 7是一元二次方程2x +7x +9=0的两根则a 5= A .3 B .-3 C .±3 D .93.设随机变量ξ服从正态分布N (μ,2δ),(δ>0)若p (ξ<0)+p (ξ<1)=1,则μ的值A .-1B .1C .-12D .124.若复数a =3+2i ,b =4+mi ,要使复数ab为纯虚数,则实数m 的值为 A .-6 B .6 C .83 D .-835.已知数列{n a },a 1=1,1n a +=n a +n ,若利用如图所示的程序框图计算该数列的第10项,则判断框内的条件是A .n ≤8?B .n ≤9?C .n ≤10?D .n ≤11? 6.曲线y =2x与直线y =x -1及x =4所围成的封闭 图形的面积为 A .2-ln2B .4-2ln2C .4-ln2D .2ln27.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是A .23cm 3B 3C .43cm 3 D .83cm 3 8.已知x ,y 满足约束条件30101x y x y ⎧⎪⎨⎪⎩+3-≤-y +≥≥-,则 z =2x -y 的最大值为A .-3B .1C .13D .159.已知sin10°=k ,则sin110°=A .1-2kB .22k -1C .1-22kD .1+22k10.过抛物线2y =4x 的焦点F 作两条互相垂直的直线l 1,l 2,l 1交C 于A 、B ,l 2交C 于M 、N .则1AB+1MN = A.B .12C D .1411.二次函数y =2x -2x +2与y =2x -+ax +b (a >0,b >0)在它们的一个交点处的切线 互相垂直,则1a +4b的最小值为 A .245 B .4 C .185 D .16512.定义[x]表示不超过x 的最大整数,若f (x )=cos (x -[x]),则下列结论中:①y =f (x )为偶函数;②y =f (x )为周期函数,周期为2π; ③y =f (x )的最小值为cos1,无最大值: ④y =f (x )无最小值,最大值为1.正确的命题的个数为A .0个B .1个C .3个D .4个第Ⅱ卷 非选择题(共90分)二、填空题:本大题共4个小题,每小题5分.共20分 13.5()x a +的展开式中3x 的系数是10,则实数a 的值为 _______________(用数字作答)14.如图,在平行四边形ABCD 中,AP ⊥BD ,垂足为P ,AP =3,则AP uu u r ·AC uuur =______________.15.已知△ABC 的三个顶点在以O 为球心的球面上,且∠B =90°, BC =1,AC =3,已知三棱锥O -ABC的体积为O 的表面积为_______________. 16.正实数列{n a }满足n a =12n n a ma --,n =3,4,…其中m 为非零实数,若a 1·a 2014=4,则 m =___________.三、解答题:本大题共6小题,共70分。
河南省豫南九校2020-2021学年高二上学期第四次联考化学试题【含答案】

河南省豫南九校2020-2021学年高二第一学期第四次联考化学试题(考试时间:90分钟试卷满分:100分)可能用到的相对原子质量:H 1 C 12 O 16 N 14 Na 23 Mg 24 S 32 Cl 35.5 Cu 64 Fe 56 Ag 108一、选择题(本大题共17小题,每小题3分,共51分。
每个小题只有一个选项符合题意)1.明代诗人于谦在《石灰吟》中写道:“千锤万凿出深山,烈火焚烧若等闲。
粉身碎骨浑不怕,要留清白在人间。
”这首脍炙人口的诗篇不仅蕴含了深刻的人文精神,还蕴藏了有趣的化学知识。
“要留清白在人间”涉及反应的化学物质中属于非电解质的是A.Ca(OH)2B.CaCO3C.CO2D.H2O2.下列关于铜锌原电池和电解氯化铜溶液的叙述正确的是A.电解氯化铜溶液时,阳极上发生还原反应B.铜锌原电池中铜片上发生氧化反应C.电解氯化铜溶液时,化学能转化为电能D.电极上同时分别发生氧化反应和还原反应,并且得失电子数相等3.下列事实,不能用勒夏特列原理解释的是A.在保存FeSO4溶液时,加入少量铁屑B.用饱和食盐水除去Cl2中的HCl气体C.可用浓氨水和氢氧化钠固体快速制取氨气D.工业合成氨采用200~500大气压的高压条件4.下列说法正确的是A.△H的大小与热化学方程式的化学计量数无关B.等量的硫蒸气和硫固体分别完全燃烧,前者放出的热量多C.在101 kPa时,1 mol氢气燃烧所放出的热量为氢气的燃烧热D.由C(石墨)→C(金刚石);△H=+119 kJ/mol可知,金刚石比石墨稳定5.只改变一个影响因素,平衡常数K与化学平衡移动的关系叙述错误的是A.K不变,平衡可能移动B.K值变化,平衡一定移动C.平衡移动,K值可能不变D.平衡移动,K值一定变化6.下列说法正确的是A.pH=6.5的溶液一定呈酸性B.用pH值表示任何溶液的酸碱性都很方便C.常温下pH=2的H2SO4溶液,升高温度pH不变D.常温下pH=12的NaOH溶液,升高温度pH不变7.100 mL浓度为2 mol/L的盐酸跟过量的锌片反应,为加快反应速率,又不影响生成氢气的量,可采用的方法是A.加入适量的6 mol/L的盐酸B.加入数滴氯化铜溶液C.加入适量蒸馏水D.加入适量的氯化钠溶液8.设N A表示阿伏加德常数的值。
河南省豫南九校2022-2023学年高三上学期第二次联考文科数学试题

豫南九校2022-2023学年上期第二次联考高三数学(文)试题(考试时间:120分钟试卷满分:150分)注意事项:1.答题前,考生务必将自己的娃名、准考证号.考场号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时.将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}22610A x x =∈<+≤N ,{}04B x x =<<,则A B ⋂=()A .{}1,2,3B .{}0,2,3C .{}1,2D .{}2,32.已知i 为虚数单位,则43i1i -=+()A .17i 22+B .17i22-C .53i 22+D .53i 22-3.已知“24x x >”是“2x m <”的充分不必要条件,则实数m 的取值范围为()A .()2,2-B .[]2,2-C .()(),22,⋃-∞-+∞D .(][),22,-∞-⋃+∞4.已知圆O 的半径为2,AB 为圆O 的直径,点C 在圆O 上,若6cos 4BOC ∠=,则OA OC ⋅= ()A .BC .D 5.已知函数()1xf x ax x =++,若()02f '=,则()2f =()A .83B .2C .53D .36.在ABC △中,内角A ,B ,C 的对边分别为a ,b ,c ,若22a b ==,且12CA CB ⋅=- ,则c =()A .2B .C D7.已知sin18m ︒=,则cos 2424︒+︒=()A .242m-B .224m-C .4D .4-8.已知{}n a 为等差数列,公差为黄金分割比512(约等于0.618),前n 项和为n S ,则()2106842a a S S -+-=()A 1-B 1+C .16D .49.2022年8月26日,河南平顶山抽干湖水成功抓捕了两只鳄雀鳝,这一话题迅速冲上热搜榜.与此同吋,关于外来物种泛滥的有害性受到了热议.为了研究某池塘里某种植物生长面积S (单位:m 2)与时间t (单位:月)之间的关系,通过观察建立了函数模型()tS t ka =(t ∈Z ,0k >,0a >且1a ≠).已知第一个月该植物的生长面积为1m 2,第3个月该植物的生长面积为4m 2,则该植物的生长面积达到100m 2,至少要经过()A .6个月B .8个月C .9个月D .11个月10.已知()e xf x x =,过1,02P ⎛⎫⎪⎝⎭作曲线()y f x =的切线,切点在第一象限,则切线的斜率为()A .3e2B .23e C .2e D11.已知函数()()sin 034f x A x πωω⎛⎫=+<< ⎪⎝⎭的最小正周期为T ,若4T f ⎛⎫= ⎪⎝⎭()f x 的图象向左平移2π个单位长度,得到奇函数()g x 的图象,则2f π⎛⎫-= ⎪⎝⎭()A .2-B .2C .D 12.已知数列{}n a 的通项公式为()2(1)n n a n n =--,前n 项和为n S ,则满足212023n S +≤-的最小正整数n 的值为()A .28B .30C .31D .32二、填空题(本大题共4小题,每小题5分,共20分)13.已知点()1,2A ,()2,3B -,则与AB垂直的单位向量的坐标为______.14.已知等差数列{}n a 的前n 项和为n S ,若945S =,且8996a a +=,则123a a +=______.15.已知函数()2sin f x x =的导函数为()f x ',()()()g x f x f x =+',则函数()g x 图象的对称中心为______.16.已知函数()231sin 3e 12xf x x π⎛⎫⎛⎫=-+-⎪ ⎪+⎝⎭⎝⎭,则()f x 在[],ππ-上的最大值与最小值之和为______.三、解答题,本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知复数z 的共轭复数为z ,()()2i 3i zm m -=+∈R (其中i 为虚数单位).(1)若6z z +=,求z ;(2)若3z z ⋅<,求m 的取值范围.18.(本小题满分12分)已知命题p :()21,02,0x a x f x xx x x ⎧++>⎪=⎨⎪+≤⎩的最小值为1-,命题q :x ∀∈R ,2420x x a -+≥恒成立.(1)若p ⌝为真,求实数a 的取值范围;(2)若()p q ∧⌝为真,求实数a 的取值范围.19.(本小题满分12分)已知在ABC △中,内角A ,B ,C 的对边分别为a ,b ,c,且sin cos a B A =.(1)若2c b =,求证:ABC △为直角三角形;(2)若ABC △的面积为6a =,求ABC △的周长.20.(本小题满分12分)已知向量()cos ,sin a x x =,()cos ,cos sin b x x x =- ,向量b 在a 上的投影记为()f x .(1)若()a ab ⊥-,求()f x 的值;(2)若()2f x =,求b .21.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且22n n s a =-.(1)求{}n a 的通项公式;(2)若()()1122n n n n a b a a ++=+⋅+,求数列{}n b 的前n 项和n T ;(3)若()10nn c n a =-,数列{}n c 的前n 项和为n A ,求n A 的最大值.22.(本小题满分12分)已知函数()()2ln exf x x k k =+∈R .(1)若1x =是()f x 的一个极值点,求()f x 的极值;(2)设()ln e x x h x =的极大值为()0h x ,且()f x 有零点,求证:02e x kx ≥-.豫南九校2022-2023学年上期第二次联考高三数学(文)参考答案123456789101112CBDAADBCBCAD1.【答案】C【解析】由题意,得{}{}220,1,2A x x =∈-<≤=N ,又{}04B x x =<<,故{}1,2A B ⋂=.故选C .2.【答案】B【解析】()()()()43i 1i 43i 17i 17i 1i 1i 1i 222----===-++-.故选B .3.【答案】D【解析】由24x x >,得04x <<,由题意,得24m≥,即(][),22,m ∈-∞-⋃+∞.故选D .4.【答案】A【解析】由cos 4BOC ∠=,得cos 4AOC ∠=-,故6224OA OC ⎛⎫⋅=⨯⨯-= ⎪ ⎪⎝⎭.故选A .5.【答案】A 【解析】由()1x f x ax x =++,得()()211f x a x +'=+,故()012f a ='+=,故1a =,故()1x f x x x =++,故()282233f =+=.故选A .6.【答案】D【解析】由12CA CB ⋅=- ,得1cos 2ab C =-.又22a b ==,故1cos 4C =-,由余弦定理,得22212cos 4122164c a bab C ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭,故c =D .7.【答案】B 【解析】()1cos 24242cos 24sin 242cos 60242cos3622⎛⎫︒+︒=⨯︒+︒=︒-︒=︒ ⎪ ⎪⎝⎭()()222212sin 1821224m m =⨯-︒=⨯-=-.故选B .8.【答案】C 【解析】设{}n a 的公差为d ,则d 是方程210x x +-=的一个解,则21d d +=,故()()()2221068424161616a a S S d d d d -+-=+=+=.故选C .9.【答案】B【解析】由题意,得()()31134S ka S ka ⎧==⎪⎨==⎪⎩,解得122k a ⎧=⎪⎨⎪=⎩,故()11222t t S t -=⨯=.令()12100t S t -=>,结合t ∈Z ,解得8t ≥,即该植物的生长面积达到100m 2时,至少要经过8个月.故选B .10.【答案】C 【解析】由()e x f x x =,得()()1e x f x x +'=,设切点坐标为()000,e x x x ,则切线方程为()()00000e 1e x x y x x x x -=+-,把点1,02P ⎛⎫ ⎪⎝⎭代入并整理,得()000112x x x ⎛⎫-=+- ⎪⎝⎭,解得01x =或012x =-(舍去),故切线斜率为()12e f '=.故选C .11.【答案】A 【解析】∵2T πω=,∴3sin 44T f A π⎛⎫==⎪⎝⎭2A =,∴()2sin 24g x x ππω⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦,∵()g x 为奇函数,∴()00g =,即()24k k ωπππ+=∈Z ,∴()122k k ω=-∈Z .又03ω<<,∴32ω=,∴()32sin 24f x x π⎛⎫=+ ⎪⎝⎭,∴2sin 222f ππ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭.故选A .12.【答案】D 【解析】由题意,得()()()()222222212143221n S n n +⎡⎤=-+-++---⎣⎦ ()()22112345221n n n ⎡⎤+--+-+-+⋅⋅⋅+-+⎣⎦()()()()()()()221124334221212(21)21n n n n n n n ⎡⎤⎡⎤⎡⎤=-⨯++-⨯++⋅⋅⋅+---+-+--+⎣⎦⎣⎦⎣⎦()()()()2222121234221121122n n n n n n n n n +=++++⋅⋅⋅+-+++=+++=-+,由212023n S +≤-,得()222023n n -+≤-,即220232n n +≥,结合*n ∈N ,解得32n ≥,故n 的最小值为32.故选D .13.【答案】10310,1010⎛⎫ ⎪ ⎪⎝⎭或10310,1010⎛⎫-- ⎪ ⎪⎝⎭【解析】由题意,得()3,1AB =- .设与AB 垂直的向量为(),a x y =,由0AB a ⋅= ,得30x y -+=,即3y x =,当a的坐标是()1,3时,可得与AB 垂直的单位向量为a a ± ,即10310,1010⎛⎫ ⎪ ⎪⎝⎭或10310,1010⎛⎫-- ⎪ ⎪⎝⎭.故答案为:10310,1010⎛⎫ ⎪ ⎪⎝⎭或10310,1010⎛⎫-- ⎪ ⎪⎝⎭.14.【答案】182【解析】因为945S =,所以()19599452a a a +==,解得55a =.又8951296a a a a +=+=,所以1291a =,所以123122182a a a +==.故答案为:182.15.【答案】(),04k k ππ⎛⎫-+∈ ⎪⎝⎭Z【解析】由()2sin f x x =,得()2cos f x x =',故()2sin 2cos 4g x x x x π⎛⎫=+=+ ⎪⎝⎭,令()4x k k ππ+=∈Z ,得()4x k k ππ=-+∈Z .故答案为:(),04k k ππ⎛⎫-+∈ ⎪⎝⎭Z .16.【答案】-6【解析】由题意,得()2321sin 31cos 3e 12e 1xx f x x x π⎛⎫⎛⎫⎛⎫=-+-=---⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭,把()f x 的图象向上平移3个单位长度,可得函数()21cos e 1x g x x ⎛⎫=-- ⎪+⎝⎭的图象.当[],x ππ∈-时,()()()221cos 1cos e 1e 1x x g x x x g x -⎛⎫⎫-=---=-=- ⎪⎪++⎝⎭⎝⎭,即()g x 为奇函数,在[],ππ-上的最大值与最小值之和为0,故()f x 在[],ππ-上的最大值与最小值之和为6-.故答案为:6-.17.【解析】由()2i 3i z m -=+,得()()()()3i 2i 3i 236i 2i 2i 2i 55m m m m z +++-+===+--+.(2分)∴236i 55m m z -+=-.(3分)(1)由6z z +=,得23265m -⨯=,解得9m =,∴33i z =+,故z ==.(6分)(2)由3z z ⋅<,得22236355m m -+⎛⎫⎛⎫+< ⎪ ⎪⎝⎭⎝⎭,(8分)即26m<,解得m <<∴m 的取值范围是(.(10分)18.(1)对于命题p ,当0x >时,()12f x x a a x=++≥+,当且仅当1x =时取等号,故当0x >时,()f x 的最小值为2a +.(2分)当0x ≤时,()()22211f x x x x =+=+-,当1x =-时,()f x 的最小值为1-.(4分)由()f x 的最小值为1-,得21a +≥-,即3a ≥-.即若命题p 为真,则3a ≥-.(5分)故若命题p ⌝为真,则3a <-,即实数a 的取值范围是(),3-∞-.(6分)(2)对于命题q ,由x ∀∈R ,2420xx a -+≥,得Δ1680a =-≤,解得2a ≥.即若命题q 为真,则2a ≥.(9分)故若q ⌝为真,则2a <.由()p q ∧⌝为真,得32a -≤<,即实数a 的取值范围为[)3,2-.(12分)19.【解析】由sin cos a B A =及正弦定理,得sin sin cos A B B A =,又sin 0B >,故tan A =()0,A π∈,故3A π=.(3分)(1)因为2c b =,所以结合余弦定理,得22222222cos 423a b c bc A b b b b =+-=+-=,所以22224ab bc +==,所以ABC △是以C 为直角的直角三角形.(6分)(2)由ABC △的面积为1sin 2bc A =8bc =,(8分)由6a =,结合余弦定理,得()()222222cos 32436a b c bc A b c bc b c =+-=+-=+-=,所以b c +=(11分)故ABC △的周长为6.(12分)20.【解析】(1)由题意,得()a b f x a b a⋅==⋅,由()a ab ⊥-,得()0a a b ⋅-=,(2分)即20a a b -⋅= ,21a b a ⋅== ,∴()1f x =.(4分)(2)由(1),得()()2215cos sin cos sin sin 2cos 2sin 222f x a b x x x x x x x ϕ=⋅=+-=+=+ (其中25sin 5ϕ=,5cos 5ϕ=).(6分)令()()55sin 222f x x ϕ=+=,得()sin 21x ϕ+=,∴()222x k k πϕπ+=+∈Z ,(8分)∴()222x k k ππϕ=+-∈Z ,(8分)∴sin 2sin 2cos 25x k ππϕϕ⎛⎫=+-== ⎪⎝⎭,cos 2cos 2sin 25x k ππϕϕ⎛⎫=+-== ⎪⎝⎭.(10分)∴b ===.(12分)21.【解析】(1)由22n n S a =-,得1122S a =,得12a =,当2n ≥时,()()111222222n n n n n n n a S S a a a a ---=-=---=-,即12n n a a -=,(2分)∴{}n a 是首项为2,公比为2的等比数列,∴{}n a 的通项公式为2n n a =.(4分)(2)由(1),得()()111211222222222n n n n n n b +++⎛⎫==- ⎪+++⋅+⎝⎭,(5分)∴11111111124661010182222n n n T +⎛⎫=⨯-+-+-+⋅⋅⋅+-⎪++⎝⎭111112422221n n+⎛⎫=⨯-=- ⎪++⎝⎭.(7分)(3)∵()()10102n nn c n a n =-=-⋅,∴当9n ≤时,0n c >;当10n =时,0n c =;当11n ≥时,0n c <.∴当9n =或10时,n A 取得最大值,且910A A =.(9分)239992827212A =⨯+⨯+⨯++⨯ .①∴234109292827212A =⨯+⨯+⨯+⋅⋅⋅+⨯.②②-①,得()923910941218222218202612A ⨯-=-+++⋅⋅⋅++=-=-,∴n A 的最大值为2026.(12分)22.【解析】(1)解法一:由()2ln e x f x x k =+,得()()2e 0xf x k x x=+>',由1x =是()f x 的一个极值点,得()10f '=,即2e 0k +=,即2ek =-.(2分)此时,()12ln 2ex f x x -=-,()()1121e 22e x x x f x x x---=-=',设()()11e 0x g x x x -=->,则()()11e 0x g x x -'=-+<,即()g x 在()0,+∞上单调递减.(3分)又()10g=,所以当()0,1x ∈时,()0g x >,即()0f x '>,当()1,x ∈+∞时,()0g x <,即()0f x '<.所以()f x 在()0,1上单调递增,在()1,+∞上单调递减,所以()f x 有极大值()12f =-,无极小值.(5分)解法二:由()2ln e x f x x k =+,得()()2e 0xf x k x x=+>',由1x =是()f x 的一个极值点,得()10f '=,即2e 0k +=,即2ek =-.(2分)此时,()12ln 2e x f x x -=-,()122e x f x x-=-',显然()f x '是减函数,又()10f '=,当()0,1x ∈时,()0f x '>,当()1,x ∈+∞时,()0f x '<.所以()f x 在()0,1上单调递增,在()1,+∞上单调递减,所以()f x 有极大值()12f =-,无极小值.(5分)(2)由()ln e x x h x =,得()()1ln 1ln 0e ex x xx x x h x x x --==>'.(6分)设()1ln x x x ϕ=-,则()ln 1x x ϕ'=--.令()0x ϕ'=,得1ex =.当10e x <<时,()0x ϕ'>,当1e x >时,()0x ϕ'<,故()x ϕ在10,e ⎛⎫ ⎪⎝⎭上单调递增,在1,e ⎛⎫+∞ ⎪⎝⎭上单调递减,故()x ϕ的极大值为1110e e ϕ⎛⎫=+>⎪⎝⎭.(8分)当10ex <<时,()0x ϕ>.又()110ϕ=>,()212ln 20ϕ=-<,故()x ϕ存在唯一的零点0x ,且()01,2x ∈.由()0001ln 0x x x ϕ=-=,得001ln x x =.(10分)当()00,x x ∈时,()0x ϕ>,即()0h >,当()0,x x ∈+∞时,()0x ϕ<,即()0h x '<,即()hx 在()00,x 上单调递增,在()0,x +∞上单调递减.故()hx 的极大值为()00000ln 1e e x x x h x x ==,(11分)令()0f x =,得2ln e 0x x k +=,即1ln 2e x xk -=.由()f x 有零点,得00112e x k x -≤,即02e x kx ≥-.(12分)。
高中必刷题第四章-1

第四章指数函数与对数函数4.1 指数4.1.1 n次方根与分数指数幂⊕4.12 无理数指数幂及其运算性质刷基础题型1 根式1.[四川成都双流中学2020高一期中]下列各式正确的是( )=3π-()*1,a n n>∈N D.()*1,na n n=>∈N2.下列说法:3±;②16的4次方根是2;③当n为大于10a≥时才有意义;④当n为大于1a∈R都有意义.正确的个数为( )A.4B.3C.2D.13.[豫南九校2020高一第二次联考]设23a<<,则( )A.1B.-1C.25a- D.52a-4.12x⎫>⎪⎭的结果是________.题型2 分数指数幂5.[江苏苏州2020高一期中]( )A.8B.4C.2D.186.[重庆南开中学2020高一期中幂表示为( )A.12a B.32a C.34a D.a7.[福建福州2020高一期中]有下列各式:①n a=;②34x-=4334a a a⋅=;④其中正确的个数是( )A.0B.1C.2D.38.[安徽黄山溪区2020高一期中]已知14a<,则( )B.D.9.已知14aa+=,则1122a a--等于( )A.2C.D.10.若()()11223223y x x=-+-+x,y分别为________,________.题型3 实数指数幂的运算性质11.[北京丰台区2020高一期中]已知0a>,则1344a a-⋅等于( )A.12a- B.316a- C.13a D.a12.[贵州黔东南2020高一期中]12164-⎛⎫=⎪⎝⎭( )A.32B.23C.25D.5213.[湖南衡阳一中2019高一联赛]若27x=,26y=,则4x y-=等于( )A.3649B.76C.67D.493614.[北京丰台区2020高一期中]计算:()230239.63 1.58--⎛⎫--+=⎪⎝⎭________.15.化简()211511336622130,03a b a b a b a b⎛⎫⎛⎫⎛⎫-÷>>⎪⎪ ⎪⎝⎭⎝⎭⎝⎭的结果是________.刷易错易错点1 化简根式时忽视根式中变量条件而致错16.[河南信阳2019高一期中]式子得( )C.D.17.[浙江温州2020高一期中]代数式恒等于( )C.D.易错点2忽略偶次根式的成立条件而致错18.的结果是( )A.25x- B.21x--C.-1D.52x-19.,则实数a的取值范围是( )A.1,2⎡⎫+∞⎪⎢⎣⎭ B.1,2⎛⎤-∞⎥⎝⎦C.11,22⎡⎤-⎢⎥⎣⎦D.R20.已知0a b<<,1n>,*n∈N,化简刷提升1.(多选)[辽宁沈阳城郊市重点联合体2020高一期中改编]下列运算正确的是( )3π- B.()22x x e e =a b -2.[海南琼海嘉积中学2020高一段考]若0a >,则76a =( )A.53a B.23aC.1D.23a -3.[江苏盐城中学2020高一质检]已知1122e e 2x x --=,则3322e ex x --的值为( )A.2B.8C.10D.144.化简2+( )A.1a -B.()21a -C.1a -D.()21a -5.[江西景德镇一中2020高一期中])0m<的结果为( ) A.B.C.- D.-6.若13a b m +=,()23106ab m m =>,则33a b +=( )A.0B.2m C.2m -D.32m 7.已知函数()()0x x a a f x a -=+>,且()13f =,则()()()012f f f ++的值是( ) A.14 B.13 C.12 D.118.设x ,y 是正数,且y x x y =,9y x =,则x 的值为( )A.19C.19.已知()f x 是奇函数,当0x >时,()21x a x f x +=⋅-,若()314f -=,则a 等于( ) A.-3B.-2C.-1D.010.计算:()1120130.2545273810.008168----⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥-⨯⨯+-⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦⎣⎦()13100.027⨯=________.11.计算:________. 12.计算:(1)[河南豫西名校2020联考]13127-⎛⎫-+⎪⎝⎭)11020.002102π---+;(2)[四川成都双流中学2020高一期中])32204311681281--⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭.13.[安徽庐巢六校联盟2020高一段考]已知函数()2x xx a f a -+=(0a >,1a ≠,a 为常数,x ∈R ). (1)若()6f m =,求()f m -的值; (2)若()13f =,求()2f ,12f ⎛⎫⎪⎝⎭的值.14.已知23236a b c d ⋅=⋅=,求证:()()11a d --=()()11b c -⋅-.4.2 指数函数 4.2.1 指数函数的概念刷基础题型1 生活中的指数函数模型1.[北京石景山区2020高一期末]池塘里浮萍的生长速度极快,它覆盖池塘的面积,每天可增加原来的一倍.若一个池塘在第30天时刚好被浮萍盖满,则浮萍覆盖池塘一半的面积是( ) A.第15天B.第20天C.第25天D.第29天2.[安徽庐巢六校联盟2020高一段考]据报道,全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度,设2010年的冬季冰雪覆盖面积为m ,从2010年起,经过x 年后,北冰洋冬季冰雪覆盖面积y 与x 的函数关系式是( ) A.500.95xy m =⋅B.5010.05xy m ⎛⎫=-⋅ ⎪⎝⎭C.500.95x y m -=⋅D.()5010.05x y m -=-⋅3.某厂2010年的生产总值为x 万元,预计生产总值每年以12%的速度递增,则该厂到2022年的生产总值是________万元.4.由于电子技术的飞速发展,计算机的成本不断降低,若每隔5年计算机的价格降低13,则现在价格为8100元的计算机经过15年价格应降为________.5.农民收入由工资性收入和其他收入两部分构成2015年某地区农民人均收入为13150元(其中工资性收入为7800元,其他收入为5350元)预计该地区自2016年起的5年内,农民的工资性收入将以每年6%的增长率增长,其他收入每年增加160元.根据以上数据,求2020年该地区农民人均收入约为多少元?(其中41.06 1.26≈,51.06 1.34≈,61.06 1.42≈)题型2 指数函数的概念6.[辽宁葫芦岛2020高一月考]下列函数不是指数函数的是( ) A.12x y +=B.3x y -=C.4x y =D.32x y =7.若函数()132x f x a a ⎛⎫=-⋅ ⎪⎝⎭是指数函数,则12f ⎛⎫ ⎪⎝⎭的值为( ) A.2B.-2C.-D.8.[吉林舒兰一中2019高一期中]若指数函数()y f x =的图像过点()2,4,则()3f 的值为( ) A.4B.8C.16D.19.已知函数()2,02,0x x a x f x x -⎧⋅≥=⎨<⎩,若()()11f f -=,则a =( )A.14B.12C.1D.210.(多选)设指数函数()x f x a =(0a >且1a ≠),则下列等式中不正确的有( ) A.()()()f x y f x f y += B.()()()f x f x y f y -=C.()()()f nx nf x n =∈QD.()()()()*nnnf xy f x f y n =∈⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦N 11.[北京石景山区2020高一期末]已知函数()f x 是指数函数,如果()()391f f =,那么()8f ________()4f .(请在横线上填写“>”“=”或“<”)12.[海南临高2020高一期中]已知函数()f x =()233x aa a -+是指数函数.(1)求()f x 的表达式;(2)判断()()()F x f x f x =--的奇偶性,并加以证明.4.2.2 指数函数的图像和性质刷基础题型1 指数函数的图像1.[江苏常州2020高一期中]已知函数()11x f x a +=+(0a >,且1a ≠)的图像恒过定点A ,则A 的坐标为( ) A.()0,1B.()1,1-C.()1,2-D.()0,22.函数()1x y a a =>的图像是( )A. B.C. D.3.[海南海口海南中学2020高一期中]函数5x y =与5x y -=的图像( ) A.关于y 轴对称 B.关于x 轴对称 C.关于原点对称D.关于直线y x =对称4.[浙江东阳2020期中]函数()21e x y x =-的图像是( )A. B.C. D.5.(多选)[安徽安庆2020高一期末改编]某数学课外兴趣小组对函数()12x f x -=的图像与性质进行了探究,得到的下列四个结论中正确的有( ) A.该函数的值域为()0,+∞ B.该函数在区间[)0,+∞上单调递增 C.该函数的图像关于直线1x =对称D.该函数的图像与直线()2y a a =-∈R 不可能有交点6.[山东潍坊2019高一期中]已知四个函数()2x f x =,()12xg x ⎛⎫= ⎪⎝⎭,()3x h x =,()13xp x ⎛⎫= ⎪⎝⎭,其中()y f x =,()y g x =的图像如图所示.(1)请在坐标系中画出()y h x =,()y p x =的图像,并根据这四个函数的图像总结出指数函数具有哪些性质?(2)举出在实际情境中能够抽象出指数函数的一个例子并说明理由.题型2 指数函数的性质 7.函数()34f x x =-( ) A.[)2,4 B.[)()2,44,+∞C.()()2,44,+∞D.[)2,+∞8.函数12x y =-,[]0,1x ∈的值域是( ) A.[]0,1B.[]1,0-C.10,2⎡⎤⎢⎥⎣⎦D.1,02⎡⎤-⎢⎥⎣⎦9.[河南豫南九校2020高一联考]设函数()()e e x x a a f x -=+∈R .若()f x 为奇函数,则实数a =________.10.[浙江浙东北联盟2020高一期中]函数12x y -=在区间()1,1k k -+内不单调,则实数k 的取值范围是________.11.知函数241y x x =-+的定义域为5212x x x -⎧⎫⎪⎪≤⎨⎬⎪⎛⎫ ⎪⎝⎭⎪⎩⎭,则该函数的值域为________.12.[江苏南京2020高一期中]已知函数()x f x a =(0a >且1a ≠)的图像经过点()2,9. (1)求实数a 的值;(2)若b ∈R ,比较()2f b 与()21f b +的大小.刷易错易错点1 忽略指数函数的值域而致错 13.函数1y =的值域为( ) A.[)1,+∞B.()1,1-C.[)1,-+∞D.[)1,1-14.函数()112x f x +⎛⎫= ⎪⎝⎭的值域是________.易错点2 忽略对指数函数的底数的分类讨论而致错 15.若函数x y a =(0a >,且1a ≠)在[]1,2上的最大值与最小值的差为2a,则a 的值为( ) A.12B.32C.23或2D.12或3216.已知函数()x f x a =(0a >,且1a ≠)在[]1,1-上恒有()2f x <,则实数a 的取值范围为________. 17.[江西南昌东湖区2020高一期中]已知函数()x f x a b =+(0a >且1a ≠),其中a ,b 均为实数. (1)若函数()f x 的图像经过点()0,2A ,()1,3B ,求函数()1y f x =的值域; (2)如果函数()f x 的定义域和值域都是[]1,0-,求a b +的值.易错点3 忽略复合函数中函数的性质而致错 18.函数()2212x xf x +⎛⎫= ⎪⎝⎭的单调递增区间是________.19.函数222x x y -+=的值域为________.易错点4 使用换元法时忽略新元的取值范围而致错 20.[福建三明2019高一期末]已知函数()42x x f x a =+⋅在区间[)2,+∞上单调递增,则实数a 的取值范围为( ) A.[)4,-+∞B.(],4-∞-C.[)8,-+∞D.(],8-∞-21.已知函数()1423x x f x +=-+的定义域为11,22⎡⎤-⎢⎥⎣⎦.求函数()f x 的值域.刷提升1.[江西抚州临川区2020高一期中]若指数函数()13xy a =-在R 上单调递减,则实数a 的取值范围是( ) A.10,3⎛⎫ ⎪⎝⎭B.()1,+∞C.RD.(),0-∞2.[四川蓉城名校联盟2019高一期中函数()xf x =在区间[]1,2上的最大值是( )C.3D.3.[北京陈经纶中学2020高一期中]若2313a ⎛⎫= ⎪⎝⎭,1323b ⎛⎫= ⎪⎝⎭,2323c ⎛⎫= ⎪⎝⎭,则( ) A.c a b << B.c b a << C.a c b << D.b a c <<4.已知函数()x f x a =(0a >,且1a ≠)在()0,2内的值域是()21,a ,则函数()y f x =的图像大致是( )A. B. C.D.5.若函数()213x f x -⎛⎫= ⎪⎝⎭,则()f x 的单调递减区间是( ) A.(],2-∞ B.[)2,+∞ C.[)2,-+∞D.(],2-∞-6.[河南豫南九校2020高一第三次联考]已知()g x 为偶函数,()h x 为奇函数,且满足()()2x g x h x -=.若存在[]1,1x ∈-,使得不等式()()0m g x h x ⋅+≤有解,则实数m 的最大值为( )A.35B.35-C.1D.-1 7.[广东揭阳2020高一期中]若直线2y a =与函数1x y a =-(0a >且1a ≠)的图像有两个公共点,则实数a 的取值范围是( )A.()0,1B.10,2⎛⎫ ⎪⎝⎭C.1,12⎛⎫ ⎪⎝⎭D.()1,28.[湖北宜昌部分示范高中教学协作体2019高一期末]已知函数()(23)43,1,1x a x a x f x a x +-+≥⎧=⎨<⎩,在R 上是增函数,则实数a 的取值范围是________.9.[福建长汀、连城一中等六校2020高一期中联考]若函数()31,01142,02x x x f x x ⎧-≥⎪⎪+=⎨⎪⨯-<⎪⎩的值域为A ,则A 为________.10.已知函数()x f x a b =+(0a >,且1a ≠)的图像过点()0,2-,()2,0. (1)求a 与b 的值;(2)求[]2,4x ∈-时,()f x 的最大值与最小值.11.[四川成都都区2020高一期中]已知函数()331x xaf x +=+为奇函数. (1)求实数a 的值;(2)判断函数()f x 的单调性,并加以证明; (3)若()g x 为偶函数,且当0x ≥时,()()g x f x =,求()g x 的解析式.刷素养12.[清华大学2019中学生标准学术能力诊断性测试]已知0x y +>,则“0x >”是“2222x y x y +>+”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件第4.1,4.2节综合训练刷能力1.若函数()33x x f x -=+与()33x x g x -=-的定义域均为R ,则( )A.()f x 与()g x 均为偶函数B.()f x 为偶函数,()g x 为奇函数C.()f x 与()g x 均为奇函数D.()f x 为奇函数,()g x 为偶函数 2.已知函数()112x b f x -⎛⎫=+ ⎪⎝⎭的图像不经过第一象限,则实数b 的取值范围是( ) A.(),1-∞- B.(],1-∞- C.(],2-∞-D.(),2-∞-3.若关于x 的不等式()2301xxa aa -<<≥的解集为A ,则函数13x y +=,x A ∈的最大值为( )A.1B.3C.6D.94.[河南豫南九校2020高一第二次联考]若()f x 满足对任意的实数a ,b 都有()()()f a b f a f b +=⋅,且()12f =,则()()()()()()()()24620181352017f f f f f f f f ++++=( ) A.1008 B.1009 C.2017 D.20185.如图,面积为8的平行四边形OABC 的对角线AC CO ⊥,AC 与BO 交于点E .若指数函数xy a =(0a >,且1a ≠)的图像经过E ,B 两点,则a 等于( )C.2D.36.[四川成都都区2020高一期中]已知0a >,设函数()[]()120202019,20201x x f x a a x ++=∈-+的最大值为M ,最小值为N ,那么M N +=( ) A.2020 B.2019 C.4040 D.40397.(多选)[安徽2020高一期中]函数()x y f x a a ==-(0a >且1a ≠)的图像可能为( )A. B.C. D.8.[安徽示范级高中2020高一期中]已知函数()y f x =满足()221xx f x=-,则()512f =________.9.已知函数()221x f x -=-在区间[]0,m 上的值域为[]0,3,则实数m 的取值范围为________.10.[福建长汀、连城一中等六校2020高一期中联考]已知函数()()11221x g x x f ⎛⎫=+⋅ ⎪-⎝⎭为偶函数,且()20f =.若不相等的两个正数x 1,x 2满足()12x x -⋅()()210f x f x ->⎡⎤⎣⎦,则不等式()()120x f x -->的解集为________.11.[广东东莞2020高一期末]已知函数()21e 1xf x =-+. (1)判断()f x 的单调性,并说明理由; (2)判断()f x 的奇偶性,并用定义法证明; (3)若不等式()()2340xx f m f -+-<对任意x ∈R 恒成立,求实数m 的取值范围.4.3 对数4.3.1 对数的概念⊕4.3.2 对数的运算刷基础题型1 对数的概念 1.有下列说法:①零和负数没有对数;②任何一个指数式都可以化成对数式; ③以10为底的对数叫做常用对数; ④以e 为底的对数叫做自然对数 中正确的个数为( ) A.1 B.2 C.3 D.42.(多选[黑龙江大庆铁人中学2020高一月考改编]下列各式中正确的有( ) A.()lg lg100= B.()lg ln e 0= C.若10lg x =,则100x = D.若251log 2x =则5x =±3.在()25log a a b -=-中,实数a 的取值范围是( )A.()(),25,-∞+∞B.()2,5C.()()2,33,5D.()3,44.[河南郑州2020高一月考]计算:3log =( ) A.12-B.12C.-1D.15.已知()23409a a =>,则23log a =( )A.2B.3C.12 D.136.[陕西西安2020月考]已知函数()f x =()2log 1,13,1xx x x -⎧->⎨≤⎩,则()()2f f -=( ) A.1 B.2 C.3 D.47.[江西抚州临川第一中学2020高一期中]已知函数23x y a -=+(0a >且1a ≠)的图像恒过定点P ,点P 在幂函数()y f x =的图像上,则()3log 3f =( ) A.-2 B.-1 C.1 D.2 题型2 对数的运算8.已知1log 2a m =,log 3a n =,则2m n a +等于( )A.3B.34C.9D.929.若lg lg 2lg 3lg x a b c =+-,则x =( )A.23a b c +-B.23a b c +-C.23ab cD.23ab c10.[天津宝坻区普通高中2019高一三校联考]计算123221log 5log 1027-⎡⎤⎛⎫-+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦的值为( ) A.-10B.-8C.10D.8 11.若41log 32x =,则2log 39x x +等于( )A.3B.5C.7D.1012.[安徽六安一中2020月考]已知272log log x y =,且14,则xy 的值是( )A.98B.49C.28D.1413.()2lg5lg2lg50+⨯=________.14.[北京石景山区2020高一期末]已知0a >,0b >,且20a b +=,则lg lg a b +的最大值为________. 题型3 对数的换底公式 15.23log 9log 4⋅=( ) A.14B.12C.2D.416.计算()2323223log 2log 3log 2log 3log 3log 2+--的值为( ) A.log 26 B.log 36 C.2 D.1 17.若235log log 4log 98x ⋅⋅=,则x 等于( ) A.8 B.25 C.16 D.4 18.[广东揭阳2020高一期中]23827log 48-⎛⎫-=⎪⎝⎭________.19.已知3log 2a =,则32log 18用a 表示为________.题型4 对数恒等式20.若4log 3a =,则22a a -+=________.21.(52log 10153++=________.刷易错易错点 忽略底数与真数的范围而致错22.使对数()log 21a a -+有意义的a 的取值范围为( ) A.()1,11,2⎛⎫+∞ ⎪⎝⎭B.10,2⎛⎫ ⎪⎝⎭C.()()0,11,+∞D.1,2⎛⎫-∞ ⎪⎝⎭23.在()31log 32a b a -=-中,实数a 的取值范围是( ) A.13,,32⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭ B.1223,,3332⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭C.13,32⎛⎫⎪⎝⎭D.23,32⎛⎫ ⎪⎝⎭24.已知()2lg 2lg lg m n m n -=+,则:m n =________.25.方程()()24log l 1og 41x x ++-=的解为________.刷提升1.求值:552log 10log 4-=( ) A.1B.log 516C.2D.log 5962.[江苏海安2020高一期中]设3log 2x =,则33223333x xx x----的值为( )A.2110B.2110-C.1710D.13103.31log 29的值是( )A.12 B.14C.2D.14.已知0ab >,给出下面四个等式:①()lg lg lg ab a b =+;②lglg lg aa b b=-; ③21lg lg 2a ab b⎛⎫= ⎪⎝⎭;④()1lg log 10ab ab =.其中正确的个数为( )A.0B.1C.2D.35.[河北廊坊高中联合体2020联考]若43m n k ==,且20m n mn +=≠,则k =( )A.18B.26C.36D.426.[湖北荆门2020高一期末]已知某抽气机每次可抽出容器内空气的60%,要使容器内的空气少于原来的0.2%,则至少要抽的次数是(参考数据:lg 20.301≈)( ) A.6B.7C.8D.97.[北京朝阳区2020高一期中]设6521m =+,452n =,则mn约等于(参考数据:lg 20.3≈) A.1020 B.103 C.106D.1098.[重庆2020高一期末]如图,点A ,C 是函数()2x f x =图像上两点,将()f x 的图像向右平移两个单位长度后得到函数()g x 的图像,点B 为()g x 图像上的点.若AB //x 轴且△ABC 为等边三角形,则点A 的横坐标为( )A.12B.logC.1D.log 239.[浙江台州2019高一期末]已知lg 3a b +=,100b a =,则lg 2a b =________.10.已知函数())ln 31f x x =+,则()lg 2f +1lg 2f ⎛⎫= ⎪⎝⎭________. 11.已知23a =,98b =,则ab 的值是________. 12.设函数()log a f x x =(0a >,且1a ≠),若()1220184f x x x =,则()()()222122018f x f x f x +++的值等于________.13.[安徽安庆2019高一期末](1)计算:2128log 3log 3-34116-⎛⎫- ⎪⎝⎭; (2)已知lg 5a =,lg 7b =,试用a ,b 表示28log 49.14.已知集合(){},,lg A x xy xy =,集合{}0,,B x y =,若A B =,求()228log x y +的值.15.已知x ,y ,z 为正数,346x y z ==,且2x py =. (1)求p 的值; (2)求证:1112z x y-=.刷素养16.[上海华东师范大学第二附属中学2020自主招生]方程ln3ln 4ln5x x x +=正实数解的个数为( ) A.0B.1C.3D.多于34.4 对数函数4.4.1 对数函数的概念⊕4.4.2 对数函数的图像和性质刷基础题型1 对数函数的概念1.[云南宣威2020高一期中]下列函数中,是对数函的有( )①()log a y x a =∈R ;②8log y x =;③ln y x =;④()log 2x y x =+;⑤42log y x =.A.1个B.2个C.3个D.4个2.满足“对定义域内任意实数x ,y ,都有()()()f xy f x f y =+”的函数()f x 可以是( )A.()2f x x =B.()2x f x =C.()2log f x x =D.()ln exf x =3.[福建龙海2020高一期末]函数()21log x y -=定义域是( ) A.()2,11,3⎛⎫+∞ ⎪⎝⎭B.()1,11,2⎛⎫+∞ ⎪⎝⎭C.2,3⎛⎫+∞ ⎪⎝⎭D.1,2⎛⎫+∞ ⎪⎝⎭4.[湖北荆门2020高一期末]函数()()25x a a f =+-log a x ⋅为对数函数,则18f ⎛⎫⎪⎝⎭等于( )A.3B.-3C.-log 36D.-log 385.设函数()21,1lg ,1x x x x f x ⎧+≤=⎨>⎩,则()()10f f 的值为( )A.lg101B.1C.2D.06.已知函数()3log f x x =,则f =________.题型2 对数函数的图像7.[山西太原2020高一期中]已知点()m, n 在函数lg y x =的图像上,则下列各点也在该函数的图像上的是( ) A.()2,2m nB.()10,10m nC.()10,1m n ++D.,110m n ⎛⎫+ ⎪⎝⎭8.若函数()1x f x a -=的图像经过点()2,4,则函数()1log 1ag x x =+的图像是( ) A.B.C.D.9.函数log a y x =,log b y x =,log c y x =,log d y x =的图像如图所示,则a ,b ,c ,d 的大小顺序是( )A.1c d a b <<<<B.1d c a b <<<<C.1c d b a <<<<D.1d c a b <<<<10.[湖南襄阳2020期末]设a ,b ,c 均为正数,且e ln a a =-,e ln b b -=-,e ln c c -=,则( ) A.a b c << B.c b a << C.c a b << D.b a c <<11.已知实数a ,b 满足等式23log log a b =,给出下列五个关系式:①1a b >>;②1b a >>;③1a b <<;④1b a <<;⑤a b =.其中可能成立的关系式是________.12.函数()log 32a y x =--的图像过的定点是________.题型3 对数函数的性质13.[安徽庐巢六校联盟2020高一段考]函数()f x 的定义域为( )A.[)1,2B.()1,+∞C.()1,2D.()2,+∞14.四川攀花2020模拟]已知123a=,2log b=,log c =,则a ,b ,c 的大小关系为( ) A.a b c >> B.a c b >> C.b a c >>D.c b a >>15.已知函数()lg f x x =,0a b <<,且()()f a f b >,则( ) A.1ab > B.01ab << C.1ab =D.()()110a b -->16.[浙江杭州西湖区2020高一期中]若定义运算(),,a a bf a b b a b≥⎧⊗=⎨<⎩,则函数()()()22log 1log 1f x x +⊗-的值域是( )A.()1,1-B.[)0,1C.[)0,+∞D.[]0,117.[河南豫南九校2020高一第二次联考]若函数74()()log 01a f x x a =<<在区间(),31a a -上单调递减,则实数a 的取值范围是________.18.已知()()0.450.45log 2log 1x x +>-,则实数x 的取值范围是________.19.定义区间[]12,x x 的长度为21x x -.若函数2log y x =的定义域为[],a b ,值域为[]0,3,则区间[],a b 长度的最大值为________.题型4 对数函数与指数函数互为反函数20.[湖南长沙开福区2020高一期中]函数()f x 与()x g x a =互为反函数,且()g x 的图像过点()2,4-,则()()12f f +=( ) A.-1B.0C.1D.1421.[陕西西安碎林区2020高一期中]若函数()y f x =与10x y =互为反函数,则()22y f x x =-的单调递减区是( ) A.()2,+∞B.(),1-∞C.()1,+∞D.(),0-∞22.已知对数函数()log a f x x =(0a >,且1a ≠),且图像过点()9,2,()f x 的反函数记为()y g x =,则()g x 的解析式是( )A.()4x g x =B.()2x g x =C.()9x g x =D.()3x g x = 23.设函数()()log a b f x x =+(0a >,且1a ≠)的图像过点()2,1,其反函数的图像过点()2,8,则a b +等于( )A.3B.4C.5D.624.设01a <<,在同一直角坐标系中,函数x y a -=与()log a y x =-的大致图像是( )A. B.C.D.刷易错易错点1 忽略对底数的讨论而致错 25.若2log 13a <,则实数a 的取值范围是( ) A.20,3⎛⎫ ⎪⎝⎭B.2,3⎛⎫+∞ ⎪⎝⎭C.2,13⎛⎫⎪⎝⎭D.()20,1,3⎛⎫+∞ ⎪⎝⎭26.若函数log a y x =(0a >,且1a ≠)在[]2,4上的最大值与最小值的差是1,则a 的值为________. 易错点2 忽略复合函数中函数的定义域而致错 27.已知函数()log 2a y ax =-在区间[]0,1上为减函数,则实数a 的取值范围是( ) A.()0,1B.()1,2C.()0,2D.()1,+∞28.函数()22log 23y x x =-++的单调递减区间为________.易错点3 忽略复合函数中函数的值域而致错 29.[河南豫南九校2020第三次联考]已知函数()()22log 3f x x ax a =-+在区间[)2,+∞上是增函数,则实数a 的取值范围是( ) A.(],4-∞B.(],2-∞C.[]4,4-D.(]4,4-30.[安徽淮北一中2020高一期中]已知函数()()213log f x x ax a =--对任意两个不相等的实数121,,2x x ⎛⎫∈-∞- ⎪⎝⎭,都满足不等式()()21210f x f x x x ->-,则实数a 的取值范围是( ) A.[)1,-+∞B.(],1-∞-C.11,2⎡⎤-⎢⎥⎣⎦D.11,2⎡⎤--⎢⎥⎣⎦31.已知2256x ≤且21log 2x ≥. (1)求x 的取值范围;(2)在(1)的条件下,求函数()22log log 24x x f x =⋅的最大值和最小值.易错点4 忽略分段函数的定义域分界点而致错 32.[福建莆田第六中学2020高一期中]已知函数()(2)1,1log ,1aa x x f x x x --≤⎧=⎨>⎩,若()f x 在(),-∞+∞上单调递增,则实数a 的取值范围为( )75A.()1,2B.()2,3C.(]2,3D.()2,+∞刷提升11.[辽宁省实验中学2019高一期中]已知函数()()2log 12x f x -+=,则函数()f x 的值域是( )A.[)0,2B.()0,+∞C.()0,2D.[)0,+∞2.给出三个数123a =,312b ⎛⎫= ⎪⎝⎭,31log 2c =,则它们的大小顺序为( )A.b c a <<B.b a c <<C.c a b <<D.c b a <<3.[重庆沙坪坝区2020高一期中]已知函数())ln21x f x -=,则()1lg 3lg 3f f ⎛⎫+=⎪⎝⎭( ) A.-1 B.0C.2D.-24.(多选)函数()()()log 201a f x x a =+<<的图像过( ) A.第一象限 B.第二象限 C.第三象限D.第四象限5.[北京101中学2020期中]设x 1,x 2,x 3均为实数,()1211log 13xx ⎛⎫=+ ⎪⎝⎭,2321log 3xx ⎛⎫= ⎪⎝⎭,3231log 3xx ⎛⎫= ⎪⎝⎭,则( ) A.132x x x << B.321x x x << C.312x x x <<D.213x x x <<6.已知()f x 是定义在R 上的偶函数,当[)0,x ∈+∞时,()22x f x =-,则不等式()2log 0f x >的解集为( ) A.102x x ⎧⎫<<⎨⎬⎩⎭B.1122x x x ⎧⎫<<>⎨⎬⎩⎭或 C.{}2x x >D.1022x x x ⎧⎫<<>⎨⎬⎩⎭或7.[福建莆田第六中学2020高一期中]已知函数()y f x =与12xy ⎛⎫= ⎪⎝⎭的图像关于直线y x =对称,则()223f x x --的单调递增区间为________.8.已知0a >且1a ≠,若函数()3,2log ,2ax x f x x x -≤⎧=⎨>⎩的值域为[)1,+∞,则a 的取值范围是________.9.[江苏常熟2020高一期中]已知函数()()log 1a x f x =-,()()log 3a g x x =+,其中01a <<. (1)解关于x 的不等式()()f x g x <;(2)若函数()()()F x f x g x =+的最小值为-4,求实数a 的值.10.[天津部分区2019高一期末]设函数()f x =()lg1aa x ∈+R ,且()10f =. (1)求a 的值; (2)求()f x 的定义域;(3)判断()f x 在区间()0,+∞上的单调性,并用单调性的定义证明.刷素养11.[北京大学等十一校2014联考自主招生]若函数()()2lg 2f x x ax a =-+的值域是R ,则a 的取值范围是( ) A.()0,1B.[]0,1C.()(),01,-∞+∞D.(][),01,-∞+∞12.[上海交通大学2019自主招生]当12x x ≠时,有()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭,则函数()f x 是“严格下76凸函数”,下列函数是“严格下凸函数”的是________. ①y x =;②y x =;③2y x =;④2log y x =.刷提升21.[重庆2020高一月考]不等式()21log 1x <+的解集为( ) A.{}01x x <<B.{}10x x -<≤C.{}10x x -<<D.{}1x x >-2.[湖北荆门2020高一期末]已知函数()f x =()2lg 32x x -+-,则函数()21f x -的定义域为( )A.()3,1,2⎛⎫-∞+∞ ⎪⎝⎭B.()1,3C.()1,2D.31,2⎛⎫⎪⎝⎭3.如果函数()log 2a f x x =-在()2,+∞上是减函数,那么()f x 在()0,2上( ) A.单调递增且无最大值 B.单调递减且无最小值 C.单调递增且有最大值D.单调递减且有最小值4.[黑龙江双鸭山第一中学2020高一期中]函数()1ln x x f x ⎛⎫- ⎪⎝⎭=的图像大致是( )A. B.C. D.5.[浙江温州新力量联盟2019高一期中]已知函数()()log 2a f x x =+,()()log 2a g x x =-,其中0a >且1a ≠,则函数()()()F x f x g x =+,()()()G x f x g x =-的奇偶性是( )A.()F x 是奇函数,()G x 是奇函数B.()F x 是偶函数,()G x 是奇函数C.()F x 是偶函数,()G x 是偶函数D.()F x 是奇函数,()G x 是偶函数6.若函数()(31)4,1log ,1aa x a x f x x x -+<⎧=⎨≥⎩对任意12x x ≠,都有()()21210f x f x x x -<-,则实数a 的取值范围是( )A.()0,1B.10,2⎛⎫⎪⎝⎭ C.1,17⎛⎤ ⎥⎝⎦D.11,73⎡⎫⎪⎢⎣⎭7.[江苏扬州2019高一期末]若函数()2log f x x =的定义域为[],a b ,值域为[]0,2,则b a -的最小值为( ) A.34B.3C.2D.328.已知对数函数()f x 的图像过点()4,2-,则不等式()()113f x f x --+>的解集为________.9.[安徽庐巢六校联盟2020高一段考]已知函数()()()lg 2lg 2f x x x =++-. (1)求函数()y f x =的定义域; (2)判断函数()y f x =的奇偶性;(3)若()()2f m f m -<,求实数m 的取值范围.10.[河北唐山2019高一期末]已知奇函数()f x =1ln1ax x +-. (1)求实数a 的值; (2)判断函数()f x 在()1,+∞上的单调性,并利用函数单调性的定义证明;(3)当[]2,5x ∈时,()()ln 1ln 1x m x +>+-恒成立,求实数m 的取值范围.774.4.3 不同函数增长的差异刷基础题型1 一次函数、指数函数和对数函数的不同增长 1.[北京石景山区2020高一期末]三个变量y 1,y 2,y 3随着变量x 的变化情况如表: x 1 3 5 7 9 11 y 1 5 135 625 1715 3635 6655 y 2 5 29 245 2189 19685 177149 y 3 5 6.10 6.61 6.95 7.20 7.40 则与x 呈对数型函数、指数型函数、幂函数型函数变化的变量依次是( ) A.y 1,y 2,y 3B.y 2,y 1,y 3C.y 3,y 2,y 1D.y 3,y 1,y 22.[广东惠州2020高一期末]下面对函数()12log f x x =,()12xg x ⎛⎫= ⎪⎝⎭与()12h x x -=在区间()0,+∞上的衰减情况说法正确的是( )A.()f x 衰减速度越来越慢,()g x 衰减速度越来越快,()h x 衰减速度越来越慢B.()f x 衰减速度越来越快,()g x 衰减速度越来越慢,()h x 衰减速度越来越快C.()f x 衰减速度越来越慢,()g x 衰减速度越来越慢,()h x 衰减速度越来越慢D.()f x 衰减速度越来越快,()g x 衰减速度越来越快,()h x 衰减速度越来越快3.四个物体同时从某一点出发向前运动,其路程()()1,2,3,4i x f i =关于时间()1x x >的函数关系是()21f x x =,()22f x x =,()32log f x x =,()42x f x =,如果它们一直运动下去,最终在最前面的物体具有的函数关系是( ) A.()21f x x =B.()22f x x =C.()32log f x x =D.()42x f x =题型2 三种函数的图像与性质应用4.[安徽省级示范高中2020高一期中]若()0,1x ∈,则下列结论正确的是( ) A.122lg x x x >> B.122lg x x x >> C.122lg x x x >>D.12lg 2xx x >>5.函数22x y x =-的图像大致是( )A B C D6.设2535a ⎛⎫= ⎪⎝⎭,3525b ⎛⎫= ⎪⎝⎭,2525c ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系是( ) A.a c b >>B.a b c >>C.c a b >>D.b c a >>7.设0x >,且1x x b a <<,则( ) A.01b a <<< B.01a b <<< C.1b a << D.1a b <<8.[山东潍坊2020高一期中]已知函数()2x f x =与()3g x x =的图像交于()11,A x y ,()22,B x y 两点,其中12x x <,若()2,1x a a ∈+,且a 为整数,则a =( )A.7B.8C.9D.109.函数2y x =与函数ln y x x =在区间()0,+∞上增长较快的一个是________.10.如图,在平面直角坐标系xOy 中,过原点O 的直线与函数3x y =的图像交于A ,B 两点,过B 作y 轴的垂线交函数9x y =的图像于点C.若AC 平行于y 轴,则点A 的坐标是________.11.已知函数()2x f x =和()3g x x =,设两个函数的图像相交于点()11,A x y 和()22,B x y ,且12x x <.若[]1,1x a a ∈+,[]2,1x b b ∈+,且,(1,2,3,4,5,6,7,a b ∈8,9,10,11,12),指出a ,b 的值,并说明理由.刷易错易错点 忽略画函数图像的准确程度而致错 12.当24x <<时,2x ,x 2,log 2x 的大小关系是( ) A.222log x x x >> B.222log x x x >> C.222log x x x >>D.22log 2x x x >>78第4.3,4.4节综合训练刷能力1.若函数()y f x =是函数x y a =(0a >,且1a ≠)的反函数,且其图像经过点)a ,则()f x =( )A.12log xB.log 2xC.12xD.x 22.设()1lg 1x f x x +=-,()1e ex x g x =+,则( )A.()f x 与()g x 都是奇函数B.()f x 是奇函数,()g x 是偶函数C.()f x 与()g x 都是偶函数D.()f x 是偶函数,()g x 是奇函数3.[广东汕头金山中学2019高一期中]函数()()21log122f x x x =+-的值域为( ) A.[)1,0- B.[)1,-+∞ C.(]0,1 D.[)1,+∞4.[河南创新发展联盟2020高一第三次联考]已知函数()f x 的图像如图所示,则函数()()12log g x x f =的单调递增区间为( )A.(],3-∞-,[]0,3B.[]3,0-,[)3,+∞C.(),5-∞-,[)0,1D.(]1,0-,()5,+∞5.[湖南衡阳第一中学2019高一期末]若函数()2log 1a y x ax =-+的定义域为R ,则实数a 的取值范围是( ) A.()0,1 B.()()0,11,2C.()1,2D.[)2,+∞6.[四川成都蓉城名校联盟2020第一次联考]若347log log log 2x y z ==<-,则( )A.347x y z <<B.743z y x <<C.437y x z <<D.734z x y <<7.[江苏苏州常熟2020高一期中]若函数()6,23log ,2a x x f x x x -+≤⎧=⎨+>⎩(0a >,且1a ≠)有最小值,则实数a 的取值范围是________.8.设常数1a >,实数x ,y 满足log 2log log a x x x a y++3=-,ya 的值为________,x 的值为________.9.[北京石景山区2020高一期末]已知函数()()()log 2log 2a a f x x x =+--(0a >,且1a ≠).(1)求函数()f x 的定义域; (2)判断函数()f x 的奇偶性; (3)解关于x 的不等式()()log 3a x f x ≥.10.已知函数()()()log 101a x a f x =+<<,函数()y g x =的图像与函数()f x 的图像关于原点对称.(1)写出函数()g x 的解析式;(2)判断函数()()f x g x -的奇偶性,并说明理由; (3)若[)0,1x ∈时,总有()()f x g x m +≤成立,求实数m 的取值范围.79专题3 指数函数、对数函数刷难关题型1 利用指数函数、对数函数的性质比较大小 1.[四川资阳2019高一期末]已知21log 3a =,35b -=,122c =,则a ,b ,c 的大小关系为( )A.a b c <<B.a c b <<C.c b a <<D.c a b <<2.[广东东莞2020高一期末]已知lg 0.3a =,0.22b =,0.60.8c =,则a ,b ,c 的大小关系是( )A.a c b <<B.c b a <<C.b a c <<D.a b c <<3.[江苏东海2020高一期中]已知 1.6log 0.6a =,0.60.6b =,0.61.6c =,则a ,b ,c 的大小关系为( )A.a b c >>B.c a b >>C.c b a >>D.b c a >>4.设2log a =0.013b =,c =( ) A.c a b << B.a b c << C.a c b << D.b a c <<题型2 指数与对数的运算 5.[河北定州2020高一期末]设0.2log 0.3a =,2log 0.3b =,则( )A.0a b +>,0ab >B.0a b +>,0ab <C.0a b +<,0ab >D.0a b +<,0ab <6.[重庆2020高一期中]计算: (1)013134210.064160.258-⎛⎫--++ ⎪⎝⎭;(2)2lg 2lg 3111lg 0.36lg823+++.7.(1401210.252-⎛⎫+⨯ ⎪⎝⎭; (2)解关于x 的方程:()()515log lo 31g 1x x --=+.8.已知函数()1lg1xf x x+=-. (1)判断并证明()f x 的奇偶性; (2)求证:()()1a b f a f b f ab +⎛⎫+= ⎪+⎝⎭;(3)已知(),1,1a b ∈-,且11a b f ab +⎛⎫= ⎪+⎝⎭,21a b fab -⎛⎫= ⎪-⎝⎭,求()f a ,()f b 的值.题型3 指数函数与对数函数的图像9.[浙江2019·6,4分]在同一直角坐标系中,函数1xy a =,1log 2a y x ⎛⎫=+ ⎪⎝⎭(0a >,且1a ≠)的图像可能是( )A. B.C. D.8010.已知函数()()log 21x a f x b =+-(0a >,且1a ≠)的图像如图所示,则a ,b 满足的关系是( )A.101a b -<<<B.101b a -<<<C.101b a -<<<D.1101a b --<<<11.[陕西渭南2020高一期末]在同一直角坐标系中,2xy =与()2log y x =-的图像可能是( )A B C D12.[河南新乡2020高一期末]已知0a >且1a ≠,则函数()222log f x x x a =-和()x g x a =在同一个平面直角坐标系的图像可能是( )A B C D 13.[云南玉溪2020高一期末]函数()()e 1e 1x x xf x +=-(其中e 为自然对数的底数)的图像大致为( )A B C D14.如图,已知点A ,B 是函数()2log 16f x x =图像上的两点,点C 是函数()2log g x x =图像上的一点,且直线BC 垂直于x 轴,若△ABC 是等腰直角三角形(其中A 为直角顶点),则点A 的横坐标为________,点B 的横坐标为________.题型 4 应用指数函数、对数函数的性质确定参数的值或范围15.已知函数()log a f x x =.若不等式()1f x >对于任意[)2,x ∈+∞恒成立,则实数a 的取值范围是( ) A.()10,1,22⎛⎫ ⎪⎝⎭ B.()10,2,2⎛⎫+∞ ⎪⎝⎭ C.()1,11,22⎛⎫ ⎪⎝⎭D.()1,12,2⎛⎫+∞ ⎪⎝⎭16.若函数()()2log 2a f x x ax =-+在区间()1,+∞上恒为正值,则实数a 的取值范围为( ) A.()1,2B.(]1,2C.()()0,11,2D.51,2⎛⎫ ⎪⎝⎭17.[福建厦门思明区2020高一期中]已知函数()()2log 1f x x =+.若()()f m f n =,m n ≠,则11m n+等于( ) A.1B.-1C.0D.218.[广东广州2020高一期末]设函数()f x =21,25,2x x x x ⎧-≤⎪⎨-+>⎪⎩,若互不相等的实数a ,b ,c 满足()()()f a f b f c ==,则222a b c ++的取值范围是( ) A.()16,32B.()18,34C.()17,35D.()6,719.已知函数()22,1log ,1x x f x x x ⎧<⎪=⎨≥⎪⎩,则()8f =________;若直线y m =与函数()f x 的图像只有1个交点,则实数m 的取值范围是________.20.[上海松江二中2020高一期末]已知()f x 是定义在[]2,2-上的奇函数,当[]0,2x ∈时,()21x f x =-,函数()22g x x x m =-+,如果对于任意的[]12,2x ∈-,总存在[]22,2x ∈-,使得()()12f x g x ≤,那么实数m 的取值范围是________.21.已知函数()()4log 41x f x kx =++与()4log g x =423xa a ⋅-⎛⎫⎪⎝⎭,其中()f x 是偶函数. (1)求实数k 的值; (2)求函数()g x 的定义域;(3)若函数()f x 与()g x 的图像有且只有一个公共点,求实数a 的取值范围.。
河南省豫南九校联盟2015届高三上学期第三次联考数学(文)

河南省豫南九校2015届高三上第三次联考数学(文)试题(考试时间:120分钟 试卷满分:150分)第Ⅰ卷 选择题(共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U =R ,集合A ={1,2,3,4,5},B ={x ∈R |23x x +-≤0},则∩B = A .{1,2} B .{x |-2≤x <3} C .{x |0≤x <3} D .{0,1} 2.已知i 是虚数单位,z =21i-+1,z 在复平面上对应的点为A ,则点A 到原点O 的距离为A .1B .2CD 3.己知向量a =(1,-2),b =(m ,-1),且a ∥b ,则实数m 的值为 A .-2 B .12C .2D .3 4.已知x 与y已求得关于y 与x A .1 B .0.85 C .0.7 D .0.5 5.已知函数f (x )=6x-2log x ,则在下列区间中,函数f (x )有零点的是 A .(0,1) B .(1,2) C .(2,4) D .(4,+∞) 6.已知数列{n a }的前n 项和为n S ,且满足n a +2=21n a +-n a ,a 5=4-a 3,则S 7= A .7 B .12 C .14 D .21 7.函数f (x )=2sin cos 1x xx +的图像大致为8.若变量x ,y 满足约束条件14040x x x y ⎧⎪⎨⎪⎩≥+y -≤-3+≤,则目标函数z =3x +y 的最大值为A .-4B .0C .4D .8 9.执行如图所示的程序框图,则输出的结果为A .4B .9C .7D .510.函数f (x )=Asin (ωx +ϕ)(其中A >0,ω>0, |ϕ|<2π)的图象如图,为了得到f (x )的图象, 则只需将g (x )=sin2x 的图象A .向右平移6π个长度单位 B .向右平移3π个长度单位 C .向左平移6π个长度单位 D .向左平移3π个长度单位11.已知双曲线2219x y m-=的一个焦点在圆22x y +-4x -5=0 上,则双曲线的离心率为 A .43 BCD .5312.已知函数f (x )在R 上可导,其导函数为()f x ',若()f x '满足()()1f x f x x '-->0,y =()x f x e关于直线x =1对称,则不等式22()f x x --<f (0)的解集是A .(-1,2)B .(1,2)C .(-1,0)∪(1,2)D .(-∞,0)∪(1,+∞)第Ⅱ卷 非选择题(共90分)二、填空题:本大题共4小题,每小题5分,共20分。
河南省豫南九校2020-2021学年高二上学期第二次联考试题 化学 含答案

豫南九校2020-2021学年上期第二次联考高二化学试题(考试时间:90分钟试卷满分:100分)可能用到的相对原子质量:H1 C12 N14 O16 Na23 Mg24 S32 K39 Cr52 Ag108一、选择题(本大题共16题,每小题3分,共48分。
每个小题只有一个选项符合题意)1.Pd-Co-硅藻土可作NaBH4释氢时的催化剂,则向释氢反应NaBH4+2H2O4H2↑+NaBO2△H=-75 kJ·mol-1中加入该催化剂后△H将A.增大B.减小C.不变D.无法判断2.一种利用蓝绿藻制氢贮氢及氢气应用的图示如下。
下列说法正确的是A.能量的转化方式只有2种B.氢气液化过程吸收能量C.蓝绿藻分解水产生H2,同时释放能量D.能量利用率:燃料电池比H2直接燃烧高3.某反应A+B=C+D在低温下能自发进行,在高温下不能自发进行,对该反应过程△H、△S的判断正确的是A.△H<0,△S>0B.△H>0,△S>0C.△H<0,△S<0D.△H>0,△S<04.《本草纲目·29卷·杏》中对药物浸出过程有如下叙述:“药液釜盛之,釜上安盆,盆上钻孔,用弦悬车辖至釜底,以纸塞孔,勿令泄气,初着糠火,一日三动车辖,以衷其汁”下列实验与文中叙述最接近的是5.常温下,下列各组离子在指定溶液中一定能大量共存的是A.0.1 mol·L-1 NaHSO4溶液:Mg2+、K+、Cr2O72-、NO3-B.滴入酚酞呈红色的溶液:Na+、Cu2+、HCO3-、NO3-C.0.1 mol·L-1 KNO,溶液:H+、K+、SO42-、I-D.0.1 mol·L-1 Na2S2O3溶液:H+、Na+、Cl-、SO42-6.H2与ICl的反应分①、②两步进行,其能量曲线如图所示,下列有关说法错误..的是A.反应①、反应②均为放热反应B.反应①、反应②均为氧化还原反应C.反应①比反应②的速率慢,与相应正反应的活化能无关D.反应①、反应②的焓变之和为△H=-218 k·mol-17.在一个不传热的恒容密闭容器中,可逆反应N 2(g)+3H2(g)2NH3(g)达到平衡的标志是①反应速率v(N2):v(H2):v(NH3)=1:3:2 ②各组分的物质的量不变③体系的压强不再发生变化④混合气体的密度不变(相同状况)⑤体系的温度不再发生变化⑥2v正(N2)=v逆(NH3)⑦单位时间内3 mol H-H键断裂的同时2 mol N-H键也断裂A.①②③⑤⑥B.②③④⑤⑥C.②③⑤⑥D.②③④⑥⑦8.25℃、101 kPa时,强酸与强碱的稀溶液发生中和反应的中和热为57.3 kJ·mol-1,辛烷的燃烧热为5518 kJ·mol-1。
2020-2021学年高二下学期期末考试联考地理试题(word版,含答案)

2020~2021学年第二学期期末三校联考高二地理第一卷单项选择题(每小题2分,共60分)我国国产科考破冰船“雪龙2”号历时5个多月,于2021年5月6日14时载着我国第37次南极科学考察队部分队员顺利返航,靠泊在上海外高桥港中国极地考察国内基地码头。
下图为该船考察期间所途径的部分地区示意图,据此完成1-3题。
1.在我国的南极科学考察站中,长城站位于中山站的()方向A.东北B.东南C.西北D.西南2.从图中可以读出,弗里曼特尔到蓬塔阿雷纳斯的最短距离大约为()A.110 km B.5500 km C.10 500 km D.15 500 km 3.“雪龙2”号返航结束时,下列说法可信的是()A.纽约(西五区)夜幕深沉B.东京(东九区)午饭刚刚开始C.莫斯科(东三区)夕阳西垂D.悉尼(东十区)华灯初上下图为某区域等高线地形图(单位:米),甲、乙两地建有养殖场,完成4-6题。
4.从图中可知()A.图中所示山峰的海拔可能为1044米B.乙地海拔可能为1025米C.图中陡崖最大相对高度可能为24米D.区域内最大高差超55米5.在②地可以看到()A.②②B.②②C.②②D.②②6.若图中建有一小型水库,甲养殖场濒临水库最高水位,则()A.水库最深可能接近10米B.水坝高度最低为15米C.库区水面大于1平方千米D.乙养殖场将污染水库印度尼西亚种植园的农民为开辟新耕地,一直有焚烧芭蕉的传统,随着种植园经济的发展,持续的毁林开荒导致“烧芭”产生的烟霾污染日益扩大,“烧芭”时节,本国及邻国新加坡烟霾污染严重,污染新加坡的烟雾主要来自苏门答腊岛的芭蕉燃烧,如图。
读图回答7-9题。
7.推测印度尼西亚“烧芭”的时间()A.12月—次年1月B.3—4月C.7—8月D.10月—11月8.新加坡降水丰富,但淡水资源匮乏,主要自然原因是()A.面积小,储水条件差B.地势低平,径流数少C.人口多,淡水需求大D.经济发达,污染严重9.苏门答腊岛产业发展方向,合理的是()A.大力推进乳畜业发展B.大力改进河网交通建设C.提升种植园农产品品质D.扩大耕地增加粮食产量图为长江、黄河、尼罗河、亚马孙河河流剖面图及水能蕴藏量表,完成10-12题。
XX省豫南九校2023届高三上学期第二次联考化学试题附解析答案完整版

豫南九校2022—2023学年上期第二次联考高三化学试题(考试时间:90分钟 试卷满分:100分)注意事项:1.答题前,考生务必将自己的姓名、准考证号、考场号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 S-32 Cl-35.5 K-39 Ca-40 Mn-55 Fe-56 Cu-64 Ba-137一、选择题(本题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.我们的生活与化学密切相关。
下列叙述正确的是()A.苏打常用于治疗胃酸过多B.燃煤中添加生石灰可减缓温室效应C.食品保鲜膜的成分为聚氯乙烯D.手机中的锂离子电池属于二次电池2.9月17日,航天员蔡旭哲、陈冬从问天实验舱成功出舱,两名出舱航天员相互配合开展舱外助力手柄安装等作业。
下列说法正确的是()A.舱外助力手柄由合金制成,该手柄材料属于化合物B.问天实验舱使用了石墨烯导热索技术,石墨烯属于新型无机非金属材料C.问天实验舱上的太阳能电池板主要材料是高纯度二氧化硅D.轻质纳米真空绝热板应用于舱内低温实验保冷设备,该绝热板为胶体3.下列说法正确的是( )A.分别将和通入溶液中,得到的沉淀不同2SO 3SO ()32Ba NOB.氯气具有强氧化性,在与其他物质反应时只能作为氧化剂C.、均能与酸和碱发生反应,二者均为两性化合物2SiO 23Al OD.将铝钠合金投入水中得无色溶液,则合金中()()Al Na n n …4.实验室模拟海水提碘的流程如下:进行操作I 和操作II ,下图实验仪器中一定用不到的是( )a. b. c. d. e. f.A.中x =1242CaC O H O x ⋅A.放电时,电流由a 极经导线流向b 极B.放电时,正极反应式为222MnO 2e 2H O Mn 4OH -+--++C.放电时,双极膜中的向右侧移动OH -D.充电时,当电路中有1mol 电子转移时,右侧石墨电极质量增加43.5g15.是制造一种功能材料的矿石主要成分,W 、X 、Y 、Z 为原子序数依次增大的短周期主族元2252Z X Y W Y ⋅素,位于三个不同周期,且X 、Y 的原子序数之和与W 、Z 的原子序数之和相等;Z 为金属元素,与X 和W 位于三个不同主族,X 的最外层电子数比内层电子数多1个。
高中数学第4章数列3、1等比数列的概念3、2等比数列的通项公式、提升训练苏教版选择性必修第一册

等比数列的概念等比数列的通项公式基础过关练题组一等比数列的概念及其应用1.有下列四个说法:①等比数列中的某一项可以为0;②等比数列中公比的取值范围是(-∞,+∞);③若一个常数列是等比数列,则这个常数列的公比为1;④若b2=ac,则a,b,c成等比数列.其中正确说法的个数为()A.0B.1C.2D.32.已知数列a,a(1-a),a(1-a)2,…是等比数列,则实数a的取值范围是()A.a≠1B.a≠0或a≠1C.a≠0D.a≠0且a≠13.(2021湖北黄石第二中学高三一模)已知函数f(x)=log k x(k为常数,k>0且k≠1).下列条件中,能使数列{a n}为等比数列的是(填序号).①数列{f(a n)}是首项为2,公比为2的等比数列;②数列{f(a n)}是首项为4,公差为2的等差数列;③数列{f(a n)}是首项为2,公差为2的等差数列的前n项和构成的数列.题组二等比数列的通项公式4.(2021江苏无锡锡山高级中学高二期中)在3和81之间插入2个数,使这4个数成等比数列,则公比q为()A.±2B.2C.±3D.35.(2021江苏镇江四校高三第一次联考)在正项等比数列{a n}中,若a6,3a5,a7依次成等差数列,则{a n}的公比为.6.(2020江苏南通高三考前模拟)已知等比数列{a n}的公比q=2,且a1·a2·a3·…·a30=1,则a3·a6·a9·…·a30=.7.(2020湖北宜昌示范高中协作体高二期末)已知数列{a n}是首项为1的等比数列,数列{b n}满足b1=2,b2=5,且a n b n+1=a n b n+a n+1.(1)求数列{a n}的通项公式;(2)求数列{b n}的前n项和S n.题组三等比中项8.(2020四川广元高一期末)两数√2+1与√2-1的等比中项是()A.1B.-1C.±1D.129.(2020重庆一中高二上期中)已知等差数列{a n}的公差为2,且a3是a1与a7的等比中项,则a1等于()A.6B.4C.3D.-110.已知a是1,2的等差中项,b是-1,-16的等比中项,则ab等于()A.6B.-6C.±6D.±1211.(多选)(2020山东临沂高二期末)已知三个数1,a,4成等比数列,则圆锥曲线x2+y2y=1的离心率可能为()A.√22B.√32C.√62D.√3题组四等比数列的性质12.(2021江苏宿迁桃州中学高二调研考试)已知各项均为正数的等比数列{a n}中,a1a2a3=5,a7a8a9=10,则a4a5a6= ()A.5√2B.7C.6D.4√213.(2021浙江十校联盟高三联考)已知数列{a n}为等比数列,则“a1<0,q>1”是“{a n}为递减数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件14.(2020四川外国语大学附属学校阶段检测)已知等比数列{a n}是递减数列,且满足a1+a4=18,a2a3=32,则a5= ()A.32B.16C.2D.115.在正项等比数列{a n}中,a1a5-2a3a5+a3a7=36,a2a4+2a2a6+a4a6=100,求数列{a n}的通项公式.能力提升练题组一等比数列的通项公式及其应用1.(2020河北保定高一期末,)已知数列a1,y2y1,…,y yy y-1,…是首项为1,公比为2的等比数列,则log2a n= ()A.n(n+1)B.y(y-1)4C.y(y+1)2D.y(y-1)22.(2021河南豫南九校高二联考,)音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代数学家、音乐理论家朱载堉创立了十二平均律,他是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音的频率之比为常数,如下表所示,其中a1,a2,…,a13表示这些半音的频率,它们满足log2(y y+1y y)12=1(i=1,2,…,12).若某一半音与D8的频率之比为√23,则该半音为()A.F8B.GC.G8D.A3.(2020江苏南京师大附中高三高考模拟,)各项均正且公差不为0的等差数列{a n}的第1项、第2项、第6项恰好是等比数列{b n}的连续三项(顺序不变),设S n=1y1y2+1y2y3+…+1y y y y+1,若对一切的n∈N*,S n≤1y1恒成立,则a1的最小值为.4.(2021江苏徐州新沂第一中学高二月考,)在各项均为正偶数的数列a1,a2,a3,a4中,前三项依次成公差为d(d>0)的等差数列,后三项依次成公比为q的等比数列.(1)若a1=4,q=32,则d=;(2)若a4-a1=88,则q的所有可能的值构成的集合为.5.(2021广东深圳、汕头、潮州、揭阳名校高三联考,)从①前n项和S n=n2+p(p∈R),②a6=11且2a n+1=a n+a n+2这两个条件中任选一个,填在下面的横线上,并完成解答.在数列{a n}中,a1=1,,其中n∈N*.(1)求数列{a n }的通项公式;(2)若a 1,a n ,a m 构成等比数列,其中m ,n ∈N *,且m >n >1,求m 的最小值.题组二 等比数列的性质及综合应用 6.(2021江苏宿迁桃州中学高二调研,)已知等比数列{a n }满足a n >0,n =1,2,…,且a 5·a 2n -5=22n (n ≥3),则当n ≥1时,log 2a 1+log 2a 3+…+log 2a 2n -1= ( )A.n (2n -1)B.(n +1)2C.n 2D.(n -1)27.(2021安徽示范高中培优联盟高二联赛,)已知数列{a n }是等比数列,数列{b n }是等差数列,若a 1·a 6·a 11=3√3,b 1+b 6+b 11=-3π4,则tan y 3+y 91-y 4·y 8的值是 ()A.-√3B.√22 C.-√22 D.18.(2020重庆第一中学高一月考,)正项数列{a n }满足:a n +a n +1+a n +2=a n a n +1a n +2,a 1+a 3=6,若前三项构成等比数列且满足a 1<a 2<a 3,S n 为数列{a n }的前n 项和,则[S 2 020]([x ]表示不超过x 的最大整数)的值为(参考数据:√5≈2.236) ( ) A.4 040 B.4 041 C.5 384 D.5 385 9.(2021江苏苏州高二期中,)已知等比数列{a n }为递增数列,若a 1+a 4=7,a 2+a 3=6,则a 1+a 2= .10.(2020广西南宁第三中学高三月考,)等差数列{a n }的前n 项和为S n ,a 3=3,其中a 1,a 3,a 9成等比数列,且数列{a n }不是常数列. (1)求数列{a n }的通项公式;(2)设b n=1,b n的前n项和为T n,求证:T n<2.y y11.(2020山西太原第五中学高二阶段测试,)已知数列{a n}的前n项和为S n,且S n=2a n-2.(1)求数列{a n}的通项公式;(2)设b n=log2a1+log2a2+…+log2a n,求使(n-8)b n≥nk对任意n∈N*恒成立的实数k的取值范围.12.(2020辽宁省实验中学高二上期中,)黄河被称为我国的母亲河,它的得名据说来自于河水的颜色,黄河因携带大量泥沙所以河水呈现黄色,黄河的水源来自青海高原,从源头开始1 000 km的河水是非常清澈的.只是在刘家峡水库附近,清澈的黄河和携带大量泥沙的洮河汇合,在两条河流的交汇处,水的颜色一清一浊,互不交融,形成了一条奇特的水中分界线,设黄河和洮河在汛期的水流量均为2 000 m3/s,黄河水的含沙量为2 kg/m3,洮河水的含沙量为20 kg/m3,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换1 000 m3的水量,即从洮河流入黄河1 000 m3的水混合后,又从黄河流入1 000 m3的水到洮河再混合.(1)求经过第二个观测点时,两股河水的含沙量;(2)从第几个观测点开始,两股河水的含沙量之差小于0.01 kg/m3?(不考虑泥沙沉淀)答案全解全析基础过关练1.B对于①,因为等比数列中的各项都不为0,所以①不正确;对于②,因为等比数列的公比不能为0,所以②不正确;对于③,若一个常数列是等比数列,则这个常数列的各项均不为0,根据等比数列的定义知此数列的公比为1,所以③正确;对于④,只有当a,b,c都不为0时,a,b,c才成等比数列,所以④不正确.因此,正确的说法只有1个,故选B.2.D由于a,a(1-a),a(1-a)2,…是等比数列,所以需同时满足a≠0,1-a≠0,所以a≠0且a ≠1.3.答案②解析①中,f(a n)=2n,即log k a n=2n,得a n=y2y,∵y y+1y y =y2y+1y2y=y2y≠常数,∴数列{a n}不是等比数列;②中,f(a n)=4+(n-1)×2=2n+2,即log k a n=2n+2,得a n=k2n+2,且a1=k4≠0,∵y y+1y y =y2(y+1)+2y2y+2=k2,且k2为非零常数,∴数列{a n}是以k4为首项,k2为公比的等比数列;③中,f(a n)=2n+y(y-1)2×2=n2+n,即log k a n=n2+n,得a n=k n(n+1),∵y y+1y y =y(y+1)(y+2)y y(y+1)=k2(n+1)≠常数,∴数列{a n}不是等比数列.4.D若使这4个数成等比数列,则81=3q3,解得q=3.故选D.5.答案 2解析设正项等比数列{a n}的公比为q,q>0,由a6,3a5,a7依次成等差数列,可得6a5=a6+a7,即有6a1q4=a1q5+a1q6,化简,得q2+q-6=0,解得q=2(q=-3舍去),则{a n }的公比为2. 6.答案 1024解析 因为{a n }为等比数列,公比q =2,且a 1·a 2·a 3·…·a 30=1,所以a 1·a 1q ·a 1q 2·…·a 1q 29=y 130q1+2+3+…+29=y 1302435=1,所以y 110=2-145,所以a 3·a 6·a 9·…·a 30=y 110q 155=y 1102155,所以a 3·a 6·a 9·…·a 30=2-145×2155=210=1024.7.解析 (1)将n =1代入已知等式,得a 1b 2=a 1b 1+a 2,∴a 2=a 1b 2-a 1b 1=3a 1. ∴{a n }是首项为1,公比为3的等比数列,∴a n =1·3n -1=3n -1. (2)由(1)及已知得b n +1-b n =y y +1y y=3,∴{b n }是首项为2,公差为3的等差数列,∴b n =2+3(n -1)=3n -1, ∴S n =y (y 1+y y )2=y (2+3y -1)2=3y 2+y2.解题模板关于a 1和q 的求法通常有以下两种:(1)根据已知条件,建立关于a 1,q 的方程组,通过解方程组求出a 1,q ,这是常规方法. (2)充分利用各项之间的关系,直接求出q 后,再求a 1,这种方法带有一定的技巧性,能简化运算.8.C 设两数的等比中项为x ,则x 2=(√2+1)·(√2-1)=1,∴x =±1,故等比中项为±1. 9.B 依题意得y 32=a 1a 7,∴(a 1+4)2=a 1(a 1+12),解得a 1=4.故选B.10.C 由题意可得a =1+22=32,b 2=(-1)×(-16)=16,解得b =±4,∴ab =±6.11.AD 由1,a ,4成等比数列,得a =±2. 当a =2时,曲线x 2+y 22=1表示焦点在y 轴上的椭圆,此时离心率为√2-1√2=√22; 当a =-2时,曲线x 2-y 22=1表示焦点在x 轴上的双曲线,此时离心率为√2+11=√3.故选AD.12.A 由等比数列的性质知a 1a 2a 3,a 4a 5a 6,a 7a 8a 9成等比数列,所以a 4a 5a 6=5√2. 13.A 若等比数列{a n }满足a 1<0,q >1,则数列{a n }为递减数列, 故“a 1<0,q >1”是“{a n }为递减数列”的充分条件;因为当等比数列{a n }满足a 1>0,0<q <1时,数列{a n }也是递减数列, 所以“a 1<0,q >1”不是“{a n }为递减数列”的必要条件.综上所述,“a 1<0,q >1”是“{a n }为递减数列”的充分不必要条件,故选A.14.D 设等比数列{a n }的公比为q.由a 2a 3=32可得a 1a 4=32,又a 1+a 4=18,且等比数列{a n }为递减数列,所以a 1=16,a 4=2,所以q 3=y 4y 1=18,故q =12,所以a 5=a 4×12=1,故选D .15.解析 设等比数列{a n }的公比为q (q >0).因为数列{a n }为等比数列,所以a 1a 5=y 32,a 3a 7=y 52,所以由题意可得y 32-2a 3a 5+y 52=36. 同理,得y 32+2a 3a 5+y 52=100.所以{(y 3-y 5)2=36,(y 3+y 5)2=100,因为a n >0, 所以{y 3-y 5=-6,y 3+y 5=10或{y 3-y 5=6,y 3+y 5=10,解得{y 3=2,y 5=8或{y 3=8,y 5=2,易得{y 1=12,y =2或{y 1=32,y =12.所以a n =12×2n -1=2n -2或a n =32×(12)y -1=26-n.能力提升练1.D 由题意可得yy y y -1=1×2n -1=2n -1(n ≥2),而a n =a 1×y 2y 1×y 3y 2×…×y y y y -1=1×21+2+…+(n -1)=2y (y -1)2(n ≥2), 当n =1时,a 1=1也满足该式,故a n =2y (y -1)2(n ∈N *),所以log 2a n =y (y -1)2,故选D .2.答案 B信息提取 (1)把八度分成13个半音;(2)相邻两个半音的频率之比是常数;(3)log 2(y y +1y y)12=1(i =1,2,…,12). 数学建模 本题是以音乐中音律的划分为背景的实际问题,由“相邻两个半音的频率之比为常数”可构建等比数列模型.实际问题可转化为已知yy y 4=√23求a n ,进而求出a n 对应的半音.根据log 2(y y +1y y)12=1可得y y +1y y=2112,即数列{a n }是公比为2112的等比数列,利用等比数列的通项公式即可求解. 解析依题意可知a n >0(n =1,2,…,12,13).由于a 1,a 2,…,a 13满足log 2(y y +1y y )12=1(i =1,2,…,12),则(y y +1y y )12=2⇒yy +1y y=2112,所以数列{a n }(n =1,2,…,12,13)为等比数列,设其公比为q ,则q =2112,D 8对应的频率为a 4,又所求半音与D 8的频率之比为√23=213=(2112)4,故所求半音对应的频率为a 4·(2112)4=a 8,其对应的半音为G. 3.答案 13解析 设等差数列{a n }的公差为d (d ≠0),由题意得y 22=a 1a 6,即(y 1+y )2=a 1(a 1+5d ), 因为d ≠0,所以d =3a 1,所以a n =a 1+(n -1)d =(3n -2)a 1,则S n =1y 1y 2+1y 2y 3+…+1y y y y +1=13y 11y 1-1y 2+1y 2-1y 3+…+1y y -1yy +1=13y 1·3yy 1y 1·(3y +1)y 1=y(3y +1)y 12,所以y(3y +1)y 12≤1y 1,则a 1≥y3y +1.因为y 3y +1=13(1-13y +1)<13,所以a 1≥13,故a 1的最小值为13. 4.答案 (1)4 (2){53,87}解析 (1)若a 1=4,q =32,则a 2=4+d ,a 3=4+2d ,y 3y 2=4+2y 4+y =32, 解得d =4.(2)根据题意,设这个数列的四项分别为a 1,a 1+d ,a 1+2d ,a 1+88,其中a 1和d 均为正偶数,根据后三项依次成等比数列,可得(a 1+2d )2=(a 1+d )(a 1+88), 整理得a 1=4y (22-y )3y -88,由a 1>0,可得(d -22)(3d -88)<0,所以22<d <883,则d 的可能值为24,26,28. 当d =24时,a 1=12,a 2=36,a 3=60,q =53;当d =26时,a 1=2085(舍);当d =28时,a 1=168,a 2=196,a 3=224,q =87.综上所述,q 的所有可能的值构成的集合为{53,87}. 方法总结判断数列{a n }是不是等比数列的方法:(1)定义法:判断y y +1y y是不是常数; (2)等比中项法:判断y y +1y y =y y y y -1(n ≥2,n ∈N *)是否成立. 5.解析 选择条件①:(1)当n =1时,由S 1=a 1=1,得p =0,故S n =n 2. 当n ≥2时,有S n -1=(n -1)2,所以a n =S n -S n -1=2n -1(n ≥2). 经检验,a 1=1符合此式,所以a n =2n -1(n ∈N *). (2)由a 1,a n ,a m 构成等比数列,得y y 2=a 1a m , 由(1)得a n =2n -1(n ∈N *),故有(2n -1)2=1×(2m -1), 化简,得m =2n 2-2n +1=2(y -12)2+12.因为m ,n 是大于1的正整数,且m >n ,所以当n =2时,m 取得最小值,最小值为5. 选择条件②:(1)由2a n +1=a n +a n +2,得a n +1-a n =a n +2-a n +1, 所以数列{a n }是等差数列,设其公差为d. 因为a 1=1,a 6=a 1+5d =11,所以d =2. 所以a n =a 1+(n -1)d =2n -1(n ∈N *).(2)因为a 1,a n ,a m 构成等比数列,所以y y 2=a 1a m ,即(2n -1)2=1×(2m -1),化简,得m =2n 2-2n +1=2(y -12)2+12. 因为m ,n 是大于1的正整数,且m >n ,所以当n =2时,m 取得最小值,最小值为5.6.C 因为{a n }为等比数列,所以a 1·a 2n -1=a 2·a 2n -2=…=a 5·a 2n -5=22n,所以log 2a 1+log 2a 3+…+log 2a 2n -1=log 2(a 1a 2n -1)y2=log 2(22y)y2=log 22y 2=n 2.故选C.7.D 在等差数列{b n }中,b 1+b 6+b 11=3b 6=-3π4,∴b 6=-π4,∴b 3+b 9=2b 6=-π2,在等比数列{a n }中,a 1·a 6·a 11=3√3,即y 63=3√3,∴a 6=√3,∴1-a 4a 8=1-(√3)2=-2,则tan y 3+y 91-y 4·y 8=tan -π2-2=tan π4=1.故选D .8.C 依题意得a 1+a 2+a 3=a 1a 2a 3,a 1+a 3=6,y 22=a 1·a 3, 故6+a 2=y 23,即(a 2-2)[(a 2+1)2+2]=0,解得a 2=2.联立{y 1+y 3=6,y 1·y 3=4,结合a 1<a 2<a 3,可解得a 1=3-√5,a 3=3+√5.依题意得a 2+a 3+a 4=a 2·a 3·a 4⇒a 4=3-√5,a 3+a 4+a 5=a 3·a 4·a 5⇒a 5=2,a 4+a 5+a 6=a 4·a 5·a 6⇒a 6=3+√5,所以数列{a n }是周期为3的周期数列,且a 1+a 2+a 3=8,故S 2020=S 673×3+1=673×8+a 1=5387-√5,又√5≈2.236,所以[S 2020]=5384.故选C . 9.答案 4解析 设等比数列{a n }的公比为q ,由题意,得{y 1(1+y 3)=7,①y 1y (1+y )=6,②②①,得y 1y (1+y )y 1(1+y 3)=y (1+y )(1+y )(1-y +y 2)=y 1-y +y 2=67, 解得q =32或q =23,经验证可知当q =23时,{a n }不是递增数列,故q =32,所以a 1+a 2=a 1(1+q )=6y =4. 10.解析 (1)设等差数列{a n }的公差为d (d ≠0). 因为a 1,a 3,a 9成等比数列, 所以y 32=a 1·a 9, 即32=(3-2d )(3+6d ), 解得d =1或d =0(舍去), 所以a n =a 3+(n -3)·1=n.(2)证明:由(1)知,a 1=1,所以S n =na 1+y (y -1)2×d =y (y +1)2,所以b n =1y y=2y (y +1)=2(1y -1y +1),则T n =b 1+b 2+…+b n =211-12+12-13+…+1y -1y +1 =2(1-1y +1)<2.11.解析 (1)由S n =2a n -2可得a 1=2. 因为S n =2a n -2,所以当n ≥2时,a n =S n -y y -1=2a n -2y y -1,即a n =2a n -1,所以数列{a n }是以2为首项,2为公比的等比数列,所以a n =2n(n ∈N *). (2)由(1)知a n =2n,所以b n =log 2a 1+log 2a 2+…+log 2a n =1+2+3+…+n =y (y +1)2.所以(n -8)b n ≥nk 对任意n ∈N *恒成立等价于(y -8)(y +1)2≥k 对任意n ∈N *恒成立,等价于k ≤[(y -8)(y +1)2]min.设c n =12(n -8)(n +1),n ∈N *,则当n =3或n =4时,c n 取得最小值-10,所以k ≤-10.12.解析 (1)在第二个观测点时,洮河流入黄河1000m 3的水混合后,黄河的含沙量为2×2000+20×10003000=8(kg/m 3),又从黄河流入1000m 3的水到洮河再混合后,洮河的含沙量为8×1000+20×10002000=14(kg/m3).(2)设在第n个观测点时黄河的含沙量为a n kg/m3,洮河的含沙量为b n kg/m3,由题意有a1=2,b1=20,且a n+1=1000y y+2000y y3000=2y y+y y3,b n+1=1000y y+1000y y+12000=y y+1+y y2=y y+2y y3,所以b n+1-a n+1=13(b n-a n),又b1-a1=18≠0,所以{b n-a n}是首项为18,公比为13的等比数列,∴b n-a n=18×(13)y-1.根据题意,有18×(13)y-1<0.01,即3n-1>1800,n∈N*,解得n>7,所以从第8个观测点开始,两股河水的含沙量之差小于0.01kg/m3.。
解析几何中的定值与定点问题-玩转压轴题(解析版)

专题5.4 解析几何中的定值与定点问题一.方法综述解析几何中的定值与定点问题近年高考中的热点问题,其解决思路下;(1)定值问题:解决这类问题时,要运用辩证的观点,在动点的“变”中寻求定值的“不变”性;一种思路是进行一般计算推理求出其结果,选定一个适合该题设的参变量,用题中已知量和参变量表示题中所涉及的定义,方程,几何性质,再用韦达定理,点差法等导出所求定值关系所需要的表达式,并将其代入定值关系式,化简整理求出结果;另一种思路是通过考查极端位置,探索出“定值”是多少,用特殊探索法(特殊值、特殊位置、特殊图形等)先确定出定值,从而找到解决问题的突破口,将该问题涉及的几何形式转化为代数形式或三角形式,证明该式是恒定的。
(2)定点问题:定点问题是动直线(或曲线)恒过某一定点的问题;一般方法是先将动直线(或曲线)用参数表示出来,再分析判断出其所过的定点.定点问题的难点是动直线(或曲线)的表示,一旦表示出来,其所过的定点就一目了然了.所以动直线(或曲线)中,参数的选择就至关重要.解题的关健在于寻找题中用来联系已知量,未知量的垂直关系、中点关系、方程、不等式,然后将已知量,未知量代入上述关系,通过整理,变形转化为过定点的直线系、曲线系来解决。
二.解题策略类型一定值问题【例1】(2020•青浦区一模)过抛物线y2=2px(p>0)的焦点作两条相互垂直的弦AB和CD,则+的值为()A.B.C.2p D.【答案】D【解析】抛物线y2=2px(p>0)的焦点坐标为(),所以设经过焦点直线AB的方程为y=k(x﹣),所以,整理得,设点A(x1,y1),B(x2,y2),所以,所以,同理设经过焦点直线CD的方程为y=﹣(x﹣),所以,整理得,所以:|CD|=p+(p+2k2p),所以,则则+=.故选:D.【点评】求定值问题常见的方法有两种:①从特殊入手,求出定值,再证明这个值与变量无关;②直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.【举一反三】1.(2020•华阴市模拟)已知F是抛物线y2=4x的焦点,过点F的直线与抛物线交于不同的两点A,D,与圆(x﹣1)2+y2=1交于不同的两点B,C(如图),则|AB|•|CD|的值是()A.2B.2C.1D.【答案】C【解析】设A(x1,y1),D(x2,y2),抛物线方程为y2=4x的焦点为F(1,0),准线方程为x=﹣1,圆(x﹣1)2+y2=1的圆心为F(1,0),圆心与焦点重合,半径为1,又由直线过抛物线的焦点F,则|AB|=x1+1﹣1=x1,|CD|=x2+1﹣1=x2,即有|AB|•|CD|=x1x2,设直线方程为x=my+1,代入抛物线方程y2=4x,可得y2﹣4my﹣4=0,则y1y2=﹣4,x1x2==1,故选:C.2.(2020温州高三月考)如图,P为椭圆上的一动点,过点P作椭圆的两条切线P A,PB,斜率分别为k1,k2.若k1•k2为定值,则λ=()A.B.C.D.【答案】C【解析】取P(a,0),设切线方程为:y=k(x﹣a),代入椭圆椭圆方程可得:(b2+a2k2)x2﹣2a3k2x+a4k2﹣a2b2λ=0,令△=4a6k4﹣4(b2+a2k2)(a4k2﹣a2b2λ)=0,化为:(a2﹣a2λ)k2=b2λ,∴k1•k2=,取P(0,b),设切线方程为:y=kx+b,代入椭圆椭圆方程可得:(b2+a2k2)x2﹣2kba2x+a2b2(1﹣λ)=0,令△=4k2b2a4﹣4(b2+a2k2)a2b2(1﹣λ)=0,化为:λa2k2=b2(1﹣λ),∴k1•k2=,又k1•k2为定值,∴=,解得λ=.故选:C.3.(2020•公安县高三模拟)已知椭圆的离心率为,三角形ABC的三个顶点都在椭圆上,设它的三条边AB、BC、AC的中点分别为D、E、F,且三条边所在直线的斜率分别为k1,k2,k3(k1k2k3≠0).若直线OD、OE、OF的斜率之和为﹣1(O为坐标原点),则=.【答案】2【解析】∵椭圆的离心率为,∴,则,得.又三角形ABC的三个顶点都在椭圆上,三条边AB、BC、AC的中点分别为D、E、F,三条边所在直线的斜率分别为k1、k2,k3,且k1、k2,k3均不为0.O为坐标原点,直线OD、OE、OF的斜率之和为﹣1,设A(x1,y1),B(x2,y2),C(x3,y3),则,,两式作差得,,则,即,同理可得,.∴==﹣2×(﹣1)=2.类型二定点问题【例2】(2020•渝中区高三模拟)已知抛物线C:x2=4y的焦点为F,A是抛物线C上异于坐标原点的任意一点,过点A的直线l交y轴的正半轴于点B,且A,B同在一个以F为圆心的圆上,另有直线l′∥l,且l′与抛物线C相切于点D,则直线AD经过的定点的坐标是()A.(0,1)B.(0,2)C.(1,0)D.(2,0)【答案】A【解析】设A(m,m2),B(0,n),∵抛物线C:x2=4y的焦点为F(0,1)又A,B同在一个以F为圆心的圆上,∴|BF|=|AF|∴n﹣1==m2+1∴n=m2+2∴直线l的斜率k==﹣∵直线l′∥l,∴直线l′的斜率为k,设点D(a,a2),∵y=x2,∴y′=x,∴k=a,∴a=﹣,∴a=﹣∴直线AD的斜率为===,∴直线AD的方程为y﹣m2=(x﹣m),整理可得y=x+1,故直线AD经过的定点的坐标是(0,1),故选:A.【点评】圆锥曲线中定点问题的两种解法(1)引进参数法:引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.(2)特殊到一般法:根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关. 【举一反三】1.(2020·全国高考模拟(理))已知抛物线28x y =,过点(),4P b 作该抛物线的切线PA ,PB ,切点为A ,B ,若直线AB 恒过定点,则该定点为( )A .()4,0B .()3,2C .()0,4-D .()4,1【答案】C【解析】设A B ,的坐标为()11x y ,,()22x y ,28x y =,4x y '=, PA PB ,的方程为()1114x y y x x -=-,()2224xy y x x -=- 由22118x y =,22228x y =,可得114x y x y =-,224x y x y =-切线PA PB ,都过点()4P b ,1144x b y ∴=⨯-,2244xb y =⨯-, 故可知过A ,B 两点的直线方程为44bx y =-, 当0x =时,4y =∴直线AB 恒过定点()04-,,故选C2.(2020·重庆高考模拟(理))已知圆22:1C x y +=,点P 为直线142x y+=上一动点,过点P 向圆C 引两条切线,,,PA PB A B 为切点,则直线AB 经过定点.( )A .11,24⎛⎫⎪⎝⎭ B .11,42⎛⎫⎪⎝⎭ C.⎫⎪⎪⎝⎭D.⎛ ⎝⎭ 【答案】B【解析】设()42,,,P m m PA PB -是圆C 的切线,,,CA PA CB PB AB ∴⊥⊥∴是圆C 与以PC 为直径的两圆的公共弦,可得以PC 为直径的圆的方程为()()22222224m m x m y m ⎛⎫⎡⎤--+-=-+ ⎪⎣⎦⎝⎭, ① 又221x y += , ②①-②得():221AB m x my -+=, 可得11,42⎛⎫⎪⎝⎭满足上式,即AB 过定点11,42⎛⎫⎪⎝⎭,故选B. 3.(2020大理一模)已知椭圆221164x y +=的左顶点为A ,过A 作两条弦AM 、AN 分别交椭圆于M 、N 两点,直线AM 、AN 的斜率记为12,k k ,满足122k k ⋅=-,则直线MN 经过的定点为___________. 【答案】28,09T ⎛⎫-⎪⎝⎭【解析】 由()2221211141616414=+4M x y k x k y k x ⎧+=-⎪⇒=⎨+⎪⎩, 同理222122214164641416N k k x k k --==++. 121814M k y k =+,1211616Nk y k -=+, 取11k =,由对称性可知,直线MN 经过x 轴上的定点28,09T ⎛⎫-⎪⎝⎭.【归纳总结】在平面直角坐标系xOy 中,过椭圆()222210x y a b a b+=>>上一定点A 作两条弦AM 、AN 分别交椭圆于M 、N 两点,直线AM 、AN 的斜率记为12,k k ,当12k k ⋅为非零常数时,直线MN 经过定点.三.强化训练1.(2020·黑龙江高三模拟)直线l 与抛物线x y C 2:2=交于B A ,两点,O 为坐标原点,若直线OB OA ,的斜率1k ,2k 满足3221=k k ,则l 的横截距( ) A .为定值3- B .为定值3 C .为定值1- D .不是定值 【答案】A【解析】设直线l 的方程为y kx b =+,由题意得22y kx b y x=+⎧⎨=⎩,则得()222220k x kb x b +-+=; 设A ,B 两点的坐标为()11,A x y ,()22,B x y ,则得12222kb x x k-+=,2122b x x k =; 又因为3221=k k ,即121223y y x x =,所以()2222222121222221222222222223k x x kb x x b kb k b k k b k b k k b k k k k x x b b b b +++--+-=++=+=== ,则得3b k =,直线l 的方程为()33y kx b kx k k x =+=+=+; 当0y =时,3x =-,所以直线l 的横截距为定值3-.故选A.2.(2020·辽宁省朝阳市第二高级中学高二期中(文))如果直线7ax by +=(0a >,0b >) 和函数()1log m f x x =+(0m >,1m ≠)的图象恒过同一个定点,且该定点始终落在圆22(1)(1)25x b y a +-++-=的内部或圆上,那么ba的取值范围是( )A .3443⎡⎤⋅⎢⎥⎣⎦B .30,4⎛⎤ ⎥⎝⎦C .4,3⎡⎫+∞⎪⎢⎣⎭D .340,,43⎛⎤⎡⎫⋃+∞ ⎪⎥⎢⎝⎦⎣⎭【答案】A【解析】根据指数函数的性质,可得函数()1log ,(0,1)m f x x m m >≠=+,恒过定点(1,1). 将点(1,1)代入7ax by +=,可得7a b +=.由于(1,1)始终落在所给圆的内部或圆上,所以2225a b +.又由227,25,a b a b +=⎧⎨+=⎩解得34a b =⎧⎨=⎩或43a b =⎧⎨=⎩,所以点(,)a b 在以(3,4)和(4,3)为端点的线段上运动, 当取点(3,4)时,43b a =,取点(4,3)时,34b a,所以b a 的取值范围是34,43⎡⎤⎢⎥⎣⎦.3.(2020·全国高三模拟)过x 轴上的点(),0P a 的直线与抛物线28y x =交于,A B 两点,若2211||||AP BP +为定值,则实数a 的值为( )A.1B.2 C .3 D .4 【答案】D【解析】设直线AB 的方程为x my a =+,代入28y x =,得2880y my a --=, 设()()1122,,,A x y B x y ,则12128,8y y m y y a +=⋅=-.()()()2222222111111AP x a y my y m y =-+=+=+,同理,()22221BP m y =+,∴()21212222222221212211111111y y y y m y y m y y AP BP+-⎛⎫+=+= ⋅⎪++⎝⎭ ()()22222264284164114m a m am a a m -⨯-+=+⋅=+,∵2211||||AP BP +为定值, 是与m 无关的常数,∴4a =.故选D .4.(2020•越城区高三期末)已知A 、B 是抛物线y 2=4x 上异于原点O 的两点,则“•=0”是“直线AB 恒过定点(4,0)”的( ) A .充分非必要条件 B .充要条件C .必要非充分条件D .非充分非必要条件【答案】B【解析】根据题意,A 、B 是抛物线y 2=4x 上异于原点O 的两点,设A (x 1,y 1),B (x 2,y 2), 若“•=0”,则设直线AB 方程为x =my +b ,将直线AB 方程代入抛物线方程y 2=4x ,可得y 2﹣4my ﹣4b =0,则y 1+y 2=4m ,y 1y 2=﹣4b , 若•=0,则•=x 1x 2+y 1y 2=()+y 1y 2=+y 1y 2=b 2﹣4b =0,解可得:b =4或b =0,又由b ≠0,则b =4,则直线AB 的方程为x =my +4,即my =x ﹣4,则直线AB 恒过定点(4,0), “•=0”是“直线AB 恒过定点(4,0)”的充分条件;反之:若直线AB 恒过定点(4,0),设直线AB 的方程为x =my +4,将直线AB 方程代入抛物线方程y 2=4x ,可得y 2﹣4my ﹣16=0,则有y 1y 2=﹣16, 此时•=x 1x 2+y 1y 2=()+y 1y 2=+y 1y 2=0,故“•=0”是“直线AB 恒过定点(4,0)”的必要条件;综合可得:“•=0”是“直线AB 恒过定点(4,0)”的充要条件;故选:B .5.(2020·湖北高考模拟)设12(,0),(,0)F c F c -是双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,点P 是C 右支上异于顶点的任意一点,PQ 是12F PF ∠的角平分线,过点1F 作PQ 的垂线,垂足为Q ,O 为坐标原点,则||OQ 的长为( ) A .定值a B .定值bC .定值cD .不确定,随P 点位置变化而变化【答案】A【解析】依题意如图,延长F 1Q ,交PF 2于点T , ∵PQ 是∠F 1PF 2的角分线.TF 1是PQ 的垂线, ∴PQ 是TF 1的中垂线,∴|PF 1|=|PT |,∵P 为双曲线2222x y a b-=1上一点,∴|PF 1|﹣|PF 2|=2a , ∴|TF 2|=2a ,在三角形F 1F 2T 中,QO 是中位线, ∴|OQ |=a . 故选:A .6.(2020·浙江省杭州第二中学高三)设点(),P x y 是圆22:2210C x y x y ++-+=上任意一点,若212x y x y a -+++--为定值,则a 的值可能为( )A .3-B .4-C .5-D .6-【答案】D【解析】圆C 标准方程为22(1)(1)1x y ++-=,圆心为(1,1)C -,半径为1r =,直线:20l x y a --=2115a---=,35a =-当35a =-+C 在直线l 上方,20x y a --≤,当=--35a C 在直线l 下方,20x y a --≥,若212x y x y a -+++--为定值,则20x y a --≥,因此35a ≤-D 满足. 故选:D.7.(2020·湖北高考模拟(理))已知圆C : 224x y +=,点P 为直线290x y +-=上一动点,过点P 向圆C 引两条切线,PA PB , ,A B 为切点,则直线AB 经过定点( )A .48,99⎛⎫⎪⎝⎭ B .24,99⎛⎫⎪⎝⎭C .()2,0D .()9,0 【答案】A【解析】设()()()112200,,,,,,A x y B x y P x y 则1122:4;:4;PA x x y y PB x x y y +=+= 即101020204;4;x x y y x x y y +=+=因此A 、B 在直线004x x y y +=上,直线AB 方程为004x x y y +=, 又00290x y +-=,所以()()0009242940y x y y y y x x -+=⇒-+-= 即8420,940,99y x x y x -=-=⇒==,直线AB 经过定点48,99⎛⎫⎪⎝⎭,选A. 8.(2020·全国高三期末(理))已知圆O :2214x y +=,直线l :y =kx +b (k ≠0),l 和圆O 交于E ,F 两点,以Ox 为始边,逆时针旋转到OE ,OF 为终边的最小正角分别为α,β,给出如下3个命题: ①当k 为常数,b 为变数时,sin (α+β)是定值; ②当k 为变数,b 为变数时,sin (α+β)是定值; ③当k 为变数,b 为常数时,sin (α+β)是定值. 其中正确命题的个数是( ) A .0 B .1C .2D .3【答案】B【解析】设点11()E x y ,,22()F x y ,,由三角函数的定义得111cos 21sin 2x y αα⎧=⎪⎪⎨⎪=⎪⎩,,221cos 21sin 2x y ββ⎧=⎪⎪⎨⎪=⎪⎩,, 将直线EF 的方程与的方程联立2214y kx b x y =+⎧⎪⎨+=⎪⎩,, 得2221(1)204k x kbx b +++-=, 由韦达定理得122212221141kb x x k b x x k ⎧+=-⎪+⎪⎨-⎪=⎪+⎩,,所以2112sin()sin cos cos sin 44x y x y αβαβαβ+=+=+=222112121222188244()4()84()11k b kb k x kx b x kx b kx x b x x k k ⎛⎫-- ⎪⎝⎭+++=++==-++,因此,当k 是常数时,sin()αβ+是常数,故选B (特值法可秒杀)9.(2020·浙江高三期末)斜率为k 的直线l 过抛物线22(0)y px p =>焦点F ,交抛物线于,A B 两点,点00(,)P x y 为AB 中点,作OQ AB ⊥,垂足为Q ,则下列结论中不正确的是( )A .0ky 为定值B .OA OB ⋅为定值C .点P 的轨迹为圆的一部分D .点Q 的轨迹是圆的一部分【答案】C【解析】设抛物线22(0)y px p =>上,A B 两点坐标分别为()()1122,,,A x y B x y ,则2211222,2,y px y px ==两式做差得,121212()()2()y y y y p x x +-=-,整理得1201212022,,2.y y p pk ky p x x y y y -=∴=∴=-+为定值,所以A 正确.因为焦点(,0)2p F ,所以直线AB 方程为()2p y k x =-.由2()22p y k x y px⎧=-⎪⎨⎪=⎩得2222244(2)0k x p k x p k -++=,则22121222(2),,4p k p x x x x k ++== 222212121212()()[()]2224p p p p y y k x x k x x x x p =--=-++=-.2121234OA OB x x y y p ∴⋅=+=-为定值.故B 正确. ,OQ AB ⊥∴点Q 的轨迹是以OF 为直径的圆的一部分,故D 正确.本题选择C 选项.10.(2020·安徽高三月考(理))已知抛物线2:8C y x =,圆22:(2)4F x y -+=,直线:(2)(0)l y k x k =-≠自上而下顺次与上述两曲线交于1234,,,M M M M 四点,则下列各式结果为定值的是( ) A .1324M M M M ⋅ B .14FM FM ⋅ C .1234M M M M ⋅ D .112FM M M ⋅【答案】C 【解析】由()228y k x y x⎧=-⎨=⎩消去y 整理得2222(48)40(0)k x k x k k -++=≠,设111422(,),(,)M x y M x y ,则21212248,4k x x x x k++==. 过点14,M M 分别作直线:2l x '=-的垂线,垂足分别为,A B , 则11422,2M F x M F x =+=+.对于A ,13241412(2)(2)(4)(4)M M M M M F M F x x ⋅=++=++12124()16x x x x =+++,不为定值,故A 不正确.对于B ,14121212(2)(2)2()4FM FM x x x x x x ⋅=++=+++,不为定值,故B 不正确. 对于C ,12341412(2)(2)4M M M M M F M F x x ⋅=--==,为定值,故C 正确.对于D ,1121111(2)(2)FM M M M F M F x x ⋅=⋅-=+,不为定值,故D 不正确.选C .11.(2020·南昌县莲塘第一中学高三月考(理))在平面直角坐标系中,两点()()111222,,,P x y P x y 间的“L -距离”定义为121212|||||.PP x x y y =-+-‖则平面内与x 轴上两个不同的定点12,F F 的“L -距离”之和等于定值(大于12|F F )的点的轨迹可以是( )A .B .C .D .【答案】A【解析】设12(,0),(,0)F c F c -,再设动点(,)M x y ,动点到定点12,F F 的“L距离”之和等于(20)m m c >>,由题意可得:x c y x c y m ++-++=,即2x c x c y m -+++=, 当,0x c y <-≥时,方程化为220x y m -+=; 当,0x c y <-<时,方程化为220x y m ++=;当,0c x c y -≤<≥时,方程化为2my c =-; 当,0c x c y -≤<<时,方程化为2my c =-;当,0x c y ≥≥时,方程化为220x y m +-=; 当,0x c y ≥<时,方程化为220x y m --=;结合题目中给出四个选项可知,选项A 中的图象符合要求,故选A . 12.(2020·东北育才学校高三月考(理))有如下3个命题;①双曲线22221(0,0)x y a b a b-=>>上任意一点P 到两条渐近线的距离乘积是定值;②双曲线2222222211(0,0)x y x y a b a b b a-=-=>>与的离心率分别是12e e 、,则22122212e e e e +是定值;③过抛物线22(0)x py p =>的顶点任作两条互相垂直的直线与抛物线的交点分别是A B 、,则直线AB 过定点;其中正确的命题有( ) A .3个 B .2个C .1个D .0个【答案】A【解析】①双曲线22221x y a b-=(a >0,b >0)上任意一点P ,设为(m ,n ),两条渐近线方程为y=±ba x=222222b m a n a b -+, 由b 2m 2﹣a 2n 2=a 2b 2,可得两个距离乘积是定值2222a b a b+; ②双曲线2222x y a b -=1与22221x y b a -=(a >0,b >0)的离心率分别是e 1,e 2,即有e 12=222a b a +,e 22=222a b b +,可得22122212e e e e +为定值1;③过抛物线x 2=2py (p >0)的顶点任作两条互相垂直的直线与抛物线的交点分别是A ,B ,可设A (s ,22s p),B (t ,22t p ),由OA ⊥OB 可得st+2224s t p=0,即有st=﹣4p 2, k AB =()222t s p t s --=2t s p +,可得直线AB 的方程为y ﹣22s p=2t s p +(x ﹣s ),即为y=2t s p +x+2p , 则直线AB 过定点(0,2p ).三个命题都正确.故选A .13.已知O 为坐标原点,点M 在双曲线22:C x y λ-=(λ为正常数)上,过点M 作双曲线C 的某一条渐近线的垂线,垂足为N ,则ON MN ⋅的值为( ) A .2λB .λC .2λD .无法确定【来源】四川省南充市2021届高三第三次模拟考试数学(文)试题 【答案】A【解析】设(,)M m n ,即有22m n λ-=,双曲线的渐近线为y x =±,可得MN =,由勾股定理可得ON ===,可得2222m n ON MN λ-⋅=== .故选:A .14.已知1F 、2F 是双曲线C :2214y x -=的左、右两个焦点,若双曲线在第一象限上存在一点P ,使得22()0OP OF F P +⋅=,O 为坐标原点,且12||||PF PF λ=,则λ的值为( ).A .13B .12C .2D .3【来源】河南省豫南九校2020-2021学年高三上学期期末联考理数试题 【答案】C 【解析】1a =,2b =,∴c =1(F,2F, 设点)P m ,∴2222()(1))1504m OP OFF P m m m +⋅=⋅=+-+=, ∴2165m =,m =,则P ±,14PF ===, ∴2122PF PF a =-=,∴12422PF PF λ===, 故选:C.15.已知1F ,2F 是双曲线221169x y -=的焦点,PQ 是过焦点1F 的弦,且PQ 的倾斜角为60︒,那么22||+-PF QF PQ 的值为A .16B .12C .8D .随α变化而变化【答案】A【解析】由双曲线方程221169x y -=知,28a =,双曲线的渐近线方程为34y x 直线PQ 的倾斜角为60︒,所以334PQ k =>,又直线PQ 过焦点1F ,如图 所以直线PQ 与双曲线的交点都在左支上.由双曲线的定义得,2128PF PF a -==…………(1),2128QF QF a -== (2)由(1)+(2)得2211()16PF QF QF PF +-+=,2216PF QF PQ ∴+-=. 故选:A16.已知椭圆()2221024x y b b+=<<,1F ,2F 分别为椭圆的左、右焦点,P 为椭圆上一点,()2,1M ,1MF 平分角12PF F ∠,则1MPF 与2MPF 的面积之和为( ) A .1B .32C .2D .3【来源】中学生标准学术能力诊断性测试2020-2021学年高三上学期1月测试理文数学(一卷)试题 【答案】C【解析】如图,椭圆()222210x y a b a b+=>>,1F ,2F 分别为椭圆的左、右焦点,P 为椭圆上一点,作一圆与线段F 1P ,F 1F 2的延长线都相切,并且与线段PF 2也相切,切点分别为D ,A ,B ,1111221122||||||||||||||||||||F D F A PF PD F F F A PF PB F F F A =⇔+=+⇔+=+, 12122212122||||||||||||||||||2||PF PB F B F F F A F B PF PF F F F A ⇔++=++⇔+=+,所以2||F A a c =-(c 为椭圆半焦距),从而点A 为椭圆长轴端点,即圆心M 的轨迹是直线x =a (除点A 外). 因点M (2,1)在12PF F ∠的平分线上,且椭圆右端点A (2,0),所以点M 是上述圆心轨迹上的点,即点M 到直线F 1P ,PF 2,F 1F 2的距离都相等,且均为1,1MPF 与2MPF 的面积之和为1212111||1||1(||||)2222PF PF PF PF ⋅⋅+⋅⋅=+=.故选:C17.已知椭圆2214x y +=的上顶点为,A B C 、为椭圆上异于A 的两点,且AB AC ⊥,则直线BC 过定点( ) A .(1,0) B .(3,0)C .10,2⎛⎫ ⎪⎝⎭D .30,5⎛⎫- ⎪⎝⎭【答案】D【解析】设直线BC 的方程为x ky m =+,()()1122,,B x y C x y 、,则由2214x ky m x y =+⎧⎪⎨+=⎪⎩整理得()2224240k y mky m +++-=, 所以212122224,44mk m y y y y k k --+==++, ()22222121212224244m mkx x k y y mk y y m k mk m k k --=+++=++++,因为()0,1A ,()()1122,1,1A x y B C x y A --==,,AB AC ⊥, 所以()()()1212121212111x x y y x x y y y y AB AC +-=-=++⋅-+22222222224242125304444m mk m mk k mk m km m k k k k k ---=+++++=+-=++++解得m k =-或35m k =, 当m k =-时,直线BC 的方程为()1x ky k k y =-=-,直线过()0,1点而()0,1A ,而,A B C 、不在同一直线上,不合题意; 当35m k =时,直线BC 的方程为3355x ky k k y ⎛⎫=+=+ ⎪⎝⎭,直线过30,5⎛⎫- ⎪⎝⎭,符合题意.故选:D.18.已知椭圆221124y x +=,圆22:4O x y +=,过椭圆上任一与顶点不重合的点G 引圆的两条切线,切点分别为,P Q ,直线PQ 与x 轴,y 轴分别交于点,M N ,则2231OMON+=( )A .54B .45C .43D .34【来源】安徽省宣城市第二中学2020-2021学年高三下学期第一次月考理科数学试题 【答案】D【解析】设112233(,),(,),(,)P x y Q x y G x y ,则切线GP 的方程为114x x y y +=,切线GQ 的方程为224x x y y +=, 因为点G 在切线,GP GQ 上,所以13134x x y y +=,23234x x y y +=,所以直线PQ 的方程为334x x y y +=, 所以3344(,0),(0,)M N x y , 因为点33(,)G x y 在椭圆221124y x +=上,所以2233312x y +=,所以22223333223311123(3)161616164x y x y OM ON+=+=+==, 故选:D19.已知椭圆22:142x y C +=的左右顶点分别为,A B ,过x 轴上点(4,0)M -作一直线PQ 与椭圆交于,P Q 两点(异于,A B ),若直线AP 和BQ 的交点为N ,记直线MN 和AP 的斜率分别为12,k k ,则12:k k =( ) A .13B .3C .12D .2【来源】湖北省“大课改、大数据、大测评”2020-2021学年高三上学期联合测评数学试题 【答案】A【解析】设(),N x y ,()11,P x y ,()22,Q x y ,设直线PQ 的方程:4x my =-由,,P N A 和,,Q N B 三点共线可知11222222y y x x y y x x ⎧=⎪++⎪⎨⎪=⎪--⎩ , 解得:()()()()()()()()1221122112211221222226222262y x y x y my y my x y x y x y my y my -++-+-==--++--+-1212122623my y y y x y y --∴=-,12121226643my y y y x y y +-+=-,(*)联立224142x my x y =-⎧⎪⎨+=⎪⎩ ,得()2228120m y my +-+=,22226448(2)16(6)0,6m m m m ∆=-+=->>,12121212228123,,()222m y y y y my y y y m m +==∴=+++, 代入(*)得121293433y y x y y -+==-,14y k x =+,22y k x =+ ,122211443k x k x x +∴==-=++.故选:A20.(2020·北京市第二中学分校高三(理))抛物线24y x =上两个不同的点A ,B ,满足OA OB ⊥,则直线AB 一定过定点,此定点坐标为__________. 【答案】(4,0).【解析】设直线l 的方程为x ty b =+代入抛物线24y x =,消去x 得2440y ty b --=,设()11,A x y ,()22,B x y ,则124y y t +=,124y y b =-,∴()()()221212121212OA OB ty b ty b y y t y y bt y y b y y ⋅=+++=++++222444bt bt b b =-++- 24b b =-=0,∴0b =(舍去)或4b =, 故直线l 过定点()4,0.21.(2020·江苏扬州中学高三月考)已知点(2,0),(4,0)A B -,圆,16)()4(:22=+++b y x C 点P 是圆C 上任意一点,若PAPB为定值,则b =________.【答案】0【解析】设(,)P x y ,PAk PB =k =, 整理得222222(1)(1)(48)4160k x k y k x k -+-+++-=, 又P 是圆C 上的任意一点,故1k ≠,圆C 的一般方程为222820x y x by b ++++=,因此20b =,22222484168,11k k b k k+-==--,解得0b =. 22.(2020·江苏海安高级中学高三)在平面直角坐标系xOy 中,A ,B 为x 轴正半轴上的两个动点,P (异于原点O )为y 轴上的一个定点.若以AB 为直径的圆与圆x 2+(y -2)2=1相外切,且∠APB 的大小恒为定值,则线段OP 的长为_____.【解析】设O 2(a ,0),圆O 2的半径为r (变量),OP=t (常数),则222222221)222tan ,tan ,2tan 141,(4,22tan 3232r a r a rOPA OPB t t a r a rrtt t APB a r t a r t a r a rt tAPB t t r r +-+∠=∠=+--∴∠==-+-++=+∴=-∴∠==-+-+∵∠APB 的大小恒为定值,∴t23.在平面直角坐标系xOy 中,椭圆22184x y +=上一点A ,点B 是椭圆上任意一点(异于点A ),过点B 作与直线OA 平行的直线l 交椭圆于点C ,当直线AB 、AC 斜率都存在时,AB AC k k +=___________. 【答案】0【解析】取特殊点B ()0,2-,则BC的方程为22y x +=,由22242y x x y ⎧+=⎪⎪⎨⎪+=⎪⎩得C ()所以202AB AC k k +==. 24.(2020·河北定州一中高三月考)P 为圆()22:15C x y -+=上任意一点,异于点()2,3A 的定点B 满足PBPA为常数,则点B 的坐标为______. 【答案】33,22⎛⎫⎪⎝⎭【解析】设()()00,,,,PA P x y B x y PBλ=,则()2215x y -+=,可得2242x y x +=+,① ()()()()222220023x x y y x y y λ⎡⎤-+-=-+-⎣⎦,②由①②得()2200002224x x y y x y --+++2222617x y λλλ=--+,可得202002220022226417x y x y λλλ⎧-=-⎪-=-⎨⎪++=⎩,解得002323212x y λ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩,B ∴点坐标为33,22⎛⎫ ⎪⎝⎭,故答案为33,22⎛⎫ ⎪⎝⎭. 25.(2020·上海长岛中学高三)在平面直角坐标系中,O 为坐标原点,M 、N 是双曲线22124x y -=上的两个动点,动点P 满足2OP OM ON =-,直线OM 与直线ON 斜率之积为2,已知平面内存在两定点1F 、2F ,使得12PF PF -为定值,则该定值为________【答案】【解析】设P (x ,y ),M (x 1,y 1),N (x 2,y 2),则由2OP OM ON =-,得(x ,y )=2(x 1,y 1)-(x 2,y 2), 即x=2x 1-x 2,y=2y 1-y 2,∵点M ,N 在双曲线22124x y -=上,所以2211124x y -=,2222124x y -=,故2x 2-y 2=(8x 12+2x 22-8x 1x 2)-(4y 12+y 22-4y 1y 2)=20-4(2x 1x 2-y 1y 2), 设k 0M ,k ON 分别为直线OM ,ON 的斜率,根据题意可知k 0M k ON =2, ∴y 1y 2-2 x 1x 2=0, ∴2x 2-y 2=20,所以P 在双曲线2x 2-y 2=20上; 设该双曲线的左,右焦点为F 1,F 2,由双曲线的定义可推断出12PF PF -为定值,该定值为26.(2020·江苏高三月考)椭圆E :22143x y +=的左顶点为A ,点,B C 是椭圆E 上的两个动点,若直线,AB AC 的斜率乘积为定值14-,则动直线BC 恒过定点的坐标为__________. 【答案】(1,0)【解析】当直线BC 的斜率存在时,设直线BC 的方程为y=kx+m ,由22143x y y kx m ⎧+=⎪⎨⎪=+⎩,消去y 得:(3+4k 2)x 2+8kmx+4m 2﹣12=0, 设B (x 1,y 1),C (x 2,y 2),则x 1+x 2=28km 34k -+,x 1x 2=2241234m k-+, 又A (﹣2,0),由题知k AB •k AC =121222y y x x ++=﹣14, 则(x 1+2)(x 2+2)+4y 1y 2=0,且x 1,x 2≠﹣2, 则x 1•x 2+2(x 1+x 2)+4+4(kx 1+m )(kx 2+m ) =(1+4k 2)x 1x 2+(2+4km )(x 1+x 2)+4m2+4=()()2221441234k m k+-++(2+4km )28km 34k -++4m2+4=0则m 2﹣km ﹣2k 2=0, ∴(m ﹣2k )(m+k )=0, ∴m=2k 或m=﹣k .当m=2k 时,直线BC 的方程为y=kx+2k=k (x+2). 此时直线BC 过定点(﹣2,0),显然不适合题意.当m=﹣k 时,直线BC 的方程为y=kx ﹣k=k (x ﹣1),此时直线BC 过定点(1,0). 当直线BC 的斜率不存在时,若直线BC 过定点(1,0),B 、C 点的坐标分别为(1,32),(1,﹣32),满足k AB •k AC =﹣14. 综上,直线BC 过定点(1,0). 故答案为:(1,0).27.已知双曲线22:13y C x -=的右焦点为F ,过点F 的直线l 与双曲线相交于P 、Q 两点,若以线段PQ为直径的圆过定点M ,则MF =______.【来源】金科大联考2020届高三5月质量检测数学(理科)试题 【答案】3【解析】点F 的坐标为()2,0,双曲线的方程可化为2233x y -=,①当直线l 的斜率不存在时,点P 、Q 的坐标分别为()2,3、()2,3-, 此时以线段PQ 为直径的圆的方程为()2229x y -+=;②当直线l 的斜率存在时,设点P 、Q 的坐标分别为()11,x y ,()22,x y , 记双曲线C 的左顶点的坐标为()1,0A -,直线l 的方程为()2y k x =-,联立方程()22332x y y k x ⎧-=⎪⎨=-⎪⎩,消去y 后整理为()()222234340kxk x k -+-+=,2422230164(3)(34)36(1)0k k k k k ⎧-≠⎨∆=+-+=+>⎩,即k ≠ 有2122212243343k x x k k x x k ⎧+=⎪⎪-⎨+⎪=⎪-⎩,()()()22121212122224y y k x x k x x x x =--=-++⎡⎤⎣⎦,222222234894333k k k k k k k ⎛⎫+=-+- ⎪---⎝⎭,()111,AP x y =+,()221,AQ x y =+,()()()1212121212111AP AQ x x y y x x x x y y ⋅=+++=+++⎡⎤⎣⎦ 22222222344931103333k k k k k k k k +-=+-+=+=----. 故以线段PQ 为直径的圆过定点()1,0M -,3MF =.28.双曲线22:143x y C -=的左右顶点为,A B ,以AB 为直径作圆O ,P 为双曲线右支上不同于顶点B 的任一点,连接PA 交圆O 于点Q ,设直线,PB QB 的斜率分别为12,k k ,若12k k λ=,则λ=_____. 【答案】34-【解析】设()()()00,,2,02,0P x y A B - 2200143x y -=,()222000331444x y x ⎛⎫=-=- ⎪⎝⎭2000200032424PA PBy y y x x k k x =⋅=+--= PA 交圆O 于点Q ,所以PA QB ⊥ 易知:33441PA PB PB QBPA QB k k k k k k λ⎧=⎪⇒==-⎨⎪⋅=-⎩即1234k k λ==-. 故答案为:34-29.过双曲线22221x y a b-=的右焦点(,0)F c 的直线交双曲线于M 、N 两点,交y 轴于P 点,若1PM MF λ=,2PN NF λ=,规定12λλ+=PM PN MF NF +,则PM PNMF NF +的定值为222a b .类比双曲线这一结论,在椭圆22221(0)x y a b a b +=>>中,PM PN MF NF+的定值为________. 【来源】贵州省铜仁市思南中学2020-2021学年高三上学期期末考试数学(理)试题【答案】222a b-【解析】如图,设椭圆()222210x y a b a b+=>>的右焦点为(),0F c ,过点(),0F c 的直线为()y k x c =-,代入椭圆的方程得:()2222222222220b a kxa k cx a k c ab +-+-=,设()11,M x y ,()22,N x y ,则22122222a k c x x b a k +=-+,2222212222a k c ab x x b a k-⋅=+, 过点,M N 分别作x 轴的垂线,垂足为,D E ,则111x PM x c MF λ==--,222=x PNx c NFλ=--,所以()()()()()1221121212122212121212122x x c x x c x x c x x x x x c x c x x c x x c x x c x x c λλ-+--+⎛⎫+=-+=-=-⎪---++-++⎝⎭将22122222a k c x x b a k +=-+,2222212222a k c ab x x b a k -⋅=+代入化简得:21222a b λλ+=-. 故答案为:222a b-.30.若M ,P 是椭圆2214x y +=两动点,点M 关于x 轴的对称点为N ,若直线PM ,PN 分别与x 轴相交于不同的两点A (m ,0),B (n ,0),则mn =_________.【来源】四川省资阳市2020-2021学年高三上学期期末数学文科试题 【答案】4 【解析】设(),M a b ,则(),N a b -,(),P c d ,则2214a b +=,2214c d +=所以PM d bk c a-=- 直线PM 的方程为()d b y b x a c a --=--,令0y =可得ad bcm d b-=- 同理有PM d b k c a+=- 直线PN 的方程为()d b y b x a c a ++=--,令0y =可得ad bcn d b+=+ 则222222ad bc ad bc a d b c mn d b d b d b -+-⎛⎫⎛⎫== ⎪⎪-+-⎝⎭⎝⎭222222111144111144a c c a c a ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=⎛⎫--- ⎪⎝⎭()2222414a c a c -==- 31.椭圆E :22143x y +=的左顶点为A ,点,B C 是椭圆E 上的两个动点,若直线,AB AC 的斜率乘积为定值14-,则动直线BC 恒过定点的坐标为__________. 【答案】(1,0)【解析】当直线BC 的斜率存在时,设直线BC 的方程为y=kx+m ,由22143x y y kx m ⎧+=⎪⎨⎪=+⎩,消去y 得:(3+4k 2)x 2+8kmx+4m 2﹣12=0, 设B (x 1,y 1),C (x 2,y 2),则x 1+x 2=28km 34k -+,x 1x 2=2241234m k -+, 又A (﹣2,0),由题知k AB •k AC =121222y y x x ++=﹣14, 则(x 1+2)(x 2+2)+4y 1y 2=0,且x 1,x 2≠﹣2, 则x 1•x 2+2(x 1+x 2)+4+4(kx 1+m )(kx 2+m ) =(1+4k 2)x 1x 2+(2+4km )(x 1+x 2)+4m2+4=()()2221441234k m k +-++(2+4km )28km 34k -++4m2+4=0则m 2﹣km ﹣2k 2=0, ∴(m ﹣2k )(m+k )=0, ∴m=2k 或m=﹣k .当m=2k 时,直线BC 的方程为y=kx+2k=k (x+2). 此时直线BC 过定点(﹣2,0),显然不适合题意.当m=﹣k 时,直线BC 的方程为y=kx ﹣k=k (x ﹣1),此时直线BC 过定点(1,0). 当直线BC 的斜率不存在时,若直线BC 过定点(1,0),B 、C 点的坐标分别为(1,32),(1,﹣32),满足k AB •k AC =﹣14. 综上,直线BC 过定点(1,0). 故答案为(1,0).。
河南省豫南九校2020-2021学年高一上学期第三次联考历史试题【含答案】

河南省豫南九校2020-2021学年高一第一学期第三次联考历史试题(考试时间:90分钟试卷满分:100分)一、选择题(本题共30小题,每小题2分,共60分。
在每小题给出的四个选项中,只有一个是符合题目要求的)1.家训是指家庭对子孙立身处世、持家治业的教诲。
家训是家庭的重要组成部分,对个人的教养、原则都有着重要的约束作用,家训或单独刊印,或附于宗谱。
家训传统传承至今说明A.家族力量仍然强大 B.宗法观念影响深远C.封建礼教束缚人性D.社会秩序遭到破坏2.公元前771年,西戎与诸侯联手杀死了周天子。
周天子的长子被扶上王位后,为了安全起见,把都城从渭河流域东迁到了现在的洛阳,其位置在黄河以南,处在中部平原的心脏地带,由此可知A.礼乐制度不复存在B.分封制度受到挑战C.王位世袭制消亡D.宗法制度开始解体3.始皇曰:“天下共苦战斗不休,以有侯王。
赖宗庙,天下初定,又复立国,是树兵也,而求其宁息,岂不难哉!”廷尉议是。
由此可知,秦朝推行A.郡国并行制B.分封制C.郡县制D.宗法制4.廷尉李斯议曰:“周文、武所封子弟同姓甚众,然后属疏远,相攻击如仇雠,诸侯更相诛伐,周天子弗能禁止。
今海内赖陛下神灵一统,皆为郡县,诸子功臣以公赋税重赏赐之,甚足易制。
天下无异意,则安宁之术也。
置诸侯不便。
”由此可知,郡县制A.形成了森严的等级制度B.利于加强对地方的直接控制C.强化了王国对中央的威胁D.使专制主义集权达到顶峰5.《汉书·高五王传》“(西汉初年),以海内初定,子弟少(年少),激秦孤立亡(无)藩辅,故大封同姓,以填(镇)天下。
”由此可知汉初推行郡国并行制A.加强了朝廷对地方的控制B.是对国情与政治反思的结果C.有利于加强中央集权D.有利于加强皇权6.唐初,三省长官议事于门下省之政事堂,唐高宗时期迁政事堂于中书省,开元十一年(723年)政事堂改称中书门下,中书省逐渐演变为撰写制救的机构。
这一变迁A.提升了门下、中书二省的地位B.使得三省政务流程与制度名存实亡C.便利了君主对朝政的全面控制D.开启中书省总理全国政务之先河7.图1、图2、图3、图4是中国古代四个历史时期(唐代、两宋、元代、明清)的科举状元籍贯统计部分摘录表。
高中数学第4章数列1_4综合拔高练苏教版选择性必修第一册

综合拔高练五年高考练考点1 等差数列及其应用 1.(2020全国Ⅱ,4,5分,)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )A.3 699块B.3 474块C.3 402块D.3 339块 2.(2020浙江,7,4分,)已知等差数列{a n }的前n 项和为S n ,公差d ≠0,且a1a ≤1.记b 1=S 2,b n +1=S 2n +2-S 2n ,n ∈N *,下列等式不可能成立的是 ( )A.2a 4=a 2+a 6B.2b 4=b 2+b 6C.a 42=a 2a 8D.a 42=b 2b 83.(2019课标全国Ⅰ,9,5分,)记S n 为等差数列{a n }的前n 项和.已知S 4=0,a 5=5,则( )A.a n =2n -5B.a n =3n -10C.S n =2n 2-8n D.S n =12n 2-2n4.(2020新高考Ⅰ,14,5分,)将数列{2n -1}与{3n -2}的公共项从小到大排列得到数列{a n },则{a n }的前n 项和为 . 5.(2020浙江,11,4分,)我国古代数学家杨辉,朱世杰等研究过高阶等差数列的求和问题,如数列{a (a +1)2}就是二阶等差数列.数列{a (a +1)2}(n ∈N *)的前3项和是 .6.(2019课标全国Ⅲ,14,5分,)记S n 为等差数列{a n }的前n 项和,若a 1≠0,a 2=3a 1,则a 10a 5= .7.(2019北京,10,5分,)设等差数列{a n }的前n 项和为S n .若a 2=-3,S 5=-10,则a 5= ,S n 的最小值为 .8.(2019课标全国Ⅰ,18,12分,)记S n 为等差数列{a n }的前n 项和.已知S 9=-a 5.(1)若a 3=4,求{a n }的通项公式;(2)若a 1>0,求使得S n ≥a n 的n 的取值范围.考点2 等比数列及其应用 9.(2020全国Ⅰ,10,5分,)设{a n }是等比数列,且a 1+a 2+a 3=1,a 2+a 3+a 4=2,则a 6+a 7+a 8=( )A.12B.24C.30D.32 10.(2018北京,4,5分,)“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于√212.若第一个单音的频率为f ,则第八个单音的频率为 ( ) A.√23f B.√223fC.√2512 fD.√2712f 11.(2019课标全国Ⅰ,14,5分,)记S n 为等比数列{a n }的前n 项和.若a 1=13,a 42=a 6,则S 5= .12.(2020全国Ⅲ文,17,12分,)设等比数列{a n }满足a 1+a 2=4,a 3-a 1=8.(1)求{a n }的通项公式;(2)记S n 为数列{log 3a n }的前n 项和.若S m +S m +1=S m +3,求m.13.(2019课标全国Ⅱ,19,12分,)已知数列{a n}和{b n}满足a1=1,b1=0,4a n+1=3a n-b n+4,4b n+1=3b n-a n-4.(1)证明:{a n+b n}是等比数列,{a n-b n}是等差数列;(2)求{a n}和{b n}的通项公式.考点3数列的综合问题14.(2020江苏,11,5分,)设{a n}是公差为d的等差数列,{b n}是公比为q的等比数列.已知数列{a n+b n}的前n项和S n=n2-n+2n-1(n∈N*),则d+q的值是.15.(2020全国Ⅰ,16,5分,)数列{a n}满足a n+2+(-1)n a n=3n-1,前16项和为540,则a1=.16.(2020新高考Ⅰ,18,12分,)已知公比大于1的等比数列{a n}满足a2+a4=20,a3=8.(1)求{a n}的通项公式;(2)记b m为{a n}在区间(0,m](m∈N*)中的项的个数,求数列{b m}的前100项和S100.考点4数学归纳法*17.(2020全国Ⅲ理,17,12分,)设数列{a n}满足a1=3,a n+1=3a n-4n.(1)计算a2,a3,猜想{a n}的通项公式并加以证明;(2)求数列{2n a n}的前n项和S n.三年模拟练应用实践1.(多选)(2020江苏盐城高二期末,)设d,S n分别为等差数列{a n}的公差与前n项和,若S10=S20,则下列判断中正确的有()A.当n=15时,S n取最大值B.当n=30时,S n=0C.当d>0时,a10+a22>0D.当d<0时,|a10|>|a22|2.(多选)(2020江苏苏州实验中学高二月考,)已知等差数列{a n }的首项为1,公差d =4,前n 项和为S n ,则下列结论成立的有( )A.数列{a aa}的前10项和为100B.若a 1,a 3,a m 成等比数列,则m =21C.若∑a =1a1a a a a +1>625,则n 的最小值为6D.若a m +a n =a 2+a 10,则1a +16a 的最小值为2512 3.(2020四川南充西南大学实验学校高一月考,)已知数列{log a b n }(a >0且a ≠1)是首项为2,公差为1的等差数列,若数列{a n }是递增数列,且满足a n =b n lg b n ,则实数a 的取值范围是( )A.(23,1) B.(2,+∞)C.(23,1)∪(1,+∞) D.(0,23)∪(1,+∞) 4.(2020山东济宁实验中学高二上期中,)古代埃及数学中有一个独特现象:除23用一个单独的符号表示以外,其他分数都可写成若干个单分数和的形式.例如25=13+115,可这样理解:有两个面包,要平均分给5个人,每人13,余13,再将这13分成5份,每人得115,这样每人分得13+115.形如22a -1(n ≥3,n ∈N *)的分数的分解:25=13+115,27=14+128,29=15+145,按此规律,22a -1=(n ≥3,n ∈N *).5.(2021河南豫南九校高二联考,)已知数列{a n }的前n 项和为S n ,数列{b n }的前n 项和为T n ,其中a 1=1,3S n =(n +m )a n (m ∈R),且a n b n =15.若对任意n ∈N *,λ>T n 恒成立,则实数λ的最小值为 .6.(2021上海交通大学附属中学高三月考,)已知等差数列{a n }(公差不为零)和等差数列{b n },如果关于x 的方程2 021x 2-(a 1+a 2+…+a 2021)x +b 1+b 2+…+b 2021=0有实数解,那么以下 2 021个方程x 2-a 1x +b 1=0,x 2-a 2x +b 2=0,x 2-a 3x +b 3=0,……,x 2-a 2 021x +b 2 021=0中,无实数解的方程最多有个.7.(2021浙江宁波宁海中学高三二模,)已知{|a n |}是首项和公差均为1的等差数列,S n 为数列{a n }的前n 项和,记m n 为|S n |的所有可能取值中的最小值,则m 1+m 2+…+m 2 020= .a n+1,②a n+1=a n+2,③8.(2021江苏南京三校高三期中联考,)在下列三个条件①a n+1=12S n=2a n-1中选择一个补充在题中横线处,并作答.设数列{a n}的前n项和为S n,a1=1,对任意的n∈N*,都有,等比数列{b n}中,对任意的n∈N*,都有b n>0,2b n+2=b n+1+3b n,且b1=1,问:是否存在k∈N*,使得对任意的n∈N*,都有a n b k≤a k b n?若存在,试求出k的值;若不存在,请说明理由.9.(2020天津耀华中学高二上期中,)在数列{a n}中,已知a1=1,其前n项和为S n,且对任意的正整数n,都有2S n=(n+1)a n成立.(1)求数列{a n}的通项公式;(2)已知关于n 的不等式a 3-2a 3·a 4-2a 4·…·a a -2a a <√2a +1对一切n ≥3,n ∈N *恒成立,求实数a 的取值范围;(3)已知c n =(11+a a)2,数列{c n }的前n 项和为T n ,试比较T n 与23的大小并证明.迁移创新10.(2019北京高考,)已知数列{a n },从中选取第i 1项、第i 2项、…、第i m 项(i 1<i 2<…<i m ),若a a 1<a a 2<…<a a a ,则称新数列a a 1,a a 2,…,a a a 为{a n }的长度为m 的递增子列.规定:数列{a n }的任意一项都是{a n }的长度为1的递增子列. (1)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;(2)已知数列{a n }的长度为p 的递增子列的末项的最小值为a a 0,长度为q 的递增子列的末项的最小值为a a 0.若p <q ,求证:a a 0<a a 0;(3)设无穷数列{a n }的各项均为正整数,且任意两项均不相等.若{a n }的长度为s 的递增子列的末项的最小值为2s -1,且长度为s 且末项为2s -1的递增子列恰有2s -1个(s =1,2,…),求数列{a n }的通项公式.4.1~4.4综合拔高练五年高考练1.C由题意可设每层有n个环,则三层共有3n个环,∴每一环扇面形石板的块数构成以a1=9为首项,9为公差的等差数列{a n},且项数为3n.不妨设上层扇面形石板总数为S1,中层总数为S2,下层总数为S3,∴S3-S2=[9(2a+1)×a+a(a-1)2×9]-9(n+1)×n+a(a-1)2×9=9n2=729,解得n =9(负值舍去).则三层共有扇面形石板(不含天心石)27×9+27×262×9=27×9+27×13×9=27×14×9=3402(块).故选C .2.D 对于A,a 2,a 4,a 6成等差数列,故A 成立;对于B,由b n +1=S 2n +2-S 2n =a 2n +2+a 2n +1,可得b n +1-b n =a 2n +2+a 2n +1-(a 2n +a 2n -1)=a 2n +2-a 2n +a 2n +1-a 2n -1=4d ,故{b n }是等差数列,则b 2,b 4,b 6也成等差数列,故B 成立;对于C,a 42=(a 1+3d )2=a 12+6a 1d +9d 2,a 2a 8=(a 1+d )·(a 1+7d )=a 12+8a 1d +7d 2,所以a 42-a 2a 8=2d 2-2a 1d =2d (d -a 1),当d =a 1时,a 42=a 2a 8成立;对于D,a 42=(a 1+a 2+12a )2=(2a 1+13d )2=4a 12+52a 1d +169d 2,b 2b 8=(a 1+a 2+4d )(a 1+a 2+28d )=(2a 1+5d )(2a 1+29d )=4a 12+68a 1d +145d 2,所以a 42-b 2b 8=24d 2-16a 1d =8d 2(3-2·a1a )≥8d 2>0,所以a 42≠b 2b 8,故D 不可能成立.故选D .3.A 设{a n }的公差为d ,依题意得,4a 1+4×32d =0①,a 1+4d =5②,联立①②,解得a 1=-3,d =2.所以a n =2n -5,S n =n 2-4n.故选A . 4.答案 3n 2-2n解析 ∵数列{2n -1}的项为1,3,5,7,9,11,13,…, 数列{3n -2}的项为1,4,7,10,13,…, ∴数列{a n }是首项为1,公差为6的等差数列, ∴a n =1+(n -1)×6=6n -5, ∴数列{a n }的前n 项和S n =(1+6a -5)×a2=3n 2-2n.5.答案 10 解析 数列{a (a +1)2}的前三项依次为1×22=1,2×32=3,3×42=6,∴所求和为1+3+6=10. 6.答案 4解析 设等差数列{a n }的公差为d , ∵a 2=3a 1,∴a 2=a 1+d =3a 1,∴d =2a 1, ∴S 10=10a 1+10×92d =100a 1,S 5=5a 1+5×42d =25a 1,又∵a 1≠0,∴a10a 5=4.7.答案 0;-10解析 解法一:设等差数列{a n }的公差为d , ∵a 2=-3,S 5=-10, ∴{a 1+a =-3,5a 1+5×42a =-10, 即{a 1+a =-3,a 1+2a =-2,解得{a 1=-4,a =1,∴a 5=a 1+4d =0,S n =na 1+a (a -1)2d =-4n +a 2-a 2=12(n 2-9n )=12(a -92)2-818,∵n ∈N *,∴n =4或n =5时,S n 取最小值,最小值为-10. 解法二:设等差数列{a n }的公差为d ,易得S 5=5(a 1+a 5)2=5a 3,∵S 5=-10,∴a 3=-2,又a 2=-3,∴d =1,∴a 5=a 3+2d =0,∴(S n )min =S 4=S 5=-10.8.解析 (1)设{a n }的公差为d. 由S 9=-a 5得a 1+4d =0. 由a 3=4得a 1+2d =4. 于是a 1=8,d =-2.因此{a n }的通项公式为a n =10-2n. (2)由(1)得a 1=-4d ,故a n =(n -5)d ,S n =a (a -9)a2.由a 1>0知d <0,故S n ≥a n 等价于n 2-11n +10≤0,解得1≤n ≤10. 所以n 的取值范围是{n |1≤n ≤10,n ∈N }. 9.D 设等比数列{a n }的公比为q , 故a 2+a 3+a 4=q (a 1+a 2+a 3), 又a 2+a 3+a 4=2,a 1+a 2+a 3=1, ∴q =2,∴a 6+a 7+a 8=q 5(a 1+a 2+a 3)=25=32,故选D .10.D 由题意知,十三个单音的频率依次构成首项为f ,公比为√212的等比数列,设该等比数列为{a n },则a 8=a 1q 7,即a 8=√2712f ,故选D .11.答案1213解析 设{a n }的公比为q ,由a 42=a 6,得a 42=a 4·q 2,∴a 4=q 2.又∵a 4=a 1·q 3,∴a 1·q 3=q 2,又a 1=13,∴q =3.由等比数列求和公式可知S 5=13×(1-35)1-3=1213.12.解析 (1)设{a n }的公比为q ,则a n =a 1q n -1. 由已知得{a 1+a 1a =4,a 1a 2-a 1=8,解得{a 1=1,a =3.所以{a n }的通项公式为a n =3n -1. (2)由(1)知log 3a n =n -1.故S n =a (a -1)2.由S m +S m +1=S m +3得m (m -1)+(m +1)m =(m +3)(m +2),即m 2-5m -6=0, 解得m =-1(舍去)或m =6.13.解析 (1)证明:由题设得4(a n +1+b n +1)=2(a n +b n ), 即a n +1+b n +1=12(a n +b n ).又因为a 1+b 1=1,所以{a n +b n }是首项为1,公比为12的等比数列. 由题设得4(a n +1-b n +1)=4(a n -b n )+8,即a n +1-b n +1=a n -b n +2. 又因为a 1-b 1=1,所以{a n -b n }是首项为1,公差为2的等差数列. (2)由(1)知,a n +b n =12a -1,a n -b n =2n -1.所以a n =12[(a n +b n )+(a n -b n )]=12a +n -12,b n =12[(a n +b n )-(a n -b n )]=12a -n +12.14.答案 4 解析易知q ≠1,则{a n +b n }的前n 项和S n =na 1+a (a -1)2d +a 1(1-a a )1-a =a 2n 2+(a 1-a 2)n -a 11-a q n +a 11-a=n 2-n +2n-1, ∴a2=1,q =2,即d =2,q =2,∴d +q =4. 15.答案 7解析 令n =2k (k ∈N *),则有a 2k +2+a 2k =6k -1(k ∈N *), ∴a 2+a 4=5,a 6+a 8=17,a 10+a 12=29,a 14+a 16=41, ∴前16项的所有偶数项和S 偶=5+17+29+41=92, ∴前16项的所有奇数项和S 奇=540-92=448, 令n =2k -1(k ∈N *),则有a 2k +1-a 2k -1=6k -4(k ∈N *).∴a2k+1-a1=(a3-a1)+(a5-a3)+(a7-a5)+…+(a2k+1-a2k-1)=2+8+14+…+6k-4=a(2+6a-4)=k(3k-1)(k∈2N*),∴a2k+1=k(3k-1)+a1(k∈N*),∴a3=2+a1,a5=10+a1,a7=24+a1,a9=44+a1,a11=70+a1,a13=102+a1,a15=140+a1,∴前16项的所有奇数项和S奇=a1+a3+…+a15=8a1+2+10+24+44+70+102+140=8a1+392=448.∴a1=7.16.解析(1)设{a n}的公比为q.由题设得a1q+a1q3=20,a1q2=8,(舍去),q2=2.解得q1=12由题设得a1=2,所以{a n}的通项公式为a n=2n.(2)由题设及(1)知b1=0,且当2n≤m<2n+1时,b m=n.所以S100=b1+(b2+b3)+(b4+b5+b6+b7)+…+(b32+b33+…+b63)+(b64+b65+…+b100)=0+1×2+2×22+3×23+4×24+5×25+6×(100-63)=480.17.解析(1)a2=5,a3=7.猜想a n=2n+1.由已知可得a n+1-(2n+3)=3[a n-(2n+1)],a n-(2n+1)=3[a n-1-(2n-1)],……a2-5=3(a1-3).因为a1=3,所以a n=2n+1.(2)由(1)得2n a n=(2n+1)2n,所以S n=3×2+5×22+7×23+…+(2n+1)×2n,①从而2S n=3×22+5×23+7×24+…+(2n+1)×2n+1,②①-②得-S n=3×2+2×22+2×23+…+2×2n-(2n+1)×2n+1,所以S n=(2n-1)2n+1+2.知识拓展解决数列的求和问题,首先要得到数列的通项公式,再根据其特点选择相应的求和方法.数列求和的方法有以下几类:(1)公式法,等差或等比数列的求和用公式法;(2)裂项相消法,形如a n =1a (a +a )(k ≠0),可裂项为a n =1a ·(1a -1a +a);(3)错位相减法,形如c n =a n ·b n ,其中{a n }是等差数列,{b n }是等比数列;(4)分组求和法,形如c n =a n +b n ,其中{a n }是等差数列,{b n }是等比数列;(5)并项求和法.三年模拟练1.BC 因为S 10=S 20,所以10a 1+10×92d =20a 1+20×192d ,解得a 1=-292d.对选项A,因为无法确定a 1和d 的正负,所以无法确定S n 是否有最大值,故A 错误. 对选项B,S 30=30a 1+30×292d =30×(-292a )+15×29d =0,故B 正确.对选项C,a 10+a 22=2a 16=2(a 1+15d )=2(-292a +15a )=d >0,故C 正确.对选项D,a 10=a 1+9d =-292d +182d =-112d ,a 22=a 1+21d =-292d +422d =132d , 因为d <0,所以|a 10|=-112d ,|a 22|=-132d ,所以|a 10|<|a 22|,故D 错误. 故选BC .2.AB 由已知可得a n =4n -3,S n =2n 2-n ,a a a =2n -1,则数列{aaa }为等差数列,则其前10项和为10×(1+19)2=100,故A 正确; 若a 1,a 3,a m 成等比数列,则a 32=a 1·a m ,所以a m =81,即a m =4m -3=81,解得m =21,故B 正确; 因为1aa a a +1=14(14a -3-14a +1),所以∑a =1a1a a a a +1=141-15+15-19+…+14a -3-14a +1=a 4a +1>625,解得n >6,因为n ∈N *,所以n 的最小值为7,故C 错误;由等差数列的性质可知m +n =12,所以1a +16a =112(1a +16a )(m +n )=1121+a a +16aa+16≥112×(17+2×4)=2512,当且仅当a a =16aa,即n =4m =485时取等号,因为m ,n ∈N *,所以n =4m =485不成立,故D 错误.故选AB.3.D 由题意得log a b 1=2,log a b n +1-log a b n =log a a a +1a a=1, ∴b 1=a 2,a a +1a a=a ,∴{b n }是以a 2为首项,a 为公比的等比数列,∴b n =a n +1.∵a n =b n lg b n ,∴a n =a n +1lg a n +1=(n +1)a n +1·lg a ,∵{a n }为递增数列,∴a n +1-a n >0,即[(n +2)a -(n +1)]a n +1·lg a >0.①当a >1时,lg a >0,a n +1>0,∴(n +2)a -(n +1)>0,即a >a +1a +2=1-1a +2,∵1a +2>0,∴1-1a +2<1,∴只需a >1即可满足[(n +2)a -(n +1)]a n +1·lg a >0.②当0<a <1时,lg a <0,a n +1>0,∴(n +2)a -(n +1)<0,即a <1-1a +2,∵1a +2≤13,∴1-1a +2≥23,∴只需0<a <23即可满足[(n +2)a -(n +1)]a n +1·lg a >0.综上所述,实数a 的取值范围为(0,23)∪(1,+∞),故选D .4.答案1a +12a 2-a解析 由题意得,25=13+115, 即22×3-1=13+13×(2×3-1),27=14+128,即22×4-1=14+14×(2×4-1),29=15+145,即22×5-1=15+15×(2×5-1), 由此归纳出22a -1=1a +1a (2a -1)(n ≥3,n ∈N *).又1a +1a (2a -1)=2a -1+1a (2a -1)=22a -1,结论成立,∴22a -1=1a +12a 2-a . 解题模板由数列的前几项归纳其通项公式时,首先要分析项的结构,然后探究结构中的各部分与项的序号n 之间的函数关系,进而求得通项公式. 5.答案 25解析 当n =1时,3S 1=3a 1=(1+m )a 1,解得m =2.当n ≥2时,由{3a a =(a +2)a a ,3a a -1=(a -1+2)a a -1得(n -1)a n =(n +1)a n -1,即a a a a -1=a +1a -1.由累乘法可得a a a 1=a (a +1)2, 又a 1=1,所以a n =a (a +1)2,由a n b n =15,得b n =25a (a +1)=25(1a -1a +1), 所以T n =251-12+(12-13)+…+(1a -1a +1)=25(1-1a +1)<25.因为对任意n ∈N *,λ>T n 恒成立,所以λ≥25,故实数λ的最小值为25. 6.答案 1010解析 设等差数列{a n }的公差为d 1,d 1≠0,等差数列{b n }的公差为d 2,则a 1+a 2+…+a 2021=2021a 1011,b 1+b 2+…+b 2021=2021b 1011, 所以原方程可变为2021x 2-2021a 1011x +2021b 1011=0,由该方程有实数解可得(-2021a 1011)2-4×20212b 1011≥0,即a 10112≥4b 1011.要使方程x 2-a i x +b i =0(i ∈N *,i ≤2021)无解, 则需Δ=(-a i )2-4b i =a a 2-4b i <0(i ∈N *,i ≤2021).设y 1=a a 2=[a 1+(a -1)a 1]2,y 2=4b i =4[b 1+(i -1)d 2](i ∈N *,i ≤2021),易得y 1的图象为开口向上的抛物线的一部分,y 2的图象为直线的一部分, 又i =1011时,y 1≥y 2,所以满足y 1<y 2的i 的取值最多可有1010个, 即无实数解的方程最多有1010个. 7.答案 1010解析 因为{|a n |}是首项和公差均为1的等差数列,所以|a n |=1+n -1=n , 根据等差数列的性质,对任意p ,q ,r ,s ∈N *,若p +q =r +s ,则|a p |+|a q |=|a r |+|a s |, 所以存在满足p +q =r +s ,有a p +a q =-(a r +a s ). 当n =4k 时,S 4k =a 1+a 2+a 3+a 4+a 5+a 6+a 7+a 8+…+a 4k -3+a 4k -2+a 4k -1+a 4k ,为使|S 4k |取得最小值,只需a 2+a 3=-(a 1+a 4),a 5+a 8=-(a 6+a 7),……,a 4k -3+a 4k =-(a 4k -2+a 4k -1), 此时S 4k =k (a 1+a 2+a 3+a 4)=0,即|S 4k |的最小值m 4k =0; 当n =4k +1时,S 4k +1=a 1+(a 2+a 3+a 4+a 5+a 6+a 7+a 8+…+a 4k -3+a 4k -2+a 4k -1+a 4k +a 4k +1),为使|S 4k +1|取得最小值,同n =4k 时,只需S 4k +1=a 1+k (a 2+a 3+a 4+a 5)=a 1, 此时S 4k +1=a 1,即|S 4k +1|的最小值m 4k +1=1; 当n =4k +2时,S 4k +2=a 1+a 2+(a 3+a 4+a 5+a 6+a 7+a 8+…+a 4k -3+a 4k -2+a 4k -1+a 4k +a 4k +1+a 4k +2),为使|S 4k +2|取得最小值,同n =4k 时,只需S 4k +2=a 1+a 2+k (a 3+a 4+a 5+a 6)=a 1+a 2, 此时S 4k +1=a 1+a 2,当a 1=1,a 2=-2时,可使|S 4k +2|取得最小值m 4k +2=1; 当n =4k +3时,S 4k +3=a 1+a 2+a 3+(a 4+a 5+a 6+a 7+a 8+…+a 4k -3+a 4k -2+a 4k -1+a 4k +a 4k +1+a 4k +2+a 4k +3),为使|S 4k +3|取得最小值,同n =4k 时,只需S 4k +3=a 1+a 2+a 3+k (a 4+a 5+a 6+a 7)=a 1+a 2+a 3,当a 1=1,a 2=2,a 3=-3时,可使|S 4k +3|取得最小值m 4k +3=0.所以m n 以4为周期,因此m 1+m 2+…+m 2020=505×(m 1+m 2+m 3+m 4)=1010.8.解析 设等比数列{b n }的公比为q.因为对任意的n ∈N *,都有2b n +2=b n +1+3b n , 所以2q 2=q +3,解得q =-1或q =32.因为对任意的n ∈N *,都有b n >0,所以q >0,从而q =32.又b 1=1,所以b n =(32)a -1.假设存在k ∈N *,使得对任意的n ∈N *,都有a n b k ≤a k b n ,即a a a a≤aa a a.记c n =aa a a,n ∈N *.下面分别选择①②③作为条件进行研究.选择①.因为a n +1=12a n +1,所以a n +1-2=12(a n -2). 又a 1=1,所以a 1-2=-1≠0,所以a n -2≠0,从而a a +1-2a a -2=12, 所以数列{a n -2}是以a 1-2=-1为首项,12为公比的等比数列,则a n -2=-(12)a -1,即a n =2-(12)a -1,所以c n =a a a a =2a -13a -1,从而a a +1a a=2a +1-13(2a -1).由2a +1-13(2a-1)≤1得2n≥2,解得n ≥1,当n =1时,c 1=c 2,当n >1时,c n +1<c n ,所以当n 的值为1或2时,c n 取得最大值,即aa a a取得最大值.所以对任意的n ∈N *,都有a a a a≤a 2a 2=a1a 1,即a n b 1≤a 1b n ,a n b 2≤a 2b n ,所以存在k 的值为1或2,使得对任意的n ∈N *,都有a n b k ≤a k b n . 选择②.因为a n +1=a n +2,所以a n +1-a n =2,所以数列{a n }是以1为首项,2为公差的等差数列,又a 1=1,所以a n =1+2(n -1)=2n -1, 所以c n =a a a a =(2n -1)(23)a -1>0,从而a a +1a a=2(2a +1)3(2a -1).由2(2a +1)3(2a -1)≤1得2n ≥5,解得n ≥52,当n ≤2时,c n +1>c n ,当n ≥3时,c n +1<c n , 又c 2=2,c 3=209,所以当n =3时,c n 取得最大值,即aa a a取得最大值.所以对任意的n ∈N *,都有a a a a≤a3a 3,即a n b 3≤a 3b n .所以存在k 的值为3,使得对任意的n ∈N *,都有a n b k ≤a k b n . 选择③.因为S n =2a n -1,所以S n +1=2a n +1-1,从而a n +1=S n +1-S n =2a n +1-1-(2a n -1)=2a n +1-2a n ,即a n +1=2a n . 又a 1=1>0,所以a n >0,且a a +1a a=2, 从而数列{a n }是以1为首项,2为公比的等比数列,所以a n =2n -1, 所以c n =a a a a =(43)a -1>0,从而a a +1a a =43>1,所以c n +1>c n ,所以不存在满足题意的k. 9.解析 (1)∵2S n =(n +1)a n ,① ∴当n ≥2时,2S n -1=na n -1,② ①-②并化简,得2a n =(n +1)a n -na n -1, 即(n -1)a n =na n -1(n ≥2), 又a 1=1≠0,∴a n ≠0,∴a a a a -1=aa -1(n ≥2), ∴a 2a 1=21,a 3a 2=32,……,a a a a -1=a a -1, ∴a n =a 2a 1·a 3a 2·…·a a a a -1·a 1=21·32·…·aa -1·1=n , 经检验,当n =1时,a 1=1也满足上式, ∴a n =n.(2)由(1)知a n =n ,设f (n )=a 3-2a 3·a 4-2a 4·…·a a -2a a·√2a +1(n ≥3,n ∈N *), 则f (n +1)-f (n )=a 3-2a 3·a 4-2a 4·…·a a -2a a ·(a a +1-2a a +1·√2a +3-√2a +1) =a 3-2a 3·a 4-2a 4·…·a a -2a a ·(a -1)√2a +3-(a +1)√2a +1a +1=a 3-2a 3·a 4-2a 4·…·a a -2a a ·√2a 3-a 2-4a +3-√2a 3+5a 2+4a +1a +1<0, ∴f (n )在n ≥3,n ∈N *上单调递减, ∴f (n )max =f (3)=√73,∴a >f (3)=√73,即实数a 的取值范围是(√73,+∞). (3)T n <23.证明如下:∵a n =n ,∴c n =(11+a a)2=(11+a )2=1a 2+2a +1<1a (a +2)=12(1a -1a +2),∴T n =c 1+c 2+c 3+…+c n =14+c 2+c 3+…+c n <14+1212-14+(13-15)+(14-16)+…+(1a -1a +2) =14+12(12+13-1a +1-1a +2) =23-12(1a +1+1a +2)<23, 即T n <23.10.解析 (1)1,3,5,6.(答案不唯一)(2)证明:设长度为q 且末项为a a 0的一个递增子列为a a 1,a a 2,…,a a a -1,a a 0. 由p <q ,得a a a ≤a a a -1<a a 0.因为{a n }的长度为p 的递增子列末项的最小值为a a 0, 且a a 1,a a 2,…,a a a 是{a n }的长度为p 的递增子列, 所以a a 0≤a a a .所以a a 0<a a 0. (3)由题设知,所有正奇数都是{a n }中的项.先证明:若2m 是{a n }中的项,则2m 必排在2m -1之前(m 为正整数). 假设2m 排在2m -1之后.设a a 1,a a 2,…,a a a -1,2m -1是数列{a n }的长度为m 且末项为2m -1的递增子列,则a a 1,a a 2,…,a a a -1,2m -1,2m 是数列{a n }的长度为m +1且末项为2m 的递增子列,与已知矛盾.再证明:所有正偶数都是{a n }中的项.假设存在正偶数不是{a n }中的项,设不在{a n }中的最小的正偶数为2m.因为2k 排在2k -1之前(k =1,2,…,m -1),所以2k 和2k -1不可能在{a n }的同一个递增子列中. 又{a n }中不超过2m +1的数为1,2,…,2m -2,2m -1,2m +1,所以{a n }的长度为m +1且末项为2m +1的递增子列个数至多为2×2×2×…×2⏟ (a -1)个×1×1=2m -1<2m,与已知矛盾.最后证明:2m 排在2m -3之后(m ≥2为整数).假设存在2m (m ≥2),使得2m 排在2m -3之前,则{a n }的长度为m +1且末项为2m +1的递增子列的个数小于2m,与已知矛盾.综上,数列{a n }只可能为2,1,4,3,…,2m -3,2m ,2m -1,…. 经验证,数列2,1,4,3,…,2m -3,2m ,2m -1,…符合条件. 所以a n ={a +1,a 为奇数,a -1,a 为偶数.主编点评本题通过对数列中新概念的理解,考查逻辑推理、知识的迁移应用能力,重点考查逻辑推理、数学抽象的核心素养,渗透数学应用与创新意识,以及由特殊到一般的分类整合思想.。
九师联盟 河南省名校联盟2020-2021学年高三9月联考语文试题

河南省名校联盟2020~2021学年高三9月质量检测语文考生注意:1.本试卷满分150分,考试时间150分钟。
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。
选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0,5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
4.本卷命题范围:高考范围。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
关于美育观念的当下认知,我们和远古时代的审美态度发生了很大的变化。
简言之,传统的审美着眼于时间性的体悟和内涵感知,可以称为“静观审美”。
网络时代逐渐产生的审美走向强调能在变化中抓人眼球,否则就难以得到关注,我们叫“流观审美”。
静观审美在观念形态上与古代的仕女画、花鸟画、宫廷画以及春秋战国时期产生的韶乐艺术相适应,创作期待的是能够察之表现的意味,创作自身的情趣融入作品之中而自得。
作品培育的是人的一种静的心态,摒弃万物的嘈杂来静默地感知美。
而我们长期熏陶或受教于这种审美观念,形成的就是对审美主要形态、主要态度和主要的观赏方式的意识。
在网络时代,AI智能的时代,不仅是虚拟世界的意识到来,就是此前兴起的二次元的年轻人意识时代,审美感知也发生了很大的变化。
流观审美在年轻一代中培育出只信赖取悦的对象,理论家推波助澜地加以眼球注意力的解释,经济取悦于这一习俗偏斜到助力的程度,绘画书法变成了拍卖确定高低,音乐以点击率多少确定走红,电视借参与之名为一些上口的通俗作品开传播之风,电影把小鲜肉当成了卖座的不二法门,纸质媒体和网络媒体将娱乐明星出位离婚作为取悦受众的关注新闻。
所谓流观审美固然有需要取得受众的合理大众需求意味,但其实质首先是动感取悦而静不下来倾听观看,人们的某种兴趣需要造就差异的凸显才能获得关注,和需要吻合的就会成为捕捉对象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省豫南九校2020-2021学年高二上学期第三次联考数学(文)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.如果a b >,那么下列不等式中正确的是( ) . A .11a b< B .22a b >C .a c b c >D .2211a bc c >++ 2.已知命题p :0x ∀>,lg 0x >,则p ⌝是() A .0x ∀>,lg 0x ≤ B .00x ∃>,0lg 0x <C .0x ∀>,lg 0x <D .00x ∃>,0lg 0x ≤3.方程221mx y +=表示焦点在y 轴上的椭圆,则m 的取值范围是( ) A .()1,+∞B .()0,∞+C .()0,1D .()0,24.在ABC 中,若(sin sin )(sin sin )sin (sin sin )A B A B C C B +-≤-,则A 的取值范围是( ) A .0,6π⎛⎤⎥⎝⎦B .,6ππ⎡⎤⎢⎥⎣⎦C .0,3π⎛⎤ ⎥⎝⎦D .,3ππ⎡⎫⎪⎢⎣⎭5.已知数列{}n a 满足递推关系:11n n n a a a +=+,112a =,则2020a =( ) A .12019B .12020 C .12021D .120226.若实数x ,y 满足约束条件22022x y x y y +-≥⎧⎪+≤⎨⎪≤⎩,则x y -的最大值等于( )A .2B .1C .-2D .-47.命题“[1,2]x ∀∈,220x a -≥”为真命题的一个充分不必要条件是( ) A .1a ≤ B .2a ≤ C .3a ≤D .4a ≤8.若直线220x y 经过椭圆的一个焦点和一个顶点,则该椭圆的标准方程为()A .2215x y +=B .22145x y +=C .2215x y +=或22145x y +=D .以上答案都不对9.已知△ABC 的内角A B C ,,的对边分别为a b c ,,,且22()a b c ab +=+,30B =︒,4a =,则ABC ∆的面积为( )A .4B .C .D .10.如图所示的数阵称为杨辉三角.斜线AB 上方箭头所示的数组成一个锯齿形的数列:12336410⋯,,,,,,,记这个数列的前n 项和为n S ,则16S 等于( ).A .128B .144C .155D .16411.已知各项都为正数的等比数列{}n a 满足7652a a a =+,存在两项,m n a a 使得14a =,则112n m n+++的最小值为( ) A .98 B .32C .256D .4312.椭圆C :22x a +22y b=1(a >b >0)的长轴长、短轴长和焦距成等差数列,若点P 为椭圆C 上的任意一点,且P 在第一象限,O 为坐标原点,F (3,0)为椭圆C 的右焦点,则OP •PF 的取值范围为( ) A .()16,10-- B .3910,4⎛⎫--⎪⎝⎭C .3916,4⎛⎤--⎥⎝⎦D .39,4⎛⎤-∞-⎥⎝⎦二、填空题13.已知等差数列{}n a 的通项公式418n a n =-,记其前n 项和为n S ,那么当n =________时,n S 取得最小值.14.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,已知6b =,6A π=,若该三角形有两解,则a 的取值范围是______.15.若∃01,22x ⎡⎤∈⎢⎥⎣⎦,使得2002+10x x λ<-成立是假命题,则实数λ的取值范围是________.16.已知椭圆C :()222210x y a b a b+=>>,1F ,2F 分别为椭圆的左、右焦点,若椭圆C 上存在点()()000,0P x y x ≥使得1260PF F ∠=︒,则椭圆的离心率的取值范围为______.三、解答题17.已知m R ∈,命题p ;存在[]01,1x ∈-,使得0112x m ⎛⎫≤- ⎪⎝⎭成立;命题q :“方程22212x y m m+=表示焦点在y 轴上的椭圆”. (1)若p 为真命题,求m 的取值范围; (2)若p q ∧为假,p q ∨为真,求m 的取值范围. 18.设函数2()2f x mx mx =--(1)若对于一切实数()0f x <恒成立,求m 的取值范围;(2)若对于[1,3],()2(1)x f x m x ∈>-+-恒成立,求m 的取值范围. 19.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足cos 2cos 22sin sin 33C A C C ππ⎛⎫⎛⎫-=+⋅- ⎪ ⎪⎝⎭⎝⎭.(1)求角A 的值;(2)若a =b a ≥,求12b c -的取值范围.20.设12,F F 分别是椭圆22221(0)x y a b a b+=>>的左右焦点,M 是C 上一点且2MF 与x 轴垂直,直线1MF 与C 的另一个交点为N .(1)若直线MN 的斜率为34,求C 的离心率;(2)若直线MN 在y 轴上的截距为2,且15MN F N =,求,a b . 21.已知数列{}n a 是首项为1,公比为12的等比数列,12n n S a a a =+++.(1)若n S 、98、1n a -成等差数列,求n 的值; (2)证明*n N ∀∈,有312112231222112n n n n a a a S S S S S S ++++++<-.22.已知椭圆2222:1x y C a b+=(0a b >>)的焦距为(2,0)A .(Ⅰ)求椭圆C 的方程;(Ⅱ)若点(0,1)B ,设P 为椭圆C 上位于第三象限内一动点,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N ,求证:四边形ABNM 的面积为定值,并求出该定值.参考答案1.D 【分析】通过反例1a =,1b =-,0c 可排除,,A B C ;利用不等式的性质可证得D 正确.【详解】若1a =,1b =-,则1111a b=>=-,221a b ==,则A ,B 错误; 若a b >,0c,则0a c b c ==,则C 错误;211c +≥ 21011c ∴<≤+,又a b > 2211a bc c ∴>++,则D 正确. 故选D 【点睛】本题考查根据不等式的性质比较大小的问题,对于此类问题通常采用排除法来进行排除,属于基础题. 2.D 【分析】根据全称命题的否定方法,结合已知中的原命题,可得答案. 【详解】∵命题p :∀x >0,总有lgx >0, ∴命题¬p 为:∃x 0>0,使得lg x 0≤0, 故选:D . 【点睛】本题考查了命题的否定,考查了推理能力,属于基础题. 3.A 【分析】将椭圆方程化为标准方程,根据题中条件列出关于m 的不等式,解出该不等式可得出实数m 的取值范围. 【详解】椭圆的标准方程为2211x y m+=,由于该方程表示焦点在y 轴上的椭圆,则101m<<,解得1m ,因此,实数m 的取值范围是()1,+∞,故选A. 【点睛】本题考查椭圆的标准方程,考查根据方程判断出焦点的位置,解题时要将椭圆方程化为标准形式,结合条件列出不等式进行求解,考查运算求解能力,属于中等题. 4.C 【分析】利用正弦定理得到222a b c bc -≤-,再利用余弦定理得到1cos 2A ≥,计算得到答案.【详解】 根据正弦定理:222(sin sin )(sin sin )sin (sin sin )A B A B C C B a b c bc +-≤-⇒-≤-根据余弦定理:2222212cos cos 023a b c bc A b c bc A A π=+-≤+-⇒≥⇒<≤ 故答案选C 【点睛】本题考查了正弦定理和余弦定理,意在考查学生对于正余弦定理的灵活运用和计算能力. 5.C 【分析】利用数列递推关系,结合等差数列的定义得数列1n a ⎧⎫⎨⎬⎩⎭是首项为2,公差为1的等差数列,再利用等差数列的通项公式计算即可. 【详解】 解:11nn n a a a +=+, 1111n na a +∴-=, 又112a =,∴数列1n a ⎧⎫⎨⎬⎩⎭是首项为2,公差为1的等差数列,即11n n a =+20201220192021a ∴=+=,即202012021a =. 故选C . 【点睛】本题考查了数列递推关系,等差数列的概念和等差数列的通项公式,属于基础题. 6.A 【解析】 【分析】作出可行域,平移目标函数,找到取最大值的点,然后可求最大值. 【详解】根据题意作出可行域如图:平移直线:0l x y -=可得在点A 处取到最大值,联立22020x y x y +-=⎧⎨+-=⎩可得(2,0)A ,代入x y -可得最大值为2,故选A.【点睛】本题主要考查线性规划,作出可行域,平移目标函数,求出最值点是主要步骤,侧重考查直观想象和数学运算的核心素养. 7.A 【分析】“[1,2]x ∀∈,220x a -≥”为真命题可转化为22,[1,2]x a x ≥∈恒成立,可得2a ≤,根据充分必要条件可选出答案. 【详解】若“[1,2]x ∀∈,220x a -≥”为真命题,可得22,[1,2]x a x ≥∈恒成立 只需()2min22a x≤=,所以1a ≤时,[1,2]x ∀∈,220x a -≥”为真命题,“[1,2]x ∀∈,220x a -≥”为真命题时推出2a ≤,故1a ≤是命题“[1,2]x ∀∈,220x a -≥”为真命题的一个充分不必要条件, 故选:A . 【点睛】本题主要考查了不等式恒成立问题,以及探求命题的充分不必要条件,属于常考题型. 8.C 【分析】利用椭圆的简单性质求解,题中没有明确焦点在x 轴还是在y 轴上,所以分情况讨论. 【详解】解:设焦点在x 轴上,椭圆的标准方程为22221(0)x ya b a b+=>>∴焦点坐标为(,0)c -,(,0)c ,顶点坐标为(0,)b ,(0,)b -;椭圆的a ,b ,c 关系:;222a c b -= 直线220x y 恒过定点()0,1和()2,0-∴直线220x y 必经过椭圆的焦点(,0)c -,和顶点(0,)b带入直线方程:222200220c b a b c -+=⎧⎪-+=⎨⎪-=⎩解得:2c =,1b =,a =∴焦点在x 轴上,椭圆的标准方程为2215x y +=; 当设焦点在y 轴,椭圆的标准方程为22221(0)y xa b a b+=>>∴焦点坐标为(0,)c -,(0,)c ,顶点坐标为(,0)b -,(,0)b ;椭圆的a ,b ,c 关系:222a c b -=直线220x y 恒过定点()0,1和()2,0-∴直线220x y 必经过椭圆的焦点(0,)c ,和顶点(,0)b -带入直线方程222022020c b a b c -+=⎧⎪-+=⎨⎪-=⎩解得:1c =,2b =,a =∴焦点在y 轴上,椭圆的标准方程为22145x y+=.故选:C . 【点睛】本题考查椭圆方程的求法,题中没有明确焦点在x 轴还是在y 轴上,要分情况讨论,解题时要注意椭圆的简单性质的合理运用,属于基础题. 9.C 【分析】根据余弦定理和三角形面积公式求解. 【详解】因为22()a b c ab +=+,即222a b c ab +-=-.所以2221cos 22a b c C ab +-==-,所以120C =︒,又30B =︒,所以30.A B ==即4a b ==,故ABC ∆的面积114422S absinC ==⨯⨯=故选C. 【点睛】本题考查运用余弦定理和面积公式解三角形,属于基础题. 10.D 【分析】由图中锯齿形数列,发现规律:奇数项的第n 项可表示成正整数的前n 项和的形式,偶数项构成以2为首项,公差是1的等差数列,由此结合等差数列的通项与求和公式,即可求出. 【详解】由图中锯齿形数列,发现:135151,312,6123,,1238a a a a ===+==++=++++,而246162,3,4,9a a a a ====,所以16[112123++1+28)](2349)S =++++++++++++()()((29)8(1827367281)1642+⨯=⨯+⨯+⨯++⨯+⨯+=, 故选D. 【点睛】本题主要考查了数列的前n 项和,等差数列的通项与求和公式,归纳推理,属于中档题. 11.B 【分析】根据7652a a a =+14a =找到mn 、的关系式,最后根据基本不等式求解112n m n+++的最小值. 【详解】因为7652a a a =+,所以2q或1q =-,又0n a >,所以2q ;14a =可知:14a =,所以6m n +=,则()28m n ++=;()2111111122+1=112282822m n n m m n n m n m n m n m n m n +++++⎛⎫⎡⎤+=+⋅++=++++ ⎪⎢⎥+++++⎝⎭⎣⎦121321218282n m m n ⎛+⎛⎫=+++≥++= ⎪ +⎝⎭⎝,取等号时+2n m =,即24m n =⎧⎨=⎩, 故选B. 【点睛】基本不等式中“1”的妙用: 已知(0)x y m m +=>,求解(0,0)a ba b x y+>>的最小值的方法:111a b a b x y a b ay bx a b a b a b x y x y m x y m x y m m ⎛⎛⎫⎛⎫⎛⎫+++=⋅+=⋅+=+++≥++= ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝,取等号时22ay bx =.12.C 【分析】根据椭圆C 的长轴长、短轴长和焦距成等差数列,(3,0)F 为椭圆C 的右焦点及椭圆中222a b c =+解方程组求得a 、b 、c ,得到椭圆方程.设出点P ,根据向量数量积转化为关于横坐标m 的二次函数,即可求得取值范围. 【详解】因为椭圆C 的长轴长、短轴长和焦距成等差数列 所以224a c b += ,即2a c b +=(3,0)F 为椭圆C 的右焦点,所以c=3在椭圆中,222a b c =+所以22223a c b a c b c ⎧=+⎪+=⎨⎪=⎩,解方程组得543a b c =⎧⎪=⎨⎪=⎩所以椭圆方程为2212516x y +=设(,)P m n ()05m <<则2212516m n +=,则22161625n m =-OP PF ⋅=()(),3,m n m n --223m m n =--221631625m m m ⎛⎫=--- ⎪⎝⎭2931625m m =-+- 2925392564m ⎛⎫=--- ⎪⎝⎭因为05m <<,所以当256m =时,OP PF ⋅取得最大值为394-当m 趋近于0时,OP PF ⋅的值趋近于-16 所以OP PF ⋅的取值范围为39(-16,-]4所以选C 【点睛】本题考查了椭圆性质的综合应用,向量在解析几何中的用法,属于中档题. 13.4. 【分析】由通项公式可知1a ,n a ,代入等差数列前n 项和公式,利用二次函数相关知识求最值即可. 【详解】因为418n a n =-, 所以114a =-,2(14418)2162n n S n nn -+-⋅==-,因为对称轴方程为4n =, 所以当4n =时,n S 取得最小值. 【点睛】本题主要考查了等差数列的通项公式与前n 项和公式,二次函数的最值,属于中档题. 14.()3,6 【分析】由正弦定理求出sin B ,三角形有两解确定B 角范围,即可求解. 【详解】∵在ABC ∆中,6b =,6A π=,∴由正弦定理得16sin 32sin b A B a a a ⨯⋅===, ∵6A π=,∴506B π<<,要使三角形有两解,得到:566B ππ<<,且2B π≠,即1sin 12B <<,∴1312a<<,解得:36a <<. 故答案为:()3,6. 【点睛】本题考查正弦定理解三角形,考查三角形解的个数求参数,属于中档题.15.(-∞【分析】将命题转化为1,22x ⎡⎤∀∈⎢⎥⎣⎦,使得12+x xλ≤恒成立是真命题,令函数()12+f x x x=,对其求导,讨论导函数取正负的区间,得出所构造的函数的单调性,从而求出最值,利用不等式恒成立的思想,得出实数λ的取值范围. 【详解】因为∃01,22x ⎡⎤∈⎢⎥⎣⎦,使得2002+10x x λ<-成立是假命题,所以1,22x ⎡⎤∀∈⎢⎥⎣⎦,使得22+10x x λ≥-恒成立是真命题,即1,22x ⎡⎤∀∈⎢⎥⎣⎦,使得12+x x λ≤恒成立是真命题,令()12+f x x x=,则()'212f x x =- ,当1,22x ⎛⎫∈ ⎪ ⎪⎝⎭时,()'0f x <,函数()f x 在1,22⎛⎫⎪ ⎪⎝⎭上单调递减,当,22x ⎛⎫∈ ⎪ ⎪⎝⎭时,()'>0f x ,函数()f x 在,22⎛⎫⎪ ⎪⎝⎭上单调递增,所以()2f x f ⎛≥=⎝⎭λ≤故答案为:(-∞.【点睛】本题考查全称命题和特称命题的关系,运用参变分离的方法求参数的范围,属于中档题. 16.10,2⎛⎤ ⎥⎝⎦【分析】根据已知,只需12PF F ∠的最大角不小于060,当动点P 在椭圆长轴端点处沿椭圆弧向短轴端点运动时12PF F ∠逐渐增大,当且仅当P 为椭圆的上(下)顶点时12PF F ∠最大,可求出,a c 不等量关系,即可求解.【详解】依题意,当点P 在椭圆的上(下)顶点处时,12PF F ∠最大. 要满足椭圆C 上存在点()()000,0P x y x ≥使得1260PF F ∠=︒, 则()12max 9060PF F ︒>∠≥︒,所以()012max 1cos90cos 602cos PF F ≤<∠︒=, 即:102c a <≤ 故椭圆离心率的取值范围为102e <≤. 故答案为:10,2⎛⎤ ⎥⎝⎦.【点睛】本题考查了直角三角形的三角函数和椭圆的简单几何性质,考查数形结合思想,属于中档题. 17.(1)1m (2)(](),01,2-∞【分析】(1)根据函数单调性,求出函数的最大值,即可得出结论;(2)求出命题,p q 为真时m 的范围,再由命题,p q 一真一假,即可求出m 的取值范围. 【详解】(1)存在[]01,1x ∈-,使得0112x m ⎛⎫≤- ⎪⎝⎭成立,∴01max 1111122x m -⎡⎤⎛⎫⎛⎫≤-=-=⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,命题p 为真时,1m . (2)命题q 为真,则220m m >>,解得:02m <<. ∵p q ∧为假,p q ∨为真,∴p ,q 中一个是真命题,一个是假命题. 当p 真q 假时,则102m m m ≤⎧⎨≤≥⎩或,解得0m ≤;当p 假q 真时,102m m >⎧⎨<<⎩,解得12m <<.综上,m 的取值范围为(](),01,2-∞.【点睛】本题考查特称命题成立求参数范围,以及椭圆的性质,考查复合命题真假判断,属于基础题. 18.(1)(8,0]-(2)2m > 【分析】(1)由不等式220mx mx --<恒成立,结合二次函数的性质,分类讨论,即可求解; (2)要使对于[1,3],()2(1)x f x m x ∈>-+-恒成立,整理得只需221xm x x >-+恒成立,结合基本不等式求得最值,即可求解. 【详解】(1)由题意,要使不等式220mx mx --<恒成立,①当0m =时,显然20-<成立,所以0m =时,不等式220mx mx --<恒成立;②当0m ≠时,只需2080m m m <⎧⎨∆=+<⎩,解得80m -<<, 综上所述,实数m 的取值范围为(8,0]-.(2)要使对于[1,3],()2(1)x f x m x ∈>-+-恒成立, 只需22mx mx m x -+>恒成立, 只需()212m x x x -+>,又因为22131024x x x ⎛⎫-+=-+> ⎪⎝⎭, 只需221xm x x >-+, 令222211111x y x x x x x x===-+-++-,则只需max m y >即可因为12x x +>=,当且仅当1x x =,即1x =时等式成立;因为[1,3]x ∈,所以max 2y =,所以2m >. 【点睛】本题主要考查了含参数的不等式的恒成立问题的求解,其中解答中把不等式的恒成立问题转化为函数的最值问题是解答的关键,着重考查了分类讨论思想,以及转化思想的应用,属于基础题.19.(1)3A π=或23π(2)⎣ 【分析】(1)利用三角函数恒等变换的应用化简已知可解得:sin A =,结合A 为ABC ∆的内角,可得A 的值.(2)由b a ≥,由(1)可得3A π=,又a =由正弦定理可得:2sin sin b cB C==,从而利用三角函数恒等变换的应用可得: 12b c-6B π⎛⎫=- ⎪⎝⎭,结合662B πππ≤-<,可得12b c -的取值范围.【详解】解:(1)由已知得2222312sin 2sin 2cos sin 44A C C C ⎛⎫-=-⎪⎝⎭,化简得sin A =,因为A 为ABC ∆的内角,所以sin 2A =,故3A π=或23π. (2)因为b a ≥,所以3A π=.由正弦定理得2sin sin sin b c a B C A===,得2sin b B =,2sin c C =,故12sin sin 2b c B C -=-=22sin sin 3B B π⎛⎫--⎪⎝⎭3sin 226B B B π⎛⎫=-=- ⎪⎝⎭. 因为b a ≥,所以233B ππ≤<,则662B πππ≤-<,所以1262b c B π⎛⎫-=-∈ ⎪⎝⎭⎣. 【点睛】本题主要考查了三角函数恒等变换的应用,考查了正弦定理,正弦函数的图象和性质在解三角形中的应用,属于中档题. 20.(1)12;(2)7,a b == 【详解】(1)记c =()()12,0,,0F c F c -,由题设可知2,b M c a ⎛⎫ ⎪⎝⎭, 则12232324MN F M b a k k b acc ===⇒=,2213,2()2c ca c ac e e a a∴-=⇒====-或舍去;(2)记直线MN 与y 轴的交点为()D 0,2,则2244bMF a=⇒=①,11135,2,12c MN F N DF F N N ⎛⎫=∴=⇒-- ⎪⎝⎭,将N 的坐标代入椭圆方程得2229114c a b+=②由①②及222c a b =-得2249,28a b ==,故7,a b ==.考点:1.椭圆方程;2.直线与椭圆的位置关系.21.(1)3n =;(2)详见解析.【分析】(1)先利用等比数列的通项公式和前n 项和公式分别求出n a 、n S ,由题意条件得出194n n S a -+=,即为111292224n n ---+=,从而解出n 的值; (2)将112k k k a S S ++裂项为()111112222k k k k k k k k k S S a S S S S S S +++++-==-,利用裂项法求出31212231222n n n a a a S S S S S S +++++,再利用放缩法可得出所证不等式.【详解】(1)由等比数列的通项公式得1111122n n n a --⎛⎫=⨯=⎪⎝⎭, 由等比数列的前n 项和公式得11111221212n n n S -⎛⎫⨯- ⎪⎝⎭==--, n S 、98、1n a -成等差数列,所以,194n n S a -+=,即121192224n n ---+=,化简得11124n -=,解得3n =; (2)()()1111122221,2,3,k k k k k k k k k S S a k S S S S S S +++++-==-=⋅⋅⋅,且11212n n n S ++-=,因此,31212231122311122222222222n n n n n n a a a S S S S S S S S S S S S S S ++++++⋅⋅⋅+=-+-++-=- 111121*********n n n n ++++=-=-<---.【点睛】本题考查等比数列通项公式与求和公式,同时也考查了裂项求和法,解题时要熟悉裂项求和法对数列通项结构的要求,考查运算求解能力,属于中等题.22.(Ⅰ)2214x y +=;(Ⅱ)四边形ABNM 的面积S 为定值2;证明见解析. 【分析】(Ⅰ)先由题意得到c =2a =,从而可求出b ,进而可得椭圆方程;(Ⅱ)先设()00,P x y (00x <,00y <),根据椭圆方程得到220044x y +=,再由题意得到直线PA 的方程为()0022y y x x =--,表示出BM ,再由直线PB 的方程为0011y y x x -=+,表示出AN ,根据四边形ABNM 的面积12S AN BM =⋅,化简整理,即可得出结论成立. 【详解】(Ⅰ)由题意,2c =,且2a =,求得c =1b =.所以椭圆C 的方程为2214x y +=;(Ⅱ)设()00,P x y (00x <,00y <),则220044x y +=.又()2,0A ,()0,1B ,所以直线PA 的方程为()0022y y x x =--. 令0x =,得0022M y y x =--,从而002112M y BM y x =-=+-.直线PB 的方程为0011y y x x -=+. 令0y =,得001N x x y =--,从而00221N x AN x y =-=+-.所以四边形ABNM 的面积()220000000000000024448411212212222x y x y x y x y S AN BM y x x y x y ⎛⎫⎛⎫++--+=⋅=+⋅+= ⎪ ⎪----+⎝⎭⎝⎭ 000000004222222x y x y x y x y --+==--+()()所以四边形ABNM 的面积S 为定值2. 【点睛】本题主要考查根据a b c ,,求椭圆方程,以及椭圆中的定值问题,熟记椭圆的标准方程,以及椭圆的简单性质,即可求解,属于常考题型.。
