人教版九年级下册第二十七章《相似》27.3《位似》同步练习
九年级数学下册第二十七章相似27.3位似习题3新版新人教版(含参考答案)

九年级数学下册练习题:位似1.两个相似的图形,如果对应顶点的连线________,对应边________,那么这两个图形叫做________,这个点叫做________.2.位似图形的性质:(1)位似图形是________图形;(2)位似图形对应顶点的连线________,对应边________;(3)位似图形对应顶点与位似中心的距离的比等于它们的________.3.位似与相似:位似图形是两个具有特殊位置关系的相似图形;位似图形一定是________图形,但相似图形不一定是________图形;相似是一种图形变换,位似也是一种图形变换,位似变换是相似变换的特例.4.已知△ABC∽△DEF,下列图形中,这两个三角形不一定存在位似关系的是( )A.B.C.D.5.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的.若AB︰FG=2︰3,则下列结论正确的是( )A.2DE=3MNB.3DE=2MNC.3∠A=2∠FD.2∠A=3∠F6.如图,A′B′∥AB,B′C′∥BC,且OA′︰A′A=4︰3,则△ABC与________是位似图形,相似比为________;△OA′B′与________是位似图形,相似比为________.7.如图,△ABC与△DEF是位似图形,相似比为23,AB=4,则DE=________.8.(1)如图①,△ABC与△A′B′C′是位似图形,且相似比是12.若AB=2cm,则A′B′=________cm在图中画出位似中心O;(2)如图②,画出以点O为位似中心,把四边形ABCD缩小到原来的12得到的图形.9.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且12 3PA PA,则AB︰A1B1的值为( )A.23B.32C.35D.5310.如图,△DEF是△ABC经过位似变换得到的,点O是位似中心,D.E.F分别是线段OA.OB.OC 的中点,则△DEF与△ABC的面积之比是( )A.1︰6B.1︰5C.1︰4D.1︰211.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′.已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是________.12.如图,△OAB与△ODC是位似图形.(1)AB与CD平行吗?请说明理由;(2)如果OB=3,OC=4,OD=3.5,试求△OAB与△ODC的相似比及OA的长.13.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.(1)画出位似中心O;(2)求△A′B′C′与△ABC的相似比.14.如图,△ABC与△A′B′C′是位似图形,点O为位似中心,点A.B.A′、B′、O共线.(1)AC与A′C′平行吗?请说明理由;(2)若AB=2A′B′,OC′=5,求CC′的长.参考答案1.相交于一点互相平行位似图形位似中心2.(1)相似(2)相交于一点互相平行(3)相似比3.相似位似4.D5.B6.△A′B′C′74△OAB 4 77.68.(1)4 如图,点O即为位似中心(2)略9.B10.C11.1 212.(1)AB∥CD 理由:∵△OAB与△ODC是位似图形,∴△OAB∽△ODC.∴∠A=∠D.∴AB ∥CD.(2)∵OB︰OC=3︰4,∴△OAB与△ODC的相似比为3 4.∴34OAOD=.∴218OA=13.(1)如图(2)△A′B′C′与△ABC的相似比为214.(1)AC∥A′C′ 理由:∵△ABC与△A′B′C′是位似图形,∴△ABC∽△A′B′C′.∴∠A=∠C′A′B′.∴AC∥A′C′.(2)∵△ABC与△A′B′C′是位似图形,∴22OC AB A BOC A B A B''==='''''.∵OC′=5,∴OC=10.∴CC′=OC-OC′=10-5=5。
九年级数学下册 第27章 图形的相似 27.3 位似同步测试 (新版)新人教版-(新版)新人教版初中
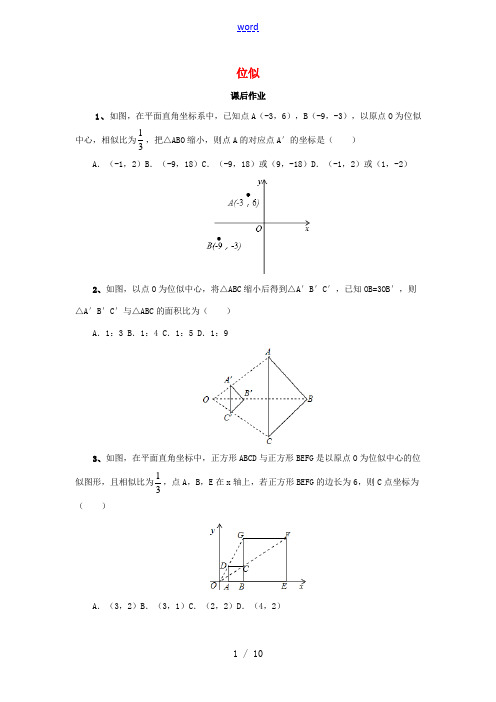
位似课后作业1、如图,在平面直角坐标系中,已知点A (-3,6),B (-9,-3),以原点O 为位似中心,相似比为31,把△ABO 缩小,则点A 的对应点A′的坐标是( ) A .(-1,2)B .(-9,18)C .(-9,18)或(9,-18)D .(-1,2)或(1,-2)2、如图,以点O 为位似中心,将△ABC 缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC 的面积比为( )A .1:3B .1:4C .1:5D .1:93、如图,在平面直角坐标中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为31,点A ,B ,E 在x 轴上,若正方形BEFG 的边长为6,则C 点坐标为( )A .(3,2)B .(3,1)C .(2,2)D .(4,2)4、如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为()A.1 B.2 C.4 D.85、如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是()A.3 B.-3 C.-4 D.46、如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是()A.P1B.P2C.P3D.P47、如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=8、如图,已知矩形OABC 与矩形ODEF 是位似图形,P 是位似中心,若点B 的坐标为(2,4),点E 的坐标为(-1,2),则点P 的坐标为9、如图,以O 为位似中心,将边长为256的正方形OABC 依次作位似变换,经第一次变化后得正方形OA 1B 1C 1,其边长OA 1缩小为OA 的21,经第二次变化后得正方形OA 2B 2C 2,其边长OA 2缩小为OA 1的21,经第三次变化后得正方形OA 3B 3C 3,其边长OA 3缩小为OA 2的21,…,依次规律,经第n 次变化后,所得正方形OA n B n 的边长为正方形OABC 边长的倒数,则n=10、已知:△ABC 在直角坐标平面内,三个顶点的坐标分别为A (0,3)、B (3,4)、C (2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC 向下平移4个单位长度得到的△A 1B 1C 1,点C 1的坐标是 ;(2)以点B 为位似中心,在网格内画出△A 2B 2C 2,使△A 2B 2C 2与△ABC 位似,且位似比为2:1,点C 2的坐标是;(3)△A 2B 2C 2的面积是 平方单位.11、如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行一次函数”(1)若函数y=kx+b的图象过点(3,1),求b的值;(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.12、如图,△ABC在方格纸中(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;(3)计算△A′B′C′的面积S.参考答案1、解析:利用位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或-k 进行求解.解:∵A (-3,6),B (-9,-3),以原点O 为位似中心,相似比为31,把△ABO 缩小, ∴点A 的对应点A′的坐标为(-3×31,6×31)或[-3×(-31),6×(-31)],即A′点的坐标为(-1,2)或(1,-2).故选D .2、解析:先求出位似比,根据位似比等于相似比,再由相似三角形的面积比等于相似比的平方即可.解:∵OB=3OB′, ∴OB ′:OB=1:3,∵以点O 为位似中心,将△ABC 缩小后得到△A′B′C′, ∴△A′B′C′∽△ABC ,∴A ′B ′:AB= OB ′:OB=1:3∴S △A ′B ′C ′:S △ABC =( A ′B ′:AB)2=1:9 故选D3、解析:直接利用位似图形的性质结合相似比得出AD 的长,进而得出△OAD ∽△OBG ,进而得出AO 的长,即可得出答案.解:∵正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为31, ∴AD:BG=1:3, ∵BG=6, ∴AD=BC=2, ∵AD ∥BG , ∴△OAD ∽△OBG , ∴OA:OB=1:3, ∴0A:(2+OA)=1:3, 解得:OA=1,∴OB=3,∴C 点坐标为:(3,2), 故选:A4、解析:根据位似变换的性质得到A 1B 1:AB=OB 1:OB ,B 1C 1∥BC ,再利用平行线分线段成比例定理得到OB 1:OB=OC 1:OC ,所以A 1B 1:AB= OC 1:OC=1:2,然后把OC 1=21OC ,AB=4代入计算即可.解:∵C 1为OC 的中点, ∴OC 1=21OC , ∵△ABC 和△A 1B 1C 1是以点O 为位似中心的位似三角形, ∴A 1B 1:AB=OB 1:OB ,B 1C 1∥BC , ∴OB 1:OB=OC 1:OC ,∴A 1B 1:AB= OC 1:OC ,A 1B 1:4= 1:2 ∴A 1B 1=2. 故选B .5、解析:根据位似变换的性质得出△ABC 的边长放大到原来的2倍,进而得出点A'的纵坐标.解:∵点C 的坐标是(-1,0).以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A′B′C,并把△ABC 的边长放大到原来的2倍. 点A′的对应点A 的纵坐标是1.5, 则点A'的纵坐标是:-3. 故选:B .6、解析:连接CA ,DB ,并延长,则交点即为它们的位似中心.继而求得答案. 解:∵如图,连接CA ,DB ,并延长,则交点即为它们的位似中心. ∴它们的位似中心是P 3.故选C .7、解析:根据位似图形的性质得出AO,DO的长,进而得出AC:DC=AB:DE=1:3,求出DE的长即可.解:∵△ABC与DEF是位似图形,它们的位似中心恰好为原点,已知A点坐标为(1,0),D点坐标为(3,0),∴AO=2,DO=5,∴AC:DC=AB:DE=1:3∵AB=1.5,∴DE=4.5.8、解析:由矩形OABC中,点B的坐标为(2,4),可求得点C的坐标,又由矩形OABC 与矩形ODEF是位似图形,P是位似中心,点C的对应点点E的坐标为(-1,2),即可求得其位似比,继而求得答案.解:∵四边形OABC是矩形,点B的坐标为(2,4),∴OC=AB=4,OA=2,∴点C的坐标为:(0,4),∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2),∴位似比为:2,∴OP:AP=OD:AB=1:2,设OP=x,则x:(x+2)=1:2,解得:x=2,∴OP=2,即点P的坐标为:(-2,0).故答案为:(-2,0).9、解析:由图形的变化规律可知正方形OAnBn 的边长为n)21(,据此即可求解. 解答: 解:由图形的变化规律可得n )21(=2561, 解得n=8. 故答案为:8.10、解析:(1)根据平移的性质得出平移后的图从而得到点的坐标; (2)根据位似图形的性质得出对应点位置,从而得到点的坐标; (3)利用等腰直角三角形的性质得出△A 2B 2C 2的面积. 试题解析:(1)如图所示:C 1(2,﹣2); 故答案为:(2,﹣2); (2)如图所示:C 2(1,0); 故答案为:(1,0); (3)∵=20,=20,=40,∴△A 2B 2C 2是等腰直角三角形, ∴△A 2B 2C 2的面积是:××=10平方单位.故答案为:10.11、解析:(1)根据平行一次函数的定义可知:k=﹣2,再利用待定系数法求出b 的值即可;(2)根据位似比为1:2可知:函数y=kx+b 与两坐标的交点坐标,再利用待定系数法求出函数y=kx+b 的表达式.解:(1)由已知得:k=﹣2,把点(3,1)和k=﹣2代入y=kx+b 中得:1=﹣2×3+b, ∴b=7;(2)根据位似比为1:2得:函数y=kx+b 的图象有两种情况:①不经过第三象限时,过(1,0)和(0,2),这时表达示为:y=﹣2x+2; ②不经过第一象限时,过(﹣1,0)和(0,﹣2),这时表达示为:y=﹣2x ﹣2; 12、解析:(1)A 点的坐标为(2,3)所以原点O 的坐标就在A 点左2个格,下3个格的点上.由此建立直角坐标系,读出B 点坐标;(2)连接OA ,OB ,OC ,并延长到OA′,OB′,OC′,使OA′,OB′,OC′的长度是OA ,OB ,OC 的2倍.然后顺次连接三点;(3)从网格上可看出三角形的底和高,利用三角形的面积公式计算. 解:(1)画出原点O ,x 轴、y 轴.(1分)B (2,1) (2)画出图形△A′B′C′. (3)S=21×4×8=16.。
初三数学下册(人教版)第二十七章相似27.3知识点总结含同步练习及答案

描述:例题:初三数学下册(人教版)知识点总结含同步练习题及答案
第二十七章 相似 27.3 位似
一、学习任务
1. 了解图形的位似,能利用位似将一个图形放大或缩小,会建立坐标系描述点的位置.
二、知识清单
位似
三、知识讲解
1.位似
两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫
做位似图形(homothetic figures ),这个点叫做位似中心.
如图, 各顶点坐标分别是:,,.以 为位似中心,在 轴下方将 放大为原来的 倍.
分析:根据位似变化的性质,即可求得 ,,的坐标,则可画出 .
解:
△ABC A (−4,4)B (−1,2)C (−5,1)O x
△ABC 2A 1B 1C 1△
A 1
B 1
C 1
()
高考不提分,赔付1万元,关注快乐学了解详情。
答案:解析:A .B .C .D .D 由题意知两矩形位似比为 ,矩形 如图所示:
4
(−2,3)
(2,−3)(3,−2)或(−2,3)
(−2,3)或(2,−3)1:2OA 'B 'C '答案:4. 如图,在平面直角坐标系中,以原点 为位中心,将 扩大到原来的 倍,得到 .
若点 的坐标是 ,则点 的坐标是
A .
B .
C .
D .C O △ABO 2△A 'B 'O A (1,2)A '(
)(2,4)
(−1,−2)(−2,−4)(−2,−1)。
九年级数学下册第二十七章相似27.3位似同步练习课件新版新人教版

解 由题意, 知胶片上的四边形与屏幕上的四边形是位似图形, 相似比为
设屏幕上的四边形的面积为x cm2, 周长为 y cm,则 解得x=3380, y=390. 答:屏幕上的四边形的面积为3380 cm2, 周长为390 cm.
锦囊妙计 理解情境构建模型
利用位似解决实际问题, 关键是将实际问 题转化为数学问 题, 把实物图转化为几何图形, 将已知条件转化为几何图形中 的条件, 将所求 的量归属在几何图形中 .
题型六 位似图形的实际应用
例题6 我们都看过电影, 其实电影放映的原理就是利用了位 似图形的 知识(示意图如图27-3-19), 光源可看作位似中心, 胶片 与屏幕的距离是6 m, 光源到 胶片的距离是0. 5 m, 胶 片上 的四边形的面积是20 cm2, 周长是30 cm, 那么屏幕 上的四边形的面积是多少? 周长是多少?
锦囊妙计 确定位似中心的技巧
(1)位似图形对应点的连线的交点就是位似 中心; (2) 若位似图形有公共顶点 , 则这个公共顶 点就是位似中心 .
题型三 应用位似图形的性质进行计算
例题3 如图27-3-15所示, 四边形ABCD 与四边形EFGH位似, 位
似中心是点O,若
则 =_________, 四边形 ABCD与四
边形EFGH的面积比为_____9_∶___49______.
分析 ∵四边形ABCD与四边形EFGH位似, 位 似中心是点O, ∴△OEF∽△OAB, △OFG∽△OBC,
∴四边形ABCD与四边形EFGH的面积比为 9∶49.
锦囊妙计 理解联系回归相似
位似是具有特殊位置关系的相似, 而有 些相似图形中的基 本图形就具有位似关系, 如 “A”字型、“X”字型图形, 所以 遇到与位似图 形相关的计算问题, 可利用相似的性质来解答.
人教版九年级数学下册27.3 位似 同步练习附答案【最新】

练习 位 似一、自主学习1.位似图形上某一对对应顶点到位中心的距离分别为5 cm 和15 cm ,则它们的相似比为_________2.如图27-33,蜡烛与成像板之间的距离为3m ,小孔纸板距蜡烛1m ,若蜡烛AB 长20cm ,则所成的像长为_________cm.图27-333.四边形ABCD 和四边形A 'B 'C 'D '是位似图形,O 为位似中心,若OA ∶OA ',=1∶2,那么AB ∶A 'B '=________,S 四边形ABCD ∶S 四边形A 'B 'C 'D '=________. 二、基础巩固4.如图27-34所示,点O 是等边△PQR 的中心,P ,Q ',R '分别是OP 、OQ 、OR 的中点,则△P 'Q 'R '与△PQR 是________,点O 是_____,相似比是________.图27-34 图27-355.如图27-35所示,矩形AOBC 与DOEF 是位似图形,且O 为位似中心,相似比为1∶2,若A(0,1)、B(2,0),则F 点的坐标为________.6.下列两个图形不是位似图形的是( )7.把△ABC 三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以3得△A 'B 'C ',的坐标A ',(0,3)、B '(6,0)、C(9,6),那么△ABC 与△A 'B 'C '是______图形,位似中心是_______,相似比为________8.把△ABC 三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以-3,得△A 'B 'C ',的坐标A '(0,-3)、B (-6,0)、C '(-9,-6),那么△ABC 与△A 'B 'C '是_____图形,位似中心是_____,相似比为_____.9.如图27-36所示,按如下方法将△ABC 的三边缩小为原来的21,任取一点O ,连AO 、BO 、CO ,并取它们的中点D 、E 、F ,则下列说法: (1)△ABC 与△DEF 是位似形. (2)△ABC ∽△DEF.(3)△ABC 与△DEF 周长的比为2∶1(4)△ABC 与△DEF 面积的比为4∶1.其中正确的个数是( )图27-36A.1B.2C.3D.410.图27-36中,△ABC 与△DEF 是位似图形.那么,DE 与AB 平行吗?为什么?EF 与BC 呢?DF 与AC 呢?11.如图27-37所示,O 为四边形ABCD 上一点,以O 为位似中心,将四边形ABCD 放大为原来的2倍.12.如图27-38所示,O 为位似中心,将△ABC 缩小为原来的32(要求对应顶点在位似中心的同旁). 13.如图27-39所示,O 为位似中心,将△ABC 放大为原来的2倍(要求对应顶点在位似中心的两旁).图27-37 图27-38 图27-39三、能力提高14.有一个正六边形,将其按比例缩小,使得缩小后的正六边形的面积为原正六边形面积的31,已知原正六边形一边为3,则后来正六边形的边长为( )A.9B.3C.3D.332 15.在任意一个三角形内部,画一个小三角形,使其各边与原三角形各边平行,则它们的位似中心是( )A.一定点B.原三角形三边垂直平分线的交点C.原三角形角平分线的交点D.位置不定的一点 16.下列说法正确的个数是( )①位似图形一定是相似图形; ②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的且相似比相等.A.1个B.2个C.3个D.4个17.若两个图形位似,则下列叙述不正确的是( )A.每对对应点所在的直线相交于同一点;B.两个图形上的对应线段之比等于相似比C.两个图形上对应线段必平行D.两个图形的面积比等于相似比的平方18.如图27-40所示,在直角坐标系中,A(1,2),B(2,4),C(4,5),D(3,1)围成四边形ABCD.作出四边形ABCD的位似图形,使得新图形与原图形对应线段的比为2∶1,位似中心是坐标原点.图27-4019.(1)如图27-41所示,作山四边形ABCD的位似图形A'B'C'D',使四边形ABCD与四边形A'B'C'D'的相似比为2∶1;(2)若已知AB=2cm,BC=3cm,∠A=60°,AB⊥BC,CD⊥DA,求四边形A'B'C'D'的面积.图27-4120.正方形ABCD各顶点的坐标分别为A(1,1),B(-1,1),C(-1,2),D(1,2),以坐标原点为位似中心,将正方形ABCD放大,使放大后的正方形A'B'C'D'的边是正方形边的3倍。
2022-2023学年人教版九年级数学下册《27-3位似》同步题型分类练习题(附答案)

2022-2023学年人教版九年级数学下册《27.3位似》同步题型分类练习题(附答案)一.位似变换1.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC的面积与△DEF的面积之比是16:9,则AO:AD的值为()A.4:7B.4:3C.6:4D.9:52.如图平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,点A,B,E在x轴上,若正方形ABCD的边长为3,则F点坐标为()A.(16.5,9)B.(18,12)C.(16.5,12)D.(16,12)3.在如图所示的网格中,以点O为位似中心,能够与四边形ABCD是位似图形的为()A.四边形NGMF B.四边形NGME C.四边形NHMF D.四边形NHME 4.如图所示,在平面直角坐标系中,A(1,0),B(0,2),C(﹣2,1),以A为位似中心,把△ABC在点A同侧按相似比1:2放大,放大后的图形记作△A'B'C',则C'的坐标为()A.(﹣6,2)B.(﹣5,2)C.(﹣4,2)D.(﹣3,2)5.如图,在直角坐标系中,矩形ABCD与矩形EFGO位似,矩形ABCD的边CD在y轴上,点B的坐标为(﹣4,4),矩形EFGO的两边都在坐标轴上,且点F的坐标为(2,1),则矩形ABCD与EFGO的位似中心的坐标是.6.如图,平面直角坐标系中,点A在x轴正半轴上,且OA=4,∠BOA=30°,∠B=90°,以点O为位似中心,在第一象限内将△AOB放大,使相似比为2:1,则点B的对应点B′的坐标为.7.如图,在平面直角坐标系中,A、B两点的坐标分别为A(﹣1,2)、B(0,2),C、D 两点的坐标分别为C(0,﹣1)、D(2,﹣1).若线段AB和线段CD是位似图形,且位似中心在y轴上,则位似中心的坐标为.8.《墨子•天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为4,以它的对角线的交点为位似中心,作它的位似图形A'B'C'D',若A'B':AB=2:1,则四边形A'B'C'D'的外接圆的周长为.9.如图,△ABC与△A1B1C1是以原点O为位似中心的位似图形,且位似比为1:2,则点A(1,2)在第一象限的对应点A1的坐标是.10.如图,在平面直角坐标系中,O是坐标原点,以点O为位似中心,△A1B1C1和△ABC 相似比为2:1,在网格中画出新图象△A1B1C1,若每个小正方形边长均为1,请写出A1,B1,C1的坐标.11.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△A n B n∁n组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…A n是OA n﹣1的中点,顶点B2,B3,…,B n.C2,C3,…,∁n都在B1C1边上.(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;(2)求出第n个三角形△A n B n∁n(n≥2)的周长.12.如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M'在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.(1)求证:四边形PQMN为正方形;(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.13.(1)对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是,若点B′表示的数是2,则点B表示的数是;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是.(2)在平面直角坐标系xOy中,已知△ABC的顶点A(﹣2,0),B(2,0),C(2,4),对△ABC及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同个实数a,将得到的点先向右平移m单位,再向上平移n个单位(m>0,n>0),得到△A′B′C′及其内部的点,其中点A,B的对应点分别为A′(1,2),B′(3,2).△ABC内部是否存在点F,使得点F经过上述操作后得到的对应点F′与点F重合,若存在,求出点F 的坐标;若不存在请说明理由.14.在平面直角坐标系中,抛物线L:y=﹣x2+x+2与y轴交于点C,与x轴交于A、B两点(点A在点B的左侧).(1)求A、B、C三点的坐标;(2)连接AC、BC,以点C为位似中心,将△ABC扩大到原来的2倍得到△A1B1C,其中点A1、B1分别是点A、B的对应点,如何平移抛物线L才能使其同时经过点A1、B1,求出所有的平移方式.二.作图-位似变换15.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是()A.4B.3C.2D.116.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为()A.(0,0),2B.(2,2),C.(2,2),2D.(1,1),17.如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为()A.(m,n+3)B.(m,n﹣3)C.(m,n+2)D.(m,n﹣2)18.如图,以点O为位似中心,把△AOB缩小后得到△COD,使△COD∽△AOB,且相似比为,已知点A(3,6),则点C的坐标为.19.如图,以点O为位似中心,把△ABC放大2倍得到△A'B'C'',①AB∥A'B';②△ABC∽△A'B'C';③AO:AA'=1:2;④点C、O、C'三点在同一直线上.则以上四种说法正确的是.20.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA =2.OC=1,则矩形AOCB的对称中心的坐标是;在第二象限内,将矩形AOCB 以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是.21.在平面直角坐标系中,△ABC的顶点A的坐标为(2,﹣5),若以原点O为位似中心,作△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的位似比为2:1,且点A1和点A 不在同一象限内,则点A1的坐标为.22.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是.23.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C (2,3).请在所给直角坐标系中按要求画图和解答下列问题:(1)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△DEF,△ABC 与△DEF的位似比为;(2)如果△ABC内部一点M的坐标为(a,b),请写出M的对应点M'的坐标(,).24.如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.(1)在平面直角坐标系中画出位似中心;(2)设点P(a,b)为△ABC内一点,确定点P在△A1B1C1内的对应点P1的坐标.25.如图,小明在学习图形的位似时,利用几何画板软件,在平面直角坐标系中画出了△ABC的位似图形△A1B1C1.(1)在图中标出△ABC和△A1B1C1的位似中心M点的位置并写出M点的坐标.(2)若以点A1为位似中心,请你帮小明在图中画出△A1B1C1的位似图形△A2B2C2,且△A1B1C1与△A2B2C2的位似比为2:1.(3)直接写出(2)中C2点的坐标.26.如图,△ABC三个顶点分别为A(0,﹣3),B(3,﹣2),C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.(1)画出△ABC向上平移5个单位得到的△A1B1C1;(2)以点C为位似中心,在网格中画出△A2B2C2,使得△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并写出A2的坐标.27.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).(1)以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1.(2)画出△ABC绕O点顺时针旋转90°后得到的△A2B2C2.28.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)直接写出△ABC与△A′B′C′的位似比;(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出△A′B′C′各顶点的坐标.参考答案一.位似变换1.解:∵△ABC与△DEF位似,∴△ABC∽△DEF,AC∥DF,∵△ABC的面积与△DEF的面积之比是16:9,∴=,∵AC∥DF,∴△AOC∽△DOF,∴==,∴AO:AD=4:7,故选:A.2.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,∴==,即==,解得:EF=12,OB=4,∴F(16,12).故选:D.3.解:如图,四边形ABCD的位似图形是四边形NGMF.故选:A.4.解:∵以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作△AB'C',∴AC=AC′,∴点C是线段AC′的中点,∵A(1,0),C(﹣2,1),∴C'的坐标为(﹣5,2).故选:B.5.解:连接BF交y轴于点P,∵C和F是对应点,∴点P为位似中心,由题意得,GF=2,AD=4,GC=4﹣1=3,∵BC∥GF,∴△BPC∽△FPG,∴=,即=2,解得,GP=1,∴OP=2,∴位似中心的坐标是(0,2),故答案为:(0,2).6.解:作BE⊥OA于E,则∠BEO=90°,∵∠ABO=90°,∠BOA=30°,∴OB=OA•cos30°=4×=2,∴BE=OB=,OE=OB•cos30°=2×=3,∴点B的坐标为:(3,),∵以点O为位似中心,在第一象限内将△AOB放大,使相似比为2:1,∴点B的对应点B'的坐标为:(3×2,×2),即(6,2),故答案为:(6,2).7.解:连接AD交BC于E,则点E为位似中心,∵A(﹣1,2)、B(0,2),C(0,﹣1)、D(2,﹣1).∴AB=1,CD=2,BC=3,∵线段AB和CD是位似图形,∴AB∥CD,∴=,即=,解得BE=1,∴OE=OB﹣BE=1,∴位似中心点E的坐标为(0,1),故答案为:(0,1).8.解:如图,连接B′D′.设B′D′的中点为O.∵正方形ABCD∽正方形A′B′C′D′,相似比为1:2,又∵正方形ABCD的面积为4,∴正方形A′B′C′D′的面积为16,∴A′B′=A′D′=4,∵∠B′A′D′=90°,∴B′D′=A′B′=4,∴正方形A′B′C′D′的外接圆的周长=4π,故答案为:4π.9.解:∵△ABC与△A1B1C1是以原点O为位似中心的位似图形,且位似比为1:2,∵A(1,2),点A(1,2)在第一象限的对应点是A1,∴点A1的坐标为:(2,4).故答案为:(2,4).10.解:如图,△A1B1C1即为所求,A1(0,8),B1(6,6),C1(6,2).11.解:(1)∵△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,∴正△A2B2C2的边长为,正△A3B3C3的边长为()2,正△A10B10C10和的边长为()9,正△A7B7C7的边长为()6,∴正△A10B10C10和正△A7B7C7的相似比==;它们的位似中心为点O;(2)∵第n个三角形△A n B n∁n(n≥2)的边长为()n﹣1,∴第n个三角形△A n B n∁n(n≥2)的周长为.12.(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,∴四边形PQMN为矩形,∵四边形P'Q'M'N'是正方形,∴PN∥P′N′,∴=,∵MN∥M′N′,∴=,∴=,而P′N′=M′N′,∴PN=MN,∴四边形PQMN为正方形;(2)解:作AD⊥BC于D,AD交PN于E,如图,∵△ABC的面积=1.5,∴AB•AC=1.5,∴AB=2,∴BC==2.5,∵BC•AD=1.5,∴AD==,设PN=x,则PQ=DE=x,AE=﹣x,∵PN∥BC,∴△APN∽△ABC,∴=,即=,解得x=,即PN的长为m.13.解:(1)点A′:﹣3×+1=﹣1+1=0,设点B表示的数为a,则a+1=2,解得a=3,设点E表示的数为b,则b+1=b,解得b=;故答案为:0,3,;(2)根据题意,得:,解得:,设点F的坐标为(x,y),∵对应点F′与点F重合,∴x+2=x,y+2=y,解得x=y=4,所以,点F的坐标为(4,4),∵点F的坐标为(4,4)不在△ABC内,故△ABC内部不存在点F,使得点F经过上述操作后得到的对应点F′与点F重合.14.解:(1)在y=﹣x2+x+2中,令y=0,即0=﹣x2+x+2,解得:x1=2,x2=﹣1,∴A(﹣1,0),B(2,0),令x=0,即y=2,∴C(0,2);(2)如图,当抛物线经过A1(2,6),B1(﹣4,6)时,设抛物线的解析式,y=﹣x2+bx+c,则有,解得,,∴抛物线的解析式为y=﹣x2﹣2x+14=﹣(x+1)2+15,当抛物线经过A2(﹣2,﹣2),B2(4,﹣2)时,同法可得抛物线的解析式为:y=﹣x2+2x+6=﹣(x﹣1)2+7.∵原来的抛物线的解析式为y=﹣(x﹣)2+,∴+1=,15﹣=,∴原来抛物线向左平移,再向上平移单位得到y=﹣x2﹣2x+14.1﹣=,7﹣=,原来抛物线向右平移单位,再向上平移单位得到y=﹣x2+2x+6.二.作图-位似变换15.解:第一个图形中的位似中心为A点,第二个图形中的位似中心为AD与BC的交点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.故选:A.16.解:如图所示:位似中心F的坐标为:(2,2),k的值为:=.故选:B.17.解:过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,设C(x,y),则CD=y﹣2、AD=﹣x,C′D′=2﹣n,AD′=m,∵△AB′C′与△ABC的位似比为2:1,∴==,即==,解得:x=﹣m,y=﹣n+3,∴点C的坐标为(﹣m,﹣n+3),故选:A.18.解:由题意得,点A与点C是对应点,△AOB与△COD的相似比是3,∴点C的坐标为(3×,6×),即(1,2),当点C值第三象限时,C(﹣1,﹣2)故答案为:(1,2)或(﹣1,﹣2).19.解:∵以点O为位似中心,把△ABC放大2倍得到△A'B'C'',∴AB∥A'B,△ABC∽△A'B'C';AO:AA'=2:1;点C、O、C'三点在同一直线上,①①②④正确,故答案为:①②④.20.解:∵OA=2.OC=1,∴B(﹣2,1),∴矩形AOCB的对称中心的坐标为(﹣1,),∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,∴B1(﹣3,),同理可得B2(﹣,),B3(﹣,),B4(﹣,),∴矩形A4OC4B4的对称中心的坐标是(﹣,).故答案为(﹣1,),(﹣,).21.解:在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),∴则点A′的坐标为:(1,﹣2.5),不在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),∴则点A′的坐标为:(﹣1,2.5),故答案为:(﹣1,2.5).22.解:如图所示:△A1B1C1和△A′B′C′与△ABC的相似比为2,点B的对应点B1的坐标是:(4,2)或(﹣4,﹣2).故答案为:(4,2)或(﹣4,﹣2).23.解:(1)如图,△DEF即为所求;(2)M′(﹣2a,﹣2b).故答案为:﹣2a,﹣2b.24.解:(1)如图点O即为位似中心;(2)设点P(a,b)为△ABC内一点,则点P在△A1B1C1内的对应点P1的坐标(2a,2b).25.解:(1)如图,点M为所作,M点的坐标为(0,2);(2)如图,△A2B2C2即为所求;(3)C2(﹣4,2).26.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.A2的坐标(﹣2.,﹣2).27.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.28.解:(1)如图,(2)2:1,(3)A′(﹣6,0),B′(﹣3,2),C′(﹣4,4).。
人教版初三数学九年级下册 第27章 相似 27.3 位似 同步训练题 含答案

第27章 相似 27.3 位似 同步训练题1. 位似图形的位似中心可以在( )A .原图形外B .原图形内C .原图形上D .以上三种可能都有2. 如图所示3个图形中是位似图形的有( )A .1个B .2个 C.3个 D .0个3. 已知:△ABC ∽△A′B′C′,下列图形中,△ABC 与△A′B′C′不存在位似关系的是( )4. 已知△ABC 中,AB =AC ,∠A =36°,以点A 为位似中心把△ABC 的各边放大2倍后得到△AB′C′,则∠B 的对应角∠B′的度数为( )A .36°B .54° C.72° D .144°5.如图是△ABC 的位似图形的几种画法,其中正确的有( )A .1个B .2个 C.3个 D .4个6. 下列图形中不是位似图形的是( )7.如图,四边形ABCD 与四边形A′B′C′D 是以O 为位似中心的位似图形,若OA ∶OA′=2∶3,则四边形ABCD 与四边形A′B′C′D 的面积比是( )A .4∶9B .2∶5 C.2∶3 D .2∶ 38. 按如下方法,将△ABC 的三边缩小到原来的12,如图,任取一点O ,连AO 、BO 、CO ,并取它们的中点D 、E 、F ,得△DEF ,则下列说法正确的个数是( ) ①△ABC 与△DEF 是位似图形;②△ABC 与△DEF 是相似图形;③△ABC 与△DEF 的周长比为1∶2;④△ABC 与△DEF 的面积比为4∶1A .1B .2 C.3 D .49. 如图,A′B′∥AB ,B′C′∥BC ,且OA′∶A′A=4∶3,则△ABC 与 是位似图形,相似比为 ;△OAB 与 是位似图形,相似比为 .10. 如图,四边形ABCD 与四边形EFGH 位似,位似中心点是O ,OE OA =35,则FG BC= .11. 如图,以点O 为位似中心,将五边形ABCDE 放大后得到五边形A′B′C′D′E′,已知OA =10cm ,OA ′=20cm ,则五边形ABCDE 的周长与五边形A′B ′C′D′E′的周长的比值是______.12. 如图,原点O 是△ABC 和△A ′B′C′的位似中心,点A(1,0)与A′(-2,0)是对应点,△ABC 的面积是32,则△A′B′C′的面积是________.13.如图,以O 为位似中心,将边长为256的正方形OABC 依次作位似变化,经第一次变化后得正方形OA 1B 1C 1,其边长OA 1缩小为OA 的12,经第二次变化后得正方形OA 2B 2C 2,其边长OA 2缩小为OA 1的12,经第三次变化后得正方形OA 3B 3C 3,其边长OA 3缩小为OA 2的12,…,依此规律,经第n 次变化后,所得正方形OA n B n C n 的边长为正方形OABC 边长的倒数,则n =________.14. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则大鱼上的一点(a ,b)对应小鱼上的点的坐标是_____________________.15. 如图,△DEO 与△ABO 是位似图形,△OEF 与△OBC 是位似图形,试说明:OD·OC=OF·OA.16. 如图,在6×8网格图中,每个小正方形边长均为1,点O 和△ABC 的顶点均在小正方形的顶点.(1)以O 为位似中心,在网格图中作△A′B′C′和△ABC 位似,且相似比为1∶2;(2)连接(1)中的AA′,求四边形AA′C′C 的周长.(结果保留根号)17. 如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作OE ⊥BC 于E 点,连接DE 交OC 于F 点,作FG ⊥BC 于G 点,则△ABC 与△FGC 是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.参考答案;1---8 DBDCD CAC9. △A′B′C′ 7∶4△OA′B′ 7∶410. 3511. 1212. 613. 814. (-0.5a ,-0.5b)15. 证明:∵△DEO 与△ABO 是位似图形,∴△DEO ∽△ABO ,∴OD OA =OE OB =DE AB,同理:OF OC =OE OB ,∴OD OA =OF OC,∴OD·OC=OF·OA. 16. 解:(1)如图(2)四边形AA′C′C 的周长为4+6 2.17. 解:△ABC 与△FGC 是位似图形,位似中心是点C.因为在矩形ABCD 中,AD∥BC ,所以∠FAD =∠FCE ,∠FDA =∠FEC ,所以△AFD ∽△CFE ,所以CF AF =CE AD.因为AD =BC ,所以CF AF =CE CB.因为∠ABC =90°,OE ⊥BC ,所以OE ∥AB.因为OA =OC ,所以CE =12BC ,所以CF AF =12,所以CF AC =13.即△ABC 与△FGC 的相似比为3∶1.。
2017-2018 人教版数学九年级下册 第二十七章 相似 27.3 位似 同步练习 含答案

人教版数学九年级下册第二十七章相似 27.3 位似同步练习1.如图,DE∥AB,CE=2BE,则△ABC与△DEC是以点为位似中心的位似图形,其相似比为.2.如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与是位似图形,位似比为,△OAB与是位似图形,位似比为. 3.如图所示,下列图形中不是位似图形的是( )4.图中两个四边形是位似图形,它们的位似中心是( )A.点M B.点NC.点O D.点P5.△ABC的顶点坐标分别是A(0,-2),B(3,0),C(0,1),将这三个点的横、纵坐标都乘以3得到△A′B′C′,则△ABC与△A′B′C′是以为位似中心的位似图形,相似比是,S△A′B′C′∶S△ABC=.6.如图所示,在平面直角坐标系xOy中,点A、B的坐标分别为(3,0),(2,-3),△AB′O′是△ABO关于点A的位似图形,且点O′的坐标为(-1,0),则点B′的坐标为.7.两个图形不仅,而且对应顶点的连线,对应边,像这样的两个图形叫做位似图形,叫做位似中心.8.位似图形上任意一对对应点到位似中心的距离之比等于,位似图形的对应边分别或.9.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于.10.在平面直角坐标系中,在作(x,y)→(kx,ky)变换时,当k>0时得到的图形是向位似图形;当k<0时,得到的图形是向位似图形.11.如图,分别按下列要求作出四边形ABCD以O点为位似中心的位似四边形A′B′C′D′.(1)沿OA的方向放大为原图的2倍;(2)沿AO的方向放大为原图的2倍.12.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).正方形网格中,每个小正方形的边长是1个单位长度.(1)画出△ABC 向下平移4个单位得到的△A 1B 1C 1,并直接写出C 1点的坐标; (2)以点B 为位似中心,在网格中画出△A 2BC 2,使△A 2BC 2与△ABC 位似,且位似比为2∶1,并直接写出C 2点的坐标及△A 2BC 2的面积. 答案: 1. C 3∶22. △A′B′C′ 7∶4 △OA′B′ 7∶43. C4. D5. O 1∶3 9∶16. (53,-4)7. 相似 相交于一点 互相平行8. 这个交点 相似比 平行 在同一条直线上 9. k 或-k 10. 同 反 11. 解:12. 解:(1)C 1(2,-2),图略; (2)如图,C 2(1,0),S△A 2BC 2=10.。
人教版九年级数学下册27.3 位似同步测试附解析学生版

人教版九年级数学下册27.2.3 相似三角形应用举例同步测试附解析学生版一、单选题(共10题;共30分)1.(3分)如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为()A.1.5m B.1.6m C.1.86m D.2.16m2.(3分)如图,放映幻灯片时通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为()A.6cm B.12cm C.18cm D.24cm3.(3分)路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E 点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是()A.6.75米B.7.75米C.8.25米D.10.75米4.(3分)如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为()A.0.36 π平方米B.0. 81 π平方米C.2 π平方米D.3.24 π平方米5.(3分)如图,为了估计某一条河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS = 60m,ST =120m,QR=80m,则这条河的宽度PQ为()A.40m B.120m C.60m D.180m6.(3分)如图,路灯距地面8m,身高 1.6m的小明从点A处沿AO所在的直线行走14m到点B时,人影长度()A.变长 3.5m B.变长 2.5m C.变短 3.5m D.变短 2.5m7.(3分)如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1 m,继续往前走3 m到达E处时,测得影子EF的长为2 m.已知王华的身高是1.5 m,那么路灯A的高度AB等于()A.4.5 m B.6 m C.7.2 m D.8 m8.(3分)如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是()A.B.C.D.9.(3分)如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是()A.4.5米B.6米C.7.2米D.8米10.(3分)某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为()A.10m B.12mC.13m D.15m二、填空题(共5题;共15分)11.(3分)如图,▱ABCD中,E是边AD的中点,BE交对角线AC于点F,那么S∠AFB :S四边形FEDC的值为12.(3分)如图,身高1.8米的轩轩从一盏路灯下的B处向前走了4米到达点C处时,发现自己在地面上的影子CE长与他的身高一样,则路灯的高AB为米.13.(3分)如图,小明为了测量高楼MN的高度,在离点N18米的点A处放了一个平面镜,小明沿NA方向后退1.5米到点C ,此时从镜子中恰好看到楼顶的点M,已知小明的眼睛(点B)到地面的高度BC是1.6米,则高楼MN的高度是.14.(3分)如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子里看到楼的顶部,如果王青身高1.55m,她估计自己眼睛距地面1.50m.同时量得LM=30cm,MS=2m,则这栋楼高m.15.(3分)如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上,若幻灯片到光源的距离为20 cm,到屏幕的距离为120 cm,且幻灯片中的图形的高度为8 cm,则屏幕上图形的高度为cm.三、解答题(共8题;共55分)16.(7分)如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连结AC并延长到点D,使CD= 12AC,连结BC并延长到点E,使CE= 12BC,连结DE.量得DE的长为15米,求池塘两端A,B的距离.17.(7分)如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。
人教版数学九年级下册 第二十七章 相似 27.3 位似 同步练习附答案学生版
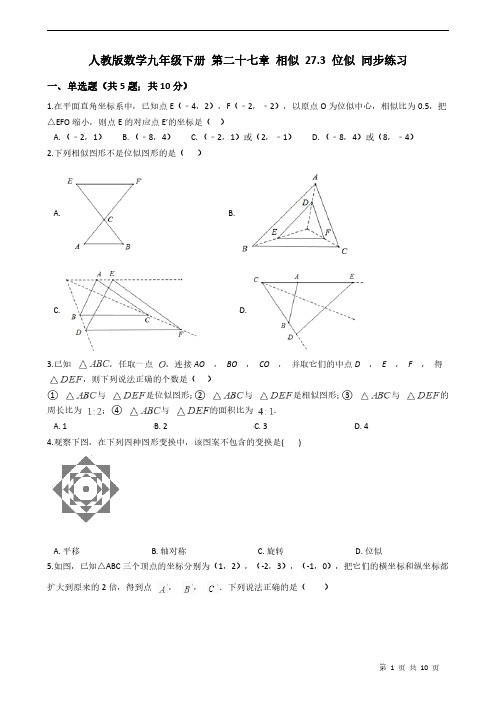
人教版数学九年级下册第二十七章相似27.3位似同步练习一、单选题(共5题;共10分)1.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是()A.(﹣2,1)B.(﹣8,4)C.(﹣2,1)或(2,﹣1)D.(﹣8,4)或(8,﹣4)2.下列相似图形不是位似图形的是()A. B.C. D.3.已知,任取一点,连接AO,BO,CO,并取它们的中点D,E,F,得,则下列说法正确的个数是()①与是位似图形;②与是相似图形;③与的周长比为;④与的面积比为.A.1B.2C.3D.44.观察下图,在下列四种图形变换中,该图案不包含的变换是()A.平移B.轴对称C.旋转D.位似5.如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点,,.下列说法正确的是()A.△与△ABC是位似图形,位似中心是点(1,0)B.△与△ABC是位似图形,位似中心是点(0,0)C.△与△ABC是相似图形,但不是位似图形D.△与△ABC不是相似图形二、填空题(共6题;共6分)6.如图,已知线段AB两个端点的坐标分别为A(4,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点D坐标为________.7.在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是________.8.在平面直角坐标系中,点A的坐标是,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为.若点恰在某一反比例函数图象上,则该反比例函数的解析式为________.9.已知:如图,,,以原点O为位似中心,相似比,把在点O另一侧缩小,则点E的对应点的坐标为________.10.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为________.11.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是________.三、作图题(共3题;共27分)12.如图,已知△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是________(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1(3)求四边形的面积.13.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.(1)画出位似中心O;(2)求出△ABC与△A′B′C′的相似比.14.如图,在网格图中,每个小正方形边长均为,点和四边形的顶点均在小正方形的顶点上.(1)以为位似中心,在网格图中作四边形和四边形位似,且位似比为;(2)根据(1)填空:________.四、综合题(共2题;共25分)15.请阅读下列材料,并完成相应的任务:在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.则有AX=BY=XY.下面是该结论的部分证明:证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.∴.同理可得.∴.∵Z'A'=Y'Z',∴ZA=YZ.任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形AXYZ的形状,并加以证明;(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成AX=BY=XY的证明过程;(3)上述解决问题的过程中,通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y 的位置,这里运用了下面一种图形的变化是.A.平移B.旋转C.轴对称D.位似16.(1)在正方形方格纸中,我们把顶点均在“格点”上的三角形称为“格点三角形”,如图△ABC是一个格点三角形,点A的坐标为(-2,2).(1)点B的坐标为________,△ABC的面积为________;(2)在所给的方格纸中,请你以原点O为位似中心,将△ABC缩小为原来的一半(仅用直尺);(3)在(2)中,若P(a,b)为线段AC上的任一点,则缩小后点P的对应点P1的坐标为________.(4)按要求作图,不要求写作法,但要保留作图痕迹.我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.①如图2,在平行四边形ABCD中,E为CD的中点,作BC的中点F.②如图3,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH.答案解析部分一、单选题1.【答案】C2.【答案】D3.【答案】C4.【答案】A5.【答案】B二、填空题6.【答案】(4,2)7.【答案】.8.【答案】9.【答案】(3,-1)10.【答案】(3,2)11.【答案】或三、作图题12.【答案】(1)(2,-2)(2)解:如图所示,以B为位似中心,画出,使与位似,且位似比为2:1,(3)解:四边形的面积是13.【答案】(1)解:(2)解:∵顶点都在格点上,B′C′=2,BC=,∴BC:B′C′=1:2∴△ABC与△A′B′C′的相似比为1:2.14.【答案】(1)解:如下图所示,四边形即为所求.(2)1:1四、综合题15.【答案】(1)解:四边形AXYZ是菱形.证明:∵ZY∥AC,YX∥ZA,∴四边形AXYZ是平行四边形.∵ZA=YZ,∴平行四边形AXYZ是菱形(2)证明:∵CD=CB,∴∠1=∠3.∵ZY∥AC,∴∠1=∠2.∴∠2=∠3.∴YB=YZ.∵四边形AXYZ是菱形,∴AX=XY=YZ.∴AX=BY=XY(3)D16.【答案】(1);4(2)解:如图,连接OA取,OA中点记作点,用同样的方法找到点和点,就得到缩小后的;(3)(4)解:①如图,连接AC、BD交于点O,连接EB交AC于点G,连接DG并延长交CB于点F,F即为所求,根据平行四边形的性质,O是BD中点,∴CO是的中线,∵E是CD中点,∴BE也是的中线,根据三条中线交于一点,所以连接DG并延长,得到的最后一条中线,则F是BC中点;②如图,分别过点B、C作的矩形对角线BD,的矩形对角线CE,,,则直线BD与CE的交点F就是的高所在直线的交点,连接AF角BC于点H,线段AH就是所求的的高.。
九年级数学下册第二十七章相似27.3位似同步练习新版新人教版

《27.3.1位似(1)》◆ 基础题1. 下列说法不正确的是 ( ) A .位似图形一定是相似图形 B. 相似图形不一定是位似图形C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比D. 位似图形中每组对应点所在的直线必相互平行2.如图,已知BC ∥DE ,则下列说法中不正确的是 ( ) A .两个三角形是位似图形 B .点A 是两个三角形的位似中心 C .AE ︰AD 是位似比 D .点B 与点E 、点C 与点D 是对应位似点3.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为________。
◆ 能力题4.将一个菱形放在2倍的放大镜下,则下列说法中不正确的是 ( ) A .菱形的边长扩大到原来的2倍 B .菱形的角的度数不变 C .菱形的面积扩大到原来的2倍 D .菱形的面积扩大到原来的4倍 5.如图,DC ∥AB ,OA =2OC ,,则OCD △与OAB △的位似比是________。
6.如图,以A 为位似中心,将△ADE 放大2倍后,得位似图形△AB C ,若1S 表示△ADE 的面积,2S 表示四边形DBCE 的面积,则21:S S =( ) A . 1︰2 B .1︰3 C .1︰4 D .2︰3提升题7.雨后操场,小明从他前面2米远的一小块积水中看到了旗杆顶端的倒影,如果旗杆底端到积水的距离为20米,小明眼睛离地面1.5米,则旗杆的高度为多少?8.在如图的方格纸中(每个小方格的边长都是1个单位)有一点O 和ABC △。
(1)请以点O 为位似中心,把ABC △缩小为原来的一半(不改变方向),得到A B C '''△。
(2)请用适当的方式描述A B C '''△的顶点A ',B ',C '的位置。
9.如图,已知△ABC中,AB=12,BC=8,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和以A、B、C为顶点的三角形相似,且相似比为13。
九年级数学下册 第二十七章 相似 27.3 位似同步导练3

第二十七章 相似27.3位似基础导练1. 下列说法不正确的是 ( )A .位似图形一定是相似图形B. 相似图形不一定是位似图形C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比D. 位似图形中每组对应点所在的直线必相互平行2. 下列说法正确的是 ( )A. 分别在△ABC 的边AB ,AC 的反向延长线上取点D ,E ,使DE ∥BC ,则△ADE 是△ABC 放大后的图形B. 两位似图形的面积之比等于位似比C. 位似多边形中对应对角线之比等于位似比D. 位似图形的周长之比等于位似比的平方3. 如图,点D E F ,,分别是()ABC AB AC >△各边的中点,下列说法中,错误..的是( )A. AD 平分BAC ∠B. 12EF BC =C. EF 与AD 互相平分D.△DEF 是△ABC 的位似图形4. 用作位似形的方法,可以将一个图形放大或缩小,位似中心 ( )A. 只能选在原图形的外部B. 只能选在原图形的内部C. 只能选在原图形的边上 D .可以选择任意位置5. 将一个菱形放在2倍的放大镜下,则下列说法中不正确的是 ( )A .菱形的边长扩大到原来的2倍B .菱形的角的度数不变C .菱形的面积扩大到原来的2倍D .菱形的面积扩大到原来的4倍6.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为________.7. 如果两个位似图形的对应线段长分别为3cm 和5cm ,且较小图形周长为30cm ,则较大图形周长为 .A B DE FC8.如图,DC ∥AB ,OA =2OC ,则OCD △与OAB △的位似比是________.能力提升9.在如图的方格纸中(每个小方格的边长都是1个单位)有一点O 和ABC △.(1)请以点O 为位似中心,把ABC △缩小为原来的一半(不改变方向),得到A B C '''△.(2)请用适当的方式描述A B C '''△的顶点A ',B ',C '的位置.10.如图,四边形ABCD 和四边形A′B′C′D′ 位似,位似比12k =,四边形A′B′C′D′和四边形A″B″C″D″位似,位似比21k =.四边形A″B″C″D″和四边形ABCD 是位似图形吗?位似比是多少?参考答案O A BC D1.D 2.C 3.A 4.D 5.C 6.2︰5 7.50cm 8.1︰2 9.略10.是位似图形,位似比为12.。
九年级数学下册 第二十七章 相似 27.3 位似同步导练1 (新版)新人教版
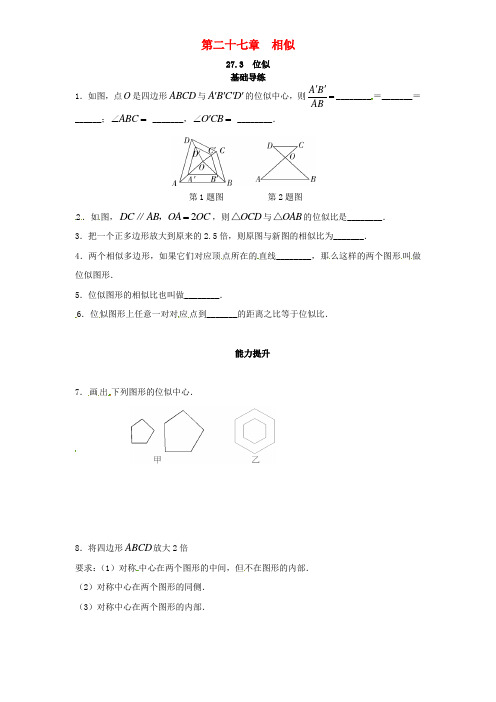
第二十七章 相似27.3 位似基础导练1.如图,点O 是四边形ABCD 与A B C D ''''的位似中心,则A B AB''=________=_______=______;ABC ∠= _______,O CB '∠= ________.第1题图 第2题图 2.如图,2DC AB OA OC =∥,,则OCD △与OAB △的位似比是________.3.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为_______.4.两个相似多边形,如果它们对应顶点所在的直线________,那么这样的两个图形叫做位似图形.5.位似图形的相似比也叫做________.6.位似图形上任意一对对应点到_______的距离之比等于位似比.能力提升7.画出下列图形的位似中心.8.将四边形ABCD 放大2倍要求:(1)对称中心在两个图形的中间,但不在图形的内部.(2)对称中心在两个图形的同侧.(3)对称中心在两个图形的内部.9.如图,四边形ABCD 和四边形A B C D ''''′位似,位似比12k =,四边形A B C D ''''和四边形A B C D ''''''''位似,位似比21k =.四边形A B C D ''''''''和四边形ABCD 是位似图形吗?位似比是多少?10.请把如图所示的图形放大2倍.11.请把如图所示的图形缩小2倍.参考答案1.B C BC '',C D CD '',D A DA '';A B C '''∠,OCB ∠2.123.254.相交于一点5.位似比6.位似中心7.略.8.略.9.是位似图形,1210.略.11.略.。
初中数学人教版九年级下册第二十七章 相似27.3 位似-章节测试习题(2)

章节测试题1.【答题】对于平面图形上的任意两点P,Q,如果经过某种变换得到新图形上的对应点P′,Q′,保持PQ=P′Q′,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是()A. 平移B. 旋转C. 轴对称D. 位似【答案】D【分析】本题考查的是平移、旋转变换、轴对称变换和位似变换,理解“等距变换”的定义、掌握平移、旋转变换、轴对称变换和位似变换的性质是解题的关键.根据平移、旋转变换、轴对称变换和位似变换的性质进行判断即可.【解答】平移的性质是把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,则平移变换是“等距变换”;旋转的性质:旋转前、后的图形全等,则旋转变换是“等距变换”;轴对称的性质:成轴对称的两个图形全等,则轴对称变换是“等距变换”;位似变换的性质:位似变换的两个图形是相似形,则位似变换不一定是等距变换,选D.2.【答题】△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是()A. 3B. 6C. 9D. 12【答案】D【分析】本题考查了位似图形的性质,利用位似图形的面积比等于位似比的平方得出是解题关键.利用位似图形的面积比等于位似比的平方,进而得出答案.【解答】∵△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,△ABC的面积是3,∴△ABC与△A′B′C′的面积比为1:4,则△A′B′C′的面积是12.选D.3.【答题】图中两个四边形是位似图形,它们的位似中心是()A. 点MB. 点NC. 点OD. 点P【答案】D【分析】本题考查了位似图形的概念,根据位似图形的位似中心位于对应点连线所在的直线上得出是解题关键.根据位似变换的定义:对应点的连线交于一点,交点就是位似中心.即位似中心一定在对应点的连线上.【解答】点P在对应点M和点N所在直线上,再利用连接另两个对应点,得出相交于P点,即可得出P为两图形位似中心,选D.4.【答题】“标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形()A. 左上B. 左下C. 右下D. 以上选项都正确【答案】B【分析】本题考查了位似变换的相关知识,位似是相似的特殊形式,平移、旋转、对称的图形都是全等形.开口向上的两个“E”形状相似,但大小不同,因此它们之间的变换属于位似变换,故最上面较大的“E”与左下的“E“是位似图形.【解答】根据位似变换的特点可知:最上面较大的“E”与左下的“E“是位似图形.选B.5.【答题】如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是()A. B. C. D.【答案】D【分析】本题考查了位似变换的性质,根据已知得出FO=a,CF=a+1,CE=(a+1),是解决问题的关键.根据位似变换的性质得出△ABC的边长放大到原来的2倍,FO=a,CF=a+1,CE=(a+1),进而得出点B的横坐标.【解答】∵点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,点B的对应点B′的横坐标是a,∴FO=a,CF=a+1,∴CE=(a+1),∴点B的横坐标是(a+1)﹣1=(a+3).选D.6.【答题】在平面直角坐标系中,点A的坐标是(﹣2,1),以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为A′.若点A'恰在某一反比例函数图象上,则该反比例函数解析式为______.【答案】【分析】本题考查了位似变换以及待定系数法求反比例函数解析式,正确得出对应点坐标是解题关键.直接利用位似图形的性质得出A′坐标,进而求出函数解析式.【解答】∵点A的坐标是(﹣2,1),以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为A′,∴A′坐标为(﹣4,2)或(4,﹣2),∵A'恰在某一反比例函数图象上,∴该反比例函数解析式为.故答案为.7.【答题】如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=______.【答案】【分析】本题考查了位似变换,正确得出对应边的比值是解题关键.直接利用位似图形的性质进而分析得出答案.【解答】∵以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,∴.故答案为.8.【答题】如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则=______.【答案】【分析】本题考查了位似变换,正确掌握位似图形的性质是解题关键.直接利用位似图形的性质结合位似比等于相似比得出答案.【解答】∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且,∴,则.故答案为.9.【答题】如图,直线y=x+1与x轴,y轴分别交于A、B两点,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:2,则点B′的坐标为______.【答案】(﹣9,﹣2)或(3,2)【分析】本题考查了一次函数的图象与性质,位似图形的性质的运用,掌握位似的概念是解决问题的关键.首先根据直线y=x+1与x轴,y轴分别交于A、B两点,解得点A和点B的坐标,再利用位似图形的性质可得点B′的坐标.【解答】∵y=x+1与x轴,y轴分别交于A、B两点,令x=0可得y=1;令y=0可得x=﹣3,∴点A和点B的坐标分别为(﹣3,0);(0,1),∵△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:2,∴,∴O′B′=2,AO′=6,∴当点B'在第一象限时,B′的坐标为(3,2);当点B'在第三象限时,B′的坐标为(﹣9,﹣2).∴B′的坐标为(﹣9,﹣2)或(3,2).故答案为(﹣9,﹣2)或(3,2).10.【答题】如图,四边形ABCD与四边形EFGH位似,位似中心点是O,,则=______.【答案】【分析】本题考查了位似变换,正确得出相似比是解题关键.直接利用位似图形的性质得出△OEF∽△OAB,△OFG∽△OBC,进而得出答案.【解答】∵四边形ABCD与四边形EFGH位似,∴△OEF∽△OAB,△OFG∽△OBC,∴,∴.故答案为.11.【答题】如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF 面积的,则AB:DE=______.【答案】2:3【分析】本题考查了位似图形的性质.注意掌握位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.由△ABC经过位似变换得到△DEF,点O是位似中心,根据位似图形的性质,即可得AB∥DE,即可求得△ABC的面积:△DEF面积=,得到AB:DE=2:3.【解答】∵△ABC与△DEF位似,位似中心为点O,∴△ABC∽△DEF,∴△ABC的面积:△DEF面积=,∴AB:DE=2:3,故答案为2:3.12.【答题】如图,△ABC与△A1B1C1为位似图形,点O是它们的位似中心,位似比是1:2,已知△ABC的面积为3,那么△A1B1C1的面积是______.【答案】12【分析】本题考查了位似图形的性质.注意位似图形是相似图形的特殊情况,注意相似三角形面积的比等于相似比的平方定理的应用.由△ABC与△A1B1C1为位似图形,位似比是1:2,即可得△ABC与△A1B1C1为相似三角形,且相似比为1:2,又由相似三角形面积的比等于相似比的平方,即可求得答案.【解答】∵△ABC与△A1B1C1为位似图形,∴△ABC∽△A1B1C1,∵位似比是1:2,∴相似比是1:2,∴△ABC与△A1B1C1的面积比为1:4,∵△ABC的面积为3,∴△A1B1C1的面积是3×4=12.故答案为12.13.【答题】如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(﹣1,1),点C的坐标为(﹣4,2),则这两个正方形位似中心的坐标是______.【答案】(2,0)或【分析】本题考查了位似图形的性质,难度一般,注意掌握每对位似对应点与位似中心共线,另外解答本题注意分情况讨论,避免漏解.两个位似图形的主要特征是:每对位似对应点与位似中心共线;不经过位似中心的对应线段平行.则位似中心就是两对对应点的延长线的交点,本题分两种情况讨论即可.【解答】①当两个位似图形在位似中心同旁时,位似中心就是CF与x轴的交点,设直线CF解析式为y=kx+b,将C(﹣4,2),F(﹣1,1)代入,得解得,即y=,令y=0得x=2,∴O′坐标是(2,0);②当位似中心O′在两个正方形之间时,可求直线OC解析式为y=,直线DE解析式为y=x+1,联立解得即.故答案为(2,0)或.14.【题文】如图,在△ABC中,AB=AC,点P在BC上.(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC.求证:PD∥AB.【答案】见解答.【分析】本题考查了作图﹣相似变换,等腰三角形的性质,平行线的判定等,熟练掌握性质定理和判定定理是解题的关键.(1)尺规作图作出∠APD=∠ABP,即可得到∠DPC=∠PAB,从而得到△PCD∽△ABP;(2)根据题意得到∠DPC=∠ABC,根据平行线的的判定即可证得结论.【解答】(1)如图:作出∠APD=∠ABP,即可得到△PCD∽△ABP;(2)证明:如图,∵∠APC=2∠ABC,∠APD=∠ABC,∴∠DPC=∠ABC,∴PD∥AB.15.【题文】如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1,请画出△A1B1C1;(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2,使它与△ABC的位似比为2:1.【答案】见解答.【分析】本题考查了位似图形的性质,旋转的性质,解题的关键是掌握所学的性质正确的做出图形.(1)根据网格结构找出点A、B、C关于原点O为旋转中心的对称点A1、B1、C1的位置,然后顺次连接即可;(2)利用位似的性质,找出点A2、B2、C2的位置,然后画出图形即可.【解答】(1)如图,△A1B1C1即为所求.(2)如图,△A2B2C2即为所求.16.【答题】如图,()图形是将已知图形按2:1放大后得到的图形.A. AB. BC. CD. D【答案】D【分析】本题考查位似图形.【解答】原图占2×3格,则放大2倍后图形应该占4×6格,选D.17.【答题】如图,△ABO与△CDO是以点O为位似中心的位似图形,若AB=4,AO=8,CO=2,则线段CD的长度为()A. B. 1 C. D. 2【答案】B【分析】本题考查位似图形.【解答】∵△ABO与△CDO是以点O为位似中心的位似图形,∴△ABO∽△CDO,∴,即,解得CD=1.选B.18.【答题】下列图形中不是位似图形的为()A. B. C. D.【答案】B【分析】本题考查位似图形.【解答】对应顶点的连线相交于一点的两个相似多边形叫位似图形.根据位似图形的概念,A、C、D三个图形中的两个图形都是位似图形;B中的两个图形不符合位似图形的概念,对应边不平行,故不是位似图形.选B.19.【答题】如图所示的是两个三角形是位似图形,它们的位似中心是()A. 点AB. 点BC. 点CD. 点D【答案】D【分析】本题考查位似图形.【解答】如图,两个三角形是位似图形,它们的位似中心是点D.选D.20.【答题】视力表用来测试一个人的视力,如图是视力表的一部分,图中的“E”均是相似图形,其中不是位似图形的是()A. ①和④B. ②和③C. ①和②D. ②和④【答案】B【分析】本题考查位似图形.【解答】①和④、①和②、②和④,两个图形是相似形、对应点的连线都经过同一点、对应边平行,都是位似图形;②和③,对应边不平行,不是位似图形,选B.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版九年级下册第二十七章《相似》27.3《位似》测试一、选择题1、下列说法不正确的是()A. 位似图形一定是相似图形B. 相似图形不一定是位似图形C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比D.位似图形中每组对应点所在的直线必相互平行2、下列说法中正确的有()①位似图形都相似;②两个等腰三角形一定相似;③两个相似多边形的面积比为4:9,则周长的比为16:81;④若一个三角形的三边分别比另一个三角形的三边长2cm,那么这两个三角形一定相似.A.1个; B.2个; C.3个; D.4个;3、如图,已知△EFH和△MNK是位似图形,那么其位似中心是()A.点AB.点BC.点C D.点D4、图中的两个四边形是位似图形,它们的位似中心是( )A.点M B.点N C.点O D.点P5、如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2 PA=3 PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )A. B. C. D.6、如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段 AB放大后得到线段CD.若点A(1,2),B (2,0),D(5,0),则点A的对应点C的坐标是()A.(2,5) B.(,5) C.(3,5) D.(3,6)7、如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是()A.3 B.﹣3 C.﹣4 D.48、如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长等于()A.6 B.5 C.9 D.9、如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C和D的坐标分别为( )A.(2,2),(3,2) B.(2,4),(3,1) C.(2,2),(3,1) D.(3,1),(2,2)10、如图,将△ABC的三边分别扩大一倍得到△(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是:()A.(-4,-3) B.(-3,-3) C.(-4,-4) D.(-3,-4)11、如图,在平面直角坐标系中,A(2,4)、B(2,0),将△OAB以O为中心缩小一半,则A对应的点的坐标()A.(1,2) B.(﹣1,﹣2) C.(1,2)或(﹣1,﹣2) D.(2,1)或(﹣2,﹣1)二、填空题12、△OAB三个顶点的坐标分别为O(0,0),A(4,6),B(3,0),以O为位似中心,将△OAB缩小为原来的,得到△OA′B′,则点A的对应点A′的坐标为.13、如图,点O是四边形ABCD和四边形EFGH的位似中心,已知AE=2,EO=1,则四边形ABCD与四边形EFGH的位似比是 .14、如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,点O是位似中心,位似比为2:1. 若五边形ABCDE的面积为17 cm2,周长为20 cm,那么五边形A′B′C′D′E′的面积为______,周长为______.15、如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:,点A的坐标为(0,),则点E的坐标是______。
16、如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是.17、如图,△ABC在平面直角坐标系内,三个顶点坐标分别为A(0,3),B(3,4),C(2,2).以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点A1的坐标是__________.18、正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为.19、如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF分别交AC、CD于P、E,则图中的位似三角形共有对.20、如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是.21、已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC向下平移4个单位长度,再向左平移1个单位长度,得到的△A1B1C1,点C1的坐标是_______;(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是_______;(3)△A2B2C2的面积是_______平方单位.三、简答题22、如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(﹣2,3),将点O,A,B,C的横坐标、纵坐标都乘以﹣2.(1)画出以变化后的四个点为顶点的四边形;(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心及与原图形的相似比.23、如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;(2)以点O为位似中心,将△ABC缩小为原来的,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2B2C2的正弦值.24、如图,在正方形网格中,每一个小正方形的边长都为1,△OAB的顶点分别为O(0,0),A(1,2),B(2,﹣1).(1)以点O(0,0)为位似中心,按位似比1:3在位似中心的同侧将△OAB放大为△OA′B′,放大后点A、B的对应点分别为A′、B′,请在图中画出△OA′B′;(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C'的坐标;(3)直接写出四边形ABA′B′的面积是.25、如图,△OAB与△ODC是位似图形,试问:(1)AB与CD平行吗?请说明理由;(2)如果OB=3,OC=4,OD=3.5,试求△OAB与△ODC的位似比及OA的长.26、如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.27、如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).(1)在图1中画出△ABC关于x轴对称的△A1B1C1;(2)在图1中画出将△ABC绕原点O按逆时针方向旋转90°所得的△A2B2C2;(3)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A3B3C3与△ABC的对应边的比为2:1(画出一种即可).直接写出点A的对应点A3的坐标.28、如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;(2)写出点A′,B′,C′的坐标:A′(),B′(),C′();(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为().参考答案一、选择题1、D2、A;3、B4、D5、B6、B【考点】位似变换;坐标与图形性质.【分析】利用位似图形的性质得出位似比,进而得出对应点坐标的关系.【解答】解:∵以原点O为位似中心,把线段 AB放大后得到线段CD,且B(2,0),D(5,0),∴=,∵A(1,2),∴C(,5).7、B【考点】位似变换;坐标与图形性质.【分析】根据位似变换的性质得出△ABC的边长放大到原来的2倍,进而得出点A'的纵坐标.【解答】解:∵点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是:﹣3.故选:B.8、A【考点】位似变换.【分析】位似是特殊的相似,位似比就是相似比,相似形对应边的比相等.【解答】解:根据题意,△ABC与△DEF位似,且AB:DE=2:3,AB=4∴DE=69、C 10、A.11、C【考点】位似变换;坐标与图形性质.【分析】根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k进行解答.【解答】解:∵以原点O为位似中心,相似比为2:1,将△OAB以O为中心缩小一半,A(2,4),则顶点A的对应点A′的坐标为(﹣1,﹣2)或(1,2),故选:C.二、填空题12、(﹣2,﹣3)或(2,3).分析:根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k进行解答.解:∵以原点O为位似中心,将△OAB缩小为原来的,A(4,6),则点A的对应点A′的坐标为(﹣2,﹣3)或(2,3),13、3:114、cm2 10 cm15、(3,3)16、(4,2)或(﹣4,﹣2).【考点】SD:作图﹣位似变换.【分析】直接利用位似图形的性质得出符合题意的图形进而得出答案.【解答】解:如图所示:△A1B1C1和△A′B′C′与△ABC的相似比为2,点B的对应点B1的坐标是:(4,2)或(﹣4,﹣2).故答案为:(4,2)或(﹣4,﹣2).17、(﹣3,2).【考点】位似变换;坐标与图形性质.【分析】利用位似图形的性质得出对应点位置,进而得出答案.【解答】解:如图所示:△A1B1C1即为所求,则点A1的坐标是:(﹣3,2).故答案为:(﹣3,2).【点评】此题主要考查了位似变换以及坐标与图形的性质,得出对应点位置是解题关键.18、(﹣1,0)或(5,﹣2).【考点】位似变换;坐标与图形性质.【专题】计算题;压轴题.【分析】由图形可得两个位似图形的位似中心必在x轴上,连接AF、DG,其交点即为位似中心,进而再由位似比即可求解位似中心的坐标.【解答】解:当位似中心在两正方形之间,连接AF、DG,交于H,如图所示,则点H 为其位似中心,且H在x轴上,∵点D的纵坐标为2,点F的纵坐标为1,∴其位似比为2:1,∴CH=2HO,即OH=OC 又C(﹣3,0),∴OC=3,OH=1,所以其位似中心的坐标为(﹣1,0);当位似中心在正方形OEFG的右侧时,如图所示,连接DE并延长,连接CF并延长,两延长线交于M,过M作MN⊥x轴,∵点D的纵坐标为2,点F的纵坐标为1,∴其位似比为2:1,∴EF=DC,即EF为△MDC的中位线,∴ME=DE,又∠DEC=∠MEN,∠DCE=∠MNE=90°,∴△DCE≌△MNE,∴CE=EN=OC+OE=3+1=4,即ON=5,MN=DC=2,则M坐标为(5,﹣2),综上,位似中心为:(﹣1,0)或(5,﹣2).故答案为:(﹣1,0)或(5,﹣2).【点评】本题主要考查了位似变换以及坐标与图形结合的问题,能够熟练运用位似的性质求解一些简单的位似计算问题.19、5 对.【考点】位似变换;平行四边形的性质.【分析】由四边形ABCD是平行四边形,则可得AD∥BC,AB∥CD,根据平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,即可证得:△ABP∽△CEP,△APF∽△CPB,△DEF∽△CEB,△DEF∽△ABF,继而可得△ABF∽△CEB,则可求得答案【解答】解:∵四边形ABCD是平行四边形∴AD∥BC,AB∥CD,∴△ABP∽△CEP,△APF∽△CPB,△DEF∽△CEB,△DEF∽△ABF,∴△ABF∽△CEB,∴此图中共有5对相似三角形.故答案为520、(0,),(﹣6,13)【考点】位似变换;坐标与图形性质.【分析】分别利用待定系数法求出一次函数解析式,再利用当B与F是对应点,以及当B与E是对应点分别求出位似中心.【解答】解:设当B与F是对应点,设直线BF的解析式为:y=kx+b,则,解得:,故直线BF的解析式为:y=﹣x+,则x=0时,y=,即位似中心是:(0,),设当B与E是对应点,设直线BE的解析式为:y=ax+c,则,解得:,故直线BE的解析式为:y=﹣2x+1,设直线HF的解析式为:y=dx+e,则,解得:,故直线HF的解析式为:y=﹣x+5,则,解得:即位似中心是:(﹣6,13),综上所述:所述位似中心为:(0,),(﹣6,13).故答案为:(0,),(﹣6,13).【点评】此题主要考查了位似图形的性质以及待定系数法求一次函数解析式,正确分类讨论得出是解题关键.21、【考点】作图-位似变换;作图-平移变换.【分析】(1)直接利用平移的性质得出各对应点位置进而得出答案;(2)利用位似图形的性质得出对应点位置进而得出答案;(3)直接利用△A2B2C2所在矩形面积减去周围三角形面积进而得出答案.【解答】解:(1)如图所示:△A1B1C1,即为所求,C1(1,﹣2);故答案为:(1,﹣2);(2)如图所示:△A2B2C2,即为所求,C2(1,0);故答案为:(1,0);(3)△A2B2C2的面积是:4×6﹣×2×6﹣×2×4﹣×2×4=10.故答案为:10.【点评】此题主要考查了位似变换以及平移变换和三角形面积求法等知识,根据题意得出对应点位置是解题关键.三、简答题22、【解答】解:(1)如图所示,四边形OA′B′C′即为所求四边形;(2)∵将点O,A,B,C的横坐标、纵坐标都乘以﹣2可得出四边形OA′B′C′,∴各对应边的比为2,对应点的连线都过原点,∴得到的四边形与四边形OABC位似,位似中心是O(0,0),与原图形的相似比为2.23、【解答】解:(1)如图所示,△A1B1C1为所求;(2)如图所示,△A2B2C2为所求,由图形可得:∠A2C2B2=∠ACB,过点A作AD⊥BC,交BC的延长线于点D,由A(2,2),C(4,﹣4),B(4,0),易得D(4,2),故AD=2,CD=6,AC==2,则sin∠ACD===,即sin∠A2C2B2=sin∠ACB=.24、如图,△OA′B′即为所求作三角形;(2分)(2)C'的坐标为:(3a,3b);(2分)(3)∴四边形ABA′B′的面积是S△A′OB′﹣S△AOB=20,答案为:20.(2分)25、解:(1)AB∥CD.理由:∵△OAB位似于△ODC,∴△OAB∽△ODC.∴∠D=∠A.∴AB∥CD(2)显然O是位似中心,位似比为OB∶OC=3∶4.∵OB∶OC=OA∶OD,即3∶4=OA∶3.5,解得OA=2.62526、如图所示:27、【考点】作图-位似变换;作图-轴对称变换;作图-旋转变换.【分析】(1)利用关于x轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可;(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2,从而得到△A2B2C2;(3)把点A、B、C的横纵坐标都乘以﹣2得到A3、B3、C3的坐标,然后描点即可.【解答】解:(1)如图1,△A1B1C1为所作;(2)如图1,△A2B2C2为所作;(3)如图2,△A3B3C3△ABC为所作,此时点A的对应点A3的坐标是(﹣4,﹣4).28、【考点】作图﹣位似变换.【分析】(1)利用位似图形的性质得出变化后图形即可;(2)利用已知图形得出对应点坐标;(3)利用各点变化规律,进而得出答案.【解答】解:(1)如图所示:四边形TA′B′C′即为所求;(2)A′(3,5),B′(5,5),C′(7,3);故答案为:(3,5),(5,5),(7,3);(3)在(1)中,∵A(2,3),B(3,3),C(4,2),A′(2×2﹣1=3,2×3﹣1=5),B′(2×3﹣1=5,2×3﹣1=5),C′(2×4﹣1=7,2×2﹣1=3);∴D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为(2a﹣1,2b﹣1).故答案为:(2a﹣1,2b﹣1).。
