微观经济学高鸿业第五版答案
微观经济学课后答案(第五版)

东方经济学——高鸿业主编第五版第二章训练题参考谜底1.曾经明白某一时代内某商品的需要函数为Qd=50-5P,供应函数为Qs=-10+5p。
〔1〕求平衡价钱Pe战争衡数目Qe,并作出几多何图形。
〔2〕假设供应函数稳定,因为花费者支出程度进步,使需要函数变为Qd=60-5P。
求出响应的平衡价钱Pe战争衡数目Qe,并作出几多何图形。
〔3〕假设需要函数稳定,因为花费技巧程度进步,使供应函数变为Qs=-5+5p。
求出响应的平衡价钱Pe战争衡数目Qe,并作出几多何图形。
〔4〕应用〔1〕〔2〕〔3〕,阐明静态剖析跟比拟静态剖析的联络跟区不。
〔5〕应用〔1〕〔2〕〔3〕,阐明需要变更跟供应变更对平衡价钱战争衡数目的妨碍.解答:(1)将需要函数Qd=50-5P跟供应函数Qs=-10+5P代入平衡前提Qd=Qs,有:50-5P=-10+5P得:Pe=6以平衡价钱Pe=6代入需要函数Qd=50-5p,得:Qe=50-5*6=20或许,以平衡价钱Pe=6代入供应函数Qe=-10+5P,得:Qe=-10+5因而,平衡价钱战争衡数目分不为Pe=6,Qe=20...如图1-1所示.(2)将因为花费者支出进步而发生的需要函数Qd=60-5p跟原供应函数Qs=-10+5P,代入平衡前提Qd=Qs,有:60-5P=-10=5P得Pe=7以平衡价钱Pe=7代入Qs=60-5p,得Qe=60-5*7=25或许,以平衡价钱Pe=7代入Qs=-10+5P,得Qe=-10+5*7=25因而,平衡价钱战争衡数目分不为Pe=7,Qe=25(3)将原需要函数Qd=50-5p跟因为技巧程度进步而发生的供应函数Qs=-5+5p,代入平衡前提Qd=Qs,有:50-5P=-5+5P得Pe=5.5以平衡价钱Pe=5.5代入Qd=50-5p,得Qe=50-5*5.5=22.5或许,以平衡价钱Pe=5.5代入Qd=-5+5P,得Qe=-5+5*5.5=22.5因而,平衡价钱战争衡数目分不为Pe=5.5,Qe=22.5.如图1-3所示.(4)所谓静态剖析是调查在既定前提下某一经济事物在经济变量的互相感化下所实现的平衡形态及其特点.也能够说,静态剖析是在一个经济模子中依照所给的外生变量来求内生变量的一种剖析办法.以(1)为例,在图1-1中,平衡点E的确是一个表达了静态剖析特点的点.它是在给定的供求力气的互相感化下所到达的一个平衡点.在此,给定的供求力气分不用给定的供应函数Qs=-10+5P跟需要函数Qd=50-5p表示,平衡点E存在的特点是:平衡价钱Pe=6且当Pe=6时,有Qd=Qs=Qe=20;同时,平衡数目Qe=20,得当Qe=20时,有Pd=Ps=Pe.也能够如此来了解静态剖析:在外生变量包含需要函数的参数(50,-5)以及供应函数中的参数(-10,5)给定的前提下,求出的内生变量分不为Pe=6,Qe=20依此类推,以上所描素的对于静态剖析的全然要点,在(2)及其图1-2跟(3)及其图1-3中的每一个独自的平衡点Ei(1,2)都掉掉了表达.而所谓的比拟静态剖析是调查当所有的前提发作变更时,原有的平衡形态会发作什么变更,并剖析比拟新旧平衡形态.也能够说,比拟静态剖析是调查在一个经济模子中外生变质变更时对内生变量的妨碍,并剖析比拟由差别数值的外生变量所决议的内生变量的差别数值,以(2)为例加以阐明.在图1-2中,由平衡点变更到平衡点,的确是一种比拟静态剖析.它表示当需要添加即需要函数发作变更时对平衡点的妨碍.非常清晰,比拟新.旧两个平衡点跟能够看到:因为需要添加由20添加为25.也能够如此了解比拟静态剖析:在供应函数坚持稳定的前提下,因为需要函数中的外生变量发作变更,即此中一个参数值由50添加为60,从而使得内生变量的数值发作变更,其结果为,平衡价钱由本来的6回升为7,同时,平衡数目由本来的20添加为25.相似的,应用(3)及其图1-3也能够阐明比拟静态剖析办法的全然请求.〔5〕由(1)跟(2)可见,当花费者支出程度进步招致需要添加,即表示为需要曲线右移时,平衡价钱进步了,平衡数目添加了.由(1)跟(3)可见,当技巧程度进步招致供应添加,即表示为供应曲线右移时,平衡价钱下落了,平衡数目添加了.总之,普通地有,需要与平衡价钱成同偏向变更,与平衡数目成同偏向变更;供应与平衡价钱成反偏向变更,与平衡数目同偏向变更.2假设表2—5是需要函数Qd=500-100P在必订价钱范畴内的需要表:〔1〔2〕依照给出的需要函数,求P=2是的需要的价钱点弹性。
高鸿业微观经济学第五版第四章答案

3.已知生产函数Q=f (L,K )=2KL-0.52L -0.52K ,假定厂商目前处于短期生产,且K=10.(1)写出短期生产中关于劳动的总产量L TP 函数、劳动的平均产量L AP 函数和劳动的边际产量L MP 函数。
(2)分别计算当劳动的总产量L TP 、劳动的平均产量L AP 和劳动的边际产量L MP 各自达到极大值时厂商的投入量。
(3)什么时候L AP =L MP ?它的值又是多少?解答:(1)由生产数Q=2KL-0.52L -0.52K ,且K=10,可得短期生产函数为:Q=20L-0.52L -0.5⋅210=20L-0.52L -50于是,根据总产量、平均产量和边际产量的定义,有以下函数:劳动的总产量函数TPL=20L-0.52L -50劳动的平均产量函数APL=20-0.5L-50/L劳动的边际产量函数MPL=20-L(2)关于总产量的最大值:20-L=0解得L=20所以,劳动投入量为20时,总产量达到极大值。
关于平均产量的最大值:-0.5+502-L =0 L=10(负值舍去)所以,劳动投入量为10时,平均产量达到极大值。
关于边际产量的最大值:由劳动的边际产量函数MPL=20-L 可知,边际产量曲线是一条斜率为负的直线。
考虑到劳动投入量总是非负的,所以,L=0时,劳动的边际产量达到极大值。
(3)当劳动的平均产量达到最大值时,一定有APL=MPL 。
由(2)可知,当劳动为10时,劳动的平均产量APL 达最大值,及相应的最大值为:APL 的最大值=10MPL=20-10=10很显然APL=MPL=105.已知生产函数为Q=min {2L,3K }求:(1)当产量Q=36时,L 与K 值分别是多少?(2)如果生产要素L P =2,K P =5,则生产480单位产量时的最小成本是多少?解答:(1)生产函数表示该函数是一个固定投入比例的生产函数,所以,厂商进行生产时,Q=2L=3K.相应的有L=18,K=12(2)由Q=2L=3K,且Q=480,可得:L=240,K=160又因为L P =2,K P =5,所以C=2⋅240+5⋅160=1280即最小成本。
西方经济学高鸿业第五版(宏观+微观)课后习题答案

第二章练习题参考答案1.已知某一时期内某商品的需求函数为Qd=50-5P,供给函数为Qs=-10+5p。
(1)求均衡价格Pe和均衡数量Qe ,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=60-5P。
求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs=-5+5p。
求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。
(4)利用(1)(2)(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)(2)(3),说明需求变动和供给变动对均衡价格和均衡数量的影响.解答:(1)将需求函数Qd=50-5P和供给函数Qs=-10+5P代入均衡条件Qd=Qs,有: 50-5P=-10+5P 得: Pe=6以均衡价格Pe=6代入需求函数Qd=50-5p ,得:Qe=50-5*6=20或者,以均衡价格Pe =6 代入供给函数Qe=-10+5P ,得:Qe=-10+5所以,均衡价格和均衡数量分别为Pe =6 , Qe=20 ...如图1-1所示.(2) 将由于消费者收入提高而产生的需求函数Qd=60-5p和原供给函数Qs=-10+5P, 代入均衡条件Qd=Qs,有: 60-5P=-10=5P 得Pe=7以均衡价格Pe=7代入Qs=60-5p ,得Qe=60-5*7=25或者,以均衡价格Pe=7代入Qs=-10+5P, 得Qe=-10+5*7=25所以,均衡价格和均衡数量分别为Pe=7,Qe=25(3) 将原需求函数Qd=50-5p 和由于技术水平提高而产生的供给函数Qs=-5+5p ,代入均衡条件Qd=Qs,有: 50-5P=-5+5P得Pe=5.5以均衡价格Pe=5.5代入Qd=50-5p ,得Qe=50-5*5.5=22.5或者,以均衡价格Pe=5.5代入Qd=-5+5P ,得Qe=-5+5*5.5=22.5所以,均衡价格和均衡数量分别为Pe=5.5,Qe=22.5.如图1-3所示.(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征.也可以说,静态分析是在一个经济模型中根据所给的外生变量来求内生变量的一种分析方法.以(1)为例,在图1-1中,均衡点E就是一个体现了静态分析特征的点.它是在给定的供求力量的相互作用下所达到的一个均衡点.在此,给定的供求力量分别用给定的供给函数Qs=-10+5P和需求函数Qd=50-5p表示,均衡点E具有的特征是:均衡价格Pe=6且当Pe=6时,有Qd=Qs=Qe=20;同时,均衡数量Qe=20,切当Qe=20时,有Pd=Ps=Pe.也可以这样来理解静态分析:在外生变量包括需求函数的参数(50,-5)以及供给函数中的参数(-10,5)给定的条件下,求出的内生变量分别为Pe=6,Qe=20 依此类推,以上所描素的关于静态分析的基本要点,在(2)及其图1-2和(3)及其图1-3中的每一个单独的均衡点Ei(1,2)都得到了体现.而所谓的比较静态分析是考察当所有的条件发生变化时,原有的均衡状态会发生什么变化,并分析比较新旧均衡状态.也可以说,比较静态分析是考察在一个经济模型中外生变量变化时对内生变量的影响,并分析比较由不同数值的外生变量所决定的内生变量的不同数值,以(2)为例加以说明.在图1-2中,由均衡点变动到均衡点,就是一种比较静态分析.它表示当需求增加即需求函数发生变化时对均衡点的影响.很清楚,比较新.旧两个均衡点和可以看到:由于需求增加由20增加为25.也可以这样理解比较静态分析:在供给函数保持不变的前提下,由于需求函数中的外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量的数值发生变化,其结果为,均衡价格由原来的6上升为7,同时,均衡数量由原来的20增加为25.类似的,利用(3)及其图1-3也可以说明比较静态分析方法的基本要求.(5)由(1)和(2)可见,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了.由(1)和(3)可见,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了.总之,一般地有,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量同方向变动.2 假定表2—5是需求函数Qd=500-100P在一定价格范围内的需求表:某商品的需求表价格(元) 1 2 3 4 5需求量400 300 200 100 0(1)求出价格2元和4元之间的需求的价格弧弹性。
西方经济学高鸿业第五版(微观)课后习题答案(3-7) 2

第三章练习题参考答案1、已知一件衬衫的价格为80元,一份肯德鸡快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德鸡快餐对衬衫的边际替代率MRS 是多少? 解:按照两商品的边际替代率MRS 的定义公式,可以将一份肯德鸡快餐对衬衫的边际替代率写成: XYMSR XY ∆∆-= 其中:X 表示肯德鸡快餐的份数;Y 表示衬衫的件数; MRS 表示在维持效用水平不变的前提下, 消费者增加一份肯德鸡快餐时所需要放弃的衬衫消费数量。
在该消费者实现关于这两件商品的效用最大化时,在均衡点上有MRSxy =Px/Py 即有MRSxy =20/80=0.25它表明:在效用最大化的均衡点上,消费者关于一份肯德鸡快餐对衬衫的边际替代率MRS 为0.25。
2 假设某消费者的均衡如图1-9所示。
其中,横轴OX1和纵轴OX2,分别表示商品1和商品2的数量,线段AB 为消费者的预算线,曲线U 为消费者的无差异曲线,E 点为效用最大化的均衡点。
已知商品1的价格P1=2元。
(1)求消费者的收入; (2)求上品的价格P2; (3)写出预算线的方程; (4)求预算线的斜率;(5)求E 点的MRS12的值。
解: (1)图中的横截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入M=2元×30=60。
(2)图中的纵截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入M=60元,所以,商品2的价格P2斜率=-P1/P2=-2/3,得P2=M /20=3元 (3)由于预算线的一般形式为:P1X1+P2X2=M 所以,由(1)、(2)可将预算线方程具体写为2X1+3X2=60。
(4)将(3)中的预算线方程进一步整理为X2=-2/3 X1+20。
很清楚,预算线的斜率为-2/3。
(5)在消费者效用最大化的均衡点E 上,有MRS12= = MRS12=P1/P2,即无差异曲线的斜率的绝对值即MRS 等于预算线的斜率绝对值P1/P2。
微观经济学高鸿业版第五章课后习题答案
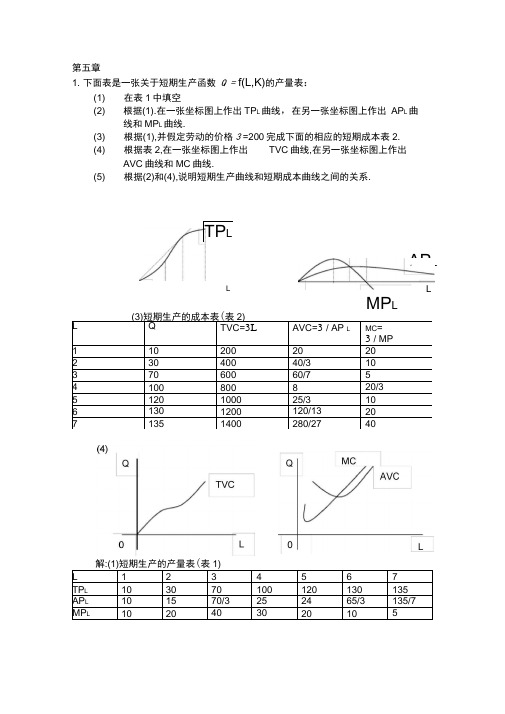
第五章1. 下面表是一张关于短期生产函数 Q = f(L,K)的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出 AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格3 =200完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出 TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.解:(1)短期生产的产量表(表1) L 1 2 3 45 6 7 TP L 10 30 70 100 120 130 135 AP L 10 15 70/3 25 24 65/3 135/7 MP L 10 2040 3020 105TP LAP LMP LL Q TVC=3L AVC=3 / AP L MC =3 / MP1 10 200 20 202 30 400 40/3 10 3 70 600 60/7 54 100 800 8 20/35 120 1000 25/3 106 130 1200 120/13 20 71351400280/2740LL(3)短期生产的成本表(表2)(5)边际产量和边际成本的关系,边际MC和边际产量MP L两者的变动方向是相反的•总产量和总成本之间也存在着对应系:当总产量TP L下凸时,总成本TC曲线和总可变成本TVC是下凹的;当总产量曲线存在一个拐点时,总成本TC曲线和总可变成本TVC也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的•MC曲线和AVC曲线的交点与MP L曲线和AP L曲线的交点是对应的•2. 下图是一张某厂商的LAC曲线和LMC曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC曲线和SMC曲线.解:在产量Q1和Q2上代表最优生产规模的SAC曲线和SMC曲线是SAC i 和SAC2以及SMC i和SMC2. SAC i和SAC?分别相切于LAC的A和B SMC i和SMC2则分别相交于LMC的A i和B i.SM LMCSAG SMC i SAC2Q2长期边际成本曲线与短期成本曲线3. 假定某企业的短期成本函数是TC(Q)=Q3-5Q2+i5Q+66:(i) 指出该短期成本函数中的可变成本部分和不变成本部分;⑵写出下列相应的函数:TVC(Q) AC(Q) AVC(Q) AFC(Q)和MC(Q).解⑴可变成本部分:Q3-5Q2+i5Q不可变成本部分:663 2(2) TVC(Q)= Q3-5Q2+i5QAC(Q)=Q2-5Q+i5+66/QAVC(Q)= Q2-5Q+i5AFC(Q)=66/QMC(Q)= 3Q2-i0Q+i53 24已知某企业的短期总成本函数是STC(Q)=0.04 Q -0.8Q +10Q+5,求最小的平均可变成本值.解:TVC(Q)=0.04 Q3-0.8Q2+10Q2AVC(Q)= 0.04Q2-0.8Q+10令AVC =0.08Q -0.8 =0得Q=10又因为AVC =0.08 0所以当Q=10 时,AVC MIN =65. 假定某厂商的边际成本函数MC=3Q 2-30Q+100且生产10单位产量时的总成本为1000.求:(1)固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数.2解:MC= 3Q -30Q+1003 2所以TC(Q)=Q -15Q +100Q+M当Q=10 时,TC=1000 =500(1) 固定成本值:500(2) TC(Q)=Q3-15Q2+100Q+500TVC(Q)= Q3-15Q2+100QAC(Q)= Q2-15Q+100+500/QAVC(Q)= Q2-15Q+1006. 某公司用两个工厂生产一种产品,其总成本函数为C=2Q12+Q22-Q1Q2,其中Q1表示第一个工厂生产的产量,Q2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合.解:构造F(Q)=2Q12+Q22-Q1Q2+ 入(G+ Q2-40):F4Q1 - Q21=0Q0^15令 --- =2Q2 -Qr + & = 0<Q2 = 25:Q2—-Q1 Q2 _40 =0C A H使成本最小的产量组合为Q1=15,Q2=257已知生产函数Q=A1/4L1/4K1/2;各要素价格分别为P A=1,P L=1.P K=2;假定厂商处于短期生产,且k二16 .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.解:因为 K =16,所以 Q =4A 1/4L 1/4(1)由(1)⑵可知L=A=Q 2/16又 TC(Q)=P A &A(Q)+P L &L(Q)+P K &16=Q 2/16+ Q 2/16+32 =Q 2/8+322AC(Q)=Q/8+32/Q TVC(Q)= Q /8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为 500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少 ? 解:(1)当 K=50 时,P K K=P K 50=500,所以P K =10.1 . .2/3 2/3L K MP L _ 6 MP K 2 L^K 」/36整理得K/L=1/1,即K=L.将其代入 Q=0.5L 1/3K 2/3,可得:L(Q)=2Q (2) STC=D ・ L(Q ) +r 50=5 2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3) 由(1)可知,K=L,且已知 K=50,所以.有 L=50•代入 Q=0.5L 1/3K 2/3,有 Q=25. 又 n =TRSTC=100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润n =1750MP L=:Q = A 1/4L ;/4;L:QMP A -:A A J /4L1/4_ P A MP L :QA 1/4L :/4_ P LQ " 3/4, 1/ 4MP AA _ L ;A.:L41所以L =A(2)MP L =1/6L MP K =2/6L -2/3K 1/3K2/3-1/3P LP K _109•假定某厂商短期生产的边际成本函数为 SMC(Q)=3Q 2-8Q+100,且已知当产量 Q=10时的总成本STC=2400,求相应的STC 函数、SAC 函数和AVC 函数。
微观经济学(高鸿业第五版)习题答案完整版
西方经济学微观部分第五版答案第二章1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(4)利用(1)、(2)和(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
西方经济学(微观部分)高鸿业第五版第四章复习与思考答案

1、下面是一张一种可变生产要素的短期生产函数的产量表:(1)、在表中填空。
答:(1)、利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系分别进行计算,其结果如(2)、所谓边际报酬递减是指短期生产中一种可变要素的边际产量在达到最高点以后开始逐步下降的这样一种普遍的生产现象。
本题的生产函数表现出边际报酬递减的现象,且从第5单位开始。
从表中可看出,当可变要素的投入量由第4单位增加到第5单位时,该要素的边际产量由原来的24下降为12。
2、用图说明短期生产函数Q=f(L,F)的TP L曲线、AP L曲线和MP L曲线的特征及其相互之间的关系。
答:如图4-1所示短期生产函数的TP L曲线、AP L曲线和MP L曲线的综合图。
图4-1中的横轴表示可变要素劳动的投入量L,纵轴表示产量Q,TP L、AP L、MP L三条曲线依次为劳动的总产量曲线、劳动的平均产量曲线和劳动的边际产量曲线。
(1)、TP L曲线。
由于MP L=dTP L/dL,所以,当MP L>0时,TP L曲线是上升的;当MP L<0时,TP L曲线是下降的;而当MP L=0时,TP L曲线达最高点。
换言之,在L=L3时,MP L曲线达到零值的B点与TP L曲线达到最大值的B’点相互对应。
(2)、AP L曲线。
由于AP L=TP L/L,所以,在L=L2时,TP L曲线有一条由原点出发的切线,其切点为C。
该切线是由原点出发与TP L曲线上所有的点的连线中斜率最大的一条连线,故该切点对应的是AP L的最大值点。
再考虑到AP L 曲线和MP L曲线一定会相交在AP L曲线饿最高点。
因此,在图中,在L=L2时,AP L曲线和MP L曲线相交于AP L曲线的最高点C’,而且与C’点相对应的是TP L曲线上的切点C。
TP L曲线和AP L曲线。
(3)、MP L曲线。
在短期生产的边际报酬递减规律的作用下,MP L曲线呈现出先上升达到最高点A以后又下降的趋势。
高鸿业微观经济学(第5版)课后习题答案 第十一章

第十一章市场失灵和微观经济政策1.什么是市场失灵?有哪几种情况会导致市场失灵?解答:在某些情况下,指市场机制会导致资源配置不当即无效率的结果,这就是市场失灵。
换句话说,市场失灵是自由的市场均衡背离帕累托最优的情况。
导致市场失灵的情况包括:垄断,外部影响,公共物品,不完全信息等。
2.垄断是如何造成市场失灵的?解答:第一,在垄断情况下,厂商的边际收益小于价格。
因此,当垄断厂商按利润最大化原则(边际收益等于边际成本)确定产量时,其价格将不是等于而是大于边际成本。
这就出现了低效率的情况。
第二,为获得和维持垄断地位从而得到垄断利润的寻租活动是一种纯粹的浪费,这进一步加剧了垄断的低效率情况。
3.外部影响的存在是如何干扰市场对资源的配置的?解答:第一,如果某个人采取某项行动的私人利益小于社会利益(即存在外部经济),则当这个人采取该行动的私人成本大于私人利益而小于社会利益时,他就不会采取这项行动,尽管从社会的角度看,该行动是有利的。
第二,如果某个人采取某项行动的私人成本小于社会成本(即存在外部不经济),则当这个人采取该行动的私人利益大于私人成本而小于社会成本时,他就会采取这项行动,尽管从社会的角度看,该行动是不利的。
第三,上述两种情况均导致了资源配置失当。
前者是生产不足,后者是生产过多。
4.如何看“科斯定理”?它在资本主义社会中适用吗?它在社会主义社会中适用吗?解答:第一,科斯定理要求财产权明确。
但是,财产权并不总是能够明确地加以规定。
有的资源,例如空气,在历史上就是大家均可使用的共同财产,很难将其财产权具体分派给谁;有的资源的财产权即使在原则上可以明确,但由于不公平问题、法律程序的成本问题等也变得实际上不可行。
第二,科斯定理要求财产权可以转让。
但是,由于信息不充分以及买卖双方不能达成一致意见等,财产权并不一定总是能够顺利地转让。
第三,即使财产权是明确的、可转让的,也不一定总能实现资源的最优配置。
转让之后的结果可能是它与原来的状态相比有所改善,但不一定为最优。
高鸿业微观经济学第五版 成本练习及答案

高鸿业微观经济学第五版成本练习及答案高鸿业微观经济学第五版成本练习及答案第五章成本理论练习一、单项选择题1、在经济学中,短期是指(d)a一年或一年以内的时期b在这一时期内所有资金投入要素均就是紧固维持不变的c在这一时期内所有资金投入要素均就是可以变动的d在这一时期内,生产者来不及调整全部生产要素的数量,至少有一种生产要素的数量是固定不变的2、在经济学中,短期和长期的分割标准就是(d)a与否可以调整产量b与否可以调整产品价格c时间长短d是否可以调整全部生产要素的数量3、在经济学中,生产的机会成本等于(d)a显性成本+隐性成本b社会成本+显性成本c财务会计成本+隐性成本da和c都对4、短期气门成本曲线随其产量减少而(a)a不断下降b不断上升c先下降再上升d先上升再下降5、某厂商生产一批产品,当生产第7个单位产品的总成本是3.5元,生产第8个单位产品总成本是4.6元,那么该厂商的边际成本是(d)a3.5元b4.6元c8.1元d1.1元6、在短期内,以下观点不恰当的一项就是(d)a总不变成本(tfc)是厂商为生产一定量的产品对不变生产要素所支付的总成本b建筑物和机器设备的折旧费属于总不变成本c总固定成本不随产量的变化而变化d当产量为零时,总固定成本也为零7、当平均成本高于边际成本时,(b)a平均值成本处在下降b平均值成本处在上升c总成本处在上升d总气门成本处在上升8、当边际成本曲线交于平均成本曲线时,下列各项不正确的是(c)a边际成本上升b平均可变成本上升c边际成本下降d总成本上升9、当边际成本曲线达到最低点时(a)a平均成本曲线呈现递减状态b平均可变成本曲线呈现递增状态c平均产量曲线达到最大值d总产量曲线达到最大值10、边际成本曲线(c)a沿着平均值总成本曲线和平均值固定成本曲线的最低点b沿着平均值气门成本曲线和平均值固定成本曲线的最低点c沿着平均值气门成本曲线和平均值成本曲线的最低点d 仅沿着平均值气门成本曲线的最低点11、当边际成本曲线上升时,其对应的平均可变成本曲线一定是(d)a上升b下降c即为不下降,也不上升d即可能将下降,又可能将上升12、当短期成本曲线以递减的速率上升时,(b)a边际成本曲线处在递增阶段b边际成本曲线处在递减阶段c边际产量曲线处在递减阶段d无法判断边际成本曲线与边际产量曲线的状态13、长期成本曲线上的各点对应的就是既定产量下的(d)a最高平均值成本b最高边际成本c平均值成本变动d最高总成本14、长期边际成本曲线呈圆形u型的原因是(c)a边际效用递减规律b边际收益递减规律c生产有规模经济向规模不经济变动d生产的一般规律15、长期成本曲线是各种产量的(a)a最高成本点的轨迹b最高平均值成本点的轨迹c最高边际成本点的轨迹d最高平均值气门成本点的轨迹16、以下关于长期边际成本曲线与长期总成本曲线之间的关系的观点恰当的就是(b)a在长期边际成本曲线下降时,长期总成本曲线以越来越快的速度下降b 在长期边际成本曲线下降时,长期总成本曲线以越来越快的速度下降c在长期边际成本曲线上升时,长期总成本曲线以越来越快的速度下降d以上均不恰当17、若某厂商的生产产量扩大1倍,而厂商生产成本的增加低于1倍,则该厂商的生产存在(a)a规模经济b规模不经济c外部性d以上均不恰当18、某日用品制造商厂单位产量所带来的边际成本大于产量增加前的平均可变成本,那么在产量增加后平均可变成本会(b)a增加b减少c维持不变d无法推论19、如某厂商的总收益为65000元,其中劳动成本为23000元,原材料成本为16500元,所有者为其他人工作可赚取14300元。
微观经济学高鸿业第五版1~5章课后习题答案
微观经济学第三章1、已知一件衬衫的价格为80元,一份肯德鸡快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德鸡快餐对衬衫的边际替代率MRS 是多少?解:按照两商品的边际替代率MRS的定义公式,可以将一份肯德鸡快餐对衬衫的边际替代率写成:XY MRS XY ∆∆-=其中:X 表示肯德鸡快餐的份数;Y 表示衬衫的件数; MRS 表示在维持效用水平不变的前提下, 消费者增加一份肯德鸡快餐时所需要放弃的衬衫消费数量。
在该消费者实现关于这两件商品的效用最大化时,在均衡点上有MRS xy =P x /P y即有MRS xy =20/80=0.25它表明:在效用最大化的均衡点上,消费者关于一份肯德鸡快餐对衬衫的边际替代率MRS 为0.25。
2 假设某消费者的均衡如图1-9所示。
其中,横轴1OX 和纵轴2OX ,分别表示商品1和商品2的数量,线段AB 为消费者的预算线,曲线U 为消费者的无差异曲线,E 点为效用最大化的均衡点。
已知商品1的价格P 1=2元。
(1)求消费者的收入; (2)求上品的价格2P ;(3)写出预算线的方程; (4)求预算线的斜率; (5)求E点的12MRS 的值。
解:(1)图中的横截距表示消费者的收入全部购买商品1的数量为30单位,且已知P 1=2元,所以,消费者的收入M =2元×30=60。
(2)图中的纵截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入M=60元,所以,商品2的价格P2斜率=-P1/P2=-2/3,得P2=M/20=3元(3)由于预算线的一般形式为:P1X1+P2X2=M所以,由(1)、(2)可将预算线方程具体写为2X1+3X2=60。
(4)将(3)中的预算线方程进一步整理为X2=-2/3X1+20。
很清楚,预算线的斜率为-2/3。
(5)在消费者效用最大化的均衡点E上,有MRS12= = MRS12=P1/P2,即无差异曲线的斜率的绝对值即MRS等于预算线的斜率绝对值P1/P2。
最新微观经济学高鸿业版第五章课后习题答案资料

第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+15OMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1Q 2长期边际成本曲线与短期成本曲线A4已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MIN AVC 5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时(1) 固定成本值:500 (2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A L A LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L (Q )+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC =100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC函数、SAC函数和AVC函数。
微观经济学课后习题答案(高鸿业)

微观经济学课后习题答案<高鸿业版>第1章课后习题详解1.回想你看到过或接触过的西方经济学著作。
它们各自属于本章所说的三种类别中的哪一种?答:第一类,企事业的经营管理方法和经验。
如行情研究、存货管理、产品质量控制、车间生产流程布局等内容。
著作有《现代企业财务管理》等。
第二类,对一个经济部门或经济问题的集中研究成果。
如资源经济学、商业经济学、农业经济学、石油经济学,对税收、财政和通货膨胀等问题的论述。
著作有《资源经济学》、《农业经济学》。
第三类,经济理论的研究和考察。
如微观经济学、数理经济学、福利经济学、经济思想史等。
著作有《宏观经济学》、《微观经济学》、《经济思想史》等。
2.为什么我国学员学习西方经济学的目的不同于西方?答:由于西方经济学具有双重性质,它既是资本主义的意识形态,由是资本主义市场经济的经验总结,这就决定了我国学员学习它所应持有的态度:在整个的理论体系上或整体倾向上对它持否定的态度,而在具体的内容上应该看到它的有用之处,是否真正有用还需要考虑到国情的差别,应结合我国的国情加以借鉴吸收,做到“弃其糟粕、取其精华、洋为中用”。
(1)我国学习下岗经济学的主要目的在于从中得到对我国有用的知识,即“学以致用”。
对西方经济学而言,“为艺术而艺术”的学习目标是不适用的。
因为,如果不是为了“实用”而学习,那么还不如去从事其它的活动。
“经济学”这一名词的英文来源是希腊文的名词“家庭管理”。
由此也可以看出西方经济学的“致用”的性质。
(2)既然学习西方经济学的目的是为了“致用”,那么就必须注意到它涉及对西方“致用”的两个特点:其一,它宣扬西方国家的意识形态,以便巩固西方社会的共识或凝聚力,即增加西方学者所说的“社会无形资本”;其二,它总结西方市场运行的经验,以便为改善其运行提供对策。
西方经济学之所以能够存在于西方,其原因即在于此;这就是说:它存在于西方的原因正是由于他对西方国家有用。
(3)在以上两个特点中,第一个特点显然对我国不但没有用处,反而会引起有害的作用。
西方经济学微观部分(高鸿业_第五版)课后习题详细问题详解

第二章需求、供给和均衡价格1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(4)利用(1)、(2)和(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
高鸿业西方经济学(微观部分)第五版2-11章课后题答案

高鸿业西方经济学(微观部分)第五版2-11章课后题答案本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March第二章需求曲线与供给曲线.............................................................................. 错误!未定义书签。
第三章效用论...................................................................................................... 错误!未定义书签。
第四章生产论...................................................................................................... 错误!未定义书签。
第五章成本论...................................................................................................... 错误!未定义书签。
第七章不完全竞争的市场.................................................................................. 错误!未定义书签。
第八章生产要素价格的决定.............................................................................. 错误!未定义书签。
第九章一般均衡论和福利经济学...................................................................... 错误!未定义书签。
(全1-23章共157页)高鸿业西方经济学微观部分第五版课后习题答案
第一章引论见本书第二十三章。
第二章需求、供给和均衡价格1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(4)利用(1)、(2)和(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
微观经济学高鸿业版第五章课后习题答案

第五章1.下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空(2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4)根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.解:(1)短期生产的产量表(表1)(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15QOMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1 Q 2长期边际成本曲线与短期成本曲线AAC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+154已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV得Q=10又因为008.0>=''C AV所以当Q=10时,6=MIN AVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时(1) 固定成本值:500 (2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A LA LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP 整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L(Q )+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L1/3K2/3, 有Q=25.又π=TR-STC=100Q-10Q-500=1750所以利润最大化时的产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC函数、SAC函数和AVC函数。
高鸿业微观经济学(第5版)课后习题答案 第七章

第七章不完全竞争的市场1. 根据图7—1(即教材第205页的图7—18)中线性需求曲线d和相应的边际收益曲线MR,试求:图7—1(1)A点所对应的MR值;(2)B点所对应的MR值。
解答:(1)根据需求的价格点弹性的几何意义,可得A点的需求的价格弹性为e d=eq \f(15-5,5)=2或者e d=eq \f(2,3-2)=2再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d))),则A点的MR值为MR=2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,2)))=1(2)与(1)类似,根据需求的价格点弹性的几何意义,可得B点的需求的价格弹性为e d=eq \f(15-10,10)=eq \f(1,2)或者e d=eq \f(1,3-1)=eq \f(1,2)再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d))),则B点的MR值为MR=1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,1/2)))=-12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线;(3)长期均衡时的利润量。
图7—2解答:本题的作图结果如图7—3所示:图7—3(1)长期均衡点为E点,因为在E点有MR=LMC。
由E点出发,均衡价格为P0,均衡数量为Q0。
(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。
在Q0的产量上,SAC曲线和LAC曲线相切;SMC曲线和LMC曲线相交,且同时与MR曲线相交。
(3)长期均衡时的利润量由图7—3中阴影部分的面积表示,即π=[AR(Q0)-SAC(Q0)]·Q 0。
高鸿业第五版微观经济学课后习题答案

.2/1 于等恒 性弹点的求需的应相,少多为 M 入收论无则,时)数常为 0>a 中其( 2Qa=M 数函入收当,现发以可,果结其即程过算计上以析分并察观
:得可,步一进
:有,是于 001/M√=Q 得可 2Q 001=M 件条知以由�解 。性 弹点入收的求需的时 0046=M 入收当�求。2Q001=M 为系关数函的间之 M 入收与 Q 量数费消的品商种某于关者费消某定假 5
的出求,下件条的定给)5,01-(数参的中数函给供及以)5-,05(数参的数函求需括包量变生外在: 析分态静解理来样这以可也.eP=sP=dP
�
GO/DG=edE�有点 e 在 GO/CG=fdE�有点 f 在
GO/BG=adE�有点 a 在 :于在由理其 edE<fdE<adE 有且,的等相不是 性弹点格价的求需的点三 f.e.a 的上线曲求需性线条三于处别分:知推地便方很以可样同,法方何几的性弹点格价的求需求据根�2�
Pd
��
Q Pd � � � dE P Qd
:为写以可性弹格价的求需的计合者费消个 001 上场市该,外此 )4( )3( 且 )04……2,1=j(P/jQ6-=Pd/jQd 即 6=)Q/P(*)Pd/Qd(-=jdE :为写以可性弹格价的 求需的 j 者费消个单,是于,6 是都性弹格价的求需的者费消个每且,买购者费消个 04 外另被品商的 3/1 场市该,意题据根再,的似类相 )2( 且
�吗同相果结的�2�与它。性弹点格价的求需的时 2=P 出求法方何几用利�形图何几的应相出作表求需或数函求需该据根�3� 。性弹点格价的求需的是 2=P 求�数函求需的出给据根�2� 。性弹弧格价的求需的间之元 4 和元 2 格价出求�1� 0 5 001 4 002 3 003 2 004 1 量求需 �元�格价 表求需的品商某 �表求需的内围范格价定一在 P001-005=dQ 数函求需是 5—2 表定假 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章需求、供给和均衡价格1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(4)利用(1)、(2)和(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E 就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s =-10+5P 和需求函数Q d=50-5P 表示,均衡点E 具有的特征是:均衡价格P e =6,且当P e =6时,有Q d =Q s=Q e =20;同时,均衡数量Q e =20,且当Q e =20时,有P d =P s=P e =6。
也可以这样来理解静态分析:在外生变量包括需求函数中的参数(50,-5)以及供给函数中的参数(-10,5)给定的条件下,求出的内生变量分别为P e =6和Q e =20。
依此类推,以上所描述的关于静态分析的基本要点,在(2)及图2—2和(3)及图2—3中的每一个单独的均衡点E i (i =1,2)上都得到了体现。
而所谓的比较静态分析是考察当原有的条件发生变化时,原有的均衡状态会发生什么变化,并分析比较新旧均衡状态。
也可以说,比较静态分析是考察在一个经济模型中外生变量变化时对内生变量的影响,并分析比较由不同数值的外生变量所决定的内生变量的不同数值,以(2)为例加以说明。
在图2—2中,由均衡点E 1变动到均衡点E 2就是一种比较静态分析。
它表示当需求增加即需求函数发生变化时对均衡点的影响。
很清楚,比较新、旧两个均衡点E 1和E 2可以看到:需求增加导致需求曲线右移,最后使得均衡价格由6上升为7,同时,均衡数量由20增加为25。
也可以这样理解比较静态分析:在供给函数保持不变的前提下,由于需求函数中的外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量的数值发生变化,其结果为,均衡价格由原来的6上升为7,同时,均衡数量由原来的20增加为25。
类似地,利用(3)及图2—3也可以说明比较静态分析方法的基本要点。
(5)由(1)和(2)可见,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了。
由(1)和(3)可见,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了。
总之,一般地,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量成同方向变动。
2. 假定表2—1(即教材中第54页的表2—5)是需求函数Q d =500-100P 在一定价格范围内的需求表:表2—1某商品的需求表价格(元) 1 2 3 4 5 需求量 400 300 200 100 0(1)求出价格2元和4元之间的需求的价格弧弹性。
(2)根据给出的需求函数,求P =2元时的需求的价格点弹性。
(3)根据该需求函数或需求表作出几何图形,利用几何方法求出P =2元时的需求的价格点弹性。
它与(2)的结果相同吗?解答:(1)根据中点公式e d =-ΔQ ΔP ·P 1+P 22,Q 1+Q 22),有e d =2002·2+42,300+1002)=1.5(2)由于当P =2时,Q d=500-100×2=300,所以,有e d =-d Q d P ·P Q =-(-100)·2300=23(3)根据图2—4,在a 点即P =2时的需求的价格点弹性为e d =GB OG =200300=23或者 e d =FO AF =23图2—4显然,在此利用几何方法求出的P =2时的需求的价格点弹性系数和(2)中根据定义公式求出的结果是相同的,都是e d =23。
3. 假定表2—2(即教材中第54页的表2—6)是供给函数Q s=-2+2P 在一定价格范围内的供给表:表2—2某商品的供给表价格(元) 2 3 4 5 6 供给量 2 4 6 8 10(1)求出价格3元和5元之间的供给的价格弧弹性。
(2)根据给出的供给函数,求P =3元时的供给的价格点弹性。
(3)根据该供给函数或供给表作出几何图形,利用几何方法求出P =3元时的供给的价格点弹性。
它与(2)的结果相同吗?解答:(1)根据中点公式e s =ΔQ ΔP ·P 1+P 22,Q 1+Q 22),有e s =42·3+52,4+82)=43(2)由于当P =3时,Q s =-2+2×3=4,所以,e s =d Q d P ·P Q =2·34=1.5。
(3)根据图2—5,在a 点即P =3时的供给的价格点弹性为e s =AB OB =64=1.5图2—5显然,在此利用几何方法求出的P =3时的供给的价格点弹性系数和(2)中根据定义公式求出的结果是相同的,都是e s =1.5。
4. 图2—6(即教材中第54页的图2—28)中有三条线性的需求曲线AB 、AC 和AD 。
图2—6(1)比较a 、b 、c 三点的需求的价格点弹性的大小。
(2)比较a 、e 、f 三点的需求的价格点弹性的大小。
解答:(1)根据求需求的价格点弹性的几何方法,可以很方便地推知:分别处于三条不同的线性需求曲线上的a 、b 、c 三点的需求的价格点弹性是相等的。
其理由在于,在这三点上,都有e d =FOAF(2)根据求需求的价格点弹性的几何方法,同样可以很方便地推知:分别处于三条不同的线性需求曲线上的a 、e 、f 三点的需求的价格点弹性是不相等的,且有e a d <e f d <e ed 。
其理由在于在a 点有:e ad =GB OG在f 点有:e f d =GCOG 在e 点有:e ed =GD OG在以上三式中,由于GB <GC <GD ,所以,e a d <e f d <e ed 。
5.利用图2—7 (即教材中第55页的图2—29)比较需求价格点弹性的大小。
(1)图(a )中,两条线性需求曲线D 1和D 2相交于a 点。
试问:在交点a ,这两条直线型的需求的价格点弹性相等吗?(2)图(b)中,两条曲线型的需求曲线D 1和D 2相交于a 点。
试问:在交点a ,这两条曲线型的需求的价格点弹性相等吗?图2—7解答:(1)因为需求的价格点弹性的定义公式为e d =-d Q d P ·P Q ,此公式的-d Qd P项是需求曲线某一点斜率的绝对值的倒数,又因为在图(a )中,线性需求曲线D 1的斜率的绝对值小于线性需求曲线D 2的斜率的绝对值,即需求曲线D 1的-d Q d P 值大于需求曲线D 2的-d Qd P值,所以,在两条线性需求曲线D 1和D 2的交点a ,在P 和Q 给定的前提下,需求曲线D 1的弹性大于需求曲线D 2的弹性。
(2)因为需求的价格点弹性的定义公式为e d =-d Q d P ·P Q ,此公式中的-d Qd P项是需求曲线某一点的斜率的绝对值的倒数,而曲线型需求曲线上某一点的斜率可以用过该点的切线的斜率来表示。
在图(b )中,需求曲线D 1过a 点的切线AB 的斜率的绝对值小于需求曲线D 2过a 点的切线FG 的斜率的绝对值,所以,根据在解答(1)中的道理可推知,在交点a ,在P 和Q 给定的前提下,需求曲线D 1的弹性大于需求曲线D 2的弹性。
6. 假定某消费者关于某种商品的消费数量Q 与收入M 之间的函数关系为M =100Q 2。
求:当收入M =6 400时的需求的收入点弹性。
解答:由已知条件M =100Q 2,可得Q =M 100于是,有d Q d M =12⎝⎛⎭⎫M 100-12·1100进一步,可得e M =d Q d M ·MQ=12⎝⎛⎭⎫M 100-12·1100·100·⎝⎛⎭⎫M 1002M 100=12观察并分析以上计算过程及其结果,可以发现,当收入函数M =aQ 2(其中a >0,为常数)时,则无论收入M 为多少,相应的需求的收入点弹性恒等于12。
7. 假定需求函数为Q =MP -N ,其中M 表示收入,P 表示商品价格,N(N >0)为常数。
求:需求的价格点弹性和需求的收入点弹性。
解答:由已知条件Q =MP -N ,可得e d =-d Q d P ·P Q =-M·(-N)·P -N -1·PMP -N =Ne M =d Q d M ·M Q =P -N ·MMP-N =1由此可见,一般地,对于幂指数需求函数Q(P)=MP -N 而言, 其需求的价格点弹性总等于幂指数的绝对值N 。
