2019-2020年九年级数学下册29.3 课题学习 制作立体模型同步练习 新人教版
人教版初中数学九年级下册《29.3 课题学习 制作立体模型》同步练习卷(1)

人教新版九年级下学期《29.3 课题学习制作立体模型》同步练习卷一.选择题(共20小题)1.如图,按照三视图确定该几何体的侧面积是(单位:cm)()A.24πcm2B.48πcm2C.60πcm2D.80πcm22.如图是某几何体的三视图,则该几何体的全面积等于()A.112B.136C.124D.843.如图,是由几个相同的小正方体组合而成的立体图形的三视图,则这个几何体的小正方体的个数是()A.5B.6C.7D.84.如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图,那么构成这个立方体图形的小正方体有()个.A.5B.6C.7D.85.如图,是一个几何体的三视图(单位:cm),则图中几何体的体积是()A.30 πcm3B.24 πcm3C.15 πcm3D.12 πcm36.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π7.一个几何体的三视图如图所示,则该几何体是()A.B.C.D.8.一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是()A.B.C.D.9.分别从正面和上面观察长方体的形状,如图所示(单位:m),则从左面观察此长方体,看到的图形的面积是()A.4m2B.12m2C.1m2D.3m210.如图是一个几何体的三视图,则这个几何体的侧面积是()A.B.2πC.4πD.411.从一个物体的不同方向看到的是如图所示的三个图形,则该物体的形状为()A.圆柱B.棱柱C.球D.圆锥12.如图是由几个大小相同的小正方体搭成的几何体从上向下看得到的平面图形,小正方形中的数字表示该位置上小正方体的个数,则从左向右看得到的平面图形是()A.B.C.D.13.如图,这是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积为()A.9πB.10πC.11πD.12π14.如图,是一个几何体的三视图,则此几何体的全面积是()A.210πcm2B.175πcm2C.320πcm2D.285πcm215.如图是一个几何体的三视图,则这个几何体的表面积是()A.60π+48B.68π+48C.48π+48D.36π+4816.如图是几个小立方块所搭的几何体俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是()A.B.C.D.17.桌上摆着一个由若干个相同正方体组成的几何体,其三视图如图所示,则组成此几何体需要正方体的个数是()A.7B.8C.9D.1018.分别从正面、左面和上面这三个方向看下面的四个几何体中的一个,得到如图所示的平面图形,那么这个几何体是()A.B.C.D.19.如图是几何体的三视图,该几何体是()A.正三棱柱B.正三棱锥C.圆柱D.圆锥20.由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数据表示该位置的小正方体的个数,则该几何体的左视图为()A.B.C.D.二.填空题(共20小题)21.如图是一个几何体的三个视图,若这个几何体的体积是24,则它的主视图的面积是.22.一个几何体有若干大小相同的小立方块搭成,如图分别是从它的正面、左面看到的形状图,则搭成该几何体最多需要个小立方块.23.若干桶方便面摆放在桌面上,如图所给出的是从不同方向看到的图形,从图形上可以看出这堆方便面共有桶.24.如图所示,是一个简单几何体的三视图,则这个几何体的侧面积等于.25.由n个相同的小正方形堆成的几何体,其视图如图所示,则n的最大值是,最小值是.26.如图,用棱长为1cm的小立方块组成一个几何体,从正面看和从上面看得到的图形如图所示,则这样的几何体的表面积的最小值是cm2.27.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要块正方体木块,至多需要块正方体木块.28.如图所示为一机器零件的三视图.若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积为.29.如图示一些小正方体木块所搭的几何体,从正面和从左面看到的图形,则搭建该几何体最多需要块正方体木块.30.如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积是.31.如图是由棱长相等的小立方体摆成的几何体的主视图与俯视图,根据视图可以判断组成这个几何体至少要个小立方体.32.如图,左边是一个由5个棱长为1的小正方体组合而成的几何图,现在增加一个小正方体,使其主视图如右,则增加后的几何体的左视图的面积为.33.如图是一个立体图形的三视图,那么这个立体图形的体积为.34.如图是某个几何体的主视图、左视图、俯视图,则该几何体是.35.一般把物体从正面看到的视图叫主视图,从左面看到的视图叫左视图,从上面看到的视图叫俯视图,一个几何体的三视图如图所示,则该几何体的侧面展开图的面积为.36.如图,是由一些相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体个数最多为个.37.如图是一些小正方体木块所搭的几何体,从正面和从上面看到的图形,则搭建该几何体最多需要块正方体木块,至少需要块正方体木块.38.用一些大小相同的小正方体搭成一个几何体,使得从正面和上面看到的这个几何体的形状如图所示,那么,组成这个几何体的小正方体的块数至少为.39.如图是某几何体的三视图,则该几何体左视图的面积为.40.一个几何体由若干个大小相同点小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是用块小立方块搭成的.三.解答题(共10小题)41.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,一摞碟子的层数与累积高度的关系如下表:(1)当一摞碟子有x层时,请写出此时的累积高度(用含x的式子表示);(2)桌子上有一些碟子,如图分别是从正面、左面和上面看到的形状图,厨房师傅想把这些碟子全部叠成一摞,求叠成一摞后的累积高度.42.如图是一个立体图形的三视图,根据图中数据,求该几何体的表面积.43.已知一个几何体的三视图如图,根据图示的数据计算该几何体的全面积及侧面展开图的圆心角(结果保留π).44.如图,的是某个几何体从三种不同方向所看到的图形.(1)说出这个立体图形的名称;(2)根据图中的有关数据,求这个几何体的侧面积.45.如图是两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸单位(毫米),求这个几何体的表面积.46.由若干个小正方体构成的几何体的主视图和左视图都是如图所示,则该几何体最多有个小正方体,最少有个小正方体.47.如图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的侧面积及全面积(结果保留π)48.一个几何体的三视图如图,求这个几何体的侧面积?49.如图是一个几何体的三视图:(1)请写出这个几何体的名称.(2)求这个几何体的侧面积.50.如图为一个几何体的三视图.(1)写出这个几何体的名称;(2)若俯视图中等边三角形的边长为4cm,主视图中大长方形的周长为28cm,求这个几何体的侧面积.人教新版九年级下学期《29.3 课题学习制作立体模型》2019年同步练习卷参考答案与试题解析一.选择题(共20小题)1.如图,按照三视图确定该几何体的侧面积是(单位:cm)()A.24πcm2B.48πcm2C.60πcm2D.80πcm2【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状,确定圆锥的母线长和底面半径,从而确定其侧面积.【解答】解:由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;根据三视图知:该圆锥的母线长为6cm,底面半径为8÷2=4cm,故侧面积=πrl=π×6×4=24πcm2.故选:A.【点评】此题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.2.如图是某几何体的三视图,则该几何体的全面积等于()A.112B.136C.124D.84【分析】由三视图可知该几何体是一个三棱柱,先根据勾股定理得到主视图三角形等边的长,再根据三棱柱的全面积=2个底面积+3个侧面积,列式计算即可求解.【解答】解:如图:由勾股定理=3,3×2=6,6×4÷2×2+5×7×2+6×7=24+70+42=136.故选:B.【点评】考查了由三视图判断几何体,由三视图求几何体的表面积,关键是由三视图得到数据的对应量.3.如图,是由几个相同的小正方体组合而成的立体图形的三视图,则这个几何体的小正方体的个数是()A.5B.6C.7D.8【分析】根据该几何体的俯视图可确定该几何体共有两行三列,再结合主视图,即可得出该几何体的小正方体的个数.【解答】解:综合三视图可知,这个几何体的底层应该有4个小正方体,第二层应该有1个小正方体,因此搭成这个几何体所用小正方体的个数是4+1=5个.故选:A.【点评】本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.4.如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图,那么构成这个立方体图形的小正方体有()个.A.5B.6C.7D.8【分析】易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.【解答】解:由从上面看到的图形易得最底层有4个正方体,第二层有1个正方体,那么共有4+1=5(个)正方体.故选:A.【点评】本题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.5.如图,是一个几何体的三视图(单位:cm),则图中几何体的体积是()A.30 πcm3B.24 πcm3C.15 πcm3D.12 πcm3【分析】根据三视图得出几何体为圆锥,再利用圆锥的体积公式解答即可.【解答】解:由三视图可得:几何体为圆锥,所以圆锥的体积=cm3,故选:D.【点评】此题考查三视图判定几何体,关键是根据三视图得出几何体为圆锥.6.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π【分析】根据圆柱体的体积公式以及对称性,即可解决问题;【解答】解:观察图象可知,几何体的体积=π•32+•π•32×6=63π,故选:B.【点评】本题考查三视图,圆柱体的体积公式等知识,解题的关键是读懂图象信息,学会利用对称性解决问题,属于中考常考题型.7.一个几何体的三视图如图所示,则该几何体是()A.B.C.D.【分析】根据三视图的形状可判断几何体的形状.【解答】解:∵该几何体的左视图和侧视图为长方形,主视图是复合图形,∴该几何体图形为,故选:C.【点评】本题考查了几何体的三视图和结构特征,根据三视图的形状可判断几何体的形状是关键.8.一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是()A.B.C.D.【分析】由已知条件可知,从正面看有3列,每列小正方数形数目分别为4,3,2;从左面看有3列,每列小正方形数目分别为1,4,3.据此可画出图形.【解答】解:由俯视图及其小正方体的分布情况知,该几何体的主视图为:该几何体的左视图为:故选:B.【点评】此题主要考查了几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视图的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.9.分别从正面和上面观察长方体的形状,如图所示(单位:m),则从左面观察此长方体,看到的图形的面积是()A.4m2B.12m2C.1m2D.3m2【分析】先根据从正面、从上面看到的形状图的相关数据可得,从左面看到的形状图是长为3m宽为1m的长方形,再根据长方形的面积公式计算即可.【解答】解:根据从正面、从上面看到的形状图的相关数据可得:从左面看到的形状图是长为3m宽为1m的长方形,则从左面看到的形状图的面积是3×1=3(m2).故选:D.【点评】此题考查了由三视图判断几何体,关键是根据从正面、从上面看到的形状图的相关数据得出从左面看到的形状图是长为3m宽为1m的长方形.10.如图是一个几何体的三视图,则这个几何体的侧面积是()A.B.2πC.4πD.4【分析】易得圆锥的底面直径为2,母线长为2,根据勾股定理可得圆锥的底母线长,根据圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求解.【解答】解:易得此几何体为圆锥,底面直径为2,母线长为2,所以圆锥的侧面积=πrl=2×1π=2π,故选:B.【点评】本题考查了由三视图判断几何体及圆锥的计算的知识,解题的关键是能够确定几何体的形状,难度不大.11.从一个物体的不同方向看到的是如图所示的三个图形,则该物体的形状为()A.圆柱B.棱柱C.球D.圆锥【分析】由主视图和左视图可得此几何体为锥体,根据俯视图是圆及圆心可判断出此几何体为圆锥.【解答】解:∵主视图和左视图都是三角形,∴此几何体为锥体,∵俯视图是一个圆及圆心,∴此几何体为圆锥,故选:D.【点评】本题考查了由三视图判断几何体的知识,用到的知识点为:由主视图和左视图可得几何体是柱体,锥体还是球体,由俯视图可确定几何体的具体形状.12.如图是由几个大小相同的小正方体搭成的几何体从上向下看得到的平面图形,小正方形中的数字表示该位置上小正方体的个数,则从左向右看得到的平面图形是()A.B.C.D.【分析】根据左视图的定义解答可得.【解答】解:由俯视图知,该几何体共2行3列,第1行自左向右依次有1个、2个、3个正方体,第2行第2列有1个正方体,其左视图如下所示:故选:A.【点评】此题考查了由三视图判断几何体,做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.13.如图,这是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积为()A.9πB.10πC.11πD.12π【分析】由三视图可判断出几何体的形状,进而利用圆锥的侧面积公式求出答案.【解答】解:由题意可得此几何体是圆锥,底面圆的半径为:2,母线长为:5,故这个几何体的侧面积为:π×2×5=10π.故选:B.【点评】此题主要考查了由三视图判断几何体的形状以及圆锥侧面积求法,正确得出几何体的形状是解题关键.14.如图,是一个几何体的三视图,则此几何体的全面积是()A.210πcm2B.175πcm2C.320πcm2D.285πcm2【分析】首先由几何体的三视图断定原几何体是一个圆锥和圆柱的组合体,进而解答即可.【解答】解:由已知可得原几何体是一个圆锥和圆柱的组合体,上部分是一个圆锥,下部分是一个圆柱,而且圆锥和圆柱的底面积相等,此几何体的全面积是=cm2,故选:A.【点评】本题考查了简单空间几何体的三视图,由三视图还原原几何体,首先是看俯视图,然后结合主视图和侧视图得原几何体,解答的关键是明白三种视图都是图形在与目光视线垂直面上的投影,此题是基础题.15.如图是一个几何体的三视图,则这个几何体的表面积是()A.60π+48B.68π+48C.48π+48D.36π+48【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,判断出几何体的形状,再根据三视图的数据,求出几何体的表面积即可.【解答】解:此几何体的表面积为π•42××2+•2π•4×6+(4+4)×6=60π+48,故选:A.【点评】此题考查了由三视图判断几何体,用到的知识点是三视图,几何体的表面积的求法,准确判断几何体的形状是解题的关键.16.如图是几个小立方块所搭的几何体俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是()A.B.C.D.【分析】由主视图的定义可得.【解答】解:这个几何体的主视图是,故选:D.【点评】本题主要考查简单几何体的三视图,熟练掌握三视图的定义是解题的关键.17.桌上摆着一个由若干个相同正方体组成的几何体,其三视图如图所示,则组成此几何体需要正方体的个数是()A.7B.8C.9D.10【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.【解答】解:根据俯视图可知该组合体共2行、4列,结合主视图和左视图知该几何体中小正方体的分布情况如图所示:则组成此几何体需要正方体的个数是8,故选:B.【点评】本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.18.分别从正面、左面和上面这三个方向看下面的四个几何体中的一个,得到如图所示的平面图形,那么这个几何体是()A.B.C.D.【分析】由主视图和左视图可得此几何体为柱体,根据俯视图是三角形可判断出此几何体为三棱柱.【解答】解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个三角形,∴此几何体为三棱柱.故选:A.【点评】本题主要考查了由三视图判断几何体,由主视图和左视图可得几何体是柱体,锥体还是球体,由俯视图可确定几何体的具体形状.19.如图是几何体的三视图,该几何体是()A.正三棱柱B.正三棱锥C.圆柱D.圆锥【分析】该几何体的俯视图与左视图均为矩形,主视图为三角形,易得出该几何体的形状.【解答】解:该几何体的左视图为矩形,俯视图亦为矩形,主视图是一个三角形,则可得出该几何体为正三棱柱.故选:A.【点评】本题主要考查的是三视图的相关知识,解得此题时要有丰富的空间想象力,是个简单题.20.由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数据表示该位置的小正方体的个数,则该几何体的左视图为()A.B.C.D.【分析】由已知条件可知,左视图有2列,每列小正方形数目分别为3,3,据此可得出图形,从而求解.【解答】解:观察图形可知,该几何体的左视图是.故选:D.【点评】本题考查由三视图判断几何体,简单组合体的三视图.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.二.填空题(共20小题)21.如图是一个几何体的三个视图,若这个几何体的体积是24,则它的主视图的面积是12.【分析】由2个视图是长方形,那么这个几何体为棱柱,另一个视图是三角形,那么可得该几何体是三棱柱,由三视图知,三棱柱的正面的高是3,根据三棱柱的体积公式得到三角形的底,根据三角形公式列式计算即可.【解答】解:由三视图知,几何体是一个三棱柱,三棱柱的正面是高为3的三角形,∵这个几何体的体积是24,∴三角形的底为=8,∴它的主视图的面积=×8×3=12,故答案为:12.【点评】此题考查了由三视图判断几何体和几何体的表面积求法,正确判断出几何体的形状是解题的关键.22.一个几何体有若干大小相同的小立方块搭成,如图分别是从它的正面、左面看到的形状图,则搭成该几何体最多需要14个小立方块.【分析】从主视图上弄清物体的上下和左右形状,从左视图上弄清楚物体的上下和前后形状,综合分析,即可得出答案.【解答】解:根据主视图和左视图可得:搭这样的几何体最多需要6+3+5=14个小正方体;故答案为:14.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图;注意主视图主要告知组成的几何体的层数和列数.23.若干桶方便面摆放在桌面上,如图所给出的是从不同方向看到的图形,从图形上可以看出这堆方便面共有6桶.【分析】从俯视图中可以看出最底层方便面的个数及摆放的形状,从主视图可以看出每一层方便面的层数和个数,从左视图可看出每一行方便面的层数和个数,从而算出总的个数.【解答】解:三摞方便面是桶数之和为:3+1+2=6.故答案为:6【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.24.如图所示,是一个简单几何体的三视图,则这个几何体的侧面积等于18.【分析】由几何体的三视图可知,该几何体是底面边长为2的等边三角形、高为3的三棱柱,再根据侧面积公式可得.【解答】解:由几何体的三视图可知,该几何体是底面边长为2的等边三角形、高为3的三棱柱,∴这个几何体的侧面积等于3×2×3=18,故答案为:18.【点评】本题考查了由三视图求几何体的侧面积,根据三视图判断几何体的形状是关键.25.由n个相同的小正方形堆成的几何体,其视图如图所示,则n的最大值是18,最小值是12.【分析】由几何体的主视图和俯视图可知,该几何体的主视图的第一列2个小正方形中每个正方形所在位置最多均可有3个小立方块,最少一个正方形所在位置有3个小立方块,另一个所在位置有1个小立方块;主视图的第二列3个小正方形中,每个小正方形所在位置最多均可有2个小立方块,最少一个正方形所在位置有2个小立方块,另两个所在位置各有1个小立方块;主视图的第三列2个小正方形所在位置最多均可有3个小立方块,最少一个正方形所在位置有3个小立方块,另一个所在位置有1个小立方块.【解答】解:这样的几何体不止一种,而有多种摆法.最多需要3×2+2×3+3×2=18(个)小立方块,最少需要7+3+2=12(个)小立方块.所以n的最大值是18,最小值是12.故答案为:18,12.【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖”就更容易得到答案.26.如图,用棱长为1cm的小立方块组成一个几何体,从正面看和从上面看得到的图形如图所示,则这样的几何体的表面积的最小值是34cm2.【分析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数,由主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.【解答】解:搭这样的几何体最少需要6+2+1=9个小正方体,最多需要6+5+2=13个小正方体;故最多需要13个小正方体,最少需要9个小正方体.最少的小正方体搭成几何体的表面积是(6+6+5)×2=34.故答案为:34;【点评】本题考查由三视图判断几何体,做这类题时要借助三种视图表示物体的特点,。
人教版数学九年级下册第29章29.1--29.3同步练习题(含答案)

人教版数学九年级下册第29章29.1--29.3同步练习题(含答案)29.1《投影》一、选择题1.关于盲区的说法正确的有()(1)我们把视线看不到的地方称为盲区(2)我们上山与下山时视野盲区是相同的(3)我们坐车向前行驶,有时会发现一些高大的建筑物会被比矮的建筑物挡住(4)人们常说“站得高,看得远”,说明在高处视野盲区要小,视野范围大A.1 个B.2个C.3个D.4个2.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是()A.越来越小B.越来越大C.大小不变D.不能确定3.如下图所示的四幅图中,灯光与影子的位置最合理的是( )4.如图,一个斜插吸管的盒装饮料的正投影是图中的( )5.如图所示,晚上小亮在路灯下散步,在小亮由A处走向B处的过程中,他在地上的影子()A.逐渐变短B.逐渐变长C.先变短后再变长D.先变长后再变短6.如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )(A)①②③④. (B)④①③②. (C)④②③①. (D)④③②①.7.下列各种现象属于中心投影现象的是( )A.上午10点时,走在路上的人的影子C.中午用来乘凉的树影D.升国旗时,地上旗杆的影子8.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子()A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短9.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )A.小明的影子比小强的影子长B.小明的影子比小强的影子短C.小明的影子和小强的影子一样长D.无法判断谁的影子长10.下列说法正确的是()A.物体在阳光下的投影只与物体的高度有关B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.D.物体在阳光照射下,影子的长度和方向都是固定不变的.11.四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L、K、C的投影中,与字母N属于同一种投影的有( )A.L、KB.答案为:C;C.KD.L、K、C12.这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为()A.0.36π平方米B.0.81π平方米C.2π平方米D.3.24π平方米二、填空题13.有下列投影:①阳光下遮阳伞的影子;②探照灯光下小明读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子.其中属于平行投影的是________.(填序号)14.如图所示,此时树的影子是在(填太阳光或灯光)下的影子.15.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为____________m.16.如图所示是两棵小树在同一时刻的影子,可以断定这是________投影,而不是_______投影.17.如图是置于水平地面上的一个球形储油罐,小敏想测量它的半径.在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(如示意图,AB=10米);同一时刻,他又测得竖直立在地面上长为1米的竹竿的影子长为2米,那么,球的半径是米.18.如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是,则排球的直径是 cm.三、解答题19.如图,已知AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.(1)请你在图中画出此时DE在阳光下的投影;(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.20.如图,晚上,小亮在广场上乘凉。
人教版九年级下册数学《课题学习:制作立体模型》学案及双基练习(含答案)

课题29.3制作立体模型(活动课)一、学习目的通过根据三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图形之间的联系。
二、工具准备刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等。
三、具体活动1、以硬纸板为主要材料,分别做出下面的两组视图所表示的立体模型。
2、按照下面给出的两组视图,用马铃薯(或萝卜)做出相应的实物模型3、下面的每一组平面图形都是由四个等边三角形组成的。
(1) (2) (3)(1)指出其中哪些可以折叠成多面体。
把上面的图形描在纸上,剪下来,叠一叠,验证你的答案;(2)画出由上面图形能折叠成的多面体的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的;(3)如果上图中小三角形的边长为1,那么对应的多面体的体积和表面积各是多少?四、课题拓广三视图和展开图都是与立体图形有关的平面图形,了解有关生产实际,结合具体例子,写一篇短文介绍三视图、展开图的应用。
29.3 课题学习──制作立体模型一、双基整合:1.小明的身高是1.6米,他的影长是2米,同一时刻古塔的影长是18米,•则古塔的高是________米.2.某同学想利用影子长度测量操场上旗杆的高度,在某一时刻,他测得自己影子长为0.8m,立即去测量旗杆的影子长为5m,•已知他的身高为1.6m,•则旗杆的高度为_______m.3.由6个大小相同的正方体搭成的几何体如图1所示,则关于它的视图说法正确的是()A.正视图的面积最大 B.左视图的面积最大C.俯视图的面积最大 D.三个视图的面积一样大(1) (5)4.在一天的生活当中,在()时其影子最短.A.6点 B.12点 C.15点 D.18点5.如图2,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m•高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB•的高为()A.5m B.6m C.7m D.8m6.如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼之间的距离AC=24m,现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?(精确到0.1m2≈1.413≈1.73)?二、探究创新7.如图3是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是()(3) (4)A.24πc m3 B.48πcm3 C.72πc m3 D.192πcm38.如图4,太阳光线与地面成60°角,一棵倾斜的大树在地面上所成的角为30°,•这时测得大树在地面上的影长约为10m,试求此大树的长约是多少?9.按照下面给出的两组视图,用马铃薯(或萝卜)做出相应的实物模型.三、智能升级10.如图这是一个几何体的二视图,求该几何体的体积( 取3.14)答案:1.14.4 2.10 3.C 4.B 5.D6.解:设甲楼的影子在乙楼上的最高点为E,作EF⊥AB于F,在Rt△BFE中,∵∠BFE=90°,∠BEF=30°,∴BF=12BE,根据勾股定理,得BF2+EF2=BE2,∴BF2+242=4BF2,即313.8m,∴CE=AF=AB-BF=16.2(m)7.B8.解:过B•作BM⊥AC于M,∵∠A=30°,∠CBE=60°,故∠ACB=30°,∴BM=12AB=5,而BC=AB=10,•∴AM=53,即AC=103≈17cm.9.略 10.解:V=V圆柱体+V长方体= (202)2×32+30×25×40=40048(cm3).答:该几何体的体积为40048c m3.。
人教版初中数学九年级下册《29.3 课题学习 制作立体模型》同步练习卷(含答案解析
人教新版九年级下学期《29.3 课题学习制作立体模型》同步练习卷一.选择题(共10小题)1.一个几何体的三视图如图所示,则这个几何体是()A.三棱锥B.三棱柱C.圆柱D.长方体2.如图是一个几何体的三视图,则这个几何体是()A.B.C.D.3.如图是某个几何体的主视图、左视图、俯视图,该几何体是()A.圆柱B.球C.圆锥D.棱锥4.一个几何体的三视图如图所示,这个几何体是()A.棱柱B.正方形C.圆柱D.圆锥5.如图是一个几何体的三视图,则该几何体的展开图可以是()A.B.C.D.6.如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是()A.B.C.D.7.如图所示是一个几何体的三视图,这个几何体的名称是()A.圆柱体B.三棱锥C.球体D.圆锥体8.一个几何体的三视图如图所示,则该几何体的形状可能是()A.B.C.D.9.一个几何体的三视图如图所示,那么这个几何体是()A.圆锥B.圆柱C.长方体D.三棱柱10.如图所示的三视图所对应的几何体是()A.B.C.D.人教新版九年级下学期《29.3 课题学习制作立体模型》同步练习卷参考答案与试题解析一.选择题(共10小题)1.一个几何体的三视图如图所示,则这个几何体是()A.三棱锥B.三棱柱C.圆柱D.长方体【分析】根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱【解答】解:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.故选:B.【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.2.如图是一个几何体的三视图,则这个几何体是()A.B.C.D.【分析】结合三视图确定小正方体的位置后即可确定正确的选项.【解答】解:结合三个视图发现,应该是由一个正方体在一个角上挖去一个小正方体,且小正方体的位置应该在右上角,故选:B.【点评】本题考查了由三视图判断几何体的知识,解题的关键是能够正确的确定小正方体的位置,难度不大.3.如图是某个几何体的主视图、左视图、俯视图,该几何体是()A.圆柱B.球C.圆锥D.棱锥【分析】根据三视图即可判断该几何体.【解答】解:由于主视图与左视图是三角形,俯视图是圆,故该几何体是圆锥,故选:C.【点评】本题考查三视图,解题的关键是熟练掌握几种常见几何体的三视图,本题属于基础题型.4.一个几何体的三视图如图所示,这个几何体是()A.棱柱B.正方形C.圆柱D.圆锥【分析】根据三视图确定该几何体是圆柱体.【解答】解:根据主视图和左视图为矩形可判断出该几何体是柱体,根据俯视图是圆可判断出该几何体为圆柱.故选:C.【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.5.如图是一个几何体的三视图,则该几何体的展开图可以是()A.B.C.D.【分析】由主视图和俯视图可得此几何体为柱体,根据左视图是圆可判断出此几何体为圆柱,再根据圆柱展开图的特点即可求解.【解答】解:∵主视图和左视图是长方形,∴该几何体是柱体,∵俯视图是圆,∴该几何体是圆柱,∴该几何体的展开图可以是.故选:A.【点评】此题考查由三视图判断几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个视图确定其具体形状.同时考查了几何体的展开图.6.如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是()A.B.C.D.【分析】解答此题首先要明确主视图是从物体正面看到的图形,然后根据几何体的主视图,判断出这个几何体可以是哪个图形即可.【解答】解:∵几何体的主视图由3个小正方形组成,下面两个,上面一个靠左,∴这个几何体可以是.故选:A.【点评】此题主要考查了三视图的概念,要熟练掌握,解答此题的关键是要明确:主视图是从物体正面看到的图形.7.如图所示是一个几何体的三视图,这个几何体的名称是()A.圆柱体B.三棱锥C.球体D.圆锥体【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:由于主视图和左视图为长方形可得此几何体为柱体,由俯视图为圆可得为圆柱体.故选:A.【点评】本题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力.8.一个几何体的三视图如图所示,则该几何体的形状可能是()A.B.C.D.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:由主视图和左视图可得此几何体上面为台,下面为柱体,由俯视图为圆环可得几何体为.故选:D.【点评】此题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.9.一个几何体的三视图如图所示,那么这个几何体是()A.圆锥B.圆柱C.长方体D.三棱柱【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:由于俯视图为三角形.主视图为两个长方形和左视图为长方形可得此几何体为三棱柱.故选:D.【点评】考查学生对圆锥三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.10.如图所示的三视图所对应的几何体是()A.B.C.D.【分析】对所给四个几何体,分别从主视图和俯视图进行判断.【解答】解:从主视图可判断A,C、D错误.故选:B.【点评】本题考查了由三视图判断几何体:由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.。
九年级数学第二十九章《制作立体模型》同步练习(含答案)
九年级数学第二十九章《制作立体模型》同步练习(含答案)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.长方体的主视图与左视图如图所示,则这个长方体的表面积是A.27cm2B.54cm2C.94cm2D.120cm2【答案】C【解析】该几何体的主视图以及左视图都是相同的矩形,俯视图也为一个矩形,可确定这个几何体是一个长方体,依题意可得这个长方体的表面积为:2×(5×4+5×3+4×3)=94(cm2).故选C.2.如图是一个几何体的三视图,则这个几何体的表面积是A.60π+48 B.68π+48C.48π+48 D.36π+48【答案】A【解析】此几何体的表面积为π•42×34×2+34•2π•4×6+(4+4)×6=60π+48,故选A.3.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三梭柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为A.16+162B.16+82C.24+162D.4+42【答案】A【解析】由三视图知,该几何体是三棱柱,其侧面积为2×22×4+4×4=16+162,故选A.二、填空题:请将答案填在题中横线上.4.用硬纸壳做一个如图所示的几何体,其底面是圆心角为300°的扇形,则该几何体的表面积为__________cm2.【答案】60+65π.5.三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为__________cm.【答案】42三、解答题:解答应写出文字说明、证明过程或演算步骤.6.根据如图视图(单位:mm),求该物体的体积.【解析】由三视图知:该几何体是两个圆柱叠放在一起,上面圆柱的底面直径为8,高为4,下面圆柱的底面直径为16,高为16,故体积为π(16÷2)2×16+π(8÷2)2×4=1088π(mm3).7.某几何体从三个方向看到的图形分别如图:(1)该几何体是__________;(2)求该几何体的体积?(结果保留π)【解析】(1)这个几何体是圆柱,故答案为:圆柱;(2)圆柱底面积=π•(22)2=π,圆柱体积V=π•3=3π.。
2019-2020学年人教版数学九年级下册29.3 课题学习 制作立体模型 同步练习A卷
2019-2020学年人教版数学九年级下册29.3 课题学习制作立体模型同步练习A卷姓名:________ 班级:________ 成绩:________一、单选题 (共13题;共26分)1. (2分)下列哪个图形是正方体的展开图()A .B .C .D .2. (2分)如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是()A . 传B . 统C . 文D . 化3. (2分)某正方体的平面展开图如图所示,则原正方体中与“春”字所在的面相对的面上的字是()A . 青B . 来C . 斗D . 奋4. (2分)如图,将长方体的表面展开,得到的平面图形不可能是()A .B .C .D .5. (2分)如图是一个正方体纸盒的展开图,每个面内都标注了字母或数字,则面a 在展开前所对的面的数字是()A . 2B . 3C . 4D . 56. (2分)如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为()A .B .C .D .7. (2分)如图是一个几何体的三视图,则这个几何体的展开图可以是()A .B .C .D .8. (2分)下列图形中可以作为一个正方体的展开图的是()A .B .C .D .9. (2分)毕业前夕,同学们准备了一份礼物送给自己的母校,现用一个正方体盒子进行包装,六个面上分别写上“祝、母、校、更、美、丽”,其中“祝”与“更”,“母”与“美”在相对的面上.则此包装盒的展开图(不考虑文字方向)不可能是()A .B .C .D .10. (2分)如图是正方体的一个平面展开图,原正方体上两个“我”字所在面的位置关系是()A . 相对B . 相邻C . 相隔D . 重合11. (2分)若一个圆柱的底面半径是1,高是3,则该圆柱的侧面展开图的面积是()A . 6B . 3πC . 6πD . 12π12. (2分)下列图形中,正方体展开后得到的图形不可能是()A .B .C .D .13. (2分)一张邮票的质量太小了,用天平称量一张邮票质量的做法可行的是()A . 称数十张邮票的质量,除以邮票的张数,可得一张邮票的质量B . 将一张邮票和一个小铁块一起称,再单独称小铁块质量,两次相减可得邮票质量C . 因为天平是测量质量的精密仪器,所以可以直接称一张邮票的质量D . 天平无论如何都不可能称出邮票质量二、填空题 (共5题;共5分)14. (1分)如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是________.15. (1分)如图,是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图折成正方体后,相对面上的两个数互为相反数,则填在B内的数为________.16. (1分)一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的的概率是________.17. (1分)一个几何体的表面展开图如图所示,则这个几何体是________.18. (1分)如图,将一张边长为6cm的正方形纸片按虚线裁剪后,恰好围成底面是正六边形的棱柱,则这个六棱柱的侧面积为________ cm2 .三、解答题 (共2题;共10分)19. (5分)如图是一个几何体的平面展开图,每个面内都注上了字母,请回答下列问题:(1)如果面B在几何体的前面,那么哪一面在后面?(2)如果面E在几何体的底部,那么哪一面在上面?(3)如果面D在前面,面F在左面,那么哪一面在上面?哪一面在右面?哪一面在底部?20. (5分)长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?四、综合题 (共1题;共2分)21. (2分)图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.(1)蜘蛛在顶点A′处.①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线.②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.(2)蜘蛛在顶点A′处.①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线.②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.(3)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.(4)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.参考答案一、单选题 (共13题;共26分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、二、填空题 (共5题;共5分)14-1、15-1、16-1、17-1、18-1、三、解答题 (共2题;共10分) 19-1、四、综合题 (共1题;共2分) 21-1、21-2、21-3、21-4、。
(含答案)九年级数学人教版下册课时练第29章《29.3 课题学习 制作立体模型》(2)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!课时练第29章投影和视图29.1投影一、选择题1.如图是某几何体的三视图,该几何体是()A.长方体B.正方体C.三棱锥D.三棱柱2.如图是某一个多面体的表面展开图,那么这个多面体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱3.下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是()A.①②B.③④C.②D.③4.一个几何体的三视图如图,那么这个几何体是()5.【2021·荆门】如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是()A.传B.因C.承D.基6.把如图所示的纸片沿着虚线折叠,可以得到的几何体是()A.三棱柱B.四棱柱C.三棱锥D.四棱锥7.下面的图形经过折叠可以围成一个棱柱的是()8.下列图形经过折叠不能围成一个棱柱的是()9.如图所示,正方体的展开图为()10.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法共有()A.7种B.4种C.3种D.2种11.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为()A.24B.25C.26D.27二、填空题12.如图1,在边长为18cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4cm,则折成的无盖长方体的容积是.13.小明用彩纸给爸爸做了一顶圆锥形生日帽,其左视图和俯视图如图所示,其中点C到AB的距离为123cm,☉C'的周长为24π,则至少需用彩纸cm2.(接口处重叠面积不计,结果保留π)14.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法有种.15.如图是一个几何体的三视图,那么这个几何体是_____________.三、解答题16.一个几何体的三视图如图所示,若其俯视图为正方形,求这个几何体的体积.17.按照下面给出的两组视图:选取合适的材料制成相应的实物模型,写出制作流程.18.(1)请画出该立体模型的三视图和表面展开图;(2)做该笔筒至少要用多少平方厘米的废纸板?19.如图是一个食品包装盒的侧面展开图.(1)请写出这个包装盒的多面体形状的名称;(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.20.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的体积和表面积.21.回答下列问题:(1)如图,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体?(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律?(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.参考答案一、选择题1234567891011 D D C A D A B D A B C二、填空题12.400cm313.288π14.415.四棱柱三、解答题16.解:观察该几何体及其三视图发现,该几何体的底面是正方形,且边长为2,高为3,则V=2×2×3=6.17.解:(1)是圆锥.制作流程:①用刻度尺度量其底面圆的半径r,高h;②用小刀把萝卜削成一个底面圆的半径为r,高为h的圆柱体;③把圆柱体加工成如图①所示的模型.(2)为正方体截去一个三棱柱,是五棱柱.制作流程:①用刻度尺度量正方体的棱长a,被截去的三棱柱的底面为直角三角形,一条直角边长为b,另一条直角边长为c;②用小刀将萝卜削成一个正方体,棱长为a;③在以这个正方体为毛坯的基础上再加工,使其截去一个三棱柱,三棱柱底面上直角三角形的两直角边长分别为b和c,做成如图②所示的模型.18.解:三视图和表面展开图如图(表面展开图画法不唯一):(2)做该笔筒至少要用多少平方厘米的废纸板?解:侧面积为(6+8+10)×14=336(cm 2),易知底面为直角三角形,直角三角形的面积为12×8×6=24(cm 2),表面积为336+24=360(cm 2).所以做该笔筒至少要用废纸板360cm 2.19.解:(1)六棱柱(2)侧面积6ab ,全面积6ab +33b 220.解:根据三视图可得上面的长方体长4mm 、高4mm 、宽2mm,下面的长方体长6mm 、宽8mm 、高2mm,∴立体图形的体积是4×4×2+6×8×2=128(mm 3),立体图形的表面积是4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm 2).21.解:(1)平面图形乙能折成长方体.(2)甲:f =6,v =6,e =10,f +v -e =2;乙:f =6,v =8,e =12,f +v -e =2.规律:面数+顶点数-棱数=2.(3)设这个多面体的面数为x.由题可得x +x +8-50=2,解得x =22,∴这个几何体的面数为22.。
九年级数学下册 29.3 课题学习 制作立体模型同步测试 (新版)新人教版
制作立体模型1. 下列各图中,经过折叠能围成一个立方体的是( A )2.把如图29-3-1中的三棱柱展开,所得到的展开图是( B )图29-3-13.如图29-3-2,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是( B )图29-3-24.如图29-3-3是一个长方体包装盒,则它的表面展开图是( A )5.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是( C )6.图29-3-4是某些多面体的表面展开图,说出这些多面体的名称:(1)__六棱锥__;(2)__三棱柱__.图29-3-4【解析】可在硬纸片上画其表面展开图,动手制成立体模型,知(1)是六棱锥,(2)是三棱柱.7.如图29-3-5是一个立体图形的三视图,则这个立体图形的名称为__圆柱__,它的体积为__250π__(结果保留π).图29-3-5【解析】 观察三视图可知,立体图形是一个圆柱,圆柱的体积为V =π×⎝ ⎛⎭⎪⎫1022×10=250π.8.已知几何体的三视图如图29-3-6,则该物体的体积为4__cm 3__.图29-3-6【解析】 观察三视图可知物体是一个正三棱柱,如图所示,底面棱长为3 cm ,高为5 cm ,于是它的体积为V =34×32×5=4534(cm 3).9. 将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是( C ) A .1 B.32C.12D.2310.如图29-3-7,将一张边长为3的正方形纸片按虚线裁剪后恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为( A )图29-3-7 A .9-3 3 B .9 C .9-52 3 D .9-323【解析】∵将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,∴这个正三角形的底面边长为1,高为12-⎝ ⎛⎭⎪⎫122=32,∴侧面为长为3,宽为3-3的长方形,面积为 9-3 3. 故选A.图29-3-811.小亮利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图29-3-8所示.(1)请画出立体模型的三视图和表面展开图; (2)做一该笔筒至少要用多少废纸板?【解析】 (1)主视图是长方形,左视图也是长方形,俯视图是一个直角三角形,表面展开图只有下底面无上底面.(2)表面积是3个矩形面积加一个直角三角形的面积. 解:(1)三视图如图(1)所示,表面展开图如图(2)所示.主视图 左视图 俯视图 (1)(2)(2)计算表面积:矩形面积为(6+8+10)×14=24×14=336(cm 2), 直角三角形面积为12×8×6=24(cm 2),表面积为336+24=360(cm 2), 所以做该笔筒至少要用废纸板360 cm 2.12.如图29-3-9是一个纸杯的三视图,你能计算出这个纸杯能装多少水吗?(π取3.14,精确到1 cm 3,不计纸的厚度)主视图 左视图 俯视图 图29-3-9【解析】 纸杯为一个圆台,圆台上底面直径为6 cm ,下底面直径为4 cm ,高为8 cm.解:如图所示,设AB为上底面直径,CD为下底面直径,则AB=6 cm,CD=4 cm, 延长AC,BD交于O,过O作OM⊥CD于N,并延长交AB于M,则OM⊥AB.∵CD∥AB,∴△OCD∽△OAB,∴CDAB=ONOM,即46=ON8+ON,∴ON=16,∴纸杯能装水的体积是V=13π×⎝⎛⎭⎪⎫622×(16+8)-13π×⎝⎛⎭⎪⎫422×16≈159(cm3).图29-3-1013.如图29-3-10,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长为多少?解:长方体侧面展开图是长方形,长为2×(2+4)=12(cm),宽为5 cm,如图,由勾股定理得蚂蚁爬行的最短路径PQ长为122+52=13(cm).。
九年级数学下册29.3课题学习制作立体模型作业2(无答案)新人教版(new)
29。
3 课题学习 制作立体模型一。
选择题:1。
一个无盖的正方体纸盒,将它展开成平面图形,可能的情况共有( ) AA.11种 B.9种 C.8种 D.7种2。
如图1,将左图的盒子展开成为一个十字型图形,它是下图中的 ( ) C3.小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽。
圆锥帽底面半径为9㎝,母线长为36㎝,请你帮助他们计算制作一个这样的生日礼帽 需要纸板的面积为( ) CA。
2648cm π B.2432cm π C。
2324cm πD。
2216cm π4.图2是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( ) BA.4 B。
6 C.12 D。
15二。
填空题:1.将图3中一块正六边形硬纸片(左图),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,见右图),需在每一个顶点处剪去一个四边形,例如图中的四边形AGA'H , 图1513图2 图3那么的大小是__________度.( 60 )2。
将一块正方形铁皮的四角各剪去一个边长为4cm 的小正方形,做成一个无盖的盒子,若盒子的容积是400cm 3,则原铁皮的边长为________㎝. ( 18 )三.解答题:1.宽多4答:90立方厘米2.图5是一纸杯,经测量纸杯上开口圆的直径为6㎝,下底面圆的直径为4㎝,母线长为8㎝,求制作这样一个纸杯需要纸多少平方厘米?(粘合部分不计)答:纸杯的侧面积为240cm π,下底面积为24cm π,故制作这样一个纸杯需要纸244cm π。
尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
人教版九年级数学下册第二十九单元制作立体模型同步练习1带答案
人教版九年级数学下册第二十九单元《制作立体模型》同步练习1带答案一、精心选一选(每题5分,共50分)1.小琳过14周岁生日,父母为她预定的生日蛋糕如下图,它的主视图应该是( )2.某物体三视图如图,那么该物体形状可能是( )(A)长方体.(B)圆锥体.(C)立方体(D)圆柱体.3.以下图是由一些相同的小正方形组成的几何体的三视图,这些相同的小正方形的个数是( )(A)4个. (B)5个. (C)6个.(D)7个.4.若是用表示1个立方体,用表示两个立方体叠加,用表示三个立方体叠加,那么以下图由6个立方体叠成的几何体的主视图是( )5.如图是一块带有圆形空洞和方形空洞的小木板,那么以下物体中既能够堵住圆形空洞,又能够堵住方形空洞的是( )6.小明从正面观看以下图所示的两个物体,看到的是( )7.有一实物如图,那么它的主视图是 ( )8.如图是正三菱柱,它的主视图正确的选项是( )9.两个物体的主视图都是圆,那么这两个物体可能是( )(A)圆柱体、圆锥体. (B)圆柱体、正方体.(C)圆柱体、球. (D)圆锥体、球.物,不同侧面观看到如下投影图,那么组成该实物的小正方体个数为 ( )(A)6. (B)7. (C)8. (D)9.二、用心想一想(每题6分,共30分)11.咱们常说的三种视图是指 .12.请写出三种视图都相同的两种几何体是 .13.棱长是1cm的小立方体组成如下图的几何体,那么那个几何体的表面积是.14.一个物体的俯视图是圆,那么该物体有可能是(写两个即可).15.一个几何体的三视图如下,那么那个几何体是 .三、解答题(每题10分,共20分)16.图中四个图形是多面体的展开图,你能说出这些多面体的名称吗?参考答案11.主视图俯视图左视图12.球、正方体214.球圆柱体圆锥体等。
最新精品人教版九年级数学29.3 课题学习 制作立体模型同步练习 精品人教版
29.3 课题学习制作立体模型
1. (2013菏泽)下列图形中,能通过折叠围成一个三棱柱的是()
2. (2013温州)下列各图中,经过折叠能围成一个立方体的是()
3. 如图,将正方体的平面展开图重新折成正方体后,“祝”字对面的字是()
A.中 B.考 C.成 D.功
4. 小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个
面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是()
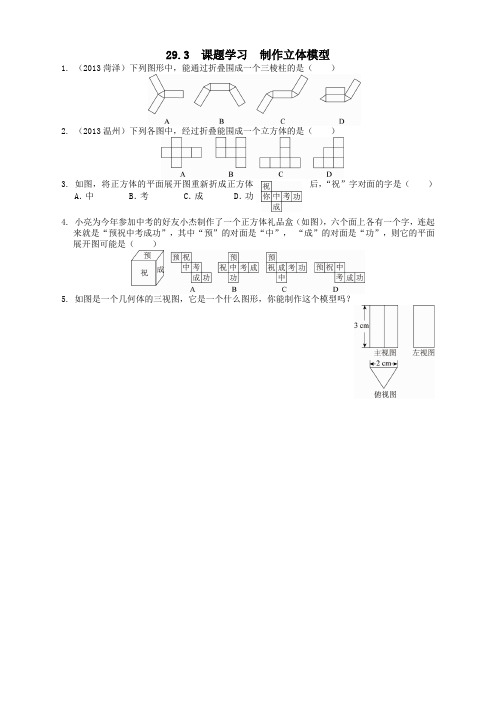
5. 如图是一个几何体的三视图,它是一个什么图形,你能制作这个模型吗?
参考答案
1.C
2.A
3.C
4.C
5.三棱柱制作模型略。
人教版九年级数学下册29.3课题学习制作立体模型练习1含答案
第二十九章投影与视图29.2 三视图 -29.3 课题学习制作立体模型测试题时限: 45 分钟姓名:分数:一、精心选一选(每题5分,共50分)1.小琳过 14 周岁诞辰,父亲母亲为她预约的诞辰蛋糕以下图,它的主视图应当是( )2.某物体三视图如图,则该物体形状可能是( )(A)长方体.(B)圆锥体.(C)立方体.(D)圆柱体.3.以下图是由一些相同的小正方形组成的几何体的三视图,这些相同的小正方形的个数是()( A)4 个.(B)5个.(C)6个.(D)7 个.4.假如用表示1个立方体,用表示两个立方体叠加,用表示三个立方体叠加,那么以下图由6 个立方体叠成的几何体的主视图是( )5. 如图是一块带有圆形空洞和方形空洞的小木板,则以下物体中既能够堵住圆形空洞,又能够堵住方形空洞的是( )6.小明从正面察看以下图所示的两个物体,看到的是( )- 1 -7.有一实物如图,那么它的主视图是( )8.如图是正三菱柱,它的主视图正确的选项是( )9.两个物体的主视图都是圆,则这两个物体可能是( )(A)圆柱体、圆锥体. (B) 圆柱体、正方体.(C) 圆柱体、球.(D)圆锥体、球.10.由若干个相同大小的正方体聚积成一个实物,不一样侧面察看到以下投影图,则组成该实物的小正方体个数为( )(A)6 .(B)7.(C)8.(D)9.二、专心想想(每题6分,共30分)11.我们常说的三种视图是指.12.请写出三种视图都相同的两种几何体是.13 .棱长是1cm 的小立方体组成如图所示的几何体,那么这个几何体的表面积是.14.一个物体的俯视图是圆,则该物体有可能是(写两个即可 ).15.一个几何体的三视图以下, 那么这个几何体是.三、解答题(每题 10 分,共 20 分)16.图中四个图形是多面体的睁开图,你能说出这些多面体的名称吗?17. 画出如图所示中立体图形的三视图.- 2 -29.2 –29.3 单元测试题参照答案1.B2.A3.D4.B5.A6.C7.B8.B9.D 10.B 11.主视图俯视图左视图2- 3 -。
2020年春人教版九年级数学下册29.3 课题学习 制作立体模型同步练习附答案
29.3 课题学习制作立体模型
1. (2013菏泽)下列图形中,能通过折叠围成一个三棱柱的是()
2. (2013温州)下列各图中,经过折叠能围成一个立方体的是()
3. 如图,将正方体的平面展开图重新折成正方体后,“祝”字对面的字是()
A.中 B.考 C.成 D.功
4. 小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个字,连起
来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是()
5. 如图是一个几何体的三视图,它是一个什么图形,你能制作这个模型吗?
参考答案
1.C
2.A
3.C
4.C
5.三棱柱制作模型略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年九年级数学下册29.3 课题学习制作立体模型同步练
习新人教版
1. (2013菏泽)下列图形中,能通过折叠围成一个三棱柱的是()
2. (2013温州)下列各图中,经过折叠能围成一个立方体的是()
3. 如图,将正方体的平面展开图重新折成正方体后,“祝”字对面的字是
()
A.中 B.考 C.成 D.功
4. 小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个
字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是()
5. 如图是一个几何体的三视图,它是一个什么图形,你能制作这个模型吗?
参考答案
1.C
2.A
3.C
4.C
5.三棱柱制作模型略。
