有限元作业第一次作业
哈工大有限元大作业

作业一一.计算程序和结果展示1.程序clearsyms a b c x E lD=E*pi*(b*x+c)^4/64;B(:,:,1)=[-6/l^2+12*x/l^3 4/l-6*x/l^2];B(:,:,2)=[6/l^2-12*x/l^3 ,2/l-6*x/l^2];n=0;for i=1:2for j=1:2n=n+1;f=B(:,:,i)*D*transpose(B(:,:,j));k(:,:,n)=int(f,x,0,l);endendk11=k(:,:,1);k12=k(:,:,2);k21=k(:,:,3);k22=k(:,:,4);K=[k11 k12;k21 k22];K=simple(K);2.结果(1)bx+cK =[ (3*pi*E*(11*b^4*l^4 + 49*b^3*c*l^3 + 84*b^2*c^2*l^2 + 70*b*c^3*l +35*c^4))/(560*l^3), -(pi*E*(19*b^4*l^4 + 84*b^3*c*l^3 + 147*b^2*c^2*l^2 + 140*b*c^3*l + 105*c^4))/(1120*l^2), -(3*pi*E*(11*b^4*l^4 + 49*b^3*c*l^3 + 84*b^2*c^2*l^2 + 70*b*c^3*l + 35*c^4))/(560*l^3), -(pi*E*(47*b^4*l^4 + 210*b^3*c*l^3 + 357*b^2*c^2*l^2 + 280*b*c^3*l + 105*c^4))/(1120*l^2)][ -(pi*E*(19*b^4*l^4 + 84*b^3*c*l^3 + 147*b^2*c^2*l^2 + 140*b*c^3*l +105*c^4))/(1120*l^2), (pi*E*(3*b^4*l^4 + 14*b^3*c*l^3 + 28*b^2*c^2*l^2 +35*b*c^3*l + 35*c^4))/(560*l), (pi*E*(19*b^4*l^4 + 84*b^3*c*l^3 + 147*b^2*c^2*l^2 +140*b*c^3*l + 105*c^4))/(1120*l^2), (pi*E*(13*b^4*l^4 + 56*b^3*c*l^3 +91*b^2*c^2*l^2 + 70*b*c^3*l + 35*c^4))/(1120*l)][ -(3*pi*E*(11*b^4*l^4 + 49*b^3*c*l^3 + 84*b^2*c^2*l^2 + 70*b*c^3*l +35*c^4))/(560*l^3), (pi*E*(19*b^4*l^4 + 84*b^3*c*l^3 + 147*b^2*c^2*l^2 + 140*b*c^3*l +105*c^4))/(1120*l^2), (3*pi*E*(11*b^4*l^4 + 49*b^3*c*l^3 + 84*b^2*c^2*l^2 +70*b*c^3*l + 35*c^4))/(560*l^3), (pi*E*(47*b^4*l^4 + 210*b^3*c*l^3 + 357*b^2*c^2*l^2 + 280*b*c^3*l + 105*c^4))/(1120*l^2)][ -(pi*E*(47*b^4*l^4 + 210*b^3*c*l^3 + 357*b^2*c^2*l^2 + 280*b*c^3*l +105*c^4))/(1120*l^2), (pi*E*(13*b^4*l^4 + 56*b^3*c*l^3 + 91*b^2*c^2*l^2 +70*b*c^3*l + 35*c^4))/(1120*l), (pi*E*(47*b^4*l^4 + 210*b^3*c*l^3 + 357*b^2*c^2*l^2 +280*b*c^3*l + 105*c^4))/(1120*l^2), (pi*E*(17*b^4*l^4 + 77*b^3*c*l^3 +133*b^2*c^2*l^2 + 105*b*c^3*l + 35*c^4))/(560*l)](2)ax^2+bx+c(将程序中D的直径换成“ax^2+bx+c”)K =[ (pi*E*(518*a^4*l^8+2233*a^3*b*l^7+2420*a^3*c*l^6+3630*a^2*b^2*l^6+7920*a^2*b*c*l^5 + 4356*a^2*c^2*l^4 +2640*a*b^3*l^5+8712*a*b^2*c*l^4+9702*a*b*c^2*l^3+3696*a*c^3*l^2 + 726*b^4*l^4 + 3234*b^3*c*l^3 + 5544*b^2*c^2*l^2 + 4620*b*c^3*l +2310*c^4))/(12320*l^3), -(pi*E*(938*a^4*l^8+4004*a^3*b*l^7+4290*a^3*c*l^6+6435*a^2*b^2*l^6+13860*a^2*b*c*l^ 5+7524*a^2*c^2*l^4+4620*a*b^3*l^5+15048*a*b^2*c*l^4+16632*a*b*c^2*l^3+6468*a*c^3*l ^2 +1254*b^4*l^4+5544*b^3*c*l^3+9702*b^2*c^2*l^2+9240*b*c^3*l+6930*c^4))/(73920*l^2), -(pi*E*(518*a^4*l^8 + 2233*a^3*b*l^7 + 2420*a^3*c*l^6 + 3630*a^2*b^2*l^6 +7920*a^2*b*c*l^5 + 4356*a^2*c^2*l^4 + 2640*a*b^3*l^5 + 8712*a*b^2*c*l^4 +9702*a*b*c^2*l^3 + 3696*a*c^3*l^2 + 726*b^4*l^4 + 3234*b^3*c*l^3 + 5544*b^2*c^2*l^2 + 4620*b*c^3*l + 2310*c^4))/(12320*l^3), -(pi*E*(2170*a^4*l^8 + 9394*a^3*b*l^7 +10230*a^3*c*l^6 + 15345*a^2*b^2*l^6 + 33660*a^2*b*c*l^5 + 18612*a^2*c^2*l^4 +11220*a*b^3*l^5 + 37224*a*b^2*c*l^4 + 41580*a*b*c^2*l^3 + 15708*a*c^3*l^2 +3102*b^4*l^4 + 13860*b^3*c*l^3 + 23562*b^2*c^2*l^2 + 18480*b*c^3*l +6930*c^4))/(73920*l^2)][ -(pi*E*(938*a^4*l^8 + 4004*a^3*b*l^7 + 4290*a^3*c*l^6 + 6435*a^2*b^2*l^6 + 13860*a^2*b*c*l^5 + 7524*a^2*c^2*l^4 + 4620*a*b^3*l^5 + 15048*a*b^2*c*l^4 +16632*a*b*c^2*l^3 + 6468*a*c^3*l^2 + 1254*b^4*l^4 + 5544*b^3*c*l^3 + 9702*b^2*c^2*l^2 + 9240*b*c^3*l + 6930*c^4))/(73920*l^2), (pi*E*(434*a^4*l^8 + 1848*a^3*b*l^7 + 1980*a^3*c*l^6 + 2970*a^2*b^2*l^6 + 6435*a^2*b*c*l^5 + 3564*a^2*c^2*l^4 +2145*a*b^3*l^5 + 7128*a*b^2*c*l^4 + 8316*a*b*c^2*l^3 + 3696*a*c^3*l^2 + 594*b^4*l^4 + 2772*b^3*c*l^3 + 5544*b^2*c^2*l^2 + 6930*b*c^3*l + 6930*c^4))/(110880*l),(pi*E*(938*a^4*l^8 + 4004*a^3*b*l^7 + 4290*a^3*c*l^6 + 6435*a^2*b^2*l^6 +13860*a^2*b*c*l^5 + 7524*a^2*c^2*l^4 + 4620*a*b^3*l^5 + 15048*a*b^2*c*l^4 +16632*a*b*c^2*l^3 + 6468*a*c^3*l^2 + 1254*b^4*l^4 + 5544*b^3*c*l^3 + 9702*b^2*c^2*l^2 + 9240*b*c^3*l + 6930*c^4))/(73920*l^2), (pi*E*(1946*a^4*l^8 + 8316*a^3*b*l^7 +8910*a^3*c*l^6 + 13365*a^2*b^2*l^6 + 28710*a^2*b*c*l^5 + 15444*a^2*c^2*l^4 +9570*a*b^3*l^5 + 30888*a*b^2*c*l^4 + 33264*a*b*c^2*l^3 + 12012*a*c^3*l^2 +2574*b^4*l^4 + 11088*b^3*c*l^3 + 18018*b^2*c^2*l^2 + 13860*b*c^3*l +6930*c^4))/(221760*l)][ -(pi*E*(518*a^4*l^8 + 2233*a^3*b*l^7 + 2420*a^3*c*l^6 +3630*a^2*b^2*l^6 + 7920*a^2*b*c*l^5 + 4356*a^2*c^2*l^4 + 2640*a*b^3*l^5 +8712*a*b^2*c*l^4 + 9702*a*b*c^2*l^3 + 3696*a*c^3*l^2 + 726*b^4*l^4 + 3234*b^3*c*l^3 +5544*b^2*c^2*l^2 + 4620*b*c^3*l + 2310*c^4))/(12320*l^3), (pi*E*(938*a^4*l^8 + 4004*a^3*b*l^7 + 4290*a^3*c*l^6 + 6435*a^2*b^2*l^6 + 13860*a^2*b*c*l^5 +7524*a^2*c^2*l^4 + 4620*a*b^3*l^5 + 15048*a*b^2*c*l^4 + 16632*a*b*c^2*l^3 +6468*a*c^3*l^2 + 1254*b^4*l^4 + 5544*b^3*c*l^3 + 9702*b^2*c^2*l^2 + 9240*b*c^3*l + 6930*c^4))/(73920*l^2), (pi*E*(518*a^4*l^8 + 2233*a^3*b*l^7 +2420*a^3*c*l^6 + 3630*a^2*b^2*l^6 + 7920*a^2*b*c*l^5 + 4356*a^2*c^2*l^4 +2640*a*b^3*l^5 + 8712*a*b^2*c*l^4 + 9702*a*b*c^2*l^3 + 3696*a*c^3*l^2 + 726*b^4*l^4 + 3234*b^3*c*l^3 + 5544*b^2*c^2*l^2 + 4620*b*c^3*l + 2310*c^4))/(12320*l^3),(pi*E*(2170*a^4*l^8 + 9394*a^3*b*l^7 + 10230*a^3*c*l^6 + 15345*a^2*b^2*l^6 +33660*a^2*b*c*l^5 + 18612*a^2*c^2*l^4 + 11220*a*b^3*l^5 + 37224*a*b^2*c*l^4 +41580*a*b*c^2*l^3 + 15708*a*c^3*l^2 + 3102*b^4*l^4 + 13860*b^3*c*l^3 +23562*b^2*c^2*l^2 + 18480*b*c^3*l + 6930*c^4))/(73920*l^2)][ -(pi*E*(2170*a^4*l^8 + 9394*a^3*b*l^7 + 10230*a^3*c*l^6 + 15345*a^2*b^2*l^6 +33660*a^2*b*c*l^5 + 18612*a^2*c^2*l^4 + 11220*a*b^3*l^5 + 37224*a*b^2*c*l^4 +41580*a*b*c^2*l^3 + 15708*a*c^3*l^2 + 3102*b^4*l^4 + 13860*b^3*c*l^3 +23562*b^2*c^2*l^2 + 18480*b*c^3*l + 6930*c^4))/(73920*l^2), (pi*E*(1946*a^4*l^8 +8316*a^3*b*l^7 + 8910*a^3*c*l^6 + 13365*a^2*b^2*l^6 + 28710*a^2*b*c*l^5 +15444*a^2*c^2*l^4 + 9570*a*b^3*l^5 + 30888*a*b^2*c*l^4 + 33264*a*b*c^2*l^3 +12012*a*c^3*l^2 + 2574*b^4*l^4 + 11088*b^3*c*l^3 + 18018*b^2*c^2*l^2 + 13860*b*c^3*l + 6930*c^4))/(221760*l), (pi*E*(2170*a^4*l^8 + 9394*a^3*b*l^7 + 10230*a^3*c*l^6 +15345*a^2*b^2*l^6 + 33660*a^2*b*c*l^5 + 18612*a^2*c^2*l^4 + 11220*a*b^3*l^5 +37224*a*b^2*c*l^4 + 41580*a*b*c^2*l^3 + 15708*a*c^3*l^2 + 3102*b^4*l^4 +13860*b^3*c*l^3 + 23562*b^2*c^2*l^2 + 18480*b*c^3*l + 6930*c^4))/(73920*l^2),(pi*E*(2282*a^4*l^8 + 9933*a^3*b*l^7 + 10890*a^3*c*l^6 + 16335*a^2*b^2*l^6 +36135*a^2*b*c*l^5 + 20196*a^2*c^2*l^4 + 12045*a*b^3*l^5 + 40392*a*b^2*c*l^4 +45738*a*b*c^2*l^3 + 17556*a*c^3*l^2 + 3366*b^4*l^4 + 15246*b^3*c*l^3 +26334*b^2*c^2*l^2 + 20790*b*c^3*l + 6930*c^4))/(110880*l)](3)b=0(等截面梁)K =[ (3*pi*E*c^4)/(16*l^3),-(3*pi*E*c^4)/(32*l^2),-(3*pi*E*c^4)/(16*l^3),-(3*pi*E*c^4)/(32*l^2)] [ -(3*pi*E*c^4)/(32*l^2), (pi*E*c^4)/(16*l), (3*pi*E*c^4)/(32*l^2), (pi*E*c^4)/(32*l)][ -(3*pi*E*c^4)/(16*l^3), (3*pi*E*c^4)/(32*l^2), (3*pi*E*c^4)/(16*l^3),(3*pi*E*c^4)/(32*l^2)] [ -(3*pi*E*c^4)/(32*l^2), (pi*E*c^4)/(32*l), (3*pi*E*c^4)/(32*l^2), (pi*E*c^4)/(16*l)]总结:将结果(3)与教材等截面梁刚度矩阵比较,发现表达式一样,侧面证明了程序的正确性。
重庆大学有限元第一次作业

有限元分析技术课程大作业科 目:有限元分析技术 教 师:姓 名: 学 号: 专 业: 机械设计及理论 类 别: 学 术 上课时间: 2016 年 11 月至 2017 年 1 月 考 生 成 绩:阅卷评语:阅卷教师 (签名)重庆大学研究生院第一章 问题提出1.1工程介绍某露天大型玻璃平面舞台的钢结构如图1所示,每个分格(图2中每个最小的矩形即为一个分格)x 方向尺寸为1m ,y 方向尺寸为1m ;分格的列数(x 向分格)=学生序号的百位数值×10+十位数值+5,分格的行数(y 向分格)=学生序号的个位数值+4,如序号为041的同学分格的列数为9,行数为5,111号同学分格的列数为16,行数为5。
钢结构的主梁(图1中黄色标记单元)为高160宽100厚14的方钢管,其空间摆放形式如图3所示;次梁(图1中紫色标记单元)为直径60厚10的圆钢管(单位为毫米),材料均为碳素结构钢Q235;该结构固定支撑点位于左右两端主梁和最中间(如不是正处于X 方向正中间,偏X 坐标小处布置)的次梁的两端,如图2中标记为UxyzRxyz 处。
玻璃采用四点支撑与钢结构连接(采用四点支撑表明垂直作用于玻璃平面的面载荷将传递作用于玻璃所在钢结构分格四周的节点处,表现为点载荷,如图4所示);试对在垂直于玻璃平面方向的22/KN m 的面载荷(包括玻璃自重、钢结构自重、活载荷(人员与演出器械载荷)、风载荷等)作用下的舞台进行有限元分析.(每分格面载荷对于每一支撑点的载荷可等效于0.5KN 的点载荷)。
1.2 作业内容(1)屏幕截图显示该结构的平面布置结构,图形中应反映所使用软件的部分界面,如图1-2;(2)该结构每个支座的支座反力;(3)该结构节点的最大位移及其所在位置;(4)对该结构中最危险单元(杆件)进行强度校核。
图1-1图1-2图1-3图1-41.3分格计算学生序号:096x向分格:9+5=14,即列数为13列;y向分格:6+4=10,即行数为10行;因此,学生作业任务是计算13×10分格的钢结构玻璃平面舞台。
有限元分析大作业

有限元大作业一题目要求:图1所示为一悬臂梁,在端部承受载荷,材料弹性模量为E,泊松比为1/3,悬臂梁的厚度(板厚)为t,若该粱被划分为两个单元,单元和节点编号如图所示,试按平面应力问题计算各个节点位移计支反力。
一、单元划分1.计算简图及单元划分如下所示:2.进行节点及单元编号节点i j m单元① 2 3 4② 3 2 13.节点坐标值节点号1 2 3 4坐标值X 2 2 0 0Y 1 0 1 0二、计算单元刚度矩阵1、计算每个单元面积△以及i b ,i c (m j i i ,,=) ①②单元的面积相等,即12121=⨯⨯=∆ 单元①的i b ,i c⎩⎨⎧=--==-=0)(1m j i m j i y x c y y b ⎩⎨⎧=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧-=--=-=-=2)(1j i mj i m y x c y y b 对平面应力问题,其表达式为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+∆-=s r s r sr s r s r s r s r s r b b uc c cb u b uc b c u c ub c c u b b u Et Krs 21212121)1(42 然后对单元①求解单元刚度子矩阵2==i r 2==i s []⎥⎦⎤⎢⎣⎡=3/1001329)1(22Et K 2==i r 3==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(23Et K2==i r 4==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(24Et K 3==j r 3==j s []⎥⎦⎤⎢⎣⎡=4003/4329)1(33Et K 3==j r 2==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(32Et K 3==j r 4==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(34Et K 4==m r 4==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)1(44Et K 4==m r 2==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(42Et K 4==m r 3==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(43Et K由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)1(Et K将单元①的单元刚度矩阵补零升阶变为单元刚度矩阵,其在总体刚度矩阵中的位置为:节点号→单元②的i b ,i c⎩⎨⎧=--=-=-=0)(1m j im j i y x c y y b ⎩⎨⎧-=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧=--==-=2)(1j i mj i m y x c y y b 然后对单元 求解单元刚度子矩阵:3==i r 3==i s []⎥⎦⎤⎢⎣⎡=3/1001329)2(33Et K 3==i r 2==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(32Et K 3==i r 1==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(31Et K 1 2 3 412[])1(22K[])1(23K[])1(24K3[])1(32K[])1(33K[])1(34K4[])1(42K[])1(43K[])1(44K2==j r 2==j s []⎥⎦⎤⎢⎣⎡=4003/4329)2(22Et K 2==j r 3==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(23Et K 2==j r 1==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(21Et K 1==m r 1==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)2(11Et K 1==m r 3==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(13Et K 1==m r 2==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(12Et K 由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)2(Et K将单元②的单元刚度矩阵补零升阶变为单元贡献矩阵,其在总体刚度矩阵中的位置为:节点号→1 2 3 41 [])2(11K[])2(12K[])2(13K2 [])2(21K[])2(22K[])2(23K3 [])2(31K [])2(32K [])2(33K 4三、计算总体刚度矩阵总体刚度矩阵是由各单元的贡献矩阵迭加而成)2()1(][][][][K K K K e +==∑四、进行节点约束处理根据节点约束情况,在总刚矩阵中可采用划行划列处理约束的方法,由题目易知,节点3和4的已知水平位移和垂直位移都为零,划去其相对应的行和列,则总刚矩阵由8阶变为4阶,矩阵如下:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------2/02/03/13043/203/73/23/443/23/133/43/23/43/43/73292211p p v u v u Et329][Et K =1 2 3 413/133/43/43/743/23/23/4----3/13/23/21----000243/23/23/4----3/13003/73/43/403/13/23/21----33/13/23/21----3/43/403/13003/743/23/23/4----40003/13/23/21----43/23/23/4----3/133/43/43/7化简⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------Et p Et p v u v u 3/1603/160130122072412213424472211 五、求解线性方程组方法:采用LU 分解法 1.求解矩阵[]U 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------75/10775/640075/6475/353007/767/27/7502447~7/877/87/7607/87/337/207/767/27/7502447~13012207241221342447⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----353/44900075/6475/353007/767/27/7502447~ 得到的[]U 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=353/44900075/6475/353007/767/27/7502447U 2.求解矩阵[]L 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----13012207241221342447353/44900075/6475/353007/767/27/75024471353/6475/767/20175/27/40017/40001 得到的[]L 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=13012207241221342447L3.进行求解⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=Et p Et p Et p y Et p Et p Ly 79425/850800225/323/1603/1603/160⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡Et p Et p Et p v u v u y v u v u U 79425/850800225/323/160353/44900075/6475/353007/7675/27/750244722112211 解得Et p v /422.82-= Et p u /497.12-= Et p v /028.91-= Et p u /897.11=于是求得各节点的位移为:⎩⎨⎧-==Etp v Etp u /028.9/897.111 ⎩⎨⎧-=-=Etp v Etp u /422.8/497.122 ⎩⎨⎧==033v u ⎩⎨⎧==044v u 六、求解相应的支反力(运用静力学的平衡方程进行求解)3号节点和4号节点的支反力如下图所示:。
(完整word版)有限元分析大作业报告要点

有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences 为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB和lineBC,设定input NDIV 为15;拾取lineAC,设定input NDIV 为20,选择网格划分方式为Tri+Mapped,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。
有限元热分析第1次大作业(16-17)

课程名称:有限元与热分析数值仿真
2016—2017学年第二学期
第一次大作业(任课教师:钱作勤)
1、简述工程热力学的三大基本定律,并深刻阐述其重要意义和应用领域。
2、一台小型化工装置采用水蒸汽再热循环。
透平蒸汽进口参数为8.5Mpa和480
度。
再热参数为1.2Mpa和440度。
凝汽压力为7kPa.。
透平和泵的效率分别为0.92和0.80。
画出该循环的T-S图。
并确定:1)每千克工质的净功;2)再热占总吸热量的百分比;3)循环热效率。
3、一稳定运行的理想蒸汽压缩制冷系统采用R134a作为工作流体,压缩机进口
是压力为0.16Mpa的饱和蒸汽。
冷凝器出口参数为0.9Mpa和32度。
质量流量为5kg/min。
压缩机等熵效率为80%。
试确定:1)压缩机功率;2)冷吨;
3)性能系数。
有限元上机作业

有限元上机作业目录1分布载荷作用下的悬臂梁应力计算 (1)1.1问题描述 (1)1.2计算模型 (1)1.2.1有限元模型及网格划分 (1)1.2.2边界条件 (1)1.2.3材料模型 (2)1.3计算结果 (2)1.4结果检验 (2)1.5小结 (3)2悬臂式连接环的应力与变形分析 (4)2.1问题描述 (4)2.2计算模型 (4)2.2.1有限元模型及网格划分 (4)2.2.2边界条件 (5)2.2.3材料模型 (5)2.3计算结果 (5)2.4结果检验 (6)2.5小结 (7)3具有中心孔的薄壁圆筒受均匀拉伸分析 (7)3.1问题描述 (7)3.2计算模型 (8)3.2.1有限元模型及网格划分 (8)3.2.2边界条件 (8)3.2.3材料模型 (8)3.3计算结果 (9)3.4结果检验 (10)3.5小结 (11)4刚架与弹簧混合建模与分析 (12)4.1问题描述 (12)4.2计算模型 (12)4.2.1有限元模型及网格划分 (12)4.2.2边界条件 (13)4.2.3材料模型 (13)4.3计算结果 (14)4.4结果检验 (15)4.5小结 (17)5过盈配合圆环受力分析 (17)5.1问题描述 (17)5.2计算模型 (18)5.2.1有限元模型及网格划分 (18)5.2.2边界条件 (18)5.2.3材料模型 (18)5.3计算结果 (19)5.4结果检验 (19)5.5小结 (20)6带中心圆孔板的热应力分析 (20)6.1问题描述 (20)6.2计算模型 (21)6.2.1有限元模型及网格划分 (21)6.2.2边界条件 (21)6.2.3材料模型 (22)6.3计算结果 (22)6.4小结 (23)7壳—梁组合结构建模计算 (24)7.1问题描述 (24)7.2计算模型 (24)7.2.1有限元模型及网格划分 (24)7.2.2边界条件 (25)7.2.3材料模型 (25)7.3计算结果 (26)7.4小结 (27)8复杂3D实体建模及受力分析 (27)8.1问题描述 (27)8.2计算模型 (28)8.2.1有限元模型及网格划分 (28)8.2.2边界条件 (28)8.2.3材料模型 (28)8.3计算结果 (29)8.4小结 (29)9含裂缝结构体的应力强度因子 (30)9.1问题描述 (30)9.2计算模型 (30)9.2.1有限元模型及网格划分 (30)9.2.2边界条件 (31)9.2.3材料模型 (31)9.3计算结果 (31)9.4小结 (32)10受热载荷的正方形烟囱建模与温度场求解 (32)10.1问题描述 (32)10.2计算模型 (33)10.2.1有限元模型及网格划分 (33)10.2.2边界条件 (33)10.2.3材料模型 (33)10.3计算结果 (34)11旋转车轮的建模与应力计算 (34)11.1问题描述 (34)11.2计算模型 (34)11.2.1有限元模型及网格划分 (34)11.2.2边界条件 (35)11.2.3材料模型 (35)11.3计算结果 (35)12U型支架的模态分析 (36)12.1问题描述 (36)12.2计算模型 (36)12.2.1有限元模型及网格划分 (36)12.2.2边界条件 (37)12.2.3材料模型 (37)12.3计算结果 (37)13异形截面梁的几何特性和扭转切应力分布 (38)13.1问题描述 (38)13.2计算模型 (39)13.2.1有限元模型及网格划分 (39)13.2.2边界条件 (40)13.2.3材料模型 (40)13.3计算结果 (40)1分布载荷作用下的悬臂梁应力计算1.1 问题描述分析模型如图1-1 所示, 梁的横截面为矩形(长x宽x高= 10x1x2 m2),受到沿长度方向线性分布载荷作用,q=(10000-1000x)N/m。
ansys命令流

工程结构有限元数值仿真学院:力学与建筑工程学院专业: 14-硕结构工程学号:TSP140601031姓名:王卓第一次作业命令流:/BATCH/input,menust,tmp,'',,,,,,,,,,,,,,,,1 WPSTYLE,,,,,,,,0/PREP7ET,1,LINK180ET,2,LINK180 MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,EX,1,,2e5 MPDATA,PRXY,1,,0.3 ETDEL,2R,1, , ,RDEL,1R,1,400, , MPTEMP,,,,,,,,MPTEMP,1,0MPDE,EX,1MPDE,PRXY,1 MPDATA,EX,1,,2E+005 MPDATA,PRXY,1,,0.3 TYPE, 1MAT, 1REAL, 1ESYS, 0 SECNUM,TSHAP,LINEET,2,LINK180ETDEL,2K,1,,,,K,2,1500,,,K,3,,1500,,K,4,1500,1500,,K,5,250,2500,,K,6,1250,2500,,K,7,250,3500,,K,8,1250,3500,,K,9,-750,4000,,K,10,2250,4000,,K,11,-1750,4000,,K,11,-1750,4500,,K,12,-750,4500,,K,13,250,4500,,K,14,1250,4500,,K,15,2250,4500,,K,16,3250,4500,,K,16,3250,4500,, LSTR, 1, 2 LSTR, 2, 4 LSTR, 1, 3 LSTR, 3, 4 LSTR, 1, 4 LSTR, 4, 6 LSTR, 3, 5 LSTR, 5, 7 LSTR, 6, 8 LSTR, 7, 8 LSTR, 5, 6 LSTR, 4, 5 LSTR, 5, 8 LSTR, 8, 10 LSTR, 10, 16 LSTR, 16, 15 LSTR, 15, 14 LSTR, 14, 13 LSTR, 13, 12 LSTR, 12, 11 LSTR, 11, 9 LSTR, 9, 7 LSTR, 7, 13 LSTR, 8, 14 LSTR, 9, 13 LSTR, 9, 12 LSTR, 10, 14 LSTR, 10, 15 LSTR, 8, 13 TYPE, 1MAT, 1REAL, 1 ESYS, 0 SECNUM,LESIZE,ALL, , ,1, ,1, , ,1, FLST,2,28,4,ORDE,2 FITEM,2,2FITEM,2,-29LMESH,P51XFLST,2,26,4,ORDE,5 FITEM,2,1FITEM,2,-14FITEM,2,17FITEM,2,-27FITEM,2,29LMESH,P51XFINISH/SOLFLST,2,1,1,ORDE,1 FITEM,2,3/GOD,P51X, , , , , ,UX,UY,UZ, , , FLST,2,1,1,ORDE,1 FITEM,2,1/GOD,P51X, , , , , ,UY,UZ, , , , FLST,2,1,1,ORDE,1 FITEM,2,15/GOF,P51X,FY,-1000FLST,2,1,1,ORDE,1 FITEM,2,10/GOF,P51X,FY,-1000SOLVEFINISH/POST1A VPRIN,0, ,ETABLE, ,LS, 1A VPRIN,0, ,ETABLE, ,LS, 2A VPRIN,0, ,ETABLE, ,U,X轴力图:变形图:第二次作业命令流:/BATCH/input,menust,tmp,'',,,,,,,,,,,,,,,,1 WPSTYLE,,,,,,,,0/input,menust,tmp,'',,,,,,,,,,,,,,,,1 WPSTYLE,,,,,,,,0/NOPRKEYW,PR_SET,1KEYW,PR_STRUC,1KEYW,PR_THERM,0KEYW,PR_FLUID,0KEYW,PR_ELMAG,0KEYW,MAGNOD,0KEYW,MAGEDG,0KEYW,MAGHFE,0KEYW,MAGELC,0KEYW,PR_MULTI,0KEYW,PR_CFD,0/GO/PREP7ET,1,BEAM188ET,2,SHELL181/MPLIB,STATMPTEMP,,,,,,,,MPTEMP,1,0MPDATA,EX,1,,3e4MPDATA,PRXY,1,,0.2 MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,DENS,1,,2.5e-9 MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,EX,2,,2.1e5MPDATA,PRXY,2,,0.3 MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,DENS,2,,7.8e-9SECTYPE, 1, BEAM, RECT, ZHU, 0 SECOFFSET, CENTSECDATA,500,500,0,0,0,0,0,0,0,0,0,0 SECTYPE, 2, BEAM, RECT, BIANLIANG, 0 SECOFFSET, CENTSECDATA,300,500,0,0,0,0,0,0,0,0,0,0 SECTYPE, 3, BEAM, I, NEILIANG, 0 SECOFFSET, CENTSECDATA,200,200,500,16,16,10,0,0,0,0,0,0 SECTYPE, 3, BEAM, I, NEILIANG, 0 SECOFFSET, CENTSECDATA,200,200,500,16,16,10,0,0,0,0,0,0 /UI,BEAM,OFFsect,4,shell,,BANsecdata, 100,1,0.0,3secoffset,MIDseccontrol,,,, , , ,K,1,,,,FLST,3,1,3,ORDE,1FITEM,3,1KGEN,3,P51X, , , ,5400, , ,0FLST,3,3,3,ORDE,2FITEM,3,1FITEM,3,-3KGEN,4,P51X, , ,5400, , , ,0FLST,3,12,3,ORDE,2FITEM,3,1FITEM,3,-12KGEN,4,P51X, , , , ,5400, ,0LSTR, 1, 13LSTR, 13, 25LSTR, 25, 37LSTR, 2, 14LSTR, 14, 26LSTR, 26, 38LSTR, 3, 15LSTR, 15, 27LSTR, 27, 39LSTR, 4, 16LSTR, 16, 28LSTR, 28, 40LSTR, 5, 17LSTR, 17, 29LSTR, 29, 41LSTR, 6, 18LSTR, 18, 30LSTR, 30, 42LSTR, 7, 19LSTR, 19, 31LSTR, 8, 20 LSTR, 20, 32 LSTR, 32, 44 LSTR, 9, 21 LSTR, 21, 33 LSTR, 33, 45 LSTR, 10, 22 LSTR, 22, 34 LSTR, 34, 46 LSTR, 11, 23 LSTR, 23, 35 LSTR, 35, 47 LSTR, 12, 24 LSTR, 24, 36 LSTR, 36, 48 LSTR, 13, 14 LSTR, 14, 15 LSTR, 16, 17 LSTR, 17, 18 LSTR, 19, 20 LSTR, 20, 21 LSTR, 22, 23 LSTR, 23, 24 LSTR, 3, 6 LSTR, 6, 9 LSTR, 9, 12 LSTR, 2, 5 LSTR, 5, 8 LSTR, 8, 11 LSTR, 1, 4 LSTR, 4, 7 LSTR, 7, 10 GPLOTLSTR, 25, 26 LSTR, 26, 27 LSTR, 37, 38 LSTR, 38, 39 LSTR, 40, 41 LSTR, 41, 42 LSTR, 42, 33 LDELE, 60 LSTR, 13, 16 LSTR, 16, 19LSTR, 14, 17 LSTR, 17, 20 LSTR, 20, 23 LSTR, 15, 18 LSTR, 18, 21 LSTR, 21, 24 LSTR, 39, 42 LSTR, 42, 45 LSTR, 45, 48 LSTR, 27, 30 LSTR, 30, 33 LSTR, 33, 36 LSTR, 38, 41 LSTR, 41, 44 LSTR, 44, 47 LSTR, 37, 40 LSTR, 40, 43 LSTR, 43, 46 LSTR, 48, 47 LSTR, 47, 46 LSTR, 45, 44 LSTR, 44, 43 LSTR, 26, 29 LSTR, 29, 32 LSTR, 32, 35 LSTR, 36, 35 LSTR, 35, 34 LSTR, 30, 29 LSTR, 29, 28 LSTR, 33, 32 LSTR, 32, 31 LSTR, 25, 28 LSTR, 28, 31 LSTR, 31, 34 FLST,2,9,4,ORDE,2 FITEM,2,45FITEM,2,-53LDELE,P51XFLST,2,4,4FITEM,2,38FITEM,2,66FITEM,2,40FITEM,2,63AL,P51X FLST,2,4,4 FITEM,2,37 FITEM,2,63 FITEM,2,39 FITEM,2,60 AL,P51X FLST,2,4,4 FITEM,2,40 FITEM,2,67 FITEM,2,42 FITEM,2,64 AL,P51X FLST,2,4,4 FITEM,2,39 FITEM,2,64 FITEM,2,41 FITEM,2,61 AL,P51X FLST,2,4,4 FITEM,2,42 FITEM,2,68 FITEM,2,44 FITEM,2,65 AL,P51X FLST,2,4,4 FITEM,2,41 FITEM,2,65 FITEM,2,43 FITEM,2,62 AL,P51X FLST,2,4,4 FITEM,2,55 FITEM,2,72 FITEM,2,90 FITEM,2,85 AL,P51X FLST,2,4,4 FITEM,2,54 FITEM,2,85 FITEM,2,91 FITEM,2,94 AL,P51X FLST,2,4,4FITEM,2,73 FITEM,2,92 FITEM,2,86 AL,P51X FLST,2,4,4 FITEM,2,91 FITEM,2,86 FITEM,2,93 FITEM,2,95 AL,P51X FLST,2,4,4 FITEM,2,92 FITEM,2,74 FITEM,2,88 FITEM,2,87 AL,P51X FLST,2,4,4 FITEM,2,93 FITEM,2,87 FITEM,2,89 FITEM,2,96 AL,P51X FLST,2,4,4 FITEM,2,57 FITEM,2,69 FITEM,2,59 FITEM,2,75 AL,P51X FLST,2,4,4 FITEM,2,56 FITEM,2,75 FITEM,2,58 FITEM,2,78 AL,P51X FLST,2,4,4 FITEM,2,59 FITEM,2,70 FITEM,2,83 FITEM,2,76 AL,P51X FLST,2,4,4 FITEM,2,58 FITEM,2,76FITEM,2,79AL,P51XFLST,2,4,4 FITEM,2,83 FITEM,2,71 FITEM,2,81 FITEM,2,77AL,P51XFLST,2,4,4 FITEM,2,84 FITEM,2,77 FITEM,2,82 FITEM,2,80AL,P51X/UI,MESH,OFF FLST,5,18,4,ORDE,2 FITEM,5,1 FITEM,5,-18CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,1 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,18,4,ORDE,2 FITEM,5,19 FITEM,5,-36CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,1 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 TYPE, 1MAT, 1 REAL,ESYS, 0SECNUM, 1/UI,MESH,OFF FLST,5,4,4,ORDE,4 FITEM,5,56 FITEM,5,-57 FITEM,5,69 FITEM,5,78CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,2 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 TYPE, 1MAT, 1 REAL,ESYS, 0 SECNUM, 1 CM,_Y,LINE LSEL, , , , 94 CM,_Y1,LINE CMSEL,S,_Y FLST,5,4,4,ORDE,4 FITEM,5,54 FITEM,5,-55 FITEM,5,72 FITEM,5,94CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,2 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,10,4,ORDE,6 FITEM,5,56 FITEM,5,-57 FITEM,5,69 FITEM,5,-71FITEM,5,78 FITEM,5,-82CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,2 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,10,4,ORDE,8 FITEM,5,54 FITEM,5,-55 FITEM,5,72 FITEM,5,-74 FITEM,5,88 FITEM,5,-89 FITEM,5,94 FITEM,5,-96CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,2 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,10,4,ORDE,8 FITEM,5,37 FITEM,5,-38 FITEM,5,43 FITEM,5,-44 FITEM,5,60 FITEM,5,-62 FITEM,5,66 FITEM,5,-68CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,1, ,1, , , ,2CMDELE,_Y CMDELE,_Y1 FLST,5,7,4,ORDE,6 FITEM,5,58 FITEM,5,-59 FITEM,5,75 FITEM,5,-77 FITEM,5,83 FITEM,5,-84 CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,2, ,1, , , ,3 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,7,4,ORDE,4 FITEM,5,85 FITEM,5,-87 FITEM,5,90 FITEM,5,-93 CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,2, ,1, , , ,3 CMSEL,S,_Y CMDELE,_Y CMDELE,_Y1 FLST,5,7,4,ORDE,4 FITEM,5,39 FITEM,5,-42 FITEM,5,63 FITEM,5,-65 CM,_Y,LINE LSEL, , , ,P51X CM,_Y1,LINE CMSEL,S,_Y CMSEL,S,_Y1 LATT,2, ,1, , , ,3CMDELE,_YCMDELE,_Y1FLST,5,18,5,ORDE,2FITEM,5,1FITEM,5,-18CM,_Y,AREAASEL, , , ,P51XCM,_Y1,AREACMSEL,S,_YCMSEL,S,_Y1AATT, 1, , 2, 0, 4 CMSEL,S,_YCMDELE,_YCMDELE,_Y1LESIZE,ALL, , ,20, ,1, , ,1,FLST,2,87,4,ORDE,4FITEM,2,1FITEM,2,-44FITEM,2,54FITEM,2,-96LMESH,P51XMSHKEY,0FLST,5,18,5,ORDE,2FITEM,5,1FITEM,5,-18CM,_Y,AREAASEL, , , ,P51XCM,_Y1,AREACHKMSH,'AREA'CMSEL,S,_YAMESH,_Y1CMDELE,_YCMDELE,_Y1CMDELE,_Y2FINISH/SOLFLST,2,12,1,ORDE,12FITEM,2,1FITEM,2,62FITEM,2,123FITEM,2,184FITEM,2,245FITEM,2,306FITEM,2,367FITEM,2,428FITEM,2,489FITEM,2,550FITEM,2,611FITEM,2,672/GOD,P51X, , , , , ,UX,UY,UZ, , , ACEL,0,0,9.8,SOLVEFINISH/POST1A VPRIN,0, ,ETABLE, ,SMISC, 1A VPRIN,0, ,ETABLE, ,SMISC, 14A VPRIN,0, ,ETABLE, ,SMISC, 2A VPRIN,0, ,ETABLE, ,SMISC, 15 ANMODE,10,0.5, ,0 ANMODE,10,0.5, ,0 ANMODE,10,0.5, ,0 ANMODE,10,0.5, ,0结构图:柱轴力图:梁弯矩图:。
有限元作业试题及答案.doc

2
答:一般选用三角形或四边形单元,在满足一定精度情况,
有限元划分网格的基本原则是:
1、拓朴正确性原则。即单元间是靠单元顶点、或单元边、或单元面连接
2、几何保形原则。即网格划分后,单元的集合为原结构近似
3、特性一致原则。即材料相同,厚度相同
4、单元形状优良原则。单元边、角相差尽可能小
c j二elcm= —a
Ni = l/a2 • a x = x/a
同理可得:Nj二y/a
有限元方法及应用试题
1
答:单元离散(划分、剖分)一单元分析一整体分析
有限元分析的主要步骤主要有:
A结构的离散化
B单元分析。选择位移函数、根据几何方程建立应变与位移的关系、根据物理方程建立应力
与位移的关系、根据虚功原理建立节点力与节点位移的关系(单元刚度方程)
C等效节点载荷计算
D整体分析,建立整体刚度方程
7、图示三角形ijni为等边三角形单元,边长为1,单位面积材料密度位P,集 中力F垂直作用于nij边的中点,集度为q的均布载荷垂直作用于im边。写出三 角形单元的节点载荷向量。
q:移到m, i点F:移到m, j点重力:移到m, I, j点
要证{8}=0
只需证,Nm = 0
Nm= 1/2A (am+bmx +cmy)
(d)平面三角形单元,29个节点,38个自由度
4、什么是等参数单元?。
如果坐标变换和位移插值采用相同的节点,并且单元的形状变换函数与位移插值的形函
数一样,则称这种变换为等参变换,这样的单元称为等参单元。
5பைடு நூலகம்
v(x, y)=
答:不能取这样的位移模式,因为在平面三节点三角形单元中,位移模式应该是呈线性的。
有限元受力分析大作业

1. 定义分析类型
Main Menu >Solution > Analysis Type > New Analysis, 选择Static 2. 定义位移约束
Main Menu >Solution> Define Loads >Apply >Structural>Displacement > On Areas, 在 弹出对话框中选Circle,点击OK后,在弹出的对话框中填入:0
后处理
1. 查看总体变形
Main Menu >General Postproc >Plot Results > Deformed shape
(2)
(2)
四. 加载和求解
1. 定义分析类型
Main Menu >Solution > Analysis Type > New Analysis, 选择Static 2. 定义位移约束
Main Menu >Solution> Define Loads >Apply >Structural>Displacement > On Areas, 在 弹出对话框中选Circle,点击OK后,在弹出的对话框中填入:0
七. 后处理
1. 查看总体变形
Main Menu >General Postproc >Plot Results > Deformed shape
S
作业三:轴承座盈利分析
1、 题目
2、建模
3、ansys前处理
导入
ansys前处理
1、定义单元类型 Main Menu>Proprocessor>Element Type >Add/Edit/Delete 弹出对话框 中后,点“Add” 。双弹出对话框,选“Solid”和“10node 92”,点 “OK”,退回到前一个对话框。
有限元上机报告一

有限元作业一上机报告20120430231 余凯峰T1243-2一、题目图示折板上端固定,右侧受力F=1000N,该力均匀分布在边缘各节点上;板厚t=2mm,材料选用低碳钢,弹性模量E=210Gpa,μ=0.33.二、有限元分析的目的1、利用ANSYS构造实体模型;2、根据结构的特点及所受载荷的情况,确定所用单元类型;正确剖分网格并施加外界条件;3、绘制结构的应力和变形图,给出最大应力和变形的位置及大小;并确定折板角点A处的应力和位移;4、研究网格密度对A处角点应力的影响;5、若在A处可用过渡圆角,研究A处圆角半径对A处角点应力的影响三、有限元模型的特点1、作业类型:平面应力2、单位制:N mm MPa3、单元类型:在Preferences选Structural,Preprocessor>ElemmentType>Add/Edit/Delete中定义单元类型为Plane-82,K3设置为Plane strs w/thk材料: EX=2.10E5MPa, PRXY=0.33 实常数:THK=2mm4、划分网格:Preprocessor—Meshing—Mesh Tool—Size Controls下的Global 点击Set—在第一行输入你要定义的网格长度—OK—点击Clear旁边的Mesh—Pick All这一步划分网格5、加载描述:Preprocessor—Loads—Define Loads—Apply—Structural—Displacement—On Lines—拾取模型被固定的上边—ok—All DOF—okPreprocessor—Loads—Define Loads—Apply—Structural—Pressure—On Lines—拾取右边线—Load pres valu输入-1000/60—ok6、后处理:网格密度设置为“3”时应力和位移图如下:网格密度设置为“4”时应力和位移图如下网格密度设置为“5”时应力和位移图如下移也减小但变化不大。
2011级南京理工大学有限元理论作业

其雅可比矩阵为:
, ,
⑵ ,
7.写出线性动力学有限元方程,并说明方程中各个符号的力学含义。简介线性动力学有限元方程的求解方法,并且说明 方法的思想和分析步骤。
解:线性动力学有限元方程为:
式中 { },{ }和{U}分别为整体节点加速度,速度和位移列阵
分别为整体质量,阻尼和刚度矩阵
4.已知集中载荷 ,试求图示六节点三角形单元的等效节点载荷列阵。
解:
5、已知材料的弹性模量 和泊松比 。计算图示四面体 单元的形函数 ;单元的刚度矩阵中的元素 和 。
解:
6、图四边形单元受到均匀的重力载荷 (单位体积载荷,沿 轴负方向)作用,已知单元的厚度 为常量,材料的弹性模量 和泊松比 。试用 阶高斯积分计算节点1处的等效节点载荷和单元刚度矩阵中的元素
其中
将上述假定代入到 时刻的平衡方程
可得到
Newmark方法分析步骤如下:
A.初始计算
(1)形成K、M和C矩阵,取 ,计算下列常数:
(2)给定位移、速度和加速度的初始值:
(3)形成有效刚度矩阵,
(4)对 阵进行三角分解,
B.对每个时间步
(1)形成有效载荷向量
解:
3.已知图示正方形薄板的边长为 ,厚度为 ,弹性模量为 ,泊松比 。现将其分成两个三角形单元,设节点2、3和4为不动点,在节点1处受到向上的集中载荷P。试求节点位移,支座反力以及单元A和单元B内的应力?
解:单元的节点编号如下:
单元节点号
i
j
m
A
1
3
4
B
4
2
1
单元A的节点坐标为:
单元B的节点坐标为:
2Hale Waihona Puke 11级南京理工大学研究生有限元理论作业
中科大有限元作业答案(第一次到第五次)

有限元作业一1、对图示杆结构,已知节点 3 的位移 10mm,试用有限元法求出各节点的节点力和节点 2 的位移。
已知两段杆的长度为 l1, l2 截面积为 A 1, A 2 ,弹性模量为 E 1, E2 。
2.求解如图所示桁架节点 1 处的水平位移和垂直位移分量以及每一杆单元的应力。
已知所有 单元 A 5106m2 , E 200GPa, L 1m。
有限元作业一1、对图示杆结构,已知节点 3 的位移 10mm,试用有限元法求出各节点的节点力和节点 2 的位移。
已知两段杆的长度为 l1, l2 截面积为 A 1, A 2 ,弹性模量为 E 1, E2 。
解:将整个杆件可以划分 3 个节点,2 个单元。
如图所示:设图中力为 F,则 1 节点所受反 作用力为-F。
对单元①,单元刚度矩阵为:ke(1) 同理,单元②的单元刚度矩阵为:1 1 AE 1 1 L1 1 1 ke(2) 将单元刚度矩阵集成,有整体刚度矩阵为:A2E2 1 1 L2 1 1 k ke(1) [k]e(2)(1) (1) k11 k12 0 0 0 0 (1) (1) (2) (2) k21 k22 0 0 k11 k12 (2) (2) 0 k21 k22 0 0 0 (1) (1) k11 k12 0 (1) (1) (2) (2) k21 k22 k11 k12 (2) (2) 0 k k 21 22 E1A EA 1 1 1 0 L L1 1 E1A EA E A EA 1 1 1 2 2 2 2 L1 L2 L2 L1 EA E2 A2 2 2 0 L2 L2 F 1x F 整体节点载荷矩阵为 R F 2x 0 , F F 3x 1x 0 整体节点位移矩阵为: 2x 2x 。
有限元作业

ci y)
cm x j (i , j , m )
A 2 A jx my mx yj 得
Ni
1 2A
[
x
j
ym
xm y j
(yj
ym )
xj
3
xm
(xm
xj)
yj
3
ym
]
1 3
Nj
1 (0 2A
yj
ym ) 3
1 3
Nj
1 (0 2A
2
x2 l
2
lx
uu12
N1
N2
uu12
B N1'
N
' 2
4x l2
l
4x l l2
E
x
E
B
uu12
,即
D
E
对于矩形截面梁单元,积分: dydz A 为单元横截面面积。
BT
EAB dx
EA
l 0
2x l2
2x
2x l2
l2
2x l2
dx
4EA
3l
4EA 3l
4EA
3l
4EA 3l
(b)、 u(x) 1x 2x2 ,由边界条件确定常数1 、2 :
}
有限元作业-内容十分详细

第一题1.题目概况矩形板尺寸如下图1,板厚为5mm。
材料弹性模量为52E=⨯泊松210N/mm μ。
选择以下一种工况讨论:比27=.0本次分析选取的是1和2两种情况。
由于1,2种情况十分类似,所以这里主要分析第一种情况的步骤。
2.模型建立2.1 单元选择及其分析本次问题中的矩形薄板的应力分析属于平面应力分析,是结构静力学问题。
定义单元类型为二维四边形单元。
(1)图2,首先在Preference菜单中定义分析类型为Structural。
图2(2)在Preprocessor/Elementtype/Add/Edit/Delet中定义单元属性为二维四边形单元,如图3所示。
图3相应的选项设置如图4所示:(3)定义材料特性:EX=200000,PRXY=0.27。
如图5,图6所示:图5(4)定义平板厚度为5,如图7所示:图72.2 模型建立及网格划分(1)图8在XY面内建立矩形,输入如图中所示数据,完成后创建的模型如图8所示。
图8图9(2)划分网格。
点击Preprocessor/Meshing/Meshingtool后,设置网格的属性。
定义四边形网格的边长为5如图10所示,点击Mesh后,开始网格划分如图10所示。
图10图112.3 载荷处理(1)定义分析类型。
点击Solution/Analysis Type/New Analysis,设为static,即结构静态分析。
如图12所示。
(2)施加约束。
点击Solution/Define Loads/Apply/Structural/Displacement/on Nodes后,点击c,d两个节点后,设置选项如图13所示,约束后的模型如图14所示。
图14(3)施加载荷。
点击Solution/Define Loads/Operate/Apply/Structual/Pressure/On lines,选择a,b边后出现选项卡后,点击设置如图15所示参数。
设置完成后载荷如图16所示。
有限元作业第一次作业

土木工程专业有限元第一次作业姓名:班级:学号:指导教师:二〇一五年6月12日题目:八节点三维规则六面体单元,已给定8个节点的坐标。
试查资料并论述:1、单元中位移函数u(x,y,z),v(x,y,z),w(x,y,z)和单元节点位移{δe }的关系式;2、[ B]矩阵的计算步骤和计算式;3、单元刚度矩阵[ k e ]的一般计算方法和计算步骤;4、论述相邻单元间公共边界上位移的连续性;5、如果已经求解得到单元8个节点的位移值{δe }怎样求单元中某一点A(x,y,z)的应力?解:1、取六面体单元的4个角点为节点,以其对称轴为,,x y z 轴。
任一节点i 有,,x y z 三个方向的位移,,i i i u v w ,此单元有8个节点,故总共有24个自由度。
如图1所示,其中原点O 取在长方体的几何中心,8个节点的编号为数学1~8,则此单元的位移列阵为:{}[]111222333444555666777888Teu v w u v w u v w u v w u v w u v w u v w u v w δ=图1该单元有8个节点,因此每个方向的位移场可以设定8个待定系数,根据确定位移模式的基本原则(从低阶到高阶、唯一确定性),选取该单元的位移模式为:123456781234567812345678(,,)(,,)(,,)u x y z a a x a y a z a xy a yz a xz a xyz v x y z b b x b y b z b xy b yz b xz b xyz w x y z c c x c y c z c xy c yz c xz c xyz=+++++++⎧⎪=+++++++⎨⎪=+++++++⎩(1-1)将8个节点的坐标值代入上式,可列出8个节点位移分量的值为:XZY O12345 678112131415116117118111212232425226227228222312333435336337338333412434445446447448444u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z =+++++++=+++++++=+++++++=+++++++512535455556557558555612636465666667668666712737475776777778777812838485886887888888u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z =+++++++=+++++++=+++++++=+++++++⎫⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎭(1-2) 由式(1-2)的8个方程中可解出18~a a ,将它们代入式(1-1),得:1122334455667788+++++++i i u N u N u N u N u N u N u N u N u N u ==∑1122334455667788+++++++i i v N v N v N v N v N v N v N v N v N v ==∑ 1122334455667788+++++++i i w N w N w N w N w N w N w N w N w N w ==∑将上式写成矩阵形式,为{}{}[]{}128e eu v N N N w δδδ⎧⎫⎪⎪===⎨⎬⎪⎪⎩⎭N I II (1-3)其中,I 为三阶单元矩阵,而N 为形状函数矩阵,由于位移u v w ,,采用同样的插值形式,故有:128128128000000000000000N N N N N N N N N ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦…N (1-4a ) 上式中,各形状函数有:12345611=111=1118811=111=1118811=111=1188x y z x y z N N a b c a b c x y z x y z N N a b c a b c x y z x y N N a b c a b ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++++ ⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++--+- ⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+-- ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭78111=111=11188z c x y z x y z N N a b c a b c ⎛⎫+ ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+----- ⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(1-4b )将式(1-4b )依次代入式(1-3),即得位移函数(,,)u x y z ,(,,)v x y z ,(,,)w x y z与单元节点位移{}eδ的关系式{}{}eδδ=N ,其中{}18eδδδ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭, {}i i i i u v w δ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭ (1,2,,8)i =2、根据空间问题的几何方程,单元应变可用节点位移表示如下:{}[]{}128=x y e ez xy yz xz εεεδδγγγ⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭ε=B B B B (2-1)其中:000=00000i i i i i i i i i i TN N N x y z N N N y x z N N N zyx ⎡⎤∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎣⎦B (2-2) 即要求出矩阵i B 中的元素i N x ∂∂,i N y ∂∂,iN z∂∂(1,2,,8)i =。
有限元分析大作业报告

有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences 为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB和lineBC,设定input NDIV 为15;拾取lineAC,设定input NDIV 为20,选择网格划分方式为Tri+Mapped,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图单元类型最小位移(mm)最大位移(mm)最小应力(Pa)最大应力(Pa)三节点0 0.0284 5460.7 392364六节点0 0.0292 0.001385 607043①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。
哈工大有限元大作业1-16S108346殷琪

有限元大作业1
一、题目
两对边简支、另两对边固支的矩形薄板(如图1),其上承受均布压力q的作用,已知:a = 1000mm, b = 500mm,板厚 h = 20mm, q=-1N/mm2,E=2.1×105N,μ = 0 .3 求对称截面上的挠度w及弯矩 Mx、My的分布曲线。
图1.矩形薄板
二、求解过程
1.进入ANSYS 2.设置计算类型 3.选择单元类型 4.定义材料参数5.确定薄板的厚度 6.生成几何模型 7.网格划分
8.模型施加约:
a 分别给两长边施加固支约束、给两短边施加简支约束
b 给薄板施加均布载荷
9.分析计算
11.弯矩Mx云图显示(如下图)
13.定义与YOZ平面和长边平行的对称面Mx上的路径14.显示对称截面Mx上的挠度(Mx)曲线(如下图)
16.定义与XOZ平面和长边平行的对称截面Mx上的路径17.显示对称截面My上的挠度(My)曲线(如下图)
三、计算结果及感受
在本次分析报告中,平面Mx为与YOZ平面平行的对称截面,平面My为与XOZ 平面平行的对称截面。
我根据《ANYSYS基础进阶》一书中所提供的步骤来做的分析,得到的结果如上面的图中所示,根据薄板Z方向的挠度云图可知,薄板的挠度为-1.08559mm。
通过这次作业感受到了陈老师所说的ANSYS等有限元分析软件只是一个工具,而真正的奥妙在有限元理论中,以前只是单纯的用智能划分网格(smart),现在知道了去想如何划分才能得到较合理分析。
有限元第一次作业2003版本
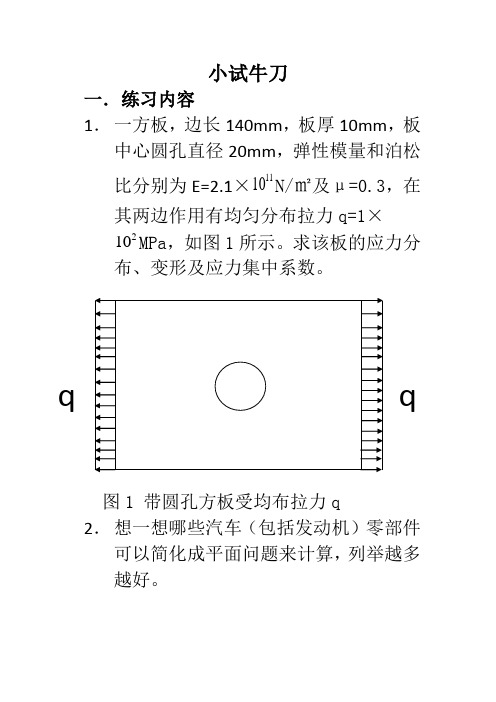
小试牛刀
一. 练习内容
1. 一方板,边长140mm ,板厚10mm ,板中心圆孔直径20mm ,弹性模量和泊松
比分别为E=2.1×1110N/㎡及μ=0.3,在
其两边作用有均匀分布拉力q=1×
210MPa ,如图1所示。
求该板的应力分
布、变形及应力集中系数。
图1 带圆孔方板受均布拉力q
2. 想一想哪些汽车(包括发动机)零部件可以简化成平面问题来计算,列举越多
越好。
q
q
二. 特别提示
1. 本课程联系总成绩R 的计算公式为
11n
i i R R n ==∑(分)
其中,n 为本课程练习的次数,为第i 次练习与检测的成绩。
2. 本次练习为开放式,要求独立完成。
如
果所交练习有k (k >1)份疑似相同,
那么每个相关同学本次练习的成绩按
下式计算:
1100R k =(分)
3. 上交时间:下周本课课间上交,过期不
计成绩。
4. 练习总成绩不及格者,本课程最终成绩
不高于60分。
2010-11-04。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
土木工程专业有限元第一次作业姓名:班级:学号:指导教师:二〇一五年 6月12日题目:八节点三维规则六面体单元,已给定8个节点的坐标。
试查资料并论述:1、单元中位移函数u(x,y,z),v(x,y,z),w(x,y,z)和单元节点位移{δe }的关系式;2、[ B]矩阵的计算步骤和计算式;3、单元刚度矩阵[ k e ]的一般计算方法和计算步骤;4、论述相邻单元间公共边界上位移的连续性;5、如果已经求解得到单元8个节点的位移值{δe}怎样求单元中某一点A(x,y,z)的应力?解:1、取六面体单元的4个角点为节点,以其对称轴为,,x y z 轴。
任一节点i 有,,x y z 三个方向的位移,,i i i u v w ,此单元有8个节点,故总共有24个自由度。
如图1所示,其中原点O 取在长方体的几何中心,8个节点的编号为数学1~8,则此单元的位移列阵为:{}[]111222333444555666777888Teu v w u v w u v w u v w u v w u v w u v w u v w δ=图1该单元有8个节点,因此每个方向的位移场可以设定8个待定系数,根据确定位移模式的基本原则(从低阶到高阶、唯一确定性),选取该单元的位移模式为:123456781234567812345678(,,)(,,)(,,)u x y z a a x a y a z a xy a yz a xz a xyz v x y z b b x b y b z b xy b yz b xz b xyz w x y z c c x c y c z c xy c yz c xz c xyz=+++++++⎧⎪=+++++++⎨⎪=+++++++⎩(1-1)将8个节点的坐标值代入上式,可列出8个节点位移分量的值为:XZY O1234 5 678112131415116117118111212232425226227228222312333435336337338333412434445446447448444u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z =+++++++=+++++++=+++++++=+++++++512535455556557558555612636465666667668666712737475776777778777812838485886887888888u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z u a a x a y a z a x y a y z a x z a x y z =+++++++=+++++++=+++++++=+++++++⎫⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎭(1-2) 由式(1-2)的8个方程中可解出18~a a ,将它们代入式(1-1),得:1122334455667788+++++++i i u N u N u N u N u N u N u N u N u N u ==∑1122334455667788+++++++i i v N v N v N v N v N v N v N v N v N v ==∑ 1122334455667788+++++++i i w N w N w N w N w N w N w N w N w N w ==∑将上式写成矩阵形式,为{}{}[]{}128e eu v N N N w δδδ⎧⎫⎪⎪===⎨⎬⎪⎪⎩⎭N I II (1-3)其中,I 为三阶单元矩阵,而N 为形状函数矩阵,由于位移u v w ,,采用同样的插值形式,故有:128128128000000000000000N N N N N N N N N ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦…N (1-4a ) 上式中,各形状函数有:12345611=111=1118811=111=1118811=111=1188x y z x y z N N a b c a b c x y z x y z N N a b c a b c x y z x y N N a b c a b ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++++ ⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++--+- ⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+-- ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭78111=111=11188z c x y z x y z N N a b c a b c ⎛⎫+ ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+----- ⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(1-4b )将式(1-4b )依次代入式(1-3),即得位移函数(,,)u x y z ,(,,)v x y z ,(,,)w x y z与单元节点位移{}eδ的关系式{}{}eδδ=N ,其中{}18eδδδ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭, {}i i i i u v w δ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭ (1,2,,8)i =2、根据空间问题的几何方程,单元应变可用节点位移表示如下:{}[]{}128=x y e ez xy yz xz εεεδδγγγ⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭ε=B B B B (2-1)其中:000=00000i i i i i i i i i i TN N N x y z N N N y x z N N N zyx ⎡⎤∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎣⎦B (2-2) 即要求出矩阵i B 中的元素i N x ∂∂,i N y ∂∂,iN z∂∂(1,2,,8)i =。
代入(1-4b )中i N 的表达式,可求出相应的i B 。
如1B 的矩阵表达式为:()()()()()()()()()()()()()()()()()()100000018000b y c z a x c z a x b y abc a x c z b y c z a x b y a x c z a x b y b y c z ⎡-++⎤⎢⎥-+⎢⎥⎢⎥-+⎢⎥=⎢⎥-+-++⎢⎥⎢⎥-+-+⎢⎥-+-++⎢⎥⎣⎦B (2-3a ) 同理,可求出任意i B 的表达式,最终可求出应变矩阵B 。
3、根据虚功原理,在任意给出的节点虚位移下,单元节点力(外力){}ep 及内力σ所做的虚功之和应等于零,即:0P A A σδδ+= (3-1)单元节点虚位移以矩阵形式表达为:{}11122888Tu v w u v u v w δ*********⎡⎤=⎣⎦…,则单元内各点将产生相应的虚位移,,u v w ***与虚应变,,,,,x y z xy yz xz εεεγγγ******,它们都是坐标,,x y z 的函数,由下式可得:{}u v w δ****⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭N , {}*δ*=B ε (3-2)单元节点力:{}111222888Tex y z x y z x y z p p p p p p p p p p ⎡⎤=⎣⎦…,则单元节点力的虚功为:{}{}TeP A p δδ*= (3-3)而内力虚功为:*eT V A dV σδ=-⎰εσ (3-4)其中: {}=eδDB σ (3-5)由此可得: *eT V A dV σδ=-⎰εσ{}(){}eTVedV δδ*=-⎰DB B{}{}eTeT V dV δδ*=-⎰B DB{}{}eTeTV dV δδ*=-⎰B DB将单元节点力虚功与内力虚功代入,得:{}{}{}{}0eTTeeT V p dV δδδ**-=⎰B DB则有: {}{}[]{}eV e ee eT p V k d δδ==⎰B DB (3-6)其中: []eeTV dV k =⎰BDB (3-7)即为所求的单元刚度矩阵。
应力矩阵B 为已知,且在三维应力状态下,弹性系数矩阵D 的一般形式为:()()()()()()1111111120001122112000021120021E μμμμμμμμμμμμμμμ⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎢⎥-⎢⎥-=⎢⎥+--⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥-⎣⎦(对称)D (3-8) 将[]ek 按节点分块可表示为:[]111218212228818288e k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦k k k k k k k k k (3-9) 其中子矩阵的计算公式为:eab cT T ij i j i j a b ck dV dxdydz ---Ω==⎰⎰⎰⎰B DB B DB (3-10)4、证明:由单元的位移表达式(1-3)可知,该单元的位移在,,x y z 方向均呈线性变化,为线性位移模式。
而因为在单元的边界上,位移是按线性变化的,且相邻单元公共节点上有相同的节点位移值,这样即可保证两个相邻单元在其公共边界面上的位移是相同的,即相邻单元公共边界面位移是连续的。
5、根据空间问题的本构方程,单元应变可用节点位移表示如下:{}{}{}=Teexyzxyyzxzσσστττδδ===D DB S σε (5-1) 由式(3-8)和式(2-2)可分别求出矩阵D 和B ,故由式(5-1),若已知单元8个节点的位移值{}eδ,可求出单元中某一点(),,A x y z 的应力σ。
