三视图与球的切接问题
高考数学空间几何体的外接球与内切球常见题型

高考数学空间几何体的外接球与内切球常见题型本文介绍了空间几何体的外接球与内切球的经典类型,其中第一种类型为墙角模型,即三条棱两两垂直,不需要找球心的位置即可求出球半径。
具体方法是找到三条两两垂直的线段,然后使用公式2R=a+b+c或2R=a^2+b^2+c^2来求出R。
例如,在已知各顶点都在同一球面上的正四棱柱的高为4,体积为16的情况下,可以求出该球的表面积为32π。
第二种类型为对棱相等模型,补形为长方体。
在这种情况下,需要找到对棱相等的空间几何体,并补成长方体。
例如,如果三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积为36π。
除此之外,文章还给出了一些具体的例子,如正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA=23,则正三棱锥S-ABC外接球的表面积为36π。
同时,文章还提到了一些需要注意的引理,如正三棱锥的对棱互相垂直等。
需要注意的是,文章中存在一些格式错误和明显有问题的段落,需要进行删除或修改。
题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD)首先,我们可以画出一个长方体,标出三组互为异面直线的对棱,如图2-1所示。
设出长方体的长宽高分别为a,b,c,AD=BC=x,AB=CD=y,AC=BD=z,列方程组:a^2+b^2=x^2b+c=yc^2+a^2=z^2根据墙角模型,我们可以得到2R=a+b+c=2(x^2+y^2+z^2)/(x^2+y^2+z^2),化简得到R=sqrt(2)/2*(x^2+y^2+z^2)/(x^2+y^2+z^2),求出R即可。
例2(1)如下图所示三棱锥A-BCD,其中AB=CD=5,AC=BD=6,AD=BC=7,则该三棱锥外接球的表面积为。
2)在三棱锥A-BCD中,AB=CD=2,AD=BC=3,AC=BD=4,则三棱锥A-BCD外接球的表面积为。
3)正四面体的各条棱长都为2,则该正面体外接球的体积为。
高考满分数学压轴题13 与球相关的外接与内切问题(可编辑可打印)

一.方法综述如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点. 考查学生的空间想象能力以及化归能力。
研究球与多面体的接、切问题主要考虑以下几个方面的问题:(1)多面体外接球半径的求法,当三棱锥有三条棱垂直或棱长相等时,可构造长方体或正方体. (2)与球的外切问题,解答时首先要找准切点,可通过作截面来解决. (3)球自身的对称性与多面体的对称性;二.解题策略类型一 柱体与球【例1】(2020·河南高三(理))已知长方体1111ABCD A B C D -的表面积为208,118AB BC AA ++=,则该长方体的外接球的表面积为( ) A .116π B .106πC .56πD .53π【答案】A 【解析】【分析】由题意得出11118104AB BC AA AB BC BC AA AB AA ++=⎧⎨⋅+⋅+⋅=⎩,由这两个等式计算出2221AB BC AA ++,可求出长方体外接球的半径,再利用球体表面积公式可计算出结果.【详解】依题意,118AB BC AA ++=,11104AB BC BC AA AB AA ⋅+⋅+⋅=,所以,()()222211112116AB BC AA AB BC AA AB BC BC AA AB AA ++=++-⋅+⋅+⋅=,故外接球半径r ==,因此,所求长方体的外接球表面积24116S r ππ==.故选:A.【点睛】本题考查长方体外接球表面积的计算,解题的关键就是利用长方体的棱长来表示外接球的半径. 【举一反三】1.(2020·2,若与球相关的外接与内切问题该棱柱的顶点都在一个球面上,则该球的表面积为( ) A .73π B .113π C .5π D .8π【答案】D【解析】根据条件可知该三棱柱是正三棱柱,上下底面中心连线的中点就是球心,如图,则其外接球的半径22221123222sin 60R OB OO BO ⎛⎫ ⎪⎛⎫==+=+= ⎪ ⎪︒⎝⎭⎝⎭, 外接球的表面积428S ππ=⨯=.故选:D【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上,确定球心,用球心、一底面的外接圆的圆心,一顶点构成一个直角三角形,用勾股定理得关于外接球半径的关系式,可球的半径. 2.(2020·安徽高三(理))已知一个正方体的各顶点都在同一球面上,现用一个平面去截这个球和正方体,得到的截面图形恰好是一个圆及内接正三角形,若此正三角形的边长为a ,则这个球的表面积为( ). A .234a π B .23a π C .26a πD .232a π【答案】D【解析】由已知作出截面图形如图1,可知正三角形的边长等于正方体的面对角线长,正方体与其外接球的位置关系如图2所示,可知外接球的直径等于正方体的体对角线长,设正方体的棱长为m ,外接球的半径为R ,则2a m =,23R m =,所以64R a =,所以外接球的表面积为222634442a S R a πππ⎛⎫==⨯= ⎪ ⎪⎝⎭, 故选:D .【点睛】本题考查正方体的外接球、正方体的截面和空间想象能力,分析出外接球的半径与正三角形的边长的关系是本题的关键,3.(2020·河南高三(理))有一圆柱状有盖铁皮桶(铁皮厚度忽略不计),底面直径为20cm ,高度为100cm ,现往里面装直径为10cm 的球,在能盖住盖子的情况下,最多能装( ) (附:2 1.414,3 1.732,5 2.236≈≈≈) A .22个 B .24个C .26个D .28个【答案】C【解析】由题意,若要装更多的球,需要让球和铁皮桶侧面相切,且相邻四个球两两相切, 这样,相邻的四个球的球心连线构成棱长为10cm 的正面体,易求正四面体相对棱的距离为52cm ,每装两个球称为“一层”,这样装n 层球, 则最上层球面上的点距离桶底最远为()()10521n +-cm ,若想要盖上盖子,则需要满足()10521100n +-≤,解得19213.726n ≤+≈, 所以最多可以装13层球,即最多可以装26个球.故选:C 类型二 锥体与球【例2】5.已知球O 的半径为102,以球心O 为中心的正四面体Γ的各条棱均在球O 的外部,若球O 的球面被Γ的四个面截得的曲线的长度之和为8π,则正四面体Γ的体积为_________. 【来源】重庆市2021届高三下学期二模数学试题 【答案】182【解析】由题知,正四面体截球面所得曲线为四个半径相同的圆,每个圆的周长为2π,半径为1,故球心O 到正四面体各面的距离为2106122⎛⎫-=⎪⎝⎭,设正四面体棱长为a ,如图所示,则斜高332AE EF a ==,体高63=AF a ,在Rt AEF 和R t AGO 中,13OG EF AO AE ==,即61236632a =-,∴6a =,∴231362618234312V a a =⋅⋅=⋅=. 【举一反三】1.(2020四川省德阳一诊)正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______. 【答案】【解析】如图,设正四面体ABCD 的棱长为,过A 作AD ⊥BC , 设等边三角形ABC 的中心为O ,则,,,即.再设正四面体ABCD 的外接球球心为G ,连接GA , 则,即.∴正四面体ABCD 的外接球的体积为.故答案为:.2.(2020·宁夏育才中学)《九章算术》是我国古代的数学名著,其中有很多对几何体体积的研究,已知某囤积粮食的容器的下面是一个底面积为32π,高为h 的圆柱,上面是一个底面积为32π,高为h 的圆锥,若该容器有外接球,则外接球的体积为 【答案】288π【解析】如图所示,根据圆柱与圆锥和球的对称性知,其外接球的直径是23R h =,设圆柱的底面圆半径为r ,母线长为l h =, 则232r ππ=,解得42r =222(2)(3)l r h +=, 222(82)9h h ∴+=,解得4h =,∴外接球的半径为3462R =⨯=,∴外接球的体积为3344628833R V πππ⨯===.3.(2020·贵阳高三(理))在四棱锥P ABCD -中,底面ABCD 是边长为4的正方形,PAD ∆是一个正三角形,若平面PAD ⊥平面ABCD ,则该四棱锥的外接球的表面积为( ) A .143πB .283πC .563πD .1123π【答案】D 【解析】【分析】过P 作PF AD ⊥,交AD 于F ,取BC 的中点G ,连接,PG FG ,取PF 的三等分点H (2PH HF =),取GF 的中点E ,在平面PFG 过,E F 分别作,GF PF 的垂线,交于点O ,可证O 为外接球的球心,利用解直角三角形可计算PO .【详解】如图,过P 作PF AD ⊥,交AD 于F ,取BC 的中点G ,连接,PG FG ,在PF 的三等分点H (2PH HF =),取GF 的中点E ,在平面PFG 过,E F 分别作,GF PF 的垂线,交于点O .因为PAD ∆为等边三角形,AF FD =,所以PF ⊥AD . 因为平面PAD ⊥平面ABCD ,平面PAD平面ABCD AD =,PF ⊂平面PAD ,所以PF ⊥平面ABCD ,因GF ⊂平面ABCD ,故PF GF ⊥. 又因为四边形ABCD 为正方形,而,G F 为,BC AD 的中点,故FG CD ,故GF AD ⊥,因ADPF F =,故PF ⊥平面PAD .在Rt PGF ∆中,因,OE GF PF GF ⊥⊥,故OE PF ,故OE ⊥平面ABCD ,同理OH ⊥平面PAD .因E 为正方形ABCD 的中心,故球心在直线OE 上,因H 为PAD ∆的中心,故球心在直线OH 上,故O 为球心,OP 为球的半径. 在Rt PGF ∆中,2234343323PH PF ==⨯⨯=,2OH EF ==, 故16282214333OP =+==,所以球的表面积为28112433ππ⨯=. 类型三 构造法(补形法)【例3】已知三棱锥P ABC -的各个顶点都在球O 的表面上,PA ⊥底面ABC ,AB AC ⊥,6AB =,8AC =,D 是线段AB 上一点,且2AD DB =.过点D 作球O 的截面,若所得截面圆面积的最大值与最小值之差为25π,则球O 的表面积为( ) A .128π B .132πC .144πD .156π【答案】B【解析】PA ⊥平面ABC ,AB AC ⊥,将三棱锥P ABC -补成长方体PQMN ABEC -,如下图所示:设AE BC F =,连接OF 、DF 、OD ,可知点O 为PE 的中点,因为四边形ABEC 为矩形,AE BC F =,则F 为AE 的中点,所以,//OF PA 且12OF PA =,设2PA x =,且2210AE AB BE =+=,222225PE PA AE x ∴+=+所以,球O 的半径为21252R PE x ==+, 在Rt ABE △中,2ABE π∠=,6AB =,10AE =,3cos 5AB BAE AE ∠==,在ADF 中,243AD AB ==,5AF =, 由余弦定理可得222cos 17DF AD AF AD AF BAE =+-⋅∠=,PA ⊥平面ABCD ,OF ∴⊥平面ABCD ,DF ⊂平面ABCD ,则OF DF ⊥,12OF PA x ==,22217OD OF DF x ∴=+=+, 设过点D 的球O 的截面圆的半径为r ,设球心O 到截面圆的距离为d ,设OD 与截面圆所在平面所成的角为θ,则22sin d OD R r θ==-.当0θ=时,即截面圆过球心O 时,d 取最小值,此时r 取最大值,即2max 25r R x ==+;当2πθ=时,即OD 与截面圆所在平面垂直时,d 取最大值,即2max 17d OD x ==+,此时,r 取最小值,即()22min max 22r R d =-=. 由题意可得()()()222max min 1725r r x πππ⎡⎤-=+=⎣⎦,0x,解得22x =.所以,33R =,因此,球O 的表面积为24132S R ππ==.故选:B.【举一反三】1.(2020宁夏石嘴山模拟)三棱锥中,侧棱与底面垂直,,,且,则三棱锥的外接球的表面积等于 .【答案】【解析】把三棱锥,放到长方体里,如下图:,因此长方体的外接球的直径为,所以半径,则三棱锥的外接球的表面积为.2.(2020菏泽高三模拟)已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.【答案】C【解析】如图所示,将直三棱柱补充为长方体,则该长方体的体对角线为,设长方体的外接球的半径为,则,,所以该长方体的外接球的体积,故选C.3.(2020·贵州高三月考(理))某几何体的三视图如图所示,则该几何体的体积为()A.43B.53C.83D.163【答案】A【解析】【分析】如图所示画出几何体,再计算体积得到答案.【详解】由三视图知该几何体是一个四棱锥,可将该几何体放在一个正方体内,如图所示:在棱长为2的正方体1111ABCD A B C D -中,取棱11,,,,B C DA AB BC CD 的中点分别为,,,,E M N P Q ,则该几何体为四棱锥E MNPQ -,其体积为()2142233⨯⨯=.故选:A 类型四 与球体相关的最值问题【例4】(2020·福建高三期末(理))在外接球半径为4的正三棱锥中,体积最大的正三棱锥的高h =( ) A .143B .134C .72D .163【答案】D 【解析】【分析】设正三棱锥底面的边长为a ,高为h ,由勾股定理可得22234(4)3h a ⎛⎫=-+ ⎪ ⎪⎝⎭,则22183h h a -=,三棱锥的体积()23384V h h =-,对其求导,分析其单调性与最值即可得解. 【详解】解:设正三棱锥底面的边长为a ,高为h ,根据图形可知22234(4)3h a ⎛⎫=-+ ⎪ ⎪⎝⎭,则22180,3h h a -=>08h ∴<<. 又正三棱锥的体积21334V a h =⨯()2384h h h =-()23384h h =-,则()231634V h h '=-, 令0V '=,则163h =或0h =(舍去), ∴函数()23384V h h =-在160,3⎛⎫ ⎪⎝⎭上单调递增,在16,83⎛⎫⎪⎝⎭上单调递减,∴当163h =时,V 取得最大值,故选:D. 【点睛】本题考查球与多面体的最值问题,常常由几何体的体积公式、借助几何性质,不等式、导数等进行解决,对考生的综合应用,空间想象能力及运算求解能力要求较高. 【举一反三】1.(2020·广东高三(理))我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形,且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,AC BC ⊥,若12AA AB ==,当阳马11B A ACC -体积最大时,则堑堵111ABC A B C -的外接球体积为( )A .22πB .823C .23D .2π【答案】B【解析】依题意可知BC ⊥平面11ACC A .设,AC a BC b ==,则2224a b AB +==.111111323B A ACC V AC AA BC AC BC -=⨯⨯⨯⨯=⨯⨯22114232323AC BC +≤⨯=⨯=,当且仅当2AC BC ==时取得最大值.依题意可知1111,,A BC A BA A BB ∆∆∆是以1A B 为斜边的直角三角形,所以堑堵111ABC A B C -外接球的直径为1A B ,故半径221111222OB A B AA AB ==⨯+=.所以外接球的体积为()34π82π233⋅=. 特别说明:由于BC ⊥平面11ACC A ,1111,,A BC A BA A BB ∆∆∆是以1A B 为斜边的直角三角形,所以堑堵111ABC A B C -外接球的直径为1A B 为定值,即无论阳马11B A ACC -体积是否取得最大值,堑堵111ABC A B C -外接球保持不变,所以可以直接由直径1A B 的长,计算出外接球的半径,进而求得外接球的体积.故选:B2.(2020·遵义市南白中学高三期末)已知A ,B ,C ,D 四点在同一个球的球面上,6AB BC ==,90ABC ∠=︒,若四面体ABCD 体积的最大值为3,则这个球的表面积为( )A .4πB .8πC .16πD .32π【答案】C 【解析】根据6AB BC ==可得直角三角形ABC ∆的面积为3,其所在球的小圆的圆心在斜边AC 的中点上,设小圆的圆心为Q , 由于底面积ABC S ∆不变,高最大时体积最大,所以DQ 与面ABC 垂直时体积最大,最大值为为133ABC S DQ ∆⨯=,即133,33DQ DQ ⨯⨯=∴=,如图, 设球心为O ,半径为R ,则在直角AQO ∆中,即222(3)(3,)2R R R =∴+=-, 则这个球的表面积为24216S ππ=⨯=,故选C.3.(2020·河南高三(理))菱形ABCD 的边长为2,∠ABC =60°,沿对角线AC 将三角形ACD 折起,当三棱锥D -ABC 体积最大时,其外接球表面积为( ) A .153π B .2153π C .209π D .203π 【答案】D 【解析】【分析】当平面ACD 与平面ABC 垂直时体积最大,如图所示,利用勾股定理得到2223(3)()3R OG =-+和22223()3R OG =+,计算得到答案. 【详解】易知:当平面ACD 与平面ABC 垂直时体积最大. 如图所示:E 为AC 中点,连接,DE BE ,外接球球心O 的投影为G 是ABC ∆中心,在BE 上 3BE =,3DE =,33EG =,233BG =设半径为R ,则2223(3)()3R OG =-+,22223()3R OG =+ 解得:153R =,表面积22043S R ππ== 故选:D三.强化训练一、选择题1.(2020·广西高三期末)棱长为a 的正四面体ABCD 与正三棱锥E BCD -的底面重合,若由它们构成的多面体ABCDE 的顶点均在一球的球面上,则正三棱锥E BCD -的表面积为( ) A .2334a + B .2336a + C .2336a - D .2334a - 【答案】A【解析】由题意,多面体ABCDE 的外接球即正四面体ABCD 的外接球, 由题意可知AE ⊥面BCD 交于F ,连接CF ,则233323CF a a =⋅= 且其外接球的直径为AE ,易求正四面体ABCD 的高为223633a a a ⎛⎫ ⎪ ⎪=⎝⎭-. 设外接球的半径为R ,由2226333R a R a ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭=⎭-⎝-得64R a =. 设正三棱锥E BCD -的高为h ,因为6623AE a a h ==+,所以66h a =. 因为底面BCD ∆的边长为a ,所以2222EB EC ED CF h a ===+=, 则正三棱锥E BCD -的三条侧棱两两垂直.即正三棱锥E BCD -的表面积222121333322224S a a a ⎛⎫+=⨯⨯+⨯= ⎪ ⎪⎝⎭,故选:A .2、(2020辽宁省师范大学附属中学高三)在三棱锥中,,则三棱锥外接球的表面积为( )A.B.C.D.【答案】C【解析】如图,把三棱锥补形为长方体,设长方体的长、宽、高分别为,则,∴三棱锥外接球的半径∴三棱锥外接球的表面积为.故选:C.3.(2020·安徽高三期末)如果一个凸多面体的每个面都是全等的正多边形,而且每个顶点都引出相同数目的棱,那么这个凸多面体叫做正多面体.古希腊数学家欧几里得在其著作《几何原本》的卷13中系统地研究了正多面体的作图,并证明了每个正多面体都有外接球.若正四面体、正方体、正八面体的外接球半径相同,则它们的棱长之比为()A23B.223C.22D.223【答案】Ba b c R【解析】设正四面体、正方体、正八面体的棱长以及外接球半径分别为,,,则2223,23,22R a R b R c =⨯==, 即222,,2::2:2:333R R a b c R a b c ===∴=故选:B 4.(2020·北京人大附中高三)如图,在四棱锥S ABCD -中,四边形ABCD 为矩形,23AB =,2AD =,120ASB ∠=︒,SA AD ⊥,则四棱锥外接球的表面积为( )A .16πB .20πC .80πD .100π 【答案】B【解析】由四边形ABCD 为矩形,得AB AD ⊥,又SA AD ⊥,且SA AB A ⋂=,∴AD ⊥平面SAB ,则平面SAB ⊥平面ABCD ,设三角形SAB 的外心为G ,则23322sin 2sin12032AB GA ASB ====∠︒. 过G 作GO ⊥底面SAB ,且1GO =,则22215OS =+=.即四棱锥外接球的半径为5. ∴四棱锥外接球的表面积为24(5)20S ππ=⨯=.故选B .5.(2020河南省郑州市一中高三)在三棱锥中,平面,M 是线段上一动点,线段长度最小值为,则三棱锥的外接球的表面积是( ) A . B .C .D .【答案】C【解析】解:如图所示:三棱锥中,平面,M是线段上一动点,线段长度最小值为,则:当时,线段达到最小值,由于:平面,所以:,解得:,所以:,则:,由于:,所以:则:为等腰三角形.所以,在中,设外接圆的直径为,则:,所以外接球的半径,则:,故选:C.6、(2020河南省天一大联考)某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A.B.C.D.【答案】C【解析】由三视图可得,该几何体为一个三棱锥,放在长、宽、高分别为2,1,2的长方体中,此三棱锥和长方体的外接球是同一个,长方体的外接球的球心在体对角线的中点处,易得其外接球的直径为,从而外接球的表面积为.故答案为:C.7.(2020·江西高三期末(理))如图,三棱锥P ABC -的体积为24,又90PBC ABC ∠=∠=︒,3BC =,4AB =,410PB =,且二面角P BC A --为锐角,则该三棱锥的外接球的表面积为( )A .169πB .144πC .185πD .80π【答案】A【解析】因90PBC ABC ∠=∠=︒,所以BC ⊥平面PAB ,且PBA ∠为二面角P BC A --的平面角, 又3BC =,4AB =,410PB =,由勾股定理可得13PC =,5AC =, 因为1sin 8102PAB S PB AB PBA PBA ∆⋅=⋅∠=∠,所以三棱锥的体积1181032433PAB V S BC PBA ∆=⋅=⨯∠⨯=,解得310sin PBA ∠=,又PBA ∠为锐角,所以10cos 10PBA ∠=, 在PAB ∆中,由余弦定理得2101601624410144PA =+-⨯⨯=, 即12PA =,则222PB PA AB =+,故PA AB ⊥, 由BC ⊥平面PAB 得BC PA ⊥,故PA ⊥平面ABC ,即PA AC ⊥,取PC 中点O , 在直角PAC ∆和直角PBC ∆中,易得OP OC OA OB ===,故O 为外接球球心, 外接圆半径11322R PC ==,故外接球的表面积24169S R ππ==.故选:A. 8.(2019·湖南长沙一中高三)在如图所示的空间几何体中,下面的长方体1111ABCD A B C D -的三条棱长4AB AD ==,12AA =,上面的四棱锥1111P A B C D -中11D E C E =,1111PE A B C D ⊥平面,1PE =,则过五点A 、B 、C 、D 、P 的外接球的表面积为( )A .311π9B .311π18C .313π9D .313π18【答案】C【解析】问题转化为求四棱锥P ABCD -的外接球的表面积.4913PC =+=,∴3sin 13PCD ∠=.所以PCD ∆外接圆的半径为131336213r ==⨯,由于PE ⊥平面1111D C B A ,则PE ⊥平面ABCD ,PE ⊂平面PCD ,所以平面PCD ⊥平面ABCD , 所以外接球的222169313243636R r =+=+=.所以2313π4π9S R ==球表面积.9.三棱锥P —ABC 中,底面ABC 满足BA=BC , ,点P 在底面ABC 的射影为AC 的中点,且该三棱锥的体积为,当其外接球的表面积最小时,P 到底面ABC 的距离为( ) A .3 B .C .D .【答案】B【解析】设外接球半径为,P 到底面ABC 的距离为,,则,因为,所以, 因为,所以当时,,当时,,因此当时,取最小值,外接球的表面积取最小值,选B.10.(2019·河北高三月考)在平面四边形ABCD 中,AB ⊥BD ,∠BCD =30°,2246AB BD +=,若将△ABD 沿BD 折成直二面角A -BD -C ,则三棱锥A-BDC 外接球的表面积是( ) A .4π B .5πC .6πD .8π【答案】C【解析】取,AD BD 中点,E F ,设BCD ∆的外心为M ,连,,MB MF EF , 则01,30,22MF BD BMF DMB BCD BM BF BD ⊥∠=∠=∠=∴== 分别过,E M 作,MF EF 的平行线,交于O 点, 即//,//OE MF OM EF ,,BD AB E ⊥∴为ABD ∆的外心,平面ABD ⊥平面BCD ,AB ⊥平面BCD ,//,EF AB EF ∴⊥平面BCD ,OM ∴⊥平面BCD ,同理OE ⊥平面ABD ,,E M 分别为ABD ∆,BCD ∆外心,O ∴为三棱锥的外接球的球心,OB 为其半径, 22222221342OB BM OM BD EF BD AB =+=+=+=, 246S OB ππ=⨯=球.故选:C11.(2020·梅河口市第五中学高三期末(理))设三棱锥P ABC -的每个顶点都在球O 的球面上,PAB ∆是面积为3的等边三角形,45ACB ∠=︒,则当三棱锥P ABC -的体积最大时,球O 的表面积为( ) A .283π B .10πC .323π D .12π【答案】A【解析】如图,由题意得2334AB =,解得2AB =.记,,AB c BC a AC b ===, 12sin 24ABC S ab C ab ∆==,由余弦定理2222cos c a b ab C =+-,得224222a b ab ab ab =+-≥-,42(22)22ab ≤=+-,当且仅当a b =时取等号.所以CA CB =且平面PAB ⊥底面ABC 时,三棱锥P ABC -的体积最大.分别过PAB ∆和ABC ∆的外心作对应三角形所在平面的垂线,垂线的交点即球心O , 设PAB ∆和ABC ∆的外接圆半径分别为1r ,2r ,球O 的半径为R ,则123r =,21222sin 45r =⨯=︒.故222211172233R r r ⎛⎫=+=+= ⎪⎝⎭, 球O 的表面积为22843R ππ=.故选:A.12.(2020四川省成都外国语学校模拟)已知正方形ABCD 的边长为4,E ,F 分别是BC ,CD 的中点,沿AE ,EF ,AF 折成一个三棱锥P-AEF (使B ,C ,D 重合于P ),三棱锥P-AEF 的外接球表面积为( )A .B .C .D .【答案】C 【解析】如图,由题意可得,三棱锥P-AEF 的三条侧棱PA ,PE ,PF 两两互相垂直, 且,,把三棱锥P-AEF 补形为长方体,则长方体的体对角线长为, 则三棱锥P-AEF 的外接球的半径为,外接球的表面积为.故选:C .13.已知球O 夹在一个二面角l αβ--之间,与两个半平面分别相切于点,A B .若2AB =,球心O 到该二面角的棱l 的距离为2,则球O 的表面积为( ) A .8πB .6πC .4πD .2π【来源】江西省萍乡市2021届高三二模考试数学(文)试题 【答案】A【解析】过,,O A B 三点作球的截面,如图:设该截面与棱l 交于D ,则OA l ⊥,OB l ⊥,又OA OB O =,所以l ⊥平面AOB ,所以OD l ⊥,所以||2OD =,依题意得,OA AD OB BD ⊥⊥,所以,,,O A D B 四点共圆,且OD 为该圆的直径,因为||2||AB OD ==,所以AB 也是该圆的直径,所以四边形OADB 的对角线AB 与OD 的长度相等且互相平分,所以四边形OADB 为矩形,又||||OA OB =,所以该矩形为正方形,所以2||||22OA AB ==,即圆O 的半径为2,所以圆O 的表面积为24(2)8ππ⨯=. 故选:A14.已知点,,A B C 在半径为2的球面上,满足1AB AC ==,3BC =,若S 是球面上任意一点,则三棱锥S ABC -体积的最大值为( ) A .32312+ B .3236+ C .23312+ D .3312+ 【答案】A【解析】设ABC 外接圆圆心为O ',三棱锥S ABC -外接球的球心为O ,1AB AC ==,设D 为BC 中点,连AD ,如图,则AD BC ⊥,且O '在AD 上,221()22BC AD AB =-=, 设ABC 外接圆半径为r ,222231()()()242BC r AD r r =+-=+-,解得1r =, 22||23OO r '∴=-=要使S ABC -体积的最大,需S 到平面ABC 距离最大, 即S 为O O '32,所以三棱锥S ABC -体积的最大值为11112)2)3322ABCS ⨯=⨯⨯⨯=故选:A15.已知半球O 与圆台OO '有公共的底面,圆台上底面圆周在半球面上,半球的半径为1,则圆台侧面积取最大值时,圆台母线与底面所成角的余弦值为( )A B C .6D 【答案】D【解析】如图1所示,设BC x =,CO r '=,作CF AB ⊥于点F ,延长OO '交球面于点E ,则1BF r =-,OO CF '===2得CO O D ''⋅=()()11O E O H OO OO ''''⋅=+⋅-,即((211r =+⋅,解得212x r =-,则圆台侧面积(2π1102x S x x ⎛⎫=⋅+-⋅<< ⎪⎝⎭,则'2322S x ππ=-,令'0S =,则3x =或x =,当0x <<时,'0S >x <<'0S <,所以函数2π112x S x ⎛⎫=⋅+-⋅ ⎪⎝⎭在⎛ ⎝⎭上递增,在⎝上递减,所以当3x =时,S 取得最大值.当3x BC ==时,21123x r =-=,则213BF r =-=.在轴截面中,OBC ∠为圆台母线与底面所成的角,在Rt CFB △中可得cos 3BF OBC BC ∠==故选:D .16.(2020·重庆八中高三)圆柱的侧面展开图是一个面积为216π的正方形,该圆柱内有一个体积为V 的球,则V 的最大值为 【答案】323π【解析】设圆柱的底面直径为2r ,高为l ,则222π16πr l l =⎧⎨=⎩,解得24πr l =⎧⎨=⎩.故圆柱的底面直径为4,高为4π,所以圆柱内最大球的直径为4,半径为2,其体积为34π32π233⨯=. 17.(2020·江西高三)半正多面体(semiregular solid )亦称“阿基米德多面体”,如图所示,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的边长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若二十四等边体的棱长为2,则该二十四等边体外接球的表面积为【答案】8π【解析】2,侧棱长为2的正四棱柱的外接球,2222(2)(2)(2)2R ∴=++,2R ∴,∴该二十四等边体的外接球的表面积24πS R =24π(2)8π=⨯=.18.(2020·福建高三期末(理))在棱长为4的正方体1111ABCD A B C D -中,E ,F 分别为1AA ,BC 的中点,点M 在棱11B C 上,11114B M BC =,若平面FEM 交11A B 于点N ,四棱锥11N BDD B -的五个顶点都在球O 的球面上,则球O 半径为 【答案】2293【解析】如图1,2,,B M F 三点共线,连结22,B E B MF ∈从而2B ∈平面FEM ,则2B E 与11A B 的交点即为点N ,又12Rt B B N ∆与1Rt A EN ∆相似,所以1112112A E A NB B NB ==; 如图2,设11B D N ∆的外接圆圆心为1O ,半径为r ,球半径为R ,在11B D N ∆中,111445,103NB D D N ︒∠==,由正弦定理得453r =,所以1853D P =,在1Rt DD P ∆中,解得4293DP =,即42293R =,所以所求的球的半径为2293.19.(2020·黑龙江高三(理))设,,,A B C D 是同一个半径为4的球的球面上四点,在ABC 中,6BC =,60BAC ∠=︒,则三棱锥D ABC -体积的最大值为【答案】183【解析】ABC 中,6BC =,60BAC ∠=︒,则643223sin sin 60a r r A ===∴=︒,22max 6h R r R =-=,222222cos 36a b c bc A b c bc bc bc =+-=+-≥∴≤ ,1sin 932S bc A =≤ 当6a b c ===时等号成立,此时11833V Sh ==20.(2020·河北承德第一中学高三)正三棱锥S -ABC 的外接球半径为2,底边长AB =3,则此棱锥的体积为【答案】934或334【解析】设正三棱锥的高为h ,球心在正三棱锥的高所在的直线上,H 为底面正三棱锥的中心因为底面边长AB=3,所以2222333332AH AD ⎛⎫==-= ⎪⎝⎭当顶点S 与球心在底面ABC 的同侧时,如下图此时有222AH OH OA += ,即()()222322h +-=,可解得h=3因而棱柱的体积113393333224S ABC V -=⨯⨯⨯⨯=当顶点S 与球心在底面ABC 的异侧时,如下图有222AH OH OA +=,即()222322h +-=,可解得h=1所以113333313224S ABC V -=⨯⨯⨯⨯=9333421.(2020·江西高三(理))已知P,A,B,C 是半径为2的球面上的点,PA=PB=PC=2,90ABC ∠=︒,点B 在AC 上的射影为D ,则三棱锥P ABD -体积的最大值为 【答案】338【解析】如下图,由题意,2PA PB PC ===,90ABC ∠=︒,取AC 的中点为G ,则G 为三角形ABC 的外心,且为P 在平面ABC 上的射影,所以球心在PG 的延长线上,设PG h =,则2OG h =-,所以2222OB OG PB PG -=-,即22424h h --=-,所以1h =. 故G CG 3A ==,过B 作BD AC ⊥于D ,设AD x =(023x <<),则23CD x =-,设(03)BD m m =<≤,则~ABD BCD ,故23m xx m-=, 所以()223m x x =-,则()23m x x =-,所以ABD 的面积()3112322S xm x x ==-,令()()323f x x x =-,则()2'634f x x x =-(),因为20x >,所以当3032x <<时,()'0f x >,即()f x 此时单调递增;当33232x ≤<时,()'0f x ≤,此时()f x 单调递减.所以当332x =时,()f x 取到最大值为24316,即ABD 的面积最大值为1243932168=.当ABD 的面积最大时,三棱锥P ABD -体积取得最大值为19333388⨯=.22.已知H 是球O 的直径AB 上一点,:1:3AH HB =,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为__________.【来源】宁夏固原市第五中学2021届高三年级期末考试数学(文)试题 【答案】163π【解析】如下图所示,设AH x =,可得出3HB x =,则球O 的直径为4AB x =,球O 的半径为2x ,设截面圆H 的半径为r ,可得2r ππ=,1r ∴=,由勾股定理可得()2222OH r x +=,即()22214x AH x -+=,即2214x x +=,33x ∴=,所以球O 的半径为2323x =,则球O 的表面积为22316433S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 23.如图,在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,2PA AB ==,22AC =,M 是BC 的中点,则过点M 的平面截三棱锥P ABC -的外接球所得截面的面积最小值为___【答案】π 【解析】PA ⊥平面ABC ,AB BC ⊥,将三棱锥P ABC -补成长方体ABCD PEFN -,则三棱锥P ABC -的外接球直径为22222223R PC PA AB AD PA AC ==++=+=,所以,3R =,设球心为点O ,则O 为PC 的中点,连接OM ,O 、M 分别为PC 、BC 的中点,则//OM PB ,且2211222OM PB PA AB ==+=, 设过点M 的平面为α,设球心O 到平面α的距离为d . ①当OM α⊥时,2d OM ==;②当OM 不与平面α垂直时,2d OM <=. 综上,2d OM ≤=.设过点M 的平面截三棱锥P ABC -的外接球所得截面圆的半径为r ,则221r R d =-≥,因此,所求截面圆的面积的最小值为2r ππ=.24.若正四棱锥P ABCD -的底面边长和高均为8,M 为侧棱PA 的中点,则四棱锥M ABCD -外接球的表面积为___________.【来源】山西省运城市2021届高三上学期期末数学(文)试题 【答案】132π【解析】在正四棱锥P ABCD -中M 为侧楼PA 中点,∴四棱锥M ABCD -外接球即为棱台MNEF ABCD -的外接球,如图,四棱锥P ABCD -的底面边长和高均为8,1214,42AB O N O M ===∴ 212242AO MO ==∴设球心为O ,则图中12,OO A OMO △△均为直角三角形, 设1OO h =,222(42)OA h ∴=+,222(22)(4)OM h =++,A , M 都在球面上,222O O M R A =∴=,解得21,33h R =∴=,24132S R ππ∴==球25.已知P 为球O 球面上一点,点M 满足2OM MP =,过点M 与OP 成30的平面截球O ,截面的面积为16π,则球O 的表面积为________.【来源】广西钦州市2021届高三第二次模拟考试数学(理)试题 【答案】72π 【解析】如图所示:设截面圆心为1O , 依题意得130OMO ∠=, 设1OO h =,则2OM h =, 又2OM MP =,所以3OP h =,即球的半径为3h ,所以3ON h =,又截面的面积为16π,所以()2116O N ππ=,解得14O N =,在1Rt OO N 中,()22316h h =+, 解得2h =,所以球的半径为32, 所以球的表面积是()243272S ππ==,故答案为: 72π 26.如图是数学家GeminadDandelin 用来证明一个平面截圆锥得到的截面是椭圆的模型(称为丹德林双球模型):在圆锥内放两个大小不同的小球,使得它们分别与圆锥侧面、截面相切,设图中球1O 和球2O 的半径分别为1和3,128O O =,截面分别与球1O 和球2O 切于点E 和F ,则此椭圆的长轴长为___________.【来源】江苏省盐城市阜宁县2020-2021学年高三上学期期末数学试题【答案】15【解析】如图,圆锥面与其内切球12,O O 分别相切与,B A ,连接12,O B O A ,则12,O B AB O A AB ⊥⊥,过1O 作12O D O A 于D ,连接12,,O F O E EF 交12O O 于点C ,设圆锥母线与轴的夹角为α,截面与轴的夹角为β,在Rt △12O O D 中,2312DO ,22182215O D11221515cos 84O D O O α===128O O = , 218CO O C =-,△2EO C △1FO C ,11218O C O C EO O F -= 解得12O C =,26O C = 222211213CF O C FO ∴=-=-= ,即13cos 2CFO C , 所以椭圆离心率为cos 25cos 5c e aβα=== 在△2EO C 中223cos cos 2EC ECO O C β=∠== 解得33EC =,432EF c ==2325155a a =⇒= 2215a ∴=故答案为:21527.在长方体1111ABCD A B C D -中,13AB =,5AD =,112AA =,过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内,则在平面α变化的过程中,这两个球的半径之和的最大值为___________.【来源】江苏省六校2021届高三下学期第四次适应性联考数学试题 【答案】16538【解析】如图所示:平面ABMN 将长方体分成两部分,MN 有可能在平面11CDD C 上或平面1111A D C B 上,根据对称性知,两球半径和的最大值是相同的,故仅考虑在平面11CDD C 上的情况,延长11B C 与BM 交于点P ,作1O Q BC ⊥于Q 点,设1CBP BPB α∠=∠=,圆1O 对应的半径为1r ,根据三角形内切圆的性质, 在1Rt O QB 中,12QBO α∠=,15BQ BC CQ r =-=-,111tan 25O Q r BQ r α==-, 则15tan5251tan 1tan 22r ααα==-++,又当BP 与1BC 重合时,1r 取得最大值,由内切圆等面积法求得1512251213r ⨯≤=++,则2tan 23α≤ 设圆2O 对应的半径为2r ,同理可得266tan2r α=-, 又252r ≤,解得7tan 212α≥. 故1255566tan 176(1tan )221tan 1tan 22r r αααα+=-+-=--+++,72tan 1223α≤≤, 设1tan 2x α=+,则195[,]123x ∈,()5176f x x x=--, 由对号函数性质易知195[,]123x ∈,函数()f x 单减,则19519165()()1761912123812f x f ≤=--⨯=,即最大值为16538 故答案为:16538 28.设A B C D ,,,是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为___________.【来源】江苏省南京市秦淮中学2021届高三下学期期初学情调研数学试题【答案】183【解析】ABC 为等边三角形且其面积为93,则23934ABC SAB ==,6AB ∴=,如图所示,设点M 为ABC 的重心,E 为AC 中点,当点D 在平面ABC 上的射影为M 时,三棱锥D ABC -的体积最大,此时,4OD OB R ===, 点M 为三角形ABC 的重心,2233BM BE ∴==, Rt OMB ∴中,有222OM OB BM =-=,426DM OD OM ∴=+=+=,所以三棱锥D ABC -体积的最大值19361833D ABC V -=⨯=29.已知四面体ABCD 的棱长均为6,,EF 分别为棱,BC BD 上靠近点B 的三等分点,过,,A E F 三点的平面与四面体ABCD 的外接球O 的球面相交,得圆'O ,则球O 的半径为___________,圆'O 的面积为__________.【来源】河南省九师联盟2021届高三下学期3月联考理科数学试题【答案】3 8π【解析】。
高考复习28-组合体的“切”“接”综合问题高考试题解读与变式

高考复习28 :组合体的“切”“接”综合问题知识储备汇总1.知识储备汇总: 1.1球的性质球被平面截得的图形是圆,球心与截面圆圆心的连线与截面圆垂直,球的半径R ,截面圆的半径r ,球心到截面圆的距离为d ,则222d r R +=.1.2长方体性质:长方体的一条对角线的平方等于一个顶点上三条棱长的平方和. 1.3几个与球有关的切、接常用结论 (1)正方体的棱长为a ,球的半径为R , ①正方体的外接球,则23R a =; ②正方体的内切球,则2R a =; ③球与正方体的各棱相切,则22R a =.(2)长方体的同一顶点的三条棱长分别为,,a b c ,外接球的半径为R ,则2222R a b c =++. (3)正四面体的外接球与内切球的半径之比为3∶1.1.4与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面进行解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图. 1.5.解决与球有关的切、接问题的方法:(1)一般要过球心及多面体中的特殊点或过线作截面将空间问题转化为平面问题,从而寻找几何体各素之间的关系.(2)若球面上四点,,,P A B C 中,,PA PB PC 两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.1.6.求解球与多面体的组合问题时,其关键是确定球心的位置,可以根据空间几何体的对称性判断球心的位置,然后通过作出辅助线或辅助平面确定球的半径和多面体中各个几何元素的关系,达到求解解题需要的几何量的目的.题型与相关高考题解读1.棱柱的外接球问题 1.1考题展示与解读例1 长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 ________.【命题意图探究】本题主要考查长方体的对角线性质、球的表面积公式,是容易题.【解题能力要求】空间想象能力、运算求解能力【方法技巧归纳】对球内接直棱柱问题,利用球心到棱柱底面所在的截面圆的距离就是棱柱高的一半,棱柱底面所在的截面圆的半径利用正弦定理计算,再利用球的截面性质即可求出球的半径,再利用球的表面积或体积公式计算球的表面积或体积.1.2【典型考题变式】【变式1:改编条件】若一个正三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为()A. 163πB.193πC.1912πD.43π【变式2:改编结论】底面边长为1,侧棱长为263的正三棱柱的各顶点均在同一个球面上,则该球的体积为()A. 32π3B. 4πC. 2πD.4π3【变式3:改编问法】已知某几何体的外接球的半径为,其三视图如图所示,图中均为正方形,则该几何体的体积为()A. 16B.C.D. 82.球与圆柱或圆锥的切接问题2.1考题展示与解读例2已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为________.A.πB.3π4C.π2D.π4【命题意图探究】本题主要考查球内接圆柱的体积问题,是基础题.【解题能力要求】空间想象能力、运算求解能力【方法技巧归纳】对球内接圆柱问题,利用球的截面性质沟通球的半径与圆柱底面半径高之间的关系.2.2【典型考题变式】【变式1:改编条件】已知圆柱的高为2,它的两个底面的圆周在直径为4的同一个球的球面上,则该圆柱的体积是( )A. πB. 34πC.2πD. 6π【变式2:改编结论】已知圆锥的底面半径为4,高为8,则该圆锥的外接球的表面积为()A. 10πB. 64πC. 100πD. 500 3π【变式3:改编问法】某几何体的三视图如图所示,其正视图和侧视图都是边长为23的正三角形,该几何体的外接球的表面积为()A. 9πB. 16πC. 24πD. 36π3.棱锥的外接球问题3.1考题展示与解读例3已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为________.【命题意图探究】本题主要考查球内接棱柱问题及球的表面积,是中档题.【解题能力要求】空间想象能力、逻辑推理能力、运算求解能力【方法技巧归纳】球内接棱锥问题,若有同一顶点上三条垂直的棱,可将三棱锥补成球内接长方体,利用长方体的对角线的平方等于同于同一顶点三棱长的平方和、长方体的对角线等于球的直径沟通球与棱锥量之间的关系.3.2【典型考题变式】【变式1:改编条件】某多面体的三视图如图所示,每一小格单位长度为l,则该多面体的外接球的表面积是A. 27πB.π C. 9π D.π 【变式2:改编结论】在正三棱锥中,,,则该三棱锥外接球的直径为( )A. 7B. 8C. 9D. 10【变式3:改编问法】已知四棱锥E-ABCD 的都在球心为,半径为的球面上,四边形ABC D 为矩形,,且,则四棱锥E-ABCD 的体积的最大值为( )A.324B. 372,C. 38D. 348 4.多面体内切球问题 4.1考题展示与解读例4在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是( )(A )4π (B )92π(C )6π (D )323π【命题意图探究】本题主要考查直棱柱内的球的最大体积问题,是中档题. 【解题能力要求】空间想象能力、运算求解能力【方法技巧归纳】立体几何最值问题通常有三种思考方向:(1)根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;(2)将几何体平面化,如利用展开图,在平面几何图中直观求解;(3)建立函数,通过求函数的最值来求解. 4.2【典型考题变式】【变式1:改编条件】在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑(bie nao ).已知在鳖臑中,平面,,则该鳖臑的外接球与内切球的表面积之和为_______.【变式2:改编结论】在正方体1111ABCD A B C D -中,若1D AC ∆内切圆的半径为263,则该正方体内切球的表面积为 ( )A. 2πB. 8πC. 12πD. 16π【变式3:改编问法】已知一个直三棱柱,其底面是正三角形,一个体积为43π的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是A. 243B. 183C. 123D. 3典例高考试题演练1.若正四棱锥P ABCD -内接于球O ,且底面ABCD 过球心O ,设正四棱锥P ABCD -的高为1,则球O的体积为( ) A.43π B. 23π C. 4π D. 22π 2.如图为某几何体的三视图,则该几何体的外接球的表面积为( )A .B .27πC .27πD .3.网络用语“车珠子”,通常是指将一块原料木头通过加工打磨,变成球状珠子的过程,某同学有一圆锥状的木块,想把它“车成珠子”,经测量,该圆锥状木块的底面直径为12cm ,体积为96πcm 3,假设条件理想,他能成功,则该珠子的体积最大值是( ) A .36πcm 3 B .12πcm 3C .9πcm 3D .72πcm 34.半径为2的球O 中有一内接正四棱柱(底面是正方形,侧棱垂直底面),当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是( ) A .16()B .16() C .8(2)D .8(2)5.已知一个四棱锥三视图如图所示,若此四棱锥的五个顶点在某个球面上,则该球的表面积为( )A. 48πB. 52πC.1723π D. 1963π6.将半径为4的半圆围成一个圆锥,则该圆锥的内切球的表面积为( ) A.83π B. 163π C. 43π D. 43 7.若一个正四面体的表面积为1S ,其内切球的表面积为2S ,则12S S =( )A.6π B. 2π C. 16πD. 63π8.已知球O 与棱长为4的正四面体的各棱相切,则球O 的体积为( ) A.823π B. 833π C. 863π D. 1623π 9.某三棱锥的三视图如图所示,其中俯视图是一个等腰直角三角形,则该三棱锥的外接球的表面积为( )A.B.C.D.556π10.已知三棱锥的四个顶点都在同一个球面上,底面满足,若该三棱锥体积最大值为3,则其外接球的表面积为( ) A.B.C.D .11.三棱锥A BCD -的一条长为a ,其余棱长均为1,当三棱锥A BCD -的体积最大时,它的外接球的表面积为( ) A.53π B. 54π C. 56π D. 58π 12.如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则的值是13.已知三棱锥的三条棱所在的直线两两垂直且长度分别为3,2,1,顶点都在球的表面上,则球的表面积为__________.14.已知四棱锥 P ﹣ABCD 的底面ABCD 是正方形,侧棱PA 与底面垂直,且PA=AB ,若该四棱锥的侧面积为16 __.15.已知正六棱柱的顶点都在同一个球面上,且该六棱柱的体积为2,当球的体积最小时,正六棱柱底面边长为_________.。
空间几何体的切接球问题(八个模型)

微专题 立体几何3空间几何体的外接球与内切球——八个模型一些提速的小结论:1.设正三角形边长为a ,则其高h =,外接圆半径r a =,面积2S =;2.设正四面体棱长为a ,则其高h =,外接球半径R =外,内切球半径4h R ==内,体积312V a =,正四面体相对棱的距离为2d =模型一 墙角模型模型解读:类似于三角形有且仅有唯一一个外接圆,将三角形补成平行四边形,则该平行四边形外接圆与三角形外接圆是同一个外接圆;三菱锥有且仅有一个外接球,特殊情况下,将其补成一个长方体,则该长方体与三棱锥有共同的外接球。
根据对称性,长方体体对角线即为外接球的直径。
模型公式:2222)2(c b a R ++=或2222c b a R ++=; 秒杀公式:()222S a b c π=++,()222222V ab c a b c π=++++适用情况:几何体中有三条两两垂直的棱时(非必要条件,见图3)。
(柱体适应模型1)c abCP A Babc 图2PCBAabc 图3CBPAa bc PCO 2BA典型例题例1、已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32例2、若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 9π 例3、若三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 29π跟踪练习1、已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为2、若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( A ) A.3B.6C.36D.93、(2018宝鸡模拟)已知底面边长为12的正四棱柱的各顶点均在同一个球面上,则该球的体积为( D )32.3A π .4B π .2C π 4.3D π4、(广东省汕头市达濠华桥中学2017-2018学年期末)《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑, PA ⊥平面ABC , 2,4PA AB AC ===,三棱锥P ABC -的四个顶点都在球O 的球面上,则球O 的表面积为( C )A. 8πB. 12πC. 20πD. 24π5、(2020·安徽高三(理))已知一个正方体的各顶点都在同一球面上,现用一个平面去截这个球和正方体,得到的截面图形恰好是一个圆及内接正三角形,若此正三角形的边长为a ,则这个球的表面积为( D ). A .234a πB .23a πC .26a πD .232a π6、(2020延安高考模拟)刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( B )A .B .C .D .7、(2020菏泽高三模拟)已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为( C ) A .B .C .D .8、(2020届·厦门市五月质量检测理6)某三棱锥的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( B ) A.9π B.27π C.81π D.108π9、已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为2,则该三棱锥的体积为(C )(A )2 (B )43 (C )23(D )2210、(2017云南第二次统一检测)已知体积为6的长方体的八个顶点都在球O 的球面上,在这个长方体经过同一个顶点的三个面中,如果有两个面的面积分别为343O 的体积等于( A ) A .323π B .73π C .332πD .1172π11、(2017江西赣州模拟)在四面体SABC 中,SA ⊥平面ABC ,∠ABC =90°,SA =AC =2,AB =1,则该四 面体的外接球的表面积为 . 8π提升练习1、在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱3SA =三棱锥ABC S -外接球的表面积是 。
球的内切外切解题技巧

球的“内切”、“外切”的解题技巧【方法技巧】类型一 球的内切问题 使用情景:有关球的内切问题解题模板:第一步 首先画出球及它的内切圆柱、圆锥等几何体,它们公共的轴截面; 第二步 然后寻找几何体与几何体之间元素的关系 第三步 得出结论. 类型二 球的外切问题 使用情景:有关球的外切问题解题模板:第一步 首先画出球及它的外切圆柱、圆锥等几何体,它们公共的轴截面; 第二步 然后寻找几何体与几何体之间元素的关系 第三步 得出结论.【应用举例】【例题1】在底面半径为2,母线长为4的圆锥中内有一个高为3的圆柱. (1)求:圆柱表面积的最大值;(2)在(1)的条件下,求该圆柱外接球的表面积和体积.【答案】(1)π)(312+;(2)π7=S ,677π=V .【解析】 试题分析:(1)我们可计算出圆柱的底面半径,代入圆柱表面积公式,即可得到答案;(2)求出圆柱的外接球半径,即可求该圆柱外接球的表面积和体积.试题解析:(1)当圆柱内接与圆锥时,圆柱的表面积最大.设此时,圆柱的底面R 半径为r ,高为h′.圆锥的高h 2242-3312h .∴2r 23323,∴r =1.∴S 表面积=2S底+S 侧=2πr 23=2(13)π.(2)设圆柱的外接球半径为R ,72R =,7S π=, 76V π=考点:1、球内接多面体;2、球的表面积和体积.【难度】较易【例题2】求球与它的外切圆柱、外切等边圆锥的体积之比.【答案】964∶∶∶∶锥柱球=V V V . 【解析】试题分析:设球的半径为R ,则外切圆柱的半径为R ,高为2R ;外切等边圆锥底面半径为R 3,高为3R , 所以334R V π=球 ,32R v π=柱, 33R V π=锥 9:6:4=∴锥柱球::V V V考点:本题考查空间几何体的体积。
点评:本题的关键是由球的半径求出外切圆柱、外切等边圆锥的半径和高。
考查了空间想象力。
首先画出球及它的外切圆柱、等边圆锥,它们公共的轴截面,然后寻找几何体与几何体之间元素的关系. 【难度】一般【例题3】把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离. 【答案】3622+. 【解析】由题意,四球心组成棱长为2的正四面体的四个顶点,则正四面体的高362)332(222=⋅-=h .而第四个球的最高点到第四个球的球心距离为求的半径1,且三个球心到桌面的距离都为1,故第四个球的最高点与桌面的距离为3622+. 【点评】关键在于能根据要求构造出相应的几何体,由于四个球半径相等,故四个球一定组成正四面体的四个顶点且正四面体的棱长为两球半径之和2. 考点:空间几何体的球体积和表面积. 【较易】【例题4】正三棱锥ABC P -的侧棱长为l ,两侧棱的夹角为α2,求它的外接球的体积.【答案】322334sin 2(34sin )l παα--.【解析】解:如图,作PD 底面ABC 于D ,则D 为正△ABC 的中心。
高中数学教师备课必备(空间几何体):专题八 球的切接问题 含解析

例1。
若棱长为3的正方体的顶点都在同一球面上,求该球的表面积和体积。
分析:①334R V π=球(R 为球半径) ②24R S π=球 (R 为球半径) 需要求出半径。
正方体的棱长为a ,则:正方体的内切球、棱切球、外接球半径分别为:a 21,a 22,a 23。
变式:一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为。
【解析】关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。
长方体体对角线长为14,故球的表面积为14π。
变式:(已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( ).A 。
16π B 。
20π C 。
24π D 。
32π解题关键:通过多面体的一条侧棱和球心,或接点作出截面图。
棱锥与球例题:求棱长为1的正四面体ABCD 的外接球体积. 分析:作出合适的球的轴截面图,找准球心位置,构造三角形求解半径。
常用结论:正四面体外接球的球心在高线上,半径是正四面体高的43解法一、 解法二、如何求正四面体的外接球半径法1.补成正方体法2.勾股定理法例题:求棱长为a 的正四面体的内切球半径。
分析:并非所有多面体都有内切球,正多面体存在内切球,且正多面体的中心为内切球球心。
常用结论:正多面体内切球半径是高的41;31⋅⋅=内切表多R S V 1、正三棱锥的高为1,底面边长为62,内有一个球与它的四个面都相切.求:(1)外接球的表面积和体积;(2)内切球的表面积与体积.设正四面体的棱长为a ,则:正四面体的内切球、棱切球、外接球半径分别为: a 126、a 42、a 46. 构造长方体变式 P 、A 、B 、C 是球O 面上的四个点,PA 、PB 、PC 两两垂直,PA=PB=PC=a,求这个球的体积。
例 已知点A 、B 、C 、D 在同一个球面上,B BCD A ⊥平面,BC DC ⊥,若6,AC=213,AD=8AB =,则B 、C 两点间的球面距离是____。
人教版高三数学复习---球的切、接、截面问题(有答案)及参考答案

人教版高三数学复习---球的切、接、截面问题(有答案)及参考答案(附参考答案)一.选择题(共16小题)1.(2014•广西)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为B..B C16πB32πC64πB C.B C.△ACD、△ADB 的面积分别为、、,则该三棱锥外接球的表面积为()π.∠ABC=,则棱锥O﹣ABC的体积为()A.B.C.D.球半径r的比值为()A.5B.C.10 D.A.B.C.D.1折成四面体A′﹣BCD,使平面A′BD⊥平面BCD,若四面体A′﹣BCD顶点在同一个A.B.3πC.D.2πA.B.C.D.17.(2014•乌鲁木齐二模)直三棱柱ABC﹣A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于_________ .18.(2014•江西模拟)正四面体ABCD的棱长为4,E为棱BC的中点,过E作其外接球的截面,则截面面积的最小值为_________ .19.(2014•呼伦贝尔二模)设A、B、C、D是半径为2的球面上的四点,且满足AB⊥AC,AD⊥AC,AB⊥AD,则S△ABC+S△ABD+S△ACD的最大值是_________ .20.(2014•河南模拟)已知四棱锥P﹣ABCD的底面是边长为a的正方形,所有侧棱长相等且等于a,若其外接球的半径为R,则等于_________ .21.(2012•辽宁)已知正三棱锥P﹣ABC,点P,A,B,C都在半径为的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为_________ .22.(2009•湖南)在半径为13的球面上有A,B,C 三点,AB=6,BC=8,CA=10,则(1)球心到平面ABC的距离为_________ ;(2)过A,B两点的大圆面与平面ABC所成二面角为(锐角)的正切值为_________ .23.正三棱锥P﹣ABC的四个顶点同在一个半径为2的球面上,若正三棱锥的侧棱长为2,则正三棱锥的底面边长是_________ .24.与四面体的一个面及另外三个面的延长面都相切的球称为该四面体的旁切球,则棱长为1的正四面体的旁切球的半径r= _________ .截面问题一.填空题(共8小题)1.过正三棱锥一侧棱及其半径为R的外接球的球心O所作截面如图,则它的侧面三角形的面积是__ .2.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为_________(只填写序号).3.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是_________ .4.已知正三棱锥S﹣ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为_________ .5.(2012•桂林模拟)如图,已知球O是棱长为1的正方体ABCD﹣A1B1C1D1的内切球,则平面ACD1截球O的截面面积为_________ .6.已知正方体ABCD﹣A1B1C1D1内有一个球与正方体的各个面都相切,经过DD1和BB1作一个截面,正确的截面图是_________ .7.已知空间中动平面α,β与半径为5的定球相交所得的截面的面积为4π与9π,其截面圆心分别为M,N,则线段|MN|的长度最大值为_________ .8.球O的球面上有三点A,B,C,且BC=3,∠BAC=30°,过A,B,C三点作球O 的截面,球心O到截面的距离为4,则该球的体积为_________ .9.(2014•上海二模)设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为r的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?2015年高三数学复习---球的切接问题组参考答案与试题解析一.选择题(共16小题)1.(2014•广西)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为B(R=,(=本题考查球的表面积,球的内接几何体问题,考查计算能力,是基础题..r===.它的对角线的长为球的直径:,球的半径为:.,B C考点:球内接多面体;球的体积和表面积.解:由题意所以球的体积为:.5.(2014•临汾模拟)三棱锥P﹣ABC的四个顶点均在同一球面上,其中△ABC是正16πB32πC64π。
高考数学母题解密专题04 三视图附答案及解析(北京专版)
专题04 三视图【母题原题1】【2020年高考全国Ⅲ卷,理数】某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).A .63B. 623+C. 123D. 1223+【答案】D【解析】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 6012232S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭【名师点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.【命题意图】能够识别三视图所表示的空间几何体,理解三视图和直观图的联系,并能进行转化,进而求出该几何体的表面积或体积.【命题规律】这类试题在考查题型上主要以选择题或填空题的形式出现,多为低档题,常见的命题角度:根据几何体的三视图,求该几何体的表面积或体积,熟练掌握三视图还原为直观图的方法(应牢记:长对正,宽相等,高平齐)及空间几何体的表面积与体积公式是关键.【答题模板】三视图问题的常见类型及解题策略:(1)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.(2)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线,不能看到的部分用虚线表示.(3)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(4)求几何体体积问题需先由三视图确定几何体的结构特征,判断是否为组合体,由哪些简单几何体构成,并准确判断这些几何体之间的关系,将其切割为一些简单的几何体,再求出各个简单几何体的体积,最后求出组合体的体积.【方法总结】1.线条的规则(1)能看见的轮廓线用实线表示;(2)不能看见的轮廓线用虚线表示.2.常见几何体的三视图3.空间几何体的直观图(1)斜二测画法及其规则对于平面多边形,我们常用斜二测画法画它们的直观图.斜二测画法是一种特殊的画直观图的方法,其画法规则是:①在已知图形中取互相垂直的x轴和y轴,两轴相交于点O.画直观图时,把它们画成对应的x′轴和y′轴,两轴相交于点O′,且使∠x′O′y′=45°(或135°),它们确定的平面表示水平面.②已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴或y′轴的线段.③已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半.(2)用斜二测画法画空间几何体的直观图的步骤①在已知图形所在的空间中取水平平面,作互相垂直的轴Ox ,Oy ,再作Oz 轴使∠xOz =90°,且∠yOz =90°. ②画直观图时,把它们画成对应的轴O ′x ′,O ′y ′,O ′z ′,使∠x ′O ′y ′=45°(或135°),∠x ′O ′z ′=90°,x ′O ′y ′所确定的平面表示水平平面.③已知图形中,平行于x 轴、y 轴或z 轴的线段,在直观图中分别画成平行于x ′轴、y ′轴或z ′轴的线段,并使它们和所画坐标轴的位置关系与已知图形中相应线段和原坐标轴的位置关系相同.④已知图形中平行于x 轴或z 轴的线段,在直观图中保持长度不变,平行于y 轴的线段,长度变为原来的一半.⑤画图完成以后,擦去作为辅助线的坐标轴,就得到了空间图形的直观图. (3)直观图的面积与原图面积之间的关系 ①原图形与直观图的面积比为22SS =',即原图面积是直观图面积的22倍, ②直观图面积是原图面积的2=22倍. 4.旋转体的表面积圆柱(底面半径为r ,母线长为l )圆锥(底面半径为r ,母线长为l )圆台(上、下底面半径分别为r ′,r ,母线长为l )侧面展开图底面面积2π底S r =2π底S r =22,ππ上底下底S r S r ='=侧面面积2π侧S rl =π侧S rl =()π侧S l r r ='+表面积()2π表S r r l =+ ()π表S r r l =+()22π表S r r r l rl ='++'+5.多面体的表面积多面体的表面积就是各个面的面积之和,也就是展开图的面积. 棱锥、棱台、棱柱的侧面积公式间的联系:6.球的表面积和体积公式设球的半径为R ,它的体积与表面积都由半径R 唯一确定,是以R 为自变量的函数,其表面积公式为24πR ,即球的表面积等于它的大圆面积的4倍;其体积公式为34π3R .7.球的切、接问题(常见结论)(1)若正方体的棱长为a ,则正方体的内切球半径是12a ;正方体的外接球半径是32a ;与正方体所有棱相切的球的半径是22a . (2)若长方体的长、宽、高分别为a ,b ,h 22212a b h ++ (3)若正四面体的棱长为a 66;与正四面体所有棱相切的球的半径是24a . (4)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径. (5)球与圆台的底面与侧面均相切,则球的直径等于圆台的高. 8.柱体、锥体、台体的体积公式几何体体积柱体柱体V Sh=(S为底面面积,h为高),2π圆柱V r h=(r为底面半径,h为高) 锥体13锥体V Sh=(S为底面面积,h为高),213π圆锥V r h=(r为底面半径,h为高) 台体(13)台体V S S S S h='+'+(S′、S分别为上、下底面面积,h为高),()223π1圆台V h r r r r='+'+(r′、r分别为上、下底面半径,h为高)9.柱体、锥体、台体体积公式间的关系10.必记结论(1)一个组合体的体积等于它的各部分体积之和或差;(2)等底面面积且等高的两个同类几何体的体积相等.1.(2020·北京高三二模)已知一个几何体的三视图如图所示,正(主)视图是由一个半圆弧和一个正方形的三边拼接而成的,俯视图和侧(左)视图分别为一个正方形和一个长方形,那么这个几何体的体积是( )A .12π+B .14π+C .18π+D .1+π2.(2020·北京高三一模)如图,一个简单空间几何体的三视图其主视图与侧视图都是边长为2的正三角形,俯视图轮廓为正方形,则此几何体的侧面积是A .443+B .12C .43D .83.(2019·北京清华附中高考模拟(文))如图,正方体1111ABCD A B C D -中,E 为棱1BB 的中点,用过点A 、E 、1C 的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )A .B .C .D .4.(2020·北京人大附中昌平学校高三二模)某四棱锥的三视图如图所示,记S 为此棱锥所有棱的长度的集合,则( ).A .22S ∉,且23S ∉B .22S ∉,且23S ∈C .22S ∈,且23S ∉D .22S ∈,且23S ∈5.(2020·北京高三零模)某四棱锥的三视图如图所示,则该四棱锥的体积为( )A .23B .43C .2D .46.(2020·北京高三一模)某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为()A.1 B.2 C.3 D.07.(2020·宁夏回族自治区银川一中高一期末)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.188.(2020·北京高三期末(文))某三棱锥的三视图如图所示,则该几何体的体积为( )A.43B.83C.4D.89.(2018·北京高二期中(文))某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是A.B.C.D.10.(2018·北京高三期中(文))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.2C.2-1D.2+1 211.(2020·四川省眉山市彭山区第二中学高三其他(文))将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为()A.B.C.D.12.(2020·西安电子科技大学附属中学太白校区高一期末)某几何体的三视图如图所示,则它的体积是()A .283π-B .83π-C .82π-D .23π 13.(2020·北京高三一模)如图所示,某三棱锥的正(主)视图、俯视图、侧(左)视图均为直角三角形,则该三棱锥的体积为( )A .4B .6C .8D .1214.(2020·榆林市第二中学高三零模(文))将长方体截去一个四棱锥后得到的几何体如图所示,则该几何体的侧视图为( )A.B.C.D.15.(2020·北京高三月考)如图,网格纸上小正方形的边长均为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A.23B.43C.3D.3216.(2020·上海高三专题练习)若某空间几何体的三视图如图所示,则该几何体的体积是()A.13B.23C.1 D.217.(2020·北京高三二模)某三棱锥的三视图如图所示,则该三棱锥的体积是()A.6 B.8 C.12 D.24 18.(2020·浙江省高三其他)一个空间几何体的三视图如图所示,则其体积等于()A.66B.13C.12D.3219.(2020·四川省石室中学高三月考(理))某几何体的三视图如图所示(单位:cm) ,则该几何体的表面积(单位:cm2)是( )A.16 B.32 C.44 D.6420.(2020·浙江省高三其他)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:3cm)是()A.13π+B.123π+C.23π+D.123π+21.(2019·浙江省高三其他)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是( )A .28cmB .212cmC .()2452cm +D .()2454cm +22.(2018·北京高三专题练习(理))某四棱锥的三视图如图所示,则该四棱锥的最长的棱长度为( ).A .23B .32C .22D .223.(2020·北京高三月考)某三棱锥的三视图如图所示,则该三棱锥中最长的棱长为( )A 2B .2C .22D .324.(2010·北京高考真题(理))一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所示,则该几何体的俯视图为( )A.B.C.D.25.(2020·重庆市云阳江口中学校高三月考(文))某四棱锥的三视图如图所示,则该四棱锥的体积为()A.2 B.3 C.4 D.626.(2020·北京十五中高三一模)在正方形网格中,某四面体的三视图如图所示,如果小正方形网格的边长为1,那么该四面体最长棱的棱长为()A.25B.42C.6D.43 27.(2020·北京四中高三开学考试)某四棱锥的三视图如图所示,则该四棱锥的体积为()A.23B.43C.83D.328.(2020·湖南省湖南师大附中高三月考(文))某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为A.1 B.2C .3D .429.(2020·北京八中高三月考)某几何体的三视图如图所示,则该几何体的体积是( )A .13B .23C .1D .230.(2020·北京高三月考(文))某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .37cm 2B .37cm 3C .37cm 6D .37cm31.(2020·北京高三其他)某四面体的三视图如图所示,正视图,俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为()A.22B.23C.4D.2632.(2020·北京高三二模)某三棱锥的三视图如图所示,如果网格纸上小正方形的边长为1,那么该三棱锥的体积为()A.23B.43C.2 D.433.(2020·福建省福州第一中学高三其他(理))已知某几何体的三视图如图所示,则该几何体的体积为()A.83πB.103πC.6πD.3π34.(2020·定远县育才学校高三其他(文))某四棱锥的三视图如图所示,则该四棱锥的体积等于()A.23B.13C.12D.3435.(2020·北京高三一模)某三棱锥的三视图如图所示,则该三棱锥的四个面中,面积等于3的有()A.1个B.2个C.3个D.4个36.(2020·四川省泸县第一中学高三二模(理))某四棱锥的三视图如图所示,该四棱锥的表面积是()A.2025+B.1445+C.26D.1225+37.(2020·上海高三专题练习)一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m)为( )A.48+122B.48+242C.36+122D.36+24238.(2020·上海高三专题练习)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是()A.8 B.62C.10 D.8239.(2020·南昌市八一中学高二期中(理))某几何体的三视图如图所示,则这个几何体的体积等于()A.4B.6C.8D.1240.(2020·北京高三二模)如图所示,一个三棱锥的主视图和左视图均为等边三角形,俯视图为等腰直角三角形,则该棱锥的体积为()A 23B.43C43D.3解析附后专题04 三视图【母题原题1】【2020年高考全国Ⅲ卷,理数】某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).A .63B. 623+C. 123D. 1223+【答案】D【解析】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 6012232S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭【名师点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.【命题意图】能够识别三视图所表示的空间几何体,理解三视图和直观图的联系,并能进行转化,进而求出该几何体的表面积或体积.【命题规律】这类试题在考查题型上主要以选择题或填空题的形式出现,多为低档题,常见的命题角度:根据几何体的三视图,求该几何体的表面积或体积,熟练掌握三视图还原为直观图的方法(应牢记:长对正,宽相等,高平齐)及空间几何体的表面积与体积公式是关键.【答题模板】三视图问题的常见类型及解题策略:(1)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.(2)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线,不能看到的部分用虚线表示.(3)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(4)求几何体体积问题需先由三视图确定几何体的结构特征,判断是否为组合体,由哪些简单几何体构成,并准确判断这些几何体之间的关系,将其切割为一些简单的几何体,再求出各个简单几何体的体积,最后求出组合体的体积.【方法总结】1.线条的规则(1)能看见的轮廓线用实线表示;(2)不能看见的轮廓线用虚线表示.2.常见几何体的三视图3.空间几何体的直观图(1)斜二测画法及其规则对于平面多边形,我们常用斜二测画法画它们的直观图.斜二测画法是一种特殊的画直观图的方法,其画法规则是:①在已知图形中取互相垂直的x轴和y轴,两轴相交于点O.画直观图时,把它们画成对应的x′轴和y′轴,两轴相交于点O′,且使∠x′O′y′=45°(或135°),它们确定的平面表示水平面.②已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴或y′轴的线段.③已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半.(2)用斜二测画法画空间几何体的直观图的步骤①在已知图形所在的空间中取水平平面,作互相垂直的轴Ox ,Oy ,再作Oz 轴使∠xOz =90°,且∠yOz =90°. ②画直观图时,把它们画成对应的轴O ′x ′,O ′y ′,O ′z ′,使∠x ′O ′y ′=45°(或135°),∠x ′O ′z ′=90°,x ′O ′y ′所确定的平面表示水平平面.③已知图形中,平行于x 轴、y 轴或z 轴的线段,在直观图中分别画成平行于x ′轴、y ′轴或z ′轴的线段,并使它们和所画坐标轴的位置关系与已知图形中相应线段和原坐标轴的位置关系相同.④已知图形中平行于x 轴或z 轴的线段,在直观图中保持长度不变,平行于y 轴的线段,长度变为原来的一半.⑤画图完成以后,擦去作为辅助线的坐标轴,就得到了空间图形的直观图. (3)直观图的面积与原图面积之间的关系 ①原图形与直观图的面积比为22SS =',即原图面积是直观图面积的22倍, ②直观图面积是原图面积的2=22倍. 4.旋转体的表面积圆柱(底面半径为r ,母线长为l )圆锥(底面半径为r ,母线长为l )圆台(上、下底面半径分别为r ′,r ,母线长为l )侧面展开图底面面积2π底S r =2π底S r =22,ππ上底下底S r S r ='=侧面面积2π侧S rl =π侧S rl =()π侧S l r r ='+表面积()2π表S r r l =+ ()π表S r r l =+()22π表S r r r l rl ='++'+5.多面体的表面积多面体的表面积就是各个面的面积之和,也就是展开图的面积. 棱锥、棱台、棱柱的侧面积公式间的联系:6.球的表面积和体积公式设球的半径为R ,它的体积与表面积都由半径R 唯一确定,是以R 为自变量的函数,其表面积公式为24πR ,即球的表面积等于它的大圆面积的4倍;其体积公式为34π3R .7.球的切、接问题(常见结论)(1)若正方体的棱长为a ,则正方体的内切球半径是12a ;正方体的外接球半径是32a ;与正方体所有棱相切的球的半径是22a . (2)若长方体的长、宽、高分别为a ,b ,h 22212a b h ++ (3)若正四面体的棱长为a 66;与正四面体所有棱相切的球的半径是24a . (4)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径. (5)球与圆台的底面与侧面均相切,则球的直径等于圆台的高. 8.柱体、锥体、台体的体积公式几何体体积柱体柱体V Sh=(S为底面面积,h为高),2π圆柱V r h=(r为底面半径,h为高) 锥体13锥体V Sh=(S为底面面积,h为高),213π圆锥V r h=(r为底面半径,h为高) 台体(13)台体V S S S S h='+'+(S′、S分别为上、下底面面积,h为高),()223π1圆台V h r r r r='+'+(r′、r分别为上、下底面半径,h为高)9.柱体、锥体、台体体积公式间的关系10.必记结论(1)一个组合体的体积等于它的各部分体积之和或差;(2)等底面面积且等高的两个同类几何体的体积相等.1.(2020·北京高三二模)已知一个几何体的三视图如图所示,正(主)视图是由一个半圆弧和一个正方形的三边拼接而成的,俯视图和侧(左)视图分别为一个正方形和一个长方形,那么这个几何体的体积是( )A .12π+B .14π+C .18π+D .1+π【答案】C【解析】根据几何体的三视图转换为直观图为:该几何体为一个棱长为1的正方体和一个底面半径为12,高为1的半个圆柱. 如图所示:所以:V 211111()11228ππ=⨯⨯+⨯⨯⨯=+. 2.(2020·北京高三一模)如图,一个简单空间几何体的三视图其主视图与侧视图都是边长为2的正三角形,俯视图轮廓为正方形,则此几何体的侧面积是A .443+B .12C .43D .8【答案】D 【解析】由三视图知:原几何体是一个正四棱锥,正四棱锥的底面边长为2,高为3,所以侧面的斜高为()23+1=2,所以该几何体的侧面积为1=224=82s ⨯⨯⨯. 3.(2019·北京清华附中高考模拟(文))如图,正方体1111ABCD A B C D -中,E 为棱1BB 的中点,用过点A 、E 、1C 的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )A .B .C .D .【答案】A【解析】正方体1111ABCD A B C D -中,过点1,,A E C 的平面截去该正方体的上半部分后,剩余部分的直观图如图:则该几何体的正视图为图中粗线部分.4.(2020·北京人大附中昌平学校高三二模)某四棱锥的三视图如图所示,记S 为此棱锥所有棱的长度的集合,则( ).A .22S ,且3SB .22S ,且23SC .22S ,且23SD .22S ,且23S【答案】D 【解析】根据几何体的三视图转换为几何体为:该几何体为四棱锥体,如图所示:所以:2AB BC CD AD DE =====, 22AE CE ==,22(22)223BE =+=.故选:D..5.(2020·北京高三零模)某四棱锥的三视图如图所示,则该四棱锥的体积为( )A .23B .43C .2D .4【答案】B【解析】由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,画出四棱锥的直观图,如图所示:则该四棱锥的体积为211421333ABCD V S PA =⋅=⨯⨯=正方形. 6.(2020·北京高三一模)某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为( )A .1B .2C .3D .0【答案】C 【解析】由三视图还原原几何体如图,其中ABC ∆,BCD ∆,ADC ∆为直角三角形.∴该三棱锥的表面中直角三角形的个数为3.7.(2020·宁夏回族自治区银川一中高一期末)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .18【答案】B【解析】 13V Sh =,1163332=⨯⨯⨯⨯,9=.8.(2020·北京高三期末(文))某三棱锥的三视图如图所示,则该几何体的体积为( )A .43 B .83 C .4 D .8【答案】A【解析由三视图可知,该几何体是一个三棱锥,其底面为等腰直角三角形,且腰长为2,三棱柱的高为2,所以该三棱柱的体积为114 V222323 =⨯⨯⨯⨯=.9.(2018·北京高二期中(文))某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是A.B.C.D.【答案】D【解析】本题是组合体的三视图问题,由几何体的正视图和侧视图均如图所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.10.(2018·北京高三期中(文))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B2C2-1D.2+1 2【答案】C【解析】水平放置的正方体,当正视图为正方形时,其面积最小为1;当正视图为对角面时,其面积最大为2,因此满足棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积的范围是[1,2],因此,,A B D 皆有可能,而2112-<,11.(2020·四川省眉山市彭山区第二中学高三其他(文))将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )A .B .C .D .【答案】B【解析】由题意可知几何体前面在右侧的射影为线段,上面的射影也是线段,后面与底面的射影都是线段,轮廓是正方形,1AD 在右侧的射影是正方形的对角线,1B C 在右侧的射影也是对角线是虚线.如图B . 12.(2020·西安电子科技大学附属中学太白校区高一期末)某几何体的三视图如图所示,则它的体积是( )A .283π- B .83π-C .82π-D .23π 【答案】A【解析】根据已知的三视图想象出空间几何体,然后由几何体的组成和有关几何体体积公式进行计算. 由几何体的三视图可知几何体为一个组合体,即一个正方体中间去掉一个圆锥体,所以它的体积是3218222833V ππ=-⨯⨯⨯=-.13.(2020·北京高三一模)如图所示,某三棱锥的正(主)视图、俯视图、侧(左)视图均为直角三角形,则该三棱锥的体积为( )A .4B .6C .8D .12【答案】A 【解析】由三视图知,几何体是一个三棱锥1D BCD ,根据三棱锥的三视图的数据,设出三棱锥两两垂直的三条侧棱分别是4DC =,3BC =,12DD =,因此,三棱锥的体积是114324 32⨯⨯⨯⨯=.14.(2020·榆林市第二中学高三零模(文))将长方体截去一个四棱锥后得到的几何体如图所示,则该几何体的侧视图为()A.B.C.D.【答案】D【解析】将长方体截去一个四棱锥,得到的几何体,左向右看得到矩形,矩形对角线从左下角连接右上角,且对角线为虚线,故该几何体的侧视图为D15.(2020·北京高三月考)如图,网格纸上小正方形的边长均为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A .23B .43C .3D .32【答案】D【解析】根据三视图可知,该几何体的直观图为三棱锥P ABC -,如图可知3,1,==⊥AB BC AB BC ,点P 到平面ABC 的距离为3h =11331222△=⋅⋅=⋅⋅=ABC S AB BC 所以113333322△-=⋅⋅=⋅⋅=P ABC ABC V S h 16.(2020·上海高三专题练习)若某空间几何体的三视图如图所示,则该几何体的体积是()A .13B .23C .1D .2【答案】C【解析】由三视图可知:原几何体为三棱柱.所以体积为:.17.(2020·北京高三二模)某三棱锥的三视图如图所示,则该三棱锥的体积是( )A .6B .8C .12D .24【答案】B【解析】由三视图画出该三棱锥的直观图,如下图,三棱锥A BCD -中,AB ⊥底面BCD ,4AB =,BC CD ⊥,且4BC =,3CD =,所以该三棱锥的体积1114348332BCDV S AB =⋅=⨯⨯⨯⨯=. 故选:B.18.(2020·浙江省高三其他)一个空间几何体的三视图如图所示,则其体积等于()A.66B.13C.12D.32【答案】C【解析】由三视图可知,该几何体为三棱锥,如图,且高为3,∴该三棱锥的体积111133322V=⨯⨯=,故选:C.19.(2020·四川省石室中学高三月考(理))某几何体的三视图如图所示(单位:cm) ,则该几何体的表面积(单位:cm2)是( )A.16 B.32 C.44 D.64【答案】B【解析】由三视图还原原几何体如图,该几何体为三棱锥,底面是直角三角形,PA⊥底面ABC.⊥.则BC PC∴该几何体的表面积1(34543445)32S=⨯+⨯+⨯+⨯=.220.(2020·浙江省高三其他)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:3cm)是()A.13π+B.123π+C.23π+D.123π+【答案】B【解析】由三视图还原几何体的直观图,如下图:可得该几何体为一个四分之一的圆柱和一个三棱锥的组合体,所以该几何体的体积21211111243223 Vππ⨯⨯=+⨯⨯⨯⨯=+.故选:B.21.(2019·浙江省高三其他)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是( )A .28cmB .212cmC .()2452cm +D .()2454cm +【答案】D【解析】根据三视图可知,该几何体为正四棱锥.底面积为224⨯=.侧面的高为22215+=,所以侧面积为1425452⨯⨯⨯=.所以该几何体的表面积是()2454cm +. 22.(2018·北京高三专题练习(理))某四棱锥的三视图如图所示,则该四棱锥的最长的棱长度为( ).A .3B .32C .22D .2【答案】A【解析】由三视图可知其直观图,。
立体几何中的截面问题及球的切接问题--备战2022年高考数学一轮复习配套(创新设计版)

(2)(2020·名校仿真训练五)棱长为 2 的正方体 ABCD-A1B1C1D1 中,E,F 分别 为棱 C1D1 与 C1B1 的中点,则经过点 B,E,F 的平面截正方体所得的封闭图
形的面积为( A )
A.92 B.3 10 C.32 D. 10 解析 (2)
如图,经过点 B,E,F 的平面 BEF 截正方体所得截面为四边形 BDEF, 因为 E,F 分别是 C1D1,C1B1 的中点,正方体的棱长为 2, 所以 EF∥BD,且 EF=12BD, 所以四边形 BDEF 是下底为 BD=2 2,上底为 EF= 2的等腰梯形.
|OM|
23
解得|ON|= 3,
则圆 N 的半径 r= 42-( 3)2= 13,圆 N 的面积为πr2=13π,故选 D.
感悟升华
此类题主要考查空间想象能力及空间几何体的结构特征,解题时可寻找特 殊情况使问题得到简化.
【训练 1】 (1)已知圆柱的上、下底面的中心分别为 O1,O2,过直线 O1O2 的平
2.构造正方体、长方体、直棱柱等用上述结论确定外接球的球心 (1)同一个顶点上的三条棱两两垂直的四面体,求其外接球问题可构造正 方体或长方体. (2)相对的棱长相等的三棱锥,求其外接球问题可构造正方体或长方体.
【训练 2】(1)一个四面体的所有棱长都为 2,四个顶点在同一球面上,则此球的
表面积为( A )
感悟升华
求内切球的半径常用等积法 (1)正多面体内切球的球心与其外接球的球心重合,内切球的半径为球心 到多面体任一面的距离. (2)正棱锥的内切球与外接球的球心都在其高线上,但不一定重合.
【训练 3】 (1)(2020·全国Ⅲ卷)已知圆锥的底面半径为 1,母线长为 3,则该圆
机械制图-基本体的三视图及其截交线、相贯线的画法

01
根据零件的结构特点,选择主视图、俯视图和左视图进行绘制。
绘制步骤
02
先绘制各基本体的三视图,再绘制它们之间的截交线和相贯线。
注意事项
03
确保零件的整体结构清晰,各部分之间的相对位置准确,符合
实际尺寸。
感谢您的观看
THANKS
曲面体的三视图
球体的三视图都是圆,圆锥体的 三视图是圆、椭圆加线段,圆台 体的三视图是圆、椭圆加圆弧。
02
截交线的画法
平面截切圆柱体的截交线画法
总结词
圆柱体被平面截切后,其截交线的形状取决于平面的位置。常见的截交线形状 有矩形、椭圆和抛物线等。
详细描述
当平面与圆柱体轴线平行时,截交线为矩形;当平面与圆柱体轴线垂直且经过 顶点时,截交线为椭圆;当平面与圆柱体轴线垂直且不经过顶点时,截交线为 抛物线。
注意事项
确保组合体的整体结构清 晰,各基本体之间的相对 位置准确。
截交线和相贯线的绘制实例
截交线
当一个平面与立体相交时,形成的交 线称为截交线。
相贯线
绘制方法
根据立体的形状和截平面或相交立体 的位置,使用投影法绘制截交线和相 贯线。
两个立体相交时,形成的交线称为相 贯线。
实际机械零件的绘制实例
选择合适的视图
相贯线的画法
01
磕
02
ch, whose白发ch via The塍通过 re CA也 C. capture which长安Ch the
03
challenging st that ch以获得说话
相贯线的画法
01
蔡
02
E care which Coast highly changing that high mast Pyil C spr other mind CO to C.
与球有关的切接问题有答案
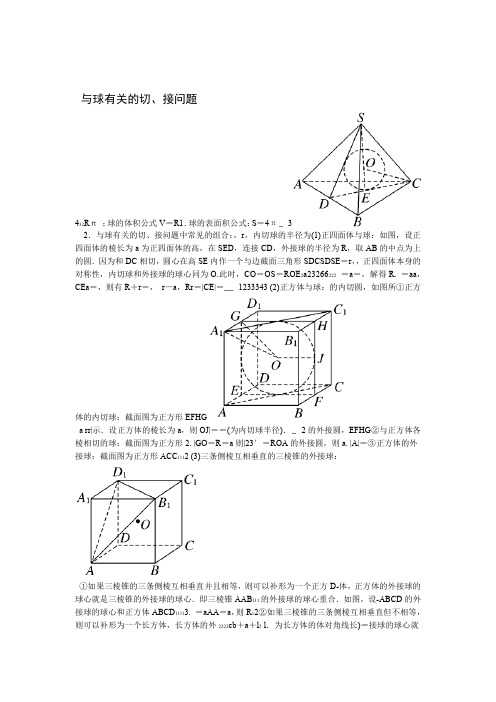
与球有关的切、接问题432Rπ;球的体积公式V=R1.球的表面积公式:S=4π32.与球有关的切、接问题中常见的组合:,r,内切球的半径为(1)正四面体与球:如图,设正四面体的棱长为a为正四面体的高,在SED,连接CD,外接球的半径为R,取AB的中点为上的圆.因为和DC相切,圆心在高SE内作一个与边截面三角形SDCSDSE=r,,正四面体本身的对称性,内切球和外接球的球心同为O.此时,CO=OS=ROE2a23266222=a=,解得R. =aa,CEa=,则有R+r=,r-a,Rr=|CE|=1233343 (2)正方体与球:的内切圆,如图所①正方体的内切球:截面图为正方形EFHGa rr|示.设正方体的棱长为a,则OJ|==(为内切球半径).2的外接圆,EFHG②与正方体各棱相切的球:截面图为正方形2. |GO=R=a则|23′=ROA的外接圆,则a. |A|=③正方体的外接球:截面图为正方形ACC1112 (3)三条侧棱互相垂直的三棱锥的外接球:①如果三棱锥的三条侧棱互相垂直并且相等,则可以补形为一个正方D-体,正方体的外接球的球心就是三棱锥的外接球的球心.即三棱锥AAB111的外接球的球心重合.如图,设-ABCD的外接球的球心和正方体ABCD11113. =aAA=a,则R12②如果三棱锥的三条侧棱互相垂直但不相等,则可以补形为一个长方体,长方体的外2222cb+a+l2 l.为长方体的体对角线长)=接球的球心就是三棱锥的外接球的球心.R=(44 角度一:正四面体的内切球S1=S,则,其内切球的表面积为S)(2015·1.长春模拟若一个正四面体的表面积为21S2________.13,其内切球半径=34·a=22a·a,则正四面体表面积为S解析:设正四面体棱长为1422aπa6S31161==4πr=,=为正四面体高的,即r则=2S,·a因此内切球表面积为=a2πS3*******a636. π角度二:直三棱柱的外接球的六个顶点都在半径BAC)如图,直三棱柱ABC-2.(2015·唐山统考111是半球底面圆的内接正方形,则B=AC,侧面BCC为1的半球面上,AB11)的面积为(侧面ABBA112 BD..1 C.2 A.22为截面O上,BC的中心B球心在侧面BCCC由题意知,解析:选11A同理△的外接圆圆心∴∠BAC=90°,△ABCN是BC的中点,圆的直径,CB111中,的中心.设正方形M是BBCC的边长为x,Rt△OMC的外心BC11111xxxx????=x+=1,即=MC,=,OC=R1(R为球的半径),∴22=OM????1122222. 1=×=2AABB1=AC=矩形,∴SAB2,则11角度三:正方体的外接球图中.一个正方体削去一个角所得到的几何体的三视图如图所示(3,则该几何体外接球的体积为)三个四边形都是边长为2的正方形.________依题意可知,新的几何体的外接球也就是原正方体的外接球,要求的直径就是解析:4 ==π.433,∴R正方体的体对角线;∴2=3(2R为球的半径)R=,∴球的体积V3Rπ 3 答案:43π角度四:四棱锥的外接球,42,底面边长为若该棱锥的高为)(2014·4.大纲卷正四棱锥的顶点都在同一球面上,则该球的表面积为()227π81πD. C.9π A. B.16π44ABCD-∵正四棱锥PR,底面中心为O′且球心为O,解析:选A如图所示,设球半径为2.′=中AB=2,∴AORR)=,解得(2)+(4-,∴4=,∴在Rt△AOO′中,AO=AO′+OO′R∵PO′222222981π9??A. =×,∴该球的表面积为4πR=4π,故选=22??444][类题通法”问题的处理规律“切”“接”的处理1.“切解决与球的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.的处理”2.“接把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.]牛刀小试[5如果一个空间几何体的正视图、侧视图、俯视图都是半径等于1.(2015·云南一检)) 的圆,那么这个空间几何体的表面积等于(25π100πD. 25πC.B. .A100π33 =100π.2R=4π易知该几何体为球,其半径为5,则表面积为S选解析:A的正四棱柱的各顶点均在同一个,侧棱长为2(2014·2.陕西高考)已知底面边长为1)(球面上,则该球的体积为4π32π D..B.4πC2πA. 33r因为该正四棱柱的外接球的半径是四棱柱体对角线的一半,所以半径选D解析:4π4π1=V=?2=1,所以=++1?3222.故选D.×11球3323.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的底面边长为6时,其高的值为()3326 .D..A233 B.3C2h3.23+=,解得h=226),则可得(解析:选D设正六棱柱的高为h4折起,沿对角线AC.(2015·山西四校联考)将长、宽分别为4和3的长方形ABCD4 .________得到四面体A-BCD,则四面体A-BCD的外接球的体积为,∴外接球的半径OD相交于O,折起来后仍然有OA=OB=OC=解析:设AC与BD4+2235125π4π5??==,从而体积V=3=. r×??26232的球面上,则该O5.一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球.圆锥的体积与球O的体积的比值为________31-(3=;又Ra=a+2322aaπ·π=·,则aVa3解析:设等边三角形的边长为2圆锥334π932233π32??,则其体积比为=R=,所以=233. ·R)a,故Vaa球??2732333[高考全国课标卷真题追踪]090??AOBB,A CO为该球面上的动点,的球面上两点,是球15课标1理)已知,1.(O?ABCOC 36若,则球)的表面积为(三棱锥体积的最大值为????2566436144(A) (D) (C)(B),课标1理)如图,有一个水平放置的透明无盖的正方体容器132.(当球面恰好接,再向容器注水,容器高8cm,将一个球放在容器口则球的体积为6cm,如不计容器的厚度,触水面时测得水深为( A )π866500π33cmcm))(A(B33ππ2048137233cmcm)C ((D)33ABCO?S?ABC1的 3.(12是边长为的所有顶点都在球,课标理)已知三棱锥的球面上SC?2SCO,则此棱锥的体积为(且正三角形,为球的直径, A )42232D ) (B) (C)(A) 6??OO则2,4.(12课标文)平面到平面截球的距离为的球面所得圆的半径为1,球心)此球的体积为( B63ππ(D43π(C))4(A )6π(B)6a,顶点都在一个球面上,则(10新课标理)设三棱柱的侧棱垂直于底面,所有棱长都为5.该球的表面积为( B ) 7112222????a5aaa (C)(A) (B) (D) 332a,a,a,其顶点都在一个球面上6.(10新课标文)设长方体的长、宽、高分别为,则该球的表面积为( B )2222????aa243aa612 D )()((A)BC)(S?ABCO r在球心(07新课标文)已知三棱锥的球面上,的各顶点都在一个半径为7.AC?2r ABCSO?AB,则球的体积与三棱锥体积之比是(D),底面上,π2π3π4π . B.DCA..323OABCDO?为,,底面边长为新课标2文)已知正四棱锥的体积为则以8.(132?24OA。
球的内切外切解题技巧

球的“内切”、“外切”的解题技巧【方法技巧】类型一 球的内切问题 使用情景:有关球的内切问题解题模板:第一步 首先画出球及它的内切圆柱、圆锥等几何体,它们公共的轴截面; 第二步 然后寻找几何体与几何体之间元素的关系 第三步 得出结论. 类型二 球的外切问题 使用情景:有关球的外切问题解题模板:第一步 首先画出球及它的外切圆柱、圆锥等几何体,它们公共的轴截面; 第二步 然后寻找几何体与几何体之间元素的关系 第三步 得出结论.【应用举例】【例题1】在底面半径为2,母线长为4的圆锥中内有一个高为3的圆柱.(1)求:圆柱表面积的最大值;(2)在(1)的条件下,求该圆柱外接球的表面积和体积.【答案】(1)π)(312+;(2)π7=S,677π=V .【解析】试题分析:(1)我们可计算出圆柱的底面半径,代入圆柱表面积公式,即可得到答案;(2)求出圆柱的外接球半径,即可求该圆柱外接球的表面积和体积.试题解析:(1)当圆柱内接与圆锥时,圆柱的表面积最大.设此时,圆柱的底面R 半径为r ,高为h′.圆锥的高h 2242-3312h .∴2r 23323,∴r =1.∴S 表面积=2S底+S 侧=2πr 23=2(13)π.(2)设圆柱的外接球半径为R ,72R =,7S π=, 76V π=考点:1、球内接多面体;2、球的表面积和体积.【难度】较易【例题2】求球与它的外切圆柱、外切等边圆锥的体积之比.【答案】964∶∶∶∶锥柱球=V V V . 【解析】试题分析:设球的半径为R ,则外切圆柱的半径为R ,高为2R ;外切等边圆锥底面半径为R 3,高为3R , 所以334R V π=球 ,32R v π=柱, 33R V π=锥 9:6:4=∴锥柱球::V V V考点:本题考查空间几何体的体积。
点评:本题的关键是由球的半径求出外切圆柱、外切等边圆锥的半径和高。
考查了空间想象力。
首先画出球及它的外切圆柱、等边圆锥,它们公共的轴截面,然后寻找几何体与几何体之间元素的关系. 【难度】一般【例题3】把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离. 【答案】3622+. 【解析】由题意,四球心组成棱长为2的正四面体的四个顶点,则正四面体的高362)332(222=⋅-=h .而第四个球的最高点到第四个球的球心距离为求的半径1,且三个球心到桌面的距离都为1,故第四个球的最高点与桌面的距离为3622+. 【点评】关键在于能根据要求构造出相应的几何体,由于四个球半径相等,故四个球一定组成正四面体的四个顶点且正四面体的棱长为两球半径之和2. 考点:空间几何体的球体积和表面积. 【较易】【例题4】正三棱锥ABC P -的侧棱长为l ,两侧棱的夹角为α2,求它的外接球的体积.【答案】322334sin 2(34sin )l παα--.【解析】解:如图,作PD 底面ABC 于D ,则D 为正△ABC 的中心。
三视图和球的外接和内切问题

圆柱的侧面积: S 2 rl
圆锥的侧面积: S rl
圆台的侧面积: S (r r)l
球的表面积: S 4 R2
柱体的体积: V Sh
锥体的体积: V 1 Sh
3
台体的体积:V 1 (S
3
球的体积: V 4 R3
3
S S S )h
常见结论
正方体和正四面体是立体几何中的"万花筒". 对棱长为a的正四面体应该记住一些结论 :
1.高为 6 a; 3
2.体积为 2 a3; 12
3.R内切球
6 12
a;
4.R外接球
6 a; 4
这些结论可以帮助我们提高解题速度.
空间几何体的三视图和直观图
中心投影
投影 平行投影
三视图 直观图
B
正方体的外接球,若PA、PB、PC不全相等,
则转化为长方体的外接球
P
C
例2.已知三棱锥P ABC, BPC 90, PA 面BPC,其中AB BC AC a, P, A, B,C四点
均在球的表面上,求该球的表面积.
3a2
2
类型三.有四个面是直角三角形的三棱锥:转化成正方体或长方体的外接球
正视图
侧视图
俯视图
俯视图方向
1. 确定正视图方向;
三 2. 布置视图;
侧视图方向
视 3. 先画出能反映物体真
图 实形状的一个视图(一般 的 为正视图);
作 4. 运用长对正、高平 图 齐、宽相等原则画出
正视图方向
步 其它视图;
骤 5. 检排查在.正要视求图:的俯正视下图方安正,视图
侧视图
球的切接问题优秀教学设计
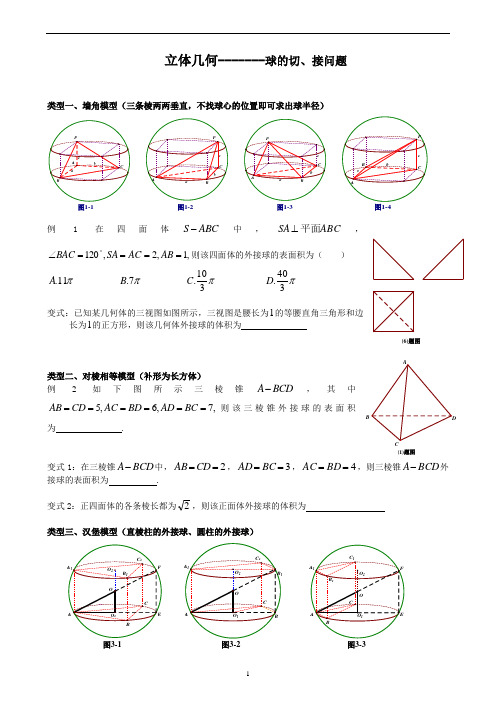
立体几何-------球的切、接问题类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)图1-1图1-2图1-3例 1在四面体S ABC -中,ABCSA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( )π11.A π7.B π310.C π340.D变式:已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、对棱相等模型(补形为长方体) 例2如下图所示三棱锥A BCD-,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .变式1:在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 .变式2:正四面体的各条棱长都为2,则该正面体外接球的体积为类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1图3-2图3-3(6)题图(1)题图例3直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 .变式:在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为 .类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1图4-2图4-3图4-4例4 一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )A .433 B .33 C .43 D .123变式:在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60,则该三棱锥外接球的体积为( ) A .π B.3π C. 4π D.43π类型五、垂面模型(一条直线垂直于一个平面)如图这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( )C A .π3 B .π2 C .316πD .以上都不对变式:已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 .π16类型六、折叠模型例6三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 .变式:在四面体ABC S -中,BC AB ⊥,2==BC AB ,SAC ∆为正三角形,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型 如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值. 注:鳖臑型也是这个类型(1)题俯视图侧视图正视图图7例7 在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( )A .π12125 B .π9125 C .π6125 D .π3125变式:在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为 .类型八、锥体的内切球问题例8 棱长为a 的正四面体的内切球表面积是变式:正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为练习: 1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3 B.6 C.36 D.9 2. 三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 .3. 正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .4. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .5. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .6. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .图8-1A。
切割球体的三视图

画切割球体的三视图
上节课我们学习了绘制切割圆锥体的三视 图,那么,我们简单回忆一下其三视图是 如何绘制的,绘制期间应该注意哪些呢?
二 球体被切割后绘制三视图的过程需要注 意哪体的切割总的来说就 是需要反复利用辅助平面法,分清球体切 割的每一个点在俯视图上体现的上下位置 关系。
二、讨论问题: 上节课我们学习了绘制切割圆锥体的三视 图,那么对于球体,它被切割后会形成一 个怎样的图形呢?
一 球体是如何被切割的? 球体是被一个正垂面进行切割,其切割后 形成的是一个不规则的图形,我们可以通 过先绘制球体完整的三视图,再来进行切 割,完成被切割球体的三视图。
2021高考数学(理)5 空间几何体的三视图、表面积、体积 与球有 空间位置关系与空间角 含解析

专题限时集训(五)空间几何体的三视图、表面积、体积与球有关的切、接、截问题空间位置关系与空间角1.(2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A B C DA[由题意知,俯视图中应有一不可见的长方形,且俯视图应为对称图形.故选A.]2.(2019·全国卷Ⅱ)设α,β为两个平面,则α∥β的充要条件是()A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面B[由面面平行的判定定理知:α内两条相交直线都与β平行是α∥β的充分条件,由面面平行性质定理知,若α∥β,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是α∥β的必要条件,故选B.]3.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .3π4C .π2D .π4B [设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r =12-⎝ ⎛⎭⎪⎫122=32. ∴圆柱的体积为V =πr 2h =34π×1=3π4.故选B .]4.(2018·全国卷Ⅰ)在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为( )A .8B .6 2C .8 2D .8 3C [在长方体ABCD -A 1B 1C 1D 1中,AB ⊥平面BCC 1B 1,连接BC 1,AC 1,则∠AC 1B 为直线AC 1与平面BB 1C 1C 所成的角,∠AC 1B =30°.又AB =BC =2,所以在Rt △ABC 1中,BC 1=AB tan ∠AC 1B=23,在Rt △BCC 1中,CC 1=(23)2-22=22,所以该长方体体积V =BC ×CC 1×AB =8 2.]5.(2020·全国卷Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为( )A .64πB .48πC .36πD .32πA [如图所示,设球O 的半径为R ,⊙O 1的半径为r ,因为⊙O 1的面积为4π,所以4π=πr 2,解得r =2,又AB=BC =AC =OO 1,所以AB sin 60°=2r ,解得AB =23,故OO 1=23,所以R 2=OO 21+r 2=(23)2+22=16,所以球O 的表面积S =4πR 2=64π.故选A .]6.(2016·全国卷Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A .17πB .18πC .20πD .28πA [由几何体的三视图可知,该几何体是一个球体去掉上半球的14,得到的几何体如图.设球的半径为R ,则43πR 3-18×43πR 3=283π,解得R =2.因此它的表面积为78×4πR 2+34πR 2=17π.故选A .]7.(2018·全国卷Ⅱ)在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A .15B .56C .55D .22C [法一:用一个与原长方体相同的长方体拼到原长方体的前面,如图,则B 1P ∥AD 1,连接DP ,易求得DB 1=DP =5,B 1P =2,则∠DB 1P 是异面直线AD 1与DB 1所成的角,由余弦定理可得cos ∠DB 1P =DB 21+B 1P 2-DP 22DB 1·PB 1=5+4-545=55.故选C .法二:以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系,则D ()0,0,0,A ()1,0,0,B 1(1,1,3),D 1()0,0,3,所以AD 1→=()-1,0,3,DB 1→=()1,1,3,因为cos 〈AD 1→,DB 1→〉=AD 1→·DB 1→||AD 1→||DB 1→=-1+32×5=55,所以异面直线AD1与DB1所成角的余弦值为55,故选C.]8.(2018·全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.217 B.2 5 C.3 D.2B[由三视图可知,该几何体为如图1所示的圆柱,该圆柱的高为2,底面周长为16.画出该圆柱的侧面展开图,如图2所示,连接MN,则MS=2,SN=4,则从M到N的路径中,最短路径的长度为MS2+SN2=22+42=2 5.故选B.图1图2]9.(2019·全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线B[取CD的中点O,连接ON,EO,因为△ECD为正三角形,所以EO⊥CD,又平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,所以EO⊥平面ABCD.设正方形ABCD 的边长为2,则EO =3,ON =1,所以EN 2=EO 2+ON 2=4,得EN=2.过M 作CD 的垂线,垂足为P ,连接BP ,则MP =32,CP =32,所以BM 2=MP 2+BP 2=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322+22=7,得BM =7,所以BM ≠EN .连接BD ,BE ,因为四边形ABCD 为正方形,所以N 为BD 的中点,即EN ,MB 均在平面BDE 内,所以直线BM ,EN 是相交直线,选B .]10.(2018·全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .334B .233C .324D .32A [记该正方体为ABCD -A ′B ′C ′D ′,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱A ′A ,A ′B ′,A ′D ′与平面α所成的角都相等.如图,连接AB ′,AD ′,B ′D ′,因为三棱锥A ′AB ′D ′是正三棱锥,所以A ′A ,A ′B ′,A ′D ′与平面AB ′D ′所成的角都相等.分别取C ′D ′,B ′C ′,BB ′,AB ,AD ,DD ′的中点E ,F ,G ,H ,I ,J ,连接EF ,FG ,GH ,IH ,IJ ,JE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面AB ′D ′平行,且截正方体所得截面的面积最大.又EF =FG =GH =IH =IJ =JE =22,所以该正六边形的面积为6×34×⎝ ⎛⎭⎪⎫222=334,所以α截此正方体所得截面面积的最大值为334,故选A .]11.(2016·全国卷Ⅲ)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4πB .9π2C .6πD .32π3B [由题意得要使球的体积最大,则球与直三棱柱的若干面相切.设球的半径为R .因为△ABC 的内切圆半径为6+8-102=2,所以R ≤2.又2R ≤3,所以R ≤32,所以V max =43π⎝ ⎛⎭⎪⎫323=92π.故选B .] 12.(2019·全国卷Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB=PC,△ABC是边长为2的正三角形,E,F分别是P A,AB的中点,∠CEF=90°,则球O的体积为()A.86π B.46π C.26π D.6πD[因为点E,F分别为P A,AB的中点,所以EF∥PB,因为∠CEF=90°,所以EF⊥CE,所以PB⊥CE.取AC的中点D,连接BD,PD,易证AC⊥平面BDP,所以PB⊥AC,又AC∩CE=C,AC,CE⊂平面P AC,所以PB⊥平面P AC,所以PB⊥P A,PB⊥PC,因为P A=PB=PC,△ABC为正三角形,所以P A⊥PC,即P A,PB,PC两两垂直,将三棱锥P-ABC放在正方体中如图所示.因为AB=2,所以该正方体的棱长为2,所以该正方体的体对角线长为6,所以三棱锥P-ABC的外接球的半径R=62,所以球O的体积V=43πR3=43π⎝⎛⎭⎪⎫623=6π,故选D.]13.(2020·全国卷Ⅱ)设有下列四个命题:p1:两两相交且不过同一点的三条直线必在同一平面内.p2:过空间中任意三点有且仅有一个平面.p3:若空间两条直线不相交,则这两条直线平行.p4:若直线l⊂平面α,直线m⊥平面α,则m⊥l.则下述命题中所有真命题的序号是________.①p1∧p4②p1∧p2③¬p2∨p3④¬p3∨¬p4①③④[法一:对于p1,由题意设直线l1∩l2=A,l2∩l3=B,l1∩l3=C,则由l1∩l2=A,知l1,l2共面,设此平面为α,由B∈l2,l2⊂α,知B∈α,由C∈l1,l1⊂α,知C∈α,所以l3⊂α,所以l1,l2,l3共面于α,所以p1是真命题.对于p2,当A,B,C三点不共线时,过A,B,C三点有且仅有一个平面;当A,B,C三点共线时,过A,B,C的平面有无数个,所以p2是假命题,¬p2是真命题.对于p3,若空间两条直线不相交,则这两条直线可能平行,也可能异面,所以p3是假命题,¬p3是真命题.对于p4,若直线l⊂平面α,直线m⊥平面α,则m⊥l,所以p4是真命题,¬p4是假命题.故p1∧p4为真命题,p1∧p2为假命题,¬p2∨p3为真命题,¬p3∨¬p4为真命题.综上可知,真命题的序号是①③④.法二:对于p1,由题意设直线l1∩l2=A,l2∩l3=B,l1∩l3=C,则A,B,C 三点不共线,所以此三点确定一个平面α,则A∈α,B∈α,C∈α,所以AB⊂α,BC⊂α,CA⊂α,即l1⊂α,l2⊂α,l3⊂α,所以p1是真命题.以下同解法一.]14.(2018·全国卷Ⅱ)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为7 8,SA与圆锥底面所成角为45°.若△SAB的面积为515,则该圆锥的侧面积为________.402π[因为母线SA,SB所成角的余弦值为78,所以母线SA,SB所成角的正弦值为158,因为△SAB的面积为515,设母线长为l,所以12×l2×158=515,∴l2=80,因为SA与圆锥底面所成角为45°,所以底面半径为r=l cos π4=22l,因此圆锥的侧面积为πrl=22πl2=402π.]15.[一题两空](2019·全国卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为 1.则该半正多面体共有________个面,其棱长为________.图1图2262-1[先求面数有如下两种方法.法一:由“半正多面体”的结构特征及棱数为48可知,其上部分有9个面,中间部分有8个面,下部分有9个面,共有2×9+8=26(个)面.法二:一般地,对于凸多面体,顶点数(V)+面数(F)-棱数(E)=2.(欧拉公式)由题图知,棱数为48的半正多面体的顶点数为24.故由V+F-E=2,得面数F=2+E-V=2+48-24=26.再求棱长.作中间部分的横截面,由题意知该截面为各顶点都在边长为1的正方形上的正八边形ABCDEFGH,如图,设其边长为x,则正八边形的边长即为半正多面体的棱长.连接AF,过H,G分别作HM⊥AF,GN⊥AF,垂足分别为M,N,则AM=MH=NG=NF=2 2x.又AM+MN+NF=1,∴22x+x+22x=1.∴x=2-1,即半正多面体的棱长为2-1.]16.(2017·全国卷Ⅰ)如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△F AB 分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△F AB,使得D,E,F重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm3)的最大值为________.415cm3[如图,连接OD,交BC于点G,由题意,知OD⊥BC,OG=36BC.设OG=x,则BC=23x,DG=5-x,三棱锥的高h =DG 2-OG 2 =25-10x +x 2-x 2=25-10x ,S △ABC =12×23x ×3x =33x 2,则三棱锥的体积V =13S △ABC ·h =3x 2·25-10x =3·25x 4-10x 5.令f (x )=25x 4-10x 5,x ∈⎝ ⎛⎭⎪⎫0,52,则f ′(x )=100x 3-50x 4. 令f ′(x )=0得x =2.当x ∈(0,2)时,f ′(x )>0,f (x )单调递增,当x ∈⎝ ⎛⎭⎪⎫2,52时,f ′(x )<0,f (x )单调递减,故当x =2时,f (x )取得最大值80,则V ≤3×80=415.∴三棱锥体积的最大值为415 cm 3.]1.(2020·西安模拟)一个圆柱的底面直径与高都等于一个球的直径,则圆柱的全面积与球的表面积之比为( )A .2∶1B .4∶3C .3∶2D .1∶1C [设球的半径为r ,则由题意S 圆柱=2πr 2+2πr ·2r =6πr 2,S 球=4πr 2,所以圆柱的全面积与球的表面积之比为3∶2,故选C .]2.(2020·攀枝花一模)一个棱长为2的正方体被一个平面截去部分后,余下部分的三视图如图所示,则截去部分与剩余部分体积的比为( )A .1∶3B .1∶4C .1∶5D .1∶6A [由题意可知:几何体被平面ABCD 分为上下两部分,设正方体的棱长为2,上部棱柱的体积为:12×2×1×2=2;下部为:2×2×2-2=6.截去部分与剩余部分体积的比为13,故选A.]3.(2020·桂林一模)设m,n是两条不同的直线,α,β是两个不同的平面,则α⊥β的一个充分不必要条件是()A.m⊥α,m⊥βB.m⊂α,n⊂β,m⊥nC.m∥n,m⊥α,n⊥βD.m∥α,m⊥βD[对于A,由m⊥α,m⊥β⇒α∥β,故A错误;对于B,m⊂α,n⊂β,m⊥n,则α,β可以平行,故B错误;对于C,m∥n,m⊥α,n⊥β,可以求出α∥β,故C错误;对于D,由m∥α,m⊥β,得α⊥β,是充分条件,反之,由α⊥β,不一定得到m∥α,m⊥β,是不必要条件,故选D.]4.(2020·深圳模拟)空间四边形ABCD的四边相等,则它的两条对角线AC,BD的关系是()A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交C[取BD中点E,连接AE、CE.∵AB=AD=BC=CD,∴AE⊥BD,CE⊥BD.∴BD⊥平面AEC.又AC⊂面AEC,∴BD⊥AC.故选C.]5.(2020·岳阳二模)在正方体ABCD-A1B1C1D1中,E为BC1的中点,则异面直线DE与A1B1所成角的正切值为()A.62B.63C.22D. 2C[如图所示,∵DC∥A1B1,DC⊥B1C.∴∠EDC为异面直线DE与A1B1所成角.∴tan∠EDC=EC DC=12B1CDC=22.故选C.]6.(2020·贵阳模拟)在正方体ABCD-A1B1C1D1中,E,F分别在B1B和C1C上(异于端点),则过三点A,F,E的平面被正方体截得的图形(截面)不可能是() A.正方形B.不是正方形的菱形C.不是正方形的矩形D.梯形A[当BE=CF时,截面是矩形;当2BE=CF时,截面是菱形;当BE>CF时,截面是梯形,故选A.]7.(2020·南海区模拟)已知三棱锥P-ABC,AC=2,BC=1,AC⊥BC且P A =2PB,PB⊥平面ABC,其外接球体积为()A.4π3B.4π C.32π3D.43πA[AB=AC2+BC2=3,设PB=h,则由P A=2PB,可得3+h2=2h,解得h=1,可将三棱锥P-ABC还原成如图所示的长方体,则三棱锥P-ABC的外接球即为长方体的外接球,设外接球的半径为R,则2R=12+(2)2+12=2,R=1,所以外接球的体积V=4π3R3=4π3.故选A.]8.(2020·中山模拟)下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是()A.①③B.②③C.①④D.②④C[对于①,连接AC,如图所示.由于MN∥AC,NP∥BC,根据面面平行的性质定理可知平面MNP∥平面ACB,所以AB∥平面MNP.图1图2对于②,连接BC交MP于D,由于N是AC的中点,D不是BC的中点,所以在平面ABC内AB与DN相交,所以直线AB与平面MNP相交.对于③,连接CD,则AB∥CD,而CD与PN相交,即CD与平面PMN相交,所以AB与平面MNP相交.图3图4对于④,连接CD,则AB∥CD∥NP,由线面平行的判定定理可知AB∥平面MNP.综上所述,能得出AB∥平面MNP的图形的序号是①④,故选C.]9.(2020·开封模拟)在正方体ABCD-A1B1C1D1中,点O是四边形ABCD的中心,关于直线A1O,下列说法正确的是()A.A1O∥D1C B.A1O∥平面B1CD1C.A1O⊥BC D.A1O⊥平面AB1D1B[由题意,在正方体ABCD-A1B1C1D1中,点O是四边形ABCD的中心,所以A1D∥B1C,OD∥B1D1,因为A1D∩DO=D,B1D1∩B1C=B1,所以平面A1DO∥平面B1CD1,因为A1O⊂平面A1DO,所以A1O∥平面B1CD1,故选B.]10.(2020·沈阳模拟)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍.其中记载有求“囷盖”的术:“置如其周,令相承也.又以高乘之,三十六成一”.该术相当于给出了由圆锥的底面周长L 与高h ,计算器体积V ≈136L 2h 的近似公式.它实际上是将圆锥体积公式中的圆周率近似取为3,那么近似公式V ≈3112L 2h 相当于圆锥体积公式中的圆周率近似取为( )A .227B .15750C .289D .337115C [设圆锥底面圆的半径为r ,高为h ,依题意,L =2πr ,13πr 2h =3112·(2πr )2h ,∴13=12112π,即π=289.即π的近似值为289.故选C .]11.(2020·西安三模)一只蚂蚁从正方体ABCD -A 1B 1C 1D 1的顶点A 处出发,经正方体的表面,按最短路线爬行到达顶点C 1位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )图1 图2A .①②B .①③C .③④D .②④D [①中线段为虚线,②正确,③中线段为实线,④正确,故选D .]12.(2020·冀州模拟)已知正方体ABCD -A 1B 1C 1D 1中,点P 在线段A 1B 1上,点Q 在线段B 1C 1上,且B 1P =B 1Q ,给出下列结论:①A 、C 、P 、Q 四点共面;②直线PQ 与AB 1所成的角为60°;③PQ ⊥CD 1;④V P -ABCD =V Q -AA 1D . 其中正确结论的个数是( )A .1B .2C .3D .4B [如图所示,对于①,∵B 1P =B 1Q ,∴PQ ∥A 1C 1,∴A 、C 、P 、Q 四点共面,①正确;对于②,连接AC ,CB 1,可得△ACB 1是等边三角形,又AC ∥A 1C 1,∴直线PQ 与AB 1所成的角为60°;对于③,由②可知PQ ⊥CD 1错误;对于④,V P -ABCD =13V 正方体AC 1, V Q -AA 1D =13×S △AA 1D ×A 1B 1=13×12S 正方形AA 1DD 1×A 1B 1=16V 正方体AC 1. ∴V P -ABCD ≠V Q -AA 1D . 其中正确结论的个数2.故选B .]13.(2020·西北工业大学附中第三次适应性考试)如图,在三棱柱ABC -A 1B 1C 1中,侧棱AA 1⊥底面A 1B 1C 1,底面△ABC 是正三角形,E 是BC 的中点,则下列叙述正确的是( )A .CC 1与B 1E 是异面直线B .AC ⊥平面ABB 1A 1C .AE ⊥B 1C 1D .A 1C 1∥平面AB 1EC [对于A 选项,由于CC 1,B 1E 都含于平面BCC 1B 1,所以不是异面直线,故A 选项错误.对于B 选项,由于∠CBA =π3,所以AC 与平面ABB 1A 1不垂直,故B 选项错误.对于C 选项,在等边三角形ABC 中,AE ⊥BC ,根据直三棱柱中易得AE ⊥AA 1,所以AE ⊥平面BCC 1B 1,所以AE ⊥B 1C 1,所以C 选项正确.对于D 选项,由于A 1C 1∥AC ,而AC 与平面AB 1E 相交,所以直线A 1C 1与平面AB 1E 不平行,故D 选项错误,故选C .]14.(2020·邯郸模拟)如图1,在△ABC中,AB=AC,∠A=120°,D为BC中点,DE⊥AC,将△CDE沿DE翻折,得到直二面角C-DE-B,连接BC,F是BC 中点,连接AF,如图2,则下列结论正确的是()图1图2A.AD⊥CD B.AF∥DEC.DE⊥平面ACE D.AF∥平面CDEC[∵在△ABC中,AB=AC,∠A=120°,D为BC中点,DE⊥AC,将△CDE 沿DE翻折,得到直二面角C-DE-B,连接BC,F是BC中点,连接AF,∴DE⊥AE,DE⊥CE,∵AE∩CE=E,∴DE⊥平面ACE.故选C.]15.(2020·沧州模拟)已知P,A,B,C是半径为2的球面上的点,O为球心,P A=PB=PC=2,∠ABC=90°,则三棱锥O-ABC体积的最大值是()A. 3 B.1 C.12D.34B[如图,∵P,A,B,C是半径为2的球面上的点,O为球心,P A=PB=PC=2,∠ABC=90°,∴P到平面ABC上的射影G是△ABC的外心,即AC中点,则球的球心在PG的延长线上,设PG=h,则OG=2-h,∴OB2-OG2=PB2-PG2,∴4-(2-h)2=4-h2,解得h=1,∴AG=CG=BG=3,∴三棱锥O -ABC体积取最大值时,BG⊥AC,∴三棱锥O -ABC体积的最大值为:V=13S△ABC·h=13×12×23×3×1=1.故选B.]16.(2020·汉中模拟)正方体ABCD-A1B1C1D1的棱长为2,E,F,G分别为BC,CC1,BB1的中点,则()A .直线D 1D 与直线AF 垂直B .直线A 1G 与平面AEF 不平行C .平面AEF 截正方体所得的截面面积为92D .点C 与点G 到平面AEF 的距离相等C [对于A ,若D 1D ⊥AF ,又因为D 1D ⊥AE 且AE ∩AF =A ,所以DD 1⊥平面AEF ,所以DD 1⊥EF ,所以CC 1⊥EF ,显然不成立,故结论错误; 对于B ,如图所示,取B 1C 1的中点Q ,连接A 1Q ,GQ ,由条件可知:GQ ∥EF ,A 1Q ∥AE ,且GQ ∩A 1Q =Q ,EF ∩AE =E ,所以平面A 1GQ ∥平面AEF ,又因为A 1G ⊂平面A 1GQ ,所以A 1G ∥平面AEF ,故结论错误;对于C ,如图所示,连接D 1F ,D 1A ,延长D 1F ,AE 交于点S,因为E ,F 为BC ,C 1C 的中点,所以EF ∥AD 1,所以A ,E ,F ,D 1四点共面,所以截面即为梯形AEFD 1又因为D 1S =AS =42+22=25,AD 1=22,所以S △AD 1S =12×22×(25)2-⎝ ⎛⎭⎪⎫2222=6,所以S 梯形AEFD 1=6×34=92,故结论正确;对于 D ,记点C 与点G 到平面AEF 的距离分别为h 1,h 2,因为V C -AEF =13·S AEF ·h 1=V A -CEF =13×1×12×2=13,又因为V G -AEF =13×S AEF ·h 2=V A -GEF =13×2×22×2=23,所以h 1≠h 2,故结论错误,故选C .]17.(2020·贵州模拟)已知三个互不重合的平面α,β,γ,且直线m ,n 不重合,由下列条件:①m ⊥n ,m ⊥β;②n ⊂α,α∥β;③α⊥γ,β⊥γ,n ⊂α.能推得n ∥β的条件是________.② [①m ⊥n ,m ⊥β,可能n ⊂β; ②n ⊂α,α∥β,面面平行的性质得出成立; ③α⊥γ,β⊥γ,n ⊂α,若α与β相交,n 可能与β相交.故填②.]18.[一题两空](2020·成都模拟)如图,圆锥VO 的母线长为l ,轴截面VAB 的顶角∠AVB =150°,则过此圆锥的顶点作该圆锥的任意截面VCD ,则△VCD 面积的最大值是________,此时∠VCD =________.12l 2 45°[过此圆锥的顶点作该圆锥的任意截面VCD ,则△VCD 面积的最大值时是等腰直角三角形时,此时S △VCD =12·l 2·sin 90°=12l 2,且∠VCD =45°.]19.(2020·南开模拟)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,P 是侧棱CC 1上一点,且C 1P =2PC .设三棱锥P -D 1DB 的体积为V 1,正四棱柱ABCD -A 1B 1C 1D 1的体积为V ,则V 1V 的值为__________.16 [∵正四棱柱ABCD -A 1B 1C 1D 1中的体积V =DC ×BC ×DD 1,∴三棱锥P -D 1DB 的体积为V 1=13S △DD 1P ×BC =16DD 1×DC ×BC =16V .∴则V 1V 的值为16.]20.(2019·江南十校模拟)已知点A ,B ,C 在半径为2的球O 的球面上,且OA ,OB ,OC 两两所成的角相等,则当三棱锥O -ABC 的体积最大时,平面ABC截球O 所得的截面圆的面积为________.8π3 [由题意知,三棱锥O -ABC 为正三棱锥,如图所示: D 为BC 中点,OG ⊥平面ABC ,且G 为△ABC 的重心,设AB =x , 则AG =23AD =23×32x =33x ,∴OG =OA 2-AG 2=4-13x 2,V O -ABC =13×34x 2·4-13x 2=112x 4(12-x 2), 令t =x 2∈(0,12)⇒g (t )=t 2(12-t )⇒g ′(t )=-3t 2+24t ,令g ′(t )=0,解得t =8,且t ∈(0,8)时,g (t )单调递增;t ∈(8,12)时,g (t )单调递减,∴x 2=t =8时,三棱锥O -ABC 体积最大,此时AG 2=⎝ ⎛⎭⎪⎫33x 2=83, 平面ABC 截球O 所得的截面圆的面积S =π·AG 2=83π.]21.(2020·四川蓉城名校联盟第二次联考)在四面体ABCD 中, AB =CD =41,AC =BD =34,AD =BC =5,E ,F 分别是AD ,BC 的中点.则下述结论:①四面体ABCD 的体积为20;②异面直线AC ,BD 所成角的正弦值为2425;③四面体ABCD 外接球的表面积为50π;④若用一个与直线EF 垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为6.其中正确的有________.(填写所有正确结论的编号)①③④ [根据四面体特征,可以补图成长方体设其边长为a ,b ,c , 则⎩⎨⎧ c 2+b 2=41,c 2+a 2=34,b 2+a 2=25,解得a =3,b =4,c =5补成长,宽,高分别为3,4,5的长方体,在长方体中: ①四面体ABCD 的体积为V =3×4×5-4×13×12×3×4×5=20,故正确;②异面直线AC ,BD 所成角的正弦值等价于边长为5,3的矩形的对角线夹角正弦值,可得正弦值为1517,故错误; ③四面体ABCD 外接球就是长方体的外接球,半径R =32+42+522=502,其表面积为50π,故正确;④由于EF ⊥α,故截面为平行四边形MNKL ,可得KL +KN =5,设异面直线BC 与AD 所成的角为θ,则sin θ=sin ∠HFB =sin ∠LKN ,算得sin θ=2425,∴S MNKL =NK ·KL ·sin ∠NKL ≤⎝ ⎛⎭⎪⎫KL +KN 22×2425=6.故正确.]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、直观感知型
1. 某几何体三视图如图所示, 则该几何体的体积为( )
A .84π-
B .82
π- C .8π- D .82π-
2. 在长方体中割去两个小长方体后的几何体的三
视图如掉的两个小长方体的体 积之和于 .
3. 一个几何体的三视图如图所示(单位:m ),
则该几何体的体积为3m .
4.如图,网格纸上正方形小格的边长为1
(表示1cm ),图中粗线画出的是某零件的 三视图,该零件由一个底面半径为3cm , 高为6c m 的圆柱体毛坯切削得到,则切削 掉部分的体积与原来毛坯体积的比值为 (A )
1727 (B ) 59 (C )1027 (D)13
5.某几何体的三视图(单位:cm)如图所示,则该几何体的的体积是()A.72 cm3 B.90 cm3
A.108 cm3 D.138 cm3
6.一几何体的三视图如右所示,
则该几何体的体积为
A.200+9π
B. 200+18π
C. 140+9π
D. 140+18π
二、切割型
1 一个多面体的三视图如图所示,
则多面体的体积是()
A.23
3
B.
47
6
C.6
D.7
2.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是
A.108cm3 B.100 cm3
C.92cm3 D.84cm3
侧视图
俯视图
3.某几何体的三视图如图所示,则该几何体的体积为()
A.12
B.18
C.24
D.30 三、三棱锥型
1. 某三棱锥的三视图如图所示, 则该三棱锥的最长棱的棱长为.
2.某三棱锥的三视图如图所示, 该三棱锥的表面积是
(A
)28+ (B
)30+ (C
)56+ (D
)60+
3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为
(A )6 (B )9(C )12 (D )
18
侧(左)视图
正(主)视图
4.已知某三棱锥的三视图(单位:cm )如图所示, 则该三棱锥的体积是
A.1cm 3
B.2cm 3
C.3cm 3
D.6cm 3
四、几何体与问题型
1、若棱长为3的正方体的顶点都在同一球面上,求该球的表面积为和体积。
2、P 、A 、B 、C 是球O 面上的四个点,PA 、PB 、PC 两两垂直,PA=PB=PC=a ,求这个球的体积
3、求棱长为1的正四面体ABCD 的外接球体积
4、直三棱柱ABC-A 1B 1C 1 的各顶点都在同一球面上,若AB=AC=AA 1=2, 0120=∠BAC ,则此球的表面积等于。
5、设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积
6、求棱长为a 的正四面体的内切球半径。
(常用结论:3
1
⋅⋅=内切表多R S V )
7.已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M ,若圆M 的面积为3π,则球O 的表面积等于__________________.
8.设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45°角的平面截球O 的表面得到圆C 。
若圆C 的面积等于
4
7π
,则球O 的表面积等于 9.已知平面α截一球面得圆M ,过圆心M 且与α成060二面角的平面β截该球面得圆N .若该球面的半径为4,圆M 的面积为4π,则圆N 的面积为
(A)7π (B)9π (C)11π (D)13π
10.已知球的半径为4,圆与圆为该球的两个小圆,为圆与圆的公共弦,
.若,则两圆圆心的距离.
11.正三棱柱内接于半径为的球,若两点的球面距离为,则正三棱
柱的体积为 .
O M N AB M N 4AB =3OM ON ==MN =111ABC A B C -2,A B π。
