最优网络结构
ELM的几种结构选择方法比较

ELM的几种结构选择方法的比较本学期我们继续讨论学习了有关Extreme Learning Machine (ELM) 的一些基础的及其扩展的论文,对ELM有了更深入的了解。
由于ELM中隐藏层和输出层的权重分别是随机和分析得到的,唯一不能确定的(需要人为指定的)是隐节点的个数,也就是网络结构的大小。
结合讨论的几篇文章,本文对当前已有的有关ELM的结构选择方法进行了简单的介绍和比较。
一.结构选择的必要性和重要性在神经网络的研究中,如何确定网络结构一直是一个公开问题。
在模式识别中,我们都知道如果我们设计的网络太小,则它不能够很好的拟合训练数据,这样的网络,我们肯定也不希望它能够很好的拟合未见数据。
另一方面,如果网络太大,它又可能会过拟合训练数据,导致不能拟合未见数据。
另外,网络太大会造成计算更复杂,对运行环境提出了更高的要求。
ELM是基于单隐藏层前馈型神经网路设计的,它的主要优势在于计算复杂度低,是一种简单和易于实现的方法。
但是,在原始的ELM中没有提供一个关于网络结构设计的有效的解,在大多数情况下,我们是通过多次试验,以训练误差为标准来选出的适当的隐节点个数。
这样做,在很多应用中就变得很乏味而且很难找到一个最优的解。
所以,很多研究人员改进了原始的ELM,通过一个学习算法来计算所需隐节点的个数。
一般来说,对于SLFNs的构造有两种启发式的方法:一是构造的方法,也就是加节点的方法;另一个就是剪枝的方法。
目前已有的方法主要有以下几种:I-ELM, EM-ELM, CS-ELM, P-ELM,和OP-ELM,前三种是构造的方法,后面两个是剪枝的方法。
接下来,对这几种方法进行简单的介绍和比较。
二.构造方法构造方法的主要思想就是先初始化一个简单(隐节点个数比所需要的少)的网络结构,然后一个个或一组组的加隐节点。
通过控制最大的隐节点个数和期望的误差,来停止学习过程,进而得到所需的网络结构。
主要有I-ELM 和EM-ELM ,下面简单的介绍这两种方法。
网络拓扑结构的自适应控制模型研究

网络拓扑结构的自适应控制模型研究随着互联网技术的迅速发展,人们对网络拓扑结构更高效的控制和管理日益迫切。
网络拓扑结构的自适应控制是一种基于控制理论和网络科学理论的新兴技术,可以帮助实现网络性能的优化和资源的高效利用。
本文将探讨网络拓扑结构的自适应控制模型研究。
一、网络拓扑结构的基本概念及分类网络拓扑结构是网络中各节点之间的连接和布局关系。
在网络科学中,常见的网络拓扑结构有星型、总线型、环型、树型、网状等,每种结构都有适合其特定应用场景的优势和劣势。
在实际应用中,往往需要选择最优的拓扑结构,以满足不同的应用需求。
二、网络拓扑结构的自适应控制模型网络拓扑结构的自适应控制模型是基于控制理论和网络科学理论的一种新型技术。
该技术通过对网络拓扑结构进行监测和分析,实现对网络自身动态变化的自适应控制,从而达到网络性能优化和资源高效利用的目的。
网络拓扑结构的自适应控制模型主要分为两种类型:基于静态模型的自适应控制模型和基于动态模型的自适应控制模型。
基于静态模型的自适应控制模型是指在网络建立初期,通过对网络拓扑结构进行分析和评估,选择最优的拓扑结构。
该模型主要基于数学模型和统计模型,在网络建立初期对网络进行优化,可实现网络性能的最大化。
基于动态模型的自适应控制模型是指在网络运行过程中,通过对网络中节点的状态信息进行监测和分析,实时调整拓扑结构。
该模型主要基于控制理论、信息论和网络科学理论,通过设计算法和策略,实现网络自适应控制,从而提高网络性能。
三、网络拓扑结构的自适应控制模型的应用场景网络拓扑结构的自适应控制模型适用于很多不同的应用场景。
例如,在大规模云计算环境中,网络中的服务器、存储设备和网络设备都需要通过网络拓扑结构的优化来实现资源的高效利用和性能优化。
又如,在分布式传感器网络中,需要通过网络拓扑结构的优化来实现能量的高效利用和数据传输的最优化。
此外,网络拓扑结构的自适应控制模型还可以应用于大规模数据中心的网络设计、机器人协作网络、物联网等领域。
网络拓扑知识:如何选择最优的网络拓扑结构

网络拓扑知识:如何选择最优的网络拓扑结构网络拓扑结构是网络系统中最为基础的组织形式,它们决定了数据包传输的路径和方式。
不同网络环境有不同的拓扑结构要求,不同的拓扑结构又会有不同的性能表现。
因此,选择最优的网络拓扑结构至关重要。
本文将从网络拓扑的概念、不同拓扑结构的特点、选择最优拓扑结构的方法等方面展开讨论。
一、网络拓扑的概念网络拓扑是指不同节点之间连接关系的组织形式,决定了节点之间通信的路径和方法。
一般来说,它可以分为以下常见类型:1.星型拓扑结构星型拓扑结构是由中心节点和若干个外围节点组成的,所有外围节点通过点对点连接到中心节点,而不与其他节点相连。
这种结构通常用于局域网中,由于只有一个中心节点掌握控制权,因此具有很好的可管理性和可靠性。
然而,如果中心节点出现故障,整个网络将会瘫痪。
2.总线拓扑结构总线拓扑结构是由一根主线连接多个节点,所有节点都通过该主线相互连接。
由于节点数量和总线长度的限制,这种拓扑结构通常只适合小型网络,如家庭或办公室网络。
缺点是如果总线出现故障,则会影响所有与之相连的节点。
3.环形拓扑结构环形拓扑结构是由以环形的方式连接多个节点,如果没有故障,数据包可以沿着环形流通。
由于它只需要少量的连接线,因此可用于小型网络。
缺点是如果环路中断,整个网络也会瘫痪。
4.网状拓扑结构网状拓扑结构是由多个节点相互连接而成,每个节点与其他节点都有连接。
这种结构因为有多条路径,因此包容性和容错性比较好。
然而,由于连接数量较多,所以建设成本较高。
二、选择最优的网络拓扑结构不同的网络环境对拓扑结构的要求是不同的,因此,我们需要根据实际情况选择最优的网络拓扑结构。
下面将介绍一些选择最优拓扑结构的方法:1.确定网络规模和布局网络规模是选择最优拓扑结构的首要考虑因素。
如果网络规模较小,例如少于10个节点,使用总线或星型拓扑结构是最佳选择。
如果网络规模较大,例如超过100个节点,使用网状拓扑结构可能是最好的选择,因为它具有较好的容错性和扩展性。
云计算中的计算存储和网络资源优化

云计算中的计算存储和网络资源优化在云计算中,计算存储和网络资源优化是两个不可忽视的关键方面。
优化这些资源的使用可以提高性能、降低成本,并增强整个云计算系统的可靠性和可扩展性。
本文将从计算存储和网络两个方面来探讨如何优化云计算中的资源。
一、计算存储资源优化1. 虚拟化技术的应用虚拟化是云计算的核心技术之一,它通过将物理资源虚拟化为多个虚拟资源,实现资源的合理分配和管理。
在计算存储方面,虚拟化可以帮助实现资源的弹性调整和动态扩展,提高整个系统的利用率。
通过使用虚拟机技术,可以将不同的计算任务分配到不同的虚拟机上,从而实现资源的最优化利用。
2. 数据冗余和压缩数据冗余是指在存储系统中存在相同或相似的数据副本,这会占用大量的存储空间。
通过使用数据冗余和压缩算法,可以有效地减少存储空间的占用,并提高存储系统的性能。
例如,可以使用压缩算法对数据进行压缩存储,从而节省存储空间并提高数据传输效率。
3. 存储层次结构的优化存储层次结构是指将数据存储在不同的存储介质中,根据数据的访问频率和重要性将其分层存储。
通过合理划分存储层次,可以提高存储系统的性能和效率。
例如,可以将频繁访问的数据存储在高速存储介质中,将不常用的数据存储在低速存储介质中,以实现最优的性能和成本平衡。
二、网络资源优化1. 负载均衡负载均衡是指将网络流量均衡地分配到多个服务器上,以提高整个系统的性能和可靠性。
通过使用负载均衡技术,可以避免单点故障,实现资源的有效利用,并提高用户的访问速度和响应时间。
例如,可以使用负载均衡器将用户请求分发到多个服务器上,以实现请求的平衡负载。
2. 带宽管理和优化带宽管理是指对网络带宽进行有效分配和调整,以提高网络的利用率和性能。
通过使用带宽管理技术,可以对网络流量进行限制和控制,避免网络拥塞和带宽浪费。
例如,可以使用流量控制和优先级队列等技术对网络流量进行管理,以确保重要数据的传输速度和可靠性。
3. 网络拓扑设计和优化网络拓扑设计是指根据实际业务需求和资源分布情况,设计最优的网络拓扑结构。
面向产量决策的多寡头网络最优结构分析

网络 的现 期利 润 随着 网络 规模 的增 加 而减 少. 最后 , 分析 了相 关研 究结果在 我 国钢铁 行 业上 的
① 收稿 日期 : 0 8一O 20 1—1 修订 1期 : 0 9一 8— 1 0; 3 20 O 3 .
古诺 产 量决 策 时 , 连接 成本 较小 时 , 完全 网络 若 则
基金项 目: 国家 自然科学基金资助项 目( 0 70 3 ; 7 5 1 1 ) 新世纪优秀人才支持计划资助项 目( C T— 6一 4 1 N E O o7 )
第 1 3卷第 5期
21 00年 5月
管
理
科
学
学
报
Vo . 3 No 5 1 1 .
M a 01 v2 0
J OUR NAL OF MANAGE MEN C E ES I HI T S I NC N C NA
面 向产 量 决 策 的 多寡 头 网络 最 优 结构 分 析①
问题 , 网络来研 究 现实 中 的各 类 系统 , 卜 用 已成
为研 究 的热 点 , 也 为分 析 多 寡 头 产 量决 策提 供 这
了一 个 全新 的视 角 . 理 学 界 已普 遍认 为 网络 化 管 是企 业 未来 发展 的必 然 趋 势 , 建 关 系 网 络具 有 构 积极 的作 用 “ . J企业 间 的关 系 网络在相 互 补充
应 用.
关键 词 :网络 结构 ; 息成 本 ;关 系成 本 ;关 系收 益 ;现期 利 润 信 中图分 类号 : 2 0 7 F 7 . 文 献标 识码 :A 文章 编 号 : 0 7— 8 7 2 1 )5— 0 3—1 10 9 0 (0 0 0 0 3 1
网络拓扑结构优化算法收敛速度评估说明

网络拓扑结构优化算法收敛速度评估说明网络拓扑结构优化算法是通过优化网络中的链路连接关系,以提高网络性能和可靠性的方法。
在实际应用中,算法的收敛速度是评估其效果的重要指标之一。
本文将从定义收敛速度、影响收敛速度的因素以及评估收敛速度的方法三个方面进行论述。
首先,什么是收敛速度?收敛速度是指网络拓扑优化算法在迭代过程中逐渐接近最优解所花费的时间。
在拓扑结构优化中,最优解往往是指网络中链路带宽利用率最大化或者时延最小化。
因此,一个快速收敛的算法意味着它能够在尽可能短的时间内达到最佳的拓扑优化状态。
其次,影响收敛速度的因素有很多,其中主要包括以下几个方面:1. 算法本身的特性:不同的算法有不同的收敛速度。
例如,梯度下降算法通常能够较快地收敛,因为它能够有效地利用目标函数的梯度信息。
而遗传算法等启发式算法则往往需要较长的时间来搜索全局最优解。
2. 网络的规模和复杂度:网络的规模越大、结构越复杂,拓扑优化算法往往需要更长的时间才能达到最优解。
这是因为大规模网络中的连接关系更加复杂,优化问题的搜索空间更大。
3. 初始拓扑状态:拓扑优化算法的初始拓扑状态也会对收敛速度产生影响。
如果初始的拓扑已经非常接近最优解,那么算法的收敛速度通常会更快。
最后,评估算法的收敛速度可以采用以下几种方法:1. 迭代次数统计:可以记录算法运行的迭代次数,并根据迭代次数来评估算法的收敛速度。
一般来说,迭代次数越少,收敛速度越快。
2. 收敛过程可视化:可以将算法的迭代过程可视化,通过观察目标函数值或者拓扑结构的变化来评估算法的收敛速度。
如果在前几次迭代中,目标函数值或者拓扑结构的变化比较大,而后续变化较小,那么算法可能已经接近最优解,收敛速度较快。
3. 算法效果评估:可以通过对比不同算法在相同条件下的优化效果来评估其收敛速度。
具体方法包括比较不同算法达到相同优化效果所需要的时间或者迭代次数。
综上所述,网络拓扑结构优化算法的收敛速度是评估其效果的重要指标之一。
最优双环网的构造

2001年12月系统工程理论与实践第12期 文章编号:100026788(2001)1220072204最优双环网的构造刘焕平1,2 杨义先3 胡铭曾1(1.哈尔滨师范大学数学系,黑龙江哈尔滨150080;2.哈尔滨工业大学计算机系,黑龙江哈尔滨 150006;3.北京邮电大学信息安全中心,北京100876)摘要: 双环网络已广泛应用于设计和实现计算机通信网、局域网以及各种大规模并行处理系统.如何设计一个最优的双环网络是人们非常关心的一个问题.本文给出了一个构造最优双环网络的快速有效的算法,从而针对有向双环网的情形解决了文献[1]提出的一个问题.关键词: 双环网;直径;最优双环网;紧优双环网中图分类号: T P393 文献标识码: A αO n the Con structi on of T igh t Doub le L oop N etw o rk s L I U H uan2p ing1,2,YAN G Y i2x ian3,H u M ing2zeng1(1.H arb in N o rm al U n iversity,H arb in150080,Ch ina;2.H arb in In stitu te of T echno logy,H arb in 150006,Ch ina;3.Beijing U n iversity of Po sts and T elecomm,Beijing100876,Ch ina)Abstract: A new fast algo rithm fo r the design of the a op ti m al doub le loop netw o rk s(DLN)is p resen ted,w h ich so lves a p rob lem listed in reference[6]fo r the directedcase.Keywords: doub le2loop netw o rk;diam eter;op ti m al;tigh t DLN1 引言一个双环网络(DLN),记为G(N;1,s),是一个有N个节点:0,1,…,(N-1)的有向图,每个节点i 相邻于节点:i+1(mod N)和i+s(mod N).这类网络广泛应用于设计和实现计算机通信网、局域网以及各种大规模并行处理系统[2].记G(N;1,s)的直径为d(N;1,s).令d(N)=m in{d(N;1,s):1<s<N}.一个双环网G(N;1, s)称为最优的(op ti m al),如果d(N;1,s)=d(N).1974年,W ong等最早研究了下述优化问题[3]:对每一个NΕ4,确定并构造出最优的G(N;1,s).从此这个问题受到了广泛深入的研究[1-9],但这一问题至今仍未得到很好的解决[1].另一个受到关注的问题是d(N)的计算,已有的研究表明,不大可能给出函数d(N)的简单显式表示,但不难得到其下界[3]:d(N)ΕU0(N)=3N- 2.自1987起,陆续找到了不少N的无限族使d(N)=U0(N).称G(N;1,s)为紧优的,如果d(N;1,s)=U0(N).显然紧优的双环网必是最优的.在一个多处理器系统中,最优的双环网络能够大大地降低处理器之间的通讯时延,因此如何构造最优双环网络一直是人们比较关心的一个问题。
深度学习中的神经网络搜索

神经网络搜索(Neural Network Search)是一种新兴的深度学习技术,旨在通过搜索算法自动发现高性能的神经网络架构,以加速模型训练和提高模型性能。
神经网络搜索基于机器学习原理,通过自动化搜索和评估不同神经网络架构的性能,最终找到最优的网络结构,从而大幅度提高深度学习的效率和效果。
神经网络搜索的核心思想是通过搜索算法自动发现最优的网络结构,而不是依赖于人工设计或简单的经验性选择。
这种技术利用了机器学习中的搜索和优化方法,结合深度学习的特性,通过大规模的数据集和计算资源进行训练和评估,以找到最优的网络结构。
神经网络搜索的主要步骤包括:1. 定义搜索空间:搜索空间是所有可能被选中的神经网络结构集合,通常包括网络层数、每层神经元数量、激活函数类型、优化器选择等。
2. 生成候选网络:从搜索空间中随机选择一组候选网络结构,通常会生成大量的候选网络。
3. 评估网络性能:对每个候选网络进行评估,通常使用预定义的评估指标,如准确率、损失值等。
4. 更新搜索空间:根据候选网络的性能,更新搜索空间,保留性能好的网络结构,剔除性能差的网络结构。
5. 终止条件:设定一定的搜索次数或达到预设的性能阈值时,停止搜索,输出最优的网络结构。
神经网络搜索的优势在于其自动化和高效性。
通过大规模的数据和计算资源进行训练和评估,神经网络搜索能够快速找到最优的网络结构,大大提高了深度学习的效率和效果。
此外,神经网络搜索还具有很强的泛化能力,即使在未见过的数据集上也能取得较好的性能。
神经网络搜索的应用场景非常广泛,包括但不限于计算机视觉、自然语言处理、语音识别等领域的模型训练。
通过神经网络搜索,可以大幅度提高模型的性能和效率,为各种应用场景提供更好的支持。
然而,神经网络搜索也存在一些挑战和限制。
首先,搜索算法的效率直接影响搜索结果的质量和速度。
其次,神经网络搜索需要大量的数据和计算资源进行训练和评估,这可能会增加成本和时间成本。
贝叶斯网络的结构学习综述

第41卷第1期2021年2月西安工业大学学报Journal of Xi'an Technological UniversityVol.41No.1Feb.2021DOI:10.16185/.2021.01.001 贝叶斯网络的结构学习综述‘吕志刚12,李叶2,王洪喜】,邸若海2(1.西安工业大学机电工程学院,西安710021;2.西安工业大学电子信息工程学院,西安710021)摘要:贝叶斯网络是一种描述变量间不确定性因果关系的概率图模型,广泛应用于预测、推理、诊断、决策风险及可靠性分析等领域。
结构学习作为构建贝叶斯网络的基础,被证实为非确定多项式难题。
文中将贝叶斯网络结构学习按照数据量大小分为完备数据和缺失数据,将完备数据下的贝叶斯网络结构学习分为近似学习算法和精确学习算法。
根据上述分类方法,对现有算法及其相关的改进算法进行总结与分析对比。
关键词:贝叶斯网络;结构学习;数据分析;非确定多项式中图号:TP181文献标志码:A文章编号:1673-9965(2021)01-0001-17 Overview of Bayesian Network Structure LearningLYU Zhtgang1'2,LI Ye2,WANG Hongxt1,DIRuohat2(1.School of Mechatronic Engineering,Xi'an Technological University,Xi'an710021,China;2.School of Electronic and Information Engineering,Xi?an Technological University,Xi'an710021,China)犃犫5狉犪":Bayesian network is a probabilistic graphical model that describes the causal relationship of uncertainty among variables.It is widely used in prediction,reasoning,diagnosis,decision-making risk, reliability analysis,etc.Structural learning,as the basis for building Bayesian networks,is proved to be anon-deterministicpolynomialproblem.Inthispaper,Bayesiannetworkstructurelearningisdividedinto completedataandmissingdataaccordingtotheamountofdata.TheBayesiannetworkstructurelearning undercomplete data is divided into approximate learning and precise learning.According to this classification,the existing algorithms and their improved algorithms are summarized,analyzed and compared.Key woix I s:bayesian networks;structural learning;data analysis;non-deterministic polynomial*收稿日期:2020-11-21基金资助:国家重点实验室基金(CEMEE2020Z0202B);陕西省自然科学基础研究计划项目(020JQ816)陕西省教育厅专项科研计划项目(20JK0680)西安市科技计划项目(2020KJRC0033)。
无线网络最优接入的研究
拓扑优化99行算法解读

拓扑优化99行算法解读
拓扑优化算法是一种常用的计算机科学算法,可以在网络和图形相关问题中求
解最优解。
拓扑优化99行算法是一种高效的算法,只需要99行代码即可实现,被广泛应用于各种领域。
该算法主要用于解决拓扑优化问题,即在给定的网络结构中,寻找一个最优的
拓扑结构,以满足特定的性能需求。
拓扑结构涉及到节点和边的连接方式,而性能需求则可以是最小化通信开销、最大化网络吞吐量或最小化传输延迟等。
拓扑优化99行算法的核心思想是通过迭代的方式,不断进行拓扑结构的调整,直到找到最优解。
算法首先定义了一个初始拓扑结构,然后通过计算当前拓扑结构的性能评价指标,如通信开销或吞吐量,来评估当前解的质量。
在每一次迭代中,算法会对当前拓扑结构进行一系列操作,如增加或删除边、
移动节点等,以生成新的拓扑结构。
然后,通过计算新拓扑结构的性能指标,与当前解进行比较,选择更优的解作为下一次迭代的起点。
拓扑优化99行算法的关键在于如何确定新的拓扑结构,并评估其性能指标。
在算法中,可以使用一些启发式方法,如局部搜索或模拟退火等,来探索可能的拓扑结构。
同时,需要定义一种合适的性能评价函数,以便准确地衡量不同拓扑结构的性能。
除了调整拓扑结构外,拓扑优化99行算法还可以考虑其他因素,如带宽限制、延迟约束等。
通过在算法中引入这些约束条件,可以实现更加现实的拓扑优化方案。
总结来说,拓扑优化99行算法是一种简洁高效的算法,用于解决拓扑结构优
化问题。
通过迭代的方式,不断调整拓扑结构,以求得最优解。
该算法可以应用于各种领域,如计算机网络、电路设计等,为问题求解提供了一种有效的方法。
面向无线传感器网络的移动最优路由算法研究

面向无线传感器网络的移动最优路由算法研究近年来,随着无线传感器网络技术的快速发展,越来越多的无线传感器应用场景涌现出来。
在这些应用场景中,移动无线传感器网络(Mobile Wireless Sensor Networks,MWSNs)由于其具有高度灵活性和可部署性的特点,获得了广泛的关注和研究。
而对于MWSNs而言,移动最优路由算法的研究则尤为重要。
MWSNs是一种由移动无线传感器组成的自组织网络,节点可以在网络中自由移动。
这种网络结构使得MWSNs可以适应各种环境,实现临时部署和快速响应。
然而,由于节点可以随意移动,网络拓扑结构的不断变化对数据传输和路由选择提出了巨大的挑战。
因此,设计一种能够在不稳定的网络环境下实现数据传输的移动最优路由算法对于MWSNs的应用至关重要。
现有的移动最优路由算法主要可以分为两大类:位置无关的和位置相关的算法。
位置无关的算法通过统计信息、网络拓扑或传感器数据等基本信息进行路由选择,而位置相关的算法则利用节点的位置信息进行相应的决策。
在位置无关的算法中,常见的有贪婪算法、集群算法和虚拟格网算法等。
贪婪算法是一种简单直观的路由选择方法,每个节点只根据邻居节点信息选择下一跳节点。
集群算法则将整个网络划分为若干个集群,每个集群内部的数据传输通过集群内的路由节点进行,跨集群的数据传输则通过集群间的路由节点。
虚拟格网算法则将网络拓扑结构抽象成为一个虚拟的方格网,每个方格内部的数据传输使用最短路径算法。
而在位置相关的算法中,常见的有基于位置预测的算法和基于位置更新的算法等。
基于位置预测的算法通过研究节点移动的规律和趋势,预测节点未来的位置,从而进行路由选择。
基于位置更新的算法则通过周期性地更新节点的位置信息,实时地进行路由选择。
尽管目前已经有了许多成熟的移动最优路由算法,但是这些算法在面对复杂的网络环境时仍然存在一些问题和挑战。
首先,网络拓扑结构的不断变化使得路由选择更加困难,需要设计更加适应动态变化的算法。
5网络最优化问题

变成两个源、两个收点的问题:从两个工厂到 西雅图和洛杉矶这两个配送中心的运输量最大。
33
BMZ问题扩展后的网络表示
两个汇
两个源
34
面对多个源、 多个汇的问题, 怎么办?
35
用Excel求解
与原来的模型相比:
增加了弧和节点 目标函数变成两个源的净流量之和
参见《Expanded BMZ.xls》
网络最优化问题
1
内容提要
1.图论简介 2.最小费用流 3.最大流 4.最短路 5.最小支撑树
2
图论简介
3
从实例引出图
5个人之间认识关系:1与2,3与4,4与5 相互认识;1认识3,3认识5,5认识2,4 认识2。
2
4
谁最爱交际? 谁最有名气?
1 5
3
4
基本概念
图 图是由一些点及一些点之间的联线所组成。连线表 示某种关系,图中点的相对位置和联线的长短曲直并 不重要。 两点之间不带箭头的联线称为边。 两点之间带箭头的联线称为弧。
在每段弧上的单位流量成本已知的前提下,通过 每一条弧的流的成本和流量成正比。
16
最小费用流解的性质
目标:在满足给定需求的条件下,使网络流的总成本最小。
决策变量:通过每一条弧的流量。
约束:
每条弧的流量都不得超过该弧的容量。 每个节点产生的净流量必须等于该节点标明的流量。
具有可行解的特征:在以上假设下,当且仅当供应点所提供 的流量总和等于需求点所需要的流量总和时,最小费用流问 题有可行解。
min f ij bij
f si=Fs , 对于供应点s i f jt=Ft , 对于需求点t j s.t. f - f =0 , 对于转运点k ki jk i j f ij cij f ij 0
最优蜘蛛网结构

数学建模网络挑战赛承诺书我们仔细阅读了第五届“认证杯”数学中国数学建模网络挑战赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们允许数学中国网站()公布论文,以供网友之间学习交流,数学中国网站以非商业目的的论文交流不需要提前取得我们的同意。
我们的参赛队号为:1739参赛队员:队员1:队员2:队员3:参赛队教练员:参赛队伍组别:数学建模网络挑战赛编号专用页参赛队伍的参赛队号:# 1739竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):2012年第五届“认证杯”数学中国数学建模网络挑战赛题 目 蜘蛛网最优模型关 键 词 蜘蛛网 螺旋线 层次分析法 能量守恒摘 要:世界上有很多种类的蜘蛛,而大部分种类的蜘蛛都是通过结网来捕食食物的。
蜘蛛网的结构主要受外因和内因的影响,本文研究并建立合理的数学模型,确定出了蜘蛛网的最优结构,得出结果与实际情况基本相符。
首先,蜘蛛织网是由一根丝完成整个工作,为了构造合理的网状,设蜘蛛只有材料L ,已知L 的情况下易知圆的面积最大,即捕食面的面积最大值,得到最大圆面积为⎰=rdr 2S 11nd d max π,其中1d 为捕丝间距。
其次,由以上可以确定S 面积只与1d 有关,根据相关生物学家的资料查得影响蜘蛛网捕丝间距的因素,主要有风、湿度、空间、温度、食物状况等。
再运用层次分析的方法计算出各个因素对1d 的权重,从而计算出捕丝的间距。
然而,以上并没有计算出放射丝的间距。
离散变量结构拓扑优化

离散变量结构拓扑优化简介离散变量结构拓扑优化是一种在离散变量结构中寻找最优拓扑结构的方法。
拓扑结构在很多领域中都有重要应用,比如计算机网络、化学分子结构、电路设计等。
通过优化拓扑结构,可以达到节省资源、提高效率的目的。
离散变量离散变量是一种具有离散取值的变量。
在拓扑结构中,离散变量可以表示节点的类型、连接状态等。
结构拓扑结构拓扑是指网络或系统中各个节点之间的连接方式和关系。
常见的结构拓扑包括星型、环型、网状等。
优化方法1. 枚举法枚举法是一种最简单、直接的优化方法。
对于给定的离散变量结构,枚举法会遍历所有可能的拓扑结构,并计算它们的性能指标。
然后从中选取最优的拓扑结构作为最终结果。
枚举法的优点是简单易懂,能够找到最优解。
然而,当离散变量较多、拓扑结构复杂时,枚举法的计算量会变得非常大,不适合大规模问题的求解。
2. 启发式算法启发式算法是一种通过启发式规则来搜索最优解的方法。
与枚举法不同,启发式算法并不是通过遍历所有可能的拓扑结构来寻找最优解,而是根据问题的特性和经验设计一些规则,从而快速找到一个较好的解。
常见的启发式算法包括遗传算法、蚁群算法、模拟退火算法等。
这些算法都有自己独特的搜索策略和优化目标。
通过不断迭代和优化,启发式算法能够逐步接近最优解,同时避免了枚举法的计算复杂度问题。
应用领域离散变量结构拓扑优化在许多领域中都有广泛应用。
1. 计算机网络在计算机网络中,通过优化网络拓扑结构可以提高网络吞吐量、降低延迟、提高容错性等。
例如,在传感器网络中,合理的拓扑结构可以减少能量消耗,延长网络寿命。
2. 化学分子结构在化学中,分子拓扑结构对于分子的性质和反应有重要影响。
通过优化分子的拓扑结构,可以改善分子的稳定性、反应活性等。
3. 电路设计在电路设计中,优化电路的拓扑结构可以提高电路的性能指标,比如功耗、响应速度等。
通过离散变量结构拓扑优化,可以找到最佳的电路连接方式和元件布局。
总结离散变量结构拓扑优化是一种通过优化离散变量结构来提高系统性能的方法。
第七章 网络最优化问题(正稿)

<= <= <= <= <= <= <= <= <= <=
= = = = = = =
$488,125
15
网络最优化问题
7.2 最大流题
Maximum Flow Problems 最大流问题
最大流问题也与网络中的流有关,但目标不是使得
流的成本最小化,而是寻找一个流的方案,使得通
过网络的流量最大
这种问题有哪些应用呢?
网络规划为描述系统各组成部分之间的关系提供了 非常有效直观和概念上的帮助,广泛应用于科学、社会 和经济活动的每个领域中。
2
网络最优化问题 Types of Network Optimization Problem 网络最优化问题类型
Minimum Cost Network Flow Model 最小费用流问题 Maximum Flow Problems 最大流问题 Shortest Path Problem 最短路问题 Minimum Spanning Tree Problem 最小支撑树问题
13
解:第一步,画出网络图
s upply nodes P1 trans shipment nodes W1 demand nodes
RO1
RO2
P2
W2
RO3
[200] P1 560 [150] 510 P2 [300]
425 [125]
[0] W1
[175]
600 [200]
[0] W2
505 [150] 490 [100] 390 [125] 410 [150] 440 [75]
想想看!
16
网络最优化问题 BMZ 公司最大流问题 案例研究1 The BMZ Maximum Flow Problem
第八讲网络最优化模型【共61张PPT】

第八讲 网络最优化模型
最短路模型
最短路模型的求解
求解最短路问题实际上就是找一条总长度最短的路 线,对于这样的最短路问题,可以建立0-1整数规划数学
模型求解(如下图)。
第八讲 网络最优化模型
最短路模型
最短路模型的求解
为简化求解过程,可以建立专门的最短路求解模型 ,用计算机求解:可以将图中各条边和每条边是的权数 直接录入到求解模型中,直接得到结果。因此可以称下 图就是一个最短路问题的数学表述模型。
条路,使两点间的总距离为最短。
第八讲 网络最优化模型
最短路模型
例8.1 如下图所示,某人每天从住处S开车到工作地T上
班,图中各弧旁的数字表示道路的长度(千米),试问 他从家出发到工作地,应选择哪条路线,才能使路上行 驶的总距离最短?
第八讲 网络最优化模型
最短路模型的基本特征
最短路模型
1、在网络中选择一条路,始于发点(源点),终于收点(目的
条道路及道路维修。工期和所需劳动力见下表。该公司共 有劳动力120人,任一工程在一个月内的劳动力投入不能超 过80人,问公司应如何分配劳动力以完成所有工程,是否能按
期完成?
工程 A.地下通道 B.人行天桥 C.新建道路 D.道路维修
工期和所需劳动力
工期 5~7月 6~7月 5~8月
8月
需要劳动力(人) 100 80 200 80
赵●
(v1)
e1
e3
钱● (v2)
●孙 (v3) e4
●李 (v4)
第八讲 网络最优化模型
基本概念
图
7、 回路 始点和终点重合的路叫做回路。上图中(v3,v5,v6
,v7,v4 ,v3)就是一条回路。
ZVS—PWM开关电源补偿网络的最优设计
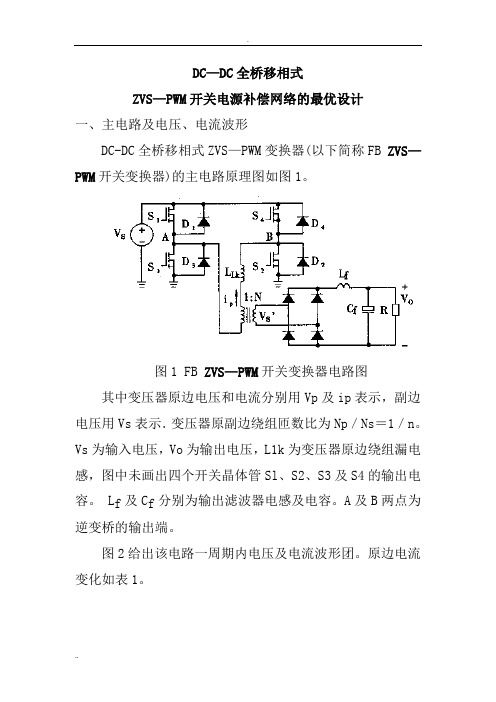
DC—DC全桥移相式ZVS—PWM开关电源补偿网络的最优设计一、主电路及电压、电流波形DC-DC全桥移相式ZVS—PWM变换器(以下简称FB ZVS—PWM开关变换器)的主电路原理图如图1。
图1 FB ZVS—PWM开关变换器电路图其中变压器原边电压和电流分别用Vp及ip表示,副边电压用Vs表示.变压器原副边绕组匝数比为Np/Ns=1/n。
Vs为输入电压,Vo为输出电压,L1k为变压器原边绕组漏电感,图中未画出四个开关晶体管Sl、S2、S3及S4的输出电容。
L f及C f分别为输出滤波器电感及电容。
A及B两点为逆变桥的输出端。
图2给出该电路一周期内电压及电流波形团。
原边电流变化如表1。
表1半周期内原边电流变化图2 FB ZVS—PWM开关变换器理论分析波形图△I=I p—I1当能量由原边传送到副边时,副边电压V s’=n V s。
由于变压器有漏感,使原边电流上升或下降一定斜率,例如t2—t4,斜率为V s/ L1k; t4—t5,斜率为(V s —V o’/L f’,L f’及V o’分别为折合到原边的L f及V o值。
原边占空比D=2 (t5—t2)/T,副边占空比或称有效占空比D eff=2(t5—t4)/T,T=2(t5—t1)。
可见由于变压器有漏感,使有效占空比D eff小于原边占空比D。
二、FB ZVS—PWM变换器小信号模型为了建立全桥FB ZVS—PWM变换器的最优控制模型,即补偿网络最优设计模型,首先应建立这类变换器的小信号等效电路模型,并推导主电路的传递函数。
已知buck型PWM变换器的连续导通模式(CCM)下小信号等效电路模型如图3。
图中忽略了电感及电容的寄生电阻。
图3 buck型PWM变换器的小信号等效电路模型FB ZVS—PWM型开关电源是由buck型PWM开关电源衍生而来的。
从工作原理分析可知,由于L1k较大,从Sl,S2(或S3,S4)导通到副边电压升到Vs需要一段时间(如图2)因此有效占空比D eff的出现是该电路的一个特殊现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在中国三大运营商都部署LTE网络并且频谱资源相同的情况下,决定最终用户体验差异的是网络的频谱效率。
频谱效率在很大程度上取决于网络内中高端SINR的占比,而中高端SINR的占比则主要由网络结构决定。
LTE速率的决定性因素—SINR
仿真和实测数据都显示,LTE的下载速率和SINR成正比,对LTE,峰值速率要求SINR能够达到25dB以上。
在一个网络中,中高端的SINR 占比越高,速率就越高,频谱效率也就越高。
对于一个蜂窝无线移动网络,为了保证业务服务连续性和切换的顺利进行,需要保证一定数量的邻接小区,邻接小区数量增加也带来干扰的增加。
所以对一个满足基本覆盖要求的LTE商用网络来说,要提升SINR,关键是要严格控制小区间重叠覆盖,降低相邻小区的干扰。
网络结构决定SINR
在实际网络中,小区间的重叠覆盖程度决定了SINR,而小区间的重叠覆盖是由网络的下倾角、方位角直接影响和决定的。
下倾角和方位角的具体取值,取决于站点高度、站间距、站点类蜂窝布局,即网络结
构。
网络结构决定了通过优化方位角、下倾角所能够获得的最高SINR 的上限。
重叠覆盖会带来导频污染,严重时近一半区域无主导信号。
如果在重叠覆盖区域共站址建设LTE网络,平均小区吞吐量较规则组网下降50%。
可见网络结构决定SINR,进而影响整个网络的性能。
如何获得最佳SINR
要获得最佳SINR,首先要确定能够尽量降低小区间的重叠覆盖的方位角和下倾角最佳取值;接下来根据方位角和下倾角数值,确定网络结构。
最优下倾角分析及实践
LTE下倾角的设置,既要使得小区间干扰最小,还要满足移动性能的要求。
天线垂直波瓣3dB宽度以外,天线增益会急剧下降;同时,小区间的重叠覆盖宽度要能够满足终端切换带的需求。
所以我们提出了最优下倾角的定义:天线上3dB的落地点位于切换带边缘,实现干扰和移动性能之间的最佳平衡。
一旦过了切换带边缘,本小区对邻小区的干扰会急剧下降,从而避免对邻区的干扰,提升SINR。
根据典型的LTE的切换时延和常规车速,计算出密集城区300米站间距情况下,不同站高对应的最优下倾角如表1所示。
在某外场,我们选择了9个小区,按照最优下倾角理论进行了优化,优化后中高端速率都有明显提升(见图1)。
最优方位角
在标准蜂窝结构中,扇区夹角都为120°,此时扇区间的重叠覆盖最小,所以最佳方位角夹角应该是120°。
但考虑到现网的站点分布不可能完全符合标准蜂窝结构,建议方位角夹角控制在90°~150°。
最优网络结构
网络结构主要是指站点高度、站间距、站点的类蜂窝布局。
在一定站高度和站间距下按照上述最优下倾角理论,可以计算出天线
下倾角取值。
当取值不可实施时,比如要求下倾角设置为16°,但天线内置电下倾为6°,需要设置机械下倾为10°,已经超出8°的限制,将产生波形畸变,说明此站点的站高过高、站间距过近或相邻站点高度相差悬殊,需要重新选址和调整站高。
站点的类蜂窝布局直接决定了扇区方位角,当站点疏密不均,没有按照蜂窝状布局时,将导致扇区的夹角不能设置为90°~150°,导致扇区间的重叠覆盖严重。
为了保证网络性能,需要在规划阶段按照最优网络结构的要求,选择合适的站点进行建设。
结合中兴通讯实际经验,最优网络结构建议为:站高在30~50m之间;城区站间距在300~500m之间,避免过近站点(站间距小于100m);尽量按照蜂窝结构分布。
