最新七年级数学上册 一次函数之动点问题讲义 (新版)鲁教版
最新学年七年级数学上册 一次函数图象的应用讲义 (新版)鲁教版(考试必备)

一次函数图象的应用(讲义)课前预习1. 我们一般从四个方面来研究一次函数,这四个方面分别是 、 、 、 . 具体来说:2. 若一次函数 y =kx +b 的图象不经过第二象限,则 k 0, b 0.3. 已知 m >0,n <0,请在如图所示的坐标系中分别作出 y =mx +n , y =nx +m 的大致图象.第 4 题图4. 如图,直线 y 12x 与直线 y 2 2x 4 相交于点 A ,请回答下列问题:当 x =-3 时, y 1 y 2 ;当 x =-1 时, y 1 y 2 ;当 x =1 时, y 1 y 2 .知识点睛1. 函数图象共存问题选定一个函数图象,根据图象性质判断 k ,b 符号,验证另一个函数图象存在的合理性.2. 数形结合求范围已知自变量 x 的取值范围求因变量 y 的取值范围:①在图上标出 x 的取值范围;②对应到函数的图象上;③根据对应的图象确定 y 的取值范围.若已知因变量 y 的取值范围求自变量 x 的取值范围,操作方式和上述类似.举例:当 x 1<x <x 2 时,y 1<y <y 2 当 x 1<x <x 2 时,y 2<y <y 1多个函数比大小:① ;② ;③ .精讲精练1. 若实数 a ,b ,c 满足 a +b +c =0,且 a <b <c ,则函数 y =ax +c 的图象可能是( )A .B .C .D .2. 一次函数 y =kx -k 的图象可能是( )A .B .C .D .3. 在同一坐标系中,正比例函数 y =kx 与一次函数 y =x -k 的图象可能是( )A .B .C .D . 4. 已知一次函数 y =mx +n 与正比例函数 y =mnx (m ,n 为常数, 且 mn ≠0),它们在同一平面直角坐标系中的图象可能是( )A .B .C .D .5. 两个一次函数 y 1=mx +n ,y 2=nx +m ,它们在同一平面直角坐标系中的图象可能是( )A .B .C .D .6. 如图,直线 y 2x 5 的图象如图所示,回答下列问题:(1)当-2<x < 1 时,y 的取值范围是 ;2(2)当-1<x ≤1 时,y 的取值范围是 .第 6 题图 第 7 题图7. 如图,直线y 2 x 4 的图象如图所示,回答下列问题:3(1)当 6<y ≤8 时,x 的取值范围是 ;(2)当-2≤y ≤2 时,x 的取值范围是 .8. 一次函数 y =kx +b (k ≠0),当-2≤x ≤5 时,对应的 y 值取值范围为 0≤y ≤7,则一次函数的解析式为 .9. 已知一次函数 y =kx +b 的图象如图所示,回答下列问题:(1)当 x <1 时,y 的取值范围是 ;(2)当 x ≥0 时,y 的取值范围是 .10. 已知一次函数 y =kx +b 的图象如图所示,回答下列问题:(1)当 y >0 时,x 的取值范围是 ;(2)当 y <2 时,x 的取值范围是 .11. 已知一次函数 y 2x 1的图象如图所示,回答下列问题:(1)当-1≤x <0 时,y 的取值范围是 ;(2)当 y >2 时,x 的取值范围是 .12. 如图,直线 y 1=kx +b 经过点 A (-1,-2)和点 B (-2,0),直线 y 2=2x过点 A ,当 y 1<y 2 时,x 的取值范围是 .第 12 题图 第 13 题图13. 如图,直线 y 1=3x +b 和 y 2=ax -3 的图象交于点 P (-2,-5),当y 1>y 2 时,x 的取值范围是 . 14. 如图所示,函数 y 1=|x |和 y 2 1 x 4 的图象相交于(-1,1), 3 3(2,2)两点.当 y 1>y 2 时,x 的取值范围是( )A .x <-1B .-1<x <2C .x >2D .x <-1 或 x >22=ax【参考答案】课前预习1. 表达式,图象,性质,计算表达式:y=kx+b(k,b 为常数,k≠0)图象:一条直线增减性:k>0,y 随x 增大而增大k<0,y 随x 增大而减小过象限:k>0,b>0,过第一、二、三象限k>0,b<0,过第一、三、四象限k<0,b>0,过第一、二、四象限k<0,b<0,过第二、三、四象限2. >,≤3. 略4. <,=,>知识点睛2. 找交点,作直线,定左右精讲精练1.A2. C3. B4.A5. C6. (1)1<y<4;(2)3<y≤77. (1)6≤x3;(2)3≤x≤98. y=x+2 或y=-x+59. (1)y<0;(2)y≥-210. (1)x<1;(2)x>0111. (1)-1≤y<1;(2)x212. x>-113. x>-214. D。
七年级数学上册 一次函数之动点问题习题 (新版)鲁教版
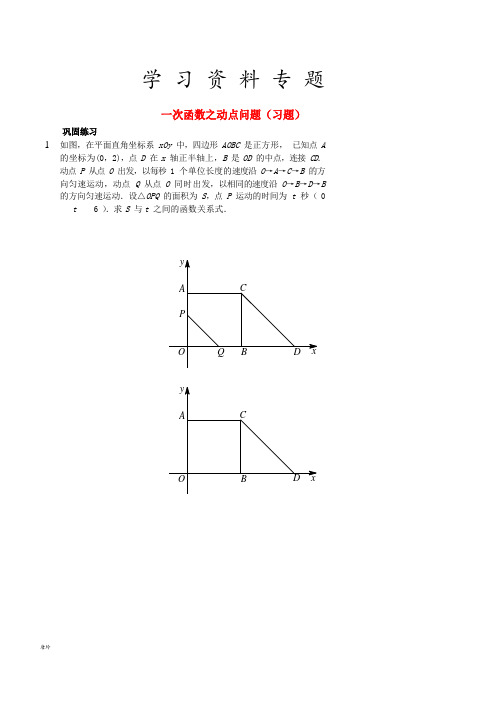
学习资料专题一次函数之动点问题(习题)巩固练习1.如图,在平面直角坐标系xOy 中,四边形AOBC 是正方形,已知点A的坐标为(0,2),点D 在x 轴正半轴上,B 是OD 的中点,连接CD.动点P 从点O 出发,以每秒 1 个单位长度的速度沿O→A→C→B 的方向匀速运动,动点Q 从点O 同时出发,以相同的速度沿O→B→D→B 的方向匀速运动.设△OPQ 的面积为S,点P 运动的时间为t 秒(0 t 6).求S 与t 之间的函数关系式.2 2. 如图,直线 y =x +4 与 x 轴、y 轴分别交于点 A ,B ,直线 y =-x +b 过点 B,且与 x 轴交于点 C .动点 P 从点 C 出发,沿 CA 方向以每秒 1 个单位长度的速度向点 A 运动,动点 Q 从点 A 同时出发,沿折线 AB -BC 以每秒 个单位长度的速度向点C 运 动,当其中一点到达终点时,另一点也随之停止.设点 P 运动的时间为 t 秒.(1)设△CPQ 的面积为 S ,求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围.(这里规定线段是面积为 0 的三角形)(2)当0 t ≤ 4 时,是否存在某一时刻,使得△APQ 是等腰三角形?若存在,求出相应的 t 值;若不存在,请说明理由.3.如图,直线y3 x23 与x 轴、y 轴分别交于点A,B,与直线y 3x 交于点C.动点P 从点A 出发,以每秒 1 个单位长度的速度沿AO-OB 向终点B 运动,动点Q 从原点O 同时出发,以相同的速度沿折线OC-CA 向终点A 运动,设点P 运动时间为t 秒.(1)设△OPQ 的面积为S,求S 与t 之间的函数关系式,并写出自变量t 的取值范围.(这里规定线段是面积为 0 的三角形)(2)当3 ≤t ≤6 时,是否存在某一时刻,使得△APQ 是等腰三角形?若存在,求出相应的t 值;若不存在,请说明理由.3思考小结什么是动点问题?由速度已知的点的运动产生的几何问题称为动点问题.一般情况下,我们如何处理动点问题?(1)研究背景图形把函数信息(坐标或表达式)转化为背景图形的信息(2)分析运动过程,分段、定范围分析运动过程常借助运动状态分析图:①起点、终点、速度——确定时间范围②状态转折点——决定分段③所求目标——明确方向(3)分析几何特征、表达、设计方案求解分段画图,表达相关线段长,列方程求解,回归范围进行验证.。
最新学年七年级数学上册 一次函数与几何综合(二)讲义 (新版)鲁教版(考试必备)

一次函数与几何综合(二)(讲义)课前预习1.如图,在平面直角坐标系xOy 中,已知A(1,2),B(3,5),C(6,3),求△ABC 的面积.2.用铅笔做讲义第 1,2 题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了2~3 分钟)重复上述动作,若仍无法解决,课堂重点听.知识点睛1. 坐标系中处理问题的两种基本方法:①从函数特征出发,设点坐标, , 借助 列方程求解.②从几何特征出发,设线段长, , 借助 列方程求解.2. 坐标系中处理面积问题,要寻找并利用 的线,通常有以下三种思路:①公式法(规则图形);②割补法(分割求和、补形作差);③转化法(例:同底等高).3. 坐标系中面积问题的处理方法举例割补求面积(铅垂法):BS △ APB 1 PM (x2B x A )精讲精练1. 如图,点 A 在直线 l 1:y =3x 上,且点 A 在第一象限,过点 A 作 AB⊥x 轴,交直线 l 2:y =x 于点 B .若 AB =3,则点 A 的坐标是 .第 1 题图 第 2 题图2. 如图,已知函数y 1 x b 的图象与 x 轴、y 轴分别交于点 A ,2B ,与函数 y =x 的图象交于点 M ,点 M 的横坐标为 2,点C 为线段 AM 上一点,过点 C 作 x 轴的垂线,垂足为点D ,交函数 y =x 的图象于点E .若 ED =4CD ,则点 E 的坐标为 .3. 如图,在平面直角坐标系中,直线 OM 经过点 A (6,6),过 A作正方形 ABCD ,在直线 OA 上有一点 E ,过 E 作正方形EFGH .已知正方形的边长与坐标轴平行,直线 OC 经过点 G , 且正方形 ABCD 的边长为 2,正方形 EFGH 的边长为 3,则点 F 的坐标为 .y 1 y =-2 x +b B y =xE MCO D A x4. 如图,在平面直角坐标系中,点 A ,C 和 B ,D 分别在直线 y 1 x 3 和 x 轴上,若△OA B ,△BC D 都是等腰直角三角形,2则点 C5. 如图,在平面直角坐标系中,已知 A (2,3),B (4,2),则△AOB 的面积为 _.第 5 题图 第 6 题图6. 如图,A ,B 是直线 y = kx 7 上的两点,点 A 的坐标为(-1,43),点 B 的横坐标为 3,则△AOB 的面积为 . 7. 如图,直线 y =-x +4 与 x 轴、y 轴分别交于点 A ,B ,点 P 的坐标为(-2,2),则 S △PAB = .第7题图 第8题图8. 如图,直线 AB :y =x +1 与 x 轴、y 轴分别交于点 A ,B ,直线CD :y =kx -2与 x 轴、y 轴分别交于点 C ,D ,直线 AB 与直线CD 交于点 P .若 S △APD =4.5,则 k 的值为 .9.如图,在平面直角坐标系中,已知A(2,4),B(6,6),C(8,2),则四边形OABC的面积为.10.如图,已知直线l1,l2 相交于点A(2,1),点B(8,4)在l1 上,l2 的表达式为y=2x-3.C 为l2 上的一个动点,且在点A 的右侧,若△ABC 的面积为 9,求点C 的坐标.11.如图,直线l1:y=x 与直线l2:y=-2x+3 相交于点A,点B 在直线l1 上,且横坐标为4.C 为l2 上的一个动点,且在点A 的左侧,若△ABC 的面积为9,则点C 的坐标为., 【参考答案】课前预习1. 13 2知识点睛1. ①坐标转线段长,几何特征②线段长转坐标,函数特征 2. 横平竖直精讲精练1. ( 39 )2 2 2. (4,4)3. (9,6)4. (30,18)5. 46. 727. 88. 529. 2410. C (4,5)11. (-1,5)。
精品学习2017-2018学年七年级数学上册 一次函数计算讲义 (新版)鲁教版

⎨ ⎨一次函数计算(讲义)课前预习1. 要画出一次函数 y kx b 的图象,需要 个点的坐标,通常找 , ;正比例函数图象经过坐标原点,因此只需再确定点即可,通常找.2.计算下列各式:2k b 0 ①b 4y 2x 3 ② y x 53.x 轴上的点 坐标等于零;y 轴上的点 坐标等于零;平行于 x 轴的直线上的点 坐标相同;平行于 y 轴的直线上的点坐标相同.4.一次函数 y =3x +4 与 y 轴的交点坐标是 ;若一次函数 y =3x +b 与 y 轴的交点为(0,4),则 b = ,一次函数的表达式为 .知识点睛一、数形结合看函数从“数”的角度看从“形”的角度看坐标(二元一次方程的一组解)平面内一点代入一次函数的表达式(二元一次方程)一条直线(一次函数的图象)联立交点坐标(二元一次方程组的解)二、特征及操作直线的交点(一次函数图象的交点)函数图象经过一点(即点在直线上),坐标代入表达式;求交点坐标,联立两个函数的表达式,解方程组;已知两点坐标求一次函数表达式,利用待定系数法.精讲精练1. 若点M 在函数y=2x-1 的图象上,则点M 的坐标可能是()A.(-1,0) B.(0,-l) C.(1,-1) D.(2,4)2. 若直线y=2x+1 经过点(m+2,1-m),则m= .3.一次函数y=-2x+3 的图象与x 轴交于点,与y 轴交于点.4.在一次函数y 1 x 1 的图象上,到y 轴的距离为 1 的点的2 2坐标为.5.若点(3,-4)在正比例函数y=kx 的图象上,那么这个函数的解析式为()待定系数法:一设、二代、三解、四还原6.若正比例函数的图象经过点(-1,2),则这个图象必经过点()A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)7.已知某个一次函数的图象经过点A(-2,0),B(0,4),求这个函数的表达式.8.已知某个一次函数的图象经过点A(3,0),B(0,-2),求这个函数的表达式.9.若一次函数y=kx+3 的图象经过点A(1,2),求这个函数的表达式.10. 若一次函数 y=2x+b 的图象经过点 A (-1,1),则 b =,该函数图象经过点 B (1, )和点 C ( ,0).11. 已知直线 y =kx +b 与直线 y =-x +1 平行,且过点(8,2),则一次函数的表达式是.12. 如图,直线 l 是一次函数 y =kx +b 的图象,填空:(1)k = ,b =;(2)当 x =4 时,y = ; (3)当 y =2 时,x = .13. 已知 y 是 x 的一次函数,下表给出了部分对应值:的值是 .14. 在同一平面直角坐标系中,一次函数 y=-x +3 与 y =3x -5 的图象交于点 M ,求点 M 的坐标.15. 若直线 y =2x+b 经过直线 y=x -2 与直线 y =3x +4 的交点,则 b的值为( ) A .-11B .-1C .1D .616. 当 b= 时,直线 y =2x +b 与 y =3x -4 的交点在 x 轴上. 17. 点 A ,B ,C ,D 的坐标如图所示,求直线 AB 与直线 CD 的交点 E 的坐标.1 21 21218. 如图,直线 l 1,l 2 相交于点 A .求 A 的坐标.19. (1)两直线l 1:y k 1x b 1 ,l 2:y k 2 x b 2 的位置关系与关于x ,y 的二元一次方程组(其中 4 个常数均不为零.每小题第一个空选填“唯一”、“无” 或“无穷多组”;其余空选填“=”或“≠”) ①当l 1 与l 2 相交时,方程组有 解, k 1k 2 . ②当l 1 与l 2 平行时,方程组 解, k 1k 2 , b 1b 2 . ③当l 1 与l 2 重合时,方程组有 解, k 1k 2, b 1 b 2 .(2)若将两直线写成l 1:a 1x b 1 y c 1 , l 2:a 2 x b 2 yc 2 的形组的角度考虑解的情况:(其中 6 个常数均不为零.每小题第一个空选填“唯一”、“无” 或“无穷多组”;其余空选填“相交”、“平行”或“重合”)①当 a 1 b 1时,方程组有 解, l 与l . a 2 b 2 ②当 a 1 b 1 c 1时,方程组 解, l 与l . a 2 b 2 c 2 ③当 a 1 b 1 = c 1时,方程组有 解, l 与l . a 2 b 2 c 2O 2 -1 -1 -254321 l A 12345 l 220. 如果方程组有无穷多组解,那么方程组 kx 2 y75x 4 y 8的解的情况是()A .唯一解B .无穷多组解C .无解D .都有可能21. 已知直线 y =x -3 与 y =2x +2 的交点为(-5,-8),则方程组的解是 ;一次函数 yx 1的图象与y2x 5 的图象的交点坐标是.① ② 【参考答案】课前预习 1. 两, (b,0) ,(0,b );一,(1,k )kk2x 22. b 4;y 73. 纵,横,纵,横4. (0 ,4) ,4, y 3x 4精讲精练 1. B2.4 3 3. ( 3,0),(0,3)24. (1,1)或(-1,0)5. B6. D7. y =2x +48. y 2x 239. y x 3 10. 3,5,3211. y =-x +1012. (1) 1,12(2)-1 (3)-2 13. -13 14. M (2,1) 15. C 16.8317. E (-2,2) 18.19. (1)①唯一,≠;②无,=,≠;③无穷多组,=,=(2)①唯一,相交;②无,平行;③无穷多组,重合20. A21. (-5,-8),(-2,-1)。
最新学年七年级数学上册 一次函数的表达式、图象、性质讲义 (新版)鲁教版(考试必备)

一次函数的表达式、图象、性质(讲义)课前预习1.在一个变化过程中,我们称数值发生变化的量为,数值始终不变的量为;变量分为和.2.表示变量之间的关系通常有三种方法,它们是、、.3.如图,在平面直角坐标系xOy 中,描出下列点的坐标:A(1,2),B(2,4),C(-1,-2),D(1,1),E(-1,3),F(1,-3).(1)作出直线BC;(2)C,D,E,F 四点中,在直线AB 上的是.知识点睛1.函数(1)一般地,如果在一个变化过程中有x 和y,并且对于任意一个x 都有的一个y 和它对应,那么我们称y 是x 的函数,其中x 是,y 是.(2)表示函数的方法一般有、和.2.一次函数(1)表达式(也称“解析式”或“关系式”).特别地,当b=0 时,称y 是x 的正比例函数(y=kx,k 为常数,k≠0).(2)图象画函数图象的一般步骤:列表、描点、连线.①一次函数图象是,因此画一次函数的图象时,只需确定点即可,通常找、;②正比例函数图象是一条经过的,因此画正比例函数的图象时,只需再确定点即可,通常找.(3)性质①k 反映图象的.当k>0 时,图象过第象限;当k<0 时,图象过第象限.若两条直线互相平行,则k 1 k2 .②b 是直线与y 轴交点的坐标.当k>0 且b>0 时,图象过第象限;当k>0 且b<0 时,图象过第象限;当k<0 且b>0 时,图象过第象限;当k<0 且b<0 时,图象过第象限.③增减性当k>0 时,y 的值随着x 值的增大而(即y 与x);当k<0 时,y 的值随着x 值的增大而(即y 与x).示意图精讲精练1. 下列各曲线中,不能表示 y 是 x 的函数的是()A .B .D .2. 已知下列函数关系式:①y =2x +1;② y1;③y =x 2-1;x④y =-8x ;⑤y =3.其中表示一次函数的有( ) A .1 个B .2 个C .3 个D .4 个3. 已知函数 y =(k -2)x +2k +1,当 k时,它是正比例函数;当 k时,它是一次函数.4. 已知函数 y =(m -2)x 2n +1-m +n ,当 m = ,n = 时,它是正比例函数;当 m ,n = 时,它是一次函数.5. (1)点(1,-1) (填“在”或“不在”)直线 y =2x -3 上;试写出直线 y =2x -3 上任意一点的坐标 . (2)满足关系式 y =2x -3 的 x ,y 所对应的点(x ,y )都在一次函数 的图象上;一次函数 y =2x -3 的图象上的点(x ,y )都满足关系式_ .6.下列四个点,在正比例函数 y 2x 的图象上的是( )5A .(2,5)B .(5,2)C .(2,-5)D .(5,-2)7.若点(m ,n )在函数 y =2x +1 的图象上,则 2m -n 的值是( )A .2B .-2C .1D .-18.(1)正比例函数 y =3x 的图象经过 象限;(2)一次函数 y =x +2 的图象经过 象限; (3)一次函数 y =-5x -3 的图象经过象限.9.已知一次函数y=kx+b 的图象经过第一、二、三象限,则b 的值可以是()A.-2 B.-1 C.0 D.210.已知一次函数y=kx+b 的图象如图所示,下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<011.一次函数y=kx+b 中,若k<0,b>0)A .第一象限B.第二象限C.第三象限D.第四象限12.下列一次函数:①y=5x-6;②y=-0.3x+3;③y=x-3;④y= ( 6)x .其中y 的值随x 的增大而减小的是.(填写序号)13.若y=kx-4 的函数值y 随x 的增大而增大,则k 的值可能是()A.-4 B.12C.0 D.314.若一次函数y=kx+b 的函数值y 随x 的增大而减小,且图象与y 轴的负半轴相交,则对k 和b 的符号判断正确的是()A.k>0,b>0 B.k>0,b<0C.k<0,b>0 D.k<0,b<015.已知一次函数y=kx-k,若y 随x 的增大而增大,则该函数的图象经过()A.第一、二、三象限B.第一、二、四象限 C.第二、三、四象限D.第一、三、四象限16.一次函数y=kx+b 满足kb>0,且y 随x 的增大而减小,则此函数的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限5 517. 已知函数 y =kx +b 的图象如图所示,则函数 y =2kx +b 的图象可能是()A .B .C .D .18. 直线 y =-x 与 y =-x +5 的位置关系是,直线 y =-x 的图象可以看作是由直线 y =-x +5 .19. 若直线y =(2m -1)x +m -2 与直线 y =-3x -1 平行,则 m =.20. 将直线 y =2x 向上平移两个单位,所得的直线是()A .y =2x +2B .y =2x -2C .y =2(x -2)D .y =2(x +2)21. 对于一次函数 y =-2x +4,下列结论错误的是()A .函数值随自变量的增大而减小B .函数的图象不经过第三象限C .函数的图象向上平移 2 个单位得到 y =-2x 的图象D .函数的图象与 y 轴的交点坐标是(0,4)【参考答案】课前预习1. 变量,常量,自变量,因变量2. 列表法,关系式法,图象法3. (1)略;(2)点 C知识点睛1. (1)两个变量,唯一,自变量,因变量(2)列表法,关系式法,图象法2. (1) y kx b (k ,b 是常数,k 0)(2)①一条直线,两, ( b,0) ,(0,b )k②原点,直线,一,(1,k )(3)①倾斜程度;一、三;二、四②纵;一、二、三;一、三、四;一、二、四;二、三、四 ③增大,同向变化;减小,反向变化精讲精练1. C2. B3.1,≠2 24. 0,0,≠2,05. (1)在,(2,1)(答案不唯一);(2)y =2x -3,y =2x -36. D7. D8. (1)第一、三;(2)第一、二、三;(3)第二、三、四 9. D 10. B11. C 12. ②④ 13. D 14. D 15. D 16. A 17. C18. 平行,向下平移 5 个单位得到的19.-120. A C 21.。
2019学年七年级数学上册 一次函数应用题讲义 (新版)鲁教版

一次函数应用题(讲义)知识点睛1.理解题意:结合图象依次分析的实际意义,把函数图象与对应起来,可借助示意图(如线段图)等梳理信息.2.利用解决问题:把所求目标转化为函数元素,利用表达式进行求解;另外,当实际场景发生变化时,要分析或者.3.结合实际场景验证所求结果.精讲精练1.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地的过程中y 与x 之间的函数关系.(1)根据图中信息,求线段AB 所在直线的函数表达式以及甲乙两地之间的距离;(2)已知两车相遇时快车比慢车多行驶 40 千米,求快车从甲地到达乙地所需的时间;(3)出发多长时间,两车相距 100 千米?O 1.5 2 ? x/小时2.一辆快车和一辆慢车分别从A,B 两站同时出发,相向而行.快车到达B 站后,停留 1 小时,然后原路原速返回 A 站,慢车到达 A 站即停运休息.如图表示的是两车之间的距离y(千米)与行驶时间x(小时)之间的函数图象.请结合图象信息,解答下列问题:(1)直接写出快车、慢车的速度及 A,B 两站间的距离;(2)求快车从 B 站返回 A 站时,y 与x 之间的函数关系式;(3)出发几小时,两车相距 200 千米?请直接写出答案.O 6 10 1115 21 x/小时3.某地发生特大暴雨灾害,受其影响,某药品的需求量急增.如图所示,平常对某种药品的需求量y1(万件)、供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+70,y2=2x-38,需求量为 0 时,即停止供应.当y1=y2 时,该药品的价格称为稳定价格,需求量称为稳定需求量.(1)求该药品的稳定价格与稳定需求量.(2)价格在什么范围内,该药品的需求量低于供应量?(3)由于灾情严重,政府部门决定对药品供应方提供价格补贴来提高供货价格,以提高供应量.根据调查统计,需将稳定需求量增加 6 万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量?y1元/件)4.甲船从 A 港出发顺流匀速驶向 B 港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向 B 港.乙船从 B 港出发逆流匀速驶向 A 港.已知救生圈漂流的速度和水流速度相同,甲、乙两船在静水中的速度相同,甲、乙两船到 A 港的距离y1,y2(km)与行驶时间x(h)之间的函数图象如图所示.(1)乙船在逆流中行驶的速度为;(2)求甲船在逆流中行驶的路程;(3)求甲船到A港的距离y1 与行驶时间x 之间的函数关系式;(4)救生圈落入水中时,甲船到 A 港的距离是多少?O?? ? 【参考答案】知识点睛1. 轴、点、线,实际场景2. 函数图象,函数图象的变化,构造函数图象精讲精练1. (1)所求函数解析式为 y =-140x +280(0≤x ≤2),甲、乙两地之间的距离是 280 千米(2)3.5 小时(3) 9 小时或19 小时7 72.(1)快车的速度是 120 千米/小时; 慢车的速度是 80 千米/小时;A ,B 两站间的距离是 1 200 千米40x 1320 (11≤ x ≤15)(2)y 120x 2520 (15< x ≤21) (3)5 小时,7 小时或 58 小时33.(1)该药品的稳定价格是 36 元/件,稳定需求量是 34 万件(2)价格 x (元/件)满足36 < x <70 时,该药品的需求量低于供应量 (3)9 元4. (1)6 km/h(2)3 km9x (0≤ x ≤2)(3) y 1 6x 30 (2< x ≤ 2.5) 15 9x 2 (4) 27 km2(2.5< x ≤3.5)。
2022秋七年级数学上册第六章一次函数全章热门考点整合应用课件鲁教版五四制
解:因为图象与y轴的交点位于原点下方,即点 (0,12-3k)位于原点下方,所以12-3k<0,可 得k>4.所以k-2>0.所以函数值随着自变量的增 大而增大.
(2)如果函数值随着自变量的增大而增大,且函数图象与y 轴的交点位于原点上方,确定满足条件的正整数k的值. 解:因为函数值随着自变量的增大而增大,所以k- 2>0,可得k>2. 因 为 函 数 图 象 与 y 轴 的 交 点 位 于 原 点 上 方 , 所 以 12 - 3k>0,可得k<4. 所以k的取值范围为2<k<4. 所以满足条件的正整数k的值为3.
6 若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=ax +c的图象可能是( A )
7 【2021·长沙明德中学月考】已知点M(1,a)和点 N(2,b)是一次函数y=-2x+1的图象上的两点, 则a与b的大小关系是( A ) A.a>b B.a=b C.a<b D.无法确定
已知一次函数的表达式是y=(k-2)x+12-3k. 8
(2)判断点C(4,-2)是否在该一次函数的图象 上,说明理由;
解:点C(4,-2)不在该一次函数的图象上. 理由如下: 对于y=-x+3,当x=4时,y=-1≠-2, 所以点C(4,-2)不在该一次函数的图象上.
(3) 若 该 一 次 函 数 的 图 象 与 x 轴 交 于 D 点 , 求 △BOD的面积.
2 求下列函数中自变量的取值范围: (1)y=-12x2-x+6;
解:x为一切实数.
(2)y=-12x1-3;
解:因为
12x-3≠0,所以
1 x≠4.
七年级数学上册一次函数之动点问题讲义(新版)鲁教版

P一次函数之动点问题(讲义)课前预习1. 由点的运动(速度已知)产生的几何问题称为动点问题. 动点问题的解决方法: (1)研究 ;(2)分析 ,分段; (3)表达,建方程.2. 根据前期训练的标准动作及上述内容,完成下题.如图,△ABC 是边长为 6 的等边三角形.动点 P 从点 A 出发, 沿折线 AB -BC 以每秒 2 个单位长度的速度运动,过点 P 作PQ ⊥AC 于点 Q .设点 P 运动的时间为 t 秒,请用含 t 的式子 分别表达出 PQ 和 AQ 的长. B思路分析: AQC( 2/ s )P : A3sB3sC ( 0 ≤ t ≤ 6)①当0 ≤ t ≤ 3 时,PQ = _,AQ =; ②当 3 t ≤ 6 时,PQ =_,AQ =.3. 用铅笔做讲义第 1,2 题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了 2~3 分钟) 重复上述动作,若仍无法解决,课堂重点听.知识点睛1.动点问题的特征是,主要考查运动的.2.一次函数背景下解决动点问题的思考方向:(1)研究背景图形把函数信息(坐标或表达式)转化为背景图形的信息(2)分析运动过程,分段、定范围分析运动过程常借助运动状态分析图:①起点、终点、速度——确定时间范围②状态转折点——决定分段③所求目标——明确方向(3)分析几何特征、表达、设计方案求解分段画图,表达相关线段长,列方程求解,回归范围进行验证.精讲精练1. 如图,直线y3x4与 x 轴、y 轴分别交于点 A ,B ,直线 BC 与 x 轴交于点 C ,∠ABC =60°.动点 P 从点 A 出发,以每秒 1 个单位长度的速度沿线段 AC 向点 C 运动(不与点 A ,C 重合),动点 Q 从点 C 同时出发,以每秒 2 个单位长度的速度沿折线 CB -BA 向点 A 运动(不与点 A ,C 重合).设△APQ 的面积为 S ,运动时间为 t (秒),求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围.32.如图,直线y x 2 与x 轴、y 轴分别交于点A,B,与直线y=x 交于点C.动点P 从原点O 出发,以每秒 2 个单位长度的速度沿O→B→A 的路线向终点A 运动(点P 不与点O,A 重合),动点Q 从点A 同时出发,以每秒 1 个单位长度的速度沿A→O→C 的路线向终点C 运动(点Q不与点A,C 重合),设点P 运动的时间为t(秒).设△APQ 的面积为S,求S 与t 之间的函数关系式,并写出自变量t 的取值范围.3.如图,直线 y 3x 2 3 与 x 轴、y 轴分别交于点 A ,B ,与 直线y 3 x 交于点 C .动点 E 从原点 O 出发,以每秒 1 个3单位长度的速度沿 OA 方向向终点 A 运动,动点 F 从点 A 同时出发,以每秒 1 个单位长度的速度沿折线 AC -CO 向终点 O 运动,设点 F 运动的时间为 t (秒).(1)设△OEF 的面积为 S ,求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围.(这里规定:线段是面积为零的三角形) (2)当1≤ t ≤ 2 时,是否存在某一时刻,使得△OEF 是等腰三角形?若存在,求出 t 的值;若不存在,请说明理由.B COABCOAyBCOA4.如图,点A 在直线y 3 x 上,过点A 作AC⊥x 轴于点C,3AC=2,过点A 作AB⊥y 轴于点B.动点P 从点O 出发,以每秒1 个单位长度的速度沿O→B→A→O 的路线向点O 运动;同时动点Q 以相同的速度沿C→A→O→C 的路线向点C 运动,设点P 运动的时间为t (秒).(1)设△OPQ 的面积为S,求S 与t 之间的函数关系式,并写出自变量t 的取值范围.(这里规定:线段是面积为零的三角形)(2)当点Q 在OC 上运动时,是否存在某一时刻,使△OPQ 是等腰三角形?若存在,求出相应的t 值;若不存在,请说明理由.AAA。
七年级数学上册 一次函数计算讲义 (新版)鲁教版

⎨ ⎨亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学 习 资 料 专 题一次函数计算(讲义)课前预习1. 要画出一次函数 y kx b 的图象,需要 个点的坐标,通常找 , ;正比例函数图象经过坐标原点,因此只需再确定点即可,通常找.2.计算下列各式:2k b 0 ①b 4y 2x 3 ② y x 53.x 轴上的点 坐标等于零;y 轴上的点 坐标等于零;平行于 x 轴的直线上的点 坐标相同;平行于 y 轴的直线上的点坐标相同.4.一次函数 y =3x +4 与 y 轴的交点坐标是 ;若一次函数 y =3x +b 与 y 轴的交点为(0,4),则 b = ,一次函数的表达式为 .知识点睛一、数形结合看函数从“数”的角度看从“形”的角度看坐标(二元一次方程的一组解)平面内一点代入一次函数的表达式(二元一次方程)一条直线(一次函数的图象)联立交点坐标(二元一次方程组的解)二、特征及操作直线的交点(一次函数图象的交点)函数图象经过一点(即点在直线上),坐标代入表达式;求交点坐标,联立两个函数的表达式,解方程组;已知两点坐标求一次函数表达式,利用待定系数法.精讲精练1. 若点M 在函数y=2x-1 的图象上,则点M 的坐标可能是()A.(-1,0) B.(0,-l) C.(1,-1) D.(2,4)2. 若直线y=2x+1 经过点(m+2,1-m),则m= .3.一次函数y=-2x+3 的图象与x 轴交于点,与y 轴交于点.4.在一次函数y 1 x 1 的图象上,到y 轴的距离为 1 的点的2 2坐标为.5.若点(3,-4)在正比例函数y=kx 的图象上,那么这个函数的解析式为()待定系数法:一设、二代、三解、四还原6.若正比例函数的图象经过点(-1,2),则这个图象必经过点()A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)7.已知某个一次函数的图象经过点A(-2,0),B(0,4),求这个函数的表达式.8.已知某个一次函数的图象经过点A(3,0),B(0,-2),求这个函数的表达式.9.若一次函数y=kx+3 的图象经过点A(1,2),求这个函数的表达式.10. 若一次函数 y=2x+b 的图象经过点 A (-1,1),则 b =,该函数图象经过点 B (1, )和点 C ( ,0).11. 已知直线 y =kx +b 与直线 y =-x +1 平行,且过点(8,2),则一次函数的表达式是.12. 如图,直线 l 是一次函数 y =kx +b 的图象,填空:(1)k = ,b =;(2)当 x =4 时,y = ; (3)当 y =2 时,x = .13. 已知 y 是 x 的一次函数,下表给出了部分对应值:的值是 .14. 在同一平面直角坐标系中,一次函数 y=-x +3 与 y =3x -5 的图象交于点 M ,求点 M 的坐标.15. 若直线 y =2x+b 经过直线 y=x -2 与直线 y =3x +4 的交点,则 b的值为( ) A .-11B .-1C .1D .616. 当 b= 时,直线 y =2x +b 与 y =3x -4 的交点在 x 轴上. 17. 点 A ,B ,C ,D 的坐标如图所示,求直线 AB 与直线 CD 的交点 E 的坐标.1 21 21218. 如图,直线 l 1,l 2 相交于点 A .求 A 的坐标.19. (1)两直线l 1:y k 1x b 1 ,l 2:y k 2 x b 2 的位置关系与关于x ,y 的二元一次方程组(其中 4 个常数均不为零.每小题第一个空选填“唯一”、“无” 或“无穷多组”;其余空选填“=”或“≠”) ①当l 1 与l 2 相交时,方程组有 解, k 1k 2 . ②当l 1 与l 2 平行时,方程组 解, k 1k 2 , b 1b 2 . ③当l 1 与l 2 重合时,方程组有 解, k 1k 2, b 1 b 2 .(2)若将两直线写成l 1:a 1x b 1 y c 1 , l 2:a 2 x b 2 yc 2 的形组的角度考虑解的情况:(其中 6 个常数均不为零.每小题第一个空选填“唯一”、“无” 或“无穷多组”;其余空选填“相交”、“平行”或“重合”)①当 a 1 b 1时,方程组有 解, l 与l . a 2 b 2 ②当 a 1 b 1 c 1时,方程组 解, l 与l . a 2 b 2 c 2 ③当 a 1 b 1 = c 1时,方程组有 解, l 与l . a 2 b 2 c 2O 2 -1 -1 -254321 l A 12345 l 220. 如果方程组有无穷多组解,那么方程组 kx 2 y75x 4 y 8的解的情况是()A .唯一解B .无穷多组解C .无解D .都有可能21. 已知直线 y =x -3 与 y =2x +2 的交点为(-5,-8),则方程组的解是 ;一次函数 yx 1的图象与y2x 5 的图象的交点坐标是.① ② 【参考答案】课前预习 1. 两, (b,0) ,(0,b );一,(1,k )kk2x 22. b 4;y 73. 纵,横,纵,横4. (0 ,4) ,4, y 3x 4精讲精练 1. B2.4 3 3. ( 3,0),(0,3)24. (1,1)或(-1,0)5. B6. D7. y =2x +48. y 2x 239. y x 3 10. 3,5,3211. y =-x +1012. (1) 1,12(2)-1 (3)-2 13. -13 14. M (2,1) 15. C 16.8317. E (-2,2) 18.19. (1)①唯一,≠;②无,=,≠;③无穷多组,=,=(2)①唯一,相交;②无,平行;③无穷多组,重合20. A21. (-5,-8),(-2,-1)。
七年级数学上册 一次函数与几何综合(二)讲义 (新版)鲁教版

一次函数与几何综合(二)(讲义)课前预习1.如图,在平面直角坐标系xOy 中,已知A(1,2),B(3,5),C(6,3),求△ABC 的面积.2.用铅笔做讲义第 1,2 题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了2~3 分钟)重复上述动作,若仍无法解决,课堂重点听.知识点睛1. 坐标系中处理问题的两种基本方法:①从函数特征出发,设点坐标, ,借助 列方程求解.②从几何特征出发,设线段长,, 借助列方程求解.2. 坐标系中处理面积问题,要寻找并利用的线,通常有以下三种思路: ①公式法(规则图形);②割补法(分割求和、补形作差); ③转化法(例:同底等高).3. 坐标系中面积问题的处理方法举例割补求面积(铅垂法):BS △ APB1PM (x2Bx A )精讲精练1. 如图,点 A 在直线 l 1:y =3x 上,且点 A 在第一象限,过点 A 作 AB ⊥x 轴,交直线 l 2:y =x 于点 B .若 AB =3,则点 A 的坐标是 .第 1 题图第 2 题图2.如图,已知函数y1x b 的图象与 x 轴、y 轴分别交于点 A ,2B ,与函数 y =x 的图象交于点 M ,点 M 的横坐标为 2,点C 为线段 AM 上一点,过点 C 作 x 轴的垂线,垂足为点D ,交函数 y =x 的图象于点E .若 ED =4CD ,则点 E 的坐标为 .3.如图,在平面直角坐标系中,直线 OM 经过点 A (6,6),过 A作正方形 ABCD ,在直线 OA 上有一点 E ,过 E 作正方形 EFGH .已知正方形的边长与坐标轴平行,直线 OC 经过点 G , 且正方形 ABCD 的边长为 2,正方形 EFGH 的边长为 3,则点 F 的坐标为 .y 1y =- 2x +bBy =x EMCOD Ax4.如图,在平面直角坐标系中,点 A ,C 和 B ,D 分别在直线y 1x 3 和 x 轴上,若△OA B ,△BC D 都是等腰直角三角形,2 则点 C5.如图,在平面直角坐标系中,已知 A (2,3),B (4,2),则△AOB 的面积为 _.第 5 题图第 6 题图6. 如图,A ,B 是直线 y = kx 7 上的两点,点 A 的坐标为(-1,43),点 B 的横坐标为 3,则△AOB 的面积为. 7.如图,直线 y =-x +4 与 x 轴、y 轴分别交于点 A ,B ,点 P 的坐标为(-2,2),则 S △PAB = .第7题图第8题图8.如图,直线 AB :y =x +1 与 x 轴、y 轴分别交于点 A ,B ,直线CD :y =kx -2与 x 轴、y 轴分别交于点 C ,D ,直线 AB 与直线 CD 交于点 P .若 S △APD =4.5,则 k 的值为 .9.如图,在平面直角坐标系中,已知A(2,4),B(6,6),C(8,2),则四边形OABC的面积为.10.如图,已知直线l1,l2 相交于点A(2,1),点B(8,4)在l1 上,l2 的表达式为y=2x-3.C 为l2 上的一个动点,且在点A 的右侧,若△ABC 的面积为 9,求点C 的坐标.11.如图,直线l1:y=x 与直线l2:y=-2x+3 相交于点A,点B 在直线l1 上,且横坐标为4.C 为l2 上的一个动点,且在点A 的左侧,若△ABC 的面积为9,则点C 的坐标为., 【参考答案】 课前预习 1. 13 2知识点睛1. ①坐标转线段长,几何特征②线段长转坐标,函数特征2. 横平竖直精讲精练1. ( 3 9 )2 2 2. (4,4) 3. (9,6) 4. (30,18) 5. 4 6. 7 2 7. 8 8. 5 2 9. 2410. C (4,5) 11. (-1,5)。
2019学年七年级数学上册 一次函数的表达式、图象、性质讲义 (新版)鲁教版

一次函数的表达式、图象、性质(讲义)课前预习1.在一个变化过程中,我们称数值发生变化的量为,数值始终不变的量为;变量分为和.2.表示变量之间的关系通常有三种方法,它们是、、.3.如图,在平面直角坐标系xOy 中,描出下列点的坐标:A(1,2),B(2,4),C(-1,-2),D(1,1),E(-1,3),F(1,-3).(1)作出直线BC;(2)C,D,E,F 四点中,在直线AB 上的是.知识点睛1. 函数(1)一般地,如果在一个变化过程中有 x 和 y ,并且对于任意一个 x 都有 的一个 y 和它对应,那么我们称 y 是 x 的函数,其中 x 是 ,y 是 . (2)表示函数的方法一般有 、 和 .2. 一次函数(1)表达式(也称“解析式”或“关系式”).特别地,当 b =0 时,称 y 是 x 的正比例函数(y =kx ,k 为常数,k≠0). (2)图象画函数图象的一般步骤:列表、描点、连线. ①一次函数图象是 ,因此画一次函数的图象时,只需确定点即可,通常找、;②正比例函数图象是一条经过 的 ,因此画正比例函数的图象时,只需再确定 点即可,通常找 . (3)性质①k 反映图象的 . 当 k >0 时,图象过第 象限;当 k <0 时,图象过第象限.若两条直线互相平行,则k 1 k 2 .②b 是直线与 y 轴交点的 坐标.当 k >0 且 b >0 时,图象过第 象限;当 k >0 且 b <0 时,图象过第 象限;当 k <0 且 b >0 时,图象过第 象限;当 k <0 且 b <0 时,图象过第 象限. ③增减性当k >0 时,y 的值随着x 值的增大而 (即y 与x );当k <0 时,y 的值随着x 值的增大而 (即y 与x).我们通常从表达式、图象、性质、计算四个方面研究函数.k >0,b >0 yxO k >0,b <0k <0,b >0精讲精练1. 下列各曲线中,不能表示 y 是 x 的函数的是()A .B .D .2. 已知下列函数关系式:①y =2x +1;② y1;③y =x 2-1;x④y =-8x ;⑤y =3.其中表示一次函数的有( ) A .1 个 B .2 个C .3 个D .4 个3. 已知函数 y =(k -2)x +2k +1,当 k时,它是正比例函数;当 k 时,它是一次函数.4. 已知函数 y =(m -2)x 2n +1-m +n ,当 m = ,n = 时,它是正比例函数;当 m,n = 时,它是一次函数.5. (1)点(1,-1) (填“在”或“不在”)直线 y =2x -3 上;试写出直线 y =2x -3 上任意一点的坐标 . (2)满足关系式 y =2x -3 的 x ,y 所对应的点(x ,y )都在一次函数 的图象上;一次函数 y =2x -3 的图象上的点(x ,y )都满足关系式_ .6.下列四个点,在正比例函数 y 2 x 的图象上的是( )5A .(2,5)B .(5,2)C .(2,-5)D .(5,-2)7.若点(m ,n )在函数 y =2x +1 的图象上,则 2m -n 的值是( )A .2B .-2C .1D .-18.(1)正比例函数 y =3x 的图象经过 象限;(2)一次函数 y =x +2 的图象经过 象限; (3)一次函数 y =-5x -3 的图象经过象限.9.已知一次函数y=kx+b 的图象经过第一、二、三象限,则b 的值可以是()A.-2 B.-1 C.0 D.210.已知一次函数y=kx+b 的图象如图所示,下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<011.一次函数y=kx+b 中,若k<0,b>0)A.第一象限BC.第三象限D.第四象限12.下列一次函数:①y=5x-6;②y=-0.3x+3;③y=x-3;④y= ( 6)x .其中y 的值随x 的增大而减小的是.(填写序号)13.若y=kx-4 的函数值y 随x 的增大而增大,则k 的值可能是()A.-4 B.12C.0 D.314.若一次函数y=kx+b 的函数值y 随x 的增大而减小,且图象与y 轴的负半轴相交,则对k 和b 的符号判断正确的是()A.k>0,b>0 B.k>0,b<0C.k<0,b>0 D.k<0,b<015.已知一次函数y=kx-k,若y 随x 的增大而增大,则该函数的图象经过()A.第一、二、三象限B.第一、二、四象限 C.第二、三、四象限D.第一、三、四象限16.一次函数y=kx+b 满足kb>0,且y 随x 的增大而减小,则此函数的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限5 517. 已知函数 y =kx +b 的图象如图所示,则函数 y =2kx +b 的图象可能是()A .B .C .D .18. 直线 y =-x 与 y =-x+5 的位置关系是,直线 y =-x 的图象可以看作是由直线 y =-x +5 .19.若直线 y =(2m -1)x +m -2 与直线 y =-3x -1 平行,则 m= .20. 将直线 y =2x 向上平移两个单位,所得的直线是()A .y =2x +2B .y =2x -2C .y =2(x -2)D .y =2(x +2)21. 对于一次函数 y =-2x +4,下列结论错误的是()A .函数值随自变量的增大而减小B .函数的图象不经过第三象限C .函数的图象向上平移 2 个单位得到 y =-2x 的图象D .函数的图象与 y 轴的交点坐标是(0,4)【参考答案】课前预习1. 变量,常量,自变量,因变量2. 列表法,关系式法,图象法3. (1)略;(2)点 C知识点睛1. (1)两个变量,唯一,自变量,因变量(2)列表法,关系式法,图象法2. (1) y kx b (k ,b 是常数,k 0)(2)①一条直线,两, ( b,0) ,(0,b )k②原点,直线,一,(1,k )(3)①倾斜程度;一、三;二、四②纵;一、二、三;一、三、四;一、二、四;二、三、四 ③增大,同向变化;减小,反向变化精讲精练1. C2. B3.1,≠2 24. 0,0,≠2,05. (1)在,(2,1)(答案不唯一);(2)y =2x -3,y =2x -36. D7. D8. (1)第一、三;(2)第一、二、三;(3)第二、三、四 9. D 10. B11. C 12. ②④ 13. D 14. D 15. D 16. A 17. C18. 平行,向下平移 5 个单位得到的19. -1 20. A 21. C 22.。
七年级数学上册 一次函数与几何综合(一)讲义 (新版)鲁教版

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题一次函数与几何综合(一)(讲义)课前预习1. 小明认为,在一次函数y=kx+b 中,x 每增加1,kx+b 就增加了k,y 也就增加了k.因此要想求出一次函数表达式中的k,只需要知道x 每增加1 个单位长度,y 增加的单位长度即可.例如:在如图所示的一次函数图象中,x 从1 变到 2 时,y 的值由3 变到 5,即x 每增加 1 个单位长度,y 就增加 2 个单位长度,因此k 的值就是 2.再结合b 为函数图象与y 轴交点纵坐标,可得b=1.故容易求出一次函数表达式为y=2x+1.请你用待定系数法验证小明的说法.请根据小明的思路,直接写出下图中一次函数的表达式.知识点睛1. 一次函数表达式:y =kx +b (k ,b 为常数,k ≠0)①k 是斜率,表示倾斜程度,可以用几何中的坡度(或坡比) 来解释.坡面的竖直高度与水平宽度的比叫坡度或坡比,如图所示,AM 即为 ,BM 即为 ,则k =AM .BM②b 是截距,表示直线与 y 轴交点的纵坐标.2. 设直线 l 1:y 1=k 1x +b 1,直线 l 2:y 2=k 2x +b 2,其中 k 1,k 2≠0.①若 k 1=k 2,且 b 1≠b 2,则直线 l 1 l 2;②若 k 1·k 2= ,则直线 l 1l 2.3. 一次函数与几何综合解题思路坐标一次函数几何图形①要求坐标, ; ②要求函数表达式, ; ③要研究几何图形,.ABM3 = 33 精讲精练 1.如图,点 B ,C 分别在直线 y =2x 和 y =kx 上,A ,D 是 x 轴上的两点,若四边形 ABCD 是正方形,则 k 的值为 .第 1 题图第 2 题图2. 如图,点 A ,B 分别在直线 y =kx 和 y =-4x 上,C ,D 是 x 轴上的两点,若四边形 ABCD 是长方形,且 AB :AD =3:2,则 k 的值为 .3.如图,已知直线 l : y3x 与 x 轴交于点 A ,与 y 轴3 交于点 B ,将△AOB 沿直线 l 折叠,点 O 落在点 C 处,则直线 AC 的表达式为 .第 3 题图第 4 题图4.已知点 A 的坐标为(5,0),直线 y =x +b (b >0)与 y 轴交于点B ,连接AB ,∠α=75°,则 b 的值为 .335.如图,△OA B 是边长为2 的等边三角形,过点A 的直线y=-x+m 与x 轴交于点C,则点C 的坐标为.6.在平面直角坐标系中,已知点P 的坐标为( ,0),直线PQ 的斜率为,则将直线PQ 绕点P 逆时针旋转90°所得直线的表达式为.7.如图,直线l1 与x 轴、y 轴分别交于点A,B,OA=m,OB=n,将△AOB 绕点O 逆时针旋转 90°得到△COD,CD 所在直线l2 与直线l1 交于点E,则l1l2;若直线l1,l2 的斜率分别为k1,k2,则k1·k2= .第7 题图第8 题图8.如图,直线y4x 8 与x 轴、y 轴分别交于点A,B,线段3AB 的垂直平分线交x 轴于点C,交AB 于点D,则直线CD的表达式为.9.如图,在平面直角坐标系 xOy 中放入一张长方形纸片 ABCO , 点 D 在 AB边上,将纸片沿 CD 翻折后,点 B 恰好落在 x 轴上的点 B ′处.若 OC =9, OC 3,则折痕 CD 所在直线的解CB 5析式为 .第 9 题图第 10 题图10.如图,直线 y 3x2 3 与 x 轴,y 轴分别交于点 A 和点 B ,D 是 y 轴上的一点,若将△DAB 沿直线 DA 折叠,点 B 恰好落在 x 轴正半轴上的点 C 处,则直线 CD 的解析式为.11.如图,在平面直角坐标系中,函数 y =x 的图象 l 是第一、三象限的角平分线.探索:若点 A 的坐标为(3,1),则它关于直线 l 的对称点 A' 的坐标为 ; 猜想:若坐标平面内任一点 P 的坐标为(m ,n ),则它关于直线 l 的对称点 P ′的坐标为 ;应用:若已知两点 B (-2,-5),C (-1,-3),试在直线 l 上确定一点 Q ,使点 Q 到 B ,C 两点的距离之和最小,则此时点 Q 的坐标为 .12.如图,已知直线l1:y 2x8与直线l2:y=-2x+16 相交于点3 3C,直线l1,l2 与x 轴分别交于点A,B,长方形DEFG 的顶点D,E 分别在l1,l2 上,顶点F,G 都在x 轴上,且点G 与点B 重合,则S 长方形DEFG : S△ABC = .33 【参考答案】课前预习1. 小明的说法正确,验证过程略y 3x 2 ,y 2x 2知识点睛1. 竖直高度,水平宽度2. ①∥;②-1,⊥3.①利用函数表达式或线段长转坐标 ②待定系数法或 k ,b 的几何意义 ③坐标转线段长或 k ,b 的几何意义精讲精练 1.2 3 2.4 5 3.y4. 3x 35. (1+ ,0)6.y3x +1 3 7. ⊥,-18. y 3 x74 49. y 1x 9310.y3x 2 3 11. (1,3);(n ,m );( 13 , 13)5 512. 8:95 333。
2019学年七年级数学上册 一次函数的表达式、图象、性质讲义 (新版)鲁教版
2019年一次函数的表达式、图象、性质(讲义)课前预习1.在一个变化过程中,我们称数值发生变化的量为,数值始终不变的量为;变量分为和.2.表示变量之间的关系通常有三种方法,它们是、、.3.如图,在平面直角坐标系xOy 中,描出下列点的坐标:A(1,2),B(2,4),C(-1,-2),D(1,1),E(-1,3),F(1,-3).(1)作出直线BC;(2)C,D,E,F 四点中,在直线AB 上的是.2019年知识点睛1.函数(1)一般地,如果在一个变化过程中有x 和y,并且对于任意一个x 都有的一个y 和它对应,那么我们称y 是x 的函数,其中x 是,y 是.(2)表示函数的方法一般有、和.2.一次函数(1)表达式(也称“解析式”或“关系式”).特别地,当b=0 时,称y 是x 的正比例函数(y=kx,k 为常数,k≠0).(2)图象画函数图象的一般步骤:列表、描点、连线.①一次函数图象是,因此画一次函数的图象时,只需确定点即可,通常找、;②正比例函数图象是一条经过的,因此画正比例函数的图象时,只需再确定点即可,通常找.(3)性质①k 反映图象的.当k>0 时,图象过第象限;当k<0 时,图象过第象限.若两条直线互相平行,则k 1 k2 .②b 是直线与y 轴交点的坐标.当k>0 且b>0 时,图象过第象限;当k>0 且b<0 时,图象过第象限;当k<0 且b>0 时,图象过第象限;当k<0 且b<0 时,图象过第象限.③增减性当k>0 时,y 的值随着x 值的增大而(即y 与x);当k<0 时,y 的值随着x 值的增大而(即y 与x).示意图精讲精练1. 下列各曲线中,不能表示 y 是 x 的函数的是()A .B .D .2. 已知下列函数关系式:①y =2x +1;② y1;③y =x 2-1;x④y =-8x ;⑤y =3.其中表示一次函数的有( ) A .1 个B .2 个C .3 个D .4 个3. 已知函数 y =(k -2)x +2k +1,当 k时,它是正比例函数;当 k时,它是一次函数.4. 已知函数 y =(m -2)x 2n +1-m +n ,当 m = ,n = 时,它是正比例函数;当 m ,n = 时,它是一次函数.5. (1)点(1,-1) (填“在”或“不在”)直线 y =2x -3 上;试写出直线 y =2x -3 上任意一点的坐标 . (2)满足关系式 y =2x -3 的 x ,y 所对应的点(x ,y )都在一次函数 的图象上;一次函数 y =2x -3 的图象上的点(x ,y )都满足关系式_ .6.下列四个点,在正比例函数 y 2x 的图象上的是( )5A .(2,5)B .(5,2)C .(2,-5)D .(5,-2)7.若点(m ,n )在函数 y =2x +1 的图象上,则 2m -n 的值是( )A .2B .-2C .1D .-18.(1)正比例函数 y =3x 的图象经过 象限;(2)一次函数 y =x +2 的图象经过 象限; (3)一次函数 y =-5x -3 的图象经过象限.9.已知一次函数y=kx+b 的图象经过第一、二、三象限,则b 的值可以是()A.-2 B.-1 C.0 D.210.已知一次函数y=kx+b 的图象如图所示,下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<011.一次函数y=kx+b 中,若k<0,b>0)A .第一象限B.第二象限C.第三象限D.第四象限12.下列一次函数:①y=5x-6;②y=-0.3x+3;③y=x-3;④y= ( 6)x .其中y 的值随x 的增大而减小的是.(填写序号)13.若y=kx-4 的函数值y 随x 的增大而增大,则k 的值可能是()A.-4 B.12C.0 D.314.若一次函数y=kx+b 的函数值y 随x 的增大而减小,且图象与y 轴的负半轴相交,则对k 和b 的符号判断正确的是()A.k>0,b>0 B.k>0,b<0C.k<0,b>0 D.k<0,b<015.已知一次函数y=kx-k,若y 随x 的增大而增大,则该函数的图象经过()A.第一、二、三象限B.第一、二、四象限 C.第二、三、四象限D.第一、三、四象限16.一次函数y=kx+b 满足kb>0,且y 随x 的增大而减小,则此函数的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限5 517. 已知函数 y =kx +b 的图象如图所示,则函数 y =2kx +b 的图象可能是()A .B .C .D .18. 直线 y =-x 与 y =-x +5 的位置关系是,直线 y =-x 的图象可以看作是由直线 y =-x +5 .19. 若直线y =(2m -1)x +m -2 与直线 y =-3x -1 平行,则 m =.20. 将直线 y =2x 向上平移两个单位,所得的直线是()A .y =2x +2B .y =2x -2C .y =2(x -2)D .y =2(x +2)21. 对于一次函数 y =-2x +4,下列结论错误的是()A .函数值随自变量的增大而减小B .函数的图象不经过第三象限C .函数的图象向上平移 2 个单位得到 y =-2x 的图象D .函数的图象与 y 轴的交点坐标是(0,4)【参考答案】课前预习1. 变量,常量,自变量,因变量2. 列表法,关系式法,图象法3. (1)略;(2)点 C知识点睛1. (1)两个变量,唯一,自变量,因变量(2)列表法,关系式法,图象法2. (1) y kx b (k ,b 是常数,k 0)(2)①一条直线,两, ( b,0) ,(0,b )k②原点,直线,一,(1,k )(3)①倾斜程度;一、三;二、四②纵;一、二、三;一、三、四;一、二、四;二、三、四 ③增大,同向变化;减小,反向变化精讲精练1. C2. B3.1,≠2 24. 0,0,≠2,05. (1)在,(2,1)(答案不唯一);(2)y =2x -3,y =2x -36. D7. D8. (1)第一、三;(2)第一、二、三;(3)第二、三、四 9. D 10. B11. C 12. ②④ 13. D 14. D 15. D 16. A 17. C18. 平行,向下平移 5 个单位得到的19.-120. A 21. C 22.。
七年级数学上册 一次函数应用题讲义 (新版)鲁教版

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题一次函数应用题(讲义)知识点睛1.理解题意:结合图象依次分析的实际意义,把函数图象与对应起来,可借助示意图(如线段图)等梳理信息.2.利用解决问题:把所求目标转化为函数元素,利用表达式进行求解;另外,当实际场景发生变化时,要分析或者.3.结合实际场景验证所求结果.精讲精练1.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地的过程中y 与x 之间的函数关系.(1)根据图中信息,求线段AB 所在直线的函数表达式以及甲乙两地之间的距离;(2)已知两车相遇时快车比慢车多行驶 40 千米,求快车从甲地到达乙地所需的时间;(3)出发多长时间,两车相距 100 千米?O 1.5 2 ? x/小时2.一辆快车和一辆慢车分别从A,B 两站同时出发,相向而行.快车到达B 站后,停留 1 小时,然后原路原速返回 A 站,慢车到达 A 站即停运休息.如图表示的是两车之间的距离y(千米)与行驶时间x(小时)之间的函数图象.请结合图象信息,解答下列问题:(1)直接写出快车、慢车的速度及 A,B 两站间的距离;(2)求快车从 B 站返回 A 站时,y 与x 之间的函数关系式;(3)出发几小时,两车相距 200 千米?请直接写出答案.O 6 10 11 15 21 x/小时3.某地发生特大暴雨灾害,受其影响,某药品的需求量急增.如图所示,平常对某种药品的需求量y1(万件)、供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+70,y2=2x-38,需求量为0 时,即停止供应.当y1=y2 时,该药品的价格称为稳定价格,需求量称为稳定需求量.(1)求该药品的稳定价格与稳定需求量.(2)价格在什么范围内,该药品的需求量低于供应量?(3)由于灾情严重,政府部门决定对药品供应方提供价格补贴来提高供货价格,以提高供应量.根据调查统计,需将稳定需求量增加6 万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量?y1元/件)4.甲船从 A 港出发顺流匀速驶向 B 港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向 B 港.乙船从 B 港出发逆流匀速驶向 A 港.已知救生圈漂流的速度和水流速度相同,甲、乙两船在静水中的速度相同,甲、乙两船到 A 港的距离y1,y2(km)与行驶时间x(h)之间的函数图象如图所示.(1)乙船在逆流中行驶的速度为;(2)求甲船在逆流中行驶的路程;(3)求甲船到A港的距离y1 与行驶时间x 之间的函数关系式;(4)救生圈落入水中时,甲船到 A 港的距离是多少?O? ? ? 【参考答案】知识点睛1. 轴、点、线,实际场景2. 函数图象,函数图象的变化,构造函数图象精讲精练1. (1)所求函数解析式为 y =-140x +280(0≤x ≤2),甲、乙两地之间的距离是 280 千米(2)3.5 小时(3) 9 小时或19 小时7 72. (1)快车的速度是 120 千米/小时; 慢车的速度是 80 千米/小时;A ,B 两站间的距离是 1 200 千米40x 1320 (11≤ x ≤15)(2)y 120x 2520 (15<x ≤21) (3)5 小时,7 小时或 58 小时33.(1)该药品的稳定价格是 36 元/件,稳定需求量是 34 万件(2)价格 x (元/件)满足36 < x <70 时,该药品的需求量低于供应量(3)9 元4. (1)6 km/h(2)3 km9x (0≤ x ≤2)(3) y 1 6x 30 (2< x ≤ 2.5) 15 9x 2 (4) 27 km2(2.5< x ≤3.5)。
2017-2018学年七年级数学上册一次函数的表达式、图象、性质讲义(新版)鲁教版

一次函数的表达式、图象、性质(讲义) 课前预习1. 在一个变化过程中,我们称数值发生变化的量为_,数值始终不变的量为_______________________ ;变量分为 __________ 禾廿________ .2. 表示变量之间的关系通常有三种方法,它们是_______________________3. 如图,在平面直角坐标系xOy中,描出下列点的坐标:A(1 , 2), B(2,4) , q-1 , -2) , D1 , 1) , E(-1 , 3), F(1 , -3).(1) 作出直线BC;(2) ____________________________________________________ C, D, E, F四点中,在直线AB上的是______________________________________知识点睛1. 函数(1)___________________________________________ 一般地,如果在一个变化过程中有 _________________________________________ x和y,并且对于任意一个x都有____________ 的一个y和它对应,那么我们称y是x的函数,其中x是____________,y是___________ .(2)________________________________ 表示函数的方法一般有___ 、 ___________________________________________ 和 _________2. 一次函数(1) 表达式(也称"解析式”或"关系式”)特别地,当b=0时,称y是x的正比例函数(y=kx, k为常数,k 丰0).(2) 图象画函数图象的一般步骤:列表、描点、连线.①一次函数图象是_________________,因此画一次函数的图象时,只需确定________ 点即可,通常找_____________ 、___________ ;②正比例函数图象是一条经过________________ 的________ ,因此画正比例函数的图象时,只需再确定__________ 点即可,通常找___________ .(3) 性质①_____________________________k反映图象的.当k>0时,图象过第________________象限;②b是直线与y轴交点的坐标.当k>0且b>0时,图象过第当k>0且b<0时,图象过第当k<0且b>0时,图象过第当k<0且b<0时,图象过第当k<0时,图象过第________________象限.若两条直线互相平行,则k i k2 .③增减性当k>0时,y的值随着x值的增大而 _______ (即y与x __________ );当k<0时,y的值随着x值的增大而 _______ (即y与x __________ ).我们通常从表达式、图象、性质、计算四个方面研究函数.精讲精练1. 下列各曲线中,不能表示y是x的函数的是(④y=-8x:⑤y=3.其中表示一次函数的有( )A. 1个B. 2个C. 3个D. 4个3. 已知函数y=(k-2) x+2k+i,当k _____________ 时,它是正比例函数;当k_____________ 时,它是一次函数.4. 已知函数y=(m-2) x2n+1- m+ n,当m=_, n= ________ 时,它是正比例函数;当m _________________ , n= ___ 时,它是一次函数.5. (1)点(1 , -1) ________ (填“在”或“不在”)直线y=2x-3上;试写出直线y=2x-3 上任意一点的坐标__________________________ .(2)满足关系式y=2x-3的x, y所对应的点(x, y)都在一次函数______________________ 的图象上;一次函数y=2x-3 的图象上的点(x ,y)都满足关系式__.6 下列四个点,在正比例函数yA. (2 , 5)B. (5 , 2)7. 若点(m, n)在函数y=2x+1的图象上,A. 2B. -28 (1)正比例函数y=3x的图象经过_ 2x的图象上的是( ) 5C. (2 , -5)D. (5 , -2)则2m n的值是() C. 1 D. -1___________________象限;_________________ 象限;象限.)2.(2)一次函数y=x+2的图象经过_(3)一次函数y=-5x-3的图象经过已知一次函数y =kx +b 的图象经过第一、 是()已知一次函数y =kx +b 的图象如图所示,下列结论正确的是 ( )A. k >0, b >0 B.k >0, b <0 C .k <0, b >0 D .k <0, b <0一次函数 y =kx +b 中,若 k <0, b >0,A.第一象限C.第三象限12 下列一次函数:①y =5x -6 :② y =-0.3 x +3;③ y =' 5 x-3 ‘④ y = (^5 严)x其中y 的值随x 的增大而减小的是 ________________ .(填写序号)13 若y =kx -4的函数值y 随x 的增大而增大,则 k 的值可能是( )14 若一次函数y =kx +b 的函数值y 随x 的增大而减小,且图象与 y 轴的负半轴相交,则对 k 和b 的符号判断正确的是(A. k >0, b >0B . k >0, b <0C. k <0, b >015 已知一次函数y =kx -k ,若y 随x 的增大而增大,则该函数的图象经 过()A.第一、二、三象限 B .第一、二、四象限 C .第二、三、四象限D.第一、三、四象限A. -2B. -1C. 0D. 21011A. -4B.C. 0D. 3D. k <0, b <0b 的值可以)D.第四象限16 一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限17 已知函数y=kx+b的图象如图所示,贝U函数y=2kx+b的图象可能是( )18 直线y=-x与y=-x+5的位置关系是_______________ ,直线y=-x的图象可以看作是由直线y=- x+5 __________________________ .19. 若直线y=(2m1) x+m-2 与直线y=-3 x-1 平行,贝U m= _______________20 将直线y=2x向上平移两个单位,所得的直线是( )A. y=2x+2B. y=2x-2C. y=2(x-2)D. y=2(x+2)21对于一次函数y=-2x+4,下列结论错误的是( )A. 函数值随自变量的增大而减小B. 函数的图象不经过第三象限C .函数的图象向上平移2个单位得到y=-2x的图象D.函数的图象与y轴的交点坐标是(0 , 4)【参考答案】课前预习1. 变量,常量,自变量,因变量2. 列表法,关系式法,图象法3. (1)略;(2)点C知识点睛1. (1)两个变量,唯一,自变量,因变量(2)列表法,关系式法,图象法2. (1)y kx b(k,b是常数,k 0)b(2)①一条直线,两,(0), (0, b)k②原点,直线,一,(1,k)(3)①倾斜程度;一、三;二、四②纵;一、二、三;一、三、四;一、二、四;二、三、四③增大,同向变化;减小,反向变化精讲精练1. C2. B13. _ ,工224. 0, 0,工2, 05. (1)在,(2 , 1)(答案不唯一);(2)y=2x-3 , y=2x-36. D7. D8. (1)第一、三;(2)第一、二、三;(3)第二、三、四9. D10. B11. C 12.②④13. D14. D15. D16. A17. C18. 平行,向下平移5个单位得到的19.-120. A21. C。
2017-2018学年七年级数学上册 一次函数的表达式、图象、性质讲义 (新版)鲁教版

一次函数的表达式、图象、性质(讲义)课前预习1.在一个变化过程中,我们称数值发生变化的量为,数值始终不变的量为;变量分为和.2.表示变量之间的关系通常有三种方法,它们是、、.3.如图,在平面直角坐标系xOy 中,描出下列点的坐标:A(1,2),B(2,4),C(—1,-2),D(1,1),E(-1,3),F(1,-3).(1)作出直线BC;(2)C,D,E,F 四点中,在直线AB 上的是.知识点睛1.函数(1)一般地,如果在一个变化过程中有x 和y,并且对于任意一个x 都有的一个y 和它对应,那么我们称y 是x 的函数,其中x 是,y 是.(2)表示函数的方法一般有、和.2.一次函数(1)表达式(也称“解析式”或“关系式”).特别地,当b=0 时,称y 是x 的正比例函数(y=kx,k 为常数,k≠0).(2)图象画函数图象的一般步骤:列表、描点、连线.①一次函数图象是,因此画一次函数的图象时,只需确定点即可,通常找、;②正比例函数图象是一条经过的,因此画正比例函数的图象时,只需再确定点即可,通常找.(3)性质①k 反映图象的.当k>0 时,图象过第象限;当k<0 时,图象过第象限.若两条直线互相平行,则k1k2 .②b 是直线与y 轴交点的坐标.当k〉0 且b>0 时,图象过第象限;当k>0 且b<0 时,图象过第象限;当k〈0 且b〉0 时,图象过第象限;当k<0 且b<0 时,图象过第象限.③增减性当k〉0 时,y的值随着x 值的增大而(即y 与x);当k<0 时,y 的值随着x 值的增大而(即y 与x).示意图k〉0,b〉0yxOk〉0,b<0k<0,b>0k〈0,b〈0我们通常从表达式、图象、性质、计算四个方面精讲精练1. 下列各曲线中,不能表示 y 是 x 的函数的是( )A .B .2. 已知下列函数关系式:①y =2x +1;② y 1;③y =x 2—1;x④y =—8x ;⑤y =3.其中表示一次函数的有( ) A .1 个 B .2 个 C .3 个 D .4 个3。
(新人教版)最新七年级数学上册 一次函数与几何综合(一)讲义 (新版)鲁教版【经典练习】

一次函数与几何综合(一)(讲义)课前预习1. 小明认为,在一次函数y=kx+b 中,x 每增加1,kx+b 就增加了k,y 也就增加了k.因此要想求出一次函数表达式中的k,只需要知道x 每增加1 个单位长度,y 增加的单位长度即可.例如:在如图所示的一次函数图象中,x 从1 变到 2 时,y 的值由3 变到 5,即x 每增加 1 个单位长度,y 就增加 2 个单位长度,因此k 的值就是 2.再结合b 为函数图象与y 轴交点纵坐标,可得b=1.故容易求出一次函数表达式为y=2x+1.请你用待定系数法验证小明的说法.请根据小明的思路,直接写出下图中一次函数的表达式.知识点睛1. 一次函数表达式:y =kx +b (k ,b 为常数,k ≠0)①k 是斜率,表示倾斜程度,可以用几何中的坡度(或坡比) 来解释.坡面的竖直高度与水平宽度的比叫坡度或坡比,如图所示,AM 即为 ,BM 即为 ,则k =AM .BM②b 是截距,表示直线与 y 轴交点的纵坐标.2. 设直线 l 1:y 1=k 1x +b 1,直线 l 2:y 2=k 2x +b 2,其中 k 1,k 2≠0.①若 k 1=k 2,且 b 1≠b 2,则直线 l 1 l 2;②若 k 1·k 2= ,则直线 l 1l 2.3. 一次函数与几何综合解题思路坐标一次函数几何图形①要求坐标, ; ②要求函数表达式, ; ③要研究几何图形,.ABM3 = 33 精讲精练 1.如图,点 B ,C 分别在直线 y =2x 和 y =kx 上,A ,D 是 x 轴上的两点,若四边形 ABCD 是正方形,则 k 的值为 .第 1 题图第 2 题图2. 如图,点 A ,B 分别在直线 y =kx 和 y =-4x 上,C ,D 是 x 轴上的两点,若四边形 ABCD 是长方形,且 AB :AD =3:2,则 k 的值为 .3.如图,已知直线 l : y3x 与 x 轴交于点 A ,与 y 轴3 交于点 B ,将△AOB 沿直线 l 折叠,点 O 落在点 C 处,则直线 AC 的表达式为 .第 3 题图第 4 题图4.已知点 A 的坐标为(5,0),直线 y =x +b (b >0)与 y 轴交于点B ,连接AB ,∠α=75°,则 b 的值为 .335.如图,△OA B 是边长为2 的等边三角形,过点A 的直线y=-x+m 与x 轴交于点C,则点C 的坐标为.6.在平面直角坐标系中,已知点P 的坐标为( ,0),直线PQ 的斜率为,则将直线PQ 绕点P 逆时针旋转90°所得直线的表达式为.7.如图,直线l1 与x 轴、y 轴分别交于点A,B,OA=m,OB=n,将△AOB 绕点O 逆时针旋转 90°得到△COD,CD 所在直线l2 与直线l1 交于点E,则l1l2;若直线l1,l2 的斜率分别为k1,k2,则k1·k2= .第7 题图第8 题图8.如图,直线y4x 8 与x 轴、y 轴分别交于点A,B,线段3AB 的垂直平分线交x 轴于点C,交AB 于点D,则直线CD的表达式为.9.如图,在平面直角坐标系 xOy 中放入一张长方形纸片 ABCO , 点 D 在 AB边上,将纸片沿 CD 翻折后,点 B 恰好落在 x 轴上的点 B ′处.若 OC =9, OC 3,则折痕 CD 所在直线的解CB 5析式为 .第 9 题图第 10 题图10.如图,直线 y 3x2 3 与 x 轴,y 轴分别交于点 A 和点 B ,D 是 y 轴上的一点,若将△DAB 沿直线 DA 折叠,点 B 恰好落在 x 轴正半轴上的点 C 处,则直线 CD 的解析式为.11.如图,在平面直角坐标系中,函数 y =x 的图象 l 是第一、三象限的角平分线.探索:若点 A 的坐标为(3,1),则它关于直线 l 的对称点 A' 的坐标为 ; 猜想:若坐标平面内任一点 P 的坐标为(m ,n ),则它关于直线 l 的对称点 P ′的坐标为 ;应用:若已知两点 B (-2,-5),C (-1,-3),试在直线 l 上确定一点 Q ,使点 Q 到 B ,C 两点的距离之和最小,则此时点 Q 的坐标为 .12.如图,已知直线l1:y 2x8与直线l2:y=-2x+16 相交于点3 3C,直线l1,l2 与x 轴分别交于点A,B,长方形DEFG 的顶点D,E 分别在l1,l2 上,顶点F,G 都在x 轴上,且点G 与点B 重合,则S 长方形DEFG : S△ABC = .33 【参考答案】课前预习1. 小明的说法正确,验证过程略y 3x 2 ,y 2x 2知识点睛1. 竖直高度,水平宽度2. ①∥;②-1,⊥3.①利用函数表达式或线段长转坐标 ②待定系数法或 k ,b 的几何意义 ③坐标转线段长或 k ,b 的几何意义精讲精练 1.2 3 2.4 5 3.y4. 3x 35. (1+ ,0)6.y3x +1 3 7. ⊥,-18. y 3 x74 49. y 1x 9310.y3x 2 3 11. (1,3);(n ,m );( 13 , 13)5 512. 8:95 333。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
一次函数之动点问题(讲义)
课前预习
1. 由点的运动(速度已知)产生的几何问题称为动点问题. 动点问
题的解决方法: (1)研究 ;
(2)分析 ,分段; (3)表达
,建方程.
2. 根据前期训练的标准动作及上述内容,完成下题.
如图,△ABC 是边长为 6 的等边三角形.动点 P 从点 A 出发, 沿折线 AB -BC 以每秒 2 个单位长度的速度运动,过点 P 作
PQ ⊥AC 于点 Q .设点 P 运动的时间为 t 秒,请用含 t 的式子 分别表达出 PQ 和 AQ 的长. B
思路分析: A
Q
C
( 2/ s )P : A
3s
B
3s
C ( 0 ≤ t ≤ 6)
①当0 ≤ t ≤ 3 时,PQ = _,AQ =
; ②当 3 t ≤ 6 时,PQ =
_,AQ =
.
3. 用铅笔做讲义第 1,2 题,并将计算、演草保留在讲义上,先看知识点
睛,再做题,思路受阻时(某个点做了 2~3 分钟) 重复上述动作,若仍无法解决,课堂重点听.
知识点睛
1.动点问题的特征是,主要考查运动的.
2.一次函数背景下解决动点问题的思考方向:
(1)研究背景图形
把函数信息(坐标或表达式)转化为背景图形的信息
(2)分析运动过程,分段、定范围
分析运动过程常借助运动状态分析图:
①起点、终点、速度——确定时间范围
②状态转折点——决定分段
③所求目标——明确方向
(3)分析几何特征、表达、设计方案求解
分段画图,表达相关线段长,列方程求解,回归范围进行验证.
精讲精练
1. 如图,直线
y
3
x
4
与 x 轴、y 轴分别交于点 A ,B ,直
线 BC 与 x 轴交于点 C ,∠ABC =60°.动点 P 从点 A 出发,以每秒 1 个
单位长度的速度沿线段 AC 向点 C 运动(不与点 A ,
C 重合),动点 Q 从点 C 同时出发,以每秒 2 个单位长度的速度沿折线 CB -BA 向点 A 运动(不与点 A ,C 重合).设△APQ 的面积为 S ,运动时间为 t (秒),求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围.
3
2.如图,直线y x 2 与x 轴、y 轴分别交于点A,B,与直线
y=x 交于点C.动点P 从原点O 出发,以每秒 2 个单位长度的速度沿O→B→A 的路线向终点A 运动(点P 不与点O,A 重合),动点Q 从点A 同时出发,以每秒 1 个单位长度的速度沿A→O→C 的路线向终点
C 运动(点Q不与点A,C 重合),设点P 运动的时间为t(秒).设△
APQ 的面积为S,求S 与
t 之间的函数关系式,并写出自变量t 的取值范围.
3.
如图,直线 y 3x 2 3 与 x 轴、y 轴分别交于点 A ,B ,与 直线
y 3 x 交于点 C .动点 E 从原点 O 出发,以每秒 1 个
3
单位长度的速度沿 OA 方向向终点 A 运动,动点 F 从点 A 同时出发,以每秒 1 个单位长度的速度沿折线 AC -CO 向终点 O 运动,设点 F 运动的时间为 t (秒).
(1)设△OEF 的面积为 S ,求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围.(这里规定:线段是面积为零的三角形) (2)当1≤ t ≤ 2 时,是否存在某一时刻,使得△OEF 是等腰三角形?若存在,求出 t 的值;若不存在,请说明理由.
B C
O
A
B
C
O
A
y
B
C
O
A
4.如图,点A 在直线y 3 x 上,过点A 作AC⊥x 轴于点C,
3
AC=2,过点A 作AB⊥y 轴于点B.动点P 从点O 出发,以每秒1 个单位长度的速度沿O→B→A→O 的路线向点O 运动;同时动点Q 以相同的速度沿C→A→O→C 的路线向点C 运动,设点P 运动的时间为t (秒).
(1)设△OPQ 的面积为S,求S 与t 之间的函数关系式,并写出自变量t 的取值范围.(这里规定:线段是面积为零的三角形)
(2)当点Q 在OC 上运动时,是否存在某一时刻,使△OPQ 是等腰三角形?若存在,求出相应的t 值;若不存在,请说明理由.
A
A
A。
