专题(三) 全等三角形判定与性质的综合运用

合集下载

全等三角形的性质及判定(经典讲义)

全等三角形的性质及判定知识要点1、全等三角形概念：两个能完全重合的三角形叫做全等三角形．2、全等三角形性质：（1）两全等三角形的对应边相等，对应角相等．（2）全等三角形的对应边上的高相等，对应边上的中线相等，对应角的平分线相等．（3）全等三角形的周长、面积相等．3、全等三角形判定方法：（1）全等判定一：三条边对应相等的两个三角形全等（SSS ）（2）全等判定二：两角和它们的夹边对应相等的两个三角形全等（ASA ）（3）全等判定三：两角及其中一个角的对边对应相等的两个三角形全等(AAS) （4）全等判定四：两边和它们的夹角对应相等的两个三角形全等（SAS ）专题一、全等图形的性质——全等图形的对应边（对应中线、角平分线、高线）、对应角、对应周长、对应面积相等例题1：下列说法，正确的是（）A.全等图形的面积相等B.面积相等的两个图形是全等形C.形状相同的两个图形是全等形D.周长相等的两个图形是全等形例题2：如图1，折叠长方形ABCD ，使顶点D 与BC 边上的N 点重合，如果AD=7cm ，DM=5cm ，∠DAM=39°，则AN =____cm ，NM =____cm ，NAB ∠= .【仿练1】如图2，已知ABC ADE ∆≅∆，AB AD =，BC DE =，那么与BAE ∠相等的角是 . 【仿练2】如图3，ABC ADE ∆≅∆，则AB= ，∠E= _．若∠BAE=120°，∠BAD=40°，则∠BAC= .、图4EDCB A图2 图3M DA NBC 图1三角形全等的判定一（SSS ）相关几何语言考点∵AE=CF ∵CM 是△的中线∴_____________( )∴____________________∴__________（）或 ∵AC=EF∴____________________∴__________（）AB=AB （）在△ABC 和△DEF 中∵⎪⎩⎪⎨⎧___________________________ ∴△ABC ≌△DEF （）例1．如图，AB ＝AD ，CB ＝CD ．△ABC 与△ADC 全等吗？为什么？例２．如图，C 是AB 的中点，AD ＝CE ，CD ＝BE ．求证△ACD ≌△CBE ．BFECAFE DCB ACMBA B A例３．如图，点B，E，C，F在一条直线上，AB=DE，AC=DF，BE=CF．求证∠A=∠D．练习1..如图，AB=CD，AD=CB，那么下列结论中错误的是（）A．∠A=∠C B．AB=AD C．AD∥BC D．AB∥CD2、如图所示，在△ABC中，AB=AC，BE=CE，则由“SSS”可以判定（）A．△ABD≌△ACD B．△BDE≌△CDEC．△ABE≌△ACE D．以上都不对3.如图，AB=AC，BD=CD，则△ABD≌△ACD的依据是（）A．SSS B．SAS C．AASD．HL4.如图,AB=AC,D为BC的中点，则△ABD≌_________.5.如图，已知AB=DE，BC=EF，若要使△ABC≌△DEF，那么还要需要一个条件，这个条件可以是：．6.如图，AB=AC，BD=DC，∠BAC=36°，则∠BAD的度数是°．7、.如图，AB=AE，AC=AD，BD=CE，求证：△ABC≌ADE。

全等三角形的性质与判定(经典讲义)

全等三角形的性质与判定的综合运用初中数学原创课件

D
B
C
当出现点共线、角共顶点时，
∴△BAD≌△CAE(AAS) . 经常会用到等量相加结果相等、
等量相减结果相等，这也是求
∴AB=AC.
两条边、两个角相等经常用到
的方法.
练习如图，B，F，C，E在一条直线上， BF=CE，AC=DF . （1）在下列条件①∠B=∠E；②∠ACB=∠DFE；③AB=DE； ④AC∥DF中，只添加一个条件就可以证得△ABC≌△DEF，则所有正确条件的序号是 _______________. （2）根据已知及（1）中添加的一个条件证明∠A=∠D .
ቐ∠ACB=∠DFE ，
∴∠A=∠D .
BC=EF ，
课堂小结
1 几何题解题习惯依题意标图、关注图形特征、挖掘隐藏条件.
2 三角形全等知识巩固判定方法，根据已知条件灵活选择判定方法.
3 几何题解题思路从结论入手，结合已知，双向推理.
课后作业
1.如图，点D在AB上，点E在AC上，BE和CD相交于点O，
∠BAD=∠CAE
AAS
∠BAC -∠CAD=∠DAE-∠CAD
D
B
C
已知∠BAC=∠DAE , AD=AE，∠ABD=∠ACE.
证明：∵∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD. 即∠BAD=∠CAE. 在△BAD和△CAE中,
A E
ABD ACE， BAD CAE， AD AE，
A
BF
CE
D
练习如图，B，F，C，E在一条直线上， BF=CE，AC=DF . （1）在下列条件①∠B=∠E；②∠ACB=∠DFE；③AB=DE；
④AC∥DF中，只添加一个条件就可以证得△ABC≌△DEF，则所有正确条件的序号是 _____________.

三角形全等的性质与判定综合应用

温故知新
复习三角形全等判定，回答下列问题 1. 我们学习了那些三角形全等的判定方法？分别是什么？边边边：三边对应相等的两个三角形全等(SSS) 边角边：两边和它们的夹角分别相等的两个三角形全等(SAS) 角边角：有两角和它们夹边对应相等的两个三角形全等(ASA）角角边：两角和其中一角的对边对应相等的两个三角形全等(AAS）
1．如图，已知BD＝CE，AB＝FD，B，D，C，E共线．若添加一个条件，
就能使△ABC≌△FDE，则下列条件中： ①AB∥DF；②AC∥EF；③∠A＝∠F；④∠A＝∠F＝90°.
满足的个数为( B ) A．1个 B．2个 C．3个 D．4个
典例精析
例1 如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，
解：∵MN∥PQ，AB⊥PQ，
∴BA⊥MN，∠EAD=∠EBC=90°
在Rt△ADE 和Rt△BEC中， DE=EC AD=EB
∴Rt△ADE ≌Rt△BEC(HL)．
∴ AE＝BC，AD=EB
∵AD＋BC＝7 ∴BE+AE=7
即AB=7.
4. 如图，点C，E，B，F在一条直线上，AB⊥CF于点B，DE⊥CF于点E，
2 如图，∠ACB＝90°，AC＝BC，BE⊥CE于点 E，AD⊥CE于点D，下面四个结论： ①∠ABE＝∠BAD；
②△CEB≌△ADC；
③AB＝CE； ④AD－BE＝DE. 其中正确的是 _①__②__④．
3 如图，MN∥PQ，AB⊥PQ，点A，D在直线MN上，点B，C在直线PQ上，
点E在AB上，AD＋BC＝7， AD＝EB，DE＝EC，则AB＝___7_____.
AC＝DF，AB＝DE.求证：CE＝BF. 证明：∵AB⊥CF，DE⊥CF，

《全等三角形》讲义（完整版）

全等三角形讲义一、知识点总结全等三角形定义：形状大小相同，并且能够完全重合的两个三角形叫做全等形三角形。

：形状大小相同，并且能够完全重合的两个三角形叫做全等形三角形。

补充说明：重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角。

：重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角。

全等三角形的性质：全等三角形的对应边相等，全等三角形的对应角相等：全等三角形的对应边相等，全等三角形的对应角相等全等三角形判定定理：（1）边边边定理：三边对应相等的两个三角形全等。

（简称SSS ）（2）边角边定理：两边和它们的夹角对应相等的两个三角形全等。

）边角边定理：两边和它们的夹角对应相等的两个三角形全等。

((简称SAS) （3）角边角定理：两角和它们的夹边对应相等的两个三角形全等。

（简称ASA ASA））（4）角角边定理：两个角和其中一个角的对边对应相等的两个三角形全等。

（简称AAS AAS））（5）斜边、直角边定理：斜边和一条直角边对应相等的两个直角三角形全等。

（简称HL HL））角平分线的性质：在角平分线上的点到角的两边的距离相等在角平分线上的点到角的两边的距离相等. .∵OP 平分∠平分∠AOB AOB AOB，，PM PM⊥⊥OA 于M ，PN PN⊥⊥OB 于N ，∴PM=PN 角平分线的判定：到角的两边距离相等的点在角的平分线上到角的两边距离相等的点在角的平分线上. .∵PM PM⊥⊥OA 于M ，PN PN⊥⊥OB 于N ，PM=PN ∴OP 平分∠平分∠AOB AOB三角形的角平分线的性质：三角形三个内角的平分线交于一点，并且这一点到三边的距离等。

二、典型例题举例A BC PMNO A BCPMN O例1、如图,△ABN ≌△ACM,∠B 和∠C 是对应角,AB 与AC 是对应边,写出其他对应边和对应角.例2、如图，△、如图，△ABC ABC 是一个钢架，是一个钢架，AB=AC AB=AC AB=AC，，AD 是连结点A 与BC 中点D 的支架．的支架．求证：△求证：△ABD ABD ABD≌△≌△≌△ACD ACD ACD．．例3、已知：点A 、F 、E 、C 在同一条直线上，AF ＝CE ，BE ∥DF ，BE ＝DF ．求证：△ABE ≌△CDF ．例4、如图：、如图：D D 在AB 上，上，E E 在AC 上，上，AB AB AB＝＝AC AC，∠，∠，∠B B ＝∠＝∠C C ．求证AD AD＝＝AE AE．．例5、如图：∠、如图：∠1=1=1=∠∠2，∠，∠3=3=3=∠∠4 求证：求证：AC=AD AC=AD例6、如图，B 、E 、F 、C 在同一直线上，AF ⊥BC 于F ，DE ⊥BC 于E ，AB=DC ，BE=CF ，你认为AB 平行于CD 吗？说说你的理由吗？说说你的理由D CB ACADB123 4例7、如图1，△ABC 的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ，连结EG ，试判断△ABC 与△AEG 面积之间的关系，并说明理由.例8、如图，OC 是∠AOB 的平分线，P 是OC 上的一点，PD ⊥OA 交OA 于D ，PE ⊥OB 交OB 于E ，F 是OC 上的另一点，连接DF ，EF ，求证DF ＝EF例9、如图，△ABC 中，AD 是它的角平分线，P 是AD 上的一点，PE ∥AB 交BC 于E ，PF ∥AC 交BC 于F ，求证：D 到PE 的距离与D 到PF 的距离相等的距离相等例10、如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC 面积是282cm ，AB ＝20cm ，AC ＝8cm，求DE 的长．AGF CBDE图1AEB DCFAB CDED C EF BA 例10、已知：BE ⊥CD ，BE ＝DE ，BC ＝DA ，求证：①，求证：① △BEC ≌△DAE ；②DF ⊥BC ．例11、如图，已知：E 是∠AOB 的平分线上一点，EC ⊥OB ，ED ⊥OA ，C ，D 是垂足，连接CD ，求证:（1）∠ECD=∠EDC ；（2）OD=OC ；（3）OE 是CD 的中垂线.三、专题版块三、专题版块专题一：专题一：全等三角形的判定和性质的应用全等三角形的判定和性质的应用例1、如图，在△ABC 中，AB=AC ， BAC=40°,分别以AB AB、AC 为边作两个等腰三角形ABD 和ACE ACE，使∠，使∠BAD=∠CAE=90°.(1)求∠DBC 的度数.(2)求证：BD=CE.例2、如图，A B ∥CD,AF CD,AF∥∥DE,BE=CF,DE,BE=CF,求证：求证：求证：AB=CD. AB=CD.例3、如图在△ABC 中，BE 、CF 分别是AC 、AB 边上的高，在BE 延长线上截取BM ＝AC ，在CF 延长线上截到CN ＝AB ，求证：AM ＝AN 。

2021年九年级数学中考一轮复习——几何专题：全等三角形性质与判定(三)

2021年九年级数学中考复习——几何专题：全等三角形性质与判定（三）1．如图，在△ABC中，AB＝AC，∠A＝108°，BE平分∠ABC交AC于点E，求证：BC＝AB+CE．2．如图2，△ABC中，∠B＝∠C，若∠A＝70°，求∠B的度数．3．如图，在△ABC中，AD⊥BC于点D，AD＝BD，点E是线段AD上一点，且ED＝CD，连接BE交AC于点F．（1）求证：∠CBF＝∠DAC；（2）若BD＝3，BF＝，求△BAF的周长．4．如图，△ABC中，AD既是中线，又是角平分线，DE⊥AB于点E，DF⊥AC于点F．（1）求证：△BDE≌△CDF；（2）你认为AD还是△ABC的高吗？如果是，请给出证明；如果不是，请说明理由．5．已知：D，A，E三点都在直线m上，在直线m的同一侧作△ABC，使AB＝AC，连接BD，CE．（1）如图①，若∠BAC＝90°，BD⊥m，CE⊥m，求证：△ABD≌△ACE；（2）如图②，若∠BDA＝∠AEC＝∠BAC，请判断BD，CE，DE三条线段之间的数量关系，并说明理由．6．已知：如图，点A、B、C、D在一条直线上，AE∥DF，AE＝DF，AB＝CD．（1）求证：∠E＝∠F；（2）若∠D＝28°，∠ECA＝100°，求∠F的度数．7．如图1，在△ABC中，AE⊥BC于点E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系和数量关系，并说明理由；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由．8．已知，在△ABC中，D是AC上一点，BF交AC于点E，连接DF．（1）如图1，BE＝EF，AB∥DF．求证：AE＝DE；（2）如图2，点D与点C重合，∠A＝90°，∠ACB＝∠ECF，∠F＝∠AEB．若CE＝3，BC＝5，求AC的长．9．如图，AB＝CD，AE⊥BC于E，DF⊥BC于F，AE＝DF．求证：（1）CE＝BF；（2）AB∥CD．10．如图，在△ACD和△BCE中，AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P，求∠ACB的度数．参考答案1．证明：如图，在BC上取BA′＝BA，连接EA′，∵∠A＝108°，AB＝AC，∴∠ABC＝∠ACB＝36°，∵BE平分∠ABC，∴∠ABE＝∠CBA＝18°，在△ABE与△A′BE中，，∴△ABE≌△A′BE（SAS），∴∠BA′E＝∠A＝108°，∴∠EA′C＝72°，∴∠A′EC＝72°，∴∠A′EC＝∠CA′E，∴CE＝CA′，∴BC＝BA′+EC＝AB+EC＝AC+EC．2．（1）证明：∵C是线段AB的中点，∴AC＝CB，在△ACD和△CBE中，∵，∴△ACD≌△CBE（SSS）；（2）解：△ABC中，∠A+∠B+∠C＝180°，∵∠B＝∠C，∴70°+∠B+∠B＝180°，∴∠B＝55°．3．解：（1）证明：∵AD⊥BC，∴∠ADC＝∠ADB＝90°，在△ACD和△BED中，，∴△ACD≌△BED（SAS），∴∠DAC＝∠CBF；（2）∵AD⊥BC，AD＝BD＝3，∴AB＝＝3，∵∠DAC＝∠CBF，∴∠DAC+∠C＝∠CBF+∠C＝90°，∴∠AFB＝90°，∴AF＝＝2，∴△BAF的周长为：AB+BF+AF＝3++2．4．（1）证明：∵AD既是中线，又是角平分线，DE⊥AB，DF⊥AC，∴BD＝CD，DE＝DF，∠DEB＝∠DFC＝90°，在Rt△BDE和Rt△CDF中，，∴Rt△BDE≌Rt△CDF（HL）；（2）AD还是△ABC的高，证明：由（1）△BDE≌△CDF，∴∠B＝∠C，∵AD既是中线，又是角平分线，∴BD＝CD，∠BAD＝∠CAD，在△BAD和△CAD中，，∴△BAD≌△CAD（AAS），∴∠ADB＝∠ADC，∵∠ADB+∠ADC＝180°，∴∠ADB＝∠ADC＝90°，即AD还是△ABC的高．5．解：（1）证明：如图①，∵D，A，E三点都在直线m上，∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵BD⊥m，CE⊥m，∴∠ADB＝∠CEA＝90°，∴∠BAD+∠ABD＝90°，∴∠ABD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（AAS）；（2）DE＝BD+CE．理由是：如图②，∵∠BDA＝∠AEC＝∠BAC，∴由三角形内角和及平角性质，得：∠BAD+∠ABD＝∠BAD+∠CAE＝∠CAE+∠ACE，∴∠ABD＝∠CAE，∠BAD＝∠ACE，在△ABD和△ACE中，，∴△ABD≌△ACE（ASA），∴BD＝AE，AD＝CE，∴DE＝AD+AE＝BD+CE．6．（1）证明：∵AE∥DF，∴∠A＝∠D，∵AB＝CD，∴AB+BC＝CD+BC，∴AC＝DB，在△EAC和△FDB中，，∴△EAC≌△FDB（SAS），∴∠E＝∠F；（2）解：由（1）得：△EAC≌△FDB，∴∠ECA＝∠FBD＝100°，∴∠F＝180°﹣∠D﹣∠FBD＝180°﹣28°﹣100°＝52°．7．解：（1）BD＝AC，BD⊥AC，理由：延长BD交AC于F．∵AE⊥BC，∴∠AEB＝∠AEC＝90°，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠DBE＝∠CAE，∵∠BED＝90°，∴∠EBD+∠BDE＝90°，∵∠BDE＝∠ADF，∴∠ADF+∠CAE＝90°，∴∠AFD＝180°﹣90°＝90°，∴BD⊥AC；（2）结论不发生变化，理由是：设AC与DE相交于点O，∵∠BEA＝∠DEC＝90°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠BDE＝∠ACE，∵∠DEC＝90°，∴∠ACE+∠EOC＝90°，∵∠EOC＝∠DOF，∴∠BDE+∠DOF＝90°，∴∠DFO＝180°﹣90°＝90°，∴BD⊥AC．8．（1）证明：∵AB∥DF，∴∠A＝∠EDF，在△ABE和△DFE中，，∴△ABE≌△DFE（AAS），∴AE＝DE；（2）解：过B作BH∥DF交CA的延长线于点H，∴∠HBE＝∠F＝∠AEB，∠H＝∠ACF＝ACB，∴BH＝EH＝BC＝5，∵CE＝3，∴CH＝HE+CE＝8，又∠BAD＝90°，∴CA＝HA＝CH＝4．9．（1）证明：∵AE⊥BC，DF⊥BC，∴∠AEB＝∠DFC＝90°，在Rt△ABE和Rt△CDF中，，∴Rt△ABE≌Rt△CDF（HL），∴BE＝CF，∴BE﹣EF＝CF﹣EF，∴CE＝BF；（2）∵Rt△ABE≌Rt△CDF，∴∠B＝∠C，∴AB∥CD．10．解：在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴∠ACD＝∠BCE，∴∠ACD﹣∠ACE＝∠BCE﹣∠ACE，即∠DCE＝∠ACB，∴∠ACB＝（∠BCD﹣∠ACE）＝（155°﹣55°）＝50°．。

八年级数学上册【满分秘诀】专题03 全等三角形(考点突破)(原卷版)

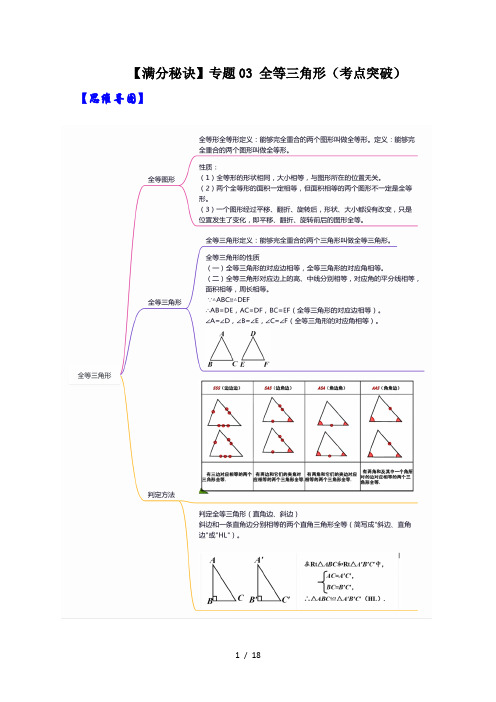
【满分秘诀】专题03 全等三角形（考点突破）【思维导图】【常见考法】【真题分点透练】【考点1 全等图形定义与性质】1．（2022春•盐湖区期末）下列各组图形中，属于全等图形的是（）A．B．C．D．2．（2021秋•信都区期末）如图，已知方格纸中是4个相同的正方形，则∠1与∠2的和为（）A．100°B．90°C．60°D．45°【考点2 全等三角形定义及性质】3．（2021秋•高阳县期末）如图，已知△ABC≌△DCB，∠A＝75°，∠DBC＝40°，则∠DCB的度数为（）A．75°B．65°C．40°D．30°4．（2021秋•重庆期末）如图，△ABC≌△AED，点E在线段BC上，∠1＝56°，则∠AED 的大小为（）A．34°B．56°C．62°D．68°5．（2022春•沙坪坝区期末）如图，点B，E，C，F在同一直线上，△ABC≌△DEF，BC ＝8，BF＝11.5，则EC的长为（）A．5B．4.5C．4D．3.56．（2022春•招远市期末）如图所示，△ABC≌△AEF．在下列结论中，不正确的是（）A．∠EAB＝∠F AC B．BC＝EF C．CA平分∠BCF D．∠BAC＝∠CAF 7．（2022春•通川区期末）如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，若△ABC ≌△A′B′C，且点A′恰好落在AB上，则∠ACA′的度数为（）A．30°B．45°C．50°D．60°8．（2021秋•民权县期末）如图，△ABC≌△ADE，且AE∥BD，∠BAD＝94°，则∠BAC 的度数的值为（）A．84°B．60°C．48°D．43°9．（2021秋•句容市期末）如图，Rt△AOB≌Rt△CDA，且点A、B的坐标分别为（﹣1，0），（0，2），则OD长是（）A．2B．5C．4D．310．（2021秋•温州期末）如图，△ABC≌△DEF，点A，B分别对应点D，E．若∠A＝70°，∠B＝50°，则∠1等于（）A．50°B．60°C．70°D．80°11．（2021秋•巢湖市期末）如图，△ACB≌△A′CB'，∠BCB'＝30°，则∠ACA'的度数为（）A．20°B．30°C．35°D．40°【考点3全等三角形判定】12．（2021秋•合肥期末）下列三角形与如图全等的三角形是（）A．B．C．D．13．（2021秋•大连期末）如图，DE⊥BA，DF⊥BC，垂足分别为E，F，DE＝DF．则△BDE≌△BDF的依据是（）A．SAS B．AAS C．SSS D．HL 14．（2021秋•汇川区期末）如图，AB∥DE，AB＝DE，添加下列条件，仍不能判断△ABC ≌△DEF的是（）A．AC＝DF B．BF＝CE C．∠A＝∠D D．AC∥DF15．（2021秋•西宁期末）下列四个三角形中，与图中的△ABC全等的是（）A．B．C．D．16．（2022春•盐湖区期末）如图，∠1＝∠2，添加下列条件，不能使△ABC≌△BAD的是（）A．∠CAB＝∠DBA B．AC＝BD C．∠C＝∠D D．AD＝BC 17．（2022春•西安期末）工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA、OB上分别在取OC＝OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线，这里构造全等三角形的依据是（）A．SSS B．ASA C．AAS D．SAS18．（2022春•文登区期末）如图，若∠B＝∠C，下列结论正确的是（）A．△BOE≌△COD B．△ABD≌△ACE C．AE＝AD D．∠AEC＝∠ADB 19．（2022春•宁德期末）如图，已知AB＝DE，AC＝DF，BE＝CF．则△ABC≌△DEF的理由是（）A．SAS B．ASA C．SSS D．AAS【考点4 全等三角形判定与性质综合应用】20．（2022春•子洲县期末）如图，点E是△ABC的边AC的中点，过点C作CF∥AB，连接FE并延长，交AB于点D，若AB＝9，CF＝6，则BD的长为（）A．2B．2.5C．3D．4.521．（2022春•通川区期末）如图，AD是△ABC的中线，CE∥AB交AD的延长线于点E，AB＝5，AC＝7，则AD的取值可能是（）A．3B．6C．8D．1222．（2022春•兰州期末）如图，在△ABC中，AB＝AC，点D是△ABC外一点，连接AD、BD、CD，且BD交AC于点O，在BD上取一点E，使得AE＝AD，∠EAD＝∠BAC，若∠ABC＝62°，则∠BDC的度数为（）A．56°B．60°C．62°D．64°22．（2022春•温县校级期末）如图，在△ABC中，AD⊥BC于点D，BE⊥AC与点E，BE 与AD交于点F，若AD＝BD＝5，CD＝3，则AF的长为（）A．3B．3.5C．2.5D．223．（2021秋•卧龙区期末）如图，E是∠AOB平分线上的一点，EC⊥OA于点C，ED⊥OB于点D，连结CD，若∠ECD＝25°，则∠AOB＝（）A．50°B．45°C．40°D．25°24．（2021秋•偃师市期末）如图，一块三角形的玻璃打碎成四块，现要到玻璃店去配一块完全一样的玻璃，最简单的办法是（）A．只带①去B．带②③去C．带①③去D．只带④去25．（2022春•沙坪坝区校级期末）如图所示，某工程队欲测量山脚两端A、B间的距离，在山旁的开阔地取一点C，连接AC、BC并分别延长至点D，点E，使得CD＝AC，CE ＝BC，测得DE的长，就是AB的长，那么判定△ABC≌△DEC的理由是（）A．SSS B．SAS C．ASA D．AAS 26．（2021秋•南宁期末）如图，点B，E，C，F在一条直线上，AC与DE相交于点O，AB＝DE，AB∥DE，BE＝CF．（1）求证：AC∥DF；（2）若∠B＝65°，∠F＝35°，求∠EOC的度数．27．（2022春•五华县期末）如图1，∠DAB＝90°，CD⊥AD于点D，点E是线段AD上的一点，若DE＝AB，DC＝AE．（1）判断CE与BE的关系是．（2）如图2，若点E在线段DA的延长线上，过点D在AD的另一侧作CD⊥AD，并保持CD＝AE，DE＝AB，连接CB，CE，BE，试说明（1）中结论是否成立，并说明理由．28．（2022春•永定区期末）如图，AD、BC相交于点O，AD＝BC，∠C＝∠D＝90°．（1）求证：△ACB≌△BDA；（2）若∠ABC＝31°，求∠CAO的度数．29．（2022春•通川区期末）如图，在四边形ABCD中，AB＝AC，BE平分∠CBA，连接AE，若AD＝AE，∠DAE＝∠CAB．（1）求证：△ADC≌△AEB；（2）若∠CAB＝36°，求证：CD∥AB．30．（2022春•泗阳县期末）如图，AB＝AE，AC＝DE，AB∥DE．（1）求证：AD＝BC；（2）若∠DAB＝70°，AE平分∠DAB，求∠B的度数．31．（2022春•新化县期末）如图，已知∠C＝∠F＝90°，BC＝EF，AE＝DB，BC与EF 交于点O．（1）求证：Rt△ABC≌Rt△DEF；（2）若∠A＝50°，求∠COE的度数．32．（2022春•鲤城区校级期末）如图，已知AB＝AC，点D，E分别是AC，AB的中点，求证：∠B＝∠C．33．（2022春•城阳区期末）已知：点A，D，C，B在同一条直线上，DF∥CE，DF＝CE，AD＝BC．求证：（1）CF＝DE；（2）AF∥EB．34．（2022春•城阳区期末）已知：OA＝OB，OC＝OD．（1）求证：△OAD≌△OBC；（2）若∠O＝85°，∠C＝25°，求∠BED的度数．35．（2022春•兴宁区期末）如图，△ABC中，AD是BC边上的中线，E，F为直线AD上的点，连接BE，CF，且BE∥CF．（1）求证：△BDE≌△CDF；（2）若AE＝13，AF＝7，试求DE的长．36．（2022春•长沙期末）如图，在△ABC中，∠B＝∠C，点D是边BC上一点，CD＝AB，点E在边AC上．（1）若∠ADE＝∠B，求证：①∠BAD＝∠CDE；②BD＝CE；（2）若BD＝CE，∠BAC＝70°，求∠ADE的度数．【考点5 角平分线性质】37．（2021秋•汇川区期末）如图，BD为∠ABC的角平分线，DE⊥BC于点E，DE＝6，∠A＝30°，则AD的长为（）A．6B．8C．12D．16 38．（2021秋•威县期末）下列各点中，到∠AOB两边距离相等的是（）A．点P B．点Q C．点M D．点N 39．（2021秋•木兰县期末）如图，BO、CO分别平分∠ABC、∠ACB，OD⊥BC于点D，OD＝2，△ABC的周长为28，则△ABC的面积为（）A．28B．14C．21D．740．（2022春•平远县期末）如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB 于点D，如果AC＝7cm，DE＝3cm，那么AE等于（）A．2cm B．3cm C．4cm D．5cm41．（2022春•岳麓区校级期末）如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是30cm2，AB＝13cm，AC＝7cm，则DE的长（）A．3cm B．4cm C．5cm D．6cm 42．（2022春•兰州期末）某镇要在三条公路围成的一块三角形平地内修建一个砂石场，如图，要使这个砂石场到三条公路的距离相等，则可供选择的地址（）A．仅有一处B．有四处C．有七处D．有无数处43．（2022春•港北区期末）如图，已知△ABC的周长是36cm，∠ABC和∠ACB的角平分线交于点O，OD⊥BC于点D，若OD＝3cm，则△ABC的面积是（）A．48cm2B．54cm2C．60cm2D．66cm2 44．（2022春•汉寿县期末）如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是20cm2，AB＝15cm，AC＝5cm，则DF的长为（）A．10cm B．5cm C．4cm D．2cm 45．（2020秋•饶平县校级期末）如图，D是∠EAF平分线上的一点，若∠ACD+∠ABD＝180°，请说明CD＝DB的理由．46.（2021秋•阳江期末）如图，点P是∠MON中一点，P A⊥OM于点A，PB⊥ON于点B，连接AB，∠P AB＝∠PBA．求证：OP平分∠MON．47.（2021秋•红桥区期末）在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F．（1）若BE＝CF，求证：AD是△ABC的角平分线．（2）若AD是△ABC的角平分线，求证：BE＝CF．【考点6 角平分线的判定与性质综合应用】48.如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．（1）说明BE＝CF的理由；（2）如果AB＝5，AC＝3，求AE、BE的长．49．（2022春•临漳县期末）如图，在四边形ABCD中，∠BAD＝α，∠BCD＝180°﹣α，BD平分∠ABC．（1）如图1，若α＝90°，根据教材中一个重要性质直接可得DA＝CD，这个性质是（2）问题解决：如图2，求证AD＝CD；（3）问题拓展：如图3，在等腰△ABC中，∠BAC＝100°，BD平分∠ABC，求证：BD+AD ＝BC．。

人教版八年级数学上册专题(三) 全等三角形判定与性质的综合运用

Rt△ODE≌Rt△OCE(AAS)，∴DE＝CE
类型三：证明两直线平行
4．如图，AC和BD相交于点O，OA＝OC，OB＝OD.求证：AB∥CD.
解：在△DOC 与△BOA 中，O∠CD＝OOC＝ A，∠BOA， OD＝OB，
∴△DOC≌△BOA(SAS)，∴∠D＝∠B，∴AB∥CD
类型四：证明两直线互相垂直 5．如图，在Rt△ABC中，∠BAC＝90°，AC＝2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A，D重合，连接BE，EC.试猜想线段BE和EC的数量及位置关系，并证明你的猜想．解：BE＝EC，BE⊥EC，证明：∵AC＝2AB，D是AC的中点，∴AB＝ AD＝CD，∵∠EAD＝∠EDA＝45°，∴∠EAB＝∠EDC＝135°，∵EA＝ ED，∴△EAB≌△EDC(SAS)，∴∠AEB＝∠DEC，EB＝EC，∴∠BED＋ ∠DEC＝∠BED＋∠AEB＝90°，∴BE⊥EC
3．如图，AC⊥AD，BC⊥BD，OE⊥CDபைடு நூலகம்AC＝BD.求证：DE＝CE.
解：∵AC⊥AD，BC⊥BD，∴∠A＝∠B＝90°，在 Rt△ADC 和 Rt△BCD 中，DACC＝＝CBDD，，∴Rt△ADC≌Rt△BCD(HL)，∴∠ACD
＝∠BDC，在 Rt△ODE 和 Rt△OCE 中，∠∠OOEDDE＝＝∠∠OOECCE＝，90°，∴ OE＝OE，
∴∠A＝∠D
类型二：证明两线段相等 2．如图，在四边形ABCD中，AD∥BC，∠A＝90°，BD＝BC， CE⊥BD于点E.求证：AD＝BE. 解：∵AD∥BC，∴∠ADB＝∠DBC，又CE⊥BD，∴∠BEC＝90°，又∵∠A＝90°，∴∠A＝∠BEC，又BD＝CB，∴△ABD≌△ECB(AAS)， ∴AD＝BE

八年级数学上册《三角形全等的判定和性质综合应用》教案、教学设计

4.归纳总结：培养学生从个别到一般、从具体到抽象的思维能力，提高学生的概括和总结能力。
（三）情感态度与价值观
1.积极主动：使学生树立积极主动的学习态度，养成良好的学习习惯，不断提高学习效率；
2.勇于探索：培养学生勇于探索、敢于创新的精神，使学生在面对困难和挑战时，能够保持积极向上的心态；
3.知识尊重：教育学生尊重知识、尊重科学，遵循客观规律，树立正确的价值观；
4.作业要求：
-学生在完成作业时，要注意书写规范，保持解答过程的简洁和清晰；
-对于提高作业和拓展作业，学生可以充分利用课余时间，进行小组合作、讨论交流，共同完成任务；
-教师将对学生的作业进行认真批改，并及时给予反馈，帮助学生发现和纠正错误。
5.作业评价：
-评价作业时，注重学生的思考过程和参与程度，鼓励创新思维和团队合作；
-提供丰富的习题和案例分析，帮助学生巩固知识，提高解题能力；
-建议学生使用几何画板等软件，进行自主探索和实验，加深对几何知识的理解。
四、教学内容与过程
（一）导入新课
1.教学活动设计：
-通过展示生活中全等三角形的实例，如建筑物的三角结构、拼图游戏等，引发学生对三角形全等的思考；
-提问：“同学们，你们在生活中遇到过全等三角形吗？它们有什么特点？”让学生分享自己的观察和发现。
4.部分学生对团队合作、交流分享的学习方式还不够熟悉，教师需在教学过程中加强引导和培养。
三、教学重难点和教学设想
（一）教学重难点
1.教学重点：
-理解并掌握三角形全等的判定方法（SSS、SAS、ASA、AAS、HL）；
-能够运用三角形全等的判定方法解决实际问题；
-培养学生的空间想象能力和逻辑推理能力。
在教学过程中，教师应注重引导学生通过自主探究、合作交流、实践操作等学习方法，培养以下过程与方法：

全等三角形的性质与判定的综合应用

全等三角形的性质与判定的综合应用全等三角形的对应角、对应边是相等的，全等三角形的判定是“SAS”、“ASA”、“AAS”、“SSS”，在说明线段相等或角相等时，常常需要综合运用全等三角形的性质和判定，下面举例予以说明。

一、说明线段相等例1、如图1，在△ABC 与△ABD 的顶点A 和D 均在BC 的同旁，AB=DC ，AC=DB ，AD 与BC 相交于O 点，则OA 与OD 相等吗若相等，请说明理由。

分析：要使OA=OD ，可分析△ABO 与△DCO 是否全等，但是条件中有一组边对应相等（AB=DC ），一组角对应相等（对顶角），显然不具备全等的条件。

但由已知条件可推出△ABC ≌△DCB ，再根据全等的性质可得∠A=∠D ，再根据全等三角形的判定“AAS”推出△ABO ≌△DCO ，从而得到OA=OD 。

解：OA=OD ，理由如下：在△ABC 和△DCB 中，因为AB=DC ，AC=BD ，BC=CB ，所以△ABC ≌△DCB （SSS ），所以∠A =∠D ，在△ABO 与△DCO 中因为∠A =∠D ，∠AOB=∠DOC ，AB=DC所以△ABO ≌△DCO ，所以OA=OD点评：本题考查了全等三角形的判定和性质。

说明两条线段相等时，可考虑着两条线段所在的两个三角形是否全等，若由已知条件不能直接说明这两个三角形全等时，可以由已知条件先推出其它的三角形全等，再由全等三角形的性质得到一些线段或角相等，为说明前面的三角形全等提供条件。

二、说明角相等例2、如图2，AB 、MN 与CD 相交于点O ，OA=OB ，OM=ON ，试问：∠D 与∠C 相等吗若相等，请进行说明理由. O D C B A 图1分析：要得到∠D=∠C，只需说明△BOD≌△AOC Array即可，但是由已知条件不能直接说明这两个三角形全等，但是由已知条件可推出△BON≌△AOM，由全等三角形的性质得到∠A=∠B，再结合OA=OB，∠AOC=∠BOD，即可说明△BOD≌△AOC。

浙教版-学年初中数学八年级上学期期末复习专题3 全等三角形的性质、判定与应用解析版

浙教版2019-2020学年初中数学八年级上学期期末复习专题3 全等三角形的性质、判定与应用一、单选题1.下列图形是全等图形的是（）A. B. C. D.2.下列选项中表示两个全等的图形的是( )A. 形状相同的两个图形B. 周长相等的两个图形C. 面积相等的两个图形D. 能够完全重合的两个图形3.下列不是利用三角形的稳定性的是（）A. 伸缩晾衣架B. 三角形房架C. 自行车的三角形车架D. 矩形门框的斜拉条4.如右图，△ABC≌△CDA，AB=4，BC=5，AC=6，则AD的长为（）A. 4B. 5C. 6D. 不能确定5.如图，用尺规作图作已知角平分线，其根据是构造两个三形全等，它所用到的判别方法是（）A. SASB. AASC. ASAD. SSS6.某实验室有一块三角形玻璃，被摔成如图所示的四块，胡老师想去店里买一块形状、大小与原来一样的玻璃，胡老师要带的玻璃编号是( )A. 1B. 2C. 3D. 47.在下列条件中，不能说明△ABC≌△A′B′C'的是( )A. ∠A=∠A′，∠C=∠C′，AC=A'C'B. ∠B=∠B′，∠C=∠C′，AB=A′B'C. ∠A=∠A′，AB=A′B′，BC=B'C'D. AB=A′B′，BC=B'C，AC=A′C'8.如图中，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，若点E，B，D到直线AC的距离分别为6、3、2，则图中实线所围成的阴影部分面积S是( )A. 50B. 44C. 38D. 329.如图，有A，B，C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（）A. 在AC，BC两边高线的交点处B. 在AC，BC两边中线的交点处C. 在AC，BC两边垂直平分线的交点处D. 在∠A，∠B内角平分线的交点处10.如图，AD是∆ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC=7 ，DE=2，AB=4，则AC的长是（）A. 3B. 4C. 5D. 6二、填空题11.如图，已知△ABC≌△DEC，∠E＝40°，∠ACB=110°，则∠D的度数为________．12.如图，已知AB∥CF，点E为DF的中点，若AB＝9 cm，CF＝5 cm，则BD＝________cm.13.如图：有一个直角三角形ABC，∠C＝90°，AC＝10，BC＝5，一条线段PQ＝AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问P点运动到离A的距离等于________时，ΔABC和ΔPQA 全等.14.如图，方格纸中△DEF的三个顶点分别在小正方形的顶点上，像这样的三个顶点都在格点上的三角形叫格点三角形，则与△DEF全等的格点（顶点在每个小格的顶点上）三角形能画________个.15.如图，△ABC中∠ABC=∠ACB，AB的垂直平分线交AC于点D．若∠A=40°，则∠DBC=________16.如图，在△ABC中，∠C＝90°，AD平分∠BAC，BC＝15，BD：CD＝3：2，则点D到AB的距离是________．三、解答题17.如图，已知△ABC（AC＜AB＜BC），请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：（1）在边BC上确定一点P，使得PA+PC=BC；（2）作出一个△DEF，使得：①△DEF是直角三角形；②△DEF的周长等于边BC的长．18.如图所示，已知点P是△ABC三条角平分线的交点，PD⊥AB，若PD=5，△ABC的周长为20，求△ABC的面积．19.已知，如图，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN 于点E；试猜测线段DE、AD、BE之间的数量关系，并说明理由．20.如图，已知AB∥CF，DE=EF（1）求证：△ADE≌△CFE；（2）若AB=7，CF=4，求BD长．21.如图：在△ABC中，己知∠ABC=45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M连接MD，过点D作DN⊥MD，交BM于点N．（1）求证：△DBN≌△DCM；（2）设CD与BM相交于点E，若点E是CD的中点，试探究线段NE、ME、CM之间的数量关系，并证明你的结论．22.在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE =∠BAC，连接CE.（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=________度；（2）设，.①如图2，当点在线段BC上移动，则，之间有怎样的数量关系？请说明理由；②当点在直线BC上移动，则，之间有怎样的数量关系？请直接写出你的结论.23.阅读理解：如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB=FC，从而把AB，AD，DC转化到△ADF中即可判断．（1）AB、AD、DC之间的等量关系为________；（2）完成（1）的证明．问题探究：如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．24.如图（1）如图①，∠MAN=90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．求证：△ABD≌△CAF；（2）如图②，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC．求证：△ABE≌△CAF；（3）如图③，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，求△ACF与△BDE的面积之和．答案解析部分一、单选题1. C解：A、两个圆不一样大，不是全等图形，不符合题意；B、两个三角形最大角分别是直角和钝角，不符合题意；C、两个图形放置的方位不一致，但图形的大小一样，形状相同，是全等图形，符合题意；D、两个正方形的大小不一样，不是全等图形；故答案为：C .【分析】只有形状相同，大小相等的两个图形才全等, 据此分别分析和判断.2.D解：A、形状相同的两个图形大小不一定相等，所以，不是全等图形，不符合题意；B、周长相等的两个图形形状、大小都不一定相同，所以，不是全等图形，不符合题意；C、面积相等的两个图形形状、大小都不一定相同，所以，不是全等图形，不符合题意；D、能够完全重合的两个图形是全等图形，符合题意．故答案为：D【分析】全等形的定义，能够完全重合的两个图形是全等形。

全等三角形性质与判定综合应用【精品】

全等三角形的性质与判定综合应用
1.如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．（1）求证：△ACD≌△BCE；
（2）若∠D=50°，求∠B的度数．
2.
如图，∠BAC=
∠DAE，∠ABD=∠ACE，BD=CE，试判断AB与AC的大小关系，并说明理由．
3.如图，已知AB=AC，AD=AE，BD=CE，且B、D、E三点共线，求证：∠3=∠1+∠2.
4.如图，已知AB⊥DC于点B，AB=DB，点E在AB上，BE=BC，延长DE，交AC于点F，求证：DE=AC，DE⊥AC．
5.如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E．AD⊥CE 于点D．
求证：DE=AD-BE ．
6.如图，已知AD∥BC，点E为CD上一点，AE、BE分别平分∠DAB、∠CBA，BE的延长线交AD的延长线于点F．（1）求证：△ABE≌△A FE；（2）求证：AD+BC=AB．
7.如图所示，Rt△ABC中，∠ABC=90°，BD⊥AC，且AE平分∠BAC，AF=AB，求证：EF∥BC。

8.如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM =CN，AM交BN于点P．（1）求证：△ABM≌△BCN；（2）求∠APN
的度数．
9.如图，已知AB=AE，BC=ED，CF=FD，AC=AD．求证：∠BAF=∠EAF.
10.如图，已知A、F、C、D四点在同一条直线上，AF=CD，AB∥DE，且AB=DE．
求证：（1）△ABC≌△DEF；（2）∠CBF=∠FEC。

全等三角形的判定及性质的综合运用

全等三角形的判定方法
SSS（边边边） SAS（边角边） ASA（角边角） AAS（角角边）
有三边对应相等的两个三角形全等.
有两边和它们的夹角对应相等的两个三角形全等.
边三有对角两应形角相全和等等它的.们两的个夹一应形有相个全两等角等角的所.和两对及个的其三边中对角
1
全等三角形的性质
• 全等三角形的对应边相等 • 全等三角形的对应角相等 • 全等三角形的面积相等 • 全等三角形的周长相等 • 全等三角形对应边上的高相等 • 全等三角形对应边上的中线相等
一.挖掘“隐含条件”判全等二.添条件判全等三.转化“间接条件”判全等
A 解：∵AE=CF(已知)
∴AE－FE=CF－EF(等量减等量，差相等)
即AF=CE
F
B
D E
C
10
例、如图，已知AB=AC，AD=AE，AB、DC相交
于点M，AC、BE相交于点N，∠1=∠2，试说明：
（1） △ABE ≌ △ACD （2）AM=AN A
12
D
E
M
N
B
C
创造条件！？ 11
总结与反思：
学习目标：
1.较熟练地掌握全等三角形判定方法以及性质在常规习题中的运用。
2.学会利用将一个复杂图形分解成有助于解题的简单图形，以及将这些简单图形在大脑中重新组合成原来的图形。
自主探究1：添条件判全等
• 独立思考以下题目，二分钟后看谁回答的准确
B
如图，已知AD平分∠BAC， A
要使△ABD≌△ACD， • 根据“SAS”需要添加条件 AB=AC ； • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C

中考数学一轮复习专题解析—全等三角形判定与性质定理

中考数学一轮复习专题解析—全等三角形判定与性质定理复习目标1.掌握全等三角形的概念和性质，能够准确地辨认全等三角形中的对应元素；2．探索三角形全等的判定方法，能利用三角形全等进行证明，掌握综合法证明的格式；考点梳理一、基本概念1.全等三角形的定义：能够完全重合的两个三角形叫做全等三角形.2.全等三角形的性质（1）全等三角形对应边相等；（2）全等三角形对应角相等.特别提醒：全等三角形的周长、面积相等；对应的高线，中线，角平分线相等.3.全等三角形的判定方法（1）三边对应相等的两个三角形全等(SSS)；（2）两角和它们的夹边对应相等的两个三角形全等（ASA）；（3）两角和其中一角的对边对应相等的两个三角形全等(AAS)；（4）两边和它们的夹角对应相等的两个三角形全等(SAS)；（5）斜边和一条直角边对应相等的两个直角三角形全等(HL).例1．如图，BD、CE分别是△ABC的边AC和AB上的高，点P在BD的延长线上，BP=AC，点Q在CE上，CQ=AB．求证：（1）AP=AQ；（2）AP△AQ．【答案】证明：（1）△BD、CE分别是△ABC的边AC和AB上的高，△△1+△CAE=90°，△2+△CAE=90°．△△1=△2,△在△AQC和△PAB中，△△AQC△△PAB．△ AP=AQ.(2)△ AP=AQ，△QAC=△P，△△PAD+△P=90°，△△PAD+△QAC=90°，即△PAQ=90°．△AP△AQ．二、灵活运用定理三角形全等是证明线段相等，角相等的最基本、最常用的方法，这不仅因为全等三角形有很多重要的角相等、线段相等的特征，还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来．应用三角形全等的判别方法注意以下几点：1. 条件充足时直接应用判定定理在证明与线段或角相等的有关问题时，常常需要先证明线段或角所在的两个三角形全等.这种情况证明两个三角形全等的条件比较充分，只要认真观察图形，结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等．2. 条件不足，会增加条件用判定定理此类问题实际是指条件开放题，即指题中没有确定的已知条件或已知条件不充分，需要补充三角形全等的条件．解这类问题的基本思路是：执果索因，逆向思维，即从求证入手，逐步分析，探索结论成立的条件，从而得出答案．3. 条件比较隐蔽时，可通过添加辅助线用判定定理在证明两个三角形全等时，当边或角的关系不明显时，可通过添加辅助线作为桥梁，沟通边或角的关系，使条件由隐变显，从而顺利运用全等三角形的判别方法证明两个三角形全等．例2．如图，已知AD为△ABC的中线，且△1＝△2,△3＝△4,求证：BE＋CF＞EF.【答案】证明：延长ED至M，使DM=DE，连接CM，MF,在△BDE和△CDM中，△△BDE△△CDM（SAS）．△BE=CM.又△△1＝△2，△3＝△4 ，△1＋△2＋△3＋△4＝180°，△△3＋△2=90°，即△EDF＝90°，△△FDM＝△EDF ＝90°．在△EDF和△MDF中△△EDF△△MDF（SAS）,△EF＝MF （全等三角形对应边相等）,△在△CMF中，CF＋CM＞MF（三角形两边之和大于第三边）,△BE＋CF＞EF.三、常见的几种辅助线添加△遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”；△遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形利用的思维模式是全等变换中的“旋转”；△遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理；△过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”；△截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分之类的题目．例3．如图所示，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF. 求证：AC=BF.【答案】证明：延长AD到H，使得DH=AD，连结BH，△ D为BC中点，△ BD=DC，在△ADC和△HDB中，△ △ADC△△HDB(SAS)，△ AC=BH, △H=△HAC，△ EA=EF，△ △HAE=△AFE，又△ △BFH=△AFE，△ BH=BF，△ BF=AC．综合训练1．（2022·长沙市雅礼实验中学九年级月考）如图，小明书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A．SSS B．SSA C．ASA D．SAS【答案】C【分析】根据全等三角形的判定方法解答即可．【详解】解：画一个三角形A′B′C′，使△A′=△A，A′B′=AB，△B′=△B，符合全等三角形的判定定理ASA，故选：C．2．（2022·全国九年级专题练习）如图G是△ABC的重心，直线过A点与BC平行．若直线CG分别与AB、交于D、E两点，直线BG与AC交于F点，则△AED 的面积：四边形ADGF的面积＝（）A．1：2B．2：1C．2：3D．3：2【答案】D【分析】根据重心的概念得出D，F分别是三角形边的中点．若设△ABC的面积是2，则△BCD的面积和△BCF的面积都是1．又因为BG：GF＝CG：GD，可求得△CGF 的面积．则四边形ADGF的面积也可求出．根据ASA可以证明△ADE△△BDC，则△ADE的面积是1．则△AED的面积：四边形ADGF的面积可求．【详解】解：设三角形ABC的面积是2，△三角形BCD的面积和三角形BCF的面积都是1，△BG：GF＝CG：GD＝2，△三角形CGF的面积是13，△四边形ADGF的面积是2−1−13＝23，△//l BC,△EAD CBD∠=∠,△,=∠=∠,BD AD ADE BDC△△ADE△△BDC（ASA）△△ADE的面积是1△△AED的面积：四边形ADGF的面积＝1：2＝3：2．3故选：D．3．（2022·重庆实验外国语学校九年级月考）如图，在正方形ABCD中，210AB=﹐E，F分别为BC，CD的中点，连接AE、BF，AE交BF于点G，将BCF△沿BF△的面积是（）翻折得到BPF△，延长FP交BA延长线于点Q，连接QG，则QGFA．25B．25C．20D．15 2【答案】D【分析】由已知可求QF=QB，在Rt△BPQ中，由勾股定理求得QB，可求出S△BQF=25，再证明△ABE△△BCF（SAS），△BGE△△BCF，由此得BF，GE，BG，过点G作GN△AB交AB于N，可证明△ANG△△ABE，再由GA=AE-GE，可求得GN，根据S△QGF=S△BQF-S△BQG即可求解．【详解】解：将BCF△，△沿BF翻折得到BPF∴PF =FC ，△PFB =△CFB ，四边形ABCD 是正方形∴△FPB =90°，CD △AB ，,90AB BC ABE BCF =∠=∠=︒△△CFB =△ABF ， △△ABF =△PFB ， △QF =QB ，△PF =FC =12CD 12AB =PB =AB 在Rt △BPQ 中，222QB BP PQ =+，△222(QB QB =+，△QB△S△BQF =1252=，△AB =BC ，BE =CF ，△ABE =△BCF =90°， △△ABE △△BCF （SAS ）， △△AEB =△BFC ，又△△EBG =△CBF ， △△BGE △△BCF ，GE BG BECF BC BF∴==， △CF，BC △BF△GEBG ，过点G 作GN △AB 交AB 于N ，△△GAN=△EAB，△ANG=△ABE=90°，△△ANG△△ABE，△GN GABE EA=△GA=AE-GE =42△GN=4105△S△BQG=12×QB×GN=1510410225⨯⨯=10，△S△QGF=S△BQF-S△BQG=25-10=15，故选：D．4．（2022·四川省宜宾市第二中学校九年级一模）如图，以ABC的三边为边分别作等边ACD△、ABE△、BCF△，则下列结论正确的是（）A．EBF DFC≌B．四边形ADFE为矩形C．四边形ADFE为菱形D ．当AB AC =，120BAC ∠=︒时，四边形ADFE 是正方形【答案】A【分析】利用SAS 得到△EBF 与△DFC 全等，利用全等三角形对应边相等得到EF ＝AC ，再由△ADC 为等边三角形得到三边相等，等量代换得到EF ＝AD ，AE ＝DF ，利用对边相等的四边形为平行四边形得到AEFD 为平行四边形，若AB ＝AC ，△BAC ＝120°，只能得到AEFD 为菱形，不能为正方形，即可得到正确的选项．【详解】解：△△ABE 、△BCF 为等边三角形，△AB ＝BE ＝AE ，BC ＝CF ＝FB ，△ABE ＝△CBF ＝60°，△△ABE −△ABF ＝△FBC −△ABF ，即△CBA ＝△FBE ，在△ABC 和△EBF 中，AB EB CBA FBE BC BF =⎧⎪∠=∠⎨⎪=⎩， △△ABC △△EBF （SAS ），△EF ＝AC ，又△△ADC 为等边三角形，△CD ＝AD ＝AC ，△EF ＝AD ＝DC ，同理可得△ABC △△DFC ，△DF ＝AB ＝AE ＝DF ，△四边形AEFD 是平行四边形，故B 、C 选项错误；△△FEA ＝△ADF ，△△FEA ＋△AEB ＝△ADF ＋△ADC ，即△FEB ＝△CDF ，在△FEB 和△CDF 中，EF DC FEB CDF EB FD =⎧⎪∠=∠⎨⎪=⎩． △△FEB △△CDF （SAS ），故选项A 正确；若AB ＝AC ，△BAC ＝120°，则有AE ＝AD ，△EAD ＝120°，此时AEFD 为菱形，选项D 错误故选A ．5．（2022·重庆实验外国语学校九年级开学考试）如图在四边形ABEC 中，BEC ∠和BAC ∠都是直角，且AB AC =．现将BEC ∆沿BC 翻折，点E 的对应点为E '，BE '与AC 边相交于D 点，恰好BE '是ABC ∠的角平分线，若1CE =，则BD 的长为（）A ．1.5B 2C ．2D 3【答案】C【分析】如图，延长CE '和BA 相交于点F ，根据翻折的性质可以证明△BE′C △△BE′F ，可得CF =2，再证明△FCA △△DBA ，可得BD =CF =2．【详解】解：如图，延长CE '和BA 相交于点F ，由翻折可知：90BE C E ∠'=∠=︒，1CE CE '==，BE '是ABC ∠的角平分线，CBE FBE ∴∠'=∠'，BE BE '='，∴()BE C BE F ASA '≅'，1E F CE ∴'='=，2CF ∴=，90FCA F ∠+∠=︒，90DBA F ∠+∠=︒，FCA DBA ∴∠=∠，90FAC DAB ∠=∠=︒，AB AC =，()FCA DBA ASA ∴≅，2BD CF ∴==．故选：C ．6．（2022·长沙市开福区青竹湖湘一外国语学校九年级三模）如图，在Rt ABC 中，90A ∠=︒，利用尺规在BA ，BC 上分别截取BD ，BE ，使BD BE =；分别以D ，E 为圆心、以大于12DE 的长为半径作弧，两弧在ABC ∠内交于点F ；作射线BF 交AC于点H．若2HA=，P为BC上一动点，则HP的最小值是（）A．12B．2C．1D．无法确定【答案】B【分析】根据作图过程可得BH平分△ABC，当HP△BC时，HP最小，根据角平分线的性质即可得HP的最小值．【详解】解：根据作图过程可知：BH平分△ABC，当HP△BC时，HP最小，△HP＝HA＝2．故选：B．7．（2022·长沙市雅礼实验中学九年级月考）如图，在Rt ABC中，90C∠=︒，以点A为圆心，适当的长度为半径画弧，分别交AC、AB于点M、N，再分别以M、N为圆心，以大于12MN的长度为半径画弧，两弧交于点O，作射线AO交BC于点D，若54B∠=︒，则CDA∠=______度．【答案】72°利用三角形内角和180°，解得36CAB ∠=︒，由角平分线性质解得18CAD ∠=︒的度数，最后根据三角形外角性质解题即可．【详解】解：90,54C B ∠=︒∠=︒905436CAB ∴∠=︒-︒=︒ AD 平分CAB ∠ 1182CAD DAB CAB ∴∠=∠=∠=︒ 185472CDA DAB B ∴∠=∠+∠=︒+︒=︒故答案为：72．8．（2022·广东深圳市南山外国语学校九年级二模）如图，在平面直角坐标系中，矩形OABC 中，3OA =，6OC =，将ABC 沿对角线AC 翻折，使点B 落在B '处，AB '与y 轴交于点D ，则点D 的坐标为______．【答案】9(0,)4-【分析】设OD m =，则6CD m =-，由题意可以求证AOD CB D '△≌△，从而得到6AD CD m ==-，再根据勾股定理即可求解．解：由题意可知：3OA BC B C '===，6OC AB ==，90B B AOD '∠=∠=∠=︒ 设OD m =，则6CD m =-，又△B DC ADO '∠=∠△()AOD CB D AAS '△≌△△6AD CD m ==-在Rt AOD △中，222AD AO OD =+，即222(6)3m m -=+ 解得：94m =△点D 的坐标为9(0,)4-故答案为9(0,)4-9．（2022·广东实验中学九年级三模）已知，ABC DCB ∠=∠，ACB DBC ∠=∠，求证：ABC DCB △≌△．【答案】证明见解析【分析】由条件△ABC ＝△DCB ，△ACB ＝△DBC ，根据ASA 证明△ABC △△DCB 即可．【详解】证明：在△ABC 和△DCB 中，ABC DCB BC CBACB DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩， △△ABC △△DCB （ASA ）；10．（2022·厦门市湖滨中学）如图，在△ABE 和△CDF 中，点C 、E 、F 、B 在同一直线上，BF ＝CE ，若AB △CD ，△A ＝△D ．求证：AB ＝CD ．【答案】见解析【分析】根据平行线的性质可得△B ＝△C ，根据已知条件可得BE ＝CD ，结合已知条件△A ＝△D ，即可证明△ABE △△DCF ，进而即可得证AB ＝CD ．【详解】解：△AB △CD ，△△B ＝△C ．△BF ＝CE ，△BF ＋EF ＝CE ＋EF ，即BE ＝CF ．△△A ＝△D ，△B ＝△C ，BE ＝CF△△ABE △△DCF （AAS ）．△AB ＝CD ．。

2021年九年级数学中考复习——几何专题：全等三角形性质与判定(三)

2021年九年级数学中考复习——几何专题：全等三角形性质与判定（三）1．如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连结CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△BCE≌△CAD；（2）若BE＝5，DA＝12，则ED的长是．2．如图，已知△ABC中，AB＝AC＝12cm，BC＝10cm，点D为AB的中点．如果点P在线段BC上以2cm/s 的速度由点B向点C运动，同时，点Q在线段AC上由点A向点C以4cm/s的速度运动．若P、Q两点分别从B、A两点同时出发，回答下列问题：（1）经过2s后，此时PB＝cm，CQ＝cm；（2）在（1）的条件下，证明：△BPD≌△CQP；（3）当△CPQ的周长为18cm时，求经过多少秒后，△CPQ为等腰三角形？3．已知：在△ABC中，AB＝AC，点D、点E在边BC上，BD＝CE，连接AD、AE．（1）如图1，求证：AD＝AE；（2）如图2，当∠DAE＝∠C＝45°时，过点B作BF∥AC交AD的延长线于点F，在不添加任何辅助线的情况下，请直接写出图2中的四个等腰三角形，使写出的每个等腰三角形的顶角都等于45°．4．如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE＝CD，AD与BE相交于点F．（1）求证：BE＝AD；（2）求∠BFD的度数．5．若△ABC和△AED均为等腰三角形，且∠BAC＝∠EAD＝90°．（1）如图（1），点B是DE的中点，判定四边形BEAC的形状，并说明理由；（2）如图（2），若点G是EC的中点，连接GB并延长至点F，使CF＝CD．求证：①EB＝DC，②∠EBG＝∠BFC．6．问题1：如图①，在四边形ABCD中，∠B＝∠C＝90°，P是BC上一点，P A＝PD，∠APD＝90°．求证：AB+CD＝BC．问题2：如图②，在四边形ABCD中，∠B＝∠C＝45°，P是BC上一点，P A＝PD，∠APD＝90°．求的值．7．如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连接CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△BCE≌△CAD；（2）请直接写出AD，BE，DE之间的数量关系：．8．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D在边BC上（不与点B、C重合），BE⊥AD，垂足为E，过点C作CF⊥CE，交线段AD于点F．（1）试说明△CAF≌△CBE的理由；（2）数学老师在课堂上提出一个问题，如果EF＝2AF，试说明CD＝BD的理由．班级同学随后进行了热烈讨论，小明同学提出了自己的想法，可以取EF的中点H，联结CH，就能得出结论，你能否能根据小明同学的想法，写出CD＝BD的理由．9．如图，四边形ABCD中，对角线AC、BD交于点O，AB＝AC，点E是BD上一点，且∠ABD＝∠ACD，∠EAD＝∠BAC．（1）求证：AE＝AD；（2）若∠ACB＝65°，求∠BDC的度数．10．如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC，D为斜边AC延长线上一点，过D点作BC的垂线交其延长线于点E，在AB的延长线上取一点F，使得BF＝CE，连接EF．（1）若AB＝2，BF＝3，求AD的长度；（2）G为AC中点，连接GF，GE，GB，求证：GE＝GF．参考答案1．证明：（1）∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA，在△BCE和△CAD中，，∴△BCE≌△CAD（AAS）；（2）解：∵△BCE≌△CAD，∴BE＝DC＝5，AD＝CE＝12，∴DE＝CE﹣CD＝12﹣5＝7．故答案为：7．2．（1）解：当P，Q两点分别从B，A两点同时出发运动2秒时，有BP＝2×2＝4cm，AQ＝4×2＝8cm，则CP＝BC﹣BP＝10﹣4＝6cm，∴CQ＝AC﹣AQ＝12﹣8＝4cm，故答案为：4，4；（2）证明：∵D是AB的中点，∴BD＝AB＝6cm，∴BP＝CQ，BD＝CP，又∵△ABC中，AB＝AC，∴∠B＝∠C，在△BPD和△CQP中，，∴△BPD≌△CQP（SAS）；（3）解：设当P，Q两点同时出发运动t秒时，有BP＝2t，CP＝10﹣2t，CQ＝12﹣4t，∴PQ＝18﹣（10﹣2t）﹣（12﹣4t）＝6t﹣4，要使△CPQ是等腰三角形，则可分为三种情况讨论：①当CP＝CQ时，则有10﹣2t＝12﹣4t，解得：t＝1；②当PQ＝PC时，则有6t﹣4＝10﹣2t解得：t＝；③当QP＝QC时，则有6t﹣4＝12﹣4t解得：t＝；综上所述，当t＝1s或s或s时，△CPQ是等腰三角形．3．（1）证明：∵AB＝AC，∵∠B＝∠C，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AD＝AE；（2）∵AD＝AE，∴∠ADE＝∠AED，∵BF∥AC，∴∠FBD＝∠C＝45°，∵∠ABC＝∠C＝∠DAE＝45°，∠BDF＝∠ADE，∴∠F＝∠BDF，∠BEA＝∠BAE，∠CDA＝∠CAD，∴满足条件的等腰三角形有：△ABE，△ACD，△DAE，△DBF．4．（1）证明：∵△ABC为等边三角形，∴∠BAE＝∠C＝60°，AB＝CA，在△ABE和△CAD中，，∴△ABE≌△CAD（SAS），∴BE＝AD；（2）解：∵∠BFD＝∠ABE+∠BAD，又∵△ABE≌△CAD，∴∠ABE＝∠CAD．∴∠BFD＝∠CAD+∠BAD＝∠BAC＝60°．5．解：（1）四边形BEAC是平行四边形，理由如下：∵△AED为等腰三角形，∠EAD＝90°，B是DE的中点，∴∠E＝∠BAE＝45°，∠ABE＝90°，∵△ABC是等腰三角形，∠BAC＝90°，∴∠ABC＝∠BAE＝45°，∠ABE＝∠BAC＝90°，∴BC∥AE，AC∥BE，∴四边形BEAC是平行四边形；（2）①∵△ABC和△AED均为等腰三角形，∠BAC＝∠EAD＝90°，∴AE＝AD，AB＝AC，∠BAE＝∠CAD，∴△AEB≌△ADC（SAS），∴BE＝CD；②延长FG至点H，使GH＝FG，∵G是EC的中点，∴EG＝DC，又∵∠EGH＝∠FGC，∴△EGH≌△CGF（SAS），∴∠BFC＝∠H，CF＝EH，∵CF＝CD，CD＝BE，∴EH＝BE，∴∠H＝∠EBG，∴∠EBG＝∠BFC．6．证明：（1）∵∠B＝∠APD＝90°，∴∠BAP+∠APB＝90°，∠APB+∠DPC＝90°，∴∠BAP＝∠DPC，又P A＝PD，∠B＝∠C＝90°，∴△BAP≌△CPD（AAS），∴BP＝CD，AB＝PC，∴BC＝BP+PC＝AB+CD；（2）如图2，过点A作AE⊥BC于E，过点D作DF⊥BC于F，由（1）可知，EF＝AE+DF，∵∠B＝∠C＝45°，AE⊥BC，DF⊥BC，∴∠B＝∠BAE＝45°，∠C＝∠CDF＝45°，∴BE＝AE，CF＝DF，AB＝AE，CD＝DF，∴BC＝BE+EF+CF＝2（AE+DF），∴＝＝．7．证明：（1）∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA，在△BCE和△CAD中，，∴△BCE≌△CAD（AAS）；（2）∵△BCE≌△CAD，∴BE＝DC，AD＝CE，∴AD＝CE＝CD+DE＝BE+DE，故答案为：AD＝BE+DE．8．解：（1）∵BE⊥AD，∴∠ACB＝∠BED＝90°，又∵∠ADC＝∠BDE，∴∠CAF＝∠CBE，∵CE⊥CF，∴∠ECF＝∠ACB＝90°，∴∠ACF＝∠BCE，又∵AC＝BC，∴△CAF≌△CBE（ASA）；（2）如图，取EF的中点H，联结CH，∵△CAF≌△CBE，∴CF＝CE，AF＝BE，∴△CEF是等腰直角三角形，∵点H是EF中点，∴CH＝FH＝EH＝EF，CH⊥EF，∵EF＝2AF，∴CH＝AF＝FH＝EH，∴CH＝BE，又∵∠CDH＝∠BDE，∠CHD＝∠BED＝90°，∴△CHD≌△BED（AAS），∴CD＝BD．9．证明：（1）∵∠BAC＝∠EAD∴∠BAC﹣∠EAC＝∠EAD﹣∠EAC即：∠BAE＝∠CAD在△ABE和△ACD中，∴△ABE≌△ACD（ASA），∴AE＝AD；（2）解：∵∠ACB＝65°，AB＝AC，∴∠ABC＝∠ACB＝65°，∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣65°﹣65°＝50°，∵∠ABD＝∠ACD，∠AOB＝∠COD，∴∠BDC＝∠BAC＝50°．10．解：（1）∵DE⊥BE，AB⊥BE，∴DE∥AB，∴△ABC∽△DEC，∵∠ABC＝90°，AB＝BC，∴△CDE为等腰直角三角形，∵CE＝BF＝3，∴CD＝3，∵AB＝2，∴AC＝2，∴AD＝AC+CD＝5；（2）证明：∵G是等腰直角△ABC斜边AC中点。

12.2全等三角形的性质与判定的综合运用教案

2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了全等三角形的基本概念、性质、判定方法及其在实际中的应用。通过实践活动和小组讨论，我们加深了对全等三角形的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
五、教学反思
在今天的教学过程中，我重点关注了全等三角形的性质与判定的综合运用。通过观察学生的反应和参与度，我有以下几点反思：
首先，我发现同学们在理解全等三角形的性质时，普遍对对应中线、对应角平分线相等的概念掌握不够扎实。在今后的教学中，我需要更加注重对这些性质的解释和举例，以便让学生更好地理解。
其次，全等三角形的判定方法是本节课的重点，但部分学生在运用这些方法时仍然感到困惑。我意识到，在讲解判定方法时，应该更加清晰地阐述各种判定方法的适用条件，并通过更多实际例题来帮助学生巩固。
在总结回顾环节，我尝试让学生自主总结全等三角形的知识点，发现他们能够较好地概括出本节课的重点内容。但我也注意到，有些同学在总结时遗漏了一些关键信息。为了帮助学生更全面地掌握知识，我计划在今后的教学中，增加课堂小结的环节，引导学生逐步完善知识结构。
-难点2：学生在判定全等三角形时，可能对各种判定方法的适用条件混淆。教师应通过对比分析，让学生明确各种判定方法的特点，并提供典型例题进行讲解；
-难点3：学生在解决实际问题时，可能难以将问题与全等三角形的知识联系起来。教师应提供具有代表性的实际问题，引导学生学会分析问题、建立数学模型，并运用全等三角形的性质与判定方法解决问题。