2019年中考数学总复习第一编教材知识梳理篇第1章数与式第4节因式分解与分式精练试题
初中数学教材知识梳理·系统复习.pdf
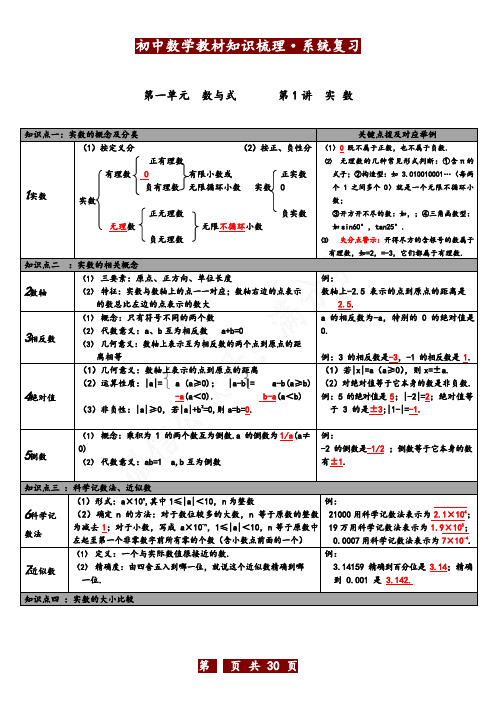
第一单元数与式第1 讲实数知识点一:实数的概念及分类关键点拨及对应举例1.实数(1)按定义分(2)按正、负性分正有理数有理数 0 有限小数或正实数负有理数无限循环小数实数0实数正无理数负实数无理数无限不循环小数负无理数(1)0 既不属于正数,也不属于负数.(2)无理数的几种常见形式判断:①含π的式子;②构造型:如 3.010010001…(每两个 1 之间多个 0)就是一个无限不循环小数;③开方开不尽的数:如,;④三角函数型:如sin60°,tan25°.(3)失分点警示:开得尽方的含根号的数属于有理数,如=2,=-3,它们都属于有理数.知识点二:实数的相关概念2.数轴(1)三要素:原点、正方向、单位长度(2)特征:实数与数轴上的点一一对应;数轴右边的点表示的数总比左边的点表示的数大例:数轴上-2.5 表示的点到原点的距离是2.5.3.相反数(1)概念:只有符号不同的两个数(2)代数意义:a、b 互为相反数a+b=0(3)几何意义:数轴上表示互为相反数的两个点到原点的距离相等a 的相反数为-a,特别的 0 的绝对值是0.例:3 的相反数是-3,-1 的相反数是1.4.绝对值(1)几何意义:数轴上表示的点到原点的距离(2)运算性质:|a|= a (a≥0);|a-b|= a-b(a≥b)-a(a<0). b-a(a<b)(3)非负性:|a|≥0,若|a|+b2=0,则a=b=0.(1)若|x|=a(a≥0),则x=±a.(2)对绝对值等于它本身的数是非负数.例:5 的绝对值是5;|-2|=2;绝对值等于 3 的是±3;|1-|=-1.5.倒数(1)概念:乘积为 1 的两个数互为倒数.a 的倒数为1/a(a≠0)(2)代数意义:ab=1 a,b 互为倒数例:-2 的倒数是-1/2 ;倒数等于它本身的数有±1.知识点三:科学记数法、近似数6.科学记数法(1)形式:a×10n,其中1≤|a|<10,n为整数(2)确定 n 的方法:对于数位较多的大数,n 等于原数的整数为减去1;对于小数,写成a×10-n,1≤|a|<10,n等于原数中左起至第一个非零数字前所有零的个数(含小数点前面的一个)例:21000用科学记数法表示为2.1×104;19万用科学记数法表示为1.9×105;0.0007用科学记数法表示为7×10-4.7.近似数(1)定义:一个与实际数值很接近的数.(2)精确度:由四舍五入到哪一位,就说这个近似数精确到哪一位.例:3.14159 精确到百分位是3.14;精确到 0.001 是3.142.知识点四:实数的大小比较8.实数的大小比较(1)数轴比较法:数轴上的两个数,右边的数总比左边的数大.(2)性质比较法:正数>0>负数;两个负数比较大小,绝对值大的反而小.(3)作差比较法:a-b>0 a>b;a-b=0 a=b;a-b<0 a<b.(4)平方法:a>b≥0a2>b2.例:把1,-2,0,-2.3 按从大到小的顺序排列结果为_ 1>0>-2>-2.3_.知识点五:实数的运算9 .常见运算乘方几个相同因数的积; 负数的偶(奇)次方为正(负)例:(1)计算:1-2-6=_-7;(-2)2=4;3-1=_1/3_;π0=__1;(2)64 的平方根是_±8 ,算术平方根是8_,立方根是4__.失分点警示:类似“的算术平方根”计算错误. 例:相互对比填一填:16的算术平方根是4,的算术平方根是_ 2 .零次幂a0=_1_(a≠0)负指数幂a-p=1/a p(a≠0,p为整数)平方根、算术平方根若x2=a(a≥0),则x= a.其中a是算术平方根.立方根若x3=a,则x=3a.10.混合运算先乘方、开方,再乘除,最后加减;同级运算,从左向右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号一次进行.计算时,可以结合运算律,使问题简单化第2 讲整式与因式分解知识点一:代数式及相关概念关键点拨及对应举例1.代数式(1)代数式:用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式.(2)求代数式的值:用具体数值代替代数式中的字母,计算得出的结果,叫做求代数式的值.求代数式的值常运用整体代入法计算.例:a-b=3,则 3b-3a=-9.2.整式(单项式、多项式)(1)单项式:表示数字与字母积的代数式,单独的一个数或一个字母也叫单项式.其中的数字因数叫做单项式的系数,所有字母的指数和叫做单项式的次数.(2)多项式:几个单项式的和.多项式中的每一项叫做多项式的项,次数最高的项的次数叫做多项式的次数.(3)整式:单项式和多项式统称为整式.(4)同类项:所含字母相同并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.例:(1)下列式子:①-2a2;②3a-5b;③x/2;④2/x;⑤7a2;⑥7x2+8x3y;⑦2017.其中属于单项式的是①③⑤⑦;多项式是②⑥;同类项是①和⑤.(2)多项式 7m5n-11mn2+1 是六次三项式,常数项是 1 .知识点二:整式的运算3.整式的加减运算(1)合并同类项法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.(2)去括号法则:若括号外是“+”,则括号里的各项都不变号;若括号外是“-”,则括号里的各项都变号.(3)整式的加减运算法则:先去括号,再合并同类项.失分警示:去括号时,如果括号外面是符号,一定要变号,且与括号内每一项相乘,不要有漏项.例:-2(3a-2b-1)=-6a+4b+2.4.幂运算法则(1)同底数幂的乘法:a m·a n=a m+n;(2)幂的乘方:(a m)n=a m n;(3)积的乘方:(a b)n=a n·b n;(4)同底数幂的除法:a m÷a n=a m-n(a≠0).其中 m,n都在整数(1)计算时,注意观察,善于运用它们的逆运算解决问题.例:已知 2m+n=2,则 3×2m×2n=6.(2)在解决幂的运算时,有时需要先化成同底数.例:2m·4m=23m.5.整式的乘除运算(1)单项式×单项式:①系数和同底数幂分别相乘;②只有一个字母的照抄. (2)单项式×多项式:m(a+b)=ma+mb.(3)多项式×多项式: (m+n)(a+b)=ma+mb+na+nb.(4)单项式÷单项式:将系数、同底数幂分别相除.(5)多项式÷单项式:①多项式的每一项除以单项式;②商相加.失分警示:计算多项式乘以多项式时,注意不能漏乘,不能丢项,不能出现变号错.例:(2a-1)(b+2)=2ab+4a-b-2.(6 )乘法公式平方差公式:(a+b)(a-b)=a2-b2.注意乘法公式的逆向运用及其变形公式的运用完全平方公式:(a±b)2=a2±2a b+b2.变形公式:a2+b2=(a±b)2∓2ab,ab=【(a+b)2-(a2+b2)】/26.混合运算注意计算顺序,应先算乘除,后算加减;若为化简求值,一般步骤为:化简、代入替换、计算.例:(a-1)2-(a+3)(a-3)-10=_-2a__.知识点五:因式分解7.因式分解(1)定义:把一个多项式化成几个整式的积的形式.(2)常用方法:①提公因式法:m a+m b+m c=m(a+b+c).②公式法:a2-b2=(a+b)(a-b);a2±2a b+b2=(a±b)2.(3)一般步骤:①若有公因式,必先提公因式;②提公因式后,看是否能用公式法分解;③检查各因式能否继续分解.(1)因式分解要分解到最后结果不能再分解为止,相同因式写成幂的形式;(2)因式分解与整式的乘法互为逆运算.第3 讲分式知识点一:分式的相关概念关键点拨及对应举例1.分式的概念A(1)分式:形如(A,B 是整式,且B 中含有字母,B≠0)B的式子.(2)最简分式:分子和分母没有公因式的分式.在判断某个式子是否为分式时,应注意:(1)判断化简之间的式子;(2)π是常数,不是字母.例:下列分式:①;②; ③;④2 x + 2 ,其中是分x2- 1式是②③④;最简分式③.A失分点警示:在解决分式的值为0,求值的问题时,一定要注意所求得的值满足分母不为0.x2-1例:当的值为0 时,则x=-1.x -1(1)无意义的条件:当B=0 时,分式无意义;B2.分式的 A(2)有意义的条件:当B≠0 时,分式有意义;B意义 A(3)值为零的条件:当A=0,B≠0 时,分式=0.B3.基本性质A A⋅C A ÷C( 1 ) 基本性质:==(C≠0).B B ⋅C B ÷C(2)由基本性质可推理出变号法则为:由分式的基本性质可将分式进行化简:x2-1x -1例:化简:= .x2+ 2 x+1 x +1A =-A=-(-A);-A=-A=A.B -B B B B -B 知识点三:分式的运算4.分式的约分和通分(1)约分(可化简分式):把分式的分子和分母中的公因式约去,am a即=;bm b(2)通分(可化为同分母):根据分式的基本性质,把异分母的分a c ac bd式化为同分母的分式,即, ⇒,b d bc bc分式通分的关键步骤是找出分式的最简公分母,然后根据分式的性质通分.例:分式1和1的最简公分母x2+x x (x-1)为x (x2- 1).5.分式的加减法(1)同分母:分母不变,分子相加减.即a±b=a±b;c c c(2)异分母:先通分,变为同分母的分式,再加减.即a±c=ad±bc.b d bd例:1+x=-1.x -1 1 -x1+1=2a.a +1 a -1 a2-16.分式的乘除法(1)乘法:a·c=ac;(2)除法:a÷c=ad;b d bd b d bc⎛a ⎫n an(3)乘方: ⎪=n(n 为正整数).⎝b ⎭b例:a⋅b=1;2÷1=2y;2b a 2 x xy⎛ 3 ⎫3 =27 .-⎪- 3⎝2x ⎭8x7.分式的混合运算(1)仅含有乘除运算:首先观察分子、分母能否分解因式,若能,就要先分解后约分.(2)含有括号的运算:注意运算顺序和运算律的合理应用.一般先算乘方,再算乘除,最后算加减,若有括号,先算括号里面的.失分点警示:分式化简求值问题,要先将分式化简到最简分式或整式的形式,再代入求值.代入数值时注意要使原分式有意义.有时也需运用到整体代入.第4 讲二次根式知识点一:二次根式关键点拨及对应举例1.有关概念(1)二次根式的概念:形如a(a≥0)的式子.(2)二次根式有意义的条件:被开方数大于或等于0.(3)最简二次根式:①被开方数的因数是整数,因式是整式(分母中不含根号);②被开方数中不含能开得尽方的因数或因式失分点警示:当判断分式、二次根式组成的复合代数式有意义的条件时,注意确保各部分都有意义,即分母不为0,被开方数大于等于01等.例:若代数式有意义,则x 的取值x -1范围是x>1.2.二次根式的性质(1)双重非负性:①被开方数是非负数,即a≥0;②二次根式的值是非负数,即a ≥0.注意:初中阶段学过的非负数有:绝对值、偶幂、算式平方根、二次根式.利用二次根式的双重非负性解题:(1)值非负:当多个非负数的和为0 时,可得各个非负数均为0.如a +1 + b -1 =0,则a=-1,b=1.(2)被开方数非负:当互为相反数的两个数同时出现在二次根式的被开方数下时,可得这一对相反数的数均为0. 如已知b= a -1 + 1-a ,则a=1,b=0.(2)两个重要性质:⎧⎪a(a≥0)①( a)2=a(a≥0);②a2=|a|=⎨;⎪⎩-a(a<0)(3)积的算术平方根:ab = a · b (a≥0,b≥0);(4)商的算术平方根:a=a(a≥0,b>0).b b例:计算:3.142=3.14;(-2)2 =2;24 =;=2 ;4=4=29 9 3知识点二:二次根式的运算3.二次根式的加减法先将各根式化为最简二次根式,再合并被开方数相同的二次根式.例:计算: 2 - 8 + 32 =3 2 .4.二次根式的乘除法(1)乘法:(2)除法:a ·ab=b = ab (a≥0,b≥0);a(a≥0,b>0).b注意:将运算结果化为最简二次根式.例:计算: 3 ⋅2 =1;32 =32 =4.2 3 2 25.二次根式的混合运算运算顺序与实数的运算顺序相同,先算乘方,再算乘除,最后算加减,有括号的先算括号里面的(或先去括号).运算时,注意观察,有时运用乘法公式会使运算简便.例:计算:( 2 +1)( 2 -1)= 1 .第二单元方程(组)与不等式(组)第5 讲一次方程(组)知识点一:方程及其相关概念关键点拨及对应举例1.等式的基本性质(1)性质1:等式两边加或减同一个数或同一个整式,所得结果仍是等式.即若a=b,则a±c=b±c .(2)性质2:等式两边同乘(或除)同一个数(除数不能为0),所得结果仍是等式.即若a=b,则ac=bc,a=b(c≠0).c c(3)性质3:(对称性)若a=b,则b=a.(4)性质4:(传递性)若a=b,b=c,则a=c.失分点警示:在等式的两边同除以一个数时,这个数必须不为0.例:判断正误.(1)若a=b,则a/c=b/c. (×)(2)若a/c=b/c,则a=b. (√)2.关于方程(1)一元一次方程:只含有一个未知数,并且未知数的次数是1,且等式两边都是整式的方程.在运用一元一次方程的定义解题时,注意一次项系数不等于0.的基本概念(2)二元一次方程:含有两个未知数,并且含有未知数的项的次例:若(a-2) x |a -1| + a = 0 是关于 x 的一元一次方程,则 a 的值为 0. 数都是 1 的整式方程.(3)二元一次方程组:含有两个未知数的两个一次方程所组成的一组方程.(4)二元一次方程组的解:二元一次方程组的两个方程的公共解.知识点二 :解一元一次方程和二元一次方程组3.解一元一次方程的步骤 (1)去分母:方程两边同乘分母的最小公倍数,不要漏乘常数项; (2)去括号:括号外若为负号,去括号后括号内各项均要变号; (3)移项:移项要变号;(4) 合并同类项:把方程化成 ax=-b(a ≠0); (5) 系数化为 1:方程两边同除以系数 a,得到方程的解 x=-b/a.失分点警示:方程去分母时,应该将分子用括号括起来,然后再去括号, 防止出现变号错误.4.二元一次 方程组的解法 思路:消元,将二元一次方程转化为一元一次方程.已知方程组,求相关代数式的值时, 需注意观察,有时不需解出方程组, 利用整体思想解决解方程组. 例: 已知⎧2x - y = 9 则 x-y 的值为 x-y=4.⎨x - 2 y = 3⎩方法:(1) 代入消元法:从一个方程中求出某一个未知数的表达式,再把 “它”代入另一个方程,进行求解;(2) 加减消元法:把两个方程的两边分别相加或相减消去一个未 知数的方法.知识点三 :一次方程(组)的实际应用5.列方程(组)解应用题的一般步骤(1)审题:审清题意,分清题中的已知量、未知量; (2)设未知数;(3)列方程(组):找出等量关系,列方程(组); (4)解方程(组);(5)检验:检验所解答案是否正确或是否满足符合题意; (6)作答:规范作答,注意单位名称.(1) 设未知数时,一般求什么设什么,但有时为了方便,也可间接设未知数.如题目中涉及到比值,可以设每一份为 x.(2) 列方程(组)时,注意抓住题目中的关键词语,如共是、等于、大(多)多少、小(少)多少、几倍、几分之几等.6.常见题型及关系式(1) 利润问题:售价=标价×折扣,销售额=售价×销量,利润=售价-进价,利润率=利润/进价×100%. (2) 利息问题:利息=本金×利率×期数,本息和=本金+利息.(3) 工程问题:工作量=工作效率×工作时间. (4) 行程问题:路程=速度×时间.①相遇问题:全路程=甲走的路程+乙走的路程;②追及问题:a.同地不同时出发:前者走的路程=追者走的路程;b.同时不同地出发:前者走的路 程+两地间距离=追者走的路程.第 6 讲 一元二次方程知识点一:一元二次方程及其解法关键点拨及对应举例1. 一元二次方程的相关概念(1) 定义:只含有一个未知数,且未知数的最高次数是 2 的整式方程. (2) 一般形式:ax 2+bx +c =0(a ≠0),其中 ax 2、bx 、c 分别叫做二次项、一次项、常数项,a 、b 、c 分别称为二次项系数、一次项系数、常数项.例:方程 axa+ 2 = 0 是关于 x 的一元二次方程,则方程的根为-1.2.一元二次 方(1)直接开平方法:形如(x +m )2=n (n ≥0)的方程,可直接开平方求解. ( 2 )因式分解法:可化为(ax +m )(bx +n )=0 的方程,用因式分解法求解.( 3 ) 公 式 法 : 一 元 二 次 方 程 ax 2 + bx + c = 0 的 求 根 公 式 为 解一元二次方程时, 注意观察, 先特殊后一般,即先考虑能否用直接开平方法和因的解法x= -b ±b2 - 4ac (b2-4ac≥0).2a(4)配方法:当一元二次方程的二次项系数为1,一次项系数为偶数时,也可以考虑用配方法.式分解法,不能用这两种方法解时,再用公式法.例:把方程x2+6x+3=0 变形为(x+h)2=k 的形式后,h=-3,k=6.知识点二:一元二次方程根的判别式及根与系数的关系(1)当Δ=b2- 4ac>0 时,原方程有两个不相等的实数根.例:方程x2+ 2x -1 = 0 的判别式3.根的判别式(2)当Δ=b2- 4ac=0 时,原方程有两个相等的实数根.等于8,故该方程有两个不相等的实数根;方程x2+ 2x + 3 = 0 的判(3)当Δ=b2- 4ac<0 时,原方程没有实数根.别式等于-8,故该方程没有实数根.*4.根与系数的关系(1)基本关系:若关于x 的一元二次方程ax2+bx+c=0(a≠0)有两个根分别为x1、x2,则x1+x2=-b/a,x1x2=c/a.注意运用根与系数关系的前提条件是△≥0.(2)解题策略:已知一元二次方程,求关于方程两根的代数式的值时,先把所求代数式变形为含有x1+x2、x1x2的式子,再运用根与系数的关系求解.与一元二次方程两根相关代数式的常见变形:(x1+1)(x2+1)=x1x2+(x1+x2)+1,x12+x22=(x1+x2)2-2x1x2, 1+1=x1+x2等.x1x2x1x2失分点警示在运用根与系数关系解题时,注意前提条件时△=b2-4ac≥0.知识点三:一元二次方程的应用(1)解题步骤:①审题;② 设未知数;③ 列一元二次方程;④解一元二次方程;⑤检验根是否有意义;⑥作答.4.列一元二次方程解应用题(2)应用模型:一元二次方程经常在增长率问题、面积问题等方面应用.①平均增长率(降低率)问题:公式:b=a(1±x)n,a 表示基数,x 表示平均增长率(降低率),n表示变化的次数,b表示变化n次后的量;②利润问题:利润=售价-成本;利润率=利润/成本×100%;③传播、比赛问题:运用一元二次方程解决实际问题时,方程一般有两个实数根,则必须要根据题意检验根是否有意义.④面积问题:a.直接利用相应图形的面积公式列方程;b.将不规则图形通过割补或平移形成规则图形,运用面积之间的关系列方程.第7 讲分式方程知识点一:分式方程及其解法关键点拨及对应举例1.定义分母中含有未知数的方程叫做分式方程.例:在下列方程中,① x2+1= 0 ;②x +y =-4 ;③1=x ,其中是分式方程的x - 1是③.程2.解分式方程方程两边同乘以最简公分母 基本思路:分式方 整式方程约去分母例:将方程 1 + 2= 2 转化为整式方程可x - 1 1 - x得:1-2=2(x -1).解法步骤:(1)去分母,将分式方程化为整式方程; (2)解所得的整式方程;(3) 检验:把所求得的 x 的值代入最简公分母中,若最 简公分母为 0,则应舍去.3.增根使分式方程中的分母为 0 的根即为增根.例:若分式方程 1= 0 有增根,则增根为x - 11.知识点二 :分式方程的应用4. 列分式方程解应用题的一般步骤(1)审题;(2)设未知数;(3) 列分式方程;(4)解分式方程;(5)检验: (6)作答.在检验这一步中,既要检验所求未知数的值是 不是所列分式方程的解,又要检验所求未知数的值是不是符合题目的实际意义.第 8 讲 一元一次不等式(组)知识点一:不等式及其基本性质 关键点拨及对应举例1.不等式的相关概念(1) 不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子. (2) 不等式的解:使不等式成立的未知数的值. (3) 不等式的解集:使不等式成立的未知数的取值范围.例:“a 与 b 的差不大于 1”用不等式表示为 a -b≤1.2.不等式 的基本性质性质 1:若 a >b,则 a ±c >b ±c ;性质 2:若 a >b,c >0,则 ac >bc , a > b ;c c性质 3:若 a >b,c <0,则 ac <bc , a < b. c c牢记不等式性质 3,注意变号.如:在不等式-2x >4 中,若将不等式两边同时除以-2,可得x <2.知识点二 :一元一次不等式 3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是 1 的, 左右两边为整式的式子叫做一元一次不等式.例:若 mx m +2 + 3 > 0 是关于 x 的一元一次不等式,则 m 的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为 1.失分点警示系数化为 1 时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x ≥a x >ax ≤a x <a知识点三 :一元一次不等式组的定义及其解法5.定义 由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元 一次不等式组. (1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集6.解法 先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式假设 a <b解集数轴表示口诀组解集的类型⎧x ≥ a ⎨x ≥ b ⎩x ≥b大大取大 情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x <1-a 的解集是 x >-1,则 a 的取值范围是 a <1.⎧x ≤ a ⎨x ≤ b ⎩x ≤a小小取小⎧x ≥ a ⎨x ≤ b ⎩a ≤x ≤b大小,小大中间找 ⎧x ≤ a ⎨x ≥ b ⎩无解大大,小小取不了知识点四 :列不等式解决简单的实际问题(1) 一般步骤:审题;设未知数;找出不等式关系;列不等式;解不 等式;验检是否有意义.(2) 应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;b.隐含不等关系:如“更省钱”、“更划算”等方案决策问题,一般 还需根据整数解,得出最佳方案注意:8.列不等列不等式解决实际问题中,设未式解应用题知数时,不应带“至少”、“最多” 等字眼,与方程中设未知数一致.第 9 讲 平面直角坐标系与函数知识点一:平面直角坐标系 关键点拨及对应举例1.相关概念(1) 定义:在平面内有公共原点且互相垂直的两条数轴构成平面直角坐标系. (2) 几何意义:坐标平面内任意一点 M 与有序实数对(x ,y )的关系是一一对应.点的坐标先读横坐标(x 轴), 再读纵坐标(y 轴).2.点的坐标特征( 1 )各象限内点的坐标的符号特征(如图所示):点 P (x,y)在第一象限⇔x >0,y >0; 点 P (x,y)在第二象限⇔x <0,y >0; 点 P (x,y )在第三象限⇔x <0,y <0; 点 P (x,y )在第四象限⇔x >0,y <0.(2) 坐标轴上点的坐标特征:①在横轴上⇔y =0;②在纵轴上⇔x =0;③原点⇔x =0,y =0.(3) 各象限角平分线上点的坐标①第一、三象限角平分线上的点的横、纵坐标相等; ②第二、四象限角平分线上的点的横、纵坐标互为相反数(4) 点 P (a ,b )的对称点的坐标特征:①关于 x 轴对称的点 P 1 的坐标为(a ,-b );②关于 y 轴对称的点 P 2 的坐标为(-a ,b ); ③关于原点对称的点 P 3 的坐标为(-a ,-b ). (5) 点 M (x,y )平移的坐标特征: M (x,yM 1(x+a ,y )M 2(x+a ,y+b )(1)坐标轴上的点不属于任何象限.(2)平面直角坐标系中图形的平移,图形上所有点的坐标变化情况相同.(3) 平面直角坐标系中求图形面积时,先观察所求图形是否为规则图形,若是, 再进一步寻找求这个图形面积的因素,若找不到,就要借助割补法,割补法的主要秘诀是过点向 x 轴、y 轴作垂线,从而将其割补成可以直接计算面积的图形来解决.3.坐标点的距离问题 (1) 点 M(a,b)到 x 轴,y 轴的距离:到 x 轴的距离为|b |;)到 y 轴的距离为|a |. (2) 平行于 x 轴,y 轴直线上的两点间的距离:点 M 1(x 1,0),M 2(x 2,0)之间的距离为|x 1-x 2|,点 M 1(x 1,y ),M 2(x 2,y )间的距离为|x 1-x 2|; 点 M 1(0,y 1),M 2(0,y 2)间的距离为|y 1-y 2|,点 M 1(x ,y 1),M 2(x ,y 2)间的距离为|y 1-y 2|.平行于 x 轴的直线上的点纵坐标相等;平行于 y 轴的直线上的点的横坐标相等.知识点二:函 数4.函数的相关概念(1) 常量、变量:在一个变化过程中,数值始终不变的量叫做常量,数值发生变化的 量叫做变量.(2) 函数:在一个变化过程中,有两个变量 x 和 y ,对于 x 的每一个值,y 都有唯一确定的值与其对应,那么就称 x 是自变量,y 是 x 的函数.函数的表示方法有:列表法、图像法、解析法.(3) 函数自变量的取值范围:一般原则为:整式为全体实数;分式的分母不为零;二 次根式的被开方数为非负数;使实际问题有意义.失分点警示函数解析式,同时有几个代数式,函数自变量的取值范围应是各个代数式中自变量的公共部分. 例:函数 y= x + 3 中自变量的取值范x - 5围是 x≥-3 且 x≠5.5.函数的图象(1) 分析实际问题判断函数图象的方法:①找起点:结合题干中所给自变量及因变量的取值范围,对应到图象中找对应点; ②找特殊点:即交点或转折点,说明图象在此点处将发生变化; ③判断图象趋势:判断出函数的增减性,图象的倾斜方向.(2) 以几何图形(动点)为背景判断函数图象的方法:①设时间为 t (或线段长为 x ),找因变量与 t(或 x)之间存在的函数关系,用含 t(或 x) 的式子表示, 再找相应的函数图象.要注意是否需要分类讨论自变量的取值范围.读取函数图象增减性的技巧:①当函数图象从左到右呈“上升”(“下降”)状态时,函数y 随x 的增大而增大(减小);②函数值变化越大,图象越陡峭;③当函数 y 值始终是同一个常数,那么在这个区间上的函数图象是一条 平行于 x 轴的线段.第 10 讲一次函数知识点一:一次函数的概念及其图象、性质关键点拨与对应举例1.一次函数的相关概念 (1) 概念:一般来说,形如 y =kx +b (k ≠0)的函数叫做一次函数.特别地,当 b =0时,称为正比例函数.(2) 图象形状:一次函数 y =kx +b 是一条经过点(0,b )和(-b/k ,0)的直线.特别地,正比例函数 y =kx 的图象是一条恒经过点(0,0)的直线.例:当 k =1 时,函数 y =kx +k-1 是正比例函数,2.一次函数的性质k ,b 符号 K >0, b >0K >0, b <0K > 0 , b=0k <0, b >0k <0, b <0k <0, b =0(1) 一次函数 y=kx+b 中,k 确定了倾斜方向和倾斜程度,b 确定了与y 轴交点的位置.(2) 比较两个一次函数函数值的大小:性质法,借助函数的图象,也可以运用数值代入法.例:已知函数 y =-2x +b ,函数值y 随 x 的增大而减小(填“增大”或 “减小”).大致图象经 过 象限 一、二、三 一、三、 四一、三 一、二、 四二、三、 四二、四图 象 性质y 随 x 的增大而增大y 随x 的增大而减小3.一次函数与(1)交点坐标:求一次函数与 x 轴的交点,只需令 y=0,解出 x 即可;求与 y 轴的交点, 例:一次函数 y =x +2 与 x 轴交点的坐标轴交点坐标-b,0只需令x=0,求出y 即可.故一次函数y=kx+b(k≠0)的图象与x 轴的交点是k ,与y 轴的交点是(0,b);(2)正比例函数y=kx(k≠0)的图象恒过点(0,0).坐标是(-2,0),与y 轴交点的坐标是(0,2).知识点二:确定一次函数的表达式4.确定一次函数表达式的条件(1)常用方法:待定系数法,其一般步骤为:①设:设函数表达式为y=kx+b(k≠0);②代:将已知点的坐标代入函数表达式,解方程或方程组;③解:求出k 与 b 的值,得到函数表达式.(2)常见类型:①已知两点确定表达式;②已知两对函数对应值确定表达式;③平移转化型:如已知函数是由y=2x平移所得到的,且经过点(0,1),则可设要求函数的解析式为 y=2x+b,再把点(0,1)的坐标代入即可.(1)确定一次函数的表达式需要两组条件,而确定正比例函数的表达式,只需一组条件即可.(2)只要给出一次函数与y 轴交点坐标即可得出b 的值,b 值为其纵坐标,可快速解题. 如:已知一次函数经过点(0,2),则可知b=2.5.一次函数图象的平移规律:①一次函数图象平移前后k 不变,或两条直线可以通过平移得到,则可知它们的k 值相同.②若向上平移h 单位,则 b 值增大h;若向下平移h 单位,则 b 值减小h.例:将一次函数 y=-2x+4 的图象向下平移 2 个单位长度,所得图象的函数关系式为y=-2x+2.知识点三:一次函数与方程(组)、不等式的关系6.一次函数与方程一元一次方程kx+b=0 的根就是一次函数y=kx+b(k、b 是常数,k≠0)的图象与x 轴交点的横坐标.例:(1)已知关于x 的方程ax+b=0的解为x=1,则函数y=ax+b 与x轴的交点坐标为(1,0).(2)一次函数 y=-3x+12 中,当x>4 时,y 的值为负数.7.一次函数与方程组二元一次方程组y=k1x+b 的解两个一次函数y=k1x+b 和y=k2x+b 图象的交点坐标.y=k2x+b8.一次函数与不等式(1)函数 y=kx+b 的函数值 y>0 时,自变量 x 的取值范围就是不等式 kx+b>0 的解集(2)函数 y=kx+b 的函数值 y<0 时,自变量 x 的取值范围就是不等式 kx+b<0 的解集知识点四:一次函数的实际应用9.一般步骤(1)设出实际问题中的变量;(2)建立一次函数关系式;(3)利用待定系数法求出一次函数关系式;(4)确定自变量的取值范围;(5)利用一次函数的性质求相应的值,对所求的值进行检验,是否符合实际意义;(6)做答. 一次函数本身并没有最值,但在实际问题中,自变量的取值往往有一定的限制,其图象为射线或线段.涉及最值问题的一般思路:确定函数表达式→ 确定函数增减性→根据自变量的取值范围确定最值.10.常见题型(1)求一次函数的解析式.(2)利用一次函数的性质解决方案问题.第11 讲反比例函数的图象和性质知识点一:反比例函数的概念及其图象、性质关键点拨与对应举例1.反比例函数的概念(1)定义:形如y=k(k≠0)的函数称为反比例函数,k 叫做比例系数,自变量x的取值范围是非零的一切实数.(2)形式:反比例函数有以下三种基本形式:①yk;②y=kx-1; ③xy=k.(其中k 为常数,且k≠0)=x例:函数y=3x m+1,当m=-2 时,则该函数是反比例函数.。
中考数学复习 第一部分 知识梳理 第一章 数与式 第2讲 整式与因式分解课件

4. 某商品的进价为a元,按标价(biāo jià)的五折出售,这
时仍可盈利25%,则这种商品的标价是_______2_._5_a元. (用
含a的式子表示)
12/9/2021
第六页,共二十二页。
5.(2018吉林)某同学化简a(a+2b)-(a+b)·(a-b)出现 了错误,解答(jiědá)过程如下: 原式=a2+2ab-(a2-b2) (第一步) =a2+2ab-a2-b2(第二步)
第十九页,共二十二页。
综合 提升 (zōnghé)
30. (2017济宁) 计算(a2)3+a2·a3-a2÷a-3得( )
D
A. 2a5-a
B. 2a5-
C. a5
D. a6
31.(2018云南)按一定规律(guīlǜ)排列的单项式:a,-a2项式是( )
(4)积的乘方:(ab)n=anbn(n为正整数).
(5) 负指数幂:a-n= .
12/9/2021
第三页,共二十二页。
3. 乘法公式:
a2-b2
(1)平方差公式:(a+b)(a-b)=_______a_2_+_2.ab+b2
(2)完全平方a2(p-í2ngafābng+)公b2 式:(a+b)2=_____________; (a-b)2=_____________.
16.(2018深圳) 分解因式:a2-9=______(__a_+_3_)__(__a_-_3_).
17. (2017安徽)因式分解:
a2b-4ab+4b=_________b_(a_-_2_)2_____.
中考数学知识点总结完整版

第一讲 数与式第1课时 实数的有关概念考点一、实数的概念及分类 〔3分〕正有理数有理数 零 有限小数和无限循环小数 实数 负有理数 正无理数无理数 无限不循环小数〔π〕、开方开不尽的数 负无理数凡能写成)0p q ,p (p q≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;考点二、实数的倒数、相反数和绝对值 〔3分〕2、数轴:数轴是规定了原点、正方向、单位长度的一条直线.3、相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4、绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 绝对值的问题经常分类讨论;5、倒数假设ab =1⇔ a 、b 互为倒数;假设ab =-1⇔a 、b 互为负倒数。
倒数等于本身的数是1和-1。
零没有倒数。
11a a-=考点三、平方根、算数平方根和立方根 〔3—10分〕 6、平方根①如果一个数的平方等于a ,那么这个数就叫做a 的平方根〔或二次方跟〕。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数a 的平方根记做“a ±〞。
②算术平方根正数a 的正的平方根叫做a 的算术平方根,记作“a 〞。
正数和零的算术平方根都只有一个,零的算术平a ,2a =;注意a 的双重非负性:0≥a a ≥07、立方根如果一个数的立方等于a ,那么这个数就叫做a 的立方根〔或a 的三次方根〕。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
2019年中考数学第一章数与式1.2整式与因式分解(讲解部分)素材

当 x=-
( ) +5 = 3.
解析㊀ 4x 2 -4x +1 = (2x) 2 -2ˑ2x +1 = (2x -1) 2 ,故选 C.
方法三 ㊀ 利用整体代换思想化简求值的方法
方法二㊀ 整式的运算方法
㊀ ㊀ 化简求值时,一般先化简,再把各字母的值代入. 有时题目并 未给出各个字母的取值,而是给几个式子的值, 这时可把这几个 式子看作一个整体,把多项式化为含有这几个式子的代数式, 再 代入求值. 运用整体代换思想,可使问题得到简化. ㊀ ㊀ 例 3㊀ 已知 x 2 -4x -1 = 0,求代数式 ( 2x - 3) 2 -( x + y ) ( x - y ) - y 2 的值. 解析㊀ (2x -3) 2 -( x + y) ( x - y) - y 2
+
化的过程.
2. 列代数式:找出数量关系, 用表示数的 ③㊀ 字母 ㊀ 将它数学 3. 代数式的值:用具体数代替代数式中的 ④㊀ 字母 ㊀ , 按运算 4. 代数式的分类 单项式 ì ï ⑤㊀ 整式㊀ ï有理式 ⑥㊀ 多项式㊀ 代数式 í 分式 ï ï无理式 î
顺序计算出的结果叫代数式的值. 求代数式的值分两步: 代数; 计算.
㊀ ㊀ 进行整式运算要以相关的运算法则为依据, 在运算过程中 要注意运算的顺序及符号的变化. 应用同底数幂的法则时, 确定 底数一定要慎重. 有些底数貌似相同,实则不同;有些底数貌似不 同,但稍作变形又相同. 对于多项式乘多项式, 结果中如有同类 项,要合并同类项,得出最简结果.
㊀4
5 年中考 3 年模拟 = 4x 2 -12x +9-( x 2 - y 2 ) - y 2 ȵ x 2 -4x -1 = 0, ʑ x 2 -4x = 1.
(1) 整式加减运算的实质是合并同类项. (2) 整式的乘法:( a+b)( m+n)= ������ ������㊀ am+an+bm+bn㊀ . ������
2019年中考数学总复习第一部分考点梳理第一章数与式第3课时分式课件

◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
◆知识清单
◆考点突破
◆课堂练兵
中考数学复习数与式知识点总结

中考数学复习数与式知识点总结第一部分:教材知识梳理-系统复第一单元:数与式第1讲:实数知识点一:实数的概念及分类1.实数是按照定义和正负性来分类的。
其中,既不属于正数也不属于负数的数是零。
无理数有几种常见形式:含π的式子是正有理数;无限不循环小数是无理数;开方开不尽的数是无理数;三角函数型的数是实数。
有理数包括正有理数、负有理数和零。
负无理数和正无理数的定义很明确。
2.在判断一个数是否为无理数时,需要注意开得尽方的含根号的数属于无理数,而开得尽的数属于有理数。
3.数轴有三个要素:原点、正方向和单位长度。
实数与数轴上的点一一对应,数轴右边的点表示的数总比左边的点表示的数大。
4.相反数是具有相反符号的两个数,它们的和为0.数轴上表示互为相反数的两个点到原点的距离相等。
5.绝对值是一个数到原点的距离。
它有非负性,即绝对值大于等于0.若|a|+b2=0,则a=b=0.绝对值等于该数本身的数是非负数。
知识点二:实数的相关概念2.数轴是一个直线,用来表示实数。
数轴上的每个点都对应着一个实数,反之亦然。
3.相反数是具有相反符号的两个数,它们的和为0.4.绝对值是一个数到原点的距离。
它有非负性,即绝对值大于等于0.5.倒数是乘积为1的两个数互为倒数。
a的倒数是1/a(a≠0)。
6.科学记数法是一种表示实数的方法,其中1≤|a|<10,n为整数。
确定n的方法是:对于数位较多的大数,n等于原数的整数位减去1;对于小数,写成a×10n,1≤|a|<10,n等于原数中左起至第一个非零数字前所有零的个数(含小数点前面的一个)。
7.近似数是一个与实际数值很接近的数。
它的精确度由四舍五入到哪一位来决定。
例:用科学记数法表示为2.1×104.19万用科学记数法表示为1.9×10^5,0.0007用科学记数法表示为7×10^-4.知识点三:科学记数法、近似数科学记数法是一种表示极大或极小数的方法,它的基本形式是a×10^n,其中1≤a<10,n为整数。
中考数学 第一部分 教材梳理 第一章 数与式 第4节 分式复习 新人教版

3. 约分:把一个分式的分子和分母的公因式约去,这种 变形称为分式的约分.
4. 通分:根据分式的基本性质,把异分母的分式化为同 分母的分式而不改变分式的值,这一过程称为分式的通分.
5. 最简公分母:一般取各分母的所有因式的最高次幂的 积作为公分母,它叫做最简公分母.
主要公式
分式的运算公式:
(1)加减法法则:
1. (2014广东)先化简再求值:
,
其中x=
.
解:原式
当x=
时,原式= .
2. (2013广东)从三个代数式:①a2-2ab+b2,②3a-3b, ③a2-b2中任意选两个代数式构造分式,然后进行化简,并求 出当a=6,b=3时该分式的值.
解:选②与③构造出分式:
原式=
当a=6,b=3时,原式=
原来的10倍,则分式的值 A. 是原来的20倍 B. 是原来的10倍
C. 是原来的 D. 不变
中的a,b的值同时扩大到
(D )
2. 不改变分式
考题预测
的值,把它的分子、分母的
各项系数都化为整数,所得结果正确的为
(C )
A.
B.
C.
D.
3. 不改变分式的值,使
的分子和分母
中x的最高次项的系数都是正数,变形正确的是
B. x=±2 D. x=0
(C )
2. (2015珠海)若分式
有意义,则x应满足 x≠5 .
考题预测
3. 使分式
有意义的x的取值为
( D)
A. x≠0
B. x≥-2 C. x≠0
D. x≠-2
4. 若分式
的值为零,则x的值为
(C )
A. -1
B. 1或-1 C. 1
(陕西专用)2019中考数学总复习第1部分教材同步复习第一章数与式课时3分式课件

内部文件,请勿外传
2. 分式的基本性质 分式的分子与分母乘 (或除以)同一个不等于 0 的整式,分式的值不变, 基本性质 A A· C A A÷ C 即 = , = (C≠0),其中 A ,B ,C 是整式 B B· C B B÷ C 公因式 约去,不改变分式的值,叫 把一个分式的分子与分母的①__________ 约分 做分式的约分 最简分式 分子与分母没有②__________ 公因式 的分式叫做最简分式 通分 最简公分母 把几个异分母的分式分别化成与原来的分式相等的同分母分式,叫做 分式的通分 一般取各分母的所有因式的最高次幂的积作公分母,这样的公分母叫 做最简公分母
2 2
15
易错点
化简求值时未注意隐含条件计算错误
2a-1 1-a2 例3 化简(a- a )÷ 2 ,并从-1,0,1,2 中选择你喜欢的数代入求值. a +a
a2-2a+1 1-a2 a-12 aa+1 错解:原式= ÷2 = a · =1-a. a a +a 1+a1-a 把 a=1 代入,原式=1-a=1-1=0;或把 a=-1 代入原式=1-a=1-(-1) =2; 或把 a=0 代入,原式=1-a=1-0=1.
14
练习 3 -2x-2=0.
x-1 x-2 2x2-x (2018· 眉山)先化简,再求值:( x - )÷ 2 ,其中 x 满足 x2 x+1 x +2x+1
x2-1 x2-2x x2x-1 解:原式=[ - ]÷ xx+1 xx+1 x+12 2x-1 x+12 = · xx+1 x2x-1 x+1 = 2 . x x+1 1 ∵x -2x-2=0,∴x =2x+2=2(x+1),∴原式= = . 2x+1 2
4
知识点二
运算
2019年中考数学第一章数与式1.2整式与因式分解(讲解部分)素材

化的过程.
3.代数式的值:用具体数代替代数式中的④ 字母 ,按运算
顺序计算出的结果叫代数式的值. 求代数式的值分两步:代数;
计算.
4.代数式的分类
{ { ìï
ï有理式
⑤ 整式
单项式 ⑥ 多项式
代数式í îïï无理式
分式
考点二 整式及其运算
1.同类项:所含字母⑦ 相同 ,并且⑧ 相同 字母的指数也 相同的项叫同类项.
解析 (2x-3) 2 -(x+y)(x-y) -y2
4 5 年中考 3 年模拟
= 4x2 -12x+9-( x2 -y2 ) -y2 = 3x2 -12x+9. ∵ x2 -4x-1 = 0, ∴ x2 -4x = 1. ∴ 原式 = 3( x2 -4x) +9 = 3×1+9 = 12.
变式训练 3 已知 x-y = 3 ,求代数式( x+1) 2 -2x+y( y-2x)
例 2 (2017 云南,9,4 分) 下列计算正确的是
( )
A.2a×3a = 6a
B.( -2a) 3 = -6a3
C.6a÷(2a)= 3a
D.( -a3 ) 2 = a6
解析 2a×3a = 6a2 ,故 A 错误;
( -2a) 3 = -8a3 ,故 B 错误;
6a÷(2a)= 3,故 C 错误;
§ 1.2 整式与因式分解
第一章 数与式 3
10
考点一 代数式
1.代数式的概念:用基本运算符号( 加、减、乘、除、乘方、开
方等)把数与① 表示数的字母 连接而成的式子叫做代数式.
注:单独一个数或一个字母② 是 ( 填 “ 是” 或 “ 不是” ) 代
数式.
2.列代数式:找出数量关系,用表示数的③ 字母 将它数学
九年级数学中考知识梳理:第一部分_第一章_第2讲_第1课时_代数式、整式与因式分解

乘法公式
平方差公式:(a+b)(a-b)=a2-b2 完全平方公式:(a±b)2=a2±2ab+b2
单项式÷ (1)系数相除;(2)同底数幂相除;(3)只在被除 单项式 式里出现的字母照抄
多项式÷ 单项式
(a+b)÷m=a÷m+b÷m
(续表)
要点
因式分解
定义
内容 把一个多项式化成几个整式的积的形式
1.(2016 年广东)已知方程 x-2y+3=8,则整式 x-2y 的值
为( )
A.5
B.10
C.12
答案:A
D.15
2.(2017 年广东)下列运算正确的是( )
A.a+2a=3a2
ห้องสมุดไป่ตู้
B.a3·a2=a5
C.(a4)2=a6
D.a4+a2=a4
答案:B
3.(2016 年广东)分解因式:m2-4=________________. 答案:(m+2)(m-2) 4.(2017 年广东)分解因式:a2+a=________________. 答案:a(a+1) 5.(2018 年广东)分解因式:x2-2x+1=________. 答案:(x-1)2 6.(2017 年广东)已知 4a+3b=1,则整式 8a+6b-3 的值为 ________. 答案:-1
答案:D
5.(2018 年山东滨州)下列运算:①a2·a3=a6,②(a3)2=a6,
③a5÷a5=a,④(ab)3=a3b3,其中结果正确的个数为( )
A.1 个
B.2 个
C.3 个
D.4 个
答案:B
整式运算
6.(2018 年四川成都)下列计算正确的是( )
A.x2+x2=x4 C.(x2y)3=x6y
2019年年中考数学总复习第一部分基础知识复习第1章数与式第4讲分式课件语文

★知识点2 ★考点2
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识要点导航 ★热点分类解析
2019年中考九年级数学总复习课件《第1章数与式》

.
因混淆平方根与算术平方根而致错 (正数有两个平方根 ,0 的平方根是 0), 而非负数的算术平方根是 , 两者切
非负数 a 的平方根为± 勿混淆.
方法帮
命题角度 5
实数的运算
1 1 10.[2018 宁夏 ]计算 |- |- 的结果是( C ) 2 4
A.1
1 B. 2
C.0 8=
1
D.-1 .
3
考点帮
考点1 考点2 考点3 考点4 考点5 考点6
实数的相关概念
名称 定义/ 几何意义 性质
数轴
注:实数与数轴上的点是一一对应的. (1)若 a,b 互为相反数,则 只有⑤ 符号 不同的 相反数 两个数互为相反数,即 实数 a 的相反数是-a. a+b=0; (2)0 的相反数是 0; (3)在数轴上,互为相反数 的两个数对应的点到原 点的距离⑥ 相等 . 几何意义:在数轴上表 绝对值 示数 a 的点与原点的距 离,记作|a|. 乘积是⑩ 1 倒数 数 a 的倒数为
=5. 写出计算结果 进行乘法运算 =4-1+2 先计算乘方、去掉绝对值符号 1 =4-5× +2 5 1 22 -5× +|-2| 5
考点2
考点3 考点4 考点5 考点6
示例
考点帮
考点1
科学记数法
把一个数写成
a×10n 的形式(其中 1 ≤|a|<10,n 为整数), 这种记数法称为科学记数法.
方法帮
提分技法
命题角度 3
实数的大小比较
比较实数大小的 5 种方法
1.数轴比较法 :将两个数表示在数轴上 ,右边的点表示的数总比左边的点表示的数大. 2.类别比较法 :正数大于零 ;负数小于零;正数大于一切负数 ;两个负数比大小 ,绝对值大的反而小 . 3.差值比较法 :设 a,b 是两个任意实数 ,则 a-b>0 ⇔a>b;a-b=0 ⇔a=b;a-b<0 ⇔a<b. 4.倒数比较法 :若 > ,ab>0,则 a<b. 5.平方比较法 :由 a>b>0,可得 题. > , 故可以把比较 与 的大小问题转化成比较 a 和 b 的大小问
2019中考数学 第一部分 教材知识梳理 第一单元 第3课时 整式及因式分解(含代数式)课件

计算求值即可.(提示:有的关系式需将已知等式
变形)
优质课件
拓展1 已知实数x,y 满足(x-1)2 +|3+y|=0,则x+y 的
值为
A.4 B.2 C.-2
(C )
D.-4
【解析】由题意得,x-1=0,y+3=0,解得x=1,y= -3,所以x+y=1+(-3)= -2.
优质课件
类型二
整式的运算 (D)
数叫做单项式的系数,所有字母的指数的和叫 次数 ;单独的一个数或一 做这个单项式的② ______ 个字母是单项式.
优质课件
(2)多项式:由几个单项式的和组成的代数式 叫做多项式.组成多项式的每个单项式叫做多项式 的项,其中不含字母的项叫常数项. 多项式中次数
最高 ③ ____的项的次数,叫做这个多项式的次数.如: 四 代数式3x2y2+2xy-1是④ _____次三项式.
优质课件
(2)公式法
A.
a b 整式乘法
2 2
因式分解
20
(a b)(a b) ____________.
2 ( a b ) 21 ______.
B.
a 2ab b 整式乘法
2 2
因式分解
优质课件
优质课件
失分点5 判断:
13
幂运算法则的运用误区
(a 3 ) 4 a 7
( ×) (×) ( ×)
14
15
a a a a 2 a3 a5
3 4
12
【名师提醒】先区分幂的乘方与同底数幂的乘法 的形式及运算法则,再进行计算.
优质课件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节 因式分解与分式
1.(2017连云港中考)化简x2x -1+x 1-x
的结果是(D ) A .x +1 B .x -1
C .-x
D .x
2.(聊城中考)把8a 3-8a 2
+2a 进行因式分解,结果正确的是(C ) A .2a(4a 2-4a +1) B .8a 2(a -1)
C .2a(2a -1)2
D .2a(2a +1)2
3.若分式|x|-1x +1
=0,则x 的值为(B ) A .-1或1 B .1
C .-1
D .1或0
4.(滨州中考)下列分式中,最简分式是( A )
A .x2-1x2+1
B .x +1x2-1
C .x2-2xy +y2x2-xy
D .x2-362x +12
5.已知a ,b 是△ABC 的两边,且a 2+b 2=2ab ,则△ABC 的形状是(A )
A .等腰三角形
B .等边三角形
C .锐角三角形
D .不确定
6.(2017廊坊中考模拟)下列各式:4x ,a 4,1x -y ,3x 4,12x 2,1a
+4,其中分式有(B ) A .2个 B .3个
C .4个
D .5个
7.下列各式中,无论x 取何值,分式都有意义的是(D )
A .12x +1
B .x 2x +1
C .
3x +1x2D .x22x2+1 8.(2017无锡中考)计算3xy24z2·⎝ ⎛⎭
⎪⎫-8z2y 等于(C ) A .6xyz B .-3xy2-8z34yz
C .-6xy
D .6x 2yz
9.(2016沧州二模)下列三个分式12x2,5x -14(m -n ),3x
的最简公分母是(D ) A .4(m -n)x B .2(m -n)x 2
C .14x2(m -n )
D .4(m -n)x 2
10.下列计算中,错误的是(A )
A .
-x +1x +1=-1 B .x -1-x +1=-1 C .n -22-n =-1 D .-n +22+n
=-1 11.(2017广安中考)当m =__8或-2__时,x 2+2(m -3)x +25是完全平方式.
12.因式分解:
(1)(丽水中考)am -3a =__a(m -3)__;
(2)(常德中考)ax 2-ay 2
=__a(x +y)(x -y)__;
(3)(安顺中考)2a 2-4a +2=__2(a -1)2__.
13.(淄博中考)计算1-4a22a +1
的结果是__1-2a__. 14.(扬州中考)当a =2 016时,分式a2-4a -2
的值是__2__018__. 15.(凉山中考)已知(2x -21)(3x -7)-(3x -7)(x -13)可分解因式为(3x +a)(x +b),其中a ,b 均为整数,则a +3b =__-31__. 16.(达州中考)化简求值:⎝ ⎛⎭
⎪⎫1+1a ÷a2-1a -2a -2a2-2a +1,a 取-1、0、1、2中的一个数. 解:原式=-1a -1
. ∵a ≠0、±1,∴a =2,∴原式=-1.
17.(滨州中考)把多项式x 2
+ax +b 分解因式,得(x +1)(x -3),则a ,b 的值分别是(B ) A .a =2,b =3
B .a =-2,b =-3
C .a =-2,b =3
D .a =2,b =-3
18.下列因式分解正确的是(B )
A .x 2-xy +x =x(x -y)
B .a 3-2a 2b +ab 2=a(a -b)2
C .x 2-2x +4=(x -1)2+3
D .ax 2-9=a(x +3)(x -3)
19.函数y =x +2x
的自变量x 的取值范围是(B ) A .x ≥-2
B .x ≥-2且x ≠0
C .x ≠0
D .x >0且x≠-2
20.(咸宁中考)a ,b 互为倒数,代数式a2+2ab +b2a +b ÷⎝ ⎛⎭⎪⎫1a +1b 的值为__1__.。
