2017春九年级数学下册2.5.2第1课时切线的判定试题(新版)湘教版

合集下载

湘教版九年级下册数学第2章圆的切线的判定

4．【模拟·张家界武陵源区】如图，CD 是⊙O 的直径， ∠A＝∠B，AD＝BD.求证：直线 AB 是⊙O 的切线．
证明：∵∠A＝∠B，∴CA＝CB，又∵AD＝BD，∴CD⊥AB. ∵CD 是⊙O 的直径，∴直线 AB 是⊙O 的切线．
5．【中考·湘潭】如图，在△ABC 中，AB＝AC，以 AB 为直径的 ⊙O 交 BC 于点 D，过点 D 作 DE⊥AC，垂足为点 E.
第2章圆
2.5.2 圆的切线第1课时圆的切线的判定
提示：点击进入习题
新知笔记
垂直
答案显示
1B
2C
3C
4 见习题 5 见习题
6C
7C
8 见习题 9 见习题 10 见习题
11 见习题 12 见习题
经过半径的外端并且___垂__直___于这条半径的直线是圆的切线．
1．下列说法中，正确的是( B ) A．与圆有公共点的直线是圆的切线 B．若圆心到直线的距离等于圆的半径，则这条直线是圆的切线 C．垂直于圆的半径的直线是圆的切线 D．过圆的半径的外端的直线是圆的切线
证明：∵BC 平分∠ABD，∴∠OBC＝∠DBC. ∵OB＝OC，∴∠OBC＝∠OCB， ∴∠OCB＝∠DBC，∴OC∥BD. ∵BD⊥CD，∴OC⊥CD. ∵OC 为⊙O 的半径，∴CD 为⊙O 的切线．
10．【中考·张家界】如图，在 Rt△ABC 中，∠ACB＝90°，以 AB 为直径作⊙O，过点 C 作直线 CD 交 AB 的延长线于点 D，使∠BCD＝∠A.
解：连接 DE，如图．易知四边形 EBCD 是⊙O 的内接四边形， ∴∠BCD＋∠DEB＝180°， ∴∠DEB＝180°－120°＝60°. ∵BE 为⊙O 的直径，∴∠BDE＝90°. 在 Rt△BDE 中，BD＝BE·sin 60°＝2 3× 23＝3.

湘教版数学九年级下册切线的判定

（1）求证：CD 是 ⊙O 的切线； (1) 证明：连接 OC，BC. ∵FC CB ，∴∠DAC ＝ ∠BAC. ∵CD ⊥ AF，∴∠ADC ＝ 90°. ∵AB 是直径，∴∠ACB ＝ 90°. ∴∠ACD ＝∠B.
∵BO ＝ OC，∴∠OCB ＝ ∠OBC. ∵∠ACO＋∠OCB ＝ 90°，∠OCB ＝ ∠OBC，
∵PE ⊥ AC，
∴PE ⊥ OP. ∴PE 为 ☉O 的切线.
5. 已知：△ABC 内接于 ☉O，过点 A 作直线 EF.
(1) 如图1，AB 为直径，要使 EF 为 ☉O 的切线，还需
添加的条件是（只需写出两种情况）：
① __B_A__⊥__E__F ；② __∠__C_A_E__=__∠__B_ . (2) 如图2，AB 是非直径的弦，∠CAE = ∠B，求证：
A
P
O
3. 如图，O 为正方形 ABCD 的对角线 AC 上一点，以 O 为圆心，OA 的长为半径的 ⊙O 与 BC 相切于点 M. 求证：CD 与 ⊙O 相切．证明：连接 OM，过点 O 作 ON⊥CD 于点 N， ∵⊙O 与 BC 相切于点 M，∴OM ⊥ BC. 又∵ON ⊥ CD，O 为正方形 ABCD 对角线 AC 上一点， ∴OM ＝ ON， ∴CD 与 ⊙O 相切．
(2) 垂直于半径的直线是圆的切线. ( × )
(3) 过直径的端点并且垂直于这条直径的直线是圆的
切线.
( √)
(4) 和圆只有一个公共点的直线是圆的切线. ( √ )
(5) 过直径一端点且垂直于直径的直线是圆的切线. ( √ )
2. 如图所示，A 是 ☉O 上一点，且 AO = 5，PO = 13， AP = 12，则 PA 与 ☉O 的位置关系是相切 .

2新湘教版初中数学九年级下册精品学案.5.2 第1课时切线的判定

CO
x
A
P
资料来源于网络仅供免费交流使用
4．已知：如图，在梯形 ABCD 中，AD∥BC，AB=DC，以 AB 为直径的⊙O 交 BC
资料来源于网络仅供免费交流使用
精品文档用心整理
于点 E，EF⊥CD，垂足为 F. 求证：（1）∠AEF=∠B；（2）EF 是⊙O 的切线.
5．已知Δ ABC 中，∠A∶∠B∶∠C=1∶2∶3，若以 B 为圆心，以 BC 长为半径作圆.求证：AC 是⊙B 的切线.
6．如图,已知:⊙D 交 y 轴于 A、B,交 x 轴于 C,过点 C 的直线:y=-2 2 -8 与 y 轴交
于点 P. (1)试判断 PC 与⊙D 的位置关系. (2)判断在直线 PC 上是否存在点 E,使得 S△ EOP=4S△ CDO,若存在,求出点 E
的坐标;若不存在,请说明理由.
y
B
D(0,1)
1.左图，等腰直角三角形 AOB 的直角顶点在圆心，AB 长等于⊙O 直径
求证：AB 是⊙O 切线
O
A
B
C
2.左图，AB 是⊙O 直径，BC 是弦，BD⊥CD 于 D，求证：CD 是⊙O 切线
D C
A
B
3．已知等边三角形边长为 a，以它的外心为圆心，当半径为_____________时，此圆与三边都相切.
精品文档用心整理
2.5.2 圆的切线
第 1 课时切线的判定
重点.难点切线的判定
教学流程 1．切线的判定定理_____________________________________________________
教师个人添加（学生学习记录）
方法 1：直线与圆有公共点：连半径，证垂直

2.5.2 第1课时切线的判定-九年级数学下册教材配套教学课件(湘教版)

∴OP∥AC.
∵PE⊥AC， ∴PE⊥OP. ∴PE为☉O的切线.
A
O
E B PC
5且.如A︵F图＝，︵FACB＝是C︵⊙B，O的连直接径AC，、点AFF、，C过是点⊙CO作上CD的⊥两A点F交，AF的延
长线于点D. （1）求证：CD是⊙O的切线；
(2)若CD＝2 3，求⊙O的半径．
(1)︵证明：︵连接OC，BC.
E
F
∵△ABC 中，AB ＝AC ，
O 是BC 中点．
∴AO 平分∠BAC，
B
O
C
又OE ⊥AB ，OF⊥AC.
∴OE ＝OF. ∵OE 是⊙O 半径，
OF ＝OE，OF ⊥ AC.
∴AC 是⊙O 的切线．
方法总结
(1) 已明确直线和圆有公共点，连结圆心和公共点，即半径，再证直线与半径垂直.简记“有交点，连半径,证垂直”;
l 离等于半径(即d=r)直线与圆相切
即：
oA AT于A
OA＝r(半径）
直线AT切圆O于A
③判定定理：经过半径的外端且垂直于这
条半径的直线是圆的切线.
OA为⊙O的半径 AT ⊥ OA于A
AT为⊙O的切线
例1 已知：如图所示，AD是圆O的直径，直线BC经过点D，并且AB=AC，∠BAD=∠CAD.
O.
l
A
l
(1)
(1)不是，因为没有垂直.
O. O
A B
l
A
(2)
(3)
(2),(3)不是，
因为没有经过半径的外端点A.
在此定理中，“经过半径的外端”和“垂直于这条半径”，两个条件缺一不可，否则就不是圆的切线.
判定直线与圆相. 切的方法

九年级数学下册第2章圆2.5直线与圆的位置关系2.5.2第1课时切线的判定同步练习1新版湘教版

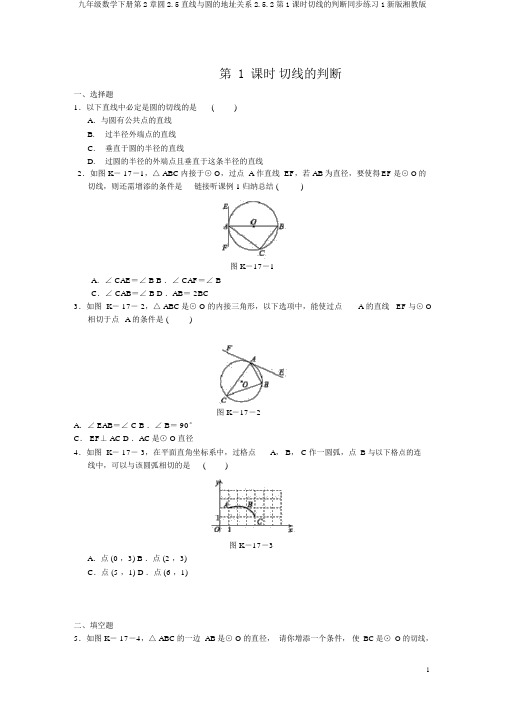
第 1 课时切线的判断一、选择题1．以下直线中必定是圆的切线的是()A．与圆有公共点的直线B.过半径外端点的直线C.垂直于圆的半径的直线D.过圆的半径的外端点且垂直于这条半径的直线2．如图 K－ 17－1，△ ABC内接于⊙ O，过点 A 作直线 EF，若 AB为直径，要使得EF 是⊙ O的切线，则还需增添的条件是链接听课例 1归纳总结 ()图 K－17－1A．∠ CAE＝∠ B B ．∠ CAF＝∠ BC．∠ CAB＝∠ B D ．AB＝ 2BC3．如图 K－ 17－ 2，△ ABC是⊙ O 的内接三角形，以下选项中，能使过点 A 的直线EF 与⊙ O 相切于点A的条件是 ()图 K－17－2A．∠ EAB＝∠ C B ．∠ B＝ 90°C． EF⊥ AC D ．AC是⊙ O直径4．如图 K－ 17－ 3，在平面直角坐标系中，过格点A， B， C 作一圆弧，点B 与以下格点的连线中，可以与该圆弧相切的是()图 K－17－3A．点 (0 ，3) B ．点 (2 ，3)C．点 (5 ，1) D ．点 (6 ，1)二、填空题5．如图 K－ 17－4，△ ABC的一边 AB是⊙ O的直径，请你增添一个条件，使BC是⊙ O的切线，你所增添的条件为________( 增添一个即可 ) ．图 K－17－46．如图 K－ 17－ 5，在△ ABC中， AB＝ AC，∠ B＝ 30°，以点 A 为圆心，以 3 cm为半径作⊙ A，当 AB＝ ________cm时， BC与⊙ A 相切．图 K－17－57．如图 K－ 17－ 6，点 A，B，D 在⊙ O上，∠ A＝ 25°， OD的延长线交直线B C于点 C，且∠ OCB ＝40°，则直线BC与⊙ O的地址关系为 ________．图 K－ 17－6三、解答题8．2018·邵阳如图K－ 17－7 所示， AB 是⊙ O的直径， C 为⊙ O上一点，过点 B 作 BD⊥ CD，垂足为 D，连接 BC，BC均分∠ ABD.求证： CD为⊙ O的切线．图 K－17－ 79．如图 K－ 17－8，在矩形 ABCD中，点 O在对角线AC上，以 OA为半径的⊙ O与 AD交于点 E，且∠ ACB＝∠ DCE.求证： CE是⊙ O的切线 . 链接听课例 2归纳总结图 K－ 17－810．如图 K－ 17－9，在正方形ABCD中， E 是 AB边上任意一点，∠ ECF＝ 45°， CF交 AD于点F，判断直线 EF 与以 C 为圆心， CD为半径的圆的地址关系，并说明原由．图 K－17－911．如图 K－17－ 10，在 Rt △ABC中，∠ ABC＝90°，以 AB 为直径作半圆O交 AC 于点 D，E 是 BC的中点，连接DE.(1)求证： DE是半圆 O的切线；(2)若∠ BAC＝ 30°， DE＝ 2，求 AD的长．图 K－ 17－ 10︵︵12．2018·永州如图K－ 17－ 11，线段 AB 为⊙ O的直径，点 C，E 在⊙ O上，BC＝ CE，CD⊥ AB，垂足为 D，连接 BE，弦 BE与线段 CD订交于点 F.(1)求证： CF＝ BF；4(2) 若 cos ∠ ABE＝，在 AB 的延长线上取一点M，使 BM＝ 4，⊙ O 的半径为 6. 求证：直线CM5是⊙ O的切线．图 K－17－ 11涵养提高思想拓展能力提高研究题如图 K－17－ 12，在矩形中，＝ 5，＝ 3.E 是上的动点，以为直径的⊙ABCD AB AD CD AEO与 AB交于点 F，过点 F 作 FG⊥ BE于点 G.(1)若 E 是 CD的中点，证明： FG是⊙ O的切线．(2)试一试究： BE能否与⊙ O相切？若能，求出此时 DE的长；若不可以，请说明原由．图 K－17－ 12教师详解详析【课时作业】[ 课堂达标 ]1．3．[ 解析 ] A如图，作直径AM，连接BM.∵ AM是直径，EF是切线，∴∠ EAM＝∠ ABM＝90°，∴∠ EAB＋∠ MAB＝ 90°，∠ M＋∠ MAB＝90°，∴∠ EAB＝∠ M.∵∠ C＝∠ M，∴∠ EAB＝∠ C. 应选 A.4． [ 解析 ] C如图，第一依据确立圆心的条件找出圆心D，此后连接DB，分别连接选项A，B， C， D 表示的点与点 B，在全部的连线中，只有点(5 ，1) 与点 B 的连线与DB垂直．故选 C.5． [ 答案 ]答案不独一，如∠ABC＝90°[ 解析 ]当△ ABC为直角三角形，即∠ABC＝ 90°时， BC与⊙ O相切．∵AB是⊙ O的直径，∠ ABC＝90°，∴BC是⊙ O的切线．6．[答案]61[ 解析 ]如图，过点 A 作 AD⊥ BC于点 D. ∵AB＝ AC，∠ B＝ 30°，∴ AD＝2AB，即 AB＝ 2AD.又∵ BC与⊙ A 相切，∴ AD就是⊙ A 的半径，∴ AD＝3 cm ，则 AB＝ 2AD＝ 6 cm. 故答案是 6. 7．[ 答案 ] 相切[ 解析 ]∵∠ BOC＝2∠ A＝50°，∠ OCB＝40°，∴在△ OBC中，∠ OBC＝ 180°－ 50°－ 40°＝ 90°，∴直线 BC与⊙ O相切．8．证明：∵ BC均分∠ ABD，∴∠ OBC＝∠ DBC.∵OB＝ OC，∴∠ OBC＝∠ OCB，∴∠ DBC＝∠ OCB，∴OC∥ BD.∵BD⊥ CD，∴ OC⊥ CD.又∵ C 为⊙ O上一点，∴CD为⊙ O的切线．9．证明：连接OE.∵ OA＝ OE，∴∠ CAD＝∠ OEA.∵四边形ABCD是矩形，∴∠ D＝ 90°， BC∥ AD，∴∠ ACB＝∠ CAE.∵∠ ACB＝∠ DCE，∴∠ OEA＝∠ DCE.∵∠ DCE＋∠ CED＝ 180°－∠ D＝ 90°，∴∠ OEA＋∠ CED＝ 90°，∴∠ OEC＝ 180°－ 90°＝ 90°，又∵ OE是⊙ O的半径，∴CE是⊙ O的切线．10．解：直线EF 与⊙ C相切．原由以下：过点C作 CH⊥ EF 于点 H.∵四边形ABCD为正方形，∴∠ B＝∠ ADC＝∠ BCD＝ 90°， CB＝ CD.将△ CBE绕点 C 顺时针旋转90°，到△ CDG的地址，则CE＝CG，∠ BCE＝∠ DCG，∴∠ GCF＝∠ BCE＋∠ FCD.∵∠ ECF＝ 45°，∴∠ BCE＋∠ FCD＝ 90°－ 45°＝ 45°，∴∠ ECF＝∠ GCF.在△ ECF与△ GCF中， CE＝ CG，∠ ECF＝∠ GCF，CF＝ CF，∴△ ECF≌△ GCF(SAS)，∴∠ EFC＝∠ DFC.而 CD⊥ FD，CH⊥ EF，∴CH＝ CD，即圆心 C到直线 EF 的距离等于⊙ C 的半径，∴直线 EF与⊙ C 相切．11．解： (1) 证明：如图，连接OD， OE， BD.∵AB为半圆 O的直径，∴∠ ADB＝∠ BDC＝ 90° .在 Rt △ BDC中， E 为斜边 BC的中点，∴ DE＝ BE.在△ OBE和△ ODE中，OB ＝OD ，OE ＝OE ， ∴△ OBE ≌△ ODE(SSS)，BE ＝DE ，∴∠ ODE ＝∠ ABC ＝ 90°. 又∵点 D 在半圆 O 上， ∴ DE 为半圆 O 的切线．(2) 在 Rt △ ABC 中，∠ BAC ＝ 30°，1∴ BC ＝ 2AC.∵ BC ＝ 2DE ＝ 4， ∴ AC ＝ 8.又∵∠ C ＝ 180°－∠ ABC －∠ BAC ＝ 60°， DE ＝EC ，∴△ DEC 为等边三角形，即 DC ＝DE ＝ 2，则 AD ＝ AC － DC ＝ 6.12．证明： (1) 延长 CD 交⊙ O 于点 G.∵ CD ⊥AB ，︵︵∴ BC ＝ BG ，︵︵ ∵ BC ＝ CE ，︵︵ ∴ CE ＝ BG ，∴∠ CBE ＝∠ GCB ， ∴ CF ＝ BF.(2) 连接 OE ，OC ， OC 交 BE 于点 H.︵︵ ∵ BC ＝ CE ，∴∠ EOC ＝∠ BOC.∵ OE ＝ OB ，∴ OC ⊥ BE.在 Rt △ OBH 中， cos ∠ OBH ＝ BH 4 ＝，OB 5 4 24 ∴ BH ＝ 5×6＝ 5 ，224 218∴ OH ＝6－（ 5）＝5. 18 OH 5 3 OB 6 3∵ ＝6 ＝，＝＝，OC 5 OM 6＋4 5OH OB∴＝，而∠ HOB ＝∠ COM ，OC OM∴△ OHB ∽△ OCM ，∴∠ OCM＝∠ OHB＝ 90°，即 OC⊥ CM.又∵ OC为⊙ O的半径，∴直线 CM是⊙ O的切线．[ 涵养提高 ]解： (1) 连接 OF， EF.∵AE是⊙O的直径，∴ AF⊥EF，∵四边形ABCD是矩形，∴∠ DAB＝∠ D＝90°， AB＝ CD，∴四边形ADEF是矩形，∴AF＝DE，∴EC＝BF.∵E 是CD的中点，∴F 是 AB的中点，∴ OF∥BE.∵FG⊥BE，∴OF⊥FG，∴FG为⊙ O的切线．(2)BE 不可以与⊙ O相切．原由：假设BE能与⊙ O相切．∵ AE是⊙ O的直径，∴AE⊥BE，∠ AEB＝ 90° .设 DE＝ x，则 EC＝ 5－ x. 由勾股定理，得AE2＋ BE2＝ AB2，即 (9 ＋x2) ＋ [(5 － x) 2＋ 9] ＝ 25，整理得 x2－ 5x＋ 9＝0. ∵ b2－4ac ＝ 25－36＝－ 11＜ 0，∴该方程无实数根，∴点 E不存在，故 BE不可以与⊙ O相切．。

2019最新九年级数学下册第2章 2.5.2 圆的切线第1课时切线的判定练习 (新版)湘教版

2.5.2 圆的切线第1课时切线的判定知|识|目|标1．通过回顾圆的切线的概念和直线与圆的位置关系，理解切线的判定定理．2．通过切线的判定定理，掌握圆的切线的作法．目标一理解切线的判定定理(1)直线与圆有公共点时证明直线是圆的切线例1 教材例2针对训练已知：如图2－5－4，在△ABC中，AB＝AC，以AB为直径的⊙O交BC 于点D，过点D作DE⊥AC于点E.求证：DE是⊙O的切线．图2－5－4【归纳总结】判定圆的切线的三种方法：(1)与圆有唯一公共点的直线是圆的切线；(2)若圆心到直线的距离等于圆的半径，则这条直线是圆的切线；(3)经过半径的外端并且垂直于这条半径的直线是圆的切线．(2)直线与圆位置关系不明时证明圆的切线例2 教材补充例题已知：如图2－5－5所示，在△ABC中，AB＝AC，O是BC的中点，OD⊥AB，垂足为D，以点O为圆心，OD为半径作⊙O.求证：AC与⊙O相切．图2－5－5【归纳总结】判定圆的切线的常用辅助线的选择：(1)如果已知直线过圆上一点，那么连接这点和圆心，得到半径，证明这条半径垂直于已知直线即可，可记为：有交点，作半径，证垂直；(2)如果已知直线与圆没有明确是否有公共点，那么过圆心作已知直线的垂线段，证明垂线段等于半径即可，可记为：无交点，作垂线，证半径．目标二掌握圆的切线的作法请回答：小涵的作图依据是________________________________________．【归纳总结】圆的切线的作法：(1)过圆外一点作圆的切线的方法：①连接圆外的点与圆心；②以连接得到的线段长为直径作圆，与已知圆交于两点；③连接圆外的点与交点，即得到过圆外一点所作的已知圆的两条切线．(2)圆的切线的作法是以圆的切线的判定定理为依据，将作切线转化为作垂线来实现，所作的直线必须满足两个基本特征：①经过半径的外端；②垂直于这条半径．知识点一切线的判定定理切线的判定定理：经过半径的______并且________________的直线是圆的切线．[注意] (1)圆的切线必须同时满足两个条件：①经过半径的外端；②垂直于这条半径．二者缺一不可．(2)“垂直于这条半径”不要省去了“这条”两个字，如图2－5－8，直线l过半径OA的外端，垂直于半径OB，但直线l不是⊙O的切线．图2－5－8(3)切线的判定方法有三种：①直线与圆有唯一公共点；②圆心到直线的距离等于半径；③切线的判定定理．知识点二过圆上一点作圆的切线步骤：(1)根据题意在圆周上取一点A ； (2)连接圆心O 与点A ；(3)过点A 作一条直线垂直于OA ，则这条直线就是所求作的圆的切线．如图2－5－9，OP 是∠AOB 的平分线，以点P 为圆心的⊙P 与OA 相切于点C.求证：⊙P 与OB 相切．图2－5－9证明：如图2－5－10，设⊙P 与OB 的公共点为D ，连接PC ，PD.图2－5－10∵OA 与⊙P 相切于点C ， ∴PC ⊥OA.又OP 平分∠AOB ， ∴∠COP ＝∠DOP. 在△COP 与△DOP 中， ⎩⎪⎨⎪⎧∠PCO ＝∠PDO ，∠COP ＝∠DOP ，OP ＝OP ，∴△COP ≌△DOP ， ∴PC ＝PD ，∴⊙P 与OB 相切．上述证明过程有无错误？若有错误，请指出错误的原因，并改正．教师详解详析【目标突破】例1 [解析] 若要证DE是⊙O的切线，只需DE满足两个条件：①DE过半径的外端点；②DE 垂直于这条半径．所以只需连接OD，则满足条件①，故只需证明DE⊥OD即可，而DE⊥AC，则只需证OD∥AC.证明：如图，连接OD，则∠OBD＝∠ODB.又∵AB＝AC，∴∠ABC＝∠ACB，∴∠ODB＝∠ACB，∴OD∥AC.∵DE⊥AC，∴DE⊥OD.又∵DE过半径OD的外端点，∴DE是⊙O的切线．例2 [解析] 要证AC是⊙O的切线，题目没有点明AC与⊙O的交点，即没有点明切点，因此，过点O作AC的垂线，垂足为E；而⊙O与AB相切于点D，所以⊙O的半径即是OD，只要证明OE＝OD问题即得解．证明：如图，连接OA，过点O作OE⊥AC，垂足为E.∵AB＝AC，O是BC的中点，∴∠BAO＝∠CAO.又∵ OD⊥AB，OE⊥AC，垂足分别为D，E，∴ OE＝OD，∴ AC与⊙O相切．例3 直径所对的圆周角是直角；经过半径的外端并且垂直于这条半径的直线是圆的切线【总结反思】[小结] 知识点一外端垂直于这条半径[反思]有错误，错误原因有两个：①条件中没有给出“⊙P与OB有公共点”；②∠PCO＝∠PDO缺乏依据．正确解答：连接PC，过点P作PD⊥OB于点D.∵OA与⊙P相切于点C，∴PC ⊥OA.又OP平分∠AOB，∴PC＝PD，∴⊙P与OB相切．。

2017春九年级数学下册2.5.2第2课时切线的性质试题新版湘教版

第2课时切线的性质知识要点切线的性质如图，⊙O 的直径AB 垂直弦CD 于E ，过点C 的切线CF 交AB 的延长线于F ，连接CO 并延长交AD 于G ，且CG ⊥AD .求证：△CEF ≌△DE A.分析：由CF 是⊙O 的切线，易得CG ⊥CF ，证得CF ∥AD ，得出∠ECF ＝∠EDA ，∠F ＝∠A ，根据垂径定理得出CE ＝DE ，然后根据AAS 即可证得△CEF ≌△DEA .方法点拨：运用切线的性质进行证明和计算时，一般连接切点与圆心，根据切线的性质转化已知条件，构造出等量关系求解．(教材P75习题T2变式)如图，AC 是⊙O 的直径，OB 是⊙O 的半径，PA 切⊙O 于点A ，PB 与AC 的延长线交于点M ，∠COB ＝∠APB .(1)求证：PB 是⊙O 的切线；(2)当OB ＝3，PA ＝PB ＝6时，求MB ，MC 的长．分析：(1)根据切线的性质，可得∠MAP ＝90°，根据直角三角形的性质，可得∠P ＋M ＝90°，根据∠COB ＝∠APB ，可得∠M ＋∠MOB ＝90°，即∠MBO ＝90°.根据切线的判定，可得答案；(2)根据相似三角形的判定与性质，可得MB AM ＝OB AP ＝OMPB，通过解方程组，可得答案．方法点拨：本题考查了切线的判定与性质，(1)利用切线的判定与性质，直角三角形的判定与性质，余角的性质；(2)利用相似三角形的判定与性质，解方程组．1.如图，已知AB 是⊙O 的直径，PB 是⊙O 的切线，则AB ____BP .若AB ＝3cm ，PB ＝4cm ，则PA ＝______.2．如图所示，AO 是△ABC 的中线，AB 切⊙O 于D ，要使⊙O 与AC 边相切，应增加的条件是___________.3．如图所示，CA 为⊙O 的切线，切点为A ，点B 在⊙O 上，如果∠CAB ＝55°，那么∠AOB 等于( )A ．120° B．110° C．90° D．55°4．如图，P 是⊙O 外一点，PA 是⊙O 的切线，PO ＝26cm ，PA ＝24cm ，则⊙O 的周长为CA ．18πcmB ．16πcmC ．20πcmD ．24πcm5．如图，△ABD 是⊙O 的内接三角形，E 是弦BD 的中点，点C 是⊙O 外一点且∠DBC ＝∠A ，连接OE 并延长与圆相交于点F ，与BC 相交于点C . (1)求证：BC 是⊙O 的切线；(2)若⊙O 的半径为6，BC ＝8，求弦BD 的长．参考答案: 要点归纳知识要点：垂直垂直平行典例导学例1 证明：∵CF 是⊙O 的切线，∴CG ⊥CF .又∵CG ⊥AD ，∴CF ∥AD ，∴∠ECF ＝∠EDA ，∠F ＝∠A .又∵AB ⊥CD ，∴CE ＝DE .在△CEF 和△DEA 中，⎩⎪⎨⎪⎧∠ECF ＝∠EDA ，∠F ＝∠A ，CE ＝DE ，∴△CEF ≌△DEA ．例2 (1)证明：∵PA 切⊙O 于点A ，∴∠MAP ＝90°，∴∠P ＋∠M ＝90°.∵∠COB ＝∠APB ，∴∠M ＋∠MOB ＝90°，∴∠MBO ＝90°，即OB ⊥PB .∵PB 经过半径的外端，∴PB 是⊙O 的切线；(2)解：∵∠COB ＝∠APB ，∠OBM ＝∠PAM ，∴△OBM ∽△PAM ，∴MB AM ＝OB AP ＝OMPM.∵AM ＝MC ＋AC ＝MC ＋2OB ＝MC ＋6，OM ＝MC ＋OC ＝MC ＋OB ＝MC ＋3，PM ＝MB ＋BP ＝MB ＋6，∴MB MC ＋6＝OBAP＝36＝12①，MC ＋3MB ＋6＝OB AP ＝12②，联立①②得⎩⎪⎨⎪⎧2MB ＝MC ＋6，2MC ＋6＝MB ＋6，解得⎩⎪⎨⎪⎧MC ＝2，MB ＝4. 当堂检测 1．⊥ 5cm2．AB ＝AC (答案不唯一) 3.B 4.C5．(1)证明：连接OB ，如图所示．∵E 是弦BD 的中点，∴BE ＝DE ，OE ⊥BD ，BF ︵＝DF ︵＝12BD ︵，∴∠BOE ＝∠A ，∠OBE ＋∠BOE ＝90°.∵∠DBC ＝∠A ，∴∠BOE ＝∠DBC ，∴∠OBE ＋∠DBC ＝90°，∴∠OBC ＝90°，即BC ⊥OB ，∴BC 是⊙O 的切线；(2)解：∵OB ＝6，BC ＝8，BC ⊥OB ，∴OC ＝OB 2＋BC 2＝10.∵△OBC 的面积＝12OC ·BE ＝12OB ·BC ，∴BE ＝OB ·BC OC ＝6×810＝4.8，∴BD ＝2BE ＝9.6，即弦BD 的长为9.6.。

2017春九年级数学下册2.5.2圆的切线第1课时切线的判定习题(新版)湘教版

2.5.2 圆的切线第1课时切线的判定基础题知识点圆的切线的判定1.下列直线中，能判定为圆的切线的是（）A. 与圆有公共点的直线B. 过圆的半径的外端点的直线C. 垂直于圆的半径的直线D. 经过直径的一个端点，且垂直于这条直径的直线2 .如图，A是圆0上一点，AO= 5, PO= 13, AP= 12,则PA与圆0的位置关系是（）A. 无法确定B. 相交C. 相切D. 相离3. __________________________________________________________________________________________________ 如图，△ ABC的一边AB是OO的直径，请你添加一个条件，使BC是OO的切线，你所添加的条件为____________________4. __________________________________________________________________________________________________ 如图，A, B是OO上的两点，AC是过A点的一条直线，如果/ AOB= 120°,那么当/ CAB的度数等于 ____________________ 度时，AC才能成为OO的切线.5. 如图，延长OO 的半径OA使OA= AB过点A作弦AC使AC= OA.求证：BC是OP的切线.6. （梅州中考）如图，在△ ABO中，OA= OB C是边AB的中点，以O为圆心的圆过点C.（1）求证：AB与OO相切；-1 B若/AOB= 120°, AB= 4 3，求OO 的面积.7.如图，已知两条射线CA CB.试画一圆，使此圆与两射线相切.C中档题8 .如图，AB是OO的直径，BC交OO于点D, DEL AC于点E,要使DE是OO的切线，还需补充一个条件，则补充的条件不正确的是（）-1 BA. DE= DOB. AB= ACC. CD= DBD. AC// OD9.（随州中考）如图，O O中，点C为両勺中点，/ ACB= 120°, 0C的延长线与AD交于点D,且/ D=Z B.求证：AD 与OO相切.10 .（宿迁中考）如图，AB是OO的弦，OPL 0A交AB于点P,过点B的直线交0P的延长线于点C,且CP= CB. （1）求证：BC 是OO的切线；⑵若OO的半径为5, OP= 1，求BC的长.参考答案综合题11.(常德中考)如图，已知OO的直径为AB, ACL AB于点A, BC与OO相交于点D,在AC上取一点E,使得ED= EA.(1)求证：ED是OO的切线;⑵当0A= 3, AE= 4时，求BC的长度.1 . D 2. C 3. AB丄BC 4. 605. 证明：T AC= OA= OC,•••/ OCA=Z OAC= 60°.又OA= AB,••• AC= AB.1•••/ ACB= -Z OAC= 30° .2•Z OCB=Z OCArZ ACB= 90°.• BC是OP的切线.6. (1)证明：连接CO.•/ AO= BQ•△ AOB是等腰三角形.••• C是边AB的中点，• OCL AB.•/ OC是OO的半径，• AB与OO相切.(2)在等腰△ AOB 中，Z AOB= 120° ,•Z A=Z B= 30 °.•/ C是边AB的中点，AB= 4 3,• AC= 2 3.在Rt△ACO中, Z ACO= 90°,Z A= 30°, AC= 2 3,• OC= #AC= 2,2• S= n X 2 = 4 n .7 .作法：(1)作Z ACB的平分线CE;⑵在CE上任取一点O;⑶作ODL CA于点D (4)以点O为圆心，以OD为半径作圆，则OO8. A9 •证明：连接OA.•/ CA= C B• CA= CB.又T Z ACB= 120°,•Z B= 30°.•Z O= 2Z B= 60°.T Z D=Z B= 30°,•Z OAD= 180°—( Z O+Z D)= 90°.• AD与OO相切.10 . (1)证明：连接OB.T OPL OA•Z A+Z OPA= 90 °.T CP= CB•Z CPB=Z CBP.又T Z APO=Z CPB•Z APO=Z CBP.T OA= OB•Z OAP=Z OBP. 即为所求.参考答案•Z OBAF Z PBC= 90°,即Z OB= 90° .• OBL BC.••• BC是OO的切线.⑵设C9 CB= x,在Rt△ OBC中, ( 5)2+ x2= (x + 1)2,解得x = 2. • BC= 2.11 . (1)证明：连接OD.•/ ACL AB•••/ BAC= 90°,即/ OA匡90° .OA= OD在厶AOE与厶DOE中，AE= DEOP OE•△ ACE^^ DOE(SSS).•••/ OAE=Z ODE= 90°,即卩ODL ED.又••• OD是OO的半径，• ED是OO的切线.(2) T AB是直径，•••/ ADB= 90° .•••/ ADC= 90° .•••/ AD冉/ CDE= 90°,/ DA冉/ ACD= 90° . •/ AE= DE,•••/ ADE=/ DAE.•••/ C DE=/ ACD.• DE= CE.又AE= DE• AE= CE.• AC= 2AE= 8.•/ OA= 3,• AB= 6.在Rt△ ABC中, BC= .A B"+ AC= ,62+ 82= 10. • BC的长度是10.。

湘教版九年级数学下册《2.5.2.1切线的判定1》同步练习(含答案解析)

2．5.2　第1课时　切线的判定知识点1　切线的判定1．下列直线中一定是圆的切线的是( )A．与圆有公共点的直线B．过半径外端点的直线C．垂直于圆的半径的直线D．过圆的半径的外端并且垂直于这条半径的直线2．如图2－5－4，A是⊙O上一点，AO＝5，PO＝13，AP＝12，则PA与⊙O的位置关系是( )　图2－5－4A．相交B．相切C．相离D．无法确定3．如图2－5－5，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为______________．图2－5－54．如图2－5－6，在△ABC中，AB＝AC，∠B＝30°，以点A为圆心，以3 cm为半径作⊙A，当AB＝________ cm时，BC与⊙A相切．图2－5－65．如图2－5－7，A，B是⊙O上的两点，AC是过点A的一条直线，如果∠AOB＝120°，那么当∠CAB的度数为________时，AC才能成为⊙O的切线．图2－5－76．如图2－5－8，点A，B，D在⊙O上，∠A＝25°，OD的延长线交直线BC于点C，且∠OCB＝40°，则直线BC与⊙O的位置关系为________．图2－5－87．教材习题2.5A组第3题变式如图2－5－9，延长⊙O的半径OA到点B，使AB＝OA，过点A作弦AC，使AC＝OA.求证：BC是⊙O的切线．图2－5－98．教材习题2.5A组第2题变式如图2－5－10，直线MN过⊙O上的一点B，△ABC内接于⊙O，∠CBM＝∠A，求证：MN是⊙O的切线．图2－5－10知识点2　切线的画法9．如图2－5－11所示，过⊙O外一点P作⊙O的切线．图2－5－1110．如图2－5－12，P是⊙O外一点，OP交⊙O于点A，OA＝AP.甲、乙两人想作一条经过点P且与⊙O相切的直线，其作法如下：甲：以点A为圆心，AP长为半径画弧，交⊙O于点B，则直线BP即为所求．乙：过点A作直线MN⊥OP，以点O为圆心，OP长为半径画弧，交射线AM于点B，连接OB，交⊙O于点C，直线CP即为所求．对于甲、乙两人的作法，下列判断正确的是( )图2－5－12A．甲正确，乙错误B．乙正确，甲错误C．两人都正确D．两人都错误11．如图2－5－13，直线AB，CD相交于点O，∠AOC＝30°，半径为1 cm的⊙P的圆心P在射线OA上，点P与点O的距离为8 cm，如果⊙P以2 cm/s的速度由A向B匀速运动，那么________s时⊙P与直线CD相切．图2－5－1312．2018·邵阳如图2－5－14所示，AB是⊙O的直径，C为⊙O上一点，过点B作BD⊥CD，垂足为D，连接BC，BC平分∠ABD.求证：CD为⊙O的切线．图2－5－1413．2018·郴州如图2－5－15，已知BC是⊙O的直径，D是BC的延长线上一点，AB＝AD，AE是⊙O的弦，∠AEC＝30°.(1)求证：直线AD是⊙O的切线；(2)若AE⊥BC，垂足为M，⊙O的半径为4，求AE的长．图2－5－1514．2017·聊城如图2－5－16，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD，CD，过点D作BC的平行线，与AB的延长线交于点P.(1)求证：PD是⊙O的切线；(2)求证：△PBD∽△DCA；(3)当AB＝6，AC＝8时，求线段PB的长．图2－5－16教师详解详析1．D 2.B3．AB ⊥BC (答案不唯一)4．6　[解析] 过点A 作AD ⊥BC 于点D .∵AB ＝AC ，∠B ＝30°，∴AD ＝AB ，即AB ＝2AD .又∵BC 与12⊙A 相切，∴AD 就是⊙A 的半径，∴AD ＝3 cm ，则AB ＝2AD ＝6 cm.5．60°　[解析] ∵在△AOB 中，OA ＝OB ，∠AOB ＝120°，∴∠OAB ＝30°，∴当∠CAB 的度数为60°时，OA ⊥AC ，AC 才能成为⊙O 的切线．6．相切　[解析] ∵∠BOC ＝2∠A ＝50°，∠OCB ＝40°，∴∠OBC ＝180°－50°－40°＝90°.又∵OB 为⊙O 的半径，∴直线BC 与⊙O 相切．7．证明：连接OC .∵AC ＝OA ＝OC ，∴∠OCA ＝∠OAC ＝60°.又OA ＝AB ，∴AC ＝AB ，∴∠ACB ＝∠OAC ＝30°，12∴∠OCB ＝∠OCA ＋∠ACB ＝90°.又∵OC 是⊙O 的半径，∴BC 是⊙O 的切线．8．证明：如图，过点B 作⊙O 的直径BD ，连接DC ，则∠D ＝∠A .又∠CBM ＝∠A ，∴∠CBM ＝∠D .∵BD 是⊙O 的直径，∴∠BCD ＝90°，∴∠D ＋∠DBC ＝90°，∴∠CBM＋∠DBC＝90°，即∠DBM＝90°，∴BD⊥MN.又BD是⊙O的直径，∴MN是⊙O的切线．9．解：作法：如图，(1)连接OP，以OP为直径作⊙O′交⊙O于A，B两点；(2)连接PA，PB，则PA，PB所在的直线即为所求作的切线．10．C　[解析] 对于甲的作法，连接OB，如图①，先判断OP为⊙A的直径，再根据圆周角定理得到∠OBP＝90°，于是根据切线的判定定理得到PB为⊙O的切线；对于乙的作法：如图②，通过证明△OAB≌△OCP得到∠OAB＝∠OCP＝90°，于是根据切线的判定定理得到PC为⊙O的切线．11．3或5　[解析] 当⊙P在点O左侧与直线CD相切时，设圆心为P′，切点为E′，∵∠AOC＝30°，P′E′＝1 cm，∴OP′＝2 cm，PP′＝8－2＝6(cm)，运动时间为6÷2＝3(s)；当⊙P在点O右侧与直线CD 相切时，同理可得PP″＝8＋2＝10(cm)，运动时间为10÷2＝5(s)．12．证明：∵BC平分∠ABD，∴∠OBC＝∠DBC.∵OC＝OB，∴∠OBC＝∠OCB.∴∠DBC ＝∠OCB .∴OC ∥BD .∵BD ⊥CD ，∴OC ⊥CD .又∵OC 为⊙O 的半径，∴CD 为⊙O 的切线．13．解：(1)证明：连接OA .因为BC 是⊙O 的直径，所以∠BAC ＝90°.因为∠AEC ＝30°，AB ＝AD ，所以∠B ＝∠D ＝30°，∠ACB ＝60°，又∠ACB ＝∠CAD ＋∠D ，所以∠CAD ＝30°，因为OC ，OA 是⊙O 的半径，所以△AOC 是等边三角形，所以∠OAC ＝60°，所以∠OAD ＝90°，即OA ⊥AD .又因为OA 是⊙O 的半径，所以AD 是⊙O 的切线．(2)因为AE ⊥BC ，垂足为M ，所以AE ＝2AM .在直角三角形AOM 中，半径OA ＝4，∠AOC ＝60°，所以AM ＝OA ·sin60°＝4×＝2 ，323所以AE ＝2AM ＝4 .314．解：(1)证明：∵圆心O 在BC 上，∴BC 是⊙O 的直径，∴∠BAC ＝90°.连接OD ，∵AD 平分∠BAC ，∴∠BAC ＝2∠DAC .∵∠DOC ＝2∠DAC ，∴∠DOC ＝∠BAC ＝90°，即OD ⊥BC .∵PD ∥BC ，∴OD ⊥PD .∵OD 是⊙O 的半径，∴PD 是⊙O 的切线．(2)证明：∵PD ∥BC ，∴∠P ＝∠ABC .∵∠ADC ＝∠ABC ，∴∠P ＝∠ADC .∵∠PBD ＋∠ABD ＝180°，∠ACD ＋∠ABD ＝180°，∴∠PBD ＝∠ACD ，∴△PBD ∽△DCA .(3)∵△ABC 是直角三角形，∴BC 2＝AB 2＋AC 2＝62＋82＝100，∴BC ＝10.∵BC 是⊙O 的直径，∴∠BDC ＝90°.∵AD 平分∠BAC ，∴＝，∴BD ＝CD .∴在Rt △BDC 中，BD 2＋CD 2＝BC 2，即BD ︵ CD ︵ 2CD 2＝BC 2＝100，∴CD ＝BD ＝5 .∵△PBD ∽△DCA ，∴＝，即PB ＝＝＝.2PB CD BD AC CD ·BD AC 5 2×5 28254。

湘教版九年级下册数学试题2.5.2 第1课时切线的判定测试卷

2.5.2 圆的切线第1课时切线的判定1．过圆上一点可以作圆的______条切线；过圆外一点可以作圆的_____条切线；•过圆内一点的圆的切线______．2．以三角形一边为直径的圆恰好与另一边相切，则此三角形是_______．3．下列直线是圆的切线的是（）A．与圆有公共点的直线B．到圆心的距离等于半径的直线C．垂直于圆的半径的直线D．过圆直径外端点的直线4．OA平分∠BOC，P是OA上任意一点（O除外），若以P为圆心的⊙P与OC相切，那么⊙P与OB的位置位置是（）A．相交B．相切C．相离D．相交或相切5．△ABC中，∠C=90°，AB=13，AC=12，以B为圆心，5为半径的圆与直线AC的位置关系是（）A．相切B．相交C．相离D．不能确定6．菱形的对角线相交于O，以O为圆心，以点O到菱形一边的距离为半径的⊙O•与菱形其它三边的位置关系是（）A．相交B．相离C．相切D．无法确定7．平面直角坐标系中，点A（3，4），以点A为圆心，5为半径的圆与直线y=－x的位置关系是（）A．相离B．相切C．相交D．以上都有可能8．如图，AB是半径⊙O的直径，弦AC与AB成30°角，且AC=CD．（1）求证：CD是⊙O的切线；（2）若OA=2，求AC的长．9．如图，AB是半圆O的直径，AD为弦，∠DBC=∠A．（1）求证：BC是半圆O的切线；（2）若OC∥AD，OC交BD于E，BD=6，CE=4，求AD的长．10．如图，AB为⊙O的直径，弦CD⊥AB于点M，过点B作BE∥CD，交AC•的延长线于点E，连结BC．（1）求证：BE为⊙O的切线；（2）如果CD=6，tan∠BCD=12，求⊙O的直径．11．如图，已知：△ABC内接于⊙O，点D在OC的延长线上，sin=12，∠D=30°．（1）求证：AD是⊙O的切线；（2）若AC=6，求AD的长．12．已知：如图，A是⊙O上一点，半径OC的延长线与过点A的直线交于B•点，OC=BC，AC=12 OB．（1）求证：AB是⊙O的切线；（2）若∠ACD=45°，OC=2，求弦CD的长．13．如图，P为⊙O外一点，PO交⊙O于C，过⊙O上一点A作弦AB⊥PO于E，若∠EAC=∠CAP，求证：PA是⊙O的切线．14．如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，G是AD的中点，连结OG并延长与BE相交于点F，延长AF•与CB的延长线相交于点P．（1）求证：BF=EF；（2）求证：PA是⊙O的切线；（3）若FG=BF，且⊙O的半径长为32，求BD和FG的长度．。

九年级数学下册 2.5.2 圆的切线第1课时切线的判定习题湘教版(2021学年)

2017春九年级数学下册 2.5．2 圆的切线第1课时切线的判定习题（新版）湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望（2017春九年级数学下册２.5.2 圆的切线第1课时切线的判定习题（新版)湘教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2０17春九年级数学下册2.5.2 圆的切线第1课时切线的判定习题(新版）湘教版的全部内容。

2．5。

2 圆的切线第1课时切线的判定基础题知识点圆的切线的判定１.下列直线中，能判定为圆的切线的是( )A．与圆有公共点的直线B．过圆的半径的外端点的直线C．垂直于圆的半径的直线D．经过直径的一个端点，且垂直于这条直径的直线2.如图，A是圆O上一点,ＡＯ＝5,ＰO=１3，ＡP＝１２,则PＡ与圆O的位置关系是（）A.无法确定Ｂ．相交C．相切D．相离３.如图,△ABC的一边AＢ是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为_＿_________＿．４.如图，A,B是⊙Ｏ上的两点，AC是过Ａ点的一条直线,如果∠AOＢ＝120°,那么当∠CAＢ的度数等于_＿______＿__＿度时，ＡC才能成为⊙Ｏ的切线．5．如图,延长⊙Ｏ的半径OA,使OA＝AB，过点Ａ作弦AC，使AC＝OA．求证:BC是⊙P的切线．６．(梅州中考）如图,在△ABＯ中，OA＝OB,C是边AB的中点,以Ｏ为圆心的圆过点Ｃ。

（１)求证:AB与⊙O相切；若∠AOB=１2０°,AB=4＼r（3)，求⊙O的面积.7.如图,已知两条射线CＡ、ＣB．试画一圆,使此圆与两射线相切．中档题８．如图,AＢ是⊙Ｏ的直径,ＢＣ交⊙O于点D,DＥ⊥AＣ于点E,要使DE是⊙O的切线,还需补充一个条件，则补充的条件不正确的是（)Ａ．ＤE＝DOＢ．AB＝ACＣ．CＤ＝DBD.AＣ∥OＤ9.(随州中考）如图,⊙O中,点C为错误!的中点，∠ACB＝１２0°，OＣ的延长线与A D交于点D,且∠D＝∠B.求证：AD与⊙Ｏ相切.10.（宿迁中考)如图,AB是⊙O的弦,ＯP⊥OA交AＢ于点Ｐ，过点Ｂ的直线交OP的延长线于点C，且CP＝CB．（1)求证：BC是⊙O的切线;（2)若⊙O的半径为＼ｒ(5)，OＰ=１，求BC的长．综合题11．（常德中考)如图,已知⊙O的直径为AB,ＡＣ⊥AＢ于点A，BC与⊙Ｏ相交于点D，在ＡC 上取一点E，使得ED=EA。

湘教版九年级下册数学切线长定理测试题

湘教版九年级数学下册测试题测试题湘教版初中数学2.5.3 切线长定理1. 如图，PA、PB分别切⊙O于点A、B，AC是⊙O的直径，连结AB、BC、OP，则与∠PAB相等的角(不包括∠PAB本身)有( )A．1个 B．2个 C．3个 D．4个第1题图第2题图2.如图，PA、PB切⊙O于点A、B，PA=8，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是（）A．8 B．18 C．16 D．143.如图，PA，PB分别是⊙O的切线，A，B分别为切点，点E是⊙O上一点，且∠AEB=60°，则∠P为（）A．120° B．60°C．30° D．45°第3题图第4题图4．如图，一圆内切于四边形ABCD，且AB=16，CD=10，则四边形ABCD 的周长为________．5.如图，AB、AC、BD是⊙O的切线，P、C、D为切点，如果AB=5，AC=3，则BD的长为 __________.第5题图第6题图6.PA、PB切⊙O于A、B两点，CD切⊙O于点E，交PA、PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是______________.7. 如图，AE、AD、BC分别切⊙O于点E、D、F，若AD=20，求△ABC 的周长．P BA O8. 如图，PA 、PB 是⊙O 的两条切线，切点分别为点A 、B ，若直径AC= 12，∠P=60o ，求弦AB 的长．9.. 如图，PA 、PB 是⊙O 的切线，A 、B 为切点，∠OAB ＝30°．（1）求∠APB 的度数；（2）当OA ＝3时，求AP 的长．初中生提高做题效率的方法厚薄读书法：复习课本要厚薄结合著名数学家华罗庚先生说:“书要能从薄读到厚,还要能从厚读到薄。

”这就是厚薄读书法。

我们在复习功课时,也可以用这种方法,具体来说分为“由薄到厚”和“由厚读薄”两个部分由薄到厚第一步要“由薄到厚”地复习课本。

2017春九年级数学下册2.5.2第1课时切线的判定试题(新版)湘教版

湘教版九年级下册数学 第2章 圆的切线的判定

湘教版数学九年级下册 切线的判定

2新湘教版初中数学九年级下册精品学案.5.2 第1课时 切线的判定

2.5.2 第1课时 切线的判定-九年级数学下册教材配套教学课件(湘教版)