山东省北镇中学、莱芜一中、德州一中2016届高三下学期4月联考数学(理)试题(附答案)(解析版)
2016年高考(538)山东德州一中等三校2016届高三4月联考

2016年高考(538)山东德州一中等三校2016届高三4月联考山东省北镇中学、莱芜一中、德州一中2016届高三4月份联考语文试题本试卷分第I卷和第II卷两部分,共8页。
满分150分,考试用时150分钟。
注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色签字笔将自己的姓名、考试号填涂在答题卡和答题纸规定的位置上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上。
第I卷(选择题36分)一、(每小题3分,共15分)阅读下面的文字,完成1~3题。
济南立城,南依泰山,北临黄河。
舜曾经耕作的历山,即今日的千佛山,座落在泉城的东南隅。
昨天上午,我趁兴登上了千佛山。
这是一处超然世外的所在,不但可以近瞰城郭,俯窥街道,还可以。
但那是过去式了,因为雾霭迷离,云气氤氲,仅勉强辨出城区的(大概/大致),至于地平线上的黄河,以及其它什么峰,什么峦,皆隐而不现,只能向记忆深处(搜寻/搜求)了。
兴冲冲上山,怏怏下山,将登缆车,忽见在城东北方位的一角,雾破云开,。
瞬间怔住,脑筋急,立马联想到学界有关华夏二字的诠释。
此番做客泉城,也拟效仿前人,为它留下一幅文字的(掠影/剪影)。
那天登千佛山,就是想借它的高度,鹰瞵鸟瞰,寻找某种创作的新鲜意象。
争奈天公不作美,只好怅然下山。
1.文中加点字的注音和字形全都正确的一项是A.座落近瞰(kn)B.雾霭氤氲(wn)C.诠释俯窥(ku)D.做客怅然(chng)1. 答案:C解析:本题考查识记现代汉语普通话常用字的字音和识记并正确书写现代常用规范汉字的能力。
A.座落应为坐落;B.氤氲应读yn;D.做客应为作客。
2.依次选用文中括号中的词语,最恰当的一项是A.大概搜寻掠影B.大概搜求剪影C.大致搜寻剪影D.大致搜求掠影2. 答案:B解析:本题考查正确使用词语(包括熟语)的能力,重点是区分实词虚词的近义词。
山东省北镇、莱芜、德州一中2016届高三下学期4月联考(DOC)
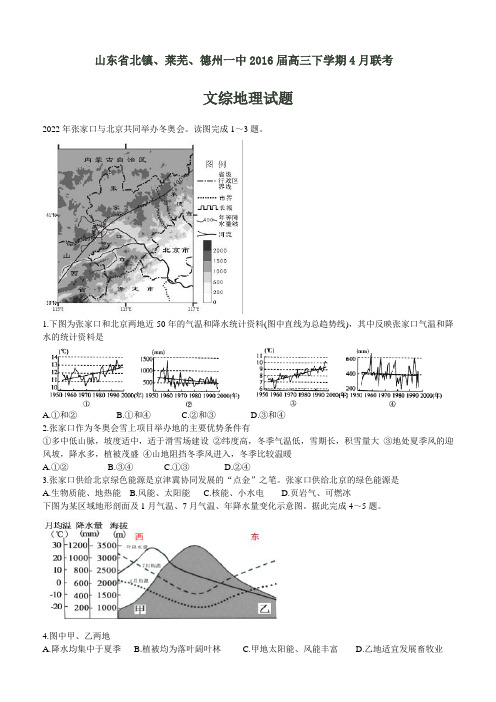
山东省北镇、莱芜、德州一中2016届高三下学期4月联考文综地理试题2022年张家口与北京共同举办冬奥会。
读图完成1~3题。
1.下图为张家口和北京两地近50年的气温和降水统计资料(图中直线为总趋势线),其中反映张家口气温和降水的统计资料是A.①和②B.①和④C.②和③D.③和④2.张家口作为冬奥会雪上项目举办地的主要优势条件有①多中低山脉,坡度适中,适于滑雪场建设②纬度高,冬季气温低,雪期长,积雪量大③地处夏季风的迎风坡,降水多,植被茂盛④山地阻挡冬季风进入,冬季比较温暖A.①②B.③④C.①③D.②④3.张家口供给北京绿色能源是京津冀协同发展的“点金”之笔。
张家口供给北京的绿色能源是A.生物质能、地热能B.风能、太阳能C.核能、小水电D.页岩气、可燃冰下图为某区域地形剖面及1月气温、7月气温、年降水量变化示意图。
据此完成4~5题。
5.图示区域可能位于A.30°S~40°S欧洲西岸B.25°N~35°N亚洲东岸C.40°N~60°N美洲西岸D.35°S~55°S美洲东岸读“宁夏农业区划图”,完成6~8题。
6.贺兰山对I区自然环境的主要影响是①阻挡西部沙漠入侵②阻挡西北寒冷气流入侵③提供冰川融水补给④抬升冬季风增加降雪量A.①②B.②③C.③④D.①③7.图中I~Ⅳ区域A.I区干旱少雨,不适宜发展种植业B.Ⅱ区水源缺乏,不宜发展畜牧业C.Ⅲ区降水丰沛,可大力发展种植业D.Ⅳ区温凉湿润,适宜发展林牧业8.从自然环境和经济水平考虑,宁夏区内人口迁移方向最有可能是A.由北向南B.由南向北C.由东向西D.由西向东依据国家区域发展新棋局,我国将依托黄金水道,建设长江经济带。
读图完成9~11题。
9.与长三角地区相比,川渝地区发展的地理优势是①水陆交通便利②矿产、水力等资源丰富③土地和用工成本低④技术力量雄厚A.①②B.①③C.②③D.③④10.为推动长江流域的综合开发,两区域在生态安全方面可以开展的合作是A.航道建设B.西电东送C.劳务输出D.水土保持11.在长江三角洲产业分工协作方面,上海应重点发展A.国际金融、文化创意、对外贸易B.机械制造、服装制造、石油化工C.原料重化工业、现代农业、旅游业D.高端装备制造、临空经济、现代物流业36.阅读图文材料,完成下列要求。
2016年4月2016届高三第三次全国大联考(山东卷)理数卷(原卷版)

【学易大联考】2016年第三次全国大联考【山东卷】理科数学试卷第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集U =R ,且11|4A x x ⎧⎫=<⎨⎬⎩⎭,|B x y ⎧==⎨⎩,则()U C A B 等于( ) A .(1,3)- B .(1,0)(3,4)- C .[0,3) D .(3,4)2. 已知复数z 满足1i i z -=(+)(i 是虚数单位),则z 在复平面内对应的点所在的象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3. 设随机变量ξ服从正态分布2(4,2)N ,且(26)0.6826P ξ≤≤=,则(6)P ξ>=( )A.0.158 8B.0.158 7C.0.158 6D.0.158 54.在底面半径为1,高为2的圆柱内随机取一点P ,则点P 到圆柱下底面的圆心的距离大于1的概率为( )A .41B .31C .32D .43 5. 已知关于x 的不等式2<6x x a -++的解集为φ,则实数a 的取值范围为( )A .(8,4)-B .(,8]-∞-C .[4,)+∞D .(,8][4,)-∞-+∞6. 已知()2115sin()42f x x x π=--,()f x '为()f x 的导函数,则()f x '的图象是( )7.已知一水平放置的长方体,其三条相邻的棱的长度分别为1,1,2,则该长方体的正视图的面积不可能等于( )A .2 B.8.等腰直角三角形ABC 中,090=A ,B A ,在双曲线D 的同一支上,且线段AB 通过双曲线的一个焦点F ,C 为双曲线D 的另一个焦点,则该双曲线的离心率为( )ABCD9. 已知变量,x y 满足02y y x y x ≥⎧⎪≤⎨⎪≤-⎩,若目标函数z ax by =+(>>0)b a 的最大值为9,则28a b +的最小值为( )A.1B.2C.10D.1210. 若函数()y f x =图象上存在不同的两点A 、B 关于y 轴对称,则称点对[,]A B 是函数()y f x =的一对“和谐点对”(注:点对[,]A B 与[,]B A 可看作同一对“和谐点对”),已知函数2e ,0()4,0x x f x x x x ⎧<⎪=⎨-+≥⎪⎩,则此函数的“和谐点对”有( )A.0对B.1对C. 2对D. 3对第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11. 某校高三(二)班某次数学的测试成绩(单位:分)的频率分布直方图如图所示,据此估计该班学生数学测试成绩的中位数为 .(保留两位小数)12. 运行如右图所示的程序框图,则输出的结果S 为 .13. 设()0sin cos k x x dx π=-⎰,若()82801281kx a a x a x a x -=+++⋅⋅⋅+,则1238a a a a +++⋅⋅⋅+= .?14. 已知直线3y =+与直线150y --=都与圆C 相交,且它们与圆C 相交所得的弦长均为8, 则圆C 的面积是15. 给出下列四个命题:①若22bm am <,则b a < ;②若错误!未找到引用源。
2016年山东省德州市高考数学一模试卷与解析word(理科)

2016年山东省德州市高考数学一模试卷(理科)一、选择题(50分)1.(5分)已知复数z满足z•i=1+i(i是虚数单位),则复数z的共轭复数在复平面内所对应的点的坐标为()A.(1,1) B.(﹣1,﹣1)C.(1,﹣1)D.(﹣1,1)2.(5分)若全集U=R,集合A={x|x2﹣x﹣2≥0},B={x|log3(2﹣x)≤1},则A ∩(∁U B)=()A.{x|x<2}B.{x|x<﹣1或x≥2}C.{x|x≥2}D.{x|x≤﹣1或x>2} 3.(5分)已知p:“直线l的倾斜角”;q:“直线l的斜率k>1”,则p是q的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(5分)不等式|x+1|﹣|x﹣5|<4的解集为()A.(﹣∞,4)B.(﹣∞,﹣4)C.(4,+∞)D.(﹣4,+∞)5.(5分)为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:附:K2=则有()的把握认为环保知识是否优秀与性别有关.A.90% B.95% C.99% D.99.9%6.(5分)函数y=的图象大致为()A.B.C.D.7.(5分)已知双曲线与椭圆的焦点重合,它们的离心率之和为,则双曲线的渐近线方程为()A.B. C. D.8.(5分)已知点A(﹣2,0),B(2,0),若圆(x﹣3)2+y2=r2(r>0)上存在点P(不同于点A,B)使得PA⊥PB,则实数r的取值范围是()A.(1,5) B.[1,5]C.(1,3]D.[3,5]9.(5分)运行如图所示的程序框图,则输出的结果是()A.e2016﹣e2015B.e2017﹣e2016C.e2015﹣1 D.e2016﹣110.(5分)f(x)是定义在(0,+∞)上单调函数,且对∀x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是()A.(0,)B.(,1)C.(1,e) D.(e,3)二、填空题(25分)11.(5分)已知两个单位向量的夹角为60°,,,若,则正实数t=.12.(5分)某三棱锥的三视图如图所示,其侧(左)视图为直角三角形,则该三棱锥外接球的表面积为.13.(5分)已知x,y满足,且z=2x﹣y的最大值是最小值的﹣2倍,则a的值是.14.(5分)(x2+x+1)(1﹣x)4展开式中x2的系数为.15.(5分)若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)①y=;②y=;③y=;④y=.三、解答题16.(12分)已知函数f(x)=2sin cos﹣2sin2(ω>0)的最小正周期为3π.(I)求函数f(x)的单调递增区间;(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c,a=2csinA,并且f(A+)=,求cosB的值.17.(12分)连续抛掷同一颗均匀的骰子,令第i次得到的点数为a i,若存在正整数k,使a1+a2+…+a k=6,则称k为你的幸运数字.(1)求你的幸运数字为3的概率;(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.18.(12分)在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4,∠CDA=120°,点N在线段PB 上,且PN=2.(1)求证:BD⊥PC;(2)求证:MN∥平面PDC;(3)求二面角A﹣PC﹣B的余弦值.19.(12分)已知数列{a n}满足a1+2a2+3a3+…+na n=n(n∈N*).(1)求数列{a n}的通项公式a n;(2)令,写出T n关于n的表达式,并求满足T n>时n的取值范围.20.(13分)设函数.(1)用含a的式子表示b;(2)令F(x)=,其图象上任意一点P(x0,y0)处切线的斜率恒成立,求实数a的取值范围;(3)若a=2,试求f(x)在区间上的最大值.21.(14分)已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3(1)求抛物线E的方程;(2)设A,B是抛物线E上分别位于x轴两侧的两个动点,且(其中O为坐标原点).①求证:直线AB必过定点,并求出该定点Q的坐标;②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.2016年山东省德州市高考数学一模试卷(理科)参考答案与试题解析一、选择题(50分)1.(5分)已知复数z满足z•i=1+i(i是虚数单位),则复数z的共轭复数在复平面内所对应的点的坐标为()A.(1,1) B.(﹣1,﹣1)C.(1,﹣1)D.(﹣1,1)【解答】解:复数z满足z•i=1+i(i是虚数单位),∴﹣i•z•i=﹣i(1+i),∴z=﹣i+1.∴=1+i,则复数z的共轭复数在复平面内所对应的点的坐标为(1,1).故选:A.2.(5分)若全集U=R,集合A={x|x2﹣x﹣2≥0},B={x|log3(2﹣x)≤1},则A ∩(∁U B)=()A.{x|x<2}B.{x|x<﹣1或x≥2}C.{x|x≥2}D.{x|x≤﹣1或x>2}【解答】解:集合A={x|x2﹣x﹣2≥0}={x|x≤﹣1或x≥2},∵log3(2﹣x)≤1=log33,∴0<2﹣x≤3,∴﹣1≤x<2,∴B={x|﹣1≤x<2},∴∁u B={x|x<﹣1或x≥2},∴A∩(∁U B)={x|x<﹣1或x≥2},故选:B.3.(5分)已知p:“直线l的倾斜角”;q:“直线l的斜率k>1”,则p是q的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:p:“直线l的倾斜角”,则直线l的斜率k=tanα>1或k<0;又q:“直线l的斜率k>1”,则p是q的必要不充分条件.故选:B.4.(5分)不等式|x+1|﹣|x﹣5|<4的解集为()A.(﹣∞,4)B.(﹣∞,﹣4)C.(4,+∞)D.(﹣4,+∞)【解答】解:x≥5时:x+1﹣x+5=6>4,不等式无解;﹣1<x<5时:x+1+x﹣5<4,解得:x<4;x≤﹣1时:﹣x﹣1+x﹣5<4恒成立.故选:A.5.(5分)为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:附:K2=则有()的把握认为环保知识是否优秀与性别有关.A.90% B.95% C.99% D.99.9%【解答】解:由题意,得K2==,则K2≈7.822>6.635,所以,有99%的把握认为环保知识是否优秀与性别有关.6.(5分)函数y=的图象大致为()A.B.C.D.【解答】解:函数的定义域为{x|x≠0且x≠±1},故排除A,∵f(﹣x)==﹣=﹣f(x),∴排除C,当x=2时,y=>0,故排除D,故选:B.7.(5分)已知双曲线与椭圆的焦点重合,它们的离心率之和为,则双曲线的渐近线方程为()A.B. C. D.【解答】解:椭圆,焦点为(4,0),(﹣4,0),离心率e=,∴双曲线离心率为﹣=2,设双曲线中c=4,可得a=2,可得b=2,故双曲线的渐近线方程为:y=.故选:D.8.(5分)已知点A(﹣2,0),B(2,0),若圆(x﹣3)2+y2=r2(r>0)上存在点P(不同于点A,B)使得PA⊥PB,则实数r的取值范围是()A.(1,5) B.[1,5]C.(1,3]D.[3,5]【解答】解:根据直径对的圆周角为90°,结合题意可得以AB为直径的圆和圆(x ﹣3)2+y2=r2有交点,显然两圆相切时不满足条件,故两圆相交.而以AB为直径的圆的方程为x2+y2=4,两个圆的圆心距为3,故|r﹣2|<3<|r+2|,求得1<r<5,故选:A.9.(5分)运行如图所示的程序框图,则输出的结果是()A.e2016﹣e2015B.e2017﹣e2016C.e2015﹣1 D.e2016﹣1【解答】解:当n=1时,满足继续循环的条件,S=e﹣1,n=2,当n=2时,满足继续循环的条件,S=e2﹣1,n=3,当n=3时,满足继续循环的条件,S=e3﹣1,n=4,…当n=k时,满足继续循环的条件,S=e k﹣1,n=k+1,…当n=2016时,满足继续循环的条件,S=e2016﹣1,n=2017,当n=2017时,不满足继续循环的条件,故输出的S值为:e2016﹣1,故选:D.10.(5分)f(x)是定义在(0,+∞)上单调函数,且对∀x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是()A.(0,)B.(,1)C.(1,e) D.(e,3)【解答】解:∵f(x)是定义在(0,+∞)上单调函数,且对∀x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,∴设f(x)﹣lnx=t,则f(t)=e+1,即f(x)=lnx+t,令x=t,则f(t)=lnt+t=e+1,则t=e,即f(x)=lnx+e,函数的导数f′(x)=,则由f(x)﹣f′(x)=e得lnx+e﹣=e,即lnx﹣=0,设h(x)=lnx﹣,则h(1)=ln1﹣1=﹣1<0,h(e)=lne﹣=1﹣>0,∴函数h(x)在(1,e)上存在一个零点,即方程f(x)﹣f′(x)=e的实数解所在的区间是(1,e),故选:C.二、填空题(25分)11.(5分)已知两个单位向量的夹角为60°,,,若,则正实数t=1.【解答】解:.∵,∴,即(t)()=0,∴t﹣t+(1﹣t2)=0,即﹣t2+=0.∵t>0,∴t=1.故答案为1.12.(5分)某三棱锥的三视图如图所示,其侧(左)视图为直角三角形,则该三棱锥外接球的表面积为50π.【解答】解:根据几何体的三视图,得:该几何体是底面为直角三角形,侧面垂直于底面,高为5的三棱锥.设三棱锥外接球的半径为R,球心到截面的距离为d,则(2.5﹣)2+(5﹣d)2=d2+2.52=R2,∴R2=∴4πR2=50π,故答案为:50π.13.(5分)已知x,y满足,且z=2x﹣y的最大值是最小值的﹣2倍,则a的值是.【解答】解:由约束条件,作出可行域如图,联立,得B(a,2﹣a),联立,得A(1,1),化目标函数z=2x﹣y为y=2x﹣z,由图可知z max=2×1﹣1=1,z min=2a﹣2+a=3a﹣2,由,解得:a=故答案为:.14.(5分)(x2+x+1)(1﹣x)4展开式中x2的系数为3.【解答】解:由于(1﹣x)4 =1﹣4x+6x2﹣4x3+x4,∴(x2+x+1)(1﹣x)4展开式中x2的系数为1﹣4+6=3,故答案为:3.15.(5分)若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是②③(填空写所有正确选项的序号)①y=;②y=;③y=;④y=.【解答】解:①函数y=﹣x﹣1,(x<0)关于原点对称的函数为﹣y=x﹣1,即y=﹣x+1,在x>0上作出两个函数的图象如图,由图象可知两个函数在x>0上的交点个数只有一个,所以函数f(x)的“伙伴点组”有1个,不满足条件.②函数y=﹣ln|x|(x<0)关于原点对称的函数为﹣y=﹣ln|﹣x|,即y=ln|x|,在x>0上作出两个函数的图象如图,由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.③函数y=﹣x2﹣4x,(x<0)关于原点对称的函数为﹣y=﹣x2+4x,即y=x2﹣4x,在x>0上作出两个函数的图象如图,由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.④函数y=e﹣x,(x<0)关于原点对称的函数为﹣y=e x,即y=﹣e x,在x>0上作出两个函数的图象如图,由图象可知两个函数在x>0上的交点个数有0个,所以函数f(x)的“伙伴点组”有0个,不满足条件.,故答案为:②③.三、解答题16.(12分)已知函数f(x)=2sin cos﹣2sin2(ω>0)的最小正周期为3π.(I)求函数f(x)的单调递增区间;(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c,a=2csinA,并且f(A+)=,求cosB的值.【解答】解:(I)由三角函数公式化简可得f(x)=2sin cos﹣2sin2=sinωx﹣1+cosωx=2sin(ωx+)﹣1,∵函数f(x)的最小正周期为T=3π,∴ω===,∴f(x)=2sin(x+)﹣1,由2kπ﹣≤x+≤2kπ+可得3kπ﹣π≤x≤3kπ+,∴函数f(x)的单调递增区间为[3kπ﹣π,3kπ+],k∈Z;(Ⅱ)∵f(A+)=,∴2sin(A++)﹣1=,∴2sin(A+)﹣1=,∴2cosA﹣1=,解得cosA=,∴sinA==,再由a=2csinA和正弦定理可得sinA=2sinCsinA,约掉sinA可得sinC=,∴C=或C=,又∵a<b<c,∴C为最大角,C=矛盾,故C=,cosC=﹣,∴cosB=﹣cos(A+C)=sinAsinC﹣cosAcosC=﹣=17.(12分)连续抛掷同一颗均匀的骰子,令第i次得到的点数为a i,若存在正整数k,使a1+a2+…+a k=6,则称k为你的幸运数字.(1)求你的幸运数字为3的概率;(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.【解答】解:(1)设“连续抛掷k次骰的和为6”为事件A,则它包含事件A1,A2,A3,其中,A1:三次恰好均为2;A2:三次恰好1,2,3各一次;A3:三次中有两次均为1,一次为4,A1,A2,A3为互斥事件,∴你的幸运数字为3的概率:P(A)=P(A1)+P(A2)+P(A3)=+=.(2)由已知得X的可能取值为5,3,1,0,P(X=5)=,P(X=3)==,P(X=1)=+=,P(X=0)=1﹣=,∴X的分布列为:EX==.18.(12分)在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4,∠CDA=120°,点N在线段PB 上,且PN=2.(1)求证:BD⊥PC;(2)求证:MN∥平面PDC;(3)求二面角A﹣PC﹣B的余弦值.【解答】证明:(1)∵△ABC是正三角形,M是AC中点,∴BM⊥AC,即BD⊥AC,又∵PA⊥平面ABCD,∴PA⊥BD,又PA∩AC=A,∴BD⊥平面PAC,∴BD⊥PC.(2)在正△ABC中,BM=6,在△ACD中,∵M为AC中点,DM⊥AC,∴AD=CD,∠ADC=120°,∴DM=2,∴=,在Rt△PAB中,PA=4,AB=4,PB=8.∴==,∴MN∥PD,又MN⊄平面PDC,PD⊂平面平面PDC,∴MN∥平面PDC.解:(Ⅲ)∵∠BAD=∠BAC+∠CAD=90°,∴AB⊥AD,以A为坐标原点,分别以AB、AD、AP所在直线为x轴,y轴,z轴,建立空间直角坐标系,∴B(4,0,0),C(2,6,0),D(0,4,0),P(0,0,4),=(2,6,﹣4),=(4,0,﹣4),由(2)知=(4,﹣4,0)是平面PAC的法向量,设平面PBC的一个法向量为=(x,y,z),则,即,取z=3,得=(),设二面角A﹣PC﹣B的平面角为θ,则cosθ===,∴二面角A﹣PC﹣B的余弦值为.19.(12分)已知数列{a n}满足a1+2a2+3a3+…+na n=n(n∈N*).(1)求数列{a n}的通项公式a n;(2)令,写出T n关于n的表达式,并求满足T n>时n的取值范围.【解答】解:(1)由a1+2a2+3a3+…+na n=n,=n﹣1(n>1),可得a1+2a2+3a3+…+(n﹣1)a n﹣1相减可得na n=1,即有a n=,(n>1),当n=1时,a1=1,上式也成立,可得a n=,(n∈N*);(2)由,结合(1)可得,b n=(2n﹣1)•()n,前n项和T n=1•+3•()2+…+(2n﹣3)•()n﹣1+(2n﹣1)•()n,T n=1•()2+3•()3+…+(2n﹣3)•()n+(2n﹣1)•()n+1,相减可得,T n=+2[()2+…+()n﹣1+()n]﹣(2n﹣1)•()n+1=+2•﹣(2n﹣1)•()n+1,化简可得,前n项和T n=3﹣.=3﹣﹣(3﹣)=,由T n﹣T n﹣1,可得数列{T n}递增,当n≥2时,T n>T n﹣1由T4=3﹣=<;T5=3﹣=>.即有n≥5时,T n≥T5>.故n的取值范围是n≥5,且n∈N*.20.(13分)设函数.(1)用含a的式子表示b;(2)令F(x)=,其图象上任意一点P(x0,y0)处切线的斜率恒成立,求实数a的取值范围;(3)若a=2,试求f(x)在区间上的最大值.【解答】解:(1)f(x)的定义域为(0,+∞),∵f′(x)=﹣ax+b,f′(1)=1﹣a+b=0,∴b=a﹣1(2)F(x)=lnx+,∴F′(x)=﹣=∴k=F′(x)=≤在(0,3]上恒成立,∴a≥(﹣x02+x0)max,x0∈(0,3],当x0=1时,﹣x02+x0的取得最大值,∴a≥(3)当a=2时,f(x)=lnx﹣x2+x,∴f′(x)=﹣2x+1=,令f′(x)=0,解得x=1或x=﹣(舍去),当0<x<1时,f′(x)>0,此时f(x)单调递增,当x>1时,f′(x)<0,此时f(x)单调递减,当c+≤1,即0<c≤时,f(x)区间上单调递增,∴f(x)max=f(c+)=ln(c+)﹣(c+)2+c+=ln(c+)+﹣c2,当.即<c<1时,f(x)在[c,1]上单调递增,在[1,c+]上单调递减,∴f(x)max=f(1)=0,当c≥1时,f(x)在[c,c+]上单调递减,∴f(x)max=f(c)=lnc﹣c2+c,综上所述,当0<c≤时,f(x)max=ln(c+)+﹣c2,当<c<1时,f(x)max=0,当c≥1时,f(x)max=lnc﹣c2+c.21.(14分)已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3(1)求抛物线E的方程;(2)设A,B是抛物线E上分别位于x轴两侧的两个动点,且(其中O为坐标原点).①求证:直线AB必过定点,并求出该定点Q的坐标;②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.【解答】(1)解:由已知可得K(﹣,0),圆C:(x﹣5)2+y2=9的圆心C(5,0),半径r=3.设MN与x轴交于R,由圆的对称性可得|MR|=于是|CR|=,即有|CK|==6,即有5+=6,解得p=2,则抛物线E的方程为y2=4x;(2)①证明:设直线AB:x=my+t,A(,y1),B(,y2),联立抛物线方程可得y2﹣4my﹣4t=0,y1+y2=4m,y1y2=﹣4t,,即有•+y1y2=,解得y1y2=﹣18或2(舍去),即﹣4t=﹣18,解得t=.则有AB恒过定点Q(,0);②解:由①可得|AB|=|y2﹣y1|=,同理|GD|=,则四边形AGBD面积S=|AB|•|GD|=4,令m2+=μ(μ≥2),则S=4是关于μ的增函数,则当μ=2时,S取得最小值,且为88.当且仅当m=±1时,四边形AGBD面积的最小值为88.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
2016届高三年级第二次四校联考理科数学试题带参考答案及评分标准

四校二联数学(理)试题 第 1 页 共 10 页2016届高三年级第二次四校联考数学(理)试题2015.12命题:康杰中学 临汾一中 忻州一中 长治二中【满分150分,考试时间为120分钟】一、选择题(5×12=60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号)1.已知集合{}|1M x x =>,集合{}2|20N x x x =-<,则M N I 等于 A .{}|12x x << B .{}|01x x << C . {}|02x x <<D .{}|2x x >2.i 是虚数单位,若21ia bi i+=++(,)a b R ∈,则lg()a b +的值是 A .2-B .1-C .0D .123. 阅读右边的程序框图,运行相应的程序.若输入x 的值为1,则输出S 的值为A. 64B. 73C. 512D. 5854. 已知等比数列{}n a 中,各项都是正数,且1321,,22a a a 成等差数列,则91078a a a a +=+A. 1B. 1C.3+D.3-5. 已知|a r |=1,|b r |=2,且()a a b ⊥-r r,则向量a 与向量b r 的夹角为A.6π B. 4π C.3πD.23π6. 某学校组织学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[)[)20,40,40,60[)[)60,80,80,100,若低于60分的人数是15人,则该班的学生人数是四校二联数学(理)试题 第 2 页 共 10 页A .45B .50C .55D .607. "0"a ≤是“函数()=(-1)f x ax x 在区间(0,+)∞内单调递增”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8. 某三棱锥的三视图如图所示,该三棱锥的表面积是A.28+ B.60+ C.56+D .30+9.将函数()sin y x x x R =+∈的图像向左平移()0m m >个单位长度后,所得到的图像关于y 轴对称,则m 的最小值是A.6π B.12π C. 3π D. 56π 10. 已知()()()()10210012101111x a a x a x a x +=+-+-++-L ,则8a 等于A .-5B .5C .90D .18011. 设抛物线2:3(0)C y px p =>的焦点为F ,点M 在C 上, 5MF =,若以MF 为直径的圆过点(0,2),则C 的方程为A .2248y x y x==或 B .2228y x y x ==或C .22416y x y x ==或D .22216y x y x ==或 12. 已知函数21()(0)2xf x x e x =+-<与()()2lng x x x a =++的图象上存在关于y 轴对称的点,则a 的取值范围是A.⎛-∞ ⎝ B.(-∞ C.⎛ ⎝ D.⎛⎝二、填空题:(本大题共4小题,每小题5分,共20分。
山东省德州市高三下学期数学4月联考试卷

山东省德州市高三下学期数学4月联考试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共14分)1. (1分) (2018高一上·佛山月考) 已知集合,,那么为________ .2. (1分) (2016高三上·六合期中) 已知复数z1=1+3i,z2=3+i(i为虚数单位).在复平面内,z1﹣z2对应的点在第________象限.3. (1分)(2016·上海模拟) 抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:运动员第一次第二次第三次第四次第五次甲8791908993乙8990918892则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.4. (1分)执行下列算法语句.若输入x=10,则输出y的值为________.5. (1分)(2013·上海理) 从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).6. (1分) (2018高三上·东区期末) 在平面直角坐标系中,为坐标原点,、是双曲线上的两个动点,动点满足,直线与直线斜率之积为2,已知平面内存在两定点、,使得为定值,则该定值为________7. (1分)等差数列{an}中,公差d≠0,且2a4﹣a72+2a10=0,数列{bn}是等比数列,且b7=a7 ,则b5b9=________.8. (1分)(2017·武汉模拟) 已知函数f(x)= (﹣3x2+3f′(2))dx,则f′(2)=________.9. (1分) (2019高二上·集宁月考) 给出以下四个命题:⑴命题,使得,则,都有;⑵已知函数f(x)=|log2x|,若a≠b,且f(a)=f(b),则ab=1;⑶若平面α内存在不共线的三点到平面β的距离相等,则平面α平行于平面β;⑷已知定义在上的函数满足函数为奇函数,则函数的图象关于点对称.其中真命题的序号为________.(写出所有真命题的序号)10. (1分) (2018高二上·山西月考) 给出下列五个命题:①当时,有;②若是锐角三角形,则;③已知是等差数列的前项和,若,则;④函数与的图像关于直线对称;⑤当时,不等式恒成立,则实数的取值范围为 .其中正确命题的序号为________.11. (1分) (2016高一上·虹口期中) 函数y=2x﹣的值域为________.12. (1分)(2017·扬州模拟) 直角△ABC的三边a,b,c,满足3≤a≤5≤b≤8≤c≤9,则△ABC面积的最大值是________.13. (1分) (2017高三下·成都期中) 已知向量 =(1,2),⊥( + ),则向量在向量方向上的投影为________.14. (1分)(2017·江苏) 设f(x)是定义在R上且周期为1的函数,在区间[0,1)上,f(x)= ,其中集合D={x|x= ,n∈N*},则方程f(x)﹣lgx=0的解的个数是________.二、解答题 (共11题;共115分)15. (10分)如图,梯形ABCD所在平面与以AB为直径的圆所在平面垂直,O为圆心,AB∥CD,∠BAD=90°,AB=2CD.若点P是⊙O上不同于A,B的任意一点.(Ⅰ)求证:BP⊥平面APD;(Ⅱ)设平面BPC与平面OPD的交线为直线l,判断直线BC与直线l的位置关系,并加以证明;(Ⅲ)求几何体DOPA与几何体DCBPO的体积之比.16. (10分) (2020高一上·遂宁期末) 已知角α的终边经过点,且为第二象限角.(1)求、、的值;(2)若,求的值.17. (10分) (2019高一上·哈尔滨月考) 若不等式的解集是 .(1)求不等式的解集;(2)已知二次不等式的解集为,求关于的不等式的解集.18. (10分) (2015高二下·双流期中) 已知椭圆的左、右焦点分别为F1、F2 ,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.(1)求椭圆的方程;(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明:为定值.(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由.19. (15分)(2018·杨浦模拟) 已知数列,其前项和为,满足,,其中,,, .(1)若,,(),求数列的前项和;(2)若,且,求证:数列是等差数列.20. (15分)(2020·甘肃模拟) 已知函数的导函数为 .(1)若曲线在处的切线与直线垂直,求的值;(2)若的两个零点从小到大依次为,,证明: .21. (10分)关于x的不等式|<0的解集为(﹣1,b).(1)求实数a,b的值;(2)若z1=a+bi,z2=cosα+isinα,且z1z2为纯虚数,求tanα的值.22. (10分)(2017·宜宾模拟) 在平面直角坐标系中,曲线C的参数方程为:(其中θ为参数).(Ⅰ)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求曲线C的极坐标方程;( II)直线l的参数方程为:(其中t为参数),直线l与曲线C分别交于A,B两点,且,求直线l的斜率.23. (5分)已知函数f(x)=(x﹣a)2+(x﹣b)2+(x﹣c)2+(a,b,c为实数)①求f(x)的最小值m(用a,b,c表示);②若a﹣b+2c=3,求(1)中m的最小值.24. (10分)(2017·龙岩模拟) 某校高一(1)(2)两个班联合开展“诗词大会进校园,国学经典润心田”古诗词竞赛主题班会活动,主持人从这两个班分别随机选出20名同学进行当场测试,他们的测试成绩按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)分组,分别用频率分布直方图与茎叶图统计如图(单位:分):高一(2)班20名学生成绩茎叶图:45526 4 5 6 870 5 5 8 8 8 8 980 0 5 59 4 5(Ⅰ)分别计算两个班这20名同学的测试成绩在[80,90)的频率,并补全频率分布直方图;(Ⅱ)分别从两个班随机选取1人,设这两人中成绩在[80,90)的人数为X,求X的分布列(频率当作概率使用).(Ⅲ)运用所学统计知识分析比较两个班学生的古诗词水平.25. (10分)如图,在正△ABC中,点D,E分别在边AC,AB上,且AD=AC,AE=AB,BD,CE相交于点F.(Ⅰ)求证:A,E,F,D四点共圆;(Ⅱ)若正△ABC的边长为2,求,A,E,F,D所在圆的半径.参考答案一、填空题 (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共11题;共115分)15-1、16-1、16-2、17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、20-2、21-1、22-1、23-1、24-1、25-1、。
山东省日照一中2016届高三下学期4月份教学质量诊断性检测(检测八)数学(理)试题含答案

俯视图侧视图正视图24212013级高三下学期教学质量诊断性检测(八)数学试题(理科)(命题人:王福宗 审题人:山世光)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|1,}A y y x x ==-+∈R ,2{|log }B y y x ==,则A B =A.(,1]-∞B.RC.∅D.[1,)+∞ 2.为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:患病 未患病 总计 服用药 10 40 50 没服用药 20 30 50 总计3070100经计算,统计量2K 的观测值 4.762k ≈,则在犯错误的概率不超过( )的前提下认为药物有效. 已知独立性检验中统计量2K 的临界值参考表为:2()P K k …0.15 0.10 0.05 0.025 0.010 0.005 0.001 k2.0722.7063.8415.0246.6357.87910.828A.0.005B.0.05C.0.010D.0.0253.已知复数∈+=a ai z (21R ),i z 212-=,若21z z为纯虚数,则=||1zA .5B .2C .3D .24.已知a 为实数,则1a ≥是关于x 的绝对值不等式1x x a +-≤有解的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件5.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为A.2π3B.π3C.2π9D.16π96.若随机变量X ~2(,)(0)N μσσ>,则有如下结论: ()0.6826P X μσμσ-<+=…, (22)0.9544P X μσμσ-<+=…, (33)0.9974P X μσμσ-<+=….某班有48名同学,一次数学考试的成绩服从正态分布,平均分为80,标准差为10,理论上说在80分到90分的人数约为A.32B.24C.8D. 16 7.设函数()f x 是定义在R 上的奇函数,且当0x ≥时,()f x 单调递减,若数列{}n a 是等差数列,且30a <,则()()()()()12345f a f a f a f a f a ++++的值A .恒为负数B .恒为正数C .恒为0D .可正可负 8.若[]x 表示不超过x 的最大整数,执行如图所示的程序框图,则输出的S 的值为 A.4 B.5 C.7 D.99.已知,,max{,},.a a b a b b a b ⎧=⎨<⎩… 设实数,x y 满足26,26,0,0,x y x y x y +⎧⎪+⎨⎪⎩……厖则max{231,22}x y x y +-++的取值范围是 A.[2,9] B.[1,9]- C.[1,8]- D.[2,8]10.已知定义域为(0,)+∞的单调函数()f x 满足:(0,)x ∀∈+∞,2(()log )3f f x x -=,则函数()()sin 2π2g x f x x =--的零点的个数为 A.1 B.2 C.3 D.4二.填空题:本大题共5小题,每小题5分,共25分.11.已知向量(1,0)a = ,(0,1)b = ,若向量()()a b a b λ+⊥-,则实数λ的值为 .12.已知函数a x x y +-=22的值域为),0[+∞,则实数a 的取值集合为 .13.已知双曲线:C 22221y x a b-=(0,0)a b >>的渐近线与圆22(2)1x y +-=相交,则双曲线C的离心率e 的取值范围是 .14.有5本不同的书,其中语文书2本,数学书2本,物理书1本,若将其随机地摆成一排,则同一科目的书均不相邻的摆法有 种. (用数字作答)15.关于函数()cos 223sin cos f x x x x =-,下列命题:①存在1x ,2x ,当12x x π-=时,()()12f x f x =成立;②()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上是单调递增; ③函数()f x 的图象关于点,012π⎛⎫⎪⎝⎭成中心对称;④将函数()f x 的图象向左平移512π个单位后将与2sin 2y x =的图象重合;其中正确的命题序号为 .三.解答题:本大题共6小题,共75分. 16.(本小题满分12分)在锐角ABC ∆中,222cos()sin cos b a c A C ac A A--+=.(I)求角A 的大小;(II)若2a =,当7sin cos()12B C π+-取得最大值时,求B 和b .0,0S n ==[]S S n =+4?n >S输出是1n n =+否结束 开始17.(本小题满分12分)如图,四棱锥P ABCD -中,PA ⊥底面ABCD , 90ABC ADC ∠=∠=︒,1CB CD ==,120BCD ∠=︒, E 为线段BP 的靠近点B 的一个四等分点,AE PC ⊥.(I)求棱PA 的长;(II)求平面PCB 与平面PCD 所成的角(锐角)的余弦值.18.(本小题满分12分)质点P 从如图放置的正方形ABCD 的顶点A 出发,根据掷骰子的情况,按照以下的规则在顶点间来回移动:如果朝上数字大于等于5,向平行于AB 边的方向移动;如果朝上数字小于等于4,向平行于AD 边的方向移动.记掷骰子*2(N )n n ∈次后质点P 回到A 点的概率为n a ,回到C 点的概率为n c . (I)求1a 的值;(II)当2n =时,设X 表示质点P 到达C 点的次数,求X 的分布列和期望; (III)当2015n =时,试比较201520151,,2a c 的大小(只需写出结论).19.(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,且152,30a S ==.数列{}n b 的前n 项和为n T ,且21n n T =-. 中学联盟网(I)求数列{}n a 、{}n b 的通项公式; (II)设()()1ln nn n n n c a b S =-+,求数列{}n c 的前n 项和.20.(本小题满分13分)在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,直线y =x 被椭圆C截得的线段长为4105.(I)求椭圆C 的方程. 山东中学联盟(II)过原点的直线与椭圆C 交于A ,B 两点(A ,B 不是椭圆C的顶点).点D 在椭圆C 上,P A B C D E且AD ⊥AB ,直线BD 与x 轴、y 轴分别交于M ,N 两点.①设直线BD ,AM 的斜率分别为k 1,k 2,证明存在常数λ使得k 1=λk 2,并求出λ的值; ②求△OMN 面积的最大值.21.(本小题满分14分)已知函数()g x =ln xx,()f x =()g x ax -. (I)求函数()g x 的单调区间; (II)若函数()f x 在区间(1,)+∞上是减函数,求实数a 的最小值;(III)若存在1x ,2x 2[,]e e ∈,(e =2.71828……是自然对数的底数)使1()f x ≤2()f x '+a ,求实数a 的取值范围.x y MND AO B2013级高三下学期教学质量诊断性检测(八)数学试题(理科)参考答案一、选择题:ABABD DBCAC 二、填空题:11.1 12.1a … 13.23(1,)314.48 15. ①③ 三、解答题:17.解:(I )解法1:因为PA ⊥底面ABCD ,BC ⊂底面ABCD ,所以PA BC ⊥.又BC AB ⊥,PA AB A = , 所以BC ⊥平面PAB .又AE ⊂平面PAB ,所以BC AE ⊥. ……………2分 又因为AE PC ⊥,PC BC C = ,所以AE ⊥平面PBC .所以AE PB ⊥. …………4分 在四边形ABCD 中,连接.BD在等腰△BCD 中,由余弦定理,222cos120 3.BD CB CD CB CD =+-⋅⋅︒=由平面几何知识,易知△ABD 为等边三角形. 所以 3.AB BD == 设PA a =,在Rt △PAB 中,3AB =,22(3)PB a =+23a =+,从而21344a BE PB +==.在Rt △PAB 中,由射影定理得2AB BE PB =⋅,即2223(3)34a a +=⋅+.解得3a =,即棱PA 的长为3.……………………………………………………6分解法2:以,AC AP所在方向分别为y 轴、z 轴的正方向,建立空间直角坐标系A xyz -.因为90ABC ADC ∠=∠=︒, 1BC DC ==,AC AC =,所以△ABC ≅△ADC .又因为120BCD ∠=︒, 所以60BCA DCA ∠=∠=︒.所以12cos 60cos 60DC AC ===︒︒. ………………2分 所以(000)A ,,,(020)C ,,,33(,,0)22B . 设PA t =,则(00,)(0)P t t >,. 所以33(,,)22BP t =-- ,133(,,)4884t BE BP ==-- .从而AE AB BE =+ 339(,,)884t =. ………………4分又因为(02)PC t =-,,,且AE PC ⊥ .所以29044t AE PC ⋅=-= ,解得3t =.所以棱PA 的长为3.………………………6分(II )设平面PCB 的一个法向量为1111(,,)n x y z =,平面PCD 的一个法向量为2222(,,).n x y z =由(020)C ,,,(00,3)P ,,33(,,0)22B ,33(,,0)22D -, 得(0,2,3)CP =- ,31(,,0)22BC =- ,31(,,0)22DC = .由110,0,n CP n BC ⎧⋅=⎪⎨⋅=⎪⎩ 得1111230,30.22y z y x -+=⎧⎪⎨-+=⎪⎩ 取13x =,得13y =,12z =.所以1(3,3,2)n =.…………………………………8分由220,0,n CP n DC ⎧⋅=⎪⎨⋅=⎪⎩ 得2222230,30.22y z y x -+=⎧⎪⎨+=⎪⎩ 取23x =,得23y =-,22z =-. 所以2(3,3,2)n =--.………………………………………………………………10分P AB CD E x yz121212cos ,||||n n n n n n ⋅<>=⋅222222333(3)2(2)(3)32(3)(3)(2)⨯+⨯-+⨯-=++⨯+-+-58=-. 所以,平面PCB 与平面PCD 所成的角(锐角)的余弦值为58.…………………12分18.20.解:(I)由题意知,a 2-b 2a =32,可得a 2=4b 2.椭圆C 的方程可简化为x 2+4y 2=a 2.将y =x 代入可得x =±5a 5. 因此2×25a 5=4105,即a =2,所以b =1,所以椭圆C 的方程为x 24+y 2=1. ……………3分(II)①设A (x 1,y 1)(x 1y 1≠0),D (x 2,y 2),则B (-x 1,-y 1).因为直线AB 的斜率k AB =y 1x 1,且AB ⊥AD ,所以直线AD 的斜率k =-x 1y 1.设直线AD 的方程为y =kx +m , 由题意知k ≠0,m ≠0.由⎩⎪⎨⎪⎧y =kx +m ,x 24+y 2=1,消去y ,得(1+4k 2)x 2+8mkx +4m 2-4=0, 所以x 1+x 2=-8mk 1+4k 2,因此y 1+y 2=k (x 1+x 2)+2m =2m1+4k 2. ……………6分 由题意知x 1≠-x 2,所以k 1=y 1+y 2x 1+x 2=-14k =y 14x 1. ……………7分所以直线BD 的方程为y +y 1=y 14x 1(x +x 1). 令y =0,得x =3x 1,即M (3x 1,0).可得k 2=-y 12x 1. ……………8分所以k 1=-12k 2,即λ=-12.因此,存在常数λ=-12使得结论成立. ……………9分②直线BD 的方程y +y 1=y 14x 1(x +x 1),令x =0,得y =-34y 1,即N ⎝⎛⎭⎫0,-34y 1. 由①知M (3x 1,0),所以△OMN 的面积S =12×3|x 1|×34|y 1|=98|x 1||y 1|. ……………11分因为|x 1||y 1|≤x 214+y 21=1,当且仅当|x 1|2=|y 1|=22时,等号成立,此时S 取得最大值98,所以△OMN 面积的最大值为98. ……………13分21. 解:(I )由0ln 0x x >⎧⎨≠⎩得, 0x >且1x ≠,则函数()g x 的定义域为()()0,11,+∞ ,且()()2ln 1ln x g x x -'=,令()0g x '=,即ln 10x -=,解得x e =当0x e <<且1x ≠时,()0g x '<;当x e >时()0g x '>,∴函数()g x 的减区间是()()0,1,1,e ,增区间是(),e +∞. …………………4分(II) 由题意得,函数()ln xf x ax x=-在()1,+∞上是减函数, ∴()()2ln 10ln x f x a x -'=-≤在()1,+∞上恒成立,即()2ln 1ln x a x -≥在()1,+∞上恒成立……6分令()()2ln 1ln x h x x -=,()1,x ∈+∞,因此()max a h x ≥即可.由()22111111()ln ln ln 244h x x x x ⎛⎫=-+=--+≤ ⎪⎝⎭,当且仅当11ln 2x =,即2x e =时等号成立,∴()max 14h x =,因此14a ≥,故a 的最小值为14. ………………8分(III)命题“若存在212,,x x e e ⎡⎤∈⎣⎦,使()()12f x f x a '≤+,”等价于“当2,x e e ⎡⎤∈⎣⎦时,有()()min max f x f x a '≤+”, ………………9分由(II)得,当2,x e e ⎡⎤∈⎣⎦时,()max 14f x a '=-,则()max 14f x a '+=, 故问题等价于:“当2,x e e ⎡⎤∈⎣⎦时,有()min 14f x ≤”, ………………10分 ()()2ln 1ln x f x a x -'=-,由(II )知2ln 110,(ln )4x x -⎡⎤∈⎢⎥⎣⎦, (1)当14a ≥时,()0f x '≤在2,e e ⎡⎤⎣⎦上恒成立,因此()f x 在2,e e ⎡⎤⎣⎦ 上为减函数,则()()222min 124e f x f e ae ==-≤,故21124a e ≥-, ………………11分(2)当0a ≤时, ()0f x '≥在2,e e ⎡⎤⎣⎦上恒成立,因此()f x 在2,e e ⎡⎤⎣⎦ 上为增函数,则()()min 14f x f e e ae e ==-≥>,不合题意 ………………12分 (3)当104a <<时,由于()2211111()ln ln ln 24f x a a x x x ⎛⎫'=-+-=--+- ⎪⎝⎭ 在2,e e ⎡⎤⎣⎦ 上为增函数,故()f x ' 的值域为()()2,f e f e ⎡⎤''⎣⎦ ,即1,4a a ⎡⎤--⎢⎥⎣⎦. 由()f x '的单调性和值域知,存在唯一()20,x e e ∈,使()00f x '=,且满足:当()0,x e x ∈时,()0f x '<,()f x 减函数;当()20,x x e ∈时,()0f x '>,()f x 增函数;所以,()()000min 01ln 4x f x f x ax x ==-≤,()20,x e e ∈, 所以,22001111111ln 4ln 4244a x x e e ≥->->-=与104a <<矛盾,不合题意. 综上,得21124a e≥-. ………………14分。
山东省北镇中学、莱芜一中、德州一中高三政治4月联考试题

北镇中学、莱芜一中、德州一中2016届高三4月份联考文综政治12.中国国家统计局2016年3月10日公布数据显示,2月消费者物价指数(CPI)同比上涨2.3%,涨幅环比提高0.5个百分点,创下2014年7月来的新高;而工业生产者出厂价格指数(PPI)同比下降4.9%,连续48个月低于上年水平。
这一经济发展趋势预示着A.央行提高基准利率,股市下跌B.央行降低基准利率,股市上涨C.经济下行压力加大,股市下跌D.经济下行压力释放,股市上涨【解析】CPI和PPI分别是消费者物价指数和生产者物价指数。
通常CPI是用来衡量通货膨胀率的指标,物价指数上涨、出厂价格指数下降时,意味着经济下行压力加大,由于人们担心经济下行压力加大,导致股市下跌,C正确入选、D错误不选。
这种情况下,央行通常不会调整货币政策来刺激经济发展,A、B无关不选。
【答案】C【考点】价格变动对经济生活的影响、股票13.加强供给侧改革,必须需求与供给“两条腿走路”。
下列经济现象中能与图1中( P为价格,Q为数量,S为供给曲线,D为需求曲线,E点为均衡价格)蕴含经济道理相符的是图1①三、四线城市控制商品房土地供应,房地产由S向S1位移②鼓励民间资本深入教育领域,社会办学由E点转向E1点③加快农民工市民化,有效需求增加,房地产S向S2位移④若E向E2位移,表明某产品供给质量和效率得到提升A.①②B.③④C.①④D.②③【解析】控制土地供应,房地产供应减少,供给曲线S向S1位移,①正确。
实行政策松绑,鼓励民间资本深入教育领域,社会办学有效供给增加,均衡价格会由E点转向E2点,②错误。
加快农民工市民化,有效需求增加,引起需求曲线D向右移动,进而引起供给量的增加,但不是供给曲线的位移,是在供给曲线上上升,③错误。
均衡价格E向E2位移,形成新的均衡价格,表明该产品有效供给增加,④正确。
故选C。
【答案】C【考点】生产与消费、影响(均衡)价格的因素14. “卡尔多•希克斯改进”是经济学家提出的一个描述收入分配和资源配置状态的经济模型,旨在确立一项衡量经济政策和行为成功与否的标准。
2016年山东省莱芜市高考一模数学试卷(理科)【解析版】

一、选择题:本大题共 10 个小题,每小题 5 分,共 50 分.在每小题给出的四 个选项中,只有一项是符合题目要求的. 1. (5 分) 已知复数 z= A.第一象限 (i 为虚数单位) , 则 z 在复平面内对应的点位于 ( B.第二象限 C.第三象限 D.第四象限 ) )
恒成立,求正整数 m 的最大值. 20. (13 分)已知函数 f(x)= ﹣aln(1+x) (a∈R) ,g(x)=x2emx(m∈R) .
(1)当 a=1,求函数 f(x)的最大值 (2)当 a<0,且对任意实数 x1,x2∈[0,2],f(x1)+1≥g(x2)恒成立,求实 数 m 的取值范围. 21. (14 分)设椭圆 C: + =1(a>b>0) ,定义椭圆 C 的“相关圆”方程
A.28+6
B.40
C.
D.30+6 )的部分图象如图所示,
7. (5 分)函数 f(x)=2sin(ωx+φ) (w>0,|φ|< 则 f(0)+f( )的值为( )
第 1 页(共 21 页)
A.2﹣
B.2+
C.1﹣
D.1+
8. (5 分)公元 263 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限 增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术” .利用“割圆 术” 刘徽得到了圆周率精确到小数点后两位的近似值 3.14, 这就是著名的 “徽 率” .如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出 n 的值 为( ) ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
(参考数据:
A.12
山东省德州市高三下学期数学4月联考试卷

山东省德州市高三下学期数学 4 月联考试卷姓名:________班级:________成绩:________一、 填空题 (共 14 题;共 14 分)1. (1 分) (2016 高一上·金台期中) 已知集合 U=R,A={x|x≥2},B={x|x<﹣1},则∁U(A∩B)=________.2. (1 分) (2016 高一上·无锡期末) 已知 M={x|﹣2≤x≤2},N={x|x<1},则(∁RM)∩N=________.3. (1 分) (2020·南京模拟) 若一组样本数据的平均数为 9,则该组数据的方差为________.4. (1 分) (2020·南京模拟) 根据如图所示伪代码,最后输出的 i 的值为________.5. (1 分) (2020·南京模拟) 从 2 名男同学和 3 名女同学中选 2 人参加某项活动,则至少有 1 名女同学被选 中的概率为________.6. (1 分) (2020·南京模拟) 双曲线的准线方程为________.7. (1 分) (2020·南京模拟) 已知为等差数列,其公差为-2,且 是 与 的等比中项,为 的前 n 项和,则 的值为________.8. (1 分) (2020·南京模拟) 已知函数 则实数 a 的取值范围为________.,若函数在区间9. (1 分) (2020·南京模拟) 给出下列命题:①若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;②若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;③若两条平行直线中的一条垂直于直线 m,那么另一条直线也与直线 m 垂直;上存在极值,第 1 页 共 16 页④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,真命题是________.(填序号)10. (1 分) (2020·南京模拟) 已知函数区间上单调递减,则 的最大值为________.的图象过点,且在11. (1 分) (2020·南京模拟) 在平面直角坐标系上的一个动点,直线分别切圆 于中,已知圆 两点,则线段,点 是直线 长的取值范围为________.12. (1 分) (2020·南京模拟) 已知正实数满足13. (1 分) (2020·南京模拟) 如图,在梯形 点, 与 交于点 .若中, ,则,则的最小值为________.且,E 为的余弦值为________.的中14. (1 分) (2020·南京模拟) 已知周期为 的函数满足,当时,,则当时( 为自然对数的底数),关于 的不等式的整数解的个数为________.在区间上二、 解答题 (共 11 题;共 115 分)15. (10 分) (2020 高二下·宜宾月考) 将三棱锥与拼接得到如图所示的多面体,其中 , , , 分别为,,,的中点,.第 2 页 共 16 页(1) 当点 在直线 上时,证明:平面;(2) 若与均为面积为 的等边三角形,求该多面体体积的最大值.16. (10 分) 在△中,角的对边分别为 、 、 ,完成下列问题:(1) 若,求证:;(2) 若,求的最大值.17. (10 分) (2018 高二上·宁波期末) 如图, 和点 D,E,F,直线 a 与 b 分别交 , , 于点 A,B,CⅠ 求证:;Ⅱ若,,,,求直线 AD 与 CF 所成的角.18. (10 分) (2020·南京模拟) 在平面直角坐标系中,椭圆 的方程为,且直线与以原点为圆心,椭圆 C 短轴长为直径的圆相切.(1) 求 b 的值;(2) 若椭圆 C 左右顶点分别为 象限,A 在线段 上.,过点作直线 与椭圆交于两点,且位于第一①若和的面积分别为,问是否存在这样的直线 使得?请说明理由;第 3 页 共 16 页②直线 定值.与直线交于点 C,连结,记直线的斜率分别为,求证: 为19. (15 分) (2020·南京模拟) 已知数列对于任意的恒成立.(1) 若,求 的值;(2) 证明:数列 是等差数列;的前 项和为 ,( 为常数)(3) 若,关于 的不等式有且仅有两个不同的整数解,求 的取值范围.20. (15 分) (2020·南京模拟) 已知函数(,且 a 为常数).(1) 若函数 (2) 若函数的图象在处的切线的斜率为( 为自然对数的底数),求 a 的值;在区间上单调递增,求 a 的取值范围;(3) 已知,且.求证:21. (10 分) (2020·南京模拟) 曲线 .(1) 求矩阵 A; (2) 求矩阵 A 的特征向量.在矩阵. 对应的变换下得到曲线22. (10 分) (2020·南京模拟) 在平面直角坐标系中,已知直线 l 的参数方程:参数),以原点为极点,x 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆 C 的极坐标方程为:(1) 将直线 的参数方程化为普通方程,圆 C 的极坐标方程化为直角坐标方程;(2) 求圆 C 上的点到直线 的距离的最小值.第 4 页 共 16 页(t 为 .23. (5 分) (2020·南京模拟) 已知为正实数,满足,求的最小值.24. (10 分) (2020·南京模拟) 五个自然数 1、2、3、4、5 按照一定的顺序排成一列.(1) 求 2 和 3 不相邻的概率;(2) 定义:若两个数的和为 6 且相邻,称这两个数为一组“友好数”.随机变量 表示上述五个自然数组成的一个排列中“友好数”的组数,求 的概率分布和数学期望.25. (10 分) (2020·南京模拟) 已知 且任意两项不相等,又对于任意的整数.,数列 ,均有(1) 当时,试求满足条件的数列 T 的个数;(2) 当,求所有满足条件的数列 T 的个数.中的每一项均在集合中,.例如时,数列 为 或第 5 页 共 16 页一、 填空题 (共 14 题;共 14 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、 13-1、 14-1、二、 解答题 (共 11 题;共 115 分)参考答案第 6 页 共 16 页15-1、第 7 页 共 16 页15-2、第 8 页 共 16 页16-1、 16-2、第 9 页 共 16 页17-1、 18-1、第 10 页 共 16 页18-2、19-1、19-2、19-3、20-1、20-2、20-3、21-1、21-2、22-1、22-2、23-1、24-1、24-2、25-1、25-2、。
山东省莱芜市高三数学4月模拟试题 理 新人教A版

莱芜一中2013年4月高三教学质量调研考试数学(理)试题本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.训练时间120分钟,满分150分,考试结束后,将本试卷和答题卡一并交回.一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知11mni i=-+,其中,m n R ∈,i 为虚数 单位,则m ni += ( ) A 、12i + B 、2i + C 、12i - D 、2i -2、如果执行右边的程序框图,那么输出的S 等于 ( )A 、2550B 、2500C 、2450D 、26523、若有直线m 、n 和平面α、β,下列四个命题中,正确的是 ( ) A 、若//m α,//n α,则//m nB 、若m α⊂,n α⊂,//m β,//n β则//αβC 、若αβ⊥,m α⊂,则m β⊥D 、若αβ⊥,m β⊥,m α⊄,则//m α4.如图所示的韦恩图中,A 、B 是非空集合,定义A *B 表示阴影部分集合.若,x y R ∈,{}22A x y x x ==-,{}3,0x B yy x ==>,则A *B =( ). A .(2,)+∞ B .[)0,1(2,)⋃+∞ C .[]0,1(2,)⋃+∞ D .[]0,1[2,)⋃+∞ 5.下列命题正确的个数 ( ) A .1B .2C .3D .4(1) 命题“2000,13x R x x ∃∈+>”的否定是“2,13x R x x ∀∈+≤”; (2)函数22()cos sin f x ax ax =-的最小正周期为π”是“1a =”的必要不充分条件; (3).22x x ax +≥在[]1,2x ∈上恒成立⇔max min 2)()2(ax x x ≥+在[]1,2x ∈上恒成立(4).“平面向量a r 与b r 的夹角是钝角”的充分必要条件是“0a b ⋅<r r ”。
山东省北镇中学、莱芜一中、德州一中2016届高三化学4月联考试题(含答案)

O OCl ClCl Cl北镇中学、莱芜一中、德州一中2016届高三4月份联考理综化学试题可能用到的相对原子质量:O 16 Li7 Co59 Fe56 Cl35.5 C12 H1 S32 Na23一、选择题(共7个小题,每题只有一个选项符合题意,每题6分)(原创,容易)7.化学与生产、生活、社会密切相关。
下列说法中正确的是( ) A .漂白粉长期放置会被空气中的氧气氧化而变质 B .不锈钢具有较强的耐腐蚀性,纯铁也有较强的耐腐蚀性C .汽车尾气中氮氧化物的产生主要是由于汽油中含有氮元素而产生的D .对石油进行分馏可以得到许多苯的同系物 【答案】B【解析】A 项漂白粉因为与空中的二氧化碳和水结合生成次氯酸,然后次氯酸光照分解,与氧气氧化无关,B 项正确,C 项汽车尾气中氮氧化物的产生是由于空气中的氮气与氧气在放电的时候生成的,D 项苯的同系物是主要由煤的干馏产生的。
【考点】化合物化学性质,认识煤及重要的烃(原创,容易)8.二噁英是一类芳香族化合物的多氯代衍生物的总称,结构稳定,难以被自然分解,是公认的最危险的致癌物质之一.如图是其中一种的结构。
下列说法中不正确的是 ( ) A .它能发生还原反应 B .它能燃烧C .它的一溴取代物只有一种D .此分子中共平面的原子最多有18个 【答案】D【解析】A 项它能与氢气发生还原反应。
B 项它能与氧气燃烧发生氧化反应,C 项它的等效氢只有一种,所以它的一溴取代物只有一种,D 项此分子中最多所有原子都共平面 【考点】有机化学物的化学性质及其反应类型(原创,容易)9.设N A 为阿伏加德罗常数的值。
下列说法正确的是( ) A .常温常压下,7.8 gNa 2S 和Na 2O 2的混合物中,阴离子所含电子数为1.8N A B .标准状况下,11.2 L 二氯甲烷中含有的分子数目为0.5N AC .常温常压下,28 g 乙烯与丙烯的混合气体含有的碳原子数目无法计算D .0.1 mol ·L -1MgCl 2溶液中含有的Mg 2+数目小于0.1N A 【答案】A【解析】A 项正确,B 项二氯甲烷在标准状况下是液体,,C 项28g 乙烯与丙烯的混合气体含有的碳原子数目为2N A,D项不知道体积。
山东省北镇中学、莱芜一中、德州一中高三物理4月联考试题

北镇中学、莱芜一中、德州一中2016届高三4月份联考理综物理试题二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.质点在xoy 平面内运动的轨迹如图所示,已知质点在y 方向的分运动是匀速运动,则关于质点速度大小的描述正确的是 ( )A .速度始终增大B .先加速运动后减速运动C .先减速运动后加速运动D .不能确定15.按右图,用玩具手枪做射击实验.先在竖直放置的靶上建立平面直角坐标系(x 轴沿水平方向).实验时,保持枪管水平,每次射击,子弹射出枪口的速度大小均相同且枪口的位置不变.第1次射击,枪口对准坐标原点O 且枪口与O 点的连线垂直于xoy 平面;第2次射击,枪口对准x=d 处;第3次射击,枪口对准x =2d 处;……;第6次射击,枪口对准x =5d 处.实验后,用光滑的曲线将靶上的这6个弹孔连接起来.则这条曲线的形状可能是下图16.一变压器原副线圈匝数比为2:1,分别将R 1、R 2与变压器的原副线圈串联如图所示,已知R 1=R 2=R ,且R 1两端的电压如图所示,则电阻R 2电压为多少A 、11VB 、22VC 、44VD 、无法确定17.如图所示为一矩形磁场区域abcd ,ab 、cd 两边足够长,ad 边长为d ,矩形区域内有一垂直纸面向外的匀强磁场,磁感应强度为B 。
在ad 边的中点P 放一粒子源,若该离子源可在纸面内向各个方向发射电荷量为q 、质量为m 、速度为v =mqBd的正粒子,粒子的重力不计。
则粒子打在cd 边上的长度为多少?A 、d )123(+ B 、d 217 C 、d D 、d 2318.某实验小组打算制作一个火箭。
甲同学设计了一个火箭质量为m ,可提供恒定的推动力,大小为F =2mg ,持续时间为t 。
乙同学对甲同学的设计方案进行了改进,采用二级推进的方式,即当质量为m 的火箭飞行经过2t 时,火箭丢弃掉2m 的质量,剩余2t 时间,火箭推动剩余的2m 继续飞行。
山东省北镇中学、莱芜一中、德州一中2016届高三下学期4月联考数学(文)试题(附答案) (1)

北镇中学、莱芜一中、德州一中2016届高三4月份联考数学(文科)试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.2.答卷前,考生务必先将自己的班级、姓名、准考证号、座号用5.0mm 黑色签字笔和2B 铅笔分别涂写在答题卡与答题纸上.3.选择题每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑;非选择题直接答在答题纸相应区域,不能答在试卷上;试题不交,请妥善保存,只交答题卡与答题纸. 参考公式:用最小二乘法求线性回归直线方程系数公式x b y a xn xy x n yx x xy y x xb ni ini ii ni ini i i∧∧====∧-=--=---=∑∑∑∑,)())((1221121.球的表面积公式24R S π=,其中R 是球的半径.如果事件B A ,互斥,那么)()()(B P A P B A P +=+;如果事件B A ,对立,那么)(1)(A P B P -=.第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是正确的.1.已知集合},{},,3{b a B a A ==,若}2{=B A ,则=B A ( )A }3,2{B }4,3{C }3,2,2{D}4,3,2{2.已知复数i 21-=a z ,i 22+=z (i 为虚数单位),若21z z为纯虚数,则实数a的值为( )A 4-B 1-C 1D 43.执行如图所示的程序框图,若输入的M 的值为55,则输出的i 的值为( )A 3B 4C 5D 64.设∈b a ,R ,则“b a <”是“0)(2<-a b a ” 的( ) A 充分不必要条件 B 必要不充分条件C 充要条件D 既不充分也不必要条件5.已知具有线性相关关系的两个变量y x ,之间的一组数据如下:且回归直线方程为6.2+=∧∧x b y ,根据模型预报当6=x 时,y 的预测值为()A 76.5B 8.6C 3.8D 46.86.函数2cos )(xxx f π=的图象大致是( )CD7.已知函数⎪⎩⎪⎨⎧≥<+=2,)31(,2),2()(x x x f x f x ,则)5log 1(3+-f 的值为( ) A151B35C 15D 328.某几何体的三视图如图所示,则该几何体外接球的表面积为( ) Aπ34 Bπ332C π4D π169.已知函数)(x f 是定义在R 上的可导函数,)('x f 为其导函数,若对于任意实数x ,都有)()('x f x f >,其中e 为自然对数的底数,则( )A )2016()2015(e f f >B )2016()2015(e f f <C )2016()2015(e f f =D )2015(e f 与)2016(f 大小关系不确定10.对于两个平面向量b a ,,定义它们的一种运算:θsin ||||b a b a ⋅=⊗(其中θ为向量,的夹角),则关于这种运算的以下结论中,不恒成立的是( )A a b b a ⊗=⊗B 若0=⊗,则//C c b c a c b a ⊗+⊗=⊗+)(D 若),(),,(2211y x y x ==,则||1221y x y x -=⊗第Ⅱ卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分.俯视图∙11.函数21)1ln(1)(x x x f -++=的定义域为________.12.若直线)0,0(2>>=-b a by ax 过圆012422=++-+y x y x 的圆心,则ab 的最大值为________.13.设△ABC 的内角C B A ,,的对边分别为c b a ,,,若B A C a sin 2sin 3,41cos ,4=-==,则=c ________.14.某企业生产甲、乙两种产品均需用B A ,两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为________万元.15.抛物线)0(21:21>=p x py C 的焦点与双曲线13:222=-y x C 的右焦点的连线交1C 于第一象限的点M .若1C在点M 处的切线平行于2C 的一条渐近线,则=p ________.三、解答题:本大题共6个小题,共75分.16.(本小题满分12分)某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康、同心共筑中国梦”主题.0.0.0.0开展全民健身活动.组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组)30,20[,第2组)40,30[,第3组)50,40[,第4组)60,50[,第5组]70,60[,得到的频率分布直方图如图所示.(Ⅰ)若电视台记者要从抽取的群众中选1人进行采访,估计被采访人恰好在第1组或第4组的概率;(Ⅱ)已知第1组群众中男性有3名,组织方要从第1组中随机抽取2名群众组成志愿者服务队,求至少有1名女性群众的概率.17.(本小题满分12分)已知函数)0(21cos cos sin 3)(2>-+⋅=ωωωωx x x x f 的两条相邻对称轴之间的距离为2π. (Ⅰ)求ω的值;(Ⅱ)将函数)(x f 的图象向左平移6π个单位,再将所得函数的图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到函数)(x g y =的图象,若函数k x g y -=)(在区间]32,6[ππ-上存在零点,求实数k 的取值范围.18.(本小题满分12分)如图,在三棱柱111C B A ABC -中,1111C A B A =,点E D ,分别是1111,B A C B 的中点,11===BD AB AA ,601=∠AB A .(Ⅰ)求证://1AC 平面BD A 1; (Ⅱ)求证:平面BDE ⊥平面111C B A .19.(本小题满分12分)已知等比数列}{n a 的前n 项和为n S ,32,01=>a a n ,且4321,1,3a a a -成等差数列. (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设数列}{n b 满足1)1(log 13=-⋅+n n S b ,求满足方程100950413221=++++n n b b b b b b 1C11ACBADE的正整数n 的值.20.(本小题满分13分)已知函数)0(21ln )2()(≤++-=a ax xx a x f . (Ⅰ)当0=a 时,求)(x f 的极值; (Ⅱ)当0<a 时,讨论)(x f 的单调性;(Ⅲ)若对于任意的)2,(],3,1[,21--∞∈∈a x x 都有3ln 2)3ln (|)()(|21-+<-a m x f x f ,求实数m 的取值范围.21.(本小题满分14分)已知椭圆)0(1:2222>>=+b a by a x C 的离心率为21,它的四个顶点构成的四边形的面积为34. (Ⅰ)求椭圆C 的方程;(Ⅱ)设椭圆C 的右焦点为F ,过F 作两条互相垂直的直线21,l l ,直线1l 与椭圆C 交于Q P ,两点,直线2l 与直线4=x 交于N 点.(i )求证:线段PQ 的中点在直线ON 上;(ii )求||||FN PQ 的取值范围.数学(文科)参考答案及评分标准说明:1.本解答仅给出了一种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容参照评分标准标准酌情赋分.2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题共10小题,每小题5分,共50分. 1.【答案】D .【解析】由}2{=B A 得B A ∈∈2,2,所以2,2==b a ,所以}2,4{},2,3{==B A ,所以}4,3,2{=B A .故选D . 【考点】元素与集合关系、集合运算. 2.【答案】C . 【解析】由题意可得,i 54522i 2i 221+--=+-=a a a z z ,因为21z z为纯虚数,所以054,0522≠+-=-a a ,所以1=a .故选C . 【考点】复数的概念、复数的代数运算. 3.【答案】D .【解析】执行程序框图,第一次2,551102=<=+⨯=i N ,第二次3,554212=<=+⨯=i N ,第三次4,5511342=<=+⨯=i N ,第四次5,55264112=<=+⨯=i N ,第五次6,55575262=>=+⨯=i N ,所以输出的i 的值为6.故选D .【考点】程序框图输出结果. 4.【答案】B .【解析】由题意可得,“0)(2<-a b a ”等价于“0,02><-a b a 或0,02<>-a b a ”,即“0,0≠<-a b a ” ,所以“b a <”是“0)(2<-a b a ” 的必要不充分条件.故选B . 【考点】充要条件、不等式性质. 5.【答案】C .【解析】由题意可得,2)43210(51=++++⨯=x ,5.4)7.68.45.43.42.2(51=++++⨯=y ,因为回归直线一定过样本点的中心),(y x ,所以6.225.4+⨯=∧b ,解得95.0=∧b .当6=x 时,y 的预测值为3.86.2695.0=+⨯.故选D .【考点】线性回归直线方程、预测值. 6.【答案】B .【解析】由题意可得,)(cos )()(cos )(22x f xxx x x f ==--=-ππ,所以)(x f 为偶函数,)(x f 的图象关于y 轴对称,可排除答案A 、C ;当1=x 时,01cos )1(<-==πf ,可排除D .故选B .【考点】函数的图象与性质. 7.【答案】A .【解析】由题意可得,135log 5log 1033<=+-<,所以315log 25log 1233<=++-<,所以151)3()31()15(log )25log 1()5log 1(115log 15log 33333====++-=+--f f f .故选A .【考点】函数值、指对运算. 8.【答案】D .【解析】由三视图可知,该几何体是底面半径为3,高为1的圆锥.设其外接球的半径为R ,则222)3()1(=--R R ,解得2=R ,所以该几何体外接球的表面积为πππ1624422=⨯==R S .故选D .【考点】三视图、组合体体积. 9.【答案】A .3R1-R1【解析】构造函数∈=x x f x F x,e )()(R ,)(x F 的导函数xx x x x f x f x f x f x F e)()()e ()e )((e )()('2'''-=-=.因为)()('x f x f >,0e >x,所以0)('<x F ,)(x F 在R 上是减函数,所以20162015e )2016()2016(e )2015()2015(f F f F =>=,所以)2016()2015(e f f >.故选A . 【考点】抽象函数单调性、比较大小. 10.【答案】C .【解析】因为θsin ||||b a b a ⋅=⊗,所以a b a b b a b a ⊗=⋅=⋅=⊗θθsin ||||sin ||||,选项A 恒成立.当0,≠b a ,0sin ||||=⋅=⊗θb a b a 时,0sin =θ,所以0=θ或πθ=,所以//;当=或=时,//恒成立,选项B 恒成立.θsin ||||⋅=⊗θ2cos 1||||-⋅=2||||⋅===212212212122222121)()())((y x y x y y x x y x y x -=+-++=||1221y x y x -=,选项D 恒成立.当⊥⊥=+===,,,1||||||时,20)(=⊗+⊗≠=⊗+,选项C 不恒成立.故选C .【考点】新定义、数量积.编者注:本题中,,在印刷体中用黑体..来表示。
山东省北镇中学、莱芜一中、德州一中2016届高三下学期4月联考数学(理)试题 含答案

北镇中学、莱芜一中、德州一中2016届高三4月份联考数学(理科)试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页.满分150分.考试用时120分钟.考试结束后,将答题卡交回.注意事项:1。
答题前,考生务必用0。
5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.2。
第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上; 如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4. 填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
参考公式:如果事件A,B互斥,那么P(A+B)=P(A)+ P(B);如果事件A,B独立,那么P(AB)=P(A)·P(B)。
第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.定义集合{}-=∈∉且,若集合{}A B x x A x B|M=1集合,2,3,4,5, {}==-∈,则集合M N-的子集个数为()N x x k k Z21,A .2B .3C .4D .无数个 【答案】C【解析】1,3,5,N ∈M N -={},42,所以集合M N -的子集个数为224=个.【考点】新定义问题、集合的运算、子集.2。
i 为虚数单位,复数2016i 的共轭复数为( )A . 1B .iC . —1D .-i【答案】A 【解析】20164504504i(i )11===,所以复数2016i 的共轭复数1。
【考点】复数四则运算及共轭复数的概念.3.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x +y 的值为( ) A .168 B .169 C .8 D .9【答案】D【解析】由题意得,甲班学生成绩的中位数为83,则x =83-80=3,乙班学生成绩的平均数是86,则86796919180818176=+++++++y ⇒6=y ,故x +y =9.【考点】茎叶图、中位数、平均数4。
山东省北镇中学等三校2016届高三下学期4月联考理综试卷(含答案)

北镇中学、莱芜一中、德州一中高三下学期4月联考理综试题1.下列有关细胞的分化、衰老、癌变的叙述正确的是()A.细胞的癌变是细胞高度分化的结果B.细胞衰老表现为酶活性降低,细胞核体积减小C.细胞分化导致基因选择性表达,细胞种类增多D.致癌因子导致正常细胞的生长和分裂失控变成癌细胞解析:本题考查细胞生命历程的有关知识,细胞癌变是原癌基因和抑癌基因突变的结果,A项不正确。
细胞衰老表现为酶活性降低,细胞核体积增大,B项不正确。
细胞分化是基因选择性表达的结果,导致细胞种类增多,C项不正确。
环境中的致癌因子会损伤细胞中的DNA分子,使原癌基因和抑癌基因发生突变,导致正常细胞的生长和分裂失控而变成癌细胞,D项正确。
答案:D说明:本题考查学生对细胞衰老、凋亡、癌变的理解,考查学生对基础知识的记忆理解。
2. 科研人员检测晴朗天气下露地栽培和大棚栽培的油桃的光合速率(Pn)日变化情况,并将检测结果绘制成下图。
下列相关说法错误的是()A.光照强度增大是导致ab段、lm段Pn增加的主要原因B.致使bc段、mn段Pn下降的原因是气孔关闭C.致使ef段、op段Pn下降的原因是光照逐渐减弱D.适时浇水、增施农家肥是提高大田作物产量的重要措施解析:早晨日出后光照强度不断增大,使得露地栽培的和大棚栽培的油桃的光合速率迅速上升。
大棚栽培条件下的油桃在bc段Pn下降,主要原因是日出后旺盛的光合作用消耗大量CO2,使大棚内密闭环境中CO2浓度迅速下降;而露地栽培的油桃在mn段Pn下降,是因环境温度过高导致气孔关闭,不能吸收CO2。
15时以后,两种栽培条件下的光合速率持续下降,是光照强度逐渐减弱所致。
适时浇水避免植物因缺水导致气孔关闭、增施农家肥从而增加土壤中CO2浓度是提高大田作物产量的可行性重要措施。
答案:B说明:本题借助曲线考查光合作用的影响因素,考查学生的综合运用能力,要求学生理论联系实际,综合运用所学知识解决生活中的生物学问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北镇中学、莱芜一中、德州一中2016届高三4月份联考数学(理科)试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页.满分150分.考试用时120分钟.考试结束后,将答题卡交回. 注意事项:1. 答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上; 如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4. 填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:如果事件A ,B 互斥,那么P(A+B )=P(A)+ P(B); 如果事件A ,B 独立,那么P(AB )=P(A)·P(B).第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.定义集合{}|A B x x A x B -=∈∉且,若集合{},2,3,4,5,M =1集合{}21,N x x k k Z ==-∈,则集合M N -的子集个数为( ) A .2 B .3 C .4 D .无数个 【答案】C【解析】1,3,5,N ∈M N -={},42,所以集合M N -的子集个数为224=个.【考点】新定义问题、集合的运算、子集.2.i 为虚数单位,复数2016i 的共轭复数为( ) A . 1 B .i C . -1 D .-i【答案】A【解析】20164504504i (i )11===,所以复数2016i 的共轭复数1. 【考点】复数四则运算及共轭复数的概念.3.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x +y 的值为( )A .168B .169C .8D .9【答案】D【解析】由题意得,甲班学生成绩的中位数为83,则x =83-80=3,乙班学生成绩的平均数是86,则86796919180818176=+++++++y ⇒6=y ,故x +y =9.【考点】茎叶图、中位数、平均数 4. 命题:,s i n ()c o s p R απαα∃∈-=;命题:"04"q a <<是”关于x 的不等式210ax ax ++>的解集是实数集"R 的充分必要条件,则下面结论正确的是( )A. p 是假命题B. q 是真命题C. ""p q ∧是假命题D. ""p q ∨是假命题 【答案】C【解析】对于命题p , ,sin()cos 4παπαα∃=-==因此命题p 是真命题; 对于命题q ,”关于x 的不等式210ax ax ++>的解集是实数集"R 的充分必要条件是0a =或240a a a >⎧⎨∆=-<⎩,即04a ≤<,所以"04"a <<是”关于x 的不等式210ax ax ++>的解集是实数集"R 的充分不必要条件,因此命题q 是假命题;""p q ∧是假命题;""p q ∨是真命题. 【考点】充要条件,简易逻辑.5. 已知变量,x y 满足约束条件230,330,10,x y x y y +-≤⎧⎪+-≥⎨⎪-≤⎩若目标函数z ax y =+ (其中0a >)仅在点(1,1)处取得最大值,则a 的取值范围为 ()A . (0,2)B .1(0,)2 C . 1(0,)3D . 11(,)32【答案】B【解析】由约束条件表示的可行域如图所示,作直线l :ax +y =0,过点(1,1)作l 的平行线l ′,则直线l ′介于直线x +2y -3=0与直线y =1之间, 因此,-12<-a <0,即0<a <12.【考点】线性规划. 6. 设,a b为正数,2311)4()a b ab a b+≤-= ,则a b += ( ) A .B .C .D . 2 【答案】B【解析】由11a b+≤得a b +≤.又2232()()44()448(),a b a b ab ab ab ab +=-+=+≥⨯=即a b +≥,所以a b +=.由不等式a b +≥成立的条件,得1ab =,所以a b +== 【考点】基本不等式.7. 如图是函数()sin()(0,0,)f x A x A x R ωϕω=+>>∈在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象,为了得到sin ()y x x R =∈的图象,只要将函数)(x f 的图象上所有的点( )A .向左平移3π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变 B .向右平移3π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变 D .向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变【答案】D【解析】由图象可知A =1,T =5π6-⎝⎛⎭⎫-π6=π,∴ω=2πT=2. ∵图象过点⎝⎛⎭⎫π3,0,且⎝⎛⎭⎫π3,0在函数的单调递减区间上, ∴sin ⎝⎛⎭⎫2π3+φ=0,∴ππϕπk 232+=+ ∴φ=π3+2k π,k ∈Z. ∴)(x f =sin ⎝⎛⎭⎫2x +π3+2k π=sin ⎝⎛⎭⎫2x +π3. 故将函数)(x f = sin ⎝⎛⎭⎫2x +π3向右平移π6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变,可得y =sin x 的图象. 法二:也可通过平移法求出φ的值. 【考点】三角函数的图象性质及图象变换.8. 某公司新招聘进8名员工,平均分给下属的甲、乙两个部门,其中两名英语翻译人员不能分给同一个部门;另三名电脑编程人员也不能分给同一个部门,则不同的分配方案种数是( ) A.18B.24C. 36D. 72【答案】C【解析】由于均分8人,所以甲、乙两个部门各4人。
完成这件事情分两类:第一类,甲部门有两名电脑编程人员,有12123318C C C =种不同的分配方案;第二类,甲部门有一名电脑编程人员,有11223318C C C =种不同的分配方案。
故共有36种不同的分配方案.选C【考点】排列组合.9. 如图,菱形ABCD 的边长为2,60A ∠=,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM AN ⋅的最大值为( )A . 3BC . 6D .9 【答案】D【解析】由平面向量的数量积的几何意义知,AM AN ⋅等于AM 与AN 在AM 方向上的投影之积,所以max 1()()()2AM AN AM AC AB AD AB AD ⋅=⋅=+⋅+22139.22AB AD AB AD =++⋅= 【考点】平面向量的数量积.10.已知0,a >且1a ≠,函数53()2)(11),1x xa f x x x a +=+-≤≤+设函数()f x 的最大值为M ,最小值为N ,则 ( ).A .8M N +=B .10M N +=C .8M N -=D .10M N -= 【答案】A【解析】53441()2)2)11x x x xxa a a f x x x a a +++-=+=+++142)(11)1x x a x x a -=++-≤≤+设1()2)(11),1x xa g x x x a -=+-≤≤+则()g x 为奇函数,所以max min ()()0.g x g x +=所以8M N +=.【考点】函数的奇偶性第Ⅱ卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分. 11.执行如图所示的程序框图,则输出的S 的值为 .【答案】2500 【解析】50(199)135992500.2S +=++++==【考点】程序框图,等差数列求和.12. 已知在正方体1111ABCD A B C D - 中,点E 是棱11A B 的中点,则直线AE 与平面11BDD B 所成角的正弦值为 .【解析】以1A 为坐标原点,分别以11111,,A B A D A A 所在直线为,,x y z 轴,建立如图所示的空间直角坐标系.设正方体的棱长为2,则(0,0,2),(2,2,2),(1,0,0)A C E ,(2,2,0),(1,0,2)AC AE ==-.1,,AC BD AC BB AC ⊥⊥∴⊥平面11BDD B ,则(2,2,0)AC =是平面11BDD B 的一个法向量.设直线AE 与平面11BDD B 所成角为θ,则10sin cos ,AC AE θ==.法二:几何法.【考点】直线与平面所成的角.13.若2a b ->,则关于x 的不等式2x a x b -+-≤的解集为___________ 【答案】∅【解析】根据绝对值的意义,x a x b -+-表示数轴上x 的对应点到a 和b 的对应点的距离之和,故最小值为a b -,所以对x R ∀∈满足2,x a x b a b -+-≥->故关于x 的不等式2x a x b -+-≤的解集为∅. 【考点】绝对值不等式14.椭圆2222:1(0)x y C a b a b +=>>的右焦点为F ,双曲线2213y x -=的一条渐近线与椭圆C 交于,A B 两点,且AF BF ⊥,则椭圆C 的离心率为 ____________.1【解析】不妨设双曲线2213y x -=的一条渐近线的渐近线为y =,记椭圆C 的左焦点为1F ,依题意得,OA OB OF c ===四边形1AFBF 为矩形,AFO ∆是正三角形,AF c =,1AF =,椭圆C的离心率为111FF e AF AF ===+.【考点】椭圆,双曲线的定义及简单几何性质. 15.对于函数()f x 给出定义:设()f x '是函数()y f x =的导数,()f x ''是函数()f x '的导数,若方程()0f x ''=有实数解0x ,则称点00(,())x f x 为函数()y f x =的“拐点”.某同学经过探究发现:任何一个三次函数32()(0)f x ax bx cx d a =+++≠都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数32115()33212f x x x x =-+-,请你根据上面探究结果,计算1232016()()()()2017201720172017f f f f ++++= . 【答案】2016【解析】32115()33212f x x x x =-+-,2()3f x x x '=-+,()210f x x ''=-=,得12x =.1()12f =,所以()f x 的“拐点”即对称中心为1(,1)2,所以()(1)2f x f x +-=. 设1232016()()()()2017201720172017S f f f f =++++, 则2016201520141()()()()2017201720172017S f f f f =++++, 两式相加得222016,2016S S =⨯=. 【考点】导数, 函数的对称性,倒序相加求和. 三、解答题:本大题共6小题,共75分. 16. (本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,cos220C C ++=. (Ⅰ)求角C 的大小;(Ⅱ)若b =,ABC ∆sin A B ,求sin A 及c 的值.【解析】(Ⅰ) cos220C C ++=∴22cos 10,C C ++=-------------------------------------------2分即21)0,C +=cos 2C ∴=----------------------------------4分 又0C π<<,3.4C π∴=-------------------------------------------5分(Ⅱ)22222cos 5,,c a b ab C a c =+-=∴=----------------------6分由正弦定理,得sin ,C A =sinA C ∴==----------------------8分1sin ,2ABC S ab C ∆=且sin ,2ABC S A B ∆=----------------------9分1sin sin 2ab C A B ∴=,sin sin sin ab C A B ∴=由正弦定理得:2()sin sin c C C=解得 1.c =----------------------12分 【考点】正弦定理,余弦定理,三角形的面积公式. 17.(本小题满分12分)2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为13,赔钱的概率是23;乙股票赚钱的概率为14,赔钱的概率为34.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元. (Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;(Ⅱ)试求袁先生2016年上半年同时投资甲、乙两只股票的总收益的分布列和数学期望. 【解析】(Ⅰ)袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率为1121313434124p =⨯+⨯==-----------------------------------------------------------------------------------4分(Ⅱ)用ξ万元表示袁先生2016年上半年同时投资甲、乙两只股票的总收益,则ξ的所有可能取值为9,0,2,11.------------------------------------------------------------------------------------5分231(9)342p ξ=-=⨯=---------------------------------------------------6分131(0)344p ξ==⨯=---------------------------------------------------7分211(2)346p ξ==⨯=---------------------------------------------------8分111(11)3412p ξ==⨯=--------------------------------------------------9分所以,ξ的分布列为-------------------------------------------------------------------------------------------------------------------10分ξ的数学期望为()11111390211246124E ξ=-⨯+⨯+⨯+⨯=--------------------------------------------------12分【考点】相互独立事件同时发生的概率,离散型随机变量的分布列及期望. 18. (本小题满分12分)如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =3,BC =2AB =2,E ,F 分别在BC ,AD 上,EF ∥AB .现将四边形ABEF 沿EF 折起,使平面ABEF ⊥平面EFDC .(Ⅰ)若12BE =,在折叠后的线段AD 上是否存在一点P ,且AP PD λ=u u u r u u u r ,使得CP ∥平面ABEF?若存在,求出λ的值;若不存在,说明理由;(Ⅱ)求三棱锥A -CDF 的体积的最大值,并求此时二面角E -AC -F 的余弦值. 【解析】(Ⅰ)因为平面ABEF ⊥平面EFDC ,平面ABEF ∩平面EFDC EF =,FD ⊥EF所以FD ⊥平面ABEF ,又AF ⊂平面ABEF , 所以FD ⊥AF -----------------------------------------1分 在折起过程中,AF ⊥EF ,同时FD ∩EF F =, 所以AF ⊥平面EFDC -----------------------------------------2分方法一:以F 为坐标原点,分别以,,FE FD FA 所在直线为,,x y z 轴,建立如图所示的空间直角坐标系. 若12BE =时,则各点坐标如下:()0,0,0F ,10,0,2A ⎛⎫ ⎪⎝⎭, 50,,02D ⎛⎫ ⎪⎝⎭, 31,,02C ⎛⎫⎪⎝⎭. 可得平面ABEF 的法向量5(0,,0)2FD =uu u v .--------------------------------------3分因为AP PD λ=u u u r u u u r ,所以1115(0,0,)(0,,0)111212FP FA FD λλλλλλ=+=+++++uu v uu v uu u v 51(0,,)2222λλλ=++所以51(0,,)2222P λλλ++,--------------------------------------4分故231(1,,)2222CP λλλ-=-++uu v .则5(23)02(22)CP FD λλ-⋅==+,解得32λ=.所以线段AD 上存在一点31(0,,)25P ,且32A P P D =u uu r u uu r ,使得CP ∥平面ABEF. --------------------------------------5分方法二:线段AD 上存在一点P ,使得CP ∥平面ABEF ,则此时32λ=.理由如下: 当32λ=时,32AP PD =uu u r uu u r ,可知35AP AD =. 过点P 作MP ∥FD 交AF 于点M ,则有35MP AP FD AD ==--------------------------------------3分 又12BE =,可得52FD =,故32MP =.又32EC =,MP ∥FD ∥EC ,所以四边形MPCE 为平行四边形.所以CP ∥ME ,--------------------------------------4分 又CP ⊄平面ABEF ,ME ⊂平面ABEF所以CP ∥平面ABEF-------------------------------------5分 (Ⅱ)设BE x =,所以(02)AF x x =<≤,3FD x =-,所以1111(3)(3)326A CDF V x x x x -=⋅⋅⋅-=-,--------------------------------------6分 所以当32x =时,A CDF V -有最大值,且最大值为38.--------------------------------------7分可得30,0,2A ⎛⎫ ⎪⎝⎭, 30,,02D ⎛⎫ ⎪⎝⎭, 11,,02C ⎛⎫ ⎪⎝⎭,()1,0,0E . 所以3(1,0,)2AE =-uu u v,13(1,,)22AC =-uuu v,3(0,0,)2FA =uu v ,1(1,,0)2FC =uu u v.设平面AEC 的一个法向量为111(,,)m x y z =,则00m AC m AE ⎧⋅=⎪⎨⋅=⎪⎩,即11111230230x y z x z +-=⎧⎨-=⎩.--------------------------------------------------8分取13x =,则(3,0,2)m =,-------------------------------------------------------9分 设平面ACF 的一个法向量为222(,,)n x y z =,则00n FA n FC ⎧⋅=⎪⎨⋅=⎪⎩,即22230,210,2z x y ⎧=⎪⎪⎨⎪+=⎪⎩--------------------------------------10分同理可得(1,2,0)n =---------------------------------------11分所以cos ,13m n m n m n⋅===所以二面角E ﹣AC ﹣F .--------------------------------------12分 【考点】线面平行与垂直的判定与性质,几何体的体积,二面角. 19.(本小题满分12分)已知数列{}n a 的前n 和为n S ,且22n S n n =+;数列{}n b 是公比大于1的等比数列,且满足149b b +=,238b b =.(Ⅰ)分别求数列{}n a ,{}n b 的通项公式;(Ⅱ)若()1nn n n n c S a b =-+,求数列{}n c 的前n 项和n T .【解析】(Ⅰ)1n =时,113a S ==------------------------------------------1分2n ≥时,()221(2)(1)2121n n n a S S n n n n n -⎡⎤=-=+--+-=+⎣⎦,又因为2113⨯+=,所以21n a n =+.---------------------------------------2分 设等比数列{}n b 的公比为q ,---------------------------------------3分由已知142398b b b b +=⎧⎨⋅=⎩,即31121198b b q b q b q ⎧+=⎪⎨⋅=⎪⎩,----------------4分解得112b q =⎧⎨=⎩,或1812b q =⎧⎪⎨=⎪⎩(舍去,因为1q >)所以,12n n b -=----------------5分(Ⅱ)()211(2)(21)2nn n c n n n -=-⋅+++⋅,---------------------------6分设数列{}1(21)2n n -+⋅的前n 项和为n G ,数列(){}21(2)nn n -⋅+的前n 项和为n R .当n 为偶数时,()2238152412(1)(2)n R n n n n ⎡⎤=-+-+---+-++⎣⎦ (521)(3)259(21)22nn n n n +++=++++==-----------------------------7分 当n 为奇数时,()21(1)2(1)n n R R n n +⎡⎤=-+++⎣⎦()2(1)(4)(1)2(1)2n n n n ++⎡⎤=-+++⎣⎦ 232n n+=---------------------------------------8分()0121325272212n n G n -=⋅+⋅+⋅+++⋅ ○1 则2n G = ()1213252(21)2212n n n n -⋅+⋅++-⋅++⋅○2----------------9分 ○1-○2得 ()0121322(222)212n n n G n --=⋅++++-+⋅()12(12)3221212n nn --=+⋅-+⋅-----------------10分()1122nn =-+-⋅ 所以()1212nn G n =+-⋅----------------11分所以,()()23212,2(3)1212,.2n n n n nn n T n n n n ⎧+-+-⋅⎪⎪=⎨+⎪++-⋅⎪⎩为奇数,为偶数----------------12分【考点】等差数列及等比数列,并项法求和,错位相减法求和. 20. (本小题满分13分)抛物线C 的方程为)0(2<=a ax y ,过抛物线C 上一点P(x 0,y 0)(x 0≠0)作斜率为k 1,k 2的两条直线分别交抛物线C 于A(x 1,y 1),B(x 2,y 2)两点(P,A,B 三点互不相同),且满足)10(012-≠≠=+λλλ且k k .(Ⅰ)求抛物线C 的焦点坐标和准线方程;(Ⅱ)设直线AB 上一点M ,满足MA BM λ=,证明线段PM 的中点在y 轴上; (Ⅲ)当λ=1时,若点P 的坐标为(1,-1),求∠PAB 为钝角时点A 的纵坐标1y 的取值范围.【解析】(Ⅰ)由抛物线C 的方程2ax y =(0<a )得,21x y a=,----------------1分 焦点坐标为)41,0(a ,准线方程为ay 41-=.----------------3分 (Ⅱ)证明:设直线PA 的方程为)(010x x k y y -=-,直线PB 的方程为)(020x x k y y -=-.点),(00y x P 和点),(11y x A 的坐标是方程组0102()y y k x x y ax-=-⎧⎪⎨=⎪⎩①②的解.将②式代入①式得000112=-+-y x k x k ax ,于是a k x x 101=+,故011x ak x -= ③----------------4分又点),(00y x P 和点),(22y x B 的坐标是方程组0202()y y k x x y ax -=-⎧⎪⎨=⎪⎩④ ⑤的解.将⑤式代入④式得000222=-+-y x k x k ax .于是220k x x a +=,故220kx x a=-.----------------5分由已知得,12k k λ-=,则012x k ax --=λ. ⑥----------------6分设点M 的坐标为),(M M y x ,由BM MA λ=,则λλ++=112x x x M .----------------7分将③式和⑥式代入上式得0001x x x x M -=+--=λλ,即00=+x x M .∴线段PM 的中点在y 轴上.----------------8分(Ⅲ)因为点)1,1(-P 在抛物线2ax y =上,所以1-=a ,抛物线方程为2x y -=.----------------9分由③式知111--=k x ,代入2x y -=得211)1(+-=k y . 将1=λ代入⑥式得211x k =-,代入2x y -=得221(1)y k =--. 因此,直线PA 、PB 分别与抛物线C 的交点A 、B 的坐标为2111(1,21)A k k k -----,2111(1,21)B k k k --+-.----------------10分于是2111(2,2)AP k k k =++,11(2,4)AB k k =,2111111112(2)4(2)2(2)(21)AP AB k k k k k k k k ⋅=+++=++.因PAB ∠为钝角且P 、A 、B 三点互不相同,故必有0AP AB ⋅<.----------------11分求得1k 的取值范围是12k <-或1102k -<<.----------------12分 又点A 的纵坐标1y 满足211(1)y k =-+,故当12k <-时,11y <-;当1102k -<<时,1114y -<<-.即11(,1)(1,)4y ∈-∞-------------------13分【考点】抛物线,直线与圆锥曲线的位置关系. 21. (本小题满分14分) 已知函数1ln(1)()(0)x f x x x++=>. (Ⅰ) 判断函数()f x 在(0,)+∞上的单调性; (Ⅱ) 若()1kf x x >+恒成立, 求整数k 的最大值; (Ⅲ)求证:23(112)(123)[1(1)]n n n e -+⨯+⨯++>.【解析】(Ⅰ)22111()[1ln(1)][ln(1)]11x f x x x x x x x '=--+=-++++----------------2分210,0,0,ln(1)0,()01x x x f x x '>∴>>+>∴<+ ()(0,)f x ∴+∞在上是减函数 ---------------- 4分 (Ⅱ)(1)[1ln(1)](),()1k x x f x h x k x x+++>=>+恒成立即恒成立,即()h x 的最小值大于k . ----------------5分21ln(1)(),x x h x x--+'=----------------6分 令()1ln(1)(0)g x x x x =--+>,则()0,()(0,)1xg x g x x '=>∴+∞+在上单调递增, ----------------7分又(2)1ln30,(3)22ln 20g g =-<=-> ,()0g x ∴=存在唯一实根a , 且满足(2,3),1ln(1)a a a ∈=++,----------------8分当x a >时,()0,()0;g x h x '>>当0x a <<时,()0,()0g x h x '<< ∴min (1)[1ln(1)]()()1(3,4)a a h x h a a a+++===+∈,故正整数k 的最大值是3 ----9分(Ⅲ)由(Ⅱ)知1ln(1)3(0)1x x x x ++>>+,∴333ln(1)12211x x x x x+>-=->-++----------------10分令(1)(*)x n n n N =+∈, 则3ln[1(1)]2(1)n n n n ++>-+ ----------------11分∴ln(112)ln(123)ln[1(1)]n n +⨯++⨯++++333111(2)(2)[2]23[]1223(1)1223(1)1323(1)232311n n n n n n n n n n >-+-++-=-+++⨯⨯+⨯⨯+=--=-+>-++----------------13分 ∴23(112)(123)[1(1)]n n n e -+⨯+⨯++> ----------------14分方法二: n 23(112)(123)[1(1)]=n n n a e-+⨯+⨯++令则当n 2n-11(1)n 2=a n n a e ++≥时,----------------10分 当n21n-1n=21,a a a a 时,<∴<----------------11分 当nn n-1n-1n 31,a a a a ≥时,>∴>----------------12分 n min 2n 21==1,1a a a e∴()>∴>----------------13分 23(112)(123)[1(1)]n n n e -+⨯+⨯++∴>----------------14分【考点】函数的单调性,函数的最值,恒成立问题的转化,构造新函数,证明不等式等.。
