2011第九届走美杯四年级

合集下载

2011年第九届走美杯初赛小学四年级(含解析)

第九届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学四年级试卷一、填空题Ⅰ(每题8分，共40分)1．2929228888⨯-=______．2．一群猴子，每只猴每天早上吃2个桃，晚上吃4个桃．一堆堆，如果这群猴子吃3个早上，2个晚上，还会余下6个桃；如果吃2个早上，3个晚上，还差8个桃．这堆猴子共有______个．3．一根绳子长1米．对折两次，用剪刀在中间剪断，得到的最长一段长______厘米．4．一个不规则木块，将它涂成红色（包括下底面），然后锯成15个小立方体木块，如图，共有______个面涂有红色．5．有7个各不相同的正整数，它们的平均数是100．将它们从小到大排列，前3个数的平均数是20，后三个数的平均数是200．最小数的最大是_______，最大的数最大是______．二、填空题Ⅱ(每题10分，共50分)6．如图，6段绳子相互连接，现在要在绳子的某处点火，如果火每分钟燃烧的距离是1，那么至少需要______分钟才能烧光这些绳子．7．小华问陈老师近年有多少岁，陈老师说：“当我像你这么大时，我的年龄是你年龄的10倍．当你像我这么大时，我已经56岁了．”，陈老师今年有______岁．8．A 、B 、C 、D 、E 五个盒子中依次放有2、4、6、8、10个小球．第一个小朋友找到放球最多的盒子，从中拿出4个放在其他盒子中各一个球．第二个小朋友也找到放球最多的盒子，从中拿出4个放在其他盒子中各一个球，依次类推，…，当2011个小朋友放完后，A 盒中放有______个球．3652849．周长为400米的跑道上，有相距100米的A、B两点．甲、乙两人分别从A、B同时反向跑步．相遇后，乙即转身与甲通向跑步，当甲跑到A时，乙恰好跑到B．当甲追上乙时，甲共跑了______米．10．如图中的两个算式中，相同的字母代表相同的数字，不同的字母代表不同的数字．则四位数ABCD= ________．三、填空题Ⅲ(每题12分，共60分)11．如图所示，四个相叠的正方形，边长分别是5、7、9、11．问灰色区与黑色区的面积的差是______．12．第一次在1、2、两数之间，写上3．第二次在1、3和3、2之间分别写上4、5．每次都在已写下的两个相邻的数之间写上这两个数之和．这样过程共重复了七次．这时所有数的和是______．13．如图部件A、B、C、D、E都是由4个11⨯的小正方形拼成，它们的单价依次为5元、4元、3元、2元、1元．现在请你用4个部件（至少用两种不同的部件）拼成一个44⨯的大正方形．并使得购买部件的花费尽可能的少，至少花______元．请将你的拼凑方案画在图中（部件可旋转或翻转）14．4个半径为1的圆中，如图放置，阴影部分的面积是______．15．在一个圆周上有1个红点和49个蓝点，所有顶点都是蓝点的凸多边形的个数，与一个有顶点是红点的凸多边形的个数，相差______．第九届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学四年级试卷参考答案1 2 3 4 5 6 7 855550 104 25 44 19；517 9 38 89 10 11 12 13 14 151000 1236 64 3282 8 4 1176参考解析一、填空题Ⅰ(每题8分，共40分)1．2929228888⨯-=______．【考点】速算巧算【难度】☆☆【答案】55550【解析】方法一：原式291012288101101(222988)25252255550=⨯⨯-⨯=⨯⨯-=⨯=；方法二：原式29101222240422(2929404)55550=⨯⨯-⨯=⨯-=．2．一群猴子，每只猴每天早上吃2个桃，晚上吃4个桃．一堆堆，如果这群猴子吃3个早上，2个晚上，还会余下6个桃；如果吃2个早上，3个晚上，还差8个桃．这堆猴子共有______个．【考点】盈亏问题【难度】☆☆【答案】104【解析】每只猴子3个早上、2个晚上共吃：322414⨯+⨯=个；每只猴子2个早上、3个晚上共吃：22+34=16⨯⨯个；猴子共有：(86)(1614)7+÷-=（只）；桃共有：1476=104⨯+（个）．3．一根绳子长1米．对折两次，用剪刀在中间剪断，得到的最长一段长______厘米．【考点】几何【难度】☆☆【答案】25【解析】如图所示100425÷=．4．一个不规则木块，将它涂成红色（包括下底面），然后锯成15个小立方体木块，如图，共有______个面涂有红色．【考点】立体几何【难度】☆☆☆【答案】44【解析】正视图：7214⨯=；侧视图：6212⨯=；俯视图：9218⨯=；所以共有：14121844++=（面）．5．有7个各不相同的正整数，它们的平均数是100．将它们从小到大排列，前3个数的平均数是20，后三个数的平均数是200．最小数的最大是_______，最大的数最大是______．【考点】平均数【难度】☆☆☆【答案】517【解析】根据题意，令a b c d e f g <<<<<<，则有：700a b c d e f g ++++++=，而题目中告诉我们：60a b c ++=，600e f g ++=，所以有：40d =，a 最大为19，g 最大为6004142517--=．二、填空题Ⅱ(每题10分，共50分)6．如图，6段绳子相互连接，现在要在绳子的某处点火，如果火每分钟燃烧的距离是1，那么至少需要______分钟才能烧光这些绳子．【考点】操作策略【难度】☆☆☆【答案】9【解析】观察可知，至少需要8分钟，这样，只有46+无法满足，则在距离B 地1的地方燃烧即可，此时共需要用：8+1=9（分钟）．365284B 3652847．小华问陈老师近年有多少岁，陈老师说：“当我像你这么大时，我的年龄是你年龄的10倍．当你像我这么大时，我已经56岁了”，陈老师今年有______岁．【考点】年龄问题【难度】☆☆☆【答案】38【解析】设当陈老师与小华一样大时，小华为1份，则陈老师为10份，此时年龄差为9份，所以现在小华为10份，陈老师为19份．当小华像陈老师一样大时，小华19份，陈老师为28份，此时1份为2，所以陈老师今年38岁．8．A 、B 、C 、D 、E 五个盒子中依次放有2、4、6、8、10个小球．第一个小朋友找到放球最多的盒子，从中拿出4个放在其他盒子中各一个球．第二个小朋友也找到放球最多的盒子，从中拿出4个放在其他盒子中各一个球，依次类推，…，当2011个小朋友放完后，A 盒中放有______个球．【考点】找规律【难度】☆☆☆ 【答案】8【解析】本题是一道操作题，则可发现规律：5个一周期(20111)54020-÷=，第2011次与第6次的相同，则是最一次A 中还有8个球．9．周长为400米的跑道上，有相距100米的A 、B 两点．甲、乙两人分别从A 、B 同时反向跑步．相遇后，乙即转身与甲通向跑步，当甲跑到A 时，乙恰好跑到B ．当甲追上乙时，甲共跑了______米．【考点】行程问题【难度】☆☆☆【答案】1000【解析】设甲、乙第一次相遇在C 地，则从同时出发到甲乙第一次相遇，甲走了弧AC ，乙弧BC 同时，从第一次相遇甲跑回A ，乙跑到B ，甲走了弧CA ，乙走了弧CB ．两次乙走的路程相等，所以两次甲走的路程相等，则AC 与CA 为200米．所以甲走200米时，乙走100米，甲比乙多走100米；现在甲要比乙多走300米，甲要再走600米，所以当甲追上乙时，甲共走了；6004001000+=米．56784456878456778457465875849753666108642第七次第六次第五次第四次第三次第二次第一次开始10．如图中的两个算式中，相同的字母代表相同的数字，不同的字母代表不同的数字．则四位数ABCD =________．【考点】数字谜【难度】☆☆【答案】1236【解析】0B E +=，推出必须又进为所以1A =，又因为B 为最高位所以B 可能为3或是2，但是则此时9C =,E 为0，而E 在首位，不能取0．所以2B =，则7E =,6C =,4F =其余的很容易推出所以1236就是ABCD ．三、填空题Ⅲ(每题12分，共60分)11．如图所示，四个相叠的正方形，边长分别是5、7、9、11．问灰色区与黑色区的面积的差是______．【考点】几何【难度】☆☆☆【答案】64【解析】利用容斥原理方法，有好多部分就相会抵消了．111177995564⨯+⨯-⨯-⨯=．12．第一次在1、2、两数之间，写上3．第二次在1、3和3、2之间分别写上4、5．每次都在已写下的两个相邻的数之间写上这两个数之和．这样过程共重复了七次．这时所有数的和是______．【考点】数论【难度】☆☆☆☆【答案】3282【解析】找规律：第0次：1、2；和为：123+=；CBA第1次：132；和为：1326333++==⨯-；第2次：14352；和为：1234515363++++==⨯-；…．事实上，每次添上新数的过程，除了外侧的两个数被加了1次外，其他的数均被加了2次．加上原来的数即新数为原数的3倍少3．所以第3次为：315342⨯-=；第4次为：3423123⨯-=；第5次为：31233366⨯-=；第6次为：336631095⨯-=；第7次为：3109533282⨯-=．13．如图部件A、B、C、D、E都是由4个11⨯的小正方形拼成，它们的单价依次为5元、4元、3元、2元、1元．现在请你用4个部件（至少用两种不同的部件）拼成一个44⨯的大正方形．并使得购买部件的花费尽可能的少，至少花______元．请将你的拼凑方案画在图中（部件可旋转或翻转）【考点】几何【难度】☆☆☆【答案】8【解析】想要最便宜就多用E,D,不行的再用贵的，这样最少用8元．14．4个半径为1的圆中，如图放置，阴影部分的面积是______．【考点】几何【难度】☆☆☆【答案】4【解析】组合完后就是一个正方形224⨯=．15．在一个圆周上有1个红点和49个蓝点，所有顶点都是蓝点的凸多边形的个数，与一个有顶点是红点的凸多边形的个数，相差______．【考点】计数【难度】☆☆☆☆【答案】1176【解析】有一个顶点是红点的凸多边形的个数就是1个红2个蓝点的三角形的个数，就是从49中选2个点的选法：494821176⨯÷=．。

小学奥数杯赛真题1312

1.小泉做一道除数是一位数的除法时，误把除数9看成6，结果算出的商是7，余数是3。

你知道正确的结果是（2012世奥（中国区）选拔赛三年级A卷）2.杨阳是班里有名的小马虎，这次在做（200×9-□）÷25+13时，又没看到题里的括号，算的结果是1788，正确的结果应该是 (2012世奥数浙江赛区四年级)。

3.袋子里有若干个球，每次拿出其中的一半又一个球，这样共操作了4次，袋中还有5个球。

袋中原有____个球（2012年第十届走美杯三年级）。

4.盒子里有若干个球。

小明每次拿出盒中的一半再放回一个球。

这样共操作了7次，袋中还有3个球。

袋中原有个球（2010年走美杯三年级）。

5.抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个球。

如此操作了2012次后, 抽屉里还剩有2个球。

那么原来抽屉里有个球（第十七届华杯赛小中组复赛）。

6.黑板上写有一个数，男同学从黑板前走过时，把他乘以3再减去14，擦去原数，换上答案，女同学从黑板前走过时，把他乘以2再减去7，擦去原数，换上答案。

全班25名男同学和15名女同学都走过后，老师把最后的数乘以5，减去5，结果是30。

那么，黑板上最初的数字是（湖北第七届创新杯）。

7.豆豆和苗苗各有一盒玻璃球，共108粒，豆豆给了苗苗10粒，豆豆剩下的玻璃比苗苗还多8粒。

原来苗苗有粒玻璃球（2010年第八届走美杯三年级）。

8.甲、乙、丙三人的平均年龄为42岁，若将甲的岁数增加7岁，乙的岁数扩大2倍，丙的岁数缩小2倍，则三人岁数相等。

丙的年龄为________岁（第四届迎春杯）。

9.甲、乙、丙、丁四人一共做了370个零件，如果把甲做的个数加上10个，乙做的个数减去20个，丙做的个数乘以2，丁做的个数除以2，四人做的零件数就正好相等。

那么乙实际做了_____ 个零件（第二届迎春杯）。

10.甲、乙、丙三所小学的学生人数的总和为1999。

已知甲校学生人数的2倍和乙校学生人数减去3人与丙校学生人数加上4人都相等。

2011年第九届走美杯初赛六年级组试题及答案

2011年第九届走美杯初赛六年级组试题一、填空题Ⅰ（每题8分，共40分）1、算式（2011－9）÷0.7÷1.1的计算结果是（）。

2、全世界胡杨90％在中国，中国胡杨90％在新疆，新疆胡杨90％在塔里木，塔里木的胡杨占全世界的（）％。

3、半径为10、20、30的三个扇形如下图放置，S2是S1的（）倍。

4、50个不同的正整数，它们的总和是2011，那么这些数里奇数至多有( )个。

5、A、B、C三队比赛篮球，A队以83∶73战胜B队，B队以88∶79战胜C队，C队以84∶76战胜A队，三队中得失分率最高的出线。

一个队的得失分率为（得的总分）／（失的总分），如，A队得失分率为（8 3+76）/（73+84）。

三队中( )队出线。

二、填空题Ⅱ（每题10分，共50分）6、如图，一个边长为120cm的等边三角形被分成了面积相等的五等份，那么，AB=( )cm。

7、某校六年级学生中男生占52％，男生中爱踢球的占80％，女生中不爱踢球的占70％。

那么，在该校六年级全体学生中，爱踢球的学生占( )％。

8、在每个方框中填入一数字，使得乘法竖式成立。

已知乘积有两种不同的得数，那么这两个得数的差是( )。

9、大小相同的金、银、铜、铁、锡正方体各一个，拼成如图的十字，一共有( )种不同的拼法（旋转后可以重合的拼法看成是相同的拼法）。

10、在右图的每个格子中填入1～6中的一个，使得每行、每列所填的数字各不相同。

每个粗框左上角的数和“＋”、“－”、“×”、“÷”分别表示粗框内所填数字的和、差、积、商（例如“600× ”表示它所在的粗框内的四个数字的乘积是600）。

三、填空题Ⅲ（每题12分，共60分）11、用1、3、5、7、9这五个数字组成若干个合数，每个数字恰好用一次。

那么，这些合数的总和最小是( ) 。

12、图1盒子高为20cm，底面数据如图2，这个盒子的容积是( )cm3。

走美杯四年级试题和答案

第三届“走美杯”四年级初赛共12道题，每题10分。

1、33×34＋34×35＋35×36＋36×37= 。

2、李东到商店买练习本，每本3角，共买9本，服务员问：“你有零钱吗？”李东说：“我带的全是5角一张的。

”服务员说：“真不巧，您没有2角一张的，我的零钱全是2角一张的，这怎么办？”你帮李东想一想，他至少应该给服务员张5角币。

3、幼儿园的老师给班里的小朋友送来40个橘子，200块饼干，120块奶糖，平均分发完毕，还剩4只橘子，20块饼干，12粒奶糖，这班里共有位小朋友。

4、有一家三口，爸爸比妈妈大3岁，他们全家今年的年龄加起来正好是58岁，而5年前他们全家人年龄加起来刚好是45岁，小孩子今年岁。

5、两个长方形如下图摆放，阴影三角形面积= 。

6、北京有一家餐馆，店号“天然居”里面有一副著名对联：客上天然居，居然天上客。

巧的很，这幅对联恰好能构成一个乘法算式（见右上图）相同的汉字代表相同的数字，不同的汉字代表不同的数字。

“天然居”表示成三位数是。

7、一个四位数给它加上小数点后比原来小2346.3，那么原四位数是。

8、用同样大小的木块堆成了如图所示的形状，这里共用了个木块。

9、下面图中有9个围棋子围成一圈，现将同色的相邻两子之间放入一个白子，在不同色的相邻两子间放入一个黑子，然后将原来的9个棋子拿掉，剩下新放入的9个棋子如右图，这算一次操作，如果继续这样操作下去，在一圈的9个子中最多有个是黑子。

10、在1999后面写一串数字，从第5个数字开始，每个数字都是它前面两个数字乘积的个位数字，这样得到1 9 8 9 2 8 6 8 4 2 ……，那么，这串数字中，前2005个数字的和是。

11、在下图的5×5方格表的空白处填入1～5中的数，使得每行、每列、每条对角线上的数各不相同。

12、甲、乙二人轮流在右上图的10个方格中，甲画“○”，乙画“×”。

09 10 11年 7 8 9届走美杯试题及答案

第七届“走进美妙的数学花园”初赛四年级试题解答一、填空题（每题8分，共40分）1、37×37+2×63×37+63×63=_10000_____2、下边的一排方格中，除9、8外，每个方格中的字都表示一个数（不同的字可以表示相同的数字），已22，则“走”+“进”+“数”+“学”+“花”+“园”=_40_3、“走美”商场有下列几种瓶装蜂蜜出售：甲，净重3kg,售价33.99元;乙，净重2kg，售价22.99元;丙，净重500g,售价5.99元，那么，_丙____种蜂蜜最贵， __甲___种蜂蜜最便宜。

4.一个数学玩具的包装盒是正方体，其表面展开图如下。

现在每方格内都填上相应的数字。

已知将这个表面展开图沿虚线折成正方体后，相对面的两数之和为“3”，则填在A、B、C内的三个数字依次是_3，1，2___。

5、某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划：该球拍每只售价为人民币60元，同时购买者可获赠1张奖券，积累3张奖券可兑换1只球拍。

由此可见，1张奖券价值为__15__元。

二、填空题（第题10分，共50分）6、（09年走美三、四、五年级都考）A,B都是整数，A大于B，且A×B=2009，那么A-B的最大值为_2008___，最小值为__8___。

7、（09年走美三、四、五年级都考）一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”。

红太狼一半路程溜达，一半路程奔跑。

灰太狼一半时间溜达，一半时间奔跑。

如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是_灰太狼______。

8、柯南家2008年一年用电10200千瓦时，上半年的月平均用电比下半年的月平均用电少100千瓦时。

柯南家下半年月平均用电为__900_____千瓦时。

9、某校A、B、C三名同学参加“走进美妙的数学花园”，其指导教师赛前预测“A获金牌，B不会获金牌，C不会获铜牌”。

结果出来后，三人之中，一人获金牌，一人获银牌，一人获铜牌，指导教师的预测只有一个人与结果相符。

走美杯三年级历年决赛真题

2011年第九届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛三年级（B 卷）一、填空题Ⅰ（每题8分，共40分）1．计算：2011990201111⨯+⨯= ．2．5个人依次领取55个苹果，从第二人起，每人比前一人多两个，第一人得个．3．某种冰激凌每个8元，这种冰激凌最近推出了“买三送一”的优惠活动，数学兴趣小组12位同学每人吃一个，他们至少需要花元钱．4．丁丁、当当、叽里、咕噜分别在A 、B 、C 、D 四个地方，他们到市中心各有一条道路，距离已标在图上（单位：米）．四个朋友相约在某处（不一定是O ）见面，每人走路的速度都是每分钟45米，他们见面最少需分钟．5．一条路的一侧有13棵树，相邻两棵之间相距5米，在路的另一侧每隔6米安装一盏路灯，需要要装盏灯（从头到尾）．二、填空题Ⅱ（每题10分，共50分）6．一根绳子对折三次，用剪刀在中间剪断，可以得到段．7．将一个周长为60厘米的正方形剪成了周长相等的两块，如图，那么每块周长是厘米．240230180150ODCBA5cm5cm8．甲、乙两人分别从相距200米的A、B两地同时出发相向而行，甲每分钟走50米，乙每分钟走40米，出发6分钟后两人相距米．9．学校组织去游览东方明珠、外滩、世纪公园、海底世界，规定每个班最少去一处，最多去两处游览，至少有个班才能保证有两个班游览的地方安全相同．10．有一个长方体木块，外表涂上红色后将它切成27个小正方体，如图，切好后，涂有1面红色的小正方体有块；涂有2面红色的小正方体有块；涂有3面红色的小正方体有块．三、填空题Ⅲ（每题12分，共60分）11．实验小学组织学生参加队列演练，开始时有50个男生、20个女生参加，后来调整队伍，每次调整减少2个男生，增加1个女生，调整次后，男、女生人数就相等了．12．如下图，四个三边长度分别为6厘米、8厘米、10厘米的直角三角形拼成一个大正方形．中间小正方形的面积是平方厘米．13．从A 到I ，只能走箭头所标的方向，共有种不同的走法．14．如图，一个等边三角形被分成了若干个同样的小等边三角形．有些小三角形已被涂黑，那么最少再涂黑个小三角形可以构成有对称轴的图形．15．点P 、Q 、R 及S 为直线上四个不同的点，其中点Q 及点R 位于点P 及点S 之间，且10PS =厘米，3QR =厘米．以这四个点为端点的所有线段长度总和为厘米．ICAQ2012年第十届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛三年级（B卷）一、填空题Ⅰ(每题8分，共40分)⨯+⨯-⨯=．1．201292012820127=⨯+，那么99@1=．a b a b2．已知@23．4个一样的宽为2厘米的长方形拼成一个大长方形．大长方形的周长是厘米．4．“走进美妙的数学花园”中，不同汉字代表不同数字．那么，走+进+美+妙+的+数+学+花+ 园的计算结果最小的是．5．请把1000表示成5个数的和，5个数中出现的数字全相同：1000=+ + + + ．二、填空题Ⅱ(每题10分，共50分)6．甲、乙、丙共有钱99元，甲的钱比乙的钱的2倍少2元，乙的钱比丙的钱的3倍少3元．甲有钱元．7．袋子里有若干个球，每次拿出其中的一半又一个球，这样共操作了4次，袋中还有5个球．袋中原有个球．8．某年6月恰有5个星期一和5个星期日，这月的15号是星期．9．如图，一个四位数加上一个三位数和为2012，这两个数的数字和等于．10．10个相同的玻璃球分给3个人，每人至少一个．有种不同的分配方法．三、填空题Ⅲ(每题12分，共60分)11．玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种．单筒玉米炮每次发射一根玉米，可以消灭8个僵尸；双筒玉米炮每次发射2根玉米，每根玉米消灭7个僵尸，三筒玉米炮每次发射3根玉米，每根玉米消灭6个僵尸．玉米炮一共开炮5次发射玉米11根，至少消灭个僵尸． 12．有五个互不相等的非零自然数．如果其中一个减少45，另外四个数都变成原先的2倍，那么得到的仍然是这五个数．这五个数的总和是． 13．一个三位数，等于它的数字和的13倍．这样的三位数有个，分别是．14．国际象棋盘中，皇后可以沿横线、竖线、斜线吃子．在44 的棋盘中最多可以放入个皇后，它们相互之间不能吃子，在图中给出你的放法(用“□”表示) ．2128515．11个方格从左至右排列，左边的5个方格中已各放了1枚棋子(3白2黑)．每次操作必须同时移动2枚相邻的黑白棋子到任2个相邻的空格中，但不能交换这2枚棋子的左右顺序．要把这5枚棋子全部移到右边5个方格中，且2枚黑子在最右边2格，至少移动次．2013年第十一届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛三年级（B卷）一、填空题I（每题8分，共40分）1．1357 (197199)++++++=．2．用运算符号将1、4、7、7组成一个算式，使结果等于24．3．将1、2、3、4、5、6这6个数字填入下左图的6个圆圈中，使每条线上三个数字之和都等于10．4．如上右图，四个一样的长方形拼成一个边长为10厘米的大正方形，中间形成了一个小正方形，每个长方形的周长是厘米．5．将10000000000减去101011后所得的答案中，数字9共出现次．二、填空题II（每题10分，共50分）6．伟伟今年8岁，爸爸34岁．再过年，爸爸的年龄是伟伟的3倍．7．红色水笔5元一支，蓝色水笔7元一支，花102元共买了16支，蓝色水笔买了支．8．五个连续偶数的和是7的倍数，这五个数之和最小等于．9．甲、乙、丙、丁四人进行乒乓球比赛（没有平局）．每两人都要赛一场，比赛结束后统计成绩，甲胜了2场，乙胜了1场，丙最多胜场．10．将黑、白各一粒围棋子放在下图方格的格点上，但两粒棋子不能在同一条线上．有种不同放法．（旋转后位置相同的算同一种）三、填空题III（每题12分，共60分）11．A、B两地相距1200米，大成从A地出发6分钟后，小功从B地出发，又过了12分钟两人相遇，大成每分钟比小功多走20米，小功每分钟走米．12．200位数M由200个1组成，2013M ，积的数字和是．13．一瓶可乐2元，两个空瓶可以再换一瓶可乐，有30元，最多可以喝瓶可乐．14．4×4的方格中应有30个正方形，下图已去掉了4个点，最少再去掉个点，才能使图中恰好只剩一个正方形．15．有6个边长为2厘米的等边三角形，2个边长为2厘米的正方形，请你选取其中的一些或全部，拼出一个八边形，在方框中画出多边形的拼法．2014年第十二届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛三年级（B卷）一、填空题Ⅰ（每题8分，共40分）1．计算：131549277⨯=．2．4个人排成一排，有种不同的排法．3．我们知道0，1，2，3，……叫做自然数，只能被1和自身整除的大于1的自然数叫做质数或素数，比如2，3，5，7，11等，按照从小到大的顺序，第10个质数是．4．“24点”游戏是很多人熟悉的数学游戏，游戏过程如下：任意从52张扑克牌（不含大小王）中抽取4张，用这4张扑克牌上的数字（从1到13，其中1Q=，A=，11J=，12 K=）通过加减乘除四则运算法则运算得出24，最先找到算法的人获胜．游戏规定4 13Q⨯⨯-张扑克牌都要用到，而且每张牌只能用一次，比如2，3，4，Q，则可以由算法(2)(43)得到24．如果在一次游戏中恰好抽到了2，5，J，Q，则你的算法是：．5．自然数1，2，……，50中，是3的倍数，但不是2的倍数的数有个．二、填空题Ⅱ（每题10分，共50分）6．下图中有个正方形．7．将一根长80厘米的细绳对折两次后，用剪刀在中点处剪开，其中最长的一段绳长是厘米．8．将一个面积为36平方厘米的正方形纸片按照下图所示方式折叠两次后对折，沿对折线剪开，得到的长方形纸片中面积最大的为平方厘米．9．古希腊的数学家们将自然数据按照以下方式与多边形联系起来，定义了多边形数：三边形数：1，3，6，10，15，……四边形数：1，4，9，16，25，……五边形数：1，5，12，22，35，……六边形数：1，6，15，28，45，…………按照上面的顺序，第10个三边形数为．10．将下图中的圆圈染色，要求有连线的两个相邻的圆圈染不同的颜色，则至少需要种颜色．三、填空题Ⅲ（每题12分，共60分）11．2015年1月1日是星期四，根据这一信息，可以算出2015年3月9日是星期．12．用1颗红珠子，2颗蓝珠子，2棵绿珠子串成一个手链，可以串成种不同的手链．13．少年宫美术班、书法班、器乐班招生．书法班招收了29名学员，在这些学员中，既报书法又报美术的有13名，既报书法又报器乐的有12人，三个科目都报的有5名．那么，只参加书法学习的学员有名．14．日常生活中经常使用十进制来表示数，要用10个数码：0，1，2，3，4，5，6，7，8，9．在电子计算机中用二进制，只要用两个数码0和1．正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进1”，于是，可以得到以下自然数的十进制与二进制表示对照表：十进制0 1 2 3 4 5 6 7 8 ……二进制 0 1 10111001011101111000 ……十进制的0在二进制中还是0，十进制的1在二进制中还是1，十进制的2在二进制中变成了1110+=，……那么，二进制中的“1111”+=，十进制的3在二进制中变成了10111用十进制表示是．15．在下面的6个圆圈中分别填入1，2，3，4，5，6，每个数字只能用一次，使各边上的三个数字的和相等．2015年第十三届“走进美妙的数学花园” 中国青少年数学论坛趣味数学解题技能展示大赛三年级（B 卷）一、填空题（每题8分，共40分）1．计算：()299999953794789⨯+⨯⨯= ．2．甲、乙、丙、丁、戊5个人排成一队，甲乙必须相邻，则一共有种不同的排法．3．现有1克、2克、3克和5克的砝码各一枚，能够称出1至11克的重量，某些重量可以有不止一种称量方法，比如3克，可以用3克的砝码称量，也可以用1克与2克的砝码称量．那么，至少需要用到3个砝码才能够称出的重量是（克）．4．我们知道0，1，2，3，……叫做自然数．只能被1和自身整除的大于1的自然数叫做质数或素数，比如2，3，5，7，11等．能够整除2015的所有质数之和为．5．一个班有30名学生，学生平均身高为140厘米，其中男生18人，男生的平均身高为144厘米，则女生平均身高是厘米．二、填空题（每题10分，共50分）6．如图所示的多面体叫做正二十面体，是5个柏拉图立体（正多面体）中的一个．这个多面体由20个面（正三角形）围成，有12个顶点，条棱．面棱顶点7．“24点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52张扑克牌（不包括大小, , , ）王）中抽取4张，用这4张扑克牌上的数字（从1到13，其中A1J=11Q=12K=13通过加减乘除四则运算得出24，最先找到算法的人获胜．游戏规定4张牌扑克都要用到，而且每张牌只能用1次，比如2，3，4，Q，则可以由算法（2×Q）×（4-3）得到24．如果在一次游戏中恰好抽到了7，9，Q，Q，则你的算法是．8．将一个面积为36平方厘米的正方形纸片按照下图所示方式对折两次后，再按对角线折叠出对角折痕，并沿折痕剪开，得到的纸片中面积最大为平方厘米．9．标准骰子六个面上点数的分布规律是相同的．请根据以下骰子能够观察到的点数信息，确定标准骰子点数的分布，并计算这5个骰子向下的面上的点数之和．10．用长9厘米、宽3厘米的相同长方形摆成下图形状，得到的图形的周长是厘米．三、填空题（每题12分，共60分）11．满足被7除余3，被9除余4，并且小于100的自然数有．12．时钟在整点1点钟敲1下，2点钟敲2下，3点钟敲3下，……，照这样敲下去，从1点到12点，再从13点钟开始敲1下，14点钟敲2下，……，这样一天到24点，时钟共敲了下．13．三年级有50名学生，他们都选择订阅甲、乙、丙三种杂志中的一种、二种或三种．则至少有名学生订阅的杂志种类相同．14．下图是一个街道的示意图，实线表示道路．从B到A，只能向右或向上或右斜上方沿着道路前进，则一共有种不同的走法．AB15．在下面的6个圆圈中分别填入1，2，3，4，5，6，每个数字只能用一次，使各边上的三个数字的和相等，称这个和为三角形边幻和．这样的三角形边幻和可以取到的值分别为．参考答案2011年第九届B 卷答案 1．2013011 2．7 3．72 4．6 5．11 6．9 7．55 8．340 9．510．6，12，8 11．10 12．4 13．17 14．3 15．332012年第十届B 卷答案 1．20120 2．199 3．28 4．365．88888888++++ 6．58 7．110 8．日 9．32 10．36 11．70 12．9313．3，117，156，195 14．4 15．42013年第十一届B 卷答案 1．10000 2．（1+7）×（7-4）=24 3．652314．20 5．7 6．5 7．11 8．70 9．3 10．9 11．28 12．120013．不借29；借瓶30 14．4 15．2014年第十二届B 卷答案 1．20140601 2．24 3．294．2×（11-5）+12 5．7 6．30 7．20 8．18 9．55 10．3 11．二 12．4 13．9 14．15 15．3541626241352015年第十三届B卷答案1．201503082．483．9，10，114．495．1346．307．（Q×9）－（Q×7）=24 8．189．1410．18011．31，9412．15613．814．2815．9，10，11，12。

小学四年级竞赛第三讲页码问题专题

第三讲页码问题一、课前热身：1、一本书共300页，这些页码共多少个数字？2、一本400页的书，它的页码中共出现了多少个数码“0”？二、典例精析：3、一本书共有200页，那么共需要个数码编页码．4、一部书，编上页码，公用了7825个数字，这部书共有页．5、一本书有123 页，在这本书的页码中，数字“1”出现了次．6、一本故事书的页码，用了49个0，问这本书共有几页？7、淘气正在读一本281页的故事书，不小心合上了，他记得刚读的连续两页页码之和是81．（1）淘气刚读完的两页页码分别是多少？（2）这本故事书还剩多少页没读？（3）如果淘气每天读20页，剩下的几天能读完？8、小刚翻开数学书，发现两页页码数的和是91，小刚翻到的是第几页和第几页呢？9、上、下两册书的页码共用了681个数码，且下册比上册多3页，则上册书有页．10、《好少年》上下两册书的页码共用了888个数码，且下册比上册多用8页，下册书有页．三、竞赛真题：11、（2011•走美杯）灰太狼给儿子买了一本叫《捕羊宝典300篇》的书，这本书共301页，这本书的页码共用了个数字．12、（2013•其他杯赛）给一本书编页码，一共用了1002个数字，这本书共有页．13、（2009•希望杯）《希望杯数学能力培训教程（四年级）》一书有160页，在它的页码中，数字“2”共出现了次．14、（2017•希望杯）张丽正在读一本181页的故事书，可是她不小心把书合上了，只记得刚读完的连续两页页码之和为81，如果张丽每天读30页，那么剩下的几天能读完？15、（2008•陈省身杯）上、下两册书的页码共用了681个数码，且下册比上册多3页，则上册书有页．四、课后练习：16、一本科幻小说共320页，问：（1）印这本科幻小说的页码共要多少个数字？（2）数字0在页码中共出现了多少次？17、一本故事书的页码共用了192个数字，这本书一共有页．18、编一本故事书的页码，一共用了 24 个数字“3”，这本故事书有页．19、一本翻开的书，这两个页码的和正好是577，你知道这两页页码分别是多少吗？20、甲、乙两册书，书页共用了777个数码，甲册比乙册多7页．那么，甲册书有页．。

走美杯四年级试题及答案

走美杯四年级试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项是正确的？A. 地球是平的B. 太阳是宇宙的中心C. 地球围绕太阳转D. 月亮是地球的卫星答案：C2. 哪个国家被称为“千岛之国”？A. 中国B. 日本C. 印度尼西亚D. 印度答案：C3. 下列哪个选项是数学中的“奇数”？A. 2B. 4C. 5D. 8答案：C4. 以下哪种动物是哺乳动物？A. 蛇B. 鳄鱼C. 鲸鱼D. 乌龟答案：C5. 世界上最高的山峰是？A. 珠穆朗玛峰B. 乞力马扎罗山C. 富士山D. 阿尔卑斯山答案：A二、填空题（每题2分，共10分）1. 一年有______个季节。

答案：四2. 地球上最大的陆地动物是______。

答案：非洲象3. 光年是长度单位，表示光在一年内通过的距离，大约是______公里。

答案：9.46万亿4. 人体最大的器官是______。

答案：皮肤5. 世界上最大的海洋是______。

答案：太平洋三、简答题（每题5分，共20分）1. 简述地球的自转和公转。

答案：地球的自转是指地球围绕自己的轴线旋转，周期约为24小时，导致了昼夜交替。

地球的公转是指地球围绕太阳的轨道运动，周期约为365.25天，导致了季节更替。

2. 请解释什么是生态系统。

答案：生态系统是由生物群落和其所在的非生物环境相互作用而形成的一个统一整体，包括了生产者、消费者和分解者等生物组成部分以及水、土壤、空气等非生物组成部分。

3. 请列举三种常见的哺乳动物。

答案：猫、狗、牛4. 描述一下水循环的过程。

答案：水循环是指地球上水分子在大气、陆地和海洋之间不断循环的过程，包括蒸发、凝结、降水和径流等环节。

四、计算题（每题10分，共20分）1. 如果一个长方形的长是8米，宽是5米，求其面积。

答案：面积 = 长× 宽 = 8米× 5米 = 40平方米2. 一个班级有40名学生，如果每名学生需要2本练习册，那么总共需要多少本练习册？答案：总练习册数 = 学生数× 每人练习册数= 40 × 2 = 80本五、阅读理解题（每题5分，共10分）阅读以下短文，回答后面的问题。

9届2011决赛走美杯的答案

四年级决赛1、（1×2×3×4×…×10×11）÷（27×25×24×22）= 。

2、运动会入场式要求运动员排成9行9列的正方形方阵。

如果去掉2行2列，每个方阵减少名运动员。

3、如图，两个边长为5的正方形放在长为12、宽为5的长方形上。

两个正方形的中心A、B4、甲、乙二人相向而行，速度相同．火车从甲身后开来，速度是人的11倍．车经过甲用18秒钟，经过乙用秒钟．5、A、B是平面上的两个定点，在平面上找一点C，使△ABC构成等腰直角三角形，这样的点C 有个。

6、甲、乙、丙、丁四人长跑。

起跑后丙领先，整个过程中丙与其他三人共有11次位置交替。

比赛结果丙不是最后一名，丙得第名。

7、20个学生的平均身高是1.5米，但身高各不相同．为了站成两排照相，摄影师给他们找来了一些高低不同的箱子，让他们站到箱子上．第一排10个人的高度都变为1.61米，而第二排10个人的高度都变为1.75米．这些箱子平均高度最多________米．8、甲、乙两人分别从A、B两地同时出发，在A、B两地间往返奔跑；出发后在距离A地600米处第一次迎面相遇；甲到B后速度提高到原来的2倍，乙到A后速度也提高到原来的2倍，结果他们在距离B地100米处第二次迎面相遇．那么，A、B间的路程是________米．9、某公司为鼓励员工，根据利润发放奖金。

利润低于或等于10万元时，发利润的10%。

利润高于10万元，而低于或等于20万元时，10万元部分按上述规定发放奖金，高于10万元的部分按8%发奖金。

利润高于20万元时，20万元部分按上述规定发放奖金，高于20万元的部分按5%发奖金。

当利润为40万元时，应发放奖金元。

10、10个小朋友手拉手围成一圈．每个人都戴着一副白色或者黑色的手套．现在将每对拉着的手上的手套交换，最少有个小朋友的手套仍然是同色的一副。

11、两个正方形边长分别是10厘米和8厘米，阴影部分面积平方厘米。

走美杯真题总结与应试技巧

计算：
【例1】(第九届走美杯第一题)
2011000－2011＝_____×999
【拓展】
20112012×20122011－20112011×20122012
几何：
【例2】(第八届走美杯第十二题)
将15个棱长为1厘米的正方体堆放在桌面上(如图)，喷上红色后再将它们分开。

涂上红色的部分，面积是____平方厘米。

数论：
【例3】(第八届走美杯第七题)
下图中，相同字母表示相同的数字，不同的字母表示不同的数字。

两位数＝______。

走美杯真题总结与应试技巧
计数：
【例4】(第六届走美杯决赛第八题)
右图共有______个正方形。

应用题：
【例5】(第八届走美杯第十题)
某人去一座商务楼的15层，4楼以下不设电梯(4楼可乘电梯)，他从1楼步行到2楼用了30秒，电梯速度是步行的10倍，请问：他到达15楼需要____秒。

杂题：
【例6】(第九届走美杯第十二题)
学校组织去游览玄武湖，中山陵，总统府，规定每个班最少去一处，最多去两处游览，那么至少有_____个班才能保证有两个班游览的地方完全相同。

走美杯常考题型：计算考点及出题方向.doc

走美杯常考题型：计算考点及出题方向
每年全国会有各种各样的竞赛陆续举办，比如希望杯、走美杯等杯赛。

很多学生都希望可以参加这些有意义的奥数竞赛。

小学频道为大家提供了走美杯常考题型，希望对大家的复习有帮助。

走美杯常考题型：计算考点及出题方向
出题方向
在三、四年级走美杯考试中计算经常从提取公因数和等差数列计算两个角度出题。

等差数列：中项定理和找规律计算是考察重点
每年走美考试中大约占总分值的8%
历年考试规律
等差数列巧算
提取公因数(乘)
凑整求和、特殊数列计算
提取公因数(公式法)
这就是为大家提供的走美杯常考题型，希望能够对大家有用，更多相关内容，请大家及时锁定!。

四年级下册数学试题-思维训练专题：09从克到吨、从毫升到升与和差倍综合问题(四年级思维训练)全国通用

已学过的重量单位有____________________。

在计量较重的物品时，通常用比千克大的单位“________”来表示，1吨可以写成1________。

在测量水、油等液体的多少时，可以用________和________做单位。

在测量较多的液体有多少时，一般用________做单位，1升可以写成1_______。

g kg t _______________1==，g g t __________8001=。

g kg kg g ______________41682=+，kg kg t kg _______822460=-。

kg t kg t kg t ____________2501403=-，kg t kg t kg t __________9508410015=+。

L mL __________680000=，mL mL L ________233=。

L mL L mL ______53524465=+，mL L mL L _____________280015=-。

mL mL L mL L ________15018504=+,mL L mL L L mL L ________8207132511=-+。

一袋大米重10（）一辆大卡车载重8（）一盒纯鲜牛奶850（）一杯茶水250（）一滴眼药水5（）最大的陆上动物是非洲象，平均重达7（）一块橡皮重约5（）一只猫的体重约2500（）9466kg →（）t 8320mL →（）L938g →（）kg 99900mL →（）L45t680 kg →（）t 2L950mL →（）L20kg89g →（）kg 69L69mL →（）L果园里有50吨苹果，如果每20千克装一箱，这些苹果一共可以装多少箱？一袋大米重25千克，一辆卡车一次最多可运160袋这样的大米，那么这辆卡车载重量是多少吨？超市搞促销，每买2袋350克的浓缩强力洗衣粉，就送1袋125克的浓缩去污洗衣粉。

05年第三届至13年第十一届走美杯试题答案 (1)

目录第三届“走美杯”答案 (2)第四届“走美杯”答案 (3)第五届“走美杯”答案 (4)第六届走美杯三年级初赛试题参考答案 (6)第六届走美杯三年级决赛试题参考答案 (9)第七届走美杯三年级初赛试题参考答案 (10)第八届走美杯三年级初赛试题参考答案 (11)第九届走美杯三年级A卷初赛试题参考答案 (13)第十届走美杯三年级B卷试题及答案详解 (14)第三届走美杯四年级试题参考答案 (18)第四届走美杯四年级试题参考答案 (19)第六届走美杯四年级初赛试题参考答案 (20)第六届走美杯四年级决赛试题参考答案 (24)第七届走美杯四年级初赛试题参考答案 (24)第八届走美杯四年级初赛试题参考答案 (25)第九届走美杯四年级A卷初赛参考答案 (27)第九届走美杯四年级B卷初赛参考答案 (28)第三届走美杯五年级试题参考答案 (33)第四届走美杯五年级试题参考答案 (34)第五届走美杯五年级初赛试题参考答案 (35)第六届走美杯五年级初赛试题参考答案 (39)第六届走美杯五年级决赛试题参考答案 (42)第七届走美杯五年级初赛试题参考答案 (43)第八届走美杯五年级初赛试题参考答案 (46)第九届走美杯五年级初赛试题参考答案 (48)第九届走美杯五年级B卷初赛试题参考答案 (52)第三届走美杯六年级试题参考答案 (52)第四届走美杯六年级试题参考答案 (53)第五届走美杯六年级试题参考答案 (54)第六届走美杯六年级决赛试题参考答案 (58)第七届走美杯六年级初赛试题参考答案 (59)第八届走美杯六年级初赛试题参考答案 (62)第九届走美杯六年级A卷初赛试题参考答案 (65)第十届2012走美杯六年级试题及答案详 (66)第六届走美杯三年级初赛试题参考答案1.22222.861；574；5733.604.155.4；36.90÷15=34－28=67.10；28.169.22210.3711.略12.361.【答案】100012.【答案】100003.【答案】404.【答案】11705.【答案】MT79366.【答案】2008；87.【答案】38.【答案】49.【答案】灰太狼10.【答案】711.【答案】105 ；312.【答案】7； 213.【答案】55；540 14.【答案】4或315.【答案】1、2 、4 、8 .第八届走美杯三年级初赛试题参考答案第九届走美杯三年级A卷初赛试题参考答案第十届走美杯三年级B卷试题及答案详解1、49042、73、364、35、46、9787、2607或23708、509、810、1203111、12、5，2，6 1 2 3 4 5 4 5 1 2 3 2 3 4 5 1 5 1 2 3 4 3 4 5 1 2第六届走美杯四年级初赛试题参考答案1.20082.64；15625（64×15625）3.2或54.155.906.200000077.168.1；2；2；39.5610.3011.147张，15块12.2100第七届走美杯四年级初赛试题参考答案1. 100002. 403. 丙；甲4. 3 、1 、25. 156. 2008；87. 灰太狼8. 9009. C.10. 1011. 55；54012. 413. 2614.55 ；259平方厘米15.21、555502、1043、254、445、19；5176、97、388、79、100010、126311、6412、328213、814、415、1176答案：1、2010012 2、19 3、0。

2011年第九届走美杯初赛小学三年级(含解析)

4．丁丁、当当、叽里、咕噜分别在、、、四个地方，他们到市中心各有一条道路，距离已标在图上（单位：米）．四个朋友相约在某处（不一定是）见面，每人走路的速度都是每分钟45米，他们见面最少需_______分钟．
5．灰太狼给儿子买了一本叫《捕羊宝典300篇》的书，这本书共301页，这本书的页码共用了______个数字．
14．、、、、、、七盏灯各自装有一个拉线开关．开始时、、亮着，一个小朋友按从到，在从到这样的顺序依次拉七盏灯的开关，一共拉了2011次，这时亮着的灯是___________．
15．如图，一张有20个小正方体组成的硬纸板，请把它分成四部分，是的每部分都能拼成一个有底无盖的正方形盒子．在图中用粗线画出分割方法．
【答案】7
【解析】考虑所有的游览方式有：（1）只去玄武湖，（2）只去中山陵，（3）只去总统府，（4）去玄武湖和中山陵，（5）去玄武湖和总统府，（6）去中山陵和总统府，所以要使保证有两个班游览的地方完全相同，则需要有个班去参加游览．
13．将五位数“54321”重复写101次，组成一个505位数“ ”，现在删去这个数所有奇数位（从左至右数）上的数字，组成一个新数，再删去新数中所有位于奇数位上的数字：按上述规律，一直删下去直到剩下一位数为止，则剩下的数字是________．
【考点】数阵图
【难度】☆☆☆
【答案】6
【解析】所有数的和为28，而图形中两个有3个数组成的线段数的和分别为11，所以剩下的一个为．
12．学校组织去游览玄武湖、中山陵、总统府，规定每个班最少去一处，最多去两处游览，那么至少有_______个班才能保证有两个班游览的地方完全相同．
【考点】最不利原理
【难度】☆☆☆
【考点】几何分割

SH四年级走美杯初赛汇总

第七届走美杯四年级初赛一、填空题Ⅰ（每题8分，共40分）1、 3737263376363⨯+⨯⨯+⨯=______2、下边的一排方格中，除9、8外，每个方格中的字都表示一个数（不同的字可以表示相同的数字），已知其中任何3个连续的方格中的数相加起来都为22，则“走”+“进”+“数”+“学”+“花”+“园”3、 “走美”商场有下列几种瓶装蜂蜜出售：甲，净重3kg ,售价33.99元;乙，净重2kg ，售价22.99元;丙，净重500g ,售价5.99元，那么，_____种蜂蜜最贵，____种蜂蜜最便宜。

4、一个数学玩具的包装盒是正方体，其表面展开图如下。

现在每方格内都填上相应的数字。

已知将这个表面展开图沿虚线折成正方体后，相对面的两数之和为“3”，则填在A 、B 、C 内的三个数字依次是________。

5、某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划：该球拍每只售价为人民币60元，同时购买者可获赠1张奖券，积累3张奖券可兑换1只球拍。

由此可见，1张奖券价值为________元。

二、填空题Ⅱ（第题10分，共50分）6、 A ,B 都是整数，A 大于B ，且2009A B ⨯=，那么A B -的最大值为________，最小值为________。

7、一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”。

红太狼一半路程溜达，一半路程奔跑。

灰太狼一半时间溜达，一半时间奔跑。

如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是___________。

8、柯南家2008年一年用电10200千瓦时，上半年的月平均用电比下半年的月平均用电少100千瓦时。

柯南家下半年月平均用电为___________千瓦时。

9、某校A 、B 、C 三名同学参加“走进美妙的数学花园”，其指导教师赛前预测“A 获金牌，B 不会获金牌，C 不会获铜牌”。

结果出来后，三人之中，一人获金牌，一人获银牌，一人获铜牌，指导教师的预测只有一个人与结果相符。

第九届走美杯

1.2828×33-7777×4=（题记不清了） PQRS2.PQRS 代表一个四位数， × 9 ,积是。

SRQP3.把1～7填入数阵图里，使三条直线上的数字之各相等，1与2已给出。

X 有（）填法。

74.记不得了。

5.正方形切去8个角，问还有几条棱？ 4 36.6段绳子如图连接。

在绳子的某处点火， 5 6火每分钟燃烧1，分钟烧光绳子。

87.王刚问张老师年龄，老师说：“我像你这么大时，我的年龄是你那时年龄的5倍，你像我这么大时，我都52岁了。

问张老师今年岁。

8.忘了。

9.甲乙两人分别在AB 两地，如果甲和乙相向而行，5分钟后相遇。

如果同向行走，甲20分钟后追上乙。

已知乙速为60米／分，求AB 两地相距米。

10.太极拳有一招式叫玉女穿梭，这个招式的方法是顺时针转180°，再逆时针转90°，再顺时针转270°，最后逆时针转90°。

如果要求一步转到相应的位置，那么应该转。

11.记不起来了。

12.第一次操作在2和3之间写上5，第二次操作在2和5之间写上7，在3和5之间写上8，以后每次操作都在两个数之间写上它们的和，问第6次操作之后，写上的所有数的和是。

13.最中间的三角形面积为12，在正六边形的每条边上画上一个正方形，再以正方形的边长画上小正三角形，部小正三角形的面积和是。

（图略）14.有6根木棒，其中5根木棒分别为25、29、33、37、41，有6根木棒搭成每边有2根的三角形。

求第6根木棒的长度有种可能。

我们把这4种三连块称之为角形。

现有7×7正方形表格，黑格有25个，白格有24个，每一次操作可以把一个角形内三个方格同时改变颜色，进行若干次操作后，黑格有可能变多，黑格最多有个。

（以上题如有误差，还请大家多多谅解，缺失的请补充）。

四年级数学竞赛拓展知识《列方程解应用题(上)》

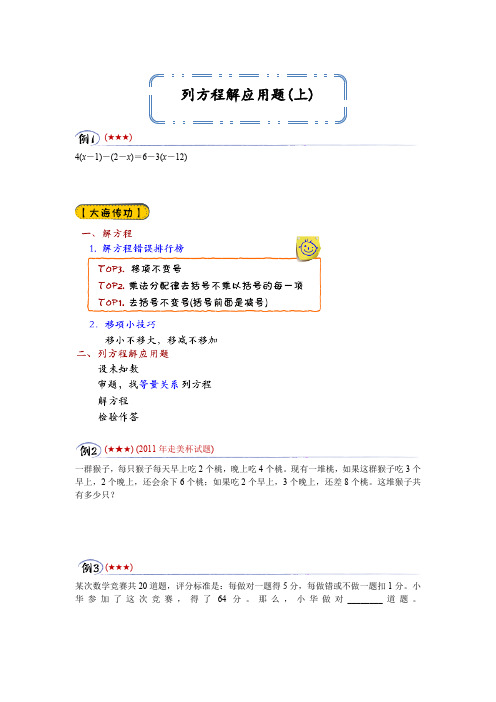
4(x －1)－(2－x )＝6－3(x －12)一群猴子，每只猴子每天早上吃2个桃，晚上吃4个桃。

现有一堆桃，如果这群猴子吃3个早上，2个晚上，还会余下6个桃；如果吃2个早上，3个晚上，还差8个桃。

这堆猴子共有多少只？某次数学竞赛共20道题，评分标准是：每做对一题得5分，每做错或不做一题扣1分。

小华参加了这次竞赛，得了64分。

那么，小华做对________道题。

(★★★)(★★★) (2011年走美杯试题)(★★★)(★★★★)⑴新学期开始，有一批新的教科书要分发到各位学生手中，这批教科书必须由一个小组的学生来搬，这批教科书如果由小组中的男生来搬，每人搬25本，那么还有15本没人搬，如果由小组中的女生来搬，每人搬20本，那么最后一名女生只需要搬10本。

已知这个小组的学生一共有8人，求男、女生各有多少名？⑵五年级一班同学参加学校植树活动，派男、女生共12人去取树苗，男同学每人拿3棵，女同学每人拿2棵，正好全部取完；如果男、女生人数调换一下，则还差2棵不能取回。

问：原来男、女生人数各是多少？(★★★★)三个连续自然数，后面两个数的积比前面两个数的积大114，求这三个数。

(★★★★★) (华杯赛试题)松鼠妈妈采松子，晴天每天可采20个，雨天每天可采12个，它一连几天采了112个松子，平均每天采14个，问，这几天当中有几天有雨？在线测试题温馨提示：请在线作答，以便及时反馈孩子的薄弱环节。

例1测：++++=(★★★)解方程：2(1)3(2)68x x xA．10B．18C．14D．16例2测：(★★★)如果把一些桃子分给一些猴子，每只猴子2个，多10个；每只猴子3个，多5个。

问：一共有多少只猴子？有多少个桃子？A．5、20B．5、22C．5、24D．4、30例3测：(★★★)某次数学竞赛共20道题，评分标准是：每做对一题得5分，每做错或不做一题扣1分。

明明参加了这次竞赛，得了70分。

那么，明明做错道题。